随机变量图形的绘制
连续型随机变量PPT课件

20
1
x
e 10 dx
1
x
e 10
20
10 1 0
10 10
e1 e2 0.2325
2021/5/11
33
3.正 态 分 布
如果连续型随机变量X 的密度函数为
f x
1
e
x 2
2 2
2
x
其中 , 0为参数
则称随机变量X 服从,参数为 , 2 的
正态分布.记作
f (x)
下面验证:
x
f x dx
1
e
x 2
2 2
dx
1
2
2021/5/11
36
密度函数的验证(续)
下面验证:
f xdx
1
x 2
e 2 2 dx 1
2
首先验证:
x dx
1
x2
e 2 dx 1
2
或验证:
x2
e 2 dx 2
2021/5/11
P 1或 2
11 dx 6 1 dx
3 9
29
24 2 99 3
2021/5/11
27
2.指 数 分 布
如果随机变量 X 的密度函数为
f
x
e
x
x0
0 x0
其中 0为常数,则称随机变量服从 参数为的指数分布.
2021/5/11
28
密度函数的验证
设X ~ 参数为的指数分布,f x是其密度函数,则有:
例 7:
设打一次电话所用的时间 X(单位:分钟)是
以 1 为参数的指数随机变量.如果某人刚
10 好在你前面走进公用电话间,求你需等待10分 钟到20分钟之间的概率.
连续型随机变量常见的几种分布

)
29
◆ 对任意区间 ( x1 , x2 ], 则有: x1 X x2 ) P ( x1 X x2 ) P ( x2 x1 ( )
(
)
30
(6) 3 原则 由标准正态分布的查表计算可以求得,
当X~N(0,1)时,
6
解: 设以7:00为起点0,以分为单位 从上午7时起, 每15分钟来 依题意, X ~ U ( 0, 30 ) 一班车,即 1 7:00,7:15, 0 x 30 f ( x ) 30 7:30 其 它 等时刻有汽 0 车到达汽站 为使候车时间X 少于 5 分钟, 乘客必须在 7:10 到 7:15 之间,或在7:25 到 7:30 之间到达车站. 故所求概率为:
2( 2) 1 2 0.9772 1 0.9544
33
例4. 从旅馆到飞机场沿 A 路走(路程短,交通拥挤)
所需时间(分钟) X ~ N (27,52 ), 沿 B 路走(路程 长,阻塞少)所需时间(分钟)Y~N (30,22 ) 若现在只有 30分钟. 问:分别选择哪一条路为好? 解: 依题意,选择所需时间超过规定时间的概率较 小的路线为好. 当只有30分钟可用时: 30 27 ) A 路: P ( X 30) 1 P ( X 30) 1 ( 5 1 (0.6) 1 0.7257 0.2743
P{10 X 15} P{25 X 30} 15 1 30 1 1 dx dx 10 30 25 30 3
7
候车时间超过10分钟,则乘客必须在7:00到7:05或 7:15到7:20之间到达车间
P (0 x 5) P (15 x 20)
常见六种随机变量分布可视化

常见六种随机变量分布可视化from scipy.stats import binomimport matplotlib.pyplot as pltimport numpy as npn = 10p = 0.3k = np.arange(0, 10)binomial = binom.pmf(k, n, p)plt.plot(k, binomial)plt.title('Binomial: n = %i, p=%0.2f' % (n, p), fontsize=15)plt.xlabel('Number of successes')plt.ylabel('Probability of sucesses', fontsize=15)plt.show()dis_2 = np.random.binomial(10,0.5,size=10000)plt.hist(dis_2,bins=10,color='r',alpha=0.4,edgecolor='y')plt.show()dis_3 = np.random.poisson(8,100000)# lam 随机事件发⽣率,size 形状 n * p = 8plt.hist(dis_3,bins=8,color='r',alpha=0.4,edgecolor='y')plt.show()1.1 离散型随机变量-(伯努利分布):1.2 离散型随机变量-(⼆项分布):1.3 离散型随机变量-(泊松分布):dis_4 = np.random.normal(0,1,100000)plt.hist(dis_4,bins=800,color='r',alpha=0.4,edgecolor='y')plt.show()dis_5 = np.random.exponential(0.125,100000)plt.hist(dis_5,bins=6000,color='r',alpha=0.4,edgecolor='y')1.4 连续型随机变量-(正态分布):1.5 连续型随机变量-(指数分布):1.6 连续型随机变量-(拉普拉斯分布):import numpy as nplaplace1 = place(0, 1, 10000)laplace2 = place(0, 2, 10000)import matplotlib.pyplot as pltfig, (ax1, ax2) = plt.subplots(1,2, sharex=True, sharey=True) ax1.hist(laplace1,bins=1000, label="lambda:1")ax1.legend()ax2.hist(laplace2, bins=1000, label="lambda:2")ax2.legend()plt.show()。
连续随机变量及其分布

0, 2 F(x)= Ax , 1,
试求: (1)系数 A;
x 0, 0 x 1, x 1.
(2)X 落在区间(0.3,0.7)内的概率; (3)X 的密度函数.
数学与信息工程系
例2:设随机变量X具有概率密度
求:(1)常数a;(2)
(3)X的分布函数F(x)
解: (1)由概率密度的性质可知
查出 ( x) ( x) 立即可得 ( x) ( x).
数学与信息工程系
第三节 连续随机变量及其分布
设 X ~ N ( , 2 ), 则有
P( X ) ? 0.6826 P( 2 X 2 ) ? 0.9544 P( 3 X 3 ) ? 0.9974
30 1 1 d x 10 30 25 30 dx 15
=1/3.
数学与信息工程系
例
X ~ U(2, 5). 现在对 X 进行三次独 立观测,试求至少有两次观测值大 于 3 的概率.
解: 记 A = { X > 3 }, 则 P(A) = P( X> 3) = 2/3
设 Y 表示三次独立观测中 A 出现的次数, 则 Y~ b(3, 2/3),所求概率为 P(Y≥2) = P(Y=2)+P(Y=3) 2 3 0 2 2 1 3 2 1 C3 C3 =20/27 3 3 3 3
f ( x)
F( x )
1
O
x
O
x
数学与信息工程系
第三节 连续随机变量及其分布
指数分布最常见的一个场合是寿命分布.
指数分布具有“无记忆性”
对于任意 s,t >0,有
3.2 离散型随机变量

1、已知分布律,求分布函数※
例3:已知X的分布律,
求 X 的分布函数。
X p Pk
1 1 4
2 1 2
3 1 8
4 1 8
F ( x) P( X x)
x 1 0, P X 1 1 , 1 x 2 4 P X 1 P X 2 3 2 x3 4 P X 1 P X 2 P X 3 7 3 x 4 8 P X 1 P X 2 P X 3 P X 4 1 4 x
例2:某人的手枪里有5发子弹,他向一个目 标独立地射击,直到首次击中才停止射击。 已知每发子弹命中目标的概率为0.6,求消耗 子弹数X的分布律。
已知离散型随机变量的分布律, 求出随机事件的概率. 练习:设随机变量 X 的分布律为
求P
X 2 , P 0 X 5/ 2, P 1 X 3
例如,袋中有5个球,编号为1,2,3,4,5,从中任取3个, 以Y表示3个球中的最大号码,则Y服从超几何分布。
本节小结:
知识点与基本要求: (1)理解离散型随机变量及其概率分布的概念,掌握 离散型随机变量的分布律的性质; (2)理解四种常见分布的实际意义,掌握四种分布(两 点分布、二项分布、泊松分布、超几何分布)及其应用; (3)理解泊松定理的结论和应用条件,了解应用泊松 分布近似表示二项分布; 教学重点:离散型随机变量的分布律性质,四种常见 分布的分布律及其应用; 教学难点:四种常见分布的分布律及其应用。
2、二项分布
设X表示n重伯努利试验中事件A发生的总次数.
X的分布律为
P( X k ) C p (1 p)
k n k
n k
生产系统建模与仿真课件--第4章--随机变量与随机分布

0 ,
Fx x ,
1 ,
x0 0 x 1 x 1
2019/9/11
1
0
1
x
(0,1)均匀分布的分布函数
30
4.2 随机数的生成方法
4.2.1 随机数的特性
仿真程序中的随机数序列必须具有以下统计特性: ① 均匀性:随机变量在其可能取值范围中任一
区间出现的概率和此区间的大小与可能值范围的比值成正 比。 ② 独立性:在某个区间内一个观测值发生
D(X )
2019/9/11
14
4.1 随机变量和随机分布概述
3.变异系数(coefficient of variation)
为了更好地描述随机变量的分散程度,引入变异系数的概 念,也称变化系数或变差系数。变异系数是指随机变量的 标准差与平均值的比值,即:
由于标准差与平均值的量纲相同,变异系数是无量纲量,
图4-9 正态分布的位置参数
2019/9/11
20
4.1 随机变量和随机分布概述
(2)比例参数 比例参数用于确定在分布范围内取值大小的比例尺度。
当比例参数的数值改变时,分布函数被压缩或扩张,分 布的范围发生改变,但分布的基本形状不会改变。
2019/9/11
21
4.1 随机变量和随机分布概述
图4-10 指数分布的比例参数
① f (x) 0
②
f (x)dx 1
F(x)为连续型随机变量的累积分布函数(CDF),它表示 随机变量小于或等于x的概率:
x
F (x) P( X x) f (x)dx
① 0 F(x) 1
② 当x1<x2时,有F(x1)≤F(x2)
1.随机变量图形的绘制 - 随机信号分析实验报告

计算机与信息工程学院验证性实验报告一、实验目的利用计算机仿真随机变量,考察其图形,以此加深对满足各种分布的随机变量的理解。
二、实验仪器或设备1、一台计算机2、MATLAB r2013a三、实验内容编程画出给定参量,随机变量的正态分布、瑞利分布、均匀分布、(0,1)分布的概率密度函数或概率分布函数曲线。
四、实验步骤1.启动MATLAB软件,运用MATLAB编写程序完成实验内容;2.对编写的程序进行调试,观察所得图形。
五、实验程序及运行结果%1.正态分布概率密度图u=1; %正态分布期望c=4; %正态分布方差x=linspace(u-5,u+5,100);y=(1/sqrt(2*pi*c))*exp(-(x-u).^2/(2*c));plot(x,y)xlabel('x');ylabel('y');title('正态分布概率密度图')-4-3-2-1012345600.050.10.150.2xy正态分布概率密度图%2.瑞利分布概率密度图 c=35; %一个大于零的常数 x=linspace(-10,c+100,1000); for i=1:length(x) if x(i)<=0 y(i)=0; elsey(i)=(x(i)/c^2).*exp(-x(i)^2./(2*c^2)); end endplot(x,y)title('瑞利分布概率密度图') xlabel('x'); ylabel('y');-2002040608010012014000.0050.010.0150.02瑞利分布概率密度图xy%3.画均匀分布概率密度图 a=-1;b=1; %在[a,b]上均匀分布 x=a:.001:b;y=1/(b-a); %在[a,b]上均匀分布xlabel('x'); ylabel('y');title('均匀分布概率密度图')-1-0.8-0.6-0.4-0.200.20.40.60.81xy均匀分布概率密度图%4.画(0,1)分布概率分布图 x=[0,1];p=0.3; %为0时概率为p y=[p,1-p]; plot(x,y,'*') xlabel('t'); ylabel('y');title('(0,1)分布概率分布图') axis([-0.5,1.5,0,1])-0.50.511.500.20.40.60.81ty(0,1)分布概率分布图%5.画泊松分布概率分布图 p=30; %参数为px=linspace(0,p,100); %1:100; s=1;j=0;for i=1:length(x) if j==0y(i)=p^j*exp(-p); elsey(i)=(p^j*exp(-p))/s;j=j+1; s=s*j; endj=0:j-1; plot(j,y) xlabel('t'); ylabel('y');title('泊松分布概率分布图')01020304050607080901000.020.040.060.08ty泊松分布概率分布图教师签名:年 月 日。
实验一随机变量图像的绘制

实验一、随机变量图像的绘制
一、实验题目:指数分布的图像绘制
二、实验器材:安装Mablab的电脑一台。
三、实验原理:
若连续型随机变量X的概率密度函数为:f={(1
θ
)∗exp(−x
θ
) x>0 0 其他
其中θ>0为常数,则称X服从参数为θ的指数分布。
四、实验内容:
1、指数分布的概率密度函数m文件编写如下:%指数分布的概率密度函数
x=0:0.01:10;
sita=2;
f=(1/sita)*exp(-x/sita);
plot(x,f)
图像如下:
2、指数分布的概率分布函数:m文件如下:
x=0:0.01:10;
sita=2;
F=1-exp(-x/sita);
plot(x,f)
图像如下:
五、实验总结:
通过实验加深了对指数分布的理解,图像能更加直观的表现出函数的性质。
指数分布的随机变量X具有以下有趣的性质:
对于任意s,t>0, 有
P{X>s+t|X>s}=P{X>t}.称为无记忆性。
随机变量图形的绘制一

一:实验题目:随机变量图形的绘制 二:实验目的:1.熟练掌握MATLAB 软件的关于概率分布作图的基本操作2.进行常用的概率密度函数和分布函数的作图3.绘制出分布律图形 三:实验要求:1.掌握MATLAB 画图命令plot2.掌握常见分布的概率密度图像和分布函数图像的画法 四:实验内容: 画正弦曲线 (1)t=0:0.1:2*pi; y=sin(t); plot(t,y) 图象如图所示:1234567-1-0.8-0.6-0.4-0.200.20.40.60.81(2)绘制随机变量为X1 X2服从正态分布的图形程序为:x1=2+randn([100000,1]);x2=4+randn([100000,1]);Y=714+807*(x1)+518*(x2)+325*(x1.^2-1)+122*(x2.^2-1)+360*x1.*x2; [f,y]=ksdensity(Y);figure;plot(y,f);图形为:(3)subplot函数把一个图形窗口分割成2×2个子区域x=0:0.1*pi:2*pi;’subplot(2,2,1)plot(x,sin(x),'-*');title('sin(x)');subplot(2,2,2)plot(x,cos(x),'--o'); title('cos(x)'); subplot(2,2,3) plot(x,sin(2*x),'-.*'); title('sin(2x)'); subplot(2,2,4); plot(x,cos(3*x),':d') title('cos(3x)’)02468-1-0.500.51sin(x)02468-1-0.500.51cos(x)2468-1-0.500.51sin(2x)2468-1-0.500.51cos(3x)。
第二章 随机变量及其分布

2. 二项分布的推导过程与说明
3. 举例( 例2,例3,例4 )
C. 泊松分布
1. 定义:如果随机变量X的概率密度如下:
P(X k)
λ k k!
e
λ
,
k =0,1,2,… ( >0) ,
(2.4)
则称X服从参数为 的泊松分布,记作:
X ~ ()
2. 说明
3. 举例
返回目录
§3 随机变量的分布函数
P{X=4}=0.218 P{X=5}=0.175 P{X=6}=0.109 P{X=7}=0.055
P{X=k} < 0.001 , 当 k ≥ 11时
P{ X=8 }=0.022 P{ X=9 }=0.007 P{X=10}=0.02
例3:
某人进行射击,设每次射击的命中率为0.02,独立射 击400次,试求至少击中两次的概率。
解:以p表示每组信号灯禁止汽车通过的概率,
X所有可能取值为0,1,2,3,4。得X的分布律 为:P{X= k}= (1-p)k p , k=0,1,2,3, P{X= 4}= (1-p)4。用表格表示如下:
X
01
2
34
pk
p (1-p) p (1-p)2 p (1-p)3 p (1-p)4
代入p=1/2可得结果,可验证此结果满足分布 律两性质。
• 而有的实验结果与数值无直接关系,我们可 以把它映射为数值来表示,如:硬币抛掷中出 现正面用“0”来表示,出现反面用“1”来表示。
例1:在一袋中装有编号分别为1,2,3的3只球,
在袋中任取一只球,放回,再取一只球,记录它 们的编号。考察两只球的编号之和。则实验的样 本空间S={e}={(i,j)} i,j=1,2,3。 i,j分别为第一,第 二次取到球的号码。 以X表示两球号码之 和,得到样本空间 的每一个样本点e, X都有一值与之对 应,如图2-1。
随机变量及其分布

随机变量及其分布一、随机变量用来表示随机现象结果的变量称为随机变量。
常用大写字母X,Y,Z等表示随机变量,而它们的取值用相应的小写字母x,y,z等表示。
假如一个随机变量仅取数轴上有限个点或可列个点(见图1.3-1),则称此随机变量为离散随机变量,或离散型随机变量。
假如一个随机变量的所有可能取值充满数轴上一个区间(a,b)(见图1.3-2),则称此随机变量为连续随机变量,或连续型随机变量,其中a可以是-∞,b可以是+∞。
[例1.3-11产品的质量特性是表征产品性能的指标,产品的性能一般都具有随机性,所以每个质量特性就是一个随机变量。
例如:(1)设X是一只铸件上的瑕疵数,则X是一个离散随机变量,它可以取0,1,2,…等值。
可用随机变量X的取值来表示事件:“X=0”表示事件“铸件上无瑕疵”,“X=2”表示事件“铸件上有两个瑕疵”,“X>2”表示事件“铸件上的瑕疵超过两个”等等。
这些事件有可能发生,也可能不发生。
因为X取0,1,2,…等值是随机的。
类似地,一平方米玻璃上的气泡数、一匹布上的疵点数、一台车床在一天内发生的故障数都是取非负整数{0,1,2,3,…}的离散随机变量。
(2)一台电视机的寿命X(单位:小时)是在[0,∞)上取值的连续随机变量:“X=0”表示事件“一台电视机在开箱时就发生故障”,“X ≤10000”表示事件“电视机寿命不超过10000小时”,“X>40000”表示事件“电视机寿命超过40000小时”。
(3)检验一个产品,结果可能是合格品,也可能是不合格品。
设X表示检验一个产品的不合格品数,则X是只能取0或1两个值的随机变量。
“X=0”表示合格品,“X= 1”表示不合格品。
类似地,检验10个产品,其中不合格品数X是仅可能取0,1,…,10等11个值的离散随机变量。
更一般的,在n个产品中的不合格品数X是可能取0,1,2,…,n等n+1个值的离散随机变量。
二、随机变量的分布随机变量的取值是随机的,但内在还是有规律性的,这个规律性可以用分布来描述。
随机变量函数曲线的动画绘制方法

随机变量函数曲线的动画绘制方法
孙晓雅
【期刊名称】《福建电脑》
【年(卷),期】2006(000)010
【摘要】针对概率论与数理统计课件制作中Powerpoint难以实现的随机变量函数曲线的绘制问题,本文运用VB以正态分布和二项分布为例,开发了随机变量函数曲线的动画绘制程序,该方法在概率课程教学中具有良好的适用性.
【总页数】2页(P199-200)
【作者】孙晓雅
【作者单位】辽宁师范大学管理学院,辽宁,大连,116029
【正文语种】中文
【中图分类】TP3
【相关文献】
1.在AutoCAD中绘制函数曲线的简易方法 [J], 胡飞嘉
2.AutoCAD中函数曲线的绘制方法 [J], 廖海平;曾翠华
3.基于梯度特征的医学体绘制传输函数曲线拟合方法 [J], 魏丽芳;齐敏;邓林;宣杭;郝重阳
4.基于AutoCAD的通用函数曲线绘制方法 [J], 吴伟中;孙建平
5.AutoCAD中绘制函数曲线的程序设计方法 [J], 熊锡义
因版权原因,仅展示原文概要,查看原文内容请购买。
随机变量简单相关系数图示的算法设计

收稿 日期 : 0 10一 4 2 1 —3l
基 金 项 目:内蒙 古 师 范 大 学 研 究 生 科 研 创 新 基 金 资 助 项 目( X J 1o 1 C Js 0 5 ) 作 者 简介 :张 衍 伟 (9 7 , , 东 省 泰 安 市 人 , 蒙 古 师 范 大 学 硕 士 研 究 生 1 8 一) 男 山 内
另一 个 圆 的圆心 在水 平 线 Y=Y/ 4上 方 , 径 R — 半
y/ X > 4 4, R.
1 1 p∈ ( 。) . 0 1
.
c
3 圆相交 的情 形 如图 1 个 所示 . 以圆 0 圆 O 和
’ 14 " /
为 例 , 关 系数 I。 相 D = 盟 , 中 S 0 一 . 直 线 其 圆] 设
使用迭代法求出a 的值后, 即可确定出圆O 的圆心的坐标为( 会一R o詈, , 心的坐标为 cs ÷)圆O 的圆
( R0 ,) 三 形A 。 中 } Ol2s等 J0J2s粤 lOI2 , 。 Ri , s 在 O 。 0。 n 。 O n = n O
WO1
0 与 01 A B的夹 角为 口 ( 口∈ ( , ) , 圆半 径 相 O 丌 )两
x x
图 l O p 1 的相 关 系 数 图 < < 时
s …
所
z 一
一
, 其
F g 1 Co r lt n c e f in i u e o < D 1 i. r ea i o fi e tf r fO o c g <
图 2 a 的 迭代 算 法 流程 值
Fi . Th l wc a to t r to l o i m t g2 ef o h r fi a in ag rt e h wi O h t
概率论与数理统计第二章--随机变量及其分布

第十四页,编辑于星期二:四点 四十二分。
由于 X的取值点 3,4,5,6将R分成五个区间,
因此我们分段讨论可得,
?0,
x ? 3,
F( x )
F (x) ? ????00..02,5,
3 ? x ? 4, 4 ? x ? 5,
1
0.5
?0.5, 5 ? x ? 6,
0.2
?
0.05
??1,
x ? 6.
且每台设备在一天内发生故障的概率都是
0.01. 为保证设备正常工作,需要配备适量 的维修人员.假设一台设备的故障可由一人 来处理,且每人每天也仅能处理一台设备. 试分别在以下两种情况下求该公司设备发生 故障而当天无人修理的概率。 (1)三名修理工每人负责包修 60台 (2)三名修理工共同负责 180台
则称 X服从参数为 p的两点 (或0-1)分布.
第十九页,编辑于星期二:四点 四十二分。
?二项分布
例4. 设射手每一次击中目标的概率为 p,现连 续射击n次,求击中次数 X 的概率分布 .
若随机变量X的概率分布为
Pn (k)
?
P
(
X
?
k)?C
k
n
p
k
(1
?
p)n?k ,
k ? 0,1,? , n
其中 0< p<1,称X服从参数为n和 p的二项分布,
第二十一页,编辑于星期二:四点 四十二分。
?泊松分布
若随机变量 X的概率分布为
P( X ? k) ?e? ? ? k , k?0,1,2,? ? ,
k!
其中λ>0为常数,则称X服从参数为λ的泊松
分布,简记为 X ~ P (? )
系统建模与仿真-第六章随机变量的生成
第六章 随机变量的生成在第四章,我们讨论产生和检验均匀随机数的方法。
因为均匀分布随机数是生成其它分布类型的随机变量的基本要素。
及进行随机仿真,必须要随机抽样,即产生服从一定分布的随机变量。
若给出随机变量的分布函数F (x ),,则可用各种方法生成服从该分布的随机变量。
本章讨论生成随机变量的方法。
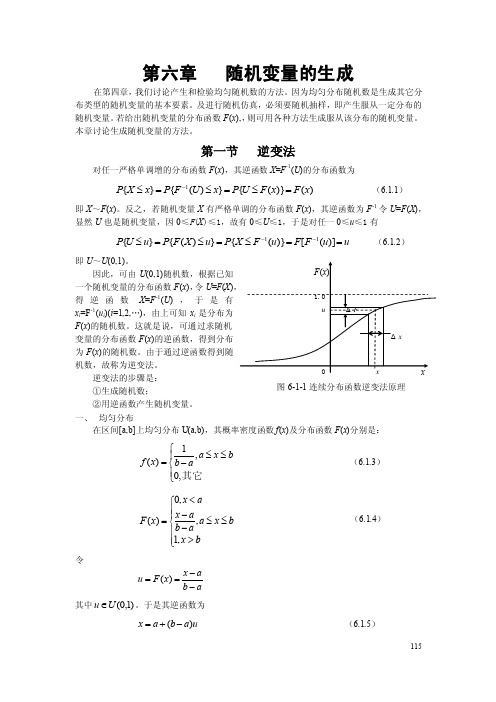
第一节 逆变法对任一严格单调增的分布函数F (x ),其逆函数X =F -1(U )的分布函数为)()}({})({}{1x F x F U P x U F P x X P =≤=≤=≤- (6.1.1) 即X ~F (x )。
反之,若随机变量X 有严格单调的分布函数F (x ),其逆函数为F -1令U =F (X ),显然U 也是随机变量,因0≤F (X )≤1,故有0≤U ≤1,于是对任一0≤u ≤1有 u u F F u F X P u X F P u U P ==≤=≤=≤--)]([)}({})({}{11 (6.1.2) 即U ~U (0,1)。
因此,可由U (0,1)随机数,根据已知一个随机变量的分布函数F (x ),令U =F (X )得逆函数X =F -1(U ),于是有x i =F -1(u i )(i =1,2,…),由上可知x i 是分布为F (x )的随机数。
这就是说,可通过求随机变量的分布函数F (x )的逆函数,得到分布为F (x )的随机数。
由于通过逆函数得到随机数,故称为逆变法。
逆变法的步骤是:①生成随机数;②用逆函数产生随机变量。
一、 均匀分布在区间[a,b]上均匀分布U(a,b),其概率密度函数f (x )及分布函数F (x )分别是:⎪⎩⎪⎨⎧≤≤-=其它,0,1)(b x a a b x f (6.1.3)⎪⎪⎩⎪⎪⎨⎧>≤≤--<=bx b x a a b ax a x x F ,1,,0)( (6.1.4) 令ab ax x F u --==)( 其中)1,0(U u ∈。
随机变量及其分布PPT课件

例8. 某类灯泡使用时数在1000小时以上 的概率是0.2,求三个灯泡在使用1000 小时以后最多只有一个坏了的概率.
解: 设X为三个灯泡在使用1000小时已坏的灯
泡数 . X ~ B (3, 0.8),
P(X k)C3k (0.8)k (0.把2)观3察k ,一个k 灯泡0,的1,2使,3用
随后单调减少.
..
0
n=13,p=0.5
..n
当(n+1)p为整数时,二项概率P(X=k) 在k=(n +1)p和k =(n+1)p-1处达到最大 值.
课下请自行证明上述结论.
31
例6. 将一枚均匀骰子抛掷3次, 令X 表示3次中出现“4”点的次数
不难求得,
X的概率分布列是:
P{
X
k}C3k
(
依题意x可取值0第i个路口遇红灯i123路口3路口2路口118x表示该汽车首次遇到红灯前已通过的路口的个数路口3路口2路口1路口3路口2路口1第i个路口遇红灯i123路口3路口2路口1第i个路口遇红灯i123某加油站替公共汽车站代营出租汽车业务每出租一辆汽车可从出租公司得到3因代营业务每天加油站要多付给职工服务费60元
一般地,我们给出如下定义:
定义1 :Байду номын сангаасxk(k=1,2, …)是离散型随 机变量X所取的一切可能值,称
P(X xk ) pk, k=1,2,… …
为离散型随机变量X的概率分布列
简称分布列, 又称分布律.
其中 pk (k=1,2, …) 满足:
(1) pk 0,
用这两条性质判断
k=1,2, … 一个函数是否是
P( X k) a k , k =0,1,2, …, 0
随机变量函数中的线性变换与平方变换的图解法

随机变量函数中的线性变换与平方变换的图解法
线性变换与平方变换是随机变量函数的一类变换,它用于描述实验中观察到的随机变量之间的关系。
本文主要介绍线性变换与平方变换的图解法,并讨论它们之间的区别和特点。
线性变换是指把一个随机变量变换成另一个同样可以表示为一组常数乘以原来随机变量的新的随机变量的变换。
它的图解法可以用四象限散点绘图来表示,如图1所示,以一个变
量Y为横轴,另一个变量X为纵轴,变换前原变量X和Y在图中表示为正方形,变换后
新变量X'和Y'形成直线,其斜率可以由图中给出,公式可表示为:Y'/X' = kY/X。
图1 线性变换的图解法
平方变换是把一个随机变量X变换为X^2的随机变量Y的变换,它的图解法可以用交叉
散点图来表示,如图2所示,以一个变量X为横轴,另一个变量Y为纵轴,表示X^2 = Y,公式可表示为Y = X^2。
综上所述,线性变换与平方变换的图解法有所不同。
前者是从一个正方形变成一条斜率,而后者是从一个点变成一条曲线。
同时,它们都是研究随机变量之间联系,表现出不同随
机变量之间的内在联系的一种变换方式。
二维随机变量数值特征及其可视化

sh_y_f_1.m【 clc,cleark=200; %计算机模拟次数z=1.4166; %期望的理论值(单位:万元)xx=zeros(1,k);yy=zeros(1,k);zz=zeros(1,k);figure(1)hndl=plot([0 0],[0,k/2],':','erasemode','xor');%实时动画要素1hold onaxis([0,2,0,1.5*k]);theAxs =axis; %取出当前坐标轴,使得后继图形保持与当前坐标相同尺度set(gca,'ytick',[0 k/3 k/2 1.5*k],'yticklabel','0|0|0|200');plot([theAxs(1),theAxs(2)],[k/3,k/3],'r:','linewidth',2); %画线标识期望理论值plot([z,z],[theAxs(3),theAxs(4)],'r-','linewidth',3); %画线标识利润期望for i=1:k %进行k次模拟x=unifrnd(10,20); %随机产生服从均匀分布U(10,20)的生产量y=unifrnd(10,20); %随机产生服从均匀分布U(10,20)的需求量xx(i)=x; yy(i)=y;%--------------------------%计算利润---------------------------- if y<=xzz(i)=0.1*y;elsezz(i)=0.05*(x+y);end%--------------------------%-----------------------------------plot([0 zz(i)],[i+k/2 i+k/2],'linewidth',1); % 将点投影到x轴,画相应的投影示意线plot(zz(i),k/3,'o'); % 画投点坐标的示意点set(hndl,'Xdata',[zz(i) zz(i)],'Ydata',[k/3,i+k/2]); %用当前数据替换图形句柄的X和Y数据drawnowif i<10 %if块语句,前几次模拟慢显示pause(0.5)endxlabel('试验重复次数n ')ylabel('每次试验的利润')endhist(zz)figure(2)plot(xx,yy,'r*')xlabel('试验模拟的进货量')ylabel('试验模拟的需求量')hold onplot([10 20 20 10 10],[10 10 20 20 10],'m-')axis([8 22 8 22])】sh_y_f_2.m【 function [E_hei E_hong p]=sh_y_f_6clc,clearnum_hei=0;num_hong=0;N=input('请输入试验次数N');NN=N;p=zeros(3,4); %分布列while N>0%---------画出盒子----------------------------------------------- axis([0 18 0 18])hold onplot([5 16],[3 3],'LineWidth',2,'color','b');plot([5 5],[3 13],'LineWidth',2,'color','b');plot([5,16],[13 13],'LineWidth',2,'color','b');plot([16 16],[3 13],'LineWidth',2,'color','b');%----------固定求的位置即大小------------------------------------ alpha=0:pi/200:2*pi;r=0.5;xx=[6 7 8 9 10 11 12 13 14 15]; %第一次抽球前球所在位置的球心横坐标yy=[4 8 7 5 9 4 7 10 12 6]; %第一次抽球前球所在位置的球心纵坐标ii=1:10;%-----------模拟抽球试验------------------------------------------ %----------第一次抽球------------------------------------------ pp1=fix(10*unifrnd(0,1))+1;%抽出的是第pp1个球,对应与第xx(pp1)所表示颜色的球[num_hei num_hong]=chouqiu(num_hei,num_hong,xx,yy,r,alpha,ii,pp1); ii=[1:pp1-1 pp1+1:10] ; %剩余的球的编号 %----------第二次抽球---------------------------------------pp11=fix(9*unifrnd(0,1))+1;pp2=ii(pp11); %抽出的是第pp2个球,对应与第xx(pp2)所表示颜色的球pp=sort([pp1 pp2]);[num_hei num_hong]=chouqiu(num_hei,num_hong,xx,yy,r,alpha,ii,pp2);ii=[1:pp(1)-1 pp(1)+1:pp(2)-1 pp(2)+1:10] ; %剩余的球的编号 %----------第三次抽球-----------------------------------------pp22=fix(8*unifrnd(0,1))+1;pp3=ii(pp22); %抽出的是第pp2个球,对应与第xx(pp2)所表示颜色的球pp=sort([pp1 pp2 pp3]);[num_hei num_hong]=chouqiu(num_hei,num_hong,xx,yy,r,alpha,ii,pp3);ii=[1:pp(1)-1 pp(1)+1:pp(2)-1 pp(2)+1:pp(3)-1 pp(3)+1:10];%剩余的球的编号N=N-1;clfif num_hei==0&&num_hong==2p(1,3)=p(1,3)+1;elseif num_hei==0&&num_hong==3p(1,4)=p(1,4)+1;elseif num_hei==1&&num_hong==1p(2,2)=p(2,2)+1;elseif num_hei==1&&num_hong==2p(2,3)=p(2,3)+1;elseif num_hei==2&&num_hong==0p(3,1)=p(3,1)+1;elseif num_hei==2&&num_hong==1p(3,2)=p(3,2)+1;enddisp('第k此模拟结果:')disp(['黑球数为num_hei=',num2str(num_hei)])disp(['红球数为num_hong=',num2str(num_hong)])num_hei=0; num_hong=0;end%----------计算N次试验中出现黑球数与红球数的期望k=sum(p'); %N次试验中出现黑球数分别为0 1 2的次数r=sum(p); %N次试验中出现红球数分别为0 1 2 3的次数E_hei=(0*k(1)+1*k(2)+2*k(3))/NN;E_hong=(0*r(1)+1*r(2)+2*r(3)+3*r(4))/NN;p=p/NN;bar3(p,'detached')title('bar3以参数detached绘制条形图')%--------------子函数--------------------------------------------- function [num_hei num_hong]=chouqiu(num_hei,num_hong,xx,yy,r,alpha,ii,pp) %-----------一次抽球的演示----------------------------------%-----------画出球-------------------------------------------n=length(ii);for i=1:nx=r*cos(alpha)+xx(ii(i));y=r*sin(alpha)+yy(ii(i));hold onplot(x,y); %半径为r的圆,x0,y0为原点坐标 axis equalif ii(i)==1||ii(i)==5 %定义该球为黑球fill(x,y,'k')elseif ii(i)==10 %定义该球为白球fill(x,y,'w')else %定义该球为红球fill(x,y,'r')endendhndl=plot(x,y,'k','EraseMode','XOR');if pp==1||pp==5hndl1=fill(x,y,'k'); %定义黑球的函数句柄num_hei=num_hei+1;elseif pp==10hndl2=fill(x,y,'w'); %定义白球的函数句柄elsehndl3=fill(x,y,'r'); %定义红球的函数句柄num_hong=num_hong+1;endfor t=0:0.5:(16-yy(pp)) %可以调节速度 0.5可变xx0=xx(pp);yy0=yy(pp)+t;x=r*cos(alpha)+xx0;y=r*sin(alpha)+yy0;set(gca,'UserData',hndl);hndl=get(gca,'UserData');set(hndl,'XData',x);set(hndl,'YData',y);if pp==1||pp==5 %抽出的是黑球set(gca,'UserData',hndl1);hndl1=get(gca,'UserData');set(hndl1,'XData',x);set(hndl1,'YData',y);elseif pp==10 %抽出的是白球set(gca,'UserData',hndl2);hndl2=get(gca,'UserData');set(hndl2,'XData',x);set(hndl2,'YData',y);else %抽出的是红球set(gca,'UserData',hndl3);hndl3=get(gca,'UserData');set(hndl3,'XData',x);set(hndl3,'YData',y);endaxis([0 18 0 18])drawnowend。
连续随机变量

x
x0 0, 2 1 / 2 x , 0 x1 F ( x) 2 1 / 2 x 2 x 1, 1 x 2 1, x2
ቤተ መጻሕፍቲ ባይዱ
P{X(0.5,1.5)}= F(1.5)-F(0.5)=3/4
例2. 设X的密度函数为
Ax(3x 2) 0 x 2 p ( x) 其他 0
f ( x )dx 2
0
1 x x e e dx 2
0
1
x
2 设随机变量X的概率密度为 f ( x) ae 求常数a.
a
1 2
例1.已知随机变量X的概率密度为
0 x1 x f ( x) 2 x 1 x 2 0 其它
15 45
解:设A—乘客候车时间超过10分钟
X—乘客于某时X分钟到达,则XU(0,60)
P( A) P{10 X 15} P(25 X 45} P{55 X 60}
5 20 5 1 60 2
2. 指数分布 Exp( ) 若r.v.X的p.d.f.为 e x , x 0
德莫佛
(I) 正态分布的定义
若X 的 p.d.f. 为
亦称高斯 (Gauss)分布
( x )2 2 2
f ( x)
1 2
e
x
, 为常数, 0 则称 X 服从参数为 , 2 的正态分布 记作 X ~ N ( , 2 ) 2 ( x ) ? 2 1 2 e dx 1 2
因为:
(4) P a X b P a X b P (a X b )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验一随机变量图形的绘制
1.实验目的
(1)掌握利用MATLAB做随机变量图形。
(2)通过作图更好的了解随机变量的分布及性质。
2.实验内容
(1)设连续随机变量X具有概率密度:
1
a<x<b
0 其他
(2)利用MATLAB做其概率密度曲线图和分布函数图程序如下:
X=0:0.1:4;
sym x;
fx=1/(4-0);
y=unifpdf(X,0,4);
y1=unifcdf(X,0,4);
subplot(1,4,1),plot(X,y);
subplot(1,4,2),plot(X,y1);
3.实验结果:
概率密度图像如下:
分布函数图像如下:
实验二随机变量统计特性的仿真
1.实验目的
(1)了解随机信号自身的特性,包括均值(数学期望)、方差。
(2)掌握随机信号的分析方法。
(3)会使用MATLAB工具进行分析,仿真。
2.实验原理
实验中涉及的函数使用
B = double(A)
返回A的双精度浮点值
subplot(m,n,p)
将一个图像窗口分为m*n个画图区域,选择第p个画图区域为画图区,这些画图区域的编号的规则是:从第一行开始排序,第一行画完之后,然后是第二行,以此类推。
plot(X,Y)
绘制线性二维图形,当Y为实数向量时,且Y的维数为m,则plot(Y)等价于plot(X,Y),其中X=1:m
当X,Y均为实数向量时,并且为维数相同,X=[X(i)],Y=[Y(i)],则plot(X,Y)先描述点(X(i),Y(i)),然后依次画线
M = mean(A)
返回沿数组中不同维的元素的平均值。
如果A是一个向量,mean(A)返回A中元素的平均值。
如果A是一个矩阵,mean(A)将中的各列视为向量,把矩阵中的每列看成一个向量,返回一个包含每一列所有元素的平均值的行向量。
V = var(X)
如果X是一个向量,返回向量X的方差。
如果X是一个矩阵,var(X)返回一个包含矩阵X每一列方差的行向量。
normrnd(mu,sigma,m,n)
生成服从均值参数为mu和标准差参数sigma的正态分布的m*n的随机数矩阵
3.实验内容
(1)设概率函数为
y=x
,a<x<b 0,其他
(2)请利用MATLAB编程给出连续随机变量X的概率密度函数、均值及方差图形。
(3)编程代码如下:
clear all;clc
X=0:.1:4;
syms x;
fx=1/(4-0);
y=unifpdf(X,0,4); %概率密度
y1=unifcdf(X,0,4); %分布函数
f=x*fx;
E=double(int(f,x,0,4)); %均值
f1=x^2*fx;
EY2=double(int(f1,x,0,4));
D=EY2-E^2; %方差
axis on;
subplot(1,4,1),plot(X,y);
title('概率密度函数');
subplot(1,4,2),plot(X,y1);
title('分布函数');
subplot(1,4,3),plot(X,E); title('随机变量X 的均值'); subplot(1,4,4),plot(X,D); title('随机变量X 的方差');
4.实验结果及结果分析
2
4
-1-0.5
0.5
1
1.5
概率密度函数0
2
4
00.1
0.20.3
0.40.5
0.60.7
0.8
0.9
1分布函数
2
4
11.21.41.61.822.22.42.62.8
3随机变量X 的均值0
2
4
随机变量X 的方差
随机变量X是在区间(a,b)上的均匀分布
均值:E(X)=(a+b)/2
方差:D(X)=(b-a)^2/12
此题方差用D(X)=E(X^2)-[E(X)]^2 公式计算
结果如图所示,在[0,4]上均匀分布的随机变量的均值E(X)=2 方差D(X)=1.333。
