含缺陷滚动轴承内部载荷分布
机械设计(9.4.1)--滚动轴承内部载荷分布及失效分析

二、失效形式
9-4 滚动轴承内部载荷分布及失效分析 一、载荷分布
1. 滚动轴承内部载荷分布
承受不偏心轴向载荷 A
承受径向载荷 R 或轴向 A 和径向 R 联 合载荷
各滚动体受力不等
一、载荷分布
9-4 滚动轴承内部载荷分布及失效分析 一、载荷分布
1. 滚动轴承内滚动轴承内部载荷分布及失效分析 一、载荷分布
1. 滚动轴承内部载荷分 布
固定套圈
一、载荷分布
9-4 滚动轴承内部载荷分布及失效分析 二、失效形式
1. 失效形式
① 疲劳点蚀
② 塑性变形
二、失效形式
9-4 滚动轴承内部载荷分布及失效分析 二、失效形式
1. 失效形式
③ 磨损
④ 套圈断裂
滚道 磨损
表征滚动轴承工作性能的要素

表征滚动轴承工作性能的要素滚动轴承的结构包括:外圈、内圈、滚动体、保持架、润滑脂和密封件。
内圈和外圈之间的对应面上设有供滚动体滚动的凹槽,根据设计要求可以有密封圈安装槽和外挡圈安装槽。
滚动轴承保持架的主要作用是将滚动体等距离分开,并引导其转动,以防止轴承运行时滚动体之间的碰撞和摩擦。
滚动体通过保持架均匀分布在内圈和外圈之间,滚动摩擦转化为滑动摩擦。
影响滚动轴承性能的主要有五个方面:轴承材料、游隙、润滑、密封条件和加工工艺。
1)轴承材料对性能的影响轴承材料是影响轴承寿命最重要的因素。
轴承的套圈和滚动体一般使用高碳铬轴承钢GCr15,不同品质的钢材原料区别主要在于氧含量和钛含量,其次为磷硫含量。
钢材中的这些非金属元素会形成非金属夹杂物,在轴承受到大载荷时会促进萌生裂纹。
其中氧含量的影响最大并且已经被证明与滚动接触疲劳寿命具有相关性,氧含量从0.0028%降低到0.0005%,其疲劳寿命可以延长一个数量级。
因为氧原子在金属中多以氧化物形式存在,氧含量高时夹杂物的颗粒大,而滚动接触疲劳寿命与最大夹杂物有关,所以控制氧含量是有效延长疲劳寿命的措施。
钢材热处理工艺对材料的组织产生影响,从而影响材料的性能。
常见的热处理质量问题有表面脱碳超标、硬度不合格、淬火裂纹以及尺寸变形等。
目前国内热处理工艺与国外的主要差距在于网状碳化物的含量、组织晶粒度大小和均匀性。
淬火温度过高(880℃)或不回火处理,会导致材料脆性较大,显微组织中的碳化物不均匀。
碳化物颗粒粗大时,基体组织中的碳化物浓度差就大,反之浓度差小,若浓度差大则浓度高和低处的寿命较低,所以平均寿命就低;碳化物的外形,细小的碳化物外形较为圆滑,粗大的碳化物外形容易有尖锐或凹凸的边缘,容易与基体产生应力集中,在受到外力作用时会成为疲劳源产生裂纹,降低使用寿命。
国外常采用电磁搅拌、均匀化退火、可控气氛连续球化退火等措施来细化均匀碳化物。
同时注意热处理后的套圈与滚动体表面硬度匹配的问题,一般滚动体的硬度控制在范围上限,而套圈的硬度控制在范围下限,保证滚动体的硬度高于套圈1~2HRC,从而达到运转过程中的“冷辗整形”作用。
深沟球轴承的载荷分布

深沟球轴承的载荷分布魏延刚;吕晶晶;刘彦奎【摘要】根据滚动轴承载荷分布理论,用传统的连续函数模型计算法、离散方法模型计算法和有限元法对深沟球轴承的载荷分布进行了计算,计算结果表明三种方法所求出的载荷分布规律相同,但计算精度不同,离散模型方法不仅计算精度最高,所给出的深沟球轴承的离散模型载荷分布计算程序,使得离散模型方法应用最为方便.【期刊名称】《大连交通大学学报》【年(卷),期】2016(037)005【总页数】5页(P62-66)【关键词】深沟球轴承;离散模型;有限元;载荷分布【作者】魏延刚;吕晶晶;刘彦奎【作者单位】大连交通大学机械工程学院,辽宁大连116028;大连交通大学机械工程学院,辽宁大连116028;大连交通大学机械工程学院,辽宁大连116028【正文语种】中文滚动轴承的载荷分布分析也是其力学特性分析的基础,如刚度、变形和承载能力、润滑状态、摩擦与温升、预期寿命等滚动轴承的一些主要性能,都是在进行载荷分布分析的基础上获得的.因此滚动轴承的载荷分布分析是确定轴承疲劳寿命和可靠性的关键因素.滚动轴承的载荷分布是指轴承在一定的载荷作用下,参与承载的滚动体数目和各受载滚动体所受载荷的大小,换句话说,也就是载荷在滚动体之间是如何分配的.实际上,滚动轴承的载荷分布不但与所受载荷的大小和方向、滚动轴承的类型和几何参数(滚动体的数目等)有关,还与滚动轴承的内部间隙、滚动体与内、外圈的变形有关.在静载荷作用下传统的滚动轴承载荷分析是在刚性套圈假设条件下进行的,并且不计摩擦力和滚动体惯性力,只考虑轴承内部间隙,滚动体与内、外圈之间的接触变形产生位移的影响(没有考虑内、外圈的整体变形的影响),而且将滚动轴承滚动体与内、外圈接触的离散模型变换为连续模型,用载荷积分这个连续函数来表示滚动轴承滚动体与内、外圈接触的位置间隙与变形的离散分布函数,为了方便应用,将载荷积分(包括径向载荷积分、轴向载荷积分和力矩载荷积分)制成表或图供设计计算时使用.这种方法是经典的滚动轴承专著采用的方法,也是国际标准所使用的方法,也就是被公认的方法[1-3].然而,经典载荷分布分析这种方法也仍然存在不足.不足之一是,实际上完全刚性的套圈是不存在的,在静载的作用下,内外套圈会不可避免的产生位移和偏离圆形的变形.不足之二是,实际上滚动体与内、外圈之间的接触是离散的,不是连续的,因此,用载荷积分这种连续函数表达离散模型必然存在一定的误差;不足之三是,实际上轴承的载荷来自轴或轴承座,轴或轴承座与轴承之间的载荷分布不是集中力,而是分布力,这种分布力必然导致轴承内、外圈产生总体变形,内外圈的总体变形对轴承的载荷分布必然会产生一定的影响.本文拟针对上述静载荷作用下传统的滚动轴承载荷分布计算的不足,一是用轴承载荷分布实际的离散模型计算轴承载荷分布,二是考虑内、外圈总体变形对滚动轴承载荷分布的影响,用有限元法对深沟球轴承的载荷分布进行计算,并比较传统的滚动轴承载荷分布计算模型、实际的离散模型计算轴承载荷分布和有限元法这三种方法的结果,从而对深沟球轴承实际的设计计算提供参考.1.1 离散模型下载荷分布数学模型与编程对于径向载荷作用下的深沟球轴承,轴承外圈固定不动,内圈在径向载荷的作用下向下移动,产生径向位移δr.以承载最大滚动体为起点,在任意角度位置滚动体的径向位移为δψ,如图1所示.由弹性力学理论可得任意角度位置ψ的滚动体所承受的径向载荷与最大承载滚动体所承受的载荷的关系为根据变形协调条件和静力平衡关系可以求出轴承所承受的径向载荷Fr与最大承载滚动体所承受的载荷的关系为式中,载荷分布系数负荷区域角度范围径向积分实际上滚动体与内、外圈之间的接触是离散的,不是连续的,因此,用载荷积分这种连续函数表达离散模型必然存在一定的误差.本文将应用轴承载荷分布离散模型进行计算,即对式直接进行求解.可应用二分法(其流程图如图2所示)求出未知量δr,从而可求出从而求出其中,为了方便计算,将深沟球轴承离散模型下的载荷分布编制VB程序,其程序框图如图3所示.1.2 两种模型下轴承载荷分布算例与结果比较以型号为209DGBB深沟球轴承为例,轴承的径向载荷为Fr=8900N,轴承内径为45mm,外径为85 mm,滚动体数目9,滚动体直径12.7 mm,弹性模量207 000 N/mm2,泊松比0.3;分别用Qψc和Qψd表示连续模型和离散模型下的深沟球轴承各个滚动体所承受的载荷,为了能够更直观的说明轴承载荷分布,将各个滚动体编号,如图4所示.在不同径向载荷Fr作用下,不同径向间隙时,传统方法和离散方法计算出的轴承的载荷分布分别在表1、表2中给出.表中列出了所有滚子的编号、与编号对应的滚子的位置角ψi、滚子所承受的载荷Qψc和Qψd;表中最后两行还给出了所有滚子所受载荷在轴承径向力方向的和力∑Fr和∑Fr与轴承径向力Fr的相对误差. 从表1中不难发现,在径向载荷Fr=4 450 N作用下,径向间隙分别为0.015、0和-0.015时,两种算法所得出的载荷分布规律一致,但受载滚子所受载荷在数值上有所不同.当径向间隙为0.015时,只有3 个滚子承受载荷,而当径向间隙为0和-0.015时,受载滚子增加为5个;而且间隙越小受载最大的滚子所受载荷越小.传统连续模型计算方法所得出所有滚子所受载荷在轴承径向力方向的和力∑Fr与轴承径向力Fr的相对误差分别约为0.98%、0.39%和0.91%,而离散模型方法所计算出的相对误差都是约为0.03%、0.01%和0.02%.当载荷Fr=8 900 N时,三个间隙下都是有5个滚子承受载荷,也是间隙越小受载最大的滚子所受载荷越小.从表2中类似的得到相应的两种算法的误差分别约为0.19%、0.36%、0.64%和0.01%、0.02%、0.005%.显然,离散模型方法所计算出的结果精度高.2.1 有限元仿真模型将深沟球轴承的内外圈和滚动体均设置为弹性体.其外圈固定,内圈转动,在其内圈的几何中心处施加Fr的径向载荷.为了提高计算效率,由于轴承几何结构的对称性,本文采用沿轴承轴线方向取有限元模型的二分之一进行计算分析,并将滚动体按照顺时针的方向进行编号.其简化后的模型如图4所示.为了在保证计算精度的同时能尽量减少计算时间,在发生接触的区域进行网格细化并设置合理的边界条件.整个轴承有限元模型共有412 068个节点和373857个单元.网格细化后的模型如图5所示.2.2 有限元仿真结果及轴承载荷分布分析对于大多数的球和滚子轴承,内滚道的法向接触应力要大于外滚道的法向应力,且内滚道与外滚道的接触应力分布规律相似.由于篇幅有限,在此仅给出径向间隙为0 mm、径向载荷为8 900N时,用有限元法进行仿真所获得的接触应力云图,见图6.由图可知,只有3号~7号滚动体承受载荷,其中5号滚动体所受的载荷最大,其最大接触应力值3 057 MPa.可以将有限元分析所得出的接触应力,通过积分的方法,将各个接触面上的应力求和,从而获得所需的每个滚动体所承受的载荷,也就是轴承的载荷分布.径向间隙分别为0 mm时,在三个大小不同的径向载荷Fr(4 450、6 675、8 900 N)作用下,三种计算方法计算出的209DGBB深沟球轴承的载荷分布在表3中给出.由表3可知,用有限元法计算出的结果与前述两种算法得出的载荷分布规律一致,但受载滚动体所受载荷在数值上有所不同.在不计接触面上的摩擦力时,有限元法计算出的相对误差分别约为1.8%、1.7%和1.7%.对深沟球轴承的载荷分布采取了三种不同的方法.分别为:传统连续型模型算法、改进后的离散模型方法以及有限元分析法.这三种方法所得出的分布规律完全相同.相比之下,离散模型算法所得出的精度最高,传统连续型模型算法次之;而根据有限元分析计算出的接触应力,通过对接触区域的接触应力进行积分所求出的结果精度相对最低,其主要原因是没有考虑接触面上摩擦力的影响.考虑到离散模型算法不但计算精度高,而且计算公式具有通用性,改变其中的一些变量即可以推广到圆柱滚子轴承和圆锥滚子轴承等其他轴承的载荷分布计算中,因此,建议应用中使用离散模型算法.【相关文献】[1]HARRIS TA, KOTZALA MN.Rolling Bearing Analysis FIFTH EDITION: Essential Concepts of Bearing Technology[M]. Boca Raton: CRC Press, 2007.[2]HARRIS TA.滚动轴承分析(第1卷):轴承技术的基本概念[M] .5版,北京:机械工业出版社,2010:104-157.[3]中华人民共和国国家标准.GB/T20060-2011滚动轴承国家标准[S].北京:中国标准出版社,2003:29-33.[4]邓四二.滚动轴承设计原理[M].北京:中国标准出版社,2004:55-68.[5]魏延刚,赵兵.四点接触球轴承接触角对接触应力的影响初探[J].大连交通大学学报, 2015,36(4):51-53..。
滚动轴承的工作情况

⑴当Fd1 +Fae > Fd2
右边压紧
Fae Fd1 Fd2
左边压紧
2
Fd2
Fae
1
Fd1
左边压紧
⑵当Fd1 +Fae < Fd2
R2 R1 右边压紧
解: 1 画安装简图→ ①画安装简图 Fd2 与 Fae同向 Fd1 同向 求Fd1,Fd2 R1 Fd1=0.68R1=0.68×5000=3400N × = Fd2=0.68R2=0.68×8000=5440N × =
只能承受纯径向载荷的轴承( 、 类 只能承受纯径向载荷的轴承(N、NA类)P=fP Fr = 只能承受纯轴向载荷的轴承( 类 只能承受纯轴向载荷的轴承(5类): P=fP Fa =
设计轴承的基本方法: 设计轴承的基本方法: 由工作条件定轴承类型→× ⑴由工作条件定轴承类型 ×0000 ⑵由结构定轴承直径→ ×00×× 由结构定轴承直径 ×× ⑶初选型号 → ××× ×× →查C、C0 查 、 验算寿命: ⑷验算寿命: 计算轴承载荷→查 、 、 计算P→计算 h 计算L 计算轴承载荷 查e、X、Y →计算 计算 计算 →分析轴承是否合格 分析轴承是否合格
┌ 两端固定→ 两端固定
1
Fae Fae
2 2
Fae指向者受力 1 Fa1= Fae , Fa2=0 固定端受力 └ 一端固定、一端游动 →固定端受力 一端固定、 α Fa 1=0 , Fa 2= Fae
2.角接触轴承 (3、7类) 角接触轴承 、 类 (1)派生轴向力 d 派生轴向力F 派生轴向力
ε ε
LP = C = 常数
1 2 3 4
L10
轴承寿命计算公式
C ε 6 L10 = ( ) × 10 (转) P 6 10 C ε 16667 C ε Lh = ( ) = ( ) (h ) 60n P n P
滚动轴承2

例1:已知齿轮轴采用一对6211轴承,已知轴承
载荷Fr 1=3500N,Fa1=1606N, Fr2=2500N,Fa2=0
fd=1.2,试求P1、P2。
解:查得:C0r=29200N
e1
0.28
0.28 0.084
0.26 0.056
n6 轴外径公差带 m6 js6 j6 k6 0
轴承内径公差带
轴承外圈与轴承座孔 基轴制:
松 ————→紧 G7,H7,JS7,J7
G7 轴承座孔公差带 H7
Js7 J7 0
轴承外径公差带
滚动轴承配合的选择原则:
1)转动圈比不动圈配合松一些 2)高速、重载、有冲击、振动时,配合应紧一些,
轴承寿命曲线:
L10
(C ) P
P L10 常数
(106 转)
1234
L10
×106(r)
轴承寿命计算公式:
L10
(C ) P
106
(转)
L10h
ห้องสมุดไป่ตู้
10 6 60n
(C ) P
(h)
或:
C P
60nL10h 106
式中:n——转速 r/min ε——寿命指数 球轴承 ε=3 滚子轴承ε=10/3
P2=fd
=5628N Fr2=1.2×2500=3000N
∵P1>P2 ∴1轴承危险, 计算1的寿命
(0.084,0.28)
(0.056,0.26)
(0.060,?)
e1
0.28
0.28 0.084
滚动轴承的判废标准

滚动轴承的判废标准内容来源自网络根据滚动轴承型式的不同,为以下几个方面:一、向心球轴承1、内外圈滚道剥落,严重磨损,内外圈有裂纹。
2、滚珠失圆或表面剥落,有裂纹。
3、保持架磨损严重。
4、转动时有杂音和振动,停止时有制根据滚动轴承型式的不同,为以下几个方面:一、向心球轴承1、内外圈滚道剥落,严重磨损,内外圈有裂纹。
2、滚珠失圆或表面剥落,有裂纹。
3、保持架磨损严重。
4、转动时有杂音和振动,停止时有制动现象及倒退反转。
5、轴承的配合间隙超过规定游隙最大值。
二、圆锥滚子轴承1、内外圈滚道剥落,严重磨损,内外圈有裂纹。
2、在滚子长方向度上,中心前移量超过1.5mm,锥形滚子前端离外圈边缘大于2~3mm。
3、保持架磨损,不能将滚子收拢在内圈上,破裂,变形无法修复。
三、向心球面滚子轴承和向心短圆柱滚子轴承1、内外圈滚道和滚子有破碎、麻点和较深的磨痕。
2、保持架变形,不能将滚子收拢在内圈上。
3、内外圈滚道与滚子的配合间隙大于0.06mm。
四、推力球轴承1、两滚道垫圈剥伤和严重磨损。
2、滚珠破碎或有麻点。
3、保持架变形严重,不能收拢滚珠。
滚动轴承的代用原则和代用方法滚动轴承的代用原则和代用方法如下:一、滚动轴承的代用原则1、轴承的工作能力系数和允许静载荷等技术参数要尽量等于原配轴承的技术参数。
2、应当选择允许极限转速等于或高于原配轴承的实际转速。
3、代用轴承的精度等级要不低于原配轴承的精度等级。
4、尺寸要相同,不能因为更换轴承而随意改变机器与轴承相配合的尺寸。
5、采用镶套方法的轴承,要保证所镶轴套的内外圆柱面的同心度,并应正确选用公差与配合。
二、滚动轴承的代用方法1、直接代用代用轴承的内径、外径和厚度尺寸与原配轴承完全相同,不需采取任何措施即可安装使用。
2、加垫代用代用轴承的内径、外径与原配轴承完全相同,仅宽度较窄时,可采用加垫代用。
所加垫圈的厚度等于原配原配轴承和代用轴承的宽度差。
垫圈内径与轴采用间隙配合,外径为轴承内圈的外径。
滚动轴承滚动体配合间隙对载荷分布的影响

Internal Combustion Engine &Parts0引言动轴承是机械领域中重要的部件之一。
其使用寿命也是人们关注的一个焦点。
轴承的使用寿命与其本身的载荷分布有着密切的关系。
因此研究滚动轴承的载荷分布对轴承而言有着重要的学术和实用价值。
滚动轴承的载荷分布,指的是轴承在一定的载荷作用下,参与承载的滚动体数目和各受载滚动体所受载荷的大小,即载荷在滚动体间的分配关系。
滚动轴承的载荷分布与许多因素有关,本文主要研究滚动体与内、外圈在不同配合状态下,载荷分布的规律。
1滚动轴承载荷分布的计算方法滚动轴承载荷分布的理论可分为三类,基于Hertz 接触理论的经典分析法、古典数值法以及以有限元、边界元为代表的现代数值法。
在静载荷作用下,传统意义上滚动轴承载荷分布,是根据理想模型计算得出的,模型中摩擦力和滚动体惯性力忽落不计,只考虑轴承内部间隙、滚动体与内外圈之间因接触变形而产生的移位的影响。
为简化计算,传统模型将滚动轴承滚动体与内、外圈接触的离散方程变换为积分函数,并将载荷积分制成表或图供设计计算时使用。
这种方法是经典的滚动轴承专著采用的方法,也是国际标准所使用的方法[1-2]。
在现实应用中,滚动体与内、外圈之间的接触是离散的,而非连续,用载荷积分这种连续函数表达离散模型必然存在一定的误差。
针对上述不足,本文采用更接近实际的离散模型对圆柱滚子轴承的载荷分布进行计算,为圆柱滚子轴承实际的设计计算提供参考。
2圆柱滚子轴承在离散模型下的载荷分布计算2.1圆柱滚子轴承离散模型下的载荷分布数学模型与编程滚动轴承在纯径向载荷作用,通常处于下方中央的滚动体承受最大载荷,其两边滚动体所承受的载荷依次减小。
某个滚动体承受载荷与否,取决于滚动体是否处于负载区域内,负载区域角度范围为[4]:径向载荷与各滚动体受载荷Q ψ之间的关系:而从而(1)ε为载荷分布系数:受载最大滚动体承受载荷:K n 为载荷位移系数,对于圆柱滚子轴承,取K i =K o =K 1δmax 是滚子的最大位移,取决于滚子与内外圈的初始间隙P d 和套圈在ψ=0°径向移动量δr ,具体为:整理得,滚子类轴承,指数n 取[5]109。
深沟球轴承载荷分布

径向载荷作用下,有确定游隙的深沟球轴承内部的载荷分布轴承以209DGBB深沟球轴承为基础,稍作调整,径向载荷为8900N。
轴承的几何参数、受力简图如下图所示。
根据滚子及滚道的曲率半径,根据下式,分别求得内圈、外圈的曲率和、差:
根据下图,分别求得内外圈的。
利用上述结果,根据下式,求得(对球轴承,n=1.5)。
将代入公式:
1 可知,在该公式中,只有与是未知量,而是求滚子最大负载的关键量。
可由下式确定:
这里,不细究的公式,它可通过查询下表并插值得:
与的关系如下:
由此,我们获得了一个非线性的三元方程组:
未知量为。
如何求解这样的方程组呢?
可以看到,,则可把第一个方程看作是仅含有的非线性方程组,且由
的物理意义可知,。
将第一个方程化作如下形式:
使用二分法,使左侧部分的值趋近于0,则可以求解出该方程组的数值解,进而求得。
利用下式,求得最大滚子负载:
再利用下式,求得不同位置角下滚子的载荷:。
滚动轴承的受力分析、载荷计算、失效和计算准则
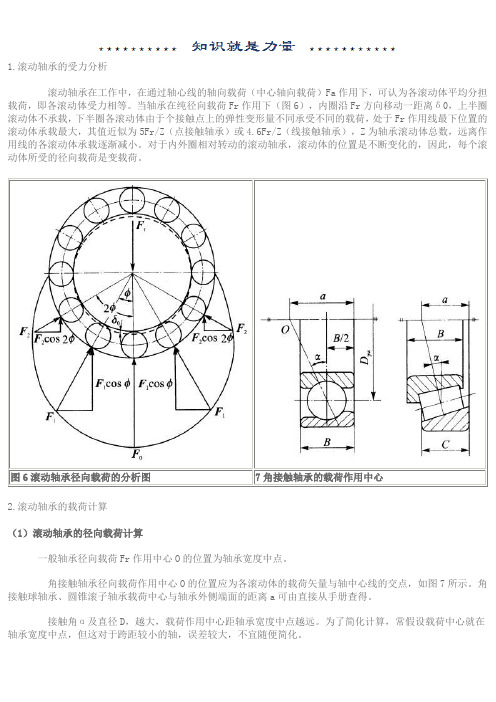
1.滚动轴承的受力分析滚动轴承在工作中,在通过轴心线的轴向载荷(中心轴向载荷)Fa作用下,可认为各滚动体平均分担载荷,即各滚动体受力相等。
当轴承在纯径向载荷Fr作用下(图6),内圈沿Fr方向移动一距离δ0,上半圈滚动体不承载,下半圈各滚动体由于个接触点上的弹性变形量不同承受不同的载荷,处于Fr作用线最下位置的滚动体承载最大,其值近似为5Fr/Z(点接触轴承)或4.6Fr/Z(线接触轴承),Z为轴承滚动体总数,远离作用线的各滚动体承载逐渐减小。
对于内外圈相对转动的滚动轴承,滚动体的位置是不断变化的,因此,每个滚动体所受的径向载荷是变载荷。
图6滚动轴承径向载荷的分析图7角接触轴承的载荷作用中心2.滚动轴承的载荷计算(1)滚动轴承的径向载荷计算一般轴承径向载荷Fr作用中心O的位置为轴承宽度中点。
角接触轴承径向载荷作用中心O的位置应为各滚动体的载荷矢量与轴中心线的交点,如图7所示。
角接触球轴承、圆锥滚子轴承载荷中心与轴承外侧端面的距离a可由直接从手册查得。
接触角α及直径D,越大,载荷作用中心距轴承宽度中点越远。
为了简化计算,常假设载荷中心就在轴承宽度中点,但这对于跨距较小的轴,误差较大,不宜随便简化。
图8角接触轴承受径向载荷产生附加轴向力1)滚动轴承的轴向载荷计算当作用于轴系上的轴向工作合力为FA,则轴系中受FA作用的轴承的轴向载荷Fa=FA,不受FA作用的轴承的轴向载荷Fa=0。
但角接触轴承的轴向载荷不能这样计算。
角接触轴承受径向载荷Fr时,会产生附加轴向力FS。
图8所示轴承下半圈第i个球受径向力Fri。
由于轴承外圈接触点法线与轴承中心平面有接触角α,通过接触点法线对轴承内圈和轴的法向反力Fi将产生径向分力Fri;和轴向分力FSi。
各球的轴向分力之和即为轴承的附加轴向力FS。
按一半滚动体受力进行分析,有FS ≈ 1.25 Frtan α(1)计算各种角接触轴承附加轴向力的公式可查表5。
表中Fr为轴承的径向载荷;e为判断系数,查表6;Y为圆锥滚子轴承的轴向动载荷系数,查表7。
货车197726型滚动轴承典型失效分析
相对于外圈降低了 58. 5% 。或者说, 前面计算的内圈 每分钟所受应力循环次数应折算为 h内 , 即 h内 = h内 / 0. 585= 407 8( 次) 。
从上述计算数据可以看出, 在同样应力状态下, 外 圈顶部应力循环次数相当于比内圈每分钟多 652 次。
所以, 疲劳剥离多发生在外圈滚道上。
K 1、K 2 —— 系数, K 1= 0. 5〔t an( -
co t( - )
) - tan 〕
时 间
表 2 段修货车滚动轴承故障调查统计表 轴 号 轴承装用时间 外观特征 轴承破损情况
K 2= 0. 5〔t an( - ) + tan 〕 cot( - )
其中: —— 轴承外圈滚道锥角, 即接
甩油 剥离 143×43×3. 5 后排保持架碎 8 块
甩油
0. 6
前排保持架碎 17 块
甩油
剥离 120×60×3 后排保持架碎 36 块
甩油
1. 0
前排保持架碎 4 块
异音
2. 0
前排保持架碎 5 块
甩油
1. 7
前排保持架碎 5 块
轴承装用 红外线测温
时间
/℃
1996. 8
正常
1996. 7
32. 1
铁路货车滚动轴承的技术状态, 是影响铁路行车 安全、车辆寿命的重要因素之一。
1 失效件的统计分析及其主要失效模式
天津铁路分局对其所属 4 个有关单位的 116 套轴
承检修记录和近 2 a 发生的滚动轴承热、切轴事故进 行了统计和分析, 结果见表 1~表 3。
通过上述统计分析可以发现, 197726 型滚动轴承 的主要失效模式有 6 种: 保持架裂损、剥离、密封失效、 滚子擦伤、密封座裂及外圈裂损。
滚动轴承的故障现象及原因分析

滚动轴承的故障现象及原因分析滚动轴承是机械设备中常用的一种轴承形式,由内圈、外圈、滚子和保持架组成。
它的主要作用是承载和传递旋转运动或轴向运动的载荷。
然而,在实际的使用过程中,滚动轴承可能会出现各种故障现象。
下面,我将从滚动轴承的故障现象和原因两个方面进行分析。
一、故障现象:1.轴承过热:滚动轴承过热通常表现为温度升高。
过高的温度会导致润滑剂失效,加剧摩擦和磨损,最终导致轴承损坏。
2.噪音:滚动轴承在工作时会发出异常的噪音。
噪音通常由于轴承的松动、减速器齿轮偏心或不平衡导致的振动引起,也可能是轴承部分损坏或磨损的结果。
3.卡住:滚动轴承可能会发生卡死现象,即不能正常转动。
卡住通常由于外部污染物进入轴承内部,或者内外圈之间的配合不当引起。
4.弹性不良:滚动轴承在运转时可能会出现弹性不良现象,即出现过大的变形或破裂。
弹性不良通常由于材料强度不足,或者过载运转和外部冲击引起。
5.寿命短:滚动轴承的使用寿命取决于材料质量、制造工艺和使用环境等因素。
如果这些方面存在问题,轴承的寿命可能会显著减少。
二、原因分析:1.润滑不良:润滑不良是导致滚动轴承故障的常见原因之一、润滑不良会导致轴承过热、摩擦增大和磨损加剧。
常见导致润滑不良的原因包括润滑油质量不合格、润滑油脂添加不足等。
2.过载运转:滚动轴承在过载运转时会受到较大的载荷,使得轴承的压力和摩擦增大,加速磨损和损坏。
过载运转通常是由于设备设计不合理、外部冲击或负载突然变化等原因引起的。
3.安装不当:滚动轴承的安装不当会导致内外圈之间的配合间隙不合适,产生轴承松动或过紧,引起摩擦增大和磨损。
安装不当还可能导致载荷不均匀分布,使得特定部位的轴承负荷过大而损坏。
5.材料质量问题:滚动轴承的材料质量直接影响其使用寿命和性能。
低质量的材料容易导致强度不足、易磨损和易断裂等问题,从而缩短滚动轴承的使用寿命。
综上所述,滚动轴承的故障现象和原因分析包括轴承过热、噪音、卡住、弹性不良、寿命短等故障现象,其原因包括润滑不良、过载运转、安装不当、环境污染和材料质量问题。
【精品】滚动轴承的额定载荷与寿命(必学)

滚动轴承寿命计算滚动轴承的额定载荷与寿命:1轴承的寿命与承载能力1.1寿命1.2基本额定载荷2根据额定动载荷选择轴承尺寸2.1轴承的当量动载荷2.2寿命公式2。
3影响轴承动载荷能力的主要因素1 / 212.4 修正额定寿命3根据额定静载荷选择轴承尺寸3.1轴承的当量静载荷3.2轴承所需额定静载荷的确定3。
3当量静载荷计算方法3.4安全因数的选取1轴承的寿命与承载能力1.1寿命轴承即使在正常的条件下使用,套圈和滚动体的滚动面也会因受到交变应力作用而发生材料疲劳,以致造2 / 21成剥落。
疲劳剥落是滚动轴承的主要失效形式,因此,轴承的寿命一般情况指其疲劳寿命.疲劳寿命的定义为:一套轴承,其中一个套圈(或垫圈)或滚动体的材料出现第一个疲劳扩展迹象之前,一个套圈(或垫圈)相对另一个套圈(或垫圈)的转数。
在某些特定情况下,轴承也可能因磨损过度或丧失必须的精度而失效,这时轴承的寿命是指磨损寿命或精度寿命,需另行考虑.此外,轴承因烧伤,磨损,裂纹,卡死,生锈等都可能无法使用,但这些应称为轴承故障,须与轴承寿命区分开.轴承选用不当,安装欠妥,润滑不良及密封不好等都是发生故障的原因,排除这些原因便可避免轴承发生故障。
(1)可靠性3 / 21实验室试验和实际应用中表明,同一结构型式和外形尺寸的一组轴承,在相同的运转条件下,实际疲劳寿命大不相同。
一批轴承的疲劳寿命服从一定的概率分布规律,所以轴承的寿命总是与其失效概率相联系。
轴承寿命的可靠性用可靠度指标衡量,它指一组在同一条件下运转的,近于相同的滚动轴承所期望达到或超过规定寿命的百分率。
单个滚动轴承的可靠度为该轴承达到或超过规定寿命的概率。
(2)基本额定寿命和修正额定寿命对于一套滚动轴承或一组在同一条件下运转的,近于相同的滚动轴承,其寿命是指与90%的可靠度,常用的材料和加工质量以及常规的运转条件相关的寿命,称之为基本额定寿命。
考虑所要求的可靠性水平,特殊的轴承性能和具体的运转条件,而对基本额定寿命进行修正所得到的寿命则称为修下正额定寿命。
滚动轴承失效分析及典型案例-印刷稿2014

大型回转支承失效案例
大型回转支承安装部位
回转支承
钢包台车
连铸机
26
大型回转支承失效案例
台车回转支承基本结构
内圈反推力 滚道1
外圈反推力 滚道4
外圈径向滚 道6
外圈主推力 滚道8
内圈主推力 滚道3
1
3
外
圈
2
内 圈
上半内圈 下半内圈
1、2-推力滚子,3-径向滚子
上半内圈 挡边5
内圈径向 滚道2
下半内圈 挡边6
轴承运行参数的收集
滚动轴承运行参数主要包括;载荷、转速,轴承在运行过程中振动、温 度、电流以及主机工作参数如轧钢过程的压下量、钢材的轧制温度等工艺 参数的变化情况以及轴承更换和实际运行时间、设备人员对设备检查记录 等。
根据上述的观察及了解基本可以分清轴承损坏原因的分析方 向,然后根据轴承损坏的形式选用相应的分析方法如:油样分析、 材料的金相分析等,进一步分析轴承损坏的根本原因
6
液压柱塞泵轴承事故案例
液压柱塞泵轴承安装部位
滚针轴承
单列圆锥滚 子轴承 30324D
驱动轴
倾斜 支承轴
柱塞 组合件
配油盘
主单列圆柱滚 子轴承 NF324
缸体
圆锥轴承外圈与座体不配合,有1mm的间隙,避免“3”点支承,圆锥轴承不承受径向载荷。 8
液压柱塞泵轴承事故案例
主要零部件的观察记录
主要零部件
圆锥滚子轴承外圈多处断裂
圆锥滚子轴承外圈断裂外貌
圆锥滚子轴承外圈断裂外貌
10
液压柱塞泵轴承事故案例
轴承照片记录-3
圆柱滚子工作表面材料剥落
圆锥滚子轴承外滚道工作表面材料剥落
圆锥滚子工作表面材料剥落
多载荷联合作用下含缺陷结构载荷比计算

Ke y wo r d s : l o a d r a t i o ; d e f e c t i v e s t r u c t u r e ; mu l t i — l o a d s c o n d i t i o n s ; s a f e t y a s s e s s me n t ; u n i t
第 4 2卷 第 6 期 2 0 1 3年 1 1 月
文 章 编 号 :1 0 0 0 — 7 4 6 6 ( 2 0 1 3 ) 0 6 — 0 0 3 8 — 0 4
石
油
化
工
设
备
Vo 1 . 4 2 No . 6
NOV .2 O1 3
P ETR( ) _ CHEM I CAL EQUI P M ENT
关 键 词 :载荷 比;缺陷结构 ;多载荷工况 ;安全评定 ;单位球方法
中 图 分 类 : A
d o i : 1 0 . 3 9 6 9 / j . i s s n . 1 0 0 0 - 7 4 6 6 . 2 0 1 3 . 0 6 . 0 0 9
来 确 定 。
这 些设 备 中有 相 当一 部分 存在缺 陷 , 若 发 生事故 , 后 果将 非 常严重 [ 1 ] 。实 际工 业 生产 中无 法对 存 在 缺 陷的设备 全部 判废并 且进 行更换 , 基 于此 , 以合乎 使 用 为原 则建立 的含 缺 陷结构完 整性评 定技 术逐 渐发
c o mb i na t i o n.H o we v e r,t he c a l c ul a t i o n me t h od s o f l oa d r a t i o ha v e no t be e n a v a i l a b l e i n t he c o nd i — t i on o f mu l t i — l oa ds . The un i t s p he r e me t ho d s ui t a bl e f o r mul t i — l o a d s c o nd i t i o ns wa s r a i s e d.By e — l a s t i c — p l a s t i c me t h o d,t he a s s ump t i o n o f un i t s phe r e mo de l wa s v a l i d a t e d i n t he c a s e o f e l b o w wi t h c i r c u mf e r e n t i a l t h r o u gh c r a c k .
游隙及载荷对滚动轴承载荷分布的影响

游隙及载荷对滚动轴承载荷分布的影响王金龙【摘要】Based on the bearing dynamic theory, the Hertz contact theory and bearing macroscopic geometry, an analysis mod-el of rolling bearings which analyzes the effect of clearance and load on the load distribution is built in this paper. The results show that the angle of bearing contact distribution increases with decrease of the radial clearance, and it decreases with de-crease of the radial load;while when the negative internal clearance of bearing appears, the relative deformation of inner and outer rings are less, but the average load of rolling elements increases, which would result in the reduction of bearing life.%基于滚动轴承动力学、Hertz弹性接触理论和轴承宏观几何学,建立了滚动轴承的分析模型。
分析游隙及载荷对滚动轴承载荷分布的影响。
分析结果表明:随着径向游隙的减小,轴承的接触分布范围角增大;随着径向载荷的减小,轴承接触分布范围角减小;当轴承出现负游隙时,轴承内、外圈相对变形量较小,但轴承中滚动体的平均载荷增加,会导致轴承寿命降低。
5滚动轴承内部的载荷分布及位移-NSK

110111max5.1 滚动轴承内部的载荷分布试想以径向载荷F r ,轴向载荷F a 加于接触角为的单列轴承(角接触球轴承、圆锥滚子轴承等)的情况,既会因F a 与F r 之差使承载区发生变化,造成滚道局部承受载荷,或者造成整个滚道圆周承受载荷。
载荷的大小由承载率ε表示。
当滚道圆周局部承载时,ε为承载区在纵轴上的投影长与滚道直径的比,此时ε≦1(见图1)。
相反,当滚道全周承载时,则为∶ε= δmax≧1式中,δmax :承受最大载荷的滚动体总弹性位移量δmin :承受最小载荷的滚动体总弹性位移量轴承任一滚动体承受的载荷Q (ψ)都与其接触面上的弹性位移δ(ψ)的t 次方成正比。
所以设ψ=0时的最大滚动体载荷为Q max ,弹性位移量为δmax ,则∶Q (ψ) =( δ(ψ) )t …………….....……(1)t =1.5(点接触), t =1.1(线接触)最大滚动体载荷Q max 与径向载荷F r ,轴向载荷F a 之间存在如下关系。
F r =J r Z Q max cos .....................(2)F a =J a Z Q max sin (3)式中,Z 是滚动体数。
J r 与J a 是按点接触或线接触方式分别由(1)推导的,与ε值对应的J r 、J a 值见表1。
当ε=0.5即半圆周承受载荷时,F a 与F r 的关系由表1得∶F a =1.216 F r tan (点接触)F a =1.260 F r tan (线接触)向心轴承的基本额定载荷,在此状态下的意义不可忽视。
当轴承的游隙Δ=0时,ε=0.5,J r 值由表1选出带入式(2),则为∶Q max =4.37 F r(点接触) (4)Q max =4.08 F r(线接触) (5)当轴承仅承受轴向载荷时,F r =0,ε=∞,J a =1,带入式(3),则为式(6)。
Q =Q max =F a ………………(6)此时,所有滚动体均承受相等的载荷。
机械设计教案-滚动轴承的工作情况

13.4滚动轴承的工作情况教学目标:通过本次课的学习,使学生掌握常用滚动轴承失效形式及计算准则教学重难点:重点:滚动轴承的疲劳点蚀难点:无教学方法与手段:1.教学方法:教师讲授、案例分析、集体讨论、个别回答、师生互动启发2.教学手段:课件演示、视频课件主要教学内容及过程一、滚动轴承的受力分析、失效形式及计算准则滚动轴承的载荷分布:实际工作时,至少达到下半圈滚动体受载,轴承工作时轴承元件上载荷与应力的变化:滚动体进入承载区后,所受的载荷由零增加到Qmax,然后再逐渐减小到零——其应力为不稳定脉动循环变化,转动套圈上各点承载情况及应力情况,也是不稳定脉动循环变应力。
固定套圈上某一点上的载荷和应力是稳定的脉动循环变应力。
滚动轴承的失效形式和计算准则:主要失效形式:1)疲劳点蚀——安装润滑和维护良好情况下的正常失效形式——主要的失效形式和轴承寿命计算的依据2)塑性变形——转速很低或作间歇摆动时的主要失效形式——引起振动、噪声、摩擦力矩增大,运转精度降低磨损——润滑不良和密封不严的情况下,或多尘条件下工作的轴承的主要失效形式。
有磨磨损和粘着磨损(烧伤)计算准则:一般轴承1)进行疲劳寿命计算(针对点蚀);2)静强度校核。
二、几个重要概念一)、基本额定寿命和基本额定动载荷1、基本额定寿命L10基本额定寿命L10——同一批轴承在相同工作条件下工作,其中90%的轴承在产生疲劳点蚀前所能运转的总转数(以106为单位)或一定转速下的工作时数基本额定动载荷C——由试验得到,轴承的基本额定寿命L10=1(106转)时,轴承所能承受的载荷称~。
在基本额定动载荷作用下,轴承可以转106转而不发生点蚀失效的可靠度为90%。
纯径向载荷——向心轴承基本额定动载荷C 纯轴向载荷——推力轴承二)、滚动轴承的当量动载荷P(实际载荷)定义:将实际载荷转换为作用效果相当并与确定基本额定动载荷的载荷条件相一致的假想载荷,该假想载荷称为:当量动载荷P在当量动载荷P作用下的轴承寿命与实际联合载荷作用下的轴承寿命相同1.对只能承受径向载荷R的轴承(N、NA轴承) P=R2.对只能承受轴向载荷A的轴承(推力球(5)和推力滚子(8)) P=A3.同时受径向载荷R 和轴向载荷A 的轴承 P=XR+YAX ——径向载荷系数,Y ——轴向载荷系数考虑冲击、振动等动载荷的影响,使轴承寿命降低,引入载荷系数fp 则: P=fRR ——受RP=fPA ——只受AP=fP(XR+YA) ——同时有R 和A三、滚动轴承的寿命计算公式载荷与寿命的关系曲线方程为:10L P ε=常数 3~球轴承ε——寿命指数 ε= 10/3——滚子轴承根据定义:)10(1610r L =,P=C (轴承所能承受的载荷为基本额定功载荷)∴110⨯=εεC L P∴ε)(10PC L = (106r ) 按小时计的轴承寿命:ε)(60106PC n L h = (h ) 考虑当工作t>120℃时,因金属组织硬度和润滑条件等的变化,轴承的基本额定动载荷C 有所下降,∴引入温度系数ft ——对C 修正,则ε)(60106PC f n L t h = (h ) 当P 、n 已知,预期寿命为h L ',则要求选取的轴承的额定动载荷C 为 ε1060h t L n f P C '= N ——选轴承型号和尺寸! 角接触球轴承和圆锥滚子轴承的轴向载荷A 的计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
σ =
[
( ) ( )]
x a
2
-
y b
2
1 2
( 4)
缺陷深度修正 本文所建的缺陷模型是深度为 h 的矩形深坑, 但实际
不至于使滚动体产生足够的离心力而 体的质量也不是很大, 对轴承内部载荷分布产生显著影响
[7 ]
。并且, 对于润滑良好
上, 当滚动体经过缺陷区域时 , 并不会瞬间落入缺陷坑内而 释放全部变形量, 离开缺陷区域时也不会瞬间跳出缺陷坑而 重新获得接触变形。在实际情况下, 滚动体进出缺陷区域以 及滚动体 - 滚道接触变形释放和重新获得是一个渐变的过 程
Load Distribution of Rolling Bearing With Localized Defect
Ding Weimin,Pan Shuaihang,Zhang Zhinan *
( School of Mechanical Engineering,Shanghai Jiao Tong University,Shanghai 200240 ,China) Abstract: This paper presents a contact dynamic model of deep groove ball bearing with a localized rectangular defect. The internal load distribution of the defective ball bearing is studied based on the model and Hertz contact theory. The effects of defect size ( length and width) on load distribution are investigated. The results show that,when a ball enters the defect,it is partly or completely unloaded while other balls in the loaded zone are loaded. The load distribution of defective ball bearing is determined by the defect size to a great extent. Key words: rolling bearing; localized defect; load distribution
[8 , 9 ]
建立了双列角接触球轴承的刚度矩阵
。轴承产品在机械装备中起着承受
并用其研 究 预 紧 力 对 轴 - 轴 承 组 件 动 力 学 性 能 的 影 响 。 Bercea 等[10] 建立了双列轴承的通用刚度矩阵表达式 , 并将 其应用于柔性 支 撑 的 圆 锥 滚 子 轴 承 。 唐 云 冰
[13 ] [12 ]
, 是研究轴承力学行为的基础 。滚动轴承缺陷对滚动轴
承内部载 荷 分 布 有 显 著 影 响 , 有必要针对这一问题展开 研究。 滚动轴承内部存在着复杂的接触状态 , 滚动体与滚道的 弹性接触 问 题 是 基 于 Hertz 接 触 理 论 来 求 解 的。1896 年, Hertz[4] 研究了两个弹性体在一点发生接触的局部应力和变 Stri形量, 对点接触与线接触问题给出了理论解 。1907 年, beck[5] 基于 Hertz 理论推导出了滚动轴承内部载荷分布 , 并 Jones 给出了最大滚动体载荷的近似公式 。1946 年, Harris 析的力学模型。而后,
2 0. 5 [ R -[ R o sin( 0 . 5 ΔΦ fc - mod( θ j - Φ f) ) ] ] - 2 0. 5 [ r2 R o sin( 0 . 5 ΔΦ fc - mod( θ j - Φ f) ) ] ] = hc ( θj ) b -[ 2 o
( 5) ( 2 ) 缺陷区域长而窄, 修正的陷落深度 d ( θ j ) 由矩形缺 陷的轴向跨度角ΔΦ fa 决定。
当滚动体经过缺陷区域时 , 滚动体与滚道间的接触变形 部分或完全释放, 同时, 滚动体和滚道的接触刚度也发生了 变化。其原因为: 滚动体与滚道的接触形式由球与曲面的点 接触变为球与线的点线接触 , 同时滚动体与局部缺陷边缘之 间的接触点数目随滚动体位置的变化而变化
[13 ]
[(
1 1 Ki
)
1 n
+
本文建立含缺陷滚动轴承二自由度接触力学模型 , 采用 静力学分析的方法, 研究其内部载荷分布, 为滚动轴承设计 评估、 寿命预测和轴承 - 转子系统振动响应研究提供参考 。
80
机械设计与研究
第 32 卷 3Q 1 - 2 πab
1
1. 1
含缺陷滚动轴承接触力学模型
轴承模型与缺陷形貌 在大多数的滚动轴承应用中 , 转速不是很高, 而且滚动 1. 2
( K (1θ ) )
f j
1 n
]
n
( 15 )
。 考虑到实
K f ( θ j ) 为滚动体与外 式中: K i 为滚动体与内滚道的接触刚度 , n = 3 / 2 ,对滚子轴承, n= 滚道的修正接触刚度, 对球轴承, 10 / 9 。 修正后的缺陷区域等效接触刚度如图 3 所示。对于图 3 所选用的几种缺陷形貌 , 轴承的径向载荷均为 1 000 N。 当 缺陷的轴向跨度为 10° 和 20° 时, 缺陷区域的滚动体仍具备 承载能力, 所以滚动体在经过缺陷区域的过程中 , 等效接触 刚度先降低后恢复。 当缺陷的轴向跨度为 30° 时, 由于陷入 其中的滚动体失去承载能力 , 滚动体与缺陷区域的等效接触 刚度降为 0 。可以看出, 缺陷的轴向跨度角很大程度上决定 了缺陷区域的等效接触刚度 。
* a* 、 b* 、 弹性体的弹性模量, δ 是量纲为 1 的几何参数, ∑ρ
为两弹性体二次曲面的曲率和 。在接触椭圆区域内, 接触压 力分布为:
▲图 2 修正的缺陷深度
第4 期 1. 3 缺陷区域接触刚度修正
丁为民等: 含缺陷滚动轴承内部载荷分布
81
其接触变形等于滚动体与每一个滚道的接触变形 滚道接触, 之和, 相当于两个串联的弹簧 。于是, 等效的接触刚度为: Kn ( θj ) =
[16 , 17 ]
的滚动轴承, 作用在滚动体和滚道间的摩擦力非常小 , 也不 本文在计算轴承内部载 足以影响轴承内部载荷分布 。因此, 荷分布过程中, 不考虑离心力和摩擦力的影响 , 也不考虑保 密封、 润滑介质等对滚动轴承静力平衡的影响 。 建立 持架、 的含缺陷滚动轴承接触力学模型如图 1a 所示。为了研究方 便起见, 将缺陷定义为矩形, 其深度为 h, 中心所在的方位角 为Φ f 。由于缺陷位于滚道曲面上 , 不能用简单的长度和宽度 来描述其形貌, 在此, 我们用环向跨度角ΔΦ fc ( 圆心为轴承形 用轴向跨度角 ΔΦ fa ( 圆心 心) 来表示缺陷的长度 ( 如图 2b ) , 为外圈滚道沟曲率中心 ) 来表示缺陷宽度( 如图 2c) 。
▲图 1 含缺陷滚动轴承接触力学模型
{
min( h c ( θ j ) h a h) if Φ f - 0 else
修正后的缺陷深度如图 2 所示, 从图中可以看出, 修正 后的缺陷边缘从直角变为平滑的曲线滚动体不会直接落入 缺陷底部。滚动体在经过缺陷区域的过程中 , 能以渐变地方 式释放与再获得接触变形 。同时可以看出, 缺陷的轴向跨度 角很大程度上决定了缺陷的深度 。 ( 1)
2 0. 5 d( θ j ) = r b - r o + [ r2 r o sin( 0 . 5 ΔΦ fa) ] ] - o -[ 2 0. 5 [ r2 r o sin( 0 . 5 ΔΦ fa) ] ] = ha b -[
( 6)
( 3 ) 缺陷区域长且宽, 滚动体可以接触到缺陷底面 , 修 正的陷落深度 d( θ j ) 就是矩形缺陷的深度 h。 d( θ j ) = h 所以, 修正的缺陷深度可表示为 : d( θ j ) = ( 7) ΔΦ fc ΔΦ fc < θj ≤ Φf + 2 2 ( 8) rb 为 式( 5 ) 至( 8 ) 中: d( θ j ) 表示角位置 θ j 处的修正缺陷深度, R o 为外滚道沟底环向半径 , r o 为外滚道沟曲率 滚动体半径, 半径。
轴承是关键机械基础件 , 在国民经济和国防建设中具有 《机械基础件、 重要地位和作用, 根据 基础制造工艺和基础材 “十二五” , 料产业 发展规划 》 到 2015 年, 我国轴承行业产值 将达到 2220 亿人民币
[1 ]
给出了球轴 承 和 滚 子 轴 承 在 任 意 载 荷 作 用 下 的 静 平 衡 载 荷 - 变形计算方法。 他们提出的分析模型被后继学者广泛 采用。Gunduz 等
*
摘 要: 建立了外滚道含矩形剥落的滚动轴承接触力学模型 , 基于 Hertz 接触理论研究了静态径向载荷作 并探究了缺陷形貌 ( 环向跨度角、 轴向跨度角 ) 对轴承内部载荷分布的影响 。 结果表 用下轴承内部载荷分布 , 明, 当滚动体经过缺陷区域时 , 其载荷部分卸载或完全卸载 , 而承载区内的其他滚动体加载 ; 缺陷形貌对滚动轴 承内部载荷分布有显著影响 。总体来说, 缺陷相貌尺寸越大, 对内部载荷分布的影响越显著 , 缺陷环向跨度角 和轴向跨度角综合决定了滚动轴承内部载荷分布 。 关键词: 滚动轴承; 缺陷; 载荷分布 中图分类号: TH124 文献标识码: A DOI:10.13952/ki.jofmdr.2016.0146
在模型中, 滚 动 体 与 滚 道 的 接 触 为 弹 性 点 接 触, 根据 Hertz 接触理论, 两弹性体在载荷 Q 的作用下发生点接触, 变 形后的接触表面是一个椭圆 , 且有 a = a*
[ [
1 - ν2 1 - ν2 1 2 + E1 E2 2 ∑ρ 3Q 1 - ν2 1 - ν2 1 2 + E1 E2 2 ∑ρ 3Q
