雨中行走问题的数学建模
人在雨中行走时的淋雨量问题

人在雨中行走时的淋雨量问题人在雨中行走时的淋雨量问题一.模型假设 1.把人看做一个长方体;2.雨滴下落的速度,方向保持不变;3.人行走一段距离的速度,方向保持不变。
4.假设主要淋雨量集中在正面,背面和头部,忽略两侧淋雨量。
即考虑总淋雨量时只考虑(正面+头部)或者(背面+头部)二.符号说明1.V 为雨速(m/s ),方向定义为朝着人正面为正。
2.D 为人在雨中行走距离。
3.R 为人在雨中行走速度3.θ为雨滴下落方向与地平面的所成角,0°≤θ≤90°。
4. h1,h2,h3分别为视人体为一个长方体时人的身高(m)、身宽(m)、厚度(m);5.总淋雨量为W (R)单位为m 3。
三.模型建立本模型是在上诉理想条件下分析人在行走时的淋雨量的大小,而淋雨量的大小取决与降雨量的大小,方向,还有人行走的速度,行走的路程。
我们的目标是求出使得人在雨中行走时淋雨量最小的条件。
即最佳行走速度。
以人为Z 轴,人行走的方向为X 轴,左边为y 轴建立空间坐标系。
则雨的降落速度可以按这个坐标系分解到x 轴,y 轴,z 轴。
得到θθθsin ,cos ,cos V Vz V Vy V Vx ===。
进一步得到θcos V R V +=相.人的头部,正面或背面的淋雨面积为h1h2,h2h3,淋雨时间为D/V.则可得到人正面或背面的淋雨量为θcos 21V R h h R D +;人头部淋雨量为θsin 32V h h RD ;进一步得总淋雨量W(R )=()θθsin 33cos 21V h h V R h h RD ++。
分析:1)当雨从人正面降落,即V 方向取正,V>0,由此得到}sin 32)cos (21{)(θθV h h V R h h R D R W ++=;对W (R)进行单调性分析可知,其一阶导数0)(<'R W 。
所以W(V)单调递减。
无最小值。
2)当雨从人后面降落,即V 方向取负,V<0,由此得到()θθsin 33cos 21)(V h h V R h h RD R W ++= =21)cos 21sin 32(h Dh RV h h V h h D --θθ,θcos 0V R -<<----------------① =θθθcos ,21)sin 32cos 21(V R h Dh RV h h V h h D -≥++;------------------② 分别讨论上诉两种情况下的一阶导数可得:2)cos 21sin 32()(R V h h V h h D R W θθ+-=' 下面对其进行极值分析:其 a )当θcos 0R R -<<时,当θθcos 21sin 32V h h V h h +>0时,。
雨中行走问题模型

数学建模之雨中行走问题模型摘要:由于降雨方向的变化,在跑步过程中尽力快跑不一定是最好的策略。
就淋雨量与跑步快慢这个问题,我们通过建立数学模型来探讨在雨中如何行走才能使淋雨量最少。
在不考虑雨的方向时,当然是跑的越快淋得越少;考虑雨的方向时,那么再分情况讨论,若雨是迎着你前进的方向落下,这时以最大的速度向前跑可使淋雨量最少;若雨是从你的背后落下,那么你应控制在雨中行走的速度,让它刚好等于落雨速度的水平分量。
关键词:淋雨量,数学模型,降雨的方向。
正文1.问题的提出要在雨中从一处沿直线跑到另一处,若雨速为常数且方向不变,试建立数学模型讨论是否跑得越快,淋雨量越少。
将人体简化成一个长方形,高a=1.5(颈部以下),宽b=0.5m,厚c=0.2m,设跑步的距离d=1000m,跑步的最大速度v m=5m/s,雨速u=4m/s,降雨量ω=2cm/h,及跑步速度为v,按以下步骤进行讨论(1)不考虑雨的方向,设降雨淋遍全身,以最大速度跑步估计跑完全程的淋雨量;(2)雨从迎面吹来,雨线与跑步方向在同一平面内,且与人体夹角为 ,问跑步速度v 为多大时可使淋雨量最少。
(3)雨从背面吹来,雨线方向跑步方向在同一平面内,且与人体的夹角为α,如图2.建立总淋雨量与速度v及参数a,b,c,d,u,ω,α之间的关系,问速度v多大,总淋雨量最小。
计算α=30°的总淋雨量.(说明:题目中所涉及的图形为网上提供)2.问题的分析总的淋雨量等于人体的各个面上的淋雨量之和。
每个面上的淋雨量等于单位面积、单位时间的淋雨量与面积以及时间的乘积。
面积由已知各边长乘积得出,时间为总路程与人前行速度的比值。
再由速度分解,合成,相对速度等知识确定各面淋雨量公式,列出总的方程,根据各变量关系,得出最优解。
淋雨量(V )=降雨量(ω)×人体淋雨面积(S )×淋浴时间(t ) ①时间(t )=跑步距离(d )÷人跑步速度(v ) ②由①② 得: 淋雨量(V )=ω×S ×d/v3.合理假设3.1模型的假设(1)人身体的表面非常复杂,为了使问题简单化,假设将人视为一个长方体,并设其高1.5m(颈部以下),宽0.5m,厚0.2m.其前、侧、顶的面积之比为1:b:c, (2)假设降雨量到一定时间时,应为定值; (3)此人在雨中跑步应为直线跑步;(4)、问题中涉及的降雨量应指天空降落到地面的雨,而不是人工,或者流失的水量,因为它可以直观的表示降雨量的多少;(5)设雨速为常速且方向不变,选择适当的空间直角坐标系,使人行走的速度为(u,0,0)设雨的速度为(,,)x y z v v v v =,人行走的距离为d=100米。
雨中行走数学建模

雨中行走问题的分析吴珍数学与应用数学二班 A班冯奎艳数学与应用数学二班 A班杨彦云数学与应用数学二班 A班摘要本文讨论了雨线方向、跑步速度与淋雨量关系的问题.针对问题一,将人视为长方体,采用物理学中流体计算的思想方法计算淋雨量,得到速度越大淋雨量越小的结论。
针对问题二,首先引入雨滴降落频率的概念,解决了用雨速来确定降雨量雨滴降落不连续的问题。
然后采用物理学中流体计算的思想方法计算淋雨量,建立跑步速度与淋雨量关系的优化模型,得到速度越大淋雨量越小的结论。
针对问题三,在问题二的基础上,改变雨线方向,采用物理学中流体计算的思想方法,建立与跑步速度与淋雨量关系的优化模型,确定淋雨量最小情况下的跑步速度.针对问题四,综合雨线方向与跑步方向夹角,跑步速度,淋雨量的关系,建立几何模型,采用数形结合的方法建立淋雨量模型。
关键词雨滴降落频率;优化模型;淋雨量一、问题重述一般情况下,行人未带雨具却突降大雨,都会选择加快行走速度以减少淋雨量,但如果考虑风速、雨速,就会发现淋雨量并不光与淋雨时间有关。
那么在雨中以何种速度跑,淋雨量最少。
现假设要在雨中从一处沿直线跑到另一处,若雨速为常数且方向不变,试建立数学模型,讨论是否跑得越快,淋雨量越少。
按以下步骤进行讨论:(1) 不考虑雨的方向,设降雨淋遍全身,以最大速度跑步,估计跑完全程的总淋雨量。
(2) 雨从迎面吹来,雨线与跑步方向在同一铅直平面内,且与人体的夹角为θ,问速度多大时,总淋雨量最少。
(3) 雨从背面吹来,雨线方向与跑步方向在同一铅直平面内,且与人体的夹角为α,问速度多大时,总淋雨量最少。
(4) 若雨线方向与跑步方向不在同一平面内即异面时,模型会有什么变化。
二、问题分析人在雨中行走时,行走时间即淋雨时间。
把人看成一个长方体,总淋雨量是各个面淋雨量之和。
为解决雨滴不是连续的,引进雨滴频率P (模型建立部分会做具体阐述)的概念。
对于问题一,在不考虑雨速方向的前提下,人的前、后、左、右以及顶部都会被淋到雨,此时淋雨量只与行走时间及单位时间内的降雨量有关。
简单优化模型10雨中行走
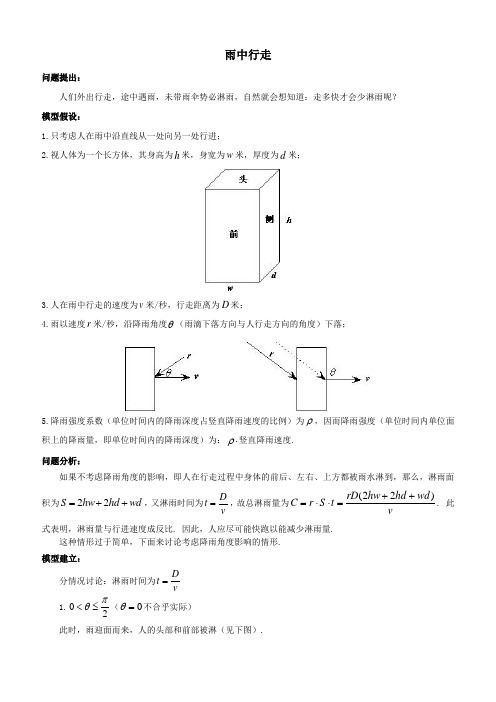
雨中行走问题提出:人们外出行走,途中遇雨,未带雨伞势必淋雨,自然就会想知道:走多快才会少淋雨呢?模型假设:1.只考虑人在雨中沿直线从一处向另一处行进;2.视人体为一个长方体,其身高为h 米,身宽为w 米,厚度为d 米;3.人在雨中行走的速度为v 米/秒,行走距离为D 米;4.雨以速度r 米/秒,沿降雨角度θ(雨滴下落方向与人行走方向的角度)下落;5.降雨强度系数(单位时间内的降雨深度占竖直降雨速度的比例)为ρ,因而降雨强度(单位时间内单位面积上的降雨量,即单位时间内的降雨深度)为:⋅ρ竖直降雨速度.问题分析:如果不考虑降雨角度的影响,即人在行走过程中身体的前后、左右、上方都被雨水淋到,那么,淋雨面积为wd hd hw S ++=22,又淋雨时间为vD t =,故总淋雨量为v wd hd hw rD t S r C )22(++=⋅⋅=. 此式表明,淋雨量与行进速度成反比. 因此,人应尽可能快跑以能减少淋雨量.这种情形过于简单,下面来讨论考虑降雨角度影响的情形.模型建立: 分情况讨论:淋雨时间为v D t =1.20πθ≤<(0=θ不合乎实际)此时,雨迎面而来,人的头部和前部被淋(见下图).头部的淋雨量:头部的面积为dw ,雨在竖直方向上的分速度为θsin r ,降雨强度为θρsin r ⋅,故淋雨量为θρθρsin sin 1dr vwD v D dw r C =⋅⋅=. 前部的淋雨量:前部的面积为wh ,雨在水平方向上的分速度为θcos r ,相对于人的速度为v r +θcos ,降雨强度为)cos (v r +⋅θρ,故淋雨量为)cos ()cos (2v r h vwD v D wh v r C +=⋅⋅+=θρθρ. 于是,总淋雨量为 [])cos (sin )cos (sin 21v r h dr vwD v r h v wD dr v wD C C C ++=++=+=θθρθρθρ. 特别地,当2πθ=(雨竖直下落)时,总淋雨量为)(hv dr vwD C +=ρ. 2.πθπ<<2(πθ=不合乎实际)此时,雨从背后落下,人的头部、后部(或前部)被淋(见下图).v令απθ+=2,则20πα<<.头部的淋雨量:头部的面积为dw ,雨在竖直方向上的分速度为αcos r ,降雨强度为αρcos r ⋅,故淋雨量为αραρcos cos 1dr vwD v D dw r C =⋅⋅=. 水平方向上的淋雨量:后部(或前部)的面积为wh ,雨在水平方向上的分速度为αsin r ,相对于人的速度为|sin |v r -α,降雨强度为|sin |v r -⋅αρ,故淋雨量为|sin ||sin |2v r h vwD v D wh v r C -=⋅⋅-=αραρ. 于是,总淋雨量为 []|sin |cos |sin |cos 21v r h dr v wDv r h v wDdr v wDC C C -+=-+=+=ααραραρ.Case (1):αsin r v ≤此时,人的行进速度不快于雨在水平方向上的分速度(雨从后方赶上人),头部和后部被淋,总淋雨量为[])sin (cos v r h dr v wDC -+=ααρ.特别地,当αsin r v =时,人的行进速度恰好等于雨在水平方向上的分速度(人刚好跟着雨向前走),仅头部被淋,总淋雨量为αρcos dr v wDC =. Case (2):αsin r v >此时,人的行进速度快于雨在水平方向上的分速度(人赶上前方的雨),头部和前部被淋,总淋雨量为[])sin (cos ααρr v h dr v wDC -+=.综上,总淋雨量为[][][]⎪⎪⎪⎩⎪⎪⎪⎨⎧><<-+≤<<-+≤<++=απθπααραπθπααρπθθθρsin ,2,)sin (cos sin ,2,)sin (cos 20,)cos (sin r v r v h dr vwD r v v r h dr vwD v r h dr v wD C 由απθ+=2得[][][]⎪⎪⎪⎩⎪⎪⎪⎨⎧-><<++-≤<<+-≤<++=θπθπθθρθπθπθθρπθθθρcos ,2,)cos (sin cos ,2,)cos (sin 20,)cos (sin r v r v h dr v wD r v v r h dr vwD v r h dr v wD C 即⎪⎪⎪⎩⎪⎪⎪⎨⎧-><<++-≤<<--≤<++=θπθπρθθρθπθπρθθρπθρθθρcos ,2,)cos sin (cos ,2,)cos sin (20,)cos sin ()(r v wDh v h d wDr r v wDh v h d wDr wDh v h d wDr v C 模型求解: 当20πθ≤<和θπθπcos ,2r v -≤<<时,)(v C 均为v 的减函数,故为使)(v C 最小,应使v 尽可能大;当θπθπcos ,2r v -><<时,)(v C 的单调性取决于θθcos sin h d +的正负,应视情况来判断.结论:要使淋雨量最小,(1)若雨迎面而来,则人应以最大可能的速度向前行进;(2)若雨从背后落下,则人应控制行进速度为雨在水平方向上的分速度.模型讨论:如果视人体为一圆柱,如何?。
数学模型论文雨中行走(1)

队号:第四队成员:刘桂清、徐丽蓉、林雪梅指导老师:刘于江老师雨中行走少淋雨问题真题摘要建一模型说明当你在雨中行走又想少淋雨时,应当如下做:(1)若你行走的方向是顺风且雨的夹角至少为,你应以雨速水平分量的速度行走,以便使雨相对于你是垂直下落的(2)在其他情况下,你都应以最快的速度行走。
关键词:少淋雨;雨速的水平分量;夹角;人速1.问题的重述当下雨时,假如你当时没带雨伞你又不得不从A地走到B地,该如何行走才能少淋到雨呢?针对这个问题,建立合理的数学模型。
讨论一下,人在顺风行走时,你以雨速的水平分量的速度走时,雨的夹角至少是多少?进而近一步讨论,在其他情况下,你都应以最快的速度行走。
2.模型的假设与符号说明2.1模型的假设(1)把人体看作长方体,底边长a米、宽为b米;高为h米;(2)风速保持不变,人速以V(m/s)匀速行走;(3)人从A地行走到B地,路程为L=1000米;2.2符号说明a 人体的宽度 (m)b 人体的厚度 (m)h 人体的身高 (m)V 人的速度(m/s)ν风速(雨速)(m/s)L 人行走的路程 (m)θ下雨的方向与人的夹角t 人在雨中行走的时间 (s)ρ降雨密度3.模型的建立与求解(1)考虑人在顺风行走时,此种情况下,如图:人淋雨的部位有头、背后,则:头顶的淋雨量:C1=VLabθρνcos侧面的淋雨量:C2=VVLbh)sin(θνρ-总淋雨量: C=C1+C2=VVhaLb)]sin(cos[θνθνρ-+结论:可以看出总淋雨量与速度.角度有关,且与人的速度成反比,当V=νsinθ时,即=θarcsinνV,总淋雨量C最小。
所以,上述情况就转化为与θ有关的问题:(1)当0=θ时C=VhV a Lb )(+νρ=ρρνLbh VLab +结论:可以看出总淋雨量与人的行走速度成反比,当速度尽可能大的时候,淋雨量越小。
(2)当4πθ=时C=VV h a Lb )]22(22[ννρ-+=VLab νρ22+h Lb ρ-Vh Lb νρ22=(Vh Lbb a ρ22)1-+h Lb ρ结论:可以看出总淋雨量与人的行走速度成反比,当速度尽可能大的时候,淋雨量越小。
关于雨中行走模型

关于雨中行走模型第六讲建模方法论(5)——建模实例(一)雨中行走问题夏季的某天,你去某地办事,接近目的地时,天空突然下起了大雨,糟糕的是你没有带雨具,且难以找到避雨的地方。
一个似乎很简单的事实是你应该在雨中尽可能的快走(跑),以减少雨淋时间。
这样做合理吗,试组建数学模型来探讨如何在雨中行走才能最大限度地减少雨淋的程度,即确定最优行走策略。
问题分析问题是在给定的降雨条件下,设计一个在雨中行走的策略(调整行走速度),使得你被雨水淋湿的程度最低。
所谓被雨水淋湿的程度,可以用其间被淋在身上的雨水量的大小来刻划,而与此有关的主要因素有:降雨的大小、风(降雨)的方向、路程的远近和行走的速度。
为了简化问题的研究,我们先做以下假设: 模型假设1(降雨的速度(即雨滴降落的速度)和降雨强度保持不变;2(行走速度恒定;3(风速及风向始终保持不变(这三项都是均匀化假设)。
4(把人的身体看成是一个呈长方体形状的物体(理想化)。
5(淋在身上的雨水被完全吸收(极端化)。
6(不考虑降雨的角度的影响,也就是说在行走的过程中身体的上方及前后左右都将淋到雨水。
7(设定变量和参数雨中行走的距离(单位:米):D;雨中行走的速度(单位:米/秒):v;人体的高度、宽度、厚度(单位:米):h,w, d被淋雨水总量(单位:升):C;降雨强度(单位:厘米/小时):I;2 身体被雨淋的面积(单位:米):S;雨中行走时间(单位:秒):t=D/v.其中,降雨强度是单位时间内平面上降雨的厚度,用以刻划降雨的大小。
在本问题中,D,d,w,h从而S是问题的参数;v,t,I是问题中的变量。
C是因变量,而v是决策变量。
模型中的参数可以通过观测和日常的调查资料得到。
模型的建立与求解按上面的分析与假设,容易知道:在雨中行走时被淋雨水总量等于被雨淋时间、被雨淋面积和降雨强度三者的乘积。
考虑到量纲一致性,并注意到I、v、D为常数,我们有C(v)=tS(米)=(米)=模型表明,被淋在身上的雨水总量与在雨中行走的速度成反比,因此在雨中最优行走策略是尽可能的快跑。
雨中行走问题数学模型案例

雨中行走问题数学模型案例
一个常见的数学模型案例是“雨中行走”问题。
在这个问题中,假设有一个人需要从一个地方到另一个地方,但是正在下雨。
人可以以一定的速度行走,但是会因为雨水而放慢速度。
问如何确定最快的路线,使得从起点到终点的时间最短。
为了建立这个数学模型,可以采用以下假设和变量:
1. 假设下雨时,人的行走速度是正常时的百分之多少,这个值称为“减速因子”。
假设减速因子为x%,则雨中行走的速度为正常速度的x%。
2. 假设人在雨中行走时的速度是与雨水的强度相关的。
可以假设速度与雨水强度成正比,即速度v与雨水强度I之间存在关系v = kI (其中k为比例常数)。
3. 假设人在雨中行走的路径是直线。
1
根据上述假设和变量,可以建立以下数学模型:
1. 定义起点和终点的坐标(x1,y1)和(x2,y2)。
2. 定义每个点(x,y)处的雨水强度I。
3. 计算人在一段距离(Δx,Δy)内花费的时间t:t = l / (v * x / 100),其中l是距离,v是速度,x是减速因子。
4. 计算从起点到终点的路线上每个点(x,y)的雨水强度I。
5. 根据模型3计算从起点到终点的每个区间的时间t,并将它们的
和作为总时间T。
6. 通过改变减速因子x,并重新计算总时间T,找到最小的总时间
对应的减速因子x,确定最快的路线。
这样,通过数学模型,可以帮助人们确定在雨中行走时最快的路线。
2。
关于淋雨数学建模

淋雨数学建模摘要:本文通过对人在雨中直线行走时雨垂直降落、从前吹来、从后吹来这三种情况的分析讨论,得到了在不同情况下淋雨总量与人的行走速度的数学模型。
并发现,当雨垂直落下和迎面吹来时,跑的速度越快淋雨越少;而当雨从背面吹来时,当人跑的速度大于等于雨速的水平分量的大小且此时夹角α满足tan caα<时,跑得越快淋雨越少,除此之外的其它情况下有当αsin u v =时,淋雨量最小。
关键词:淋雨 直线行走一 问题重述人在雨中从一处沿直线跑到另一处,若雨速为常数且方向不变。
试建立数学模型讨论是否跑得越快,淋雨量越少,并用MATLAB 编程实现。
假设跑步距离d=100米,跑步最大速度为m v =5 m/s ,雨速u=4m/s ,降雨量为w=2cm/h 。
(1)不考虑雨的方向,设降雨淋遍全身,以最大速度跑步,估计跑完全程的淋雨量。
(2)雨从迎面吹来,雨线与跑步方向在同一平面内,且与人体夹角为θ,问跑步速度v 为多大?淋雨量最少。
二 问题的分析人在雨中行走时可能出现以下三种情形:情形一:雨垂直下落,人以速度v 前行,此时降雨淋遍全身(如图1所示)图 1情形二:雨迎面吹来,雨线与跑步方向在同一平面内,与人的正面夹角为θ,此时后背淋不到雨(如图2所示)图2情形三:雨从背面吹来,雨线方向与跑步方向在同一平面内,与人的背后夹角为α,此时正面淋不到雨(如图3所示)图 3我们知道当人在雨中前行的时候,人和雨相对地面都是运动的,故知人与雨是相对运动的。
为此我们选择人作为参考系,再考虑雨的相对速度及其与人体方向(即与人体夹角θ、α)对总淋雨量的影响。
三合理的假设3.1 将人体看成一个长方体;3.2 雨速为常数且方向不变;3.3 降雨量为一定值;3.4 考虑雨的方向与人体前进的方向在同一平面内;3.5 符号的假定:a: 身高(颈部以下) b: 身宽 c: 身厚v: 跑步最大速度d: 跑步距离 v: 跑步速度mw: 降雨量 u: 雨速 Q: 总淋雨量θ: 雨迎面吹来与人的夹角α: 雨背面吹来与人的夹角s:有效淋雨面积v:以人为参考系时的相对雨速四模型的建立我们先考虑如下情形,现有一块土地面积为s,雨垂直降落,雨速及方向不变,且降雨量为一常数w ,则有时间t内该土地的淋雨量为Q stw=。
数学建模雨中行走

数学建模⾬中⾏⾛摘要夏天⽇益临近,天⽓情况也逐渐变幻莫测。
我们常常遇到过这样的问题,我们⾛在⼤街上,突然下起⼤⾬,⽬的地离我们不远,所以我们并不准备避⾬。
这是我们就遇到⼀个问题,是按照正常速度前⾏,还是⼤步奔跑地前进,以减少⾝上的淋⾬量。
按照常理,我们⼤多数⼈都会奔跑前⾏。
但是,这样果真能够减少被淋湿的程度吗?1.问题重述⼀个⾬天,你有件急事需要从家中要从家中到学校去,学校离家不远,仅⼀公⾥,况且事情紧急,你来不及花时间去翻找⾬具,决定碰⼀下运⽓,顶着⾬去学校。
假设刚刚出发⾬就⼤了,但你不打算再回去了,⼀路上,你将被⼤⾬淋湿。
⼀个似乎很简单事情是你应该在⾬中尽可能地快⾛,以减少淋⾬时间。
但如果考虑将与⽅向的变化,在全部距离上尽⼒地快跑不⼀定是最好的策略。
试建⽴数学模型来探讨如何在⾬中⾏⾛才能减少淋⾬的程度。
2.建模准备建模⽬标:在给定的降⾬条件下,设计⼀个⾬中⾏⾛的策略,使得你被⾬⽔淋湿的程度最少。
主要因素:淋⾬量,降⾬的⼤⼩,降⾬的⽅向(风),路程的远近,⾏⾛的速度。
3.模型假设即符号说明(1)把⼈体视为长⽅体,⾝⾼h⽶,宽度w⽶,厚度d⽶。
淋浴总量⽤C升来记。
(2)降⾬⼤⼩⽤降⾬强度I(cm/h)来描述,降⾬强度指单位时间平⾯上的降下⽔的厚度。
在这⾥可视为⼀常量。
(3)风速保持不变。
(4)你⼀定速度v(m/s)跑完全程D⽶。
4.模型建⽴与计算(1)不考虑⾬的⽅向,此时你的前后左右和上下都将被淋⾬。
淋⾬⾯积:S=2wh+2dh+wd(⽶2)⾬中⾏⾛的时间:t=(秒)降⾬强度:I(厘⽶/时)=0.01I(⽶/时)=(⽶/秒)淋⾬量:C=(⽶3)=(升)(模型中D,I,S为参数,⽽v为变量)结论:淋⾬量与速度成反⽐。
这也验证了尽可能快跑能减少淋⾬量。
若取参数D=1000m, I=2cm/h, h=1.5m, w=0.5m, d=0.2m时,则有S=2.2m2 .若你在⾬中⾏⾛的最⼤速度v=6m/s, 则计算得你在⾬中⾏⾛了167秒,即2分47秒。
数学建模数学建模之雨中行走问题模型

正文:数学建模之雨中行走问题模型摘要:考虑到降雨方向的变化,在全部距离上尽力地快跑不一定是最好的策略。
试建立数学模型来探讨如何在雨中行走才能减少淋雨的程度。
若雨是迎着你前进的方向向你落下,这时的策略很简单,应以最大的速度向前跑;若雨是从你的背后落下,你应控制你在雨中的行走速度,让它刚好等于落雨速度的水平分量。
① 当αsin r v <时,淋在背上的雨量为[]v vh rh pwD -αsin ,雨水总量()[]v v r h dr pwD C -+=ααsin cos .② 当αsin r v =时,此时02=C .雨水总量αcos v pwDdr C =,如030=α,升24.0=C这表明人体仅仅被头顶部位的雨水淋湿.实际上这意味着人体刚好跟着雨滴向前走,身体前后将不被淋雨.③ 当αsin r v >时,即人体行走的快于雨滴的水平运动速度αsin r .此时将不断地赶上雨滴.雨水将淋胸前(身后没有),胸前淋雨量()v r v pwDh C αsin 2-=关键词:淋雨量, 降雨的大小,降雨的方向(风),路程的远近,行走的速度1.问题的重述人们外出行走,途中遇雨,未带雨伞势必淋雨,自然就会想到,走多快才会少淋雨呢?一个简单的情形是只考虑人在雨中沿直线从一处向另一处进行时,雨的速度(大小和方向)已知,问行人走的速度多大才能使淋雨量最少?2.问题的分析.由于没带伞而淋雨的情况时时都有,这时候大多人都选择跑,一个似乎很简单的事情是你应该在雨中尽可能地快走,以减少雨淋的时间。
但如果考虑到降雨方向的变化,在全部距离上尽力地快跑不一定是最好的策略。
,一、我们先不考虑雨的方向,设定雨淋遍全身,以最大速度跑的话,估计总的淋雨量;二、再考虑雨从迎面吹来,雨线与跑步方向在同一平面内,且与人体的夹角为 ,如图1,建立总淋雨量与速度v 及参数a,b,c,d,u,w,θ之间的关系,问速度v 多大,总淋雨量最少,计算=0,=090时的总淋雨量;θθθ三、再是雨从背面吹来,雨线方向与跑步方向在同一平面内,且与人体的夹角为α,如图2.,建立总淋雨量与速度v及参数a , b , c, d , u , w , α之间的关系,问速度多大,总淋雨量最少;四、以总淋雨量为纵轴,对(三)作图,并解释结果的实际意义;五、若雨线方向不在同一平面内,模型会有什么变化;按照这五个步骤,我们可以进行研究了。
数学建模淋雨模型

淋雨量模型一、问题概述要在雨中从一处沿直线跑到另一处,若雨速为常数且方向不变,试建立数学模型讨论是否跑得越快,淋雨量越少;将人体简化成一个长方体,高a=颈部以下,宽b=,厚c=,设跑步的距离d=1000m,跑步的最大速度v m=5m/s,雨速u=4m/s,降雨量ω=2cm/h,及跑步速度为v,按以下步骤进行讨论17:1、不考虑雨的方向,设降雨淋遍全身,以最大速度跑步,估计跑完全程的总淋雨量;2、雨从迎面吹来,雨线与跑步方向在同一平面内,且与人体的夹角为θ,如图1.建立总淋雨量与速度v及参数a,b,c,d,u,ω,θ之间的关系,问速度v多大,总淋雨里最少;计算θ=0,θ=30°的总淋雨量.3、雨从背面吹来,雨线方向跑步方向在同一平面内,且与人体的夹角为α,如图2.建立总淋雨量与速度v及参数a,b,c,d,u,ω,α之间的关系,问速度v多大,总淋雨量最小;计算α=30°的总淋雨量.说明:题目中所涉及的图形为网上提供(4)、以总淋雨量为纵轴,速度v为横轴,对3作图考虑α的影响,并解释结果的实际意义.(5)、若雨线方向跑步方向不在同一平面内,试建立模型二、问题分析淋雨量是指人在雨中行走时全身所接收到得雨的体积,可表示为单位时间单位面积上淋雨的多少与接收雨的面积和淋雨时间的乘积;可得:淋雨量V=降雨量ω×人体淋雨面积S×淋浴时间t ①时间t=跑步距离d÷人跑步速度v ②由①②得:淋雨量V=ω×S×d/v三、模型假设1、将人体简化成一个长方体,高a=颈部以下,宽b=,厚c=.设跑步距离d=1000m,跑步最大速度v m=5m/s,雨速u=4m/s,降雨量ω=2cm/h,记跑步速度为v;参考2、假设降雨量到一定时间时,应为定值;3、此人在雨中跑步应为直线跑步;4、问题中涉及的降雨量应指天空降落到地面的雨,而不是人工,或者流失的水量,因为它可以直观的表示降雨量的多少;四、模型求解:一、模型Ⅰ建立及求解:设不考虑雨的方向,降雨淋遍全身,则淋雨面积:S=2ab+2ac+bc雨中奔跑所用时间为:t=d/v总降雨量V =ω×S ×d/vω=2cm/h=2×10-2/3600 m/s将相关数据代入模型中,可解得:S =㎡V = cm3= L(二)、模型Ⅱ建立及求解:若雨从迎面吹来,雨线与跑步方向在同一平面内,且与人体的夹角为θ.,则淋雨量只有两部分:顶部淋雨量和前部淋雨量. 如图1设雨从迎面吹来时与人体夹角为θ. ,且 0°<θ<90°,建立a,b,c,d,u,ω,θ之间的关系为:1、考虑前部淋雨量:由图可知雨速的水平分量为θsin u ⋅且方向与v 相反,故人相对于雨的水平速度为:则前部单位时间单位面积淋雨量为:又因为前部的淋雨面积为:b a ⋅,时间为: d/v于是前部淋雨量V 2为 :即:()()v u /v sin u a V 2⋅+⋅⋅⋅⋅=θωd b ①2、考虑顶部淋雨量:由图可知雨速在垂直方向只有向下的分量, 且与v 无关,所以顶部单位时间单位面积淋雨量为()θωcos ⋅,顶部面积为()c b ⋅ ,淋雨时间为()v /d ,于是顶部淋雨量为:v /cos b V 1θω⋅⋅⋅⋅=d c ②由①②可算得总淋雨量 :代入数据求得:由Vv 函数可知:总淋雨量V 与人跑步的速度v 以及雨线与人的夹角θ两者有关;对函数Vv 求导,得:显然:V '<0, 所以V 为v 的减函数,V 随v 增大而减小;因此,速度v=v m =5m/s ,总淋雨量最小;Ⅰ当θ=0,代入数据,解得:V 3≈LⅡ当θ=30°,代入数据,解得:V =m3≈L三、模型Ⅲ建立及求解:若雨从背面吹来,雨线方向与跑步方向在同一平面内,且与人体的夹角为α则淋雨量只有两部分:顶部淋雨量和后部淋雨量.如图2设雨从背部吹来时与人体夹角为α, 且0°<α﹤90°,建立a,b,c,d,u,α,ω之间的关系为:1、先考虑顶部淋雨量:当雨从背面吹来,而对于人顶部的淋雨量 V 1 ,它与模型①中一样,雨速在垂直方向只有向下的分量,同理可得:2、后部淋雨量:人相对于雨的水平速度为:⎩⎨⎧⋅>⋅-⋅≤-⋅ααααsin u v sin v sin u v v sin ,,u u从而可得,人背部单位时间单位面积淋雨量为:()()⎩⎨⎧⋅>⋅-⋅⋅≤-⋅⋅ααωααωsin u v u /sin u v sin u v u /v sin ,,u 可得人背部淋雨量为: ()()⎩⎨⎧⋅>⋅-⋅⋅⋅⋅=⋅≤-⋅⋅⋅⋅⋅=ααωααωsin u v u /sin u v a V sin u v u /v sin a V 33,,d b u d b而总淋雨量:V=V 1+ V 3从而有:⎩⎨⎧⋅>⋅-⋅⋅⋅⋅+⋅⋅⋅⋅=⋅≤-⋅⋅⋅⋅⋅+⋅⋅⋅⋅=ααωαωααωαωsin u v u /)sin u v (d b a v /cos c b V sin u v u /)v sin (d b a v /cos c b V ,,d u d ③ 化简③式得:()()⎩⎨⎧⋅>+⋅-⋅⋅⋅⋅=⋅≤-⋅+⋅⋅⋅⋅=αααωαααωsin u v /a v /sin cos b V sin u v /a v /sin cos b V ,,u a c d u a c d ④ 代入相关数据化简得:()[]()[]⎩⎨⎧⋅>+-=⋅≤-+=ααααααsin u v 360/375.0v /1.5sin cos 2.0V sin u v 360/375.0v /1.5sin cos 2.0V ,, ⑤ 由Vv 函数可知:总淋雨量V 与人跑步的速度v 以及雨线与人的夹角α两者有关;Ⅰ、 当αsin u v ⋅≤时,且0°<α﹤90°,可得:c cos α+a sin α>0对⑤式求导,易知V '<0;所以,总淋雨量V 随着速度v 的增加而减少,因此,αsin u v ⋅= 总淋雨量最小;Ⅱ、当v >u sin α时,且0°<α﹤90°,对⑤式求导,解得:2v 180cos 2.0sin 5.1V )(⋅-='αα ⅰ、当α- cos α<0时,即 :tan α<2/15,即V`<0;从而推出,总淋雨量V 随着速度v 的增加而减少,所以,速度v=v m ,总淋雨量最小;ⅱ、当α- cos α>0时,即 :tan α>2/15,即V`>0;从而推出,总淋雨量V 随着速度v 的增加而增加,所以,当速度v 取最小,即v=u sin α 总淋雨量最小;当α=30°,tan α>2/15 ,由模型⑶分析的,当v=u sin α=4×1/2=2m/s总淋雨量最小,且V=m3=L五、结果分析:1在该模型中考虑到雨的方向问题,这个模型跟模型二相似,将模型二与模型三综合起来跟实际的生活就差不多很相似了; 由这三个模型可以得出在一定的速度下人跑的越快淋雨量就越少; 2若雨迎面吹来时,跑得越快越好3若雨从背面吹来时,分为两种情况:当tanα>c/a时,跑步速度v=u sinα时V最小;当tanα<c/a时,跑得越快越好;但是该模型只是考虑雨线方向与人的跑步方向在同一平面内,若是雨线方向与人的跑步方向不在同一平面内建立坐标系上,对于这种情况,我们认为在本质和考虑问题的思想上来说模型是不变的,应分别对几个淋雨面进行以上同样方法建立求解模型, 但是解算的过程,我想应该更复杂; 参考文献:1 姜启源, 数学模型第三版M, 高等教育出版社,2。
初等数学建模试题极其答案

1.你要在雨中从一处沿直线走到另一处.雨速是常数.方向不变。
你是否走得越快.淋雨量越少呢?2.假设在一所大学中.一位普通教授以每天一本的速度开始从图书馆借出书。
再设图书馆平均一周收回借出书的1/10.若在充分长的时间内.一位普通教授大约借出多少年本书?3.一人早上6:00从山脚A上山.晚18:00到山顶B;第二天.早6:00从B下山.晚18:00到A。
问是否有一个时刻t,这两天都在这一时刻到达同一地点?4.如何将一个不规则的蛋糕I平均分成两部分?5.兄妹二人沿某街分别在离家3公里与2公里处同向散步回家.家中的狗一直在二人之间来回奔跑。
已知哥哥的速度为3公里/小时.妹妹的速度为2公里/小时.狗的速度为5公里/小时。
分析半小时后.狗在何处?6.甲乙两人约定中午12:00至13:00在市中心某地见面.并事先约定先到者在那等待10分钟.若另一个人十分钟内没有到达.先到者将离去。
用图解法计算.甲乙两人见面的可能性有多大?7.设有n个人参加某一宴会.已知没有人认识所有的人.证明:至少存在两人他们认识的人一样多。
8.一角度为60度的圆锥形漏斗装着10端小孔的面积为0.5平方厘米.9.假设在一个刹车交叉口.所有车辆都是由东驶上一个1/100的斜坡.计算这种情下的刹车距离。
如果汽车由西驶来.刹车距离又是多少?10. 水管或煤气管经常需要从外部包扎以便对管道起保护作用。
包扎时用很长的带子缠绕在管道外部。
为了节省材料.如何进行包扎才能使带子全部包住管道而且带子也没有发生重叠。
:顶=1:a:b.选坐.v>0,而设语雨L(1q -+v x ),v≤x Q(v)=L(v x -q +1),v>x2.解:由于教授每天借一本书.即一周借七本书.而图书馆平均每周收回书的1/10.设教授已借出书的册数是时间t 的函数小x(t)的函数.则它应满足(时间t 以周为单位)其中 初始条件表示开始时教授借出数的册数为0。
解该线性题得X(t) =70[1-e t 10 ]由于当t ∞时.其极限值为70,故在充分长的时间内.一位普通教授大约已借出70本书。
数学建模 雨中行走问题

数学模型论文学校:班级:姓名:学号:雨中行走问题摘要当我们在雨中冒雨行走时总会下意思的加快速度,似乎跑得越快淋雨量就会越小。
但事实上会是这种情况吗?在这里,我们将给予综合性的考虑,来解释不同情况下的淋雨量。
在不考虑风向的情况下,若人的全身都受到雨淋,理所当然人跑的越快所淋的雨就会越少。
那么模型也可算出淋雨量。
当雨线从正面和人的跑步方向在同一平面时,并且考虑风向的影响,雨线方向和竖直方向成θ角。
因为迎着雨的方向跑,所以全身都会淋到雨,由于有夹角,可以将雨分成竖直方向和水平方向两部分。
便可根据题的要求解出模型。
当雨线从后面和人的跑步方向在同一平面时,并且考虑风向的影响,雨线方向和竖直方向成α角。
因为背着雨的方向跑,所以全身不一定都会淋到雨。
可分几种情况分别来说。
关键词人速;雨速;风向;夹角1.问题的重述当人们在雨中行走时,是不是走的越快就会淋越少的雨呢?对于这个问题,建立合理的数学模型。
讨论一下,在不考虑风向时,人的淋雨量为多少;进而进一步讨论一下,在考虑雨线方向与人的跑步方向在同一平面内成不同角度时的淋雨量。
2.问题的分析当人在雨中行走时,是否跑的越快所淋的雨量就越少那,答案当然不是。
人在雨中所淋到的雨量和风向有关,因为风向的不同会导致雨线和人成不同的角度。
从而使人所淋到的雨量有所不同。
3.模型的假设与符号说明3.1模型的假设(1)把人体视为长方体,身高h米,身宽w米,身厚d米,淋雨总量C升。
(2)把降雨强度视为常量,记为:I(cm h)。
(3)风速保持不变。
v m s跑完全程D。
(4)以定速度()3.2符号说明h人体的身高(m)w 人体的宽度(m)d 人体的厚度(m)D 人跑步的全程(m)v 人跑步的速度(m/s)i 降雨强度(cm/h)c 人在跑步中的淋雨总量(L)s 人在雨中会被雨淋的面积 (㎡)t 人在雨中跑步的时间 (s)v 雨滴下落速度 (m/s)θ 雨滴反方向与人速度方向的夹角ρ 雨滴密度4.模型的建立与求解(1)不考虑雨的方向,此种情况,人的前后左右都会淋雨。
雨中行走问题数学建模

雨中行走问题数学建模摘要:1.引言:雨中行走的背景和问题描述2.数学建模的基本概念和方法3.雨中行走问题的数学模型建立4.雨中行走问题的求解方法5.雨中行走问题的实际应用6.结论:数学建模在解决实际问题中的重要性正文:1.引言雨中行走是一个日常生活中常见的场景,然而,在雨中行走时,人们往往会面临一个问题:如何选择一条路径,使得行走的时间最短或者淋雨的程度最小?这个问题看似简单,实际上涉及到复杂的数学问题。
数学建模就是利用数学方法来解决实际问题,它已经成为各个领域解决实际问题的重要手段。
本文将从雨中行走这个问题出发,介绍数学建模的基本概念和方法。
2.数学建模的基本概念和方法数学建模是运用数学理论、方法和工具对实际问题进行抽象、描述和求解的过程。
它主要包括以下几个步骤:(1)问题分析:了解问题的背景,明确问题的目标,为建立数学模型奠定基础。
(2)建立模型:根据问题分析的结果,建立数学模型,将实际问题转化为数学问题。
(3)求解模型:运用数学方法求解模型,得到实际问题的解。
(4)模型检验:将求解得到的结果反演到实际问题中,检验模型的有效性和准确性。
(5)模型应用:将求解结果应用到实际问题中,为实际问题的解决提供理论依据。
3.雨中行走问题的数学模型建立为了解决雨中行走问题,我们首先需要建立一个数学模型。
假设一个人要从A 地走到B 地,途中会遇到降雨,降雨的强度可以用降雨量表示。
假设这个人的行走速度为v,降雨量为r,那么,他走完这段路程所需的时间为t=d/v,其中d 表示A 地到B 地的距离。
另外,他在行走过程中淋雨的量为Q=rt,其中r 表示降雨的强度,t 表示行走的时间。
4.雨中行走问题的求解方法为了求解雨中行走问题,我们需要构建一个目标函数,用来描述行走时间和淋雨量的关系。
假设我们的目标是最小化行走时间,那么目标函数可以表示为:min t。
根据目标函数,我们可以建立一个线性规划模型,用来求解雨中行走问题。
数学建模

淋雨数学模型一、提出问题当你在雨中行走又想少淋雨时,应当如何做?假设一人在雨中沿直线从一处走向另一处,雨速为常数且方向不变,但雨下降的方向不同,所以就降雨的方向与人行走方向考虑建立数学模型,讨论是否走得越快,淋雨量就越少。
将人体看成一个立方体,高(身高)a,长(身宽)b,宽(身厚)c。
二、分析问题从两类情形考虑:(1)若你行走的方向是顺风与雨保持一定的角度,且以雨速水平分量的速度行走,使雨相对于人是垂直下落的,可以将人看成质点考虑。
(2)而在其他情况下,在三维空间里,我们应从三个方面来考虑:1)当雨垂直下落时,淋雨面积考虑顶部、前后两面与两侧面。
2)当雨迎面吹来时,淋雨面积考虑人体顶部、前面与两侧面。
3) 当雨从背面吹来时,淋雨面积考虑人体顶部、后面与两侧面。
三、模型假设与符号说明(1)将人看成立方体(2)雨速为常数且方向不变(3)人以一定的速度匀速前行(4)降雨量为常数(5)不考虑风对人产生任何外在影响(如:风过大而无法前行)c ba符号说明:长方体的高、长、宽分别为a,b,c。
(如上图):v: 行走速度 ; u: 雨速 ; w: 降雨量;d: 走路距离 ; Q:总淋雨量 ; s: 有效淋雨面积; v: 以人为参考系时的相对速度;mv:人的最大速度;θ:降雨方向与人行走方向的夹角;α:雨迎面吹来与人体方向的夹角;β:雨从背面吹来与人体方向的夹角。
四、模型假设第一类情形:(图形如下)当v ≥ u水平时,人的淋雨量不考虑水平方向,只考虑竖直方向,且当 v =u水平时淋雨量最少。
∴ v=u*sinθ∴ θ=arcsin(u v)Oy人行走 方向第二类情形:1) 当雨垂直下落时: (如下图)v abc有效淋雨面积:s=2*ab+2*ac+bc淋雨时间: t=vd总淋雨量: Q=stw=(2*ab+2*ac+bc)*w*vd(1)2) 当雨迎面吹来时:(如下图)c由于在三维空间考虑,所以人的顶部、迎面部分和两侧面为有效淋雨面积,记顶部面积s 1=bc,迎面部分面积s 2=ab ,侧面面积s 3=2*ac淋雨时间 t=vd雨速水平分量 v1= u*sin α雨速竖直分量 v 2= u*cos α雨水相对速度 v = u*sin α+v顶部淋雨量Q1=s1*t*w* cosα=bc*v d*w* cosα迎面淋雨量Q2=s2*t*w*u v- =ab*v d*w* u v+sin*uα侧面淋雨量Q3=s3*t*w*sinα=2*ac*v d*w*cosα总淋雨量为:Q= Q1+Q2+Q3=vd*W*(bc* cosα+ ab* uv+sin*uα+2*ac*conα) (2)3)当雨从背面吹来时:(如下图)c同理,人的顶部、背面部分和两侧面为有效淋雨面积,记顶部面积为s4= bc,背面部分面积为s5=ab,侧面面积s6=2*ac淋雨时间: t=vd雨速水平分量v1= u*sinβ雨速竖直分量v2= u*cosβ雨水相对速度v=u*sinβ-v顶部淋雨量Q4=s4*t*w* cosβ=bc*v d*w* cosβ背面淋雨量Q5=s5*t*w*u v- =ab*v d*w* u v-sin*uβ侧面淋雨量Q6=s6*t*w*sinβ=2*ac*v d*w*cosβ总淋雨量为:Q= Q1+Q2+Q3=vd*W*(bc*cosβ+ ab* uv-sin*uβ+2*ac*sinβ) (3)五、模型求解运用数学分析中求函数最值的知识,对于以上所建的模型我们求解得到不同情况下人的淋雨量Q与行走速度v的具体关系如下:第一类情形:当 v ≥ u*sin(θ)时,虑竖直方向,且当 v=u*sin(θ)时,淋雨量最少。
数学建模-淋雨模型

建模论文|淋雨模型姓名:王瑜班级:服工112学号:1人在雨中行走的速度与淋雨量关系摘要本文在给定的降雨条件下,分别建立相应的数学模型,分析人体在雨中行走时淋雨多少与行走速度、降雨方向等因素的关系。
其中文中所涉及到的降雨量是指从天空降落到地面上的雨水,未经蒸发、渗透、流失而在水面上积聚的水层深度,它可以直观地表示降雨的多少。
淋雨量,是指人在雨中行走时全身所接收到得雨的体积,可表示为单位时间单位面积上淋雨的多少与接收雨的面积和淋雨时间的乘积。
针对问题一,设降雨淋遍全身不考虑雨的方向,经简化假设得人淋雨面积为前后左右及头顶面积之和。
针对问题二,雨迎面吹来,雨线方向与行走方向在同一平面,人淋雨面积为前方和头顶面积之和。
因各个方向上降雨速度分量不同,故分别计算头顶和前方的淋雨量后相加即为总的淋雨量。
据此可列出总淋雨量W与行走速度v之间的v时,淋雨量最少。
函数关系。
分析表明当行走速度为max针对问题三,雨从背面吹来,雨线与行走方向在同一平面内,人淋雨量与人和雨相对速度有关。
列出函数关系式分析并求解。
关键词淋雨量;降雨的大小;降雨的方向(风);路程的远近;行走的速度;一、问题重述生活中的我们常常会遇到下雨而没带雨具的时刻,我们在那时会有很多选择,其中之一就是淋雨,往往好多人会在雨中快走或奔跑而使自己身体淋雨量最小化,但往往很多人会感觉到淋雨量并不会因为快走或奔跑而减少多少,反而有时候淋雨量倒有所增加,淋雨量和速度等有关参数的关系如何,是否人走得越快雨淋得越少,让我们假设一数学模型模拟计算真实情况。
当我们在雨中从一处沿直线跑到另一处时,如果雨速为常数,走的时候身体的动作的大小和暴露在雨中的面积大小影响着淋雨的多少,并且行走速度也同样影响着淋雨量Q,将人体简化成一个长方体,高a=1.5米,宽b=0.5米,厚c=0.2m,行走距离D,雨速u,降雨量I,行走速度为ν。
1、当我们不考虑风,即雨滴垂直下落时,淋雨量和人行走速度之间的关系?2、当雨滴从前方(斜的)下落时,即雨滴与人体的夹角为θ,建立总淋雨量与速度v及其它参数之间的关系,此时速度与淋雨量的关系?3、当雨从人的背面吹来,即雨滴与人体的夹角为θ,建立总淋雨量与速度v之间的关系?二、模型的假设与符号说明2.1 基本假设1、假设人行走的路线是直线;2、不考虑风的方向(即假定前后左右都淋雨),这是一种较为理想的假设,主要为了建模的方便,并且假设雨滴的速度为常数;3、为计算淋雨面积的方便,把人体表面积看成长方体,长用a表示,宽用b表示,厚度用c 表示,且abc都是定值。
数学建模数学建模之雨中行走问题模型

数学建模雨中行走模型系别:班级:姓名:学号:正文:数学建模之雨中行走问题模型摘要:考虑到降雨方向的变化,在全部距离上尽力地快跑不一定是最好的策略。
试建立数学模型来探讨如何在雨中行走才能减少淋雨的程度。
若雨是迎着你前进的方向向你落下,这时的策略很简单,应以最大的速度向前跑;若雨是从你的背后落下,你应控制你在雨中的行走速度,让它刚好等于落雨速度的水平分量。
① 当αsin r v <时,淋在背上的雨量为[]v vh rh pwD -αsin ,雨水总量()[]v v r h dr pwD C -+=ααsin cos .② 当αsin r v =时,此时02=C .雨水总量αcos v pwDdr C =,如030=α,升24.0=C这表明人体仅仅被头顶部位的雨水淋湿.实际上这意味着人体刚好跟着雨滴向前走,身体前后将不被淋雨.③ 当αsin r v >时,即人体行走的快于雨滴的水平运动速度αsin r .此时将不断地赶上雨滴.雨水将淋胸前(身后没有),胸前淋雨量()v r v pwDh C αsin 2-= 关键词:淋雨量, 降雨的大小,降雨的方向(风),路程的远近,行走的速度1.问题的重述人们外出行走,途中遇雨,未带雨伞势必淋雨,自然就会想到,走多快才会少淋雨呢一个简单的情形是只考虑人在雨中沿直线从一处向另一处进行时,雨的速度(大小和方向)已知,问行人走的速度多大才能使淋雨量最少2.问题的分析.由于没带伞而淋雨的情况时时都有,这时候大多人都选择跑,一个似乎很简单的事情是你应该在雨中尽可能地快走,以减少雨淋的时间。
但如果考虑到降雨方向的变化,在全部距离上尽力地快跑不一定是最好的策略。
,一、我们先不考虑雨的方向,设定雨淋遍全身,以 最大速度跑的话,估计总的淋雨量;二、再考虑雨从迎面吹来,雨线与跑步方向在同一平面内,且与人体的夹角为θ ,如图1,建立总淋雨量与速度v 及参数a,b,c,d,u,w,θ之间的关系,问速度v 多大,总淋雨量最少,计算θ=0,θ=090时的总淋雨量;三、再是雨从背面吹来,雨线方向与跑步方向在同一平面内,且与人体的夹角为α,如图2.,建立总淋雨量与速度v及参数a , b , c, d , u , w , α之间的关系,问速度多大,总淋雨量最少;四、以总淋雨量为纵轴,对(三)作图,并解释结果的实际意义;五、若雨线方向不在同一平面内,模型会有什么变化;按照这五个步骤,我们可以进行研究了。
关于人在雨中行走的数学模型

关于人在雨中行走的数学模型第一篇:关于人在雨中行走的数学模型关于人在雨中行走的数学模型摘要本题在给定的降雨条件下,分别建立相应的数学模型,分析人体在雨中行走时淋雨多少与行走速度、降雨方向等因素的关系。
其中题中所涉及到的降雨量是指从天空降落到地面上的雨水,未经蒸发、渗透、流失而在水面上积聚的水层深度,它可以直观地表示降雨的多少。
淋雨量,是指人在雨中行走时全身所接收的雨的体积,可表示为单位时间单位面积上淋雨的多少与接收雨的面积和淋雨时间的乘积。
利用MATLAB软件对各个问题进行求解。
对于问题一,设降雨淋遍全身不考虑雨的方向,经简化假设人淋雨面积为前后左右及头顶面积之和。
对于问题二,雨迎面吹来,雨线方向与行走方向在同一平面,人淋雨面积为前方和头顶面积之和。
因各个方向上降雨速度分量不同,故分别计算头顶和前方的淋雨量后相加即为总的淋雨量。
据此可列出总淋雨量w与行走速度v之间的函数关系。
分析表明当行走速度为vm 时,淋雨量最少。
对于问题三,雨从背面吹来,雨线与行走在同一平面内,人淋雨量于人和雨相对速度有关,列出函数关系式分析并求解。
关键词:淋雨量,降雨的大小,降雨的方向(风),路程的远近,行走的速度,雨滴下落的速度,角度,降雨强度问题重述要在雨中从一处沿直线跑到另一处,若雨速为常数且方向不变,试建立数学模型讨论是否跑得越快,淋雨量越少。
将人体简化成一个长方体,高a=1.5m(颈部以下),宽b=0.5m,厚c=0.2m.设跑步距离d=1000m,跑步最大速度vm=5m/s,雨速u=4m/s,降雨量w=2cm/h,记跑步速度为v.按以下步骤进行讨论:(1)不考虑雨的方向,设降雨淋遍全身,以最大速度跑步,估计跑完全程的总淋雨量。
(2)雨从迎面吹来,雨线与跑步方向在同一平面内,且与人体的夹角为θ,如图1.建立总淋雨量与速度v及参数a,b,c,d,u,w,θ之间的关系,问速度v多大,总淋雨量最少。
计算θ=0,θ=30ο时的总淋雨量。
雨中行走问题(数学问题解决)

雨中行走问题(数学问题解决)-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN科目:数学问题解决摘要:雨天,你有件急事需要从家中到学校去,学校离家不远,仅有一公里,况且事情紧急,你不准备花时间翻找雨具,决定碰一下运气,顶着雨去学校。
假设刚刚出发雨就大了,但你也不打算再回去了。
一路上,你将被大雨淋湿。
一个似乎很简单的事实是你应该在雨中尽可能地快走,以减少雨淋的时间。
但是如果考虑到降雨方向的变化,在全部距离上尽力地快跑不一定是最好的策略。
通过建立数学模型来探讨如何在雨中行走才能减少淋雨的程度,分别从雨与人的方向以及是否在同一平面等情况找出如何在雨中行走才能淋雨最少。
一.问题的提出对于雨中行走这个实际的问题,它的背景是简单的,人人皆知无需进一步讨论。
我们的问题是:要在给定的降雨条件下,设计一个雨中行走的策略,使得你被雨水淋湿的程度最低。
显然它可以按确定性模型处理。
分析参与这一问题的因素,主要有:①降雨的大小;②风(降雨)的方向;③路程的远近与你跑的快慢。
二、模型假设1、降雨的速度(即雨滴下落速度)和降水强度(单位时间平面上降下雨水的厚度)保持不变;2、你以定常的速度跑完全程;3、风速始终保持不变;4、把人体看成一个长方体的物体;三、模型的建立与求解1、不考虑降雨的角度的影响即在你行走的过程中身体的前后左右和上方都将淋到雨水。
参数与变量::d雨中行走的距离;t雨中行走的时间;::v雨中行走的速度;:a你的身高;:b你的宽度;:c你的厚度;:q你身上被淋的雨水的总量;:w降水强度(降雨的大小,即单位时间平面上降下雨水的厚度,厘米/时)行走距离d,身体尺寸不变,从而身体被雨淋的面积22s ba ca bc=++是不变的,可认为是问题的参数。
雨中行走的速度v,从而在雨中行走的时间/t d v=及降雨强度的大小在问题中是可以调节、分析的,是问题中的变量。
考虑到各参数取值单位的一致性,可得在整个雨中行走期间整个身体被淋的雨水的总量是:()3(/3600)0.01()/(/3600)10() q t w S d v w S=⋅⋅⋅=⋅⋅⋅米升模型中的参数可以通过观测和日常的调查资料得到。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
雨中行走问题的数学建模
要在雨中沿直线从一处跑到另一处,若雨速为常数且方向不变,试建立数学模型讨论是否跑得越快,淋雨量越少。
将人体简化为长方体,高a=1.5米(颈部以下),宽b=0.5米,厚c=0.2米,设跑步距离d=1000米,跑步最大速度Vm=5米/秒,雨速u=4米/秒,降雨量w=2cm/h,记跑步速度为v,按一下步骤进行讨论。
(1)不考虑雨的方向,设降雨淋遍全身,以最大速度跑步,估计跑完全程的总淋雨量。
(2)雨从迎面吹来,雨线与跑步方向在同一平面内,且与人体的夹角为x,如图一,建
立总淋雨量与速度v以及参数a、b、c、d、u、w、x之间关系,问速度v多大,总淋雨量最少,计算x=0,x=30时的总淋雨量。
(3)雨从背面吹来,雨线方向与跑步方向在同一平面内,且与人体的夹角为y,如图2,建立总淋雨量与速度v以及参数a、d、c、d、u、w、y之间的关系,问速度v多大,总淋雨量最少,计算y=30时的总淋雨量。
(4)以总淋雨量为纵轴,速度v为横轴,对(3)进行作图,并解释结果的实际意义。
(5)若雨线方向与跑步方向不在同一平面内,模型会有什么变化。
问题分析:在我们的日常生活中,下雨天气是不可避免的,当我们遇到此类的天气且身上没有携带避雨的雨具时,是否快跑就会减少身上的淋雨量呢?就此问题我们做一个模型假设查探我们的问题。
模型假设:将人体简化成一个长方体,高a=1.5m,宽b=0.5m.厚c=0.2m;设跑步的距离为1000m,跑步的最大速度Vm=5m/s,雨速u=4m/s,降雨量w=2cm/h
模型建立:
模型一:(1)题中所述不考虑雨的方向,假设降雨淋遍全身,此时的雨速也是均匀下落,由假设人体为长方体可知,该人体的表面积s=2ab+2ac+bc,因为跑步距离d=1000m,所以该人在雨中的淋雨时间t=d/Vm,在该时间内的降雨量w=2cm/h=(0.0001/18)m/s 所以,总淋雨量Q=s*t*w。
模型二:(2)
《1》当雨迎面吹来时该人只有头顶和迎面淋雨,设头顶部淋雨量为Q1,由图一可知淋雨面积s1=bc,淋雨的时间t1=d/v,淋雨量(降雨方向与雨速方向应在一条线上)为w*cosx,由此可知淋雨总量Q1=s1*t1*w*cosx。
《2》由图一可知,雨速在水平方向上的水平分量为u*sinx(方向与v相反),设定参照物后水平方向上的合成速度为u*sinx+v,淋雨面积s2=a*b,淋雨的时间t2=d/v,淋雨量为w*sinx+w*v/u(即本身的淋雨量加上人相对雨速的淋雨量),迎面淋雨量Q2=s2*t2*w*(usinx+v)/u。
由此可以得到该人在单位时间和单位面积内的总淋雨量Q=Q1+Q2=(0.01cosx)/(18*v)+[0.075*(4sinx+v)]/(18*v)
模型三:
(3)当雨从背面吹来,雨线方向与跑步方向一致时,设定参照物后人参考速度|u*siny-v|,当u*siny-v>0时,即雨速在水平上的分量小于人的速度,此时在水平方向上的合成速度是v-u*siny,此时的人的淋雨总量可分为两部分:头顶部分Q3和背面部分Q4,;
《1》头顶部淋雨量为Q3,由图二可知淋雨面积s1=bc,淋雨的时间t3=d/v,淋雨量(降雨方向与雨速方向应在一条线上)为w*cosx,由此可知该人在单位时间和单位面积内的淋雨总量Q3= s1*t1*w*cosx。
《2》由图二可知,雨速在水平方向上的水平分量为u*sinx(方向与v相反),设定参照物后人的参考速度为v-u*siny,淋雨面积s2=a*b,淋雨的时间t2=d/v,降雨量w=w*(v/u)-wsiny,所以该人在单位时间和面积内的总的淋雨量Q4=s2*t2*w*(v-u*siny)/u=abdw(v-u*siny)/uv=0.0010461(1-siny/v)。
所以降雨总量Q=Q3+Q4=(0.01cosy)/(18*v)+0.0010461(1-siny/v)
当u*siny-v>0时,即雨速在水平上的分量大于人的速度,此时的人的淋雨总量可分为两部分:头顶部分Q5和背面部分Q6。
《3》头顶部淋雨量为Q5,由图二可知淋雨面积s1=bc,淋雨的时间t3=d/v,淋雨量(降雨方向与雨速方向应在一条线上)为w*cosx,由此可知淋雨总量Q5= s1*t1*w*cosx
《4》由图二可知,雨速在水平方向上的水平分量为u*siny-v(方向与v相反),此时在水平方向上的合成速度为u*siny-v,淋雨面积s2=a*b,淋雨的时间t2=d/v,,降雨量w=wsinx-w*v/u,此时该人的淋雨总量Q6= s2*t2*w*(usinx+v)/u所以降雨总量Q=Q5+Q6=0.0027778*[(0.2cosy-1.5siny)/v+1.5]
4:根据三中所求的降雨总量然后对式子分别求导可以可画出图如下:
模型求解:由于该模型是在理想情况下假设的,由以上模型(1 (2(3可求出下列数值:
(1)带入数据可求出以下未知量:表面积s=2ab+2ac+bc=2*1.5*0.5+2*1.5*0.2+0.5*0.2=2.2 跑步的时间t=d/vm=1000/5=200s, 总的淋雨量Q=s*t*w=2.44L
结果分析:由这些数值可知:随着人跑步的速度逐渐变快,人的淋雨量越少,跟我们在实际生活中相差不大,只是这是在理想模型下建立的求解,因为在实际的生活中人的跑步速度不肯能是匀速的,而且人的速度也不可能是一直增加的。
(2)带入数据可求出以下未知量:头顶淋雨量:Q3=s1*t1*w*cosx =(0.01cosx)/(18*v) 迎面淋雨量:Q4= s2*t2*w*(usinx+v)/u =0.0010461(1-siny/v)总的淋雨量Q=Q3+Q4=0.01cosy/(18*v)+0.0010461(1-siny/v)=0.00069445[(0.2cosy-1.5siny)/v+1.5]
由题可知该人在雨中的最大速度是v=vm,所以当v=vm时,Q最小,此时带入数据可知Q=0.694*[(0.8cosx+6sinx)/v+1.5],
x=0,速度v=vm=5m/s,Q=1.152L
x=30, 速度v=vm=5m/s,Q=1.554L
结果分析:在该模型中只考虑到了顶面和人的迎雨面,可以看出在该模型下人跑的越快,淋雨就越少,这个与模型二很相似,可是在实际情况我们也应该考虑到人的背面是否淋雨,在模型三中就解释了这个问题。
(3)带入数据可求出下列:
头顶淋雨量:Q5=s1*t1*w*cosx =(0.01cosy)/(18*v)
迎雨面淋雨量:Q6= s2*t2*w*(usinx+v)/u=abdw(u*siny-v)/uv
总的淋雨量:Q=Q5+Q6=0.0027778*[(0.2cosy-1.5siny)/v+1.5]
若c*cosy-a*siny<0.即tany>c/a,此时v=usiny时Q最小,当y=30时,v=usiny=4*sin30=2m/s, 此时Q=0.0027778*[(0.2cos30-1.5sin30)/v+1.5]=0.24L,当v=vm时,y=30,Q=0.93L.由此可知,当v=usiny时,淋雨量是最小的。
结果分析:在该模型中考虑到雨的方向问题,这个模型跟模型二相似,将模型二与模型三综合起来跟实际的生活就差不多很相似了。
由这三个模型可以得出在一定的速度下人跑的越快淋雨量就越少。
4:当雨从人体背面吹来时,根据模型三可知道只要满足c*cosy-a*siny<0即tany>c/a,而此时v=usiny的Q最小,即人体淋雨量最少,此时该人只有背面与头顶部淋雨。
5:若是雨线方向与跑步方向不在同一平面内,建立坐标系然后分别对几个淋雨面进行以上同样方法建立求解模型,在本质和考虑问题的思想上来说模型是不变的,只是解算的过程复杂了!。
