结构力学第2章习题及参考答案
结构力学2考试题和答案

结构力学2考试题和答案一、单项选择题(每题2分,共20分)1. 在结构力学中,下列哪一项不是结构分析的基本假设?A. 平面假设B. 小变形假设C. 材料均匀性假设D. 材料非线性假设答案:D2. 确定结构的内力时,通常采用哪种分析方法?A. 能量法B. 弯矩分配法C. 弯矩图法D. 极限平衡法答案:C3. 在结构力学中,以下哪种类型的结构是超静定结构?A. 简支梁B. 悬臂梁C. 连续梁D. 刚架答案:C4. 梁的剪力图和弯矩图的零点位置关系是什么?A. 剪力图的零点与弯矩图的极值点重合B. 弯矩图的零点与剪力图的极值点重合C. 剪力图的零点与弯矩图的零点重合D. 剪力图的极值点与弯矩图的零点重合答案:A5. 以下哪种情况下,结构的稳定性分析是必要的?A. 荷载较小B. 荷载较大C. 荷载恒定D. 荷载变化答案:B6. 确定结构的位移时,通常采用哪种方法?A. 弯矩分配法B. 弯矩图法C. 虚拟力法D. 能量法答案:C7. 在结构力学中,以下哪种结构是静定结构?A. 三铰拱B. 刚架C. 连续梁D. 悬臂梁答案:D8. 以下哪种方法可以用来求解超静定结构?A. 弯矩分配法B. 弯矩图法C. 能量法D. 所有以上方法答案:D9. 结构力学中,以下哪种荷载属于分布荷载?A. 集中荷载B. 均布荷载C. 点荷载D. 线荷载答案:B10. 在结构力学中,以下哪种情况下结构会发生屈曲?A. 荷载较小B. 荷载较大C. 荷载恒定D. 荷载变化答案:B二、填空题(每题2分,共20分)1. 结构力学中,结构的内力包括______、______和______。
答案:轴力、剪力、弯矩2. 梁的挠度计算中,通常采用的两种方法是______和______。
答案:弯矩分配法、能量法3. 结构的稳定性分析中,______是衡量结构稳定性的一个重要参数。
答案:屈曲荷载因子4. 在结构力学中,______是结构分析的基本假设之一。
结构力学课后习题答案(朱慈勉)

朱慈勉 结构力学 第2章课后答案全解2-2 试求出图示体系的计算自由度,并分析体系的几何构造。
(a)(ⅠⅡ)(ⅠⅢ)舜变体系ⅠⅡⅢ(b)W=5×3 - 4×2 – 6=1>0几何可变(c)有一个多余约束的几何不变体系(d)W=3×3 - 2×2 – 4=1>0可变体系2-3 试分析图示体系的几何构造。
(a)(ⅡⅢ)Ⅲ几何不变2-4 试分析图示体系的几何构造。
(a)几何不变(b)W=4×3 -3×2 -5=1>0几何可变体系(ⅠⅢ)(ⅡⅢ)几何不变(d)Ⅲ(ⅠⅢ)有一个多余约束的几何不变体(ⅠⅢ)(ⅡⅢ)(ⅠⅡ)舜变体系(f)(ⅠⅢ)(ⅡⅢ)无多余约束内部几何不变(h)二元体W=3×8 - 9×2 – 7= -1, 有1个多余约束2-5 试从两种不同的角度分析图示体系的几何构造。
(a)(ⅠⅢ)ⅠⅡⅢ(ⅠⅡ)(ⅡⅢ)舜变体系(b)Ⅲ(ⅡⅢ)(ⅠⅢ)同济大学朱慈勉 结构力学 第3章习题答案3-2 试作图示多跨静定梁的弯矩图和剪力图。
(a)2P F a 2P F a4P F Q34P F 2P F(b)aa aaa2m6m2m4m2m2020Q10/326/310(c)18060(d)3m2m2m3m3m4m3m2m 2m2mA2m2m2m2m7.5514482.524MQ3-3 试作图示刚架的内力图。
(a)242018616MQ18(b)4kN ·m3m3m6m1k N /m2kN A CBD6m10kN3m3m 40kN ·mABC D30303011010QM 210(c)45MQ(d)3m3m6m6m2m 2m444444/32MQN(e)4481``(f)4m4m2m3m4m222220M3-4 试找出下列各弯矩图形的错误之处,并加以改正。
(a)F P(b)(c)(d)(e)(f)F3-5 试按图示梁的BC 跨跨中截面的弯矩与截面B 和C 的弯矩绝对值都相等的条件,确定E 、F两铰的位lx l lx置。
《结构力学》课后习题答案__重庆大学出版社

第1章 绪论(无习题)第2章 平面体系的几何组成分析习题解答习题2.1 是非判断题(1) 若平面体系的实际自由度为零,则该体系一定为几何不变体系。
( )(2) 若平面体系的计算自由度W =0,则该体系一定为无多余约束的几何不变体系。
( ) (3) 若平面体系的计算自由度W <0,则该体系为有多余约束的几何不变体系。
( ) (4) 由三个铰两两相连的三刚片组成几何不变体系且无多余约束。
( )(5) 习题2.1(5) 图所示体系去掉二元体CEF 后,剩余部分为简支刚架,所以原体系为无多余约束的几何不变体系。
( )B DACEF习题 2.1(5)图(6) 习题2.1(6)(a)图所示体系去掉二元体ABC 后,成为习题2.1(6) (b)图,故原体系是几何可变体系。
( )(7) 习题2.1(6)(a)图所示体系去掉二元体EDF 后,成为习题2.1(6) (c)图,故原体系是几何可变体系。
()(a)(b)(c)AEBFCD习题 2.1(6)图【解】(1)正确。
(2)错误。
0W 是使体系成为几何不变的必要条件而非充分条件。
(3)错误。
(4)错误。
只有当三个铰不共线时,该题的结论才是正确的。
(5)错误。
CEF 不是二元体。
(6)错误。
ABC 不是二元体。
(7)错误。
EDF 不是二元体。
习题2.2 填空(1) 习题2.2(1)图所示体系为_________体系。
习题2.2(1)图(2) 习题2.2(2)图所示体系为__________体系。
习题2-2(2)图(3) 习题 2.2(3)图所示4个体系的多余约束数目分别为_______、________、__________、__________。
习题2.2(3)图(4) 习题2.2(4)图所示体系的多余约束个数为___________。
习题2.2(4)图(5) 习题2.2(5)图所示体系的多余约束个数为___________。
习题2.2(5)图(6) 习题2.2(6)图所示体系为_________体系,有_________个多余约束。
结构力学习题及答案

构造力学习题第2章平面体系的几何组成分析2-1~2-6 试确定图示体系的计算自由度。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图2-7~2-15 试对图示体系进展几何组成分析。
假设是具有多余约束的几何不变体系,那么需指明多余约束的数目。
题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图题2-13图题2-14图题2-15图题2-16图题2-17图题2-18图题2-19图题2-20图题2-21图2-11=W2-1 9-W=2-3 3-W=2-4 2-W=2-5 1-W=2-6 4-W=2-7、2-8、2-12、2-16、2-17无多余约束的几何不变体系2-9、2-10、2-15具有一个多余约束的几何不变体系2-11具有六个多余约束的几何不变体系2-13、2-14几何可变体系为2-18、2-19 瞬变体系2-20、2-21具有三个多余约束的几何不变体系第3章静定梁和静定平面刚架的内力分析3-1 试作图示静定梁的内力图。
〔a〕〔b〕(c) (d)习题3-1图3-2 试作图示多跨静定梁的内力图。
〔a〕〔b〕(c)习题3-2图3-3~3-9 试作图示静定刚架的内力图。
习题3-3图习题3-4图习题3-5图习题3-6图习题3-7图习题3-8图习题3-9图3-10 试判断图示静定构造的弯矩图是否正确。
(a)(b)(c)(d)局部习题答案3-1〔a 〕m kN M B ⋅=80〔上侧受拉〕,kN F RQB 60=,kN F L QB 60-=〔b 〕m kN M A ⋅=20〔上侧受拉〕,m kN M B ⋅=40〔上侧受拉〕,kN F RQA 5.32=,kN F L QA 20-=,kN F LQB 5.47-=,kN F R QB 20=(c)4Fl M C =〔下侧受拉〕,θcos 2F F L QC =3-2 (a)0=E M ,m kN M F ⋅-=40〔上侧受拉〕,m kN M B ⋅-=120〔上侧受拉〕〔b 〕m kN M RH ⋅-=15(上侧受拉),m kN M E ⋅=25.11〔下侧受拉〕〔c 〕m kN M G ⋅=29(下侧受拉),m kN M D ⋅-=5.8(上侧受拉),m kN M H ⋅=15(下侧受拉) 3-3 m kN M CB ⋅=10〔左侧受拉〕,m kN M DF ⋅=8〔上侧受拉〕,m kN M DE ⋅=20〔右侧受拉〕 3-4 m kN M BA ⋅=120〔左侧受拉〕3-5 m kN M F ⋅=40〔左侧受拉〕,m kN M DC ⋅=160〔上侧受拉〕,m kN M EB ⋅=80(右侧受拉) 3-6 m kN M BA ⋅=60〔右侧受拉〕,m kN M BD ⋅=45〔上侧受拉〕,kN F QBD 46.28=3-7 m kN M C ⋅=70下〔左侧受拉〕,m kN M DE ⋅=150〔上侧受拉〕,m kN M EB ⋅=70(右侧受拉) 3-8 m kN M CB ⋅=36.0〔上侧受拉〕,m kN M BA ⋅=36.0〔右侧受拉〕 3-9 m kN M AB ⋅=10〔左侧受拉〕,m kN M BC ⋅=10〔上侧受拉〕 3-10 〔a 〕错误 〔b 〕错误 〔c 〕错误 〔d 〕正确第4章 静定平面桁架和组合构造的内力分析4-1 试判别习题4-1图所示桁架中的零杆。
结构力学第2章习题及参考答案
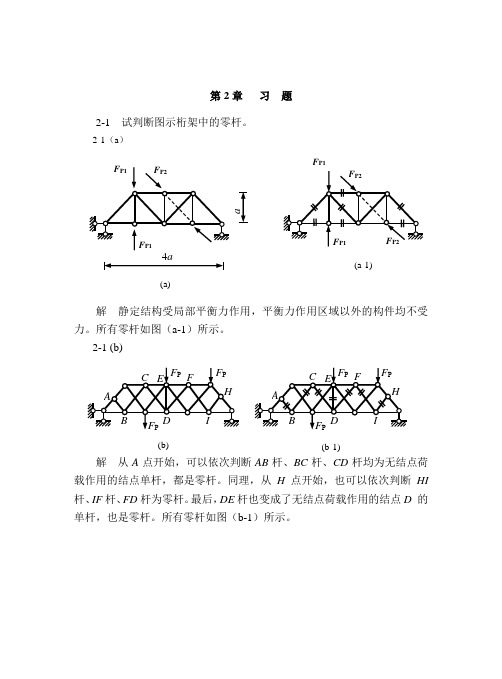
解悬臂刚架,梁部分先求杆端控制弯矩,再区段叠加。柱剪力为零,弯矩图为常数。
2-21(b)
解两刚片三支杆组成单体刚架,先求支座反力,再作弯矩图。注意二杆结点有外力偶作用时,杆端弯矩将产生突变,突变值等于力偶值。
2-21(c)
解(1)铰附近截面作用有集中力偶时,弯矩值等于力偶值,据此,可知顶铰左右两侧截面的弯矩为M,上侧受拉。又因为横梁上没有竖向集中力作用,弯矩图应是一条直线。考虑本题结构对称,荷载也对称,则横梁上的弯矩图为一条水平线。
2-14试作图示多跨静定梁内力图。
解:(1)确定求解顺序:EF→CDE→ABC
(2)求支座反力及各部分之间的相互作用力。结果如图(b)所示。
(3)分别画出每一部分的内力图,组合在一起就是原结构的内力图,如图(c)和(d)所示。
2-15试作图示多跨静定梁弯矩图。
解:(1)确定求解顺序。DEF→DCB→AB。
(2)二杆刚结点上,若无集中力偶作用时,则两个杆的杆端弯矩应该相等,且同时外侧受拉。这样就可以画出两个柱子的弯矩图了。
2-21(d)
解本题为基——附型结构,先算上部、后算下部。两个部分均三铰刚架,分别求解即可。
2-21(e)
2-22试作图示组合结构的弯矩图和轴力图。
FN12= -75kN,FN34=75kN
100kn100kn50kn2520251875knm202550kn截面内力5mcos3025sincos187525295kncossin5050188knsincos5050683kn5m305m5m213求图示三铰拱结构的支座反力链杆轴力并求指定截面k1求支座反力10kn10kn取ceb部分为隔离体截面的弯矩取kad部分为隔离体40knayed20kn4m4m4m4m214试作图示多跨静定梁内力图
南京航空航天大学_结构力学_课后习题答案_第2章

第二章 薄板的弯曲(习题解答)2-1 写出2-1图所示矩形薄板的边界条件。
OA 为简支边,并作用有分布的弯矩M 。
BC 边为固支边,OC 边为简支边。
AB 边为自由边。
解:OA 边:M x w Dyw u x w D M w x x x x x -=∂∂-=∂∂+∂∂-======0220222200)(0;OC 边:0)(00220222200=∂∂-=∂∂+∂∂-======y y y y y y wD x w u y w D M w ;BC 边:00=∂∂===ax a x xww ;AB 边:0)(2222=∂∂+∂∂-===b y by yx wu y w D M0])2([)(2333=∂∂∂-+∂∂-=∂∂+==by by yx y y x w u y w D xM Q2-2 如图2-2所示,矩形薄板OA 边和OC 边为简支边,AB 和BC 为自由边,在点B 受向下的横向集中力P 。
试证w mxy =可作为该薄板的解答,并确定常数m 、内力及边界处反力。
解:mxy w =满足平衡微分方程0/4==∇D q wOC 边上:0)(0022220=;==∂∂+∂∂-=y y x wu y w D wOA 边上:0)(0022220=;==∂∂+∂∂-=x x y wu x w DwAB 边上:0])2([0)(23332222=∂∂∂-+∂∂-=∂∂+∂∂-==by b y y x wu y w D x w u y w D ;BC 边上:0])2([0)(23332222=∂∂∂-+∂∂-=∂∂+∂∂-==ax a x y x wu x w D y w u x w D ;在B 点上:P m u D y x wu D by a x -=--=∂∂∂--==)1(2)()1(2,2)1(2u D Pm -=⇒所以)1(2u D Pxyw -=0)(2222=∂∂+∂∂-=y wu x w D M x ;0)(2222=∂∂+∂∂-=x w u y w D M y ;2)1(2P y x w u D M xy-=∂∂∂--= ;02=∇∂∂-=w xD Q x ;02=∇∂∂-=w y D Q y P R R P y x wu D R O C AA ==-=∂∂∂--=;)()1(222-3 如图2-3所示,半椭圆形薄板,直线边界为简支边,曲线边界ACB 为固支边,承受横向载荷0q=q xa 。
结构力学第2章习题参考答案_khdaw

2
w.
13 FN6 = 1.352 1FP
案 网
sin α =
1
cos α =
2
sin β =
2
cos β =
3
FN6 sin β + FN5 cos α − FN4 sin θ = 0
2.5Fp
Fp
Fp
∑Fy = 0
2 FP , ∑M K = 0 2 FN1 = 4 FP , ∑ Fx = 0
FN 4 = −4.5 FP
y
∑F
x
=0 FN2 = 0
FN1 = 0
取 1、2 杆相交结点为隔离体,可求得:
2-6(f) 取隔离体图(a)所示,求得支座反力。再取隔离体图(b)列方程有: G F E 0 A 1 B 2 H
答
FN3
F
w.
H FN2
案 网
da
D C 2 FN5 D Fp Fp Fp (b)隔离体图
后
FN4
Fp
kh
w.
kh
da
课
后
答
w.
案 网
Fp l=8×a
co
A D E B (d)
m
Fp
N
O
P
Q
U
V
H
课后答案网
2-2 答:
11 9 10
1 0 8
12
13 6
4 5
7 4×2.5 m
17.5 kN 依次取结点为隔离体,受力图如下所示。 10 kN FN1 FN2
32.5 kN
2×1.25 m
课后答案网
2-6(a) 答:取图(a)所示隔离体,列方程有: 80 kN 45o FN1 (a)隔离体 2 FN1 (b)隔离体 FN2 80 kN K
南京航空航天大学 结构力学 课后习题答案 第2章

第二章 薄板的弯曲(习题解答)2-1 写出2-1图所示矩形薄板的边界条件。
OA 为简支边,并作用有分布的弯矩M 。
BC 边为固支边,OC 边为简支边。
AB 边为自由边。
解:OA 边:M x w D y w u x w D M w x x x x x -=∂∂-=∂∂+∂∂-======0220222200)(0;OC 边:0)(00220222200=∂∂-=∂∂+∂∂-======y y y y y y wD x w u y w D M w ;BC 边:00=∂∂===ax a x xww ;AB 边:0)(2222=∂∂+∂∂-===b y by yx wu y w D M0])2([)(2333=∂∂∂-+∂∂-=∂∂+==by by yx y y x w u y w D xM Q2-2 如图2-2所示,矩形薄板OA 边和OC 边为简支边,AB 和BC 为自由边,在点B 受向下的横向集中力P 。
试证w mxy =可作为该薄板的解答,并确定常数m 、内力及边界处反力。
解:mxy w =满足平衡微分方程0/4==∇D q wOC 边上:0)(0022220=;==∂∂+∂∂-=y y x wu y w D wOA 边上:0)(0022220=;==∂∂+∂∂-=x x y wu x w D wAB 边上:0])2([0)(23332222=∂∂∂-+∂∂-=∂∂+∂∂-==by b y y x wu y w D x w u y w D ;BC 边上:0])2([0)(23332222=∂∂∂-+∂∂-=∂∂+∂∂-==ax a x y x wu x w D y w u x w D ;在B 点上:P m u D y x wu D by a x -=--=∂∂∂--==)1(2)()1(2,2)1(2u D Pm -=⇒所以)1(2u D Pxyw -=0)(2222=∂∂+∂∂-=y wu x w D M x ;0)(2222=∂∂+∂∂-=x w u y w D M y ;2)1(2P y x w u D M xy-=∂∂∂--= ;02=∇∂∂-=w xD Q x ;02=∇∂∂-=w y D Q y P R R P y x wu D R O C AA ==-=∂∂∂--=;)()1(222-3 如图2-3所示,半椭圆形薄板,直线边界为简支边,曲线边界ACB 为固支边,承受横向载荷0q=q xa 。
《结构力学》课后习题答案__重庆大学出版社

第1章 绪论(无习题)第2章 平面体系的几何组成分析习题解答习题2.1 是非判断题(1) 若平面体系的实际自由度为零,则该体系一定为几何不变体系。
( )(2) 若平面体系的计算自由度W =0,则该体系一定为无多余约束的几何不变体系。
( ) (3) 若平面体系的计算自由度W <0,则该体系为有多余约束的几何不变体系。
( ) (4) 由三个铰两两相连的三刚片组成几何不变体系且无多余约束。
( )(5) 习题2.1(5) 图所示体系去掉二元体CEF 后,剩余部分为简支刚架,所以原体系为无多余约束的几何不变体系。
( )B DACEF习题 2.1(5)图(6) 习题2.1(6)(a)图所示体系去掉二元体ABC 后,成为习题2.1(6) (b)图,故原体系是几何可变体系。
( )(7) 习题2.1(6)(a)图所示体系去掉二元体EDF 后,成为习题2.1(6) (c)图,故原体系是几何可变体系。
()(a)(b)(c)AEBFCD习题 2.1(6)图【解】(1)正确。
(2)错误。
0W 是使体系成为几何不变的必要条件而非充分条件。
(3)错误。
(4)错误。
只有当三个铰不共线时,该题的结论才是正确的。
(5)错误。
CEF 不是二元体。
(6)错误。
ABC 不是二元体。
(7)错误。
EDF 不是二元体。
习题2.2 填空(1) 习题2.2(1)图所示体系为_________体系。
习题2.2(1)图(2) 习题2.2(2)图所示体系为__________体系。
习题2-2(2)图(3) 习题 2.2(3)图所示4个体系的多余约束数目分别为_______、________、__________、__________。
习题2.2(3)图(4) 习题2.2(4)图所示体系的多余约束个数为___________。
习题2.2(4)图(5) 习题2.2(5)图所示体系的多余约束个数为___________。
习题2.2(5)图(6) 习题2.2(6)图所示体系为_________体系,有_________个多余约束。
结构力学第二章答案
2-4f
Ⅲ
O13
Ⅰ O12
Ⅱ O23
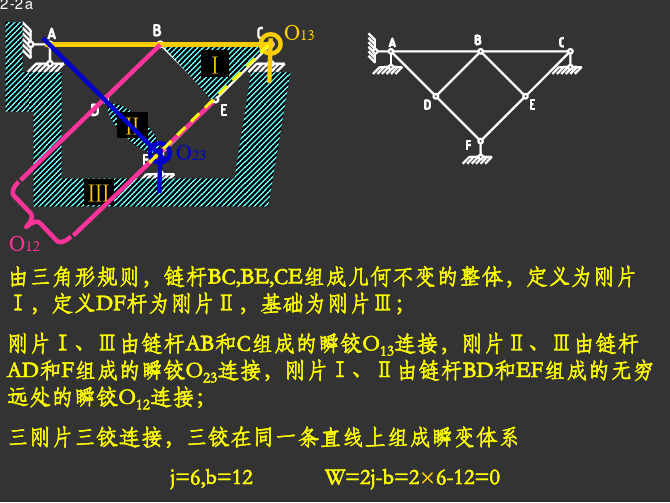
由三角形规则,链杆AC,CD,DA组成几何不变的整体,定义为刚片 Ⅰ,同理,定义链杆BG,GF,FB为刚片Ⅱ,定义链杆HE,EJ,JH为刚 片Ⅲ; 刚片Ⅰ、Ⅱ由链杆AG,BC组成的瞬铰O12连接,刚片Ⅰ、Ⅲ由链杆 HC,DE组成的瞬铰O13连接,刚片Ⅱ、Ⅲ由链杆JG,EF组成的瞬铰 O23连接; 三刚片三铰连接,三铰不在同一条直线上,组成内部几何不变体 系,且无多余约束。 j=9,b=15 W=2j-b=2×9-5=3 (内部几何不变体)
由三角形规则定义DFH组成刚片,在此基础上加二元体(D-E-H)组 成扩大刚片定义为刚片Ⅰ,定义刚片AC为刚片Ⅱ 。
刚片Ⅰ和Ⅱ 由三根平行链杆AD,BE,和DC连接,组成瞬变体系。
三刚片三铰连接,三铰在同一条 直线上,组成瞬变体系。 Ⅱ
Ⅰ
Ⅲ
O12
O13
2-5b
Ⅱ Ⅰ O12 O13
Ⅲ
三刚片三铰连接,三铰不在同一条直线上, 组成内部几何不变且无多余约束体系。 Ⅱ Ⅰ
Ⅲ
O23
O13
O12
O23
2-9a、b
Ⅲ
O12 Ⅱ O13 O23 Ⅰ O13
Ⅲ
O23
Ⅱ
Ⅰ
三刚片三铰连接,三铰不 在同一条直线上,组成几 何不变且无多余约束体 系。
2-4e
Ⅲ Ⅰ Ⅱ
O13
O12
O23
由三角形规则,链杆AB,BE,EA组成几何不变的整体,定义为刚片 Ⅰ,同理,定义链杆BC,CF,FB为刚片Ⅱ,定义链杆HG为刚片Ⅲ; 刚片Ⅰ、Ⅱ由实铰B(O12)连接,刚片Ⅰ、Ⅲ由链杆AH,GE组成的瞬 铰A(O13)连接,刚片Ⅱ、Ⅲ由链杆CH,GF组成的瞬铰C(O23)连接; 三刚片三铰连接,三铰在同一条直线上,组成瞬变体系。 j=7,b=11 W=2j-b=2×7-11=3 (微小位移后为内部几何不变体)
结构力学章节习题及参考答案

第1章绪论(无习题)之阳早格格创做第2章仄里体系的机动领会习题解问习题利害推断题(1) 若仄里体系的本质自由度为整,则该体系一定为几许稳定体系.( )(2) 若仄里体系的估计自由度W=0,则该体系一定为无多余拘束的几许稳定体系.( )(3) 若仄里体系的估计自由度W<0,则该体系为有多余拘束的几许稳定体系.( )(4) 由三个铰二二贯串的三刚刚片组成几许稳定体系且无多余拘束.( )(5) 习题2.1(5) 图所示体系去掉二元体CEF后,结余部分为简收刚刚架,所以本质系为无多余拘束的几许稳定体系.( )习题 2.1(5)图(6) 习题2.1(6)(a)图所示体系去掉二元体ABC后,成为习题2.1(6) (b)图,故本质系是几许可变体系.( )(7) 习题2.1(6)(a)图所示体系去掉二元体EDF后,成为习题2.1(6) (c)图,故本质系是几许可变体系.( )习题 2.1(6)图习题挖空(1) 习题2.2(1)图所示体系为_________体系.习题2.2(1)图(2) 习题2.2(2)图所示体系为__________体系.习题 2-2(2)图(3) 习题2.2(3)图所示4个体系的多余拘束数目分别为_______、________、__________、__________.习题 2.2(3)图(4) 习题 2.2(4)图所示体系的多余拘束个数为___________.习题 2.2(4)图(5) 习题 2.2(5)图所示体系的多余拘束个数为___________.习题 2.2(5)图(6) 习题 2.2(6)图所示体系为_________体系,有_________个多余拘束.习题 2.2(6)图(7) 习题 2.2(7)图所示体系为_________体系,有_________个多余拘束.习题 2.2(7)图对付习题2.3图所示各体系举止几许组成领会.第3章静定梁与静定刚刚架习题解问习题利害推断题(1) 正在使用内力图特性画制某受直杆段的直矩图时,必须先供出该杆段二端的端直矩.()(2) 区段叠加法仅适用于直矩图的画制,不适用于剪力图的画制.()(3) 多跨静定梁正在附属部分受横背荷载效率时,必会引起基础部分的内力.()(4) 习题3.1(4)图所示多跨静定梁中,CDE战EF部分均为附属部分.()习题3.1(4)图习题挖空(1)习题3.2(1)图所示受荷的多跨静定梁,其定背通联C所传播的直矩M C的大小为______;截里B的直矩大小为______,____侧受推.习题3.2(1)图(2) 习题3.2(2)图所示风载效率下的悬臂刚刚架,其梁端直矩M AB=______kN·m,____侧受推;左柱B截里直矩M B=______kN·m,____侧受推.习题3.2(2)图习题做图所示单跨静定梁的M图战F图.Q(a) (b)(c) (d)(e) (f)习题做图所示单跨静定梁的内力图.(c) 习题做图所示斜梁的内力图.习题做图所示多跨梁的内力图.(a)(a)习题改正图所示刚刚架的直矩图中的过失部分.(a) (b) (c)(d) (e) (f)习题做图所示刚刚架的内力图.(a)(b)第4章静定拱习题解问习题4.1利害推断题(1) 三铰拱的火仄推力不但是与三个铰的位子有关,还与拱轴线的形状有关.()(2) 所谓合理拱轴线,是指正在任性荷载效率下皆能使拱处于无直矩状态的轴线. ( )(3) 改变荷载值的大小,三铰拱的合理拱轴线形状也将爆收改变. ( )习题4.2挖空(1) 习题3.2(3)图所示三铰拱的火仄推力F H 等于.习题3.2(3)图习题4.3供图所示三铰拱收反力战指定截里K 的内力.已知轴线圆程24()f y x l x l =-.第5章 静定仄里桁架习题解问习题5.1 利害推断题(1) 利用结面法供解桁架结构时,可从任性结面启初. ( ) 习题5.2挖空(1)习题3.2(4)图所示桁架中有根整杆.习题3.2(4)图习题5.3 试用结面法供图所示桁架杆件的轴力.(a) (b)习题5.4 推断图所示桁架结构的整杆.(a) (b)(c)习题5.5 用截里法供解图所示桁架指定杆件的轴力.(a)(b)第6章 结构的位移估计习题解问习题6.1 利害推断题(1) 变形骸真功本理仅适用于弹性体系,不适用于非弹性体系.( )(2) 真功本理中的力状态战位移状态皆是真设的.( )(3) 功的互等定理仅适用于线弹性体系,不适用于非线弹性体系.( )(4) 反力互等定理仅适用于超静定结构,不适用于静定结构.( )(5) 对付于静定结构,有变形便一定有内力.( )(6) 对付于静定结构,有位移便一定有变形.( )(7) 习题4.1(7)图所示体系中各杆EA 相共,则二图中C 面的火仄位移相等.( )(8) M P 图,M 图如习题4.1(8)图所示,EI =常数.下列图乘截止是精确的:4)832(12l l ql EI ⨯⨯⨯ ( )(9) M P 图、M (9)图所示,下列图乘截止是精确的:033202201111)(1y A EI y A y A EI ++ ( )(10) (10)图所示结构的二个仄稳状态中,有一个为温度变更,此时功的互等定理不可坐.( )习题 4.1(7)图习题 4.1(8)图 习题4.1(9)图习题 4.1(10)图习题6.2挖空题(1) 习题4.2(1)图所示刚刚架,由于收座B 下重所引起D 面的火仄位移D H =______. (2) 真功本理有二种分歧的应用形式,即_______本理战_______本理.其中,用于供位移的是_______本理.(3) 用单位荷载法估计位移时,假制状态中所加的荷载应是与所供广义位移相映的________.(4) 图乘法的应用条件是:__________且M P 与M 图中起码有一个为直线图形.(5) 已知刚刚架正在荷载效率下的M P 图如习题4.2(5)图所示,直线为二次扔物线,横梁的抗直刚刚度为2EI ,横杆为EI ,则横梁中面K 的横背位移为________.(6) 习题4.2(6)图所示拱中推杆AB 比本安排少度短了,由此引起C 面的横背位移为________;引起收座A 的火仄反力为________.(7) 习题4.2(7)图所示结构,当C 面有F P =1(↓)效率时,D 面横背位移等于(↑),当E 面有图示荷载效率时,C 面的横背位移为________.(8) 习题 4.2(8)图(a )所示连绝梁收座B 的反力为)(1611R ↑=B F ,则该连绝梁正在收座B 下重B =1时(如图(b )所示),D 面的横背位移D δ=________.习题 4.2(1)图 习题 4.2(5)图习题 4.2(6)图 习题 4.2(7)图习题 4.2(8)图习题6.3C V .EI 为常数.1)供C V习题4.3(1)图2)供C V习题4.3(2)图3)供C V习题4.3(3)图4)供A习题4.3(4)图习题6.4 分别用积分法战图乘法供习题4.4(a)图所示刚刚架C 面的火仄位移C H .已知EI =常数.习题6.5 习题4.5(a)图所示桁架各杆截里均为A =2×103m 2,E ×108kN/m 2,F P =30kN ,d =2m.试供C 面的横背位移V C .第7章 力法习题解问习题7.1利害推断题(1)习题5.1(1)图所示结构,当收座A 爆收转化时,D q l l B A C lA B lD C A BC22ql 2ql 281ql 2(b)图M P M 图(c)(a)xx1l各杆均爆收内力.()习题5.1(1)图习题5.1(2)图(2)习题 5.1(2)图所示结构,当内中侧均降下t1℃时,二杆均只爆收轴力.()(3)习题 5.1(3)图(a)战(b)所示二结构的内力相共.()习题5.1(3)图(4)习题 5.1(3)图(a)战(b)所示二结构的变形相共.()习题7.2 挖空题(1)习题5.2(1) 图(a)所示超静定梁的收座A爆收转角,若选图(b)所示力法基础结构,则力法圆程为_____________,代表的位移条件是______________,其中=_________;若选图(c)所示力法基础结构时,力法圆1c程为____________,代表的位移条件是______________,其中1c=_________.习题5.2(1)图(2)习题5.2(2)图(a)所示超静定结构,当基础体系为图(b)时,力法圆程为____________________,=________;当基础体系为图(c)时,力法圆程为1P____________________,1P=________.习题5.2(2)图(3)习题5.2(3)图(a)所示结构各杆刚刚度相共且为常数,AB杆中面直矩为________,____侧受推;图(b)所示结构M BC=________,____侧受推.习题5.2(3)图(4)连绝梁受荷载效率时,其直矩图如习题5.2(4)图所示,则D面的挠度为________,位移目标为____.习题5.2(4)图习题7.3试决定习题5.3图所示结构的超静定次数.图习题7.4用力法估计习题5.4图所示各超静定梁,并做出直矩图战剪力图.图习题7.5用力法估计习题5.5图所示各超静定刚刚架,并做出内力图.图习题7.6利用对付称性,估计习题5.12图所示各结构的内力,并画直矩图.图习题7.7画出习题5.17图所示各结构直矩图的大概形状.已知各杆EI=常数.图第8章位移法习题解问习题8.1决定用位移法估计图所示结构的基础已知量数目,并画出基础结构.(除证明者中,其余杆的EI为常数.)(a) (b) (c) (d)图习题8.2利害推断(1)位移法基础已知量的个数与结构的超静定次数无关.()(2)位移法可用于供解静定结构的内力.()(3)用位移法估计结构由于收座移动引起的内力时,采与与荷载效率时相共的基础结构.()(4)位移法只可用于供解连绝梁战刚刚架,不克不迭用于供解桁架.()习题8.3用位移法估计习题6.6图所示连绝梁,做直矩图战剪力图,EI=常数.(1)(2)习题8.4用位移法估计结构,做直矩图,EI=常数.(1)(2)第9章渐近法习题解问习题9.1利害推断题(1)力矩调配法不妨估计所有超静定刚刚架的内力.()(2)习题7.1(2)图所示连绝梁的蜿蜒刚刚度为EI,杆少为l,杆端直矩M BC<M.()习题7.1(2)图习题7.1(3)图(3)习题7.1(3)图所示连绝梁的线刚刚度为i,欲使A端爆收逆时针单位转角,需施加的力矩M A>3i.()习题9.2挖空题(1)习题7.2(1)图所示刚刚架EI=常数,各杆少为l,杆端直矩M AB =________.(2)习题7.2(2)图所示刚刚架EI=常数,各杆少为l,杆端直矩M AB =________.(3)习题7.2(3)图所示刚刚架各杆的线刚刚度为i,欲使结面B爆收逆时针的单位转角,应正在结面B施加的力矩M B =______.习题7.2(1)图习题7.2(2)图习题7.2(3)图(4)用力矩调配法估计习题7.2(4)图所示结构(EI=常数)时,传播系数C BA =________,C BC =________.习题7.2(4)图习题9.3用力矩调配法估计习题7.3图所示连绝梁,做直矩图战剪力图,并供收座B的反力.(1)(2)习题9.4用力矩调配法估计习题7.4图所示连绝梁,做直矩图.(1)(2)习题9.5用力矩调配法估计习题7.5图所示刚刚架,做直矩图.(1)(2)第11章效率线及其应用习题解问习题11.1利害推断题(1)习题8.1(1)图示结构BC杆轴力的效率线应画正在BC杆上.()习题8.1(1)图习题8.1(2)图(2) 习题8.1(2)图示梁的M C效率线、F Q C效率线的形状如图(a)、(b)所示.(3) 习题8.1(3)图示结构,利用M C效率线供牢固荷载F P1、F P2、F P3效率下M C的值,可用它们的合力F R去代替,即M C= F P1y1+ F P2y2+ F P3y3=F R y.( )习题8.1(3)图(4) 习题8.1(4)图中的(a)所示主梁F Q C左的效率线如图(b)所示.( )习题8.1(4)图(5)习题8.1(5)图示梁F R A的效率线与F Q A左的效率线相共.( )习题8.1(5)图(6) 简收梁的直矩包络图为活载效率下各截里最大直矩的连线.( )习题11.2挖空题(1) 用静力法做效率线时,其效率线圆程是.用机动法做静定结构的效率线,其形状为机构的.(2) 直矩效率线横目标量目是.(3)习题8.2(3)图所示结构,F P=1沿AB移动,M D的效率线正在B面的横标为,F Q D的效率线正在B面的横标为.习题8.2(3)图(4) 习题8.2(4)图所示结构,F P=1沿ABC移动,则M D 效率线正在B面的横标为.习题8.2(4)图(5)习题8.2(5)图所示结构,F P=1沿AC移动,截里B的轴力F N B的效率线正在C面的横标为.习题8.2(5)图习题11.3单项采用题(1)习题8.3(1)图所示结构中收座A左侧截里剪力效率线的形状为( ).习题8.3(1)图(2) 习题8.3(2)图所示梁止家列荷载效率下,反力F R A的最大值为( ).(a) 55kN (b) 50kN (c) 75kN (d) 90kN习题8.3(2)图(3)习题8.3(3)图所示结构F Q C效率线(F P=1正在BE上移动)BC、CD段横标为( ).(a) BC,CD均不为整; (b) BC,CD均为整;(c) BC为整,CD不为整;(d) BC不为整,CD为整.习题8.3(3)图(4)习题8.3(4)图所示结构中,收座B左侧截里剪力效率线形状为( ).习题8.3(4)图(5)习题8.3(5)图所示梁止家列荷载效率下,截里K的最大直矩为( ).(a) 15kN·m(b) 35 kN·m(c) 30 kN·m(d) kN·m习题8.3(5)图习题11.4做习题8.4(a)图所示悬臂梁F R A、M C、F Q C的效率线.习题11.5做习题8.5(a)图所示结构中F N BC、M D的效率线,F P =1正在AE上移动.习题11.6做习题8.6(a)图所示伸臂梁的M A、M C、F Q A 左、F Q A左的效率线.习题11.7做习题8.7(a)图所示结构中截里C的M C、F Q C的效率线.习题11.8(a)图所示静定多跨梁的F R B、M E、F Q B左、F Q B左、F Q C的效率线.习题11.9(a)图所示牢固荷载效率下截里K的内力M K战F Q K左.习题11.10(a)图所示连绝梁M K、M B、F Q B左、F Q B左效率线的形状.若梁上有随意安插的均布活荷载,请画出使截里K爆收最大直矩的荷载安插.第2章仄里体系的机动领会习题解问习题利害推断题(1) 若仄里体系的本质自由度为整,则该体系一定为几许稳定体系.( )(2) 若仄里体系的估计自由度W=0,则该体系一定为无多余拘束的几许稳定体系.( )(3) 若仄里体系的估计自由度W<0,则该体系为有多余拘束的几许稳定体系.( )(4) 由三个铰二二贯串的三刚刚片组成几许稳定体系且无多余拘束.( )(5) 习题2.1(5) 图所示体系去掉二元体CEF后,结余部分为简收刚刚架,所以本质系为无多余拘束的几许稳定体系.( )习题 2.1(5)图(6) 习题2.1(6)(a)图所示体系去掉二元体ABC后,成为习题2.1(6) (b)图,故本质系是几许可变体系.( )(7) 习题2.1(6)(a)图所示体系去掉二元体EDF后,成为习题2.1(6) (c)图,故本质系是几许可变体系.( )习题 2.1(6)图【解】(1)精确.(2)过失.0W 是使体系成为几许稳定的需要条件而非充分条件.(3)过失.(4)过失.惟有当三个铰不共线时,该题的论断才是精确的.(5)过失.CEF不是二元体.(6)过失.ABC不是二元体.(7)过失.EDF不是二元体.习题挖空(1) 习题2.2(1)图所示体系为_________体系.习题2.2(1)图(2) 习题2.2(2)图所示体系为__________体系.习题 2-2(2)图(3) 习题2.2(3)图所示4个体系的多余拘束数目分别为_______、________、__________、__________.习题 2.2(3)图(4) 习题 2.2(4)图所示体系的多余拘束个数为___________.习题 2.2(4)图(5) 习题 2.2(5)图所示体系的多余拘束个数为___________.习题 2.2(5)图(6) 习题 2.2(6)图所示体系为_________体系,有_________个多余拘束.习题 2.2(6)图(7) 习题 2.2(7)图所示体系为_________体系,有_________个多余拘束.习题 2.2(7)图【解】(1)几许稳定且无多余拘束.安排二边L形杆及大天分别动做三个刚刚片.(2)几许常变.中间三铰刚刚架与大天形成一个刚刚片,其与左边倒L形刚刚片之间惟有二根链杆相联,缺少一个拘束.(3)0、1、2、3.末尾一个启关的圆环(大概框)里里有3个多余拘束.(4)4.表层可瞅做二元体去掉,下层多余二个铰.(5)3.下层(包罗大天)几许稳定,为一个刚刚片;与表层刚刚片之间用三个铰相联,多余3个拘束.(6)里里几许稳定、0.将左上角火仄杆、左上角铰交三角形战下部铰交三角形分别动做刚刚片,根据三刚刚片准则领会.(7)里里几许稳定、3.中围启关的正圆形框为有3个多余拘束的刚刚片;里里铰交四边形可选一对付仄止的对付边瞅做二个刚刚片;根据三刚刚片准则即可领会.对付习题2.3图所示各体系举止几许组成领会.【解】(1)如习题解2.3(a)图所示,刚刚片AB与刚刚片I 由铰A战收杆①相联组成几许稳定的部分;再与刚刚片BC 由铰B战收杆②相联,故本质系几许稳定且无多余拘束.习题解2.3(a)图(2)刚刚片Ⅰ、Ⅱ、Ⅲ由不共线三铰A、B、(Ⅰ,Ⅲ)二二相联,组成几许稳定的部分,如习题解2.3(b)图所示.正在此部分上增加二元体C-D-E,故本质系几许稳定且无多余拘束.习题解2.3(b)图(3)如习题解2.3(c)图所示,将左、左二端的合形刚刚片瞅成二根链杆,则刚刚片Ⅰ、Ⅱ、Ⅲ由不共线三铰(Ⅰ,Ⅱ)、(Ⅱ,Ⅲ)、(Ⅰ,Ⅲ)二二相联,故体系几许稳定且无多余拘束.习题解2.3(c)图(4)如习题解2.3(d)图所示,刚刚片Ⅰ、Ⅱ、Ⅲ由不共线的三铰二二相联,产死大刚刚片;该大刚刚片与天基之间由4根收杆贯串,有一个多余拘束.故本质系为有一个多余拘束的几许稳定体系.习题解2.3(d)图(5)如习题解2.3(e)图所示,刚刚片Ⅰ、Ⅱ、Ⅲ组成几许稳定且无多余拘束的体系,为一个大刚刚片;该大刚刚片与天基之间由仄止的三根杆①、②、③相联,故本质系几许瞬变.习题解2.3(e)图(6)如习题解2.3(f)图所示,由三刚刚片准则可知,刚刚片Ⅰ、Ⅱ及天基组成几许稳定且无多余拘束的体系,设为夸大的天基.刚刚片ABC与夸大的天基由杆①战铰C相联;刚刚片CD与夸大的天基由杆②战铰C相联.故本质系几许稳定且无多余拘束.习题解2.3(f)图第3章静定梁与静定刚刚架习题解问习题利害推断题(1) 正在使用内力图特性画制某受直杆段的直矩图时,必须先供出该杆段二端的端直矩.()(2) 区段叠加法仅适用于直矩图的画制,不适用于剪力图的画制.()(3) 多跨静定梁正在附属部分受横背荷载效率时,必会引起基础部分的内力.()(4) 习题3.1(4)图所示多跨静定梁中,CDE战EF部分均为附属部分.()习题3.1(4)图【解】(1)精确;(2)过失;(3)精确;(4)精确;EF为第二条理附属部分,CDE为第一条理附属部分;习题挖空(1)习题3.2(1)图所示受荷的多跨静定梁,其定背通联C所传播的直矩M C的大小为______;截里B的直矩大小为______,____侧受推.习题3.2(1)图(2) 习题3.2(2)图所示风载效率下的悬臂刚刚架,其梁端直矩M AB=______kN·m,____侧受推;左柱B截里直矩M B=______kN·m,____侧受推.习题3.2(2)图【解】(1)M C = 0;M C = F P l,上侧受推.CDE部分正在该荷载效率下自仄稳;(2)M AB=288kN·m,左侧受推;M B=32kN·m,左侧受推;习题做图所示单跨静定梁的M图战F图.Q(a) (b)(c) (d)(e) (f)【解】M图(单位:kN·m)F Q图(单位:kN)(a)M图F Q图(b)M图F Q 图(c)M图F Q图(d)M图F Q图(e)M图(单位:kN·m)F Q图(单位:kN)(f)习题做图所示单跨静定梁的内力图.(c) 【解】M图(单位:kN·m)F Q图(单位:kN)(c)习题做图所示斜梁的内力图.【解】M图(单位:kN·m)F Q图(单位:kN)F N图(单位:kN)习题做图所示多跨梁的内力图.(a)【解】M图(单位:kN·m)F Q图(单位:kN)(a)习题3.7 改正图所示刚刚架的直矩图中的过失部分.(a) (b) (c)(d) (e) (f)【解】(a) (b) (c)(d) (e) (f)习题做图所示刚刚架的内力图.(a)(b)【解】M图(单位:kN·m)F Q图(单位:kN)F N图(单位:kN)(a)M图(单位:kN·m)F Q图(单位:kN)F N图(单位:kN)(b)第4章静定拱习题解问习题4.1利害推断题(1) 三铰拱的火仄推力不但是与三个铰的位子有关,还与拱轴线的形状有关.()(2) 所谓合理拱轴线,是指正在任性荷载效率下皆能使拱处于无直矩状态的轴线. ()(3) 改变荷载值的大小,三铰拱的合理拱轴线形状也将爆收改变. ( ) 【解】(1)过失.从公式0H /C F M f =可知,三铰拱的火仄推力与拱轴线的形状无关;(2)过失.荷载爆收改变时,合理拱轴线将爆收变更; (3)过失.合理拱轴线与荷载大小无关; 习题4.2挖空(1) 习题3.2(3)图所示三铰拱的火仄推力F H 等于.习题3.2(3)图【解】(1)F P /2;习题4.3供图所示三铰拱收反力战指定截里K 的内力.已知轴线圆程24()fy x l x l=-.【解】H H 16kN A B F F ==;VA 8kN()F =↑;V 24kN()B F =↑ 15kN m K M =-⋅;Q 1.9kN K F =;N 17.8kN K F =-第5章 静定仄里桁架习题解问习题5.1 利害推断题(1) 利用结面法供解桁架结构时,可从任性结面启初. ( ) 【解】(1)过失.普遍从仅包罗二个已知轴力的结面启初. 习题5.2挖空(1)习题3.2(4)图所示桁架中有根整杆.习题3.2(4)图【解】(1)11(仅横背杆件中有轴力,其余均为整杆). 习题5.3 试用结面法供图所示桁架杆件的轴力.(a) (b)【解】 (1)提示:根据整杆判别规则有:N13N430F F ==;根据等力杆判别规则有:N24N46F F =.而后分别对付结面2、3、5列力仄稳圆程,即可供解局部杆件的内力. (2) 提示:根据整杆判别规则有:N18N17N16N27N36N450F F F F F F ======;根据等力杆判别规则有:N12N23N34F F F ==;N78N76N65F F F ==.而后与结面4、5列力仄稳圆程,即可供解局部杆件的内力.习题5.4 推断图所示桁架结构的整杆.(a) (b) (c)【解】(a) (b) (c)提示:(c)题需先供出收座反力后,截与Ⅰ.Ⅰ截里以左为断绝体,由30M =∑,可得N120F =,而后再举止整杆推断. 习题5.5 用截里法供解图所示桁架指定杆件的轴力.(a)(b)【解】(1) N P 32a F F =-;N P 12b F F =;N Pc F F =提示:截与Ⅰ.Ⅰ截里可得到N b F 、N c F ;根据整杆推断规则,杆26、杆36为整杆,则通过截与Ⅱ.Ⅱ截里可得到N a F . (2)N 0a F =;N P b F =;N 0c F =提示:截与Ⅰ.Ⅰ截里可得到N b F ;由结面1可知N 0a F =;截与Ⅱ.Ⅱ截里,与圆圈以内为摆脱体,对付2面与矩,则N 0c F =.第6章 结构的位移估计习题解问习题6.1 利害推断题(1) 变形骸真功本理仅适用于弹性体系,不适用于非弹性体系.( )(2) 真功本理中的力状态战位移状态皆是真设的.( )(3) 功的互等定理仅适用于线弹性体系,不适用于非线弹性体系.( )(4) 反力互等定理仅适用于超静定结构,不适用于静定结构.( )(5) 对付于静定结构,有变形便一定有内力.( ) (6) 对付于静定结构,有位移便一定有变形.( ) (7) 习题4.1(7)图所示体系中各杆EA 相共,则二图中C 面的火仄位移相等.( )(8) M P 图,M 图如习题4.1(8)图所示,EI =常数.下列图乘截止是精确的:4)832(12l l ql EI ⨯⨯⨯ ( )(9) M P 图、M (9)图所示,下列图乘截止是精确的:033202201111)(1y A EI y A y A EI ++ ( )(10) (10)图所示结构的二个仄稳状态中,有一个为温度变更,此时功的互等定理不可坐.( ) 习题 4.1(7)图习题 4.1(8)图 习题 4.1(9)图习题 4.1(10)图【解】(1)过失.变形骸真功本理适用于弹性战非弹性的所有体系.(2)过失.惟有一个状态是真设的. (3)精确.(4)过失.反力互等定理适用于线弹性的静定战超静定结构.(5)过失.譬如静定结构正在温度变更效率下,有变形但是不内力.(6)过失.譬如静定结构正在收座移动效率下,有位移但是稳定形.(7)精确.由桁架的位移估计公式可知.(8)过失.由于与0y 的M 图为合线图,应分段图乘.(9)精确. (10)精确.习题6.2挖空题(1) 习题4.2(1)图所示刚刚架,由于收座B 下重所引起D 面的火仄位移D H =______.(2) 真功本理有二种分歧的应用形式,即_______本理战_______本理.其中,用于供位移的是_______本理.(3) 用单位荷载法估计位移时,假制状态中所加的荷载应是与所供广义位移相映的________.(4) 图乘法的应用条件是:__________且M P 与M 图中起码有一个为直线图形.(5) 已知刚刚架正在荷载效率下的M P 图如习题4.2(5)图所示,直线为二次扔物线,横梁的抗直刚刚度为2EI ,横杆为EI ,则横梁中面K 的横背位移为________.(6) 习题4.2(6)图所示拱中推杆AB 比本安排少度短了,由此引起C 面的横背位移为________;引起收座A 的火仄反力为________.(7) 习题4.2(7)图所示结构,当C 面有F P =1(↓)效率时,D 面横背位移等于(↑),当E 面有图示荷载效率时,C 面的横背位移为________.(8) 习题 4.2(8)图(a )所示连绝梁收座B 的反力为)(1611R ↑=B F ,则该连绝梁正在收座B 下重B =1时(如图(b )所示),D 面的横背位移Dδ=________.习题 4.2(1)图 习题 4.2(5)图习题 4.2(6)图 习题 4.2(7)图习题 4.2(8)图【解】(1)()3∆→.根据公式R ΔF c =-∑估计.(2)真位移、真力;真力 . (3)广义单位力.(4)EI 为常数的直线杆.(5)48.875()EI↓.先正在K 面加单位力并画M 图,而后利用图乘法公式估计.(6)1.5cm ↑;0.C 面的横背位移用公式NΔF l =∆∑估计;制制缺面不会引起静定结构爆收反力战内力.(7)()a∆↑.由位移互等定理可知,C 面效率单位力时,E面沿M 目标的位移为21a∆δ=-.则E 面效率单位力M =1时,C面爆收的位移为12a∆δ=-.(8)11()16↓.对付(a )、(b )二个图示状态,应用功的互等定理可得截止.C V .EI为常数.【解】1)供C V习题4.3(1)图(1) 积分法画M P 图,如习题4.3(1)(b)图所示.正在C 面加横背单位力F P =1,并画M 图如习题4.3(1)(c)图所示.由于该二个直矩图对付称,可估计一半,再将截止乘以2.AC 段直矩为12M x =,P P 12M F x =则(2) 图乘法 2)供C V习题4.3(2)图(1) 积分法画M P 图,如习题4.3(2)(b)图所示.正在C 面加横背单位力并画M 图,如习题4.3(2)(c)图所示.以C 面为坐标本面,x 轴背左为正,供得AC 段(0≤x ≤2)直矩为M x =,2P 10(2)M x =⨯+则(2) 图乘法由估计位移的图乘法公式,得3)供C V习题4.3(3)图(1) 积分法画M P 图,如习题4.3(3)(b)图所示.正在C 面加横背单位力并画M 图,如习题4.3(3)(c)图所示.根据图中的坐标系,二杆的直矩(按下侧受推供)分别为 AB 杆12M x =-,2P 142ql M x qx =-CB 杆M x =,P 2ql M x =则(2)图乘法 4)供A习题4.3(4)图(1)积分法画M P 图,如习题4.3(4)(b)图所示.正在A 面加单位力奇并画M 图,如习题4.3(4)(c)图所示.以A 为坐标本面,x 轴背左为正,直矩表白式(以下侧受推为正)为113M x l=-,2P 3122M qlx qx =-则358ql EI=( ) (2) 图乘法由估计位移的图乘法公式,得358ql EI=( ) 分别用积分法战图乘法供习题 4.4(a)图所示刚刚架C 面的火仄位移C H .已知EI =常数.【解】1)积分法P M 、M图分别如习题 4.4(b )、(c )图所示,修坐坐标系如(c )图所示.各杆的直矩用x 表示,分别为 CD 杆M x =,P 12M qlx =AB 杆M x =,2P 12M qlx qx =-代进公式估计,得2)图乘法习题 4.5(a)图所示桁架各杆截里均为A =2×103m 2,E ×108kN/m 2,F P =30kN ,d =2m.试供C 面的横背位移V C ∆.D ql lBAC lA B lD CABD C22ql 2ql281ql 2(b)图M P M 图(c)(a)xx1ll【解】画NP F 图,如习题4.5(b)图所示.正在C 面加横背单位力,并画N F 图,如习题4.5(c)图所示. 由桁架的位移估计公式N NP F F Δl EA=∑,供得 第7章 力法习题解问利害推断题(1)习题5.1(1)图所示结构,当收座A 爆收转化时,各杆均爆收内力.( )习题5.1(1)图习题5.1(2)图(2)习题 5.1(2)图所示结构,当内中侧均降下t 1℃时,二杆均只爆收轴力.( )(3)习题 5.1(3)图(a)战(b)所示二结构的内力相共.( )习题5.1(3)图(4)习题 5.1(3)图(a)战(b)所示二结构的变形相共.( )【解】(1)过失.BC 部分是静定的附属部分,爆收刚刚体位移,而无内力.(2)过失.刚刚结面会沿左上圆爆收线位移,从而引起所连梁柱的蜿蜒.(3)精确.二结构中梁二跨的抗直刚刚度比值均为1:1,果此二结构内力相共.(4)过失.二结构内力相共,但是图(b)结构的刚刚度是图(a)的一倍,所以变形惟有图(a)的一半.习题7.2 挖空题(1)习题5.2(1) 图(a)所示超静定梁的收座A 爆收转角,若选图(b)所示力法基础结构,则力法圆程为_____________,代表的位移条件是______________,其中1c =_________;若选图(c)所示力法基础结构时,力法圆程为____________,代表的位移条件是______________,其中1c =_________.习题5.2(1)图(2)习题5.2(2)图(a)所示超静定结构,当基础体系为图(b)时,力法圆程为____________________,1P =________;当基础体系为图(c)时,力法圆程为____________________,1P =________.习题5.2(2)图(3)习题5.2(3)图(a)所示结构各杆刚刚度相共且为常数,AB 杆中面直矩为________,____侧受推;图(b)所示结构M BC =________,____侧受推.习题5.2(3)图(4)连绝梁受荷载效率时,其直矩图如习题5.2(4)图所示,则D 面的挠度为________,位移目标为____.习题5.2(4)图【解】(1)1111c 0X δ∆+=,沿X 1的横背位移等于整,-2l ;1111c X δ∆θ+=,沿X 1的转角等于,0.(2)11111P X X k δ∆+=-,458ql EI -;1111P 0X δ∆+=,3242ql q EI k+. (3)28ql ,下侧;2M ,下侧.可利用对付称性简化估计. (4)52EI,背下.选三跨简收梁动做基础结构,正在其上D 面加横背单位力并画M 图,图乘即可.试决定习题5.3图所示结构的超静定次数.图【领会】结构的超静定次数等于其估计自由度的千万于值,大概者使用“排除多余拘束法”直交领会.【解】(a )1;(b )2;(c )5;(d )3.用力法估计习题5.4图所示各超静定梁,并做出直矩图战剪力图.图【解】(1)本结构为1次超静定结构.采用基础体系如习题解5.4(1)图(a)所示,基础圆程为1111P 0X δ∆+=.系数战自由项分别为114EI δ=,1P 54EI∆=- 解得113.5kN m X =⋅.直矩图战剪力图分别如习题解5.4(1)图(d)战(e)所示. 习题解5.4(1)图用力法估计习题5.5图所示各超静定刚刚架,并做出内力图.图【解】(3)本结构为2次超静定结构.采用基础体系如习题解5.5(3)图(a)所示,基础圆程为系数战自由项分别为112503EI δ=,12210δδ==,226083EI δ=,1P 625EI ∆=,2P 20003EI∆= 解得17.5kN X =-,2 3.29kN X =-.内力图分别如习题解 5.5(3)图(e)~(g)所示. 习题解5.5(3)图利用对付称性,估计习题5.12图所示各结构的内力,并画直矩图.图【解】(2)将本结构所受普遍荷载领会为对付称战阻挡。
《结构力学》课后习题答案__重庆大学出版社

第1章 绪论(无习题)第2章 平面体系的几何组成分析习题解答习题2.1 是非判断题(1) 若平面体系的实际自由度为零,则该体系一定为几何不变体系。
( )(2) 若平面体系的计算自由度W =0,则该体系一定为无多余约束的几何不变体系。
( ) (3) 若平面体系的计算自由度W <0,则该体系为有多余约束的几何不变体系。
( ) (4) 由三个铰两两相连的三刚片组成几何不变体系且无多余约束。
( )(5) 习题2.1(5) 图所示体系去掉二元体CEF 后,剩余部分为简支刚架,所以原体系为无多余约束的几何不变体系。
( )B DACEF习题 2.1(5)图(6) 习题2.1(6)(a)图所示体系去掉二元体ABC 后,成为习题2.1(6) (b)图,故原体系是几何可变体系。
( )(7) 习题2.1(6)(a)图所示体系去掉二元体EDF 后,成为习题2.1(6) (c)图,故原体系是几何可变体系。
()(a)(b)(c)AEBFCD习题 2.1(6)图【解】(1)正确。
(2)错误。
0W 是使体系成为几何不变的必要条件而非充分条件。
(3)错误。
(4)错误。
只有当三个铰不共线时,该题的结论才是正确的。
(5)错误。
CEF 不是二元体。
(6)错误。
ABC 不是二元体。
(7)错误。
EDF 不是二元体。
习题2.2 填空(1) 习题2.2(1)图所示体系为_________体系。
习题2.2(1)图(2) 习题2.2(2)图所示体系为__________体系。
习题2-2(2)图(3) 习题 2.2(3)图所示4个体系的多余约束数目分别为_______、________、__________、__________。
习题2.2(3)图(4) 习题2.2(4)图所示体系的多余约束个数为___________。
习题2.2(4)图(5) 习题2.2(5)图所示体系的多余约束个数为___________。
习题2.2(5)图(6) 习题2.2(6)图所示体系为_________体系,有_________个多余约束。
结构力学第2章习题参考答案_khdaw

C A
E
F
J A B C Fp
K D
(c)
ww
(a) 三杆结点、结点无荷载,单杆为零杆。因此杆件 AB、BC、CD、DE、DF、FG、GH 为 零杆,共计 7 根轴力为零的杆件。 (b) 竖向荷载下水平反力为零,因此属对称结构对称荷载情况。从三杆结点、结点无荷载 单杆为零杆,对称轴结点无荷载非垂直对称轴的两杆为零杆可知,杆件 AC、FG、EB、LM、 ID、JD 为零杆。在 NGCHPON,RKELTSR 两个三角形部分中,可有多种分析判断方法证明 GO、GH、HO、SK、KL、SL 为零杆。其一种方法是,因为 O、H、G 三点都是两杆共线的 四杆结点,从垂直共线杆方向投影应该平衡的角度,可以证明 GO、GH、HO 三杆为零杆, 另三杆同理。故本题共计 12 根轴力为零的杆件。 (c) 利用减二元体、三杆结点、结点无荷载,单杆为零杆,分析可得杆件 AN、NO、OJ、 OP、JB、JC、KC、KQ、KD、ER 为零杆,考虑对称,则另一侧的 SL、LF、LG、GM、MU、 MH、TU、UV、VI 也为零杆。因此,共计 19 根轴力为零的杆件。 (d) 从 B、C、E、G、D 三点是三杆结点、结点无荷载,单杆为零杆,在考虑两杆结点无荷 载,可得杆件 AC、CD、CF、FD、FG、GD、GH、DE、DB 为零杆,共计 9 根轴力为零的 杆件。
2
A
∑Fy = 0
取 I 结点隔离体有:
FA y = 15.33 kN
FNID = −8 kN
再取 D 结点为隔离体有: FN1 = 4 2 NEF
ww
w.
kh
da
课
后
答
w.
案 网
用截面从杆 2、JK、EF 截开,取右侧为隔离体, 列投影方程有: ∑ F y = 0 FN 2 = 5FB y = 28.33 kN
《结构力学》课后习题答案__重庆大学出版社

第1章 绪论(无习题)第2章 平面体系的几何组成分析习题解答习题2.1 是非判断题(1) 若平面体系的实际自由度为零,则该体系一定为几何不变体系。
( )(2) 若平面体系的计算自由度W =0,则该体系一定为无多余约束的几何不变体系。
( ) (3) 若平面体系的计算自由度W <0,则该体系为有多余约束的几何不变体系。
( ) (4) 由三个铰两两相连的三刚片组成几何不变体系且无多余约束。
( )(5) 习题2.1(5) 图所示体系去掉二元体CEF 后,剩余部分为简支刚架,所以原体系为无多余约束的几何不变体系。
( )B DACEF习题 2.1(5)图(6) 习题2.1(6)(a)图所示体系去掉二元体ABC 后,成为习题2.1(6) (b)图,故原体系是几何可变体系。
( )(7) 习题2.1(6)(a)图所示体系去掉二元体EDF 后,成为习题2.1(6) (c)图,故原体系是几何可变体系。
()(a)(b)(c)AEBFCD习题 2.1(6)图【解】(1)正确。
(2)错误。
0W 是使体系成为几何不变的必要条件而非充分条件。
(3)错误。
(4)错误。
只有当三个铰不共线时,该题的结论才是正确的。
(5)错误。
CEF 不是二元体。
(6)错误。
ABC 不是二元体。
(7)错误。
EDF 不是二元体。
习题2.2 填空(1) 习题2.2(1)图所示体系为_________体系。
习题2.2(1)图(2) 习题2.2(2)图所示体系为__________体系。
习题2-2(2)图(3) 习题 2.2(3)图所示4个体系的多余约束数目分别为_______、________、__________、__________。
习题2.2(3)图(4) 习题2.2(4)图所示体系的多余约束个数为___________。
习题2.2(4)图(5) 习题2.2(5)图所示体系的多余约束个数为___________。
习题2.2(5)图(6) 习题2.2(6)图所示体系为_________体系,有_________个多余约束。
结构力学第二版课后习题答案

结构力学第二版课后习题答案结构力学第二版课后习题答案结构力学是一门研究物体受力情况和力学性质的学科,它在工程领域中有着广泛的应用。
结构力学的学习不仅需要理论的掌握,还需要通过实际的习题来加深对知识的理解和运用。
本文将为大家提供《结构力学》第二版课后习题的答案,希望能够帮助大家更好地学习和应用结构力学知识。
第一章弹性力学基础1.1 弹性力学的基本概念1. 弹性力学是研究物体在外力作用下发生形变时,恢复到原来形态的力学学科。
2. 牛顿第二定律:物体所受合外力等于物体质量乘以加速度。
3. 弹性体:在外力作用下,物体发生形变,当外力消失后,物体能够完全恢复到原来的形态。
4. 弹性力学的基本假设:线弹性假设、小变形假设、平面假设。
1.2 应力和应变1. 应力:单位面积上的力,即单位面积上的力的大小。
2. 应变:物体在外力作用下发生的形变程度。
3. 线弹性假设下的应力-应变关系:胡克定律,即应力与应变成正比。
4. 应力张量:描述物体内部各点上的应力状态,是一个二阶张量。
1.3 弹性体的本构关系1. 本构关系:描述物体应力和应变之间的关系。
2. 弹性体的本构关系:胡克定律。
3. 弹性模量:描述物体对应力的敏感程度。
4. 剪切模量:描述物体对剪切应力的敏感程度。
第二章弹性力学的基本方程2.1 平衡方程与应力平衡方程1. 平衡方程:描述物体在力的作用下的平衡状态。
2. 应力平衡方程:描述物体在外力作用下的应力分布情况。
2.2 应变平衡方程1. 应变平衡方程:描述物体在外力作用下的应变分布情况。
2.3 弹性力学基本方程1. 弹性力学基本方程:包括平衡方程、应力平衡方程和应变平衡方程。
第三章弹性体的力学性质3.1 弹性体的应力分析1. 弹性体的平面应力问题:在一个平面上受力的弹性体。
2. 弹性体的平面应变问题:在一个平面上发生应变的弹性体。
3.2 弹性体的弯曲1. 弹性体的弯曲:在外力作用下,物体发生弯曲变形。
2. 弯曲方程:描述弯曲变形的关系。
结构力学章节习题与参考答案

第1章绪论(无习题)第2章平面体系的机动分析习题解答习题2.1是非判断题(1) 若平面体系的实际自由度为零,则该体系一定为几何不变体系。
( )(2) 若平面体系的计算自由度W=0,则该体系一定为无多余约束的几何不变体系。
( )(3) 若平面体系的计算自由度W<0,则该体系为有多余约束的几何不变体系。
( )(4) 由三个铰两两相连的三刚片组成几何不变体系且无多余约束。
( )(5) 习题2.1(5) 图所示体系去掉二元体CEF后,剩余部分为简支刚架,所以原体系为无多余约束的几何不变体系。
( )习题2.1(5)图(6) 习题2.1(6)(a)图所示体系去掉二元体ABC后,成为习题2.1(6) (b)图,故原体系是几何可变体系。
( )(7) 习题2.1(6)(a)图所示体系去掉二元体EDF后,成为习题2.1(6) (c)图,故原体系是几何可变体系。
()(a)(b)(c)习题2.1(6)图习题2.2填空(1) 习题2.2(1)图所示体系为_________体系。
习题2.2(1)图(2) 习题2.2(2)图所示体系为__________体系。
习题2-2(2)图(3) 习题2.2(3)图所示4个体系的多余约束数目分别为_______、________、__________、__________。
习题2.2(3)图(4) 习题2.2(4)图所示体系的多余约束个数为___________。
习题 2.2(4)图(5) 习题2.2(5)图所示体系的多余约束个数为___________。
习题 2.2(5)图(6) 习题2.2(6)图所示体系为_________体系,有_________个多余约束。
习题 2.2(6)图(7) 习题2.2(7)图所示体系为_________体系,有_________个多余约束。
习题 2.2(7)图习题2.3 对习题2.3图所示各体系进行几何组成分析。
(a)(b)(c)(d)(e)(f)(h)(g)(i)(j)(k)(l)习题2.3图第3章 静定梁与静定刚架习题解答习题3.1 是非判断题(1) 在使用力图特征绘制某受弯杆段的弯矩图时,必须先求出该杆段两端的端弯矩。
《结构力学》习题解答(内含解答图)

习题2-13试对图示体系进行几何组成分析。
习题2-13图习题2-13解答图
解:将原图结点进行编号,并将支座6换为单铰,如图(b)。取基础为刚片Ⅰ,△134为刚片Ⅱ,△235为刚片Ⅲ,由规则一知,三刚片用三个不共线的铰联结组成几何不变体。在此基础上增加二元体674、785,而杆38看作多余约束。杆910由铰联结着链杆10,可看作二元体,则整个体系为有一个多余约束的几何不变体系。
习题2-7试对图示体系进行几何组成分析。
习题2-7图习题2-7解答图
解:将题中的折杆用直杆代替,如图(b)所示。杆CD和链杆1由铰D联结构成二元体可以去掉;同理,去掉二元体杆CE和链杆2,去掉二元体ACB,则只剩下基础,故整个体系为几何不变体系,且无多余约束。
另外也可用基础与杆AC、杆BC是由不共线的三个铰联结,组成几何不变体,在此几何不变体上增加二元体杆CD和链杆1、杆CE和链杆2的方法分析。,
习题2-8试对图示体系进行几何组成分析。
习题2-8图习题2-8解答图
解:为了便于分析,对图中的链杆和刚片进行编号,分析过程见图2-21(b)。首先去掉二元体NMI、JNI,然后分析剩余部分。杆AD由固定支撑与基础联结形成一体,构成几何不变体,在此基础上增加二元体DEB、EFC、EHF形成刚片Ⅰ(注意固定铰支座与铰相同);铰结△GIJ为刚片Ⅱ;刚片I与刚片Ⅱ之间用不交于一点的杆DI、杆GI、杆HJ相连,组成几何不变体。
习题2-18试对图示体系进行几何组成分析。
解:将原图结点进行编号,并将固定铰支座换为单铰,如图(b)。折杆AD上联结杆EF,从几何组成来说是多余约束;同理,折杆CD上联结杆EF也是多余约束。取基础为刚片Ⅰ,折杆AD为刚片Ⅱ,折杆CD为刚片Ⅲ。刚片Ⅰ与刚片Ⅱ是由链杆A和杆BD相连,刚片Ⅰ与刚片Ⅲ是由链杆C相连,注意,杆BD只能使用一次。由规则二知,体系为几何可变体系。
李廉锟版 结构力学 第二章 平面体系的机动分析 习题参考答案

结构力学习题参考答案第二章平面体系的机动分析复习思考题习题8. 图2-27所示体系因A、B、C三铰共线所以是瞬变的,这样分析正确否?为什么?解:【这道题对理解思路挺有帮助的。
】第一步:计算计算自由度WW=3m-(2h+r)=3×6-7×2=4>3 所以结构是常变体系。
第二步:分析几何构造性。
去二元体(I刚片和1杆),剩下部分是II、III刚片通过2根杆相连,是常变体系。
但是,为什么会得到如题中的结论呢?是因为2杆重复利用了,相当于在体系中多加了一根杆,增加一个联系,从而得出错误结论。
几何构造性分析,所有杆件不能重复、不能遗漏。
解:第一步:计算计算自由度WW=2j-(b+r)=2×10-(17+4)=-1,有一个多余联系。
第二步:分析几何构造性。
从上至下依次去二元体,最后发现有一根杆是多余的。
该体系是有一个多于联系的几何不变体系。
习题2-2 试对图示平面体系进行机动分析。
解:第一步:计算计算自由度WW=2j-(b+r)=2×14-(25+3)=0这表明体系具有几何不变所需最少的联系数目。
第二步:分析几何构造性。
去掉二元体后如图所示,分别在三角形基础上依次增加二元体从而形成刚片I、II,此刚片I、II通过一铰和一根不通过此铰的杆相连,得到的体系是几何不变的,且没有多余联系。
解:第一步:计算计算自由度3(2)321(2303)0W m h r =−+=×−×+=或者2()212(213)0W j b r =−+=×−+= 这表明体系具有几何不变所需最少的联系数目。
第二步:分析几何构造性此体系的支座链杆只有三根,且不完全平行也不交于一点,若体系为一刚片,则他与地基是按两刚片规则组成的,因此只需分析体系本身是不是一个几何不变的刚片即可。
去掉M 和C 两个二元体。
在b 图中,KFL 刚片、ABF 刚片和GEJ 刚片通过不共线的三个铰(Ⅰ,Ⅱ)、(Ⅱ,Ⅲ)和(Ⅰ,Ⅲ)两两连接,由三刚片规则可知,体系为几何不变体系,且无多余联系。
结构力学 第2章习题参考答案

FN3 FN2
0
1
45o Fp
0
w.
45
o
FN2
FN4 45o FN3
Fp
Fp
K
(a)隔离体图
3.5Fp
da
30 kN 3×2m 2 3 30 kN 30 kN
(b)隔离体图
FN2 +FP × cos 45D = 0
FN2 = −
取隔离体图(b)所示,列方程有:
∑ M K = 0 FN4 × 2d + FN3 cos 45D × 2d + 3.5FP × 2d − FP × d = 0 FN4 = −4 FP
∑F
y
= 0 FN3 sin 45D − FN2 sin 45D − 3.5 FP + 2 FP = 0
FN1 + FN3 sin 45D = 0 , FN1 = − FP
ww
(b)对称情况 (a)反对称情况 根据隔离体图(a) 依次利用结点法可求得 1、2、3 杆轴力:
FN1 = 30 kN
FN 2 = −30 2 kN=42.42 kN
隔离体 (c)
cos β = 5 13 FN1 = −1.802 8 FP
5
本题是对称结构对称荷载情况,只须计算一半杆件即可。由隔离体图(a)列投影方程如下 FN1 cos β + FN2 sin α + FP = 0 FN1 sin β + FN2 cos α = 0 可得
FN2 = 1.118 0 FP
2 FP 2
FN3 = 2 FP
1
m
l
∑M
FN2 × 2 m+FN1 × sin 45D × 2 m = 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8 kN 20 kN
HI
J ⅠK
L
2 1
AC
D
E ⅠF
G
B
2.5m6 15m
2.5 m
(a)
K
LD
FNJK D
FN2
FNEF FD
G
B
FBy (b
)
解:(1)判断零杆。如图(a)所示。
(2)求支座反力
F x 0 , FAx 0
M A 0 , FB y 12.67 kN
F y 0 , FA y 15.33 kN
5 29
MK
M
0 K
FH yK
510 130 3 120
kN
m
FQK FQ0K cosK FH sinK 52
5 130 29
2 0 29
FNK FN0K sinK FH cosK 52
2 130 29
5 140 kN 29
2-12 图示圆弧三饺拱,求支座反力及截面 D 的 M 、FQ 、FN 值。 20kN/m
D
C
5m
5m
FH
30
A 5m
B 5m
FH
FAy
FBy
习题 2-12 图
解 (1)求支座反力。
FB y 100 kN , FA y 100 kN , FH 50 kN
(2)求等代梁 D 截面内力
M
0 D
FAy
2.5
1 2
20 2.52
187.5kNm
FQ0D FAy 20 2.5 50 kN
30 kN A 4 B 30 kN
3×2m
N 1
N
D
N
CN 2 E
N3
30 kN N
4×2mN N (b-2)反对称荷载组
30 kN N
N
解 (1)荷载分组。将荷载与支座反力分解成对称和反对称情况。
(2)求指定杆轴力。对称情况 1、2、3 杆轴力为零。反对称情况 4 杆
轴力为零。由 A 结点的平衡条件,得
(3)求三铰拱 D 截面内力
yD 5mcos30 2.5 3 m
D 30, tan D
3 3
, sin D
1 2
,cos
D
3 2
MD
M
0 D
FH yD
187.5 2.5
3 29.5 kN m
FQD FQ0D cosD FH sinD 50
3 50 1 18.8 kN
2
2
FN D
FN0D
2-11 求图示抛物线( y 4 fx(l x) / l 2 ) 三铰拱距左支座 5m 的截面内力。
y
FH A
x
FAy
20 kN/m
K
C
40 kN·m Q
4m
10 m×2=20m
习题 2-11 图
B 5m
FH
FBy
解 (1)求支座反力
FB y 48 kN , FA y 152 kN , FH 130 kN
I
3 (a-2)3
3
N
N
N
解 (1)判断零杆 ①二杆结点的情况。N、V 结点为无结点荷载作用的二杆结点,故 NA、 NO 杆件和 VI、VU 杆件都是零杆;接着,O、U 结点又变成无结点荷载作用 的二杆结点,故 OP、OJ、UT、UM 杆件也是零杆。②结点单杆的情况。BJ、 DK、QK、RE、HM、SL、LF 杆件均为无结点荷载作用的结点单杆,都是零杆; 接着,JC、CK、GM、LG 杆件又变成了无结点荷载作用的结点单杆,也都是 零杆。所有零杆如图(a-1)所示。去掉零杆后的简化体系如图(a-2)所示。
(2)求指定杆轴力。 Ⅰ-Ⅰ截面(图(b)):
F y 0 , FN3
2 2
FP
M K 0 , FN1 4FP
Fx 0 , FN4 4.5FP
Ⅱ-Ⅱ截面(图(c))
F y 0 , FN2 0.5FP
2-5 用截面法求图示桁架中指定杆的轴力。
10kN 10kN 10kN 10kN
(a)
20 kN
20 kN
(b)
解 (1)求支座反力 FAy FB y 20 kN
(2)判断零杆。去掉零杆得图(b)所示简化体系。 (3)求杆件轴力
结点 E:
FNAC FNBD 20 kN
Fy 0 , FNEC 33.33kN
结点 C
Fx 0 , FNEF 26.67 kN
由对称性可知
Ⅱ—Ⅱ截面(图(b)):将 FN 4 滑移到 B 点
M D 0 : FN4x 9 4 3 4 3 2 5 2 7 1 3 0
由比例关系
FN 4x
1 kN 3
FN4
10.52 3
32
FN 4 x
1.21kN , FN4 y
10.5 3
FN
4
x
1.17 kN
F x 0 , FN2 3.3kN
F y 0 : FN1 FN
2 2
FN 4 y
2
2
0
,
FN1
2.83 kN
2-10 选用较简捷的方法计算图示桁架中指定杆的轴力。
4m 4m
H G 1E D
4kN
4
2
A
3F C B
FAy
1kN 2kN 2kN 2kN 1kN
FBy
K 3m6 18m
习题 2-10 图
H G FN1E D
FN 2
2kN 2kN
2m 2m 3m 3m
习题 2—9 图
FN 3
FN 6
C
1kN 2kN
FN 5
(a)Ⅰ—Ⅰ截面
1kN
D
FN1
2kN 4kNFN 2
FN4 4kN
B FN4 (a)Ⅱ—Ⅱ截面
解 Ⅰ—Ⅰ截面(图(a))
F y 0 , FN5 4 kN ; M C 0 , FN3 5 kN
F x 0 , FN6 3 kN
FNOG=-FNOH 同理,G、H 结点也为“K”结点,故
(a)
FNOG=-FNGH FNHG=-FNOH 由式(a)、(b)和(c)得
(b) (c)
FNOG=FNGH=FNOH=0 同理,可判断在 TRE 三角形中
FNSK=FNKL=FNSL=0 D 结点也是“K”结点,且处于对称荷载作用下的对称轴上,故 ID、JD
FNTL FNLE 0.5 2FP , FNTS FNSR 2FP
至此已求出对称轴右侧所有杆件的轴力,对称轴左侧杆件的轴力可由
对称性很方便地得到。
2-2(b)
F GH
Fp
Fp
H Fp
aa
C
E
D
A
B
E D
A
B
l=2×a
(b)
(b-1)
(b-2)
解 (1)判断零杆。零杆如图(b-1)所示,去掉零杆后的简化体系如 图(b-2)所示。
解 Ⅰ-Ⅰ截面(图(a-1))
F x 0 , FN1 80 2 kN
Ⅱ-Ⅱ截面(图(a-2))
M K 0 , FN2 = 80 kN
2-8 (b)
60 kN
1
N
2
N
3
N 4×2 m
(b) N
3×2 m
30 kN
N 1
N
30 kN N 2
30 kN N
N3
(b-1)对称N荷载组 N
30 kN N
2-1(c) 2Fp
aa
Fp l=6×a
Fp
(c)
2Fp
N O PQ
RS T
F AG
HI
J
C Fp
D
(c-1)
M
K
L
E Fp B
解 该结构在竖向荷载下,水平反力为零。因此,本题属对称结构承受
对称荷载的情况。AC、FG、EB 和 ML 均为无结点荷载作用的结点单杆,都
是零杆。
在 NCP 三角形中,O 结点为“K”结点,所以
5kN
Ⅰ
FN1x
A
25kN
D Ⅰ FN2y
FN2x FN2
(b)
ⅡC
FN3
Ⅱ
B 10kN
(c)
解 (1)求支座反力 FAx 0 , FBy 10 kN , FAy 25kN
(2)求指定杆轴力 Ⅰ—Ⅰ截面(图(b))
MD 0 , FN1x 30kN , FN1
5 2
FN1x
15
5 kN
M A 0 , FN2y 5kN , FN2
FN 3 F C B
2kN 1kN
FBy
(a)Ⅰ—Ⅰ截面
解 (1)求支座反力
FBy
44 9
kN
4.89 kN ,
FAy
28 9
kN
3.11kN
(2)求指定杆轴力
结点 C:去掉零杆 CD
F y 0 : FN2 y 1kN , FN2
13 2
FN 2 y
1.8 kN
结点 G
F y 0 , FN4 1kN
(3)求指定杆轴力
由 I 结点的平衡条件,得
由 D 结点的平衡条件,得
FNID 8 kN
Ⅰ-Ⅰ截面(图(b))
FN1 8 2 kN
F y 0 , FN2 5FB y 28.32 kN
0.75 m 0.75m
2-7 试用对称性求图示桁架各杆轴力。
C
D
A
E
F
B
20 kN 1m8 8m
20 kN
Ⅰ—Ⅰ截面(图(a))
M F 0 : FN1 4 FN2 y 3 FBy 6 1 3 0
