一维最大类间方差法

合集下载

基于最大类间类内方差比法的图像分割

4、本实验对不同图像的处理方法：
针对灰度图像，笔者打算根据如下的实验步骤进行实验仿真；对于彩色图像，笔者打算分别将原图三通道提取出来，然后按照如下的实验步骤分别对单通道分割，然后对处理后的三个通道进行整合，得到新的分割图像。
四、实验步骤
1、给定一个初始阈值 Th=Th0，将图像分成 C1 和 C2 两类； 2、分别按下列公式计算两类中的方差σ1^2 和σ2^2，灰度均值 μ1 和μ2，以及图像的总体均值μ；
由于最大类间、类内方差比法是基于图像灰度分布的阈值方法。数学模型如下：
设原图像为 f(x,y),经过分割处理后的图像为 g(x,y),g(x,y) 为二值图像，则有
g
(
x,
y)
1
0
f (x, y) Th f (x, y) Th
（3-1）
2、最大类间方差法与最大类间、类内方差比法的不同：
最大类间方差法又叫大津法,简称 OTSU。它是按图像的灰度特性, 将图像分成背景和目标 2 部分。背景和目标之间的类间方差越大,说明构成图像的 2 部分的差别越大。它只需处理类间方差，在 Matlab 中 grathresh()即为最大类间方差函数，用来寻找阈值。
p1
N c2 N im age
(4 4)
4、计算类间方差σb^2=和类内方差σin^2；
b2 p1 (1 )2 p2 (2 )2
2 in
p1பைடு நூலகம்
2 1
p2
2 2
(4 5) (4 6)
5、选择最佳阈值 Th=Th*，使得图像按照该阈值分成 C1 和 C2 后，
满足两者方差比最大：
max
b=zeros(m,n);
%新建二维矩阵 b 用来显示分割后的图像

最大类间方差法

最大类间方差法是由日本学者大津于1979年提出的,是一种自适应的阈值确定的方法,又叫大津法,简称OTSU。

它是按图像的灰度特性，将图像分成背景和目标2部分。

背景和目标之间的类间方差越大,说明构成图像的2部分的差别越大,当部分目标错分为背景或部分背景错分为目标都会导致2部分差别变小。

因此,使类间方差最大的分割意味着错分概率最小.对于图像I(x，y），前景(即目标)和背景的分割阈值记作T，属于前景的像素点数占整幅图像的比例记为ω0，其平均灰度μ0；背景像素点数占整幅图像的比例为ω1,其平均灰度为μ1。

图像的总平均灰度记为μ,类间方差记为g。

假设图像的背景较暗，并且图像的大小为M×N，图像中像素的灰度值小于阈值T的像素个数记作N0，像素灰度大于阈值T的像素个数记作N1，则有：ω0=N0/ M×N （1)ω1=N1/ M×N (2）N0+N1=M×N (3）ω0+ω1=1 (4）μ=ω0*μ0+ω1*μ1 （5）g=ω0(μ0—μ）^2+ω1（μ1-μ)^2 （6)将式(5）代入式（6)，得到等价公式: g=ω0ω1（μ0-μ1)^2 (7)采用遍历的方法得到使类间方差最大的阈值T,即为所求。

Otsu算法步骤如下：设图象包含L个灰度级(0,1…,L—1)，灰度值为i的的象素点数为Ni ,图象总的象素点数为N=N0+N1+。

..+N（L-1）.灰度值为i的点的概为：P(i) = N(i）/N.门限t将整幅图象分为暗区c1和亮区c2两类，则类间方差σ是t的函数：σ=a1*a2(u1—u2)^2 （2)式中，aj 为类cj的面积与图象总面积之比，a1 = sum(P(i)）i—>t, a2 = 1—a1；uj为类cj的均值，u1 = sum（i＊P（i）)/a1 0->t,u2 = sum(i＊P（i））/a2，t+1-〉L—1该法选择最佳门限t^ 使类间方差最大，即：令Δu=u1—u2，σb = max{a1(t)＊a2(t)Δu^2} OTSU方法计算图像二值化的自适应阈值int otsu (unsigned char ＊image，int rows, int cols, int x0，int y0，int dx, int dy，int vvv）{unsigned char *np；// 图像指针int thresholdValue=1; // 阈值int ihist[256］; // 图像直方图，256个点int i，j，k；// various countersint n，n1，n2，gmin，gmax;double m1, m2，sum, csum, fmax，sb;// 对直方图置零...memset（ihist, 0，sizeof（ihist));gmin=255; gmax=0；// 生成直方图for （i = y0 + 1；i < y0 + dy - 1; i++）{np = &image[i＊cols+x0+1］；for (j = x0 + 1; j 〈x0 + dx - 1; j++）{ihist[＊np］++;if(*np > gmax）gmax=＊np;if(*np < gmin）gmin=＊np;np++；}}// set up everythingsum = csum = 0。

4.2 一维随机变量的方差

2
+∞
2
1
−
( x−µ )2 2σ 2
dx
令 σ
2
=t，
+∞ −∞
EX =
∫
(µ + σt) 2 ⋅
+∞ t2 − 2
1 e 2π
−
t2 2
dt
te dt + σ
t2 − 2 2
=µ
2
∫
−∞
1 2µσ e dt + 2π 2π
∫
+∞
−∞
∫
+∞
−∞
t e dt 2π
2
t2 − 2
=µ −
2
σ
2
2π
te
λ
⋅e
− λx + ∞ 0
=
2
DX = EX − (EX ) =
2
2
λ2
λ
2
−( ) =
2
1
1
λ
λ2
1 2 X 注意：注意：若已知随机变量 ~e(θ ) ， DX = θ
x 1 −θ e , x >0 X 的分布密度为ϕ(x) = θ 随机变量 0, x x ≤0 +∞ 1 −θ 2
vk = ∑ xik pi , pi = P{ X = xi } 离散：离散：
i
连续：连续： vk = ∫
+∞
−∞
x kϕ ( x ) dx, ϕ ( x )是X的密度函数
特别： v 1 = EX （期望）， v 2 = EX 2
µk = E( X − EX )k 阶中心矩：随机变量的k 阶中心矩：
EX 2 = 0 × 0.6 + 1 × 0.3 + 2 × 01 = 0.5 . 2 EX 2 = 02 × 0.6 + 12 × 0.3 + 2 2 × 01 = 0.7 .

Otsu算法(大律法或最大类间方差法)

Otsu算法(大律法或最大类间方差法)一、Otsu最大类间方差法原理利用阈值将原图像分成前景，背景两个图象。

前景：用n1,csum,m1来表示在当前阈值下的前景的点数，质量矩，平均灰度后景：用n2, sum-csum,m2来表示在当前阈值下的背景的点数，质量矩，平均灰度当取最佳阈值时，背景应该与前景差别最大，关键在于如何选择衡量差别的标准，而在otsu算法中这个衡量差别的标准就是最大类间方差（英文简称otsu，这也就是这个算法名字的来源），在本程序中类间方差用sb表示，最大类间方差用fmax 关于最大类间方差法（otsu）的性能:类间方差法对噪音和目标大小十分敏感，它仅对类间方差为单峰的图像产生较好的分割效果。

当目标与背景的大小比例悬殊时，类间方差准则函数可能呈现双峰或多峰，此时效果不好，但是类间方差法是用时最少的。

最大类间方差法（otsu）的公式推导：记t为前景与背景的分割阈值，前景点数占图像比例为w0，平均灰度为u0；背景点数占图像比例为w1，平均灰度为u1。

则图像的总平均灰度为：u=w0*u0+w1*u1。

前景和背景图象的方差：g=w0*(u0-u)*(u0-u)+w1*(u1-u)*(u1-u)=w0*w1*(u0-u1)*(u0-u1),此公式为方差公式。

可参照概率论课本上面的g的公式也就是下面程序中的sb的表达式。

当方差g最大时，可以认为此时前景和背景差异最大，此时的灰度t是最佳阈值sb = w1*w2*(u1-u0)*(u0-u1)算法实现1：unsafe public int GetThreshValue(Bitmap image){BitmapData bd = image.LockBits(new Rectangle(0, 0, image.Width, image.Height), ImageLockMode.WriteOnly, image.PixelFormat);byte* pt = (byte*)bd.Scan0;int[] pixelNum = new int[256]; //图象直方图，共256个点byte color;byte* pline;int n, n1, n2;int total; //total为总和，累计值double m1, m2, sum, csum, fmax, sb; //sb为类间方差，fmax存储最大方差值int k, t, q;int threshValue = 1; // 阈值int step = 1;switch (image.PixelFormat){case PixelFormat.Format24bppRgb:step = 3;break;case PixelFormat.Format32bppArgb:step = 4;break;case PixelFormat.Format8bppIndexed:step = 1;break;}//生成直方图for (int i = 0; i < image.Height; i++){pline = pt + i * bd.Stride;for (int j = 0; j < image.Width; j++){color = *(pline + j * step); //返回各个点的颜色，以RGB表示pixelNum[color]++; //相应的直方图加1}}//直方图平滑化for (k = 0; k <= 255; k++){total = 0;for (t = -2; t <= 2; t++) //与附近2个灰度做平滑化，t值应取较小的值{q = k + t;if (q < 0) //越界处理q = 0;if (q > 255)q = 255;total = total + pixelNum[q]; //total为总和，累计值}//平滑化，左边2个+中间1个+右边2个灰度，共5个，所以总和除以5，后面加0.5是用修正值pixelNum[k] = (int)((float)total / 5.0 + 0.5);}//求阈值sum = csum = 0.0;n = 0;//计算总的图象的点数和质量矩，为后面的计算做准备for (k = 0; k <= 255; k++){//x*f(x)质量矩，也就是每个灰度的值乘以其点数（归一化后为概率），sum为其总和sum += (double)k * (double)pixelNum[k];n += pixelNum[k]; //n为图象总的点数，归一化后就是累积概率}fmax = -1.0; //类间方差sb不可能为负，所以fmax初始值为-1不影响计算的进行n1 = 0;for (k = 0; k < 255; k++) //对每个灰度（从0到255）计算一次分割后的类间方差sb{n1 += pixelNum[k]; //n1为在当前阈值遍前景图象的点数if (n1 == 0) { continue; } //没有分出前景后景n2 = n - n1; //n2为背景图象的点数//n2为0表示全部都是后景图象，与n1=0情况类似，之后的遍历不可能使前景点数增加，所以此时可以退出循环if (n2 == 0) { break; }csum += (double)k * pixelNum[k]; //前景的“灰度的值*其点数”的总和m1 = csum / n1; //m1为前景的平均灰度m2 = (sum - csum) / n2; //m2为背景的平均灰度sb = (double)n1 * (double)n2 * (m1 - m2) * (m1 - m2); //sb为类间方差if (sb > fmax) //如果算出的类间方差大于前一次算出的类间方差{fmax = sb; //fmax始终为最大类间方差（otsu）threshValue = k; //取最大类间方差时对应的灰度的k就是最佳阈值}}image.UnlockBits(bd);image.Dispose();return threshValue;}算法实现2：Otsu算法步骤如下：设图象包含L个灰度级(0,1…,L-1)，灰度值为i的的象素点数为Ni ，图象总的象素点数为N=N0+N1+...+N(L-1)。

otsu算法——图像分割

前景比例：
背景比例：
像素点总数：
前景和背景概率之和：
平均灰度值：
类间方差：
将公式（4）和（5）带入（6）可以得到等价公式：
核心代码：Histogram[data[i*srcimage.step + j]]++;//step指向每行的字节总量，date访问每个像素的值for (int i = 1; i < 255 ;i++)//从1开始遍历，寻找最合适的值{//每次遍历前需要初始化各变量w0 = 0; u0 = 0; w1 = 0; u1 = 0;for (int j = 0; j <= i; j++)//背景部分各值计算 { w0 += Histogram[j]; //背景部分像素点总数 u0 += j*Histogram[j]; //背景部分像素总灰度和 } u0 = u0 / w0; //背景像素平均灰度 w0 = w0 / number; //背景部分像素点所占比例}double varValueI = w1*w2*(u1 - u2)*(u1 - u2); //类间方差计算
算法过程：（1）设K(x,y)=f(x,y)/g(x,y)为像素点的斜率，其中f(x,y)为点(x,y)的灰度值， g(x,y)为点(x,y)周围点的平均值。（2）设阈值t1，t2将二维直方图分为A、B、 C三个区域。其中B区域代表前景和背景像素点部分，而A、C代表边界点和噪声点部分。
算法过程：（1）对于图像I(x,y),将前景与背景的分割阈值设为T。（2）将属于前景的像素点的个数占整个图像的比例设为w0，其平均灰度设为u0。（3）将属于背景的像素点的个数占整个图像的比例设为w1，其平均灰度设为u1。（4）图像的总平均灰度设为u，类间方差设为S。假设图片的大小为M*N，图像中像素灰度值小于阈值T的像素个数记为N0，像素灰度大于阈值T的像素个数记为N1。则它们之间的关系如下。

一维最大类间方差法

由Otsu(大津展之)于1978年提出的最大类间方差法，是引起较多关注的一种阈值选取方法。

它是在判决分析或最小二乘原理的基础上推导出来的。

参考文献：[1] Otsu N. A threshold selection method from gray-level histogram. IEEE Trans,1979;SMC-9;62-66 下载地址算法思想：假设一幅图像有L个灰度级[1,2,…,L]。

灰度级为i的像素点的个数为n i，那么总的像素点个数就应该为N=n1+n2+…+n L。

为了讨论方便，我们使用归一化的灰度级直方图并且视为这幅图像的概率分布:现在假设我们通过一个灰度级为k的门限将这些像素点划分为两类:C0和C1(背景和目标,或者反之亦然)；C0表示灰度级为[1,…,k]的像素点，C1表示灰度级为[k+1,…,L]的像素点。

那么，每一类出现的概率以及各类的平均灰度级分别由下面的式子给出：以及其中，分别为灰度级从1到k的累积出现概率和平均灰度级（一阶累积矩），而是整幅图像的平均灰度级。

我们可以很容易验证，对于任意选定的k，都有：这两类的类内方差由下面的公式给出：这需要二阶累积矩(second-order cumulative moment，统计学概念)。

为了评价(灰度级k)这个门限“好”的程度，我们需要引入判别式分析中使用的判别式标准来测量（类的分离性测量）：其中：又根据式(9)，可以得出：这三个式子分别是类内方差、类间方差和灰度级的总方差。

然后，我们的问题就简化为一个优化问题，即寻找一个门限k使(12)式中给出的一个目标函数取最大值。

这个观点是出于这样一个猜想，一个好的阈值将会把灰度级分为两类，那么反过来说，就是如果一个门限能够在灰度级上将图像分割为最好的两类的话，那么这个门限就是最好的门限。

上面给出的判别式标准是分别求取λ、κ和η的最大值。

然而，对于κ而言，它又等于另外一个，比如κ=λ+1；而对于λ而言，又有η=λ/(λ+1)，因为始终存在下面的基本关系：效果展示：算法评价：就最大类间方差算法而言，优点是算法简单，当目标与背景的面积相差不大时，能够有效地对图像进行分割。

阈值确定方法

阈值确定⽅法⼀、问题重述图形（或图像）在计算机⾥主要有两种存储和表⽰⽅法。

⽮量图是使⽤点、直线或多边形等基于数学⽅程的⼏何对象来描述图形，位图则使⽤像素来描述图像。

⼀般来说，照⽚等相对杂乱的图像使⽤位图格式较为合适，⽮量图则多⽤于⼯程制图、标志、字体等场合。

⽮量图可以任意放缩，图形不会有任何改变。

⽽位图⼀旦放⼤后会产⽣较为明显的模糊，线条也会出现锯齿边缘等现象。

⽮量图从本质上只是使⽤曲线⽅程对图形进⾏的精确描述，在以像素为基本显⽰单元的显⽰器或打印机上是⽆法直接表现的。

将⽮量图转换成以像素点阵来表⽰的信息，再加以显⽰或打印，这个过程称之为栅格化（Rasterization），见图1。

栅格化的逆过程相对⽐较困难。

假设有⼀个形状较为简单的图标，保存成⼀定分辨率的位图⽂件。

我们希望将其⽮量化，请你建⽴合理的数学模型，尽量准确地提取出图案的边界线条，并将其⽤⽅程表⽰出来。

⼆、问题分析本题的要求是完成位图的⽮量化，通过建⽴合理的数学模型，将⼀个有⼀定分辨率的位图⽂件尽量准确地提取出图案的边界线条，最终将位图⽤⽅程的形式表⽰出来。

解决本问题的流程图见下图。

⾸先，通过MATLAB读取位图的各个像素的像素值（0-1），得到位图各个点的灰度值，通过最⼤类间⽅差法和最⼤熵法确定阈值，完成灰度的⼆值化，使各个像素点的灰度值全部由0或1表⽰。

其次，将位图的轮廓通过合适的算法提取出来，根据特征值对轮廓进⾏拟合。

最后，根据拟合的函数完成位图的⽮量图，完成其⽮量化过程，并通过对⽐⽮量图和原始位图对应的。

三、问题假设及符号说明3.1问题假设3.2符号说明四、模型建⽴4.1模型准备本题要求将⼀个形状较为简单的图标，保存成⼀定分辨率的位图⽂件，即将位图⽮量化。

阈值：指释放⼀个⾏为反应所需要的最⼩刺激强度，本⽂指像素点灰度值⼆值化的临界值。

4.2阈值的确定⽅法 4.2.1最⼤类间⽅差法最⼤类间⽅差法的基本思想是将待分割图像看作是由两类组成的整体，⼀类是背景，⼀类是⽬标[6]。

otsu阈值最大类间方差法

Otsu阈值最大类间方差法是一种确定阈值的算法，通过将图像分成前景和背景两部分，以最大化这两部分之间的方差。

这种方法是在判决分析最小二乘法原理的基础上推导得出的。

具体来说，Otsu算法首先基于直方图得到每个分割特性值的发生概率，并以阈值变量将分割特征值分为两类。

然后，算法计算出每一类的类内方差及类间方差，选取使类间方差最大或类内方差最小的阈值T作为最佳阈值。

当目标与背景的大小比例悬殊时，类间方差准则函数可能呈现双峰或多峰，此时效果不好。

但总体来说，Otsu阈值最大类间方差法在图像分割、二值化等方面具有高效性，且该算法的稳定性能够得到保证。

一维熵和二维熵

图像的熵是一种特征的统计形式，它反映了图像中平均信息量的多少。

图像的一维熵表示图像中灰度分布的聚集特征所包含的信息量，令P i表示图像中灰度值为i的像素所占的比例，则定义灰度图象的一元灰度熵为：H= - E i=0255P i lnP i(其中，E i=0255表示从灰度0到255进行求和运算，因为公式无法输入，暂且这样表示)图象的一维熵可以表示图像灰度分布的聚集特征，却不能反映图像灰度分布的空间特征，为了表征这种空间特征，可以在一维熵的基础上引入能够反映灰度分布空间特征的特征量来组成图像的二维熵。

选择图像的邻域灰度均值作为灰度分布的空间特征量，与图像的像素灰度组成特征二元组，记为(i,j)，其中i表示像素的灰度值(0<=i<=255)，j表示领域灰度均值(0<=j<=255),P ij=(f(i,j))/N2即可反应某像素位置上的灰度值与其周围像素的灰度分布的综合特征，其中f(i, j)为特征二元组(i,j)出现的频数，N为图像的尺度，定义离散的图像二维熵为：H= - E i=0255E j=0255 (P ij lnP ij )依此构造的图像二维熵可以在反映图像所包含的信息量的前提下，突出反映图像中像素位置的灰度信息和像素邻域内灰度分布的综合特征；本文是Li和Lee关于一维最小交叉熵图像阈值分割的原文。

这里进行了简单翻译，有不足的地方请大家一起讨论完善。

后续有文章对信息熵学进行初窥，敬请期待。

摘要：通过最小化图像与其部分区域之间的交叉熵解决了图像分割中的阈值选取问题。

其中交叉熵基于两幅图像之间的像素运算得到，同时提出一种基于统计直方图的实现算法。

该方法提出了一种信息理论意义上针对二值图像的无偏估计，因而不需要了解图像灰度分布的先验知识。

1、介绍在众多的模式识别系统中，图像阈值化是重要的一个初步环节。

其中阈值的选取会影响到后期图像分割的精度以及效率。

本文的方法假设图像中的背景和待分割目标可以通过将图像的灰度值与选定的一个合适的阈值对比而区分。

图像分割最大类间方差法

OPENCV的二值化操作中，有一种“大津阈值处理”的方法，使用函数cvThreshold(image,image2,0,255,CV_THRESH_OTSU) 实现，该函数就会使用大律法OTSU得到的全局自适应阈值来进行二值化图片，而参数中的threshold不再起作用。

OTSU算法OTSU算法也称最大类间差法，有时也称之为大津算法，由大津于1979年提出，被认为是图像分割中阈值选取的最佳算法，计算简单，不受图像亮度和对比度的影响，因此在数字图像处理上得到了广泛的应用。

它是按图像的灰度特性,将图像分成背景和前景两部分。

因方差是灰度分布均匀性的一种度量,背景和前景之间的类间方差越大,说明构成图像的两部分的差别越大,当部分前景错分为背景或部分背景错分为前景都会导致两部分差别变小。

因此,使类间方差最大的分割意味着错分概率最小。

设灰度图像灰度级是L，则灰度范围为[0,L-1]，利用OTSU算法计算图像的最佳阈值为：t = Max[w0(t) * (u0(t) - u)^2 + w1(t) * (u1(t) - u)^2)]其中的变量说明：当分割的阈值为t时，w0为背景比例，u0为背景均值，w1为前景比例，u1为前景均值，u为整幅图像的均值。

使以上表达式值最大的t，即为分割图像的最佳阈值。

以下是一段在OpenCV中实现的C语言程序，即一个使用OTSU算法提取图像阈值的函数，输入参数为一个图像指针，返回分割该图像的最佳阈值。

其中的变量说明：当分割的阈值为t时w0为背景像素点占整幅图像的比例u0为w0平均灰度w1为前景像素点占整幅图像的比例u1为w1平均灰度u为整幅图像的平均灰度公式:g = w0*pow((u-u0),2) + w1*pow((u-u1),2)int MyAutoFocusDll::otsuThreshold(IplImage *frame){const int GrayScale = 256;int width = frame->width;int height = frame->height;int pixelCount[GrayScale];float pixelPro[GrayScale];int i, j, pixelSum = width * height, threshold = 0;uchar* data = (uchar*)frame->imageData; //指向像素数据的指针for(i = 0; i < GrayScale; i++){pixelCount[i] = 0;pixelPro[i] = 0;}//统计灰度级中每个像素在整幅图像中的个数for(i = 0; i < height; i++){for(j = 0;j < width;j++){pixelCount[(int)data[i * width + j]]++; //将像素值作为计数数组的下标 }}//计算每个像素在整幅图像中的比例float maxPro = 0.0;int kk=0;for(i = 0; i < GrayScale; i++){pixelPro[i] = (float)pixelCount[i] / pixelSum;if( pixelPro[i] > maxPro ){maxPro = pixelPro[i];kk = i;}}//遍历灰度级[0,255]float w0, w1, u0tmp, u1tmp, u0, u1, u, deltaTmp, deltaMax = 0;for(i = 0; i < GrayScale; i++) // i作为阈值{w0 = w1 = u0tmp = u1tmp = u0 = u1 = u = deltaTmp = 0;for(j = 0; j < GrayScale; j++){if(j <= i) //背景部分{w0 += pixelPro[j];u0tmp += j * pixelPro[j];}else //前景部分{w1 += pixelPro[j];u1tmp += j * pixelPro[j];}}u0 = u0tmp / w0;u1 = u1tmp / w1;u = u0tmp + u1tmp;deltaTmp = w0 * pow((u0 - u), 2) + w1 * pow((u1 - u), 2);if(deltaTmp > deltaMax){deltaMax = deltaTmp;threshold = i;}}return threshold;}接下来介绍OTSU方法的原理：********************************************************************* ********************************************************************* *********************OTSU法对于具有双峰性质的灰度图像或是彩色图像的某一通道的分割效果很好,程序为了增加健壮性加了个可以根据实际情况确定的修正值th_set.********************************************************************* ********************************************************************* ********************function y1=OTSU(image,th_set)image=imread('color1.bmp');gray=rgb2gray(image);%原图像的灰度图low_high=stretchlim(gray);%增强图像，似乎也不是一定需要gray=imadjust(gray,low_high,[]);% subplot(224);imshow(gray);title('after adjust');count=imhist(gray);[r,t]=size(gray);n=r*t;l=256;count=count/n;%各级灰度出现的概率for i=2:lif count(i)~=0st=i-1;breakendend%以上循环语句实现寻找出现概率不为0的最小灰度值for i=l:-1:1if count(i)~=0;nd=i-1;breakendend%实现找出出现概率不为0的最大灰度值f=count(st+1:nd+1);p=st;q=nd-st;%p和分别是灰度的起始和结束值u=0;for i=1:q;u=u+f(i)*(p+i-1);ua(i)=u;end%计算图像的平均灰度值for i=1:q;w(i)=sum(f(1:i));end%计算出选择不同k的时候，A区域的概率d=(u*w-ua).^2./(w.*(1-w));%求出不同k值时类间方差[y,tp]=max(d);%求出最大方差对应的灰度级th=tp+p;if th<th_setth=tp+p;elseth=th_set; %根据具体情况适当修正门限endy1=zeros(r,t);for i=1:rfor j=1:tx1(i,j)=double(gray(i,j));endendfor i=1:rfor j=1:tif (x1(i,j)>th)y1(i,j)=x1(i,j);elsey1(i,j)=0;endendend%上面一段代码实现分割% figure,imshow(y1);% title('灰度门限分割的图像');接下来介绍OTSU方法的原理以及用Ｃ语言实现：阈值将原图像分成前景、背景两个图像。

坦克目标红外图像分割算法研究

则此时µ(x)由窗宽 c=2∆q 及参数 q 决定，一旦选定了窗宽 c， γ(X)就只与参数 q 有关，此时使γ(X)获最小值的参数 q 就是最终的阈值。由于 q 在灰度区间[0,L]上是遍历的，当 c 取值不同时才影响γ(X)，进而影响阈值选取，所以 c 的大小对分割结果的好坏起决定作用。Murthy 等人在参考文献[7]中证明了当窗宽 c 小于两峰间距离时，必定存在最小模糊率；反之，就可能丢失其间的阈值。此后，
第 36 卷，增刊 Vol.36 Supplement
红外与激光工程
Infrared and Laser Engineering
2007 年 9 月 Sep.2007
坦克目标红外图像分割算法研究
蒋一明，王克勇，郑（北京理工大学链，宋承天 100081）
宇航科学技术学院，北京
摘要：图像分割技术在图像处理和计算机视觉中具有重要意义。首先介绍了一维 Otsu 方法和模糊阈值分割算法的基本原理。针对坦克红外图像目标——景间对比度较小，边缘模糊等特点，提出了一种结合图像空间相关信息的自适应模糊阈值分割算法。实验结果表明，该算法具有更好的分割效果和更强的鲁棒性。关键词：图像分割；模糊阈值；空间相关信息中图分类号：TP391 文献标识码：A 文章编号：1007-2276(2007)增(探测与制导)-0275-04
通过从 1~L 改变 t 可求得最佳灰度分割阈值 topt。实验证明，无论图像直方图有无明显的双峰特性，使用此方法都可得到较好的结果。基于一维 Otsu 方法的阈值分割算法计算简单、运算速度快，特别是不同物体或结构之间有较大的强度对比时，能够得到很好的分割效果。然而，由于该算法在考虑像素本身灰度值的同时并不考虑图像的空间分布，因此其分割结果对噪声很敏感。

常用一维搜索算法

无约束优化：不对定义域或值域做任何限制的情况下，求解目标函数的最小值。

这是因为实际应用中，许多情形被抽象为函数形式后均为凸函数，对于凸函数来说局部最小值点即为全局最小值点，因此只要能求得这类函数的一个最小值点，该点一定为全局最小值。

（直接法：又称数值方法，它只需计算目标函数驻点的函数数值，而不是求其倒数，如坐标轮换法，单纯型法等。

间接法：又称解析法，是应用数学极值理论的解析方法。

首先计算出目标函数的一阶或一阶、二阶导数，然后根据梯度及海赛矩阵提供的信息，构造何种算法，从而间接地求出目标函数的最优解，如牛顿法、最速下降法共轭梯度法及变尺度法。

）在优化算法中保证整体收敛的重要方法就是线搜索法与信赖域法,这两种算法既相似又有所不同。

根据不同的线搜索准则就延伸出不同的线搜索算法,譬如比较常见和经典的最速下降法,牛顿法,拟牛顿法以及共辄梯度法等。

一维搜索又称线性搜索(Line Search),就是指单变量函数的最优化,它是多变量函数最优化的基础,是求解无约束非线性规划问题的基本方法之一。

一维搜索技术既可独立的用于求解单变量最优化问题,同时又是求解多变量最优化问题常用的手段,虽然求解单变量最优化问题相对比较简单,但其中也贯穿了求解最优化问题的基本思想。

由于一维搜索的使用频率较高,因此努力提高求解单变量问题算法的计算效率具有重要的实际意义。

在多变量函数的最优化中,迭代格式Xk+1=Xk+akdk其关键就是构造搜索方向dk和步长因子ak设Φ(a)=f(xk+adk)这样从凡出发,沿搜索方向dk,确定步长因子ak,使Φ(a)<Φ(0)的问题就是关于步长因子a的一维搜索问题。

其主要结构可作如下概括:首先确定包含问题最优解的搜索区间，然后采用某种分割技术或插值方法缩小这个区间，进行搜索求解。

一维搜索通常分为精确的和不精确的两类。

如果求得ak使目标函数沿方向dk达到极小,即使得f (xk+akdk)=minf(xk+adk) (a>0)则称这样的一维搜索为最优一维搜索,或精确一维搜索,ak叫最优步长因子;如果选取ak使目标函数f得到可接受的下降量,即使得下降量f(xk)一f(xk+akdk)>0是用户可接受的,则称这样的一维搜索为近似一维搜索,或不精确一维搜索,或可接受一维搜索。

类间方差法2

类间方差法
利用阈值将原图像分成前景，背景两个图象。

前景：用n1,csum,m1 来表示在当前阈值下的前景的点数，质量矩，平均灰度
后景：用n2, sum-csum,m2 来表示在当前阈值下的背景的点数，质量矩，平均灰度
当取最佳阈值时，背景应该与前景差别最大，关键在于如何选择衡量差别的标准，而在otsu 算法中这个衡量差别的标准就是最大类间方差（英文简称otsu，这也就是这个算法名字的来源），在本程序中类间方差用sb 表示，最大类间方差用fmax
关于最大类间方差法（otsu）的性能：
类间方差法对噪音和目标大小十分敏感，它仅对类间方差为单峰的图像产生较好的分割效果。

当目标与背景的大小比例悬殊时，类间方差准则函数可能呈现双峰或多峰，此时效果不好，但是类间方差法是用时最少的。

类间方差σ2B(k)和类内方差σ2A(k)定义如下:
σ2B=W1(M1-Mr)2+W2(M2-Mr)2=W1W2(M1-Mr)2,
σ2A=W1σ21+W2σ22.
模式分类理论中,不同类别之间可分性度量有三个标准:散布矩阵、散度和Battacharyya距离[6]，类间方差与类内方差的比值对应于散布矩阵，反映了各类模式在模式空间的分布情况。

类间方差越大，类内方差越小，则说明分类结果类与类之间距离大，每类自身各像素性质相似度越大，即模式分类结果越好。

基于最大类间、类内方差比法的图像分割

3、本实验阈值 Th 的确定方法：
由于最大类间、类内方差比法图像分割的核心是阈值 Th 的确定，即要处理类间方差和类内方差的比值，找出最大的比值，此时满足最大比值的 Th 即为所求。我们可以将所有类间、类内方差的比值放在一个矩阵中，然后使用 find 函数找出矩阵的最大值，对应的 Th 即为所求，。
由于最大类间、类内方差比法是基于图像灰度分布的阈值方法。数学模型如下：设原图像为 f(x,y),经过分割处理后的图像为 g(x,y),g(x,y) 为二值图像，则有
1 g ( x, y ) 0
f ( x, y ) Th f ( x, y ) Th
（3-1）
2、最大类间方差法与最大类间、类内方差比法的不同：
f ( x, y ) Th* f ( x, y ) Th*
(4 8)
五、基于 MATLAB 的实验仿真 1、应用于灰度图像分割代码
clear all; close all; a=imread('D:\我的图片\3.jpg'); a=rgb2gray(a); figure; imshow(a); title('此为原图'); a=double(a); [m,n]=size(a); th=zeros(1,254); %建立一维零矩阵存放类间类内方差比的值；我们需要对灰
(4 3)
j 1
3、按下式计算两类在图像中的分布概率 p1 和 p2；
p1
N N
c1
p1
N c2 N im a g e
(4 4)
im a g e
4、计算类间方差σb^2=和类内方差σin^2；
b2 p1 (1 )2 p2 (2 )2

halcon 二值化阈值

halcon 二值化阈值在图像处理中，二值化是一种常见且重要的操作。

通过将图像中的像素灰度值映射为黑白两种颜色，从而将图像转化为只有黑白两种颜色的二值图像。

在Halcon软件中，二值化操作是非常常用的，并且Halcon提供了多种二值化阈值的计算方法，以适应不同的图像处理需求。

一、二值化简介二值化是将一幅图像转换为只有两种颜色的图像的过程。

这两种颜色通常是黑色和白色，也可以是其他两种特定的颜色。

二值化可以分割图像中的目标物体和背景，减少图像中的信息量，提取所需的目标特征，用于后续的图像处理和分析。

二、Halcon二值化方法Halcon提供了多种二值化阈值的计算方法，下面将分别介绍常用的几种方法。

1. 固定阈值法固定阈值法是最简单、最直接的二值化方法之一。

通过选择一个固定的灰度值作为阈值，大于该灰度值的像素设为白色，小于该灰度值的像素设为黑色。

具体操作步骤如下：①使用read_image函数将图像读入Halcon中。

②使用threshold函数进行固定阈值化处理，指定阈值。

③使用write_image函数将二值化后的图像保存。

2. 标准差法标准差法是根据图像灰度值的标准差进行二值化的方法。

通过计算整个图像的灰度标准差，将标准差的一定倍数作为阈值进行二值化。

具体操作步骤如下：①使用read_image函数将图像读入Halcon中。

②使用deviation_image函数计算图像的标准差。

③选择适当的倍数作为阈值放入threshold函数中进行二值化处理。

④使用write_image函数将二值化后的图像保存。

3. 迭代方法迭代方法是根据图像灰度直方图的波峰和波谷进行二值化的方法。

通过找到波峰和波谷之间的最佳阈值，进行二值化处理。

具体操作步骤如下：①使用read_image函数将图像读入Halcon中。

②使用gray_histo函数计算图像的灰度直方图。

③使用regulate函数对灰度直方图进行处理，得到平滑的直方图。

农产品检测中的图像分割算法

交流Experience ExchangeI G I T C W 经验278DIGITCW2020.05图像分割是一个经典的机器视觉处理问题，其目的是将图像分割为若干个相关的区域，从而提取出感兴趣的区域或者轮廓特征。

图像分割的准确性直接作用于目标物测量的准确性，其效率直接影响生产的效率，因而，一个快速准确图像分割算法是目标识别，分级分类任务面临的首要问题。

在农业产品分级分类任务中，图像分割的目的是将工业相机采集到的图片中的农产品准确的提取出来，为进一步的尺寸测量，分类任务做好准备。

对于农产品图像分割算法来说，由于受到生产设备成像质量，灰尘污渍，光照条件，阴影等外部因素影响，造成分割的不准确。

本文通过对比不同图像分割算法，阐述各类算法的优缺点，以及各自合适的应用场景。

1 传统提取算法阙值提取法是图像分割中使用较为广泛的方法，通过阙值的设置，将处于阙值区间内的像素区域归纳为同一区域，从而分割图像。

此类算法的缺陷在于只考虑了目标的灰度信息，从而缺少鲁棒性。

在这类算法中，如何获取一个合理的阙值是算法成功的关键，手动选取阙值无法具备通用性，易受环境变化的影响，主流的选取阙值的方法有最大类间方差法和最大熵阙值分割法。

最大类间方差法根据图像的灰度特性寻找阙值，使分割出的图像区域之间的差别最大，用于判断分割图像区域之间的差别是其各区域间的内部方差。

最大类间方差法极易受到噪音的影响，如阴影，但在单纯背景条件下，适用于初步的获取目标物的位置。

最大熵阙值法与最大类间方差原理类似，将图像通过信息熵分为不同区域。

信息熵在混乱无序的系统中较大，在确定有序的系统中较小，根据信息熵的特性，可将图像分割为不同的区域。

徐海，秦立峰等人在黄瓜叶部角斑病提取任务中，使用最大类间方差法初分割，继而使用最大熵发二次分割提取病虫害区域。

另外，彩色图片中，使用色彩信息分割图像也是常用的手段，常见的色彩信息表示方式有BGR 和HSV ，通过设置色值区间可提取农作物病变区域。

SPSS与数理统计之一维方差分析

F分布的形状
接受域
拒绝域
方差分析的逻辑思想
• 多个样本通过实验会得到有差异的数据，即数据间存在着变异，即参差不齐。造成变异的因素是多方面的，有些可能是由于实验不同方法产生的，有些可能是由于随机抽样误差及其他未知因素造成的。例如把18名学生随机分成三组，每组接受一种教学方法实验，结果如下：
2 2 ( 80 81 ) ......( 87 81 ) 组内变异SSw= (85 862 ) ....(90 86) 2
(84 792 ) ....(72 79) 2
=288
三种变异的关系为SSt= SSb+ SSw
F=
• 总自由度dft=N-1=17, N为总人数
Means for groups in homogeneous subsets are displayed. a. Uses Harmonic Mean Sample Size = 6.000.
教学方法3与教学方法2取得的成绩属于不同的子集，所以教学方法3与教学方法2取得的成绩具有显著性差异。
在方差分析中，研究者关心的是组间均方是否显著大于组内均方，所以就算F值，计算组间均方与组内均方的比值。
F>F0.05(2,15)=3.68
分子自由度
分母自由度
ANOVA 成绩 Sum of Squares 156.000 288.000 444.000 df 2 15 17 Mean Square 78.000 19.200 F 4.063 Sig. .039
总变异=组间变异+组内变异
2 85 82)2 .....( 84 822 ) ....(72 82)2 • 总变异SSt= (80 82) ......( =444

一维数据聚类算法

一维数据聚类算法一维数据聚类算法是一种将一维数据划分为多个簇（或者称为类）的方法，以实现数据的分组和分类。

这种算法常用于时间序列分析、图像处理、数据挖掘等领域。

本文将介绍三种常见的一维数据聚类算法：K-Means算法、层次聚类算法和密度聚类算法。

1. K-Means算法K-Means算法是一种迭代的、基于距离的聚类算法。

它的步骤如下：1)随机选择K个数据点作为初始的聚类中心；2)根据每个数据点与聚类中心的距离，将数据点分配给离它最近的聚类中心所在的簇；3)更新每个簇的聚类中心为簇中所有数据点的均值；4)重复步骤2和步骤3，直到聚类中心不再变化或达到最大迭代次数。

K-Means算法适用于数据集的簇形状较为规则、大小相近，并且簇间的距离较大的情况。

但它对噪声和异常值比较敏感，并且需要事先指定簇的个数K。

2.层次聚类算法层次聚类算法通过逐步合并或分割簇来构建聚类层次结构。

它的步骤如下：1)将每个数据点作为一个初始的簇；2)根据簇间的距离（如欧式距离、相关系数等），合并距离最近的两个簇，形成一个新的簇；3)重复步骤2，直到所有数据点都合并到一个簇中，或者达到设定的簇个数。

层次聚类算法不需要事先指定簇的个数，但它的计算复杂度较高，尤其是当数据集较大时。

3.密度聚类算法密度聚类算法通过将密度相连的数据点划分为一个簇，适用于数据集中簇的形状和大小不规则的情况。

其中，最常用的密度聚类算法是DBSCAN（Density-Based Spatial Clustering of Applications with Noise）算法。

DBSCAN算法的步骤如下：1)随机选择一个未被访问的数据点；2)判断该点的密度是否大于设定的阈值，如果是，则将该点及其密度可达的所有点划分为一个簇，并标记为已访问；3)重复步骤2，直到所有数据点都被访问。

DBSCAN算法能够自动处理噪声和异常值，并且不需要事先指定簇的个数，但对参数的设置较为敏感。

python---简单最大类间方差法（OTSU）算法

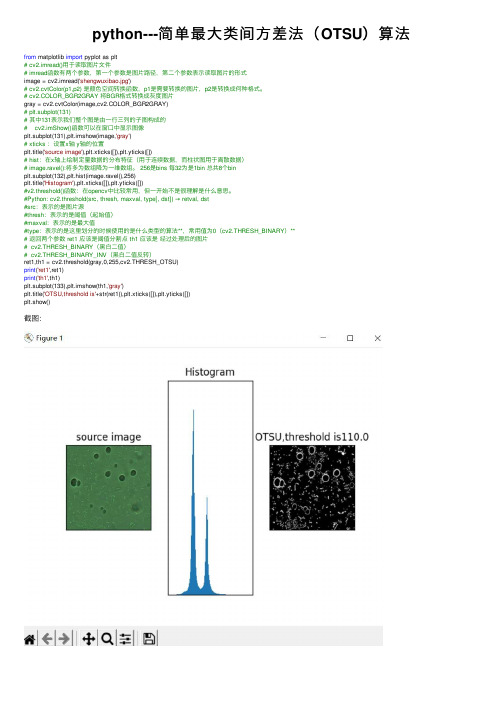
python---简单最⼤类间⽅差法（OTSU）算法from matplotlib import pyplot as plt# cv2.imread()⽤于读取图⽚⽂件# imread函数有两个参数，第⼀个参数是图⽚路径，第⼆个参数表⽰读取图⽚的形式image = cv2.imread('shengwuxibao.jpg')# cv2.cvtColor(p1,p2) 是颜⾊空间转换函数，p1是需要转换的图⽚，p2是转换成何种格式。

# cv2.COLOR_BGR2GRAY 将BGR格式转换成灰度图⽚gray = cv2.cvtColor(image,cv2.COLOR_BGR2GRAY)# plt.subplot(131)# 其中131表⽰我们整个图是由⼀⾏三列的⼦图构成的# cv2.imShow()函数可以在窗⼝中显⽰图像plt.subplot(131),plt.imshow(image,'gray')# xticks ：设置x轴 y轴的位置plt.title('source image'),plt.xticks([]),plt.yticks([])# hist：在x轴上绘制定量数据的分布特征（⽤于连续数据，⽽柱状图⽤于离散数据）# image.ravel():将多为数组降为⼀维数组。

256是bins 每32为是1bin 总共8个binplt.subplot(132),plt.hist(image.ravel(),256)plt.title('Histogram'),plt.xticks([]),plt.yticks([])#v2.threshold()函数：在opencv中⽐较常⽤，但⼀开始不是很理解是什么意思。

#Python: cv2.threshold(src, thresh, maxval, type[, dst]) → retval, dst#src：表⽰的是图⽚源#thresh：表⽰的是阈值（起始值）#maxval：表⽰的是最⼤值#type：表⽰的是这⾥划分的时候使⽤的是什么类型的算法**，常⽤值为0（cv2.THRESH_BINARY）**# 返回两个参数 ret1 应该是阈值分割点 th1 应该是经过处理后的图⽚# cv2.THRESH_BINARY（⿊⽩⼆值）# cv2.THRESH_BINARY_INV（⿊⽩⼆值反转）ret1,th1 = cv2.threshold(gray,0,255,cv2.THRESH_OTSU)print('ret1',ret1)print('th1',th1)plt.subplot(133),plt.imshow(th1,'gray')plt.title('OTSU,threshold is'+str(ret1)),plt.xticks([]),plt.yticks([])plt.show()截图：。