雷达成像基本算法
机载聚束模式合成孔径雷达的成像算法

基于图像聚焦与运动补偿的改进算法
总结词
详细描述
该算法通过引入图像聚焦和运动补偿技术, 实现了对运动目标和复杂背景的高分辨率成 像。
基于图像聚焦与运动补偿的改进算法,通过 对运动目标和复杂背景进行聚焦和补偿处理 ,提高了成像的分辨率和对比度。该算法具 有较高的计算复杂度,但能够提供高质量的 SAR图像,适用于对运动目标和复杂背景的
实验结果展示与分析
结果展示
将机载聚束模式合成孔径雷达的原始回波数据转化为 地物图像,并进行对比分析。
结果分析
通过与实地采集的地物图像进行对比,验证了机载聚 束模式合成孔径雷达的成像效果。
成像算法性能评估与对比分析
性能评估:评估机载聚束模式合成孔径雷达的成像算法在分辨率、对比度、清晰度等方面的性能指 标。
机载聚束模式合成孔径雷达 的成像算法
2023-11-06
目 录
• 成像算法概述 • 聚束模式SAR基本成像算法 • 改进型聚束模式SAR成像算法 • 成像算法的优化与实现 • 成像算法验证与分析 • 结论与展望
01
成像算法概述
合成孔径雷达(SAR)基本原理
合成孔径雷达是一种雷达成像技术,通过在飞行器上安装雷达天线,利用目标的 反射信号,生成高分辨率的图像。
数据输出与显示
将成像结果和目标信息进行输出和 显示,为后续任务提供决策支持。
05
成像算法验证与分析
实验场景与数据采集
实验场景
机载聚束模式合成孔径雷达(CS-SAR)在城市、农田、 山丘等典型地物场景中进行实验。
数据采集
采集不同飞行高度、速度、姿态等条件下的雷达回波数 据,以及对应的地物图像数据。
除了军事应用外,该成像算法也可应用于民用航空领域,例如机场跑道检测、地形测绘、 气象观测等方面,具有广泛的应用前景。
雷达成像rd算法积分旁瓣比

雷达成像rd算法积分旁瓣比
雷达成像是一种利用雷达技术进行目标成像的方法,而积分旁
瓣比是评价雷达成像质量的重要指标之一。
积分旁瓣比是指成像过
程中目标信号与旁瓣(或者说杂波)信号之间的比值。
在雷达成像中,旁瓣通常是指由于雷达天线方向图、波束形状等因素引起的非
期望信号。
从技术角度来看,雷达成像中的积分旁瓣比是由雷达系统的性
能参数、成像算法以及目标场景等多个因素共同决定的。
首先,雷
达系统的天线方向图和波束形状会直接影响到旁瓣的产生,因此天
线设计和波束控制是影响积分旁瓣比的重要因素。
其次,成像算法
的设计也会对积分旁瓣比产生影响,比如在成像算法中采用的滤波、聚焦等处理方式会影响到目标信号和旁瓣信号的分离程度。
此外,
目标场景的复杂程度也会对积分旁瓣比产生影响,比如目标的反射
特性、背景干扰等因素都会影响到成像质量。
另外,从应用角度来看,积分旁瓣比的大小直接关系到雷达成
像的清晰度和目标分辨率。
较高的积分旁瓣比意味着目标信号相对
于旁瓣信号更突出,成像质量更高,目标的细节信息能够更加清晰
地呈现出来。
因此,在实际的雷达成像应用中,工程师们通常会根
据具体的成像要求和场景特点来调整雷达系统参数和优化成像算法,以获得更好的积分旁瓣比,从而获得更高质量的雷达成像结果。
总之,雷达成像中的积分旁瓣比是一个综合了技术、算法和应
用等多方面因素的重要指标,对于评价雷达成像质量和优化成像效
果具有重要意义。
雷达成像技术(保铮word版)第五章 合成孔径雷达成像算法

第五章 合成孔径雷达成像算法SAR 成像处理最初用光学处理,后来采用数字处理。
与光学处理相比,数字处理更精确、更灵活,在距离徙动校正、运动补偿、几何校正和坐标转换等方面有明显的优势。
SAR 成像处理主要有两个问题,一是距离徙动校正,二是运动补偿。
距离徙动可分解一次的线性分量和二次以上(包括二次)的弯曲分量,线性分量称为距离走动,弯曲分量称为距离弯曲。
这一章主要讨论针对不同距离徙动程度情况下,需要采用的不同成像算法,运动补偿将在下一章讨论。
5.1 距离徙动距离徙动对合成孔径雷达成像是一个重要的问题,虽然在前面已多次提及,这里还要对它作比较系统的介绍。
θ∆波束Qθ∆BR B ALxBR ROmvt x图5.1正侧视时距离徙动的示意图距离徙动的情况对不同的波束指向会有所不同,首先讨论正侧视的情况,这时距离徙动可用图5.1来说明。
所谓距离徙动是雷达直线飞行对某一点目标(如图中的Q 点)观测时的距离变化。
如图5.1所示,天线的波束宽度为θ∆,当载机飞到A 点时波束前沿触及Q 点,而当载机飞到B 点时,波束后沿离开Q 点,A 到B 的长度即有效合成孔径L ,Q 点对A 、B 的转角即相干积累角,它等于波束宽度θ∆。
Q 点到航线的垂直距离为最近距离B R 。
这种情况下的距离徙动通常以合成孔径边缘的斜距R 与最近距离B R 之差表示,即BB B q R R R R R -∆=-=2secθ (5.1)在合成孔径雷达里,波束宽度θ∆一般较小,2)(2112secθθ∆+≈∆,而相干积累角θ∆与横向距离分辨率a ρ有以下关系:θλρ∆=2a 。
利用这些关系,(5.1)式可近似写成:22232)(81aBB q R R R ρλθ=∆≈(5.2)假设条带场景的幅宽为W ,即场景近、远边缘与航线的最近距离分别为2W R B -和2W R B +,得场景两端的距离徙动差为2232a q WR ρλ=∆ (5.3)距离徙动和距离徙动差的影响表现在它们与距离分辨率r ρ的相对值,如果它们比r ρ小得多,就无需作包络移动补偿。
sar 常用成像算法

sar 常用成像算法SAR(Synthetic Aperture Radar)是合成孔径雷达的缩写,是一种利用雷达技术进行成像的方法。
常用成像算法是指在SAR成像过程中常用的数据处理方法,用于从原始雷达数据中提取目标信息并生成可视化图像。
本文将介绍几种常用的SAR成像算法。
一、Range-Doppler算法Range-Doppler算法是最基础、最常用的SAR成像算法之一。
它通过两个主要步骤来实现成像:距离向(Range)压缩和多普勒向(Doppler)压缩。
首先,进行距离向压缩,将接收到的信号与发射的信号进行相关运算,得到目标在距离上的分布信息。
然后,进行多普勒向压缩,根据目标的运动情况对信号进行频率调整,得到目标在速度上的分布信息。
最后,将两个方向上的信息进行合成,得到最终的成像结果。
二、Chirp Scaling算法Chirp Scaling算法是一种用于高分辨率SAR成像的算法。
它通过对原始SAR数据进行频率调整,实现对目标的高精度成像。
具体而言,该算法通过对接收到的信号进行线性调频,使得距离上的分布信息与目标的距离成线性关系。
然后,对调频后的信号进行快速傅里叶变换,得到目标在频谱上的分布信息。
最后,对频谱信息进行逆变换,得到目标在距离上的高分辨率成像结果。
三、Omega-K算法Omega-K算法是一种用于高分辨率SAR成像的频域算法。
它通过对SAR数据进行快速傅里叶变换,将时域数据转换为频域数据,然后根据目标的运动情况对频域数据进行调整,实现高分辨率成像。
具体而言,该算法通过对频域数据进行插值,使得目标的速度信息与频率成线性关系。
然后,对插值后的数据进行逆傅里叶变换,得到目标在距离上的高分辨率成像结果。
四、Polar Format算法Polar Format算法是一种用于SAR成像的快速算法。
它通过将SAR数据从直角坐标系转换为极坐标系,实现对目标的快速成像。
具体而言,该算法首先将原始SAR数据进行极坐标变换,得到距离和方位两个维度上的数据。
毫米波雷达成像算法

毫米波雷达成像算法
毫米波雷达成像算法主要包括以下步骤:
1.信号采集:通过雷达系统发射毫米波信号并接收目标反射的回波信号,获取包含目标信息的回波数据。
2.信号处理:对回波数据进行预处理,包括滤波、去噪、补偿等操作,以提高信号质量。
3.距离像估计:对处理后的回波数据进行距离像估计,得到每个目标点的距离像数据。
4.成像处理:对距离像数据进行成像处理,包括运动补偿、多普勒补偿、聚焦等操作,以提高成像质量。
5.目标检测与跟踪:在成像结果中检测并跟踪目标,提取目标的位置、速度、姿态等信息。
6.特征提取与分类:对目标进行特征提取和分类,以实现目标识别和分类。
在毫米波雷达成像算法中,信号处理和成像处理是关键步骤。
常用的信号处理算法包括匹配滤波器、自适应滤波器等;常用的成像处理算法包括频域成像、时域成像等。
为了提高算法性能,需要不断优化算法和参数选择,以适应不同的场景和应用需求。
雷达点目标成像
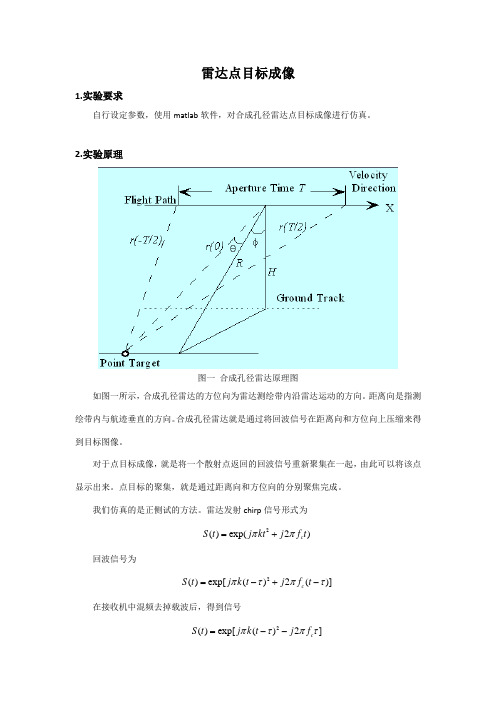
雷达点目标成像1.实验要求自行设定参数,使用matlab 软件,对合成孔径雷达点目标成像进行仿真。
2.实验原理图一 合成孔径雷达原理图如图一所示,合成孔径雷达的方位向为雷达测绘带内沿雷达运动的方向。
距离向是指测绘带内与航迹垂直的方向。
合成孔径雷达就是通过将回波信号在距离向和方位向上压缩来得到目标图像。
对于点目标成像,就是将一个散射点返回的回波信号重新聚集在一起,由此可以将该点显示出来。
点目标的聚集,就是通过距离向和方位向的分别聚焦完成。
我们仿真的是正侧试的方法。
雷达发射chirp 信号形式为2()exp(2)c S t j kt j f t ππ=+回波信号为2()exp[()2()]c S t j k t j f t πτπτ=-+-在接收机中混频去掉载波后,得到信号2()exp[()2]c S t j k t j f πτπτ=--可得信号的距离向信号形式为2exp[(2/)]j k t r c π-方位向信号形式为exp[4/]c j f r c π-其中()r t =当v t R 时有2()()2vt r t R R ≈+,知回波信号在方位向上也是线性调频信号,其调频率为22v Rλ,λ为载波波长。
对于成像算法,我们采用经典的距离多普勒算法,即SD 算法。
他的基本思想是基本思想是将二位处理分解为两个一维处理的级联方式,即分别压缩距离向和方位向。
由于雷达的飞行线路接近直线,所以方位向和距离向相互有影响,要对数据进行徙动校正。
但是由于机载SAR 飞行范围小,距离弯曲量很小,故可以不用考虑徙动校正。
SD 算法的具体流程图如图二所示。
图二 SD 算法的具体流程图4.实验过程参数设置:飞机飞行高度:10000m下视角:45度飞机的飞行速度:100m/s合成孔径时间:1sPRF :500HzK :113010⨯Hz/s脉冲宽度:10us载波频率: 10510Hz ⨯回波点阵大小:501X501对数据进行距离向压缩,得到图一。
雷达成像积分旁瓣比公式

雷达成像积分旁瓣比公式
雷达成像积分旁瓣比是衡量雷达成像系统图像质量的重要指标之一,它描述了成像系统在成像过程中对于干扰源的抑制能力。
积分旁
瓣比越大,表示成像系统对于干扰源的抑制能力越强,图像质量越好。
雷达成像积分旁瓣比的计算公式为:
SIR = 10 * log10(I_main / I_side)
其中,SIR表示积分旁瓣比,I_main表示主瓣内的能量,I_side
表示旁瓣内的能量。
积分旁瓣比的单位通常是分贝(dB)。
拓展:
雷达成像积分旁瓣比的大小受到多种因素的影响。
其中,主要因
素包括雷达天线的辐射特性、系统噪声、散射目标的分布以及采用的
成像算法等。
为了提高雷达成像积分旁瓣比,可以采取以下措施:
1.优化雷达天线辐射特性:通过调整天线方向图、天线孔径大小、天线波束宽度等参数,减小旁瓣的能量。
2.降低系统噪声:采用低噪声放大器、有效的信噪比增益技术等,以提高系统的信噪比,从而减小旁瓣的能量。
3.优化成像算法:选择适合的成像算法,如谱分析法、波束形成
方法等,以提高图像的分辨率和对干扰源的抑制能力。
4.控制散射目标分布:通过对目标的选取、分类、滤波等处理,
减小干扰目标对成像结果的影响,进而提高积分旁瓣比。
综上所述,雷达成像积分旁瓣比是一个衡量雷达成像系统图像质
量的指标,通过优化天线辐射特性、降低系统噪声、优化成像算法以
及控制散射目标分布等手段,可以提高积分旁瓣比,从而改善雷达成
像系统的成像效果。
SAR成像及成像算法

SAR成像及成像算法
SAR(Synthetic Aperture Radar),即合成孔径雷达,是一种具有视距的雷达成像技术,它利用通过雷达发射的电磁波的返回信号来构建成像,是今天最受欢迎的遥感成像技术之一、它是由空间技术应用罗列公司(STARS)于1970年首次研制完成的。
由于它的无损探测、低成本、通用性强、快速更新和相当高的精度等优点,使SAR成像广泛应用于地表特性探测、航空和海洋地理资源监测、地表热分辨观测、大气和气候研究等多种领域,并取得了突出的成果。
SAR成像的本质是利用雷达发射的电磁波探测地表物质的反射状态,从而构建三维图像。
SAR成像算法主要分成基线分析、多普勒解析和像元投影三个过程。
首先,基线分析是处理多普勒解析的基本步骤,它识别SAR图像的物理位置,将地表物质的反射信号与它们在同一物理位置的多普勒频率作对比,从而计算出相应的基线;其次,多普勒解析处理SAR图像所涉及的空间结构,它可以利用反射信号的多普勒频率,将不同波段中的多普勒信号重建成三维定量数据;最后,像元投影过程会将三维数据转换成二维图像,以实现SAR成像。
当前。
cs成像处理算法_chirpscaling基本原理

cs成像处理算法_chirpscaling基本原理
Chirp scaling(扫频比例调制)是一种用于合成孔径雷达(SAR)成像的算法,其基本原理如下:
1. 生成虚拟波控制(Virtual Waveform Synthesis):根据SAR 系统的参数,生成一个虚拟的传输波形(通常是线性调频信号),该波形在距离与时间上是完全对应的,可以看作是输入信号。
2. 快速傅里叶变换(FFT):将接收到的SAR数据进行FFT 变换,将时域数据转换为频域数据。
3. 范围压缩(Range Compression):将频域数据进行傅里叶变换,以将散射信号从距离域转换为频率域,同时进行相位校正和距离校正。
4. 脉冲压缩(Pulse Compression):将范围压缩后的数据与虚拟波形进行相关运算,以增强散射信号并抑制杂散干扰。
5. 幅度调制(Amplitude Modulation):将脉冲压缩后的数据乘以一个复数调制函数,以调制图像的幅度。
6. 幅度控制和灰度映射(Gain Control and Gray Scale Mapping):通过调整增益,使图像的动态范围适应显示设备的能力,并将数据映射到灰度显示。
Chirp scaling算法利用了线性调频(chirp)信号在时域和频域
上的性质,通过合适的信号设计和处理方法,实现了SAR图像的高分辨率成像。
雷达成像中的傅里叶变换

雷达成像中的傅里叶变换
在雷达成像中,通过对回波信号进行快速傅里叶变换(FFT)或离散傅里叶变换(DFT),可以将信号从时域转换到频域。
这有助于识别和提取信号中的有用信息,例如目标的距离、速度和方向等。
傅里叶变换是一种数学方法,用于将信号从时域转换到频域。
它可以将复杂的信号分解为简单的正弦波分量,这些正弦波分量的频率和振幅与原始信号的频率和振幅相关。
通过分析这些分量,可以提取信号的特征,并识别其中包含的目标信息。
在雷达成像中,回波信号通常是一个复数信号,它包含了目标的距离、速度和方向等信息。
通过对回波信号进行快速傅里叶变换或离散傅里叶变换,可以将信号从时域转换到频域。
在频域中,回波信号的能量通常集中在一些特定的频率上,这些频率对应于目标的特征。
通过对这些频率的能量进行分析,可以提取目标的距离、速度和方向等信息。
此外,通过对回波信号进行逆傅里叶变换,可以将信号从频域转换回时域。
这有助于将目标的距离、速度和方向等信息转换为目标的位置和形状信息,从而实现雷达成像。
在雷达成像中,常用的傅里叶变换算法有快速傅里叶变换(FFT)和离散傅里叶变换(DFT)。
FFT 是一种高效的算法,可以在短时间内完成傅里叶变换,适用于处理实时性要求较高的场景。
DFT 是一种更加准确的算法,适用于处理频率分辨率更高的场景。
在实际应用中,需要根据具体的需求选择合适的傅里叶变换算法。
(完整版)各种SAR成像算法总结

各种SAR成像算法总结1 SAR成像原理SAR成像处理的目的是要得到目标区域散射系数的二维分布,它是一个二维相关处理过程,通常可以分成距离向处理和方位向处理两个部分。
在处理过程中,各算法的区别在于如何定义雷达与目标的距离模型以及如何解决距离-方位耦合问题,这些问题直接导致了各种算法在成像质量和运算量方面的差异。
一般来说,忽略多普勒频移所引起的距离向相位变化,距离向处理变为一维的移不变过程且相关核已知,即退化为一般的脉冲压缩处理;同时将雷达与目标的距离按2阶Taylor展开并忽略高次项,则方位向处理也是一个一维的移不变过程,并退化为一般的脉冲压缩处理,这就是经典的距离多普勒(Range-Doppler RD)算法的实质。
若考虑多普勒频移对距离向相位的影响,同时精确的建立雷达与目标的距离模型,则不论距离向处理还是方位向处理都变为二维的移变相关过程。
线性调频尺度变换(Chirp-Scaling CS)算法即在此基础之上将二维数据变换到频域,利用Chirp Scaling原理及频域的相位校正方法,对二维数据进行距离徙动校正处理、距离向及方位向的聚焦处理,最终完成二维成像处理。
当方位向数据积累延迟小于全孔径时间(即方位向为子孔径数据)的情况下,方位向处理必须使用去斜(dechirp)处理及频谱分析的方法。
在RD和CS 算法的基础之上,采用dechirp处理及频谱分析的方法完成方位向处理的算法分别称为频谱分析(SPECAN)算法和扩展CS(Extended Chirp Scaling ECS)算法。
1.1 SAR成像原理本节以基本的正侧视条带工作模式为例,对SAR的成像原理进行分析和讨论。
正侧视条带SAR 的空间几何关系如下图所示。
图中,αoβ平面为地平面,oγ垂直于αoβ平面。
SAR 运动平台位于S 点,其在地面的投影为G 点。
SAR运动平台的运动方向Sx 平行于oβ,速度大小为a v 。
SAR 天线波束中心与地面的交点为C ,CG 与运动方向Sx 垂直;S 与C 的距离为s R ,12B SB ∠称为天线波束的方位向宽度,大小为a β。
雷达成像的原理和方法

雷达成像的原理和方法
雷达成像是利用雷达系统发送连续波或脉冲波到目标上,然后接收目标反射回来的信号,并基于接收到的信号,重建目标的空间位置和形状。
雷达成像的原理和方法主要有以下几点:
1. 雷达方程:雷达方程是描述雷达反射回波的数学表达式,基于雷达方程可以计算目标到雷达的距离、方位角和仰角,从而确定目标在三维空间中的位置。
2. 双向测距:雷达发送连续波或脉冲波到目标上,然后接收目标反射回来的信号。
利用以目标为中心的球坐标系,测量从雷达到目标的距离。
3. 方位角测量:通过测量雷达发射时刻和接收时刻之间的差别,可以得到目标的方位角。
4. 仰角测量:通过测量接收到的信号的相位差,可以得到目标的仰角。
5. 多普勒效应:目标的运动会导致接收到的信号频率的变化,利用多普勒效应可以获取目标的速度信息。
雷达成像的方法主要包括以下几种:
1. 时域成像:通过测量雷达发射和接收信号的时刻,可以得到不同目标点的距
离信息,并通过距离信息重建目标的位置和形状。
2. 频域成像:通过测量接收到的信号的频谱信息,可以得到目标的多普勒频移和速度信息,并基于速度信息重建目标的位置和形状。
3. 合成孔径雷达(SAR):利用合成孔径雷达技术,通过叠加多个雷达扫描周期的数据,可以提高空间分辨率,获得高质量的雷达图像。
4. 多普勒雷达成像(MTI):利用多普勒效应,除去地面散射和杂波信号,提取目标的多普勒信息,从而实现对目标的空间成像。
总结而言,雷达成像通过发送和接收信号,结合雷达方程和测量技术,可以实现对目标的空间位置、形状和速度等信息的获取,并通过相应的算法和处理方法,重建目标的图像。
双基SAR成像算法

03
数据处理系统对接收到的信号 进行处理,得到目标的高分辨 率图像。
双基SAR系统分类
根据发射站的数目,双基SAR可以分为两站SAR 和多站SAR。
多站SAR则有多个发射站和多个接收站,可以提 供更高的成像分辨率和更广的覆盖范围。
两站SAR是最简单的双基SAR,只有一个发射站 和一个接收站。
根据工作方式,双基SAR可以分为同步SAR和异 步SAR。同步SAR要求各接收站与发射站同步接 收信号,而异步SAR则不要求严格的时间同步。
实例
例如,可以采用基于小波变换的成像算法提 高图像质量和分辨率;采用基于压缩感知的 成像算法降低采样率和数据处理量;采用基 于深度学习的目标检测算法提高目标检测的
准确性和鲁棒性。
05
双基SAR系统实现与验证
系统硬件组成与工作模式
发射和接收天线
双基SAR系统需要使用两个 不同的天线,一个用于发射 射频信号,另一个用于接收 反射信号。发射天线通常采 用线性或圆形天线阵列,而 接收天线则采用高灵敏度的 接收器。
06
双基SAR应用与发展趋势
双基SAR在战场侦察与监视中的应用
战场侦察
双基SAR算法可以用于生成高分辨率的战场环境图像,帮助指 挥官了解敌方阵地和武器部署情况。
目标识别
双基SAR算法可以结合其他传感器数据,对目标进行分类和识 别,提高打击精度。
动态监视
双基SAR可以实时获取地面动态变化信息,如车辆移动、人员 聚集等,为决策提供支持。
双基SAR在灾害监测与救援中的应用
01
02
03
灾害预警
灾后评估
救援导航
双基SAR可以快速获取灾区图像 ,帮助有关部门及时发现灾情并 做出响应。
雷达成像的RD算法

for i=1:Nr
sig(:,i)=ifft(sig(:,i));
end
figure
contour(abs(sig));
gama=B/Tp; % range chirp rate
delta_theta=k_a*lamda/2/res_a; % required azimuth opening angle
% corresponding to processed bandwith
for i=1:Nr
sig(:,i)=fftshift(fft(sig(:,i)));
end
disp('end of azimuth fft')
fdr=-2*va*va/lamda/Ra;
dfa=prf/Na;
fa=((0:Na-1)-Na/2)*dfa;
figure
prf=100.; % PRF
%%%(II) echo return modelling(point target)
na=fix(Ta*prf/2); % azimuth sampling number
ta=-na:na;
ta=ta/prf; % slow time along azimuth
end
rmax=max(max(ra)); % max. slant range
rmin=min(min(ra)); % min. slant range
rmc=fix((rmax-rmin)/bin_r); % range migration
rg=0*ra;
lamda=c/fc; % wavelength
雷达成像算法的研究与应用

雷达成像算法的研究与应用雷达成像是一种基于雷达反射信号进行成像的技术,可以用于目标检测、目标识别、目标跟踪等领域。
雷达成像算法是指对雷达反射信号进行处理、分析和综合,从而得到图像信息的方法和技术。
近年来,随着雷达技术的不断发展和应用领域的不断扩大,雷达成像算法的研究和应用也越来越重要。
一、雷达成像算法概述雷达成像算法可以分为两类:合成孔径雷达(SAR)成像和相控阵雷达(Phased Array Radar,PAR)成像。
其中,SAR成像是指利用合成孔径技术对距离向分辨率进行综合,并通过合成调制方法提高成像的虚拟光圈长度,从而实现高分辨率成像的技术。
而PAR成像则是通过相控阵指向并综合多个天线的输出信号,实现对目标的高速成像和跟踪的技术。
在SAR成像中,最常用的成像算法是基于飞行器或卫星运动的正向逆向重建算法,该算法可以实现高分辨率并且具有良好的抗噪性能。
而在PAR成像中,则常采用逆合成波束算法,该算法不仅能够实现目标成像,还可以提供目标跟踪的性能。
二、雷达成像应用领域雷达成像技术的应用领域非常广泛,主要包括军事、民用、海洋、科研等领域。
1. 军事领域在军事应用中,雷达成像技术常用于舰船、飞机、导弹等目标的探测、跟踪和定位。
此外,雷达成像技术还可以用于抗干扰和隐身性能的提高,保证军队对目标进行有效侦察和打击。
2. 民用领域在民用领域中,雷达成像技术可用于气象预报、地质勘探、城市规划、交通安全等领域。
例如,在气象预报中可以使用雷达成像技术进行降雨量预测和天气风险评估;在地质勘探中可以使用雷达成像技术进行地质储层的勘探和资源开发。
3. 海洋领域在海洋领域中,雷达成像技术可用于海洋水流、潮汐、浪高、风速等海洋环境监测和海上船只的智能导航与安全管理。
同时,雷达成像技术也可以为海洋研究提供重要的数据来源,例如海上物理实验、海上生物学研究等领域。
4. 科研领域在科研领域中,雷达成像技术可以用于遥感、地形信息获取、智能交通等领域。
sar成像算法时域 频域 波数域

SAR成像算法是合成孔径雷达(Synthetic Aperture Radar)技术的重要组成部分。
该算法主要是通过对雷达信号进行处理和分析,从而得到目标区域的高分辨率成像结果。
在SAR成像算法中,常常涉及到时域、频域和波数域等不同的数据处理方法。
本文将针对这三个主题展开详细的介绍和分析。
一、时域处理时域处理是SAR成像算法中最基本的数据处理方法之一。
时域处理主要是对雷达接收到的信号进行时域分析,包括距离-时间图像(Range-Time Image)的形成、脉冲压缩(Pulse Compression)等。
时域处理的关键是对信号的时延进行精确测量和定位,从而实现对目标的定位和成像。
在时域处理中,常用的算法包括FFt变换、匹配滤波等,这些算法可以提高雷达系统的距离分辨率和速度分辨率,从而实现对目标的高精度成像。
二、频域处理频域处理是SAR成像算法中另一个重要的数据处理方法。
频域处理主要是通过对雷达信号进行频谱分析,从而得到目标的频谱特征和频率分布信息。
频域处理可以通过傅里叶变换等算法将时域信号转换为频域信号,从而实现对信号的频率分辨率和频谱分布的分析。
在频域处理中,常用的算法包括FFT变换、滤波器设计等,这些算法可以对雷达信号进行频谱分析和滤波处理,从而提高SAR系统的信噪比和成像质量。
三、波数域处理波数域处理是SAR成像算法中较为复杂和高级的数据处理方法。
波数域处理主要是通过对雷达信号进行波数域分析,从而得到目标的波数分布和散射特征。
波数域处理可以通过波数变换、波数域滤波等算法实现对雷达信号的波数分布和散射特征的提取。
在波数域处理中,常用的算法包括快速波数变换算法、极化分析算法等,这些算法可以对雷达信号进行全波数域分析和波数域成像,从而实现对目标的高分辨率成像和三维重构。
时域、频域和波数域是SAR成像算法中常用的数据处理方法,它们各自具有特定的优点和适用范围,通过合理的组合和应用,可以实现对目标的高分辨率成像和高精度测量。
探地雷达成像算法研究

资料范本本资料为word版本,可以直接编辑和打印,感谢您的下载探地雷达成像算法研究地点:__________________时间:__________________说明:本资料适用于约定双方经过谈判,协商而共同承认,共同遵守的责任与义务,仅供参考,文档可直接下载或修改,不需要的部分可直接删除,使用时请详细阅读内容探地雷达成像算法研究摘要探地雷达(Ground Penetrating Radar,简称GPR)集无损检测、穿透能力强、分辨率高等众多优点而成为检测和识别地下目标的一种有效技术手段。
性能优良的探地雷达成像方法有助于精确定位地下目标,同时提高对目标的检测和识别能力,从而推动探地雷达在城市质量监控、地质灾害、考古挖掘、高速公路无损检测、地雷探测等各个方面得到更广泛的应用。
本文以中国电波传播研究所的探地雷达LD-2000为实验设备,从中读取探测数据。
以MATLAB为软件平台,实现了探地雷达数据的显示、处理、成像几个部分。
其中数据显示方式包括数据的波形堆积图,剖面面色阶图以及带数据波形图;数据处理部分包括直达波的去除、背景噪声的去除、振幅增益等;雷达成像算法部分主要采用波前成像算法和投影层析成像算法。
Imaging Algorithm of Ground Penetrating RadarABSTRACTGPR (Ground Penetrating Radar, referred GPR) set of non-destructive testing, penetration ability, many advantages of high resolution detection and identification of underground and become the target of an effective technical means. Excellent performance GPR imaging approach helps pinpoint underground targets, while increasing the target detection and identification capabilities, thereby promoting the quality of ground penetrating radar surveillance in the city, geological disasters, archaeological excavation, highway nondestructive testing, mine detection, etc. aspects to be more widely used.In this paper, China Institute of Radiowave Propagation GPR LD-2000 for the experimental apparatus, reads probe data. MATLAB as the software platform to achieve a ground-penetrating radar data display, processing, imaging several parts. Wherein the data includes a datawaveform display stacked, with a cross-sectional side view and a gradation data waveform; data processing section includes the removal of the direct wave, the background noise removal, the amplitude gain, etc.; radar imaging algorithm some of the major imaging algorithm and the wavefront projection tomography algorithms.1 绪论1.1 选题的背景及意义雷达是利用电磁波探测目标的电子设备。
雷达成像信号处理算法研究及实现

雷达成像信号处理算法研究及实现近年来,雷达技术在军事、航空、交通等领域得到了广泛的应用。
雷达成像是一种重要的目标识别技术。
在雷达成像中,信号处理算法的优劣直接影响到图像质量和成像效果。
雷达成像信号雷达成像信号是高频脉冲信号,其波形难以用常规的连续函数描述。
传统的Fourier 变换无法处理此类信号。
通常,雷达成像信号可以考虑离散化,从而使用离散 Fourier 变换(DFT)来处理。
DFT 算法DFT 是一种将离散信号转换为频域信号的算法。
对于一个长度为 N 的离散信号 s(n), 其 DFT 的计算公式如下:FN-1S(k) = ∑s(n) * exp [-2πik * n / N], 0≤k≤N-1, n=0其中,k 表示频域的索引,n 表示时间域的索引。
S(k) 表示信号在频域内的值。
DFT 算法计算量较大,时间复杂度 O(N^2),不适用于处理大规模数据。
FFT (快速 Fourier 变换)是一种优化的 DFT 算法,它可以将时间复杂度降低至 O(Nlog N),被广泛应用于信号处理领域。
距离测量距离测量是雷达成像信号处理的核心问题。
在雷达成像中,需要测量目标到雷达的距离。
距离的测量可以通过分析雷达成像信号中的周期性波形完成。
如下图所示,雷达发射高频脉冲(1),经过空气传播(2)后,遇到目标物体反射回来,并由接收器接收(3)。
在接收到反射的信号后,需要计算目标物距离。
对于单频率的波形,周期性可以用来估算距离。
可以通过计算从发射到接收所需时间(Time Of Flight,TOF),然后将其与光速相乘得到目标物距离。
TOF 可以通过两个采样点之间的时间差计算得到。
根据采样定理,采样的时间间隔必须小于等于波形周期的一半。
脉冲压缩对于雷达成像信号,当目标物位于大距离处时,接收到的信号强度较小。
这使得信噪比(SNR)与目标距离成反比。
相控阵雷达多波束形成成像算法

相控阵雷达多波束形成成像算法相控阵雷达(Phased Array Radar)是一种采用多个雷达天线单元,通过精确的相位控制实现波束的形成和多波束成像的雷达系统。
相控阵雷达具有快速扫描、高度定位精度和抗干扰能力强等优势,被广泛应用于军事和民用领域。
在相控阵雷达中,多波束成像算法是实现目标探测和识别的关键技术之一多波束成像算法通过采集多个波束的回波信号,并将其综合分析,提取目标的信息。
常见的多波束成像算法包括波达矢量法(Wavenumber Vector Algorithm)、最大似然法(Maximum Likelihood Method)、最小二乘法(Least Squares Method)等。
波达矢量法是一种常用的多波束成像算法。
它基于多通道相控阵雷达的输出数据,对每个源波束进行相干合成,得到新的波束,以获得更高分辨率的成像结果。
具体步骤如下:1.在相控阵雷达中,多个天线单元分别接收到目标的回波信号,并将信号进行变频处理,转换为基带信号。
2.对于每个源波束,通过给每个天线单元施加不同的相位延迟,实现波束的方向性选择。
通过相位延迟控制,可以控制波束的形成方向。
3.对接收到的回波信号进行时域和频域处理,获得目标的空时信息。
4.对每个源波束的输出信号进行相干合成,得到新的波束。
5.对新的波束进行后续的信号处理和成像算法,获得目标的成像结果。
最大似然法是一种基于统计学的多波束成像算法。
它假设目标的回波信号满足高斯分布,并利用最大似然估计方法,通过最大化似然函数,计算出目标的位置和幅度信息。
最小二乘法是一种通过最小化误差平方和的方法,进行多波束成像的算法。
它根据每个源波束的输出信号和目标位置的关系,建立数学模型,通过求解最小二乘问题,得到目标的位置和幅度估计结果。
总之,多波束成像算法是相控阵雷达中的重要技术,通过采集多个波束的回波信号,并利用合适的算法进行信号处理和成像分析,可以实现目标的快速探测和精确定位。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2Vr2 f 0 f 。 cR0
1.2.2 一般情况下的信号频谱
为了获得双曲距离等式的信号频谱,可进行如下操作:(1) 距离向 FFT;(2) 方位 向 FFT;(3) 距离向逆 FFT。其中前两步得到二维频域表达式,最后一步得到距离多普 勒域表达式。 将信号进行距离向 FFT,利用驻定相位原理,得到 距离频域的表达式
D2 df f , f , Vr 1
c 2 f2 4Vr2 f 0 f c 2 f2 4Vr2 f 0 f
2 2
,则
Vr2 2 R 2
1
(1.2.13)
由于 D2df(fτ, fη, Vr)就是直线几何中方位时刻 η 时的斜视角 θr 的余弦值,且距离徙动可以 表示为 R0 / cosθr 的形式,因此,D2df(fτ, fη, Vr)称为二维频域中的徙动因子。为了给出不 同相位项的显示表达式,令 D f , Vr 1
c 2 f2 4Vr2 f 02
,则二维频域的表达式为
s2 df f , f A0 A1 A2Wr f Wa f fc f2 4 R0 f 0 exp j exp j Kr c
2 f f2 2 f0 f0 (1.2.14)
c 2 f2
可以忽略。第一项代表方位向调制,第二项代表距离徙动,第三项代表距离和方位的交 叉耦合。下面,可以直接写出傅立叶积分中的相位
c 2 f2 f2 f f2 4 R0 f 0 2 3 2 f (1.2.16) D f , Vr c 4Vr2 f 02 K r f D f V f D f V , 2 , 0 0 r r
其中,常数 A1 含有一个 / 4 的相位,但它对下面的分析并不重要。 将信号进行方位向 FFT,利用驻定相位原理处理时,公式比较繁琐,下面给出推导 过程。傅立叶积分中的相位为
4 f 0 f R f2 2 f c Kr
(1.2.9)
(1.2.2)
将信号进行方位向 FFT,利用驻定相位原理,得到 普勒域的频谱
,从而可以得到距离多
2 Rrd f Wa f fc srd , f A0r c 2 2 Rrd f f2 4 exp j R exp j exp j K r c 0 Ka
下面给出典型的机载和星载条带 SAR 的参数。 表 1-1 机载和星载 SAR 的典型参数 参数 距离向参数 景中心距离 高度 发射脉冲时宽 距离脉冲调频率 信号带宽 距离采样率 斜距条带宽度 方位向参数 雷达有效速度 雷达工作频率 雷达工作波长 方位调频率 合成孔径长度
6
符号
机载
星载
单位
R(ηc) Tr Kr Fr
信号的二维频域表达式可以表示为
(1.2.10)
cR0 f 2 f 0 f Vr2 1 c 2 f2 4Vr2 f 0 f
2
。于是,
f2 s2 df f , f A0 A1 A2Wr f Wa f fc exp j Kr c 2 f2 4 R0 f 0 f exp j 1 2 2 c 4Vr f 0 f
(1.2.4)
其中,Rrd 为该域中的距离徙动量,其表达式为 Rrd f R0 这是一条关于 fη 的抛物线。 对 距 离 多 普 勒 域 的 信 号 进 行 距 离 向 FFT , 利 用 驻 定 相 位 原 理 , 得 到
2 R0
8V
2 r
f2
(1.2.5)
f 2 Rrd f ,从而可以得到二维频域的频谱 Kr c
4 f 0 f R f2 s0 f , A0 AW exp j (1.2.8) 1 r f a c exp j Kr c
f 2 R ,从而可以得到 Kr c
(1.2.11)
其中,包络 Wa 的表达式为
4
cR0 f Wa f a c 2 f2 2 2 2 f 0 f Vr 1 2 4Vr f 0 f
(1.2.12)
用符号 D2df(fτ, fη, Vr)表示根号项 1
1 Kr
2Vr2 f 03 D 3 f , Vr
Kr cR0 f2
2 R0 ,代入积分表达式,得到 cD f V , r
距离多普勒域的表达式为
2 R0 srd , f A0 A1 A2 A3r K m Wa f fc cD f ,Vr 2 2 R0 4 R0 D f ,Vr f 0 exp j exp j K m c cD f , V r
c 2 f2 f f2 2 f f2 2 D f , Vr D f , Vr f0 f0 f 0 D f , Vr 2 f 02 D 3 f , Vr 4Vr2 f 02
2
2
(1.2.15)
2 f f2 该近似是对根式的 Taylor 展开,当 D f , Vr 1 2 2 2 时,展开的高次项 4Vr f 0 f0 f0
(1.2.6)
假设 f0 >> |fτ|,Ka 中的距离向频率 f0 由 f0 + fτ 所代替,则二维频域的频谱可以简化为
3
s2 df f , f A0Wr f Wa f fc
(1.2.7)
f2 4 f 0 f f2 R0 exp j exp j exp j Kr c Ka '
f
因此,θ(fτ)对 fτ 的导数为
cR0 f2 d f 4 R0 2 f f 2 2 2 3 3 df Kr cD f ,Vr 2Vr f 0 D f ,Vr
(1.2.17)
5
令
d f 0 ,则 f df
第1章 条带模式合成孔径雷达
1.1 基本定义和几何模型
图 1-1 单站条带 SAR 几何模型
1.2 回波信号频谱
基于处理效率考虑,大多数 SAR 处理算法都工作在频域,其中匹配滤波和距离徙 动校正(RCMC)是首要考虑的效率因素。在方位频域,最短斜距相同的目标具有一致的 距离徙动轨迹,这样使得在该域中应用 RCMC 较为方便。因此,对距离多普勒域和二 维频域中的 SAR 信号频谱的推导是十分有用的。 1.2.1 信号频谱的抛物线近似 对于诸如 ERS 或 RADARSAT 这样具有小斜视角和中等孔径长度的传感器, 双曲距
D 2 f ,Vr
其中,常数 A2 含有一个无关紧要的 / 4 的相位。在数字处理器实现中,先进行距离向
FFT 还是方位向 FFT 并不重要。在任何情况下,二维信号频谱都可以用以上等式精确表
达。 对二维频域的信号进行距离向逆 FFT,直接应用驻定相位原理,会导致出现 fτ 的四 次方程,使得代数求解过程冗长。为避免繁琐的代数处理,作如下近似
目标照射时间 天线长度 多普勒带宽 方位采样率(PRF) 斜视角
Ta La Δfdop Fa θr,c
3.4 1 443 600 <8
0.64 10 1338 1700 <4
s m Hz Hz °
根据典型的机载和星载参数,我们画出回波信号在不同域中的图形,如下:
(a)
(b)
7
(c)
(d)
图 1-2 典型机载参数的 SAR 回波:(a) 正调频时域回波信号(相位);(b) 负调频时域回 波信号(相位);(c) 回波信号的二维频域(幅度);(d) 回波信号的距离-多普勒域(幅度)
将瞬时斜距表达式代入,得到 θ(η)对 η 的导数为
d 4 f 0 f Vr2 2 f d c R02 Vr2 2 2Vr2 f 0 f d 令 0 ,则 f 或 d c R02 Vr2 2
第一步,将回波信号通过二维 FFT,将数据变换到二维频域,结果如下
s2 df f , f AWr f Wa f fc
(1.3.1)
f2 4 f R0 4 R0 exp j exp j D f ,Vr exp j Km cD f , Vr
(1.2.18)
其中, K m
1 Kr
2Vr2 f 03 D 3 f , Vr
Kr cR0 f2
为新的距离调频率,常数 A3 含有一个无关紧要的
/ 4 的相位。距离向包络 ωr 表示距离徙动,第一个指数项为有距离徙动引起的方位向
调制,第二个指数项为距离向调制。
1.2.3 条带 SAR 的典型参数
(a)
8
(b)
(c)
(d)
图 1-3 典型机载参数的 SAR 回波:(a) 正调频时域回波信号(相位);(b) 负调频时域回 波信号(相位);(c) 回波信号的二维频域(幅度);(d) 回波信号的距离-多普勒域(幅度)
9
1.3 Range-Doppler 成像算法
1.3.1 Range-Dopper 算法流程
2
离等式可以进行抛物线近似 R R02 Vr2 2 R0 于是,基带接收信号可以近似为 2 R s0 , A0r a c c 2 2 R 4 2 exp j R0 exp j K a exp j K r c 其中方位向调频率 Ka 为 Ka 2Vr2 2Vr2 f 0 R0 cR0 f Ka (1.2.3) Vr2 2 2 R0 (1.2.1)
