第六章 随机数生成器
第六章 随机数生成器

不可少的 基本元素 (0,1)均匀分布随机数是产生其他许多分布 的随机数的基础 一个随机数序列必须满足两个重要的统计性质: 均匀性和独立性
随机数的性质
均匀性 如果将区间[0,1]分为n个等长的子区间,那 么在每个区间的期望观测次数为N/n,其中N 为观测的总次数 独立性 观测值落在某个特定区间的概率与以前的观测 值无关
线性同余随机数生成器(LCG)
Zi (aZi 1 c)(mod m)
其中,a称为乘法因子,c称为加法因子,m为 模数 当a=1时,为加同余法; 当c=0时,为乘同余法; 当a≠1、c≠0时,为混合同余法
例:
使用线性同余法产生随机数序列,其中Z0=27、 a=17、c=43、m=100。 解:Zk=(aZk-1+c)mod m Z1=(17×27+43) mod 100=502mod100=2 Z2=(17×2+43) mod 100=77mod100=77 Z3=(17×77+43) mod 100=1352mod100=52 …… U1=2/100=0.02, U2=77/100=0.77, U3=0.52
当Xi=Ui时,E(Ui) 1/ 2,V(Ui)=1/12 E ( X i X i j ) 1/ 4 所以, j 12E ( X i X i j ) 3 1/12
相关性检验
12 h j U1 kj U1 (k 1) j 3, h 1 k 0
定理:
LCG具有满周期,当且仅当以下3个条件成立:
1. m和c互质;
2. 存在一个质数q,能够同时整除m和a-1; 3. m和a-1能够被4整除。
用Python编程语言编写随机数生成器程序示例

用Python编程语言编写随机数生成器程序示例标题: 用Python编程语言编写随机数生成器程序示例介绍:这个示例程序将演示如何使用Python编程语言生成随机数。
随机数在很多领域都有应用,例如游戏开发、数据分析、密码学等。
我们将使用Python内置的random模块来生成随机数。
这个模块提供了多种生成随机数的方法。
以下是一个简单的示例代码,它将生成一个介于0和1之间的随机浮点数:```pythonimport randomrandom_number = random.random()print("随机数:", random_number)```在这个示例中,我们首先导入了random模块。
然后,使用random()函数来生成一个介于0和1之间的随机浮点数,并将结果保存在变量random_number中。
最后,我们使用print函数将随机数打印出来。
如果你需要生成一个特定范围内的随机整数,你可以使用randint()函数。
以下是一个示例代码,它将生成一个介于1和10之间的随机整数:```pythonimport randomrandom_integer = random.randint(1, 10)print("随机整数:", random_integer)```在这个示例中,我们使用randint()函数生成一个介于1和10之间的随机整数,并将结果保存在变量random_integer中。
除了这些方法,random模块还提供了其他许多生成随机数的函数,例如生成随机选择的样本、生成随机浮点数、生成随机字节等。
总结:这个示例程序展示了如何使用Python编程语言生成随机数。
通过使用random模块中提供的函数,我们可以轻松地生成随机数,并在不同的应用中使用它们。
无论是生成随机整数、浮点数还是随机选择样本等,Python的random模块都提供了丰富的函数来满足各种需求。
真随机数生成器原理-概述说明以及解释

真随机数生成器原理-概述说明以及解释1.引言1.1 概述在引言部分的概述中,我们将介绍真随机数生成器的原理。
随机数在许多领域中起着重要的作用,如密码学、模拟实验和数据加密等。
然而,传统的伪随机数生成器在生成随机数时存在一定的规律性和可预测性,这可能会导致数据的不安全性和模拟实验的误差。
因此,为了解决这一问题,真随机数生成器应运而生。
本文将深入探讨真随机数的定义、真随机数的重要性以及真随机数生成器的原理。
首先,我们将介绍真随机数的定义,即无法以任何方式预测或确定的数值。
接着,我们将探讨真随机数在密码学、模拟实验和数据加密等领域的重要性,说明为什么需要使用真随机数生成器。
随后,我们将详细讨论真随机数生成器的原理。
真随机数生成器是一种能够利用物理或环境噪声生成真正随机数的设备或算法。
我们将介绍一些常见的真随机数生成器方法,例如基于硬件设备的真随机数生成器和基于环境噪声的真随机数生成器。
我们将探究它们的工作原理和优缺点,并讨论如何确保生成的随机数具有高度的真实性和随机性。
最后,我们将总结本文的主要内容,并展望真随机数生成器的应用前景。
真随机数生成器在密码学中的应用可以加强数据的安全性,而在模拟实验中的应用可以提高结果的准确性。
此外,真随机数生成器还有望在数据加密、随机抽样和随机算法等领域发挥更重要的作用。
综上所述,真随机数生成器具有广泛的应用前景,值得进一步研究和探索。
通过本文的阅读,读者将能够了解到真随机数生成器的原理和应用,进一步认识到真随机数的重要性,并对相关领域的发展和应用提供有益的参考。
1.2 文章结构本文将从引言、正文和结论三个部分来探讨真随机数生成器的原理。
具体来说,文章结构如下:引言部分将简要介绍本文的背景和目的。
首先,我们会概述真随机数的定义以及其在各个领域的重要性。
接下来,我们会明确文章的结构,并简要介绍各个章节的内容。
正文部分将详细探讨真随机数生成器的原理。
首先,我们会对真随机数的定义进行进一步解释,包括其与伪随机数的区别和随机性的特征。
随机数生成器公式

随机数生成器公式随机数生成器公式,这玩意儿听起来是不是有点神秘又有点高大上?其实啊,它在我们的生活和学习中还挺常见的。
先来说说啥是随机数。
随机数啊,就像是老天爷闭着眼睛随便扔出来的数字,没有啥规律可言。
比如说抽奖的时候,电脑随机抽出的中奖号码,那就是随机数。
那随机数生成器公式是咋回事呢?简单来说,就是通过一些数学的方法和规则,让计算机或者其他工具能够“制造”出看起来像是随机出现的数字。
咱们就拿一个简单的例子来说吧。
假设我们要在 1 到 100 之间生成随机数,有一种常见的方法是用编程语言里的随机函数。
就像在Python 里,可以用“random.randint(1, 100)”这个命令,每次运行,它都会给出一个 1 到 100 之间的随机数。
我记得有一次,我们班上搞活动,要通过随机数来决定谁先上台表演节目。
我就用电脑上的随机数生成器来操作,同学们那叫一个紧张又兴奋,眼睛都紧紧盯着屏幕,等着看谁是那个幸运儿。
当第一个随机数出来的时候,被选中的同学先是一愣,然后满脸通红地走上台,大家都哈哈大笑。
再深入一点说,随机数生成器公式可不只是这么简单。
有些更复杂的公式,是为了让生成的随机数更符合真正的随机特性。
比如说,要避免出现连续出现相同数字的情况,或者要保证每个数字出现的概率都差不多。
还有啊,随机数生成器在科学研究里也大有用处。
比如说做模拟实验的时候,需要用随机数来模拟各种不确定的因素。
像研究天气变化、金融市场的波动,都得靠随机数生成器来帮忙。
在游戏开发中,随机数生成器也是不可或缺的。
想象一下,要是游戏里的怪物出现、宝藏掉落都是固定的,那多没意思啊!有了随机数,每次玩游戏都有新的惊喜和挑战。
不过,随机数生成器也不是完美无缺的。
有时候,由于算法的限制,可能会出现一些不太随机的情况。
比如说,在某些情况下,可能会出现一小段数字看起来有规律的现象。
总之,随机数生成器公式虽然看起来有点复杂,但它真的给我们的生活和各种领域带来了很多有趣和有用的东西。
概率模拟使用随机数生成器进行概率模拟

概率模拟使用随机数生成器进行概率模拟概率模拟:使用随机数生成器进行概率模拟概率模拟是一种通过生成随机事件来模拟研究概率问题的方法。
为了有效进行概率模拟,我们常常使用随机数生成器来产生符合一定概率分布的随机数。
本文将介绍概率模拟的基本原理,并详细说明如何使用随机数生成器进行概率模拟。
一、概率模拟基本原理概率模拟是基于概率论的一种分析方法,通过模拟随机事件的发生情况来预测其概率分布。
在现实世界中,很多事件的结果是不确定的,无法通过精确计算得到其概率。
这时候,我们可以通过随机数生成器模拟一系列随机事件,然后根据模拟结果统计频率,从而推断真实概率。
概率模拟的基本原理可以用以下步骤总结:1. 定义随机试验:明确研究对象、试验过程和结果。
2. 设定概率分布:根据实际情况,假设事件的概率分布。
3. 生成随机数:使用随机数生成器生成符合设定概率分布的随机数。
4. 进行模拟:多次独立地重复试验,并记录事件发生的频率。
5. 统计频率:根据模拟结果统计频率分布,推断真实概率。
二、随机数生成器的选择随机数生成器是概率模拟的关键工具,它能够生成满足特定概率分布的随机数序列。
在选择随机数生成器时,需要考虑以下几个因素:1. 均匀性:生成的随机数应该具有均匀分布特性,保证随机性。
2. 独立性:生成的随机数应该相互独立,避免序列中的随机数之间存在相关性。
3. 有效性:生成的随机数应该能够满足模拟的需求,有足够的精度和范围。
常用的随机数生成器包括线性同余法、Mersenne Twister算法等。
三、使用随机数生成器进行概率模拟的步骤使用随机数生成器进行概率模拟通常包括以下几个步骤:1. 确定模拟的随机事件和概率分布。
在进行概率模拟前,首先需要明确研究对象和所关注的随机事件,并根据实际情况设定相应的概率分布。
2. 设定随机数生成器参数。
根据所选择的随机数生成器,设定相应的参数,如随机数种子、生成的随机数范围等。
3. 生成随机数序列。
C语言程序设计 – 第 06 章课后习题

C语言程序设计– 第六章课后习题电子13-02班王双喜一、选择题1. C语言中一维数组的定义方式为:类型说明符数组名(C)A. [整型常量]B. [整型表达式]C. [整型常量]或[整型常量表达式]D. [常量表达式]2. C语言中引用数组元素时,下标表达式的类型为(C)A. 单精度型B. 双精度型C. 整型D. 指针型3. 若有定义:int a[3][4];,则对a数组元素的非法引用是(D)A. a[0][3*1]B. a[2][3]C. a[1+1][0]D. a[0][4](解释:A、B、C均正确,D看起来引用不太妥当,但其亦有其意义(a[0][4]等价于a[1][0]))4. 若有定义:int a[][3] = {1, 2, 3, 4, 5, 6, 7, 8, 9};,则a数组的第一维大小是(C)A. 1B. 2C. 3D. 4(解释:共9个元素,除以3即可得第一维大小是3;若有余数,则应加1)5. 若有定义:int a[] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};,则值为5的表达式是(C)A. a[5]B. a[a[4]]C. a[a[3]]D. a[a[5]]6. 要求定义包含8个int类型元素的一维数组,以下错误的定义语句是(A)A. int N = 8;int a[N]; B. #define N 3while (a[2*N+2];C. int a[] = {0, 1, 2, 3, 4, 5, 6, 7};D. int a[1+7] = {0};(解释:数组的大小必须是整型常量或整型常量表达式)7. 若二维数组a有m列,则在a[i][j]前的元素个数为(A)A. i * m + jB. j * m + iC. i * m + i - 1D. i * m + j - 18. 下面是对数组s的初始化,其中不正确的是(D)A. char s[5] = {"abc"};B. char s[5] = {'a', 'b', 'c'};C. char s[5] = "";D. char s[5] = "abcdef";(解释:D中元素个数太多,算上'\0'共六个,非法)9. 下面程序段的运行结果是(B)char c[] = "\t\v\\\0will\n";printf("%d", strlen(c));A. 14B. 3C. 9D. 字符串中有非法字符,输出值不确定(解释:字符串中第四个是'\0'即结束标志,因此字符串长度是3)10. 判断字符串s1是否等于s2,应当使用(D)A. if (s1 == s2)B. if (s1 = s2)C. if (strcpy(s1, s2))D. if (strcmp(s1, s2) == 0)(解释:对于字符串来讲,其名字的内容是该字符串的起始地址,不能通过比较名字来比较相等,而应该用专用的函数进行逐字符匹配)二、写出程序的执行结果1. 程序一:# include <stdio.h>main(){int a[3][3] = {1, 3, 5, 7, 9, 11, 13, 15, 17};int sum = 0, i, j;for (i = 0; i < 3; i++)for (j = 0; j < 3; j++){a[i][j] = i + j;if (i == j) sum = sum + a[i][j];}printf("sum = %d", sum);}执行结果:打印sum = 6.(解释:a中各个元素的值是其行和列数字之和,sum内保存a中对角线元素之和,即sum = 0 + 2 + 4)2. 程序二:# include <stdio.h>main(){int i, j, row, col, max;int a[3][4] = {{1, 2, 3, 4}, {9, 8, 7, 6}, {-1, -2, 0, 5}};max = a[0][0]; row = 0; col = 0;for (i = 0; i < 3; i++)for (j = 0; j < 4; j++)if (a[i][j] > max){max = a[i][j];row = i;col = j;}printf("max = %d, row = %d, col = %d\n", max, row, col);}执行结果:打印max = 9, row = 1, col = 0.(解释:此程序的功能是逐行逐列扫描元素,总是将最大的元素赋给max,并保存该元素的行数和列数;因此执行完毕后,max是最大的元素(9),row是其行数(1),col是其列数(0))3. 程序三:# include <stdio.h>main(){int a[4][4], i, j, k;for (i = 0; i < 4; i++)for (j = 0; j < 4; j++)a[i][j] = i - j;for (i = 0; i < 4; i++){for (j = 0; j <= i; j++)printf("%4d", a[i][j]);printf("\n");}}执行结果:第一行打印0;第二行打印1 0;第三行打印2 1 0;第四行打印3 2 1 0。
第六章伪随机序列生成器

n
l (n)
l ( n)
; n 1
l (n)
6.2 伪随机序列生成器的定义和性质
定义 6.5 一个伪随机序列生成器是一个确定性多项式 时间算法G满足下列两个条件: 1)延伸性,存在一个正整数函数 l (n) n(n 1,2,) 使得对一 切 x 0,1*有 G( x) l ( x ) ; 2)伪随机性,随机变量序列 G(U n ); n 1是伪随机的,即 U l ( n) ; n 1 是多项式时间不 它与均匀分布随机变量序列 可区分的。 生成器G的输入x称为它的种子,要求将长n比特的种 子延伸为长l(n)比特的序列,且该序列与长l(n)的随机 比特序列是多项式时间不可区分的。l(n)>n称为的延 伸因子。
i i i 1
(3)不可预测性。 定义 6.6 随机变量序列X n ; n 1称为多项式时间 不可预测的若对每个多项式时间概率算法M’, 每个正多项式p(n)和一切充分大的n有 1 1 PrM (1 , X ) next ( X ) (6.4) 2 p ( n) 定理 6.3 一个随机变量序列X ; n 1是伪随机的 (参看定义6.4)当且仅当它是多项式时间不 可预测的。 (4)单向函数性。 定理 6.4 设G为一延伸因子l(n)的伪随机序列生 成器,若对每对 x, y 0,1满足 x y ,定义函数 f ( x, y) G( x) ,则f为一强单向函数。
第六章 伪随机序列生成器
6.1 计算不可区分性
* 0 , 1 定义 6.1 一个概率分布族是由 的一个无穷 子集I,称为指标集,和每个指标 i I 对应一个 概率分布p ( x) : D [0,1], p ( x) 0, p ( x) 1 构成,其中 * 0 , 1 Di为 的一个有穷子集。 定义 6.2 两个随机变量族 X | x D , i I 和Y | y E , i I 称为多项式时间不可区分,若对每个多项 式时间概率算法M’,每个正多项式p(n)和一切 充分大的n有 PrM ' ( X i , i) 1 PrM ' (Yi , i) 1 1 (6.1) p( i )
随机数生成器原理

随机数生成器原理随机数生成器是计算机科学中一个非常重要的概念,它在密码学、模拟实验、统计学等领域都有着广泛的应用。
随机数生成器的原理是如何产生一系列看似无规律、不可预测的数字序列,这些数字序列被认为是随机的。
在现代计算机系统中,随机数生成器是一个至关重要的组成部分,它为计算机提供了随机性,使得计算机能够执行各种复杂的任务。
本文将介绍随机数生成器的原理及其在计算机科学中的应用。
随机数生成器的原理可以分为伪随机数生成器和真随机数生成器两种。
伪随机数生成器是通过一定的算法产生一系列近似随机的数字序列,这些数字序列在一定程度上具有随机性,但是其实质是确定性的。
真随机数生成器则是通过一些物理过程产生真正的随机性,比如利用量子力学的原理来产生随机数。
在实际应用中,由于真随机数生成器的成本较高,大部分情况下我们使用的是伪随机数生成器。
伪随机数生成器的原理是基于一个种子(seed)和一个确定性的算法来产生随机数序列。
种子是一个初始值,通过对种子进行一系列的数学运算,比如加法、乘法、取模等,就可以产生一系列的伪随机数。
在计算机中,通常使用当前的系统时间作为种子,以保证每次生成的随机数序列都是不同的。
当然,在一些特定的应用中,我们也可以自己指定种子来产生确定的随机数序列。
随机数生成器在计算机科学中有着广泛的应用。
在密码学中,随机数生成器被用来产生加密密钥,以保证数据的安全性。
在模拟实验中,随机数生成器可以用来模拟各种随机事件,比如赌博游戏、天气模拟等。
在统计学中,随机数生成器可以用来进行抽样调查,以获取一定的样本数据。
总的来说,随机数生成器在计算机科学中扮演着非常重要的角色。
在实际应用中,我们需要注意随机数生成器的质量。
一个好的随机数生成器应该具有均匀性、独立性和周期性。
均匀性是指随机数生成器产生的随机数应该服从均匀分布,即每个数值的概率应该是相同的。
独立性是指随机数生成器产生的随机数应该是相互独立的,一个随机数不应该受到其他随机数的影响。
随机数生成器

随机数的原理与计算机实现摘要:随机数在计算机网络信息安全中起着至关重要的作用。
本文将对随机数,随机数产生器如何用计算机语言(JAVA )实现做简要介绍。
Abstract :Random number in the computer network information security plays a vital role. This will be random numbers, random number generator to use the computer language (JAVA) to achieve a brief introduction.关键字:随机数、计算机网络信息安全、JAVA 、随机数产生器Keyword :Random numbers, computer network and information security, JAVA, random number generator一、随机数简介什么叫随机数呢?由具有已知分布的总体中抽取简单子样,在蒙特卡罗方法中占有非常重要的地位。
总体和子样的关系,属于一般和个别的关系,或者说属于共性和个性的关系。
由具有已知分布的总体中产生简单子样,就是由简单子样中若干个性近似地反映总体的共性。
随机数是实现由已知分布抽样的基本量,在由已知分布的抽样过程中,将随机数作为已知量,用适当的数学方法可以由它产生具有任意已知分布的简单子样。
在连续型随机变量的分布中,最简单而且最基本的分布是单位均匀分布。
由该分布抽取的简单子样称,随机数序列,其中每一个体称为随机数。
单位均匀分布也称为[0,1]上的均匀分布,其分布密度函数为:分布函数为 :由于随机数在蒙特卡罗方法中占有极其重要的位置,我们用专门的符号ξ表示。
由随机数序列的定义可知,ξ1,ξ2,…是相互独立且具有相同单位均匀分布的随机数序列。
也就是说,独立性、均匀性是随机数必备的两个特点。
随机数具有非常重要的性质:对于任意自然数s ,由s 个随机数组成的s 维空间上的点(ξn+1,ξn+2,…ξn+s )在s 维空间的单位立方体G s 上均匀分布,即对任意的a i ,如下等式成立:⎩⎨⎧≤≤=其他,010,1)(x x f ⎪⎩⎪⎨⎧>≤≤<=1,110,0,0)(x x x x x F si a i ,,2,1,10 =≤≤∏=+==≤si ii i n a s i a P 1),,1,( ξ其中P (·)表示事件·发生的概率。
真随机数生成器原理

真随机数生成器原理全文共四篇示例,供读者参考第一篇示例:真随机数生成器(TRNG)是指通过利用无法预测的物理或生物过程生成的随机数的设备。
相较于伪随机数生成器(PRNG),真随机数生成器生成的随机数更具有随机性和不可预测性,能够在安全性要求高的领域发挥重要作用。
在计算机科学、密码学、模拟计算等领域,真随机数生成器广泛应用。
真随机数生成器的工作原理主要基于物理或生物过程的不可预测性。
常用的物理过程包括量子效应、热噪声、光电效应等;生物过程则包括人类感知、动物运动等。
通过利用这些过程,可以获取到具有高度随机性的数据,从而生成真随机数。
量子效应是一种常用的真随机数生成器的物理原理。
在量子物理学中,一个系统的状态可以是多个状态的线性叠加,而当这个系统被观测时,其状态会坍缩为一个确定的状态。
量子效应的不可预测性保证了生成的随机数的高度随机性。
通过利用量子效应,可以构建基于量子比特的真随机数生成器。
另一个常用的真随机数生成器原理是热噪声。
在物理系统中,由于温度的存在,会导致电子的不规则运动和碰撞,产生电子在电路中随机分布的现象。
通过测量这些不规则的电信号,可以获取到高度随机的数据,从而生成真随机数。
热噪声真随机数生成器具有结构简单、易实现的特点,被广泛应用于各种场景。
光电效应也是一种常用的真随机数生成器原理。
在光电转换器件中,当光子撞击材料表面时,会引发电子的光电发射现象。
由于光子的不可预测性,引发的光电发射现象也是不可预测的,从而可以作为真随机数生成器的输入源。
光电效应真随机数生成器具有高速、实时性强的特点,适用于要求高速随机数生成的场景。
在生物过程方面,人类感知也可以作为真随机数生成器的原理。
在密码学中,可以利用人类对随机性的感知来生成真随机数。
通过让人类在一组随机数中选择特定的数字或位置,可以获取到高度随机的数据。
由于人类的感知能力是不可预测的,因此生成的随机数也具有高度的随机性。
除了以上介绍的几种原理外,还有许多其他物理或生物过程可以作为真随机数生成器的原理,例如原子核衰变、混沌系统等。
随机数生成器工具的程序设计及代码示例

随机数生成器工具的程序设计及代码示例随机数生成器是计算机科学中常用的工具,用于生成不可预测的随机数序列。
这在许多应用中都是十分重要的,比如密码学、模拟实验、游戏开发等等。
本文将介绍随机数生成器的程序设计原理,并给出一个代码示例供参考。
一、随机数生成器的原理随机数生成器的原理通常基于一个起始点,通过一系列的计算操作,生成一个似乎无序的数列。
这个数列根据所用的算法可以是伪随机序列,但在实际应用中已经足够满足需求。
随机数生成器的设计需要考虑以下几个因素:1. 常数种子值:随机数生成器需要一个种子值作为起点。
这个种子值可以是用户输入的,也可以是从系统时间获取的。
种子值越随机,生成的随机数序列越随机。
2. 随机数算法:常用的随机数算法有线性同余算法、梅森旋转算法等。
在选择算法时,需要考虑算法的效率和生成的随机数的质量。
3. 生成范围:随机数生成器需要指定生成的随机数的范围。
在实际应用中,常常需要生成整数或者在一定范围内的浮点数。
二、随机数生成器的代码示例下面是一个使用Python编写的随机数生成器的简单示例。
```pythonimport timeclass RandomNumberGenerator:def __init__(self, seed=None):if seed is None:seed = int(time.time())self.seed = seeddef generate(self):a = 1103515245c = 12345m = 2 ** 31self.seed = (a * self.seed + c) % mreturn self.seed# 示例代码rng = RandomNumberGenerator()for _ in range(10):print(rng.generate())```在这个示例代码中,我们定义了一个RandomNumberGenerator类,其中包含了一个generate方法用于生成随机数。
系统建模与仿真-第六章随机变量的生成
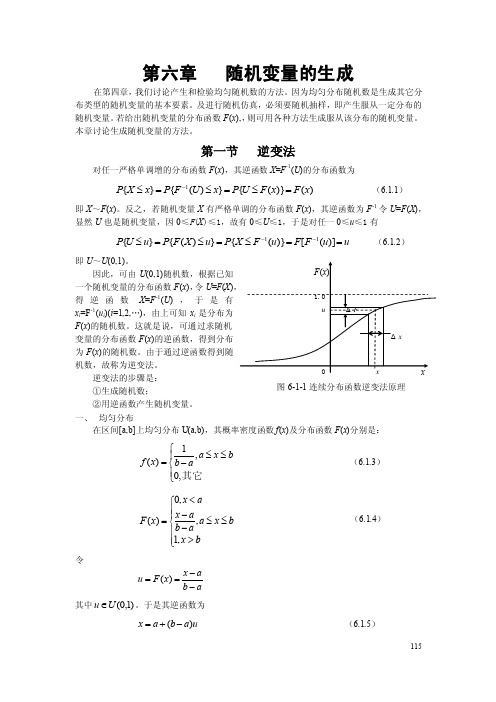
第六章 随机变量的生成在第四章,我们讨论产生和检验均匀随机数的方法。
因为均匀分布随机数是生成其它分布类型的随机变量的基本要素。
及进行随机仿真,必须要随机抽样,即产生服从一定分布的随机变量。
若给出随机变量的分布函数F (x ),,则可用各种方法生成服从该分布的随机变量。
本章讨论生成随机变量的方法。
第一节 逆变法对任一严格单调增的分布函数F (x ),其逆函数X =F -1(U )的分布函数为)()}({})({}{1x F x F U P x U F P x X P =≤=≤=≤- (6.1.1) 即X ~F (x )。
反之,若随机变量X 有严格单调的分布函数F (x ),其逆函数为F -1令U =F (X ),显然U 也是随机变量,因0≤F (X )≤1,故有0≤U ≤1,于是对任一0≤u ≤1有 u u F F u F X P u X F P u U P ==≤=≤=≤--)]([)}({})({}{11 (6.1.2) 即U ~U (0,1)。
因此,可由U (0,1)随机数,根据已知一个随机变量的分布函数F (x ),令U =F (X )得逆函数X =F -1(U ),于是有x i =F -1(u i )(i =1,2,…),由上可知x i 是分布为F (x )的随机数。
这就是说,可通过求随机变量的分布函数F (x )的逆函数,得到分布为F (x )的随机数。
由于通过逆函数得到随机数,故称为逆变法。
逆变法的步骤是:①生成随机数;②用逆函数产生随机变量。
一、 均匀分布在区间[a,b]上均匀分布U(a,b),其概率密度函数f (x )及分布函数F (x )分别是:⎪⎩⎪⎨⎧≤≤-=其它,0,1)(b x a a b x f (6.1.3)⎪⎪⎩⎪⎪⎨⎧>≤≤--<=bx b x a a b ax a x x F ,1,,0)( (6.1.4) 令ab ax x F u --==)( 其中)1,0(U u ∈。
随 机 数 生 成 器

随机数生成器与线性同余法产生随机数1、随机数生成器与-dev-random:随机数生成器,顾名思义就是能随机产生数字,不能根据已经产生的数预测下次所产生的数的“器”(器存在软件与硬件之分),真正的随机数生成器其产生的随机数具有随机性、不可预测性、不可重现性。
什么是真正的随机数生成器?指的是由传感器采集设备外部温度、噪声等不可预测的自然量产生的随机数。
比如Linux的-dev-random设备文件其根据设备中断(键盘中断、鼠标中断等)来产生随机数,由于鼠标的操作(移动方向、点击)是随机的、不可预测的也是不可重现的,所以产生的随机数是真随机数。
-dev-random即所谓的随机数池,当通信过程(如https安全套接层SSL)需要加密密钥时,就从随机数池中取出所需长度的随机数作为密钥,这样的密钥就不会被攻击者(Attacker)猜测出。
但是由于-dev-random是采集系统中断来生成随机数的,所以在无系统中断时,读取-dev-random是处于阻塞状态的,如下所示(鼠标移动与否决定了cat -dev-random的显示结果,cat -dev-random | od -x先显示的4行是查看该设备文件前,系统中断被采集而产生的随机数,而之后的随机数则是鼠标移动锁产生的随机数):cat读取-dev-radom测试效果.gif在Linux上还存在随机数生成器-dev-urandom,而读取该随机数池是不会阻塞的,因为其不受实时变化的因素影响,所以-dev-urandom是一个伪随机数生成器,而C语言的rand()库函数所产生的随机数也是伪随机数。
-dev-random与-dev-urandom的区别在于一个阻塞一个非阻塞,一个更安全一个较安全。
对于-dev-random来说,如果需要的随机数长度小于随机数池中的随机数,则直接返回获取到的随机数,并且池中的随机数长度减去获取长度,如果要获取的随机数长度大于池中已有的长度,则获取的进程处于阻塞状态等待新的生成的随机数部分注入池中。
随机数生成器原理

随机数生成器原理随机数生成器是计算机科学中非常重要的一个概念,它可以用来产生一系列看似无规律的数字,但实际上却具有一定的规律性。
在计算机编程、密码学、模拟实验等领域,随机数生成器都扮演着至关重要的角色。
那么,随机数生成器的原理是什么呢?随机数生成器的原理主要分为伪随机数生成器和真随机数生成器两种。
首先,我们来看伪随机数生成器。
伪随机数生成器是通过一定的算法,根据一个起始值,计算出一系列的数字。
这些数字看上去是随机的,但实际上是可以被复现的。
伪随机数生成器的核心在于随机种子的选择和算法的设计。
常见的伪随机数生成算法包括线性同余发生器、梅森旋转算法等。
这些算法都可以根据一个种子值,生成一系列的数字。
但是,由于算法本身的局限性,伪随机数生成器并不能产生真正意义上的随机数。
接着,我们来看真随机数生成器。
真随机数生成器是通过利用物理过程来产生随机数的。
常见的真随机数生成器包括基于热噪声、量子效应、大气噪声等。
这些真随机数生成器利用了自然界中的随机性,产生的随机数是真正意义上的随机数,不受任何规律性的约束。
真随机数生成器在密码学、安全通信等领域有着重要的应用,因为它们能够提供高质量的随机数,从而增强系统的安全性。
无论是伪随机数生成器还是真随机数生成器,它们都在计算机科学中扮演着非常重要的角色。
在实际应用中,我们需要根据具体的需求来选择合适的随机数生成器。
如果只是需要一些看似随机的数字,那么伪随机数生成器是一个不错的选择。
但如果需要高质量的随机数,那么真随机数生成器则是更好的选择。
总的来说,随机数生成器的原理涉及到数学、物理等多个领域,它们的设计和实现都需要深入的专业知识。
随机数生成器的选择对于系统的安全性和性能有着直接的影响,因此在实际应用中需要慎重考虑。
希望通过本文的介绍,读者能对随机数生成器的原理有所了解,并在实际应用中做出明智的选择。
随机数生成器

随机数⽣成器随机数⽣成器⼀、随机数1.1随机数的概念数学上是这样定义随机数的:在连续型随机变量的分布中,最简单⽽且最基本的分布是单位均匀分布。
由该分布抽取的简单⼦样称为随机数序列,其中每⼀个体称为随机数。
单位均匀分布即[0,1]上的均匀分布。
由随机数序列的定义可知,ξ1,ξ2,…是相互独⽴且具有相同单位均匀分布的随机数序列。
也就是说,独⽴性、均匀性是随机数必备的两个特点。
1.2随机数的分类随机数⼀般分为伪随机数和真随机数。
利⽤数学算法产⽣的随机数属于伪随机数。
利⽤物理⽅法选取⾃然随机性产⽣的随机数可以看作真随机数。
实⽤中是使⽤随机数所组成的序列,根据所产⽣的⽅式,随机数序列再可以分为两类:1.伪随机数序列伪随机数序列由数学公式计算所产⽣。
实质上,伪随机数并不随机,序列本⾝也必然会重复,但由于它可以通过不同的设计产⽣满⾜不同要求的序列且可以复现(相同的种⼦数将产⽣相同的序列),因⽽得到⼴泛的应⽤。
由伪随机数发⽣器所产⽣的伪随机数序列,只要它的周期⾜够长并能通过⼀系列检验,就可以在⼀定的范围内将它当作真随机数序列来使⽤。
2.真随机数序列真随机数序列是不可预计的,因⽽也不可能出现周期性重复的真正的随机数序列。
它只能由随机的物理过程所产⽣,如电路的热噪声、宇宙噪声、放射性衰变等。
按照不同的分类标准,随机数还可分为均匀随机数和⾮均匀随机数,例如正态随机数。
1.3随机数的衡量标准在实际模拟过程中,我们⼀般只需要产⽣区间[0,1]上的均匀分布随机数,因为其他分布的随机数都是由均匀分布的随机数转化来的。
实⽤中的均匀随机数主要通过以下三个⽅⾯来衡量其随机性能的⾼低。
1.周期性伪随机数序列是由具有周期性的数学公式计算产⽣,其本⾝也必然会表现出周期性,即序列中的⼀段⼦序列与另⼀段⼦序列相同。
它的周期必须⾜够长,才能为应⽤提供⾜够多的可⽤数据。
只有真随机数序列才能提供真正的、永不重复的随机数序列。
2.相关性随机数发⽣器所产⽣的⼀个随机数序列中的各个随机数应该不相关,所产⽣的各个随机数序列中的随机数也应该不相关。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
随机数的产生方法
物理方法:利用某些物理过程来产生均匀分布 随机数
随机数表:利用物理过程得到的大量随机数, 制成随机数表
随机数产生程序:按照一定的算法计算出具有 类似于均匀分布随机变量的独立取样值性质的 数
伪随机数
计算机产生随机数的要求
49
19
13
61
55
14
25
11
15
5
15
16
1
3
随机数的检验
为了检验产生的随机数序列是否满足均匀性和 独立性,有必要进行一系列的检验:
均匀性检验(频率检验) 序列检验 游程检验 相关性检验
均匀性检验
2检验
2 n (Oi Ei )2
i 1
Ei
其中,Oi为第i组中数据的观测值个数,Ei为第i 组中数据的期望个数,n为组数。
维均匀性,以此判断随机数序列的独立性。
假设Ui是独立同分布U(0,1)的随机变量,则构 造n个d维随机变量:
U1=(U1,U2,…,Ud), U2=(Ud+1,Ud+2,…,U2d),… 将[0,1]等分为k个子区间,则在d维空间中共有 kd个子区间,n个随机变量落在每个区间的个 数期望值(期望频度)为n/kd。设fj1,j2,…,jd为落 在子区间j1j2…jd的观测值个数(观测频度),
平方取中法
20世纪40年代由冯·诺依曼提出的第一个随机 数生成器
例:设有一个4位正整数Z0,对之取平方得到 一个8位正整数(如果不够8位数,可以在左侧 加上0补足8位)。而后取中间的4位获得一个 新的4位正整数Z1。将Z1/10000得到一个[0,1] 之间的小数,则获得第一个“随机数”U1。然 后基于Z1重复上述操作,得到Z2和U2,依次类 推……
2采样分布近似等于有n 1个自由度的 2分布
均匀性检验
2检验
H0:Ri服从U[0,1] H1:Ri不服从U[0,1] 检验方法:选定一个显著性水平 (如 =0.05)
如果2 k1,2,就接受H0,认为符合均匀性
序列检验
序列检验是运用 2检验来检验随机数序列的n
游程检验
aij, bi的取值见书第149,150页
如果n足够大(n≥4000),R近似满足自由度为6 的 2分布。
相关性检验
0.12 0.01 0.23 0.28 0.89 0.31 0.64 0.28 0.83 0.93 0.99 0.15 0.33 0.35 0.91 0.41 0.60 0.27 0.75 0.88 0.68 0.49 0.05 0.43 0.95 0.58 0.19 0.36 0.69 0.87
例:使用不同种子的周期
使用乘同余法,对a=13、m=26=64且 Z0=1,2,3,4, 求产生器的周期。
i
Xi
Xi
Xi
Xi
0
1
2
3
4
1
13
26
39
52
2
41
18
59
36
3
21
42
63
20
4
17
34
51
4
5
29
58
23
6
57
50
43
7
37
10
47
8
33
2
35
9
45
7
10
9
27
11
53
31
12
序列检验
则
2 (d) kd n
kk
k
...
j1 1 j2 1 jd
(f j1 , j2 ,... jd
n kd
)2
2 (d)服从自由度为kd 1的 2分布。
游程检验
游程检验是一种对独立性假设的更为直接的检 验。
对Ui序列进行检验,以得到Ui的不间断子序列, 每个子序列都是Ui单调增长的最长子序列,每 个子序列称为游程。 例:[0.86], [0.11, 0.23], [0.03, 0.13], [0.06, 0.55, 0.64, 0.87], [0.10]
第六章 随机数生成器
随机数
在离散系统仿真中,随机数是一个必不可少的 基本元素
(0,1)均匀分布随机数是产生其他许多分布 的随机数的基础
一个随机数序列必须满足两个重要的统计性质: 均匀性和独立性
随机数的性质
均匀性 如果将区间[0,1]分为n个等长的子区间,那 么在每个区间的期望观测次数为N/n,其中N 为观测的总次数
游程检验
给定一个有n个Ui的序列,对长度为1,2,3,4,5,2,3,4,5
ri
长度
6的游程,
i=6,7,...
则可构造如下检验统计量:
1 6 6
R
n
i1
aij (ri nbi )(rj nb j )
j1
定理:
LCG具有满周期,当且仅当以下3个条件成立: 1. m和c互质; 2. 存在一个质数q,能够同时整除m和a-1; 3. m和a-1能够被4整除。
模数m的取值
为了使LCG的周期足够长,m的取值应该较大; 为了加快计算机的处理速度,选择m=2b,其
中b为计算机CPU一次能处理的最大位数;目 前b=32-1=31
产生的随机数要尽可能的逼近理想的均匀性和 独立性统计性质
产生的随机数要有足够长的周期 产生随机数的速度要快,占用的内存空间要小 随机数必须是可重复的
对于给定的起始点或初始条件,应当能够产生 相同的随机数序列,而且与正被仿真的系统完 全无关
产生随机数的算法是利用递推公式:
X n f ( X n1, X n2 ,..., X nk )
LCG的周期
用LCG方法产生的随机数序列会出现周期循环 的现象,一旦Zi取值和以前出现的某个值相同, 此后的随机数序列就开始循环。循环的长度称 为生成器的周期;
由于0≤Zi≤m-1,因此最大周期是m,称之为满 周期;
为了产生成百上千的随机数,必须采用周期足 够长的LCG,最好是满周期的生成器,这样对 随机数的均匀性也很有利。
线性同余随机数生成器(LCG)
Zi (aZi1 c)(mod m)
其中,a称为乘法因子,c称为加法因子,m为 模数
当a=1时,为加同余法; 当c=0时,为乘同余法; 当a≠1、c≠0时,为混合同余法
例:
使用线性同余法产生随机数序列,其中Z0=27、 a=17、c=43、m=100。
解:Zk=(aZk-1+c)mod m Z1=(17×27+43) mod 100=502mod100=2 Z2=(17×2+43) mod 100=77mod100=77 Z3=(17×77+43) mod 100=1352mod100=52 …… U1=2/100=0.02, U2=77/100=0.77, U3=0.52
