(完整版)2020中考数学九年级下册锐角三角函数在实际问题中的应用(含答案)

合集下载

九年级数学第二十八章《锐角三角函数——应用举例》同步练习(含答案)

九年级数学第二十八章《锐角三角函数——应用举例》同步练习（含答案）一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的．1．如图，在综合实践活动中，小明在学校门口的点C处测得树的顶端A仰角为37°，同时测得BC=15米，则树的高AB(单位：米)为A．15tan37︒B．15sin37︒C．15tan 37°D．15sin 37°【答案】C【解析】如图，在Rt△ABC中，∠B=90°，∠C=37°，BC=15，∴tan C=ABBC，则AB=BC•tan C=15tan37°．故选C．【名师点睛】本题考查了解直角三角形的应用﹣仰角俯角问题．解决此类问题要了解角之间的关系，找到与已知和未知相关联的直角三角形，当图形中没有直角三角形时，要通过作高或垂线构造直角三角形，当问题以一个实际问题的形式给出时，要善于读懂题意，把实际问题划归为直角三角形中边角关系问题加以解决．2．如图，在海拔200米的小山顶A处，观察M，N两地，俯角分别为30°，45°，则M，N两地的距离为A．200米B．2003米C．400米D．200（3+1）米【答案】D【解析】过A作AB⊥MN于B,在Rt △ABM 中, 90,200,30ABM AB M ∠==∠=，tan AB M BM∴∠=， 2003BM ∴=，在Rt △ABN 中, 90,45ABN N BAN ∠=∠=∠=，∴BN =AB =200，()200320020031MN ∴=+=+米.故选D.3．如图是一张简易活动餐桌，测得30cm OA OB ==，50cm OC OD ==，B 点和O 点是固定的．为了调节餐桌高矮，A 点有3处固定点，分别使OAB ∠为30，45，60，问这张餐桌调节到最低时桌面离地面的高度是（不考虑桌面厚度）A ．402cmB ．40cmC ．403cmD ．30cm【答案】B【解析】过点D 作DE ⊥AB 于点E ，∵∠OAB =30时，桌面离地面最低， ∴DE 的长即为最低长度， ∵OA =OB =30cm ，OC =OD =50cm ， ∴AD =OA +OD =80cm ，在Rt △ADE 中，∵∠OAB =30，AD =80cm ， ∴140cm.2DE AD ==故选:B.4．如图，某水库堤坝横截面迎水坡AB的坡度是1:3，堤坝高为40m，则迎水坡面AB的长度是A．80m B．803mC．40m D．403m【答案】A5．如图，铁路MN和公路PQ在点O处交汇，∠QON=30°.公路PQ上A处距O点240米．如果火车行驶时，周围200米以内会受到噪音的影响．那么火车在铁路MN上沿ON方向以72千米/时的速度行驶时，A 处受噪音影响的时间为A．409秒B．16秒C．403秒D．24秒【答案】B【解析】如图，以点A为圆心，取AB＝AD＝200米为半径，过点A作AC⊥MN,∵∠QON＝30°，OA＝240米，∴AC＝120米，当火车到B点时开始对A处产生噪音影响，到点D时结束影响，此时AB＝200米，∵AB＝200米，AC＝120米，∴由勾股定理得: BC＝160米∴BD＝2BC＝320米,∵72千米/小时＝20米/秒,∴影响时间应是320÷20＝16 (秒)，故选B.6．如图，在A、B两地之间要修一条笔直的公路，从A地测得公路走向是北偏东48°，A，B两地同时开工，若干天后公路准确接通，若公路AB长8千米，另一条公路BC长是6千米，且BC的走向是北偏西42°，则A地到公路BC的距离是A．6千米B．8千米C．10千米D．14千米【答案】B【解析】∵∠ABG＝48°，∠CBE＝42°，∴∠ABC＝180°－48°－42°＝90°，∴A到BC的距离就是线段AB的长度，∴AB＝8千米.BE=，她7．如图，小颖利用有一锐角是30的三角板测量一棵树的高度，已知她与树之间的水平距离6mAB=，那么这棵树高的眼睛距地面的距离 1.5m23 1.5mA．23m B．()32 1.5m D．4.5mC．()【答案】B【解析】在直角三角形ACD中，∠CAD=30°，AD=6m，∴CD=AD tan30°=6×33=23，∴CE=CD+DE=23+1.5（m）．故选B．8．如图，在小山的东侧A点有一个热气球，由于受风的影响，以30米/分的速度沿与地面成75°角的方向飞行，25分钟后到达C处，此时热气球上的人测得小山西侧B点的俯角为30°，则小山东西两侧A，B 两点间的距离为多少米．A．7502B．3752C．3756D．7506【答案】A二、填空题：请将答案填在题中横线上．9．如图，长4m的楼梯AB的倾斜角∠ABD为60°，为了改善楼梯的安全性能，准备重新建造楼梯，使其倾斜角∠ACD为45°，则调整后楼梯AC长为_____m．【答案】26【解析】在Rt△ABD中，∵sin∠ABD=AD AB，∴AD=4sin60°=23（m），在Rt△ACD中，∵sin∠ACD=AD AC，∴AC=23sin45=26（m）．故答案是：26．10．我国海域辽阔，渔业资源丰富．如图，现有渔船B在海岛A，C附近捕鱼作业，已知海岛C位于海岛A 的北偏东45°方向上．在渔船B上测得海岛A位于渔船B的北偏西30°的方向上，此时海岛C恰好位于渔船B的正北方向18（1+3）nmile处，则海岛A，C之间的距离为______nmile．【答案】2【解析】作AD⊥BC于D，设AC=x海里，在Rt△ACD中，AD=AC×sin∠ACD=22x，则CD=22x，在Rt△ABD中，BD=6 tan2ADABD=∠x，则22x+62x=18（1+3），解得，x=182，答：A，C之间的距离为182海里．故答案为：182.11．如图，一轮船由南向北航行到O处时，发现与轮船相距40海里的A岛在北偏东33方向．已知A岛周围20海里水域有暗礁，如果不改变航向，轮船________（填“有”或“没有”）触暗礁的危险．（可使用科学记算器）【答案】没有【解析】已知OA=40，∠O=33°，则AB=40•sin33°≈21.79＞20．所以轮船没有触暗礁的危险．故答案为: 没有．12．数学组活动，老师带领学生去测塔高，如图，从B点测得塔顶A的仰角为60，测得塔基D的仰角为45，已知塔基高出测量仪20m，（即20mDC=），则塔身AD的高为________米．【答案】()2031-【解析】在Rt △ABC 中，AC =3BC ．在Rt △BDC 中有DC =BC =20，∴AD =AC−DC =3BC−BC =20（3−1）米．故答案为：20（3−1）．三、解答题：解答应写出文字说明、证明过程或演算步骤．13．某中学九年级数学兴趣小组想测量建筑物AB 的高度.他们在C 处仰望建筑物顶端A 处，测得仰角为45，再往建筑物的方向前进6米到达D 处，测得仰角为60，求建筑物的高度.(测角器的高度忽略不计，结果精确到0.1米，3 1.732≈，2 1.414)≈【解析】设AB x =米， ∵∠C =45°，∴在Rt ABC △中，BC AB x ==米，60ADB ∠=， 6CD =米，∴在Rt ADB △中tan ∠ADB =ABBD， tan60°=6xx -，解得)333114.2x =≈米答，建筑物的高度为14.2米．14．如图，一个热气球悬停在空中，从热气球上的P点测得直立于地面的旗杆AB的顶端A与底端B的俯角分别为34°和45°，此时P点距地面高度PC为75米，求旗杆AB的高度（结果精确到0.1米）．（参考数据：sin34°=0.56，cos34°=0.83，tan34°=0.67）15．太阳能光伏发电因其清洁、安全、便利、高效等特点，已成为世界各国普遍关注和重点发展的新兴产业．如图是太阳能电池板支撑架的截面图，其中线段AB、CD、EF表示支撑角钢，太阳能电池板紧贴在支撑角钢AB上且长度均为300cm，AB的倾斜角为30°，BE=CA=50cm，支撑角钢CD、EF与地面接触点分别为D、F，CD垂直于地面，FE⊥AB于点E．点A到地面的垂直距离为50cm，求支撑角钢CD和EF的长度各是多少．（结果保留根号）【解析】如图所示，延长BA交FD延长线于点G，过点A作AH⊥DG于点H．由题意知，AB=300cm，BE=AC=50cm，AH=50cm，∠AGH=30°．在Rt△AGH中，∵AG=2AH=100cm，∴CG=AC+AG=150cm，则CD=12CG=75cm．∵EG=AB﹣BE+AG=300﹣50+100=350（cm）．在Rt△EFG中，EF=EG tan∠EGF=350tan30°=350×33503（cm）．答：支撑角钢CD的长为75cm，EF 3503．。

2024中考数学专题5.9三角函数在实际生活中的应用 (全国通用)

考向5.9 三角函数在实际生活中的应用【知识要点】1、在直角三角形中，除直角外，一共有五个元素，即三条边和二个锐角。

由直角三角形中除直角外的已知元素，求出所有未知元素的过程，叫做解直角三角形。

2、如图1，当从低处观测高处的目标时，视线与水平线所成的锐角称为仰角当从高处观测低处的目标时，视线与水平线所成的锐角称为俯角3、如图2，坡面与水平面的夹角叫做仰角 (或叫做坡比)。

用字母i 表示，即tan h i A l==4、从某点的指北方向按顺时针转到目标方向的水平角，叫做方位角。

如图3，OA 、OB 、OC 的方位角分别为45°、135°、225°。

5、指北或指南方向线与目标方向线所成的小于90°的水平角，叫做方位角。

如图4，OA 、OB 、OC 、OD 的方向角分别是：北偏东30°，南偏东45°(东南方向)、南偏西为60°，北偏西60°。

7.测量物体高度的方法：（1）.利用全等三角形的知识；（2）利用相似三角形的对应边成比例；（3）.利用三角函数的知识例1、如图，某无人机爱好者在一小区外放飞无人机，当无人机飞行到一定高度D 点处时，无人机测得操控者A 的俯角为75︒，测得小区楼房BC 顶端点C 处的俯角为45︒．已知操控者A 和小区楼房BC 之间的距离为45米，小区楼房BC的高度为（1）求此时无人机的高度；（2）在（1）条件下，若无人机保持现有高度沿平行于AB 的方向，并以5米/秒的速度继续向前匀速飞行．问：经过多少秒时，无人机刚好离开了操控者的视线？（假定点A ，B ，C ，D 都在同一平面内．参考数据：tan 752︒=tan152︒=．计算结果保留根号）图1图2hA图3 图4解：如图1，过D 点作DH ⊥AB ，垂足为点H ，过C 点作CE ⊥DH ，垂足为点E ，可知四边形EHBC 为矩形，∴EH =CB ，CE =HB ，∵无人机测得小区楼房BC 顶端点C 处的俯角为45︒，测得操控者A 的俯角为75︒，DM ∥AB ，∴∠ECD =45°，∠DAB =75°，∴∠CDE =∠ECD =45°，∴CE =DE ，设CE =DE =HB =x ，∴AH =45-x ，DH =DE +EH =x +在Rt △DAH 中，DH =tan75°×AH =(()245x -，即(()245x x +=-，解得：x =30，∴DH = 30+∴此时无人机的高度为()30米；（2）如图2所示，当无人机飞行到图中F 点处时，操控者开始看不见无人机，此时AF 刚好经过点C ，过A 点作AG ⊥DF ，垂足为点G ，此时，由（1）知，AG =30（米），∴°=tan 75AG DG ；∵tan =BC CAB AB ∠=∴°=30CAB ∠∵DF ∥AB ，∴∠DFA =∠CAB =30°，∴°45tan 30GA GF ==,∴=30DF GF DG -=+,因为无人机速度为5米/秒，6+（秒）；所以经过()6秒时，无人机刚好离开了操控者的视线．一、单选题1．（2021·广东深圳·二模）“儿童放学归来早，忙趁东风放纸鸢”，小明周末在龙潭公园草坪上放风筝，已知风筝拉线长100米且拉线与地面夹角为65︒（如图所示，假设拉线是直的，小明身高忽略不计），则风筝离地面的高度可以表示为（）A．100sin65︒B．100cos65︒C．100tan65︒D．100 sin65︒2．（2021·浙江温州·一模）如图，小慧的眼睛离地面的距离为1.6m，她用三角尺测量广场上的旗杆高度，仰角恰与三角板60︒角的边重合，量得小慧与旗杆之间的距离BC为5m，则旗杆AD的高度（单位：m）为（）A．6.6B．11.6C．1.6D．1.6+3．（2021·河北唐山·二模）如图，某停车场入口的栏杆AB，从水平位置绕点O旋转到A′B′的位置，已知AO 的长为4米．若栏杆的旋转角∠AOA′＝α，则栏杆A端升高的高度为（）A ．4sin α米B ．4sin α米C ．4cos α米D ．4cos α米4．（2021·广东云浮·一模）如图，是一水库大坝横断面的一部分，坝高60m h =，迎水斜坡100m AB =，斜坡的坡角为a ，则tan a 的值为（）A ．43B ．34C ．35D ．455．（2021·重庆市永川区教育科学研究所一模）鹅岭公园是重庆最早的私家园林，前身为礼园，是国家级AAA 旅游景区，园内有一瞰胜楼，登上高楼能欣赏到重庆的优美景色．周末，李明同学游览鹅岭公园，如图，在点A 观察到瞰胜楼楼底点C 的仰角为12°，楼顶点D 的仰角为13°，测得斜坡BC 的坡面距离BC =510米，斜坡BC 的坡度8:15i =．则瞰胜楼的高度CD 是（）米．（参考数据：tan12°≈0.2，tan13°≈0.23）A ．30B ．32C ．34D ．366．（2021·山东·济宁学院附属中学二模）如图，在某监测点B 处望见一艘正在作业的渔船在南偏西15°方向的A 处，若渔船沿北偏西75°方向以60海里/小时的速度航行，航行半小时后到达C 处，在C 处观测到B 在C 的北偏东60°方向上，则B 、C 之间的距离为（）A ．30海里B ．C ．20海里D ．7．（2021·河北唐山·一模）如图，电线杆的高度为CD ＝m ，两根拉线AC 与BC 互相垂直（A ，D ，B在同一条直线上），若∠CBA ＝α，则拉线AC 的长度可以表示为（）A ．sin mαB ．cos mαC ．m cosαD ．tan mα8．（2021·江苏无锡·一模）如图，胡同左右两侧是竖直的墙，一架BC 斜靠在右侧墙壁上，测得梯子与地面的夹角为45°，此时梯子顶端B 恰巧与墙壁顶端重合．因梯子阻碍交通，故将梯子底端向右移动一段距离到达D 处，此时测得梯子AD 与地面的夹角为60°，则胡同左侧的通道拓宽了（）AB ．3米C ．(3米D ．(3米9．（2021·重庆一中三模）如图，小欢同学为了测量建筑物AB 的高度，从建筑物底端点B 出发，经过一段坡度1:2.4i =的斜坡，到达C 点，测得坡面BC 的长度为15.6米，再沿水平方向行走30米到达点D （A ，B ，C ，D 均在同一平面内）．在点D 处测得建筑物顶端A 的仰角为37︒，则建筑物AB 的高度约为（参考数据：sin 370.60︒≈，cos370.80︒≈，tan 370.75︒≈）（）A ．27.3米B ．28.4米C ．33.3米D ．38.4米10．（2021·江苏南通·二模）如图，某大楼DE 楼顶挂着“众志成城，抗击疫情”的大型宣传牌，为了测量宣传牌的高度CD ，小江从楼底点E 向前行走30米到达点A ，在A 处测得宣传牌下端D 的仰角为60°．小江再沿斜坡AB 行走26米到达点B ，在点B 测得宣传牌的上端C 的仰角为43°，已知斜坡AB 的坡度i＝1：2.4，点A 、B 、C 、D 、E 在同一平面内，CD ⊥AE ，宣传牌CD 的高度约为（）（参考数据：sin43°≈0.68，cos43°≈0.73，tan43°≈0.93）A ．8.3米B ．8.5米C ．8.7米D ．8.9米11．（2021·重庆八中二模）如图，一棵松树AB 挺立在斜坡CB 的顶端，斜坡CB 长为52米，坡度为i ＝12：5，小张从与点C 相距60米的点D 处向上爬12米到达观景台DE 的顶端点E ，在此测得松树顶端点A 的仰角为39°，则松树的高度AB 约为（）（参考数据：sin39°≈0.63，cos39°≈0.78，tan39°≈0.81）A ．16.8米B ．28.8米C ．40.8米D ．64.2米12．（2021·重庆·字水中学三模）白沙镇有一望夫塔，小明在与塔底中心的D 同一水平线的A 处，测得24AD =米，沿坡度0.75:1i =的斜坡AB 走到B 点，测得塔顶E 仰角为37°，再沿水平方向走22米到C 处，测得塔顶E 的仰角为22°，则塔高DE 为（）米．（结果精确到十分位）（sin 370.60︒≈，cos370.80︒≈，tan 370.75︒≈，sin 220.37︒≈，cos 220.93︒≈，tan 220.40︒≈，）A ．18.3米B ．19.7米C ．20.7米D ．22.3米二、填空题13．（2021·广东·深圳市南山区太子湾学校二模）如图，一楼房AB 后有一假山，其斜面坡度为i ＝1（斜面坡度是指坡面的铅直高度与水平宽度的比），山坡坡面上点E 处有一休息亭，测得假山坡脚C 与楼房水平距离BC ＝25米，与亭子距离CE ＝20米，小丽从楼房顶测得E 点的俯角为45°，则楼房AB的高为_____米．14．（2021·广东·广州市第六十五中学一模）小颖家住在甲楼，她所居住的楼房前面有一座乙楼．冬天，阳光入射角是30°，两楼距离20米，小颖家的阳台距地面7米，乙楼高18米，那么影子的顶端距她家阳台还有_________米.（精确到0.1米）15．（2021·山东·郓城县教学研究室一模）如图，在一笔直的海岸线l上有相距2km的A、B两个观测站，B站在A站的正东方向上，从A站测得船C在北偏东60°的方向上，从B站测得船C在北偏东30°的方向上，则船C到海岸线l的距离是__km．16．（2021·吉林长春·二模）如图，在A处看建筑物CD的顶端C的仰角为α，且tanα＝0.8，向前行进3米到达B处，从B处看顶端C的仰角为45°（图中各点均在同一平面内，A、B、D三点在同一条直线上，CD⊥AD，则建筑物CD的高度为_____米．17．（2021·广东·佛山市华英学校一模）如图，直立于地面上的电线杆AB，在阳光下落在水平地面和坡面上的影子分别是BC，CD．测得BC＝9m，CD＝6m，斜坡CD的坡度i＝1D处测得电线杆顶端A 的仰角为30°，则电线杆AB的高度为_____．18．（2021·湖南·长沙市开福区青竹湖湘一外国语学校二模）如图，某同学在楼房的A处测得荷塘的一端B 处的俯角为30°，荷塘另一端点D与点C，B在同一直线上，已知楼房AC＝32米，CD＝16米，则荷塘的宽BD为________米．19．（2021·山东·庆云县渤海中学一模）如图，在大楼AB的正前方有一斜坡CD，CD＝4米，坡角∠DCE＝30°，小红在斜坡下的点C处测得楼顶B的仰角为60°，在斜坡上的点D处测得楼顶B的仰角为45°，其中点A、C、E在同一直线上．则大楼AB的高度_____．（结果保留根号）20．（2021·湖北咸宁·模拟预测）如图，建筑物BC上有一高为8m的旗杆AB，从D处观测旗杆顶部A的仰角为53︒，观测旗杆底部B 的仰角为45︒，则建筑物BC 的高约为_____m （结果保留小数点后一位）．（参考数据sin 530.80︒≈，cos530.60︒≈，tan 53 1.33︒≈）三、解答题21．（2021·贵州六盘水·模拟预测）位于我市的北盘江大桥是世界第一高桥，大桥采用低塔斜拉桥桥型（如图1），桥长1341.4米，桥面至江面垂直距离565.4米．图2是从图1中抽象出的平面图，测得拉索AB 与水平桥面的夹角是30°，拉索DE 与水平桥面的夹角是60°，两拉索顶端的距离BE 为55米，两拉索底端距离AD 为240米．(1)求DC EC的值；（结果保留根号）(2)求立柱BC 的长．（结果精确到0.1≈1.732）22．（2021·贵州·仁怀市教育研究室一模）如图，两座建筑物AD 与BC ，其地面距离CD 为60m ，从AD 的顶点A 测得BC 顶部B 的仰角30α=︒，测得其底部C 的俯角45β=︒，求建筑物BC 的高（结果保留根号）．23．（2021·河南商丘·三模）在一次实弹演习中，我国参演红军需轰炸蓝军的一个桥梁，如图，红军飞行员驾驶战机飞到A 处时发现桥梁BC 并测得B 、C 两点的俯角分别为45°、35°．已知飞机、桥梁BC 与地面在同一水平面上，其桥梁BC 长度为800m ．请求出此时飞机离地面的高度．（结果保留整数．参考数据：sin35°≈712，cos35°≈56，tan35°≈710）一、单选题1．（2021·吉林长春·中考真题）如图是净月潭国家森林公园一段索道的示意图．已知A 、B 两点间的距离为30米，A α∠=，则缆车从A 点到达B 点，上升的高度（BC 的长）为（）A ．30sin α米B ．30sin α米C ．30cos α米D ．30cos α米2．（2021·福建·中考真题）如图，某研究性学习小组为测量学校A 与河对岸工厂B 之间的距离，在学校附近选一点C ，利用测量仪器测得60,90,2km A C AC ∠=︒∠=︒=．据此，可求得学校与工厂之间的距离AB 等于（）A ．2kmB ．3kmC ．D ．4km3．（2021·湖南衡阳·中考真题）如图是某商场营业大厅自动扶梯的示意图．自动扶梯AB 的倾斜角为37︒，大厅两层之间的距离BC 为6米，则自动扶梯AB 的长约为（sin 370.6,cos370.8,tan 370.75︒≈︒≈︒≈）（）．A ．7.5米B ．8米C ．9米D ．10米4．（2021·山东济南·中考真题）无人机低空遥感技术已广泛应用于农作物监测．如图，某农业特色品牌示范基地用无人机对一块试验田进行监测作业时，在距地面高度为135m 的A 处测得试验田右侧出界N 处俯角为43︒，无人机垂直下降40m 至B 处，又测得试验田左侧边界M 处俯角为35︒，则M ，N 之间的距离为（参考数据：tan 430.9︒≈，sin 430.7︒≈，cos 350.8︒≈，tan 350.7︒≈，结果保留整数）（）A ．188mB ．269mC ．286mD ．312m5．（2021·浙江金华·中考真题）如图是一架人字梯，已知2AB AC ==米，AC 与地面BC 的夹角为α，则两梯脚之间的距离BC 为（）A ．4cos α米B ．4sin α米C ．4tan α米D ．4cos α米6．（2021·广东深圳·中考真题）如图，在点F 处，看建筑物顶端D 的仰角为32°，向前走了15米到达点E 即15EF =米，在点E 处看点D 的仰角为64°，则CD 的长用三角函数表示为（）A ．15sin 32︒B ．15tan 64︒C ．15sin 64︒D ．15tan 32︒7．（2021·山东日照·中考真题）如图，在一次数学实践活动中，小明同学要测量一座与地面垂直的古塔AB 的高度，他从古塔底部点B 处前行30m 到达斜坡CE 的底部点C 处，然后沿斜坡CE 前行20m 到达最佳测量点D 处，在点D 处测得塔顶A 的仰角为30 ，已知斜坡的斜面坡度i =A ，B ，C ，D ，E 在同一平面内，小明同学测得古塔AB 的高度是（）A ．()20m +B ．()10mC ．D ．40m8．（2021·贵州毕节·中考真题）如图，拦水坝的横断面为梯形ABCD ．其中//AD BC ，45ABC ∠=︒，30DCB ∠=︒，斜坡AB 长8m ．则斜坡CD 的长为（）A ．B ．C ．D 9．（2021·湖北十堰·中考真题）如图，小明利用一个锐角是30 的三角板测量操场旗杆的高度，已知他与旗杆之间的水平距离BC 为15m ，AB 为1.5m （即小明的眼睛与地面的距离），那么旗杆的高度是（）A ．3m 2⎛⎫ ⎪⎝⎭B ．C ．D ．3m 2⎛⎫+ ⎪⎝⎭10．（2021·湖北随州·中考真题）如图，某梯子长10米，斜靠在竖直的墙面上，当梯子与水平地面所成角为α时，梯子顶端靠在墙面上的点A 处，底端落在水平地面的点B 处，现将梯子底端向墙面靠近，使梯子与地面所成角为β，已知3sin cos 5αβ==，则梯子顶端上升了（）A ．1米B ．1.5米C ．2米D ．2.5米11．（2021·重庆·中考真题）如图，在建筑物AB 左侧距楼底B 点水平距离150米的C 处有一山坡，斜坡CD 的坡度（或坡比）为1:2.4i =，坡顶D 到BC 的垂直距离50DE =米（点A ，B ，C ，D ，E 在同一平面内），在点D 处测得建筑物顶A 点的仰角为50°，则建筑物AB 的高度约为（参考数据：sin 500.77︒≈；cos500.64︒≈；tan 50 1.19︒≈）A．69.2米B．73.1米C．80.0米D．85.7米12．（2021·山东泰安·中考真题）如图，为了测量某建筑物BC的高度，小颖采用了如下的方法：先从与建筑物底端B在同一水平线上的A点出发，沿斜坡AD行走130米至坡顶D处，再从D处沿水平方向继续前行若干米后至点E处，在E点测得该建筑物顶端C的仰角为60°，建筑物底端B的俯角为45°，点A、B、i=．根据小颖的测量数据，计算出建筑物BC的高度约为C、D、E在同一平面内，斜坡AD的坡度1:2.4（ 1.732≈）A．136.6米B．86.7米C．186.7米D．86.6米二、填空题13．（2021·广西百色·中考真题）数学活动小组为测量山顶电视塔的高度，在塔的椭圆平台遥控无人机．当无人机飞到点P处时，与平台中心O点的水平距离为15米，测得塔顶A点的仰角为30°，塔底B点的俯角为60°，则电视塔的高度为_________米．14．（2021·广西梧州·中考真题）某市跨江大桥即将竣工，某学生做了一个平面示意图（如图），点A到桥的距离是40米，测得∠A＝83°，则大桥BC的长度是___米．（结果精确到1米）（参考数据：sin83°≈0.99，cos83°≈0.12，tan83°≈8.14）15．（2021·江苏无锡·中考真题）一条上山直道的坡度为1：7，沿这条直道上山，则前进100米所上升的高度为________米．16．（2021·四川乐山·中考真题）如图，为了测量“四川大渡河峡谷”石碑的高度，佳佳在点C处测得石碑顶A点的仰角为30 ，她朝石碑前行5米到达点D处，又测得石顶A点的仰角为60︒，那么石碑的高度AB的长=________米．（结果保留根号）17．（2021·贵州遵义·中考真题）小明用一块含有60°（∠DAE＝60°）的直角三角尺测量校园内某棵树的高度，示意图如图所示，若小明的眼睛与地面之间的垂直高度AB为1.62m，小明与树之间的水平距离BC为4m，则这棵树的高度约为___m．（结果精确到0.1m≈1.73）18．（2021·内蒙古赤峰·中考真题）某滑雪场用无人机测量雪道长度．如图，通过无人机的镜头C测一段水平雪道一端A处的俯角为50°，另一端B处的俯角为45°，若无人机镜头C处的高度CD为238米，点A，︒≈，D，B在同一直线上，则通道AB的长度为_________米．(结果保留整数，参考数据sin500.77︒≈)cos500.64︒≈，tan50 1.1919．（2021·广西来宾·中考真题）如图，从楼顶A 处看楼下荷塘C 处的俯角为45︒，看楼下荷塘D 处的俯角为60︒，已知楼高AB 为30米，则荷塘的宽CD 为__________米．（结果保留根号）20．（2021·湖北黄石·中考真题）如图，直立于地面上的电线杆AB ，在阳光下落在水平地面和坡面上的影子分别是BC 、CD ，测得5BC =米，4CD =米，150BCD ∠=︒，在D 处测得电线杆顶端A 的仰角为45︒，则电线杆AB 的高度约为______米．（参考数据： 1.414≈ 1.732≈，结果按四舍五入保留一位小数）21．（2021·湖北荆州·中考真题）如图1是一台手机支架，图2是其侧面示意图，AB ，BC 可分别绕点A ，B 转动，测量知8cm BC =，16cm AB =．当AB ，BC 转动到60=︒∠BAE ，50ABC ∠=︒时，点C 到AE 的距离为_____________cm ．（结果保留小数点后一位，参考数据：sin 700.94︒≈ 1.73≈）22．（2021·湖北武汉·中考真题）如图，海中有一个小岛A ，一艘轮船由西向东航行，在B 点测得小岛A 在北偏东60︒方向上；航行12n mile 到达C 点，这时测得小岛A 在北偏东30︒方向上．小岛A 到航线BC 的距离是__________n mile 1.73≈，结果用四舍五入法精确到0.1）．三、解答题23．（2021·山东青岛·中考真题）某校数学社团开展“探索生活中的数学”研学活动，准备测量一栋大楼BC 的高度．如图所示，其中观景平台斜坡DE 的长是20米，坡角为37︒，斜坡DE 底部D 与大楼底端C 的距离CD 为74米，与地面CD 垂直的路灯AE 的高度是3米，从楼顶B 测得路灯AE 项端A 处的俯角是42.6︒．试求大楼BC 的高度．（参考数据：3sin 375︒≈，4cos375≈︒，3tan 374︒≈，17sin 42.625︒≈，34cos 42.645︒≈，9tan 42.610︒≈）24．（2021·广西河池·中考真题）如图，小明同学在民族广场A 处放风筝，风筝位于B 处，风筝线AB 长为100m ，从A 处看风筝的仰角为30︒，小明的父母从C 处看风筝的仰角为50︒．（1）风筝离地面多少m ？（2）AC 相距多少m ？（结果保留小数点后一位，参考数据：sin300.5︒=，cos300.8660︒＝，tan300.5774︒＝，sin500.7760︒＝，cos500.6428︒＝，tan50 1.1918︒＝）25．（2021·四川巴中·中考真题）学校运动场的四角各有一盏探照灯，其中一盏探照灯B的位置如图所示，已知坡长AC＝12m，坡角α为30°，灯光受灯罩的影响，最远端的光线与地面的夹角β为27°，最近端的光线恰好与地面交于坡面的底端C处，且与地面的夹角为60°，A、B、C、D在同一平面上．（结果精确到0.1m.参考数据：sin27°≈0.45，cos27°≈0.89，tan27°≈0.50 1.73．）（1）求灯杆AB的高度；（2）求CD的长度．1．A【解析】【分析】过点A 作AC ⊥BC 于C ，根据正弦的定义解答即可．【详解】解：如图，过点A 作AC ⊥BC 于C ，在Rt △ABC 中，sin B =AC AB，则AC =AB •sin B =100sin65°（米），故选：A ．【点拨】本题考查的是解直角三角形的应用—坡度坡角问题，掌握锐角三角函数的定义是解题的关键．2．D【解析】【分析】根据题意可知 1.6BE CD ==米，60ABC ∠=︒．再利用特殊角的三角函数解直角三角形即可求出AC 长，从而求出AD 长．【详解】根据题意可知 1.6BE CD ==米，60ABC ∠=︒．∵60ABC ∠=︒，∴在Rt ABC 中，tan 60AC BC =︒= 米．∴ 1.6)AD AC CD =+=米．故选D ．【点拨】本题考查解直角三角形的实际应用．掌握特殊角的三角函数值是解答本题的关键．3．B【解析】【分析】过点A′作A′C ⊥AB 于点C ，根据锐角三角函数的定义即可求出答案．【详解】解：如答图，过点A′作A′C ⊥AB 于点C ．在Rt △OCA′，sinα＝A C A O''，所以A′C ＝A′O·sinα．由题意得A′O ＝AO ＝4，所以A′C ＝4sinα，因此本题选B ．【点拨】本题考查解直角三角形，解题的关键是熟练运用锐角三角函数的定义，本题属于基础题型．4．B【解析】【分析】直接利用勾股定理得出BC ，再利用锐角三角函数关系得出答案．【详解】解：过点A 作AC ⊥BD ，垂足为C ，∵坝高h =60m ，迎水斜坡AB =100m ，∴BC ==80（m ），则tanα=603804= ．故选：B ．【点拨】此题主要考查了解直角三角形的应用，正确掌握边角关系是解题关键．5．D【解析】【分析】由斜坡BC 的坡度8:15i =，设8CE x =、15BE x =，由勾股定理可知17BC x =，BC =510，求得30x =，据此可知AE 、DE 的长，再根据DC DE CE =-可得答案．【详解】由斜坡BC 的坡度8:15i =，设8CE x =、15BE x =，在Rt BCE 中，17BC x ===，由17510BC x ==求得30x =，∴240CE =米、450BE =米，在Rt ACE △中，2401200tan tan12CE AE CAE ===∠︒（米），在Rt ADE △中，tan 1200tan13276DE AE DAE =∠=⨯︒=（米），则27624036DC DE CE =-=-=（米）．故选：D ．【点拨】本题主要考查解直角三角形的应用能力，注意能借助仰角和俯角构造直角三角形并解直角三角形是解决本题的关键．6．D【解析】【分析】根据时间、速度、距离之间的关系求出AC ，根据等腰直角三角形的性质解答即可．【详解】解：如图：由题意得，AC ＝60×0.5＝30海里，∵CD ∥BF ，∴∠CBF ＝∠DCB ＝60°，又∠ABF ＝15°，∴∠ABC ＝45°，∵AE ∥BF ，∴∠EAB ＝∠FBA ＝15°，又∠EAC ＝75°，∴∠CAB ＝90°，∴sin 45AC BC ︒=∴BC ＝海里，故选：D ．【点拨】本题考查的是解直角三角形的应用−方向角问题，正确标注方向角、熟记锐角三角函数的定义是解题的关键．7．B【解析】【分析】根据同角的余角相等得∠ACD ＝∠CBD ，由cos ∠ACD ＝CD AC ，即可求出AC 的长度．【详解】解：∵∠ACD +∠BCD ＝90°，∠CBD +∠BCD ＝90°，∴∠ACD ＝∠CBD ，在Rt △ACD 中，∵cos ∠ACD ＝CD AC，∴AC ＝cos cos CD m ACD α=∠．故选：B ．【点拨】本题主要考查解直角三角形的应用，熟练掌握同角的余角相等和三角函数的定义是解题的关键．8．D【解析】【分析】根据等腰直角三角形的性质分别求出E C 、EB ，根据正切的定义求出DE ，结合图形计算得到答案．【详解】解：在Rt EBC 中，45BCE ∠=︒，3EC EB ∴====（米)，在Rt BDE △中，tan BE BDE DE ∠=，tan BE DE BDE ∴==∠（米)，(3CD EC DE ∴=-=米，故选：D ．【点拨】本题考查的是解直角三角形的应用—坡度坡角问题，掌握坡度的概念、熟记锐角三角函数的定义是解题的关键．9．A【解析】【分析】延长AB 与DC 相交与点E ，由题意和三角函数可求得EC 的长度，根据37°角的三角函数求得AE 的长度，进而可求出建筑物AB 的高度．【详解】如图，延长AB 与DC 相交于点E ，∵15.6BC =，斜坡BC 的坡度i =1：2.4=512，∴12cos 13BCE =∠，5sin 13BCE =∠，∴12cos 15.6=14.413EC BC BCE =∙=⨯∠，5sin 15.6613BE BC BCE =∙=⨯=∠，∴==14.430=44.4ED EC CD ++，又∵D ∠=37°，∴=tan 37=44.40.75=33.3AE ED ∙︒⨯，∴33.3627.3AB AE BE =-=-=，故选：A ．【点拨】此题考查了三角函数应用题，仰角和坡度的概念，做出辅助线是解答本题的关键．10．A【解析】【分析】过B 分别作AE 、DE 的垂线，设垂足为F 、G ．分别在Rt △ABF 和Rt △ADE 中，通过解直角三角形求出BF 、AF 、DE 的长，再求出EF 即BG 的长；在Rt △CBG 中求出CG 的长，根据CD =CG +GE -DE 即可求出宣传牌的高度．【详解】解：过B 作BF ⊥AE ，交EA 的延长线于F ，作BG ⊥DE 于G ．Rt △ABF 中，i =tan ∠BAF =BF AF ＝12.4，AB =26米，∴BF =10（米），AF =24（米），∴BG =AF +AE =54（米），Rt △BGC 中，∠CBG =43°，∴CG =BG •tan43°≈54×0.93=50.22（米），Rt △ADE 中，∠DAE =60°，AE =30米，∴∴CD =CG +GE -DE（米）．故选：A ．【点拨】此题考查了仰角、坡度的定义，能够正确地构建出直角三角形，将实际问题化归为解直角三角形的问题是解答此类题的关键．11．B【解析】【分析】延长AB交DC的延长线于H，作EF⊥AH于F，根据矩形的性质得到FH＝DE＝12，EF＝DH，根据坡度的概念分别求出CH、BH，根据正切的定义求出AF，结合图形计算即可．【详解】解：延长AB交DC的延长线于H，作EF⊥AH于F，则四边形EDHF为矩形，∴FH＝DE＝12米，EF＝DH，∵斜坡CB的坡度为t＝12：5，∴设BH＝12x，CH＝5x，由勾股定理得，（5x）2+（12x）2＝522，解得，x＝4，则BH＝12x＝48米，CH＝5x＝20米，则EF＝DH＝DC+CH＝60+20＝80（米），在Rt△AEF中，tan∠AEF＝AF EF，则AF＝EF•tan∠AEF≈80×0.81＝64.8（米），∴AB＝AF+HF﹣BH＝64.8+12﹣48＝28.8（米），故选：B．【点拨】本题考查的是解直角三角形的应用-仰角俯角问题、坡度坡角问题，掌握仰角俯角、坡度坡角的概念、熟记锐角三角函数的定义是解题的关键．12．B【解析】【分析】连接DE，作BF⊥DE于F，BG⊥DA于G，设BG=3x m，则AG=4x m，BF=DG=24+4x（m），CF=BF+BC=46+4x（m），由三角函数定义得出EF=tan37°（24+4x），EF=tan22°（46+4x），得出0.75（24+4x）=0.40（46+4x ），解得27x =，求出DF 、EF ，即可得出答案．【详解】解：连接DE ，作BF ⊥DE 于F ，BG ⊥DA 于G ，如图：则DF =BG ，BF =DG =AD +AG ，∵AB =斜坡AB 的坡度0.75BG i AG==，∴设BG =3x m ，则AG =4x m ，BF =DG =24+4x （m ），CF =BF +BC =24+4x +22=46+4x （m ），由题意得：∠EBF =37°，∠ECF =22°，∵tan ∠BEF =244EF EF BF x =+，tan ∠ECF =464EF EF CF x=+，∴EF =tan 37°（24+4x ），EF =tan 22°（46+4x ），∴0.75（24+4x ）=0.40（46+4x ），解得：27x =，∴DF =BG =3x =67（m ），EF =0.40（46+4x ）=1327（m ），∴DE =DF +EF =613213819.7777+=≈；故选：B ．【点拨】本题考查的是解直角三角形的应用-仰角俯角问题、坡度坡角问题，掌握仰角俯角的概念、坡度坡角分概念、熟记锐角三角函数的定义是解题的关键．13．（）．【解析】【分析】过点E 作EF ⊥BC 的延长线于F ，EH ⊥AB 于点H ，解直角三角形即可求解．【详解】解：过点E 作EF ⊥BC 的延长线于F ，EH ⊥AB 于点H ，在Rt △CEF 中，∵i ＝EF CF tan ∠ECF ，∴∠ECF ＝30°，∴EF ＝12CE ＝10米，CF ＝∴BH ＝EF ＝10米，HE ＝BF ＝BC +CF ＝（在Rt △AHE 中，∵∠HAE ＝45°，∴AH＝HE ＝（∴AB ＝AH +HB ＝（答：楼房AB 的高为（故答案为：（【点拨】本题考查了解直角三角形的应用，涉及俯角及坡度的知识，构造直角三角形是解题的关键．14．0.6【解析】【分析】如图，解直角三角形ABC 可以求得AB 的长，求出乙楼的影子在甲楼上的高度CD ，再求影子的顶端距她家阳台的距离.【详解】解：如图，△ABC 中，∠ABC=90°，∠ACB=30°，BC=20米，所以AB=BC•tan ∠ACB ＝20•tan30°＝（米），CD=18-11.55=6.45（米），∴影子的顶端距她家阳台还有7-6.45≈0.6（米）．故答案为0.6.【点拨】本题考查特殊角的三角函数值，解直角三角形，根据BC 求出AB 的值是解题的关键．15【解析】【分析】根据题意可证得△ABC 为等腰三角形，即可求出BC 的长，然后再解直角三角形CBD 即可求得．【详解】解：如图，过点C 作CD ⊥AB 于点D ，根据题意得：∠CAD =90°−60°=30°，∠CBD =90°−30°=60°，∴∠ACB =∠CBD −∠CAD =60°-30°=30°，∴∠CAB =∠ACB ，∴BC =AB =2km ，在Rt △CBD 中，sin 602CD BC =⋅︒==，【点拨】本题考查了等腰三角形的判定与性质及解直角三角形的应用，解决本题的关键是证出△ABC 是等腰三角形．16．12【解析】【分析】根据∠DBC =45°可得BD CD =，根据tan α＝0.8，可得3810CD CD =+，进而即可求得CD 的长．【详解】∵∠DBC =45°，∴BD =CD tan 45⨯︒=CD ，tanα=，3AD AB BD CD =+=+,则3810CD CD =+，解得CD =12．经检验：符合题意故答案为12．【点拨】本题考查了解直角三角形的应用，掌握正切的意义是解题的关键．17．(6m+【解析】【分析】延长AD 交BC 的延长线于F ，作DG ⊥BF 于G ，根据直角三角形的性质和勾股定理求出DC 、CG 的长，根据正切的定义解答即可．【详解】解：如图，延长AD 交BC 的延长线于F ，作DG ⊥BF 于G ，∵∠ADE ＝30°，∴∠AFB ＝30°，∵CD ＝6m ，斜坡CD 的坡度i ＝1∴tan ∠DCG ＝DG CG ∴∠DCG ＝30°，∴DG ＝3m ，CG ＝，∴∠DFC ＝∠DCF ＝30°，∴DF ＝DC ，∵DG ⊥BF ，∴FG ＝CG ＝，∴FC＝，∴FB ＝FC +BC ＝（）m ，∴AB ＝BF ×tan ∠AFB ＝（）m ．故答案为：（m ．【点拨】本题主要考查了勾股定理，坡比和解直角三角形，解题的关键在于能够熟练掌握相关知识进行求解．18．16【解析】【分析】根据已知条件转化为直角三角形ABC 中的有关量，由锐角三角函数的定义可求出BC ，根据BD =BC -CD 可得出答案．【详解】解：由题意知，∠ABC =30°，∠ACB =90°，AC =32米，tan tan 30,AC ABC BC ︒∠==tan 30AC BC ︒∴===（米）∵CD =16米，∴BD =BC -CD=16米．故答案为：16．【点拨】本题考查了解直角三角形的应用，解题的关键是利用仰俯角的定义将题目中的相关量转化为直角三角形ABC 中的有关元素．19．（【解析】【分析】在直角三角形DCE 中，利用锐角三角函数定义求出DE 的长，过D 作DF 垂直于AB ，交AB 于点F ，可得出三角形BDF 为等腰直角三角形，设BF =DF =x (米)，表示出BC ，BD ，DC ，由题意得到三角形BCD 为直角三角形，利用勾股定理列出关于x 的方程，求出方程的解得到x 的值，即可确定出AB 的长．【详解】解：在Rt △DCE 中，DC ＝4米，∠DCE ＝30°，∠DEC ＝90°，∴DE 12=DC ＝2(米)，过D 作DF ⊥AB ，交AB 于点F，∵∠BFD ＝90°，∠BDF ＝45°，∴∠FBD ＝45°，即△BFD 为等腰直角三角形，设BF ＝DF ＝x 米，∵四边形DEAF 为矩形，∴AF ＝DE ＝2米，即AB ＝（x +2）米，在Rt △ABC 中，∠ABC ＝30°，∴cos30B AB C ===︒BD =米，DC ＝4米，∵∠DCE ＝30°，∠ACB ＝60°，∴∠DCB ＝90°，在Rt △BCD 中，根据勾股定理得：22(24)2163x x +=+ ，解得：x ＝则AB ＝（故答案为：（【点拨】此题考查了解直角三角形的实际应用--仰角俯角问题，坡度坡角问题，熟练掌握解直角三角形的方法是解本题的关键．20．24.2【解析】【分析】先根据等腰直角三角形的判定与性质可得BC CD =，设m BC CD x ==，从而可得(8)m AC x =+，再在Rt ACD △中，利用正切三角函数解直角三角形即可得．【详解】解：由题意得：,8m,53,45AC CD AB ADC BDC ⊥=∠=︒∠=︒，Rt BCD ∴ 是等腰直角三角形，BC CD ∴=，设m BC CD x ==，则(8)m AC x =+，在Rt ACD △中，tan AC ADC CD∠=，即8tan 53 1.33x x +=︒≈，解得24.2(m)x ≈，经检验，是所列分式方程的解，且符合题意，即建筑物BC 的高约为24.2m ，故答案为：24.2．【点拨】本题考查了等腰直角三角形的判定与性质、解直角三角形的应用，熟练掌握解直角三角形的方法是解题关键．21．(2)180.3米【解析】【分析】对于（1），由特殊角三角函数值得出答案；对于（2），设DC ＝x 米，再根据特殊角三角函数值得CE =（米），AC ＝（3x ）（米），再由AC ＝AD +DC ，得关于x 的方程，求出x 的值，即可解决问题．(1)∵∠ECD ＝90°，∠EDC ＝60°，∴∠DEC ＝90°﹣∠EDC ＝30°，∴tan tan 30∠==︒=DC DEC EC ，即DC EC (2)设DC ＝x 米，∵∠EDC ＝60°，∠ECD ＝90°，∴tan 60CE DC =⋅︒=（米），∴(55)=+=BC BE CE （米）.∵∠A ＝30°，∴3)==AC x （米）.∵AC ＝AD +DC ，∴3240=+x x ，。

初三数学锐角三角函数含答案

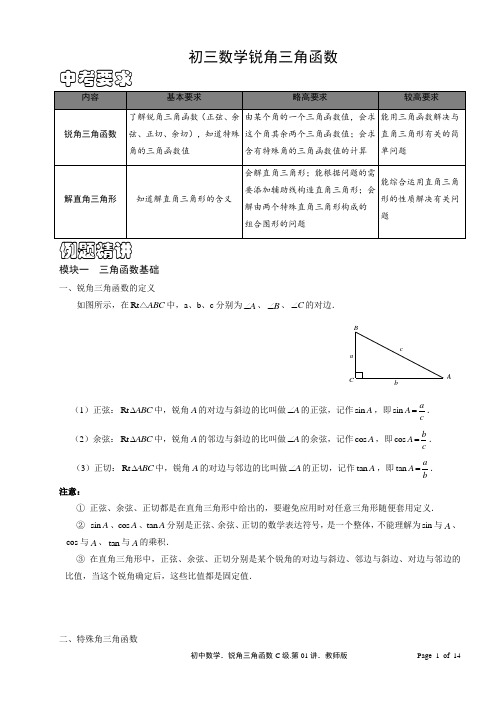
初三数学锐角三角函数中考要求例题精讲模块一三角函数基础一、锐角三角函数的定义如图所示，在Rt ABC △中，a 、b 、c 分别为A ∠、B ∠、C ∠的对边．（1）正弦：Rt ABC ∆中，锐角A 的对边与斜边的比叫做A ∠的正弦，记作sin A ，即sin aA c=．（2）余弦：Rt ABC ∆中，锐角A 的邻边与斜边的比叫做A ∠的余弦，记作cos A ，即cos b A c =．（3）正切：Rt ABC ∆中，锐角A 的对边与邻边的比叫做A ∠的正切，记作tan A ，即tan a A b=．注意：① 正弦、余弦、正切都是在直角三角形中给出的，要避免应用时对任意三角形随便套用定义． ② sin A 、cos A 、tan A 分别是正弦、余弦、正切的数学表达符号，是一个整体，不能理解为sin 与A 、cos 与A 、tan 与A 的乘积．③ 在直角三角形中，正弦、余弦、正切分别是某个锐角的对边与斜边、邻边与斜边、对边与邻边的比值，当这个锐角确定后，这些比值都是固定值．二、特殊角三角函数a A这些特殊角的三角函数值一定要牢牢记住！三、锐角三角函数的取值范围在Rt ABC ∆中，90C ∠=︒，000a b c a c b c >>><<，，，，，又sin a A c =，cos b A c =，tan aA b=，所以 0sin 10cos 1tan 0A A A <<<<>，，．四、三角函数关系 1．同角三角函数关系： 22sin cos 1A A +=，sin tan cos AA A= 2．互余角三角函数关系：(1) 任意锐角的正弦值等于它的余角的余弦值：()sin cos 90A A =︒-；(2) 任意锐角的余弦值等于它的余角的正弦值：()cos sin 90A A =︒-； (3) 任意锐角的正切值等于它的余角的余切值：()tan cot 90A A =︒-． 3．锐角三角函数值的变化规律：(1)A 、B 是锐角，若A >B ，则sin A >sin B ；若A <B ，则sin A <sin B(2) A 、B 是锐角，若A >B ，则cos A <cos B ；若A <B ，则cos A >cos B (3) A 、B 是锐角，若A >B ，则tan tan A B >；若A <B ，则tan tan A B < 【例1】已知在ABC △中，A B ∠∠、是锐角，且5sin tan 22913A B AB cm ===，，，则ABC S =△ ．【解析】过C 作CD AB ⊥于D ，这样由三角函数定义得到线段的比：5sin tan 213CD CDA B AC BD====，，设5132CD m AC m CD n BD n ====，，，，解题的关键是求出m n 、值．51222CD BD n m AD m ====，所以529122922AB AD BD m m m =+=+==所以12101452ABC m CD S AB CD ===⋅=，，△ 小结：设ABC △中，a b c 、、为A B C ∠∠∠、、的对边，R 为ABC △外接圆的半径，不难证明：与锐角三角函数相关的几个重要结论：（1）111sin sin sin 222ABC S bc A ac B ab C ===△；（2）2sin sin sin a b c R A B C===．【答案】145【巩固】如图，点A 在半径为R 的O 上，以A 为圆心，r 为半径作A ，设O 的弦PQ 与A 相切，求证PA QA ⋅为定值．【答案】证明线段乘积为定值，联想到三角形的面积，可以和三角函数联系起来．∵1sin 2APQ S PA QA A =⋅△，12APQ S r PQ =⋅△， ∴sin PA QA A r PQ ⋅⋅=⋅．在APQ △中，sin 2PQ A R =，∴2PQPA QA r PQ R⋅=⋅÷，∴2PA QA Rr ⋅=为定值．【例2】求tan1tan2tan3tan89︒⋅︒⋅︒⋅⋅︒的值【答案】∵tan cot 1αα=，tan cot(90)αα=︒-∴tan1tan89tan1cot11︒︒=︒︒=，tan2tan88tan2cot 21︒︒=︒︒=， tan44tan46tan44cot 441︒︒=︒︒=，而tan451︒=，∴tan1tan2tan3tan891︒⋅︒⋅︒⋅⋅︒=．【巩固】化简：22sin cos sin 1tan sin cos αααααα++-- 【解析】原式()2222cos sin cos sin cos sin sin cos αααααααα+=+--22cos sin sin cos cos sin αααααα-==--．【答案】sin cos αα-【例3】已知tan α1）221cos sin cos 1sin cos sin a ααααα-+-+（2090α︒<<︒）．【答案】⑴221cos sin cos 1sin cos sin a ααααα-+-+()()222222sin sin sin sin cos sin sin cos sin cos cos 3cos cos cos sin cos cos cos sin cos sin sin αααααααααααααααααααααα⎛⎫+ ⎪++⎝⎭====+⎛⎫++ ⎪⎝⎭，1sin 2cos αα-=OQPA【巩固】已知tan 2α=，求4sin 2cos 5cos 3sin αααα-+．【答案】4sin 2cos 5cos 3sin αααα-+4sin 24226cos 3sin 532115cos αααα-⨯-===+⨯+．【例4】已知α为锐角，且22sin 5cos 10αα-+=，求α的度数．【答案】∵22sin cos 1αα+=∴22(1cos )5cos 10αα--+=，即：22cos 5cos 30αα+-=． ∴(2cos 1)(cos 3)0αα-+=．解得：cos 3α=-或1cos 2α=． ∵0cos 1α≤≤，∴1cos 2α=，∴60α=︒．【巩固】若α为锐角，且22cos 7sin 50αα+-=，求α的度数．【答案】由α为锐角，可知0sin 1α<<．又由22cos 7sin 50αα+-=，22sin cos 1αα+=可知22sin 7sin 30αα-+=，解之得1sin 302αα=⇒=︒．【例5】已知sin cos αα+（α为锐角），求作以1sin α和1cos α为两根的一元二次方程．【解析】∵sin cos αα+=，两边平方得：22sin cos 2sin cos 2αααα++=又∵22sin cos 1αα+=，∴1sin cos 2αα⋅=．∴11sin cos sin cos sin cos αααααα++==112sin cos αα⋅= ∴以1sin α和1cos α为两根的一元二次方程为：220x -+=【答案】220x -+=【巩固】若方程222210x ax a -+-=的一个根是sin α，则它的另一个根必是cos α或cos α-．【答案】不妨设方程的另一根为m ，由一元二次方程的根系关系可知sin m a α+=，21sin 2a m α-=，故2(sin )1sin 2m m αα+-=，整理可得22sin (sin )1m m αα=+-，即22sin 1m α+=，又22sin cos 1αα+=，故cos m α=±．【巩固】已知：ABC △中，方程2(sin sin )(sin sin )(sin sin )0B A x A C x C B -+-+-=的两根相等，求证60B <︒．【答案】两根相等则判别式为0，但是观察系数的规律，是否有其他的好办法呢？∵此方程系数之和为0，∴1x =必为此方程的根．又∵此方程两根相等，∴121x x ==，∴12sin sin 1sin sin C Bx x B A-==-．又由正弦定理，有c b b a -=-，∴2c ab +=．再由余弦定理，有22222222()3()26212cos 22882c a a c c a ba c ca ca ca B caca ca ca ++-+-+--====≥．∴60B ︒≤，且等号不会成立，否则方程就不存在了．【巩固】在ABC △中，60A =︒，最大边与最小边的边长分别是方程2327320x x -+=的两个根，求ABC △的外接圆半径和内切圆的面积．【答案】题目中涉及到边长的关系，以及外接圆半径，这为正弦定理提供了便利条件．∵60A =︒，且显然此三角形有两边不等（即以已知方程为根的两边）， ∴ABC △中，A 既不是最大角也不是最小角，不防设b 为最大边，c 为最小边，由韦达定理，有3293b c bc +==，，又由余弦定理，有：2222cos a b c bc A =+-222()3b c bc b c bc =+-=+- 813249=-=．∴7a =（7a =-舍去）又由正弦定理，有2sin aR A===∴7916a b c ++=+=． 1sin 2S bc A P r ==⋅（其中2a b cP ++=，r 为内切圆半径）即132822r =⨯，∴r =∴内切圆面积21ππ3S r ==．【例6】若0°<θ<30°，且1sin 3km θ=+(k 为常数，且k <0)，则m 的取值范是．【答案】∵0°<θ<30°∴sin 0°<sin θ<sin 30°，即0<sin θ<12∴0<13km +<12，所以1136km -<<，又因为0k <∴1163m k k<<-．模块二解直角三角形一、解直角三角形的概念根据直角三角形中已知的量（边、角）来求解未知的量（边、角）的过程就是解直角三角形．二、直角三角形的边角关系如图，直角三角形的边角关系可以从以下几个方面加以归纳：（1）三边之间的关系：222a b c += (勾股定理) （2）锐角之间的关系：90A B ∠+∠=︒（3）边角之间的关系：sin cos ,cos sin ,tan a b aA B A B A c c b=====三、解直角三角形的四种基本类型（1）已知斜边和一直角边(如斜边c ，直角边a )，由sin aA c=求出A ∠，则90B A ∠=︒-∠，b =；（2）已知斜边和一锐角(如斜边c ，锐角A )，求出90B A ∠=︒-∠，sin a c A =，cos b c A =；（3）已知一直角边和一锐角(如a 和锐角A )，求出90B A ∠=︒-∠，tan b a B =，sin ac A=；（4）已知两直角边(如a 和b )，求出c =tan aA b=，得90B A ∠=︒-∠．具体解题时要善于选用公式及其变式，如sin a A c =可写成sin a c A =，sin a c A=等．四、解直角三角形的方法解直角三角形的方法可概括为：“有斜(斜边)用弦(正弦，余弦)，无斜用切(正切，余切)，宁乘毋除，取原避中”．这几句话的意思是：当已知或求解中有斜边时，就用正弦或余弦；无斜边时，就用正切或余切；当所求的元素既可用乘法又可用除法时，则用乘法，不用除法；既可由已知数据又可用中间数据求得时，则用原始数据，尽量避免用中间数据．五、解直角三角形的技巧及注意点在Rt ABC ∆中，90A B ∠+∠=︒，故sin cos(90)cos A A B =︒-=，cos sin A B =．利用这些关系式，可在解题时进行等量代换，以方便解题．六、如何解直角三角形的非基本类型的题型对解直角三角形的非基本类型的题型，通常是已知一边长及一锐角三角函数值，可通过解方程(组)来转化为四种基本类型求解；（1）如果有些问题一时难以确定解答方式，可以依据题意画图帮助分析；（2）对有些比较复杂的问题，往往要通过作辅助线构造直角三角形，作辅助线的一般思路是：①作垂线构成直角三角形；②利用图形本身的性质，如等腰三角形顶角平分线垂直于底边等．七、直角三角形中其他重要概念（1）仰角与俯角：在视线与水平线所成的角中，视线在水平线上方的叫做仰角，在水平线下方的叫做俯角．如图⑴．（2）坡角与坡度：坡面的垂直高度h 和水平宽度l 的比叫做坡度（或叫做坡比），用字母表示为hi l=，坡面与水平面的夹角记作α，叫做坡角，则tan hi lα==．坡度越大，坡面就越陡．如图⑵． cb aC BA（3）方向角（或方位角）：方向角一般是指以观测者的位置为中心，将正北或正南方向作为起始方向旋转到目标的方向线所成的角（一般指锐角），通常表达为北（南）偏东（西）××度．如图⑶．八、解直角三角形应用题的解题步骤及应注意的问题：（1）分析题意，根据已知条件画出它的平面或截面示意图，分清仰角、俯角、坡角、坡度、水平距离、垂直距离等概念的意义；（2）找出要求解的直角三角形．有些图形虽然不是直角三角形，但可添加适当的辅助线，把它们分割成一些直角三角形和矩形（包括正方形）；（3）根据已知条件，选择合适的边角关系式解直角三角形；（4）按照题目中已知数据的精确度进行近似计算，检验是否符合实际，并按题目要求的精确度取近似值，注明单位．【例7】如图，某高层楼房与上海东方明珠电视塔隔江想望，甲、乙两学生分别在这楼房的A B ，两层，甲在A 层测得电视塔塔顶D 的仰角为α，塔底C 的俯角为β，乙在B 层测得塔顶D 的仰角为θ，由于塔底的视线被挡住，乙无法测得塔底的俯角，已知A B ，之间的高度差为a ，求电视塔高CD （用含a αβθ，，，的代数式表示）【解析】作AE CD ⊥于E ，BF CD ⊥于F ，设DE x = 在Rt ADE ∆中，由tan DE AE α=，得tan tan DE xAE αα==，在Rt DBF ∆中，由tan DFBFθ=，得 tan tan DF x aBF θθ+==，因为AE BF =，所以tan tan x x a αθ+=，解得tan tan tan a x αθα⋅=-，从而tan tan aAE θα=- 在Rt AEC ∆中，由tan EC AE β=，得tan tan tan tan a EC AE ββθα=⋅=- 所以()tan tan tan tan tan tan tan tan tan tan a a a CD DE EC αβαβθαθαθα+=+=+=--- 【答案】()tan tan tan tan a αβθα+-【例8】一座建于若干年前的水库大坝的横断面如图所示，其中背水面的整个坡面是长为90米、宽为5图(3)图(2)图(1)俯角仰角视线视线水平线铅垂线米的矩形．现需将其整修并进行美化，方案如下：① 将背水坡AB 的坡度由1:0.75改为；② 用一组与背水坡面长边垂直的平行线将背水坡面分成9块相同的矩形区域，依次相间地种草与栽花．（1）求整修后背水坡面的面积；（2）如果栽花的成本是每平方米25元，种草的成本是每平方米20元，那么种植花草至少需要多少元？【答案】（1）作AE BC ⊥于E ．∵ 原来的坡度是1:0.75，∴ 140.753AE EB == ．设4AE k =，3BE k =， ∴ 5AB k =，又 ∵ 5AB =米， ∴1k =，则4AE =米．设整修后的斜坡为AB '，由整修后坡度为，有AE EB ='，∴∠AB E '=30°， ∴ 28AB AE '==米． ∴ 整修后背水坡面面积为908720⨯=米2 ．（2）将整修后的背水坡面分为9块相同的矩形，则每一区域的面积为80米2 ．解法一：∵ 要依次相间地种植花草，有两种方案：第一种是种草5块，种花4块，需要20×5×80+25×4×80=16000元；第二种是种花5块，种草4块，需要20×4×80+25×5×80=16400元． ∴ 应选择种草5块、种花4块的方案，需要花费16000元．解法二：∵ 要依次相间地种植花草，则必然有一种是5块，有一种是4块，而栽花的成本是每平方米25元，种草的成本是每平方米20元，∴ 两种方案中，选择种草5块、种花4块的方案花费较少．即：需要花费20×5×80+25×4×80=16000元．【例9】如图，在某海域内有三个港口A 、D 、C ．港口C 在港口A 北偏东60︒方向上，港口D 在港口A北偏西60︒方向上．一艘船以每小时25海里的速度沿北偏东30︒的方向驶离A 港口3小时后到达B 点位置处，此时发现船舱漏水，海水以每5分钟4吨的速度渗入船内．当船舱渗入的海水总量超过75吨时，船将沉入海中．同时在B 处测得港口C 在B 处的南偏东75︒方向上．若船上的抽水机每小时可将8吨的海水排出船外，问此船在B 处至少应以怎样的航行速度驶向最近的港口停靠，才能保证船在抵达港口前不会沉没（要求计算结果保留根号）？并指出此时船的航行方向．DCBA【解析】连结AC、AD、BC、BD，延长AT，过B作BT AT⊥于T，AC与BT交于点E．过B作BP AC⊥于点P．由已知得90BAD∠=︒，30BAC∠=︒，32575AB=⨯=（海里），在BEP∆和AET∆中，90BPE ATE∠=∠=︒，AET BEP∠=∠，∴30EBP EAT∠=∠=︒．∵60BAT∠=︒，∴30BAP∠=︒，从而17537.52BP=⨯=（海里）．∵港口C在B处的南偏东75︒方向上，∴45CBP∠=︒．在等腰Rt CBP∆中，BC==，∴BC<AB．BAD∆是Rt∆，∴BD AB>．综上，可得港口C离B点位置最近．∴此船应转向南偏东75︒方向上直接驶向港口C．设由B驶向港口C船的速度为每小时x海里，548)5÷⨯-<7，解不等式，得x>．答：此船应转向沿南偏东75︒的方向向港口C航行，且航行速度至少不低于每小时能保证船在抵达港口前不会沉没．【答案】此船应转向沿南偏东75︒的方向向港口C航行，且航行速度至少不低于每小时证船在抵达港口前不会沉没．【巩固】海面上B处有一货轮正在向正南方向航行，其航行路线是当它到达正南方C时，在驶向正西方的目的地A处，且200CA CB==海里，在AB中点O处有一客轮，其速度为货轮的一半，现在客轮要截住货轮取一件货物，于是选择某一航向行驶去截住货轮，那么当客轮截住客轮时至少航行了多少海里，它所选择了怎样的方向角？（路程保留整数海里，角度精确到度）【解析】如图，由题意可知，ABC∆为等腰直角三角形，假设客轮截住货轮的地点在BC边上时，过OD BC⊥于D，OD为客轮到达BC边的最短距离，即客轮航行的路程为OD，由货轮速度为客轮的2倍可知，货轮航行的距离为2OD BC=，即货轮此时到达了C点，∴客轮截住货轮的地点不可能在BC边上．∴客轮截住货轮的地点在AC 边上．设在AC 边上的F 点两船相遇，设客轮航行的距离为x ，即OE x =，则2BC CE x +=， ∴2200CE x =-，过O 作OF AC ⊥于F ，则11002OF BC ==海里，11002FC AC ==海里， ∴3002EF x =-在Rt DEF ∆中，222OF EF OE +=，即222100(3002)x x +-=，解得x =1282x ≈，2118x ≈∴141OE OA ≤=∴1282x ≈不符合题意，∴118x ≈ 即当客轮截住货轮时，航行了118海里．在Rt OEF ∆中，100cos 0.8475118EOF ∠=≈ ∴32EOF ∠=︒∴客轮的航行方向应为南偏东32︒．【答案】客轮的航行方向应为南偏东32︒课堂检测1．（辽宁竞赛）如图，湖心岛上有一凉亭，现欲利用湖岸边的开阔平整地带，测量凉亭顶端到湖面所在平面的高度AB (见示意图)，可供使用的工具有测倾器、皮尺．（1）请你根据现有条件，设计一个测量凉亭顶端到湖面所在平面的高度AB 的方案，画出测量方案的平面示意图，并将测量的数据标注在图形上（所测的距离用m ，n 表示，角用α，β表示，测倾器高度忽略不计）；（2）根据你所测量的数据，计算凉亭到湖面的高度AB (用字母表示)．F EDOC BA【解析】（1）如图所示，在点C 测得ACB α∠=，在点D 测得ADB β∠=，测得DC m =（2）在Rt ABC ∆中，设AB x =，tan x BC α=在Rt ABD ∆中，tan xBD β= BD BC m -=，即tan tan x xm βα-= 解得tan tan tan tan x m αβαβ⋅=-【答案】（1）DC m =；（2）tan tan tan tan m αβαβ⋅-2．化简：222tan1tan 2....tan89sin 1sin 2...sin 89︒⋅︒︒︒+︒++︒【解析】tan1tan2....tan89tan451︒⋅︒︒=︒=()()22222222sin 1sin 2...sin 89sin 1cos 1sin 2cos 2...sin 45︒+︒++︒=︒+︒+︒+︒++︒1894422=+=，故原式289=．【答案】2893．如图1、图2，是一款家用的垃圾桶，踏板AB （与地面平行）或绕定点P （固定在垃圾桶底部的某一位置）上下转动（转动过程中始终保持''AP A P BP B P ==，）．通过向下踩踏点A 到'A （与地面接触点）使点B 上升到点'B ，与此同时传动杆BH 运动到''B H 的位置，点H 绕固定点D 旋转（DH 为旋转半径）至点'H ，从而使桶盖打开一个张角'HDH ∠．如图3，桶盖打开后，传动杆''H B 所在的直线分别与水平直线AB DH 、垂直，垂足为点M C 、，设''H C B M =．测得6cm 12cm '8cm AP PB DH ===，，．要使桶盖张开的角度'HDH ∠不小于60︒，那么踏板AB 离地面的高度至少等于多少cm ？（结果保留两位有效数字）【解析】过点'A 作'A N AB ⊥垂足为N 点，在Rt 'H CD ∆中，若'HDH ∠不小于60︒，则'3sin 60'H C H D ≥︒=，即3''43H C H D ≥=， ∴''43B M H C =≥， ∵Rt 'Rt 'A NP B MP ∆∆∽ ∴''''A N A PB M B P=， ∴''643'23 3.5cm 'A P B M A N B P ⋅⨯=≥=≈，∴踏板AB 离地面的高度至少等于3.5cm ．【答案】踏板AB 离地面的高度至少等于3.5cm课后作业1．化简求值：1sin 1sin 1cos 1cos 1sin 1sin 1cos 1cos αααααααα⎛⎫⎛⎫-+-+-- ⎪⎪ ⎪⎪+-+-⎝⎭⎝⎭（090α︒<<︒）【解析】原式()()()()222222221sin 1sin 1cos 1cos 1sin 1sin 1cos 1cos αααααααα⎡⎤⎡⎤-+-+⎢⎥⎢⎥=-⋅-⎢⎥⎢⎥----⎣⎦⎣⎦由090α︒<<︒可知，0cos 1α<<，0sin 1α<<．故原式1sin 1sin 1cos 1cos cos cos sin sin αααααααα-+-+⎛⎫⎛⎫=-- ⎪⎪⎝⎭⎝⎭2sin 2cos 4cos sin αααα--=⋅=．图3图2C MAA'P BB'HDH'H'DHB'BPA'A（图1）NCMA'PBB'HDH'【答案】42．若045α︒<<︒，且sin cos αα=sin α的值．【解析】方法1：由2263sin cos sin cos 256αααα==，结合22sin cos 1αα+=，可得 2226397sin (1sin )sin 2561616ααα-=⇒=或．由045α︒<<︒可知221sin sin 452α<︒=，故27sin sin 16αα=⇒=．方法2：由sin cos 2sin cos αααα=，结合22sin cos 1αα+=，可得sin cos αα+==cos sin αα-=，故sin α．3．（2011甘肃兰州）通过学习三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化．类似的，可以在等腰三角形中建立边角之间的联系．我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad ）．如图①在ABC △中，AB AC =，顶角A 的正对记作sadA ，这时=BCsadA AB=底边腰．容易知道一个角的大小与这个角的正对值也是相互唯一确定的．根据上述角的正对定义，解下列问题：（1）60sad ︒= ．（2）对于0180A ︒<<︒，∠A 的正对值sadA 的取值范围是．（3）如图②，已知3sin 5A =，其中A ∠为锐角，试求sadA 的值．【解析】（1）1（2）02sadA <<（3）设53AB a BC a ==，，则4AC a =．在AB 上取4AD AC a ==，作DE AC ⊥于点E ．则312416164sin 4cos 44555555DE AD A a a AE AD A a a CE a a =⋅=⋅==⋅=⋅==-=，，，CD =图②图①C BAC B A∴CDsadAAC==EDCBA。

2020-2021中考数学锐角三角函数综合题含答案解析

2020-2021中考数学锐角三角函数综合题含答案解析一、锐角三角函数1．已知：如图，在四边形 ABCD 中， AB ∥CD ， ∠ACB =90°， AB=10cm ， BC=8cm ， OD 垂直平分 A C ．点 P 从点 B 出发，沿 BA 方向匀速运动，速度为 1cm/s ；同时，点 Q 从点 D 出发，沿 DC 方向匀速运动，速度为 1cm/s ；当一个点停止运动，另一个点也停止运动．过点 P 作 PE ⊥AB ，交 BC 于点 E ，过点 Q 作 QF ∥AC ，分别交 AD ， OD 于点 F ， G ．连接 OP ，EG ．设运动时间为 t ( s )（0＜t ＜5），解答下列问题：（1）当 t 为何值时，点 E 在BAC 的平分线上？（2）设四边形 PEGO 的面积为 S(cm 2) ，求 S 与 t 的函数关系式；（3）在运动过程中，是否存在某一时刻 t ，使四边形 PEGO 的面积最大？若存在，求出t 的值；若不存在，请说明理由；（4）连接 OE ， OQ ，在运动过程中，是否存在某一时刻 t ，使 OE ⊥OQ ？若存在，求出t 的值；若不存在，请说明理由．【答案】（1）4s t =；（2）PEGO S 四边形2315688t t =-++ ，(05)t <<；（3）52t =时，PEGO S 四边形取得最大值；（4）165t =时，OE OQ ⊥. 【解析】【分析】（1）当点E 在∠BAC 的平分线上时，因为EP ⊥AB ，EC ⊥AC ，可得PE=EC ，由此构建方程即可解决问题．（2）根据S 四边形OPEG =S △OEG +S △OPE =S △OEG +（S △OPC +S △PCE -S △OEC ）构建函数关系式即可．（3）利用二次函数的性质解决问题即可．（4）证明∠EOC=∠QOG ，可得tan ∠EOC=tan ∠QOG ，推出EC GQOC OG=，由此构建方程即可解决问题．【详解】（1）在Rt △ABC 中，∵∠ACB=90°，AB=10cm ，BC=8cm ， ∴22108-=6（cm ）， ∵OD 垂直平分线段AC ， ∴OC=OA=3（cm ），∠DOC=90°， ∵CD ∥AB ，∴∠BAC=∠DCO ， ∵∠DOC=∠ACB ， ∴△DOC ∽△BCA ， ∴AC AB BCOC CD OD ==， ∴61083CD OD==， ∴CD=5（cm ），OD=4（cm ）， ∵PB=t ，PE ⊥AB ，易知：PE=34t ，BE=54t ，当点E 在∠BAC 的平分线上时， ∵EP ⊥AB ，EC ⊥AC ， ∴PE=EC ，∴34t=8-54t ，∴t=4．∴当t 为4秒时，点E 在∠BAC 的平分线上．（2）如图，连接OE ，PC ．S 四边形OPEG =S △OEG +S △OPE =S △OEG +（S △OPC +S △PCE -S △OEC ） =1414153154338838252524524t t t t t ⎡⎛⎫⎛⎫⎛⎫⎛⎫⨯-⨯+⨯⨯-+⨯-⨯-⨯⨯- ⎪ ⎪ ⎪ ⎪⎢⎝⎭⎝⎭⎝⎭⎝⎭⎣ =281516(05)33t t t -++<<．（3）存在．∵28568(05)323S t t ⎛⎫=--+<< ⎪⎝⎭，∴t=52时，四边形OPEG 的面积最大，最大值为683．（4）存在．如图，连接OQ ． ∵OE ⊥OQ ，∴∠EOC+∠QOC=90°，∵∠QOC+∠QOG=90°，∴∠EOC=∠QOG，∴tan∠EOC=tan∠QOG，∴EC GQOC OG=，∴358544345ttt-=-，整理得：5t2-66t+160=0，解得165t=或10（舍弃）∴当165t=秒时，OE⊥OQ．【点睛】本题属于四边形综合题，考查了解直角三角形，相似三角形的判定和性质，锐角三角函数，多边形的面积等知识，解题的关键是学会利用参数构建方程解决问题.2．在正方形ABCD中，对角线AC，BD交于点O，点P在线段BC上（不含点B），∠BPE=12∠ACB，PE交BO于点E，过点B作BF⊥PE，垂足为F，交AC于点G．（1）当点P与点C重合时（如图1）．求证：△BOG≌△POE；（2）通过观察、测量、猜想：BFPE=，并结合图2证明你的猜想；（3）把正方形ABCD改为菱形，其他条件不变（如图3），若∠ACB=α，求BFPE的值．（用含α的式子表示）【答案】（1）证明见解析（2）12BFPE=（3）1tan2BFPEα=【解析】解：（1）证明：∵四边形ABCD是正方形，P与C重合，∴OB="OP" ，∠BOC=∠BOG=90°．∵PF⊥BG ，∠PFB=90°，∴∠GBO=90°—∠BGO，∠EPO=90°—∠BGO．∴∠GBO=∠EPO ．∴△BOG≌△POE（AAS）．（2）BF1PE2=．证明如下：如图，过P作PM//AC交BG于M，交BO于N，∴∠PNE=∠BOC=900，∠BPN=∠OCB．∵∠OBC=∠OCB =450，∴∠NBP=∠NPB．∴NB=NP．∵∠MBN=900—∠BMN，∠NPE=900—∠BMN，∴∠MBN=∠NPE．∴△BMN≌△PEN（ASA）．∴BM=PE．∵∠BPE=12∠ACB，∠BPN=∠ACB，∴∠BPF=∠MPF．∵PF⊥BM，∴∠BFP=∠MFP=900．又∵PF=PF，∴△BPF≌△MPF（ASA）．∴BF="MF" ，即BF=12 BM．∴BF=12PE，即BF1PE2=．（3）如图，过P作PM//AC交BG于点M，交BO于点N，∴∠BPN=∠ACB=α，∠PNE=∠BOC=900．由（2）同理可得BF=12BM，∠MBN=∠EPN．∵∠BNM=∠PNE=900，∴△BMN∽△PEN．∴BM BNPE PN=．在Rt△BNP中，BNtan=PNα，∴BM=tanPEα，即2BF=tanPEα．∴BF 1=tan PE 2α．（1）由正方形的性质可由AAS 证得△BOG ≌△POE ．（2）过P 作PM//AC 交BG 于M ，交BO 于N ，通过ASA 证明△BMN ≌△PEN 得到BM=PE ，通过ASA 证明△BPF ≌△MPF 得到BF=MF ，即可得出BF 1PE 2=的结论．（3）过P 作PM//AC 交BG 于点M ，交BO 于点N ，同（2）证得BF=12BM ， ∠MBN=∠EPN ，从而可证得△BMN ∽△PEN ，由BM BN PE PN =和Rt △BNP 中BNtan =PNα即可求得BF 1=tan PE 2α．3．如图（1），在平面直角坐标系中，点A （0，﹣6），点B （6，0）．Rt △CDE 中，∠CDE=90°，CD=4，DE=4，直角边CD 在y 轴上，且点C 与点A 重合．Rt △CDE 沿y 轴正方向平行移动，当点C 运动到点O 时停止运动．解答下列问题：（1）如图（2），当Rt △CDE 运动到点D 与点O 重合时，设CE 交AB 于点M ，求∠BME 的度数．（2）如图（3），在Rt △CDE 的运动过程中，当CE 经过点B 时，求BC 的长．（3）在Rt △CDE 的运动过程中，设AC=h ，△OAB 与△CDE 的重叠部分的面积为S ，请写出S 与h 之间的函数关系式，并求出面积S 的最大值．【答案】（1）∠BME=15°；（2BC=4；（3）h≤2时，S=﹣h 2+4h+8，当h≥2时，S=18﹣3h ．【解析】试题分析：（1）如图2，由对顶角的定义知，∠BME=∠CMA ，要求∠BME 的度数，需先求出∠CMA 的度数．根据三角形外角的定理进行解答即可；（2）如图3，由已知可知∠OBC=∠DEC=30°，又OB=6，通过解直角△BOC 就可求出BC 的长度；（3）需要分类讨论：①h≤2时，如图4，作MN ⊥y 轴交y 轴于点N ，作MF ⊥DE 交DE 于点F ，S=S △EDC ﹣S △EFM ；②当h≥2时，如图3，S=S △OBC ．试题解析：解：（1）如图2，∵在平面直角坐标系中，点A（0，﹣6），点B（6，0）．∴OA=OB，∴∠OAB=45°，∵∠CDE=90°，CD=4，DE=4，∴∠OCE=60°，∴∠CMA=∠OCE﹣∠OAB=60°﹣45°=15°，∴∠BME=∠CMA=15°；如图3，∵∠CDE=90°，CD=4，DE=4，∴∠OBC=∠DEC=30°，∵OB=6，∴BC=4；（3）①h≤2时，如图4，作MN⊥y轴交y轴于点N，作MF⊥DE交DE于点F，∵CD=4，DE=4，AC=h，AN=NM，∴CN=4﹣FM，AN=MN=4+h﹣FM，∵△CMN∽△CED，∴，∴，解得FM=4﹣，∴S=S△EDC﹣S△EFM=×4×4﹣（44﹣h）×（4﹣）=﹣h2+4h+8，②如图3，当h≥2时，S=S△OBC=OC×OB=（6﹣h）×6=18﹣3h．考点：1、三角形的外角定理；2、相似；3、解直角三角形4．如图，将一副直角三角形拼放在一起得到四边形ABCD，其中∠BAC=45°，∠ACD=30°，点E为CD边上的中点，连接AE，将△ADE沿AE所在直线翻折得到△AD′E，D′E交AC于F 点．若AB=6cm．（1）AE的长为 cm；（2）试在线段AC上确定一点P，使得DP+EP的值最小，并求出这个最小值；（3）求点D′到BC的距离．【答案】（1）；（2）12cm；（3）cm．【解析】试题分析：（1）首先利用勾股定理得出AC的长，进而求出CD的长，利用直角三角形斜边上的中线等于斜边的一半进而得出答案：∵∠BAC=45°，∠B=90°，∴AB=BC=6cm，∴AC=12cm．∵∠ACD=30°，∠DAC=90°，AC=12cm，∴（cm）．∵点E为CD边上的中点，∴AE=DC=cm．（2）首先得出△ADE为等边三角形，进而求出点E，D′关于直线AC对称，连接DD′交AC 于点P，根据轴对称的性质，此时DP+EP值为最小，进而得出答案．（3）连接CD′，BD′，过点D′作D′G⊥BC于点G，进而得出△ABD′≌△CBD′（SSS），则∠D′BG=45°，D′G=GB，进而利用勾股定理求出点D′到BC边的距离．试题解析：解：（1）．（2）∵Rt△ADC中，∠ACD=30°，∴∠ADC=60°，∵E为CD边上的中点，∴DE=AE．∴△ADE为等边三角形．∵将△ADE沿AE所在直线翻折得△AD′E，∴△AD′E为等边三角形，∠AED′=60°．∵∠EAC=∠DAC﹣∠EAD=30°，∴∠EFA=90°，即AC所在的直线垂直平分线段ED′．∴点E，D′关于直线AC对称．如答图1，连接DD′交AC于点P，∴此时DP+EP值为最小，且DP+EP=DD′．∵△ADE是等边三角形，AD=AE=，∴，即DP+EP最小值为12cm．（3）如答图2，连接CD′，BD′，过点D′作D′G⊥BC于点G，∵AC垂直平分线ED′，∴AE=AD′，CE=CD′，∵AE=EC，∴AD′=CD′=．在△ABD′和△CBD′中，∵，∴△ABD′≌△CBD′（SSS）．∴∠D′BG=∠D′BC=45°．∴D′G=GB．设D′G长为xcm，则CG长为cm，在Rt△GD′C中，由勾股定理得，解得：（不合题意舍去）．∴点D′到BC边的距离为cm．考点：1．翻折和单动点问题；2．勾股定理；3．直角三角形斜边上的中线性质；4．等边三角形三角形的判定和性质；5．轴对称的应用（最短线路问题）；6．全等三角形的判定和性质；7．方程思想的应用．5．（2013年四川攀枝花12分）如图，在平面直角坐标系中，四边形ABCD是梯形，AB∥CD，点B（10，0），C（7，4）．直线l经过A，D两点，且sin∠DAB=22．动点P在线段AB上从点A出发以每秒2个单位的速度向点B运动，同时动点Q从点B出发以每秒5个单位的速度沿B→C→D的方向向点D运动，过点P作PM垂直于x轴，与折线A→D→C相交于点M，当P，Q两点中有一点到达终点时，另一点也随之停止运动．设点P，Q运动的时间为t秒（t＞0），△MPQ的面积为S．（1）点A的坐标为，直线l的解析式为；（2）试求点Q与点M相遇前S与t的函数关系式，并写出相应的t的取值范围；（3）试求（2）中当t为何值时，S的值最大，并求出S的最大值；（4）随着P，Q两点的运动，当点M在线段DC上运动时，设PM的延长线与直线l相交于点N，试探究：当t为何值时，△QMN为等腰三角形？请直接写出t的值．【答案】解：（1）（﹣4，0）；y=x+4．（2）在点P、Q运动的过程中：①当0＜t≤1时，如图1，过点C作CF⊥x轴于点F，则CF=4，BF=3，由勾股定理得BC=5．过点Q作QE⊥x轴于点E，则BE=BQ•cos∠CBF=5t•35=3t．∴PE=PB﹣BE=（14﹣2t）﹣3t=14﹣5t，S=12PM•PE=12×2t×（14﹣5t）=﹣5t2+14t．②当1＜t≤2时，如图2，过点C、Q分别作x轴的垂线，垂足分别为F，E，则CQ=5t﹣5，PE=AF﹣AP﹣EF=11﹣2t﹣（5t﹣5）=16﹣7t．S=1 2PM•PE=12×2t×（16﹣7t）=﹣7t2+16t．③当点M与点Q相遇时，DM+CQ=CD=7，即（2t﹣4）+（5t﹣5）=7，解得t=167．当2＜t＜167时，如图3，MQ=CD﹣DM﹣CQ=7﹣（2t﹣4）﹣（5t﹣5）=16﹣7t，S=12PM•MQ=12×4×（16﹣7t）=﹣14t+32．综上所述，点Q与点M相遇前S与t的函数关系式为()()225t14t0<t1S{7t16t1<t21614t322<t<7-+≤=-+≤⎛⎫-+ ⎪⎝⎭．（3）①当0＜t≤1时，22749S5t14t5t55⎛⎫=-+=--+⎪⎝⎭，∵a=﹣5＜0，抛物线开口向下，对称轴为直线t=75，∴当0＜t≤1时，S随t的增大而增大．∴当t=1时，S有最大值，最大值为9．②当1＜t≤2时，22864S7t16t7t77⎛⎫=-+=--+⎪⎝⎭，∵a=﹣7＜0，抛物线开口向下，对称轴为直线t=87，∴当t=87时，S有最大值，最大值为647．③当2＜t＜167时，S=﹣14t+32∵k=﹣14＜0，∴S随t的增大而减小．又∵当t=2时，S=4；当t=167时，S=0，∴0＜S＜4．综上所述，当t=87时，S有最大值，最大值为647．（4）t=209或t=125时，△QMN为等腰三角形．【解析】（1）利用梯形性质确定点D的坐标，由sin∠DAB=22，利用特殊三角函数值，得到△AOD为等腰直角三角形，从而得到点A的坐标；由点A、点D的坐标，利用待定系数法求出直线l的解析式：∵C（7，4），AB∥CD，∴D（0，4）．∵sin∠DAB=22，∴∠DAB=45°．∴OA=OD=4．∴A（﹣4，0）．设直线l的解析式为：y=kx+b，则有4k b0{b4-+==，解得：k1{b4==．∴y=x+4．∴点A坐标为（﹣4，0），直线l的解析式为：y=x+4．（2）弄清动点的运动过程分别求解：①当0＜t≤1时，如图1；②当1＜t≤2时，如图2；③当2＜t＜167时，如图3．（3）根据（2）中求出的S表达式与取值范围，逐一讨论计算，最终确定S的最大值．（4）△QMN为等腰三角形的情形有两种，需要分类讨论：①如图4，点M在线段CD上，MQ=CD﹣DM﹣CQ=7﹣（2t﹣4）﹣（5t﹣5）=16﹣7t，MN=DM=2t﹣4，由MN=MQ，得16﹣7t=2t﹣4，解得t=209．②如图5，当点M运动到C点，同时当Q刚好运动至终点D，此时△QMN为等腰三角形，t=125．∴当t=209或t=125时，△QMN为等腰三角形．考点：一次函数综合题，双动点问题，梯形的性质，锐角三角函数定义，特殊角的三角函数值，由实际问题列函数关系式，一次函数和二次函数的性质，等腰三角形的性质，分类思想的应用．6．如图，矩形OABC中，A(6，0)、C(0，23)、D(0，33)，射线l过点D且与x轴平行，点P、Q分别是l和x轴的正半轴上的动点，满足∠PQO＝60º．(1)点B的坐标是，∠CAO＝ º，当点Q与点A重合时，点P的坐标为；(2)设点P的横坐标为x，△OPQ与矩形OABC重叠部分的面积为S，试求S与x的函数关系式和相应的自变量x的取值范围．【答案】（1）（6，3）． 30．（3，3）（2）()()()()243x 430x 3331333x x 3x 5232S {23x 1235x 93543x 9x +≤≤-+-<≤=-+<≤>【解析】解：（1）（6，23）． 30．（3，33）．（2）当0≤x≤3时，如图1，OI=x ，IQ=PI•tan60°=3，OQ=OI+IQ=3+x ；由题意可知直线l ∥BC ∥OA ，可得EF PE DC 31==OQ PO DO 333==，∴EF=13（3+x ），此时重叠部分是梯形，其面积为：EFQO 14343S S EF OQ OC 3x x 43233==+⋅=+=+梯形（）（）当3＜x≤5时，如图2，)HAQ EFQO EFQO 221S S S S AH AQ243331333 3x 3=∆=-=-⋅⋅=+---梯形梯形当5＜x≤9时，如图3，12S BE OAOC 312x 2323 =x 1233=+⋅=--+（）（）。

2020-2021中考数学压轴题专题复习——锐角三角函数的综合及答案解析

2020-2021中考数学压轴题专题复习——锐角三角函数的综合及答案解析一、锐角三角函数1．如图，山坡上有一棵树AB，树底部B点到山脚C点的距离BC为63米，山坡的坡角为30°．小宁在山脚的平地F处测量这棵树的高，点C到测角仪EF的水平距离CF=1米，从E处测得树顶部A的仰角为45°，树底部B的仰角为20°，求树AB的高度．（参考数值：sin20°≈0.34，cos20°≈0.94，tan20°≈0.36）【答案】6.4米【解析】解：∵底部B点到山脚C点的距离BC为6 3 米，山坡的坡角为30°．∴DC=BC•cos30°=3==米，639∵CF=1米，∴DC=9+1=10米，∴GE=10米，∵∠AEG=45°，∴AG=EG=10米，在直角三角形BGF中，BG=GF•tan20°=10×0.36=3.6米，∴AB=AG-BG=10-3.6=6.4米，答：树高约为6.4米首先在直角三角形BDC中求得DC的长，然后求得DF的长，进而求得GF的长，然后在直角三角形BGF中即可求得BG的长，从而求得树高2．在△ABC中，AB=BC，点O是AC的中点，点P是AC上的一个动点（点P不与点A，O，C重合）．过点A，点C作直线BP的垂线，垂足分别为点E和点F，连接OE，OF．（1）如图1，请直接写出线段OE与OF的数量关系；（2）如图2，当∠ABC=90°时，请判断线段OE与OF之间的数量关系和位置关系，并说明理由（3）若|CF﹣AE|=2，3△POF为等腰三角形时，请直接写出线段OP的长．【答案】（1）OF =OE；（2）OF⊥EK，OF=OE，理由见解析；（3）OP的长为62或233.【解析】【分析】（1）如图1中，延长EO交CF于K，证明△AOE≌△COK，从而可得OE=OK，再根据直角三角形斜边中线等于斜边一半即可得OF=OE；（2）如图2中，延长EO交CF于K，由已知证明△ABE≌△BCF，△AOE≌△COK，继而可证得△EFK是等腰直角三角形，由等腰直角三角形的性质即可得OF⊥EK，OF=OE；（3）分点P在AO上与CO上两种情况分别画图进行解答即可得.【详解】（1）如图1中，延长EO交CF于K，∵AE⊥BE，CF⊥BE，∴AE∥CK，∴∠EAO=∠KCO，∵OA=OC，∠AOE=∠COK，∴△AOE≌△COK，∴OE=OK，∵△EFK是直角三角形，∴OF=12EK=OE；（2）如图2中，延长EO交CF于K，∵∠ABC=∠AEB=∠CFB=90°，∴∠ABE+∠BAE=90°，∠ABE+∠CBF=90°，∴∠BAE=∠CBF，∵AB=BC，∴△ABE≌△BCF，∴BE=CF，AE=BF，∵△AOE≌△COK，∴AE=CK，OE=OK，∴FK=EF，∴△EFK是等腰直角三角形，∴OF⊥EK，OF=OE；（3）如图3中，点P在线段AO上，延长EO交CF于K，作PH⊥OF于H，∵|CF﹣AE|=2，EF=23，AE=CK，∴FK=2，在Rt△EFK中，tan∠FEK=3，∴∠FEK=30°，∠EKF=60°，∴EK=2FK=4，OF=12EK=2，∵△OPF是等腰三角形，观察图形可知，只有OF=FP=2，在Rt△PHF中，PH=12PF=1，HF=3，OH=2﹣3，∴OP=()2212362+-=-.如图4中，点P在线段OC上，当PO=PF时，∠POF=∠PFO=30°，∴∠BOP=90°，∴323综上所述：OP6223.【点睛】本题考查了全等三角形的判定与性质、直角三角形斜边中线等于斜边一半、等腰直角三角形的判定与性质、解直角三角形等，综合性较强，正确添加辅助线是解题的关键.3．如图，从地面上的点A看一山坡上的电线杆PQ，测得杆顶端点P的仰角是45°，向前走6m到达B点，测得杆顶端点P和杆底端点Q的仰角分别是60°和30°．（1）求∠BPQ的度数；（2）求该电线杆PQ的高度（结果精确到1m）．备用数据：，【答案】（1）∠BPQ=30°；（2）该电线杆PQ的高度约为9m．【解析】试题分析：（1）延长PQ交直线AB于点E，根据直角三角形两锐角互余求得即可；（2）设PE=x米，在直角△APE和直角△BPE中，根据三角函数利用x表示出AE和BE，根据AB=AE-BE即可列出方程求得x的值，再在直角△BQE中利用三角函数求得QE的长，则PQ的长度即可求解．试题解析：延长PQ交直线AB于点E，（1）∠BPQ=90°-60°=30°；（2）设PE=x米．在直角△APE中，∠A=45°，则AE=PE=x米；∵∠PBE=60°∴∠BPE=30°在直角△BPE中，BE=33PE=33x米，∵AB=AE-BE=6米，则3，解得：3则BE=（3）米．在直角△BEQ中，QE=33BE=33（33+3）=（3+3）米．∴PQ=PE-QE=9+33-（3+3）=6+23≈9（米）．答：电线杆PQ的高度约9米．考点：解直角三角形的应用-仰角俯角问题．4．（6分）某海域有A，B两个港口，B港口在A港口北偏西30°方向上，距A港口60海里，有一艘船从A港口出发，沿东北方向行驶一段距离后，到达位于B港口南偏东75°方向的C处，求该船与B港口之间的距离即CB的长（结果保留根号）．【答案】．【解析】试题分析：作AD⊥BC于D，于是有∠ABD=45°，得到AD=BD=，求出∠C=60°，根据正切的定义求出CD的长，得到答案．试题解析：作AD⊥BC于D，∵∠EAB=30°，AE∥BF，∴∠FBA=30°，又∠FBC=75°，∴∠ABD=45°，又AB=60，∴AD=BD=，∵∠BAC=∠BAE+∠CAE=75°，∠ABC=45°，∴∠C=60°，在Rt△ACD中，∠C=60°，AD=，则tanC=，∴CD==，∴BC=．故该船与B港口之间的距离CB的长为海里．考点：解直角三角形的应用-方向角问题．5．在等腰△ABC中，∠B=90°，AM是△ABC的角平分线，过点M作MN⊥AC于点N，∠EMF=135°．将∠EMF绕点M旋转，使∠EMF的两边交直线AB于点E，交直线AC于点F，请解答下列问题：（1）当∠EMF绕点M旋转到如图①的位置时，求证：BE+CF=BM；（2）当∠EMF绕点M旋转到如图②，图③的位置时，请分别写出线段BE，CF，BM之间的数量关系，不需要证明；（3）在（1）和（2）的条件下，tan∠BEM=，AN=+1，则BM=，CF=．【答案】（1）证明见解析（2）见解析（3）1，1+或1﹣【解析】【分析】(1)由等腰△ABC中，∠B=90°，AM是△ABC的角平分线，过点M作MN⊥AC于点N，可得BM=MN，∠BMN=135°，又∠EMF=135°，可证明的△BME≌△NMF，可得BE=NF，NC=NM=BM进而得出结论；（2）①如图②时，同（1）可证△BME≌△NMF，可得BE﹣CF=BM，②如图③时，同（1）可证△BME≌△NMF，可得CF﹣BE=BM；(3) 在Rt△ABM和Rt△ANM中，，可得Rt△ABM≌Rt△ANM，后分别求出AB、 AC、 CN 、BM、 BE的长，结合（1）（2）的结论对图①②③进行讨论可得CF的长.【详解】（1）证明：∵△ABC是等腰直角三角形，∴∠BAC=∠C=45°，∵AM是∠BAC的平分线，MN⊥AC，∴BM=MN，在四边形ABMN中，∠，BMN=360°﹣90°﹣90°﹣45°=135°，∵∠ENF=135°，，∴∠BME=∠NMF，∴△BME≌△NMF，∴BE=NF，∵MN⊥AC，∠C=45°，∴∠CMN=∠C=45°，∴NC=NM=BM，∵CN=CF+NF，∴BE+CF=BM；（2）针对图2，同（1）的方法得，△BME≌△NMF，∴BE=NF，∵MN⊥AC，∠C=45°，∴∠CMN=∠C=45°，∴NC=NM=BM，∵NC=NF﹣CF，∴BE﹣CF=BM；针对图3，同（1）的方法得，△BME≌△NMF，∴BE=NF，∵MN⊥AC，∠C=45°，∴∠CMN=∠C=45°，∴NC=NM=BM，∵NC=CF﹣NF，∴CF﹣BE=BM；（3）在Rt△ABM和Rt△ANM中，，∴Rt△ABM≌Rt△ANM（HL），∴AB=AN=+1，在Rt△ABC中，AC=AB=+1，∴AC=AB=2+，∴CN=AC﹣AN=2+﹣（+1）=1，在Rt△CMN中，CM=CN=，∴BM=BC﹣CM=+1﹣=1，在Rt△BME中，tan∠BEM===，∴BE=，∴①由（1）知，如图1，BE+CF=BM，∴CF=BM﹣BE=1﹣②由（2）知，如图2，由tan∠BEM=，∴此种情况不成立；③由（2）知，如图3，CF﹣BE=BM，∴CF=BM+BE=1+，故答案为1，1+或1﹣．【点睛】本题考查三角函数与旋转与三角形全等的综合，难度较大，需综合运用所学知识求解.6．如图13，矩形的对角线，相交于点，关于的对称图形为．（1）求证：四边形是菱形；（2）连接，若，．①求的值；②若点为线段上一动点（不与点重合），连接，一动点从点出发，以的速度沿线段匀速运动到点，再以的速度沿线段匀速运动到点，到达点后停止运动．当点沿上述路线运动到点所需要的时间最短时，求的长和点走完全程所需的时间．【答案】（1）详见解析；（2）①②和走完全程所需时间为【解析】试题分析：（1）利用四边相等的四边形是菱形；（2）①构造直角三角形求；②先确定点沿上述路线运动到点所需要的时间最短时的位置，再计算运到的时间.试题解析：解：（1）证明：四边形是矩形.与交于点O,且关于对称四边形是菱形.（2）①连接,直线分别交于点,交于点关于的对称图形为在矩形中，为的中点，且O为AC的中点为的中位线同理可得：为的中点，②过点P作交于点由运动到所需的时间为3s由①可得，点O以的速度从P到A所需的时间等于以从M运动到A即：由O运动到P所需的时间就是OP+MA和最小.如下图，当P运动到,即时，所用时间最短.在中，设解得：和走完全程所需时间为考点：菱形的判定方法；构造直角三角形求三角函数值；确定极值时动点的特殊位置7．问题探究：（一）新知学习：圆内接四边形的判断定理：如果四边形对角互补，那么这个四边形内接于圆（即如果四边形EFGH的对角互补，那么四边形EFGH的四个顶点E、F、G、H都在同个圆上）．（二）问题解决：已知⊙O的半径为2，AB，CD是⊙O的直径．P是上任意一点，过点P分别作AB，CD 的垂线，垂足分别为N，M．（1）若直径AB⊥CD，对于上任意一点P（不与B、C重合）（如图一），证明四边形PMON内接于圆，并求此圆直径的长；（2）若直径AB⊥CD，在点P（不与B、C重合）从B运动到C的过程汇总，证明MN的长为定值，并求其定值；（3）若直径AB与CD相交成120°角．①当点P运动到的中点P1时（如图二），求MN的长；②当点P（不与B、C重合）从B运动到C的过程中（如图三），证明MN的长为定值．（4）试问当直径AB与CD相交成多少度角时，MN的长取最大值，并写出其最大值．【答案】（1）证明见解析，直径OP=2；（2）证明见解析，MN的长为定值，该定值为2；（3）①MN=；②证明见解析；（4）MN取得最大值2．【解析】试题分析：（1）如图一，易证∠PMO+∠PNO=180°，从而可得四边形PMON内接于圆，直径OP=2；（2）如图一，易证四边形PMON是矩形，则有MN=OP=2，问题得以解决；（3）①如图二，根据等弧所对的圆心角相等可得∠COP1=∠BOP1=60°，根据圆内接四边形的对角互补可得∠MP1N=60°．根据角平分线的性质可得P1M=P1N，从而得到△P1MN是等边三角形，则有MN=P1M．然后在Rt△P1MO运用三角函数就可解决问题；②设四边形PMON的外接圆为⊙O′，连接NO′并延长，交⊙O′于点Q，连接QM，如图三，根据圆周角定理可得∠QMN=90°，∠MQN=∠MPN=60°，在Rt△QMN中运用三角函数可得：MN=QN•sin∠MQN，从而可得MN=OP•sin∠MQN，由此即可解决问题；（4）由（3）②中已得结论MN=OP•sin∠MQN可知，当∠MQN=90°时，MN最大，问题得以解决．试题解析：（1）如图一，∵PM⊥OC，PN⊥OB，∴∠PMO=∠PNO=90°，∴∠PMO+∠PNO=180°，∴四边形PMON内接于圆，直径OP=2；（2）如图一，∵AB⊥OC，即∠BOC=90°，∴∠BOC=∠PMO=∠PNO=90°，∴四边形PMON是矩形，∴MN=OP=2，∴MN的长为定值，该定值为2；（3）①如图二，∵P1是的中点，∠BOC=120°，∴∠COP1=∠BOP1=60°，∠MP1N=60°，∵P1M⊥OC，P1N⊥OB，∴P1M=P1N，∴△P1MN是等边三角形，∴MN=P1M．∵P1M=OP1•sin∠MOP1=2×sin60°=，∴MN=；②设四边形PMON的外接圆为⊙O′，连接NO′并延长，交⊙O′于点Q，连接QM，如图三，则有∠QMN=90°，∠MQN=∠MPN=60°，在Rt△QMN中，sin∠MQN=，∴MN=QN•sin∠MQN，∴MN=OP•sin∠MQN=2×sin60°=2×=，∴MN是定值．（4）由（3）②得MN=OP•sin∠MQN=2sin∠MQN．当直径AB与CD相交成90°角时，∠MQN=180°﹣90°=90°，MN取得最大值2．考点：圆的综合题．8．在正方形ABCD中，BD是一条对角线.点P在射线CD上（与点C，D不重合），连接AP，平移△ADP，使点D移动到点C，得到△BCQ，过点Q作QH⊥BD于点H，连接AH、PH.（1）若点P在线CD上，如图1，①依题意补全图1；②判断AH与PH的数量关系与位置关系并加以证明；（2）若点P在线CD的延长线上，且∠AHQ＝152°，正方形ABCD的边长为1，请写出求DP长的思路.（可以不写出计算结果）【答案】（1）①如图；②AH＝PH，AH⊥PH．证明见解析（2）或【解析】试题分析：（1）①如图（1）；②（1）法一：轴对称作法，判断：AH＝PH，AH⊥PH．连接CH，根据正方形的每条对角线平分一组对角得：△DHQ等腰Rt△，根据平移的性质得DP＝CQ，证得△HDP≌△△HQC，全等三角形的对应边相等得PH＝CH，等边对等角得∠HPC＝∠HCP，再结合BD是正方形的对称轴得出∠AHP＝180°－∠ADP＝90°，∴AH＝PH且AH⊥PH．四点共圆作法，同上得：∠HPC＝∠DAH，∴A、D、P、H共向，∴∠AHP＝90°，∠APH＝∠ADH＝45°，∴△APH等腰Rt△．（2）轴对称作法同（1）作HR⊥PC于R，∵∠AHQ＝152°，∴∠AHB＝62°，∴∠DAH＝17°∴∠DCH＝17°．设DP＝x，则.由代入HR，CR解方程即可得出x的值. 四点共圆作法，A、H、D、P共向，∴∠APD＝∠AHB＝62°，∴．试题解析：（1）①法一：轴对称作法，判断：AH＝PH，AH⊥PH证：连接CH，得：△DHQ等腰Rt△，又∵DP＝CQ，∴△HDP≌△△HQC，∴PH＝CH，∠HPC＝∠HCPBD为正方形ABCD对称轴，∴AH＝CH，∠DAH＝∠HCP，∴AH＝PH，∠DAH＝∠HPC，∴∠AHP＝180°－∠ADP＝90°，∴AH＝PH且AH⊥PH．法二：四点共圆作法，同上得：∠HPC＝∠DAH，∴A、D、P、H共向，∴∠AHP＝90°，∠APH＝∠ADH＝45°，∴△APH等腰Rt△．（2）法一：轴对称作法考虑△DHQ等腰Rt△，PD＝CQ，作HR⊥PC于R，∵∠AHQ＝152°，∴∠AHB＝62°，∴∠DAH＝17°∴∠DCH＝17°．设DP＝x，则.由得：，∴．即PD=法二：四点共向作法，A、H、D、P共向，∴∠APD＝∠AHB＝62°，∴．考点：全等三角形的判定；解直角三角形；正方形的性质；死电脑共圆9．如图，矩形OABC中，A(6，0)、C(0，23)、D(0，33)，射线l过点D且与x轴平行，点P、Q分别是l和x轴的正半轴上的动点，满足∠PQO＝60º．(1)点B的坐标是，∠CAO＝ º，当点Q与点A重合时，点P的坐标为；(2)设点P 的横坐标为x ，△OPQ 与矩形OABC 重叠部分的面积为S ，试求S 与x 的函数关系式和相应的自变量x 的取值范围．【答案】（1）（6，23）． 30．（3，33）（2）()()()()243x 430x 3331333x x 3x 5232S {23x 1235x 93543x 9x+≤≤-+-<≤=-+<≤> 【解析】解：（1）（6，23）． 30．（3，33）．（2）当0≤x≤3时，如图1，OI=x ，IQ=PI•tan60°=3，OQ=OI+IQ=3+x ；由题意可知直线l ∥BC ∥OA ，可得EF PE DC 31==OQ PO DO 333==，∴EF=13（3+x ），此时重叠部分是梯形，其面积为：EFQO 14343S S EF OQ OC 3x x 432==+⋅=+=+梯形（）（）当3＜x≤5时，如图2，()HAQ EFQO EFQO 221S S S S AH AQ 243331333 x 43x 3=x x 32232∆=-=-⋅⋅=+---+-梯形梯形。

中考数学复习《锐角三角函数及其实际应用》经典题型及测试题(含答案)

中考数学复习《锐角三角函数及其实际应用》经典题型及测试题（含答案）命题点分类集训命题点1 特殊角的三角函数值【命题规律】1.考查内容：主要考查 30°，45°，60°角的正弦，余弦，正切值的识记、正余弦的转换及由三角函数值求出角度. 2.考查形式：①三类特殊角的三角函数值识记；②与非负性结合，通过三角函数值求角度；③正弦余弦、正切余切之间的相互转化，判断关系式是否成立；④在实数运算中涉及三类特殊角的三角函数值运算(具体试题见实数的运算部分)．【命题预测】特殊角的三角函数值作为识记内容在实数运算中考查的可能性比较大，而单独考查也会出现．1. sin 60°的值等于( ) A . 12B .22 C . 32D . 3 1. C2. 下列式子错误．．的是( ) A . cos 40°＝sin 50° B . tan 15°·tan 75°＝1 C . sin 225°＋cos 225°＝1 D . sin 60°＝2sin 30°2. D 【解析】逐项分析如下：选项逐项分析正误 A cos40°＝sin(90°－40°)＝sin50° √ B tan15°·tan75°＝1tan75°×tan75°＝1√ C sin 2A ＋cos 2A ＝1√ D∵sin60°＝32，2sin30°＝2×12＝1，∴sin60°≠2sin30° ×3. 已知α，β均为锐角，且满足|sin α－12|＋（tan β－1）2＝0，则α＋β＝________．3. 75° 【解析】由于绝对值和算术平方根都是非负数，而这两个数的和又为零，于是它们都为零．根据题意，得|sin α－12|＝0，（tan β－1）2＝0，则sin α ＝12，tan β ＝1，又因为α、β均为锐角，则α＝30°，β＝45°，所以α＋β＝30°＋45°＝75°. 命题点2 直角三角形的边角关系【命题规律】1.考查内容：在直角三角形中，三边与两个锐角之间关系的互化.2.考查形式：已知一边及某锐角的三角函数值，求其他量，或结合直角坐标系求锐角三角函数值．【命题预测】直角三角形的边角关系是解直角三角形实际应用问题的基础，值得关注．4. 如图，在平面直角坐标系中，点A 的坐标为(4，3)，那么cos α的值是( ) A . 34B . 43C . 35D . 454. D 【解析】如解图，过点A 作AB ⊥x 轴于点B ，∵A (4，3)，∴OB ＝4，AB ＝3，∴OA ＝32＋42＝5，∴cos α＝OB OA ＝45.5. 在Rt △ABC 中，∠C ＝90°，sin A ＝45，AC ＝6 cm .则BC 的长度为( )A . 6 cmB . 7 cmC . 8 cmD . 9 cm5. C 【解析】∵sin A ＝BC AB ＝45，∴设BC ＝4a ，则AB ＝5a ，AC ＝（5a ）2－（4a ）2＝3a ，∴3a ＝6，即a ＝2，故BC ＝4a ＝8 cm.6. 已知：如图，在锐角△ABC 中，AB ＝c ，BC ＝a ，AC ＝b ，AD ⊥BC 于D. 在Rt △ABD 中，sin ∠B ＝ADc ，则AD ＝c sin ∠B ；在Rt △ACD 中，sin ∠C ＝________，则AD ＝________．所以c sin ∠B ＝b sin ∠C ，即bsin B ＝csin C ，进一步即得正弦定理：asin A ＝b sin B ＝c sin C.(此定理适合任意锐角三角形) 参照利用正弦定理解答下题：在△ABC 中，∠B ＝75°，∠C ＝45°，BC ＝2，求AB 的长．6. 解：∵sin C ＝AD AC ＝ADb ，∴AD ＝b sin C ，由正弦定理得：BC sin A ＝ABsin C ，∵∠B ＝75°， ∠C ＝45°， ∴∠A ＝60°， ∴2sin 60°＝ABsin 45°，∴AB ＝2×22÷32＝263.命题点3 锐角三角函数的实际应用【命题规律】1.考查内容：主要考查利用几何建模思想，将实际问题抽象为几何中的直角三角形的有关问题，并根据直角三角形的边角关系解决实际问题.2.考查形式：①仰角、俯角问题；②方位角问题；③坡度、坡角问题；④测量问题等．【命题预测】锐角三角函数的实际应用是将实际问题转化为几何问题并加以解决的数学建模题型，是全国命题的趋势．7. 小明利用测角仪和旗杆的拉绳测量学校旗杆的高度．如图，旗杆PA 的高度与拉绳PB 的长度相等，小明将PB 拉到PB′的位置，测得∠PB′C＝α(B′C 为水平线)，测角仪B′D 的高度为1米，则旗杆PA 的高度为( )A .11－sin α B . 11＋sin α C . 11－cos α D . 11＋cos α7. A 【解析】在Rt △PCB ′中，sin α＝PCPB ′，∴PC ＝PB ′·sin α，又∵B ′D ＝AC ＝1，则PB ′·sin α＋1＝P A ，而PB ′＝P A ，∴P A ＝11－sin α.8. 如图①是小志同学书桌上的一个电子相框，将其侧面抽象为如图②所示的几何图形，已知BC ＝BD ＝15 cm ，∠CBD ＝40°，则点B 到CD 的距离为________cm (参考数据：sin 20°≈0.342，cos 20°≈0.940，sin 40°≈0.643，cos 40°≈0.766.结果精确到0.1 cm ，可用科学计算器)．8. 14.1 【解析】如解图，过点B 作BE ⊥CD 于点E ，∵BC ＝BD ＝15 cm ，∠CBD ＝40°，∴∠CBE ＝20°，在Rt △CBE 中，BE ＝BC ·cos ∠CBE ≈15×0.940＝14.1(cm)．第8题图第9题图第10题图9. 如图，一艘渔船位于灯塔P 的北偏东30°方向，距离灯塔18海里的A 处，它沿正南方向航行一段时间后，到达位于灯塔P 的南偏东55°方向上的B 处，此时渔船与灯塔P 的距离约为________海里．(结果取整数．参考数据：sin 55°≈0.8，cos 55°≈0.6，tan 55°≈1.4)9. 11 【解析】∵∠A ＝30°，∴PM ＝12PA ＝9海里．∵∠B ＝55°， sin B ＝PM PB ，∴0.8＝9PB ，∴PB ≈11海里．10. 如图，在一次数学课外实践活动中，小聪在距离旗杆10 m 的A 处测得旗杆顶端B 的仰角为60°，测角仪高AD 为1 m ，则旗杆高BC 为__________m ．(结果保留根号)10. 103＋1 【解析】如解图，过点A 作AE ⊥BC ，垂足为点E ，则AE ＝CD ＝10 m ，在Rt △AEB 中，BE ＝AE·tan 60°＝10×3＝10 3 m ，∴BC ＝BE ＋EC ＝BE ＋AD ＝(103＋1)m . 11. 如图，大楼AB 右侧有一障碍物，在障碍物的旁边有一幢小楼DE ，在小楼的顶端D 处测得障碍物边缘点C 的俯角为30°，测得大楼顶端A 的仰角为45°(点B 、C 、E 在同一水平直线上)，已知AB ＝80 m ，DE ＝10 m ，求障碍物B 、C 两点间的距离．(结果精确到0.1 m ，参考数据：2≈1.414，3≈1.732)11. 解：如解图，过点D 作DF ⊥AB ，垂足为点F ，则四边形FBED 为矩形，∴FD ＝BE ，BF ＝DE ＝10，FD ∥BE ，由题意得：∠FDC ＝30°，∠ADF ＝45°，∵FD ∥BE ， ∴∠DCE ＝∠FDC ＝30°，在Rt △DEC 中，∠DEC ＝90°，DE ＝10，∠DCE ＝30°， ∵tan ∠DCE ＝DE CE ，∴CE ＝10tan 30°＝103，在Rt △AFD 中，∠AFD ＝90°，∠ADF ＝∠FAD ＝45°， ∴FD ＝AF ，又∵AB ＝80，BF ＝10，∴FD ＝AF ＝AB －BF ＝80－10＝70，∴BC ＝BE －CE ＝FD －CE ＝70－103≈52.7(m )．答：障碍物B 、C 两点间的距离约为52.7 m ．12.某地的一座人行天桥如图所示，天桥高为6米，坡面BC 的坡度为1∶1，为了方便行人推车过天桥，有关部门决定降低坡度，使新坡面AC 的坡度为1∶ 3. (1)求新坡面的坡角α；(2)天桥底部的正前方8米处(PB 的长)的文化墙PM 是否需要拆除？请说明理由．12. 解：(1)∵新坡面AC 的坡度为1∶3，∴tan α＝13＝33， ∴α＝30°.答：新坡面的坡角α的度数为30°.(2)原天桥底部正前方8米处的文化墙PM 不需要拆除．理由如下：如解图所示，过点C 作CD ⊥AB ，垂足为点D ， ∵坡面BC 的坡度为1∶1， ∴BD ＝CD ＝6米，∵新坡面AC 的坡度为1∶3， ∴CD ∶AD ＝1∶3， ∴AD ＝63米，∴AB ＝AD －BD ＝(63－6)米＜8米，故正前方的文化墙PM 不需拆除．答：原天桥底部正前方8米处的文化墙PM 不需要拆除．13.如图，某无人机于空中A 处探测到目标B ，D ，从无人机A 上看目标B ，D 的俯角分别为30°，60°，此时无人机的飞行高度AC 为 60 m ，随后无人机从A 处继续水平飞行30 3 m 到达A′处． (1)求A ，B 之间的距离；(2)求从无人机A′上看目标D 的俯角的正切值．13. 解：(1)如解图，过点D 作DE ⊥AA′于点E ，由题意得，AA ′∥BC ，∴∠B ＝∠FAB ＝30°，又∵AC ＝60 m ，在Rt △ABC 中，sin B ＝AC AB ，即12＝60AB，∴AB ＝120 m .答：A ，B 之间的距离为120 m ．(2)如解图，连接A′D ，作A′E ⊥BC 交BC 延长线于E ， ∵AA ′∥BC ，∠ACB ＝90°， ∴∠A ′AC ＝90°，∴四边形AA′EC 为矩形， ∴A ′E ＝AC ＝60 m ，又∵∠ADC ＝∠FAD ＝60°，在Rt △ADC 中，tan ∠ADC ＝AC CD ，即5＝60CD，∴CD ＝20 3 m ，∴DE ＝DC ＋CE ＝AA′＋DC ＝303＋203＝50 3 m ， ∴tan ∠AA ′D ＝tan ∠A ′DE ＝A′E DE ＝60503＝235，答：从无人机A′上看目标D 的俯角的正切值为235.中考冲刺集训一、选择题1.一个公共房门前的台阶高出地面1.2米，台阶拆除后，换成供轮椅行走的斜坡，数据如图所示，则下列关系或说法正确的是( )A . 斜坡AB 的坡度是10° B . 斜坡AB 的坡度是tan 10°C . AC ＝1.2tan 10° 米D . AB ＝ 1.2cos 10°米第1题图第2题图第3题图2.如图，以O 为圆心，半径为1的弧交坐标轴于A ，B 两点，P 是AB ︵上一点(不与A ，B 重合)，连接OP ，设∠POB＝α，则点P 的坐标是( )A . (sin α，sin α)B . (cos α，cos α)C . (cos α，sin α)D . (sin α，cos α)3.一座楼梯的示意图如图所示，BC 是铅垂线，CA 是水平线，BA 与CA 的夹角为θ.现要在楼梯上铺一条地毯，已知CA ＝4米，楼梯宽度1米，则地毯的面积至少需要( )A . 4sin θ 米2B . 4cos θ 米2C . (4＋4tan θ) 米2 D . (4＋4tan θ) 米24.如图是由边长相同的小正方形组成的网格，A ，B ，P ，Q 四点均在正方形网格的格点上，线段AB ，PQ 相交于点M ，则图中∠QMB 的正切值是( )A . 12B . 1C . 3D . 2第4题图第5题图第6题图5.如图所示，某办公大楼正前方有一根高度是15米的旗杆ED ，从办公大楼顶端A 测得旗杆顶端E 的俯角α是45°，旗杆底端D 到大楼前梯坎底边的距离DC 是20米，梯坎坡长BC 是12米，梯坎坡度i ＝1∶3，则大楼AB 的高度约为(精确到0.1米，参考数据：2≈1.41，3≈1.73，6≈2.45)( )A . 30.6B . 32.1C . 37.9D . 39.46. 如图，钓鱼竿AC 长6 m ，露在水面上的鱼线BC 长3 2 m ，某钓鱼者想看看鱼钩上的情况，把鱼竿AC 转到AC′的位置，此时露在水面上的鱼线B ′C ′为3 3 m ，则鱼竿转过的角度是( )A . 60°B . 45°C . 15°D . 90°二、填空题7. 如图，点A(3，t)在第一象限，射线OA 与x 轴所夹的锐角为α，tan α＝32，则t 的值是________．第7题图第8题图第9题图8. 如图是矗立在高速公路边水平地面上的交通警示牌，经测量得到如下数据：AM＝4米，AB＝8米，∠MAD ＝45°，∠MBC＝30°，则警示牌的高CD为______米．(结果精确到0.1米，参考数据：2≈1.41，3≈1.73) 9. 如图，航拍无人机从A处测得一幢建筑物顶部B的仰角为30°，测得底部C的俯角为60°，此时航拍无人机与该建筑物的水平距离AD为90米，那么该建筑物的高度BC约为________米．(精确到1米，参考数据：3≈1.73)三、解答题10. 如图，在数学活动课中，小敏为了测量校园内旗杆CD的高度，先在教学楼的底端A点处，观测到旗杆顶端C的仰角∠CAD＝60°，然后爬到教学楼上的B处，观测到旗杆底端D的俯角是30°. 已知教学楼AB高4米．(1)求教学楼与旗杆的水平距离AD；(结果保留根号．．．．．．)(2)求旗杆CD的高度．11. 图为放置在水平桌面上的台灯的平面示意图，灯臂AO长为40 cm，与水平面所形成的夹角∠OAM为75°，由光源O射出的边缘光线OC，OB与水平面所形成的夹角∠OCA，∠OBA分别为90°和30°，求该台灯照亮水平面的宽度BC(不考虑其他因素，结果精确到0.1 cm.温馨提示：sin75°≈0.97，cos75°≈0.26，3≈1.73)．12. 阅读材料：关于三角函数还有如下的公式：sin (α±β)＝sin αcos β±cos αsin β tan (α±β)＝tan α±tan β1∓tan α tan β利用这些公式可以将一些不是特殊角的三角函数转化为特殊角的三角函数来求值，例如：tan 75°＝tan (45°＋30°)＝tan 45°＋tan 30°1－tan 45°tan 30°＝1＋331－1×33＝2＋ 3 根据以上阅读材料，请选择适当的公式计算下列问题： (1)计算sin 15°；(2)某校在开展爱国主义教育活动中，来到烈士纪念碑前缅怀和纪念为国捐躯的红军战士．李三同学想用所学知识来测量如图纪念碑的高度，已知李三站在离纪念碑底7米的C 处，在D 点测得纪念碑碑顶的仰角为75°，DC 为 3 米，请你帮助李三求出纪念碑的高度．答案与解析：1. B第2题解图2. C 【解析】如解图，过点P 作PC ⊥OB 于点C ，则在Rt △OPC 中，OC ＝OP ·cos ∠POB ＝1×cos α＝cos α，PC ＝OP ·sin ∠POB ＝1×sin α＝sin α，即点P 的坐标为(cos α，sin α)．3. D 【解析】在Rt △ABC 中，∠BAC ＝θ，CA ＝4米，∴BC ＝CA ·tan θ＝4tan θ.地毯长为(4＋4tan θ)米，宽为1米，其面积为(4＋4tan θ)×1＝(4＋4tan θ)米2.4. D 【解析】如解图，将AB 平移到PE 位置，连接QE, 则PQ ＝210，PE ＝22，QE ＝42，∵△PEQ 中，PE 2＋QE 2＝PQ 2，则∠PEQ ＝90°，∴tan ∠QMB ＝tan ∠P ＝QEPE＝2.第4题解图第5题解图5. D 【解析】如解图，设AB 与DC 的延长线交于点G ，过点E 作EF ⊥AB 于点F ，过点B 作BH ⊥ED 于点H ，则可得四边形GDEF 为矩形．在Rt △BCG 中，∵BC ＝12，i BC ＝BG CG ＝33，∴∠BCG ＝30°，∴BG ＝6，CG ＝63，∴BF ＝FG －BG ＝DE －BG ＝15－6＝9，∵∠AEF ＝α＝45°，∴AF ＝EF ＝DG ＝CG ＋CD ＝63＋20，∴AB ＝BF ＋AF ＝9＋20＋63≈39.4(米)．6. C 【解析】∵sin ∠CAB ＝BC AC ＝326＝22，∴∠CAB ′＝45°，∵sin ∠C ′AB ′＝B ′C ′AC ′＝336＝32，∴∠C ′AB ′＝60°，∴∠CAC ′＝60°－45°＝15°，即鱼竿转过的角度是15°.第7题解图7. 92【解析】如解图，过点A 作AB ⊥x 轴于点B.∵点A(3，t)在第一象限，∴OB ＝3，AB ＝t ，在11 Rt △ABO 中，tan α＝AB OB ＝t 3＝32，解得t ＝92. 8. 2.9 【解析】在Rt △AMD 中，DM ＝tan ∠DAM ×AM ＝tan 45°×4＝4米，在Rt △BMC 中，CM ＝tan ∠MBC ×BM ＝tan 30°×12＝4 3 米，故CD ＝CM －DM ＝43－4≈2.9米．9. 208 【解析】在Rt △ABD 中，BD ＝AD·tan ∠BAD ＝90×tan 30°＝303，在Rt △ACD 中，CD ＝AD·tan ∠CAD ＝90×tan 60°＝903，BC ＝BD ＋CD ＝303＋903＝1203≈208(米)．10. 解：(1)∵在教学楼B 点处观测旗杆底端D 处的俯角是30°，∴∠ADB ＝30°，在Rt △ABD 中，∠BAD ＝90°，∠ADB ＝30°，AB ＝4(米)，∴AD ＝AB tan ∠ADB ＝4tan 30°＝43(米)．答：教学楼与旗杆的水平距离是4 3 米．(也可先求∠ABD ＝60°，利用tan 60°去计算得到结论)(2)∵在Rt △ACD 中，∠ADC ＝90°，∠CAD ＝60°，AD ＝4 3 米，∴CD ＝AD·tan 60°＝43×3＝12(米)．答：旗杆CD 的高度是12米．11. 解：∵tan ∠OBC ＝tan 30°＝OC BC ＝33， ∴OC ＝33BC ， ∵sin ∠OAC ＝sin 75°＝OC OA≈0.97， ∴33BC 40≈0.97， ∴BC ≈67.1(cm )．12. 解：(1)sin 15°＝sin (45°－30°)＝sin 45°cos 30°－cos 45°sin 30° ＝22×32－22×12 ＝6－24. (2)在Rt △BDE 中，∠BDE ＝75°，DE ＝CA ＝7，tan ∠BDE ＝BE DE ，即tan 75°＝BE 7＝2＋3， ∴ BE ＝14＋73，又∵AE ＝DC ＝3，∴AB ＝BE ＋AE ＝14＋73＋3＝14＋83(米)，答：纪念碑的高度是(14＋83)米．。

2020锐角三角函数-九年级数学人教版(下)(解析版)

sin A
A的对边斜边
，
cosA
A的邻边斜边
， tanA
A的对边 .
A的邻边
8．把 △ ABC 的各边长都增加两倍，则锐角 A 的正弦值
A．增加 2 倍
B．增加 4 倍
C．不变
D ．不能确定
【答案】 C
9．如图，在平面直角坐标系中，点是
A 的坐标为（ 3,4），那么 sin 的值
A． 3
5
B． 3
4
C． 4
5
D． 4
3
【答案】 C
【解析】作 AB⊥x 轴交 x 轴于点 B，
∵A（ 3，4），
∴AB=4 ， BO=3 ， ∴AO= AB2 BO2 = 42 32 =5 ，
∴sin = AB = 4 .
AO 5
故选 C.
【名师点睛】要求一个角的三角函数值，如果图中没有现成的直角三
角形，我们一般通过构造垂线将要求的角放入直角三角形中求解
【解析】原式 = 27 3 +8×1 ﹣ 1+2×3 =3+4 ﹣1+ 3 =6+ 3 ．
2
2
【名师点睛】本题考查了二次根式的混合运算：先把各二次根式化
简为最简二次根式，然后进行二次根式的乘除运算，再合并即可．在
二次根式的混合运算中，如能结合题目特点，灵活运用二次根式的
性质，选择恰当的解题途径，往往能事半功倍．
AB 13
tan B= AC 12 ．
BC 5
故答案为： 5 ； 12 ．
13 5
【名师点睛】本题考查锐角三角函数的定义：在直角三角形中，锐
角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边．

2020-2021全国中考数学锐角三角函数的综合中考真题汇总及详细答案

2020-2021全国中考数学锐角三角函数的综合中考真题汇总及详细答案一、锐角三角函数1．如图，海上观察哨所B 位于观察哨所A 正北方向，距离为25海里．在某时刻，哨所A 与哨所B 同时发现一走私船，其位置C 位于哨所A 北偏东53°的方向上，位于哨所B 南偏东37°的方向上．（1）求观察哨所A 与走私船所在的位置C 的距离；（2）若观察哨所A 发现走私船从C 处以16海里/小时的速度向正东方向逃窜，并立即派缉私艇沿北偏东76°的方向前去拦截．求缉私艇的速度为多少时，恰好在D 处成功拦截．（结果保留根号）（参考数据：sin37°＝cos53°≈，cos37 ＝sin53°≈去，tan37°≈2，tan76°≈）【答案】（1）观察哨所A 与走私船所在的位置C 的距离为15海里；（2）当缉私艇以每小时617D 处成功拦截.【解析】【分析】（1）先根据三角形内角和定理求出∠ACB ＝90°，再解Rt △ABC ，利用正弦函数定义得出AC 即可；（2）过点C 作CM ⊥AB 于点M ，易知，D 、C 、M 在一条直线上．解Rt △AMC ，求出CM 、AM ．解Rt △AMD 中，求出DM 、AD ，得出CD ．设缉私艇的速度为x 海里/小时，根据走私船行驶CD 所用的时间等于缉私艇行驶AD 所用的时间列出方程，解方程即可．【详解】（1）在ABC △中，180180375390ACB B BAC ︒︒︒︒︒∠=-∠-∠=--=.在Rt ABC V 中，sin AC B AB =，所以3sin 3725155AC AB ︒=⋅=⨯=（海里）. 答：观察哨所A 与走私船所在的位置C 的距离为15海里.（2）过点C 作CM AB ⊥，垂足为M ，由题意易知，D C M 、、在一条直线上. 在Rt ACM V 中，4sin 15125CM AC CAM =⋅∠=⨯=，3cos 1595AM AC CAM =⋅∠=⨯=. 在Rt ADM △中，tan MD DAM AM∠=，所以tan 7636MD AM ︒=⋅=. 所以222293691724AD AM MD CD MD MC =+=+==-=，.设缉私艇的速度为v海里/小时，则有2491716=，解得617v=.经检验，617v=是原方程的解.答：当缉私艇以每小时617海里的速度行驶时，恰好在D处成功拦截.【点睛】此题考查了解直角三角形的应用﹣方向角问题，结合航海中的实际问题，将解直角三角形的相关知识有机结合，体现了数学应用于实际生活的思想．2．问题背景:如图（a）,点A、B在直线l的同侧，要在直线l上找一点C，使AC与BC的距离之和最小，我们可以作出点B关于l的对称点B′,连接A B′与直线l交于点C，则点C即为所求.（1）实践运用：如图(b)，已知，⊙O的直径CD为4，点A 在⊙O 上，∠ACD=30°，B 为弧AD 的中点，P为直径CD上一动点，则BP+AP的最小值为．（2）知识拓展：如图(c)，在Rt△ABC中，AB=10，∠BAC=45°，∠BAC的平分线交BC于点D，E、F分别是线段AD和AB上的动点，求BE+EF的最小值，并写出解答过程．【答案】解：（1）2．（2）如图，在斜边AC上截取AB′=AB，连接BB′．∵AD平分∠BAC，∴点B与点B′关于直线AD对称．过点B′作B′F⊥AB,垂足为F，交AD于E，连接BE．则线段B′F的长即为所求 (点到直线的距离最短) ．在Rt△AFB/中，∵∠BAC=450, AB/="AB=" 10，∴．∴BE+EF的最小值为【解析】试题分析：（1）找点A或点B关于CD的对称点，再连接其中一点的对称点和另一点，和MN的交点P就是所求作的位置，根据题意先求出∠C′AE，再根据勾股定理求出AE，即可得出PA+PB的最小值：如图作点B关于CD的对称点E，连接AE交CD于点P，此时PA+PB最小，且等于A．作直径AC′，连接C′E，根据垂径定理得弧BD=弧DE．∵∠ACD=30°，∴∠AOD=60°，∠DOE=30°．∴∠AOE=90°．∴∠C′AE=45°．又AC为圆的直径，∴∠AEC′=90°．∴∠C′=∠C′AE=45°．∴C′E=AE=AC′=2．∴AP+BP的最小值是22（2）首先在斜边AC上截取AB′=AB，连接BB′，再过点B′作B′F⊥AB，垂足为F，交AD于E，连接BE，则线段B′F的长即为所求．3．（本题满分14分，第（1）小题满分4分，第（2）小题满分5分，第（3）小题满分5分）CD AB，动点P、Q分别在线段OC、CD已知：如图，AB是半圆O的直径，弦//上，且DQ OP =，AP 的延长线与射线OQ 相交于点E 、与弦CD 相交于点F （点F 与点C 、D 不重合），20AB =，4cos 5AOC ∠=．设OP x =，CPF ∆的面积为y ．（1）求证：AP OQ =；（2）求y 关于x 的函数关系式，并写出它的定义域；（3）当OPE ∆是直角三角形时，求线段OP 的长．【答案】（1）证明见解析；（2）236030050(10)13x x y x x -+=<<；（3）8OP = 【解析】【分析】（1）证明线段相等的方法之一是证明三角形全等，通过分析已知条件，OP DQ =，联结OD 后还有OA DO =，再结合要证明的结论AP OQ =，则可肯定需证明三角形全等，寻找已知对应边的夹角，即POA QDO ∠=∠即可；（2）根据PFC ∆∽PAO ∆，将面积转化为相似三角形对应边之比的平方来求；（3）分成三种情况讨论，充分利用已知条件4cos 5AOC ∠=、以及（1）（2）中已证的结论，注意要对不符合（2）中定义域的答案舍去．【详解】（1）联结OD ，∵OC OD =，∴OCD ODC ∠=∠，∵//CD AB ，∴OCD COA ∠=∠，∴POA QDO ∠=∠．在AOP ∆和ODQ ∆中， {OP DQPOA QDO OA DO=∠=∠=，∴AOP ∆≌ODQ ∆，∴AP OQ =；（2）作PH OA ⊥，交OA 于H ，∵4cos 5AOC ∠=， ∴4455OH OP x ==，35PH x =， ∴132AOP S AO PH x ∆=⋅=． ∵//CD AB ，∴PFC ∆∽PAO ∆， ∴2210()()AOP yCP x S OP x∆-==， ∴2360300x x y x-+=，当F 与点D 重合时， ∵42cos 210165CD OC OCD =⋅∠=⨯⨯=， ∴101016x x =-，解得5013x =， ∴2360300x x y x-+=50(10)13x <<；（3）①当90OPE ∠=o 时，90OPA ∠=o ， ∴4cos 1085OP OA AOC =⋅∠=⨯=； ②当90POE ∠=o 时，1010254cos cos 25OC CQ QCO AOC ====∠∠， ∴252OP DQ CD CQ CD ==-=-2571622=-=， ∵501013OP <<， ∴72OP =（舍去）； ③当90PEO ∠=o 时，∵//CD AB ，∴AOQ DQO ∠=∠，∵AOP ∆≌ODQ ∆，∴DQO APO ∠=∠，∴AOQ APO ∠=∠，∴90AEO AOP ∠=∠=o ，此时弦CD 不存在，故这种情况不符合题意，舍去；综上，线段OP 的长为8．4．如图，矩形OABC 中，A(6，0)、C(0，23)、D(0，33)，射线l 过点D且与x 轴平行，点P 、Q 分别是l 和x 轴的正半轴上的动点，满足∠PQO ＝60º．(1)点B 的坐标是，∠CAO ＝ º，当点Q 与点A 重合时，点P 的坐标为；(2)设点P 的横坐标为x ，△OPQ 与矩形OABC 重叠部分的面积为S ，试求S 与x 的函数关系式和相应的自变量x 的取值范围．【答案】（1）（6，23）． 30．（3，33）（2）()()()()243x 430x 3331333x x 3x 5S {23x 1235x 93543x 9+≤≤-+-<≤=-+<≤> 【解析】解：（1）（6，23）． 30．（3，33）．（2）当0≤x≤3时，如图1，OI=x ，IQ=PI•tan60°=3，OQ=OI+IQ=3+x ；由题意可知直线l ∥BC ∥OA ，可得EF PE DC31==OQ PO DO333==，∴EF=13（3+x），此时重叠部分是梯形，其面积为：EFQO14343S S EF OQ OC3x x43 233==+⋅=+=+梯形（）（）当3＜x≤5时，如图2，()HAQEFQO EFQO221S S S S AH AQ243331333x43x3=x x32232∆=-=-⋅⋅=+---+-梯形梯形。

2020中考数学九年级下册锐角三角函数在实际问题中的应用(含答案)

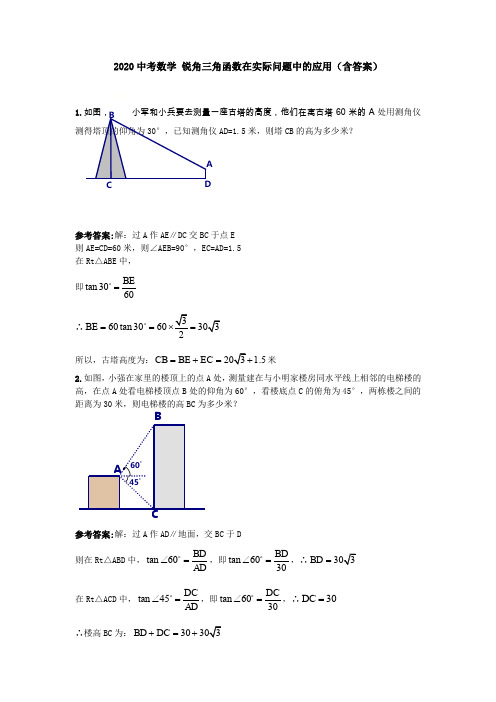
2020中考数学锐角三角函数在实际问题中的应用（含答案）1.如图，小军和小兵要去测量一座古塔的高度，他们在离古塔60米的A 处用测角仪测得塔顶的仰角为30°，已知测角仪AD=1.5米，则塔CB 的高为多少米？参考答案:解：过A 作AE ∥DC 交BC 于点E 则AE=CD=60米，则∠AEB=90°，EC=AD=1.5 在Rt △ABE 中，即tan 3060BE=∴60tan 3060BE === 所以，古塔高度为： 1.5CB BE EC =+=米2.如图，小强在家里的楼顶上的点A 处，测量建在与小明家楼房同水平线上相邻的电梯楼的高，在点A 处看电梯楼顶点B 处的仰角为60°，看楼底点C 的俯角为45°，两栋楼之间的距离为30米，则电梯楼的高BC 为多少米？参考答案:解：过A 作AD ∥地面，交BC 于D 则在Rt △ABD 中，tan 60BD AD ∠=，即tan 6030BD∠=，∴BD =在Rt △ACD 中，tan 45DC AD ∠=，即tan 6030DC ∠=，∴30DC = ∴楼高BC 为：30BD DC +=+AD BC3.小明在热气球A 上看到正前方横跨河流两岸的大桥BC ，并测得B ，C 两点的俯角分别为45°，35°。

已知大桥BC 与地面在同一水平面上，其长度为100米，请求出热气球离地面的高度。

（结果保留整数，参考数据：7sin 3512≈，5cos356≈，7tan 3510≈）参考答案:解：过A 作AD ⊥BC 于点D则AD 即为热气球的高度，且∠1=∠2=45∴可设AD=BD=x 则CD=x+100 在Rt △ADC 中tan AD C DC =，即tan 35100xx =+得：7003x =即热气球的高度为7003AD =米 4.如图，某建筑物BC 顶部有一旗杆AB ，且点A ，B ，C 在同一直线上．小红在D 处观测旗杆顶部A 的仰角为47°，观测旗杆底部B 的仰角为42°．已知点D 到地面的距离DE 为1.56m ，EC=21m ，求旗杆AB 的高度和建筑物BC 的高度（结果保留小数点后一位，参考数据：tan47°≈1.07，tan42°≈0.90）．参考答案:解：根据题意，DE=1.56,EC=21,∠ACE=90°,∠DEC=90°．过点D 作DF ⊥AC,垂足为F ．则∠DFC=90°,∠ADF=47°,∠BFD=42°．1.41≈ 1.73≈）参考答案:解：过C 作CD ⊥AB 于点D ，则∠DBC=45°=∠BCD ∴可设BD=CD=x在Rt △ACD 中可得：tan DCDAC AD∠=即：tan 302x x =+得1 2.73x =≈即，点C 与探测面的距离大约为2.73米。

2020-2021全国中考数学锐角三角函数的综合中考真题汇总含详细答案

2020-2021全国中考数学锐角三角函数的综合中考真题汇总含详细答案一、锐角三角函数1．图1是一种折叠式晾衣架．晾衣时，该晾衣架左右晾衣臂张开后示意图如图2所示，两支脚OC＝OD＝10分米，展开角∠COD＝60°，晾衣臂OA＝OB＝10分米，晾衣臂支架HG ＝FE＝6分米，且HO＝FO＝4分米．当∠AOC＝90°时，点A离地面的距离AM为_______分米；当OB从水平状态旋转到OB′（在CO延长线上）时，点E绕点F随之旋转至OB′上的点E′处，则B′E′﹣BE为_________分米．【答案】553【解析】【分析】如图，作OP⊥CD于P，OQ⊥AM于Q，FK⊥OB于K，FJ⊥OC于J．解直角三角形求出MQ，AQ即可求出AM，再分别求出BE，B′E′即可．【详解】解：如图，作OP⊥CD于P，OQ⊥AM于Q，FK⊥OB于K，FJ⊥OC于J．∵AM⊥CD，∴∠QMP＝∠MPO＝∠OQM＝90°，∴四边形OQMP是矩形，∴QM＝OP，∵OC＝OD＝10，∠COD＝60°，∴△COD是等边三角形，∵OP⊥CD，∠COD＝30°，∴∠COP＝12∴QM＝OP＝OC•cos30°＝3∵∠AOC＝∠QOP＝90°，∴∠AOQ＝∠COP＝30°，∴AQ＝1OA＝5（分米），2∴AM＝AQ＋MQ＝5＋3∵OB∥CD，∴∠BOD＝∠ODC＝60°在Rt△OFK中，KO＝OF•cos60°＝2（分米），FK＝OF•sin60°＝23（分米），在Rt△PKE中，EK＝22EF FK-＝26（分米），∴BE＝10−2−26＝（8−26）（分米），在Rt△OFJ中，OJ＝OF•cos60°＝2（分米），FJ＝23（分米），在Rt△FJE′中，E′J＝2263-（2）＝26，∴B′E′＝10−（26−2）＝12−26，∴B′E′−BE＝4．故答案为：5＋53，4．【点睛】本题考查解直角三角形的应用，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，属于中考常考题型．2．在矩形ABCD中，AD＞AB，点P是CD边上的任意一点（不含C，D两端点），过点P 作PF∥BC，交对角线BD于点F．（1）如图1，将△PDF沿对角线BD翻折得到△QDF，QF交AD于点E．求证：△DEF是等腰三角形；（2）如图2，将△PDF绕点D逆时针方向旋转得到△P'DF'，连接P'C，F'B．设旋转角为α（0°＜α＜180°）．①若0°＜α＜∠BDC，即DF'在∠BDC的内部时，求证：△DP'C∽△DF'B．②如图3，若点P是CD的中点，△DF'B能否为直角三角形？如果能，试求出此时tan∠DBF'的值，如果不能，请说明理由．【答案】（1）证明见解析；（2）①证明见解析；②123【解析】【分析】（1）根据翻折的性质以及平行线的性质可知∠DFQ=∠ADF ，所以△DEF 是等腰三角形；（2）①由于PF ∥BC ，所以△DPF ∽△DCB ，从而易证△DP′F′∽△DCB ；②由于△DF'B 是直角三角形，但不知道哪个的角是直角，故需要对该三角形的内角进行分类讨论．【详解】（1）由翻折可知：∠DFP=∠DFQ ， ∵PF ∥BC ， ∴∠DFP=∠ADF ， ∴∠DFQ=∠ADF ， ∴△DEF 是等腰三角形；（2）①若0°＜α＜∠BDC ，即DF'在∠BDC 的内部时， ∵∠P′DF′=∠PDF ，∴∠P′DF′﹣∠F′DC=∠PDF ﹣∠F′DC ， ∴∠P′DC=∠F′DB ，由旋转的性质可知：△DP′F′≌△DPF ， ∵PF ∥BC ， ∴△DPF ∽△DCB ， ∴△DP′F′∽△DCB ∴''DC DP DB DF = ， ∴△DP'C ∽△DF'B ；②当∠F′DB=90°时，如图所示， ∵DF′=D F=12BD ， ∴'12DF BD =， ∴tan ∠DBF′='12DF BD =；当∠DBF′=90°，此时DF′是斜边，即DF′＞DB ，不符合题意；当∠DF′B=90°时，如图所示， ∵DF′=DF=12BD ，∴∠DBF′=30°，∴tan∠DBF′=3.【点睛】本题考查了相似三角形的综合问题，涉及旋转的性质，锐角三角函数的定义，相似三角形的性质以及判定等知识，综合性较强，有一定的难度，熟练掌握相关的性质与定理、运用分类思想进行讨论是解题的关键.3．已知Rt△ABC中，AB是⊙O的弦，斜边AC交⊙O于点D，且AD=DC，延长CB交⊙O 于点E．（1）图1的A、B、C、D、E五个点中，是否存在某两点间的距离等于线段CE的长？请说明理由；（2）如图2，过点E作⊙O的切线，交AC的延长线于点F．①若CF=CD时，求sin∠CAB的值；②若CF=aCD（a＞0）时，试猜想sin∠CAB的值．（用含a的代数式表示，直接写出结果）【答案】（1）AE=CE；（2）①；②．【解析】试题分析：（1）连接AE、DE，如图1，根据圆周角定理可得∠ADE=∠ABE=90°，由于AD=DC，根据垂直平分线的性质可得AE=CE；（2）连接AE、ED，如图2，由∠ABE=90°可得AE是⊙O的直径，根据切线的性质可得∠AEF=90°，从而可证到△ADE∽△AEF，然后运用相似三角形的性质可得=AD•AF．①当CF=CD 时，可得，从而有EC=AE=CD ，在Rt △DEC 中运用三角函数可得sin ∠CED=，根据圆周角定理可得∠CAB=∠DEC ，即可求出sin ∠CAB 的值；②当CF=aCD （a ＞0）时，同①即可解决问题．试题解析：（1）AE=CE ．理由：连接AE 、DE ，如图1，∵∠ABC=90°，∴∠ABE=90，∴∠ADE=∠ABE=90°，∵AD=DC ，∴AE=CE ；（2）连接AE 、ED ，如图2，∵∠ABE=90°，∴AE 是⊙O 的直径，∵EF 是⊙OO 的切线，∴∠AEF=90°，∴∠ADE=∠AEF=90°，又∵∠DAE=∠EAF ，∴△ADE ∽△AEF ，∴，∴=AD•AF ．①当CF=CD 时，AD=DC=CF ，AF=3DC ，∴=DC•3DC=，∴AE=DC ，∵EC=AE ，∴EC=DC ，∴sin ∠CAB=sin ∠CED===；②当CF=aCD （a ＞0）时，sin ∠CAB=．∵CF=aCD ，AD=DC ，∴AF=AD+DC+CF=（a+2）CD ，∴=DC•（a+2）DC=（a+2），∴AE=DC ，∵EC=AE ，∴EC=DC ，∴sin ∠CAB=sin ∠CED==．考点：1．圆的综合题；2．探究型；3．存在型．4．如图，反比例函数() 0k y k x=≠ 的图象与正比例函数 2y x = 的图象相交于A (1,a ),B 两点，点C 在第四象限，CA ∥y 轴，90ABC ∠=︒. (1)求k 的值及点B 的坐标； (2)求tanC 的值.【答案】（1）2k =，()1,2B --；（2）2. 【解析】【分析】（1）先根据点A 在直线y=2x 上，求得点A 的坐标，再根据点A 在反比例函数()0ky k x=≠ 的图象上，利用待定系数法求得k 的值，再根据点A 、B 关于原点对称即可求得点B 的坐标；（2）作BH ⊥AC 于H ，设AC 交x 轴于点D ，根据90ABC ∠=︒ ， 90BHC ∠=︒ ，可得C ABH ∠∠=，再由已知可得AOD ABH ∠∠=，从而得C AOD ∠∠=，求出Ctan 即可.【详解】（1）∵点A (1，a )在2y x =上， ∴a =2，∴A (1，2)，把A (1，2)代入 ky x= 得2k =， ∵反比例函数()0ky k x=≠ 的图象与正比例函数 2y x = 的图象交于A ，B 两点， ∴A B 、两点关于原点O 中心对称，∴()12B --，；（2）作BH ⊥AC 于H ，设AC 交x 轴于点D ，∵90ABC ∠=︒ ， 90BHC ∠=︒ ，∴C ABH ∠∠=，∵CA ∥y 轴，∴BH ∥x 轴，∴AOD ABH ∠∠=，∴C AOD ∠∠=，∴AD 22OD 1tanC tan AOD =∠===.【点睛】本题考查了反比例与一次函数综合问题，涉及到待定系数法、中心对称、三角函数等知识，熟练掌握和应用相关知识是解题的关键，（2）小题求出∠C=∠AOD是关键.5．问题探究：（一）新知学习：圆内接四边形的判断定理：如果四边形对角互补，那么这个四边形内接于圆（即如果四边形EFGH的对角互补，那么四边形EFGH的四个顶点E、F、G、H都在同个圆上）．（二）问题解决：已知⊙O的半径为2，AB，CD是⊙O的直径．P是上任意一点，过点P分别作AB，CD 的垂线，垂足分别为N，M．（1）若直径AB⊥CD，对于上任意一点P（不与B、C重合）（如图一），证明四边形PMON内接于圆，并求此圆直径的长；（2）若直径AB⊥CD，在点P（不与B、C重合）从B运动到C的过程汇总，证明MN的长为定值，并求其定值；（3）若直径AB与CD相交成120°角．①当点P运动到的中点P1时（如图二），求MN的长；②当点P（不与B、C重合）从B运动到C的过程中（如图三），证明MN的长为定值．（4）试问当直径AB与CD相交成多少度角时，MN的长取最大值，并写出其最大值．【答案】（1）证明见解析，直径OP=2；（2）证明见解析，MN的长为定值，该定值为2；（3）①MN=；②证明见解析；（4）MN取得最大值2．【解析】试题分析：（1）如图一，易证∠PMO+∠PNO=180°，从而可得四边形PMON内接于圆，直径OP=2；（2）如图一，易证四边形PMON是矩形，则有MN=OP=2，问题得以解决；（3）①如图二，根据等弧所对的圆心角相等可得∠COP1=∠BOP1=60°，根据圆内接四边形的对角互补可得∠MP1N=60°．根据角平分线的性质可得P1M=P1N，从而得到△P1MN是等边三角形，则有MN=P1M．然后在Rt△P1MO运用三角函数就可解决问题；②设四边形PMON的外接圆为⊙O′，连接NO′并延长，交⊙O′于点Q，连接QM，如图三，根据圆周角定理可得∠QMN=90°，∠MQN=∠MPN=60°，在Rt△QMN中运用三角函数可得：MN=QN•sin∠MQN，从而可得MN=OP•sin∠MQN，由此即可解决问题；（4）由（3）②中已得结论MN=OP•sin∠MQN可知，当∠MQN=90°时，MN最大，问题得以解决．试题解析：（1）如图一，∵PM⊥OC，PN⊥OB，∴∠PMO=∠PNO=90°，∴∠PMO+∠PNO=180°，∴四边形PMON内接于圆，直径OP=2；（2）如图一，∵AB⊥OC，即∠BOC=90°，∴∠BOC=∠PMO=∠PNO=90°，∴四边形PMON是矩形，∴MN=OP=2，∴MN的长为定值，该定值为2；（3）①如图二，∵P1是的中点，∠BOC=120°，∴∠COP1=∠BOP1=60°，∠MP1N=60°，∵P1M⊥OC，P1N⊥OB，∴P1M=P1N，∴△P1MN是等边三角形，∴MN=P1M．∵P1M=OP1•sin∠MOP1=2×sin60°=，∴MN=；②设四边形PMON的外接圆为⊙O′，连接NO′并延长，交⊙O′于点Q，连接QM，如图三，则有∠QMN=90°，∠MQN=∠MPN=60°，在Rt△QMN中，sin∠MQN=，∴MN=QN•sin∠MQN，∴MN=OP•sin ∠MQN=2×sin60°=2×=，∴MN 是定值．（4）由（3）②得MN=OP•sin ∠MQN=2sin ∠MQN ．当直径AB 与CD 相交成90°角时，∠MQN=180°﹣90°=90°，MN 取得最大值2．考点：圆的综合题．6．（本题满分14分，第（1）小题满分4分，第（2）小题满分5分，第（3）小题满分5分）已知：如图，AB 是半圆O 的直径，弦//CD AB ，动点P 、Q 分别在线段OC 、CD 上，且DQ OP =，AP 的延长线与射线OQ 相交于点E 、与弦CD 相交于点F （点F 与点C 、D 不重合），20AB =，4cos 5AOC ∠=．设OP x =，CPF ∆的面积为y ．（1）求证：AP OQ =；（2）求y 关于x 的函数关系式，并写出它的定义域；（3）当OPE ∆是直角三角形时，求线段OP 的长．【答案】（1）证明见解析；（2）236030050(10)13x x y x x -+=<<；（3）8OP =【解析】【分析】（1）证明线段相等的方法之一是证明三角形全等，通过分析已知条件，OP DQ =，联结OD 后还有OA DO =，再结合要证明的结论AP OQ =，则可肯定需证明三角形全等，寻找已知对应边的夹角，即POA QDO ∠=∠即可；（2）根据PFC ∆∽PAO ∆，将面积转化为相似三角形对应边之比的平方来求；（3）分成三种情况讨论，充分利用已知条件4cos 5AOC ∠=、以及（1）（2）中已证的结论，注意要对不符合（2）中定义域的答案舍去．【详解】（1）联结OD ，∵OC OD =， ∴OCD ODC ∠=∠， ∵//CD AB ， ∴OCD COA ∠=∠，∴POA QDO ∠=∠．在AOP ∆和ODQ ∆中，{OP DQPOA QDO OA DO=∠=∠=， ∴AOP ∆≌ODQ ∆， ∴AP OQ =；（2）作PH OA ⊥，交OA 于H ， ∵4cos 5AOC ∠=， ∴4455OH OP x ==，35PH x =， ∴132AOP S AO PH x ∆=⋅=． ∵//CD AB ， ∴PFC ∆∽PAO ∆， ∴2210()()AOPy CP x S OP x∆-==， ∴2360300x x y x-+=，当F 与点D 重合时，∵42cos 210165CD OC OCD =⋅∠=⨯⨯=， ∴101016x x =-，解得5013x =， ∴2360300x x y x-+=50(10)13x <<；（3）①当90OPE ∠=o 时，90OPA ∠=o ， ∴4cos 1085OP OA AOC =⋅∠=⨯=； ②当90POE ∠=o 时，1010254cos cos 25OC CQ QCO AOC ====∠∠，∴252OP DQ CD CQ CD ==-=-2571622=-=， ∵501013OP <<， ∴72OP =（舍去）；③当90PEO ∠=o 时，∵//CD AB ， ∴AOQ DQO ∠=∠， ∵AOP ∆≌ODQ ∆， ∴DQO APO ∠=∠， ∴AOQ APO ∠=∠，∴90AEO AOP ∠=∠=o ，此时弦CD 不存在，故这种情况不符合题意，舍去；综上，线段OP 的长为8．7．如图，在Rt △ABC 中，∠BAC=90°，∠B=60°，BC=16cm ，AD 是斜边BC 上的高，垂足为D ，BE=1cm ．点M 从点B 出发沿BC 方向以1cm/s 的速度运动，点N 从点E 出发，与点M 同时同方向以相同的速度运动，以MN 为边在BC 的上方作正方形MNGH ．点M 到达点D 时停止运动，点N 到达点C 时停止运动．设运动时间为t （s ）．（1）当t 为何值时，点G 刚好落在线段AD 上？（2）设正方形MNGH 与Rt △ABC 重叠部分的图形的面积为S ，当重叠部分的图形是正方形时，求出S 关于t 的函数关系式并写出自变量t 的取值范围．（3）设正方形MNGH 的边NG 所在直线与线段AC 交于点P ，连接DP ，当t 为何值时，△CPD 是等腰三角形？【答案】（1）3；（2）；（3）t=9s 或t=（15﹣6）s.【解析】试题分析：（1）求出ED 的距离即可求出相对应的时间t.（2）先求出t 的取值范围，分为H 在AB 上时，此时BM 的距离，进而求出相应的时间．同样当G 在AC 上时，求出MN 的长度，继而算出EN 的长度即可求出时间，再通过正方形的面积公式求出正方形的面积.（3）分DP=PC 和DC=PC 两种情况，分别由EN 的长度便可求出t 的值．试题解析：∵∠BAC=90°，∠B=60°，BC=16cm ∴AB=8cm ，BD=4cm ，AC=8cm ，DC=12cm ，AD=4cm.（1）∵当G 刚好落在线段AD 上时，ED=BD ﹣BE=3cm ∴t=s=3s ．（2）∵当MH 没有到达AD 时，此时正方形MNGH 是边长为1的正方形，令H 点在AB上，则∠HMB=90°，∠B=60°，MH=1∴BM=cm.∴t=s.当MH到达AD时，那么此时的正方形MNGH的边长随着N点的继续运动而增大，令G点在AC上，设MN=xcm，则GH=DH=x，AH=x，∵AD=AH+DH=x+x=x=4，∴x=3．当≤t≤4时，S MNGN=1cm2．当4＜t≤6时，S MNGH=（t﹣3）2cm2∴S关于t的函数关系式为：.（3）分两种情况：①∵当DP=PC时，易知此时N点为DC的中点，∴MN=6cm∴EN=3cm+6cm=9cm.∴t=9s故当t=9s的时候，△CPD为等腰三角形；②当DC=PC时，DC=PC=12cm∴NC=6cm∴EN=16cm﹣1cm﹣6cm=（15﹣6）cm∴t=（15﹣6）s故当t=（15﹣6）s时，△CPD为等腰三角形．综上所述，当t=9s或t=（15﹣6）s时，△CPD为等腰三角形．考点：1.双动点问题；2.锐角三角函数定义；3.特殊角的三角函数值；4.正方形的性质；5.由实际问题列函数关系式；6.等腰三角形的性质；7.分类思想的应用.8．（2013年四川攀枝花12分）如图，在平面直角坐标系中，四边形ABCD是梯形，AB∥CD，点B（10，0），C（7，4）．直线l经过A，D两点，且sin∠DAB=22．动点P在线段AB上从点A出发以每秒2个单位的速度向点B运动，同时动点Q从点B出发以每秒5个单位的速度沿B→C→D的方向向点D运动，过点P作PM垂直于x轴，与折线A→D→C相交于点M，当P，Q两点中有一点到达终点时，另一点也随之停止运动．设点P，Q运动的时间为t秒（t＞0），△MPQ的面积为S．（1）点A的坐标为，直线l的解析式为；（2）试求点Q与点M相遇前S与t的函数关系式，并写出相应的t的取值范围；（3）试求（2）中当t为何值时，S的值最大，并求出S的最大值；（4）随着P，Q两点的运动，当点M在线段DC上运动时，设PM的延长线与直线l相交于点N，试探究：当t为何值时，△QMN为等腰三角形？请直接写出t的值．【答案】解：（1）（﹣4，0）；y=x+4．（2）在点P、Q运动的过程中：①当0＜t≤1时，如图1，过点C作CF⊥x轴于点F，则CF=4，BF=3，由勾股定理得BC=5．过点Q作QE⊥x轴于点E，则BE=BQ•cos∠CBF=5t•35=3t．∴PE=PB﹣BE=（14﹣2t）﹣3t=14﹣5t，S=12PM•PE=12×2t×（14﹣5t）=﹣5t2+14t．②当1＜t≤2时，如图2，过点C、Q分别作x轴的垂线，垂足分别为F，E，则CQ=5t﹣5，PE=AF﹣AP﹣EF=11﹣2t﹣（5t﹣5）=16﹣7t．S=12PM•PE=12×2t×（16﹣7t）=﹣7t2+16t．③当点M与点Q相遇时，DM+CQ=CD=7，即（2t﹣4）+（5t﹣5）=7，解得t=167．当2＜t＜167时，如图3，MQ=CD﹣DM﹣CQ=7﹣（2t﹣4）﹣（5t﹣5）=16﹣7t，S=12PM•MQ=12×4×（16﹣7t）=﹣14t+32．综上所述，点Q与点M相遇前S与t的函数关系式为()()225t14t0<t1S{7t16t1<t21614t322<t<7-+≤=-+≤⎛⎫-+ ⎪⎝⎭．（3）①当0＜t≤1时，22749S5t14t5t55⎛⎫=-+=--+⎪⎝⎭，∵a=﹣5＜0，抛物线开口向下，对称轴为直线t=75，∴当0＜t≤1时，S随t的增大而增大．∴当t=1时，S有最大值，最大值为9．②当1＜t≤2时，22864S7t16t7t77⎛⎫=-+=--+⎪⎝⎭，∵a=﹣7＜0，抛物线开口向下，对称轴为直线t=87，∴当t=87时，S有最大值，最大值为647．③当2＜t＜167时，S=﹣14t+32∵k=﹣14＜0，∴S随t的增大而减小．又∵当t=2时，S=4；当t=167时，S=0，∴0＜S＜4．综上所述，当t=87时，S有最大值，最大值为647．（4）t=209或t=125时，△QMN为等腰三角形．【解析】（1）利用梯形性质确定点D的坐标，由sin∠DAB=22，利用特殊三角函数值，得到△AOD为等腰直角三角形，从而得到点A的坐标；由点A、点D的坐标，利用待定系数法求出直线l的解析式：∵C（7，4），AB∥CD，∴D（0，4）．∵sin∠DAB=22，∴∠DAB=45°．∴OA=OD=4．∴A（﹣4，0）．设直线l的解析式为：y=kx+b，则有4k b0{b4-+==，解得：k1{b4==．∴y=x+4．∴点A坐标为（﹣4，0），直线l的解析式为：y=x+4．（2）弄清动点的运动过程分别求解：①当0＜t≤1时，如图1；②当1＜t≤2时，如图2；③当2＜t＜167时，如图3．（3）根据（2）中求出的S表达式与取值范围，逐一讨论计算，最终确定S的最大值．（4）△QMN为等腰三角形的情形有两种，需要分类讨论：①如图4，点M在线段CD上，MQ=CD﹣DM﹣CQ=7﹣（2t﹣4）﹣（5t﹣5）=16﹣7t，MN=DM=2t﹣4，由MN=MQ，得16﹣7t=2t﹣4，解得t=209．②如图5，当点M运动到C点，同时当Q刚好运动至终点D，此时△QMN 为等腰三角形，t=125． ∴当t=209或t=125时，△QMN 为等腰三角形．考点：一次函数综合题，双动点问题，梯形的性质，锐角三角函数定义，特殊角的三角函数值，由实际问题列函数关系式，一次函数和二次函数的性质，等腰三角形的性质，分类思想的应用．9．如图，某公园内有一座古塔AB ，在塔的北面有一栋建筑物，某日上午9时太阳光线与水平面的夹角为32°，此时塔在建筑物的墙上留下了高3米的影子CD ．中午12时太阳光线与地面的夹角为45°，此时塔尖A 在地面上的影子E 与墙角C 的距离为15米（B 、E 、C 在一条直线上），求塔AB 的高度．（结果精确到0.01米）参考数据：sin32°≈0.5299，cos32°≈0.8480，tan32°≈0.6249，2 1.4142≈．【答案】塔高AB 约为32.99米. 【解析】【分析】过点D 作DH ⊥AB ，垂足为点H ，设AB ＝x ，则 AH ＝x ﹣3，解直角三角形即可得到结论．【详解】解：过点D 作DH ⊥AB ，垂足为点H ．由题意，得 HB = CD = 3，EC = 15，HD = BC ，∠ABC =∠AHD = 90°， ∠ADH = 32°．设AB = x ，则 AH = x – 3．在Rt △ABE 中，由 ∠AEB = 45°，得 tan tan451ABAEB EB∠=︒==． ∴ EB = AB = x ．∴ HD = BC = BE + EC = x + 15．在Rt △AHD 中，由 ∠AHD = 90°，得 tan AHADH HD∠=．即得 3tan3215x x -︒=+．解得 15tan32332.991tan32x ⋅︒+=≈-︒．∴ 塔高AB 约为32.99米．【点睛】本题考查的是解直角三角形的应用，根据题意作出辅助线，构造出直角三角形是解答此题的关键．10．许昌芙蓉湖位于许昌市水系建设总体规划中部，上游接纳清泥河来水，下游为鹿鸣湖等水系供水，承担着承上启下的重要作用，是利用有限的水资源、形成良好的水生态环境打造生态宜居城市的重要部分．某校课外兴趣小组想测量位于芙蓉湖两端的A ，B 两点之间的距离他沿着与直线AB 平行的道路EF 行走，走到点C 处，测得∠ACF=45°，再向前走300米到点D 处，测得∠BDF=60°．若直线AB 与EF 之间的距离为200米，求A ，B 两点之间的距离（结果保留一位小数）【答案】215.6米．【解析】【分析】过A 点做EF 的垂线，交EF 于M 点，过B 点做EF 的垂线，交EF 于N 点，根据Rt △ACM 和三角函数tan BDF ∠求出CM 、DN ，然后根据MN MD DN AB =+=即可求出A 、B 两点间的距离. 【详解】解：过A 点做EF 的垂线，交EF 于M 点，过B 点做EF 的垂线，交EF 于N 点在Rt △ACM 中，∵45ACF ∠=︒， ∴AM=CM=200米，又∵CD=300米，所以100MD CD CM =-=米，在Rt △BDN 中，∠BDF=60°，BN=200米 ∴115.6tan 60BNDN =≈o米， ∴215.6MN MD DN AB =+=≈米即A ，B 两点之间的距离约为215.6米．【点睛】本题主要考查三角函数，正确做辅助线是解题的关键.11．如图，在正方形ABCD 中，E 是边AB 上的一动点，点F 在边BC 的延长线上，且CF AE =，连接DE ，DF ，EF . FH 平分EFB ∠交BD 于点H .（1）求证：DE DF ⊥；（2）求证：DH DF =：（3）过点H 作HM EF ⊥于点M ，用等式表示线段AB ，HM 与EF 之间的数量关系，并证明.【答案】（1）详见解析；（2）详见解析；（3）22EF AB HM =-，证明详见解析. 【解析】【分析】（1）根据正方形性质， CF AE =得到DE DF ⊥.（2）由AED CFD △△≌，得DE DF =.由90ABC ∠=︒，BD 平分ABC ∠，得45DBF ∠=︒.因为FH 平分EFB ∠，所以EFH BFH ∠=∠.由于45DHF DBF BFH BFH ∠=∠+∠=︒+∠,45DFH DFE EFH EFH ∠=∠+∠=︒+∠, 所以DH DF =.（3）过点H 作HN BC ⊥于点N ，由正方形ABCD 性质，得222BD AB AD AB =+=.由FH 平分,EFB HM EF HN BC ∠⊥⊥，，得HM HN =.因为4590HBN HNB ∠=︒∠=︒，，所以22sin 45HNBH HN HM ===︒.由22cos 45DFEF DF DH ===︒，得22EF AB HM =-.【详解】（1）证明：∵四边形ABCD 是正方形， ∴AD CD =，90EAD BCD ADC ∠=∠=∠=︒. ∴90EAD FCD ∠=∠=︒. ∵CF AE =。

2020-2021全国中考数学锐角三角函数的综合中考真题汇总含答案

2020-2021全国中考数学锐角三角函数的综合中考真题汇总含答案一、锐角三角函数1．如图，从地面上的点A看一山坡上的电线杆PQ，测得杆顶端点P的仰角是45°，向前走6m到达B点，测得杆顶端点P和杆底端点Q的仰角分别是60°和30°．（1）求∠BPQ的度数；（2）求该电线杆PQ的高度（结果精确到1m）．备用数据：，【答案】（1）∠BPQ=30°；（2）该电线杆PQ的高度约为9m．【解析】试题分析：（1）延长PQ交直线AB于点E，根据直角三角形两锐角互余求得即可；（2）设PE=x米，在直角△APE和直角△BPE中，根据三角函数利用x表示出AE和BE，根据AB=AE-BE即可列出方程求得x的值，再在直角△BQE中利用三角函数求得QE的长，则PQ的长度即可求解．试题解析：延长PQ交直线AB于点E，（1）∠BPQ=90°-60°=30°；（2）设PE=x米．在直角△APE中，∠A=45°，则AE=PE=x米；∵∠PBE=60°∴∠BPE=30°在直角△BPE中，33米，∵AB=AE-BE=6米，则3，解得：3则BE=（33+3）米．在直角△BEQ中，QE=33BE=33（33+3）=（3+3）米．∴PQ=PE-QE=9+33-（3+3）=6+23≈9（米）．答：电线杆PQ的高度约9米．考点：解直角三角形的应用-仰角俯角问题．2．（6分）某海域有A，B两个港口，B港口在A港口北偏西30°方向上，距A港口60海里，有一艘船从A港口出发，沿东北方向行驶一段距离后，到达位于B港口南偏东75°方向的C处，求该船与B港口之间的距离即CB的长（结果保留根号）．【答案】．【解析】试题分析：作AD⊥BC于D，于是有∠ABD=45°，得到AD=BD=，求出∠C=60°，根据正切的定义求出CD的长，得到答案．试题解析：作AD⊥BC于D，∵∠EAB=30°，AE∥BF，∴∠FBA=30°，又∠FBC=75°，∴∠ABD=45°，又AB=60，∴AD=BD=，∵∠BAC=∠BAE+∠CAE=75°，∠ABC=45°，∴∠C=60°，在Rt△ACD中，∠C=60°，AD=，则tanC=，∴CD==，∴BC=．故该船与B港口之间的距离CB的长为海里．考点：解直角三角形的应用-方向角问题．3．在正方形ABCD中，对角线AC，BD交于点O，点P在线段BC上（不含点B），∠BPE=12∠ACB，PE交BO于点E，过点B作BF⊥PE，垂足为F，交AC于点G．（1）当点P与点C重合时（如图1）．求证：△BOG≌△POE；（2）通过观察、测量、猜想：BFPE=，并结合图2证明你的猜想；（3）把正方形ABCD改为菱形，其他条件不变（如图3），若∠ACB=α，求BF PE的值．（用含α的式子表示）【答案】（1）证明见解析（2）12BFPE=（3）1tan2BFPEα=【解析】解：（1）证明：∵四边形ABCD是正方形，P与C重合，∴OB="OP" ，∠BOC=∠BOG=90°．∵PF⊥BG ，∠PFB=90°，∴∠GBO=90°—∠BGO，∠EPO=90°—∠BGO．∴∠GBO=∠EPO ．∴△BOG≌△POE（AAS）．（2）BF1PE2=．证明如下：如图，过P作PM//AC交BG于M，交BO于N，∴∠PNE=∠BOC=900，∠BPN=∠OCB．∵∠OBC=∠OCB =450，∴∠NBP=∠NPB．∴NB=NP．∵∠MBN=900—∠BMN，∠NPE=900—∠BMN，∴∠MBN=∠NPE．∴△BMN≌△PEN（ASA）．∴BM=PE．∵∠BPE=12∠ACB ，∠BPN=∠ACB ，∴∠BPF=∠MPF ． ∵PF ⊥BM ，∴∠BFP=∠MFP=900．又∵PF=PF ， ∴△BPF ≌△MPF （ASA ）．∴BF="MF" ，即BF=12BM ． ∴BF=12PE ，即BF 1PE 2=．（3）如图，过P 作PM//AC 交BG 于点M ，交BO 于点N ，∴∠BPN=∠ACB=α，∠PNE=∠BOC=900．由（2）同理可得BF=12BM ， ∠MBN=∠EPN ． ∵∠BNM=∠PNE=900，∴△BMN ∽△PEN ．∴BM BNPE PN=．在Rt △BNP 中，BN tan =PN α， ∴BM =tan PE α，即2BF=tan PEα． ∴BF 1=tan PE 2α．（1）由正方形的性质可由AAS 证得△BOG ≌△POE ．（2）过P 作PM//AC 交BG 于M ，交BO 于N ，通过ASA 证明△BMN ≌△PEN 得到BM=PE ，通过ASA 证明△BPF ≌△MPF 得到BF=MF ，即可得出BF 1PE 2=的结论．（3）过P 作PM//AC 交BG 于点M ，交BO 于点N ，同（2）证得BF=12BM ， ∠MBN=∠EPN ，从而可证得△BMN ∽△PEN ，由BM BN PE PN =和Rt △BNP 中BNtan =PNα即可求得BF 1=tan PE 2α．4．如图（1），在平面直角坐标系中，点A （0，﹣6），点B （6，0）．Rt △CDE 中，∠CDE=90°，CD=4，DE=4，直角边CD 在y 轴上，且点C 与点A 重合．Rt △CDE 沿y 轴正方向平行移动，当点C 运动到点O 时停止运动．解答下列问题：（1）如图（2），当Rt △CDE 运动到点D 与点O 重合时，设CE 交AB 于点M ，求∠BME的度数．（2）如图（3），在Rt△CDE的运动过程中，当CE经过点B时，求BC的长．（3）在Rt△CDE的运动过程中，设AC=h，△OAB与△CDE的重叠部分的面积为S，请写出S与h之间的函数关系式，并求出面积S的最大值．【答案】（1）∠BME=15°；（2BC=4；（3）h≤2时，S=﹣h2+4h+8，当h≥2时，S=18﹣3h．【解析】试题分析：（1）如图2，由对顶角的定义知，∠BME=∠CMA，要求∠BME的度数，需先求出∠CMA的度数．根据三角形外角的定理进行解答即可；（2）如图3，由已知可知∠OBC=∠DEC=30°，又OB=6，通过解直角△BOC就可求出BC的长度；（3）需要分类讨论：①h≤2时，如图4，作MN⊥y轴交y轴于点N，作MF⊥DE交DE于点F，S=S△EDC﹣S△EFM；②当h≥2时，如图3，S=S△OBC．试题解析：解：（1）如图2，∵在平面直角坐标系中，点A（0，﹣6），点B（6，0）．∴OA=OB，∴∠OAB=45°，∵∠CDE=90°，CD=4，DE=4，∴∠OCE=60°，∴∠CMA=∠OCE﹣∠OAB=60°﹣45°=15°，∴∠BME=∠CMA=15°；如图3，∵∠CDE=90°，CD=4，DE=4，∴∠OBC=∠DEC=30°，∵OB=6，∴BC=4；（3）①h≤2时，如图4，作MN⊥y轴交y轴于点N，作MF⊥DE交DE于点F，∵CD=4，DE=4，AC=h，AN=NM，∴CN=4﹣FM，AN=MN=4+h﹣FM，∵△CMN∽△CED，∴，∴，解得FM=4﹣，∴S=S△EDC﹣S△EFM=×4×4﹣（44﹣h）×（4﹣）=﹣h2+4h+8，②如图3，当h≥2时，S=S△OBC=OC×OB=（6﹣h）×6=18﹣3h．考点：1、三角形的外角定理；2、相似；3、解直角三角形5．已知：如图，在Rt△ABC中，∠ACB=90°，点M是斜边AB的中点，MD∥BC，且MD=CM，DE⊥AB于点E，连结AD、CD．（1）求证：△MED∽△BCA；（2）求证：△AMD≌△CMD；（3）设△MDE的面积为S1，四边形BCMD的面积为S2，当S2=175S1时，求cos∠ABC的值．【答案】（1）证明见解析；（2）证明见解析；（3）cos∠ABC=5 7 .【解析】【分析】（1）易证∠DME=∠CBA，∠ACB=∠MED=90°，从而可证明△MED∽△BCA；（2）由∠ACB=90°，点M是斜边AB的中点，可知MB=MC=AM，从而可证明∠AMD=∠CMD，从而可利用全等三角形的判定证明△AMD≌△CMD；（3）易证MD=2AB，由（1）可知：△MED∽△BCA，所以2114ACBS MDS AB⎛⎫==⎪⎝⎭V，所以S△MCB=12S△ACB=2S1，从而可求出S△EBD=S2﹣S△MCB﹣S1=25S1，由于1EBDS MES EB=V，从而可知52MEEB=，设ME=5x，EB=2x，从而可求出AB=14x，BC=72，最后根据锐角三角函数的定义即可求出答案．【详解】（1）∵MD∥BC，∴∠DME=∠CBA，∵∠ACB=∠MED=90°，∴△MED∽△BCA；（2）∵∠ACB=90°，点M是斜边AB的中点，∴MB=MC=AM，∴∠MCB=∠MBC，∵∠DMB=∠MBC，∴∠MCB=∠DMB=∠MBC，∵∠AMD=180°﹣∠DMB，∠CMD=180°﹣∠MCB﹣∠MBC+∠DMB=180°﹣∠MBC，∴∠AMD=∠CMD，在△AMD与△CMD中，MD MD AMD CMD AM CM =⎧⎪∠=∠⎨⎪=⎩， ∴△AMD ≌△CMD （SAS ）；（3）∵MD=CM ， ∴AM=MC=MD=MB ， ∴MD=2AB ，由（1）可知：△MED ∽△BCA ， ∴2114ACB S MD S AB ⎛⎫== ⎪⎝⎭V ， ∴S △ACB =4S 1， ∵CM 是△ACB 的中线， ∴S △MCB =12S △ACB =2S 1， ∴S △EBD =S 2﹣S △MCB ﹣S 1=25S 1， ∵1EBDS MES EB=V ， ∴1125S MEEB S =，∴52ME EB =，设ME=5x ，EB=2x ， ∴MB=7x ， ∴AB=2MB=14x ，∵12MD ME AB BC ==， ∴BC=10x ，∴cos ∠ABC=105147BC x AB x ==. 【点睛】本题考查相似三角形的综合问题，涉及直角三角形斜边中线的性质，全等三角形的性质与判定，相似三角形的判定与性质，三角形面积的面积比，锐角三角函数的定义等知识，综合程度较高，熟练掌握和灵活运用相关的性质及定理进行解题是关键.6．如图①，抛物线y ＝ax 2+bx+c 经过点A （﹣2，0）、B （4，0）、C （0，3）三点．（1）试求抛物线的解析式；（2）点P 是y 轴上的一个动点，连接PA ，试求5PA+4PC 的最小值；（3）如图②，若直线l 经过点T （﹣4，0），Q 为直线l 上的动点，当以A 、B 、Q 为顶点所作的直角三角形有且仅有三个时，试求直线l 的解析式．【答案】（1）233384y x x =-++；（2）5PA+4PC 的最小值为18；（3）直线l 的解析式为334y x =+或334y x =--.【解析】【分析】（1）设出交点式，代入C 点计算即可（2）连接AC 、BC ，过点A 作AE ⊥BC 于点E ，过点P 作PD ⊥BC 于点D ，易证△CDP ∽△COB ，得到比例式PC PD BC OB =，得到PD=45PC ，所以5PA+4PC ＝5（PA+45PC ）＝5（PA+PD ），当点A 、P 、D 在同一直线上时，5PA+4PC ＝5（PA+PD ）＝5AE 最小，利用等面积法求出AE=185，即最小值为18 （3）取AB 中点F ，以F 为圆心、FA 的长为半径画圆, 当∠BAQ ＝90°或∠ABQ ＝90°时，即AQ 或BQ 垂直x 轴，所以只要直线l 不垂直x 轴则一定找到两个满足的点Q 使∠BAQ ＝90°或∠ABQ ＝90°，即∠AQB ＝90°时，只有一个满足条件的点Q ，∴直线l 与⊙F 相切于点Q 时，满足∠AQB ＝90°的点Q 只有一个；此时，连接FQ ，过点Q 作QG ⊥x 轴于点G ，利用cos ∠QFT 求出QG ，分出情况Q 在x 轴上方和x 轴下方时，分别代入直接l 得到解析式即可【详解】解：（1）∵抛物线与x 轴交点为A （﹣2，0）、B （4，0） ∴y ＝a （x+2）（x ﹣4）把点C （0，3）代入得：﹣8a ＝3 ∴a ＝﹣38∴抛物线解析式为y ＝﹣38（x+2）（x ﹣4）＝﹣38x 2+34x+3 （2）连接AC 、BC ，过点A 作AE ⊥BC 于点E ，过点P 作PD ⊥BC 于点D ∴∠CDP ＝∠COB ＝90°∵∠DCP ＝∠OCB ∴△CDP ∽△COB ∴PC PDBC OB= ∵B （4，0），C （0，3）∴OB＝4，OC ＝3，BC ∴PD ＝45PC ∴5PA+4PC ＝5（PA+45PC ）＝5（PA+PD ） ∴当点A 、P 、D 在同一直线上时，5PA+4PC ＝5（PA+PD ）＝5AE 最小 ∵A （﹣2，0），OC ⊥AB ，AE ⊥BC ∴S △ABC ＝12AB•OC ＝12BC•AE ∴AE ＝631855AB OC BC ⨯==n ∴5AE ＝18∴5PA+4PC 的最小值为18．（3）取AB 中点F ，以F 为圆心、FA 的长为半径画圆当∠BAQ ＝90°或∠ABQ ＝90°时，即AQ 或BQ 垂直x 轴，∴只要直线l 不垂直x 轴则一定找到两个满足的点Q 使∠BAQ ＝90°或∠ABQ ＝90° ∴∠AQB ＝90°时，只有一个满足条件的点Q∵当Q 在⊙F 上运动时（不与A 、B 重合），∠AQB ＝90° ∴直线l 与⊙F 相切于点Q 时，满足∠AQB ＝90°的点Q 只有一个此时，连接FQ ，过点Q 作QG ⊥x 轴于点G ∴∠FQT ＝90°∵F 为A （﹣2，0）、B （4，0）的中点 ∴F （1，0），FQ ＝FA ＝3 ∵T （﹣4，0） ∴TF ＝5，cos ∠QFT ＝35FQ TF = ∵Rt △FGQ 中，cos ∠QFT ＝35FG FQ = ∴FG ＝35FQ ＝95∴x Q ＝1﹣9455=-，QG 125==①若点Q 在x 轴上方，则Q （41255-，）设直线l解析式为：y＝kx+b∴40 412 55 k bk b-+=⎧⎪⎨-+=⎪⎩解得：343kb⎧=⎪⎨⎪=⎩∴直线l：334y x=+②若点Q在x 轴下方，则Q（41255--，）∴直线l：334y x=--综上所述，直线l的解析式为334y x=+或334y x=--【点睛】本题是二次函数与圆的综合题，同时涉及到三角函数、勾股定理等知识点，综合度比较高，需要很强的综合能力，第三问能够找到满足条件的Q点是关键，同时不要忘记需要分情况讨论7．如图1，以点M（－1，0）为圆心的圆与y轴、x轴分别交于点A、B、C、D，直线y＝－x－与⊙M相切于点H，交x轴于点E，交y轴于点F．（1）请直接写出OE、⊙M的半径r、CH的长；（2）如图2，弦HQ交x轴于点P，且DP:PH＝3:2，求cos∠QHC的值；（3）如图3，点K为线段EC上一动点（不与E、C重合），连接BK交⊙M于点T，弦AT 交x轴于点N．是否存在一个常数a，始终满足MN·MK＝a，如果存在，请求出a的值；如果不存在，请说明理由．【答案】（1）OE=5，r=2，CH=2（2）；（3）a=4【解析】【分析】（1）在直线y＝－x－中，令y=0，可求得E的坐标，即可得到OE的长为5；连接MH，根据△EMH与△EFO相似即可求得半径为2；再由EC=MC=2，∠EHM=90°，可知CH 是RT△EHM斜边上的中线，根据直角三角形斜边上的中线等于斜边的一半即可得出CH的长；（2）连接DQ、CQ．根据相似三角形的判定得到△CHP∽△QPD，从而求得DQ的长，在直角三角形CDQ中，即可求得∠D的余弦值，即为cos∠QHC的值；（3）连接AK，AM，延长AM，与圆交于点G，连接TG，由圆周角定理可知，∠GTA=90°，∠3=∠4，故∠AKC=∠MAN，再由△AMK∽△NMA即可得出结论．【详解】（1）OE=5，r=2，CH=2（2）如图1，连接QC、QD，则∠CQD =90°，∠QHC =∠QDC，易知△CHP∽△DQP，故，得DQ=3，由于CD=4，；（3）如图2，连接AK，AM，延长AM，与圆交于点G，连接TG，则，由于，故，；而，故在和中，；故△AMK∽△NMA;即：故存在常数，始终满足常数a="4"解法二：连结BM，证明∽得8．如图，在▱ABCD中，AC与BD交于点O，AC⊥BC于点C，将△ABC沿AC翻折得到△AEC，连接DE．（1）求证：四边形ACED是矩形；（2）若AC＝4，BC＝3，求sin∠ABD的值．【答案】（1）证明见解析（2）613【解析】【分析】（1）根据▱ABCD中，AC⊥BC，而△ABC≌△AEC，不难证明；（2）依据已知条件，在△ABD或△AOC作垂线AF或OF，求出相应边的长度，即可求出∠ABD的正弦值．【详解】（1）证明：∵将△ABC沿AC翻折得到△AEC，∴BC＝CE，AC⊥CE，∵四边形ABCD是平行四边形，∴AD∥BC，AD＝BC，∴AD＝CE，AD∥CE，∴四边形ACED是平行四边形，∵AC⊥CE，∴四边形ACED是矩形．（2）解：方法一、如图1所示，过点A作AF⊥BD于点F，∵BE＝2BC＝2×3＝6，DE＝AC＝4，∴在Rt△BDE中，2222BD BE DE64213=+=+=∵S△BDE＝12×DE•AD＝12AF•BD，∴AF61313213=，∵Rt△ABC中，AB2234+5，∴Rt△ABF中，sin ∠ABF ＝sin ∠ABD ＝61361313655AF AB ==．方法二、如图2所示，过点O 作OF ⊥AB 于点F ，同理可得，OB ＝1132BD =， ∵S △AOB ＝11OF AB OA BC 22⋅=⋅， ∴OF ＝23655⨯=， ∵在Rt △BOF 中，sin ∠FBO ＝0613513F OB ==， ∴sin ∠ABD ＝613．【点睛】本题考查直角三角形翻折变化后所得图形的性质，矩形的判定和性质，平行四边形的性质和解直角三角形求线段的长度，关键是正确添加辅助线和三角形面积的计算公式求出sin ∠ABD ．9．如图，AB 为O e 的直径，C 、D 为O e 上异于A 、B 的两点，连接CD ，过点C 作CE DB ⊥，交CD 的延长线于点E ，垂足为点E ，直径AB 与CE 的延长线相交于点F .（1）连接AC 、AD ，求证：180DAC ACF ∠+∠=︒.（2）若2ABD BDC ∠=∠.①求证：CF 是O e 的切线.②当6BD =，3tan 4F =时，求CF 的长. 【答案】（1）详见解析；（2）①详见解析；② 203CF =. 【解析】【分析】（1）根据圆周角定理证得∠ADB=90°，即AD ⊥BD ，由CE ⊥DB 证得AD ∥CF ，根据平行线的性质即可证得结论；（2）①连接OC ．先根据等边对等角及三角形外角的性质得出∠3=2∠1，由已知∠4=2∠1，得到∠4=∠3，则OC ∥DB ，再由CE ⊥DB ，得到OC ⊥CF ，根据切线的判定即可证明CF 为⊙O 的切线；②由CF ∥AD ，证出∠BAD=∠F ，得出tan ∠BAD=tan ∠F=BD AD =34，求出AD=43BD=8，利用勾股定理求得AB=10，得出OB=OC=，5，再由tanF=OC CF =34，即可求出CF ．【详解】解：（1）AB 是O e 的直径，且D 为O e 上一点， 90ADB ∴∠=︒，CE DB ⊥Q ，90DEC ∴∠=︒，//CF AD ∴，180DAC ACF ∴∠+∠=︒.（2）①如图，连接OC .OA OC =Q ，12∴∠=∠.312∠=∠+∠Q ，321∴∠=∠.42BDC Q ∠=∠，1BDC ∠=∠，421∴∠=∠，43∴∠=∠，//OC DB ∴.CE DB ⊥Q ，OC CF ∴⊥.又OC Q 为O e 的半径，CF ∴为O e 的切线.②由（1）知//CF AD ，BAD F ∴∠=∠， 3tan tan 4BAD F ∴∠==， 34BD AD ∴=. 6BD =Q483AD BD ∴==， 226810AB ∴=+=，5OB OC ==.OC CF Q ⊥，90OCF ∴∠=︒，3tan 4OC F CF ∴==，解得203CF =. 【点睛】本题考查了切线的判定、解直角三角形、圆周角定理等知识；本题综合性强，有一定难度，特别是（2）中，需要运用三角函数、勾股定理和由平行线得出比例式才能得出结果．10．如图，在Rt △ABC 中，∠C ＝90°，∠A ＝30°，AB ＝4，动点P 从点A 出发，沿AB 以每秒2个单位长度的速度向终点B 运动．过点P 作PD ⊥AC 于点D (点P 不与点A ，B 重合)，作∠DPQ ＝60°，边PQ 交射线DC 于点Q ．设点P 的运动时间为t 秒．（1）用含t的代数式表示线段DC的长：_________________；（2）当t =__________时，点Q与点C重合时；（3）当线段PQ的垂直平分线经过△ABC一边中点时，求出t的值．【答案】（1）；（2）1；（3）t的值为或或.【解析】【分析】（1）先求出AC，用三角函数求出AD，即可得出结论；（2）利用AQ=AC，即可得出结论；（3）分三种情况，利用锐角三角函数，即可得出结论．【详解】（1）∵AP= , AB=4,∠A＝30°∴AC= , AD=∴CD=；（2）AQ=2AD=当AQ=AC时，Q与C重合即=∴t=1；（3）①如图，当PQ的垂直平分线过AB的中点F时，∴∠PGF＝90°，PG＝PQ＝AP＝t，AF＝AB＝2.∵∠A＝∠AQP＝30°，∴∠FPG＝60°，∴∠PFG＝30°，∴PF＝2PG＝2t，∴AP＋PF＝2t＋2t＝2，∴t＝②如图，当PQ的垂直平分线过AC的中点N时，∴∠QMN ＝90°，AN＝AC＝，QM＝PQ＝AP＝t.在Rt△NMQ中，∵AN＋NQ＝AQ，∴③如图，当PQ的垂直平分线过BC的中点F时，∴BF ＝BC ＝1，PE ＝PQ ＝t ，∠H ＝30°.∵∠ABC ＝60°，∴∠BFH ＝30°＝∠H ，∴BH ＝BF ＝1.在Rt △PEH 中，PH ＝2PE ＝2t.∵AH ＝AP ＋PH ＝AB ＋BH ，∴2t ＋2t ＝5，∴t ＝.即当线段PQ 的垂直平分线经过△ABC 一边中点时，t 的值为或或.【点睛】此题是三角形综合题，主要考查了等腰三角形的判定和性质，锐角三角函数，垂直平分线的性质，正确作出图形是解本题的关键．11．如图①,在菱形ABCD 中,60B ︒∠= ，4AB =.点P 从点A 出发以每秒2个单位的速度沿边AD 向终点D 运动，过点P 作PQ AC ⊥交边AB 于点Q ，过点P 向上作//PN AC ，且3PN PQ =，以PN 、PQ 为边作矩形PQMN .设点P 的运动时间为t （秒），矩形PQMN 与菱形ABCD 重叠部分图形的面积为S .（1）用含t 的代数式表示线段PQ 的长.（2）当点M 落在边BC 上时，求t 的值.（3）当0t 1<<时，求S 与t 之间的函数关系式，（4）如图②,若点O 是AC 的中点，作直线OM .当直线OM 将矩形PQMN 分成两部分图形的面积比为12：时，直接写出t 的值【答案】（1）23PQ t =；（2）45；（3）2193403163t t -+-；（4） 23t = 或87t = ．【解析】【分析】（1）由菱形性质得∠D=∠B=60°，AD=AB=CD=4，△ACD 是等边三角形，证出△APQ 是等腰三角形，得出PF=QF，PF=PA•sin60°=3t，即可得出结果；（2）当点M落在边BC上时，由题意得：△PDN是等边三角形，得出PD=PN，由已知得PN=3PQ=3t，得出PD=3t，由题意得出方程，解方程即可；（3）当0＜t≤45时，PQ=23t，PN=3PQ=3t，S=矩形PQMN的面积=PQ×PN，即可得出结果；当45＜t＜1时，△PDN是等边三角形，得出PE=PD=AD-PA=4-2t，∠FEN=∠PED=60°，得出NE=PN-PE=5t-4，FN=3NE=3（5t-4），S=矩形PQMN的面积-2△EFN的面积，即可得出结果；（4）分两种情况：当0＜t≤45时，△ACD是等边三角形，AC=AD=4，得出OA=2，OG是△MNH的中位线，得出OG=4t-2，NH=2OG=8t-4，由面积关系得出方程，解方程即可；当45＜t≤2时，由平行线得出△OEF∽△MEQ，得出EF OFEQ MQ=，即233ttEF t-=+，解得EF=2332t t-，得出EQ=23323t tt-+，由三角形面积关系得出方程，解方程即可．【详解】（1）∵在菱形ABCD中，∠B=60°，∴∠D=∠B=60°，AD=AB=CD=4，△ACD是等边三角形，∴∠CAD=60°，∵PQ⊥AC，∴△APQ是等腰三角形，∴PF=QF，PF=PA•sin60°=2t×32=3t，∴PQ=23t；（2）当点M落在边BC上时，如图2所示：由题意得：△PDN是等边三角形，∴PD=PN，∵333t=3t，∴PD=3t，∵PA+PD=AD，即2t+3t=4，解得：t=45．（3）当0＜t≤45时，如图1所示：PQ=23t，PN=3PQ=3×23t=3t，S=矩形PQMN的面积=PQ×PN=23t×3t=63t2；当45＜t＜1时，如图3所示：∵△PDN是等边三角形，∴PE=PD=AD-PA=4-2t，∠FEN=∠PED=60°，∴NE=PN-PE=3t-（4-2t）=5t-4，∴335t-4），∴S=矩形PQMN的面积-2△EFN的面积32-2×1235t-4）2=-19t233，即S=-19t233（4）分两种情况：当0＜t≤45时，如图4所示：∵△ACD 是等边三角形， ∴AC=AD=4， ∵O 是AC 的中点，∴OA=2，OG 是△MNH 的中位线， ∴OG=3t-（2-t ）=4t-2，NH=2OG=8t-4， ∴△MNH 的面积=12MN×NH=12×23t×（8t-4）=13×63t 2，解得：t=23；当45＜t≤2时，如图5所示：∵AC ∥QM ， ∴△OEF ∽△MEQ ，∴EF OF EQ MQ =233tt EF t -=+，解得：2332t t -，∴23323t t t -∴△MEQ 的面积=12×3t×23323t t t -+=1332，解得：t=87；综上所述，当直线OM 将矩形PQMN 分成两部分图形的面积比为1：2时，t 的值为23或87．【点睛】本题是四边形综合题目，考查了菱形的性质、矩形的性质、等边三角形的判定与性质、勾股定理、相似三角形的判定与性质、三角形中位线定理等知识；本题综合性强，难度较大，熟练掌握菱形和矩形的性质，综合运用知识，进行分类讨论是解题的关键．12．如图，△ABC中，AC＝BC＝10，cosC＝35，点P是AC边上一动点（不与点A、C重合），以PA长为半径的⊙P与边AB的另一个交点为D，过点D作DE⊥CB于点E．（1）当⊙P与边BC相切时，求⊙P的半径．（2）连接BP交DE于点F，设AP的长为x，PF的长为y，求y关于x的函数解析式，并直接写出x的取值范围．（3）在（2）的条件下，当以PE长为直径的⊙Q与⊙P相交于AC边上的点G时，求相交所得的公共弦的长.【答案】（1）409R=;（2）25880320xy x xx=-++（3）505-【解析】【分析】（1）设⊙P与边BC相切的切点为H，圆的半径为R，连接HP，则HP⊥BC，cosC＝35，则sinC＝45，sinC＝HPCP＝10RR-＝45，即可求解；（2）首先证明PD∥BE，则EB BFPD PF=，即：2024588x yxxxy-+-=，即可求解；（3）证明四边形PDBE为平行四边形，则AG＝EP＝BD，即：AB＝DB+AD＝AG+AD＝5【详解】（1）设⊙P与边BC相切的切点为H，圆的半径为R，连接HP，则HP⊥BC，cosC＝35，则sinC＝45，sinC＝HPCP＝10RR-＝45，解得：R＝409；（2）在△ABC中，AC＝BC＝10，cosC＝35，设AP＝PD＝x，∠A＝∠ABC＝β，过点B作BH⊥AC，则BH＝ACsinC＝8，同理可得：CH＝6，HA＝4，AB＝45，则：tan∠CAB＝2，BP＝228+(4)x-＝2880x x-+，DA＝25x，则BD＝45﹣25x，如下图所示，PA＝PD，∴∠PAD＝∠CAB＝∠CBA＝β，tanβ＝2，则cosβ5，sinβ5，EB ＝BDcosβ＝（45﹣25x ）×5＝4﹣25x ，∴PD ∥BE ，∴EB BFPD PF=，即：2024588x y x xx y-+--=，整理得：y ＝25xx 8x 803x 20-++；（3）以EP 为直径作圆Q 如下图所示，两个圆交于点G ，则PG ＝PQ ，即两个圆的半径相等，则两圆另外一个交点为D ， GD 为相交所得的公共弦， ∵点Q 是弧GD 的中点， ∴DG ⊥EP ， ∵AG 是圆P 的直径， ∴∠GDA ＝90°， ∴EP ∥BD ，由（2）知，PD ∥BC ，∴四边形PDBE 为平行四边形， ∴AG ＝EP ＝BD ，∴AB ＝DB+AD ＝AG+AD ＝5 设圆的半径为r ，在△ADG 中， AD ＝2rcosβ5DG 5AG ＝2r ， 5＝52r 51+，则：DG 550﹣5 相交所得的公共弦的长为50﹣5 【点睛】本题考查的是圆知识的综合运用，涉及到解直角三角形、勾股定理等知识，其中（3），要关键是根据题意正确画图，此题用大量的解直角三角形的内容，综合难度很大．13．如图，直线与轴交于点，与轴交于点，抛物线经过点，．点为轴上一动点，过点且垂直于轴的直线分别交直线及抛物线于点，．（1）填空：点的坐标为，抛物线的解析式为；（2）当点在线段上运动时（不与点，重合），①当为何值时，线段最大值，并求出的最大值；②求出使为直角三角形时的值；（3）若抛物线上有且只有三个点到直线的距离是，请直接写出此时由点，，，构成的四边形的面积．【答案】（1），；（2）①当时，有最大值是3；②使为直角三角形时的值为3或；（3）点，，，构成的四边形的面积为：6或或.【解析】【分析】（1）把点A坐标代入直线表达式y＝，求出a＝−3，把点A、B的坐标代入二次函数表达式，即可求解；（2）①设：点P（m，），N（m，）求出PN值的表达式，即可求解；②分∠BNP＝90°、∠NBP＝90°、∠BPN＝90°三种情况，求解即可；（3）若抛物线上有且只有三个点N到直线AB的距离是h，则只能出现：在AB直线下方抛物线与过点N的直线与抛物线有一个交点N，在直线AB上方的交点有两个，分别求解即可．【详解】解：（1）把点坐标代入直线表达式，解得：，则：直线表达式为：，令，则：，则点坐标为，将点的坐标代入二次函数表达式得：，把点的坐标代入二次函数表达式得：，解得：，故：抛物线的解析式为：，故：答案为：，；（2）①∵在线段上，且轴，∴点，，∴，∵，∴抛物线开口向下，∴当时，有最大值是3，②当时，点的纵坐标为-3，把代入抛物线的表达式得：，解得：或0（舍去），∴；当时，∵，两直线垂直，其值相乘为-1，设：直线的表达式为：，把点的坐标代入上式，解得：，则：直线的表达式为：，将上式与抛物线的表达式联立并解得：或0（舍去），当时，不合题意舍去，故：使为直角三角形时的值为3或；（3）∵，，在中，，则：，，∵轴，∴，若抛物线上有且只有三个点到直线的距离是，则只能出现：在直线下方抛物线与过点的直线与抛物线有一个交点，在直线上方的交点有两个.当过点的直线与抛物线有一个交点，点的坐标为，设：点坐标为：，则：，过点作的平行线，则点所在的直线表达式为：，将点坐标代入，解得：过点直线表达式为：，将拋物线的表达式与上式联立并整理得：，，将代入上式并整理得：，解得：，则点的坐标为，则：点坐标为，则：，∵，，∴四边形为平行四边形，则点到直线的距离等于点到直线的距离，即：过点与平行的直线与抛物线的交点为另外两个点，即：、，直线的表达式为：，将该表达式与二次函数表达式联立并整理得：，解得：，则点、的横坐标分别为，，作交直线于点，则，作轴，交轴于点，则：，，，则：，同理：，故：点，，，构成的四边形的面积为：6或或.【点睛】本题考查的是二次函数知识的综合运用，涉及到一次函数、解直角三角形等相关知识，其中（3）中确定点N 的位置是本题的难点，核心是通过△＝0，确定图中N 点的坐标．14．已知：如图，在Rt △ABO 中，∠B =90°，∠OAB =30°，OA =3．以点O 为原点，斜边OA 所在直线为x 轴，建立平面直角坐标系，以点P （4，0）为圆心，PA 长为半径画圆，⊙P 与x 轴的另一交点为N ，点M 在⊙P 上，且满足∠MPN =60°．⊙P 以每秒1个单位长度的速度沿x 轴向左运动，设运动时间为ts ，解答下列问题：（发现）（1）MN n的长度为多少；（2）当t =2s 时，求扇形MPN （阴影部分）与Rt △ABO 重叠部分的面积．（探究）当⊙P 和△ABO 的边所在的直线相切时，求点P 的坐标．（拓展）当MN n与Rt △ABO 的边有两个交点时，请你直接写出t 的取值范围．【答案】【发现】（1）MN n的长度为π3；（23P 的坐标为10（，）；或230）或230（）；【拓展】t 的取值范围是23t ≤＜或45t ≤＜，理由见解析．【解析】【分析】发现：（1）先确定出扇形半径，进而用弧长公式即可得出结论；（2）先求出PA =1，进而求出PQ ，即可用面积公式得出结论；探究：分圆和直线AB 和直线OB 相切，利用三角函数即可得出结论；拓展：先找出·MN和直角三角形的两边有两个交点时的分界点，即可得出结论．【详解】 [发现]（1）∵P （4，0），∴OP =4．∵OA =3，∴AP =1，∴·MN的长度为6011803ππ⨯=．故答案为3π；（2）设⊙P 半径为r ，则有r =4﹣3=1，当t =2时，如图1，点N 与点A 重合，∴PA =r =1，设MP 与AB 相交于点Q ．在Rt △ABO 中，∵∠OAB =30°，∠MPN =60°． ∵∠PQA =90°，∴PQ 12=PA 12=，∴AQ =AP ×cos30°32=，∴S 重叠部分=S △APQ 12=PQ ×AQ 38=．即重叠部分的面积为38． [探究]①如图2，当⊙P 与直线AB 相切于点C 时，连接PC ，则有PC ⊥AB ，PC =r =1． ∵∠OAB =30°，∴AP =2，∴OP =OA ﹣AP =3﹣2=1； ∴点P 的坐标为（1，0）；②如图3，当⊙P 与直线OB 相切于点D 时，连接PD ，则有PD ⊥OB ，PD =r =1，∴PD ∥AB ，∴∠OPD =∠OAB =30°，∴cos ∠OPD PD OP =，∴OP 12330cos ==︒，∴点P 的坐标为（23，0）； ③如图4，当⊙P 与直线OB 相切于点E 时，连接PE ，则有PE ⊥OB ，同②可得：OP 233=； ∴点P 的坐标为（23-，0）；[拓展]t 的取值范围是2＜t ≤3，4≤t ＜5，理由：如图5，当点N 运动到与点A 重合时，·MN与Rt △ABO 的边有一个公共点，此时t =2；当t＞2，直到⊙P运动到与AB相切时，由探究①得：OP=1，∴t411-==3，·MN与Rt△ABO的边有两个公共点，∴2＜t≤3．如图6，当⊙P运动到PM与OB重合时，·MN与Rt△ABO的边有两个公共点，此时t=4；直到⊙P运动到点N与点O重合时，·MN与Rt△ABO的边有一个公共点，此时t=5；∴4≤t＜5，即：t的取值范围是2＜t≤3，4≤t＜5．【点睛】本题是圆的综合题，主要考查了弧长公式，切线的性质，锐角三角函数，三角形面积公式，作出图形是解答本题的关键．15．如图，半圆O的直径AB＝20，弦CD∥AB，动点M在半径OD上，射线BM与弦CD 相交于点E（点E与点C、D不重合），设OM＝m．（1）求DE的长（用含m的代数式表示）；（2）令弦CD所对的圆心角为α，且sin4 =25α．①若△DEM的面积为S，求S关于m的函数关系式，并求出m的取值范围；②若动点N在CD上，且CN＝OM，射线BM与射线ON相交于点F，当∠OMF＝90°时，求DE的长．【答案】（1）DE＝10010mm-；（2）①S＝2360300m mm-+，（5013＜m＜10），②DE＝5 2 .【解析】【分析】（1）由CD∥AB知△DEM∽△OBM，可得DE DMOB OM=，据此可得；（2）①连接OC、作OP⊥CD、MQ⊥CD，由OC＝OD、OP⊥CD知∠DOP＝12∠COD，据此可得sin ∠DOP ＝sin ∠DMQ ＝45、sin ∠ODP ＝35，继而由OM ＝m 、OD ＝10得QM ＝DM sin ∠ODP ＝35（10﹣m ），根据三角形的面积公式即可得；如图2，先求得PD ＝8、CD ＝16，证△CDM ∽△BOM 得CD DM BO OM =，求得OM ＝5013，据此可得m 的取值范围； ②如图3，由BM ＝OB sin ∠BOM ＝10×35＝6，可得OM ＝8，根据（1）所求结果可得答案．【详解】（1）∵CD ∥AB ，∴△DEM ∽△OBM ， ∴DE DM OB OM =，即1010DE m m-=， ∴DE ＝10010m m -；（2）①如图1，连接OC 、作OP ⊥CD 于点P ，作MQ ⊥CD 于点Q ，∵OC ＝OD 、OP ⊥CD ，∴∠DOP ＝12∠COD ， ∵sin 2α＝45， ∴sin ∠DOP ＝sin ∠DMQ ＝45，sin ∠ODP ＝35， ∵OM ＝m 、OD ＝10，∴DM ＝10﹣m ，∴QM ＝DM sin ∠ODP ＝35（10﹣m ），则S △DEM ＝12DE •MQ ＝12×10010m m -×35（10﹣m ）＝2360300m m m-+，如图2，∵PD ＝OD sin ∠DOP ＝10×45＝8， ∴CD ＝16，∵CD ∥AB ，∴△CDM ∽△BOM ，∴CD DM BO OM =，即1610=10OM OM-，解得：OM ＝5013， ∴5013＜m ＜10， ∴S ＝2360300m m m-+，（5013＜m ＜10）． ②当∠OMF ＝90°时，如图3，则∠BMO ＝90°，在Rt △BOM 中，BM ＝OB sin ∠BOM ＝10×35＝6，则OM ＝8，由（1）得DE ＝100108582-⨯=．【点睛】本题主要考查圆的综合题，解题的关键是熟练掌握圆的有关性质、相似三角形的判定与性质及解直角三角形的能力．。

2020-2021中考数学锐角三角函数综合题及详细答案

2020-2021中考数学锐角三角函数综合题及详细答案一、锐角三角函数1．如图，在平行四边形ABCD中，平分，交于点，平分，交于点，与交于点，连接，.（1）求证：四边形是菱形；（2）若，，，求的值.【答案】（1）证明见解析（2）【解析】试题分析：（1）根据AE平分∠BAD、BF平分∠ABC及平行四边形的性质可得AF=AB=BE，从而可知ABEF为平行四边形，又邻边相等，可知为菱形（2）由菱形的性质可知AP的长及∠PAF=60°，过点P作PH⊥AD于H，即可得到PH、DH 的长，从而可求tan∠ADP试题解析：(1)∵AE平分∠BAD BF平分∠ABC∴∠BAE=∠EAF ∠ABF=∠EBF∵AD//BC∴∠EAF=∠AEB ∠AFB=∠EBF∴∠BAE=∠AEB ∠AFB=∠ABF∴AB=BE AB=AF∴AF=AB=BE∵AD//BC∴ABEF为平行四边形又AB=BE∴ABEF为菱形（2）作PH⊥AD于H由∠ABC=60°而已（1）可知∠PAF=60°，PA=2，则有PH=，AH=1，∴DH=AD-AH=5∴tan∠ADP=考点：1、平行四边形；2、菱形；3、直角三角形；4、三角函数2．如图，在△ABC中，AB=7.5，AC=9，S△ABC=814．动点P从A点出发，沿AB方向以每秒5个单位长度的速度向B点匀速运动，动点Q从C点同时出发，以相同的速度沿CA方向向A点匀速运动，当点P运动到B点时，P、Q两点同时停止运动，以PQ为边作正△PQM （P、Q、M按逆时针排序），以QC为边在AC上方作正△QCN，设点P运动时间为t秒．（1）求cosA的值；（2）当△PQM与△QCN的面积满足S△PQM=95S△QCN时，求t的值；（3）当t为何值时，△PQM的某个顶点（Q点除外）落在△QCN的边上．【答案】（1）coaA=45；（2）当t=35时，满足S△PQM=95S△QCN；（3）当t=273326-s或2733+s时，△PQM的某个顶点（Q点除外）落在△QCN的边上．【解析】分析：（1）如图1中，作BE⊥AC于E．利用三角形的面积公式求出BE，利用勾股定理求出AE即可解决问题；（2）如图2中，作PH⊥AC于H．利用S△PQM=95S△QCN构建方程即可解决问题；（3）分两种情形①如图3中，当点M落在QN上时，作PH⊥AC于H．②如图4中，当点M在CQ上时，作PH⊥AC于H．分别构建方程求解即可；详解：（1）如图1中，作BE⊥AC于E．∵S △ABC =12•AC•BE=814， ∴BE=92，在Rt △ABE 中，AE=22=6AB BE -， ∴coaA=647.55AE AB ==．（2）如图2中，作PH ⊥AC 于H ．∵PA=5t ，PH=3t ，AH=4t ，HQ=AC-AH-CQ=9-9t ，∴PQ 2=PH 2+HQ 2=9t 2+（9-9t ）2，∵S △PQM =95S △QCN ， ∴34•PQ 2=9354⨯•CQ 2， ∴9t 2+（9-9t ）2=95×（5t ）2，整理得：5t 2-18t+9=0，解得t=3（舍弃）或35． ∴当t=35时，满足S △PQM =95S △QCN ．（3）①如图3中，当点M 落在QN 上时，作PH ⊥AC 于H ．易知：PM ∥AC ，∴∠MPQ=∠PQH=60°，∴PH=3HQ ， ∴3t=3（9-9t ），∴t=273326-． ②如图4中，当点M 在CQ 上时，作PH ⊥AC 于H ．同法可得PH=3QH ，∴3t=3（9t-9），∴t=27+33，综上所述，当t=2733-s 或27+3326s 时，△PQM 的某个顶点（Q 点除外）落在△QCN 的边上．点睛：本题考查三角形综合题、等边三角形的性质、勾股定理锐角三角函数、解直角三角形等知识，解题的关键是灵活运用所学知识解决问题，学会用分类讨论的思想思考问题，属于中考常考题型．3．在矩形ABCD 中，AD ＞AB ，点P 是CD 边上的任意一点（不含C ，D 两端点），过点P 作PF ∥BC ，交对角线BD 于点F ．（1）如图1，将△PDF 沿对角线BD 翻折得到△QDF ，QF 交AD 于点E ．求证：△DEF 是等腰三角形；（2）如图2，将△PDF 绕点D 逆时针方向旋转得到△P'DF'，连接P'C ，F'B ．设旋转角为α（0°＜α＜180°）．①若0°＜α＜∠BDC ，即DF'在∠BDC 的内部时，求证：△DP'C ∽△DF'B ．②如图3，若点P 是CD 的中点，△DF'B 能否为直角三角形？如果能，试求出此时tan ∠DBF'的值，如果不能，请说明理由．【答案】（1）证明见解析；（2）①证明见解析；②12 【解析】【分析】（1）根据翻折的性质以及平行线的性质可知∠DFQ=∠ADF ，所以△DEF 是等腰三角形；（2）①由于PF ∥BC ，所以△DPF ∽△DCB ，从而易证△DP′F′∽△DCB ；②由于△DF'B 是直角三角形，但不知道哪个的角是直角，故需要对该三角形的内角进行分类讨论．【详解】（1）由翻折可知：∠DFP=∠DFQ ，∵PF ∥BC ，∴∠DFP=∠ADF ，∴∠DFQ=∠ADF ，∴△DEF 是等腰三角形；（2）①若0°＜α＜∠BDC ，即DF'在∠BDC 的内部时，∵∠P′DF′=∠PDF ，∴∠P′DF′﹣∠F′DC=∠PDF ﹣∠F′DC ，∴∠P′DC=∠F′DB ，由旋转的性质可知：△DP′F′≌△DPF ，∵PF ∥BC ，∴△DPF ∽△DCB ，∴△DP′F′∽△DCB ∴''DC DP DB DF = ， ∴△DP'C ∽△DF'B ；②当∠F′DB=90°时，如图所示，∵DF ′=DF=12BD ， ∴'12DF BD =， ∴tan ∠DBF′='12DF BD =；当∠DBF′=90°，此时DF′是斜边，即DF′＞DB，不符合题意；当∠DF′B=90°时，如图所示，∵DF′=DF=1BD，2∴∠DBF′=30°，∴tan∠DBF′=3.【点睛】本题考查了相似三角形的综合问题，涉及旋转的性质，锐角三角函数的定义，相似三角形的性质以及判定等知识，综合性较强，有一定的难度，熟练掌握相关的性质与定理、运用分类思想进行讨论是解题的关键.4．下图是某儿童乐园为小朋友设计的滑梯平面图.已知BC=4 m,AB=6 m,中间平台宽度DE=1 m,EN,DM,CB为三根垂直于AB的支柱,垂足分别为N,M,B,∠EAB=31°,DF⊥BC于点F,∠CDF=45°,求DM和BC的水平距离BM的长度.(结果精确到0.1 m.参考数据:sin31°≈0.52,cos 31°≈0.86,tan 31°≈0.60)【答案】2.5m.【解析】试题分析：设DF=x，在Rt△DFC中，可得CF=DF=x，则BF=4-x，根据线段的和差可得AN=5-x，EN=DM=BF=4－，在Rt△ANE中，∠EAB=，利用∠EAB的正切值解得x的值．试题解析：解：设DF=，在Rt△DFC中，∠CDF=，∴CF=tan·DF=，又∵CB=4，∴BF=4－，∵AB=6，DE=1，BM= DF=，∴AN=5－，EN=DM=BF=4－，在Rt△ANE中，∠EAB=，EN=4－，AN=5－，tan==0．60，解得=2．5，答：DM和BC的水平距离BM为2．5米．考点：解直角三角形．5．如图，AB是⊙O的直径，弦CD⊥AB于H，过CD延长线上一点E作⊙O的切线交AB 的延长线于切点为G，连接AG交CD于K．（1）求证：KE=GE；（2）若KG2=KD•GE，试判断AC与EF的位置关系，并说明理由；（3）在（2）的条件下，若sinE=，AK=，求FG的长．【答案】（1）证明见解析；（2）AC∥EF，证明见解析；（3）FG= ．【解析】试题分析：（1）如图1，连接OG．根据切线性质及CD⊥AB，可以推出∠KGE=∠AKH=∠GKE，根据等角对等边得到KE=GE；（2）AC与EF平行，理由为：如图2所示，连接GD，由∠KGE=∠GKE，及KG2=KD•GE，利用两边对应成比例且夹角相等的两三角形相似可得出△GKD与△EKG相似，又利用同弧所对的圆周角相等得到∠C=∠AGD，可推知∠E=∠C，从而得到AC∥EF；（3）如图3所示，连接OG，OC，先求出KE=GE，再求出圆的半径，根据勾股定理与垂径定理可以求解；然后在Rt△OGF中，解直角三角形即可求得FG的长度．试题解析：（1）如图1，连接OG．∵EG为切线，∴∠KGE+∠OGA=90°，∵CD⊥AB，∴∠AKH+∠OAG=90°，又∵OA=OG，∴∠OGA=∠OAG，∴∠KGE=∠AKH=∠GKE，∴KE=GE．（2）AC∥EF，理由为连接GD，如图2所示．∵KG2=KD•GE，即，∴，又∵∠KGE=∠GKE，∴△GKD∽△EGK，∴∠E=∠AGD，又∵∠C=∠AGD，∴∠E=∠C，∴AC∥EF；（3）连接OG，OC，如图3所示，∵EG为切线，∴∠KGE+∠OGA=90°，∵CD⊥AB，∴∠AKH+∠OAG=90°，又∵OA=OG，∴∠OGA=∠OAG，∴∠KGE=∠AKH=∠GKE，∴KE=GE．∵sinE=sin∠ACH=，设AH=3t，则AC=5t，CH=4t，∵KE=GE，AC∥EF，∴CK=AC=5t，∴HK=CK-CH=t．在Rt△AHK中，根据勾股定理得AH2+HK2=AK2，即（3t）2+t2=（2）2，解得t=．设⊙O半径为r，在Rt△OCH中，OC=r，OH=r-3t，CH=4t，由勾股定理得：OH2+CH2=OC2，即（r-3t）2+（4t）2=r2，解得r= t=．∵EF为切线，∴△OGF为直角三角形，在Rt△OGF中，OG=r=，tan∠OFG=tan∠CAH=，∴FG=【点睛】此题考查了切线的性质，相似三角形的判定与性质，垂径定理，勾股定理，锐角三角函数定义，圆周角定理，平行线的判定，以及等腰三角形的判定，熟练掌握定理及性质是解本题的关键．6．在正方形ABCD中，BD是一条对角线.点P在射线CD上（与点C，D不重合），连接AP，平移△ADP，使点D移动到点C，得到△BCQ，过点Q作QH⊥BD于点H，连接AH、PH.（1）若点P在线CD上，如图1，①依题意补全图1；②判断AH与PH的数量关系与位置关系并加以证明；（2）若点P在线CD的延长线上，且∠AHQ＝152°，正方形ABCD的边长为1，请写出求DP长的思路.（可以不写出计算结果）【答案】（1）①如图；②AH＝PH，AH⊥PH．证明见解析（2）或【解析】试题分析：（1）①如图（1）；②（1）法一：轴对称作法，判断：AH＝PH，AH⊥PH．连接CH，根据正方形的每条对角线平分一组对角得：△DHQ等腰Rt△，根据平移的性质得DP＝CQ，证得△HDP≌△△HQC，全等三角形的对应边相等得PH＝CH，等边对等角得∠HPC＝∠HCP，再结合BD是正方形的对称轴得出∠AHP＝180°－∠ADP＝90°，∴AH＝PH且AH⊥PH．四点共圆作法，同上得：∠HPC＝∠DAH，∴A、D、P、H共向，∴∠AHP＝90°，∠APH＝∠ADH＝45°，∴△APH等腰Rt△．（2）轴对称作法同（1）作HR⊥PC于R，∵∠AHQ＝152°，∴∠AHB＝62°，∴∠DAH＝17°∴∠DCH＝17°．设DP＝x，则.由代入HR，CR解方程即可得出x的值. 四点共圆作法，A、H、D、P共向，∴∠APD＝∠AHB＝62°，∴．试题解析：（1）①法一：轴对称作法，判断：AH＝PH，AH⊥PH证：连接CH，得：△DHQ等腰Rt△，又∵DP＝CQ，∴△HDP≌△△HQC，∴PH＝CH，∠HPC＝∠HCPBD为正方形ABCD对称轴，∴AH＝CH，∠DAH＝∠HCP，∴AH＝PH，∠DAH＝∠HPC，∴∠AHP＝180°－∠ADP＝90°，∴AH＝PH且AH⊥PH．法二：四点共圆作法，同上得：∠HPC＝∠DAH，∴A、D、P、H共向，∴∠AHP＝90°，∠APH＝∠ADH＝45°，∴△APH等腰Rt△．（2）法一：轴对称作法考虑△DHQ 等腰Rt △，PD ＝CQ ，作HR ⊥PC 于R ，∵∠AHQ ＝152°，∴∠AHB ＝62°，∴∠DAH ＝17°∴∠DCH ＝17°．设DP ＝x ，则.由得：，∴．即PD=法二：四点共向作法，A 、H 、D 、P 共向，∴∠APD ＝∠AHB ＝62°，∴．考点：全等三角形的判定；解直角三角形；正方形的性质；死电脑共圆7．如图①，抛物线y ＝ax 2+bx+c 经过点A （﹣2，0）、B （4，0）、C （0，3）三点．（1）试求抛物线的解析式；（2）点P 是y 轴上的一个动点，连接PA ，试求5PA+4PC 的最小值；（3）如图②，若直线l 经过点T （﹣4，0），Q 为直线l 上的动点，当以A 、B 、Q 为顶点所作的直角三角形有且仅有三个时，试求直线l 的解析式．【答案】（1）233384y x x =-++；（2）5PA+4PC 的最小值为18；（3）直线l 的解析式为334y x=+或334y x=--.【解析】【分析】（1）设出交点式，代入C点计算即可（2）连接AC、BC，过点A作AE⊥BC于点E，过点P作PD⊥BC于点D，易证△CDP∽△COB，得到比例式PC PDBC OB=，得到PD=45PC，所以5PA+4PC＝5（PA+45PC）＝5（PA+PD），当点A、P、D在同一直线上时，5PA+4PC＝5（PA+PD）＝5AE最小，利用等面积法求出AE=185，即最小值为18 （3）取AB中点F，以F为圆心、FA的长为半径画圆, 当∠BAQ＝90°或∠ABQ＝90°时，即AQ或BQ垂直x轴，所以只要直线l不垂直x轴则一定找到两个满足的点Q使∠BAQ＝90°或∠ABQ＝90°，即∠AQB＝90°时，只有一个满足条件的点Q，∴直线l与⊙F相切于点Q时，满足∠AQB＝90°的点Q只有一个；此时，连接FQ，过点Q作QG⊥x轴于点G，利用cos∠QFT求出QG，分出情况Q在x轴上方和x轴下方时，分别代入直接l得到解析式即可【详解】解：（1）∵抛物线与x轴交点为A（﹣2，0）、B（4，0）∴y＝a（x+2）（x﹣4）把点C（0，3）代入得：﹣8a＝3∴a＝﹣38∴抛物线解析式为y＝﹣38（x+2）（x﹣4）＝﹣38x2+34x+3（2）连接AC、BC，过点A作AE⊥BC于点E，过点P作PD⊥BC于点D ∴∠CDP＝∠COB＝90°∵∠DCP＝∠OCB∴△CDP∽△COB∴PC PDBC OB=∵B（4，0），C（0，3）∴OB＝4，OC＝3，BC∴PD＝45PC∴5PA+4PC＝5（PA+45PC）＝5（PA+PD）∴当点A、P、D在同一直线上时，5PA+4PC＝5（PA+PD）＝5AE最小∵A（﹣2，0），OC⊥AB，AE⊥BC∴S △ABC ＝12AB•OC ＝12BC•AE ∴AE ＝631855AB OC BC ⨯==n ∴5AE ＝18∴5PA+4PC 的最小值为18．（3）取AB 中点F ，以F 为圆心、FA 的长为半径画圆当∠BAQ ＝90°或∠ABQ ＝90°时，即AQ 或BQ 垂直x 轴，∴只要直线l 不垂直x 轴则一定找到两个满足的点Q 使∠BAQ ＝90°或∠ABQ ＝90° ∴∠AQB ＝90°时，只有一个满足条件的点Q∵当Q 在⊙F 上运动时（不与A 、B 重合），∠AQB ＝90° ∴直线l 与⊙F 相切于点Q 时，满足∠AQB ＝90°的点Q 只有一个此时，连接FQ ，过点Q 作QG ⊥x 轴于点G ∴∠FQT ＝90°∵F 为A （﹣2，0）、B （4，0）的中点 ∴F （1，0），FQ ＝FA ＝3 ∵T （﹣4，0） ∴TF ＝5，cos ∠QFT ＝35FQ TF = ∵Rt △FGQ 中，cos ∠QFT ＝35FG FQ = ∴FG ＝35FQ ＝95∴x Q ＝1﹣9455=-，QG125==①若点Q 在x 轴上方，则Q （41255-，）设直线l 解析式为：y ＝kx+b∴4041255k b k b -+=⎧⎪⎨-+=⎪⎩ 解得：343k b ⎧=⎪⎨⎪=⎩ ∴直线l ：334y x =+ ②若点Q 在x 轴下方，则Q （41255--，） ∴直线l ：334y x =-- 综上所述，直线l 的解析式为334y x =+或334y x =--【点睛】本题是二次函数与圆的综合题，同时涉及到三角函数、勾股定理等知识点，综合度比较高，需要很强的综合能力，第三问能够找到满足条件的Q点是关键，同时不要忘记需要分情况讨论8．如图，AB是⊙O的直径，PA、PC与⊙O分别相切于点A，C，PC交AB的延长线于点D，DE⊥PO交PO的延长线于点E．(1)求证：∠EPD=∠EDO；(2)若PC=3，tan∠PDA=34，求OE的长．【答案】（1）见解析；（25.【解析】【分析】（1）由切线的性质即可得证.（2）连接OC，利用tan∠PDA=34，可求出CD=2,进而求得OC=32，再证明△OED∽△DEP，根据相似三角形的性质和勾股定理即可求出OE的长.【详解】（1）证明：∵PA，PC与⊙O分别相切于点A，C，∴∠APO=∠CPO, PA⊥AO，∵DE⊥PO，∴∠PAO=∠E=90°，∵∠AOP=∠EOD，∴∠APO=∠EDO，∴∠EPD=∠EDO.（2）连接OC，∴PA=PC=3，∵tan∠PDA=34，∴在Rt△PAD中，AD=4，PD=22PA AD+=5，∴CD=PD-PC=5-3=2，∵tan∠PDA=34，∴在Rt△OCD中，OC=32，OD=22OC CD+=52，∵∠EPD=∠ODE，∠OCP=∠E=90°，∴△OED∽△DEP，∴PDDO =PEDE=DEOE=2，∴DE=2OE,在Rt△OED中，OE2+DE2=OD2，即5OE2=252⎛⎫⎪⎝⎭=254，∴OE=5．【点睛】本题考查了切线的性质；锐角三角函数；勾股定理和相似三角形的判定与性质，充分利用tan∠PDA=34，得线段的长是解题关键.9．阅读下面材料：观察与思考：阅读下列材料，并解决后面的问题．在锐角△ABC 中，∠A 、∠B 、∠C 的对边分别是a 、b 、c ，过A 作AD ⊥BC 于D （如图），则sin B ＝AD c ，sin C ＝ADb，即AD ＝c sin B ，AD ＝b sin C ，于是c sin B ＝b sin C ，即sin sin b c B C = ．同理有：sin sin c aC A=，sin sin a b A B=，所以sin sin sin a b cA B C ==．即：在一个三角形中，各边和它所对角的正弦的比相等．在锐角三角形中，若已知三个元素（至少有一条边），运用上述结论和有关定理就可以求出其余三个未知元素．根据上述材料，完成下列各题．（1）如图，△ABC 中，∠B ＝75°，∠C ＝45°，BC ＝60，则AB ＝；（2）如图，一货轮在C 处测得灯塔A 在货轮的北偏西30°的方向上，随后货轮以60海里/时的速度按北偏东30°的方向航行，半小时后到达B 处，此时又测得灯塔A 在货轮的北偏西75°的方向上（如图），求此时货轮距灯塔A 的距离AB ．（3）在（2）的条件下，试求75°的正弦值．（结果保留根号）【答案】（1）6；（2）6海里；（36+2【解析】【分析】（1）根据材料：在一个三角形中，各边和它所对角的正弦的比相等，写出比例关系，代入数值即可求得AB 的值.（2）此题可先由速度和时间求出BC 的距离，再由各方向角得出∠A 的角度，过B 作BM ⊥AC 于M ，求出∠MBC=30°，求出MC ，由勾股定理求出BM ，求出AM 、BM 的长，由勾股定理求出AB 即可；（3）在三角形ABC 中，∠A=45，∠ABC=75，∠ACB=60，过点C 作AC 的垂线BD ，构造直角三角形ABD ，BCD ，在直角三角形ABD 中可求出AD 的长，进而可求出sin75°的值．【详解】解：（1）在△ABC 中，∠B=75°，∠C=45°，BC=60，则∠A=60°， ∵AB sinC =sin BCA，∴45AB sin o=60sin60o，即2 =3，解得：AB=206. （2）如图，依题意：BC=60×0.5=30（海里） ∵CD ∥BE ， ∴∠DCB+∠CBE=180° ∵∠DCB=30°， ∴∠CBE=150° ∵∠ABE=75°． ∴∠ABC=75°， ∴∠A=45°，在△ABC 中，sin AB ACB ∠=BC sin A ∠ 即60?ABsin =3045?sin ，解之得：6．答：货轮距灯塔的距离6海里．（3）过点B 作AC 的垂线BM ，垂足为M.在直角三角形ABM中，∠A=45°，AB=156，所以AM=153，在直角三角形BDC中，∠BCM=60°，BC=30°，可求得CM=15，所以AC=153+15，由题意得，15315＝156，sin75°=6+2．【点睛】本题考查方向角的含义，三角形的内角和定理，含30度角的直角三角形，等腰三角形的性质和判定等知识点，解题关键是熟练掌握解直角三角形方法．10．兰州银滩黄河大桥北起安宁营门滩，南至七里河马滩，是黄河上游的第一座大型现代化斜拉式大桥如图，小明站在桥上测得拉索AB与水平桥面的夹角是31°，拉索AB的长为152米，主塔处桥面距地面7.9米（CD的长），试求出主塔BD的高．（结果精确到0.1米，参考数据：sin31°≈0.52，cos31°≈0.86，tan31°≈0.60）【答案】主塔BD的高约为86.9米．【解析】【分析】根据直角三角形中由三角函数得出BC相应长度，再由BD=BC+CD可得出.【详解】在Rt△ABC中，∠ACB=90°，sin BCA AB=． ∴sin 152sin311520.5279.04BC AB A ︒=⨯=⨯=⨯=．79.047.986.9486.9BD BC CD =+=+=≈（米）答：主塔BD 的高约为86.9米．【点睛】本题考察了直角三角形与三角函数的结合，熟悉掌握是解决本题的关键.11．如图，在平面直角坐标系中，菱形ABCD 的边AB 在x 轴上，点B 坐标（﹣6，0），点C 在y 轴正半轴上，且cos B ＝35，动点P 从点C 出发，以每秒一个单位长度的速度向D 点移动（P 点到达D 点时停止运动），移动时间为t 秒，过点P 作平行于y 轴的直线l 与菱形的其它边交于点Q ．（1）求点D 坐标；（2）求△OPQ 的面积S 关于t 的函数关系式，并求出S 的最大值；（3）在直线l 移动过程中，是否存在t 值，使S ＝320ABCDS 菱形？若存在，求出t 的值；若不存在，请说明理由．【答案】（1）点D 的坐标为（10，8）．（2）S 关于t 的函数关系式为S ＝24(04)220(410)33t t t t t ⎧⎪⎨-+<⎪⎩剟…，S 的最大值为503．（3）3或7. 【解析】【分析】（1）在Rt △BOC 中，求BC,OC,根据菱形性质再求D 的坐标；（2）分两种情况分析：①当0≤t ≤4时和②当4＜t ≤10时，根据面积公式列出解析式，再求函数的最值；（3）分两种情况分析：当0≤t ≤4时，4t ＝12，；当4＜t ≤10时，22201233t t -+= 【详解】解：（1）在Rt △BOC 中，∠BOC ＝90°，OB ＝6，cos B ＝35，10cos OBBC B∴==8OC ∴==∵四边形ABCD 为菱形，CD ∥x 轴，∴点D 的坐标为（10，8）．（2）∵AB ＝BC ＝10，点B 的坐标为（﹣6，0）， ∴点A 的坐标为（4，0）．分两种情况考虑，如图1所示． ①当0≤t ≤4时，PQ ＝OC ＝8，OQ ＝t ，∴S ＝12PQ •OQ ＝4t ， ∵4＞0，∴当t ＝4时，S 取得最大值，最大值为16；②当4＜t ≤10时，设直线AD 的解析式为y ＝kx +b （k ≠0），将A （4，0），D （10，8）代入y ＝kx +b ，得：4k b 010k b 8+=⎧⎨+=⎩，解得：4k 316b 3⎧=⎪⎪⎨⎪=-⎪⎩， ∴直线AD 的解析式为41633y x =-．当x ＝t 时，41633y t =-， 41648(10)333PQ t t ⎛⎫∴=--=- ⎪⎝⎭21220233S PQ OP t t ∴=⋅=-+ 22202502(5),033333S t t t =-+=--+-<Q ∴当t ＝5时，S 取得最大值，最大值为503．综上所述：S 关于t 的函数关系式为S ＝24(04)220(410)33t t t t t ⎧⎪⎨-+<⎪⎩剟…，S 的最大值为503．（3）S 菱形ABCD ＝AB •OC ＝80．当0≤t ≤4时，4t ＝12，解得：t ＝3；当4＜t ≤10时，222033t t -+＝12，解得：t 1＝5﹣7（舍去），t 2＝5+ 7．综上所述：在直线l 移动过程中，存在t 值，使S ＝320ABCD S 菱形，t 的值为3或5+7．【点睛】考核知识点：一次函数和二次函数的最值问题.数形结合，分类讨论是关键.12．如图，AB 为O e 的直径，C 、D 为O e 上异于A 、B 的两点，连接CD ，过点C 作CE DB ⊥，交CD 的延长线于点E ，垂足为点E ，直径AB 与CE 的延长线相交于点F .（1）连接AC 、AD ，求证：180DAC ACF ∠+∠=︒. （2）若2ABD BDC ∠=∠. ①求证：CF 是O e 的切线. ②当6BD =，3tan 4F =时，求CF 的长. 【答案】（1）详见解析；（2）①详见解析；② 203CF =. 【解析】【分析】（1）根据圆周角定理证得∠ADB=90°，即AD ⊥BD ，由CE ⊥DB 证得AD ∥CF ，根据平行线的性质即可证得结论；（2）①连接OC ．先根据等边对等角及三角形外角的性质得出∠3=2∠1，由已知∠4=2∠1，得到∠4=∠3，则OC ∥DB ，再由CE ⊥DB ，得到OC ⊥CF ，根据切线的判定即可证明CF 为⊙O 的切线；②由CF ∥AD ，证出∠BAD=∠F ，得出tan ∠BAD=tan ∠F=BD AD =34，求出AD=43BD=8，利用勾股定理求得AB=10，得出OB=OC=，5，再由tanF=OC CF =34，即可求出CF ．【详解】解：（1）AB 是O e 的直径，且D 为O e 上一点，90ADB ∴∠=︒， CE DB ⊥Q ， 90DEC ∴∠=︒， //CF AD ∴，180DAC ACF ∴∠+∠=︒. （2）①如图，连接OC . OA OC =Q ，12∴∠=∠. 312∠=∠+∠Q ， 321∴∠=∠.42BDC Q ∠=∠，1BDC ∠=∠， 421∴∠=∠， 43∴∠=∠， //OC DB ∴. CE DB ⊥Q ， OC CF ∴⊥.又OC Q 为O e 的半径， CF ∴为O e 的切线.②由（1）知//CF AD ，BAD F ∴∠=∠， 3tan tan 4BAD F ∴∠==， 34BD AD ∴=. 6BD =Q483AD BD ∴==， 226810AB ∴=+=，5OB OC ==.OC CF Q ⊥， 90OCF ∴∠=︒，3tan 4OC F CF ∴==，解得203CF =. 【点睛】本题考查了切线的判定、解直角三角形、圆周角定理等知识；本题综合性强，有一定难度，特别是（2）中，需要运用三角函数、勾股定理和由平行线得出比例式才能得出结果．13．如图，直线与轴交于点，与轴交于点，抛物线经过点，．点为轴上一动点，过点且垂直于轴的直线分别交直线及抛物线于点，．（1）填空：点的坐标为，抛物线的解析式为；（2）当点在线段上运动时（不与点，重合），①当为何值时，线段最大值，并求出的最大值；②求出使为直角三角形时的值；（3）若抛物线上有且只有三个点到直线的距离是，请直接写出此时由点，，，构成的四边形的面积．【答案】（1），；（2）①当时，有最大值是3； ②使为直角三角形时的值为3或；（3）点，，，构成的四边形的面积为：6或或.【解析】【分析】（1）把点A 坐标代入直线表达式y ＝，求出a ＝−3，把点A 、B 的坐标代入二次函数表达式，即可求解；（2）①设：点P （m ，），N （m ，）求出PN 值的表达式，即可求解；②分∠BNP ＝90°、∠NBP ＝90°、∠BPN ＝90°三种情况，求解即可；（3）若抛物线上有且只有三个点N到直线AB的距离是h，则只能出现：在AB直线下方抛物线与过点N的直线与抛物线有一个交点N，在直线AB上方的交点有两个，分别求解即可．【详解】解：（1）把点坐标代入直线表达式，解得：，则：直线表达式为：，令，则：，则点坐标为，将点的坐标代入二次函数表达式得：，把点的坐标代入二次函数表达式得：，解得：，故：抛物线的解析式为：，故：答案为：，；（2）①∵在线段上，且轴，∴点，，∴，∵，∴抛物线开口向下，∴当时，有最大值是3，②当时，点的纵坐标为-3，把代入抛物线的表达式得：，解得：或0（舍去），∴；当时，∵，两直线垂直，其值相乘为-1，设：直线的表达式为：，把点的坐标代入上式，解得：，则：直线的表达式为：，将上式与抛物线的表达式联立并解得：或0（舍去），当时，不合题意舍去，故：使为直角三角形时的值为3或；（3）∵，，在中，，则：，，∵轴，∴，若抛物线上有且只有三个点到直线的距离是，则只能出现：在直线下方抛物线与过点的直线与抛物线有一个交点，在直线上方的交点有两个.当过点的直线与抛物线有一个交点，点的坐标为，设：点坐标为：，则：，过点作的平行线，则点所在的直线表达式为：，将点坐标代入，解得：过点直线表达式为：，将拋物线的表达式与上式联立并整理得：，，将代入上式并整理得：，解得：，则点的坐标为，则：点坐标为，则：，∵，，∴四边形为平行四边形，则点到直线的距离等于点到直线的距离，即：过点与平行的直线与抛物线的交点为另外两个点，即：、，直线的表达式为：，将该表达式与二次函数表达式联立并整理得：，解得：，则点、的横坐标分别为，，作交直线于点，则，作轴，交轴于点，则：，，，则：，同理：，故：点，，，构成的四边形的面积为：6或或.【点睛】本题考查的是二次函数知识的综合运用，涉及到一次函数、解直角三角形等相关知识，其中（3）中确定点N 的位置是本题的难点，核心是通过△＝0，确定图中N 点的坐标．14．如图，在航线l 的两侧分别有观测点A 和B ，点B 到航线l 的距离BD 为4km ，点A 位于点B 北偏西60°方向且与B 相距20km 处．现有一艘轮船从位于点A 南偏东74°方向的C 处，沿该航线自东向西航行至观测点A 的正南方向E 处．求这艘轮船的航行路程CE 的长度．（结果精确到0.1km ）（参考数据：3≈1.73，sin74°≈0.96，cos74°≈0.28，tan74°≈3.49）【答案】20.9km 【解析】分析：根据题意，构造直角三角和相似三角形的数学模型，利用相似三角形的判定与性质和解直角三角形即可. 详解：如图，在Rt △BDF 中，∵∠DBF=60°，BD=4km ，∴BF=cos 60BDo=8km ， ∵AB=20km ， ∴AF=12km ，∵∠AEB=∠BDF ，∠AFE=∠BFD ， ∴△AEF ∽△BDF ，∴AE BDAF BF ， ∴AE=6km ，在Rt △AEF 中，CE=AE•tan74°≈20.9km ．故这艘轮船的航行路程CE 的长度是20.9km ．点睛：本题考查相似三角形，掌握相似三角形的概念，会根据条件判断两个三角形相似.15．已知：在△ABC 中，∠ACB=90°，CD ⊥AB 于D ，BE ：AB=3：5，若CE= 2 ，cos ∠ACD=45，求tan ∠AEC 的值及CD 的长．【答案】tan ∠AEC=3, CD=12125【解析】解：在RT △ACD 与RT △ABC 中∵∠ABC+∠CAD=90°, ∠ACD+∠CAD=90°∴∠ABC=∠ACD, ∴cos ∠ABC=cos ∠ACD=45在RT △ABC 中，45BC AB = 令BC=4k,AB=5k 则AC=3k 由35BE AB = ,BE=3k 则CE=k,且2 则2，2 ∴RT △ACE 中，tan ∠AEC=ACEC=3 ∵RT △ACD 中cos ∠ACD=45CD AC = ,，12125。

专题07 利用锐角三角函数解实际问题(教师版含解析) -2021年中考数学复习重难点与压轴题型训练

备战2021年中考复习重难点与压轴题型专项训练专题07 利用锐角三角函数解实际问题【专题训练】一、解答题1．(2020·江西中考真题)如图1是一种手机平板支架，由托板、支撑板和底座构成，手机放置在托板上，图2是其侧面结构示意图，量得托板长AB =120mm ，支撑板长CD =80mm ，底座长DE =90mm ，托板AB 固定在支撑板顶端点C 处，且CB =40mm ，托板AB 可绕点C 转动，支撑板CD 可绕点D 转动．(结果保留小数点后一位)(1)若∠DCB =80°，∠CDE =60°，求点A 到直线DE 的距离；(2)为了观看舒适，在(1)的情况下，把AB 绕点C 逆时针旋转10°后，再将CD 绕点D 顺时针旋转，使点B 落在直线DE 上即可，求CD 旋转的角度．(参考数据：sin 400.643,cos 400.766︒︒≈≈，tan 400.839︒≈，sin 26.60.448≈，cos 26.60.894,tan 26.60.500︒︒≈≈ 1.732≈)【答案】(1)如图所示，过点A 作AMDE ⊥，CN DE ⊥，CP AM ⊥，则90CPM CMD CND ∠=∠=∠=︒,∵120mm AB =，40mm CB =，∵80mm =AC ，又∵80DCB ︒∠=，60CDE ︒∠=，∵100ACD ∠=︒，120CDM∠=︒， ∵360909012060PCD∠=︒-︒-︒-︒=︒， ∵1006040ACP∠=︒-︒=︒, ∵sin 40800.64351.44mm AP AC =︒=⨯=，又∵60CDN =︒,80mm CD =，∵sin 608069.28CN CD =︒=⨯=≈mm ， ∵69.2851.44120.72120.7AM mm =+=≈．∵点A 到直线DE 的距离是120.7mm ．(2)如图所示，根据题意可得90DCE ∠=︒，40mm CB =，80mm CD =， ∵401tan 802BC CDB DC ∠===， ∵26.6CDB ∠=︒，根据(1)可得60CDE ︒∠=，∵CD 旋转的角度=60-26.6=33.4︒︒︒．【点睛】本题主要考查了解直角三角形的应用，准确的构造直角三角形，利用三角函数的定义求解是解题的关键．2．(2020·浙江宁波市·中考真题)图1是一种三角车位锁，其主体部分是由两条长度相等的钢条组成．当位于顶端的小挂锁打开时，钢条可放入底盒中(底盒固定在地面下)，此时汽车可以进入车位；当车位锁上锁后，钢条按图1的方式立在地面上，以阻止底盘高度低于车位锁高度的汽车进入车位．图2是其示意图，经测量，钢条AB ＝AC ＝50cm ，∵ABC ＝47°．(1)求车位锁的底盒长BC ．(2)若一辆汽车的底盘高度为30cm ，当车位锁上锁时，问这辆汽车能否进入该车位?(参考数据：sin 47°≈0.73，cos 47°≈0.68，tan 47°≈1.07)【答案】解：(1)过点A作AH∵BC于点H，∵AB＝AC，∵BH＝HC，在Rt∵ABH中，∵B＝47°，AB＝50，∵BH＝ABcosB＝50cos47°≈50×0.68＝34，∵BC＝2BH＝68cm．(2)在Rt∵ABH中，∵AH＝ABsinB＝50sin47°≈50×0.73＝36.5，∵36.5＞30，∵当车位锁上锁时，这辆汽车不能进入该车位．【点睛】本题考查解直角三角形，解题的关键是熟练运用锐角函数的定义，本题属于基础题型．3．(2020·浙江绍兴市·中考真题)如图1为搭建在地面上的遮阳棚，图2、图3是遮阳棚支架的示意图．遮阳棚支架由相同的菱形和相同的等腰三角形构成，滑块E，H可分别沿等长的立柱AB，DC上下移动，AF＝EF＝FG＝1m．(1)若移动滑块使AE＝EF，求∵AFE的度数和棚宽BC的长．(2)当∵AFE由60°变为74°时，问棚宽BC是增加还是减少？增加或减少了多少？(结果精确到0.1m≈1.73，sin37°≈0.60，cos37°≈0.80，tan37°≈0.75)【答案】解：(1)∵AE＝EF＝AF＝1,∵∵AEF是等边三角形,∵∵AFE＝60°,连接MF并延长交AE于K，则FM＝2FK,∵∵AEF是等边三角形,∵AK＝1 2,∵FK==,∵FM＝2FK∵BC＝4FM＝6.92≈6.9(m); (2)∵∵AFE＝74°,∵∵AFK＝37°,∵KF＝AF•cos37°≈0.80,∵FM＝2FK＝1.60,∵BC＝4FM＝6.40＜6.92,6.92﹣6.40＝0.5,答：当∵AFE由60°变为74°时,棚宽BC是减少了，减少了0.5m.【点睛】本题主要考查了解直角三角形的应用,观察图形,发现直角三角形是解题的关键.4．(2020·浙江中考真题)有一种升降熨烫台如图1所示，其原理是通过改变两根支撑杆夹角的度数来调整熨烫台的高度．图2是这种升降熨烫台的平面示意图．AB和CD是两根相同长度的活动支撑杆，点O是它们的连接点，OA=OC，h(cm)表示熨烫台的高度．(1)如图2﹣1．若AB=CD=110cm，∵AOC=120°，求h的值；(2)爱动脑筋的小明发现，当家里这种升降熨烫台的高度为120cm时，两根支撑杆的夹角∵AOC是74°(如图2﹣2)．求该熨烫台支撑杆AB的长度(结果精确到lcm)．(参考数据：sin37°≈0.6，cos37°≈0.8，sin53°≈0.8，cos53°≈0.6．)【答案】(1)过点B作BE∵AC于E，∵OA=OC，∵AOC=120°，∵∵OAC=∵OCA=1801202︒︒-=30°，∵h=BE=AB•sin30°=110×12=55；(2)过点B作BE∵AC于E，∵OA=OC，∵AOC=74°，∵∵OAC=∵OCA=180742︒︒-=53°，∵AB=BE÷sin53°=120÷0.8=150(cm)，即该熨烫台支撑杆AB的长度约为150cm．【点睛】本题考查了解直角三角形的应用，作出辅助线构造直角三角形，弄清题中的数据是解本题的关键．5．(2020·四川广安市·中考真题)如图所示的是某品牌太阳能热水器的实物图和横断面示意图，己知真空集热管AB与支架CD 所在直线相交于水箱横断面∵O的圆心，支架CD与水平线AE垂直，AB=154cm，∵A=30°，另一根辅助支架DE=78cm，∵E=60°．(1)求CD的长度．(结果保留根号)(2)求OD 的长度．(≈1.414≈1.732)【答案】解：(1)在Rt CDE △中，6078cm CED DE ∠=︒=，，·60CD DE sin ∴=︒=答：CD 的长度为；(2)设水箱半径OD 的长度为x 厘米，则CO =(x )厘米，AO =(154+x )厘米， ∵∵A =30°，∵CO =12AO ，x =12(154+x )，解得：x =154-154-135.096≈18.9cm ．答：OD 的长度为18.9cm ．【点睛】此题考查的是解直角三角形的应用和圆的基本性质，掌握利用锐角三角函数解直角三角形和圆的半径相等是解题关键． 6．(2020·湖南衡阳市·中考真题)小华同学将笔记本电脑水平放置在桌子上，当是示屏的边缘线OB 与底板的边缘线OA 所在水平线的夹角为120°时，感觉最舒适(如图①)．侧面示意图为图②；使用时为了散热，他在底板下面垫入散热架，如图③，点B 、O 、C 在同一直线上，24cm OA OB ==，BC AC ⊥，30OAC ∠=︒．(1)求OC 的长；(2)如图④，垫入散热架后，要使显示屏的边缘线OB 与水平线的夹角仍保持120°，求点B '到AC 的距离．(结果保留根号)【答案】解：(1)∵24cm OA =，BC AC ⊥，30OAC ∠=︒ ∵1122OC OA cm ==．即OC 的长度为12cm ．(2)如图，过点O 作OM ∵AC ，过点B ′作B ′E ∵AC 交AC 的延长线于点E ，交OM 于点D ，B ′E 即为点B '到AC 的距离，∵OM ∵AC ，B ′E ∵AC ， ∵B ′E ∵OD ，∵MN ∵AC ，∵∵NOA =∵OAC =30°，∵∵AOB =120°，∵∵NOB =90°，∵∵NOB ′=120°，∵∵BOB ′=120°-90°=30°，∵BC ∵AC ，B ′E ∵AE ，MN ∵AE ，∵BC ∵B ′E ，四边形OCED 为矩形，∵∵OB ′D =∵BOB ′=30°，DE =OC =12cm ，在Rt ∵B ′OD 中，∵∵OB ′D =30°，B ′O =BO =24cm ，∵B'D cos OB'D==B'O 2∠B ′D = ，B ′E =B ′D +DE = ()12cm ，答：点B '到AC 的距离为()12cm ．【点睛】本题考查解直角三角形的应用、矩形的判定和性质和直角三角形中30度角所对的直角边长度是斜边的一半，解题的关键是灵活应用所学知识解决问题，属于中考常考题型．7．(2020·湖南益阳市·中考真题)沿江大堤经过改造后的某处横断面为如图所示的梯形ABCD ，高DH =12米，斜坡CD 的坡度1:1i =，此处大堤的正上方有高压电线穿过，PD 表示高压线上的点与堤面AD 的最近距离(P 、D 、H 在同一直线上)，在点C 处测得26DCP ∠=︒．(1)求斜坡CD 的坡角α(2)电力部门要求此处高压线离堤面AD 的安全距离不低于18米，请问此次改造是否符合电力部门的安全要求？(参考数据：sin 260.44≈，tan 260.49≈，sin 710.95≈，tan 71 2.90≈)【答案】解(1)∵tan 1:11i α===，∵=45α︒；(2)延长AD 交PC 于点E ，过点E 作EF ∵BC 于F ，如图，则四边形DEFH 是矩形，∵EF =DH =12m ，DE =HF ，∵HDE =∵EFH =∵DHF =90°，∵α=45°，∵∵HDC =45°，∵HC =DH =12m ，又∵PCD =26°，∵∵ECF =45°+26°=71°，∵tan 71EF FC ︒=，即12 4.14tan 71 2.90EF FC ==≈︒m ， ∵HF =HC -CF =12-4.14=7.86m ，∵DE =7.86m ，∵AE //BC ，∵∵PED =∵PCH =71°，在Rt ∵PDE 中，tan PD PED DE ∠=，即 tan 717.86PD ︒=， ∵7.86 2.9022.8018PD =⨯≈＞m ，∵此次改造符合电力部门的安全要求．【点睛】本题考查的是解直角三角形的应用-仰角俯角问题，根据题意作出辅助线，构造出直角三角形是解答此题的关键． 8．(2020·辽宁葫芦岛市·中考真题)如图，小明利用学到的数学知识测量大桥主架在水面以上的高度AB ，在观测点C 处测得大桥主架顶端A 的仰角为30°，测得大桥主架与水面交汇点B 的俯角为14°，观测点与大桥主架的水平距离CM 为60米，且AB 垂直于桥面．(点A ,B ,C ,M 在同一平面内)(1)求大桥主架在桥面以上的高度AM ；(结果保留根号)(2)求大桥主架在水面以上的高度AB ．(结果精确到1米)(参考数据sin140.24,cos140.97,tan14 1.73︒︒︒≈≈≈≈)【答案】解：(1)AB 垂直于桥面90︒∴∠=∠=AMC BMC在Rt AMC △中，60,30︒=∠=CM ACMtan ∠=AM ACM CMtan 3060︒∴=⋅==AM CM (米)答：大桥主架在桥面以上的高度AM 为(2)在Rt BMC △中，60,14︒=∠=CM BCMtan ∠=MBBCM CMtan14600.2515︒∴=⋅=⨯≈MB CM=+AB AM MB1550∴≈+≈AB (米)答：大桥主架在水面以上的高度AB 约为50米．【点睛】本题考查直角三角形的边角关系，锐角三角函数的意义，掌握锐角三角函数的意义是解决问题的前提．9．(2020·四川内江市·中考真题)为了维护我国海洋权力，海监部门对我国领海实行了常态化巡航管理．如图，正在执行巡航任务的海监船以每小时60海里的速度向正东方向航行，在A处测得灯塔P在北偏东60°方向上，海监船继续向东航行1小时到达B处，此时测得灯塔P在北偏东30方向上．(1)求B处到灯塔P的距离；(2)已知灯塔P的周围50海里内有暗礁，若海监船继续向正东方向航行是否安全？【答案】(1)过点P作PD∵AB于点D，由题意得，AB=60(海里)，∵P AB=30°，∵PBD=60°，∵∵APB=∵PBD-∵P AB=60°-30°=30°=∵P AB，∵PB=AB=60(海里)，答：B处到灯塔P的距离为60海里；(2)由(1)可知∵APB=∵P AB=30°，∵PB=AB=60(海里)在Rt∵PBD中，PD=BPsin60°=60=海里)，∵50>，∵海监船继续向正东方向航行是安全的．【点睛】本题考查了解直角三角形的应用-方向角问题，正确根据题意画出图形、准确标注方向角、熟练掌握锐角三角函数的概念是解题的关键．10．(2020·湖北随州市·中考真题)如图，某楼房AB 顶部有一根天线BE ，为了测量天线的高度，在地面上取同一条直线上的三点C ，D ，A ，在点C 处测得天线顶端E 的仰角为60︒，从点C 走到点D ，测得CD =5米，从点D 测得天线底端B 的仰角为45°，已知A ，B ，E 在同一条垂直于地面的直线上，AB =25米．(1)求A 与C 之间的距离；(2)求天线BE 的高度．( 1.73≈，结果保留整数)【答案】(1)依题意可得，在Rt ABD △中，45ADB ∠=︒ ，25AD AB ∴==米，5CD =米，25530AC AD CD ∴=+=+=米.即,A C 之间的距离为30米．(2)在Rt ACE △中，60ACE ∠=︒，30AC =米，30tan 60AE ∴=⋅︒=米)，25AB =米，25)(BE AE AB ∴=-=-米．173≈．．并精确到整数可得27BE ≈米．即天线BE 的高度约为27米．【点睛】(1)本题主要考查等腰直角三角形的性质，掌握等腰直角三角形的性质是解答本题的关键．(2)本题主要考查三角函数的灵活运用，正确运用三角函数是解答本题的关键．11．(2020·湖北鄂州市·中考真题)鄂州市某校数学兴趣小组借助无人机测量一条河流的宽度CD ．如图所示，一架水平飞行的无人机在A 处测得正前方河流的左岸C 处的俯角为α，无人机沿水平线AF 方向继续飞行50米至B 处，测得正前方河流右岸D 处的俯角为30°．线段AM 的长为无人机距地面的铅直高度，点M 、C 、D 在同一条直线上．其中tan 2,MC α==米． (1)求无人机的飞行高度AM ；(结果保留根号)(2)求河流的宽度CD ．(结果精确到1 1.73≈≈)【答案】(1)由题意可得AF∵MD∵∵ACM=∵F AC=αα==米);在Rt∵ACM中，AM=CMtan∵ACM=CM tan2(2)如图，过点B作BH∵MD，在Rt∵BDH中，∵BDH=∵FBD=30°，BH=∵DH=BH÷tan30°=300米，∵AM∵DM，AM∵AF∵四边形ABHM是矩形∵MH=AB=50米∵CH=CM-MH=50(米)∵CD=DH-CH=300-(50)=350-263(米)故河流的宽度CD为263米．【点睛】此题主要考查三角函数的应用，解题的关键是熟知解直角三角形的方法．12．(2020·山东临沂市·中考真题)如图．要想使人安全地攀上斜靠在墙面上的梯子的顶端，梯子与地面所成的角α一般要满足6075α︒︒，现有一架长5.5m 的梯子．(1)使用这架梯子最高可以安全攀上多高的墙(结果保留小数点后一位)？(2)当梯子底端距离墙面2.2m 时，α等于多少度(结果保留小数点后一位)？此时人是否能够安全使用这架梯子？(参考数据：sin 750.97︒=，cos750.26︒=，tan 75 3.73︒=，sin 23.60.40︒=，cos56.40.40︒=，tan 21.80.40︒=)【答案】解：(1)当∵ABC =75°时，梯子能安全使用且它的顶端最高；在Rt ∵ABC 中，有sin ∵ABC =AC AB∵AC =AB •sin ∵ABC =5.5×sin 75°≈5.3；答：安全使用这个梯子时，梯子的顶端距离地面的最大高度AC 约为5.3m(2)在Rt ∵ABC 中，有cos ∵ABC =BC AB =2.25.5=0.4 由题目给的参考数据cos56.40.40︒=，可知∵ABC =56.4° ∵56.4°＜60°，不在安全角度内；∵这时人不能安全使用这个梯子，答：人不能够安全使用这个梯子．【点睛】此题考查的是解直角三角形的实际应用，熟练掌握并能灵活运用各锐角三角函数是解答此类题的关键．13．(2020·贵州贵阳市·中考真题)脱贫攻坚工作让老百姓过上了幸福的生活．如图①是政府给贫困户新建的房屋，如图②是房屋的侧面示意图，它是一个轴对称图形，对称轴是房屋的高AB 所在的直线．为了测量房屋的高度，在地面上C 点测得屋顶A 的仰角为35°，此时地面上C 点、屋檐上E 点、屋顶上A 点三点恰好共线，继续向房屋方向走8m 到达点D 时，又测得屋檐E 点的仰角为60°，房屋的顶层横梁EF =12m ，EF ∥CB ，AB 交EF 于点G (点C ，D ，B 在同一水平线上)．(参考数据：sin350.6︒≈，cos350.8︒≈，tan350.7︒≈ 1.7≈)(1)求屋顶到横梁的距离AG ；(2)求房屋的高AB (结果精确到1m )．【答案】解：(1)∵房屋的侧面示意图是轴对称图形，AB 所在直线是对称轴，EF ∥CB ，∵AG EF ⊥，162EG EF ==，35AEG ACB ∠=∠=︒．在Rt AGE ∆中，90AGE ∠=︒，35AEG ∠=°，∵tan AEG AG EG∠=，6EG =，tan350.7︒≈． ∵6tan3542AG =≈°(米)答：屋顶到横梁的距离AG 约是4.2米．(2)过点E 作EH CB ⊥于点H ，设EH x =，在Rt EDH ∆中，90EHD ∠=︒，60EDH∠=°， ∵tan EHEDH DH ∠=，∵tan 60x DH =°，在Rt ECH ∆中，90EHC ∠=︒，35ECH ∠=°， ∵tan EHECH CH ∠=，∵tan 35x CH =°． ∵8CH DH CD -==， ∵8tan 35tan 60x x -=°°，∵tan350.7︒≈， 1.7≈，解得9.52x ≈．∵ 4.29.5213.7214AB AG BG =+=+=≈(米)答：房屋的高AB 约是14米．【点睛】本题主要考查了仰角的定义及其解直角三角形的应用，解题时首先正确理解仰角的定义，然后构造直角三角形利用三角函数和已知条件列方程解决问题．14．(2020·河南中考真题)位于河南省登封市境内的元代观星台，是中国现存最早的天文台，也是世界文化遗产之一．某校数学社团的同学们使用卷尺和自制的测角仪测量观星台的高度．如图所示，他们在地面一条水平步道MP上架设测角仪，先在点M处测得观星台最高点A的仰角为22°，然后沿MP方向前进16m到达点N处，测得点A的仰角为45°．测角仪的高度为1.6m，(1)求观星台最高点A距离地面的高度(结果精确到0.1m．参考数据：︒≈︒≈︒≈≈)；220.37,220.93,22 1.41sin cos tan(2)“景点简介”显示，观星台的高度为12.6m，请计算本次测量结果的误差，并提出一条减小误差的合理化建议．【答案】解：(1)如图，过点A作AE∵MN交MN的延长线于点E，交BC的延长线于点D，设AD的长为xm，∵AE∵ME，BC∵MN，∵AD∵BD，∵ADC=90°，∵∵ACD=45°，∵CD=AD=xm，BD=BC+CD=(16+x)m，由题易得，四边形BMNC为矩形，∵四边形CNED 为矩形，∵DE =CN =BM =1.6m ，在Rt ∵ABD 中，tan ABD=0.4016AD x BD x==+∠，解得：10.7x ≈，即AD =10.7m ，AE =AD +DE =10.7+1.6=12.3m ，答：观星台最高点A 距离地面的高度为12.3m ．(2)本次测量结果的误差为：12.6-12.3=0.3m ，减小误差的合理化建议：多次测量，求平均值．【点睛】本题考查解直角三角形的实际应用，根据题意作出辅助线，构造出直角三角形是解答此题的关键．15．(2020·四川攀枝花市·中考真题)实验学校某班开展数学“综合与实践”测量活动．有两座垂直于水平地面且高度不一的圆柱，两座圆柱后面有一斜坡，且圆柱底部到坡脚水平线MN 的距离皆为100cm ．王诗嬑观测到高度90cm 矮圆柱的影子落在地面上，其长为72cm ；而高圆柱的部分影子落在坡上，如图所示．已知落在地面上的影子皆与坡脚水平线MN 互相垂直，并视太阳光为平行光，测得斜坡坡度1:0.75i =，在不计圆柱厚度与影子宽度的情况下，请解答下列问题：(1)若王诗嬑的身高为150cm ，且此刻她的影子完全落在地面上，则影子长为多少cm ？(2)猜想：此刻高圆柱和它的影子与斜坡的某个横截面一定同在一个垂直于地面的平面内．请直接回答这个猜想是否正确？(3)若同一时间量得高圆柱落在坡面上的影子长为100cm ，则高圆柱的高度为多少cm ？解：(1)设王诗嬑的影长为xcm ，由题意可得：9015072x=，解得：x =120，经检验：x =120是分式方程的解，王诗嬑的的影子长为120cm ；(2)正确，因为高圆柱在地面的影子与MN 垂直，所以太阳光的光线与MN 垂直，则在斜坡上的影子也与MN 垂直，则过斜坡上的影子的横截面与MN 垂直，而横截面与地面垂直，高圆柱也与地面垂直，∵高圆柱和它的影子与斜坡的某个横截面一定同在一个垂直于地面的平面内；(3)如图，AB 为高圆柱，AF 为太阳光，∵CDE 为斜坡，CF 为圆柱在斜坡上的影子，过点F 作FG ∵CE 于点G ，由题意可得：BC =100，CF =100，∵斜坡坡度1:0.75i =， ∵140.753DE FG CE CG ===， ∵设FG =4m ，CG =3m ，在∵CFG 中，()()22243100m m +=，解得：m =20， ∵CG =60，FG =80，∵BG=BC+CG=160，过点F作FH∵AB于点H，∵同一时刻，90cm矮圆柱的影子落在地面上，其长为72cm，FG∵BE，AB∵BE，FH∵AB，可知四边形HBGF为矩形，∵9072AH AHHF BG==，∵AH=9090160 7272BG⨯=⨯=200，∵AB=AH+BH=AH+FG=200+80=280，故高圆柱的高度为280cm.【点睛】本题考查了解分式方程，解直角三角形，平行投影，矩形的判定和性质等知识，解题的关键是理解实际物体与影长之间的关系解决问题，属于中考常考题型．。

九年级数学锐角三角函数（带答案）

九年级数学锐角三角函数（带答案）锐角三角函数与解直角三角形【考纲要求】1.理解锐角三角函数的定义、性质及应用，特殊角三角函数值的求法，运用锐角三角函数解决与直角三角形有关的实际问题.题型有选择题、填空题、解答题，多以中、低档题出现；2.命题的热点为根据题中给出的信息构建图形，建立数学模型，然后用解直角三角形的知识解决问题.【知识网络】【考点梳理】考点一、锐角三角函数的概念如图所示，在Rt △ABC 中，∠C ＝90°，∠A 所对的边BC 记为a ，叫做∠A 的对边，也叫做∠B 的邻边，∠B 所对的边AC 记为b ，叫做∠B 的对边，也是∠A 的邻边，直角C 所对的边AB 记为c ，叫做斜边．锐角A 的对边与斜边的比叫做∠A 的正弦，记作sinA ，即sin A aA c ∠==的对边斜边；锐角A 的邻边与斜边的比叫做∠A 的余弦，记作cosA ，即cos A bA c ∠==的邻边斜边；锐角A 的对边与邻边的比叫做∠A 的正切，记作tanA ，即tan A aA A b∠==∠的对边的邻边.同理sin B b B c ∠==的对边斜边；cos B a B c∠==的邻边斜边；tan B bB B a ∠==∠的对边的邻边．要点诠释：(1)正弦、余弦、正切函数是在直角三角形中定义的，反映了直角三角形边与角的关系，是两条线段的比值．角的度数确定时，其比值不变，角的度数变化时，比值也随之变化．A B Ca b c(2)sinA，cosA，tanA分别是一个完整的数学符号，是一个整体，不能写成，，，不能理解成sin与∠A，cos与∠A，tan与∠A的乘积．书写时习惯上省略∠A的角的记号“∠”，但对三个大写字母表示成的角(如∠AEF)，其正切应写成“tan∠AEF”，不能写成“tanAEF”；另外，、、常写成、、．(3)任何一个锐角都有相应的锐角三角函数值，不因这个角不在某个三角形中而不存在．(4)由锐角三角函数的定义知：当角度在0°＜∠A＜90°之间变化时，，，tanA＞0．考点二、特殊角的三角函数值利用三角函数的定义，可求出0°、30°、45°、60°、90°角的各三角函数值，归纳如下：要点诠释：(1)通过该表可以方便地知道0°、30°、45°、60°、90°角的各三角函数值，它的另一个应用就是：如果知道了一个锐角的三角函数值，就可以求出这个锐角的度数，例如：若，则锐角．(2)仔细研究表中数值的规律会发现：、、、、sin90?的值依次为0、、、、1，而c o s0?、s i n0、、、cos90?的值的顺序正好相反，、、的值依次增大，其变化规律可以总结为：当角度在0°＜∠A＜90°之间变化时，①正弦、正切值随锐角度数的增大(或减小)而增大(或减小)②余弦值随锐角度数的增大(或减小)而减小(或增大)．考点三、锐角三角函数之间的关系如图所示，在Rt△ABC中，∠C=90°．(1)互余关系：，；(2)平方关系：；(3)倒数关系：或；(4)商数关系：．要点诠释：锐角三角函数之间的关系式可由锐角三角函数的意义推导得出，常应用在三角函数的计算中，计算时巧用这些关系式可使运算简便．考点四、解直角三角形在直角三角形中，由已知元素(直角除外)求未知元素的过程，叫做解直角三角形.在直角三角形中，除直角外，一共有5个元素，即三条边和两个锐角.设在Rt△ABC中，∠C=90°，∠A、∠B、∠C所对的边分别为a、b、c，则有：①三边之间的关系：a2+b2=c2(勾股定理).②锐角之间的关系：∠A+∠B=90°.③边角之间的关系：，，，，，.④，h为斜边上的高.要点诠释：(1)直角三角形中有一个元素为定值(直角为90°)，是已知的值.(2)这里讲的直角三角形的边角关系指的是等式，没有包括其他关系(如不等关系).(3)对这些式子的理解和记忆要结合图形，可以更加清楚、直观地理解.考点五、解直角三角形的常见类型及解法已知条件解法步骤Rt△ABC两边两直角边(a，b)由求∠A，∠B=90°－∠A，斜边，一直角边(如c，a)由求∠A，∠B=90°－∠A，一边一角一直角边和一锐角锐角、邻边(如∠A，b)∠B=90°－∠A，，锐角、对边(如∠A，a)∠B=90°－∠A ，，斜边、锐角(如c，∠A)∠B=90°－∠A，，要点诠释：1．在遇到解直角三角形的实际问题时，最好是先画出一个直角三角形的草图，按题意标明哪些元素是已知的，哪些元素是未知的，然后按先确定锐角、再确定它的对边和邻边的顺序进行计算.2．若题中无特殊说明，“解直角三角形”即要求出所有的未知元素，已知条件中至少有一个条件为边.考点六、解直角三角形的应用解直角三角形的知识应用很广泛，关键是把实际问题转化为数学模型，善于将某些实际问题中的数量关系化归为直角三角形中的边角关系是解决实际应用问题的关键.解这类问题的一般过程是：(1)弄清题中名词、术语的意义，如仰角、俯角、坡度、坡角、方向角等概念，然后根据题意画出几何图形，建立数学模型.(2)将已知条件转化为几何图形中的边、角或它们之间的关系，把实际问题转化为解直角三角形的问题.(3)根据直角三角形(或通过作垂线构造直角三角形)元素(边、角)之间的关系解有关的直角三角形.(4)得出数学问题的答案并检验答案是否符合实际意义，得出实际问题的解.拓展：在用直角三角形知识解决实际问题时，经常会用到以下概念：(1)坡角：坡面与水平面的夹角叫做坡角，用字母表示.坡度(坡比)：坡面的铅直高度h和水平距离的比叫做坡度，用字母表示，则，如图，坡度通常写成=∶的形式.(2)仰角、俯角：视线与水平线所成的角中，视线中水平线上方的叫做仰角，在水平线下方的叫做俯角，如图.(3)方位角：从某点的指北方向线按顺时针转到目标方向的水平角叫做方位角，如图①中，目标方向PA，PB，PC的方位角分别为是40°，135°，245°.(4)方向角：指北或指南方向线与目标方向线所成的小于90°的水平角，叫做方向角，如图②中的目标方向线OA，OB，OC，OD的方向角分别表示北偏东30°，南偏东45°，南偏西80°，北偏西60°.特别如：东南方向指的是南偏东45°，东北方向指的是北偏东45°，西南方向指的是南偏西45°，西北方向指的是北偏西45°.要点诠释：1．解直角三角形实际是用三角知识，通过数值计算，去求出图形中的某些边的长或角的大小，最好画出它的示意图.2．非直接解直角三角形的问题，要观察图形特点，恰当引辅助线，使其转化为直角三角形或矩形来解.例如：3．解直角三角形的应用题时，首先弄清题意(关键弄清其中名词术语的意义)，然后正确画出示意图，进而根据条件选择合适的方法求解.【典型例题】类型一、锐角三角函数的概念与性质1．(1)如图所示，在△ABC中，若∠C＝90°，∠B＝50°，AB＝10，则BC的长为( )．A．102tan50° B．102cos50° C．102sin50° D．10 sin50°(2)如图所示，在△ABC中，∠C＝90°，sinA＝35，求cosA+tanB的值．(3)如图所示的半圆中，AD是直径，且AD＝3，AC＝2，则sinB 的值等于________．【思路点拨】(1)在直角三角形中，根据锐角三角函数的定义，可以用某个锐角的三角函数值和一条边表示其他边．(2)直角三角形中，某个内角的三角函数值即为该三角形中两边之比．知道某个锐角的三角函数值就知道了该角的大小，可以用比例系数k表示各边．(3)要求sinB的值，可以将∠B转化到一个直角三角形中．【答案与解析】(1)选B．(2)在△ABC，∠C＝90°，3sin5 BCAAB==．设BC＝3k，则AB＝5k(k＞0)．由勾股定理可得AC＝4k，∴4432 cos tan5315k kA Bk k+=+=．(3)由已知，AD是半圆的直径，连接CD，可得∠ACD＝90°∠B＝∠D，所以sinB＝sinD＝23 ACAD=．【总结升华】已知一个角的某个三角函数值，求同角或余角的其他三角函数值时，常用的方法是：利用定义，根据三角函数值，用比例系数表示三角形的边长；(2)题求cosA时，还可以直接利用同角三角函数之间的关系式sin2 A+cos2 A＝1，读者可自己尝试完成．举一反三：【变式】Rt △ABC 中，∠C=90°，a 、b 、c 分别是∠A 、∠B 、∠C 的对边，那么c 等于( ) (A) a cos A bsin B + (B) a sin A bsin B + (C)a b sin A sin B + (D) a bcos A sin B+ 【答案】选B.过点C 作CD ⊥AB 于D,在Rt △ACD 中, AD ADcos A AC b==,所以AD=bcosA,同理,BD=acosB,所以c=AB=AD+BD=bcosA+acosB,又∠A+∠B=90°,所以cosA=sinB,cosB=sinA,所以c=asinA+bsinB.类型二、特殊角的三角函数值2．解答下列各题： (1)化简求值：tan 60tan 45sin 45sin 30sin 60cos30cos 45--++°°°°°°°；(2)在△ABC 中，∠C ＝90°，化简12sin cos A A -．【思路点拨】第(2)题可以先利用关系式sin 2 A+cos 2A ＝1对根号内的式子进行变形，配成完全平方的形式．【答案与解析】解 (1)tan 60tan 45sin 45sin 30sin 60cos30cos 45--++°°°°°°°311331112323322--=-+=-++13-23=(2)∵12sin cos A A -22sin cos 2sin cos A A A A =+-2(sin cos )|sin cos |A A A A =-=-，∴12sin cos A A -cos sin (045)sin cos (4590)A A A A A A --<【总结升华】由第(2)题可得到今后常用的一个关系式：1±2sin αcos α=(sin α±cos α)2．例如，若设sin α+cos α＝t ，则21sin cos (1)2t αα=-．举一反三：【变式】若3sin22α=，cos sinβα=，(2α，β为锐角)，求2tan()3β的值.【答案】∵3sin22α，且2α为锐角，∴2α＝60°，α＝30°．∴12 cos sin22βα===，∴β＝45°．∴23 tan()tan3033β==°．3．(1)如图所示，在△ABC中，∠ACB＝105°，∠A＝30°，AC＝8，求AB和BC的长；(2)在△ABC中，∠ABC＝135°，∠A＝30°，AC＝8，如何求AB和BC的长?(3)在△ABC中，AC＝17，AB＝26，锐角A满足12sin13A=，如何求BC的长及△ABC的面积？若AC＝3，其他条件不变呢?【思路点拨】第(1)题的条件是“两角一夹边”．由已知条件和三角形内角和定理，可知∠B＝45°；过点C作CD ⊥AB于D，则Rt△ACD是可解三角形，可求出CD的长，从而Rt△CDB可解，由此得解；第(2)题的条件是“两角一对边”；第(3)题的条件是“两边一夹角”，均可用类似的方法解决．【答案与解析】解： (1)过点C作CD⊥AB于D．∵∠A＝30°，∠ACD＝105°，∴∠B＝45°．∵AC2sinA＝CD＝BC2sin B，∴sin8sin3042sin sin45AC ABCB===°°．∴AB＝AD+BD＝AC2cosA+BC2cosB＝8cos30°+42cos45°＝443+．(2)作CD ⊥AB 的延长线于D ，则AB ＝434-，42BC =． (3)作BD ⊥AC 于D ，则BC ＝25，ABC S =△204．当AC ＝3时，∠ACB 为钝角，BC ＝25，36ABC S =△．【总结升华】对一个斜三角形，通常可以作一条高，将它转化为两个直角三角形，并且要尽量使直角三角形中含有特殊的锐角(如30°、45°、60°的角)，然后通过解直角三角形得到原来斜三角形的边、角的大小．类型三、解直角三角形及应用4．如图所示，D 是AB 上一点，且CD ⊥AC 于C ，:2:3ACD CDB S S =△△，4cos 5DCB ∠=， AC+CD ＝18，求tanA 的值和AB 的长．【思路点拨】解题的基本思路是将问题转化为解直角三角形的问题，转化的目标主要有两个，一是构造可解的直角三角形；二是利用已知条件通过设参数列方程．【答案与解析】解：作DE ∥AC 交CB 于E ，则∠EDC ＝∠ACD ＝90°．∵4cos 5CD DCE CE =∠=，设CD ＝4k(k ＞0)，则CE ＝5k ，由勾股定理得DE ＝3k ．∵△ACD 和△CDB 在AB 边上的高相同，∴AD:DB ＝:2:3ACD CDB S S =△△．即553533AC DE k k ==?=．∴44tan 55CD k A AC k ===．∵AC+CD ＝18，∴5k+4k ＝18，解得k ＝2．∴2241241AD AC CD k =+==．∴AB ＝AD+DB ＝AD+32AD ＝541．【总结升华】在解直角三角形时，常用的等量关系是：勾股定理、三角函数关系式、相等的线段、面积关系等．专题总结及应用一、知识性专题专题1：锐角三角函数的定义【专题解读】锐角三角函数定义的考查多以选择题、填空题为主．例1 如图28－123所示，在Rt △ABC 中，∠ACB ＝90°，BC ＝1，AB ＝2，则下列结论正确的是 ( ) A ．sin A ＝32 B ．tan A ＝12 C ．cos B ＝32D ．tan B ＝3 分析 sin A ＝BC AB ＝12，tan A ＝BC AC ＝33，cos B ＝BC AB ＝12．故选D.例2 在△ABC 中，∠C ＝90°，cos A ＝35,则tan A 等于 ( )A ．35 B ．45 C ．34 D ．43分析在Rt △ABC 中，设AC ＝3k ，AB ＝5k ，则BC ＝4k ，由定义可知tan A ＝4433BC k AC k ==．故选D.分析在Rt △ABC 中，BC ＝222254AB AC -=-＝3，∴sin A ＝35BC AB =．故填35．专题2 特殊角的三角函数值【专题解读】要熟记特殊角的三角函数值．例4 计算|－3|＋2cos 45°－(3－1)0．分析cos 45°＝22．解：原式＝3＋2322－1＝2＋2．例5 计算－12??-＋9＋(－1)2007－cos 60°．分析cos 60°＝12．解：原式＝12＋3＋(－1)－12＝3－1＝2．例6 计算|－2|＋(cos 60°－tan 30°)0＋8．分析 cos 60°＝12，tan 30°＝33，∴cos 60°－tan 30°≠0，∴(cos 60°－tan 30°)0＝1，解：原式＝2＋1十＋22＝32＋1．例7 计算312-??－(π－3.14)0－|1－tan 60°|－132-.分析tan 60°＝3.解：原式＝8－1－3＋1＋3＋2＝10.专题3 锐角三角函数与相关知识的综合运用【专题解读】锐角三角函数常与其他知识综合起来运用，考查综合运用知识解决问题的能力.例8 如图28－124所示，在△ABC 中，AD 是BC 边上的高，E 为AC 边的中点，BC ＝14，AD ＝12，sin B ＝45． (1)求线段DC 的长； (2)求t an ∠EDC 的值.分析在Rt △ABD 中，由sin B ＝ADAB，可求得BD ，从而求得CD ．由直角三角形斜边上的中线等于斜边的一半，得DE ＝12AC ＝EC ，则∠EDC ＝∠C ，所以求tan ∠EDC 可以转化为求tan C .解：(1)∵AD 是BC 边上的高，∴AD ⊥BC在Rt △ABD 中，sin B ＝ADAB．∵AD ＝12，sin B ＝45，∴AB ＝15，∴BD ＝22AB AD -＝221512-＝9．∵BC ＝14，∴CD ＝5．(2)在Rt △ADC 中，∵AE ＝EC ，∴DE ＝12AC ＝EC ，∴∠EDC ＝∠C∵tan C ＝AD DC＝125,∴tan ∠EDC ＝tan C ＝125．例9 如图28－125所示，在△ABC 中，AD 是BC 边上的高，tan B ＝cos ∠DAC . (1)求证AC ＝BD ；(2)若sin C ＝1213，BC ＝12，求AD 的长．分析 (1)利用锐角三角函数的定义可得AC ＝BD ．(2)利用锐角三角函数与勾股定理可求得AD 的长．证明：(1)∵AD 是BC 边上的高，∴AD ⊥BC ，∴∠ADB ＝90°，∠ADC ＝90°．在Rt △ABD 和Rt △ADC 中，∵tan B ＝AD BD ，cos ∠DAC ＝ADAC，tan B ＝cos ∠DAC ，∴AD BD ＝AD AC，∴AC ＝BD . 解：(2)在Rt △ADC 中，sin C ＝1213，设AD ＝12k ，AC ＝13k ，∴CD ＝22AC AD -＝5k ．∵BC ＝BD ＋CD ，AC ＝BD ，∴BC ＝13k ＋5k ＝18k ．由已知BC ＝12，∴18k ＝12，k ＝23，∴AD ＝12k ＝12323＝8．例10 如图28－126所示，在△ABC 中，∠B ＝45°，∠C ＝30°，BC ＝30＋303，求AB 的长．分析过点A 作AD ⊥BC 于D ，把斜三角形转化为直角三角形，利用AD 是两个直角三角形的公共边，设AD ＝x ，把BD ，DC 用含x 的式子表示出来，再由BD ＋CD ＝BC 这一等量关系列方程，求得AD ，则AB 可在Rt △ABD 中求得．解：过点A 作AD ⊥BC 于D ，设AD ＝x .在Rt △ADB 中，tan B ＝AD BD ，∴BD ＝tan tan 45AD ADB =?＝x ，在Rt △ADC 中，tan C ＝AD CD ，∴CD ＝tan AD C ＝tan30AD＝3x ．又∵BD ＋CD ＝BC ，BC ＝30＋303，∴x ＋3x ＝30＋303 ,∴x ＝30．在Rt △ABD 中，sin B ＝ADAB，∴AB ＝30sin sin 45AD B =＝3022＝302. 专题4 用锐角三角函数解决实际问题【专题解读】加强数学与实际生活的联系，提高数学的应用意识，培养应用数学的能力是当今数学改革的方向，围绕本章内容，纵观近几年各地的中考试题，与解直角三角形有关的应用问题逐步成为命题的热点，其主要类型有轮船定位问题、堤坝工程问题、建筑测量问题、高度测量问题等，解决各类应用问题时要注意把握各类图形的特征及解法．例13 如图28－131所示，我市某中学数学课外活动小组的同学利用所学知识去测量沱江流经我市某段的河宽．小凡同学在点A 处观测到对岸C 点，测得∠CAD ＝45°，又在距A 处60米远的B 处测得∠CB A ＝30°，请你根据这些数据算出河宽是多少?(结果保留小数点后两位)分析本题可作CE ⊥AB ，垂足为E ，求出CE 的长即为河宽．解：如图28－131所示，过点C 作CE ⊥AB 于E ，则CE 即为河宽，设CE ＝x (米)，则BE ＝x ＋60(米)．在Rt △BCE 中，tan30°＝CE EB ，即33＝60x x +,解得x ＝30(3＋1)≈81.96(米)．答：河宽约为81．96米．【解题策略】解本题的关键是设CE ＝x ，然后根据BE ＝AB ＋AE 列方程求解．例14 如图28－132所示，某边防巡逻队在一个海滨浴场岸边的A 点处发现海中的B 点有人求救，便立即派三名救生员前去营救．1号救生员从A 点直接跳入海中；2号救生员沿岸边(岸边可以看成是直线)向前跑到C 点再跳入海中；3号救生员沿岸边向前跑300米到离B 点最近的D 点，再跳入海中，救生员在岸上跑的速度都是6米／秒，在水中游泳的速度都是2米/秒．若∠BAD ＝45°，∠BCD ＝60°，三名救生员同时从A 点出发，请说明谁先到达营救地点B ．(参考数据2≈1.4，3≈1.7)分析在Rt △ABD中，已知∠A ＝45°和AD ，可求AB ，BD ，在Rt △BCD 中，可利用求出的BD 和∠BCD ＝60°求出BC ，然后根据计算出的数据判断谁先到达．解：在Rt △ABD 中，∠A ＝45°，∠D ＝90°，AD ＝300，∴AB ＝AD 300cos 4522=＝3002.BDAD＝tan 45°，即BD ＝AD 2tan 45°＝300．在Rt △BCD 中，∠BCD ＝60°，∠D ＝90°，∴BC ＝300sin 6032BD =＝2003，CD ＝tan 60BD＝3003＝1003 . 1号救生员到达B 点所用的时间为30022＝1502≈210(秒)，2号救生员到达 B 点所用的时间为3001003200362-+＝50＋25033≈192(秒)，3号救生员到达B 点所用的时间为3006＋3002＝200(秒)．∵192＜200＜210.∴2号求生员先到达营救地点B .【解题策略】本题为阅读理解题，题目中的数据比较多，正确分析题意是解题的关键．例15 如图28－133所示，某货船以24海里/时的速度将一批重要物资从A 处运往正东方向的M 处，在点A 处测得某岛C 在它的北偏东60°方向上，该货船航行30分钟后到达B 处，此时再测得该岛在它的北偏东30°方向上；已知在C 岛周围9海里的区域内有暗礁，若货船继续向正东方向航行，该货船有无触礁危险?试说明理由．分析本题可作CD ⊥AM 于点D ，在Rt △BCD 中求出CD 即可．解：过点C 作CD ⊥AM ，垂足为点D ，由题意得∠CBD ＝60°，∠CAB ＝30°, ∴∠ACB ＝30°，∠CAB ＝∠ACB ，∴BC ＝AB ＝24312＝12(海里)．在R t △BCD 中，CD ＝BC 3sin 60°＝63(海里)．∵63＞9，∴货船继续向正东方向航行无触礁危险．【解题策略】此题实际上是通过⊙C (半径为9海里)与直线AM 相离判断出无触礁危险. 例16 如图28－134所示，某幢大楼顶部有一块广告牌CD ，甲、乙两人分别在相距8米的A ， B 两处测得D 点和C 点的仰角分别为45°和60°，且A ，B ，F 三点在一条直线上，若BE ＝15米，求这块广告牌的高度．(3≈1.73，结果保留整数) 分析由于CD ＝CE －DE ，所以可分别在R t △AED 和Rt △BEC 中求DE ，CE 的长，从而得出结论．解：∵AB ＝8，BE ＝15，∴AE ＝23．在Rt △AED 中，∠DAE ＝45°，∴DE ＝AE ＝23．在Rt △BEC 中，∠CBE ＝60°，∴CE ＝BE 2tan 60°＝153，∴CD ＝CE －DE ＝153－23≈3，即这块广告牌的高度约为3米．例17 如图28－135所示，某水库大坝的横断面是梯形，坝顶宽AD ＝2.5m ，坝高4 m ，背水坡的坡度是1：1，迎水坡的坡度是1：1.5，求坝底宽BC .分析坡度即坡角的正切值，所以分别过A ，D 两点向坝底引垂线，把梯形转化为两个直角三角形和一个矩形．解：过A 作AE ⊥BC 于E ，过D 作DF ⊥BC 于F ，由题意可知tan B ＝1，tan C ＝11.5，在Rt △ABE 中，AE ＝4，tan B ＝AEBE＝1，∴BE ＝AE ＝4，在Rt △DFC 中，DF ＝AE ＝4，tan C ＝11.5DF CF =，∴CF ＝1．5DF ＝1.534＝6．又∵EF ＝AD ＝2.5，∴BC ＝BE ＋EF ＋FC ＝4＋2.5＋6＝12．5．答：坝底宽BC 为12．5 m ．【解题策略】背水坡是指AB ，而迎水坡是指CD .例18 如图28－136所示，山顶建有一座铁塔，塔高CD ＝30m ，某人在点A 处测得塔底C 的仰角为20°，塔顶D 的仰角为23°，求此人距CD 的水平距离AB ．(参考数据：sin 20°≈0.342，cos 20°≈0.940，tan 20°≈0.364，sin 23°≈0.391，cos 23°≈0.921，tan 23°≈0.424)分析要求AB 的值，由于两个直角三角形中都只有角的已知条件，不能直接求解，所以设AB 为未知量，即用AB 表示BD 和BC ，根据BD －BC ＝CD ＝30，列出关于AB 的方程．解：在Rt △ABC 中，∠CAB ＝20°，∴BC ＝AB tan ∠CAB ＝AB tan 20°．在Rt △ABD 中，∠DAB ＝23°，∴BD ＝AB tan ∠DAB ＝AB tan 23°．∴CD ＝BD －BC ＝AB tan 23°－AB tan 20°＝AB (tan 23°－tan 20°)．∴AB ＝tan 23tan 20CD ?-?≈300.4240.364-＝500(m)．答：此人距CD 的水平距离AB 约为500 m ．二、规律方法专题专题5 公式法【专题解读】本章的公式很多，熟练掌握公式是解决问题的关键．例19 当0°＜α＜90°时，求21sin cos αα-的值．分析由sin 2α＋cos 2α＝1，可得1－sin 2α＝cos 2α解：∵sin 2α＋cos 2α＝1，∴cos 2α＝1－sin 2α．∴221sin cos |cos |cos cos cos αααααα-==.∵0°＜a ＜90°，∴cos α＞0．∴原式＝cos cos αα＝1．【解题策略】以上解法中，应用了关系式sin 2α＋cos 2α＝1(0°＜α＜90°)，这一关系式在解题中经常用到，应当牢记，并灵活运用．三、思想方法专题专题6 类比思想【专题解读】求方程中未知数的过程叫做解方程，求直角三角形中未知元素的过程叫做解直角三角形，因此对解直角三角形的概念的理解可类比解方程的概念．我们可以像解方程(组)一样求直角三角形中的未知元素．例20 在Rt △ABC 中，∠C＝90°，∠A ，∠B ，∠C 的对边分别为a ，b ，c ，已知a ＝52，b ＝152，解这个直角三角形．分析已知两直角边长a ，b ，可由勾股定理c ＝22a b +求出c ，再利用sin A ＝ac求出∠A ，进而求出∠B ＝90°－∠A ．解：∵∠C ＝90°，∴a 2＋b 2＝c 2．∴c ＝222515+522a b +==2（）（）. 又∵sin A ＝51225a c ==，∴∠A ＝30°．∴∠B ＝90°－∠A ＝60°．【解题策略】除直角外，求出Rt △ABC 中的所有未知元素就是解直角三角形．专题7 数形结合思想【专题解读】由“数”思“形”，由“形”想“数”，两者巧妙结合，起到互通、互译的作用，是解决几何问题常用的方法之一．例21 如图28－137所示，已知∠α的终边OP ⊥AB ，直线AB 的方程为y ＝－33x ＋33，则cos α等于 ( ) A ．12 B ．22 C ．32 D ．33分析∵y ＝－33x ＋33，∴当x ＝0时，y ＝33，当y ＝0时，x ＝1，∴A (1，0)，B 30,3?? ? ???，∴OB ＝33，OA ＝1，∴AB ＝22OB OA +＝233，∴cos ∠OBA ＝12OB AB =. ∴OP ⊥AB ，∴∠α＋∠OAB ＝90°，又∵∠OBA ＋∠OAB ＝90°，∴∠α＝∠OBA ．∴cos α＝cos ∠OBA ＝12．故选A.专题8 分类讨论思想【专题解读】当结果不能确定，且有多种情况时，对每一种可能的情况都要进行讨论．例22 一条东西走向的高速公路上有两个加油站A，B，在A的北偏东45°方向上还有一个加油站C，C到高速公路的最短距离是30 km，B，C间的距离是60 km．要经过C修一条笔直的公路与高速公路相交，使两路交叉口P到B，C的距离相等，求交叉口P与加油站A的距离．(结果可保留根号)解：①如图28－138(1)所示，在Rt△BDC中，∵CD＝30，CB＝60，∴∠B＝30°．又PC＝PB，∴∠CPD＝60°，∴DP＝103．故AP＝AD＋DP＝(30＋103)km．②同理，如图28－138(2)所示，可求得AP＝(30－103)km，故交叉口P与加油站A的距离为(30＋103)km或(30－103)km．【解题策略】此题针对P点的位置分两种情况进行讨论，即点P 在线段AB上或点P在线段BA的延长线上．专题9 转化思想例24 如图28－140所示，A，B两城市相距100 km．现计划在这两座城市中间修筑一条高速公路(即线段AB)，经测量，森林保护中心P在A城市的北偏东30°和B城市的北偏西45°的方向上．已知森林保护区的范围在以P点为圆心，50 km为半径的圆形区域内．请问计划修筑的这条高速公路会不会穿越保护区．为什么?(参考数据：3≈1.732，2≈1.414)解：过点P作PC⊥AB，C是垂足，则∠APC＝30°，∠BPC＝45°，AC＝PC2tan 30°，BC＝PC2tan 45°，∵AC＋BC＝AB，∴PC2tan 30°＋PC2tan 45°＝100，∴(33＋1)PC＝100，∴PC＝50(3－3)≈503(3－1.732)≈63．4＞50．答：森林保护区的中心与直线AB的距离大于保护区的半径，所以计划修筑的这条高速公路不会穿越保护区．例25 小鹃学完解直角三角形知识后，给同桌小艳出了一道题：“如图28－141所示，把一张长方形卡片ABCD放在每格宽度为12 mm的横格纸中，恰好四个顶点都在横格线上．已知α＝36°，求长方形卡片的周长．”请你帮小艳解答这道题．(结果保留整数；参考数据：sin 36°≈0．6，cos 36°≈0．8，tan 36°≈0.7)解：作BE⊥l于点E，DF⊥l于点F．∵α＋∠DAF＝180°－∠BAD＝180°－90°＝90°，∠ADF ＋∠DAF ＝90°，∴∠ADF ＝α＝36°．根据题意，得BE ＝24 mm ，DF ＝48 mm ．在Rt △ABE 中，sin α＝BEAB，∴AB ＝sin36BE ?≈240.6＝40(mm)．在Rt △ADF 中，cos ∠ADF ＝DFAD，∴AD ＝cos36DF ?≈480.8＝60(mm)．∴矩形ABCD 的周长＝2(40＋60)＝200(mm)．例26 如图28－142所示，某居民楼I 高20米，窗户朝南．该楼内一楼住户的窗台离地面距离CM 为2米，窗户CD 高1．8米．现计划在I 楼的正南方距1楼30米处新建一居民楼Ⅱ．当正午时刻太阳光线与地面成30°角时，要使Ⅱ楼的影子不影响I 楼所有住户的采光，新建Ⅱ楼最高只能盖多少米?解：设正午时光线正好照在I 楼的一楼窗台处，此时新建居民楼Ⅱ高x 米．过C 作CF ⊥l 于F ，在Rt △ECF 中，EF ＝(x －2)米，FC ＝30米，∠ECF ＝30°，∴tan 30°＝230x -,∴＝103＋2．答：新建居民楼Ⅱ最高只能建(103＋2)米．。

中考数学专题复习10锐角三角函数及其运用(解析版)

锐角三角函数及其运用复习考点攻略考点一锐角三角函数1. 锐角三角函数的定义：在Rt △ABC 中.∠C =90°.AB =c .BC =a .AC =b .正弦：sin A =∠的对边=斜边A ac ；余弦：cos A =∠的邻边=斜边A bc；正切：tanA =∠的对边=邻边A ab．【注意】根据定义求三角函数值时.一定要根据题目图形来理解.严格按照三角函数的定义求解.有时需要通过辅助线来构造直角三角形.2【例2】A ．BCD ．1【答案】C 【解析】把sin45°=代入原式得：原式=2×．故选C ．考点三解直角三角形1．在直角三角形中.求直角三角形所有未知元素的过程叫做解直角三角形． 2．解直角三角形的常用关系：在Rt △ABC 中.∠C =90°.则：（1）三边关系：a 2+b 2=c 2；（2）两锐角关系：∠A +∠B =90°；（3）边与角关系：sin A =cos B =a c .cos A =sin B =b c .tan A =ab；（4）sin 2A +cos 2A =1．3．科学选择解直角三角形的方法口诀：已知斜边求直边.正弦、余弦很方便；已知直边求直边.理所当然用正切；已知两边求一边.勾股定理最方便；已知两边求一角.函数关系要记牢；已知锐角求锐角.互余关系不能少；已知直边求斜边.用除还需正余弦.【例3】如图.我市在建高铁的某段路基横断面为梯形ABCD .DC ∥AB ,BC 长为6米.坡角β为45°.AD 的坡角α为30°.则AD 的长为 ________ 米（结果保留根号）2sin 222【答案】62【解析】解：过C 作CE ⊥AB 于E.DF ⊥AB 于F.可得矩形CEFD 和Rt △CEB 与Rt △DFA. ∵BC=6.∴CE=2sin 456322BC ︒=⨯=.∴DF=CE=32.∴62sin 30DF AD ==︒.故答案为：62．【例4】如图.大海中有A 和B 两个岛屿.为测量它们之间的距离.在海岸线PQ 上点E 处测得74AEP =︒∠.30BEQ =︒∠；在点F 处测得60AFP =︒∠.60BFQ =︒∠.1km EF =．⑴ 判断AB 、AE 的数量关系.并说明理由⑵ 求两个岛屿A 和B 之间的距离（结果精确到0.1km ）．（参考数据：3 1.73≈. sin740.96︒≈.cos740.28︒≈.tan74 3.49︒≈.sin760.97︒≈.cos760.24︒≈）【答案】（1）见解析；（2）3.6km【解析】（1）相等.证明：∵30BEQ =︒∠.60BFQ =︒∠.∴30EBF =︒∠.EF BF =．又∵60AFP =︒∠.∴60BFA =︒∠．在AEF △与ABF △中.EF BF =.AFE AFB =∠∠.AF AF =. ∴AEF ABF △≌∠.∴AB AE =．（2）作AH PQ ⊥.垂足为H .设AE x =.则sin74AH x =︒.cos74HE x =︒.cos741HF x =︒+．Rt AHF △中.tan60AH HF =⋅︒.∴()cos74cos741tan 60x x ︒=︒+⋅︒.即()0.960.281 1.73x x =+⨯. ∴ 3.6x ≈.即 3.6km AB ≈．考点四锐角三角函数的应用1．仰角和俯角：仰角：在视线与水平线所成的角中.视线在水平线上方的角叫做仰角．俯角：在视线与水平线所成的角中.视线在水平线下方的角叫做俯角． 2．坡度和坡角坡度：坡面的铅直高度h 和水平宽度l 的比叫做坡面的坡度（或坡比）.记作i =h l．坡角：坡面与水平面的夹角叫做坡角.记作α.i =tan α．坡度越大.α角越大.坡面越陡． 3．方向角（或方位角）指北或指南方向线与目标方向线所成的小于90°的水平角叫做方向角．4．解直角三角形中“双直角三角形”的基本模型：5．解直角三角形实际应用的一般步骤（1）弄清题中名词、术语.根据题意画出图形.建立数学模型；（2）将条件转化为几何图形中的边、角或它们之间的关系.把实际问题转化为解直角三角形问题；（3）选择合适的边角关系式.使运算简便、准确；（4）得出数学问题的答案并检验答案是否符合实际意义.从而得到问题的解．6.解直角三角形应用题应注意的问题：（1）分析题意.根据已知条件画出它的平面或截面示意图.分清仰角、俯角、坡角、坡度、水平距离、垂直距离等概念的意义；（2）找出要求解的直角三角形．有些图形虽然不是直角三角形.但可添加适当的辅助线.把它们分割成一些直角三角形和矩形（包括正方形）；（3）根据已知条件.选择合适的边角关系式解直角三角形；（4）按照题目中已知数据的精确度进行近似计算.检验是否符合实际.并按题目要求的精确度取近似值.注明单位．【例5】如图.一名滑雪爱好者先从山脚下A处沿登山步道走到点B处.再沿索道乘坐缆车到达顶部C．已知在点A处观测点C.得仰角为35°.且A.B的水平距离AE＝1000米.索道BC 的坡度i＝1：1.长度为2600米.求山的高度（即点C到AE的距离）（参考数据：sin35°≈0.57.cos35°≈0.82.tan35°≈0.70.≈1.41.结果保留整数）【答案】1983米【解析】：如图.作CD⊥AE于点D.BF⊥CD于点F．又∵BE⊥AD.∴四边形BEDF是矩形．在Rt△BCF中.∵BC的坡度i＝1：1.∴∠CBF＝45°．∵BC＝2600米.∴米．∴米．∵A.B的水平距离AE＝1000米.∴米．∵∠CAD＝35°.∴（米）．答：山高CD约为1983米．【例6】如图.一艘海轮位于灯塔P的南偏东30°方向.距离灯塔100海里的A处.它计划沿正北方向航行.去往位于灯塔P的北偏东45°方向上的B处．（1）问B处距离灯塔P有多远？（结果精确到0.1海里）（2）假设有一圆形暗礁区域.它的圆心位于射线PB上.距离灯塔150海里的点O处．圆形暗礁区域的半径为60海里.进入这个区域.就有触礁的危险．请判断海轮到达B处是否有触礁的危险？如果海伦从B处继续向正北方向航行.是否有触礁的危险？并说明理由．（参考数据：≈1.414.≈1.732）【答案】（1）71海里；（2）见解析【解析】解：（1）过点P作PD⊥AB于点D．依题意可知.P A＝100.∠APD＝60°.∠BPD＝45°．∴∠A＝30°．∴PD＝50．在△PBD中.BD＝PD＝50.∴PB ＝50≈71．答：B 处距离灯塔P 约71海里．（2）依题意知：OP ＝150.OB ＝150﹣71＝79＞60． ∴海轮到达B 处没有触礁的危险．海伦从B 处继续向正北方向航行.有触礁的危险．第一部分选择题一、选择题（本题有10小题.每题3分.共30分）1. 比萨斜塔是意大利的著名建筑.其示意图如图所示．设塔顶中心点为点B .塔身中心线AB 与垂直中心线AC 的夹角为A ∠.过点B 向垂直中心线AC 引垂线.垂足为点D ．通过测量可得AB 、BD 、AD 的长度.利用测量所得的数据计算A ∠的三角函数值.进而可求A ∠的大小．下列关系式正确的是（）A ．sin BDA AB= B ．cos ABA AD=C ．tan ADA BD=D ．sin ADA AB=【答案】A【解析】由题可知.△ABD 是直角三角形.90BDA ∠=︒.sin BD A AB ∴=.cos AD A AB=,tan BDA AD =．∴选项B 、C 、D 都是错误的.故答案选A ． 2. 如图.在ABC 中.∠C ＝90°.设∠A .∠B .∠C 所对的边分别为a .b .c .则（）A ．c ＝b sinB B ．b ＝c sin BC ．a ＝b tan BD ．b ＝c tan B【答案】B【解析】∵Rt ABC 中.90C ∠=︒.A ∠、B 、C ∠所对的边分别为a 、b 、c ∴sin bB c=.即sin b c B =.则A 选项不成立.B 选项成立 tan bB a=.即tan b a B =.则C 、D 选项均不成立故选：B ． 3. 已知α是锐角.sin α=cos60°.则α等于（） A ．30° B ．45°C ．60°D ．不能确定4. 若∠A 是锐角.且sinA= 3.则（）A. 0°<∠A<30°B. 30°<∠A<45°C. 45°<∠A<60°D. 60°<∠A<90° 【答案】 A【解析】∵sin0°＝0.sinα＝ 13.sin30°＝ 12.又0＜ 13＜ 12.∴0°＜α＜30°．故答案为：A ．5. 点（-sin60°.cos60°）关于y 轴对称的点的坐标是（）A. （√32.12） B. （-√32.12） C. （-√32.-12） D. （- 12.- 32）【答案】 A 【解析】∵sin60°=√32.cos60°=12.∴（-sin60°.cos60°）=（-√32. 12）.关于y 轴对称点的坐标是（ √32.12）．故答案为：A ．6. 在Rt △ABC 中.∠C ＝90°.BC ＝5.AC ＝12.则sinB 的值是（）A ．512B ．125C ．513D ．1213【答案】D【解析】解：如图所示：∵∠C ＝90°.BC ＝5.AC ＝12.∴13AB =. ∴12sin 13AC B AB ==．故选：D ．7. 如图.某停车场入口的栏杆AB.从水平位置绕点O 旋转到A′B′的位置.已知AO 的长为4米．若栏杆的旋转角∠AOA′＝α.则栏杆A 端升高的高度为（） A ．米 B ．4sinα米 C ．米 D ．4cosα米【答案】B【解析】解：如答图.过点A′作A′C ⊥AB 于点C ．在Rt △OCA′.sinα＝.所以A′C ＝A′O ·sinα．由题意得A′O ＝AO ＝4.所以A′C ＝4sinα.因此本题选B ．8. 菱形ABCD 的对角线AC =10cm.BD =6cm.那么tan为（）【解析】如图.由题意得.AO ⊥BO .AO =AC =5cm.BO =BD =3cm. 4sin α4cos αA CA O''2B1212则tan=tan ∠OBA .故选A.9. 如图.AB 是圆锥的母线.BC 为底面直径.已知BC ＝6 cm.圆锥的侧面积为15π cm 2 . 则sin∠ABC 的值为（）A.34B.35C.45 D. 53【答案】 C【解析】解：设圆锥的母线长为R.由题意得： 15π=π6R.解得：R=5. ∴圆锥的高为4. ∴.故答案为：C.10. 如图.四边形ABCD 是一张平行四边形纸片.其高2cm AG =.底边6cm BC .45B ∠=︒.沿虚线EF 将纸片剪成两个全等的梯形.若30BEF ∠=︒.则AF 的长为（）2B53AO BO ==A ．1cm B．cm 3C．3)cm - D．(2-【答案】D【解析】如图所示.过点F 作FM BC ⊥交BC 于点M.∵AG BC ⊥.45B ∠=︒.AG=2.∴BG=FM=2.AF=GM.令AF=x. ∵两个梯形全等.∴AF=GM=EC=x.又∵30BEF ∠=︒.∴2=tan 30FMME =︒.∴ME =.又∵BC=6.∴26BC BG GM ME EC x x =+++=+++=.∴2x =-D ．第二部分填空题二、填空题（本题有6小题.每题4分.共24分）11..若tan （α–15°）= .则锐角α的度数是________．【答案】 75°【解析】【解答】由tan(α−15°)= √3.得 α−15°=60°. 解得α=75°. 故答案为：75°12.如图.在Rt △ABC 中.∠C =90°.BC =12.tan A =.则sin B =___________．125【答案】【解析】在Rt △ABC 中.∠C =90°.BC =12.tan A =.得.即. ∴AC =5．由勾股定理.得AB．所以sin B =. 故答案为：．13. 如图.A.B.C 是O上的三点.若OBC ∆是等边三角形.则cos A ∠=___________．【解析】解：∵△OBC 是等边三角形∴∠COB=60° ∴∠A=12COB ∠=30°∴cos cos30A ∠= 14. 如图是某商场营业大厅自动扶梯示意图．自动扶梯AB 的倾斜角为30.在自动扶梯下方地面C 处测得扶梯顶端B 的仰角为60︒.A 、C 之间的距离为4m ．则自动扶梯的垂直高度BD =_________m ．（结果保留根号）【答案】【解析】∵∠BAC+∠ABC=∠BCD=60°.∠BAC=30°. ∴∠ABC=30°.∴∠ABC=∠BAC.∴BC=AC=4. 在Rt △BCD 中.BD=BCsin60°=4×2=故答案为： 513125125BC AC =12125AC =513AC AB =51315. 如图所示.在四边形ABCD 中.90B ∠=︒.2AB =.8CD =．连接AC .AC CD ⊥.若1sin 3ACB ∠=.则AD 长度是_________．【答案】10【解析】解：在Rt ABC 中.∵12,sin 3AB AB ACB AC =∠==.∴1263AC =÷=．在Rt ADC 中.AD ==10=．故答案为：10．16. 如图.某校教学楼后面紧邻着一个山坡.坡上面是一块平地．//,BC AD BE AD ⊥.斜坡AB 长26m .斜坡AB 的坡比为12∶5．为了减缓坡面.防止山体滑坡.学校决定对该斜坡进行改造．经地质人员勘测.当坡角不超过50°时.可确保山体不滑坡．如果改造时保持坡脚A 不动.则坡顶B 沿BC 至少向右移________m 时.才能确保山体不滑坡．（取tan50 1.2︒=）【答案】10【解析】解：如图.设点B 沿BC 向右移动至点H.使得∠HAD=50°.过点H 作HF ⊥AD 于点F.∵AB=26.斜坡AB 的坡比为12∶5.则设BE=12a.AE=5a.∴()()22212526a a +=.解得：a=2.∴BE=24.AE=10.∴HF=BE=24.∵∠HAF=50°.则24tan50 1.2HFAF AF︒===.解得：AF=20.∴BH=EF=20-10=10.故坡顶B沿BC至少向右移10m时.才能确保山体不滑坡.故答案为：10．第三部分解答题二、解答题（本题有7小题.共46分）17. 如图.在ABC中.90,tanC A ABC∠==∠的平分线BD交AC于点.D CD=AB的长？【答案】6【解析】解：在Rt ABC中.90,3C tanA∠==30,60,A ABC∴∠=∠=BD是ABC∠的平分线.30,CBD ABD∴∠=∠=︒又3,CD=330CDBCtan∴==.在Rt ABC中.90,30∠=︒∠=︒C A.630BCABsin∴==︒．故答案为：6．18. 已知：如图.在菱形ABCD中.AE⊥BC.垂足为E.对角线BD=8.tan∠CBD=．（1）求边AB的长；（2）求cos∠BAE的值．12【答案】（1）2√5 ；（2）35【解析】（1）连接AC .AC 与BD 相交于点O .∵四边形ABCD 是菱形.∴AC ⊥BD .BO =BD =4. ∵Rt △BOC 中.tan ∠CBD ==.∴OC =2. ∴AB =BC（2）∵AE ⊥BC.∴S 菱形ABCD =BC ·AE=BD ·AC . ∵AC=2OC =4.∴=×8×4.∴AE =.∴BE. ∴cos ∠ABE ==．19. 如图.小明利用学到的数学知识测量大桥主架在水面以上的高度AB .在观测点C 处测得大桥主架顶端A 的仰角为30°.测得大桥主架与水面交汇点B 的俯角为14°.观测点与大桥主架的水平距离CM 为60米.且AB 垂直于桥面．（点,,,A B C M 在同一平面内）12OC OB 1212125BE AB 35（1）求大桥主架在桥面以上的高度AM ；（结果保留根号）（2）求大桥主架在水面以上的高度AB ．（结果精确到1米）（参考数据sin140.24,cos140.97,tan14 1.73︒︒︒≈≈≈≈）【答案】（1）大桥主架在桥面以上的高度AM 为（2）大桥主架在水面以上的高度AB 约为50米．【解析】解：（1）AB 垂直于桥面90︒∴∠=∠=AMC BMC在Rt AMC △中.60,30︒=∠=CM ACMtan ∠=AM ACM CM tan 30603︒∴=⋅=⨯=AM CM （米）答：大桥主架在桥面以上的高度AM 为（2）在Rt BMC △中.60,14︒=∠=CM BCMtan ∠=MBBCM CMtan14600.2515︒∴=⋅=⨯≈MB CM=+AB AM MB 1550∴≈+≈AB （米）答：大桥主架在水面以上的高度AB 约为50米．20. 如图.某船向正东航行.在A 处望见海岛C 在北偏东60°.前进6海里到B 点.此时测得海岛C 在北偏东45°.已知在该岛周围6海里内有暗礁.问船继续向正东航行.有触礁的危险吗?【答案】见解析【解析】解：如图.过点C 作CD ⊥AB 于点D.∵∠CAD=90°-60°=30°.∠CBD=90°-45°=45°.∴BD=CD.设CD=x.∴AD=AB+6=6+x.在Rt△CAD中.tan∠CAD=CD AD.∴√33= xx+6.3x=6 √3+ √3x.（3-√3）x=6 √3.解得x=3 √3+3＞6.答：若船继续向东航行.无触礁危险。

2020-2021中考数学综合题专题复习【锐角三角函数】专题解析含详细答案

2020-2021中考数学综合题专题复习【锐角三角函数】专题解析含详细答案一、锐角三角函数1．如图，山坡上有一棵树AB，树底部B点到山脚C点的距离BC为63米，山坡的坡角为30°．小宁在山脚的平地F处测量这棵树的高，点C到测角仪EF的水平距离CF=1米，从E处测得树顶部A的仰角为45°，树底部B的仰角为20°，求树AB的高度．（参考数值：sin20°≈0.34，cos20°≈0.94，tan20°≈0.36）【答案】6.4米【解析】解：∵底部B点到山脚C点的距离BC为6 3 米，山坡的坡角为30°．∴DC=BC•cos30°=3639=⨯=米，∵CF=1米，∴DC=9+1=10米，∴GE=10米，∵∠AEG=45°，∴AG=EG=10米，在直角三角形BGF中，BG=GF•tan20°=10×0.36=3.6米，∴AB=AG-BG=10-3.6=6.4米，答：树高约为6.4米首先在直角三角形BDC中求得DC的长，然后求得DF的长，进而求得GF的长，然后在直角三角形BGF中即可求得BG的长，从而求得树高2．如图，在△ABC中，∠ABC=∠ACB，以AC为直径的⊙O分别交AB、BC于点M、N，点P在AB的延长线上，且∠CAB=2∠BCP．（1）求证：直线CP是⊙O的切线．（2）若BC=2，sin∠BCP=，求点B到AC的距离．（3）在第（2）的条件下，求△ACP的周长．【答案】（1）证明见解析（2）4（3）20【解析】试题分析：（1）利用直径所对的圆周角为直角，2∠CAN=∠CAB，∠CAB=2∠BCP判断出∠ACP=90°即可；（2）利用锐角三角函数，即勾股定理即可．试题解析：（1）∵∠ABC=∠ACB，∴AB=AC，∵AC为⊙O的直径，∴∠ANC=90°，∴∠CAN+∠ACN=90°，2∠BAN=2∠CAN=∠CAB，∵∠CAB=2∠BCP，∴∠BCP=∠CAN，∴∠ACP=∠ACN+∠BCP=∠ACN+∠CAN=90°，∵点D在⊙O上，∴直线CP是⊙O的切线；（2）如图，作BF⊥AC∵AB=AC，∠ANC=90°，∴CN=CB=，∵∠BCP=∠CAN，sin∠BCP=，∴sin∠CAN=，∴∴AC=5，∴AB=AC=5，设AF=x，则CF=5﹣x，在Rt△ABF中，BF2=AB2﹣AF2=25﹣x2，在Rt△CBF中，BF2=BC2﹣CF2=2O﹣（5﹣x）2，∴25﹣x2=2O﹣（5﹣x）2，∴x=3，∴BF2=25﹣32=16，∴BF=4，即点B到AC的距离为4．考点：切线的判定3．如图（1），在平面直角坐标系中，点A（0，﹣6），点B（6，0）．Rt△CDE中，∠CDE=90°，CD=4，DE=4，直角边CD在y轴上，且点C与点A重合．Rt△CDE沿y轴正方向平行移动，当点C运动到点O时停止运动．解答下列问题：（1）如图（2），当Rt△CDE运动到点D与点O重合时，设CE交AB于点M，求∠BME 的度数．（2）如图（3），在Rt△CDE的运动过程中，当CE经过点B时，求BC的长．（3）在Rt△CDE的运动过程中，设AC=h，△OAB与△CDE的重叠部分的面积为S，请写出S与h之间的函数关系式，并求出面积S的最大值．【答案】（1）∠BME=15°；（2BC=4；（3）h≤2时，S=﹣h2+4h+8，当h≥2时，S=18﹣3h．【解析】试题分析：（1）如图2，由对顶角的定义知，∠BME=∠CMA，要求∠BME的度数，需先求出∠CMA的度数．根据三角形外角的定理进行解答即可；（2）如图3，由已知可知∠OBC=∠DEC=30°，又OB=6，通过解直角△BOC就可求出BC的长度；（3）需要分类讨论：①h≤2时，如图4，作MN⊥y轴交y轴于点N，作MF⊥DE交DE于点F，S=S△EDC﹣S△EFM；②当h≥2时，如图3，S=S△OBC．试题解析：解：（1）如图2，∵在平面直角坐标系中，点A（0，﹣6），点B（6，0）．∴OA=OB，∴∠OAB=45°，∵∠CDE=90°，CD=4，DE=4，∴∠OCE=60°，∴∠CMA=∠OCE﹣∠OAB=60°﹣45°=15°，∴∠BME=∠CMA=15°；如图3，∵∠CDE=90°，CD=4，DE=4，∴∠OBC=∠DEC=30°，∵OB=6，∴BC=4；（3）①h≤2时，如图4，作MN⊥y轴交y轴于点N，作MF⊥DE交DE于点F，∵CD=4，DE=4，AC=h，AN=NM，∴CN=4﹣FM，AN=MN=4+h﹣FM，∵△CMN∽△CED，∴，∴，解得FM=4﹣，∴S=S△EDC﹣S△EFM=×4×4﹣（44﹣h）×（4﹣）=﹣h2+4h+8，②如图3，当h≥2时，S=S△OBC=OC×OB=（6﹣h）×6=18﹣3h．考点：1、三角形的外角定理；2、相似；3、解直角三角形4．如图，AB是⊙O的直径，弦CD⊥AB于H，过CD延长线上一点E作⊙O的切线交AB 的延长线于切点为G，连接AG交CD于K．（1）求证：KE=GE；（2）若KG2=KD•GE，试判断AC与EF的位置关系，并说明理由；（3）在（2）的条件下，若sinE=，AK=，求FG的长．【答案】（1）证明见解析；（2）AC∥EF，证明见解析；（3）FG= ．【解析】试题分析：（1）如图1，连接OG．根据切线性质及CD⊥AB，可以推出∠KGE=∠AKH=∠GKE，根据等角对等边得到KE=GE；（2）AC与EF平行，理由为：如图2所示，连接GD，由∠KGE=∠GKE，及KG2=KD•GE，利用两边对应成比例且夹角相等的两三角形相似可得出△GKD与△EKG相似，又利用同弧所对的圆周角相等得到∠C=∠AGD，可推知∠E=∠C，从而得到AC∥EF；（3）如图3所示，连接OG，OC，先求出KE=GE，再求出圆的半径，根据勾股定理与垂径定理可以求解；然后在Rt△OGF中，解直角三角形即可求得FG的长度．试题解析：（1）如图1，连接OG．∵EG为切线，∴∠KGE+∠OGA=90°，∵CD⊥AB，∴∠AKH+∠OAG=90°，又∵OA=OG，∴∠OGA=∠OAG，∴∠KGE=∠AKH=∠GKE，∴KE=GE．（2）AC∥EF，理由为连接GD，如图2所示．∵KG2=KD•GE，即，∴，又∵∠KGE=∠GKE，∴△GKD∽△EGK，∴∠E=∠AGD，又∵∠C=∠AGD，∴∠E=∠C，∴AC∥EF；（3）连接OG，OC，如图3所示，∵EG为切线，∴∠KGE+∠OGA=90°，∵CD⊥AB，∴∠AKH+∠OAG=90°，又∵OA=OG，∴∠OGA=∠OAG，∴∠KGE=∠AKH=∠GKE，∴KE=GE．∵sinE=sin∠ACH=，设AH=3t，则AC=5t，CH=4t，∵KE=GE，AC∥EF，∴CK=AC=5t，∴HK=CK-CH=t．在Rt△AHK中，根据勾股定理得AH2+HK2=AK2，即（3t）2+t2=（2）2，解得t=．设⊙O半径为r，在Rt△OCH中，OC=r，OH=r-3t，CH=4t，由勾股定理得：OH2+CH2=OC2，即（r-3t）2+（4t）2=r2，解得r= t=．∵EF为切线，∴△OGF为直角三角形，在Rt△OGF中，OG=r=，tan∠OFG=tan∠CAH=，∴FG=【点睛】此题考查了切线的性质，相似三角形的判定与性质，垂径定理，勾股定理，锐角三角函数定义，圆周角定理，平行线的判定，以及等腰三角形的判定，熟练掌握定理及性质是解本题的关键．5．如图，二次函数y＝x2+bx﹣3的图象与x轴分别相交于A、B两点，点B的坐标为（3，0），与y轴的交点为C，动点T在射线AB上运动，在抛物线的对称轴l上有一定点D，其纵坐标为23，l与x轴的交点为E，经过A、T、D三点作⊙M．（1）求二次函数的表达式；（2）在点T的运动过程中，①∠DMT的度数是否为定值？若是，请求出该定值：若不是，请说明理由；②若MT＝12AD，求点M的坐标；（3）当动点T在射线EB上运动时，过点M作MH⊥x轴于点H，设HT＝a，当OH≤x≤OT 时，求y的最大值与最小值（用含a的式子表示）．【答案】（1）y＝x2﹣2x﹣3（2）①在点T的运动过程中，∠DMT的度数是定值②（0，3）（3）见解析【解析】【分析】（1）把点B的坐标代入抛物线解析式求得系数b的值即可；（2）①如图1，连接AD．构造Rt△AED，由锐角三角函数的定义知，tan∠DAE＝3．即∠DAE＝60°，由圆周角定理推知∠DMT＝2∠DAE＝120°；②如图2，由已知条件MT＝12AD，MT＝MD，推知MD＝12AD，根据△ADT的外接圆圆心M在AD的中垂线上，得到：点M是线段AD的中点时，此时AD为⊙M的直径时，MD＝12AD．根据点A、D的坐标求得点M的坐标即可；（3）如图3，作MH⊥x于点H，则AH＝HT＝12AT．易得H（a﹣1，0），T（2a﹣1，0）．由限制性条件OH≤x≤OT、动点T在射线EB上运动可以得到：0≤a﹣1≤x≤2a﹣1．需要分类讨论：（i）当2111(1)211aa a-⎧⎨----⎩……，即413a<„，根据抛物线的增减性求得y的极值．（ii）当0112111(1)211aaa a<-⎧⎪->⎨⎪--<--⎩…，即43＜a≤2时，根据抛物线的增减性求得y的极值．（iii）当a﹣1＞1，即a＞2时，根据抛物线的增减性求得y的极值．【详解】解：（1）把点B（3，0）代入y＝x2+bx﹣3，得32+3b﹣3＝0，解得b＝﹣2，则该二次函数的解析式为：y＝x2﹣2x﹣3；（2）①∠DMT的度数是定值．理由如下：如图1，连接AD．∵抛物线y＝x2﹣2x﹣3＝（x﹣1）2﹣4．∴抛物线的对称轴是直线x＝1．又∵点D的纵坐标为∴D（1，由y＝x2﹣2x﹣3得到：y＝（x﹣3）（x+1），∴A（﹣1，0），B（3，0）．在Rt△AED中，tan∠DAE＝DEAE==．∴∠DAE＝60°．∴∠DMT＝2∠DAE＝120°．∴在点T的运动过程中，∠DMT的度数是定值；②如图2，∵MT＝12AD．又MT＝MD，∴MD＝12AD．∵△ADT的外接圆圆心M在AD的中垂线上，∴点M是线段AD的中点时，此时AD为⊙M的直径时，MD＝12AD．∵A（﹣1，0），D（1，∴点M的坐标是（0（3）如图3，作MH⊥x于点H，则AH＝HT＝12 AT．又HT＝a，∴H（a﹣1，0），T（2a﹣1，0）．∵OH≤x≤OT，又动点T在射线EB上运动，∴0≤a﹣1≤x≤2a﹣1．∴0≤a﹣1≤2a﹣1．∴a≥1，∴2a﹣1≥1．（i）当2111(1)211aa a-⎧⎨----⎩……，即14a3剟时，当x＝a﹣1时，y最大值＝（a﹣1）2﹣2（a﹣1）﹣3＝a2﹣4a；当x＝1时，y最小值＝4．（ii）当0112111(1)211aaa a<-⎧⎪->⎨⎪--<--⎩„，即43＜a≤2时，当x＝2a﹣1时，y最大值＝（2a﹣1）2﹣2（2a﹣1）﹣3＝4a2﹣8a．当x＝1时，y最小值＝﹣4．（iii）当a﹣1＞1，即a＞2时，当x＝2a﹣1时，y最大值＝（2a﹣1）2﹣2（2a﹣1）﹣3＝4a2﹣8a．当x＝a﹣1时，y最小值＝（a﹣1）2﹣2（a﹣1）﹣3＝a2﹣4a．【点睛】主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养．要会利用数形结合的思想把代数和几何图形结合起来，利用点的坐标的意义表示线段的长度，从而求出线段之间的关系；另外，解答（3）题时，一定要分类讨论，以防漏解或错解．6．如图，在平面直角坐标系中，点O 为坐标原点，直线4y kx =+交x 轴、y 轴分别于点A 、点B ，且ABO ∆的面积为8.（1）求k 的值；（2）如图，点P 是第一象限直线AB 上的一个动点，连接PO ，将线段OP 绕点O 顺时针旋转90°至线段OC ，设点P 的横坐标为t ，点C 的横坐标为m ，求m 与t 之间的函数关系式（不要求写出自变量t 的取值范围）；（3）在（2）的条件下，过点B 作直线BM OP ⊥，交x 轴于点M ，垂足为点N ，点K 在线段MB 的延长线上，连接PK ，且0PK KB P +=，2PMB KPB ∠=∠，连接MC ，求四边形BOCM 的面积.【答案】（1）1k =；（2）4m t =+；（3）32BOCM S =Y .【解析】【分析】（1）先求出A 的坐标，然后利用待定系数法求出k 的值；(2) 过点P 作PD x ⊥轴，垂足为D ，过点C 作CE x ⊥轴，垂足为E ，证POD OCE ∆≅∆可得OE PD =，进一步得出m 与t 的函数关系式；（3）过点O 作直线OT AB ⊥，交直线BM 于点Q ，垂足为点T ，连接QP ，先证出QTB PTO ∆≅∆；再证出KPB BPN ∠=∠；设KPB x ∠=︒，通过计算证出PO PM =；再过点P 作PD x ⊥轴，垂足为点D ，根据tan tan OPD BMO ∠=∠得到OD BO PD MO =，列式可求得t=4；所以OM=8进一步得出四边形BOCM 是平行四边形，最后可得其面积为32.【详解】解：（1）把0x =代入4y kx =+，4y =，∴4BO =，又∵4ABO S ∆=， ∴142AO BO ⋅=，4AO =， ∴(4,0)A -，把4x =-，0y =代入4y kx =+，得044k =-+，解得1k =.故答案为1；（2）解：把x t =代入4y x =+，4y t =+， ∴(,4)P t t +如图，过点P 作PD x ⊥轴，垂足为D ，过点C 作CE x ⊥轴，垂足为E ，∴90PDO CEO ∠=∠=︒，∴90POD OPD ∠+∠=︒，∵线段OP 绕点O 顺时针旋转90°至线段OC ，∴90POC ∠=︒，OP OC =，∴90POD EOC ∠+∠=︒，∴OPD EOC ∠=∠，∴POD OCE ∆≅∆，∴OE PD =，4m t =+.故答案为4m t =+.（3）解：如图，过点O 作直线OT AB ⊥，交直线BM 于点Q ，垂足为点T ，连接QP ，由（1）知，4AO BO ==，90BOA ∠=︒，∴ABO ∆为等腰直角三角形，∴45ABO BAO ∠=∠=︒，9045BOT ABO ABO ∠=︒-∠=︒=∠，∴BT TO =，∵90BTO ∠=︒，∴90TPO TOP ∠+∠=︒，∵PO BM ⊥，∴90BNO ∠=︒，∴BQT TPO ∠=∠，∴QTB PTO ∆≅∆，∴QT TP =，PO BQ =，∴PQT QPT ∠=∠，∵PO PK KB =+，∴QB PK KB =+，QK KP =，∴KQP KPQ ∠=∠，∴PQT KQP QPT KPQ ∠-∠=∠-∠，TQB TPK ∠=∠，∴KPB BPN ∠=∠，设KPB x ∠=︒，∴BPN x ∠=︒，∵2PMB KPB ∠=∠，∴2PMB x ∠=︒，45POM PAO APO x ∠=∠+∠=︒+︒，9045NMO POM x ∠=︒-∠=︒-︒， ∴45PMO PMB NMO x POM ∠=∠+∠=︒+︒=∠，∴PO PM =，过点P 作PD x ⊥轴，垂足为点D ，∴22OM OD t ==，9045OPD POD x BMO ∠=︒-∠=︒-︒=∠，tan tan OPD BMO ∠=∠， OD BO PD MO =，442t t t =+， 14t =，22t =-（舍）∴8OM =，由（2）知，48m t OM =+==，∴CM y P 轴，∵90PNM POC ∠=∠=︒，∴BM OC P ，∴四边形BOCM 是平行四边形，∴4832BOCM S BO OM =⨯=⨯=Y .故答案为32.【点睛】本题考查了一次函数和几何的综合题，全等三角形的判定和性质，解直角三角形，添加适当的辅助线构造全等三角形是本题的关键．7．如图，直线y ＝12x +2与x 轴交于点A ，与y 轴交于点B ，抛物线y ＝﹣12x 2+bx +c 经过A 、B 两点，与x 轴的另一个交点为 C ．（1）求抛物线的解析式；（2）根据图象，直接写出满足12x +2≥﹣12x 2+bx +c 的x 的取值范围；（3）设点D 为该抛物线上的一点、连结AD ，若∠DAC ＝∠CBO ，求点D 的坐标．【答案】（1）213222y x x =--+；（2）当x ≥0或x ≤﹣4；（3）D 点坐标为（0，2）或（2，﹣3）．【解析】【分析】（1）由直线y ＝12x +2求得A 、B 的坐标，然后根据待定系数法即可求得抛物线的解析式；（2）观察图象，找出直线在抛物线上方的x 的取值范围；（3）如图，过D 点作x 轴的垂线，交x 轴于点E ，先求出CO ＝1，AO ＝4，再由∠DAC ＝∠CBO ，得出tan ∠DAC ＝tan ∠CBO ，从而有，DE CO AE BO =,最后分类讨论确定点D 的坐标．【详解】解：（1）由y ＝12x +2可得：当x ＝0时，y ＝2；当y ＝0时，x ＝﹣4，∴A （﹣4，0），B （0，2），把A 、B 的坐标代入y ＝﹣12x 2+bx +c 得： 322b c ⎧=-⎪⎨⎪=⎩，， ∴抛物线的解析式为：213222y x x =--+ （2）当x ≥0或x ≤﹣4时，12x +2≥﹣12x 2+bx +c （3）如图，过D 点作x 轴的垂线，交x 轴于点E ，由213222y x x =-+令y ＝0，解得：x 1＝1，x 2＝﹣4，∴CO ＝1，AO ＝4，设点D 的坐标为（m ，213222m m --+）， ∵∠DAC ＝∠CBO ，∴tan ∠DAC ＝tan ∠CBO ，∴在Rt △ADE 和Rt △BOC 中有DE CO AE BO =，当D 在x 轴上方时，213212242--+=+m m m 解得：m 1＝0，m 2＝﹣4（不合题意，舍去），∴点D 的坐标为（0，2）．当D 在x 轴下方时，213(2)12242---+=+m m m解得：m1＝2，m2＝﹣4（不合题意，舍去），∴点D的坐标为（2，﹣3），故满足条件的D点坐标为（0，2）或（2，﹣3）．【点睛】本题是二次函数综合题型，主要考查了一次函数图象上点的坐标特征，待定系数法求二次函数解析式．解题的关键是能够熟练掌握一次函数和二次函数的有关知识解决问题，分类讨论是第（3）题的难点．8．如图，AB是圆O的直径，O为圆心，AD、BD是半圆的弦，且∠PDA=∠PBD．延长PD 交圆的切线BE于点E(1)判断直线PD是否为⊙O的切线，并说明理由；(2)如果∠BED=60°，PD=3，求PA的长；(3)将线段PD以直线AD为对称轴作对称线段DF，点F正好在圆O上，如图2，求证：四边形DFBE为菱形．【答案】（1）证明见解析；（2）1；（3）证明见解析.【解析】【分析】（1）连接OD，由AB是圆O的直径可得∠ADB=90°，进而求得∠ADO+∠PDA=90°，即可得出直线PD为⊙O的切线；（2）根据BE是⊙O的切线，则∠EBA=90°，即可求得∠P=30°，再由PD为⊙O的切线，得∠PDO=90°，根据三角函数的定义求得OD，由勾股定理得OP，即可得出PA；（3）根据题意可证得∠ADF=∠PDA=∠PBD=∠ABF，由AB是圆O的直径，得∠ADB=90°，设∠PBD=x°，则可表示出∠DAF=∠PAD=90°+x°，∠DBF=2x°，由圆内接四边形的性质得出x 的值，可得出△BDE是等边三角形．进而证出四边形DFBE为菱形．【详解】（1）直线PD为⊙O的切线，理由如下：如图1，连接OD，∵AB是圆O的直径，∴∠ADB=90°，∴∠ADO+∠BDO=90°，又∵DO=BO，∴∠BDO=∠PBD，∵∠PDA=∠PBD，∴∠BDO=∠PDA，∴∠ADO+∠PDA=90°，即PD⊥OD，∵点D在⊙O上，∴直线PD为⊙O的切线；（2）∵BE是⊙O的切线，∴∠EBA=90°，∵∠BED=60°，∴∠P=30°，∵PD为⊙O的切线，∴∠PDO=90°，在Rt△PDO中，∠P=30°，3∴0 tan30ODPD=，解得OD=1，∴22PO PD OD+，∴PA=PO﹣AO=2﹣1=1；（3）如图2，依题意得：∠ADF=∠PDA，∠PAD=∠DAF，∵∠PDA=∠PBD∠ADF=∠ABF，∴∠ADF=∠PDA=∠PBD=∠ABF，∵AB是圆O的直径，∴∠ADB=90°，设∠PBD=x°，则∠DAF=∠PAD=90°+x°，∠DBF=2x°，∵四边形AFBD内接于⊙O，∴∠DAF+∠DBF=180°，即90°+x+2x=180°，解得x=30°，∴∠ADF=∠PDA=∠PBD=∠ABF=30°，∵BE、ED是⊙O的切线，∴DE=BE，∠EBA=90°，∴∠DBE=60°，∴△BDE是等边三角形，∴BD=DE=BE，又∵∠FDB=∠ADB﹣∠ADF=90°﹣30°=60°∠DBF=2x°=60°，∴△BDF是等边三角形，∴BD=DF=BF，∴DE=BE=DF=BF，∴四边形DFBE为菱形.【点睛】本题是一道综合性的题目，考查了切线的判定和性质，圆周角定理和菱形的性质，是中档题，难度较大．9．如图1，以点M（－1，0）为圆心的圆与y轴、x轴分别交于点A、B、C、D，直线y＝－x－与⊙M相切于点H，交x轴于点E，交y轴于点F．（1）请直接写出OE、⊙M的半径r、CH的长；（2）如图2，弦HQ交x轴于点P，且DP:PH＝3:2，求cos∠QHC的值；（3）如图3，点K为线段EC上一动点（不与E、C重合），连接BK交⊙M于点T，弦AT 交x轴于点N．是否存在一个常数a，始终满足MN·MK＝a，如果存在，请求出a的值；如果不存在，请说明理由．【答案】（1）OE=5，r=2，CH=2（2）；（3）a=4【解析】【分析】（1）在直线y＝－x－中，令y=0，可求得E的坐标，即可得到OE的长为5；连接MH，根据△EMH与△EFO相似即可求得半径为2；再由EC=MC=2，∠EHM=90°，可知CH 是RT△EHM斜边上的中线，根据直角三角形斜边上的中线等于斜边的一半即可得出CH的长；（2）连接DQ、CQ．根据相似三角形的判定得到△CHP∽△QPD，从而求得DQ的长，在直角三角形CDQ中，即可求得∠D的余弦值，即为cos∠QHC的值；（3）连接AK，AM，延长AM，与圆交于点G，连接TG，由圆周角定理可知，∠GTA=90°，∠3=∠4，故∠AKC=∠MAN，再由△AMK∽△NMA即可得出结论．【详解】（1）OE=5，r=2，CH=2（2）如图1，连接QC、QD，则∠CQD =90°，∠QHC =∠QDC，易知△CHP∽△DQP，故，得DQ=3，由于CD=4，；（3）如图2，连接AK，AM，延长AM，与圆交于点G，连接TG，则，由于，故，；而，故在和中，；故△AMK∽△NMA;即：故存在常数，始终满足常数a="4"解法二：连结BM，证明∽得10．兰州银滩黄河大桥北起安宁营门滩，南至七里河马滩，是黄河上游的第一座大型现代化斜拉式大桥如图，小明站在桥上测得拉索AB与水平桥面的夹角是31°，拉索AB的长为152米，主塔处桥面距地面7.9米（CD的长），试求出主塔BD的高．（结果精确到0.1米，参考数据：sin31°≈0.52，cos31°≈0.86，tan31°≈0.60）【答案】主塔BD的高约为86.9米．【解析】【分析】根据直角三角形中由三角函数得出BC相应长度，再由BD=BC+CD可得出.【详解】在Rt△ABC中，∠ACB=90°，sin BCAAB=．∴sin152sin311520.5279.04BC AB A︒=⨯=⨯=⨯=．79.047.986.9486.9BD BC CD=+=+=≈（米）答：主塔BD的高约为86.9米．【点睛】本题考察了直角三角形与三角函数的结合，熟悉掌握是解决本题的关键.11．如图，在平面直角坐标系中，菱形ABCD的边AB在x轴上，点B坐标（﹣6，0），点C在y轴正半轴上，且cos B＝35，动点P从点C出发，以每秒一个单位长度的速度向D点移动（P点到达D点时停止运动），移动时间为t秒，过点P作平行于y轴的直线l与菱形的其它边交于点Q．（1）求点D坐标；（2）求△OPQ的面积S关于t的函数关系式，并求出S的最大值；（3）在直线l移动过程中，是否存在t值，使S＝320ABCDS菱形？若存在，求出t的值；若不存在，请说明理由．【答案】（1）点D 的坐标为（10，8）．（2）S 关于t 的函数关系式为S ＝24(04)220(410)33t t t t t ⎧⎪⎨-+<⎪⎩剟…，S 的最大值为503．（3）3或7. 【解析】【分析】（1）在Rt △BOC 中，求BC,OC,根据菱形性质再求D 的坐标；（2）分两种情况分析：①当0≤t ≤4时和②当4＜t ≤10时，根据面积公式列出解析式，再求函数的最值；（3）分两种情况分析：当0≤t ≤4时，4t ＝12，；当4＜t ≤10时，22201233t t -+= 【详解】解：（1）在Rt △BOC 中，∠BOC ＝90°，OB ＝6，cos B ＝35， 10cos OBBC B∴== 228OC BC OB ∴=-=∵四边形ABCD 为菱形，CD ∥x 轴， ∴点D 的坐标为（10，8）．（2）∵AB ＝BC ＝10，点B 的坐标为（﹣6，0）， ∴点A 的坐标为（4，0）．分两种情况考虑，如图1所示．①当0≤t ≤4时，PQ ＝OC ＝8，OQ ＝t ，∴S ＝12PQ •OQ ＝4t ，∵4＞0，∴当t ＝4时，S 取得最大值，最大值为16；②当4＜t ≤10时，设直线AD 的解析式为y ＝kx +b （k ≠0），将A （4，0），D （10，8）代入y ＝kx +b ，得：4k b 010k b 8+=⎧⎨+=⎩，解得：4k 316b 3⎧=⎪⎪⎨⎪=-⎪⎩，∴直线AD 的解析式为41633y x =-．当x ＝t 时，41633y t =-， 41648(10)333PQ t t ⎛⎫∴=--=- ⎪⎝⎭21220233S PQ OP t t ∴=⋅=-+ 22202502(5),033333S t t t =-+=--+-<Q ∴当t ＝5时，S 取得最大值，最大值为503．综上所述：S 关于t 的函数关系式为S ＝24(04)220(410)33t t t t t ⎧⎪⎨-+<⎪⎩剟…，S 的最大值为503．（3）S 菱形ABCD ＝AB •OC ＝80．当0≤t ≤4时，4t ＝12，解得：t ＝3；当4＜t ≤10时，222033t t -+＝12，解得：t 1＝5﹣7（舍去），t 2＝5+ 7．综上所述：在直线l 移动过程中，存在t 值，使S ＝320ABCD S 菱形，t 的值为3或5+7．【点睛】考核知识点：一次函数和二次函数的最值问题.数形结合，分类讨论是关键.12．超速行驶是引发交通事故的主要原因．上周末，小明和三位同学尝试用自己所学的知识检测车速，如图，观测点设在到万丰路（直线AO ）的距离为120米的点P 处．这时，一辆小轿车由西向东匀速行驶，测得此车从A 处行驶到B 处所用的时间为5秒且∠APO ＝60°，∠BPO ＝45°．（1）求A 、B 之间的路程；（2）请判断此车是否超过了万丰路每小时65千米的限制速度？请说明理由．（参考数据：2 1.414,3 1.73≈≈）．【答案】【小题1】73.2【小题2】超过限制速度．【解析】解：（1）100(31)AB =-73.2 (米)．…6分(2) 此车制速度v==18.3米/秒13．如图，在ABC △中，10AC BC ==，3cos 5C =,点P 是BC 边上一动点（不与点,A C 重合），以PA 长为半径的P e 与边AB 的另一个交点为D ，过点D 作DE CB ⊥于点E .()1当P e 与边BC 相切时，求P e 的半径；()2联结BP 交DE 于点F ，设AP 的长为x ，PF 的长为y ，求y 关于x 的函数解析式，并直接写出x 的取值范围；()3在()2的条件下，当以PE 长为直径的Q e 与P e 相交于AC 边上的点G 时，求相交所得的公共弦的长.【答案】（1）409；（2）)25880010x x x y x -+=<<；（3）105- 【解析】【分析】（1）设⊙P 与边BC 相切的切点为H ，圆的半径为R ，连接HP ，则HP ⊥BC ，cosC=35，则sinC=45，sinC=HP CP =R 10R -=45，即可求解；（2）PD∥BE，则EBPD＝BFPF，即：2248805x x x yx y--+-=，即可求解；（3）证明四边形PDBE为平行四边形，则AG=GP=BD，即：AB=DB+AD=AG+AD=45，即可求解．【详解】（1）设⊙P与边BC相切的切点为H，圆的半径为R，连接HP，则HP⊥BC，cosC=35，则sinC=35，sinC=HPCP=R10R-=45，解得：R=409；（2）在△ABC中，AC=BC=10，cosC=35，设AP=PD=x，∠A=∠ABC=β，过点B作BH⊥AC，则BH=ACsinC=8，同理可得：CH=6，HA=4，5tan∠()2284x+-2880x x-+25，则525，如下图所示，PA=PD ，∴∠PAD=∠CAB=∠CBA=β， tanβ=2，则cosβ=5，sinβ=5， EB=BDcosβ=（45-25x ）×5=4-25x ，∴PD ∥BE ，∴EB PD ＝BFPF，即：2248805x x x y x--+-=，整理得：y=()25x x 8x 800x 103x 20-+<<+；（3）以EP 为直径作圆Q 如下图所示，两个圆交于点G ，则PG=PQ ，即两个圆的半径相等，则两圆另外一个交点为D ，GD 为相交所得的公共弦， ∵点Q 时弧GD 的中点， ∴DG ⊥EP ， ∵AG 是圆P 的直径， ∴∠GDA=90°， ∴EP ∥BD ，由（2）知，PD ∥BC ，∴四边形PDBE 为平行四边形， ∴AG=EP=BD ，∴5设圆的半径为r ，在△ADG 中，AD=2rcosβ=5，DG=5，AG=2r ，5+2r=45，解得：2r=51+，则：DG=5=10-25，相交所得的公共弦的长为10-25．【点睛】本题考查的是圆知识的综合运用，涉及到解直角三角形、勾股定理等知识，其中（3），要关键是根据题意正确画图，此题用大量的解直角三角形的内容，综合难度很大．14．已知：如图，在Rt △ABO 中，∠B =90°，∠OAB =30°，OA =3．以点O 为原点，斜边OA 所在直线为x 轴，建立平面直角坐标系，以点P （4，0）为圆心，PA 长为半径画圆，⊙P 与x 轴的另一交点为N ，点M 在⊙P 上，且满足∠MPN =60°．⊙P 以每秒1个单位长度的速度沿x 轴向左运动，设运动时间为ts ，解答下列问题：（发现）（1）MN n的长度为多少；（2）当t =2s 时，求扇形MPN （阴影部分）与Rt △ABO 重叠部分的面积．（探究）当⊙P 和△ABO 的边所在的直线相切时，求点P 的坐标．（拓展）当MN n与Rt △ABO 的边有两个交点时，请你直接写出t 的取值范围．【答案】【发现】（1）MN n的长度为π3；（2）重叠部分的面积为38；【探究】：点P 的坐标为10（，）；或230）或230（）；【拓展】t 的取值范围是23t ≤＜或45t ≤＜，理由见解析．【解析】【分析】发现：（1）先确定出扇形半径，进而用弧长公式即可得出结论；（2）先求出PA =1，进而求出PQ ，即可用面积公式得出结论；探究：分圆和直线AB 和直线OB 相切，利用三角函数即可得出结论；拓展：先找出·MN和直角三角形的两边有两个交点时的分界点，即可得出结论．【详解】[发现]（1）∵P （4，0），∴OP =4．∵OA =3，∴AP =1，∴·MN的长度为6011803ππ⨯=．故答案为3π；（2）设⊙P 半径为r ，则有r =4﹣3=1，当t =2时，如图1，点N 与点A 重合，∴PA =r =1，设MP 与AB 相交于点Q ．在Rt △ABO 中，∵∠OAB =30°，∠MPN =60°． ∵∠PQA =90°，∴PQ 12=PA 12=，∴AQ =AP ×cos30°3=，∴S 重叠部分=S △APQ 12=PQ ×AQ 3=．即重叠部分的面积为38． [探究]①如图2，当⊙P 与直线AB 相切于点C 时，连接PC ，则有PC ⊥AB ，PC =r =1． ∵∠OAB =30°，∴AP =2，∴OP =OA ﹣AP =3﹣2=1； ∴点P 的坐标为（1，0）；②如图3，当⊙P 与直线OB 相切于点D 时，连接PD ，则有PD ⊥OB ，PD =r =1，∴PD ∥AB ，∴∠OPD =∠OAB =30°，∴cos ∠OPD PD OP =，∴OP 12330cos ==︒∴点P 的23，0）； ③如图4，当⊙P 与直线OB 相切于点E 时，连接PE ，则有PE ⊥OB ，同②可得：OP 23=； ∴点P 的坐标为（23，0）；[拓展]t的取值范围是2＜t≤3，4≤t＜5，理由：如图5，当点N运动到与点A重合时，·MN与Rt△ABO的边有一个公共点，此时t=2；当t＞2，直到⊙P运动到与AB相切时，由探究①得：OP=1，∴t411-==3，·MN与Rt△ABO的边有两个公共点，∴2＜t≤3．如图6，当⊙P运动到PM与OB重合时，·MN与Rt△ABO的边有两个公共点，此时t=4；直到⊙P运动到点N与点O重合时，·MN与Rt△ABO的边有一个公共点，此时t=5；∴4≤t＜5，即：t的取值范围是2＜t≤3，4≤t＜5．【点睛】本题是圆的综合题，主要考查了弧长公式，切线的性质，锐角三角函数，三角形面积公式，作出图形是解答本题的关键．15．如图，半圆O的直径AB＝20，弦CD∥AB，动点M在半径OD上，射线BM与弦CD 相交于点E（点E与点C、D不重合），设OM＝m．（1）求DE的长（用含m的代数式表示）；（2）令弦CD所对的圆心角为α，且sin4 =25α．①若△DEM的面积为S，求S关于m的函数关系式，并求出m的取值范围；②若动点N在CD上，且CN＝OM，射线BM与射线ON相交于点F，当∠OMF＝90°时，求DE的长．【答案】（1）DE ＝10010m m -；（2）①S ＝2360300m m m-+，（5013＜m ＜10），②DE ＝52. 【解析】【分析】（1）由CD ∥AB 知△DEM ∽△OBM ，可得DE DMOB OM=，据此可得；（2）①连接OC 、作OP ⊥CD 、MQ ⊥CD ，由OC ＝OD 、OP ⊥CD 知∠DOP ＝12∠COD ，据此可得sin ∠DOP ＝sin ∠DMQ ＝45、sin ∠ODP ＝35，继而由OM ＝m 、OD ＝10得QM ＝DM sin ∠ODP ＝35（10﹣m ），根据三角形的面积公式即可得；如图2，先求得PD ＝8、CD ＝16，证△CDM ∽△BOM 得CD DM BO OM =，求得OM ＝5013，据此可得m 的取值范围； ②如图3，由BM ＝OB sin ∠BOM ＝10×35＝6，可得OM ＝8，根据（1）所求结果可得答案．【详解】（1）∵CD ∥AB ， ∴△DEM ∽△OBM ， ∴DE DM OB OM =，即1010DE mm-=， ∴DE ＝10010mm-；（2）①如图1，连接OC 、作OP ⊥CD 于点P ，作MQ ⊥CD 于点Q ，∵OC ＝OD 、OP ⊥CD ， ∴∠DOP ＝12∠COD ， ∵sin2α＝45，∴sin ∠DOP ＝sin ∠DMQ ＝45，sin ∠ODP ＝35， ∵OM ＝m 、OD ＝10，∴DM ＝10﹣m ，∴QM ＝DM sin ∠ODP ＝35（10﹣m ），则S △DEM ＝12DE •MQ ＝12×10010m m -×35（10﹣m ）＝2360300m m m-+，如图2，∵PD ＝OD sin ∠DOP ＝10×45＝8， ∴CD ＝16，∵CD ∥AB ，∴△CDM ∽△BOM ，∴CD DM BO OM =，即1610=10OM OM-，解得：OM ＝5013， ∴5013＜m ＜10， ∴S ＝2360300m m m-+，（5013＜m ＜10）． ②当∠OMF ＝90°时，如图3，则∠BMO ＝90°，在Rt△BOM中，BM＝OB sin∠BOM＝10×35＝6，则OM＝8，由（1）得DE＝100108582-⨯=．【点睛】本题主要考查圆的综合题，解题的关键是熟练掌握圆的有关性质、相似三角形的判定与性质及解直角三角形的能力．。

2023中考九年级数学分类讲解 -第九讲直角三角形、锐角三角函数及其应用(含答案)(全国通用版)

第九讲直角三角形、锐角三角函数及其应用专项一直角三角形知识清单1. 直角三角形的性质（1）直角三角形的两个锐角；（2）直角三角形斜边上的中线等于斜边的；（3）勾股定理：如果直角三角形的两条直角边长分别为a，b，斜边长为c，那么a，b，c满足；（4）直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的．2. 直角三角形的判定（1）有一个角是直角的三角形是直角三角形；（2）有两个角的三角形是直角三角形；（3）勾股定理的逆定理：如果三角形的三边长a，b，c满足，那么这个三角形是直角三角形；（4）如果一个三角形一边上的中线等于这条边的，那么这个三角形是直角三角形．（这个结论在做填空、选择题时可直接用）3. 勾股数：能够成为的三个正整数，称为勾股数．考点例析例1 如图1，AB∥CD，CE⊥AD，垂足为E．若∠A＝40°，则∠C的度数为（）A．40°B．50°C．60°D．90°图1分析：根据平行线的性质，得∠D＝∠A＝40°，再在Rt△CED中，根据“直角三角形的两个锐角互余”即可求得∠C的度数．例2 如图2，在Rt△ABC中，∠ABC＝90°，BF是AC边上的中线，DE是△ABC的中位线．若DE＝6，则BF的长为（）A．6 B．4 C．3 D．5图2分析：根据三角形的中位线定理可求出AC 的长，再根据“直角三角形斜边上的中线等于斜边的一半”即可求得BF 的长．例3 如图3，在Rt △ABC 中，∠C ＝90°，∠B ＝30°，AB ＝8．若E ，F 是BC 边上的两个动点，以EF 为边的等边三角形EFP 的顶点P 在△ABC 的内部或边上，则等边三角形EFP 的周长的最大值为．图3分析：当点F 与点C 重合，点P 落在AB 边上时，△EFP 的边长最长，周长也最长，根据“直角三角形中，30°角所对的直角边等于斜边的一半”可求出AC 的长，再利用三角函数，或求出AP 利用勾股定理均可求得△EFP 边长的最大值，进而得解．例4 如图4，某港口P 位于东西方向的海岸线上，甲、乙轮船同时离开港口，各自沿一固定方向航行，甲、乙轮船每小时分别航行12海里和16海里，1小时后两船分别位于点A ，B 处，且相距20海里．若甲船沿北偏西40°方向航行，则乙船沿方向航行．图4分析：由题意，知AP ＝12，BP ＝16，AB ＝20，根据勾股定理的逆定理，可推出△APB 是直角三角形，且∠APB ＝90°，结合甲船的航行方向可推出乙船的航行方向．例5 如图5，在Rt △ABC 中，∠ACB ＝90°，以该三角形的三条边为边向外作正方形，正方形的顶点E ，F ，G ，H ，M ，N 都在同一个圆上．记该圆的面积为S 1，△ABC 的面积为S 2，则12S S 的值是（） A ．5π2 B ．3π C ．5π D ．11π2图5分析：设Rt △ABC 的三边长为a ，b ，c ，其中c 为斜边，设⊙O 的半径为r ，根据图形的特点找出a ，b ，c，r的等量关系，用含c的式子表示S1和S2，即可求出比值．跟踪训练1.如图，△ABC中，∠ACB＝90°，AC＝8，BC＝6，将△ADE沿DE翻折，使点A与点B重合，则CE的长为（）A．198B．2 C．254D．74第1题图第2题图第3题图2.如图，已知A（8，0），C（-2，0），以点A为圆心，AC长为半径画弧，交y轴正半轴于点B，则点B 的坐标为（）A.（0，5）B.（5，0）C.（6，0）D.（0，6）3.（2021·成都）如图，图中数字代表所在正方形的面积，则A所代表的正方形的面积为．4.（2021·西宁）如图，在Rt△ABC中，∠BAC＝90°，D，E分别是AB，BC的中点，连接AE，DE．若DE＝92，AE＝152，则点A到BC的距离是．第4题图第5题图5.如图，在▱ABCD中，点E在AD上，且EC平分∠BED．若∠EBC＝30°，BE＝10，则▱ABCD的面积为．6.对角线互相垂直的四边形叫做“垂美”四边形，现有如图所示的“垂美”四边形ABCD，对角线AC，BD交于点O．若AD＝2，BC＝4，则AB2+CD2＝．第6题图第7题图7.如图，在四边形ABCD中，AB∥CD，∠ABC＝60°，AD＝BC＝CD＝4．若M是四边形ABCD内的一个动点，满足∠AMD＝90°，则点M到直线BC的距离的最小值为．专项二锐角三角函数知识清单1. 锐角三角函数如图，在Rt△ABC中，∠C＝90°，∠A，∠B，∠C的对边长分别为a，b，c，则∠A的正弦：sin A＝ac；∠A的余弦：cos A＝；∠A的正切：tan A＝．∠A的正弦、余弦、正切都是∠A的锐角三角函数．2. 特殊角的三角函数值考点例析例1如图1，点A，B，C在边长为1的正方形网格格点上，下列结论错误的是（）A．1sin3B=B．25sin C C．1tan2B=D．22sin sin1B C+=图1分析：利用正方形网格的特点，由勾股定理得出AB，AC，BC的长，进而利用勾股定理的逆定理推出△ABC 是直角三角形，最后根据锐角三角函数的定义对选项逐一判断即可．归纳：锐角三角函数使用的前提一定是直角三角形，并能准确地找出某个角的对边、邻边和斜边．例2 如图2，在Rt△ABC中，∠ACB＝90°，CE是斜边AB上的中线，过点E作EF⊥AB交AC于点F．若BC＝4，△AEF的面积为5，则sin∠CEF的值为（）A．35B5C．45D25三角函数α30°45°60°sin αcos αtan α图2分析：根据“直角三角形斜边上的中线等于斜边的一半”，得CE ＝AE ＝BE ，进而得到∠BEC ＝2∠A ，连接BF ，由EF ⊥AB ，得∠BFC ＝2∠A ，所以∠BEC ＝∠BFC ，从而有∠CEF ＝∠CBF ．根据三角形的面积公式求出AF 的长，在Rt △BCF 中，利用勾股定理求出CF ，再根据锐角三角函数的定义求解即可．归纳：一个锐角的三角函数值仅与这个锐角的大小有关，而与这个锐角在何处、在何种三角形中无关（即与三角形三边的长短无关）．当一个锐角的三角函数值求解较烦琐或不易直接求得时，可转化为求与其相等的角的三角函数值．跟踪训练1.tan 30°的值等于（）A B C ．1 D ．22.如图，在平面直角坐标系内有一点P （3，4），连接OP ，则OP 与x 轴正方向所夹锐角α的正弦值是（）A ．34B ．43C ．35D ．45第2题图第3题图第4题图3.如图，在△ABC 中，O 是角平分线AD ，BE 的交点．若AB ＝AC ＝10，BC ＝12，则tan ∠OBD 的值是（）A ．12B ．2CD 4.如图，在正方形网格中，每个小正方形的边长都是1，⊙O 是△ABC 的外接圆，点A ，B ，O 在网格线的交点上，则sin ∠ACB 的值是．专项三解直角三角形知识清单解直角三角形的几种常见类型及解法：考点例析例1 在△ABC 中，∠ABC ＝90°．若AC ＝100，sin A ＝35，则AB 的长是（） A ．5003 B ．5035 C ．60 D ．80分析：利用锐角三角函数的定义求出BC 的长，然后再利用勾股定理即可求得AB 的长．例2 如图，△ABC 底边BC 上的高为h 1，△PQR 底边QR 上的高为h 2，则有（）A ．h 1＝h 2B ．h 1＜h 2C ．h 1＞h 2D ．以上都有可能分析：分别作出△ABC 底边BC 上的高和△PQR 底边QR 上的高，再利用锐角三角函数分别表示出h 1和h 2，即可确定其大小关系．跟踪训练1.如图，在△ABC 中，∠B ＝45°，∠C ＝60°，AD ⊥BC 于点D ，BD 若E ，F 分别为AB ，BC 的中点，则EF 的长为（）A B C ．1 D第1题图第2题图2.如图，△ABC 的顶点B ，C 的坐标分别是（1，0），(，且∠ABC ＝90°，∠A ＝30°，则顶点A 的坐标是．3.在△ABC 中，∠A ＝45°，AB ＝BC ＝5，则△ABC 的面积为．4.在锐角三角形ABC 中，∠A ，∠B ，∠C 的对边分别为a ，b ，c ，边角总满足关系式：sin sin sin a b c A B C ==．（1）如图①，若a ＝6，∠B ＝45°，∠C ＝75°，求b 的值；（2）某公园准备在园内一个锐角三角形水池ABC 中建一座小型景观桥CD （如图②所示）．若CD ⊥AB ，AC ＝14米，AB ＝10米，sin ∠ACB ，求景观桥CD 的长度．① ②第4题图专项四锐角三角函数的实际应用知识清单锐角三角函数的实际应用主要是测量物体的高度、测量两点之间的距离等，常用到下面几个概念：1. 仰角、俯角如图1，在视线与水平线所成的锐角中，视线在水平线上方的角叫做，视线在水平线下方的角叫做．图1 图2 图32. 坡度、坡角如图2，坡面的铅直高度h 和水平宽度l 的比叫做坡面的坡度（或坡比），用字母i 表示；坡面与水平面的夹角α叫做坡角，i ＝＝，坡度越大，α越，坡面越．3. 方位角一般是指以观测者的位置为中心，将正北或正南方向作为起始方向，旋转到目标的方向所成的小于90°的角．如图3，点A位于点O的北偏东方向，点B位于点O的60°方向，点C位于点O的（或）方向．考点例析例1 无人机低空遥感技术已广泛应用于农作物监测．如图1，某农业特色品牌示范基地用无人机对一块试验田进行监测作业时，在距地面高度为135 m的A处测得试验田右侧边界N处的俯角为43°，无人机垂直下降40 m至B处，又测得试验田左侧边界M处的俯角为35°，则M，N之间的距离为（参考数据：tan 43°≈0.9，sin 43°≈0.7，cos 35°≈0.8，tan 35°≈0.7）（）A．188 m B．269 m C．286 m D．312 m图1分析：在Rt△AON中，由AO的长和∠N的度数求出ON的长，再在Rt△BOM中，由BO的长和∠M的度数求出MO的长，结合MN＝MO+ON即可求得M，N之间的距离．例2 某商场准备改善原有楼梯的安全性能，把坡角由37°减至30°．已知原楼梯长为5米，调整后的楼梯会加长（参考数据：sin 37°≈0.6，cos 37°≈0.8，tan 37°≈0.75）（）A．6米B．3米C．2米D．1米分析：画出示意图如图2所示，在Rt△BAD中，由AB＝5，∠BAD＝37°，求出BD的长，在Rt△BCD中，根据“直角三角形中，30°角所对的直角边等于斜边的一半”求出BC的长，进而得解．图2例3 如图3，一艘轮船位于灯塔P的南偏东60°方向，距离灯塔50海里的A处，它沿正北方向航行一段时间后，到达位于灯塔P的北偏东45°方向上的B处，此时B处与灯塔P的距离为海里．（结果保留根号）图3分析：过点P作PC⊥AB于点C，在Rt△APC中，由P A的长和∠A的度数求出PC的长，再在Rt△BPC 中，由PC的长和∠B的度数即可求得PB的长．跟踪训练1.如图，在点F处，看建筑物顶端D的仰角为32°，向前走了15米到达点E处，即EF＝15米，在点E处看点D的仰角为64°，则CD的长用三角函数表示为（）A．15sin 32°B．15tan 64°C．15sin 64°D．15tan 32°第1题图第2题图第3题图2.如图，为了测量某建筑物BC的高度，小颖采用了如下的方法：先从与建筑物底端B在同一水平线上的A 点出发，沿斜坡AD行走130米至坡顶D处，再从D处沿水平方向继续前行若干米后至点E处，在E点测得该建筑物顶端C的仰角为60°，建筑物底端B的俯角为45°，点A，B，C，D，E在同一平面内，斜坡AD的坡度i＝1∶2.4．根据小颖的测量数据，计算筑物BC）（）A．136.6米B．86.7米C．186.7米D．86.6米3.某景区A，B两个景点位于湖泊两侧，游客从景点A到景点B必须经过C处才能到达．观测得景点B在景点A的北偏东30°方向，从景点A出发向正北方向步行600米到达C处，测得景点B在C的北偏东75°方向．（1）求景点B和C处之间的距离；（结果保留根号）（2）当地政府为了便捷游客游览，打算修建一条从景点A到景点B的笔直的跨湖大桥．大桥修建后，从景点A到景点B）专项五锐角三角函数中的建模思想知识清单根据实际问题建立数学模型，再通过解决数学问题达到解决实际问题的目的，这种思想被称为建模思想．考点例析例一种可折叠的医疗器械放置在水平地面上，这种医疗器械的侧面结构如图实线所示，底座为△ABC，点B，C，D在同一条直线上，测得∠ACB＝90°，∠ABC＝60°，AB＝32 cm，∠BDE＝75°，其中一段支撑杆CD＝84 cm，另一段支撑杆DE＝70 cm．求支撑杆上的点E到水平地面的距离EF是多少？（结果保留整数；参考数据：sin 15°≈0.26，cos 15°≈0.97，tan 15°≈0.27）分析：过点D作DM⊥EF于点M，DN⊥BA交BA的延长线于点N，解Rt△ABC求出BC的长，再解Rt△BDN 求出DN的长，易得四边形MFND是矩形，利用矩形的性质可得MF＝DN及∠BDM的度数，进而求得∠EDM，最后解Rt△EMD求出EM的长，进而得解．解：归纳：解直角三角形的前提是在直角三角形中进行，对于非直角三角形问题，要注意观察图形特点，作恰当的辅助线，将其转化为直角三角形求解．跟踪训练1.如图①是一台手机支架，图②是其侧面示意图，AB，BC可分别绕点A，B转动，测量知BC＝8 cm，AB ＝16 cm．当AB，BC转动到∠BAE＝60°，∠ABC＝50°时，点C到AE的距离为cm．（结果精确到0.1 cm；参考数据：sin 70°≈0.94）①②①②③第1题图第2题图2.某种落地灯如图①所示，AB为立杆，其高为84 cm；BC为支杆，可绕点B旋转，其中BC长为54 cm；DE为悬杆，滑动悬杆可调节CD的长度．已知支杆BC与悬杆DE之间的夹角∠BCD为60°．（1）如图②，当支杆BC与地面垂直，且CD的长为50 cm时，求灯泡悬挂点D距离地面的高度；（2）在图②所示的状态下，将支杆BC绕点B顺时针旋转20°，同时调节CD的长（如图③），此时测得灯泡悬挂点D到地面的距离为90 cm，求CD的长．（结果精确到1 cm；参考数据：sin 20°≈0.34，cos 20°≈0.94，tan 20°≈0.36，sin 40°≈0.64，cos 40°≈0.77，tan 40°≈0.84）参考答案专项一直角三角形例1 B 例2 A 例3例4 北偏东50°例5 C 解析：如图，取AB的中点O，AC的中点D，连接OC，OD，OE，OG．因为圆心在线段EF和MN的垂直平分线上，所以点O为圆心．设AC＝a，BC＝b，AB＝c，则a2+b2＝c2．在Rt△ABC中，O为AB的中点，所以OA＝OB＝OC．又D为AC的中点，所以OD∥BC．所以OD⊥AC．因为OG，OE为⊙O的半径，所以OD2+DG2＝OB2+BE2，即2222222a cb cb⎛⎫⎛⎫⎛⎫++=+⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭．整理，得a＝b．所以215π4Sc=，224Sc=．所以12SS＝5π．1．D 2．D 3．100 4．3655．50 6．20 7．2专项二锐角三角函数例1 A例2 A 解析：连接BF．在Rt△ABC中，CE是斜边AB上的中线，所以CE＝AE＝BE，所以∠A＝∠ACE．所以∠BEC＝2∠A．因为EF⊥AB，所以EF是AB的垂直平分线．所以S△BEF＝S△AEF＝5，∠FBA＝∠A．所以∠BFC＝2∠A．所以∠BEC＝∠BFC．又∠BEF＝∠BCF＝90°，所以∠CEF＝∠CBF．因为S △AFB ＝2S △AEF ＝10，所以12AF ·BC ＝10．因为BC ＝4，所以AF ＝BF ＝5．所以CF 3．所以sin ∠CEF ＝sin ∠CBF ＝35CF BF =．1．A 2．D 3．A 4 专项三解直角三角形例1 D 例2 A1．C 2．( 3．2或144．解：（1）因为∠B ＝45°，∠C ＝75°，所以∠A ＝180°-∠B -∠C ＝60°．所以6sin 60sin 45b =︒︒，解得b ＝（2）因为sin sin AB AC ACB B =∠14sin B =，解得sin B ．所以∠B ＝60°．所以tan B ＝CD BD =BD CD ．在Rt △ACD 中，AC 2＝CD 2+AD 2，即196＝CD 2+210⎛⎫ ⎪ ⎪⎝⎭，解得CD ＝CD ＝-（舍去）．所以景观桥CD 的长度为专项四锐角三角函数的实际应用例1 C 例2 D 例3 1．C 2．A3．解：（1）过点C 作CD ⊥AB 于点D ．在Rt △ACD 中，∠A ＝30°，AC ＝600，所以CD ＝12AC ＝300．在Rt △BCD 中，∠B ＝75°-∠A ＝45°，所以BC ＝sin 45CD ︒＝．答：景点B 和C 处之间的距离为m ．（2）在Rt △ACD 中，∠A ＝30°，AC ＝600，所以AD ＝AC ·cos 30°＝．在Rt △BCD 中，∠B ＝45°，所以BD ＝CD ＝300．所以AB ＝AD +BD ＝．所以AC +BC -AB ＝600+-（300+≈205（m ）．答：大桥修建后，从景点A 到景点B 比原来少走约205 m ．专项五锐角三角函数中的建模思想例过点D 作DM ⊥EF 于点M ，DN ⊥BA 交BA 的延长线于点N ．在Rt △ABC 中，∠ABC ＝60°，AB ＝32，所以BC ＝AB ·cos 60°＝16．因为CD ＝84，所以BD ＝BC +CD ＝16+84＝100．在Rt △BDN 中，DN ＝BD ·sin 60°＝＝．易得四边形MFND 是矩形，所以MF ＝DN ＝，MD ∥FN ．所以∠BDM ＝∠ABC ＝60°．因为∠BDE ＝75°，所以∠EDM ＝∠BDE -∠BDM ＝75°-60°＝15°．在Rt △EMD 中，DE ＝70，所以EM ＝DE ·sin 15°≈70×0.26＝18.2．所以EF ＝EM +MF ＝18.2+≈105．答：支撑杆上的点E 到水平地面的距离EF 约是105 cm ．1．6.32．解：（1）如图①，过点D 作DF ⊥BC 于点F ．在Rt △DCF 中，CD ＝50，∠FCD ＝60°，所以FC ＝CD ·cos 60°＝25．所以F A ＝AB +BC -FC ＝84+54-25＝113（cm ）．答：灯泡悬挂点D 距离地面的高度为113 cm ．（2）如图②，过点C 作CG 垂直于地面于点G ，过点B 作BN ⊥CG 于点N ，过点D 作DM ⊥CG 于点M ．在Rt △BCN 中，BC ＝54，∠BCN ＝20°，所以CN ＝BC ·cos 20°≈54×0.94＝50.76．所以CM ＝CN +NG -MG ＝CN +AB -MG ＝50.76+84-90＝44.76．在Rt △DCM 中，∠DCM ＝∠BCD -∠BCN ＝40°，所以CD ＝cos40CM ≈44.760.77≈58（cm ）．答：CD 的长约为58 cm ．① ②第2题图。

【解析版】华师大版九年级数学下册课后练习：锐角三角函数的应用+课后练习二及详解

cos BCD
cos55 o
70.2
∴ t甲 = 57.2 10=38.6（秒）， t乙 = 70.2 =35.1（秒）
2
2
∴ t甲 >t乙
答：乙先到达 B 处
满分冲刺题一：
答案： D
详解：如图，在 Rt△ AFG中， tan AFG
AG ，∠ AFG=60°，
FG
∴ FG
AG tan 60o
详解： 1 如图，分别过 A、 D作 AF⊥ BC， DG⊥BC，垂点分别为 F、G
在 Rt△ ABF中， AB=16 米，∠ B=60°， sin B
AF
，
AB
∴ AF 16
3 8 3 ，即 DG= 8 3
2
S 又∵ CE=8，∴ △DCE 1 CE DG 1 8 8 3 32 3
2
2
又∵需加固的大坝长为 150 米，∴需要填方： 150 32 3=4800 3
思维拓展
题面：小明想测量一棵树的高度，他发现树的影子恰好落在地面和一斜坡上；如图，此时测
得地面上的影长为 8 米，坡面上的影长为 4 米．已知斜坡的坡角为 30°，同一时刻，一根
长为 l 米、垂直于地面放置的标杆在地面上的影长为
2 米，则树的高度为
A. (6 3) 米 B.12 米 C. (4 2 3) 米 D ． 10 米
秒后赶到海岸线上的 D处，再向 B 处游去若 CD=40 米， B 在 C的北偏东 35°方向，甲乙的
游泳速度都是 2 米 / 秒问谁先到达 B处？请说明理由
( 参考数据： sin 55°≈ 0.82 ， cos 55°≈ 0.57 ， tan55 °≈ 1.43)
满分冲刺

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2020 中考数学锐角三角函数在实际问题中的应用（含答案）1. 如图，B小军和小兵要去测量一座古塔的高度，他们在离古塔60米的A处用测角仪参考答案:解：过A作AE∥DC交BC于点 E 则AE=CD=60米，则∠ AEB=90°，EC=AD=1.5 在Rt △ ABE中，BE即tan30o60∴ BE 60tan30o 60 330 32所以，古塔高度为：CB BE EC 20 3 1.5 米2. 如图，小强在家里的楼顶上的点A处，测量建在与小明家楼房同水平线上相邻的电梯楼的高，在点A处看电梯楼顶点 B 处的仰角为60°，看楼底点C的俯角为45°，两栋楼之间的距离为30 米，则电梯楼的高BC为多少米？BC参考答案:解：过A作AD∥地面，交BC于D则在Rt △ ABD中，tan 60o BD，即tan 60o BD，∴ BD30 3 AD30在Rt △ ACD中，tan 45o DC，DC即tan 60o，∴DC30AD30∴楼高BC为：BD DC 30 30 3AD=1.5 米，则塔CB的高为多少米？3. 小明在热气球 A 上看到正前方横跨河流两岸的大桥 BC ，并测得 B ，C 两点的俯角分别为 45°， 35°。

已知大桥 BC 与地面在同一水平面上，其长度为 100 米，请求出热气球离地面即热气球的高度为 AD 700 米34. 如图，某建筑物 BC 顶部有一旗杆 AB ，且点 A ，B ，C 在同一直线上．小红在 D 处观测旗杆顶部 A 的仰角为 47°，观测旗杆底部 B 的仰角为 42°．已知点 D 到地面的距离 DE 为1.56m ， EC=21m ，求旗杆 AB 的高度和建筑物 BC 的高度（结果保留小数点后一位，参考数据： tan47 ° ≈1.07 ，tan42 °≈ 0.90 ）．的高度。

（结果保留整数，参考数据：sin35o 172，cos35o6，tan3510)参考答案 : 解：过 A 作 AD ⊥BC 于点 D 则AD 即为热气球的高度，且∠ 1=∠ 2=45°∴可设 AD=BD=x 则 CD=x+100 在 Rt △ ADC 中AD o x tanC，即 tan35o DC x 100 得： x700参考答案 : 解：根据题意， DE=1.56,EC=21, ∠ACE=90° , ∠DEC=90°．过点 D 作 DF ⊥AC,垂足为 F ．则∠ DFC=90°, ∠ ADF=47° , ∠BFD=42°．可得四边形 DECF 为矩形． ∴DF=EC=21,FC=DE=．1 56．∴AF=DF · tan47 °≈ 21×107=22.47 ．在 Rt △ DFB 中， tan BDFDF ∴BF=DF · tan42 °≈ 21×0.90=18.90 ．于是， AB=AF-BF=22.47-18.90=3.57 ≈3.6, BC=BF+FC=18.90+1.56=20.46≈20.5 ．5. 如图所示，探测出某建筑物废墟下方点 C 处有生命迹象．在废墟一侧面上选两探测点A 、B ，AB 相距 2 米，探测线与该面的夹角分别是 30°和 45°（如图）．试确定生命所在点C 与探测面的距离．（参考数据 2 1.41, 3 1.73 ）参考答案 : 解：过 C 作 CD ⊥AB 于点 D ，则∠ DBC=45° =∠ BCD ∴可设 BD=CD=x得 x 3 1 2.73即，点 C 与探测面的距离大约为 2.73 米。

6. 如图所示，如图所示，我市某中学课外活动小组的同学利用所学知识去测量釜溪河沙湾段的宽度。

小宇同学在 A 处观测对岸 C 点，测得∠ CAD ＝45°，小英同学在距 A 处 50 米远的 B在 Rt △ DFA 中， tan ADFAFDF在 Rt △ ACD 中可得： tan DACDCAD即： tan30ox x2处测得∠ CBD ＝30°，请你根据这些数据算出河宽。

（精确到 0.01 米，参考数据， 21.414 ，参考答案 :解：在 Rt △ ACE 中，∠ CAE=45° ∴可设 CE=EA=x在 Rt △ BCE 中， tanB CE ，即 tan30ox，得 x 25 3 25 43.3 25 68.3BE x 50即，河宽约为 68.3 米7.如图，甲、乙为两座建筑物，它们之间的水平距离 BC 为30m ，在A 点测得 D 点的仰角∠ EAD 为 45°，在 B 点测得 D 点的仰角∠ CBD 为 60°，求这两座建筑物的高度（结果保留根号）BC参考答案 :解：如图，过 A 作AF ⊥CD 于点 F ，在 Rt △ BCD 中，∠ DBC=6°0 ， BC=30m ， ∵ tan DBCBC∴CD=BC?tan6°0 =30 3 m ， ∴乙建筑物的高度为 30 3 m ；在 Rt △AFD 中，∠DAF=45°，∴DF=AF=BC=30，m3 1.732 )DD∴ AB=CF=C﹣DDF=30 3 30 m，∴甲建筑物的高度为30 3 30 m．8. 如图所示，在某海域，一艘指挥船在C处收到渔船在B处发出的求救信号，经确定，遇险抛锚的渔船所在的 B 处位于 C 处的南偏西 45°方向上，且 BC ＝60 海里；指挥船搜索发现，在 C 处的南偏西 60°方向上有一艘海监船 A ，恰好位于 B 处的正西方向．于是命令海监船 A 前往搜救，已知海监船 A 的航行速度为 30 海里/小时，问渔船在 B 处需要等待多长时间才能得到海监船 A 的救援？ (参考数据： 2 1.41， 3 1.73 ， 6 2.45，结果精确到 0.1 小时 )参考答案 :解：因为 A 在B 的正西方，延长 AB 交南北轴于点 D ，则 AB ⊥CD 于点 D∵∠ BCD ＝45°， BD ⊥ CD ∴BD ＝CDCD 在 Rt △BDC 中，∵ cos ∠BCD ＝，BC ＝60海里 BC即 cos45°＝CD2，解得 CD ＝30 2 海里60 2∴ BD ＝CD ＝ 30 2 海里∵AB ＝AD －BD∴ AB ＝ 30 6－30 2 ＝30( 6 2)海里 ∵海监船 A 的航行速度为 30 海里/ 小时AB 30 6 2 则渔船在 B 处需要等待的时间为 AB＝＝ 6 2 ≈2.45 －1.41 ＝30 301.04 ≈1.0 小时∴渔船在 B 处需要等待 1.0 小时旅游项目，我市对某山区进行调查，发现一瀑布．为测量它的高度，测量人员在瀑布的对面山上 D 点处测得瀑布顶端 A 点的仰角是 30°，测得瀑布底端 B 点的在 Rt △ ADC 中， ∵tan ∠ ACD ＝ ADCD即 tan60AD 30 23，解得 AD ＝30 6 海里9. 随着人们生活水平的不断提高，旅游已成为人们的一种生活时尚．为开发新的北东俯角是10°，AB与水平面垂直．又在瀑布下的水平面测得CG＝27m，GF＝17.6 m（注：C、G、F三点在同一直线上，CF⊥AB于点F）．斜坡CD＝20m，坡角∠ ECD＝40°．求瀑布AB的高度．（参考数据： 3 ≈1.73 ，sin40 °≈0.64 ，cos40°≈0.77 ，tan40 °≈0.84 ，sin10 ° ≈0.17 ，cos10°≈0.98 ，tan10 °≈0.18）参考答案:解：过点D作DM⊥CE，交CE于点M，作DN⊥AB，交AB于点N，如图所示．在Rt△CMD中，CD＝20m，∠DCM＝40°，∠ CMD＝90°，∴CM＝CD?cos40°≈15.4m，DM＝CD?sin40 ° ∴DN＝MF＝CM＋CG＋GF＝60m．在Rt△BDN中，∠ BDN＝10°，∠BND＝90° ∴BN＝DN?tan10 °≈10.8 m．在Rt△ADN中，∠ ADN＝30°，∠ AND＝90° ∴AN＝DN?tan30 °≈34.6 m．∴AB＝AN＋BN＝45.4m．答：瀑布AB的高度约为45.4 米．10. 如图，斜坡BE，坡顶B到水平地面的距离处，E处分别测得CD顶部点D 的仰角AB为3米，坡底AE为18米，在B ，60°，求CD的高度．（结果3 解得： x ＝9 3＋32，则 CD ＝9 3＋23＋3＝9 3＋92（米）．答： CD 的高度是 9 3＋9米．211. 如图，站在高出海平面 100m 的悬崖 C 处，俯视海平面上一搜捕鱼船 A ，并测得其俯角为 30°，则船与观察者之间的水平距离是多少？船向观察者方向行进了一段距离到达B 处，此参考答案 : 解：由题可知∠ CAD=30°，∠ CBD=60°， CD=100 在 Rt △ ADC 中，tan CADCDAD，即 tan30oCDAD100 ，∴AD，∴AD 100 3CDoCD 100100 3在 Rt △ BDCtan CBD即 tan60o，∴ BDBD，BD BD3在直角△ ABF 中， tanDEC ＝ DECC，则EC ＝tan DCDEC3x tan 60o3(x 3) 米．∵ BF －CE ＝AE ，即 3x 3(x 3) 18 ．3∴船与观察者之间的水平距离为：AD 100 3 ，船航行了100 3100 3 200 3 3312. 有一艘渔轮在海上 C 处作业时，发生故障，立即向搜救中心发出救援信号，此时搜救中心的两艘救助轮救助一号和救助二号分别位于海上 A 处和 B 处， B 在 A 的正东方向，且相距 100 里，测得地点 C 在 A 的南偏东 60°，在 B 的南偏东 30°方向上，如图所示，若救助一号和救助二号的速度分别为 40里/小时和 30 里/小时，问搜救中心应派那艘救助轮才能尽早赶到 C 处救援？（ 3 ≈1.7 ）参考答案 :解：作 CD ⊥ AB 交 AB 延长线于 D ，由已知得：∠ EAC=60°，∠ FBC=30°， ∴∠ 1=30°，∠ 2=90° -3 0°=60°，北北∵∠ 1+∠ 3=∠ 2，∴∠ 3=30°， AB∴∠ 1=∠ 3， 122 ∴AB=BC=100， EF1在Rt △BDC 中， BD 21BC 50，∴ CDBC 2 BD 2 50 3 ，∵AD=AB+BD=15，0 ∴在 Rt △ACD 中， ACAD 2 CD 2 =100 3 ，AC 5∴t 1号 A 40C=25 3 4.25，t 2号10<4.25∴搜救中心应派 2 号艘救助轮才能尽早赶到 C 处救援．13. 一艘渔船位于港口 A 的北偏东 60°方向，距离港口 20海里 B 处，它沿北偏西BC 10 30 337°方向航行至 C 处突然出现故障，在 C 处等待救援， B ，C 之间的距离为 10海里，救援船从港口 A 出发 20 分钟到达 C 处，求救援的艇的航行速度 . （sin37 ° ≈0.6 ，cos37°≈ 0.8 ， 3 ≈1.732 ，结果取整数）参考答案 : 解：辅助线如图所示：BD ⊥AD ，BE ⊥CE ，CF ⊥AF ，有题意知，∠ FAB=60°，∠ CBE=3°7 ， ∴∠ BAD=3°0 ， ∵AB=20海里， ∴BD=10海里，在 Rt △ ABD 中， AD AB 2 BD 2 10 3 17.32ACAF 2 FC 2 182 11.322 21.26在 Rt △BCE 中， sin37CEBCAE在 Rt △ AFC 中，21.26×3≈64海里/ 小时. 答：救援的艇的航行速度大约是 64 海里/ 小时 . 14. 今年，我国海关总署严厉打击“洋垃圾”违法行动，坚决把“洋垃圾”拒于国门之外．如图，某天我国一艘海监船巡航到 A 港口正西方的 B 处时，发现在 B 的北偏东60o 方向，相距 150海里处的 C 点有一可疑船只正沿 CA 方向行驶，C 点在 A 港口的北偏东 30o 方向上，海监船向 A 港口发出指令，执法船立即从 A 港口沿 AC 方向驶出，在D 处成功拦截可疑船只，此时 D 点与 B 点的距离为 75 2 海里．AH 25 32 DH BD 2 2 BH 2 75 BAH 180 BAC 60 在 Rt ABH 中， tan BAH B A H H 31）求 B 点到直线 CA 的距离；2) BD 75 2BH=75AD DH AH 75 25 3 （海里）答：执法船从 A 到D 航行了75 25 3 海里。