弯矩二次分配法.docx
弯矩二次分配法及后续弯矩剪力轴力计算表

3
32.684 31.363 21.35
3
32.684 31.363 -21.35
3
32.329 32.022 21.45
3
32.329 32.022 -21.45
3
30.022 31.755 20.59
3
30.022 31.755 -20.59
3
32.594 37.707 23.43
3
32.594 37.707 -23.43
24.263 12.132
-4.640
31.755
-76.30 24.263 27.773 12.971 -10.511
-4.640 -5.311
32.594 -64.349
0.34 0.272 0.388
25.942 12.132 -0.367 37.707
20.754
-0.293 20.460
-76.30 29.604 -11.053 -0.419 -58.167
剪力
V1
q
b
V0
剪力
MC
q
b
V5AB 47.26 17.66
0.3
44.61 M5AB 25.058 44.61
0.3
V5BA 53.40 17.66
0.3
50.75 M5BA 42.545 50.75
0.3
V5BC 11.81 9.84
0.3
10.33 M5BC 16.562 10.33 0.3
V4AB 72.77 28.18
-76.30 27.773 -10.511 -4.654 -63.692
0.318 0.318 0.364
24.263 12.132 -4.373 32.022
结构设计弯矩2次分配法计算

上柱
下柱 0.433
-24.59 -8.40 -0.37 -33.35
右梁 0.26 -13.35 -14.76 -4.91 -0.22 -33.24
0.215 68.95 -11.96 9.85 0.41 67.25
0.302
-16.79 0.00 0.57 -16.22
0.302
-16.79 -8.40 0.57 -24.62
0.362 18.48 -6.69 -5.03 2.89 9.65
0.362 18.48 -6.69 -5.03 4.46 11.21
0.362 18.48 -6.69 -5.03 4.15 10.90
0.425 18.48 -7.85 -5.95 3.78 8.46
0.469
-8.67 -2.95 4.84 -6.77
1.77 -1.91
-0.95
上柱
0.319
-5.89 0.00 2.55 -3.35
0.319
-5.89 -4.33 3.93 -6.30
0.319
-5.89 -2.95 3.65 -5.19
0.376
-6.95 -2.95 3.35 -6.55
D
左梁
下柱
上柱
0.531 18.48 -9.81 -7.38 5.48 6.77
-2.99 0.00 9.41 6.42
0.402 10.00 -4.02 -31.47 -2.41 -27.90 0.402 10.00 -4.02 -31.47 12.65 -12.84
0.299
-2.99 -1.75 10.38 5.64
0.402 10.00 -4.02 -31.47 13.95 -11.54
恒载作用下弯矩二次分配法

土木0 6 1 2 1 1 2 0 4 3许志刚---弯矩二次分
配
弯
矩
二
分
配
法
计
算
器
在计算竖向恒载和活载作用下框架结构弯矩时要多次使用弯矩二次分配法,此表为恒载作用下12轴线框架的计算过程,如果大家也是三跨的梁可以参用这个计算器,输入每一层的各节点梁柱分配系数和各节点固端弯矩,即可自动计算生成所有其他数据,注意千万不要改动了表上除各节点梁柱分配系数和各节点固端弯矩以外的数
据,否则公式被取消了就无法得出正确结果!!!!(计算的各节点最终弯矩代数和均为0,有的为0.01的是因为四舍五入造成的)
图5-29 恒载作用下的框架弯矩内力二次分配图。
《弯矩二次分配法》课件

02 弯矩二次分配法的基本原 理
弯矩与应力的关系
弯矩是使梁产生弯曲变形的力 矩,与梁的截面和跨度等因素 有关。
应力是由于弯矩引起的梁截面 上的正应力和剪应力,与弯矩 的大小和梁的材料属性有关。
弯矩与应力的关系可以通过材 料力学中的弯曲正应力公式和 剪切应力公式来描述。
弯矩二次分配法的计算步骤
03 弯矩二次分配法的实现过 程
建立模型
确定结构形式和支承条件
确定单元类型和节点
根据实际工程情况,确定结构的跨度 、高度、材料等参数,分为若干个 单元,确定节点位置和数量。
建立计算简图
根据结构形式和支承条件,建立计算 简图,简化实际结构,便于计算分析 。
内存占用减少
优化算法以降低内存占用 ,使其在处理大规模问题 时更加高效。
精度控制
引入误差控制机制,确保 计算结果在可接受的精度 范围内。
应用范围拓展
多跨连续梁
将弯矩二次分配法应用于多跨连 续梁,解决复杂结构的内力分析
问题。
考虑剪切变形
在方法中考虑剪切变形的影响, 以更精确地模拟实际结构的受力
情况。
06 结论与展望
弯矩二次分配法的总结
弯矩二次分配法是一种有效的结构分 析方法,适用于求解连续梁和刚架结 构的弯矩分布情况。
弯矩二次分配法在工程实践中得到了 广泛应用,为结构设计提供了重要的 依据和支持。
该方法基于结构力学的基本原理,通 过迭代计算,对结构的弯矩进行二次 分配,得到更为精确的结果。
优化改进
根据对比分析结果,对计算方法进 行优化改进,提高计算精度和可靠 性。
04 弯矩二次分配法的应用实 例
桥梁工程中的应用
总结词
竖向荷载计算(弯矩二次分配法)实例

05
结论
竖向荷载计算的重要性
确保结构安全
竖向荷载计算是结构设计中的重要环节,准确计 算竖向荷载对于保证结构安全至关重要。
提高结构性能
合理的竖向荷载计算有助于优化结构设计,提高 结构的承载能力、稳定性和抗震性能。
降低成本
竖向荷载计算的误差可能导致结构加固或重建, 准确计算可降低不必要的成本。
弯矩二次分配法的限制条件
01
假定楼板为刚性,不考虑楼板的变形和位移。
ቤተ መጻሕፍቲ ባይዱ02
仅适用于规则的结构,对于不规则的结构需要进行 特殊处理。
03
对于节点平衡条件,仅考虑节点左右两侧的平衡, 不考虑上下平衡。
弯矩二次分配法的优化建议
01 考虑楼板的变形和位移,采用有限元法或其他数 值方法进行计算。
02 对于不规则的结构,采用特殊处理方法,如引入 弹性支座或采用有限元模型进行模拟。
弯矩二次分配法的优势与局限性
优势
局限性
弯矩二次分配法计算过程较为复杂,需要耗费较多 时间和计算资源,对于大型复杂结构可能不适用。
弯矩二次分配法能够考虑各杆件之间的相互 作用和影响,计算结果相对准确,适用于多 种结构形式。
适用范围
弯矩二次分配法适用于梁、柱等杆系结构, 但对于板、壳等连续介质,需要采用其他方 法进行计算。
03
竖向荷载计算实例
实例一:简单框架结构
总结词
简单框架结构适用于跨度较小、层数较少的建筑,其竖向荷载计算相对简单。
详细描述
简单框架结构通常由梁和柱组成,竖向荷载通过梁传递至柱,再由柱传递至基 础。弯矩二次分配法在此类结构中应用广泛,能够快速准确地计算出各构件的 弯矩值。
六层三跨荷载作用下弯矩二次分配法有附加弯矩.xls

-72.52 9.78 -4.29 -0.15 -67.17
0.35 0.253
0.00 23.76 -11.88 -0.54 11.34
17.18 8.59 -0.39 25.37
0.253 0.144
4.62 17.18 9.13 -0.39 25.92
-72.52 9.78 -4.29 -0.22 -67.25
0.99 0.76 -23.01 -11.94
-4.62 -17.18 -8.59 0.26 -25.51
0.00 -23.76 11.88 0.35 -11.53
0.144 0.253 0.253 0.35
72.52 -9.78 4.29 0.22 67.25
-17.18 -8.59 0.39 -25.37
-4.62 -17.18 -9.13 0.39 -25.92
0.00 -23.76 11.88 0.54 -11.34
左梁 0.468
0 6.58 -3.29 -1.89 1.40
上柱
下柱 0.339 偏心矩 1.16 4.77 8.59 -1.37 11.99
右梁 0.193
-15.23 2.72 -1.26 -0.78 -14.55
0.35 0.253
0.00 23.77 -11.89 1.82 13.71
0.222
-43.05 8.57 -4.89 -2.41 -41.78
左梁 0.193
15.23 -2.72 1.26 0.78 14.55
上柱
下柱 0.339 偏心矩 -1.16 -4.77 -8.59 1.37 -11.99
右梁 0.468
0.00 -6.58 3.29 1.89 -1.40
力矩分配法两跨弯矩二次分配xls
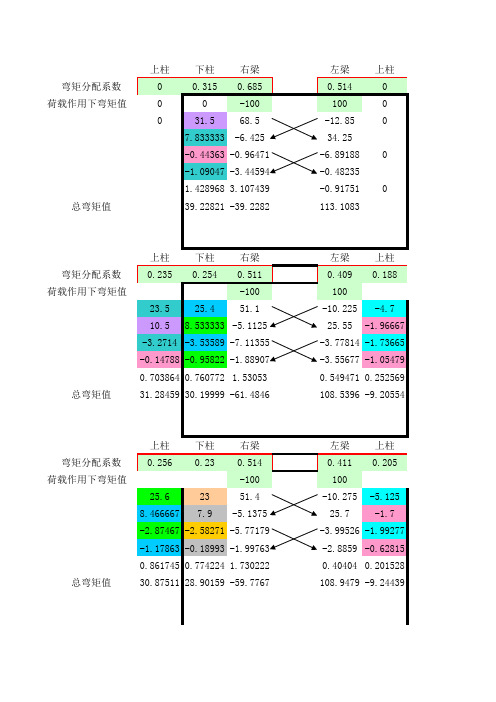
上柱下柱右梁左梁上柱弯矩分配系数00.3150.6850.5140荷载作用下弯矩值00-1001000031.568.5-12.8507.833333-6.42534.25-0.44363-0.96471-6.891880-1.09047-3.44594-0.482351.4289683.107439-0.917510总弯矩值39.22821-39.2282113.1083上柱下柱右梁左梁上柱弯矩分配系数0.2350.2540.5110.4090.188荷载作用下弯矩值-10010023.525.451.1-10.225-4.710.58.533333-5.112525.55-1.96667-3.2714-3.53589-7.11355-3.77814-1.73665-0.14788-0.95822-1.88907-3.55677-1.054790.7038640.760772 1.530530.5494710.252569总弯矩值31.2845930.19999-61.4846108.5396-9.20554上柱下柱右梁左梁上柱弯矩分配系数0.2560.230.5140.4110.205荷载作用下弯矩值-10010025.62351.4-10.275-5.1258.4666677.9-5.137525.7-1.7-2.87467-2.58271-5.77179-3.99526-1.99277-1.17863-0.18993-1.99763-2.8859-0.628150.8617450.7742241.7302220.404040.201528总弯矩值30.8751128.90159-59.7767108.9479-9.24439上柱下柱右梁左梁上柱弯矩分配系数0.2370.2340.5290.4210.188荷载作用下弯矩值-10010023.723.452.9-10.525-4.77.666667-5.262526.45-1.53333-0.56979-0.56258-1.2718-4.91693-2.19568-0.8609-2.45846-0.6359-0.596210.786690.7767321.755945-0.25314-0.11304总弯矩值30.7226723.61416-54.3368110.119-9.13827柱底弯矩值左梁宽(m)0.3000.300左梁高(m)0.5000.000中框架梁惯性矩I。
弯矩二次分配法excel

弯矩二次分配法excel弯矩二次分配法(Moment Distribution Method)是一种用于计算连续梁和框架结构内力的方法。
它的原理是通过数值迭代的方式来逐步分配弯矩,直到收敛为止。
这种方法在工程实践中广泛应用,其计算结果精确可靠。
弯矩二次分配法的基本步骤如下:1. 绘制结构的荷载图和剪力图首先,根据结构的几何形状和荷载情况,绘制出整个结构的荷载图和剪力图。
这些图用于确定结构中各个节点的边界条件和外力作用点。
2. 划分初始刚度矩阵将结构按照其自由度进行划分,建立初始的刚度矩阵。
每个节点的自由度包括水平位移和转角,而每个单元的自由度包括剪力和弯矩。
刚度矩阵记录了结构中各个单元之间的刚度关系。
3. 进行弯矩分配根据结构的初始刚度矩阵以及节点的边界条件,通过弯矩分配的方法来逐步计算每个单元的剪力和弯矩。
首先,将全局外力施加到结构上,然后根据初始刚度矩阵和外力计算出每个单元的初始剪力和弯矩。
接下来,按照一定的迭代顺序,将每个单元的剪力和弯矩按照一定的比例分配给相邻的单元,然后更新刚度矩阵。
直到满足一定的收敛条件,即剪力和弯矩的分配趋于稳定,这个过程称为弯矩分配。
4. 计算节点位移在进行了弯矩分配之后,根据节点边界条件和每个单元的位移,可以计算出每个节点的位移。
这里使用弯矩二次分配法的一个重要假设,即梁在弯曲作用下可以看作刚性倍增杆,因此弯曲刚度与柔度成反比。
5. 更新刚度矩阵根据已知的节点位移和单元位移,可以更新刚度矩阵。
通过多次迭代计算,直到满足一定的收敛条件。
6. 计算内力最后,在完成弯矩分配和节点位移计算之后,根据梁的基本原理和弯矩分配法的结果,可以得到结构中各个节点和单元的内力。
以上是弯矩二次分配法的基本步骤,通过这种方法可以计算得到结构中各个节点和单元的内力分布。
这种方法在实际工程中广泛应用,尤其是对于复杂结构的计算分析非常有用。
在Excel中,可以通过建立相应的计算模型和公式来实现弯矩二次分配法的计算。
弯矩二次分配法

梁端弯矩调幅
(1) 为何要进行调幅
框架构造梁端弯矩较大,配筋较多,因而不便施 工。而框架中允许梁端出现塑性铰。所以,在梁中可 考虑塑性内力重分布,一般是降低支座弯矩(梁端弯 矩),以减小支座处旳配筋。
(2) 怎样进行调幅 ① 根据工程经验,对钢筋混凝土框架,可取
调幅系数:
钢筋混凝土装配式框架 钢筋混凝土现浇式框架
因为框架构造对称、荷载对称,故可取如下图(b)所示半边构造计算。 ① 梁旳线刚度
其他层柱:
梁、柱转动刚度及相对转动刚度见表3.3。
(2)计算分配系数: 分配系数按下式计算:
(4)弯矩分配与传递
弯矩分配与传递如图所示。首先将各节点旳分配系数填在相 应方框内,将梁旳固端弯矩填写在框架横梁相应位置上,然后 将节点放松,把各节点不平衡弯矩“同步”进行分配。
二、弯矩二次分配法
对六层下列无侧移旳框架,此法较为以便。
详细计算环节:
(1)计算框架各杆旳线刚度及分配系数。 (2)计算框架各层梁端在竖向荷载作用下旳固端弯矩。 (3)计算框架各节点处旳不平衡弯矩,并将每一节点处旳不平
衡弯矩同步进行分配并向远端传递,传递系数为1/2。 (4)进行两次分配后结束(仅传递一次,但分配两次) (5)将各杆端旳固端弯矩、第一。 这么,在支座出现塑性铰后来,不会造成跨中截面 承载力不足。一般,跨中弯矩可乘以1.1~1.2旳调 整系数(见下图)。
为了确保梁旳安全,跨中弯矩还必须满足下列条 件:
图 框架梁塑性调幅
M1' M1
M 2 ' M 2 M 0 ' M 0.5 (M1 M 2 )
二、弯矩二次分配法
对六层下列无侧移旳框架,此法较为以便。 基本假定:
① 框架梁、柱正交; ② 框架梁连续且贯穿整个楼层; ③ 不考虑轴向变形; ④ 框架侧移忽视不计。
2016新编弯矩二次分配法
2016新编弯矩二次分配法按弯矩二次分配法计算例题5-2钢筋混凝土框架的弯矩,并绘出弯矩图。
屋面和楼面荷载标准值见下表7。
表7 例题5-3框架屋面和楼面荷载【解】(1)计算梁、柱转动刚度因为框架结构对称、荷载对称,又属奇数跨,故在对称轴上梁的截面只有竖向位移(沿对称轴方向),没有转角。
所以可取如图4所示半边结构计算。
对称截面处可取为滑动端。
梁、柱转动刚度及相对转动刚度如表8所示。
图4 [例题5,3]计算简图表8 粱、柱转动刚度及相对转动刚度(2)计算分配系数分配系数按下式计算:其中各节点杆件分配系数见表9。
表9 分配系数(3)荷载分析1)屋面梁上线荷载设计值?恒载:1.2[(2.93+1.00+2.60) ×4.5+0.25×0.60×25×1.2]=40.67kN/m 活载:(?式中系数1.2为考虑梁挑檐及抹灰重的系数)q=45.08 kN/m 12)楼面梁上线荷载设计值教室恒载:1.2[(1.10+1.00+2.60) ×4.5+0.25×0.60×25×1.2]=30.78kN/m 活载:(?系数0.9为屋面及楼而活荷载折减系数。
)q=42.12 kN/m 2走道恒载:=30.78kN/m活载:q=44.96 kN/m 3(4)梁端固端弯矩M F顶层边跨梁(教室):中跨梁(走道):其他层边跨梁(教室):中跨梁(走道):(5)弯矩分配与传递弯矩分配与传递按图5的方法进行。
首先将各节点的分配系数填在相应方框内;将梁的固端弯矩填写在框架横梁相应位置上。
然后将节点放松,把各节点不平衡弯矩同时进行分配。
假定远端固定进行传递(不向滑动端传递):右(左)梁分配弯矩向左(右)梁传递;上(下)柱分配弯矩向下(上)柱传递(传递系数均为1,2)。
第一次分配弯矩传递后,再进行第二次弯矩分配,然后不再传递。
实际上,弯矩二次分配法,只将不平衡弯矩分配两次,将分配弯矩传递一次。
弯矩二次分配法

弯矩二次分配法弯矩二次分配法是一种用于处理多成分系统优化问题的方法。
它结合了反比例定律、动态规划和解析几何学等多学科技术,可以有效地解决多成分系统优化问题。
它为解决复杂的在线优化问题提供了新的解决思路。
弯矩二次分配法的基本思想是将优化的多成分系统组合成弯矩函数,然后借助反比例定律和动态规划,将多变量的优化问题转换为弯矩函数的极值问题。
弯矩函数在极值问题中,可以采用解析几何学方法来求得极值点,从而获得问题的最优解。
它还可以使用改进的动态规划方法,将极值问题转换为搜索问题,从而有效解决高维的优化问题。
弯矩二次分配法的应用很广泛,包括工业优化、金融优化、机器学习优化等方面。
它主要用于多成分系统的优化,比如交通系统的优化、资源配置的优化等等。
针对上述问题,弯矩二次分配法可以采用反比例定律,将多变量问题转换为相关弯矩函数的极值问题,然后借助动态规划和解析几何学等技术来求解,从而获得问题的最优解。
弯矩二次分配法的另一个重要应用是定价的优化。
在定价优化中,有很多变量,如定价、促销时间、折扣等,它们之间是复杂的相互关系,由于其多变量性,单纯地采用传统的动态规划方法很难得到高效的最优解,而采用弯矩二次分配法可以有效解决这个问题。
此外,弯矩二次分配法在多终端视频压缩技术中也有广泛的应用。
多终端视频压缩技术涉及多终端网络和视频通道,多个终端网络之间的压缩参数有复杂的相互关系,由于其多变量性,单纯地采用传统的动态规划方法无法得到高效的最优解,而采用弯矩二次分配法可以有效地解决这个问题。
总的来说,弯矩二次分配法是一种实用的多成分系统优化方法,它结合了反比例定律、动态规划和解析几何学等多学科技术,在多成分系统优化问题中取得了很大的进展,并可以有效解决复杂的在线优化问题。
由于其多功能性,它也被广泛应用于工业优化、金融优化和机器学习优化等多个领域,为解决复杂优化问题提供了有用的解决方案。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
按弯矩二次分配法计算例题
5-2钢筋混凝土框架的弯矩,并绘岀弯矩图。
屋面和楼面荷载标准值见下表
7
表7例题5-3框架屋面和楼面荷载
荷载性质 荷载类别 屋面荷载(kN / n l )
楼面荷tt(tπ∕m 5) 熬
室
走 道
活
载
使用荀载 0.70 2,00
雷荷載 0.30 —
—— 恒 载
地面材料重 2.93 1.10 1.10 誓合层重 1.00 1.00
1.00 预制板重
2.60
2.60
2.60
【解】
⑴计算梁、柱转动刚度
因为框架结构对称、荷载对称,又属奇数跨,故在对称轴上梁的截面只有竖向位移 取如图4所示半边结构计算。
对称截面处可取为滑动端。
梁、柱转动刚度及相对转动刚度如表
8所示。
图4 [例题5 - 3]计算简图
表8 粱、柱转动刚度及相对转动刚度
⅞3 ~44.
9QK7∣h
Qj=4Ξ. 12Wni ππππm
誓严兰!牛
I
y∏⅛
¾ =44. 96kN∕m ⅛
Hin y 丄山斛山H
IIiTnrnlnlInhiimniiIii
(沿对称轴方向),没有转角。
所以可
构件宕称
转动刚度SM ・沁
相对转动刚度F
框架梁
边跨
4Xk 尸4X 24
X 10⅛6・ 64X IO 1
1.072 中» Ξ×k b -2X½90X 10⅛l t BOXID l 1,019 框架柱
首S
4×k e =4×Ξ2. 53XlO 3=QO. 12×103 1.000 其他层
4 Xk 尸4 × 28,48 X 1O 3=113,92× IO 3
1, 264
(2)计算分配系数
分配系数按下式计算:
其中各节点杆件分配系数见表
9
-M- ⅛
∑⅛
d 左梁
□右梁
"上柱
d 下柱
5 1*O7Ξ÷L. 264=2. 33
6 --- 0.459 — 0. 541 4 1.072+1.204X2-3.600
0. 293 0.351 0. 351 3 1.072+1. 264×S=3.600 — O T 298 0.351 0. 351 2 1.CW2+1. 264+1.00=3.336 — 0. 321 0.379 6 300 10 I i 072+1.019+1. 2^4=3. 355 0. 320 0. 303 — 0. 377 9 1.072+1.019+1. 2S4×2=4.619 0+ Ξ3≡ 0. 220 0*274 0. 274 8 1.072+1,019+1- 264× 2=4.619
O t 232 Q,22O 0.274 0, 274
1,072+1.019+1. Ξ64+l. Ooo=4. 355
0. 246
0. 234
0.290
0. 230
(3)荷载分析
1)屋面梁上线荷载设计值
①
×.5+0.25 ×0.60 ×25×1.2 ]=40.67kN∕m
1.4×D.70×4.5=4.41 kN/m
(①式中系数1.2为考虑梁挑檐及抹灰重的系数)
q 1=45.08 kN/m
2)楼面梁上线荷载设计值
教室
恒载:1.2[(2.93+1.00+2.60)
活载:
恒载:1.2[(1.10+1.00+2.60) ×.5+0.25 ×0.60 ×25×1.2]=30.78kN∕m 活载: 1.4χ2 00⅛4 5χ0.9s =11.34 kN/m
(②系数0.9为屋面及楼而活荷载折减系数。
)
q 2=42.12 kN/m
走道
恒载:=30.78kN∕m
活载:
1.4x
2.50x4.5x0.9=14.18 kN/m
q 3=44.96 kN/m
(4)梁端固端弯矩 M F
顶层
1 1
=
=-×45^2× - =33.81⅛Λr -w
中跨梁(走道):
’「
■ 一
二 其他层
M F =
= —×42 12×5.7r = 114 04⅛V -^2
边跨梁(教室):
L
(5)弯矩分配与传递
弯矩分配与传递按图 5的方法进行。
首先将各节点的分配系数填在相应方框内;将梁的固端弯矩填写在框架横梁 相应位置上。
然后将节点放松,把各节点不平衡弯矩同时进行分配。
假定远端固定进行传递 (不向滑动端传递):右
(左)
梁分配弯矩向左(右)梁传递;上(下)柱分配弯矩向下(上)柱传递(传递系数均为
1 /2)。
第一次分配弯矩传递后,再进行 第二次弯矩分配,然后不再传递。
实际上,弯矩二次分配法,
只将不平衡弯矩分配两次,将分配弯矩传
边跨梁(教室):
◎詁22.皿
中跨梁 (走道):
(6)作弯矩图
将杆端弯矩按比例画在杆件受拉一侧。
对于无荷载直接作用的杆件 (如柱),将杆端弯矩连以直线,即为该杆的弯矩图;
对于有荷载直接作用的杆件 (如梁),以杆端弯矩的连线为基线,叠加相应简支梁的弯矩图,即为该杆件的弯矩图。
例如顶层
边跨横梁B 5, 10的跨中弯矩为
=-×45.08x5 72-(S2.86+116.38)^=83 46fcV-w
8 ' Z
框架的弯矩图(设计值)如图6所示。
上柱下柱右粱
0.541 0,459
-122 05
O 351
40.03 33.02 -15.35 ST.' 70
3 . 351 ⅛O. 03
2^.02 -11.34 46.71 43.22 -3. 84 59.40
66.03
56.02 20. 02 -1⅛. 1£ -3. 19 -2.71 Θ2. 06 T2.冊 -114.04
40 03
20.02 -⅛.32 -15.35 -13. Ol
TT T S ~-ιoe.4i
0.351 O. 2Sβ -114.04
⅛0- tt¾ Γjg J 8 TTbl Σ9Γ32^
-11.3⅛ -¾53 飞 6
Cbi
j 1
0.300 0.321
-114 04
34.21 3&吕1 -9.8S
-3 C¼ 郎
31,17
-90.5T
左粱上柱下柱右梁
0.377 0.303 122. 05 -28.24
20.01 -5.44 116.3B
0.232 M 274
114 04 -18. S3 -22.01
1L4.S7 35 T3
0.232 0.Z74 114.04
-18,63 -22.01 -33.91
-33. 27 -26.T4 -11.01 -6 41 一5-15 -50.69
-65 70
O 274 0. 220 -33.T2
-22.01 -IT J ST
-Ilol 2.θ2 2.34 -30.10
-49. 05
0.2T4
0.220 -33.72 -22.01 -1T.S7 -11.70
113.T3
-31 45
-32. 14 -50」:
j 0. 246 0.2⅛0 0.230 0.234 114 04
-Ifi I re -23-391 -13.47
-33H 72 -13. BO 16,31 -IeO -IiOI
'2. 12
'1,58
-ITl IloTe
-36. ⅛ -Zi 15
-54.23
-10.08
图5 弯矩分配与传递
0.320
16.99 -11 Ol
1.5T
1,£5
图6中括号内的数字为梁端弯矩调幅后相应截面弯矩数值 (调幅系数为0 • 8)
图6框架弯矩图计算值
框架结构梁端弯矩较大,配筋较多,因而不便施工。
由于超静定钢 筋混凝土结构具有塑性内力重分布的性质,所以在重力荷载作用下可 乘以调幅系数β,适当降低梁端弯矩。
根据工程经验,对现浇钢筋混 凝土框架,可取β =0.40.9,梁端弯矩降低后,跨中弯矩增加。
这样, 梁端弯矩调幅后,不仅可以减少梁端配筋数量,达到方便施工的目的, 而且还可以提高柱的安全储备,以满足“强柱弱梁”的设计原则。
i99 0K7⅛ 2∖}
50 ∣(∣
5i ∣ fΛJ
31.45
5c ?
Θ
(b
>11 30
M f»| (kN
¢)
116 ISOl MJ)
A2 H6{66 29)
∣∣C.4KM ∣
⅛3)
(⅛l -<w M 4⅛ 4ft.71
UOTO (W. 9N)
113 H
吻
r 一 <i f .
I OTAfJQ i √κ
4S.7L
IlO 7⅛
00.J7 31 17
j⅛ 52
∣4 (I
创
W
o r 2fi.i5
LO
54 2J
15 W。
