几何变换——旋转变换
数学几何变换的方法

数学几何变换的方法几何变换是数学中一项重要的研究内容,通过对图形进行不同的操作,可以实现平移、旋转、缩放等效果。
这些变换方法不仅在几何学中有着广泛的应用,还在计算机图形学、机器人学等领域发挥着重要作用。
本文将介绍几何变换的常见方法及其应用。
一、平移变换平移变换是指将图形沿着指定方向上移动一定距离的操作。
其数学表达式为:平移后的坐标 = 原坐标 + 平移矢量平移矢量的大小和方向决定了平移的距离和方向。
平移变换常用于游戏开发、图像处理等领域,可以实现图形的移动、平移动画效果等。
二、旋转变换旋转变换是指将图形围绕某个中心点按一定角度进行旋转的操作。
其数学表达式为:旋转后的坐标 = 中心点坐标 + R * (原坐标 - 中心点坐标)其中,R为旋转矩阵,通过矩阵乘法将原坐标进行旋转。
旋转变换常用于计算机图形学中,实现图像的旋转、三维模型的变换等。
三、缩放变换缩放变换是指改变图形的尺寸大小的操作。
其数学表达式为:缩放后的坐标 = 原坐标 * 缩放因子缩放因子可以是一个比例因子,用于确定缩放的大小,也可以是一个矩阵,对各个坐标轴进行不同程度的缩放。
缩放变换常用于计算机辅助设计、图像处理等领域,可以实现图形的放大、缩小、图像的拉伸等效果。
四、对称变换对称变换是指将图形绕着中心轴进行镜像翻转的操作。
其数学表达式为:对称后的坐标 = 中心轴坐标 + S * (原坐标 - 中心轴坐标)其中,S为对称矩阵,通过矩阵乘法将原坐标进行对称。
对称变换常用于图像处理中,实现图像的镜像翻转、对称图案的生成等。
五、投影变换投影变换是指将三维物体投影到二维平面上的操作,常见的有透视投影和正交投影两种形式。
投影变换常用于计算机图形学中,实现三维物体的绘制和显示。
总结:数学几何变换的方法包括平移、旋转、缩放、对称和投影等。
这些变换方法在各个领域中都有重要应用,比如游戏开发、图像处理、计算机辅助设计等。
掌握几何变换的方法对于理解和应用相关领域的技术具有重要意义。
中考数学专题复习旋转类几何变换
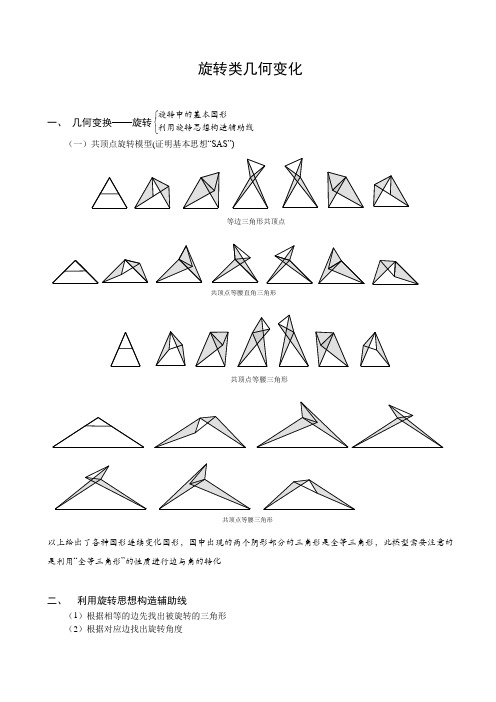
旋转类几何变化一、几何变换——旋转旋转中的基本图形利用旋转思想构造辅助线⎧⎨⎩(一)共顶点旋转模型(证明基本思想“SAS”)等边三角形共顶点共顶点等腰直角三角形共顶点等腰三角形共顶点等腰三角形以上给出了各种图形连续变化图形,图中出现的两个阴影部分的三角形是全等三角形,此模型需要注意的是利用“全等三角形”的性质进行边与角的转化二、利用旋转思想构造辅助线(1)根据相等的边先找出被旋转的三角形(2)根据对应边找出旋转角度(3)根据旋转角度画出对应的旋转的三角形三 、 旋转变换前后具有以下性质:(1)对应线段相等,对应角相等 (2)对应点位置的排列次序相同(3)任意两条对应线段所在直线的夹角都等于旋转角θ.考点一 旋转与最短路程☞考点说明:旋转与最短路程问题主要是利用旋转的性质转化为两点之间线段最短的问题,同时与旋转有关路程最短的问题,比较重要的就是费马点问题,涉及费马点问题,视学生程度进行选择性讲解。
【例1】 如图,四边形ABCD 是正方形,ABE ∆是等边三角形,M 为对角线BD 上任意一点,将BM 绕点B逆时针旋转60︒得到BN ,连接AM 、CM 、EN . ⑴求证:AMB ENB ∆∆≌⑵①当M 点在何处时,AM CM +的值最小;②当M 点在何处时,AM BM CM ++的值最小,并说明理由; ⑶当AM BM CM ++的最小值为31+时,求正方形的边长.ENMDCB A【例2】 阅读下列材料对于任意的ABC ∆,若三角形内或三角形上有一点P ,若PA PB PC ++有最小值,则取到最小值时,点P 为该三角形的费马点。
①若三角形内有一个内角大于或等于120︒,这个内角的顶点就是费马点②若三角形内角均小于120︒,则满足条件120APB BPC APC ∠=∠=∠=︒时,点P 既为费马点 解决问题:⑴如图,ABC ∆中,三个内角均小于120︒,分别以AB 、AC 为边向外作等边ABD ∆、ACE ∆,连接CD 、BE 交于点P ,证明:点P 为ABC ∆的费马点。
几何形的旋转和对称变换

几何形的旋转和对称变换几何形的旋转和对称变换是数学中常见的概念和技巧。
通过旋转和对称变换,我们可以改变几何形的位置和形状,展现出不同的视觉效果和特性。
本文将介绍旋转和对称变换的定义、性质以及在实际问题中的应用。
一、旋转变换旋转变换是指将几何形绕某个点或某条直线旋转一定角度,从而改变形状和位置。
1. 定义设点A(x, y)绕点O(a, b)逆时针旋转θ度,则旋转后点A的坐标为A’(x', y')。
根据旋转变换的定义,有以下公式:x' = a + (x-a)cosθ - (y-b)sinθy' = b + (x-a)sinθ + (y-b)cosθ2. 性质- 旋转变换不改变几何形的大小。
- 旋转变换保持直线上的点的相对位置关系。
- 旋转角度可以是正数或负数,正数表示逆时针旋转,负数表示顺时针旋转。
3. 应用旋转变换在计算机图形学、机器人学和物理学等领域有广泛的应用。
在设计制图中,旋转变换可以用于生成各种艺术效果、模拟物体的运动轨迹等。
在机器人学中,旋转变换可以应用于机器人的路径规划和姿态控制。
在物理学中,旋转变换可以用于分析刚体的运动和转动。
二、对称变换对称变换是指将几何形围绕着某个轴线或中心对称,从而保持形状不变或形状镜像对称。
1. 定义- 轴对称:如果一个几何形上的任意一点到轴的距离和该点的镜像到轴的距离相等,那么这个几何形关于该轴对称。
常见的轴对称有水平轴对称、垂直轴对称和斜对称。
- 中心对称:如果一个几何形上的任意一点关于某个点对称后仍然位于几何形上,那么这个几何形关于该点中心对称。
中心对称即是以某个点为中心,投影方向相反的对称。
2. 性质- 对称变换保持几何形的面积和周长不变。
- 轴对称保持几何形的形状相同,而中心对称保持几何形的形状镜像对称。
- 轴对称和中心对称可以叠加使用,得到更复杂的变换效果。
3. 应用对称变换在几何学、物理学和图像处理等领域具有重要的应用。
旋转平移翻折的几何变换与性质

旋转平移翻折的几何变换与性质旋转、平移和翻折是几何中常见的基本变换方式,它们在空间和平面几何中发挥着重要的作用。
本文将介绍旋转平移翻折的几何变换及其性质,推导其数学表达式,并通过具体的实例来说明其应用。
一、旋转变换旋转是指将平面或空间中的图形按照一定角度绕着旋转中心进行旋转的操作。
对于平面上的点(x, y),其绕原点逆时针旋转θ度后的新坐标可以由以下公式计算得出:x' = x*cosθ - y*sinθy' = x*sinθ + y*cosθ其中,x'和y'分别表示旋转后点的坐标,θ为旋转角度。
二、平移变换平移是指将平面或空间中的图形沿着指定的方向和距离进行移动的操作。
平移变换可以用一个向量来表示。
对于平面上的点(x, y),其平移(dx, dy)后的新坐标可以由以下公式计算得出:x' = x + dxy' = y + dy其中,(dx, dy)为平移向量,x'和y'分别表示平移后点的坐标。
三、翻折变换翻折是指将平面或空间中的图形沿着指定的轴进行对称的操作。
对于平面上的点(x, y),其关于直线y=k翻折后的新坐标可以由以下公式计算得出:x' = xy' = 2k - y其中,(x', y')为翻折后点的坐标,k为翻折轴的位置。
以上是旋转、平移和翻折的几何变换的数学表达式。
下面将通过实例说明它们在几何问题中的应用。
实例一:旋转变换假设有一张平面上的三角形ABC,顶点分别为A(1, 2),B(3, 4)和C(5, 6)。
现在需要将该三角形绕原点顺时针旋转60度,求旋转后各顶点的坐标。
根据旋转变换的公式,旋转角度θ=60°,原点为旋转中心,可以计算得出旋转后的各顶点坐标为:A'(1*cos60° - 2*sin60°, 1*sin60° + 2*cos60°) = (0.5, 2.598)B'(3*cos60° - 4*sin60°, 3*sin60° + 4*cos60°) = (-1.133, 4.330)C'(5*cos60° - 6*sin60°, 5*sin60° + 6*cos60°) = (1.333, 7.464)实例二:平移变换假设有一条直线L,其方程为y = 2x - 1。
旋转变换-高中数学知识点讲解

旋转变换1.旋转变换【知识点的知识】1、线性变换我们把形如{푥푦′′ == 푎푐 푥푥 ++ 푑푏푦푦(※)的几何变换叫做线性变换,(※)式叫做这个线性变换的坐标变换公式,P ′(x ′,y ′)是 P (x ,y )在这个线性变换作用下的像.(2)常见的线性变换有旋转变换、反射变换、伸缩变换、投影变换、切变变换.(3)对同一个直角坐标平面内的两个线性变换σ、ρ,如果对平面内任意一点 P ,都有σ(P )=ρ(P ),则称这 个两个线性变换相等,简记为σ=ρ,设,所对应的二阶矩阵分别为 A ,B ,则 A =B .2、旋转变换P (x ,y )绕原点逆时针旋转 180°得到 P ′(x ′,y ′),称 P ′为 P 在此旋转变换作用下的象.变换的坐标 公式和二阶矩阵为:【解题方法点拨】1.几种常见的线性变换(1)恒等变换矩阵 M = ;(2)旋转变换 R θ 对应的矩阵是 M = ;1 / 2(3)反射变换要看关于哪条直线对称.例如若关于x 轴对称,则变换对应矩阵为M1=;若关于y 轴对称,则变换对应矩阵为M2=;若关于坐标原点对称,则变换对应矩阵M3=;(4)伸压变换对应的二阶矩阵M=,表示将每个点的横坐标变为原来的k1 倍,纵坐标变为原来的k2 倍,k1,k2 均为非零常数;(5)投影变换要看投影在什么直线上,例如关于x 轴的投影变换的矩阵为M=;(6)切变变换要看沿什么方向平移,若沿x 轴平移|ky|个单位,则对应矩阵M=,若沿y 轴平移|kx|个单位,则对应矩阵M=.(其中k 为非零常数).2.线性变换的基本性质设向量α=,规定实数λ与向量α的乘积λα=;设向量α=,β=,规定向量α与β的和α+β=.(1)设M是一个二阶矩阵,α、β是平面上的任意两个向量,λ是一个任意实数,则①M(λα)=λMα,②M(α+β)=Mα+Mβ.(2)二阶矩阵对应的变换(线性变换)把平面上的直线变成直线(或一点).2/ 2。
几何形的旋转平移和对称变换

几何形的旋转平移和对称变换几何形的旋转、平移和对称变换几何形的旋转、平移和对称变换是几何学中的基础概念和操作,它们在数学和实际应用中都扮演着重要的角色。
通过这些变换,我们可以改变和调整图形的位置、方向和形状,使得几何问题的解决变得更加灵活和方便。
本文将对几何形的旋转、平移和对称变换进行详细介绍。
1. 旋转变换旋转变换是指沿着一个固定点旋转图形一定的角度。
在平面几何中,我们通常以原点为中心,按照逆时针方向旋转来描述旋转变换。
旋转变换可以保持图形的大小和形状不变,只改变其方向和位置。
常见的旋转角度有90度、180度和360度。
旋转变换的数学表示式为:x' = x*cosθ - y*sinθy' = x*sinθ + y*cosθ其中,(x, y)是旋转前的点的坐标,(x', y')是旋转后的点的坐标,θ是旋转的角度。
2. 平移变换平移变换是指将图形沿着平行于坐标轴的方向移动一定的距离。
平移变换只改变图形的位置,保持其大小、形状和方向不变。
平移变换可以用向量来表示,其中向量的分量表示图形在x轴和y轴上的位移。
平移变换的数学表示式为:x' = x + dxy' = y + dy其中,(x, y)是平移前的点的坐标,(x', y')是平移后的点的坐标,(dx, dy)是平移的距离。
3. 对称变换对称变换是指将图形绕着某个轴线或某个点进行翻转,使得图形在变换前后保持镜像对称关系。
常见的对称变换有关于x轴、y轴和原点的对称。
对称变换的数学表示式为:关于x轴对称:(x, y) -> (x, -y)关于y轴对称:(x, y) -> (-x, y)关于原点对称:(x, y) -> (-x, -y)4. 综合应用几何形的旋转、平移和对称变换在许多领域有着广泛的应用,如建筑设计、计算机图形学、机器人学等等。
通过这些变换,我们可以灵活地处理图形的位置和形状,满足不同需求的设计和计算要求。
三维几何中的旋转变换

三维几何中的旋转变换在三维几何中,旋转变换是一种重要的几何操作,它可以用来描述物体在三维空间中的旋转运动。
旋转变换在计算机图形学、机器人学、航空航天等领域都有广泛的应用。
本文将介绍旋转变换的基本原理、表示方法以及应用案例。
一、旋转变换的基本原理在三维几何中,旋转变换是指将一个点或物体绕某一旋转轴旋转一定角度的操作。
旋转变换可以通过旋转矩阵来描述,旋转矩阵是一个3×3的矩阵,表示了三维空间中的旋转变换。
旋转矩阵可以由旋转轴和旋转角度来确定,旋转轴可以用一个单位向量来表示。
二、旋转变换的表示方法旋转变换可以用欧拉角、四元数和旋转矩阵等方式来表示。
欧拉角是一种简单直观的表示方法,它将旋转变换分解为绕X轴、Y轴和Z轴的连续旋转。
四元数是一种更高效的表示方法,它可以用一个四维向量来表示旋转变换。
旋转矩阵是一种常用的表示方法,它直接描述了旋转变换的矩阵形式。
三、旋转变换的应用案例1. 计算机图形学中的旋转变换在计算机图形学中,旋转变换被广泛用于三维模型的变换和动画效果的实现。
通过对三维模型进行旋转变换,可以改变模型的朝向、角度和位置,从而实现各种复杂的视觉效果。
2. 机器人学中的旋转变换在机器人学中,旋转变换用于描述机器人末端执行器的运动。
通过对机器人执行器进行旋转变换,可以实现机器人的姿态调整、运动轨迹规划以及运动学逆解等功能。
3. 航空航天中的旋转变换在航空航天领域中,旋转变换广泛应用于飞行器的姿态控制和导航系统。
通过对飞行器的姿态进行旋转变换,可以实现飞行器的稳定飞行、精确导航以及目标跟踪等功能。
四、总结旋转变换是三维几何中的重要操作,它可以描述物体在三维空间中的旋转运动。
旋转变换可以用旋转矩阵、欧拉角和四元数等方式来表示,不同的表示方法适用于不同的应用场景。
通过对旋转变换的研究和应用,可以实现计算机图形学、机器人学和航空航天等领域的相关技术发展。
几何证明旋转变换

旋转变换学习指导:旋转变换是初中几何图形变换的一种类型,利用旋转的特征是几何证明中常用的一种形式,在各地中考中,渐渐出现有关旋转变换的证明试题,该类试题有利于提高学生观察图形的能力和逻辑推理能力。
重点:1.掌握旋转的性质2.掌握中心对称、中心对称图形的性质3.能利用旋转变换证明有关结论难点:利用旋转变换证明有关结论。
[范例]如图1所示:已知,点M,N分别在正方形ABCD的边BC、CD上,已知AB=a,的周长为2a,求证:∠MAN=45°。
[点拨]欲求∠MAN=45°,关键是要将△MCN的周长与正方形的周长联系起来,考虑到AB=AD,∠B+∠D=180°,故可将△ABM绕A点逆时针旋转90°,再来转化∠MAN。
[证明]将△ABM绕A点逆时针旋转90°后,M点落在M’处。
则△ABM≌ADM’∴DM’=BM,AM’=AM在正方形ABCD中,∵∠B=∠ADC=90°,AB=AD∴∠ADM’+∠AND=90°+90°=180°∴M’、D、N三点共线∵AB=a,C△AMN =2a∴MC+NC+MN+CD+BC=CM+BM+CN+DN∴MN=DN+BM=DN+DM’=MN’在△AMN和△AMN’中AM=AM’MN=M’NAN=AN∴△AMN≌△AMN’∴∠MAN=∠M’AN∵∠1=∠2∴∠MAN+∠2+∠3=∠MAN+∠1+∠3=∠MAN+∠M’AN=2∠MAN=90°∴∠MAN=45°[同类变式](一)如图2所示,从正方形ABCD的顶点A作∠EAF=45°,交DC于点E,BC于点F 。
(1)问DE+BF=EF吗?请说明理由;(2)过点A作AP⊥EF于P,求证:AP=AB(二)如图3所示,已知点E、F分别在正方形ABCD的边BC、CD上,并且∠DAF=∠EAF求证:BE+DF=AE(三)如图4所示,已知△ABC是边长为2的等边三角形,点D为△ABC外一点,BD=DC,∠BDC=120°,以D为顶点作60°的角交AB、AC于点M、N.求△AMN的周长.(四)如图5所示,△ABC中,∠ABC=90°,AB=BC,斜边AC上有D、E两点,且∠DBE=45°,试判断:AD、DE、EC这三边能否构成直角三角形?(五)如图6所示,已知M是直角三角形ABC斜边上的中点,P、Q分别在AB、AC上,且PM⊥QM.试判断:BP、PQ、QC这三边能否构成直角三角形?(六)如图7所示,△ABC中,D为BC中点,E、F分别为AB、AC上的点,且ED⊥DF求证:BE+CF>EF.(七)如图8所示,△ABC中,∠ACB=90°, BC=AC, D、E,且M是AB中点求证:△MDE是等腰三角形.(八)如图9所示,四边形ABCD和OMNE都是边长为1的正方形.正方形OMNE的顶点O是正方形ABCD的对角线的交点.求证:当正方形OMNE绕O点旋转时,两个正方形的重叠面积是一个定值(巩固延伸一)如图10所示,正方形ABEF和ACGH在△ABC的外侧,M是BC中点求证:FH=2AM(巩固延伸二)如图11所示,分别以△ABC的AB、AC为一边向两边作正方形ABFH和正方形ACDE.连结EF,作AI⊥BC,I为垂足。
几何形的旋转了解形的旋转变换及其性质

几何形的旋转了解形的旋转变换及其性质几何形的旋转:了解形的旋转变换及其性质几何学是一门研究形状、大小和相对位置关系的学科。
其中,形的旋转变换是一种常见的变换方式,通过对几何形进行旋转来达到不同的目的。
本文将介绍形的旋转变换以及它的性质。
1. 形的旋转变换概述形的旋转变换是指将一个几何形绕着一个点作圆周运动,保持其大小、形状和方向不变。
旋转变换可以分为顺时针旋转和逆时针旋转两种情况。
旋转中心可以是任意点,被旋转的几何形叫做原形,旋转后的几何形称为像形。
2. 旋转的基本性质(1)保角性质:旋转变换不改变角的大小。
(2)保持距离性质:旋转变换保持原始形与新形之间的线段长度不变。
(3)保直线性质:旋转变换保持原始形与新形之间的直线仍然是直线。
3. 旋转的角度与方向几何形的旋转可以通过角度来衡量。
顺时针旋转的角度为正,逆时针旋转的角度为负。
旋转角度可以是任意实数,也可以是特定的角度如90°、180°等。
不同的旋转角度会带来不同的效果和形状变化。
4. 旋转的中心旋转的中心可以是形状自身的一个点,也可以是外部指定的一点。
对于正多边形,旋转中心通常是形状的中心点,而对于任意多边形,则可以选择不同的旋转中心,从而得到不同的旋转变换。
5. 旋转的应用旋转变换在现实生活中有许多应用。
比如,地球绕着自转轴旋转,产生白昼和黑夜交替;风车的叶片沿着中心旋转,产生动力;艺术家可以运用旋转变换创作出绚丽多彩的图案等等。
6. 旋转的组合变换旋转变换可以与其他几何变换如平移、缩放和镜像等进行组合,得到更加复杂的变换效果。
通过适当选择变换的顺序和参数,可以实现多样化的几何形变。
7. 旋转的数学表示旋转变换可以通过矩阵乘法来表示。
对于二维空间中以原点为中心旋转的变换,可以使用如下的矩阵表示:[cosθ -sinθ][sinθ cosθ]其中θ表示旋转的角度,cosθ和sinθ分别为旋转角度θ的余弦和正弦值。
通过矩阵乘法,可以将原始形的坐标与旋转矩阵相乘,得到旋转后形的坐标。
几何形的旋转和相似变换

几何形的旋转和相似变换几何形的旋转和相似变换是数学中重要的几何变换方法。
通过这些变换,我们可以通过改变角度和尺度来改变几何形的位置和形状。
在本文中,我们将介绍几何形的旋转和相似变换的概念、性质和应用。
一、旋转变换旋转变换是将几何形沿着某一点或某一直线旋转一定角度的操作。
旋转变换可以是顺时针或逆时针方向,旋转角度可以是任意实数。
旋转变换可以改变几何形的位置和方向,但不改变形状和大小。
旋转变换的特点如下:1. 旋转中心:旋转变换的中心是固定不变的点,几何形中的每个点都绕着该中心进行旋转。
2. 旋转角度:旋转变换的角度决定了几何形旋转的方向和程度。
角度为正表示顺时针旋转,角度为负表示逆时针旋转。
3. 旋转中心与点的距离关系:旋转变换后,几何形上的点到旋转中心的距离保持不变。
这意味着旋转变换不改变几何形的大小。
旋转变换广泛应用于几何学、物理学和工程学等领域。
在几何学中,旋转变换用于研究几何形的对称性、相似性和拓扑结构。
在物理学中,旋转变换用于描述刚体的运动和转动力学。
在工程学中,旋转变换用于设计和分析机械部件、轮胎和风力装置等。
二、相似变换相似变换是一种同时改变几何形的位置、形状和大小的变换。
相似变换是通过对几何形进行等比例缩放和旋转来实现的。
相似变换可以将几何形放大或缩小,但保持几何形的形状和比例关系不变。
相似变换的特点如下:1. 缩放因子:相似变换通过缩放因子来改变几何形的大小。
缩放因子是一个实数,大于1表示放大,小于1表示缩小。
2. 相似比例:相似变换保持几何形的形状和比例关系不变。
这意味着几何形中的每个线段在相似变换后,其长度与其他线段的长度之比相等。
3. 旋转变换:相似变换可以包含旋转变换,通过旋转几何形来改变其方向。
相似变换在几何学、统计学、计算机图形学和艺术设计等领域具有广泛的应用。
在几何学中,相似变换用于研究几何形的相似性和尺度不变性。
在统计学中,相似变换用于数据分析和模式识别。
在计算机图形学中,相似变换用于生成和变换图像和三维模型。
中考数学 专题22 几何三大变换问题之旋转(中心对称)问题(含解析)

专题22 几何三大变换问题之旋转(中心对称)问题轴对称、平移、旋转是平面几何的三大变换。
旋转变换是指在同一平面内,将一个图形(含点、线、面)整体绕一固定点旋转一个定角,这样的图形变换叫做图形的旋转变换,简称旋转。
旋转由旋转中心、旋转的方向和角度决定。
经过旋转,旋转前后图形的形状、大小不变,只是位置发生改变;旋转前、后图形的对应点到旋转中心的距离相等,即旋转中心在对应点所连线段的垂直平分线上; 旋转前、后的图形对应点与旋转中心所连线段的夹角等于旋转角。
把一个图形绕着某一定点旋转一个角度360°/n(n 为大于1的正整数)后,与初始的图形重合,这种图形就叫做旋转对称图形,这个定点就叫做旋转对称中心,旋转的角度叫做旋转角。
特别地,中心对称也是旋转对称的一种的特别形式。
把一个图形绕着某一点旋转180°,如果它能与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心,这两个图形的对应点叫做关于中心的对称点。
如果把一个图形绕某一点旋转180度后能与自身重合,这个图形是中心对称图形。
在初中数学以及日常生活中有着大量的旋转变换的知识,是中考数学的必考内容。
中考压轴题中旋转问题,包括直线(线段)的旋转问题;三角形的旋转问题;四边形旋转问题;其它图形的问题。
一. 直线(线段)的旋转问题1. 如图,直线l :y 3x 3=-+与y 轴交于点A ,将直线l 绕点A 顺时针旋转75º后,所得直线的解析式为【 】A .y 33=B .y x 3=+.y x 3=-+ D .y x 3=【答案】B 。
【考点】旋转的性质,待定系数法,直线上点的坐标与方程的关系,锐角三角函数定义,特殊角的三角函数值。
【分析】如图,由已知,可求直线y3x3=-+与x、y轴的交点分别为B(1,0),A(0,3),2.根据要求,解答下列问题:(1)已知直线l1的函数表达式为y x1=+,直接写出:①过原点且与l1垂直的直线l2的函数表达式;②过点(1,0)且与l1垂直的直线l2的函数表达式;(2)如图,过点(1,0)的直线l4向上的方向与x轴的正方向所成的角为600,①求直线l4的函数表达式;②把直线l4绕点(1,0)按逆时针方向旋转900得到的直线l5,求直线l5的函数表达式;(3)分别观察(1)(2)中的两个函数表达式,请猜想:当两直线垂直时,它们的函数表达式中自变量的系数之间有何关系?请根据猜想结论直接写出过点(1,1)且与直线11y x55=-垂直的直线l6的函数表达式。
解析几何旋转变换公式

解析几何旋转变换公式解析几何这门学问里,旋转变换公式可是个相当重要的家伙!咱们今天就来好好说道说道。
记得我以前教过一个学生,叫小李。
这孩子吧,脑子挺灵,就是一碰到旋转变换公式就犯迷糊。
有一次做作业,碰到一道要用旋转变换公式解决的题,他愣是在那苦思冥想了半天,最后写出来的答案还是错得离谱。
我问他:“小李啊,你到底是咋想的?”他挠挠头说:“老师,我觉得这公式太复杂了,绕来绕去的,我都被绕晕了。
”其实啊,旋转变换公式没那么可怕。
咱们先来说说平面直角坐标系中的旋转变换。
假设点 P(x, y) 绕原点逆时针旋转θ 角度得到点 P'(x', y'),那么这其中的公式就是x' = x * cosθ - y * sinθ,y' = x * sinθ + y * cosθ 。
咱们来仔细瞅瞅这公式。
你看,cosθ 和sinθ 就像是两个小助手,帮助我们完成点的旋转。
比如说,当θ = 90° 时,cos90° = 0,sin90° = 1,这时候 x' = -y,y' = x,这不就是把点逆时针旋转了 90 度嘛!再比如说,在一个具体的图形中,有个三角形 ABC,A 点坐标是(1, 0),B 点坐标是(0, 1),C 点坐标是(-1, 0)。
现在要把这个三角形绕原点逆时针旋转 45°,那咱们就可以用这旋转变换公式来算算新的顶点坐标啦。
经过一番计算,A 点新坐标变成了(√2/2, √2/2),B 点新坐标变成了(-√2/2, √2/2),C 点新坐标变成了(-√2/2, -√2/2)。
你瞧,通过公式,咱们就能清晰地看到图形旋转后的样子。
回到开头提到的小李同学,后来我给他仔仔细细地讲解了几遍,还让他自己动手多做了几道题,慢慢地,他也不再害怕这旋转变换公式了,做题的准确率也提高了不少。
在实际生活中,旋转变换公式也有不少用处呢。
比如说设计一个旋转的摩天轮,工程师就得用这公式来确定座舱的位置变化;再比如在计算机图形学中,要让一个图像旋转,也得靠这公式帮忙。
旋转变换与几何关系解析

旋转变换与几何关系解析旋转变换是几何学中常用的一种变换方式,通过旋转一个图形或物体,可以得到不同的几何关系。
本文将从几何关系的角度对旋转变换进行解析,并探讨其应用和实际意义。
一、旋转变换的基本概念旋转变换是指通过旋转将一个图形或物体转换为另一个图形或物体的变换方式。
在几何学中,旋转变换通常以一个点为轴心,将其他点绕轴心旋转一定角度后得到新的点。
旋转变换可以在平面内进行,也可以在三维空间中进行。
二、旋转变换与几何关系的解析1. 平面旋转变换在平面旋转变换中,我们以一个点为轴心,将其他点绕轴心旋转一定角度。
这种旋转变换可以改变图形的位置、形状和方向。
几何关系的解析包括以下几个方面:(1) 位置关系:旋转后的图形相对于原图形的位置关系可以通过坐标变换来解析。
设原图形中的点A(x, y)经过旋转变换后得到点A'(x', y'),则有以下关系:x' = x*cosθ - y*sinθy' = x*sinθ + y*cosθ其中,θ表示旋转角度。
(2) 形状关系:旋转变换可以改变图形的形状,例如,一个矩形绕一个点旋转后可以变成一个椭圆。
通过解析旋转变换的坐标变换公式,可以得到旋转后的图形的形状关系。
(3) 方向关系:旋转变换也可以改变图形的方向。
通过解析旋转变换的角度变换公式,可以得到旋转后的图形的方向关系。
2. 空间旋转变换在三维空间中,旋转变换与平面旋转变换类似,都是以一个点为轴心将其他点绕轴心旋转一定角度。
不同之处在于,旋转变换同时涉及到三个坐标轴的旋转。
几何关系的解析主要包括以下几个方面:(1) 位置关系:类似于平面旋转变换,位置关系可以通过坐标变换来解析。
设原空间中的点A(x, y, z)经过旋转变换后得到点A'(x', y', z'),则有以下关系:x' = x*cosθ - y*sinθy' = x*sinθ + y*cosθz' = z其中,θ表示旋转角度。
几何相关问题的旋转变换方法总结

几何相关问题的旋转变换方法总结几何学是研究空间和形状的学科,其中旋转变换是一种常见的操作,它可以改变图形的方向和位置,从而帮助我们解决各种几何问题。
在本文中,我们将总结几何相关问题的旋转变换方法,探讨其应用和意义。
一、旋转变换的基本概念旋转变换是指将一个图形绕着某个中心点旋转一定角度,从而改变图形的方向和位置。
在几何学中,我们通常使用角度来表示旋转的大小,其中正角表示逆时针旋转,负角表示顺时针旋转。
旋转变换的基本要素有三个:旋转中心、旋转角度和旋转方向。
旋转中心是图形旋转的中心点,旋转角度是图形旋转的大小,旋转方向则决定了图形是顺时针还是逆时针旋转。
二、旋转变换的基本公式在几何学中,我们可以使用矩阵来表示旋转变换。
设一个点P(x, y)绕着原点旋转α角度后得到的新点为P'(x', y'),则有以下旋转变换的基本公式:x' = x * cosα - y * sinαy' = x * sinα + y * cosα其中,cosα和sinα分别表示旋转角度α的余弦和正弦值。
三、旋转变换的应用举例1. 图形的旋转旋转变换可以帮助我们改变图形的方向和位置。
例如,我们可以将一个矩形绕着其中心点旋转90度,从而得到一个新的矩形。
同样地,我们也可以将一个三角形或者任意多边形进行旋转变换,从而得到不同的图形。
2. 坐标系的旋转旋转变换还可以帮助我们改变坐标系的方向和位置。
例如,我们可以将一个平面坐标系绕着原点旋转45度,从而得到一个新的坐标系。
这种变换可以简化计算,使得问题的求解更加方便。
3. 物体的旋转旋转变换在物体的建模和动画设计中有着重要的应用。
例如,在计算机图形学中,我们可以通过旋转变换来模拟物体的旋转运动,从而实现逼真的动画效果。
此外,旋转变换还可以用于计算物体的表面积、体积和惯性矩等物理性质。
四、旋转变换的意义和局限性旋转变换在几何学和相关学科中具有广泛的应用和重要的意义。
几何变换之旋转的性质

旋转那些事儿旋转,是三大几何变换中考察最多、难度最大的那个,平移、对称从图像观察角度来说直接显然,对应的结论也很容易用到.而旋转,变换得到的图形相对复杂些,有时候解题的突破口隐藏得更深,导致无从下手.本篇将从基本的性质开始,到一些常见的模型,最后说说关于构造旋转能给我们带来什么,全方位了解旋转在中考题中的考察.一、旋转的基本性质如下图,将△ABC 绕点A 旋转一定角度得到△ADE .性质一:对应边相等 结论:AB =AD ,AC =AE .补充:当然还可以得到BC =DE ,但这并没有什么用,因为BC 与DE 并没有特殊位置关系.性质二:对应角相等结论:∠B =∠D ,∠C =∠E ,∠BAC =∠DAE .补充:如果不是特殊角,此性质并没有什么用,但由性质二可以推性质三.性质三:旋转角都相等 结论:∠BAD =∠CAE =∠BFD . 补充:∠BAD =∠CAE 易证,∠BAD =∠BFD 可用“8字”模型证明: ∵∠BAD +∠B =∠BFD +∠D ,且∠B =∠D , ∴∠BAD =∠BFD .且第三组对应边往往用得最多.ABCDEFαααE DCBA【中考真题-关于三角形的旋转】1.(2019·眉山)如图,在Rt ABC ∆中,90B ∠=︒,5AB =,12BC =,将ABC ∆绕点A 逆时针旋转得到ADE ∆,使得点D 落在AC 上,则tan ECD ∠的值为 .【分析】对应边相等求线段长,即可得所求角的正切值. 由题意得:AD =AB =5,EN =CB =12, ∴CD =AC -AD =13-5=8, ∴123tan 82ECD ∠==.2.(2019·内江)如图,在△ABC 中,AB =2,BC =3.6,∠B =60°,将△ABC 绕点A 顺时针旋转得到△ADE ,当点B 的对应点D 恰好落在BC 边上时,则CD 的长为( )A .1.6B .1.8C .2D .2.6【分析】利用对应边相等、对应角相等可得特殊图形. 由题意得:△ABC ≌△ADE ,∴AB =AD , 又∠B =60°,∴△ABD 是等边三角形, ∴BD =AB =2,又BC =3.6, ∴CD =1.6.故选A .ABCDEABCE3.(2019·阜新)如图,在ABC ∆中,AC BC =,将ABC ∆绕点A 逆时针旋转60︒,得到ADE ∆.若2AB =,30ACB ∠=︒,则线段CD 的长度为 .【分析】连接EC ,由题意可得△ACE 是等边三角形,∴EC =AC =BC =ED ,易证△ECD ≌△EAD ,∴CD =AD =AB =2, 故CD 的长为2.4.(2019·包头)如图,在ABC ∆中,55CAB ∠=︒,25ABC ∠=︒,在同一平面内,将ABC∆绕A 点逆时针旋转70︒得到ADE ∆,连接EC ,则tan DEC ∠的值是 .【分析】已知角度,必可求出∠DEC 的度数,且应该是个特殊角. 由题意得:∠EAC =70°,∴∠AEC =∠ACE =55°, 又∠EAD =∠CAB =55°,∴∠CAD =15°,∵∠ACE +∠CAD =∠ADE +∠DEC ,∴∠DEC =45°, ∴tan ∠DEC =1.ABCDEABCDEABCDE5.(2018·镇江)如图,ABC ∆中,90BAC ∠>︒,5BC =,将ABC ∆绕点C 按顺时针方向旋转90︒,点B 对应点B '落在BA 的延长线上.若9sin 10B AC ∠'=,则AC = .【分析】题目给出'B AC ∠的正切值,故构造包含'B AC ∠的直角三角形. 过点C 作CH ⊥'BB 交'BB 于点H,则5CH ==,根据9sin 10B AC '∠=,即910CH AC =,可得:101099AC CH ===6.(2019·山西)如图,在ABC ∆中,90BAC ∠=︒,10AB AC cm ==,点D 为ABC ∆内一点,15BAD ∠=︒,6AD cm =,连接BD ,将ABD ∆绕点A 按逆时针方向旋转,使AB 与AC 重合,点D 的对应点为点E ,连接DE ,DE 交AC 于点F ,则CF 的长为 cm .【分析】特殊特殊度数必然有特殊图形. ∵15BAD ∠=︒,∴15CAE ∠=︒,∴60AFH ∠=︒ 过点A 作AH ⊥DE 交DE 于H 点,∵AD =6cm,∴AH =cm,HF =cm ,∴AF =cm,10CF =-,故CF的长为10-.B'A'ABH B'A'A BCABC DE FHFEDCBA【中考真题-关于四边形的旋转】7.(2017·吉林)如图,在矩形ABCD中,5AB=,3AD=.矩形ABCD绕着点A逆时针旋转一定角度得到矩形AB C D'''.若点B的对应点B'落在边CD上,则B C'的长为.【分析】无论图形是什么,抓住旋转的重点来分析.过点B'作B H'⊥AB交AB于H点,则AH=4,BH=1,∴1B C'=.8.(2019·梧州)如图,在菱形ABCD中,2AB=,60BAD∠=︒,将菱形ABCD绕点A逆时针方向旋转,对应得到菱形AEFG,点E在AC上,EF与CD交于点P,则DP的长是.【分析】特殊的菱形旋转特殊的角度必然得到其他特殊的图形.连接DE,易证△PDE是等腰直角三角形,∵AB=2,∴AC=∵2 AE AB==,∴2CE=,∴1PE=,∴1PD.D'C'B'BCDHD'C'B'A BCDA BCDEFG PA BCDEFG P9.(2018·陇南)如图,点E 是正方形ABCD 的边DC 上一点,把ADE ∆绕点A 顺时针旋转90︒到ABF ∆的位置,若四边形AECF 的面积为25,2DE =,则AE 的长为( )A .5 BC .7D【分析】旋转可以改变图形位置,或许会形成新的特殊图形. 易证△ADE ≌△ABF ,∴正方形ABCD 面积为25,所以边长AD =5, 又DE =2,∴AE D .10.(2019·贺州)如图,正方形ABCD 的边长为4,点E 是CD 的中点,AF 平分BAE∠交BC 于点F ,将ADE ∆绕点A 顺时针旋转90︒得ABG ∆,则CF 的长为 .【分析】方法较多,举一种与旋转相关的做法. 设EAF BAF α∠=∠=,DAE BAG β∠=∠=,则GAF GFA αβ∠=+=∠,∴GF =GA =EA=∴6CF CG GF =-=-,∴CF的长为6-AB CDEFGAB CDEF α+ββαβαGA BCDEF11.(2019·营口)如图,ABC ∆是等边三角形,点D 为BC 边上一点,122BD DC ==,以点D 为顶点作正方形DEFG ,且DE BC =,连接AE ,AG .若将正方形DEFG 绕点D 旋转一周,当AE 取最小值时,AG 的长为 .【分析】如图,当D 、A 、E 三点共线时,AE 最小, 过点A 作AM ⊥BC 交BC 于M 点,∵DM =1,AM =∴AD ==此时8AG ==,故AG 的长为8.ABCDEFGMABCE FG。
空间几何中的旋转与平移变换

平移矩阵的性质: 平移矩阵是线性 变换的一种,具 有线性变换的特 性,如矩阵乘法 可交换、可结合 等。
添加标题
平移矩阵是线性变换的一种,保持向量的加法性质不变 平移矩阵不改变向量的模长 平移矩阵不改变向量的方向 平移矩阵可以表示为矩阵与向量的乘积
平移矩阵的定义:表示物体在 空间中沿某一方向移动一定距 离的矩阵。
观状态的变化
实例分析:气体 分子的无规则运
动和扩散现象
结论:旋转和平 移变换是熵增加 的必要条件,与 热力学第二定律
密切相关
添加标题
添加标题
添加标题
添加标题
汇报人:XX
旋转矩阵是正 交矩阵
旋转矩阵的行 列式值为1
旋转矩阵的逆 矩阵等于其转 置矩阵
旋转矩阵对应 于一个旋转变 换
0
0
0
0
1
2
3
4
旋转矩阵的定义:一个由三个复 数构成的矩阵,表示在三维空间 中绕轴旋转的角度。
旋转矩阵的性质:转置矩阵等于 原矩阵的逆矩阵,即转置矩阵的 行列式值为1。
旋转矩阵的运算规则:矩阵乘法、 加法、数乘等基本运算规则。
平移距离两个参数。
旋转和平移变Βιβλιοθήκη 都是可逆 的,即变换前后的物体可以相互转换。
旋转和平移变换都是刚性 变换,即变换前后物体的 形状和大小不会发生变化。
旋转和平移变换都是仿 射变换,即变换后物体 与原物体在同一直线上 的点仍然在同一直线上。
旋转:物体绕某点转动, 各点距离该点距离相等
平移:物体沿某方向移动, 各点距离起点长度相等
在量子力学中,旋转和 平移变换被用来描述粒 子状态的变换,从而影 响粒子的能量和动量。
旋转和平移变换可以影响 物体的能量和动量,从而
平面几何的旋转变换

平面几何的旋转变换旋转是平面几何中常见的一种变换,通过旋转可以改变图形的方向和位置。
在本文中,我们将探讨平面几何中的旋转变换以及其相关性质和特点。
一、旋转的定义旋转是指将一个图形绕着一个固定点旋转一定角度,从而改变原图形的位置和方向。
在平面几何中,旋转变换可以用一个旋转中心和一个旋转角度来表示。
旋转中心是一个固定点,旋转角度是图形绕旋转中心旋转的角度。
二、旋转的性质1. 旋转不改变图形的大小和形状,只改变其位置和方向;2. 旋转是保角变换,即旋转前后,图形内部的角度大小保持不变;3. 若两个图形是相似的,那么它们可以通过旋转变换互相转化。
三、旋转的实例下面我们通过一些实例来展示旋转的具体应用。
例1:将一个三角形绕着一个固定点旋转45度。
解:假设三角形的顶点分别为A、B、C,旋转中心为O,旋转角度为45度。
我们可以按照如下步骤进行旋转:1. 将点A、B、C与旋转中心O连接;2. 以线段OA为半径,在逆时针方向上画一个45度的弧,交于点A';3. 以线段OB为半径,在逆时针方向上画一个45度的弧,交于点B';4. 以线段OC为半径,在逆时针方向上画一个45度的弧,交于点C';那么,经过旋转变换后,原三角形ABC将变为三角形A'B'C',且A'B'C'与ABC相似。
例2:将一个正方形绕着中心点旋转90度。
解:假设正方形的四个顶点分别为A、B、C、D,中心点为O,旋转角度为90度。
按照下面的步骤进行旋转:1. 将点A、B、C、D与中心点O连接;2. 以线段OA为半径,在逆时针方向上画一个90度的弧,交于点A';3. 以线段OB为半径,在逆时针方向上画一个90度的弧,交于点B';4. 以线段OC为半径,在逆时针方向上画一个90度的弧,交于点C';5. 以线段OD为半径,在逆时针方向上画一个90度的弧,交于点D';那么,经过旋转变换后,原正方形ABCD将变为正方形A'B'C'D',且A'B'C'D'与ABCD相似。
几何变换的基本概念与方法

几何变换的基本概念与方法几何变换是指通过一定的操作将图形或空间中的点、线、面等按照一定规律进行改变的过程。
几何变换在数学、计算机图形学、物理学等领域都有广泛的应用。
下面将介绍几何变换的基本概念和常用的方法。
一、基本概念1. 平移变换:平移变换是指通过平移向量对图形中的每个点进行位移,使得整个图形整体移动到新的位置上,而形状和大小不变。
平移变换可以用矩阵形式表示为:(x', y') = (x, y) + (dx, dy)其中,(x, y)是原始点的坐标,(dx, dy)是平移向量,(x', y')是平移后点的坐标。
2. 旋转变换:旋转变换是指通过旋转中心和旋转角度对图形中的每个点进行旋转,使得整个图形绕着旋转中心进行旋转。
旋转变换可以用矩阵形式表示为:(x', y') = (x, y) * R其中,(x, y)是原始点的坐标,(x', y')是旋转后点的坐标,R是旋转矩阵,可以通过求解得到。
3. 缩放变换:缩放变换是指通过缩放因子对图形中的每个点进行缩放,使得整个图形按照一定比例进行放大或缩小。
缩放变换可以用矩阵形式表示为:(x', y') = (x, y) * S其中,(x, y)是原始点的坐标,(x', y')是缩放后点的坐标,S是缩放矩阵,可以通过求解得到。
4. 对称变换:对称变换是指通过对称轴将图形中的每个点映射到对称位置,使得整个图形关于对称轴对称。
对称变换可以用矩阵形式表示为:(x', y') = (x, y) * M其中,(x, y)是原始点的坐标,(x', y')是对称后点的坐标,M是对称矩阵,可以通过求解得到。
二、常用方法1. 坐标变换法:将原始图形的每个点的坐标进行变换,根据不同的变换方式,选择相应的变换矩阵进行计算,得到变换后的图形。
2. 向量变换法:将原始图形看作由线段或向量组成,通过对每个线段或向量进行变换,得到变换后的线段或向量,并重新组合为变换后的图形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
几何变换一
——旋转变换
1.在四边形ABCD 中,对角线AC 平分∠DAB .
(1) 如图1,当∠DAB =120°,∠B =∠D =90°时,求证:AB+AD=AC . (1) 如图2,当∠DAB =120°,∠B 与∠D 互补时,线段AB 、AD 、AC 有怎样的数量关系?写出你的猜想,并给予证明; (2)如图3,当∠DAB =90°时,∠B 与∠D 互补时,线段AB 、AD 、AC 有怎样的数量关系?写出你的猜想,不需证明 .
2.(1)已知:如图1,A B C ∆是⊙O 的内接正三角形,点P 为弧BC 上一动点, 求证:P A P B P C =+
(2) 如图2,四边形A B C D 是⊙O 的内接正方形,点P 为弧BC 上一动点, 求证
: PA PC =+
(3) 如图3,六边形A B C D E F 是⊙O 的内接正六边形,点P 为弧BC 上一动点,请探究P A P B P C 、、三者之间有何数量关系,并给予证明.
3.正方形ABCD 中,E 为BC 上的一点,F 为CD 上一点,如果BE+DF=EF ,求∠EAF 的度数。
A B
C
D
图2
A
B C
D
图1
A
B
C
D 图3
图1
图2
图3
4.请阅读下列材料:
已知:如图(1)在Rt △ABC 中,∠BAC =90°,AB = AC ,点D 、E 分别为线段BC 上两动点,若∠DAE =45°.探究线段BD 、DE 、EC 三条线段之间的数量关系. 小明的思路是:把△AEC 绕点A 顺时针旋转90°,得到△ABE′,连结E′D , 使问题得到解决.请你参考小明的思路探究并解决下列问题: (1)猜想BD 、DE 、EC 三条线段之间存在的数
量关系式,并对你的猜想给予证明; 图(1) (2)当动点E 在线段BC 上,动点D 运动在线
段CB 延长线上时,如图(2),其它条件 不变,(1)中探究的结论是否发生改变? 请说明你的猜想并给予证明.
5.(1)如图1,图2,图3,在A B C △中,分别以A B A C ,为边,向A B C △外作正三角形,正四边形,正五边形,B E C D ,相交于点O .
①如图1,求证:A B E A D C △≌△; ②探究:如图1,B O C ∠= ; 如图2,B O C ∠= ;
如图3,B O C ∠= .
(2)如图4,已知:A B A D ,是以A B 为边向A B C △外所作正n 边形的一
组邻边;A C A E
,的延长
△外所作正n边形的一组邻边.B E C D ,是以A C为边向A B C
相交于点O.
①猜想:如图4,B O C
∠= (用含n的式子表示);
②根据图4证明你的猜想.
6.(1)如图3,四边形ABCD中,CB
=
ABC,︒
ADC,请你猜
∠120
∠60
AB=,︒
=
想线段DA、DC之和与线段BD的数量关系,并证明你的结论;
(2)如图4,四边形ABCD中,BC
ABC,若点P为四边形ABCD
∠60
=
AB=,︒
内一点,且︒
APD,请你猜想线段PA、PD、PC之和与线段BD的数量关系,
∠120
=
并证明你的结论.
图3
图4。
