数值分析第一次作业_1_
数值分析作业及参考答案

数值分析第一次作业及参考答案1. 设212S gt =,假定g 是准确的,而对t 的测量有0.1±秒的误差,证明当t 增加时S 的绝对误差增加,而相对误差却减少。
解:2**22211()0.122()0.10.2()1122,(),().r r e S S S gt gt gt e S gt e S t gt gt t e S e S =-=-====∴↑↑↓2. 设2()[,]f x C a b ∈且()()0f a f b ==,求证2''1max ()()max ().8a x ba xb f x b a f x ≤≤≤≤≤-解:由112,0),(,0)()()0()00.a b L x l x l x =⨯+⨯=(两点线性插值 插值余项为"111()()()()()()[,]2R x f x L x f x a x b a b ξξ=-=--∈ [,].x a b ∴∀∈有12211()()"()()()max "()[()()]221()()1max "()[]()max "().228a x ba xb a x b f x R x f x a x b f x x a b x x a b x f x b a f x ξ≤≤≤≤≤≤==--≤---+-≤=-21max ()()max "()8a xb a x b f x b a f x ≤≤≤≤∴≤-3. 已测得函数()y f x =的三对数据:(0,1),(-1,5),(2,-1),(1)用Lagrange 插值求二次插值多项式。
(2)构造差商表。
(3)用Newton 插值求二次插值多项式。
解:(1)Lagrange 插值基函数为0(1)(2)1()(1)(2)(01)(02)2x x l x x x +-==-+-+-同理 1211()(2),()(1)36l x x x l x x x =-=+ 故2202151()()(1)(2)(2)(1)23631i i i p x y l x x x x x x x x x =-==-+-+-++=-+∑(2)令0120,1,2x x x ==-=,则一阶差商、二阶差商为0112155(1)[,]4,[,]20(1)12f x x f x x ---==-==-----0124(2)[,,]102f x x x ---==-22()1(4)(0)1*(0)(1)31P x x x x x x =+--+-+=-+4. 在44x -≤≤上给出()xf x e =的等距节点函数表,若用二次插值求x e 的近似值,要使截断误差不超过610-,问使用函数表的步长h 应取多少?解:()40000(),(),[4,4],,,, 1.x k x f x e f x e e x x h x x h x x th t ==≤∈--+=+≤考察点及(3)200044343()()[(()]()[()]3!(1)(1)(1)(1)3!3!.(4,4).6f R x x x h x x x x h t t t e t h th t h e h e ξξ=----+-+≤+⋅⋅-=≤∈-则436((1)(1)100.006.t t t h --+±<< 在点 得5. 求2()f x x =在[a,b ]上的分段线性插值函数()h I x ,并估计误差。
数值分析大作业一

数值分析大作业一一、算法设计方案1、求λ1和λ501的值:思路:采用幂法求出按模最大特征值λmax,该值必为λ1或λ501,若λmax小于0,则λmax=λ1;否则λmax=λ501。
再经过原点平移,使用幂法迭代出矩阵A-λmax I的特征值,此时求出的按模最大特征值即为λ1和λ501的另一个值。
2、求λs的值:采用反幂法求出按模最小的特征值λmin即为λs,其中的方程组采用LU分解法进行求解。
3、求与μk最接近的特征值:对矩阵A采用带原点平移的反幂法求解最小特征值,其中平移量为:μk。
4、A的条件数cond(A)=| λmax/λmin|;5、A的行列式的值:先将A进行LU分解,再求U矩阵对角元素的乘积即为A 行列式的值。
二、源程序#include<iostream>#include<iomanip>#include<math.h>#define N 501#define E 1.0e-12 //定义精度常量#define r 2#define s 2using namespace std;double a[N];double cc[5][N];void init();double mifa();double fmifa();int max(int aa,int bb);int min(int aa,int bb);int max_3(int aa,int bb,int cc);void LU();void main(){double a1,a2,d1,d501=0,ds,det=1,miu[39],lamta,cond;int i,k;init();/*************求λ1和λ501********************/a1=mifa();if(a1<0)d1=a1; //若小于0则表示λ1的值elsed501=a1; //若大于0则表示λ501的值for(i=0;i<N;i++)a[i]=a[i]-a1;a2=mifa()+a1;if(a2<0)d1=a2; //若小于0则表示λ1的值elsed501=a2; //若大于0则表示λ501的值cout<<"λ1="<<setiosflags(ios::scientific)<<setprecision(12)<<d1<<"\t";cout<<"λ501="<<setiosflags(ios::scientific)<<setprecision(12)<<d501<<endl;/**************求λs*****************/init();ds=fmifa();cout<<"λs="<<setiosflags(ios::scientific)<<setprecision(12)<<ds<<endl;/**************求与μk最接近的特征值λik**************/cout<<"与μk最接近的特征值λik:"<<endl;for(k=0;k<39;k++){miu[k]=d1+(k+1)*(d501-d1)/40;init();for(i=0;i<N;i++)a[i]=a[i]-miu[k];lamta=fmifa()+miu[k];cout<<"λi"<<k+1<<"\t\t"<<setiosflags(ios::scientific)<<setprecision(12)<<lamta<<en dl;}/**************求A的条件数**************/cout<<"矩阵A的条件式";cond=abs(max(abs(d1),abs(d501))/ds);cout<<"cond="<<setiosflags(ios::scientific)<<setprecision(12)<<cond<<endl;/**************求A的行列式**************/cout<<"矩阵A的行列式";init();LU();for(i=0;i<N;i++){det*=cc[2][i];}cout<<"det="<<setiosflags(ios::scientific)<<setprecision(12)<<det<<endl;system("pause");}/**************初始化函数,给a[N]赋值*************/void init(){int i;for(i=1;i<=501;i++)a[i-1]=(1.64-0.024*i)*sin((double)(0.2*i))-0.64*exp((double)(0.1/i)); }/**************幂法求最大绝对特征值**************/double mifa(){int i,k=0;double u[N],y[N]={0},b=0.16,c=-0.064,Beta_=0,error;for(i=0;i<501;i++)u[i]=1; //令u[N]=1for(k=1;k<2000;k++) //控制最大迭代次数为2000{/***求y(k-1)***/double sum_u=0,gh_sum_u;for(i=0;i<N;i++){sum_u+=u[i]*u[i]; }gh_sum_u=sqrt(sum_u);for(i=0;i<N;i++){y[i]=u[i]/gh_sum_u;}/****求新的uk****/u[0]=a[0]*y[0]+b*y[1]+c*y[2];u[1]=b*y[0]+a[1]*y[1]+b*y[2]+c*y[3]; //前两列和最后两列单独拿出来求中D间的循环求for(i=2;i<N-2;i++){u[i]=c*y[i-2]+b*y[i-1]+a[i]*y[i]+b*y[i+1]+c*y[i+2];}u[N-2]=c*y[N-4]+b*y[N-3]+a[N-2]*y[N-2]+b*y[N-1];u[N-1]=c*y[N-3]+b*y[N-2]+a[N-1]*y[N-1];/***求beta***/double Beta=0;for(i=0;i<N;i++){Beta+=y[i]*u[i];}//cout<<"Beta"<<k<<"="<<Beta<<"\t"; 输出每次迭代的beta /***求误差***/error=abs(Beta-Beta_)/abs(Beta);if(error<=E) //若迭代误差在精度水平内则可以停止迭代{return Beta;} //控制显示位数Beta_=Beta; //第个eta的值都要保存下来,为了与后个值进行误差计算 }if(k==2000){cout<<"error"<<endl;return 0;} //若在最大迭代次数范围内都不能满足精度要求说明不收敛}/**************反幂法求最小绝对特¬征值**************/double fmifa(){int i,k,t;double u[N],y[N]={0},yy[N]={0},b=0.16,c=-0.064,Beta_=0,error;for(i=0;i<501;i++)u[i]=1; //令u[N]=1for(k=1;k<2000;k++){double sum_u=0,gh_sum_u;for(i=0;i<N;i++){sum_u+=u[i]*u[i]; }gh_sum_u=sqrt(sum_u);for(i=0;i<N;i++){y[i]=u[i]/gh_sum_u;yy[i]=y[i]; //用重新赋值,避免求解方程组的时候改变y的值}/****LU分解法解方程组Au=y,求新的***/LU();for(i=2;i<=N;i++){double temp_b=0;for(t=max(1,i-r);t<=i-1;t++)temp_b+=cc[i-t+s][t-1]*yy[t-1];yy[i-1]=yy[i-1]-temp_b;}u[N-1]=yy[N-1]/cc[s][N-1];for(i=N-1;i>=1;i--){double temp_u=0;for(t=i+1;t<=min(i+s,N);t++)temp_u+=cc[i-t+s][t-1]*u[t-1];u[i-1]=(yy[i-1]-temp_u)/cc[s][i-1];}double Beta=0;for(i=0;i<N;i++){Beta+=y[i]*u[i];}error=abs(Beta-Beta_)/abs(Beta);if(error<=E){return (1/Beta);}Beta_=Beta;}if(k==2000){cout<<"error"<<endl;return 0;} }/**************求两数最大值的子程序**************/int max(int aa,int bb){return(aa>bb?aa:bb);}/**************求两数最小值的子程序**************/int min(int aa,int bb){return(aa<bb?aa:bb);}/**************求三数最大值的子程序**************/int max_3(int aa,int bb,int cc){ int tt;if(aa>bb)tt=aa;else tt=bb;if(tt<cc) tt=cc;return(tt);}/**************LU分解**************/void LU(){int i,j,k,t;double b=0.16,c=-0.064;/**赋值压缩后矩阵cc[5][501]**/for(i=2;i<N;i++)cc[0][i]=c;for(i=1;i<N;i++)cc[1][i]=b;for(i=0;i<N;i++)cc[2][i]=a[i];for(i=0;i<N-1;i++)cc[3][i]=b;for(i=0;i<N-2;i++)cc[4][i]=c;for(k=1;k<=N;k++){for(j=k;j<=min(k+s,N);j++){double temp=0;for(t=max_3(1,k-r,j-s);t<=k-1;t++)temp+=cc[k-t+s][t-1]*cc[t-j+s][j-1];cc[k-j+s][j-1]=cc[k-j+s][j-1]-temp;}//if(k<500){for(i=k+1;i<=min(k+r,N);i++){double temp2=0;for(t=max_3(1,i-r,k-s);t<=k-1;t++)temp2+=cc[i-t+s][t-1]*cc[t-k+s][k-1];cc[i-k+s][k-1]=(cc[i-k+s][k-1]-temp2)/cc[s][k-1];}}}}三、程序结果。
数值分析课第一次作业答案answer1

计算机习题: 1. 作多项式 p,以 −1,0,1 为零点,首项系数为 2,并计算 p(3)。 4
答案:p = poly ([−1, 0, 1]),s = polyval(p, 3)。 2. 已知函数在下列各点的值为 xi 0.2 0.4 0.6 0.8 1.0
2
a 6 6e+154 0 1 1
b 10 10e+154 1 -1e+5 -4
c -4 -4e+154 1 1 3.999999
-1e+155 -7e+155 1e+155 答案:第二种方法更准确,因为第一种方法是一个累加的过程。 matlab 的 x = a : h : b 和 x = a + (0 : n) ∗ h 是第二种方法实现的。 代码: format long e a = 0; b = 8; n = 9; h = (b-a)/n; x(1) = a; y(1) = a; for j = 1:n, x(j+1) = x(j) + h; y(j+1) = y(1) + j*h; end [x',y',(a:h:b)',a+(0:n)’*h] 第二章 插值法 1. 当 x = 1, −1, 2 时,f (x) = 0, −3, 4,求 f (x) 的二次插值多项式。 (计算两遍,分别用拉格朗日插值和牛顿插值)
5
f (xi ) 0.98 0.92 0.81 0.64 0.38 求 4 次牛顿插值多项式 P4 (x) 并画图。 答案: 代码: x=0.2:0.2:1.0; y=[0.98,0.92,0.81,0.64,0.38]; n = length(y); if length(x)~=n, error('x and y are not compatible'); end D = zeros(n,n); D(:,1)=y(:); for j=2:n for i=j:n D(i,j) = (D(i,j-1)-D(i-1,j-1))/(x(i)-x(i-j+1)); end end p=D(1,1)*[zeros(1,n-1),1]; for k=2:n p=p+D(k,k)*[zeros(1,n-k),poly(x(1:k-1))]; end x=0.2:0.01:1.0; z=polyval(p,x); plot(x,z) 比较:p = polyf it(x, y, 4)。
数值分析大作业

数值分析上机作业(一)一、算法的设计方案1、幂法求解λ1、λ501幂法主要用于计算矩阵的按模最大的特征值和相应的特征向量,即对于|λ1|≥|λ2|≥.....≥|λn|可以采用幂法直接求出λ1,但在本题中λ1≤λ2≤……≤λ501,我们无法判断按模最大的特征值。
但是由矩阵A的特征值条件可知|λ1|和|λ501|之间必然有一个是最大的,通过对矩阵A使用幂法迭代一定次数后得到满足精度ε=10−12的特征值λ0,然后在对矩阵A做如下的平移:B=A-λ0I由线性代数(A-PI)x=(λ-p)x可得矩阵B的特征值为:λ1-λ0、λ2-λ0…….λ501-λ0。
对B矩阵采用幂法求出B矩阵按模最大的特征值为λ∗=λ501-λ0,所以λ501=λ∗+λ0,比较λ0与λ501的大小,若λ0>λ501则λ1=λ501,λ501=λ0;若λ0<λ501,则令t=λ501,λ1=λ0,λ501=t。
求矩阵M按模最大的特征值λ的具体算法如下:任取非零向量u0∈R nηk−1=u T(k−1)∗u k−1y k−1=u k−1ηk−1u k=Ay k−1βk=y Tk−1u k(k=1,2,3……)当|βk−βk−1||βk|≤ε=10−12时,迭终终止,并且令λ1=βk2、反幂法计算λs和λik由已知条件可知λs是矩阵A 按模最小的特征值,可以应用反幂法直接求解出λs。
使用带偏移量的反幂法求解λik,其中偏移量为μk=λ1+kλ501−λ140(k=1,2,3…39),构造矩阵C=A-μk I,矩阵C的特征值为λik−μk,对矩阵C使用反幂法求得按模最小特征值λ0,则有λik=1λ0+μk。
求解矩阵M按模最小特征值的具体算法如下:任取非零向量u 0∈R n ηk−1= u T (k−1)∗u k−1y k−1=u k−1ηk−1 Au k =y k−1βk =y T k−1u k (k=1,2,3……)在反幂法中每一次迭代都要求解线性方程组Au k =y k−1,当K 足够大时,取λn =1βk 。
(完整版)数值分析第一次作业

问题1:20.给定数据如下表:试求三次样条插值S(x),并满足条件 (1)S`(0.25)=1.0000,S`(0.53)=0.6868; (2)S ’’(0.25)=S ’’(0.53)=0。
分析:本问题是已知五个点,由这五个点求一三次样条插值函数。
边界条件有两种,(1)是已知一阶倒数,(2)是已知自然边界条件。
对于第一种边界(已知边界的一阶倒数值),可写出下面的矩阵方程。
⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡432104321034322110d M M M M M 200020000020022d d d d λμμλμλμλ其中μj =j1-j 1-j h h h +,λi=j1-j j h h h +,dj=6f[x j-1,x j ,x j+1], μn =1,λ0=1对于第一种边界条件d 0=0h 6(f[x 0,x 1]-f 0`),d n =1-n h 6(f`n-f `[x n-1,x n ]) 解:由matlab 计算得:由此得矩阵形式的线性方程组为:⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡ 2.1150-2.4286-3.2667-4.3143-5.5200-M M M M M 25714.00001204286.000004000.026000.0006429.023571.0001243210解得 M 0=-2.0286;M 1=-1.4627;M 2= -1.0333; M 3= -0.8058; M 4=-0.6546S(x)=⎪⎪⎩⎪⎪⎨⎧∈-+-+-∈-+-+-∈-+-+-∈-+-+-]53.0,45.0[x 5.40x 9.1087x 35.03956.8.450-x 1.3637-x .5301.67881- ]45.0,39.0[x 9.30x 11.188x 54.010.418793.0-x 2.2384-x .450(2.87040-]39.0,30.0[x 03.0x 6.9544x 9.30 6.107503.0-x 1.9136-x .3902.708779-]30.0,25.0[x 5.20x 10.9662x 0.3010.01695.20-x 4.8758-x .3006.76209-33333333),()()()(),()()()),()()()(),()()()(Matlab 程序代码如下:function tgsanci(n,s,t) %n代表元素数,s,t代表端点的一阶导。
JZX高等数值分析第一次实验作业
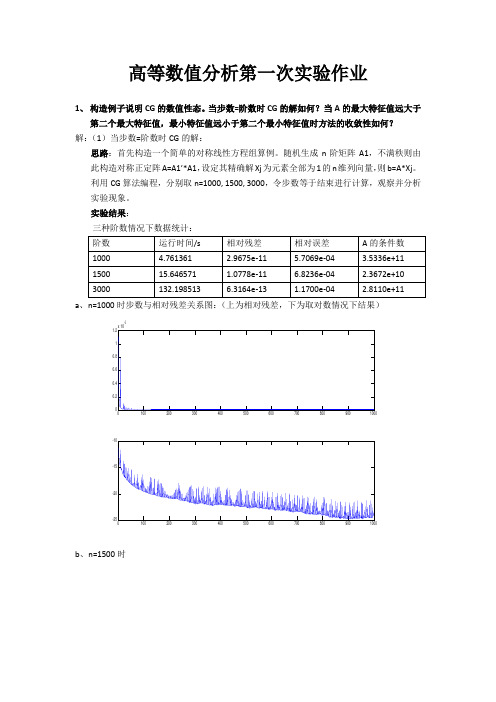
相对残差 6.1302e-16 8.7797e-09 8.0295e-09 8.5677e-09 9.1433e-09
a、 m=1 (左为相对残差,右为取对数情况)
1 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1
0 1
1.5
0
-5
-10
-15
-20
-25
-30
-35
-40
1000
4.761361
2.9675e-11
5.7069e-04
3.5336e+11
1500
15.646571
1.0778e-11
6.8236e-04
2.3672e+10
3000
132.198513
6.3164e-13
1.1700e-04
2.8110e+11
a、n=1000 时步数与相对残差关系图:(上为相对残差,下为取对数情况下结果)
(2)当 A 最大特征值远大于第二个特征值,最小特征值远小于第二个最小特征值时收敛
性情况。
思路:构造题目要求的矩阵 A。首先随机生成 n 阶矩阵 B,B 不满秩,构造对角阵 A1(最
大特征值远大于第二个最大特征值,最小特征值远小于第二个最小特征值),则由此构
造出对称正定矩阵 A: b1=B’*B; A=b1’*A1*b1。同样设定精确解 Xj 为元素全部为 1 的 n
5、 构造对称不定的矩阵,验证 Lanczos 方法的近似中断,观察收敛曲线中的峰点个数和特
征值的分布关系;观察当出现峰点时,MINRES 方法的收敛性态怎样。
解:思路:类似前两题,首先构造出一个 n 阶对角阵 D,其对角线上有 m 个负值,再对随
数值分析第一次作业

《数值分析》计算作业院系:航空科学与工程学院学号: SY1005512姓名:王天龙日期: 2010年10月31日计算实习说明书目的:训练运用计算机进行科学与工程计算的能力。
要求:1.独立进行算法设计、程序设计和上机运算,并得出正确的结果。
2.编制程序时全部采用双精度,要求按题目的要求设计输出,并执行打印。
3.只能根据题目给出的信息并且只允许一次计算得出全部结果。
题目:第一题 设有501×501的矩阵123499500501a b c b a b cc b a b c A c b a b c c b a b c ba ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦其中0.1(1.640.024)s i n (0.2)0.64 (125i i a i i e i =--= ,,,;0.16b =;0.064c =-。
矩阵A 的特征值12501()ii λ= ,,,满足 125011501||min ||S i i λλλλλ≤≤<<<= ,试求:1.1λ,501λ和S λ的值。
2.A 的与数5011140k kλλμλ-=+最接近的特征值(1239)ik k λ= ,,,。
3.A 的(谱范数)条件数2()cond A 和行列式det A 。
说明:1.在所有的算法中,凡是要给出精度水平ε的,都取1210ε-=。
2.选择算法时,应使A 的所有零元素都不存储。
3.打印以下内容: (1)算法的设计方案。
(2)全部源程序(要求注明主程序和每个子程序的功能)。
(3)特征值1λ,501λ,S λ和(1239)ik k λ= ,,,以及2()cond A ,det A 的值。
4.采用e 型输出所有计算结果,并至少显示12位有效数字。
一、程序算法的设计算法设计方案如下:二、全部源程序编程软件:Fortran:三、计算结果1.特征值1λ,501λ,S λ1-.107001135582E+02λ=,501 .972463398616E+01λ=,-.555823879237E-02S λ=2. (1239)ik k λ= ,,,如下表所示(ZK 代表ik λ)3.A 的条件数2()cond A 和行列式det A 的值2() .192509100000E+04cond A =,det .277059968428+119A =五、讨论这里选取的初始向量为X(i)=1,X={x1,x2,x3,,,,,,,x501},当初始向量与特征向量较近时,收敛较快,若初始向量与特征向量正交,则求解可能失真。
北航数值分析大作业一

北京航空航天大学数值分析大作业一学院名称自动化专业方向控制工程学号ZY*******学生姓名许阳教师孙玉泉日期2021 年11月26 日设有501501⨯的实对称矩阵A ,⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=5011A a b c b c c b c b a其中,064.0,16.0),501,,2,1(64.0)2.0sin()024.064.1(1.0-==⋅⋅⋅=--=c b i e i i a ii 。
矩阵A 的特征值为)501,,2,1(⋅⋅⋅=i i λ,并且有||min ||,501150121i i s λλλλλ≤≤=≤⋅⋅⋅≤≤1λ,501λ和s λ的值。
A 的与数4015011λλλμ-+=kk 最接近的特征值)39,,2,1(⋅⋅⋅=k k i λ。
A 的(谱范数)条件数2)A (cond 和行列式detA 。
一 方案设计1 求1λ,501λ和s λ的值。
s λ为按模最小特征值,||min ||5011i i s λλ≤≤=。
可使用反幂法求得。
1λ,501λ分别为最大特征值及最小特征值。
可使用幂法求出按模最大特征值,如结果为正,即为501λ,结果为负,那么为1λ。
使用位移的方式求得另一特征值即可。
2 求A 的与数4015011λλλμ-+=kk 最接近的特征值)39,...,2,1(=k k i λ。
题目可看成求以k μ为偏移量后,按模最小的特征值。
即以k μ为偏移量做位移,使用反幂法求出按模最小特征值后,加上k μ,即为所求。
3 求A 的(谱范数)条件数2)(A cond 和行列式detA 。
矩阵A 为非奇异对称矩阵,可知,||)(min max2λλ=A cond(1-1)其中m ax λ为按模最大特征值,min λ为按模最小特征值。
detA 可由LU 分解得到。
因LU 均为三角阵,那么其主对角线乘积即为A 的行列式。
二 算法实现1 幂法使用如下迭代格式:⎪⎪⎩⎪⎪⎨⎧⋅===⋅⋅⋅=------||max |)|sgn(max ||max /),,(111111)0()0(10k k k k k k k k Tn u u Ay u u u y u u u β任取非零向量 (2-1)终止迭代的控制理论使用εβββ≤--||/||1k k k , 实际使用εβββ≤--||/||||||1k k k(2-2)由于不保存A 矩阵中的零元素,只保存主对角元素a[501]及b,c 值。
数值分析上机作业1-1解析

数值计算方法上机题目11、实验1. 病态问题实验目的:算法有“优”与“劣”之分,问题也有“好”和“坏”之别。
所谓坏问题就是问题本身的解对数据变化的比较敏感,反之属于好问题。
希望读者通过本实验对此有一个初步的体会。
数值分析的大部分研究课题中,如线性代数方程组、矩阵特征值问题、非线性方程及方程组等都存在病态的问题。
病态问题要通过研究和构造特殊的算法来解决,当然一般要付出一些代价(如耗用更多的机器时间、占用更多的存储空间等)。
问题提出:考虑一个高次的代数多项式∏=-=---=201)()20)...(2)(1()(k k x x x x x p (E1-1)显然该多项式的全部根为l ,2,…,20,共计20个,且每个根都是单重的(也称为简单的)。
现考虑该多项式方程的一个扰动0)(19=+xx p ε (E1-2)其中ε是一个非常小的数。
这相当于是对(E1-1)中19x 的系数作一个小的扰动。
我们希望比较(E1-1)和(E1-2)根的差别,从而分析方程(E1-1)的解对扰动的敏感性。
实验内容:为了实现方便,我们先介绍两个 Matlab 函数:“roots ”和“poly ”,输入函数u =roots (a )其中若变量a 存储1+n 维的向量,则该函数的输出u 为一个n 维的向量。
设a 的元素依次为121,...,,+n a a a ,则输出u 的各分量是多项式方程0...1121=++++-n n n n a x a x a x a的全部根,而函数b=poly(v)的输出b 是一个n +1维变量,它是以n 维变量v 的各分量为根的多项式的系数。
可见“roots ”和“Poly ”是两个互逆的运算函数.ve=zeros(1,21); ve(2)=ess;roots(poly(1:20))+ve)上述简单的Matlab 程序便得到(E1-2)的全部根,程序中的“ess ”即是(E1-2)中的ε。
实验要求:(1)选择充分小的ess ,反复进行上述实验,记录结果的变化并分析它们。
清华大学高等数值分析 第一次实验作业

10
-10
0
100
200
300
400
500
600
700
800
900
迭代次数
图9
m=100时,Lanczos法求解Ax=b的收敛曲线
高等数值分析实验作业一
10
4
Lanzcos 算法的收敛曲线 (阶数 n=1002)
10
2
10
0
||rk||/||b||
10
-2
10
-4
10
-6
10
-8
10
-10
0
200
迭代次数
图12 m=10时,Minres法求解Ax=b的收敛曲线
10
2
Minres 算法的收敛曲线 (阶数 n=1002)
10
0
10
-2
||rk||/||b||
10
-4
10
-6
10
-8
10
-10
0
100
200
300
400
500
600
700
迭代次数
图13
10
2
m=50时,Minres法求解Ax=b的收敛曲线
10
0
Lanzcos 算法的收敛曲线 (阶数 n=1002)
m=10 m=50 m=100 m=400 m=800
10
-2
10
-4
||rk||/||b||
10
-6
10
-8
10
-10
10
-12
0
2
4
6
8
10
12
14
16
贾忠孝高等数值分析第一次上机作业

【运行结果】 当 m=300 时,下图表示实验结果,其中 k 为停机循环次数
当 m=995 时,停机循环次果表明当 m 越小时,收敛速度越快,在有限精度下,停机循环次数越小。这 与 Lanczos 方法最多 m 步找到准确解这一结论相吻合。
4. 取初始近似解为零向量, 右端项 b 仅由 A 的 m 个不同个特征向量的线性组 合表示时, Lanczos 方法的收敛性如何? 数值计算中方法的收敛性和m 的大小关 系如何? 【程序】 clc clear clf n=1000; rs=10^(-10); %停机准则 m=10; disp('Lanczos 算法') %定义对称正定阵与 b
1 1000, 2 59.8858, 999 10.0961, 1000 0.01,
经过 k=100,基本收敛达到精度要求。
【结论】 后者的收敛速度要大于前者。说明当 A 的最大特征值远大于第二个最大特征 值, 最小特征值远小于第二个最小特征值时,收敛速度只与 2. 对于同样的例子, 比较 CG 和 Lanczos 的计算结果. 【程序】
高等数值分析实验作业一
机械系 光辉 2014310205
1. 构造例子说明 CG 的数值性态 . 当步数 = 阶数时 CG 的解如何 ? 当 A 的最 大特征值远大于第二个最大特征值, 最小特征值远小于第二个最小特征值时 方 法的收敛性如何? 问题 1 【程序】 clc clear n=1000; %定义对称正定阵与 b lans=sort(rand(n,1),'descend'); D=diag(lans); Q=orth(rand(1000,1000)); A=Q*D*Q'; b=rand(n,1); %初始情况 x0=eye(n,1); r0=b-A*x0; p(:,1)=r0; %执行第一步 af(1)=dot(r0,r0)/dot(p(:,1),A*p(:,1)); x(:,1)=x0+af(1)*p(:,1); r(:,1)=b-A*x(:,1); bat(2)=dot(r(:,1),r(:,1))/dot(r0,r0); p(:,2)=r(:,1)+bat(2)*p(:,1); %执行 k 步 K=n; for k=2:1:K k af(k)=dot(r(:,k-1),r(:,k-1))/dot(A*p(:,k),p(:,k)); x(:,k)=x(:,k-1)+af(k)*p(:,k); r(:,k)=b-A*x(:,k);
(完整版)数值分析第一次作业

问题1:20.给定数据如下表:试求三次样条插值S(x),并满足条件 (1)S`(0.25)=1.0000,S`(0.53)=0.6868; (2)S ’’(0.25)=S ’’(0.53)=0。
分析:本问题是已知五个点,由这五个点求一三次样条插值函数。
边界条件有两种,(1)是已知一阶倒数,(2)是已知自然边界条件。
对于第一种边界(已知边界的一阶倒数值),可写出下面的矩阵方程。
⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡432104321034322110d M M M M M 200020000020022d d d d λμμλμλμλ其中μj =j1-j 1-j h h h +,λi=j1-j j h h h +,dj=6f[x j-1,x j ,x j+1], μn =1,λ0=1对于第一种边界条件d 0=0h 6(f[x 0,x 1]-f 0`),d n =1-n h 6(f`n-f `[x n-1,x n ]) 解:由matlab 计算得:由此得矩阵形式的线性方程组为:⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡ 2.1150-2.4286-3.2667-4.3143-5.5200-M M M M M 25714.00001204286.000004000.026000.0006429.023571.0001243210解得 M 0=-2.0286;M 1=-1.4627;M 2= -1.0333; M 3= -0.8058; M 4=-0.6546S(x)=⎪⎪⎩⎪⎪⎨⎧∈-+-+-∈-+-+-∈-+-+-∈-+-+-]53.0,45.0[x 5.40x 9.1087x 35.03956.8.450-x 1.3637-x .5301.67881- ]45.0,39.0[x 9.30x 11.188x 54.010.418793.0-x 2.2384-x .450(2.87040-]39.0,30.0[x 03.0x 6.9544x 9.30 6.107503.0-x 1.9136-x .3902.708779-]30.0,25.0[x 5.20x 10.9662x 0.3010.01695.20-x 4.8758-x .3006.76209-33333333),()()()(),()()()),()()()(),()()()(Matlab 程序代码如下:function tgsanci(n,s,t) %n代表元素数,s,t代表端点的一阶导。
北航数值分析-实习作业1(C语言详细注释)

《数值分析》计算实习作业《一》北航第一题 设有501501⨯的矩阵⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=501500499321a bc b a b cc b a b ccb a bc c b a b c b a A其中.064.0,16.0);501,2,1(64.0)2.0sin()024.064.1(1.0-===--=c b i e i i a i i 矩阵的特征值)501,,2,1( =i i λ满足||min ||,501150121i i s λλλλλ≤≤=<<<试求1. 5011,λλ和s λ的值2. 的与数4015011λλκλμ-+=k 最接近的特征值)39,,2,1( =K κλi3. 的(谱范数)条件数2)A (cond 和行列式A det 要求1. 算法的设计方案(A 的所有零元素都不能存储)2. 全部源程序(详细注释)。
变量为double ,精度-1210=ε,输出为e 型12位有效数字3. 特征值s 5011,,λλλ和)39,,2,1( =K κλi 以及A cond det ,)A (2的值4. 讨论迭代初始向量的选取对计算结果的影响,并说明原因解答:1. 算法设计对于s λ满足||min ||5011i i s λλ≤≤=,所以s λ是按模最小的特征值,直接运用反幂法可求得。
对于5011,λλ,一个是最大的特征值,一个是最小的特征值,不能确定两者的绝对值是否相等,因此必须首先假设||||5011λλ≠,然后运用幂法,看能否求得一个特征值,如果可以求得一个,证明A 是收敛的,求得的结果是正确的,然后对A 进行带原点平移的幂法,偏移量是前面求得的特征值,可以求得另一个特征值,最后比较这两个特征值,较大的特征值是501λ,较小的特征值就是1λ。
如果在假设的前提下,无法运用幂法求得按模最大的特征值,即此时A 不收敛,则需要将A 进行带原点平移的幂法,平移量可以选取1,再重复上述步骤即可求得两个特征值。
数值分析作业1

拉格朗日插值法摘要:本篇综述是从插值法的原理入手,通过线性插值(一次插值) 、抛物线插值(二次插值)的分析,从特殊到一般,从简单到复杂,引入拉格朗日插值多项式。
关键词:插值法线性插值抛物插值拉格朗日插值一、引言在科学研究和其他许多实际问题中,常常有函数不便于处理和计算的情形。
有时候函数关系没有明显的解析表达式,需要根据实验观测或其他方法来确定与自变量的某些值相对应的函数值;有时函数虽有解析表达式,但是使用很不方便。
因此,希望对这些问题中的函数建立一个简单的便于计算和处理的近似表达式,即用一个简单的函数来近似代替这些不变处理的函数。
与用近似数代替准确数一样,这也是数值计算方法中最基本的概念和方法之一,也就是插值法。
二、插值法的基本原理1. 插值法设函数y =f(x)定义在区间〔a , b ]上,x°,X i,…,X n是la , b 1上取定的n+1个互异的节点,且在这些点处的函数值f (X o),f (xj,…,f (X n)为已知,即y i二f(X i),若存在一个f(x)的近似函数P(X),满足p(Xi)= yi i = 0, 1,2, , , n。
( 1),则称p( x )为f (x)的插值函数。
(1)式称为插值条件,f ( x )称为被插函数,[a , b ]称为插值区间,求p ( x )的方法就是插值法。
插值函数p ( x )在n+1个互异插值节点X i ( i = 0, 1, 2, , , n)处与f (x )相等,在其他点x就用p( x )的值作为f (x)的近似值。
这一过程称为插值,点x称为插值点。
换句话说,插值就是根据被插函数给出的函数表“插出”所要点的函数值。
用p ( X )的值作为f (x)的近似值。
不仅希望p ( X )能较好的逼近f(X),而且还希望它简单。
由于代数多项式计算既简单又便于计算,这是我们选择用多项式作为插值函数的原因。
我们数值分析课主要学习了代数多项式插值。
数值分析第一次作业答案

作业1.用如下数值表构造不超过3次的插值多项式2. P55 11题.给出概率积分⎰-=xxdxey 022π的数据表用2次插值计算,试问:(1) 当x = 0.472时,积分值等于多少? (2) 当x 为何值时,积分值等于0.5? 解:(1) 取x 0 = 0.47, x 1 = 0.48, x 2 = 0.4980.4955530040.04093346-80.1809899240.355496540.51166830.50274980.4937452=+=----⨯+----⨯+----⨯==----+----+----≈)48.049.0)(47.049.0()48.0472.0)(47.0472.0()49.048.0)(47.048.0()49.0472.0)(47.0472.0()49.0472.0)(48.047.0()49.0472.0)(48.0472.0()472.0())(())(())(())(())(())(()472.0(2120210221120121210y Lxx xx xxy x x x x x x y x x x x x x x x x x x x y(2)90.4769359350.05272367-80.4362204360.093439170.50274980.51166830.49374520.51166830.50274980.49374520.49 0.51166830.50274980.49374520.50274980.51166830.49374520.48 0.51166830.49374520.50274980.49374520.51166830.50274980.47=+=----⨯+----⨯+----⨯==----+----+----≈))(()5.0)(5.0())(()5.0)(5.0())(()5.0)(5.0()5.0())(())(())(())(())(())(()5.0(212210221120121210Lyyy y yy xy y yy y y xyyyy yy xy y y y y y x3. 证明方程e x +10x -2=0在区间[0,1]内有一个根,如果使用二分法求该区间内的根,且误差不超过10-6,试问需要二分区间[0,1]多少次?4. 设x t =451.01为准确值,x a =451.023为x t 的近似值,试求出x a 有效数字的位数及相对误差 作业答案1.解:N 2(x ) = f (0)+f [0,1](x -0)+ f [0,1,2](x -0) (x -1) 1+1×(x -0) +3×(x -0) (x -1)=3x 2-2x +1 为求得P 3(x ),根据插值条件知,P 3(x )应具有下面的形式 P 3(x )=N 2(x )+k (x -0) (x -1) (x -2),这样的P 3(x )自然满足:P 3(x i )= f (x i )由P 3’(1 )=3P 3’(1 )= N 2’(1 )+k (1-0) (1-2) =N 2’(1 )-k = 4-k=3∴ k =1∴ P 3(x )=N 2(x )+ (x -0) (x -1) (x -2)=x 3+1 3. 证明 令f (x )=e x +10x -2,∵ f (0)=-1<0,f (1)=e+8> 0∴ f (x )= e x +10x -2 =0在[0,1]有根。
北航数值分析实习题目第一题

《数值分析B》大作业一ZY1515105 樊雪松一.算法设计方案:1.矩阵A的存储与检索将带状线性矩阵A[501][501]转存为一个矩阵MatrixC[5][501] 。
在数组MatrixC[5][501]中检索A的带内元素a ij的方法是:A的带内元素a ij=C中的元素c i-j+2,j。
2.求解λ1,λ501,λs1、首先分别使用幂法和反幂法迭代求出矩阵按摸最大和最小的特征值λmax和λmin。
λmin即为λs;如果λ max>0,则λ501=λmax;如果λmax<0,则λ1=λmax。
2、使用带原点平移的幂法(mifa()函数),令平移量p=λmax,求出对应的按摸最大的特征值λ’max,如果λ max>0,则λ1=λ’max+p;如果λmax<0,则λ501=λ’max+p。
3、求解A的与数μk=λ1+k(λ501-λ1)/40 的最接近的特征值λik (k=1,2,…,39)。
使用带原点平移的反幂法,令平移量p=μk,即可求出与μk最接近的特征值λ ik。
4、求解A的(谱范数)条件数cond(A)2和行列式detA。
cond(A)2=|λ1/λn|,其中λ1和λn分别是矩阵A的模最大和最小特征值。
求解矩阵A的行列式,可先对矩阵A进行LU分解后,detA等于U所有对角线上元素的乘积。
二.源程序#include<stdio.h>#include<math.h>#include<conio.h>//定义A中元素double C[5][501];double a[501];double b;double c;//声明所有函数void YaSuoJZ(double C[5][501],double a[501],double b,double c) ;//压缩矩阵函数double mifa(double C[5][501]); //幂法函数void daizhuangLU(double A[5][501]); //带状矩阵的LU分解double fanmifa(double C[5][501]);//反幂法函数//最值函数int max2(int x,int y);int max3(int x,int y,int z);int min(int x,int y);//最值函数int max2(int x,int y) //求2个数的最大值{int z;z=x>y?x:y;return(z);}int max3(int x,int y,int z) //求3个数的最大值{int w;w = z > max2(x,y)? z:max2(x,y);return(w);}int min(int x,int y) //求2个数的最小值{int z;z=x>y?y:x;return(z);}//将矩阵A压缩存储在矩阵C中void YaSuoJZ(double C[5][501],double a[501],double b,double c) {int i;for(i=0;i<=500;i++){if(i>=2) C[0][i]=c;else C[0][i]=0;if(i>=1) C[1][i]=b;else C[1][i]=0;if(i<=499) C[3][i]=b;else C[3][i]=0;if(i<=498) C[4][i]=c;else C[4][i]=0;C[2][i]=a[i];}}//幂法函数:用幂法求矩阵模最大的特征值double mifa(double C[5][501]){double u[501];double y[501]={0},η=0;double β,βk=0;double ε=1;// ε为精度double sumu=0,sumAY=0;int i,j,k=1; //k为循环次数for (i=0;i<=500;i++) //取任一非零向量u0u[i] = 1.0;while(ε>=1e-12){for(i=0;i<=500;i++) //求u(k-1)的2范数ηsumu=sumu+u[i]*u[i];η=sqrt(sumu);sumu=0;for(i=0;i<=500;i++) //求y(k-1)y[i]=u[i]/η;for(i=0;i<=500;i++) //求u(k)的各分量u[i]{for(j=max2(0,i-2);j<=min(i+2,500);j++)sumAY=sumAY+C[i-j+2][j]*y[j];u[i]=sumAY;sumAY=0;}//求幂法中的βkβ=βk; //将β(k-1)放在β中βk=0;for(i=0;i<=500;i++) //求βkβk=βk+y[i]*u[i];if(k>=2)ε=fabs(βk-β)/fabs(βk);k++;}return(βk);}//带状矩阵的LU分解void daizhuangLU(double A[5][501]){int i,j,k,m,t;double sumukj=0,sumlik=0;for(k=0;k<=500;k++){for(j=k;j<=min(k+2,500);j++) //求ukj并存在A[k-j+2][j]中{for(t=max3(0,k-2,j-2);t<=k-1;t++)sumukj=sumukj+A[k-t+2][t]*A[t-j+2][j];A[k-j+2][j]=A[k-j+2][j]-sumukj;sumukj=0;}if(k<500)for(i=k+1;i<=min(k+2,500);i++) //求lik并存在A[i-k+2][k]中{for(m=max3(0,i-2,k-2);m<=k-1;m++)sumlik=sumlik+A[i-m+2][m]*A[m-k+2][k];A[i-k+2][k]=(A[i-k+2][k]-sumlik)/A[2][k];sumlik=0;}}}//反幂法函数:用反幂法求矩阵的模最小的特征值double fanmifa(double M[5][501]){double u[501];double y[501]={0},x[501],η=0;double fβ,fβk=0;double ε=1;double fsumu=0,sumLX=0,sumUu=0;int i,t,m,k=1;for(i=0;i<=500;i++) //任取一非零向量u0u[i]=1;daizhuangLU(M); //对A进行LU分解A=LU,Au(k)=y(k-1)等价于Uu(k)=x和Lx=y(k-1) while(ε>=1e-12){for(i=0;i<=500;i++) //求u(k-1)的2范数ηfsumu=fsumu+u[i]*u[i];η=sqrt(fsumu);fsumu=0;for(i=0;i<=500;i++) //求y(k-1)y[i]=u[i]/η;for(i=0;i<=500;i++) //求中间向量xx[i]=y[i];for(i=1;i<=500;i++){for(t=max2(0,i-2);t<=i-1;t++)sumLX=sumLX+M[i-t+2][t]*x[t];x[i]=x[i]-sumLX;sumLX=0;}u[500]=x[500]/C[2][500]; //求u(k)的各分量u[i]for(i=499;i>=0;i--){for(m=i+1;m<=min(i+2,500);m++)sumUu=sumUu+M[i-m+2][m]*u[m];u[i]=(x[i]-sumUu)/M[2][i];sumUu=0;}//求反幂法中的βkfβ=fβk; //将fβ(k-1)放在fβ中fβk=0;for(i=0;i<=500;i++) //求fβkfβk=fβk+y[i]*u[i];if(k>=2)ε=fabs(1/fβk-1/fβ)/fabs(1/fβk);k++;}return(1/fβk);}//主函数void main(){int i,j,k;double λ1,λ501,λm,λm1,λm2,λs,λ,p;double cond,detA=1;for(i=1;i<=501;i++)a[i-1]=(1.64-0.024*i)*sin(0.2*i)-0.64*exp(0.1/i);b=0.16;c=-0.064;YaSuoJZ(C,a,b, c); //将矩阵A中元素压缩存储在C中λm1=mifa(C); //对A用幂法求出模最大的特征值λm1λs=fanmifa(C); //对A用反幂法求出模最小的特征值λsYaSuoJZ(C,a,b, c); //还原矩阵A中元素并压缩存储在C中for(j=0;j<=500;j++) //对A进行平移,平移量为λm1,平移后矩阵元素压缩存储在C中C[2][j]=C[2][j]-λ?m1;λm=mifa(C);λm2=λm1+λm; //λm1与λm2是矩阵的最大最小特征值if(λm1>λm2) //判断A最大最小特征值{λ501=λm1;λ1=λm2;}else{λ501=λm2;λ1=λm1;}printf("数值分析计算实习第一题\n\n ZY1515105 樊雪松\n\n (1)A的最大最小以及模最小的特征值\n");printf("A的最小特征值λ1=%.13e\n",λ1);printf("A的最大特征值λ501=%.13e\n",λ501);printf("A的模最小特征值λs=%.13e\n",λs);printf("\n(2)与数μk最接近的特征值\n");printf("\t要求接近的值\t\t\t实际求得的特征值\n");YaSuoJZ(C,a,b, c); //还原矩阵A中元素并压缩存储在C中for(k=1;k<=39;k++){p=λ1+k*(λ501-λ1)/40;for(j=0;j<=501;j++)C[2][j]=C[2][j]-p;λ=fanmifa(C)+p;printf("μ%d=%.13e λ%d=%.13e\n",k,p,k,λ);YaSuoJZ(C,a,b, c); //还原矩阵A中元素并压缩存储在C中}printf("\n(3)计算A的条件数cond(A)和行列式detA\n");cond=λm1/λs;daizhuangLU(C);for(j=0;j<=500;j++)detA=detA*C[2][j];printf("A的条件数cond(A)=%.13e\n",cond);printf("A的行列式detA=%.13e\n",detA);getch();}三、运行结果数值分析计算实习第一题ZY1515105 樊雪松(1)A的最大最小以及模最小的特征值A的最小特征值λ1=-1.0700113615018e+001A的最大特征值λ501=9.7246340987773e+000A的模最小特征值λs=-5.5579107942295e-003(2)与数μk最接近的特征值要求接近的值实际求得的特征值μ1=-1.0189494922173e+001 λ1=-1.0182934033146e+001 μ2=-9.6788762293280e+000 λ2=-9.5857074250676e+000 μ3=-9.1682575364831e+000 λ3=-9.1726724239280e+000 μ4=-8.6576388436383e+000 λ4=-8.6522840078976e+000 μ5=-8.1470201507934e+000 λ5=-8.0934838086753e+000 μ6=-7.6364014579485e+000 λ6=-7.6594054076924e+000 μ7=-7.1257827651036e+000 λ7=-7.1196846486912e+000 μ8=-6.6151640722588e+000 λ8=-6.6117643393973e+000 μ9=-6.1045453794139e+000 λ9=-6.0661032265951e+000 μ10=-5.5939266865690e+000 λ10=-5.5851010526284e+000 μ11=-5.0833079937241e+000 λ11=-5.1140835298122e+000 μ12=-4.5726893008792e+000 λ12=-4.5788721768651e+000 μ13=-4.0620706080344e+000 λ13=-4.0964709262599e+000 μ14=-3.5514519151895e+000 λ14=-3.5542112157508e+000 μ15=-3.0408332223446e+000 λ15=-3.0410900181333e+000 μ16=-2.5302145294997e+000 λ16=-2.5339703111304e+000 μ17=-2.0195958366549e+000 λ17=-2.0032307695635e+000μ18=-1.5089771438100e+000 λ18=-1.5035576112274e+000μ19=-9.9835845096511e-001 λ19=-9.9355860600754e-001μ20=-4.8773975812023e-001 λ20=-4.8704267388496e-001μ21=2.2878934724645e-002 λ21=2.2317362495748e -002μ22=5.3349762756952e-001 λ22=5.3241747420686e -001μ23=1.0441163204144e+000 λ23=1.0528989626935e+000μ24=1.5547350132593e+000 λ24=1.5894458818809e+000μ25=2.0653537061042e+000 λ25=2.0603304602743e+000μ26=2.5759723989490e+000 λ26=2.5580755970728e+000μ27=3.0865910917939e+000 λ27=3.0802405093071e+000μ28=3.5972097846388e+000 λ28=3.6136208676923e+000μ29=4.1078284774837e+000 λ29=4.0913785104506e+000μ30=4.6184471703285e+000 λ30=4.6030353782791e+000μ31=5.1290658631734e+000 λ31=5.1329242838984e+000μ32=5.6396845560183e+000 λ32=5.5949063480833e+000μ33=6.1503032488632e+000 λ33=6.0809338570269e+000μ34=6.6609219417080e+000 λ34=6.6803540921116e+000μ35=7.1715406345529e+000 λ35=7.2938774481266e+000μ36=7.6821593273978e+000 λ36=7.7171117142356e+000μ37=8.1927780202427e+000 λ37=8.2252200140502e+000μ38=8.7033967130876e+000 λ38=8.6486660651935e+000μ39=9.2140154059324e+000 λ39=9.2542003445750e+000(3)计算A 的条件数cond(A)和行列式detAA 的条件数cond(A)=1.9252042739022e+003A 的行列式detA=2.7727861417521e+118四、结果分析设A 的n 个线性无关的特征向量为1x ,2x ,…,n x ,其相对应的特征值满足的关系为n λλλλ≥≥≥> 321。
北航数值分析作业第一题

数值分析作业第一题一、 算法设计方案利用带状Dollittle 分解,将A[501][501]转存到数组C[5][501],以节省存储空间1、计算λ1和λ501首先使用幂法求出矩阵的按模最大的特征值λ0:如果λ0>0,则其必为按模最大值,因此λ501=λ0,然后采用原点平移法,平移量为λ501,使用幂法迭代求出矩阵A -λ501I 的按模最大的特征值,其特征值按从小到大排列应为λ1-λ501、λ2-λ501、……、0。
因此A-λ501I 的按模最大的特征值应为λ1-λ501。
又因为λ501的值已求得,由此可直接求出λ1。
2、计算λSλS 为矩阵A 按模最小的特征值,可以通过反幂法直接求出。
3、计算λikλik 是对矩阵A 进行λik 平移后,再用反幂法求出按模最小的特征值λmin ,λik =λik +λmin 。
4、计算矩阵A 的条件数计算cond (A )2和行列式det(A)矩阵A 的条件数为n12cond λλ)( A ,其中λ1和λn 分别是矩阵A 的模最大和最小特征值,直接利用上面求得的结果直接计算。
矩阵A 的行列式可先对矩阵A 进行LU 分解后,det(A)等于U 所有对角线上元素的乘积。
二、源程序:#include<math.h>#include<stdio.h>#include<stdlib.h>#include<iostream.h>#define s 2#define r 2int Max(int v1,int v2);int Min(int v1,int v2);int maxt(int v1,int v2,int v3);void storage(double C[5][501],double b,double c);double mifa(double C[5][501]);void LU(double C[5][501]);double fmifa(double C[5][501]);int Max(int v1,int v2) //求两个数的最大值{ return((v1>v2)?v1:v2);}int Min(int v1,int v2) //求两个数最小值{ return ((v1<v2)?v1:v2);}int maxt(int v1,int v2,int v3) //求三个数最大值{ int t;if(v1>v2) t=v1;else t=v2;if(t<v3) t=v3;return(t);}/***将矩阵值转存在一个数组里,以节省存储空间***/void storage(double C[5][501],double b,double c){ int i=0,j=0;C[i][j]=0,C[i][j+1]=0;for(j=2;j<=500;j++)C[i][j]=c;i++;j=0;C[i][j]=0;for(j=1;j<=500;j++)C[i][j]=b;i++;for(j=0;j<=500;j++)C[i][j]=(1.64-0.024*(j+1))*sin(0.2*(j+1))-0.64*exp(0.1/(j+1));i++;for(j=0;j<=499;j++)C[i][j]=b;C[i][j]=0;i++;for(j=0;j<=498;j++)C[i][j]=c;C[i][j]=0,C[i][j+1]=0;}//用于求解最大的特征值,幂法double mifa(double C[5][501]){ int m=0,i,j;double b2,b1=0,sum;double u[501],y[501];for (i=0;i<501;i++){ u[i] = 1.0;}do{ sum=0;if(m!=0)b1=b2;m++;for(i=0;i<=500;i++)sum+=u[i]*u[i];for(i=0;i<=500;i++)y[i]=u[i]/sqrt(sum);for(i=0;i<=500;i++){ u[i]=0;for(j=Max(i-r,0);j<=Min(i+s,500);j++)u[i]=u[i]+C[i-j+s][j]*y[j];}b2=0;for(i=0;i<=500;i++)b2=b2+y[i]*u[i];}while(fabs(b2-b1)/fabs(b2)>=1.0e-12);return b2;}/*****行列式LU分解*****/void LU(double C[5][501]){ double sum;int k,i,j;for(k=1;k<=501;k++){ for(j=k;j<=Min(k+s,501);j++){ sum=0;for(i=maxt(1,k-r,j-s);i<=k-1;i++)sum+=C[k-i+s][i-1]*C[i-j+s][j-1];C[k-j+s][j-1]-=sum;}for(j=k+1;j<=Min(k+r,501);j++){ sum=0;for(i=maxt(1,j-r,k-s);i<=k-1;i++)sum+=C[j-i+s][i-1]*C[i-k+s][k-1];C[j-k+s][k-1]=(C[j-k+s][k-1]-sum)/C[s][k-1];}}}/***带状DOOLITE分解,并且求解出方程组的解***/void solve(double C[5][501],double x[501],double b[501]){ int i,j,k,t;double B[5][501],c[501];for(i=0;i<=4;i++){ for(j=0;j<=500;j++)B[i][j]=C[i][j];}for(i=0;i<=500;i++)c[i]=b[i];for(k=0;k<=500;k++){ for(j=k;j<=Min(k+s,500);j++){ for(t=Max(0,Max(k-r,j-s));t<=k-1;t++)B[k-j+s][j]=B[k-j+s][j]-B[k-t+s][t]*B[t-j+s][j];}for(i=k+1;i<=Min(k+r,500);i++){ for(t=Max(0,Max(i-r,k-s));t<=k-1;t++)B[i-k+s][k]=B[i-k+s][k]-B[i-t+s][t]*B[t-k+s][k];B[i-k+s][k]=B[i-k+s][k]/B[s][k];}}for(i=1;i<=500;i++)for(t=Max(0,i-r);t<=i-1;t++)c[i]=c[i]-B[i-t+s][t]*c[t];x[500]=c[500]/B[s][500];for(i=499;i>=0;i--){ x[i]=c[i];for(t=i+1;t<=Min(i+s,500);t++)x[i]=x[i]-B[i-t+s][t]*x[t];x[i]=x[i]/B[s][i];}}//用于求解模最大的特征值,反幂法double fmifa(double C[5][501]){ int m=0,i;double b2,b1=0,sum=0,u[501],y[501];for (i=0;i<=500;i++){ [i] = 1.0;}do{ if(m!=0)b1=b2;m++;sum=0;for(i=0;i<=500;i++)sum+=u[i]*u[i];for(i=0;i<=500;i++)y[i]=u[i]/sqrt(sum);solve(C,u,y);b2=0;for(i=0;i<=500;i++)b2+=y[i]*u[i];}while(fabs(b2-b1)/fabs(b2)>=1.0e-12);return 1/b2;}/***主程序***/void main(){ double b=0.16,c=-0.064,det=1.0;int i;double C[5][501],cond;storage(C,b,c); //进行C的赋值cout.precision(12); //定义输出精度double k1=mifa(C); //利用幂法计算矩阵的最大特征值和最小特征值if(k1<0)printf("λ1=%.12e\n",k1);else if(k1>=0)printf("λ501=%.12e\n",k1);for(i=0;i<501;i++)C[2][i]=C[2][i]-k1;double k2=mifa(C)+k1;if(k2<0)printf("λ1=%.12e\n",k2);else if(k2>=0)printf("λ501=%.12e\n",k2);storage(C,b,c);double k3=fmifa(C); //利用反幂法计算矩阵A的按模最小特征值printf("λs=%.12e\n",k3);storage(C,b,c); //计算最接近特征值double u[39]={0};for(i=0;i<39;i++){ u[i]=k1+(i+1)*(k2-k1)/40;C[2][i]=C[2][i]-u[i];u[i]=fmifa(C)+u[i];printf("与数u%d 最接近的特征值λ%d: %.12e\n",i+1,i+1,u[i]);}if(k1>0) //计算矩阵A的条件数,取2范数cond=fabs(k1/k3);else if(k1<0)cond=fabs(k2/k3);storage(C,b,c);LU(C); //利用LU分解计算矩阵A的行列式for(i=0;i<501;i++)det*=C[2][i];printf("\ncond(A)=%.12e\n",cond);printf("\ndet(A)=%.12e\n",det);}三、计算结果:四、结果分析迭代初始向量的选择对果有一定的影响,选择不同的初始向量可能会得到不同阶的特征值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数值分析第一次作业(1)
1.已测得函数()
y f x
=的三对数据:(0,1),(-1,5),(2,-1),
(1)用Lagrange插值求二次插值多项式。
(2)构造差商表。
(3)用Newton插值求二次插值多项式。
2.在44
x
-≤≤上给出()x
f x e
=的等距节点函数表,若用二次插值求x e的近似值,要使截断误差不超过6
10-,问使用函数表的步长h应取多少?
3.求2
()
f x x
=在[a,b]上的分段线性插值函数()
h
I x,并估计误差。
4.已知单调连续函数()
y f x
=的如下数据
用插值法计算x约为多少时() 1.
f x=(小数点后至少保留4位)
5.设函数()
f x在区间[0,3]上具有四阶连续导数,试用埃尔米特插值法,求一个次
数不高于3的多项式
3()
P x,使其满足
3(0)0
P=,
3(1)1
P=,
3'(1)3
P=,
3(2)1
P=。
并写出误差估计式。
6.设函数()
y f x
=在节点0,1,2,3
x=的函数值均为零,试分别求满足下列边界条件下的三次样条插值函数()
S x:
(1)''
(0)1,(3)0
f f
==(2)''''
(0)1,(3)0
f f
==
7.编程实现题:
在微电机设计计算中需要查磁化曲线表,通常给出的表是磁密B每间隔100高斯磁路每厘米长所需安匝数at的值,下面要解决B从4000至11000区间的查表问题。
为节省计算机存储单元,采用每500高斯存入一个at值,在利用差分公式计算。
从差分表中看到三阶差分近似于0,计算时只需两阶差分。
当4000≤B≤10500时用牛顿前插公式;当10500≤B≤11000时用牛顿后插公式;
试在计算机上编程实现求任一在区间[4000,11000]内的函数值。
