冲击响应谱计算的matlab程序
Z2.11 Matlab求解冲激响应和阶跃响应

2
Xidian University, ICIE. All Rights Reserved
2.2 冲激响应与阶跃响应
第二章 连续系统的时域分析
例 求以下系统的冲激响应和阶跃响应。
7y”(t) + 4y’(t) + 6y(t) = f’(t)+ f(t)
第二章 连续系统的时域分析
Z2.11 Matlab求解冲激响应和阶跃响应
MATLAB提供了专门用于求LTI系统的冲激响应和阶跃响应
的函数。设LTI系统的微分方程为:
n
m
ai y (i) (t) bi f (i) (t)
i 1
j 1
求LTI系统的冲激响应的函数为:
impulse(b, a)
求LTI系统的阶跃响应的函数为:
2.2 冲激响应与阶跃响应
知识点Z2.11
第二章 连续系统的时域分析源自Matlab求解冲激响应和阶跃响应
主要内容:
Matlab求解冲激响应和阶跃响应的函数
基本要求:
了解冲激响应和阶跃响应的Matlab求解方法
1
Xidian University, ICIE. All Rights Reserved
2.2 冲激响应与阶跃响应
解:
a=[7 4 6];
Impulse Response
%构0.2 造系数向量
Amplitude
b=[1 1]; subplot(2,1,1) impulse(b,a);
0
-0.2
0
2
4
6
8
10 12 14 16 18 20
Time (sec)
液体火箭发动机冲击响应谱分析计算方法

为 x ( t) . 一般情况下 , 冲击加速度的测量比较容易 实现 , 因此当基础受到加速度作用时 , 质量块 m 的 运动方程可表示为
mx + cx + kx = ku ( t) + cu ( t)
.. . ..
( 1)
. 因此了解发动机工作状态下的
冲击特性 ,制定相应的抗冲击策略 , 直接关系到全 箭的结构可靠性 . 冲击响应谱在结构分析方面的用 途主要用来衡量冲击作用的效果 ,估计冲击对结构 的损伤势 [ 3 ] . 根据冲击响应谱 , 可以计算在特定冲 击作用下发动机结构零件的强度和发动机自身的 安全性 . 某新型大推力液体火箭发动机在地面试验 过程中 ,测得了全程段的时域数据 , 因测试软件功 能所限 ,不能进行冲击响应谱分析 . 基于此 ,文中从 冲击响应谱概念着手 , 基于 Matlab 软件包开发了 冲击响应谱分析软件 , 力图快速 、 方便的对液体火 箭发动机地面试验数据进行冲击响应谱分析 ,为地 面试验数据的深入分析提供辅助手段 .
3 发动机地面试验冲击响应谱计算
在对某型液体火箭发动机多次地面试验时域 数据进行分析时 ,发现燃气发生器点火时所测的冲 击响应均较大 . 考虑到发动机自身的安全性 , 以及 该启动冲击对全箭结构的影响 ,有必要对发生器启 动冲击进行冲击响应谱分析 . 因发动机地面试验数据采集软件功能所限 ,不 能进行冲击响应谱分析 ,因此地面试验结束后对所 采集的时域数据利用文中开发的 Vibsr s 冲击响应 谱分析软件进行计算 ,所得计算结果导出为 t xt 文 文中件供深入分析地面试验数据时参考 . 考虑到篇 幅所限 ,只给出燃气发生器上一个三向加速度传感 器所测的发生器启动时的冲击响应谱分析结果 . 图 3~5 分别为轴向 、 径向 、 切向加速度传感器所测的 冲击响应及利用 Vibsr s 计算得到的最大冲击响应 谱 . 计算过程中时间范围根据冲击响应的时域图形 给定 ,频率范围选择为 0. 1 ~ 10 k Hz , 其他选项采
matlab冲激响应

Matlab冲激响应引言冲激响应是信号处理中的一个重要概念,用于描述线性时不变系统的响应特性。
在Matlab中,我们可以使用不同的方法来计算和分析系统的冲激响应。
本文将介绍冲激响应的概念、Matlab中计算冲激响应的方法,并通过实例演示如何使用Matlab来计算系统的冲激响应。
冲激响应的概念冲激响应是描述系统对单位冲激信号的响应的函数。
单位冲激信号通常表示为δ(t),它在t=0时刻取值为1,其他时刻取值为0。
冲激响应由系统对单位冲激信号的响应构成,可以用数学公式表示为h(t)。
Matlab中计算冲激响应的方法在Matlab中,我们可以使用多种方法来计算系统的冲激响应,其中包括时域方法、频域方法和离散方法。
以下是常用的几种方法:时域方法时域方法是通过求解系统的微分方程来计算冲激响应。
Matlab提供了lsim函数来计算连续系统和离散系统的冲激响应。
通过传入系统的差分方程和单位冲激信号作为输入,lsim函数可以返回系统的冲激响应。
频域方法频域方法是通过系统的传递函数来计算冲激响应。
Matlab提供了freqresp函数和impulse函数来计算连续系统和离散系统的冲激响应。
通过传入系统的传递函数和频率向量作为输入,freqresp函数可以返回系统的冲激响应。
离散方法离散方法是通过系统的差分方程来计算冲激响应。
Matlab提供了impulse函数来计算离散系统的冲激响应。
通过传入系统的差分方程和单位冲激信号作为输入,impulse函数可以返回系统的冲激响应。
Matlab中计算冲激响应的实例为了更好地理解如何使用Matlab来计算冲激响应,我们将通过一个实例演示。
假设存在一个连续系统的传递函数为H(s),我们想要计算该系统的冲激响应。
步骤1:定义系统的传递函数首先,我们需要使用Matlab的tf函数来定义系统的传递函数。
假设系统的传递函数为H(s)=1/(s+1),代码如下所示:num = 1;den = [1 1];H = tf(num, den);步骤2:计算冲激响应接下来,我们可以使用lsim函数来计算系统的冲激响应。
利用matlab由开环传递函数求闭环传递函数并求其单位冲击和阶跃响应.docx

利用matlab 由开环传递函数求闭环传递函数并求其单位冲击和阶跃响应并绘制输出阶跃响应曲线和脉冲响应曲线 解:编程(见:\work\CT_tch\resp_2_20110522)clear all;close all;%%%%%%%%%%%%%%a0 = [00000.8];bl = [10];b2 = [0.3 1 ];b3 = [0.5 0.7 1];bO = conv(bl,conv(b2,b3)); % bO:开环传递函数分母多项式系数 %%%%闭环传递函数aa = a0;% aa :闭环传递函数分了多项式系数 bb = bO + aO; % bb :闭环传递函数分了多项式系数 disp ('System Closed Loop Transfer Function is :*)aabb%%%%计算:阶跃响应t = 0:0.1 :20y = step (aa, bb, t);% 阶跃响应%%%%绘制:阶跃响应figure(l)plot(t ,y);title 。
阶跃响应); xlabelC时间 /s');ylabel(1S 值);grid ; %%%%计算:figure(2)yy = impulse (aa, bb, t);% 标题:脉冲响应plot(t, yy); titlcC 脉冲响应); xlabelC 时间/s); ylabel(1S 值);grid; %网格%%%%绘制:脉冲响应wt = logspace (-1,1); % 对数空间「0.1, 10)例:设有一个系统的开环传递函数如下函数, 01 %aO:开环传递函数分子多项式系数 % s % % (0.5 s2 + 0.7s+ 1) %标题:阶跃响应 %横坐标 %纵坐标 % io,!! 脉冲响应[mag,phase] = bode (a0 ,b0 ,wt); % 计算:Bode111的幅值和相位[Gm,Pm,Wcg,Wcm] = margin(aO,bO); % 计算:稳定裕度disp ('System Gain Margin and its associated frequency areGm %模值稳定裕度Wcg %幅值穿越频率,剪切频率,1/sdisp ('System Phase Margin and its associated frequency are : Pm %相位稳定裕度Wcm % ■兀相位穿越频率,1/s%%%%绘制:Bode图figure(3)Subplot (211); %对数幅值■频率图amp = 20*logl0(mag); % 20*log(mag), dBsemilogx(wt,amp);title C对数幅值■频率图);xlabel C频率 / rad*); ylabel f 幅值 / dB);grid;subplot (212); %相位-频率图semilogx(wt,phase);title C相位-频率图);xlabel ('频率/ rad*); ylabel('相位/ degree*);grid;运行该程序可得系统的单位阶跃和脉冲响应曲线如下,W 15图1系统的单位阶跃响应曲线系统的Bode图如F,图2 系统的脉冲响应曲线系统怕篦图幅频系统伯律图相麹:-300•■»、1—10图3 系统的Bode图。
matlab由差分方程求冲击响应

matlab由差分方程求冲击响应冲击响应是指系统在接受一个瞬时力或冲击时的反应。
在MATLAB中,可以使用差分方程来求解系统的冲击响应。
本文将介绍如何使用MATLAB进行差分方程求解,以及如何求取系统的冲击响应。
首先,我们需要了解差分方程的基本概念和表示。
差分方程是一种离散时间系统的描述方法,其以当前时刻的输入和之前时刻的输出为基础,通过递推关系来求解下一个时刻的输出。
差分方程可以表示为:y(n) = a1 * y(n-1) + a2 * y(n-2) + ... + aN * y(n-N) + b0 * x(n) + b1 * x(n-1) + ... + bM * x(n-M)其中,y(n)为当前时刻的输出,y(n-1)到y(n-N)为之前时刻的输出,x(n)到x(n-M)为当前时刻的输入,aN和bM为系数。
在MATLAB中,我们可以使用filter函数来求解差分方程。
filter函数的语法如下:y = filter(b,a,x)其中,b和a分别为差分方程中的b系数和a系数,x为输入信号。
函数的输出y为差分方程的响应结果。
假设我们有一个差分方程为:y(n) = 2 * y(n-1) - 3 * y(n-2) + x(n)其中,初始条件为y(0)=1,y(1)=2。
我们想要求解该差分方程的冲击响应。
首先,我们需要定义差分方程的系数和输入信号。
在MATLAB中,可以使用向量或矩阵来表示。
假设输入信号为冲击函数,即只在n=0时为1,其他时刻为0。
我们可以定义输入信号x如下:x = [1 zeros(1,99)];接下来,我们需要定义差分方程的系数。
根据差分方程的形式,我们可以得到a=[1 -2]和b=[1]。
我们可以将它们定义为向量:a = [1 -2];b = [1];然后,我们可以使用filter函数来求解差分方程的响应。
即:y = filter(b,a,x);最后,我们可以绘制差分方程的冲击响应图像。
matlab求冲激响应和阶跃响应数值解

matlab求冲激响应和阶跃响应数值解标题:深度探讨matlab求冲激响应和阶跃响应数值解的方法一、前言在信号与系统课程中,我们经常会遇到需要求解系统的冲激响应和阶跃响应的问题。
而在实际工程实践中,我们往往需要利用计算机进行数值求解。
在本文中,我们将重点探讨如何利用matlab对系统的冲激响应和阶跃响应进行数值求解,并结合个人观点,深入探讨其中的数学原理和工程应用。
二、matlab求解冲激响应的数值解1. 离散系统的冲激响应在信号与系统中,我们经常会遇到离散系统的冲激响应求解问题。
离散系统的冲激响应可以通过卷积求解,而在matlab中,我们可以利用conv函数来进行计算。
具体来说,在matlab中,我们可以定义系统的传递函数H(z),然后利用impulse函数生成单位脉冲输入序列,再利用conv函数与传递函数H(z)进行卷积运算,即可得到离散系统的冲激响应序列。
2. 个人观点与实践应用对于离散系统的冲激响应,我个人认为在实际工程中,常常需要对数字滤波器进行设计和分析。
而利用matlab求解冲激响应可以帮助工程师们更好地理解数字滤波器的特性,从而进行参数调整和性能优化。
三、matlab求解阶跃响应的数值解1. 连续系统的阶跃响应在连续系统中,阶跃响应是指系统在接受单位阶跃输入后的响应。
在matlab中,我们可以利用step函数来求解连续系统的阶跃响应。
具体来说,我们可以利用tf函数定义连续系统的传递函数G(s),然后利用step函数对系统进行仿真,即可得到连续系统的阶跃响应曲线。
2. 个人观点与实践应用对于连续系统的阶跃响应,我认为在控制系统工程中具有重要的应用价值。
控制系统工程师们往往需要对系统的阶跃响应进行分析和优化,而利用matlab进行阶跃响应的数值求解,可以帮助工程师们更好地理解系统的动态特性,从而提高系统的稳定性和性能。
四、总结与回顾通过对matlab求解冲激响应和阶跃响应的数值解的深入探讨,我们不仅对系统的动态特性有了更深入的理解,同时也学会了如何利用matlab来进行系统动态特性的数值分析。
用Matlab求冲激响应的几种方法

则 系统 函数 为
G ㈤ = =
然 后输 人 Ma t l a b程 序 :
y l= d s o l v e f ‘D2 y+2 Dy + 5 0 Y : He a v i —
6 ,一 0 . 0 8 ,0 . 1 2 ] ) ;屏幕 上 就会 显示 与 图 1 一 样
的结果 。
图 2 先 求 阶跃 响应 然 后 求 导
采用直接调用 i mp u l s e函数 的方 法 求 解 。
Ma t l a b程 序 为 :
s i d e ’ , ’D y( 0) =0,Y ( 0 ) =0’ ) ;
a= [ 1 ,2,5 0] ;
y 2=d i f( y 1 ) ;
运行可得 : y 2=1 / 7 e x p (一t ) ¥s i n( 7 t ) 再 输 入 He a v i s i d e
b= [ 1 ] ;
i mp u l s e( b ,a ) ;
● 第 一作 者 : 贺 富 堂 ( 1 9 5 7一) , 男 ,工 学 硕 士 , 高 级 工 程 师 ,多 年 来 主 要 从 事 电 路 、 电 磁 场 及 信 号 与 系 统 的 实 验 教 学
工作。 ● 收稿 日期 :2 0 1 5一 O 1 —0 6
称 冲激 响 应 。笔 者 常 常 遇 到 对 同 一 上 机 题 目,学 生
用 不 同 的方 法 解 出 的 结 果 似 乎 不 同 的情 况 ,具 体 题
目是 : 已知 微 分 方 程
Y ( t ) +2 Y ( t ) + 5 0 y( t ) =x ( t ) 果 。本 题 有 3种 解 法 。 ( 0 )
matlab 冲击响应谱

matlab 冲击响应谱冲击响应谱(shock response spectrum, SRS)是一种对于结构体系进行受冲击载荷响应分析的工具,用于评估结构在受到冲击载荷作用下的响应情况。
Matlab可以用于计算和绘制冲击响应谱。
要计算冲击响应谱,首先需要定义冲击载荷的时间历程和结构物的动力特性。
假设冲击载荷的时间历程为A(t),结构物的动力特性为d(t),则冲击响应谱可以通过以下步骤来计算:1. 计算结构物的频率响应函数(Frequency Response Function, FRF),用于描述结构物对频率激励的响应情况。
可以使用Matlab内置的函数`freqresp`来计算FRF,例如:```matlabsys = tf(A, B, C, D); % 定义结构物的传递函数w = logspace(-2, 2, 1000); % 定义频率范围G = freqresp(sys, w); % 计算频率响应函数```2. 根据冲击载荷的时间历程和结构物的动力特性,计算结构物的动力响应。
可以使用Matlab内置的函数`lsim`来模拟结构物的动力响应,例如:```matlabt = linspace(0, 10, 1000); % 定义时间范围x = A.*exp(-0.5*(t-5).^2/2); % 定义冲击载荷的时间历程y = lsim(sys, x, t); % 计算结构物的动力响应```3. 根据结构物的动力响应,计算冲击响应谱。
可以使用Matlab内置的函数`abs`来计算动力响应的绝对值,在频域上进行峰值计算,例如:```matlabSRS = abs(G).*max(abs(y)); % 计算冲击响应谱```4. 将冲击响应谱绘制成图形。
可以使用Matlab内置的函数`semilogx`来绘制半对数坐标系下的图形,例如:```matlabsemilogx(w, SRS); % 绘制冲击响应谱xlabel('Frequency (Hz)'); % 设置x轴标签ylabel('Shock Response (g)'); % 设置y轴标签title('Shock response spectrum'); % 设置图形标题```利用上述步骤,可以使用Matlab计算和绘制冲击响应谱,从而评估结构在受到冲击载荷作用下的响应情况。
matlab信号与系统冲击阶跃响应报告

matlab信号与系统冲击阶跃响应报告信号与系统是电子信息工程专业的重要课程之一,也是科学技术领域中的基础理论之一。
在信号与系统的学习中,冲击响应和阶跃响应是非常重要的概念。
通过对这两种响应的研究,我们可以更好地理解信号与系统的性质,从而应用到实际工程中。
在本文中,我将针对matlab中信号与系统的冲击响应和阶跃响应进行深入探讨,并分析其在实际应用中的重要性。
1. 冲击响应的概念和特点冲击响应是指系统对冲击信号(也称为单位脉冲信号)的响应。
在matlab中,我们可以通过使用impulse函数来获取系统的冲击响应。
冲击响应具有以下几个特点:- 冲击响应是系统的自由响应,不受外部信号的影响。
- 冲击响应是系统的固有特性,可以反映系统的动态响应能力。
- 冲击响应是系统的重要性能指标之一,可以用来评估系统的稳定性和动态特性。
2. 阶跃响应的概念和特点阶跃响应是指系统对阶跃信号(也称为单位阶跃信号)的响应。
在matlab中,我们可以通过使用step函数来获取系统的阶跃响应。
阶跃响应具有以下几个特点:- 阶跃响应是系统对输入信号的稳定响应,可以反映系统的静态特性和稳定性。
- 阶跃响应可以用来评估系统的超调量、上升时间和稳定状态误差等性能指标。
- 阶跃响应在控制系统和滤波器设计中具有重要应用,是系统分析和设计的基础。
3. matlab中的信号与系统分析在matlab中,我们可以利用信号与系统工具箱来进行冲击响应和阶跃响应的分析和计算。
通过调用相应的函数,我们可以得到系统的冲击响应和阶跃响应,并对其进行进一步的分析和处理。
在实际工程中,我们可以利用matlab来进行系统建模、性能分析和参数优化,从而实现对系统行为的深入理解和控制。
4. 个人观点和理解在我看来,信号与系统的冲击响应和阶跃响应是非常重要的概念,对于理解系统的动态和静态特性具有重要意义。
通过对冲击响应和阶跃响应的研究,我们可以更好地理解系统的内在特性,从而在实际工程中进行系统设计和控制。
用matlab求解某已知的差分方程的单位冲激响应全过程

⽤matlab求解某已知的差分⽅程的单位冲激响应全过程⽤matlab求解某已知的差分⽅程的单位冲激响应全过程(2008-11-24 20:39:56)转载▼标签:冲激响应差分⽅程matlabz变换教育ⅰ.设计题⽬:已知某LIT系统的差分⽅程为:3y(n)-4y(n-1)+2y(n-2)=x(n)+2x(n-1)计算n=[-20:100]时的系统单位冲激响应。
ⅱ.设计要求:本课程设计应满⾜以下要求:1. 实⽤性:设计的典型函数应该能够正确运⾏.2. 可读性:源程序代码清晰,有层次,主要程序段有注释.ⅲ.设计⽬的:在学习了数字信号处理这门课程后,按照基本原理,综合运⽤所学的知识,利⽤Matlab ,掌握系统的单位冲激响应内容,由给定的差分⽅程求解系统的单位冲激响应h(n).ⅳ.设计原理:根据给定的差分⽅程:3y(n)-4y(n-1)+2y(n-2)=x(n)+2x(n-1)利⽤z变换,求出H(z),再通过求其逆变换,得到系统单位冲激响应h(n)。
ⅴ.具体算法:第⼀步,根据差分⽅程:3y(n)-4y(n-1)+2y(n-2)=x(n)+2x(n-1)⽤z变换求出H(z)的表达式,原式可化为:源程序::ⅵ.MATLAB源程序计算系统单位冲激响应源程序:num=[1,2,0];den=[3,-4,2];n=[-20:100];hn=dimpulse(num,den)hn=dimpulse(num,den);stem(hn);title('LTI系统的单位冲激响应')ⅶ.系统仿真结果:(1).LTI系统的单位冲激响应的计算结果:h(n) =0.3333 1.1111 1.2593 0.9383 0.4115 -0.0768 -0.3768 -0.4512 -0.3504 -0.1664 0.0117 0.1266 0.1609 0.1302 0.0663 0.0016 -0.0421 -0.0571 -0.0482 -0.0261 -0.0027 0.0138 0.0202 0.0177 0.0102 0.0018 -0.0045 -0.0071 -0.0065 -0.0039 -0.0009 0.0014 0.0025 0.0024LTI系统的单位冲激响应的结果图:ⅷ.运算结果验证:在matlab中输⼊以下程序进⾏验证:num=[1,2,0];den=[3,-4,2];disp(‘系统传递函数H(z)’);printsys(num,den,‘z’);disp(‘转为零极点增益模型’);[z1,p1,k1]=tf2zp(num,den)disp(‘转为零极点留数模型’);[r1,p1]=residue(num,den)h(n)=dimpulse(num,den)输出结果为:系统传递函数H(z)num/den =z^2 + 2 z---------------3 z^2 -4 z + 2转为零极点增益模型z1 = 0-2p1 =0.6667 + 0.4714i0.6667 - 0.4714ik1 =0.3333转为零极点留数模型r1 =0.5556 - 0.5500i0.5556 + 0.5500ip1 =0.6667 + 0.4714i0.6667 - 0.4714ih(n)=0.3333 1.1111 1.2593 0.93830.4115 -0.0768 -0.3768 -0.4512-0.3504 -0.1664 0.0117 0.12660.1609 0.1302 0.0663 0.0016 -0.0421 -0.0571 -0.0482 -0.0261 -0.0027 0.0138 0.0202 0.0177 0.0102 0.0018 -0.0045 -0.0071 -0.0065 -0.0039 -0.0009 0.00140.0025 0.0024ⅸ.对其进⾏理论验证:当n=0时,当n=1时,同理可证,当n=2,3,……时,结果均与源程序运⾏结果相符,此实践课题已正确完成。
系统的基本函数。因为MATLAB基本函数中没有冲击函数,
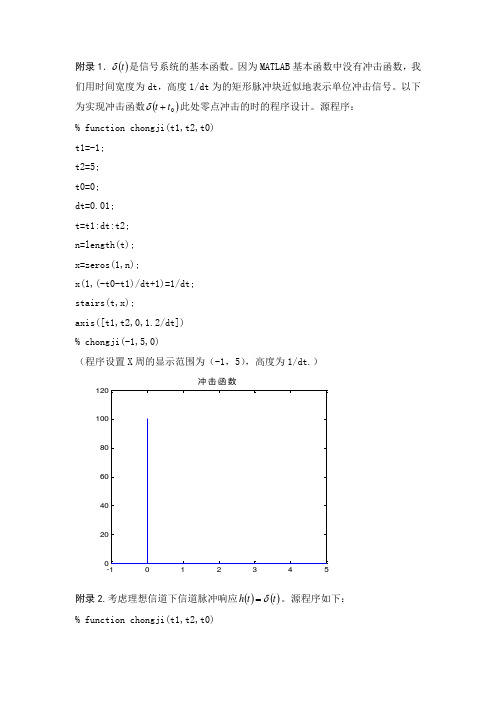
附录1.()t δ是信号系统的基本函数。
因为MATLAB 基本函数中没有冲击函数,我们用时间宽度为dt ,高度1/dt 为的矩形脉冲块近似地表示单位冲击信号。
以下为实现冲击函数()0t t +δ此处零点冲击的时的程序设计。
源程序:% function chongji(t1,t2,t0)t1=-1;t2=5;t0=0;dt=0.01;t=t1:dt:t2;n=length(t);x=zeros(1,n);x(1,(-t0-t1)/dt+1)=1/dt;stairs(t,x);axis([t1,t2,0,1.2/dt])% chongji(-1,5,0)(程序设置X 周的显示范围为(-1,5),高度为1/dt.)-1012345020406080100120冲击函数附录2.考虑理想信道下信道脉冲响应()()t t h δ=。
源程序如下:% function chongji(t1,t2,t0)t2=5;t0=0;dt=10^(-9);t=t1:dt:t2;n=length(t);x=zeros(1,n);x(1,(-t0-t1)/dt+1)=1/dt;x1=x;stairs(t,x1);% chongji(-1,5,0)-101234500.20.40.60.81单位冲击函数附录3.实现从光源到接收机的0次脉冲响应h(t)。
源程序:clearAr=1/10000;c=3e8;D=sqrt(10.25);G0=(Ar*4)/(pi*D^4)dt=10^(-9);t1=0;t2=60*10^(-9);t=t1:dt:t2;n=length(t);x=zeros(1,n);x(1,round((t0-t1)/dt+1))=1/dt;x1=x.*G0;figure,stairs(t,x1);xlabel('时间(s)');ylabel('脉冲响应h(t)');grid on60102119.1-⨯=G 9.12110=h附录4.h1为房间内一次反射的脉冲响应,由于考虑到发射机和接收机的视场问题所以只计算了4面墙。
matlab冲击响应谱

matlab冲击响应谱冲击响应谱是用于评估结构在地震或冲击载荷作用下的响应能力的一种方法。
MATLAB是一种常用的数值计算和数据可视化软件,可以用于分析和绘制冲击响应谱。
在MATLAB中,可以使用信号处理工具箱或结构动力学工具箱来计算冲击响应谱。
下面是一个示例代码,展示了如何计算和绘制冲击响应谱:matlab.% 导入地震波数据。
load earthquake_data.mat.acceleration = earthquake_data; % 地震加速度数据。
% 定义系统参数。
mass = 1000; % 质量。
damping_ratio = 0.05; % 阻尼比。
natural_frequency = 10; % 自振频率。
% 计算冲击响应谱。
omega = logspace(-1, 2, 1000); % 频率范围。
spectrum = zeros(size(omega));for i = 1:length(omega)。
H = 1 / sqrt((1 (omega(i)/natural_frequency)^2)^2 + (2damping_ratio(omega(i)/natural_frequency))^2);spectrum(i) = max(abs(fft(acceleration . H)));end.% 绘制冲击响应谱。
figure;loglog(omega, spectrum);xlabel('频率 (rad/s)');ylabel('冲击响应谱');title('冲击响应谱');grid on;上述代码中,首先导入地震波数据,然后定义了系统的质量、阻尼比和自振频率。
接下来,通过计算冲击响应谱的公式,使用logspace函数生成一系列频率值,并在循环中计算每个频率下的冲击响应谱值。
最后,使用loglog函数将频率和冲击响应谱绘制成对数坐标图。
matlab由差分方程求冲击响应

文章题目:从差分方程到冲击响应:探究MATLAB在信号处理中的应用一、引言在信号处理领域,差分方程和冲击响应是重要的概念和工具。
MATLAB作为一种强大的数学软件,可以有效地应用于差分方程求解和冲击响应计算。
本文将从差分方程的基本概念入手,深入探讨MATLAB在求解差分方程和计算冲击响应方面的应用,并结合案例分析和个人观点,全面展示这一主题的深度和广度。
二、差分方程的基本概念差分方程是离散时间系统建模和分析的基础。
它描述了系统中信号在传输过程中随时间发生的变化。
对于一个一阶离散时间系统,差分方程一般形式为:\[y[n] = a_1 * x[n] + a_2 * x[n-1] + ... + a_k * x[n-k] + b_0 * y[n-1] + b_1 * y[n-2] + ... + b_m * y[n-m]\]其中,\[x[n]\]为输入信号,\[y[n]\]为输出信号,\[a_1, a_2, ..., a_k\]和\[b_0, b_1, ..., b_m\]为系统的系数。
三、MATLAB中的差分方程求解MATLAB提供了一系列函数和工具,用于对差分方程进行求解和分析。
通过MATLAB,可以直接输入差分方程,进行系统参数的设定和求解,得到系统的响应。
使用MATLAB中的`filter`函数可以对离散时间系统进行差分方程求解,求得系统的输出响应。
四、冲击响应的计算冲击响应是对系统进行冲击激励后的输出响应。
在信号处理中,冲击响应是评估系统性能和特性的重要方式。
对于一般的差分方程系统,可以使用MATLAB中的`impz`函数来计算系统的冲击响应。
这一函数可以帮助我们直观地了解系统对冲击激励的响应情况,从而评估系统的稳定性和频率特性。
五、MATLAB在信号处理中的应用案例以一阶离散时间系统为例,假设系统差分方程为:\[y[n] = 0.5 * x[n] + 0.2 * x[n-1] + 0.1 * y[n-1]\],我们可以通过MATLAB求解该系统的冲击响应。
lsdyna冲击响应谱

lsdyna冲击响应谱
LS-DYNA中可以计算冲击响应谱(Shock Response Spectrum,SRS)的模块是*Dynain*。
使用LS-DYNA进行冲击响应谱分析的步骤如下:
1. 在LS-DYNA中创建包含冲击载荷的模型,并定义模型的几
何形状和材料特性。
2. 指定约束和边界条件,确保模型能够适当地响应冲击载荷。
3. 定义冲击分析的时间步长和总时长。
4. 运行LS-DYNA模拟,获得模型的响应结果。
5. 在Dynain模块中,选择冲击响应曲线/冲击动力学(Shock Response Curve/Shock Dynamics)计算冲击响应谱。
6. 定义冲击响应谱的参数,如SRS分析的频率范围、周期窗
口等。
7. 运行冲击响应谱分析,LS-DYNA将自动计算并输出响应结果。
需要注意的是,LS-DYNA中计算冲击响应谱的结果是基于模
型在给定冲击载荷下的响应。
因此,正确定义冲击载荷并进行
准确的模型构建非常重要,以确保所得到的冲击响应谱具有实际可靠性。
matlab求冲激响应和阶跃响应

一、 已知微分方程:()7()10()()6'()4()y t y t y t e t e t e t '''''++=++1、使用M 语言编辑求解其冲激响应、阶跃响应,绘制图形,并求对应的时域连续解。
◆ 分析建模对微分方程进行Laplace 变换,就可得到系统函数即传递函数:2264()710s s h s s s ++=++ 计算系统冲激响应冲激函数的Laplace 变换为u(s)=1,则系统对冲激函数的响应的Laplace 变换为y(s)=h(s)u(s),冲激响应就是h(s)的拉普拉斯反变换,可以把h(s)展开为极点留数式,由于分母多项式没有重根,故有k p t e ∑nk k=1h(t)=r计算系统阶跃响应阶跃函数的Laplace 变换为u(s)=1/s ,则系统对阶跃函数的响应的Laplace 变换为y(s)=h(s)u(s),阶跃响应就是h(s)/s 的拉普拉斯反变换。
◆ 源程序function hipeer01clear;clc;a=[1,7,10];b=[1,6,4];sys=tf(b,a);t=0:0.1:10;h=impulse(sys,t );%求冲激响应plot( h );grid on;title('冲激响应');xlabel('t');ylabel('h(t)');%画冲激响应图endfunction hipeer02clear;clc;a=[1,7,10];b=[1,6,4];sys=tf(b,a);t=0:0.1:10;g=step( sys,t ) %求阶跃响应plot( g );grid on;title('阶跃响应');xlabel('t');ylabel('g(t)');%画阶跃响应图end◆ 结果冲激响应的时域解:2541()()()()33t t h t t e e u t δ--=+-+阶跃响应的时域解:25212()()()3155t t g t e e u t --=-+2、 使用sinnlink 工具箱,求其在幅值为1,周期为1s , 5s ,10s 的方波信号使用下的响应,要求在同一图形窗口中绘制激励和响应波形。
matlab冲激响应

matlab冲激响应一、概述Matlab是一种强大的数学软件,用于计算、数据分析和可视化等方面。
在信号处理领域中,Matlab被广泛用于设计数字滤波器和分析滤波器的性能。
冲激响应是数字滤波器中一个重要的概念,本文将详细介绍如何在Matlab中计算冲激响应。
二、什么是冲激响应在数字信号处理中,滤波器可以看作是一个系统,输入信号经过该系统后输出另一个信号。
冲激响应就是指当输入信号为一个单位脉冲时,系统的输出信号。
因为单位脉冲包含了所有频率成分,所以通过计算单位脉冲的输出可以得到该系统的频率响应。
三、如何计算冲激响应1. 理论计算对于离散时间系统而言,其输入和输出可以表示为序列的形式。
设输入序列为x[n],输出序列为y[n],则离散时间系统可以表示为:y[n]=T{x[n]}其中T表示该系统的传输函数。
如果我们将x[n]设置为一个单位脉冲序列,则有:x[n]={1,0,0,0,...}此时,输出序列y[n]即为该系统的冲激响应。
但是,在实际应用中,很难直接求出系统的传输函数,因此需要采用其他方法计算冲激响应。
2. Matlab计算在Matlab中,可以使用以下命令计算数字滤波器的冲激响应:h = impz(b,a)其中b和a分别为数字滤波器的分子和分母系数,h即为所求的冲激响应。
例如,如果要计算一个二阶低通Butterworth滤波器的冲激响应,则可以使用以下代码:[b,a] = butter(2,0.5);h = impz(b,a);这里butter函数表示生成Butterworth滤波器的函数,第一个参数2表示该滤波器为二阶,第二个参数0.5表示截止频率为0.5。
四、绘制冲激响应曲线在得到数字滤波器的冲激响应后,我们可以通过绘制其曲线来直观地了解该系统对不同频率成分的信号进行过滤。
可以使用以下命令绘制数字滤波器的冲激响应曲线:stem(h)其中stem函数表示绘制离散数据点图形。
例如,在上述例子中,我们可以使用以下代码绘制该Butterworth滤波器的冲激响应曲线:stem(h)五、总结本文介绍了Matlab中计算数字滤波器冲激响应的方法,并给出了绘制冲激响应曲线的示例。
冲击响应谱计算的matlab程序

冲击响应谱计算的m a t l a b程序(总8页)本页仅作为文档封面,使用时可以删除This document is for reference only-rar21year.Marchdisp(' ')disp(' ver July 3, 2006')disp(' by Tom Irvine Email')disp(' ')disp(' This program calculates the shock response spectrum')disp(' of an acceleration time history, which is pre-loaded into Matlab.') disp(' The time history must have two columns: time(sec) & acceleration') disp(' ')%clear t;clear y;clear yy;clear n;clear fn;clear a1;clear a2clear b1;clear b2;clear jnum;clear THM;clear resp;clear x_pos;clear x_neg;%iunit=input(' Enter acceleration unit: 1= G 2= m/sec^2 ');%disp(' ')disp(' Select file input method ');disp(' 1=external ASCII file ');disp(' 2=file preloaded into Matlab ');file_choice = input('');%if(file_choice==1)[filename, pathname] = uigetfile('*.*');filename = fullfile(pathname, filename);%fid = fopen(filename,'r');THM = fscanf(fid,'%g %g',[2 inf]);THM=THM';elseTHM = input(' Enter the matrix name: ');end%t=double(THM(:,1));y=double(THM(:,2));%tmx=max(t);tmi=min(t);n = length(y);%out1 = sprintf('\n %d samples \n',n);disp(out1)%dt=(tmx-tmi)/(n-1);sr=1./dt;%out1 = sprintf(' SR = %g samples/sec dt = %g sec \n',sr,dt); disp(out1)%fn(1)=input(' Enter the starting frequency (Hz) ');if fn(1)>sr/30.fn(1)=sr/30.;end%idamp=input(' Enter damping format: 1= damping ratio 2= Q '); %disp(' ')if(idamp==1)damp=input(' Enter damping ratio (typically ');elseQ=input(' Enter the amplification factor (typically Q=10) ');damp=1./(2.*Q);end%disp(' ')disp(' Select algorithm: ')disp(' 1=Kelly-Richman 2=Smallwood ');ialgorithm=input(' ');%tmax=(tmx-tmi) + 1./fn(1);limit = round( tmax/dt );n=limit;yy=zeros(1,limit);for i=1:length(y)yy(i)=y(i);end%disp(' ')disp(' Calculating response..... ')%% SRS engine%for j=1:1000%omega=2.*pi*fn(j);omegad=omega*sqrt(damp^2));cosd=cos(omegad*dt);sind=sin(omegad*dt);domegadt=damp*omega*dt;%if(ialgorithm==1)a1(j)=2.*exp(-domegadt)*cosd;a2(j)=-exp(-2.*domegadt);b1(j)=2.*domegadt;b2(j)=omega*dt*exp(-domegadt);b2(j)=b2(j)*( (omega/omegad)*.*(damp^2))*sind -2.*damp*cosd ); b3(j)=0;%elseE=exp(-damp*omega*dt);K=omegad*dt;C=E*cos(K);S=E*sin(K);Sp=S/K;%a1(j)=2*C;a2(j)=-E^2;b1(j)=;b2(j)=2.*(Sp-C);b3(j)=E^2-Sp;endforward=[ b1(j), b2(j), b3(j) ];back =[ 1, -a1(j), -a2(j) ];%resp=filter(forward,back,yy);%x_pos(j)= max(resp);x_neg(j)= min(resp);%jnum=j;if fn(j) > sr/8.breakfn(j+1)=fn(1)*(2. ^ (j*(1./12.)));end%% Output options%disp(' ')disp(' Select output option ');choice=input(' 1=plot only 2=plot & output text file ' );disp(' ')%if choice == 2%%[writefname, writepname] = uiputfile('*','Save SRS data as');writepfname = fullfile(writepname, writefname);writedata = [fn' x_pos' (abs(x_neg))' ];fid = fopen(writepfname,'w');fprintf(fid,' %g %g %g\n',writedata');fclose(fid);%%% disp(' Enter output filename ');% SRS_filename = input(' ','s');%% fid = fopen(SRS_filename,'w');% for j=1:jnum% fprintf(fid,'% % % \n',fn(j),x_pos(j),abs(x_neg(j)));% end% fclose(fid);end%% Plot SRS%disp(' ')disp(' Plotting output..... ')%% Find limits for plot%srs_max = max(x_pos);if max( abs(x_neg) ) > srs_maxsrs_max = max( abs(x_neg ));endsrs_min = min(x_pos);if min( abs(x_neg) ) < srs_minsrs_min = min( abs(x_neg ));%figure(1);plot(fn,x_pos,fn,abs(x_neg),'-.');%if iunit==1ylabel('Peak Accel (G)');elseylabel('Peak Accel (m/sec^2)');endxlabel('Natural Frequency (Hz)');Q=1./(2.*damp);out5 = sprintf(' Acceleration Shock Response Spectrum Q=%g ',Q);title(out5);grid;set(gca,'MinorGridLineStyle','none','GridLineStyle',':','XScale','log','YScale','log'); legend ('positive','negative',2);%ymax= 10^(round(log10(srs_max)+);ymin= 10^(round(log10(srs_min));%fmax=max(fn);fmin=fmax/10.;%fmax= 10^(round(log10(fmax)+);%if fn(1) >=fmin=;endif fn(1) >= 1fmin=1;endif fn(1) >= 10fmin=10;endif fn(1) >= 100fmin=100;endaxis([fmin,fmax,ymin,ymax]);%disp(' ')disp(' Plot pseudo velocity ');vchoice=input(' 1=yes 2=no ' );if(vchoice==1)figure(2);%% Convert to pseudo velocity%for j=1:jnumif iunit==1x_pos(j)=386.*x_pos(j)/(2.*pi*fn(j));x_neg(j)=386.*x_neg(j)/(2.*pi*fn(j));elsex_pos(j)=x_pos(j)/(2.*pi*fn(j));x_neg(j)=x_neg(j)/(2.*pi*fn(j));endend%srs_max = max(x_pos);if max( abs(x_neg) ) > srs_maxsrs_max = max( abs(x_neg ));endsrs_min = min(x_pos);if min( abs(x_neg) ) < srs_minsrs_min = min( abs(x_neg ));end%plot(fn,x_pos,fn,abs(x_neg),'-.');%if iunit==1ylabel('Velocity (in/sec)');elseylabel('Velocity (m/sec)');endxlabel('Natural Frequency (Hz)');Q=1./(2.*damp);out5 = sprintf(' Pseudo Velocity Shock Response Spectrum Q=%g ',Q);title(out5);grid;set(gca,'MinorGridLineStyle','none','GridLineStyle',':','XScale','log','YScale','log'); legend ('positive','negative',2);%ymax= 10^(round(log10(srs_max)+);ymin= 10^(round(log10(srs_min));%axis([fmin,fmax,ymin,ymax]);end。
实验3 利用matlab求LTI连续系统的响应

实验3 利用matlab 求LTI 连续系统的响应一. 实验目的:1. 了解LTI 系统的冲激响应h(t)及matlab 实现; 2. 了解LTI 系统的阶跃响应g(t)及matlab 实现; 3. 了解LTI 系统的零状态响应; 二. 实验原理:设描述连续系统的微分方程为:()()()()∑∑===Mj j jN i i i t f bt y a 0则可以用向量a 和b 来表示该系统,即: ],,,,[011a a a a a N N -= ],,,,[011b b b b b M M -=注意:在用向量来表示微分方程描述的连续系统时,向量a 和b 的元素一定要以微分方程时间求导的降幂次序来排列,且缺项要用零来补齐。
1. impulse()函数函数impulse()将绘出由向量a 和b 表示的连续系统在指定时间范围内的冲激响应h(t)的时域波形,并能求出指定时间范围内冲激响应的数值解。
impulse()函数有如下几种调用格式:● impulse(b,a) ● impulse(b,a,t)● impulse(b,a,t1:p:t2) ● y= impulse(b,a,t1:p:t2) 详细用法可查阅帮助文件。
2. Step()函数 函数step()将绘出由向量a 和b 表示的连续系统在指定时间范围内的阶跃响应g(t)的时域波形,并能求出指定时间范围内阶跃响应的数值解。
step()函数有如下几种调用格式:● step(b,a) ● step(b,a,t)● step(b,a,t1:p:t2) ● y= step(b,a,t1:p:t2) 3.lsim()函数 函数lsim()将绘出由向量a 和b 表示的连续系统在指定时间范围内对函数x(t)响应的时域波形,并能求出指定时间范围内响应的数值解。
lsim()函数有如下几种调用格式:● lsim(b,a,x,t) ● y=lsim(b,a,x,t) 三. 范例程序已知描述某电路的微分方程是()()()()()()t e t e t e t r t i t i 46107'"'''++=++由理论方法可推导出系统的冲激响应)(t h 和阶跃响应)(t g 为()()t u e e t t h t t )3134()(52--+-+=δ()t u e e t g t t )5215132()(52+-=--下面演示MATLAB 求解冲激响应和阶跃响应的两种方法,以及lsim 函数的多种调用方式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
disp(' ')disp(' srs.m ver 2.0 July 3, 2006')disp('byTomIrvineEmail:*****************')disp(' ')disp(' This program calculates the shock response spectrum')disp(' of an acceleration time history, which is pre-loaded into Matlab.') disp(' The time history must have two columns: time(sec) & acceleration') disp(' ')%clear t;clear y;clear yy;clear n;clear fn;clear a1;clear a2clear b1;clear b2;clear jnum;clear THM;clear resp;clear x_pos;clear x_neg;%iunit=input(' Enter acceleration unit: 1= G 2= m/sec^2 ');%disp(' ')disp(' Select file input method ');disp(' 1=external ASCII file ');disp(' 2=file preloaded into Matlab ');file_choice = input('');%if(file_choice==1)[filename, pathname] = uigetfile('*.*');filename = fullfile(pathname, filename);%fid = fopen(filename,'r');THM = fscanf(fid,'%g %g',[2 inf]);THM=THM';elseTHM = input(' Enter the matrix name: ');end%t=double(THM(:,1));y=double(THM(:,2));%tmx=max(t);tmi=min(t);n = length(y);%out1 = sprintf('\n %d samples \n',n);disp(out1)%dt=(tmx-tmi)/(n-1);sr=1./dt;%out1 = sprintf(' SR = %g samples/sec dt = %g sec \n',sr,dt); disp(out1)%fn(1)=input(' Enter the starting frequency (Hz) ');if fn(1)>sr/30.fn(1)=sr/30.;end%idamp=input(' Enter damping format: 1= damping ratio 2= Q '); %disp(' ')if(idamp==1)damp=input(' Enter damping ratio (typically 0.05) ');elseQ=input(' Enter the amplification factor (typically Q=10) '); damp=1./(2.*Q);end%disp(' ')disp(' Select algorithm: ')disp(' 1=Kelly-Richman 2=Smallwood ');ialgorithm=input(' ');%tmax=(tmx-tmi) + 1./fn(1);limit = round( tmax/dt );n=limit;yy=zeros(1,limit);for i=1:length(y)yy(i)=y(i);end%disp(' ')disp(' Calculating response..... ')%% SRS engine%for j=1:1000%omega=2.*pi*fn(j);omegad=omega*sqrt(1.-(damp^2));cosd=cos(omegad*dt);sind=sin(omegad*dt);domegadt=damp*omega*dt;%if(ialgorithm==1)a1(j)=2.*exp(-domegadt)*cosd;a2(j)=-exp(-2.*domegadt);b1(j)=2.*domegadt;b2(j)=omega*dt*exp(-domegadt);b2(j)=b2(j)*( (omega/omegad)*(1.-2.*(damp^2))*sind -2.*damp*cosd );b3(j)=0;%elseE=exp(-damp*omega*dt);K=omegad*dt;C=E*cos(K);S=E*sin(K);Sp=S/K;%a1(j)=2*C;a2(j)=-E^2;b1(j)=1.-Sp;b2(j)=2.*(Sp-C);b3(j)=E^2-Sp;endforward=[ b1(j), b2(j), b3(j) ];back =[ 1, -a1(j), -a2(j) ];%resp=filter(forward,back,yy);%x_pos(j)= max(resp);x_neg(j)= min(resp);%jnum=j;if fn(j) > sr/8.breakendfn(j+1)=fn(1)*(2. ^ (j*(1./12.)));end%% Output options%disp(' ')disp(' Select output option ');choice=input(' 1=plot only 2=plot & output text file ' );disp(' ')%if choice == 2%%[writefname, writepname] = uiputfile('*','Save SRS data as');writepfname = fullfile(writepname, writefname);writedata = [fn' x_pos' (abs(x_neg))' ];fid = fopen(writepfname,'w');fprintf(fid,' %g %g %g\n',writedata');fclose(fid);%%% disp(' Enter output filename ');% SRS_filename = input(' ','s');%% fid = fopen(SRS_filename,'w');% for j=1:jnum% fprintf(fid,'%7.2f %10.3f %10.3f\n',fn(j),x_pos(j),abs(x_neg(j)));% end% fclose(fid);end%% Plot SRS%disp(' ')disp(' Plotting output..... ')%% Find limits for plot%srs_max = max(x_pos);if max( abs(x_neg) ) > srs_maxsrs_max = max( abs(x_neg ));endsrs_min = min(x_pos);if min( abs(x_neg) ) < srs_minsrs_min = min( abs(x_neg ));end%figure(1);plot(fn,x_pos,fn,abs(x_neg),'-.');%if iunit==1ylabel('Peak Accel (G)');elseylabel('Peak Accel (m/sec^2)');endxlabel('Natural Frequency (Hz)');Q=1./(2.*damp);out5 = sprintf(' Acceleration Shock Response Spectrum Q=%g ',Q);title(out5);grid;set(gca,'MinorGridLineStyle','none','GridLineStyle',':','XScale','log ','YScale','log');legend ('positive','negative',2);%ymax= 10^(round(log10(srs_max)+0.8));ymin= 10^(round(log10(srs_min)-0.6));%fmax=max(fn);fmin=fmax/10.;%fmax= 10^(round(log10(fmax)+0.5));%if fn(1) >= 0.1fmin=0.1;endif fn(1) >= 1fmin=1;endif fn(1) >= 10fmin=10;endif fn(1) >= 100fmin=100;endaxis([fmin,fmax,ymin,ymax]);%disp(' ')disp(' Plot pseudo velocity? ');vchoice=input(' 1=yes 2=no ' );if(vchoice==1)figure(2);%% Convert to pseudo velocity%for j=1:jnumif iunit==1x_pos(j)=386.*x_pos(j)/(2.*pi*fn(j));x_neg(j)=386.*x_neg(j)/(2.*pi*fn(j));elsex_pos(j)=x_pos(j)/(2.*pi*fn(j));x_neg(j)=x_neg(j)/(2.*pi*fn(j));endend%srs_max = max(x_pos);if max( abs(x_neg) ) > srs_maxsrs_max = max( abs(x_neg ));endsrs_min = min(x_pos);if min( abs(x_neg) ) < srs_minsrs_min = min( abs(x_neg ));end%plot(fn,x_pos,fn,abs(x_neg),'-.');%if iunit==1ylabel('Velocity (in/sec)');elseylabel('Velocity (m/sec)');endxlabel('Natural Frequency (Hz)');Q=1./(2.*damp);out5 = sprintf(' Pseudo Velocity Shock Response Spectrum Q=%g ',Q); title(out5);grid;set(gca,'MinorGridLineStyle','none','GridLineStyle',':','XScale','log ','YScale','log');legend ('positive','negative',2);%ymax= 10^(round(log10(srs_max)+0.8));ymin= 10^(round(log10(srs_min)-0.6));%axis([fmin,fmax,ymin,ymax]); end。
