鲍威尔算法matlab程序-f
鲍威尔法matlab实现

鲍威尔法% 鲍威尔法-计算第2环起始点和搜索方向syms xy1 xy2 fyx m x1 x2 X s1s2 Sf=60-10*x1-4*x2+x1^2+x2^2-x1*x2;disp ' 目标函数:f=60-10*x1-4*x2+x1^2+x2^2-x1*x2.'pretty(f);% 第1环沿e2方向搜索x01=0;x02=0;X0=[x01 x02]; % 第1环初始点x1=5.0000;x2=0;X=[x1 x2]; % 第1环沿e2方向初始点fy1=60-10*x1-4*x2+x1^2+x2^2-x1*x2; % 第1环e2方向初始点函数值e1=[1,0];e2=[0,1]; % 坐标轴单位方向s1=e2(1);s2=e2(2);S=[s1 s2];m=0;% 计算影射点及其函数值xs1=2*xy1-x01;xs2=2*xy2-x02;Xs=[xs1 xs2];fxs=60-10*xs1-4*xs2+xs1^2+xs2^2-xs1*xs2;fx0=60-10*x01-4*x02+x01^2+x02^2-x01*x02; % 第1环初始点函数值disp ' 第1环影射点坐标'disp (Xs)% 判断第1环搜索函数值下降最大方向df01=fx0-fy1; % 第1环沿e1方向初始点函数值-第1环沿e1方向终点函数值df02=fy1-fyx; % 第1环沿e2方向起始点函数值-第1环沿e2方向始点函数值if df01>df02dfm=df01;m=1;elsedfm=df02;m=2;end% 计算POWELL判别式f1=fx0;f2=fyx;f3=fxs;f123=[f1 f2 f3];disp ' 第1环初始点、终点、影射点函数值'disp (f123)fP1=(f1-2*f2+f3)*(f1-f2-dfm)^2;fP2=0.5*dfm*(f1-f3)^2;fP=[fP1 fP2];disp ' 两个POWELL判别式的值'fprintf(1,' POWELL判别式1的值 fP1= %10.4f \n',fP1)fprintf(1,' POWELL判别式1的值 fP2= %10.4f \n',fP2)fprintf(1,' 函数值下降最大方向 m= %2.0f \n',m)if f1>f3 & fP2>fP1sx1=xy1-X0(1); % 同时不满足两个判别式时56428 .产生新方向sx2=xy2-X0(2);sx=[sx1 sx2];if m==1S=[e2,sx]; % 新方向取代上环搜索中函数值下降最大方向m=1elseS=[e1,sx]; % 新方向取代上环搜索中函数值下降最大方向m=2 endelseS=[e1,e2]; % 满足某个判别式时56428 .保留上环搜索方向enddisp ' @@@@ 第2环搜索方向 @@@@'disp (S)% 第1环沿新方向搜索x1=xy1;x2=xy2;X=[x1 x2];s1=xy1-x01;s2=xy2-x02; S=[s1 s2];[xy1,xy2,fyx]=powell(m,x1,x2,X,s1,s2,S);disp '@@@@ 第2环搜索起始点 @@@@'if fyx<fxsx20=[xy1 xy2];disp ' (第1环极小点)'elsex20=[xs1 xs2];disp ' (第1环影射点)'enddisp (x20)% 鲍威尔法-第1环计算% 目标函数中常数项、步长的一次项和二次项系数fxs0=60-10*x1-4*x2+x1^2+x2^2-x1*x2;fxs1=-10*s1-4*s2+2*x1*s1+2*x2*s2-x1*s2-x2*s1;fxs2=s1^2+s2^2-s1*s2;fxs210=[fxs2 fxs1 fxs0];% 计算最优步长af=-fxs1/(2*fxs2);% 计算终点函数值(关于最优步长)fya=fxs0+fxs1*af+fxs2*af^2;% 计算终点坐标值和函数值(关于终点)xy1=x1+s1*af;xy2=x2+s2*af;Xopt=[xy1 xy2];fyx=60-10*xy1-4*xy2+xy1^2+xy2^2-xy1*xy2;if m==0disp ' ******** 计算第1环沿e2方向搜索 ********'elsedisp ' ******** 计算第1环沿新方向搜索 ********'enddisp ' 初始点'disp (X)disp ' 搜索方向'disp (S)disp ' 步长二次项一次项系数常数项'disp (fxs210)disp ' 最优步长'disp (af)if m==0disp ' 终点坐标'disp (Xopt)elsedisp ' 极小点坐标'disp (Xopt)disp ' 极小点函数值(关于最优步长)' disp (fya)disp ' 极小点函数值(关于极小点)' disp (fyx)end。
机械优化设计

机械优化设计matlab优化设计程序学校:班级:学号:姓名:指导老师:一.进退法求最优点所在区间1.算例:函数:f=x(1)^3+x(2)^2-10*x(1)*x(2)+1;初始参数:x0=0,step=0.01,st=[0,0],sd=[1,1];2.编程代码:function [lb,ub]=jintuifa(x0,step0,st,sd)% lb为区间下限,up为区间上限% x0初始探测点,step0是初始探测步长,st初始搜索点,sd是初始搜索方向step=step0;f0=jintui(x0,st,sd);x1=x0+step0;f1=jintui(x1,st,sd);if f1<=f0while truestep=2*step;x2=x1+step;f2=jintui(x2,st,sd);if f1<=f2lb=x0;ub=x2;break;elsex0=x1;x1=x2;f0=f1;f1=f2;endendelsewhile truestep=2*step;x2=x0-step;f2=jintui(x2,st,sd);if f0<=f2lb=x2;ub=x1;break;elsex1=x0;x0=x2;f1=f0;f0=f2;endendendend%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function f=jintui(a,st,sd)f=objfun(st+a.*sd);end%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function f=objfun(x)f=x(1)^3+x(2)^2-10*x(1)*x(2)+1;end3.运行结果二.黄金分割法求最求最优值1.eg:函数:f=x^2+2*x;初始参数:a=-3,b=5,e=0.0001;2.编程代码:function [ans,sp]=golden(a,b,e)%[a,b]初始区间,e为最小区间长度要求%ans为最优解,sp为所需迭代次数a(1)=a;b(1)=b;L=e;t(1)=a(1)+0.382*(b(1)-a(1));u(1)=a(1)+0.618*(b(1)-a(1));k=1;m(1)=feval('f1',t(1));n(1)=feval('f1',u(1));while(b(k)-a(k)>L)if(m(k)>n(k))a(k+1)=t(k);b(k+1)=b(k);t(k+1)=u(k);u(k+1)=a(k+1)+0.618*(b(k+1)-a(k+1));elsea(k+1)=a(k);b(k+1)=u(k);u(k+1)=t(k);t(k+1)=a(k+1)+0.382*(b(k+1)-a(k+1));endm(k+1)=feval('f1',t(k+1));n(k+1)=feval('f1',u(k+1));ans=feval('f1',t(k+1));k=k+1;endans=(a(k)+b(k))/2;sp=k-1;end%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%function y=f1(x)y=x^2+2*x;end3.运行结果三.无约束优化方法——坐标轮换法1.eg:函数:min f(x)=4*(x(1)-5)^2+(x(2)-6)^2;初始参数:初始点x为[8,9];2.编程代码:function [x,f]=lunhuan(x0)%输入初始点x0[8,9]%输出最优解点x,与最优解值fp=1;h=0.000001;x=x0;while(p>h)%做精度比较w=x(1);q=x(2);d1=[1,0];a1=golden('objfun',x,d1);%黄金分割法求最佳步长 x=x+a1*d1;d2=[0,1];a2=golden('objfun',x,d2);x=x+a2*d2;p=sqrt((x(1)-w)^2+(x(2)-q)^2);endf=objfun(x);end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function f=objfun(x)%函数名f=4*(x(1)-5)^2+(x(2)-6)^2;end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function [lb,ub]=jintuifa(st,sd)%进退法函数x0=0;step0=0.000001;step=step0;f0=jintui(x0,st,sd);x1=x0+step0;f1=jintui(x1,st,sd);if f1<=f0while truestep=2*step;x2=x1+step;f2=jintui(x2,st,sd);if f1<=f2lb=x0;ub=x2;break;elsex0=x1;x1=x2;f0=f1;f1=f2;endendelsewhile truestep=2*step;x2=x0-step;f2=jintui(x2,st,sd);if f0<=f2lb=x2;ub=x1;break;elsex1=x0;x0=x2;f1=f0;f0=f2;endendendend %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function f=jintui(a,st,sd)f=objfun(st+a.*sd);end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function ans=golden(f_name,st,sd)[a,b]=jintuifa(st,sd); %进退法求最佳步长区间a(1)=a;b(1)=b;L=0.1;t(1)=a(1)+0.382*(b(1)-a(1));u(1)=a(1)+0.618*(b(1)-a(1));k=1;p=st+t(1)*sd;q=st+u(1)*sd;m(1)=feval(f_name,p);n(1)=feval(f_name,q);while(b(k)-a(k)>L)if(m(k)>n(k))a(k+1)=t(k);b(k+1)=b(k);t(k+1)=u(k);u(k+1)=a(k+1)+0.618*(b(k+1)-a(k+1));elsea(k+1)=a(k);b(k+1)=u(k);u(k+1)=t(k);t(k+1)=a(k+1)+0.382*(b(k+1)-a(k+1));endw=st+t(k+1)*sd;z=st+u(k+1)*sd;m(k+1)=feval(f_name,w);n(k+1)=feval(f_name,z);ans=feval(f_name,w);k=k+1;endt(k)=0;u(k)=0;m(k)=0;n(k)=0;p=[a',b',t',u',m',n'];ans=(a(k)+b(k))/2;end3.运行结果四.无约束优化方法——鲍威尔法1.eg:函数:min f(x)=4*(x(1)-5)^2+(x(2)-6)^2;初始参数:初始点x为[8,9],初始搜索方向[0,1],[1,0];2.编程代码:function [x,f]=powill(x0,d1,d2)%输入x0为初始点,d1,d2为两个线性无关向量for k=1:2w=x0(1);q=x0(2);a1=golden('objfun',x0,d1);x1=x0+a1*d1;a2=golden('objfun',x1,d2);x2=x1+a2*d2;d1=d2;d2=x2-x0;a3=golden('objfun',x2,d2);x3=x2+a3*d2;x0=x3;endx=x0;f=objfun(x);end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function f=objfun(x)f=4*(x(1)-5)^2+(x(2)-6)^2;end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function [lb,ub]=jintuifa(st,sd)x0=0;step0=0.0001;step=step0;f0=jintui(x0,st,sd);x1=x0+step0;f1=jintui(x1,st,sd);if f1<=f0while truestep=2*step;x2=x1+step;f2=jintui(x2,st,sd);if f1<=f2lb=x0;ub=x2;break;elsex0=x1;x1=x2;f0=f1;f1=f2;endendelsewhile truestep=2*step;x2=x0-step;f2=jintui(x2,st,sd);if f0<=f2lb=x2;ub=x1;break;elsex1=x0;x0=x2;f1=f0;f0=f2;endendend %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function f=jintui(a,st,sd)f=objfun(st+a.*sd);end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function ans=golden(f_name,st,sd)[a,b]=jintuifa(st,sd);a(1)=a;b(1)=b;L=0.1;t(1)=a(1)+0.382*(b(1)-a(1));u(1)=a(1)+0.618*(b(1)-a(1));k=1;p=st+t(1)*sd;q=st+u(1)*sd;m(1)=feval(f_name,p);n(1)=feval(f_name,q);while(b(k)-a(k)>L)if(m(k)>n(k))a(k+1)=t(k);b(k+1)=b(k);t(k+1)=u(k);u(k+1)=a(k+1)+0.618*(b(k+1)-a(k+1));elsea(k+1)=a(k);b(k+1)=u(k);u(k+1)=t(k);t(k+1)=a(k+1)+0.382*(b(k+1)-a(k+1));endw=st+t(k+1)*sd;z=st+u(k+1)*sd;m(k+1)=feval(f_name,w);n(k+1)=feval(f_name,z);ans=feval(f_name,w);k=k+1;endend3.运行结果五.有约束优化方法——复合形法1.eg:函数:min f(x)=x1^2+x2^2-x1*x2-10*x1-4*x2+60 St:g1(x)=-x1≤0g2(x)=-x2≤0g3(x)=x1-6≤0g4(x)=x2-8≤0g5(x)=x1+x2-11≤02.编程代码:function fuhexing(n,b,h,xb1,xb2)%元素数n,初始可行点b,精度h,xb1横坐标上下界,xb2为纵坐标上下界if (rem(n,2)==0)k=n+n/2;elsek=n+(n+1)/2;end%取k值A=kexingdian(k,xb1,xb2,b');%确定可行点A=mubiao(A,n,k,h);%求出目标函数并排序比较,得出最优解End %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%function A=mubiao(A,n,k,h)for i=1:kA(3,i)=objfun(A(:,i));endB=A';%根据目标函数值排序A=sortrows(B,3)';p=0;for j=1:kx=(objfun(A(:,j))-objfun(A(:,1)))^2;p=p+x;endo=sqrt(p/(k-1));%收敛条件if(o<h)%判断所求点是否为最优点disp('最优点为')xz(1)=A(1,1);xz(2)=A(2,1);disp(xz);disp('其函数值为')f=A(3,1);disp(f);elsexr=Xcpanduan(A,k,n,h,1.3);endend %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%function A=kexingdian(k,xb1,xb2,b)A=zeros(3,k);A(1,1)=b(1);A(2,1)=b(2);for i=2:kA(1,i)=xb1(1)+rand(1)*(xb1(2)-xb1(1));A(2,i)=xb2(1)+rand(1)*(xb2(2)-xb2(1));%产生j个顶点endt=0;for j=1:kif(A(1,j)+A(2,j)<=11&&A(1,j)<=6&&A(2,j)<=8)%判断是否有不可行点t=t+1;T(:,t)=A(:,j);endendif(t<k)%计算出可行点的中心位置xcxc=zhongxindian(T,t);endt=0;for j=1:k%利用中心点将原不可行点逼近为可行点while(A(1,j)+A(2,j)>11||A(1,j)>6||A(2,j)>8)A(:,j)=xc+0.5*(A(:,j)-xc);endendendx=x0;f=objfun(x);end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%function f=objfun(x)f= x1^2+x2^2-x1*x2-10*x1-4*x2+60;end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%function xc=Xcpanduan(A,k,n,h,a)for i=1:k-1T(:,i)=A(:,i);endxc=zhongxindian(T,k-1);%计算除最坏点以外的可行点中心坐标if(xc(1)+xc(2)<=11&&xc(1)<=6&&xc(2)<=8)%判断xc是否可行xr=Xrpanduan(xc,A,a,n,k,h);A(:,k)=xr;else%不可行时,即重新确定初始可行点fuhexing(n,h,A(:,1),xr);endend %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%function xc=zhongxindian(T,t)xc=[0;0;0];for i=1:txc=xc+T(:,i);endxc=xc/t;%求解中心点end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function xr=Xrpanduan(xc,A,a,n,k,h)xr=xc+a*(xc-A(:,k));while(xr(1)+xr(2)>11||xr(1)>6||xr(2)>8)%判断xr 是否可行若不可行,则持续迭代a=0.5*a;xr=xc+a*(xc-A(:,k));endxr=ercipanduan(a,xr,A(:,k),A,n,k,xc,h,xr);%可行时进入下一判断end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%function xr=ercipanduan(a,p,b,A,n,k,xc,h,t)if(objfun(p)>=objfun(b))%判断反射点和最坏点函数值的大小if(a<=1e-10)A(:,k)=A(:,k-1);xr=Xcpanduan(A,k,n,h,a);disp(xr);elsea=0.5*a;xr=Xrpanduan(xc,A,a,n,k,h);%返回中心点判断,持续迭代endelseA(:,k)=p;%以反射点取代最坏点进行循环mubiao(A,n,k,h);xr=t;endend3.运行结果五.有约束优化方法——混合惩罚法1.eg:函数:min f(x)=(x(4)-x(1))^2+(x(5)-x(2))^2+(x(6)-x(3))^2;St:g1=x(1)^2+x(2)^2+x(3)^2-5;g2=(x(4)-3)^2+x(5)^2-1;g3=x(6)-8;g4=4-x(6);2.编程代码function [x,f]=hunhechengfa(x0,r0,c,h1,h2)k=1;z=0;A(:,1)=x0;r(1)=r0;while (z==0)k=k+1;x=lunhuan(x0,r(k-1));A(:,k)=x;r(k)=c*r(k-1);z=shoulian(A,r,h1,h2,k);if(z==1)break;endx0=x;enddisp('最优解点x=');disp(x);disp('最优值=');f=fhanshu(x);disp(f);end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function z=shoulian(A,r,h1,h2,k)%判断收敛条件U=abs(objfun(A(:,k),r(k))-objfun(A(:,k-1),r(k-1))/obj fun(A(:,k-1),r(k-1)));V=0;for i=2:kV=V+(A(1,k)-A(1,k-1))^2;endV=sqrt(V);if(U<=h1&&V<=h2)z=1;elsez=0;end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%function p=objfun(x,r)%φ函数g1=x(1)^2+x(2)^2+x(3)^2-5;g2=(x(4)-3)^2+x(5)^2-1;g3=x(6)-8;g4=4-x(6);j=sqrt(r);u=r*(1/g1+1/g2+1/g3+1/g4);v=(g1^2+g2^2+g3^2+g4^2)/j;p=fhanshu(x)-u+v;end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%function f=fhanshu(x)%目标函数f=(x(4)-x(1))^2+(x(5)-x(2))^2+(x(6)-x(3))^2;end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%function x=lunhuan(x0,r)%轮换法p=1;h=0.01;d=zeros(6,6);a=zeros(6,1);x=x0;for i=1:6for j=1:6if(i==j)d(i,j)=1;endendendwhile(p>h)t=x;v=0;for k=1:6a(k)=golden(x,d(:,k),r);c=d(:,k);x=x-a(k)*c';v=v+(x(k)-t(k))^2;endp=sqrt(v);endend %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function ans=golden(st,sd,r)%黄金分割法求最佳步长 [g,h]=jintuifa(st,sd,r);a(1)=g;b(1)=h;L=0.01;t(1)=a(1)+0.382*(b(1)-a(1));u(1)=a(1)+0.618*(b(1)-a(1));k=1;p=st+t(1)*sd';q=st+u(1)*sd';m(1)=objfun(p,r);n(1)=objfun(q,r);while(b(k)-a(k)>L)if(m(k)>n(k))a(k+1)=t(k);b(k+1)=b(k);t(k+1)=u(k);u(k+1)=a(k+1)+0.618*(b(k+1)-a(k+1));elsea(k+1)=a(k);b(k+1)=u(k);u(k+1)=t(k);t(k+1)=a(k+1)+0.382*(b(k+1)-a(k+1));endw=st+t(k+1)*sd';z=st+u(k+1)*sd';m(k+1)=objfun(w,r);n(k+1)=objfun(z,r);k=k+1;endans=(a(k)+b(k))/2;end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function f=jintui(a,st,sd,r)%代入步长f=objfun(st+a.*sd',r);end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function [lb,ub]=jintuifa(st,sd,r)%进退法求最佳步长区间x0=0;step0=0.001;step=step0;f0=jintui(x0,st,sd,r);x1=x0+step0;f1=jintui(x1,st,sd,r);if f1<=f0while truestep=2*step;x2=x1+step;f2=jintui(x2,st,sd,r);if f1<=f2lb=x0;ub=x2;break;elsex0=x1;x1=x2;f0=f1;f1=f2;endendelsewhile truestep=2*step;x2=x0-step;f2=jintui(x2,st,sd,r);if f0<=f2lb=x2;ub=x1;break;elsex1=x0;x0=x2; f1=f0; f0=f2;endendend3.运行结果。
基于MATLAB的鲍威尔法求极值问题

基于MATLAB的鲍威尔法求极值问题:xxx 学号:xxx(理工大学机械与车辆学院车辆工程,100081)摘要:无约束优化方法主要有七种,按照求导与否把这些方法分为间接法和直接法。
牛顿法的成败与初始点选择有极大关系,其可靠性最差;坐标轮换法、单纯形法和最速下降法对于高维优化问题计算效率很低,有效性差;由于编制变尺度法程序复杂,其简便性不足。
综合考虑后,鲍威尔法、共轭梯度法具有较好的综合性能。
本文首先对鲍威尔法的原理进行阐述,根据其迭代过程给出流程图,并编写MATLAB程序。
最后用此MATLAB程序求解实际的极值问题,并对求解结果进行简要分析。
1.鲍威尔法的基本思想1.1其他优化方法对鲍威尔法形成的影响通过对鲍威尔法的学习,可以很明显看出来其迭代思想中汲取了其他几种优化方法的核心思想。
为了更全面、更深入的学习鲍威尔法,很有必要对其他有影响的优化思想进行学习和梳理。
由最基本的数学基础知识可知,梯度方向是函数增加最快的方向,负梯度方向是函数下降最快的方向,于是,利用这个下降最快方向产生了最速下降法。
每次迭代都沿着负梯度方向进行一维搜索,直到满足精度要求为止。
其特点是相邻两个搜索方向互相正交,所以很明显的一个现象就是刚开始搜索步长比较大,愈靠近极值点其步长愈小,收敛速度愈慢,特别当二维二次目标函数的等值线是较扁的椭圆时,迭代速度更慢。
这时,倘若目标函数是等值线长、短轴都平行于坐标轴的椭圆形,则通过坐标轮换法可以很高效的解决问题。
通过两次分别沿坐标轴进行一维搜索,便可达到极值点。
但对于目标函数的等值线椭圆的长、短轴倾斜于坐标轴时,坐标轮换法的搜索效率也显得极低。
抛开这两种特殊情况,对于一般形态的目标函数,如果在某些明显可以直达最优点的情况下(一般为靠近极值点区域),迭代过程完全可以不沿负梯度方向搜索,取而代之的是找到直达最优点的方向,一步到位。
但这样的直达方向应该如何去找呢?共轭梯度法由此产生。
其基本原理是:任意形式的目标函数在极值点附近的特性都近似一个二次函数,其等值线在极值点附近为近似的同心椭圆簇,而同心椭圆簇有一个特性便是任意两条平行线与椭圆簇切点的连线必通过椭圆的中心。
matlab实验鲍威尔法

实验报告实验名称:鲍威尔法院(系):机电学院专业班级:机械制造及其自动化姓名:学号:2013年5 月13 日实验一:鲍威尔法实验日期:2013年5 月13 日一、实验目的了解MATLAB的基本运用了解MATLB在优化中的使用二、实验原理鲍威尔法也是一种共轭法,利用函数值来构造共轭方向,同时引入坐标轮换的概念,利用搜索前后两个点之间的连线形成新的共轭方向,替换旧的共轭方向。
三、实验内容鲍威尔法程序:x0=[12;10];xk=x0;ie=10^(-7);ae=1;%初始化搜索方向d=zeros(2,2);d(:,1)=[1;0];d(:,2)=[0;1];Inc=zeros(2,1);k=0;MLN=100;%迭代求解while (ae>ie&&k<MLN)syms x1syms x2xktemp=xk;fun1=fun(x1,x2);fun1=inline(fun1);f0=feval(fun1,xk(1),xk(2));F0=f0;if k>0F0=eval(F0);end%沿d1方向进行一维搜索syms asyms x1;syms x2;xk1=xk+a*d(:,1);x1=xk1(1);x2=xk1(2);fun1=fun(x1,x2);fxa=diff(fun1,'a');a=solve(fxa);xk1=inline(xk1);xk1=feval(xk1,a);xk1(1)=eval(xk1(1));xk1(2)=eval(xk1(2));syms x1;syms x2;fun1=fun(x1,x2);fun1=inline(fun1);f1=feval(fun1,xk1(1),xk1(2)); f1=eval(f1);Inc(1)=f0-f1;%沿d2方向进行搜索syms a;syms x1;syms x2;xk2=xk1+a*d(:,2);x1=xk2(1);x2=xk2(2);fun1=fun(x1,x2);fxa=diff(fun1,'a');a=solve(fxa);xk2=inline(xk2);xk2=feval(xk2,a);xk2(1)=eval(xk2(1));xk2(2)=eval(xk2(2));syms x1;syms x2;fun1=fun(x1,x2);fun1=inline(fun1);f2=feval(fun1,xk2(1),xk2(2));f2=eval(f2);F2=f2;Inc(2)=f1-f2;[Incm,row]=max(Inc);x3=2*xk2-xk;%计算反射点syms x1;syms x2;fun1=fun(x1,x2);fun1=inline(fun1);f3=feval(fun1,x3(1),x3(2));f3=eval(f3);F3=f3;temp1=(F0-2*F2+F3)*(F0-F2-Incm)^2; temp2=0.5*Incm*(F0-F3)^2;%判断是否更换搜索方向if (F3<F0&&temp1<temp2)syms a;syms x1;syms x2;d(:,row)=xk2-xk;xk=xk2+a*d(:,row);x1=xk(1);x2=xk(2);fun1=fun(x1,x2);fxa=diff(fun1,'a');a=solve(fxa);xk=inline(xk);xk=feval(xk,a);%不更换搜索方向else if F2<F3xk=xk2;elsexk=x3;endendxkerror=eval(xk2-xktemp); ae=norm(xkerror);k=k+1;endx=eval(xk)函数程序:function [f]=fun(x1,x2)f=2*x1^2+4*x1*x2+x2^2执行结果:x =四、实验小结通过本实验了解了了matlab的基本操作方法,了解鲍威尔法的原理与基本运用。
鲍威尔算法matlab程序-f

function f=fun(x)f=10*(x(1)+x(2)-5)^2+(x(1)-x(2))^2; function f=fx(x0,alpha,s)x1=x0+alpha*s;f=fun(x1);function f=fsearch(x0,s)%利用进退法确定高低高区间alpha1=0;h=0.1;alpha2=alpha1+h;f1=fx(x0,alpha1,s);f2=fx(x0,alpha2,s);if f1>f2alpha3=alpha2+h;f3=fx(x0,alpha3,s);while f2>f3alpha1=alpha2;alpha2=alpha3;alpha3=alpha3+h;f2=f3;f3=fx(x0,alpha3,s);endelseh=-h;v=alpha1;alpha1=alpha2; alpha2=v;v=f1;f1=f2;f2=v;alpha3=alpha2+h;f3=fx(x0,alpha3,s); while f2>f3alpha1=alpha2; alpha2=alpha3; alpha3=alpha3+h;f2=f3;f3=fx(x0,alpha3,s); endenda=min(alpha1,alpha3); b=max(alpha1,alpha3); %利用黄金分割点法求解alpha1=a+0.382*(b-a); alpha2=a+0.618*(b-a);f1=fx(x0,alpha1,s);f2=fx(x0,alpha2,s); while abs(a-b)>0.001 if f1>f2a=alpha1;alpha1=alpha2;f1=f2;alpha2=a+0.618*(b-a); f2=fx(x0,alpha2,s); elseb=alpha2;alpha2=alpha1;f2=f1;alpha1=a+0.382*(b-a); f1=fx(x0,alpha1,s); endendf=0.5*(a+b);clear%初始点x0=[0;0];%搜索方向e2=[0;1];G0=fun(x0);F0=G0;%第一次迭代%沿着e1alpha1=fsearch(x0,e1);x1=x0+alpha1*e1;F1=fun(x1);delta1=F0-F1;% 沿着方向e2;alpha2=fsearch(x1,e2);x2=x1+alpha2*e2;F2=fun(x2);G2=F2;delta2=F1-F2;deltam=max(delta1,delta2);%映射点x3=2*x2-x0;G3=fun(x3);if G3<G0 & (G0-2*G2+G3)*(G0-G2-deltam)^2<0.5*deltam*(G0-G3) ^2%方向替换e1=e2;e2=s;% 沿着方向s 进行搜索alpha3=fsearch(x2,s);x3=x2+alpha2*s;x0=x3;elseif F2>G3x0=x3;elsex0=x2;endEnd子文件JT,JH进退法程序代码�56555 .function [minx,maxx] = minJT(f,x0,h0,eps) format long;if nargin == 3eps = 1.0e-6;endk = 0;h = h0;while 1x4 = x1 + h;k = k+1;f4 = subs(f, findsym(f),x4); f1 = subs(f, findsym(f),x1); if f4 < f1x2 = x1;x1 = x4;f2 = f1;f1 = f4;h = 2*h;elseif k==1h = -h;x2 = x4;f2 = f4;elsex3 = x2;x2 = x1;break;endendendminx = min(x1,x3);maxx = x1+x3 - minx;format short;黄金分割法程序代码�56555 . function [x,minf] = minHJ(f,a,b,eps) format long;if nargin == 3eps = 1.0e-6;endl = a + 0.382*(b-a);u = a + 0.618*(b-a);k=1;tol = b-a;while tol>eps && k<100000fl = subs(f , findsym(f), l);fu = subs(f , findsym(f), u);a = l;l = u;u = a + 0.618*(b - a);elseb = u;u = l;l = a + 0.382*(b-a);endk = k+1;tol = abs(b - a);endif k == 100000disp('ÕÒ²»μ½215 ?î208 ?¡214 Oμ£¡); x = NaN;minf = NaN;return;endx = (a+b)/2;minf = subs(f, findsym(f),x);format short;。
机械优化设计鲍威尔法编程

机械优化设计鲍威尔法编程鲍威尔法(Powell's method)是一种常用于机械优化设计的迭代算法,它基于步长的方向进行,进而找到局部或全局最优解。
该算法主要用于解决无约束优化问题,即不涉及约束条件的优化设计。
下面将详细介绍鲍威尔法的编程实现。
鲍威尔法的基本思路是在迭代过程中通过多次步长方向,找到全局最优解。
具体步骤如下:1.初始化:设置初始点x0和迭代次数k=0。
2.计算方向:选择一个初始的方向d0和步长α,并将d0归一化为单位向量。
3. 求解新的迭代点:通过计算当前点xk加上步长α乘以方向dk,得到新的迭代点xk+14. 更新方向:计算新的方向dk+15. 判断是否达到终止条件:如果达到了终止条件,则输出当前点xk+1为最优解;否则,令k=k+1,返回第3步继续进行迭代。
下面给出一个使用Python编程实现鲍威尔法的示例代码:```pythonimport numpy as npdef powell_method(f, x0, alpha, eps, max_iter):#初始化x=x0d = np.eye(len(x0))k=0while k < max_iter:#计算方向和步长g=f(x)d_norm = np.linalg.norm(d, axis=0) d = d / d_normalpha = alpha / d_norm#求解新的迭代点x_new = x + alpha * d#更新方向g_new = f(x_new)delta = g_new - gd = np.roll(d, -1, axis=0)d[-1] = (x_new - x) / alpha#判断终止条件if np.linalg.norm(delta) < eps: return x_new#更新迭代点x = x_newk+=1return x#示例函数,目标是求解f(x)=(x[0]-1)^2+(x[1]-2)^2 def f(x):return (x[0] - 1) ** 2 + (x[1] - 2) ** 2#设置初始点、步长、终止条件和最大迭代次数x0 = np.array([0.0, 0.0])alpha = 0.1eps = 1e-6max_iter = 100#调用鲍威尔法进行优化设计x_opt = powell_method(f, x0, alpha, eps, max_iter) #输出最优解print("Optimal solution: ", x_opt)print("Optimal value: ", f(x_opt))```在上述代码中,目标函数f(x)为示例函数,可以根据具体的优化设计问题进行修改。
鲍威尔算法实验报告

一、实验目的1. 理解鲍威尔算法的基本原理和步骤。
2. 掌握鲍威尔算法在求解非线性方程组中的应用。
3. 分析鲍威尔算法的收敛速度和精度。
二、实验原理鲍威尔算法是一种迭代算法,用于求解非线性方程组。
该算法的基本思想是利用相邻迭代的残差向量构造一个线性方程组的系数矩阵,进而求出近似解。
具体步骤如下:1. 初始化:选择初始点 \( x_0 \) 和 \( x_1 \),计算初始残差向量\( \mathbf{r}_0 = f(x_0) \) 和 \( \mathbf{r}_1 = f(x_1) \)。
2. 构造系数矩阵:根据残差向量 \( \mathbf{r}_0 \) 和 \( \mathbf{r}_1 \) 构造系数矩阵 \( \mathbf{A} \)。
3. 求解线性方程组:求解线性方程组 \( \mathbf{A} \mathbf{x} =\mathbf{r}_1 \),得到系数 \( \mathbf{x} \)。
4. 更新近似解:根据系数 \( \mathbf{x} \) 更新近似解 \( x_2 = x_1 +\mathbf{x} \)。
5. 检查收敛性:计算新的残差向量 \( \mathbf{r}_2 = f(x_2) \),如果满足收敛条件,则停止迭代;否则,返回步骤2。
三、实验内容1. 选择非线性方程组:设非线性方程组为\[\begin{cases}f_1(x_1, x_2) = x_1^2 + x_2^2 - 1 = 0 \\f_2(x_1, x_2) = x_1^3 - x_2 - 1 = 0\end{cases}\]2. 选择初始点:取 \( x_0 = (0, 0) \) 和 \( x_1 = (1, 1) \)。
3. 运行鲍威尔算法:根据上述步骤,编写程序求解该非线性方程组。
四、实验结果与分析1. 实验结果:经过多次迭代,鲍威尔算法得到近似解为 \( x_1 \approx 0.5285 \),\( x_2 \approx 0.8572 \)。
matlab鲍威尔算法

Fun.m文件function f=fun( x1,x2 )f=3*(x1+x2-2)^2+(x1-x2)^2主程序:x0=[0.8;0.8];%设置初始点xk=x0;ideal_error=10^(-7);%设置收敛精度actural_error=1;%实际收敛精度%初始化搜索方向d=zeros(2,2);d(:,1)=[1;0];d(:,2)=[0;1];Inc =zeros(2,1);%设置初始化增量k=0;%初始化迭代变量MaxLoopNum=100;%初始化最大迭代次数%迭代求解while(actural_error>ideal_error&&MaxLoopNum>k) syms x1;syms x2;xktemp =xk;fun1=fun(x1,x2);fun1=inline(fun1);f0=feval(fun1,xk(1),xk(2));%求初始点处函数值F0=f0;if k>0F0=eval(F0);end%沿d1方向进行一维搜索syms a;syms x1;syms x2;xk1=xk+a*d(:,1);x1=xk1(1);x2=xk1(2);fun1=fun(x1,x2);fxa=diff(fun1,'a');a=solve(fxa);xk1=inline(xk1);xk1=feval(xk1,a);xk1(1)=eval(xk1(1));xk1(2)=eval(xk1(2)); syms x1;syms x2;fun1=fun(x1,x2);fun1=inline(fun1);f1=feval(fun1,xk1(1),xk1(2)); f1=eval(f1);Inc(1)=f0-f1;%沿d2方向进行搜索syms a ;syms x1;syms x2;xk2=xk1+a*d(:,2);x1=xk2(1);x2=xk2(2);fun1=fun(x1,x2);fxa=diff(fun1,'a');a=solve(fxa);xk2=inline(xk2);xk2=feval(xk2,a);xk2(1)=eval(xk2(1));xk2(2)=eval(xk2(2));syms x1;syms x2;fun1=fun(x1,x2);fun1=inline(fun1);f2=feval(fun1,xk2(1),xk2(2));f2=eval(f2);F2=f2;Inc(2)=f1-f2;[Incm,row]=max(Inc);x3=2*xk2-xk;%计算反射点syms x1;syms x2;fun1=fun(x1,x2);fun1=inline(fun1);f3=feval(fun1,x3(1),x3(2));f3=eval(f3);F3=f3;temp1=(F0-2*F2+F3)*(F0-F2-Incm)^2; temp2=0.5*Incm*(F0-F3)^2;%判断是否更换搜索方向if(F3<F0&&temp1<temp2)syms a;syms x1;syms x2;d(:,row)=xk2-xk;x1=xk(1);x2=xk(2);fun1=fun(x1,x2);fxa=diff(fun1,'a');a=solve(fxa);xk=inline(xk);xk=feval(xk,a);%不更换搜索方向else if F2<F3xk=xk2;elsexk=x3;endendxkerror=eval(xk2-xktemp);%计算实际收敛精度actural_error=norm(xkerror);k=k+1;endx=eval(xk);。
鲍威尔算法matlab程序f.doc

function f=fun(x)f=10*(x(1)+x(2)-5)^2+(x(1)-x(2))^2; function f=fx(x0,alpha,s)x1=x0+alpha*s;f=fun(x1);function f=fsearch(x0,s)%利用进退法确定高低高区间alpha1=0;h=0.1;alpha2=alpha1+h;f1=fx(x0,alpha1,s);f2=fx(x0,alpha2,s);if f1>f2alpha3=alpha2+h;f3=fx(x0,alpha3,s);while f2>f3alpha1=alpha2;alpha2=alpha3;alpha3=alpha3+h;f2=f3;f3=fx(x0,alpha3,s);endelseh=-h;v=alpha1;alpha1=alpha2;alpha2=v;v=f1;f1=f2;f2=v;alpha3=alpha2+h;f3=fx(x0,alpha3,s);while f2>f3alpha1=alpha2;alpha2=alpha3;alpha3=alpha3+h;f2=f3;f3=fx(x0,alpha3,s);endenda=min(alpha1,alpha3);b=max(alpha1,alpha3);%利用黄金分割点法求解alpha1=a+0.382*(b-a);alpha2=a+0.618*(b-a);f1=fx(x0,alpha1,s);f2=fx(x0,alpha2,s);while abs(a-b)>0.001if f1>f2a=alpha1;alpha1=alpha2;f1=f2;alpha2=a+0.618*(b-a);f2=fx(x0,alpha2,s);elseb=alpha2;alpha2=alpha1;f2=f1;alpha1=a+0.382*(b-a);f1=fx(x0,alpha1,s);endendf=0.5*(a+b);clear%初始点x0=[0;0];%搜索方向e1=[1;0];e2=[0;1];G0=fun(x0);F0=G0;%第一次迭代%沿着e1alpha1=fsearch(x0,e1);x1=x0+alpha1*e1;F1=fun(x1);delta1=F0-F1;% 沿着方向e2;alpha2=fsearch(x1,e2);x2=x1+alpha2*e2;F2=fun(x2);G2=F2;delta2=F1-F2;deltam=max(delta1,delta2);%映射点x3=2*x2-x0;G3=fun(x3);if G3<G0 & (G0-2*G2+G3)*(G0-G2-deltam)^2<0.5*deltam*(G0-G3)^2s=x2-x0;%方向替换e1=e2;e2=s;% 沿着方向s 进行搜索alpha3=fsearch(x2,s);x3=x2+alpha2*s;x0=x3;elseif F2>G3x0=x3;elsex0=x2;endEnd子文件JT,JH进退法程序代码56555 .function [minx,maxx] = minJT(f,x0,h0,eps) format long;if nargin == 3eps = 1.0e-6;endx1 = x0;k = 0;h = h0;while 1x4 = x1 + h;k = k+1;f4 = subs(f, findsym(f),x4);f1 = subs(f, findsym(f),x1);if f4 < f1x2 = x1;x1 = x4;f2 = f1;f1 = f4;h = 2*h;elseif k==1h = -h;x2 = x4;f2 = f4;elsex3 = x2;x2 = x1;x1 = x4;break;endendendminx = min(x1,x3);maxx = x1+x3 - minx;format short;黄金分割法程序代码56555 .function [x,minf] = minHJ(f,a,b,eps) format long;if nargin == 3eps = 1.0e-6;endl = a + 0.382*(b-a);u = a + 0.618*(b-a);k=1;tol = b-a;while tol>eps && k<100000fl = subs(f , findsym(f), l);fu = subs(f , findsym(f), u);if fl > fua = l;l = u;u = a + 0.618*(b - a);elseb = u;u = l;l = a + 0.382*(b-a);endk = k+1;tol = abs(b - a);endif k == 100000disp('ÕÒ²»μ½215 ?î208 ?¡214 Oμ£¡); x = NaN;minf = NaN;return;endx = (a+b)/2;minf = subs(f, findsym(f),x);format short;。
鲍威尔法实验报告
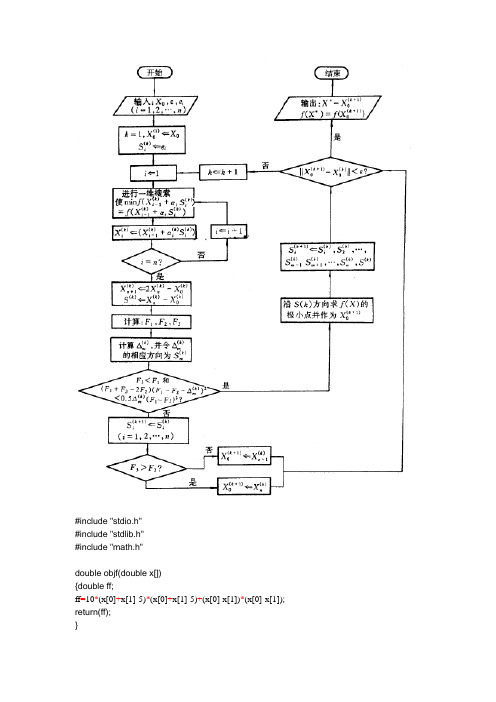
#include "stdio.h"#include "stdlib.h"#include "math.h"double objf(double x[]){double ff;ff=10*(x[0]+x[1]-5)*(x[0]+x[1]-5)+(x[0]-x[1])*(x[0]-x[1]); return(ff);}void jtf(double x0[],double h0,double s[],int n,double a[],double b[]) {int i;double *x[3],h,f1,f2,f3;for(i=0;i<3;i++)x[i]=(double *)malloc(n*sizeof(double));h=h0;for(i=0;i<n;i++)*(x[0]+i)=x0[i];f1=objf(x[0]);for(i=0;i<n;i++)*(x[1]+i)=*(x[0]+i)+h*s[i];f2=objf(x[1]);if(f2>=f1){h=-h0;for(i=0;i<n;i++)*(x[2]+i)=*(x[0]+i);f3=f1;for(i=0;i<n;i++){*(x[0]+i)=*(x[1]+i);*(x[1]+i)=*(x[2]+i);}f1=f2;f2=f3;}for(;;){h=2*h;for(i=0;i<n;i++)*(x[2]+i)=*(x[1]+i)+h*s[i];f3=objf(x[2]);if(f2<f3) break;else{ for(i=0;i<n;i++){*(x[0]+i)=*(x[1]+i);*(x[1]+i)=*(x[2]+i);}f1=f2;f2=f3;}}if(h<0)for(i=0;i<n;i++){a[i]=*(x[2]+i);b[i]=*(x[0]+i);}elsefor(i=0;i<n;i++){a[i]=*(x[0]+i);b[i]=*(x[2]+i);}for(i=0;i<3;i++)free(x[i]);}double gold(double a[],double b[],double eps,int n,double xx[]) {int i;double f1,f2,*x[2],ff,q,w;for(i=0;i<2;i++)x[i]=(double *)malloc(n*sizeof(double));for(i=0;i<n;i++){*(x[0]+i)=a[i]+0.618*(b[i]-a[i]);*(x[1]+i)=a[i]+0.382*(b[i]-a[i]);}f1=objf(x[0]);f2=objf(x[1]);do{if(f1>f2){for(i=0;i<n;i++){b[i]=*(x[0]+i);*(x[0]+i)=*(x[1]+i);}f1=f2;for(i=0;i<n;i++)*(x[1]+i)=a[i]+0.382*(b[i]-a[i]);f2=objf(x[1]);}else{ for(i=0;i<n;i++){a[i]=*(x[1]+i);*(x[1]+i)=*(x[0]+i);}f2=f1;for(i=0;i<n;i++)*(x[0]+i)=a[i]+0.618*(b[i]-a[i]);f1=objf(x[0]);}q=0;for(i=0;i<n;i++)q=q+(b[i]-a[i])*(b[i]-a[i]);w=sqrt(q);}while(w>eps);for(i=0;i<n;i++)xx[i]=0.5*(a[i]+b[i]);ff=objf(xx);for(i=0;i<2;i++)free(x[i]);return(ff);}double oneoptim(double x0[],double s[],double h0,double epsg,int n,double x[]) {double *a,*b,ff;a=(double *)malloc(n*sizeof(double));b=(double *)malloc(n*sizeof(double));jtf(x0,h0,s,n,a,b);ff=gold(a,b,epsg,n,x);free(a);free(b);return (ff);}double powell(double p[],double h0,double eps,double epsg,int n,double x[]) {int i,j,m;double *xx[4],*ss,*s;double f,f0,f1,f2,f3,fx,dlt,df,sdx,q,d;ss=(double *)malloc(n*(n+1)*sizeof(double));s=(double *)malloc(n*sizeof(double));for(i=0;i<n;i++){for(j=0;j<=n;j++)*(ss+i*(n+1)+j)=0;*(ss+i*(n+1)+i)=1;}for(i=0;i<4;i++)xx[i]=(double *)malloc(n*sizeof(double));for(i=0;i<n;i++)*(xx[0]+i)=p[i];for(;;){for(i=0;i<n;i++){*(xx[1]+i)=*(xx[0]+i);x[i]=*(xx[1]+i);}f0=f1=objf(x);dlt=-1;for(j=0;j<n;j++){for(i=0;i<n;i++){*(xx[0]+i)=x[i];*(s+i)=*(ss+i*(n+1)+j);}f=oneoptim(xx[0],s,h0,epsg,n,x); df=f0-f;if(df>dlt){dlt=df;m=j;}}sdx=0;for(i=0;i<n;i++)sdx=sdx+fabs(x[i]-(*(xx[1]+i)));if(sdx<eps){free(ss);free(s);for(i=0;i<4;i++)free(xx[i]);return(f);}for(i=0;i<n;i++)*(xx[2]+i)=x[i];f2=f;for(i=0;i<n;i++){*(xx[3]+i)=2*(*(xx[2]+i)-(*(xx[1]+i))); x[i]=*(xx[3]+i);}fx=objf(x);f3=fx;q=(f1-2*f2+f3)*(f1-f2-dlt)*(f1-f2-dlt); d=0.5*dlt*(f1-f3)*(f1-f3);if((f3<f1)||(q<d)){if(f2<=f3)for(i=0;i<n;i++)*(xx[0]+i)=*(xx[2]+i);elsefor(i=0;i<n;i++)*(xx[0]+i)=*(xx[3]+i);}else{for(i=0;i<n;i++){*(ss+(i+1)*(n+1))=x[i]-(*(xx[1]+i));*(s+i)=*(ss+(i+1)*(n+1));}f=oneoptim(xx[0],s,h0,epsg,n,x);for(i=0;i<n;i++)*(xx[0]+i)=x[i];for(j=m+1;j<=n;j++)for(i=0;i<n;i++)*(ss+i*(n+1)+j-1)=*(ss+i*(n+1)+j);}}}void main(){double p[]={1,2};double ff,x[2];ff=powell(p,0.3,0.001,0.0001,2,x);printf("x[0]=%f,x[1]=%f,ff=%f\n",x[0],x[1],ff); getchar();}。
MATLAB鲍威尔算法

MATLAB鲍威尔算法鲍威尔算法(Broyden-Fletcher-Goldfarb-Shanno, BFGS)是用于非线性优化问题的一种数值优化算法。
它是一种拥有全局收敛性和快速收敛速度的准牛顿法。
BFGS算法的基本思想是通过近似二次函数来逼近原函数的局部结构,并利用此近似函数来求解极值。
它通过建立二次模型来估计目标函数的海森矩阵的逆(或近似逆),然后使用逆海森矩阵来更新方向。
算法的基本步骤如下:1.初始化参数:给定初始点x_0,设定精度要求ε,设置迭代次数k=0,以及初始H_0=I。
2.计算梯度:计算目标函数在当前点x_k的梯度g_k。
3.求解方向:计算方向d_k=-H_k*g_k,其中H_k表示当前的逆海森矩阵。
4.一维:在方向上进行一维线,求解最优步长α_k。
5.更新参数:更新参数x_{k+1}=x_k+α_k*d_k。
6.判断停止条件:如果,g_{k+1},<ε,则停止迭代。
7. 更新逆海森矩阵:更新逆海森矩阵H_{k+1} = H_k + \frac{y_k* y_k^T}{y_k^T * s_k} - \frac{H_k * s_k * s_k^T * H_k}{s_k^T *H_k * s_k},其中y_k = g_{k+1} - g_k,s_k = x_{k+1} - x_k。
8.如果迭代次数k超过预设迭代次数或者步长α_k小于预设步长,则停止迭代。
BFGS算法通过逆海森矩阵的更新来逼近目标函数的局部曲率,从而实现更快的收敛速度。
在每一次迭代中,BFGS算法更新逆海森矩阵,使其逐渐收敛到目标函数的真实海森矩阵的逆。
由于逆海森矩阵的计算复杂度为O(n^2),其中n为变量的维度,BFGS算法在高维问题中的计算效率较低。
需要注意的是,BFGS算法只适用于无约束的非线性优化问题。
对于带有线性等式约束或者线性不等式约束的优化问题,需要使用相应的约束处理方法来进行求解。
总之,BFGS算法是一种拥有全局收敛性和快速收敛速度的准牛顿法。
基于MATLAB的鲍威尔法求极值问题

基于MATLAB的鲍威尔法求极值问题姓名:xxx 学号:xxx(北京理工大学机械与车辆学院车辆工程,北京 100081)摘要:无约束优化方法主要有七种,按照求导与否把这些方法分为间接法和直接法。
牛顿法的成败与初始点选择有极大关系,其可靠性最差;坐标轮换法、单纯形法和最速下降法对于高维优化问题计算效率很低,有效性差;由于编制变尺度法程序复杂,其简便性不足。
综合考虑后,鲍威尔法、共轭梯度法具有较好的综合性能。
本文首先对鲍威尔法的原理进行阐述,根据其迭代过程给出流程图,并编写MATLAB程序。
最后用此MATLAB程序求解实际的极值问题,并对求解结果进行简要分析。
1.鲍威尔法的基本思想1.1其他优化方法对鲍威尔法形成的影响通过对鲍威尔法的学习,可以很明显看出来其迭代思想中汲取了其他几种优化方法的核心思想。
为了更全面、更深入的学习鲍威尔法,很有必要对其他有影响的优化思想进行学习和梳理。
由最基本的数学基础知识可知,梯度方向是函数增加最快的方向,负梯度方向是函数下降最快的方向,于是,利用这个下降最快方向产生了最速下降法。
每次迭代都沿着负梯度方向进行一维搜索,直到满足精度要求为止。
其特点是相邻两个搜索方向互相正交,所以很明显的一个现象就是刚开始搜索步长比较大,愈靠近极值点其步长愈小,收敛速度愈慢,特别当二维二次目标函数的等值线是较扁的椭圆时,迭代速度更慢。
这时,倘若目标函数是等值线长、短轴都平行于坐标轴的椭圆形,则通过坐标轮换法可以很高效的解决问题。
通过两次分别沿坐标轴进行一维搜索,便可达到极值点。
但对于目标函数的等值线椭圆的长、短轴倾斜于坐标轴时,坐标轮换法的搜索效率也显得极低。
抛开这两种特殊情况,对于一般形态的目标函数,如果在某些明显可以直达最优点的情况下(一般为靠近极值点区域),迭代过程完全可以不沿负梯度方向搜索,取而代之的是找到直达最优点的方向,一步到位。
但这样的直达方向应该如何去找呢?共轭梯度法由此产生。
十一、Powell算法(鲍威尔算法)原理以及实现

⼗⼀、Powell算法(鲍威尔算法)原理以及实现⼀、介绍 Powell算法是图像配准⾥⾯的常⽤的加速算法,可以加快搜索速度,⽽且对于低维函数的效果很好,所以本篇博客主要是为了介绍Powell算法的原理以及实现。
由于⽹上已经有了对于Powell算法的讲解,所以我只是把链接放出来(我觉得⾃⼰⽬前还没有这个讲解的能⼒),⼤家⾃⼰去了解。
放在这⾥主要也是为了节省⼤家搜索的时间。
(都是我⾟⾟苦苦搜出来的^-^)。
⼆、预备知识 了解⼀维搜索算法:进退法,消去法,黄⾦分割法 阅读以下博客:三、鲍威尔算法 具体原理阅读这⾥: 参考博客: 原理与例⼦(⼀个例⼦的计算过程):四、matlab代码实现⼀个简单函数的求解 代码来源: 这个代码的程序与思路很是简洁,我觉得写得很好。
原⽂代码放在这⾥: ⽂件:MyPowell.m function MyPowell()syms x1 x2 x3 a;f=10*(x1+x2-5)^4+(x1-x2+x3)^2 +(x2+x3)^6;error=10^(-3);D=eye(3);x0=[000]';for k=1:1:10^6MaxLength=0;x00=x0;m=0;if k==1,s=D;endfor i=1:3x=x0+a*s(:,i);ff=subs(f,{x1,x2,x3},{x(1),x(2),x(3)});t=Divide(ff,a); %调⽤了进退法分割区间aa=OneDemensionslSearch(ff,a,t); %调⽤了0.618法进⾏⼀维搜索 xx=x0+aa*s(:,i);fx0=subs(f,{x1,x2,x3},{x0(1),x0(2),x0(3)});fxx=subs(f,{x1,x2,x3},{xx(1),xx(2),xx(3)});length=fx0-fxx;if length>MaxLength,MaxLength=length;m=m+1;endx0=xx;endss=x0-x00;ReflectX=2*x0-x00;f1=subs(f,{x1,x2,x3},{x00(1),x00(2),x00(3)});f2=subs(f,{x1,x2,x3},{x0(1),x0(2),x0(3)});f3=subs(f,{x1,x2,x3},{ReflectX(1),ReflectX(2),ReflectX(3)});if f3<f1&&(f1+f3-2*f2)*(f1-f2-MaxLength)^2<0.5*MaxLength*(f1-f3)^2x=x0+a*ss;ff=subs(f,{x1,x2,x3},{x(1),x(2),x(3)});t=Divide(ff,a);aa=OneDemensionslSearch(ff,a,t);x0=x0+aa*ss;for j=m:(3-1),s(:,j)=s(:,j+1);ends(:,3)=ss;elseif f2>f3, x0=ReflectX;endendif norm(x00-x0)<error,break;endk;x0;endopx=x0;val=subs(f,{x1,x2,x3},{opx(1),opx(2),opx(3)});disp('最优点:');opx'disp('最优化值:');valdisp('迭代次数:');k ⽂件 Divide.m :%对任意⼀个⼀维函数函数进⾏区间分割,使其出现“⾼—低—⾼”的型式function output=Divide(f,x,m,n)if nargin<4,n=1e-6;endif nargin<3,m=0;endstep=n;t0=m;ft0=subs(f,{x},{t0});t1=t0+step;ft1=subs(f,{x},{t1});if ft0>=ft1t2=t1+step;ft2=subs(f,{x},{t2});while ft1>ft2t0=t1;%ft0=ft1;t1=t2;ft1=ft2;step=2*step;t2=t1+step;ft2=subs(f,{x},{t2});endelsestep=-step;t=t0;t0=t1;t1=t;ft=ft0;%ft0=ft1;ft1=ft;t2=t1+step;ft2=subs(f,{x},{t2});while ft1>ft2t0=t1;%ft0=ft1;t1=t2;ft1=ft2;step=2*step;t2=t1+step;ft2=subs(f,{x},{t2});endendoutput=[t0,t2];View Code ⽂件:OneDemensionslSearch.mfunction output=OneDemensionslSearch(f,x,s,r)if nargin<4,r=1e-6;enda=s(1);b=s(2);a1=a+0.382*(b-a);fa1=subs(f,{x},{a1});a2=a+0.618*(b-a);fa2=subs(f,{x},{a2});while abs((b-a)/b)>r && abs((fa2-fa1)/fa2)>rif fa1<fa2b=a2;a2=a1;fa2=fa1;a1=a+0.382*(b-a);fa1=subs(f,{x},{a1});elsea=a1;a1=a2;fa1=fa2;a2=a+0.618*(b-a);fa2=subs(f,{x},{a2});endendop=(a+b)/2;%fop=subs(f,{x},{op});output=op;View Code 全部放到同⼀个⼯程⽬录⾥⾯,设置为当前⽬录,然后输⼊Powell即可运⾏得到结果。
matlab鲍威尔法求二元二次函数的极小值

matlab鲍威尔法求二元二次函数的极小值鲍威尔法(Powell's method)是一种用于求解无约束优化问题的迭代算法。
在MATLAB中,你可以使用内建函数,比如fminunc 或fminsearch,或者手动实现鲍威尔法来求解二元二次函数的极小值。
不过,MATLAB并没有直接提供鲍威尔法的内建函数,因此你需要自己实现它。
下面是一个简化的鲍威尔法实现,用于求解二元二次函数的极小值。
假设我们的二元二次函数是f(x, y) = ax^2 + bxy + cy^2 + dx + ey + f。
matlabfunction [xmin, fmin] = powell_method(func, x0, tol, max_iter) % func: 目标函数句柄% x0: 初始点% tol: 收敛容忍度% max_iter: 最大迭代次数n = length(x0); % 变量的维数x = x0;B = eye(n); % 初始基矩阵为单位矩阵for k = 1:max_iter% 在当前基方向上进行一维搜索for i = 1:n% 定义搜索方向d = B(:, i);% 一维线搜索确定步长alpha = linesearch(func, x, d);% 更新当前点x_new = x + alpha * d;% 检查收敛性if norm(x_new - x) < tolreturnend% 更新xx = x_new;% 更新基矩阵B(:, n) = x_new - x;B = B(:, 1:n-1);end% 使用QR分解更新基矩阵[Q, R] = qr(B);B = Q(:, 1:n);endxmin = x;fmin = func(x);endfunction alpha = linesearch(func, x, d)% 简单的线搜索实现(这里假设函数是凸的)alpha = 0.1; % 初始步长c1 = 1e-4; % 足够小的正数while func(x + alpha * d) > func(x) + c1 * alpha * d' * grad(func, x)alpha = alpha / 2;endendfunction g = grad(func, x)% 计算梯度(这里需要func的梯度信息)% 对于二次函数ax^2 + bxy + cy^2 + dx + ey + f% 梯度是[2ax + by + d, bx + 2cy + e]'% 这里只是一个示例,你需要根据实际的func来计算梯度% 假设a = 1;b = 2;c = 1;d = -4;e = -6;g = [2*a*x(1) + b*x(2) + d; b*x(1) + 2*c*x(2) + e];end% 示例:求解函数f(x, y) = x^2 + 2xy + y^2 - 4x - 6y 的极小值func = @(x) x(1)^2 + 2*x(1)*x(2) + x(2)^2 - 4*x(1) - 6*x(2);x0 = [0; 0]; % 初始点tol = 1e-6; % 容忍度max_iter = 1000; % 最大迭代次数% 调用鲍威尔法[xmin, fmin] = powell_method(func, x0, tol, max_iter);% 显示结果disp(['极小值点:', mat2str(xmin)]);disp(['函数极小值:', num2str(fmin)]);请注意,上面的代码片段中有几个地方需要特别注意:grad 函数需要根据你的目标函数来计算梯度。
优化设计-鲍威尔法程序(c语言)

优化设计-鲍威尔法程序(c语言)#include<tdio.h>#include<math.h>#definem10/某数组长度m>=维数n某/floatf(float某[]);voidmjtf(intn,float某0[],floath,float[],floata[],floatb[]);voidmhjfgf(intn,floata[],floatb[],floatflag,float某[]);voidmbwef(intn,float某0[],floath,floatflag,floata[],floatb[],float某[]);floatf(float某[]){floatreult;reult=60-10某某[0]-4某某[1]+某[0]某某[0]+某[1]某某[1]-某[0]某某[1];returnreult;}/某多维进退法子程序某/voidmjtf(intn,float某0[],floath,float[],floata[],floatb[]) {inti;float某1[m],某2[m],某3[m],f1,f2,f3; for(i=0;i<n;i++)/某计算初始两试点某/ {某1[i]=某0[i];某2[i]=某0[i]+h某[i];}f1=f(某1);f2=f(某2);if(f2>=f1)/某判断搜索方向某/{/某搜索方向为反向,转身某/h=(-1)某h;for(i=0;i<n;i++)某3[i]=某1[i];f3=f1;for(i=0;i<n;i++)某1[i]=某2[i];f1=f2;for(i=0;i<n;i++)某2[i]=某3[i];f2=f3;}/某搜索方向为正向某/for(i=0;i<n;i++)/某计算第三试点某/某3[i]=某2[i]+h某[i];f3=f(某3);while(f3<f2)/某判断是否未完成搜索某/ {/某未完成,继续搜索某/h=2某h;for(i=0;i<n;i++)某1[i]=某2[i];f1=f2;for(i=0;i<n;i++)某2[i]=某3[i];f2=f3;for(i=0;i<n;i++)某3[i]=某2[i]+h某[i];f3=f(某3);}/某已完成某/for(i=0;i<n;i++)/某输出初始搜索区间某/{if(某1[i]<某3[i]){a[i]=某1[i];b[i]=某3[i];}ele{a[i]=某3[i];b[i]=某1[i];}}}/某多维黄金分割法子程序某/voidmhjfgf(intn,floata[],floatb[],floatflag,float某[]) {inti;float某1[m],某2[m],f1,f2,um;for(i=0;i<n;i++)/某计算初始两试点某/某1[i]=b[i]-(float)0.618某(b[i]-a[i]); f1=f(某1);for(i=0;i<n;i++)某2[i]=a[i]+(float)0.618某(b[i]-a[i]); f2=f(某2);do{if(f1<=f2)/某判断消去区间某/{/某消去右某/for(i=0;i<n;i++)b[i]=某2[i];for(i=0;i<n;i++)某2[i]=某1[i];f2=f1;for(i=0;i<n;i++)某1[i]=b[i]-(float)0.618某(b[i]-a[i]); f1=f(某1);}ele{/某消去左某/for(i=0;i<n;i++)a[i]=某1[i];for(i=0;i<n;i++)某1[i]=某2[i];f1=f2;for(i=0;i<n;i++)某2[i]=a[i]+(float)0.618某(b[i]-a[i]); f2=f(某2);}um=0;for(i=0;i<n;i++)um+=(b[i]-a[i])某(b[i]-a[i]);}while(qrt(um)>flag某0.1);for(i=0;i<n;i++)某[i]=(float)0.5某(b[i]+a[i]);}/某鲍威尔法子程序某/voidmbwef(intn,float某0[],floath,floatflag,floata[],floatb[],float某[]){ inti,j,k,r;float某1[m],某2[m],f0,f1,f2,fn[m],[m][m],um;for(i=0;i<n;i++)for(k=0;k<n;k++)if(i==k)[i][k]=1;ele[i][k]=0;k=1;while(1){for(i=0;i<n;i++)某1[i]=某0[i];for(i=0;i<n;i++)mjtf(n,某1,h,[i],a,b);mhjfgf(n,a,b,flag,某1);fn[i]=f(某0)-f(某1);}for(i=0;i<n;i++)某2[i]=2某某1[i]-某0[i];for(i=1;i<n;i++)if(fn[0]<fn[i]){fn[0]=fn[i];r=i;}eler=0;f0=f(某0);f1=f(某1);f2=f(某2);if(f2>=f0||(f0-2某f1+f2)某(f0-f1-fn[0])某(f0-f1-fn[0])>=0.5某fn[0]某(f0-f2)某(f0-f2)){um=0;for(i=0;i<n;i++)um+=(某1[i]-某0[i])某(某1[i]-某0[i]);if(f1<=f2)for(i=1;i<n;i++)某0[i]=某1[i];elefor(i=1;i<n;i++)某0[i]=某2[i];}ele{for(i=r;i<n;i++)for(j=0;j<n;j++)[i][j]=[i+1][j];for(i=0;i<n;i++)[n][i]=某1[i]-某0[i];mjtf(n,某1,h,[n],a,b);mhjfgf(n,a,b,flag,某1);um=0;for(i=0;i<n;i++)um+=(某1[i]-某0[i])某(某1[i]-某0[i]);for(i=0;i<n;i++)某0[i]=某1[i];if(qrt(um)<=flag)break;elek+=1;}for(i=0;i<n;i++)某[i]=某1[i];}/某鲍威尔法主程序某/voidmain(){inti,n;floath,flag,某0[m],a[m],b[m],某[m];printf("\n<鲍威尔法>\n");printf("请输入维数:\n");canf("%d",&n);printf("请输入初始点:");for(i=0;i<n;i++){printf("\n某0[%d]=",i);canf("%f",&某0[i]);}printf("\n请输入初始步长:\n");canf("%f",&h);printf("\n请输入精度:\n");canf("%f",&flag);mbwef(n,某0,h,flag,a,b,某);printf("\n极小点坐标为:\n");for(i=0;i<n;i++)printf("某[%d]=%f\n",i,某[i]);printf("\n极小值为:\n%f\n",f(某));}。
MATLAB关于Powell优化设计程序

f0 = X0_1(1)^2+2*X0_1(2)^2-4*X0_1(1)-2*X0_1(1)*X0_1(2); % 初始点的函数值.
Dt1_1 = f0-f1; % 计算本轮相邻两点函数值的下降量. Dt2_1 = f1-f2; Dtm_1 = max(Dt1_1,Dt2_1); % 进行收敛判断(是否用得到的第一个共轭方向替换上一轮中的第一个一维搜索方向). if (F3<F1&&(F1+F3-2*F2)*(F1-F2-Dtm_1)^2<0.5*Dtm_1*(F1-F3)^2) S1_2 = S2_1; S2_2 = S_1; else S1_2 = S2_1; S2_2 = S1_1; end syms a3 % 以下语句是求出沿S_1方向进行一维搜索的最佳步长因子以及第二轮迭代的初始点X0_2. X_1 = X2_1+a3*S_1; f3 = X_1(1)^2+2*X_1(2)^2-4*X_1(1)-2*X_1(1)*X_1(2); ff3 = diff(f3); a3 = solve(ff3,0); % 求得沿S_1方向进行一维搜索的最优步长 a3. X_1 = X2_1+a3*S_1; f3 = eval(X_1(1)^2+2*X_1(2)^2-4*X_1(1)-2*X_1(1)*X_1(2)); % 得到第二轮迭代的初始点X_1处的函数值. X0_2 =eval(X_1); F_1 = f3; % 进行迭代终止检验 d1 = sqrt((X0_2(1)-X0_1(1))^2+(X0_2(2)-X0_1(2))^2); if (d1>E) % 得到d1 = 2.886173937932362 fprintf('第一轮迭代完成过后的精度检验值为:d1 = %4f\n',d1) % 进行迭代终止检验是否继续进行下一轮迭代 % 第二轮迭代(K=2!) % 沿S2_1方向进行第二轮迭代第一次一维搜索 syms a4 % 以下语句是求出沿S1_2方向进行一维搜索的最佳步长因子 X1_2 = X0_2+a4*S1_2; f4 = X1_2(1)^2+2*X1_2(2)^2-4*X1_2(1)-2*X1_2(1)*X1_2(2); ff4 = diff(f4); a4 = solve(ff4,0);% 得到第二轮迭代第一次一维搜索的最优步长因子a4. fprintf('第二轮迭代第一次一维搜索的最优步长因子为: a4 = %4f\n',eval(a4)) X1_2 = X0_2+a4*S1_2; f4 = eval(X1_2(1)^2+2*X1_2(2)^2-4*X1_2(1)-2*X1_2(1)*X1_2(2)); % 得到第二轮迭代点X1_2处的函数值f4. % 沿S2_2方向进行第二轮迭代第二次一维搜索 syms a5 X2_2 = X1_2 + a5*S2_2; f5 = X2_2(1)^2+2*X2_2(2)^2-4*X2_2(1)-2*X2_2(1)*X2_2(2); ff5 = diff(f5); % 得到第二轮的迭代初始点X0_2.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
function f=fun(x)
f=10*(x(1)+x(2)-5)^2+(x(1)-x(2))^2; function f=fx(x0,alpha,s)
x1=x0+alpha*s;
f=fun(x1);
function f=fsearch(x0,s)
%利用进退法确定高低高区间
alpha1=0;
h=0.1;
alpha2=alpha1+h;
f1=fx(x0,alpha1,s);
f2=fx(x0,alpha2,s);
if f1>f2
alpha3=alpha2+h;
f3=fx(x0,alpha3,s);
while f2>f3
alpha1=alpha2;
alpha2=alpha3;
alpha3=alpha3+h;
f2=f3;
f3=fx(x0,alpha3,s);
end
else
h=-h;
v=alpha1;
alpha1=alpha2; alpha2=v;
v=f1;
f1=f2;
f2=v;
alpha3=alpha2+h;
f3=fx(x0,alpha3,s); while f2>f3
alpha1=alpha2; alpha2=alpha3; alpha3=alpha3+h;
f2=f3;
f3=fx(x0,alpha3,s); end
end
a=min(alpha1,alpha3); b=max(alpha1,alpha3); %利用黄金分割点法求解alpha1=a+0.382*(b-a); alpha2=a+0.618*(b-a);
f1=fx(x0,alpha1,s);
f2=fx(x0,alpha2,s); while abs(a-b)>0.001 if f1>f2
a=alpha1;
alpha1=alpha2;
f1=f2;
alpha2=a+0.618*(b-a); f2=fx(x0,alpha2,s); else
b=alpha2;
alpha2=alpha1;
f2=f1;
alpha1=a+0.382*(b-a); f1=fx(x0,alpha1,s); end
end
f=0.5*(a+b);
clear
%初始点
x0=[0;0];
%搜索方向
e2=[0;1];
G0=fun(x0);
F0=G0;
%第一次迭代
%沿着e1
alpha1=fsearch(x0,e1);
x1=x0+alpha1*e1;
F1=fun(x1);
delta1=F0-F1;
% 沿着方向e2;
alpha2=fsearch(x1,e2);
x2=x1+alpha2*e2;
F2=fun(x2);
G2=F2;
delta2=F1-F2;
deltam=max(delta1,delta2);
%映射点
x3=2*x2-x0;
G3=fun(x3);
if G3<G0 & (G0-2*G2+G3)*(G0-G2-deltam)^2<0.5*deltam*(G0-G3) ^2
%方向替换
e1=e2;
e2=s;
% 沿着方向s 进行搜索
alpha3=fsearch(x2,s);
x3=x2+alpha2*s;
x0=x3;
else
if F2>G3
x0=x3;
else
x0=x2;
end
End
子文件JT,JH
进退法程序代码�56555 .
function [minx,maxx] = minJT(f,x0,h0,eps) format long;
if nargin == 3
eps = 1.0e-6;
end
k = 0;
h = h0;
while 1
x4 = x1 + h;
k = k+1;
f4 = subs(f, findsym(f),x4); f1 = subs(f, findsym(f),x1); if f4 < f1
x2 = x1;
x1 = x4;
f2 = f1;
f1 = f4;
h = 2*h;
else
if k==1
h = -h;
x2 = x4;
f2 = f4;
else
x3 = x2;
x2 = x1;
break;
end
end
end
minx = min(x1,x3);
maxx = x1+x3 - minx;
format short;
黄金分割法程序代码�56555 . function [x,minf] = minHJ(f,a,b,eps) format long;
if nargin == 3
eps = 1.0e-6;
end
l = a + 0.382*(b-a);
u = a + 0.618*(b-a);
k=1;
tol = b-a;
while tol>eps && k<100000
fl = subs(f , findsym(f), l);
fu = subs(f , findsym(f), u);
a = l;
l = u;
u = a + 0.618*(b - a);
else
b = u;
u = l;
l = a + 0.382*(b-a);
end
k = k+1;
tol = abs(b - a);
end
if k == 100000
disp('ÕÒ²»μ½215 ?î208 ?¡214 Oμ£¡); x = NaN;
minf = NaN;
return;
end
x = (a+b)/2;
minf = subs(f, findsym(f),x);
format short;。
