找单位1列数量关系式
分数除法解决问题例

• 摩托车的速度比汽车的速度快 1 。 12
• 现在每台电视的价钱比原来降低了 2 。
• 一本书,看了总页数的 3 。
7
5
① 若全书共有X页,还剩多少页没有看?
② 若已经看了18页,全书共多少页?
二、看图列方程。 “1”
货物A: 货物B:
1
X吨
5
18吨
----------
三、解决问题。
1. 一本课外书,我读了35页,还剩 2 没有读, 这本书一共多少页? 7
2. 农药厂5月份生产农药165吨,比4月 份增产 2 ,4月份生产农药多少吨? 9
四、补充条件并解答
• 一 ,_________ , 5
这堆沙子一共多少吨?
Thank You ! 不尽之处,恳请指正!
• 找出单位“1”。
• 对应量÷对应分率=单位“1”的量
• 遇到不对应的分率,要想办法把不对 应的分率变为对应的分率。
分数应用题解决方法(方程法)
• 找出单位“1”,把未知的单位“1” 设为
• 单位“1”的量×对应分率=对应量
• 遇到不对应的分率,要想办法把不对 应的分率变为对应的分率。
• 一、列出数量关系。
分数除法解决问题例
解决分数除法应用题的一般步骤:
(1)审题; (2)找准单位“1”; (3)画线段图分析; (4)找出数量关系式; (5)列出算式。
看图列方程
4 9
“1”
女生480人 全校 X人
看图列方程
篮球: 足球:
“ 1”
----------
45个 ?个
1 4
_____
?个
分数应用题解决方法:(算术法)
找单位“1”写数量关系式

)
)
数量关系式是:
= 1 33、松树的棵树是杨树 2 。把 3数量关系式是: 4、文艺书的本书占图书总数的 1 6 单位“1”。 数量关系式是: = 。把 =
看作单位“1”。
看作
2 5、武汉长江大桥相当于黄浦江大桥的 。把 9 作单位“1”。 数量关系式是: =
看
先判断把哪个量看作单位“1”,再根据分 数乘法的意义列出关系式。
3 女生人数相当于全班人数的 。把( 5 看作单位“1”。 数量关系式是: =
)
先判断把哪个量看作单位“1”,再根据分数乘法 的意义列出关系式。
9 1、十月份的用电量是九月份的 10 。把( 看作单位“1”。 数量关系式是: = 1 2、第一季度的产量占全年产量的 。把( 3 看作单位“1”。
新人教版六年级上册数学第三单元分数除法应用题例5

解:设爸爸的体重为x kg。 8 8 x- x=35 小明的体重比爸爸轻 15 15 爸爸: 7 x=35 是爸爸体重的几分之几? ?千克 15 15 小明: x=35× 7 35千克 x=75 问题:①你们能借助线段图理解这个等量关系式和方程的意思吗?
“ 1”
②图中哪部分是小明体重比爸爸轻的部分? ③他是怎样求小明体重比爸爸轻的部分的?
答:合唱队女生有24人。
返回目录
(3) 白兔的只数比黑兔多 2 ,白兔有450
3
只,黑兔有多少只?这道题把( 黑兔的只数 ) 看作单位 “1”,如果黑兔的只数用χ表示,
2χ 白兔比黑兔多了( 3 2χ 以表示为( χ+ 3
)只,白兔的只数就可
)。
8 比爸爸的体重轻 ,小明爸爸的体重 15
是多少千克?
单位“1” ×分率=对应量
对应量÷分率=单位“1” 单位“1” ×(1-少着的分率)=对应量 对应量÷(1-少着的分率)= 单位 “ 1” 单位“1” ×(1+多着的分率)=对应量
对应量÷(1+多着的分率)= 单位 “1”
我会看图列式并解答:
解:设故事书有χ本。 3χ χ- =20 8 5χ =20 5χ 85 5 8 ÷ 8 =20÷ 8 χ=32
②小红买了一本书和一枝钢笔,书的价格 是10元,正好比钢笔价格少 3 ,钢笔的 8 价格是多少元?
2 ③白兔的只数比黑兔多 ,白兔有450 3 只,黑兔有多少只?
水的质
8.在通常情况下,体积相等的冰的质量比水的 1 质量少10 。现有一块重9千克的冰,如果有一桶 水的体积和这块冰的体积相等,这桶水有多重?
美术小组有 25 人,美术小组的人数比
1 航模小组多 。航模小组有多少人? 4
第一单元寻找单位“1”和列出等量关系式“提高型”专项练习(解析版)人教版

【分析】我们通常把“比”后的量看作单位“1”,求比一个数多几分之几的数是多少,用乘法计算。据此解答。
【详解】由分析可知:
“红花有90朵,黄花的朵数比红花的朵数多 ”是把红花的朵数看作单位“1”。
黄花的数量是:
90×(1+ )
=90×
=120(朵)
【点睛】本题考查分数乘法的计算,找准单位“1”是解题的关键。
【详解】童话书比故事书多 ,是把故事书的本数看作单位“1”,并把单位“1”平均分成7份。童话书比故事书多的本数相当于其中的1份。
【点睛】本题考查判断单位“1”的方法,关键是找清楚分率比赛的是“谁”的几分之几,“谁”就是单位“1”。
12.“小强的身高是 m,比妈妈的身高矮 ”。这句话中把( )看作单位“1”,数量关系式是( )。
240÷ =420(棵)
则梨树棵树的 与桃树同样多,是将梨树的棵数看作单位“1”,如果桃树有240棵,则梨树有420棵。
【点睛】本题考查已知一个数的几分之几是多少,求这个数,明确用除法是解题的关键。
16.学校图书室今年新进图书300本,今年比去年增长了 ,是把()看作单位“1”,今年是去年的 。
【答案】去年新进图书的数量;
【点睛】在确定单位“1”,一般是“谁、占谁”是单位“1”。
11.童话书比故事书多 ,是把( )看作了单位“1”,并把单位“1”平均分成( )份。童话书比故事书多的本数相当于其中的( )份。
【答案】 故事书的本数 7 1
【分析】根据题意,童话书比故事书多 ,童话书比故事书多的数量是故事书的 ,所以是把故事书看作单位“1”,结合题意分析解答即可。
【分析】根据判断单位“1”的方法:一般是把“比、占、是、相当于”后面的量看作单位“1”,即分数“的”字前面的量看作单位“1”,进行解答即可。
寻找单位“1”

闫雨晴最近学的用分数四则混合运算应用题,真有趣。
有趣的同时,也带来了一些难度,所以,我决定,就这个话题,仔细的研究一番,一方面巩固一下自己的知识,一方面把关于分数四则混合运算的应用题研究明白。
下面是我的研究过程。
单位一就是把一个量看做是一个整体,不管它的值是多少,都把它看成是十分之十,也就是单位一比如是修路,可以把修路看成是一个整体,如果甲修这条路需要X天完成,那么他每天就修X分之一,共修X天,X乘以X分之一,不就是一吗?那么他的效率就是X分之一同样的道理,乙的效率就是1/Y他们合起来每天就修(1/X+1/Y),再乘以他们合作的天数N就是所修的路的整体,就是单位一. 我列了这道题:阳光水果超市运来一批水果,第一天卖出9/20,第二天卖出120千克,这时卖出了全部水果的3/4,还剩几千克没卖出去?思路分析:这道题的类型和上一道题基本差不多,只是这道题是求单位一的几分之几是多少罢了。
用全部水果的3/4减9/20,得数,就是相对应的分率。
再用单位一乘没卖的分率,就可以了。
一百二十除以四分之三减二十分之九的差乘一减四分之三的差等于一百(千克)这道题主要是理解题意。
这就是我对单位一地理解!最近学的用有关分数单位一的应用题,真有趣。
有趣的同时,也带来了一些难度,所以,我决定,就这个话题,仔细的研究一番,一方面巩固一下自己的知识,一方面把关于分数四则混合运算的应用题研究明白。
下面是我的研究过程。
单位一就是把一个量看做是一个整体,不管它的值是多少, 都把它看成是十分之十,也就是单位一比如是修路,可以把修路看成是一个整体,如果甲修这条路需要X天完成,那么他每天就修X分之一,共修X天,X乘以X分之一,不就是一吗?那么他的效率就是X分之一同样的道理,乙的效率就是1/Y他们合起来每天就修(1/X+1/Y),再乘以他们合作的天数N就是所修的路的整体,就是单位一. 我列了这道题:阳光水果超市运来一批水果,第一天卖出9/20,第二天卖出120千克,这时卖出了全部水果的3/4,还剩几千克没卖出去?思路分析:这道题的类型和上一道题基本差不多,只是这道题是求单位一的几分之几是多少罢了。
在题目中标出单位“1”,画出线段图,写出数量关系,并列出算式

在题目中标出单位“1”,画出线段图,写出数量关系,并列出算式1、一堆煤,运走了1/2
2、一根绳子,第一次减去1/4
3、一批水泥,第一天运了2/5
4、空气中的氧气约占1/5
5、2/7的鸡是母鸡
在题目中标出单位“1”,画出线段图,写出数量关系,并列出算式1、一堆煤,运走了1/2
2、一根绳子,第一次减去1/4
3、一批水泥,第一天运了2/5
4、空气中的氧气约占1/5
5、2/7的鸡是母鸡
6、水果店运来一批水果。
桔子占1/4
7、国家拨款800万元,其中4/5用于退耕还林
8、小艾的身高是小云的8/9
9、爸爸工资的6/7等于妈妈的工资
10、红气球的个数相当于绿气球的4/5
11、红旗数量占总数的7/10
6、水果店运来一批水果。
桔子占1/4
7、国家拨款800万元,其中4/5用于退耕还林
8、小艾的身高是小云的8/9
9、爸爸工资的6/7等于妈妈的工资
10、红气球的个数相当于绿气球的4/5
11、红旗数量占总数的7/10。
六年级分数除法之量率对应(基础)
量率对应
分数应用题,首先要确定单位“1”。
单位“1”确定以后,一个具体数量总
与一个具体分数(分率)相对应,这种对应关系叫“量率对应”,画线段图比较容易理解量率对应。
数量关系式
已知量÷对应分率=单位“1”
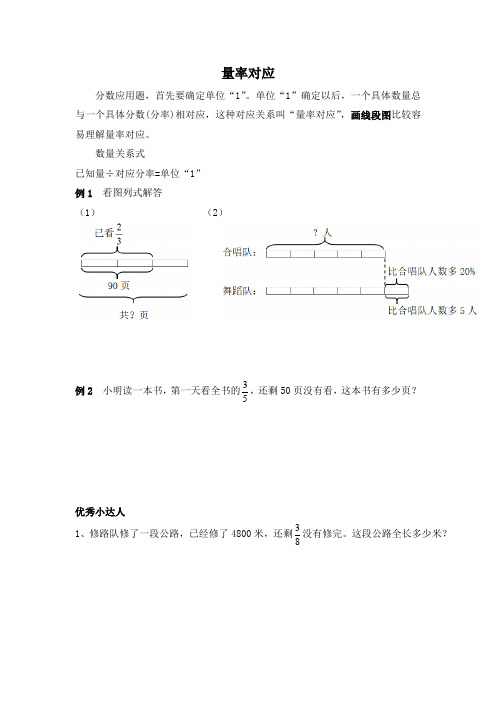
例1 看图列式解答
(1) (2)
例2 小明读一本书,第一天看全书的53,还剩50页没有看,这本书有多少页?
优秀小达人
1、修路队修了一段公路,已经修了4800米,还剩8
3没有修完。
这段公路全长多少米?
例3 一批原料,第一天用去它的
41,第二天又用去它的5
1,两天共用去原料27吨。
这批原料一共有多少吨?
优秀小达人 1、一堆水泥,第一天运走总数的51,第二天运走总数的3
1,还剩70吨。
这堆水泥原有多少吨?
例4 琳琳有一些零花钱,买学习用品用去了5
2,她又买了一本《科幻世界》用去了18元,这时正好用去了她所有零花钱的一半,琳琳原来有零花钱多少元?
优秀小达人
1、黄霏霏看一本漫画书,第一天看了60页,第二天看了这本书的25%,两天正好看了这本书的
2011,这本书一共有多少页?。
六年级数学-求单位1练习题

求单位“1”练习题一、想一想,再用你喜欢的符号标出表示单位“1”的量。
1. 生物组的人数是美术组的31。
2. 母鸡的43是小鸡的只数。
3. 汽车的辆数相当于自行车辆数的32。
4. 甲数的83相当于乙数。
二、照样子,写一写。
例:苹果的个数是桃子个数的61。
数量关系式:桃子个数×61=苹果的个数 1. 妈妈的年龄是爸爸年龄的43。
数量关系式:2. 女生占全班人数的53。
数量关系式:3. 篮球个数的73相当于足球的个数。
数量关系式:4. 文艺书本数的65和科技书同样多。
数量关系式: 三、看图列算式(或方程)并解答。
列式:列式:120千米23?千米36枝钢笔:是钢笔的73?枝四、列式计算。
1. 一个数的43是2112,这个数是多少?2. 一个数的54是20,这个数的258是多少?五、找朋友(问题、算式一线牵)。
妈妈今年40岁,妈妈的年龄是爸爸年龄的98,明明的年龄是妈妈年龄的51。
40×51 爸爸今年多少岁? 40÷98妈妈和明明一共多少岁?40+40×51 妈妈和爸爸一共多少岁?40+40÷98 明明今年多少岁? 六、走进生活,解决问题。
1. 小岩买了一瓶橙汁,喝了53,正好是300毫升,这瓶橙汁总量是多少毫升?2. 实验小学参加艺术班的学生有1080人,占全校学生总数的52,全校共有学生多少人?3. 同学们做了16朵红花,做的黄花的朵数是红花的45,又是蓝花的1110。
做的蓝花有多少朵?七、智力大比拼!你能根据所给的算式编出数学应用题吗?赶快试一试吧! 90÷43 120×52。
小学六年级数学应用题一题多解

仙桃市干河小学
一、复习导入
找出下列各题中的单位“1”并列出数量 关系式
(4)女生人数 男生人数
二、解题方法探究 例一
方法一
方法二
方法三
答:运来的大米有300千克
对应的数量 除以对应的 分率等于单 位“1”的量
例二
方法一
方法二
答:运来的大米有450千克
例三方法一Fra bibliotek法二运来的大米 运来的面粉
“1” ?
160千克
对应的数量除以对应的分率等于单位“1”的量
对应总数量 对应分率和
小结
1)找准单位“1” 2)分析题意,确定解题的方法
单位“1”的量已知,用乘法 单位“1”的量未知,用除法或 列方程解答 3)用除法解答时,要根据对应的数量 除以对应的分率等于单位“1”的量 用方程解答时,要能准确写出数量关 系式,根据数量关系式列出方程并解答
三、巩固与提高 答:小齿轮每分钟转490周
答:课桌和椅子的单价各是75元,45元。
涉及“1”的计算分类

六年级数学(上册)第二单元涉及单位“1”的计算(分类及方法)第一类:题目中只有一个量,这个量是整体量,要根据题目中的数量关系来列式计算。
列式的时候可借用线段图来直观地理清数量关系,从而想出相应的数量关系式,进一步在数量关系式中标出已知量和未知量,最终列式解答。
要千万注意搞清楚题目中已知数量的对应分率(即讲求“对应”)。
这类题目的列式方法还可以简单地记忆如下:①已知单位“1”,用“”法;②要求单位“1”,用“”法▲运用这个记忆方法的前提是对数量关系式足够熟练,简记方法是“果”,数量关系式才是“因”,切忌本末倒置。
初学者应多思考数量关系式,根据数量关系式来列式,从而加深理解,以便逐步过渡到不列数量关系式也能熟练理清数量关系,直接写算式计算。
【例题演练】1、一条绳子,剪去了它的,还剩下40厘米,这条绳子原来的长度是多少厘米?2、一辆汽车从甲地开往乙地,已经行驶了全程的,恰好行驶了156千米,甲乙两地的相距多少千米?3、书店里原有一批故事书,第一周卖出了故事书量的,第二周卖出了故事书总量的,这时还剩下140本故事书,这个书店里原有故事书多少本?第二类:题目中有主要有两个量(其中一个量是已知量,而另一个量是未知量),他们之间存在着某种分数关系(即题目会有“一个量是另一个量的几分之几”这样的条件)。
在解决这类问题时,关键是要搞清楚以下两个问题:①哪一个量是单位“1”?②这个单位“1”是已知量还是要求的未知量?已知单位“1”,用“”法;要求单位“1”,用“”法【注意】(1)这是简单判断的方法,做题时可以直接运用。
但是同学们在做完每一题后都应该多进行复习,并且在复习的时候做到结合数量关系式来理解这个过程,才能有更深层次的理解和掌握,做到将知识升华。
(2)当题目中出现三个量时,中间有一个是过渡量,联系着已知量和待求量,可先将三个量分开前后两对来独立思考数量关系,再列式计算,方法同上。
(3)做题时要细心地查看题目最终所求的问题是什么,计算出其中的一个量有可能只是中间的某一个过程,要避免大意失分。
百分数的应用练习

百分数的应用练习一、细心填写:1、先找单位“1”,再列出数量关系式。
(1)男生人数占全班人数的几分之几?把()看作单位“1”()÷()=()(2)小明做题的正确率是几分之几?把()看作单位“1”()÷()=()2、32人是50人的()%;45分占1小时的()%;甲数是乙数的4,甲数是乙数的()%;乙数是甲数的()%。
53、种子发芽率是求()是()的百分之几。
零件合格率是求()是()的百分之几。
小麦出粉率是求()是()的百分之几。
胡麻出油率是求()是()的百分之几。
二、准确计算:55254372-50%60%某1-÷5+-6767793811125%某-某=28(1+40%)某=981-20%某=1+20%某=44三、解决问题:1、把8克糖放入92克水中,糖水的浓度是百分之几?2、601班共50人,体育锻炼达标的有48人。
求达标率;未达标的人数占全班的百分之几?3、学校植树绿化,种了120棵树,成活了102棵。
求成活率。
4、602班昨天1人有事请假、2人生病没有到校上课,到校上课的有57人。
求昨天的出席率。
一、把下面的分数化成百分数:113123======244555541371======5888810二、谨慎选择:1、口算测验时,小明做对100题,错了4题,小明计算的正确率是()A96%B100%C96.2%2、401班有50人,昨天有4人缺席,昨天出席率是()A92.6%B92%C8%三、细心填写:1、求“去年产值是今年的百分之几”应该用()÷(),再把求出的结果化成百分数。
2、花生出油率是求()是()的百分之几。
子弹命中率是求()是()的百分之几。
考试及格率是求()是()的百分之几。
3、某学校今天六年级400人全部到校,今天六年级的出席率是()%。
四、解决问题:1、电视机厂去年计划生产彩电20万台,4、李兵参加数学竞赛,做对了18题错结果生产25万台。
巧用单位“1”解决分数、百分数问题

巧用单位“1”解决分数、百分数问题分数、百分数的解题方法,大致是相同的。
步骤如下:一、寻找单位“1”1、表示数量关系的分数或百分数前面的量,就是单位“1”。
例如:“儿子的年龄比爸爸年龄的多4岁”,单位“1”是前的量“爸爸的年龄”;“男生60人,女生80人,男生人数比女生多百分之几?”单位“1”是“百分之几前的量:女生人数。
2、如果叙述比较简洁,需根据题意将句子补充完整。
例如:解决“8月份用水100吨,10月份节约15%,10月份用水多少吨?”时,把“10月份节约15%”补充成“10月份比8月份节约15%”。
单位“1”就是15%前的量:8月份的用水量。
解决“一种手机原价1200元,现在降低了,现价多少钱?”时,需将“现在降低了”补充成“现价比原价降低了” ,单位“1”就是前面的量:原价。
二、选择合适的方法。
(一)不求单位“1”1、分数,百分数前有多,增加等字样,用乘加。
例如:五年级师生向希望小学捐书150本,六年级比五年级多捐20% 。
六年级师生捐书多少本?分析:单位“1”是五年级师生捐书数。
不求单位“1”,前有“多”,用乘加。
列式150×(1+20% )2、分数,百分数前有少,降低,短等字样,用乘减。
例如:五年级师生向希望小学捐书150本,六年级比五年级少捐20%。
六年级师生捐书多少本?分析:单位“1”是五年级师生捐书数。
不求单位“1”,20%前有“少”,用乘减。
列式150×(1-20% )3、分数,百分数前无多无少。
直接用乘法。
例如:五年级师生向希望小学捐书150本,六年级捐书数是五年级的80%。
六年级师生捐书多少本?分析:单位“1”是五年级师生捐书数。
不求单位“1”,80%前无多无少字样,直接用乘法。
列式150×80%(二)求单位“1”1、分数,百分数前有多,增加等字样,用除加。
例如:图书馆有科技书400本,比故事书多20% ,故事书有多少本?分析:单位“1”是故事书册数,求单位“1”。
单位1的确定及转化教学案+练习

六数〔上〕单位“1〞确实定及转化——教学案+练习教学目标:(一)理解单位“1〞的含义和在实际问题中的表现形式,能判断问题中的单位“1〞的对应数量是的还是未知的,能将各数量准确地与分率相对应;(二)熟练应用数量关系式:单位“1〞的数量×分率〔或倍数〕=分率〔或倍数〕的对应数量,其中两者,求其三;教学重点:(一)确定单位“1〞,理清数量关系〔通过画线段图或列文字等式,熟练后可在大脑中构建数量关系等式〕;(二)正确判断复杂分数应用题的题型特征并应用正确的方法解决问题。
教学难点:1、熟悉分数应用题中特有的数学语言;2、在理解的根底上熟练运用根本运算原那么;3、培养正确的思维习惯〔注意审题,具体问题,具体分析,切实理清题意中的数量关系〕,熟练运用分析及解题的常用工具〔能清晰地用线段图表示题意中地数量关系并用算术式或列方程解题〕;知识点:确定单位“1〞、数量关系核心公式:〔1〕单位1时,对应量= 标准量×对应分率〔注意;此公式是用来求对应量,前提条件单位1必须是的〕〔2〕单位1未知时,标准量=对应量÷对应分率( 注意;此公式是用来求标准量,前提条件单位1必须是的)以上两个公式的共同点是找分率〔3〕题目里如果有几个单位1时,要统一单位1,题目里真正的单位1就是题目里的不变量,找准这个不变量,把其他几个假单1后面的分率转化成真分率,再用相关公式解决就可以了。
【典型例题讲练】题型一,找单位1,1,仓库里有化肥30吨,第一次取出总数的15 ,第二次取出余下的13,第二次取出多少吨?(单位1是 )2、晶晶三天看完一本书,第一天看了全书的14 ,第二天看了余下的25,第二天比第一天多看了15页,这本书共有多少页?(单位1是 )题型二;找分率1,乙数是甲数的23 ,丙数是乙数的45,丙数是甲数的几分之几?2、乙数是甲数的34 ,丙数是乙数的35,丙数是甲数的几分之几?3、一根管子,第一次截去全长的14 ,第二次截去余下的12,两次共截去全长的几分之几?4、一个旅客从甲城坐火车到乙城,火车行了全程的一半时旅客睡着了。
分数乘法应用1

分数乘法应用题知识要点:分数乘法应用题的基本题就是求一个数的几分之几是多少。
关键是通过分析题意,找到是求谁的几分之几,然后根据乘法的意义列出算式。
数量关系式是:单位1的量×对应分率=分率对应的量1、育才小学有男生120人。
男生是女生的35,女生有多少人?(2)女生是男生的35,女生有多少人?(3)女生比男生多35,女生有多少人?(4)男生比女生少35,女生有多少人?(5)男生占全校的35,女生有多少人?(6)女生占总数的35,全校有多少人?2、先用直线划出单位“1”的量,再把数量关系式补充完整。
(1)皮球的个数比足球多52。
()的个数×52=()的个数(2)实际用水量比原计划节约91。
()用水量×91=()用水量(3)一桶油用去53,正好用去12千克。
这桶油重多少千克?()的千克数×53=()的千克数(4)学校饲养组养黑兔12只,是白兔只数的32。
饲养组养白兔多少只?( )的只数×32=( )的只数 3、一段长3米的布,第一次剪去它的31,第二次又剪去31米,两次一共剪去多少米?还剩多少米?4、周大婶收了532吨南瓜,收的冬瓜比南瓜多815。
收的冬瓜比南瓜多多少吨?5、(1)一本书450页,第一天看了全书的15,第二天看了65页,第三天应该从第几页看起?(2)一根铁丝长12米,第一次用去了全长的14,第二次用去了全长的13,两次一共用去了多少米?(3)一根铁丝长12米,第一次用去了全长的14,第二次用去了13米,两次一共用去了多少米?6(1)学校一月份用电800度,二月份比一月份节约了15,二月少用电多少度?(2)学校一月份用电800度,二月份比一月份节约了15度,二月份用电多少度?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
找单位“1”列数量关系式专项练习
一、
(1)“已经修了全长的43
”,
把( )看作单位“1”,( )×43
=( )
(2)“一袋大米,吃去52
”,
把( )看作单位“1”,( )×52
=( )
(3)甲数31
的与乙数相等,
把( )看作单位“1”,( )×31
=( )
(4)一件上衣的价钱比一条裤子便宜72
,
把( )看作单位“1”,( )×72
=( )
(5)“实际用水量比计划节约91
”,
把( )看作单位“1”,( )×91
=( )
(6)水结成冰后,体积增加101
,
把( )看作单位“1”,( )×101
=( )
(7)冰化成水后,体积减少111
,
把( )看作单位“1”,( )×111
=( )
二、
(1)“一根绳子,截去32
”,这里把( )看作单位“1”,求截去多少,就是求(
)的32是多少?
(2)“长的54
等于宽”,这里把( )看作单位“1”,求宽多少,就是求( )的54是多少?
三、应用题。
1、修路队计划每天修路65千米,上午修了32
,上午修了多少千米?
2、修路队计划每天修路65千米,上午修了32
,还剩几分之几没有修?
3、修路队计划每天修路
65千米,实际每天多修32,实际每天多修多少千米?
4、一堆煤有30吨,用去了
52,用去了多少吨?(写出数量关系式,画出线段图)
5、滨海小学去年有24个班,今年的班级数比去年增加83,今年增加了多少个班?(写出数量关系式,画出线段图)
6、一种毛衣原价56元,现价比原价降低了
72,降价多少元?(写出数量关系式,画出线段图)
7、(1)学校买了48个排球,买的足球比排球多41,买的足球比排球多多少个?(写出数量关系式,画出线段图)
(2)学校买了48个排球,买的足球是排球的
45,买了多少个足球?(写出数量关系式,画出线段图)
8、某工厂一月份用电4800度,二月份比一月份节约用电101,二月份比一月份节约用电多少度?二月份实际用电多少度?。
