导电媒质中平面电磁波
导电媒质中的平面电磁波

vp
2
2
可见,良导体中相速为频率的函数,是色散波,且电导率越大,相 速越慢。
3. 趋肤效应
高频电磁波从表面进入导电媒质越深,场的幅度就越小,能量就越小, 即能量趋于表面,这就是趋肤效应,或集肤效应或趋表效应。
趋肤深度(或集肤深度、穿透深度):当场从表面进入导电媒质中一 段距离后,使得其幅度衰减到表面幅度的1/e倍时,这段距离(或深度) 叫做趋肤深度δ。即
常数。
3. 波阻抗
导电媒质中的波阻抗为
g
c
Ex
g
Hy
j
c
1 j
c e j
可见 c为复数,其模值和相位分别为
c
[1
(
)
2
]
1 4
0
1 arctg 2
0,
4
由上式可知,c 有非零相角,意味着电场与磁场具有不同的相位,相
位差为θ,故(可4)改写为
g
g
H
uuv E
ey
m
vp
1
2
1
2
1
1
2π
2
2π
1
2
1
2π 2π
k
由上可知:
(1)导电媒质中相速要比理想介质中慢,波长要比理想介质中短;
(2)σ愈大,相速vp越慢,波长λ越短; (3)相速与频率有关,故电磁波中不同的频率分量将以不同的相速传播,
经过一定距离后,它们的相位发生不同变化,从而导致信号失真,比,除有微弱损耗引起的振幅
衰减外,其余参量近似相同。
2. 良导体中的均匀平面波
对于良导体:
tg c
?
1
物理意义表示电介质中的传导电流远大于位移电流,相关参数有:
平面电磁波

例如铜:
f 1MHz, c 66106 m
f 30GHz, c 0.38106 m
4.4 电磁波的极化
本节要点
极化 线极化 圆极化 椭圆极化
1. 极化(polarization)
金属导体 金属导体
导体上的感应电 动势等于零
导体上的感应电 动势最大
无耗媒质中电场、磁场与功率流
4.2 无限大导电媒质中的平面电磁波
本节要点
复介电常数 导电媒质中的平面波 色散及其对通信的影响
1.复介电常数(complex permittivity)
无限大导电媒质中复介电常数
~ 1 j
实部代表位移电流的贡 献,不会引起能量消耗。
+z轴方向传播的均匀平面波 -z轴方向传播的均匀平面波
4. 均匀平面波的基本概念
如果电介质区无限延伸,则电场矢量可一般地表示为 E ax E0e jkz 时域表达式为 Ex z, t E0 cost kz 0
下面,我们对平面波进行较为详细的分析。
代表场的波动状态,称为电磁波的相位。它由三部分构成:
~ 将无耗媒质的相位常数及波阻抗中的 均以 来取代,即 得导电媒质中的复相位常数为
~ ~ k j
~ 1 j
2 1 1 1 2 1 2
~ 1 j
2
2.导体中均匀平面电磁波
导体中均匀平面波的电磁场及平均坡印廷矢量为
Ex E0ez e jz
Hy
E0e z e jz e j / 4
9. 平面波解析

的存在与否,将波分为三种类型 和H 根据 E
z
z
1.TEM 波
( Ez 0, H z 0,
Kc 0)
说明任一时刻,在xoy平面上场的分布与稳态场相同
0, H 0 ),亦称横电波 2.TE 波( E
z z
3.TM 波(
z 0, H z 0 E
),亦称横磁波
(9 - 2 - 1)
图 9-1 均匀平面电磁波的传播
综上可见,可取:
E e x Ex ( z, t )
E x ( z, t ) 1 E x ( z, t ) 2 0 2 2 z t
2 2
(9-2-2)
此方程的通解为
Ex ( z, t ) f1 ( z t ) f 2 ( z t )
E E E 2 t t
2 2
(9-1-2)
类似的推导可得
H H H 2 t t
2 2
(9-1-3)
相量形式的波动方程:
E +k E 0
2 2 2
H +k H 0
2
(9-1-4)
其中:
k c
2
c j 1 j
Z(z)=A+ ez + A-ez
2 T E0 ( x, y )+K c 2 E0 ( x, y ) 0 2 T H0 ( x, y )+K c 2 H0 ( x, y ) 0
(9-1-5)
K c c +
2 2
2
(9-1-5)分成纵向成分和横向成分:
2 T E0T ( x, y )+Kc 2 E0T ( x, y ) 0 2 T H0T ( x, y )+Kc 2 H0T ( x, y ) 0 2 T E0z ( x, y )+Kc 2 E0z ( x, y ) 0 2 T H0z ( x, y )+Kc 2 H0z ( x, y ) 0
导电媒质均匀平面波
7.2 导电介质中的均匀平面波——2、导电媒质中均匀平面波的传播特性3)媒质导电性对场的影响媒质的导电性由比值 γ < 10 2 wε 1/ 2 γ γ Q K = w με c = w με 1 j ≈ w με 1 j wε 2 wε γ 决定,不仅与媒质特性有关,还与频率有关 wε(1)良介质μ μ γ = ηc = 1 j εc ε wε 1 / 2≈μ γ 1+ j ε 2 wε γ μ 1 , β ≈ w με , V p ≈ α ≈ 2 ε με 1 μ γ μ λ ≈ f με , η c = ε 1 + j 2 wε ≈ ε 平面波在良介质中的传播特性与理想介质中的平面波十分相似 只有微弱损耗引起的衰减,E和H时间相位差极小近似为07.2 导电介质中的均匀平面波——2、导电媒质中均匀平面波的传播特性(1)良导体γ Q K = w με c = w με 1 j wε γ > 100 wε1/ 2γ ≈ w με j 2 wε 1/ 2= wμγ e jπ / 4 = (1 j ) j2 γ = w με e 2 wε wμγπ1/ 22μ μ γ = ηc = 1 j εc ε wε 1 / 2μ γ ≈ j ε wε 1 / 2≈wμγejπ4= (1 + j )wμ 2γ7.2 导电介质中的均匀平面波——2、导电媒质中均匀平面波的传播特性 πf wμγ w 2w Vp = ≈ α≈β ≈ = πfμγ , =2 μγ β μγ 2 wμ j π wμ 2 π λ = 2π ≈ 2π 4 e = (1 + j ) , ηC = =2 wμγ fμγ β γ 2γ 良导体中,均匀平面波为色散波γ越大,电磁波的传播速度越慢,波长越短f=465MHz的电磁波在铜(γ=6.8×107s/m)中传播,其相速为 283.15m/s,波长为0.018mm电场相位超前磁场相位π/4, |ηc|<<1 wm>>we, 平均功率流密度沿波的传播方向按指数规律e-2αz衰减,而场的振幅 按e-αz衰减, γ越大衰减越快(趋肤效应)v 1 v v * v 1 2 γ 2αz Sc = E × H = ez E0 e (1 + j ) 2 2 2 μwv 1 2 γ 2αz S av = e z E 0 e 2 2 μw7.2 导电介质中的均匀平面波——2、导电媒质中均匀平面波的传播特性例7-2-1 有一均匀平面波,在海水中(εr=80,μr=1,γ=4s/m),v v 7 沿+z方向传播,在z=0处,E = e x 100 cos 10 π t(2)确定E的振幅衰减为z=0处的1%时的z值;() (V / m )(1)求其衰减常数α,相位常数β,相速Vp,波长λ及波阻抗ηc; (3)写出E(z,t)和H(z,t)在z=0.8m处的函数表示式分 析:v v Q E (z = 0 , t ) = e x 100 cos 10 7 π t() w = 10 7 πγ γ 4 = = = 180 > 100,为良导体 1 w ε w ε 0ε r 107 π × 10 9 × 80 36πwμγ 107 π × 4π × 10 7 × 4 (1)α ≈ β ≈ = = 8.89 ( Np / m ) 2 2 2π 2π w 107 π = = 0.707(m ) λ= Vp = = = 3.53 × 10 6 (m / s ) β 8.89 β 8.89ηC =wμγejπ4π j 107 π × 4π × 10-7 j π = e 4 = πe 4 (Ω ) 47.2 导电介质中的均匀平面波——2、导电媒质中均匀平面波的传播特性(2)波的振幅按 e αz 规律衰减,设 z = z1处,波的振幅衰减为 z = 0处的1%e( 3)α v v Q E (z = 0 , t ) = e x 100 cos 10 7 π t v v E (z , t ) = e x 100 e α z cos 10 7 π t - β z v v 100 α z H (z , t ) = e y e cos 10 7 π t - β z - θ , η c = η c e jθ αz1= 0.01 z1 = ln 0.01=ηc( ( (4.605 = 0.518(m ) 8.89)))v v (z = 0 .8 , t ) = e x 100 e 8 .89 × 0 .8 cos 10 7 π t - 8 .89 × 0 .8 ∴E v 082 = e x 0。
导电媒质中的波阻抗

2 2
H H
x y
(r (r
) )
k k
2H 2H
x y
(r) (r)
0 0
2H z (r) k 2H z (r) 0
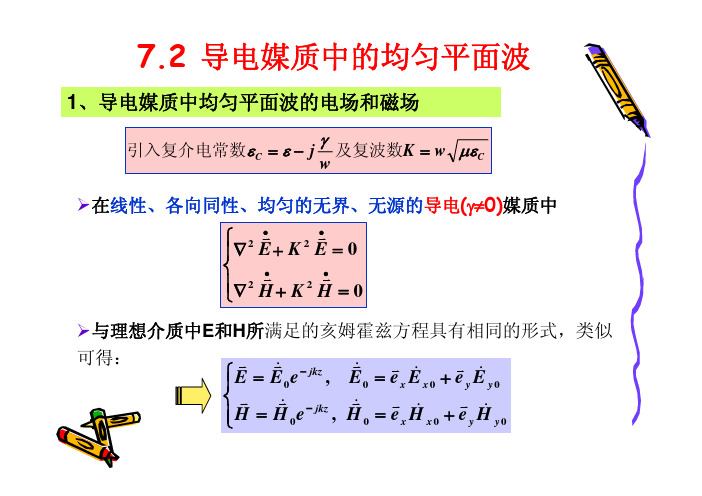
这些方程称为齐次标量亥姆霍兹方程。
由于各个分量方程结构相同,它们的解具有同一形式。
在直角坐标系中,若时变电磁场的场量仅与一个坐标变量有关, 则该时变电磁场的场量不可能具有该坐标分量。
3 z 2
可见,电磁波向正 z 方向传播。
上式中 t 称为时间相位。kz 称
为空间相位。空间相位相等的点组成 的曲面称为波面。
由上式可见, z = 常数的平面为 波面。因此,这种电磁波称为平面波。
因 Ex(z) 与 x, y 无关,在 z = 常 数的波面上,各点场强振幅相等。因 此,这种平面波又称为均匀平面波。
ez
E x z
得
H
e
y
j
E x z
eyHy
Hy
j
E x z
已知电场强度分量 Ex 满足齐次标量亥姆霍兹方程,考虑到
E x x
E x y
0
得
d2Ex dz 2
k 2Ex
0
这是一个二阶常微分方程,其通解为
Ex Ex0e jkz Ex0e jkz
上式第一项代表向正 z 轴方向传播的波,第二项反之。
首先仅考虑向正 z 轴方向传播的波,即 Ex (z) Ex0e jkz
式中Ex0 为 z = 0 处电场强度的有效值。
Ex(z) 对应的瞬时值为
Ez(z, t)
O
2
t1 = 0
t2
T 4
t3
T 2
Ex (z,t) 2Ex0 sin( t kz)
电磁场与电磁波——第六章 6-3 导电煤质

al 1n E1 E2
(Np)
工程上又常用dB来计算衰减量, 其定义为
al 10 lg P1 20lg E1 (dB)
P2
E2
当|E1|/|E2|=e=2.718, 衰减量为1Np, 或20lg 2.718 3=8.686dB, 故
β称为相位常数, α称为衰减常数。 两边平方后有
2 2 j
j
2 a2 2 上式两边的实部和虚部应分别相等, 即 2a
由上二方程解得
1/ 2
2
1
2
1
1/ 2
2
1
2
1
6.3.3 平面波在导电媒质中的传播特性
采用等效复介电常数 e 后, 平面波在导电媒质中的场表达式
和传播参数可仿照理想介质情况来得出。 在无源区, 设其时谐电
磁场的电场复矢量为 E exEx , Ex的波动方程为:
2 Ex
2
kc Ex
0
kc
e
( j )
对于沿+z方向传播的波, 解的形式 E ex E0e jkcz
传播常数 jKc j
电场复数表达式
E exE0e z exE0eze jz
同相。此时磁场强度复矢量为
磁场强度复矢量为
H
ey
E0
e
e jkcz
ey
E0
e
eaze j ze j
其瞬时值为
H (t) ey
E0
e
eaz
cos(t z )
磁场滞后电场, 二者不再同相。
导电媒质中的平面波
磁场强度的方向与电场强度相垂直, 并都垂直于传播方向Zˆ , 因此导电媒质中的平面波是横电磁波。这个性质与理想介质中 的平面电磁波是相同的。
平面电磁波在两种不同媒质中传播特性的比较

电磁波 的应用范 围很广 , 实中几乎无处 不 现
在 。 代 电子技术 如通讯 、 现 广播 、 电视 、 导航 、 达 、 雷 测
( 正或负向) 传播的波。 由平面电磁波的特点可知 , 对于沿 z 轴正向传播的均匀平面电磁波的电磁场场
量 和驯 随时间t 变化外 , 只与波传播方向的坐标 z 有关 , 而与 , 无关, Y 写成数学表达式为
E = (,) H =日(,) tz , tz (. ) 14
控、 电子仪器和测量系统 , 都离不开电磁波的传播 。 电磁波在不同媒质 中传播特性不 同, 在实际生活 中 的应用更是非常广泛 。 下面即在线性、 各向同性、 均
匀的介质 中只有传导电流和位移 电流的情况下, 由
电场强度 和磁 场强度 H 满足 的波 动方 程 出发 , 研
, e
]= c ( t oc一 so
经计算可得出上方程的一般解是
(z [ £ )= ,
+ 2 )
e
]:  ̄ c ( t I. , 一 ;o c o
(. ) 16
由此可得 , 振相沿 正 z 向传播 的速度即波的传播 方 相速度是
=
其中 =七
, 和g f 是任意函数, 其具体形式由初
第2 期
Ma . o 7 r2 o V0. 7 No 2 11 .
平面 电磁波在两种不 同媒质 中传播特性 的 比较
杨延玲L , 刘辉兰 于家峰 ,
(. 1 山东师范大学 物理与微 电子学院, 山东 济南 2 10 ;. 500 2 德州学院 物理 系, 山东 德 州 2 32 ) 50 3
d
可
11 . 无损媒质的特点 无损媒质又称无耗媒质 , 其
5 电磁波在导电媒质中的传播解读

令
i
,称之为复介电常数,则上式写成:
k 2 2
由于k’是复数,则可以分解成实数部分和虚数部分,即: k
a ib
其中a, b为实数,代入上式,可以得到:
i t ax ibx E ( x , t ) E0 e bx i t ax E ( x , t ) E0 e e
则得到:
E B t
2
将麦克斯韦方程组的第一式代入上式中,得: 2 E E 2 E 2 t t 2 E E 2 E 2 0 t t 用同样的方法可得到: 因为:
2
2 令 k 2 i
2
k n
,称为复波数,则上面两式可以写成:
2 2 E ( r ) k E ( r ) 0 2 2 B(r ) k B(r ) 0
非导电媒质 (7.7-2)
此为导电媒质中电磁场满足的赫姆霍兹方程。
(7.7-1)
上式也称为波动方程,只是多了一个与时间一次导数有关的项,这一 项与导电媒质的电导率有关,即为一消耗项,表示电磁波在导电媒质中传 播时是衰减的。
2、单色电磁波的波动方程
i t E ( r , t ) E ( r )e it 设: B ( r , t ) B ( r )e
2 B B 2 B 2 0 t t
1
E 1 2 E 2 t B 1 2 B 2 t E 0 2 t 2B 0 t 2
2
所以上式可以写成:
7.7 电磁波在导电媒质中的传播
第5章--时变电磁场和平面电磁波--导电媒质中的平面波

1)(电)介质: 1
2)不良导体: 1
3)良导体: 1
图5.5-1 几种媒质的 与频率的关系(对数坐标)
第五章 时变电磁场和平面电磁波
二、平面波在导电媒质中的传播特性
§5.5 导电媒质中的平面波
a) 导电媒质中波动方程的解
在无源区,设时谐电场复矢量为 E xˆEx
※相速还与频率有关,携带信号的电磁波,其不同的频率分量将以不同的相速传播,
经过一段距离后,信号的相位将发生变化,从而导致信号失真。这种现象称为色散。
※因此导电媒质是色散媒质。
第五章 时变电磁场和平面电磁波
§5.5 导电媒质中的平面波
导电媒质中平面波的波长为
2π
k
2π
2
第五章 时变电磁场和平面电磁波
§5.5 导电媒质中的平面波
表5.5-3 ;理想介质和导电媒质传播特性的比较 ( p.154)
• 演示:理想介质和导电媒质传播特性
第五章 时变电磁场和平面电磁波
§5.5 导电媒质中的平面波
三、弱导电媒质(低损耗介质)中的均匀平面波
弱导电媒质: 1
kc
讨论内容
一.导电媒质的分类 二.导电媒质中的均匀平面波 三.弱导电媒质中的均匀平面波 四.良导体中的均匀平面波
第五章 时变电磁场和平面电磁波
一、导电媒质的分类
§5.5 导电媒质中的平面波
等效复介电常数
在无源区
在理想介质中: 0 在有耗媒质中: 0
H j E H Jc j E E j E
1 j
1
2
平面电磁波

入射波
i
r
反射波
x
法 t 折射波 线
1 1 2 2
z y
斯耐尔定律:
①入射线,反射线及折射线位于同一平面;
② 入射角 i 等于反射角 r ; ③ 折射角 t 与入射角 i 的关系为
sin i k2 sin t k1
k1 1 1
Ex Ex 0e jkz H y H y 0e jkz
写成瞬时形式为:
Ez ( z , t ) Ez 0 cos(t kz ) H y ( z , t ) H y 0 cos(t kz )
传播方向
理想介质中均匀平面波的电场和磁场
当 c 2 c1时,R<0,在分界面上电场为最小值,
磁场为最大值
三, ①导电媒质 (1,1,1 0) 对②导电煤
质 ( 2,2, 2 0) 的垂直入射
一区合成波:
E1 ex E (e
i x0
1z
Re )
1z
衰减
入射波,反射波在传播过程中都在衰减 折射波在传播过程中也一样在衰减
则合成场强的大小为
E E E Em
2 x 2 y
合成场强的方向与x轴的夹角有如下关系:
tg Ey Ex sin(t kz y ) cos(t kz y ) tg (t kz y )
右旋圆极化: 时间t越大,合成场强与x 轴的夹角越大,合成波矢 量随着时间的旋转方向与
i x0
i x0
电磁波垂直入射到理想导体表面,电磁波产生 全反射,第一煤质中的电磁波为驻波,具有驻 波的性质!!
二,①为理想介质(1,1 ) ②为理想介质( 2,2)
电磁场(山东大学)智慧树知到答案2024年山东大学

电磁场(山东大学)山东大学智慧树知到答案2024年第一章测试1.已知如图所示半径为R的半圆柱面均匀分布面电荷密度为s,假设该半圆柱面轴向长度为无限长,放置在真空中,则半圆柱轴线上的电场强度E大小为()。
A: B: C: D:答案:C2.两同心金属球内外半径分别为a和b,中间为理想电介质e=3e0,内、外球面之间的电压为U,则介质中的外球表面(半径为b)电位移矢量D大小为( )。
A: B: C: D:答案:A3.电场强度E通过一个闭合曲面的通量等于零,意味着( )。
A:该闭合曲面内正电荷等于负电荷 B:该闭合曲面内正电荷多于负电荷 C:该闭合曲面内极化电荷等于零 D:该闭合曲面内负电荷多于正电荷答案:A4.A:不确定 B:能 C:不能 D:其余选项都有可能对答案:C5.半径为a的长直圆柱导线通恒定电流I。
外面包一层半径为b的绝缘材料,磁导率为m ¹ m0,绝缘层内表面(半径为a)中的极化强度M大小为()。
A: B: C: D:答案:B6.下面关于磁感应强度方向的说法哪些是正确的( )。
A:与产生磁场的电流方向以及电流流经导线的受力方向共同构成的平面垂直B:与产生磁场的电流成右手螺旋关系 C:平行于产生磁场的电流 D:与产生磁场的电流成左手螺旋关系答案:AB7.极化电荷的存在使得介质内部的电场强度增大。
A:对 B:错答案:B8.长直载流导线附近有一单匝矩形线框与其共面,如图所示。
设电流i(t)= I0,线框以速度v0向右平行移动,此时回路中的感应电动势大小为()。
A:B:C:D:答案:B9.关于D的下列公式中,对于任何介质都成立是()。
A: B: C: D:答案:D10.时变电磁场基本方程组中J.C.Maxwell贡献最大的是()。
A: B:C: D:答案:B第二章测试1.已知半径为R的无限长圆柱体内均匀分布体电荷ρ,介电常数为ε,圆柱内外的电场强度与距离圆柱轴心的径向距离有何关系?()A:柱内外电场强度均随距离增大而减小 B:柱内电场强度随距离增大而增大,柱外电场强度随距离增大而减小 C:柱内电场强度随距离增大而减小,柱外电场强度随距离增大而增大 D:柱内外电场强度均随距离增大而增大答案:B2.任意对称形状的单个导体都可以通过默认另外一个电极在无穷远处,利用电容的定义式进行单个导体电容值的计算。
平面电磁波

第六章主平面电磁波要 内 容 9学时平面电磁波电磁波:变化的电磁场脱离场源后在空间的传播 平面电磁波:等相位面为平面构成的电磁波 均匀平面电磁波:等相位面上E、H 处处相等的 电磁波 若电磁波沿 x 轴方向传播,则H=H(x,t),E=E(x,t) 平面电磁波知识结构框图电磁场基本方程组 电磁波动方程 均匀平面电磁波的传播特性平面电磁波的基本特性1. 理想介质中的均匀平面波 2. 损耗媒质中的均匀平面波 3. 均匀平面波的极化 4. 均匀平面波对平面边界的垂直入射 5. 均匀平面波对平面边界的斜入射 6. 各向异性媒质中的均匀平面波1-120 2-120理想介质中均匀平面波 平面电磁波的极化导电媒质中均匀平面波平面电磁波的垂直入射平面电磁波的斜入射各向异性媒质中的均匀平面波x方向传播的一组均匀平面波3-120平面电磁波知识结构框图数的媒质, σ → ∞ 的媒质称为理想导体。
σ 介 于两者之间的媒质称为有损耗媒质或导电媒质。
6.1 理想介质中的均匀平面波 理想介质是指电导率 σ = 0 ,ε 、 μ 为实常6.1.1波动方程的解其通解为假设电磁场沿着 Z 轴方向传播,且电场仅有指向 X 轴 的方向分量,则磁场必只有 Y 方向的分量,即:z z E x = f1 (t − ) + f 2 (t + ) v v ∂ 2 Ex + β 2 Ex = 0 ∂z 2对于时谐变电磁场:E = ex E x ( z, t )波动方程H = ey H y (z,t)其通解为 则平面波是指波前面,即等相位面或者波前 阵是平面的波。
均匀平面波是指波前面上场量振 幅处处相等的波。
本节介绍最简单的情况,即介绍无源、均 匀(homogeneous)(媒质参数与位置无关)、 线性(linear)(媒质参数与场强大小无关)、 各向同性(isotropic)(媒质参数与场强方向无 关)的无限大理想介质中的时谐平面波。
4-120 5-120则∂E 2 =0 ∂t 2 ∂E 2 ∇ 2 E x − με 2x = 0 ∂t 2 ∂ E x 1 ∂E x2 − =0 ∂z 2 v 2 ∂t 2 ∇ 2 E − με其中: v =其中: β = ω μ εEx = Ex + e− jβ z + Ex − e+ jβ zE x = E x+ cos(ω t − β z ) + E x− cos(ω t + β z )对应的磁场为1∇ × E = −μ6-120με∂H ∂t∂H y ∂E x = −μ ∂z ∂t对应的磁场为∇ × E = −μ其通解为∂H ∂t∂H y ∂E x = −μ ∂z ∂t考察电场的一个分量 ,瞬时值表达式为:Ex ( z, t ) = Ex+ cos(ωt − β z + ϕx )其中Hy =β ⎡ E + cos(ω t − β z ) − E x− cos(ω t + β z ) ⎤ ⎦ ωμ ⎣ xωt 为时间相位 , β z 为空间相位 , ϕ x 是初始相位。
整理《电磁场与电磁波》答案(6) 一选择题

《电磁场与电磁波》自测试题整理表姓名:职业工种:申请级别:受理机构:填报日期:A4打印/ 修订/ 内容可编辑《电磁场与电磁波》自测试题1.介电常数为的均匀线性介质中,电荷的分布为,则空间任一点____________,_____________。
2. ;1. 线电流与垂直穿过纸面,如图所示。
已知,试问__ _______;若,则_____ ____。
2. ;1A1. 镜像法是用等效的代替原来场问题的边界,该方法的理论依据是___。
2. 镜像电荷;唯一性定理1. 在导电媒质中,电磁波的相速随频率改变的现象称为_____________,这样的媒质又称为_________ 。
2. 色散;色散媒质1. 已知自由空间一均匀平面波,其磁场强度为,则电场强度的方向为__________,能流密度的方向为__________。
2. ;1. 传输线的工作状态有________ ____、_______ _____、____________三种,其中________ ____状态不传递电磁能量。
2. 行波;驻波;混合波;驻波1. 真空中有一边长为的正六角形,六个顶点都放有点电荷。
则在图示两种情形下,在六角形中心点处的场强大小为图中____________________;图中____________________。
2. ;1. 平行板空气电容器中,电位(其中a、b、c 与d为常数),则电场强度__________________,电荷体密度_____________________。
2. ;1. 在静电场中,位于原点处的电荷场中的电场强度线是一族以原点为中心的__________________线,等位线为一族_________________。
2. 射;同心圆1. 损耗媒质中的平面波 , 其传播系数可表示为__________ 的复数形式,其中表示衰减的为___________。
2.;1. 在无损耗传输线上,任一点的输入功率都 _______,并且等于_______ 所得到的功率。
04-导电媒质中均匀平面波的传播特性PDF

2
1
2
1
3)相位常数 4)波长
2
1
2
1
21
f
2
1
2
1
5)波阻抗 理想介质
Z
(实数,纯电阻性质)
Ɛ替换为Ɛc
导电媒质
Zc
c
j
Zc ej
Zc
1 tan1 2
0
~
4
(呈电阻电感性)
6)相位速度(波速)
理想媒质中:v
k
1
损耗媒质中:
媒质损耗使波的传播速度变慢,波长变短 损耗媒质中波的相速与媒质参数、频率有关 色散现象:波的传播速度(相速)随频率改变而改变 具有色散效应的波称为色散波,有损媒质是色散媒质
导电媒质中均匀平面波 的参数和传播特性
谭阳红教授
导电媒质中均匀平面电磁波的方程
kc c
z
E(z,t) exExme cos(t z)
H (z, t)
ey
Exmezcos(t z)
Zc
凡是出现 Ɛ 的地方,都替换为Ɛc
1 导电媒质中均匀平面电磁波的参数
1)波数
kc c j
2)衰减常数
快于场量 =传播方向
3 导电媒质中传输特性总结
2 振幅呈指数 衰减,频率越 大,衰减越快
3 E=|Zc |H 4 波阻抗 是复数
1 横电磁波
导电媒质中
的均匀平面波
5 磁场滞后电
场,滞后角随
8 能流密度
频率变化
方向即传 播方向
7 磁场能大于 电场能,能
6 相速与媒 质和频率有
量衰减快于 关,色散波
场量
携带信号的电磁波的不同频率分量将以不同的 相速度传播,经过一段距离之后,不同频率分 量之间的相位关系将发生变化,导致信号失真
地球物理场论题库

《地球物理场论》题库与答案一、填空题 (每小题 1分,共30)1. 场是时空坐标的函数。
2. 在矢量场A 分布的空间中,有向面元dS 与该面元处的A 两个矢量的点乘是矢量场A通过dS 的 通量 。
3. 矢量场的散度是一个标量场。
4. 矢量场的散度是空间坐标的函数。
5. 矢量场的散度代表矢量场的通量源的分布特性。
6. 若矢量场A(x,y,z)的散度为f(x,y,z),且f 不全为0,则该矢量场称为有源场。
7. 若矢量场A(x,y,z)的散度为f(x,y,z),则称f(x,y,z)为源密度。
8. 在场矢量A 空间中一有向闭合路径l ,则称A 沿l 积分的结果称为矢量A 沿l 的环流。
9. 一个矢量场的旋度是另外一个为矢量场。
10. 矢量在空间某点处的旋度表征矢量场在该点处的漩涡源密度11. 对一个矢量场进行旋度变换后再进行散度变化,运算结果等于012. 标量场的梯度表征标量场变化规律:其方向为标量场增加最快的方向,其幅度表示标量场的最大增加率。
13. 在有限区域内,任意矢量场由矢量场的散度、旋度和边界条件唯一确定。
14. 若矢量场A 的散度和旋度值在某区域V 内处处有为0,称该矢量场A 为调和场。
15. 描述电荷在三维空间中分布状态的函数是电荷体密度。
16. 描述电荷在二维空间的面上分布状态的函数是电荷面密度。
17. 电流密度矢量描述空间电流分布的状态。
18. 电流连续性方程描述了电荷密度 与电流密度矢量两者之间的关系。
19. 电场是在电荷周围形成的一种物质。
20. 产生电场的源泉有2个。
21. 电场的特性是对处于其中的电荷产生力的作用。
22. 处在电场中的电荷所受的作用力与电场强度大小成正比。
23. 磁场是在电流周围形成的一种物质。
24. 在磁场中运动电荷所受到的作用力的方向由电荷运动方向和磁场方向共同确定。
25. 线电流元Idl 在距其R 产生的磁感应强度为:03()4Idl R dB Rμπ⨯=⋅。
第20讲 均匀平面电磁波的传播(2)

ε=ε0、ζ = 5.8×107 S/m。 解:对于频率范围的低端 fL =10kHz ,有 假 5.8 107 设 1.04 1014 1 L 2 104 1 109 不 36 好 对于频率范围的高端 fH =100MHz ,有
良导体
5.8 107 1.04 1010 1 H 2 108 1 109 36
第20讲
均匀平面电磁波的传播(2)
——均匀平面波在导电媒质中传播
目录
均匀平面波在 导电媒质中的 传播 色散与群速 各向异性媒质中 传播(简介)
一般导电媒质 弱导电媒质
良导电媒质
1 导电媒质中的均匀平面波
导电媒质的典型特征是电导率 ≠ 0
电磁波在导电媒质中传播时,有传导电流 J = E 存在,同时
z Ε ( z ) ex Εxm e ex Εxm e z e jz 瞬时值形式 E ( z, t ) ex Exm e z cos(t z )
令 jkc j ,则均匀平面波解为
称为电磁波的传播常数,单位:1/m
e z 是衰减因子, 称为衰减常数,单位:Np/m(奈培/米) jz是相位因子, 称为相位常数,单位:rad/m(弧度/米) e
合成波电场
E ( z, t ) E1 ( z, t ) E2 ( z, t ) ex 2 Em cos(t z ) cos(0t 0 z )
振幅,包络波,以角频率 缓慢变化
行波因子,代表沿 z 轴传播的行波
E ( z, t ) E1 ( z, t ) E2 ( z, t ) ex 2Em cos(t z) cos(0t 0 z)
平面电磁波 第六章

• 解出 E 就可用Maxwell方程组求出 H ,故只须解 E 。
• 不失一般性,可作一些假设,使求解更方便: ˆ (1)设 E 只有x方向的分量,即 E r E x x ; ˆ (2)设 E 只随z 坐标变化,即 E r E x z x ; x • E x z 满足的常微分方程:
vp
6、从行波角度理解电磁波各参数的物理意义: 相速度 ( vp ):等相位面在一秒钟之内前进的距离 波长(λ):等相位面在一个周期 T 之内前进的距离 2 2 v pT k k 周期(T ):等相位面前进一个波长所需的时间
vp T
频率( f ):等相位面在一秒钟之内前进的波长数 vp 1 f T
E:
H:
x y z
某时刻的三个 等相位面
• 均匀平面波每个等相位面上的场矢量处处相等。 • 任意固定时刻,空间中不同等相位面上的场值不同。 (除非两个等相位面间距为波长的整数倍)
5、Poynting矢量:
• 瞬时Poynting矢量: 1 2 ˆ S r , t Em cos2 t kz z
真空中: 0
0 120 377 0
• 波阻抗只是一个比值,单位与电阻相同,它并不意味 着存在能量损耗。 • 波阻抗仅由媒质参数决定,与场矢量值无关。 • 电场、磁场的互求公式:
ˆ z E H
1 ˆ zH E
ˆ z为 传 播 方 向
等相位面上的场分布情况 4、场结构:
m/s
v0 2 2 m k f
Hm Em 0 10 0
ˆ H 为 - x方 向
电磁场与电磁波第20讲极化导电媒质平面波坡印亭矢量

关于无损耗媒质中平面波的推导和讨论可以应用于损耗媒质中波传 播的情况,只要用kc 替换 k 就可以了。 然而,为了与传输线理论中 的记号一致,习惯上定义一个传播常数 ,使得
jkc j c (m-1 )
得
1/ 2 j j c =j ( ) j (1 ) j j
c (rad/m)
d 2 Ex 2 k 0 Ex 0 2 dz
k0 0 0
Ex ( z) Ex ( z) Ex ( z) E0e jk0 z E0e jk0 z
jk0 z jt Ex ( z , t ) Re E e e E 0 cos(t k 0 z ) (V/m) 0
有
2 E 2 E
E E 0
2 2
齐次矢量亥姆霍兹方程。
H j E E 0 H 0
12
在简单的,导电的无源媒质中, =0,0, 时谐场:
H E j E j ( ) E j c E j
1/ 2 j j (1 ) j
1 j 1 j 2 8
2
j j '(1 j
'' 1/2 ) '
2 '' 1 '' j ' 1 j 2 ' 8 '
E j H H J j E E / H 0 E j H
right : j H = j ( H ) j ( j E ) 2 E so : 2 E 2 E
导电媒质中均匀平面电磁波的e、h相位关系

导电媒质中均匀平面电磁波的e、h相位关系在导电媒质里均匀平面电磁波的e和h那关系可有点意思呢。
就好像两个人在跳一种特别的舞蹈,彼此之间有着独特的默契。
咱先说说这个e它就像是一个领舞者。
你看,e在导电媒质里传播的时候,可不是随随便便的。
它有着自己的一套节奏和步伐,就像一个经验丰富的舞者在舞台上尽情展现自己的风采。
那h呢?h就像是跟随着e的伴舞。
这俩在这个导电媒质的大舞台上共同演绎着电磁波的故事。
有人可能会问,这e和h到底是怎么个相位关系呢?这就好比白天和黑夜的关系。
虽然它们不完全一样,但却有着一种内在的联系。
e和h的相位不是同步的,就像两个人走路,一个人先迈出一步,另一个人再跟着迈出一步,不过步子大小和速度还不太一样呢。
在导电媒质里,e的相位总是比h的相位超前一点。
这就像是在一场接力赛里,e先拿到接力棒跑了一段,然后h才开始跑起来。
你要是把e和h想象成两个小伙伴一起去旅行的话。
e就像是那个急性子的小伙伴,早早地就出发了,沿着既定的路线前行。
h呢,则像是那个稍微慢一点的小伙伴,虽然出发晚一点,但是也朝着相同的方向前进。
而且它们在旅途中的状态也不太一样。
e的能量变化和h的能量变化就像是两个人的心情起伏。
e的能量变化会影响到h的能量变化,反过来也是一样。
这就像两个好朋友之间,一个人的情绪会感染到另一个人。
咱们再深入一点来看这个事儿。
在导电媒质这种特殊的环境里,e和h的这种相位关系可不是毫无意义的。
它就像汽车的两个轮子,虽然一个在前一个在后,但却共同推动着汽车前进。
如果没有这种特定的相位关系,那均匀平面电磁波在导电媒质里就没办法好好传播了。
这就好比两个人跳舞,如果没有配合好节奏和步伐,那就乱套了,观众可就要喝倒彩了。
有时候我们可能会觉得这种相位关系很复杂,很难理解。
其实只要我们换个角度去想,就像看一幅画一样。
一幅好画里有各种各样的元素,单独看每个元素可能没什么特别的,但是当它们组合在一起的时候,就形成了一幅美丽的画卷。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ey
m
c
e ze j ze j
其瞬时值为
uuv H
uuv ey
Em c
e z
cos(t
z
0 )
第6页/共21页
1 arctg 2
可知,σ愈大,则θ愈大,表示磁场强度比电场强度的相位滞后越 多,尽管电场与磁场有相位差,但二者仍然保持互相垂直,且都垂直于 传播方向。
Ex
因为电场强度与磁场强度的相位不
j
E0e ze jt
联立可得
2
1
2
1
2
1
2
1
可见,传播常数γ的
实部β决定相位变化
量,虚部z α决定幅度
变化量。
由(3)、(4)式可知,导电媒质中电场和磁场的振幅均按e-αz随
传播距离衰减,每传播单位长度(z=1)振幅衰减为原来的e-α倍,故
α称为衰减常数,另外β表示相位随传播距离的变化量,故β称为相位
第10页/共21页
6. 损耗角
复介电常数
c
1
j
j
虚部与实部之比为
g
E E
J
g
D
传导电流 位移电流
t
传导电流越大,损耗越大,定义导电媒质的损耗角 c 。
tg c
可见,损耗角与频率、媒质参数有关。
根据损耗角可将导电媒质分为弱导电媒质(电介质)、强导电媒质 (良导体)和一般的导电媒质(不良导体)。
高频电磁波从表面进入导电媒质越深,场的幅度就越小,能量就越小, 即能量趋于表面,这就是趋肤效应,或集肤效应或趋表效应。
对于良导体:
tg c
?
1
物理意义表示电介质中的传导电流远大于位移电流,相关参数有:
2
c
1 j
2
e
j 4
由此可见,电阻部分和电抗(呈感性)部分相等,即c 的相角为45o。
vp
2
2
可见,良导体中相速为频率的函数,是色散波,且电导率越大,相 速越慢。
第13页/共21页
3. 趋肤效应
g
g
Ex Em e j z
其中
g
Em Eme j0
设 j
g
g
g
则
Ex
E e j( -j )z m
Em e ze j z
(3)
uv
uuv
uuv
其瞬时值为 E z,t exEx z,t exEmez cos(t z 0) (3)
第3页/共21页
g
g
由方程 E j H得
常数。
第5页/共21页
3. 波阻抗
导电媒质中的波阻抗为
g
c
Ex
g
Hy
j
c
1 j
c e j
可见 c为复数,其模值和相位分别为
c
[1
(
)
2
]
1 4
0
1 arctg 2
0,
4
由上式可知,c 有非零相角,意味着电场与磁场具有不同的相位,相
位差为θ,故(可4)改写为
g
g
H
uuv E
主要内容
❖ 导电媒质中均匀平面波的传播特性 ❖ 集肤效应
学习目的
❖ 掌握导电媒质与无耗媒质中均匀平面波的区别 ❖ 掌握集肤效应、趋肤深度、表面电阻的定义
第1页/共21页
6.2 导电媒质中的平面电磁波
6.2.1导电媒质中平面电磁波的传播特性
1. 复介电常数
无源、无界的导电媒质中麦克斯韦方程的复数形式为
同,复能流密度的实部及虚部均不会
z 为零,这就意味着平面波在导电媒质
中传播时,既有单向流动的传播能量,
Hy
又有来回流动的交换能量。
第7页/共21页
4. 相速度和波长
导电媒质中均匀平面波的相速为
波长为
vp
1
2
1
2
1
1
2π
2
2π
1
2
1
2π 2π
k
由上可知:
第11页/共21页
6.2.2 趋肤深度和表面电阻
1. 电介质中的均匀平面波
对于电介质:
tg
c
=
1
物理意义表示电介质中的传导电流远小于位移电流,相关参数有:
2
由于电介质σ极小,故与理想介质相比,除有微弱损耗引起的振幅
衰减外,其余参量近似相同。
第12页/共21页
2. 良导体中的均匀平面波
g
g
2 H 2c H 0
g
g
2 H 2 H 0 (2)
对于均匀平面电磁波,设沿z轴传播,电场强度只有x分量,则由上节
可计算出式(1)的解为:
用γ替代无耗 媒质解中的k
g
2 Ex z 2
2
g
Ex
0
g
g
g
Ex Em e j z Em e j z
对于沿z轴正方向传播的均匀平面波,其解为:
2
we
1 2
Ex2
1 2
Hy
2
1 2
H
2 y
1 2
H
2 y
wm
由上式表明,理想介质中波阻抗为纯阻,电场与磁场相位相同,而导
电媒质下:
we
1 2
Ex2
wm
1 2
H
2 y
1 2
Ex c
2
1 2
c
2
Ex2
1 2
c
Ex2
1 2
Ex2
j
1 2
Ex2
1
2
we
1
2
we
可见,导电媒质中 wm we ,其波阻抗呈电阻、电感性质。
(1)导电媒质中相速要比理想介质中慢,波长要比理想介质中短;
(2)σ愈大,相速vp越慢,波长λ越短; (3)相速与频率有关,故电磁波中不同的频率分量将以不同的相速传播,
经过一定距离后,它们的相位发生不同变化,从而导致信号失真,这种现
象称为色散。
第8页/共21页
5. 电场能量和磁场能量
在理想介质中,电场与磁场能量密度是相等的,即
g
g
H
1 j
g
E
uuv ey
1 j
Ex z
将(3)式代入上式得
g uuv H ey 其瞬时值形式为
g
E m
e ze j z
j
uuv uuv H ey
Em
ez cos(t z 0 )
j
(4) (4)
第4页/共21页
2 传播常数γ
E0e jt
x
O
由于
2
2c
2 (
j )
第9页/共21页
从以上分析可以看到,导电媒质中的平面波与理想介质中的平面波 相比具有以下特点: (1)导电媒质中的电磁波是衰减波,频率越高或电导率越大,α就越大, 衰减也就越快。 (2)导电媒质中平面波的波阻抗c 为复数,呈现电阻、电感特性。 (3)c 表明导电媒质中电场和磁场的相位不同,出现相位差。 (4)导电媒质中电磁波的相速度不再是常数,而是随频率变化的函数,有 色散现象。 (5)导电媒质中平均磁场能量密度 wav,m 大于平均电场能量密度 wav,e 。
g
g
g
H E j E
定义
j
1
j
g
E
g
jc E
c
1
j
j
导电媒质的等效 复介电常数
引入εc后方程形式与无耗媒质中麦克斯韦方程具有完全相同的形式,
可将导电媒质看做具有复介电常数εc的介质。
第2页/共21页
这2样Eg 可 得2到cEEg、H0满足2的zE2g令x亥姆jk2霍2兹Egx2方0程c (解即为复2数EEgg波x动2Eg方Emg e程 j0kz)为Egm(e j1kz)传播常数
