高考模拟试题一
模拟高考各科试题及答案

模拟高考各科试题及答案一、语文试题及答案1. 阅读下面一段文言文,完成(1)-(3)题。
(1)下列词语解释不正确的一项是:A. 觥筹交错(酒杯和酒筹相互错杂)B. 箪食瓢饮(用瓢盛水喝)C. 夙兴夜寐(早起晚睡)D. 箪食壶浆(用壶盛酒)答案:D(2)下列句子中,加点词的意义和用法相同的一项是:A. 吾谁与归B. 吾从子游C. 吾与点也D. 吾谁欺答案:A(3)翻译文中划线的句子。
句子:不以物喜,不以己悲。
翻译:不因为物质的得失而感到高兴或悲伤。
2. 现代文阅读,回答问题。
(1)文章中“他”为什么坚持要回家?答案:因为他思念家乡和亲人。
(2)文章中“她”对“他”的态度是怎样的?答案:她对“他”既关心又有些无奈。
(3)文章的主题是什么?答案:文章的主题是思乡之情。
二、数学试题及答案1. 已知函数f(x)=2x^2-3x+1,求f(2)的值。
答案:f(2)=2*(2^2)-3*2+1=52. 解方程:x^2-5x+6=0。
答案:x=2或x=33. 计算定积分:∫(0到1) (2x+3)dx。
答案:(2/2)x^2+3x | 0到1 = 2+3-0 = 5三、英语试题及答案1. 根据句意,选择填空。
I don't think it is necessary to ________ the matter.A. look intoB. look upC. look outD. look over答案:A2. 翻译句子。
句子:他决定去旅行,放松一下。
翻译:He decided to go on a trip to relax.3. 阅读理解,回答问题。
(1)文章中提到了哪些旅游目的地?答案:文章提到了巴黎、伦敦和纽约。
(2)作者对旅游的态度是什么?答案:作者认为旅游是一种放松和学习的方式。
四、物理试题及答案1. 已知一个物体的质量为2kg,受到的重力为19.6N,求物体的加速度。
答案:a=F/m=19.6N/2kg=9.8m/s^22. 一个电容器的电容为4μF,通过它的电流为2A,求电容器的电压。
2024年高考数学模拟试题含答案(一)

2024年高考数学模拟试题含答案(一)一、选择题(每题5分,共40分)1. 若函数f(x) = 2x - 1在区间(0,2)上是增函数,则实数a的取值范围是()A. a > 0B. a ≥ 1C. a ≤ 1D. a < 0【答案】C【解析】由题意知,f'(x) = 2 > 0,所以函数在区间(0,2)上是增函数。
又因为f(0) = -1,f(2) = 3,所以f(x)在区间(0,2)上的取值范围是(-1,3)。
要使得f(x)在区间(0,2)上是增函数,只需保证a ≤ 1。
2. 已知函数g(x) = x² - 2x + 1,则下列结论正确的是()A. 函数g(x)在区间(-∞,1)上是增函数B. 函数g(x)在区间(1,+∞)上是减函数C. 函数g(x)的对称轴为x = 1D. 函数g(x)的顶点坐标为(1,0)【答案】D【解析】函数g(x) = x² - 2x + 1 = (x - 1)²,所以函数的顶点坐标为(1,0),对称轴为x = 1。
根据二次函数的性质,当x > 1时,函数g(x)递增;当x < 1时,函数g(x)递减。
3. 已知数列{an}的前n项和为Sn,且满足Sn =2an - 1,则数列{an}的通项公式是()A. an = 2^n - 1B. an = 2^nC. an = 2^n + 1D. an = 2^(n-1)【答案】D【解析】由Sn = 2an - 1,得an = (Sn + 1) / 2。
当n = 1时,a1 = (S1 + 1) / 2 = 1。
当n ≥ 2时,an = (Sn + 1) / 2 = (2an - 1 + 1) / 2 = 2an-1。
所以数列{an}是首项为1,公比为2的等比数列,通项公式为an = 2^(n-1)。
4. 已知函数h(x) = |x - 2| - |x + 1|,则函数h(x)的图像是()A. 两条直线B. 两条射线C. 一个三角形D. 一个抛物线【答案】B【解析】函数h(x) = |x - 2| - |x + 1|表示数轴上点x到点2的距离减去点x到点-1的距离。
广东省2024届高三春季高考模拟卷(1)数学试题含解析

2024年第一次广东省普通高中学业水平合格性考试数学冲刺卷(一)答案解析一、选择题:本大题共12小题,每小题6分,共72分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{}2,0,1,2A =-,{}21B x x =-≤≤∣,则A B = ()A.{}2- B.{}1 C.{}2,0,1- D.{}0,1,2【答案】C 【解析】【分析】根据集合交集运算求解即可.【详解】解:因为{}2,0,1,2A =-,{}21B xx =-≤≤∣,所以A B = {}2,0,1-故选:C2.已知角α的终边过点()1,2P -,则tan α等于()A.2 B.2- C.12-D.12【答案】B 【解析】【分析】由正切函数的定义计算.【详解】由题意2tan 21α==--.故选:B .3.下列函数中是减函数且值域为R 的是()A.1()f x x= B.1()f x x x=-C.()ln f x x= D.3()f x x=-【答案】D 【解析】【分析】由幂函数及对数函数的图象与性质即可求解.【详解】解:对A :函数()f x 的值域为()(),00,-∞⋃+∞,故选项A 错误;对B :函数()f x 为(),0∞-和()0,∞+上的增函数,故选项B 错误;对C :函数()ln ,0()ln ln ,0x x f x x x x >⎧==⎨-<⎩,所以()f x 在()0,∞+上单调递增,在(),0∞-上单调递减,故选项C 错误;对D :由幂函数的性质知()f x 为减函数且值域为R ,故选项D 正确;故选:D.4.不等式22150x x -++≤的解集为()A .532x x ⎧⎫-≤≤⎨⎬⎩⎭B.52x x ⎧≤-⎨⎩或}3x ≥C.532x x ⎧⎫-≤≤⎨⎬⎩⎭D.{3x x ≤-或52x ⎫≥⎬⎭【答案】B 【解析】【分析】将式子变形再因式分解,即可求出不等式的解集;【详解】解:依题意可得22150x x --≥,故()()2530x x +-≥,解得52x ≤-或3x ≥,所以不等式的解集为52x x ⎧≤-⎨⎩或}3x ≥故选:B .5.化简:AB OC OB +-=()A.BAB.CAC.CBD.AC【答案】D 【解析】【分析】根据向量的线性运算法则,准确运算,即可求解.【详解】根据向量的线性运算法则,可得()AB OC OB AB OC OB AB BC AC +-=+-=+=.故选:D.6.方程()234xf x x =+-的零点所在的区间为()A.()1,0- B.10,2⎛⎫ ⎪⎝⎭C.1,12⎛⎫ ⎪⎝⎭D.41,3⎛⎫⎪⎝⎭【答案】C 【解析】【分析】分析函数()f x 的单调性,利用零点存在定理可得出结论.【详解】因为函数2x y =、34y x =-均为R 上的增函数,故函数()f x 在R 上也为增函数,因为()10f -<,()00f <,15022f ⎛⎫=<⎪⎝⎭,()110f =>,由零点存在定理可知,函数()f x 的零点所在的区间为1,12⎛⎫⎪⎝⎭.故选:C.7.已知扇形的半径为1,圆心角为60 ,则这个扇形的弧长为()A.π6B.π3C.2π3D.60【答案】B 【解析】【分析】根据扇形的弧长公式计算即可.【详解】易知π603=,由扇形弧长公式可得ππ133l =⨯=.故选:B8.把黑、红、白3张纸牌分给甲、乙、丙三人,则事件“甲分得红牌”与“乙分得红牌”是()A.对立事件B.互斥但不对立事件C.不可能事件D.必然事件【答案】B 【解析】【分析】根据题意,分析可得“甲分得红牌”与“乙分得红牌”不会同时发生,但除了这2个事件外,还有事件“丙分得红牌”,由对立事件与互斥事件的概念,可得答案.【详解】根据题意,把黑、红、白3张纸牌分给甲、乙、丙三人,事件“甲分得红牌”与“乙分得红牌”不会同时发生,则两者是互斥事件,但除了“甲分得红牌”与“乙分得红牌”之外,还有“丙分得红牌”,则两者不是对立事件,则事件“甲分得红牌”与“乙分得红牌”是互斥但不对立事件;故选:B .【点睛】本题考查对立事件与互斥事件的概念,要注意对立一定互斥,但互斥不一定对立,属于基础题.9.要得到函数4y sinx =-(3π)的图象,只需要将函数4y sin x =的图象A.向左平移12π个单位B.向右平移12π个单位C.向左平移3π个单位D .向右平移3π个单位【答案】B 【解析】【详解】因为函数sin 4sin[4()]312y x x ππ⎛⎫=-=- ⎪⎝⎭,要得到函数43y sin x π⎛⎫=- ⎪⎝⎭的图象,只需要将函数4y sin x =的图象向右平移12π个单位.本题选择B 选项.点睛:三角函数图象进行平移变换时注意提取x 的系数,进行周期变换时,需要将x 的系数变为原来的ω倍,要特别注意相位变换、周期变换的顺序,顺序不同,其变换量也不同.10.已知两条直线l ,m 与两个平面α,β,下列命题正确的是()A.若//l α,l m ⊥,则m α⊥B.若//αβ,//m α,则//m βC.若//l α,//m α,则//l mD.若l α⊥,l //β,则αβ⊥【答案】D 【解析】【分析】A.利用线面的位置关系判断;B.利用线面的位置关系判断;C.利用直线与直线的位置关系判断;D.由l //β,过l 作平面γ,有m γβ= ,利用线面平行的性质定理得到得到//l m ,再利用面面垂直的判定定理判断.【详解】A.若//l α,l m ⊥,则//,m m αα⊂或,m α相交,故错误;B.若//αβ,//m α,则//m β或m β⊂,故错误;C.若//l α,//m α,则//l m ,l ,m 相交或异面,故错误;D.若l //β,过l 作平面γ,有m γβ= ,则//l m ,因为l α⊥,所以m α⊥,又m β⊂,则αβ⊥,故正确.故选:D11.已知函数()122,0,log ,0,x x f x x x ⎧≤⎪=⎨>⎪⎩则()()2f f -=()A.-2B.-1C.1D.2【答案】D 【解析】【分析】先根据分段函数求出()2f -,再根据分段函数,即可求出结果.【详解】因为()21224f --==,所以()()12112log 244f f f ⎛⎫-=== ⎪⎝⎭.故选:D.12.已知37log 2a =,1314b ⎛⎫= ⎪⎝⎭,135log c =,则a 、b 、c 的大小关系为()A.a b c >> B.a c b>> C.b a c>> D.c b a>>【答案】A 【解析】【分析】利用对数函数、指数函数的单调性结合中间值法可得出a 、b 、c 的大小关系.【详解】因为337log log 312a =>=,13110144b ⎛⎫⎛⎫<=<= ⎪ ⎪⎝⎭⎝⎭,1133log 5log 10c =<=,因此,a b c >>.故选:A.二、填空题:本大题共6小题,每小题6分,共36分.13.已知i 是虚数单位,则复数4i1i-+的虚部为__________.【答案】2-【解析】【分析】先把复数化简为22i --,再根据虚部定义得出即可.【详解】()()()()224i 1i 4i 1i 4i4i 4i =22i 1i 1i 1i 1i 2------===--++--,则复数的虚部为2-.故答案为:2-.14.函数51x y a -=+且((0a >且1a ≠)的图象必经过定点______________.【答案】(5,2)【解析】【分析】由指数函数的性质分析定点【详解】令50x -=,得5x =,此时2y =故过定点(5,2)15.如果函数()()sin 06f x x πωω⎛⎫=-> ⎪⎝⎭的最小正周期为2π,则ω的值为______________.【答案】4【解析】【分析】根据正弦型函数的周期计算公式2T πω=即可求解.【详解】2T πω=,∴2242Tππωπ===.故答案为:4.16.已知圆柱的底面直径与高都等于球的直径,若该球的表面积为48π,则圆柱的侧面积为_____.【答案】48π.【解析】【分析】先由球的表面积为48π求出球的半径,然后由圆柱的侧面积公式算出即可【详解】因为球的表面积24π48πS R ==所以R所以圆柱的底面直径与高都为所以圆柱的侧面积:2π⨯故答案为:48π【点睛】本题考查的是空间几何体表面积的算法,较简单.17.某工厂生产甲、乙、丙、丁四种不同型号的产品,产量分别为200,400,300,100件,为检验产品的质量,现用分层抽样的方法从以上所有的产品中抽取60件进行检验,则应从丙种型号的产品中抽取________件.【答案】18【解析】【详解】应从丙种型号的产品中抽取30060181000⨯=件,故答案为18.点睛:在分层抽样的过程中,为了保证每个个体被抽到的可能性是相同的,这就要求各层所抽取的个体数与该层所包含的个体数之比等于样本容量与总体的个体数之比,即n i ∶N i =n ∶N .18.已知()f x 是定义在R 上的偶函数,当x ≥0时,()22xf x =-,则不等式()2f x ≤的解集是_______;【答案】[]22-,【解析】【分析】判断函数当0x ≥时的单调性,利用函数奇偶性和单调性的关系将不等式进行转化求解即可.【详解】∵当x ≥0时,()22xf x =-,∴偶函数()f x 在[0,+∞)上单调递增,且()2=2f ,所以()2f x ≤,即()()2fx f ≤,∴2x ≤,解得22x -≤≤.故答案为:[]22-,.三、解答题:本大题共4小题,第19~21题各10分,第22题12分,共42分.解答需写出文字说明,证明过程和演算步骤.19.在△ABC 中,角A ,B ,C 的对边分别是,,a b c ,已知46,5,cos 5a b A ===-(1)求角B 的大小;(2)求三角形ABC 的面积.【答案】(1)B=300(2)93122ABC S ∆-=【解析】【详解】分析:(1)由同角三角函数关系先求3sin 5A =,由正弦定理可求sinB 的值,从而可求B 的值;(2)先求得()()sin 30C sin A B sin A =+=+的值,代入三角函数面积公式即可得结果.详解:(1)由正弦定理又∴B 为锐角sinA=35,由正弦定理B=300(2)()()sin 30C sin A B sin A =+=+,∴19312bsin 22ABC S a C -==点睛:以三角形和为载体,三角恒等变换为手段,正弦定理、余弦定理为工具,对三角函数及解三角形进行考查是近几年高考考查的一类热点问题,一般难度不大,但综合性较强.解答这类问题,两角和与差的正余弦公式、诱导公式以及二倍角公一定要熟练掌握并灵活应用,特别是二倍角公式的各种变化形式要熟记于心.20.某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用比例分配的分层随机抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:[)20,30,[)30,40,⋅⋅⋅,[]80,90,并整理得到如下频率分布直方图:(1)根据频率分布直方图估计分数的样本数据的70%分位数;(2)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等.试估计总体中女生的人数.【答案】(1)77.5;(2)160(人).【解析】【分析】(1)根据分位数的概念,结合题给频率分布直方图计算得出结果即可;(2)根据频率分布直方图计算出样本中分数不小于70的人数,进而计算出样本中男生及女生的人数,最后求出总体中女生的人数.【详解】(1)由频率分布直方图可知,样本中分数不小于70的频率为()0.020.04100.6+⨯=,从而有:样本中分数小于70的频率为10.60.4-=,又由频率分布直方图可得:样本中分数小于80的频率为0.8,所以样本数据的70%分位数必定位于[)70,80之间.计算为:0.70.4701077.50.80.4-+⨯=-所以其分数的样本数据的70%分位数估计值为77.5.(2)由题知,样本中分数不小于70的学生人数为()0.020.041010060+⨯⨯=,从而有,样本中分数不小于70的男生人数为160302⨯=,进而得,样本中的男生人数为30260⨯=,女生人数为1006040-=,所以总体中女生人数为40400160100⨯=(人).21.某市出租车的票价按以下规则制定:起步公里为2.6公里,收费10元;若超过2.6公里的,每公里按2.4元收费.(1)设A 地到B 地的路程为4.1公里,若搭乘出租车从A 地到B 地,需要付费多少?(2)若某乘客搭乘出租车共付费16元,则该出租车共行驶了多少公里?【答案】(1)13.6元(2)5.1公里【解析】【分析】(1)设出租车行驶x 公里,根据题设写出付费额()f x 的分段函数形式,进而求从A 地到B 地需要的付费;(2)由题意出租车行驶公里数 2.6x >,结合解析式列方程求该出租车共行驶的公里数.【小问1详解】设出租车行驶x 公里,则付费额10,0 2.6()10 2.4( 2.6), 2.6x f x x x <≤⎧=⎨+->⎩,所以(4.1)10 2.4(4.1 2.6)13.6f =+⨯-=元.【小问2详解】由题意,出租车行驶公里数 2.6x >,令10 2.4( 2.6)16x +-=,则 5.1x =公里.22.如图,在三棱锥V-ABC 中,平面VAB ⊥平面ABC ,VAB 为等边三角形,AC BC ⊥,且AC=BC=,O,M分别为AB,VA 的中点.(1)求证:VB //平面MOC ;(2)求三棱锥V-ABC 的体积.【答案】(1)证明见解析;(2)33.【解析】【详解】试题分析:(1)要证明线面平行,就是要证线线平行,题中有中点,由中位线定理易得线线平行,注意得出线面平行结论时,必须把判定定理的条件写全;(2)要求三棱锥的体积,首先要确定高,本题中有面面垂直,由此易得VO 与底面ABC 垂直,因此VO 就是高,求出其长,及ABC 面积,可得体积.试题解析:(1)证明: 点O,M 分别为AB,VA 的中点//OM VB ∴又,OM MOC VB MOC ⊂⊄平面平面//VB MOC∴平面(2)解:连接VO ,则由题知VO ⊥平面AB C,∴VO 为三棱锥V-ABC 的高.又112ABC S VO === ,11.1333V ABC ABC V S VO -∴==⨯=考点:线面平行的判断,体积.。
新高考全国 I 卷语文模拟试题(附答案)

新高考全国I 卷语文模拟试题(附答案)一、现代文阅读(35 分)(一)现代文阅读I(本题共 5 小题,17 分)阅读下面的文字,完成1~5 题。
材料一:中国古典诗歌中的意象,是诗人情感与客观物象的融合,是诗人心灵的映照。
意象的运用,使诗歌具有了丰富的内涵和独特的艺术魅力。
诗歌中的意象往往具有特定的象征意义。
比如,梅花常被赋予高洁、坚贞的品质;菊花象征着淡泊、隐逸;杨柳则代表着离别、思念。
诗人通过这些意象,传达出自己的情感和思想。
意象的组合也能创造出丰富的意境。
不同的意象组合在一起,可以形成不同的意境。
如“明月松间照,清泉石上流”,明月、青松、清泉、山石等意象的组合,营造出一种清幽、宁静的意境。
此外,意象还可以通过比喻、拟人、夸张等修辞手法来增强表现力。
例如,“忽如一夜春风来,千树万树梨花开”,将雪花比作梨花,生动地描绘出了雪景的美丽。
材料二:在现代诗歌中,意象的运用也非常广泛。
现代诗人常常通过独特的意象来表达自己对生活、对世界的感悟。
与古典诗歌相比,现代诗歌中的意象更加多样化和个性化。
现代诗人可以从日常生活中的各种事物中选取意象,如汽车、高楼、电脑等。
同时,现代诗歌中的意象也更加注重对内心世界的挖掘和表达。
现代诗歌中的意象组合也更加自由和灵活。
诗人可以根据自己的创作意图,随意组合各种意象,创造出独特的意境。
然而,无论是古典诗歌还是现代诗歌,意象都是诗歌的灵魂。
它能够激发读者的联想和想象,使读者更好地理解诗歌的内涵。
1. 下列关于材料中“意象” 的表述,不正确的一项是(3 分)A. 意象是诗人情感与客观物象的融合,能使诗歌具有丰富内涵和独特艺术魅力。
B. 古典诗歌中的意象往往有特定象征意义,如梅花代表高洁坚贞,菊花象征淡泊隐逸。
C. 现代诗歌中的意象更加多样化和个性化,可从日常生活事物中选取,也更注重内心世界表达。
D. 古典诗歌和现代诗歌中的意象组合都很自由灵活,能创造出独特意境,激发读者联想想象。
2025年高考(新高考)模拟试卷英语试题(一)(含听力音频和答案)

2025年高考(新高考)模拟试题卷英语听力音频 双击收听.mp3本试卷共12页,考试用时150分钟,满分150分;广东省考生无需答听力部分,考试用时120分钟,满分120分。
注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
第一部分听力(共两节,满分30分)做题时,先将答案标在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
例:How much is the shirt?A. £19.15.B. £9.18.C. £9.15.答案是C。
1.What does the woman think of the movie?A.It’s amusing B.It’s exciting C.It’s disappointing 2.How will Susan spend most of her time in France?A.Traveling around B.Studying at a school C.Looking after her aunt 3.What are the speakers talking about?A.Going out B.Ordering drinks C.Preparing for a party 4.Where are the speakers?A.In a classroom B.In a library C.In a bookstore 5.What is the man going to do?A.Go on the Internet B.Make a phone call C.Take a train trip第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
2023年普通高等学校招生全国统一模拟考试示范性试题(一)

2023年普通高等学校招生全国统一模拟考试英语科示范试题(一)本试卷满分150分考试用时120分钟【本示范卷说明:本卷由全国新高考地区各级优秀英语教师选编而成,试题排版严格按照高考试题排布。
命题质量高,仅供高三一线教学老师参考使用以便了解2023年高考命题动向,不作其他使用】第一部分:听力(共两节,满分30分)做题时,先将答案标在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题纸上。
第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1.Which gate should the woman go to?A.Gate20.B.Gate30.C.Gate35.2.What type of book is the woman reading?A.Science fiction.B.Horror fiction.C.Romantic fiction. 3.Where does the conversation take place?A.In a restaurant.B.In a shop.C.In a cinema. 4.What day is it when they are talking?A.Tuesday.B.Wednesday.C.Thursday.5.What are the speakers mainly talking about?A.A stranger.B.An artwork.C.A suspect.第二节(共15小题:每小题1.5分,满分22.5分)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟:听完后,各小题将给出5秒钟的作答时间。
高考模拟试题大全及答案

高考模拟试题大全及答案一、选择题1. 下列关于细胞结构的描述,哪项是错误的?A. 细胞核是细胞的控制中心B. 线粒体是细胞的能量工厂C. 细胞壁只存在于植物细胞中D. 细胞膜具有选择性通透性答案:C2. 在化学反应中,下列哪种物质不是催化剂?A. 硫酸B. 氢氧化钠C. 酶D. 氧化铁答案:A二、填空题1. 光合作用是植物通过______将光能转化为化学能的过程。
答案:叶绿体2. 根据题目所给的化学反应方程式,如果反应物A的摩尔质量是B的2倍,且反应物A和B按照1:2的摩尔比参与反应,那么生成物C的摩尔质量是______。
答案:B的3倍三、简答题1. 简述牛顿第二定律的内容及其应用。
答案:牛顿第二定律指出,物体的加速度与作用在其上的合力成正比,与物体的质量成反比。
公式表示为:\[ F = ma \]。
这一定律在物理学中广泛应用于分析和计算物体在受力情况下的运动状态。
2. 描述水的三态变化及其影响因素。
答案:水的三态包括固态(冰)、液态(水)和气态(水蒸气)。
水的三态变化受温度影响,当温度降低时,水会从液态转变为固态;当温度升高时,水会从液态转变为气态。
此外,压力也会影响水的相变。
四、计算题1. 已知某物体在水平面上受到的摩擦力是其重力的0.25倍,求物体在水平面上的加速度,假设物体的质量为10kg。
答案:首先计算物体的重力:\[ F_{重力} = m \times g = 10\times 9.8 \] N。
摩擦力为:\[ F_{摩擦} = 0.25 \times F_{重力} \]。
根据牛顿第二定律,\[ F_{摩擦} = m \times a \],解得加速度\( a = \frac{F_{摩擦}}{m} = \frac{0.25 \times 10 \times9.8}{10} = 2.45 \) m/s²。
2. 某化学反应的速率常数 \( k \) 为0.05 s⁻¹,如果反应物的初始浓度为1 mol/L,求10秒后反应物的浓度。
2023届山东省高考模拟练习(一)数学试题

2023高考模拟练习(一)数学一、单选题:本题共8小题 每小题5分 共40分。
在每小题给出的四个选项中 只有一项是符合题目要求的.1.设全集{}2,1,0,1,2U =-- 集合()lg 22A x y x x ⎧=∈=-⎨+⎩N 则U A =( )A .{}2,1,2--B .{}2,2-C .∅D .{}2,1,0,2--2.已知复数231i z =- 且2z a bz =+ 其中a b 为实数 则a b -=( )A .12-B .12 C .32D .2 3.已知向量a b 满足323a b a b ==-= 则a a b ⋅-=( )A .8B .9C .14D .234.“角谷猜想”首先流传于美国 不久便传到欧洲 后来一位名叫角谷静夫的日本人又把它带到亚洲 因而人们就顺势把它叫作“角谷猜想”.“角谷猜想”是指一个正整数 如果是奇数就乘以3再加1 如果是偶数就除以2 这样经过若干次运算 最终回到1.对任意正整数0a .记按照述规则实施第n 次运算的结果为()n a n ∈N 若51a = 且()1,2,3,4i a i =均不为1 则0a =( )A .5或16B .5或32C .3或8D .7或325.已知函数()f x 的部分图象如图所示 则()f x 的解析式可能为( )A .()()cos π1f x x x =+B .()()1cos πf x x x =-C .()()1sin πf x x x =-D .()3221f x x x x =-+-6.已知正四棱锥(底面为正方形 且顶点在底面的射影为正方形的中心的棱锥为正四棱锥)P -ABCD 的底面正方形边长为2 其内切球O 的表面积为π3动点Q 在正方形ABCD 内运动 且满足OQ OP = 则动点Q 形成轨迹的周长为( ) A .2π11B .3π11C .4π11 D .5π117.2022年7月24日14时22分 搭载我国首个科学实验舱问天实验舱的长征五号B 遥三运载火箭成功发射 令世界瞩目.为弘扬航天精神 M 大学举办了“逐梦星辰大海——航天杯”知识竞赛 竞赛分为初赛和复赛 初赛通过后进入复赛 复赛通过后颁发相应荣誉证书和奖品.为鼓励学生积极参加 学校后勤部给予一定的奖励:只参加了初赛的学生奖励50元的奖品 参加了复赛的学生再奖励100元的奖品.现有A B C 三名学生报名参加了这次竞赛 已知A 通过初赛、复赛的概率分别为12 13;B 通过初赛、复赛的概率分别为23 12C 通过初赛和复赛的概率与B 完全相同.记这三人获得后勤部的奖品总额为X 元 则X 的数学期望为( ) A .300元B .10003元 C .350元 D .20003元 8.过椭圆C :22143x y +=上的点()11,A x y ()22,B x y 分别作C 的切线 若两切线的交点恰好在直线l :4x =上 则12y y ⋅的最小值为( )A .32-B .94-C .-9D .94二、选择题:本题共4小题 每小题5分 共20分.在每小题给出的四个选项中 有多项符合题目要求.全部选对的得5分 部分选对的得2分 有选错的得0分.9.在新冠疫情防控常态化的背景下 为提高疫情防控意识 某学校举办了一次疫情防控知识竞赛(满分100分) 并规定成绩不低于90分为优秀.现该校从高一、高二两个年级分别随参赛学生分数高一 7478 84 89 89 93 95 97 99 100 高二 7778 84 87 88 91 94 94 95 96 A .高一年级所抽取参赛学生成绩的中位数为91分 B .高二年级所抽取参赛学生成绩的众数为94分 C .两个年级所抽取参赛学生的优秀率相同 D .两个年级所抽取参赛学生的平均成绩相同10.已知抛物线C :()220y px p =>的焦点为()4,0F 点A B 在C 上 且弦AB 的中点到直线2x =-的距离为5 则( ) A .16p = B .线段AB 的长为定值 C .A B 两点到C 的准线的距离之和为14 D .AF BF ⋅的最大值为4911.如图 在直四棱柱1111ABCD A B C D -中 底面ABCD 为菱形 且1DE A C ⊥ 垂足为E 则( )A .1AA BD ⊥B .1AA ∥平面BDEC .平面BDE ⊥平面1A CDD .BE ⊥平面1A CD12.已知函数()4f x +是定义在R 上的奇函数 函数()2g x +是定义在R 上的偶函数 且满足()()()21g x x f x =-- ()()3426g g =+= 则( ) A .()f x 的图象关于点()1,0对称B .()f x 是周期为3的周期函数C .()10f =D .()202618i f i ==∑三、填空题:本题共4小题 每小题5分 共20分.13.中国共产党第二十次全国代表大会在北京召开期间 将含甲、乙在内的8名工作人员平均分配到A B 两个省代表厅从事服务工作 则甲、乙两人不分在同一省代表厅的概率为______.14.已知圆22x y a +=与圆22420x y x y b ++++=交于M N 两点 若855MN =则实数a b 的一对值可以为a =______ b =______.(写出满足条件的一组即可)15.已知函数2(1),0(),(1),0x xx e x f x x x e ⎧+<⎪=⎨+≥⎪⎩若关于x 的方程()()20f x a f x -=⎡⎤⎣⎦有3个不相等的实数根 则实数a 的取值范围是_______________16.已知双曲线222:1(0)4y x C b b -=>的上顶点、下焦点分别为M F 以M 为圆心 b 为半径的圆与C 的一条渐近线交于A B 两点 若60AMB ∠=︒ AB 的中点为Q (Q 在第一象限) 点P 在双曲线的下支上 则当||||PF PQ +取得最小值时 直线PQ 的斜率为__________. 四、解答题:本题共6小题 共70分。
2024届广东省深圳市高三下学期高考模拟卷全真演练物理试题(一)(基础必刷)
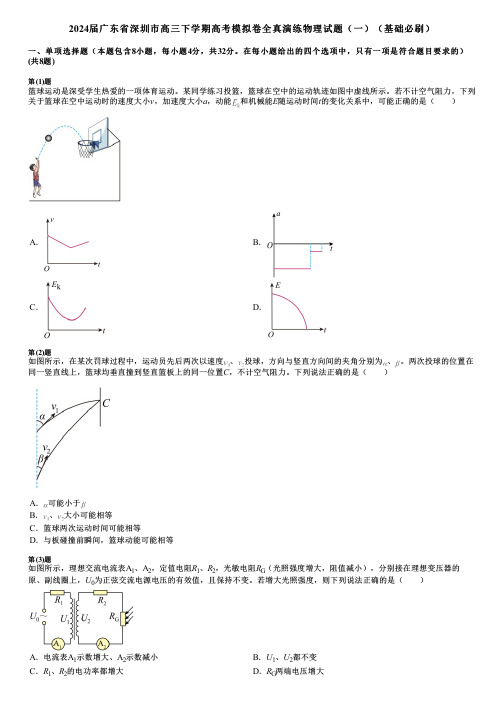
2024届广东省深圳市高三下学期高考模拟卷全真演练物理试题(一)(基础必刷)一、单项选择题(本题包含8小题,每小题4分,共32分。
在每小题给出的四个选项中,只有一项是符合题目要求的)(共8题)第(1)题篮球运动是深受学生热爱的一项体育运动。
某同学练习投篮,篮球在空中的运动轨迹如图中虚线所示。
若不计空气阻力,下列关于篮球在空中运动时的速度大小v,加速度大小a,动能和机械能E随运动时间t的变化关系中,可能正确的是( )A.B.C.D.第(2)题如图所示,在某次罚球过程中,运动员先后两次以速度、投球,方向与竖直方向间的夹角分别为、。
两次投球的位置在同一竖直线上,篮球均垂直撞到竖直篮板上的同一位置C,不计空气阻力。
下列说法正确的是( )A.可能小于B.、大小可能相等C.篮球两次运动时间可能相等D.与板碰撞前瞬间,篮球动能可能相等第(3)题如图所示,理想交流电流表A1、A2,定值电阻R1、R2,光敏电阻R G(光照强度增大,阻值减小),分别接在理想变压器的原、副线圈上,U0为正弦交流电源电压的有效值,且保持不变。
若增大光照强度,则下列说法正确的是( )A.电流表A1示数增大、A2示数减小B.U1、U2都不变C.R1、R2的电功率都增大D.R G两端电压增大第(4)题半圆柱玻璃砖的截面如图所示,O点为圆心,与直径AB垂直,一束与成(较小)角的白光沿半径方向入射到O点,紧贴A点有一与AB垂直的光屏,下列说法正确的是( )A.光屏上A点上、下各有一个白色光斑B.光屏上A点上、下各有一个彩色光带C.光屏上A点上方有一彩色光带,下方有一白色光斑D.光屏上A点上方有一白色光斑,下方有一彩色光带第(5)题如图所示是光线由空气射入横截面为半圆形的玻璃砖,再由玻璃砖射入空气中的光路图,O点是半圆形玻璃砖的圆心,可能正确的光路是()A.①、③B.②、④C.②、③D.①、④第(6)题2023年10月26日,中国自主研发的神舟十七号载人飞船发射成功,并实现了与中国空间站的快速对接。
天津市 2024届高考模拟预测全真演练物理试题(一)

天津市 2024届高考模拟预测全真演练物理试题(一)一、单选题:本题共7小题,每小题4分,共28分 (共7题)第(1)题吸烟有害健康,烟草中含有放射性元素钋210,衰变方程为,衰变产生的粒子对肺组织会造成损伤。
下列说法正确的是( )A.粒子很容易从肺穿到体外B.核的核子数是82个C.核的比结合能比的大D.升高温度可以加快的衰变第(2)题2022年冬奥会在北京成功举行,其中跳台滑雪项目是一项勇敢者的运动。
如图所示为某跳台滑雪运动员从助滑道滑下,然后从跳台a处沿水平方向飞出,在斜坡b处着陆的示意图,其中E k-t图像是运动员从a到b飞行时的动能随飞行时间变化的关系图像,不计空气阻力的作用,重力加速度g取10m/s2,则下列说法中正确的是( )A.运动员在a处的速度大小为20m/sB.运动员在b处时,重力的瞬时功率为1.2×104WC.斜坡的倾角为30°D.t=2s时,运动员在空中离坡面的距离最大第(3)题下列若干叙述中,不正确的是( )A.黑体辐射电磁波的强度按波长分布只与黑体的温度有关B.对于同种金属产生光电效应时,逸出光电子的最大初动能与照射光的频率成线性关系C.一块纯净的放射性元素矿石,经过一个半衰期以后,它的总质量仅剩下一半D.按照玻尔理论,氢原子核外电子从半径较小的轨道跃迁到半径较大的轨道时,电子的动能减小,原子的能量增加第(4)题取一条较长的软绳,用手握住一端拉平后连续向上,向下抖动长绳,可以看到如图所示的一列波,此时波刚好传播至质点,质点在平衡位置。
则( )A.质点将向右运动B.质点的起振方向向上C.此后质点的速度始终相同D.质点比滞后半个周期振动第(5)题在x轴上有两个点电荷和分别位于坐标原点和x1处,它们共同产生的电场在x轴上的电势分布如图所示,处电势为0,规定无穷远处为零势能位置,已知点电荷在空间中任意点的电势分布公式为(其中k为静电力常量,q为电荷量,r为该点到点电荷的距离)。
2024年全国1卷高考语文模拟试题及答案

2024年全国1卷高考语文模拟试题及答案2024年全国1卷高考语文模拟试题及答案一、选择题1、下列词语中,字形和读音全部正确的一项是:()A. 订正、汲取教训、锲而不舍、撒手锏B. 修茸、一筹莫展、越俎代庖、狙击手C. 针砭、明察秋毫、咎由自取、口头禅D. 矍铄、言简意赅、气冲霄汉、洗脚婢2、下列句子中,没有语病的一项是:()A. 我们既要传承传统文化,又要与时俱进,以适应新的时代环境。
B. 大量的事实告诉我们,环境恶化导致生物灭绝,人类要善待大自然。
C. 有关部门高度重视人民的意见,以确保“禁烟令”的顺利实施。
D. 即使生活再艰辛,我也要坚持不懈地努力,因为我的梦想就是成为一个科学家。
3、下列作品中,属于鲁迅小说集《呐喊》的是:()A. 《孔乙己》B. 《背影》C. 《荷塘月色》D. 《葫芦僧判断葫芦案》二、阅读理解阅读下面的文言文,完成4-6题。
未几,夫恬上前,问所欲言。
王曰:“吾欲言南尚可斗太守恶其无状。
”恬曰:“前日恬罪甚重,郎中令劳赐如令,是恬与并得罪。
”夫恬曰:“死未晚也。
”恬闻天下之至苦也莫苦于狱吏而吏道也莫患于无文而止在促捕之众也幸而道不携犹破折锐首而折左股而话之犹无所羞而夫恬为上相与为朝廷之法而以贾竖受货为资而挛拘牵张于辞语者恶独安?窃见郡县之吏徒以阿坐为毕能郡之大者也吏安得不悉虎狼还以道为尚父且父之不德而咎若曹罪乃大矣陷乃公独痴牧羊而道苦索则何?”恬不为理,引首以塞其气。
相与营当引太守舍,驾不能过半涂,良市卒正言于从者曰:“可与杀牛茵茵也。
”而恬得兵甚备,因恬请曰:“窃闻恬为人臣,佞而无骨,畏强怀弱,以货自免。
骄君甚则贵而求逆,暴君甚则利而求逆。
恬不知为死计,而尚与贾竖受货。
”恬得死诚节矣!4、下列句子中,断句正确的一项是:()A. 前日/恬罪甚重B. 贾竖/受货为资/而挛拘牵张于辞语者/恶独安C. 引首以塞/其气D. 可与杀牛茵茵也5、下列关于文章内容的理解,正确的一项是:()A. 夫恬认为自己的罪行很重,所以觉得自己应该被处死。
2024届陕西省宝鸡市高三上学期高考模拟检测(一)语文试题及答案

2024年宝鸡市高考模拟检测(一)语文注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、现代文阅读(36分)(一)论述类文本阅读(本题共3小题,9分)阅读下面的文字,完成1~3题。
对科学而言,存在一种已经建立的框架,使得任何科学家都可以证明别人是错误的,而且能确保所有人都能够知道这一点。
因此我觉得似乎是社会的混乱和人类的缺陷帮助了科学事业的存在与发展。
科学家有时也会犯错误,他们常会犯选择性观察的错误,因为他们有时过分主观,倾向于记住那些成功的经历而忽视了另外一些情况。
但是,在很多情况下,这些错误往往蕴含着正确的部分,或是能够激励其他人去发现真正正确的东西。
弗雷德·霍伊尔是当代最杰出的天文物理学家之一,他在恒星演化、宇宙学及其他许多问题上做出了不可磨灭的贡献。
与此同时,他也提出了不少错误的古怪观点,以致观察人员与实验人员觉得必须去验证。
尽管这些验证胜败交错,但几乎在每个问题上这些努力都将相应领域的研究向前大大推进了。
例如,他曾提出流感病毒和艾滋病病毒来源于彗星,认为星际灰尘颗粒是些细菌。
在论证或反驳其观点的过程中,研究人员获得了丰富的和有意义的新知识,尽管最终没有找到任何证据证明这些特别的见解。
列出一些科学家犯错误的例子对科学家不无益处,揭去科学神秘的面纱将有助于启迪年轻的科学家。
在历史上,即使是像牛顿、达尔文、爱因斯坦这样伟大的科学家也曾犯过严重的错误。
幸运的是,正因为科学事业是一种集体的事业,所以任何个人的影响和作用都不能超过集体。
因此,即使那些最有才华的科学家犯了错误,这些错误也能被其他远不如他们的科学家发现并弥补。
不同的科学家有着不同的思考习惯,有一些可能更谨慎一些。
2024届陕西省宝鸡市高考模拟监测(一) 理科综合试题

2024届陕西省宝鸡市高考模拟监测(一)理科综合试题一、单项选择题(本题包含8小题,每小题4分,共32分。
在每小题给出的四个选项中,只有一项是符合题目要求的)(共8题)第(1)题小明同学用欧姆表测电阻,选择开关置于“×100”挡时,表针停在图中的100与500之间的中间位置上。
为了使测量结果比较精确,下列操作正确的是()A.直接读数并乘上100即可B.换“×100”挡,无需重新欧姆调零C.换“×1k”挡,需重新进行欧姆调零D.选择任意挡都行,但需进行欧姆调零第(2)题如图(a),纸面内,圆形金属框通过长导线与平行金属板MN和PQ连接框内有如图(b)所示周期性变化的磁场(规定垂直纸面向里为磁场的正方向)导线上c、d接有电阻R,O1、O2是金属板上正对的两个小孔。
t=0时刻,从O1孔内侧由静止释放一个离子(不计重力)离子能够在时间△t内到达O2孔,已知△t>2T,规定从c经R到d为电流I的正方向,从O1指向O2为离子速度v的正方向,则下列图像可能正确的是( )A.B.C.D.第(3)题如图所示,空气中有一折射率为的玻璃柱体,其横截面是圆心角为90o、半径为R的扇形OAB、一束平行光平行于横截面,以45o入射角射到OA上,OB不透光,若考虑首次入射到圆弧上的光,则上有光透出的部分的弧长为( )A.B.C.D.第(4)题如图所示,竖直细杆O点处固定有一水平横杆,在横杆上有A、B两点,且,在A、B两点分别用两根等长的轻质细线悬挂两个相同的小球a和b,将整个装置绕竖直杆匀速转动,则a、b两球稳定时的位置关系可能正确的是( )A .B .C .D .第(5)题霍尔推进器将来可能安装在飞船上用于星际旅行,其简化的工作原理如图所示,放电通道两端电极间存在加速电场,该区域内有与电场近似垂直的约束磁场(未画出)用于提高工作物质被电离的比例,工作时,工作物质氙气进入放电通道后被电离为氙离子,再经电场加速喷出,形成推力,某次测试中,氙气被电离的比例为,氙离子喷射速度为,推进器产生的推力为,推进器质量,已知氙离子的比荷为;计算时,取氙离子的初速度为零,忽略磁场对离子的作用力及粒子之间的相互作用,则( )A .将该推进器用于宇宙航行时,飞船获得的加速度B .氙离子的加速电压约为C.氙离子向外喷射形成的电流约为D.每秒进入放电通道的氙气质量约为第(6)题在地面上以初速度竖直上抛一物体A 后,又以初速度v0在同一地点竖直上抛另一物体B ,若要使两物体能在空中相遇,则两物体抛出的时间间隔必须满足什么条件(已知,不计空气阻力)( )A .B .C .D .第(7)题如图所示,手握绳端在竖直方向做简谐运动,形成的一列简谐横波以速度沿轴正向传播,时刻,在轴上、间的简谐横波如图所示,从此时刻开始,点处质点经过时间刚好第3次到达波峰,则下列说法正确的是( )A .时刻,绳端正在向下振动B .绳端的振动频率为C .若将波的振动频率增大一倍,则波的传播速度也增大一倍D .若将波的振动频率增大为原来的2倍,则简谐波的波长也会增大为原来的2倍第(8)题如图所示,平行板电容器充电后断开电源,上极板接地,在板间点处固定一个试探电荷q,现将下极板向下平移一小段距离,用表示试探电荷在点所受的电场力,用E表示极板间的电场强度,用表示点的电势,用表示试探电荷在点的电势能,则下列物理量随与下极板的距离的变化关系图线中,可能正确的是( )A.B.C.D.二、多项选择题(本题包含4小题,每小题4分,共16分。
高考数学模拟试题含答案

高考数学模拟试题 (一)一、选择题(本题共12个小题,每题5分,共60分,在每小题给出的四个选项中,只有一项是符合要求的,请把符合要求一项的字母代号填在题后括号内.)1.已知集合M={x∣-3x -28 ≤0},N = {x|-x-6>0},则M∩N 为()A.{x| 4≤x<-2或3<x≤7}B. {x|-4<x≤-2或3≤x<7 }C.{x|x≤-2或x>3 }D. {x|x<-2或x≥3}2.在映射f的作用下对应为,求-1+2i的原象()A.2-iB.-2+iC.iD.23.若,则()A.a>b>c B.b>a>c C.c>a>b D.b>c>a4.要得到函数y=sin2x的图像,可以把函数的图像()A.向左平移个单位B. 向右平移个单位C.向左平移个单位D. 向右平移个单位5. 如图,是一程序框图,则输出结果中()A. B.C. D.6.平面的一个充分不必要条件是()A.存在一条直线B.存在一个平面C.存在一个平面D.存在一条直线7.已知以F1(-2,0),F2(2,0)为焦点的椭圆与直线有且仅有一个交点,则椭圆的长轴长为()A. B. C. D.8.O是平面上一定点,A、B、C是平面上不共线的三个点,动点P满足,则p的轨迹一定通过△ABC的()A.外心B. 重心C.内心D. 垂心9.设{a n}是等差数列,从{a1,a2,a3,…,a20}中任取3个不同的数,使这3个数仍成等差数列,则这样不同的等差数列最多有()A.90个 B.120个C.180个 D.200个10.下列说法正确的是 ( )A.“x2=1”是“x=1”的充分不必要条件B.“x=-1”是“x2-5x-6=0”的必要不充分条件C.命题“使得”的否定是:“均有”D.命题“若α=β,则sinα=sinβ”的逆否命题为真命题11.设等比数列的公比q=2,前n项和为,则()A. 2B. 4C.D.12.设曲线在点(3,2)处的切线与直线ax+y+1=0垂直,则a=()A.2 B.-2 C. D.二、填空题(本大题共4小题,每小题5分,满分20分.把答案直接填在题中的横线上.)13. 已知,,则的最小值.14. 如图是一个几何体的三视图,根据图中数据可得几何体的表面积为.15. 已知(1+x)+(1+x)2+(1+x)3+…+(1+x)n=a0+a1x+a2x+…+a n x n,若a1+a2+…+a n-1=29-n,则自然数n等于.16.有以下几个命题:①曲线x2-(y+1)2=1按a=(-1,2)平移可得曲线(x+1)2-(y+3)2=1②与直线相交,所得弦长为2③设A、B为两个定点,m为常数,,则动点P的轨迹为椭圆④若椭圆的左、右焦点分别为F1、F2,P是该椭圆上的任意一点,则点F2关于∠F1PF2的外角平分线的对称点M的轨迹是圆其中真命题的序号为(写出所有真命题的序号).三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤)17.(本小题满分12分)求函数y=7-4sinxcosx+4cos2x-4cos4x的最大值与最小值.18.(本小题满分12分)同时抛掷3个正方体骰子,各个面上分别标以数(1,2,3,4,5,6),出现向上的三个数的积被4整除的事件记为A.(1)求事件A发生的概率P(A);(2)这个试验重复做3次,求事件A至少发生2次的概率;(3)这个试验反复做6次,求事件A发生次数ξ的数学期望.19.(本小题满分12分)如图所示,已知四棱锥P-ABCD的底面是直角梯形, ∠ABC=∠BCD=90°,AB=BC=PB=PC=2CD=2,侧面PBC⊥底面ABCD,O是BC的中点,AO交BD于E.(1)求证:PA⊥BD;(2)求证:平面PAD⊥平面PAB;(3)求二面角P-DC-B.20. (本小题满分12分)如图,M是抛物线y2=x上的一点,动弦ME、MF分别交x轴于A、B两点,且MA=MB.(1)若M为定点,证明直线EF的斜率为定值;(2)若M为动点,且∠EMF=90°,求△EMF的重心G的轨迹方程.21.(本小题满分12分)已知函数的图象与直线相切,切点的横坐标为1.(1)求函数f(x)的表达式和直线的方程;(2)求函数f(x)的单调区间;(3)若不等式f(x)≥2x+m对f(x)定义域内的任意x恒成立,求实数m的取值范围.请考生在第22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分.作答时用2B铅笔在答题卡上把所选题目对应的题号涂黑.22.(本小题满分10分)[几何证明选讲]如图,E是圆内两弦AB和CD的交点,直线EF//CB,交AD的延长线于F,FG切圆于G,求证:(1)∽;(2)EF=FG.23.[选修4-4:坐标系与参数方程]已知曲线C:(t为参数), C:(为参数).(1)化C,C的方程为普通方程,并说明它们分别表示什么曲线;(2)若C上的点P对应的参数为,Q为C上的动点,求PQ中点M到直线(t为参数)距离的最小值.24.【不等式选讲】解不等式:参考答案1.A2.D3.A4.A5.D6.D7.C8.B9.C 10.D 11.C 12.B13. 3 14. 12π15.4 16.④17.解:y=7-4sinxcosx+4cos2x-4cos4x=7-2sin2x+4cos2x(1-cos2x)=7-2sin2x+4cos2xsin2x=7-2sin2x+sin22x=(1-sin2x)2+6.由于函数z=(u-1)2+6在[-1,1]中的最大值为z max=(-1-1)2+6=10,最小值为z min=(1-1)2+6=6,故当sin2x=-1时y取得最大值10,当sin2x=1时y取得最小值6.18.解:(1)解法1先考虑事件A的对立事件,共两种情况:①3个都是奇数;②只有一个是2或6,另两个都是奇数,.解法2 事件的发生有以下五种情况:三个整数都是4:;有两个整数是4,另一个不是4:;只有一个数是4,另两个不是4:;三个数都是2或6:;有两个数是2或6,另一个数是奇数:故得.(2).(3).19.解法一:(1)证明:∵PB=PC,∴PO⊥BC.又∵平面PBC⊥平面ABCD,平面PBC∩平面ABCD=BC,∴PO⊥平面ABCD.在梯形ABCD中,可得Rt△ABO≌Rt△BCD,∴∠BEO=∠OAB+∠DBA=∠DBC+∠DBA=90°,即AO⊥BD.∵PA在平面ABCD内的射影为AO,∴PA⊥BD.(2)证明:取PB的中点N,连接CN.∵PC=BC, ∴CN⊥PB.①∴AB⊥BC,且平面PBC⊥平面ABCD.∴AB⊥平面PBC.∵AB平面PAB,∴平面PBC⊥平面PAB.②由①、②知CN⊥平面PAB,连接DM、MN,则由MN∥AB∥CD,得四边形MNCD为平行四边形,∴DM⊥平面PAB.∵DC⊥BC,且平面PBC⊥平面ABCD,∴DC⊥平面PBC,∵PC平面PBC.∴DC⊥PC.∴∠PCB为二面角P-DC-B的平面角.∵三角形PBC是等边三角形,∴∠PCB=60°,即二面角P-DC-B的大小为60°.∵DM平面PAD,∴平面PAD⊥平面PAB.解法二:取BC的中点O,因为三角形PBC是等边三角形,由侧面PBC⊥底面ABCD,得PO⊥底面ABCD.以BC中点O为原点,以BC所在直线为x轴,过点O与AB平行的直线为y轴,建立空间直角坐标系O-xyz.(1)证明:∵CD=1,则在直角梯形中,AB=BC=2,在等边三角形PBC中,.(2)证明:,(3)显然所夹角等于所示二面角的平面角.20. 解:(1)设M(y02,y0),直线ME的斜率为k(k>0),则直线MF的斜率为-k,所以直线ME的方程为y-y0=k(x-y02).....所以直线EF的斜率为定值.(2)当∠EMF=90°时,∠MAB=45°,所以k=1.∴直线ME的方程为:y-y0=x-y02..同理可得.设重心消去得21.解:(1). ∴f(1)=1.∴节点为(1,1).∴1=-2×1+c.∴c=3.∴直线l的方程为y=-2x+3.(2).(3)令,由得,在上是减函数,在上是增函数...22.解: EF//CB,∽.FG是圆的切线.故FG=EF.23.解:(Ⅰ).为圆心是,半径是1的圆,为中心是坐标原点,焦点在轴上,长半轴长是8,短半轴长是3的椭圆.(Ⅱ)当时,,故,为直线.精品文档. M到的距离 .从而当时,d取得最小值.24.解:(1)时,得,解得,所以,;(2)时,得,解得,所以,;(3)时,得,解得,所以,无解.综上,不等式的解集为.。
2024届山东省济南市高三新高考第一次模拟考试物理试题

2024届山东省济南市高三新高考第一次模拟考试物理试题一、单选题 (共6题)第(1)题如图所示,真空中的正四面体边长为,在两点分别固定电荷量大小均为的异种电荷,已知静电力常量为,无穷远处电势为零。
则下列说法正确的是( )A.点的电场强度大小为B.点和点电场强度大小相等、方向相反C.将一个带电粒子沿直线从点移动到点,电势能先增大后减小D.将一带电粒子从无穷远处移动到点,电场力做功为零第(2)题如图所示,在同一竖直平面内,一根均匀的橡皮筋跨过光滑的定滑轮P,一端固定在O点,另一端跟一可视为质点且质量为m的物块相连,橡皮筋的原长等于OP,受到的弹力跟伸量成正比(比例系数为k),先让物块静止在粗糙水平面上的位置A点,AP竖直向上,此时物块挤压水平面,然后给物块一个初速度,物块恰能运动到B点,重力加速度为g,橡皮筋一直在弹性限度内,C点是AB的中点。
下列关于物块向右运动的说法正确的是( )A.物块受到的摩擦力一直在增大B.物块做匀减速运动C.物块经过C点时的速度等于D.物块经过C点时的速度大于第(3)题超声波加湿器利用水槽底部雾化器模块将电能转换成机械能,高频电信号由图甲电路产生,通过压电陶瓷转换成同频率的高频声信号,发出超声波。
两列超声波信号叠加后,会出现振动加强点,图乙为某时刻两列超声波在水中传播的波形图,分别为两列波的前端,已知声波在水中传播的速度为。
下列说法正确的是( )A.该超声波加湿器所发出的超声波信号频率为B.两列波传播稳定后,坐标原点O的振幅是C.沿x轴上的M、N两点间(包括M、N两点),振动加强点的位置有4个D.拔出图甲线圈中的铁芯,沿x轴上的M、N两点间振动加强点的个数减少第(4)题近年来,我国在新能源汽车领域取得了巨大的突破和发展。
目前,核能汽车处于试验阶段,车上主要搭载了核动力电池,利用原子核衰变释放的核能转化为电池的电能。
某种核动力电池利用了钚的衰变,衰变方程为,下列说法正确的是( )A.X为粒子B .该反应的发生需要吸收能量C.的结合能大于的结合能D.的原子核比的原子核更加稳定第(5)题铑106的半衰期约370天,衰变方程为,下列说法正确的是( )A.根据题中方程式无法判断X粒子的种类B.采取低温冷冻的措施可适当降低辐射风险和辐射剂量C.的比结合能比的比结合能大,衰变时释放能量D.任意370天中,1000个原子核将会有500个发生衰变第(6)题某发射星云可认为完全由氢原子构成,其发光机理可简化为:能量为12.09eV的紫外光子照射该星云时,会使其氢原子从基态跃迁到激发态,处于激发态的氢原子会辐射光子。
1. 《2024年高考数学模拟试题及答案》

1. 《2024年高考数学模拟试题及答案》一、选择题(本大题共 12 小题,每小题 5 分,共 60 分)1、已知集合 A ={x |-2 < x < 3},B ={x | x² 5x + 4 <0},则A ∩ B =()A {x | 1 < x < 3}B {x |-2 < x < 1}C {x | 1 < x < 4}D {x |-2 < x < 4}2、复数 z =(1 + i)(2 i)在复平面内对应的点位于()A 第一象限B 第二象限C 第三象限D 第四象限3、已知向量 a =(1, 2),b =(m, -1),若 a ⊥ b,则 m =()A -2B 2C -1/2D 1/24、某中学高一年级有学生 1000 人,高二年级有学生 800 人,高三年级有学生 600 人,现采用分层抽样的方法从该校抽取一个容量为 n的样本,若从高二年级抽取了 80 人,则 n 的值为()A 200B 240C 280D 3205、函数 f(x) = log₂(x² 4x + 3)的单调递增区间是()A (∞, 1)B (∞, 2)C (2, +∞)D (3, +∞)6、若直线 l₁:ax + 2y + 6 = 0 与直线 l₂:x +(a 1)y + a² 1= 0 平行,则 a =()A -1B 2C -1 或 2D 17、已知等差数列{aₙ}的前 n 项和为 Sₙ,若 a₁= 2,S₃= S₅,则公差 d =()A -2B 0C 2D 48、已知圆 C:(x 1)²+(y 2)²= 4 与直线 l:x y + 1 = 0 相交于 A,B 两点,则弦长|AB| =()A 2√2B 2√3C 4D 69、一个几何体的三视图如图所示,则该几何体的体积为()(正视图和侧视图是等腰三角形,底边为 4,高为 4;俯视图是边长为 4 的正方形)A 32B 64C 128/3D 256/310、设函数 f(x) =sin(ωx +φ)(ω > 0,|φ| <π/2)的最小正周期为π,且f(π/8) =√2/2,则()A f(x)在(0, π/2)上单调递减B f(x)在(π/8, 3π/8)上单调递增C f(x)在(0, π/2)上单调递增D f(x)在(π/8, 3π/8)上单调递减11、已知函数 f(x) = x³ 3x,若过点 M(2, t)可作曲线 y = f(x)的三条切线,则实数 t 的取值范围是()A (-6, -2)B (-4, -2)C (-6, 2)D (0, 2)12、已知双曲线 C:x²/a² y²/b²= 1(a > 0,b > 0)的左、右焦点分别为 F₁,F₂,过 F₂作双曲线 C 的一条渐近线的垂线,垂足为 H,若|F₂H| = 2a,则双曲线 C 的离心率为()A √5B 2C √3D √2二、填空题(本大题共 4 小题,每小题 5 分,共 20 分)13、已知函数 f(x) = 2sin(2x +π/6),则 f(x)的最小正周期为_____14、若 x,y 满足约束条件 x +y ≥ 1,x y ≥ -1,2x y ≤ 2,则 z= x + 2y 的最大值为_____15、已知抛物线 y²= 2px(p > 0)的焦点为 F,点 A(4, 2)在抛物线上,且|AF| = 5,则 p =_____16、已知数列{aₙ}满足 a₁= 1,aₙ₊₁= 2aₙ + 1,则 a₅=_____三、解答题(本大题共 6 小题,共 70 分)17、(10 分)在△ABC 中,角 A,B,C 所对的边分别为 a,b,c,已知 a = 3,b = 5,c = 7、(1)求角 C 的大小;(2)求△ABC 的面积18、(12 分)已知数列{aₙ}是等差数列,a₁= 1,a₃+ a₅=14、(1)求数列{aₙ}的通项公式;(2)设数列{bₙ}满足 bₙ = aₙ × 2ⁿ,求数列{bₙ}的前 n 项和 Sₙ19、(12 分)如图,在四棱锥 P ABCD 中,底面 ABCD 是平行四边形,PA ⊥底面 ABCD,PA = AB = 2,AD = 4,∠BAD = 60°(1)证明:BD ⊥平面 PAC;(2)求二面角 P BD A 的余弦值20、(12 分)某工厂生产甲、乙两种产品,已知生产每吨甲产品要用 A 原料 3 吨,B 原料 2 吨;生产每吨乙产品要用 A 原料 1 吨,B原料 3 吨。
河北省衡水市第二中学2024届高三高考模拟一数学试题(含答案解析)

河北省衡水市第二中学2024届高三高考模拟一数学试题学校:___________姓名:___________班级:___________考号:___________一、单选题1.已知集合{}2120,{23},P xx x Q x m x m P Q =--≤=≤≤-=∅ ∣∣,则实数m 的取值范围是().A .{0m m <∣或4}m >B .{04}m m <<∣C .{3mm <∣或4}m >D .{34}mm <<∣2.某同学统计最近5次考试成绩,发现分数恰好组成一个公差不为0的等差数列,设5次成绩的平均分数为x ,第60百分位数为m ,当去掉某一次的成绩后,4次成绩的平均分数为y ,第60百分位数为n .若y x =,则()A .m n >B .m n=C .m n<D .m 与n 大小无法判断3.吹气球时,气球的体积V (单位:L )与半径r (单位:dm )之间的关系是343V r π=.当4L 3V π=时,气球的瞬时膨胀率为()A .1dm /L 4πB .1dm /L3C .3L /dmD .4L /dmπ4.设实数x ,y 满足22154x y +=)A .B .2-C .D .前三个答案都不对5.记数列{}n a 的前n 项和为n S ,设甲:{}n a 是公比不为1的等比数列;乙:存在一个非零常数t ,使1n S t ⎧⎫+⎨⎬⎩⎭是等比数列,则()A .甲是乙的充要条件B .甲是乙的充分不必要条件C .甲是乙的必要不充分条件D .甲是乙的既不充分也不必要条件6.六氟化硫,化学式为6SF ,在常压下是一种无色、无臭、无毒、不燃的稳定气体,有良好的绝缘性,在电器工业方面具有广泛用途.六氟化硫分子结构为正八面体结构(正八面体每个面都是正三角形,可以看作是将两个棱长均相等的正四棱锥将底面粘接在一起的几何体).如图所示,正八面体E ABCD F --的棱长为a ,下列说法中正确的个数有()①此八面体的表面积为2;②异面直线AE 与BF 所成的角为45 ;③此八面体的外接球与内切球的体积之比为④若点P 为棱EB 上的动点,则AP CP +的最小值为.A .1个B .2个C .3个D .4个7.在ABC V 中,2AB AC =,AD 是A ∠的平分线,交BC 于点D ,且AC tAD =,则t 的取值范围是A .3,4⎛⎫+∞ ⎪⎝⎭B .3,14⎛⎫⎪⎝⎭C .1,2⎛⎫+∞ ⎪⎝⎭D .1,12⎛⎫⎪⎝⎭8.已知,,(1,)a b c ∈+∞,且e 9ln11,e 10ln10,e 11ln 9a b c a b c ===,则,,a b c 的大小关系为()A .a b c >>B .c a b >>C .b c a>>D .c b a>>二、多选题9.下列四个命题正确的是()A .若1i 1z +-=,则1i z --的最大值为3B .若复数12,z z满足12122,2,1z z z z ==+=,则12z z -=C .若()sin sin C A AB A AB B AC C P λλ⎛⎫ ⎪=+∈ ⎪⎝⎭R,则点P 的轨迹经过ABC V 的重心D .在ABC V 中,D 为ABC V 所在平面内一点,且1132+= AD AB AC ,则16BCD ABDS S =△△10.由倍角公式2cos 22cos 1x x =-可知,cos 2x 可以表示为cos x 的二次多项式.一般地,存在一个()*n n ∈N 次多项式()110n n n n n P t a t a t a --=+++ (0a ,1a ,…,n a ∈R ),使得()cos cos n nx P x =,这些多项式()n P t 称为切比雪夫(P .L .Tschebyscheff )多项式.运用探究切比雪夫多项式的方法可得()A .()3343P t t t=-+B .()424881P t t t =-+C.1sin 544+︒=D.1cos546︒=11.已知n S 是数列{}n a 的前n 项和,且21n n S S n +=-+,则下列选项中正确的是().A .121n n a a n ++=-(2n ≥)B .22n n a a +-=C .若10a =,则1004950S =D .若数列{}n a 单调递增,则1a 的取值范围是11,43⎛⎫- ⎪⎝⎭三、填空题12.已知:平面l αβ= ,A l ∈,B l ∈,4AB =,C β∈,CA l ⊥,3AC =,D α∈,DB l ⊥,3.DB =直线AC 与BD 的夹角是60︒,则线段CD 的长为.13.数列{}满足()2*114,13n n n a a a a n N +==-+∈,则122017111a a a +++ 的整数部分是.14.极线是高等几何中的重要概念,它是圆锥曲线的一种基本特征.对于圆222x y r +=,与点()00,x y 对应的极线方程为200x x y y r +=,我们还知道如果点()00,x y 在圆上,极线方程即为切线方程;如果点()00,x y 在圆外,极线方程即为切点弦所在直线方程.同样,对于椭圆22221x y a b +=,与点()00,x y 对应的极线方程为00221x x y y a b +=.如上图,已知椭圆C :22143x y +=,()4,P t -,过点P 作椭圆C 的两条切线PA ,PB ,切点分别为A ,B ,则直线AB 的方程为;直线AB 与OP 交于点M ,则sin PMB ∠的最小值是.四、解答题15.在数列{}n a 中,已知321212222n n a a a a n -++++= .(1)求数列{}n a 的通项公式;(2)在数列{}n a 中的1a 和2a 之间插入1个数11x ,使1112,,a x a 成等差数列;在2a 和3a 之间插入2个数2122,x x ,使221223,,,a x x a 成等差数列;…;在n a 和1n a +之间插入n 个数12,,,n n nn x x x ,使121,,,,,n n n nn n a x x x a + 成等差数列,这样可以得到新数列{}1112212233132334:,,,,,,,,,,,n n b a x a x x a x x x a a ,设数列{}n b 的前n 项和为n S ,求55S (用数字作答).16.已知椭圆2222:1(0)x y C a b a b+=>>的右焦点为F ,左顶点为A ,短轴长为点31,2⎛⎫ ⎪⎝⎭.(1)求椭圆C 的方程;(2)过点F 的直线l (不与x 轴重合)与C 交于,P Q 两点,直线,AP AQ 与直线4x =的交点分别为,M N ,记直线,MF NF 的斜率分别为12,k k ,证明:12k k ⋅为定值.17.在四棱锥P ABCD -中,底面ABCD 是边长为2的正方形,E 是BC 的中点,点F 在棱AD 上,且PA AD ⊥,2cos5PAE ∠=-,PA =(1)若平面PAB ⋂平面PCD l =,证明://l 平面ABCD ;(2)求平面PEF 与平面PCD 的夹角的余弦值的最大值.18.近年来,购买盲盒成为当下年轻人的潮流之一,为了引导青少年正确消费,国家市场监管总局提出,盲盒经营行为应规范指引,经营者不能变相诱导消费.盲盒最吸引人的地方,是因为盒子上没有标注,只有打开才会知道自己买到了什么,这种不确定性的背后就是概率.几何分布是概率论中非常重要的一个概率模型,可描述如下:在独立的伯努利(Bernoulli )试验中,若所考虑事件首次出现,则试验停止,此时所进行的试验次数X 服从几何分布,事件发生的概率p 即为几何分布的参数,记作()~X G p .几何分布有如下性质:分布列为()()11k P X k p p -==-,1,2,,,k n =⋅⋅⋅⋅⋅⋅,期望()()1111k k E X k p p p+∞-==-⋅=∑.现有甲文具店推出四种款式不同、单价相同的文具盲盒,数量足够多,购买规则及概率规定如下:每次购买一个,且买到任意一种款式的文具盲盒是等可能的.(1)现小嘉欲到甲文具店购买文具盲盒.①求他第二次购买的文具盲盒的款式与第一次购买的不同的概率;②设他首次买到两种不同款式的文具盲盒时所需要的购买次数为Y ,求Y 的期望;(2)若甲文具店的文具盲盒的单价为12元,乙文具店出售与甲文具店款式相同的非盲盒文具且单价为18元.小兴为了买齐这四种款式的文具,他应选择去哪家文具店购买更省钱,并说明理由.19.牛顿在《流数法》一书中,给出了代数方程的一种数值解法——牛顿法.具体做法如下:如图,设r 是()0f x =的根,首先选取0x 作为r 的初始近似值,若()f x 在点00(,())x f x 处的切线与x 轴相交于点1(,0)x ,称1x 是r 的一次近似值;用1x 替代0x 重复上面的过程,得到2x ,称2x 是r 的二次近似值;一直重复,可得到一列数:012,,,,,n x x x x .在一定精确度下,用四舍五入法取值,当()*1,N n n x x n -∈近似值相等时,该值即作为函数()f x 的一个零点r .(1)若32()33f x x x x =++-,当00x =时,求方程()0f x =的二次近似值(保留到小数点后两位);(2)牛顿法中蕴含了“以直代曲”的数学思想,直线常常取为曲线的切线或割线,求函数()e 3x g x =-在点(2,(2))g 处的切线,并证明:23ln31e <+;(3)若()(1ln )h x x x =-,若关于x 的方程()h x a =的两个根分别为1212,()x x x x <,证明:21e e x x a ->-.参考答案:题号12345678910答案C CACBBADABCBC题号11答案AC1.C【分析】化简集合A 后,根据P Q =∅ 分类讨论即可.【详解】由{}2120[3,4]P xx x =--≤=-∣,P Q =∅ ,当Q =∅时,需满足23m m >-,解得3m <;当Q ≠∅时,需满足34m m ≥⎧⎨>⎩,解得4m >,综上3m <或4m >.故选:C 2.C【分析】依题意不妨设这5次的分数从小到大分别为a 、a d +、2a d +、3a d +、4a d +()0,0a d >>,即可求出x 、m ,要使去掉一个数据之后平均数不变,则去掉的一定是2a d +,从而求出n ,即可判断.【详解】依题意不妨设这5次的分数从小到大分别为a 、a d +、2a d +、3a d +、4a d +()0,0a d >>,所以()123425x a a d a d a d a d a d =++++++++=+,又560%3⨯=,所以第60百分位数为23522a d a d m a d +++==+,要使4次成绩的平均分数为y 且y x =,则去掉的数据一定是2a d +,即还剩下a 、a d +、3a d +、4a d +()0,0a d >>,又460% 2.4⨯=,所以第60百分位数为3n a d =+,因为0d >,所以n m >.故选:C 3.A【分析】气球膨胀率指的是气球体积变化的值与半径变化值之间的比值,即rV∆∆,但此题所求的时瞬时变化率,故需要利用导数求解.【详解】因为343V r π=,所以r =,所以12333143r π-⎛⎫'=⨯ ⎪⎝⎭,所以,当43V π=时,12123333314313131433434344r ππππππ-⎛⎫⎛⎫⎛⎫⎛⎫'=⨯=⨯=⨯= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭dm /L .故选:A 4.C【分析】转化为动点到两定点之间距离和,再利用焦点三角形的性质可求最小值.,点(,)P x y 是椭圆22:154x y C +=上的点,设(1,0),(1,0),(0,1)E F A -,如图.记题中代数式为M ,则||||||||||M PA PF PA PE AE =+=+≥=等号当点E ,A ,P 依次共线时取得.因此所求最小值为故选:C.5.B【分析】利用等比数列前n 项和公式,结合充分条件、必要条件的定义判断即得.【详解】设数列{}n a 的首项和公比分别为1a ,(1)≠q q ,则111n n q S a q -=⋅-,取11a t q =-,得1n n S q t +=,显然数列{1}n S t +是等比数列;反之,取1t =,0n a =,此时11n S +=,数列{1}nS t+为等比数列,而{}n a 不是等比数列,所以甲是乙的充分不必要条件.故选:B 6.B【分析】对①:计算出一个三角形面积后乘8即可得;对②:借助等角定理,找到与AE 平行,与BF 相交的线段,计算即可得;对③:借助外接球与内切球的性质计算即可得;对④:空间中的距离和的最值问题可将其转化到同意平面中进行计算.【详解】对①:由题意可得2284S =⨯=表,故①正确;对②:连接AC ,取AC 中点O ,连接OE 、OF ,由题意可得OE 、OF 为同一直线,A 、E 、C 、F 四点共面,又AE EC CF FA ===,故四边形AECF 为菱形,故//AE CF ,故异面直线AE 与BF 所成的角等于直线CF 与BF 所成的角,即异面直线AE 与BF 所成的角等于60CFB ∠=,故②错误;对③:由四边形ABCD 为正方形,有2222222AC BC AB EC AE a =+=+=,故四边形AECF 亦为正方形,即点O 到各顶点距离相等,即此八面体的外接球球心为O,半径为2aR =,设此八面体的内切球半径为r ,则有2112233E ABCD F E ABCD V S r V a ---=⨯==⨯⨯⨯表r =,则此八面体的外接球与内切球的体积之比为33R r ⎛⎫⎪⎛⎫== ⎪⎝⎭对④:将AEB 延EB 折叠至平面EBC中,如图所示:则在新的平面中,A 、P 、C 三点共线时,AP CP +有最小值,则()min 22AP CP a +=⨯=,故④错误.故选:B.【点睛】关键点点睛:本题④中,关键点在于将不共面的问题转化为同一平面的问题.7.A【解析】在ABC V 中,2AB AC =,AD 是A ∠的平分线,由角平分线性质可得2BD ABCD AC==,利用cos cos BAD CAD ∠=∠结合余弦定理化简可得22212CD AC AD =-,再代入cos CAD ∠的式子中消去CD ,通过AC tAD =,化简整理得出3cos 4CAD t∠=,即可得到t 的取值范围.【详解】在ABC V 中,2AB AC =,AD 是A ∠的平分线,∴由角平分线的性质可得2BD ABCD AC==,BAD CAD ∠=∠,在ABD △中,由余弦定理得222cos 2AB AD BD BAD AB AD +-∠=⋅,在ACD 中,由余弦定理得222cos 2AC AD CD CAD AC AD +-∠=⋅,∴22222222AB AD BD AC AD CD AB AD AC AD+-+-=⋅⋅,化简得22222AD AC CD =-,即22212CD AC AD =-,∴22223332cos 2244AD AC AD CD AD CAD AC AD AC AD AC t+-∠===⋅⋅而0,2CAD π⎛⎫∠∈ ⎪⎝⎭,故()3cos 0,14CAD t ∠=∈,∴3,4t ⎛⎫∈+∞ ⎪⎝⎭.故选:A.【点睛】本题考查了三角形内角平分线的性质以及余弦定理在解三角形中的应用,考查了转化能力与计算能力,属于中档题.8.D【分析】构造函数()()e ,1,xf x x x∞=∈+,利用导数讨论其单调性,将问题转化为比较,,,再转化为比较9ln11,10ln10,11ln 9,构造函数()()20ln g x x x =-,利用导数讨论其单调性,利用单调性即可得答案.【详解】由题知,e e e 9ln11,10ln10,11ln 9a b ca b c ===,记()()e ,1,x f x x x ∞=∈+,则()()21e x x f x x-'=,当()1,x ∈+∞时,()0f x '>,()f x 单调递增,故比较,,a b c 的大小关系,只需比较,,的大小关系,即比较9ln11,10ln10,11ln 9的大小关系,记()()20ln ,1g x x x x =->,则()20ln 1g x x x=-+-',记()20ln 1h x x x =-+-,则()21200h x x x=--<',所以()h x 在()1,+∞上单调递减,又()220338ln 81ln 8ln e 0822h =-+-=-<-<,所以,当()8,x ∈+∞时,()0h x <,()g x 单调递减,所以()()()11109g g g <<,即9ln1110ln1011ln 9<<,所以()()()f a f b f c <<,所以a b c <<.故选:D【点睛】本题难点在于构造函数()()e ,1,xf x x x∞=∈+,将问题转化成比较,,的大小关系后,需要再次构造函数()()20ln ,1g x x x x =->,对学生观察问题和分析问题的能力有很高的要求,属于难题.9.ABC【分析】A 根据复数模的几何意义及圆的性质判断;B 利用复数的运算和模的运算求解即可;C 结合重心的性质进行判断;D 利用平面向量基本定理,判断出D 点位置,进而可求.【详解】对A ,由1i 1z +-=的几何意义,知复数z 对应的动点Z 到定点(1,1)-的距离为1,即动点Z 的轨迹以(1,1)-为圆心,1为半径的圆,1i z --表示动点点Z 的轨迹以(1,1)的距离,由圆的性质知:max |i |z --==113,A 正确;对B ,设i,i,(,,,R)z m n z c d m n c d =+=+∈12,因为12122,2,1z z z z ==+=,所以,m n c d +=+=222244,,m c n d +=+=1,所以mc nd +=-2,所以12()()i z z m c n d -=-+-====,B 正确;对C ,由正弦定理的sin sin AC C AB B ⋅=⋅,即||sin ||sin AC C AB B =,()sin sin sin AB AC AP AB AC AB B AC C AB B λλ⎛⎫ ⎪∴==+ ⎪⎝⎭,设BC 中点为E ,如图:则AB +AC =2AE,则||sin AP AE AB Bλ=2 ,由平面向量的共线定理得,,A P E 三点共线,即点P 在边BC 的中线上,故点P 的轨迹经过ABC V 的重心,C 正确;对D ,如图由已知点D 在ABC V 中与AB 平行的中位线上,且靠近BC 的三等分点处,故有,,ABD ABC ACD ABC BCD S S S S S ===1123 1111236ABC ABC S S ⎛⎫--= ⎪⎝⎭ ,所以13BCD ABDS S =△△,D 错误.故选:ABC 10.BC【分析】根据两角和的余弦公式,以及二倍角的正余弦公式化简可得3cos34cos 3cos x x x =-,根据定义即可判断A 项;根据二倍角公式可推得()424cos 8cos 8cos 1P x x x =-+,即可得出B 项;根据诱导公式以及A 的结论可知,3cos544cos 183cos18︒=︒-︒,2sin 54cos 362cos 181︒=︒=︒-.平方相加,即可得出25cos 188︒+=,进而求出C 项;假设D 项成立,结合C 项,检验即可判断.【详解】对于A 项,()cos3cos 2cos 2cos sin 2sin =+=-x x x x x x x ()222cos 1cos 2cos sin x x x x=--()()222cos 1cos 2cos 1cos x x x x =---34cos 3cos x x =-.由切比雪夫多项式可知,()3cos3cos x P x =,即()33cos 4cos 3cos P x x x =-.令cos t x =,可知()3343P t t t =-,故A 项错误;对于B 项,()cos 4cos 22x x =⨯()2222cos 2122cos 11x x =-=⨯--428cos 8cos 1x x =-+.由切比雪夫多项式可知,()4cos 4cos x P x =,即()424cos 8cos 8cos 1P x x x =-+.令cos t x =,可知()424881P t t t =-+,故B 项正确;对于C 项,因为36218︒=⨯︒,54318︒=⨯︒,根据A 项3cos34cos 3cos x x x =-,可得3cos 544cos 183cos18︒=︒-︒,2cos 362cos 181︒=︒-.又cos 36sin 54︒=︒,所以2222cos 36cos 54sin 54cos 541︒+︒=︒+︒=,所以,()()22324cos 183cos182cos 1811︒-︒+︒-=.令cos180t =︒>,可知()()223243211t tt -+-=,展开即可得出642162050t t t -+=,所以42162050t t -+=,解方程可得258t ±=.因为cos18cos320t =︒>︒,所以258t =,所以,2cos 362cos 181︒=︒-512184=⨯=,所以,sin 54cos36︒=︒=C 项正确;对于D 项,假设1cos546︒=,因为1sin 544︒=,则22221si c s n o 5445⎫︒=+≠⎪⎪⎝⎭⎝⎭︒+,显然不正确,故假设不正确,故D 项错误.故选:BC.【点睛】方法点睛:根据题意多项式的定义,结合两角和以及二倍角的余弦公式,化简可求出()()34cos ,cos P x P x ,换元即可得出()()34,P t P t .11.AC【分析】对于A ,由21n n S S n +=-+,多写一项,两式相减即可得出答案.对于B ,由121n n a a n ++=-(2n ≥),多递推一项,两式相减即可得出答案少了条件2n ≥.对于C ,由分析知22n n a a +-=,所以{}n a 奇数项是以10a =为首项,2为公差的等差数列,偶数项是以21a =为首项,2为公差的等差数列,由等差数列得前n 项和公式即可得出答案.对于D ,因为数列{}n a 单调递增,根据1234n a a a a a <<<<< ,即可求出1a 的取值范围.【详解】对于A ,因为21n n S S n +=-+,当()2121n n n S S n -≥=-+-,,两式相减得:121n n a a n ++=-(2n ≥),所以A 正确.对于B ,因为121n n a a n ++=-(2n ≥),所以()+122+11=21n n a a n n ++=-+,两式相减得:22n n a a +-=(2n ≥),所以B 不正确.对于C ,21n n S S n +=-+ ,令1n =,则211S S =-+,1211a a a +=-+,因为10a =,所以21a =.令2n =,则324S S =-+,112324a a a a a ++=--+,所以32a =.因为22n n a a +-=(2n ≥),而312a a -=,所以22n n a a +-=.所以{}n a 奇数项是以10a =为首项,2为公差的等差数列.偶数项是以21a =为首项,2为公差的等差数列.则:()()10012399100139924100=+++S a a a a a a a a a a a =+++++++++ 5049504950025012=495022⨯⨯⎛⎫⎛⎫=⨯+⨯+⨯+⨯ ⎪ ⎪⎝⎭⎝⎭,所以C 正确.对于D ,21n n S S n +=-+,令1n =,则211S S =-+,1211a a a +=-+,则2121a a =-+又因为+12=21n n a a n +++,令1n =则23=3a a +,所以()3211=332122a a a a -=--+=+,同理:()4311=552223a a a a -=-+=-+,()5411=772324a a a a -=--+=+,因为数列{}n a 单调递增,所以1234n a a a a a <<<<< ,解12a a <得:113a <,解23a a <得:114a >-,解34a a <得:114a <,解45a a <得:114a >-,解56a a <得:114a <,所以1a 的取值范围是11,44⎛⎫- ⎪⎝⎭,所以D 不正确.故选:AC.【点睛】本题考查的是等差数列的知识,解题的关键是利用121n n a a n ++=-,得出{}n a 的奇数项、偶数项分别成等差数列,考查学生的逻辑推理能力和运算求解能力,属于难题.12.5【分析】作//AE BD 且AE BD =,连接,ED EC ,则CAE ∠(或其补角)为异面直线,AC BD 所成的角,所以60CAE ∠=︒或120CAE ∠=︒,证明DE EC ⊥,先求出EC ,再得CD .【详解】如图,作//AE BD 且AE BD =,连接,ED EC ,则CAE ∠(或其补角)为异面直线,AC BD 所成的角,所以60CAE ∠=︒或120CAE ∠=︒,因为//AE BD 且AE BD =,所以ABDE 是平行四边形,所以//DE AB ,4DE AB ==,因为,AB AC AB BD ⊥⊥,所以,ED AC ED AE ⊥⊥,AC AE A ⋂=,所以BD ⊥平面AEC ,CE ⊂平面AEC ,所以ED CE ⊥,3AC AE ==,若60CAE ∠=︒,则3CE =,5CD ==,若120CAE ∠=︒,则23sin 60CE =⨯︒=,CD =故答案为:5【点睛】本题考查异面直线所成角的应用,都可空间两点间的距离.解题关键是作出异面直线所成的角.构造三角形,在三角形中求线段长.13.2【详解】因为()2*114,13n n n a a a a n N +==-+∈,所以211(1)0n n n n n a a a a a ++-=->⇒>,数列{}单调递增,所以1(11)0n n n a a a +-=->,所以111(1)1111n n n n na a a a a +--=--=,所以121122111111111111()()()11111n n n n n S a a a a a a a a a a a =+++=-+-++-=------ ,所以20172017131m S a ==--,因为143a =,所以22223444131313133133133()1,()1,()12,33999818181a a a =-+==-+==-+> ,所以20172016201542a a a a >>>>> ,所以201711a ->,所以20171011a <<-,所以201512331a <-<-,因此m 的整数部分是2.点睛:本题考查了数列的综合应用问题,其中解答中涉及到数列的通项公式,数列的裂项求和,数列的单调性的应用等知识点的综合应用,着重考查了学生分析问题和解答问题的能力,以及推理与运算能力,试题有一定的难度,属于难题,本题的借助数列递推关系,化简数列为111111n n na a a +=---,再借助数列的单调性是解答的关键.14.103tyx -+-=(或330x ty -+=);【分析】(1)根据已知直接写出直线AB 的方程;(2)求出cos ,OP n →→〈〉=sin PMB ∠利用基本不等式求解.【详解】解:(1)由题得AB :4143x ty-+=,即103ty x -+-=,(2)()4,OP t →=-,3k AB t→=,∴AB →的方向向量(),3n t = ,所以cos ,OP nOP n OP n→→→→→→⋅〈〉==sin PMB ∠==,即()min sin PMB ∠=.故答案为:103tyx -+-=.15.(1)2n n a =(2)14337【分析】(1)根据数列的前n 项和求数列的通项公式,一定要分1n =和2n ≥讨论.(2)首先弄清楚新数列前55项的构成,再转化为错位相减法求和.【详解】(1)当1n =时,12a =;当2n ≥时,3312211121222222222n n n n n n a a a a a a a a a ----⎛⎫⎛⎫=++++-++++ ⎪ ⎪⎝⎭⎝⎭()2212n n =--=,所以122nn a -=⇒2n n a =,2n ≥.当1n =时,上式亦成立,所以:2n n a =.(2)由()123155n n ⎡⎤+++++-=⎣⎦ ⇒10n =.所以新数列前55项中包含数列的前10项,还包含,11x ,21x ,22x ,31x ,32x ,L ,98x ,99x .且12112a a x +=,()23212222a a x x ++=,()3431323332a a x x x +++=,()91091929992a a x x x ++++=.所以()()()239101255121029222a a a a a a S a a a +++=+++++++123910357191122a a a a a ++++=+ .设123935719T a a a a =++++ 1239325272192=⨯+⨯+⨯++⨯ 则234102325272192T =⨯+⨯+⨯++⨯ ,所以()1239102322222192T T T -=-=⨯+⨯+++-⨯ 101722=-⨯-.故:101722T =⨯+.所以1010955172211228211433722S ⨯+=+⨯=⨯+=.【点睛】关键点点睛:本题的关键是要弄清楚新数列前55项的构成.可先通过列举数列的前几项进行观察得到规律.16.(1)22143x y +=;(2)证明见解析.【分析】(1)由题意得b =,将点3(1,)2代入椭圆的方程可求得2a 的值,进而可得椭圆的方程;(2)设:1l x ty =+,1(P x ,1)y ,2(Q x ,2)y ,联立直线l 和椭圆的方程,可得122634ty y t +=-+,122934y y t =-+,直线PA 的方程为11(2)2y y x x =++,令4x =,得116(4,2y M x +,同理226(4,)2y N x +,由斜率公式计算即可.【详解】(1)因为2b =b =,再将点31,2⎛⎫ ⎪⎝⎭代入22213x y a +=得21314a +=,解得24a =,故椭圆C 的方程为22143x y +=;(2)由题意可设()()1122:1,,,,l x ty P x y Q x y =+,由221143x ty x y =+⎧⎪⎨+=⎪⎩可得()2234690t y ty ++-=,易知0∆>恒成立,所以12122269,3434t y y y y t t +=-=-++,又因为−2,0,所以直线PA 的方程为=+2,令4x =,则1162=+y y x ,故1164,2y M x ⎛⎫⎪+⎝⎭,同理2264,2y N x ⎛⎫⎪+⎝⎭,从而()()111212126266,413333y x y y k k ty ty +===-++,故()()()212121222212121222363643419189333993434y y y y t k k t t ty ty t y y t y y t t -+====-+++++--+++为定值.17.(1)证明见解析(2)14【分析】(1)证明出//CD 平面PAB ,利用线面平行的性质可得出//CD l ,再利用线面平行的判定定理可证得结论成立;(2)计算出cos PAB ∠的值,以A 为坐标原点,AB 、AD 所在直线分别为x 、y 轴,建立空间直角坐标系,设()0,,0F a ()02a ≤≤,利用空间向量法结合二次函数的基本性质可求得平面PEF 与平面PCD 的夹角的余弦值的最大值.【详解】(1)证明:因为四边形ABCD 正方形,所以//AB CD .因为CD ⊂/平面PAB ,AB ⊂平面PAB ,所以//CD 平面PAB .又因为CD ⊂平面PCD ,平面PAB ⋂平面PCD l =,所以//CD l .因为l ⊂/平面ABCD ,CD ⊂平面ABCD ,所以//l 平面ABCD .(2)解:由题意可得AE ==,PE =因为四边形ABCD 是正方形,所以AB AD ⊥.又因为PA AD ⊥,PA AB A = ,PA 、AB ⊂平面PAB ,所以AD ⊥平面PAB .因为//AD BC ,所以⊥BC 平面PAB ,因为PB ⊂平面PAB ,所以,BC PB⊥.则PB ===.所以,222cos 2PA AB PB PAB PA AB +-∠==⋅以A 为坐标原点,AB 、AD 所在直线分别为x 、y 轴,建立如图所示的空间直角坐标系.点P 到平面yAz的距离为()cos π1AP PAB -∠=,点P 到平面xAy2==.则()1,0,2P -,()2,2,0C ,()0,2,0D ,()2,1,0E ,设()0,,0F a ()02a ≤≤,则()3,2,2PC =-,()2,0,0CD =- ,设平面PCD 的法向量为()111,,x n y z = ,则1111322020PC n x y z CD n x ⎧⋅=+-=⎪⎨⋅=-=⎪⎩,取11y =,可得()0,1,1n = .设平面PEF 的法向量为()222,,m x y z = ,()3,1,2PE =-,()1,,2PF a =- ,则22222232020PE m x y z PF m x ay z ⎧⋅=+-=⎪⎨⋅=+-=⎪⎩,取24y =,可得()22,4,31m a a =-- .设平面PEF 与平面PCD 的夹角为α,则cos m n m nα⋅==⋅ 令[]11,3a t +=∈,则cosα==.当1512t =时,211484013t t ⎛⎫-⨯+⎪⎝⎭取得最小值,最小值为143,所以cos α75a =.故平面PEF 与平面PCD 的夹角的余弦值的最大值为14.18.(1)①34;②73(2)应该去乙店购买非盲盒文具,理由见解析【分析】(1)①明确第二次只需买到其余的三种文具盲盒的任意一款即可求解;②结合已知由几何分布的性质即可求解.(2)由随机变量以及相应的均值结合几何分布的性质即可求解.【详解】(1)①由题意可知,当第一次购买的文具盲盒已经确定时,第二次只需买到其余的三种文具盲盒的任意一款即可,所以34p =;②设从第一次购买文具后直到购买到两种不同款式的文具盲盒所需要的购买次数为X ,则由题意可知3~4X G ⎛⎫ ⎪⎝⎭,又1Y X =+,所以()()()4711133E Y E X E X =+=+=+=.(2)由题意,在乙店买齐全部文具盲盒所花费的费用为18472⨯=元,设从甲店买齐四种文具盲盒所需要的购买次数为Z ,从第一次购买到1i -种不同款式的文具开始,到第一次购买到i 种不同款式的文具盲盒所需要的购买次数为随机变量i Z ,则5~4i i Z G -⎛⎫ ⎪⎝⎭,其中1,2,3,4i =,而1234Z Z Z Z Z =+++,所以()()()441234114425124533i i i E Z E Z Z Z Z E Z i===+++===+++=-∑∑,所以在甲店买齐全部文具盲盒所需费用的期望为()1210072E Z =>,所以应该去乙店购买非盲盒文具.19.(1)1.83(2)22e e 30x y ---=,证明见解析(3)证明见解析【分析】(1)根据题意分别计算出12,x x ,取2x 得近似值即为方程()0f x =的二次近似值;(2)分别求出(2)g ,(2)g ',即可写出函数()g x 在点(2,(2))g 处的切线方程;设2()ln 1,1ex m x x x =-->,证明出2()(e )m x m ≤,得出2(3)(e )m m <,即可证明;(3)先判断出1201e x x <<<<,然后辅助证明两个不等式()()()1e 1e 1e h x x x ≥-≤≤-和()(01)h x x x ≥<≤即可.【详解】(1)2()361f x x x '=++,当00x =时,(0)1f '=,()f x 在点(0,3)-处的切线方程为3y x +=,与x 轴的交点横坐标为(3,0),所以13x =,(3)46f '=,()f x 在点(3,54)处的切线方程为5446(3)y x -=-,与x 轴的交点为42(,0)23,所以方程()0f x =的二次近似值为1.83.(2)由题可知,2(2)e 3g =-,()e x g x '=,2(2)e g '=,所以()g x 在(2,(2))g 处的切线为22(e 3)e (2)y x --=-,即22e e 30x y ---=;设2()ln 1,1e x m x x x =-->,则211()em x x '=-,显然()m x '单调递减,令()0m x '=,解得2e x =,所以当2(1,e )x ∈时,()0m x '>,则()m x 在2(1,e )单调递增,当2(e ,)x ∈+∞时,()0m x '<,则()m x 在2(e ,)+∞单调递减,所以2222e ()(e )ln e 10em x m ≤=--=,所以2(3)(e )m m <,即2233ln 310ln 31e e --<⇔<+.(3)由()ln h x x x x =-,得()ln h x x '=-,当01x <<时,ℎ′>0;当1x >时,ℎ′<0,所以ℎ在0,1上单调递增,在1,+∞上单调递减,所以1x =是ℎ的极大值点,也是ℎ的最大值点,即()max ()11h x h ==,又0e x <<时,()0h x >,e x >时,()0h x <,所以当方程()h x a =有两个根时,必满足1201e x x <<<<;曲线()y h x =过点()1,1和点()e,0的割线方程为1(e)1e y x =--,下面证明()()()1:e 1e 1e h x x x ≥-≤≤-,设()()()()1e 1e 1eu x h x x x =--≤≤-,则()1e 11ln ln lne e 1u x x x -⎛⎫=-+=-'- ⎪-⎝⎭,所以当1e 11e x -<<时,()0u x '>;当1e 1e e x -<<时,()0u x '<,所以()u x 在1e 11,e -⎛⎫ ⎪⎝⎭上单调递增,()()10u x u ≥=;在1e 1e ,e -⎛⎫ ⎪⎝⎭上()u x 单调递减,()()e 0u x u ≥=,所以当1e x ≤≤时,()0u x ≥,即()1()e (1e)1ef x x x ≥-≤≤-(当且仅当1x =或e x =时取等号),由于21e x <<,所以()()221e 1e a f x x =>--,解得2e e x a a >-+;①下面证明当01x <≤时,()h x x ≥,设()()ln ,01n x h x x x x x =--<≤=,因为ln 0x ≤,所以当01x <≤时,()f x x ≥(当且仅当1x =时取等号),由于101x <<所以()11a h x x =>,解得1x a ->-,②①+②,得21e e x x a ->-.【点睛】关键点睛:第三问的难点在于辅助构造出两个函数不等式,这样再利用函数单调性,得到相关不等式,然后进行估计21x x -的范围.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高考模拟试题一年级__________ 班级_________ 学号_________ 姓名__________ 分数____总分 一 二 三 四一、填空题(共0题,题分合计0分)二、多项选择题(共22题,题分合计22分)1.绿色植物在暗室中生长可以消耗的物质是 A .ATP B .葡萄糖 C .C02 D .O 22.控制下列生物性状的遗传物质的传递,不遵循孟德尔遗传定律的有A .大肠杆菌中抗青霉素性状的遗传B .紫荣莉花枝条的绿色和白色性状的遗传C .人类的苯丙酮尿症的遗传D .玉米果皮和种皮性状的遗传3.根据现代对ATP 代谢的研究,反应式:ATPADP+Pi+能量。
不能简单地看作是一个可逆反应,下面是这个结论的有关理由,其中正确的是 A .酶1和酶2是不同的B .酶1和酶2催化的反应,在细胞内的场所是不同的 C. ADP 和Pi 这两种物质是不能被重复利用的D .酶1催化的反应释放出的能量不能用到酶2催化的反应中去4.下列有关免疫的论述正确的是A. 胸腺在特异性免疫中的作用是诱导淋巴干细胞发育分化成T 淋巴细胞 B .已免疫的机体,在再次接受相同刺激时所发生的反应叫做过敏反应C. 记忆B 淋巴细胞受到抗原刺激后会迅速克隆出大量的能够产生相应抗体的B 淋巴细胞得分 阅卷人得分 阅卷人D.巨噬细胞.T细胞.B细胞.记忆细胞.效应B细胞均能识别抗原5.细胞周期包括G1.S.G2和M四个时期,在S期进行下列工作实践可取得良好效果的是A.植物组织培养B.作物(如小麦.水稻)诱变育种C.肿瘤的某些药物治疗D.作物的人工授粉6.鉴定脱脂奶粉是否为伪劣产品,需要的化学试剂是A.斐林试剂 B. 双缩脲试剂 C. 碘-碘化钾试剂 D. 苏丹III试剂7.以基因型为AABB和aabb二倍体植物为亲本,欲培育出基因型为AAaaBBbb的植株,可能的途径有A.F1不断自交 B.以秋水仙素处理F1C.利用F1的花药进行离体培养 D.运用植物体细胞杂交技术培育8.科学家将含人的抗胰蛋白酶基因的DNA片断,注射到羊的受精卵中,该受精卵发育的羊能分泌含抗胰蛋白酶的奶。
这一过程涉及A.DNA按照碱基互补配对原则自我复制B.RNA以自身为模板自我复制C.DNA以其一条链为模板合成RNAD.按照RNA密码子的排列顺序合成蛋白质9.基因工程中获取真核细胞中的目的基因时,一般是用人工合成基因的方法。
这一方法涉及:A.以信使RNA为模板反转录合成互补的单链DNAB.根据已知的蛋白质的氨基酸序列,推测信使RNA的碱基序列C.按照RNA密码子的排列顺序合成蛋白质D.用限制酶将供体DNA切成许多片段并转入受体细胞进行复制10.下列关于病毒与人类关系的描述中,正确的是有A.病毒必须从人体内环境中获得营养物质,营寄生生活B.SARS病毒的遗传物质为RNA,容易出现变种,故疫苗研制工作比较困难C.爱滋病病毒的核酸种类与人体细胞相同,故易感染人体D.在转基因工程中,某些病毒能携带某些基因进入受体细胞11.番茄的果皮红色对黄色显性。
番茄甲自交全部结红果,番茄乙自交全部结黄果,现将甲的花粉接到乙的柱头上。
下列叙述正确的是A.上述杂交所得果实全呈红色 B.上述杂交所得果实全呈黄色C.番茄甲肯定是纯合子 D.番茄乙肯定是纯合子12.下列与微生物生长.代谢.繁殖有关的说法中,不正确的是A.细菌的细胞质里悬浮着多种颗粒状的内含物,但无细胞器B.当病毒侵入宿主细胞以后,只能合成一种类型的蛋白质C.与酶合成的调节相比,酶活性的调节是一种快速精细的调节方式D.连续培养有利于微生物尽快将代谢产物释放到培养基中13.下列实例中,涉及基因重组的是A.我国著名育种专家袁隆平利用杂交技术培育出的超级水稻品种B.英国科学家利用细胞核移植技术克隆出小绵羊C.荷兰科学家将人乳高铁蛋白基因移植到牛体内并获得成功D.乘宇宙飞船上过太空的辣椒种子结出的果实较平常的大一倍以上14.关于下列微生物所需要的氮源物质的说法正确的是①分子态氮②氨③铵盐④硝酸盐⑤尿素⑥牛肉膏⑦蛋白胨A.③④等是微生物最常用的氮源B.固氮微生物把②转变为①C.⑤⑥⑦既是氮源又是碳源D.氮源用于合成蛋白质.核酸及其他含氮物质15.如图所示是一个渗透作用的实验装置,在烧杯内装有蒸馏水,在下部封有半透膜的长颈漏斗内装有麦芽糖和NaCl混合溶液,已知半透膜上的小孔只能允许水分子及比水分子小的物质通过。
实验开始时,漏斗内的液面略高于烧杯内蒸馏水的液面,过一段时间后,用新制的氢氧化铜溶液和硝酸银溶液分别检验蒸馏水中的物质。
在整个实验过程中,所观察到的现象是A.漏斗内的液面下降B.烧杯内液体遇硝酸银溶液有白色沉淀C.漏斗内的液面上升D.烧杯内溶液遇新制的氢氧化铜溶液经加热后有砖红色沉淀NaCl16.下列关于构成细胞的化合物功能的叙述,错误的是A.生命活动都由蛋白质调节 B.干种子因缺乏自由水不能萌发C.多糖是细胞的能源物质 D.生物的遗传物质是DNA17.有关细胞全能性的叙述,正确的是A.受精卵在自然条件下能使后代细胞形成完整个体,因此全能性最高B.生物体内已分化的细胞也表达出了全能性C.卵细胞与受精卵一样,细胞未分化,全能性很高D.植物细胞离体培养,在一定条件下能表现出全能性18.下列行为与垂体分泌的激素有关的是A.照顾幼仔行为 B.巨人症C.性行为 D.蜜蜂采蜜行动19.美国得克萨斯州科学家在2002年2月14日宣布,他们已经培育出世界上第一只克隆猫。
这只名为CC的小猫毛色花白,看上去完全不像生养它的花斑猫妈妈,也不完全像为它提供细胞的基因猫妈妈。
正确的解释可能是A.表现型是基因型和环境共同作用的结果B.发生了基因重组所造成的结果C.提供卵细胞的雌猫细胞质基因的调控作用D.生养它的花斑猫妈妈的基因的调控作用20.下列高科技成果中,根据基因重组原理进行的是A.我国科学家袁隆平利用杂交技术培育出超级水稻B.我国科学家将苏云金杆菌的某些基因移植到棉花体内,培育出抗虫棉C.我国科学家通过返回式卫星搭载种子培育出太空椒D.我国科学家通过体细胞克隆技术培养出克隆牛21.按自由组合定律遗传的具有两对相对性状的纯合体杂交,F2中出现的性状重组类型的个体占总数的比例可能为:A.3\8B.5\8C.1\16D.1\822.在DNA粗提取的实验过程中,两次向烧杯中加入蒸馏水的作用是:A.稀释血液、冲洗样品B.使血细胞破裂C.降低NACl溶液的浓度D.冲洗DNA,去掉杂质得分阅卷人三、单项选择题(共157题,题分合计157分)1.下列对真核生物基因结构的认识中,不正确的是A. 编码区完整转录并加工后形成的信使RNA,参与蛋白质合成B. 启动转录和终止转录的有关信息就包括在编码区中C. 真核生物基因中的平均核苷酸数量比原核生物基因中的核苷酸数量要多得多D. 编码区转录后,内含子的切除和外显子的拼接是在细胞核中进行的2.某科学家在研究细胞膜运输物质时发现有下列四种关系,分别用四种曲线表示。
在研究具体的物质X时,发现与曲线②和④相符,试问:细胞膜运输物质X的方式是A. 主动运输B. 自由扩散C. 内吞和外排D. 无法判断3.下列有关人体内蛋白质代谢过程的叙述,下正确的是A.在健康成年人体内,蛋白质的合成和分解是平衡的B.在一个健康人的尿液中尿素的含量较高,说明其食物结构中含有较多的蛋白质C.丙氨酸、甘氨酸等氨基酸不能通过转按基再作用合成D.通过脱氨基作用生成的氨必须转变成尿素才能排出体外4.甲培养基中含有15N标记尿嘧啶核糖核苷酸,乙培养基中含有3H标记胸腺嘧啶脱氧核苷酸,分别用这两种培养基培养正在发育的人体细胞,你认为正在发育的细胞对这两种物质的吸收量A.甲大于乙 B. 乙大于甲 C. 甲等于乙 D. 无法确定5.对细胞内各种生物膜的结构和组成的叙述错误的是A.主要由蛋白质、脂类和少量糖类组成B.磷脂双分子层是各种生物膜的基本骨架C.不同生物膜上的蛋白质的种类和数量不同D.内质网膜能生成高尔基体膜,说明两者化学组成完全相同6.用大肠杆菌生产干扰素,需要应用的生物工程的组合是①基因工程②细胞工程③发酵工程④酶工程A. ①②③B. ①②④C. ①③④D. ②③④7.核酸是一切生物的遗传物质,小麦的遗传物质由几种核苷酸组成A. 2种B. 4种C. 5种D. 8种8.如果你在载玻片上用钢笔点上一个直径约为1mm的小圆点,在光镜下选用6倍目镜和5倍物镜进行观察,则视野内所看到的小圆点A.面积约为30mm2 B. 直径约为3cm C. 面积扩大3 D. 直径约为11mm9.ATP与DNA共有的组成成分为A.核糖和磷酸基 B. 脱氧核糖和磷酸基C. 腺嘌呤和磷酸基D. 腺嘌呤和高能磷酸键10.下列哪种细胞器直接作用于核膜的形成A. DNAB. RNAC. 内质网D. 高尔基体11.雄蛙和雌蛙的性染色体组成分别为XY和XX,假定一只正常的XX蝌蚪在外界环境的影响下,变成了一只能生育的雄蛙,用此雄蛙与正常雌蛙交配,问:其子代中的雌蛙(♀)和雄蛙(♂)的比例是A.♀:♂=1:1 B. ♀ : ♂=2 : 1 C. ♀ : ♂=3 : 1 D. ♀: ♂=1 : 012.在一个随机交配的中等大小的种群中,经调查发现控制某性状的基因型只有两种:AA基因型的频率为60%,Aa基因型的频率为40%。
试问:随机交配繁殖一代后AA基因型的个体占A. 2/3 B. 1/3 C. 36% D. 48%13.关于微生物对环境的净化作用的正确叙述是A.微生物可分解各种有机污染物B.净化污水的微生物为多种厌氧型生物C.微生物把污水中的有机物分解成CO2和H2O及含有N、P的无机盐D.纤维素比人畜粪尿更易于被微生物分解14.如图所示为面包霉体内合成氨基酸的途径。
若在发酵工程中利用面包霉来大量合成氨基酸A,应采取的最佳措施是A.改变面包霉的细胞膜通透性B.在高温高压下进行发酵C.对面包霉进行诱变处理,选育出不能合成②酶的菌种D.对面包霉进行诱变处理,选育出不能合成③酶的菌种15.现有二种固体培养基,已知其配制时所加的成分如下用这两种培养基分别去分离土壤中A.甲培养基适于分离自养型自生固氮菌;乙培养基适于分离异养型自生固氮菌B.甲培养基适于分离酵母菌;乙培养基适于分离真菌C.甲培养基适于分离异养型自生固氮菌;乙培养基适于分离自养型自生固氮菌D.甲培养基适于分离自养型共生细菌;乙培养基适于分离异养型共生固氮菌16.对三株大小、长势相同的植株分别进行如下处理:甲连续光照5h;l乙先光照1h,再在黑暗中1h,连续交替共10h:丙先光照5s,再在黑暗中5s,连续交替10h。
在其他条件相同情况下,光照结束时它们体内有机物含量是A. 丙 = 乙 > 甲 B.甲 = 乙 = 丙 C. 丙 > 甲 > 乙 D.甲 > 乙 > 丙17.下列不是染色体变异和基因突变的主要区别有A. 染色体结构变异是DNA上比较大的区段发生改变,而基因突变则是DNA分子上个别核苷酸的改变B.基因突变可发生回复突变,染色体结构变异则不能发生回复突变C.基因突变一般是微小突变,其遗传效应小,而染色体结构变异是较大的变异,其遗传效应大D.染色体结构变异可通过细胞学检查进行鉴别,而基因突变则不能鉴别18.火灾常给森林带来较大危害,但是在某些国家有时对寒带地区森林中的残枝落叶等进行有限度的人工火烧,以对森林进行资源管理,这种人工火烧的主要目的是A.消灭森林病虫害,形成烟雾 B.提高森林的蓄水能力C.刺激林木种子的萌发 D.加速生态系统的分解过程19.生活在不同纬度地区的动物,其动物个体大小是不一样的。
