博弈论作业.
博弈论作业——精选推荐

博弈论作业1.海盗分金中如果假设需要同意的人超过半数提议才能通过,则理性结局又会是什么?如果200个人参加(只要半数即可通过)又将如何?500人呢?解:半数即可通过——倒推分析结果如下(1000,0)(999,0,1)(999,0,1,0)(998,0,1,0,1)下一步的分钱方案中,只需要把上一步得钱非0的强盗的得钱数改为0,而其它强盗则反之。
进而有非0和0的间隔分布,除了提出方案的强盗外,其它得钱非0的强盗得到1块钱。
因此有200个强盗分1000个金币的情形为 ( X, 0, 1, …, 0 )可得X=901因此有500个强盗分1000个金币的情形为 ( X, 0, 1, …, 0 )可得X=751超过半数才可通过——倒推结果如下(0,1000)(999,1,0)(997,0,2,1)(997,0,1,0,2)因此,5个强盗分1000个金币的情形为(997,0,1,0,2)2.在无限期的鲁宾斯坦模型中,假设分割只能是0.01的整数倍,即X只能为0,0.01;0.02;…….0.99或1,求δ=0.5和δ非常接近于1时的子博弈完美均衡(假设两个人的折现因子相同)两个人要分一块冰淇淋,甲将分得冰淇淋的x份额(x ≥ 0),乙将得到1-x的份额(1-x ≥ 0)。
两人进行轮流出价。
首先,甲提出一个划分方法(x,1-x),乙可以接受或拒绝这个提议,如果他接受了,则博弈结束,他们按照这种划分去切割冰淇淋;如果乙拒绝这个提议,那么他会提出一个划分方法(y,1-y),甲可以接受或者拒绝,博弈过程将这个方式持续进行下去,直到他们达成一个协议。
每当协议的达成拖延时,他们的得益会有一个折扣(贴现),两人的贴现因子由iδ (0<iδ<1)表示。
这种折扣代表了讨价还价的成本。
其它条件相同,对参与者而言,达成一个协议所需的时间越长,冰淇淋就会越小。
两人贴现相同,如果假定1δ=2δ=δ的话,上述讨价还价博弈的唯一的均衡结果将会是(1 / (1 + δ), δ / (1 + δ))。
博弈论例题

选择题在一个零和博弈中,如果玩家A的收益为+5,那么玩家B的收益必然是:A. +5B. -5(正确答案)C. 0D. 无法确定下列哪个策略组合是纳什均衡的一个特征?A. 每个玩家都选择对自己最不利的策略B. 给定其他玩家的策略,每个玩家都无法通过改变自己的策略来改善境遇(正确答案)C. 所有玩家都获得相同的收益D. 博弈中不存在优势策略在囚徒困境中,如果两个囚徒都选择合作,他们的总刑期将:A. 比都选择背叛时更长B. 比都选择背叛时更短(正确答案)C. 与都选择背叛时相同D. 无法比较博弈论中的“支付矩阵”用于表示:A. 玩家的先后顺序B. 不同策略组合下各玩家的收益或损失(正确答案)C. 博弈的公平程度D. 玩家之间的信任度在重复博弈中,以下哪种行为可能促进合作?A. 一次性博弈后的报复威胁(正确答案)B. 总是选择背叛C. 忽视对方之前的行动D. 不考虑未来收益主导策略(Dominant Strategy)是指:A. 无论对手如何选择,都能带来最大收益的策略(正确答案)B. 只有在对手选择特定策略时才有效的策略C. 收益总是低于其他策略的策略D. 博弈中最后一个被采用的策略在双人零和博弈中,如果增加了一个可选策略给双方,那么:A. 纳什均衡一定不存在B. 纳什均衡可能增加、减少或保持不变(正确答案)C. 纳什均衡数量一定增加D. 纳什均衡数量一定减少在拍卖博弈中,第二价格密封拍卖(Vickrey Auction)的赢家支付的是:A. 自己报出的最高价B. 所有报价中的第二高价(正确答案)C. 拍卖品的真实价值D. 拍卖前设定的底价。
“博弈论”习题及参考答案

《博弈论》习题一、单项选择题1.博弈论中,局中人从一个博弈中得到的结果常被称为()。
A. 效用B. 支付C. 决策D. 利润2.博弈中通常包括下面的内容,除了()。
A.局中人B.占优战略均衡C.策略D.支付3.在具有占优战略均衡的囚徒困境博弈中()。
A.只有一个囚徒会坦白B.两个囚徒都没有坦白C.两个囚徒都会坦白D.任何坦白都被法庭否决了4.在多次重复的双头博弈中,每一个博弈者努力()。
A.使行业的总利润达到最大B.使另一个博弈者的利润最小C.使其市场份额最大D.使其利润最大5.一个博弈中,直接决定局中人支付的因素是()。
A. 策略组合B. 策略C. 信息D. 行动6.对博弈中的每一个博弈者而言,无论对手作何选择,其总是拥有惟一最佳行为,此时的博弈具有()。
A.囚徒困境式的均衡B.一报还一报的均衡C.占优策略均衡D.激发战略均衡7.如果另一个博弈者在前一期合作,博弈者就在现期合作;但如果另一个博弈者在前一期违约,博弈者在现期也违约的策略称为()。
A.一报还一报的策略B.激发策略C.双头策略D.主导企业策略8.在囚徒困境的博弈中,合作策略会导致()。
A.博弈双方都获胜B.博弈双方都失败C.使得先采取行动者获胜D.使得后采取行动者获胜9.在什么时候,囚徒困境式博弈均衡最可能实现()。
A. 当一个垄断竞争行业是由一个主导企业控制时B.当一个寡头行业面对的是重复博弈时C.当一个垄断行业被迫重复地与一个寡头行业博弈时D. 当一个寡头行业进行一次博弈时10.一个企业采取的行为与另一个企业在前一阶段采取的行为一致,这种策略是一种()。
A.主导策略B.激发策略C.一报还一报策略D.主导策略11.关于策略式博弈,正确的说法是()。
A. 策略式博弈无法刻划动态博弈B. 策略式博弈无法表明行动顺序C. 策略式博弈更容易求解D. 策略式博弈就是一个支付矩阵12.下列关于策略的叙述哪个是错误的():A. 策略是局中人选择的一套行动计划;B. 参与博弈的每一个局中人都有若干个策略;C. 一个局中人在原博弈中的策略和在子博弈中的策略是相同的;D. 策略与行动是两个不同的概念,策略是行动的规则,而不是行动本身。
博弈论作业

博弈论作业博弈论作业一、 下面的得益矩阵表示博弈方之间的一个静态博弈。
该博弈有没有纯策略纳什均衡?博弈的结果是什么?博弈方 2L C R博弈 T 方 M 1 B 答:此博弈有两个纳什均衡:1、ML 得益(3,4)2、TR 得益(4,2)二、 求出下图中得益矩阵所表示的博弈中的混合策略纳什均衡与得益。
博弈方 2L R博弈 T 方 B 1答:(一)求混合策略均衡1、博弈方1的概率P则对博弈方2而言,有1×P +2(1-P )=2×P +0(1-P )2-P =2PP =2/3当P ﹤2/3,2-P ﹥2P ,则q ﹡=1是最合适的策略,即选择L 。
当P =2/3,2-P =2P ,则q ﹡∈(0,1)是最适合反应。
当P ﹥2/3,2-P ﹤2P ,则q ﹡=0是最适合策略,即选择R 。
2、给定博弈方2的概率q则对博弈方1而言,有2×q +0(1-q )=1×q +3(1-q )2q =3-2qq =3/4当q ﹤3/4,2q ﹤3-2q ,则P ﹡=0是最合适的策略,即选择B 。
当q =3/4,2q =3-2q ,则P ﹡∈(0,1)是最适合反应。
当q ﹥3/4,2q ﹥3-2q ,则P ﹡=1是最适合策略,即选择T 。
所以:混合策略的均衡点为(2/3,3/4)。
(二)得益:∪1=2×P ×q +0×P ×(1-q)+1×(1-P)×q+3(1-P)(1-q)=2×2/3×3/4+1×1/3×3/4+3×1/3×1/4=3/2∪2=1×P ×q +2×P ×(1-q)+2×(1-P)×q+0(1-P)(1-q)=1×2/3×3/4+2×2/3×1/4+2×1/3×3/4=4/3三、 设一四阶段两博弈方之间的动态博弈如下图所示。
§博弈论作业题4道

企业战略决策和管理中的博弈作业:一、优利公司和埃克森公司是生产一种非常精密的摄象机的仅有的两家公司。
他们在商业杂志上投入或高或低的广告费。
他们的赢得矩阵如下所示:(单位:万美元)埃克森低高┏━━━━━━┳━━━━━┓低┃1200,1300┃1100,1200┃优利┣━━━━━━╋━━━━━┫高┃1300,1200┃1200,1100┃┗━━━━━━┻━━━━━┛1、优利公司在商业杂志上的广告支出是高还是低?答:在优利公司广告支出低的情况下:如果埃克森公司也支出低,优利公司可赢得1200万,如果埃克森公司支出高,优利公司则赢得1100万。
在优利公司广告支出高的情况下:如果埃克森公司支出低,优利公司可赢得1300万,如果埃克森公司支出高,优利公司则赢得1200万。
因此,优利公司为获得尽可能高的利润,只有选择广告支出高的策略。
2、埃克森公司的广告支出是高还是低?答:在埃克森公司广告支出低的情况下:优利公司支出低,埃克森公司可赢得1300万,如果优利公司支出高,埃克森公司则赢得1200万;在埃克森公司广告支出高时: 如果优利公司支出低,埃克森公司赢得1200万,如果优利公司支出高,埃克森公司仅赢得1100万。
因此,埃克森公司应选择低的广告支出策略。
3、每家公司是否都存在占优(最优)策略?答:埃克森公司与优利公司都存在各自的占优策略。
二、两家肥皂制造商:富特纳公司和梅森公司,在即将到来的广告战中或侧重于报纸,或侧重于杂志。
他们的赢得矩阵如下所示:(单位:万美元)梅森报纸杂志┏━━━━━┳━━━━━┓报纸┃800,900┃700,800┃富特纳┣━━━━━╋━━━━━┫杂志┃900,800┃800,700┃┗━━━━━┻━━━━━┛1、对每家公司来说是否存在占优策略?如果存在,各是什么?答:富特纳公司与梅森公司都存在占优策略。
富特纳公司广告投入侧重于杂志,梅森公司侧重于报纸。
2、每家公司的利润各是多少?答:富特纳公司与梅森公司在各自占优策略下的利润均为900万美元。
博弈论作业——精选推荐
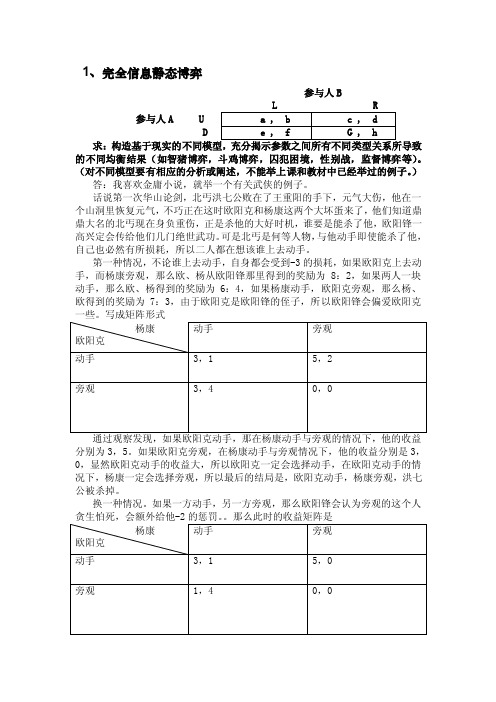
1、完全信息静态博弈参与人B参与人A UD求:的不同均衡结果(如智猪博弈,斗鸡博弈,囚犯困境,性别战,监督博弈等)。
(对不同模型要有相应的分析或阐述,不能举上课和教材中已经举过的例子。
)答:我喜欢金庸小说,就举一个有关武侠的例子。
话说第一次华山论剑,北丐洪七公败在了王重阳的手下,元气大伤,他在一个山洞里恢复元气,不巧正在这时欧阳克和杨康这两个大坏蛋来了,他们知道鼎鼎大名的北丐现在身负重伤,正是杀他的大好时机,谁要是能杀了他,欧阳锋一高兴定会传给他们几门绝世武功。
可是北丐是何等人物,与他动手即使能杀了他,自己也必然有所损耗,所以二人都在想该谁上去动手。
第一种情况,不论谁上去动手,自身都会受到-3的损耗,如果欧阳克上去动手,而杨康旁观,那么欧、杨从欧阳锋那里得到的奖励为8:2,如果两人一块动手,那么欧、杨得到的奖励为6:4,如果杨康动手,欧阳克旁观,那么杨、欧得到的奖励为7:3,由于欧阳克是欧阳锋的侄子,所以欧阳锋会偏爱欧阳克分别为3,5。
如果欧阳克旁观,在杨康动手与旁观情况下,他的收益分别是3,0,显然欧阳克动手的收益大,所以欧阳克一定会选择动手,在欧阳克动手的情况下,杨康一定会选择旁观,所以最后的结局是,欧阳克动手,杨康旁观,洪七公被杀掉。
换一种情况。
如果一方动手,另一方旁观,那么欧阳锋会认为旁观的这个人可见,如果欧阳克动手,那在杨康动手与旁观的情况下,他的收益分别为3,5。
如果欧阳克旁观,那在杨康动手与旁观的情况下,他的收益分别为1,0。
所以他一定会选择动手,对杨康来说,动手的收益分别为1,4,旁观的收益分别是0,0,所以他一定会选择动手,最终的结果一定是,欧、杨两人一起动手杀掉七公。
第三种情况。
由于洪七公是天下第一大帮丐帮帮主,杀掉他的人一定会得罪丐帮,得罪天下武林同道,以后难以立足江湖,自身会受到-3的损伤,此时的如果杨康选择旁观,那么它的收益分别为0,0。
所以杨康一定不会动手。
同样,欧阳克选择动手,收益分别是-1,1.如果选择旁观收益分别为1,0。
博弈论基础作业及答案

博弈论基础作业、名词解释纳什均衡占优战略均衡纯战略混合战略子博弈精炼纳什均衡贝叶斯纳什均衡精炼贝叶斯纳什均衡共同知识见PPT二、问答题1. 举出囚徒困境和智猪博弈的现实例子并进行分析。
囚徒困境的例子:军备竞赛;中小学生减负;几个大企业之间的争相杀价等等;以中小学生减负为例:在当前的高考制度下,给定其他学校对学生进行减负,一个学校最好不减负,因为这样做,可以带来比其他学校更高的升学率。
给定其他学校不减负,这个学校的最佳应对也是不减负。
否则自己的升学率就比其他学校低。
因此,不论其他学校如何选择,这个学校的最佳选择都是不减负。
每个学校都这样想,所以每个学校的最佳选择都是不减负,因此学生的负担越来越重。
请用同样的方法分析其他例子。
智猪博弈的例子:大企业开发新产品;小企业模仿;股市中,大户搜集分析信息,散户跟随大户的操作策略以股市为例:给定散户搜集资料进行分析,大户的最佳选择是跟随。
而给定散户跟随,大户的最佳选择是自己搜集资料进行分析。
但是不论大户是选择分析还是跟随,散户的最佳选择都是跟随。
因此如果大户和散户是聪明的,并且大户知道散户也是聪明的,那么大户就会预见到散户会跟随,而给定散户跟随,大户只有自己分析。
请用同样的方法分析其他例子。
2. 请用博弈论来说明“破釜沉舟”和“穷寇勿追”的道理。
破釜沉舟是一个承诺行动。
目的是要断绝自己的退路,让自己无路可退,让自己决一死战变得可以置信。
也就是说与敌人对决时,只有决一死战,这样才可以取得胜利。
否则,如果不破釜沉舟,那么遇到困难时,就很有可能退却,也就无法取得胜利。
穷寇勿追就是要给对方一个退路,由于有退路,对方就不会殊死抵抗。
否则,对方退无可退,只有坚决抵抗一条路,因而必然决一死战。
自己也会付出更大的代价。
3. 当求职者向企业声明自己能力强时, 企业未必相信。
但如果求职者拿出自 己的各种获奖证书时,却能在一定程度上传递自己能力强的信息。
这是为什么? 由于口头声明几乎没有成本,因此即便是能力差的求职者也会向企业声明自 己能力强。
博弈论作业及答案浙江财经大学张老师作业答案.docx

第 1 次作业1、考虑一个工作申请的博弈。
两个学生同时向两家企业申请工作,每家企业只有一个工作岗位。
工作申请规则如下: 每个学生只能向其中一家企业申请工 作;如果一家企业只有一个学生申请, 该学生获得工作; 如果一家企业有两个学 生申请,则每个学生获得工作的概率为 1/2 。
现在假定每家企业的工资满足:W1/2<W2<2W1 ,则问:a .写出以上博弈的战略式描述b .求出以上博弈的所有纳什均衡(包括混合策略均衡 )2、设古诺模型中有 n 家厂商。
q i 为厂商 i 的产量, Qq 1 q 2 L q n 为市场总产量。
P 为市场出清价格,且已知 PP(Q)aQ (当 Qa时,否则 P0 )。
假设厂商 i 生产产量 q i 的总成本为 C iC i(q i ) cq i,也就是说没有固定成本且各厂的边际成本都相同,为常数 c(ca) 。
假设各厂同时选择产量,该模型的纳什均衡是什么?当趋向于无穷大时博弈分析是否仍然有效?3、两 个 厂商 生产 一种 完 全同质的 商品 ,该 商品 的市 场需 求函数为Q 100 P ,设厂商 1 和厂商 2 都没有固定成本。
若他们在相互知道对方边际成本的情况下, 同时作出产量决策是分别生产 20 单位和 30 单位。
问这两个厂商的边际成本各是多少?各自的利润是多少?4、五户居民都可以在一个公共的池塘里放养鸭子。
每只鸭子的收益v 是鸭子总数N的函数,并取决于N是否超过某个临界值N;如果NN,收益v v( N )50N;如果NN时,v(N)0 。
再假设每只鸭子的成本为 c 2元。
若所有居民同时决定养鸭的数量,问该博弈的纳什均衡是什么?5、三对夫妻的感情状态可以分别用下面三个得益矩阵对应的静态博弈来表示。
问:这三个博弈的纳什均衡分别是什么?这三对夫妻的感情状态究竟如何?矩阵 1:妻子丈夫活着死了活着1, 1-1, 0死了0, -10,0矩阵 2:妻子活着死了丈夫活着0, 01,0死了0, 10,0矩阵 3:妻子活着死了丈夫活着-1,-11,0死了0, 10,06、两个个体一起参加某项工程,每个人的努力程度e i [0,1] (i1,2) ,成本为c(e i ) (i1,2) ,该项目的产出为f (e1,e2)。
博弈论习题2

《博弈论》习题一、选择题1. 博弈论中,局中人从一个博弈中得到的结果常被称为(B):A. 效用;B. 损益;C. 决策;D. 利润2. 下列关于策略的叙述哪个是错误的(C):A. 策略是局中人选择的一套行动计划;B. 参与博弈的每一个局中人都有若干个策略;C. 一个局中人在原博弈中的策略和在子博弈中的策略是相同的;D. 策略与行动是两个不同的概念,策略是行动的规则,而不是行动本身。
3. 囚徒困境说明(A):A. 双方都独立依照自己的利益行事,则双方不能得到最好的结果;B. 如果没有某种约束,局中人也可在(抵赖,抵赖)的基础上达到均衡;C. 双方都依照自己的利益行事,结果一方赢,一方输;D、每个局中人在做决策时,不需考虑对手的反应4. 一个博弈中,直接决定局中人损益的因素是(A):A. 策略组合;B. 策略;C. 信息;D. 行动。
5、策略式博弈,正确的说法是(B):A. 策略式博弈无法刻划动态博弈;B. 策略式博弈无法表明行动顺序;C. 策略式博弈更容易求解;D. 策略式博弈就是一个支付矩阵。
6. 下列有关策略和纳什均衡的叙述正确的有(ABCD):A. 纯策略是博弈方采取“要么做,要么不做”的策略形式;B. 混合策略是博弈方根据一组选定的概率,在两种或两种以上可能的行为中随机选择的策略;C. 有些博弈不存在纯策略纳什均衡,但存在混合策略的纳什均衡;D. 有些博弈既存在纯策略纳什均衡,也存在混合策略的纳什均衡。
7、古诺模型体现了寡头企业的( C )决策模型。
A 成本B 价格C 产量D 质量8、伯特兰德模型体现了寡头企业的什么决策模型。
BA 成本B 价格C 产量D 质量9、用囚徒困境来说明两个寡头企业的情况,说明了:(C)A、每个企业在做决策时,不需考虑竞争对手的反应B、一个企业制定的价格对其它企业没有影响C、企业为了避免最差的结果,将不能得到更好的结果D、一个企业制定的产量对其它企业的产量没有影响10、子博弈精炼纳什均衡(C ):A. 不是一个一般意义上的纳什均衡;B. 和纳什均衡没有什么关系;C. 要求某一策略组合在每一个子博弈上都构成一个纳什均衡;D. 要求某一策略组合在原博弈上都构成一个纳什均衡。
博弈论作业

第1次作业1、考虑一个工作申请的博弈。
两个学生同时向两家企业申请工作,每家企业只有一个工作岗位。
工作申请规则如下:每个学生只能向其中一家企业申请工作;如果一家企业只有一个学生申请,该学生获得工作;如果一家企业有两个学生申请,则每个学生获得工作的概率为1/2。
现在假定每家企业的工资满足:W1/2<W2<2W1,则问:a .写出以上博弈的战略式描述b .求出以上博弈的所有纳什均衡(包括混合策略均衡)2、设古诺模型中有n 家厂商。
i q 为厂商i 的产量,12n Q q q q =+++L 为市场总产量。
P 为市场出清价格,且已知Q a Q P P-==)((当a Q <时,否则0=P )。
假设厂商i 生产产量i q 的总成本为i i i i cq q C C ==)(,也就是说没有固定成本且各厂的边际成本都相同,为常数)(a c c <。
假设各厂同时选择产量,该模型的纳什均衡是什么?当趋向于无穷大时博弈分析是否仍然有效?3、两个厂商生产一种完全同质的商品,该商品的市场需求函数为P Q -=100,设厂商1和厂商2都没有固定成本。
若他们在相互知道对方边际成本的情况下,同时作出产量决策是分别生产20单位和30单位。
问这两个厂商的边际成本各是多少?各自的利润是多少?4、五户居民都可以在一个公共的池塘里放养鸭子。
每只鸭子的收益v 是鸭子总数N 的函数,并取决于N 是否超过某个临界值N ;如果N N<,收益N N v v -==50)(;如果N N ≥时,0)(≡N v 。
再假设每只鸭子的成本为2=c 元。
若所有居民同时决定养鸭的数量,问该博弈的纳什均衡是什么?5、三对夫妻的感情状态可以分别用下面三个得益矩阵对应的静态博弈来表示。
问:这三个博弈的纳什均衡分别是什么?这三对夫妻的感情状态究竟如何?6、两个个体一起参加某项工程,每个人的努力程度[0,1](1,2)i e i ∈=,成本为()(1,2)i c e i =,该项目的产出为12(,)f e e 。
博弈论作业

第1次作业1、考虑一个工作申请的博弈。
两个学生同时向两家企业申请工作,每家企业只有一个工作岗位。
工作申请规则如下:每个学生只能向其中一家企业申请工作;如果一家企业只有一个学生申请,该学生获得工作;如果一家企业有两个学生申请,则每个学生获得工作的概率为1/2。
现在假定每家企业的工资满足:W1/2<W2<2W1,则问:a .写出以上博弈的战略式描述b .求出以上博弈的所有纳什均衡(包括混合策略均衡)2、设古诺模型中有n 家厂商。
i q 为厂商i 的产量,12n Q q q q =+++L 为市场总产量。
P 为市场出清价格,且已知Q a Q P P-==)((当a Q <时,否则0=P )。
假设厂商i 生产产量i q 的总成本为i i i i cq q C C ==)(,也就是说没有固定成本且各厂的边际成本都相同,为常数)(a c c <。
假设各厂同时选择产量,该模型的纳什均衡是什么?当趋向于无穷大时博弈分析是否仍然有效?3、两个厂商生产一种完全同质的商品,该商品的市场需求函数为P Q -=100,设厂商1和厂商2都没有固定成本。
若他们在相互知道对方边际成本的情况下,同时作出产量决策是分别生产20单位和30单位。
问这两个厂商的边际成本各是多少?各自的利润是多少?4、五户居民都可以在一个公共的池塘里放养鸭子。
每只鸭子的收益v 是鸭子总数N 的函数,并取决于N 是否超过某个临界值N ;如果N N<,收益N N v v -==50)(;如果N N ≥时,0)(≡N v 。
再假设每只鸭子的成本为2=c 元。
若所有居民同时决定养鸭的数量,问该博弈的纳什均衡是什么?5、三对夫妻的感情状态可以分别用下面三个得益矩阵对应的静态博弈来表示。
问:这三个博弈的纳什均衡分别是什么?这三对夫妻的感情状态究竟如何?矩阵1: 妻子丈夫 活着 死了活着 1,1 -1,0死了 0,-1 0,0矩阵2: 妻子丈夫 活着 死了活着 0,0 1,0死了 0,1 0,0矩阵3: 妻子丈夫活着 死了 活着 -1,-1 1,0 死了0,10,06、两个个体一起参加某项工程,每个人的努力程度[0,1](1,2)i e i ∈=,成本为()(1,2)i c e i =,该项目的产出为12(,)f e e 。
博弈论基础作业及答案

博弈论基础作业一、名词解释纳什均衡占优战略均衡纯战略混合战略子博弈精炼纳什均衡贝叶斯纳什均衡精炼贝叶斯纳什均衡共同知识见PPT二、问答题1.举出囚徒困境和智猪博弈的现实例子并进行分析。
囚徒困境的例子:军备竞赛;中小学生减负;几个大企业之间的争相杀价等等;以中小学生减负为例:在当前的高考制度下,给定其他学校对学生进行减负,一个学校最好不减负,因为这样做,可以带来比其他学校更高的升学率。
给定其他学校不减负,这个学校的最佳应对也是不减负。
否则自己的升学率就比其他学校低。
因此,不论其他学校如何选择,这个学校的最佳选择都是不减负。
每个学校都这样想,所以每个学校的最佳选择都是不减负,因此学生的负担越来越重。
请用同样的方法分析其他例子。
智猪博弈的例子:大企业开发新产品;小企业模仿;股市中,大户搜集分析信息,散户跟随大户的操作策略以股市为例:给定散户搜集资料进行分析,大户的最佳选择是跟随。
而给定散户跟随,大户的最佳选择是自己搜集资料进行分析。
但是不论大户是选择分析还是跟随,散户的最佳选择都是跟随。
因此如果大户和散户是聪明的,并且大户知道散户也是聪明的,那么大户就会预见到散户会跟随,而给定散户跟随,大户只有自己分析。
请用同样的方法分析其他例子。
2.请用博弈论来说明“破釜沉舟”和“穷寇勿追”的道理。
破釜沉舟是一个承诺行动。
目的是要断绝自己的退路,让自己无路可退,让自己决一死战变得可以置信。
也就是说与敌人对决时,只有决一死战,这样才可以取得胜利。
否则,如果不破釜沉舟,那么遇到困难时,就很有可能退却,也就无法取得胜利。
穷寇勿追就是要给对方一个退路,由于有退路,对方就不会殊死抵抗。
否则,对方退无可退,只有坚决抵抗一条路,因而必然决一死战。
自己也会付出更大的代价。
3.当求职者向企业声明自己能力强时,企业未必相信。
但如果求职者拿出自己的各种获奖证书时,却能在一定程度上传递自己能力强的信息。
这是为什么?由于口头声明几乎没有成本,因此即便是能力差的求职者也会向企业声明自己能力强。
博弈论作业

第1次作业1、考虑一个工作申请的博弈。
两个学生同时向两家企业申请工作,每家企 业只有一个工作岗位。
工作申请规则如下:每个学生只能向其中一家企业申请工 作;如果一家企业只有一个学生申请, 该学生获得工作;如果一家企业有两个学 生申请,则每个学生获得工作的概率为 1/2。
现在假定每家企业的工资满足: W1/2VW2V2W1,则问:a.写出以上博弈的战略式描述b 求出以上博弈的所有纳什均衡(包括混合策略均衡)3、两个厂商生产一种完全同质的商品,该商品的市场需求函数为 Q 100P ,设厂商1和厂商2都没有固定成本。
若他们在相互知道对方 边际成本的情况下,同时作出产量决策是分别生产20单位和30单位。
问这两个 厂商的边际成本各是多少?各自的利润是多少?4、五户居民都可以在一个公共的池塘里放养鸭子。
每只鸭子的收益 _ v 是鸭 子总数N 的函数,并取决于N 是否超过某个临界值N ;如果N N ,收益 v v(N)50 N ;如果N N 时,v(N) 0。
再假设每只鸭子的 成本为c 2元。
若所有居民同时决定养鸭的数量,问该博弈的纳什均衡是什 么?矩阵2:5、三对夫妻的感情状态可以分别用下面三个得益矩阵对应的静态博弈来表 问:这三个博弈的纳什均衡分别是什么?这三对夫妻的感情状态究竟如何? 矩阵1:7示2、设古诺模型中有n 家厂商。
q i 为厂商i 的产 场总产量。
P 为市场出清价格,且已知P P(Q) a Q (当Q否则P 0)0假设厂商i 生产产量q j 的总成本为C i C i (q i ) cq i ,也就 是说没有固定成本且各厂的边际成本都相同, 为常数c(c a) o 假设各厂同时 选择产量,该模型的纳什均衡是什么?当趋向于无穷大时博弈分析是否仍然有 效?量。
量,量, Q q i q 2 L q n 为市a 时,矩阵3:6两个个体一起参加某项工程,每个人的努力程度 e [0,1] (i 1,2),成本为c (e )(i 1,2),该项目的产出为f (61,62)。
博弈论作业

-10,0 -8,-8
A
坦白
作业6
乙 不犯 甲 不犯 犯 不犯 犯 甲 犯
写出甲的策略集
作业7:田忌赛马
田忌和齐王各有三个马, 下马, 田忌和齐王各有三个马,上,中,下马,齐王 的上中下马分别比田忌的上中下马要好, 的上中下马分别比田忌的上中下马要好,但田 忌的上马比齐王的中马要好, 忌的上马比齐王的中马要好,田忌的中马比齐 王的下马要好。 王的下马要好。 赛三场,每马只能出场一次,胜一场得1分 赛三场,每马只能出场一次,胜一场得 分, 负一场得-1分 负一场得 分。 请写出博弈的标准式, 请写出博弈的标准式,博弈有没有纯策略纳什 均衡? 均衡
作业14 作业
两个厂商生产同质产品,厂商1先定价,厂 两个厂商生产同质产品,厂商 先定价, 先定价 商2后定价,分别为p1,p2 后定价,分别为 后定价 边际成本同为c 边际成本同为 q1=a1-b1p1+d1p2 q2=a2-b2p2+d2p1 求解SPNE 求解
作业15:三个厂商的动态博弈 作业 三个厂商的动态博弈
作业16:三个厂商的动态博弈 作业 三个厂商的动态博弈
P(Q)=a-Q,Q=q1+q2+q3,每个厂商的 每个厂商的 边际成本为C,没有固定成本。 边际成本为 ,没有固定成本。企业按照以 下顺序进行产出决策,( ,(1)企业1和企业 和企业2 下顺序进行产出决策,( )企业 和企业 同时决策产量q1, ,( ,(2)企业3观察 同时决策产量 ,q2,( )企业 观察 到q1,q2后,决策产量 。求解此博弈 , 后 决策产量q3。 的SPNE
a L R
T
1,1 0,0
L b
0,0 0,0
R
B
T
博弈论作业一

博弈论作业一一、判断题1.合作和协调是两个重要的社会问题,协调和合作的关键在于预期。
2.一项改革如果是帕累托改进,则该项改革肯定能够推行;如果仅仅是希克斯—卡而多意义上的改进,则改革不一定能够推行,3.如果交易成为零,则产权结构对资源配置效率无任何影响;如果交易成本为正,则产权结构一定会影响资源配置。
4.法律是一种激励机制,民法和刑法的关键区别在于外部性、制裁的可置信和复仇问题。
5.一个博弈一般由参与人、战略、信息、行动、支付和结果组成,而参与人、战略和支付称为博弈规则。
6.“人不犯我,我不犯人,人若犯我,我必犯人”是一个战略,而“犯人”是一个行动。
7.在单人决策中,一个人能够选择的行动越朵越好;在多人博弈中,一个人能够选择越多不一定越好。
8.在赤壁之战中,如果共同知识是成立的,则苦肉计不可行。
9.一个协议如果是纳什均衡,双方肯定会遵守协议。
因此,执行协议肯定对双方都有利。
10.如果一个博弈存在占优均衡,则均衡一定唯一的;如果剔除严格劣战略可解,均衡也是唯一的。
二简答题1.警察抓小偷. 在十字路口,小偷选择逃往左还是右边。
警察到达时不知道小偷逃跑方向。
他只能选择追过去还是不追。
警察能否抓到小偷完全取决于开始追的方向是正确还是错误,如果开始追对了方向则肯定能追到小偷,反之则不能。
如果警察停止追小偷他的支付为零,如果抓到小偷则支付为1,而如果追了没有追到支付为-1。
小偷被抓到则支付为-1,而没有抓到为1。
现在要求写出该博弈的战略式(标准式)。
2.a.求解所有的纳什均衡b.指出帕累托有效配置,该配置是否可以达到并说明理由。
3.a.该博弈是否有占优战略均衡?b.该博弈是否剔除严格劣战略可解?c.用以上博弈说明剔除严格劣战略的顺序与均衡结果无关。
4..丈夫(player 1)和妻子(player 2)必须独立决定出门是否带伞,下雨和不下雨的概率相同。
每个人的支付规则相同,如果下雨,带伞得-2,不带伞的得-5;如果不下雨,带伞的得-1,不带伞得1。
博弈论试题及答案

博弈论试题及答案一、单项选择题(每题2分,共20分)1. 博弈论的创始人是()。
A. 约翰·纳什B. 亚当·斯密C. 弗朗西斯·培根D. 约翰·梅纳德·凯恩斯答案:A2. 在零和博弈中,一方的损失等于另一方的收益,因此双方的总和为()。
A. 零B. 正数C. 负数D. 任意数答案:A3. 博弈论中,当参与者的策略相互依赖时,我们称之为()。
A. 独立博弈B. 合作博弈C. 非合作博弈D. 竞争博弈答案:C4. 囚徒困境中,如果两个参与者都选择合作,那么他们将()。
A. 获得最大收益B. 获得最小收益C. 获得中等收益D. 被惩罚答案:A5. 在博弈论中,纳什均衡是指()。
A. 所有参与者都选择最优策略B. 所有参与者都选择次优策略C. 至少有一个参与者选择最优策略D. 至少有一个参与者选择次优策略答案:A6. 博弈论中的“混合策略”是指参与者()。
A. 随机选择策略B. 总是选择最优策略C. 总是选择次优策略D. 总是选择固定策略答案:A7. 博弈论中的“完全信息”意味着()。
A. 所有参与者都知道所有可能的策略B. 所有参与者都不知道任何策略C. 至少有一个参与者不知道所有策略D. 至少有一个参与者不知道其他参与者的策略答案:A8. 在博弈论中,如果参与者的收益只取决于他们自己的选择,而与其他参与者的选择无关,则这种博弈被称为()。
A. 零和博弈B. 非零和博弈C. 合作博弈D. 非合作博弈答案:B9. 博弈论中的“重复博弈”是指()。
A. 博弈只进行一次B. 博弈进行有限次C. 博弈进行无限次D. 博弈进行任意次数答案:C10. 在博弈论中,如果参与者可以做出承诺,并且这些承诺是可信的,则这种博弈被称为()。
A. 有限博弈B. 无限博弈C. 有承诺博弈D. 无承诺博弈答案:C二、多项选择题(每题3分,共15分)1. 以下哪些是博弈论的基本概念?()A. 纳什均衡B. 混合策略C. 完全信息D. 零和博弈答案:A B C D2. 在非合作博弈中,以下哪些因素会影响参与者的决策?()A. 参与者的收益B. 参与者的策略C. 参与者的偏好D. 参与者的预期答案:A B C D3. 在博弈论中,以下哪些情况可能导致参与者选择合作?()A. 重复博弈B. 参与者之间的信任C. 参与者的收益结构D. 参与者的策略选择答案:A B C4. 以下哪些是博弈论的应用领域?()A. 经济学B. 政治学C. 军事战略D. 心理学答案:A B C D5. 在博弈论中,以下哪些策略被认为是非理性的?()A. 总是选择最优策略B. 总是选择次优策略C. 总是选择固定策略D. 随机选择策略答案:B C三、简答题(每题5分,共20分)1. 请简述博弈论在经济学中的应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1次作业1、考虑一个工作申请的博弈。
两个学生同时向两家企业申请工作,每家企业只有一个工作岗位。
工作申请规则如下:每个学生只能向其中一家企业申请工作;如果一家企业只有一个学生申请,该学生获得工作;如果一家企业有两个学生申请,则每个学生获得工作的概率为1/2。
现在假定每家企业的工资满足:W1/2<W2<2W1,则问:a .写出以上博弈的战略式描述b .求出以上博弈的所有纳什均衡(包括混合策略均衡)2、设古诺模型中有n 家厂商。
i q 为厂商i 的产量,12n Q q q q =+++为市场总产量。
P 为市场出清价格,且已知Q a Q P P-==)((当a Q <时,否则0=P )。
假设厂商i 生产产量i q 的总成本为i i i i cq q C C ==)(,也就是说没有固定成本且各厂的边际成本都相同,为常数)(a c c <。
假设各厂同时选择产量,该模型的纳什均衡是什么?当趋向于无穷大时博弈分析是否仍然有效?3、两个厂商生产一种完全同质的商品,该商品的市场需求函数为P Q -=100,设厂商1和厂商2都没有固定成本。
若他们在相互知道对方边际成本的情况下,同时作出产量决策是分别生产20单位和30单位。
问这两个厂商的边际成本各是多少?各自的利润是多少?4、五户居民都可以在一个公共的池塘里放养鸭子。
每只鸭子的收益v 是鸭子总数N 的函数,并取决于N 是否超过某个临界值N ;如果N N<,收益N N v v -==50)(;如果N N ≥时,0)(≡N v 。
再假设每只鸭子的成本为2=c 元。
若所有居民同时决定养鸭的数量,问该博弈的纳什均衡是什么?5、三对夫妻的感情状态可以分别用下面三个得益矩阵对应的静态博弈来表示。
问:这三个博弈的纳什均衡分别是什么?这三对夫妻的感情状态究竟如何?6、两个个体一起参加某项工程,每个人的努力程度[0,1](1,2)i e i ∈=,成本为()(1,2)i c e i =,该项目的产出为12(,)f e e 。
个体的努力程度不影响到项目的分配方法,项目的产出在2个体之间均分。
试回答以下问题: 1、如果1212(,)3f e e e e =,2()(1,2)i i c e e i ==,试求此博弈的的Nash均衡(即两个个体选择的最优努力程度)。
2、如果1212(,)4f e e e e =,()(1,2)i i c e e i ==,试求此博弈的的Nash均衡。
第2次作业1、企业甲和企业乙都是彩电制造商,都可以选择生产低档产品或高档产品,每个企业在四种不同的情况下的利润如以下得益矩阵所示。
如果企业甲先于企业乙进行产品选择并投入生产,即企业乙在决定产品时已经知道企业甲的选择,而且这一点双方都清楚。
(1)用扩展型表示这一博弈。
2、两个寡头企业进行价格竞争博弈,企业1的利润函数是q c aq p ++--=21)(π,企业2的利润函数是p b q +--=22)(π,其中p 是企业1的价格,q 是企业2的价格。
求:(1)两个企业同时决策的纯策略纳什均衡; (2)企业1先决策的子博弈完美纳什均衡; (3)企业2先决策的子博弈完美纳什均衡;(4)是否存在参数c b a ,,的特定值或范围,使两个企业都希望自己先决策?3、考虑如下的双寡头市场战略投资模型:企业1和企业2目前情况下的生产成本都是2=c。
企业1可以引进一项新技术使单位成本降低到1=c ,该项技术需要投资f 。
在企业1作出是否投资的决策(企业2可以观察到)后,两个企业同时选择产量。
假设市场需求函数为q q p -=14)(,其中p 是市场价格,q 是两个企业的总产量。
问上述投资额f处于什么水平时,企业1会选择引进新技术?4、在市场进入模型中,市场逆需求函数为p =13-Q ,进入者和在位者生产的边际成本都为1,固定成本为0,潜在进入者的进入成本为4。
博弈时序为:在位者首先决定产量水平;潜在进入者在观察到在位者的产量水平之后决定是否进入;如果不进入,则博弈结束,如果进入,则进入者选择产量水平。
求解以上博弈精炼纳什均衡。
5、在三寡头的市场中,市场的逆需求函数为三家产量之和Q Q a p ,-=,每家企业的不变边际成本为c ,固定成本为0。
如果企业1首先选择产量,企业2和企业3观察到企业1的产量后同时选择产量,则均衡时的市场价格。
第三次作业1、两个人合作开发一项产品,能否成功与两个人的工作态度有关,设成功概率如下:单位的利益。
问该博弈无限次重复博弈的均衡是什么?2、两寡头古诺产量竞争模型中厂商的利润函数为()i i i j i q t q q π=--,1,2i =。
若11t =是两个厂商的共同知识,而2t 则是厂商2的私人信息,厂商1只知道23/4t =或24/5t =,且2t 取这两个值的概率相等。
若两个厂商同时选择产量,请找出该博弈的纯策略贝叶斯均衡。
3、两个厂商生产相同产品在市场上进行竞争性销售。
第1个厂商的成本函数为11q c =,其中1q 为厂商1的产量。
第2个厂商的成本函数为22cq c =,其中2q 为厂商2的产量,c 为其常数边际成本。
两个厂商的固定成本都为零。
厂商2的边际成本c 是厂商2的“私人信息”,厂商1认为c 在⎥⎦⎤⎢⎣⎡23,21上呈均匀分布。
设市场需求函数为214q q P --=,其中P 为价格,两个厂商都以其产量为纯战略,问纯战略贝叶斯均衡为何?。
4、两个企业同时决定是否进入一个市场,企业i 的进入成本),0[∞∈i θ是私人信息,i θ是服从分布函数)(i F θ的随机变量以及分布密度)(i f θ严格大于零,并且1θ和2θ两者独立。
如果只有一个企业进入,进入企业i 的利润函数为m i πθ-;如果两个企业都进入,则企业i 的利润函数为i d θπ-;如果没有企业进入,利润为零。
假定mπ和dπ是共同知识,且mπ>dπ>0,试计算此博弈的贝叶斯均衡。
博弈论第1次作业1、a .写出以上博弈的战略式描述b .求出以上博弈的所有纳什均衡(包括混合策略均衡)①存在两个纯战略纳什均衡:分别为(企业1,企业2),收益为)2,1(W W 。
(企业2,企业1),收益为)1,2(W W 。
②存在一个混合策略均衡:令学生A 选择企业1的概率为p ,选择企业2的概率为p -1;学生B 选择企业1的概率为q ,选择企业2的概率为q -1。
当学生A 以)1,(p p -的概率选择时,学生B 选择企业1的期望收益应该与选择企业2的期望收益相等,即:221).1(2.1)1(121.W p W p W p W p -+=-+ 解得:21212W W W W p +-=,211221W W W W p +-=-同理求出:221).1(2.1)1(121.W q W q W q W q -+=-+ 解得:21212W W W W q +-=,211221W W W W q +-=-所以,混合策略纳什均衡为:学生A 、B 均以)21122,21212(W W W W W W W W +-+-的概率选择企业1,企业2。
2、该模型的纳什均衡是什么?当趋向于无穷大时博弈分析是否仍然有效?各厂商的利润函数为:ink k i i i i i i q q c a q c Q a q c q Q a C q P u ).().(.).(.1∑=--=--=--=-=求解:i nk k q i q q q c a u ii).(max max 1∑=--=对其求导,令导数为0,解得反应函数为:()]......[211121n i i i q q q q q c a q ++++++--=+-纳什均衡),...,,(**2*1n q q q ,必是n 条反应函数的交点)...([21**3*2*1n q q q c a q +++--=)...([21**3*1*2n q q q c a q +++--=.....)......([21**1*1*2*1*n i i iq q q q q c a q ++++++--=+-......)...([21*1*2*1*-+++--=n nq q q c a q得到:1...**2*1+-====n ca q q q n,且为唯一的纳什均衡。
当趋向于无穷大时博弈分析无效。
01lim lim *=+-=∞→∞→n ca q n in ,此时为完全竞争市场,此时博弈分析无效。
3、问这两个厂商的边际成本各是多少?各自的利润是多少? 设:边际成本不变,为1c ,2c 。
计算得市场出清价格为: )(100100)(21q q Q Q P P +-=-==两个厂商的利润函数为:1211111111)].(100[).(..q q q c q c P q c q P u +--=-=-= 2212222222)].(100[).(..q q q c q c P q c q P u +--=-=-=求解:12111)].(100[max max 11q q q c u q q +--=22122)].(100[max max 22q q q c u q q +--=对其求导,令导数为0,解得反应函数为:)100(21)(21211q c q R q --==)100(21)(12122q c q R q --==纳什均衡),(*2*1q q ,即(20,30)为两条反应函数的交点)30100(21201--=c)20100(21302--=c得到: 301=c ,202=c 。
此时:4001=u ,9002=u 。
4、若所有居民同时决定养鸭的数量,问该博弈的纳什均衡是什么?设居民i 选择的养鸭数目为in )5,4,3,2,1(=i ,则总数为∑==51i inN 。
假设:N N <居民的得益函数为:i i i i i i i n n n c V n c n V u ).48().(..51∑=-=-=-=计算:i i i u i u n n u ii).48(max max 51∑=-=得到反应函数:)......(212451121n n n n n R n i i i i ++++-==+-5、反应函数的交点),,,,(*5*4*3*2*1n n n n n 是博弈的纳什均衡。
将),,,,(*5*4*3*2*1n n n n n 带入反应函数,得:8*5*4*3*2*1=====n n n n n 。
此时:64=i u 。
此时,40=N然后讨论下N①若40>N ,则N N <,上述博弈成立。
②若40≤N ,则]5[NN =5、问:这三个博弈的纳什均衡分别是什么?这三对夫妻的感情状态究竟如何?矩阵3:用划线法得出三个矩阵的纳什均衡分别为: 矩阵1:(活着,活着) (死了,死了)可以看出这对夫妻间感情十分深厚。
