(2)计算机数制转换数的表示
计算机基础进制转换

计算机基础进制转换计算机基础之进制转换一、引言计算机基础是每个计算机科学学生必修的一门课程,其中进制转换是其中的重要内容之一。
进制转换是指将一个数字从一种进制表示转换为另一种进制表示的过程。
本文将介绍常见的进制转换方法及其应用。
二、十进制与二进制的转换1. 十进制转二进制十进制是我们常用的一种进制,而二进制是计算机中最基本的进制。
将十进制数转换为二进制数的方法是通过不断除以2来进行的。
具体步骤如下:(1)将十进制数除以2,得到商和余数;(2)将得到的余数从下往上按顺序排列,得到的就是转换后的二进制数。
2. 二进制转十进制将二进制数转换为十进制数的方法是通过按权展开法进行的。
具体步骤如下:(1)将二进制数从右往左按位数编号,最右边为第0位;(2)将每一位的数乘以权重2的n次方,n为该位的编号;(3)将各位乘积相加,得到的和就是转换后的十进制数。
三、十进制与八进制的转换1. 十进制转八进制将十进制数转换为八进制数的方法是通过不断除以8来进行的。
具体步骤如下:(1)将十进制数除以8,得到商和余数;(2)将得到的余数从下往上按顺序排列,得到的就是转换后的八进制数。
2. 八进制转十进制将八进制数转换为十进制数的方法是通过按权展开法进行的。
具体步骤如下:(1)将八进制数从右往左按位数编号,最右边为第0位;(2)将每一位的数乘以权重8的n次方,n为该位的编号;(3)将各位乘积相加,得到的和就是转换后的十进制数。
四、十进制与十六进制的转换1. 十进制转十六进制将十进制数转换为十六进制数的方法是通过不断除以16来进行的。
具体步骤如下:(1)将十进制数除以16,得到商和余数;(2)将得到的余数从下往上按顺序排列,得到的就是转换后的十六进制数。
其中,余数大于9时,可以用A、B、C、D、E、F来表示。
2. 十六进制转十进制将十六进制数转换为十进制数的方法是通过按权展开法进行的。
具体步骤如下:(1)将十六进制数从右往左按位数编号,最右边为第0位;(2)将每一位的数乘以权重16的n次方,n为该位的编号;(3)将各位乘积相加,得到的和就是转换后的十进制数。
计算机基础——进制与进制的转换

计算机基础——进制与进制的转换进制是计量系统中用来表示数字的一种方法,主要包括十进制、二进制、八进制和十六进制。
在计算机科学中,不同进制的转换是基础中的基础,对于理解计算机内部的数据表示方式以及进行编程、网络通信等方面都具有重要作用。
本文将详细介绍不同进制的表示方法和转换方式。
一、进制的定义和表示1. 十进制(Decimal)十进制是我们平时最常用的进制,使用0-9这10个数字来表示数值。
每位的权重是10的n次方,从右到左依次是10的0次方、10的1次方、10的2次方,依此类推。
例如,数值256在十进制中表示为2*10^2+5*10^1+6*10^0=200+50+6=2562. 二进制(Binary)二进制是计算机内部最基本的进制,只使用0和1这两个数字来表示数值。
每位的权重是2的n次方,从右到左依次是2的0次方、2的1次方、2的2次方,依此类推。
例如,数值101在二进制中表示为1*2^2+0*2^1+1*2^0=4+0+1=53. 八进制(Octal)八进制使用0-7这8个数字来表示数值。
每位的权重是8的n次方,从右到左依次是8的0次方、8的1次方、8的2次方,依此类推。
例如,数值73在八进制中表示为7*8^1+3*8^0=56+3=614. 十六进制(Hexadecimal)十六进制使用0-9和A-F这16个数字来表示数值,其中A表示10,B表示11,以此类推。
每位的权重是16的n次方,从右到左依次是16的0次方、16的1次方、16的2次方,依此类推。
例如,数值3F在十六进制中表示为3*16^1+F*16^0=48+15=63二、进制之间的转换十进制到二进制的转换原理是将十进制数不断除以2,直到商为0,然后将每次的余数倒序排列。
例如,将十进制数19转换为二进制:19/2=9余19/2=4余14/2=2余02/2=1余01/2=0余1二进制到十进制的转换原理是将二进制数的每位与对应的权重相乘,然后将乘积相加。
二进制八进制十进制十六进制转换符号口诀

二进制八进制十进制十六进制转换符号口诀标题:探索二进制、八进制、十进制及十六进制转换的符号口诀导语:在计算机科学和信息技术领域,进制转换是一项基础而重要的技能。
掌握不同进制之间的转换可以帮助我们更好地理解计算机系统的工作原理,以及更高效地处理数字数据。
本文将介绍二进制、八进制、十进制和十六进制转换的符号口诀,帮助读者轻松掌握这一技能。
一、二进制(Binary)1. 符号口诀:2进1摸、0、1解析:二进制是一种仅由0和1组成的进制系统。
符号口诀中的“2进1摸、0、1”意味着每个二进制位表示的是2的n次方,其中n表示该位置的权重。
从右至左的二进制位权重分别为1、2、4、8、16...,而对应的二进制值只能是0或1。
二、八进制(Octal)1. 符号口诀:8进1摸、0~7解析:八进制是一种由数字0至7组成的进制系统。
符号口诀中的“8进1摸、0~7”表示每个八进制位的权重为8的n次方,而每个位置上的值范围是0至7。
三、十进制(Decimal)1. 符号口诀:10进1摸、0~9解析:十进制是我们日常生活中最常用的进制系统,由0至9的数字组成。
符号口诀中的“10进1摸、0~9”表示每个十进制位的权重为10的n次方,而每个位置上的值范围是0至9。
四、十六进制(Hexadecimal)1. 符号口诀:16进1摸、0~9 A~F解析:十六进制是一种容易与二进制转换的进制系统,由0至9以及A至F的16个字符组成。
符号口诀中的“16进1摸、0~9 A~F”表示每个十六进制位的权重为16的n次方,而每个位置上的值范围是0至9和A至F。
二进制、八进制、十进制和十六进制间的转换:转换是理解不同进制的关键部分,下面将介绍在各进制之间进行转换的方法。
1. 二进制转八进制和十六进制:- 先将二进制数按照3(八进制)或4(十六进制)位一组进行分组。
- 将每组的二进制数转换为对应的八进制或十六进制值。
2. 八进制和十六进制转二进制:- 分别将八进制和十六进制数的每一位转换为对应的三位二进制数(八进制)或四位二进制数(十六进制)。
二进制 八进制 十进制 的转化关系

二进制八进制十进制的转化关系二进制、八进制和十进制是常见的数制系统,用于表示数字和进行数值计算。
它们之间有着特定的转化关系,可以相互转换。
本文将介绍二进制、八进制和十进制的概念以及它们之间的转换方法。
一、二进制(Binary System)二进制是一种使用0和1表示数字的数制系统。
每一位数字称为一个比特(bit),可以表示两种状态:0或1。
二进制数从右往左依次表示2^0、2^1、2^2、2^3...的权值。
例如,二进制数1101表示:1 * 2^0 + 0 * 2^1 + 1 * 2^2 + 1 * 2^3 = 13。
二、八进制(Octal System)八进制是一种使用0-7表示数字的数制系统。
每一位数字称为一个八进制位。
八进制数从右往左依次表示8^0、8^1、8^2、8^3...的权值。
例如,八进制数27表示:7 * 8^0 + 2 * 8^1 = 23。
三、十进制(Decimal System)十进制是我们常用的数制系统,使用0-9表示数字。
每一位数字称为一个十进制位。
十进制数从右往左依次表示10^0、10^1、10^2、10^3...的权值。
例如,十进制数123表示:3 * 10^0 + 2 * 10^1 + 1 * 10^2 = 123。
四、二进制和八进制的转换二进制和八进制之间的转换比较简单。
将二进制数从右往左每3位分组,每组转换为一个八进制位。
不足3位的在左边补0。
例如,二进制数110101011转换为八进制:001 101 010 11,即转换为八进制数1523。
反之,将八进制数每一位转换为3位的二进制数即可。
五、二进制和十进制的转换二进制和十进制之间的转换也比较简单。
将二进制数从右往左每一位与对应的权值相乘,然后求和。
例如,二进制数1101转换为十进制:1 * 2^0 + 0 * 2^1 + 1 * 2^2 + 1 * 2^3 = 13。
反之,将十进制数不断除以2,直到商为0,然后将每一步的余数从下往上排列即可得到二进制数。
计算机数学之进制数之间的转换 (进阶)

(A)53
(B)32
(C)23
(D)46
9.十六进制数FF.1转换成十进制数是__C__。 (A)255.625 (B)250.1625 (C)255.0625 (D)250.0625
10.在下列字Z
(B)9
(C)空格字符
(D)a
今天课就上到这里,欢迎大家多提意见。 讲的不好的地方希望大家谅解!谢谢!
项相加)
(10011)2
2 91
2
41
2
20
2
10
0 1 高位
(19)10=(10011)2
=1*2 4
+1*2 1
这里的权 值是2的i次
方
+1*2 0
=16+2+1 =19
注意:2 的0次方 等于1,
不是0
*十进制数与八进制整数间的转换
A. “十进制”转“八 进制”(除8取余)
8
19 余数 低位
6.二进制数10011010.1011转换成八进制数是__A___。 (A)232.54 (B)232.13 (C)232.51 (D)232.52
7.12 十进制小数0.625转换成十六进制小数是___A___。
(A)0.A
(B)0.1
(C)0.01
(D)0.A1
8.二进制数10111转换成十进制数是___C___。
二.十进制→八进制 (整数部分除8取余, 小数部分乘8取整)
三.十进制→十六进制 (整数部分除16取余, 小数部分乘16取整)
四.十六进制→二进制 (每一位十六进制数表示 四位二进制数)
五.八进制→二进制 (每一位八进制数表示 三位二进制数)
补充
权值:整数部分按权展开:i的取值范围i≥0 小数部分按权展开:i的取值范围i<0
计算机进制之间的转换

计算机进制之间的转换进制是计算机中用于表示数值的一组符号系统,包括二进制、八进制、十进制和十六进制等。
在计算机科学中,进制转换是一种常见且重要的操作。
本文将详细介绍计算机进制之间的转换方法。
1. 二进制 (Binary) 转换为十进制 (Decimal):方法1:将二进制数从右往左按位展开,每一位的值与2的幂相乘,然后将得到的结果相加。
例如,二进制数1101转换为十进制,计算过程如下:(1*2^3)+(1*2^2)+(0*2^1)+(1*2^0)=13方法2:使用公式法。
将二进制数从高位到低位按权展开,并将每一位的值乘以相应权重,然后将结果相加。
例如,二进制数1101转换为十进制,计算过程如下:(1*2^3)+(1*2^2)+(0*2^1)+(1*2^0)=132. 十进制 (Decimal) 转换为二进制 (Binary):方法1:使用除二取余法。
将十进制数从右往左不断除以2,直到商为0。
最后,将得到的余数按照从下往上的顺序排列,即为二进制数。
例如,十进制数13转换为二进制,计算过程如下:13÷2=商6、余16÷2=商3、余03÷2=商1、余11÷2=商0、余1将得到的余数按从下往上的顺序排列,即为二进制数1101方法2:使用公式法。
将十进制数转换为相应的二进制幂的和。
例如,十进制数13转换为二进制,计算过程如下:13=(2^3)+(2^2)+(2^0)=11013. 十进制 (Decimal) 转换为八进制 (Octal):方法1:使用除八取余法。
将十进制数从右往左不断除以8,直到商为0。
最后,将得到的余数按从下往上的顺序排列,即为八进制数。
例如,十进制数86转换为八进制,计算过程如下:86÷8=商10、余610÷8=商1、余21÷8=商0、余1将得到的余数按从下往上的顺序排列,即为八进制数126方法2:使用公式法。
将十进制数转换为相应的八进制幂的和。
计算机数制及转化
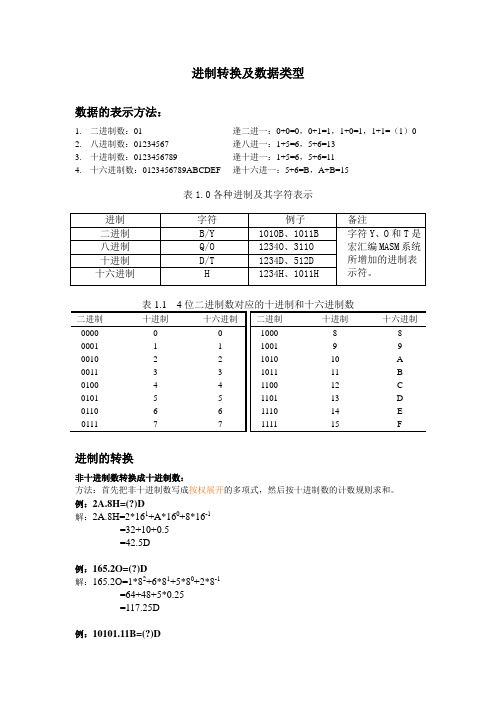
进制转换及数据类型数据的表示方法:1.二进制数:01 逢二进一:0+0=0,0+1=1,1+0=1,1+1=(1)02.八进制数:01234567 逢八进一:1+5=6,5+6=133.十进制数:0123456789 逢十进一:1+5=6,5+6=114.十六进制数:0123456789ABCDEF 逢十六进一:5+6=B,A+B=15表1.0各种进制及其字符表示进制的转换非十进制数转换成十进制数:方法:首先把非十进制数写成按权展开的多项式,然后按十进制数的计数规则求和。
例:2A.8H=(?)D解:2A.8H=2*161+A*160+8*16-1=32+10+0.5=42.5D例:165.2O=(?)D解:165.2O=1*82+6*81+5*80+2*8-1=64+48+5*0.25=117.25D例:10101.11B=(?)D解:10101.11B=1*24+0*23+1*22+0*21+1*20+1*2-1+1*2-2=16+0+4+0+1+0.5+0.25=21.75D十进制数转换其它进制数:1.整数转换方法:整数转换,采用基数连除法。
把十进制整数N 转换成R 进制数的步骤:1) 将N 除以R ,记下所得的商和余数2) 将上一步所得的商再除以R ,记下所得商和余数 3) 重复做第2步直到商为04) 将各个余数转换成R 进制的数码,并按照和运算过程相反的顺序把各个余数排列起来,即为R 进制数。
例:427D=(?)H 解:427D=1ABH 例:427D=(?)O 解:427D=653O 例:11D=(?)B 解:11D=1011B2.纯小数转换纯小数转换,采用基数连乘法。
把十进制的纯小数M 转换成R 进制数的步骤: 1) 将M 乘以R ,记下整数部分2) 将上一步乘积中的小数部分再乘以R ,记下整数部分3) 重复做第2步,直到小数部分为0或者满足精度要求为止4) 将各步求得的整数转换成R 进制的数码,并按照和运算过程相同的顺序排列起来,即为所求的R 进制数。
二进制、十进制、八进制、十六进制四种进制之间相互的转换

二进制、十进制、八进制、十六进制四种进制之间相互的转换一.在计算机应用中,二进制使用后缀b表示;十进制使用后缀d表示八制使用后缀Q表示,十六制使用后缀H表示。
二.二进制,十六进制与十进制的计算转换1.二进制转换为十进制计算公式:二进制数据X位数字乘以2的X-1次方的积的总和例:10101011b=( )d相应的十进制值即为:27 +25+23+21+20=128+32+8+2+1=1712.十六进制转换十进制计算公式:二进制数据X位数字乘以16的X-1次方的积的总和(与二进制转换十制进同理的,将底数换为16)注意:在十六进制中,10-15依次用A,B,C,D,E,F表示例:1F3E H=()d计算:1*16的3次方+15*16的2次方+3*16的1次方+14*16的0次方=1*4096+15*256+3*16+14=7998三.十进制与二进制,十六制的计算转换1.十进制转换为二进制十进制数据数字除以2的余数的逆序组合例:404d=( )b2|404余02|202余02|101余02|50余12|25余02|12余12|6余02|3余12|1计算结果便是:1101010002.十进制转换十六进制。
与上面同理,注意的是10以上的数字用字母表示,除数是16十六进制与二进制的转换,建议通过十进制来进行中转。
带小数点的十进制转换为二进制时同理,小数店后的数位指数为负指数===================================================================== =================关于“进制之间的转换”问题的分析指导在计算机文化一书中,在其中一个章节里面详细介绍了进制之间的转换,而且在考试中进制转换也占了一定的比例,虽然分数不是很多,但是因为平时大家接触的不多,并且有点繁复,所以很多学员在做这种题目,要么选择猜答案,要么选择放弃。
笔者觉得只要掌握了方法,其实这些题目也很简单的,下面我就对进制的转换进行具体的分析和讲解,以供大家参考。
计算机进制之间相互转换

计算机进制之间的相互转换一、进位计数制所谓进位计数制是指按照进位的方法进行计数的数制,简称进位制。
在计算机中主要采用的数制是二进制,同时在计算机中还存在八进制、十进制、十六进制的数据表示法。
下面先来介绍一下进制中的基本概念:1、基数数制是以表示数值所用符号的个数来命名的,表明计数制允许选用的基本数码的个数称为基数,用R表示。
例如:二进制数,每个数位上允许选用0和1,它的基数R=2;十六进制数,每个数位上允许选用1,2,3,…,9,A,…,F共16个不同数码,它的基数R=16。
2、权在进位计数制中,一个数码处在数的不同位置时,它所代表的数值是不同的。
每一个数位赋予的数值称为位权,简称权。
权的大小是以基数R为底,数位的序号i为指数的整数次幂,用i表示数位的序号,用Ri表示数位的权。
例如,543.21各数位的权分别为102、101、100、10-1和10-2。
3、进位计数制的按权展开式在进位计数制中,每个数位的数值等于该位数码与该位的权之乘积,用Ki表示第i位的系数,则该位的数值为KiRi。
任意进位制的数都可以写成按权展开的多项式和的形式。
二、计算机中的常用的几种进制。
在计算机中常用的几种进制是:二进制、八进制、十进制和十六进制。
二进制数的区分符用字母B表示,八进制数的区分符用字母O表示,十进制数的区分符用字母D表示或不用区分符,十六进制数的区分符用字母H表示。
1、二进制(Binary System)二进制数中,是按“逢二进一”的原则进行计数的。
其使用的数码为0,1,二进制数的基为“2”,权是以2为底的幂。
2、八进制(Octave System)八进制数中,是按“逢八进一”的原则进行计数的。
其使用的数码为0,1,2,3,4,5,6,7,八进制数的基为“8”,权是以8为底的幂。
3、十进制(Decimal System)十进制数中,是按“逢十进一”的原则进行计数的。
其使用的数码为1,2,3,4,5,6,7,8,9,0,十进制数的基为“10”,权是以10为底的幂。
进制换算

一。
进制概念1。
十进制十进制使用十个数字(0、1、2、3、4、5、6、7、8、9)记数,基数为10,逢十进一。
历史上第一台电子数字计算机ENIAC是一台十进制机器,其数字以十进制表示,并以十进制形式运算。
设计十进制机器比设计二进制机器复杂得多。
而自然界具有两种稳定状态的组件普遍存在,如开关的开和关,电路的通和断,电压的高和低等,非常适合表示计算机中的数。
设计过程简单,可靠性高。
因此,现在改为二进制计算机。
2。
二进制二进制以2为基数,只用0和1两个数字表示数,逢2进一。
二进制与遵循十进制数遵循一样的运算规则,但显得比十进制更简单。
例如:(1)加法:0+0=0 0+1=1 1+0=1 1+1=0(2)减法:0-0=0 1-1=01-0=1 0-1=1(3)乘法:0*0=0 0*1=01*0=0 1*1=1(4)除法:0/1=0 1/1=1,除数不能为03。
八进制所谓八进制,就是其基数为8,基数值可以取0、1、2、3、4、5、6、7共8个值,逢八进一。
八进制与十进制运算规则一样。
那么为什么要用八进制呢?难道要设计八进制的计算机么?实际上,八进制与十六进制的引用,主要是为了书写和表示方便,因为二进制表示位数比较长。
如:(1024)10 用二进制表示为(10000000000)2,共有11个数字,用八进制表示为(2000)8。
更重要的是,由于二进制与八进制存在在一种对等关系,每三位二进制与一位八进制数完全对等(23=8)。
所以二进制和十进制在运算上无区别,而时进制不具备这一优点。
4。
十六进制十六进制应用也是非常广泛的一种计数制。
在使用者看来,十六进制是二进制数的一种更加紧凑的一种表示方法。
基数为:0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F,逢十进一。
在十六进制系统中,数值为10到15的数分别用A、B、C、D、E、F表示。
二进制数及与之等值的八进制、十进制和十六进制数二进制八进制十进制十六进制0000 0 0 00001 1 1 10010 2 2 20011 3 3 30100 4 4 40101 5 5 50110 6 6 60111 7 7 71000 10 8 81001 11 9 91010 12 10 A1011 13 11 B1100 14 12 C1101 15 13 D1110 16 14 E1111 17 15 F二。
各进制之间的转换方法及表格

各进制之间的转换方法及表格进制之间的转换方法及表格:在计算机科学和数学领域中,进制是使用不同的基数来表示数字的一种方法。
常见的进制包括二进制、八进制、十进制和十六进制。
在这些进制之间进行转换非常重要,因为不同的进制在不同的场景中具有不同的优势和适用性。
下面我将详细介绍各种进制之间的转换方法,并提供一个表格以方便参考。
1.二进制转换为十进制:-方法:将二进制数每一位与2的幂相乘,然后求和。
2.十进制转换为二进制:-方法:使用短除法将十进制数连续除以2,直到商为0为止,然后依次取所得余数,从最后一个除数开始。
3.十进制转换为八进制:-方法:使用短除法将十进制数连续除以8,直到商为0为止,然后依次取所得余数,从最后一个除数开始。
-示例:将十进制数219转换为八进制数:219÷8=27余3,27÷8=3余3,3÷8=0余3、所以219的八进制表示为3334.八进制转换为十进制:-方法:将八进制数每一位与8的幂相乘,然后求和。
-示例:将八进制数333转换为十进制数:(3*8^2)+(3*8^1)+(3*8^0)=2195.十进制转换为十六进制:-方法:使用短除法将十进制数连续除以16,直到商为0为止,然后依次取所得余数,从最后一个除数开始。
十六进制中的10到15分别用字母A到F表示。
-示例:将十进制数255转换为十六进制数:255÷16=15余15,15÷16=0余15、所以255的十六进制表示为FF。
6.十六进制转换为十进制:-方法:将十六进制数每一位与16的幂相乘,然后求和。
十六进制中的A到F分别用数字10到15表示。
-示例:将十六进制数3FF转换为十进制数:(3*16^2)+(15*16^1)+(15*16^0)=1023下面是一个表格,展示了各种进制之间的转换方法和示例:进制转换,二进制,十进制,八进制,十六进制---------,----------,-------,-------,---------十进制转二进制,/,47,/,/十进制转八进制,/,219,333,/八进制转十进制,/,333,/,/十进制转十六进制,/,255,/,FF十六进制转十进制,/,3FF,/,/通过上述的转换方法和表格,我们可以在不同的进制之间进行转换,进而满足不同场景下对数据的需求。
进制之间的转换方法

进制之间的转换方法进制是计算机科学中非常重要的概念之一。
进制之间的转换方法是在计算机科学中非常基础、重要的技能,它是计算机编程和数据处理必备的知识之一。
在本文档中,将介绍如何在不同进制之间进行转换,包括二进制、八进制、十进制和十六进制,并提供相关的实例。
二进制(Binary)在计算机科学中,二进制是最常见的进制,因为计算机中的所有数据处理都是在二进制的基础上完成的。
二进制表示的是由 0 和 1 组成的数字系统。
在二进制中,每一位上的数字的权值都是 2 的幂次方,从右往左依次为1、2、4、8、16……如下表所示。
2^7 2^6 2^5 2^4 2^3 2^2 2^1 2^0128 64 32 16 8 4 2 1因此,一个八位的二进制数可以表示 0 ~ 255 的十进制数。
例如,二进制数 01100100 表示的是十进制数100 。
二进制转八进制将一个二进制数转换成八进制数,可以将二进制数每三位分为一组(从右往左),然后将每一组转换成相应的八进制数。
例如,将二进制数 11010 转换成八进制,可以按下面的方法进行:1. 将二进制数每三位分为一组:011 010 。
因为二进制数是从右往左数的,所以最后一组的位数不足三位,需要在最高位补 0 使其成为三个二进制位。
2. 将每组的二进制数转换成相应的八进制数。
011 对应的八进制数是 3,010 对应的八进制数是 2。
因此,11010 的八进制表示为 32。
二进制转十进制将一个二进制数转换成十进制数,可以将每一位上的数字乘以相应的权值,然后将所有的结果相加。
例如,将二进制数 101010 转换成十进制数,可以按下面的方法进行:1. 将每一位上的数字乘以相应的权值,从右往左依次为 1、2、4、8、16、32。
因此,101010 转换成十进制数为:0x20 + 2x16 + 0x8 + 1x4 + 0x2 + 1x1 = 42。
二进制转十六进制将一个二进制数转换成十六进制数,可以将二进制数每四位分为一组(从右往左),然后将每一组转换成相应的十六进制数。
计算机进制之间相互转换

计算机进制之间的相互转换一、进位计数制所谓进位计数制是指按照进位的方法进行计数的数制,简称进位制.在计算机中主要采用的数制是二进制,同时在计算机中还存在八进制、十进制、十六进制的数据表示法。
下面先来介绍一下进制中的基本概念:1、基数数制是以表示数值所用符号的个数来命名的,表明计数制允许选用的基本数码的个数称为基数,用R表示。
例如:二进制数,每个数位上允许选用0和1,它的基数R=2;十六进制数,每个数位上允许选用1,2,3,…,9,A,…,F共16个不同数码,它的基数R=16。
2、权在进位计数制中,一个数码处在数的不同位置时,它所代表的数值是不同的.每一个数位赋予的数值称为位权,简称权。
权的大小是以基数R为底,数位的序号i为指数的整数次幂,用i表示数位的序号,用Ri表示数位的权.例如,543.21各数位的权分别为102、101、100、10-1和10—2.3、进位计数制的按权展开式在进位计数制中,每个数位的数值等于该位数码与该位的权之乘积,用Ki表示第i位的系数,则该位的数值为KiRi。
任意进位制的数都可以写成按权展开的多项式和的形式。
二、计算机中的常用的几种进制。
在计算机中常用的几种进制是:二进制、八进制、十进制和十六进制。
二进制数的区分符用字母B表示,八进制数的区分符用字母O表示,十进制数的区分符用字母D表示或不用区分符,十六进制数的区分符用字母H表示。
1、二进制(Binary System)二进制数中,是按“逢二进一”的原则进行计数的。
其使用的数码为0,1,二进制数的基为“2”,权是以2为底的幂。
2、八进制(Octave System)八进制数中,是按“逢八进一”的原则进行计数的。
其使用的数码为0,1,2,3,4,5,6,7,八进制数的基为“8”,权是以8为底的幂。
3、十进制(Decimal System)十进制数中,是按“逢十进一”的原则进行计数的.其使用的数码为1,2,3,4,5,6,7,8,9,0,十进制数的基为“10”,权是以10为底的幂。
进制转换的知识点

进制转换的知识点一、数制的基本概念。
1. 十进制(Decimal)- 十进制是我们日常生活中最常用的数制。
它的基数是10,使用0 - 9这十个数字来表示数。
- 例如,数字234,它可以表示为2×10^2+3×10^1+4×10^0。
2. 二进制(Binary)- 二进制是计算机中最基本的数制,基数为2,只使用0和1两个数字。
- 例如,二进制数101,它表示为1×2^2+0×2^1+1×2^0=4 + 0+1 = 5(转换为十进制)。
3. 八进制(Octal)- 八进制的基数是8,使用0 - 7这八个数字。
- 例如,八进制数34,它表示为3×8^1+4×8^0=24 + 4=28(转换为十进制)。
4. 十六进制(Hexadecimal)- 十六进制的基数是16,使用0 - 9和A - F(或a - f)这十六个字符来表示数,其中A - F(a - f)分别表示10 - 15。
- 例如,十六进制数2A,它表示为2×16^1+10×16^0=32+10 = 42(转换为十进制)。
二、进制转换方法。
1. 十进制转二进制。
- 除2取余法。
- 将十进制数除以2,取余数,然后将商继续除以2,直到商为0。
- 例如,将十进制数13转换为二进制:- 13÷2 = 6·s·s1- 6÷2 = 3·s·s0- 3÷2 = 1·s·s1- 1÷2 = 0·s·s1- 然后将余数从下往上排列,得到二进制数1101。
2. 二进制转十进制。
- 位权展开法。
- 如前面二进制数101转换为十进制的例子,将二进制数的每一位乘以2的相应位权(从右往左,位权依次为2^0,2^1,2^2,·s)然后相加。
3. 十进制转八进制。
计算机中的二进制、八进制、十进制、十六进制

计算机中的⼆进制、⼋进制、⼗进制、⼗六进制1.1 进制⼆进制:逢⼆进⼀,数值只有0和1。
⼋进制:逢⼋进⼀,数值有0,1,2,3,4,5,6,7⼗进制:逢⼗进⼀,数值有0,1,2,3,4,5,6,7,8,9⼗六进制:逢⼗六进⼀,数值有0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F1.2 进制转换⼆进制、⼋进制、⼗六进制转为⼗进制⼗进制转为⼆进制、⼋进制、⼗六进制1.3 原码,反码,补码1.3.1 机器数和真值机器数:⼀个数在计算机中的⼆进制表⽰形式。
叫做这个数的机器数。
机器数是带符号的,最⾼位0表⽰正数,1表⽰负数。
⽰例:⽐如10进制中的+3,计算机长度为8位。
转为⼆进制是0000 0011。
⽐如-3,转为⼆进制是1000 0011。
真值:因为第⼀位是符号位,所以机器数的形式值就不等于真正的数值。
⽐如1000 0011,作为负数可以是-3,作为正数可以说131.为了区分,将带符号位的计算数对应的真正的数值称为机器数的真值。
1.3.2 原码,反码,补码原码:就是符号位加上真值的绝对值,即第⼀位表⽰符号位,其余位表⽰值。
+1 = [0000 0001]原-1 = [1000 0001]原原码是⼈脑最容易理解和计算的表⽰⽅式.反码:正数的反码是其本⾝,负数的反码是在其原码的基础上,符号位不变,其余各位按位取反。
+1 = [0000 0001]原 = [0000 0001]反-1 = [1000 0001]原 = [1111 1110]反⼀个反码表⽰的是负数, ⼈脑⽆法直观的看出来它的数值. 通常要将其转换成原码再计算。
补码:正数的补码是其本⾝,负数的补码是在原码的基础上,符号位不变,其余各位取反后+1。
+1 = [0000 0001]原 = [0000 0001]反 = [0000 0001]补-1 = [1000 0001]原 = [1111 1110]反 = [1111 1111]补对于负数, 补码表⽰⽅式也是⼈脑⽆法直观看出其数值的. 通常也需要转换成原码在计算其数值.于是⼈们开始探索将符号位参与运算, 并且只保留加法的⽅法. ⾸先来看原码。
进制转换

在高速发展的现代社会,计算机浩浩荡荡地成为了人们生活中不可缺少的一部分,帮助人们解决通信,联络,互动等各方面的问题。
今天我就给大家讲讲与计算机甚至日常生活有密切相关的“进制转换”问题。
我们以(25.625)(十)为例讲解一下进制之间的转化问题。
1. 十-----> 二给你一个十进制,比如:6,如果将它转换成二进制数呢?10进制数转换成二进制数,这是一个连续除2的过程:把要转换的数,除以2,得到商和余数,将商继续除以2,直到商为0。
最后将所有余数倒序排列,得到数就是转换结果。
听起来有些糊涂?我们结合例子来说明。
比如要转换6为二进制数。
“把要转换的数,除以2,得到商和余数”。
那么:十转二示意图要转换的数是6, 6 ÷ 2,得到商是3,余数是0。
“将商继续除以2,直到商为0……”现在商是3,还不是0,所以继续除以2。
那就: 3 ÷ 2, 得到商是1,余数是1。
“将商继续除以2,直到商为0……”现在商是1,还不是0,所以继续除以2。
那就: 1 ÷ 2, 得到商是0,余数是1“将商继续除以2,直到商为0……最后将所有余数倒序排列”好极!现在商已经是0。
我们三次计算依次得到余数分别是:0、1、1,将所有余数倒序排列,那就是:110了!6转换成二进制,结果是110。
把上面的一段改成用表格来表示,则为:被除数计算过程商余数6 6/2 3 03 3/2 1 11 1/2 0 1(在计算机中,÷用 / 来表示)2. 二----> 十二进制数转换为十进制数二进制数第0位的权值是2的0次方,第1位的权值是2的1次方……所以,设有一个二进制数:0110 0100,转换为10进制为:下面是竖式:0110 0100 换算成十进制" ^ " 为次方第0位 0 * 2^0 = 0第1位 0 * 2^1 = 0第2位 1 * 2^2 = 4第3位 0 * 2^3 = 0第4位 0 * 2^4 = 0第5位 1 * 2^5 = 32第6位 1 * 2^6 = 64第7位 0 * 2^7 = 0 +---------------------------100用横式计算为:0 * 2 ^ 0 + 0 * 2 ^ 1 + 1 * 2 ^ 2 + 0 * 2 ^ 3 + 0 * 2 ^ 4 + 1 * 2 ^ 5 + 1 * 2 ^ 6 + 0 * 2 ^ 7 = 1000乘以多少都是0,所以我们也可以直接跳过值为0的位:1 *2 ^ 2 + 1 * 2 ^ 5 + 1 * 2 ^ 6 = 1003. 十----> 八10进制数转换成8进制的方法,和转换为2进制的方法类似,唯一变化:除数由2变成8。
计算机进制之间的转换

56
十六进制与二进制之间的转换
十六进制转为二进制数
学习项目 记一记 看一看 练一练 想一想
通过介绍十六进制 转为二进制数的方法, 使学生掌握转换过程。
58
十六进制转为二进制数方法
方法:
将每一位十六进制数转为四 位二进制数,不足四位时: 进行左补零。
59
十六进制转为二进制数例题
1、(0.75)10=( 0.11
)2
2、(2.23)10=( 10.001 )2三位小数
欢迎进入高等测试
28
十进制转为二进制数注意事项
十进制整数
方法:除2取余
倒序回
除数为0止
十进制小数
方法:规则- 乘2取整
正序回
小数位为0止
不规则-乘2取整
正序回
保留有效位数
十进制数既含整数又含小数时:分别对整数和小数进行转 换,最后将结果进行相加即可
①电子器件的实现很容易。电路开关的闭合与 断开、电灯的亮与灭、二极管的导通与截止、 高电平与低电平等。
②二进制运算简单。运算器结构大大简化,控 制简单
③便于进行逻辑运算。二进制的0、1两种状态, 可以代表逻辑运算中的“假”和“真”两种值
④可靠性高。二进制的0、1两种状态,在传输 和处理时不容易出错。
3、数制表示
❖制数表示:一般用括号后加数字下标2、8、 10、16来分别表示二进制、八进制、十进 制和十六进制数字,如(5)l0=表示10进制5; (101)2表示2进制101。
11
❖对于r进制的数,在数值的后面使用特定的 字母标注
(101) 2 Binary (101) 8 Octal (101) 10 Decimal (101) 16 Hexadecimal
计算机各进制换算

计算机各进制换算计算机中常用的进制包括十进制、二进制、八进制和十六进制。
换算不同进制之间的方法是很基础和重要的,下面我们来看一下如何进行这些进制之间的转换。
1.十进制转二进制:十进制数可以被2整除或除2取余数的方式转为二进制数。
具体步骤如下:-将十进制数除以2,得到的商再除以2,如此类推,直到商为0。
将得到的余数从下往上排列,就得到了对应的二进制数。
例如,十进制数10转为二进制数:10÷2=5,余数为0,5÷2=2,余数为1,2÷2=1,余数为0,1÷2=0,余数为1、所以10的二进制表示为1010。
2.二进制转十进制:二进制数可以通过加权求和的方式转为十进制数。
具体步骤如下:-从二进制数的最右边(低位)开始,依次对每一位乘以2的n次方(n为该位的索引)。
-将得到的结果相加,即可得到对应的十进制数。
例如,二进制数1010转为十进制数:1x2^3+0x2^2+1x2^1+0x2^0=8+0+2+0=10。
3.十进制转八进制:十进制数可以被8整除或除8取余数的方式转为八进制数。
具体步骤如下:-将十进制数除以8,得到的商再除以8,如此类推,直到商为0。
将得到的余数从下往上排列,就得到了对应的八进制数。
例如,十进制数25转为八进制数:25÷8=3,余数为1,3÷8=0,余数为3、所以25的八进制表示为314.八进制转十进制:八进制数可以通过加权求和的方式转为十进制数。
具体步骤与二进制转十进制相同,只是将每一位乘以8的n次方(n为该位的索引)。
例如,八进制数31转为十进制数:3x8^1+1x8^0=24+1=255.十进制转十六进制:十进制数可以被16整除或除16取余数的方式转为十六进制数。
-将十进制数除以16,得到的商再除以16,如此类推,直到商为0。
将得到的余数从下往上排列,用A表示10、B表示11、C表示12、D表示13、E表示14、F表示15,就得到了对应的十六进制数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0
0 1
1
1 1
例:!1 || 0 && 1 = ?
0 || 0 && 1 0 || 0 0
2、八进制数
数字符号:0,1,2,3,4,5,6,7
基数:8 进位制:逢八进一 3、十六进制数 数字符号:0,1,2,3,4,5,6,7,8,9, A,B,C,D,E,F
基数:16
进位制:逢十六进一
数制之间的转换
商
余数
(2)二进制的逻辑运算: 二进制的逻辑运算实际一种按位运算,是对 因果关系进行分析的一种运算。 三种逻辑运算符是:
非
(NOT) 高
与
(AND)
或
(OR) 低 (运算优先级)
逻辑运算真值表(C语言)
a 0
b 0
!a 1
!b 1
a&&b a||b 0 0
0:假
1:真
0
1 1
1
0 1
1
0 0
0
1 0
1、定点表示法
指数的小数点的位置是固定的。
通常将小数点固定在数值部分的最高位之前或最
低位之后。
前者表示成纯小数,后者表示成整数。
数的定点表示法有定点小数和定点整数两种。
定点小数 定点整数
数符SM 数符SM
. 尾数M 尾数M .
表示数的正、负 “0”表示正数
“1”表示负数
例1:设某微型机字长为8位,若有两数,
例:
X1 = +1011,
X2 = -1011
[X1]原 = 01011, [X2]原 = 11011
[X1]反 = 01011, [X2]反 = 10100
3、补码
补码表示法的符号部分同原码。
补码的数值部分与它的符号位有关: 对于正数:补码的数值与原码相同。 对于负数:补码的数值是将原码数值按位求反, 再在最低位加1。
字长:一般说来,计算机在同一时间内处理的一组二进制数称为一个计算机的 “字”,而这组二进制数的位数就是“字长”。字长与计算机的功能和用途有很 大的关系,是计算机的一个重要技术指标。字长直接反映了一台计算机的计算精 度,为适应不同的要求及协调运算精度和硬件造价间的关系,大多数计算机均支
持变字长运算,即机内可实现半字长、全字长(或单字长)和双倍字长运算。在
进制之间有简单的对应关系: 十六进制: 0 1 2 … 7 8 9
二进制:0000 0001 0010 0111 1000 1001
十六进制: A
B
C
D
E
F
二进制:1010 1011 1100 1101 1110 1111
转换方法:以小数点为界,将二进制数的整数部分
从低位开始,小数部分从高位开始,每四位分成一组,
第二讲 计算机数制转换、 运算、数据表示方法
一、计算机的定义(COMPUTER)
电子计算机:一种能够高速、准确、自动完成对各种数
字化信息进行算术和逻辑运算的电子设备。
计算机的特点
1、运算速度快 巨型机的运算速度已达到几千亿次/秒。 海量运算:天气预报,大地测量、 运载火箭参数的计算等 2、计算精度高 计算精度与机器字长有关,机器字越长,精度越高。 字:字长是直接用二进制代码指令表达的计算机语言,指令是用0和1组成的 一串代码,它们有一定的位数,并分成若干字长段,各段的编码表示不同的含义, 例如某台计算机字长为16位,即有16个二进制数合成一条指令或其它信息。16个 0和1可组成各种排列组合,通过线路变成电信号,让计算机执行各种不同的操作。 2
D、11101 . 1010
2、二进制数
十进制数
方法:按权相加法
将各位的数值与权相乘后,再相加。例:
( 1101.101 )2 = ( ? )10
解:( 1101.101 )2 = 1*23 + 1*22 + 0*21 + 1*20
+ 1*2-1 + 0*2-2 + 1*2-3 = 8+4+1+1/2+1/8 =( 13.625 )10
(0.6875 ) 10= (0. 1011) 2
1
高
0
1
1
低
十进制小数不一定都能转化成完全等值的二进制
小数,有时要取近似值,看精度要求是几位小数。
例:将十进制数29.6351转化成二进制数,精确
到小数点后四位是( )
A、11100 . 1011
B、11101 . 1011
C、11010 . 1001
1、十进制数 二进制数
方法:整数:除 2 取余法
小数:乘 2 取整法
例:( 25.6875 )10 = ( ? )2
整数:除 2 取余法
2
2 2 2 2
25
12 6 3 1 0
1 低
0 0 1 1 高
所以 ( 25 ) 10= ( 11001) 2
小数:乘 2 取整法
0.6875 * 2 1.3750 0.375 * 2 0.750 0.75 * 2 1.50 0.5 * 2 1.0
其他指标相同时,字长越大计算机的处理数据的速度就越快。 计算机的字长有:8位、16位、32位、64位。 3、存储功能强 依靠计算机的存储器完成,可以存储原始数据、中间结果、最终结果等。存储
容量是计算机的一个重要的技术指标。
例:硬盘:160GB、320GB、800GB、1TB、2TB、3TB、4TB等 内存:512MB、1GB、2GB、4GB、8GB、16GB等
例:( 11010.1101 )2 = ( ? )8
011010.110100
3
2 . 6
4
二进制数
4、八进制数
例:( 357.6)8 = ( ? )2
3
5
7
.
6
011 101 111 . 110
5、二进制数
十六进制数
由于一位十六进制的16个数字符号正好相应于四
位二进制数的十六种不同组合,所以十六进制与二
补-补:0 0 1 0 0 1 0 1 1 0 0 1 0 0 0 0
规格化:使尾数数值部分最高位为1。
四、计算机中信息数据的表示
数值数据
文字数据 图像数据
声音数据
视频数据
信息的数字化表示
1.ASCII编码
2.中文编码
3.BCD编码 4.图像编码 5.声音编码 6.视频编码
计算机中常用的编码 非数值信息 0、1代码
一个带符号的二进制数由两部分组成,即数
的符号部分与数的数值部分。 在计算机中,0表示“+”,1表示“-”
例:
N1 = +1011,
N2 = -1011 1 1011
在计算机中 0 1 0 1 1 符号 数值
机器数:将数的符号数字化了的数据表示形式。 真值: 带有“+”、“-”号的数据表示形式。
3、二进制数
八进制数
由于一位八进制的8个数字符号正好相应于三位二进制数的 八种不同组合,所以八进制与二进制之间有简单的对应关系:
八进制: 0
1
2
3
4
5
6
7
二进制:000 001 010 011 100 101 110 111
转换方法:以小数点为界,将二进制数的整数部分从低位开始, 小数部分从高位开始,每三位分成一组,头尾不足三位的补0, 然后将每组的三位二进制数转换为一位八进制数。
[N4]补 = 1 0 0 1 1 0 0 0
2、浮点表示法
指数的小数点的位置不是固定的,是浮动的。
任何一个二进制数N总可以表示成如下的浮点形式:
N = 2E * M
其中:E:N的阶码,为整数,小数点实际位置。 M:N的尾数,为小数,表示N的有效数字。 一个浮点数在机器中的表示如下:
SE ቤተ መጻሕፍቲ ባይዱ符
E 阶码
头尾不足四位的补0,然后将每组的四位二进制数转
换为一位十六进制数。
例:( 1010110110.110111 )2 = ( ? )16
001010110110.11011100 2 B 6 . D C
6、十六进制数
二进制数
例:( 5D . 6E )16 = ( ? )2
5 D . 6 E
01011101.01101110
机器数常用的表示方法有三种:
1、原码
2、反码
3、补码
这三种机器数的表示形式中,符号部分的规定 是相同的,所不同的是数值部分的表示形式。
1、原码
原码表示法是一种较简单的表示法,符号用“0”表 示“+”,“1”表示“-”,数值部分以真值形式表示。
例:X1 = 1101, X2 = -1101,
[X1]原 = 01101 [X2]原 = 11101
N1=+1101,N2=-1101,
采用定点整数如何在机器中表示?
解:
N1 = +1101, N2 = -1101
[N1]原 = 0 0 0 0 1 1 0 1
[N1]补 = 0 0 0 0 1 1 0 1 [N2]原 = 1 0 0 0 1 1 0 1
[N2]补 = 1 1 1 1 0 0 1 1
4、具有逻辑判断能力
逻辑判断:对文字、符号进行判断和比较。
例:A>B AND B>C (即A>B>C)
结果:TRUE FALSE
1 5、能进行自动控制
0
结果:FALSE(0)
若:A=10,B=5,C=6
计算机内部的操作运算全是根据人们事先编制好的程 序自动控制进行的。
二、计算机中数据的表示、运算和存储
例2:设某微型机字长为8位,若有两数,
