初二数学面积法几何专题
面积几何知识点总结初中

面积几何知识点总结初中一、平行四边形的面积平行四边形的面积公式为:S=底×高其中,底表示平行四边形的任意一条边的长度,高表示底到对角线的距离。
二、长方形、正方形和矩形的面积长方形、正方形和矩形都属于平行四边形,因此它们的面积公式也可以通过底和高来计算。
长方形的面积公式为:S=长×宽正方形的面积公式为:S=边长×边长矩形的面积公式为:S=长×宽三、三角形的面积三角形的面积公式为:S=底×高÷2其中,底表示三角形的底边长度,高表示底边到顶点的垂直距离。
四、梯形的面积梯形的面积公式为:S=(上底+下底)×高÷2其中,上底和下底分别表示梯形的上底和下底的长度,高表示梯形的高度。
五、圆的面积圆的面积公式为:S=πr²其中,r表示圆的半径,π表示圆周率,约等于3.14。
以上是初中阶段学习的常见平面图形的面积计算公式,接下来我们将介绍一些面积性质和应用。
六、平面图形面积的性质1. 同样是四边形,其它条件相同时,长方形的面积最大,正方形次之,矩形最小。
2. 三角形的面积与底和高的乘积成正比。
3. 圆的面积与半径的平方成正比。
七、面积的应用1. 在日常生活中,人们常常需要测量房屋、土地的面积,以便做出合理的规划和设计。
2. 在商业活动中,面积的计算也是非常重要的,比如建筑物的施工、地毯的铺设等。
3. 在科学研究中,许多领域需要对空间的面积进行计算,比如地理学、农业学、建筑学等。
总之,面积是一个常见的几何量,它涉及到多种平面图形的计算和性质,对我们的日常生活和工作都有很大的影响。
因此,学习面积几何知识是非常重要的,它不仅可以提高我们的数学素养,还能帮助我们更好地理解和应用数学知识。
希望同学们能够认真学习面积几何知识,灵活运用它们,提高数学成绩,为将来的学习和工作打下坚实的基础。
八年级数学暑假专题—怎样证明面积问题以及用面积法解几何问题 人教版

一 教学内容:暑假专题——怎样证明面积问题以及用面积法解几何问题教学目标:1 使学生灵活掌握证明几何图形中的面积的方法。
2 培养学生分析问题、解决问题的能力。
二 重点、难点:重点:证明面积问题的理论依据和方法技巧。
难点:灵活运用所学知识证明面积问题。
教学过程:(一)证明面积问题常用的理论依据1 三角形的中线把三角形分成两个面积相等的部分。
2 同底同高或等底等高的两个三角形面积相等。
3 平行四边形的对角线把其分成两个面积相等的部分。
4 同底(等底)的两个三角形面积的比等于高的比。
同高(或等高)的两个三角形面积的比等于底的比。
5 三角形的面积等于等底等高的平行四边形的面积的一半。
6. 三角形的中位线截三角形所得的三角形的面积等于原三角形面积的。
147. 14三角形三边中点的连线所成的三角形的面积等于原三角形面积的。
8 有一个角相等或互补的两个三角形的面积的比等于夹角的两边的乘积的比。
(二)证明面积问题常用的证题思路和方法1 分解法:通常把一个复杂的图形,分解成几个三角形。
2 作平行线法:通过平行线找出同高(或等高)的三角形。
3 利用有关性质法:比如利用中点、中位线等的性质。
4 还可以利用面积解决其它问题。
【典型例题】(一)怎样证明面积问题 1 分解法例1 从△ABC 的各顶点作三条平行线AD 、BE 、CF ,各与对边或延长线交于D 、E 、F ,求证:△DEF 的面积=2△ABC 的面积。
FEAB D C分析:从图形上观察,△DEF 可分为三部分,其中①是△ADE ,它与△ADB 同底等高,故S S ADE ADB ∆∆=②二是△,和上面一样,ADF S S ADF ADC ∆∆=③三是△AEF ,只要再证出它与△ABC 的面积相等即可 由S △CFE =S △CFB故可得出S △AEF =S △ABC 证明:∵AD 作平行线法 例 2 已知:在梯形ABCD 中,DC求证:S S ADM ABCD ∆=12A BS S S MN h S AMD DMN AMN ABCD ∆∆∆=+=⋅=1212MN DC AB=+2则S MN h ABCD =⋅又 S S S MN h AMD AMN MND ∆∆∆=+=⋅12∴=S S ADM ABCD∆12证线段之积相等例3 设AD 、BE 和CF 是△ABC 的三条高,求证:AD ·BC =BE ·AC =CF ·ABAFEB D C分析:从结论可看出,AD 、BE 、CF 分别是BC 、AC 、AB 三边上的高,故可联想到可用面积法。
初中数学面积问题总结归纳

初中数学面积问题总结归纳
在初中数学中,面积问题主要涉及到平面图形的面积计算。
以下是在初中数学中常见的面积问题总结归纳:
1. 矩形的面积计算:矩形的面积可以通过长度和宽度的乘积来计算,即面积 = 长 ×宽。
2. 正方形的面积计算:正方形的边长相等,所以正方形的面积可以通过边长的平方来计算,即面积 = 边长 ×边长。
3. 三角形的面积计算:三角形的面积可以通过底边长和高的乘积再除以2来计算,即面积 = 底边长度 ×高 ÷ 2。
4. 平行四边形的面积计算:平行四边形的面积可以通过底边长和高的乘积来计算,即面积 = 底边长度 ×高。
5. 梯形的面积计算:梯形的面积可以通过上底与下底之和的一半再乘以高来计算,即面积 = (上底 + 下底) ×高 ÷ 2。
6. 圆的面积计算:圆的面积可以通过半径的平方再乘以π(pi)来计算,即面积 = 半径 ×半径× π。
在解决这些面积问题时,需要注意图形的参数,如边长、底边长、高、半径等,并且对于复杂图形,可能需要将其分解为多个基本图形来计算面积。
此外,也要注意单位的转换和精确计算的问题。
初二求面积的题

初二求面积的题目及解答
一、矩形面积
例题:一个矩形的长是6厘米,宽是4厘米,求它的面积。
解答:矩形的面积可以通过长乘以宽来计算,即6厘米×4厘米=24平方厘米。
二、三角形面积
例题:一个三角形的底边长是6厘米,高是4厘米,求它的面积。
解答:三角形的面积可以通过底边长乘以高再除以2来计算,即(6厘米×4厘米)/2=12平方厘米。
三、圆形面积
例题:一个圆的半径是3厘米,求它的面积。
解答:圆的面积可以通过π乘以半径的平方来计算,即π×(3厘米)^2=27π平方厘米。
四、扇形面积
例题:一个扇形的半径是5厘米,圆心角是72度,求它的面积。
解答:扇形的面积可以通过圆的面积乘以圆心角与360度的比值来计算,即π×(5厘米)^2×(72度/360度)=25π平方厘米。
五、组合图形面积
例题:求下图组合图形的面积(单位:厘米)
解答:通过数格子的方法,我们可以求得组合图形的面积为:100平方厘米。
八年级数学竞赛例题专题讲解:面积法

八年级数学竞赛例题专题讲解:面积法阅读与思考平面几何学的产生源于人们测量土地面积的需要,面积关联着几何图形的重要元素边与角.所谓面积法是指借助面积有关的知识来解决一些直接或间接与面积问题有关的数学问题的一种方法.有许多数学问题,虽然题目中没有直接涉及面积,但由于面积联系着几何图形的重要元素,所以借助于有关面积的知识求解,常常简捷明快.用面积法解题的基本思路是:对某一平面图形面积,采用不同方法或从不同角度去计算,就可得到一个含边或角的关系式,化简这个面积关系式就可得到求解或求证的结果.下列情况可以考虑用面积法:(1)涉及三角形的高、垂线等问题;(2)涉及角平分线的问题.例题与求解【例1】如图,从等边三角形内一点向三边作垂线,已知这三条垂线段的长分别为1,3,5,则这个等边三角形的边长为______________.(全国初中数学联赛试题) 解题思路:从寻求三条垂线段与等边三角形的高的关系入手.等腰三角形底边上任一点到两腰距离之和等于一腰上的高,那么等边三角形呢?等腰梯形呢?【例2】如图,△AOB中,∠O=,OA=OB,正方形CDEF的顶点C在DA上,点D在OB上,点F在AB上,如果正方形CDEF的面积是△AOB的面积的,则OC:OD等于( )A.3:1 B.2:1C.3:2 D.5:3解题思路:由面积关系,可能想到边、角之间的关系,这时通过设元,即可把几何问题代数化来解决.【例3】如图,在□ABCD中,E为AD上一点,F为AB上一点,且BE=DF,BE与DF交于G,求证:∠BGC=∠DGC.(长春市竞赛试题)解题思路:要证∠BGC=∠DGC,即证CG为∠BGD的平分线,不妨用面积法寻找证题的突破口.【例4】如图,设P为△ABC内任意一点,直线AP,BP,CP交BC,CA,AB于点D、E、F.求证:(1);(2).(南京市竞赛试题)解题思路:过P点作平行线,产生比例线段.【例5】如图,在△ABC中,E,F,P分别在BC,CA,AB上,已知AE,BF,CP相交于一点D,且,求的值.解题思路:利用上例的结论,通过代数恒等变形求值.(黄冈市竞赛试题)【例6】如图,设点E,F,G,H分别在面积为1的四边形ABCD的边AB,BC,CD,DA上,且(是正数),求四边形EFGH的面积.(河北省竞赛试题)解题思路:连对角线,把四边形分割成三角形,将线段的比转化为三角形的面积比.线段比与面积比的相互转化,是解面积问题的常用技巧.转化的基本知识有:(1) 等高三角形面积比,等于它们的底之比;(2) 等底三角形面积比,等于它们的高之比;(3) 相似三角形面积比,等于它们相似比的平方.能力训练1.如图,正方形ABCD的边长为4cm,E是AD的中点,BM⊥EC,垂足为M,则BM=______.(福建省中考试题)2.如图,矩形ABCD中,P为AB上一点,AP=2BP,CE⊥DP于E,AD=,AB=,则CE=__________.(南宁市中考试题)第1题图第2题图第3题图3.如图,已知八边形ABCDEFGH中四个正方形的面积分别为25,48,121,114,PR=13,则该八边形的面积为____________.(江苏省竞赛试题) 4. 在△ABC中,三边长为,,,表示边上的高的长,,的意义类似,则(++)的值为____________. (上海市竞赛试题)5.如图,△ABC的边AB=2,AC=3,Ⅰ,Ⅱ,Ⅲ分别表示以AB,BC,CA为边的正方形,则图中三个阴影部分的面积之和的最大值是__________.(全国竞赛试题) 6.如图,过等边△ABC内一点P向三边作垂线,PQ=6,PR=8,PS=10,则△ABC的面积是 ( ).A. B.C.D.(湖北省黄冈市竞赛试题)第5题图第6题图第7题图7.如图,点D是△ABC的边BC上一点,若∠CAD=∠DAB=,AC=3,AB=6,则AD的长是( ).A.2 B. C.3 D.8.如图,在四边形ABCD中,M,N分别是AB,CD的中点,AN,BN,DM,CM划分四边形所成的7个区域的面积分别为,,,,,,,那么恒成立的关系式是( ).A.+=B.+=C.+= D.+=9.已知等边△ABC和点P,设点P到△ABC三边AB,AC,BC的距离分别为,,,△ABC的高为.若点P在一边BC上(如图1),此时,可得结论:++=.请直接用上述信息解决下列问题:当点P在△ABC内(如图2)、点P在△ABC外(如图3)这两种情况时,上述结论是否还成立?若成立.请给予证明;若不成立,,,与之间又有怎样的关系?请写出你的猜想,不需证明.(黑龙江省中考试题)10.如图,已知D,E,F分别是锐角△ABC的三边BC,CA,AB上的点,且AD、BE、CF相交于P点,AP=BP=CP=6,设PD=,PE=,PF=,若,求的值.(“希望杯”邀请赛试题)11.如图,在凸五边形ABCDE中,已知AB∥CE,BC∥AD,BE∥CD,DE∥AC,求证:AE∥BD.(加拿大数学奥林匹克试题)12.如图,在锐角△ABC中,D,E,F分别是AB,BC,CA边上的三等分点. P,Q,R分别是△ADF,△BDE,△CEF的三条中线的交点.(1) 求△DEF与△ABC的面积比;(2) 求△PDF与△ADF的面积比;(3) 求多边形PDQERF与△ABC的面积比.13.如图,依次延长四边形ABCD的边AB,BC,CD,DA至E,F,G,H,使,若,求的值.(上海市竞赛试题)14.如图,一直线截△ABC的边AB,AC及BC的延长线分别交于F,E,D三点,求证:.(梅涅劳斯定理)15.如图,在△ABC中,已知,求的值.(“华罗庚金杯”少年数学邀请赛试题)。
初中数学重点梳理:面积问题与面积方法(二)
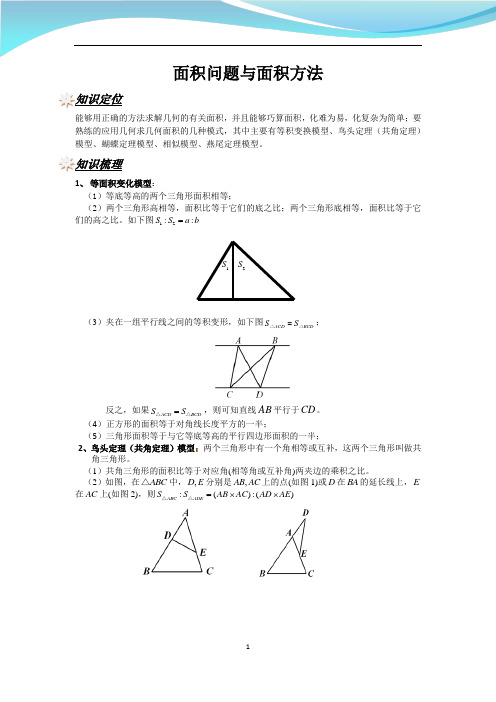
面积问题与面积方法知识定位能够用正确的方法求解几何的有关面积,并且能够巧算面积,化难为易,化复杂为简单;要熟练的应用几何求几何面积的几种模式,其中主要有等积变换模型、鸟头定理(共角定理)模型、蝴蝶定理模型、相似模型、燕尾定理模型。
知识梳理1、 等面积变化模型:(1)等底等高的两个三角形面积相等;(2)两个三角形高相等,面积比等于它们的底之比;两个三角形底相等,面积比等于它们的高之比。
如下图12::S S a b =(3)夹在一组平行线之间的等积变形,如下图ACD BCD S S =△△;反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD 。
(4)正方形的面积等于对角线长度平方的一半;(5)三角形面积等于与它等底等高的平行四边形面积的一半;2、鸟头定理(共角定理)模型:两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
(1)共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。
(2)如图,在ABC △中,,D E 分别是,AB AC 上的点(如图1)或D 在BA 的延长线上,E 在AC 上(如图2),则:():()ABC ADE S S AB AC AD AE =⨯⨯△△1S 2S3、蝴蝶定理模型:任意四边形中的比例关系。
蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系。
① 1243::S S S S =1324S S S S ⨯=⨯ ② ()()1243::AO OC S S S S =++ 4、相似模型:相似三角形:相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:(1)相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; (2)相似三角形的面积比等于它们相似比的平方。
(完整版)初二几何面积法

专题复习一、面积法何谓面积法在求解平面几何问题的时候,根据有关几何量与涉及的有关图形面积之间的内在联系,用面积或面积之间的关系表示有关线段间的关系,从而把要论证的线段之间的关系转化为面积的关系,并通过图形面积的等积变换对所论问题来进行求解的方法,称之为面积法。
(一)证明面积问题常用的理论依据用面积法解几何问题常用到下列性质:1、全等三角形的面积相等;2、三角形的中线把三角形分成面积相等的两部分;3、同底同高或等底等高的两个三角形面积相等。
4、同底(等底)的两个三角形面积的比等于高的比。
同高(或等高)的两个三角形面积的比等于底的比。
一、证线段相等1、已知:△ABC 中,∠A 为锐角,AB=AC ,BD ⊥AC 于D ,CE ⊥AB 于E ,求证:BD=CEED C B A2、已知:等腰△ABC 中,AB=AC ,D 为底边BC 的中点,DE ⊥AB ,DF ⊥AC ,垂足分别为E 、F.求证:DE=DF.3、(1)已知: △ABC 中,AB=AC ,P 为底边BC 上一点,PD ⊥AB 于D ,PE ⊥AC 于E ,BF ⊥AC 于F ,求证:PD+PE=BF.P(2)若P 为 △ABC 的底边BC 的延长线上一点,其他条件不变,请画出图形,并猜想(1)中的结论仍然成立吗?若成立,请说明理由;若不成立,请写出正确的结论,并证明。
F ED CB AP A B C4、(1)已知等边△ABC 内有一点P ,PD ⊥AB ,PE ⊥BC ,PF ⊥CA ,垂足分别为D 、E 、F ,又AH 为△ABC 的高,求证:PD+PE+PF=AH. PH F E D C B A(2)若P 是等边△ABC 外部一点,其他条件不变,(1)中的结论仍然成立吗?若成立,请说明理由;若不成立,请写出正确的结论,并说明理由。
AB C DE F H P二、证角相等5、点C 是线段AB 上一点,分别以AC 、BC 为边在AB 同侧作等边△ACD 和等边△BCE ,连接BD 、AE 交于O 点,再连接OC ,求证:∠AOC=∠BOC.1、Rt △ABC 中,∠BAC=90°,AB=3,M 为边BC 上一点,连接AM ,若将△ABM 沿直线AM 翻折后,点B 恰好落在边AC 的中点B ′处,那么点M 到AC 的距离是 。
初二数学知识点专题讲解与练习23---面积的计算(培优版)

A
EF
D
5
8
10
B 例1图 C
【例 2】如图,在△ABC 中,已知 BD 和 CE 分别是两边上的中线,并且 BD⊥CE,BD=4,CE=6,
那么△AAB.C 的12面积等于 (
.)
B 14
.C 16
(全国初中数学联赛) .D 18
BG
上,ABCD
和
DEFG
都是正方形,面积分别为
7cm2
和
,则△ 11cm2
CDE
的面
积等于___________cm2.
(武汉市竞赛试题)
2.如图,P 为正方形 ABCD 内一点,PA=PB=10,并且 P 到 CD 边的距离也等于 10,那么正方形
的面积是 ABCD
_______________.
A
D
K
M
B 第 10 题图 C
11.如图 , , 1 AB CD 是两条线段,M 是 AB 的中点, , , △ △ △ S DMC S DAC S DBC 分别表示△DMC,△DAC,
△ 的面积,当 ∥ 时,有 = + ① DBC
AB CD
△S DMC △S DAC 2 S△DBC……….. .
(1) 如图 2,若图 1 中 AB 与 CD 不平行时,①式是否成立?请说明理由.
秒,AE 的长为 y.
(1) 求出 y 关于 x 的函数关系式,并写出自变量 x 的取值范围;
(2) 当 x 为何值时,△BDE 的面积 S 有最大值,最大值为多少?
(江西省中考试题)
解题思路:对于(1)利用△ADE∽△ABC 可得 y 与 x 的关系式;对于(2)先写出 S 关于 x 的函数关系式,
初二数学等面积法压轴题

初二数学等面积法压轴题
等面积法是解决几何问题的一种重要方法,特别是在求解压轴题时。
以下是一道典型的初二数学等面积法压轴题:
题目:
已知矩形ABCD,AB = 3,AD = 2,以A为圆心作图,设⊙A的半径为r,用等面积法求证:r > 2 - √7。
证明:
第一步,由于题目没有明确说明哪些图形与圆相切,我们首先考虑与圆相切的特殊情况。
假设⊙A与线段CD相切于点E,则AE为半径,即r = AE。
第二步,根据矩形的性质和勾股定理,我们有AE² + DE² = AD²。
代入已知的AB、AD和AE的值,我们可以得到一个关于DE的二次方程。
第三步,解这个二次方程,我们得到DE = √7 - 1。
由于DE < CD(因为CD = AB = 3),我们知道这种情况是不可能的。
第四步,为了证明r > 2 - √7,我们需要找到一个与⊙A相切且使得r满足这个不等式的切线。
考虑到线段CD与⊙A相切的情况,我们可以使用等面积法来找到这条切线。
第五步,根据等面积法,我们知道矩形的面积等于圆的面积加上四分之一圆的面积。
即3 × 2 = πr² - (1/4)πr²。
解这个方程,我们得到r = 2 + √7。
第六步,根据第五步的结果,我们得到r > 2 - √7。
综上,我们证明了r > 2 - √7。
初中几何模型与解法中考几何专题:等面积法
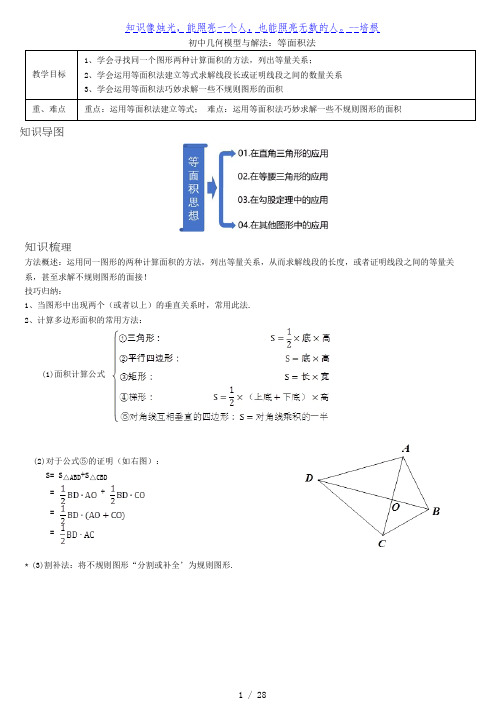
初中几何模型与解法:等面积法教学目标1、学会寻找同一个图形两种计算面积的方法,列出等量关系;2、学会运用等面积法建立等式求解线段长或证明线段之间的数量关系3、学会运用等面积法巧妙求解一些不规则图形的面积重、难点重点:运用等面积法建立等式;难点:运用等面积法巧妙求解一些不规则图形的面积知识导图知识梳理方法概述:运用同一图形的两种计算面积的方法,列出等量关系,从而求解线段的长度,或者证明线段之间的等量关系,甚至求解不规则图形的面接!技巧归纳:1、当图形中出现两个(或者以上)的垂直关系时,常用此法.2、计算多边形面积的常用方法:(1)面积计算公式(2)对于公式⑤的证明(如右图):S=S △ABD +S △CBD===*(3)割补法:将不规则图形“分割或补全’为规则图形.+=又∵ABC =AC AB∴该直角三角形斜边AB上的高CD=导学一:等面积法在直角三角形的应用知识点讲解1在直角三角形中,两条直角边、斜边以及斜边上的高,知道任意两个可以运用勾股定理、等面积思想求出剩余两个。
如图:基本公式:①勾股定理:②等面积法:证明②:即:,例题1.如图,在Rt ABC ,∠C=90°,当直角边AC =4,斜边AB =5时,求该直角三角形斜边AB上的高CD ?【参考答案】=2.如图,在Rt ABC (BC AC ),∠C=90°,当斜边AB =10cm,斜边AB上的高CD =4.8cm 时,求该直角三角形直角边AC和BC的长度?【参考答案】解:设AC =x,BC =y,(y由勾股定理:==100又∵ABC =AC AB ∴x y=48再由.得到解得:答:AC =6,BC =8同步练习1.如图,在Rt ABC,∠C=90°,且AC=24,BC=7,作ABC的三个内角的角平分线交于点P,再过点P依次作PD⊥AB于D,作PE⊥BC于E,作PF⊥AC于F.(1)求证:PD=PE=PF;(2)求出:PD的值.【参考答案】(1)证明∵AP平分∠CAB,且PD⊥AB,PF⊥AC∴PD=PF同理,PD=PE综上,PD=PE=PF(2)解:C、=5设:PD=PE=PF=dABC =AC =84sp;ABC&en=APBBPC CPA 84=++d =3,PD=32.如图,△ABC的顶点A,B,C在边长为1的正方形网格的格点上,则BC边长的高为()B、D、A、【参考答案】C 解:∵S△ABC =3×4−×2×3−×2×1−×2×4=4∵BC==,∴BC边长的高==故选:C.导学二:等面积法在等腰三角形的应用知识点讲解1在等腰三角形中,可以运用“割补法”的等面积思想,先建立有关“腰以及腰上的高”的等式,再通过等式两边约分来探索出线段之间的数量关系!例题1.如图,在△ABC中,AB=AC,AC边上的高BD=10cm.(1)如图1,求AB边上高CE的长;(2)如图2,若点P为BC边上任意一点,PM⊥AB于点M,PN⊥AC于点N,求PM+PN的值;(3)如图3,若点P为BC延长线上任意一点,PM⊥AB于M,PN⊥AC于点N,在①PM+PN;②PM PN中有一个是定值,判断出来并求值.【参考答案】(1)由S△ABC=×AB×CE=×AC×BD∵AB=AC,BD=10∴CE=10(2)如图,连接AP由S△ABP+S△ACP=S△ABC×AB×PM+×AC×PD=×AC×BD∵AB=AC,BD=10∴PM+PN=10(3)如图,连接APPM−PN是定值理由如下:连接AP,由S△ABP−S△ACP=S△ABC×AB×PM−×AC×PD=×AC×BD∵AB=AC,BD=10∴PM−PN=102.已知等边△ABC和内部一点P,设点P到△ABC三边的AB、BC、AC的距离分别是h1,h2,h3,△ABC的高为h,问h1、h2、h3与h之间有怎样的数量关系?请说明理由。
人教版八年级数学下册专题复习(十一) 几何图形的面积等分

思维特训(十一)几何图形的面积等分方法点津面积等分基本模型:1.三角形的中线把三角形面积等分;2.夹在两条平行线间的距离相等,同底等高的两个三角形面积相等;3.过平行四边形对角线中点(对称中心)的任意一条直线把平行四边形面积等分.典题精练类型一作一个图形的面积等于已知图形1.(1)如图11-S-1①,已知直线m∥n,点A,B在直线n上,点C,P在直线m上.①写出图①中面积相等的三角形:________;②当点P在直线m上移动到任一位置时,总有________与△ABC的面积相等;(2)如图11-S-1②,已知一个五边形ABCDE,你能否过点E作一条直线交BC(或其延长线)于点M,使四边形ABME的面积等于五边形ABCDE的面积?图11-S-1类型二等分面积2.阅读下列材料:小明遇到一个问题:AD是△ABC的中线,M为BC边上任意一点(不与点D重合),过点M作一直线,使其等分△ABC的面积.他的作法是:如图11-S-2①,连接AM,过点D作DN∥AM交AC于点N,作直线MN,直线MN即为所求直线.请你参考小明的作法,解决下列问题:(1)如图②,在四边形ABCD中,AE平分四边形ABCD的面积,M为CD边上一点,过点M作一直线MN,使其等分四边形ABCD的面积(要求:在图②中画出直线MN,并保留作图痕迹);(2)如图③,求作过点A的直线AE,使其等分四边形ABCD的面积(要求:在图③中画出直线AE,并保留作图痕迹).图11-S-23.有一些几何图形可以被某条直线分成面积相等的两部分,我们将“把一个几何图形分成面积相等的两部分的直线叫做该图形的二分线”,如三角形的中线所在的直线一定是三角形的“二分线”.解决下列问题:(1)在图11-S-3①中,试用三种不同的方法分别画出平行四边形ABCD的“二分线”;(2)解决问题:兄弟俩分家时,有原来共同承包的一块平行四边形田地ABCD,现要进行平均划分,由于在这块地里有一口井P,如图②所示,为了兄弟俩都能方便使用这口井,兄弟俩在划分时犯难了,聪明的你能帮他们解决这个问题吗(画图,并说明结果)?图11-S-34.我们把能平分四边形面积的直线称为“好线”.利用下面的作图,可以得到四边形的“好线”:如图11-S-4①,在四边形ABCD中,取对角线BD的中点O,连接OA,OC,AC.显然,折线AOC能平分四边形ABCD的面积,再过点O作OE∥AC交CD于点E,则直线AE即为一条“好线”.(1)试说明:直线AE是“好线”的理由;(2)如图②,AE为一条“好线”,F为AD边上的一点,请作出经过点F的“好线”,并对画图作适当说明(不需要说明理由).图11-S-45.自定义:在一个图形上画一条直线,若这条直线既平分该图形的面积,又平分该图形的周长,我们称这条直线为这个图形的“等分积周线”.(1)如图11-S-5①,已知△ABC,AC≠BC,过点C能否画出△ABC的一条“等分积周线”?若能,说出确定的方法;若不能,请说明理由.(2)如图②,在四边形ABCD中,∠B=∠C=90°,EF垂直平分AD,垂足为F,交BC 于点E,已知AB=3,BC=8,CD=5.求证:直线EF为四边形ABCD的“等分积周线”.(3)如图③,在△ABC中,AB=BC=6,AC=8,请你作出△ABC的一条“等分积周线”EF(要求:直线EF不过△ABC的顶点,交边AC于点F,交边BC于点E),并说明理由.图11-S-5典题讲评与答案详析1.解:(1)①图①中符合条件的三角形有:△CAB与△P AB,△BCP与△APC,△ACO 与△BPO.②△P AB(2)如图,连接EC,过点D作直线DM∥EC交BC的延长线于点M,作直线EM,直线EM即为所求的直线.2.解:(1)如图①,连接AM,过点E作EN∥AM,交AD于点N,再作直线MN即可.(2)如图②,取对角线BD的中点O,连接AO,CO,AC,过点O作OE∥AC交CD于点E,直线AE就是所求直线.3.解:(1)答案不唯一,示例如下:(2)能解决这个问题.连接AC,BD相交于点O,过点O,P作直线与DC,AB分别交于点E,F,如图所示.则一人分四边形ADEF,一人分四边形CEFB.4.解:(1)∵OE∥AC,∴S△AOE=S△COE,∴S△AOF=S△CEF.又∵折线AOC能平分四边形ABCD的面积,∴直线AE平分四边形ABCD的面积,即AE是“好线”.(2)连接EF,过点A作EF的平行线交CD于点G,连接FG,则FG为一条“好线”.∵AG∥EF,∴S△AGE=S△AFG. 设AE与FG的交点是O,则S△AOF=S△GOE.又∵AE为一条“好线”,∴FG为一条“好线”.5.解:(1)不能.理由:如图①,取AB的中点D,连接CD,则S△ADC=S△DBC,且过点C只能画CD一条直线平分△ABC的面积.∵AC≠BC,∴AD+AC≠BD+BC,∴过点C不能画出△ABC的一条“等分积周线”.(2)证明:如图②,连接AE,DE,设BE=x,∵EF垂直平分AD,∴AE=DE,AF=DF,S△AEF=S△DEF.∵∠B=∠C=90°,AB=3,BC=8,CD=5,∴在Rt△ABE和Rt△DCE中,根据勾股定理,得AB2+BE2=CE2+DC2,即32+x2=(8-x)2+52,解得x=5,∴BE=5,CE=3,∴AB+BE=CE+DC,S△ABE=S△DCE.∴AF+AB+BE=DF+CE+DC.∵S四边形ABEF=S△ABE+S△AEF,S四边形DCEF=S△DEF+S△DCE,∴S四边形ABEF=S四边形DCEF,∴直线EF为四边形ABCD的“等分积周线”.(3)如图③,在AC上取一点F,使得FC=AB=6,在BC上取一点E,使得BE=2,作直线EF,则直线EF是△ABC的“等分积周线”.理由:由作图可得AF=AC-FC=8-6=2,在CB上取一点G,使得CG=AF=2.∵AB =BC,∴∠A=∠C.在△ABF和△CFG中,AF=CG,∠A=∠C,AB=CF,∴△ABF≌△CFG(SAS),∴S△ABF=S△CFG.又易得BE=EG=2,∴S△BFE=S△EFG,∴S△EFC=S四边形ABEF,AF+AB+BE=CE+CF=10,∴直线EF是△ABC的“等分积周线”.。
专题 在平面直角坐标系中求图形的面积(四大题型)(原卷版)

(苏科版)八年级上册数学《第5章 平面直角坐标系》专题训练 在平面直角坐标系中求图形的面积【例题1】(2023春•青龙县期中)如图,已知三角形ABC 如图所示放置在平面直角坐标系中,其中C (﹣4,4).则三角形ABC的面积是( )A.4B.6C.8D.1【变式1-1】如图,已知三角形ABC如图所示放置在平面直角坐标系中,其中C(﹣4,4).则三角形ABC的面积是( )A.4B.6C.12D.24【变式1-2】(2023•岳麓区校级开学)如图,△ABC的三个顶点坐标分别为A(﹣3,2),B(0,3),C(0,﹣1),则△ABC的面积为( )A.4B.6C.4.5D.5【变式1-3】(2023春•思明区校级期中)已知点A(1,2a+1),B(﹣a,a﹣3),若线段AB∥x轴,则三角形AOB的面积为( )A.21B.28C.14D.10.5【变式1-4】(2022春•巴音郭楞州期末)如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中,三角形ABC的三个顶点A(5,2)、B(5,5)、C(1,1)均在格点上.(1)将三角形ABC向左平移5个单位,再向下平移3个单位得到三角形A1B1C1,画出平移后的图形,并写出点A1的坐标;(2)求三角形ABC的面积.【变式1-5】如图所示,将图中的点(﹣5,2),(﹣3,4),(﹣1,2),(﹣4,2),(﹣2,2),(﹣2,3),(﹣4,3)做如下变化:(1)横坐标不变,纵坐标分别减4,再将所得的点用线段依次连接起来,所得的图形与原来的图形相比有什么变化?(2)纵坐标不变,横坐标分别加6,再将所得的点用线段依次连接起来,所得的图形与原来的图形相比有什么变化?(3)求出以点(﹣5,2),(﹣3,4),(﹣1,2)为顶点的三角形的面积?【例题2】如图,A(3,0),B(0,3),C(1,4),求△ABC的面积.【变式2-1】如图,已知:A(3,2),B(5,0),E(4,1),求△AOE的面积.【变式2-2】在如图所示的正方形网格中,每个小正方形的单位长度均为1,△ABC的三个顶点恰好是正方形网格的格点.(1)写出图中所示△ABC各顶点的坐标.(2)求出此三角形的面积.【变式2-3】(2023春•双柏县期中)在直角坐标系中,已知A(﹣3,4),B(﹣1,﹣2),O(0,0),画出三角形并求三角形AOB的面积.【变式2-4】(2022春•雷州市期末)如图,△ABC在直角坐标系中,(1)请写出△ABC各点的坐标;.(2)求出S△ABC【变式2-5】在如图所示的正方形网格中,每个小正方形的边长均为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A、C的坐标分别为(﹣4,5)、(﹣1,3).(1)请在如图所示的网格平面内画出平面直角坐标系;(2)请把三角形ABC先向右平移5个单位长度,再向下平移3个单位长度得到三角形A′B′C′,在图中画出三角形A′B′C′;(3)求三角形ABC的面积.【变式2-6】(2023秋•浏阳市期中)如图,在平面直角坐标系xOy 中,点A 的坐标为(﹣4,4),点B 的坐标为(﹣2,0),点C 的坐标为(﹣1,2).(1)请面出△ABC 关于y 轴的对称图形△A 1B 1C 1;(2)直接写出A 1,B 1,C 1三点的坐标;(3)求△ABC 的面积.【例题3】(2022春•长安区校级月考)如图所示,在平面直角坐标系中,点A (4,0),B (3,4),C (0,2),则四边形ABCO 的面积为( )A .9B .10C .11D .12【变式3-1】(2022春•商南县期末)如图,有一块不规则的四边形图形ABCD,各个顶点的坐标分别为A (﹣2,8),B(﹣11,6),C(﹣14,0),D(0,0)(比例尺为1:100),现在想对这块地皮进行规划,需要确定它的面积.(1)确定这个四边形的面积(2)如果把原来四边形ABCD的各个顶点的纵坐标保持不变,横坐标加2,所得的四边形面积又是多少?【变式3-2】(2022秋•高明区月考)已知:A(﹣5,﹣2),B(﹣1,2),C(5,4),D(6,﹣2).(1)在坐标系中描出各点,画出四边形ABCD;(2)求四边形ABCD的面积.【变式3-3】如图,四边形ABCD四个顶点的坐标分别为A(﹣2,0),B(1,7),C(5,5),D(7,0).试求这个四边形的面积.【变式3-4】如图,面积为12cm 2的△ABC 向x 轴正方向平移至△DEF 的位置,相应的坐标如图所示(a ,b 为常数),(1)求点D 、E 的坐标;(2)求四边形ACED 的面积.【变式3-5】如图,在平面直角坐标系xOy 中,已知A (2,4),B (6,6),C (8,2),求四边形OABC 的面积.【例题4】(2021秋•围场县期末)已知点O (0,0),点A (﹣3,2),点B 在y 轴上,若△AOB 的面积为12,则点B 的坐标为( )A .(0,8)B .(0,4)C .(8,0)D .(0,﹣8)或(0,8)【变式4-1】已知点A(1,0),B(0,2),点P在x轴的负半轴上,且△PAB的面积为5,则点P的坐标为( )A.(0,﹣4)B.(0,﹣8)C.(﹣4,0)D.(6,0)【变式4-2】(2022春•路南区期末)如图,已知A(﹣2,3)、B(4,3)、C(﹣1,﹣3)(1)求点C到x轴的距离;(2)求△ABC的面积;(3)点P在y轴上,当△ABP的面积为6时,请直接写出点P的坐标.【变式4-3】如图,在平面直角坐标系中,点A(4,0),B(3,4),C(0,2).(1)求S;四边形ABCO;(2)连接AC,求S△ABC=8?若存在,请求点P坐标.(3)在x轴上是否存在一点P,使S△PAB【变式4-4】(2022•天津模拟)如图,A(﹣1,0),C(1,4),点B在x轴上,且AB=3.(1)求点B的坐标;(2)求△ABC的面积;(3)在y轴上是否存在点P,使以A、B、P三点为顶点的三角形的面积为10?若存在,请直接写出点P 的坐标;若不存在,请说明理由.【变式4-5】(2022秋•渭滨区期末)如图所示,在平面直角坐标系中,已知A(0,1)、B(2,0)、C (4,3).(1)在平面直角坐标系中画出△ABC,则△ABC的面积是 ;(2)若点D与点C关于y轴对称,则点D的坐标为 ;(3)已知P为x轴上一点,若△ABP的面积为1,求点P的坐标.【变式4-6】(2022•天津模拟)如图,在平面直角坐标系中,已知A(a,0),B(b,0),其中a,b满足|a+1|+(b﹣3)2=0.(1)填空:a= ,b= ;(2)若在第三象限内有一点M(﹣2,m),请用含m的式子表示△ABM的面积;(3)在(2)条件下,当m=−32时,在x轴上是否存在点P(不与点A重合),使得S三角形PBM=S三角形ABM,若存在请求出点P的坐标,不存在说明理由.1.(2022春•湖北期末)已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.(1)在图中画出△A′B′C′;(2)写出点A′、B′的坐标;(3)连接A′A、C′C,求四边形A′ACC′的面积.2.已知A(0,3),B(﹣4,0),C(﹣2,﹣3),D(4,﹣1),求图中四边形ABCD的面积.专题难点突破练3.(2022春•黄石期末)如图,在平面直角坐标系中,线段AB的坐标分别为A(﹣4,1),B(﹣1,﹣3),把线段AB先向右平移5个单位长度,再向上平移4个单位长度得到线段CD(其中点A与点D、点B与点C是对应点)(1)画出平移后的线段CD,写出点C的坐标为( , ).(2)连接AD、BC,四边形ABCD的面积为 .(3)点E在线段AD上,CE=6,点F是线段CE上一动点,线段BF的最小值为 .4.(2022春•船营区校级期末)如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(3,c)三点,其中a、b、c满足关系式:|a﹣2|+(b﹣3)2+0.(1)求a、b、c的值;(2)如果在第二象限内有一点P(m,12),请用含m的式子表示四边形ABOP的面积;(3)在(2)的条件下,是否存在负整数m,使四边形ABOP的面积等于△AOP面积的两倍?若存在,求出所有满足条件的点P的坐标,若不存在,请说明理由.5.(2022秋•竞秀区期末)已知,如图,方格纸中每个小方格都是边长为1个单位长度的正方形,现有A,B,C三点,其中点A坐标为(﹣4,1),点B坐标为(1,1).(1)请根据点A,B的坐标在方格纸中建立平面直角坐标系,并直接写出点C坐标为 ;(2)依次连接A,B,C,A,得到△ABC,请判断△ABC的形状,并说明理由;(3)若点C关于直线AB的对称点为点D.则点D的坐标为 ;(4)在y轴上找一点F,使△ABF的面积等于△ABD的面积,点F的坐标为 .6.(2022春•青羊区校级月考)在外面直角坐标系中,O为原点,点A(0,2),B(﹣2,0),C(4,0).(1)如图1,△ABC的面积为 ;(2)如图2,将点B向右平移7个单位长度,再向上平移4个单位长度,得到对应点D.①求△ACD的面积;②已知点P(1,m)是一动点,若△PAC的面积等于△ACD的面积,请求出点P的坐标.7.(2022春•梁平区期中)如图1,以长方形ABCD的中心O为原点,平行于BC的直线为x轴建立平面直角坐标系,若点D的坐标为(6,3).(1)直接写出A、B、C的坐标;(2)设AD的中点为E,点M是y轴上的点,且△CME的面积是长方形ABCD面积的16,求点M的坐标;(3)如图2,若点P从C点出发向CB方向匀速移动(不超过点B),点Q从B点出发向BA方向匀速移动(不超过点A),且点Q的速度是P的一半,P、Q两点同时出发,已知当移动时间为t秒时,P点的横坐标为6﹣2t,此时①CP= ,AQ= (用含t的式子表示).②在点P、Q移动过程中,四边形PBQD的面积是否发生变化?若不变,求其值;若变化,求其变化范围.8.(2023春•涵江区期中)如图1,点A(0,a),B(b,0),且a,b满足(a﹣4)2=0.(1)求点A和点B的坐标;(2)如图2,点C(m,n)在线段AB上,且满足n﹣m=5,点D在y轴负半轴上,连接CD交x轴负半轴于点M,且S△MBC =S△MOD,求点D的坐标;(3)平移直线AB,交x轴正半轴于点E,交y轴于点F,P为直线EF上且位于第三象限内的一个点,过点P作PG⊥x轴于点G,若S△PAB=20,且GE=12,求点P的坐标.9.(2023春•武汉期中)在平面直角坐标系中,点A 、B 分别是x 轴和y 轴的正半轴上的点,C 点在第一象限,它们的坐标分别是A (a ,0),B (0,b ),C (a ﹣1,2b ),且满足|a−4|+=0.(1)直接写出四边形AOBC 的面积 ;(2)点P 是x 轴上一个动点,当△APC 的面积等于8时,求点P 的坐标;(3)将线段AC 平移至线段MN (点A 的对应点为M ,点C 的对应点为N ),且点M 在线段OB 上,当△MAC 的面积为152时,求点N 的坐标.。
2024年北师大版八年级上册数学期末复习专题六 坐标系中的图形面积

面积的一半,点 P 的坐标为(0, )或(0,- ).
的距离为5,
所以△ ABC 的面积= ×4×5=10.
1
2
3
4
5
6
专题
(2)若点 P (0, m )在 y 轴上,试用含 m 的代数式表示△
ABP 的面积;
【解】当 m >0时,△ ABP 的面积= ×4 m =2 m ;
当 m <0时,△ ABP 的面积= ×4×(- m )=-2 m .
面积” S .
【解】三点的“水平底” a =1-(-3)=4,“铅垂
高” h =5-1=4.所以 “矩面积” S = ah =4×4=16.
1
2
3
4
5
6
专题
(2)若点 A (1,2), B (-3,1), P (0, t )的“矩面积” S 为
12,求点 P 的坐标.
【解】三点的“水平底” a =1-(-3)=4,“矩面
积” S 为12.当1≤ t ≤2时, h =2-1=1,则“矩面
积” S =1×4=4≠12,不合题意;当 t >2时, h = t -
1,则4( t -1)=12,解得 t =4,所以点 P 的坐标为(0,
4).当 t <1时, h =2- t ,则4(2- t )=12,解得 t =
-1,所以点 P 的坐标为(0,-1).
坐标差的最大值,“铅垂高” h :任意两点纵坐标差的最
大值,则“矩面积” S = ah .
1
2
3
4
5
6
专题
例如:三点坐标分别为 A (1,2), B (-3,1), C (2,-
平面几何面积法 专题

专题27 面积法阅读与思考平面几何学的产生源于人们测量土地面积的需要,面积关联着几何图形的重要元素边与角.所谓面积法是指借助面积有关的知识来解决一些直接或间接与面积问题有关的数学问题的一种方法.有许多数学问题,虽然题目中没有直接涉及面积,但由于面积联系着几何图形的重要元素,所以借助于有关面积的知识求解,常常简捷明快.用面积法解题的基本思路是:对某一平面图形面积,采用不同方法或从不同角度去计算,就可得到一个含边或角的关系式,化简这个面积关系式就可得到求解或求证的结果. 下列情况可以考虑用面积法:(1)涉及三角形的高、垂线等问题; (2)涉及角平分线的问题.例题与求解【例1】 如图,从等边三角形内一点向三边作垂线,已知这三条垂线段的长分别为1,3,5,则这个等边三角形的边长为______________.(全国初中数学联赛试题)解题思路:从寻求三条垂线段与等边三角形的高的关系入手.等腰三角形底边上任一点到两腰距离之和等于一腰上的高,那么等边三角形呢?等腰梯形呢?DEFA BC P【例2】 如图,△AOB 中,∠O =090,OA =OB ,正方形CDEF 的顶点C 在DA 上,点D 在OB 上,点F 在AB 上,如果正方形CDEF 的面积是△AOB 的面积的52,则OC :OD 等于( ) A .3:1 B .2:1 C .3:2 D .5:3解题思路:由面积关系,可能想到边、角之间的关系,这时通过设元,即可把几何问题代数化来解决.EFAOBDC【例3】 如图,在□ABCD 中,E 为AD 上一点,F 为AB 上一点,且BE =DF ,BE 与DF 交于G ,求证:∠BGC =∠DGC .(长春市竞赛试题)解题思路:要证∠BGC =∠DGC ,即证CG 为∠BGD 的平分线,不妨用面积法寻找证题的突破口.GDBC A F E【例4】 如图,设P 为△ABC 内任意一点,直线AP ,BP ,CP 交BC ,CA ,AB 于点D 、E 、F .求证:(1)1=++CF PFBE PE AD PD ; (2)2=++CFPCBE PB AD PA . (南京市竞赛试题)解题思路:过P 点作平行线,产生比例线段.EPBAC DF【例5】 如图,在△ABC 中,E ,F ,P 分别在BC ,CA ,AB 上,已知AE ,BF ,CP 相交于一点D ,且1994=++DP CD DF BD DE AD ,求DPCDDF BD DE AD ⋅⋅的值. 解题思路:利用上例的结论,通过代数恒等变形求值.(黄冈市竞赛试题)FDABC EP【例6】如图,设点E ,F ,G ,H 分别在面积为1的四边形ABCD 的边AB ,BC ,CD , DA上,且k HADHGD CG FC BF EB AE ====(k 是正数),求四边形EFGH 的面积. (河北省竞赛试题)解题思路:连对角线,把四边形分割成三角形,将线段的比转化为三角形的面积比. 线段比与面积比的相互转化,是解面积问题的常用技巧.转化的基本知识有: (1) 等高三角形面积比,等于它们的底之比; (2) 等底三角形面积比,等于它们的高之比; (3) 相似三角形面积比,等于它们相似比的平方.ABCDHEFG能力训练1.如图,正方形ABCD 的边长为4cm ,E 是AD 的中点,BM ⊥EC ,垂足为M ,则BM =______.(福建省中考试题)2.如图,矩形ABCD 中,P 为AB 上一点,AP = 2BP ,CE ⊥DP 于E ,AD =a ,AB =b ,则CE =__________.(南宁市中考试题)MEADBCEDACBP1214814425CBAHGF DEQ TPR第1题图 第2题图 第3题图3.如图,已知八边形ABCDEFGH 中四个正方形的面积分别为25,48,121,114,PR =13,则该八边形的面积为____________.(江苏省竞赛试题)4. 在△ABC 中,三边长为3=a ,4=b ,6=c ,a h 表示a 边上的高的长,b h ,c h 的意义类似,则(a h +b h +c h )⋅⎪⎪⎭⎫⎝⎛++c b ah h h 111的值为____________. (上海市竞赛试题)5.如图,△ABC 的边AB =2,AC =3,Ⅰ,Ⅱ,Ⅲ分别表示以AB ,BC ,CA 为边的正方形,则图中三个阴影部分的面积之和的最大值是__________.(全国竞赛试题)6.如图,过等边△ABC 内一点P 向三边作垂线,PQ =6,PR =8,PS =10,则△ABC 的面积是 ( ).A. 3192B. 3190C. 3194D.3196(湖北省黄冈市竞赛试题)ⅢⅠⅡEBADCRSQAPCBDBCA第5题图 第6题图 第7题图 7.如图,点D 是△ABC 的边BC 上一点,若∠CAD =∠DAB =060,AC =3,AB =6,则AD 的长是( ).A .2 B. 212 C.3 D. 2138.如图,在四边形ABCD 中,M ,N 分别是AB ,CD 的中点,AN ,BN ,DM ,CM 划分四边形所成的7个区域的面积分别为1S ,2S ,3S ,4S ,5S ,6S ,7S ,那么恒成立的关系式是( ).A. 2S +6S =4SB.1S +7S =4SC. 2S +3S =4S D .1S +6S =4SS 1S 2S 6S 7S 5S 3S 4NMAB DC9.已知等边△ABC 和点P ,设点P 到△ABC 三边AB ,AC ,BC 的距离分别为1h ,2h ,3h ,△ABC 的高为h .若点P 在一边BC 上(如图1),此时03 h ,可得结论:1h +2h +3h =h . 请直接用上述信息解决下列问题:当点P 在△ABC 内(如图2)、点P 在△ABC 外(如图3)这两种情况时,上述结论是否还成立?若成立.请给予证明;若不成立,1h ,2h ,3h 与h 之间又有怎样的关系?请写出你的猜想,不需证明.(黑龙江省中考试题)图3图2图1MM M F E DAF E DA EDA BCPBC P BCP10.如图,已知D ,E ,F 分别是锐角△ABC 的三边BC ,CA ,AB 上的点,且AD 、BE 、CF 相交于P 点,AP =BP =CP =6,设PD =x ,PE =y ,PF =z ,若28=++zx yz xy ,求xyz 的值.(“希望杯”邀请赛试题)EPDACBF11.如图,在凸五边形ABCDE 中,已知AB ∥CE,BC ∥AD ,BE ∥CD ,DE ∥AC ,求证:AE ∥BD .(加拿大数学奥林匹克试题)DABC ER P Q E DC B A F 12.如图,在锐角△ABC 中,D ,E ,F 分别是AB ,BC ,CA 边上的三等分点. P ,Q ,R 分别是△ADF ,△BDE ,△CEF 的三条中线的交点.(1) 求△DEF 与△ABC 的面积比;(2) 求△PDF 与△ADF 的面积比;(3) 求多边形PDQERF 与△ABC 的面积比.13.如图,依次延长四边形ABCD 的边AB ,BC ,CD ,DA 至E ,F ,G ,H ,使m DAAHCD DG BC CF AB BE ====, 若ABCD EFGH S S 四边形四边形2=,求m 的值. (上海市竞赛试题)HEFGAD CB14. 如图,一直线截△ABC 的边AB ,AC 及BC 的延长线分别交于F ,E ,D 三点,求证:1=⋅⋅FBAFEA CE DC BD . (梅涅劳斯定理)EBDA CF15.如图,在△ABC 中,已知21===FA FB EC EA DB DC ,求ABC GHI S S ∆∆的值.(“华罗庚金杯”少年数学邀请赛试题)。
初中数学几何模型(九)面积模型
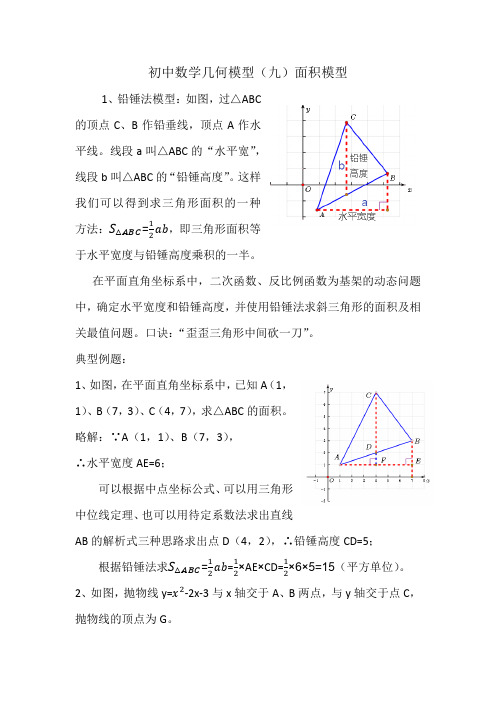
初中数学几何模型(九)面积模型1、铅锤法模型:如图,过△ABC的顶点C、B作铅垂线,顶点A作水平线。
线段a叫△ABC的“水平宽”,线段b叫△ABC的“铅锤高度”。
这样我们可以得到求三角形面积的一种方法:S△ABC=12ab,即三角形面积等于水平宽度与铅锤高度乘积的一半。
在平面直角坐标系中,二次函数、反比例函数为基架的动态问题中,确定水平宽度和铅锤高度,并使用铅锤法求斜三角形的面积及相关最值问题。
口诀:“歪歪三角形中间砍一刀”。
典型例题:1、如图,在平面直角坐标系中,已知A(1,1)、B(7,3)、C(4,7),求△ABC的面积。
略解:∵A(1,1)、B(7,3),∴水平宽度AE=6;可以根据中点坐标公式、可以用三角形中位线定理、也可以用待定系数法求出直线AB的解析式三种思路求出点D(4,2),∴铅锤高度CD=5;根据铅锤法求S△ABC=12ab=12×AE×CD=12×6×5=15(平方单位)。
2、如图,抛物线y=x2-2x-3与x轴交于A、B两点,与y轴交于点C,抛物线的顶点为G。
(1)求△ABC和△BCG的面积;(2)若点D在直线BC下方抛物线上运动,求△BCD面积的最大值。
(3)若点D在直线BC下方抛物线上运动,求四边形ACDB面积的最大值。
2、等积模型:用不同方法表示同一个图形的面积,结果相等。
(1)当所表示的图形是“规则”图形时,不同的方法指的是:①直接用面积公式表示;②用其他图形面积的和或差表示。
(2)当所表示的图形是“不规则”的图形时,不同方法指的是:用割补法来表示。
典型例题:1、在Rt△ABC中,∠C=90°,CD是斜边上的高,用直角三角形的三边表示斜边上的高CD。
解:∵S △ABC =12ch ,S △ABC =12ab ,∴12ch =12ab ,∴h=ab c。
结论:直角三角形斜边上的高等于两直角边的乘积除以斜边。
2、(1)如图①,已知△ABC 中,AB=AC ,点P 是BC 上的一点,PN ⊥AC 于点N ,PM ⊥AB 于点M ,CG ⊥AB 于点G ,求证:CG=PM+PN 。
初中数学八年级专题复习专题23 面积的计算

专题23 面积的计算○阅 ○读 ○与 ○思 ○考计算图形的面积是几何问题中一种重要题型,计算图形的面积必须掌握如下与面积有关的重要知识: 1.常见图形的面积公式;2.等积定理:等底等高的两个三角形面积相等; 3.等比定理:(1) 同底(或等底)的两个三角形面积之比等于等于对应高之比;同高(或等高)的两个三角形面积之比等于等于对应底之比.(2) 相似三角形的面积之比等于对应线段之比的平方. 熟悉下列基本图形、基本结论:例 题 与 求 解【例1】如图,△ABC 内三个三角形的面积分别为5,8,10,四边形AEFD 的面积为x ,则x =________.(黄冈市竞赛试题)解题思路:图中有多对小三角形共高,所以可将面积比转化为线段之比作为解题突破口.【例2】如图,在△ABC 中,已知BD 和CE 分别是两边上的中线,并且BD ⊥CE ,BD =4,CE =6,那么△ABC 的面积等于 ( ) (全国初中数学联赛)A .12B .14C .16D .18 解题思路:由中点想到三角形中位线,这样△ABC 与四边形BCDE 面积存在一定的关系.例1图C例2图C【例3】如图,依次延长四边形ABCD 的边AB ,BC ,CD ,DA 至E ,F ,G ,H ,使BE AB =CF BC =DG CD =AH DA=m ,若S 四边形EFGH =2S 四边形ABCD ,求m 的值.解题思路:添加辅助线将四边形分割成三角形,充分找出图形面积比与线段比之间的关系,建立关于m 的方程.【例4】如图,P ,Q 是矩形ABCD 的边BC 和CD 延长线上的两点,P A 与CQ 相交于点E ,且∠P AD=∠QAD ,求证:S 矩形ABCD =S △APQ .解题思路:图形含全等三角形、相似三角形,能得到相等的线段、等积式,将它们与相应图形联系起来,促使问题的转化.【例5】如图,在Rt △ABC 中,∠A =90°,AB =8,AC =6,若动点D 从点B 出发,沿线段BA 运动到点A 为止,移动速度为每秒2个单位长度. 过点D 作DE ∥BC 交AC 于点E ,设动点D 运动的时间为x 秒,AE 的长为y .(1) 求出y 关于x 的函数关系式,并写出自变量x 的取值范围;(2) 当x 为何值时,△BDE 的面积S 有最大值,最大值为多少? (江西省中考试题) 解题思路:对于(1)利用△ADE ∽△ABC 可得y 与x 的关系式;对于(2)先写出S 关于x 的函数关系式,再求最大值.例3图例4图例5图C【例6】如图,设P 为△ABC 内任意一点,直线AP ,BP ,CP 交BC ,CA ,AB 于点D ,E ,F . 求证:(1)PD AD +PE BE +PFCF=1; (2)P A AD +PB BE +PC CF=2 解题思路:过点A ,P 分别作BC 的垂线,这样既可得到平行线,产生比例线段,又可以与面积联系起来,把P AAD转化为面积比,利用面积法证明.○能 ○力 ○训 ○练A 级1.如图,ABCD 中,AE ∶BE =1∶2,S △AEF =6cm 2,则S △CDF 的值为________. (济南市中考试题) 2.如图,正六边形ABCDEF 的边长为23cm ,P 为正六边形内任一点,则点P 到各边距离之和为_______.3.如图,P 是边长为8的正方形ABCD 外一点,PB =PC ,△PBD 的面积等于48,则△PBC 的面积为_____________. (北京市竞赛试题)4.如图,已知△BOF ,△AOF ,△BOD ,△COE 的面积分别为30,40,35,84,则△ABC 的面积为________.(浙江省竞赛试题)5.如图,已知AD 是Rt △ABC 斜边BC 上的高,DE 是Rt △ADC 斜边上的高,如果DC ∶AD =1∶2, S △DCE =a ,那么S △ABC 等于 ( ) (金华市中考试题)A .4aB .9aC .16aD .25a例6图D第2题图CF第1题图第3题图P6.如图,已知M 是ABCD 边AB 的中点,CM 交BD 于点E ,则图中阴影部分面积与ABCD 的面积之比为( ) (山西省中考试题)A .16B .14C .13D .5127.如图,在△ABC 中,DE ∥BC ,DE 分别交AB ,AC 于点D ,E ,若S △ADE =2S △DCE ,则S △ADES △ABC等于( )(浙江省宁波市中考试题) A .14 B .12 C .23 D .498.如图,△ABC 是边长为6cm 的等边三角形,被一平行于BC 的矩形所截,AB 被截成三等分,则图中阴影部分面积面积为( )cm 2. (广东省竞赛试题)A .4B .2 3C .3 3D .4 39.如图,平面上有两个边长相等的正方形ABCD 和 A ′B ′C ′D ′,且正方形A ′B ′C ′D ′的顶点A ′在正方形ABCD 的中心,当正方形A ′B ′C ′D ′绕A ′ 转动时,两个正方形重合部分的面积必然是一个定值. 这个结论对吗?证明你的判断. (“希望杯”邀请赛试题)10.如图,设凸四边形ABCD 的一组对边AB ,CD 的中点分别为K ,M .求证:S 四边形ABCD =S △ABM +S △DCK..第8题图第5题图DC第4题图D第6题图CM第7题图C第9题图C'11.如图1,AB ,CD 是两条线段,M 是AB 的中点,S △DMC ,S △DAC ,S △DBC 分别表示△DMC ,△DAC ,△DBC 的面积,当AB ∥CD 时,有S △DMC =S △DAC +S △DBC2………..①.(1) 如图2,若图1中AB 与CD 不平行时,①式是否成立?请说明理由.(2) 如图3,若图1中AB 与CD 相交于点O 时, 问S △DMC 与S △DAC 和S △DBC 有何相等关系?试证明你的结论. (安徽省中考试题)图2图1图312.如图,在△ABC 中,∠ACB =90°,∠ABC =30°,将△ABC 绕顶点C 顺时针旋转,旋转角为θ(0°<θ<180°),得到△A ′B ′C ′.(1) 如图1,当AB ∥CB ′时,设A ′B ′与CB 相交于点D ,证明:△A ′CD 是等边三角形;(2) 如图2,连接A ′A ,B ′B ,设△ACA ′和△BCB ′的面积分别为S △ACA ′和S △BCB ′.求证:S △ACA ′∶S △BCB ′=1∶3. (3) 如图3,设AC 的中点为E ,A ′B ′的中点为P ,AC =a ,连接EP ,当θ=_____时,EP 长度最大,最大值是____________. (安徽省中考试题)图2图1图3第10题图B 级1.如图,A 在线段BG 上,ABCD 和DEFG 都是正方形,面积分别为7cm 2和11cm 2,则△CDE 的面积等于___________cm 2. (武汉市竞赛试题)2.如图,P 为正方形ABCD 内一点,P A =PB =10,并且P 到CD 边的距离也等于10,那么正方形ABCD 的面积是_______________. (北京市竞赛试题)3.如图,四边形ABCD 中,点E ,F 分别在BC ,DC 上,DF FC =1,CEBE =2,若△ADF 的面积为m ,四边形AECF 的面积为n (n >m ),则四边形ABCD 的面积为___________. (全国初中数学联赛试题)4.如图,图形ABCD 中,AB ∥CD ,AC 和BD 相交于点O ,若AC =5,BD =12,中位线长为132,△AOB的面积为S 1,△OCD 的面积为S 2,则S 1+S 2=_________. (山东省竞赛试题)5.如图,分别延长△ABC 的三边AB ,BC ,CA 至A ′,B ′,C ′,使得AA ′=3AB ,BB ′=3BC ,CC ′=3AC ,若S △ABC =1,则S △A ′B ′C ′等于 ( ).A .18B .19C .24D .27(山东省竞赛试题) 6.如图,若ABCD 是2×2的正方形,E 是AB 的中点,F 是BC 的中点,AF 与DE 相交于点I ,BD 和AF 相交于点H ,那么四边形BEIH 的面积是 ( )A .13B .52 C .715 D .815(江苏省竞赛试题)7.如图,矩形ABCD 中,E 是BC 上的一点,F 是CD 上的点,已知S △ABE =S △ADF =13S ABCD ,则S △AEF S △CEF的值等于 ( ) (北京市竞赛试题)A .2B .3C .4D .5第6题图F第4题图第3题图B第2题图第1题图FA第5题图第7题图A BEF8.(1) 探究:如图1,在ABCD 的形外分别作等腰直角三角形ABF 和等腰直角三角形ADE ,∠F AB =∠EAD =90°,连接AC ,EF. 在图中找一个与△F AE 全等的三角形,并加以证明.(2) 应用:以ABCD 的四条边为边,在其形外分别作正方形,如图2,连接EF ,GH ,IJ ,KL ,若ABCD 的面积为5,则图中阴影部分四个三角形的面积之和为____________. (长春市中考试题)图1图2BJ9.如图,在梯形ABCD 中,AD ∥BC ,AB =AD =DC =2cm ,BC =4cm ,在等腰△PQR 中,∠QPR =120°,底边QR =6cm , 点B ,C ,Q ,R 在同一条直线l 上,且C ,Q 两点重合,如果等腰△PQR 以1cm/s 的速度沿直线l 箭头所示方向匀速运动,t 秒时梯形ABCD 与等腰△PQR 重合部分的面积记为S cm 2.(1) 当t =4时,求S 的值;(2) 当4≤t ≤10时,求S 与t 的函数关系式,并求出S 的最大值. (广州市中考试题)10.有一根直尺的短边长为2cm ,长边长为10cm ,还有一块锐角为45°的直角三角纸板,它的斜边长为12cm ,如图1将直尺的短边DE 放置与直角三角纸板的斜边AB 重合,且点D 与点A 重合 将直尺沿AB 方向平移,如图2,设平移的长为x cm(0≤x ≤10),直尺与三角形纸板重叠部分(图中阴影部分)的面积S cm 2.(1) 当x =0时,S =________,当10=x 时,S =________; (2) 当0<x ≤4时,求S 关于x 的函数关系式;(3) 当4<x <10时,求S 关于x 的函数关系式,并求出S 的最大值. (徐州市中考试题)图1图2E11.如图,设H 是等腰三角形ABC 的三边上的高线的交点,在底边BC 保持不变的情况下,让顶点A 至底边BC 的距离变小(仍保持三角形为等腰三角形),这时HBC ABC S S ∆∆⋅的值变大、变小、还是不变?证第9题图BC(Q)R明你的结论. (全国初中数学联赛试题)12.(1) 请你在图1中作一条直线,使它将矩形ABCD分成面积相等的两部分;(2) 如图2,点M是矩形ABCD内一定点,请你在图2中过点M作一条直线,使它将矩形ABCD分成面积相等的两部分;(3) 如图3,在平面直角坐标系中,直角梯形OBCD是某市将要筹建的高新技术开发区用地示意图,其中DC∥OB,OB=6,BC=4,CD=4. 开发区综合服务管理委员会(其占地面积不计)设在点P(4,2)处. 为了方便驻区单位,准备过点P修一条笔直的道路(路的宽不计),并且使这条路所在的直线l将直角梯形OBCD分成面积相等的两部分. 你认为直线l是否存在?若存在,求出直线l的表达式;若不存在,请说明理由. (陕西省中考试题)图1图2图3专题23 面积的计算例1.22 提示:连接AF.例2.选C提示:连接DE.例3提示:连接GA,HB,EC,FD,AC,BD,则(1)(1)HAE HAB ABDS m S m mS=+=+∙△△△,同理(1)FCG BCDS m m S=+△△,故+(1)HAE FCG ABCDS S m m S=+∙△△,同理+(1)EBF GDH ABCDS S m m S=+△△.例4.提示:过E作EF∥BC交AB于F,△AEF≌△ADE≌△ADQ,又△AED∽△PEC,则AD DEPC CE=,积AD·CE=PC·DE.例5.提示:(1)362y x=-+(0≤x≤4)第11题图(2)22336(2)622S x x x =-+=--+,当x =2时,S 最大值=6. 例6.(1)如图,分别过P ,A 作BC 的垂线,垂足为P 1,A 1.11111212PBCABCBC PP S PP PD S AA AD BC AA ===△△则. 同理PCA ABC S PE BE S =△△,=PABABCS PF CF S △△, 故++=1BPC PCA PAB ABCS S S PD PE PF AD BE CF S ++=△△△△. (2)=3()2PD PB PC PD PE PFAD BE CF AD BE CF++-++=. A 级1.54cm2.18cm3.324.3155.C6.C7.D 8.C9.提示:当正方形ABCD 与正方形A ’B ’C ’D ’的对应边平行时,两者重合部分面积为正方形面积的14;转动后,两者重合面积仍为定值. 10. 提示:过A 、K 、B 分别作CD 的垂线. 11.(1)结论仍然成立,证明略. (2)2DBC DACDMC S S S -=△△△12.(1)略 (2)△ACA ’∽△BCB ’2213ACA BCB S AC S BC ''==△△ (3)120°,32aB 级12.256 3.3122n m + 4提示:S 梯形ABCD=2+5.B 6.C 7.D 8.(1)略 (2)10 9.提示:(1)当t =4时,Q 与B 重合,P 与D 重合,如图a ,重合部分是△BDC ,S △BDC=122⨯⨯=. (2)①当4≤t ≤6时,如图b ,BQ =t -4,CR =6-4, 由△PQR ∽△BQM ∽△CRN ,得22(),CRN PQRS CR SPQ ==PQRBQM S S ∆∆=(PQ BQ )2=(324-t )2, ∴S =S △PQR -S △BQM -S △CRN =235)5(32+--t .当t =5时,S 最大值=325.②当6<t ≤10时,如图c ,BR =10-t ,BK ⊥RK ,且∠KRB =30°,所以BK =21BR =21(10-t ),KR =23(10-t ),S =21BK ·KR =83(10-t )2.当t =6时,S 最大值=23. 综合①②,当t =5时,S 最大值=325.图c图b图aA10.提示:(1)S =2cm 2;S =2cm 2.(2)当0<x ≤4时,如图a ,DG =AD =x ,AE =EF =x +2,S =2)(DEDG EF ⨯+=2x +2cm 2.(3)当4<x <10时,应分两种情况进行讨论:①当4<x <6时,如图b ,DG =AD =x ,EF =BE =12-x -2=10-x ,S =S △ABC -S △ADG -S △BEF =-x 2+10x -14=-(x -5)2+11,故当x =5时,S 最大值=11.②当6≤x <10时,如图c ,BD =DG =12-x ,EF =BE =10-x ,S =22-x ,当x =6时,S 最大值=10. 综上所述,4<x <10时,S 的最大值为11cm 2.图a图b图c11.∵∠HBD =∠HAE ,∴Rt △BDH ∽Rt △ADC .∴HDDC BD AD =.又BD =DC =21BC , ∴AD ·HD =BD ·DC =41BC 2.∴S △ABC ·S △HBC =(21AD ·BC )(21HD ·BC )=161BC 4.而BC 是不变的,∴当点A 至BC 的距离变小时,乘积S △ABC ·S △HBC 保持不变.12.(1)(2)略(3)如图,存在符合条件的直线l .过点D 作DA ⊥OB 于A ,则点P (4,2)为矩形ABCD 的对称中心. ∴过点P 的直线只要平分△DOA 的面积即可.易知,在OD 边上必存在点H ,使得直线PH 将△DOA 的面积平分,从而,直线PH 平分梯形OBCD 的面积,直线PH 即为所求直线l .设直线PH 的表达式为y =kx +b ,且点P (4,2), ∴2=4k +b ,即b =2-4k ,∴y =kx +2-4k .∵直线OD 的表达式为y =2x , ∴⎩⎨⎧=-+=x y k kx y 242,解得⎪⎪⎩⎪⎪⎨⎧--=--=k k y k k x 284242, ∴点H 的坐标为(k k --242,kk --284). ∴PH 与线段AD 的交点F 的坐标为(2,2-2k ),∴0<2-2k <4,∴-1<k <1. ∴S △DHF =21(4-2+2k )·(2-kk --242)=21×21×2×4,解得k =2313-(k =2313--不合题意,舍去).∴b =8-213,∴直线l 的表达式为y =2313-x +8-213.。
初中数学重点梳理:面积问题的解决方法
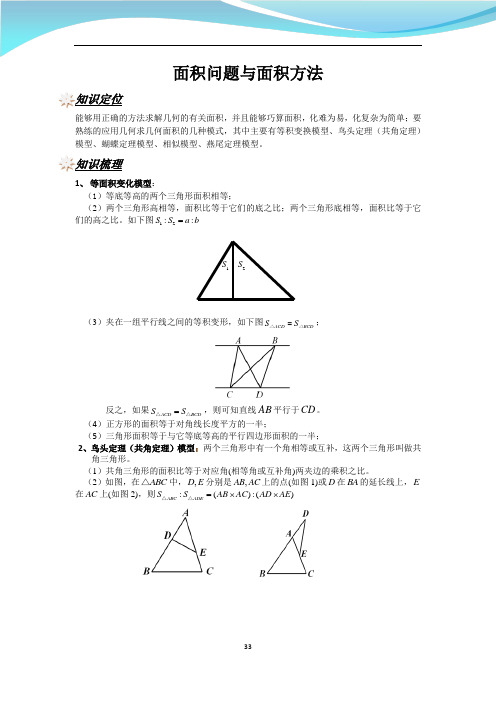
面积问题与面积方法知识定位能够用正确的方法求解几何的有关面积,并且能够巧算面积,化难为易,化复杂为简单;要熟练的应用几何求几何面积的几种模式,其中主要有等积变换模型、鸟头定理(共角定理)模型、蝴蝶定理模型、相似模型、燕尾定理模型。
知识梳理1、 等面积变化模型:(1)等底等高的两个三角形面积相等;(2)两个三角形高相等,面积比等于它们的底之比;两个三角形底相等,面积比等于它们的高之比。
如下图12::S S a b =(3)夹在一组平行线之间的等积变形,如下图ACD BCD S S =△△;反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD 。
(4)正方形的面积等于对角线长度平方的一半;(5)三角形面积等于与它等底等高的平行四边形面积的一半;2、鸟头定理(共角定理)模型:两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
(1)共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。
(2)如图,在ABC △中,,D E 分别是,AB AC 上的点(如图1)或D 在BA 的延长线上,E 在AC 上(如图2),则:():()ABC ADE S S AB AC AD AE =⨯⨯△△1S 2S3、蝴蝶定理模型:任意四边形中的比例关系。
蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系。
① 1243::S S S S =1324S S S S ⨯=⨯ ② ()()1243::AO OC S S S S =++ 4、相似模型:相似三角形:相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:(1)相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; (2)相似三角形的面积比等于它们相似比的平方。
武汉市七一中学八年级数学专题——面积问题(含答案)

武汉市七一中学八年级数学专题——面积问题(含答案)平面几何学的产生起源于人们对土地面积的测量,面积是平面几何中一个重要的概念,联系着几何图形中的重要元素边与角.计算图形的面积是几何问题中一种常见问题,求面积的基本方法有:1.直接法:根据面积公式和性质直接进行运算.2.割补法:通过分割或补形,把不规则图形或不易求解的问题转化为规则图形或易于求解的问题.3.等积法:根据面积的等积性质进行转化求解,常见的有同底等高、同高等底和全等的等积转化.4.等比法:将面积比转化为对应线段的比.熟悉以下基本图形中常见的面积关系:注等积定理:等底等高的两个三角形面积相等.等比定理:(1)同底(或等底)的两个三角形面积之比等于对应高之比,同高(或等高)的两个三角形面积之比等于对应底之比; (2)相似三角形面积之比等于对应线段的平方比. 例题求解【例1】 在梯形ABCD 中,AB ∥CD ,AC 、BD 相交于点O ,若AC=5,BD=12,中位线长为213,△AOB 的面积为S 1,△COD 的面积为S 2,则21S S += .(山东省竞赛题)思路点拨 本例综合了梯形、面积等丰富的知识,图形中有重要面积的关系:S △AOD =S △BOC =21S S ,S梯形ABCD=S 1+S 2+212S S =221)(S S +(读者证明),于是将问题转化为求梯形ABCD 的面积.【例2】 如图,在△ABC 中,已知BD 和CE 分别是两边上的中线,并且BD ⊥CE ,BD =4,CE=6,那么△ABC 的面积等于( ) A .12 B .14 C .16 D .18 (全国初中数学联赛试题)思路点拨由中点想到三角形中位线,这样△ABC与四边形BCDE 面积存在一定的关系,只要求出四边形BCDE面积即可.【例3】如图,P、Q是矩形ABCD的边BC和CD延长线上的两点,AP与CQ相交于点E,且∠PAD=∠QAD,求证:S矩形ABCD=S△APQ. (重庆市竞赛题)思路点拨把面积用相应的线段表示,面积的证明问题就转化为线段的等积式的证明.注意等线段的代换.【例4】如图甲,AB、CD是两条线段,M是AB的中点,S△DMC、S△DAC、S△DBC分别表示△DMC、△DAC、△DBC的面积,当AB∥CD时,有S△DMC =2DBCDAC SS∆∆+·(1)如图乙,若图甲中AB不平行CD,①式是否成立?请说明理由;(2)如图丙,若图甲中A月与CD相交于点O时,问S△DMC和S△DAC和S △DBC有何种相等关系?试证明你的结论. (安徽省中考题)思路点拨 对于(1),因△DMC 、△DAC 、△DBC 同底,要判断①式是否成立,只需寻找它们的高之间的关系:对于(2),由于M 为AB 中点,可利用等积变换得到相等的面积关系,通过建立含S △DMC 、S △DAC 、S △DBC 的等式寻找它们的关系.注 本例综合了三角形、梯形中位线、等积变形等知识,要求我们在动态型数学情景下进行观察、分析、探索、猜想和论证. 通过强化或弱化条件,改变图形的位置等方式进一步探究问题是发展几何问题的重要途径.【例5】如图,设P 为△ABC 内任意一点,直线AP 、BP 、CP 交BC 、CA 、AB 于点D 、E 、F .求证:(1)1=++CFPF BEPE ADPD ;(2)2=++CFPC BEPB ADPA .思路点拨过P点、A点分别作BC的垂线,这样既可得到平行线,产生比例线段,又可与面积联系起来,把羔转化为面积比,利用面积法证明.注有些几何问题,虽然题目中没有直接涉及面积,但由于面积关联着边角两个重要元素,所以我们可从面积角度思考问题,这就是常说的面积法.用面积法解题的基本步骤是:(1)用不同方法或从不同角度计算某一图形面积,得到一个含边或舍角的关系式.(2)化简这个面积关系式,直至得到求解或求证的结果.当问题涉及三角形的高、垂线或角平分线时,不妨用面积法试一试.学力训练1.如图,是一个圆形花坛,中间的鲜花构成了一个菱形图案(图中尺寸单位为米),如果每平方米种植鲜花20株,那么这个菱形图案中共有鲜花株.(第14届“希望杯”邀请赛试题)2.如图,矩形内有两个相邻的正方形面积分别为4和2,那么阴影部分的面积为.(2003年上海市中考题)3.如图,在△ABC 中,∠B=∠CAD ,23=ACBD ,则CADABD S S ∆∆= .(重庆市竞赛题)4.如图,梯形ABCD 中,AB ∥CD ,AB =a ,CD=b(a<b),对角线AC 与BD 相交于O ,△BOC 的面积为梯形ABCD 的面积的92,则ba = .5.如图,在四边形ABCD 中,∠A =135°,∠B=∠D=90°,BC=23,AD=2,则四边形ABCD 的面积为( ) A .42B .43C .4D .6 (湖北省荆州市中考题)6.ABCD 是边长为1的正方形,△BPC 是等边三角形,则厶BPD 的面积为( ) A .41 B .413- C .81 D .8132- (武汉市选拔赛题)7.如图,在△ABC中,∠ACB=90°,分别以AC、AB为边,在△ABC 外作正方形ACEF和正方形AGHB,作CK⊥AB分别交AB和GH于D和K,则正方形ACEF的面积S1与矩形AGKD的面积S2的大小关系为( )AC的大 A.S1=S2 B.S1>S2 C.S1<S2 D.不能确定,与AB小有关(2002年8.有一块缺角矩形地皮ABCDE(如图),其中AB=110m,BC=80m,CD=90m,∠EDC=135°.现准备用此块地建一座地基为长方形(图中用阴影部分表示)的教学大楼,以下四个方案中,地基面积最大的是( )(2003年广州市中考题)9.今有一块正方形土地,要在其上修筑两条笔直的道路,使道路将这块土地分成形状相同且面积相等的4部分.若道路的宽度可忽略不计,请设计4种不同的修筑方案.(2000年山东省竞赛题)10.如图,已知梯形ABCD的面积为34cm2,AE=BF,CE与DF相交于O,△OCD的面积为11cm2,求蝶形(阴影部分)的面积.11.探究规律:如图a,已知:直线m∥ n,A、B为直线n上两点,C、P为直线m 上两点.(1)请写出图a中,面积相等的各对三角形;(2)如果A、B、C为三个定点,点P在m上移动,那么,无论P点移动到任何位置,总有与△ABC的面积相等.理由是:.解决问题:如图b,五边形ABCDE是张大爷十年前承包的一块土地的示意图.经过多年开垦荒地,现已变成如图c所示的形状,但承包土地与开垦荒地的分界小路(即图c中折线CDE)还保留着.张大爷想过正点修一条直路,直路修好后,要保持直路左边的土地面积与承包时的一样多,右边的土地面积与开垦的荒地面积一样多.请你用有关的几何知识,按张大爷的要求设计出修路方案.(不计分界小路与直路的占地面积)(1)写出设计方案,并在图c 中画出相应的图形; (2)说明方案设计理由. (河北省中考题)12.如图,△ABC 中,AD 与BE 相交于F ,已知S △AFB =12cm 2,S △BFD =9cm 2,S △AFE =6cm 2,那么四边形CDFE 的面积为 cm 2.(我爱数学夏令营竞赛题)13.如图,分别延长△ABC 的三边AB 、BC 、CA 至A ′、B ′、C ′,使得AA ′=3AB ,BB ′=3BC ,CC ′=3AC ,若S △ABC =1,则S △A'B'C'= . 14.如图,设△ABC 的面积是1,D 是边BC 上一点,且21 DCBD ,若在边AC 上取一点,使四边形ABDE 的面积为54,则ECAE 的值为 . (天津市竞赛题)15.如图,从等边三角形内一点向三边作垂线,已知这三条垂线段的长分别为1、3、5,则这个等边三角形的边长为 . (全国初中数学联赛试题)16.如图,E 、F 分别是矩形ABCD 的边AB 、BC 的中点,连结AF 、CE ,设AF 与CE 的交点为G ,则ABCDAGCD S S 矩形四边形等于( )A .65 B .54 C .43 D .32 (全国初中数学竞赛题)17.如图,AE ⊥AB 且AE =AB ,BC ⊥CD 且BC=CD ,请按照图中所标注的数据,计算图中实线所围成的图形的面积S 是( ) A .50 B .62 C .65 D .68 (山东省竞赛题)18.如图,在△ADC 中,EF ∥BC ,S △AEF =S △BCE ,若S △ABC =1,则S △CEF 等于( )A .41 B .51 C .25- D .233-(四川省竞赛题)19.已知菱形ABCD 的两条对角线AC 、BD 的乘积等于菱形的一条边长的平方,则菱形的一个钝角的大小是( )A .165° D .135° C . 150° D .120° (“希望杯”邀请赛试题)20.如图,在锐角△ABC中,D、E、F分别是AB、BC、CA边上的三等分点,P、Q、R分别是△ADF、△BDE、△CEF的三条中线的交点.(1)求△DEF与△ABC的面积比;(2)求△PDF与△ADF的面积比;(3)求多边形PDQERF与△ABC的面积比.( “希望杯”邀请赛试题)21.如图,设凸四边形ABCD的一组对边AB、CD的中点分别为K、M,求证:S四边形ABCD=S△ABM+S△DCK.22.如图,已知D、E、F分别是锐角△ABC的三边BC、CA、AB上的点,且AD、BE、CF相交于P点,AP=BP=CP=6,设PD =x,PE=y,PF=z,若xy+yz+ z x=28,求xyz的值.23.如图,在△ABC中是否存在一点P,使得过P点的任意一直线都将△ABC分成等积的两部分?为什么?24.如图,以△ABC的三边为边向形外分别作正方形ABDE,CAFG,BCHK,连结EF,GH,KD,求证:以EF,GH,KD为边可以构成一个三角形,并且所构成的三角形的面积等于△ABC 面积的3倍. (北京市竞赛题)思考 如图,设G(也称重心)为△ABC 三条中线AD 、BE 、CF 的交点,则2===GFCG GE BG GD AG ,请读者证明.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初二数学面积法几何专题初二数学---面积法解题【本讲教育信息】【讲解内容】——怎样证明面积问题以及用面积法解几何问题【教学目标】1. 使学生灵活掌握证明几何图形中的面积的方法。
2. 培养学生分析问题、解决问题的能力。
【重点、难点】:重点:证明面积问题的理论依据和方法技巧。
难点:灵活运用所学知识证明面积问题。
【教学过程】(一)证明面积问题常用的理论依据1. 三角形的中线把三角形分成两个面积相等的部分。
2. 同底同高或等底等高的两个三角形面积相等。
3. 平行四边形的对角线把其分成两个面积相等的部分。
4. 同底(等底)的两个三角形面积的比等于高的比。
同高(或等高)的两个三角形面积的比等于底的比。
5. 三角形的面积等于等底等高的平行四边形的面积的一半。
③三是△AEF ,只要再证出它与△ABC 的面积相等即可由S △CFE =S △CFB故可得出S △AEF =S △ABC 证明:∵AD//BE//CF∴△ADB 和△ADE 同底等高 ∴S △ADB =S △ADE同理可证:S △ADC =S △ADF ∴S △ABC =S △ADE +S △ADF 又∵S △CEF =S △CBF ∴S △ABC =S △AEF∴S △AEF +S △ADE +S △ADF =2S △ABC ∴S △DEF =2S △ABC2. 作平行线法例2. 已知:在梯形ABCD 中,DC//AB ,M 为腰BC 上的中点求证:S S ADM ABCD ∆=12分析:由M 为腰BC 的中点可想到过M 作底的平行线MN ,则MN 为其中位线,再利用平行线间的距离相等,设梯形的高为hD CN MA BS S S MN h S AMD DMN AMN ABCD ∆∆∆=+=⋅=1212证明:过M 作MN//AB∵M 为腰BC 的中点 ∴MN 是梯形的中位线 设梯形的高为h MN DC AB=+2则S MN h ABCD =⋅又 S S S MN h AMD AMN MND ∆∆∆=+=⋅12∴=S S ADM ABCD ∆12(二)用面积法解几何问题有些几何问题,往往可以用面积法来解决,用面积法解几何问题常用到下列性质: 性质1:等底等高的三角形面积相等 性质2:同底等高的三角形面积相等性质3:三角形面积等于与它同底等高的平行四边形面积的一半性质4:等高的两个三角形的面积比等于底之比性质5:等底的两个三角形的面积比等于高之比1. 证线段之积相等例3. 设AD 、BE 和CF 是△ABC 的三条高,求证:AD ·BC =BE ·AC =CF ·ABAFEB D C分析:从结论可看出,AD 、BE 、CF 分别是BC 、AC 、AB 三边上的高,故可联想到可用面积法。
证明:∵AD 、BE 、CF 是△ABC 的三条高 ∴=⋅=⋅=⋅S AD BC BE AC CF ABABC ∆222∴⋅=⋅=⋅AD BC BE AC CF AB2. 证等积问题例4. 过平行四边形ABCD 的顶点A 引直线,和BC 、DC 或其延长线分别交于E 、F ,求证:S △ABF =S △ADEA DB E CF分析:因为AB//DF ,所以△ABF 与△ABC 是同底AB 和等高的两个三角形,所以这两个三角形的面积相等。
证明:连结AC ∵CF//AB∴==S S S ABF ABC ABCD ∆∆12平行四边形又∵CE//AD∴==S S S ADE ACD ABCD ∆∆12平行四边形 ∴=S S ABFADE∆∆3. 证线段之和例5. 已知△ABC 中,AB =AC ,P 为底边BC上任一点,PE ⊥AB ,PF ⊥AC ,BH ⊥AC ,求证:PE+PF =BHAHF EB P C分析:已知有垂线,就可看作三角形的高,连结AP ,则S S S AB PE AC PF ABC ABP APC ∆∆∆=+=⋅+⋅1212又由,所以AB AC S AC PE PF ABC ==⋅+∆12()又S AC BHABC ∆=⋅12 故PE+PF =BH 证明:连结AP ,则 S S S ABCABPAPC∆∆∆=+∵AB =AC ,PE ⊥AB ,PF ⊥AC∴=⋅+⋅=⋅+S AB PE AC PF AC PE PF ABC ∆121212()又∵BH ⊥AC∴=⋅S AC BH ABC ∆12∴⋅+=⋅1212AC PE PF AC BH () ∴PE+PF =BH4. 证角平分线例6. 在平行四边形ABCD 的两边AD 、CD 上各取一点F 、E ,使AE =CF ,连AE 、CF 交于P ,求证:BP 平分∠APC 。
F PA B分析:要证BP 平分∠APC ,我们可以考虑,只要能证出B 点到PA 、PC 的距离相等即可,也就是△ABE 和△BFC 的高相等即可,又由已知AE =FC 可联想到三角形的面积,因此只要证出S △ABE =S △BCF 即可由平行四边形ABCD 可得S △ABE =S △ABC ,S △BFC =S △ABC所以S △ABE =S △BFC ,因此问题便得解。
证明:连结AC 、BE 、BF∵四边形ABCD 是平行四边形 ∴S △ABE =S △ABC S △BFC =S △ABC ∴S △ABE =S △BFC 又∵AE =CF而△ABE 和△BFC 的底分别是AE 、CF ∴△ABE 和△BFC 的高也相等 即B 到PA 、PC 的距离相等 ∴B 点在∠APC 的平分线上 ∴PB 平分∠APC【模拟试题】(答题时间:25分钟)1. 在平行四边形ABCD 中,E 、F 点分别为BC 、CD 的中点,连结AF 、AE ,求证:S △ABE =S △ADFD F CEA B2. 在梯形ABCD 中,DC//AB ,M 为腰BC 上的中点,求证:S S S ADMDCMABM∆∆∆=+D CMA B3. Rt △ABC 中,∠ACB =90°,a 、b 为两直角边,斜边AB 上的高为h ,求证:111222a b h +=Cb a hA D B4. 已知:E 、F 为四边形ABCD 的边AB 的三等分点,G 、H 为边DC 的三等分点,求证:S S EFGH ABCD =13D A G EF HB C5. 在△ABC 中,D 是AB 的中点,E 在AC上,且CEAC13,CD和BE交于G,求△ABC和四边形ADGE的面积比。
ADG EB C【试题答案】1. 证明:连结AC ,则S S ABCADC∆∆=又∵E 、F 分别为BC 、CD 的中点∴=S S ABE ABC ∆∆12S S ADF ADC ∆∆=12∴=S S ABEADF∆∆2. 证明:过M 作MN//DC//ABD CN MA∵M 为腰BC 上的中点∴△DCM 和△ABM 的高相等,设为h 1 ∴+=⋅+⋅=+⋅S S DC h AB h DC AB h DCM ABM ∆∆121212111() 又∵△DMN 与△AMN 的高也为h 1 ∴=+S S S ADMDMNAMN∆∆∆=⋅+⋅=+=⋅12121211111MN h MN h MN h h MN h ()∵MN 为梯形的中位线∴MN AB CD =+12() ∴=+S S S ADMDCMABM∆∆∆3. 证明:∵在Rt △ABC 中,∠ACB =90°,CD ⊥AB∴==⋅S ab AB h ABC ∆1212∴=⋅ab AB h∴=⋅=+⋅a b AB h a b h 2222222()∴两边同时除以a b 22+得:111222a b h +=4. 证明:连结FD 、FG 、FCA G EF H则由已知可得S S FGH DFC ∆∆=13①作DM//AB ,设它们之间的距离为h ,G 到DM 的距离为a ,则由已知可得H 、C 到DM 的距离分别为2a 、3a ∴=+S EF h a EFG ∆12()S S AF h BF h a AFD BFC ∆∆+=⋅+⋅+12123()=⋅+⋅+⋅EF h EF h EF a1232=⋅+⋅3232EF h EF a=⋅+⋅31212()EF h EF a=⋅⋅+312EF h a ()=3S EFG∆即S S S EFG AFD BFC ∆∆∆=+13()②①+②得:S S EFGH ABCD =135. 证明:作DF//AC 交BE 于FDG EFB C可得△DFG ≌△CEG∴==⋅S S ABE CEG DFG ∆∆∆1412=⋅⋅=141223112S S ABC ABC∆∆而S S S S ADGEABC ABC ABC=-=12112512∆∆∆∴△ABC 和四边形ADGE 的面积比是12:5。
