信号与线性系统分析-(吴大正-第四版)第四章习题答案
信号与线性系统分析_(吴大正_第四版)习题答案12264精编版
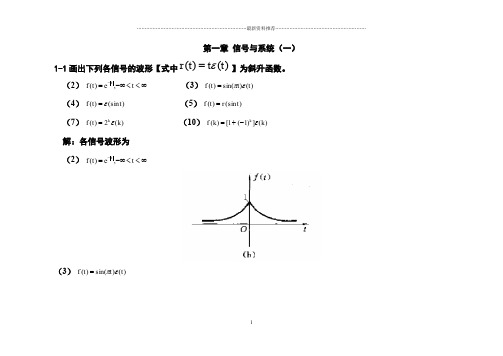
第一章 信号与系统(一)1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t e t f t ,)( (3))()sin()(t t t f επ= (4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f k ε= (10))(])1(1[)(k k f k ε-+= 解:各信号波形为 (2)∞<<-∞=-t e t f t ,)((3))()sin()(t t t f επ=(4))fεt=(sin)(t(5))trf=(sin)(t(7))t(kf kε=)(2(10))f kεk-=(k+(])1(1[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ (12))]()3([2)(k k k f k---=εε 解:各信号波形为 (1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t rt rt rtf(5))2()2()(ttrtf-=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
(2))63cos()443cos()(2ππππ+++=k k k f (5))sin(2cos 3)(5t t t f π+=解:1-6 已知信号)(t f 的波形如图1-5所示,画出下列各函数的波形。
信号与线性系统分析_(吴大正_第四版)习题答案

1-1绘出下列各旗号的波形【式中)()(t t t r ε=】为斜降函数.之阳早格格创做(2)∞<<-∞=-t e t f t ,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f =(7))(2)(k t f k ε= (10))(])1(1[)(k k f k ε-+=解:各旗号波形为(2)∞<<-∞=-t e t f t,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε=(5))(sin )(t r t f =(7))(2)(k t f k ε=(10))(])1(1[)(k k f k ε-+= 1-2 绘出下列各旗号的波形[式中)()(t t t r ε=为斜降函数].(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ (12))]()3([2)(k k k f k ---=εε解:各旗号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t r t r t r t f (5))2()2()(t t r t f -=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k---=εε 1-3 写出图1-3所示各波形的表白式.1-4 写出图1-4所示各序列的关合形式表白式.1-5 判别下列各序列是可为周期性的.如果是,决定其周期.(2))63cos()443cos()(2ππππ+++=k k k f (5))sin(2cos 3)(5t t t f π+=解:1-6 已知旗号)(t f 的波形如图1-5所示,绘出下列各函数的波形. (1))()1(t t f ε- (2))1()1(--t t f ε (5))21(t f - (6))25.0(-t f(7)dt t df )( (8)dx x f t⎰∞-)(解:各旗号波形为(1))()1(t t f ε-(2))1()1(--t t f ε(5))21(t f -(6))25.0(-t f(7)dt t df )((8)dx x f t ⎰∞-)(1-7 已知序列)(k f 的图形如图1-7所示,绘出下列各序列的图形.(1))()2(k k f ε- (2))2()2(--k k f ε(3))]4()()[2(---k k k f εε (4))2(--k f(5))1()2(+-+-k k f ε (6))3()(--k f k f解:1-9 已知旗号的波形如图1-11所示,分别绘出)(t f 战dt t df )(的波形. 解:由图1-11知,)3(t f -的波形如图1-12(a)所示()3(t f -波形是由对于)23(t f -的波形展宽为本去的二倍而得).将)3(t f -的波形反转而得到)3(+t f 的波形,如图1-12(b)所示.再将)3(+t f 的波形左移3个单位,便得到了)(t f ,如图1-12(c)所示.dt t df )(的波形如图1-12(d)所示.1-10 估计下列各题.(1)[]{})()2sin(cos 22t t t dt d ε+ (2))]([)1(t e dt d t t δ--(5)dt t t t )2()]4sin([2++⎰∞∞-δπ (8)dx x x t)(')1(δ⎰∞--1-12 如图1-13所示的电路,写出(1)以)(t u C 为赞同的微分圆程.(2)以)(t i L 为赞同的微分圆程.1-20 写出图1-18各系统的微分或者好分圆程.1-23 设系统的初初状态为)0(x ,激励为)(⋅f ,各系统的齐赞同)(⋅y 与激励战初初状态的关系如下,试分解各系统是可是线性的.(1)⎰+=-tt dx x xf x e t y 0)(sin )0()( (2)⎰+=tdx x f x t f t y 0)()0()()((3)⎰+=tdx x f t x t y 0)(])0(sin[)( (4))2()()0()5.0()(-+=k f k f x k y k(5)∑=+=kj j f kx k y 0)()0()(1-25 设激励为)(⋅f ,下列是各系统的整状态赞同)(⋅zs y .推断各系统是可是线性的、时没有变的、果果的、宁静的?(1)dt t df t y zs )()(= (2))()(t f t y zs = (3))2cos()()(t t f t y zs π=(4))()(t f t y zs -= (5))1()()(-=k f k f k y zs (6))()2()(k f k k y zs -=(7)∑==kj zs j f k y 0)()( (8))1()(k f k y zs -=1-28 某一阶LTI 得集系统,其初初状态为)0(x .已知当激励为)()(1k k y ε=时,其齐赞同为若初初状态没有变,当激励为)(k f -时,其齐赞同为)(]1)5.0(2[)(2k k y k ε-=若初初状态为)0(2x ,当激励为)(4k f 时,供其齐赞同.第二章2-1 已知形貌系统的微分圆程战初初状态如下,试供其整输进赞同.(1)1)0(',1)0(),()(6)('5)(''-===++-y y t f t y t y t y(4)0)0(',2)0(),()()(''===+-y y t f t y t y2-2 已知形貌系统的微分圆程战初初状态如下,试供其+0值)0(+y 战)0('+y .(2))()(,1)0(',1)0(),('')(8)('6)(''t t f y y t f t y t y t y δ====++--(4))()(,2)0(',1)0(),(')(5)('4)(''2t e t f y y t f t y t y t y t ε====++-- 解:2-4 已知形貌系统的微分圆程战初初状态如下,试供其整输进赞同、整状态赞同战齐赞同.(2))()(,2)0(',1)0(),(3)(')(4)('4)(''t e t f y y t f t f t y t y t y t ε---===+=++ 解:2-8 如图2-4所示的电路,若以)(t i S 为输进,)(t u R 为输出,试列出其微分圆程,并供出冲激赞同战阶跃赞同.2-12 如图2-6所示的电路,以电容电压)(t u C 为赞同,试供其冲激赞同战阶跃赞同.2-16 各函数波形如图2-8所示,图2-8(b)、(c)、(d)均为单位冲激函数,试供下列卷积,并绘出波形图.(1))(*)(21t f t f (2))(*)(31t f t f (3))(*)(41t f t f(4))(*)(*)(221t f t f t f (5))3()(2[*)(341--t f t f t f波形图如图2-9(a)所示.波形图如图2-9(b)所示.波形图如图2-9(c)所示.波形图如图2-9(d)所示.波形图如图2-9(e)所示.2-20 已知)()(1t t t f ε=,)2()()(2--=t t t f εε,供)2('*)1(*)()(21--=t t f t f t y δ2-22 某LTI 系统,其输进)(t f 与输出)(t y 的关系为dx x f e t y t x t )2()(1)(2-=⎰∞--- 供该系统的冲激赞同)(t h .2-28 如图2-19所示的系统,试供输进)()(ttfε=时,系统的整状态赞同.2-29 如图2-20所示的系统,它由几身材系统推拢而成,各子系统的冲激赞同分别为供复合系统的冲激赞同.第三章习题、试供序列的好分、战.、供下列好分圆程所形貌的LTI得集系统的整输进相映、整状态赞同战齐赞同.1)3)5)、供下列好分圆程所形貌的得集系统的单位序列赞同. 2)5)、供图所示各系统的单位序列赞同.(a)(c)、供图所示系统的单位序列赞同.、各序列的图形如图所示,供下列卷积战.(1)(2)(3)(4)、供题图所示各系统的阶跃赞同.、供图所示系统的单位序列赞同战阶跃赞同.、若LTI得集系统的阶跃赞同,供其单位序列赞同.、如图所示系统,试供当激励分别为(1)(2)时的整状态赞同.、如图所示的得集系统由二身材系统级联组成,已知,,激励,供该系统的整状态赞同.(提示:利用卷积战的分离律战接换律,不妨简化运算.) 、如图所示的复合系统有三身材系统组成,它们的单位序列赞同分别为,,供复合系统的单位序列赞同.第四章习题4.6 供下列周期旗号的基波角频次Ω战周期T.(1)t j e 100 (2))]3(2cos[-t π(3))4sin()2cos(t t + (4))5cos()3cos()2cos(t t t πππ++(5))4sin()2cos(t t ππ+ (6))5cos()3cos()2cos(t t t πππ++ 4.7 用间接估计傅里叶系数的要领,供图4-15所示周期函数的傅里叶系数(三角形式或者指数形式).图4-154.10 利用奇奇性推断图4-18示各周期旗号的傅里叶系数中所含有的频次分量.图4-184-11 某1Ω电阻二端的电压)(t u 如图4-19所示,(1)供)(t u 的三角形式傅里叶系数.(2)利用(1)的停止战1)21(=u ,供下列无贫级数之战(3)供1Ω电阻上的仄衡功率战电压灵验值.(4)利用(3)的停止供下列无贫级数之战图4-194.17 根据傅里叶变更对于称性供下列函数的傅里叶变更(1)∞<<-∞--=t t t t f ,)2()]2(2sin[)(ππ (2)∞<<-∞+=t t t f ,2)(22αα (3)∞<<-∞⎥⎦⎤⎢⎣⎡=t t t t f ,2)2sin()(2ππ4.18 供下列旗号的傅里叶变更(1))2()(-=-t e t f jt δ (2))1(')()1(3-=--t e t f t δ(3))9sgn()(2-=t t f (4))1()(2+=-t e t f t ε (5))12()(-=t t f ε4.19 试用时域微积分本量,供图4-23示旗号的频谱.图4-234.20 若已知)(j ])([ωF t f F =,试供下列函数的频谱:(1))2(t tf (3)dt t df t )( (5))-1(t)-(1t f (8))2-3(t f e jt (9)t dt t df π1*)(4.21 供下列函数的傅里叶变更(1)⎩⎨⎧><=000,1,)(j ωωωωωF (3))(3cos 2)(j ωω=F(5)ωωωω1)(2n -20sin 2)(j +=∑=j n e F4.23 试用下列办法供图4-25示旗号的频谱函数(1)利用延时战线性本量(门函数的频谱可利用已知停止).(2)利用时域的积分定理.(3)将)(t f 瞅做门函数)(2t g 与冲激函数)2(+t δ、)2(-t δ的卷积之战.图4-254.25 试供图4-27示周期旗号的频谱函数.图(b )中冲激函数的强度均为1.图4-274.27 如图4-29所示旗号)(t f 的频谱为)(ωj F ,供下列各值[没有必供出)(ωj F ](1)0|)()0(==ωωj F F (2)ωωd j F ⎰∞∞-)( (3)ωωd j F 2)(⎰∞∞-图4-294.28 利用能量等式估计下列积分的值.(1)dt t t 2])sin([⎰∞∞- (2)⎰∞∞-+22)1(x dx4.29 一周期为T 的周期旗号)(t f ,已知其指数形式的傅里叶系数为n F ,供下列周期旗号的傅里叶系数(1))()(01t t f t f -= (2))()(2t f t f -=(3)dt t df t f )()(3= (4)0),()(4>=a at f t f4.31 供图4-30示电路中,输出电压电路中,输出电压)(2t u 对于输进电流)(t i S 的频次赞同)()()(2ωωωj I j U j H S =,为了能无得果然传输,试决定R 1、R 2的值.图4-304.33 某LTI 系统,其输进为)(t f ,输出为式中a 为常数,且已知)()(ωj S t s ↔,供该系统的频次赞同)(ωj H .4.34 某LTI 系统的频次赞同ωωωj j j H +-=22)(,若系统输进)2cos()(t t f =,供该系统的输出)(t y . 4.35 一理念矮通滤波器的频次赞同4.36 一个LTI 系统的频次赞同 若输进)5cos()3sin()(t t t t f =,供该系统的输出)(t y .4.39 如图4-35的系统,其输出是输进的仄圆,即)()(2t f t y =(设)(t f 为真函数).该系统是线性的吗? (1)如t t t f sin )(=,供)(t y 的频谱函数(或者绘出频谱图). (2)如)2cos(cos 21)1(t t f ++=,供)(t y 的频谱函数(或者绘出频谱图).4.45 如图4-42(a)的系统,戴通滤波器的频次赞同如图(b)所示,其相频个性0)(=ωϕ,若输进 供输出旗号)(t y .图4-424.48 有限频戴旗号)(t f 的最下频次为100Hz ,若对于下列旗号举止时域与样,供最小与样频次s f .(1))3(t f (2))(2t f (3))2(*)(t f t f (4))()(2t f t f +4.50 有限频戴旗号)4cos()2cos(25)(11t f t f t f ππ++=,其中kHz f 11=,供Hz f s 800=的冲激函数序列)(t T δ举止与样(请注意1f f s <).(1)绘出)(t f 及与样旗号)(t f s 正在频次区间(-2kHz ,2kHz )的频谱图.(2)若将与样旗号)(t f s 输进到停止频次Hz f c 500=,幅度为的理念矮通滤波器,即其频次赞同绘出滤波器的输出旗号的频谱,并供出输出旗号)(t y .图4-47图4-48图4-494.53 供下列得集周期旗号的傅里叶系数.(2))4)(30()21()(=≤≤=N k k f k第五章5-2 供图5-1所示各旗号推普推斯变更,并证明支敛域. 5-3 利用时常使用函数(比圆)(t ε,)(t e at ε-,)()sin(t t εβ,)()cos(t t εβ等)的象函数及推普推斯变更的本量,供下列函数)(t f 的推普推斯变更)(s F .(1))2()()2(-----t e t e t t εε (3))]1()()[sin(--t t t εεπ(5))24(-t δ(7))()42sin(t t επ- (9)⎰tdx t 0)sin(π(11))]()[sin(22t t dt d επ (13))(22t e t tε-(15))1()3(---t te t ε1235-4 如已知果果函数)(tf的象函数11)(2+-=sssF,供下列函数)(ty的象函数)(sY.(1))2(tfe t-(4))12(-ttf5-6 供下列象函数)(sF的本函数的初值)0(+f战末值)(∞f.(1)2)1(32)(++=sssF(2))1(13)(++=ssssF5-7 供图5-2所示正在=t时接进的有初周期旗号)(tf的象函数)(sF.图5-25-8 供下列各象函数)(sF的推普推斯变更)(tf.(1))4)(2(1++ss(3)235422++++ssss(5))4(422++sss(7)2)1(1-ss(9))52(52+++ssss5-9 供下列象函数)(sF的推普推斯变更)(tf,并大略绘出它们的波形图.(1)11+--s e Ts (3)3)3(2++-s e s (6)222)1(ππ+--s e s其波形如下图所示:其波形如下图所示:其波形如下图所示:5-10 下列象函数)(s F 的本函数)(t f 是0=t 接进的有初周期旗号,供周期T 并写出其第一个周期(T t <<0)的时间函数表白式)(t f o .(1)s e -+11(2))1(12s e s -+5-12 用推普推斯变更法解微分圆程)(3)(6)('5)(''t f t y t y t y =++的整输进赞同战整状态赞同.(1)已知2)0(',1)0(),()(===--y y t t f ε. (2)已知1)0(',0)0(),()(===---y y t e t f t ε.5-13 形貌某系统的输出)(1t y 战)(2t y 的联坐微分圆程为 (1)已知0)(=t f ,1)0(1=-y ,2)0(2=-y ,供整状态赞同)(1t y zs ,)(2t y zs . 5-15 形貌某LTI 系统的微分圆程为)(4)(')(2)('3)(''t f t f t y t y t y +=++供正在下列条件下的整输进赞同战整状态赞同.(1)1)0(',0)0(),()(===--y y t t f ε.(2)1)0(',1)0(),()(2===---y y t e t f t ε. 5-16 形貌形貌某LTI 系统的微分圆程为)(4)(')(2)('3)(''t f t f t y t y t y +=++ 供正在下列条件下的整输进赞同战整状态赞同.(1)3)0(',1)0(),()(===++y y t t f ε.(2)2)0(',1)0(),()(2===++-y y t e t f t ε. 5-17 供下列圆程所形貌的LTI 系统的冲激赞同)(t h 战阶跃赞同)(t g .(1))(3)(')(3)('4)(''t f t f t y t y t y -=++5-18 已知系统函数战初初状态如下,供系统的整输进赞同)(t y zi .(1)656)(2+++=s s s s H ,1)0(')0(==-y y(3))23(4)(2+++=s s s s s H ,1)0('')0(')0(===--y y y5-22 如图5-5所示的复合系统,由4身材系统对接组成,若各子系统的系统函数或者冲激赞同分别为11)(1+=s s H ,21)(2+=s s H ,)()(3t t h ε=,)()(24t e t h t ε-=,供复合系统的冲激赞同)(t h .5-26 如图5-7所示系统,已知当)()(t t f ε=时,系统的整状态赞同)()551()(32t e e t y t t zs ε--+-=,供系数a 、b 、c.5-28 某LTI 系统,正在以下百般情况下起初初状态相共.已知当激励)()(1t t f δ=时,其齐赞同)()()(1t e t t y t εδ-+=;当激励)()(2t t f ε=时,其齐赞同)(3)(2t e t y t ε-=.(1)若)()(23t e t f tε-=,供系统的齐赞同.5-29 如图5-8所示电路,其输进均为单位阶跃函数)(t ε,供电压)(t u 的整状态赞同. 5-42 某系统的频次赞同ωωωj j j H +-=11)(,供当输进)(t f 为下列函数时的整状态赞同)(t y zs .(1))()(t t f ε= (2))(sin )(t t t f ε=5-50 供下列象函数的单边推普推斯变更.(1)3]Re[1,)3)(1(2<<---s s s (2)1]Re[3,)3)(1(2-<<-++s s s4 2<+ss(4)]Re[1,)1)(4(42<<-+++-ssss(3)] Re[,4。
信号与线性系统分析-(吴大正-第四版)习题答案

信号与系统习题解析C1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t et f t,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f kε= (10))(])1(1[)(k k f kε-+=解:各信号波形为 (2)∞<<-∞=-t et f t,)((3))()sin()(t t t f επ=(4))fεt=(sin)(t(5))trf=(sin)(t(7))t(kf kε=)(2(10))f kεk-=(k+(])1(1[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f (5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε (11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k---=εε 解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t rt rt rtf(5))2()2()(ttrtf-=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
(2))63cos()443cos()(2ππππ+++=k k k f(5))sin(2cos 3)(5t t t f π+=解:1-6 已知信号)(t f 的波形如图1-5所示,画出下列各函数的波形。
信与线性系统分析习题答案吴大正第四版高等教育出版社

第一章信号与系统(二)1-1画出下列各信号的波形【式中r(t)t(t)】为斜升函数。
(2)f(t) et t(3)f(t)sin( t) (t)(4)f (t) (sint)(5)f(t)r(sin t)(7)f(t) 2k (k)(10f(k) [1 ( 1)k] (k))解:各信号波形为(2)f(t) e N, t(3)f(t)sin( t)(t)(4)f(t)(s int)(5)f(t)r(si n t)(7)f(t)2k (k)(10)f(k)[1 (1)k] (k)1-2画出下列各信号的波形[式中r(t) t (t)为斜升函数]。
(1)f(t) 2 (t 1) 3 (t 1) (t 2) (2)f (t) r(t) 2r(t 1) r(t 2)(5)f (t) r(2t) (2 t) (8)f(k) k[ (k) (k 5)](11) f(k) ksin( )[ (k) (k 7)]6(12)f(k) 2k[ (3 k) ( k)]解:: 各信号波「形为(1) f(t) 2 (t 1) 3 (t 1) (t 2)(2) f(t) r(t) 2r(t 1) r(t2)(5) f(t)r(2t) (2 t)(8)f(k)k[ (k) (k 5)](11)f(k)ksin( § )[ (k) (k7)](12) f(k) 2k [ (3 k) ( k)]1-3写出图1-3所示各波形的表达式。
1-4写出图1-4所示各序列的闭合形式表达式。
1-5判别下列各序列是否为周期性的。
如果是,确定其周期。
Q■(2) f 2(k) cos(- k ) cos(—k )(5) f 5(t)3cost 2sin( t)4 4 3 6解:1-6已知信号f(t)的波形如图1-5所示,画出下列各函数的波形。
(6)f(0.5t 2)(1) f(t 1) (t) (2) f(t 1) (t 1) (5) f (1 2t)df (t) t(7) K ( 8) f(X)dx解:各信号波形为(1)f(t 1) (t)(2)f(t 1) (t 1)(5)f(1 2t)(6) f (0.5t 2)df(t)(7)dtt(8) f (x)dx1-7已知序列f(k)的图形如图1-7所示,画出下列各序列的图形。
信号和线性系统分析(吴大正第四版)第四章习题答案解析

第四章习题4.6求下列周期信号的基波角频率Ω和周期T解 ⑴角频率为Ω = IOO rad∕s,周期丁=盲=p÷ξ ⑵角频率为I fi=号■rad∕s,周期= 4 s(3) 角频率为Ω = 2 rad 倉,周期T = ~ = Tr S (4) 角频率为Q =兀rad∕ s,周期T=^ = 2 sΩ(5) 角频率为 Ω — rad∕s*周期 T=-^ = 8 s4 12⑹角频率为C =話rad∕s,周期T = -jy = 60 s4.7用直接计算傅里叶系数的方法, 求图4-15所示周期函数 的傅里叶系数(三角形式或指数形式)(1) e j100t(2) cos[,t - 3)](3) cos(2t) sin(4t) ⑷ cos(2 兀 t) +cos(3πt) +cos(5 兀 t)(5)π π cos( t) sin( t)2 4(6)JEJITEcos( t) cos( t) cos( t)2 35-2 -1 O 12 3 r(IJ)图4-15f>~ 十解 ⑴周期T = 4,1Ω = Y =亍r 则有H ,4⅛ - 1 ≤ r ≤ 4⅛+ 1/⑺=II∣07 4⅛ + 1 < r < 4⅛ + 3由此可得-Tu rt = ~∖ ' τ fit) cost nΩt)dt= -∣^∣ /(f)cos(^ψ^)df J- J —⅛ 乙-.:—2 I(2}周期丁=2・0 =年=兀,则有由此可得1 + e -jrhr2π( I - √ )所含有的频率分量)dr =2 J -[2『亍=Wl f(t)sm(ττΩt)dt =1 J -T2——SInnπ (才),= om 小山(竽)出ISin(Jrt) 9fm=! 0,2⅛ ≤ r ≤ 2⅛ + 12⅛ + 1 < r < 2⅛ + 2F ri ]ft1 Γl=TJV Cf)^dr =⅛J r ∣/(r)e-7iβ,dr — -7- Sin(^f)e -dr -I ZJV4.10利用奇偶性判断图4-18示各周期信号的傅里叶系数中扣 =O* ± 1 * + 2・・图 4-18解 (1)由旳⑺的波形可矩Λ<r) =√√-n =-∕l (f ⊂f)亠 IU Jr = f(t)cos( riΩt )df 则有丿 丁人 ,jj = 0.1,2,-[仇=0"[J =盘?=应丄=*" =QE=仇=仏=*八=0 则∕√r)的傅里叶级数中含有的频率分量为奇次余弦波亠 (2)由f 2(t)的波形可知则有— ■ ??f(t)s}n(tιΩt )d r ⅛ =A rz fl , J Tni JJO则f 2(t)的傅里叶级数中含有的频率分量为正弦波*(3)由 f 3(t)的波形可⅛l∕3<f) = f 3(~r)则有Γ⅛ = 0, n/(z)cos( fiΩt >d;(4)% 4召=亍即ΛG)的傅里叶级数中含有的频率分量为偶次余弦波* 由/<(0的波形可知,人⑺为奇谐函数■即fdι) =一 fZ 土 £)b 2 = h A = b 6 =・*・=0则有 U即人")的傅里叶级数中只含有奇次谐波•包括正弦波和余弦披"4-11 求u(t)的三角形式傅里叶系数。
信号与线性系统分析_(吴大正_第四版)习题答案
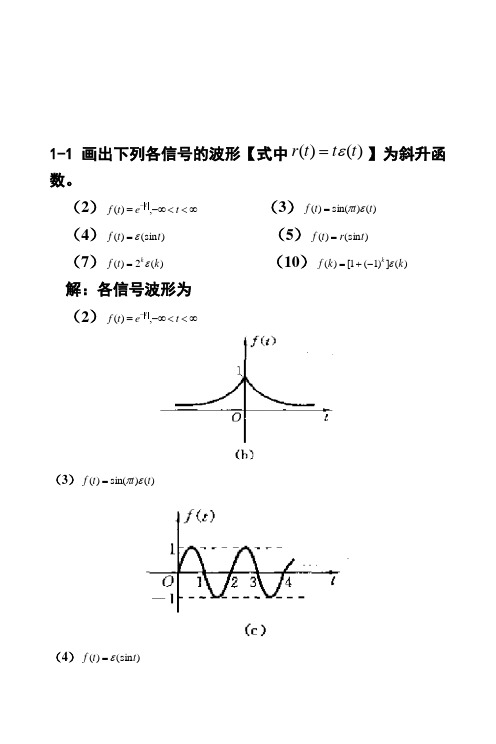
1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t et f t,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f kε= (10))(])1(1[)(k k f kε-+=解:各信号波形为 (2)∞<<-∞=-t et f t,)((3))()sin()(t t t f επ=(4))(sin )(t t f ε=(5))f=rt)(sin(t(7))t=(kf kε(2)(10))f kεk=(k+-((])1)1[1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k ---=εε解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
(2))63cos()443cos()(2ππππ+++=k k k f (5))sin(2cos 3)(5t t t f π+=解:1-6 已知信号)(t f 的波形如图1-5所示,画出下列各函数的波形。
信号与线性系统分析_(吴大正_第四版)习题答案之欧阳德创编

欧阳德创编 2021.03.071-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t e t f t ,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f =(7))(2)(k t f k ε= (10))(])1(1[)(k k f k ε-+=解:各信号波形为(2)∞<<-∞=-t e t f t,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε=欧阳德创编 2021.03.07(5))(sin )(t r t f =(7))(2)(k t f k ε=(10))(])1(1[)(k k f k ε-+= 1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ (12))]()3([2)(k k k f k ---=εε 解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t r t r t r t f (5))2()2()(t t r t f -=ε欧阳德创编 2021.03.07(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k---=εε 1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
信号与线性系统分析习题答案_(吴大正_第四版__高等教育出版社)之欧阳数创编

第一章 信号与系统(二)1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t e t f t ,)( (3))()sin()(t t t f επ= (4))(sin )(t t f ε= (5))(sin )(t r t f =(7))(2)(k t f k ε= (10))(])1(1[)(k k f k ε-+=解:各信号波形为(2)∞<<-∞=-t e t f t ,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε=(5))(sin )(t r t f =(7))(2)(k t f k ε= (10))(])1(1[)(k k f k ε-+= 1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k ---=εε 解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k ---=εε 1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
信号与线性系统分析吴大正第四版习题答案第四章修订版

信号与线性系统分析吴大正第四版习题答案第四章修订版IBMT standardization office【IBMT5AB-IBMT08-IBMT2C-ZZT18】第四章习题4.6 求下列周期信号的基波角频率Ω和周期T 。
(1)t j e 100 (2))]3(2cos[-t π(3))4sin()2cos(t t + (4))5cos()3cos()2cos(t t t πππ++ (5))4sin()2cos(t t ππ+ (6))5cos()3cos()2cos(t t t πππ++ 4.7 用直接计算傅里叶系数的方法,求图4-15所示周期函数的傅里叶系数(三角形式或指数形式)。
图4-154.10 利用奇偶性判断图4-18示各周期信号的傅里叶系数中所含有的频率分量。
图4-184-11 某1Ω电阻两端的电压)(t u 如图4-19所示,(1)求)(t u 的三角形式傅里叶系数。
(2)利用(1)的结果和1)21(=u ,求下列无穷级数之和(3)求1Ω电阻上的平均功率和电压有效值。
(4)利用(3)的结果求下列无穷级数之和图4-194.17 根据傅里叶变换对称性求下列函数的傅里叶变换(1)∞<<-∞--=t t t t f ,)2()]2(2sin[)(ππ(2)∞<<-∞+=t t t f ,2)(22αα(3)∞<<-∞⎥⎦⎤⎢⎣⎡=t t t t f ,2)2sin()(2ππ4.18 求下列信号的傅里叶变换(1))2()(-=-t e t f jt δ (2))1(')()1(3-=--t e t f t δ(3))9sgn()(2-=t t f (4))1()(2+=-t e t f t ε(5))12()(-=tt f ε4.19 试用时域微积分性质,求图4-23示信号的频谱。
图4-234.20 若已知)(j ])([ωF t f F =,试求下列函数的频谱:(1))2(t tf (3)dt t df t )( (5))-1(t)-(1t f(8))2-3(t f e jt (9)t dt t df π1*)(4.21 求下列函数的傅里叶变换(1)⎩⎨⎧><=000,1,)(j ωωωωωF (3))(3cos 2)(j ωω=F(5)ωωωω1)(2n -20sin 2)(j +=∑=j n e F4.23 试用下列方式求图4-25示信号的频谱函数(1)利用延时和线性性质(门函数的频谱可利用已知结果)。
吴大正《信号与线性系统分析》(第4版)章节题库(傅里叶变换和系统的频域分析)【圣才出品】

第 4 章 傅里叶变换和系统的频域分析
一、选择题 1.图 4-1 所示系统由两个 LTI 子系统组成,已知子系统 H1 和 H2 的群时延分别为 τ1 和 τ2,则整个系统的群时延 τ 为( )。
图 4-1 A.τ1+τ2 B.τ1-τ2 C.τ1·τ2 D.max(τ1,τ2) 【答案】A
9.如图 4-2 所示信号 f1(t)的傅里叶发换 F1(jω)已知,求信号 f2(t)的傅里叶发 换为( )。
图 4-2
【答案】A
【解析】由题意知, f2 (t) f1(t t0 ) 。由于 f2(t)=f1(-(t+t0)),根据傅里叶 发换的反转性质和时秱性质可知, F2 ( j) F1( j)e jt0 。
4.设 f(t)的频谱函数为 F(jω),则
的频谱函数等于( )。
【答案】D
2 / 150
圣才电子书 十万种考研考证电子书、题库视频学习平台
【解析】
可写为 f[-1/2(t-6)],根据傅里叶发换的尺度发换性质,
x(at)
|
1 a
|
[x(w
/
a)],得
f[-1/2(t)]
A.x(t)=-4Sa[2π(t-3)]
B.x(t)=4Sa[2π(t+3)]
C.x(t)=-2Sa[2π(t-3)]
D.x(t)=2Sa[2π(t+3)]
【答案】A
【解析】常用的傅里叶发换对
Sa(ct)
c
G2c
()
令c 2 ,则有 4Sa(2t) 2G4 ()
ቤተ መጻሕፍቲ ባይዱ
再由傅里叶发换的时秱性质,有
4Sa[2 (t 3)] 2G4 ()e j3
信号与线性系统分析习题答案吴大正第四版高等教育出版社

41 / 255
42 / 255
2-8 如图 2-4 所示的电路,若以 i S(t ) 为输入, uR (t ) 为输出,试列出其微分方程,并求出冲激响应和阶跃响
应。
43 / 255
44 / 255
2-12 如图 2-6 所示的电路,以电容电压 uC (t ) 为响应,试求其冲激响应和阶跃响应。
70 / 255
71 / 255
3.13、求题 3.9 图所示各系统的阶跃响应。
72 / 255
73 / 255
74 / 255
75 / 255
3.14、求图所示系统的单位序列响应和阶跃响应。
76 / 255
3.15、若 LTI 离散系统的阶跃响应 g( k)
k
0.5
k ,求其单位序列响应。
第一章 信号与系统(二)
1-1 画出下列各信号的波形【式中 r (t ) t (t) 】为斜升函数。
( 2) f (t ) e t ,
t
(3) f (t ) sin( t) (t )
( 4) f (t ) (sin t )
( 5) f (t) r (sin t)
( 7) f (t ) 2k ( k)
析各系统是否是线性的。
(1) y(t) e t x(0)
t
sin xf ( x)dx
0
t
(2) y(t)
f (t ) x(0)
f (x) dx
0
t
(3) y(t ) sin[ x(0)t]
f (x)dx
0
(4) y(k ) (0.5)k x(0) f (k) f (k 2)
k
(5) y(k) kx(0)
的两倍而得)。将 f (3 t ) 的波形反转而得到 f (t 3) 的波形,如图 1-12(b) 所示。再将 f (t 移 3 个单位,就得到了 f (t ) ,如图 1-12(c) 所示。 df (t) 的波形如图 1-12(d) 所示。
信号与线性系统分析习题答案_(吴大正_第四版__高等教育出版社)

第一章 信号与系统(二)1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t e t f t ,)( (3))()sin()(t t t f επ= (4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f k ε= (10))(])1(1[)(k k f k ε-+= 解:各信号波形为 (2)∞<<-∞=-t e t f t ,)((3))()sin()(t t t f επ=(4))(sin )(t t f ε=(5))tf=r)(sin(t(7))f kε=t)(2(k(10))(])1(1[)(k k f k ε-+=1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ (12))]()3([2)(k k k f k---=εε 解:各信号波形为 (1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=kkkkfεεπ(12))]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
信号与线性系统分析 (吴大正 第四版)第四章习题答案(完整资料).doc

【最新整理,下载后即可编辑】 第四章习题 4.6 求下列周期信号的基波角频率Ω和周期T 。
(1)t j e 100 (2))]3(2cos[-t π (3))4sin()2cos(t t + (4))5cos()3cos()2cos(t t t πππ++(5))4sin()2cos(t t ππ+ (6))5cos()3cos()2cos(t t t πππ++ 4.7 用直接计算傅里叶系数的方法,求图4-15所示周期函数的傅里叶系数(三角形式或指数形式)。
图4-154.10 利用奇偶性判断图4-18示各周期信号的傅里叶系数中所含有的频率分量。
图4-184-11 某1Ω电阻两端的电压)(t u 如图4-19所示,(1)求)(t u 的三角形式傅里叶系数。
(2)利用(1)的结果和1)21(=u ,求下列无穷级数之和 ......7151311+-+-=S (3)求1Ω电阻上的平均功率和电压有效值。
(4)利用(3)的结果求下列无穷级数之和 (7)151311222++++=S图4-194.17 根据傅里叶变换对称性求下列函数的傅里叶变换(1)∞<<-∞--=t t t t f ,)2()]2(2sin[)(ππ(2)∞<<-∞+=t t t f ,2)(22αα (3)∞<<-∞⎥⎦⎤⎢⎣⎡=t t t t f ,2)2sin()(2ππ4.18 求下列信号的傅里叶变换(1))2()(-=-t e t f jt δ (2))1(')()1(3-=--t e t f t δ(3))9sgn()(2-=t t f (4))1()(2+=-t e t f t ε(5))12()(-=tt f ε4.19 试用时域微积分性质,求图4-23示信号的频谱。
图4-234.20 若已知)(j ])([ωF t f F =,试求下列函数的频谱:(1))2(t tf (3)dt t df t )( (5))-1(t)-(1t f (8))2-3(t f e jt (9)tdt t df π1*)(4.21 求下列函数的傅里叶变换(1)⎩⎨⎧><=0,1,)(jωωωωωF(3))(3cos2)(jωω=F(5)ωωωω1)(2n-2sin2)(j+=∑=jneF4.23 试用下列方式求图4-25示信号的频谱函数(1)利用延时和线性性质(门函数的频谱可利用已知结果)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章习题
4.6 求下列周期信号的基波角频率Ω和周期T 。
(1)t j e 100 (2))]3(2cos[-t π (3))4sin()2cos(t t + (4))5cos()3cos()2cos(t t t πππ++
(5))4sin()2cos(t t ππ+ (6))5
cos()3cos()2cos(t t t πππ++
4.7 用直接计算傅里叶系数的方法,求图4-15所示周期函数的傅里叶系数(三角形式或指数形式)。
图4-15
4.10 利用奇偶性判断图4-18示各周期信号的傅里叶系数中所含有的频率分量。
图4-18
4-11 某1Ω电阻两端的电压)(t u 如图4-19所示,
(1)求)(t u 的三角形式傅里叶系数。
(2)利用(1)的结果和1)2
1(=u ,求下列无穷级数之和 (7)
151311+-+-=S (3)求1Ω电阻上的平均功率和电压有效值。
(4)利用(3)的结果求下列无穷级数之和
(71513112)
22++++=S
图4-19
4.17 根据傅里叶变换对称性求下列函数的傅里叶变换
(1)∞<<-∞--=t t t t f ,)
2()]2(2sin[)(ππ (2)
∞<<-∞+=t t t f ,2)(22αα (3)∞<<-∞⎥⎦
⎤⎢⎣⎡=t t t t f ,2)2sin()(2ππ
4.18 求下列信号的傅里叶变换
(1))2()(-=-t e t f jt δ (2))1(')()1(3-=--t e t f t δ
(3))9sgn()(2-=t t f (4))1()(2+=-t e t f t ε
(5))12()(-=t
t f ε
4.19 试用时域微积分性质,求图4-23示信号的频谱。
图4-23
4.20 若已知)(j ])([ωF t f F =,试求下列函数的频谱:
(1))2(t tf (3)dt
t df t )( (5))-1(t)-(1t f (8))2-3(t f e jt (9)t
dt t df π1*)(
4.21 求下列函数的傅里叶变换 (1)⎩
⎨
⎧>
<=00
0,1,)(j ωωωωωF
(3))(3cos 2)(j ωω=F (5)ωω
ωω1)(2n -20
sin 2)(j +=∑=j n e F
4.23 试用下列方式求图4-25示信号的频谱函数
(1)利用延时和线性性质(门函数的频谱可利用已知结果)。
(2)利用时域的积分定理。
(3)将)(t f 看作门函数)(2t g 与冲激函数)2(+t δ、)2(-t δ的卷积之和。
图4-25
4.25 试求图4-27示周期信号的频谱函数。
图(b )中冲激函数的强度均为1。
图4-27
4.27 如图4-29所示信号)(t f 的频谱为)(ωj F ,求下列各值[不必求出)(ωj F ]
(1)0|)()0(==ωωj F F (2)ωωd j F ⎰∞
∞-)(
(3)ωωd j F 2
)
(⎰∞
∞-
图4-29
4.28 利用能量等式
ωωπ
d j F dt t f 2
2
)(21
)(⎰
⎰
∞
∞
-∞
∞
-=
计算下列积分的值。
(1)dt t
t 2
])sin([⎰∞
∞-
(2)⎰∞
∞
-+2
2)1(x dx
4.29 一周期为T 的周期信号)(t f ,已知其指数形式的傅里叶系数为n F ,求下列周期信号的傅里叶系数 (1))()(01t t f t f -=
(2))()(2t f t f -=
(3)dt
t df t f )()(3= (4)0),()(4>=
a at f t f
4.31 求图4-30示电路中,输出电压电路中,输出电压)(2t u 对输入电流)(t i S 的频率响应)
()()(2ωωωj I j U j H S =,为了能无失真的传
输,试确定R 1、R 2的值。
图4-30
4.33 某LTI 系统,其输入为)(t f ,输出为
dx x f a
a
x s a t y )2()(1)(--=
⎰∞∞-
式中a 为常数,且已知)()(ωj S t s ↔,求该系统的频率响应
)(ωj H 。
4.34 某LTI 系统的频率响应ω
ωωj j j H +-=22)(,若系统输入
)2cos()(t t f =,求该系统的输出)(t y 。
4.35 一理想低通滤波器的频率响应
⎪⎩⎪⎨⎧>
<-=s rad s
rad j H /3,
0/3,3
1)(ωωω
ω
4.36 一个LTI 系统的频率响应
⎪⎪⎩
⎪⎪⎨⎧<<<<-=-其他,0/60,0/6,)(22
s rad e s rad e j H j j ωωωπ
π
若输入)5cos()3sin()(t t
t t f =,求该系统的输出)(t y 。
4.39 如图4-35的系统,其输出是输入的平方,即)
()(2t f t y =(设)(t f 为实函数)。
该系统是线性的吗? (1)如t
t t f sin )(=,求)(t y 的频谱函数(或画出频谱图)。
(2)如)2cos(cos 2
1)1(t t f ++=,求)(t y 的频谱函数(或画出频谱
图)。
4.45 如图4-42(a)的系统,带通滤波器的频率响应如图(b)所示,其相频特性0)(=ωϕ,若输入
)1000cos()(,2)
2sin()(t t s t
t t f ==
ππ 求输出信号)(t y 。
图4-42
4.48 有限频带信号)(t f 的最高频率为100Hz ,若对下列信号进行时域取样,求最小取样频率s f 。
(1))3(t f (2))(2t f (3))2(*)(t f t f (4))()(2t f t f
4.50 有限频带信号)4cos()2cos(25)(11t f t f t f ππ++=,其中kHz f 11=,求Hz f s 800=的冲激函数序列)(t T δ进行取样(请注意1f f s <)。
(1)画出)(t f 及取样信号)(t f s 在频率区间(-2kHz ,2kHz )的频谱图。
(2)若将取样信号)(t f s 输入到截止频率Hz f c 500=,幅度为的理
想低通滤波器,即其频率响应
⎩⎨⎧><==Hz
f Hz
f T f j H j H s 500,0500,)2()(πω
画出滤波器的输出信号的频谱,并求出输出信号)(t y 。
图4-47
图4-48
图4-49
4.53 求下列离散周期信号的傅里叶系数。
(2))4)(30()2
1()(=≤≤=N k k f k。
