线段差的最大值与线段和的最小值问题
一次函数综合—线段和差、存在性问题解析
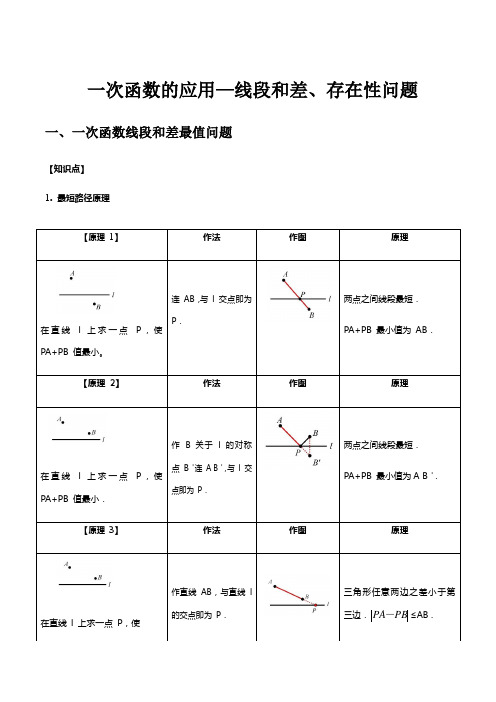
一次函数的应用—线段和差、存在性问题一、一次函数线段和差最值问题【知识点】1. 最短路径原理【原理1】作法作图原理在直线l 上求一点P,使PA+PB 值最小。
连AB,与l 交点即为P.两点之间线段最短.PA+PB 最小值为AB.【原理2】作法作图原理在直线l 上求一点P,使PA+PB 值最小.作 B 关于l 的对称点B'连A B',与l 交点即为P.两点之间线段最短.PA+PB 最小值为A B'.【原理3】作法作图原理在直线l 上求一点P,使作直线AB,与直线l的交点即为P.三角形任意两边之差小于第三边.≤AB .PBPA-(1)求线段和最小时动点坐标或直线解析式; (2)求三角形周长最小值;(3)求线段差最大时点的坐标或直线解析式。
3. 口诀:“和小异,差大同”(一)一次函数线段和最小值问题【例题讲解】★★☆例题1.在平面直角坐标系xOy 中,y 轴上有一点P ,它到点(4,3)A ,(3,1)B 的距离之和最小,则点P 的坐标是( ) A .(0,0)B .4(0,)7C .5(0,)7D .4(0,)5【答案】C的值最大 .【原理 4】作法作图原理在直线 l 上求一点 P ,使的值最大 .作 B 关于 l 的对称点 B '作直线 A B ',与 l 交点即为 P .三角形任意两边之差小于第三边.≤A B ' .PB PA -PB PA -PB PA -【解析】解:作A 关于y 轴的对称点C ,连接BC 交y 轴于P ,则此时AP PB +最小,即此时点P 到点A 和点B 的距离之和最小,(4,3)A ,(4,3)C ∴-,设直线CB 的解析式是y kx b =+,把C 、B 的坐标代入得:3413k bk b =-+⎧⎨-=+⎩,解得:47k =-,57b =,4577y x ∴=-+,把0x =代入得:57y =, 即P 的坐标是5(0,)7,故选:C .【备注】本题考查了轴对称-最短路线问题,一次函数的解析式,坐标与图形性质等知识点,关键是能画出P 的位置,题目比较典型,是一道比较好的题目.★★☆练习1.如图,在平面直角坐标系中,已知点(2,3)A ,点(2,1)B -,在x 轴上存在点P 到A ,B 两点的距离之和最小,则P 点的坐标是 .【答案】(1,0)-【解析】解:作A 关于x 轴的对称点C ,连接BC 交x 轴于P ,则此时AP BP +最小,A 点的坐标为(2,3),B 点的坐标为(2,1)-,(2,3)C ∴-,设直线BC 的解析式是:y kx b =+,把B 、C 的坐标代入得:2123k b k b -+=⎧⎨+=-⎩解得11k b =-⎧⎨=-⎩.即直线BC 的解析式是1y x =--,当0y =时,10x --=,解得:1x =-,P ∴点的坐标是(1,0)-.故答案为:(1,0)-.【备注】本题考查了一次函数图象上点的坐标特征,用待定系数法求一次函数的解析式,轴对称-最短路线问题的应用,关键是能找出P 点,题目具有一定的代表性,难度适中.★★☆练习2.如图,直线34120x y +-=与x 轴、y 轴分别交于点B 、A 两点,以线段AB 为边在第一象限内作正方形ABCD .若点P 为x 轴上的一个动点,求当PC PD +的长最小时点P 的坐标.【答案】详见解析【解析】解:直线34120x y +-=与x 轴、y 轴分别交于点B 、A 两点,则点A 、B 的坐标分别为:(0,3),(4,0),如图所示,过点C 作CH x ⊥轴交于点H ,90ABO BAO ∠+∠=︒,90ABO CBH ∠+∠=︒,CBH BAO ∴∠=∠,又90AOB CHB ∠=∠=︒,AB BC =,()AOB BHC AAS ∴∆≅∆,4CH OB ∴==,3HB OA ==,故点(7,4)C ,同理可得点(3,7)D ,确定点C 关于x 轴的对称点(7,4)C '-,连接C D '交x 轴于点P ,则此时PC PD +的长最小,将点C '、D 的坐标代入一次函数表达式并解得: 直线CD 的表达式为:116144y x =-+, 当0y =时,6111x =,故点61P,0).(11【备注】本题考查的是一次函数上坐标点的特征,涉及到点的对称性、正方形性质等,本题的难点在于:通过证明三角形全等,确定点C、D的坐标.★★☆例题2.在平面直角坐标系中,矩形OACB的顶点O在坐标原点,顶点A、B分别在x轴、y轴的正半轴上,3OB=,D为边OB的中点,若E为x轴上的一个动点,当CDE∆的周长最小时,求点E OA=,4的坐标()A.(3,0)-B.(1,0)C.(0,0)D.(3,0)【答案】B【解析】解:如图,作点D关于x轴的对称点D',连接CD'与x轴交于点E,连接DE.若在边OA上任取点E'与点E不重合,连接CE'、DE'、D E''由DE CE D E CE CD D E CE DE CE'+'=''+'>'='+=+,可知CDE∆的周长最小.OB=,D为边OB的中点,42∴=,OD∴,(0,2)D在矩形OACB 中,3OA =,4OB =,D 为OB 的中点,3BC ∴=,2D O DO '==,6D B '=,//OE BC ,Rt ∴△D OE Rt '∽△D BC ',∴OE D OBC D B '=' 即236OE = 1OE =,∴点E 的坐标为(1,0)故选:B .【备注】此题主要考查轴对称--最短路线问题,解决此类问题,一般都是运用轴对称的性质,将求折线问题转化为求线段问题,其说明最短的依据是三角形两边之和大于第三边.★★☆练习1.如图,在平面直角坐标系中,点A 、B 的坐标分别为(1,4)和(3,0),点C 是y 轴上的一个动点,连接AC 、BC ,当ABC ∆的周长最小值时,ABC ∆的面积为 .【答案】3【解析】解:如图,作点A 关于y 轴的对称点A ',连接A B '交y 轴于点C ',此时ABC ∆'的周长最小,设直线A B ' 的解析式为y kx b =+,(1,4)A '-,(3,0)B ,∴430k b k b -+=⎧⎨+=⎩,1k ∴=-,3b =,∴直线A B ' 的解析式为3y x =-+,当0x =时,3y =,(0,3)C ∴',ABC AA BAA C S SS∆'''∴=-11242122=⨯⨯-⨯⨯ 413=-=.所以ABC ∆'的面积为3.故答案为:3.【备注】本题考查了轴对称、最短路线问题、坐标与图形性质、三角形的面积,解决本题的关键是掌握轴对称的性质.★★☆练习2.如图,在平面直角坐标系中,直线122y x =+与x 轴、y 轴分别交于A 、B 两点,以AB 为边 在第二象限内作正方形ABCD .(1)求点A 、B 的坐标,并求边AB 的长;(2)求点C 和点D 的坐标;(3)在x 轴上找一点M ,使MDB ∆的周长最小,请求出M 点的坐标,并直接写出MDB ∆的周长最小值.【答案】详见解析【解析】解: (1)对于直线122y x =+, 令0x =,得到2y =;令0y =,得到4x =-,(4,0)A ∴-,(0,2)B ,即4OA =,2OB =, 则224225AB =+=;(2)过D 作DE x ⊥轴,过C 作CF y ⊥轴,四边形ABCD 为正方形,AB BC AD ∴==,90ABC BAD BFC DEA AOB ∠=∠=∠=∠=∠=︒,90FBC ABO ∠+∠=︒,90ABO BAO ∠+∠=︒,90DAE BAO ∠+∠=︒,FBC OAB EDA ∴∠=∠=∠,()DEA AOB BFC AAS ∴∆≅∆≅∆,2AE OB CF ∴===,4DE OA FB ===,即426OE OA AE =+=+=,246OF OB BF =+=+=,则(6,4)D -,(2,6)C -;(3)如图所示,连接BD ,找出B 关于y 轴的对称点B ',连接DB ',交x 轴于点M ,此时BM MD DM MB DB +=+'='最小,即BDM ∆周长最小,(0,2)B ,(0,2)B ∴'-,设直线DB '解析式为y kx b =+,把(6,4)D -,(0,2)B '-代入得:642k b b -+=⎧⎨=-⎩,解得:1k =-,2b =-,∴直线DB '解析式为2y x =--,令0y =,得到2x =-,则M 坐标为(2,0)-, 此时MDB ∆的周长为21062+.【备注】本题属于一次函数综合题,涉及的知识有:待定系数法求一次函数解析式,坐标与图形性质,勾 股定理,全等三角形的判定与性质,正方形的性质,对称性质,以及一次函数与坐标轴的交点,熟练掌握 性质及定理是解本题的关键(二)一次函数线段差最大值问题【例题讲解】★★☆例题1.已知,如图点(1,1)A ,(2,3)B -,点P 为x 轴上一点,当||PA PB -最大时,点P的坐标为( )A .1(,0)2B .5(,0)4C .1(,0)2-D .(1,0)【答案】A【解析】解:作A 关于x 轴对称点C ,连接BC 并延长交x 轴于点P , (1,1)A ,C ∴的坐标为(1,1)-,连接BC ,设直线BC 的解析式为:y kx b =+,∴123k b k b +=-⎧⎨+=-⎩, 解得:21k b =-⎧⎨=⎩, ∴直线BC 的解析式为:21y x =-+, 当0y =时,12x =, ∴点P 的坐标为:1(2,0),当B ,C ,P 不共线时,根据三角形三边的关系可得:||||PA PB PC PB BC -=-<,∴此时||||PA PB PC PB BC -=-=取得最大值.故选:A .【备注】此题考查了轴对称、待定系数法求一次函数的解析式以及点与一次函数的关系.此题难度较大,解题的关键是找到P 点,注意数形结合思想与方程思想的应用.★★☆练习1.平面直角坐标系中,已知(4,3)A 、(2,1)B ,x 轴上有一点P ,要使PA PB -最大,则P 点坐 标为【答案】(1,0)【解析】解:(4,3)A 、(2,1)B ,x 轴上有一点P ,||PA PB AB ∴-,∴当A ,B ,P 三点共线时,PA PB -最大值等于AB 长,此时,设直线AB 的解析式为y kx b =+,把(4,3)A 、(2,1)B 代入,可得3412k b k b =+⎧⎨=+⎩, 解得11k b =⎧⎨=-⎩, ∴直线AB 的解析式为1y x =-,令0y =,则1x =,P ∴点坐标为(1,0),故答案为:(1,0). 【备注】本题主要考查了坐标与图形性质,利用待定系数法求得直线AB 的解析式是解决问题的关键. ★★☆练习2.如图,在平面直角坐标系中,点A 的坐标为(0,4),点B 的坐标为(6,0),点P 在一次函数1322y x =+的图象上运动,则PB PA -的最大值为( )A .2B .233C .4D .143【答案】C【解析】解:如图,作点A 关于直线1322y x =+的对称点K ,连接AK 交直线于H ,连接PK .AK PH ⊥,(0,4)A ,∴直线AK 的解析式为24y x =-+,由132224y x y x ⎧=+⎪⎨⎪=-+⎩,解得12x y =⎧⎨=⎩, (1H ∴,20,AH KH =,(2,0)K ∴.PB PA PB PK KB ∴-=-,∴当点P 在BK 的延长线上时,P B P K BK '-'=的值最大,最大值为624-=,故选:C .【备注】本题考查一次函数图象上的点的特征、轴对称等知识,解题的关键是学会利用对称解决最值问题 属于中考常考题型.【题型知识点总结】一次函数最短路径问题注意事项:1. 根据“和小异,差大同”判断是否需要作对称;2. 作对称时注意要选取动点运动的直线为对称轴作某一定点的对称点。
初中几何中线段和差的最大值与最小值典型分析(最全)

初中几何中线段和差的最大值与最小值典型分析(最全)-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN初中几何中线段和(差)的最值问题一、两条线段和的最小值。
基本图形解析:(对称轴为:动点所在的直线上)一)、已知两个定点:1、在一条直线m 上,求一点P ,使PA+PB 最小; (1)点A 、B 在直线m 两侧:(2)点A 、B 在直线同侧:A 、A ’ 是关于直线m 的对称点。
2、在直线m 、n 上分别找两点P 、Q ,使PA+PQ+QB 最小。
(1)两个点都在直线外侧:(2)一个点在内侧,一个点在外侧: (3)两个点都在内侧:mm A Bm B mA Bmnmnnmn(4)、台球两次碰壁模型变式一:已知点A 、B 位于直线m,n 的内侧,在直线n 、m 分别上求点D 、E 点,使得围成的四边形ADEB 周长最短.填空:最短周长=________________变式二:已知点A 位于直线m,n 的内侧, 在直线m 、n 分别上求点P 、Q 点PA+PQ+QA 周长最短.二)、一个动点,一个定点: (一)动点在直线上运动:n点B 在直线n 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、两点在直线两侧:2、两点在直线同侧:(二)动点在圆上运动点B 在⊙O 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B )1、点与圆在直线两侧:2、点与圆在直线同侧:m nmnmnmmm三)、已知A 、B 是两个定点,P 、Q 是直线m 上的两个动点,P 在Q 的左侧,且PQ 间长度恒定,在直线m 上要求P 、Q 两点,使得PA+PQ+QB 的值最小。
(原理用平移知识解)(1)点A 、B 在直线m 两侧:过A 点作AC ∥m,且AC 长等于PQ 长,连接BC,交直线m 于Q,Q 向左平移PQ 长,即为P 点,此时P 、Q 即为所求的点。
线段和差最值问题-经典模型

For personal use only in study and research; not for commercial use线段和(差)的最值问题此类问题特点:1.两个定点,一个定点;2. 线段和最小值,线段差最大值一、线段和最小值问题若在一条直线m上,求一点P,使PA+PB最小;(1)两侧/异侧型:定点A、B在直线m(动点P所在直线)两侧:直接连接A、B两点交直线m于一点P,该点P即为所求点。
(PA+PB=AB)(2)同侧型:定点A、B在动点P所在直线m同侧:(方法:一找二作三连):一找:找定点A、B,动点P及动点所在的直线m;二作:任选一个定点做对称;三连:连接对称点与另一个定点,其连线交动点所在直线于一点P,该点P即为所求。
(PA+PB=PA’+PB=A’B)二、线段差最大值问题若在一条直线m上,求一点P,使得最大(1)同侧型:定点A、B在直线m(动点P所在直线)两侧:直接连接A、B两点交直线m于一点P,该点P即为所求点。
()(2)两侧/异侧型:定点A、B在直线m(动点P所在直线)两侧:任选一个定点做对称;三连:连接对称点与另一个定点,其连线交动点所在直线m于一点P,该点P即为所求点。
()线段和最小值练习题1.如图1,在锐角三角形ABC中,AB=,∠BAC=45°,∠BAC的平分线交BC于点D,M,N分别是AD和AB上的动点,则BM+MN的最小值为?????????????.2. 如图2所示,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC边上一点.若AE=2,EM+CM的最小值为?????????.3.如图3,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AD=4,AB=5,BC=6,点P是AB上一个动点,当PC+PD的和最小时,PB的长为__________.图1 图2 图3 图44. 如图4,菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值为????????????.5. 如图5,圆柱形玻璃杯,高为12cm,底面周长为18cm,在杯内离杯底3cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为________cm.6.已知正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.则PB +PE的最小值是7. 如图6,已知正方形ABCD的边长为8,点M在DC上,且DM=2,N是AC上的一个动点,则DN+MN的最小值为?????????? ?.8.如图7,在边长为2cm的正方形ABCD中,点Q为BC边的中点,点P为对角线AC上一动点,连接PB、PQ,则△PBQ 周长的最小值为????????????????????cm.(结果不取近似值)图5 图6 图79. 如图8,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,则PA+PC的最小值是.10. 如图9,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,B为AN弧的中点,P是直径MN上一动点,则PA+PB的最小值为______.如图8 如图9解答题1.如图,一元二次方程x2+2x-3=0的二根x1,x2(x1<x2)是抛物线y=ax2+bx+c与x轴的两个交点B,C 的横坐标,且此抛物线过点A(3,6).(1)求此二次函数的解析式;(2)设此抛物线的顶点为P,对称轴与AC相交于点Q,求点P和点Q的坐标;(3)在x轴上有一动点M,当MQ+MA取得最小值时,求M点的坐标.?2.如图,在平面直角坐标系中,点A的坐标为(1,),△AOB的面积是.(1)求点B的坐标;(2)求过点A、O、B的抛物线的解析式;(3)在(2)中抛物线的对称轴上是否存在点C,使△AOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由;?3. 如图,在平面直角坐标系中,矩形的顶点O在坐标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点.(1)若E为边OA上的一个动点,当△CDE的周长最小时,求点E的坐标;(2)若E、F为边OA上的两个动点,且EF=2,当四边形CDEF的周长最小时,求点E、F的坐标.4. 如图,已知直线y=x+1与y轴交于点A,与x轴交于点D,抛物线y=x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).(1)求该抛物线的解析式;(2)在抛物线的对称轴上找一点M,使|AM-MC|的值最大,求出点M的坐标.5.抛物线的解析式为,交x轴与A与B,交y轴于C。
初中几何中线段和差的最大值与最小值典型分析(最全)

初中几何中线段和(差)的最值问题一、两条线段和的最小值。
基本图形解析:(对称轴为:动点所在的直线上)一)、已知两个定点:1、在一条直线m 上,求一点P ,使PA+PB 最小; (1)点A 、B 在直线m 两侧:(2)点A 、B 在直线同侧:A 、A ’ 是关于直线m 的对称点。
2、在直线m 、n 上分别找两点P 、Q ,使PA+PQ+QB 最小。
(1)两个点都在直线外侧:(2)一个点在内侧,一个点在外侧:m m mmABmn m nnmn(3)两个点都在内侧:(4)、台球两次碰壁模型变式一:已知点A 、B 位于直线m,n 的内侧,在直线n 、m 分别上求点D 、E 点,使得围成的四边形ADEB 周长最短.填空:最短周长=________________变式二:已知点A 位于直线m,n 的内侧, 在直线m 、n 分别上求点P 、Q 点PA+PQ+QA 周长最短.二)、一个动点,一个定点: (一)动点在直线上运动:点B 在直线n 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、两点在直线两侧:nnm Bnn2、两点在直线同侧:(二)动点在圆上运动点B 在⊙O 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、点与圆在直线两侧:2、点与圆在直线同侧:三)、已知A 、B 是两个定点,P 、Q 是直线m 上的两个动点,P 在Q 的左侧,且PQ 间长度恒定,在直线m 上要求P 、Q 两点,使得PA+PQ+QB 的值最小。
(原理用平移知识解) (1)点A 、B 在直线m 两侧:mnmmmmm过A 点作AC ∥m,且AC 长等于PQ 长,连接BC,交直线m 于Q,Q 向左平移PQ 长,即为P 点,此时P 、Q 即为所求的点。
(2)点A 、B 在直线m 同侧: 练习题1.如图,∠AOB =45°,P 是∠AOB 内一点,PO =10,Q 、R 分别是OA 、OB 上的动点,求△PQR 周长的最小值为 .2、 如图1,在锐角三角形ABC 中,AB=4,∠BAC=45°,∠BAC 的平分线交BC 于点D ,M,N 分别是AD 和AB 上的动点,则BM+MN 的最小值为 . 3、如图,在锐角三角形ABC 中 ,AB=52,∠BAC=45,BAC 的平分线交BC 于D ,M 、N 分别是AD 和AB 上的动点,则BM+MN 的最小值是多少mABB'EQ PmABQPQ4、如图4所示,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC边上一点.若AE=2,EM+CM的最小值为.5、如图3,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AD=4,AB=5,BC=6,点P是AB 上一个动点,当PC+PD的和最小时,PB的长为__________.6、如图4,等腰梯形ABCD中,AB=AD=CD=1,∠ABC=60°,P是上底,下底中点EF直线上的一点,则PA+PB的最小值为.7、如图5菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值为.8、如图,菱形ABCD的两条对角线分别长6和8,点P是对角线AC上的一个动点,点M、N分别是边AB、BC的中点,则PM+PN的最小值是9、如图,圆柱形玻璃杯,高为12cm,底面周长为18cm,在杯内离杯底3cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为________cm.10、如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为11、如图,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.则PB+PE的最小值是12、如图6所示,已知正方形ABCD的边长为8,点M在DC上,且DM=2,N是AC上的一个动点,则DN+MN的最小值为.13、如图,正方形ABCD的边长是2,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值为.14、如图7,在边长为2cm的正方形ABCD中,点Q为BC边的中点,点P为对角线AC上一动点,连接PB、PQ,则△PBQ周长的最小值为cm.(结果不取近似值).15、如图,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,则PA+PC的最小值是.16、如图8,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,B为AN弧的中点,P是直径MN上一动点,则PA+PB的最小值为( )(A)2 (B) (C)1 (D)2解答题1、如图9,正比例函数y=x的图象与反比例函数y=(k≠0)在第一象限的图象交于A 点,过A点作x轴的垂线,垂足为M,已知三角形OAM的面积为1.(1)求反比例函数的解析式;(2)如果B为反比例函数在第一象限图象上的点(点B与点A不重合),且B点的横坐标为1,在x轴上求一点P,使PA+PB最小.2、如图,一元二次方程x2+2x-3=0的二根x1,x2(x1<x2)是抛物线y=ax2+bx+c 与x轴的两个交点B,C的横坐标,且此抛物线过点A(3,6).(1)求此二次函数的解析式;(2)设此抛物线的顶点为P,对称轴与AC相交于点Q,求点P和点Q的坐标;(3)在x轴上有一动点M,当MQ+MA取得最小值时,求M点的坐标.3、如图10,在平面直角坐标系中,点A的坐标为(1,),△AOB的面积是.(1)求点B的坐标;(2)求过点A、O、B的抛物线的解析式;(3)在(2)中抛物线的对称轴上是否存在点C,使△AOC的周长最小若存在,求出点C的坐标;若不存在,请说明理由;4.如图,抛物线y =35x 2-185x +3和y 轴的交点为A ,M 为OA 的中点,若有一动点P ,自M点处出发,沿直线运动到x 轴上的某点(设为点E ),再沿直线运动到该抛物线对称轴上的某点(设为点F ),最后又沿直线运动到点A ,求使点P 运动的总路程最短的点E ,点F 的坐标,并求出这个最短路程的长.5.如图,已知在平面直角坐标系xOy 中,直角梯形OABC 的边OA 在y 轴的正半轴上,OC 在x 轴的正半轴上,OA =AB =2,OC =3,过点B 作BD ⊥BC ,交OA 于点D .将∠DBC 绕点B 按顺时针方向旋转,角的两边分别交y 轴的正半轴、x 轴的正半轴于点E 和F . (1)求经过A 、B 、C 三点的抛物线的解析式; (2)当BE 经过(1)中抛物线的顶点时,求CF 的长;(3)在抛物线的对称轴上取两点P 、Q (点Q 在点P 的上方),且PQ =1,要使四边形BCPQ 的周长最小,求出P 、Q 两点的坐标.6.如图,已知平面直角坐标系,A,B两点的坐标分别为A(2,-3),B(4,-1)若C(a,0),D(a+3,0)是x轴上的两个动点,则当a为何值时,四边形ABDC的周长最短.7、如图11,在平面直角坐标系中,矩形的顶点O在坐标原点,顶点A、B分别在x 轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点.(1)若E为边OA上的一个动点,当△CDE的周长最小时,求点E的坐标;(2)若E、F为边OA上的两个动点,且EF=2,当四边形CDEF的周长最小时,求点E、F的坐标.v1.0 可编辑可修改二、求两线段差的最大值问题 (运用三角形两边之差小于第三边) 基本图形解析:1、在一条直线m 上,求一点P ,使PA 与PB 的差最大; (1)点A 、B 在直线m 同侧:解析:延长AB 交直线m 于点P ,根据三角形两边之差小于第三边,P ’A —P ’B <AB ,而PA —PB=AB 此时最大,因此点P 为所求的点。
中考数学 考点系统复习 第七章 作图与图形变换 微专题(七) 利用“两点之间线段最短”求最值

模型三:“两点两线”型(两个动点+两个定点) (一)利用垂直平分线的性质求四边形周长最小值 【模型分析】 点 P,Q 是∠AOB 内部的两定点,在 OA 上找点 M,在 OB 上找点 N,使得四 边形 PQNM 周长最小. 思路点拨:
8.★如图,在矩形 ABCD 中,AB=4,AD=6,AE=4,AF=2,点 G,H 分 别是边 BC,CD 上的动点,则四边形 EFGH 周长的最小值为 22 5+10+10.
【模型演变】 两定点 A,B 位于直线 l 异侧,在直线 l 上找一点 P,使得|PA-PB|值最 大. 思路点拨:将两定点异侧转化为同侧问题,同“基础模型”即可解决, 作点 B 关于直线 l 的对称点 B′,连接 AB′并延长,与直线 l 交于点 P, 点 P 即为所求.
5.★如图,在正方形 ABCD 中,AB=6,点 F 是对角线 BD 上靠近点 B 的
2.★如图,在△ABC 中,AB=AC,AB 的垂直平分线交 AB 于点 N,交 AC 于点 M,P 是直线 MN 上一动点,H 为 BC 的中点,若 AB=13,△ABC 的周 长是 36.则 PB+PH 的最小值为 112 2.
3.★如图,在矩形 ABCD 中,AB=6,AD=3,点 P 为矩形 ABCD 内一点,
【模型演变】 两定点 A,B 位于直线 l 同侧,在直线 l 上找一点 P,使得 PA+PB 值最小. 思路点拨:将两定点同侧转化为异侧问题,同“基础模型”即可解决, 作点 B 关于直线 l 的对称点 B′,连接 AB′,与直线 l 交于点 P,点 P 即 为所求.
1.如图,等边三角形 AD 边 上的动点,E 是 AB 边上一点,且 AE=2,则线段 EF+CF 的最小值为 22 3 .
1 且动点 P 满足 S△PAB=3S 矩形 ABCD,则点 P 到 A,B 两点距离之和的最小值为 22 13 .
2024成都中考数学二轮复习微专题 利用两点之间线段最短解决最值问题(含答案)

2024成都中考数学二轮复习微专题利用两点之间线段最短解决最值问题模型一“一线两点”型(一个动点+两个定点)类型一线段和最小值问题模型分析问题:两定点A、B位于直线l异侧,在直线l上找一点P,使PA+PB的值最小.解题思路:根据两点之间线段最短,PA+PB的最小值即为线段AB的长.连接AB交直线l 于点P,点P即为所求.模型演变问题:两定点A、B位于直线l同侧,在直线l上找一点P,使PA+PB的值最小.解题思路:将两定点同侧转化为异侧问题,同“模型分析”即可解决.作点B关于l的对称点B′,连接AB′,与直线l交于点P.注:也可以作点A关于直线l的对称点A′,连接A′B,与直线l交于点P′.模型应用1.如图,四边形ABCD是菱形,对角线AC、BD相交于点O,AC=63,BD=6,点P是AC上一动点,点E是AB的中点,则PD+PE的最小值为________.第1题图S矩形ABCD,2.如图,在矩形ABCD中,AB=5,AD=3,点P是矩形内一动点,满足S△P AB=13则PA+PB的最小值为________.第2题图模型迁移3.如图,一次函数y=kx+b的图象与反比例函数y=mx的图象相交于A(3,5)、B(a,-3)两点,与x轴交于点C.第3题图(1)求反比例函数和一次函数的表达式;(2)若点P为y轴上的动点,当PB+PC取最小值时,求△BPC的面积.4.如图,已知抛物线y=-x2-2x+3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.点P是该抛物线对称轴l上的一个动点,求△PBC周长的最小值.第4题图类型二线段差最大值问题模型分析问题:两定点A、B位于直线l同侧,在直线l上找一点P,使得|PA-PB|的值最大.解题思路:根据两边之差小于第三边,|PA-PB|最大值即AB的长,连接AB并延长,与直线l交于点P,点P即为所求.模型演变问题:两定点A、B位于直线l异侧,在直线l上找一点P,使得|PA-PB|的值最大.解题思路:将两定点异侧转化为同侧问题,同“模型分析”即可解决.作点B关于l的对称点B′,连接AB′并延长与直线l交于点P.模型应用5.如图,在△ABC中,AB=3,AC=4,BC=5,EF是BC的垂直平分线,点P是EF上的动点,则|PA-PB|的最大值为________.第5题图6.如图,在等边△ABC中,AB=4,AD是中线,点E是AD的中点,点P是AC上一动点,则BP-EP的最大值为________.第6题图7.如图,在正方形ABCD中,AB=8,AC与BD交于点O,N是AO的中点,点M在BC 边上,且BM=6,P为对角线BD上一动点,则PM-PN的最大值为________.第7题图模型迁移8.已知抛物线y=x2-2x-8与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,P 是抛物线对称轴上的一个动点,当|PB-PC|有最大值时,求点P的坐标.模型二“一点两线”型(两个动点+一个定点)类型一两条线段的和最小值问题模型分析问题:点P是∠AOB的边OB上一定点,在OA上找一点M,在OB上找一点N,使得PM +MN的值最小.解题思路:要使PM+MN的值最小,设法将PM、MN转化到同一条直线上,利用垂线段最短即可解决.作点P关于OA的对称点P′,过点P′作OB的垂线,分别与OA,OB交于点M、N.模型应用9.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是∠BAC的平分线.若P,Q 分别是AD,AC上的动点,则PC+PQ的最小值为________.第9题图10.如图,在菱形ABCD中,AB=6,∠A=120°,点M,N分别为BD,CD上的动点,则CM+MN的最小值为________.第10题图类型二周长最小值问题模型分析问题:点P是∠AOB的内部一定点,在OA上找一点M,在OB上找一点N,使得△PMN 的周长最小.解题思路:要使△PMN的周长最小,即PM+MN+PN的值最小,根据两点之间线段最短,将三条线段转化到同一直线上即可解决.分别作点P关于OA、OB的对称点P′、P″,连接P′P″交OA、OB于点M、N.模型应用11.如图,在△ABC中,AB=AC,∠BAC=90°,点D为AB上一定点,点E,F分别为边AC,BC上的动点,当△DEF的周长最小时,则∠FDE=________.第11题图12.如图,在Rt△ABC中,∠C=90°,∠B=60°,点D在BC上,且AD=4,点E,F分别为边AC,AB上的动点,则△DEF周长的最小值为________.第12题图模型三“一定长+两定点”型类型一异侧线段和最小值问题(“造桥”问题)模型分析问题:已知l1∥l2,l1,l2之间距离为d,在l1,l2上分别找M,N两点,使得MN⊥l1,且AM +MN+NB的值最小.解题思路:要求AM+MN+NB的最小值,MN为定值,即要求AM+NB的最小值,通过平移构造平行四边形,将AM、NB转化到同一条直线上.将点A向下平移d个单位到点A′,连接A′B交直线l2于点N,过点N作MN⊥l1于点M.模型应用13.如图,已知直线a∥b,a,b之间的距离为4,点P到直线a的距离为4,点Q到直线b的距离为2,PQ=241.在直线a上有一动点A,直线b上有一动点B,满足AB⊥b,且PA +AB+BQ最小,则PA+BQ=________.第13题图类型二同侧线段和最小值问题(平移型问题)模型应用14.如图,菱形ABCD的边长为3,∠BAD=60°,点E,F在对角线AC上(点E在点F的左侧),且EF=1,则DE+BF的最小值为________.第14题图15.如图,四边形ABCD是平行四边形,AB=4,BC=12,∠ABC=60°,点E、F是AD边上的动点,且EF=2,则四边形BEFC周长的最小值为________.第15题图模型迁移16.如图,已知点A(3,1),B(1,0),PQ是直线y=x上的一条动线段,且PQ=2(点Q在点P的下方),当AP+PQ+QB取得最小值时,求点Q的坐标.第16题图参考答案1.33【解析】如解图,连接DE ,则PD +PE ≥DE ,设DE 交AC 于点M ,当点P 与点M 重合时PD +PE 取得最小值,且最小值为DE .∵在菱形ABCD 中,AC =63,BD =6,∴AO =33,OD =3,AC ⊥BD ,∴AD =OA 2+OD 2=6,∴AD =BD =AB ,∴∠BAD =60°,∵点E 为AB 的中点,∴DE ⊥AB ,∴DE =AD ·sin60°=3 3.第1题解图2.41【解析】如解图,设△PAB 底边AB 上的高为h ,∵S △P AB =13S 矩形ABCD ,∴12AB ·h =13AB ·AD ,∴h =2,即h 为定值,在AD 上截取AE =2,作EF ∥AB ,交CB 于点F ,故点P 在直线EF 上运动,作点A 关于直线EF 的对称点A ′,连接A ′B ,交直线EF 于点P ,此时PA +PB 最小,即为A ′B 的长.由对称得AA ′=2AE =4,∴A ′B =AA ′2+AB 2=42+52=41,即PA +PB 的最小值为41.第2题解图3.解:(1)把点A (3,5)代入y =m x可得m =3×5=15,∴反比例函数的表达式为y =15x,把点B (a ,-3)代入y =15x,可得a =-5,∴B (-5,-3).把点A (3,5),B (-5,-3)代入y =kx +b k +b =55k +b =-3=1=2,∴一次函数的表达式为y =x +2;(2)∵一次函数的表达式为y =x +2,令y =0,则x =-2,∴C (-2,0),如解图,作点C 关于y 轴的对称点C ′,则C ′(2,0),即CC ′=4,连接BC ′交y 轴于点P ,此时PC +PB 有最小值,最小值为BC ′,设直线BC ′的表达式为y =k ′x +b ′,5k ′+b ′=-3k ′+b ′=0,′=37′=-67,则BC ′的表达式为y =37x -67,∴P (0,-67),即OP =67,此时S △BPC =S △BCC ′-S △PCC ′=12×4×3-12×4×67=307.第3题解图4.解:当y =0时,-x 2-2x +3=0,解得x 1=-3,x 2=1,∴点A 坐标为(-3,0),点B 坐标为(1,0).当x =0时,y =3,∴点C 坐标为(0,3).∵△PBC 的周长为PB +PC +BC ,BC 为定值,∴当PB +PC 最小时,△PBC 的周长最小.∵点A ,点B 关于抛物线的对称轴l 对称,∴连接AC ,交l 于点P ,点P 即为所求的点.∵AP =BP ,∴PB +PC +BC =AC +BC .∵A (-3,0),B (1,0),C (0,3),∴AC =32,BC =10,∴△PBC 周长的最小值为32+10.5.3【解析】如解图,延长BA 交EF 于P ′,当点P 位于P ′处时|PA -PB |的值最大,∴|PA -PB |的最大值为AB =3.第5题解图6.7【解析】如解图,连接BE 并延长交AC 于点P ′,此时BP -EP 取得最大值为BE ,在等边△ABC 中,AD 是中线,∴BD =DC =2,∴AD =BD ·tan60°=2×3=23,∵E 为AD的中点,∴DE =12AD =3.∴在Rt △BDE 中,BE =BD 2+DE 2=22+(3)2=7,∴BP -EP 的最大值为7.第6题解图7.2【解析】如解图,以BD 为对称轴作点N 的对称点N ′,连接MN ′并延长交BD 于点P ,连接NP ,根据轴对称性质可知PN =PN ′,∴PM -PN =PM -PN ′≤MN ′,当P ,M ,N ′三点共线时,PM -PN 取得最大值,最大值为MN ′的长,∵正方形的边长为8,∴AC =2AB =82,∵O 为AC 中点,∴AO =OC =42,∵N 为OA 中点,∴ON =22,∴ON ′=CN ′=22,∴AN ′=62,∵BM =6,∴CM =AB -BM =8-6=2,∴CM BM =CN ′AN ′=13,∵∠MCN ′=∠BCA ,∴△CMN ′∽△CBA ,∴∠CMN ′=∠CBA =90°,∵∠N ′CM =45°,∴△N ′CM 为等腰直角三角形,∴MN ′=CM =2,即PM -PN 的最大值为2.第7题解图8.解:如解图,连接PA ,则PA =PB ,当x =0时,y =x 2-2x -8=-8,则C (0,-8),当y =0时,x 2-2x -8=0,解得x 1=-2,x 2=4,则A (-2,0),B (4,0),∴抛物线的对称轴为直线x =1,∴|PB -PC |=|PA -PC |≤AC (当点A 、C 、P 共线时取等号),延长AC 交直线x =1于点P ′,设直线AC 的解析式为y =mx +n (m ≠0),把A (-2,0),C (0,-8)代入得2m +n =0=-8=-4=-8,∴直线AC 的解析式为y =-4x -8,当x =1时,y =-4-8=-12,即P ′(1,-12),∴当|PB -PC |有最大值时,点P 的坐标为(1,-12).第8题解图9.245【解析】如解图,过点C作CM⊥AB交AB于点M,交AD于点P,过点P作PQ⊥AC 于点Q,∵AD是∠BAC的平分线.∴PQ=PM,∴PC+PQ=PC+PM=CM,根据垂线段最短可知,此时PC+PQ有最小值,即为CM,∵AC=6,BC=8,∠ACB=90°,∴AB=AC2+BC2=62+82=10,∵S△ABC=12AB·CM=12AC·BC,∴CM=AC·BCAB=6×810=245.第9题解图10.33【解析】如解图,过点A作CD的垂线,垂足为N,与DB的交点记为M,∵四边形ABCD为菱形,∴点A与点C关于对角线BD对称,∴AM=CM,∴CM+MN=AM+MN =AN,根据垂线段最短可知,此时CM+MN有最小值,最小值为AN.∵AB=6,∠A=120°,∴∠ADC=60°,AD=6,∴AN=AD·sin60°=33,∴CM+MN的最小值为3 3.第10题解图11.90°【解析】如解图,作D关于AC的对称点D′,关于BC的对称点D″,连接D′D″交AC于点E,交BC于点F,此时,△DEF的周长最小,最小为D′D″,∵AB=AC,∠BAC =90°,∴∠B=45°,DD′⊥AC,DD″⊥BC,∴∠BDD′=45°,∴∠D′DD″=135°,∴∠D′+∠D″=45°,∵ED′=ED,DF=D″F,∴∠D′=∠D′DE,∠D″=∠D″DF,∴∠D″DF+∠D′DE=45°,∴∠FDE=90°.第11题解图12.4【解析】如解图,作点D关于直线AC的对称点D′,点D关于直线AB的对称点D″,连接D′D″交AC于点E,交AB于点F,此时△DEF的周长最小,最小值为D′D″的长,连接AD′、AD″,在Rt△ABC中,∵∠C=90°,∠B=60°,∴∠BAC=30°,∵∠DAB=∠D″AB,∠DAC=∠D′AC,∴∠D′AD″=2∠BAC=60°,∵AD′=AD,AD″=AD,∴AD′=AD″,∴△AD′D″是等边三角形,∴D′D″=AD′=AD=4,∴△DEF的周长的最小值为4.第12题解图13.10【解析】如解图,过点P作PF⊥b交a于点E,交b于点F,在PF上截取PC=4,连接QC交b于点B,过点B作BA⊥a于点A,此时PA+AB+BQ最短.过点Q作QD⊥PF 于点D.在Rt△PQD中,∵∠D=90°,PQ=241,PD=10,∴DQ=PQ2-PD2=8,CD =PD-PC=6,∵AB=PC=4,AB∥PC,∴四边形ABCP是平行四边形,∴PA=BC,∴PA +BQ=CB+BQ=QC=DQ2+CD2=10.第13题解图14.10【解析】如解图,作DM∥AC,使得DM=EF=1,连接BM交AC于点F,连接BD,∵DM∥AC,∴∠BDM=90°,∵DM=EF,DM∥EF,∴四边形DEFM是平行四边形,∴DE=FM,∴DE+BF=FM+FB=BM,根据两点之间线段最短可知,此时DE+FB最短,∵四边形ABCD是菱形,AB=3,∠BAD=60°,∴△ABD是等边三角形,∴BD=AB=3,在Rt△BDM中,BM=12+32=10,∴DE+BF的最小值为10.第14题解图15.14+237【解析】如解图,将点B沿BC向右平移2个单位长度得到点B′,作点B′关于AD的对称点B″,连接CB″,交AD于点F,在AD上截取EF=2,连接B′F,四边形EBB′F为平行四边形,则BE=B′F,B″F=B′F,此时四边形BEFC的周长为BE+EF+FC+BC=B″F+EF+FC+BC=B″C+EF+BC,当点C、F、B″三点共线时,四边形BEFC的周长最小.∵AB=4,BB′=2,∠ABC=60°,∴B′B″经过点A.∴AB′=2 3.∴B′B″=4 3.∵BC=12,∴B ′C =10.∴B ″C =B ′B ″2+B ′C 2=237.∴B ″C +EF +BC =14+237.∴四边形BEFC 周长的最小值为14+237.第15题解图16.解:如解图,过点A 作直线MN ∥直线y =x ,将点A (3,1)沿MN 向下平移2个单位后得到A ′(2,0),作点B (1,0)关于直线y =x 的对称点B ′(0,1),连接A ′B ′交直线y =x 于点Q .∵AA ′=PQ =2,AA ′∥PQ ,∴四边形APQA ′是平行四边形,∴AP =A ′Q .∴AP +PQ +QB =A ′Q +PQ +B ′Q ,且PQ =2,∴当A ′Q +B ′Q 值最小时,AP +PQ +QB 值最小,根据两点之间线段最短,即A ′,Q ,B ′三点共线时A ′Q +B ′Q 值最小.∵B ′(0,1),A ′(2,0),∴直线A ′B ′的解析式y =-12x +1,=x=-12x +1,=23=23,∴点Q 的坐标为(23,23).第16题解图。
线段差的最大值的原理

线段差的最大值的原理线段差的最大值是指在一组给定的线段中,找出两条线段之间长度的差值的最大值。
这个问题在数学和计算几何中经常出现,对于解决实际问题具有重要意义。
在本文中,我们将介绍线段差的最大值的原理以及如何通过数学方法进行求解。
首先,我们来看一下线段差的最大值的定义。
给定一组线段,每个线段都有一个长度,我们需要找出其中两条线段之间长度的差值的最大值。
换句话说,我们需要找到两个线段的长度之差的最大值。
为了更直观地理解这个问题,我们可以通过一个简单的例子来说明。
假设我们有一组线段,它们的长度分别为3、5、7、9、11。
我们需要找出其中两条线段之间长度的差值的最大值。
在这个例子中,最大的差值显然是11-3=8,因此线段差的最大值为8。
接下来,我们将介绍线段差的最大值的原理。
假设我们有n条线段,它们的长度分别为L1、L2、L3、...、Ln。
我们需要找出其中两条线段之间长度的差值的最大值。
为了求解这个问题,我们可以采用以下方法:1. 首先,我们可以对给定的线段进行排序,从小到大排列。
这样可以方便我们找出最大值和最小值。
2. 然后,我们可以遍历所有的线段对,计算它们之间的长度差值,并找出其中的最大值。
3. 最后,我们得到的最大值就是线段差的最大值。
通过上述方法,我们可以比较容易地求解线段差的最大值。
当然,在实际问题中,我们可能会遇到更复杂的情况,例如线段不是按照长度排序的,或者线段的数量非常大。
针对这些情况,我们可以采用更高效的算法来求解线段差的最大值,例如动态规划算法或者贪心算法。
总之,线段差的最大值是一个重要的数学问题,它在实际问题中具有广泛的应用。
通过本文的介绍,我们了解了线段差的最大值的原理以及求解方法,希望能对读者有所帮助。
在实际问题中,我们可以根据具体情况选择合适的算法来求解线段差的最大值,从而更好地解决实际问题。
初中几何中线段和差的最大值与最小值模型解析学习资料
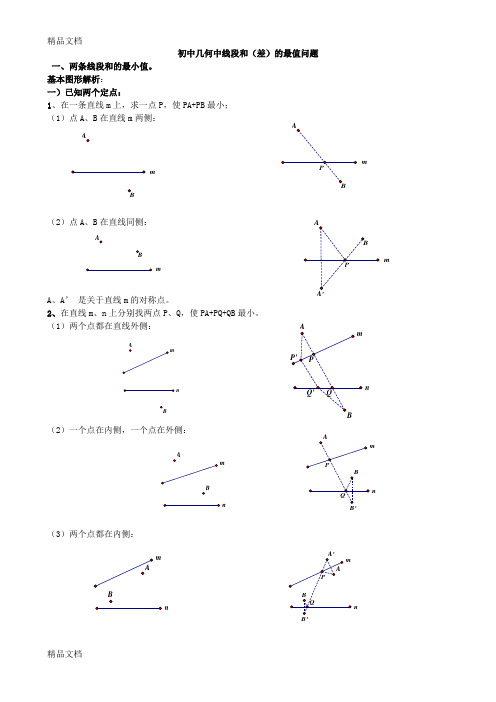
精品文档初中几何中线段和(差)的最值问题一、两条线段和的最小值。
基本图形解析:一)已知两个定点:1、在一条直线m 上,求一点P ,使PA+PB 最小; (1)点A 、B 在直线m 两侧:(2)点A 、B 在直线同侧:A 、A ’ 是关于直线m 的对称点。
2、在直线m 、n 上分别找两点P 、Q ,使PA+PQ+QB 最小。
(1)两个点都在直线外侧:(2)一个点在内侧,一个点在外侧:(3)两个点都在内侧:mmB mA Bmn mnnmnnnm(4)台球两次碰壁模型变式一:已知点A、B位于直线m,n 的内侧,在直线n、m分别上求点D、E点,使得围成的四边形ADEB周长最短.填空:最短周长=________________变式二:已知点A位于直线m,n 的内侧, 在直线m、n分别上求点P、Q点PA+PQ+QA周长最短.二)一个动点,一个定点:(一)动点在直线上运动:点B在直线n上运动,在直线m上找一点P,使PA+PB最小(在图中画出点P和点B)1、两点在直线两侧:2、两点在直线同侧:(二)动点在圆上运动点B在⊙O上运动,在直线m上找一点P,使PA+PB最小(在图中画出点P和点B)1、点与圆在直线两侧:mnmnmnmm m精品文档2、点与圆在直线同侧:(三)已知A 、B 是两个定点,P 、Q 是直线m 上的两个动点,P 在Q 的左侧,且PQ 间长度恒定,在直线m 上要求P 、Q 两点,使得PA+PQ+QB 的值最小。
(原理用平移知识解) (1)点A 、B 在直线m 两侧:过A 点作AC ∥m,且AC 长等于PQ 长,连接BC,交直线m 于Q,Q 向左平移PQ 长,即为P 点,此时P 、Q 即为所求的点。
(2)点A 、B 在直线m 同侧:二、求两线段差的最大值问题 (运用三角形两边之差小于第三边) 基本图形解析:1、在一条直线m 上,求一点P ,使PA 与PB 的差最大;(1)点A 、B 在直线m 同侧:解析:延长AB 交直线m 于点P ,根据三角形两边之差小于第三边,P ’A —P ’B <AB ,而PA —PB=AB 此时最大,因此点P 为所求的点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
线段差的最大值与线段和的最小值问题
有关线段差的最大值与线段和的最小值问题的主要应用原理是:1、两点这间线段最短。
2、三角形的任意两边之和大于第三边(找和的最小值)。
3、三角形的任意两边之差小于第三边(找差的最大值)。
作图找点的关键:充分利用轴对称,找出对称点,然后,使三点在一条直线上。
即利用线段的垂直平分线定理可以把两条线段、三条线段、四条线段搬在同一条直线上。
证明此类问题,可任意另找一点,利用以上原理来证明。
一两条线段差的最大值:
(1)两点同侧:如图,点P在直线L上运动,画出一点P,使︱PA-PB︱取最大值。
作法:连结AB并延长AB交直线L于点P。
点P即为所求。
︱PA-PB︱=AB
证明:在直线L上任意取一点P。
,连结PA、PB,︱PA-PB︱<AB
p'
(2两点异侧:如图,如图,点P在直线L上运动,画出一点P,使︱PA-PB︱取最大值。
作法:1、作B关于直线L的对称点B。
B
2、连结AB并延长AB交直线L于点P。
点P即为所求。
︱PA-PB︱=AB
证明:在直线L上任意取一点P。
,连结PA、PB、PB。
︱PA-PB︱=︱PA-PB︱<AB
(三角形任意两边之差小于第三边)
二、两条线段和的最小值问题:
(1))两点同侧:如图,点P在直线L上运动,画出一点P使P A+PB取最小值。
(三角形的任意两边之和大于第三边(找和的最小值),P A+PB=AB
(2)两点异侧:如图,点P在直线L上运动,画出一点P使P A+PB取最小值。
(两点之间线段最短)
三、中考考点:
08年林金钟老师的最后一题:如图,在矩形ABCO中,B(3,2),E(3,1),F(1,2)在X轴与Y轴上是否分别存在点M、N,使得四边形EFNM的周长最小?若存在,请求出周长的最小值,若不存在,请说明理由。
提示:EF长不变。
即求F N+NM+MF的最小值。
利用E关于X轴的对称点E,F的对称点F,把这三条线段搬到同一条直线上。
一、以正方形为载体,求线段和的最小值
例1. 如图1,四边形ABCD 是正方形,边长是4,E 是BC 上一点,且CE =1,P 是对角线BD 上任一点,则PE +PC 的最小值是_____________。
例2. 如图2,正方形ABCD 的边长为8,点E 、F 分别在AB 、BC 上,AE =3,CF =1,P 是对角线AC 上的一个动点,则PE +PF 的最小值是( )
C
N
二、以菱形为载体,求线段和的最小值
例3. (05,南充)如图3,点P是边长为1的菱形ABCD对角线AC上一个动点,M、N分别是AB,BC边上的中点,PM+PN的最小值是()
三、以等腰梯形为载体,求线段和的最小值
例4.(05,河南)如图4,在梯形ABCD中,AD∥BC,AB=CD=AD=1,∠B=60°,直线MN为梯形ABCD的对称轴,P为MN上一点,那么PC+PD的最小值为_____________。
