您的位置：360文档中心› Matlab中竖曲线计算程序

Matlab中竖曲线计算程序

合集下载

竖曲线运算步骤及公式讲解

竖曲线运算步骤及公式讲解

1 / 2
竖曲线上高程计算
已知：①第一坡度：i 1(上坡为“＋”，下坡为“－”)
②第二坡度：i 2(上坡为“＋”，下坡为“－”)
③变坡点桩号：S Z
④变坡点高程：H Z
⑤竖曲线的切线长度：T
⑥待求点桩号：S
计算过程：
1、切线上任意点与竖曲线间的竖距h 通过推导可得：
==PQ h )()(2112li y l x R y y A A q p ---=-R
l 22= 2、竖曲线曲线长： L = R ω
3.竖曲线切线长： T= T A =T B ≈ L/2 =
2
ωR 4、竖曲线的外距： E =R T 22
5. 竖曲线上任意点至相应切线的距离：R
x y 22
= 式中：x —为竖曲任意点至竖曲线起点（终点）的距离, m ；
R —为竖曲线的半径，m 。

竖曲线计算的目的是确定设计纵坡上指定桩号的路基设计标高，其计算步骤
如下：
（1）计算竖曲线的基本要素：竖曲线长：L ；切线长：T ；外距：E 。

（2）计算竖曲线起终点的桩号： 竖曲线起点的桩号 = 变坡点的桩号－T
（3）计算竖曲线上任意点切线标高及改正值：
切线标高 = 变坡点的标高±（x T -）⨯i ；改正值：y=R
x 22 （4）计算竖曲线上任意点设计标高
某桩号在凹形竖曲线的设计标高 = 该桩号在切线上的设计标高 + y
某桩号在凸形竖曲线的设计标高 = 该桩号在切线上的设计标高－ y
-----精心整理，希望对您有所帮助!。

4800竖曲线计算放样程序

4800竖曲线计算放样程序

4800竖曲线计算放样程序SJBGJS(主程序)Lb1 1:｛KB X｝:Prog“YSJG”:N=-V－W:N>0＝＞N=-1:≠＞S=0.14L÷（0.07+0.035I）：Y=（0.07+0.035I）÷LC=Abs（K-Q）:K>Q＝＞C<T＝＞D=（K-Q+T）2÷（2RLb1 2:C<T＝＞D=（K-Q-T）2÷（2RLb1 3:K<Q＝＞P=V÷100: ≠＞P=W÷＝＞Prog“123”NormProg“BBBB”:Goto 1123K<J-L＝＞Prog“11”: ≠＞K<J＝＞Prog“22”: ≠＞K≤○＝＞Prog “33”: ≠＞K≤○+L＝＞Prog“22”: ≠＞Prog“11”33G=G+0.01I（MB）11G=G-Abs B×0.0222M=1＝＞Prog“44”: ≠＞Prog“55”44K≤J-L+S＝＞Prog“E”: ≠＞K<J＝＞Prog“C”: ≠＞K<○+L-S＝＞Prog“C”: ≠＞Prog“F”55K≤J-L+S＝＞Prog“A”: ≠＞K<J＝＞Prog“C”: ≠＞K<J＝＞Prog “C”: ≠＞K<○+L-S＝＞Prog“C”: ≠＞Prog“B”EB≤0＝＞G=G+0.02B: ≠＞G=G+B((K-J+L)×Y-0.07)÷FB≤0＝＞G=G+0.02B: ≠＞G=G+B((○+L-K)×Y-0.07)÷CK<J＝＞G=G((K-J+L)×Y-0.07)÷3.5×MB: ≠＞G=G+((○+L-K)×Y-0.07)÷3.5×AB>0＝＞G=G-0.02B: ≠＞G=G-B((K-J+L)×Y-0.07)÷BB>0＝＞G=G-0.02B: ≠＞G=G-B((○+L-K)×Y-0.07)÷BBBBLb1 0:｛Z｝H=G-Z:H>0＝＞Prog“BBB”: ≠＞Prog“SBB”Fix 3:C=C+0.0001:“LL=”:Pause 0BBF“P11”U“P22”H≥-10＝＞C=Abs B+1.9-（H+0.03）F: ≠＞C=Abs B+1.9+9.97F+1-（H+10.03）H<8＝＞C=Abs B+1.5H+0.3: ≠＞H≤16＝＞C=Abs B+13.433+（H-8）×1.5+0.3: ≠＞Abs B+26.865+（H-16）×ACB>0＝＞G=G-○×B: ≠＞G=G-B((K-J+L)×Y-0)÷BCB>0＝＞G=G-○×B: ≠＞G=G-B((○+L-K)×Y-0)÷SBBF“P11”U“P22”H≥-10＝＞C=Abs B+1.9-（H+0.03）F: ≠＞H≥-20＝＞C=Abs B+1.9+9.97F+1-（H+10.03）U：≠＞H≥-30＝＞C=Abs B+1.9+9.97F+9.97U+2-（H+20.03）U: ≠＞H≥-40＝＞………SJGK≤30231.33＝＞Q=30350:A=311.580:R=15000:T=105.061:V=-0.967: W=+2.368:J=30049.62:○=30141.33:L=90:M=+1:I=7:Goto 1: ≠＞K ≤30594.22＝＞Q=30350:A=311.580:R=15000:T=105.061:V=-0.967:W =+2.368:J=30311.33:○=30391.27:L=80:M=+1:I=7:Goto 1: ≠＞K≤31123.63＝＞Q=30350:A=311.580:R=15000:T=105.061:V=-0.967:W=+ 2.368:J=30674.22:○=30768.06:L=80:M=+1:I=7:Goto 1: ≠＞K≤31 123.63＝＞………Lb1 1Q----为该段竖曲线的变坡点桩号A----变坡点高程R----竖曲线半径R----竖曲线切线长E----竖曲线外距P1---变坡点前一个纵坡坡率P2---变坡点后一个纵坡坡率N----竖曲线纵要素因子，凸为-1，凹为+1 K0---直线直线段边桩放样辅助程序BBBBBB（主程序）Defm 3Lb1 0:｛G ,Z｝H=G-Z:H>0＝＞Prog“BBBBB”: ≠＞Prog“BBBB”Goto 0BBBBBH<12＝＞L=9+1.5H: ≠＞H≤20＝＞L=9+8×1.5+1.5+（H-8）×1.75: H ≤20＝＞L=9+8×1.5+1.5+8×1.75+3+（H-16）×2:BBBBC“P1”:D“P2”:S“P3”H>-12＝＞L=11.25-（H+0.045）C: ≠＞H>-20＝＞L=11.25+9.955 C+1.5-（H+10+0.045）D: ≠＞L=11.25+9.955 C+9.955 D+3-（H+20+0.045）说明：G---路肩设计高Z---实测高L---理论宽度H---填挖值。

5800平曲线和竖曲线计算程序。以验证过

5800平曲线和竖曲线计算程序。以验证过

5800平曲线和竖曲线计算程序。

以验证过5800平曲线程序1.主程序Lbl 4："1.SZ => XY"："2.XY => SZ"：？N：？S：Prog“SUB0”↙1÷P→C: (P-R)÷(2HPR) →D:180÷∏→E:N=1 => Goto1：Goto2：↙Lbl 1:? Z：Abs(S-O) →W：Prog "SUB1"："XS="：X◢"YS="：Y◢F-90→F：“FS=”：F▲DMS◢D:X+DCos(F)→X: "X=":X◢Y+DSin(F)→Y: "Y="：Y◢Goto4↙Lbl 2：？X：？Y：X→I：Y→J：Prog“SUB2”：O+W→S：“S=”：S◢“Z=”：Z◢Goto4↙2. 正算子程序(SUB1)0.1739274226→A：0.3260725774→B：0.0694318442→K：0.3300094782→L：1-L→F：1-K→M：U+W(Acos(G+QEKW(C+KWD))+Bcos(G+QELW(C+LWD))+B cos(G+QEFW(C+FWD))+Acos(G+QEMW(C+MWD))) →X：V+W(Asin(G+QEKW(C+KWD))+Bsin(G+QELW(C+LWD))+Bsin(G+QEFW(C+FWD))+Asin(G+QE MW(C+MW D))) →Y：G+QEW(C+WD)+90→F：X+Zcos（F）→X：Y+Zsin（F）→Y2. 反算子程序(SUB2)G-90→T：Abs((Y-V)cosT-(X-U)sinT) →W：0→Z：Lbl 0：Prog "SUB1"：T+QEW(C+WD) →L：(J-Y)cos（L）-(I-X)sin（L）→Z：IF Abs （Z）<10-6：T hen Goto1：Else W+Z→W：Goto 0：IfEndLb1 1：0→Z：Prog "SUB1" ：(J-Y)÷sin（F）→ZSUB0 数据库子程序Goto1↙同时保存多个曲线时的指针Lbl 1：IF S<***（线元终点里程）:Then***→G（线元起点方位角）:***→O（线元起点里程）:***→U（线元起点X）:***→V（线元起点Y）:***→P（线元起点曲率半径）:***→R（线元终点曲率半径）: ***→H（线元起点至终点长度）：0或1、-1→Q：Return:IfEnd↙Lbl 1：IF S<***（线元终点里程）:Then***→G（线元起点方位角）:***→O（线元起点里程）:***→U（线元起点X）:***→V（线元起点Y）:***→P（线元起点曲率半径）:***→R（线元终点曲率半径）: ***→H（线元起点至终点长度）：0或1、-1→Q：Return:IfEnd ……………..为了便于解读，每增加一个线元增加一行语句，每增加一条曲线增加一个Lbl，每增加个工程增加一个文件。

5800全线竖曲线程序(带数据库)

5800全线竖曲线程序(带数据库)

5800全线竖曲线程序（带数据库）
Lbl 0：“DK”？L回车
If L﹤0:Then Goto 4:IfEnd回车
If L﹤下一线元起点里程（本线元终点里程）：Then 本线元起点里程→E：本线元起点内轨顶面高程→K：本线元坡度→F：Goto 3:IfEnd 回车
If L﹤下一线元起点里程：Then 本线元起点里程→E：本线元起点内轨顶面高程→K:竖曲线半径→R：本线元坡度→F：Goto 2:IfEnd回车。

Goto 0：If End回车(第N-1线元数据要素)。

Goto 0：If End回车(第N线元数据要素)
注：1、有竖曲线时凸曲线时返回Goto 2:IfEd回车
2、有竖曲线时凹曲线时返回Goto 1:IfEd回车
3、一般坡度时返回Goto 3：IfEnd回车
Lbl 1：L-E→S:“H=”：S*tan（tan1-(F)+90*S÷（∏*R））+K→H▲Goto 4回车
Lbl 2：L-E→S:“H=”：S*tan（tan1-(F)-90*S÷（∏*R））+K→H▲Goto 4回车
Lbl 3：“H=”:K+（L-E）*F→H▲
Goto 4回车
Lbl 4：“LH=”？J：“I”?I：“D”?D：H+J+I*D→V回车
“BH=”：V→V▲
Lbl 5：Goto 0：IfEnd回车
说明：
输入部分：1、DK？为所求的里程；
2、LH?为所求点高程距内轨顶面的垂直距离；
3、I?为所求的横坡坡比；
4、D?为所求高程点距中线的边距。

显示结果：1、所求里程对应的内轨顶面高程；
2、BH=为所求点或边坡点的高程
席崇辉
2010年3月26日。

竖曲线计算示意图及说明

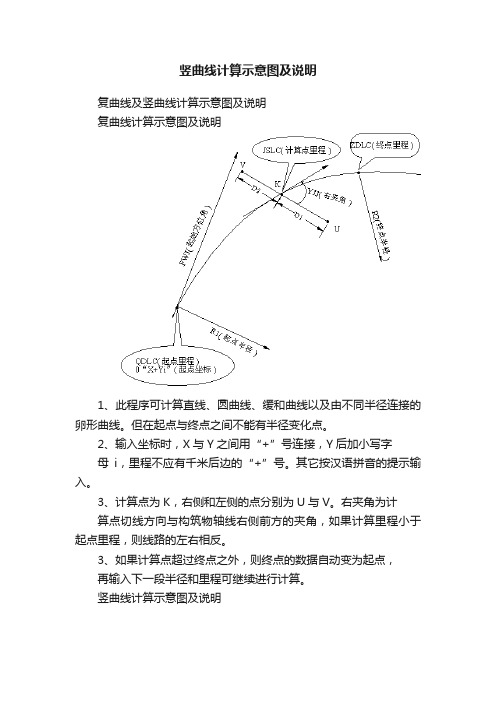
竖曲线计算示意图及说明

竖曲线计算示意图及说明
复曲线及竖曲线计算示意图及说明
复曲线计算示意图及说明
1、此程序可计算直线、圆曲线、缓和曲线以及由不同半径连接的卵形曲线。

但在起点与终点之间不能有半径变化点。

2、输入坐标时，X与Y之间用“+”号连接，Y后加小写字
母i，里程不应有千米后边的“+”号。

其它按汉语拼音的提示输入。

3、计算点为K，右侧和左侧的点分别为U与V。

右夹角为计
算点切线方向与构筑物轴线右侧前方的夹角，如果计算里程小于起点里程，则线路的左右相反。

3、如果计算点超过终点之外，则终点的数据自动变为起点，
再输入下一段半径和里程可继续进行计算。

竖曲线计算示意图及说明
1、竖曲线只能计算两个变坡点之间的高程。

按上图中所示的汉语拼音提示输入数据。

2、如果计算里程超过终点里程，则终点自动变为起点，然后再按提示输入下一个变坡点的数据，继续进行计算。

竖曲线的高程计算 matlab

竖曲线的高程计算 matlab

竖曲线的高程计算 matlab
竖曲线的高程计算matlab
竖曲线的高程计算&lpar;matlab&rpar;
%任一斜曲线的高程排序(未知变坡点的桩号和高程),须要输出的数据存有：已知数据：i1、i2、r、z0、k0
建议点的桩号数据：k1
k1=1371;%要求点的桩号
i1=0.004;%前段切线的坡度
i2=-0.0053;%后段切线的坡度
r=50000;
z0=144.531;%变坡点高程
k0=1371;%变坡点桩号
w=i1-i2;
e=t^2/(2*r);
k2=k0-t;%竖曲线起点的桩号
k3=k0+t;%斜曲线终点的桩号
t1=k1-k2;%要求点距离k2的橫距
e1=(t1)^2/(2*r);%建议点的竖距
z1=z0-(k0-k1)*i1-e1;
t1=k1-k3;%建议点距离k3的橫距
e1=(t1)^2/(2*r);%要求点的竖距
z1=z0-(k0-k1)*i2-e1;
求出来的z1只是中心线上的某点高程。

这是在matlab里运行的程序，只要红色部分的字就好。

我建议最好先把红色部分字复制下来再粘贴到txt文档里，在txt文档里检查
下格式，如果没问题，就可以从txt文档里复制下来粘贴到matlab里。

记住：别忘记替换你想替换的数据了哦。

竖曲线运算步骤及公式讲解

竖曲线运算步骤及公式讲解

竖曲线上高程计算
已知：①第一坡度：i 1(上坡为“＋”，下坡为“－”)
②第二坡度：i 2(上坡为“＋”，下坡为“－”)
③变坡点桩号：S Z
④变坡点高程：H Z
⑤竖曲线的切线长度：T
⑥待求点桩号：S
计算过程：
1、切线上任意点与竖曲线间的竖距h 通过推导可得：
==PQ h )()(2112li y l x R y y A A q p ---=-R
l 22= 2、竖曲线曲线长： L = R ω
3.竖曲线切线长： T= T A =T B ≈ L/2 =
2ωR
4、竖曲线的外距： E =R
T 22
5. 竖曲线上任意点至相应切线的距离：R
x y 22= 式中：x —为竖曲任意点至竖曲线起点（终点）的距离, m ；
R —为竖曲线的半径，m 。

竖曲线计算的目的是确定设计纵坡上指定桩号的路基设计标高，其计算步骤如下：
（1）计算竖曲线的基本要素：竖曲线长：L ；切线长：T ；外距：E 。

（2）计算竖曲线起终点的桩号： 竖曲线起点的桩号 = 变坡点的桩号－T
（3）计算竖曲线上任意点切线标高及改正值：
切线标高 = 变坡点的标高±（x T -）⨯i ；改正值：y=R
x 22 （4）计算竖曲线上任意点设计标高
某桩号在凹形竖曲线的设计标高 = 该桩号在切线上的设计标高 + y 某桩号在凸形竖曲线的设计标高 = 该桩号在切线上的设计标高－ y。

FX5800竖曲线程序(无名草编制)

FX5800竖曲线程序(无名草编制)
序号
程序内容 SQ-CG
主程序
备注
1 2 3 4 5 6 7 8 9 10 11 1 2 3 4 5 1 2 3 4 5 6
Nrom 2:Deg “LX?[1-10]”?A Lbl 0 "KP="?K "BP="?B Prog"SQ":Prog"CG" If J≠O:Then "IP=":Fix4:J ⊿ "HP=":Fix3:H ⊿ Else "HP=":Fix3:H ⊿ IfEnd Goto 0 SQ Prog"SQ-DATA" P-2T→F:P-T→G If T=0: Then S-I(G-K)→D Else If K≤F: Then S-I(G-K)→D: Else SIT+I(K-F)+R(K-F)²→D IfEnd CG If B=0:Then 0→J:D→H Else "LB="?M:"HB="?N Prog"CG-DATA" X+(Y-X)(K-Q)/(Z-Q）→J D+N+J(Abs(B)-M)→H IfEnd SQ-DATA
数据库 可有可无
备注
1
56.013→W:63.101→P:If K≥W And K≤P:Then 40.139→S:0→T:0→R:0.02594→ I:Return:IfEnd P→W:136.899→P:If K≥W And K≤P:Then 41.096→S:36.899→T:+1/(2*8493.67)→ R:0.02594→I:Return:IfEnd P→W:431.535→P:If K≥W And K≤P:Then 50.965→S:46.535→T:-1/(2*2499.982)→ R:0.03463→I:Return:Ifend If K<56.013 Or K>431.535:Then Cls：Locate 5,2,"KP ERROR"⊿ Stop IfEnd 路线起点桩号（或上一段数据库终点桩号）→W: 第一段竖曲线起点桩号（或竖曲线终点桩号)→ P:If K≥W And K≤P:Then 第一段竖曲线起点高 程（或竖曲线变坡点高程） →S:第一段为0（或 竖曲线切线长）→T:第一段为0（或竖曲线半 径）→R:前坡度→I:Return:IfEnd

matlab设计曲线方程

matlab设计曲线方程

matlab设计曲线方程在MATLAB中设计曲线方程的方法有很多种，下面是一些常见的方法：使用内置函数：MATLAB提供了一些内置函数来创建特定的曲线，例如正弦、余弦、指数、对数等函数。

例如，要创建一个y = sin(x)的曲线，你可以使用以下代码：matlab复制代码x = 0:0.01:2*pi; % 创建一个从0到2*pi的x数组，步长为0.01y = sin(x); % 计算每个x值的正弦值plot(x, y); % 绘制曲线使用多项式：如果你需要设计一个多项式曲线，你可以使用polyfit和polyval函数。

例如，要拟合一个二次多项式，你可以使用以下代码：matlab复制代码x = 0:0.1:10; % 创建一个从0到10的x数组，步长为0.1y = 2*x.^2 + 3*x + 1; % 定义一个二次多项式p = polyfit(x, y, 2); % 使用polyfit函数拟合多项式y_fit = polyval(p, x); % 使用polyval函数计算拟合值plot(x, y, 'o', x, y_fit); % 绘制原始数据和拟合曲线自定义函数：如果你需要的曲线方程不能由MATLAB的内置函数表示，你可以定义自己的函数。

例如，要定义一个y = exp(-x)的函数，你可以使用以下代码：matlab复制代码function y = my_func(x)y = exp(-x);end然后，你可以像使用内置函数一样使用这个自定义函数：matlab复制代码x = 0:0.01:1; % 创建一个从0到1的x数组，步长为0.01y = my_func(x); % 计算每个x值的函数值plot(x, y); % 绘制曲线。

matlab点到线段的垂直距离

matlab点到线段的垂直距离

Matlab是一种高级技术计算语言和交互式环境，用于学术、工程和科学计算。

在Matlab中，点到线段的垂直距离是一个常见的问题，本文将介绍如何使用Matlab计算点到线段的垂直距离。

二、问题描述点到线段的垂直距离是指从给定点到线段的垂直距离。

给定一个线段AB和一个点C，求点C到线段AB的垂直距离。

这是一个在工程、地理信息系统等领域经常遇到的问题。

三、计算方法计算点到线段的垂直距离的方法有很多种，其中一种比较常用的方法是利用点C到线段AB的投影点。

具体计算步骤如下：1. 计算线段AB的方向向量2. 计算点C到线段AB起点A的向量AC3. 计算AC在AB上的投影点P4. 计算CP的长度，即为点C到线段AB的垂直距离四、Matlab实现在Matlab中，可以使用向量和矩阵运算来实现点到线段的垂直距离计算。

以下是一个简单的Matlab代码示例：```matlab定义线段AB和点C的坐标B = [3, 4];C = [1, 2];计算线段AB的方向向量AB = B - A;计算点C到线段AB起点A的向量ACAC = C - A;计算AC在AB上的投影点Pt = dot(AC, AB) / dot(AB, AB);P = A + t * AB;计算CP的长度，即为点C到线段AB的垂直距离distance = norm(C - P);```五、实例演示接下来，我们通过一个具体的实例来演示Matlab计算点到线段的垂直距离。

假设线段AB的起点为A(0, 0)，终点为B(3, 4)，点C的坐标为C(1, 2)。

根据上述Matlab代码，可以计算出点C到线段AB的垂直距离为1。

六、注意事项在实际应用中，需要注意以下几点：1. 确保线段AB的始点和终点坐标正确2. 确保点C的坐标正确3. 注意处理线段退化为点或线的特殊情况七、总结通过本文的介绍，读者可以了解如何使用Matlab计算点到线段的垂直距离。

这对于需要进行空间分析和计算的工程师、科学家和研究人员来说，是一个非常有用的技巧。

基于JAVA和MATLAB的线路工程坐标计算程序设计

基于JAVA和MATLAB的线路工程坐标计算程序设计

基于JAVA和MATLAB的线路工程坐标计算程序设计作者：金蕾南有杰陈凯红岳迎春来源：《绿色科技》2018年第10期摘要：结合MATLAB数值计算能力和JAVA的多线程网络编程能力，开发出了具有线路工程放样数据计算功能的WEB程序。

该程序无需客户端，实现了多程序设计用户通过浏览器访问指定地址即可。

关键词：线路工程放样数据计算;MATLAB软件;JAVA语言;混合编程中图分类号：TU997文献标识码：A文章编号：1674-9944（2018）10-0225-031引言线路工程由直线和曲线构成，放样前要计算线路细部点坐标，这些坐标计算可用编程计算器或软件处理。

计算器内存小，计算效率低且不易完成复杂计算;软件有GPS系统软件、ARCGIS软件、AUTO-CAD软件等，这些软件中都有一些内置功能模块能实现计算，但它们的共性是计算模式固定，缺少灵活性，且通用性和移植性很差，对运行环境要求苛刻;而类似互联网上的一些小型程序安装包，因易感染BUG不放心使用。

为此开发具有移植性、通用性的软件有一定实际应用价值。

MATLAB具有高性能数值计算能力，JAVA具备多线程网络编程能力，结合二者的特点开发出一款具有线路工程坐标计算功能的WEB程序，部署在自建服务器上，实现多程序设计用户通过浏览器按指定地址异步访问，无需客户端，程序通用、方便、安全可靠，解决了以前一些方法应用中存在的问题。

2程序设计原理2.1语言介绍MATLAB是由MathWork公司推出的一种具有高性能的数值计算功能和可视化的软件，是目前在科研领域和工程界中较为流行的计算工具。

它集矩阵计算、符号运算、数值计算等功能于一体，并且附带有针对不同领域的MATLAB工具箱，为各个领域的应用提供了极大便利。

该编程语言语法简单，功能强大。

JAVA是由SUN公司发布的一种面向对象的程序设计语言，在数据处理和分析方面的能力不足，但其语言本身安全性较高，拥有MATLAB所不具备的网络编程与多线程功能。

路线竖曲线高程计算小程序(JMB)

路线竖曲线高程计算小程序(JMB)

竖曲线起点（桩号）: 竖曲线终点（桩号）: 竖曲线起点高程（米）: 所求点桩号 桩号 K26+600.000 K26+583.500 K26+616.500 K26+600.000 K26+583.500 K5+320.000 K5+325.000 K5+330.000 K5+335.000 K5+340.000 K5+345.000 K5+350.000 K5+355.000 K5+360.000 K5+365.000 K5+370.000 K5+375.000 K5+380.000 K5+385.000 K5+390.000
域输入数据。
式：若为K10+352.5,则输入10352.5。
所求桩号是否在竖曲线范围内，若否，则计算结果错误。
编共享程序，本人不对计算结果负责！若有需要，请自行改进程序。
2016/1/29 17:50
（若需查看当前时间，请按F9刷新）
使用提示：
1、请在黄色区域输入数据。源自变 坡 点 前 坡 度 : 变 坡 点 后 坡 度 : 竖曲线半径 坡 曲 曲 切 外 线 线 线 距 凸 凹 （米）: 差 : 性: 长（米）: 长（米）: （米）:
2、桩号输入方式：若为K10+352.5,则输入
3、请自行判断所求桩号是否在竖曲线范围
4、本程序为自编共享程序，本人不对计算
竖曲线高程计算程序
LZGD—ZT206—WangXiaosheng 变 坡 点 桩 号: K26+600.000 1500.012 0.20% 2.50% 3000.00 2.30% 凹形竖曲线 69.00 34.50 0.1984 K26+565.500 K26+634.500 1499.94 所求点高程(米) 曲线点 1500.210 1500.033 1500.479 1500.210 1500.033 1457.452 1457.462 1457.472 1457.482 1457.492 1457.502 1457.512 1457.522 1457.532 1457.542 1457.552 1457.562 1457.572 1457.582 1457.592 打开程序时间： 2016/1/29 17:50 变坡点高程 （米）:

matlab竖直直线方程

matlab竖直直线方程

matlab竖直直线方程摘要：一、引言1.介绍MATLAB 软件2.说明竖直直线方程在数学和工程领域的重要性二、MATLAB 中竖直直线方程的表示方法1.一般式竖直直线方程2.斜率截距式竖直直线方程3.两点式竖直直线方程三、MATLAB 中竖直直线方程的绘制1.绘制一般式竖直直线方程2.绘制斜率截距式竖直直线方程3.绘制两点式竖直直线方程四、MATLAB 中竖直直线方程的求解1.使用plot 函数绘制竖直直线方程并求解2.使用其他MATLAB 内置函数求解竖直直线方程五、竖直直线方程在实际问题中的应用1.工程问题中的应用2.数学问题中的应用六、总结1.回顾竖直直线方程的表示方法和绘制方法2.强调竖直直线方程在实际问题中的重要性正文：一、引言MATLAB 是一款功能强大的数学软件，广泛应用于工程和科学研究领域。

竖直直线方程是数学和工程领域中常见的一种直线方程形式，掌握其表示和应用方法对于解决实际问题具有重要意义。

本文将介绍MATLAB 中竖直直线方程的相关知识。

二、MATLAB 中竖直直线方程的表示方法竖直直线方程通常表示为y = k (x - x0)，其中k 为直线的斜率，(x0, y0) 为直线上的一点。

在MATLAB 中，竖直直线方程可以表示为以下三种形式：1.一般式竖直直线方程：y = mx + b，其中m 为斜率，b 为y 轴截距。

2.斜率截距式竖直直线方程：y = mx + n，其中m 为斜率，n 为y 轴截距。

3.两点式竖直直线方程：y - y1 = m(x - x1)，其中(x1, y1) 为直线上的一点，m 为斜率。

三、MATLAB 中竖直直线方程的绘制在MATLAB 中，可以使用plot 函数绘制竖直直线方程。

例如，绘制斜率截距式竖直直线方程y = 2x + 1，可以输入以下命令：```matlabplot(x, 2*x + 1);```此外，还可以使用其他MATLAB 内置函数绘制竖直直线方程，如scatter 函数、quiver 函数等。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

sqx=sortrows(yssj,4); %%原始数据按变坡点里程排序，输入顺序为（R,i1,i2,变坡点里程，变坡点设计高程）
[r1,d1]=size(sqx); %%sq矩阵中第一行数据顺序 R,i1,i2,变坡点里程，变坡点设计高程
for i=1:r1
sqxjg=10; %%曲线上两点间隔距离
sqx(i,6)=sqx(i,3)-sqx(i,2); %%计算坡度差
sqx(i,7)=(abs(sqx(i,1)* sqx(i,6)))/2; %%计算竖曲线切线长
sqx(i,8)=((sqx(i,7))^2)/(2*sqx(i,1)); %%计算外距
sqx(i,9)=sqx(i,5)-sqx(i,7)*sqx(i,2); %%计算起始点高程
sqx(i,10)=sqx(i,4)-sqx(i,7); %%计算起始点里程
qxfyd(2*i-1,1)=sqx(i,10); %%起始点里程
qxfyd(2*i,1)=sqx(i,9); %%起始点设计高程
a=floor(sqx(i,7)/sqxjg); %%jg米一桩,坡桩个数
for j=1:a
if sqx(i,6)<0; %%判断竖曲线类型凸形
qxfyd(2*i-1,j+1)=qxfyd(2*i-1,1)+j*sqxjg; %%前坡放样点里程
qxfyd(2*i,j+1)=qxfyd(2*i,1)+sqx(i,2)*j*sqxjg-((j*10)^2)/(2*sqx(i,1));
%%前坡放样点设计高程
qxfyd(2*i-1,a+2)=sqx(i,4); %%变坡点里程
qxfyd(2*i,a+2)=sqx(i,5)-sqx(i,8); %%变坡点设计高程
qxfyd(2*i-1,j+2+a)=qxfyd(2*i-1,a+2)+sqxjg*j; %%后坡桩放样点里程
qxfyd(2*i,j+2+a)=sqx(i,5)+sqx(i,3)*(j*sqxjg)-(sqx(i,7)-j*sqxjg)^2/(2* sqx(i,1));%%后坡桩放样点设计高程
qxfyd(2*i-1,j+3+a)=sqx(i,10)+2*sqx(i,7); %%终点里程
qxfyd(2*i,j+3+a)=sqx(i,5)+sqx(i,7)*sqx(i,3); %%终点设计高
end
if sqx(i,6)>0; %%判断竖曲线类型凹形
qxfyd(2*i-1,j+1)=qxfyd(2*i-1,1)+j*sqxjg; %%前坡放样点里程
qxfyd(2*i,j+1)=qxfyd(2*i,1)+sqx(i,2)*j*sqxjg+((j*10)^2)/(2*sqx(i,1));
%%前坡放样点设计高程
qxfyd(2*i-1,a+2)=sqx(i,4); %%变坡点里程
qxfyd(2*i,a+2)=sqx(i,5)+sqx(i,8); %%变坡点设计高程
qxfyd(2*i-1,j+2+a)=qxfyd(2*i-1,a+2)+sqxjg*j; %%后坡桩放样点里程
qxfyd(2*i,j+2+a)=sqx(i,5)+sqx(i,3)*(j*sqxjg)+(sqx(i,7)-j*sqxjg)^2/(2* sqx(i,1));%%后坡桩放样点设计高程
qxfyd(2*i-1,j+3+a)=sqx(i,10)+2*sqx(i,7); %%终点里程
qxfyd(2*i,j+3+a)=sqx(i,5)+sqx(i,7)*sqx(i,3); %%终点设计高程
end
end
zxfy(2*i-1,2)=qxfyd(2*i-1,3+2*a); %%提取曲线终点里程
zxfy(2*i,2)=qxfyd(2*i,3+2*a); %%提取曲线终点高程
zxfy(1:2*i,1)=qxfyd(1:2*i,1); %%提取曲线起点里程和高程
end
for i=1:r1-1;
zxjg=50; %%直线上放样点间距
b=floor((zxfy(2*i+1,1)-zxfy(2*i-1,2))/zxjg); %%直线上放样点的个数for k=1:b;
zxfyd(2*i-1,k)=zxfy(2*i-1,2)+zxjg*k; %%直线上放样点的里程
zxfyd(2*i,k)=zxfy(2*i,2)+zxjg*k*sqx(i,3); %%直线上放样点的高程
end
end
[r2,c2]=size(qxfyd);
sqxfy1=zeros(2,(r2*c2)/2);
sqxfy1(1,1:c2)=qxfyd(1,1:c2);
sqxfy1(2,1:c2)=qxfyd(2,1:c2);
for n=2:(r2/2);
e1=(n-1)*c2+(n-1);
d1=n*c2+(n-1);
sqxfy1(1,e1:d1-1)=qxfyd(2*n-1,1:c2);
sqxfy1(2,e1:d1-1)=qxfyd(2*n,1:c2);
end
%%上个循环是将每个曲线段上的放样点的里程和高程放在两行里面，第一行为曲线段上各点的里程；第二行为曲线段上各点的高程
[r3,c3]=size(zxfyd);
sqxfy2=zeros(2,(r3*c3)/2);
sqxfy2(1,1:c3)=zxfyd(1,1:c3);
sqxfy2(2,1:c3)=zxfyd(2,1:c3);
for m=2:(r3/2);
e2=(m-1)*c3+(m-1);
d2=m*c3+(m-1);
sqxfy2(1,e2:d2-1)=zxfyd(2*m-1,1:c3);
sqxfy2(2,e2:d2-1)=zxfyd(2*m,1:c3);
end
%%上个循环是将每个直线段上的放样点的里程和高程放在两行里面，第一行为曲线段上各点的里程；第二行为曲线段上各点的高程
sqxfy3=zeros(2,((r2*c2)+(r3*c3))/2);
sqxfy3(1:2,1:(r2*c2)/2)=sqxfy1(1:2,1:(r2*c2)/2);
sqxfy3(1:2,((r2*c2)/2+1):((r2*c2)/2+(r3*c3)/2))=sqxfy2(1:2,1:(r3*c3)/ 2);
%%将直线段和曲线段整理到一起，但为横行排列，第一行为竖曲线上各点的里程；第二行为竖曲线上各点的高程
sqxfy4=sqxfy3'; %%得到竖曲线的所有放样点，两列数据，第一列为竖曲线上各点的里程；第二列为竖曲线上各点的高程
sqxfy5=sortrows(sqxfy4,1); %%将竖曲线的所有放样点数据按里程进行排序
[r4,c4]=size(sqxfy5);
for ts=1:r4;
sy1=sqx(1,4);
sy2=sqxfy5(ts,1);
if sy2==sy1;
sy3=ts;
end%%找出排列好的放样数据矩阵中第一个曲线段的变坡点，即线路的起点
sy4=sqx(r1,4);
sy5=sqxfy5(ts,1);
if sy5==sy4;
sy6=ts;
end%%找出排列好的放样数据矩阵中最后一个曲线段的变坡点，即线路的终点
end
liu=sy6-sy3+1
sqxfysj(1:liu,1:2)=sqxfy5(sy3:sy6,1:2);
x=sqx(:,4);
y=sqx(:,5);
plot(x,y,'-bo'); %%竖曲线变坡点的连线图
hold on
x=sqxfysj(:,1);
y=sqxfysj(:,2);
plot(x,y,'-r*'); %%竖曲线全程放样点设计高程图
title('竖曲线高程设计图');
xlabel('逐桩里程/m');
ylabel('逐桩设计高程/m');
legend('竖曲线设计图','变坡点图形',1);
save('sqxfysjfile','sqxfysj');
msgbox '计算完毕！';。

相关文档
最新文档