实验三 Mathematica的综合程序设计
Mathematica编程

实验报告
实验3 Mathematica编程
3.1 实验目的
通过本实验了解Mathematica编程的基本概念,掌握Mathematica中程序设计的一般方法。
培养编程与上机调试能力。
3.2 实验内容
3.2.1 编写一个程序,用以寻求边长为相邻整数,面积也为整数的三角形。
算法描述:
3.2.2 编写程序,输入两个正整数,用“辗转相除法”求它们的最大公约数。
辗转相除法:
(1) 以大数m作被除数,小数n做除数,相除后余数为r。
(2) 若r ≠0,则m ←n,n ←r,继续相除得到新的r。
若仍有r ≠0,则重复此过程,直到r = 0为止。
(3) 最后的n就是最大公约数。
算法描述:
3.2.3 编写程序,求Fibonacci 数列的前20项 Fibonacci 数列的定义:
⎩⎨⎧>-+-==2)2()1(2
,11)(n n F n F n n F
据此给出算法描述,并编程。
3.3 实验步骤
1、打开mathematica 。
2、对照实验要求,编写对应代码。
3、运行修改。
4、保存。
3.3.1 代码
1
2
3、
3.3.2 实验结果
1、
2、
3、
3.4 实验体会。
mathematica 数学实验报告

数学实验报告实验一数学与统计学院信息与计算科学(1)班郝玉霞201171020107数学实验一一、实验名:微积分基础二、实验目的:学习使用Mathematica的一些基本功能来验证或观察得出微积分学的几个基本理论。
三、实验环境:学校机房,工具:计算机,软件:Mathematica。
四、实验的基本理论和方法:利用Mathematica作图来验证高中数学知识与大学数学内容。
五、实验的内容和步骤及结果内容一、验证定积分dttsx⎰=11与自然对数xb ln=是相等的。
步骤1、作积分dttsx⎰=11的图象;语句:S[x_]:=NIntegrate[1/t,{t,1,x}]Plot[S[x],{x,0.1,10}]实验结果如下:21图1dttsx⎰=11的图象步骤2、作自然对数xb ln=的图象语句:Plot[Log[x],{x,0.1,10}] 实验结果如下:2 1图2xb ln=的图象步骤3、在同一坐标系下作以上两函数的图象语句:Plot[{Log[x],S[x]},{x,0.1,10}] 实验结果如下:21图3dttsx⎰=11和xb ln=的图象内容二、观察级数与无穷乘积的一些基本规律。
(1)在同一坐标系里作出函数xy sin=和它的Taylor展开式的前几项构成的多项式函数3!3xxy-=,!5!353xxxy+-=,⋅⋅⋅的图象,观察这些多项式函数的图象向xy sin=的图像逼近的情况。
语句1:s[x_,n_]:=Sum[(-1)^(k-1)x^(2k-1)/((2k-1)!),{k,1,n}]Plot[{Sin[x],s[x,2]},{x,-2Pi,2Pi},PlotStyle->{RGB[0,0,1]}] 实验结果如下:64242图4x y sin =和它的二阶Taylor 展开式的图象语句2:s[x_,n_]:=Sum[(-1)^(k-1)x^(2k-1)/((2k-1)!),{k,1,n}]Plot[{Sin[x],s[x,3]},{x,-2Pi,2Pi},PlotStyle->{RGB[0,1,1]}] 实验结果如下:642321图5x y sin =和它的三阶Taylor 展开式的图象语句3:s[x_,n_]:=Sum[(-1)^(k-1)x^(2k-1)/((2k-1)!),{k,1,n}]Plot[{Sin[x],s[x,4]},{x,-2Pi,2Pi},PlotStyle->{RGB[0,1,0]}] 实验结果如下:642321图6x y sin =和它的四阶Taylor 展开式的图象语句4:s[x_,n_]:=Sum[(-1)^(k-1)x^(2k-1)/((2k-1)!),{k,1,n}]Plot[{Sin[x],s[x,5]},{x,-2Pi,2Pi},PlotStyle->{RGB[1,0,0]}] 实验结果如下:642321图7x y sin =和它的五阶Taylor 展开式的图象语句5:s[x_,n_]:=Sum[(-1)^(k-1)x^(2k-1)/((2k-1)!),{k,1,n}] Plot[{Sin[x],s[x,2],s[x,3],s[x,4],s[x,5] },{x,-2Pi,2Pi}] 实验结果如下: 6422图8xy sin=和它的二、三、四、五阶Taylor展开式的图象(2)分别取n=10,20,100,画出函数xkkynk)12sin(1211--=∑=在区间[-3π,3π]上的图像,当n→∞时,这个函数趋向于什么函数?语句1:f[x_,n_]:=Sum[Sin[k*x]/k,{k,1,n,2}]Plot[f[x,10],{x,-2Pi,2Pi},PlotStyle->{RGB[0,0,1]}]实验结果如下:6420.5图9 n=10时,xkkynk)12sin(1211--=∑=的图像语句2:f[x_,n_]:=Sum[Sin[k*x]/k,{k,1,n,2}]Plot[f[x,20],{x,-2Pi,2Pi},PlotStyle->{RGB[0,0,1]}] 实验结果如下:6420.5图10 n=20时,xk k y nk )12sin(1211--=∑=的图像语句3:f[x_,n_]:=Sum[Sin[k*x]/k,{k,1,n,2}]Plot[f[x,100],{x,-2Pi,2Pi},PlotStyle->{RGB[0,0,1]}] 实验结果如下:6420.5图11 n=100时,xk k y nk )12sin(1211--=∑=的图像(3)分别取5,15,100,,在同一坐标系里作出函数x x f sin )(=与∏=-⋅=nk k x x x p 1222)1()(π在区间[-2π,2π]上的图像。
mathematica实验报告

mathematica实验报告《使用Mathematica进行实验报告:探索数学的奥秘》Mathematica是一款强大的数学软件,它不仅可以进行数学计算和图形绘制,还可以进行数据分析和模拟实验。
在本实验报告中,我们将使用Mathematica来探索数学的奥秘,展示其强大的功能和应用。
首先,我们将使用Mathematica进行数学计算。
通过输入数学表达式和方程式,我们可以快速地进行数值计算和符号运算。
Mathematica还提供了丰富的数学函数和算法,可以帮助我们解决复杂的数学问题,如微积分、线性代数和离散数学等。
其次,我们将利用Mathematica进行图形绘制。
通过输入函数表达式和参数设置,我们可以绘制出各种数学图形,如函数图像、曲线图和三维图形等。
Mathematica还提供了丰富的绘图工具和选项,可以帮助我们定制和美化图形,使其更加直观和具有艺术感。
接下来,我们将利用Mathematica进行数据分析。
通过输入数据集和统计方法,我们可以进行数据的可视化和分析,帮助我们发现数据的规律和趋势。
Mathematica还提供了丰富的数据处理和建模工具,可以帮助我们进行数据挖掘和预测分析,为决策和规划提供有力的支持。
最后,我们将利用Mathematica进行模拟实验。
通过输入模型和参数设置,我们可以进行各种科学和工程问题的模拟实验,帮助我们理解和预测实际现象。
Mathematica还提供了丰富的模拟工具和仿真方法,可以帮助我们进行虚拟实验和验证假设,为科学研究和工程设计提供有力的工具支持。
总之,Mathematica是一款强大的数学软件,它可以帮助我们探索数学的奥秘,解决数学问题,展示数学图形,分析数学数据,进行数学模拟实验,为科学研究和工程应用提供有力的支持。
希望本实验报告可以激发更多人对数学和科学的兴趣,让我们一起来探索数学的奥秘吧!。
Mathematica数学实验报告 实验三

数学实验报告实验三学院:数学与统计学院班级:信息与计算科学(1)班姓名:郝玉霞学号:201171020107实验三一、实验名:最佳分数近似值二、实验目的:研究怎样用分数近似值去给定的无理数作最佳逼近。
“最佳”就是既要误差小,又要分母小。
我们首先需要对“最佳”定出具体而明确的标准,还要寻找一个求最佳分数近似值的简单易行的算法。
三、实验环境:学校机房,Mathematica 软件。
四、实验的基本理论和方法:1、根据高中数学及大学数学中所学内容,经过分析研究,得出基本结论,利用Mathematica 来进行验证,并寻找一个求最佳分数近似值的简单易行的算法。
2、计算圆周率π“连分数展开”方法,并且利用特定的函数来展开其他数。
五、实验的内容和步骤实验步骤: 1、计算对数值对给定的正实数b ,N 且b ≠1,要求对数值a=N b log ,也就是求实数a 使a b =N ,如果能找到整数p ,q 使q pN b≈,则N b qp ≈,N b log qp≈,以lg2为例:由102=1024≈1000=310可得lg2≈103=0.3,再要提高精确度,就要找出更大的q 使q2更接近10的某个幂q10,也就是使p q32更接近于1。
练习题1:让q 依次取遍1到10000的所有的正整数,对每一个q ,按如下的递推法则求出一个正整数p=p(q)使实数p qq 102)(=λ最接近于1:q=1时,p(1)=0,λ(1)=01102=2.设已对q 求出p(q)和λ(q),计算2λ(q),如果2λ(q)<10,则取p(q+1)=p(q),λ(q+1)=2λ(q),如果2λ(q )≥10,则取p(q+1)=p(q)+1,λ(q+1)=10)(2q λ. 如果λ(q)比以前所有的λ(i)(11-≤≤q i )都更接近1,即|λ(q)-1|<|λ(i)-1|对所有3、Mathematica 中常用的展开数与多项式的函数的使用;的1≤i ≤q-1成立,就取qp都是最佳逼近lg2的的分数近似值,它们可以展开成小数近似值。
Mathematica实验报告

Mathematica 实验报告【实验名称】利用MA THEMA TICA 作图、运算及编程.【实验目的】1。
掌握用MA THEMATICA 作二维图形,熟练作图函数Plot 、ParametricPlot 等应用,对图形中曲线能做简单的修饰.2。
掌握用MATHEMA TICA 做三维图形,对于一些二元函数能做出其等高线图等,熟练函数Plot3D ,ParametricPlot 的用法。
3、掌握用MA THEMATICA 进行微积分基本运算:求极限、导数、积分等。
【实验原理】1.二维绘图命令:二维曲线作图:Plot[fx,{x ,xmin,xmax}],二维参数方程作图:ParametricPlot[{fx ,fy},{t ,tmin ,tmax}]2.三维绘图命令:三维作图plot3D [f,{x ,xmin ,xmax},{y,ymin ,ymax}],三维参数方程作图:ParameticaPlot3D[{fx,fy ,fz },{t ,tmin,tmax }]【实验内容】(含基本步骤、主要程序清单及异常情况记录等)1。
作出函数)sin(22y x z +=π的图形. 步骤: z=Sin [Pi Sqrt[x^2+y^2]];Plot3D [z ,{x,-1,1},{y,—1,1},PlotPoints →30,Lighting →True]2。
椭球面()⎪⎪⎩⎪⎪⎨⎧=∈⎪⎭⎫ ⎝⎛-∈==u z v u v u y v u x R R R R R R sin ,,,2,0,2,2,sin cos cos cos 332121πππ自行给定,作图. 步骤:ParametricPlot3D [{4Cos[u ]Cos[v],3Cos [u]Sin[v],2Sin[u]},{u ,—Pi/2,Pi/2},{v,0,2Pi}]3.做出极坐标描绘的图形:)cos 1(4θ+=r步骤:r [t_]:=4(1+Cos[t ]);ParametricPlot [{r [t ]Cos[t],r [t ]Sin [t]},{t,0,2Pi}]【实验结果】结果1:结果2:结果3:【总结与思考】MATHEMATICA作图的常见错误:General::spell1: Possible spelling error,因为在MATHEMATICA中作图函数大小写有区别.由于拼写间要有空格,易导致错误。
MATHEMATICA程序设计

顺序结构
顺序结构就是复合 全局变量和局部变量 顺序结构 循环结构 分枝结构 转向结构 输入、输出函数 程序的跟踪与调试 程序包 表达式
顺序结 构就 是复 合表 达式 顺序结 构就 是复 合表 达式 顺序结 构就 是复 合表 达式 顺序结 构就 是复 合表 达式
如果在表达式后面 加分号“;”则运 算 结果不显示,但会 自动加一个Null.
循环结构
全局变量和局部变量 顺序结构 循环结构 分枝结构 转向结构 输入、输出函数 程序的跟踪与调试 程序包
1、While循环 2、For循环 3、Do循环 4、不动点FixedPoint 5、表达式替代 6、Nest函数
分枝结构
1 If [条件,表达式] 条件,表达式]
全局变量和局部变量 顺序结构 循环结构 分枝结构 转向结构 输入、输出函数 程序的跟踪与调试 程序包
调用外挂程序包
全局变量和局部变量 顺序结构 循环结构 分枝结构 转向结构 输入、输出函数 程序的跟踪与调试 程序包
线性代数软件包 Graphics软件包 球面参数方程式的 绘图函数 三维图形的投影
自己编制程序包
全局变量和局部变量 顺序结构 循环结构 分枝结构 转向结构 输入、输出函数 程序的跟踪与调试 程序包
if条件表达式1表达式2当条件为true时求表达式1的值当条件为false时求表达式2的程序包流程控制breaklablenamegotoname程序包输入函数1getname2readname3input程序包出错信息1输入错误或语法错误2逻辑错误或功能使用不当3利用跟踪可以了解每次迭代的结果程序包线性代数软件包graphics软件包球面参数方程式的绘图函数三维图形的投影程序包上下文的概念程序包的格式mycijmmtelchm矩阵的初等变换感谢您使用本课件
数学实验综合实验报告

一、实验目的:1、初步认识迭代,体会迭代思想的重要性。
2、通过在mathematica 环境下编写程序,利用迭代的方法求解方程的根、线性方程组的解、非线性方程组的解。
3、了解分形的的基本特性及利用mathematica 编程生成分形图形的基本方法, 在欣赏由mathematica 生成的美丽的分形图案的同时对分形几何这门学科有一个直观的了解。
从哲理的高度理解这门学科诞生的必然性,激发读者探寻科学真理的兴趣。
4、从一个简单的二次函数的迭代出发,利用mathematica 认识混沌现象及其所 蕴涵的规律。
5、.进一步熟悉Mathematic 软件的使用,复习总结Mathem atic 在数学作图中的应用,为便于研究数学图像问题提供方便,使我们从一个新的视角去理解数学问题以及问题的实际意义。
6、在学习和运用迭代法求解过程中,体会各种迭代方法在解决问题的收敛速度上的异同点。
二、实验的环境:学校机房,mathematica4环境三、实验的基本理论和方法:1、迭代(一)—方程求解函数的迭代法思想:给定实数域上光滑的实值函数)(x f 以及初值0x 定义数列1()n n x f x +=, ,3,2,1,0=n , (1)n x , ,3,2,1,0=n ,称为)(x f 的一个迭代序列。
(1)方程求根给定迭代函数)(x f 以及初值0x 利用(1)迭代得到数列n x , ,3,2,1,0=n .如果数列收敛到某个*x ,则有)(**x f x =. (2)即*x 是方程)(x f x =的解。
由此启发我们用如下的方法求方程0)(=x g 的近似解。
将方程0)(=x g 改写为等价的方程)(x f x =, (3) 然后选取一初值利用(1)做迭代。
迭代数列n x 收敛的极限就是方程0)(=x g 的解。
为了使得迭代序列收敛并尽快收敛到方程0)(=x g 的某一解的条件是迭代函数)(x f 在解的附近的导数将的绝对值尽量小,因此迭代方程修订成x x f x h x )1()()(λλ-+== (4) 选取λ使得|)(|x h '在解的附近尽量小. 为此, 我们可以令,01)()(=-+'='λλx f x h得)(11x f '-=λ. 于是 1)()()(-'--=x f x x f x x h . 特别地,如果取x x g x f +=)()(, 则可得到迭代公式 .,1,0,)()(1 ='-=+n x g x g x x n n n n (5) (2)线性方程组的数值解的迭代求解理论与矩阵理论给定一个n 元线性方程组⎪⎩⎪⎨⎧=++=++,,1111111n n nn n n n b x a x a b x a x a (6)或写成矩阵的形式,b Ax = (7) 其中)(ij a A =是n 阶方阵,T n x x x x ),,(21 =及T n b b b b ),,,(21 =均为n 维列向量.熟知,当矩阵A 的行列式非零时,以上的方程组有唯一解.如何有效,快速地寻求大型的线性方程组的数值解释科学工程计算中非常重要的任务.而迭代法常常是求解这些问题的有效方法之一。
mathematica实验报告

mathematica实验报告Mathematica 实验报告一、实验目的本实验旨在深入了解和掌握 Mathematica 软件的基本功能和操作方法,通过实际的案例和问题解决,提升运用 Mathematica 进行数学计算、数据分析、图形绘制以及编程的能力。
二、实验环境操作系统:Windows 10Mathematica 版本:121三、实验内容与步骤(一)数学计算1、基本运算在 Mathematica 中,直接输入数学表达式进行计算,例如:计算 2+ 3 4 的结果,输入`2 + 3 4` ,得到结果 14。
2、函数计算使用内置函数进行复杂的数学运算,如计算正弦函数`SinPi / 6`的值,结果为 05。
(二)数据分析1、数据导入通过`Import` 函数导入外部数据文件,如 CSV 格式的数据文件。
假设我们有一个名为`datacsv` 的文件,包含两列数据`x` 和`y` ,使用`data = Import"datacsv"`即可将数据导入。
2、数据处理对导入的数据进行处理,如计算平均值、方差等统计量。
可以使用`Meandata` 计算平均值,`Variancedata` 计算方差。
(三)图形绘制1、二维图形绘制简单的函数图形,如`PlotSinx, {x, 0, 2 Pi}`绘制正弦函数在`0` 到`2 Pi` 区间的图形。
2、三维图形绘制三维图形,如`Plot3Dx^2 + y^2, {x, -2, 2},{y, -2, 2}`绘制一个抛物面。
(四)编程实践1、定义函数使用`Function` 关键字定义自己的函数,例如定义一个计算阶乘的函数`factorialn_ := Ifn == 0, 1, n factorialn 1` 。
2、循环结构使用`For` 循环和`While` 循环实现重复操作,例如使用`For`循环计算 1 到 10 的和,`sum = 0; Fori = 1, i <= 10, i++, sum += i; sum` 。
Mathematica实验报告
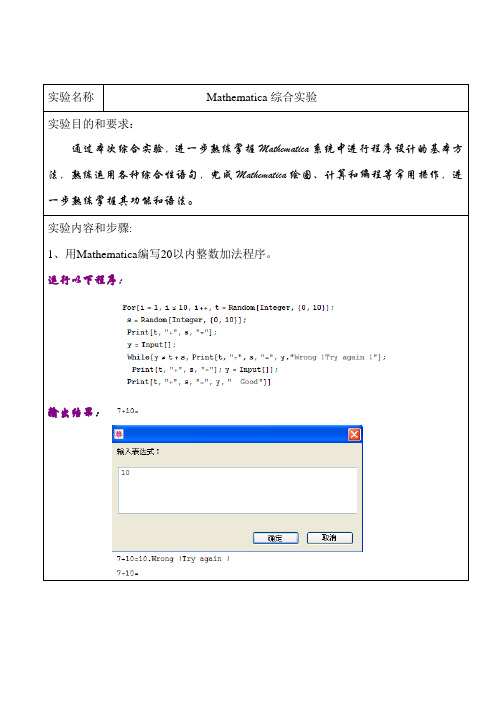
实验名称Mathematica综合实验实验目的和要求:通过本次综合实验,进一步熟练掌握Mathematica系统中进行程序设计的基本方法,熟练运用各种综合性语句,完成Mathematica绘图、计算和编程等常用操作,进一步熟练掌握其功能和语法。
实验内容和步骤:1、用Mathematica编写20以内整数加法程序。
运行以下程序:输出结果:2、编写程序,列出9*9的乘法表来。
输入程序:9*9乘法表3、编写程序,输入两个正整数,用“辗转相除法”求它们的最大公约数。
辗转相除法:(1) 以大数m作被除数,小数n做除数,相除后余数为r。
(2) 若r ≠ 0,则m ← n,n ← r,继续相除得到新的r。
若仍有r ≠ 0,则重复此过程,直到r = 0为止。
(3) 最后的n就是最大公约数。
Mathematica代码如下:运行结果4、统计一个班级某次考试个分数段的人数。
输入程序:运行结果:5、编写程序用切线法求方程的解。
Mathematica语句和运行结果如下:6、编写Mathematica程序显示二维码图像。
输入程序:二维码图像7、用0~8这九个数字,组成一个二位数和一个三位数相乘使他们的积恰好是四位数.数字不能重复。
即□□×□□□=□□□□输入以下Mathematica程序:输出结果:8、用Mathematica编写程序绘制一个围棋棋盘.输入以下程序:围棋棋牌9、假设新开辟的国家公园里没有兔子和狐狸,现引进兔子和狐狸个50只,n 个月后兔子和狐狸的数量分别记为n R 和n F ,假定有⎩⎨⎧+=-=++nn n n n n F R F F R R 6.02.02.01.111Mathematica 程序如下:运行结果如下:注释:在一段时间内,兔子和狐狸的数量均会减少,但最终均会趋于一个稳定值。
10、有一个木工、一个电工和一个油漆工,三人协商合作装修他们的房子,并达成如下协议:a.每人总共工作10天(包括给自己家干活);b.每人日工资根据市场价确定在60 80 元之间;c.每人的总支出与每人的总收入相等。
Mathematica程序设计

上页 下页 退出
哈 工 程 大 学 数 值 计 算 软 件
1、全局变量与局部变量 如果不使用Clear[]等命令删除的话,全局变量在 等命令删除的话, 如果不使用 等命令删除的话 整个程序中都存在,而使用Module[]或者 或者Block[]定义 整个程序中都存在,而使用 或者 定义 的变量称为局部变量(称为模块 称为模块), 的变量称为局部变量 称为模块 ,它只在所定义的模 块内是可见的。实际上, 块内是可见的。实际上,模块就是其它计算机语言中 的函数或者子程序。 的函数或者子程序。 Module[{x,y,…},body] 建立模块,并且申请局部变量 建立模块, x,y,… Module[{x=x0,y=y0,…},body] 同上,但已经给局部变 同上, 量赋初值 Block[{x,y,…},body] 建立模块,并且申请局部变量 建立模块, x,y,… Block[{x=x0,y=y0,…},body] 同上,但已经给局部变 同上, 量赋初值
D DDD D @ @@@ LH@L @ H D @ @ D D
在Mathematica中,用于条件判断的逻辑运算符 中 语言是一致的,它们是>、 、 、 、 、 、 与C语言是一致的,它们是 、>=、<、<=、==、!=、 &&、||。 、 。
上页 下页 退出
哈 工 程 大 学 数 值 计 算 软 件
@ @8 <8< @ D 8D D < @ 8@ < D
For循环与C语言中的for(;;)语句用法一样,只不过现 循环与C语言中的 语句用法一样, 循环与 语句用法一样 在变成了For[,,,]的形式,下面是有关 的形式, 循环的例子: 在变成了 的形式 下面是有关For循环的例子 循环的例子
Mathematica程序设计

Mathematica 程序设计江门职业技术学院 教育与教育技术系 10数学2班 黄殿遥( 1. A,B 可为数,也可为表达式 2. 结果为真则 True , 假False )二 逻辑算符三 条件语句1)If 语句 If[条件,语句1,语句2]如果条件成立,执行语句1,否则执行语句2。
(注:语句2可省)2)Which 语句 Whih[条件1,语句1,条件2,语句2,….]如果条件1成立,执行语句1,条件2成立,执行语句2,……例如 1》 输入:x=2 ; If[x>3 , Print[“x>3”] , Print[“x<=3”]]输出: x<=32》定义分段函数 f(x)= ,并在区间[-2,2] 画图。
输入: f[x_]=If[x>0 , 2x-1 , x^2-1];Plot[f[x] , {x , -2 , 2}] 3》定义分段函数 f(x)= ,并在区间[-2,2] 画图。
方法一 输入:f[x_]=If[x <-1 , -1 , If[x>1 , 1 ,x]];Plot[f[x] , {x , -2 , 2}] 方法二 输入:f[x_]=Which[x>1 , 1 , -1<=x<=1 , x , x<-1 , -1]; Plot[f[x] , {x , -2 , 2}]四 循环语句1) For 语句For[i=s1 , i<=n , i=i+s2 , 循环体语句]流程图:例如: 输入: For[i=1 , i<=10 , i=i+2 ,m=0,m=m+i^2,mPrint[i]]输出: 1 3 5 7 92)Do语句Do[循环体语句,{n , s1 , s2 , s3}]等价于 For[n=s1 , n<=s2 , n=n+s3 , 循环体语句] 例如:输入: Do[Print[1/n] , {n , 2 , 10 , 3}]输出:3)While语句While[条件语句,表达式]例如 n=0;While[n<3 , Print[n];n=n+1] 输出: 012注:1》加粗部分不能省;否则,进入死循环。
mathematica 实验报告

Mathematica实验报告引言Mathematica是一款功能强大的数学软件,广泛应用于数学、科学和工程等领域。
本实验报告旨在介绍Mathematica软件的使用方法,并通过一系列实例演示其在数学问题求解中的应用。
实验步骤步骤一:安装和启动Mathematica首先,我们需要下载并安装Mathematica软件。
根据操作系统的不同,可以从官方网站或其他可靠来源获取安装文件。
安装完成后,双击启动Mathematica软件。
步骤二:创建新的NotebookMathematica使用Notebook作为工作环境,可以将其类比为一个电子文档。
在Mathematica启动后,点击“File”菜单,选择“New”并选择“Notebook”,即可创建一个新的Notebook。
步骤三:编写代码在Notebook中,我们可以编写Mathematica代码。
Mathematica的代码由一系列的函数、变量和运算符组成。
以下是一个简单的示例代码,用于计算平方根:a = 9;Sqrt[a]在上述代码中,我们首先定义了变量a的值为9,然后使用Sqrt函数计算变量a的平方根。
要执行代码,可以按下“Shift” + “Enter”键,Mathematica将输出计算结果。
步骤四:编辑和运行代码在Mathematica中,可以随时编辑和运行代码。
例如,我们可以更改变量a的值,并重新计算平方根。
只需修改代码为:a = 16;Sqrt[a]然后再次按下“Shift” + “Enter”键,Mathematica将根据新的变量a的值重新计算平方根。
步骤五:绘制图表Mathematica还提供了强大的绘图功能,可以可视化数据和函数。
以下是一个简单的示例代码,用于绘制正弦函数的图表:Plot[Sin[x], {x, 0, 2Pi}]在上述代码中,我们使用Plot函数绘制了正弦函数在0到2π范围内的图表。
执行代码后,Mathematica将显示出相应的图表。
mathematica实验报告3(图形绘制)

2.运行结果()A准确,表现效果好;B正确;C部分结果不准确;D有较严重错误.
3.其它问题______________________________________________________________________.
4.综合评定()A优秀;B良好;C合格;D不合格;E有明显抄袭或雷同现象.
三、实验内容
1.绘制下列显式平面曲线(可选项取默认值)。
(1) ;
(2) 。
2.绘制下列隐函数平面曲线(可选项取默认值)。
(1) ;
(2) 。
3.绘制下列极坐标式平面曲线(可选项取默认值)。
(1) ;
(2) 。
4.绘制下列Байду номын сангаас间曲线。
(1) ;
(2) 。
5.绘制下列曲面。
(1) ,在矩形域 上;
(2) ,在矩形域 上。
新疆财经大学《数学软件》实验报告
实验3图形绘制
班级专业:数学-08-01姓名:崔仁霞李海燕学号:*******************日期:成绩:
一、实验目的
1.熟悉Mathematica绘图命令;
2.掌握平面图形及空间图形的绘制方法及图形的控制方法。
二、实验准备
命令:Plot、ParametricPlot、ImplicitPlot、PolarPlot、ListPlot、Show、PlotStyle、ParametricPlot3D、Plot3D、ListPlot3D等命令。
6.已知 个 值的数据为:
试绘制此数据曲面的图形。
四、程序、命令与结果
一,(1)命令:
结果:
(2)命令:
结果:
二,(1)命令:
mathematica 实验报告

mathematica 实验报告Mathematica 实验报告引言:Mathematica 是一款强大的数学软件,它能够帮助用户进行各种数学计算、数据分析和可视化等工作。
本实验报告将介绍我在使用 Mathematica 进行实验时的一些经验和心得。
一、实验目的本次实验的目的是通过使用 Mathematica,掌握其基本操作和功能,了解其在数学计算和数据处理方面的应用。
二、实验步骤1. 安装和启动 Mathematica首先,我在官方网站下载了 Mathematica 的安装包,并按照提示完成了安装。
然后,我启动了 Mathematica 软件,进入了主界面。
2. 基本操作在主界面中,我发现 Mathematica 提供了一个强大的交互式界面,用户可以通过键入命令和运行代码来实现各种功能。
我尝试了一些基本操作,比如进行简单的数学计算、定义变量和函数等。
3. 数据处理和分析Mathematica 提供了丰富的数据处理和分析功能,使得用户可以轻松处理和分析各种数据。
我使用了一些内置的函数和工具,对一些实验数据进行了处理和分析。
例如,我使用了 ListPlot 函数绘制了一些实验数据的散点图,并使用了Fit 函数进行了数据拟合。
4. 可视化Mathematica 还提供了强大的可视化功能,用户可以通过绘制图表和图形来展示数据和结果。
我使用了 Plot 函数绘制了一些函数的图像,并使用了 Graphics 函数绘制了一些几何图形。
5. 编程和自动化Mathematica 具有强大的编程功能,用户可以编写自己的函数和程序来实现复杂的计算和操作。
我尝试了一些简单的编程,比如编写了一个计算斐波那契数列的函数。
此外,我还了解到 Mathematica 支持自动化操作,可以通过编写脚本和批处理文件来实现自动化的计算和分析。
三、实验结果与分析通过使用 Mathematica,我成功完成了实验的各项任务,并取得了一些令人满意的结果。
Mathematica程序设计

哈 工 程 大 学 数 值 计 算 软 件 电 子 教 案
3、条件语句 Mathematica提供了多种设置条件的方法,对于 编程来说很方便。 •lhs=rhs/;test 当test为True时,执行lhs=rhs •If[test,then,else] 若test为True,执行then,否则执行 else •Which[test1,value1,test2,value2,…] 返回首个testi为 True时的valuei值 •Switch[expr,form1,value1,form2,value2,…] 先计算 expr的值,然后依次与formi比较,返回首个与formi 匹配的valuei的值,如果没有匹配项则返回Null •Switch[expr,form1,value1,form2,value2,…,def] 同上, 但如果没有匹配则返回def
上页 下页 退出
如果将刚才的程序变为如下形式:
哈 工 程 大 学 数 值 计 算 软 件 电 子 教 案
则它就是一个即有输入又有输出的子程序,其中的 f[x_,y_]中的下划线是必不可少的,如果你对其它计算 机语言很熟悉,你一定要问一个问题: 程序中的参数x,y是什么类型的变量? 实际上,它是mathematica中任一合法表达式.
上页 下页 退出
ቤተ መጻሕፍቲ ባይዱ
哈 工 程 大 学 数 值 计 算 软 件 电 子 教 案
其中body中可含有多个语句,除最后一个语句外, 各语句间以分号结尾,可以多个语句占用一行,也可 一个语句占用多行。但这两个命令略有差别,当 Module[]申请的局部变量与全局变量重名时,它会在 内存中重新建立一个新的变量,Module[]运行完毕, 这个新的局部变量也会从内存中消失,而Block[]此时 不会建立新的变量,它将重名的全局变量的值存起来, 然后使用全局变量作为局部变量,当Block[]运行完毕 后,再恢复全局变量的值。 另外,如果在Module[]或Block[]中有Return[expr] 命令,则程序执行到Return[expr]后,将会跳出模块, 并返回expr的值;则模块中无Return[]命令,则返回 模块中最后一个语句的计算结果(注:最后一个语句不 能用分号结束,否则将返回Null,即空信息)。
1.4.1 Mathematica 程序设计简介
1.4.1 Ma the matica程序设计简介(王积社)1.4.1.1 Mathematica程序设计功能1.4.1.1.1 模块模块,相当于C语言的子程序.即是把能够实现一定的功能的一系列表达式语句“集成”在一块,称之为一个模块,从而使Mathematica程序能更加清晰.另外,使用模块,也可更好地控制变量的属性.一般情况下,Mathematica假设所有变量都为全局变量.实际上这样做可能会使程序不具有通用性,也可能在调用程序时陷入混乱状态.于是就需要局部变量的功能,这需要用模块来控制.Mathematica的模块工作很简单,在模块中可定义它的局部变量,局部变量有唯一的名字,互不冲突,可有效地保护模块内外的每个变量的作用范围.常用模块函数有:Module与Block,其格式见下表:Body为执行体,包含合法的Mathematica语句,多个语句之间用“;”间隔,最后一个值为此模块的值.分析下面的例子,注意区分Module与Block的功能.输入:t=10;Module[{t},t=8;Print[t]]Print[t]结果如右图:可见模块中的t为局部变量,它独立于全局变量t(尽管模块内部有语句“t=8”且其Print[t]输出8,但是模块外的Print[t]仍输出10).再看Block例子,输入:y=x^2+1Block[{x=1},Print[y]]计算结果如右图:可见在模块Block中用局部变量x的值计算了全局变量y的值,于是如果希望把模块中局部变量作为全局变量使用时,可以用Block[]函数.然而在Module中却不能,见右图结果:总之,Module[vars,body]在执行时要检查模块体body,把其中出现变量vats都看作是局部的;而Block[vats,body]并不查看模块体body的形式,而在整个计算Body的过程中,只管使用vars的局部值.强调:在程序设计时,应该使程序中的各个部分尽可能地独立,以使程序易读、易改、易维护,主要方法是设置具有一定作用域的变量,这就需要模块的功能.1.4.1.1.2 逻辑运算与:&& expr1 && expr2 && … && exprn计算expri,直到其中有一个为假为止.或:|| exprl || expr2 || … || exprn计算expri,直到其中有一个为真为止1.4.1.1.3 一些特殊的赋值方式1.4.1.1.4条件结构常用的条件结构函数有:1.4.1.1.5 符号条件在Mathemahca 中,有一种可能的情况就是所给出的条件结果既不是真也不为假,请看右例:下面给出处理符号条件的函数.因x=x,故Mathematica 给出结果为真:1.4.1.1.6 循环结构 1) Do 循环.2) While 与For 循环在Mathematica 程序中,Do 是以结构方式进行循环的,然而有时你需要生成非结构循环,此时,运用函数While 和For是合适的.下面是While 和For 函数的循环结构形式:While 是“当”循环,当条件满足时,循环体一直进行,因此为了防止死循环,在循环体中应包括命令能改变循环条件语句.While 和For 循环是在执行循环体前对循环条件进行测试,一旦测试结果为假,就中止While 和For 循环. 例:(1) 用Do 循环计算n !,输入:m=1;n=10;Do[m=m*k,{k,n}] m计算结果见右图.(2) 用While 循环计算n !,输入:m=1;n=10;Whil e[n>0,m=m*n;n--]m计算结果见右图.(3)用For循环计算n!,输入:For[m = 1; n = 1, n ≤ 10, n++, m = n*m]m计算结果见右图.(4)多重循环示例,输入:Do[Print[i*j], {i,1,5}, {j,1,i}]计算结果如下:3) 重复运用函数我们除了可用Do、While、For等进行循环计算外,我们还重复运用函数.下面给出重复运用函数的方式.下面例子对函数x2迭代3次:例如(1)输入: Nest[f, x, 5]则输出:f[f[f[f[f[x]]]]](1)输入: g[x_]:=x^2; Nest[g, x, 3]则输出:8x(3)输入: FixedPoint [f, x, 5]则输出:f[f[f[f[f[x]]]]]输入: FixedPoint [g, x, 5]则输出:32x4) 流程控制函数程序结构的流程控制一般来说比较简单,但在应用While或For等循环时就比较复杂,这是因为他们的流程控制依赖于表达式的值.而且在这样的循环中,流程的控制并不依赖于循环体中表达式的值,有时在编制Mathematica程序时,流程控制受某一过程或循环体执行结果的影响,这时,我们可用流程控制函数来控制流程.这些函数的工作过程与C语言中的很相似.常用的流程控制函数:例如(1)输入: t = 1Do[t *= k; Print[t]; If[t > 5, Break[]], {k, 10}]计算结果为:(2)输入:t=1Do[t*=k;Print[t];If[k<5,Continue[]];t+=2,{k,5}]计算结果为:(3)输入:f[x_]:=(If[x>5,Return[5]];t=x^3;Return[t-5])f[10]f[2]计算结果为:1.4.1.2 MATHEMATICA程序设计中的几个问题1.4.1.2.1程序的注释为了增加程序的可读性,常常需要在程序中加入一些用作解释性的文字或与程序执行无关的字符串,当我们用“(* 注释内容*)”将其括起来时,程序将不执行它,并把它当作一个空格.1.4.1.2.2程序执行的跟踪On[名字]:打开对这个函数或变量的跟踪,对其每一次调用,它的参数,计算结果都将显示.On[ ]:打开对所有函数或变量的跟踪.On[Set]:打开对赋值操作的跟踪.由于所有变量的值的改变都要通过它因此,是最常用的跟踪命令.*)Off[]:关闭跟踪功能例如1.4.1.2.3 程序调试的机制Mathematica中程序调试的机制比较复杂,初学者不议掌握,这里介绍两种常用的方法,其一是分段加注释方法,把程序后面部分注释,一段一段地调试,这种方法需要读者在实际中体会.其二是用Trace[].Trace[]的使用形式是Trace[表达式,模式],这里的模式其过滤作用,得到的结果是一个表,表里留下的结果是表达式求值过程中与模式匹配的表达式,从中可以找出求值过程中的错误,如用下面的输入可以看到求值过程中的所有赋值:例求解一元二次方程程序设计:(1)算法分析:设方程是22 (-0)++=++≠的形式ax bx c dx ex f a d于是在执行程序时,需要分别输入方程的两边(用表{左边,右边}保存输入结果),输入后用一个模块对所输入的内容进行处理和求解,并把此模块定义为一个函数.模块中,需要对方程进行整理、提取系数,再用求根公式进行求解,然后返回所求得结果.(2)程序框图:(3)程序设计:s[xr_List]:= (* 输入{方程左边,方程右边 }*)Module[{v,w,a,b,c},a=Coefficient[w,v^2];b=Coefficient[w,v];c=w/.v->0;If [a==0,Return[{-c/b}]];{(-b+Sqrt[b^2-4 a c])/(2 a),(-b-Sqrt[b^2-4 a c])/(2 a)} ];s[{x^2+3 x+5, x+4}]Trace[s[{x^2+3 x+5, x+4}],_=_]11。
数学分析实验-Mathematica 软件的应用

七、自定义函数
格式 f[x_]:=… f[x_,y_]:=… f[x_,y_,…]:= … Clear[f] 意义 定义一元函数 f(x) 定义二元函数 f(x,y) 定义多元函数 f(x,y,…) 取消对 f 的定义
(1) 出现在 f[x_]中的x是一类实体,用来表示函数定 义中的变量。x_可以用任何形式的参数来替代,右端定 义式中的x将会随之变化。看下面的例子:
1
三、函数与变量的命名规则
在Mathematica系统中,变量名和函数名遵从如下命 名规则: (1) 以字母开头的任意长度的字符或数字串; (2) 区分大小写; (3) 为与系统函数相区别,通常以小写字母开头; (4) 函数的形式为f[x].
四、变量赋值与变量替换
举例如下: x=5; ( 赋值) x=. (取消赋值) /. x ->3 (变量替换,计算时用3暂时替换x的值) Clear[x] (清除x的定义及其赋值)
H(n)-ln(n) 0.5777155816 0.5774656441 0.5773823223 0.5773406597 0.577315661 0.5772989959
7000
8000 9000 10000
9.430952520
9.564474984 9.682251076 9.787606036
5 4 3 2 1
20
40
60
80ቤተ መጻሕፍቲ ባይዱ
100
猜测1 调和数列的前n项和H(n)是发散数列,它的数值与 ln(n)+C 很接近。
猜测2 数列H(n)- ln(n)可能是收敛的。
Step5 用计算数据作印证 对充分大的n,计算H(n)-ln(n)的值: t2=Table[N[{n,H[n],Log[n],H[n]-Log[n]},10], {n,1000,10000,1000}]
综合数学实验报告(mathematica)

综合数学实验报告(mathematica)数学综合实验报告学院:数学与统计学院专业:数学与应用数学姓名:##########学号:##########班级:##########综合实验实验一:观察数列极限一、实验目的利用数形结合的方法观察数列的极限,可以从点图上看出数列的收敛性,以及近似地观察出数列的收敛值;通过编程可以输出数列的任意多项值,以此来得到数列的收敛性。
通过此实验对数列极限概念的理解形象化、具体化。
二.实验环境学校机房,Mathematica 4.0软件三、实验的基本理论和方法1、Mathematica中常用的函数及函数调用的方法;2、对Fabonacci数列、调和级数以及3n+1问题规律的掌握。
四、实验内容及步骤设为实数列,为定数.若对任给的正数,总存在正整数,使得当时有,则称数列收敛于定数称为数列的极限,并记作或。
下面,我们以求为例进行实验,程序编写及运行如下:程序运行结果如下:五、实验结果和结果分析由运行结果和图像可知,发现在时,函数值无限靠近2.7左右。
实验二:函数图像绘制一、实验目的通过函数图形来认识函数,运用函数的图形来观察和分析函数的有关性态,建立数形结合的思想。
二.实验环境学校机房,Mathematica 4.0软件三、实验的基本理论和方法1、Mathematica中常用绘图函数Plot在绘制一元函数时的方法;2、函数迭代法的基本理论以及在Mathematica中的使用。
四、实验内容及步骤1、求的所有根(先画图再求解)。
2、求方程与的根。
3、求下列各题的解。
(1);(2),求;(3)(精确到17位有效数字);(4);(5)将在处展开(最高次幂为8);(6),求。
4、作sinx的n阶Taylor展开(n=10,30,60)并比较图像5、已知函数,作出并比较当分别取-1,0,1,2,3时的图形,并从图形上观察极值点、驻点、单调区间、凹凸区间以及渐近线。
在mathematica中输入下面语句:Do[Plot[1/(x^2+2x+c),{x,-5,4},GridLines→Automatic,Frame→True,PlotStyle→RGBColor[1,0,0]],{c,-1,3}]程序运行结果如下:实验结果和结果分析观察图可得:第一幅图:极大值点为,驻点为,单调区间为增、,减、,凸区间为、,凹区间为,渐近线为水平,垂直, .第二幅图:极大值点为,驻点为,单调区间为增、,减、,凸区间为、,凹区间.第三幅图:没有极值点,没有驻点,单调增区间为,单调减区间为,凸区间为、.第四、五幅图:极大值点为,驻点为,单调区间为增,减,凸区间为、.实验三:泰勒公式与函数逼近一、实验目的利用Mathematica计算函数的各阶泰勒多项式,并通过绘制曲线图形,根据图形观察泰勒展开的误差,进一步掌握泰勒展开与函数逼近的思想,并对泰勒公式与原函数作出比较。
数学实验mathematic_初步实验报告

For, Do,While,If,Switch等
【实验环境】
Mathematica5
二、实验内容:
【实验方案】
1.积分的求解
2.图形的绘制
【实验过程】(实验步骤、记录、数据、分析)
1.求积分
(1)
解:
( 2)
解:
2.将 在 处和 处展成9阶泰勒公式形式
解:(1)在 处(2)在源自处3、解方程(组)Graphics
【实验结论】(结果)
用Mathematica计算出了函数不定积分和定积分;很好的掌握了解方程(组)的方法;理解和掌握把函数展成泰勒公式的方法;掌握了用Mathematica绘制一元函数、二元函数以及参数函数图形的方法。
【实验小结】(收获体会)
深刻体会到Mathematica是一个功能强大的常用数学软件。以符号计算见长,也具有高精度的数值计算功能和强大的图形功能。并掌握了Mathematica的几种基本操作命令。
(1)
解:Solve[{Log[a+x]= =5,Cos(a-x)= =0.5},{a,x}]
(2)
解:
4、做作出下列函数的图形
(1)
解:Plot[Which[x 1,2 x,0 x 1,2,x<0,Cos[x]+1],{x,-8,8}]
Graphics
(2)
SurfaceGraphics
(3)
解:ParametricPlot[{3Cos[t]^3,3 Sin[t]^3},{t,-3 ,3 }]
新乡学院数学与信息科学系
实验报告
实验项目名称mathematic初步试验
所属课程名称数学实验
实验类型基础性试验
实验日期2013-4-12
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验三:Mathematica的综合程序设计1.验证角谷猜想.如果一个自然数,是偶数,就把它除以2,如果是奇数,就把它乘以3加1, 这样下去,经过若干次之后,必定得到数字1.试编写程序验证这一猜想.In[ ]:= n=Input["n="];Print["n=",n];k=0;While[n!=1,k++;If[EvenQ[n],n=n/2,n=3n+1]];Print["k=",k]Out[ ]= n= 23k= 152.求一个整数的所有因子方法一:因子竖着放的In[ ]:= n=Input["n="];Print["n=",n];For[i=1,i<=n,i++,If[Mod[n,i]==0,Print[i]]]In[ ]:= n= 12Out[ ]= 1234612方法二:借助于列表,横着排放In[ ]:= n=Input["n="];Print["n=",n];t={};For[i=1,i<=n,i++,If[Mod[n,i]==0,AppendTo[t,i]]];tIn[ ]:= n= 12Out[ ]= {1,2,3,4,6,12}3.验证Nn=p1*p2*...*pn+1是不是素数此题,n不宜过大,以免溢出.In[ ]:= For[k=1;n=1,n<=30,n++,k=k*Prime[n];If[PrimeQ[k+1],Print["N[",n,"]=",k+1," is a Prime"],Print["N[",n,"] =",k+1," is not a Prime"]]]4.Fermat数是不是素数,欧拉证明了n=5不是.试试看.nIn[ ]:= f[n_] := 221In[ ]:= f[{1,2,3,4,5,6,7,8}]Out[ ]= {5,17,257,65537,4294967297,18446744073709551617,340282366920938463463374 607431768211457,1157920892373161954235709850086879078532699846656405640394575840 07913129639937 }In[ ]:= PrimeQ[%]Out[ ]= {True,True,True,True,False,False,False,False}5.求所有完全数方法一In[ ]:= For[n=2,n<=1000,n++,t={};For[i=1,i<=n,i++,If[Mod[n,i]==0,AppendTo[t,i]]];t;If[(Plus@@t)==2n,Print[n," yes"]]]Out[ ]= 6 yes28 yes496 yes方法二In[ ]:= For[n=2,n<=1000,n++,s=0;For[i=1,i<=n-1,i++,If[Mod[n,i]==0,s=s+i]]; If[s== n,Print[n," yes"]]] Out[ ]= 6 yes28 yes496 yesIn[ ]:= For[n=2,n<=1000,n++,s=0;For[i=1,i<=n/2,i++,If[Mod[n,i]==0,s=s+i]]; If[s== n,Print[n," yes"]]] Out[ ]= 6 yes28 yes496 yes我们来观察一下时间的长短In[ ]:= For[n=2,n<=1000,n++,s=0;For[i=1,i<=n-1,i++,If[Mod[n,i]==0,s=s+i]];If[s==n,Print[n," yes"]]]//TimingOut[ ]= 6 yes28 yes496 yes{2.023 Second,Null}In[ ]:= For[n=2,n<=1000,n++,s=0;For[i=1,i<=n/2,i++,If[Mod[n,i]==0,s=s+i]];If[s==n,Print[n," yes"]]]//TimingOut[ ]= 6 yes28 yes496 yes{1.382 Second,Null}6.利用牛顿迭代法求下列方程的解(1) x^3 - 2 x - 5 = 0, x0 = 2In[ ]:= f[x_] := x^3 - 2 x - 5x0 = 2.0;For[i = 1, i<= 5, i++,x1 = x0 - f[x0] / f'[x0]; Print[i, " ", x1]; x0 = x1]Out[ ]= 1 2.12 2.094573 2.094554 2.094555 2.09455(2) x^41 + x ^3 - 1 = 0, x0 = 1In[ ]:= f[x_] := x^41 + x ^3 - 1x0 = 1.0;For[i = 1, i<= 8, i++, x1 = x0 - f[x0] /f'[x0]; Print[i, " ", x1]; x0 = x1]Out[ ]= 1 0.9772732 0.9604613 0.9533914 0.9524965 0.9524846 0.9524847 0.9524848 0.952484(3) x^3 - x - 1 = 0, x0 = 1.5In[ ]:= f[x_] := x^3 - x - 1x0 = 1.5;For[i = 1, i<= 5,i++,x1 = x0 - f[x0] /f' [x0]; Print[i, " ", x1]; x0 = x1]Out[ ]= 1 1.347832 1.32523 1.324724 1.324725 1.32472(4) x^3 - x^2 - 1 = 0, x0 = 1.5In[ ]:= f[x_] := x^3 -x^2 - 1x0 = 1.5;For[i = 1, i<=5,i++,x1 = x0 - f[x0] /f' [x0]; Print[i, " ", x1]; x0 = x1]Out[ ]= 1 1.466672 1.465573 1.465574 1.465575 1.465577.求孪生素数方法一:多重循环的编程In[ ]:= k=0;For[n=3,n<1000,n=n+2,flag1=1;(*标志,1,是,0,不是*)For[i=2,i<=Round[Sqrt[n]],i++,If[n/i==Floor[n/i],flag1=0;Break[]]];If[flag1==1,(*表明n是素数,现在再来判断n+2是不是素数*) flag2=1;m=n+2;For[j=2,j<=Round[Sqrt[m]],j++,If[m/j==Floor[m/j],flag2=0;Break[]]];If[flag2==1,k=k+1;(*计数器*)Print["k=",k," ",n," ",m]]]]Out[ ]= k= 1 3 5k= 2 5 7k= 3 11 13k= 4 17 19k= 5 29 31k= 6 41 43k= 7 59 61k= 8 71 73k= 9 101 103k= 10 107 109k= 11 137 139k= 12 149 151k= 13 179 181k= 14 191 193k= 15 197 199k= 16 227 229k= 17 239 241k= 18 269 271k= 19 281 283k= 20 311 313k= 21 347 349k= 22 419 421k= 23 431 433k= 24 461 463k= 25 521 523k= 26 569 571k= 27 599 601k= 28 617 619k= 29 641 643k= 30 659 661k= 31 809 811k= 32 821 823k= 33 827 829k= 34 857 859k= 35 881 883方法二:直接利用PrimeQ,不建议使用.In[ ]:= k=0;For[n=3,n<1000,n=n+2,If[PrimeQ[n] && PrimeQ[n+2],k++;Print["k=",k," ",n," ",n+2]]] Out[ ]= k= 1 3 5k= 2 5 7k= 3 11 13k= 4 17 19k= 5 29 31k= 6 41 43k= 7 59 61k= 8 71 73k= 9 101 103k= 10 107 109k= 11 137 139k= 12 149 151k= 13 179 181k= 14 191 193k= 15 197 199k= 16 227 229k= 17 239 241k= 18 269 271k= 19 281 283k= 20 311 313k= 21 347 349k= 22 419 421 k= 23 431 433 k= 24 461 463 k= 25 521 523 k= 26 569 571 k= 27 599 601 k= 28 617 619 k= 29 641 643 k= 30 659 661 k= 31 809 811 k= 32 821 823 k= 33 827 829 k= 34 857 859 k= 35 881 883。
