减小ADC量化噪声的技术
ADC芯片介绍

ADC芯片介绍ADC,即模数转换器(Analog-to-Digital Converter),是一种将模拟信号转换成数字信号的电子设备。
它是数字系统中的重要组成部分,广泛应用于通信系统、仪器仪表、工业自动化、医疗设备等领域。
本文将介绍ADC芯片的基本原理、分类、特点以及应用领域等相关内容。
一、ADC芯片的基本原理1.采样:采样是指将模拟信号在一定时间间隔内取样,即在一段时间内获取一系列的模拟信号值。
采样过程中需要考虑采样频率和抗混叠滤波等问题。
2.量化:量化是指将采样到的模拟信号值转换为具有离散数值的数字信号。
量化过程中需要确定量化位数和量化级数等参数,并利用ADC芯片内部的比较器和计数器等电路实现。
通过采样和量化两个过程,ADC芯片可以将模拟信号转换为数字信号,进而被数字系统所处理。
二、ADC芯片的分类根据其工作原理和结构,ADC芯片可以分为几种不同的类型。
1.逐次逼近型ADC:逐次逼近型ADC芯片是一种常见的ADC芯片类型,它通过逐次逼近的方式进行模拟信号到数字信号的转换。
逐次逼近型ADC芯片具有较高的分辨率和较低的功耗,适用于对精度要求较高的应用领域。
2.并行型ADC:并行型ADC芯片是一种将模拟信号同时转换为多个比特的数字信号的ADC芯片类型。
它具有高速和高精度的特点,但功耗较大。
并行型ADC芯片适用于对采样速度要求较高的应用场景,如通信系统中的信号处理和无线电频谱分析等。
3. Sigma-Delta型ADC:Sigma-Delta型ADC芯片主要应用于对信噪比要求较高的应用场景。
它通过过采样和累积量化的方式实现高精度的模数转换。
Sigma-Delta型ADC芯片适用于音频处理、音频编解码等领域。
三、ADC芯片的特点1.分辨率高:ADC芯片的分辨率是指其能够表示的电压值的最小差值。
分辨率越高,ADC芯片对模拟信号的转换精度越高。
2.采样速度快:ADC芯片的采样速度是指其每秒钟能够进行的采样次数。
高性能sigma-deltaADC的设计与研究

西安电子科技大学博士学位论文高性能sigma-delta ADC的设计与研究姓名:***申请学位级别:博士专业:微电子学与固体电子学指导教师:***20100401摘要i摘要高性能的模数转换器是当今微电子模拟领域研究的热点之一。
基于过采样技术和sigma-delta调制机制的模数转换器(Analog to Digital Converter,ADC)广泛使用在数字音频、综合业务数字网(Integrated Services Digital Network,ISDN)、数字电话等系统中。
这种高精度的模数转换器,通过采用过采样技术,增加调制器系统的信噪比,提高其实现的精度;通过使用sigma-delta噪声整形技术,降低了信号带内的量化噪声功率。
sigma-delta ADC由模拟调制器和数字抽取滤波器组成,而模拟调制器的噪声整形性能决定了整个转换器系统的精度。
本文首先对sigma-delta ADC的系统设计进行了深入的研究,采用MATLAB软件进行系统建模和仿真,并由此总结了一套完整的系统设计方法。
根据过采样率、精度和动态性能的要求,得出调制器所需的阶数以及前馈因子、反馈因子和积分器增益因子等参数。
然后再通过MATLAB系统仿真,预测出实际调制器可以达到的性能。
在模拟调制器的设计中,各种非理想因素会极大地影响模拟调制器的性能。
因此,对各种非理想因素进行系统的、量化的分析是必要的。
本文对各种非理想因素,如运放有限直流增益、有限带宽和摆率、输出摆幅限制、开关非线性,时钟抖动、采样电容kT/C噪声等都进行了量化分析,从而为随后的电路设计提供了设计依据。
sigma-delta ADC的结构主要分为单环(Single-Loop)结构和级联结构(Multi-stAge-noise-SHaping,MASH)两种,这两种结构具有各自的优缺点。
针对这两种结构,本文分别设计了一个高阶单环一位结构的sigma-delta ADC和一个级联多位(MASH24b-24b)结构的sigma-delta ADC。
单片机ADC模数转换原理及精度提升策略

单片机ADC模数转换原理及精度提升策略概述:单片机中的ADC(Analog to Digital Converter)电路是将模拟信号转换为数字信号的重要组成部分。
ADC模数转换原理是基于采样和量化的原理实现的。
本文将介绍单片机ADC模数转换的原理,并探讨提高转换精度的策略。
1. ADC模数转换原理:ADC模数转换原理分为三个步骤:采样、量化和编码。
首先,采样器将输入的模拟信号按照一定频率进行采样,得到一系列离散的采样值。
然后,量化器将采样值按照一定的精度进行量化,将连续的模拟信号转换为离散的数字信号。
最后,编码器将量化后的数字信号编码为二进制码,以便单片机进行处理。
2. 提高ADC转换精度的策略:(1)增加采样频率:采样频率越高,获得的采样值越多,可以更准确地还原原始的模拟信号。
因此,可以通过提高ADC的采样频率来提高转换精度。
(2)优化参考电压:ADC的转换精度受到参考电压的影响。
参考电压应为稳定、精确的电压源,以确保ADC转换的准确性。
可以通过使用参考电压源或外部参考电压电路来提高转换精度。
(3)降低噪声:噪声会影响ADC的转换精度。
噪声可以来自电源、引脚等,因此需要采取措施来降低噪声水平。
例如,使用滤波电路和屏蔽措施来降低噪声对ADC转换的干扰。
(4)校准和校正:由于元件参数的不均匀性和时间漂移等原因,ADC的转换精度可能会发生偏差。
因此,需要进行校准和校正,以提高转换精度。
可以使用校准电路或软件校准的方法来进行校准。
(5)增加分辨率和位数:增加ADC的分辨率和位数可以提高转换精度。
分辨率是指ADC可以分辨的最小电压变化量,位数则代表了ADC转换结果的位数。
增加分辨率和位数可以获得更准确的转换结果。
(6)差分输入:使用差分输入可以减少共模噪声对ADC转换精度的影响。
差分输入可以通过采取差分双终端输入的方式来实现,将信号的差值作为转换信号输入。
3. 总结:单片机ADC模数转换原理是通过采样、量化和编码实现了模拟信号向数字信号的转换。
adc滤波的10种经典算法

adc滤波的10种经典算法ADC(模数转换器)滤波算法是将采样得到的模拟信号进行数字化处理时常用的方法。
滤波的目的是去除噪声和不必要的频率成分,以提高信号质量。
下面列举了10种经典的ADC滤波算法:1. 均值滤波器:将一组采样值取平均值,用于平滑信号,减小噪声的影响。
该算法简单且易于实现,但对于快速变化的信号可能会引入较大的误差。
2. 中值滤波器:将一组采样值排序,取中间值作为输出值。
中值滤波器能够有效地去除脉冲噪声,对于非线性噪声具有良好的去除效果。
3. 限幅滤波器:将采样值限制在一定范围内,超出范围的值替换为最大或最小值。
该滤波器适用于信号中存在脉冲噪声的情况,能够有效去除异常值。
4. 低通滤波器:只允许低频信号通过,抑制高频信号。
常用的低通滤波器包括巴特沃斯滤波器、布脱沃斯滤波器等。
低通滤波器可应用于去除高频噪声,平滑信号。
5. 高通滤波器:只允许高频信号通过,抑制低频信号。
高通滤波器可用于去除低频噪声,突出高频信号。
6. 带通滤波器:只允许一定频率范围内的信号通过,抑制其他频率的信号。
带通滤波器可用于突出某个频段的信号。
7. 自适应滤波器:根据输入信号的特点自动调整滤波参数,适应不同的信号环境。
自适应滤波器能够实时调整滤波效果,适应信号的变化。
8. 卡尔曼滤波器:利用系统的状态方程和观测方程,通过最小化预测误差和观测误差的加权和,实现对信号的滤波。
卡尔曼滤波器适用于线性系统,能够对系统状态进行较准确的估计。
9. 无限脉冲响应(IIR)滤波器:在滤波过程中利用反馈,具有较窄的通带和较宽的阻带。
IIR滤波器具有较好的频率响应特性,但容易引入稳定性问题。
10. 有限脉冲响应(FIR)滤波器:滤波过程中不利用反馈,仅利用输入信号和滤波器的系数进行计算。
FIR滤波器具有较好的稳定性和线性相位特性,适用于需要精确频率响应的应用。
这些经典的ADC滤波算法在不同的应用场景中有着各自的优势和适用性。
在实际应用中,需要根据信号的特点和要求选择合适的滤波算法,以达到最佳的滤波效果。
单片机ADC技术原理及精度提升方法探讨

单片机ADC技术原理及精度提升方法探讨摘要:本文首先介绍了单片机ADC技术的原理和基本概念,然后探讨了提高ADC精度的常用方法,包括增加参考电压精度、降低噪声干扰、使用运算放大器和滤波器等。
通过深入研究和分析这些方法,可以帮助工程师们更好地理解和应用单片机ADC技术,提升系统的测量精度。
1. 引言ADC(Analog-to-Digital Converter)是将模拟信号转换为数字信号的核心器件,广泛应用于通信、仪器仪表、工业自动化等领域。
单片机ADC技术在嵌入式系统中发挥着重要作用,因其集成度高、成本低、功耗小、易于编程等特点而备受工程师们的青睐。
2. 单片机ADC原理单片机ADC的基本原理是通过采样和量化过程将连续模拟信号转换为离散数字信号。
首先,外部模拟信号经过模拟开关传递给采样电容,然后经过采样保持电路固定时间后,再由电压比较器比较采样保持电压与参考电压的大小,进而产生一个数字输出。
通常情况下,单片机ADC的参考电压是一个固定值,其精度对于整个系统的准确度至关重要。
3. 单片机ADC精度的影响因素在实际应用中,单片机ADC的精度会受到多种因素的影响。
以下是几个常见的影响因素:3.1 参考电压的精度参考电压的精度直接影响着ADC转换结果的准确度。
如果参考电压精度较低,那么ADC的测量结果会存在较大的误差。
因此,为了提高ADC精度,可以选择高稳定性、高准确度的参考电压源。
3.2 噪声干扰噪声干扰是影响ADC转换精度的另一个主要因素。
噪声可以来自各种源,包括电源噪声、地线噪声、射频干扰等。
为了降低噪声干扰对ADC性能的影响,可以采取一系列措施,如提高电源滤波能力、合理布线、使用屏蔽罩等。
3.3 电源稳定性供电电源的稳定性对于ADC的精度有着重要影响。
当供电电压波动较大时,ADC的参考电压和转换结果都会受到影响,导致转换精度下降。
因此,应该尽量保证供电电源的稳定性,如使用稳压器或电池供电。
4. 提高ADC精度的方法为了提高单片机ADC的精度,工程师们可以采取以下几种常用方法:4.1 增加参考电压精度参考电压的精度直接影响ADC转换结果的准确度。
噪声整形SAR_ADC设计

噪声整形SAR_ADC设计噪声整形SAR_ADC是一种用于模拟信号数字化转换的关键电路,它在许多应用领域中发挥着重要作用。
本文将介绍噪声整形SAR_ADC的设计原理、工作原理以及其在电子系统中的应用。
噪声是电子系统中不可避免的现象,它来自于各种源头,如电源噪声、电路元件的热噪声以及外部干扰等。
在信号的采集和处理过程中,噪声会对信号的准确性和精度产生不良影响。
因此,噪声整形SAR_ADC的设计就是为了尽可能地降低噪声的干扰,提高信号的采集精度。
噪声整形SAR_ADC的设计原理基于逐次逼近寻找最佳比较电压来实现信号的模拟信号数字化转换。
其工作原理可以简要描述如下:首先,输入的模拟信号经过采样保持电路进行采样,然后由比较器与DAC进行逐次逼近比较,以找到最佳比较电压。
接着,通过数字控制逻辑电路对比较结果进行编码,最终输出数字信号。
在整个转换过程中,噪声整形电路起到了关键作用,它通过滤波、抑制和校准等技术手段来降低噪声的干扰,提高信号的采集质量。
噪声整形SAR_ADC在许多电子系统中都有广泛的应用。
在通信系统中,它被用于信号的调制和解调;在医疗设备中,它用于生物信号的采集和处理;在工业控制系统中,它被用于传感器信号的采集和反馈控制等。
通过合理设计和优化,噪声整形SAR_ADC可以实现高速、高精度和低功耗的特性,适应不同应用场景的需求。
总之,噪声整形SAR_ADC的设计是电子系统中不可或缺的一部分。
它通过降低噪声的干扰,提高信号的采集精度,为信号的后续处理和应用提供了可靠的数据基础。
随着科技的不断进步和应用需求的不断提高,噪声整形SAR_ADC的设计将继续发展和创新,为电子系统的性能提升和功能扩展提供更好的支持。
ADC采样误差分析

ADC采样误差分析摘要本文将介绍ADC(模数转换器)采样过程中产生的误差,并分析其对数据准确性的影响。
首先,我们将回顾ADC的工作原理和采样流程。
接着,将介绍ADC采样误差的分类及其原因。
最后,将讨论一些解决ADC采样误差的方法。
1. ADC工作原理和采样流程回顾ADC是一种将模拟信号转换为数字信号的器件。
它通常由样本保持电路(Sample and Hold Circuit)、模拟到数字转换器(Analog-to-Digital Converter)和数字数据处理电路等组成。
ADC采样过程包括采样、保持和转换三个步骤。
在采样阶段,ADC对模拟信号进行离散化,即按一定时间间隔对输入信号进行采样。
采样过程中需要考虑信号的带宽、信噪比等因素。
在保持阶段,样本保持电路将采样到的信号保持在一个稳定的电压上,以便转换器能够准确地对信号进行转换。
保持阶段对信号保持时间的控制十分重要,过长或过短的保持时间都会引起误差。
在转换阶段,模拟信号被转换为数字信号。
转换器的精度和速度对转换结果的准确性有着重要影响。
ADC通常使用逐次逼近(Successive Approximation)或逐次逼近寻找法(SAR-ADC)进行模拟到数字的转换。
2. ADC采样误差的分类及原因ADC采样过程中会产生各种误差,主要包括量化误差、采样保持误差、线性度误差和噪声误差等。
2.1 量化误差量化误差是由于数字化过程中对模拟信号进行离散化所引起的误差。
在ADC 中,模拟信号被划分为多个离散的电平,每个电平对应一个数字代码。
量化误差即为模拟信号与其对应的数字代码之间的差值。
量化误差的主要原因是ADC的分辨率有限,即能够表示的电平数目是有限的。
2.2 采样保持误差采样保持误差是由于样本保持电路在信号保持阶段引入的误差。
样本保持电路在保持信号的过程中,可能会存在保持电容的不均匀性、采样切换的延迟等问题,导致采样信号与原始信号之间产生差异。
2.3 线性度误差线性度误差是指ADC在转换过程中由于非线性特性引起的误差。
ADC有哪些实际应用-如何利用噪声扰动提高ADC无杂散动态范围-

ADC有哪些实际应用?如何利用噪声扰动提高ADC无杂散动态范围?ADC是模数转换器的简称,在本文中不是游戏中的ADC哦。
为了增进大家对ADC的认识,本文将基于两个方面介绍ADC:1.ADC的实际应用、2.如何利用噪声扰动提高ADC无杂散动态范围。
如果你对ADC具有兴趣,不妨和我一起继续往下阅读哦。
一、ADC实际应用1.音乐录制模数转换器是2000年代音乐再现技术和基于数字音频工作站的声音记录所不可或缺的。
人们通常使用模拟记录在计算机上制作音乐,因此需要模数转换器来创建脉冲码调制(PCM)数据流,该数据流会进入光盘和数字音乐文件。
当前用于音乐的模数转换器可以以高达192 kHz的速率采样。
在这些问题上存在大量文献,但是商业考虑通常起着重要作用。
许多录音棚采用24位/ 96 kHz(或更高)脉冲编码调制(PCM)或直接流数字录音(DSD)格式,然后对信号进行下采样或抽取,以进行光盘数字音频制作(44.1 kHz),对于常用的广播和电视广播应用,由于人类的奈奎斯特频率和听觉范围,将其降低到48 kHz 。
2.数字信号处理要求ADC处理,存储或传输几乎任何数字形式的模拟信号。
例如,电视调谐卡使用快速视频模数转换器。
慢速片上8、10、12或16位模数转换器在微控制器中很常见。
数字存储示波器需要非常快速的模数转换器,这对于软件定义的无线电及其新应用也至关重要。
3.科学仪器数字成像系统通常使用模数转换器将像素数字化。
一些雷达系统通常使用模数转换器将信号强度转换为数字值,以进行后续信号处理。
许多其他原位和遥感系统通常使用类似技术。
所得数字化数值中的二进制位数反映了分辨率,xxx的离散量化级数(信号处理)。
模拟信号和数字信号之间的对应关系取决于量化误差。
量化过程必须以足够的速度进行,这可能会限制数字信号的分辨率。
科学仪器中的许多传感器都会产生模拟信号。
温度、压力、pH、光强度等。
所有这些信号都可以放大并馈送到模数转换器,以产生与输入信号成比例的数字。
sigma-delta ADC

Σ-Δ ADCsigma-delta ADC 的基本思想是先对信号进行过采样,接着用负反馈网络对量化噪声进行低频衰减,高频放大,把大部分噪声功率整形到信号频带之外,最后用数字滤波器滤除带外噪声,达到提高精度的目的。
在介绍Σ-Δ ADC 之前,我们先对传统ADC 进行量化噪声分析ADC 输入的模拟量是连续的,而输出的数字量是离散的,用离散的数字量表示连续的模拟量,需要经过量化和编码,由于数字量只能取有限位,故量化过程会引入误差,量化误差也称量化噪声。
数字量用N 位二进制数表示时最多可有N 2个不同编码。
在输入模拟信号归一化为0~1之间数值的情况下,对应输出码的一个最低有效位发生变化的最小输入模拟量的变化量为: N q 21=,对量化噪声的频域分析表明,若输入信号的最小幅度大于量化器的量化阶梯q,则量化噪声的总功率与采样频率fs 无关是个常数,且功率谱密度在0-fs/2频带内均匀分布,为白噪声,其在以±q/2量化单位所划分的各量化电平内的分布是一样的,量化噪声功率可表示为121][22/2/222q de e q e E q q e ===⎰-σ由于量化噪声均匀散布在fs 宽度的频带内(-fs/2—fs/2),所以量化噪声的功率谱密度可以表示为fsfs q f D N 222*12112)(== 由该方程可知,要想得到高信噪比信号,有两种方法,增加分辨位数N 或者采样频率fs ,当提高采样频率K 倍,N K 22=时,相当于提高N 位的分辨率,Σ-Δ ADC 就用到了提高采样频率的方法来增强信噪比,称为过采样法。
如果在过采样同时还能够对量化噪声的分布做出改变,使其不再是在fs 频带内均匀分布,而是与信号所在频带分离开来,那么通过频域滤波就能有效除去量化噪声,进一步提高信噪比,这种方式称作噪声整形,在Σ-Δ ADC 中,噪声整形是通过Σ-Δ 调制来实现的。
sigma-delta ADC 的基本原理框图描述如下其中,抗混叠滤波器是一个简单的模拟低通滤波器,其作用是抑制输入信号中超过奈奎斯特频率的高频噪声,避免因频率混叠对输出造成干扰。
高精度ADC与DAC电路设计考核试卷

B.权电阻DAC
C. R-2R梯形DAC
D. PWM C
15.以下哪种技术可以用来提高ADC的抗干扰能力?()
A.差分输入
B.单端输入
C.交流耦合
D.直流耦合
16.在ADC转换过程中,以下哪个步骤不是必须的?()
A.采样
B.量化
C.编码
D.过采样
17.对于一个理想的DAC,其输出与理想输出之间的最大偏差称为?()
A.绝对误差
B.相对误差
C.线性误差
D.非线性误差
18.在实际应用中,以下哪种因素可能会导致ADC的实际分辨率低于理想分辨率?()
A.量化噪声
B.转换速度
C.电源波动
D.采样频率
19.关于ADC和DAC的同步工作,以下描述正确的是?()
A.同步工作可以提升转换速率
B.同步工作会降低转换精度
C.同步工作有利于减小噪声
12.在高精度ADC与DAC电路中,以下哪些措施有助于减小电源噪声的影响?()
A.使用模拟地和数字地分离
B.使用差分信号路径
C.增加去耦电容
D.使用低噪声电源
13.以下哪些因素会影响ADC的动态范围?()
A.转换器的位数
B.输入信号幅度
C.量化噪声
D.采样频率
14.在DAC的设计中,以下哪些结构可以提供更高的线性度?()
高精度ADC与DAC电路设计考核试卷
考生姓名:__________答题日期:_______年__月__日得分:____________判卷人:__________
一、单项选择题(本题共20小题,每小题1分,共20分,在每小题给出的四个选项中,只有一项是符合题目要求的)
ADC噪声分析与消除

ADC的输入噪声:好噪声,坏噪声和丑噪声。
有些噪声怎样可以是好噪声?美国模拟器件公司Walt Kester(walt.kester@)引言所有模数转换器(ADC)都有一定数量的折合到输入端的噪声——它被看作一种与无噪声ADC 的输入端串联的噪声源模型。
不能把折合到输入端的噪声与量化噪声相混淆,量化噪声仅在ADC 处理随时间变化的信号时有意义。
在大多数情况下,输入噪声越小越好;但是在有些情况下,输入噪声实际上对提高分辨率是有帮助的。
如果现在你觉得这似乎没有道理,那么请阅读本文以弄明白有些噪声怎样可以是好噪声。
折合到输入端的噪声(编码变迁噪声)实际的ADC在许多方面与理想的ADC有偏差。
折合到输入端的噪声(又称作有效输入噪声)无疑是偏离理想值,它对ADC总传递函数的影响如图1所示。
当模拟输入电压增加时,“理想的”ADC(如图1a所示)保持一个恒定的输出编码直到达到一个变迁区,在那一点上输出编码立刻跳变到下一个量化值,并且一直保持到达到下一个变迁区域。
理论上理想的ADC具有零编码变迁噪声,并且变迁区域的宽度等于零。
实际的ADC有一定数量的编码变迁噪声,因而具有有限的变迁区域宽度。
图1b示出编码变迁噪声宽度约为一个最低有效位(LSB)峰峰值(P-P)噪声的情况。
(Translation of Figure 1)IDEAL ADC = 理想的ADCACTUAL ADC = 实际的ADCDIGITAL OUTPUT = 数字输出ANALOG INPUT = 模拟输入图1. 编码变迁噪声(折合到输入端的噪声)及其对ADC传递函数的影响从内部结构来看,所有ADC电路都会由于电阻器噪声和“kT/C”噪声而产生一定数量的有效值(RMS)噪声。
这种噪声,甚至对于直流输入信号也会出现,认为是造成编码变迁噪声的原因,现在通常称作折合到输入端的噪声。
折合到输入端的噪声最常用的表征方法是检查大量输出采样的直方图,同时ADC的输入端保持在一个恒定的直流值。
ADC原理及的应用
高精度Delta-Sigma A/D转换器的原理及其应用本次在线座谈主要介绍TI的高精度Delta-Sigma A/D转换器的原理及其应用,Delta-Sigma转换器的特点是将绝大多数的噪声从动态转移到阻态,通常Delta-Sigma转换器被用于对成本与精度有要求的低频场合。
本文首先将对TI的高精度Delta-Sigma A/D转换器进行综述性介绍,而后将介绍噪声的测量及芯片ADS1232等。
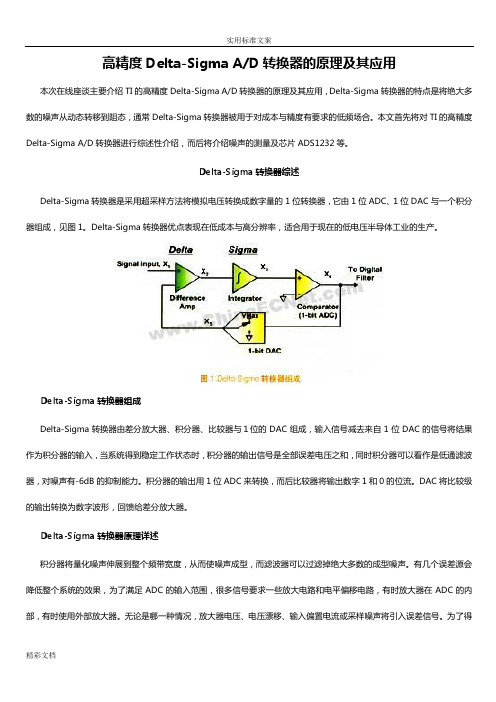
Delta-Sigma转换器综述Delta-Sigma转换器是采用超采样方法将模拟电压转换成数字量的1位转换器,它由1位ADC、1位DAC与一个积分器组成,见图1。
Delta-Sigma转换器优点表现在低成本与高分辨率,适合用于现在的低电压半导体工业的生产。
Delta-Sigma转换器组成Delta-Sigma转换器由差分放大器、积分器、比较器与1位的DAC组成,输入信号减去来自1位DAC的信号将结果作为积分器的输入,当系统得到稳定工作状态时,积分器的输出信号是全部误差电压之和,同时积分器可以看作是低通滤波器,对噪声有-6dB的抑制能力。
积分器的输出用1位ADC来转换,而后比较器将输出数字1和0的位流。
DAC将比较级的输出转换为数字波形,回馈给差分放大器。
Delta-Sigma转换器原理详述积分器将量化噪声伸展到整个频带宽度,从而使噪声成型,而滤波器可以过滤掉绝大多数的成型噪声。
有几个误差源会降低整个系统的效果,为了满足ADC的输入范围,很多信号要求一些放大电路和电平偏移电路,有时放大器在ADC的内部,有时使用外部放大器。
无论是哪一种情况,放大器电压、电压漂移、输入偏置电流或采样噪声将引入误差信号。
为了得到精确的ADC转换结果,放大器的误差应该通过调整来消除或减少。
积分器对输入低频或直流信号内置一个低通滤波器,从而极大地降低了通道内的噪声。
典型的半导体放大器的噪声分为两个部分,1/F噪声和对地噪声,Delta-Sigma ADC的主要应用是在低频场合,因此1/F噪声的影响占主要地位。
adc模块的工作原理

adc模块的工作原理ADC模块(Analog-to-Digital Converter,模数转换器)是一种电子模块,用于将模拟信号转换为数字信号。
其工作原理包括采样、量化和编码三个步骤。
下面将详细介绍ADC模块的工作原理。
首先是采样(Sampling)过程。
模拟信号是连续的,而数字信号是离散的,所以在进行模数转换之前,需要对模拟信号进行采样。
采样就是周期性地获取模拟信号的瞬时值。
ADC模块中会有一个采样保持电路,用于将输入模拟信号的电压值保持在一个稳定的电容上,并在采样时刻进行采样。
采样时间的持续时间取决于采样率,也就是每秒采样的次数。
常见的采样率有8kHz、16kHz、32kHz、48kHz等。
接着是量化(Quantization)过程。
模拟信号经过采样后,还需要将连续的模拟信号分为离散的级别。
ADC模块中通常会使用一个比较器电路来比较采样电压与参考电压的大小关系,并将其转换为相应的数字量。
量化过程需要确定量化水平的数目,也就是基本的量化级别数目。
量化级别数目越多,模拟信号的精度越高,但同时也会需要更多的位数来表示采样后的信号。
一般来说,ADC模块的分辨率通常在8位至24位之间。
分辨率为n位的ADC模块可以产生2^n个量化级别。
最后是编码(Encoding)过程。
编码是将量化后的信号转换为数字量并输出的过程。
ADC模块中一般采用二进制编码形式,即把量化值转换为相应的二进制码。
编码方式有两种常用的类型:直接编码和差分编码。
直接编码是采用二进制补码形式表示,其中最低有效位(LSB)为量化水平之间的等间距,最高有效位(MSB)为符号位。
差分编码是相邻两个采样点之间的差值进行编码。
差分编码可以减小量化噪声的影响,并且能够使得编码结果更加准确。
编码后的数字信号可以通过并行输出或串行输出的方式传递给其他电路进行处理。
总结起来,ADC模块的工作原理包括采样、量化和编码三个步骤。
它能够将模拟信号转换为数字信号,实现数字系统与模拟信号的接口。
噪声整形SAR_ADC的建模

噪声整形SAR_ADC的建模近年来,随着科技的发展,模拟信号变换为数字信号的过程变得越来越重要。
SAR_ADC(Successive Approximation Register Analog-to-Digital Converter)作为一种常见的模拟-数字转换器,被广泛应用于通信、测量和控制系统中。
然而,SAR_ADC并非完美无缺,其中一个主要问题是噪声。
噪声是指ADC的输出信号中与输入信号无关的不相关信号。
噪声会导致ADC的输出结果偏离真实值,从而降低了系统的精度和可靠性。
为了解决这个问题,人们提出了噪声整形技术。
噪声整形旨在通过一系列的电路和算法,减小SAR_ADC中的噪声干扰,提高系统的性能。
噪声整形的核心思想是通过对输入信号的采样和量化,以及对量化结果的处理,减小ADC输出中的噪声。
具体来说,噪声整形包括以下几个方面:首先,采样过程是噪声整形的第一步。
合理的采样方式可以降低输入信号中的噪声。
常用的采样方式包括均匀采样和随机采样。
均匀采样是指以固定的时间间隔对输入信号进行采样,而随机采样则是以不规则的时间间隔对输入信号进行采样。
这两种采样方式都可以有效地降低噪声。
其次,量化过程是噪声整形的关键步骤。
ADC将连续的模拟信号转换为离散的数字信号,这个过程中会引入量化误差。
为了减小量化误差,可以采用高精度的ADC和过采样技术。
高精度的ADC可以提高量化的精度,而过采样技术则可以增加采样点的数量,从而减小量化误差。
最后,在量化结果的处理过程中,可以采用数字滤波器或者数字后处理技术来进一步减小噪声。
数字滤波器可以通过滤波器的设计和参数设置,滤除ADC输出中的噪声成分。
数字后处理技术则可以通过对量化结果的处理,进一步降低噪声。
总的来说,噪声整形技术是为了提高SAR_ADC的性能而提出的一种方法。
通过合理的采样、量化和处理,可以减小ADC 输出中的噪声干扰,提高系统的精度和可靠性。
随着技术的不断发展,相信噪声整形技术将在各个领域发挥更大的作用,推动模拟-数字转换技术的进一步发展。
Σ-Δ ADC的工作原理

ADC主流类型有: Σ-Δ型(Sigma-Delta)、逐次比较型(SAR)、流水线型(Pipeline)、并行比较型(Flash)。
下图为这四种类型主要特点的对比。
越来越多的应用,诸如音频、测量等,都需要高分辨率、高集成度和价格低廉的ADC。
新型Σ-Δ转换技术恰好可以满足上述需求。
下面介绍Σ-Δ ADC的工作原理,其主要过程包括:过采样、噪声成形、数字滤波和抽取。
1、过采样对于一个Nbit ADC,由SNR的公式:SNR=6.02N+1.76dB可知,为了改善SNR和更为精确地再现输入信号,对于传统ADC来讲,必须增加位数。
将采样频率提高一个过采样系数k,即采样频率为Kfs,则由FFT分析显示噪声基线降低,SNR值未变,但噪声能量分散到一个更宽的频率范围。
Σ-Δ转换器正是利用了这一原理,具体方法是紧接着1bit ADC之后进行数字滤波。
大部分噪声被数字滤波器滤掉,这样,RMS噪声就降低了,从使得Σ-Δ转换器能够从一个低分辨率ADC 获得宽动态范围。
图2 N位ADC以频率kfs采样单音信号的频谱分析图3 数字滤波器对噪声频谱的滤除效应2、噪声成形通过下图所示的一阶Σ-Δ调制器的工作原理,可以理解噪声成形的工作机制。
Σ-Δ调制器包含1个差分放大器、1个积分器、1个比较器以及1个由1bit DAC(1个简单的开关,可以将差分放大器的反相输入接到正或负参考电压)构成的反馈环。
反馈DAC的作用是使积分器的平均输出电压接近于比较器的参考电平。
调制器输出中“1”的密度将正比于输入信号,如果输入电压上升,比较器必须产生更多数量的“1”,反之亦然。
积分器用来对误差电压求和,对于输入信号表现为一个低通滤波器,而对于量化噪声则表现为高通滤波。
这样,大部分量化噪声就被推向更高的频段。
和前面的简单过采样相比,总的噪声功率没有改变,但噪声的分布发生了变化.图4 Σ-Δ调制器框图在Σ-Δ调制器中采用更多的积分与求和环节,可以提供更高阶数的量化噪声成形。
高精度sigma-delta ADC的研究与设计

高精度sigma-delta ADC的研究与设计高精度sigma-delta ADC的研究与设计摘要:随着现代通信技术的发展,对高精度的模拟-数字转换(ADC)器件的需求日益增加。
sigma-delta ADC作为一种高精度、高速的转换器,在各个领域得到了广泛的应用。
本文将对高精度sigma-delta ADC的研究与设计进行探讨。
首先,概述了sigma-delta ADC的基本原理,并深入剖析了其优缺点。
然后,详细介绍了sigma-delta ADC的设计流程,包括模拟前端设计、数字滤波器设计、数字后处理等方面。
最后,通过实际案例验证了设计的可行性和有效性。
本文旨在为高精度sigma-delta ADC的研究与设计提供参考,希望能够对相关领域的研究人员提供一定的帮助。
一、引言近年来,模拟-数字转换技术在通信、医疗、工业控制等领域得到了广泛的应用。
高精度的ADC器件是实现这些应用的关键。
sigma-delta ADC由于其高精度、高动态范围、低功耗等优点,成为了各领域广泛采用的ADC芯片。
本文将对高精度sigma-delta ADC进行研究与设计,以满足近年来对高精度ADC的需求。
二、sigma-delta ADC的基本原理sigma-delta ADC是一种基于过采样和噪声整形的ADC技术。
其基本原理是通过将输入信号过采样,并利用高阶模拟滤波器抑制高频噪声,将输入信号的动态范围转移到更低频率范围内,从而增加了ADC的分辨率。
sigma-delta ADC主要分为模拟前端和数字后端两个部分,通过这两个部分的协同工作,实现了高精度的模拟-数字转换。
三、sigma-delta ADC的优缺点1. 优点:(1)由于过采样和高阶滤波器的使用,sigma-delta ADC具有较高的分辨率和动态范围;(2)sigma-delta ADC可以利用硬件结构的优化和数字滤波器的后处理,实现较高的抗干扰能力;(3)sigma-delta ADC的功耗较低,适用于低功耗应用。
减小ADC量化噪声的技术

减小ADC量化噪声的技术关键字:采样噪声功率周期电压转换器数模转换器(ADC)提供了许多系统中模拟信号到数字信号的重要转换。
它们完成一个模拟输入信号到二元有限长度输出命令的振幅量化,范围通常在6到18b 之间,是一个固有的非线性过程。
该非线性特性表现为ADC二元输出中的宽带噪声,称作量化噪声,它限制了一个ADC的动态范围。
本文描述了两种时下最流行的方法来改善实际ADC应用中的量化噪声性能:过采样和高频抖动。
为理解量化噪声缩减法,首先让我们回顾一下,一个理想的N位ADC的信号与量化噪声比为(单位dB)SNR Q=6.02N+4.77+20log10(L F)dB,其中:L F=ADC的输入模拟电压级的加载因子测量(SNR Q由参考资料1提供)。
参数L F定义为模拟输入电压的均方根(RMS)除以ADC的峰值输入电压。
当ADC的输入电压为一个可以覆盖转换器满量程电压的正弦曲线,L F=0.707。
假如那样的话,SNR Q等式中的最后一项变为?3dB,并且ADC的最大输出信号与噪声比为:SNR Q-max=6.02N+4.77?3=6.02N+1.77dB。
在技术文献中非常普遍的SNR Q-max公式说明了为什么工程师要对ADC的SNR使用一个经验值6dB/b。
作为一个应用问题,SNR Q-max公式是不切实际的乐观。
首先,SNR公式描绘了一个在现实世界中不存在的理想ADC。
第二,在实际应用中,ADC的输入极少会覆盖全部值。
现实世界的模拟信号通常实际上是脉冲信号,而促使ADC的输入变为饱和引发了可大大减小ADC输出SNR的信号切割。
但是,本文将假设一个使用大部分输入模拟电压范围的高品质ADC而非研究最坏情况下的场景。
假定ADC的SNR为6dB/b,下一步是考虑作为可能改进SNR Q的过采样法。
减小ADC量化噪声的过采样过程简单直观。
模拟信号在f s采样率被数字化,该采样率高于满足Nyquist标准(两倍输入模拟信号带宽)所需的最小采样率,然后被低通过滤。
Digital Dither技术简析

Digital Dither技术简析【摘要】本文介绍了数字抖动的量化定理,给出了其应用的范畴及性质,分布形态近似满足正态分布,并简单阐述了数字Dither对截位误差的抑制作用和对微分非线性的改善作用。
其中数字Dither的特征函数是一个基础性公式。
【关键词】数字抖动;量化定理;正态分布;应用0 引言Dither的中文意思为“抖动”,当前,Dither技术是用来抑制模数转换器ADC 量化噪声QN,提高ADC的性能指标较有效的方法,并产生了大量的相关理论和方法。
但是,现有的Dither技术及其理论方法处理的信号基本是时间和幅度上都连续的模拟信号,然而,随着数字信号处理DSP和计算机技术的大力发展,用有限的字长来表征模拟信号使之数字化是未来技术的发展趋势和必然要求。
因此,有必要研究数字通信系统中的DigitalDither技术。
通常对数字Dither采用一种“重量化”技术,先将Dither信号转换成一些离散的中间变量,以便于存储和处理。
在第2次量化之前,将转化的Dither信号值添加到待处理的信号之中,以达到数字化处理的要求。
另外一种方法,用伪随机数发生器来产生Dither采样信号,经过数模转换器DAC转换成模拟信号,按照传统方法加入到输入信号中,再进行量化。
这两种方法没有好坏之分,可通过对ADC的性能指标进行分析,以便得到最优的数字Dither信号。
作为一篇综述性文章,主要探讨了数字Dither的量化理论和重要应用,从而为后续的研究提供了一定的参考。
1 有效性采样和量化1.1 数字Dither量化定理2000年,美国科学家Wannamaker、Lipshitz 等提出了一个有趣的问题:严格来说,几乎没有数字Dither能够完全地消除量化噪声,加入数字Dither只可使量化噪声尽可能变小而不能为0。
从他们的工作中总结出数字抖动量化定理QTDD,该定理在实际的应用可作为指导性条件[1]。
r-1阶加型二进制数字Dither系统中,Φd(u)为Dither信号的特征函数,对u求导,有如下量化定理:■|■=0 t=0,1,…,r-1量化定理指出:对Dither的特征函数做任意阶数次求导,其值为0。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2008-07-13 15:05:17 减小ADC 量化噪声的技术作者:RichardLyons 来源:电子系统设计关键字:采样噪声功率周期电压转换器数模转换器(ADC)提供了许多系统中模拟信号到数字信号的重要转换。
它们完成一个模拟输入信号到二元有限长度输出命令的振幅量化,范围通常在6到18b 之间,是一个固有的非线性过程。
该非线性特性表现为 ADC 二元输出中的宽带噪声,称作量化噪声,它限制了一个 ADC 的动态范围。
本文描述了两种时下最流行的方法来改善实际 ADC 应用中的量化噪声性能:过采样和高频抖动。
为理解量化噪声缩减法,首先让我们回顾一下,一个理想的N 位ADC 的信号与量化噪声比为(单位dB)SNR Q =6.02N+4.77+20log 1o (L F)dB ,其中:L F =ADC 的输入模拟电压级的加载因子测量(SNR Q 由参考资料1提供)。
参数L F 定义为模拟输入电压的均方根(RMS) 除以ADC 的峰值输入电压。
当ADC 的输入电压为一个可以覆盖转换器满量程电压的正弦曲线, L F =0.707。
假如那样的话,SNR Q等式中的最后一项变为?3dB ,并且ADC 的最大输出信号与噪声比为:SNR Q-max =6.02N+4.77?3=6.02N+1.77dB 。
在技术文献中非常普遍的 SNR Q-max 公式说明了为什么工程师要对 ADC 的SNR 使用一个经验值6dB/b 。
作为一个应用问题,SNR Q-max 公式是不切实际的乐观。
首先, SNR 公式描绘了一个在现实世界中不存在的理想 ADC 。
第二,在实际应用中,ADC 的输入极少会覆盖全部值。
现实世界的模拟信号通常实际上是脉冲信号,而促使 ADC 的输入变为饱和引发了可大大减小 ADC 输出SNR 的信号切割。
但是,本文将假设一个使用大部分输入模拟电压范围的高品质 ADC 而非研究最坏情况下的场景。
假定ADC 的SNR 为6dB/b ,下一步是考虑作为可能改进 SNR Q 的过采样法。
减小ADC 量化噪声的过采样过程简单直观。
模拟信号在f s 采样率被数字化,该采样率高于满足Nyquist 标准(两倍输入模拟信号带宽)所需的最小采样率,然后被低通过滤。
过采样基于如下假设:一个 ADC 的总量化噪声功率(方差)为转换器最小有效位(LSB)电压的平方除以12 : 总量化噪声功率=<T 2=(LSB value)/12过采样同样假设量化噪声值是真实随机的;这意味着在频率范围内,量化噪声有一个平滑的频谱。
(如果ADC 是由一个覆盖转换器模拟输入电压范围重要部分的模拟信号驱动且周期性不明显,该假设有效)。
图1显示了量化噪声的另一方面,功率频谱密度(PSD)。
这是在每Hz 噪声功率下测量的量化噪声的频率范围特征。
利用PSD ,量化噪声可以被表示为每单位带宽的功率大小。
随机噪声假设得到的总量化噪声(基于转换器LSB 电压的固定值)被均匀分布在PSDShaded region*lim the sameareaFreq naloganti aliasing kwvpass filterDigrtalconverter lawpass―filterDecimation频率范围内,从?f s/2到+f s/2,如图1所示。
该量化噪声 PSD的振幅为总量化噪声功率除以总带宽f s,其中振幅出现在总带宽上:PSD noise =[(LSB value) 2/12](1/f s)=(LSB value) 2/12f s单位为W/Hz。
下一个问题是:怎样才能减小PSD noise等级?”利用一个具有附加位分解的 ADC,可以减小分子中的LSB值,这个ADC将减小LSD值同样也减小PSD noise。
不过这是一个昂贵的解决办法。
更好的办法是用更高采样率来增大分母。
采用更高采样率的结果在图2(a)中用低级离散信号表示。
通过将 ADC的f s,old采样率增加到某一更高值f s,new (过采样),总噪声功率(一个不变值)被分布在一个广泛的频率范围内[图2(b)]。
由于一个转换器的总量化噪声功率仅依赖于位数而不是采样率,图2(a)和2(b)中阴暗曲线下的面积相等。
将一个低通过率器放在转换器的输出来减小量化噪声等级对信号的损害。
S >gna I ofinterestantLowpa ss filterresponse^⑹ 、|////必N The concept of oversampling can be shown means of (a) twlae PSD al U|dd rale;(b) noise PSD at tfie higher f fr|n fiW rate, and ^c) processing steps.通过过采样得到改进的信号与量化噪声比为,以dB为单位:SNR Q-gain =10IOg 10 (f s,new /f s,old ) oSNR Q-gain表达式的出处在参考资料1中提供。
作为一个SNR的函数,N位ADC的位数大约是SNR/6,因此总有效位数为10log(M)/6+N ,其中M=f s,new /f s old ,o这意味着如果采样率 M为2,则ADC的有效位数是N os=0.5+N。
利用因数为2的过采样,可获得在有效 SNR中的一半位。
获得一个特殊的K额外有效位数所需的过采样率M由式子M=4 K得出,因而有效位数为 N os=K+N o(a)1 0 Isb 0.5 1st!-OJ Isb -1,0 Isb .Converter _ output code--------------(c)i.oisb 05 I 曲Converterquantization error^八一一…一 一…一-0.5 Isb■■豐-1.0 Isb ..................... .... . ........................................3. Quantization errors can occur >when a sampled (a) lortJevel anatog signal is converted to {b) an AUU output sequence, resulting in highly penodic quantization noise (cj.举例说明,如果 f s,oid =100kHz ,且 f s ,new=400kHz , SNR Q-gain =10log 10(4)=6.02dB 。
这样,因数为 4 的过采样(和过滤)将量化噪声减小到1b 。
从而,有可能由一个 N 位ADC 得到N+1位的性能,因为信号振幅分解是以更高采样速度为代价得到 的。
经过数字过滤后,输出信号可以被减小到低级f s,old 而不会有损改进了的 SNR 。
当然,为了能从过采样方案中受益,用于低通滤波器系数和寄存器的位数必需超过 ADC 的初始位数。
通过利用依赖于用x(t)表示的干扰模拟噪声的数字低通过率器,就有可能采用图 2(c)中与低采样率下所需的模拟过滤器相对的低性能(更简单)模拟抗混迭滤波器。
第二个用来最小化 ADC 量化噪声影响的技术是高频抖动,它在进行模拟数字转换前将噪声加入模拟信号。
一个例子是,图 3(a)中显示的数字化低级模拟正弦信号。
该信号的峰值电压刚刚超过了单个ADC 的LSB 电压级,引起转换器输出x 1 (n)个样本。
由于高峰值正弦电压级,x 1(n)输出序列被省略,并且在其频谱范围内产生谱谐波,该谐波与图 3(c)中的量化噪声周期一样很明显。
A Ki(n)-▼•■呼r ■■呼叩于甲 ................i i v i t t P i v i- 4.L ・ A 」.」L J-1.4. L J ------------ -------- I d ft I I I I Illi p i ■ | t t I | l |i I丄上 .................... .... ........ KW 亡■ a ■ * * —H K{H)J J LftandomanalogDigitalpsei-idorHndorn notse £enerat<?r4 These spectra show a discrete sinusoid with: (a) no dithering and (b) wkiti ditheiing.图4(a)显示x i(n)的频谱,以dB为单位,在那里乱真量化噪声谐波非常明显。
平均多频谱不可能将某些频谱关注的部分提升到那些乱真谐波级之上,注意到这点很有所值。
因为量化噪声与输入正弦波紧密相关,量化噪声的时间周期与输入正弦波一样,频谱平均同样也会提高噪声谐波级。
然而高频抖动将提供帮助。
高频抖动的结果为一个越过附加转换器LSB界限且产生更随机量化噪声的噪声模拟信号,以及降低不希望出现的频谱谐波级[图4(b)]。
抖动提高了平均频谱噪声基数但却使SNR2增加。
抖动迫使量化噪声丧失其与初始输入信号的一致性,如果想要的话,该一致性将会从平均化中受益。
当数字化低振幅模拟信号,长周期模拟信号(比如在采样时间间隔中有偶数周期的正弦波),和变化缓慢的(低频或DC)模拟信号时,高频抖动十分有用。
图5(a)显示了高频抖动的标准执行。
由噪声二极管或噪声产生器集成电路提供,用于该过程的大量随机宽带模拟噪声具有一个峰到峰值为1/3-to-1LSB 电压级。
Wannamaker已经表示使用TPDF的抖动处理会导致具有不变零均值和独立于输入信号特征的不变(非零)功率的量化噪声。
这些都是量化噪声非常期待的特性;前者保证数字转换器的输出平均起来等于输入;后者保证将不会出现噪声调制”噪声调制在量化噪声的功率依赖于信号或者被信号调制时出现。
这对音频信号来说具有感性意义,而且通常是不需要的。
对苛求的高性能音频应用来说,工程师已经发现该类型的抖动是理想的。
它可以通过从两个分离的,独立的,均匀分布的(也称作矩形PDF)噪声产生器增加抖动噪声产生。
两个独立噪声源之和的PDF是它们各自PDF的卷积。
因为两个矩形函数的卷积是三角形的,这个双噪声源抖动方案产生所需的TPDF。
理想的TPDF抖动噪声具有刚好两个 LSB电压级的峰对峰级。
5. The two forms of dithering are standard or non-subtractive dithering <a) andsubtractive djltiehng (b).在关注信号占据了全频带 0 到 f s/2 中某些已明确定义部分的情况下,发射具有等同于 4 到 6LSB 电压级的峰对峰值,和具有信号带外部频谱能量的频谱状抖动噪声将是有益的。
