七年级下册数学压轴题集锦 (1) 2
(完整版)人教版数学七年级下册期末几何压轴题考试题(一)

一、解答题1.如图所示,A (1,0)、点B 在y 轴上,将三角形OAB 沿x 轴负方向平移,平移后的图形为三角形DEC ,且点C 的坐标为(﹣3,2).(1)直接写出点E 的坐标 ;(2)在四边形ABCD 中,点P 从点B 出发,沿“BC→CD”移动.若点P 的速度为每秒1个单位长度,运动时间为t 秒,回答下列问题:①当t= 秒时,点P 的横坐标与纵坐标互为相反数;②求点P 在运动过程中的坐标,(用含t 的式子表示,写出过程);③当点P 运动到CD 上时,设∠CBP=x°,∠PAD=y°,∠BPA=z°,试问 x ,y ,z 之间的数量关系能否确定?若能,请用含x ,y 的式子表示z ,写出过程;若不能,说明理由.2.如图,直线//PQ MN ,点C 是PQ 、MN 之间(不在直线PQ ,MN 上)的一个动点.(1)如图1,若1∠与2∠都是锐角,请写出C ∠与1∠,2∠之间的数量关系并说明理由; (2)把直角三角形ABC 如图2摆放,直角顶点C 在两条平行线之间,CB 与PQ 交于点D ,CA 与MN 交于点E ,BA 与PQ 交于点F ,点G 在线段CE 上,连接DG ,有BDF GDF ∠=∠,求AEN CDG∠∠的值; (3)如图3,若点D 是MN 下方一点,BC 平分PBD ∠, AM 平分CAD ∠,已知25PBC ∠=︒,求ACB ADB ∠+∠的度数.3.已知,AB ∥CD ,点E 为射线FG 上一点.(1)如图1,若∠EAF =25°,∠EDG =45°,则∠AED = .(2)如图2,当点E 在FG 延长线上时,此时CD 与AE 交于点H ,则∠AE D 、∠EAF 、∠EDG 之间满足怎样的关系,请说明你的结论;(3)如图3,当点E 在FG 延长线上时,DP 平分∠EDC ,∠AED =32°,∠P =30°,求∠EKD 的度数.4.已知直线AB //CD ,点P 、Q 分别在AB 、CD 上,如图所示,射线PB 按逆时针方向以每秒12°的速度旋转至PA 便立即回转,并不断往返旋转;射线QC 按逆时针方向每秒3°旋转至QD 停止,此时射线PB 也停止旋转.(1)若射线PB 、QC 同时开始旋转,当旋转时间10秒时,PB '与QC '的位置关系为 ; (2)若射线QC 先转15秒,射线PB 才开始转动,当射线PB 旋转的时间为多少秒时,PB ′//QC ′.5.已知,//AE BD ,A D ∠=∠.(1)如图1,求证://AB CD ;(2)如图2,作BAE ∠的平分线交CD 于点F ,点G 为AB 上一点,连接FG ,若CFG ∠的平分线交线段AG 于点H ,连接AC ,若ACE BAC BGM ∠=∠+∠,过点H 作HM FH ⊥交FG 的延长线于点M ,且3518E AFH ∠-∠=︒,求EAF GMH ∠+∠的度数.6.已知:AB //CD .点E 在CD 上,点F ,H 在AB 上,点G 在AB ,CD 之间,连接FG ,EH ,GE ,∠GFB =∠CEH .(1)如图1,求证:GF //EH ;(2)如图2,若∠GEH =α,FM 平分∠AFG ,EM 平分∠GEC ,试问∠M 与α之间有怎样的数量关系(用含α的式子表示∠M )?请写出你的猜想,并加以证明.7.请观察下列等式,找出规律并回答以下问题.111122=-⨯,1112323=-⨯,1113434=-⨯,1114545=-⨯,…… (1)按照这个规律写下去,第5个等式是:______;第n 个等式是:______. (2)①计算:11111223344950⨯⨯⨯⨯++++. ②若a 30b -=,求:()()()()()()()()111111122339797ab a b a b a b a b +++++++++++++. 8.阅读下面文字:对于5231591736342⎛⎫⎛⎫⎛⎫-+-++- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 可以如下计算:原式()()()5231591736342⎡⎤⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-+-+++-+- ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦⎣⎦ ()()()5231591736342⎡⎤⎛⎫⎛⎫⎛⎫=-+-++-+-+-++-⎡⎤ ⎪ ⎪ ⎪⎢⎥⎣⎦⎝⎭⎝⎭⎝⎭⎣⎦ 1014⎛⎫=+- ⎪⎝⎭114=- 上面这种方法叫拆项法,你看懂了吗?仿照上面的方法,计算:(1)115112744362⎛⎫⎛⎫-+-++- ⎪ ⎪⎝⎭⎝⎭(2)235120192018201720163462⎛⎫⎛⎫-++-+ ⎪ ⎪⎝⎭⎝⎭ 9.探究与应用:观察下列各式:1+3= 21+3+5= 21+3+5+7=21+3+5+7+9=2……问题:(1)在横线上填上适当的数;(2)写出一个能反映此计算一般规律的式子;(3)根据规律计算:(﹣1)+(﹣3)+(﹣5)+(﹣7)+…+(﹣2019).(结果用科学记数法表示)10.观察下列各式:(x-1)(x+1)=x2-1(x-1)(x2+x+1)=x3-1(x-1)(x3+x2+x+1)=x4-1……(1)根据以上规律,则(x-1)(x6+x5+x4+x3+x2+x+1)=__________________.(2)你能否由此归纳出一般性规律(x-1)(x n+x n-1+x n-2+…+x+1)=____________.(3)根据以上规律求1+3+32+…+349+350的结果.11.如图1,把两个边长为1的小正方形沿对角线剪开,所得的4个直角三角形拼成一个面积为2的大正方形.由此得到了一种能在数轴上画出无理数对应点的方法.(1)图2中A、B两点表示的数分别为___________,____________;(2)请你参照上面的方法:①把图3中51⨯的长方形进行剪裁,并拼成一个大正方形.在图3中画出裁剪线,并在图4的正方形网格中画出拼成的大正方形,该正方形的边长a=___________.(注:小正方形边长都为1,拼接不重叠也无空隙)a-.(图②在①的基础上,参照图2的画法,在数轴上分别用点M、N表示数a以及3中标出必要线段的长)12.2此2的小数部分我们不可能全部写出来,于是小明用21-来表示2的小数部分,事实上,小明的表示方法是有道理的,因为2的整数部分是1,将这个数减去其整数部分,差就是2的小数部分,又例如:∵()232273<<,即273<<,∴7的整数部分为2,小数部分为()72-。
初一数学下学期压轴题精选

1.(1)如图1,把△ABC 沿DE 折叠,使点A 落在点A’处,试探索△1+△2与△A 的关系.(不必证明).(2)如图2,BI 平分△ABC ,CI 平分△ACB ,把△ABC 折叠,使点A 与点I 重合,若△1+△2=130°,求△BIC 的度数;(3)如图3,在锐角△ABC 中,BF△AC 于点F ,CG△AB 于点G ,BF 、CG 交于点H ,把△ABC 折叠使点A 和点H 重合,试探索△BHC 与△1+△2的关系,并证明你的结论.2.己知ABC ∆的三边长a 、b 、c 都是正整数,且满足22614580a b a b +--+=(1)求a 、b 的值;(2)求ABC ∆的周长的最小值.3. 9岁的小芳身高1.36米,她的表姐明年想报考北京的大学.表姐的父母打算今年暑假带着小芳及其表姐先去北京旅游一趟,对北京有所了解.他们四人7月31日下午从苏州出发,1日到4日在北京旅游,8月5日上午返回苏州.苏州与北京之间的火车票和飞机票价如下:火车 (高铁二等座) 全票524元,身高1.1~1.5米的儿童享受半价票;飞机 (普通舱) 全票1240元,已满2周岁未满12周岁的儿童享受半价票.他们往北京的开支预计如下:假设他们四人在北京的住宿费刚好等于上表所示其他三项费用之和,7月31日和8月5日合计按一天计算,不参观景点,但产生住宿、伙食、市内交通三项费用.(1) 他们往返都坐火车,结算下来本次旅游总共开支了13668元,求x ,y 的值;(2) 他们往返都坐飞机 (成人票五五折),其他开支不变,至少要准备多少元?(3) 他们去时坐火车,回来坐飞机 (成人票五五折),其他开支不变,准备了14000元,是否够用? 如果不够,他们准备不再增加开支,而是压缩住宿的费用,请问他们预定的标准间房价每天不能超过多少元?4. 如图1,一副三角板的两个直角重叠在一起,△A =30°,△C =45°△COD 固定不动,△AOB 绕着O 点顺时针旋转α°(0°< α <180° )(1)若△AOB 绕着O 点旋转图2的位置,若△BOD =60°,则△AOC =________;(2)若0°<α<90°,在旋转的过程中△BOD +△AOC 的值会发生变化吗?若不变化,请求出这个定值;(3)若90°< α <180° ,问题(2)中的结论还成立吗?说明理由;(4)将△AOB 绕点O 逆时针旋转α度(0°< α <180°),问当α为多少度时,两个三角形至少有一组边所在直线垂直?(请直接写出所有答案).5. 阅读材料:方程x 2﹣x ﹣2=0中,只含有一个未知数且未知数的次数为2.像这样的方程叫做一元二次方程.把方程的左边分解因式得到(x ﹣2)(x+1)=0.我们知道两个因式乘积为0,其中有一个因式为0即可,因此方程可以转化为:x ﹣2=0或x+1=0.解这两个一次方程得:x=2或x=﹣1.所以原方程的解为:x=2或x=﹣1.上述将方程x 2﹣x ﹣2=0转化为x ﹣2=0或x+1的过程,是将二次降为一次的“降次”过程,从而使得问题得到解决.仿照上面降次的方法,解决下列问题:(1)解方程x 2﹣3x=0;(2)2a 2﹣a ﹣3=0;(3)解方程组:. 图1 A B D C 图2 B D C A O O。
初中七年级下册期末压轴题数学附答案(一)

初中七年级下册期末压轴题数学附答案(一)一、解答题1.如图所示,A (1,0)、点B 在y 轴上,将三角形OAB 沿x 轴负方向平移,平移后的图形为三角形DEC ,且点C 的坐标为(﹣3,2).(1)直接写出点E 的坐标;(2)在四边形ABCD 中,点P 从点B 出发,沿“BC→CD”移动.若点P 的速度为每秒1个单位长度,运动时间为t 秒,回答下列问题:①当t=秒时,点P 的横坐标与纵坐标互为相反数;②求点P 在运动过程中的坐标,(用含t 的式子表示,写出过程);③当点P 运动到CD 上时,设∠CBP=x°,∠PAD=y°,∠BPA=z°,试问x ,y ,z 之间的数量关系能否确定?若能,请用含x ,y 的式子表示z ,写出过程;若不能,说明理由.2.已知直线//AB CD ,点P 为直线AB 、CD 所确定的平面内的一点.(1)如图1,直接写出APC ∠、A ∠、C ∠之间的数量关系;(2)如图2,写出APC ∠、A ∠、C ∠之间的数量关系,并证明;(3)如图3,点E 在射线BA 上,过点E 作//EF PC ,作PEG PEF ∠∠=,点G 在直线CD 上,作BEG ∠的平分线EH 交PC 于点H ,若30APC ∠= ,140PAB ∠= ,求PEH ∠的度数.3.问题情境:如图1,AB ∥CD ,∠PAB =130°,∠PCD =120°.求∠APC 的度数.小明的思路是:过P 作PE ∥AB ,通过平行线性质,可得∠APC =∠APE +∠CPE =50°+60°=110°.问题解决:(1)如图2,AB ∥CD ,直线l 分别与AB 、CD 交于点M 、N ,点P 在直线I 上运动,当点P 在线段MN 上运动时(不与点M 、N 重合),∠PAB =α,∠PCD =β,判断∠APC 、α、β之间的数量关系并说明理由;(2)在(1)的条件下,如果点P 在线段MN 或NM 的延长线上运动时.请直接写出∠APC 、α、B 之间的数量关系;(3)如图3,AB ∥CD ,点P 是AB 、CD 之间的一点(点P 在点A 、C 右侧),连接PA 、PC ,∠BAP 和∠DCP 的平分线交于点Q .若∠APC =116°,请结合(2)中的规律,求∠AQC 的度数.4.已知,如图1,射线PE 分别与直线AB ,CD 相交于E 、F 两点,∠PFD 的平分线与直线AB 相交于点M ,射线PM 交CD 于点N ,设∠PFM =α°,∠EMF =β°,且(40﹣2α)2+|β﹣20|=0(1)α=,β=;直线AB 与CD 的位置关系是;(2)如图2,若点G 、H 分别在射线MA 和线段MF 上,且∠MGH =∠PNF ,试找出∠FMN 与∠GHF 之间存在的数量关系,并证明你的结论;(3)若将图中的射线PM 绕着端点P 逆时针方向旋转(如图3),分别与AB 、CD 相交于点M 1和点N 1时,作∠PM 1B 的角平分线M 1Q 与射线FM 相交于点Q ,问在旋转的过程中1FPN Q∠∠的值是否改变?若不变,请求出其值;若变化,请说明理由.5.如图1,已AB ∥CD ,∠C =∠A .(1)求证:AD ∥BC ;(2)如图2,若点E 是在平行线AB ,CD 内,AD 右侧的任意一点,探究∠BAE ,∠CDE ,∠E 之间的数量关系,并证明.(3)如图3,若∠C =90°,且点E 在线段BC 上,DF 平分∠EDC ,射线DF 在∠EDC 的内部,且交BC 于点M ,交AE 延长线于点F ,∠AED +∠AEC =180°,①直接写出∠AED 与∠FDC 的数量关系:.②点P 在射线DA 上,且满足∠DEP =2∠F ,∠DEA ﹣∠PEA =514∠DEB ,补全图形后,求∠EPD 的度数6.已知,AB ∥CD ,点E 为射线FG 上一点.(1)如图1,若∠EAF =25°,∠EDG =45°,则∠AED =.(2)如图2,当点E 在FG 延长线上时,此时CD 与AE 交于点H ,则∠AE D 、∠EAF 、∠EDG 之间满足怎样的关系,请说明你的结论;(3)如图3,当点E 在FG 延长线上时,DP 平分∠EDC ,∠AED =32°,∠P =30°,求∠EKD 的度数.7.规定:求若干个相同的有理数(均不等于0)的除法运算叫做除方,如2÷2÷2,(-3)÷(-3)÷(-3)÷(-3)等.类比有理数的乘方,我们把2÷2÷2记作2③,读作“2的圈3次方”,(-3)÷(-3)÷(-3)÷(-3)记作(-3)④,读作“-3的圈4次方”,一般地,把n aa a a a ÷÷÷⋯÷ 个(a≠0)记作a ⓝ,读作“a 的圈n 次方”.(初步探究)(1)直接写出计算结果:2③=___,(12)⑤=___;(2)关于除方,下列说法错误的是___A .任何非零数的圈2次方都等于1;B .对于任何正整数n ,1ⓝ=1;C .3④=4③;D .负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数.(深入思考)我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?(1)试一试:仿照上面的算式,将下列运算结果直接写成幂的形式.(-3)④=___;5⑥=___;(-12)⑩=___.(2)想一想:将一个非零有理数a 的圈n 次方写成幂的形式等于___;(3)算一算:212÷(−13)④×(−2)⑤−(−13)⑥÷338.(概念学习)规定:求若干个相同的有理数(均不等于0)的除法运算叫做除方,如2÷2÷2,(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)等.类比有理数的乘方,我们把2÷2÷2记作2③,读作“2的圈3次方”,(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)记作(﹣3)④,读作“﹣3的圈4次方”,一般地,把n 个a (a ≠0)记作a ⓝ,读作“a 的圈n 次方”.(初步探究)(1)直接写出计算结果:2③=,(﹣12)⑤=;(深入思考)我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?(1)试一试:仿照上面的算式,将下列运算结果直接写成乘方的形式.(﹣3)④=;5⑥=;(﹣12)⑩=.(2)想一想:将一个非零有理数a 的圈n 次方写成乘方的形式等于;9.规定:求若干个相同的有理数(均不等于0)的除法运算叫做除方,如2÷2÷2,(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)等,类比有理数的乘方,我们把2÷2÷2记作2③,读作“2的圈3次方,”(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)记作(﹣3)④,读作:“(﹣3)的圈4次方”.一般地,把个记作a ⓝ,读作“a 的圈n 次方”(初步探究)(1)直接写出计算结果:2③,(﹣12)③.(深入思考)2④21111112222222⎛⎫=⨯⨯⨯=⨯= ⎪⎝⎭我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?(2)试一试,仿照上面的算式,将下列运算结果直接写成幂的形式.5⑥;(﹣12)⑩.(3)猜想:有理数a (a≠0)的圈n (n≥3)次方写成幂的形式等于多少.(4)应用:求(-3)8×(-3)⑨-(﹣12)9×(﹣12)⑧10.已知,在计算:()()12++++N N N 的过程中,如果存在正整数N ,使得各个数位均不产生进位,那么称这样的正整数N 为“本位数”.例如:2和30都是“本位数”,因为2349++=没有进位,30313293++=没有进位;15和91都不是“本位数”,因为15161748++=,个位产生进位,919293276++=,十位产生进位.则根据上面给出的材料:(1)下列数中,如果是“本位数”请在后面的括号内打“√”,如果不是“本位数”请在后面的括号内画“×”.106();111();400();2015().(2)在所有的四位数中,最大的“本位数”是,最小的“本位数”是.(3)在所有三位数中,“本位数”一共有多少个?11.阅读下面的文字,解答问题.对于实数a ,我们规定:用符号[a ]表示不大于a 的最大整数;用{a }表示a 减去[a ]所得的差.例如:=1,[2.2]=2,1,{2.2}=2.2﹣2=0.2.(1)仿照以上方法计算:={5}=;(2)若=1,写出所有满足题意的整数x 的值:.(3)已知y 0是一个不大于280的非负数,且满足}=0.我们规定:y 1=],y 2=],y 3=],…,以此类推,直到y n 第一次等于1时停止计算.当y 0是符合条件的所有数中的最大数时,此时y 0=,n =.12.阅读下列材料:小明为了计算22019202012222+++++ 的值,采用以下方法:设22019202012222s =+++++ ①则22020202122222s =++++ ②②-①得,2021221s s s -==-请仿照小明的方法解决以下问题:(1)291222++++= ________;(2)220333+++= _________;(3)求231n a a a a ++++ 的和(1a >,n 是正整数,请写出计算过程).13.如图1,在平面直角坐标系中,点A 为x 轴负半轴上一点,点B 为x 轴正半轴上一点,()0,C a ,(),D b a ,其中a 、b 满足关系式:24(1)0a b a ++--=.()1a =______,b =______,BCD 的面积为______;()2如图2,石AC BC ⊥于点C ,点P 是线段OC 上一点,连接BP ,延长BP 交AC 于点.Q 当CPQ CQP ∠=∠时,求证:BP 平分ABC ∠;(提示:三角形三个内角和等于180) ()3如图3,若AC BC ⊥,点E 是点A 与点B 之间上一点连接CE ,且CB 平分.ECF ∠问BEC ∠与BCO ∠有什么数量关系?请写出它们之间的数量关系并请说明理由.14.如图,已知//AB CD ,CN 是BCE ∠的平分线.(1)若CM 平分BCD ∠,求MCN ∠的度数;(2)若CM 在BCD ∠的内部,且CM CN ⊥于C ,求证:CM 平分BCD ∠;(3)在(2)的条件下,过点B 作BP BQ ⊥,分别交CM 、CN 于点P 、Q ,PBQ ∠绕着B 点旋转,但与CM 、CN 始终有交点,问:BPC BQC ∠+∠的值是否发生变化?若不变,求其值;若变化,求其变化范围.15.在平面直角坐标系xOy 中,如图正方形ABCD 的顶点A ,B 坐标分别为()1,0A -,()3,0B ,点E ,F 坐标分别为(),0E m ,()3,0F m ,且12m -<≤,以EF 为边作正方形EFGH .设正方形EFGH 与正方形ABCD 重叠部分面积为S .(1)①当点F 与点B 重合时,m 的值为______;②当点F 与点A 重合时,m 的值为______.(2)请用含m 的式子表示S ,并直接写出m 的取值范围.16.中国传统节日“端午节”期间,某商场开展了“欢度端午,回馈顾客”的让利促销活动,对部分品牌的粽子进行了打折销售,其中甲品牌粽子打八折,乙品牌粽子打七五折.已知打折前,买6盒甲品牌粽子和3盒乙品牌粽子需660元;打折后,买5盒甲品牌粽子和4盒乙品牌粽子需520元.(1)打折前,每盒甲、乙品牌粽子分别为多少元?(2)在商场让利促销活动期间,某敬老院准备购买甲、乙两种品牌粽子共40盒,总费用不超过2300元,问敬老院最多可购买多少盒乙品牌粽子?17.对于平面直角坐标系xOy 中的图形G 和图形G 上的任意点P (x ,y ),给出如下定义:将点P (x ,y )平移到P '(x +t ,y ﹣t )称为将点P 进行“t 型平移”,点P '称为将点P 进行“t 型平移”的对应点;将图形G 上的所有点进行“t 型平移”称为将图形G 进行“t 型平移”.例如,将点P (x ,y )平移到P '(x +1,y ﹣1)称为将点P 进行“l 型平移”,将点P (x ,y )平移到P '(x ﹣1,y +1)称为将点P 进行“﹣l 型平移”.已知点A (2,1)和点B (4,1).(1)将点A (2,1)进行“l 型平移”后的对应点A '的坐标为.(2)①将线段AB 进行“﹣l 型平移”后得到线段A 'B ',点P 1(1.5,2),P 2(2,3),P 3(3,0)中,在线段A ′B ′上的点是.②若线段AB 进行“t 型平移”后与坐标轴有公共点,则t 的取值范围是.(3)已知点C (6,1),D (8,﹣1),点M 是线段CD 上的一个动点,将点B 进行“t 型平移”后得到的对应点为B ',当t 的取值范围是时,B 'M 的最小值保持不变.18.如图1,以直角AOC △的直角顶点O 为原点,以OC ,OA 所在直线为x 轴和y 轴建立平面直角坐标系,点()0,A a ,(),0C b 80b -=.(1)直接写出点A ,点C 的坐标;(2)如图1,坐标轴上有两动点P ,Q 同时出发,点P 从点C 出发沿x 轴负方向以每秒2个单位长度的速度匀速运动,点Q 从点O 出发沿y 轴正方向以每秒1个单位长度的速度匀速运动,当点P 到达点O 整个运动随之结束;线段AC 的中点D 的坐标是()4,3D ,设运动时间为t 秒.是否存在t ,使得DOP △与DOQ △的面积相等?若存在,求出t 的值;若不存在,说明理由;(3)如图2,在(2)的条件下,若DOC DCO ∠=∠,点G 是第二象限中一点,并且OA 平分DOG ∠,点E 是线段OA 上一动点,连接CE 交OD 于点H ,当点E 在OA 上运动的过程中,探究DOG ∠,OHC ∠,ACE ∠之间的数量关系,直接写出结论.19.题目:满足方程组3512332x y kx y k+=+⎧⎨+=-⎩的x与y的值的和是2,求k的值.按照常规方法,顺着题目思路解关于x,y的二元一次方程组,分别求出xy的值(含有字母k),再由x+y=2,构造关于k的方程求解,从而得出k值.(1)某数学兴趣小组对本题的解法又进行了探究利用整体思想,对于方程组中每个方程变形得到“x+y”这个整体,或者对方程组的两个方程进行加减变形得到“x+y”整体值,从而求出k值请你运用这种整体思想的方法,完成题目的解答过程.(2)小勇同学的解答是:观察方程①,令3x=k,5y=1解得y=15,3x+y=2,∴x=95∴k=3×95=275把x=95,y=15代入方程②得k=﹣35所以k的值为275或﹣35.请诊断分析并评价“小勇同学的解答”.20.如图,已知∠a和β∠的度数满足方程组223080αββα︒︒⎧∠+∠=⎨∠-∠=⎩,且CD//EF,AC AE⊥.(1)分别求∠a和β∠的度数;(2)请判断AB与CD的位置关系,并说明理由;(3)求C∠的度数.21.一个四位正整数,若其千位上与百位上的数字之和等于十位上与个位上的数字之和,都等于k,那么称这个四位正整数为“k类诚勤数”,例如:2534,因为25347+=+=,所以2534是“7类诚勤数”.(1)请判断7441和5436是否为“诚勤数”并说明理由;(2)若一个四位正整数A为“5类诚勤数”且能被13整除,请求出的所有可能取值.22.在平面直角坐标系中,若点P (x ,y )的坐标满足x ﹣2y +3=0,则我们称点P 为“健康点”:若点Q (x ,y )的坐标满足x +y ﹣6=0,则我们称点Q 为“快乐点”.(1)若点A 既是“健康点”又是“快乐点”,则点A 的坐标为;(2)在(1)的条件下,若B 是x 轴上的“健康点”,C 是y 轴上的“快乐点”,求△ABC 的面积;(3)在(2)的条件下,若P 为x 轴上一点,且△BPC 与△ABC 面积相等,直接写出点P 的坐标.23.如图,在平面直角坐标系中,点O 为坐标原点,A 点的坐标为()1A m n -,,B 点的坐标为()0n -,,其中,m n 是二元一次方程组2202m n m n +=⎧⎨-=-⎩的解,过点A 作x 轴的平行线交y 轴于点C .(1)求点,A B 的坐标;(2)动点P 从点B 出发,以每秒4个单位长度的速度沿射线BO 的方向运动,连接PC ,设点P 的运动时间为t 秒,三角形OPC 的面积为()0S S ≠,请用含t 的式子表示S (不用写出相应的t 的取值范围);(3)在(2)的条件下,在动点P 从点B 出发的同时,动点Q 从点C 出发以每秒1个单位长度的速度沿线段CA 的方向运动.过点O 作直线PC 的垂线,点G 为垂足;过点Q 作直线PC 的垂线,点H 为垂足.当2OG QH =时,求t 的值.24.如图,在平面直角坐标系中,已知,点()0,A a ,(),0B b ,()0,C c ,a ,b ,c 满足()28212a b -+-=,(1)直接写出点A ,B ,C 的坐标及ABC 的面积;(2)如图2,过点C 作直线//l AB ,已知(),D m n 是l 上的一点,且152ACD S ≤△,求n 的取值范围;(3)如图3,(),M x y 是线段AB 上一点,①求x ,y 之间的关系;②点N 为点M 关于y 轴的对称点,已知21BCN S =△,求点M 的坐标.25.阅读材料:形如2213x <+<的不等式,我们就称之为双连不等式.求解双连不等式的方法一,转化为不等式组求解,如221213x x <+⎧⎨+<⎩;方法二,利用不等式的性质直接求解,双连不等式的左、中、右同时减去1,得122x <<,然后同时除以2,得1112x <<.解决下列问题:(1)请你写一个双连不等式并将它转化为不等式组;(2)利用不等式的性质解双连不等式2235x ≥-+>-;(3)已知532x -≤<-,求35x +的整数值.26.阅读材料:如果x 是一个有理数,我们把不超过x 的最大整数记作[x ].例如,[3.2]=3,[5]=5,[-2.1]=-3.那么,x =[x ]+a ,其中0≤a <1.例如,3.2=[3.2]+0.2,5=[5]+0,-2.1=[-2.1]+0.9.请你解决下列问题:(1)[4.8]=,[-6.5]=;(2)如果[x ]=3,那么x 的取值范围是;(3)如果[5x -2]=3x +1,那么x 的值是;(4)如果x =[x ]+a ,其中0≤a <1,且4a =[x ]+1,求x 的值.27.阅读理解:例1.解方程|x |=2,因为在数轴上到原点的距离为2的点对应的数为±2,所以方程|x |=2的解为x =±2.例2.解不等式|x ﹣1|>2,在数轴上找出|x ﹣1|=2的解(如图),因为在数轴上到1对应的点的距离等于2的点对应的数为﹣1或3,所以方程|x ﹣1|=2的解为x =﹣1或x =3,因此不等式|x ﹣1|>2的解集为x <﹣1或x >3.参考阅读材料,解答下列问题:(1)方程|x ﹣2|=3的解为;(2)解不等式:|x ﹣2|≤1.(3)解不等式:|x ﹣4|+|x +2|>8.(4)对于任意数x ,若不等式|x +2|+|x ﹣4|>a 恒成立,求a 的取值范围.28.如图①,在平直角坐标系中,△ABO 的三个顶点为A (a ,b ),B (﹣a ,3b ),O(0,0|b ﹣2|=0,线段AB 与y 轴交于点C .(1)求出A ,B 两点的坐标;(2)求出△ABO 的面积;(3)如图②,将线段AB 平移至B 点的对应点B '落在x 轴的正半轴上时,此时A 点的对应点为A ',记△A B C ''的面积为S ,若24<S <32,求点A '的横坐标的取值范围.29.已知关于x 、y 的二元一次方程23,3 3.x y a x y a +=-⎧⎨-=-⎩①②(1)若方程组的解x 、y 满足0,1x y ≤<,求a 的取值范围;(2)求代数式638x y +-的值.30.如图,在平面直角坐标系中,已知△ABC,点A 的坐标是(4,0),点B 的坐标是(2,3),点C 在x 轴的负半轴上,且AC=6.(1)直接写出点C 的坐标.(2)在y 轴上是否存在点P ,使得S △POB =23S △ABC 若存在,求出点P 的坐标;若不存在,请说明理由.(3)把点C 往上平移3个单位得到点H ,作射线CH,连接BH ,点M 在射线CH 上运动(不与点C 、H 重合).试探究∠HBM ,∠BMA ,∠MAC 之间的数量关系,并证明你的结论.【参考答案】***试卷处理标记,请不要删除一、解答题1.(1)(-2,0);(2)①t=2;②当点P在线段BC上时,点P的坐标(-t,2),当点P在线段CD上时,点P的坐标(-3,5-t);③能确定,z=x+y.【分析】(1)根据平移的性质即可得到结论;(2)①由点C的坐标为(-3,2).得到BC=3,CD=2,由于点P的横坐标与纵坐标互为相反数;于是确定点P在线段BC上,有PB=CD,即可得到结果;②当点P在线段BC上时,点P的坐标(-t,2),当点P在线段CD上时,点P的坐标(-3,5-t);③如图,过P作PF∥BC交AB于F,则PF∥AD,根据平行线的性质即可得到结论.【详解】解:(1)根据题意,可得三角形OAB沿x轴负方向平移3个单位得到三角形DEC,∵点A的坐标是(1,0),∴点E的坐标是(-2,0);故答案为:(-2,0);(2)①∵点C的坐标为(-3,2)∴BC=3,CD=2,∵点P的横坐标与纵坐标互为相反数;∴点P在线段BC上,∴PB=CD,即t=2;∴当t=2秒时,点P的横坐标与纵坐标互为相反数;故答案为:2;②当点P在线段BC上时,点P的坐标(-t,2),当点P在线段CD上时,点P的坐标(-3,5-t);③能确定,如图,过P作PF∥BC交AB于F,则PF∥AD,∠1=∠CBP=x°,∠2=∠DAP=y°,∴∠BPA=∠1+∠2=x°+y°=z°,∴z=x+y.【点睛】本题考查了坐标与图形的性质,坐标与图形的变化-平移,平行线的性质,正确的作出辅助线是解题的关键.2.(1)∠A+∠C+∠APC=360°;(2)见解析;(3)55°【分析】(1)首先过点P作PQ∥AB,则易得AB∥PQ∥CD,然后由两直线平行,同旁内角互补,即可证得∠A+∠C+∠APC=360°;(2)作PQ∥AB,易得AB∥PQ∥CD,根据两直线平行,内错角相等,即可证得∠APC=∠A+∠C;(3)由(2)知,∠APC=∠PAB-∠PCD,先证∠BEF=∠PQB=110°、∠PEG=12∠FEG,∠GEH=12∠BEG,根据∠PEH=∠PEG-∠GEH可得答案.【详解】解:(1)∠A+∠C+∠APC=360°如图1所示,过点P作PQ∥AB,∴∠A+∠APQ=180°,∵AB∥CD,∴PQ∥CD,∴∠C+∠CPQ=180°,∴∠A+∠APQ+∠C+∠CPQ=360°,即∠A+∠C+∠APC=360°;(2)∠APC=∠A+∠C,如图2,作PQ∥AB,∴∠A=∠APQ,∵AB∥CD,∴PQ∥CD,∴∠C=∠CPQ,∵∠APC=∠APQ-∠CPQ,∴∠APC=∠A-∠C;(3)由(2)知,∠APC=∠PAB-∠PCD,∵∠APC=30°,∠PAB=140°,∴∠PCD=110°,∵AB∥CD,∴∠PQB=∠PCD=110°,∵EF∥BC,∴∠BEF=∠PQB=110°,∵EF∥BC,∴∠BEF=∠PQB=110°,∵∠PEG=∠PEF,∴∠PEG=12∠FEG,∵EH平分∠BEG,∴∠GEH=12∠BEG,∴∠PEH=∠PEG-∠GEH=1 2∠FEG-12∠BEG=12∠BEF=55°.【点睛】此题考查了平行线的性质以及角平分线的定义.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.3.(1)∠APC=α+β,理由见解析;(2)∠APC=α-β或∠APC=β-α;(3)58°【分析】(1)过点P作PE∥AB,根据平行线的判定与性质即可求解;(2)分点P在线段MN或NM的延长线上运动两种情况,根据平行线的判定与性质及角的和差即可求解;(3)过点P,Q分别作PE∥AB,QF∥AB,根据平行线的判定与性质及角的和差即可求解.【详解】解:(1)如图2,过点P作PE∥AB,∵AB∥CD,∴PE∥AB∥CD,∴∠APE=α,∠CPE=β,∴∠APC=∠APE+∠CPE=α+β.(2)如图,在(1)的条件下,如果点P在线段MN的延长线上运动时,∵AB∥CD,∠PAB=α,∴∠1=∠PAB=α,∵∠1=∠APC+∠PCD,∠PCD=β,∴α=∠APC+β,∴∠APC=α-β;如图,在(1)的条件下,如果点P在线段NM的延长线上运动时,∵AB∥CD,∠PCD=β,∴∠2=∠PCD=β,∵∠2=∠PAB+∠APC,∠PAB=α,∴β=α+∠APC ,∴∠APC =β-α;(3)如图3,过点P ,Q 分别作PE ∥AB ,QF ∥AB ,∵AB ∥CD ,∴AB ∥QF ∥PE ∥CD ,∴∠BAP =∠APE ,∠PCD =∠EPC ,∵∠APC =116°,∴∠BAP +∠PCD =116°,∵AQ 平分∠BAP ,CQ 平分∠PCD ,∴∠BAQ =12∠BAP ,∠DCQ =12∠PCD ,∴∠BAQ +∠DCQ =12(∠BAP +∠PCD )=58°,∵AB ∥QF ∥CD ,∴∠BAQ =∠AQF ,∠DCQ =∠CQF ,∴∠AQF +∠CQF =∠BAQ +∠DCQ =58°,∴∠AQC =58°.【点睛】此题考查了平行线的判定与性质,添加辅助线将两条平行线相关的角联系到一起是解题的关键.4.(1)20,20,//AB CD ;(2)180FMN GHF ∠+∠=︒;(3)1FPN Q ∠∠的值不变,12FPN Q=∠∠【分析】(1)根据2(402)|20|0αβ-+-=,即可计算α和β的值,再根据内错角相等可证//AB CD ;(2)先根据内错角相等证//GH PN ,再根据同旁内角互补和等量代换得出180FMN GHF ∠+∠=︒;(3)作1PEM ∠的平分线交1M Q 的延长线于R ,先根据同位角相等证//ER FQ ,得1FQM R =∠∠,设PER REB x ==∠∠,11PM R RM B y ==∠∠,得出12EPM R ∠=∠,即可得12FPN Q=∠∠.【详解】解:(1)2(402)|20|0αβ-+-= ,4020α∴-=,200β-=,20αβ∴==,20PFM MFN ∴∠=∠=︒,20EMF ∠=︒,EMF MFN ∴∠=∠,//AB CD ∴;故答案为:20、20,//AB CD ;(2)180FMN GHF ∠+∠=︒;理由:由(1)得//AB CD ,MNF PME ∴∠=∠,MGH MNF ∠=∠ ,PME MGH ∴∠=∠,//GH PN ∴,GHM FMN ∴∠=∠,180GHF GHM ∠+∠=︒ ,180FMN GHF ∴∠+∠=︒;(3)1FPN Q ∠∠的值不变,12FPN Q=∠∠;理由:如图3中,作1PEM ∠的平分线交1M Q 的延长线于R ,//AB CD ,1PEM PFN ∴∠=∠,112PER PEM ∠=∠ ,12PFQ PFN =∠,PER PFQ ∴∠=∠,//ER FQ ∴,1FQM R ∴∠=∠,设PER REB x ==∠∠,11PM R RM B y ==∠∠,则有:122y x R y x EPM =+∠⎧⎨=+∠⎩,可得12EPM R ∠=∠,112EPM FQM ∴∠=∠,∴112EPM FQM ∠=∠.【点睛】本题主要考查平行线的判定与性质,熟练掌握内错角相等证平行,平行线同旁内角互补等知识是解题的关键.5.(1)见解析;(2)∠BAE+∠CDE=∠AED,证明见解析;(3)①∠AED-∠FDC=45°,理由见解析;②50°【分析】(1)根据平行线的性质及判定可得结论;(2)过点E作EF∥AB,根据平行线的性质得AB∥CD∥EF,然后由两直线平行内错角相等可得结论;(3)①根据∠AED+∠AEC=180°,∠AED+∠DEC+∠AEB=180°,DF平分∠EDC,可得出2∠AED+(90°-2∠FDC)=180°,即可导出角的关系;②先根据∠AED=∠F+∠FDE,∠AED-∠FDC=45°得出∠DEP=2∠F=90°,再根据∠DEA-∠PEA=514∠DEB,求出∠AED=50°,即可得出∠EPD的度数.【详解】解:(1)证明:AB∥CD,∴∠A+∠D=180°,∵∠C=∠A,∴∠C+∠D=180°,∴AD∥BC;(2)∠BAE+∠CDE=∠AED,理由如下:如图2,过点E作EF∥AB,∵AB∥CD∴AB∥CD∥EF∴∠BAE=∠AEF,∠CDE=∠DEF即∠FEA+∠FED=∠CDE+∠BAE∴∠BAE+∠CDE=∠AED;(3)①∠AED-∠FDC=45°;∵∠AED+∠AEC=180°,∠AED+∠DEC+∠AEB=180°,∴∠AEC=∠DEC+∠AEB,∴∠AED=∠AEB,∵DF平分∠EDC∠DEC=2∠FDC∴∠DEC=90°-2∠FDC,∴2∠AED+(90°-2∠FDC)=180°,∴∠AED-∠FDC=45°,故答案为:∠AED-∠FDC=45°;②如图3,∵∠AED=∠F+∠FDE,∠AED-∠FDC=45°,∴∠F=45°,∴∠DEP=2∠F=90°,∵∠DEA-∠PEA=514∠DEB=57∠DEA,∴∠PEA=27∠AED,∴∠DEP=∠PEA+∠AED=97∠AED=90°,∴∠AED=70°,∵∠AED+∠AEC=180°,∴∠DEC+2∠AED=180°,∴∠DEC=40°,∵AD∥BC,∴∠ADE=∠DEC=40°,在△PDE中,∠EPD=180°-∠DEP-∠AED=50°,即∠EPD=50°.【点睛】本题主要考查平行线的判定和性质,熟练掌握平行线的判定和性质,角平分线的性质等知识点是解题的关键.6.(1)70°;(2)EAF AED EDG∠=∠+∠,证明见解析;(3)122°【分析】(1)过E 作//EF AB ,根据平行线的性质得到25EAF AEH ∠=∠=︒,45EAG DEH ∠=∠=︒,即可求得AED ∠;(2)过过E 作//EM AB ,根据平行线的性质得到180EAF MEH ∠=︒-∠,180EDG AED MEH ∠+∠=︒-,即EAF AED EDG ∠=∠+∠;(3)设EAI x ∠=,则3BAE x ∠=,通过三角形内角和得到2EDK x ∠=-︒,由角平分线定义及//AB CD 得到33224x x =︒+-︒,求出x 的值再通过三角形内角和求EKD ∠.【详解】解:(1)过E 作//EF AB ,//AB CD ,//EF CD ∴,25EAF AEH ∴∠=∠=︒,45EAG DEH ∠=∠=︒,70AED AEH DEH ∴∠=∠+∠=︒,故答案为:70︒;(2)EAF AED EDG ∠=∠+∠.理由如下:过E 作//EM AB ,//AB CD ,//EM CD ∴,180EAF MEH ∴∠+∠=︒,180EDG AED MEH ∠+∠+=︒,180EAF MEH ∴∠=︒-∠,180EDG AED MEH ∠+∠=︒-,EAF AED EDG ∴∠=∠+∠;(3):1:2EAP BAP ∠∠= ,设EAP x ∠=,则3BAE x ∠=,32302AED P ∠-∠=︒-︒=︒ ,DKE AKP ∠=∠,又180EDK DKE DEK ∠+∠+∠=︒ ,180KAP KPA AKP ∠+∠+∠=︒,22EDK EAP x ∴∠=∠-︒=-︒,DP 平分EDC ∠,224CDE EDK x ∴∠=∠=-︒,//AB CD ,EHC EAF AED EDG ∴∠=∠=∠+∠,即33224x x =︒+-︒,解得28x =︒,28226EDK ∴∠=︒-︒=︒,1802632122EKD ∴∠=︒-︒-︒=︒.【点睛】本题主要考查了平行线的性质和判定,正确做出辅助线是解决问题的关键.7.初步探究:(1)12,8;(2)C ;深入思考:(1)213,415,82;(2)21n a -;(3)-5.【分析】初步探究:(1)根据除方运算的定义即可得出答案;(2)根据除方运算的定义逐一判断即可得出答案;深入思考:(1)根据除方运算的定义即可得出答案;(2)根据(1)即可总结出(2)中的规律;(3)先按照除方的定义将每个数的圈n 次方算出来,再根据有理数的混合运算法则即可得出答案.【详解】解:初步探究:(1)2③=2÷2÷2=12(12)⑤=11111822222÷÷÷÷=(2)A :任何非零数的圈2次方就是两个相同数相除,所以都等于1,故选项A 错误;B :因为多少个1相除都是1,所以对于任何正整数n ,1ⓝ都等于1,故选项B 错误;C :3④=3÷3÷3÷3=19,4③=4÷4÷4=14,3④≠4③,故选项C 正确;D :负数的圈奇数次方,相当于奇数个负数相除,则结果是负数;负数的圈偶数次方,相当于偶数个负数相除,则结果是正数,故选项D 错误;故答案选择:C.深入思考:(1)(-3)④=(-3)÷(-3)÷(-3)÷(-3)=2135⑥=5÷5÷5÷5÷5÷5=415(-12)⑩=8111111111122222222222⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫-÷-÷-÷-÷-÷-÷-÷-÷-÷-=⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭(2)a ⓝ=a÷a÷a…÷a=21n a -(3)原式=()4252621111442711233---÷⨯-÷-⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭=1144981278⎛⎫÷⨯--÷ ⎪⎝⎭=23--=-5【点睛】本题主要考查了除方运算,运用到的知识点是有理数的混合运算,掌握有理数混合运算的法则是解决本题的关键.8.初步探究:(1)12,-8;深入思考:(1)(−13)2,(15)4,82;(2)21n a -⎛⎫⎪⎝⎭【分析】初步探究:(1)分别按公式进行计算即可;深入思考:(1)把除法化为乘法,第一个数不变,从第二个数开始依次变为倒数,由此分别得出结果;(2)结果前两个数相除为1,第三个数及后面的数变为1a,则11n a a a -⎛⎫=⨯ ⎪⎝⎭ⓝ;【详解】解:初步探究:(1)2③=2÷2÷2=12,111111-=-----222222⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫÷÷÷÷ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⑤111=1---222⎛⎫⎛⎫⎛⎫÷÷÷ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭()11-2--22⎛⎫⎛⎫÷÷ ⎪ ⎪⎝⎭⎝⎭=-8;深入思考:(1)(-3)④=(-3)÷(-3)÷(-3)÷(-3)=1×(−13)2=(−13)2;5⑥=5÷5÷5÷5÷5÷5=(15)4;同理可得:(﹣12)⑩=82;(2)21n a a -⎛⎫= ⎪⎝⎭ⓝ【点睛】本题是有理数的混合运算,也是一个新定义的理解与运用;一方面考查了有理数的乘除法及乘方运算,另一方面也考查了学生的阅读理解能力;注意:负数的奇数次方为负数,负数的偶数次方为正数,同时也要注意分数的乘方要加括号,对新定义,其实就是多个数的除法运算,要注意运算顺序.9.(1)12,-2;(2)(15)4,(﹣2)8;(3)n-21a⎛⎫⎪⎝⎭;(4)7-28.【分析】(1)分别按公式进行计算即可;(2)把除法化为乘法,第一个数不变,从第二个数开始依次变为倒数,由此分别得出结果;(3)结果前两个数相除为1,第三个数及后面的数变为1a,则aⓝ=a×(1a)n-1;(4)将第二问的规律代入计算,注意运算顺序.【详解】解:(1)2③=2÷2÷2=12,(﹣12)③=﹣12÷(﹣12)÷(﹣12)=﹣2;(2)5⑥=5×15×15×15×15×15=(15)4,同理得;(﹣12)⑩=(﹣2)8;(3)aⓝ=a×1a×1a×…×n-211a a⎛⎫= ⎪⎝⎭;(4)(-3)8×(-3)⑨-(﹣12)9×(﹣12)⑧=(-3)8×(1-3)7-(﹣12)9×(-2)6=-3-(-12)3=-3+1 8=7 -2 8.【点睛】本题是有理数的混合运算,也是一个新定义的理解与运用;一方面考查了有理数的乘除法及乘方运算,另一方面也考查了学生的阅读理解能力;注意:负数的奇数次方为负数,负数的偶数次方为正数,同时也要注意分数的乘方要加括号,对新定义,其实就是多个数的除法运算,要注意运算顺序.10.(1)×,√,×,×;(2)3332;1000;(3)36(个).【分析】(1)根据“本位数”的定义即可判断;(2)要想保证不进位,千位、百位、十位最大只能是3,个位最大只能是2,故最大的四位“本位数”是3332;千位最小为1,百位、十位、个位最小为0,故最小的“本位数”是1000;(3)要想构成“本位数”,百位可以为1,2,3,十位可以为0,1,2,3,个位可以为0,1,2,所有的三位数中,“本位数”一共有34336⨯⨯=(个).【详解】解:(1)106107108321++=有进位;111112113336++=没有进位;4004014021203++=有进位;2015201620176048++=有进位;故答案为:×,√,×,×.(2)要想保证不进位,千位、百位、十位最大只能是3,个位最大只能是2,故最大的四位“本位数”是3332;千位最小为1,百位、十位、个位最小为0,故最小的“本位数”是1000,故答案为:3332,1000.(3)要想构成“本位数”,百位可以为1,2,3,十位可以为0,1,2,3,个位可以为0,1,2,所有的三位数中,“本位数”一共有34336⨯⨯=(个).【点睛】本题考查了新定义计算题,准确理解新定义的内涵是解题的关键.11.(1)2;32)1、2、3;(3)256,4【分析】(1)依照定义进行计算即可;(2)由题可知,04x <<,则可得满足题意的整数的x 的值为1、2、3;(3)由0=,可知,0y 是某个整数的平方,又0y 是符合条件的所有数中最大的数,则0256y =,再依次进行计算.【详解】解:(1)由定义可得,2=,[52=,{53∴=.故答案为:2;3.(2)1= ,2∴<,即04x <<,∴整数x 的值为1、2、3.故答案为:1、2、3.(3)0= ,即0=-=,∴2t ,且t 是自然数,0y 是符合条件的所有数中的最大数,0256y ∴=,1[16]16y ∴===,2[4]4y ===,3[2]2y ===,41y ===,即4n =.故答案为:256,4.【点睛】本题属于新定义类问题,主要考查估算无理数大小,无理数的整数部分和小数部分,理解定义内容是解题关键.12.(1)1021-;(2)21332-;(3)111n a a +--【分析】(1)设式子等于s ,将方程两边都乘以2后进行计算即可;(2)设式子等于s ,将方程两边都乘以3,再将两个方程相减化简后得到答案;(3)设式子等于s ,将方程两边都乘以a 后进行计算即可.【详解】(1)设s=291222++++ ①,∴2s=29102222++++ ②,②-①得:s=1021-,故答案为:1021-;(2)设s=220333+++ ①,∴3s=22021333+++ ②,②-①得:2s=2133-,∴21332s -=,故答案为:21332-;(3)设s=231n a a a a ++++ ①,∴as=231n n a a a a a +++++ ②,②-①得:(a-1)s=11n a +-,∴s=111n a a +--.【点睛】此题考查代数式的规律计算,能正确理解已知的代数式的运算规律是难点,依据规律对于每个式子变形计算是关键.13.(1)4-;3-;6;(2)证明见解析;(3)2BEC BCO ∠=∠,理由见解析.【详解】分析:(1)求出CD 的长度,再根据三角形的面积公式列式计算即可得解;(2)根据等角的余角相等解答即可;(3)首先证明∠ACD=∠ACE ,推出∠DCE=2∠ACD ,再证明∠ACD=∠BCO ,∠BEC=∠DCE=2∠ACD 即可解决问题;【解答】(1)解:如图1中,∵|a+4|+(b-a-1)2=0,∴a=-4,b=-3,∵点C(0,-4),D(-3,-4),∴CD=3,且CD∥x轴,∴△BCD的面积=12×4×3=6;故答案为-4,-3,6.(2)如图2中,∵∠CPQ=∠CQP=∠OPB,AC⊥BC,∴∠CBQ+∠CQP=90°,又∵∠ABQ+∠CPQ=90°,∴∠ABQ=∠CBQ,∴BQ平分∠CBA.(3)如图3中,结论:∠BEC=2∠BCO.理由:∵AC⊥BC,∴∠ACB=90°,∴∠ACD+∠BCF=90°,∵CB 平分∠ECF ,∴∠ECB=∠BCF ,∴∠ACD+∠ECB=90°,∵∠ACE+∠ECB=90°,∴∠ACD=∠ACE ,∴∠DCE=2∠ACD ,∵∠ACD+∠ACO=90°,∠BCO+∠ACO=90°,∴∠ACD=∠BCO ,∵C (0,-4),D (-3,-4),∴CD ∥AB ,∠BEC=∠DCE=2∠ACD ,∴∠BEC=2∠BCO ,点睛:本题考查了坐标与图形性质,三角形的角平分线,三角形的面积,三角形的内角和定理,三角形的外角性质等知识,熟记性质并准确识图是解题的关键.14.(1)90°;(2)见解析;(3)不变,180°【分析】(1)根据邻补角的定义及角平分线的定义即可得解;(2)根据垂直的定义及邻补角的定义、角平分线的定义即可得解;(3)180BPC BQC ∠+∠=︒,过Q ,P 分别作//QG AB ,//PH AB ,根据平行线的性质及平角的定义即可得解.【详解】解(1)CN ,CM 分别平分BCE ∠和BCD ∠,12BCN BCE ∴=∠,12BCM BCD ∠=∠,180BCE BCD ∠+∠=︒ ,111()90222MCN BCN BCM BCE BCD BCE BCD ∴∠=∠+∠=∠+∠=∠+∠=︒;(2)CM CN ⊥ ,90MCN ∴∠=︒,即90BCN BCM ∠+∠=︒,22180BCN BCM ∴∠+∠=︒,CN 是BCE ∠的平分线,2BCE BCN ∴∠=∠,2180BCE BCM ∴∠+∠=︒,又180BCE BCD ∠+∠=︒ ,2BCD BCM ∴∠=∠,又CM 在BCD ∠的内部,CM ∴平分BCD ∠;(3)如图,不发生变化,180BPC BQC ∠+∠=︒,过Q ,P 分别作//QG AB ,//PH AB ,。
人教版七年级下册数学期末解答题压轴题题含答案

人教版七年级下册数学期末解答题压轴题题含答案一、解答题1.(1)如图1,分别把两个边长为1cm的小正方形沿一条对角线裁成4个小三角形拼成一个大正方形,则大正方形的边长为______cm;(2)若一个圆的面积与一个正方形的面积都是22πcm,设圆的周长为C圆.正方形的周长为C正,则C圆______C正(填“=”,或“<”,或“>”)(3)如图2,若正方形的面积为2900cm,李明同学想沿这块正方形边的方向裁出一块面积为2740cm的长方形纸片,使它的长和宽之比为5:4,他能裁出吗?请说明理由?2.如图,这是由8个同样大小的立方体组成的魔方,体积为64.(1)求出这个魔方的棱长;(2)图中阴影部分是一个正方形ABCD,求出阴影部分的边长.3.张华想用一块面积为400cm2的正方形纸片,沿着边的方向剪出一块面积为300cm2的长方形纸片,使它的长宽之比为3:2.他不知能否裁得出来,正在发愁.李明见了说:“别发愁,一定能用一块面积大的纸片裁出一块面积小的纸片.”你同意李明的说法吗?张华能用这块纸片裁出符合要求的纸片吗?4.求下图44⨯的方格中阴影部分正方形面积与边长.5.有一块正方形钢板,面积为16平方米.(1)求正方形钢板的边长.(2)李师傅准备用它裁剪出一块面积为12平方米的长方形工件,且要求长宽之比为3:2,问李师傅能办到吗?若能,求出长方形的长和宽;若不能,请说明理由.(参考数≈).2 1.414≈3 1.732二、解答题6.已知AB //CD .(1)如图1,E 为AB ,CD 之间一点,连接BE ,DE ,得到∠BED .求证:∠BED =∠B +∠D ;(2)如图,连接AD ,BC ,BF 平分∠ABC ,DF 平分∠ADC ,且BF ,DF 所在的直线交于点F .①如图2,当点B 在点A 的左侧时,若∠ABC =50°,∠ADC =60°,求∠BFD 的度数. ②如图3,当点B 在点A 的右侧时,设∠ABC =α,∠ADC =β,请你求出∠BFD 的度数.(用含有α,β的式子表示)7.(1)(问题)如图1,若//AB CD ,40AEP ∠=︒,130PFD ∠=︒.求EPF ∠的度数; (2)(问题迁移)如图2,//AB CD ,点P 在AB 的上方,问PEA ∠,PFC ∠,EPF ∠之间有何数量关系?请说明理由;(3)(联想拓展)如图3所示,在(2)的条件下,已知EPF α∠=,PEA ∠的平分线和PFC ∠的平分线交于点G ,用含有α的式子表示G ∠的度数.8.已知,AB ∥CD .点M 在AB 上,点N 在CD 上.(1)如图1中,∠BME 、∠E 、∠END 的数量关系为: ;(不需要证明) 如图2中,∠BMF 、∠F 、∠FND 的数量关系为: ;(不需要证明)(2)如图3中,NE 平分∠FND ,MB 平分∠FME ,且2∠E +∠F =180°,求∠FME 的度数;(3)如图4中,∠BME =60°,EF 平分∠MEN ,NP 平分∠END ,且EQ ∥NP ,则∠FEQ 的大小是否发生变化,若变化,请说明理由,若不变化,求出∠FEQ 的度数.9.如图1,把一块含30°的直角三角板ABC 的BC 边放置于长方形直尺DEFG 的EF 边上. (1)根据图1填空:∠1= °,∠2= °; (2)现把三角板绕B 点逆时针旋转n °.①如图2,当n =25°,且点C 恰好落在DG 边上时,求∠1、∠2的度数;②当0°<n <180°时,是否会存在三角板某一边所在的直线与直尺(有四条边)某一边所在的直线垂直?如果存在,请直接写出所有n 的值和对应的那两条垂线;如果不存在,请说明理由.10.如图,已知//AB CD ,CN 是BCE ∠的平分线. (1)若CM 平分BCD ∠,求MCN ∠的度数;(2)若CM 在BCD ∠的内部,且CM CN ⊥于C ,求证:CM 平分BCD ∠;(3)在(2)的条件下,过点B 作BP BQ ⊥,分别交CM 、CN 于点P 、Q ,PBQ ∠绕着B 点旋转,但与CM 、CN 始终有交点,问:BPC BQC ∠+∠的值是否发生变化?若不变,求其值;若变化,求其变化范围.三、解答题11.为更好地理清平行线相关角的关系,小明爸爸为他准备了四根细直木条AB 、BC 、CD 、DE ,做成折线ABCDE ,如图1,且在折点B 、C 、D 处均可自由转出.(1)如图2,小明将折线调节成50B ∠=︒,85C ∠=︒,35D ∠=︒,判断AB 是否平行于ED ,并说明理由;(2)如图3,若35C D ∠=∠=︒,调整线段AB 、BC 使得//AB CD 求出此时B 的度数,要求画出图形,并写出计算过程.(3)若85C ∠=︒,35D ∠=︒,//AB DE ,请直接写出此时B 的度数. 12.如图1所示:点E 为BC 上一点,∠A =∠D ,AB ∥CD (1)直接写出∠ACB 与∠BED 的数量关系;(2)如图2,AB ∥CD ,BG 平分∠ABE ,BG 的反向延长线与∠EDF 的平分线交于H 点,若∠DEB 比∠GHD 大60°,求∠DEB 的度数;(3)保持(2)中所求的∠DEB 的度数不变,如图3,BM 平分∠EBK ,DN 平分∠CDE ,作BP ∥DN ,则∠PBM 的度数是否改变?若不发生变化,请求它的度数,若发生改变,请说明理由.(本题中的角均为大于0°且小于180°的角).13.如图1,E 点在BC 上,∠A =∠D ,AB ∥CD . (1)直接写出∠ACB 和∠BED 的数量关系 ;(2)如图2,BG 平分∠ABE ,与∠CDE 的邻补角∠EDF 的平分线交于H 点.若∠E 比∠H 大60°,求∠E ;(3)保持(2)中所求的∠E 不变,如图3,BM 平分∠ABE 的邻补角∠EBK ,DN 平分∠CDE ,作BP ∥DN ,则∠PBM 的度数是否改变?若不变,请求值;若改变,请说理由.14.已知,如图①,∠BAD =50°,点C 为射线AD 上一点(不与A 重合),连接BC . (1)[问题提出]如图②,AB ∥CE ,∠BCD =73 °,则:∠B = .(2)[类比探究]在图①中,探究∠BAD 、∠B 和∠BCD 之间有怎样的数量关系?并用平行....线的性质....说明理由.(3)[拓展延伸]如图③,在射线BC上取一点O,过O点作直线MN使MN∥AD,BE平分OG BE交AD于G点,当C点沿着射∠ABC交AD于E点,OF平分∠BON交AD于F点,//线AD方向运动时,∠FOG的度数是否会变化?若变化,请说明理由;若不变,请求出这个不变的值.15.如图1,D是△ABC延长线上的一点,CE//AB.(1)求证:∠ACD=∠A+∠B;(2)如图2,过点A作BC的平行线交CE于点H,CF平分∠ECD,FA平分∠HAD,若∠BAD=70°,求∠F的度数.(3)如图3,AH//BD,G为CD上一点,Q为AC上一点,GR平分∠QGD交AH于R,QN 平分∠AQG交AH于N,QM//GR,猜想∠MQN与∠ACB的关系,说明理由.四、解答题16.如图①,将一副直角三角板放在同一条直线AB上,其中∠ONM=30°,∠OCD=45°.(1)将图①中的三角板OMN沿BA的方向平移至图②的位置,MN与CD相交于点E,求∠CEN的度数;(2)将图①中的三角板OMN绕点O按逆时针方向旋转,使∠BON=30°,如图③,MN 与CD相交于点E,求∠CEN的度数;(3)将图①中的三角板OMN绕点O按每秒30°的速度按逆时针方向旋转一周,在旋转的过程中,在第____________秒时,直线MN恰好与直线CD垂直.(直接写出结果)17.操作示例:如图1,在△ABC中,AD为BC边上的中线,△ABD的面积记为S1,△ADC 的面积记为S2.则S1=S2.解决问题:在图2中,点D、E分别是边AB、BC的中点,若△BDE的面积为2,则四边形ADEC的面积为 .拓展延伸:(1)如图3,在△ABC中,点D在边BC上,且BD=2CD,△ABD的面积记为S1,△ADC的面积记为S2.则S1与S2之间的数量关系为.(2)如图4,在△ABC中,点D、E分别在边AB、AC上,连接BE、CD交于点O,且BO=2EO,CO=DO,若△BOC的面积为3,则四边形ADOE的面积为 .18.直线MN与直线PQ垂直相交于O,点A在射线OP上运动,点B在射线OM上运动,A、B不与点O重合,如图1,已知AC、BC分别是∠BAP和∠ABM角的平分线,(1)点A、B在运动的过程中,∠ACB的大小是否发生变化?若发生变化,请说明理由;若不发生变化,试求出∠ACB的大小.(2)如图2,将△ABC沿直线AB折叠,若点C落在直线PQ上,则∠ABO=________,如图3,将△ABC沿直线AB折叠,若点C落在直线MN上,则∠ABO=________(3)如图4,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及其反向延长线交于E、F,则∠EAF=;在△AEF中,如果有一个角是另一个角的32倍,求∠ABO的度数.19.如图,△ABC和△ADE有公共顶点A,∠ACB=∠AED=90°,∠BAC=45°,∠DAE=30°.(1)若DE//AB,则∠EAC=;(2)如图1,过AC上一点O作OG⊥AC,分别交A B、A D、AE于点G、H、F.①若AO =2,S △AGH =4,S △AHF =1,求线段OF 的长;②如图2,∠AFO 的平分线和∠AOF 的平分线交于点M ,∠FHD 的平分线和∠OGB 的平分线交于点N ,∠N +∠M 的度数是否发生变化?若不变,求出其度数;若改变,请说明理由.20.已知AB //CD ,点E 是平面内一点,∠CDE 的角平分线与∠ABE 的角平分线交于点F . (1)若点E 的位置如图1所示.①若∠ABE =60°,∠CDE =80°,则∠F = °; ②探究∠F 与∠BED 的数量关系并证明你的结论;(2)若点E 的位置如图2所示,∠F 与∠BED 满足的数量关系式是 .(3)若点E 的位置如图3所示,∠CDE 为锐角,且1452E F ∠≥∠+︒,设∠F =α,则α的取值范围为 .【参考答案】一、解答题1.(1);(2)<;(3)不能,理由见解析 【分析】(1)根据所拼成的大正方形的面积为2即可求得大正方形的边长;(2)由圆和正方形的面积公式可分别求的圆的半径及正方形的边长,进而可求得圆和正方形的解析:(122)<;(3)不能,理由见解析 【分析】(1)根据所拼成的大正方形的面积为2即可求得大正方形的边长;(2)由圆和正方形的面积公式可分别求的圆的半径及正方形的边长,进而可求得圆和正方形的周长,利用作商法比较这两数大小即可;(3)利用方程思想求出长方形的长边,与正方形边长比较大小即可; 【详解】解:(1)∵小正方形的边长为1cm , ∴小正方形的面积为1cm 2, ∴两个小正方形的面积之和为2cm 2, 即所拼成的大正方形的面积为2 cm 2, 设大正方形的边长为x cm , ∴22x = , ∴x∴; (2)设圆的半径为r , ∴由题意得22r ππ=, ∴r = ∴=22C r π=圆 设正方形的边长为a ∵22a π=, ∴a∴=4C a =正∴1C C ===<圆正 故答案为:<;(3)解:不能裁剪出,理由如下: ∵正方形的面积为900cm 2, ∴正方形的边长为30cm∵长方形纸片的长和宽之比为5:4, ∴设长方形纸片的长为5x ,宽为4x , 则54740x x ⋅=, 整理得:237x =,∴22(5)252537925900x x ==⨯=>, ∴22(5)30x >, ∴530x >,∴长方形纸片的长大于正方形的边长, ∴不能裁出这样的长方形纸片. 【点睛】本题通过圆和正方形的面积考查了对算术平方根的应用,主要是对学生无理数运算及比较大小进行了考查.2.(1)棱长为4;(2)边长为:(或) 【分析】(1)由立方体的体积为棱长的立方可以得到答案;(2)用勾股定理直接计算得到答案.【详解】解:(1)设正方体的棱长为,则,所以,即正方体的棱长为4.解析:(1)棱长为4;(2【分析】(1)由立方体的体积为棱长的立方可以得到答案;(2)用勾股定理直接计算得到答案.【详解】解:(1)设正方体的棱长为x,则364x=,即正方体的棱长为4.x=,所以4(2)因为正方体的棱长为4,所以AB=【点睛】本题考查的是立方根与算术平方根的理解与计算,由实际的情境去理解问题本身就是求一个数的立方根与算术平方根是关键.3.不同意,理由见解析.【详解】试题分析:设面积为300平方厘米的长方形的长宽分为3x厘米,2x厘米,则3x•2x=300,x2=50,解得x=,而面积为400平方厘米的正方形的边长为20厘米,由于解析:不同意,理由见解析.【详解】试题分析:设面积为300平方厘米的长方形的长宽分为3x厘米,2x厘米,则3x•2x=300,x2=50,解得x=400平方厘米的正方形的边长为20厘米,由于20,所以用一块面积为400平方厘米的正方形纸片,沿着边的方向裁不出一块面积为300平方厘米的长方形纸片,使它的长宽之比为3:2.试题解析:解:不同意李明的说法.设长方形纸片的长为3x(x>0)cm,则宽为2x cm,依题意得:3x•2x=300,6x2=300,x2=50,∵x>0,∴x∴长方形纸片的长为cm,∵50>49,∴7,∴21,即长方形纸片的长大于20cm,由正方形纸片的面积为400 cm2,可知其边长为20cm,∴长方形纸片的长大于正方形纸片的边长.答:李明不能用这块纸片裁出符合要求的长方形纸片.点睛:本题考查了算术平方根的定义:一个正数的正的平方根叫这个数的算术平方根;0的算术平方根为0.也考查了估算无理数的大小.4.8;【分析】用大正方形的面积减去4个小直角三角形的面积可得到所求的正方形的面积为8,然后利用正方形面积公式求8的算术平方根即可.【详解】解:正方形面积=4×4-4××2×2=8;正方形的边解析:8;【分析】用大正方形的面积减去4个小直角三角形的面积可得到所求的正方形的面积为8,然后利用正方形面积公式求8的算术平方根即可. 【详解】解:正方形面积=4×4-4×12×2×2=8;正方形的边长 【点睛】本题考查了算术平方根:一般地,如果一个正数x 的平方等于a ,即x 2=a ,那么这个正数x叫做a5.(1)4米 (2)见解析 【分析】(1)根据正方形边长与面积间的关系求解即可;(2)设长方形的长宽分别为米、米,由其面积可得x 值,比较长方形的长和宽与正方形边长的大小可得结论. 【详解】 解解析:(1)4米 (2)见解析 【分析】(1)根据正方形边长与面积间的关系求解即可;(2)设长方形的长宽分别为3x 米、2x 米,由其面积可得x 值,比较长方形的长和宽与正方形边长的大小可得结论. 【详解】解:(1)正方形的面积是16平方米, ∴4=米;(2)设长方形的长宽分别为3x 米、2x 米, 则3212x x •=, 22x =,x34x =,24x =<,∴长方形长是4米,所以李师傅不能办到.【点睛】本题考查了算术平方根的实际应用,灵活的利用算术平方根表示正方形和长方形的边长是解题的关键.二、解答题6.(1)见解析;(2)55°;(3) 【分析】(1)根据平行线的判定定理与性质定理解答即可;(2)①如图2,过点作,当点在点的左侧时,根据,,根据平行线的性质及角平分线的定义即可求的度数;②如图解析:(1)见解析;(2)55°;(3)1118022αβ︒-+ 【分析】(1)根据平行线的判定定理与性质定理解答即可;(2)①如图2,过点F 作//FE AB ,当点B 在点A 的左侧时,根据50ABC ∠=︒,60ADC ∠=︒,根据平行线的性质及角平分线的定义即可求BFD ∠的度数;②如图3,过点F 作//EF AB ,当点B 在点A 的右侧时,ABC α∠=,ADC β∠=,根据平行线的性质及角平分线的定义即可求出BFD ∠的度数.【详解】解:(1)如图1,过点E 作//EF AB ,则有BEF B ∠=∠,//AB CD ,//EF CD ∴,FED D ∴∠=∠,BED BEF FED B D ∴∠=∠+∠=∠+∠;(2)①如图2,过点F 作//FE AB ,有BFE FBA ∠=∠.//AB CD ,//EF CD ∴.EFD FDC ∴∠=∠.BFE EFD FBA FDC ∴∠+∠=∠+∠.即BFD FBA FDC ∠=∠+∠,BF 平分ABC ∠,DF 平分ADC ∠,1252FBA ABC ∴∠=∠=︒,1302FDC ADC ∠=∠=︒, 55BFD FBA FDC ∴∠=∠+∠=︒.答:BFD ∠的度数为55︒;②如图3,过点F 作//FE AB ,有180BFE FBA ∠+∠=︒.180BFE FBA ∴∠=︒-∠,//AB CD ,//EF CD ∴.EFD FDC ∴∠=∠.180BFE EFD FBA FDC ∴∠+∠=︒-∠+∠.即180BFD FBA FDC ∠=︒-∠+∠,BF 平分ABC ∠,DF 平分ADC ∠, 1122FBA ABC α∴∠=∠=,1122FDC ADC β∠=∠=, 1118018022BFD FBA FDC αβ∴∠=︒-∠+∠=︒-+. 答:BFD ∠的度数为1118022αβ︒-+. 【点睛】本题考查了平行线的判定与性质,解决本题的关键是熟练掌握平行线的判定与性质. 7.(1)90°;(2)∠PFC=∠PEA+∠P ;(3)∠G=α【分析】(1)根据平行线的性质与判定可求解;(2)过P 点作PN ∥AB ,则PN ∥CD ,可得∠FPN=∠PEA+∠FPE ,进而可得∠PF 解析:(1)90°;(2)∠PFC =∠PEA +∠P ;(3)∠G =12α【分析】(1)根据平行线的性质与判定可求解;(2)过P 点作PN ∥AB ,则PN ∥CD ,可得∠FPN =∠PEA +∠FPE ,进而可得∠PFC =∠PEA +∠FPE ,即可求解;(3)令AB 与PF 交点为O ,连接EF ,根据三角形的内角和定理可得∠GEF +∠GFE =12∠PEA +12∠PFC +∠OEF +∠OFE ,由(2)得∠PEA =∠PFC -α,由∠OFE +∠OEF =180°-∠FOE =180°-∠PFC 可求解.【详解】解:(1)如图1,过点P作PM∥AB,∴∠1=∠AEP.又∠AEP=40°,∴∠1=40°.∵AB∥CD,∴PM∥CD,∴∠2+∠PFD=180°.∵∠PFD=130°,∴∠2=180°-130°=50°.∴∠1+∠2=40°+50°=90°.即∠EPF=90°.(2)∠PFC=∠PEA+∠P.理由:过P点作PN∥AB,则PN∥CD,∴∠PEA=∠NPE,∵∠FPN=∠NPE+∠FPE,∴∠FPN=∠PEA+∠FPE,∵PN∥CD,∴∠FPN=∠PFC,∴∠PFC=∠PEA+∠FPE,即∠PFC=∠PEA+∠P;(3)令AB与PF交点为O,连接EF,如图3.在△GFE中,∠G=180°-(∠GFE+∠GEF),∵∠GEF=12∠PEA+∠OEF,∠GFE=12∠PFC+∠OFE,∴∠GEF+∠GFE=12∠PEA+12∠PFC+∠OEF+∠OFE,∵由(2)知∠PFC=∠PEA+∠P,∴∠PEA=∠PFC-α,∵∠OFE+∠OEF=180°-∠FOE=180°-∠PFC,∴∠GEF+∠GFE=12(∠PFC−α)+12∠PFC+180°−∠PFC=180°−12α,∴∠G=180°−(∠GEF+∠GFE)=180°−180°+12α=12α.【点睛】本题主要考查平行线的性质与判定,灵活运用平行线的性质与判定是解题的关键.8.(1)∠BME=∠MEN﹣∠END;∠BMF=∠MFN+∠FND;(2)120°;(3)不变,30°【分析】(1)过E作EH∥AB,易得EH∥AB∥CD,根据平行线的性质可求解;过F作FH∥AB解析:(1)∠BME=∠MEN﹣∠END;∠BMF=∠MFN+∠FND;(2)120°;(3)不变,30°【分析】(1)过E作EH∥AB,易得EH∥AB∥CD,根据平行线的性质可求解;过F作FH∥AB,易得FH∥AB∥CD,根据平行线的性质可求解;(2)根据(1)的结论及角平分线的定义可得2(∠BME+∠END)+∠BMF-∠FND=180°,可求解∠BMF=60°,进而可求解;(3)根据平行线的性质及角平分线的定义可推知∠FEQ=12∠BME,进而可求解.【详解】解:(1)过E作EH∥AB,如图1,∴∠BME=∠MEH,∵AB∥CD,∴HE∥CD,∴∠END=∠HEN,∴∠MEN=∠MEH+∠HEN=∠BME+∠END,即∠BME=∠MEN﹣∠END.如图2,过F作FH∥AB,∴∠BMF=∠MFK,∵AB∥CD,∴FH∥CD,∴∠FND=∠KFN,∴∠MFN=∠MFK﹣∠KFN=∠BMF﹣∠FND,即:∠BMF=∠MFN+∠FND.故答案为∠BME=∠MEN﹣∠END;∠BMF=∠MFN+∠FND.(2)由(1)得∠BME=∠MEN﹣∠END;∠BMF=∠MFN+∠FND.∵NE平分∠FND,MB平分∠FME,∴∠FME=∠BME+∠BMF,∠FND=∠FNE+∠END,∵2∠MEN+∠MFN=180°,∴2(∠BME+∠END)+∠BMF﹣∠FND=180°,∴2∠BME+2∠END+∠BMF﹣∠FND=180°,即2∠BMF+∠FND+∠BMF﹣∠FND=180°,解得∠BMF=60°,∴∠FME=2∠BMF=120°;(3)∠FEQ的大小没发生变化,∠FEQ=30°.由(1)知:∠MEN=∠BME+∠END,∵EF平分∠MEN,NP平分∠END,∴∠FEN=12∠MEN=12(∠BME+∠END),∠ENP=12∠END,∵EQ∥NP,∴∠NEQ=∠ENP,∴∠FEQ=∠FEN﹣∠NEQ=12(∠BME+∠END)﹣12∠END=12∠BME,∵∠BME=60°,∴∠FEQ=12×60°=30°.【点睛】本题主要考查平行线的性质及角平分线的定义,作平行线的辅助线是解题的关键.9.(1)120,90;(2)①∠1=120°-n°,∠2=90°+n°;②见解析【分析】(1)根据邻补角的定义和平行线的性质解答;(2)①根据邻补角的定义求出∠ABE,再根据两直线平行,同位角相解析:(1)120,90;(2)①∠1=120°-n°,∠2=90°+n°;②见解析【分析】(1)根据邻补角的定义和平行线的性质解答;(2)①根据邻补角的定义求出∠ABE,再根据两直线平行,同位角相等可得∠1=∠ABE,根据两直线平行,同旁内角互补求出∠BCG,然后根据周角等于360°计算即可得到∠2;②结合图形,分A B、B C、AC三条边与直尺垂直讨论求解.【详解】解:(1)∠1=180°-60°=120°,∠2=90°;故答案为:120,90;(2)①如图2,∵∠ABC=60°,∴∠ABE=180°-60°-n°=120°-n°,∵DG∥EF,∴∠1=∠ABE=120°-n°,∠BCG=180°-∠CBF=180°-n°,∵∠ACB+∠BCG+∠2=360°,∴∠2=360°-∠ACB-∠BCG=360°-90°-(180°-n°)=90°+n°;②当n=30°时,∵∠ABC=60°,∴∠ABF=30°+60°=90°,AB⊥DG(EF);当n=90°时,∠C=∠CBF=90°,∴BC⊥DG(EF),AC⊥DE(GF);当n =120°时,∴AB ⊥DE (GF ).【点睛】本题考查了平行线角的计算,垂线的定义,主要利用了平行线的性质,直角三角形的性质,读懂题目信息并准确识图是解题的关键.10.(1)90°;(2)见解析;(3)不变,180°【分析】(1)根据邻补角的定义及角平分线的定义即可得解;(2)根据垂直的定义及邻补角的定义、角平分线的定义即可得解; (3),过,分别作,,根据解析:(1)90°;(2)见解析;(3)不变,180°【分析】(1)根据邻补角的定义及角平分线的定义即可得解;(2)根据垂直的定义及邻补角的定义、角平分线的定义即可得解;(3)180BPC BQC ∠+∠=︒,过Q ,P 分别作//QG AB ,//PH AB ,根据平行线的性质及平角的定义即可得解.【详解】解(1)CN ,CM 分别平分BCE ∠和BCD ∠,12BCN BCE ∴=∠,12BCM BCD ∠=∠, 180BCE BCD ∠+∠=︒,111()90222MCN BCN BCM BCE BCD BCE BCD ∴∠=∠+∠=∠+∠=∠+∠=︒; (2)CM CN ⊥,90MCN ∴∠=︒,即90BCN BCM ∠+∠=︒,22180BCN BCM ∴∠+∠=︒, CN 是BCE ∠的平分线,2BCE BCN ∴∠=∠,2180BCE BCM ∴∠+∠=︒,又180BCE BCD ∠+∠=︒,2BCD BCM ∴∠=∠,又CM 在BCD ∠的内部,CM ∴平分BCD ∠;(3)如图,不发生变化,180BPC BQC ∠+∠=︒,过Q ,P 分别作//QG AB ,//PH AB ,则有//////QG AB PH CD ,BQG ABQ ∴∠=∠,CQG ECQ ∠=∠,BPH FBP ∠=∠,CPH DCP ∠=∠, ⊥BP BQ ,CP CQ ⊥,90PBQ PCQ ∴∠=∠=︒,180ABQ PBQ FBP ∠+∠+=︒,180ECQ PCQ DCP ∠+∠+∠=︒,180ABQ FBP ECQ DCP ∴∠+∠+∠+∠=︒,BPC BQC BPH CPH BQG CQG ∴∠+∠=∠+∠+∠+∠180ABQ FBP ECQ DCP =∠+∠+∠+∠=︒,180BPC BQC ∴∠+∠=︒不变.【点睛】此题考查了平行线的性质,熟记平行线的性质及作出合理的辅助线是解题的关键.三、解答题11.(1)平行,理由见解析;(2)35°或145°,画图、过程见解析;(3)50°或130°或60°或120°【分析】(1)过点C 作CF ∥AB ,根据∠B=50°,∠C=85°,∠D=35°,即可得C解析:(1)平行,理由见解析;(2)35°或145°,画图、过程见解析;(3)50°或130°或60°或120°【分析】(1)过点C 作CF ∥AB ,根据∠B =50°,∠C =85°,∠D =35°,即可得CF ∥ED ,进而可以判断AB 平行于ED ;(2)根据题意作AB ∥CD ,即可∠B =∠C =35°;(3)分别画图,根据平行线的性质计算出∠B 的度数.【详解】解:(1)AB 平行于ED ,理由如下:如图2,过点C 作CF ∥AB ,∴∠BCF=∠B=50°,∵∠BCD=85°,∴∠FCD=85°-50°=35°,∵∠D=35°,∴∠FCD=∠D,∴CF∥ED,∵CF∥AB,∴AB∥ED;(2)如图,即为所求作的图形.∵AB∥CD,∴∠ABC=∠C=35°,∴∠B的度数为:35°;∵A′B∥CD,∴∠ABC+∠C=180°,∴∠B的度数为:145°;∴∠B的度数为:35°或145°;(3)如图2,过点C作CF∥AB,∵AB∥DE,∴CF∥DE,∴∠FCD=∠D=35°,∵∠BCD=85°,∴∠BCF=85°-35°=50°,∴∠B=∠BCF=50°.答:∠B的度数为50°.如图5,过C作CF∥AB,则AB∥CF∥CD,∴∠FCD=∠D=35°,∵∠BCD=85°,∴∠BCF=85°-35°=50°,∵AB∥CF,∴∠B+∠BCF=180°,∴∠B=130°;如图6,∵∠C=85°,∠D=35°,∴∠CFD=180°-85°-35°=60°,∵AB∥DE,∴∠B=∠CFD=60°,如图7,同理得:∠B=35°+85°=120°,综上所述,∠B 的度数为50°或130°或60°或120°. 【点睛】本题考查了平行线的判定与性质,解决本题的关键是区分平行线的判定与性质,并熟练运用.12.(1) ;(2) ;(3)不发生变化,理由见解析 【分析】(1)如图1,延长DE 交AB 于点F ,根据平行线的性质推出;(2)如图2,过点E 作ES ∥AB ,过点H 作HT ∥AB ,根据AB ∥CD ,AB ∥E解析:(1) +180ACB BED ∠∠=︒;(2) 100︒;(3)不发生变化,理由见解析 【分析】(1)如图1,延长DE 交AB 于点F ,根据平行线的性质推出+180ACB BED ∠∠=︒; (2)如图2,过点E 作ES ∥AB ,过点H 作HT ∥AB ,根据AB ∥CD ,AB ∥ES 推出BED ABE CDE ∠=∠+∠,再根据AB ∥TH ,AB ∥CD 推出GHD THD THB ∠=∠-∠,最后根据BED ∠比BHD ∠大60︒得出BED ∠的度数;(3)如图3,过点E 作EQ ∥DN ,根据DEB CDE ABE ∠=∠+∠得出βα-的度数,根据条件再逐步求出PBM ∠的度数. 【详解】(1)如答图1所示,延长DE 交AB 于点F . AB ∥CD ,所以D EFB ∠=∠,又因为A D ∠=∠,所以A EFB ∠=∠,所以AC ∥DF ,所以ACB CED ∠=∠. 因为+180CED BED ∠∠=︒,所以+180ACB BED ∠∠=︒. (2)如答图2所示,过点E 作ES ∥AB ,过点H 作HT ∥AB . 设ABG EBG α∠=∠=,FDH EDH β∠=∠=,因为AB ∥CD ,AB ∥ES ,所以ABE BES ∠=∠,SED CED ∠=∠, 所以21802BED BES SED ABE CDE αβ∠=∠+∠=∠+∠=+︒-, 因为AB ∥TH ,AB ∥CD ,所以ABG THB ∠=∠,FDH DHT ∠=∠,所以GHD THD THB βα∠=∠-∠=-,因为BED ∠比BHD ∠大60︒,所以2+1802()60αββα︒---=︒,所以40βα-=︒,所以40BHD ∠=︒,所以100BED ∠=︒(3)不发生变化如答图3所示,过点E 作EQ ∥DN .设CDN EDN α∠=∠=,EBM KBM β∠=∠=,由(2)易知DEB CDE ABE ∠=∠+∠,所以2+1802100αβ︒-=︒,所以40βα-=︒,所以180()180DEB CDE EDN EBM PBM PBM αβ∠=∠+∠+︒-∠+∠=+︒--∠, 所以80()40PBM βα∠=︒--=︒.【点睛】本题考查了平行线的性质,求角的度数,正确作出相关的辅助线,根据条件逐步求出角度的度数是解题的关键.13.(1)∠ACB+∠BED=180°;(2)100°;(3)40° 【分析】(1)如图1,延长DE 交AB 于点F ,根据ABCD 可得∠DFB=∠D ,则∠DFB=∠A ,可得ACDF ,根据平行线的性质得∠A解析:(1)∠ACB +∠BED =180°;(2)100°;(3)40° 【分析】(1)如图1,延长DE 交AB 于点F ,根据AB //CD 可得∠DFB =∠D ,则∠DFB =∠A ,可得AC //DF ,根据平行线的性质得∠ACB +∠CEF =180°,由对顶角相等可得结论;(2)如图2,作EM //CD ,HN //CD ,根据AB //CD ,可得AB //EM //HN //CD ,根据平行线的性质得角之间的关系,再根据∠DEB 比∠DHB 大60°,列出等式即可求∠DEB 的度数; (3)如图3,过点E 作ES //CD ,设直线DF 和直线BP 相交于点G ,根据平行线的性质和角平分线定义可求∠PBM 的度数. 【详解】解:(1)如图1,延长DE 交AB 于点F ,//AB CD ,DFB D ∴∠=∠,A D ∠=∠,A DFB ∴∠=∠,//AC DF ∴,180ACB CEF ∴∠+∠=︒, 180ACB BED ∴∠+∠=︒,故答案为:180ACB BED ∠+∠=︒;(2)如图2,作//EM CD ,//HN CD ,//AB CD ,//////AB EM HN CD ∴,1180EDF ∴∠+∠=︒,MEB ABE ∠=∠,BG 平分ABE ∠,12ABG ABE ∴∠=∠,//AB HN , 2ABG ∴∠=∠,//CF HN ,23β∴∠+∠=∠,∴132ABE β∠+∠=∠,DH 平分EDF ∠,132EDF ∴∠=∠,∴1122ABE EDF β∠+∠=∠,1()2EDF ABE β∴∠=∠-∠,2EDF ABE β∴∠-∠=∠,设DEB α∠=∠,1180180()1802MEB EDF ABE EDF ABE αβ∠=∠+∠=︒-∠+∠=︒-∠-∠=︒-∠,DEB ∠比DHB ∠大60︒,60αβ∴∠-︒=∠, 1802(60)αα∴∠=︒-∠-︒,解得100α∠=︒.DEB ∴∠的度数为100︒;(3)PBM ∠的度数不变,理由如下:如图3,过点E 作//ES CD ,设直线DF 和直线BP 相交于点G ,BM 平分EBK ∠,DN 平分CDE ∠,12EBM MBK EBK ∴∠=∠=∠,12CDN EDN CDE ∠=∠=∠,//ES CD ,//AB CD ,////ES AB CD ∴, DES CDE ∴∠=∠,180BES ABE EBK ∠=∠=︒-∠, G PBK ∠=∠,由(2)可知:100DEB ∠=︒,180100CDE EBK ∴∠+︒-∠=︒, 80EBK CDE ∴∠-∠=︒, //BP DN , CDN G ∴∠=∠,12PBK G CDN CDE ∴∠=∠=∠=∠,PBM MBK PBK ∴∠=∠-∠1122EBK CDE =∠-∠ 1()2EBK CDE =∠-∠ 1802=⨯︒ 40=︒.【点睛】本题考查了平行线的性质,解决本题的关键是掌握平行线的性质.14.(1);(2),见解析;(3)不变, 【分析】(1)根据平行线的性质求出,再求出的度数,利用内错角相等可求出角的度数;(2)过点作∥,类似(1)利用平行线的性质,得出三个角的关系; (3)运用解析:(1)23︒;(2)BCD A B ∠=∠+∠,见解析;(3)不变, 25FOG ∠=︒ 【分析】(1)根据平行线的性质求出50A DCE ∠=∠=︒,再求出BCE ∠的度数,利用内错角相等可求出角的度数;(2)过点C 作CE ∥AB ,类似(1)利用平行线的性质,得出三个角的关系;(3)运用(2)的结论和平行线的性质、角平分线的性质,可求出FOG ∠的度数,可得结论. 【详解】(1)因为CE ∥AB ,所以50A DCE ∠=∠=︒,B BCE ∠=∠ 因为∠BCD =73 °,所以23BCE BCD DCE ∠=∠-∠=︒, 故答案为:23︒ (2)BCD A B ∠=∠+∠, 如图②,过点C 作CE ∥AB , 则A DCE ∠=∠,B BCE ∠=∠. 因为BCD DCE BCE ∠=∠+∠, 所以BCD BAD B ∠=∠+∠, (3)不变, 设ABE x ∠=, 因为BE 平分ABC ∠, 所以CBE ABE x ∠=∠=.由(2)的结论可知BCD BAD ABC ∠=∠+∠,且50BAD ︒∠=, 则:502BCD x ∠=︒+. 因为MN ∥AD ,所以502BON BCD x ∠=∠=︒+, 因为OF 平分BON ∠,所以1252COF NOF BON x ∠=∠=∠=︒+.因为OG ∥BE , 所以COG CBE x ∠=∠=,所以2525FOG COF COG x x ∠=∠-∠=+-=︒︒. 【点睛】本题考查了平行线的性质和角平分线的定义,解题关键是熟练运用平行线的性质证明角相等,通过等量代换等方法得出角之间的关系.15.(1)证明见解析;(2)∠F=55°;(3)∠MQN =∠ACB ;理由见解析. 【分析】(1)首先根据平行线的性质得出∠ACE =∠A ,∠ECD =∠B ,然后通过等量代换即可得出答案; (2)首先根据角解析:(1)证明见解析;(2)∠F=55°;(3)∠MQN =12∠ACB ;理由见解析. 【分析】(1)首先根据平行线的性质得出∠ACE =∠A ,∠ECD =∠B ,然后通过等量代换即可得出答案;(2)首先根据角平分线的定义得出∠FCD =12∠ECD ,∠HAF =12∠HAD ,进而得出∠F =12(∠HAD+∠ECD ),然后根据平行线的性质得出∠HAD+∠ECD 的度数,进而可得出答案;(3)根据平行线的性质及角平分线的定义得出12QGR QGD ∠=∠,12NQG AQG ∠=∠,180MQG QGR ∠+∠=︒ ,再通过等量代换即可得出∠MQN =12∠ACB .【详解】解:(1)∵CE //AB , ∴∠ACE =∠A ,∠ECD =∠B , ∵∠ACD =∠ACE+∠ECD , ∴∠ACD =∠A+∠B ;(2)∵CF 平分∠ECD ,FA 平分∠HAD , ∴∠FCD =12∠ECD ,∠HAF =12∠HAD ,∴∠F =12∠HAD+12∠ECD =12(∠HAD+∠ECD ), ∵CH //AB , ∴∠ECD =∠B , ∵AH //BC , ∴∠B+∠HAB =180°, ∵∠BAD =70°,110B HAD ∴∠+∠=︒,∴∠F =12(∠B+∠HAD )=55°; (3)∠MQN =12∠ACB ,理由如下:GR 平分QGD ∠,12QGR QGD ∴∠=∠.GN 平分AQG ∠,12NQG AQG ∴∠=∠.//QM GR ,180MQG QGR ∴∠+∠=︒ .∴∠MQN =∠MQG ﹣∠NQG =180°﹣∠QGR ﹣∠NQG =180°﹣12(∠AQG+∠QGD )=180°﹣12(180°﹣∠CQG+180°﹣∠QGC ) =12(∠CQG+∠QGC ) =12∠ACB . 【点睛】本题主要考查平行线的性质和角平分线的定义,掌握平行线的性质和角平分线的定义是解题的关键.四、解答题16.(1)105°;(2)135°;(3)5.5或11.5.【分析】(1)在△CEN中,用三角形内角和定理即可求出;(2)由∠BON=30°,∠N=30°可得MN∥CB,再根据两直线平行,同旁内角解析:(1)105°;(2)135°;(3)5.5或11.5.【分析】(1)在△CEN中,用三角形内角和定理即可求出;(2)由∠BON=30°,∠N=30°可得MN∥CB,再根据两直线平行,同旁内角互补即可求出∠CEN的度数.(3)画出图形,求出在MN⊥CD时的旋转角,再除以30°即得结果.【详解】解:(1)在△CEN中,∠CEN=180°-∠ECN-∠CNE=180°-45°-30°=105°;(2)∵∠BON=30°,∠N=30°,∴∠BON=∠N,∴MN∥CB.∴∠OCD+∠CEN=180°,∵∠OCD=45°∴∠CEN=180°-45°=135°;(3)如图,MN⊥CD时,旋转角为360°-90°-45°-60°=165°,或360°-(60°-45°)=345°,所以在第165°÷30°=5.5或345°÷30°=11.5秒时,直线MN恰好与直线CD垂直.【点睛】本题以学生熟悉的三角板为载体,考查了三角形的内角和、平行线的判定和性质、垂直的定义和旋转的性质,前两小题难度不大,难点是第(3)小题,解题的关键是画出适合题意的几何图形,弄清求旋转角的思路和方法,本题的第一种情况是将旋转角∠DOM放在四边形DOMF中,用四边形内角和求解,第二种情况是用周角减去∠DOM的度数.17.解决问题:6;拓展延伸:(1)S1=2S2 (2)10.5【解析】试题分析:解决问题:连接AE,根据操作示例得到S△ADE=S△BDE,S△ABE=S△AEC,从而得到结论;拓展延伸:(1)解析:解决问题:6;拓展延伸:(1)S1=2S2(2)10.5【解析】试题分析:解决问题:连接AE,根据操作示例得到S△ADE=S△BDE,S△ABE=S△AEC,从而得到结论;拓展延伸:(1)作△ABD的中线AE,则有BE=ED=DC,从而得到△ABE的面积=△AED的面积=△ADC的面积,由此即可得到结论;(2)连接AO.则可得到△BOD的面积=△BOC的面积,△AOC的面积=△AOD的面积,△EOC的面积=△BOC的面积的一半,△AOB的面积=2△AOE的面积.设△AOD的面积=a,△AOE的面积=b,则a+3=2b,a=b+1.5,求出a、b的值,即可得到结论.试题解析:解:解决问题连接AE.∵点D、E分别是边AB、BC的中点,∴S△ADE=S△BDE,S△ABE=S△AEC.∵S△BDE =2,∴S△ADE =2,∴S△ABE=S△AEC=4,∴四边形ADEC的面积=2+4=6.拓展延伸:解:(1)作△ABD的中线AE,则有BE=ED=DC,∴△ABE的面积=△AED的面积=△ADC的面积= S2,∴S1=2S2.(2)连接AO.∵CO=DO,∴△BOD的面积=△BOC的面积=3,△AOC的面积=△AOD的面积.∵BO=2EO,∴△EOC的面积=△BOC的面积的一半=1.5,△AOB的面积=2△AOE的面积.设△AOD的面积=a,△AOE的面积=b,则a+3=2b,a=b+1.5,解得:a=6,b=4.5,∴四边形ADOE的面积为=a+b=6+4.5=10.5.18.(1)∠AEB的大小不会发生变化,∠ACB=45°;(2)30°,60°;(3)60°或72°.【分析】(1)由直线MN与直线PQ垂直相交于O,得到∠AOB=90°,根据三角形的外角的性质得到∠解析:(1)∠AEB的大小不会发生变化,∠ACB=45°;(2)30°,60°;(3)60°或72°.【分析】(1)由直线MN与直线PQ垂直相交于O,得到∠AOB=90°,根据三角形的外角的性质得到∠PAB+∠ABM=270°,根据角平分线的定义得到∠BAC=12∠PAB,∠ABC=12∠ABM,于是得到结论;(2)由于将△ABC沿直线AB折叠,若点C落在直线PQ上,得到∠CAB=∠BAQ,由角平分线的定义得到∠PAC=∠CAB,即可得到结论;根据将△ABC沿直线AB折叠,若点C落在直线MN上,得到∠ABC=∠ABN,由于BC平分∠ABM,得到∠ABC=∠MBC,于是得到结论;(3)由∠BAO与∠BOQ的角平分线相交于E可得出∠E与∠ABO的关系,由AE、AF分别是∠BAO和∠OAG的角平分线可知∠EAF=90°,在△AEF中,由一个角是另一个角的32倍分情况进行分类讨论即可.【详解】解:(1)∠ACB的大小不变,∵直线MN与直线PQ垂直相交于O,∴∠AOB=90°,∴∠OAB+∠OBA=90°,∴∠PAB+∠ABM=270°,∵AC、BC分别是∠BAP和∠ABM角的平分线,∴∠BAC=12∠PAB,∠ABC=12∠ABM,∴∠BAC+∠ABC=12(∠PAB+∠ABM)=135°,∴∠ACB=45°;(2)∵将△ABC沿直线AB折叠,若点C落在直线PQ上,∴∠CAB=∠BAQ,∵AC平分∠PAB,∴∠PAC=∠CAB,∴∠PAC=∠CAB=∠BAO=60°,∵∠AOB=90°,∴∠ABO=30°,∵将△ABC沿直线AB折叠,若点C落在直线MN上,∴∠ABC=∠ABN,。
七年级下数学压轴题

七年级下数学压轴题一、相交线与平行线。
题1:如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE,∠AOD:∠BOE = 4:1,求∠AOF的度数。
解析:设∠BOE = x,因为OE平分∠BOD,所以∠BOD = 2∠BOE=2x。
又因为∠AOD + ∠BOD = 180°,且∠AOD:∠BOE = 4:1,所以∠AOD = 4x。
则4x + 2x=180°,6x = 180°,解得x = 30°。
所以∠COE = 180° - ∠BOE = 150°。
因为OF平分∠COE,所以∠COF=(1)/(2)∠COE = 75°。
∠AOC=∠BOD = 60°,所以∠AOF=∠AOC+∠COF = 60°+ 75°=135°。
题2:已知直线l_1∥ l_2,直线l_3和直线l_1、l_2交于点C和D,在C、D之间有一点P。
(1)如果P点在C、D之间运动时,问∠PAC,∠APB,∠PBD之间的关系是否发生变化。
(2)若点P在C、D两点的外侧运动时(P点与点C、D不重合),试探索∠PAC,∠APB,∠PBD之间的关系又是如何?解析:(1)过点P作PE∥ l_1,因为l_1∥ l_2,所以PE∥ l_2。
∠PAC = ∠APE,∠PBD=∠BPE。
所以∠APB = ∠APE+∠BPE = ∠PAC + ∠PBD。
(2)当点P在l_1上方时,过点P作PF∥ l_1,因为l_1∥ l_2,所以PF∥ l_2。
∠PAC = ∠APF,∠PBD + ∠BPF=180°,所以∠PBD = 180°-(∠APB - ∠PAC),即∠PAC=∠APB + ∠PBD。
当点P在l_2下方时,过点P作PG∥ l_2,同理可得∠PBD = ∠APB+∠PAC。
二、实数。
题3:已知a、b满足√(2a + 8)+| b - √(3)|=0,解关于x的方程(a + 2)x + b^2=a - 1。
七年级(下册)数学压轴题集锦
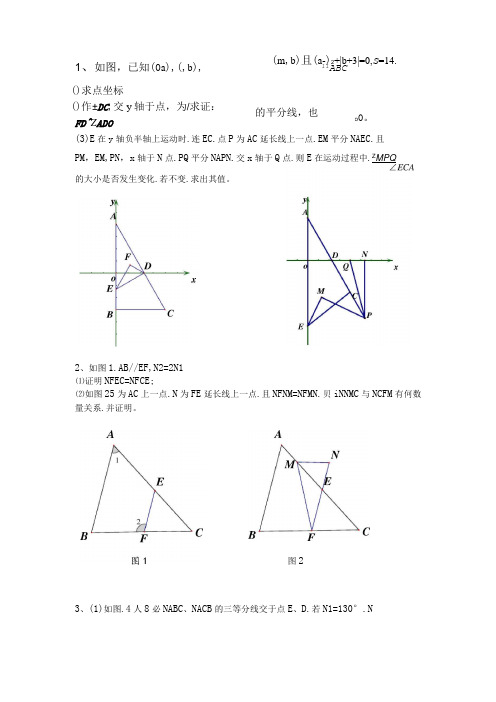
1、如图,已知(0a ),(,b ),()求点坐标()作±DC ,交y 轴于点,为/求证:FD^Z ADO (m ,b )且(a-)2+|b+3|=0,S =14. 11ABC(3)E 在y 轴负半轴上运动时.连EC.点P 为AC 延长线上一点.EM 平分NAEC.且 PM ,EM,PN ,x 轴于N 点.PQ 平分NAPN.交x 轴于Q 点.则E 在运动过程中.Z MPQ2、如图1.AB//EF,N2=2N1⑴证明NFEC=NFCE;⑵如图25为AC 上一点.N 为FE 延长线上一点.且NFNM=NFMN.贝iNNMC 与NCFM 有何数量关系.并证明。
3、(1)如图.4人8必NABC 、NACB 的三等分线交于点E 、D.若N1=130°.N的平分线,也 o 0。
的大小是否发生变化.若不变.求出其值。
图22=110°.求NA的度数。
(2)如图.△ABC,NABC的三等分线分别与NACB的平分线交于点D,E若N1=110°.N2=130°.求NA的度数。
4、如图.NABC+NADC=180°.OE、OF分别是角平分线.则判断OE、OF的位置关系为?5、已知NA=NC=90°.(1)如图.NABC的平分线与NADC的平分线交于点E.试问BE与DE有何位置关系?说明你的理由。
(2)如图.试问NABC的平分线BE与NADC的外角平分线DF有何位置关系?说明你的理由。
(3)如图.若NABC的外角平分线与NADC的外角平分线交于点E.试问BE与DE有何位置关系?说明你的理由。
6.(1)如图.点E在AC的延长线上.NBAC与NDCE的平分线交于点F.NB=60NF=56°,求NBDC的度数。
(2)如图.点E在CD的延长线上.NBAD与NADE的平分线交于点F.试问NF、NB和NC之间有何数量关系?为什么?7.已知NABC与NADC的平分线交于点E。
期中解答题压轴必刷常考题七年级数学下学期期中期末满分必刷常考压轴题人教版

解答题压轴必刷常考题【压轴题题必考】1.(安溪)如图,将一条数轴在原点O和点B处各折一下,AO∥BC,得到一条“折线数轴”.图中点A表示﹣20,点B表示20,点C表示36.动点M从点A出发,以2个单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点N从点C出发,以1个单位/秒的速度沿着“折线数轴”的负方向运动,从点B运动到点O期间的速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为t秒.(1)填空:点A和点C在数轴上相距56个单位长度;(2)当t为何值时,点M与点N相遇?(3)当t为何值时,M、O两点在数轴上相距的长度与N、B两点在数轴上相距的长度相等.【答案】(1)56 (2)t=(3)t的值为4或13或22或34【解答】解:(1)∵点A表示﹣20,点C表示36,∴点A和点C在数轴上相距36﹣(﹣20)=56(个单位长度),故答案为:56;(2)由题意知,N从C到B需16s,M从A到O需10s,∴M、N在OB段相遇,根据题意得:20+(t﹣10)+16+2(t﹣16)=56,解得t=,答:t为时,点M与点N相遇;(3)分四种情况:①当点M在AO上,点N在CB上时,OM=20﹣2t,BN=16﹣t,∴20﹣2t=16﹣t,解得t=4,②当M在OB上,N在CB上时,OM=t﹣10,BN=16﹣t,∴t﹣10=16﹣t,解得t=13,③当M在OB上,N在OB上时,OM=t﹣10,BN=2(t﹣16),∴t﹣10=2(t﹣16),解得t=22,④当M在BC上,N在OA上时,20+2(t﹣30)=20+(t﹣26),解得t=34,综上所述,t的值为4或13或22或34时,M、O两点在数轴上相距的长度与N、B两点在数轴上相距的长度相等.2.(朝阳)将一副三角板中的两块直角三角尺的直角顶点C按如图1方式叠放在一起,其中∠A=60°,∠D=30°,∠E=∠B=45°.(1)若∠1=25°,则∠2的度数为;(2)直接写出∠1与∠3的数量关系:;(3)直接写出∠2与∠ACB的数量关系:;(4)如图2,当∠ACE<180°且点E在直线AC的上方时,将三角尺ACD固定不动,改变三角尺BCE的位置,但始终保持两个三角尺的顶点C重合,这两块三角尺是否存在一组边互相平行?请直接写出∠ACE角度所有可能的值.【答案】(1)65°(2)∠1=∠3;(3)∠2+∠ACB=180°(4)30°或45°或120°或135°或165°.【解答】解:(1)∵∠1=25°,∠ACD=90°,∴∠2=∠ACD﹣∠1=65°,故答案为:65°;(2)∵∠1+∠2=∠ACD=90°,∠2+∠3=∠BCE=90°,∴∠1+∠2=∠2+∠3,∴∠1=∠3,故答案为:∠1=∠3;(3)∵∠ACD=∠BCE=90°,∴∠ACB+∠2=∠1+∠2+∠3+∠2=∠ACD+∠BCE=180°,即∠2+∠ACB=180°,故答案为:∠2+∠ACB=180°;(4)存在,①当BC∥AD时,∵BC∥AD,∴∠BCD=∠D=30°,∴∠ACB=90°+30°=120°,∴∠ACE=∠ACB﹣∠BCE=120°﹣90°=30°;②当BE∥AC时,如图,∵BE∥AC,∴∠ACE=∠E=45°;③当AD∥CE时,如图,∵AD∥CE,∴∠DCE=∠D=30°,∴∠ACE=90°+30°=120°;④当BE∥CD时,如图,∵BE∥CD,∴∠DCE=∠E=45°,∴∠ACE=∠ACD+∠DCE=135°;⑤当BE∥AD时,如图,过点C作CF∥AD,∵BE∥AD,CF∥AD,∴BE∥AD∥CF,∴∠ECF=∠E=45°,∠DCF=∠D=30°,∴∠DCE=30°+45°=75°,∴∠ACE=90°+75°=165°.综上所述:当∠ACE=30°或45°或120°或135°或165°时,有一组边互相平行.故答案为:30°或45°或120°或135°或165°.3.(淇县)如图(1),AB∥CD,猜想∠BPD与∠B、∠D的关系,说出理由.解:猜想∠BPD+∠B+∠D=360°理由:过点P作EF∥AB,∴∠B+∠BPE=180°(两直线平行,同旁内角互补)∵AB∥CD,EF∥AB,∴EF∥CD,(如果两条直线都和第三条直线平行,那么这两条直线也互相平行.)∴∠EPD+∠D=180°(两直线平行,同旁内角互补)∴∠B+∠BPE+∠EPD+∠D=360°∴∠B+∠BPD+∠D=360°(1)依照上面的解题方法,观察图(2),已知AB∥CD,猜想图中的∠BPD与∠B、∠D的关系,并说明理由.(2)观察图(3)和(4),已知AB∥CD,猜想图中的∠BPD与∠B、∠D的关系,不需要说明理由.【答案】(1)∠BPD=∠B+∠D(2)∠BPD=∠B﹣∠D.【解答】解:(1)∠BPD=∠B+∠D.理由:如图2,过点P作PE∥AB,∵AB∥CD,∴PE∥AB∥CD,∴∠1=∠B,∠2=∠D,∴∠BPD=∠1+∠2=∠B+∠D;(2)如图(3):∠BPD=∠D﹣∠B.理由:∵AB∥CD,∴∠1=∠D,∵∠1=∠B+∠P,∴∠D=∠B+∠P,即∠BPD=∠D﹣∠B;如图(4):∠BPD=∠B﹣∠D.理由:∵AB∥CD,∴∠1=∠B,∵∠1=∠D+∠P,∴∠B=∠D+∠P,即∠BPD=∠B﹣∠D.4.(西乡塘)如图,已知DC∥FP,∠1=∠2,∠DEF=30°,∠AGF=70°,FH平分∠EFG.(1)求证:DC∥AB;(2)求∠PFH的度数.【答案】(1)略(2)∠PFH的度数为20°【解答】解:(1)∵DC∥FP,∴∠C=∠2,又∵∠1=∠2,∴∠C=∠1,∴DC∥AB;(2)∵DC∥FP,DC∥AB,∠DEF=30°,∴∠DEF=∠EFP=30°,AB∥FP,又∵∠AGF=70°,∴∠AGF=∠GFP=70°,∴∠GFE=∠GFP+∠EFP=70°+30°=100°,又∵FH平分∠EFG,∴∠GFH=∠GFE=50°,∴∠PFH=∠GFP﹣∠GFH=70°﹣50°=20°.答:∠PFH的度数为20°.5.(海勃湾)如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.(1)试判断直线AB与直线CD的位置关系,并说明理由;(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN 上一点,且GH⊥EG,求证:PF∥GH;(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ 平分∠EPK,求∠HPQ的度数.【答案】(1)AB∥CD(2)PF∥GH(3)∠HPQ的度数为45°【解答】解:(1)AB∥CD,理由如下:∵∠1与∠2互补,∴∠1+∠2=180°,又∵∠1=∠AEF,∠2=∠,∴∠AEF+∠CFE=180°,∴AB∥CD;(2)由(1)知,AB∥CD,∴∠BEF+∠EFD=180°.又∵∠BEF与∠EFD的角平分线交于点P,∴,∴∠EPF=90°,即EG⊥PF.∵GH⊥EG,∴PF∥GH;(3)∵∠PHK=∠HPK,∴∠PKG=2∠HPK.又∵GH⊥EG,∴∠KPG=90°﹣∠PKG=90°﹣2∠HPK.∴∠EPK=180°﹣∠KPG=90°+2∠HPK.∵PQ平分∠EPK,∴.∴∠HPQ=∠QPK﹣∠HPK=45°.答:∠HPQ的度数为45°.6.(黔江)(1)如图1,已知AB∥CD,则∠AEC=∠BAE+∠DCE成立吗?请说明理由;(2)如图2,已知AB∥CD,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E,若∠F AD=60°,∠ABC=40°,求∠BED的度数;(3)如图3,已知AB∥CD,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E,若∠F AD=α,∠ABC=β,请你求出∠BED的度数(用含α,β的式子表示).【答案】(1)成立(2)∠BED=50°(3)【解答】解:(1)成立,理由:如图1中,作EF//AB,则有EF//CD,∴∠1=∠BAE,∠2=∠DCE∴∠AEC=∠1+∠2=∠BAE+∠DCE;(2)如图2,过点E作EH//AB,∵AB//CD,∠F AD=60°,∴∠F AD=∠ADC=60°,∵DE平分∠ADC,∠ADC=60°,∴,∵BE平分∠ABC,∠ABC=40°,∴,∵AB//CD,∴AB//CD//EH,∴∠ABE=∠BEH=20°,∠CDE=∠DEH=30°,∴∠BED=∠BEH+∠DEH=50°.(3)如图3,过点E作EG//AB,∵BE平分∠ABC,DE平分∠ADC,∠ABC=β,∠ADC=∠F AD=α,∴,,∵AB//CD,∴AB//CD//EG,∴,,∴.7.(拱墅)小明同学在完成七年级下册数学第1章的线上学习后,遇到了一些问题,请你帮他解决一下.(1)如图1,已知AB∥CD,则∠AEC=∠BAE+∠DCE成立吗?请说明理由.(2)如图2,已知AB∥CD,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E,若∠F AD=50°,∠ABC=40°,求∠BED的度数.【答案】(1)∠AEC=∠BAE+∠DCE.(2)∠BED=45°【解答】解:(1)∠AEC=∠BAE+∠DCE成立,理由:过点E作EF∥AB,如图,∵EF∥AB,∴∠A=∠AEF.∵EF∥AB,AB∥CD,∴FE∥CD.∴∠C=∠CEF.∵∠AEC=∠AEF+∠CEF,∴∠AEC=∠BAE+∠DCE.(2)过点E作EH∥AB,如图,由(1)的结论可得:∠BED=∠ABE+∠EDC,∵BE平分∠ABC,∠ABC=40°,∴∠ABE=∠ABC=20°.∵∠F AD=50°,AB∥CD,∴∠ADC=∠F AD=50°.∵DE平分∠ADC,∴∠EDC=∠ADC=25°.∴∠BED=20°+25°=45°.8.(宜兴)如图①,已知PQ∥MN,且∠BAM=2∠BAN.(1)填空:∠PBA=°;(2)如图(1)所示,射线AM绕点A开始顺时针旋转至AN便立即按原速度回转至AM 位置,射线BP绕点B开始顺时针旋转至BQ便立即按原速度回转至BP位置.若AM转动的速度是每秒2度,BP转动的速度是每秒1度,若射线BP先转动30秒,射线AM才开始转动,在射线BP到达BQ之前,射线AM转动几秒,两射线互相平行?(3)如图(2),若两射线分别绕点A,B顺时针方向同时转动,速度同题(2),在射线AM到达AN之前,若两射线交于点C,过C作∠ACD交PQ于点D,且∠ACD=120°,则在转动过程中,请探究∠BAC与∠BCD的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.【答案】(1)120(2)AM转动30秒或110秒(3)∠BAC=2∠BCD【解答】解:(1)∵∠BAM=2∠BAN,∠BAM+∠BAN=180°,∴∠BAM=120°.∵PQ∥MN,∴∠PBA=∠BAM=120°.故答案为:120;(2)设射线AM转动t秒,两射线互相平行,当0<t<90时,如图,AM′和BP′为经过t秒后AM,BP旋转的位置,则∠MAM′=2t°,∠PBP′=(t+30)°,∵PQ∥MN,∴∠BM′A=∠MAM′=2t°,∵AM′∥BP′,∴∠AM′B=∠PBP′.∴2t=t+30.解得:t=30;当90<t<150时,如图,AM′和BP′为经过t秒后AM,BP旋转的位置,则∠MAM′=(360﹣2t)°,∠PBP′=(t+30)°,∵PQ∥MN,∴∠BM′A=∠MAM′=2t°,∵AM′∥BP′,∴∠AM′B=∠PBP′.∴360﹣2t=t+30.解得:t=110.综上所述,当射线AM转动30秒或110秒时,两射线互相平行.(3)∠BAC与∠BCD的数量关系不会发生变化,∠BAC=2∠BCD.理由:设射线AM,BP转动时间为m秒,∴∠BAC=(2m﹣120)°,∠ABC=(120﹣t)°,∴∠ACB=180°﹣(2m﹣120)°﹣(120﹣m)°=(180﹣m)°.∵∠ACD=120°,∴∠BCD=120°﹣(180﹣m)°=(m﹣60)°.∵2m﹣120=2(m﹣60),∴∠BAC=2∠BCD.∴∠BAC与∠BCD的数量关系不会发生变化,∠BAC=2∠BCD.9.(仁寿)如图①.已知AM∥CN,点B为平面内一点,AB⊥BC于点B,过点B作BD⊥AM于点D,设∠BCN=α.(1)若α=30°,求∠ABD的度数;(2)如图②,若点E、F在DM上,连接BE、BF、CF,使得BE平分∠ABD、BF平分∠DBC,求∠EBF的度数;(3)如图③,在(2)问的条件下,若CF平分∠BCH,且∠BFC=3∠BCN,求∠EBC 的度数.【答案】(1)30°(2)45°(3)97.5°.【解答】解:(1)延长DB,交NC于点H,如图,∵AM∥CN,BD⊥AM,∴DH⊥NC.∴∠BHC=90°.∵∠BCN=α=30°,∴∠HBC=90°﹣∠BCN=60°.∵AB⊥BC,∴∠ABC=90°.∴∠ABD=180°﹣∠ABC﹣∠HBC=30°;(2)延长DB,交NC于点H,如图,∵AM∥CN,BD⊥AM,∴DH⊥NC.∴∠BHC=90°.∵∠BCN=α,∴∠HBC=90°﹣α.∵AB⊥BC,∴∠ABC=90°.∴∠ABD=180°﹣∠ABC﹣∠HBC=α.∵BE平分∠ABD,∴∠DBE=∠ABE=α.∵∠HBC=90°﹣α,∴∠DBC=180°﹣∠HBC=90°+α.∵BF平分∠DBC,∴∠DBF=∠CBF=∠DBC=45°+α.∴∠EBF=∠DBF﹣∠DBE=45°+α﹣α=45°;(3)∵∠BCN=α,∴∠HCB=180°﹣∠BCN=180°﹣α.∵CF平分∠BCH,∴∠BCF=∠HCF=∠HCB=90°﹣α.∵AM∥CN,∴∠DFC=∠HCF=90°﹣α.∵∠BFC=3∠BCN,∴∠BFC=3α.∴∠DFB=∠DFC﹣∠BFC=90°﹣α.由(2)知:∠DBF=45°+α.∵BD⊥AM,∴∠D=90°.∴∠DBF+∠DFB=90°.∴45°+α+90°﹣α=90°.解得:α=15°.∴∠FBC=∠DBF=45°+α=52.5°.∴∠EBC=∠FBC+∠EBF=52.5°+45°=97.5°.10.(邵东)点A、B在数轴上分别表示实数a、b,A、B两点之间的距离记作AB.当A、B 两点中有一点为原点时,不妨设A点在原点.如图①所示,则AB=OB=|b|=|a﹣b|.当A、B两点都不在原点时:(1)如图②所示,点A、B都在原点的右边,不妨设点A在点B的左侧,则AB=OB﹣OA=|b|﹣|a|=b﹣a=|b﹣a|=|a﹣b|(2)如图③所示,点A、B都在原点的左边,不妨设点A在点B的右侧,则AB=OB﹣OA=|b|﹣|a|=﹣b﹣(﹣a)=a﹣b=|a﹣b|(3)如图④所示,点A、B分别在原点的两边,不妨设点A在点O的右侧,则AB=OB+OA =|b|+|a|=a+(﹣b)=|a﹣b|回答下列问题:(1)综上所述,数轴上A、B两点之间的距离AB=.(2)数轴上表示2和﹣4A和B之间的距离AB=.(3)数轴上表示x和﹣2的两点A和B之间的距离AB=| ,如果AB=2,则x的值为.(4)若代数式|x+2|+|x﹣3|有最小值,则最小值为.【答案】(1)AB=|a﹣b|(2)6 (3)0或﹣4 (4)5【解答】解:(1)综上所述,数轴上A、B两点之间的距离AB=|a﹣b|;(2)数轴上表示2和﹣4的两点A和B之间的距离AB=2﹣(﹣4)=2+4=6;(3)数轴上表示x和﹣2的两点A和B之间的距离AB=|x+2|,如果AB=2,则x的值为0或﹣4;(4)若代数式|x+2|+|x﹣3|有最小值,则最小值为5.故答案为:(1)|a﹣b|;(2)6;(3)|x+2|;0或﹣4;(4)511.(广安)点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|,例如:数轴上表示﹣1与﹣2的两点间的距离=|﹣1﹣(﹣2)|=﹣1+2=1;而|x+2|=|x﹣(﹣2)|,所以|x+2|表示x与﹣2两点间的距离.利用数形结合思想回答下列问题:(1)数轴上表示﹣2和5两点之间的距离.(2)若数轴上表示点x的数满足|x﹣1|=3,那么x=.(3)若数轴上表示点x的数满足﹣4<x<2,则|x﹣2|+|x+4|=.【答案】(1)76(2)﹣2或4(3)6【解答】解:(1)根据题意知数轴上表示﹣2和5两点之间的距离为5﹣(﹣2)=7,故答案为:7;(2)∵|x﹣1|=3,即在数轴上到表示1和x的点的距离为3,∴x=﹣2或x=4,故答案为:﹣2或4;(3)∵|x﹣2|+|x+4|表示在数轴上表示x的点到﹣4和2的点的距离之和,且x位于﹣4到2之间,∴|x﹣2|+|x+4|=2﹣x+x+4=6,故答案为:6.12.(兴宁)如图,在数轴上有两个长方形ABCD和EFGH,这两个长方形的宽都是3个单位长度,长方形ABCD的长AD是6个单位长度,长方形EFGH的长EH是10个单位长度,点E在数轴上表示的数是5.且E、D两点之间的距离为14.(1)填空:点H在数轴上表示的数是,点A在数轴上表示的数是.(2)若线段AD的中点为M,线段EH上一点N,EN=EH,M以每秒4个单位的速度向右匀速运动,N以每秒3个单位的速度向左运动,设运动时间为x秒,原点为O.当OM=2ON时,求x的值.(3)若长方形ABCD以每秒2个单位的速度向右匀速运动,长方形EFGH固定不动,设长方形ABCD运动的时间为t(t>0)秒,两个长方形重叠部分的面积为S,当S=12时,求此时t的值.【答案】(1)15;﹣15(2)或.(3)t的值为9或13.【解答】解:(1)由题意可得,点H在数轴上表示的数为:5+10=15;点A在数轴上表示的数为:5﹣14﹣6=﹣15.故答案为:15;﹣15.(2)∵点M是线段AD的中点,∴点M表示的数为5﹣14﹣=﹣12,又∵EN=EH,∴点N在数轴上表示的数为:5+(15﹣5)=,由题意可得,x秒时,点M在数轴上表示的数为:﹣12+4x,点N在数轴上表示的数为:﹣3x,∴OM=|4x﹣12|,ON=|3x﹣|,∵OM=2ON,∴|4x﹣12|=2|3x﹣|∴4x﹣12=2(3x﹣)或4x﹣12=﹣2(3x﹣),解得x=或x=.故答案为:或.(3)当CD与EF重合时,所用时间为=7秒,由题意得:AD与EH重合的部分为=4,如图1所示,设长方形ABCD从EF运动到AD与EH重叠部分为4时,所用的时间为t1秒,∴t1==2,∴第一次重叠面积为12时,时间t为2+7=9(秒);当AD与EH重叠部分为4时,如图2所示,设长方形ABCD从EF运动到AD与EH重叠部分为4时,所用的时间为t2秒,∴t2==6,∴第二次重叠面积S=12时,时间t为6+7=13(秒);∴当长方形ABCD与长方形EFGH重叠部分的面积为12时,t的值为9或13.13.(宣化)如图,一只蚂蚁从点A沿数轴向右爬了2个单位长度到达点B,点A表示﹣,设点B所表示的数为m.(1)实数m的值是;(2)求|m+1|+|m﹣1|的值;(3)在数轴上还有C、D两点分别表示实数c和d,且有|2c+d|与互为相反数,求2c﹣3d的平方根.【答案】(1)2﹣(2)2 (3)±4.【解答】解:(1)m=﹣+2=2﹣;(2)∵m=2﹣,则m+1>0,m﹣1<0,∴|m+1|+|m﹣1|=m+1+1﹣m=2;答:|m+1|+|m﹣1|的值为2.(3)∵|2c+d|与互为相反数,∴|2c+d|+=0,∴|2c+d|=0,且=0,解得:c=﹣2,d=4,或c=2,d=﹣4,①当c=﹣2,d=4时,所以2c﹣3d=﹣16,无平方根.②当c=2,d=﹣4时,∴2c﹣3d=16,∴2c﹣3d的平方根为±4,答:2c﹣3d的平方根为±4.14.(锦江)阅读下面材料:点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为|AB|.当A、B两点中有一点在原点时,不妨设点A在原点,如图1,|AB|=|OB|=|b|=|a﹣b|;当A、B两点都不在原点时,如图2,点A、B都在原点的右边,|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|;如图3,当点A、B都在原点的左边,|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣(﹣a)=|a﹣b|;如图4,当点A、B在原点的两边,|AB|=|OB|+|OA|=|a|+|b|=a+(﹣b)=|a﹣b|.回答下列问题:(1)数轴上表示1和6的两点之间的距离是数轴上表示2和﹣3的两点之间的距离是.(2)数轴上若点A表示的数是x,点B表示的数是﹣4,则点A和B之间的距离是,若|AB|=3,那么x为.(3)当x是时,代数式|x+2|+|x﹣1|=7.(4)若点A表示的数﹣1,点B与点A的距离是10,且点B在点A的右侧,动点P、Q 同时从A、B出发沿数轴正方向运动,点P的速度是每秒3个单位长度,点Q的速度是每秒个单位长度,求运动几秒后,B、P、Q三点中,有一点恰好是另两点所连线段的中点?(请写出必要的求解过程).【答案】(1)5,5(2)﹣1或﹣7 (3)﹣4或3 (4)运动或或5秒【解答】解:(1)数轴上表示1和6的两点之间的距离是|6﹣1|=5,数轴上表示2和﹣3的两点之间的距离是|2﹣(﹣3)|=5.(2)数轴上若点A表示的数是x,点B表示的数是﹣4,则点A和B之间的距离是|x+4|,若|AB|=3,则|x+4|=3,解得x=﹣1或﹣7.(3)当x>1时,|x+2|+|x﹣1|=x+2+x﹣1=7,2x=6,x=3,当x<﹣2时,|x+2|+|x﹣1|=﹣x﹣2+1﹣x=7,﹣2x=8,x=﹣4,当﹣2≤x≤1时,|x+2|+|x﹣1|=x+2+1﹣x=3≠7,∴当x=﹣4或3时,代数式|x+2|+|x﹣1|=7.(4)设运动t秒后,有一点恰好是另两点所连线段的中点,由题意,得①点B为线段PQ中点时,,解得,②点P为线段BQ中点时,,解得,③点Q为线段BP中点时,,解得t=5.答:运动或或5秒后,B、P、Q三点中,有一点恰好是另两点所连线段的中点.15.(宣化)阅读下面的文字,解答问题.大家知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能完全地写出来,于是小明用﹣1来表示的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为的整数部分是1,用这个数减去其整数部分,差就是小数部分.请解答下列问题:(1)求出+2的整数部分和小数部分;(2)已知:10+=x+y,其中x是整数,且0<y<1,请你求出(x﹣y)的相反数.【答案】(1)3,﹣1 (2)﹣14【解答】解:(1)∵1<<2,∴3<+2<4,∴+2的整数部分是1+2=3,+2的小数部分是﹣1;(2)∵2<<3,∴12<10+<13,∴10+的整数部分是12,10+的小数部分是10+﹣12=﹣2,即x=12,y=﹣2,∴x﹣y=12﹣(﹣2)=12﹣+2=14﹣,则x﹣y的相反数是﹣14.16.(靖江)在平面直角坐标系xOy中,对于点P(x,y),若点Q的坐标为(ax+y,x+ay),则称点Q是点P的“a阶派生点”(其中a为常数,且a≠0).例如:点P(1,4)的“2阶派生点”为点Q(2×1+4,1+2×4),即点Q(6,9).(1)若点P的坐标为(﹣1,5),则它的“3阶派生点”的坐标为;(2)若点P的“5阶派生点”的坐标为(﹣9,3),求点P的坐标;(3)若点P(c+1,2c﹣1)先向左平移2个单位长度,再向上平移1个单位长度后得到了点P1.点P1的“﹣4阶派生点”P2位于坐标轴上,求点P2的坐标.【答案】(1)(2,14)(2)(﹣2,1);(3)(0,﹣15)或(,0).【解答】解:(1)3×(﹣1)+5=2;﹣1+3×5=14,∴点P的坐标为(﹣1,5),则它的“3级派生点”的坐标为(2,14).故答案为:(2,14);(2)设点P的坐标为(a,b),由题意可知,解得:,∴点P的坐标为(﹣2,1);(3)由题意,P1(c﹣1,2c),∴P1的“﹣4阶派生点“P2为:(﹣4(c﹣1)+2c,c﹣1﹣8c),即(﹣2c+4,﹣7c﹣1),∵P2在坐标轴上,∴﹣2c+4=0或﹣7c﹣1=0,∴c=2或c=﹣,∴P2(0,﹣15)或(,0).17.(黄山)在平面直角坐标系xOy中,对于P,Q两点给出如下定义:若点P到x、y轴的距离中的最大值等于点Q到x、y轴的距离中的最大值,则称P,Q两点为“等距点”.下图中的P,Q两点即为“等距点”.(1)已知点A的坐标为(﹣3,1),①在点E(0,3),F(3,﹣3),G(2,﹣5)中,为点A的“等距点”的是;②若点B的坐标为B(m,m+6),且A,B两点为“等距点”,则点B的坐标为;(2)若T1(﹣1,﹣k﹣3),T2(4,4k﹣3)两点为“等距点”,求k的值.【答案】(1)①E、F;②(﹣3,3);(2)1或2【解答】解:(1)①∵点A(﹣3,1)到x、y轴的距离中最大值为3,∴与A点是“等距点”的点是E、F.②当点B坐标中到x、y轴距离其中至少有一个为3的点有(3,9)、(﹣3,3)、(﹣9,﹣3),这些点中与A符合“等距点”的是(﹣3,3).故答案为①E、F;②(﹣3,3);(2)T1(﹣1,﹣k﹣3),T2(4,4k﹣3)两点为“等距点”,①若|4k﹣3|≤4时,则4=﹣k﹣3或﹣4=﹣k﹣3解得k=﹣7(舍去)或k=1.②若|4k﹣3|>4时,则|4k﹣3|=|﹣k﹣3|解得k=2或k=0(舍去).根据“等距点”的定义知,k=1或k=2符合题意.即k的值是1或2.18.(延长)在平面直角坐标系中,O为坐标原点,过点A(8,6)分别作x轴、y轴的平行线,交y轴于点B,交x轴于点C,点P是从点B出发,沿B→A→C以2个单位长度/秒的速度向终点C运动的一个动点,运动时间为t(秒).(1)直接写出点B和点C的坐标B(,)、C(,);(2)当点P运动时,用含t的式子表示线段AP的长,并写出t的取值范围;(3)点D(2,0),连接PD、AD,在(2)条件下是否存在这样的t值,使S△APD=S,若存在,请求出t值,若不存在,请说明理由.四边形ABOC【答案】(1)0、6,8、0 (2)AP=8﹣2t(0≤t<4);AP=2t﹣8(4≤t≤7).(3)当t为3秒和5秒时S△APD=S四边形ABOC【解答】解:(1)B(0,6),C(8,0),故答案为:0、6,8、0;(2)当点P在线段BA上时,由A(8,6),B(0,6),C(8,0)可得:AB=8,AC=6∵AP=AB﹣BP,BP=2t,∴AP=8﹣2t(0≤t<4);当点P在线段AC上时,∵AP=点P走过的路程﹣AB=2t﹣8(4≤t≤7).(3)存在两个符合条件的t值,当点P在线段BA上时∵S△APD=AP•AC S四边形ABOC=AB•AC∴(8﹣2t)×6=×8×6,解得:t=3<4,当点P在线段AC上时,∵S△APD=AP•CD CD=8﹣2=6∴(2t﹣8)×6=×8×6,解得:t=5<7,综上所述:当t为3秒和5秒时S△APD=S四边形ABOC,19.(齐齐哈尔)如图①,在平面直角坐标系中,点A、B在x轴上,AB⊥BC,AO=OB=2,BC=3(1)写出点A、B、C的坐标.(2)如图②,过点B作BD∥AC交y轴于点D,求∠CAB+∠BDO的大小.(3)如图③,在图②中,作AE、DE分别平分∠CAB、∠ODB,求∠AED的度数.【答案】(1)A(﹣2,0),B(2,0),C(2,3);(2)90°(3)45°【解答】解:(1)依题意得:A(﹣2,0),B(2,0),C(2,3);(2)∵BD∥AC,∴∠ABD=∠BAC,∴CAB+∠BDO=∠ABD+∠BDO=90°;(3):∵BD∥AC,∴∠ABD=∠BAC,∵AE,DE分别平分∠CAB,∠ODB,∴∠CAE+∠BDE=(∠BAC+∠BDO)=(∠ABD+∠BDO)=×90°=45°,过点E作EF∥AC,则∠CAE=∠AEF,∠BDE=∠DEF,∴∠AED=∠AEF+∠DEF=∠CAE+∠BDE=45°.20.(随县)如图,在平面直角坐标系中,已知点A(0,2),B(4,0),C(4,3)三点.(1)求△ABC的面积;(2)如果在第二象限内有一点P(m,1),且四边形ABOP的面积是△ABC的面积的两倍;求满足条件的P点坐标.【答案】(1)6(2)P(﹣8,1)【解答】解:(1)∵B(4,0),C(4,3),∴BC=3,∴S△ABC=×3×4=6;(2)∵A(0,2)(4,0),∴OA=2,OB=4,∴S四边形ABOP=S△AOB+S△AOP=×4×2+×2(﹣m)=4﹣m,又∵S四边形ABOP=2S△ABC=12,∴4﹣m=12,解得:m=﹣8,∴P(﹣8,1).。
七年级下数学压轴题精选二

北京市七年级下数学压轴题精选21.在等边ABC ∆的两边AB 、AC 所在直线上分别有两点M 、N ,D 为△ABC 外一点,且︒=∠60MDN ,︒=∠120BDC ,BD=DC . 探究:当M 、N 分别在直线AB 、AC 上移动时,BM 、NC 、MN 之间的数量关系及AMN ∆的周长Q 与等边ABC ∆的周长L 的关系.(1)如图1,当点M 、N 边AB 、AC 上,且DM=DN 时,BM 、NC 、MN 之间的数量关系是 ; 此时=LQ;(2)如图2,点M 、N 在边AB 、AC 上,且当DM ≠DN 时,猜想(I )问的两个结论还成立吗?若成立请直接写出你的结论;若不成立请说明理由.(3) 如图3,当M 、N 分别在边AB 、CA 的延长线上时,探索BM 、NC 、MN 之间的数量关系如何?并给出证明.图 1NM DC BA图 2NMDCBA图3NMDCB A2.如图, 已知四边形ABCD 中,AD //BC,CD=BC ,∠C =∠EAB =60°,∠DAE =28°,求∠EBC 的度数.3、已知△ABC 。
(1)如图,AC ⊥AB ,点D 为BC 上一点,∠ABD=∠BAD ,∠EAC=∠CAD ,求证:AE ∥BC 。
(2)如图,点P 是BC 上一点,且∠APC <90°,以AP 为一边作正方形APMN ,若NC ⊥BC ,则∠ACB=_____________°,并证明你的结论。
EDC B A4.如图,已知在锐角△ABC 中,∠B =2∠C ,∠B 的平分线与A D 垂直于D ,求证:AC=2BD .E DCBA5.(1)如图1,四边形ABCD 中,CB AB =,︒=∠60ABC ,︒=∠120ADC ,请你猜想线段DA 、DC 之和与线段BD 的数量关系,直接写出你的结论;(2分)(2)如图2,四边形ABCD 中,BC AB =,︒=∠60ABC ,若点P 为四边形ABCD 内一点,且︒=∠120APD ,请你猜想线段PA 、PD 、PC 之和与线段BD 的数量关系,并证明你的结论.(6分)6. 在ABC ∆中,BO 平分ABC ∠,点P 为直线AC 上一动点,BO PO ⊥于点O 。
七年级下册数学几何压轴题

七年级下册数学几何压轴题
1. 把一个长方形沿x轴正方向移动m个单位,求移动前后阴影的面积差。
2. 一个小正方体沿着x轴正方向移动,它的一面在x轴上翻转,求翻转前后阴影的面积比值。
3. 一个方形沿着y轴正方向移动,移动到一个圆的周围,求圆和方形的阴影面积比值。
4. 把一个正方形沿对角线方向移动,它最后完全重合的时候恰好覆盖了一个面积为S的等腰三角形,求三角形面积S。
5. 把一个正方形沿着y轴正方向移动,移动m个单位的时候与另外一个正方形刚好重合,求另外一个正方形的边长。
6. 一个矩形沿x轴正方向移动,移动到另外一个矩形的正上方还有b个单位,求两个矩形的阴影面积比值。
7. 把一个半圆形沿y轴正方向移动,移动到正方形的中心时,求正方形面积和半圆形面积的阴影面积比值。
8. 把一个梯形沿y轴正方向移动,移动到一个与梯形相似的大梯形上面靠着底边的位置,求阴影的面积比值。
9. 把一个正三角形沿着x轴正方向移动,相邻两次的位移满足一个等差数列,第一次移动2个单位,第三次移动8个单位,求正三角形的边长。
10. 一个椭圆形沿y轴正方向移动,移动到一个长方形上方恰好横跨长方形的两个端点,求已经移动了多少个单位。
七年级数学下册期末压轴题训练

七年级数学下册期末压轴题训练1.如图1,E点在BC上,∠A=∠D,∠ACB+∠BED=180°.(1)求证:AB∥CD;(2)如图2,AB∥CD,BG平分∠ABE,与∠EDF的平分线交于H点,若∠DEB比∠DHB大60°,求∠DEB的度数.(3)保持(2)中所求的∠DEB的度数不变,如图3,BM平分∠EBK,DN平分∠CDE,作BP∥DN,则∠PBM的度数是否改变?若不变,请求值;若改变,请说明理由.2.如图1,△ABC是等腰直角三角形,∠BAC=90°,BC=5cm,D是BC的中点,点P 从A点出发,以2cm/s的速度沿着射线CA方向运动,连接PD交AB于点E,过点D作PD的垂线交直线AC于点F,交直线AB于点G,若运动时间为t(s).(1)当t=1.5时,则BG=cm;(2)在点P的运动过程中,试探究线段PF与EG的数量关系,并说明理由;(3)如图2,连接EF,EF上是否存在点H使得△DCF与△F AH全等,若存在,求出此时t的值;若不存在,请说明理由.3.在△ABC中,BD平分∠ABC,CE平分∠ACB,BD和CE交于点O,其中令∠BAC=x,∠BOC=y.(1)【计算求值】如图1,①如果x=50°,则y=;②如果y=130°,则x=.(2)【猜想证明】如图2请你根据(1)中【计算求值】的心得猜想写出y与x的关系式为y=,并请你说明你的猜想的正确性.(3)【解决问题】如图3,某校园内有一个如图2所示的三角形的小花园,花园中有两条小路,BD和CE为三角形的角平分线,交点为点O,在O处建有一个自动浇水器,需要在BC边取一处接水口F,经过测量得知∠BAC=120°,OD•OE=12000米2,BC﹣BE ﹣CD=170米,请你求出水管OF至少要多长?(结果取整数)4.在△ABC中,AB=AC,∠BAC=90°,点D为AC上一动点.(1)如图1,点E、点F均是射线BD上的点并且满足AE=AF,∠EAF=90°.求证:△ABE≌△ACF;(2)在(1)的条件下,求证:CF⊥BD;(3)由(1)我们知道∠AFB=45°,如图2,当点D的位置发生变化时,过点C作CF ⊥BD于F,连接AF.那么∠AFB的度数是否发生变化?请证明你的结论.5.如图:在△ABC中,∠BAC=110°,AC=AB,射线AD、AE的夹角为55°,过点B作BF⊥AD于点F,直线BF交AE于点G,连接CG.(1)如图1,若射线AD、AE都在∠BAC的内部,且点B与点B′关于AD对称,求证:CG=B'G;(2)如图2,若射线AD在∠BAC的内部,射线AE在∠BAC的外部,其他条件不变,求证:CG=BG﹣2GF;(3)如图3,若射线AD、AE都在∠BAC的外部,其他条件不变,若CG=GF,AF =4,S△ABG=12,求BF的长.6.如图,CD是经过∠BCA顶点C的一条直线,CA=CB,E、F分别是直线CD上两点,且∠BEC=∠CF A=α.(1)若直线CD经过∠BCA的内部,且E、F在射线CD上.①如图1,若∠BCA=90°,α=90°,则BE CF;②如图2,若0°<∠BCA<180°,请添加一个关于α与∠BCA关系的条件,使①中的结论仍然成立,并说明理由;(2)如图3,若直线CD经过∠BCA的外部,α=∠BCA,请提出关于EF,BE,AF三条线段数量关系的合理猜想,并简述理由.7.小明同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来则形成一组全等的三角形,小明把具有这个规律的图形称为“手拉手”图形.(1)问题发现:如图1,若△ABC和△ADE均是顶角为40°的等腰三角形,BC、DE 分别是底边,求证:BD=CE;(2)拓展探究:如图2,若△ACB和△DCE均为等边三角形,点A、D、E在同一条直线上,连接BE,则∠AEB的度数为;线段BE与AD之间的数量关系是;(3)解决问题:如图3,若△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一条直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB 的度数及线段CM、AE、BE之间的数量关系并说明理由.8.材料阅读:如图1所示,已知直角梯形BCDE中,A是CD上一点,CB=a,AC=b,AB =c,且AB⊥AE,AB=AE,现需探究直角三角形ABC的三边a、b、c之间的数量关系:【初步探究】(1)猜想ABC是否与ADE全等,若是,请说明理由;【问题解决】(2)请用两种含有a,b,c的代数式的方法表示直角梯形BCDE的面积:S梯形BCDE=.S梯形BCDE=.由此,你能得到的a、b、c的数量关系是:.【拓展应用】(3)如图2,等腰三角形ABC中,D是底边BC上的中点,BC=12,AB=10,E、F分别是线段AD和AC上的两个动点,求:CE+EF的最小值.9.【问题背景】如图1,在等边△ABC中,D、E分别为边BC、AC上任意一点,连接AD、BE,AD与BE相交于点O,且BD=CE.请直接写出线段AD与BE之间的数量关系:;∠AOE=.【推广探究】如图2,在等边△ABC中,P、M分别为边AB、AC上的点,且AM=BP,过点P作PQ ∥BE交AC于点Q,过点M作MN∥AD交BC于点N,PQ与MN交于点F.(1)∠MFQ=;(2)求证:PQ=MN.【深入探究】如图3,在“推广探究”的条件下,令四边形APFM的周长为C1,四边形CNFQ的周长为C2,MF=a,FQ=b,FN=c,则C1﹣C2=(请用含有a、b的代数式表示).10.【初步探索】(1)如图1:在四边形ABCD中,AB=AD,∠B=∠ADC=90°,E、F分别是BC、CD 上的点,且EF=BE+FD,探究图中∠BAE、∠F AD、∠EAF之间的数量关系.小王同学探究此问题的方法是:延长FD到点G,使DG=BE.连接AG,先证明△ABE ≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是;【灵活运用】(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E、F分别是BC、CD 上的点,且EF=BE+FD,上述结论是否仍然成立,并说明理由;【拓展延伸】(3)如图3,已知在四边形ABCD中,∠ABC+∠ADC=180°,AB=AD,若点E在CB 的延长线上,点F在CD的延长线上,如图3所示,仍然满足EF=BE+FD,请写出∠EAF 与∠DAB的数量关系,并给出证明过程.。
七年级下册数学压轴题集锦

七年级下册数学压轴题集锦(一)1、如图,已知A(0,a),B (0,b ),C (m ,b )且(a -4)2+|b +3|=0,S △ABC =14. (1)求C 点坐标(2)作DE ⊥DC ,交y 轴于E 点,EF 为∠AED 的平分线,且∠DFE =900.求证:FD 平分∠ADO ; (3)E 在y 轴负半轴上运动时,连EC ,点P 为AC 延长线上一点,EM 平分∠AEC ,且PM ⊥EM ,PN ⊥x轴于N 点,PQ 平分∠APN ,交x 轴于Q 点,则E 在运动过程中,∠MPQ∠ECA 的大小是否发生变化,若不变,求出其值.2、如图1,AB ∥EF ,∠2=2∠1(1)证明∠FEC =∠FCE ;图1(2)如图2,M 为AC 上一点,N 为FE 延长线上一点,且∠FNM =∠FMN ,则∠NMC 与∠CFM 有何数量关系,并证明。
图2B C B3、(1)如图,△ABC, ∠ABC 、∠ACB 的三等分线交于点E 、D ,若∠1=130°,∠2=110°,求∠A 的度数。
(2)如图,△ABC,∠ABC 的三等分线分别与∠ACB 的平分线交于点D,E 若∠1=110°,∠2=130°,求∠A 的度数。
4、如图,∠ABC+∠ADC=180°,OE 、OF 分别是角平分线,则判断OE 、OF 的位置关系为?5、已知∠A=∠C=90°.(1)如图,∠ABC 的平分线与∠ADC 的平分线交于点E ,试问BE 与DE 有何位置关系?说明你的理由。
(2)如图,试问∠ABC 的平分线BE 与∠ADC 的外角平分线DF 有何位置关系?说明你的理由。
(3)如图,若∠ABC 的外角平分线与∠ADC 的外角平分线交于点E ,试问BE 与DE 有何位置关系?说明你的理由。
BA B6、(1)如图,点E 在AC 的延长线上,∠BAC 与∠DCE 的平分线交于点F ,∠B=60°,∠F=56°,求∠BDC 的度数。
北师大七年级下册数学压轴题集锦

北师大七年级下册数学压轴题集锦集团标准化小组:[VVOPPT-JOPP28-JPPTL98-LOPPNN]北师大七年级下册数学压轴题集锦1、如图1,AB//EF, ∠2=2∠1;(1)证明∠FEC=∠FCE ;(2)如图2,M 为AC 上一点,N 为FE 延长线上一点,且∠FNM=∠FMN ,则∠NMC 与∠CFM 有何数量关系,并证明。
图22、(1)如图,△ABC, ∠ABC 、∠ACB 的三等分线交于点E 、D ,若∠1=130°,∠2=110°, 求∠A 的度数。
(2)如图,△ABC,∠ABC 的三等分线分别与∠ACB 的平分线交于点D 、E ,若∠1=110°,∠2=130°,求∠A 的度数。
3、如图,∠ABC+∠ADC=180°,OE 、OF 分别是角平分线,则判断OE 、OF 的位置关系为?4、已知∠A=∠C=90°。
(1)如图,∠ABC 的平分线与∠ADC 的平分线交于点E ,试问BE 与DE 有何位置关系?说明你的理由。
(2)如图,试问∠ABC 的平分线BE 与∠ADC 的外角平分线DF 有何位置关系?说明你的理由。
(3)如图,若∠ABC 的外角平分线与∠ADC 的外角平分线交于点E ,试问BE 与DE 有何位置关系?说明你的理由。
5.(1)如图,点E 在AC 的延长线上,∠BAC 与∠DCE 的平分线交于点F ,∠B=60°,∠F=56°,CBB求∠BDC的度数。
(2)如图,点E在CD的延长线上,∠BAD与∠ADE的平分线交于点F,试问∠F、∠B 和∠C之间有何数量关系?为什么?6.已知∠ABC与∠ADC的平分线交于点E。
(1)如图,试探究∠E、∠A与∠C之间的数量关系,并说明理由。
(2)如图,是探究∠E、∠A与∠C之间的数量关系,并说明理由。
8.(1)如图,点E是AB上方一点,MF平分∠AME,若点G恰好在MF的反向延长线上,且NE平分∠CNG,2∠E与∠G互余,求∠AME的大小。
七年级数学版下册压轴题

七年级数学版下册压轴题第一题:分数的加减乘除运算题目要求:请计算以下数式的值,并将答案化简至最简形式。
1.(1/3) + (2/5)2.(4/7) - (1/5)3.(2/3) × (3/8)4.(5/6) ÷ (1/4)答案及解析1.(1/3) + (2/5)解法:首先最小公倍数为15,将分数的分母变为15,得到(5/15) + (6/15) = 11/15,所以答案为11/15。
2.(4/7) - (1/5)解法:首先最小公倍数为35,将分数的分母变为35,得到(20/35) - (7/35) = 13/35,所以答案为13/35。
3.(2/3) × (3/8)解法:将分数相乘得到(2×3)/(3×8) = 6/24,将6/24化简为最简形式,得到1/4,所以答案为1/4。
4.(5/6) ÷ (1/4)解法:将除法转化为乘法,得到(5/6) × (4/1)= (5×4)/(6×1) = 20/6,将20/6化简为最简形式,得到10/3,所以答案为10/3。
第二题:解一元一次方程题目要求:解下列一元一次方程。
1.2x - 3 = x + 42.3(x + 5) = 6x - 93.2(x + 3) - 4(x - 2) = 5(2x - 1)答案及解析1.2x - 3 = x + 4解法:将方程中的变量合并在一起,得到2x - x = 4 + 3,化简得到x = 7,所以方程的解为x = 7。
2.3(x + 5) = 6x - 9解法:先将方程中的括号展开,得到3x + 15 = 6x - 9,将变量合并在一起,得到3x - 6x = -9 - 15,化简得到-3x = -24,再将方程两边同时除以-3,得到x = 8,所以方程的解为x = 8。
3.2(x + 3) - 4(x - 2) = 5(2x - 1)解法:先将方程中的括号展开,得到2x + 6 - 4x + 8 = 10x - 5,将变量合并在一起,得到-2x + 14 = 10x - 5,将方程中的常数项合并在一起,得到-2x - 10x = -5 - 14,化简得到-12x = -19,再将方程两边同时除以-12,得到x =19/12,所以方程的解为x = 19/12。
(完整版)人教版初一数学下册期末压轴题试题(带答案) (一)
一、解答题1.对于平面直角坐标系xOy 中的图形G 和图形G 上的任意点P (x ,y ),给出如下定义: 将点P (x ,y )平移到P '(x +t ,y ﹣t )称为将点P 进行“t 型平移”,点P '称为将点P 进行“t 型平移”的对应点;将图形G 上的所有点进行“t 型平移”称为将图形G 进行“t 型平移”.例如,将点P (x ,y )平移到P '(x +1,y ﹣1)称为将点P 进行“l 型平移”,将点P (x ,y )平移到P '(x ﹣1,y +1)称为将点P 进行“﹣l 型平移”.已知点A (2,1)和点B (4,1).(1)将点A (2,1)进行“l 型平移”后的对应点A '的坐标为 .(2)①将线段AB 进行“﹣l 型平移”后得到线段A 'B ',点P 1(1.5,2),P 2(2,3),P 3(3,0)中,在线段A ′B ′上的点是 .②若线段AB 进行“t 型平移”后与坐标轴有公共点,则t 的取值范围是 .(3)已知点C (6,1),D (8,﹣1),点M 是线段CD 上的一个动点,将点B 进行“t 型平移”后得到的对应点为B ',当t 的取值范围是 时,B 'M 的最小值保持不变.2.如图1,点E 在直线AB 、DC 之间,且180DEB ABE CDE ∠+∠-∠=︒.(1)求证://AB DC ;(2)若点F 是直线BA 上的一点,且BEF BFE ∠=∠,EG 平分DEB ∠交直线AB 于点G ,若20D ∠=︒,求FEG ∠的度数;(3)如图3,点N 是直线AB 、DC 外一点,且满足14CDM CDE ∠=∠,14ABN ABE ∠=∠,ND 与BE 交于点M .已知()012CDM αα∠=︒<<︒,且//BN DE ,则NMB ∠的度数为______(请直接写出答案,用含α的式子表示).3.如图,直线//PQ MN ,一副直角三角板,ABC DEF ∆∆中,90,45,30,60ACB EDF ABC BAC DFE DEF ︒︒︒︒∠=∠=∠=∠=∠=∠=.(1)若DEF ∆如图1摆放,当ED 平分PEF ∠时,证明:FD 平分EFM ∠.(2)若,ABC DEF ∆∆如图2摆放时,则PDE ∠=(3)若图2中ABC ∆固定,将DEF ∆沿着AC 方向平移,边DF 与直线PQ 相交于点G ,作FGQ ∠和GFA ∠的角平分线GH FH 、相交于点H (如图3),求GHF ∠的度数.(4)若图2中DEF ∆的周长35,5cm AF cm =,现将ABC ∆固定,将DEF ∆沿着CA 方向平移至点F 与A 重合,平移后的得到''D E A ∆,点D E 、的对应点分别是''D E 、,请直接写出四边形'DEAD 的周长.(5)若图2中DEF ∆固定,(如图4)将ABC ∆绕点A 顺时针旋转,1分钟转半圈,旋转至AC 与直线AN 首次重合的过程中,当线段BC 与DEF ∆的一条边平行时,请直接写出旋转的时间.4.如图,∠EBF =50°,点C 是∠EBF 的边BF 上一点.动点A 从点B 出发在∠EBF 的边BE 上,沿BE 方向运动,在动点A 运动的过程中,始终有过点A 的射线AD ∥BC .(1)在动点A 运动的过程中, (填“是”或“否”)存在某一时刻,使得AD 平分∠EAC ? (2)假设存在AD 平分∠EAC ,在此情形下,你能猜想∠B 和∠ACB 之间有何数量关系?并请说明理由;(3)当AC ⊥BC 时,直接写出∠BAC 的度数和此时AD 与AC 之间的位置关系.5.已知,//AE BD ,A D ∠=∠.(1)如图1,求证://AB CD ;(2)如图2,作BAE ∠的平分线交CD 于点F ,点G 为AB 上一点,连接FG ,若CFG ∠的平分线交线段AG 于点H ,连接AC ,若ACE BAC BGM ∠=∠+∠,过点H 作HM FH ⊥交FG 的延长线于点M ,且3518E AFH ∠-∠=︒,求EAF GMH ∠+∠的度数.6.如图,直线HD //GE ,点A 在直线HD 上,点C 在直线GE 上,点B 在直线HD 、GE 之间,∠DAB =120°.(1)如图1,若∠BCG =40°,求∠ABC 的度数;(2)如图2,AF 平分∠HAB ,BC 平分∠FCG ,∠BCG =20°,比较∠B ,∠F 的大小; (3)如图3,点P 是线段AB 上一点,PN 平分∠APC ,CN 平分∠PCE ,探究∠HAP 和∠N 的数量关系,并说明理由.7.请观察下列等式,找出规律并回答以下问题.111122=-⨯,1112323=-⨯,1113434=-⨯,1114545=-⨯,…… (1)按照这个规律写下去,第5个等式是:______;第n 个等式是:______. (2)①计算:11111223344950⨯⨯⨯⨯++++. ②若a 30b -=,求:()()()()()()()()111111122339797ab a b a b a b a b +++++++++++++. 8.阅读理解:计算1111234⎛⎫+++ ⎪⎝⎭×11112345+++⎛⎫ ⎪⎝⎭﹣111112345⎛⎫++++ ⎪⎝⎭×111234++⎛⎫ ⎪⎝⎭时,若把11112345+++⎛⎫ ⎪⎝⎭与111234++⎛⎫ ⎪⎝⎭分别各看着一个整体,再利用分配律进行运算,可以大大简化难度.过程如下:解:设111234++⎛⎫ ⎪⎝⎭为A ,11112345+++⎛⎫ ⎪⎝⎭为B , 则原式=B (1+A )﹣A (1+B )=B+AB ﹣A ﹣AB=B ﹣A=15.请用上面方法计算: ①11111123456⎛⎫+++++ ⎪⎝⎭×111111234567⎛⎫+++++ ⎪⎝⎭-1111111234567⎛⎫++++++ ⎪⎝⎭×1111123456⎛⎫++++ ⎪⎝⎭②111123n ⎛⎫++++ ⎪⎝⎭111231n ⎛⎫+++ ⎪+⎝⎭-1111231n ⎛⎫++++ ⎪+⎝⎭11123n ⎛⎫+++ ⎪⎝⎭. 9.如图1,把两个边长为1的小正方形沿对角线剪开,所得的4个直角三角形拼成一个面积为2的大正方形.由此得到了一种能在数轴上画出无理数对应点的方法.(1)图2中A 、B 两点表示的数分别为___________,____________;(2)请你参照上面的方法:①把图3中51⨯的长方形进行剪裁,并拼成一个大正方形.在图3中画出裁剪线,并在图4的正方形网格中画出拼成的大正方形,该正方形的边长a=___________.(注:小正方形边长都为1,拼接不重叠也无空隙)②在①的基础上,参照图2的画法,在数轴上分别用点M、N表示数a以及3a-.(图中标出必要线段的长)10.我们知道,任意一个正整数n都可以进行这样的分解:n p q=⨯(p,q是正整数,且p q≤),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的完美分解.并规定:()pF nq=.例如18可以分解成1×18,2×9或3×6,因为18-1>9-2>6-3,所以3×6是18的完美分解,所以F(18)=31 62 =.(1)F(13)=,F(24)=;(2)如果一个两位正整数t,其个位数字是a,十位数字为1b-,交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为36,那么我们称这个数为“和谐数”,求所有“和谐数”;(3)在(2)所得“和谐数”中,求F(t)的最大值.11.如果有一列数,从这列数的第2个数开始,每一个数与它的前一个数的比等于同一个非零的常数,这样的一列数就叫做等比数列(Geometric Sequences).这个常数叫做等比数列的公比,通常用字母q表示(q≠0).(1)观察一个等比列数1,1111,,,24816,…,它的公比q=;如果a n(n为正整数)表示这个等比数列的第n项,那么a18=,a n=;(2)如果欲求1+2+4+8+16+…+230的值,可以按照如下步骤进行:令S=1+2+4+8+16+…+230…①等式两边同时乘以2,得2S=2+4+8+16++32+…+231…②由② ﹣①式,得2S﹣S=231﹣1即(2﹣1)S=231﹣1所以3131212121S-==--请根据以上的解答过程,求3+32+33+…+323的值;(3)用由特殊到一般的方法探索:若数列a1,a2,a3,…,a n,从第二项开始每一项与前一项之比的常数为q,请用含a1,q,n的代数式表示a n;如果这个常数q≠1,请用含a1,q,n的代数式表示a1+a2+a3+…+a n.12.阅读下列材料:小明为了计算22019202012222+++++的值,采用以下方法:设22019202012222s=+++++①则22020202122222s=++++②②-①得,2021221s s s-==-请仿照小明的方法解决以下问题:(1)291222++++=________;(2)220333+++=_________;(3)求231na a a a++++的和(1a>,n是正整数,请写出计算过程).13.如图,在平面直角坐标系中,已知△ABC,点A的坐标是(4,0),点B的坐标是(2,3),点C在x轴的负半轴上,且AC=6.(1)直接写出点C的坐标.(2)在y轴上是否存在点P,使得S△POB=23S△ABC若存在,求出点P的坐标;若不存在,请说明理由.(3)把点C往上平移3个单位得到点H,作射线CH,连接BH,点M在射线CH上运动(不与点C、H重合).试探究∠HBM,∠BMA,∠MAC之间的数量关系,并证明你的结论.14.已知点C在射线OA上.(1)如图①,CD//OE,若∠AOB=90°,∠OCD=120°,求∠BOE的度数;(2)在①中,将射线OE沿射线OB平移得O′E'(如图②),若∠AOB=α,探究∠OCD 与∠BO′E′的关系(用含α的代数式表示)(3)在②中,过点O′作OB的垂线,与∠OCD的平分线交于点P(如图③),若∠CPO′=90°,探究∠AOB与∠BO′E′的关系.15.在平面直角坐标系xOy 中,如图正方形ABCD 的顶点A ,B 坐标分别为()1,0A -,()3,0B ,点E ,F 坐标分别为(),0E m ,()3,0F m ,且12m -<≤,以EF 为边作正方形EFGH .设正方形EFGH 与正方形ABCD 重叠部分面积为S .(1)①当点F 与点B 重合时,m 的值为______;②当点F 与点A 重合时,m 的值为______.(2)请用含m 的式子表示S ,并直接写出m 的取值范围.16.阅读下列材料:我们知道||x 的几何意义是在数轴上数x 对应的点与原点的距离,即|||0|x x =-,也就是说,12||x x -表示在数轴上数1x 与数2x 对应的点之间的距离;例 1.解方程||2x =,因为在数轴上到原点的距离为2的点对应的数为2±,所以方程||2x =的解为2x =±.例 2.解不等式|1|2x ->,在数轴上找出|1|2x -=的解(如图),因为在数轴上到1对应的点的距离等于2的点对应的数为1-或3,所以方程|1|2x -=的解为1x =-或3x =,因此不等式|1|2x ->的解集为1x <-或3x >.参考阅读材料,解答下列问题:(1)方程|3|5x +=的解为 ;(2)解不等式:|2|3x -≤;(3)解不等式:428x x -++>.17.在如图所示的平面直角坐标系中,A(1,3),B(3,1),将线段A平移至CD,C (m,-1),D(1,n)(1)m=_____,n=______(2)点P的坐标是(c,0)①设∠ABP=α,请写出∠BPD和∠PDC之间的数量关系(用含α的式子表示,若有多种数量关系,选择一种加以说明)②当三角形PAB的面积不小于3且不大于10,求点p的横坐标C的取值范围(直接写出答案即可)18.如图1,已知,点A(1,a),AH⊥x轴,垂足为H,将线段AO平移至线段BC,点B(b,0),其中点A与点B对应,点O与点C对应,a、b满足24(3)0a b-+-=.(1)填空:①直接写出A、B、C三点的坐标A(________)、B(________)、C(________);②直接写出三角形AOH的面积________.(2)如图1,若点D(m,n)在线段OA上,证明:4m=n.(3)如图2,连OC,动点P从点B开始在x轴上以每秒2个单位的速度向左运动,同时点Q从点O开始在y轴上以每秒1个单位的速度向下运动.若经过t秒,三角形AOP与三角形COQ的面积相等,试求t的值及点P的坐标.19.题目:满足方程组3512332x y kx y k+=+⎧⎨+=-⎩的x与y的值的和是2,求k的值.按照常规方法,顺着题目思路解关于x,y的二元一次方程组,分别求出xy的值(含有字母k),再由x+y=2,构造关于k的方程求解,从而得出k值.(1)某数学兴趣小组对本题的解法又进行了探究利用整体思想,对于方程组中每个方程变形得到“x+y”这个整体,或者对方程组的两个方程进行加减变形得到“x+y”整体值,从而求出k值请你运用这种整体思想的方法,完成题目的解答过程.(2)小勇同学的解答是:观察方程①,令3x=k,5y=1解得y=15,3x+y=2,∴x=95∴k=3×95=275把x=95,y=15代入方程②得k=﹣35所以k的值为275或﹣35.请诊断分析并评价“小勇同学的解答”.20.某工厂接受了20天内生产1200台GH型电子产品的总任务.已知每台GH型产品由4个G型装置和3个H型装置配套组成.工厂现有80名工人,每个工人每天能加工6个G 型装置或3个H型装置.工厂将所有工人分成两组同时开始加工,每组分别加工一种装置,并要求每天加工的G、H型装置数量正好全部配套组成GH型产品.(1)按照这样的生产方式,工厂每天能配套组成多少套GH型电子产品?请列出二元一次方程组解答此问题.(2)为了在规定期限内完成总任务,工厂决定补充一些新工人,这些新工人只能独立进行G型装置的加工,且每人每天只能加工4个G型装置.设原来每天安排x名工人生产G型装置,后来补充m名新工人,求x的值(用含m的代数式表示)21.(1)阅读下列材料并填空:对于二元一次方程组4354{336x yx y+=+=,我们可以将x,y的系数和相应的常数项排成一个数表4354 () 1336,求得的一次方程组的解{x ay b==,用数表可表示为10)01ab(.用数表可以简化表达解一次方程组的过程如下,请补全其中的空白:从而得到该方程组的解为x=,y=.(2)仿照(1)中数表的书写格式写出解方程组236{2x yx y+=+=的过程.22.在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,b满足|a+b﹣2|25a b-+0,现同时将点A,B分别向右平移1个单位,再向上平移2个单位,分别得到点A,B的对应点为C,D.(1)请直接写出A、B、C、D四点的坐标.(2)点E在坐标轴上,且S△BCE=S四边形ABDC,求满足条件的点E的坐标.(3)点P 是线段BD 上的一个动点,连接PC ,PO ,当点P 在线段BD 上移动时(不与B ,D 重合)求:DCP BOP CPO∠+∠∠的值.23.某校为了丰富同学们的课外活动,决定给全校20个班每班配4副乒乓球拍和若干乒乓球,两家体育用品商店对同一款乒乓球拍和乒乓球推出让利活动,甲商店买一副乒乓球拍送10个乒乓球,乙商店所有商品均打九折(按标价的90%)销售,已知2副乒乓球拍和10个乒乓球110元,3副乒乓球拍和20个乒乓球170元。
【初中数学】七年级下册压轴题专项练习(解析版)

一、解答题1.如图,用两个面积为200cm 2七年级下册数学压轴题专题练习(解析版)的小正方形拼成一个大的正方形.(1)则大正方形的边长是;(2)若沿着大正方形边的方向裁出一个长方形,能否使裁出的长方形纸片的长宽之比为4:3,且面积为360cm 2?2.如图,在9⨯9网格中,每个小正方形的边长均为1,正方形ABCD 的顶点都在网格的格点上.(1)求正方形ABCD 的面积和边长;(2)建立适当的平面直角坐标系,写出正方形四个顶点的坐标.3.已知在4⨯4的正方形网格中,每个小正方形的边长为1.(1)计算图①中正方形ABCD 的面积与边长.(2)利用图②中的正方形网格,作出面积为8的正方形,并在此基础上建立适当的数轴,在数轴上表示实数8和-8.4.小丽想用一块面积为400cm 2的正方形纸片,沿着边的方向裁处一块面积为300cm 2的长方形纸片.(1)请帮小丽设计一种可行的裁剪方案;(2)若使长方形的长宽之比为3:2,小丽能用这块纸片裁处符合要求的纸片吗?若能,请帮小丽设计一种裁剪方案,若不能,请简要说明理由.5.某市在招商引资期间,把已倒闭的油泵厂出租给外地某投资商,该投资商为减少固定资产投资,将原来的400m 2的正方形场地改建成300m 2的长方形场地,且其长、宽的比为5:3.(1)求原来正方形场地的周长;(2)如果把原来的正方形场地的铁栅栏围墙全部利用,围成新场地的长方形围墙,那么这些铁栅栏是否够用?试利用所学知识说明理由.二、解答题6.如图,MN//GH,点A、B分别在直线MN、GH上,点O在直线MN、GH之间,若∠NAO=116︒,∠OBH=144︒.(1)∠AOB=︒;(2)如图2,点C、D是∠NAO、∠GBO角平分线上的两点,且∠CDB=35︒,求∠ACD的度数;(3)如图3,点F是平面上的一点,连结FA、FB,E是射线FA上的一点,若∠MAE=n∠OAE,∠HBF=n∠OBF,且∠AFB=60︒,求n的值.7.如图,∠EBF=50°,点C是∠EBF的边BF上一点.动点A从点B出发在∠EBF的边BE 上,沿BE方向运动,在动点A运动的过程中,始终有过点A的射线AD∥BC.(1)在动点A运动的过程中,(填“是”或“否”)存在某一时刻,使得AD平分∠EAC?(2)假设存在AD平分∠EAC,在此情形下,你能猜想∠B和∠ACB之间有何数量关系?并请说明理由;(3)当AC⊥BC时,直接写出∠BAC的度数和此时AD与AC之间的位置关系.8.如图,已知直线AB//射线CD,∠CEB=100︒.P是射线EB上一动点,过点P作PQ//EC交射线CD于点Q,连接CP.作∠PCF=∠PCQ,交直线AB于点F,CG平分∠ECF.(1)若点P,F,G都在点E的右侧,求∠PCG的度数;(2)若点P,F,G都在点E的右侧,∠EGC-∠ECG=30︒,求∠CPQ的度数;(3)在点P的运动过程中,是否存在这样的情形,使∠EGC:∠EFC=4:3?若存在,求出∠CPQ的度数;若不存在,请说明理由.9.已知:AB∥CD,截线MN分别交AB、CD于点M、N.(1)如图①,点B在线段MN上,设∠EBM=α°,∠DNM=β°,且满足a-30+(β﹣60)2=0,求∠BEM的度数;(2)如图②,在(1)的条件下,射线DF平分∠CDE,且交线段BE的延长线于点F;请写出∠DEF与∠CDF之间的数量关系,并说明理由;(3)如图③,当点P在射线NT上运动时,∠DCP与∠BMT的平分线交于点Q,则∠Q与∠CPM的比值为(直接写出答案).10.问题情境:(1)如图1,AB//CD,∠PAB=128︒,∠PCD=119︒.求∠APC度数.小颖同学的解题思路是:如图2,过点P作PE//AB,请你接着完成解答.问题迁移:(2)如图3,AD//BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠PCE=∠β.试判断∠CPD、∠α、∠β之间有何数量关系?(提示:过点P作PF//AD),请说明理由;(3)在(2)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你猜想∠CPD、∠α、∠β之间的数量关系并证明.三、解答题11.已知:直线l 1∥l 2,A 为直线l 1上的一个定点,过点A 的直线交l 2于点B ,点C 在线段BA 的延长线上.D ,E 为直线l 2上的两个动点,点D 在点E 的左侧,连接AD ,AE ,满足∠AED =∠DAE .点M 在l 2上,且在点B 的左侧(2)射线AF 为∠CAD 的角平分线.①如图2,当点D 在点B 右侧时,用等式表示∠EAF 与∠ABD 之间的数量关系,并证明;②当点D 与点B 不重合,且∠ABM +∠EAF =150°时,直接写出∠EAF 的度数..(1)如图1,若∠BAD =25°,∠AED =50°,直接写出∠ABM 的度数;12.阅读下面材料:小颖遇到这样一个问题:已知:如图甲,AB //CD ,E 为AB ,CD 之间一点,连接BE ,DE ,∠B =35︒,∠D =37︒,求∠BED 的度数.她是这样做的:过点E 作EF //AB ,则有∠BEF =∠B ,因为AB //CD ,所以EF //CD .①所以∠FED =∠D ,所以∠BEF +∠FED =∠B +∠D ,即∠BED =_;1.小颖求得∠BED的度数为__;2.上述思路中的①的理由是__;3.请你参考她的思考问题的方法,解决问题:已知:直线a//b,点A,B在直线a上,点C,D在直线b上,连接AD,BC,BE平分∠ABC,DE 平分∠ADC,且BE,DE所在的直线交于点E.(1)如图1,当点B在点A的左侧时,若∠ABC=α,∠ADC=β,则∠BED的度数为;(用含有α,β的式子表示).(2)如图2,当点B在点A的右侧时,设∠ABC=α,∠ADC=β,直接写出∠BED的度数(用含有α,β的式子表示).13.如图1,AB//CD,E是AB、CD之间的一点.(1)判定∠BAE,∠CDE与∠AED之间的数量关系,并证明你的结论;(2)如图2,若∠BAE、∠CDE的两条平分线交于点F.直接写出∠AFD与∠AED之间的数量关系;(3)将图2中的射线DC沿DE翻折交AF于点G得图3,若∠AGD的余角等于2∠E的补角,求∠BAE的大小.14.(1)学习了平行线以后,香橙同学想出了过一点画一条直线的平行线的新方法,她是通过折纸做的,过程如(图1).①请你仿照以上过程,在图2中画出一条直线b,使直线b经过点P,且b//a,要求保留折纸痕迹,画出所用到的直线,指明结果.无需写画法:②在(1)中的步骤(b)中,折纸实际上是在寻找过点P的直线a的线.(2)已知,如图3,AB//CD,BE平分∠ABC,CF平分∠BCD.求证:BE//CF(写出每步的依据).15.如图所示,已知AM//BN,点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C、D,且∠CBD=60︒(1)求∠A的度数.(2)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.四、解答题16.在ABC中,射线AG平分∠BAC交BC于点G,点D在BC边上运动(不与点G重合),过点D作DE//AC交AB于点E.(1)如图1,点D在线段CG上运动时,DF平分∠EDB.①若∠BAC=100︒,∠C=30︒,则∠AFD=_____;若∠B=40︒,则∠AFD=_____;②试探究∠AFD与B之间的数量关系?请说明理由;(2)点D在线段BG上运动时,∠BDE的角平分线所在直线与射线AG交于点F.试探究∠AFD与B之间的数量关系,并说明理由.17.己知:如图①,直线MN⊥直线PQ,垂足为O,点A在射线OP上,点B在射线OQ上(A、B不与O点重合),点C在射线ON上且OC=2,过点C作直线l//PQ.点D在点C的左边且CD=3(1)直接写出的∆BCD面积 ;(2)如图②,若AC⊥BC,作∠CBA的平分线交OC于E,交AC于F,试说明∠CEF=∠CFE;(3)如图③,若∠ADC=∠DAC,点B在射线OQ上运动,∠ACB的平分线交DA的延长线于点H,在点B运动过程中∠H的值是否变化?若不变,求出其值;若变化,求出变化范围.∠ABC18.Rt△ABC中,∠C=90°,点D、E分别是△ABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.(1)若点P在线段AB上,如图(1)所示,且∠α=50°,则∠1+∠2=°;(2)若点P在边AB上运动,如图(2)所示,则∠α、∠1、∠2之间的关系为:;(3)若点P运动到边AB的延长线上,如图(3)所示,则∠α、∠1、∠2之间有何关系?猜想并说明理由.(4)若点P运动到△ABC形外,如图(4)所示,则∠α、∠1、∠2之间的关系为:. 19.直线MN与直线PQ垂直相交于O,点A在射线OP上运动,点B在射线OM上运动,A、B不与点O重合,如图1,已知AC、BC分别是∠BAP和∠ABM角的平分线,(1)点A、B在运动的过程中,∠ACB的大小是否发生变化?若发生变化,请说明理由;若不发生变化,试求出∠ACB的大小.(2)如图2,将△ABC沿直线AB折叠,若点C落在直线PQ上,则∠ABO=________,如图3,将△ABC沿直线AB折叠,若点C落在直线MN上,则∠ABO=________(3)如图4,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及其反3向延长线交于E、F,则∠EAF=;在△AEF中,如果有一个角是另一个角的倍,求∠ABO2的度数.20.如果三角形的两个内角α与β满足2α+β=90︒,那么我们称这样的三角形是“准互余三角形”.(1)如图1,在Rt ABC中,∠ACB=90︒,BD是ABC的角平分线,求证:△ABD是“准互余三角形”;(2)关于“准互余三角形”,有下列说法:①在ABC中,若∠A=100︒,∠B=70︒,∠C=10︒,则ABC是“准互余三角形”;②若ABC是“准互余三角形”,∠C>90︒,∠A=60︒,则∠B=20︒;③“准互余三角形”一定是钝角三角形.其中正确的结论是___________(填写所有正确说法的序号);(3)如图2,B,C为直线l上两点,点A在直线l外,且∠ABC=50︒.若P是直线l上一点,且△ABP是“准互余三角形”,请直接写出∠APB的度数.【参考答案】一、解答题1.(1);(2)无法裁出这样的长方形.【分析】(1)先计算两个小正方形的面积之和,在根据算术平方根的定义,即可求解;(2)设长方形长为cm,宽为cm,根据题意列出方程,解方程比较4x与20的大小解析:(1)20;(2)无法裁出这样的长方形.【分析】(1)先计算两个小正方形的面积之和,在根据算术平方根的定义,即可求解;(2)设长方形长为4x cm,宽为3x cm,根据题意列出方程,解方程比较4x与20的大小即可.【详解】解:(1)由题意得,大正方形的面积为200+200=400cm2,∴边长为:400=20cm;(2)根据题意设长方形长为4x cm,宽为3x cm,4x⋅3x=360由题:则x2=30x0∴x=30∴长为430430>20∴无法裁出这样的长方形.【点睛】本题考查了算术平方根,根据题意列出算式(方程)是解决此题的关键.2.(1)面积为29,边长为;(2),,,,图见解析.【分析】(1)面积等于一个大正方形的面积减去四个直角三角形的面积,再利用算术平方根定义求得边长即可;(2)建立适当的坐标系后写出四个顶点的坐标解析:(1)面积为29,边长为29;(2)A (0,5),B (2,0),C (7,2),D (5,7),图见解析.【分析】(1)面积等于一个7⨯7大正方形的面积减去四个直角三角形的面积,再利用算术平方根定义求得边长即可;(2)建立适当的坐标系后写出四个顶点的坐标即可.【详解】解:(1)正方形的面积S正方形ABCD =72-4⨯⨯2⨯5=29,正方形边长为S =29;(2)建立如图平面直角坐标系,则A (0,5),B (2,0),C (7,2),D (5,7).12【点睛】本题考查了算术平方根及坐标与图形的性质及割补法求面积,从图形中整理出直角三角形是进一步解题的关键.3.(1)正方形的面积为10,正方形的边长为;(2)见解析【分析】(1)利用正方形的面积减去4个直角三角形的面积即可求出正方形的面积,然后根据算术平方根的意义即可求出边长;(2)根据(1)的方法画解析:(1)正方形ABCD 的面积为10,正方形ABCD 的边长为10;(2)见解析【分析】(1)利用正方形的面积减去4个直角三角形的面积即可求出正方形ABCD 的面积,然后根据算术平方根的意义即可求出边长;(2)根据(1)的方法画出图形,然后建立数轴,根据算术平方根的意义即可表示出结论.【详解】解:(1)正方形ABCD 的面积为4×4-4×2×3×1=10则正方形ABCD 的边长为10;(2)如下图所示,正方形的面积为4×4-4×2×2×2=8,所以该正方形即为所求,如图建立数轴,以数轴的原点为圆心,正方形的边长为半径作弧,分别交数轴于两点11∴正方形的边长为8∴弧与数轴的左边交点为-8,右边交点为8,实数8和-8在数轴上如图所示.【点睛】此题考查的是求网格中图形的面积和实数与数轴,掌握算术平方根的意义和利用数轴表示无理数是解题关键.4.(1)可以以正方形一边为长方形的长,在其邻边上截取长为15cm 的线段作为宽即可裁出符合要求的长方形;(2)不能,理由见解析.【解析】(1)解:设面积为400cm2的正方形纸片的边长为a cm∴解析:(1)可以以正方形一边为长方形的长,在其邻边上截取长为15cm 的线段作为宽即可裁出符合要求的长方形;(2)不能,理由见解析.【解析】(1)解:设面积为400cm 2的正方形纸片的边长为a cm∴a 2=400又∵a >0∴a =20又∵要裁出的长方形面积为300cm 2∴若以原正方形纸片的边长为长方形的长,则长方形的宽为:300÷20=15(cm )∴可以以正方形一边为长方形的长,在其邻边上截取长为15cm 的线段作为宽即可裁出符合要求的长方形(2)∵长方形纸片的长宽之比为3:2∴设长方形纸片的长为3x cm ,则宽为2x cm∴6x 2=300∴x 2=50又∵x >0∴x =52∴长方形纸片的长为152又∵152()2=450>202即:152>20∴小丽不能用这块纸片裁出符合要求的纸片5.(1)原来正方形场地的周长为80m ;(2)这些铁栅栏够用.【分析】(1)正方形边长=面积的算术平方根,周长=边长×4,由此解答即可;(2)长、宽的比为5:3,设这个长方形场地宽为3am ,则长为解析:(1)原来正方形场地的周长为80m ;(2)这些铁栅栏够用.【分析】(1)正方形边长=面积的算术平方根,周长=边长×4,由此解答即可;(2)长、宽的比为5:3,设这个长方形场地宽为3am ,则长为5am ,计算出长方形的长与宽可知长方形周长,同理可得正方形的周长,比较大小可知是否够用.【详解】解:(1)400=20(m ),4×20=80(m ),答:原来正方形场地的周长为80m ;(2)设这个长方形场地宽为3am ,则长为5am .由题意有:3a ×5a =300,解得:a =±20,∵3a 表示长度,∴a >0,∴a =20,∴这个长方形场地的周长为 2(3a +5a )=16a =1620(m ),∵80=16×5=16×25>1620,∴这些铁栅栏够用.【点睛】本题考查了算术平方根的实际应用,解答本题的关键是明确题意,求出长方形和正方形的周长.二、解答题6.(1)100;(2)75°;(3)n=3.【分析】(1)如图:过O作OP//MN,由MN//OP//GH得∠NAO+∠POA=180°,∠POB+∠OBH=180°,即∠NAO+∠AOB+∠OB解析:(1)100;(2)75°;(3)n=3.【分析】(1)如图:过O作OP//MN,由MN//OP//GH得∠NAO+∠POA=180°,∠POB+∠OBH=180°,即∠NAO+∠AOB+∠OBH=360°,即可求出∠AOB;(2)如图:分别延长AC、CD交GH于点E、F,先根据角平分线求得∠NAC=58︒,再根据平行线的性质得到∠CEF=58︒;进一步求得∠DBF=18︒,∠DFB=17︒,然后根据三角形外角的性质解答即可;(3)设BF交MN于K,由∠NAO=116°,得∠MAO=64°,故∠MAE=∠OBH=144°,∠HBF=n∠OBF,得∠FBH=∠FKN=∠F+∠FAK,得【详解】解:(1)如图:过O作OP//MN,∵MN//GHl∴MN//OP//GH∴∠NAO+∠POA=180°,∠POB+∠OBH=180°∴∠NAO+∠AOB+∠OBH=360°∵∠NAO=116°,∠OBH=144°∴∠AOB=360°-116°-144°=100°;n⨯64︒,同理n+1n n⨯144︒,从而∠BKA=∠FBH=⨯144︒,又n+1n+1n n⨯144︒=60︒+⨯64︒,即可求n.n+1n+1(2)分别延长AC、CD交GH于点E、F,∵AC平分∠NAO且∠NAO=116︒,∴∠NAC=58︒,又∵MN//GH,∴∠CEF=58︒;∵OBH144,OBG 36∵BD 平分OBG ,∴DBF18,又∵CDB35,∴DFBCDB DBF 351817;∴ACD DFB AEF 175875;(3)设FB 交MN 于K ,∵NAO116,则MAO 64;∴MAEn 64n 1n n 144,BKA =FBH 144,n+1n 1∵OBH144,∴FBH 在△FAK 中,BKAFKA F ∴n n 1446460,n 1n 1n 6460,n 1∴n 3.经检验:n 3是原方程的根,且符合题意.【点睛】本题主要考查平行线的性质及应用,正确作出辅助线、构造平行线、再利用平行线性质进行求解是解答本题的关键.7.(1)是;(2)∠B =∠ACB ,证明见解析;(3)∠BAC =40°,AC⊥AD .【分析】(1)要使AD 平分∠EAC ,则要求∠EAD =∠CAD ,由平行线的性质可得∠B =∠EAD ,∠ACB =∠CAD解析:(1)是;(2)∠B =∠ACB ,证明见解析;(3)∠BAC =40°,AC⊥AD .【分析】(1)要使AD 平分∠EAC ,则要求∠EAD =∠CAD ,由平行线的性质可得∠B =∠EAD ,∠ACB =∠CAD ,则当∠ACB =∠B 时,有AD 平分∠EAC ;(2)根据角平分线可得∠EAD =∠CAD ,由平行线的性质可得∠B =∠EAD ,∠ACB =∠CAD ,则有∠ACB =∠B ;(3)由AC⊥BC ,有∠ACB =90°,则可求∠BAC =40°,由平行线的性质可得AC⊥AD .【详解】解:(1)是,理由如下:要使AD平分∠EAC,则要求∠EAD=∠CAD,由平行线的性质可得∠B=∠EAD,∠ACB=∠CAD,则当∠ACB=∠B时,有AD平分∠EAC;故答案为:是;(2)∠B=∠ACB,理由如下:∵AD平分∠EAC,∴∠EAD=∠CAD,∵AD∥BC,∴∠B=∠EAD,∠ACB=∠CAD,∴∠B=∠ACB.(3)∵AC⊥BC,∴∠ACB=90°,∵∠EBF=50°,∴∠BAC=40°,∵AD∥BC,∴AD⊥AC.【点睛】此题考查了角平分线和平行线的性质,熟练掌握角平分线和平行线的有关性质是解题的关键.8.(1)40°;(2)65°;(3)存在,56°或20°【分析】(1)依据平行线的性质以及角平分线的定义,即可得到∠PCG的度数;(2)依据平行线的性质以及角平分线的定义,即可得到∠ECG=∠G解析:(1)40°;(2)65°;(3)存在,56°或20°【分析】(1)依据平行线的性质以及角平分线的定义,即可得到∠PCG的度数;(2)依据平行线的性质以及角平分线的定义,即可得到∠ECG=∠GCF=25°,再根据PQ∥CE,即可得出∠CPQ=∠ECP=65°;(3)设∠EGC=4x,∠EFC=3x,则∠GCF=4x-3x=x,分两种情况讨论:①当点G、F在点E 的右侧时,②当点G、F在点E的左侧时,依据等量关系列方程求解即可.【详解】解:(1)∵∠CEB=100°,AB∥CD,∴∠ECQ=80°,∵∠PCF=∠PCQ,CG平分∠ECF,∴∠PCG=∠PCF+∠FCG=2∠QCF+2∠FCE=2∠ECQ=40°;(2)∵AB∥CD111∴∠QCG=∠EGC,∠QCG+∠ECG=∠ECQ=80°,∴∠EGC+∠ECG=80°,又∵∠EGC-∠ECG=30°,∴∠EGC=55°,∠ECG=25°,∴∠ECG=∠GCF=25°,∠PCF=∠PCQ=2(80°-50°)=15°,∵PQ∥CE,∴∠CPQ=∠ECP=65°;(3)设∠EGC=4x,∠EFC=3x,则∠GCF=∠FCD=4x-3x=x,①当点G、F在点E的右侧时,1则∠ECG=x,∠PCF=∠PCD=∵∠ECD=80°,3 x,233∴x+x+x+x=80°,22解得x=16°,3∴∠CPQ=∠ECP=x+x+x=56°;2②当点G、F在点E的左侧时,则∠ECG=∠GCF=x,∵∠CGF=180°-4x,∠GCQ=80°+x,∴180°-4x=80°+x,解得x=20°,∴∠FCQ=∠ECF+∠ECQ=40°+80°=120°,∴∠PCQ=2∠FCQ=60°,∴∠CPQ=∠ECP=80°-60°=20°.【点睛】本题主要考查了平行线的性质,解题时注意:两直线平行,同旁内角互补;两直线平行,1内错角相等.9.(1)30°;(2)∠DEF+2∠CDF =150°,理由见解析;(3)【分析】(1)由非负性可求α,β的值,由平行线的性质和外角性质可求解;(2)过点E 作直线EH ∥AB ,由角平分线的性质和平行解析:(1)30°;(2)∠DEF +2∠CDF =150°,理由见解析;(3)2【分析】(1)由非负性可求α,β的值,由平行线的性质和外角性质可求解;(2)过点E 作直线EH ∥AB ,由角平分线的性质和平行线的性质可求∠DEF =180°﹣30°﹣2x °=150°﹣2x °,由角的数量可求解;(3)由平行线的性质和外角性质可求∠PMB =2∠Q +∠PCD ,∠CPM =2∠Q ,即可求解.【详解】解:(1)∵∵AB ∥CD ,∴∠AMN =∠MND =60°,∵∠AMN =∠B +∠BEM =60°,∴∠BEM =60°﹣30°=30°;(2)∠DEF +2∠CDF =150°.理由如下:过点E 作直线EH ∥AB ,1α-30+(β﹣60)2=0,∴α=30,β=60,∵DF 平分∠CDE ,∴设∠CDF =∠EDF =x °;∵EH ∥AB ,∴∠DEH =∠EDC =2x °,∴∠DEF =180°﹣30°﹣2x °=150°﹣2x °;∴∠DEF =150°﹣2∠CDF ,即∠DEF +2∠CDF =150°;(3)如图3,设MQ 与CD 交于点E ,∵MQ 平分∠BMT ,QC 平分∠DCP ,∴∠BMT =2∠PMQ ,∠DCP =2∠DCQ ,∵AB ∥CD ,∴∠BME =∠MEC ,∠BMP =∠PND ,∵∠MEC =∠Q +∠DCQ ,∴2∠MEC =2∠Q +2∠DCQ ,∴∠PMB =2∠Q +∠PCD ,∵∠PND =∠PCD +∠CPM =∠PMB ,∴∠CPM =2∠Q ,∴∠Q 与∠CPM 的比值为2,故答案为:2.【点睛】本题主要考查了平行线的性质、角平分线的性质,准确计算是解题的关键.1110.(1)见解析;(2),理由见解析;(3)①当在延长线时(点不与点重合),;②当在之间时(点不与点,重合),.理由见解析【分析】(1)过P 作PE ∥AB ,构造同旁内角,利用平行线性质,可得∠APC=解析:(1)见解析;(2)∠CPD =∠α+180︒-∠β,理由见解析;(3)①当P 在BA 延长线时(点P 不与点A 重合),∠CPD =180︒-∠β-∠α;②当P 在BO 之间时(点P 不与点B ,O 重合),∠CPD =∠α-180︒+∠β.理由见解析【分析】(1)过P 作PE ∥AB ,构造同旁内角,利用平行线性质,可得∠APC =113°;(2)过过P 作PF //AD 交CD 于F ,,推出AD //PF //BC ,根据平行线的性质得出BCP 180,即可得出答案;(3)画出图形(分两种情况:①点P 在BA 的延长线上,②当P 在BO 之间时(点P 不与点B ,O 重合)),根据平行线的性质即可得出答案.【详解】解:(1)过P 作PE //AB ,AB //CD ,∴PE //AB //CD ,APE PAB =180,∠CPE +∠PCD =180︒,∠PAB =128︒,∠PCD =119︒∴∠APE=52︒,∠CPE=61︒,∴∠APC=52︒+61︒=113︒;(2)∠CPD=∠α+180︒-∠β,理由如下:如图3,过P作PF//AD交CD于F,AD//BC,∴AD//PF//BC,∴∠ADP=∠DPF,∠BCP=∠CPF,∠BCP+∠PCE=180︒,∠PCE=∠β,∴∠BCP=180︒-∠β又∠ADP=∠αCPD DPF CPF=180;(3)①当P在BA延长线时(点P不与点A重合),∠CPD=180︒-∠β-∠α;理由:如图4,过P作PF//AD交CD于F,AD//BC,∴AD//PF//BC,∴∠ADP=∠DPF,∠BCP=∠CPF,∠BCP+∠PCE=180︒,∠PCE=∠β,∴∠BCP=180︒-∠β,又∠ADP=∠α,∴∠CPD=∠CPF-∠DPF=180︒-∠α-∠β;②当P在BO之间时(点P不与点B,O重合),∠CPD=∠α-180︒+∠β.理由:如图5,过P作PF//AD交CD于F,AD//BC,∴AD//PF//BC,∴∠ADP=∠DPF,∠BCP=∠CPF,∠BCP+∠PCE=180︒,∠PCE=∠β,∴∠BCP=180︒-∠β,又∠ADP=∠α∴∠CPD=∠DPF-∠CPF=∠α+∠β-180︒.【点睛】本题考查了平行线的性质的应用,主要考查学生的推理能力,解决问题的关键是作辅助线构造内错角以及同旁内角.三、解答题11.(1);(2)①,见解析;②或【分析】(1)由平行线的性质可得到:,,再利用角的等量代换换算即可;(2)①设,,利用角平分线的定义和角的等量代换表示出对比即可;②分类讨论点在的左右两侧的情况,解析:(1)125︒;(2)①∠ABD=2∠EAF,见解析;②30或110︒【分析】(1)由平行线的性质可得到:∠DEA=∠EAN,∠MBA=∠BAN,再利用角的等量代换换算即可;(2)①设∠EAF=α,∠AED=∠DAE=β,利用角平分线的定义和角的等量代换表示出∠ABD对比即可;②分类讨论点D在B的左右两侧的情况,运用角的等量代换换算即可.【详解】.解:(1)设在l1上有一点N在点A的右侧,如图所示:∵l1//l2∴∠DEA=∠EAN,∠MBA=∠BAN∴∠AED=∠DAE=∠EAN=50︒∴∠BAN=∠BAD+∠DAE+∠EAN=25︒+50︒+50︒=125︒∠BAM=125︒(2)①∠ABD=2∠EAF.证明:设∠EAF=α,∠AED=∠DAE=β.∴∠FAD=∠EAF+∠DAE=α+β.∵AF为∠CAD的角平分线,∴∠CAD=2∠FAD=2α+2β.∵l1l2,∴∠EAN=∠AED=β.∴∠CAN=∠CAD-∠DAE-∠EAN=2α+2β-β-β=2α.∴∠ABD=∠CAN=2α=2∠EAF.②当点D在点B右侧时,如图:由①得:∠ABD=2∠EAF又∵∠ABD+∠ABM=180︒∴∠ABM+2∠EAF=180︒∵∠ABM+∠EAF=150︒∴∠EAF=180︒-150︒=30︒当点D在点B左侧,E在B右侧时,如图:∵AF为∠CAD的角平分线1∴∠DAF=∠CAD2∵l1l 2∴∠AED=∠NAE,∠CAN=∠ABE∵∠DAE=∠AED=∠NAE11∴∠DAE=(∠DAE+∠NAE)=∠DAN2211∴∠EAF=∠DAF+∠DAE=(∠CAD+∠DAN)=(360︒-∠CAN)221=180︒-∠ABE2∵∠ABE+∠ABM=180︒11∴∠EAF=180︒-(180︒-∠ABM)=90︒+∠ABM22又∵∠EAF+∠ABM=150︒11∴∠EAF=90︒+⨯(150︒-∠EAF)=165︒-∠EAF22∴∠EAF=110︒当点D和F在点B左侧时,设在l2上有一点G在点B的右侧如图:11此时仍有∠DAE=∠DAN,∠DAF=∠CAD2211(360︒-∠CAN)=180︒-∠ABG22∴11=180︒-(180︒-∠ABM)=90︒+∠ABM22∠EAF=∠DAE+∠DAF=∴∠EAF=110︒综合所述:∠EAF=30︒或110︒【点睛】本题主要考查了平行线的性质,角平分线的定义,角的等量代换等,灵活运用平行线的性质和角平分线定义等量代换出角的关系是解题的关键.12.;2.平行于同一条直线的两条直线平行;3.(1);(2).【分析】1、根据角度和计算得到答案;2、根据平行线的推论解答;3、(1)根据角平分线的性质及1的结论证明即可得到答案;(2)根据B11解析:1.72;2.平行于同一条直线的两条直线平行;3.(1)α+β;(2)2211180-α+β.22【分析】1、根据角度和计算得到答案;2、根据平行线的推论解答;3、(1)根据角平分线的性质及1的结论证明即可得到答案;11(2)根据BE平分∠ABC,DE平分∠ADC,求出∠ABE=α,∠CDE=β,过点E作2211EF∥AB,根据平行线的性质求出∠BEF=α,∠DEF=180︒-∠CDE=180︒-β,再利用22周角求出答案.【详解】1、过点E作EF//AB,则有∠BEF=∠B,因为AB//CD,所以EF//CD.①所以∠FED=∠D,所以∠BEF+∠FED=∠B+∠D,即∠BED=72;故答案为:72;2、过点E作EF//AB,则有∠BEF=∠B,因为AB//CD,所以EF∥CD(平行于同一条直线的两条直线平行),故答案为:平行于同一条直线的两条直线平行;3、(1)∵BE平分∠ABC,DE平分∠ADC,1111∴∠ABE=∠ABC=α,∠CDE=∠ADC=β,2222过点E作EF∥AB,由1可得∠BED=∠BEF+∠FED=∠ABE+∠CDE,11∴∠BED=α+β,2211故答案为:α+β;22(2)∵BE平分∠ABC,DE平分∠ADC,1111∴∠ABE=∠ABC=α,∠CDE=∠ADC=β,22221过点E作EF∥AB,则∠ABE=∠BEF=α,2∵AB//CD,∴EF∥CD,∴∠CDE+∠DEF=180︒,1∴∠DEF=180︒-∠CDE=180︒-β,21111∴∠BED=360︒-∠DEF-∠BEF=360︒-(180︒-β)-α=180-α+β.2222【点睛】此题考查平行线的性质:两直线平行内错角相等,两直线平行同旁内角互补,平行线的推论,正确引出辅助线是解题的关键.13.(1),见解析;(2);(3)60°【分析】(1)作EF//AB,如图1,则EF//CD,利用平行线的性质得∠1=∠BAE,∠2=∠CDE,从而得到∠BAE+∠CDE=∠AED;(2)如图2,1解析:(1)∠BAE+∠CDE=∠AED,见解析;(2)∠AFD=∠AED;(3)60°2【分析】(1)作EF//AB,如图1,则EF//CD,利用平行线的性质得∠1=∠BAE,∠2=∠CDE,从而得到∠BAE+∠CDE=∠AED;(2)如图2,由(1)的结论得∠AFD=∠BAF+∠CDF,根据角平分线的定义得到∠BAF=1 2∠BAE,∠CDF=2∠CDE,则∠AFD=2(∠BAE+∠CDE),加上(1)的结论得到111∠AFD=2∠AED;(3)由(1)的结论得∠AGD=∠BAF+∠CDG,利用折叠性质得∠CDG=4∠CDF,再利用3等量代换得到∠AGD=2∠AED-∠BAE,加上90°-∠AGD=180°-2∠AED,从而可计算2出∠BAE的度数.【详解】解:(1)∠BAE+∠CDE=∠AED理由如下:作EF//AB,如图1,AB//CD,∴EF//CD.∴∠1=∠BAE,∠2=∠CDE,∴∠BAE+∠CDE=∠AED;(2)如图2,由(1)的结论得∠AFD=∠BAF+∠CDF,∠BAE、∠CDE的两条平分线交于点F,11∴∠BAF=∠BAE,∠CDF=∠CDE,221∴∠AFD=(∠BAE+∠CDE),2∠BAE+∠CDE=∠AED,1∴∠AFD=∠AED;2(3)由(1)的结论得∠AGD=∠BAF+∠CDG,而射线DC沿DE翻折交AF于点G,∴∠CDG=4∠CDF,11∴∠AGD=∠BAF+4∠CDF=∠BAE+2∠CDE=∠BAE+2(∠AED-∠BAE)=2232∠AED-∠BAE,290︒-∠AGD=180︒-2∠AED,3∴90︒-2∠AED+∠BAE=180︒-2∠AED,2∴∠BAE=60︒.【点睛】本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.14.(1)①见解析;②垂;(2)见解析【分析】(1)①过点折纸,使痕迹垂直直线,然后过点折纸使痕迹与前面的痕迹垂直,从而得到直线;②步骤(b)中,折纸实际上是在寻找过点的直线的垂线.(2)先根据解析:(1)①见解析;②垂;(2)见解析【分析】(1)①过P点折纸,使痕迹垂直直线a,然后过P点折纸使痕迹与前面的痕迹垂直,从而得到直线b;②步骤(b)中,折纸实际上是在寻找过点P的直线a的垂线.(2)先根据平行线的性质得到∠ABC=∠BCD,再利用角平分线的定义得到∠2=∠3,然后根据平行线的判定得到结论.【详解】(1)解:①如图2所示:②在(1)中的步骤(b)中,折纸实际上是在寻找过点P的直线a的垂线.故答案为垂;(2)证明:BE平分∠ABC,CF平分∠BCD(已知),∴∠1=∠2,∠3=∠3(角平分线的定义),AB//CD(已知),∴∠ABC=∠BCD(两直线平行,内错角相等),∴2∠2=2∠3(等量代换),∴∠2=∠3(等式性质),∴BE//CF(内错角相等,两直线平行).【点睛】本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了平行线的性质与判定.15.(1);(2)不变化,,理由见解析;(3)【分析】(1)结合题意,根据角平分线的性质,得;再根据平行线的性质计算,即可得到答案;(2)根据平行线的性质,得,;结合角平分线性质,得,即可完成求解解析:(1)∠A=60;(2)不变化,∠APB=2∠ADB,理由见解析;(3)∠ABC=30【分析】(1)结合题意,根据角平分线的性质,得∠ABN;再根据平行线的性质计算,即可得到答案;(2)根据平行线的性质,得∠APB=∠PBN,∠ADB=∠DBN;结合角平分线性质,得∠APB=2∠ADB,即可完成求解;(3)根据平行线的性质,得∠ACB=∠CBN;结合∠ACB=∠ABD,推导得∠ABC=∠DBN;再结合(1)的结论计算,即可得到答案.【详解】(1)∵BC,BD分别评分∠ABP和∠PBN,11∴∠CBP=∠ABP,∠DBP=∠PBN,22∴∠ABN=2∠CBD又∵∠CBD=60,∴∠ABN=120∵AM//BN,∴∠A+∠ABN=180∴∠A=60;(2)∵AM//BN,∴∠APB=∠PBN,∠ADB=∠DBN又∵BD平分∠PBN∴∠PBN=2∠DBN,∴∠APB=2∠ADB;∴∠APB与∠ADB之间的数量关系保持不变;(3)∵AD//BN,∴∠ACB=∠CBN又∵∠ACB=∠ABD,∴∠CBN=∠ABD,∵∠ABC+∠CBN=∠ABD+∠DBN∴∠ABC=∠DBN由(1)可得∠CBD=60,∠ABN=1201∴∠ABC=⨯(120-60)=30.2【点睛】本题考查了角平分线、平行线的知识;解题的关键是熟练掌握角平分线、平行线的性质,从而完成求解.四、解答题16.(1)①115°,110°;②,证明见解析;(2),证明见解析.【解析】【分析】(1)①根据角平分线的定义求得∠CAG=∠BAC=50°;再由平行线的性质可得∠EDG=∠C=30°,∠FMD=1︒解析:(1)①115°,110°;②∠AFD=90+∠B,证明见解析;(2)21∠AFD=90︒-∠B,证明见解析.2【解析】【分析】1(1)①根据角平分线的定义求得∠CAG=∠BAC=50°;再由平行线的性质可得2∠EDG=∠C=30°,∠FMD=∠GAC=50°;由三角形的内角和定理求得∠AFD的度数即可;已知1AG平分∠BAC,DF平分∠EDB,根据角平分线的定义可得∠CAG=∠BAC,21∠FDM=∠EDG;由DE//AC,根据平行线的性质可得∠EDG=∠C,∠FMD=∠GAC;即可得211111∠FDM +∠FMD=∠EDG +∠GAC=∠C+∠BAC=(∠BAC+∠C)=×140°=70°;再由三22222角形的内角和定理可求得∠AFD=110°;1②∠AFD=90°+∠B,已知AG平分∠BAC,DF平分∠EDB,根据角平分线的定义可得211∠CAG=∠BAC,∠FDM=∠EDG;由DE//AC,根据平行线的性质可得∠EDG=∠C,221111∠FMD=∠GAC;由此可得∠FDM +∠FMD=∠EDG +∠GAC=∠C+∠BAC=222211(∠BAC+∠C)=×(180°-∠B)=90°-∠B;再由三角形的内角和定理可得221∠AFD=90°+∠B;21(2)∠AFD=90°-∠B,已知AG平分∠BAC,DF平分∠EDB,根据角平分线的定义可得2111∠CAG=∠BAC,∠NDE=∠EDB,即可得∠FDM=∠NDE=∠EDB;由DE//AC,根据平行2221线的性质可得∠EDB=∠C,∠FMD=∠GAC;即可得到∠FDM=∠NDE=∠C,所以∠FDM211111+∠FMD =∠C+∠BAC=(∠BAC+∠C)=×(180°-∠B)=90°-∠B;再由三角形外角222221的性质可得∠AFD=∠FDM +∠FMD=90°-∠B.2【详解】(1)①∵AG平分∠BAC,∠BAC=100°,1∴∠CAG=∠BAC=50°;2∵DE//AC,∠C=30°,∴∠EDG=∠C=30°,∠FMD=∠GAC=50°;∵DF平分∠EDB,1∴∠FDM=∠EDG=15°;2∴∠AFD=180°-∠FMD-∠FDM=180°-50°-15°=115°;∵∠B=40°,∴∠BAC+∠C=180°-∠B=140°;∵AG平分∠BAC,DF平分∠EDB,11∴∠CAG=∠BAC,∠FDM=∠EDG,22∵DE//AC,∴∠EDG=∠C,∠FMD=∠GAC;11111∴∠FDM +∠FMD=∠EDG +∠GAC=∠C+∠BAC=(∠BAC+∠C)=×140°=70°;22222∴∠AFD=180°-(∠FDM +∠FMD)=180°-70°=110°;故答案为115°,110°;1②∠AFD=90°+∠B,理由如下:2∵AG平分∠BAC,DF平分∠EDB,11∴∠CAG=∠BAC,∠FDM=∠EDG,22∵DE//AC,∴∠EDG=∠C,∠FMD=∠GAC;11111∴∠FDM +∠FMD=∠EDG +∠GAC=∠C+∠BAC=(∠BAC+∠C)=×(180°-∠B)22222 1=90°-∠B;211∴∠AFD=180°-(∠FDM +∠FMD)=180°-(90°-∠B)=90°+∠B;221(2)∠AFD=90°-∠B,理由如下:2如图,射线ED交AG于点M,∵AG平分∠BAC,DF平分∠EDB,11∴∠CAG=∠BAC,∠NDE=∠EDB,221∴∠FDM=∠NDE=∠EDB,2∵DE//AC,∴∠EDB=∠C,∠FMD=∠GAC;1∴∠FDM=∠NDE=∠C,211111∴∠FDM +∠FMD =∠C+∠BAC=(∠BAC+∠C)=×(180°-∠B)=90°-∠B;222221∴∠AFD=∠FDM +∠FMD=90°-∠B.2【点睛】本题考查了角平分线的定义、平行线的性质、三角形的内角和定理及三角形外角的性质,根据角平分线的定义、平行线的性质、三角形的内角和定理及三角形外角的性质确定各角之间的关系是解决问题的关键.17.(1)3; (2)见解析; (3)见解析【详解】分析:(1)因为△BCD的高为OC,所以S△BCD=CD•OC,(2)利用∠CFE+∠CBF=90°,∠OBE+∠OEB=90°,求出∠CEF=∠解析:(1)3; (2)见解析; (3)见解析【详解】。
(完整版)七年级下册期末压轴题数学试题及解析(一)解析

一、解答题1.如图1,在平面直角坐标系中,(,0),(,2)A a C b ,且满足2(2)|2|0a b ++-=,过C 作CB x ⊥轴于B .(1)求ABC ∆的面积.(2)若过B 作//BD AC 交y 轴于D ,且,AE DE 分别平分,CAB ODB ∠∠,如图2,求AED ∠的度数.(3)在y 轴上存在点P 使得ABC ∆和ACP ∆的面积相等,请直接写出P 点坐标.2.已知AB ∥CD ,∠ABE 与∠CDE 的角分线相交于点F .(1)如图1,若BM 、DM 分别是∠ABF 和∠CDF 的角平分线,且∠BED =100°,求∠M 的度数;(2)如图2,若∠ABM =13∠ABF ,∠CDM =13∠CDF ,∠BED =α°,求∠M 的度数; (3)若∠ABM =1n ∠ABF ,∠CDM =1n∠CDF ,请直接写出∠M 与∠BED 之间的数量关系3.如图1,把一块含30°的直角三角板ABC 的BC 边放置于长方形直尺DEFG 的EF 边上. (1)根据图1填空:∠1= °,∠2= °;(2)现把三角板绕B 点逆时针旋转n °.①如图2,当n =25°,且点C 恰好落在DG 边上时,求∠1、∠2的度数;②当0°<n <180°时,是否会存在三角板某一边所在的直线与直尺(有四条边)某一边所在的直线垂直?如果存在,请直接写出所有n 的值和对应的那两条垂线;如果不存在,请说明理由.4.如图,已知//AB CD ,CN 是BCE ∠的平分线.(1)若CM 平分BCD ∠,求MCN ∠的度数;(2)若CM 在BCD ∠的内部,且CM CN ⊥于C ,求证:CM 平分BCD ∠;(3)在(2)的条件下,过点B 作BP BQ ⊥,分别交CM 、CN 于点P 、Q ,PBQ ∠绕着B 点旋转,但与CM 、CN 始终有交点,问:BPC BQC ∠+∠的值是否发生变化?若不变,求其值;若变化,求其变化范围.5.综合与探究(问题情境)王老师组织同学们开展了探究三角之间数量关系的数学活动(1)如图1,//EF MN ,点A 、B 分别为直线EF 、MN 上的一点,点P 为平行线间一点,请直接写出PAF ∠、PBN ∠和APB ∠之间的数量关系;(问题迁移)(2)如图2,射线OM 与射线ON 交于点O ,直线//m n ,直线m 分别交OM 、ON 于点A 、D ,直线n 分别交OM 、ON 于点B 、C ,点P 在射线OM 上运动,①当点P 在A 、B (不与A 、B 重合)两点之间运动时,设ADP α∠=∠,BCP β∠=∠.则CPD ∠,α∠,β∠之间有何数量关系?请说明理由.②若点P 不在线段AB 上运动时(点P 与点A 、B 、O 三点都不重合),请你画出满足条件的所有图形并直接写出CPD ∠,α∠,β∠之间的数量关系.6.如图,直线HD //GE ,点A 在直线HD 上,点C 在直线GE 上,点B 在直线HD 、GE 之间,∠DAB =120°.(1)如图1,若∠BCG =40°,求∠ABC 的度数;(2)如图2,AF 平分∠HAB ,BC 平分∠FCG ,∠BCG =20°,比较∠B ,∠F 的大小; (3)如图3,点P 是线段AB 上一点,PN 平分∠APC ,CN 平分∠PCE ,探究∠HAP 和∠N 的数量关系,并说明理由.7.阅读下面文字: 对于5231591736342⎛⎫⎛⎫⎛⎫-+-++- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 可以如下计算:原式()()()5231591736342⎡⎤⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-+-+++-+- ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦⎣⎦ ()()()5231591736342⎡⎤⎛⎫⎛⎫⎛⎫=-+-++-+-+-++-⎡⎤ ⎪ ⎪ ⎪⎢⎥⎣⎦⎝⎭⎝⎭⎝⎭⎣⎦ 1014⎛⎫=+- ⎪⎝⎭ 114=- 上面这种方法叫拆项法,你看懂了吗?仿照上面的方法,计算:(1)115112744362⎛⎫⎛⎫-+-++- ⎪ ⎪⎝⎭⎝⎭(2)235120192018201720163462⎛⎫⎛⎫-++-+ ⎪ ⎪⎝⎭⎝⎭ 8.阅读下面的文字,解答问题 22的小数部分我们不可能全部212 21,将这个数减去其整数部分,差就是小数部分.23,∴22)请解答:(1整数部分是,小数部分是.(2a b,求|a﹣b(3)已知:x+y,其中x是整数,且0<y<1,求x﹣y的相反数.9.据说,我国著名数学家华罗庚在一次访问途中,看到飞机邻座的乘客阅读的杂志上有一道智力题:一个数32768,它是一个正数的立方,希望求它的立方根,华罗庚不假思索给出了答案,邻座乘客非常惊奇,很想得知其中的奥秘,你知道华罗庚是怎样准确计算出的吗?请按照下面的问题试一试:<<______位(1)由33==,因为1000327681000000101000,1001000000数;(2)由32768的个位上的数是8________,划去327683=27,4=64后面的三位数768得到32,因为33_____________-分别是两个数的立方,仿照上面的计算过程,请计算:(3)已知13824和110592=________10.对于实数a,我们规定:用符号为a的根整=,=3.数,例如:3(1)仿照以上方法计算:=______;=_____.=,写出满足题意的x的整数值______.(2)若1如果我们对a连续求根整数,直到结果为1为止.例如:对10连续求根整数2次3=→=1,这时候结果为1.(3)对100连续求根整数,____次之后结果为1.(4)只需进行3次连续求根整数运算后结果为1的所有正整数中,最大的是____.11.阅读下面的文字,解答问题.对于实数a,我们规定:用符号[a]表示不大于a的最大整数;用{a}表示a减去[a]所得的差.例如:=1,[2.2]=2,1,{2.2}=2.2﹣2=0.2.(1)仿照以上方法计算:]={5=;(2)若]=1,写出所有满足题意的整数x的值:.(3)已知y0是一个不大于280的非负数,且满足}=0.我们规定:y1=],y2=,y3=],…,以此类推,直到y n第一次等于1时停止计算.当y0是符合条件的所有数中的最大数时,此时y0=,n=.12.对于有理数a 、b ,定义了一种新运算“※”为:()()223a b a b a b a b a b ⎧-≥⎪=⎨-<⎪⎩※ 如:532537=⨯-=※,2131313=-⨯=-※. (1)计算:①()21-=※______;②()()43--=※______;(2)若313m x =-+※是关于x 的一元一次方程,且方程的解为2x =,求m 的值; (3)若3241A x x x =-+-+,3262B x x x =-+-+,且3A B =-※,求322x x +的值. 13.如图,以直角三角形AOC 的直角顶点O 为原点,以OC 、OA 所在直线为x 轴和y 轴建立平面直角坐标系,点A (0,a ),C (b ,0)满足2a b -+|b ﹣2|=0,D 为线段AC 的中点.在平面直角坐标系中,以任意两点P (x 1,y 1)、Q (x 2,y 2)为端点的线段中点坐标为(122x x +,122y y +).(1)则A 点的坐标为 ;点C 的坐标为 ,D 点的坐标为 .(2)已知坐标轴上有两动点P 、Q 同时出发,P 点从C 点出发沿x 轴负方向以1个单位长度每秒的速度匀速移动,Q 点从O 点出发以2个单位长度每秒的速度沿y 轴正方向移动,点Q 到达A 点整个运动随之结束.设运动时间为t (t >0)秒.问:是否存在这样的t ,使S △ODP =S △ODQ ,若存在,请求出t 的值;若不存在,请说明理由.(3)点F 是线段AC 上一点,满足∠FOC =∠FCO ,点G 是第二象限中一点,连OG ,使得∠AOG =∠AOF .点E 是线段OA 上一动点,连CE 交OF 于点H ,当点E 在线段OA 上运动的过程中,请确定∠OHC ,∠ACE 和∠OEC 的数量关系,并说明理由.14.已知AB ∥CD ,线段EF 分别与AB ,CD 相交于点E ,F .(1)请在横线上填上合适的内容,完成下面的解答:如图1,当点P 在线段EF 上时,已知∠A =35°,∠C =62°,求∠APC 的度数;解:过点P 作直线PH ∥AB ,所以∠A =∠APH ,依据是 ;因为AB ∥CD ,PH ∥AB ,所以PH ∥CD ,依据是 ;所以∠C =( ),所以∠APC =( )+( )=∠A +∠C =97°.(2)当点P ,Q 在线段EF 上移动时(不包括E ,F 两点):①如图2,∠APQ +∠PQC =∠A +∠C +180°成立吗?请说明理由;②如图3,∠APM =2∠MPQ ,∠CQM =2∠MQP ,∠M +∠MPQ +∠PQM =180°,请直接写出∠M ,∠A 与∠C 的数量关系.15.如图,在长方形ABCD 中,AB =8cm ,BC =6cm ,点E 是CD 边上的一点,且DE =2cm ,动点P 从A 点出发,以2c m/s 的速度沿A →B →C →E 运动,最终到达点E .设点P 运动的时间为t 秒.(1)请以A 点为原点,AB 所在直线为x 轴,1cm 为单位长度,建立一个平面直角坐标系,并用t 表示出点P 在不同线段上的坐标.(2)在(1)相同条件得到的结论下,是否存在P 点使△APE 的面积等于20cm 2时,若存在,请求出P 点坐标;若不存在,请说明理由.16.某地葡萄丰收,准备将已经采摘下来的11400公斤葡萄运送杭州,现有甲、乙、丙三种车型共选择,每辆车运载能力和运费如表表示(假设每辆车均满载)车型甲 乙 丙 汽车运载量(公斤/辆)600 800 900 汽车运费(元/辆) 500 600 700 辆?(2)为了节省运费,现打算用甲、乙、丙三种车型都参与运送,已知它们的总辆数为15辆,你能分别求出这三种车型的辆数吗?怎样安排运费最省?17.如图,在下面直角坐标系中,已知()0,A a ,(),0B b ,(),C b c 三点,其中a ,b ,c 满足关系式()22340a b c ---=.(1)求a,b,c的值;(2)如果在第二象限内有一点1,2P m⎛⎫⎪⎝⎭,请用含m的式子表示四边形ABOP的面积;(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积与三角形ABC的面积相等?若存在,求出点P的坐标,若不存在,请说明理由.18.在平面直角坐标系xOy中,对于给定的两点P,Q,若存在点M,使得△MPQ的面积等于1,即S△MPQ=1,则称点M为线段PQ的“单位面积点”,解答下列问题:如图,在平面直角坐标系xOy中,点P的坐标为(1,0).(1)在点A(1,2),B(﹣1,1),C(﹣1,﹣2),D(2,﹣4)中,线段OP的“单位面积点”是;(2)已知点E(0,3),F(0,4),将线段OP沿y轴向上平移t(t>0)个单位长度,使得线段EF上存在线段OP的“单位面积点”,直接写出t的取值范围.(3)已知点Q(1,﹣2),H(0,﹣1),点M,N是线段PQ的两个“单位面积点”,点M在HQ的延长线上,若S△HMN≥2S△PQN,求出点N纵坐标的取值范围.19.题目:满足方程组3512332x y kx y k+=+⎧⎨+=-⎩的x与y的值的和是2,求k的值.按照常规方法,顺着题目思路解关于x,y的二元一次方程组,分别求出xy的值(含有字母k),再由x+y=2,构造关于k的方程求解,从而得出k值.(1)某数学兴趣小组对本题的解法又进行了探究利用整体思想,对于方程组中每个方程变形得到“x+y”这个整体,或者对方程组的两个方程进行加减变形得到“x+y”整体值,从而求出k值请你运用这种整体思想的方法,完成题目的解答过程.(2)小勇同学的解答是:观察方程①,令3x =k ,5y =1解得y =15,3x +y =2,∴x =95 ∴k =3×95=275把x =95,y =15代入方程②得k =﹣35 所以k 的值为275或﹣35. 请诊断分析并评价“小勇同学的解答”.20.两个两位数的和是68,在较大的两位数的右边接着写较小的两位数,得到一个四位数;在较大的两位数的左边写上较小的两位数,也得到一个四位数.已知前一个四位数比后一个四位数大990.若设较大的两位数为x ,较小的两位数为y ,回答下列问题: (1)可得到下列哪一个方程组?A .68,1010990.x y x y y x +=⎧⎨+-+=⎩B .()()68,1010990.x y x y y x +=⎧⎨+-+=⎩C .()()68,100100990.x y x y y x +=⎧⎨+-+=⎩D .()()1068,100100990.x y x y y x +=⎧⎨+-+=⎩(2)解所确定的方程组,求这两个两位数.21.我国传统数学名著《九章算术》记载:“今有牛五、羊二,直金十九两;牛二、羊五,直金十六两.问牛、羊各直金几何?”译文:“假设有5头牛、2只羊,值19两银子;2头牛、5只羊,值16两银子.问每头牛、每只羊分别值银子多少两?”根据以上译文,提出以下两个问题:(1)求每头牛、每只羊各值多少两银子?(2)若某商人准备用20两银子买牛和羊(要求既有牛也有羊,且银两须全部用完),请问商人有几种购买方法?列出所有的可能.22.为了加强公民的节水意识,合理利用水资源,某城市规定用水收费标准如下:每户每月用水量不超过6米3时,水费按a 元/米3收费;每户每月用水量超过6米3时,不超过的部分每立方米仍按a 元收费,超过的部分按c 元/米3收费,该市某用户今年3、4月份的用水量和水费如下表所示:系式;(2)已知某户5月份的用水量为8米3,求该用户5月份的水费.23.已知AM ∥CN ,点B 为平面内一点,AB ⊥BC 于B .(1)如图1,过点B 作BD ⊥AM 于点D ,∠BAD 与∠C 有何数量关系,并说明理由; (2)如图2,在(1)问的条件下,点E ,F 在DM 上,连接BE ,BF ,CF ,若BF 平分∠DBC ,BE 平分∠ABD ,∠FCB+∠NCF =180°,∠BFC =5∠DBE ,求∠ABE 的度数. 24.如图,在平面直角坐标系中,点O 为坐标原点,A 点的坐标为()1A m n -,,B 点的坐标为()0n -,,其中,m n 是二元一次方程组2202m n m n +=⎧⎨-=-⎩的解,过点A 作x 轴的平行线交y 轴于点C .(1)求点,A B 的坐标;(2)动点P 从点B 出发,以每秒4个单位长度的速度沿射线BO 的方向运动,连接PC ,设点P 的运动时间为t 秒,三角形OPC 的面积为()0S S ≠,请用含t 的式子表示S (不用写出相应的t 的取值范围);(3)在(2)的条件下,在动点P 从点B 出发的同时,动点Q 从点C 出发以每秒1个单位长度的速度沿线段CA 的方向运动.过点O 作直线PC 的垂线,点G 为垂足;过点Q 作直线PC 的垂线,点H 为垂足.当2OG QH =时,求t 的值.25.某治污公司决定购买10台污水处理设备.现有甲、乙两种型号的设备可供选择,其中每台的价格与月处理污水量如下表:甲型 乙型 价格(万元/台)x y 处理污水量(吨/月) 300 260经调查:购买一台甲型设备比购买一台乙型设备多2万元,购买3台甲型设备比购买4台乙型设备少2万元.(1)求x ,y 的值;(2)如果治污公司购买污水处理设备的资金不超过91万元,求该治污公司有哪几种购买方案;(3)在(2)的条件下,如果月处理污水量不低于2750吨,为了节约资金,请为该公司设计一种最省钱的购买方案.26.材料1:我们把形如ax by c +=(a 、b 、c 为常数)的方程叫二元一次方程.若a 、b 、c 为整数,则称二元一次方程ax by c +=为整系数方程.若c 是a ,b 的最大公约数的整倍数,则方程有整数解.例如方程342,735,426x y x y x y +=-=+=都有整数解;反过来也成立.方程6310421x y x y +=-=和都没有整数解,因为6,3的最大公约数是3,而10不是3的整倍数;4,2的最大公约数是2,而1不是2的整倍数.材料2:求方程56100x y +=的正整数解. 解:由已知得:1006100520555y y y y x y ---===--……① 设5y k =(k 为整数),则5y k =……② 把②代入①得:206x k =-.所以方程组的解为2065x k y k =-⎧⎨=⎩, 根据题意得:206050k k ->⎧⎨>⎩. 解不等式组得0<k <103.所以k 的整数解是1,2,3. 所以方程56100x y +=的正整数解是:145x y =⎧⎨=⎩,810x y =⎧⎨=⎩,215x y =⎧⎨=⎩. 根据以上材料回答下列问题:(1)下列方程中:① 3911x y +=,② 15570x y -=,③ 63111x y +=,④27999x y -=,⑤ 9126169x -=,⑥ 22121324x y +=.没有整数解的方程是 (填方程前面的编号);(2)仿照上面的方法,求方程3438x y +=的正整数解;(3)若要把一根长30m 的钢丝截成2m 长和3m 长两种规格的钢丝(两种规格都要有),问怎样截才不浪费材料?你有几种不同的截法?(直接写出截法,不要求解题过程) 27.在平面直角坐标系xOy 中.点A ,B ,P 不在同一条直线上.对于点P 和线段AB 给出如下定义:过点P 向线段AB 所在直线作垂线,若垂足Q 落在线段AB 上,则称点P 为线段AB 的内垂点.若垂足Q 满足|AQ -BQ |最小,则称点P 为线段AB 的最佳内垂点.已知点A (﹣2,1),B (1,1),C (﹣4,3).(1)在点P1(2,3)、P2(﹣5,0)、P3(﹣1,﹣2),P4(﹣12,4)中,线段AB的内垂点为;(2)点M是线段AB的最佳内垂点且到线段AB的距离是2,则点M的坐标为;(3)点N在y轴上且为线段AC的内垂点,则点N的纵坐标n的取值范围是;(4)已知点D(m,0),E(m+4,0),F(2m,3).若线段CF上存在线段DE的最佳内垂点,求m的取值范围.28.如图①,在平直角坐标系中,△ABO的三个顶点为A(a,b),B(﹣a,3b),O (0,0),且满足3a++|b﹣2|=0,线段AB与y轴交于点C.(1)求出A,B两点的坐标;(2)求出△ABO的面积;(3)如图②,将线段AB平移至B点的对应点B'落在x轴的正半轴上时,此时A点的对应点为A',记△A B C''的面积为S,若24<S<32,求点A'的横坐标的取值范围.29.已知关于x、y的二元一次方程23,3 3. x y ax y a+=-⎧⎨-=-⎩①②(1)若方程组的解x 、y 满足0,1x y ≤<,求a 的取值范围; (2)求代数式638x y +-的值. 30.如图,在平面直角坐标系中,点的坐标分别是,现同时将点分别向上平移2个单位长度,再向右平移2个单位长度,得到的对应点.连接.(1)写出点的坐标并求出四边形的面积. (2)在轴上是否存在一点,使得的面积是面积的2倍?若存在,请求出点的坐标;若不存在,请说明理由. (3)若点是直线上一个动点,连接,当点在直线上运动时,请直接写出与的数量关系.【参考答案】***试卷处理标记,请不要删除一、解答题1.(1)4;(2)45︒;(2)(0,3)P 或(0,1)-. 【分析】(1)根据非负数的性质易得2a =-,2b =,然后根据三角形面积公式计算; (2)过E 作//EF AC ,根据平行线性质得////BD AC EF ,且1312CAB ∠=∠=∠,1422ODB ∠=∠=∠,所以112()2AED CAB ODB ∠=∠+∠=∠+∠;然后把90CAB ODB ∠+∠=︒ 代入计算即可;(3)分类讨论:设(0,)P t ,当P 在y 轴正半轴上时,过P 作//MN x 轴,//AN y 轴,//BM y 轴,利用4APC ANP CMP MNAC S S S S ∆∆∆=--=梯形可得到关于t 的方程,再解方程求出t ;当P 在y 轴负半轴上时,运用同样方法可计算出t . 【详解】解:(1)2(2)20a b ++-=,20a ∴+=,20b -=, 2a ∴=-,2b =,CB AB ⊥(2,0)A ∴-,(2,0)B ,(2,2)C , ABC ∆∴的面积12442=⨯⨯=;(2)解://CB y 轴,//BD AC ,5CAB ∴∠=∠,又∵590ODB ∠+∠=︒, ∴90CAB ODB ∠+∠=︒, 过E 作//EF AC ,如图①,//BD AC ,////BD AC EF ∴,31∴∠=∠,42∠=∠AE ∵,DE 分别平分CAB ∠,ODB ∠,即:132CAB ∠=∠,142ODB ∠=∠,112()452AED CAB ODB ∴∠=∠+∠=∠+∠=︒;(3)(0,1)P -或(0,3).解:①当P 在y 轴正半轴上时,如图②,设(0,)P t ,过P 作//MN x 轴,//AN y 轴,//BM y 轴,4APC ANP CMP MNAC S S S S ∆∆∆=--=梯形,∴4(2)(2)42t t t t -+---=,解得3t =,②当P 在y 轴负半轴上时,如图③4APC ANP CMP MNAC S S S S ∆∆∆=--=梯形∴4(2)(2)42t t t t -+-+--=,解得1t =-, 综上所述:(0,3)P 或(0,1)-. 【点睛】本题考查了平行线的判定与性质:两直线平行,内错角相等.也考查了非负数的性质、坐标与图形性质以及三角形面积公式.构造矩形求三角形面积是解题关键. 2.(1)65°;(2)3606α︒-︒;(3)2n ∠M +∠BED =360° 【分析】(1)首先作EG ∥AB ,FH ∥AB ,连结MF ,利用平行线的性质可得∠ABE +∠CDE =260°,再利用角平分线的定义得到∠ABF +∠CDF =130°,从而得到∠BFD 的度数,再根据角平分线的定义和三角形外角的性质可求∠M 的度数;(2)先由已知得到∠ABE =6∠ABM ,∠CDE =6∠CDM ,由(1)得∠ABE +∠CDE =360°-∠BED ,∠M =∠ABM +∠CDM ,等量代换即可求解; (3)由(2)的方法可得到2n ∠M +∠BED =360°. 【详解】解:(1)如图1,作//EG AB ,//FH AB ,连结MF ,//AB CD ,//////EG AB FH CD ∴,ABF BFH ∴∠=∠,CDF DFH ∠=∠,180ABE BEG ∠+∠=︒,180GED CDE ∠+∠=︒,360ABE BEG GED CDE ∴∠+∠+∠+∠=︒,100BED BEG DEG ∠=∠+∠=︒, 260ABE CDE ∴∠+∠=︒,ABE ∠和CDE ∠的角平分线相交于E ,130ABF CDF ∴∠+∠=︒, 130BFD BFH DFH ∴∠=∠+∠=︒,BM 、DM 分别是ABF ∠和CDF ∠的角平分线,12MBF ABF ∴∠=∠,12MDF CDF ∠=∠,65MBF MDF ∴∠+∠=︒, 1306565BMD ∴∠=︒-︒=︒;(2)如图1,13ABM ABF ∠=∠,13CDM CDF ∠=∠,3ABF ABM ∴∠=∠,3CDF CDM ∠=∠,ABE ∠与CDE ∠两个角的角平分线相交于点F ,6ABE ABM ∴∠=∠,6CDE CDM ∠=∠, 66360ABM CDM BED ∴∠+∠+∠=︒,BMD ABM CDM ∠=∠+∠, 6360BMD BED ∴∠+∠=︒,3606BMD α︒-︒∴∠=; (3)由(2)结论可得,22360n ABM n CDM E ∠+∠+∠=︒,M ABM CDM ∠=∠+∠, 则2360n M BED ∠+∠=︒. 【点睛】本题主要考查了平行线的性质和四边形的内角和,关键在于掌握两直线平行同位角相等,内错角相等,同旁内角互补的性质.3.(1)120,90;(2)①∠1=120°-n °,∠2=90°+n °;②见解析 【分析】(1)根据邻补角的定义和平行线的性质解答;(2)①根据邻补角的定义求出∠ABE ,再根据两直线平行,同位角相等可得∠1=∠ABE ,根据两直线平行,同旁内角互补求出∠BCG ,然后根据周角等于360°计算即可得到∠2; ②结合图形,分A B 、B C 、AC 三条边与直尺垂直讨论求解. 【详解】解:(1)∠1=180°-60°=120°, ∠2=90°;故答案为:120,90; (2)①如图2,∵∠ABC=60°,∴∠ABE=180°-60°-n°=120°-n°,∵DG∥EF,∴∠1=∠ABE=120°-n°,∠BCG=180°-∠CBF=180°-n°,∵∠ACB+∠BCG+∠2=360°,∴∠2=360°-∠ACB-∠BCG=360°-90°-(180°-n°)=90°+n°;②当n=30°时,∵∠ABC=60°,∴∠ABF=30°+60°=90°,AB⊥DG(EF);当n=90°时,∠C=∠CBF=90°,∴BC⊥DG(EF),AC⊥DE(GF);当n=120°时,∴AB⊥DE(GF).【点睛】本题考查了平行线角的计算,垂线的定义,主要利用了平行线的性质,直角三角形的性质,读懂题目信息并准确识图是解题的关键. 4.(1)90°;(2)见解析;(3)不变,180° 【分析】(1)根据邻补角的定义及角平分线的定义即可得解;(2)根据垂直的定义及邻补角的定义、角平分线的定义即可得解;(3)180BPC BQC ∠+∠=︒,过Q ,P 分别作//QG AB ,//PH AB ,根据平行线的性质及平角的定义即可得解. 【详解】解(1)CN ,CM 分别平分BCE ∠和BCD ∠,12BCN BCE ∴=∠,12BCM BCD ∠=∠,180BCE BCD ∠+∠=︒,111()90222MCN BCN BCM BCE BCD BCE BCD ∴∠=∠+∠=∠+∠=∠+∠=︒;(2)CM CN ⊥,90MCN ∴∠=︒,即90BCN BCM ∠+∠=︒,22180BCN BCM ∴∠+∠=︒,CN 是BCE ∠的平分线,2BCE BCN ∴∠=∠, 2180BCE BCM ∴∠+∠=︒,又180BCE BCD ∠+∠=︒,2BCD BCM ∴∠=∠,又CM 在BCD ∠的内部,CM ∴平分BCD ∠;(3)如图,不发生变化,180BPC BQC ∠+∠=︒,过Q ,P 分别作//QG AB ,//PH AB ,则有//////QG AB PH CD ,BQG ABQ ∴∠=∠,CQG ECQ ∠=∠,BPH FBP ∠=∠,CPH DCP ∠=∠,⊥BP BQ ,CP CQ ⊥,90PBQ PCQ ∴∠=∠=︒,180ABQ PBQ FBP ∠+∠+=︒,180ECQ PCQ DCP ∠+∠+∠=︒, 180ABQ FBP ECQ DCP ∴∠+∠+∠+∠=︒, BPC BQC BPH CPH BQG CQG ∴∠+∠=∠+∠+∠+∠180ABQ FBP ECQ DCP =∠+∠+∠+∠=︒,180BPC BQC ∴∠+∠=︒不变.【点睛】此题考查了平行线的性质,熟记平行线的性质及作出合理的辅助线是解题的关键. 5.(1)360PAF PBN APB ∠+∠+∠=°;(2)①CPD αβ∠=∠+∠,理由见解析;②图见解析,CPD βα∠=∠-∠或CPD αβ∠=∠-∠ 【分析】(1)作PQ ∥EF ,由平行线的性质,即可得到答案;(2)①过P 作//PE AD 交CD 于E ,由平行线的性质,得到DPE α∠=∠,CPE β∠=∠,即可得到答案;②根据题意,可对点P 进行分类讨论:当点P 在BA 延长线时;当P 在BO 之间时;与①同理,利用平行线的性质,即可求出答案. 【详解】解:(1)作PQ ∥EF ,如图:∵//EF MN , ∴////EF MN PQ ,∴180PAF APQ ∠+∠=°,180PBN BPQ ∠+∠=°, ∵APB APQ BPQ ∠=∠+∠ ∴360PAF PBN APB ∠+∠+∠=°; (2)①CPD αβ∠=∠+∠; 理由如下:如图,过P 作//PE AD 交CD 于E , ∵//AD BC ,∴////AD PE BC ,∴DPE α∠=∠,CPE β∠=∠, ∴CPD DPE CPE αβ∠=∠+∠=∠+∠; ②当点P 在BA 延长线时,如备用图1:∵PE ∥AD ∥BC ,∴∠EPC=β,∠EPD =α, ∴CPD βα∠=∠-∠;当P 在BO 之间时,如备用图2:∵PE ∥AD ∥BC , ∴∠EPD =α,∠CPE =β, ∴CPD αβ∠=∠-∠. 【点睛】本题考查了平行线的性质,解题的关键是熟练掌握两直线平行同旁内角互补,两直线平行内错角相等,从而得到角的关系.6.(1)∠ABC =100°;(2)∠ABC >∠AFC ;(3)∠N =90°﹣12∠HAP ;理由见解析. 【分析】(1)过点B 作BM //HD ,则HD //GE //BM ,根据平行线的性质求得∠ABM 与∠CBM ,便可求得最后结果;(2)过B 作BP //HD //GE ,过F 作FQ //HD //GE ,由平行线的性质得,∠ABC =∠HAB +∠BCG ,∠AFC =∠HAF +∠FCG ,由角平分线的性质和已知角的度数分别求得∠HAF ,∠FCG ,最后便可求得结果;(3)过P 作PK //HD //GE ,先由平行线的性质证明∠ABC =∠HAB +∠BCG ,∠AFC =∠HAF +∠FCG ,再根据角平分线求得∠NPC 与∠PCN ,由后由三角形内角和定理便可求得结果.【详解】解:(1)过点B作BM//HD,则HD//GE//BM,如图1,∴∠ABM=180°﹣∠DAB,∠CBM=∠BCG,∵∠DAB=120°,∠BCG=40°,∴∠ABM=60°,∠CBM=40°,∴∠ABC=∠ABM+∠CBM=100°;(2)过B作BP//HD//GE,过F作FQ//HD//GE,如图2,∴∠ABP=∠HAB,∠CBP=∠BCG,∠AFQ=∠HAF,∠CFQ=∠FCG,∴∠ABC=∠HAB+∠BCG,∠AFC=∠HAF+∠FCG,∵∠DAB=120°,∴∠HAB=180°﹣∠DAB=60°,∵AF平分∠HAB,BC平分∠FCG,∠BCG=20°,∴∠HAF=30°,∠FCG=40°,∴∠ABC=60°+20°=80°,∠AFC=30°+40°=70°,∴∠ABC>∠AFC;(3)过P作PK//HD//GE,如图3,∴∠APK=∠HAP,∠CPK=∠PCG,∴∠APC=∠HAP+∠PCG,∵PN平分∠APC,∴∠NPC=12∠HAP+12∠PCG,∵∠PCE=180°﹣∠PCG,CN平分∠PCE,∴∠PCN=90°﹣12∠PCG,∵∠N +∠NPC +∠PCN =180°,∴∠N =180°﹣12∠HAP ﹣12∠PCG ﹣90°+12∠PCG =90°﹣12∠HAP ,即:∠N =90°﹣12∠HAP .【点睛】本题考查了角平分线的定义,平行线性质和判定:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想与方程思想的应用,理清各角度之间的关系是解题的关键,也是本题的难点.7.(1)14-(2)124- 【分析】(1)根据例子将每项的整数部分相加,分数部分相加即可解答;(2)根据例子将每项的整数部分相加,分数部分相加即可解答.【详解】(1)115112744362⎛⎫⎛⎫-+-++- ⎪ ⎪⎝⎭⎝⎭()115112744362⎛⎫=--+-+--+- ⎪⎝⎭ 104⎛⎫=+- ⎪⎝⎭ 14=- (2)原式()235120192018201720163462⎛⎫=-+-++-+-+ ⎪⎝⎭ 124⎛⎫=-+- ⎪⎝⎭ 124=- 【点睛】此题考察新计算方法,正确理解题意是解题的关键,根据例子即可仿照计算.8.(1)7;(2)5;(3)【分析】(1(2)分别确定出a 、b 的值,代入原式计算即可求出值;(3)根据题意确定出等式左边的整数部分得出y 的值,进而求出y 的值,即可求出所求.【详解】解:(1)∵78, ∴7.故答案为:7.(2)∵34,∴a,3∵23,∴b=2∴=5(3)∵23∴11<12,∵,其中x是整数,且0﹤y<1,∴x=11,y=,∴x-y==【点睛】本题考查的是无理数的小数部分和整数部分及其运算.估算无理数的整数部分是解题关键.9.(1)两;(2)2,3;(3)24,-48.【分析】(1)根据题中所给的分析方法先求出这32768的立方根都是两位数;(2)继续分析求出个位数和十位数即可;(3)利用(1)(2)中材料中的过程进行分析可得结论.【详解】解:(1)由103=1000,1003=1000000,∵1000<32768<100000,∴10100,∴故答案为:两;(2)∵只有个位数是2的立方数是个位数是8,∴2划去32768后面的三位数768得到32,因为33=27,43=64,∵27<32<64,∴3040.∴3.故答案为:2,3;(3)由103=1000,1003=1000000,1000<13824<1000000,∴10100,∴∵只有个位数是4的立方数是个位数是4,∴4划去13824后面的三位数824得到13,因为23=8,33=27,∵8<13<27,∴2030.∴;由103=1000,1003=1000000,1000<110592<1000000,∴10100,∴∵只有个位数是8的立方数是个位数是2,∴8,划去110592后面的三位数592得到110,因为43=64,53=125,∵64<110<125,∴4050.∴;故答案为:24,-48.【点睛】此题考查立方根,解题关键在于理解一个数的立方的个位数就是这个数的个位数的立方的个位数.10.(1)2;5;(2)1,2,3;(3)3;(4)255【分析】(1(2)根据定义可知x<4,可得满足题意的x的整数值;(3)根据定义对120进行连续求根整数,可得3次之后结果为1;(4)最大的正整数是255,根据操作过程分别求出255和256进行几次操作,即可得出答案.【详解】解:(1)∵22=4, 62=36,52=25,∴56,∴,,故答案为2,5;(2)∵12=1,22=4,且=1,∴x=1,2,3,故答案为1,2,3;(3)第一次:,第二次:,第三次:,故答案为3;(4)最大的正整数是255,理由是:∵,,,∴对255只需进行3次操作后变为1,∵,,,,∴对256只需进行4次操作后变为1,∴只需进行3次操作后变为1的所有正整数中,最大的是255,故答案为255.【点睛】本题考查了估算无理数的大小的应用,主要考查学生的阅读能力和猜想能力,同时也考查了一个数的平方数的计算能力.11.(1)2;32)1、2、3;(3)256,4【分析】(1)依照定义进行计算即可;(2)由题可知,04x <<,则可得满足题意的整数的x 的值为1、2、3;(3)由0=,可知,0y 是某个整数的平方,又0y 是符合条件的所有数中最大的数,则0256y =,再依次进行计算.【详解】解:(1)由定义可得,2=,[52=,{53∴=故答案为:2;3.(2)[]1x =,2∴<,即04x <<,∴整数x 的值为1、2、3.故答案为:1、2、3.(3)0{}0y =,即0==,∴2t =,且t 是自然数,0y 是符合条件的所有数中的最大数,0256y ∴=,1[16]16y ∴===,2[4]4y ===,3[2]2y ===,41y ===,即4n =.故答案为:256,4.【点睛】本题属于新定义类问题,主要考查估算无理数大小,无理数的整数部分和小数部分,理解定义内容是解题关键.12.(1)①5;②2-;(2)1;(3)16.【分析】(1)根据题中定义代入即可得出;(2)根据2x =,讨论3和 m 的两种大小关系,进行计算;(3)先判定A 、B 的大小关系,再进行求解.【详解】(1)根据题意:∵21>-,∴()()212215-=⨯--=※,∵43-<-,∴()()()243434223--=--⨯-=-+=-※. (2)∵2x =,∴31325m =-+⨯=※,① 若3m >,则235m ⨯-=,解得1m =,②若3m <, 则2353m -⨯=,解得3m =-(不符合题意), ∴1m =.(3)∵()()323224162210A B x x x x x x x -=-+-+--+-+=--<,∴A B <, ∴()3232224162333A B A B x x x x x x =-=-+-+--+-+=-※, 得380x x +-=,∴3222816x x +=⨯=.【点睛】本题考查了一种新运算,读懂题意掌握新运算并能正确化简是解题的关键.13.(1)(0,4)A ,(2,0)C ,(1,2)D ;(2)存在,1t =;(3)2OHC ACE OEC ∠∠∠+=【分析】(1)根据绝对值和算术平方根的非负性,求得a ,b 的值,得出点A ,C 的坐标,再运用中点公式求出点D 的坐标;(2)根据题意可得CP =t ,OP =2-t ,OQ =2t ,AQ =4-2t ,再根据S △ODP =S △ODQ ,列方程求解即可;(3)过点H 作HP ∥AC 交x 轴于点P ,先证明OG ∥AC ,再根据角的和差关系以及平行线性质,得出∠PHO =∠GOF =∠1+∠2,∠OHC =∠OHP +∠PHC =∠GOF +∠4=∠1+∠2+∠4,最后代入可得2OHC ACE OEC ∠∠∠+=.【详解】解:(1)2|2|0a b b -+-=,20a b ∴-=,20b -=,4a ∴=,2b =,)4(0,A ∴,(2,0)C ,设(,)D x y ,D 为线段AC 的中点.0212x +∴==,4022y +==, (1,2)D ∴,故答案为:(0,4)A ,(2,0)C ,(1,2)D ;(2)存在,1t =.由条件可知:点P 从点C 运动到点O 需要时间为2秒,点Q 从点O 运动到点A 需要时间2秒,02t ∴<,点Q 在线段AO 上,CP t ∴=,2OP t =-,2OQ t =,42AQ t =-,11(2)2222ODP D S OP y t t ∆∴=⋅=-⨯=-, 112122ODQ D S OQ x t t ∆=⋅=⨯⨯=, ODP ODQ S S ∆∆=,2t t ∴-=,1t ∴=.(3)如图2,2390∠+∠=︒,12∠=∠,3FCO ∠=∠,180GOC ACO ∴∠+∠=︒,//OG AC ∴,1CAO ∴∠=∠,414OEC CAO ∴∠=∠+∠=∠+∠,如图,过点H 作//HP AC 交x 轴于点P ,则4PHC ∠=∠,//PH OG ,12PHO GOF ∴∠=∠=∠+∠,4124OHC OHP PHC GOF ∴∠=∠+∠=∠+∠=∠+∠+∠,∴()12442142OHC ACE OEC ∠+∠=∠+∠+∠+∠=∠+∠=∠.【点睛】本题考查了平行线的性质,三角形面积,非负数的性质,中点坐标公式等,是一道三角形综合题,解题关键是学会添加辅助线,运用转化的思想思考问题.14.(1)两直线平行,内错角相等;平行于同一条直线的两条直线平行;∠CPH ;∠APH ,∠CPH ;(2)①∠APQ +∠PQC =∠A +∠C +180°成立,理由见解答过程;②3∠PMQ +∠A +∠C =360°.【分析】(1)根据平行线的判定与性质即可完成填空;(2)结合(1)的辅助线方法即可完成证明;(3)结合(1)(2)的方法,根据∠APM =2∠MPQ ,∠CQM =2∠MQP ,∠PMQ +∠MPQ +∠PQM =180°,即可证明∠PMQ ,∠A 与∠C 的数量关系.【详解】解:过点P 作直线PH ∥AB ,所以∠A =∠APH ,依据是两直线平行,内错角相等;因为AB ∥CD ,PH ∥AB ,所以PH ∥CD ,依据是平行于同一条直线的两条直线平行;所以∠C =(∠CPH ),所以∠APC =(∠APH )+(∠CPH )=∠A +∠C =97°.故答案为:两直线平行,内错角相等;平行于同一条直线的两条直线平行;∠CPH ;∠APH ,∠CPH ;(2)①如图2,∠APQ +∠PQC =∠A +∠C +180°成立,理由如下:过点P作直线PH∥AB,QG∥AB,∵AB∥CD,∴AB∥CD∥PH∥QG,∴∠A=∠APH,∠C=∠CQG,∠HPQ+∠GQP=180°,∴∠APQ+∠PQC=∠APH+∠HPQ+∠GQP+∠CQG=∠A+∠C+180°.∴∠APQ+∠PQC=∠A+∠C+180°成立;②如图3,过点P作直线PH∥AB,QG∥AB,MN∥AB,∵AB∥CD,∴AB∥CD∥PH∥QG∥MN,∴∠A=∠APH,∠C=∠CQG,∠HPQ+∠GQP=180°,∠HPM=∠PMN,∠GQM=∠QMN,∴∠PMQ=∠HPM+∠GQM,∵∠APM=2∠MPQ,∠CQM=2∠MQP,∠PMQ+∠MPQ+∠PQM=180°,∴∠APM+∠CQM=∠A+∠C+∠PMQ=2∠MPQ+2∠MQP=2(180°﹣∠PMQ),∴3∠PMQ+∠A+∠C=360°.【点睛】考核知识点:平行线的判定和性质.熟练运用平行线性质和判定,添加适当辅助线是关键.15.(1)建立直角坐标系见解析,当0<t≤4时,即当点P在线段AB上时,其坐标为:P(2t,0),当4<t≤7时,即当点P在线段BC上时,其坐标为:P(8,2t﹣8),当7<t≤10时,即当点P在线段CE上时,其坐标为:P(22﹣2t,6);(2)存在,当点P的坐标分别为:P(203,0)或P(8,4)时,△APE的面积等于220cm.【分析】(1)建立平面直角坐标系,根据点P的运动速度分别求出点P在线段AB,BC,CE上的坐标;(2)根据(1)中得到的点P 的坐标以及220APE Scm =,分别列出三个方程并解出此时t的值再进行讨论.【详解】(1)正确画出直角坐标系如下:当0<t ≤4时,点P 在线段AB 上,此时P 点的横坐标为22t t ⨯=,其纵坐标为0; ∴此时P 点的坐标为:P (2t ,0);同理:当4<t ≤7时,点P 在线段BC 上,此时P 点的坐标为:P (8,2t ﹣8);当7<t ≤10时,点P 在线段CE 上,此时P 点的坐标为:P (22﹣2t ,6).(2)存在,①如图1,当0<t ≤4时,点P 在线段AB 上, 126202APE S t =⨯⨯=,解得:t 103=(s ); ∴P 点的坐标为:P (203,0). ②如图2,当4<t ≤7时,点P 在线段BC 上,APE ADE ABP PCE S AB BC S S S =⨯---;∴1112048628(28)6(142)222t t =-⨯⨯-⨯⨯--⨯⨯-; 解得:t =6(s );∴点P 的坐标为:P (8,4).③如图3,当7<t ≤10时,点P 在线段CE 上,16(202)202APE S t =⨯⨯-=; 解得:t 203=(s ); ∵203<7,∴t 203=(应舍去), 综上所述:当P 点的坐标为:P (203,0)或 P (8,4)时,△APE 的面积等于220cm . 【点睛】 本题考查了三角形的面积的计算公式,12S =⨯⨯三角形底高,在本题计算的过程中根据动点的坐标正确地求出三角形的底边长度和高是解题的关键.16.(1)甲3辆,乙12辆;(2)有三种方案,具体见解析,甲4辆,乙9辆,丙2辆最省钱.【分析】(1)设需要甲x 辆,乙y 辆,根据运送11400公斤和需运费8700元,可列出方程组求解.(2)设需要甲x 辆,乙y 辆,则丙(15﹣x ﹣y )辆,根据甲汽车运载量+乙汽车运载量+丙汽车运载量=11400,列方程,化简后,根据甲、乙、丙三种车型都参与运送,即x >0,y >0,15﹣x ﹣y >0,解不等式即可求出x 的范围,进而得出方案.计算出每种方案需要的运费,比较即可得出运费最省的方案.【详解】(1)设需要甲x 辆,乙y 辆,根据题意得:600800114005006008700x y x y +=⎧⎨+=⎩ 解得:312x y =⎧⎨=⎩. 答:甲3辆,乙12辆;(2)设需要甲x 辆,乙y 辆,则丙(15﹣x ﹣y )辆,根据题意得:600x +800y +900(15﹣x ﹣y )=11400化简得:y =21﹣3x .∵x >0,y =21﹣3x >0,15﹣x ﹣y =2x -6>0,解得:3<x <7.∵x 为整数,∴x =4,5,6.因此方案有三种:方案①:甲4辆,乙9辆,丙2辆;。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、2a b m b a-+b+3=0=14.ABCA S如图,已知(0,),B (0,),C (,)且(4),o y =DC FD ADO ⊥∠∠∠(1)求C 点坐标(2)作DE ,交轴于E 点,EF 为AED 的平分线,且DFE 90。
求证:平分;(3)E 在y 轴负半轴上运动时,连EC ,点P 为AC 延长线上一点,EM 平分∠AEC ,且PM ⊥EM,PN ⊥x 轴于N 点,PQ 平分∠APN ,交x 轴于Q 点,则E 在运动过程中,MPQECA ∠∠的大小是否发生变化,若不变,求出其值。
x2、如图1,AB//EF, ∠2=2∠1 (1)证明∠FEC=∠FCE;(2)如图2,M 为AC 上一点,N 为FE 延长线上一点,且∠FNM=∠FMN ,则∠NMC 与∠CFM 有何数量关系,并证明。
图1 图2B C B C3、(1)如图,△ABC, ∠ABC 、∠ACB 的三等分线交于点E 、D ,若∠1=130°,∠2=110°,求∠A 的度数。
BC(2)如图,△ABC,∠ABC 的三等分线分别与∠ACB 的平分线交于点D,E 若∠1=110°,∠2=130°,求∠A 的度数。
AC4、如图,∠ABC+∠ADC=180°,OE 、OF 分别是角平分线,则判断OE 、OF 的位置关系为?FA5、已知∠A=∠C=90°.(1)如图,∠ABC 的平分线与∠ADC 的平分线交于点E ,试问BE 与DE 有何位置关系?说明你的理由。
(2)如图,试问∠ABC 的平分线BE 与∠ADC 的外角平分线DF 有何位置关系?说明你的理由。
(3)如图,若∠ABC 的外角平分线与∠ADC 的外角平分线交于点E ,试问BE 与DE 有何位置关系?说明你的理由。
6.(1)如图,点E 在AC 的延长线上,∠BAC 与∠DCE 的平分线交于点F ,∠B=60°,∠F=56°,求∠BDC 的度数。
AE(2)如图,点E 在CD 的延长线上,∠BAD 与∠ADE 的平分线交于点F ,试问∠F 、∠B 和∠C 之间有何数量关系?为什么?EAD7.已知∠ABC 与∠ADC 的平分线交于点E 。
BB(1)如图,试探究∠E、∠A与∠C之间的数量关系,并说明理由。
B C(2)如图,是探究∠E、∠A与∠C之间的数量关系,并说明理由。
B C8.(1)如图,点E是AB上方一点,MF平分∠AME,若点G恰好在MF的反向延长线上,且NE平分∠CNG,2∠E与∠G互余,求∠AME的大小。
A(2)如图,在(1)的条件下,若点P是EM上一动点,PQ平分∠MPN,NH平分∠PNC,交AB于点H,PJ//NH,当点P在线段EM上运动时,∠JPQ的度数是否改变?若不变,求出其值;若改变,请说明你的理由。
D9.如图,已知MA//NB,CA平分∠BAE,CB平分∠ABN,点D是射线AM上一动点,连DC ,当D 点在射线AM (不包括A 点)上滑动时,∠ADC+∠ACD+∠ABC 的度数是否发生变化?若不变,说明理由,并求出度数。
BN10.如图,AB//CD ,PA 平分∠BAC ,PC 平分∠ACD ,过点P 作PM 、PE 交CD 于M ,交AB 于E ,则(1)∠1+∠2+∠3+∠4不变;(2)∠3+∠4-∠1-∠2不变,选择正确的并给予证明。
11.如图,在平面直角坐标系中,已知点A (-5,0),B (5.0),D (2,7), (1)求C 点的坐标;(2)动点P 从B 点出发以每秒1个单位的速度沿BA 方向运动,同时动点Q 从C 点出发也以每秒1个单位的速度沿y 轴正半轴方向运动(当P 点运动到A 点时,两点都停止运动)。
设从出发起运动了x 秒。
①请用含x 的代数式分别表示P,Q 两点的坐标; ②当x=2时,y 轴上是否存在一点E ,使得△AQE 的面积与△APQ 的面积相等?若存在,求E 的坐标,若不存在,说明理由?12.如图,在平面直角坐标系中,∠ABO=2∠BAO ,P 为x 轴正半轴上一动点,BC 平分xx∠ABP ,PC 平分∠APF ,OD 平分∠POE 。
(1)求∠BAO 的度数;(2)求证:∠C=15°+∠OAP ;(3)P 在运动中,∠C+∠D 的值是否变化,若发生变化,说明理由,若不变求其值。
x13.如图,A 为x 轴负半轴上一点,C (0,-2),D (-3,-2)。
(1)求△BCD 的面积;(2)若AC ⊥BC ,作∠CBA 的平分线交CO 于P ,交CA 于Q ,判断∠CPQ 与∠CQP 的大小关系,并说明你的结论。
(3)若∠ADC=∠DAC ,点B 在x 轴正半轴上任意运动,∠ACB 的平分线CE 交DA 的延长线于点E ,在B 点的运动过程中,的值是否变化?若不变,求出其值;若变化,说明理由。
14.如图,已知点A (-3,2),B (2,0),点C 在x 轴上,将△ABC 沿x 轴折叠,使点A 落在点D 处。
(1)写出D 点的坐标并求AD 的长;xxx(2)EF 平分∠AED ,若∠ACF-∠AEF=15º,求∠EFB 的度数。
xy FGEDBAoC15.(1)在平面直角坐标系中,如图1,将线段AB 平移至线段CD ,连接AC 、BD 。
①直接写出图中相等的线段、平行的线段; ②已知A (-3,0)、B (-2,-2),点C 在y 轴的正半轴上,点D 在第一象限内,且=5,求点C 、D 的坐标;y DBAoC(2)在平面直角坐标系中,如图,已知一定点M (1,0),两个动点E (a ,2a+1)、F (b ,-2b+3),请你探索是否存在以两个动点E 、F 为端点的线段EF 平行于线段OM 且等于线段OM 。
若存在,求以点O 、M 、E 、F 为顶点的四边形的面积,若不存在,请说明理由。
yoM16.如图,在直角坐标系中,已知B (b ,0),C (0,a ),且+(2c-8)²=0.(1)求B 、C 的坐标;(2)如图,AB//CD ,Q 是CD 上一动点,CP 平分∠DCB ,BQ 与CP 交于点P ,求的值。
yPC BoDAQ17.如图,A 、B 两点同时从原点O 出发,点A 以每秒m 个单位长度沿x 轴的负方向运动,点B 以每秒n 个单位长度沿y 轴的正方向运动。
(1)若|x+2y-5|+|2x-y|=0,试分别求出1秒钟后A 、B 两点的坐标。
yoAB(2)如图,设∠BAO 的邻补角和∠ABO 的邻补角平分线相交于点P ,问:点A 、B 在运动的过程中,∠P 的大小是否会发生变化?若不发生变化,请求出其值;若发生变化,请说明理由。
yPoAB(3)如图,延长BA 至E ,在∠ABO 的内部作射线BF 交x 轴于点C ,若∠EAC 、∠FCA 、∠ABC 的平分线相交于点G ,过点G 作BE 的垂线,垂足为H ,试问∠AGH 和∠BGC 的大小关系如何?请写出你的结论并说明理由。
yB18、如图,在平面直角坐标系中,A (a ,0),C (b ,2),且满足(a+b )²+|a-b+4|=0,过C 作CBx 轴于B 。
(1)求三角形ABC 的面积。
xyCBAo(2)若过B 作BD//AC 交y 轴于D ,且AE 、DE 分别平分∠CAB ,∠ODB ,如图,求∠AED 的度数。
xyEDC BAo(3)在y 轴上是否存在点P ,使得ABC 和ACP 的面积相等,若存在,求出P 点的坐标;若不存在,请说明理由。
xyCBAo19.已知:在△ABC 和△XYZ 中,Y+∠Z=95°,将△XYZ 如图摆放,使得∠X 的两条边分别经过点B 和点C 。
(1)将△XYZ 如图1摆放时,则∠ABX+∠ACX= 度;(2)将△XYZ 如图2摆放时,请求出∠ABX+∠ACX 的度数,并说明理由;(3)能否将△XYZ 摆放到某个位置时,使得BX 、CX 同时平分∠ABC 和∠ACB ?请写出你的结论。
ZX一、细心选一选(每小题3分,共30分)1、对于下列式子①ab;②;③;④;⑤,以下判断正确的是()A、①③是单项式B、②是多项式C、①⑤是整式D、②④是多项式2、如图,由∠1=∠2,则可得出()A、AD‖BCB、AB‖CDC、AD‖BC且AB‖CDD、∠3=∠43、下列各式的计算中,正确的是()A 、B、a4 +a5 =a9C、D、4、对于四舍五入得到的近似数3.20×105,下列说法正确的是()A、有3个有效数字,精确到百分位B、有6个有效数字,精确到个位C、有2个有效数字,精确到万位D、有3个有效数字,精确到千位5、已知:如图AB‖CD,CE平分∠ACD,∠A=110°,则∠ECD等于()A、110°B、70°C、55°D、35°6、如果x+y=-5,xy=3,那么x2+y2 的值是()A、25B、-25C、19D、-197、下列各题中的数,是准确数的是()A、初一年级有800名同学B、月球离地球的距离为38万千米C、小明同学身高148cmD、今天气温估计28℃8、一幅扑克牌去掉大小王后,从中任抽一张是红桃的概率是()A、B、C、D、9、1纳米相当于1根头发丝直径的六万分之一。
则利用科学记数法来表示,头发丝的半径是()A、6万纳米B、6×104纳米C、3×10-6米D、3×10-5米10、x16 可写成( )A、x8 +x8 B 、x8 x2 C 、x8x8 D、x4x4二、专心填一填(每空格2分,共24分)1.如图,在直线DE与∠O的两边相交,则∠O的同位角是。
∠8的内错角是。
∠1的同旁内角是。
2.单项式的系数是3.用科学记数法表示:①,② .4.女生两人,男生一人,站成一排,女生不相邻的概率是______________。
若围成一圈,女生不相邻的概率是___________。
5.∠1与∠2互余,∠2与∠3互补,∠1=63°,那么∠3= 。
6.(-4a3+12a2b-6abc)÷(-4a2 ) = _____________________________。
7.三个连续偶数,如果中间一个数是t ,则它们的积为______________________.8.22004×(-0.5)2004 =_________________。
三、认真算一算(1━4每题5分,第5题6分,共26分)1、(2x+y)(x-y)2、(a+b-3)(a+b+3)3、104 ×100 ÷10-24、5、先化简再求值(6分),其中x = 10,y =四、用心画一画(本题4分)1、如图:打台球时,小球由A点出发撞击到台球桌边CD的点O处,请用尺规作图的方法作出小球反弹后的运动方向(不写作法,但要保留作用痕迹)五、耐心做一做(共16分)1、(6分)一个小妹妹将10盒蔬菜的标签全部撕掉了。
