初一下册数学压轴题精练答案

合集下载

数学初一下学期数学期末复习压轴题解答题试卷带答案

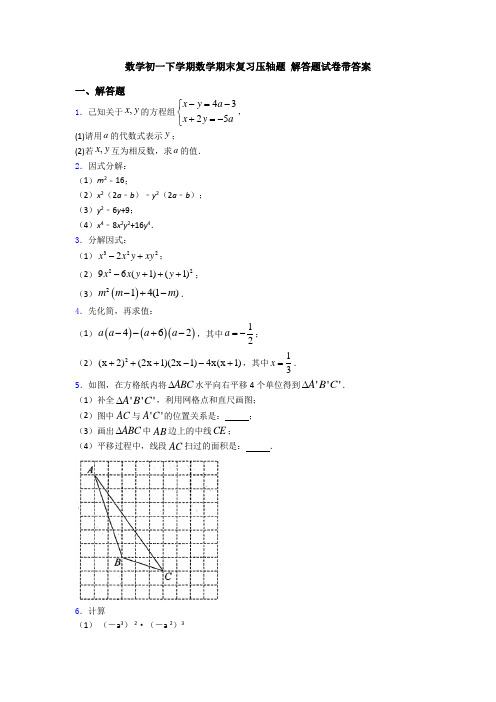
数学初一下学期数学期末复习压轴题解答题试卷带答案一、解答题1．己知关于,x y 的方程组4325x y a x y a -=-⎧⎨+=-⎩， (1)请用a 的代数式表示y ；(2)若,x y 互为相反数，求a 的值．2．因式分解：（1）m 2﹣16；（2）x 2（2a ﹣b ）﹣y 2（2a ﹣b ）；（3）y 2﹣6y +9；（4）x 4﹣8x 2y 2+16y 4．3．分解因式：（1）3222x x y xy -+；（2）2296(1)(1)x x y y -+++；（3）()214(1)m m m -+-．4．先化简，再求值：（1）()()()462a a a a --+-，其中12a =-；（2）2(x 2)(2x 1)(2x 1)4x(x 1)+++--+，其中13x =． 5．如图，在方格纸内将ABC ∆水平向右平移4个单位得到'''A B C ∆．（1）补全'''A B C ∆，利用网格点和直尺画图；（2）图中AC 与''A C 的位置关系是：；（3）画出ABC ∆中AB 边上的中线CE ；（4）平移过程中，线段AC 扫过的面积是：．6．计算（1）（－a 3） 2·（－a 2）3（2）（2x -3y ）2-（y+3x ）（3x -y ）（3） ()()()102323223π--⎛⎫+-+-+- ⎪⎝⎭ 7．因式分解：（1）43312x x -（2）2()a b x a b -+-（3）2169x -（4）(1)(5)4x x +++8．计算：（1）2a （a ﹣2a 2）；（2）a 7＋a ﹣（a 2）3；（3）（3a ＋2b ）（2b ﹣3a ）；（4）（m ﹣n ）2﹣2m （m ﹣n ）．9．已知关于x 的方程3m x +=的解满足325x y a x y a -=-⎧⎨+=⎩，若15y -<<，求实数m 的取值范围．10．先化简，再求值：(a －1)(2a +1)+(1+a )(1－a )，其中a =2．11．解不等式(组)(1)解不等式 114136x x x +-+≤-，并把解集在数轴上．．．．表示出来． (2)解不等式835113x x x x ->⎧⎪+⎨≥-⎪⎩，并写出它的所有整数解． 12．如图，已知ABC 中，,AD AE 分别是ABC 的高和角平分线．若44B ∠=︒，12DAE ∠=︒，求C ∠的度数．13．分解因式(1)321025a a a ++；(2)(1)(2)6t t ++- ．14．如图，△ABC 中，AE 是△ABC 的角平分线，AD 是BC 边上的高．（1）若∠B ＝35°，∠C ＝75°，求∠DAE 的度数；（2）若∠B ＝m °，∠C ＝n °，（m ＜n ），则∠DAE ＝ °（直接用m 、n 表示）．15．如图1是一个长为 4a ，宽为 b 的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后用四块小长方形拼成的一个“回形”正方形（如图2）．（1）图2中的阴影部分的面积为；（2）观察图2请你写出 ()2a b +，()2a b -，ab 之间的等量关系是；（3）根据（2）中的结论，若 6x y +=，114x y ⋅=，则 x y -= ；（4）实际上我们可以用图形的面积表示许多恒等式，下面请你设计一个几何图形来表示恒等式()()2222252a b a b a ab b ++=++．在图形上把每一部分的面积标写清楚． 16．如图，在每个小正方形边长为1的方格纸中，△ABC 的顶点都在方格纸格点上．将△ABC 向左平移2格，再向上平移4格．(1)请在图中画出平移后的△A ′B ′C ′；(2)再在图中画出△ABC 的高CD ；(3)在图中能使S △PBC ＝S △ABC 的格点P 的个数有个(点P 异于A )17．把下列各式分解因式：（1）4x 2-12x 3（2）x 2y +4y -4xy（3）a 2(x -y )+b 2(y -x )18．如图，CD ⊥AB ，EF ⊥AB ，垂足分别为D 、F ，∠1＝∠2，若∠A ＝65°，∠B ＝45°，求∠AGD 的度数．19．如图，边长为1的正方形ABCD 被两条与边平行的线段EF ，GH 分割成四个小长方形，EF 与GH 交于点P ，设BF 长为a ，BG 长为b ，△GBF 的周长为m ，(1)①用含a ，b ，m 的式子表示GF 的长为；②用含a ，b 的式子表示长方形EPHD 的面积为；(2)已知直角三角形两直角边的平方和等于斜边的平方，例如在图1，△ABC 中，∠ABC=900，则222AB BC AC +=，请用上述知识解决下列问题：①写出a ，b ，m 满足的等式；②若m=1，求长方形EPHD 的面积；③当m 满足什么条件时，长方形EPHD 的面积是一个常数？20．当,m n 都是实数，且满足28m n =+，就称点21,2n P m +⎛⎫- ⎪⎝⎭为“爱心点”．（1）判断点()5,3A 、()4,8B 哪个点为“爱心点”，并说明理由；（2）若点(),4A a -、()4,B b 是“爱心点”，请判断A 、B 两点的中点C 在第几象限？并说明理由；（3）已知P 、Q 为有理数，且关于x 、y的方程组3x y q x y q⎧+=+⎪⎨-=-⎪⎩解为坐标的点(),B x y 是“爱心点”，求p 、q 的值．【参考答案】***试卷处理标记，请不要删除一、解答题1．（1）31y a =-+；（2）12a =-．【分析】（1）通过消元的方法，消去x ，即可用a 的代数式表示y ；（2）令y x =-，再将x 、x -代入方程组，即可求解．【详解】解：（1）由43x y a -=-得：43x a y =-+，将其代入25x y a +=-得：4325a y y a -++=-，整理得：393y a =-+，即31y a =-+．故答案为31y a =-+．（2）若x 、y 互为相反数，则y x =- 再将x 、y 代入方程组：4325x x a x x a+=-⎧⎨-=-⎩ ，解得12a =-．故答案为12a =-．【点睛】本题考查次二元一次方程组的运用，难度一般，熟练掌握消元法是顺利解题的关键．2．（1）（m +4）（m ﹣4）；（2）（2a ﹣b ）（x +y ）（x ﹣y ）；（3）（y ﹣3）2；（4）（x +2y ）2（x ﹣2y ）2【分析】（1）原式利用平方差公式因式分解即可；（2）原式提取公因式，再利用平方差公式因式分解即可；（3）原式利用完全平方公式因式分解即可；（4）原式利用完全平方公式，以及平方差公式因式分解即可．【详解】解：（1）原式＝（m+4）（m﹣4）；（2）原式＝（2a﹣b）（x2﹣y2）＝（2a﹣b）（x+y）（x﹣y）；（3）原式＝（y﹣3）2；（4）原式＝（x2﹣4y2）2＝（x+2y）2（x﹣2y）2．【点睛】此题考查的是因式分解，掌握利用提公因式法和公式法因式分解是解决此题的关键．3．（1）x（x-y）2；（2）（3x-y-1）2；（3）（m-1）（m+2）（m-2）．【分析】（1）首先提公因式x，然后利用完全平方公式即可分解；（2）根据完全平方公式进行因式分解即可；（3）首先提公因式（m-1）然后利用平方差公式即可分解．【详解】解：（1）原式=x（x2-2xy+y2）=x（x-y）2；（2）原式=（3x）2-2×（3x）（y+1）+（y+1）2=（3x-y-1）2；（3）原式=（m-1）（m2-4）=（m-1）（m+2）（m-2）．【点睛】本题考查了用提公因式法和公式法进行因式分解，将式子分解彻底是解题关键．4．（1）-8a+12，16；（2）x2+3，1 3 9【分析】（1）直接利用多项式乘法去括号，进而合并同类项，再将已知数据代入求出答案；（2）直接利用多项式乘法去括号，进而合并同类项,再将已知数据代入求出答案．【详解】解：（1）原式=a2-4a-（a2-2a+6a-12）=a2-4a-（a2+4a-12）=a2-4a-a2-4a+12=-8a+12把12a=-代入得：原式=-8×（1-2）+12=16；（2）原式=x2+4x+4+4x2-1-4x2-4x =x2+3把13x=代入得：原式=（13）2+3=139．【点睛】本题考查了多项式乘法，合并同类项，平方差公式和完全平方公式．细心运算是解题关键．5．（1）图见详解；（2）平行且相等；（3）图见详解；（4）28．【分析】（1）根据图形平移的性质画出△A B C '''即可；（2）根据平移的性质可得出AC 与A C ''的关系；（3）先取AB 的中点E ，再连接CE 即可；（4）线段AC 扫过的面积为平行四边形AA C C ''的面积，根据平行四边形的底为4，高为7，可得线段AC 扫过的面积．【详解】解：（1）如图所示，△A B C '''即为所求；（2）由平移的性质可得，AC 与A C ''的关系是平行且相等；故答案为：平行且相等；（3）如图所示，线段CE 即为所求；（4）如图所示，连接AA '，CC '，则线段AC 扫过的面积为平行四边形AA C C ''的面积，由图可得，线段AC 扫过的面积4728=⨯=．故答案为：28．【点睛】本题主要考查了利用平移变换进行作图，作图时要先找到图形的关键点，分别把这几个关键点按照平移的方向和距离确定对应点后，再顺次连接对应点即可得到平移后的图形．6．（1）-12a ；（2）-522x 10y 12xy +-；（3）1034．【分析】（1）先计算幂的乘方，然后计算同底数幂相乘，即可得到答案；（2）先计算完全平方公式和平方差公式，然后合并同类项，即可得到答案；（3）先计算负整数指数幂，零指数幂，绝对值，然后合并同类项，即可得到答案．【详解】解：（1）32236612()()()a a a a a -•-=•-=-；（2）2(23)(3)(3)x y y x x y --+-=22224129(9)x xy y x y -+--=2251210x xy y --+；（3）()()()102323223π--⎛⎫+-+-+- ⎪⎝⎭ =311824+++ =3104；【点睛】本题考查了负整数指数幂，零指数幂，完全平方公式，平方差公式，以及同底数幂的乘法，解题的关键是熟练掌握运算法则进行解题．7．（1）3x 3（x ﹣4）；（2）（a ﹣b ）（1+2x ）；（3）（4﹣3x ）（4+3x ）；（4）2(3)x +．【分析】（1）原式提取公因式3x 3即可；（2）原式提取公因式-a b 即可；（3）原式利用平方差公式分解即可；（4）原式变形后，利用完全平方公式分解即可．【详解】解：（1）原式＝3x 3（x ﹣4）；（2）原式＝（a ﹣b ）（1+2x ）；（3）原式＝（4﹣3x ）（4+3x ）；（4）原式＝2554x x x ++++＝269x x ++＝2(3)x +．【点睛】此题考查了提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．8．（1）2a 2﹣4a 3；（2）a 7＋a ﹣a 6；（3）4b 2﹣9a 2；（4）n 2﹣m 2【分析】（1）由题意根据单项式乘以多项式法则求出即可；（2）根据题意先算乘方，再合并同类项即可；（3）由题意直接根据平方差公式求出即可；（4）由题意先根据完全平方公式和单项式乘以多项式进行计算，再合并同类项即可．【详解】解：（1）2a （a ﹣2a 2）＝2a 2﹣4a 3；（2）a 7＋a ﹣（a 2）3＝a 7＋a ﹣a 6；（3）（3a ＋2b ）（2b ﹣3a ）＝4b 2﹣9a 2；（4）（m ﹣n ）2﹣2m （m ﹣n ）＝m 2﹣2mn ＋n 2﹣2m 2＋2mn＝n 2﹣m 2．【点睛】本题考查整式的混合运算，乘法公式等知识点，能正确根据整式的运算法则进行化简是解此题的关键．9．21m -<<【分析】先解方程组325x y a x y a-=-⎧⎨+=⎩，消去a 用含x 的式子表示y,再将x=3-m 代入y 中，从而得到用含m 的式子表示y,在根据15y -<<，解关于m 的不等式组，求出m 的取值范围.【详解】解：325x y a x y a -=-⎧⎨+=⎩①②，①5⨯+②得6315x y -=即25y x =-③ 由3m x +=得3x m =-，代入③得，12y m =-又因为15y -<<，则1125m -<-<，解得21m -<<【点睛】本题主要考查了分式方程的解以及二元一次方程组的解，解题时需要掌握解二元一次方程和一元一次不等式的方法．10．a 2－a ，2【分析】分别根据多项式的乘法法则和平方差公式计算每一项，再合并同类项，然后把a 的值代入化简后的式子计算即可．【详解】解：(a －1)(2a +1)+(1+a )(1－a )=2a 2－a －1+1－a 2= a 2－a ，当a =2时，原式=22－2=2．【点睛】本题考查了整式的混合运算和代数式求值，属于基本题型，熟练掌握多项式的乘法法则是解题的关键．11．（1）x ≤2，图见详解；（2）22x -≤<；-2、-1、0、1.【分析】（1）由题意直接根据解不等式的步骤逐步进行计算求解，并把解集在数轴上表示出来即可．（2）根据题意分别解出两个不等式，取公共部分得出其解集从而写出它的所有整数解即可．【详解】解：（1）去分母，得 6x+2（x+1）≤6-（x-14），去括号，得 6x+2x+2≤6-x+14，移项，合并同类项，得 9x ≤18，两边都除以9，得 x ≤2.解集在数轴上表示如下：（2）835113x x x x ->⎧⎪⎨+≥-⎪⎩①②解①得：2x <，解②得：2x ≥-，则不等式组的解集是：22x -≤<.它的所有整数解有：-2、-1、0、1.【点睛】本题考查的是一元一次不等式（组）的解法，注意掌握求不等式（组）的解集，应遵循以下原则：同大取较大，同小取较小，小大大小中间找，大大小小解不了．12．68︒【分析】根据已知首先求得∠BAD 的度数，进而可以求得∠BAE ，而∠CAE=∠BAE ，在△ACD 中利用内角和为180°，即可求得∠C ．【详解】解：∵AD 是△ABC 的高，∠B=44︒，∴∠ADB=∠ADC =90︒，在△ABD 中，∠BAD=180︒-90︒-44︒=46︒，又∵ AE 平分∠BAC ，∠DAE=12︒，∴∠CAE=∠BAE=46︒-12︒=34︒，而∠CAD=∠CAE-∠DAE=34︒-12︒=22︒，在△ACD 中，∠C=180︒-90︒-22︒=68︒．故答案为68︒．【点睛】本题考查三角形中角度的计算，难度一般，熟记三角形内角和为180°是解题的关键．13．（1）()25a a +；（2）()()41t t +-．【分析】（1）首先利用提公因式法，提出a ，再利用公式法，即可分解因式；（2）首先将两个多项式的乘积展开，合并同类项后，再利用十字相乘法即可分解因式．【详解】解：（1）()()23221025=10255a a a a a a a a ++++=+；（2）()()22(1)(2)6=3263441t t t t t t t t ++-++-=+-=+-．【点睛】本题考查因式分解，难度不大，是中考的常考点，熟练掌握分解因式的方法是顺利解题的关键．14．（1）20°；（2）1122n m - 【分析】（1）根据∠DAE ＝∠EAC ﹣∠DAC ，求出∠EAC ，∠DAC 即可．（2）计算方法与（1）相同．【详解】解：（1）∵∠B ＝35°，∠C ＝75°，∴∠BAC ＝180°﹣35°﹣75°＝70°，∵AE 平分∠BAC ，∴∠CAE ＝12∠CAB ＝35°， ∵AD ⊥BC ，∴∠ADC ＝90°，∴∠DAC ＝90°﹣75°＝15°，∴∠DAE ＝∠EAC ﹣∠DAC ＝35°﹣15°＝20°．（2）∵∠B ＝m °，∠C ＝n °，∴∠BAC ＝180°﹣m °﹣n °，∵AE 平分∠BAC ，∴∠CAE ＝12∠CAB ＝90°﹣（12m ）°﹣（12n ）°， ∵AD ⊥BC ，∴∠ADC ＝90°，∴∠DAC ＝90°﹣n °，∴∠DAE ＝∠EAC ﹣∠DAC ＝（12n ﹣12m ）°，故答案为：（12n ﹣12m ）．【点睛】本题考查三角形内角和定理角平分线的定义，三角形的高的性质等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．15．（1）2()b a -；（2）22()()4a b a b ab +=-+；（3）±5；（4）详见解析【分析】（1）表示出阴影部分正方形的边长，然后根据正方形的面积公式列式即可；（2）根据大正方形的面积减去小正方形的面积等于四个小长方形的面积列式即可；（3）将（x -y ）2变形为（x +y ）2—4xy ，再代入求值即可；（4）由已知的恒等式，画出相应的图形，如图所示．【详解】解：（1）阴影部分为一个正方形，其边长为b -a ，∴其面积为：2()b a -，故答案为：2()b a -；（2）大正方形面积为：()2a b +小正方形面积为：2()b a -=2()a b -，四周四个长方形的面积为：4ab ，∴22()()4a b a b ab +=-+，故答案为：22()()4a b a b ab +=-+；（3）由（2）知，22()()4x y x y xy +=-+， ∴22()()4x y x y xy -=+-， ∴2()4x y x y xy -=±+-=2116454±-⨯=±，故答案为：±5；（4）符合等式()()2222252a b a b a ab b ++=++的图形如图所示，【点睛】本题考查了完全平方公式的几何背景，此类题目关键在于同一个图形的面积用两种不同的方法表示．16．（1）见解析；（2）见解析；（3）4．【分析】整体分析：（1）根据平移的要求画出△A´B´C´；（2）延长AB ，过点C 作AB 延长线的垂线段；（3）过点A 作BC 的平行线，这条平行线上的格点数（异于点A ）即为结果．【详解】（1）如图所示（2）如图所示．（3）如图，过点A 作BC 的平行线，这条平行线上的格点数除点A 外有4个，所以能使S △ABC =S △PBC 的格点P 的个数有4个，故答案为4．17．（1）4x 2（1-3x ）（2）y (x -2)2（2）(x -y )(a +b )(a -b ) 【分析】（1）直接利用提公因式法分解因式即可；（2）先提取公因式，然后利用完全平方公式分解因式即可；（3）先提取公因式，然后利用平方差公式分解因式即可.【详解】（1）()232412413x x x x =--；（2）()()22244442x y y xy y x x y x +-=+-=-；（3）()()()()()2222()()a x y b y x x y a b x y a b a b =--=-+--+-.【点睛】本题考查了分解因式，解题的关键是熟练掌握提取公因式法和公式法分解因式. 18．70°【分析】由CD ⊥AB ，EF ⊥AB 可得出∠CDF=∠EFB=90°，利用“同位角相等，两直线平行”可得出CD ∥EF ，利用“两直线平行，同位角相等”可得出∠DCB=∠1，结合∠1=∠2可得出∠DCB=∠2，利用“内错角相等，两直线平行”可得出DG ∥BC ，利用“两直线平行，同位角相等”可得出∠ADG 的度数，在△ADG 中，利用三角形内角和定理即可求出∠AGD 的度数.【详解】解：∵CD ⊥AB ，EF ⊥AB ，∴∠CDF ＝∠EFB ＝90°，∴CD ∥EF ，∴∠DCB ＝∠1．∵∠1＝∠2，∴∠DCB ＝∠2，∴DG ∥BC ，∴∠ADG ＝∠B ＝45°．又∵在△ADG 中，∠A ＝65°，∠ADG ＝45°，∴∠AGD ＝180°﹣∠A ﹣∠ADG ＝70°【点睛】本题考查了平行线的判定与性质以及三角形内角和定理，利用平行线的性质求出∠ADG 的度数是解题的关键.19．（1）①m a b --；②1a b ab --+；（2）①22220m ma mb ab --+=；②12；③m=1 【分析】（1）①直接根据三角形的周长公式即可；②根据BF 长为a ，BG 长为b ，表示出EP ，PH 的长，根据求长方形EPHD 的面积；（2）①直接根据直角三角形两直角边的平方和等于斜边的平方，表示出a ，b ，m 之间的关系式；②根据线段之间的关系利用勾股定理求出长方形EPHD 的面积的值；③结合①的结论和②的作法即可求解.【详解】（1）①∵BF 长为a ，BG 长为b ，△GBF 的周长为m ，∴GF m a b =--，故答案为：m a b --；②∵正方形ABCD 的边长为1 ，∴AB=BC=1，∵BF 长为a ，BG 长为b ，∴AG=1-b ，FC=1-a ，∴EP=AG=1-b ，PH=FC=1-a ，∴长方形EPHD 的面积为：(1)(1)1a b a b ab --=--+，故答案为：1a b ab --+；（2）①△ABC 中，∠ABC=90°，则222AB BC AC +=，∴在△GBF 中， GF m a b =--，∴()222m a b a b --=+，化简得，22220m ma mb ab --+=故答案为：22220m ma mb ab --+=；②∵BF=a ，GB=b ，∴FC=1-a ，AG=1-b ，在Rt △GBF 中，22222GF BF BG a b ==+=+，∵Rt △GBF 的周长为1，∴1BF BG GF a b ++=+=即1a b =--，即222212(()b a b a b a +=-+++)，整理得12220a b ab --+= ∴12a b ab +-=， ∴矩形EPHD 的面积••S PH EP FC AG ==()()11a b =--1a b ab =--+11122=-=． ③由①得： 22220m ma mb ab --+=， ∴212ab ma mb m =+-. ∴矩形EPHD 的面积••S PH EP FC AG == ()()11a b =--1a b ab =--+2112ma mb a m b +-=--+ ()()211121m a m m b =--+-+， ∴要使长方形EPHD 的面积是一个常数，只有m=1．【点睛】本题考查了正方形的特殊性质和勾股定理，根据正方形的特殊性质和勾股定理推出22220m ma mb ab --+=是解题的关键．20．（1）()5,3A 为爱心点，理由见解析；（2）第四象限，理由见解析；（3）0p =，q =23- 【分析】（1）分别把A 、B 点坐标，代入（m ﹣1，22n +）中，求出m 和n 的值，然后代入2m ＝8+n 检验等号是否成立即可；（2）把点A（a，﹣4）、B（4，b）各自代入（m﹣1，22n+）中，分别用a、b表示出m、n，再代入2m＝8+n中可求出a、b的值，则可得A和B点的坐标，再根据中点坐标公式即可求出C点坐标，然后即可判断点C所在象限；（3）解方程组，用q和p表示x和y，然后代入2m＝8+n可得关于p和q的等式，再根据p，q为有理数，即可求出p、q的值．【详解】解：（1）A点为“爱心点”，理由如下：当A（5，3）时，m﹣1＝5，22n+＝3，解得：m＝6，n＝4，则2m＝12，8+n＝12，所以2m＝8+n，所以A（5，3）是“爱心点”；当B（4，8）时，m﹣1＝4，22n+＝8，解得：m＝5，n＝14，显然2m≠8+n，所以B点不是“爱心点”；（2）A、B两点的中点C在第四象限，理由如下：∵点A（a，﹣4）是“爱心点”，∴m﹣1＝a，22n+＝﹣4，解得：m＝a+1，n＝﹣10．代入2m＝8+n，得2（a+1）＝8﹣10，解得：a＝﹣2，所以A点坐标为（﹣2，﹣4）；∵点B（4，b）是“爱心点”，同理可得m＝5，n＝2b﹣2，代入2m＝8+n，得：10=8+2b﹣2，解得：b＝2．所以点B坐标为（4，2）．∴A、B两点的中点C坐标为（2442,22-+-+），即（1，﹣1），在第四象限．（3）解关于x，y的方程组3x y qx y q⎧+=+⎪⎨-=-⎪⎩，得：2x qy q⎧=-⎪⎨=⎪⎩．∵点B（x，y）是“爱心点”，∴m﹣1﹣q，22n+＝2q，解得：m﹣q+1，n＝4q﹣2．代入2m＝8+n，得：﹣2q+2＝8+4q﹣2，整理得﹣6q＝4．∵p，q为有理数，若使p﹣6q结果为有理数4，则P＝0，所以﹣6q＝4，解得：q＝﹣23．所以P＝0，q＝﹣23．【点睛】本题是新定义题型，以“爱心点”为载体，主要考查了解二元一次方程组、中点坐标公式等知识以及阅读理解能力和迁移运用能力，正确理解题意、熟练掌握二元一次方程组的解法是关键．。

初中七年级下册期末压轴题数学附答案(一)

初中七年级下册期末压轴题数学附答案（一）一、解答题1．如图所示，A （1，0）、点B 在y 轴上，将三角形OAB 沿x 轴负方向平移，平移后的图形为三角形DEC ，且点C 的坐标为（﹣3，2）．（1）直接写出点E 的坐标；（2）在四边形ABCD 中，点P 从点B 出发，沿“BC→CD”移动．若点P 的速度为每秒1个单位长度，运动时间为t 秒，回答下列问题：①当t=秒时，点P 的横坐标与纵坐标互为相反数；②求点P 在运动过程中的坐标，（用含t 的式子表示，写出过程）；③当点P 运动到CD 上时，设∠CBP=x°，∠PAD=y°，∠BPA=z°，试问x ，y ，z 之间的数量关系能否确定？若能，请用含x ，y 的式子表示z ，写出过程；若不能，说明理由．2．已知直线//AB CD ，点P 为直线AB 、CD 所确定的平面内的一点．（1）如图1，直接写出APC ∠、A ∠、C ∠之间的数量关系；（2）如图2，写出APC ∠、A ∠、C ∠之间的数量关系，并证明；（3）如图3，点E 在射线BA 上，过点E 作//EF PC ，作PEG PEF ∠∠=，点G 在直线CD 上，作BEG ∠的平分线EH 交PC 于点H ，若30APC ∠= ，140PAB ∠= ，求PEH ∠的度数．3．问题情境：如图1，AB ∥CD ，∠PAB ＝130°，∠PCD ＝120°．求∠APC 的度数．小明的思路是：过P 作PE ∥AB ，通过平行线性质，可得∠APC ＝∠APE +∠CPE ＝50°+60°＝110°．问题解决：（1）如图2，AB ∥CD ，直线l 分别与AB 、CD 交于点M 、N ，点P 在直线I 上运动，当点P 在线段MN 上运动时（不与点M 、N 重合），∠PAB ＝α，∠PCD ＝β，判断∠APC 、α、β之间的数量关系并说明理由；（2）在（1）的条件下，如果点P 在线段MN 或NM 的延长线上运动时．请直接写出∠APC 、α、B 之间的数量关系；（3）如图3，AB ∥CD ，点P 是AB 、CD 之间的一点（点P 在点A 、C 右侧），连接PA 、PC ，∠BAP 和∠DCP 的平分线交于点Q ．若∠APC ＝116°，请结合（2）中的规律，求∠AQC 的度数．4．已知，如图1，射线PE 分别与直线AB ，CD 相交于E 、F 两点，∠PFD 的平分线与直线AB 相交于点M ，射线PM 交CD 于点N ，设∠PFM ＝α°，∠EMF ＝β°，且（40﹣2α）2＋|β﹣20|＝0（1）α＝，β＝；直线AB 与CD 的位置关系是；（2）如图2，若点G 、H 分别在射线MA 和线段MF 上，且∠MGH ＝∠PNF ，试找出∠FMN 与∠GHF 之间存在的数量关系，并证明你的结论；（3）若将图中的射线PM 绕着端点P 逆时针方向旋转（如图3），分别与AB 、CD 相交于点M 1和点N 1时，作∠PM 1B 的角平分线M 1Q 与射线FM 相交于点Q ，问在旋转的过程中1FPN Q∠∠的值是否改变？若不变，请求出其值；若变化，请说明理由．5．如图1，已AB ∥CD ，∠C ＝∠A ．（1）求证：AD ∥BC ；（2）如图2，若点E 是在平行线AB ，CD 内，AD 右侧的任意一点，探究∠BAE ，∠CDE ，∠E 之间的数量关系，并证明．（3）如图3，若∠C ＝90°，且点E 在线段BC 上，DF 平分∠EDC ，射线DF 在∠EDC 的内部，且交BC 于点M ，交AE 延长线于点F ，∠AED +∠AEC ＝180°，①直接写出∠AED 与∠FDC 的数量关系：．②点P 在射线DA 上，且满足∠DEP ＝2∠F ，∠DEA ﹣∠PEA ＝514∠DEB ，补全图形后，求∠EPD 的度数6．已知，AB ∥CD ，点E 为射线FG 上一点．（1）如图1，若∠EAF ＝25°，∠EDG ＝45°，则∠AED =．（2）如图2，当点E 在FG 延长线上时，此时CD 与AE 交于点H ，则∠AE D 、∠EAF 、∠EDG 之间满足怎样的关系，请说明你的结论；（3）如图3，当点E 在FG 延长线上时，DP 平分∠EDC ，∠AED ＝32°，∠P ＝30°，求∠EKD 的度数．7．规定：求若干个相同的有理数（均不等于0）的除法运算叫做除方，如2÷2÷2，（-3）÷（-3）÷（-3）÷（-3）等．类比有理数的乘方，我们把2÷2÷2记作2③，读作“2的圈3次方”，（-3）÷（-3）÷（-3）÷（-3）记作（-3）④，读作“-3的圈4次方”，一般地，把n aa a a a ÷÷÷⋯÷ 个（a≠0）记作a ⓝ，读作“a 的圈n 次方”．（初步探究）（1）直接写出计算结果：2③=___，（12）⑤=___；（2）关于除方，下列说法错误的是___A ．任何非零数的圈2次方都等于1；B ．对于任何正整数n ，1ⓝ=1；C ．3④=4③；D ．负数的圈奇数次方结果是负数，负数的圈偶数次方结果是正数．（深入思考）我们知道，有理数的减法运算可以转化为加法运算，除法运算可以转化为乘法运算，有理数的除方运算如何转化为乘方运算呢？（1）试一试：仿照上面的算式，将下列运算结果直接写成幂的形式．（-3）④=___；5⑥=___；（-12）⑩=___．（2）想一想：将一个非零有理数a 的圈n 次方写成幂的形式等于___；（3）算一算：212÷(−13)④×(−2)⑤−(−13)⑥÷338．（概念学习）规定：求若干个相同的有理数（均不等于0）的除法运算叫做除方，如2÷2÷2，（﹣3）÷（﹣3）÷（﹣3）÷（﹣3）等．类比有理数的乘方，我们把2÷2÷2记作2③，读作“2的圈3次方”，（﹣3）÷（﹣3）÷（﹣3）÷（﹣3）记作（﹣3）④，读作“﹣3的圈4次方”，一般地，把n 个a （a ≠0）记作a ⓝ，读作“a 的圈n 次方”．（初步探究）（1）直接写出计算结果：2③＝，（﹣12）⑤＝；（深入思考）我们知道，有理数的减法运算可以转化为加法运算，除法运算可以转化为乘法运算，有理数的除方运算如何转化为乘方运算呢？（1）试一试：仿照上面的算式，将下列运算结果直接写成乘方的形式．（﹣3）④＝；5⑥＝；（﹣12）⑩＝．（2）想一想：将一个非零有理数a 的圈n 次方写成乘方的形式等于；9．规定：求若干个相同的有理数（均不等于0）的除法运算叫做除方，如2÷2÷2，（﹣3）÷（﹣3）÷（﹣3）÷（﹣3）等，类比有理数的乘方，我们把2÷2÷2记作2③，读作“2的圈3次方，”（﹣3）÷（﹣3）÷（﹣3）÷（﹣3）记作（﹣3）④，读作：“（﹣3）的圈4次方”．一般地，把个记作a ⓝ，读作“a 的圈n 次方”（初步探究）（1）直接写出计算结果：2③，（﹣12）③．（深入思考）2④21111112222222⎛⎫=⨯⨯⨯=⨯= ⎪⎝⎭我们知道，有理数的减法运算可以转化为加法运算，除法运算可以转化为乘法运算，有理数的除方运算如何转化为乘方运算呢？（2）试一试，仿照上面的算式，将下列运算结果直接写成幂的形式．5⑥；（﹣12）⑩．（3）猜想：有理数a （a≠0）的圈n （n≥3）次方写成幂的形式等于多少．(4)应用：求（-3）8×（-3）⑨-（﹣12）9×（﹣12）⑧10．已知，在计算：()()12++++N N N 的过程中，如果存在正整数N ，使得各个数位均不产生进位，那么称这样的正整数N 为“本位数”．例如：2和30都是“本位数”，因为2349++=没有进位，30313293++=没有进位；15和91都不是“本位数”，因为15161748++=，个位产生进位，919293276++=，十位产生进位．则根据上面给出的材料：（1）下列数中，如果是“本位数”请在后面的括号内打“√”，如果不是“本位数”请在后面的括号内画“×”．106（）；111（）；400（）；2015（）．（2）在所有的四位数中，最大的“本位数”是，最小的“本位数”是．（3）在所有三位数中，“本位数”一共有多少个？11．阅读下面的文字，解答问题．对于实数a ，我们规定：用符号[a ]表示不大于a 的最大整数；用{a }表示a 减去[a ]所得的差．例如：＝1，[2.2]＝2，1，{2.2}＝2.2﹣2＝0.2．（1）仿照以上方法计算：＝{5}＝；（2）若＝1，写出所有满足题意的整数x 的值：．（3）已知y 0是一个不大于280的非负数，且满足}＝0．我们规定：y 1＝]，y 2＝]，y 3＝]，…，以此类推，直到y n 第一次等于1时停止计算．当y 0是符合条件的所有数中的最大数时，此时y 0＝，n ＝．12．阅读下列材料：小明为了计算22019202012222+++++ 的值，采用以下方法：设22019202012222s =+++++ ①则22020202122222s =++++ ②②-①得，2021221s s s -==-请仿照小明的方法解决以下问题：（1）291222++++= ________；（2）220333+++= _________；（3）求231n a a a a ++++ 的和（1a >，n 是正整数，请写出计算过程）.13．如图1，在平面直角坐标系中，点A 为x 轴负半轴上一点，点B 为x 轴正半轴上一点，()0,C a ，(),D b a ，其中a 、b 满足关系式：24(1)0a b a ++--=．()1a =______，b =______，BCD 的面积为______；()2如图2，石AC BC ⊥于点C ，点P 是线段OC 上一点，连接BP ，延长BP 交AC 于点.Q 当CPQ CQP ∠=∠时，求证：BP 平分ABC ∠；(提示：三角形三个内角和等于180) ()3如图3，若AC BC ⊥，点E 是点A 与点B 之间上一点连接CE ，且CB 平分.ECF ∠问BEC ∠与BCO ∠有什么数量关系？请写出它们之间的数量关系并请说明理由．14．如图，已知//AB CD ，CN 是BCE ∠的平分线．（1）若CM 平分BCD ∠，求MCN ∠的度数；（2）若CM 在BCD ∠的内部，且CM CN ⊥于C ，求证：CM 平分BCD ∠；（3）在（2）的条件下，过点B 作BP BQ ⊥，分别交CM 、CN 于点P 、Q ，PBQ ∠绕着B 点旋转，但与CM 、CN 始终有交点，问：BPC BQC ∠+∠的值是否发生变化？若不变，求其值；若变化，求其变化范围．15．在平面直角坐标系xOy 中，如图正方形ABCD 的顶点A ，B 坐标分别为()1,0A -，()3,0B ，点E ，F 坐标分别为(),0E m ，()3,0F m ，且12m -<≤，以EF 为边作正方形EFGH .设正方形EFGH 与正方形ABCD 重叠部分面积为S .（1）①当点F 与点B 重合时，m 的值为______；②当点F 与点A 重合时，m 的值为______.（2）请用含m 的式子表示S ，并直接写出m 的取值范围.16．中国传统节日“端午节”期间，某商场开展了“欢度端午，回馈顾客”的让利促销活动，对部分品牌的粽子进行了打折销售，其中甲品牌粽子打八折，乙品牌粽子打七五折．已知打折前，买6盒甲品牌粽子和3盒乙品牌粽子需660元；打折后，买5盒甲品牌粽子和4盒乙品牌粽子需520元．（1）打折前，每盒甲、乙品牌粽子分别为多少元？（2）在商场让利促销活动期间，某敬老院准备购买甲、乙两种品牌粽子共40盒，总费用不超过2300元，问敬老院最多可购买多少盒乙品牌粽子？17．对于平面直角坐标系xOy 中的图形G 和图形G 上的任意点P （x ，y ），给出如下定义：将点P （x ，y ）平移到P '（x +t ，y ﹣t ）称为将点P 进行“t 型平移”，点P '称为将点P 进行“t 型平移”的对应点；将图形G 上的所有点进行“t 型平移”称为将图形G 进行“t 型平移”．例如，将点P （x ，y ）平移到P '（x +1，y ﹣1）称为将点P 进行“l 型平移”，将点P （x ，y ）平移到P '（x ﹣1，y +1）称为将点P 进行“﹣l 型平移”．已知点A （2，1）和点B （4，1）．（1）将点A （2，1）进行“l 型平移”后的对应点A '的坐标为．（2）①将线段AB 进行“﹣l 型平移”后得到线段A 'B '，点P 1（1.5，2），P 2（2，3），P 3（3，0）中，在线段A ′B ′上的点是．②若线段AB 进行“t 型平移”后与坐标轴有公共点，则t 的取值范围是．（3）已知点C （6，1），D （8，﹣1），点M 是线段CD 上的一个动点，将点B 进行“t 型平移”后得到的对应点为B '，当t 的取值范围是时，B 'M 的最小值保持不变．18．如图1，以直角AOC △的直角顶点O 为原点，以OC ，OA 所在直线为x 轴和y 轴建立平面直角坐标系，点()0,A a ，(),0C b 80b -=．（1）直接写出点A ，点C 的坐标；（2）如图1，坐标轴上有两动点P ，Q 同时出发，点P 从点C 出发沿x 轴负方向以每秒2个单位长度的速度匀速运动，点Q 从点O 出发沿y 轴正方向以每秒1个单位长度的速度匀速运动，当点P 到达点O 整个运动随之结束；线段AC 的中点D 的坐标是()4,3D ，设运动时间为t 秒．是否存在t ，使得DOP △与DOQ △的面积相等？若存在，求出t 的值；若不存在，说明理由；（3）如图2，在（2）的条件下，若DOC DCO ∠=∠，点G 是第二象限中一点，并且OA 平分DOG ∠，点E 是线段OA 上一动点，连接CE 交OD 于点H ，当点E 在OA 上运动的过程中，探究DOG ∠，OHC ∠，ACE ∠之间的数量关系，直接写出结论．19．题目：满足方程组3512332x y kx y k+=+⎧⎨+=-⎩的x与y的值的和是2，求k的值．按照常规方法，顺着题目思路解关于x，y的二元一次方程组，分别求出xy的值（含有字母k），再由x＋y＝2，构造关于k的方程求解，从而得出k值．（1）某数学兴趣小组对本题的解法又进行了探究利用整体思想，对于方程组中每个方程变形得到“x＋y”这个整体，或者对方程组的两个方程进行加减变形得到“x＋y”整体值，从而求出k值请你运用这种整体思想的方法，完成题目的解答过程．（2）小勇同学的解答是：观察方程①，令3x＝k，5y＝1解得y＝15，3x＋y＝2，∴x＝95∴k＝3×95＝275把x＝95，y＝15代入方程②得k＝﹣35所以k的值为275或﹣35．请诊断分析并评价“小勇同学的解答”．20．如图，已知∠a和β∠的度数满足方程组223080αββα︒︒⎧∠+∠=⎨∠-∠=⎩，且CD//EF,AC AE⊥.(1)分别求∠a和β∠的度数；(2)请判断AB与CD的位置关系，并说明理由；(3)求C∠的度数．21．一个四位正整数，若其千位上与百位上的数字之和等于十位上与个位上的数字之和，都等于k，那么称这个四位正整数为“k类诚勤数”，例如：2534，因为25347+=+=，所以2534是“7类诚勤数”．（1）请判断7441和5436是否为“诚勤数”并说明理由；（2）若一个四位正整数A为“5类诚勤数”且能被13整除，请求出的所有可能取值．22．在平面直角坐标系中，若点P （x ，y ）的坐标满足x ﹣2y +3＝0，则我们称点P 为“健康点”：若点Q （x ，y ）的坐标满足x +y ﹣6＝0，则我们称点Q 为“快乐点”．（1）若点A 既是“健康点”又是“快乐点”，则点A 的坐标为；（2）在（1）的条件下，若B 是x 轴上的“健康点”，C 是y 轴上的“快乐点”，求△ABC 的面积；（3）在（2）的条件下，若P 为x 轴上一点，且△BPC 与△ABC 面积相等，直接写出点P 的坐标．23．如图，在平面直角坐标系中，点O 为坐标原点，A 点的坐标为()1A m n -,，B 点的坐标为()0n -,，其中,m n 是二元一次方程组2202m n m n +=⎧⎨-=-⎩的解，过点A 作x 轴的平行线交y 轴于点C ．（1）求点,A B 的坐标；（2）动点P 从点B 出发，以每秒4个单位长度的速度沿射线BO 的方向运动，连接PC ，设点P 的运动时间为t 秒，三角形OPC 的面积为()0S S ≠，请用含t 的式子表示S （不用写出相应的t 的取值范围）；（3）在（2）的条件下，在动点P 从点B 出发的同时，动点Q 从点C 出发以每秒1个单位长度的速度沿线段CA 的方向运动．过点O 作直线PC 的垂线，点G 为垂足；过点Q 作直线PC 的垂线，点H 为垂足．当2OG QH =时，求t 的值．24．如图，在平面直角坐标系中，已知，点()0,A a ，(),0B b ，()0,C c ，a ，b ，c 满足()28212a b -+-=，（1）直接写出点A ，B ，C 的坐标及ABC 的面积；（2）如图2，过点C 作直线//l AB ，已知(),D m n 是l 上的一点，且152ACD S ≤△，求n 的取值范围；（3）如图3，(),M x y 是线段AB 上一点，①求x ，y 之间的关系；②点N 为点M 关于y 轴的对称点，已知21BCN S =△，求点M 的坐标．25．阅读材料：形如2213x <+<的不等式，我们就称之为双连不等式.求解双连不等式的方法一，转化为不等式组求解，如221213x x <+⎧⎨+<⎩；方法二，利用不等式的性质直接求解，双连不等式的左、中、右同时减去1，得122x <<，然后同时除以2，得1112x <<．解决下列问题：（1）请你写一个双连不等式并将它转化为不等式组；（2）利用不等式的性质解双连不等式2235x ≥-+>-；（3）已知532x -≤<-，求35x +的整数值．26．阅读材料：如果x 是一个有理数，我们把不超过x 的最大整数记作[x ]．例如，[3.2]=3，[5]=5，[－2.1]=－3．那么，x =[x ]+a ，其中0≤a ＜1．例如，3.2=[3.2]+0.2，5=[5]+0，－2.1=[－2.1]+0.9．请你解决下列问题：（1）[4.8]=，[－6.5]=；（2）如果[x ]=3，那么x 的取值范围是；（3）如果[5x －2]=3x +1，那么x 的值是；（4）如果x =[x ]+a ，其中0≤a ＜1，且4a =[x ]+1，求x 的值．27．阅读理解：例1．解方程|x |＝2，因为在数轴上到原点的距离为2的点对应的数为±2，所以方程|x |＝2的解为x ＝±2．例2．解不等式|x ﹣1|＞2，在数轴上找出|x ﹣1|＝2的解（如图），因为在数轴上到1对应的点的距离等于2的点对应的数为﹣1或3，所以方程|x ﹣1|＝2的解为x ＝﹣1或x ＝3，因此不等式|x ﹣1|＞2的解集为x ＜﹣1或x ＞3．参考阅读材料，解答下列问题：（1）方程|x ﹣2|＝3的解为；（2）解不等式：|x ﹣2|≤1．（3）解不等式：|x ﹣4|+|x +2|＞8．（4）对于任意数x ，若不等式|x +2|+|x ﹣4|＞a 恒成立，求a 的取值范围．28．如图①，在平直角坐标系中，△ABO 的三个顶点为A （a ，b ），B （﹣a ，3b ），O（0，0|b ﹣2|＝0，线段AB 与y 轴交于点C ．（1）求出A ，B 两点的坐标；（2）求出△ABO 的面积；（3）如图②，将线段AB 平移至B 点的对应点B '落在x 轴的正半轴上时，此时A 点的对应点为A '，记△A B C ''的面积为S ，若24＜S ＜32，求点A '的横坐标的取值范围．29．已知关于x 、y 的二元一次方程23,3 3.x y a x y a +=-⎧⎨-=-⎩①②（1）若方程组的解x 、y 满足0,1x y ≤<，求a 的取值范围；（2）求代数式638x y +-的值．30．如图，在平面直角坐标系中，已知△ABC,点A 的坐标是(4，0)，点B 的坐标是(2，3)，点C 在x 轴的负半轴上,且AC=6.(1)直接写出点C 的坐标.(2)在y 轴上是否存在点P ，使得S △POB =23S △ABC 若存在,求出点P 的坐标;若不存在，请说明理由.(3)把点C 往上平移3个单位得到点H ，作射线CH,连接BH ，点M 在射线CH 上运动(不与点C 、H 重合).试探究∠HBM ，∠BMA ，∠MAC 之间的数量关系，并证明你的结论.【参考答案】***试卷处理标记，请不要删除一、解答题1．（1）（-2，0）；（2）①t=2；②当点P在线段BC上时，点P的坐标（-t，2），当点P在线段CD上时，点P的坐标（-3，5-t）；③能确定，z=x+y．【分析】（1）根据平移的性质即可得到结论；（2）①由点C的坐标为（-3，2）．得到BC=3，CD=2，由于点P的横坐标与纵坐标互为相反数；于是确定点P在线段BC上，有PB=CD，即可得到结果；②当点P在线段BC上时，点P的坐标（-t，2），当点P在线段CD上时，点P的坐标（-3，5-t）；③如图，过P作PF∥BC交AB于F，则PF∥AD，根据平行线的性质即可得到结论．【详解】解：（1）根据题意，可得三角形OAB沿x轴负方向平移3个单位得到三角形DEC，∵点A的坐标是（1，0），∴点E的坐标是（-2，0）；故答案为：（-2，0）；（2）①∵点C的坐标为（-3，2）∴BC=3，CD=2，∵点P的横坐标与纵坐标互为相反数；∴点P在线段BC上，∴PB=CD，即t=2；∴当t=2秒时，点P的横坐标与纵坐标互为相反数；故答案为：2；②当点P在线段BC上时，点P的坐标（-t，2），当点P在线段CD上时，点P的坐标（-3，5-t）；③能确定，如图，过P作PF∥BC交AB于F，则PF∥AD，∠1=∠CBP=x°，∠2=∠DAP=y°，∴∠BPA=∠1+∠2=x°+y°=z°，∴z=x+y．【点睛】本题考查了坐标与图形的性质，坐标与图形的变化-平移，平行线的性质，正确的作出辅助线是解题的关键．2．（1）∠A+∠C+∠APC=360°；（2）见解析；（3）55°【分析】（1）首先过点P作PQ∥AB，则易得AB∥PQ∥CD，然后由两直线平行，同旁内角互补，即可证得∠A+∠C+∠APC=360°；（2）作PQ∥AB，易得AB∥PQ∥CD，根据两直线平行，内错角相等，即可证得∠APC=∠A+∠C；（3）由（2）知，∠APC=∠PAB-∠PCD，先证∠BEF=∠PQB=110°、∠PEG=12∠FEG，∠GEH=12∠BEG，根据∠PEH=∠PEG-∠GEH可得答案．【详解】解：（1）∠A+∠C+∠APC=360°如图1所示，过点P作PQ∥AB，∴∠A+∠APQ=180°，∵AB∥CD，∴PQ∥CD，∴∠C+∠CPQ=180°，∴∠A+∠APQ+∠C+∠CPQ=360°，即∠A+∠C+∠APC=360°；（2）∠APC=∠A+∠C，如图2，作PQ∥AB，∴∠A=∠APQ，∵AB∥CD，∴PQ∥CD，∴∠C=∠CPQ，∵∠APC=∠APQ-∠CPQ，∴∠APC=∠A-∠C；（3）由（2）知，∠APC=∠PAB-∠PCD，∵∠APC=30°，∠PAB=140°，∴∠PCD=110°，∵AB∥CD，∴∠PQB=∠PCD=110°，∵EF∥BC，∴∠BEF=∠PQB=110°，∵EF∥BC，∴∠BEF=∠PQB=110°，∵∠PEG=∠PEF，∴∠PEG=12∠FEG，∵EH平分∠BEG，∴∠GEH=12∠BEG，∴∠PEH=∠PEG-∠GEH=1 2∠FEG-12∠BEG=12∠BEF=55°．【点睛】此题考查了平行线的性质以及角平分线的定义．此题难度适中，注意掌握辅助线的作法，注意掌握数形结合思想的应用．3．（1）∠APC=α+β，理由见解析；（2）∠APC=α-β或∠APC=β-α；（3）58°【分析】（1）过点P作PE∥AB，根据平行线的判定与性质即可求解；（2）分点P在线段MN或NM的延长线上运动两种情况，根据平行线的判定与性质及角的和差即可求解；（3）过点P，Q分别作PE∥AB，QF∥AB，根据平行线的判定与性质及角的和差即可求解．【详解】解：（1）如图2，过点P作PE∥AB，∵AB∥CD，∴PE∥AB∥CD，∴∠APE=α，∠CPE=β，∴∠APC=∠APE+∠CPE=α+β．（2）如图，在（1）的条件下，如果点P在线段MN的延长线上运动时，∵AB∥CD，∠PAB=α，∴∠1=∠PAB=α，∵∠1=∠APC+∠PCD，∠PCD=β，∴α=∠APC+β，∴∠APC=α-β；如图，在（1）的条件下，如果点P在线段NM的延长线上运动时，∵AB∥CD，∠PCD=β，∴∠2=∠PCD=β，∵∠2=∠PAB+∠APC，∠PAB=α，∴β=α+∠APC ，∴∠APC =β-α；（3）如图3，过点P ，Q 分别作PE ∥AB ，QF ∥AB ，∵AB ∥CD ，∴AB ∥QF ∥PE ∥CD ，∴∠BAP =∠APE ，∠PCD =∠EPC ，∵∠APC =116°，∴∠BAP +∠PCD =116°，∵AQ 平分∠BAP ，CQ 平分∠PCD ，∴∠BAQ =12∠BAP ，∠DCQ =12∠PCD ，∴∠BAQ +∠DCQ =12（∠BAP +∠PCD ）=58°，∵AB ∥QF ∥CD ，∴∠BAQ =∠AQF ，∠DCQ =∠CQF ，∴∠AQF +∠CQF =∠BAQ +∠DCQ =58°，∴∠AQC =58°．【点睛】此题考查了平行线的判定与性质，添加辅助线将两条平行线相关的角联系到一起是解题的关键．4．（1）20，20，//AB CD ；（2）180FMN GHF ∠+∠=︒；（3）1FPN Q ∠∠的值不变，12FPN Q=∠∠【分析】（1）根据2(402)|20|0αβ-+-=，即可计算α和β的值，再根据内错角相等可证//AB CD ；（2）先根据内错角相等证//GH PN ，再根据同旁内角互补和等量代换得出180FMN GHF ∠+∠=︒；（3）作1PEM ∠的平分线交1M Q 的延长线于R ，先根据同位角相等证//ER FQ ，得1FQM R =∠∠，设PER REB x ==∠∠，11PM R RM B y ==∠∠，得出12EPM R ∠=∠，即可得12FPN Q=∠∠．【详解】解：（1）2(402)|20|0αβ-+-= ，4020α∴-=，200β-=，20αβ∴==，20PFM MFN ∴∠=∠=︒，20EMF ∠=︒，EMF MFN ∴∠=∠，//AB CD ∴；故答案为：20、20，//AB CD ；（2）180FMN GHF ∠+∠=︒；理由：由（1）得//AB CD ，MNF PME ∴∠=∠，MGH MNF ∠=∠ ，PME MGH ∴∠=∠，//GH PN ∴，GHM FMN ∴∠=∠，180GHF GHM ∠+∠=︒ ，180FMN GHF ∴∠+∠=︒；（3）1FPN Q ∠∠的值不变，12FPN Q=∠∠；理由：如图3中，作1PEM ∠的平分线交1M Q 的延长线于R ，//AB CD ，1PEM PFN ∴∠=∠，112PER PEM ∠=∠ ，12PFQ PFN =∠，PER PFQ ∴∠=∠，//ER FQ ∴，1FQM R ∴∠=∠，设PER REB x ==∠∠，11PM R RM B y ==∠∠，则有：122y x R y x EPM =+∠⎧⎨=+∠⎩，可得12EPM R ∠=∠，112EPM FQM ∴∠=∠，∴112EPM FQM ∠=∠．【点睛】本题主要考查平行线的判定与性质，熟练掌握内错角相等证平行，平行线同旁内角互补等知识是解题的关键．5．（1）见解析；（2）∠BAE+∠CDE=∠AED，证明见解析；（3）①∠AED-∠FDC=45°，理由见解析；②50°【分析】（1）根据平行线的性质及判定可得结论；（2）过点E作EF∥AB，根据平行线的性质得AB∥CD∥EF，然后由两直线平行内错角相等可得结论；（3）①根据∠AED+∠AEC=180°，∠AED+∠DEC+∠AEB=180°，DF平分∠EDC，可得出2∠AED+（90°-2∠FDC）=180°，即可导出角的关系；②先根据∠AED=∠F+∠FDE，∠AED-∠FDC=45°得出∠DEP=2∠F=90°，再根据∠DEA-∠PEA=514∠DEB，求出∠AED=50°，即可得出∠EPD的度数．【详解】解：（1）证明：AB∥CD，∴∠A+∠D=180°，∵∠C=∠A，∴∠C+∠D=180°，∴AD∥BC；（2）∠BAE+∠CDE=∠AED，理由如下：如图2，过点E作EF∥AB，∵AB∥CD∴AB∥CD∥EF∴∠BAE=∠AEF，∠CDE=∠DEF即∠FEA+∠FED=∠CDE+∠BAE∴∠BAE+∠CDE=∠AED；（3）①∠AED-∠FDC=45°；∵∠AED+∠AEC=180°，∠AED+∠DEC+∠AEB=180°，∴∠AEC=∠DEC+∠AEB，∴∠AED=∠AEB，∵DF平分∠EDC∠DEC=2∠FDC∴∠DEC=90°-2∠FDC，∴2∠AED+（90°-2∠FDC）=180°，∴∠AED-∠FDC=45°，故答案为：∠AED-∠FDC=45°；②如图3，∵∠AED=∠F+∠FDE，∠AED-∠FDC=45°，∴∠F=45°，∴∠DEP=2∠F=90°，∵∠DEA-∠PEA=514∠DEB=57∠DEA，∴∠PEA=27∠AED，∴∠DEP=∠PEA+∠AED=97∠AED=90°，∴∠AED=70°，∵∠AED+∠AEC=180°，∴∠DEC+2∠AED=180°，∴∠DEC=40°，∵AD∥BC，∴∠ADE=∠DEC=40°，在△PDE中，∠EPD=180°-∠DEP-∠AED=50°，即∠EPD=50°．【点睛】本题主要考查平行线的判定和性质，熟练掌握平行线的判定和性质，角平分线的性质等知识点是解题的关键．6．（1）70°；（2）EAF AED EDG∠=∠+∠，证明见解析；（3）122°【分析】（1）过E 作//EF AB ，根据平行线的性质得到25EAF AEH ∠=∠=︒，45EAG DEH ∠=∠=︒，即可求得AED ∠；（2）过过E 作//EM AB ，根据平行线的性质得到180EAF MEH ∠=︒-∠，180EDG AED MEH ∠+∠=︒-，即EAF AED EDG ∠=∠+∠；（3）设EAI x ∠=，则3BAE x ∠=，通过三角形内角和得到2EDK x ∠=-︒，由角平分线定义及//AB CD 得到33224x x =︒+-︒，求出x 的值再通过三角形内角和求EKD ∠．【详解】解：（1）过E 作//EF AB ，//AB CD ，//EF CD ∴，25EAF AEH ∴∠=∠=︒，45EAG DEH ∠=∠=︒，70AED AEH DEH ∴∠=∠+∠=︒，故答案为：70︒；（2）EAF AED EDG ∠=∠+∠．理由如下：过E 作//EM AB ，//AB CD ，//EM CD ∴，180EAF MEH ∴∠+∠=︒，180EDG AED MEH ∠+∠+=︒，180EAF MEH ∴∠=︒-∠，180EDG AED MEH ∠+∠=︒-，EAF AED EDG ∴∠=∠+∠；（3）:1:2EAP BAP ∠∠= ，设EAP x ∠=，则3BAE x ∠=，32302AED P ∠-∠=︒-︒=︒ ，DKE AKP ∠=∠，又180EDK DKE DEK ∠+∠+∠=︒ ，180KAP KPA AKP ∠+∠+∠=︒，22EDK EAP x ∴∠=∠-︒=-︒，DP 平分EDC ∠，224CDE EDK x ∴∠=∠=-︒，//AB CD ，EHC EAF AED EDG ∴∠=∠=∠+∠，即33224x x =︒+-︒，解得28x =︒，28226EDK ∴∠=︒-︒=︒，1802632122EKD ∴∠=︒-︒-︒=︒．【点睛】本题主要考查了平行线的性质和判定，正确做出辅助线是解决问题的关键．7．初步探究：（1）12，8;（2）C ；深入思考：（1）213，415，82；（2）21n a -；（3）-5.【分析】初步探究：（1）根据除方运算的定义即可得出答案；（2）根据除方运算的定义逐一判断即可得出答案；深入思考：（1）根据除方运算的定义即可得出答案；（2）根据（1）即可总结出（2）中的规律；（3）先按照除方的定义将每个数的圈n 次方算出来，再根据有理数的混合运算法则即可得出答案.【详解】解：初步探究：（1）2③=2÷2÷2=12（12）⑤=11111822222÷÷÷÷=（2）A ：任何非零数的圈2次方就是两个相同数相除，所以都等于1，故选项A 错误;B ：因为多少个1相除都是1，所以对于任何正整数n ，1ⓝ都等于1，故选项B 错误；C ：3④=3÷3÷3÷3=19，4③=4÷4÷4=14，3④≠4③，故选项C 正确；D ：负数的圈奇数次方，相当于奇数个负数相除，则结果是负数；负数的圈偶数次方，相当于偶数个负数相除，则结果是正数，故选项D 错误；故答案选择：C.深入思考：（1）（-3）④=(-3)÷(-3)÷(-3)÷(-3)=2135⑥=5÷5÷5÷5÷5÷5=415（-12）⑩=8111111111122222222222⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫-÷-÷-÷-÷-÷-÷-÷-÷-÷-=⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭（2）a ⓝ=a÷a÷a…÷a=21n a -（3）原式=()4252621111442711233---÷⨯-÷-⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭=1144981278⎛⎫÷⨯--÷ ⎪⎝⎭=23--=-5【点睛】本题主要考查了除方运算，运用到的知识点是有理数的混合运算，掌握有理数混合运算的法则是解决本题的关键.8．初步探究：（1）12，-8；深入思考：（1）(−13)2，(15)4，82；（2）21n a -⎛⎫⎪⎝⎭【分析】初步探究：（1）分别按公式进行计算即可；深入思考：（1）把除法化为乘法，第一个数不变，从第二个数开始依次变为倒数，由此分别得出结果；（2）结果前两个数相除为1，第三个数及后面的数变为1a，则11n a a a -⎛⎫=⨯ ⎪⎝⎭ⓝ；【详解】解：初步探究：（1）2③=2÷2÷2=12，111111-=-----222222⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫÷÷÷÷ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⑤111=1---222⎛⎫⎛⎫⎛⎫÷÷÷ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭()11-2--22⎛⎫⎛⎫÷÷ ⎪ ⎪⎝⎭⎝⎭=-8；深入思考：（1）（-3）④=（-3）÷（-3）÷（-3）÷（-3）=1×(−13)2=(−13)2；5⑥=5÷5÷5÷5÷5÷5=(15)4；同理可得：（﹣12）⑩＝82；（2）21n a a -⎛⎫= ⎪⎝⎭ⓝ【点睛】本题是有理数的混合运算，也是一个新定义的理解与运用；一方面考查了有理数的乘除法及乘方运算，另一方面也考查了学生的阅读理解能力；注意：负数的奇数次方为负数，负数的偶数次方为正数，同时也要注意分数的乘方要加括号，对新定义，其实就是多个数的除法运算，要注意运算顺序．9．（1）12，-2；（2）（15）4，（﹣2）8；（3）n-21a⎛⎫⎪⎝⎭；（4）7-28.【分析】（1）分别按公式进行计算即可；（2）把除法化为乘法，第一个数不变，从第二个数开始依次变为倒数，由此分别得出结果；（3）结果前两个数相除为1，第三个数及后面的数变为1a，则aⓝ=a×(1a)n-1；（4）将第二问的规律代入计算，注意运算顺序．【详解】解：（1）2③=2÷2÷2=12，（﹣12）③=﹣12÷（﹣12）÷（﹣12）=﹣2；（2）5⑥=5×15×15×15×15×15=（15）4，同理得；（﹣12）⑩=（﹣2）8；（3）aⓝ=a×1a×1a×…×n-211a a⎛⎫= ⎪⎝⎭；(4)（-3）8×（-3）⑨-（﹣12）9×（﹣12）⑧=（-3）8×（1-3）7-（﹣12）9×（-2）6=-3-(-12)3=-3+1 8=7 -2 8.【点睛】本题是有理数的混合运算，也是一个新定义的理解与运用；一方面考查了有理数的乘除法及乘方运算，另一方面也考查了学生的阅读理解能力；注意：负数的奇数次方为负数，负数的偶数次方为正数，同时也要注意分数的乘方要加括号，对新定义，其实就是多个数的除法运算，要注意运算顺序．10．（1）×，√，×，×；（2）3332；1000；（3）36（个）．【分析】（1）根据“本位数”的定义即可判断；（2）要想保证不进位，千位、百位、十位最大只能是3，个位最大只能是2，故最大的四位“本位数”是3332；千位最小为1，百位、十位、个位最小为0，故最小的“本位数”是1000；（3）要想构成“本位数”，百位可以为1，2，3，十位可以为0，1，2，3，个位可以为0，1，2，所有的三位数中，“本位数”一共有34336⨯⨯=（个）．【详解】解：（1）106107108321++=有进位；111112113336++=没有进位；4004014021203++=有进位；2015201620176048++=有进位；故答案为：×，√，×，×．（2）要想保证不进位，千位、百位、十位最大只能是3，个位最大只能是2，故最大的四位“本位数”是3332；千位最小为1，百位、十位、个位最小为0，故最小的“本位数”是1000，故答案为：3332，1000．（3）要想构成“本位数”，百位可以为1，2，3，十位可以为0，1，2，3，个位可以为0，1，2，所有的三位数中，“本位数”一共有34336⨯⨯=（个）．【点睛】本题考查了新定义计算题，准确理解新定义的内涵是解题的关键．11．（1）2；32）1、2、3；（3）256，4【分析】（1）依照定义进行计算即可；（2）由题可知，04x <<，则可得满足题意的整数的x 的值为1、2、3；（3）由0=，可知，0y 是某个整数的平方，又0y 是符合条件的所有数中最大的数，则0256y =，再依次进行计算．【详解】解：（1）由定义可得，2=，[52=，{53∴=．故答案为：2；3．（2）1= ，2∴<，即04x <<，∴整数x 的值为1、2、3．故答案为：1、2、3．（3）0= ，即0=-=，∴2t ，且t 是自然数，0y 是符合条件的所有数中的最大数，0256y ∴=，1[16]16y ∴===，2[4]4y ===，3[2]2y ===，41y ===，即4n =．故答案为：256，4．【点睛】本题属于新定义类问题，主要考查估算无理数大小，无理数的整数部分和小数部分，理解定义内容是解题关键．12．（1）1021-；（2）21332-；（3）111n a a +--【分析】（1）设式子等于s ，将方程两边都乘以2后进行计算即可；（2）设式子等于s ，将方程两边都乘以3，再将两个方程相减化简后得到答案；（3）设式子等于s ，将方程两边都乘以a 后进行计算即可.【详解】（1）设s=291222++++ ①，∴2s=29102222++++ ②，②-①得：s=1021-，故答案为：1021-；（2）设s=220333+++ ①，∴3s=22021333+++ ②，②-①得：2s=2133-，∴21332s -=,故答案为：21332-；（3）设s=231n a a a a ++++ ①，∴as=231n n a a a a a +++++ ②，②-①得：（a-1）s=11n a +-，∴s=111n a a +--.【点睛】此题考查代数式的规律计算，能正确理解已知的代数式的运算规律是难点，依据规律对于每个式子变形计算是关键.13．（1）4-；3-；6；（2）证明见解析；（3）2BEC BCO ∠=∠，理由见解析.【详解】分析：（1）求出CD 的长度，再根据三角形的面积公式列式计算即可得解；（2）根据等角的余角相等解答即可；（3）首先证明∠ACD=∠ACE ，推出∠DCE=2∠ACD ，再证明∠ACD=∠BCO ，∠BEC=∠DCE=2∠ACD 即可解决问题；【解答】（1）解：如图1中，∵|a+4|+（b-a-1）2=0，∴a=-4，b=-3，∵点C（0，-4），D（-3，-4），∴CD=3，且CD∥x轴，∴△BCD的面积=12×4×3=6；故答案为-4，-3，6．（2）如图2中，∵∠CPQ=∠CQP=∠OPB，AC⊥BC，∴∠CBQ+∠CQP=90°，又∵∠ABQ+∠CPQ=90°，∴∠ABQ=∠CBQ，∴BQ平分∠CBA．（3）如图3中，结论：∠BEC=2∠BCO．理由：∵AC⊥BC，∴∠ACB=90°，∴∠ACD+∠BCF=90°，∵CB 平分∠ECF ，∴∠ECB=∠BCF ，∴∠ACD+∠ECB=90°，∵∠ACE+∠ECB=90°，∴∠ACD=∠ACE ，∴∠DCE=2∠ACD ，∵∠ACD+∠ACO=90°，∠BCO+∠ACO=90°，∴∠ACD=∠BCO ，∵C （0，-4），D （-3，-4），∴CD ∥AB ，∠BEC=∠DCE=2∠ACD ，∴∠BEC=2∠BCO ，点睛：本题考查了坐标与图形性质，三角形的角平分线，三角形的面积，三角形的内角和定理，三角形的外角性质等知识，熟记性质并准确识图是解题的关键．14．（1）90°；（2）见解析；（3）不变，180°【分析】（1）根据邻补角的定义及角平分线的定义即可得解；（2）根据垂直的定义及邻补角的定义、角平分线的定义即可得解；（3）180BPC BQC ∠+∠=︒，过Q ，P 分别作//QG AB ，//PH AB ，根据平行线的性质及平角的定义即可得解．【详解】解（1）CN ，CM 分别平分BCE ∠和BCD ∠，12BCN BCE ∴=∠，12BCM BCD ∠=∠，180BCE BCD ∠+∠=︒ ，111()90222MCN BCN BCM BCE BCD BCE BCD ∴∠=∠+∠=∠+∠=∠+∠=︒；（2）CM CN ⊥ ，90MCN ∴∠=︒，即90BCN BCM ∠+∠=︒，22180BCN BCM ∴∠+∠=︒，CN 是BCE ∠的平分线，2BCE BCN ∴∠=∠，2180BCE BCM ∴∠+∠=︒，又180BCE BCD ∠+∠=︒ ，2BCD BCM ∴∠=∠，又CM 在BCD ∠的内部，CM ∴平分BCD ∠；（3）如图，不发生变化，180BPC BQC ∠+∠=︒，过Q ，P 分别作//QG AB ，//PH AB ，。

初一下学期数学期末复习压轴题解答题试卷带答案

初一下学期数学期末复习压轴题解答题试卷带答案一、解答题1．解方程或不等式（组）（1）24231x y x y +=⎧⎨-=⎩ （2）2151132x x -+-≥ （3）312(2)15233x x x x +<+⎧⎪⎨-≤+⎪⎩ 2．已知，关于x 、y 二元一次方程组237921x y a x y -=-⎧⎨+=-⎩的解满足方程2x-y=13，求a 的值．3．如图，已知AB ∥CD ， 12∠=∠，BE 与CF 平行吗？4．因式分解：（1）16x 2－9y 2（2）(x 2+y 2)2－4x 2y 25．计算：（1）022019()32020-- （2）4655x x x x ⋅+⋅6．如图，△ABC 的顶点都在方格纸的格点上，将△ABC 向下平移3格，再向右平移4格.（1）请在图中画出平移后的△A′B′C′；（2）在图中画出△A′B′C′的高C′D′.7．先化简，再求值：（2a +b ）2﹣（2a +3b ）（2a ﹣3b ），其中a ＝12，b ＝﹣2．8．计算：（1）201()2016|5|2----；（2）（3a 2）2﹣a 2•2a 2+（﹣2a 3）2+a 2．9．解不等数组：3(2)41213x x x x --≤-⎧⎪+⎨>-⎪⎩，并在数轴上表示出它的解集． 10．探究与发现：如图1所示的图形，像我们常见的学习用品﹣﹣圆规．我们不妨把这样图形叫做“规形图”，那么在这一个简单的图形中，到底隐藏了哪些数学知识呢？下面就请你发挥你的聪明才智，解决以下问题：（1）观察“规形图”，试探究∠BDC 与∠A 、∠B 、∠C 之间的关系，并说明理由；（2）请你直接利用以上结论，解决以下三个问题：①如图2，把一块三角尺XYZ 放置在△ABC 上，使三角尺的两条直角边XY 、XZ 恰好经过点B 、C ，若∠A ＝50°，则∠ABX+∠ACX ＝ °；②如图3，DC 平分∠ADB ，EC 平分∠AEB ，若∠DAE ＝50°，∠DBE ＝130°，求∠DCE 的度数；③如图4，∠ABD ，∠ACD 的10等分线相交于点G 1、G 2…、G 9，若∠BDC ＝140°，∠BG 1C ＝77°，求∠A 的度数．11．已知关于x 、y 的二元一次方程组21322x y x y k +=⎧⎪⎨-=-⎪⎩(k 为常数)． (1)求这个二元一次方程组的解(用含k 的代数式表示)；(2)若()2421y x +=，求k 的值； (3)若14k ≤，设364m x y =+，且m 为正整数，求m 的值． 12．疫情初期，武汉物资告急，全国一心，各地纷纷运送物资到武汉。

(完整版)人教版七年级数学下册期末复习压轴题-解答题试卷及答案

(完整版)人教版七年级数学下册期末复习压轴题解答题试卷及答案一、解答题1. 仔细阅读下列解题过程:若 , 求的值．解：2222690a ab b b ++-+=222222690()(3)003033a ab b b b a b b a b b a b ∴+++-+=∴++-=∴+=-=∴=-=，，根据以上解题过程, 试探究下列问题:（1）已知 , 求的值；（2）已知 , 求的值；（3）若 , 求的值.2. 启秀中学初一年级组计划将本书奖励给本次期中考试中取得优异成绩的名同学, 如果每人分本, 那么还剩下本；如果每人分本, 那么最后一人分得的书不足本, 但不少于本. 最终, 年级组讨论后决定, 给名同学每人发本书, 那么将剩余多少本书？3．在南通市中小学标准化建设工程中, 某校计划购进一批电脑和电子白板, 经过市场考察得知, 购买台电脑和台电子白板需要万元, 购买台电脑和台电子白板需要万元．（1）求每台电脑、每台电子白板各多少万元；（2）根据学校实际, 需购进电脑和电子白板共台, 若总费用不超过万元, 则至多购买电子白板多少台？4．已知关于 , 的二元一次方程组它的解是正数．（1）求m 的取值范围；（2）化简: ；5. 已知 , , 求的平方根.6. 定义: 若实数x, y 满足 , , 且x ≠y, 则称点M(x, y)为“好点”. 例如, 点(0, －2)和 (－2, 0)是“好点”. 已知: 在直角坐标系xOy 中, 点P(m, n).(1)P1(3, 1)和P2(－3, 1)两点中, 点________________是“好点”.(2)若点P(m, n)是“好点”, 求m+n 的值.(3)若点P 是“好点”, 用含t 的代数式表示mn, 并求t 的取值范围.7. 已知有理数满足: , 且 , 求的值.8. 如图, 在方格纸内将水平向右平移4个单位得到 .（1）补全 , 利用网格点和直尺画图；（2）图中与的位置关系是: ；（3）画出ABC ∆中AB 边上的中线CE ；（4）平移过程中, 线段扫过的面积是: .9. 如图所示, A(2, 0), 点 B 在 y 轴上, 将三角形 OAB 沿 x 轴负方向平移, 平移后的图形为三角形 DEC, 且点 C 的坐标为(-6, 4) .(1)直接写出点E 的坐标；(2)在四边形 ABCD 中, 点 P 从点 B 出发, 沿“BC→CD”移动. 若点 P 的速度为每秒 2 个单位长度, 运动时间为 t 秒, 回答下列问题:①求点 P 在运动过程中的坐标, (用含 t 的式子表示, 写出过程)；②当 3 秒＜t＜5 秒时, 设∠CBP＝x°, ∠PAD＝y°, ∠BPA＝z°, 试问 x, y, z 之间的数量关系能否确定？若能, 请用含 x, y 的式子表示 z, 写出过程；若不能, 说明理由．10. 问题1: 现有一张△ABC纸片, 点D.E分别是△ABC边上两点, 若沿直线DE折叠. （1）探究1: 如果折成图①的形状, 使A点落在CE上, 则∠1与∠A的数量关系是；（2）探究2: 如果折成图②的形状, 猜想∠1+∠2和∠A的数量关系是；（3）探究3：如果折成图③的形状, 猜想∠1、∠2和∠A的数量关系, 并说明理由．（4）问题2: 将问题1推广, 如图④, 将四边形ABCD纸片沿EF折叠, 使点A.B落在四边形EFCD的内部时, ∠1+∠2与∠A.∠B之间的数量关系是 .11．已知a ＋b=5, ab=－2．求下列代数式的值:（1）；（2） .12．如图, 在方格纸内将水平向右平移4个单位得到△ ．（1）画出△；（2）画出边上的中线和高线；（利用网格点和直尺画图）（3）的面积为 .13. 如果ac ＝b, 那么我们规定（a, b ）＝c. 例如；因为23＝8, 所以（2, 8）＝3.（1）根据上述规定填空: （3, 27）＝ , （4, 1）＝ , （2, 0.25）＝；（2）记（3, 5）＝a, （3, 6）＝b, （3, 30）＝c. 判断a, b, c 之间的等量关系, 并说明理由.14. 先化简, 再求值：（x ﹣2y ）（x ＋2y ）﹣（x ﹣2y ）2, 其中x ＝3, y ＝﹣1.15．已知： , ．求下列代数式的的值．(1)xy ；(2)224x xy y ++；(3) . 16. 装饰公司为小明家设计电视背景墙时需要A.B 型板材若干块, A型板材规格是a(b, B 型板材规格是b(b.现只能购得规格是150(b 的标准板材.（单位: cm ）（1）若设a(60cm, 裁法一裁法二裁法三b(30cm．一张标准板材尽可能多的裁出A型、B型板材,共有下表三种裁法, 下图是裁法一的裁剪示意图．A型板材块数120B型板材块数3m n则上表中, m=___________, n=__________；（2）为了装修的需要, 小明家又购买了若干C型板材, 其规格是a(a, 并做成如下图的背景墙．请写出下图中所表示的等式：__________；(3)若给定一个二次三项式2a2(5ab(3b2, 试用拼图的方式将其因式分解. （请仿照（2）在几何图形中标上有关数量）17．已知关于x、y的方程组与有相同的解, 求a、b的值．18. 计算：（1）（12）﹣3﹣20160﹣|﹣5|；（2）（3a2）2﹣a2•2a2+（﹣2a3）2+a2；（3）（x+5）2﹣（x﹣2）（x﹣3）；（4）（2x+y ﹣2）（2x+y+2）.19. 已知关于、的二元一次方程组 (k 为常数).(1)求这个二元一次方程组的解(用含k 的代数式表示)；(2)若 , 求k 的值；(3)若 , 设 , 且m 为正整数, 求m 的值．20. 解下列方程组或不等式组（1）24231x y x y +=⎧⎨-=⎩ （2）()211113x x x x ⎧--≤⎪⎨+>-⎪⎩【参考答案】***试卷处理标记, 请不要删除一、解答题1. （1）；（2）；（3） .【分析】（1）首先把第3项裂项, 拆成 , 再用完全平方公式因式分解, 利用非负数的性质求得代入求得数值；（2）首先把第2项裂项, 拆成 , 再用完全平方公式因式分解, 利用非负数的性质求得代入求得数值；（3）先把代入 , 得到关于和的式子, 再仿照（1）（2）题．【详解】解: （1）2222210x xy y y y ∴-++-+=22()(1)0x y y ∴-+-=010x y y ∴-=-=，，11x y ∴==，，23x y ∴+=；（2）2254210a b ab b +--+=22244210a b ab b b ∴+-+-+=22(2)(1)0a b b ∴-+-=2010a b b ∴-=-=，21a b ∴==，；（3）4m n =+，2(4)8200n n t t ∴++-+=22448160n n t t ∴+++-+=22(2)(4)0n t ∴++-=2040n t ∴+=-=，24n t ∴=-=，42m n ∴=+=20(2)1m t n -∴=-=【点睛】本题考查的分组分解法、配方法和非负数的性质, 对于项数较多的多项式因式分解, 分组分解法是一个常用的方法.首先要观察各项特征, 寻找熟悉的式子, 熟练掌握平方差公式和完全平方公式是基础.2．38本【分析】先表示书的总量, 利用不等关系列不等式组, 求不等式组的正整数解即可得到答案.【详解】解: 由题意得:由①得:由②得:不等式组的解集是:为正整数,20,n ∴=478158,m n ∴=+=15820638.∴-⨯=答: 剩下本书.【点睛】本题考查的是不等式组的应用, 掌握利用不等关系列不等式组是解题的关键.3．（1）电脑万元, 电子白板万元；（2）台【分析】（1）设每台电脑元, 每台电子白板元, 根据题意列出方程组, 解方程组即可；（2）设购进电子白板台, 则购进电脑台, 根据总费用不超过万元, 列出不等式, 根据实际意义即可求解．【详解】（1）设每台电脑元, 每台电子白板元, 则 , 解得故每台电脑万元, 每台电子白板万元；（2）设购进电子白板台, 则购进电脑台, 由题意得1.50.5(31)30m m +-≤解得 , 又因为是正整数, 则 , 故至多购买电子白板台.【点睛】本题考查了二元一次方程组应用, 一元一次不等式应用, 综合性较强, 难度不大, 根据题意列出二元一次方程组、一元一次不等式是解题关键.4. （1）（2）m -【分析】（1）先解方程组, 用含m 的式子表示出x 、y, 再根据方程组的解时一对正数列出关于m 的不等式组, 解之可得；（2）根据m 的取值范围判断出m-2<0、m+1>0,m-1<0, 再根据绝对值性质去绝对值符号、合并同类项即可得．【详解】解: （1）解方程组 ,得321x m y m =+⎧⎨=-⎩因为解为正数, 则 , 解得；（2）原式2(1)(1)m m m m =--+--=-.【点睛】本题考查了二元一次方程组及解法、一元一次不等式组及解法. 解题的关键是根据题意列出关于m 的不等式组及绝对值的性质.5．【分析】根据题意得到三元一次方程组, 解方程组, 求出 , 最后求平方根即可.【详解】∵ , ,∴ , ,∴2113024010y x x y z -+-=⎧⎪-+=⎨⎪-=⎩，解得231x y z =⎧⎪=⎨⎪=⎩，则6x y z ++=，∴ 平方根为 .【点睛】本题考查相反数的意义, 非负数的表达, 解三元一次方程组, 求平方根等知识, 综合性较强, 解题关键是根据题意列出三元一次方程组.6. (1) ；(2) ；(3)【分析】(1)将P1(3, 1)和P2(－3, 1)分别代入等式即可得出结果；(2)将点P(m, n)代入等式即可得出m+n 的值；(3)根据“好点”的定义, 将P 点代入即可得到关于m 和n 的等式, 将两个等式结合即可得出结果．【详解】解: (1)对于 , ,对于 , , , 所以是“好点”(2)∵点是好点,∴222,2m n t n m t =+=+， 222()m n n m -=-，∴2m n +=-(3)∵ ,2222m n n t m t -=+--①，2222m n m t n t +=+++②，得()()2()0m n m n m n -++-=，即()(2)0m n m n -++=，由题知, ,由②得 ,∴4242,4mn t mn t -=-+=-，∵ , ∴ ,∴2()40m n mn +->，∴44(4)0t -->，所以3t >，【点睛】本题主要考查的是新定义“好点”, 正确的掌握整式的乘法解题的关键.7. 【分析】利用将整理求出的值, 然后将利用完全平方公式变形, 将各自的值代入计算即可求出值．【详解】∵221x y ， ∴化简得: ,∵1x y -=，∴ 可化为: ,即有： ,∴2222313516x xy y x y xy ．【点睛】此题考查了整式的混合运算化简求值, 熟练掌握运算法则是解本题的关键.8. （1）图见详解；（2）平行且相等；（3）图见详解；（4）28.【分析】（1）根据图形平移的性质画出△A B C '''即可；（2）根据平移的性质可得出AC 与A C ''的关系；（3）先取的中点 , 再连接即可；（4）线段扫过的面积为平行四边形的面积, 根据平行四边形的底为4, 高为7, 可得线段扫过的面积．【详解】解: （1）如图所示, △ 即为所求；（2）由平移的性质可得, 与的关系是平行且相等；故答案为: 平行且相等；（3）如图所示, 线段即为所求；（4）如图所示, 连接 , , 则线段扫过的面积为平行四边形的面积,由图可得, 线段扫过的面积．故答案为：28.【点睛】本题主要考查了利用平移变换进行作图, 作图时要先找到图形的关键点, 分别把这几个关键点按照平移的方向和距离确定对应点后, 再顺次连接对应点即可得到平移后的图形.9．（1）（2）1）点P 在线段BC 上时, , 2）点P 在线段CD 上时, ；（3）能确定, , 证明见解析【分析】（1）根据平移的性质即可得到结论；（2）①分两种情况: 1）点P 在线段BC 上时, 2）点P 在线段CD 上时；②如图, 作P 作交于AB 于E, 则 , 根据平行线的性质即可得到结论．【详解】（1）∵点B 的横坐标为0, 点C 的横坐标为-6,∴将A(2, 0)向左平移6个单位长度得到点E∴()4,0E -；（2）①∵6,4BC CD ==∴1）点P 在线段BC 上时,(),4P t -；2）点P 在线段CD 上时,()6,10P t --；②能确定如图, 作P 作交于AB 于E, 则∴1,2CBP x DAP y ==︒==︒∠∠∠∠ ∴1+2BPA x y z ==︒+︒=︒∠∠∠ ∴z x y =+．【点睛】本题考查了平行线的问题, 掌握平移的性质、代数式的用法、平行线的性质以及判定定理是解题的关键.10. （1） ;（2） ;（3）见解析;（4）【分析】（1）根据三角形外角性质可得；（2）在四边形中, 内角和为360°, ∠BDA=∠CEA=180°, 利用这两个条件, 进行角度转化可得关系式；（3）如下图, 根据（1）可得∠1=2∠ , ∠2=2∠ , 从而推导出关系式；（4）根据平角的定义以及四边形的内角和定理, 与（2）类似思路探讨, 可得关系式．【详解】（1）∵△'EDA 是△EDA 折叠得到∴∠A=∠A '∵∠1是△'ADA 的外角∴∠1=∠A+∠A '∴12A ∠=∠；（2）∵在四边形中, 内角和为360°∴∠A+A '+∠A DA '+∠A EA '=360°同理, ∠A=∠∴2∠A+∠A DA '+∠A EA '=360°∵∠BDA=∠CEA=180∴∠1+∠A DA '+∠A EA '+∠2=360°∴122A ∠+∠=∠ ；（3）数量关系:理由：如下图, 连接由（1）可知: ∠1=2∠ , ∠2=2∠∴212()2EAA DAA DAE ∠-∠=∠-=∠'∠'；（4）由折叠性质知: ∠2=180°－2∠AEF, ∠1=180°－2∠BFE相加得： .【点睛】本题考查角度之间的关系, （4）问的解题思路是相同的, 主要运用三角形的内角和定理和四边形的内角和定理进行角度转换.11. （1）29；（2）64.【分析】（1）根据完全平方公式得到 , 然后整体代入计算即可；（2）根据完全平方公式得到 , 然后整体代入计算即可．【详解】解: （1）；（2） .【点睛】本题考查了代数式求值, 完全平方公式和整体代入的思想, 熟练掌握完全平方公式是解题的关键.12. (1)见解析； (2) 见解析；(3) 4.【解析】【分析】（1）根据图形平移的性质画出△A′B′C′即可；（2）先取AB 的中点D, 再连接CD 即可；过点C 作CD ⊥AB 交AB 的延长线于点E, CE 即为所求；（3）利用割补法计算△ABC 的面积.【详解】（1）如图所示:(2)如图所示；（3）S△BCD=20-5-1-10=4.13. （1）3, 0, ﹣2；（2）a+b＝c, 理由见解析.【分析】（1）直接根据新定义求解即可；（2）先根据新定义得出关于a, b, c的等式, 然后根据幂的运算法则求解即可.【详解】（1）∵33＝27,∴（3, 27）＝3,∵40＝1,∴（4, 1）＝0,∵2﹣2＝,∴（2, 0. 25）＝﹣2.故答案为: 3, 0, ﹣2；（2）a+b＝c.理由: ∵（3, 5）＝a, （3, 6）＝b, （3, 30）＝c,∴3a＝5, 3b＝6, 3c＝30,∴3a×3b＝5×6＝3c＝30,∴3a×3b＝3c,∴a+b＝c.【点睛】本题考查了新定义运算, 明确新定义的运算方法是解答本题的关键, 本题也考查了有理数的乘方、同底数幂的乘法运算.14．4xy﹣8y2, ﹣20【分析】先根据整式的乘法法则和乘法公式算乘法, 再合并同类项, 最后代入求出即可.【详解】（x﹣2y）（x＋2y）﹣（x﹣2y）2＝x2﹣4y2﹣（x2﹣4xy＋4y2）＝x2﹣4y2﹣x2＋4xy﹣4y2＝4xy﹣8y2,当x＝3, y＝﹣1时,原式＝4×3×（﹣1）﹣8×（﹣1）2＝﹣20.【点睛】本题考查整式的化简求值, 涉及平方差公式、完全平方公式、合并同类项等知识, 熟练掌握整式的乘法运算法则和乘法公式的运用是解答的关键.15. （1）3；（2）31；（3）25.【分析】（1）把多项式乘积展开, 再将已知代入, 即可求解；（2）根据（1）得到 , 再利用完全平方公式, 即可求解；（3）根据将用来表示, 再代入 , 合并同类项即可求解．【详解】解: （1）∵ , 而 ,∴ ()=324=3254=3xy x y -++--+⨯-．故答案为 .（2）由（1）知 ,∴ ()22224=2=523=31x xy y x y xy +++++⨯．故答案为 .（3）∵ , 得 ,则()()22225=55525105525x xy y y y y y y y y y y ++-+-+=-++-+=．故答案为 .【点睛】本题目考查整式的乘法, 难度一般, 是常考知识点, 熟练掌握代数式之间的转化是顺利解题的关键.16．（1）m(1, n(5；（2）（a(2b ）2(a2(4ab(4b2；（3）2a2(5ab(3b2((a(b)(2a(3b), 详见解析【分析】（1）结合图形和条件分析可以得出按裁法二裁剪时, 可以裁出B 型板1块, 按裁法三裁剪时, 可以裁出5块B 型板；（2）看图即可得出所求的式子；（3）通过画图能更好的理解题意, 从而得出结果. 由于构成的是长方形, 它的面积等于所给图片的面积之和, 从而因式分解.【详解】（1）按裁法二裁剪时, 2块A 型板材块的长为120cm, 150-120=30, 所以可裁出B 型板1块, 按裁法三裁剪时, 全部裁出B 型板, 150÷30=5, 所以可裁出5块B 型板； ∴m=1, n=5.故答案为：1, 5；（2）如下图:发现的等式为: （a(2b ）2(a2(4ab(4b2；故答案为: （a(2b ）2(a2(4ab(4b2.（3）按题意画图如下:∵构成的长方形面积等于所给图片的面积之和,∴2a 2+5ab +3b 2=(a +b )(2a +3b ).【点睛】本题考查了完全平方公式和几何图形的应用及一元一次方程的应用, 关键是根据学生的画图能力, 计算能力来解答.17．149299a b ⎧=⎪⎪⎨⎪=⎪⎩【分析】因为两个方程组有相同的解, 故只需把两个方程组中不含未知数和含未知数的方程分别组成方程组, 求出未知数的值, 再代入另一组方程组即可.【详解】354526x y ax by -=⎧⎨+=-⎩①③ 和2348x y ax by +=-⎧⎨-=⎩②④ 解: 联立①②得:解得：12x y =⎧⎨=-⎩将代入③④得: 解得：149299a b ⎧=⎪⎪⎨⎪=⎪⎩【点睛】此题考查了二元一次方程组的解, 方程组的解即为能使方程组中两方程都成立的未知数的值.18. （1）2；（2）7a4+4a6+a2；（3）15x+19；（4）4x2+4xy+y2﹣4【分析】（1）首先利用负整数指数幂的性质、零次幂的性质、绝对值的性质进行计算, 再算加减即可；（2）首先利用积的乘方的计算法则、单项式乘以单项式计算法则计算, 再合并同类项即可；（3）首先利用完全平方公式、多项式乘以多项式计算法则计算, 再合并同类项即可；（4）首先利用平方差计算, 再利用完全平方公式进行计算即可．【详解】解: （1）原式＝8﹣1﹣5＝2；（2）原式＝9a4﹣2a4+4a6+a2,＝7a4+4a6+a2；（3）原式＝x2+10x+25﹣（x2﹣3x﹣2x+6）,＝x2+10x+25﹣x2+3x+2x﹣6,＝15x+19；（4）原式＝（2x+y）2﹣4,＝4x2+4xy+y2﹣4.【点睛】本题考查的是实数的运算, 幂的运算及合并同类项, 整式的混合运算, 掌握以上知识点是解题的关键.19. （1）；（2）或；（3）1或2.【分析】（1）根据题意直接利用加减消元法进行计算求解即可；（2）由题意根据和以及（n为整数）得到三个关于k的方程, 求出k即可；（3）根据题意用含m的代数式表示出k, 根据, 确定m的取值范围, 由m为正整数, 求得m的值即可．【详解】解: （1）,①+②得: , 解得: ,①-②得：, 解得：,∴二元一次方程组的解为: .（2）∵, ,∴, 即, 解得: ；∵, ,∴, 即, 解得: ；∵（n为正整数）, ,∴为偶数, 即, 解得: ；当时, , 为奇数, 不合题意, 故舍去．综上52k=或12k=-.（3）∵, 即,∴2114mk-=，∵14k≤，∴, 解得,∵m为正整数,∴m=1或2.【点睛】本题考查解二元一次方程组以及解一元一次不等式, 根据题意列出不等式是解题的关键.20. （1）（2）【分析】（1）运用加减消元法先消除x, 求y的值后代入方程②求x得解；（2）先分别解每个不等式, 然后求公共部分, 确定不等式组的解集．【详解】解: （1）①×2-②, 得 7y=7,∴y=1.把y=1代入②, 得 x=2．∴21 xy=⎧⎨=⎩．（2）解不等式得.解不等式得.∴不等式组的解集为.【点睛】此题考查解方程组和不等式组, 属常规基础题, 难度不大．。

2024年人教版中学七7年级下册数学期末解答题压轴题卷含答案

2024年人教版中学七7年级下册数学期末解答题压轴题卷含答案一、解答题1．如图，在99网格中，每个小正方形的边长均为1，正方形ABCD的顶点都在网格的格点上．（1）求正方形ABCD的面积和边长；（2）建立适当的平面直角坐标系，写出正方形四个顶点的坐标．2．如图是一块正方形纸片．（1）如图1，若正方形纸片的面积为1dm2，则此正方形的对角线AC的长为dm．（2）若一圆的面积与这个正方形的面积都是2πcm2，设圆的周长为C圆，正方形的周长为C正，则C圆C正(填“＝”或“＜”或“＞”号)（3）如图2，若正方形的面积为16cm2，李明同学想沿这块正方形边的方向裁出一块面积为12cm2的长方形纸片，使它的长和宽之比为3：2，他能裁出吗？请说明理由？3．如图，用两个边长为103的小正方形拼成一个大的正方形.(1)求大正方形的边长？(2)若沿此大正方形边的方向出一个长方形，能否使裁出的长方形的长宽之比为3:2，且面积为480cm2？4．如图，纸上有五个边长为1的小正方形组成的图形纸，我们可以把它剪开拼成一个正方形．（1）拼成的正方形的面积与边长分别是多少？（2）如图所示，以数轴的单位长度的线段为边作一个直角三角形，以数轴的-1点为圆心，直角三角形的最大边为半径画弧，交数轴正半轴于点A ，那么点A 表示的数是多少？点A 表示的数的相反数是多少？（3）你能把十个小正方形组成的图形纸，剪开并拼成正方形吗？若能，请画出示意图，并求它的边长5．如图用两个边长为18cm 的小正方形纸片拼成一个大的正方形纸片，沿着大正方形纸片的边的方向截出一个长方形纸片，能否使截得的长方形纸片长宽之比为3:2，且面积为30cm 2请说明理由．二、解答题6．如图①，将一张长方形纸片沿EF 对折，使AB 落在''A B 的位置；（1）若1∠的度数为a ，试求2∠的度数（用含a 的代数式表示）；（2）如图②，再将纸片沿GH 对折，使得CD 落在''C D 的位置．①若//'EF C G ，1∠的度数为a ，试求3∠的度数（用含a 的代数式表示）； ②若''B F C G ⊥，3∠的度数比1∠的度数大20︒，试计算1∠的度数．7．如图1，点A 在直线MN 上，点B 在直线ST 上，点C 在MN ，ST 之间，且满足MAC ACB SBC ∠+∠+∠360=︒．（1）证明：//MN ST ；（2）如图2，若60ACB ∠=︒，//AD CB ，点E 在线段BC 上，连接AE ，且2DAE CBT ∠=∠，试判断CAE ∠与CAN ∠的数量关系，并说明理由；（3）如图3，若180ACB n︒∠=（n 为大于等于2的整数），点E 在线段BC 上，连接AE ，若MAE n CBT ∠=∠，则:CAE CAN ∠∠=______．8．综合与实践课上，同学们以“一个直角三角形和两条平行线”为背景开展数学活动，如图，已知两直线,a b ，且,a b ABC //是直角三角形，90BCA ∠=︒，操作发现：（1）如图1．若148∠=︒，求2∠的度数；（2）如图2，若30,1A ∠=︒∠的度数不确定，同学们把直线a 向上平移，并把2∠的位置改变，发现21120∠-∠=︒，请说明理由．（3）如图3，若∠A =30°，AC 平分BAM ∠，此时发现1∠与2∠又存在新的数量关系，请写出1∠与2∠的数量关系并说明理由．9．（1）（问题）如图1，若//AB CD ，40AEP ∠=︒，130PFD ∠=︒．求EPF ∠的度数；（2）（问题迁移）如图2，//AB CD ，点P 在AB 的上方，问PEA ∠，PFC ∠，EPF ∠之间有何数量关系？请说明理由；（3）（联想拓展）如图3所示，在（2）的条件下，已知EPF α∠=，PEA ∠的平分线和PFC ∠的平分线交于点G ，用含有α的式子表示G ∠的度数．10．如图，直线//PQ MN ，点C 是PQ 、MN 之间（不在直线PQ ，MN 上）的一个动点．（1）如图1，若1∠与2∠都是锐角，请写出C ∠与1∠，2∠之间的数量关系并说明理由；（2）把直角三角形ABC 如图2摆放，直角顶点C 在两条平行线之间，CB 与PQ 交于点D ，CA 与MN 交于点E ，BA 与PQ 交于点F ，点G 在线段CE 上，连接DG ，有BDF GDF ∠=∠，求AENCDG∠∠的值；（3）如图3，若点D 是MN 下方一点，BC 平分PBD ∠， AM 平分CAD ∠，已知25PBC ∠=︒，求ACB ADB ∠+∠的度数．三、解答题11．为更好地理清平行线相关角的关系，小明爸爸为他准备了四根细直木条AB 、BC 、CD 、DE ，做成折线ABCDE ，如图1，且在折点B 、C 、D 处均可自由转出．（1）如图2，小明将折线调节成50B ∠=︒，85C ∠=︒，35D ∠=︒，判断AB 是否平行于ED ，并说明理由；（2）如图3，若35C D ∠=∠=︒，调整线段AB 、BC 使得//AB CD 求出此时B 的度数，要求画出图形，并写出计算过程．（3）若85C ∠=︒，35D ∠=︒，//AB DE ，请直接写出此时B 的度数． 12．如图1，E 点在BC 上，∠A ＝∠D ，AB ∥CD ．（1）直接写出∠ACB 和∠BED 的数量关系；（2）如图2，BG 平分∠ABE ，与∠CDE 的邻补角∠EDF 的平分线交于H 点．若∠E 比∠H 大60°，求∠E ；（3）保持（2）中所求的∠E 不变，如图3，BM 平分∠ABE 的邻补角∠EBK ，DN 平分∠CDE ，作BP ∥DN ，则∠PBM 的度数是否改变？若不变，请求值；若改变，请说理由．13．如图1，//AB CD ，E 是AB 、CD 之间的一点．（1）判定BAE ∠，CDE ∠与AED ∠之间的数量关系，并证明你的结论；（2）如图2，若BAE ∠、CDE ∠的两条平分线交于点F ．直接写出AFD ∠与AED ∠之间的数量关系；（3）将图2中的射线DC 沿DE 翻折交AF 于点G 得图3，若AGD ∠的余角等于2E ∠的补角，求BAE ∠的大小．14．如图，//AC BD ，BC 平分ABD ∠，设ACB ∠为α，点E 是射线BC 上的一个动点．（1）若30α=︒时，且BAE CAE ∠=∠，求CAE ∠的度数；（2）若点E 运动到1l 上方，且满足100BAE ∠=︒，:5:1BAE CAE ∠∠=，求α的值；（3）若:()1BAE CAE n n ∠∠=>，求CAE ∠的度数（用含n 和α的代数式表示）． 15．已知：ABC 和同一平面内的点D ．（1）如图1，点D 在BC 边上，过D 作//DE BA 交AC 于E ，//DF CA 交AB 于F ．根据题意，在图1中补全图形，请写出EDF ∠与BAC ∠的数量关系，并说明理由；（2）如图2，点D 在BC 的延长线上，//DF CA ，EDF BAC ∠=∠．请判断DE 与BA 的位置关系，并说明理由．（3）如图3，点D 是ABC 外部的一个动点．过D 作//DE BA 交直线AC 于E ，//DF CA 交直线AB 于F ，直接写出EDF ∠与BAC ∠的数量关系，并在图3中补全图形．四、解答题16．（1）如图1，∠BAD 的平分线AE 与∠BCD 的平分线CE 交于点E ，AB ∥CD ，∠ADC =50°，∠ABC =40°，求∠AEC 的度数；（2）如图2，∠BAD的平分线AE与∠BCD的平分线CE交于点E，∠ADC=α°，∠ABC=β°，求∠AEC的度数；（3）如图3，PQ⊥MN于点O，点A是平面内一点，AB、AC交MN于B、C两点，AD平分∠BAC交PQ于点D，请问ADPACB ABC∠∠-∠的值是否发生变化？若不变，求出其值；若改变，请说明理由．17．模型与应用.（模型）（1）如图①，已知AB∥CD，求证∠1＋∠MEN＋∠2＝360°.（应用）（2）如图②，已知AB∥CD，则∠1+∠2+∠3+∠4+∠5+∠6的度数为．如图③，已知AB∥CD，则∠1+∠2+∠3+∠4+∠5+∠6＋…＋∠n的度数为．（3）如图④，已知AB∥CD，∠AM1M2的角平分线M1 O与∠CM n M n－1的角平分线M n O交于点O，若∠M1OM n＝m°．在（2）的基础上，求∠2+∠3+∠4+∠5+∠6＋……＋∠n－1的度数．（用含m、n的代数式表示）18．操作示例：如图1，在△ABC中，AD为BC边上的中线，△ABD的面积记为S1，△ADC 的面积记为S2．则S1=S2．解决问题：在图2中，点D、E分别是边AB、BC的中点，若△BDE的面积为2，则四边形ADEC的面积为 .拓展延伸：（1）如图3，在△ABC中，点D在边BC上，且BD=2CD，△ABD的面积记为S1，△ADC的面积记为S2．则S1与S2之间的数量关系为．（2）如图4，在△ABC中，点D、E分别在边AB、AC上，连接BE、CD交于点O，且BO=2EO，CO=DO，若△BOC的面积为3，则四边形ADOE的面积为 .19．Rt△ABC中，∠C=90°，点D、E分别是△ABC边AC、BC上的点，点P是一动点.令∠PDA=∠1，∠PEB=∠2，∠DPE=∠α.（1）若点P在线段AB上，如图（1）所示，且∠α=50°，则∠1+∠2=°；（2）若点P在边AB上运动，如图（2）所示，则∠α、∠1、∠2之间的关系为：；（3）若点P 运动到边AB 的延长线上，如图（3）所示，则∠α、∠1、∠2之间有何关系？猜想并说明理由.（4）若点P 运动到△ABC 形外，如图（4）所示，则∠α、∠1、∠2之间的关系为： . 20．已知AB //CD ，点E 是平面内一点，∠CDE 的角平分线与∠ABE 的角平分线交于点F ．（1）若点E 的位置如图1所示．①若∠ABE =60°，∠CDE =80°，则∠F = °； ②探究∠F 与∠BED 的数量关系并证明你的结论；（2）若点E 的位置如图2所示，∠F 与∠BED 满足的数量关系式是．（3）若点E 的位置如图3所示，∠CDE 为锐角，且1452E F ∠≥∠+︒，设∠F =α，则α的取值范围为．【参考答案】一、解答题1．（1）面积为29，边长为；（2），，，，图见解析．【分析】（1）面积等于一个大正方形的面积减去四个直角三角形的面积，再利用算术平方根定义求得边长即可；（2）建立适当的坐标系后写出四个顶点的坐标解析：（1）面积为29292）(0,5)A ，(2,0)B ，(7,2)C ，(5,7)D ，图见解析．【分析】（1）面积等于一个77⨯大正方形的面积减去四个直角三角形的面积，再利用算术平方根定义求得边长即可；（2）建立适当的坐标系后写出四个顶点的坐标即可．【详解】解：（1）正方形的面积217425292ABCD S =-⨯⨯⨯=正方形，正方形边长为29S =；（2）建立如图平面直角坐标系，则(0,5)A ，(2,0)B ，(7,2)C ，(5,7)D ．【点睛】本题考查了算术平方根及坐标与图形的性质及割补法求面积，从图形中整理出直角三角形是进一步解题的关键．2．（1）；（2）＜；（3）不能；理由见解析．【分析】（1）由正方形面积，易求得正方形边长，再由勾股定理求对角线长；（2）由圆面积公式，和正方形面积可求周长，比较两数大小可以采用比商法；（3）采解析：（122）＜；（3）不能；理由见解析．【分析】（1）由正方形面积，易求得正方形边长，再由勾股定理求对角线长；（2）由圆面积公式，和正方形面积可求周长，比较两数大小可以采用比商法；（3）采用方程思想求出长方形的长边，与正方形边长比较大小即可. 【详解】解：（1）由已知AB 2＝1，则AB ＝1，由勾股定理，AC 2； 2（22，周长为222π．221424C C ππππ<圆正；即C 圆<C 正；故答案为：＜（3）不能；由已知设长方形长和宽为3xcm和2xcm∴长方形面积为：2x•3x＝12解得x∴长方形长边为＞4∴他不能裁出．【点睛】本题主要考查了算术平方根在正方形、圆、长方形面积中的应用，灵活的进行算术平方根的计算与无理数大小比较是解题的关键.3．（1）大正方形的边长是；（2）不能【分析】（1）根据已知正方形的面积求出大正方形的面积，即可求出边长；（2）先求出长方形的边长，再判断即可．【详解】（1）大正方形的边长是（2）设长方形纸解析：（1）大正方形的边长是2）不能【分析】（1）根据已知正方形的面积求出大正方形的面积，即可求出边长；（2）先求出长方形的边长，再判断即可．【详解】（1）大正方形的边长是（2）设长方形纸片的长为3xcm，宽为2xcm，则3x•2x=480，解得：因为片的长宽之比为2：3，且面积为480cm2．【点睛】本题考查算术平方根，解题的关键是能根据题意列出算式．4．（1）5；；（2）；；（3）能，．【分析】（1）易得5个小正方形的面积的和，那么就得到了大正方形的面积，求得面积的算术平方根即可为大正方形的边长．（2）求出斜边长即可．（3）一共有10个小正解析：（1）521；13（1）易得5个小正方形的面积的和，那么就得到了大正方形的面积，求得面积的算术平方根即可为大正方形的边长．（2）求出斜边长即可．（3）一共有10个小正方形，那么组成的大正方形的面积为10，边长为10的算术平方根，画图．【详解】试题分析：解：（1）拼成的正方形的面积与原面积相等1×1×5=5，边长为5，如图（1）（2）斜边长=222222+=，故点A表示的数为：222-；点A表示的相反数为：222-（3）能，如图拼成的正方形的面积与原面积相等1×1×10=1010考点：1．作图—应用与设计作图；2．图形的剪拼．5．不能截得长宽之比为，且面积为cm2的长方形纸片，见解析【分析】根据拼图求出大正方形的边长，再根据长方形的长、宽之比为3：2，计算长方形的长与宽进行验证即可．【详解】解：不能，因为大正方形纸解析：不能截得长宽之比为3:2，且面积为30cm2的长方形纸片，见解析【分析】根据拼图求出大正方形的边长，再根据长方形的长、宽之比为3：2，计算长方形的长与宽进行验证即可．解：不能，2+2=36（cm 2），所以大正方形的边长为6cm ，设截出的长方形的长为3b cm ，宽为2b cm ，则6b 2=30，所以b所以3b所以不能截得长宽之比为3：2，且面积为30cm 2的长方形纸片．【点睛】本题考查了算术平方根，理解算术平方根的意义是正确解答的关键．二、解答题6．（1）；（2）① ；②【分析】(1)由平行线的性质得到，由折叠的性质可知，∠2=∠BFE ，再根据平角的定义求解即可；(2) ①由（1）知，，根据平行线的性质得到，再由折叠的性质及平角的定义解析：（1）1902a ︒- ；（2）①1454a ︒+ ；②50︒ 【分析】(1)由平行线的性质得到4'B FC a ∠=∠=，由折叠的性质可知，∠2=∠BFE ，再根据平角的定义求解即可；(2) ①由（1）知，1902BFE a ∠=︒-，根据平行线的性质得到1BFE C'GB 902a ∠=∠=︒- ，再由折叠的性质及平角的定义求解即可；②由（1）知，∠BFE = 19012EFB '∠=︒-∠，由''B F C G ⊥可知：''90B FC FGC ∠+∠=︒，再根据条件和折叠的性质得到''11402190B FC FGC +=∠+∠=∠︒-∠︒，即可求解．【详解】解：（1）如图，由题意可知'//'A E B F ，∴14a ∠=∠=，∵//AD BC ，∴4'B FC a ∠=∠=，180BFB a '∴∠=︒-，∴由折叠可知1129022BFE BFB a '∠=∠=∠=︒-．（2）①由题（1）可知1902BFE a ∠=︒- ， ∵//'EF C G ，1902BFE C'GB a ∴∠=∠=︒-，再由折叠可知：113180*********HGC C GB a a ⎛⎫∠+∠=︒-∠=︒-︒-=︒+ ⎪⎝⎭'， 13454HGC a ∴∠=∠=︒+；②由''B F C G ⊥可知：''90B FC FGC ∠+∠=︒，由（1）知19012BFE ∠=︒-∠， 11802180290112B FC BFE ⎛⎫'∴∠=︒-∠=︒-︒-∠=∠ ⎪⎝⎭，又3∠的度数比1∠的度数大20︒，∴3=1+20∠∠︒，()18023180212014021FGC '∴∠=︒-∠=︒-∠+︒=︒-∠，''11402190B FC FGC +=∴∠+∠=∠︒-∠︒，1=50∴∠︒．【点睛】此题考查了平行线的性质，属于综合题，有一定难度，熟记“两直线平行，同位角相等”、“两直线平行，内错角相等”及折叠的性质是解题的关键．7．（1）见解析；（2）见解析；（3）n-1【分析】（1）连接AB ，根据已知证明∠MAB+∠SBA=180°，即可得证；（2）作CF ∥ST ，设∠CBT=α，表示出∠CAN ，∠ACF ，∠BCF ，根据解析：（1）见解析；（2）见解析；（3）n -1【分析】（1）连接AB ，根据已知证明∠MAB +∠SBA =180°，即可得证；（2）作CF ∥ST ，设∠CBT =α，表示出∠CAN ，∠ACF ，∠BCF ，根据AD ∥BC ，得到∠DAC =120°，求出∠CAE 即可得到结论；（3）作CF ∥ST ，设∠CBT =β，得到∠CBT =∠BCF =β，分别表示出∠CAN 和∠CAE ，即可得到比值．【详解】解：（1）如图，连接AB ，，360MAC ACB SBC ∠+∠+∠=︒，180ACB ABC BAC ∠+∠+∠=︒，180MAB SBA ∴∠+∠=︒，//MN ST ∴（2）2CAE CAN ∠=∠，理由：作//CF ST ，则////,MN CF ST 如图，设CBT α∠=，则2DAE α∠=．BCF CBT α∠=∠=，60CAN ACF α∠=∠=︒-，//AD BC ，180120DAC ACB ∠=︒-∠=︒，12012022(60)2CAE DAE CAN αα∴∠=︒-∠=︒-=︒-=∠．即2CAE CAN ∠=∠．（3）作//CF ST ，则////,MN CF ST 如图，设CBT β∠=，则MAE n β∠=．//CF ST ，CBT BCF β∴∠=∠=，180180n ACF CAN n nββ︒︒-∠=∠=-=， 1801180180(180)n CAE MAE CAN n n n n βββ︒-∠=︒-∠-∠=︒--+=︒-， 11::1n CAE CAN n n n-∠∠==-，故答案为1n -．【点睛】本题主要考查平行线的性质和判定，解题关键是角度的灵活转换，构建数量关系式． 8．（1）42°；（2）见解析；（3）∠1=∠2，理由见解析【分析】（1）由平角定义求出∠3=42°，再由平行线的性质即可得出答案；（2）过点B 作BD ∥a ．由平行线的性质得∠2+∠ABD=180°解析：（1）42°；（2）见解析；（3）∠1=∠2，理由见解析【分析】（1）由平角定义求出∠3=42°，再由平行线的性质即可得出答案；（2）过点B 作BD ∥a ．由平行线的性质得∠2+∠ABD =180°，∠1=∠DBC ，则∠ABD =∠ABC -∠DBC =60°-∠1，进而得出结论；（3）过点C 作CP ∥a ，由角平分线定义得∠CAM =∠BAC =30°，∠BAM =2∠BAC =60°，由平行线的性质得∠1=∠BAM =60°，∠PCA =∠CAM =30°，∠2=∠BCP =60°，即可得出结论．【详解】解：（1）∵∠1=48°，∠BCA =90°，∴∠3=180°-∠BCA -∠1=180°-90°-48°=42°，∵a ∥b ，∴∠2=∠3=42°；（2）理由如下：过点B 作BD ∥a ．如图2所示：则∠2+∠ABD =180°，∵a ∥b ，∴b ∥BD ，∴∠1=∠DBC ，∴∠ABD =∠ABC -∠DBC =60°-∠1，∴∠2+60°-∠1=180°，（3）∠1=∠2，理由如下：过点C作CP∥a，如图3所示：∵AC平分∠BAM∴∠CAM=∠BAC=30°，∠BAM=2∠BAC=60°，又∵a∥b，∴CP∥b，∠1=∠BAM=60°，∴∠PCA=∠CAM=30°，∴∠BCP=∠BCA-∠PCA=90°-30°=60°，又∵CP∥a，∴∠2=∠BCP=60°，∴∠1=∠2．【点睛】本题是三角形综合题目，考查了平移的性质、直角三角形的性质、平行线的判定与性质、角平分线定义、平角的定义等知识；本题综合性强，熟练掌握平移的性质和平行线的性质是解题的关键．9．（1）90°；（2）∠PFC=∠PEA+∠P；（3）∠G=α【分析】（1）根据平行线的性质与判定可求解；（2）过P点作PN∥AB，则PN∥CD，可得∠FPN=∠PEA+∠FPE，进而可得∠PF 解析：（1）90°；（2）∠PFC=∠PEA+∠P；（3）∠G=12α【分析】（1）根据平行线的性质与判定可求解；（2）过P点作PN∥AB，则PN∥CD，可得∠FPN=∠PEA+∠FPE，进而可得∠PFC=∠PEA+∠FPE，即可求解；（3）令AB与PF交点为O，连接EF，根据三角形的内角和定理可得∠GEF+∠GFE＝1 2∠PEA+12∠PFC+∠OEF+∠OFE，由（2）得∠PEA=∠PFC-α，由∠OFE+∠OEF=180°-∠FOE=180°-∠PFC可求解．【详解】解：（1）如图1，过点P作PM∥AB，又∠AEP=40°，∴∠1=40°．∵AB∥CD，∴PM∥CD，∴∠2+∠PFD=180°．∵∠PFD=130°，∴∠2=180°-130°=50°．∴∠1+∠2=40°+50°=90°．即∠EPF=90°．（2）∠PFC=∠PEA+∠P．理由：过P点作PN∥AB，则PN∥CD，∴∠PEA=∠NPE，∵∠FPN=∠NPE+∠FPE，∴∠FPN=∠PEA+∠FPE，∵PN∥CD，∴∠FPN=∠PFC，∴∠PFC=∠PEA+∠FPE，即∠PFC=∠PEA+∠P；（3）令AB与PF交点为O，连接EF，如图3．在△GFE中，∠G=180°-（∠GFE+∠GEF），∵∠GEF＝12∠PEA+∠OEF，∠GFE＝12∠PFC+∠OFE，∴∠GEF+∠GFE＝12∠PEA+12∠PFC+∠OEF+∠OFE，∵由（2）知∠PFC=∠PEA+∠P，∴∠PEA=∠PFC-α，∵∠OFE+∠OEF=180°-∠FOE=180°-∠PFC，∴∠GEF+∠GFE＝12(∠PFC−α)+12∠PFC+180°−∠PFC＝180°−12α，∴∠G＝180°−(∠GEF+∠GFE)＝180°−180°+12α＝12α．【点睛】本题主要考查平行线的性质与判定，灵活运用平行线的性质与判定是解题的关键．10．（1）见解析；（2）；（3）75°【分析】（1）根据平行线的性质、余角和补角的性质即可求解．（2）根据平行线的性质、对顶角的性质和平角的定义解答即可．（3）根据平行线的性质和角平分线的定义以解析：（1）见解析；（2）12；（3）75°【分析】（1）根据平行线的性质、余角和补角的性质即可求解．（2）根据平行线的性质、对顶角的性质和平角的定义解答即可．（3）根据平行线的性质和角平分线的定义以及三角形内角和解答即可．【详解】解：（1）∠C=∠1+∠2，证明：过C作l∥MN，如下图所示，∵l∥MN，∴∠4=∠2（两直线平行，内错角相等），∵l∥MN，PQ∥MN，∴l∥PQ，∴∠3=∠1（两直线平行，内错角相等），∴∠3+∠4=∠1+∠2，∴∠C=∠1+∠2；（2）∵∠BDF=∠GDF，∵∠BDF=∠PDC，∴∠GDF=∠PDC，∵∠PDC+∠CDG+∠GDF=180°，∴∠CDG+2∠PDC=180°，∴∠PDC=90°-12∠CDG，由（1）可得，∠PDC+∠CEM=∠C=90°，∴∠AEN=∠CEM，∴190(90)90122CDGAEN CEM PDCCDG CDG CDG CDG︒-︒-∠∠∠︒-∠====∠∠∠∠，（3）设BD交MN于J．∵BC平分∠PBD，AM平分∠CAD，∠PBC=25°，∴∠PBD=2∠PBC=50°，∠CAM=∠MAD，∵PQ∥MN，∴∠BJA=∠PBD=50°，∴∠ADB=∠AJB-∠JAD=50°-∠JAD=50°-∠CAM，由（1）可得，∠ACB=∠PBC+∠CAM，∴∠ACB+∠ADB=∠PBC+∠CAM+50°-∠CAM=25°+50°=75°．【点睛】本题考查了平行线的性质、余角和补角的性质，解题的关键是根据平行找出角度之间的关系．三、解答题11．（1）平行，理由见解析；（2）35°或145°，画图、过程见解析；（3）50°或130°或60°或120°【分析】（1）过点C作CF∥AB，根据∠B=50°，∠C=85°，∠D=35°，即可得C解析：（1）平行，理由见解析；（2）35°或145°，画图、过程见解析；（3）50°或130°或60°或120°【分析】（1）过点C作CF∥AB，根据∠B=50°，∠C=85°，∠D=35°，即可得CF∥ED，进而可以判断AB平行于ED；（2）根据题意作AB∥CD，即可∠B=∠C=35°；（3）分别画图，根据平行线的性质计算出∠B的度数．【详解】解：（1）AB平行于ED，理由如下：如图2，过点C作CF∥AB，∴∠BCF=∠B=50°，∵∠BCD=85°，∴∠FCD=85°-50°=35°，∵∠D=35°，∴∠FCD=∠D，∴CF∥ED，∵CF∥AB，∴AB∥ED；（2）如图，即为所求作的图形．∵AB∥CD，∴∠ABC=∠C=35°，∴∠B的度数为：35°；∵A′B∥CD，∴∠ABC+∠C=180°，∴∠B的度数为：145°；∴∠B的度数为：35°或145°；（3）如图2，过点C作CF∥AB，∵AB∥DE，∴CF∥DE，∴∠FCD=∠D=35°，∵∠BCD=85°，∴∠BCF=85°-35°=50°，∴∠B=∠BCF=50°．答：∠B的度数为50°．如图5，过C作CF∥AB，则AB∥CF∥CD，∴∠FCD=∠D=35°，∵∠BCD=85°，∴∠BCF=85°-35°=50°，∵AB∥CF，∴∠B+∠BCF=180°，∴∠B=130°；如图6，∵∠C=85°，∠D=35°，∴∠CFD=180°-85°-35°=60°，∵AB∥DE，∴∠B=∠CFD=60°，如图7，同理得：∠B=35°+85°=120°，综上所述，∠B的度数为50°或130°或60°或120°．【点睛】本题考查了平行线的判定与性质，解决本题的关键是区分平行线的判定与性质，并熟练运用．12．（1）∠ACB+∠BED=180°；（2）100°；（3）40°【分析】（1）如图1，延长DE 交AB 于点F ，根据ABCD 可得∠DFB=∠D ，则∠DFB=∠A ，可得ACDF ，根据平行线的性质得∠A解析：（1）∠ACB +∠BED =180°；（2）100°；（3）40°【分析】（1）如图1，延长DE 交AB 于点F ，根据AB //CD 可得∠DFB =∠D ，则∠DFB =∠A ，可得AC //DF ，根据平行线的性质得∠ACB +∠CEF =180°，由对顶角相等可得结论；（2）如图2，作EM //CD ，HN //CD ，根据AB //CD ，可得AB //EM //HN //CD ，根据平行线的性质得角之间的关系，再根据∠DEB 比∠DHB 大60°，列出等式即可求∠DEB 的度数；（3）如图3，过点E 作ES //CD ，设直线DF 和直线BP 相交于点G ，根据平行线的性质和角平分线定义可求∠PBM 的度数．【详解】解：（1）如图1，延长DE 交AB 于点F ，//AB CD ，DFB D ∴∠=∠，A D ∠=∠，A DFB ∴∠=∠，//AC DF ∴，180ACB CEF ∴∠+∠=︒，180ACB BED ∴∠+∠=︒，故答案为：180ACB BED ∠+∠=︒；（2）如图2，作//EM CD ，//HN CD ，//AB CD ，//////AB EM HN CD ∴，1180EDF ∴∠+∠=︒，MEB ABE ∠=∠， BG 平分ABE ∠，12ABG ABE ∴∠=∠， //AB HN ，//CF HN ，23β∴∠+∠=∠， ∴132ABE β∠+∠=∠， DH 平分EDF ∠，132EDF ∴∠=∠， ∴1122ABE EDF β∠+∠=∠，1()2EDF ABE β∴∠=∠-∠， 2EDF ABE β∴∠-∠=∠，设DEB α∠=∠，1180180()1802MEB EDF ABE EDF ABE αβ∠=∠+∠=︒-∠+∠=︒-∠-∠=︒-∠，DEB ∠比DHB ∠大60︒，60αβ∴∠-︒=∠，1802(60)αα∴∠=︒-∠-︒，解得100α∠=︒．DEB ∴∠的度数为100︒；（3）PBM ∠的度数不变，理由如下：如图3，过点E 作//ES CD ，设直线DF 和直线BP 相交于点G ，BM 平分EBK ∠，DN 平分CDE ∠，12EBM MBK EBK ∴∠=∠=∠， 12CDN EDN CDE ∠=∠=∠， //ES CD ，//AB CD ，////ES AB CD ∴，DES CDE ∴∠=∠，180BES ABE EBK ∠=∠=︒-∠，G PBK ∠=∠，由（2）可知：100DEB ∠=︒，180100CDE EBK ∴∠+︒-∠=︒，80EBK CDE ∴∠-∠=︒，//BP DN ，12PBK G CDN CDE ∴∠=∠=∠=∠， PBM MBK PBK ∴∠=∠-∠1122EBK CDE =∠-∠ 1()2EBK CDE =∠-∠ 1802=⨯︒ 40=︒．【点睛】本题考查了平行线的性质，解决本题的关键是掌握平行线的性质．13．（1），见解析；（2）；（3）60°【分析】（1）作EF//AB ，如图1，则EF//CD ，利用平行线的性质得∠1＝∠BAE ，∠2＝∠CDE ，从而得到∠BAE ＋∠CDE ＝∠AED ；（2）如图2，解析：（1）BAE CDE AED ∠+∠=∠，见解析；（2）12AFD AED ∠=∠；（3）60° 【分析】（1）作EF //AB ，如图1，则EF //CD ，利用平行线的性质得∠1＝∠BAE ，∠2＝∠CDE ，从而得到∠BAE ＋∠CDE ＝∠AED ；（2）如图2，由（1）的结论得∠AFD ＝∠BAF ＋∠CDF ，根据角平分线的定义得到∠BAF ＝12∠BAE ，∠CDF ＝12∠CDE ，则∠AFD ＝12（∠BAE ＋∠CDE ），加上（1）的结论得到∠AFD ＝12∠AED ；（3）由（1）的结论得∠AGD ＝∠BAF ＋∠CDG ，利用折叠性质得∠CDG ＝4∠CDF ，再利用等量代换得到∠AGD ＝2∠AED －32∠BAE ，加上90°－∠AGD ＝180°－2∠AED ，从而可计算出∠BAE 的度数．【详解】解：（1）BAE CDE AED ∠+∠=∠理由如下：作//EF AB ，如图1，//AB CD ，//EF CD ∴．1BAE ∴∠=∠，2CDE ∠=∠，BAE CDE AED ∴∠+∠=∠；（2）如图2，由（1）的结论得AFD BAF CDF ∠=∠+∠，BAE ∠、CDE ∠的两条平分线交于点F ，12BAF BAE ∴∠=∠，12CDF CDE ∠=∠， 1()2AFD BAE CDE ∴∠=∠+∠， BAE CDE AED ∠+∠=∠，12AFD AED ∴∠=∠；（3）由（1）的结论得AGD BAF CDG ∠=∠+∠，而射线DC 沿DE 翻折交AF 于点G ，4CDG CDF ∴∠=∠，11422()22AGD BAF CDF BAE CDE BAE AED BAE ∴∠=∠+∠=∠+∠=∠+∠-∠= 322AED BAE ∠-∠， 901802AGD AED ︒-∠=︒-∠，390218022AED BAE AED ∴︒-∠+∠=︒-∠， 60BAE ∴∠=︒．【点睛】本题考查了平行线性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．14．（1）60°；（2）50°；（3）或【分析】（1）根据平行线的性质可得的度数，再根据角平分线的性质可得的度数，应用三角形内角和计算的度数，由已知条件，可计算出的度数；（2）根据题意画出图形，先解析：（1）60°；（2）50°；（3）18021n α︒--或18021n α︒-+【分析】（1）根据平行线的性质可得CBD ∠的度数，再根据角平分线的性质可得ABE 的度数，应用三角形内角和计算BAC ∠的度数，由已知条件BAE CAE ∠=∠，可计算出CAE ∠的度数；（2）根据题意画出图形，先根据:5:1BAE CAE ∠∠=可计算出CAE ∠的度数，由100BAE ∠=︒可计算出BAC ∠的度数，再根据平行线的性质和角平分线的性质，计算出CBD ∠的度数，即可得出结论；（3）根据题意可分两种情况，①若点E 运动到1l 上方，根据平行线的性质由α可计算出CBD ∠的度数，再根据角平分线的性质和平行线的性质，计算出BAC ∠的度数，再:BAE CAE n ∠∠=，BAE BAC CAE ∠=∠+∠，列出等量关系求解即可等处结论；②若点E 运动到1l 下方，根据平行线的性质由α可计算出CBD ∠的度数，再根据角平分线的性质和平行线的性质，计算出BAC ∠的度数，再:BAE CAE n ∠∠=，BAE BAC CAE ∠=∠-∠列出等量关系求解即可等处结论．【详解】解：（1）30α=︒，//AC BD ，30CBD ∴∠=︒， BC 平分ABD ∠，30ABE CBD ∴∠=∠=︒，1801803030120BAC ABE α∴∠=︒-∠-=︒-︒-︒=︒，又BAE CAE ∠=∠， 111206022CAE BAC ∴∠=∠=⨯︒=︒；（2）根据题意画图，如图1所示，100BAE ∠=︒，:5:1BAE CAE ∠∠=，20CAE ∴∠=︒，1002080BAC BAE CAE ∴∠=∠-∠=︒-︒=︒，//AC BD ，180100ABD BAC ∴∠=︒-∠=︒，又BC 平分ABD ∠，111005022CBD ABD ∴∠=∠=⨯︒=︒， 50CBD α∴=∠=︒；（3）①如图2所示，//AC BD ，CBD ACB α∴∠=∠=，BC 平分ABD ∠，22ABD CBD α∴∠=∠=，1801802BAC ABD α∴∠=︒-∠=︒-，又:BAE CAE n ∠∠=，():BAC CAE CAE n ∴∠+∠∠=，(1802):CAE CAE n α︒-+∠∠=，解得18021CAE n α︒-∠=-；②如图3所示，//AC BD ，CBD ACB α∴∠=∠=，BC 平分ABD ∠，22ABD CBD α∴∠=∠=，1801802BAC ABD α∴∠=︒-∠=︒-，又:BAE CAE n ∠∠=，():BAC CAE CAE n ∴∠-∠∠=，(1802):CAE CAE n α︒--∠∠=，解得18021CAE n α︒-∠=+．综上CAE ∠的度数为18021n α︒--或18021n α︒-+．【点睛】本题主要考查平行线的性质和角平分线的性质，两直线平行，同位角相等．两直线平行，同旁内角互补．两直线平行，内错角相等．合理应用平行线的性质是解决本题的关键． 15．（1）图见解析，，理由见解析；（2），理由见解析；（3）图见解析，或．【分析】（1）根据平行线的画法补全图形即可得，根据平行线的性质可得，由此即可得；（2）如图（见解析），先根据平行线的性质可解析：（1）图见解析，EDF BAC ∠=∠，理由见解析；（2）//DE BA ，理由见解析；（3）图见解析，EDF BAC ∠=∠或180EDF BAC ∠+∠=︒．【分析】（1）根据平行线的画法补全图形即可得，根据平行线的性质可得F=，由此即可得；∠=∠∠∠D AC,EDF BFD B B∠=∠，再根据等量代换可得（2）如图（见解析），先根据平行线的性质可得BAC BODEDF BOD∠=∠，然后根据平行线的判定即可得；（3）先根据点D的位置画出如图（见解析）的两种情况，再分别利用平行线的性质、对顶角相等即可得．【详解】（1）由题意，补全图形如下：∠=∠，理由如下：EDF BACDE BA，//∴∠=∠，EDF BFD//DF CA，∴∠=∠，BABFD C∴∠=∠；EDF BACDE BA，理由如下：（2）//如图，延长BA交DF于点O，//DF CA，∴∠=∠，BAC BODEDF BAC∠=∠，∴∠=∠，EDF BODDE BA∴；//（3）由题意，有以下两种情况：∠=∠，理由如下：①如图3-1，EDF BACDE BA，//∴∠+∠=︒，180E EAFDF CA，//∴∠+∠=︒，180E EDFEAF EDF ∴∠=∠，由对顶角相等得：BAC EAF ∠=∠，EDF BAC ∴∠=∠；②如图3-2，180EDF BAC ∠+∠=︒，理由如下：//DE BA ，180EDF F ∴∠+∠=︒，//DF CA ，BAC F ∴∠=∠，180EDF BAC ∴∠+∠=︒．【点睛】本题考查了平行线的判定与性质等知识点，较难的是题（3），正确分两种情况讨论是解题关键．四、解答题16．（1）∠E=45°；（2）∠E=；（3）不变化，【分析】（1）由三角形内角和定理，可得∠D+∠ECD=∠E+∠EAD ，∠B+∠EAB=∠E+∠ECB ，由角平分线的性质，可得∠ECD=∠ECB=∠解析：（1）∠E =45°；（2）∠E =2βα-；（3）不变化，12【分析】（1）由三角形内角和定理，可得∠D+∠ECD=∠E+∠EAD ，∠B+∠EAB=∠E+∠ECB ，由角平分线的性质，可得∠ECD=∠ECB=12∠BCD ，∠EAD=∠EAB=12∠BAD ，则可得∠E= 12（∠D+∠B ），继而求得答案；（2）首先延长BC 交AD 于点F ，由三角形外角的性质，可得∠BCD=∠B+∠BAD+∠D ，又由角平分线的性质，即可求得答案．（3）由三角形内角和定理，可得90ADP ACB DAC ∠+︒=∠+∠ADP DFO ABC OEB ∠+∠=∠+∠，利用角平分线的性质与三角形的外角的性质可得答案．【详解】解：（1）∵CE 平分∠BCD ，AE 平分∠BAD∴∠ECD=∠ECB=12∠BCD ，∠EAD=∠EAB=12∠BAD ， ∵∠D+∠ECD=∠E+∠EAD ，∠B+∠EAB=∠E+∠ECB ， ∴∠D+∠ECD+∠B+∠EAB=∠E+∠EAD+∠E+∠ECB ∴∠D+∠B=2∠E ，∴∠E=12（∠D+∠B ）， ∵∠ADC=50°，∠ABC=40°，∴∠AEC=12×（50°+40°）=45°；（2）延长BC 交AD 于点F ，∵∠BFD=∠B+∠BAD ，∴∠BCD=∠BFD+∠D=∠B+∠BAD+∠D ， ∵CE 平分∠BCD ，AE 平分∠BAD∴∠ECD=∠ECB=12∠BCD ，∠EAD=∠EAB=12∠BAD ， ∵∠E+∠ECB=∠B+∠EAB ，∴∠E=∠B+∠EAB －∠ECB=∠B+∠BAE －12∠BCD =∠B+∠BAE －12（∠B+∠BAD+∠D ） = 12（∠B －∠D ）， ∠ADC =α°，∠ABC =β°，即∠AEC=.2βα-（3）ADP ACB ABC ∠∠-∠的值不发生变化，1.2ADP ACB ABC ∠∴=∠-∠ 理由如下：如图，记AB 与PQ 交于E ，AD 与CB 交于F ，,PQ MN ⊥90,DOC BOE ∴∠=∠=︒90ADP ACB DAC ∠+︒=∠+∠①，ADP DFO ABC OEB ∠+∠=∠+∠②，∴ ①－②得：90,DFO ACB ABC DAC OEB ︒-∠=∠-∠+∠-∠90,DFO OEB DAC ACB ABC ∴︒-∠+∠-∠=∠-∠90,,ADP DFO OEB EAD ADP ∠=︒-∠∠-∠=∠AD 平分∠BAC ，,BAD CAD ∴∠=∠,OEB CAD ADP ∴∠-∠=∠2,ADP ACB ABC ∠=∠-∠1.2ADP ACB ABC ∠∴=∠-∠【点睛】此题考查了三角形内角和定理、三角形外角的性质以及角平分线的定义．此题难度较大，注意掌握整体思想与数形结合思想的应用．17．（1）证明见解析；（2）900°，180°(n－1)；（3）(180n－180－2m)°【详解】【模型】（1）证明：过点E作EF∥CD，∵AB∥CD，∴EF∥AB，∴∠1＋∠MEF解析：（1）证明见解析；（2）900°，180°(n－1)；（3）(180n－180－2m)°【详解】【模型】（1）证明：过点E作EF∥CD，∵AB∥CD，∴EF∥AB，∴∠1＋∠MEF＝180°，同理∠2＋∠NEF＝180°∴∠1＋∠2＋∠MEN＝360°【应用】（2）分别过E点，F点，G点，H点作L1，L2，L3，L4平行于AB，利用（1）的方法可得∠1+∠2+∠3+∠4+∠5+∠6=180×5=900°；由上面的解题方法可得：∠1+∠2+∠3+∠4+∠5+∠6＋…＋∠n=180°(n－1)，故答案是：900°， 180°(n－1)；（3）过点O作SR∥AB，∵AB∥CD，∴SR∥CD，∴∠AM1O＝∠M1OR同理∠C M n O＝∠M n OR∴∠A M1O＋∠CM n O＝∠M1OR＋∠M n OR，∴∠A M1O＋∠CM n O＝∠M1OM n＝m°，∵M1O平分∠AM1M2，∴∠AM1M2＝2∠A M1O，同理∠CM n M n-1＝2∠CM n O，∴∠AM1M2＋∠CM n M n-1＝2∠AM1O＋2∠CM n O＝2∠M1OM n＝2m°，又∵∠A M1M2＋∠2+∠3+∠4+∠5+∠6＋……＋∠n－1＋∠CM n M n-1＝180°(n－1)，∴∠2+∠3+∠4+∠5+∠6＋…＋∠n－1＝(180n－180－2m)°点睛：本题考查了平行线的性质，角平分线的定义，解决此类题目，过拐点作平行线是解题的关键，准确识图理清图中各角度之间的关系也很重要．18．解决问题：6；拓展延伸：（1）S1=2S2 （2）10.5【解析】试题分析：解决问题：连接AE，根据操作示例得到S△ADE=S△BDE，S△ABE=S△AEC，从而得到结论；拓展延伸：（1）解析：解决问题：6；拓展延伸：（1）S1=2S2（2）10.5【解析】试题分析：解决问题：连接AE，根据操作示例得到S△ADE=S△BDE，S△ABE=S△AEC，从而得到结论；拓展延伸：（1）作△ABD的中线AE，则有BE=ED=DC，从而得到△ABE的面积=△AED的面积=△ADC的面积，由此即可得到结论；（2）连接AO．则可得到△BOD的面积=△BOC的面积，△AOC的面积=△AOD的面积，△EOC的面积=△BOC的面积的一半，△AOB的面积=2△AOE的面积．设△AOD的面积=a，△AOE的面积=b，则a+3=2b，a=b+1.5，求出a、b的值，即可得到结论．试题解析：解：解决问题连接AE．∵点D、E分别是边AB、BC的中点，∴S△ADE=S△BDE，S△ABE=S△AEC．∵S△BDE =2，∴S△ADE =2，∴S△ABE=S△AEC=4，∴四边形ADEC的面积=2+4=6．拓展延伸：解：（1）作△ABD的中线AE，则有BE=ED=DC，∴△ABE的面积=△AED的面积=△ADC的面积= S2，∴S1=2S2．（2）连接AO．∵CO=DO，∴△BOD的面积=△BOC的面积=3，△AOC的面积=△AOD的面积．∵BO=2EO，∴△EOC的面积=△BOC的面积的一半=1.5，△AOB的面积=2△AOE的面积．设△AOD的面积=a，△AOE的面积=b，则a+3=2b，a=b+1.5，解得：a=6，b=4.5，∴四边形ADOE的面积为=a+b=6+4.5=10.5．19．（1）140°；（2）∠1+∠2=90°+α；（3）∠1=90°+∠2+α,理由见解析;(4)∠2=90°+∠1﹣α．【详解】试题分析：（1）根据四边形内角和定理以及邻补角的定义，得出∠1+∠2解析：（1）140°；（2）∠1+∠2=90°+α；（3）∠1=90°+∠2+α,理由见解析;(4)∠2=90°+∠1﹣α．【详解】试题分析：（1）根据四边形内角和定理以及邻补角的定义，得出∠1+∠2=∠C+∠α，进而得出即可；（2）利用（1）中所求的结论得出∠α、∠1、∠2之间的关系即可；（3）利用三角外角的性质，得出∠1=∠C+∠2+α=90°+∠2+α；（4）利用三角形内角和定理以及邻补角的性质可得出∠α、∠1、∠2之间的关系．试题分析：（1）∵∠1＋∠2＋∠CDP＋∠CEP＝360°，∠C＋∠α＋∠CDP＋∠CEP＝360°，∴∠1＋∠2＝∠C ＋∠α，∵∠C ＝90°，∠α＝50°，∴∠1＋∠2＝140°，故答案为140；（2）由(1)得∠α＋∠C ＝∠1＋∠2，∴∠1＋∠2＝90°＋∠α.故答案为∠1＋∠2＝90°＋∠α.（3）∠1＝90°＋∠2＋∠α.理由如下：如图③，设DP 与BE 的交点为M ，∵∠2＋∠α＝∠DME ，∠DME ＋∠C ＝∠1，∴∠1＝∠C ＋∠2＋∠α＝90°＋∠2＋∠α.（4）如图④，设PE 与AC 的交点为F ，∵∠PFD ＝∠EFC ，∴180°－∠PFD ＝180°－∠EFC ，∴∠α＋180°－∠1＝∠C ＋180°－∠2，∴∠2＝90°＋∠1－∠α.故答案为∠2＝90°＋∠1－∠α点睛：本题考查了三角形内角和定理和外角的性质、对顶角相等的性质，熟练掌握三角形外角的性质是解决问题的关键.20．（1）①70；②∠F=∠BED ，证明见解析；（2）2∠F+∠BED=360°；（3）【分析】（1）①过F 作FG//AB ，利用平行线的判定和性质定理得到∠DFB=∠DFG+∠BFG=∠CDF+∠A解析：（1）①70；②∠F =12∠BED ，证明见解析；（2）2∠F+∠BED =360°；（3）3045α︒≤<︒ 【分析】（1）①过F 作FG//AB ，利用平行线的判定和性质定理得到。

七年级数学下册期末考试压轴训练题(附答案解析)

七年级数学下册期末考试压轴训练题(附答案解析)1．如图，点A、B的坐标分别为（a，0），（b，0），且满足（2a+2）2+√b−3=0，现同时将A、B分别向上平移2个单位，再向右平移1个单位，分别得到A、B对应点C、D，连接AC、BD．(1)求点A、B的坐标；(2)如图1，点P（0，m）是y轴负半轴上一动点，连接AP、PD，其中直线PD交x轴于E点，若S△P AE＝S△BDE，求m的值；(3)如图2，连接BC，在直线BC上取一点F，使BF＝3CF，求点F的坐标．2．如图1，在平面直角坐标系中，点A、B的坐标分别为A（a，0），B（0，b）2a-+√b+3＝0，现同时将点A、B分别向上平移3个单位长度，再向右平移6个单位，分别得到点A、B的对应点D，C，连接AD，BC，CD．（1）求点C，D的坐标；（2）在y轴上是否存在一点P，使三角形P AC的面积等于四边形ABCD的面积？若存在，请求出点P的坐标，请说明理由；（3）如图2，设点E是直线CD上一动点（点不与点C、D重合），连接AE、BE，请直接写出∠DAE，∠CBE和∠AEB之间的数量关系．3．如图①，在平面直角坐标系中，点A(0,a)，C(b,0)，其中，a是16的算术平方根，b3=8，线段GO由线段AC平移所得，并且点G与点A对应，点O与点C对应．（1）点A的坐标为；点C的坐标为；点G的坐标为；（2）如图②，F是线段AC上不同于AC的任意一点，求证：∠OFC=∠OAF+∠AOF；（3）如图③，若点F满足FOC FCO∠=∠，点E是线段OA上一动点（与点O、A不重合），连CE交OF于点H，在点E运动的过程中，∠OHC+∠ACE=2∠OEC是否总成立？请说明理由．4．已知，在平面直角坐标系中，AB⊥x轴于点B，点A(a,b)满足√a−4+|b−2|=0，平移线段AB使点A 与原点重合，点B的对应点为点C．（1）则a＝，b＝，点C坐标为；（2）如图1，点D（m，n）在线段BC上，求m，n满足的关系式；（3）如图2，E是线段OB上一动点，以OB为边作∠BOG＝∠AOB，交BC于点G，连CE交OG于点F，当点E在线段OB上运动过程中，∠OFC+∠FCG的值是否会发生变化？若变化请说明理由，若不变，请求出其∠OEC值．5．如图，在平面直角坐标系，点A、B的坐标分别为（a，0），（0，b）．且|a﹣8b0，将点B向右平移24个单位长度得到C．（1）求A、B两点的坐标；（2）点P、Q分别为线段BC、OA两个动点，P自B点向C点以2个单位长度/秒向右运动，同时点Q自A 点向O点以4个单位长度/秒向左运动，设运动的时间为t，连接PQ，当PQ恰好平分四边形BOAC的面积时，求t的值；（3）点D是直线AC上一点，连接QD，作∠QDE＝120°，边DE与BC的延长线相交于点E，DM平分∠CDE，DN平分∠ADQ，当点Q运动时，∠MDN的度数是否变化？请说明理由．6．如图1，在平面直角坐标系中，A（a，0）是x轴正半轴上一点，C是第四象限一点，CB∠y轴，交y轴负半轴于B（0，b），且（a﹣3）2+|b+4|＝0，S四边形AOBC＝16．（1）求C点坐标；（2）如图2，设D为线段OB上一动点，当AD∠AC时，∠ODA的角平分线与∠CAE的角平分线的反向延长线交于点P，求∠APD的度数．（3）如图3，当D点在线段OB上运动时，作DM∠AD交BC于M点，∠BMD、∠DAO的平分线交于N点，则D点在运动过程中，∠N的大小是否变化？若不变，求出其值，若变化，说明理由．7．如图，已知AM∠BN，∠A＝64°．点P是射线AM上一动点（与点A不重合），BC、BD分别平分∠ABP 和∠PBN，分别交射线AM于点C，D．（1）∠∠ABN的度数是；∠∠AM∠BN，∠∠ACB＝∠；（2）求∠CBD的度数；（3）当点P运动时，∠APB与∠ADB之间的数量关系是否随之发生变化？若不变化，请写出它们之间的关系，并说明理由：若变化，请写出变化规律；（4）当点P运动到使∠ACB＝∠ABD时，∠ABC的度数是．8．在平面直角坐标系中，D（0，﹣3），M（4，﹣3），直角三角形ABC的边与x轴分别相交于O、G两点，与直线DM分别交于E、F点，∠ACB＝90°．（1）将直角三角形如图1位置摆放，如果∠AOG＝46°，则∠CEF＝；（2）将直角三角形ABC如图2位置摆放，N为AC上一点，∠NED+∠CEF＝180°，请写出∠NEF与∠AOG 之间的等量关系，并说明理由．（3）将直角三角形ABC如图3位置摆放，若∠GOC＝140°，延长AC交DM于点Q，点P是射线GF上一动点，探究∠POQ，∠OPQ与∠PQF的数量关系，请直接写出结论（题中的所有角都大于0°小于180°）．9．在平面直角坐标系中，A（a，0），B（b，0），C（﹣1，c）（见图1），且|2a+b+1|+√a+2b−4+(c−2)2=0．（1）求a、b、c的值；（2）①在x轴的正半轴上存在一点M，使三角形COM的面积是三角形ABC的面积的一半，求出点M的坐标；②在坐标轴的其它位置是否存在点M，使三角形COM的面积三角形ABC的面积的一半仍然成立? 若存在，请直接写出符合条件的点M的坐标；（3）如图2，过点C作CD⊥y轴交y轴于点D，点P为线段CD延长线上的一动点，连接OP，OE平分∠AOP，OF⊥OE．当点P运动时，∠OPD的值是否会改变？若不变，求其值；若改变，说明理由．∠DOE10．已知：b是立方根等于本身的负整数，且a、b满足(a+2b)2+|c+1|=0，请回答下列问题：2（1）请直接写出a、b、c的值：a=_______，b=_______，c=_______．（2）a、b、c在数轴上所对应的点分别为A、B、C，点D是B、C之间的一个动点(不包括B、C两点)，|=________．其对应的数为m，则化简|m+12（3）在（1）、（2）的条件下，点A、B、C开始在数轴上运动，若点B、点C都以每秒1个单位的速度向左运动，同时点A以每秒2个单位长度的速度向右运动，假设t秒钟过后，若点A与点C之间的距离表示为AC，点A与点B之间的距离表示为AB，请问：AB−AC的值是否随着时间t的变化而改变？若变化，请说明理由；若不变，请求出AB−AC的值．x y，都是二元一次方程x−4y= 11．如图①，在平面直角坐标系中，点A在x轴上，直线OC上所有的点坐标(,)x y，都是二元一次方程x+2y=6的解，过C作x轴的平行线，交y轴0的解，直线AC上所有的点坐标(,)与点B．（1）求点A、B、C的坐标；（2）如图∠，点M、N分别为线段BC，OA上的两个动点，点M从点C以每秒1个单位长度的速度向左运动，同时点N从点O以每秒1．5个单位长度的速度向右运动，设运动时间为t秒，且0＜t＜4，试比较四边形MNAC的面积与四边形MNOB的面积的大小．12．已知点A（1，a），将线段OA平移至线段BC，B（b，0），a是m+6n的算术平方根，2m＝3，n＝√4，且m＜n，正数b满足（b+1）2＝16．（1）直接写出A、B两点坐标为：A，B；（2）如图1，连接AB、OC，求四边形AOCB的面积；（3）如图2，若∠AOB＝a，点P为y轴正半轴上一动点，试探究∠CPO与∠BCP之间的数量关系．13．如图，MN ∥OP ，点A 为直线MN 上一定点，B 为直线OP 上的动点，在直线MN 与OP 之间且在线段AB 的右方作点D ，使得AD ⊥BD ．设(DAB αα∠=为锐角)． (1)求NAD ∠与∠PBD 的和；(提示过点D 作EF ∥MN) (2)当点B 在直线OP 上运动时，试说明90OBD NAD ∠-∠=︒；(3)当点B 在直线OP 上运动的过程中，若AD 平分∠NAB ，AB 也恰好平分∠OBD ，请求出此时α的值14．如图1，在平面直角坐标系中，点A （a ，0），B （b ，3），C （c ，0），满足√a +b +|a −b +6|+(c −4)2=0．（1）分别求出点A ，B ，C 的坐标及三角形ABC 的面积．（2）如图2．过点C 作CD ⊥AB 于点D ，F 是线段AC 上一点，满足∠FDC =∠FCD ，若点G 是第二象限内的一点，连接DG ，使∠ADG =∠ADF ，点E 是线段AD 上一动点（不与A 、D 重合），连接CE 交DF 于点H ，点E 在线段AD 上运动的过程中，∠DHC+∠ACE∠CED的值是否会变化？若不变，请求出它的值；若变化，请说明理由．（3）如图3，若线段AB 与y 轴相交于点F ，且点F 的坐标为（0，32），在坐标轴上是否存在一点P ，使三角形ABP 和三角形ABC 的面积相等？若存在，求出P 点坐标．若不存在，请说明理由．（点C 除外）15．如图，在平面直角坐标系中，点A，B的坐标分别为（－1，0），（3，0），现同时将点A，B分别向上平移2个单位长度，再向右平移1个单位长度，分别得到点A，B的对应点C，D．连接AC，BD．（1）写出点C，D的坐标及四边形ABDC的面积．（2）在y轴上是否存在一点P，连接P A，PB，使S三角形P AB＝S四边形ABDC？若存在，求出点P的坐标，若不存在，试说明理由；（3）点Q是线段BD上的动点，连接QC，QO，当点Q在BD上移动时（不与B，D重合），给出下列结论：①∠DCQ+∠BOQ∠CQO的值不变；②∠DCQ+∠COQ∠BQO的值不变，其中有且只有一个正确，请你找出这个结论并求值．16．如图1，已知直角梯形ABCO中，∠AOC＝90°，AB∠x轴，AB＝6，若以O为原点，OA，OC所在直线为y轴和x轴建立如图所示直角坐标系，A(0，a)，C(c，0)中a，c满足|a+c﹣7c-＝0（1）求出点A、B、C的坐标；（2）如图2，若点M从点C出发，以2单位/秒的速度沿CO方向移动，点N从原点出发，以1单位/秒的速度沿OA方向移动，设M、N两点同时出发，且运动时间为t秒，当点N从点O运动到点A时，点M同时也停止运动，在它们的移动过程中，当2S△ABN≤S△BCM时，求t的取值范围：（3）如图3，若点N是线段OA延长上的一动点，∠NCH＝k∠OCH，∠CNQ＝k∠BNQ，其中k＞1，NQ∠CJ，求HCJABN∠∠的值（结果用含k的式子表示）．17．问题情境（1）如图1，已知AB∠CD，∠PBA＝125°，∠PCD＝155°，求∠BPC的度数．佩佩同学的思路：过点P作PG∠AB，进而PG∠CD，由平行线的性质来求∠BPC，求得∠BPC＝问题迁移（2）图2．图3均是由一块三角板和一把直尺拼成的图形，三角板的两直角边与直尺的两边重合，∠ACB ＝90°，DF∠CG，AB与FD相交于点E，有一动点P在边BC上运动，连接PE，P A，记∠PED＝∠α，∠P AC ＝∠β．∠如图2，当点P在C，D两点之间运动时，请直接写出∠APE与∠α，∠β之间的数量关系；∠如图3，当点P在B，D两点之间运动时，∠APE与∠α，∠β之间有何数量关系？请判断并说明理由；拓展延伸（3）当点P在C，D两点之间运动时，若∠PED，∠P AC的角平分线EN，AN相交于点N，请直接写出∠ANE 与∠α，∠β之间的数量关系．18．如图1，在平面直角坐标系中，A(6,a)，B(b,0)，且(a−6)2+√b−2=0.（1）求点A、B的坐标；=15，请求出P点的坐标；（2）如图1，P点为y轴正半轴上一点，连接BP，若SΔPAB（3）如图2，已知AB=√52，若C点是x轴上一个动点，是否存在点C，使BC=AB，若存在，请直接写出所有符合条件的点C的坐标；若不存在，请说明理由．A ，点B与点A关于y轴对称.19．已知平面直角坐标系内两点A、B，点(3,4)（1）则点B的坐标为________；（2）动点P、Q分别从A点、B点同时出发，沿直线AB向右运动，同向而行，点P的速度是每秒4个单位长度，点Q的速度是每秒2个单位长度，设P、Q的运动时间为t秒，用含t的代数式表示ΔOPQ的面积S，并写出t的取值范围；SΔABO.求m的取值范围.（3）在平面直角坐标系中存在一点M(m,−m)，满足SΔMOB≤2320．如图1，O为平面直角坐标系的原点，点A坐标为（4，0），同时将点A，O分别向上平移2个单位，再向左平移1个单位，得到对应点B，C．（1）求四边形OABC的面积；（2）在y轴上是否存在一点M，使△MOA的面积与四边形OABC的面积相等？若存在这样一点，求出点M的坐标，若不存在，请说明理由；（3）如图2，点P在OA边上，且∠CBP=∠CPB，Q是AO延长线上一动点，∠PCQ的平分线CD交BP的延长线于点D，在点Q运动的过程中，求∠D和∠CQP的数量关系．参考答案：1．(1)解：∵(2a+2)2+√b−3=0，(2a+2)2≥0，√b−3≥0，∴2a+2=0，b−3=0，1a∴=-，b=3，(1,0),(3,0)A B∴-；(2)∠将A、B分别向上平移2个单位，再向右平移1个单位，分别得到A、B对应点C、D，∴C(0,2)，D(4,2)，∴AO=1,OB=3,CD=4,OC=2，∵点P（0，m）是y轴负半轴上一动点，∴PO=−m，PC=2−m，∵S△P AE＝S△BDE，S梯形OCDB=S梯形OCDE+S△DBE=S 梯形OCDE+APES= S梯形OCDE+S△POE+S△APO=S△PCD+S△APO，∴12(OB+CD)OC=12PCCD+12AOPO，即：12(3+4)×2=12×4×(2−m)+12×1×(−m)，整理得：52m=−3，∴m=−65；(3)分如下两种情况进行讨论：①当F在BC中间，如图所示：过F作FM⊥AB于M，NF⊥OC于N，过点O作OG BC⊥于G，∵BF＝3CF，AO=1,OB=3,CD=4,OC=2，∴S△COFS△BOF =12OGCF12OGBF=13，∵S△BOC=12OBOC=12×3×2=3，∴S△COF=14S△BOC=34，∴12CONF=34，∴NF=34，∵S△BOF=34S△BOC=94，∴12OBFM=94，∴FM=32，∴F(34,32 )，②当F在BC延长线上，则只能在第二象限，如图所示：过F作FP⊥AB于P，FQ⊥OC于Q，过点O作OH⊥BC于H，∵BF＝3CF，AO=1,OB=3,CD=4,OC=2，∴S△COFS△BOF =12OHCF12OHBF=13，∴S△COF=12S△OBC，∵S△BOC=12OBOC=12×3×2=3，∴S△COF=12S△BOC=32，∴12COFQ=32，∴FQ=32，S△BOF=S△OCF+S△BOC=92，∴12OBPF=92，∴PF=3，∵F在第二象限，∴F(−32,3) ，综上所述：F(34,32)或者F(−32,3)．2．（1）∵2a -+√b +3＝0，|a −2|≥0，√b +3≥0，∴a −2=0,b +3=0解得a =2,b =−3∴A(2,0),B(0,−3)将点A 、B 分别向上平移3个单位长度，再向右平移6个单位，分别得到点A 、B 的对应点D ，C ，由平移的性质可知，即将A 、B 的横坐标+6，纵坐标+3，∴D(2+6,0+3),C(0+6,−3+3)，即D(8,3),C(6,0)；（2）存在，理由如下：设P(0,m)，(2,0)A ，(6,0)C ，∴AC =6−2=4，三角形P AC 的面积为12AC ×|y P |=12×4×|m |=2|m |，四边形ABCD 的面积为12AC ×(|y D |+|y B |)=12×4×(3+3)=12，∴2|m |=12，解得m =±6，∴(0,6)P 或者P(0,−6)；（3）如图，过点E 作EM //AD ，∴∠DAE =∠AEM ，∵A,B 平移后对应的点分别为D,C ，∴AD //BC ，∵EM //AD ，∴EM //BC ，∠CBE =∠BEM ，∴∠DAE +∠CBE =∠AEM +∠BEM =∠AEB ．∴∠DAE+∠CBE=∠AEB．3．（1）连接GA∵a是16的算术平方根∴a=4∴A(0,4)∴AO=4∵b3=8∴b=2∴C(2,0)∴OC=2∵线段GO由线段AC平移所得，并且点G与点A对应，点O与点C对应∴GA=OC=2，GA//OCG∴(2,4)故答案为：(0,4)，(2,0)，(−2,4)；（2）∵线段GO由线段AC平移所得∴OG//CA，∴∠OFC=∠GOF∵∠GOF=∠GOA+∠AOF∴∠OFC=∠GOA+∠AOF∵OG//CA∴∠GOA=∠OAF∴∠OFC=∠OAF+∠AOF（3）∵OG//CA∴∠GOC+∠ACO=180°∵∠GOC=∠GOA+∠AOC∴∠GOA+∠AOC+∠ACO=180°∵∠AOC=90°∴∠GOA+90°+∠ACO=180°，即∠GOA+∠ACO=90°∵OG//CA∴∠GOA=∠OAC∴∠OAC+∠ACO=90°∵∠AOC=∠AOF+∠FOC=90°∴∠AOF+∠FOC=∠OAC+∠ACO∵FOC FCO∠=∠，∠ACO=∠FCO∴∠AOF=∠OAC由（2）的结论得：∠OHC=∠OEH+∠EOH，∠OEC=∠EAC+∠ACE∵∠OEH=∠OEC，∠EOH=∠AOF=∠OAC∴∠OHC=∠OEC+∠OAC∴∠OHC+∠ACE=∠OEC+∠OAC+∠ACE∵∠EAC=∠OAC∴∠OEC=∠OAC+∠ACE∴∠OHC+∠ACE=2∠OEC∴在点E运动的过程中，∠OHC+∠ACE=2∠OEC总成立．4．（1）解：∵√a−4+|b−2|=0，∴a−4=0,b−2=0,∴a=4,b=2,∵AB=OC=2,且C在y轴负半轴上，∴C(0,−2),故填：4,2,(0,−2)；（2）如图1，过点D分别作DM∠x轴于点M，DN∠y轴于点N，连接OD．∵AB ⊥ x 轴于点B ，且点A ，D ，C 三点的坐标分别为：(4,2),(m,n),(0,−2) ∴OB =4,OC =2,MD =−n,ND =m ，∴S △BOC =12OBOC =4,又∠S △BOC = S △BOD ＋S △COD=12OB ×MD ＋12OC ×ND=12×4×(−n)+12×m ×2=m −2n ，∴m −2n =4；（3）解：∠OFC+∠FCG ∠OEC 的值不变，值为2．理由如下：如图所示，分别过点E ，F 作EP ∠OA ， FQ ∠OA 分别交y 轴于点P ，点Q ，∠线段OC 是由线段AB 平移得到，∠BC ∠OA ，又∠EP ∠OA ，∠EP ∠BC ，∠∠GCF =∠PEC ，∠EP ∠OA ，∠∠AOE =∠OEP ，∠∠OEC =∠OEP +∠PEC =∠AOE +∠GCF ，同理：∠OFC =∠AOF +∠GCF ，又∠∠AOB =∠BOG ，∠∠OFC =2∠AOE +∠GCF ，∴∠OFC+∠FCG ∠OEC=∠OFC +∠FCG ∠AOE +∠FCG =2∠AOE +2∠FCG ∠AOE +∠FCG=2．5．解：（1）∵|a ﹣8b -0，|a −26|≥080b -≥， ∴|a −26|=0，√8−b =0∴{a −26=08−b =0，解得：{a =26b =8∴点A 、B 的坐标分别为（26，0），（0，8）；（2）∠点B 向右平移24个单位长度得到C ，∠C （24，8），设BP =2t ，PC =24−2t ，OQ =26−4t ，AQ =4t ，∵PQ 平分四边形BOAC 的面积，∴S 梯形OBPQ =S 梯形QACP∴BP+OQ 2BO =CP+QA 2BO∴BP +OQ =CP +QA∴2t +26−4t =4t +24−2t解得t =12；（3）当点Q 运动时，∠MDN 的度数不变，理由如下：如图，当D 在线段CA 的延长线上时，∠DM 平分∠CDE ，DN 平分∠ADQ ，∴∠NDC =12∠QDA ，∠MDC =12∠CDE ，∴∠MDN =∠NDC +∠MDC =12(∠QDA +∠CDE)=12∠QDE ， ∵∠QDE =120°，∠∠MDN =60°；同理求得当D在线段AC的延长线上时，∠MDN=60°；当点D在线段AC上时，∠DM平分∠CDE，DN平分∠ADQ，∴∠NDQ=12∠QDA，∠MDC=12∠CDE，设∠CDE=x∵∠QDE=120°∠∠QDC=120°-x，∠∠ADQ=180°-∠QDC=60°+x，∴∠MDN=∠MDC+∠QDC+∠NDQ=12x+120o−x+12(60o+x)=150o，综上所述：∠MDN=60°或150°.6．解：（1）∠（a﹣3）2+|b+4|＝0，∠a﹣3＝0，b+4＝0，∠a＝3，b＝﹣4，∠A（3，0），B（0，﹣4），∠OA＝3，OB＝4，∠S四边形AOBC＝16．∴1（OA+BC）×OB＝16，2（3+BC）×4＝16，∴12∴BC＝5，∠C是第四象限一点，CB∠y轴，∠C（5，﹣4）；（2）如图，延长CA，∠AF是∠CAE的角平分线，∠CAE，∴∠CAF＝12∵∠CAE＝∠OAG，∠OAG，∴∠CAF＝12∵AD∠AC，∠∠DAO+∠OAG＝∠PAD+∠PAG＝90°，∠∠AOD＝90°，∠∠DAO+∠ADO＝90°，∠∠ADO＝∠OAG，∠ADO，∴∠CAF＝12∵DP是∠ODA的角平分线∠∠ADO＝2∠ADP，∠∠CAF＝∠ADP，∠∠CAF＝∠PAG，∠∠PAG＝∠ADP，∠∠APD＝180°﹣（∠ADP+∠PAD）＝180°﹣（∠PAG+∠PAD）＝180°﹣90°＝90°即：∠APD＝90°；（3）不变，∠ANM＝45°理由：如图，∠∠AOD ＝90°，∠∠ADO+∠DAO ＝90°，∠DM∠AD ，∠∠ADO+∠BDM ＝90°，∠∠DAO ＝∠BDM ，∠NA 是∠OAD 的平分线，∴∠DAN ＝12∠DAO ＝12∠BDM ，∵CB∠y 轴，∠∠BDM+∠BMD ＝90°，∴∠DAN ＝12（90°﹣∠BMD ），∵MN 是∠BMD 的角平分线，∴∠DMN ＝12∠BMD ，∴∠DAN+∠DMN ＝12（90°﹣∠BMD ）+12∠BMD ＝45° 在∠DAM 中，∠ADM ＝90°，∠∠DAM+∠DMA ＝90°，在∠AMN 中，∠ANM ＝180°﹣（∠NAM+∠NMA ）＝180°﹣（∠DAN+∠DAM+∠DMN+∠DMA ）＝180°﹣[（∠DAN+DMN ）+（∠DAM+∠DMA ）] ＝180°﹣（45°+90°）＝45°，∠D 点在运动过程中，∠N 的大小不变，求出其值为45°． 7．解：（1）∠∠AM //BN ，∠A ＝64°，∠∠ABN ＝180°﹣∠A ＝116°，故答案为：116°；∠∠AM //BN ，∠∠ACB ＝∠CBN ，故答案为：CBN；（2）∠AM//BN，∠∠ABN+∠A＝180°，∠∠ABN＝180°﹣64°＝116°，∠∠ABP+∠PBN＝116°，∠BC平分∠ABP，BD平分∠PBN，∠∠ABP＝2∠CBP，∠PBN＝2∠DBP，∠2∠CBP+2∠DBP＝116°，∠∠CBD＝∠CBP+∠DBP＝58°；（3）不变，∠APB：∠ADB＝2：1，∠AM//BN，∠∠APB＝∠PBN，∠ADB＝∠DBN，∠BD平分∠PBN，∠∠PBN＝2∠DBN，∠∠APB：∠ADB＝2：1；（4）∠AM//BN，∠∠ACB＝∠CBN，当∠ACB＝∠ABD时，则有∠CBN＝∠ABD，∠∠ABC+∠CBD＝∠CBD+∠DBN∠∠ABC＝∠DBN，由（1）∠ABN＝116°，∠∠CBD＝58°，∠∠ABC+∠DBN＝58°，∠∠ABC＝29°，故答案为：29°．8．（1）如图1，作CP∠x轴，∠D（0，﹣3），M（4，﹣3），∠DM∠x轴，∠CP∠DM∠x轴，∠∠AOG＝∠1，∠2+∠CEF＝180°，∠∠2＝180°﹣∠CEF，∠∠1+∠2＝90°，∠∠AOG+180°﹣∠CEF＝90°，∠∠AOG＝46°，∠∠CEF＝136°，故答案为136°；（2）∠AOG+∠NEF＝90°．理由如下：如图2，作CP∠x轴，∠CP∠DM∠x轴，∠∠AOG＝∠1，∠2+∠CEF＝180°，而∠NED+∠CEF＝180°，∠∠2＝∠NED，∠∠1+∠2＝90°，∠∠AOG +∠NEF ＝90°；（3）如图3，当点P 在GF 上时，过点P 作PN ∠OG ，∠NP ∠OG ∠DM ，∠∠GOP ＝∠OPN ，∠PQF ＝∠NPQ ，∠∠OPQ ＝∠GOP +∠PQF ，∠∠OPQ ＝140°﹣∠POQ +∠PQF ；如图4，当点P 在线段GF 的延长线上时，过点P 作PN ∠OG ，∠NP ∠OG ∠DM ，∠∠GOP ＝∠OPN ，∠PQF ＝∠NPQ ，∠∠OPN ＝∠OPQ +∠QPN ，∠∠GOP ＝∠OPQ +∠PQF ，∠140°﹣∠POQ ＝∠OPQ +∠PQF ．9．（1）因为|2a +b +1|+√a +2b −4+(c −2)2=0，根据绝对值、二次根式和平方的非负性，可以得到{2a +b +1=0a +2b −4=0，（c -2）2=0，解{2a +b +1=0a +2b −4=0得到a =-2，b =3；因为（c -2）2=0，所以c=2，故a =-2，b =3，c=2；（2）解：由（1）可知A （-2，0），B （3，0），则分情况讨论点M ：①当M 在x 轴上时，设M （m ，0），由题意：12•|m |•2=12 12×5×2，∴m =±52，∴M （52，0）或（-52，0）．②当M 在y 轴上时，设M （0，m ），由题意：12•|m |•1=12 12×5×2，∴m =±5，∠M （5，0）或（0，-5），综上所述，满足条件的点M 坐标为M （52，0）或（-52，0）或（0，5）或（0，-5）．（3）解：如图中，结论：∠OPD ∠DOE 的值是定值，∠OPD ∠DOE=2．理由：∠OE ∠OF ，∠∠EOF =90°，∠∠AOE +∠FOG =90°，∠∠AOE =∠EOP ，∠EOP +∠POF =90°，∠∠FOG =∠POF ，∠∠DOE +∠AOE =90°，∠AOE +∠FOG =90°，∠∠DOE =∠FOG ，∠CP ∠AG ，∠∠OPD =∠POG =2∠FOG ，∠∠OPD =2∠FOG ，∴∠OPD ∠DOE=2． 10．解：（1）∠b 是立方根等于本身的负整数，∠b=-1∵(a+2b)2+|c+12|=0，(a+2b)2≥0，|c+12|≥0∴a+2b=0，c+12=0解得：a=2，c=−12故答案为：2；-1；−12；（2）∵b=-1，c=−12，b 、c 在数轴上所对应的点分别为B 、C ，点D 是B 、C 之间的一个动点(不包括B 、C 两点)，其对应的数为m ，∴-1＜m ＜−12∴m+12＜0∴|m+12|= -m -12故答案为：-m -12；（3）运动前AB=2－（-1）=3，AC=2－（−12）=52由题意可知：运动后AB=3＋2t ＋t=3＋3t ，AC=52＋2t ＋t=52＋3t∴AB －AC=（3＋3t ）－（52＋3t ）=12∴AB−AC 的值不会随着时间t 的变化而改变，AB －AC=12．11．（1）令y =0，则x +2×0=6，解得x =6， (6,0)A ∴．{x −4y =0x +2y =6解得{x =4y =1 ∴C(4,1)．∵BC //x 轴，∴点B 的纵坐标与点C 的纵坐标相同，(0,1)B ∴ ；（2）∵A(6,0)，B(0,1)，C(4,1)，∴OA =6,BC =4．∵点M 从点C 以每秒1个单位长度的速度向左运动，同时点N 从点O 以每秒1.5个单位长度的速度向右运动，∴MC =t,ON =1.5t ，∴BM =4−t,NA =6−1.5t ，∴S 四边形MNOB =12(BM +ON)⋅OB =12×(4−t +1.5t)×1=t 4+2，S 四边形MNAC =12(MC +NA)⋅OB =12×(t +6−1.5t)×1=−t 4+3．当t 4+2>−t 4+3时，即t >2时，S 四边形MNOB >S 四边形MNAC ；当t 4+2=−t 4+3时，即t =2时，S 四边形MNOB =S 四边形MNAC ；当t 4+2<−t 4+3时，即t <2时，S 四边形MNOB <S 四边形MNAC ． 12．（1）∵a 是m +6n 2m ＝3，n ＝√4，且m ＜n ，正数b 满足（b +1）2＝16．∴m ＝﹣3，n ＝2，a ＝3，b ＝3，∠A （1，3），B （3，0）；故答案为：A（1，3）；B（3，0）；（2）如图1所示：由题意知：C（2，﹣3），∠B（3，0），∠OB＝3，∴S四边形AOCB＝S△AOB+S△BOC＝12×3×3+12×3×3=9，故答案为：9；（3）过点P作PD∠OA，如图2所示：∠OA∠BC，∠PD∠OA∠BC∠∠BCP＝∠DPC，∠DPO＝∠AOP．∠∠AOB＝a，∠∠AOP＝90°﹣∠AOB＝90°﹣a．∠∠DPO＝90°﹣a．∠∠DPC＝∠DPO+∠CPO，∠∠BCP＝∠CPO+90°﹣a，即∠BCP﹣∠CPO＝90°﹣a，故答案为：∠BCP﹣∠CPO＝90°﹣a．13．解：（1）过点D作EF∠MN，如下图所示∵MN//OP∴EF∠OP∠∠NAD=∠ADE，∠PBD=∠BDE∵AD⊥BD∴∠ADB=90°∠∠ADE＋∠BDE=∠ADB=90°∠∠NAD＋∠PBD=90°（2）∠∠NAD＋∠PBD=90°∠∠PBD=90°－∠NAD∠∠OBD＋∠PBD=180°，∠∠OBD＋90°－∠NAD=180°∠90OBD NAD∠-∠=︒；（3）∵AD平分∠NAB，AB也恰好平分∠OBD，∠DAB=α∴∠NAD=∠DAB=α，∠NAB=2∠DAB=2α，∠OBD=2∠OBA ∵MN//OP∴∠OBA=∠NAB=2α∴∠OBD=4α由（2）知90OBD NAD∠-∠=︒即4α−α=90°解得：α=30°14．解：（1）∵√a+b+|a−b+6|+(c−4)2=0，∴{a+b=0a−b+6=0c−4=0，解得：a=−3,b=3,c=4，∴A(−3,0)，B(3,3)，(4,0)C如图，过点B作BM⊥AC，则AC=7，BM=3，∴S△ABC=12ACBM=12×7×3=212，（2）不变，∵CD ⊥AB ，∴∠ADC =90°，∠∠DAC +∠FCD =90°，∠FDC +∠ADF =90°，∵∠FDC =∠FCD∴∠DAC =∠ADF ，∠∠CED =∠ACE +∠DAC∠DHC =∠CED +∠ADF =∠ACE +∠DAC +∠DAC =∠ACE +2∠DAC∴∠DHC+∠ACE ∠CED =∠ACE+2∠DAC+∠ACE ∠ACE+∠DAC =2， ∴∠DHC+∠ACE ∠CED 的值不变，∠DHC+∠ACE ∠CED =2；（3）存在，①当点P 在x 轴上时，则AF =AC =7，因为点P 不与点C 重合，所以点P(−10,0)； ②当点P 在y 轴上时，设P （0,t ）则PF =|t −32|,∴S △ABP =S △AFP +S △BFP =12×3×|t −32|+12×3×|t −32| =4∴|t −32|=43，解得t =16或t =176，所以P(0,16)或P(0,176)综上，存在一点P ，使三角形ABP 和三角形ABC 的面积相等，点P(−10,0)或(0,16)或(0,176)． 15．（1）∠将点A ，B 分别向上平移2个单位长度，再向右平移1个单位长度， ∠C （0，2），D （4，2），AB ∠CD 且AB =CD =4，∠四边形ABDC 是平行四边形，∠S 四边形ABCD ＝4×2＝8．（2）存在，设点P的坐标为（0，y），根据题意，得12×4×|y|＝8．解得y＝4或y＝－4．∠点P的坐标为（0，4）或（0，－4）．（3）结论∠正确．过点Q作QE∠AB，交CO于点E．∠AB∠CD，∠QE∠CD．∠∠DCQ＝∠EQC，∠BOQ＝∠EQO．∠∠EQC＋∠EQO＝∠CQO，∠∠DCQ＋∠BOQ＝∠CQO．∴∠DCQ+∠BOQ∠CQO＝1．16．(1)∵|a+c﹣10|7c =0∴a+c﹣10=0，且c﹣7=0，∴c=7，a+c=10，∴c=3，∴A(0，3)，C(7，0)，∵AB∥x轴，AB=6，∴B(6，3)；(2)∵A(0，3)，C(7，0)，∴OA=3，OC=7，由题意得：ON=t，CM=2t，∴AN=3﹣t，∵2S△ABN≤S△BCM，∴2×12×(3﹣t)×6≤12×2t×3，解得：t≥2，∵当点N从点O运动到点A时，点M同时也停止运动，∴0≤t≤3，∴t的取值范围为：2≤t≤3；(3)设AB与CN交于点D，如图所示：∠AB∠OC，∠∠BDC=∠OCD，∠∠BDC=∠BND+∠ABN，∠CNQ=k∠BNQ，∠NCH=k∠OCH，∠∠BDC=(k+1)∠BNQ+∠ABN，∠OCD=(k+1)∠OCH，∠(k+1)∠BNQ+∠ABN=(k+1)∠OCH，∠∠ABN═(k+1)∠OCH﹣(k+1)∠BNQ=(k+1)(∠OCH﹣∠BNQ)，∠NQ∠CJ，∠∠NCJ=∠CNQ=k∠BNQ，∠∠HCJ+∠NCJ=∠NCH=k∠OCH，∠∠HCJ=k∠OCH﹣∠NCJ=k∠OCH﹣k∠BNQ=k(∠OCH﹣∠BNQ)，∴∠HCJ∠ABN =k(∠OCH﹣∠BNQ)(k+1)(∠OCH﹣∠BNQ)=kk+1．17．解：（1）∵PG∥AB,∠PBA=125°，∴∠BPG=180°−∠PBA=55°，∵AB∥CD，∴PG∥CD，∴∠CPG=180°−∠PCD=25°，∴∠BPC=∠BPG+∠CPG=80°，故答案为：80°；（2）①∠APE=∠α+∠β，理由如下：如图，过点P作PQ∥DF，∴∠QPE=∠α，∵DF∥CG，∴PQ∥CG，∴∠QPA=∠β，∴∠APE=∠QPE+∠QPA=∠α+∠β；②∠APE=∠β−∠α，理由如下：如图，过点P作PQ∥DF，∴∠QPE=∠α，∵DF∥CG，∴PQ∥CG，∴∠QPA=∠β，∴∠APE=∠QPA−∠QPE=∠β−∠α；（3）∠ANE=12(∠α+∠β)，理由如下：∵EN,AN分别平分∠PED,∠PAC，∴∠NED=12∠PED=12∠α,∠NAC=12∠PAC=12∠β，如图，过点N作NQ∥DF，∴∠QNE=∠NED=12∠α，∵DF∥CG，∴NQ∥CG，∴∠QNA=∠NAC=12∠β，∴∠ANE=∠QNE+∠QNA=12∠α+12∠β=12(∠α+∠β)．18．解：（1）60a-=，b−2=0∴a=6，b=2∴A(6,6)，B(2,0)（2）作AM⊥x轴于点M，如图所示设P(0,y)，且y>0∴SΔPAB=S梯形OMAP−SΔPOB−SΔABM=12×(y+6)×6−12×2×y−12×4×6=2y+6若SΔPAB=15即2y+6=15∴y=92∴P(0,92)（3）存在，C1(2+√52,0)，C2(2−√52,0)∵AB=√52，B(2,0)，BC=AB∴当C点在x正半轴上时，坐标为C1(2+√52,0)，当C点在x负半轴上时，坐标为C2(2−√52,0)故答案为C1(2+√52,0)，C2(2−√52,0).19．解：（1）∠A（-3，4），A、B两点关于y轴对称，∠点B的坐标为（3，4）．故答案为（3，4）．（2）∠AP=4t，BQ=2t，AB=6，当P与Q相遇时4t=6+2t解得t=3∴当0⩽t⩽3时，PQ=6+2t-4t=6-2t；当t＞3时，PQ=4t-6-2t=2t-6(6−2t)=12−4t∴当0⩽t⩽3时, S=42(2t−6)=4t−12当t>3时, S=42（3）如图，设AB交y轴于D．∠点M的坐标为（m，-m），∠点M在二四象限的角平分线上，∠当m＜-4时，显然不存在．∠当-4＜m＜0时，M在第二象限；S△OMB=S△ODB+S△ODM−S△BDM=12×4×3+12×4×（−m）−12×3×（4+m）=−72m∵S△AOB=12×6×4=12∴−72m≤23×12∴m≥−16 7∴−167≤m＜0③当m＞0时，M在第四象限；S△OBM=S△DBM+S△DOM−S△BDO=12×4×m+12×3×（4+m）−12×4×3=72m由题意可得72m≤23×12∴m≤167∴0＜m≤16 7综上所述，满足条件的m的值为：−167≤m＜0或0＜m≤16720．（1）如图1中，由题意B（3，2），C（-1，2），∠BC∠OA，BC=OA，∠四边形ABCO是平行四边形．∠S平行四边形ABCD=4×2=8．（2）存在．理由：如图1中，设M（0，m）由题意S△AOM=8，∴12×4×|m|=8∴m=±4，∠M（0，4）或（0，-4）．（3）结论：∠CQP=2∠D．理由：如图3中，延长CP到K．∠BC∠OA，∠∠CBP=∠DPQ，∠∠CBP=∠CPB，∠CPB=∠DPK，∠∠DPQ=∠DPK，设∠DPQ=∠DPK=x，∠DCQ=∠DCP=y，则有{2x=2y+∠CQP①x=y+∠D②，①-2×∠得到∠CQP=2∠D．。

七年级下册数学期末复习压轴题解答题试题及答案解答doc

七年级下册数学期末复习压轴题解答题试题及答案解答doc一、解答题1．计算：（1）2a （a ﹣2a 2）；（2）a 7＋a ﹣（a 2）3；（3）（3a ＋2b ）（2b ﹣3a ）；（4）（m ﹣n ）2﹣2m （m ﹣n ）．2．因式分解：（1）m 2﹣16；（2）x 2（2a ﹣b ）﹣y 2（2a ﹣b ）；（3）y 2﹣6y +9；（4）x 4﹣8x 2y 2+16y 4．3．计算：（1）0201711(2)(1)()2--+--；（2）()()()3243652a a a +-•- 4．解不等式-3+3+121-3-18-x x x x ⎧≥⎪⎨⎪<⎩（）5．已知△ABC中，∠A =60°，∠ACB =40°，D 为BC 边延长线上一点，BM 平分∠ABC ，E 为射线BM 上一点．（1）如图1，连接CE ，①若CE ∥AB ，求∠BEC 的度数；②若CE 平分∠ACD ，求∠BEC 的度数．（2）若直线CE 垂直于△ABC 的一边，请直接写出∠BEC 的度数．6．疫情初期，武汉物资告急，全国一心，各地纷纷运送物资到武汉．已知3辆大货车与2辆小货车可以一次运货17吨，5辆大货车与4辆小货车可以一次运货29吨，则2辆大货车与1辆小货车可以一次运货多少吨？7．如图，点D 、E 、F 分别是△ABC 三边上的点，DF ∥AC ，∠BFD=∠CED ，请写出∠B 与∠CDE 之间的数量关系，并说明理由．8．已知a +a 1-=3，求（1）a 2+21a（2）a 4+41a 9．阅读材料：求1+2+22+23+24+…+22020的值．解：设S ＝1+2+22+23+24+…+22020，将等式两边同时乘以2得，2S ＝2+22+23+24+25+ (22021)将下式减去上式，得2S ﹣S ＝22021﹣1，即S ＝22021﹣1．即1+2+22+23+24+…+22020＝22021﹣1仿照此法计算：（1）1+3+32+33+ (320)（2）2310011111 (2222)+++++． 10．先化简，再求值：（x ﹣2y ）（x ＋2y ）﹣（x ﹣2y ）2，其中x ＝3，y ＝﹣1．11．实验中学要为学校科技活动小组提供实验器材，计划购买A 型、B 型两种型号的放大镜．若购买100个A 型放大镜和150个B 型放大镜需用1500元；若购买120个A 型放大镜和160个B 型放大镜需用1720元．(1)求每个A 型放大镜和每个B 型放大镜各多少元；(2)学校决定购买A 型放大镜和B 型放大镜共75个，总费用不超过570元，那么最多可以购买多少个A 型放大镜？12．解方程或不等式（组）（1）24231x y x y +=⎧⎨-=⎩ （2）2151132x x -+-≥ （3）312(2)15233x x x x +<+⎧⎪⎨-≤+⎪⎩ 13．疫情初期，武汉物资告急，全国一心，各地纷纷运送物资到武汉。

人教版七年级下数学期末复习不等式压轴题训练（含答案）

人教版七年级下数学期末复习不等式压轴题训练（含答案）七年级下数学期末复习不等式压轴题训练（含答案）1.定义新运算：对于任意实数a，b，都有a⊕b＝a(a－b)+1，等式右边是通常的加法、减法及乘法运算，比如：2⊕5＝2′(2－5)+1＝2′(－3)+1＝－6+1＝－5.（1）求（－2）⊕3的值（2）若3⊕x的值小于13，求x的取值范围，并在图示的数轴上表示出来.2.例题试确定实数a的取值范围，使不等式组恰有两个整数解．解：由不等式两边同乘以6得到3x+2（x+1）＞0，可以求出x＞－，由不等式两边都乘以3得到3x+5a+4＞4x+4+3a可以解出x＜2a，所以不等式组的解集为，因为该不等式组恰有有两个整数解，所以1＜2a≤2，所以＜a≤1．仿照例题完成下题试确定实数a的取值范围，使不等式组恰有两个整数解．3.阅读材料，并回答问题如图，有一根木棒MN放置在数轴上，它两端M、N分别落在点A、B．将木棒在数轴上水平移动，当点M移动到点B时，点N所对应的数为20，当点N移动到点A时，点M所对应的数为5．（单位：cm）由此可得，木棒长为__________cm ．借助上述方法解决问题：一天，美羊羊去问村长爷爷的年龄，村长爷爷说：“我若是你现在这么大，你还要40年才出生呢，你若是我现在这么大，我已经是老寿星了，116岁了，哈哈！”美羊羊纳闷，村长爷爷到底是多少岁？（1）请你画出示意图，求出村长爷爷和美羊羊现在的年龄．（2）若羊村中的小羊均与美羊羊同岁，老羊均与村长爷爷同岁．灰太狼计划为全家抓5只羊，综合考虑口感和生长周期等因素，决定所抓羊的年龄之和不超过112岁且高于34岁．请问灰太狼有几种抓羊方案？4.x取哪些正整数时，不等式x+3>6与2x-1<10都成立？5.已知多项式a2-5a-7减去多项式a2-11a+9的差等于不等式5-4x<0的最小正整数解，求a的值．6..一件由黄金与白银制成的首饰重a克,商家称其中黄金含量不低于90%,黄金和白银的密度分别是19.3和10.5,列出不等式表示这件首饰的体积应满足什么条件.(提示:质量=密度×体积.)7.某自行车保管站在某个星期日接受保管的自行车共有3500辆次，其中变速车保管费是每辆0.5元，一般车保管费是每辆0.3元．（1）若设一般车停放辆次数为x，总的保管费收入为y元，试写出y与x的关系式．（2）若估计前来停放3500辆自行车中，变速车的辆次不小于25%，但不大于40%，试求该保管站这个星期日收入保管费总数的取值范围．答案：1定义新运算：对于任意实数a，b，都有a⊕b＝a(a－b)+1，等式右边是通常的加法、减法及乘法运算，比如：2⊕5＝2′(2－5)+1＝2′(－3)+1＝－6+1＝－5.（1）求（－2）⊕3的值（2）若3⊕x的值小于13，求x的取值范围，并在图示的数轴上表示出来.【22题答案】【答案】（1）11（2）x＞－1．数轴表示如图所示：【解析】【详解】分析：（1）按照定义新运算a⊕b=a（a-b）+1，求解即可．（2）先按照定义新运算a⊕b=a（a-b）+1，得出3⊕x，再令其小于13，得到一元一次不等式，解不等式求出x的取值范围，即可在数轴上表示．不等式的解集在数轴上表示的方法：＞，≥向右画；＜，≤向左画，在表示解集时“≥”，“≤”要用实心圆点表示；“＜”，“＞”要用空心圆点表示．解：（1）∵a⊕b=a（a－b）＋1，∴（－2）⊕3=－2（－2－3）＋1=10＋1=11．（2）∵3⊕x＜13，∴3（3－x）＋1＜13，9－3x＋1＜13，－3x＜3，∴x＞－1．数轴表示如图所示：2.例题试确定实数a的取值范围，使不等式组恰有两个整数解．解：由不等式两边同乘以6得到3x+2（x+1）＞0，可以求出x＞－，由不等式两边都乘以3得到3x+5a+4＞4x+4+3a可以解出x＜2a，所以不等式组的解集为，因为该不等式组恰有有两个整数解，所以1＜2a≤2，所以＜a≤1．仿照例题完成下题试确定实数a的取值范围，使不等式组恰有两个整数解．【23题答案】【答案】＜a≤【解析】【详解】试题分析：先求出不等式组的解集，再根据整数解的情况，得到a的取值范围.试题解析：解不等式组得：2-3a 以＜a≤．3.阅读材料，并回答问题如图，有一根木棒MN放置在数轴上，它的两端M、N分别落在点A、B．将木棒在数轴上水平移动，当点M移动到点B时，点N所对应的数为20，当点N移动到点A时，点M所对应的数为5．（单位：cm）由此可得，木棒长为__________ cm．借助上述方法解决问题：一天，美羊羊去问村长爷爷的年龄，村长爷爷说：“我若是你现在这么大，你还要40年才出生呢，你若是我现在这么大，我已经是老寿星了，116岁了，哈哈！”美羊羊纳闷，村长爷爷到底是多少岁？（1）请你画出示意图，求出村长爷爷和美羊羊现在的年龄．（2）若羊村中的小羊均与美羊羊同岁，老羊均与村长爷爷同岁．灰太狼计划为全家抓5只羊，综合考虑口感和生长周期等因素，决定所抓羊的年龄之和不超过112岁且高于34岁．请问灰太狼有几种抓羊方案？【24题答案】【答案】（1）村长64岁，美羊羊12岁（2）抓四只小羊一只老羊或抓五只小羊【解析】【详解】试题分析：（1）在求村长爷爷年龄时，借助数轴，把美羊羊与村长爷爷的年龄差看做木棒MN，类似村长爷爷比美羊羊大时看做当N点移动到A点时，此时M点所对应的数为-40，美羊羊比村长爷爷大时看做当M点移动到B点时，此时N点所对应的数为116，所以可知爷爷比美羊羊大[116-（-40）]÷3=52，可知爷爷的年龄．（2）设抓小羊x只，则老羊为(5-x)只，再根据抓羊的年龄之和不超过112岁且高于34岁，列不等式组，解不等式组，得出其整数解即可试题解析：（1）如图：点A表示美羊羊现在的年龄，点B表示村长爷爷现在的年龄，木棒MN的两端分别落在点A、B．由题意可知，当点N移动到点A时，点M所对应的数为-40，当点M移动到点B时，点N所对应的数为116．可求MN=52．所以点A所对应的数为12，点B所对应的数为64．即美羊羊今年12岁，村长爷爷今年64岁．（2）设抓小羊x只，则老羊为(5-x)只，依题意得：解得：，则x=4或x=5,即抓四只小羊一只老羊或抓五只小羊【点睛】此题考查了数轴，解题的关键是把村长爷爷与美羊羊的年龄差看做一个整体（木棒MN），而后把此转化为上一题中的问题．4.x取哪些正整数时，不等式x+3>6与2x-1<10都成立？【20题答案】【答案】4或5【解析】【详解】试题分析：解x+3>6和2x-1<10，求出解集的公共部分，再从解集中找出正整数即可.解x+3>6得，x>3;解2x-1<10得，x<5.5;∴3，∴x=4或5.5.已知多项式a2-5a-7减去多项式a2-11a+9的差等于不等式5-4x<0的最小正整数解，求a的值．【21题答案】【答案】a=3【解析】【详解】试题分析：先解不等式5-4x<0，求出解集，从而从解集中找出最小正整数，然后列方程求解.∵5-4x<0，∴，∴不等式5-4x<0的最小正整数解是2，∴(a2-5a-7)-(a2-11a+9)=a2-5a-7-a2+11a-9=6a-16=2,∴6a=18,∴a=3.6..一件由黄金与白银制成的首饰重a克,商家称其中黄金含量不低于90%,黄金和白银的密度分别是19.3和10.5,列出不等式表示这件首饰的体积应满足什么条件.(提示:质量=密度×体积.)【22题答案】【答案】【解析】【详解】试题分析：由质量=密度×体积可得,据此表示出当黄金含量为90％时V的取值范围,进而得出答案.解：如果其中黄金的含量为90%,则首饰的体积V()为.如果其中黄金的含量为100%(注意仅仅是如果!),则首饰的体积V()为.∴主要考查了由实际问题抽象出一元一次不等式,根据质量、密度、体积之间的关系表示出V的最大值是解题关键.7.某自行车保管站在某个星期日接受保管的自行车共有3500辆次，其中变速车保管费是每辆0.5元，一般车保管费是每辆0.3元．（1）若设一般车停放的辆次数为x，总的保管费收入为y元，试写出y与x的关系式．（2）若估计前来停放的3500辆自行车中，变速车的辆次不小于25%，但不大于40%，试求该保管站这个星期日收入保管费总数的取值范围．【23题答案】【答案】（1）y＝－0.2x＋1750；（2）这个星期天保管费的收入在1225元至1330元之间．【解析】【分析】（1）根据总的保管费y=一般车辆人保管费+变速车的保管费列出方程，化简即可．（2）根据3500辆自行车中，变速车的辆次不小于25%，但不大于40%可确定变速车的辆数范围，再根据辆数确定保管费收费范围即可．【小问1详解】由题意，得y＝0.3x＋0.5(3500－x)，即y＝－0.2x＋1750．【小问2详解】∵变速车停放的辆次不小于3500的25%，但不大于3500的40%，∴一般自行车停放的辆次是在3500×60%与3500×75%之间．当x＝3500×60%＝2100时，y＝－0.2×2100＋1750＝1330；当x＝3500×75%＝2625时，y＝－0.2×2625＋1750＝1225；∴这个星期天保管费的收入在1225元至1330元之间．【点睛】本题主要考查了一次函数的实际应用，准确根据题意求解析式是解题的关键．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

初一下册数学压轴题精练答案参考答案与试题解析一．解答题（共9小题）1．如图1，在平面直角坐标系中，△AOB是直角三角形，∠AOB=90°，斜边AB与y轴交于点C．（1）若∠A=∠AOC，求证：∠B=∠BOC；（2）如图2，延长AB交x轴于点E，过O作OD⊥AB，若∠DOB=∠EOB，∠A=∠E，求∠A 的度数；（3）如图3，OF平分∠AOM，∠BCO的平分线交FO的延长线于点P，∠A=40°，当△ABO 绕O点旋转时（斜边AB与y轴正半轴始终相交于点C），问∠P的度数是否发生改变若不变，求其度数；若改变，请说明理由．考点：三角形内角和定理；坐标与图形性质．专题：证明题．分析：（1）由直角三角形两锐角互余及等角的余角相等即可证明；（2）由直角三角形两锐角互余、等量代换求得∠DOB=∠EOB=∠OAE=∠E；然后根据外角定理知∠DOB+∠EOB+∠OEA=90°；从而求得∠DOB=30°，即∠A=30°；（3）由角平分线的性质知∠FOM=45°﹣∠AOC ①，∠PCO=∠A+∠AOC ②，根据①②解得∠PCO+∠FOM=45°+∠A，最后根据三角形内角和定理求得旋转后的∠P的度数．解答：（1）证明：∵△AOB是直角三角形，∴∠A+∠B=90°，∠AOC+∠BOC=90°，∵∠A=∠AOC，∴∠B=∠BOC；解：（2）∵∠A+∠ABO=90°，∠DOB+∠ABO=90°，∴∠A=∠DOB，又∵∠DOB=∠EOB，∠A=∠E，∴∠DOB=∠EOB=∠OAE=∠OEA，∵∠DOB+∠EOB+∠OEA=90°，∴∠A=30°；（3）∠P的度数不变，∠P=25°．理由如下：（只答不变不得分）∵∠AOM=90°﹣∠AOC，∠BCO=∠A+∠AOC，又∵OF平分∠AOM，CP平分∠BCO，∴∠FOM=45°﹣∠AOC ①，∠PCO=∠A+∠AOC ②，①+②得：∠PCO+∠FOM=45°+∠A，∴∠P=180°﹣（∠PCO+∠FOM+90°）=180°﹣（45°+∠A+90°）=180°﹣（45°+20°+90°）=25°．点评：本题综合考查了三角形内角和定理、坐标与图形的性质．解答时，需注意，△ABO旋转后的形状与大小均无变化．2．在平面直角坐标系中，A（﹣1，0），B（0，2），点C在x轴上．（1）如图（1），若△ABC的面积为3，则点C的坐标为（2，0）或（﹣4，0）．（2）如图（2），过点B点作y轴的垂线BM，点E是射线BM上的一动点，∠AOE的平分线交直线BM于F，OG⊥OF且交直线BM于G，当点E在射线BM上滑动时，的值是否变化若不变，请求出其值；若变化，请说明理由．考点：三角形内角和定理；坐标与图形性质；垂线；平行线的性质；三角形的面积；三角形的外角性质．分析：（1）利用A，B点坐标，△ABC的面积为3，得出AC的长，进而得出C点坐标；（2）首先根据已知得出∠EOG=∠EOx，进而得出FM∥x轴，再利用已知得出∠BOF=∠EGO，即可得出∠BEO=2∠BOF，得出答案即可．解答：解：（1）∵A（﹣1，0），B（0，2），点C在x轴上．△ABC的面积为3，∴AC的长为3，则点C的坐标为（2，0）或（﹣4，0）；故答案为：（2，0）或（﹣4，0）；（2）∵∠AOE+∠EOx=180°，∴∠AOE+∠EOx=90°，即∠EOF+∠EOx=90°∵∠EOF+∠EOG=90°，∴∠EOG=∠EOx，∴FM∥x轴，∴∠GOx=∠EGO，∴∠EOG=∠EGO，∴∠BEO=2∠EGO，∵∠FOG=90°，∴∠EGO+∠OFG=90°，∵FM⊥y轴，∴∠BOF+∠OFG=90°，∴∠BOF=∠EGO，∴∠BEO=2∠BOF，∴=2．点评：此题主要考查了三角形内角和定理应用以及平行线的判定和三角形面积求法等知识，根据已知得出FM∥x轴以及∠BOF=∠EGO是解题关键．3．如图1，在平面直角坐标系中，A（a，0），B（b，0），C（﹣1，2），且|2a+b+1|+（a+2b ﹣4）2=0．（1）求a，b的值；（2）①在x轴的正半轴上存在一点M，使△COM的面积=△ABC的面积，求出点M的坐标；②在坐标轴的其它位置是否存在点M，使△COM的面积=△ABC的面积仍然成立若存在，请直接写出符合条件的点M的坐标；（3）如图2，过点C作CD⊥y轴交y轴于点D，点P为线段CD延长线上一动点，连接OP，OE平分∠AOP，OF⊥OE．当点P运动时，的值是否会改变若不变，求其值；若改变，说明理由．考点：三角形内角和定理；非负数的性质：绝对值；非负数的性质：偶次方；解二元一次方程组；三角形的面积；三角形的外角性质．分析：（1）根据非负数的性质即可列出关于a，b的方程组求得a，b的值；（2）①过点C做CT⊥x轴，CS⊥y轴，垂足分别为T、S，根据三角形的面积公式即可求得OM的长，则M的坐标即可求得；②根据三角形的面积公式，即可写出M的坐标；（3）利用∠BOF根据平行线的性质，以及角平分线的定义表示出∠OPD和∠DOE即可求解．解答：解：（1）∵|2a+b+1|+（a+2b﹣4）2=0，又∵|2a+b+1|≥0，（a+2b﹣4）2≥0，∴|2a+b+1|=0且（a+2b﹣4）2=0．∴∴即a=﹣2，b=3．（2）①过点C做CT⊥x轴，CS⊥y轴，垂足分别为T、S．∵A（﹣2，0），B（3，0），∴AB=5，因为C（﹣1，2），∴CT=2，CS=1，△ABC的面积=AB•CT=5，要使△COM的面积=△ABC的面积，即△COM的面积=，所以OM•CT=，∴OM=．所以M的坐标为（，0）．②存在．点M的坐标为（0，5）或（﹣，0）或（0，﹣5）．（3）的值不变，理由如下：∵CD⊥y轴，AB⊥y轴∴∠CDO=∠DOB=90°∴AB∥CD∴∠OPD=∠POB∵OF⊥OE∴∠POF+∠POE=90°，∠BOF+∠AOE=90°∵OE平分∠AOP∴∠POE=∠AOE∴∠POF=∠BOF∴∠OPD=∠POB=2∠BOF∵∠DOE+∠DOF=∠BOF+∠DOF=90°∴∠DOE=∠BOF∴∠OPD=2∠BOF=2∠DOE∴．点评：本题考查了非负数的性质，三角形的面积公式，以及角平分线的定义，平行线的性质，求点的坐标问题常用的方法就是转化成求线段的长的问题．4．长方形OABC，O为平面直角坐标系的原点，OA=5，OC=3，点B在第三象限．（1）求点B的坐标；（2）如图1，若过点B的直线BP与长方形OABC的边交于点P，且将长方形OABC的面积分为1：4两部分，求点P的坐标；（3）如图2，M为x轴负半轴上一点，且∠CBM=∠CMB，N是x轴正半轴上一动点，∠MCN 的平分线CD交BM的延长线于点D，在点N运动的过程中，的值是否变化若不变，求出其值；若变化，请说明理由．考点：平行线的判定与性质；坐标与图形性质；三角形的面积．分析：（1）根据第三象限点的坐标性质得出答案；（2）利用长方形OABC的面积分为1：4两部分，得出等式求出AP的长，即可得出P 点坐标，再求出PC的长，即可得出OP的长，进而得出答案；（3）首先求出∠MCF=2∠CMB，即可得出∠CNM=∠NCF=∠MCF﹣∠NCM=2∠BMC﹣2∠DCM，得出答案．解答：解：（1）∵四边形OABC为长方形，OA=5，OB=3，且点B在第三象限，∴B（﹣5，﹣3）．（2）若过点B的直线BP与边OA交于点P，依题意可知：×AB×AP=×OA×OC，即×3×AP=×5×3，∴AP=2∵OA=5，∴OP=3，∴P（﹣3，0），若过点B的直线BP与边OC交于点P，依题意可知：×BC×PC=×OA×OC，即×5×PC=×5×3，∴PC=∵OC=3，∴OP=，∴P（0，﹣）．综上所述，点P的坐标为（﹣3，0）或（0，﹣）．（3）延长BC至点F，∵四边形OABC为长方形，∴OA∥BC．∴∠CBM=∠AMB，∠AMC=∠MCF．∵∠CBM=∠CMB，∴∠MCF=2∠CMB．过点M作ME∥CD交BC于点E，∴∠EMC=∠MCD．又∵CD平分∠MCN，∴∠NCM=2∠EMC．∴∠D=∠BME=∠CMB﹣∠EMC，∠CNM=∠NCF=∠MCF﹣∠NCM=2∠BMC﹣2∠DCM=2∠D，∴=．点评：此题主要考查了平行线的性质以及矩形的性质、图形面积求法等知识，利用数形结合得出的是解题关键．5．如图，直线AB∥CD．（1）在图1中，∠BME、∠E，∠END的数量关系为：∠E=∠BME+∠END；（不需证明）在图2中，∠BMF、∠F，∠FND的数量关系为：∠BMF=∠F+∠FND；（不需证明）（2）如图3，NE平分∠FND，MB平分∠FME，且2∠E与∠F互补，求∠FME的大小．（3）如图4中，∠BME=60°，EF平分∠MEN，NP平分∠END，EQ∥NP，则∠FEQ的大小是否发生变化若变化，说明理由；若不变化，求∠FEQ的度数．考点：平行线的性质．分析：（1）过点E作EF∥AB，根据两直线平行，内错角相等可得∠BME=∠1，∠END=∠2，然后相加即可得解；先根据两直线平行，同位角相等求出∠3=∠FND，再根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解；（2）设∠END=x°，∠BNE=y°，根据（1）的结论可得x+y=∠E，2x+∠F=y，然后消掉x 并表示出y，再根据2∠E与∠F互补求出y，然后根据角平分线的定义求解即可；（3）根据（1）的结论表示出∠MEN，再根据角平分线的定义表示出∠FEN和∠ENP，再根据两直线平行，内错角相等可得∠NEQ=∠ENP，然后根据∠FEQ=∠FEN﹣∠NEQ 整理即可得解．解答：解：（1）如图1，过点E作EF∥AB，∵AB∥CD，∴AB∥EF∥CD，∴∠BME=∠1，∠END=∠2，∴∠1+∠2=∠BME+∠END，即∠E=∠BME+∠END；如图2，∵AB∥CD，∴∠3=∠FND，∴∠BMF=∠F+∠3=∠F+∠FND，即∠BMF=∠F+∠FND；故答案为：∠E=∠BME+∠END；∠BMF=∠F+∠FND；（2）如图3，设∠END=x°，∠BNE=y°，由（1）的结论可得x+y=∠E，2x+∠F=y，消掉x得，3y=2∠E+∠F，∵2∠E与∠F互补，∴2∠E+∠F=180°，∴3y=180°，解得y=60°，∵MB平分∠FME，∴∠FME=2y=2×60°=120°；（3）由（1）的结论得，∠MEN=∠BME+∠END，∵EF平分∠MEN，NP平分∠END，∴∠FEN=∠MEN=（∠BME+∠END），∠ENP=∠END，∵EQ∥NP，∴∠NEQ=∠ENP，∴∠FEQ=∠FEN﹣∠NEQ=（∠BME+∠END）﹣∠END=∠BME，∵∠BME=60°，∴∠FEQ=×60°=30°．点评：本题考查了平行线的性质，三角形的一个外角等于与它不相邻的两个内角的和的性质，角平分线的定义，此类题目，过拐点作平行线是解题的关键，准确识图理清图中各角度之间的关系也很重要．6．在平面直角坐标系中，点B（0，4），C（﹣5，4），点A是x轴负半轴上一点，S四边形AOBC=24．（1）线段BC的长为5，点A的坐标为（﹣7，0）；（2）如图1，BM平分∠CBO，CM平分∠ACB，BM交CM于点M，试给出∠CMB与∠CAO 之间满足的数量关系式，并说明理由；（3）若点P是在直线CB与直线AO之间的一点，连接BP、OP，BN平分∠CBP，ON平分∠AOP，BN交ON于N，请依题意画出图形，给出∠BPO与∠BNO之间满足的数量关系式，并说明理由．考点：三角形内角和定理；坐标与图形性质；三角形的面积；三角形的外角性质．专题：分类讨论．分析：（1）根据点B、C的横坐标求出BC的长度即可；再根据四边形的面积求出OA的长度，然后根据点A在y轴的负半轴写出点A的坐标；（2）根据两直线平行，同旁内角互补用∠CAO表示出∠ACB，再根据角平分线的定义表示出∠MAB和∠MBC，然后利用三角形的内角和定理列式整理即可得解；（3）分①点P在OB的左边时，根据三角形的内角和定理表示出∠PBO+∠POB，再根据两直线平行，同旁内角互补和角平分线的定义表示出∠NBP+∠NOP，然后在△NBO 中，利用三角形的内角和定理列式整理即可得解；②点P在OB的右边时，求出∠CBP+∠AOP+∠BPO=360°，再根据角平分线的定义表示出∠PBN+∠PON，然后利用四边形的内角和定理列式整理即可得解．解答：解：（1）∵点B（0，4），C（﹣5，4），∴BC=5，S四边形AOBC=（BC+OA）•OB=（5+OA）•4=24，解得OA=7，所以，点A的坐标为（﹣7，0）；（2）∵点B、C的纵坐标相同，∴BC∥OA，∴∠ACB=180°﹣∠CAO，∠CBO=90°，∵BM平分∠CBO，CM平分∠ACB，∴∠MCB=（180°﹣∠CAO）=90°﹣∠CAO，∠MBC=∠CBO=×90°=45°，在△MBC中，∠CMB+∠MCB+∠MBC=180°，即∠CMB+90°﹣∠CAO+45°=180°，解得∠CMB=45°+∠CAO；（3）①如图1，当点P在OB左侧时，∠BPO=2∠BNO．理由如下：在△BPO中，∠PBO+∠POB=180°﹣∠BPO，∵BC∥OA，BN平分∠CBP，ON平分∠AOP，∴∠NBP+∠NOP=（180°﹣∠PBO﹣∠POB），在△NOB中，∠BNO=180°﹣（∠NBP+∠NOP+∠PBO+∠POB），=180°﹣[（180°﹣∠PBO﹣∠POB）+∠PBO+∠POB]，=90°﹣（∠PBO+∠POB），=90°﹣（180°﹣∠BPO），=∠BPO，∴∠BPO=2∠BNO；②如图2，当点P在OB右侧时，∠BNO+∠BPO=180°．理由如下：∵BC∥OA，∴∠CBP+∠AOP+∠BPO=360°，∵BN平分∠CBP，ON平分∠AOP，∴∠PBN+∠PON+∠BPO=×360°=180°，∴∠PBN+∠PON=180°﹣∠BPO，在四边形BNOP中，∠BNO=360°﹣∠PBN﹣∠PON﹣∠BPO=360°﹣（180°﹣∠BPO）﹣∠BPO=180°﹣∠BPO，∴∠BNO+∠BPO=180°．点评：本题考查了三角形的内角和定理，角平分线的定义，平行线的性质，以及坐标与图形性质，准确识图理清图中各角度之间的关系是解题关键，（3）要注意分情况讨论．7．如图1，在平面直角坐标系中，四边形OBCD各个顶点的坐标分别是O（0，0），B（2，6），C（8，9），D（10，0）；（1）三角形BCD的面积=30（2）将点C平移，平移后的坐标为C′（2，8+m）；①若S△BDC′=32，求m的值；②当C′在第四象限时，作∠C′OD的平分线OM，OM交于C′C于M，作∠C′CD的平分线CN，CN交OD于N，OM与CN相交于点P（如图2），求的值．考点：作图-平移变换；坐标与图形性质；三角形内角和定理．分析：（1）三角形BCD的面积=正方形的面积﹣3个小三角形的面积；（2）①分平移后的坐标为C′在B点的上方；在B点的下方两种情况讨论可求m的值；②利用外角以及角平分线的性质得出∠ODC+∠CC′O=2∠P，即可得出答案．解答：解：（1）三角形BCD的面积为：×6×10=30；故答案为：30；（2）①当C在x轴上方，如图1所示：∵S△BDC′=32，D到BC″的距离为8，∴BC″=8，∵B（2，6），∴8+m=14，∴m=6，∵AB=6，BC′=8，∴C′在x轴下方，且AC′=2，∴8+m=﹣2，∴m=﹣10，即m=6或m=﹣10；②如图2，在△OC′M中，∵∠OMC是∠OMC′的外角，∴∠2+∠6=∠OMC，在△PMC中，∵∠OMC是∠CMP的外角，∴∠4+∠P=∠OMC，∴∠2+∠6=∠4+∠P，在△CND中，∵∠ONC是∠CND的外角，∴∠3+∠7=∠ONC，在△ONP中，∵∠ONC是∠ONP的外角，∴∠1+∠P=∠ONC，∴∠3+∠7=∠1+∠P，∴∠3+∠7+∠2+∠6=∠4+∠P+∠1+∠P，∵∠2=∠1，∠3=∠4，∴∠6+∠7=2∠P，∴∠ODC+∠CC′O=2∠P，∴=．点评：此题主要考查了外角的性质以及三角形面积求法和点坐标性质等知识，利用数形结合得出C′的不同位置是解题关键．8．如图，四边形ABCD中，AD∥BC，DE平分∠ADB，∠BDC=∠BCD．（1）求证：∠1+∠2=90°；（2）若∠ABD的平分线与CD的延长线交于F，且∠F=55°，求∠ABC；（3）若H是BC上一动点，F是BA延长线上一点，FH交BD于M，FG平分∠BFH，交DE 于N，交BC于G．当H在BC上运动时（不与B点重合），的值是否变化如果变化，说明理由；如果不变，试求出其值．考点：等腰三角形的性质；角平分线的定义；平行线的性质．专题：综合题．分析：本题考查了等腰三角形的性质、角平分线的性质以及平行线的性质，解决问题的关键在于熟悉掌握知识要点，并且善于运用角与角之间的联系进行传递．（1）由AD∥BC，DE平分∠ADB，得∠ADC+∠BCD=180，∠BDC=∠BCD，得出∠1+∠2=90°；（2）由DE平分∠ADB，CD平分∠ABD，四边形ABCD中，AD∥BC，∠F=55°，得出∠ABC=∠ABD+∠DBC=∠ABD+∠ADB，即∠ABC=70°；（3）在△BMF中，根据角之间的关系∠BMF=180°﹣∠ABD﹣∠BFH，得∠GND=180°﹣∠AED﹣∠BFG，再根据角之间的关系得∠BAD=﹣∠DBC，在综上得出答案．解答：（1）证明：AD∥BC，∠ADC+∠BCD=180，∵DE平分∠ADB，∠BDC=∠BCD，∴∠ADE=∠EDB，∠BDC=∠BCD，∵∠ADC+∠BCD=180°，∴∠EDB+∠BDC=90°，∠1+∠2=90°．解：（2）∠FBD+∠BDE=90°﹣∠F=35°，∵DE平分∠ADB，BF平分∠ABD，∴∠ADB+∠ABD=2（∠FBD+∠BDE）=70°，又∵四边形ABCD中，AD∥BC，∴∠DBC=∠ADB，∴∠ABC=∠ABD+∠DBC=∠ABD+∠ADB，即∠ABC=70°；（3）的值不变．证明：在△BMF中，∠BMF=∠DMH=180°﹣∠ABD﹣∠BFH，又∵∠BAD=180°﹣（∠ABD+∠ADB），∠DMH+∠BAD=（180°﹣∠ABD﹣∠BFH）+（180°﹣∠ABD﹣∠ADB），=360﹣∠BFH﹣2∠ABD﹣∠ADB，∠DNG=∠FNE=180°﹣∠BFH﹣∠AED，=180°﹣∠BFH﹣∠ABD﹣∠ADB，=（∠DMH+∠BAD），∴=2．点评：本题考查等腰三角形的性质及三角形内角和定理；此题为探索题，比较新颖，实际涉及的知识不多．9．如图（1）所示，一副三角板中，含45°角的一条直角边AC在y轴上，斜边AB交x轴于点G．含30°角的三角板的顶点与点A重合，直角边AE和斜边AD分别交x轴于点F、H．（1）若AB∥ED，求∠AHO的度数；（2）如图2，将三角板ADE绕点A旋转．在旋转过程中，∠AGH的平分线GM与∠AHF的平分线HM相交于点M，∠COF的平分线ON与∠OFE的平分线FN相交于点N．①当∠AHO=60°时，求∠M的度数；②试问∠N+∠M的度数是否发生变化若改变，求出变化范围；若保持不变，请说明理由．考点：三角形内角和定理；角平分线的定义；平行线的性质；三角形的外角性质．专题：综合题．分析：（1）由AB∥ED可以得到∠BAD=∠D=60°，即∠BAC+∠CAD=60°，然后根据已知条件即可求出∠AHO；（2）①由∠AHO+∠AHF=180°，∠AHO=60°，可以求出∠AHF，而HM是∠AHF的平分线，GM是∠AGH的平分线，∠MHF=∠MGH+∠M，由此即可求出∠M；②∠N+∠M的度数不变，当∠BAC与∠DAE没有重合部分时，∠GAH﹣∠OAF=（45°+∠OAH）﹣（30°+∠OAH）=15°；当AC与AD在一条直线上时，∠GAH﹣∠OAF=45°﹣30°=15°；当∠BAC与∠DAE有重合部分时，∠GAH﹣∠OAF=（45°﹣∠OAH）﹣（30°﹣∠OAH）=15°，即∠GAH﹣∠OAF=15°．而根据已知条件∠M=∠MHF﹣∠MGH=∠AHF﹣∠AGH=∠GAH，∠N=180°﹣（∠OFE+90°）=180°﹣（∠OAF+90°）﹣90°=90°﹣∠OAF，由此即可得到结论．解答：解：（1）∵AB∥ED∴∠BAD=∠D=60°（两直线平行，内错角相等），即∠BAC+∠CAD=60°．∵∠BAC=45°，∴∠CAD=60°﹣45°=15°，∠AHO=90°﹣∠CAD=75°；（2）①∵∠AHO+∠AHF=180°，∠AHO=60°，∴∠AHF=180°﹣60°=120°∵HM是∠AHF的平分线，∴∠MHF=∠AHF=60°（角平分线的定义）．∵GM是∠AGH的平分线，∠AGH=45°，∴∠MGH=∠AGH=°，∵∠MHF=∠MGH+∠M，∴∠M=60°﹣°=°；②∠N+∠M的度数不变，理由是：当∠BAC与∠DAE没有重合部分时，∠GAH﹣∠OAF=（45°+∠OAH）﹣（30°+∠OAH）=15°；当AC与AD在一条直线上时，∠GAH﹣∠OAF=45°﹣30°=15°；当∠BAC与∠DAE有重合部分时，∠GAH﹣∠OAF=（45°﹣∠OAH）﹣（30°﹣∠OAH）=15°；∴∠GAH﹣∠OAF=15°．易得出∠M=∠MHF﹣∠MGH=∠AHF﹣∠AGH=∠GAH，∠N=180°﹣（∠OFE+90°）=180°﹣（∠OAF+90°）﹣90°=90°﹣∠OAF，∴∠M+∠N=∠GAH+90°﹣∠OAF=90°+×15°=°（定值）．。