七年级数学下册压轴题(汇编)
完整版七年级下册数学压轴题集锦

、2如图,已知(A0,a),B(0,b),C(m,b)且(a-4)+b+3=0,S=14.1ABCV(1)求C点坐标o。
90DFE=为?AED的平分线,且?点,(2)作DE?DC,交y轴于EEF求证:FD平分?ADO;(3)E在y轴负半轴上运动时,连EC,点P为AC延长线上一点,EM平分∠AEC,且PM⊥EM,PN⊥x轴于N点,PQ平分∠APN,交x轴于Q点,则E在运动过程?MPQ中,?ECA的大小是否发生变化,若不变,求出其值。
y yA A ND F oQ D x oxE MC CB PE1 2=2∠∠、如图1,AB//EF,2FCE;FEC=∠(1)证明∠NMC,则∠FNM=∠FMNN为AC上一点,为FE延长线上一点,且∠M(2)如图2,有何数量关系,并证明。
与∠CFMAN1MEE2CCB BFF2 1 图图1(1)如图,∠ABC的平分线与∠ADC的平分线交于点E,试问BE与DE有何位置关系?说明你的理由。
(2)如图,试问∠ABC的平分线BE与∠ADC的外角平分线DF有何位置关系?说明你的理由。
(3)如图,若∠ABC的外角平分线与∠ADC的外角平分线交于点E,试问BE与DE有何位置关系?说明你的理由。
N G DE D DM BF C B BC C EA A EA,B=60∠°DCE的平分线交于点F,∠1()如图,点E在AC的延长线上,BAC与∠6. BDC的度数。
F=56°,求∠∠FBDEC、试问∠F的平分线交于点与∠ADEF,∠E2()如图,点在CD的延长线上,BAD 之间有何数量关系?为什么?和∠∠BC ABFECD。
的平分线交于点与∠已知∠7.ABCADCE3(1)如图,试探究∠E、∠A与∠C之间的数量关系,并说明理由。
AEDCB(2)如图,是探究∠E、∠A与∠C之间的数量关系,并说明理由。
DAECB的反向延MF,若点G恰好在MF)如图,点E是AB上方一点,平分∠AME8.(1 互余,求∠AME的大小。
压轴题02:相交线与平行线综合专练20题(解析版)-年七年级数学下学期期末精选题汇编(北师大版)
压轴题02:相交线与平行线综合专练20题(解析版)一、单选题1.如图a是长方形纸带,∠DEF=26°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE 的度数是()A.102°B.108°C.124°D.128°【答案】A【分析】先由矩形的性质得出∠BFE=∠DEF=26°,再根据折叠的性质得出∠CFG=180°-2∠BFE,∠CFE=∠CFG-∠EFG即可.【详解】∠四边形ABCD是矩形,∠AD∠BC,∠∠BFE=∠DEF=26°,∠∠CFE=∠CFG-∠EFG=180°-2∠BFE-∠EFG=180°-3×26°=102°,故选A.【点睛】本题考查了翻折变换(折叠问题)、矩形的性质、平行线的性质;熟练掌握翻折变换和矩形的性质,弄清各个角之间的关系是解决问题的关键.2.定义:平面内的直线l1与l2相交于点O,对于该平面内任意一点M,点M到直线l1、l2的距离分别为a、b,则称有序非负实数对(a,b)是点M的“距离坐标”,根据上述定义,距离坐标为(2,1)的点的个数有()A.2个B.3个C.4个D.5个【答案】C【分析】首先根据题意,可得距离坐标为(2,1)的点是到l1的距离为2,到l2的距离为1的点;然后根据到l1的距离为2的点是两条平行直线,到l2的距离为1的点也是两条平行直线,可得所求的点是以上两组直线的交点,一共有4个,据此解答即可.【详解】解:如图1,,到l 1的距离为2的点是两条平行直线l 3、l 4,到l 2的距离为1的点也是两条平行直线l 5、l 6,∠两组直线的交点一共有4个:A 、B 、C 、D ,∠距离坐标为(2,1)的点的个数有4个.故选C .【点睛】此题主要考查了点的坐标,以及对“距离坐标”的含义的理解和掌握,解答此题的关键是要明确:到l 1的距离为2的点是两条平行直线,到l 2的距离为1的点也是两条平行直线.3.如图1n //AB CB ,则∠1+∠2+∠3+…+∠n=( )A .540°B .180°nC .180°(n-1)D .180°(n+1)【答案】C【分析】 根据题意,作21//DB AB ,31//EB AB ,41//FB AB ,由两直线平行,同旁内角互补,即可求出答案.【详解】解:根据题意,作21//DB AB ,31//EB AB ,41//FB AB ,∠1n //AB CB ,∠121180B B D ∠+∠=︒,2323180DB B B B E ∠+∠=︒,3434180EB B B B F ∠+∠=︒,……∠122323343411803B B D DB B B B E EB B B B F ∠+∠+∠+∠+∠+∠=︒⨯,……∠123180(1)n n ∠+∠+∠++∠=︒⨯-;故选:C .【点睛】本题考查了平行线的性质,解题的关键是正确作出辅助线,熟练运用两直线平行同旁内角互补进行证明.4.如果两个角的两边分别平行,而其中一个角比另一个角的3倍少20°,那么这两个角是( ) A .50°、130°B .都是10°C .50°、130°或10°、10°D .以上都不对 【答案】C【分析】首先由两个角的两边分别平行,可得这两个角相等或互补.然后设其中一角为x °,由其中一个角比另一个角的3倍少20°,然后分别从两个角相等与互补去分析,即可求得答案,注意别漏解.【详解】解:∠两个角的两边分别平行,∠这两个角相等或互补.设其中一角为x °,若这两个角相等,则x =3x ﹣20,解得:x =10,∠这两个角的度数是10°和10°;若这两个角互补,则180﹣x =3x ﹣20,解得:x =50,∠这两个角的度数是50°和130°.∠这两个角的度数是50°、130°或10°、10°.故选:C .【点睛】此题考查了平行线的性质与一元一次方程的解法.此题难度适中,解题的关键是掌握如果两个角的两边分别平行,则这两个角相等或互补,注意方程思想的应用.5.如图,已知//AB CD ,M 为平行线之间一点连接AM ,CM ,N 为AB 上方一点,连接AN ,CN ,E 为NA 延长线上一点.若AM ,CM 分别平分BAE ∠,DCN ∠,则M ∠与N ∠的数量关系为( ).A .90M N ∠-∠=︒B .2180M N ∠-∠=︒C .180M N ∠+∠=︒D .2180M N ∠+∠=︒【答案】B【分析】 过点M 作//MO AB ,过点N 作//NP AB ,则//////MO AB CD NP ,根据平行线的性质可得12AMC ∠=∠+∠,223CNE ∠=∠-∠,318021∠=︒-∠,即可得出结论.【详解】解:过点M 作//MO AB ,过点N 作//NP AB ,//AB CD ,//////MO AB CD NP ∴,1AMO ∴∠=∠,OMC MCD ∠=∠, AM ,CM 分别平分BAE ∠,DCN ∠,21BAE ∴∠=∠,22NCD ∠=∠,2MCD ∠=∠,12AMC ∴∠=∠+∠,//CD NP ,22PNC NCD ∴∠=∠=∠,223CNE ∴∠=∠-∠,//NP AB ,∴∠=∠=︒-∠,NAB31802122(18021)2(12)1802180CNE AMC ∴∠=∠-︒-∠=∠+∠-︒=∠-︒,2180AMC CNE ∴∠-∠=︒,故选:B .【点睛】本题考查了平行线的性质,邻补角的定义,解题的关键是熟练掌握平行线的性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.6.如图,△ABC 中,∠ACB =90°,AC =3,BC =4,AB =5,P 为直线AB 上一动点,连接PC ,则线段PC 的最小值是( )A .3B .2.5C .2.4D .2【答案】C【分析】 当PC ∠AB 时,PC 的值最小,利用面积法求解即可.【详解】解:在Rt △ABC 中,∠ACB =90°,AC =3,BC =4,AB =5,∠当PC ∠AB 时,PC 的值最小,此时:△ABC 的面积=12•AB •PC =12•AC •BC ,∠5PC =3×4,∠PC =2.4,故选:C .【点睛】本题主要考查了垂线段最短和三角形的面积公式,解题的关键是学会利用面积法求高.7.如图,已知直线AB 、CD 被直线AC 所截,//AB CD ,E 是平面内任意一点(点E 不在直线AB 、CD 、AC 上),设BAE α∠=,DCE β∠=.下列各式:∠αβ+,∠αβ-,∠a β-,∠360αβ︒--,AEC ∠的度数可能是( )A.∠∠B.∠∠C.∠∠∠D.∠∠∠∠【答案】D【分析】由题意根据点E有6种可能位置,分情况进行讨论,依据平行线的性质以及三角形外角性质进行计算求解即可.【详解】解:(1)如图1,由AB∠CD,可得∠AOC=∠DCE1=β,∠∠AOC=∠BAE1+∠AE1C,∠∠AE1C=β-α.(2)如图2,过E2作AB平行线,则由AB∠CD,可得∠1=∠BAE2=α,∠2=∠DCE2=β,∠∠AE2C=α+β.(3)如图3,由AB∠CD,可得∠BOE3=∠DCE3=β,∠∠BAE3=∠BOE3+∠AE3C,∠∠AE3C=α-β.(4)如图4,由AB∠CD,可得∠BAE4+∠AE4C+∠DCE4=360°,∠∠AE4C=360°-α-β.(5)(6)当点E在CD的下方时,同理可得∠AEC=α-β或β-α.综上所述,∠AEC的度数可能为β-α,α+β,α-β,360°-α-β,即∠∠∠∠.故选:D.【点睛】本题主要考查平行线的性质的运用,解题时注意两直线平行,同位角相等;两直线平行,内错角相等以及分类讨论.8.∠如图1,AB∥CD,则∠A+∠E+∠C=180°;∠如图2,AB∥CD,则∠E=∠A+∠C;∠如图3,AB ∥CD,则∠A+∠E-∠1=180°;∠如图4,AB∥CD,则∠A=∠C+∠P.以上结论正确的个数是()A.∠∠∠∠B.∠∠∠C.∠∠∠D.∠∠∠【答案】C【分析】∠过点E作直线EF AB∥,由平行线的性质即可得出结论;∠过点E作直线EF AB∥,由平行线的性质即可得出结论;∠过点E作直线EF AB∥,由平行线的性质可得出∠A+∠E-∠1=180°;∠先过点P作直线PF AB∥,再根据两直线平行,内错角相等和同位角相等即可作出判断.【详解】∥,解:∠过点E作直线EF AB∥∥,∠∠A+∠1=180°,∠2+∠C=180°,∠AB CD∥,∠AB CD EF∠∠A+∠C+∠AEC=360°,故∠错误;∠过点E作直线EF AB∥,∠AB CD∥,∥∥,∠∠A=∠1,∠2=∠C,∠AB CD EF∠∠AEC=∠A+∠C,即∠AEC=∠A+∠C,故∠正确;∠过点E作直线EF AB∥,∥∥,∠∠A+∠3=180°,∠1=∠2,∠AB CD∥,∠AB CD EF∠∠A+∠AEC-∠2=180°,即∠A+∠AEC-∠1=180°,故∠正确;∠如图,过点P作直线PF AB∥,∠AB CD∥∥,∥,∠AB CD PF∠∠1=∠FP A,∠C=∠FPC,∠∠FP A=∠FPC+∠CP A,∠∠1=∠C+∠CP A,∠AB ∠CD ,∠∠A =∠1,即∠A =∠C+∠C P A ,故∠正确.综上所述,正确的小题有∠∠∠.故选:C .【点睛】本题考查的是平行线的性质及平行公理的推论,根据题意作出辅助线是解答此题的关键. 9.如图,//,AD BC D ABC ∠=∠,点E 是边DC 上一点,连接AE 交BC 的延长线于点H ,点F 是边AB 上一点,使得FBE FEB ∠=∠,作FEH ∠的角平分线EG 交BH 于点G ,若100DEH ︒∠=,则BEG ∠的度数是( ).A .30︒B .40︒C .50︒D .60︒【答案】B【分析】 AD ∠BC ,∠D =∠ABC ,则AB ∠CD ,则∠AEF =180°-∠AED -∠BEG =180°-2β,在△AEF 中,100°+2α+180°-2β=180°,故β-α=40°,即可求解.【详解】解:设FBE =∠FEB =α,则∠AFE =2α,∠FEH 的角平分线为EG ,设∠GEH =∠GEF =β,∠AD ∠BC ,∠∠ABC +∠BAD =180°,而∠D =∠ABC ,∠∠D +∠BAD =180°,∠AB ∠CD ,∠DEH=100°,则∠CEH=∠F AE=80°,∠AEF=180°-∠FEG-∠BEG=180°-2β,在∠AEF中,在∠AEF中,80°+2α+180-2β=180°,故β-α=40°,而∠BEG=∠FEG-∠FEB=β-α=40°,故选:B.【点睛】此题考查平行线的性质,解题关键是落脚于∠AEF内角和为180°,即100°+2α+180°-2β=180°,题目难度较大.10.如图,直线AB MN∥,点C为直线MN上一点,连接AC、BC,∠CAB=40°,∠ACB=90°,∠BAC 的角平分线交MN于点D,点E是射线AD上的一个动点,连接CE、BE,∠CED的角平分线交MN于点F.当∠BEF=70°时,令ECMα∠=,用含α的式子表示∠EBC为().A.52αB.10α︒-C.1102α︒-D.1102α-︒【答案】D【分析】先求出∠ABC,再延长CE,交AB于点G,结合平行线的性质表示出∠BCE,然后根据三角形内角和定理表示∠CED,再根据角平分线得定义表示出∠CEB,最后根据三角形内角和定理得出答案.【详解】在∠ABC中,∠CAB=40°,∠ACB=90°,∠∠ABC=50°.延长CE,交AB于点G,∠MN BA∥,∠EGBα∠=,∠ACM=∠BAC=40°,∠∠ACE=α-40°,∠∠BCE=90°-(α-40°)=130°-α.∠∠CEA=180°-∠CAE-∠ACE,∠∠CED=180°-∠CEA=∠CAE+∠ACE=20°+(α-40°)=α-20°.∠EF平分∠CED,∠∠CEF=111022CEDα∠=-︒,∠∠CEB=1110706022αα-︒+︒=+︒,∠∠EBC=11180(60)(130)10 22ααα︒-+︒-︒-=-︒.故选:D.【点睛】本题主要考查了角平分线的定义,三角形内角和定理,平行线的性质,将待求角转化到适合的三角形是解题的关键.二、填空题11.如图,已知,∠ABG为锐角,AH∠BG,点C从点B(C不与B重合)出发,沿射线BG的方向移动,CD∠AB交直线AH于点D,CE∠CD交AB于点E,CF∠AD,垂足为F(F不与A重合),若∠ECF =n°,则∠BAF的度数为_____度.(用n来表示)【答案】n或180﹣n【分析】分两种情况讨论:当点M在线段BC上;点C在BM延长线上,根据平行线的性质,即可得到结论.【详解】解:过A作AM∠BC于M,如图1,当点C在BM延长线上时,点F在线段AD上,∠AD∠BC,CF∠AD,∠CF∠BG,∠∠BCF=90°,∠∠BCE+∠ECF=90°,∠CE∠AB,∠∠BEC=90°,∠∠B+∠BCE=90°,∠∠B=∠ECF=n°,∠AD∠BC,∠∠BAF=180°﹣∠B=180°﹣n°,过A作AM∠BC于M,如图2,当点C在线段BM上时,点F在DA延长线上,∠AD∠BC,CF∠AD,∠CF∠BG,∠∠BCF=90°,∠∠BCE+∠ECF=90°,∠CE∠AB,∠∠BEC=90°,∠∠B+∠BCE=90°,∠∠B=∠ECF=n°,∠AD∠BC,∠∠BAF=∠B=n°,综上所述,∠BAF的度数为n°或180°﹣n°,故答案为:n或180﹣n.【点睛】本题主要考查了平行线的性质的运用,解题时注意:两直线平行,同旁内角互补;两直线平行,内错角相等.12.镇江市旅游局为了亮化某景点,在两条笔直且互相平行的景观道MN、QP上分别放置A、B两盏激光灯,如图所示.A灯发出的光束自AM逆时针旋转至AN便立即回转;B灯发出的光束自BP逆时针旋转至BQ便立即回转,两灯不间断照射,A灯每秒转动12°,B灯每秒转动4°.B灯先转动12秒,A灯才开始转动.当B灯光束第一次到达BQ之前,两灯的光束互相平行时A灯旋转的时间是.【答案】6秒或19.5秒【分析】设A灯旋转t秒,两灯光束平行,B灯光束第一次到达BQ需要180÷4=45(秒),推出t≤45−12,即t≤33.利用平行线的性质,结合角度间关系,构建方程即可解答.【详解】解:设A灯旋转t秒,两灯的光束平行,B灯光束第一次到达BQ需要180÷4=45(秒),∠t≤45﹣12,即t≤33.由题意,满足以下条件时,两灯的光束能互相平行:∠如图,∠MAM'=∠PBP',12t=4(12+t),解得t=6;∠如图,∠NAM'+∠PBP'=180°,12t﹣180+4(12+t)=180,解得t=19.5;综上所述,满足条件的t的值为6秒或19.5秒.故答案为:6秒或19.5秒.【点睛】本题主要考查平行线的性质,解题的关键是熟练掌握基本知识,属于中考常考题型.13.如图,已知AD∥CE,∠BCF=∠BCG,CF与∠BAH的平分线交于点F,若∠AFC的余角等于2∠B 的补角,则∠BAH的度数是_____.【答案】60°##60度【分析】首先设∠BAF=x°,∠BCF=y°,过点B作BM AD,过点F作FN AD,根据平行线的性质,可得∠AFC =(x+2y)°,∠ABC=(2x+y)°,又由∠F的余角等于2∠B的补角,可得方程:90﹣(x+2y)=180﹣2(2x+y),继而求得答案.【详解】解:设∠BAF=x°,∠BCF=y°,∠∠BCF=∠BCG,CF与∠BAH的平分线交于点F,∠∠HAF=∠BAF=x°,∠BCG=∠BCF=x°,∠BAH=2x°,∠GCF=2y°,过点B作BM AD,过点F作FN AD,如图所示:∠AD CE,∠AD FN BM CE ,∠∠AFN =∠HAF =x °,∠CFN =∠GCF =2y °,∠ABM =∠BAH =2x °,∠CBM =∠GCB =y °,∠∠AFC =(x +2y )°,∠ABC =(2x +y )°,∠∠F 的余角等于2∠B 的补角,∠90﹣(x +2y )=180﹣2(2x +y ),解得:x =30,∠∠BAH =60°.故答案为:60°【点睛】此题考查了平行线的性质与判定以及余角、补角的定义.此题难度适中,注意掌握辅助线的作法,掌握数形结合思想与方程思想的应用.14.如图,已知AB //CD ,BE 、DE 的交点为E ,现作如下操作:第一次操作,分别作∠ABE 和∠CDE 的平分线,交点为E 1,第二次操作,分别作∠ABE 1和∠CDE 1的平分线,交点为E 2,第三次操作,分别作∠ABE 2和∠CDE 2的平分线,交点为E 3,...第n (n ≥2)次操作,分别作∠ABEn ﹣1和∠CDEn ﹣1的平分线,交点为En ,若∠En =α度,则∠BED =___度.【答案】2n a【分析】先过E 作//EF AB ,确定BED ABE CDE ∠=∠+∠,再根据角平分线的性质确定n E ∠与BED ∠的关系,即可求解.【详解】解:如下图,过E 作//EF AB ,∠//AB CD ,∠////AB EF CD ,∠B BEF D DEF ∠=∠∠=∠,,∠BED BEF DEF ∠=∠+∠,∠BED ABE CDE ∠=∠+∠;如下图,∠ABE ∠和CDE ∠的平分线交点为1E ∠111111222DE B ABE CDE ABE CDE BED ∠=∠+∠=∠+∠=∠ ∠1ABE ∠和1CDE ∠的平分线交点为2E , ∠22211111122412BE ABE CDE ABE CD E D E DE B B D ∠=∠+∠=∠+∠∠=∠=; ∠2ABE ∠和2CDE ∠的平分线交点为3E , ∠33322211122812BE ABE CDE ABE CD E D E DE B B D ∠=∠+∠=∠+∠∠=∠=; … 以此类推,12n n E BED ∠=∠ ∠当n E α∠=度时,2n BED α∠=度.故答案为2n α .【点睛】本题主要考查了角平分线的定义以及平行线性质:两直线平行,内错角相等的运用.解决问题的关键是作平行线构造内错角,找到角之间的关系.15.如图,直线,,AB CD EF 与直线,,GH IJ KL 分别相交,图中的同位角共有__________对.【答案】156【分析】观察图形,直线 GH,IJ,KL 上,每条直线有5个交点,直线AB,CD,EF 上,每条直线有3个交点,每个交点存在4个角,根据每2个交点可以构成4对同位角,分别求得直线GH,IJ,KL 和AB,CD,EF 上的同位角的对数即可.【详解】观察图形,直线,,GH IJ KL 上,每条直线有5个交点,直线,,AB CD EF 上,每条直线有3个交点,每个交点存在4个角,则直线,,GH IJ KL 上存在的同位角的个数是:5(51)4310434031202-⨯⨯=⨯⨯=⨯=对,同理直线,,AB CD EF 上存在的同位角的个数是:3(31)43362-⨯⨯=对, 则总数是12036156+=对.故答案为:156.【点睛】 本题考查了找同位角,分类讨论是解题的关键.三、解答题16.探究并尝试归纳:(1)如图1,已知直线a 与直线b 平行,夹在平行线间的一条折线形成一个角∠A ,试求∠1+∠2+∠A 的度数,请加以说明.(2)如图2,已知直线a 与直线b 平行,夹在平行线间的一条折线增加一个折,形成两个角∠A 和∠B,请直接写出∠1+∠2+∠A +∠B = 度.(3)如图3,已知直线a 与直线b 平行,夹在平行线间的一条折线每增加一个折,就增加一个角.当形成n 个折时,请归纳并写出所有角与∠1、∠2的总和: 【结果用含有n 的代数式表示,n 是正整数,不用证明】【答案】(1)360°(2)540(3)180(1)n ⋅+︒【分析】(1)过A 作AB //直线a ,再根据平行线的性质即可得到结论;(2)过A 作AC //直线a ,BD //直线a ,则AC//BD //直线b ,根据平行线的性质即可得到结论; (3)根据平行线的性质即可得到结论.(1)解:过A 作AB //直线a ,则AB //直线b ,1342180∴∠+∠=∠+∠=︒,12360MAN ∴∠+∠+∠=︒;(2)解:过A 作AC //直线a ,BD //直线a ,则AC //BD //直线b ,135642180∴∠+∠=∠+∠=∠+∠=︒,12540MAB ABN ∴∠+∠+∠+∠=︒,故答案为:540;(3)解:由(1),(2)知,当形成1个折时,所有角与1∠、2∠的总和180(11)360=⋅+︒=︒,当形成2个折时,所有角与1∠、2∠的总和180(21)540=⋅+︒=︒,当形成n 个折时,所有角与1∠、2∠的总和180(1)n =⋅+︒,故答案为:180(1)n ⋅+︒.【点睛】本题考查了平行线的性质,正确的作出图形是解题的关键.17.如图,已知AB CD ∥,E 、F 分别在AB CD 、上,点G 在AB 、CD 之间,连接GE GF 、.(1)当40BEG ∠=︒时,EP 平分,BEG FP ∠平分DFG ∠;∠如图1,当EG FG ⊥时,则P ∠=______°;∠如图2,在CD 的下方有一点Q ,若EG 恰好平分,BEQ FD ∠恰好平分GFQ ∠,求2Q P ∠+∠的度数;(2)在AB 的上方有一点O ,若FO 平分GFC ∠.线段GE 的延长线平分OEA ∠,则当100EOF EGF ∠+∠=︒时,直接写出OEA ∠与OFC ∠的关系.【答案】(1)∠45;∠140︒(2)3160OEA OFC ∠-∠=︒【分析】(1)根据平行线的性质,以及角平分线的定义即可求解;(2)过点O 作OT AB ∥,则OT CD ∥设OFC OFG ∠=∠β=,OEH HEA α∠=∠=,1802G BEG GFD αβ∠=∠+∠=+︒-,根据平行线的性质求得80αβ+=︒,进而根据()33222160OEA OFC ββαβα∠-∠=--=+=︒即可求解.(1)∠如图,分别过点,G P 作,GN AB PM AB ∥∥,BEG EGN ∴∠=∠,AB CD ∥,NGF GFD ∴∠=∠,EGF BEG GFD ∴∠=∠+∠,同理可得EPF BEP PFD ∠=∠+∠,EG FG ⊥,90EGF ∴∠=︒,EP 平分,BEG FP ∠平分DFG ∠;11,22BEP BEG PFD GFD ∴∠=∠∠=∠, ∴()114522EPP BEG GFD EGF ∠=∠+∠=∠=︒, 故答案为:45,∠如图,过点Q 作QR CD ∥,40BEG ∠=︒,EG 恰好平分,BEQ FD ∠恰好平分GFQ ∠,40GEQ BEG ∴∠=∠=︒,GFQ QFD ∠=∠,设GFQ QFD ∠=∠α=,QR CD ∥,AB CD ∥,1801802100EQR QEB QEG ∴∠=︒-∠=︒-∠=︒,CD QR ∥,180DFQ FQR ∴∠+∠=︒,180FQR α∴+∠=︒,100FQE α∴+∠=︒,100FQE α∴∠=︒-,由(1)可知240G P BEG EFD α∠=∠=∠+∠=︒+,210040140FQE P αα∴∠+∠=︒-+︒+=︒;(2)如图,在AB 的上方有一点O ,若FO 平分GFC ∠,线段GE 的延长线平分OEA ∠,设H 为线段GE 的延长线上一点,则OFC OFG ∠=∠,OEH HEA ∠=∠设OFC OFG ∠=∠β=,OEH HEA α∠=∠=如图,过点O 作OT AB ∥,则OT CD ∥TOF OFC β∴∠=∠=,2TOE OEA α∠=∠=2EOF βα∴∠=-HEA BEG α∠=∠=,1802GFD β∠=︒-由(1)可知1802G BEG GFD αβ∠=∠+∠=+︒-100EOF EGF ∠+∠=︒∴2βα-+1802αβ+︒-100=︒80αβ∴+=︒2,OFC OEA βα∠=-∠=β()33222160OEA OFC ββαβα∴∠-∠=--=+=︒即3160OEA OFC ∠-∠=︒【点睛】本题考查了平行线的性质,以及角平分线的定义,掌握平行线的性质是解题的关键.18.点O 是直线AB 上的一点,射线OC 从OA 出发绕点O 顺时针方向旋转,旋转到OB 停止,设AOC α∠=(0180α︒≤≤︒),射线OD OC ⊥,作射线OE 平分BOD ∠.(1)如图1,若40α=︒,且OD 在直线AB 的上方,求DOE ∠的度数(要求写出简单的几何推理过程).(2)射线OC 顺时针旋转一定的角度得到图2,当射线OD 在直线AB 的下方时,其他条件不变,请你用含α的代数式表示DOE ∠的度数,(要求写出简单的几何推理过程).(3)射线OC 从OA 出发绕点O 顺时针方向旋转到OB ,在旋转过程中你发现DOE ∠与AOC∠(01800180AOC DOB ︒≤∠≤︒︒≤∠≤︒,)之间有怎样的数量关系?请你直接用含α的代数式表示DOE ∠的度数.【答案】(1)25DOE ∠=︒ (2)1452DOE α∠=-︒ (3)1452DOE AOC ∠=︒-∠即1452DOE α∠=︒-或1452DOE AOC ∠=︒+∠即1452DOE α∠=︒+或11352DOE AOC ∠=︒-∠即11352DOE α∠=︒-或1452DOE AOC ∠=∠-︒即1452DOE α∠=-︒ 【分析】(1)根据40α=︒,∠COD =90°,求出∠BOD =50°,根据OE 平分∠BOD ,即可得出结果;(2)先用α表示出∠BOC ,再根据∠COD =90°表示出∠BOD ,根据OE 平分∠BOD ,即可得出结果; (3)分四种情况进行讨论,分别求出∠DOE 与∠AOC 的关系,用含α的代数式表示∠DOE 的度数即可.(1)解:∠OD ∠OC ,∠∠COD =90°,∠40α=︒,即40AOC ∠=︒,∠18050BOD COD AOC ∠=︒-∠-∠=︒,∠OE 平分∠BOD , ∠1252DOE BOD ∠=∠=︒. (2)AOC α∠=,180BOC α∴∠=︒-,∠OD ∠OC ,∠∠COD =90°,∠BOD COD BOC ∠=∠-∠()90180α=︒-︒-90α=-︒∠OE 平分∠BOD , ∠114522DOE BOD α∠=∠=-︒. (3)∠当090AOC ︒≤∠≤︒,OD 在直线AB 的上方时,如图所示:180BOD COD AOC ∠=︒-∠-∠18090AOC =︒-︒-∠90AOC =︒-∠,∠OE 平分∠BOD , ∠114522DOE BOD AOC ∠=∠=︒-∠, 即1452DOE α∠=︒-. ∠当090AOC ︒≤∠≤︒,OD 在直线AB 的下方时,如图所示:∠90AOD COD AOC AOC ∠=∠-∠=︒-∠,∠18090BOD AOD AOC∠=︒-∠=︒+∠,∠OE平分∠BOD,∠114522DOE BOD AOC ∠=∠=︒+∠,即1452 DOEα∠=︒+.∠当90180AOC︒∠≤︒<,OD在直线AB的上方时,如图所示:180BOC AOC∠=︒-∠,BOD DOC BOC∴∠=∠+∠90180AOC=︒+︒-∠270AOC=︒-∠,∠OE平分∠BOD,∠1113522DOE BOD AOC ∠=∠=︒-∠,即11352 DOEα∠=︒-.∠当90180AOC︒∠≤︒<,OD在直线AB的下方时,如图所示:∠180BOC AOC ∠=︒-∠,BOD COD BOC ∴∠=∠-∠()90180AOC =︒-︒-∠90AOC =∠-︒,∠OE 平分∠BOD , ∠114522DOE BOD AOC ∠=∠=∠-︒, 即1452DOE α∠=-︒. 综上分析可知,1452DOE AOC ∠=︒-∠即1452DOE α∠=︒-或1452DOE AOC ∠=︒+∠即1452DOE α∠=︒+或11352DOE AOC ∠=︒-∠即11352DOE α∠=︒-或1452DOE AOC ∠=∠-︒即1452DOE α∠=-︒. 【点睛】本题主要考查了角平分线的定义,垂直的定义,根据α的大小和OD 的位置分类讨论,是解决本题的关键.19.如图,AD //BC ,127DAC ∠=︒,15ACF ∠=︒,142EFC ∠=︒.(1)求证:EF //AD ;(2)连接CE ,若CE 平分∠BCF ,求∠FEC 的度数.【答案】(1)证明见解析(2)19FEC ∠=︒【分析】(1)先根据平行线的性质,得到∠ACB 的度数,进而得出∠FCB 的度数,再根据∠EFC =140°,即可得到∠EFC =142°,即可得到EF ∠BC ,进而得出EF ∠AD ;(2)先根据CE 平分∠BCF ,可得∠BCE =19°,再根据EF ∠BC ,即可得到∠FEC =19°.(1)证明:∠AD BC ∥∠180ACB DAC ∠+∠=︒∠127DAC ∠=︒∠53ACB ∠=︒又∠15ACF ∠=︒∠38FCB ACB ACF ∠=∠-∠=︒∠142EFC ∠=︒∠180FCB EFC ∠+∠=︒∠EF BC ∥又∠AD BC ∥∠EF AD ∥(2)解:∠CF 平分∠BCF ∠1192BCE FCB ∠=∠=︒ ∠EF BC ∥∠19FEC ECB ∠=∠=︒答:∠FEC 的度数19°.【点睛】本题考查平行线的判定,三角形内角和定理,角平分线定义,三角形的外角性质,邻补角定义,能综合运用定理运行推理是解此题的关键,难度适中.20.已知点B ,D 分别在AK 和CF 上,且∥CF AK .(1)如图1,若25CDE ∠=︒,80DEB ∠=︒,则ABE ∠的度数为________;(2)如图2,BG 平分ABE ∠,GB 的延长线与EDF ∠的平分线交于H 点,若DEB ∠比DHB ∠大60︒,求DEB ∠的度数;(3)保持(2)中所求的DEB ∠的度数不变,如图3,BM 平分EBK ∠,DN 平分CDE ∠,作∥BP DN ,则PBM ∠的度数是否改变?若不变,请求值;若改变,请说明理由.【答案】(1)55°(2)100°(3)不变,40°【分析】(1)过点E 作ES CF ,根据∥CF AK ,则ES CF AK ,运用平行线的性质计算即可.(2) 延长DE ,交AB 于点M ,则∠DEB =∠EMB +∠EBM ,利用平行线的性质,角平分线的定义,三角形外角的性质计算即可.(3) 过点E 作EQ DN ,则EQ DN BP ,利用前面的结论和方法,进行等量代换并推理计算即可.(1)解:如图1,过点E 作ES CF ,∠∥CF AK ,∠ES CF AK ,∠∠CDE =∠DES ,∠SEB =∠ABE ,∠∠CDE +∠ABE =∠DES +∠SEB =∠DEB ,∠∠CDE =25°,∠DEB =80°,∠∠ABE =∠DEB -∠CDE =80°-25°=55°.故答案为:55°.(2)解:如图2,延长DE ,交AB 于点M ,则∠DEB =∠EMB +∠EBM ,∠∥CF AK ,BG 平分ABE ∠,∠∠EMB =180°-∠MDF ,∠EBM =2∠ABG =2∠HBN ,∠MDH =∠HDF =∠HNK =12∠MDF ,∠∠HBN +∠DHB =∠HNK ,∠∠DEB =(180°-∠MDF ) +2∠HBN =180°-∠MDF +122MDF DHB ⎛⎫⨯∠-∠ ⎪⎝⎭, ∠∠DEB =180°-∠MDF +∠MDF -2∠DHB =180°-2∠DHB ,∠DEB ∠60DHB -∠=︒,∠∠DEB =180°-2(∠DEB -60°),∠3∠DEB =300°,解得∠DEB =100°.(3)解:过点E作EQ DN,则EQ DN BP,根据(1)得,∠DEB=∠CDE+∠ABE,∠BM平分EBK∠,∠,DN平分CDE∠∠DEB=2∠NDE+180°-2∠EBM,∠∠DEB=100°,∠∠EBM-∠NDE=40°,∠EQ DN,∠∠DEQ=∠NDE,∠∠EBM =40°+∠DEQ,,,∠EQ DN DN BP∠EQ BP,∠∠EBM+∠PBM +∠BEQ =180°,∠40°+∠DEQ+∠PBM +∠BEQ =180°,∠40°+∠DEB+∠PBM =180°,∠∠PBM =180°-100°-40°=40°,∠∠PBM 的度数不变,值为40°.【点睛】本题考查了平行线的判定和性质,三角形外角的性质,角的平分线定义,熟练掌握平行线的判定和性质是解题的关键.。
七年级下数学压轴题

七年级下数学压轴题一、相交线与平行线。
题1:如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE,∠AOD:∠BOE = 4:1,求∠AOF的度数。
解析:设∠BOE = x,因为OE平分∠BOD,所以∠BOD = 2∠BOE=2x。
又因为∠AOD + ∠BOD = 180°,且∠AOD:∠BOE = 4:1,所以∠AOD = 4x。
则4x + 2x=180°,6x = 180°,解得x = 30°。
所以∠COE = 180° - ∠BOE = 150°。
因为OF平分∠COE,所以∠COF=(1)/(2)∠COE = 75°。
∠AOC=∠BOD = 60°,所以∠AOF=∠AOC+∠COF = 60°+ 75°=135°。
题2:已知直线l_1∥ l_2,直线l_3和直线l_1、l_2交于点C和D,在C、D之间有一点P。
(1)如果P点在C、D之间运动时,问∠PAC,∠APB,∠PBD之间的关系是否发生变化。
(2)若点P在C、D两点的外侧运动时(P点与点C、D不重合),试探索∠PAC,∠APB,∠PBD之间的关系又是如何?解析:(1)过点P作PE∥ l_1,因为l_1∥ l_2,所以PE∥ l_2。
∠PAC = ∠APE,∠PBD=∠BPE。
所以∠APB = ∠APE+∠BPE = ∠PAC + ∠PBD。
(2)当点P在l_1上方时,过点P作PF∥ l_1,因为l_1∥ l_2,所以PF∥ l_2。
∠PAC = ∠APF,∠PBD + ∠BPF=180°,所以∠PBD = 180°-(∠APB - ∠PAC),即∠PAC=∠APB + ∠PBD。
当点P在l_2下方时,过点P作PG∥ l_2,同理可得∠PBD = ∠APB+∠PAC。
二、实数。
题3:已知a、b满足√(2a + 8)+| b - √(3)|=0,解关于x的方程(a + 2)x + b^2=a - 1。
初一数学第二学期期中压轴题汇编(人教版)

(3)若方程组
的解是
,求 m 的值,并判断该方程组是否符合(2)中
的规律.
第 3 页(共 50 页)
网校新初二数学赵云辉老师主编
11、△ ABC 中有两个角相等,AD 是它的高,∠CAD=40°,求∠BAD.
12、规定,满足(1)各边互不相等且均为整数,(2)最短边上的高与最长边上的高的比值
为整数 k,这样的三角形称为比高三角形、其中 k 叫做比高系数.根据规定解答下列问题:
第 2 页(共 50 页)
网校新初二数学赵云辉老师主编
8、已知:A(4,0),B(1,﹣x),C(1,3),△ ABC 的面积为 6,求代数式 2x2﹣5x+x2+4x ﹣3x2﹣2 的值.
9、根据下列提供的信息,列方程组,求每支网球拍的单价和每支乒乓球拍的单价,小明带 了 500 元,想买这样的 5 只网球拍,4 只乒乓球拍,能否如愿?
(1)周长为 13 的比高系数 k=
.
(2)写出一个只有 4 个比高系数的比高三角形的周长,周长为
.
(3)比高△ ABC 三边与它的比高系数 k 之间满足 BC﹣AC=AC﹣AB=k2,求△ ABC 的周长.
13、已知△ ABC 中的两角之差为 20°,过△ ABC 顶点的一条直线把这个三角形分成了两个 等腰三角形,写出△ ABC 中最大角.(只写出结果不要求过程)
七年级下册数学几何压轴题

七年级下册数学几何压轴题
1. 把一个长方形沿x轴正方向移动m个单位,求移动前后阴影的面积差。
2. 一个小正方体沿着x轴正方向移动,它的一面在x轴上翻转,求翻转前后阴影的面积比值。
3. 一个方形沿着y轴正方向移动,移动到一个圆的周围,求圆和方形的阴影面积比值。
4. 把一个正方形沿对角线方向移动,它最后完全重合的时候恰好覆盖了一个面积为S的等腰三角形,求三角形面积S。
5. 把一个正方形沿着y轴正方向移动,移动m个单位的时候与另外一个正方形刚好重合,求另外一个正方形的边长。
6. 一个矩形沿x轴正方向移动,移动到另外一个矩形的正上方还有b个单位,求两个矩形的阴影面积比值。
7. 把一个半圆形沿y轴正方向移动,移动到正方形的中心时,求正方形面积和半圆形面积的阴影面积比值。
8. 把一个梯形沿y轴正方向移动,移动到一个与梯形相似的大梯形上面靠着底边的位置,求阴影的面积比值。
9. 把一个正三角形沿着x轴正方向移动,相邻两次的位移满足一个等差数列,第一次移动2个单位,第三次移动8个单位,求正三角形的边长。
10. 一个椭圆形沿y轴正方向移动,移动到一个长方形上方恰好横跨长方形的两个端点,求已经移动了多少个单位。
七年级下册数学的压轴题

1.下面哪个数是 8 和 12 的最小公倍数?
A.24
B.36
C.48
D.60
2.如果 3x - 7 = 11,那么 x 的值是多少?
A. 4
B. 6
C.8
D.9
3.一个三角形的三个内角分别为 50°、60°和多少度?
A.70°
B.80°
C.90°
D.100°
4.一辆汽车以每小时 60 公里的速度行驶,4 小时后行驶了多少公里?
A.120 公里
B.180 公里
C.240 公里
D.300 公里
5.一个正方形的边长是 7 厘米,它的面积是多少平方厘米?
A.49 平方厘米
B.54 平方厘米
C.56 平方厘米
D.63 平方厘米
6.如果一个圆的半径是 5 厘米,则它的直径是多少厘米?
A. 5 厘米
B.10 厘米
C.15 厘米
D.20 厘米
7.下列哪个数是 7 的平方?
A.49
B.56
C.64
D.72
8.一个长方体的长是 8 厘米,宽是 5 厘米,高是 4 厘米,它的体积是多少立方厘米?
A.160 立方厘米
B.180 立方厘米
C.200 立方厘米
D.240 立方厘米
9.如果一个数的 25% 是 15,那么这个数是多少?
A.50
B.60
C.75
D.80。
七年级下册数学期末复习压轴题 解答题试题及答案解答

七年级下册数学期末复习压轴题解答题试题及答案解答1.如图,AB∥CD,点E、F在直线AB上,G在直线CD 上,且∠EGF=90°,∠BFG=140°,求∠XXX的度数.解:由XXX,得∠XXX∠CGE,又∠BFG=140°,所以∠CGE=140°.2.已知x+$\frac{1}{x}$=$\frac{2}{3}$,求值;解:将x+$\frac{1}{x}$=$\frac{2}{3}$两边同时乘以x,得x²+1=$\frac{2}{3}$x,移项化简得3x²-2x-3=0,解得x=1或x=-$\frac{3}{2}$,所以所求值为1或-$\frac{3}{2}$.3.已知关于x、y的二元一次方程组begin{cases} 2x+y=k\\ x+2y=-1 \end{cases}$的解互为相反数,求k的值。
解:设x=-a,y=a,代入方程组得begin{cases} -2a+y=k\\ x-2a=-1 \end{cases}$解得a=$\frac{1}{3}$,y=-$\frac{1}{3}$,k=$\frac{4}{3}$.4.分解因式:1) x²-2xy+xy=x²-xy;2) 9x²-6x(y+1)+(y+1)=(3x-1)(3x-y-1);3) m²(m-1)+4(1-m)=-(m-2)².5.某口罩加工厂有A,B两组工人共150人,A组工人每人每小时可加工口罩70只,B组工人每小时可加工口罩50只,A,B两组工人每小时一共可加工口罩9300只。
1)求A、B两组工人各有多少人?2)由于疫情加重,A、B两组工人均提高了工作效率,一名A组工人和一名B组工人每小时共可生产口罩200只,若A、B两组工人每小时至少加工只口罩,那么A组工人每人每小时至少加工多少只口罩?解:(1)设A组工人有x人,B组工人有150-x人,则70x+50(150-x)=9300解得x=90,150-x=60,所以A组工人有90人,B组工人有60人.2)设A组工人每人每小时可加工a只口罩,B组工人每人每小时可加工b只口罩,则a+b=20070a+50b≥解得a≥100,所以A组工人每人每小时至少加工100只口罩.6.已知下列等式:①32-12=8。
七年级下期末数学压轴题

1.已知三个非负数a 、b 、c 满足325a b c ++=和231a b c +−=,若37m a b c +−,求m 的最大值和最小值.【答案】提示:由已知条件得325213a b c a b c +=−+=+ ,解得73711a c b c =− =− ,则32m c =−,由000a b c≥≥≥得73071100c c c −−≥≥≥,解得37711c ≤≤.故m 的最大值为111−,最小值为57−.2.将若干由l 开始的连续自然数写在纸上,然后删去其中一个数,则余下的数的平均数为4537,问删去的那个数是多少?分析 设所写的数为l ,2,…,n ,删去其中的()1a a n ≤≤,则余下的数的平均数为1245317n a n +++−=− ,由1a n ≤≤,建立n 的不等式组.解 1a n ∴≤≤,()()()1231231231111n n n a n n n n ++++−++++−++++−∴<<−−−即()()()1112142253171n n n n n n −+−<<−−,解得1110510777n ≤≤,106n =或107.当106n =时,46a =;当107n =时,a 为非整数,舍去.3.若正数a 、b 、c 满足不等式组1126352351124c a b c a b c a b a c b <+<<+< <+<,则a 、b 、c 的大小关系是( )A .a b c <<B .b c a <<C .c a b <<D .不确定【答案】B 提示:175871581736232436a c a b c c a a b c a b a b c b c <++<<++<<++<>,,,,517734826a c c cbc b b >>>>>,,. 4.玩具厂用于生产的全部劳力为450个工时,原料为400个单位,生产一个小熊要使用15个工时、20个单位的原料,售价为80元;生产一个小猫要使用10个工时、5个单位的原料,售价为45元.在芳力和原料的限制下合理安排生产小熊、小猫的个数,可以使小熊和小猫总售价尽可能高,请用你所学过的数学知识分析,总售价是否可能达到2200元?【答案】提示:设小熊和小猫的个数分别为x y 、,总售价为z ,则()804551691510450205400z x y x y x y x y =+=++ +≤≤.当总售价为2200z =元时,即为1694403290480x y x y x y += + + ≤≤,也即440163909440164809x x x x − + − + ≤≤,解得1414x ≤≤,故14x =.此时24y =,当1424x y ==,时,801445242200z =×+×=(元) 故安排生产小熊14个、小猫24个可达到总售价2200元.5. (l )把26(1)x x −+展开后得121121211210...a x a x a x a x a +++++,则121086420a a a a a a a ++++++=________;(2)已知2232012...(1)(7)(2)(2)x x a a x a x +−=++++++88(2)a x +,则1234567a a a a a a a −+−+−+【答案】(1)365 【提示】令1x =,由已知等式得12112101a a a a a +++++= ① 令1x =−,由已知等式午1211210729a a a a a −++−+=② ①+②得()1210202730a a a a ++++= ,即121020365a a a a ++++= . (2)58− 提示:令3x =−,得01234567832a a a a a a a a a =−+−+−+−+,令2x =−,得027a −=,比较两边x 的最高次项系数可得81a =,原式2713258=−+−=−. 6.已知252000x =,802000y =,则11x y+等于( ). A .2B .1C .12D .32【答案】B 【提示】252000xy y = ①,802000xy x = ②,①×②得()25802000xyx y +×=,得xy x y =+.7.已知252510a b c d ⋅−⋅=,求证:()()()()1111a d b c −−=−−).【提示】由已知有251025a b ⋅==×,得11251a b −−⋅=,故()1111251d a b d −−−−⋅=.同理可得()1111251b c d b −−−−⋅=,从而()()()()()()()()111111112525a d b d c b d b −×−−−−×−−−⋅=⋅,即()()()()111122a d c b −−−−=,故()()()()1111a d c b −−=−−.8.若非零实数a b ,(a b ≠)满足220070a a −+=,220070b b −+=,则11a b+=____________. 【答案】12007【提示】两式相减得1a b +=,两式相加得2007ab =. 9.已知3ax by +=,5ay bx −=,则()()2222a b x y ++的值为_________.【答案】34 【提示】原式()()22ax by ay bx =++−10.若a b 、满足5||7b =,则3||s b =−的取值范围是___________.【答案】211453−s ≤≤【提示】由条件得215191430=+=−s b s ,,则21501430+− s s ≥≥,解得211453−s ≤≤ 11.已知实数m n p 、、满足等式⋅,求p 的值.分析0,a ≥0)挖掘隐含条件. 解 由19901990m n m n −+ −−≥≥得199199m n +≤≤,∴199m n +=①0= 又由非负数性质,得3520230m n p m n p +−−=+−= ① ② 解由①②③联立的方程组得201p =.12.如图,已知B 是线段AC 上的一点,M 是线段AB 的中点,N 是线段AC 的中点,P 为NA的中点,Q 为MA 的中点,则MN PQ ∶等于( ).A .1B .2C .3D .4【答案】B 提示:1()2MN AN AM PQ PA QA AN AM =−=−=−,. 思路点拨 利用中点,设法把MN PQ 、用含相同线段的代数式表示.13.如图,C 是线段AB 的中点,D 是线段AC 的中点,已知图中所有线段的长度之和为23,求线段AC 的长度.【答案】7313 提示:设AC x =,则32222x x AD AB x DC DB x CB x =====,,,,,由题意得:113223222x x x x x x +++++=. 14.平面内有若干条直线,当下列情况时,可将乎面最多分成几部分? (1)有一条直线时,最多可分成2部分. (2)有两条直线时,最多可分成4部分.CB NM P QADCBA(3)有三条直线时,最多可分成____部分. (4)有n 条直线时,最多可分成____部分.【答案】7;222n n ++ 15.把一张长方形纸条按图中那样折叠后,若得到70AOB ∠′=°,则B OG ∠′=______.【答案】55°16. (1)O 为平面上一点,过点O 在这个平面上引2005条不同的直线1l ,2l ,3l ,…,2005l ,则可形成______对以点O 为顶点的对顶角.(2)若平面上4条直线两两相交,且无三线共点,则一共有_____对同旁内角.【答案】(1)设过O 点的n 条不同直线可形成n a 对对顶角,2n =时,223a n ==,时,32224a a n +×,时, 4323...a a =+×,,20052004220042200422003...24232221a a =+×=×+×++×+×+×+×200520044018020=×=.(2)共有12条线段,有21224×=对同旁内角.17.如图,直线AB CD ∥,30EFA ∠°=, 90FGH ∠=°,30HMN ∠=°,50CNP ∠=°,则GHM ∠的大小是______.【答案】40° 提示:过G 作RG ∥AB ,过点H 作HT CD 交MN 于T ,则GHM GHT MHT ∠=∠−∠.18.分解因式:32(21)x a x ++2(21)a a x ++−2(1)a +−.分析 因a 的最高次数低于x 的最高次数,故将原式整理成字母a 的二次三项式.(第3题)B 'C ' GODC BAa 30°50° M GH P N FE DCBA (第14题)解 原式2232(1)(22)(1)x a x x a x x x =+++++−− 22(1)2(1)(1)(1)x a x x a x x =+++++− 22(1)(21)x x ax a =+++− (1)(1)(1)x x a x a =++++−19.分解因式:2(1)(3)(5)12x x x −+++= .【答案】22(43)(41)x x x x +−++ 20.把下列各式分解因式:(1)4271x x −+;(2)42221x x ax a +++−; (3)4322321x x x x ++++.思路点拨 所给多项式,或有两项的平方和、或有两项的积的2倍,只需配上缺项,就能用配方法恰当分解.【答案】(1)原式422222219(1)(3)x x x x x =++−=+−22(31)(31)x x x x =++−+ (2)原式=4222222212(1)()x x x ax a x x a ++−+−=+−−=2(1)x x a ++−2(1)x x a −++ (3)原式=22(1)x x ++21.计算下列各题:(1)(252)(472)(692)(8112)(199419972)(142)(362)(582)(7102)(199319962)++++++++++××××…×××××…×;(2)32322000220001998200020002001−−+−×; (3)4444444444(764)(1564)(2364)(3164)(3964)(364)(1164)(1964)(2764)(3564)++++++++++. 思路点拨 观察分子、分母数字间的特点,用字母表示数,从一般情形考虑,通过分解变形,寻找复杂数值下隐含的规律.对于(3),运用44222222264(1664)16(8)(4)(48)(48)a a a a a a a a a a +=++−=+−=++−+的结果.【答案】()()()()21232312+−=++=++n n n n n n 考虑一般性:()()()()()()()()()()34567891019951996998.2345678919941995×⋅××⋅××=×⋅×××⋅×× 原式=(2)设2000=a ,则原式()()()322322a 2a a 2(a 2)a 1a 21998666.a a (a 1)a 12001667a 1(a 1)−−−−−−=−===+−+++−(3)原式=(378)(7118)(11158)(15198)(35398)(39438)(138)(378)(7118)(11158)(31358)(35398)×+×+×+×+×+×+−×+×+×+×+×+×+39438337138×+=−×+. 22. (1)当x 分别取值12007,12006,…,12,1,2,…,2006,2007时,求出代数式2211x x −+的值,将所得的结果相加,其和等于( ). A .-1 B .1 C .0 D .2007(2)已知0a b c ++=,1114a b c ++=−,那么222111a b c++的值为( ). 思路点拨 对于(1),取值成对互为倒数,不妨先计算2222111111x x x x− − +++ ;对于(2),由222222111111a b c a b c ++=++想到完全平方公式. 【答案】().01111111111 122222222=+−++−=+−++−x x x x x x x x C 提示:选().162161112111 22=++×−= ++− ++abc c b a bc ac ab c b a C 提示:原式=选 23. (1)若x 取整数.则使分式6321x x +−的值为整数的x 的值有 个. (2)求最大的正整数n ,使得3n +100能被n +10整除. 分析 因相关分式中分子的次数大于或等于分母的次数,故可用分离整数法解题.对于(2),通过将整式整除的问题转化为一个分式问题来加以解决. 解 (1)原式=3+621x −,由题意得(21)x −|6,2x -1=±1,±2,±3,±6,只有当2x -1=±1,±3,x 才为整数,即满足条件的x 有4个.(2)∵332100(1000)90090010100101010n n n n n n n ++−==−+−+++为整数, ∴(n +10)|900,从而x 的最大值为890. 24.(1)设a 、b 、c 均为非零实数,并且2()ab a b =+,3()bc b c =+,4()ca c a =+,则a b c ++= ;(2)(上海市竞赛题)计算:222212110050022005000+++−+−+221005000k k k +−+22999999005000−+. 解 (1)对已知三式取倒数,得112()ab a b =+,113()bc b c =+,114()ca c a =+.∴111211131114a b b c c a +=+=+=解得245a =,247b =,24c =.∴24241128245735a b c ++=++=. (2)∵2222(100)1005000(100)100(100)5000n n n n n n −+−+−−−+=222200100001005000n n n n −+−+=2,而225050501005000−×+=1∴原式=49×2+1=99.25.(1)若使分式241312a a a−++没有意义,则a 的值为 .(2)若分式22123b b b −−−的值为0,则b 的值为 .【答案】(1)0或15− (2)126.已知115x y+=,则2522x xy yx xy y −+++= . 【答案】5727.若2310x x −+=,则2421x x x ++的值为 . 【答案】18提示:由条件可得13x x +=. 28.甲、乙两个公司用相同的价格购粮,他们各购两次,已知两次的价格不同,甲公司每次购粮1万千克,乙公司每次用1万元购粮,那么两次平均价格较低的是哪个公司?【答案】这两次购粮的价格分别为x 元/千克和y 元/千克(x y ≠),则甲公司两次购粮的平均价格为:1000010000200002x y x y++=,乙公司两次购粮的平均价格为:2000021000010000xy x y x y =++.因22()022()x y xy x y x y x y +−−=>++,故两次平均价格较低的是乙公司.29. (1)如果242114x x x =++,那么42251553x x x −+= ; (2)若a b c d b c d a ===,则a b c da b c d−+−+−+的值是 .思路点拨 对于(1),由条件出发,先求出221x x +的值;对于(2),引入参数,利用参数寻找a 、b 、c 、d 的关系.【答案】()03)31(5,31122=−+=+x x xx 原式=由条件得. (2)设a b c dk b c d a ====,则2d ak c dk a k ===⋅,,34b c k a k a b k a k =⋅=⋅=⋅=⋅,,得41k =,即1k =±,当1k =时,a b c d ===,原式=0;当1k =−时,原式=2−.30.(1)若关于x 的方程1221(1)(2)x x ax x x x x ++−=+−−+无解,求a 的值. 分析 原方程“无解”内涵丰富:可能是化得的整式方程无解.亦可能是求得的整式方程的解为增根,故须全面讨论. 解 原方程化为(2)3a a +=−, ①∵原方程无解,∴20a +=或10x −=,20x +=, 得2a =−或1,2x x ==−.把1,2x x ==−分别代入①,得15,2a a =−=−, 综上知a =-2,-5或12−.(2)解下列分式方程: ① 18272938x x x x x x x x +++++=+++++; ②222111132567124x x x x x x x ++=+++++++.思路点拨 若去分母化为整式方程,则显然较繁.对于(1),分别计算等号左右两边或分离整数;对于(2),把等号左边的每个分式拆项.【答案】(2)①,811311911211+−++−=+−++−x x x x 原方程化为 即1111-,(x 2)(x 3)(x 8)(x 9),329x 8x x x −=++=++++++进一步化为 11x -. 2=解并检验得 ②111111112,,122334444x x x x x x x x x −++−==+++++++++原方程化为--即 2.x =解并检验得31.已知:1ax by cz ===,求444444111111111111a b c x y z +++++++++++的值. 【答案】由条件有:111x y z a b c===,,,于是 44444441111111111111a a x a a a a +=+=+=++++++,原式=3.32.已知实数p 、q 、r 满足26p q r ++=,11131p q r++=,则p q r p r q p r p r q p +++++= .【答案】803 提示:把条件中的两个等式相乘.33.已知x y z uy z u z u x u x y x y z ===++++++++,求x y y z z u u x z u u x x y y z +++++++++++的值. 【答案】由条件,得.x y z u x y z u x y z u x y z uy z u z u x u x y x y z ++++++++++++===++++++++(1)0,111 1 4x y z u x y z u +++≠===+++若,则由分母推得原式==。
七年级数学版下册压轴题

七年级数学版下册压轴题第一题:分数的加减乘除运算题目要求:请计算以下数式的值,并将答案化简至最简形式。
1.(1/3) + (2/5)2.(4/7) - (1/5)3.(2/3) × (3/8)4.(5/6) ÷ (1/4)答案及解析1.(1/3) + (2/5)解法:首先最小公倍数为15,将分数的分母变为15,得到(5/15) + (6/15) = 11/15,所以答案为11/15。
2.(4/7) - (1/5)解法:首先最小公倍数为35,将分数的分母变为35,得到(20/35) - (7/35) = 13/35,所以答案为13/35。
3.(2/3) × (3/8)解法:将分数相乘得到(2×3)/(3×8) = 6/24,将6/24化简为最简形式,得到1/4,所以答案为1/4。
4.(5/6) ÷ (1/4)解法:将除法转化为乘法,得到(5/6) × (4/1)= (5×4)/(6×1) = 20/6,将20/6化简为最简形式,得到10/3,所以答案为10/3。
第二题:解一元一次方程题目要求:解下列一元一次方程。
1.2x - 3 = x + 42.3(x + 5) = 6x - 93.2(x + 3) - 4(x - 2) = 5(2x - 1)答案及解析1.2x - 3 = x + 4解法:将方程中的变量合并在一起,得到2x - x = 4 + 3,化简得到x = 7,所以方程的解为x = 7。
2.3(x + 5) = 6x - 9解法:先将方程中的括号展开,得到3x + 15 = 6x - 9,将变量合并在一起,得到3x - 6x = -9 - 15,化简得到-3x = -24,再将方程两边同时除以-3,得到x = 8,所以方程的解为x = 8。
3.2(x + 3) - 4(x - 2) = 5(2x - 1)解法:先将方程中的括号展开,得到2x + 6 - 4x + 8 = 10x - 5,将变量合并在一起,得到-2x + 14 = 10x - 5,将方程中的常数项合并在一起,得到-2x - 10x = -5 - 14,化简得到-12x = -19,再将方程两边同时除以-12,得到x =19/12,所以方程的解为x = 19/12。
压轴题01:整式的乘除综合专练20题(原卷版)-七年级数学下学期期末精选题汇编(北师大版)

压轴题01:整式的乘除综合专练20题(原卷版)一、单选题1.在数学中,为了书写简便,18世纪数学家欧拉就引进了求和符号“∑”.如记1nk k =∑=1+2+3+…+(n ﹣1)+n ,3()n k x k =+∑=(x +3)+(x +4)+…+(x +n );已知()()23133nk x k x k x x m =⎡⎤+-+=++⎣⎦∑,则m 的值是( ) A .﹣62 B .﹣38 C .﹣40 D .﹣202.计算100501111122222⋅⋅⋅-⋅⋅⋅个个其结果用幂的形式可表示为( )A .25033333⋅⋅⋅个B .26033333⋅⋅⋅个C .27033333⋅⋅⋅个D .28033333⋅⋅⋅个3.如图,长方形内的阴影部分是由四个半圆围成的图形,则阴影部分的面积是( ).A .21π(2)4ab b - B .21π(2)2ab b -C .221π()4b a -D .221π()8b a -4.计算()()()242018(21)212121++++的结果是( )A .403621+B .403621-C .201821-D .403625.观察等式:2+22=23﹣2;2+22+23=24﹣2;2+22+23+24=25﹣2;…已知按一定规律排列的一组数:2100,2101,2102,…,2199,2200,若2100=S ,用含S 的式子表示这组数据的和是( ) A .2S 2﹣S B .2S 2+SC .2S 2﹣2SD .2S 2﹣2S ﹣26.如图,在长方形ABCD 中放入一个边长为8的大正方形ALMN 和两个边长为6的小正方形(正方形DEFG 和正方形HIJK ).3个阴影部分的面积满足31222S S S +-=,则长方形ABCD 的面积为( )A .100B .96C .90D .867.观察下列等式:()()2111x x x -+=-,()()23111x x x x -++=-,()()324111x x x x x -+++=-,……,利用你发现的规律回答:若()()65432112x x x x x x x -++++++=-,则2016x 的值是( )A .-1B .0C .1D .220168.已知在216()()x mx x a x b +-=++中,a 、b 为整数,能使这个因式分解过程成立的m 的值共有( )个 A .4 B .5 C .8 D .10二、填空题9.如图,在我国南宋数学家杨辉所著的《详解九章算术》一书中,介绍了()na b +展开式的系数规律,称为“杨辉三角”.如第5行的5个数是1,4,10,4,1,恰好对应着()4432234464a b a a b a b ab b +=++++展开式中的各项系数.利用上述规律计算:432101410161014101-⨯+⨯-⨯=______.()()()()()()01234511 11 2 11 3 3 11 4 6 4 11 5 10 10 5 1a b a b a b a b a b a b ⋯⋯++++++⋯⋯10.将边长为1的正方形纸片按如图所示方法进行对折,记第1次对折后得到的图形面积为1S ,第2次对折后得到的图形面积为2S ,…,第n 次对折后得到的图形面积为n S ,请根据图2化简, 12320192020S S S S S +++++=________.11.如图,在长方形 ABCD 中,E 为 AB 中点,以 BE 为边作正方形 BEFG ,边 EF 交 CD 于点 H ,在边 BE 上取点 M 使 BM =BC ,作 MN ∥BG 交 CD 于点 L ,交 FG 于点 N .欧几里得在《几何原本》中利用该图解释了()()22a b a b a b +-=-.连结DE ,记∥EDH 的面积为 S 1,图中阴影部分的面积为S 2.若72a b =,则12S S 的值为__________.12.若2()()6x a x b x mx ++=++,其中,,a b m 均为整数,则m 的值为_______.13.()()()24321(31)3131312+++⋯++的值为_______.14.现有如图∥的小长方形纸片若干块,已知小长方形的长为a(cm),宽为b(cm),用3个如图∥的完全相同的图形和8个如图∥的小长方形,拼成如图∥的大长方形,则图∥中阴影部分面积与整个图形的面积之比为________.15.若两正方体所有棱长之和为48,表面积之和为72,则体积之和为_______________.三、解答题16.若x 满足()()944x x --=,求()()2249x x -+-的值.解:设9,4x a x b -=-=,则()()()()944,945x x ab a b x x --==+=-+-=, ∥()()()22222249252417x x a b a b ab -+-=+=+-=-⨯=. 请仿照上面的方法求解下面问题:(1)若x 满足()()222004200731x x -+-=,求()()20042007x x --的值;(2)已知正方形ABCD 的边长为x ,E ,F 分别是,AD DC 上的点,且1,3AE CF ==,长方形EMFD 的面积是48,分别,MF DF 作正方形MFRN 和正方形GFDH ,求阴影部分的面积.17.若整式A 只含有字母x ,且A 的次数不超过3次,令A =ax 3+bx 2+cx +d ,其中a ,b ,c ,d 为整数,在平面直角坐标系中,我们定义:M (b +d ,a +b +c +d )为整式A 的关联点,我们规定次数超过3次的整式没有关联点.例如,若整式A =2x 2﹣5x +4,则a =0,b =2,c =﹣5,d =4,故A 的关联点为(6,1). (1)若A =x 3+x 2﹣2x +4,则A 的关联点坐标为 .(2)若整式B 是只含有字母x 的整式,整式C 是B 与(x ﹣2)(x +2)的乘积,若整式C 的关联点为(6,﹣3),求整式B 的表达式.(3)若整式D =x ﹣3,整式E 是只含有字母x 的一次多项式,整式F 是整式D 与整式E 的平方的乘积,若整式F 的关联点为(﹣200,0),请直接写出整式E 的表达式.18.阅读下列材料:小明为了计算22020202112222+++⋅⋅⋅++的值,采用以下方法: 设22020202112222S +++⋅⋅⋅++=∥则22021202222222S =++⋅⋅⋅++∥ ∥-∥得,2022221S S S -==-. 请仿照小明的方法解决以下问题: (1)220222++⋅⋅⋅+=______; (2)求2501111222+++⋅⋅⋅++=______;(3)求()()()2100222-+-+⋅⋅⋅+-的和;(请写出计算过程)(4)求2323n a a a na +++⋅⋅⋅+的和(其中0a ≠且1a ≠).(请写出计算过程)19.【知识生成】通常情况下,通过用两种不同的方法计算同一个图形的面积,可以得到一个恒等式.如图1,在边长为a 的正方形中剪掉一个边长为b 的小正方形()a b >.把余下的部分沿虚线剪开拼成一个长方形(如图2).图1中阴影部分面积可表示为:a 2-b 2,图2中阴影部分面积可表示为(a +b )(a -b ),因为两个图中的阴影部分面积是相同的,所以可得到等式:a 2-b 2=(a +b )(a -b );【拓展探究】图3是一个长为2a ,宽为2b 的长方形,沿图中虚线用剪刀平均分成四个小长方形,然后按图4的形状拼成一个正方形.(1)用两种不同方法表示图4中阴影部分面积:方法1: ,方法2: ;(2)由(1)可得到一个关于(a +b )2、(a -b )2、ab 的的等量关系式是 ; (3)若a +b =10,ab =5,则(a -b )2= ; 【知识迁移】(4)如图5,将左边的几何体上下两部分剖开后正好可拼成如右图的一个长方体.根据不同方法表示它的体积也可写出一个代数恒等式: .20.数学家波利亚说过:“为了得到一个方程,我们必须把同一个量以两种不同的方法表示出来,即将一个量算两次,从而建立相等关系,”这就是“算两次”原理,也称为富比尼(G .Fubini )原理,例如:对于一个图形,通过不同的方法计算图形的面积可以得到一个数学等式.【教材片段】:计算如图1的面积,把图1看做一个大正方形,它的面积是()2a b +,如果把图1看做是由2个长方形和2个小正方形组成的,它的面积为222a ab b ++,由此得到:()2222a b a ab b +=++.(1)如图2,用不同的代数式表示大正方形的而积,由此得到的等式为__________;(用a 、b 表示) (2)利用上面结论解决问题:若6,2x y xy +==,则()2x y -=__________;(3)如图3,用不同的代数式表示大正方形的面积,由此得到的等式为__________;(用a 、b 、c 表示)(4)利用上面结论解决问题:已知7,14a b c ab bc ac ++=++=,则222a b c ++=__________;(5)如图4,用不同的代数式表示大正方形的面积(里面是边长为c的小正方形),由此得到的等式为__________;(用a、b、c表示)(6)若22=-==+,请通过计算说明a、b、c满足上面结论.a nb nc n1,2,1。
七年级(下册)数学压轴题集锦

1、2a b m b a-+b+3=0=14.ABCA S如图,已知(0,),B (0,),C (,)且(4),o y =DC FD ADO ⊥∠∠∠(1)求C 点坐标(2)作DE ,交轴于E 点,EF 为AED 的平分线,且DFE 90。
求证:平分;(3)E 在y 轴负半轴上运动时.连EC.点P 为AC 延长线上一点.EM 平分∠AEC.且PM ⊥EM,PN ⊥x 轴于N 点.PQ 平分∠APN.交x 轴于Q 点.则E 在运动过程中.MPQECA∠∠的大小是否发生变化.若不变.求出其值。
2、如图1.AB//EF, ∠2=2∠1 (1)证明∠FEC=∠FCE;(2)如图2.M 为AC 上一点.N 为FE 延长线上一点.且∠FNM=∠FMN.则∠NMC 与∠CFM 有何数量关系.并证明。
图1 图2 3、(1)如图.△ABC, ∠ABC 、∠ACB 的三等分线交于点E 、D.若∠1=130°.∠B C B C2=110°.求∠A 的度数。
(2)如图.△ABC,∠ABC 的三等分线分别与∠ACB 的平分线交于点D,E 若∠1=110°.∠2=130°.求∠A 的度数。
4、如图.∠ABC+∠ADC=180°.OE 、OF 分别是角平分线.则判断OE 、OF 的位置关系为?5、已知∠A=∠C=90°.BCCFA(1)如图.∠ABC 的平分线与∠ADC 的平分线交于点E.试问BE 与DE 有何位置关系?说明你的理由。
(2)如图.试问∠ABC 的平分线BE 与∠ADC 的外角平分线DF 有何位置关系?说明你的理由。
(3)如图.若∠ABC 的外角平分线与∠ADC 的外角平分线交于点E.试问BE 与DE 有何位置关系?说明你的理由。
6.(1)如图.点E 在AC 的延长线上.∠BAC 与∠DCE 的平分线交于点F.∠B=60°,∠F=56°,求∠BDC 的度数。
【初中数学】七年级下册压轴题专项练习(解析版)

一、解答题1.如图,用两个面积为200cm 2七年级下册数学压轴题专题练习(解析版)的小正方形拼成一个大的正方形.(1)则大正方形的边长是;(2)若沿着大正方形边的方向裁出一个长方形,能否使裁出的长方形纸片的长宽之比为4:3,且面积为360cm 2?2.如图,在9⨯9网格中,每个小正方形的边长均为1,正方形ABCD 的顶点都在网格的格点上.(1)求正方形ABCD 的面积和边长;(2)建立适当的平面直角坐标系,写出正方形四个顶点的坐标.3.已知在4⨯4的正方形网格中,每个小正方形的边长为1.(1)计算图①中正方形ABCD 的面积与边长.(2)利用图②中的正方形网格,作出面积为8的正方形,并在此基础上建立适当的数轴,在数轴上表示实数8和-8.4.小丽想用一块面积为400cm 2的正方形纸片,沿着边的方向裁处一块面积为300cm 2的长方形纸片.(1)请帮小丽设计一种可行的裁剪方案;(2)若使长方形的长宽之比为3:2,小丽能用这块纸片裁处符合要求的纸片吗?若能,请帮小丽设计一种裁剪方案,若不能,请简要说明理由.5.某市在招商引资期间,把已倒闭的油泵厂出租给外地某投资商,该投资商为减少固定资产投资,将原来的400m 2的正方形场地改建成300m 2的长方形场地,且其长、宽的比为5:3.(1)求原来正方形场地的周长;(2)如果把原来的正方形场地的铁栅栏围墙全部利用,围成新场地的长方形围墙,那么这些铁栅栏是否够用?试利用所学知识说明理由.二、解答题6.如图,MN//GH,点A、B分别在直线MN、GH上,点O在直线MN、GH之间,若∠NAO=116︒,∠OBH=144︒.(1)∠AOB=︒;(2)如图2,点C、D是∠NAO、∠GBO角平分线上的两点,且∠CDB=35︒,求∠ACD的度数;(3)如图3,点F是平面上的一点,连结FA、FB,E是射线FA上的一点,若∠MAE=n∠OAE,∠HBF=n∠OBF,且∠AFB=60︒,求n的值.7.如图,∠EBF=50°,点C是∠EBF的边BF上一点.动点A从点B出发在∠EBF的边BE 上,沿BE方向运动,在动点A运动的过程中,始终有过点A的射线AD∥BC.(1)在动点A运动的过程中,(填“是”或“否”)存在某一时刻,使得AD平分∠EAC?(2)假设存在AD平分∠EAC,在此情形下,你能猜想∠B和∠ACB之间有何数量关系?并请说明理由;(3)当AC⊥BC时,直接写出∠BAC的度数和此时AD与AC之间的位置关系.8.如图,已知直线AB//射线CD,∠CEB=100︒.P是射线EB上一动点,过点P作PQ//EC交射线CD于点Q,连接CP.作∠PCF=∠PCQ,交直线AB于点F,CG平分∠ECF.(1)若点P,F,G都在点E的右侧,求∠PCG的度数;(2)若点P,F,G都在点E的右侧,∠EGC-∠ECG=30︒,求∠CPQ的度数;(3)在点P的运动过程中,是否存在这样的情形,使∠EGC:∠EFC=4:3?若存在,求出∠CPQ的度数;若不存在,请说明理由.9.已知:AB∥CD,截线MN分别交AB、CD于点M、N.(1)如图①,点B在线段MN上,设∠EBM=α°,∠DNM=β°,且满足a-30+(β﹣60)2=0,求∠BEM的度数;(2)如图②,在(1)的条件下,射线DF平分∠CDE,且交线段BE的延长线于点F;请写出∠DEF与∠CDF之间的数量关系,并说明理由;(3)如图③,当点P在射线NT上运动时,∠DCP与∠BMT的平分线交于点Q,则∠Q与∠CPM的比值为(直接写出答案).10.问题情境:(1)如图1,AB//CD,∠PAB=128︒,∠PCD=119︒.求∠APC度数.小颖同学的解题思路是:如图2,过点P作PE//AB,请你接着完成解答.问题迁移:(2)如图3,AD//BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠PCE=∠β.试判断∠CPD、∠α、∠β之间有何数量关系?(提示:过点P作PF//AD),请说明理由;(3)在(2)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你猜想∠CPD、∠α、∠β之间的数量关系并证明.三、解答题11.已知:直线l 1∥l 2,A 为直线l 1上的一个定点,过点A 的直线交l 2于点B ,点C 在线段BA 的延长线上.D ,E 为直线l 2上的两个动点,点D 在点E 的左侧,连接AD ,AE ,满足∠AED =∠DAE .点M 在l 2上,且在点B 的左侧(2)射线AF 为∠CAD 的角平分线.①如图2,当点D 在点B 右侧时,用等式表示∠EAF 与∠ABD 之间的数量关系,并证明;②当点D 与点B 不重合,且∠ABM +∠EAF =150°时,直接写出∠EAF 的度数..(1)如图1,若∠BAD =25°,∠AED =50°,直接写出∠ABM 的度数;12.阅读下面材料:小颖遇到这样一个问题:已知:如图甲,AB //CD ,E 为AB ,CD 之间一点,连接BE ,DE ,∠B =35︒,∠D =37︒,求∠BED 的度数.她是这样做的:过点E 作EF //AB ,则有∠BEF =∠B ,因为AB //CD ,所以EF //CD .①所以∠FED =∠D ,所以∠BEF +∠FED =∠B +∠D ,即∠BED =_;1.小颖求得∠BED的度数为__;2.上述思路中的①的理由是__;3.请你参考她的思考问题的方法,解决问题:已知:直线a//b,点A,B在直线a上,点C,D在直线b上,连接AD,BC,BE平分∠ABC,DE 平分∠ADC,且BE,DE所在的直线交于点E.(1)如图1,当点B在点A的左侧时,若∠ABC=α,∠ADC=β,则∠BED的度数为;(用含有α,β的式子表示).(2)如图2,当点B在点A的右侧时,设∠ABC=α,∠ADC=β,直接写出∠BED的度数(用含有α,β的式子表示).13.如图1,AB//CD,E是AB、CD之间的一点.(1)判定∠BAE,∠CDE与∠AED之间的数量关系,并证明你的结论;(2)如图2,若∠BAE、∠CDE的两条平分线交于点F.直接写出∠AFD与∠AED之间的数量关系;(3)将图2中的射线DC沿DE翻折交AF于点G得图3,若∠AGD的余角等于2∠E的补角,求∠BAE的大小.14.(1)学习了平行线以后,香橙同学想出了过一点画一条直线的平行线的新方法,她是通过折纸做的,过程如(图1).①请你仿照以上过程,在图2中画出一条直线b,使直线b经过点P,且b//a,要求保留折纸痕迹,画出所用到的直线,指明结果.无需写画法:②在(1)中的步骤(b)中,折纸实际上是在寻找过点P的直线a的线.(2)已知,如图3,AB//CD,BE平分∠ABC,CF平分∠BCD.求证:BE//CF(写出每步的依据).15.如图所示,已知AM//BN,点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C、D,且∠CBD=60︒(1)求∠A的度数.(2)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.四、解答题16.在ABC中,射线AG平分∠BAC交BC于点G,点D在BC边上运动(不与点G重合),过点D作DE//AC交AB于点E.(1)如图1,点D在线段CG上运动时,DF平分∠EDB.①若∠BAC=100︒,∠C=30︒,则∠AFD=_____;若∠B=40︒,则∠AFD=_____;②试探究∠AFD与B之间的数量关系?请说明理由;(2)点D在线段BG上运动时,∠BDE的角平分线所在直线与射线AG交于点F.试探究∠AFD与B之间的数量关系,并说明理由.17.己知:如图①,直线MN⊥直线PQ,垂足为O,点A在射线OP上,点B在射线OQ上(A、B不与O点重合),点C在射线ON上且OC=2,过点C作直线l//PQ.点D在点C的左边且CD=3(1)直接写出的∆BCD面积 ;(2)如图②,若AC⊥BC,作∠CBA的平分线交OC于E,交AC于F,试说明∠CEF=∠CFE;(3)如图③,若∠ADC=∠DAC,点B在射线OQ上运动,∠ACB的平分线交DA的延长线于点H,在点B运动过程中∠H的值是否变化?若不变,求出其值;若变化,求出变化范围.∠ABC18.Rt△ABC中,∠C=90°,点D、E分别是△ABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.(1)若点P在线段AB上,如图(1)所示,且∠α=50°,则∠1+∠2=°;(2)若点P在边AB上运动,如图(2)所示,则∠α、∠1、∠2之间的关系为:;(3)若点P运动到边AB的延长线上,如图(3)所示,则∠α、∠1、∠2之间有何关系?猜想并说明理由.(4)若点P运动到△ABC形外,如图(4)所示,则∠α、∠1、∠2之间的关系为:. 19.直线MN与直线PQ垂直相交于O,点A在射线OP上运动,点B在射线OM上运动,A、B不与点O重合,如图1,已知AC、BC分别是∠BAP和∠ABM角的平分线,(1)点A、B在运动的过程中,∠ACB的大小是否发生变化?若发生变化,请说明理由;若不发生变化,试求出∠ACB的大小.(2)如图2,将△ABC沿直线AB折叠,若点C落在直线PQ上,则∠ABO=________,如图3,将△ABC沿直线AB折叠,若点C落在直线MN上,则∠ABO=________(3)如图4,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及其反3向延长线交于E、F,则∠EAF=;在△AEF中,如果有一个角是另一个角的倍,求∠ABO2的度数.20.如果三角形的两个内角α与β满足2α+β=90︒,那么我们称这样的三角形是“准互余三角形”.(1)如图1,在Rt ABC中,∠ACB=90︒,BD是ABC的角平分线,求证:△ABD是“准互余三角形”;(2)关于“准互余三角形”,有下列说法:①在ABC中,若∠A=100︒,∠B=70︒,∠C=10︒,则ABC是“准互余三角形”;②若ABC是“准互余三角形”,∠C>90︒,∠A=60︒,则∠B=20︒;③“准互余三角形”一定是钝角三角形.其中正确的结论是___________(填写所有正确说法的序号);(3)如图2,B,C为直线l上两点,点A在直线l外,且∠ABC=50︒.若P是直线l上一点,且△ABP是“准互余三角形”,请直接写出∠APB的度数.【参考答案】一、解答题1.(1);(2)无法裁出这样的长方形.【分析】(1)先计算两个小正方形的面积之和,在根据算术平方根的定义,即可求解;(2)设长方形长为cm,宽为cm,根据题意列出方程,解方程比较4x与20的大小解析:(1)20;(2)无法裁出这样的长方形.【分析】(1)先计算两个小正方形的面积之和,在根据算术平方根的定义,即可求解;(2)设长方形长为4x cm,宽为3x cm,根据题意列出方程,解方程比较4x与20的大小即可.【详解】解:(1)由题意得,大正方形的面积为200+200=400cm2,∴边长为:400=20cm;(2)根据题意设长方形长为4x cm,宽为3x cm,4x⋅3x=360由题:则x2=30x0∴x=30∴长为430430>20∴无法裁出这样的长方形.【点睛】本题考查了算术平方根,根据题意列出算式(方程)是解决此题的关键.2.(1)面积为29,边长为;(2),,,,图见解析.【分析】(1)面积等于一个大正方形的面积减去四个直角三角形的面积,再利用算术平方根定义求得边长即可;(2)建立适当的坐标系后写出四个顶点的坐标解析:(1)面积为29,边长为29;(2)A (0,5),B (2,0),C (7,2),D (5,7),图见解析.【分析】(1)面积等于一个7⨯7大正方形的面积减去四个直角三角形的面积,再利用算术平方根定义求得边长即可;(2)建立适当的坐标系后写出四个顶点的坐标即可.【详解】解:(1)正方形的面积S正方形ABCD =72-4⨯⨯2⨯5=29,正方形边长为S =29;(2)建立如图平面直角坐标系,则A (0,5),B (2,0),C (7,2),D (5,7).12【点睛】本题考查了算术平方根及坐标与图形的性质及割补法求面积,从图形中整理出直角三角形是进一步解题的关键.3.(1)正方形的面积为10,正方形的边长为;(2)见解析【分析】(1)利用正方形的面积减去4个直角三角形的面积即可求出正方形的面积,然后根据算术平方根的意义即可求出边长;(2)根据(1)的方法画解析:(1)正方形ABCD 的面积为10,正方形ABCD 的边长为10;(2)见解析【分析】(1)利用正方形的面积减去4个直角三角形的面积即可求出正方形ABCD 的面积,然后根据算术平方根的意义即可求出边长;(2)根据(1)的方法画出图形,然后建立数轴,根据算术平方根的意义即可表示出结论.【详解】解:(1)正方形ABCD 的面积为4×4-4×2×3×1=10则正方形ABCD 的边长为10;(2)如下图所示,正方形的面积为4×4-4×2×2×2=8,所以该正方形即为所求,如图建立数轴,以数轴的原点为圆心,正方形的边长为半径作弧,分别交数轴于两点11∴正方形的边长为8∴弧与数轴的左边交点为-8,右边交点为8,实数8和-8在数轴上如图所示.【点睛】此题考查的是求网格中图形的面积和实数与数轴,掌握算术平方根的意义和利用数轴表示无理数是解题关键.4.(1)可以以正方形一边为长方形的长,在其邻边上截取长为15cm 的线段作为宽即可裁出符合要求的长方形;(2)不能,理由见解析.【解析】(1)解:设面积为400cm2的正方形纸片的边长为a cm∴解析:(1)可以以正方形一边为长方形的长,在其邻边上截取长为15cm 的线段作为宽即可裁出符合要求的长方形;(2)不能,理由见解析.【解析】(1)解:设面积为400cm 2的正方形纸片的边长为a cm∴a 2=400又∵a >0∴a =20又∵要裁出的长方形面积为300cm 2∴若以原正方形纸片的边长为长方形的长,则长方形的宽为:300÷20=15(cm )∴可以以正方形一边为长方形的长,在其邻边上截取长为15cm 的线段作为宽即可裁出符合要求的长方形(2)∵长方形纸片的长宽之比为3:2∴设长方形纸片的长为3x cm ,则宽为2x cm∴6x 2=300∴x 2=50又∵x >0∴x =52∴长方形纸片的长为152又∵152()2=450>202即:152>20∴小丽不能用这块纸片裁出符合要求的纸片5.(1)原来正方形场地的周长为80m ;(2)这些铁栅栏够用.【分析】(1)正方形边长=面积的算术平方根,周长=边长×4,由此解答即可;(2)长、宽的比为5:3,设这个长方形场地宽为3am ,则长为解析:(1)原来正方形场地的周长为80m ;(2)这些铁栅栏够用.【分析】(1)正方形边长=面积的算术平方根,周长=边长×4,由此解答即可;(2)长、宽的比为5:3,设这个长方形场地宽为3am ,则长为5am ,计算出长方形的长与宽可知长方形周长,同理可得正方形的周长,比较大小可知是否够用.【详解】解:(1)400=20(m ),4×20=80(m ),答:原来正方形场地的周长为80m ;(2)设这个长方形场地宽为3am ,则长为5am .由题意有:3a ×5a =300,解得:a =±20,∵3a 表示长度,∴a >0,∴a =20,∴这个长方形场地的周长为 2(3a +5a )=16a =1620(m ),∵80=16×5=16×25>1620,∴这些铁栅栏够用.【点睛】本题考查了算术平方根的实际应用,解答本题的关键是明确题意,求出长方形和正方形的周长.二、解答题6.(1)100;(2)75°;(3)n=3.【分析】(1)如图:过O作OP//MN,由MN//OP//GH得∠NAO+∠POA=180°,∠POB+∠OBH=180°,即∠NAO+∠AOB+∠OB解析:(1)100;(2)75°;(3)n=3.【分析】(1)如图:过O作OP//MN,由MN//OP//GH得∠NAO+∠POA=180°,∠POB+∠OBH=180°,即∠NAO+∠AOB+∠OBH=360°,即可求出∠AOB;(2)如图:分别延长AC、CD交GH于点E、F,先根据角平分线求得∠NAC=58︒,再根据平行线的性质得到∠CEF=58︒;进一步求得∠DBF=18︒,∠DFB=17︒,然后根据三角形外角的性质解答即可;(3)设BF交MN于K,由∠NAO=116°,得∠MAO=64°,故∠MAE=∠OBH=144°,∠HBF=n∠OBF,得∠FBH=∠FKN=∠F+∠FAK,得【详解】解:(1)如图:过O作OP//MN,∵MN//GHl∴MN//OP//GH∴∠NAO+∠POA=180°,∠POB+∠OBH=180°∴∠NAO+∠AOB+∠OBH=360°∵∠NAO=116°,∠OBH=144°∴∠AOB=360°-116°-144°=100°;n⨯64︒,同理n+1n n⨯144︒,从而∠BKA=∠FBH=⨯144︒,又n+1n+1n n⨯144︒=60︒+⨯64︒,即可求n.n+1n+1(2)分别延长AC、CD交GH于点E、F,∵AC平分∠NAO且∠NAO=116︒,∴∠NAC=58︒,又∵MN//GH,∴∠CEF=58︒;∵OBH144,OBG 36∵BD 平分OBG ,∴DBF18,又∵CDB35,∴DFBCDB DBF 351817;∴ACD DFB AEF 175875;(3)设FB 交MN 于K ,∵NAO116,则MAO 64;∴MAEn 64n 1n n 144,BKA =FBH 144,n+1n 1∵OBH144,∴FBH 在△FAK 中,BKAFKA F ∴n n 1446460,n 1n 1n 6460,n 1∴n 3.经检验:n 3是原方程的根,且符合题意.【点睛】本题主要考查平行线的性质及应用,正确作出辅助线、构造平行线、再利用平行线性质进行求解是解答本题的关键.7.(1)是;(2)∠B =∠ACB ,证明见解析;(3)∠BAC =40°,AC⊥AD .【分析】(1)要使AD 平分∠EAC ,则要求∠EAD =∠CAD ,由平行线的性质可得∠B =∠EAD ,∠ACB =∠CAD解析:(1)是;(2)∠B =∠ACB ,证明见解析;(3)∠BAC =40°,AC⊥AD .【分析】(1)要使AD 平分∠EAC ,则要求∠EAD =∠CAD ,由平行线的性质可得∠B =∠EAD ,∠ACB =∠CAD ,则当∠ACB =∠B 时,有AD 平分∠EAC ;(2)根据角平分线可得∠EAD =∠CAD ,由平行线的性质可得∠B =∠EAD ,∠ACB =∠CAD ,则有∠ACB =∠B ;(3)由AC⊥BC ,有∠ACB =90°,则可求∠BAC =40°,由平行线的性质可得AC⊥AD .【详解】解:(1)是,理由如下:要使AD平分∠EAC,则要求∠EAD=∠CAD,由平行线的性质可得∠B=∠EAD,∠ACB=∠CAD,则当∠ACB=∠B时,有AD平分∠EAC;故答案为:是;(2)∠B=∠ACB,理由如下:∵AD平分∠EAC,∴∠EAD=∠CAD,∵AD∥BC,∴∠B=∠EAD,∠ACB=∠CAD,∴∠B=∠ACB.(3)∵AC⊥BC,∴∠ACB=90°,∵∠EBF=50°,∴∠BAC=40°,∵AD∥BC,∴AD⊥AC.【点睛】此题考查了角平分线和平行线的性质,熟练掌握角平分线和平行线的有关性质是解题的关键.8.(1)40°;(2)65°;(3)存在,56°或20°【分析】(1)依据平行线的性质以及角平分线的定义,即可得到∠PCG的度数;(2)依据平行线的性质以及角平分线的定义,即可得到∠ECG=∠G解析:(1)40°;(2)65°;(3)存在,56°或20°【分析】(1)依据平行线的性质以及角平分线的定义,即可得到∠PCG的度数;(2)依据平行线的性质以及角平分线的定义,即可得到∠ECG=∠GCF=25°,再根据PQ∥CE,即可得出∠CPQ=∠ECP=65°;(3)设∠EGC=4x,∠EFC=3x,则∠GCF=4x-3x=x,分两种情况讨论:①当点G、F在点E 的右侧时,②当点G、F在点E的左侧时,依据等量关系列方程求解即可.【详解】解:(1)∵∠CEB=100°,AB∥CD,∴∠ECQ=80°,∵∠PCF=∠PCQ,CG平分∠ECF,∴∠PCG=∠PCF+∠FCG=2∠QCF+2∠FCE=2∠ECQ=40°;(2)∵AB∥CD111∴∠QCG=∠EGC,∠QCG+∠ECG=∠ECQ=80°,∴∠EGC+∠ECG=80°,又∵∠EGC-∠ECG=30°,∴∠EGC=55°,∠ECG=25°,∴∠ECG=∠GCF=25°,∠PCF=∠PCQ=2(80°-50°)=15°,∵PQ∥CE,∴∠CPQ=∠ECP=65°;(3)设∠EGC=4x,∠EFC=3x,则∠GCF=∠FCD=4x-3x=x,①当点G、F在点E的右侧时,1则∠ECG=x,∠PCF=∠PCD=∵∠ECD=80°,3 x,233∴x+x+x+x=80°,22解得x=16°,3∴∠CPQ=∠ECP=x+x+x=56°;2②当点G、F在点E的左侧时,则∠ECG=∠GCF=x,∵∠CGF=180°-4x,∠GCQ=80°+x,∴180°-4x=80°+x,解得x=20°,∴∠FCQ=∠ECF+∠ECQ=40°+80°=120°,∴∠PCQ=2∠FCQ=60°,∴∠CPQ=∠ECP=80°-60°=20°.【点睛】本题主要考查了平行线的性质,解题时注意:两直线平行,同旁内角互补;两直线平行,1内错角相等.9.(1)30°;(2)∠DEF+2∠CDF =150°,理由见解析;(3)【分析】(1)由非负性可求α,β的值,由平行线的性质和外角性质可求解;(2)过点E 作直线EH ∥AB ,由角平分线的性质和平行解析:(1)30°;(2)∠DEF +2∠CDF =150°,理由见解析;(3)2【分析】(1)由非负性可求α,β的值,由平行线的性质和外角性质可求解;(2)过点E 作直线EH ∥AB ,由角平分线的性质和平行线的性质可求∠DEF =180°﹣30°﹣2x °=150°﹣2x °,由角的数量可求解;(3)由平行线的性质和外角性质可求∠PMB =2∠Q +∠PCD ,∠CPM =2∠Q ,即可求解.【详解】解:(1)∵∵AB ∥CD ,∴∠AMN =∠MND =60°,∵∠AMN =∠B +∠BEM =60°,∴∠BEM =60°﹣30°=30°;(2)∠DEF +2∠CDF =150°.理由如下:过点E 作直线EH ∥AB ,1α-30+(β﹣60)2=0,∴α=30,β=60,∵DF 平分∠CDE ,∴设∠CDF =∠EDF =x °;∵EH ∥AB ,∴∠DEH =∠EDC =2x °,∴∠DEF =180°﹣30°﹣2x °=150°﹣2x °;∴∠DEF =150°﹣2∠CDF ,即∠DEF +2∠CDF =150°;(3)如图3,设MQ 与CD 交于点E ,∵MQ 平分∠BMT ,QC 平分∠DCP ,∴∠BMT =2∠PMQ ,∠DCP =2∠DCQ ,∵AB ∥CD ,∴∠BME =∠MEC ,∠BMP =∠PND ,∵∠MEC =∠Q +∠DCQ ,∴2∠MEC =2∠Q +2∠DCQ ,∴∠PMB =2∠Q +∠PCD ,∵∠PND =∠PCD +∠CPM =∠PMB ,∴∠CPM =2∠Q ,∴∠Q 与∠CPM 的比值为2,故答案为:2.【点睛】本题主要考查了平行线的性质、角平分线的性质,准确计算是解题的关键.1110.(1)见解析;(2),理由见解析;(3)①当在延长线时(点不与点重合),;②当在之间时(点不与点,重合),.理由见解析【分析】(1)过P 作PE ∥AB ,构造同旁内角,利用平行线性质,可得∠APC=解析:(1)见解析;(2)∠CPD =∠α+180︒-∠β,理由见解析;(3)①当P 在BA 延长线时(点P 不与点A 重合),∠CPD =180︒-∠β-∠α;②当P 在BO 之间时(点P 不与点B ,O 重合),∠CPD =∠α-180︒+∠β.理由见解析【分析】(1)过P 作PE ∥AB ,构造同旁内角,利用平行线性质,可得∠APC =113°;(2)过过P 作PF //AD 交CD 于F ,,推出AD //PF //BC ,根据平行线的性质得出BCP 180,即可得出答案;(3)画出图形(分两种情况:①点P 在BA 的延长线上,②当P 在BO 之间时(点P 不与点B ,O 重合)),根据平行线的性质即可得出答案.【详解】解:(1)过P 作PE //AB ,AB //CD ,∴PE //AB //CD ,APE PAB =180,∠CPE +∠PCD =180︒,∠PAB =128︒,∠PCD =119︒∴∠APE=52︒,∠CPE=61︒,∴∠APC=52︒+61︒=113︒;(2)∠CPD=∠α+180︒-∠β,理由如下:如图3,过P作PF//AD交CD于F,AD//BC,∴AD//PF//BC,∴∠ADP=∠DPF,∠BCP=∠CPF,∠BCP+∠PCE=180︒,∠PCE=∠β,∴∠BCP=180︒-∠β又∠ADP=∠αCPD DPF CPF=180;(3)①当P在BA延长线时(点P不与点A重合),∠CPD=180︒-∠β-∠α;理由:如图4,过P作PF//AD交CD于F,AD//BC,∴AD//PF//BC,∴∠ADP=∠DPF,∠BCP=∠CPF,∠BCP+∠PCE=180︒,∠PCE=∠β,∴∠BCP=180︒-∠β,又∠ADP=∠α,∴∠CPD=∠CPF-∠DPF=180︒-∠α-∠β;②当P在BO之间时(点P不与点B,O重合),∠CPD=∠α-180︒+∠β.理由:如图5,过P作PF//AD交CD于F,AD//BC,∴AD//PF//BC,∴∠ADP=∠DPF,∠BCP=∠CPF,∠BCP+∠PCE=180︒,∠PCE=∠β,∴∠BCP=180︒-∠β,又∠ADP=∠α∴∠CPD=∠DPF-∠CPF=∠α+∠β-180︒.【点睛】本题考查了平行线的性质的应用,主要考查学生的推理能力,解决问题的关键是作辅助线构造内错角以及同旁内角.三、解答题11.(1);(2)①,见解析;②或【分析】(1)由平行线的性质可得到:,,再利用角的等量代换换算即可;(2)①设,,利用角平分线的定义和角的等量代换表示出对比即可;②分类讨论点在的左右两侧的情况,解析:(1)125︒;(2)①∠ABD=2∠EAF,见解析;②30或110︒【分析】(1)由平行线的性质可得到:∠DEA=∠EAN,∠MBA=∠BAN,再利用角的等量代换换算即可;(2)①设∠EAF=α,∠AED=∠DAE=β,利用角平分线的定义和角的等量代换表示出∠ABD对比即可;②分类讨论点D在B的左右两侧的情况,运用角的等量代换换算即可.【详解】.解:(1)设在l1上有一点N在点A的右侧,如图所示:∵l1//l2∴∠DEA=∠EAN,∠MBA=∠BAN∴∠AED=∠DAE=∠EAN=50︒∴∠BAN=∠BAD+∠DAE+∠EAN=25︒+50︒+50︒=125︒∠BAM=125︒(2)①∠ABD=2∠EAF.证明:设∠EAF=α,∠AED=∠DAE=β.∴∠FAD=∠EAF+∠DAE=α+β.∵AF为∠CAD的角平分线,∴∠CAD=2∠FAD=2α+2β.∵l1l2,∴∠EAN=∠AED=β.∴∠CAN=∠CAD-∠DAE-∠EAN=2α+2β-β-β=2α.∴∠ABD=∠CAN=2α=2∠EAF.②当点D在点B右侧时,如图:由①得:∠ABD=2∠EAF又∵∠ABD+∠ABM=180︒∴∠ABM+2∠EAF=180︒∵∠ABM+∠EAF=150︒∴∠EAF=180︒-150︒=30︒当点D在点B左侧,E在B右侧时,如图:∵AF为∠CAD的角平分线1∴∠DAF=∠CAD2∵l1l 2∴∠AED=∠NAE,∠CAN=∠ABE∵∠DAE=∠AED=∠NAE11∴∠DAE=(∠DAE+∠NAE)=∠DAN2211∴∠EAF=∠DAF+∠DAE=(∠CAD+∠DAN)=(360︒-∠CAN)221=180︒-∠ABE2∵∠ABE+∠ABM=180︒11∴∠EAF=180︒-(180︒-∠ABM)=90︒+∠ABM22又∵∠EAF+∠ABM=150︒11∴∠EAF=90︒+⨯(150︒-∠EAF)=165︒-∠EAF22∴∠EAF=110︒当点D和F在点B左侧时,设在l2上有一点G在点B的右侧如图:11此时仍有∠DAE=∠DAN,∠DAF=∠CAD2211(360︒-∠CAN)=180︒-∠ABG22∴11=180︒-(180︒-∠ABM)=90︒+∠ABM22∠EAF=∠DAE+∠DAF=∴∠EAF=110︒综合所述:∠EAF=30︒或110︒【点睛】本题主要考查了平行线的性质,角平分线的定义,角的等量代换等,灵活运用平行线的性质和角平分线定义等量代换出角的关系是解题的关键.12.;2.平行于同一条直线的两条直线平行;3.(1);(2).【分析】1、根据角度和计算得到答案;2、根据平行线的推论解答;3、(1)根据角平分线的性质及1的结论证明即可得到答案;(2)根据B11解析:1.72;2.平行于同一条直线的两条直线平行;3.(1)α+β;(2)2211180-α+β.22【分析】1、根据角度和计算得到答案;2、根据平行线的推论解答;3、(1)根据角平分线的性质及1的结论证明即可得到答案;11(2)根据BE平分∠ABC,DE平分∠ADC,求出∠ABE=α,∠CDE=β,过点E作2211EF∥AB,根据平行线的性质求出∠BEF=α,∠DEF=180︒-∠CDE=180︒-β,再利用22周角求出答案.【详解】1、过点E作EF//AB,则有∠BEF=∠B,因为AB//CD,所以EF//CD.①所以∠FED=∠D,所以∠BEF+∠FED=∠B+∠D,即∠BED=72;故答案为:72;2、过点E作EF//AB,则有∠BEF=∠B,因为AB//CD,所以EF∥CD(平行于同一条直线的两条直线平行),故答案为:平行于同一条直线的两条直线平行;3、(1)∵BE平分∠ABC,DE平分∠ADC,1111∴∠ABE=∠ABC=α,∠CDE=∠ADC=β,2222过点E作EF∥AB,由1可得∠BED=∠BEF+∠FED=∠ABE+∠CDE,11∴∠BED=α+β,2211故答案为:α+β;22(2)∵BE平分∠ABC,DE平分∠ADC,1111∴∠ABE=∠ABC=α,∠CDE=∠ADC=β,22221过点E作EF∥AB,则∠ABE=∠BEF=α,2∵AB//CD,∴EF∥CD,∴∠CDE+∠DEF=180︒,1∴∠DEF=180︒-∠CDE=180︒-β,21111∴∠BED=360︒-∠DEF-∠BEF=360︒-(180︒-β)-α=180-α+β.2222【点睛】此题考查平行线的性质:两直线平行内错角相等,两直线平行同旁内角互补,平行线的推论,正确引出辅助线是解题的关键.13.(1),见解析;(2);(3)60°【分析】(1)作EF//AB,如图1,则EF//CD,利用平行线的性质得∠1=∠BAE,∠2=∠CDE,从而得到∠BAE+∠CDE=∠AED;(2)如图2,1解析:(1)∠BAE+∠CDE=∠AED,见解析;(2)∠AFD=∠AED;(3)60°2【分析】(1)作EF//AB,如图1,则EF//CD,利用平行线的性质得∠1=∠BAE,∠2=∠CDE,从而得到∠BAE+∠CDE=∠AED;(2)如图2,由(1)的结论得∠AFD=∠BAF+∠CDF,根据角平分线的定义得到∠BAF=1 2∠BAE,∠CDF=2∠CDE,则∠AFD=2(∠BAE+∠CDE),加上(1)的结论得到111∠AFD=2∠AED;(3)由(1)的结论得∠AGD=∠BAF+∠CDG,利用折叠性质得∠CDG=4∠CDF,再利用3等量代换得到∠AGD=2∠AED-∠BAE,加上90°-∠AGD=180°-2∠AED,从而可计算2出∠BAE的度数.【详解】解:(1)∠BAE+∠CDE=∠AED理由如下:作EF//AB,如图1,AB//CD,∴EF//CD.∴∠1=∠BAE,∠2=∠CDE,∴∠BAE+∠CDE=∠AED;(2)如图2,由(1)的结论得∠AFD=∠BAF+∠CDF,∠BAE、∠CDE的两条平分线交于点F,11∴∠BAF=∠BAE,∠CDF=∠CDE,221∴∠AFD=(∠BAE+∠CDE),2∠BAE+∠CDE=∠AED,1∴∠AFD=∠AED;2(3)由(1)的结论得∠AGD=∠BAF+∠CDG,而射线DC沿DE翻折交AF于点G,∴∠CDG=4∠CDF,11∴∠AGD=∠BAF+4∠CDF=∠BAE+2∠CDE=∠BAE+2(∠AED-∠BAE)=2232∠AED-∠BAE,290︒-∠AGD=180︒-2∠AED,3∴90︒-2∠AED+∠BAE=180︒-2∠AED,2∴∠BAE=60︒.【点睛】本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.14.(1)①见解析;②垂;(2)见解析【分析】(1)①过点折纸,使痕迹垂直直线,然后过点折纸使痕迹与前面的痕迹垂直,从而得到直线;②步骤(b)中,折纸实际上是在寻找过点的直线的垂线.(2)先根据解析:(1)①见解析;②垂;(2)见解析【分析】(1)①过P点折纸,使痕迹垂直直线a,然后过P点折纸使痕迹与前面的痕迹垂直,从而得到直线b;②步骤(b)中,折纸实际上是在寻找过点P的直线a的垂线.(2)先根据平行线的性质得到∠ABC=∠BCD,再利用角平分线的定义得到∠2=∠3,然后根据平行线的判定得到结论.【详解】(1)解:①如图2所示:②在(1)中的步骤(b)中,折纸实际上是在寻找过点P的直线a的垂线.故答案为垂;(2)证明:BE平分∠ABC,CF平分∠BCD(已知),∴∠1=∠2,∠3=∠3(角平分线的定义),AB//CD(已知),∴∠ABC=∠BCD(两直线平行,内错角相等),∴2∠2=2∠3(等量代换),∴∠2=∠3(等式性质),∴BE//CF(内错角相等,两直线平行).【点睛】本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了平行线的性质与判定.15.(1);(2)不变化,,理由见解析;(3)【分析】(1)结合题意,根据角平分线的性质,得;再根据平行线的性质计算,即可得到答案;(2)根据平行线的性质,得,;结合角平分线性质,得,即可完成求解解析:(1)∠A=60;(2)不变化,∠APB=2∠ADB,理由见解析;(3)∠ABC=30【分析】(1)结合题意,根据角平分线的性质,得∠ABN;再根据平行线的性质计算,即可得到答案;(2)根据平行线的性质,得∠APB=∠PBN,∠ADB=∠DBN;结合角平分线性质,得∠APB=2∠ADB,即可完成求解;(3)根据平行线的性质,得∠ACB=∠CBN;结合∠ACB=∠ABD,推导得∠ABC=∠DBN;再结合(1)的结论计算,即可得到答案.【详解】(1)∵BC,BD分别评分∠ABP和∠PBN,11∴∠CBP=∠ABP,∠DBP=∠PBN,22∴∠ABN=2∠CBD又∵∠CBD=60,∴∠ABN=120∵AM//BN,∴∠A+∠ABN=180∴∠A=60;(2)∵AM//BN,∴∠APB=∠PBN,∠ADB=∠DBN又∵BD平分∠PBN∴∠PBN=2∠DBN,∴∠APB=2∠ADB;∴∠APB与∠ADB之间的数量关系保持不变;(3)∵AD//BN,∴∠ACB=∠CBN又∵∠ACB=∠ABD,∴∠CBN=∠ABD,∵∠ABC+∠CBN=∠ABD+∠DBN∴∠ABC=∠DBN由(1)可得∠CBD=60,∠ABN=1201∴∠ABC=⨯(120-60)=30.2【点睛】本题考查了角平分线、平行线的知识;解题的关键是熟练掌握角平分线、平行线的性质,从而完成求解.四、解答题16.(1)①115°,110°;②,证明见解析;(2),证明见解析.【解析】【分析】(1)①根据角平分线的定义求得∠CAG=∠BAC=50°;再由平行线的性质可得∠EDG=∠C=30°,∠FMD=1︒解析:(1)①115°,110°;②∠AFD=90+∠B,证明见解析;(2)21∠AFD=90︒-∠B,证明见解析.2【解析】【分析】1(1)①根据角平分线的定义求得∠CAG=∠BAC=50°;再由平行线的性质可得2∠EDG=∠C=30°,∠FMD=∠GAC=50°;由三角形的内角和定理求得∠AFD的度数即可;已知1AG平分∠BAC,DF平分∠EDB,根据角平分线的定义可得∠CAG=∠BAC,21∠FDM=∠EDG;由DE//AC,根据平行线的性质可得∠EDG=∠C,∠FMD=∠GAC;即可得211111∠FDM +∠FMD=∠EDG +∠GAC=∠C+∠BAC=(∠BAC+∠C)=×140°=70°;再由三22222角形的内角和定理可求得∠AFD=110°;1②∠AFD=90°+∠B,已知AG平分∠BAC,DF平分∠EDB,根据角平分线的定义可得211∠CAG=∠BAC,∠FDM=∠EDG;由DE//AC,根据平行线的性质可得∠EDG=∠C,221111∠FMD=∠GAC;由此可得∠FDM +∠FMD=∠EDG +∠GAC=∠C+∠BAC=222211(∠BAC+∠C)=×(180°-∠B)=90°-∠B;再由三角形的内角和定理可得221∠AFD=90°+∠B;21(2)∠AFD=90°-∠B,已知AG平分∠BAC,DF平分∠EDB,根据角平分线的定义可得2111∠CAG=∠BAC,∠NDE=∠EDB,即可得∠FDM=∠NDE=∠EDB;由DE//AC,根据平行2221线的性质可得∠EDB=∠C,∠FMD=∠GAC;即可得到∠FDM=∠NDE=∠C,所以∠FDM211111+∠FMD =∠C+∠BAC=(∠BAC+∠C)=×(180°-∠B)=90°-∠B;再由三角形外角222221的性质可得∠AFD=∠FDM +∠FMD=90°-∠B.2【详解】(1)①∵AG平分∠BAC,∠BAC=100°,1∴∠CAG=∠BAC=50°;2∵DE//AC,∠C=30°,∴∠EDG=∠C=30°,∠FMD=∠GAC=50°;∵DF平分∠EDB,1∴∠FDM=∠EDG=15°;2∴∠AFD=180°-∠FMD-∠FDM=180°-50°-15°=115°;∵∠B=40°,∴∠BAC+∠C=180°-∠B=140°;∵AG平分∠BAC,DF平分∠EDB,11∴∠CAG=∠BAC,∠FDM=∠EDG,22∵DE//AC,∴∠EDG=∠C,∠FMD=∠GAC;11111∴∠FDM +∠FMD=∠EDG +∠GAC=∠C+∠BAC=(∠BAC+∠C)=×140°=70°;22222∴∠AFD=180°-(∠FDM +∠FMD)=180°-70°=110°;故答案为115°,110°;1②∠AFD=90°+∠B,理由如下:2∵AG平分∠BAC,DF平分∠EDB,11∴∠CAG=∠BAC,∠FDM=∠EDG,22∵DE//AC,∴∠EDG=∠C,∠FMD=∠GAC;11111∴∠FDM +∠FMD=∠EDG +∠GAC=∠C+∠BAC=(∠BAC+∠C)=×(180°-∠B)22222 1=90°-∠B;211∴∠AFD=180°-(∠FDM +∠FMD)=180°-(90°-∠B)=90°+∠B;221(2)∠AFD=90°-∠B,理由如下:2如图,射线ED交AG于点M,∵AG平分∠BAC,DF平分∠EDB,11∴∠CAG=∠BAC,∠NDE=∠EDB,221∴∠FDM=∠NDE=∠EDB,2∵DE//AC,∴∠EDB=∠C,∠FMD=∠GAC;1∴∠FDM=∠NDE=∠C,211111∴∠FDM +∠FMD =∠C+∠BAC=(∠BAC+∠C)=×(180°-∠B)=90°-∠B;222221∴∠AFD=∠FDM +∠FMD=90°-∠B.2【点睛】本题考查了角平分线的定义、平行线的性质、三角形的内角和定理及三角形外角的性质,根据角平分线的定义、平行线的性质、三角形的内角和定理及三角形外角的性质确定各角之间的关系是解决问题的关键.17.(1)3; (2)见解析; (3)见解析【详解】分析:(1)因为△BCD的高为OC,所以S△BCD=CD•OC,(2)利用∠CFE+∠CBF=90°,∠OBE+∠OEB=90°,求出∠CEF=∠解析:(1)3; (2)见解析; (3)见解析【详解】。
七年级下册数学压轴题集锦
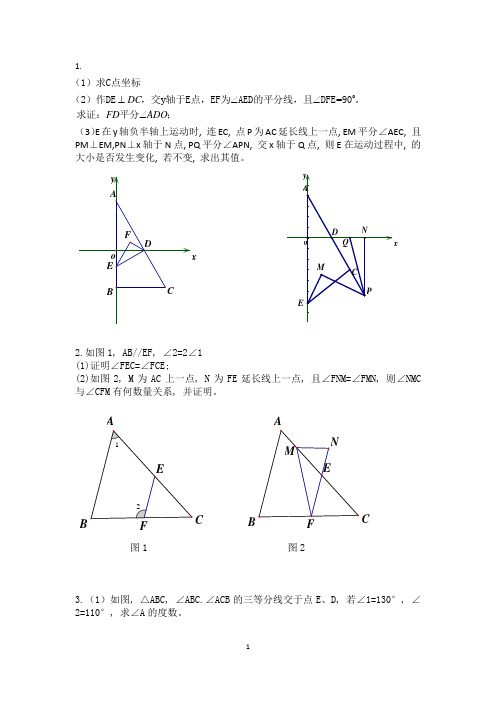
1.o y =DC FD ADO ⊥∠∠∠(1)求C 点坐标(2)作DE ,交轴于E 点,EF 为AED 的平分线,且DFE 90。
求证:平分;(3)E 在y 轴负半轴上运动时, 连EC, 点P 为AC 延长线上一点, EM 平分∠AEC, 且PM ⊥EM,PN ⊥x 轴于N 点, PQ 平分∠APN, 交x 轴于Q 点, 则E 在运动过程中, 的大小是否发生变化, 若不变, 求出其值。
x2.如图1, AB//EF, ∠2=2∠1 (1)证明∠FEC=∠FCE;(2)如图2, M 为AC 上一点, N 为FE 延长线上一点, 且∠FNM=∠FMN, 则∠NMC 与∠CFM 有何数量关系, 并证明。
图1 图23.(1)如图, △ABC, ∠ABC.∠ACB 的三等分线交于点E 、D, 若∠1=130°, ∠2=110°, 求∠A 的度数。
B C B CBC(2)如图, △ABC,∠ABC 的三等分线分别与∠ACB 的平分线交于点D,E 若∠1=110°, ∠2=130°, 求∠A的度数。
AC4.如图, ∠ABC+∠ADC=180°, OE 、OF 分别是角平分线, 则判断OE 、OF 的位置关系为?FEA5.已知∠A=∠C=90°.(1)如图, ∠ABC 的平分线与∠ADC 的平分线交于点E, 试问BE 与DE 有何位置关系? 说明你的理由。
(2)如图, 试问∠ABC 的平分线BE 与∠ADC 的外角平分线DF 有何位置关系?说明你的理由。
(3)如图, 若∠ABC 的外角平分线与∠ADC 的外角平分线交于点E, 试问BE 与DE 有何位置关系?说明你的理由。
A(2)如图, 点E 在CD 的延长线上, ∠BAD 与∠ADE 的平分线交于点F, 试问∠F 、∠B 和∠C 之间有何数量关系? 为什么?EAD7.已知∠ABC 与∠ADC 的平分线交于点E 。
七年级下学期数学期末压轴题精选(汇编)
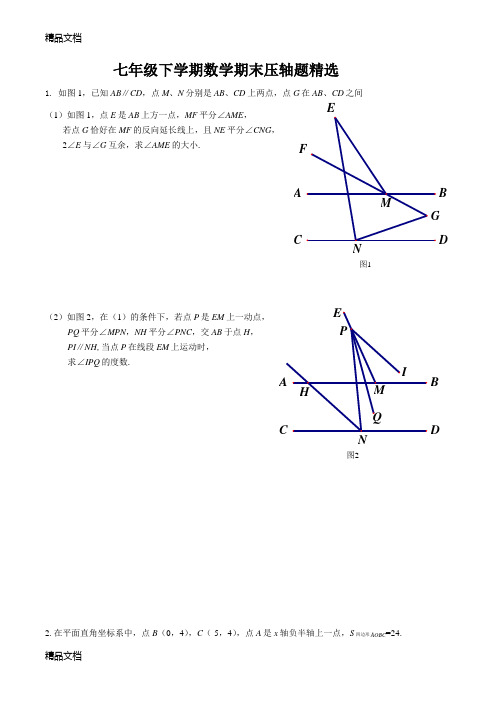
图1AB CDE N图2BDN七年级下学期数学期末压轴题精选1. 如图1,已知AB ∥CD ,点M 、N 分别是AB 、CD 上两点,点G 在AB 、CD 之间 (1)如图1,点E 是AB 上方一点,MF 平分∠AME ,若点G 恰好在MF 的反向延长线上,且NE 平分∠CNG , 2∠E 与∠G 互余,求∠AME 的大小.(2)如图2,在(1)的条件下,若点P 是EM 上一动点,PQ 平分∠MPN ,NH 平分∠PNC ,交AB 于点H , PI ∥NH ,当点P 在线段EM 上运动时, 求∠IPQ 的度数.2. 在平面直角坐标系中,点B (0,4),C (-5,4),点A 是x 轴负半轴上一点,S 四边形AOBC =24.图1图2xy yxO FDEO HBACBAC(1)线段BC 的长为 ,点A 的坐标为 ; (2)如图1,EA 平分∠CAO ,DA 平分∠CAH ,CF ⊥AE 点F ,试给出∠ECF 与∠DAH 之间 满足的数量关系式,并说明理由;(3)若点P 是在直线CB 与直线AO 之间的一点,连接BP 、OP ,BN 平分CBP ∠,ON 平分AOP ∠, BN 交ON 于N ,请依题意画出图形,给出BPO ∠与BNO ∠之间满足的数量关系式,并说明理由.FABC DEN3. 如图,AC ∥BD ,点D 在点B 的右侧,BE ⊥AB ,∠EBD 、∠ACD 的平分线交于点F (点F 不与点B 、C 重合). ∠ABD = m ,∠ACD = n .(1)若点A 在点C 的右侧,求∠BFC ,并直接写出12BFC ABEABD ACD∠-∠∠+∠的值;(2)将(1)中的线段CD 沿BD 方向平移,当点C 移动到点A 的右侧时,求∠BFC ,并直接写出∠BFC 、∠ABD 、∠ACD 之间的关系.4. 如图,MN ∥AB ,点C 、D 在直线MN 上运动,∠CBD 的平分线交射线AC 于点E .(1)当点D 在点C 的右侧运动时,①若∠ACB =∠A ,求AEBCDB∠∠②若∠ACB 比∠A 大30°,AEBCDB∠∠的值是否发生变化,若不变,求出其值;若变化,请探究∠AEB 与∠CDB(2)当点D 在点C 的左侧运动时,若∠ACB =∠A ,请直接写出∠AEB 与∠CDB 之间的关系.图2图1xyDEFBCOAGH5. 线段AB是直角三角形ABC的斜边,将ABC∆放置在平面直角坐标系中,线段AB交y轴于点D. (1)如图1,若点C与点O重合,已知(,)(,)A t aB t b-、,且a b+=D的坐标;(2)如图2,将ABC∆沿着AC方向平移,边AB、BC交平行于y轴的直线于E、F,直线EF交x轴于点G, 点H是边AC上一点,连接FH,①若∠CFH+∠CFE=200°,请写出∠AOD与∠HFE之间的关系,并证明你的结论;②若12+2002CFH CFE∠∠=,请直接写出∠AOD与∠HFE之间的关系.6. 如图1,CD∥AB,12ABF EBF∠=∠, CF平分∠DCE, ∠F的2倍与∠E的余角的和为108°. (1)(2)2,点G、H分别是CD、BE 上一点,3BHI GHI ∠=∠, GJ ∥HI , GK 平分∠DGH ,下列结论:①KGJHGJ∠∠的值为定值,②KGJ HGJ ∠-∠的值为定值,有且只有一个结论正确,请判断,并求出其定值.。
七年级数学下学期期末试卷压轴题整理

1.三角形的两条边长分别是3cm 和4cm ,一个内角为,那么满足条件,且彼此不全等的三角形共有个. 2.如图,把△ABC 纸片沿DE 折叠,当点A 落在四边形BCDE 的外部时,则∠A 与∠1、∠2之间的数量关系是( )A .∠A =∠1-∠2B .2∠A =∠1-∠2C .3∠A =2∠1-∠2D .3∠A =2(∠1-∠2)3.(本题10分)经过顶点的一条直线,.分别是直线 上两点,且.(1)若直线经过的内部,且在射线上,请解决下面的问题:①如图1,若,, 则 ; |BE -AF |(填“”,“”或“”);②如图2,将(1)中的已知条件改成∠BCA=60°,∠=120°,其它条件不变,(1)中的结论__________。
(填“成立”、“不成立”)③若,请添加一个关于与关系的条件 ,使①中的两个结论仍然成立,并证明两个结论成立.(2)如图3,若直线经过的外部,,请提出三条线段数量关系的合理猜想(不要求证明)____________________.9a ,纸若成重,方形的面积,写出一个代数1( E D C BA2 (第18题)恒等式______________________;(2)试选用图①中的纸片(每种纸片至少用一次)在下面的方框中拼成与图②不同的一个长方形,(拼出的图中必须保留拼图的痕迹),标出此长方形的长和宽,并利用拼成的长方形面积写出一个代数恒等式.8。
如图3,在△ABC 中,两条角平分线BD 和CE 相交于点O ,若∠BOC =118°,那么∠A 的度数是 .9.如图4,∠ACB =∠DFE ,BC =EF ,,才能使得△ABC≌△DEF 。
18.(6分)(1)如图5—1);(2)如图5—2,长是 ,面积是 (写成多项式乘法的形式); (3)比较左、右两图的阴影部分面积,可以得到乘法公式 (用式子表达).10.(11分)数学课上,老师让同学们按要求折叠长方形纸片.第一步:先将长方形的四个顶点标上字母A ,B ,C ,D (如图12); 第二步:折叠纸片,使AB 与CD 重合,折出纸痕MN ,然后打开铺平; 第三步:过点D 折叠纸片,使A 点落在折痕MN上的A'处,折痕是DL .这时,老师说:“A ’L 的长度一定等于LD 的一半.”同学们经过测量果然如此.为了解开其中的奥秘,老师设置了几个思考题,请同学们完成: (1)△ALD 与△A ’LD 关于LD 对称吗?(2)AD =A'D 吗?∠ADL =∠A ’DL 吗?∠LA ’D 是直角吗? (3)连接AA',△A'AN 与△A ’DN 对称吗? (4)A'A =A ’D 吗?△A ’AD 是什么三角形?(5)请同学们完整地说明A ’L =LD 的理由. 11.如图2,在等边△ABC 中,取BD =CE =AF ,且D ,E ,F 非所在边中点,由图中找出3个全等三角形组成一组,这样的全等三角形的组数有( ).A.2B.3 C 。
(完整版)七年级下册数学压轴题
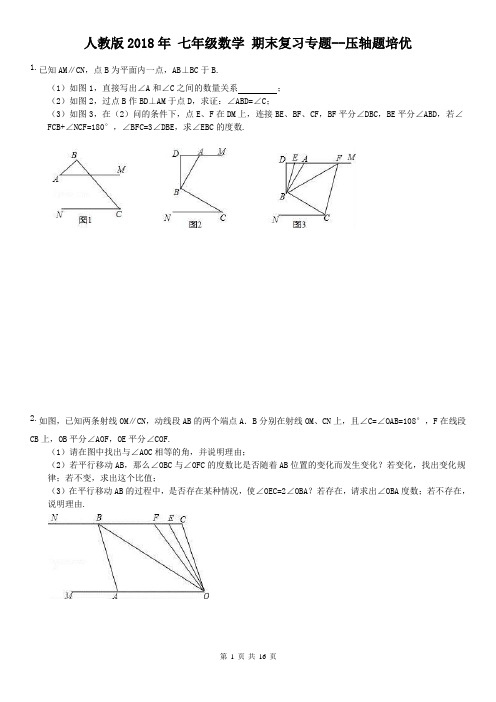
人教版2018年七年级数学期末复习专题--压轴题培优1.已知AM∥CN,点B为平面内一点,AB⊥BC于B.(1)如图1,直接写出∠A和∠C之间的数量关系;(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;(3)如图3,在(2)问的条件下,点E、F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.2.如图,已知两条射线OM∥CN,动线段AB的两个端点A.B分别在射线OM、CN上,且∠C=∠OAB=108°,F在线段CB上,OB平分∠AOF,OE平分∠COF.(1)请在图中找出与∠AOC相等的角,并说明理由;(2)若平行移动AB,那么∠OBC与∠OFC的度数比是否随着AB位置的变化而发生变化?若变化,找出变化规律;若不变,求出这个比值;(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=2∠OBA?若存在,请求出∠OBA度数;若不存在,说明理由.3.已知AB∥CD,线段EF分别与AB、CD相交于点E、F.(1)如图①,当∠A=25°,∠APC=70°时,求∠C的度数;(2)如图②,当点P在线段EF上运动时(不包括E、F两点),∠A.∠APC与∠C之间有什么确定的相等关系?试证明你的结论.(3)如图③,当点P在线段FE的延长线上运动时,(2)中的结论还成立吗?如果成立,说明理由;如果不成立,试探究它们之间新的相等关系并证明.4.如图1,在平面直角坐标系中,A(a,0)是x轴正半轴上一点,C是第四象限一点,CB⊥y轴,交y轴负半轴于B(0,b),且(a-3)2+|b+4|=0,S四边形AOBC=16.(1)求C点坐标;(2)如图2,设D为线段OB上一动点,当AD⊥AC时,∠ODA的角平分线与∠CAE的角平分线的反向延长线交于点P,求∠APD的度数.(3)如图3,当D点在线段OB上运动时,作DM⊥AD交BC于M点,∠BMD、∠DAO的平分线交于N点,则D点在运动过程中,∠N的大小是否变化?若不变,求出其值,若变化,说明理由.5.已知BC∥OA,∠B=∠A=100°.试回答下列问题:(1)如图1所示,求证:OB∥AC;(2)如图2,若点E、F在BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF.试求∠EOC的度数;(3)在(2)的条件下,若平行移动AC,如图3,那么∠OCB:∠OFB的值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
AEBDFC七年级数学下册期中压轴题1、如图,一条直线1l ,最多将平面分成两块,两条直线1l 、2l 相交,最多将平面分成4块,三条直线1l 、2l 、3l 最多将平面分成7块,…,则9条直线1l 、2l 、…,9l 最多将平面分成( )块。
A .49 B .48C .47D .462、已知直线AB ∥CD ,交直线EF 于E 、F 两点,点P 为直线EF 右边平面上一点,且∠AEP=160°,∠EPF=45° ,则∠CFP 的度数为 .3、已知如图,△ABC 中,A (m ,n ),B (-4,-1),C (a ,b ),且满足条件22+-=b a ,032=-++n m (本题11分)(1)写出A 、C 的坐标,并画出△ABC. (3分) 1l1l2l1l2l3l(2)P 为坐标轴上一点,且△PBC 的面积等于6,直接写出满足条件的所有P 的坐标,并根据所学过的初一、小学知识选一个P 点坐标写出求解过程.(5分)(3)将AB 平移到A′B′使B′(4,0).现让点C 沿x 轴负方向运动,点N 从点A′出发,沿A′A 方向运动,且点N 的速度比点C 慢.当点C 到达点(-3,0)时,点C 、N 同时停止(自己在坐标系中完成图形). 问:点N 、C 在运动过程中,AB N ACN B CN BAC ''∠+∠'∠+∠的值是否变化?如不变,求其值;如变化,说明理由.(3分)NMH G FE D CBA4、学习了平行线后,小敏想出了过己知直线外一点画这条直线的平行线的新方法,她是通过折一张半透明的纸得到的(如图(1)~(4)),从图中可知,小敏画平行线的依据有( ) ①两直线平行,同位角相等;②两直线平行,内错角相等; ③同位角相等,两直线平行;④内错角相等,两直线平行. A .①② B .②③ C .③④ D .①④5、如图,直线AB∥CD,∠EFA=30°,∠FGH=90°,∠HMN=30°,∠MND=50°,则∠GHM 的大小是 .6、如图1,已知AB ∥CD ,点M 、N 分别是AB 、CD 上两点,点G 在AB 、CD 之间 (1)求证:∠BMG+∠GND=∠MGN.(2)如图2,点E 是AB 上方一点,MF 平分∠AME ,若点G 恰好在MF 的反向延长线上,且NE 平分∠CNG ,2∠E 与∠G 互余,求∠AME 的大小(3)如图3,在(2)的条件下,若点P 是EM 上一动点,PQ 平分∠MPN ,NH 平分∠PNC ,交AB 于点H ,PJ ∥NH 当点P 在线段EM 上运动时,∠JPQ 的度数是7、在平面直角坐标系中,点B (0,4),C (-5,4),点A 是x 轴负半轴上一点,S 四边形AOBC =24. (1)线段BC 的长为 ,点A 的坐标为 ;GNMDCBAABCDACN(2)如图1,EA 平分∠CAO ,DA 平分∠CAH ,CF ⊥AE 点F ,试给出∠ECF 与∠DAH 之间满足的数量关系式,并说明理由;(3)若点P 是在直线CB 与直线AO 之间的一点,连接BP 、OP ,BN 平分CBP ∠,ON 平分AOP ∠,BN 交ON 于N ,请依题意画出图形,给出BPO ∠与BNO ∠之间满足的数量关系式,并说明理由.8、江汉区某中学组织七年级同学参加校外活动,原计划租用45座客车若干辆,但有15人没有座位;如果租用同样数量的60座客车,则多出一辆,且其余客车刚好坐满.已知45座和60座客车的租金分别为220元/辆和300元/辆.(1)设原计划租45座客车x 辆,七年级共有学生y 人,则y = (用含x 的式子表示);若租用60座客车,则y = (用含x 的式子表示); (2)七年级共有学生多少人?(3)若同时租用两种型号的客车或只租一种型号的客车,每辆客车恰好坐满并且每个同学都有座位,共有哪几种租车方案?哪种方案更省钱?9、如图1,在平面直角坐标系中,A (a ,0),B (b ,0),C (-1,2),且221(24)0a b a b ++++-=.(1)求a ,b 的值;(2)①在x 轴的正半轴上存在一点M ,使△COM 的面积=12△ABC 的面积,求出点M 的坐标;②在坐标轴的其它位置是否存在点M ,使△COM 的面积=12△ABC 的面积仍然成立,若存在,请直接写出符合条件的点M 的坐标;(3)如图2,过点C 作CD ⊥y 轴交y 轴于点D ,点P 为线段CD 延长线上一动点,连接OP ,OE 平分∠AOP ,OF ⊥OE .当点P 运动时,DOEOPD∠∠的值是否会改变?若不变,求其值;若改变,说明理由.F EDCBA10、已知,四边形ABCD 中,AD ∥BC ,∠A =∠BCD =∠ABD ,DE 平分∠ADB ,下列说法:①AB ∥CD ;② ED ⊥CD ;③S △EDF =S △BCF .其中错误的说法有( )A .0个B .1个C .2个D .3个11、如图,直线EF ∥GH ,点B 、A 分别在直线EF 、GH 上,连接AB ,在AB 左侧作三角形ABC ,其中∠ACB = 90°,且∠DAB =∠BAC ,直线BD 平分∠FBC 交直线GH 于D . (1)若点C 恰在EF 上,如图1,则∠DBA =________.(2)将A 点向左移动,其它条件不变,如图2,则(1)中的结论还成立吗?若成立,证明你的结论;若不成立,说明你的理由. CABDFHEGCBFEGADH图1 图2(3)若将题目条件“∠ACB = 90°”,改为:“∠ACB = 120°”,其它条件不变,那么∠DBA = _________.(直接写出结果,不必证明) (2分)12、如图1,在平面直角坐标系中,A (a ,0),C (b ,2),且满足02)2(2=-++b a ,过C 作CB ⊥x 轴于B .(1)求三角形ABC的面积.(2)若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,如图2,求∠AED的度数.(3)在y轴上是否存在点P,使得三角形ABC和三角形ACP的面积相等,若存在,求出P 点坐标;若不存在,请说明理由.图1 图2 备用图13、已知∠AOB 与∠BOC 互为邻补角,且∠BOC >∠AOB . OD 平分∠AOB ,射线OE 使12BOE EOC ∠=∠,当∠DOE =72°时,则∠EOC 的度数为( )A .72°B .108°C .72°或108°D .以上都不对14、如图,点E 在直线BH 、DC 之间,点A 为BH 上一点,且AE ⊥CE ,∠DCE-∠HAE=90°.(1)求证:BH ∥CD.(2)如图:直线AF 交DC 于F ,AM 平分∠EAF ,AN 平分∠BAE.试探究∠MAN ,∠AFG 的数量关系. EHA BGC DBAH15、如图,点A(a,6)在第一象限,点B(0,b)在y轴负半轴上,且a,b满足:2a b-++=.(|4|0(1)求△AOB的面积.(2)若线段AB与x轴相交于点C,在点C的右侧,x轴的上是否存在点D,使S△ACD=S△BOC,若存在,求出D点坐标,若不存在,请说明理由.(3)若∠AOx轴=60°,射线OA绕O点以每秒4°的速度顺时针旋转到OA′,射线OB绕B 点以每秒10°的速度顺时针旋转到O′B,当OB转动一周时两者都停止运动. 若两射线同时开始运动,在旋转过程中,经过多长时间,OA′∥O′B?16、如图:AB ∥CD ,OE 平分∠BOC ,OF ⊥OE ,OP ⊥CD , ∠ABO =40°,则下列结论:①OF 平分∠BOD ②∠POE =∠BOF ③∠BOE =70° ④∠POB =2∠DOF ,其中结论正确的序号是( ) A .①②③④ B .只有①③④ C .只有①②③ D .只有①④17、如图:已知在平面直角坐标系中点A (a ,b )点B (a ,0),且满足+=0.(1)求点A 、B 的坐标.(2)已知点C (0,b ),点P 从点B 出发沿x 轴正方向以1个单位每秒的速度移动,同时点Q 从点C 出发沿y 轴负方向以2个单位每秒的速度移动,某一时刻,如 FPEODCBA图所示且S阴=S四边形OCAB,求点P移动的时间.18、A.64B.49C.100D.811920、21、AB∥CD,点C在点D的右侧,∠ABC,∠ADC的平分线交于点E(不与B,D点重合).∠ABC=n°,∠ADC=80°.(1)若点B在点A的左侧,求∠BED的度数(用含n的代数式表示);(2)将(1)中的线段BC沿DC方向平移,当点B移动到点A右侧时,请画出图形并判断∠BED的度数是否改变.若改变,请求出∠BED的度数(用含n的代数式表示);若不变,请说明理由.BAEDC22、长方形OABC,O为平面直角坐标系的原点,OA=5,OC=3,点B在第三象限.(1)求点B的坐标;(2)如图1,若过点B的直线BP与长方形OABC的边交于点P,且将长方形OABC的面积分为1:4两部分,求点P的坐标;(3)如图2,M为x轴负半轴上一点,且∠CBM=∠CMB,N是x轴正半轴上一动点,∠MCN的平分线CD交BM的延长线于点D,在点N运动的过程中,D CNM ∠∠的值是否变化?若不变,求出其值;若变化,请说明理由.图1 图223、24、25、26、精品文档精品文档。
