初一下数学压轴题汇总

合集下载

初一数学下学期压轴题精选

1．（1）如图1，把△ABC 沿DE 折叠，使点A 落在点A’处，试探索△1+△2与△A 的关系．（不必证明）．（2）如图2，BI 平分△ABC ，CI 平分△ACB ，把△ABC 折叠，使点A 与点I 重合，若△1+△2=130°，求△BIC 的度数；（3）如图3，在锐角△ABC 中，BF△AC 于点F ，CG△AB 于点G ，BF 、CG 交于点H ，把△ABC 折叠使点A 和点H 重合，试探索△BHC 与△1+△2的关系，并证明你的结论．2.己知ABC ∆的三边长a 、b 、c 都是正整数，且满足22614580a b a b +--+=(1)求a 、b 的值;(2)求ABC ∆的周长的最小值.3. 9岁的小芳身高1．36米，她的表姐明年想报考北京的大学．表姐的父母打算今年暑假带着小芳及其表姐先去北京旅游一趟，对北京有所了解．他们四人7月31日下午从苏州出发，1日到4日在北京旅游，8月5日上午返回苏州．苏州与北京之间的火车票和飞机票价如下：火车 (高铁二等座) 全票524元，身高1．1～1．5米的儿童享受半价票；飞机 (普通舱) 全票1240元，已满2周岁未满12周岁的儿童享受半价票．他们往北京的开支预计如下：假设他们四人在北京的住宿费刚好等于上表所示其他三项费用之和，7月31日和8月5日合计按一天计算，不参观景点，但产生住宿、伙食、市内交通三项费用．(1) 他们往返都坐火车，结算下来本次旅游总共开支了13668元，求x ，y 的值；(2) 他们往返都坐飞机 (成人票五五折)，其他开支不变，至少要准备多少元?(3) 他们去时坐火车，回来坐飞机 (成人票五五折)，其他开支不变，准备了14000元，是否够用? 如果不够，他们准备不再增加开支，而是压缩住宿的费用，请问他们预定的标准间房价每天不能超过多少元?4. 如图1，一副三角板的两个直角重叠在一起，△A =30°，△C =45°△COD 固定不动，△AOB 绕着O 点顺时针旋转α°（0°< α <180° ）（1）若△AOB 绕着O 点旋转图2的位置，若△BOD =60°，则△AOC =________；（2）若0°<α<90°，在旋转的过程中△BOD +△AOC 的值会发生变化吗?若不变化，请求出这个定值；（3）若90°< α <180° ，问题（2）中的结论还成立吗?说明理由；（4）将△AOB 绕点O 逆时针旋转α度（0°< α <180°），问当α为多少度时，两个三角形至少有一组边所在直线垂直?（请直接写出所有答案）．5. 阅读材料：方程x 2﹣x ﹣2=0中，只含有一个未知数且未知数的次数为2．像这样的方程叫做一元二次方程．把方程的左边分解因式得到（x ﹣2）（x+1）=0．我们知道两个因式乘积为0，其中有一个因式为0即可，因此方程可以转化为：x ﹣2=0或x+1=0．解这两个一次方程得：x=2或x=﹣1．所以原方程的解为：x=2或x=﹣1．上述将方程x 2﹣x ﹣2=0转化为x ﹣2=0或x+1的过程，是将二次降为一次的“降次”过程，从而使得问题得到解决．仿照上面降次的方法，解决下列问题：（1）解方程x 2﹣3x=0；（2）2a 2﹣a ﹣3=0；（3）解方程组：．图1 A B D C 图2 B D C A O O。

七年级下期末真题精选(压轴60题19个考点专练)(原卷版)

七年级下期末真题精选（压轴60题19个考点专练）一．幂的乘方与积的乘方（共1小题）1．（2021春•西湖区校级期末）已知a，b，c为自然数，且满足2a×3b×4c＝192，则a+b+c的取值不可能是（）A．5B．6C．7D．8二．多项式乘多项式（共1小题）2．（2021春•鄞州区校级期末）若（x﹣3）（x+m）＝x2+nx﹣15，求的值．三．完全平方公式的几何背景（共2小题）3．（2021春•奉化区校级期末）如图，将几个小正方形与小长方形拼成一个边长为（a+b+c）的正方形．（1）若用不同的方法计算这个边长为（a+b+c）的正方形面积，就可以得到一个等式，这个等式可以为（只要写出一个即可）；（2）请利用（1）中的等式解答下列问题：①若三个实数a，b，c满足a+b+c＝11，ab+bc+ac＝38，求a2+b2+c2的值；②若三个实数x，y，z满足2x×4y÷8z＝，x2+4y2+9z2＝44，求2xy﹣3xz﹣6yz的值．4．（2017春•庆元县期末）如图所示，图甲由长方形①，长方形②组成，图甲通过移动长方形②得到图乙．（1）S甲＝，S乙＝（用含a、b的代数式分别表示）；（2）利用（1）的结果，说明a2、b2、（a+b）（a﹣b）的等量关系；（3）现有一块如图丙尺寸的长方形纸片，请通过对它分割，再对分割的各部分移动，组成新的图形，画出图形，利用图形说明（a+b）2、（a﹣b）2、ab三者的等量关系．四．完全平方式（共1小题）5．（2022春•拱墅区期末）如图，用1块边长为a的大正方形，4块边长为b的小正方形和4块长为a，宽为b的长方形（a＞b），密铺成正方形ABCD，已知ab＝2，正方形ABCD的面积为S，（）A．若a＝2b+1，则S＝16B．若a＝2b+2，则S＝25C．若S＝25，则a＝2b+3D．若S＝16，则a＝2b+4五．整式的混合运算（共4小题）6．（2022春•宁波期末）如图，将两张长为a，宽为b的长方形纸片按图1，图2两种方式放置，图1和图2中两张长方形纸片重叠部分分别记为①和②，正方形ABCD中未被这两张长方形纸片覆盖部分用阴影表示，图1和图2中阴影部分的面积分别记为S1和S2．若知道下列条件，仍不能求S1﹣S2值的是（）A．长方形纸片长和宽的差B．长方形纸片的周长和面积C．①和②的面积差D．长方形纸片和①的面积差7．（2021春•镇海区校级期末）下列计算正确的是（）A．a5+a5＝2a10B．a3•2a2＝2a6C．（a+1）2＝a2+1D．（﹣2ab）2＝4a2b28．（2020春•义乌市期末）如图，长方形ABCD的边BC＝13，E是边BC上的一点，且BE＝BA＝10．F，G分别是线段AB，CD上的动点，且BF＝DG，现以BE，BF为边作长方形BEHF，以DG为边作正方形DGIJ，点H，I均在长方形ABCD内部．记图中的阴影部分面积分别为S1，S2，长方形BEHF和正方形DGIJ的重叠部分是四边形KILH，当四边形KILH的邻边比为3：4时，S1+S2的值为．9．（2019春•江北区期末）一张如图1的长方形铁皮，四个角都剪去边长为30厘米的正方形，再四周折起，做成一个有底无盖的铁盒如图2，铁盒底面长方形的长是4a（cm），宽是3a（cm），这个无盖铁盒各个面的面积之和称为铁盒的全面积．（1）请用a的代数式表示图1中原长方形铁皮的面积；（2）若要在铁盒的各个外表面漆上某种油漆，每元钱可漆的面积为（cm2），则油漆这个铁盒需要多少钱（用a的代数式表示）？（3）铁盒的底面积是全面积的几分之几（用a的代数式表示）？若铁盒的底面积是全面积的，求a的值；（4）是否存在一个正整数a，使得铁盒的全面积是底面积的正整数倍？若存在，请求出这个a，若不存在，请说明理由．六．因式分解的应用（共6小题）10．（2019春•嘉兴期末）在日常生活中如取款、上网等都需要密码，有一种用“因式分解法”产生的密码，方便记忆，原理是对于多项x4﹣y4，因式分解的结果是（x﹣y）（x+y）（x2+y2），若取x＝9，y＝9时，则各个因式的值是：（x+y）＝18，（x﹣y）＝0，（x2+y2）＝162，于是就可以把“180162”作为一个六位数的密码，对于多项式9x3﹣xy2，取x＝10，y＝10时，用上述方法产生的密码是（写出一个即可）．11．（2022春•金东区期末）通常情况下，a+b不一定等于ab，观察下列几个式子：第1个：2+2＝2×2；第2个：3+＝3×；第3个：4+＝4×…我们把符合a+b＝ab的两个数叫做“和积数对”．（1）写出第4个式子．（2）写出第n个式子，并检验．（3）若m，n是一对“和积数对”，求代数式的值．12．（2021春•婺城区校级期末）小刚同学动手剪了如图①所示的正方形与长方形纸片若干张．（1）他用1张1号、1张2号和2张3号卡片拼出一个新的图形（如图②）．根据这个图形的面积关系写出一个你所熟悉的乘法公式，这个乘法公式是；（2）如果要拼成一个长为（a+2b），宽为（a+b）的大长方形，则需要2号卡片张，3号卡片张；（3）当他拼成如图③所示的长方形，根据6张小纸片的面积和等于大纸片（长方形）的面积可以把多项式a2+3ab+2b2分解因式，其结果是；（4）动手操作，请你依照小刚的方法，利用拼图分解因式a2+5ab+6b2＝画出拼图．13．（2021春•婺城区校级期末）材料一：一个正整数x能写成x＝a2﹣b2（a，b均为正整数，且a≠b），则称x为“雪松数”，a，b为x的一个平方差分解，在x的所有平方差分解中，若a2+b2最大，则称a，b为x的最佳平方差分解，此时F（x）＝a2+b2．例如：24＝72﹣52，24为雪松数，7和5为24的一个平方差分解，32＝92﹣72，32＝62﹣22，因为92+72＞62+22，所以9和7为32的最佳平方差分解，F（32）＝92+72材料二：若一个四位正整数，它的千位数字与个位数字相同，百位数字与十位数字相同，但四个数字不全相同，则称这个四位数为“南麓数”．例如4334，5665均为“南麓数”．根据材料回答：（1）请直接写出两个雪松数，并分别写出它们的一对平方差分解；（2）试证明10不是雪松数；（3）若一个数t既是“雪松数”又是“南麓数”，并且另一个“南麓数”的前两位数字组成的两位数与后两位数字组成的两位数恰好是t的一个平方差分解，请求出所有满足条件的数t中F（t）的最大值．14．（2018春•鄞州区期末）教科书中这样写道：“我们把多项式a2+2ab+b2及a2﹣2ab+b2叫做完全平方式”，如果一个多项式不是完全平方式，我们常做如下变形：先添加一个适当的项，使式子中出现完全平方式，再减去这个项，使整个式子的值不变，这种方法叫做配方法．配方法是一种重要的解决问题的数学方法，不仅可以将一个看似不能分解的多项式分解因式，还能解决一些与非负数有关的问题或求代数式最大值，最小值等．例如：分解因式x2+2x﹣3＝（x2+2x+1）﹣4＝（x+1）2﹣4＝（x+1+2）（x+1﹣2）＝（x+3）（x﹣1）；例如求代数式2x2+4x﹣6的最小值.2x2+4x﹣6＝2（x2+2x﹣3）＝2（x+1）2﹣8．可知当x＝﹣1时，2x2+4x﹣6有最小值，最小值是﹣8，根据阅读材料用配方法解决下列问题：（1）分解因式：m2﹣4m﹣5＝．（2）当a，b为何值时，多项式a2+b2﹣4a+6b+18有最小值，并求出这个最小值．（3）当a，b为何值时，多项式a2﹣2ab+2b2﹣2a﹣4b+27有最小值，并求出这个最小值．15．（2016春•慈溪市期末）利用我们学过的知识，可以导出下面这个形式优美的等式：a2+b2+c2﹣ab﹣bc﹣ac＝[（a﹣b）2+（b﹣c）2+（a﹣c）2]该等式从左到右的变形，不仅保持了结构的对称性，还体现了数学的和谐、简洁美．（1）请你说明这个等式的正确性；（2）若a＝2014，b＝2015，c＝2016，你能很快求出a2+b2+c2﹣ab﹣bc﹣ac的值；（3）已知实数x，y，z，a满足x+a2＝2014，y+a2＝2015，z+a2＝2016，且xyz＝36．求代数式++﹣﹣﹣的值．七．分式的定义（共1小题）16．（2021春•奉化区校级期末）定义：如果一个分式能化成一个整式与一个分子为常数的分式的和的形式，则称这个分式为“和谐分式”．如＝＝+＝1+，＝＝a﹣1+，则和都是“和谐分式”．（1）下列各式中，属于“和谐分式”的是：（填序号）；①；②；③；④（2）将“和谐分式化成一个整式与一个分子为常数的分式的和的形为：＝．（3）应用：已知方程组有正整数解，求整数m的值．八．分式的化简求值（共2小题）17．（2021春•鄞州区校级期末）已知abc＝1，a+b+c＝2，a2+b2+c2＝3，则的值为（）A．﹣1B．C．2D．18．（2019春•鄞州区期末）已知：a﹣b＝m，b﹣c＝n．（1）m＝3，n＝4，求代数式（a﹣c）2，a2+b2+c2﹣ab﹣bc﹣ca的值．（2）若m＜0，n＜0，判断代数式的值与0的大小关系并说明理由．九．二元一次方程组的解（共1小题）19．（2021春•奉化区校级期末）已知关于x，y的方程组给出下列结论：①当a＝1时，方程组的解也是x+y＝2a+1的解；②无论a取何值，x，y的值不可能是互为相反数；③x，y都为自然数的解有4对；④若2x+y＝8，则a＝2．正确的有几个（）A．1B．2C．3D．4一十．二元一次方程组的应用（共3小题）20．（2019春•北仑区期末）宁波杨梅季，本地慈溪杨梅在宁波人的心中是一种家乡的味道．今年是杨梅大年，某杨梅种植大户为了能让居民品尝到物美价廉的杨梅，对1000斤的杨梅进行打包方式优惠出售，打包方式及售价如下：圆篮每篮8斤，售价160元；方篮每篮18斤，售价270元．假如用这两种打包方式恰好全部装完这1000斤杨梅．（1）若销售a篮圆篮和a篮方篮共收入8600元，求a的值；（2）当销售总收入为16760元时，①若这批杨梅全部售完，请问圆篮共包装了多少篮，方篮共包装了多少篮？②若杨梅大户留下b（b＞0）篮圆篮送人，其余的杨梅全部售出，求b的值；（3）为了让更多的人及时吃到杨梅，几家种植大户联合，一起拼车用大、中两种快递送货车运送方形篮杨梅720篮，大车每车比中车每车多送30篮，若一半杨梅用大车送货，一半杨梅用中车装．运送完这批杨梅大中货车运送车次比为3：4，求每辆大、中货车各运送方形杨梅几篮？21．（2018春•宁波期末）用如图所示的甲、乙、丙三块木板做一个长、宽、高分别为x厘米，y厘米和30厘米的长方体木箱，其中甲块木板锯成两块刚好能做箱底和一个长侧面，乙块木板锯成两块刚好能做一个长侧面和一个短侧面，丙块木块锯成两块刚好能做箱盖和剩下的一个短侧面（厚度忽略不计，x＞y）．（1）用含x，y的代数式表示这三块木板的面积；（2）若甲块木块的面积比丙块木块的面积大300平方厘米，乙块木块的面积为1800平方厘米，求x，y 的值；（3）如果购买一块长120厘米，宽为（x+y）的长方形木板做这个木箱，木板的利用率为，试求+的值．22．（2021春•奉化区校级期末）某公园的门票价格规定如表：购票人数1～50人51～100人100以上票价10元/人8元/人5元/人（1）某校七年级甲、乙两班共100多人去该公园举行联欢活动，其中甲班50多人，乙班不足50人．如果以班为单位分别买票，两个班一共应付920元；如果两个班联合起来作为一团体购票，一共只要付515元．问：甲、乙两班分别有多少人？（2）若有A、B两个团队共160人，以各自团队为单位分别买票，共用950元，问A、B两个团队各有多少人？一十一．解分式方程（共1小题）23．（2022春•宁波期末）我们把形如x+＝a+b（a，b不为零），且两个解分别为x1＝a，x2＝b的方程称为“十字分式方程”．例如x+＝4为十字分式方程，可化为x+＝1+3，∴x1＝1，x2＝3．再如x+＝﹣6为十字分式方程，可化为x+＝（﹣2）+（﹣4），∴x1＝﹣2，x2＝﹣4．应用上面的结论解答下列问题：（1）若x+＝﹣5为十字分式方程，则x1＝，x2＝．（2）若十字分式方程x﹣＝﹣2的两个解分别为x1＝m，x2＝n，求的值．（3）若关于x的十字分式方程x﹣＝﹣k﹣1的两个解分别为x1，x2（k＞0，x1＞x2），求的值．一十二．分式方程的应用（共6小题）24．（2021春•奉化区校级期末）商家常将单价不同的A、B两种糖混合成“什锦糖”出售，记“什锦糖”的单价为：A、B两种糖的总价与A、B两种糖的总质量的比．现有两种“什锦糖”：一种是由相同千克数的A种糖和B种糖混合而成的“什锦糖”甲，另一种是由相同金额数的A种糖和B种糖混合而成的“什锦糖”乙．若B种糖比A种糖的单价贵40元/千克，“什锦糖”甲比“什锦糖”乙的单价贵5元/千克，则A 种糖的单价为（）A．50元/千克B．60元/千克C．70元/千克D．80元/千克25．（2021春•婺城区校级期末）某工厂承接了一批纸箱加工任务，用如图1所示的长方形和正方形纸板（长方形的宽与正方形的边长相等）加工成如图所示的竖式与横式两种无盖的长方形纸箱．（加工时接缝材料不计）（1）该工厂原计划用若干天加工纸箱200个，后来由于对方急需要货，实际加工时每天加工速度是原计划的1.5倍，这样提前2天超额完成了任务，且总共比原计划多加工40个，问原计划每天加工纸箱多少个；（2）若该厂购进正方形纸板1000张，长方形纸板2000张．问竖式纸盒，横式纸盒各加工多少个，恰好能将购进的纸板全部用完；（3）该工厂某一天使用的材料清单上显示，这天一共使用正方形纸板50张，长方形纸板a张，全部加工成上述两种纸盒，且120＜a＜136，试求在这一天加工两种纸盒时，a的所有可能值．26．（2021春•婺城区校级期末）“十•一”期间，某商场举行促销活动，活动期间规定：商场内所有商品按标价的80%出售；同时，当顾客在该商场消费满一定金额后，按如下方案获得相应金额的奖券：200≤p＜400400≤p＜500500≤p＜700700≤p＜900…消费金额p（元）的范围3060100130…获得奖券金额（元）根据上述促销方法，顾客在该商场购物可获得双重优惠．例如，购买标价为450元的商品，则消费金额为450×0.8＝360（元），获得优惠额为：450×0.2+30＝120（元）．设购买商品的优惠率＝．试问：（1）购买一件标价为800元的商品，顾客得到的优惠率是多少？（2）若一顾客购买了一套西装，得到的优惠率为，已知该套西装的标价高于700元，低于850元，该套西装的标价是多少元？27．（2021春•奉化区校级期末）某服装店购进一批甲、乙两种款型时尚T恤衫，甲种款型共用了7800元，乙种款型共用了6400元，甲种款型的件数是乙种款型件数的1.5倍，甲种款型每件的进价比乙种款型每件的进价少30元．（1）甲、乙两种款型的T恤衫各购进多少件？（2）商店进价提高60%标价销售，销售一段时间后，甲款型全部售完，乙款型剩余一半，商店决定对乙款型按标价的五折降价销售，很快全部售完，求售完这批T恤衫商店共获利多少元？28．（2021春•南浔区期末）某商场在一楼至二楼间安装了一部自动扶梯，以匀速向上行驶．甲、乙两同学同时从扶梯上匀速走到二楼，且甲每分钟走动的级数是乙的两倍．已知甲走了24级到扶梯顶部，乙走了16级到扶梯顶部（甲、乙两同学每次只跨一级台阶）．（1）扶梯露在外面的部分有多少级？（2）如果与扶梯并排有一从二楼到一楼的楼梯道，台阶数与扶梯级数相同，甲、乙各自到扶梯顶部后按原速再下楼梯到楼梯底部再乘扶梯，若楼梯与扶梯之间的距离忽略不计，问甲第1次追上乙时是在扶梯上还是在楼梯上？他已经走动的级数是多少级？29．（2015春•杭州期末）某工厂承接了一批纸箱加工任务，用如图1所示的长方形和正方形纸板（长方形的宽与正方形的边长相等）加工成如图所示的竖式与横式两种无盖的长方形纸箱．（加工时接缝材料不计）（1）该工厂原计划用若干天加工纸箱200个，后来由于对方急需要货，实际加工时每天加工速度时原计划的1.5倍，这样提前2天超额完成了任务，且总共比原计划多加工40个，问原计划每天加工纸箱多少个；（2）若该厂购进正方形纸板1000张，长方形纸板2000张．问竖式纸盒，横式纸盒各加工多少个，恰好能将购进的纸板全部用完．一十三．平行线的性质（共15小题）30．（2021春•奉化区校级期末）如图，AD∥BC，∠D＝∠ABC，点E是边DC上一点，连接AE交BC的延长线于点H．点F是边AB上一点．使得∠FBE＝∠FEB，作∠FEH的角平分线EG交BH于点G，若∠DEH＝100°，则∠BEG的度数为（）A．30°B．40°C．50°D．60°31．（2021春•奉化区校级期末）如图，AB∥CD，CF平分∠DCG，GE平分∠CGB交FC的延长线于点E，若∠E＝34°，则∠B的度数为．32．（2021春•乐清市期末）将一副三角板如图1所示摆放，直线GH∥MN，现将三角板ABC绕点A以每秒1°的速度顺时针旋转，同时三角板DEF绕点D以每秒2°的速度顺时针旋转，设时间为t秒，如图2，∠BAH＝t°，∠FDM＝2t°，且0≤t≤150，若边BC与三角板的一条直角边（边DE，DF）平行时，则所有满足条件的t的值为．33．（2021春•奉化区校级期末）如图，AB∥CD，∠DCE的角平分线CG的反向延长线和∠ABE的角平分线BF交于点F，∠E﹣∠F＝33°，则∠E＝．34．（2021春•奉化区校级期末）如图，已知直线l1∥l2，且l3和l1、l2分别交于A、B两点，点P在直线AB 上．（1）∠1、∠2、∠3之间的关系为；（2）如果点P在A、B两点之间运动时，∠1、∠2、∠3之间的关系为；（3）如果点P（点P和A、B不重合）在A、B两点外侧运动时，∠1、∠2、∠3之间关系为．35．（2022春•婺城区期末）如图，已知AB∥CD，直线MN交AB于点M，交CD于点N．点E是线段MN 上一点，P，Q分别在射线MA，NC上，连接PE，QE，PF平分∠MPE，QF平分∠CQE．（1）如图1，若PE⊥QE，∠EQN＝64°，则∠MPE＝°，∠PFQ＝°．（2）如图2，求∠PEQ与∠PFQ之间的数量关系，并说明理由．（3）如图3，当PE⊥QE时，若∠APE＝150°，∠MND＝110°，过点P作PH⊥QF交QF的延长线于点H．将直线MN绕点N顺时针旋转，速度为每秒5°，直线MN旋转后的对应直线为M′N，同时△FPH绕点P逆时针旋转，速度为每秒10°，△FPH旋转后的对应三角形为△F′PH′，当直线MN首次落到CD上时，整个运动停止．在此运动过程中，经过t秒后，直线M′N恰好平行于△F′PH′的一条边，请直接写出所有满足条件的t的值．36．（2021春•奉化区校级期末）如图，已知直线AB∥射线CD，∠CEB＝100°．P是射线EB上一动点，过点P作PQ∥EC交射线CD于点Q，连接CP．作∠PCF＝∠PCQ，交直线AB于点F，CG平分∠ECF．（1）若点P，F，G都在点E的右侧．①求∠PCG的度数；②若∠EGC﹣∠ECG＝40°，求∠CPQ的度数．（2）在点P的运动过程中，是否存在这样的情形，使？若存在，求出∠CPQ的度数；若不存在，请说明理由．37．（2021春•镇海区校级期末）已知：直线a∥b，点A，B在直线a上，点C，D在直线b上，（1）连接AD，BC，BE平分∠ABC，DE平分∠ADC，且BE，DE所在的直线交于点E．①如图1，若∠ABC＝60°，∠ADC＝70°，则∠BED的度数为；②如图2，设∠ABC＝α，∠ADC＝β，则∠BED的度数为（用含有α，β的式子表示）．（2）如图3，EF平分∠MEN，NP平分∠END，EQ∥NP，则∠FEQ和∠BME的数量关系是．（3）如图4，若∠BAP＝∠BAC，∠DCP＝∠ACD，且AE平分∠BAP，CF平分∠DCP，猜想∠E+∠F的结果并且证明你的结论；38．（2021春•慈溪市期末）如图，直线CD∥EF，点A，B分别在直线CD，EF上（自左至右分别为C，A，D和E，B，F），∠ABF＝60°．射线AM自射线AB的位置开始，绕点A以每秒1°的速度沿逆时针方向旋转，同时，射线BN自射线BE开始以每秒5°的速度绕点B沿顺时针方向旋转，当射线BN旋转到BF的位置时，两者停止运动．设旋转时间为x秒．（1）如图1，直接写出下列答案：①∠BAD的度数；②射线BN过点A时的x的值．（2）如图2，求当AM∥BN时的x的值．（3）若两条射线AM和BN所在的直线交于点P．①如图3，若P在CD与EF之间，且∠APB＝126°，求x的值．②若x＜24，求∠APB的度数（直接写出用含x的代数式表示的结果）．39．（2021春•镇海区期末）已知直线AB∥CD．（1）如图1，直接写出∠BME、∠E、∠END的数量关系为；（2）如图2，∠BME与∠CNE的角平分线所在的直线相交于点P，试探究∠P与∠E之间的数量关系，并证明你的结论；（3）如图3，∠ABM＝∠MBE，∠CDN＝∠NDE，直线MB、ND交于点F，则＝．40．（2020春•奉化区期末）已知EM∥BN．（1）如图1，求∠E+∠A+∠B的大小，并说明理由．（2）如图2，∠AEM与∠ABN的角平分线相交于点F．①若∠A＝120°，∠AEM＝140°，则∠EFD＝．②试探究∠EFD与∠A的数量关系，并说明你的理由．（3）如图3，∠AEM与∠ABN的角平分线相交于点F，过点F作FG⊥BD交BN于点G，若4∠A＝3∠EFG，求∠EFB的度数．41．（2021春•奉化区校级期末）已知，直线AB∥DC，点P为平面上一点，连接AP与CP．（1）如图1，点P在直线AB、CD之间，当∠BAP＝60°，∠DCP＝20°时，求∠APC．（2）如图2，点P在直线AB、CD之间，∠BAP与∠DCP的角平分线相交于点K，写出∠AKC与∠APC之间的数量关系，并说明理由．（3）如图3，点P落在CD外，∠BAP与∠DCP的角平分线相交于点K，∠AKC与∠APC有何数量关系？并说明理由．42．（2021春•越城区期末）如图1，已知直线CD∥EF，点A、B分别在直线CD与EF上．P为两平行线间一点．（1）求证∠APB＝∠DAP+∠FBP；（2）利用（1）的结论解答：①如图2，AP1、BP1分别平分∠DAP、∠FBP，请你直接写出∠P与∠P1的数量关系是．②如图3，AP2、BP2分别平分∠CAP、∠EBP，若∠APB＝80°，则∠AP2B的度数是．43．（2021春•婺城区校级期末）已知直线AB∥CD．（1）如图1，直接写出∠ABE，∠CDE和∠BED之间的数量关系是．（2）如图2，BF，DF分别平分∠ABE，∠CDE，那么∠BFD和∠BED有怎样的数量关系？请说明理由．（3）如图3，点E在直线BD的右侧，BF，DF仍平分∠ABE，∠CDE，请直接写出∠BFD和∠BED的数量关系．44．（2016春•嵊州市期末）已知：直线a∥b，点A，B分别是a，b上的点，APB是a，b之间的一条折弦，且∠APB＜90°，Q是a，b之间且在折线APB左侧的一点，如图．（1）若∠1＝33°，∠APB＝74°，则∠2＝度．（2）若∠Q的一边与P A平行，另一边与PB平行，请探究∠Q，∠1，2间满足的数量关系并说明理由．（3）若∠Q的一边与P A垂直，另一边与PB平行，请直接写出∠Q，∠1，2之间满足的数量关系．一十四．平行线的判定与性质（共7小题）45．（2021春•奉化区校级期末）如图，PQ∥MN，A，B分别为直线MN、PQ上两点，且∠BAN＝45°，若射线AM绕点A顺时针旋转至AN后立即回转，射线BQ绕点B逆时针旋转至BP后立即回转，两射线分别绕点A、点B不停地旋转，若射线AM转动的速度是a°/秒，射线BQ转动的速度是b°/秒，且a、b 满足|a﹣5|+（b﹣1）2＝0．若射线AM绕点A顺时针先转动18秒，射线BQ才开始绕点B逆时针旋转，在射线BQ到达BA之前，问射线AM再转动秒时，射线AM与射线BQ互相平行．46．（2022春•鄞州区期末）如图，已知CD平分∠ACB，∠1＝∠2．（1）求证：DE∥AC；（2）若∠3＝30°，∠B＝25°，求∠BDE的度数．47．（2021春•奉化区校级期末）课题学习：平行线的“等角转化”功能．阅读理解：如图1，已知点A是BC外一点，连接AB，AC．求∠BAC+∠B+∠C的度数．（1）阅读并补充下面推理过程．解：过点A作ED∥BC，所以∠B＝，∠C＝．又因为∠EAB+∠BAC+∠DAC＝180°．所以∠B+∠BAC+∠C＝180°．解题反思：从上面的推理过程中，我们发现平行线具有“等角转化”的功能，将∠BAC，∠B，∠C“凑”在一起，得出角之间的关系，使问题得以解决．方法运用：（2）如图2，已知AB∥ED，求∠B+∠BCD+∠D的度数．提示：过点C作CF∥AB．深化拓展：（3）已知AB∥CD，点C在点D的右侧，∠ADC＝70°，BE平分∠ABC，DE平分∠ADC，BE，DE所在的直线交于点E，点E在AB与CD两条平行线之间．如图3，点B在点A的左侧，若∠ABC＝60°，则∠BED的度数为°．48．（2021春•奉化区校级期末）[感知]如图①，AB∥CD，∠AEP＝40°，∠PFD＝130°，求∠EPF的度数．小明想到了以下方法：解；（1）如图①，过点P作PM∥AB，∴∠1＝∠AEP＝40°（两直线平行，内错角相等）∵AB∥CD（已知），∴PM∥CD（平行于同一条直线的两直线平行），∴∠2+∠PFD＝180°（两直线平行，同旁内角互补）．∵∠PFD＝130°（已知），∴∠2＝180°﹣130°＝50°（等式的性质），∴∠1+∠2＝40°+50°＝90°（等式的性质）．即∠EPF＝90°（等量代换）．[探究]如图②，AB∥CD，∠AEP＝50°，∠PFC＝120°，求∠EPF的度数．[应用]如图③所示，在[探究]的条件下，∠PEA的平分线和∠PFC的平分线交于点G，则∠G的度数是°．49．（2021春•奉化区校级期末）（1）如图1，已知直线l1∥l2，且l3和l1，l2分别交于A，B两点，点P在线段AB上，则∠1，∠2，∠3之间的等量关系是；如图2，点A在B处北偏东40°方向，在C处的北偏西45°方向，则∠BAC＝°．（2）如图3，∠ABD和∠BDC的平分线交于E，BE交CD于点F，∠1+∠2＝90°，试说明：AB∥CD；并探究∠2与∠3的数量关系．50．（2020春•诸暨市期末）如图，在三角形ABC中，D，E，F三点分别在AB，AC，BC上，过点D的直线与线段EF的交点为点M，已知2∠1﹣∠2＝150°，2∠2﹣∠1＝30°．（1）求证：DM∥AC；（2）若DE∥BC，∠C＝50°，求∠3的度数．51．（2019春•拱墅区期末）如图，AD∥EC．（1）若∠C＝40°，AB平分∠DAC，求∠DAB的度数．（2）若AE平分∠DAB，BF平分∠ABC，试说明AE∥BF的理由．一十五．平移的性质（共2小题）52．（2022春•西湖区校级期末）如图，直线AB∥CD，直线EF与AB、CD分别交于点G、H，∠EHD＝α（0°＜α＜90°）．小安将一个含30°角的直角三角板PMN按如图①放置，使点N、M分别在直线AB、CD上，且在点G、H的右侧，∠P＝90°，∠PMN＝60°．（1）填空：∠PNB+∠PMD∠P（填“＞”“＜”或“＝”）；（2）若∠MNG的平分线NO交直线CD于点O，如图②．①当NO∥EF，PM∥EF时，求α的度数；②小安将三角板PMN保持PM∥EF并向左平移，在平移的过程中求∠MON的度数（用含α的式子表示）．53．（2017春•上虞区期末）如图1所示，已知BC∥OA，∠B＝∠A＝120°（1）说明OB∥AC成立的理由．（2）如图2所示，若点E，F在BC上，且∠FOC＝∠AOC，OE平分∠BOF，求∠EOC的度数．（3）在（2）的条件下，若左右平移AC，如图3所示，那么∠OCB：∠OFB的比值是否随之发生变化？若变化，请说明理由；若不变，请求出这个比值．（4）在（3）的条件下，当∠OEB＝∠OCA时，求∠OCA的度数．一十六．频数（率）分布直方图（共1小题）54．（2018春•嘉兴期末）某市抽查部分家庭每月水电费的开支（单位：元），得到下面的频数分布直方图（每一组含前一个边界值，不含后一个边界值）．请根据该直方图，回答下列问题：（1）被抽查的家庭共有多少户？（2）自左至右第二组的频数、频率分别是多少？（3）小明同学说：“由图中信息可知，被抽查家庭的每月水电费最低开支至少是100元”你认为小明的说法对吗？为什么？一十七．条形统计图（共4小题）55．（2021春•奉化区校级期末）某中学举行“庆祝中华人民共和国成立70周年”知识预赛，学生会把成绩x（分）分成五组：A组：50≤x＜60；B组：60≤x＜70；C组：70≤x＜80；D组：80≤x＜90；E组：90≤x＜100．统计后绘制成如下两个统计图（不完整）．（1）直接填空：①m的值为；②在图2中，C组的扇形圆心角的度数为．（2）在图1中，画出60≤x＜70所对应的条形图；（3）若学生会计划从预赛中选拔前30名进入复赛，则进入复赛的成绩应不低于多少分？56．（2018春•拱墅区期末）以下是某网络书店1～4月关于图书销售情况的两个统计图：某网络书店1﹣4月销售总额统计图绘本类图书销售额占该书店当月销售总额的百分比统计图（1）求1月份该网络书店绘本类图书的销售额．（2）若已知4月份与1月份这两个月的绘本类图书销售额相同，请补全统计图2．（3）有以下两个结论：①该书店第一季度的销售总额为182万元．②该书店1月份到3月份绘本类图书销售额的月增长率相等．请你判断以上两个结论是否正确，并说明理由．57．（2021春•镇海区期末）牡丹江管局教育局为了解九年级学生每学期参加综合实践活动的情况，随机抽样调查某校九年级学生一个学期参加综合实践活动的天数，并用得到的数据绘制了下面两幅不完整的统计图．请你根据图中提供的信息，回答下列问题：（1）求出该校九年级学生总数；（2）分别求出活动时间为5天的学生人数和7天的学生人数，并补全图②；（3）求该校九年级学生一个学期参加综合实践活动天数在5天以上（含5天）的人数是多少？58．（2022春•南浔区期末）某校研究性学习小组以“学生到学校交通工具类型”为主题对全校学生进行随机抽样调查，调查的项目有：公共汽车、小车、摩托车、自行车、其它（每位同学仅选一项）．根据调查。

(完整版)七年级下学期数学期末压轴题精选

图1AB CDE N图2BDN七年级下学期数学期末压轴题精选1. 如图1，已知AB ∥CD ，点M 、N 分别是AB 、CD 上两点，点G 在AB 、CD 之间（1）如图1，点E 是AB 上方一点，MF 平分∠AME ，若点G 恰好在MF 的反向延长线上，且NE 平分∠CNG ， 2∠E 与∠G 互余，求∠AME 的大小.（2）如图2，在（1）的条件下，若点P 是EM 上一动点，PQ 平分∠MPN ，NH 平分∠PNC ，交AB 于点H ， PI ∥NH ,当点P 在线段EM 上运动时，求∠IPQ 的度数.图1图2xy yxO FDEO HBACBAC2. 在平面直角坐标系中，点B （0，4），C （-5，4），点A 是x 轴负半轴上一点，S 四边形AOBC =24. （1）线段BC 的长为，点A 的坐标为；（2）如图1，EA 平分∠CAO ，DA 平分∠CAH ，CF ⊥AE 点F ，试给出∠ECF 与∠DAH 之间满足的数量关系式，并说明理由；（3）若点P 是在直线CB 与直线AO 之间的一点，连接BP 、OP ，BN 平分CBP ∠，ON 平分AOP ∠， BN 交ON 于N ，请依题意画出图形，给出BPO ∠与BNO ∠之间满足的数量关系式，并说明理由.FABC DEN3. 如图，AC ∥BD ,点D 在点B 的右侧，BE ⊥AB ,∠EBD 、∠ACD 的平分线交于点F (点F 不与点B 、C 重合). ∠ABD = m ，∠ACD = n .（1）若点A 在点C 的右侧，求∠BFC ,并直接写出12BFC ABEABD ACD∠-∠∠+∠的值；（2）将（1）中的线段CD 沿BD 方向平移，当点C 移动到点A 的右侧时，求∠BFC ,并直接写出∠BFC 、∠ABD 、∠ACD 之间的关系.4. 如图，MN ∥AB ,点C 、D 在直线MN 上运动，∠CBD 的平分线交射线AC 于点E .（1）当点D 在点C 的右侧运动时，①若∠ACB =∠A ，求AEBCDB∠∠②若∠ACB 比∠A 大30°，AEBCDB∠∠的值是否发生变化，若不变，求出其值；若变化，请探究∠AEB 与∠CDB（2）当点D 在点C 的左侧运动时，若∠ACB =∠A ，请直接写出∠AEB 与∠CDB 之间的关系.图2图1xy DE F BCO AGH图1图25. 线段AB 是直角三角形ABC 的斜边，将ABC ∆放置在平面直角坐标系中，线段AB 交y 轴于点D . （1）如图1，若点C 与点O 重合，已知(,)(,)A t a B t b -、，且a b +=D 的坐标；（2）如图2，将ABC ∆沿着AC 方向平移，边AB 、BC 交平行于y 轴的直线于E 、F ，直线EF 交x 轴于点G , 点H 是边AC 上一点，连接FH ，①若∠CFH +∠CFE =200°，请写出∠AOD 与∠HFE 之间的关系，并证明你的结论；②若12+2002CFH CFE ∠∠=，请直接写出∠AOD 与∠HFE 之间的关系.6. 如图1，CD ∥AB ,12ABF EBF ∠=∠, CF 平分∠DCE , ∠F 的2倍与∠E 的余角的和为108°.（1）求∠ABE 的度数；（2）如图2，点G 、H 分别是CD 、BE 上一点，3BHI GHI ∠=∠, GJ ∥HI , GK 平分∠DGH ,下列结论：①KGJHGJ∠∠的值为定值，②KGJ HGJ ∠-∠的值为定值，有且只有一个结论正确，请判断，并求出其定值.。

2023-2024学年七年级数学下册实数压轴题(十大题型)(原卷版)

(1)如图1，当2n =时，拼成的大正方形ABCD 的边长为
如图2，当5n =时，拼成的大正方形1111D C B A 的边长为
如图3，当10n =时，拼成的大正方形2222A B C D 的边长为
(2)小李想沿着正方形纸片1111D C B A 边的方向能否裁出一块面积为()22.42dm
的长方形纸片，使它的长宽之比
为21：？他能裁出吗？请说明理由．
(1)仿照康康上述的方法，探究7
(2)继续仿照上述方法，在（1）中得到的
确，精确到0.001（画出示意图，标明数据，并写出求解过程）
(3)综合上述具体探究，已知非负整数
的估算值．
(1)有44⨯的网格，每个方格的边长为1，把正方形ABCD画在网格中，要求顶点在格点上．
(2)如图，把正方形ABCD放到数轴上，使得点A与数1-重合，边
为________．
任务：
(1)在图3中画图确定表示10的点M．
(2)把5个小正方形按图中位置摆放，并将其进行裁剪，拼成一个大正方形．请在图中画出裁剪线，并在图中画出所拼得的大正方形的示意图．
(3)小丽想用一块面积为36cm
它的长是宽的2倍．小丽能用这块纸片裁出符合要求的纸片吗？请你通过计算说明理由．
(4)在图6中的数轴上分别标出表示数。

七年级数学下册期末考试压轴训练题(附答案解析)

七年级数学下册期末考试压轴训练题(附答案解析)1．如图，点A、B的坐标分别为（a，0），（b，0），且满足（2a+2）2+√b−3=0，现同时将A、B分别向上平移2个单位，再向右平移1个单位，分别得到A、B对应点C、D，连接AC、BD．(1)求点A、B的坐标；(2)如图1，点P（0，m）是y轴负半轴上一动点，连接AP、PD，其中直线PD交x轴于E点，若S△P AE＝S△BDE，求m的值；(3)如图2，连接BC，在直线BC上取一点F，使BF＝3CF，求点F的坐标．2．如图1，在平面直角坐标系中，点A、B的坐标分别为A（a，0），B（0，b）2a-+√b+3＝0，现同时将点A、B分别向上平移3个单位长度，再向右平移6个单位，分别得到点A、B的对应点D，C，连接AD，BC，CD．（1）求点C，D的坐标；（2）在y轴上是否存在一点P，使三角形P AC的面积等于四边形ABCD的面积？若存在，请求出点P的坐标，请说明理由；（3）如图2，设点E是直线CD上一动点（点不与点C、D重合），连接AE、BE，请直接写出∠DAE，∠CBE和∠AEB之间的数量关系．3．如图①，在平面直角坐标系中，点A(0,a)，C(b,0)，其中，a是16的算术平方根，b3=8，线段GO由线段AC平移所得，并且点G与点A对应，点O与点C对应．（1）点A的坐标为；点C的坐标为；点G的坐标为；（2）如图②，F是线段AC上不同于AC的任意一点，求证：∠OFC=∠OAF+∠AOF；（3）如图③，若点F满足FOC FCO∠=∠，点E是线段OA上一动点（与点O、A不重合），连CE交OF于点H，在点E运动的过程中，∠OHC+∠ACE=2∠OEC是否总成立？请说明理由．4．已知，在平面直角坐标系中，AB⊥x轴于点B，点A(a,b)满足√a−4+|b−2|=0，平移线段AB使点A 与原点重合，点B的对应点为点C．（1）则a＝，b＝，点C坐标为；（2）如图1，点D（m，n）在线段BC上，求m，n满足的关系式；（3）如图2，E是线段OB上一动点，以OB为边作∠BOG＝∠AOB，交BC于点G，连CE交OG于点F，当点E在线段OB上运动过程中，∠OFC+∠FCG的值是否会发生变化？若变化请说明理由，若不变，请求出其∠OEC值．5．如图，在平面直角坐标系，点A、B的坐标分别为（a，0），（0，b）．且|a﹣8b0，将点B向右平移24个单位长度得到C．（1）求A、B两点的坐标；（2）点P、Q分别为线段BC、OA两个动点，P自B点向C点以2个单位长度/秒向右运动，同时点Q自A 点向O点以4个单位长度/秒向左运动，设运动的时间为t，连接PQ，当PQ恰好平分四边形BOAC的面积时，求t的值；（3）点D是直线AC上一点，连接QD，作∠QDE＝120°，边DE与BC的延长线相交于点E，DM平分∠CDE，DN平分∠ADQ，当点Q运动时，∠MDN的度数是否变化？请说明理由．6．如图1，在平面直角坐标系中，A（a，0）是x轴正半轴上一点，C是第四象限一点，CB∠y轴，交y轴负半轴于B（0，b），且（a﹣3）2+|b+4|＝0，S四边形AOBC＝16．（1）求C点坐标；（2）如图2，设D为线段OB上一动点，当AD∠AC时，∠ODA的角平分线与∠CAE的角平分线的反向延长线交于点P，求∠APD的度数．（3）如图3，当D点在线段OB上运动时，作DM∠AD交BC于M点，∠BMD、∠DAO的平分线交于N点，则D点在运动过程中，∠N的大小是否变化？若不变，求出其值，若变化，说明理由．7．如图，已知AM∠BN，∠A＝64°．点P是射线AM上一动点（与点A不重合），BC、BD分别平分∠ABP 和∠PBN，分别交射线AM于点C，D．（1）∠∠ABN的度数是；∠∠AM∠BN，∠∠ACB＝∠；（2）求∠CBD的度数；（3）当点P运动时，∠APB与∠ADB之间的数量关系是否随之发生变化？若不变化，请写出它们之间的关系，并说明理由：若变化，请写出变化规律；（4）当点P运动到使∠ACB＝∠ABD时，∠ABC的度数是．8．在平面直角坐标系中，D（0，﹣3），M（4，﹣3），直角三角形ABC的边与x轴分别相交于O、G两点，与直线DM分别交于E、F点，∠ACB＝90°．（1）将直角三角形如图1位置摆放，如果∠AOG＝46°，则∠CEF＝；（2）将直角三角形ABC如图2位置摆放，N为AC上一点，∠NED+∠CEF＝180°，请写出∠NEF与∠AOG 之间的等量关系，并说明理由．（3）将直角三角形ABC如图3位置摆放，若∠GOC＝140°，延长AC交DM于点Q，点P是射线GF上一动点，探究∠POQ，∠OPQ与∠PQF的数量关系，请直接写出结论（题中的所有角都大于0°小于180°）．9．在平面直角坐标系中，A（a，0），B（b，0），C（﹣1，c）（见图1），且|2a+b+1|+√a+2b−4+(c−2)2=0．（1）求a、b、c的值；（2）①在x轴的正半轴上存在一点M，使三角形COM的面积是三角形ABC的面积的一半，求出点M的坐标；②在坐标轴的其它位置是否存在点M，使三角形COM的面积三角形ABC的面积的一半仍然成立? 若存在，请直接写出符合条件的点M的坐标；（3）如图2，过点C作CD⊥y轴交y轴于点D，点P为线段CD延长线上的一动点，连接OP，OE平分∠AOP，OF⊥OE．当点P运动时，∠OPD的值是否会改变？若不变，求其值；若改变，说明理由．∠DOE10．已知：b是立方根等于本身的负整数，且a、b满足(a+2b)2+|c+1|=0，请回答下列问题：2（1）请直接写出a、b、c的值：a=_______，b=_______，c=_______．（2）a、b、c在数轴上所对应的点分别为A、B、C，点D是B、C之间的一个动点(不包括B、C两点)，|=________．其对应的数为m，则化简|m+12（3）在（1）、（2）的条件下，点A、B、C开始在数轴上运动，若点B、点C都以每秒1个单位的速度向左运动，同时点A以每秒2个单位长度的速度向右运动，假设t秒钟过后，若点A与点C之间的距离表示为AC，点A与点B之间的距离表示为AB，请问：AB−AC的值是否随着时间t的变化而改变？若变化，请说明理由；若不变，请求出AB−AC的值．x y，都是二元一次方程x−4y= 11．如图①，在平面直角坐标系中，点A在x轴上，直线OC上所有的点坐标(,)x y，都是二元一次方程x+2y=6的解，过C作x轴的平行线，交y轴0的解，直线AC上所有的点坐标(,)与点B．（1）求点A、B、C的坐标；（2）如图∠，点M、N分别为线段BC，OA上的两个动点，点M从点C以每秒1个单位长度的速度向左运动，同时点N从点O以每秒1．5个单位长度的速度向右运动，设运动时间为t秒，且0＜t＜4，试比较四边形MNAC的面积与四边形MNOB的面积的大小．12．已知点A（1，a），将线段OA平移至线段BC，B（b，0），a是m+6n的算术平方根，2m＝3，n＝√4，且m＜n，正数b满足（b+1）2＝16．（1）直接写出A、B两点坐标为：A，B；（2）如图1，连接AB、OC，求四边形AOCB的面积；（3）如图2，若∠AOB＝a，点P为y轴正半轴上一动点，试探究∠CPO与∠BCP之间的数量关系．13．如图，MN ∥OP ，点A 为直线MN 上一定点，B 为直线OP 上的动点，在直线MN 与OP 之间且在线段AB 的右方作点D ，使得AD ⊥BD ．设(DAB αα∠=为锐角)． (1)求NAD ∠与∠PBD 的和；(提示过点D 作EF ∥MN) (2)当点B 在直线OP 上运动时，试说明90OBD NAD ∠-∠=︒；(3)当点B 在直线OP 上运动的过程中，若AD 平分∠NAB ，AB 也恰好平分∠OBD ，请求出此时α的值14．如图1，在平面直角坐标系中，点A （a ，0），B （b ，3），C （c ，0），满足√a +b +|a −b +6|+(c −4)2=0．（1）分别求出点A ，B ，C 的坐标及三角形ABC 的面积．（2）如图2．过点C 作CD ⊥AB 于点D ，F 是线段AC 上一点，满足∠FDC =∠FCD ，若点G 是第二象限内的一点，连接DG ，使∠ADG =∠ADF ，点E 是线段AD 上一动点（不与A 、D 重合），连接CE 交DF 于点H ，点E 在线段AD 上运动的过程中，∠DHC+∠ACE∠CED的值是否会变化？若不变，请求出它的值；若变化，请说明理由．（3）如图3，若线段AB 与y 轴相交于点F ，且点F 的坐标为（0，32），在坐标轴上是否存在一点P ，使三角形ABP 和三角形ABC 的面积相等？若存在，求出P 点坐标．若不存在，请说明理由．（点C 除外）15．如图，在平面直角坐标系中，点A，B的坐标分别为（－1，0），（3，0），现同时将点A，B分别向上平移2个单位长度，再向右平移1个单位长度，分别得到点A，B的对应点C，D．连接AC，BD．（1）写出点C，D的坐标及四边形ABDC的面积．（2）在y轴上是否存在一点P，连接P A，PB，使S三角形P AB＝S四边形ABDC？若存在，求出点P的坐标，若不存在，试说明理由；（3）点Q是线段BD上的动点，连接QC，QO，当点Q在BD上移动时（不与B，D重合），给出下列结论：①∠DCQ+∠BOQ∠CQO的值不变；②∠DCQ+∠COQ∠BQO的值不变，其中有且只有一个正确，请你找出这个结论并求值．16．如图1，已知直角梯形ABCO中，∠AOC＝90°，AB∠x轴，AB＝6，若以O为原点，OA，OC所在直线为y轴和x轴建立如图所示直角坐标系，A(0，a)，C(c，0)中a，c满足|a+c﹣7c-＝0（1）求出点A、B、C的坐标；（2）如图2，若点M从点C出发，以2单位/秒的速度沿CO方向移动，点N从原点出发，以1单位/秒的速度沿OA方向移动，设M、N两点同时出发，且运动时间为t秒，当点N从点O运动到点A时，点M同时也停止运动，在它们的移动过程中，当2S△ABN≤S△BCM时，求t的取值范围：（3）如图3，若点N是线段OA延长上的一动点，∠NCH＝k∠OCH，∠CNQ＝k∠BNQ，其中k＞1，NQ∠CJ，求HCJABN∠∠的值（结果用含k的式子表示）．17．问题情境（1）如图1，已知AB∠CD，∠PBA＝125°，∠PCD＝155°，求∠BPC的度数．佩佩同学的思路：过点P作PG∠AB，进而PG∠CD，由平行线的性质来求∠BPC，求得∠BPC＝问题迁移（2）图2．图3均是由一块三角板和一把直尺拼成的图形，三角板的两直角边与直尺的两边重合，∠ACB ＝90°，DF∠CG，AB与FD相交于点E，有一动点P在边BC上运动，连接PE，P A，记∠PED＝∠α，∠P AC ＝∠β．∠如图2，当点P在C，D两点之间运动时，请直接写出∠APE与∠α，∠β之间的数量关系；∠如图3，当点P在B，D两点之间运动时，∠APE与∠α，∠β之间有何数量关系？请判断并说明理由；拓展延伸（3）当点P在C，D两点之间运动时，若∠PED，∠P AC的角平分线EN，AN相交于点N，请直接写出∠ANE 与∠α，∠β之间的数量关系．18．如图1，在平面直角坐标系中，A(6,a)，B(b,0)，且(a−6)2+√b−2=0.（1）求点A、B的坐标；=15，请求出P点的坐标；（2）如图1，P点为y轴正半轴上一点，连接BP，若SΔPAB（3）如图2，已知AB=√52，若C点是x轴上一个动点，是否存在点C，使BC=AB，若存在，请直接写出所有符合条件的点C的坐标；若不存在，请说明理由．A ，点B与点A关于y轴对称.19．已知平面直角坐标系内两点A、B，点(3,4)（1）则点B的坐标为________；（2）动点P、Q分别从A点、B点同时出发，沿直线AB向右运动，同向而行，点P的速度是每秒4个单位长度，点Q的速度是每秒2个单位长度，设P、Q的运动时间为t秒，用含t的代数式表示ΔOPQ的面积S，并写出t的取值范围；SΔABO.求m的取值范围.（3）在平面直角坐标系中存在一点M(m,−m)，满足SΔMOB≤2320．如图1，O为平面直角坐标系的原点，点A坐标为（4，0），同时将点A，O分别向上平移2个单位，再向左平移1个单位，得到对应点B，C．（1）求四边形OABC的面积；（2）在y轴上是否存在一点M，使△MOA的面积与四边形OABC的面积相等？若存在这样一点，求出点M的坐标，若不存在，请说明理由；（3）如图2，点P在OA边上，且∠CBP=∠CPB，Q是AO延长线上一动点，∠PCQ的平分线CD交BP的延长线于点D，在点Q运动的过程中，求∠D和∠CQP的数量关系．参考答案：1．(1)解：∵(2a+2)2+√b−3=0，(2a+2)2≥0，√b−3≥0，∴2a+2=0，b−3=0，1a∴=-，b=3，(1,0),(3,0)A B∴-；(2)∠将A、B分别向上平移2个单位，再向右平移1个单位，分别得到A、B对应点C、D，∴C(0,2)，D(4,2)，∴AO=1,OB=3,CD=4,OC=2，∵点P（0，m）是y轴负半轴上一动点，∴PO=−m，PC=2−m，∵S△P AE＝S△BDE，S梯形OCDB=S梯形OCDE+S△DBE=S 梯形OCDE+APES= S梯形OCDE+S△POE+S△APO=S△PCD+S△APO，∴12(OB+CD)OC=12PCCD+12AOPO，即：12(3+4)×2=12×4×(2−m)+12×1×(−m)，整理得：52m=−3，∴m=−65；(3)分如下两种情况进行讨论：①当F在BC中间，如图所示：过F作FM⊥AB于M，NF⊥OC于N，过点O作OG BC⊥于G，∵BF＝3CF，AO=1,OB=3,CD=4,OC=2，∴S△COFS△BOF =12OGCF12OGBF=13，∵S△BOC=12OBOC=12×3×2=3，∴S△COF=14S△BOC=34，∴12CONF=34，∴NF=34，∵S△BOF=34S△BOC=94，∴12OBFM=94，∴FM=32，∴F(34,32 )，②当F在BC延长线上，则只能在第二象限，如图所示：过F作FP⊥AB于P，FQ⊥OC于Q，过点O作OH⊥BC于H，∵BF＝3CF，AO=1,OB=3,CD=4,OC=2，∴S△COFS△BOF =12OHCF12OHBF=13，∴S△COF=12S△OBC，∵S△BOC=12OBOC=12×3×2=3，∴S△COF=12S△BOC=32，∴12COFQ=32，∴FQ=32，S△BOF=S△OCF+S△BOC=92，∴12OBPF=92，∴PF=3，∵F在第二象限，∴F(−32,3) ，综上所述：F(34,32)或者F(−32,3)．2．（1）∵2a -+√b +3＝0，|a −2|≥0，√b +3≥0，∴a −2=0,b +3=0解得a =2,b =−3∴A(2,0),B(0,−3)将点A 、B 分别向上平移3个单位长度，再向右平移6个单位，分别得到点A 、B 的对应点D ，C ，由平移的性质可知，即将A 、B 的横坐标+6，纵坐标+3，∴D(2+6,0+3),C(0+6,−3+3)，即D(8,3),C(6,0)；（2）存在，理由如下：设P(0,m)，(2,0)A ，(6,0)C ，∴AC =6−2=4，三角形P AC 的面积为12AC ×|y P |=12×4×|m |=2|m |，四边形ABCD 的面积为12AC ×(|y D |+|y B |)=12×4×(3+3)=12，∴2|m |=12，解得m =±6，∴(0,6)P 或者P(0,−6)；（3）如图，过点E 作EM //AD ，∴∠DAE =∠AEM ，∵A,B 平移后对应的点分别为D,C ，∴AD //BC ，∵EM //AD ，∴EM //BC ，∠CBE =∠BEM ，∴∠DAE +∠CBE =∠AEM +∠BEM =∠AEB ．∴∠DAE+∠CBE=∠AEB．3．（1）连接GA∵a是16的算术平方根∴a=4∴A(0,4)∴AO=4∵b3=8∴b=2∴C(2,0)∴OC=2∵线段GO由线段AC平移所得，并且点G与点A对应，点O与点C对应∴GA=OC=2，GA//OCG∴(2,4)故答案为：(0,4)，(2,0)，(−2,4)；（2）∵线段GO由线段AC平移所得∴OG//CA，∴∠OFC=∠GOF∵∠GOF=∠GOA+∠AOF∴∠OFC=∠GOA+∠AOF∵OG//CA∴∠GOA=∠OAF∴∠OFC=∠OAF+∠AOF（3）∵OG//CA∴∠GOC+∠ACO=180°∵∠GOC=∠GOA+∠AOC∴∠GOA+∠AOC+∠ACO=180°∵∠AOC=90°∴∠GOA+90°+∠ACO=180°，即∠GOA+∠ACO=90°∵OG//CA∴∠GOA=∠OAC∴∠OAC+∠ACO=90°∵∠AOC=∠AOF+∠FOC=90°∴∠AOF+∠FOC=∠OAC+∠ACO∵FOC FCO∠=∠，∠ACO=∠FCO∴∠AOF=∠OAC由（2）的结论得：∠OHC=∠OEH+∠EOH，∠OEC=∠EAC+∠ACE∵∠OEH=∠OEC，∠EOH=∠AOF=∠OAC∴∠OHC=∠OEC+∠OAC∴∠OHC+∠ACE=∠OEC+∠OAC+∠ACE∵∠EAC=∠OAC∴∠OEC=∠OAC+∠ACE∴∠OHC+∠ACE=2∠OEC∴在点E运动的过程中，∠OHC+∠ACE=2∠OEC总成立．4．（1）解：∵√a−4+|b−2|=0，∴a−4=0,b−2=0,∴a=4,b=2,∵AB=OC=2,且C在y轴负半轴上，∴C(0,−2),故填：4,2,(0,−2)；（2）如图1，过点D分别作DM∠x轴于点M，DN∠y轴于点N，连接OD．∵AB ⊥ x 轴于点B ，且点A ，D ，C 三点的坐标分别为：(4,2),(m,n),(0,−2) ∴OB =4,OC =2,MD =−n,ND =m ，∴S △BOC =12OBOC =4,又∠S △BOC = S △BOD ＋S △COD=12OB ×MD ＋12OC ×ND=12×4×(−n)+12×m ×2=m −2n ，∴m −2n =4；（3）解：∠OFC+∠FCG ∠OEC 的值不变，值为2．理由如下：如图所示，分别过点E ，F 作EP ∠OA ， FQ ∠OA 分别交y 轴于点P ，点Q ，∠线段OC 是由线段AB 平移得到，∠BC ∠OA ，又∠EP ∠OA ，∠EP ∠BC ，∠∠GCF =∠PEC ，∠EP ∠OA ，∠∠AOE =∠OEP ，∠∠OEC =∠OEP +∠PEC =∠AOE +∠GCF ，同理：∠OFC =∠AOF +∠GCF ，又∠∠AOB =∠BOG ，∠∠OFC =2∠AOE +∠GCF ，∴∠OFC+∠FCG ∠OEC=∠OFC +∠FCG ∠AOE +∠FCG =2∠AOE +2∠FCG ∠AOE +∠FCG=2．5．解：（1）∵|a ﹣8b -0，|a −26|≥080b -≥， ∴|a −26|=0，√8−b =0∴{a −26=08−b =0，解得：{a =26b =8∴点A 、B 的坐标分别为（26，0），（0，8）；（2）∠点B 向右平移24个单位长度得到C ，∠C （24，8），设BP =2t ，PC =24−2t ，OQ =26−4t ，AQ =4t ，∵PQ 平分四边形BOAC 的面积，∴S 梯形OBPQ =S 梯形QACP∴BP+OQ 2BO =CP+QA 2BO∴BP +OQ =CP +QA∴2t +26−4t =4t +24−2t解得t =12；（3）当点Q 运动时，∠MDN 的度数不变，理由如下：如图，当D 在线段CA 的延长线上时，∠DM 平分∠CDE ，DN 平分∠ADQ ，∴∠NDC =12∠QDA ，∠MDC =12∠CDE ，∴∠MDN =∠NDC +∠MDC =12(∠QDA +∠CDE)=12∠QDE ， ∵∠QDE =120°，∠∠MDN =60°；同理求得当D在线段AC的延长线上时，∠MDN=60°；当点D在线段AC上时，∠DM平分∠CDE，DN平分∠ADQ，∴∠NDQ=12∠QDA，∠MDC=12∠CDE，设∠CDE=x∵∠QDE=120°∠∠QDC=120°-x，∠∠ADQ=180°-∠QDC=60°+x，∴∠MDN=∠MDC+∠QDC+∠NDQ=12x+120o−x+12(60o+x)=150o，综上所述：∠MDN=60°或150°.6．解：（1）∠（a﹣3）2+|b+4|＝0，∠a﹣3＝0，b+4＝0，∠a＝3，b＝﹣4，∠A（3，0），B（0，﹣4），∠OA＝3，OB＝4，∠S四边形AOBC＝16．∴1（OA+BC）×OB＝16，2（3+BC）×4＝16，∴12∴BC＝5，∠C是第四象限一点，CB∠y轴，∠C（5，﹣4）；（2）如图，延长CA，∠AF是∠CAE的角平分线，∠CAE，∴∠CAF＝12∵∠CAE＝∠OAG，∠OAG，∴∠CAF＝12∵AD∠AC，∠∠DAO+∠OAG＝∠PAD+∠PAG＝90°，∠∠AOD＝90°，∠∠DAO+∠ADO＝90°，∠∠ADO＝∠OAG，∠ADO，∴∠CAF＝12∵DP是∠ODA的角平分线∠∠ADO＝2∠ADP，∠∠CAF＝∠ADP，∠∠CAF＝∠PAG，∠∠PAG＝∠ADP，∠∠APD＝180°﹣（∠ADP+∠PAD）＝180°﹣（∠PAG+∠PAD）＝180°﹣90°＝90°即：∠APD＝90°；（3）不变，∠ANM＝45°理由：如图，∠∠AOD ＝90°，∠∠ADO+∠DAO ＝90°，∠DM∠AD ，∠∠ADO+∠BDM ＝90°，∠∠DAO ＝∠BDM ，∠NA 是∠OAD 的平分线，∴∠DAN ＝12∠DAO ＝12∠BDM ，∵CB∠y 轴，∠∠BDM+∠BMD ＝90°，∴∠DAN ＝12（90°﹣∠BMD ），∵MN 是∠BMD 的角平分线，∴∠DMN ＝12∠BMD ，∴∠DAN+∠DMN ＝12（90°﹣∠BMD ）+12∠BMD ＝45° 在∠DAM 中，∠ADM ＝90°，∠∠DAM+∠DMA ＝90°，在∠AMN 中，∠ANM ＝180°﹣（∠NAM+∠NMA ）＝180°﹣（∠DAN+∠DAM+∠DMN+∠DMA ）＝180°﹣[（∠DAN+DMN ）+（∠DAM+∠DMA ）] ＝180°﹣（45°+90°）＝45°，∠D 点在运动过程中，∠N 的大小不变，求出其值为45°． 7．解：（1）∠∠AM //BN ，∠A ＝64°，∠∠ABN ＝180°﹣∠A ＝116°，故答案为：116°；∠∠AM //BN ，∠∠ACB ＝∠CBN ，故答案为：CBN；（2）∠AM//BN，∠∠ABN+∠A＝180°，∠∠ABN＝180°﹣64°＝116°，∠∠ABP+∠PBN＝116°，∠BC平分∠ABP，BD平分∠PBN，∠∠ABP＝2∠CBP，∠PBN＝2∠DBP，∠2∠CBP+2∠DBP＝116°，∠∠CBD＝∠CBP+∠DBP＝58°；（3）不变，∠APB：∠ADB＝2：1，∠AM//BN，∠∠APB＝∠PBN，∠ADB＝∠DBN，∠BD平分∠PBN，∠∠PBN＝2∠DBN，∠∠APB：∠ADB＝2：1；（4）∠AM//BN，∠∠ACB＝∠CBN，当∠ACB＝∠ABD时，则有∠CBN＝∠ABD，∠∠ABC+∠CBD＝∠CBD+∠DBN∠∠ABC＝∠DBN，由（1）∠ABN＝116°，∠∠CBD＝58°，∠∠ABC+∠DBN＝58°，∠∠ABC＝29°，故答案为：29°．8．（1）如图1，作CP∠x轴，∠D（0，﹣3），M（4，﹣3），∠DM∠x轴，∠CP∠DM∠x轴，∠∠AOG＝∠1，∠2+∠CEF＝180°，∠∠2＝180°﹣∠CEF，∠∠1+∠2＝90°，∠∠AOG+180°﹣∠CEF＝90°，∠∠AOG＝46°，∠∠CEF＝136°，故答案为136°；（2）∠AOG+∠NEF＝90°．理由如下：如图2，作CP∠x轴，∠CP∠DM∠x轴，∠∠AOG＝∠1，∠2+∠CEF＝180°，而∠NED+∠CEF＝180°，∠∠2＝∠NED，∠∠1+∠2＝90°，∠∠AOG +∠NEF ＝90°；（3）如图3，当点P 在GF 上时，过点P 作PN ∠OG ，∠NP ∠OG ∠DM ，∠∠GOP ＝∠OPN ，∠PQF ＝∠NPQ ，∠∠OPQ ＝∠GOP +∠PQF ，∠∠OPQ ＝140°﹣∠POQ +∠PQF ；如图4，当点P 在线段GF 的延长线上时，过点P 作PN ∠OG ，∠NP ∠OG ∠DM ，∠∠GOP ＝∠OPN ，∠PQF ＝∠NPQ ，∠∠OPN ＝∠OPQ +∠QPN ，∠∠GOP ＝∠OPQ +∠PQF ，∠140°﹣∠POQ ＝∠OPQ +∠PQF ．9．（1）因为|2a +b +1|+√a +2b −4+(c −2)2=0，根据绝对值、二次根式和平方的非负性，可以得到{2a +b +1=0a +2b −4=0，（c -2）2=0，解{2a +b +1=0a +2b −4=0得到a =-2，b =3；因为（c -2）2=0，所以c=2，故a =-2，b =3，c=2；（2）解：由（1）可知A （-2，0），B （3，0），则分情况讨论点M ：①当M 在x 轴上时，设M （m ，0），由题意：12•|m |•2=12 12×5×2，∴m =±52，∴M （52，0）或（-52，0）．②当M 在y 轴上时，设M （0，m ），由题意：12•|m |•1=12 12×5×2，∴m =±5，∠M （5，0）或（0，-5），综上所述，满足条件的点M 坐标为M （52，0）或（-52，0）或（0，5）或（0，-5）．（3）解：如图中，结论：∠OPD ∠DOE 的值是定值，∠OPD ∠DOE=2．理由：∠OE ∠OF ，∠∠EOF =90°，∠∠AOE +∠FOG =90°，∠∠AOE =∠EOP ，∠EOP +∠POF =90°，∠∠FOG =∠POF ，∠∠DOE +∠AOE =90°，∠AOE +∠FOG =90°，∠∠DOE =∠FOG ，∠CP ∠AG ，∠∠OPD =∠POG =2∠FOG ，∠∠OPD =2∠FOG ，∴∠OPD ∠DOE=2． 10．解：（1）∠b 是立方根等于本身的负整数，∠b=-1∵(a+2b)2+|c+12|=0，(a+2b)2≥0，|c+12|≥0∴a+2b=0，c+12=0解得：a=2，c=−12故答案为：2；-1；−12；（2）∵b=-1，c=−12，b 、c 在数轴上所对应的点分别为B 、C ，点D 是B 、C 之间的一个动点(不包括B 、C 两点)，其对应的数为m ，∴-1＜m ＜−12∴m+12＜0∴|m+12|= -m -12故答案为：-m -12；（3）运动前AB=2－（-1）=3，AC=2－（−12）=52由题意可知：运动后AB=3＋2t ＋t=3＋3t ，AC=52＋2t ＋t=52＋3t∴AB －AC=（3＋3t ）－（52＋3t ）=12∴AB−AC 的值不会随着时间t 的变化而改变，AB －AC=12．11．（1）令y =0，则x +2×0=6，解得x =6， (6,0)A ∴．{x −4y =0x +2y =6解得{x =4y =1 ∴C(4,1)．∵BC //x 轴，∴点B 的纵坐标与点C 的纵坐标相同，(0,1)B ∴ ；（2）∵A(6,0)，B(0,1)，C(4,1)，∴OA =6,BC =4．∵点M 从点C 以每秒1个单位长度的速度向左运动，同时点N 从点O 以每秒1.5个单位长度的速度向右运动，∴MC =t,ON =1.5t ，∴BM =4−t,NA =6−1.5t ，∴S 四边形MNOB =12(BM +ON)⋅OB =12×(4−t +1.5t)×1=t 4+2，S 四边形MNAC =12(MC +NA)⋅OB =12×(t +6−1.5t)×1=−t 4+3．当t 4+2>−t 4+3时，即t >2时，S 四边形MNOB >S 四边形MNAC ；当t 4+2=−t 4+3时，即t =2时，S 四边形MNOB =S 四边形MNAC ；当t 4+2<−t 4+3时，即t <2时，S 四边形MNOB <S 四边形MNAC ． 12．（1）∵a 是m +6n 2m ＝3，n ＝√4，且m ＜n ，正数b 满足（b +1）2＝16．∴m ＝﹣3，n ＝2，a ＝3，b ＝3，∠A （1，3），B （3，0）；故答案为：A（1，3）；B（3，0）；（2）如图1所示：由题意知：C（2，﹣3），∠B（3，0），∠OB＝3，∴S四边形AOCB＝S△AOB+S△BOC＝12×3×3+12×3×3=9，故答案为：9；（3）过点P作PD∠OA，如图2所示：∠OA∠BC，∠PD∠OA∠BC∠∠BCP＝∠DPC，∠DPO＝∠AOP．∠∠AOB＝a，∠∠AOP＝90°﹣∠AOB＝90°﹣a．∠∠DPO＝90°﹣a．∠∠DPC＝∠DPO+∠CPO，∠∠BCP＝∠CPO+90°﹣a，即∠BCP﹣∠CPO＝90°﹣a，故答案为：∠BCP﹣∠CPO＝90°﹣a．13．解：（1）过点D作EF∠MN，如下图所示∵MN//OP∴EF∠OP∠∠NAD=∠ADE，∠PBD=∠BDE∵AD⊥BD∴∠ADB=90°∠∠ADE＋∠BDE=∠ADB=90°∠∠NAD＋∠PBD=90°（2）∠∠NAD＋∠PBD=90°∠∠PBD=90°－∠NAD∠∠OBD＋∠PBD=180°，∠∠OBD＋90°－∠NAD=180°∠90OBD NAD∠-∠=︒；（3）∵AD平分∠NAB，AB也恰好平分∠OBD，∠DAB=α∴∠NAD=∠DAB=α，∠NAB=2∠DAB=2α，∠OBD=2∠OBA ∵MN//OP∴∠OBA=∠NAB=2α∴∠OBD=4α由（2）知90OBD NAD∠-∠=︒即4α−α=90°解得：α=30°14．解：（1）∵√a+b+|a−b+6|+(c−4)2=0，∴{a+b=0a−b+6=0c−4=0，解得：a=−3,b=3,c=4，∴A(−3,0)，B(3,3)，(4,0)C如图，过点B作BM⊥AC，则AC=7，BM=3，∴S△ABC=12ACBM=12×7×3=212，（2）不变，∵CD ⊥AB ，∴∠ADC =90°，∠∠DAC +∠FCD =90°，∠FDC +∠ADF =90°，∵∠FDC =∠FCD∴∠DAC =∠ADF ，∠∠CED =∠ACE +∠DAC∠DHC =∠CED +∠ADF =∠ACE +∠DAC +∠DAC =∠ACE +2∠DAC∴∠DHC+∠ACE ∠CED =∠ACE+2∠DAC+∠ACE ∠ACE+∠DAC =2， ∴∠DHC+∠ACE ∠CED 的值不变，∠DHC+∠ACE ∠CED =2；（3）存在，①当点P 在x 轴上时，则AF =AC =7，因为点P 不与点C 重合，所以点P(−10,0)； ②当点P 在y 轴上时，设P （0,t ）则PF =|t −32|,∴S △ABP =S △AFP +S △BFP =12×3×|t −32|+12×3×|t −32| =4∴|t −32|=43，解得t =16或t =176，所以P(0,16)或P(0,176)综上，存在一点P ，使三角形ABP 和三角形ABC 的面积相等，点P(−10,0)或(0,16)或(0,176)． 15．（1）∠将点A ，B 分别向上平移2个单位长度，再向右平移1个单位长度， ∠C （0，2），D （4，2），AB ∠CD 且AB =CD =4，∠四边形ABDC 是平行四边形，∠S 四边形ABCD ＝4×2＝8．（2）存在，设点P的坐标为（0，y），根据题意，得12×4×|y|＝8．解得y＝4或y＝－4．∠点P的坐标为（0，4）或（0，－4）．（3）结论∠正确．过点Q作QE∠AB，交CO于点E．∠AB∠CD，∠QE∠CD．∠∠DCQ＝∠EQC，∠BOQ＝∠EQO．∠∠EQC＋∠EQO＝∠CQO，∠∠DCQ＋∠BOQ＝∠CQO．∴∠DCQ+∠BOQ∠CQO＝1．16．(1)∵|a+c﹣10|7c =0∴a+c﹣10=0，且c﹣7=0，∴c=7，a+c=10，∴c=3，∴A(0，3)，C(7，0)，∵AB∥x轴，AB=6，∴B(6，3)；(2)∵A(0，3)，C(7，0)，∴OA=3，OC=7，由题意得：ON=t，CM=2t，∴AN=3﹣t，∵2S△ABN≤S△BCM，∴2×12×(3﹣t)×6≤12×2t×3，解得：t≥2，∵当点N从点O运动到点A时，点M同时也停止运动，∴0≤t≤3，∴t的取值范围为：2≤t≤3；(3)设AB与CN交于点D，如图所示：∠AB∠OC，∠∠BDC=∠OCD，∠∠BDC=∠BND+∠ABN，∠CNQ=k∠BNQ，∠NCH=k∠OCH，∠∠BDC=(k+1)∠BNQ+∠ABN，∠OCD=(k+1)∠OCH，∠(k+1)∠BNQ+∠ABN=(k+1)∠OCH，∠∠ABN═(k+1)∠OCH﹣(k+1)∠BNQ=(k+1)(∠OCH﹣∠BNQ)，∠NQ∠CJ，∠∠NCJ=∠CNQ=k∠BNQ，∠∠HCJ+∠NCJ=∠NCH=k∠OCH，∠∠HCJ=k∠OCH﹣∠NCJ=k∠OCH﹣k∠BNQ=k(∠OCH﹣∠BNQ)，∴∠HCJ∠ABN =k(∠OCH﹣∠BNQ)(k+1)(∠OCH﹣∠BNQ)=kk+1．17．解：（1）∵PG∥AB,∠PBA=125°，∴∠BPG=180°−∠PBA=55°，∵AB∥CD，∴PG∥CD，∴∠CPG=180°−∠PCD=25°，∴∠BPC=∠BPG+∠CPG=80°，故答案为：80°；（2）①∠APE=∠α+∠β，理由如下：如图，过点P作PQ∥DF，∴∠QPE=∠α，∵DF∥CG，∴PQ∥CG，∴∠QPA=∠β，∴∠APE=∠QPE+∠QPA=∠α+∠β；②∠APE=∠β−∠α，理由如下：如图，过点P作PQ∥DF，∴∠QPE=∠α，∵DF∥CG，∴PQ∥CG，∴∠QPA=∠β，∴∠APE=∠QPA−∠QPE=∠β−∠α；（3）∠ANE=12(∠α+∠β)，理由如下：∵EN,AN分别平分∠PED,∠PAC，∴∠NED=12∠PED=12∠α,∠NAC=12∠PAC=12∠β，如图，过点N作NQ∥DF，∴∠QNE=∠NED=12∠α，∵DF∥CG，∴NQ∥CG，∴∠QNA=∠NAC=12∠β，∴∠ANE=∠QNE+∠QNA=12∠α+12∠β=12(∠α+∠β)．18．解：（1）60a-=，b−2=0∴a=6，b=2∴A(6,6)，B(2,0)（2）作AM⊥x轴于点M，如图所示设P(0,y)，且y>0∴SΔPAB=S梯形OMAP−SΔPOB−SΔABM=12×(y+6)×6−12×2×y−12×4×6=2y+6若SΔPAB=15即2y+6=15∴y=92∴P(0,92)（3）存在，C1(2+√52,0)，C2(2−√52,0)∵AB=√52，B(2,0)，BC=AB∴当C点在x正半轴上时，坐标为C1(2+√52,0)，当C点在x负半轴上时，坐标为C2(2−√52,0)故答案为C1(2+√52,0)，C2(2−√52,0).19．解：（1）∠A（-3，4），A、B两点关于y轴对称，∠点B的坐标为（3，4）．故答案为（3，4）．（2）∠AP=4t，BQ=2t，AB=6，当P与Q相遇时4t=6+2t解得t=3∴当0⩽t⩽3时，PQ=6+2t-4t=6-2t；当t＞3时，PQ=4t-6-2t=2t-6(6−2t)=12−4t∴当0⩽t⩽3时, S=42(2t−6)=4t−12当t>3时, S=42（3）如图，设AB交y轴于D．∠点M的坐标为（m，-m），∠点M在二四象限的角平分线上，∠当m＜-4时，显然不存在．∠当-4＜m＜0时，M在第二象限；S△OMB=S△ODB+S△ODM−S△BDM=12×4×3+12×4×（−m）−12×3×（4+m）=−72m∵S△AOB=12×6×4=12∴−72m≤23×12∴m≥−16 7∴−167≤m＜0③当m＞0时，M在第四象限；S△OBM=S△DBM+S△DOM−S△BDO=12×4×m+12×3×（4+m）−12×4×3=72m由题意可得72m≤23×12∴m≤167∴0＜m≤16 7综上所述，满足条件的m的值为：−167≤m＜0或0＜m≤16720．（1）如图1中，由题意B（3，2），C（-1，2），∠BC∠OA，BC=OA，∠四边形ABCO是平行四边形．∠S平行四边形ABCD=4×2=8．（2）存在．理由：如图1中，设M（0，m）由题意S△AOM=8，∴12×4×|m|=8∴m=±4，∠M（0，4）或（0，-4）．（3）结论：∠CQP=2∠D．理由：如图3中，延长CP到K．∠BC∠OA，∠∠CBP=∠DPQ，∠∠CBP=∠CPB，∠CPB=∠DPK，∠∠DPQ=∠DPK，设∠DPQ=∠DPK=x，∠DCQ=∠DCP=y，则有{2x=2y+∠CQP①x=y+∠D②，①-2×∠得到∠CQP=2∠D．。

七年级下数学压轴题

七年级下数学压轴题一、相交线与平行线。

题1：如图，直线AB、CD相交于点O，OE平分∠BOD，OF平分∠COE，∠AOD：∠BOE = 4：1，求∠AOF的度数。

解析：设∠BOE = x，因为OE平分∠BOD，所以∠BOD = 2∠BOE=2x。

又因为∠AOD + ∠BOD = 180°，且∠AOD：∠BOE = 4：1，所以∠AOD = 4x。

则4x + 2x=180°，6x = 180°，解得x = 30°。

所以∠COE = 180° - ∠BOE = 150°。

因为OF平分∠COE，所以∠COF=(1)/(2)∠COE = 75°。

∠AOC=∠BOD = 60°，所以∠AOF=∠AOC+∠COF = 60°+ 75°=135°。

题2：已知直线l_1∥ l_2，直线l_3和直线l_1、l_2交于点C和D，在C、D之间有一点P。

(1)如果P点在C、D之间运动时，问∠PAC，∠APB，∠PBD之间的关系是否发生变化。

(2)若点P在C、D两点的外侧运动时（P点与点C、D不重合），试探索∠PAC，∠APB，∠PBD之间的关系又是如何？解析：(1)过点P作PE∥ l_1，因为l_1∥ l_2，所以PE∥ l_2。

∠PAC = ∠APE，∠PBD=∠BPE。

所以∠APB = ∠APE+∠BPE = ∠PAC + ∠PBD。

(2)当点P在l_1上方时，过点P作PF∥ l_1，因为l_1∥ l_2，所以PF∥ l_2。

∠PAC = ∠APF，∠PBD + ∠BPF=180°，所以∠PBD = 180°-(∠APB - ∠PAC)，即∠PAC=∠APB + ∠PBD。

当点P在l_2下方时，过点P作PG∥ l_2，同理可得∠PBD = ∠APB+∠PAC。

二、实数。

题3：已知a、b满足√(2a + 8)+| b - √(3)|=0，解关于x的方程(a + 2)x + b^2=a - 1。

七年级下学期压轴题集

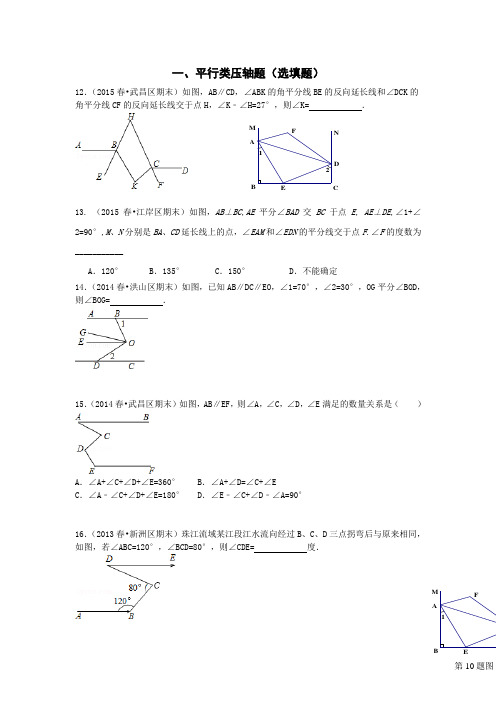
一、平行类压轴题（选填题）12．（2015春•武昌区期末）如图，AB ∥CD ，∠ABK 的角平分线BE 的反向延长线和∠DCK 的角平分线CF 的反向延长线交于点H ，∠K ﹣∠H=27°，则∠K= ．13. （2015春•江岸区期末）如图，AB ⊥BC ,AE 平分∠BAD 交BC 于点E , AE ⊥DE ,∠1+∠2=90°,M 、N 分别是BA 、CD 延长线上的点，∠EAM 和∠EDN 的平分线交于点F .∠F 的度数为___________A ．120°B ．135°C ．150°D ．不能确定14．（2014春•洪山区期末）如图，已知AB ∥DC ∥EO ，∠1=70°，∠2=30°，OG 平分∠BOD ，则∠BOG= ．15．（2014春•武昌区期末）如图，AB ∥EF ，则∠A ，∠C ，∠D ，∠E 满足的数量关系是（）A ．∠A+∠C+∠D+∠E=360°B ．∠A+∠D=∠C+∠EC ．∠A ﹣∠C+∠D+∠E=180°D ．∠E ﹣∠C+∠D ﹣∠A=90° 16．（2013春•新洲区期末）珠江流域某江段江水流向经过B 、C 、D 三点拐弯后与原来相同，如图，若∠ABC=120°，∠BCD=80°，则∠CDE= 度．M 1FEBA第10题图NM 21FE DCBA17．（3分）（2012春•武昌区期末）如图，在△ABC 中，∠ABC 的平分线与∠ACB 的外角平分线交于点E ，EC 延长线交∠ABC 的外角平分线于点D ，若∠D 比∠E 大10°，则∠A 的度数是．18．（2014春•硚口区期末）如图，BD 平分∠ABC ，AF 平分∠BAD ，∠EAD=2∠DBC ，∠BDC=∠AFB ，下列结论：①AD ∥BC ；②∠AFB=90°；③∠FAG=∠DCG ，其中正确的是（）A ．①②③B ．①②C ．①D ．②③19.（2014春•二中期末）如图，点P 的坐标为（0,2），PF ∥CD ，OE 平分∠AOC ，OE ⊥OF 。

七年级下册数学动点问题及压轴题(带答案)

七年级下册动点问题及压轴题1．如图1，在平面直角坐标系中，A（a，0）是x轴正半轴上一点，C是第四象限一点，CB⊥y轴，交y轴负半轴于B（0，b），且（a﹣3）2+|b+4|=0，S四边形AOBC=16．（1）求C点坐标；（2）如图2，设D为线段OB上一动点，当AD⊥AC时，∠ODA的角平分线与∠CAE 的角平分线的反向延长线交于点P，求∠APD的度数．（3）如图3，当D点在线段OB上运动时，作DM⊥AD交BC于M点，∠BMD、∠DAO的平分线交于N点，则D点在运动过程中，∠N的大小是否变化？若不变，求出其值，若变化，说明理由．【解答】解：（1）∵（a﹣3）2+|b+4|=0，∴a﹣3=0，b+4=0，∴a=3，b=﹣4，∴A（3，0），B（0，﹣4），∴OA=3，OB=4，∵S四边形AOBC=16．∴（OA+BC）×OB=16，∴（3+BC）×4=16，∴BC=5，∵C是第四象限一点，CB⊥y轴，∴C（5，﹣4）（2）如图，延长CA，∵AF是∠CAE的角平分线，∴∠CAF=∠CAE，∵∠CAE=∠OAG，∴∠CAF=∠OAG，∵AD⊥AC，∴∠DAO+∠OAG=∠PAD+∠PAG=90°，∵∠AOD=90°，∴∠DAO+∠ADO=90°，∴∠ADO=∠OAG，∴∠CAF=∠ADO，∵DP是∠ODA的角平分线∴∠ADO=2∠ADP，∴∠CAF=∠ADP，∵∠CAF=∠PAG，∴∠PAG=∠ADP，∴∠APD=180°﹣（∠ADP+∠PAD）=180°﹣（∠PAG+∠PAD）=180°﹣90°=90°即：∠APD=90°（3）不变，∠ANM=45°理由：如图，∵∠AOD=90°，∴∠ADO+∠DAO=90°，∵DM⊥AD，∴∠ADO+∠BDM=90°，∴∠DAO=∠BDM，∵NA是∠OAD的平分线，∴∠DAN=∠DAO=∠BDM，∵CB⊥y轴，∴∠BDM+∠BMD=90°，∴∠DAN=（90°﹣∠BMD），∵MN是∠BMD的角平分线，∴∠DMN=∠BMD，∴∠DAN+∠DMN=（90°﹣∠BMD）+∠BMD=45°在△DAM中，∠ADM=90°，∴∠DAM+∠DMA=90°，在△AMN中，∠ANM=180°﹣（∠NAM+∠NMA）=180°﹣（∠DAN+∠DAM+∠DMN+∠DMA）=180°﹣[（∠DAN+DMN）+（∠DAM+∠DMA）]=180°﹣（45°+90°）=45°，∴D点在运动过程中，∠N的大小不变，求出其值为45°2．如图1，直线MN与直线AB、CD分别交于点E、F，∠1与∠2互补．（1）试判断直线AB与直线CD的位置关系，并说明理由；（2）如图2，∠BEF与∠EFD的角平分线交于点P，EP与CD交于点G，点H是MN上一点，且GH⊥EG，求证：PF∥GH；（3）如图3，在（2）的条件下，连接PH，K是GH上一点使∠PHK=∠HPK，作PQ平分∠EPK，问∠HPQ的大小是否发生变化？若不变，请求出其值；若变化，说明理由．【考点】JB：平行线的判定与性质．【分析】（1）利用对顶角相等、等量代换可以推知同旁内角∠AEF、∠CFE互补，所以易证AB∥CD；（2）利用（1）中平行线的性质推知°；然后根据角平分线的性质、三角形内角和定理证得∠EPF=90°，即EG⊥PF，故结合已知条件GH⊥EG，易证PF∥GH；（3）利用三角形外角定理、三角形内角和定理求得∠4=90°﹣∠3=90°﹣2∠2；然后由邻补角的定义、角平分线的定义推知∠QPK=∠EPK=45°+∠2；最后根据图形中的角与角间的和差关系求得∠HPQ的大小不变，是定值45°．【解答】解：（1）如图1，∵∠1与∠2互补，∴∠1+∠2=180°．又∵∠1=∠AEF，∠2=∠CFE，∴∠AEF+∠CFE=180°，∴AB∥CD；（2）如图2，由（1）知，AB∥CD，∴∠BEF+∠EFD=180°．又∵∠BEF与∠EFD的角平分线交于点P，∴∠FEP+∠EFP=（∠BEF+∠EFD）=90°，∴∠EPF=90°，即EG⊥PF．∵GH⊥EG，∴PF∥GH；（3）∠HPQ的大小不发生变化，理由如下：如图3，∵∠1=∠2，∴∠3=2∠2．又∵GH⊥EG，∴∠4=90°﹣∠3=90°﹣2∠2．∴∠EPK=180°﹣∠4=90°+2∠2．∵PQ平分∠EPK，∴∠QPK=∠EPK=45°+∠2．∴∠HPQ=∠QPK﹣∠2=45°，∴∠HPQ的大小不发生变化，一直是45°．3.如图①，在矩形ABCD中，AB=10cm，BC=8cm，点P从A出发，沿A→B→C→D 路线运动，到D停止，点P的速度为每秒1cm，a秒时点P改变速度，变为每秒bcm，图②是点P出发x秒后△APD的面积S（cm2）与x（秒）的关系图象，（1）参照图②，求a、b及图②中的c值；（2）设点P离开点A的路程为y（cm），请写出动点P改变速度后y与出发后的运动时间x（秒）的关系式，并求出点P到达DC中点时x的值．（3）当点P出发多少秒后，△APD的面积是矩形ABCD面积的．4．星光橱具店购进电饭煲和电压锅两种电器进行销售，其进价与售价如表：进价（元/台）售价（元/台）电饭煲200250电压锅160200（1）一季度，橱具店购进这两种电器共30台，用去了5600元，并且全部售完，问橱具店在该买卖中赚了多少钱？（2）为了满足市场需求，二季度橱具店决定用不超过9000元的资金采购电饭煲和电压锅共50台，且电饭煲的数量不少于电压锅的，问橱具店有哪几种进货方案？并说明理由；（3）在（2）的条件下，请你通过计算判断，哪种进货方案橱具店赚钱最多？【考点】一元一次不等式组的应用；二元一次方程组的应用．【分析】（1）设橱具店购进电饭煲x台，电压锅y台，根据图表中的数据列出关于x、y的方程组并解答即可，等量关系是：这两种电器共30台；共用去了5600元；（2）设购买电饭煲a台，则购买电压锅（50﹣a）台，根据“用不超过9000元的资金采购电饭煲和电压锅共50台，且电饭煲的数量不少于电压锅的”列出不等式组；（3）结合（2）中的数据进行计算．【解答】解：（1）设橱具店购进电饭煲x台，电压锅y台，依题意得，解得，所以，20×+10×=1400（元）．答：橱具店在该买卖中赚了1400元；（2）设购买电饭煲a台，则购买电压锅（50﹣a）台，依题意得，解得22≤a≤25．又∵a为正整数，∴a可取23，24，25．故有三种方案：①防购买电饭煲23台，则购买电压锅27台；②购买电饭煲24台，则购买电压锅26台；③购买电饭煲25台，则购买电压锅25台．（3）设橱具店赚钱数额为W元，当a=23时，W=23×+27×=2230；当a=24时，W=24×+26×=2240；当a=25时，W=25×+25×=2250；综上所述，当a=25时，W最大，此时购进电饭煲、电压锅各25台．5．（本题12分）已知：在平面直角坐标系中，直线AB 分别与x 轴负半轴、y 轴正半轴交于点B (b ，0)、点A (0，a )，且a 、b 满足0|32|34=++++--b a b a ，点D (h ，m )是直线AB 上且不与A 、B 两点重合的动点(1) 求△AOB 的面积;(2) 如图1，点P 、点T 分别是线段OA 、x 轴正半轴上的动点，过T 作TE ∥AB ，连接TP ．若∠ABO ＝n °，请探究∠APT 与∠PTE 之间的数量关系？（注：可用含n 的式子表达并说明理由）(3) 若32S △BOD ≥S △AOD ，求出m 的取值范围.。

期中解答题压轴必刷常考题七年级数学下学期期中期末满分必刷常考压轴题人教版

解答题压轴必刷常考题【压轴题题必考】1．（安溪）如图，将一条数轴在原点O和点B处各折一下，AO∥BC，得到一条“折线数轴”．图中点A表示﹣20，点B表示20，点C表示36．动点M从点A出发，以2个单位/秒的速度沿着“折线数轴”的正方向运动，从点O运动到点B期间速度变为原来的一半，之后立刻恢复原速；同时，动点N从点C出发，以1个单位/秒的速度沿着“折线数轴”的负方向运动，从点B运动到点O期间的速度变为原来的两倍，之后也立刻恢复原速．设运动的时间为t秒．（1）填空：点A和点C在数轴上相距56个单位长度；（2）当t为何值时，点M与点N相遇？（3）当t为何值时，M、O两点在数轴上相距的长度与N、B两点在数轴上相距的长度相等．【答案】（1）56 （2）t＝（3）t的值为4或13或22或34【解答】解：（1）∵点A表示﹣20，点C表示36，∴点A和点C在数轴上相距36﹣（﹣20）＝56（个单位长度），故答案为：56；（2）由题意知，N从C到B需16s，M从A到O需10s，∴M、N在OB段相遇，根据题意得：20+（t﹣10）+16+2（t﹣16）＝56，解得t＝，答：t为时，点M与点N相遇；（3）分四种情况：①当点M在AO上，点N在CB上时，OM＝20﹣2t，BN＝16﹣t，∴20﹣2t＝16﹣t，解得t＝4，②当M在OB上，N在CB上时，OM＝t﹣10，BN＝16﹣t，∴t﹣10＝16﹣t，解得t＝13，③当M在OB上，N在OB上时，OM＝t﹣10，BN＝2（t﹣16），∴t﹣10＝2（t﹣16），解得t＝22，④当M在BC上，N在OA上时，20+2（t﹣30）＝20+（t﹣26），解得t＝34，综上所述，t的值为4或13或22或34时，M、O两点在数轴上相距的长度与N、B两点在数轴上相距的长度相等．2．（朝阳）将一副三角板中的两块直角三角尺的直角顶点C按如图1方式叠放在一起，其中∠A＝60°，∠D＝30°，∠E＝∠B＝45°．（1）若∠1＝25°，则∠2的度数为；（2）直接写出∠1与∠3的数量关系：；（3）直接写出∠2与∠ACB的数量关系：；（4）如图2，当∠ACE＜180°且点E在直线AC的上方时，将三角尺ACD固定不动，改变三角尺BCE的位置，但始终保持两个三角尺的顶点C重合，这两块三角尺是否存在一组边互相平行？请直接写出∠ACE角度所有可能的值．【答案】（1）65°（2）∠1＝∠3；（3）∠2+∠ACB＝180°（4）30°或45°或120°或135°或165°．【解答】解：（1）∵∠1＝25°，∠ACD＝90°，∴∠2＝∠ACD﹣∠1＝65°，故答案为：65°；（2）∵∠1+∠2＝∠ACD＝90°，∠2+∠3＝∠BCE＝90°，∴∠1+∠2＝∠2+∠3，∴∠1＝∠3，故答案为：∠1＝∠3；（3）∵∠ACD＝∠BCE＝90°，∴∠ACB+∠2＝∠1+∠2+∠3+∠2＝∠ACD+∠BCE＝180°，即∠2+∠ACB＝180°，故答案为：∠2+∠ACB＝180°；（4）存在，①当BC∥AD时，∵BC∥AD，∴∠BCD＝∠D＝30°，∴∠ACB＝90°+30°＝120°，∴∠ACE＝∠ACB﹣∠BCE＝120°﹣90°＝30°；②当BE∥AC时，如图，∵BE∥AC，∴∠ACE＝∠E＝45°；③当AD∥CE时，如图，∵AD∥CE，∴∠DCE＝∠D＝30°，∴∠ACE＝90°+30°＝120°；④当BE∥CD时，如图，∵BE∥CD，∴∠DCE＝∠E＝45°，∴∠ACE＝∠ACD+∠DCE＝135°；⑤当BE∥AD时，如图，过点C作CF∥AD，∵BE∥AD，CF∥AD，∴BE∥AD∥CF，∴∠ECF＝∠E＝45°，∠DCF＝∠D＝30°，∴∠DCE＝30°+45°＝75°，∴∠ACE＝90°+75°＝165°．综上所述：当∠ACE＝30°或45°或120°或135°或165°时，有一组边互相平行．故答案为：30°或45°或120°或135°或165°．3．（淇县）如图（1），AB∥CD，猜想∠BPD与∠B、∠D的关系，说出理由．解：猜想∠BPD+∠B+∠D＝360°理由：过点P作EF∥AB，∴∠B+∠BPE＝180°（两直线平行，同旁内角互补）∵AB∥CD，EF∥AB，∴EF∥CD，（如果两条直线都和第三条直线平行，那么这两条直线也互相平行．）∴∠EPD+∠D＝180°（两直线平行，同旁内角互补）∴∠B+∠BPE+∠EPD+∠D＝360°∴∠B+∠BPD+∠D＝360°（1）依照上面的解题方法，观察图（2），已知AB∥CD，猜想图中的∠BPD与∠B、∠D的关系，并说明理由．（2）观察图（3）和（4），已知AB∥CD，猜想图中的∠BPD与∠B、∠D的关系，不需要说明理由．【答案】（1）∠BPD＝∠B+∠D（2）∠BPD＝∠B﹣∠D．【解答】解：（1）∠BPD＝∠B+∠D．理由：如图2，过点P作PE∥AB，∵AB∥CD，∴PE∥AB∥CD，∴∠1＝∠B，∠2＝∠D，∴∠BPD＝∠1+∠2＝∠B+∠D；（2）如图（3）：∠BPD＝∠D﹣∠B．理由：∵AB∥CD，∴∠1＝∠D，∵∠1＝∠B+∠P，∴∠D＝∠B+∠P，即∠BPD＝∠D﹣∠B；如图（4）：∠BPD＝∠B﹣∠D．理由：∵AB∥CD，∴∠1＝∠B，∵∠1＝∠D+∠P，∴∠B＝∠D+∠P，即∠BPD＝∠B﹣∠D．4．（西乡塘）如图，已知DC∥FP，∠1＝∠2，∠DEF＝30°，∠AGF＝70°，FH平分∠EFG．（1）求证：DC∥AB；（2）求∠PFH的度数．【答案】（1）略（2）∠PFH的度数为20°【解答】解：（1）∵DC∥FP，∴∠C＝∠2，又∵∠1＝∠2，∴∠C＝∠1，∴DC∥AB；（2）∵DC∥FP，DC∥AB，∠DEF＝30°，∴∠DEF＝∠EFP＝30°，AB∥FP，又∵∠AGF＝70°，∴∠AGF＝∠GFP＝70°，∴∠GFE＝∠GFP+∠EFP＝70°+30°＝100°，又∵FH平分∠EFG，∴∠GFH＝∠GFE＝50°，∴∠PFH＝∠GFP﹣∠GFH＝70°﹣50°＝20°．答：∠PFH的度数为20°．5.（海勃湾）如图1，直线MN与直线AB、CD分别交于点E、F，∠1与∠2互补．（1）试判断直线AB与直线CD的位置关系，并说明理由；（2）如图2，∠BEF与∠EFD的角平分线交于点P，EP与CD交于点G，点H是MN 上一点，且GH⊥EG，求证：PF∥GH；（3）如图3，在（2）的条件下，连接PH，K是GH上一点使∠PHK＝∠HPK，作PQ 平分∠EPK，求∠HPQ的度数．【答案】（1）AB∥CD（2）PF∥GH（3）∠HPQ的度数为45°【解答】解：（1）AB∥CD，理由如下：∵∠1与∠2互补，∴∠1+∠2＝180°，又∵∠1＝∠AEF，∠2＝∠，∴∠AEF+∠CFE＝180°，∴AB∥CD；（2）由（1）知，AB∥CD，∴∠BEF+∠EFD＝180°．又∵∠BEF与∠EFD的角平分线交于点P，∴，∴∠EPF＝90°，即EG⊥PF．∵GH⊥EG，∴PF∥GH；（3）∵∠PHK＝∠HPK，∴∠PKG＝2∠HPK．又∵GH⊥EG，∴∠KPG＝90°﹣∠PKG＝90°﹣2∠HPK．∴∠EPK＝180°﹣∠KPG＝90°+2∠HPK．∵PQ平分∠EPK，∴．∴∠HPQ＝∠QPK﹣∠HPK＝45°．答：∠HPQ的度数为45°．6．（黔江）（1）如图1，已知AB∥CD，则∠AEC＝∠BAE+∠DCE成立吗？请说明理由；（2）如图2，已知AB∥CD，BE平分∠ABC，DE平分∠ADC，BE、DE所在直线交于点E，若∠F AD＝60°，∠ABC＝40°，求∠BED的度数；（3）如图3，已知AB∥CD，BE平分∠ABC，DE平分∠ADC，BE、DE所在直线交于点E，若∠F AD＝α，∠ABC＝β，请你求出∠BED的度数（用含α，β的式子表示）．【答案】（1）成立（2）∠BED＝50°（3）【解答】解：（1）成立，理由：如图1中，作EF//AB，则有EF//CD，∴∠1＝∠BAE，∠2＝∠DCE∴∠AEC＝∠1+∠2＝∠BAE+∠DCE；（2）如图2，过点E作EH//AB，∵AB//CD，∠F AD＝60°，∴∠F AD＝∠ADC＝60°，∵DE平分∠ADC，∠ADC＝60°，∴，∵BE平分∠ABC，∠ABC＝40°，∴，∵AB//CD，∴AB//CD//EH，∴∠ABE＝∠BEH＝20°，∠CDE＝∠DEH＝30°，∴∠BED＝∠BEH+∠DEH＝50°．（3）如图3，过点E作EG//AB，∵BE平分∠ABC，DE平分∠ADC，∠ABC＝β，∠ADC＝∠F AD＝α，∴，，∵AB//CD，∴AB//CD//EG，∴，，∴．7．（拱墅）小明同学在完成七年级下册数学第1章的线上学习后，遇到了一些问题，请你帮他解决一下．（1）如图1，已知AB∥CD，则∠AEC＝∠BAE+∠DCE成立吗？请说明理由．（2）如图2，已知AB∥CD，BE平分∠ABC，DE平分∠ADC，BE、DE所在直线交于点E，若∠F AD＝50°，∠ABC＝40°，求∠BED的度数．【答案】（1）∠AEC＝∠BAE+∠DCE．（2）∠BED＝45°【解答】解：（1）∠AEC＝∠BAE+∠DCE成立，理由：过点E作EF∥AB，如图，∵EF∥AB，∴∠A＝∠AEF．∵EF∥AB，AB∥CD，∴FE∥CD．∴∠C＝∠CEF．∵∠AEC＝∠AEF+∠CEF，∴∠AEC＝∠BAE+∠DCE．（2）过点E作EH∥AB，如图，由（1）的结论可得：∠BED＝∠ABE+∠EDC，∵BE平分∠ABC，∠ABC＝40°，∴∠ABE＝∠ABC＝20°．∵∠F AD＝50°，AB∥CD，∴∠ADC＝∠F AD＝50°．∵DE平分∠ADC，∴∠EDC＝∠ADC＝25°．∴∠BED＝20°+25°＝45°．8．（宜兴）如图①，已知PQ∥MN，且∠BAM＝2∠BAN．（1）填空：∠PBA＝°；（2）如图（1）所示，射线AM绕点A开始顺时针旋转至AN便立即按原速度回转至AM 位置，射线BP绕点B开始顺时针旋转至BQ便立即按原速度回转至BP位置．若AM转动的速度是每秒2度，BP转动的速度是每秒1度，若射线BP先转动30秒，射线AM才开始转动，在射线BP到达BQ之前，射线AM转动几秒，两射线互相平行？（3）如图（2），若两射线分别绕点A，B顺时针方向同时转动，速度同题（2），在射线AM到达AN之前，若两射线交于点C，过C作∠ACD交PQ于点D，且∠ACD＝120°，则在转动过程中，请探究∠BAC与∠BCD的数量关系是否发生变化？若不变，请求出其数量关系；若改变，请说明理由．【答案】（1）120（2）AM转动30秒或110秒（3）∠BAC＝2∠BCD【解答】解：（1）∵∠BAM＝2∠BAN，∠BAM+∠BAN＝180°，∴∠BAM＝120°．∵PQ∥MN，∴∠PBA＝∠BAM＝120°．故答案为：120；（2）设射线AM转动t秒，两射线互相平行，当0＜t＜90时，如图，AM′和BP′为经过t秒后AM，BP旋转的位置，则∠MAM′＝2t°，∠PBP′＝（t+30）°，∵PQ∥MN，∴∠BM′A＝∠MAM′＝2t°，∵AM′∥BP′，∴∠AM′B＝∠PBP′．∴2t＝t+30．解得：t＝30；当90＜t＜150时，如图，AM′和BP′为经过t秒后AM，BP旋转的位置，则∠MAM′＝（360﹣2t）°，∠PBP′＝（t+30）°，∵PQ∥MN，∴∠BM′A＝∠MAM′＝2t°，∵AM′∥BP′，∴∠AM′B＝∠PBP′．∴360﹣2t＝t+30．解得：t＝110．综上所述，当射线AM转动30秒或110秒时，两射线互相平行．（3）∠BAC与∠BCD的数量关系不会发生变化，∠BAC＝2∠BCD．理由：设射线AM，BP转动时间为m秒，∴∠BAC＝（2m﹣120）°，∠ABC＝（120﹣t）°，∴∠ACB＝180°﹣（2m﹣120）°﹣（120﹣m）°＝（180﹣m）°．∵∠ACD＝120°，∴∠BCD＝120°﹣（180﹣m）°＝（m﹣60）°．∵2m﹣120＝2（m﹣60），∴∠BAC＝2∠BCD．∴∠BAC与∠BCD的数量关系不会发生变化，∠BAC＝2∠BCD．9．（仁寿）如图①．已知AM∥CN，点B为平面内一点，AB⊥BC于点B，过点B作BD⊥AM于点D，设∠BCN＝α．（1）若α＝30°，求∠ABD的度数；（2）如图②，若点E、F在DM上，连接BE、BF、CF，使得BE平分∠ABD、BF平分∠DBC，求∠EBF的度数；（3）如图③，在（2）问的条件下，若CF平分∠BCH，且∠BFC＝3∠BCN，求∠EBC 的度数．【答案】（1）30°（2）45°（3）97.5°．【解答】解：（1）延长DB，交NC于点H，如图，∵AM∥CN，BD⊥AM，∴DH⊥NC．∴∠BHC＝90°．∵∠BCN＝α＝30°，∴∠HBC＝90°﹣∠BCN＝60°．∵AB⊥BC，∴∠ABC＝90°．∴∠ABD＝180°﹣∠ABC﹣∠HBC＝30°；（2）延长DB，交NC于点H，如图，∵AM∥CN，BD⊥AM，∴DH⊥NC．∴∠BHC＝90°．∵∠BCN＝α，∴∠HBC＝90°﹣α．∵AB⊥BC，∴∠ABC＝90°．∴∠ABD＝180°﹣∠ABC﹣∠HBC＝α．∵BE平分∠ABD，∴∠DBE＝∠ABE＝α．∵∠HBC＝90°﹣α，∴∠DBC＝180°﹣∠HBC＝90°+α．∵BF平分∠DBC，∴∠DBF＝∠CBF＝∠DBC＝45°+α．∴∠EBF＝∠DBF﹣∠DBE＝45°+α﹣α＝45°；（3）∵∠BCN＝α，∴∠HCB＝180°﹣∠BCN＝180°﹣α．∵CF平分∠BCH，∴∠BCF＝∠HCF＝∠HCB＝90°﹣α．∵AM∥CN，∴∠DFC＝∠HCF＝90°﹣α．∵∠BFC＝3∠BCN，∴∠BFC＝3α．∴∠DFB＝∠DFC﹣∠BFC＝90°﹣α．由（2）知：∠DBF＝45°+α．∵BD⊥AM，∴∠D＝90°．∴∠DBF+∠DFB＝90°．∴45°+α+90°﹣α＝90°．解得：α＝15°．∴∠FBC＝∠DBF＝45°+α＝52.5°．∴∠EBC＝∠FBC+∠EBF＝52.5°+45°＝97.5°．10．（邵东）点A、B在数轴上分别表示实数a、b，A、B两点之间的距离记作AB．当A、B 两点中有一点为原点时，不妨设A点在原点．如图①所示，则AB＝OB＝|b|＝|a﹣b|．当A、B两点都不在原点时：（1）如图②所示，点A、B都在原点的右边，不妨设点A在点B的左侧，则AB＝OB﹣OA＝|b|﹣|a|＝b﹣a＝|b﹣a|＝|a﹣b|（2）如图③所示，点A、B都在原点的左边，不妨设点A在点B的右侧，则AB＝OB﹣OA＝|b|﹣|a|＝﹣b﹣（﹣a）＝a﹣b＝|a﹣b|（3）如图④所示，点A、B分别在原点的两边，不妨设点A在点O的右侧，则AB＝OB+OA ＝|b|+|a|＝a+（﹣b）＝|a﹣b|回答下列问题：（1）综上所述，数轴上A、B两点之间的距离AB＝．（2）数轴上表示2和﹣4A和B之间的距离AB＝．（3）数轴上表示x和﹣2的两点A和B之间的距离AB＝| ，如果AB＝2，则x的值为．（4）若代数式|x+2|+|x﹣3|有最小值，则最小值为．【答案】（1）AB＝|a﹣b|（2）6 （3）0或﹣4 （4）5【解答】解：（1）综上所述，数轴上A、B两点之间的距离AB＝|a﹣b|；（2）数轴上表示2和﹣4的两点A和B之间的距离AB＝2﹣（﹣4）＝2+4＝6；（3）数轴上表示x和﹣2的两点A和B之间的距离AB＝|x+2|，如果AB＝2，则x的值为0或﹣4；（4）若代数式|x+2|+|x﹣3|有最小值，则最小值为5．故答案为：（1）|a﹣b|；（2）6；（3）|x+2|；0或﹣4；（4）511．（广安）点A、B在数轴上分别表示有理数a、b，A、B两点之间的距离表示为AB，在数轴上A、B两点之间的距离AB＝|a﹣b|，例如：数轴上表示﹣1与﹣2的两点间的距离＝|﹣1﹣（﹣2）|＝﹣1+2＝1；而|x+2|＝|x﹣（﹣2）|，所以|x+2|表示x与﹣2两点间的距离．利用数形结合思想回答下列问题：（1）数轴上表示﹣2和5两点之间的距离．（2）若数轴上表示点x的数满足|x﹣1|＝3，那么x＝．（3）若数轴上表示点x的数满足﹣4＜x＜2，则|x﹣2|+|x+4|＝．【答案】（1）76（2）﹣2或4（3）6【解答】解：（1）根据题意知数轴上表示﹣2和5两点之间的距离为5﹣（﹣2）＝7，故答案为：7；（2）∵|x﹣1|＝3，即在数轴上到表示1和x的点的距离为3，∴x＝﹣2或x＝4，故答案为：﹣2或4；（3）∵|x﹣2|+|x+4|表示在数轴上表示x的点到﹣4和2的点的距离之和，且x位于﹣4到2之间，∴|x﹣2|+|x+4|＝2﹣x+x+4＝6，故答案为：6．12．（兴宁）如图，在数轴上有两个长方形ABCD和EFGH，这两个长方形的宽都是3个单位长度，长方形ABCD的长AD是6个单位长度，长方形EFGH的长EH是10个单位长度，点E在数轴上表示的数是5．且E、D两点之间的距离为14．（1）填空：点H在数轴上表示的数是，点A在数轴上表示的数是．（2）若线段AD的中点为M，线段EH上一点N，EN＝EH，M以每秒4个单位的速度向右匀速运动，N以每秒3个单位的速度向左运动，设运动时间为x秒，原点为O．当OM＝2ON时，求x的值．（3）若长方形ABCD以每秒2个单位的速度向右匀速运动，长方形EFGH固定不动，设长方形ABCD运动的时间为t（t＞0）秒，两个长方形重叠部分的面积为S，当S＝12时，求此时t的值．【答案】（1）15；﹣15（2）或．（3）t的值为9或13．【解答】解：（1）由题意可得，点H在数轴上表示的数为：5+10＝15；点A在数轴上表示的数为：5﹣14﹣6＝﹣15．故答案为：15；﹣15．（2）∵点M是线段AD的中点，∴点M表示的数为5﹣14﹣＝﹣12，又∵EN＝EH，∴点N在数轴上表示的数为：5+（15﹣5）＝，由题意可得，x秒时，点M在数轴上表示的数为：﹣12+4x，点N在数轴上表示的数为：﹣3x，∴OM＝|4x﹣12|，ON＝|3x﹣|，∵OM＝2ON，∴|4x﹣12|＝2|3x﹣|∴4x﹣12＝2（3x﹣）或4x﹣12＝﹣2（3x﹣），解得x＝或x＝．故答案为：或．（3）当CD与EF重合时，所用时间为＝7秒，由题意得：AD与EH重合的部分为＝4，如图1所示，设长方形ABCD从EF运动到AD与EH重叠部分为4时，所用的时间为t1秒，∴t1＝＝2，∴第一次重叠面积为12时，时间t为2+7＝9（秒）；当AD与EH重叠部分为4时，如图2所示，设长方形ABCD从EF运动到AD与EH重叠部分为4时，所用的时间为t2秒，∴t2＝＝6，∴第二次重叠面积S＝12时，时间t为6+7＝13（秒）；∴当长方形ABCD与长方形EFGH重叠部分的面积为12时，t的值为9或13．13．（宣化）如图，一只蚂蚁从点A沿数轴向右爬了2个单位长度到达点B，点A表示﹣，设点B所表示的数为m．（1）实数m的值是；（2）求|m+1|+|m﹣1|的值；（3）在数轴上还有C、D两点分别表示实数c和d，且有|2c+d|与互为相反数，求2c﹣3d的平方根．【答案】（1）2﹣（2）2 （3）±4．【解答】解：（1）m＝﹣+2＝2﹣；（2）∵m＝2﹣，则m+1＞0，m﹣1＜0，∴|m+1|+|m﹣1|＝m+1+1﹣m＝2；答：|m+1|+|m﹣1|的值为2．（3）∵|2c+d|与互为相反数，∴|2c+d|+＝0，∴|2c+d|＝0，且＝0，解得：c＝﹣2，d＝4，或c＝2，d＝﹣4，①当c＝﹣2，d＝4时，所以2c﹣3d＝﹣16，无平方根．②当c＝2，d＝﹣4时，∴2c﹣3d＝16，∴2c﹣3d的平方根为±4，答：2c﹣3d的平方根为±4．14．（锦江）阅读下面材料：点A、B在数轴上分别表示实数a、b，A、B两点之间的距离表示为|AB|．当A、B两点中有一点在原点时，不妨设点A在原点，如图1，|AB|＝|OB|＝|b|＝|a﹣b|；当A、B两点都不在原点时，如图2，点A、B都在原点的右边，|AB|＝|OB|﹣|OA|＝|b|﹣|a|＝b﹣a＝|a﹣b|；如图3，当点A、B都在原点的左边，|AB|＝|OB|﹣|OA|＝|b|﹣|a|＝﹣b﹣（﹣a）＝|a﹣b|；如图4，当点A、B在原点的两边，|AB|＝|OB|+|OA|＝|a|+|b|＝a+（﹣b）＝|a﹣b|．回答下列问题：（1）数轴上表示1和6的两点之间的距离是数轴上表示2和﹣3的两点之间的距离是．（2）数轴上若点A表示的数是x，点B表示的数是﹣4，则点A和B之间的距离是，若|AB|＝3，那么x为．（3）当x是时，代数式|x+2|+|x﹣1|＝7．（4）若点A表示的数﹣1，点B与点A的距离是10，且点B在点A的右侧，动点P、Q 同时从A、B出发沿数轴正方向运动，点P的速度是每秒3个单位长度，点Q的速度是每秒个单位长度，求运动几秒后，B、P、Q三点中，有一点恰好是另两点所连线段的中点？（请写出必要的求解过程）．【答案】（1）5，5（2）﹣1或﹣7 （3）﹣4或3 （4）运动或或5秒【解答】解：（1）数轴上表示1和6的两点之间的距离是|6﹣1|＝5，数轴上表示2和﹣3的两点之间的距离是|2﹣（﹣3）|＝5．（2）数轴上若点A表示的数是x，点B表示的数是﹣4，则点A和B之间的距离是|x+4|，若|AB|＝3，则|x+4|＝3，解得x＝﹣1或﹣7．（3）当x＞1时，|x+2|+|x﹣1|＝x+2+x﹣1＝7，2x＝6，x＝3，当x＜﹣2时，|x+2|+|x﹣1|＝﹣x﹣2+1﹣x＝7，﹣2x＝8，x＝﹣4，当﹣2≤x≤1时，|x+2|+|x﹣1|＝x+2+1﹣x＝3≠7，∴当x＝﹣4或3时，代数式|x+2|+|x﹣1|＝7．（4）设运动t秒后，有一点恰好是另两点所连线段的中点，由题意，得①点B为线段PQ中点时，，解得，②点P为线段BQ中点时，，解得，③点Q为线段BP中点时，，解得t＝5．答：运动或或5秒后，B、P、Q三点中，有一点恰好是另两点所连线段的中点．15．（宣化）阅读下面的文字，解答问题．大家知道是无理数，而无理数是无限不循环小数，因此的小数部分我们不可能完全地写出来，于是小明用﹣1来表示的小数部分，你同意小明的表示方法吗？事实上，小明的表示方法是有道理的，因为的整数部分是1，用这个数减去其整数部分，差就是小数部分．请解答下列问题：（1）求出+2的整数部分和小数部分；（2）已知：10+＝x+y，其中x是整数，且0＜y＜1，请你求出（x﹣y）的相反数．【答案】（1）3，﹣1 （2）﹣14【解答】解：（1）∵1＜＜2，∴3＜+2＜4，∴+2的整数部分是1+2＝3，+2的小数部分是﹣1；（2）∵2＜＜3，∴12＜10+＜13，∴10+的整数部分是12，10+的小数部分是10+﹣12＝﹣2，即x＝12，y＝﹣2，∴x﹣y＝12﹣（﹣2）＝12﹣+2＝14﹣，则x﹣y的相反数是﹣14．16．（靖江）在平面直角坐标系xOy中，对于点P（x，y），若点Q的坐标为（ax+y，x+ay），则称点Q是点P的“a阶派生点”（其中a为常数，且a≠0）．例如：点P（1，4）的“2阶派生点”为点Q（2×1+4，1+2×4），即点Q（6，9）．（1）若点P的坐标为（﹣1，5），则它的“3阶派生点”的坐标为；（2）若点P的“5阶派生点”的坐标为（﹣9，3），求点P的坐标；（3）若点P（c+1，2c﹣1）先向左平移2个单位长度，再向上平移1个单位长度后得到了点P1．点P1的“﹣4阶派生点”P2位于坐标轴上，求点P2的坐标．【答案】（1）（2，14）（2）（﹣2，1）；（3）（0，﹣15）或（，0）．【解答】解：（1）3×（﹣1）+5＝2；﹣1+3×5＝14，∴点P的坐标为（﹣1，5），则它的“3级派生点”的坐标为（2，14）．故答案为：（2，14）；（2）设点P的坐标为（a，b），由题意可知，解得：，∴点P的坐标为（﹣2，1）；（3）由题意，P1（c﹣1，2c），∴P1的“﹣4阶派生点“P2为：（﹣4（c﹣1）+2c，c﹣1﹣8c），即（﹣2c+4，﹣7c﹣1），∵P2在坐标轴上，∴﹣2c+4＝0或﹣7c﹣1＝0，∴c＝2或c＝﹣，∴P2（0，﹣15）或（，0）．17．（黄山）在平面直角坐标系xOy中，对于P，Q两点给出如下定义：若点P到x、y轴的距离中的最大值等于点Q到x、y轴的距离中的最大值，则称P，Q两点为“等距点”．下图中的P，Q两点即为“等距点”．（1）已知点A的坐标为（﹣3，1），①在点E（0，3），F（3，﹣3），G（2，﹣5）中，为点A的“等距点”的是；②若点B的坐标为B（m，m+6），且A，B两点为“等距点”，则点B的坐标为；（2）若T1（﹣1，﹣k﹣3），T2（4，4k﹣3）两点为“等距点”，求k的值．【答案】（1）①E、F；②（﹣3，3）；（2）1或2【解答】解：（1）①∵点A（﹣3，1）到x、y轴的距离中最大值为3，∴与A点是“等距点”的点是E、F．②当点B坐标中到x、y轴距离其中至少有一个为3的点有（3，9）、（﹣3，3）、（﹣9，﹣3），这些点中与A符合“等距点”的是（﹣3，3）．故答案为①E、F；②（﹣3，3）；（2）T1（﹣1，﹣k﹣3），T2（4，4k﹣3）两点为“等距点”，①若|4k﹣3|≤4时，则4＝﹣k﹣3或﹣4＝﹣k﹣3解得k＝﹣7（舍去）或k＝1．②若|4k﹣3|＞4时，则|4k﹣3|＝|﹣k﹣3|解得k＝2或k＝0（舍去）．根据“等距点”的定义知，k＝1或k＝2符合题意．即k的值是1或2．18．（延长）在平面直角坐标系中，O为坐标原点，过点A（8，6）分别作x轴、y轴的平行线，交y轴于点B，交x轴于点C，点P是从点B出发，沿B→A→C以2个单位长度/秒的速度向终点C运动的一个动点，运动时间为t（秒）．（1）直接写出点B和点C的坐标B（，）、C（，）；（2）当点P运动时，用含t的式子表示线段AP的长，并写出t的取值范围；（3）点D（2，0），连接PD、AD，在（2）条件下是否存在这样的t值，使S△APD＝S，若存在，请求出t值，若不存在，请说明理由．四边形ABOC【答案】（1）0、6，8、0 （2）AP＝8﹣2t（0≤t＜4）；AP＝2t﹣8（4≤t≤7）．（3）当t为3秒和5秒时S△APD＝S四边形ABOC【解答】解：（1）B（0，6），C（8，0），故答案为：0、6，8、0；（2）当点P在线段BA上时，由A（8，6），B（0，6），C（8，0）可得：AB＝8，AC＝6∵AP＝AB﹣BP，BP＝2t，∴AP＝8﹣2t（0≤t＜4）；当点P在线段AC上时，∵AP＝点P走过的路程﹣AB＝2t﹣8（4≤t≤7）．（3）存在两个符合条件的t值，当点P在线段BA上时∵S△APD＝AP•AC S四边形ABOC＝AB•AC∴（8﹣2t）×6＝×8×6，解得：t＝3＜4，当点P在线段AC上时，∵S△APD＝AP•CD CD＝8﹣2＝6∴（2t﹣8）×6＝×8×6，解得：t＝5＜7，综上所述：当t为3秒和5秒时S△APD＝S四边形ABOC，19．（齐齐哈尔）如图①，在平面直角坐标系中，点A、B在x轴上，AB⊥BC，AO＝OB＝2，BC＝3（1）写出点A、B、C的坐标．（2）如图②，过点B作BD∥AC交y轴于点D，求∠CAB+∠BDO的大小．（3）如图③，在图②中，作AE、DE分别平分∠CAB、∠ODB，求∠AED的度数．【答案】（1）A（﹣2，0），B（2，0），C（2，3）；（2）90°（3）45°【解答】解：（1）依题意得：A（﹣2，0），B（2，0），C（2，3）；（2）∵BD∥AC，∴∠ABD＝∠BAC，∴CAB+∠BDO＝∠ABD+∠BDO＝90°；（3）：∵BD∥AC，∴∠ABD＝∠BAC，∵AE，DE分别平分∠CAB，∠ODB，∴∠CAE+∠BDE＝（∠BAC+∠BDO）＝（∠ABD+∠BDO）＝×90°＝45°，过点E作EF∥AC，则∠CAE＝∠AEF，∠BDE＝∠DEF，∴∠AED＝∠AEF+∠DEF＝∠CAE+∠BDE＝45°．20．（随县）如图，在平面直角坐标系中，已知点A（0，2），B（4，0），C（4，3）三点．（1）求△ABC的面积；（2）如果在第二象限内有一点P（m，1），且四边形ABOP的面积是△ABC的面积的两倍；求满足条件的P点坐标．【答案】（1）6（2）P（﹣8，1）【解答】解：（1）∵B（4，0），C（4，3），∴BC＝3，∴S△ABC＝×3×4＝6；（2）∵A（0，2）（4，0），∴OA＝2，OB＝4，∴S四边形ABOP＝S△AOB+S△AOP＝×4×2+×2（﹣m）＝4﹣m，又∵S四边形ABOP＝2S△ABC＝12，∴4﹣m＝12，解得：m＝﹣8，∴P（﹣8，1）．。

初一下数学期末压轴题

期末复习解答压轴题专项训练1．（2022春·安徽滁州·七年级校考期末）已知点B，D分别在AK和CF上，且CF∥AK．（1）如图1，若∠CDE=25°，∠DEB=80°，则∠ABE的度数为________；（2）如图2，BG平分∠ABE，GB的延长线与∠EDF的平分线交于H点，若∠DEB比∠DHB大60°，求∠DEB的度数；（3）保持（2）中所求的∠DEB的度数不变，如图3，BM平分∠EBK，DN平分∠CDE，作BP∥DN，则∠PBM的度数是否改变？若不变，请求值；若改变，请说明理由．【思路点拨】（1）过点E作ES∥CF，根据CF∥AK，则ES∥CF∥AK，运用平行线的性质计算即可．（2）延长DE，交AB于点M，则∠DEB=∠EMB+∠EBM，利用平行线的性质，角平分线的定义，三角形外角的性质计算即可．（3）过点E作EQ∥DN，则EQ∥DN∥BP，利用前面的结论和方法，进行等量代换并推理计算即可．【解题过程】（1）解：如图1，过点E作ES∥CF，∵CF∥AK，∴ES∥CF∥AK，∴∠CDE=∠DES，∠SEB=∠ABE，∴∠CDE+∠ABE =∠DES+∠SEB=∠DEB，∵∠CDE=25°，∠DEB=80°，∴∠ABE =∠DEB-∠CDE=80°-25°=55°．故答案为：55°．（2）解：如图2，延长DE，交AB于点M，则∠DEB=∠EMB+∠EBM，∵CF∥AK，BG平分∠ABE，∴∠EMB=180°-∠MDF，∠EBM=2∠ABG=2∠HBN，∠MDH=∠HDF=∠HNK=1∠MDF，2∵∠HBN+∠DHB=∠HNK，∠MDF−∠DHB)，∴∠DEB=(180°-∠MDF) +2∠HBN=180°-∠MDF+2×(12∴∠DEB=180°-∠MDF+∠MDF-2∠DHB=180°-2∠DHB，∵∠DEB−∠DHB=60°，∴∠DEB=180°-2(∠DEB-60°)，∴3∠DEB=300°，解得∠DEB=100°．（3）解：过点E作EQ∥DN，则EQ∥DN∥BP，根据（1）得，∠DEB=∠CDE+∠ABE，∵BM平分∠EBK，DN平分∠CDE，∴∠DEB=2∠NDE+180°-2∠EBM，∵∠DEB=100°，∴∠EBM-∠NDE=40°，∵EQ∥DN，∴∠DEQ=∠NDE，∴∠EBM =40°+∠DEQ，∵EQ∥DN，DN∥BP，∴EQ∥BP，∴∠EBM+∠PBM +∠BEQ =180°，∴40°+∠DEQ+∠PBM +∠BEQ =180°，∴40°+∠DEB+∠PBM =180°，∴∠PBM =180°-100°-40°=40°，∴∠PBM 的度数不变，值为40°．2．（2022春·广西南宁·七年级统考期末）综合与实践：问题情境：如图1，AB∥CD，∠PAB=25°，∠PCD=37°，求∠APC的度数，小明的思路是：过点P作PE∥AB，通过平行线性质来求∠APC问题解决：（1）按小明的思路，易求得∠APC 的度数为°；问题迁移：如图2，AB∥CD，点P 在射线OM 上运动，记∠PAB=α，∠PCD=β．（2）当点P 在B，D 两点之间运动时，问∠APC 与α，β 之间有何数量关系？请说明理由；拓展延伸：（3）在（2）的条件下，如果点P 在B，D 两点外侧运动时（点P 与点O，B，D 三点不重合）请你直接写出当点P 在线段OB 上时，∠APC 与α，β 之间的数量关系，点P 在射线DM 上时，∠APC 与α，β 之间的数量关系．【思路点拨】（1）根据平行线的性质，得到∠APE=∠PAB=25°，∠CPE=∠PCD=37°，即可得到∠APC；（2）过P作PE∥AD交AC于E，推出AB∥PE∥DC，根据平行线的性质得出∠APE=α，∠CPE=β，即可得出答案；（3）分两种情况：P在BD延长线上；P在DB延长线上，分别画出图形，根据平行线的性质得出∠α=∠APE，∠β=∠CPE，即可得出答案；【解题过程】解：(1)如图1，过P作PE∥AB，∵AB∥CD，∴PE∥AB∥CD，∴∠APE=∠PAB=25°，∠CPE=∠PCD=37°，∴∠APC=25°+37°=62°；故答案为：62；(2)∠APC与α,β之间的数量关系是：∠APC=α+β；理由：如图，过点P作PE//AB交AC于点E，∵AB//CD，∴AB//PE//CD,∴α=∠APE,β=∠CPE,∴∠APC=∠APE+∠CPE=a+β；(3)如图3，所示，当P在射线DM上时，过P作PE∥AB，交AC于E，∵AB∥CD，∴AB∥PE∥CD，∴∠1=∠PAB=α，∵∠1=∠APC+∠PCD，∴∠APC=∠1−∠PCD，∴∠APC=α−β，∴当P在射线DM上时，∠APC=α−β；如图4所示，当P在线段OB上时，同理可得：∠APC=β−α，∴当P在线段OB上时，∠APC=β−α．故答案为：∠APC=β−α；∠APC=α−β.3．（2022春·江苏扬州·七年级统考期末）汛期即将来临，防汛指挥部在某水域一危险地带两岸各安置了一探照灯，便于夜间查看河水及两岸河堤的情况．如图，灯A射出的光束自AM顺时针旋转至AN便立即回转，灯B射出的光束自BP顺时针旋转至BQ便立即回转，两灯不停交叉照射巡视．若灯A射出的光束转动的速度是a°/秒，灯B射出的光束转动的速度是b°/秒，且a、b满足|a−3b|+(a+b−4)2=0．假定这一带水域两岸河堤是平行的，即PQ∥MN，且∠BAN=45°．(1)求a、b的值；(2)如图2，两灯同时转动，在灯A射出的光束到达AN之前，若两灯射出的光束交于点C，过C作CD⊥AC交PQ于点D，若∠BCD=20°，求∠BAC的度数；(3)若灯B射线先转动30秒，灯A射出的光束才开始转动，在灯B射出的光束到达BQ之前，A灯转动几秒，两灯的光束互相平行？【思路点拨】（1）根据|a−3b|+(a+b−4)2=0，可得a−3b=0，且a+b−4=0，进而得出a、b的值；（2）设灯A射线转动时间为t秒，根据∠BCD=90°﹣∠BCA=90°−(180°−2t)=2t−90°=20°可得t的值，根据∠BAC=45°−(180°−3t)=3t−135°可得∠BAC；（3）设A灯转动t秒，两灯的光束互相平行，分两种情况进行讨论：①在灯A射线转到AN之前，②在灯A 射线转到AN之后，分别求得t的值即可．【解题过程】（1）∵|a−3b|+(a+b−4)2=0．又∵|a﹣3b|≥0，(a+b−4)2≥0．∴a=3，b=1；（2）设A灯转动时间为t秒，如图，作CE//PQ，而PQ//MN,∴PQ//CE//MN,∴∠ACE=∠CAN=180°−3t°，∠BCE=∠CBD=t°，∴∠BCA=∠CBD+∠CAN=t+180°−3t=180°−2t，∵∠ACD=90°，∴∠BCD=90°﹣∠BCA=90°−(180°−2t)=2t−90°=20°，∴t=55°，∵∠CAN=180°−3t，∴∠BAC=45°−(180°−3t)=3t−135°=165°−135°=30°；（3）设A灯转动t秒，两灯的光束互相平行．依题意得0<t<150①当0<t<60时，3t=(30+t)×1，解得t=15；②当60<t<120时，3t−3×60+(30+t)×1=180，解得t=82.5；③当120<t<150时，3t−360=t+30，解得t=195>150(不合题意)综上所述，当t=15秒或82.5秒时，两灯的光束互相平行．4．（2022春·湖南永州·七年级统考期末）如图，直线AB∥CD，直线EF与AB、CD分别交于点G、H，∠EHD=α(0°<α<90°)．小安将一个含30°角的直角三角板PMN按如图①放置，使点N、M分别在直线AB、CD上，且在点G、H的右侧，∠P=90°，∠PMN=60°．(1)填空：∠PNB+∠PMD∠P（填“>”“<”或“=”）；(2)若∠MNG的平分线NO交直线CD于点O，如图②．①当ON∥EF，PM∥EF时，求α的度数；②当PM∥EF时，求∠MON的度数（用含α的式子表示）．【思路点拨】（1）过P点作PQ∥AB，根据平行线的性质可得∠PNB=∠NPQ，∠PMD=∠QPM，进而可求解；（2）①由平行线的性质可得∠ONM=∠PMN=60°，结合角平分线的定义可得∠ANO=∠ONM=60°，再利用平行线的性质可求解；②可分两种情况：点N在G的右侧时，点N在G的左侧时，利用平行线的性质及角平分线的定义计算可求解．【解题过程】（1）解：过P点作PQ∥AB，∴∠PNB=∠NPQ，∵AB∥CD，∴PQ∥CD，∴∠PMD=∠QPM，∴∠PNB+∠PMD=∠NPQ+∠QPM=∠MPN，故答案为：=（2）①∵ON∥EF，PM∥EF，∴PO∥PM，∴∠ONM=∠NMP，∵∠PMN=60°，∴∠ONM=∠PMN=60°，∵NO平分∠MNO，∴∠ANO=∠ONM=60°，∵AB∥CD，∴∠NOM=∠ANO=60°，∴α=∠NOM=60°；②点N在G的右侧时，如图②，∵PM∥EF，∠EHD=α，∴∠PMD=α，∴∠NMD=60°+α，∵AB∥CD，∴∠ANM=∠NMD=60°+α，∵NO平分∠ANM，∴∠ANO=12∠ANM=30°+12α，∵AB∥CD，∴∠MON=∠ANO=30°+12α；点N在G的左侧时，如图，∵PM∥EF，∠EHD=α，∴∠PMD=α，∴∠NMD=60°+α，∵AB∥CD，∴∠BNM+∠NMO=180°，∠BNO=∠MON，∵NO平分∠MNG，∴∠BNO=12[180°−(60°+α)]=60°−12α，∴∠MON=60°−12α，综上所述，∠MON的度数为30°+12α或60°−12α．5．（2022秋·重庆沙坪坝·七年级统考期末）已知：如图，直线a∥b，AC⊥BC于点C，连接AB且分别交直线a、b于点E、F．（1）如图①，若∠DEF和∠EFG的角平分线EM、FM交于点M，请求∠M的度数；（2）如图②，若∠EDC的角平分线DM分别和直线b及∠FGC的角平分线GQ的反向延长线交于点N和点M，试说明：∠1+∠2=135°；(3)如图③，点M为直线a上一点，连结MF，∠MFE的角平分线FN交直线a于点N，过点N作NQ⊥NF交∠HFM 的角平分线FQ于点Q，若∠DEA记为β，请直接用含β的代数式来表示∠MNQ+∠HFQ．【思路点拨】（1）由平行线的性质及角平分线的定义可得∠DEF+∠GFE=180°，∠DEM=12∠DEF；∠GFM=12∠GFE，即∠DEM+∠GFM=12(∠DEF+∠GFE)=90°，过点M作直线l∥a交AB于点H，可得∠HME=∠DEM,∠HMF=∠GFM，进而可得∠EMF=∠HME+∠HMF=∠DEM+∠GFM=90°．（2）过点C作直线l∥a，由平行线的性质可得∠FGC+∠4=180°,∠EDC+∠5=180°，由题意得∠4+∠5=90°，可得∠FGC+∠FGC=270°，由角平分线的定义可得∠6+∠7=12(∠FGC+∠FGC)=135°，由a∥b得∠6=∠3=∠2，由对顶角相等可得∠7=∠1，可得∠1+∠2=135°；（3）由题意可知∠MEF=∠DEA=β，根据平行线的性质及角平分线的定义可得∠HFE=180°−β，∠EFN=∠MFN=12∠MFE=x，∠HFQ=∠MFQ=12∠HFM=y，，进而可得x+y=180°−β2，由a∥b，NQ⊥NF∠HFN+∠MNF=180°，∠QNF=90°，即∠MNQ+∠QNF+∠MFN+∠MFQ+∠HFQ=180°，可得∠MNQ= 90°−x−2y，进而可求∠MNQ+∠HFQ．【解题过程】（1）∵a∥b，∴∠DEF+∠GFE=180°．∵EM、FM分别平分∠DEF和∠GFE，∴∠DEM=12∠DEF；∠GFM=12∠GFE，∴∠DEM+∠GFM=12(∠DEF+∠GFE)=90°，过点M作直线l∥a交AB于点H，∵a∥b，∴l∥b，∴∠HME=∠DEM,∠HMF=∠GFM，∴∠EMF=∠HME+∠HMF=∠DEM+∠GFM=90°．（2）过点C作直线l∥a，∵a∥b，∴l∥b，∴∠FGC+∠4=180°,∠EDC+∠5=180°.又∵∠4+∠5=90°∴∠FGC+∠FGC=270°又∵GQ、DM分别平分∠FGC和∠EDC，∴∠6+∠7=12(∠FGC+∠FGC)=135°∵a∥b，∴∠6=∠3=∠2又∵∠7=∠1∴∠1+∠2=135°．（3）∠MNQ +∠HFQ =β2．理由如下：由题意可知∠MEF =∠DEA =β， ∵a ∥b ，∴∠MEF +∠HBE =180°，即∠HFE =180°−β， ∵FN 平分∠MFE ，FQ 平分∠HFM ，∴∠EFN =∠MFN =12∠MFE =x ，∠HFQ =∠MFQ =12∠HFM =y ，∴∠HFE =180°−β=2(∠EFN +∠MFQ )=2(x +y )，即x +y =180°−β2，∵a ∥b ，NQ ⊥NF∴∠HFN +∠MNF =180°，∠QNF =90°，则∠MNQ +∠QNF +∠MFN +∠MFQ +∠HFQ =180°， ∴∠MNQ =90°−x −y −y =90°−x −2y ，∴∠MNQ +∠HFQ =90°−x −2y +y =90°−x −y =90°−180°−β2=β2．6．（2022秋·四川宜宾·七年级统考期末）几何模型在解题中有着重要作用，例如美味的“猪蹄模型”．（1）导入：如图①，已知AB∥CD∥EF ，如果∠A =26°，∠C =34°，那么 ∠AEC = °；（1）发现：如图②，已知AB∥CD，请判断∠AEC与∠A，∠C之间的数量关系，并说明理由；（3）运用：(i)如图③，已知AB∥CD，∠AEC=88°，点M、N分别在AB、CD上，MN∥AE，如果∠C=28°，那么∠MND=°；(ii)如图④，已知AB∥CD，点M、N分别在AB、CD上，ME、NE分别平分∠AMF和∠CNF．如果∠E=116°，那么∠F=°；(iii)如图⑤，已知AB∥CD，点M、N分别在AB、CD上，MF、NG分别平分∠BME和∠CNE，且EG∥MF．如果∠MEN=α，那么∠EGN=．(用含α的代数式表示)【思路点拨】（1）根据平行线的性质得出∠A=∠AEF,∠C=∠FEC，进而根据∠AEC=∠AEF+∠CEF，即可求解；（2）过点E作EF∥AB，根据（1）的方法即可求解；（3）（i）由（2）可得∠AEC=∠A+∠C=88°，∠C=28°，得出∠A=60°，根据∠MND=180°−∠BMN，即可求解；（ii）由“猪蹄模型”，可得∠E=∠AME+∠CNE=116°，∠F=∠BMF+∠DNF，根据角平分线的性质得出∠AME=12∠AMF,∠CNE=12∠CNF，继而根据∠F=∠BMF+∠DNF=128°，即可求解；（iii）如图所示，延长GE交AB于点H，设∠ENG=β，∠HME−θ，根据平行线的性质得出∠MHE=∠BMF=180−θ2=90°−θ2，α=θ+2β，根据∠EGN=∠GNC+∠AHE=∠GNC+∠AMF，即可得出结论．【解题过程】（1）解：如图1，∵AB∥CD∥EF∴∠A=∠AEF,∠C=∠FEC∵∠A=26°，∠C=34°，∴∠AEC=∠AEF+∠CEF=∠A+∠B=26°+34°=60°∴∠AEC=60°故答案为：60．（2）∠AEC=∠A+∠C,如图所示，过点E作EF∥AB，∵EF∥AB，∴∠A=∠AEF，∵EF∥AB，AB∥CD，∴EF∥CD，∴∠FEC=∠C，∴∠AEC=∠AEF+∠FEC=∠A+∠C；（3）解：（i）由（2）可得∠AEC=∠A+∠C=88°，∠C=28°，∴∠A=60°，∵MN∥AE，∴∠BMN=∠A=60°，∵AB∥CD，∴∠MND=180°−∠BMN=180°−60°=120°，故答案为：120．（ii）解：如图所示，∵AB∥CD由“猪蹄模型”，可得∠E=∠AME+∠CNE=116°，∠F=∠BMF+∠DNF；∵ME、NE分别平分∠AMF和∠CNF∴∠AME=12∠AMF,∠CNE=12∠CNF∴∠AMF+∠CNF=116°×2=232°∴∠MBF+∠DNF=360°−232°=128°，∴∠F=∠BMF+∠DNF=128°,故答案为：128．（iii ）解：如图所示，延长GE 交AB 于点H ，设∠ENG =β，∠HME −θ∵MF 、NG 分别平分∠BME 和∠CNE ，∴∠BMF =12∠BME =12(180°−θ)=90°−θ2,∠CNE =2∠ENG =2β，∵HG∥MF∴∠MHE =∠BMF =180−θ2=90°−θ2，∵AB∥CD∴∠MEN =∠AME +∠CNE ，∴α=θ+2β∴∠EGN =∠GNC +∠AHE =∠GNC +∠AMF =β+θ+90°−θ2=β+90°+θ2=90°+α2．7．（2022秋·海南海口·七年级校考期末）点E 在射线DA 上，点F 、G 为射线BC 上两个动点，满足∠DBF =∠DEF ，∠BDG =∠BGD ，DG 平分∠BDE ．(1)如图1，当点G在点F右侧时，①试说明：BD∥EF；②试说明∠DGE=∠BDG−∠FEG；(2)如图2，当点G在点F左侧时，（1）中的结论②是否成立，若不成立，请写出正确结论；（不用说理）(3)如图3，在（2）的条件下，P为BD延长线上一点，DM平分∠BDG，交BC于点M，DN平分∠PDM，交EF于点N，连接NG，若DG⊥NG，∠B−∠DNG=∠EDN，求∠B的度数．【思路点拨】（1）①根据角平分线的定义即可得到∠BDG＝∠ADG，从而可得∠ADG＝∠DGB，则AB∥BC，可得∠DEF ＝∠EFG，即可得到∠DBF＝∠EFG，从而证明BD∥EF；②过点G作GH∥DB交DA于点H，根据平行线的性质求解即可；（2）过点G作GK∥DB交AD于K，则KG∥EF，可得∠BDG＝∠DGK，∠GEF＝∠KGE，即可得到∠DGE ＝∠BDG＋∠FEG；（3）设∠BDM=∠MDG=α，则∠BDG=∠EDG=∠DGB=2α∠PDE=180∘−4α，∠PDM=180°−α，由角平分线的定义可得∠PDN=∠MDN=12∠PDM=90∘−α2，然后分别求出∠EDN=72α−90∘，∠DNG=32α，∠B−∠DNG=∠EDN进行求解即可．【解题过程】（1）证明：①∵DG平分∠BDE，∴∠BDG＝∠ADG，又∵∠BDG＝∠BGD，∴∠ADG＝∠DGB，∴AD∥BC，∴∠DEF＝∠EFG，∵∠DBF＝∠DEF，∴∠DBF＝∠EFG，∴BD∥EF；②过点G作GH∥DB交DA于点H，由①得BD∥EF，∴GH∥DB∥EF，∴∠BDG＝∠DGH，∠FEG＝∠EGH，∴∠DGE＝∠DGH-∠EGH，∴∠DGE=∠BDG-∠FEG；（2）解：过点G作GK∥DB交AD于K，同理可证BD∥EF，∴KG∥EF，∴∠BDG＝∠DGK，∠GEF＝∠KGE，∴∠DGE＝∠DGK＋∠KGE，∴∠DGE＝∠BDG＋∠FEG；（3）解：设∠BDM=∠MDG=α，则∠BDG=∠EDG=∠DGB=2α，∠PDE=180∘−∠BDE=180∘−4α，∠PDM=180°−α，∵DN平分∠PDM，∴∠PDN=∠MDN=12∠PDM=90∘−α2，∴∠EDN=∠PDN−∠PDE=90∘−α2−(180∘−4α)=72α−90∘，∠GDN=∠MDN−∠MOG=90∘−α2−α=90∘−32α，∵DG⊥NG，∴∠DGN=90∘，∴∠DNG=90∘−∠GDN=90∘−(90∘−32α)=32α，∵DE∥BF，∴∠B=∠PDE=180∘−4α，∵∠B−∠DNG=∠EDN，∴180∘−4α−32α=72α−90∘，∴α=30∘，∴∠B=180∘−4α=60∘．8．（2022春·湖北武汉·七年级统考期末）直线AB∥CE，BE—EC是一条折线段，BP平分∠ABE．(1)如图1，若BP∥CE，求证：∠BEC+∠DCE=180°；(2)CQ平分∠DCE，直线BP，CQ交于点F．①如图2，写出∠BEC和∠BFC的数量关系，并证明；②当点E在直线AB，CD之间时，若∠BEC=40°，直接写出∠BFC的大小．【思路点拨】（1）延长DC交BE于K，交BP于T，由AB∥CD，BP平分∠ABE，可得∠BTK=∠TBK，又BP∥CE，故∠KCE=∠KEC，即可得∠BEC+∠DCE=180°；（2）①延长AB交FQ于M，延长DC交BE于N，设∠ABP=∠EBP=α，∠DCQ=∠ECQ=β，可得∠F=180°-∠FBM-∠FMB=180°-（α+β），∠E=180°-∠NCE-∠CNE=180°-（180°-2β）-（180°-2α）=2（α+β）-180°，故∠E+2∠F=180°；②由∠E+2∠F=180°，即可得∠F=70°．【解题过程】（1）解：证明：延长DC交BE于K，交BP于T，如图：∵AB∥CD，∴∠ABT=∠BTK，∵BP平分∠ABE，∴∠ABT=∠TBK，∴∠BTK=∠TBK，∵BP∥CE，∴∠BTK=∠KCE，∠TBK=∠KEC，∴∠KCE=∠KEC，∵∠KCE+∠DCE=180°，∴∠KEC+∠DCE=180°，即∠BEC+∠DCE=180°；（2）①∠E+2∠F=180°，证明如下：延长AB交FQ于M，延长DC交BE于N，如图：∵射线BP、CQ分别平分∠ABE，∠DCE，∴∠ABP=∠EBP，∠DCQ=∠ECQ，设∠ABP=∠EBP=α，∠DCQ=∠ECQ=β，∴∠FBM=∠ABP=α，∠MBE=180°-2α，∠NCE=180°-2β，∠FCN=∠DCQ=β，∵AB∥DC，∴∠CNE=∠MBE=180°-2α，∴∠F=180°-∠FBM-∠FMB=180°-（α+β），∠E=180°-∠NCE-∠CNE=180°-（180°-2β）-（180°-2α）=2（α+β）-180°，∴∠E+180°=2（180°-∠F），∴∠E+2∠F=180°；②由①知∠E+2∠F=180°，∵∠BEC=40°，∴∠F=70°．9．（2022春·山东德州·七年级统考期末）如图1，AD∥BC，∠BAD的平分线交BC于点G，∠BCD=90°．(1)试说明：∠BAG=∠BGA；(2)如图2，点F在AG的反向延长线上，连接CF交AD于点E，若∠BAG−∠F=45°，求证：CF平分∠BCD；(3)如图3，线段AG上有点P，满足∠ABP=3∠PBG，过点C作CH∥AG.若在直线AG上取一点M，使∠PBM=的值．∠DCH，求∠ABM∠GBM【思路点拨】（1）先根据平行线的性质可得∠GAD=∠BGA，再根据角平分线的定义可得∠BAG=∠GAD，然后根据等量代换即可得证；（2）过点F作FM∥BC于M，先根据平行线的性质可得∠BGA=∠MFG,∠BCF=∠MFC，从而可得∠BAG−∠GFC=∠MFC，则∠BCF=∠MFC=45°，再根据角平分线的定义即可得证；（3）设∠ABC=4x(x>0)，则∠ABP=3x，∠PBG=x，先根据平行线的性质可得∠BAD=180°−4x，从而可得∠BGA=90°−2x，再根据平行线的性质可得∠BCH=∠BGA=90°−2x，从而可得∠PBM=∠DCH= 2x，然后分①点M在BP的下方和②点M在BP的上方两种情况，根据角的和差可得∠ABM和∠GBM的值，由此即可得．【解题过程】（1）证明：∵AD∥BC，∴∠GAD=∠BGA，∵AG平分∠BAD，∴∠BAG=∠GAD，∴∠BAG=∠BGA．（2）证明：如图，过点F作FM∥BC于M，∴∠BGA=∠MFG,∠BCF=∠MFC，由（1）已证：∠BAG=∠BGA，∴∠BAG=∠MFG=∠MFC+∠GFC，即∠BAG−∠GFC=∠MFC，又∵∠BAG−∠GFC=45°，∴∠MFC=45°，∴∠BCF=45°，又∵∠BCD=90°，∴CF平分∠BCD．（3）解：设∠ABC=4x(x>0)，∵∠ABP=3∠PBG，∴∠ABP=3x，∠PBG=x，∵AD∥BC，∴∠BAD=180°−∠ABC=180°−4x，由（1）已得：∠BGA=∠BAG=12∠BAD=90°−2x，∵AG∥CH，∴∠BCH=∠BGA=90°−2x，∵∠BCD=90°，∴∠PBM=∠DCH=90°−(90°−2x)=2x，由题意，分以下两种情况：①如图，当点M在BP的下方时，∴∠ABM=∠ABP+∠PBM=3x+2x=5x，∠GBM=∠PBM−∠PBG=2x−x=x，∴∠ABM∠GBM =5xx=5；②如图，当点M在BP的上方时，∴∠ABM=∠ABP−∠PBM=3x−2x=x，∠GBM=∠PBM+∠PBG=2x+x=3x，∴∠ABM∠GBM =x3x=13；综上，∠ABM∠GBM 的值是5或13．10．（2022春·河南安阳·七年级统考期末）猜想说理：（1）如图，AB∥CD∥EF，分别就图1、图2、图3写出∠A，∠C，∠AFC的关系，并任选其中一个图形说明理由：拓展应用：（2）如图4，若AB∥CD，则∠A+∠C+∠AFC=度；（3）在图5中，若A1B∥A n D，请你用含n的代数式表示∠1+∠2+∠3+∠4+⋯+∠n的度数．【思路点拨】（1）根据平行线的性质可直接得到结论；（2）过点F作AB的平行线，利用平行线的性质，计算出∠A＋∠C＋∠AFC的度数；（3）过点E作AB的平行线，过点F作AB的平行线，利用平行线的性质，计算出∠A＋∠AEF＋∠EFC＋∠C度数；通过前面的计算，找出规律．利用规律得到有n个折点的结论；【解题过程】解：（1）如图1：∠A＋∠C＝∠AFC，如图2：∠A−∠C＝∠AFC，如图3：∠C−∠A＝∠AFC，如图1说明理由如下：∵AB∥CD∥EF，∴∠A＝∠AFE，∠C＝∠EFC，∴∠A＋∠C＝∠AFE＋∠EFC，即∠A＋∠C＝∠AFC；（2）如下图：过F作FH∥AB，∴∠A＋∠AFH＝180°，又∵AB∥CD，∴CD∥FH，∴∠C＋∠CFH＝180°，∴∠A＋∠AFH＋∠C＋∠CFH＝360°，即∠A＋∠C＋∠AFC＝360°；故答案为：360；（3）如下图：AB∥CD，过E作EG∥AB，过F作FH∥AB，∵AB∥CD，∴AB∥EG∥FH∥CD，∴∠A＋∠AEG＝180°，∠GEF＋∠EFH＝180°，∠HFC＋∠C＝180°，∴∠A＋∠AEG＋∠GEF＋∠EFH＋∠HFC＋∠C＝180°×3，即∠A＋∠AEF＋∠EFC＋∠C＝540°；综上所述：由当平行线AB与CD间没有点的时候，∠A＋∠C＝180°，当A、C之间加一个折点F时，∠A＋∠AFC＋∠C＝2×180°；当A、C之间加二个折点E、F时，则∠A＋∠AEF＋∠EFC＋∠C＝3×180°；以此类推，如图5，A1B∥A n D，当A1、A5之间加三个折点A2、A3、A4时，则∠A1+∠A2＋∠A3＋∠A4＋∠A5＝4×180°；…当A1、A n之间加n个折点A2、A3、…A n−1时，则∠A1＋∠A2＋∠A3＋…∠A n＝（n-1）×180°，即∠1＋∠2＋∠3＋∠4＋⋯＋∠n的度数是（n-1）×180°．11．（2022春·黑龙江·七年级统考期末）点E在射线DA上，点F、G为射线BC上两个动点，满足∠DBF=∠DEF，∠BDG=∠BGD，DG平分∠BDE．(1)如图1，当点G在F右侧时，求证：BD//EF；(2)如图2，当点G在F左侧时，求证：∠DGE=∠BDG+∠FEG；(3)如图3，在(2)的条件下，P为BD延长线上一点，DM平分∠BDG，交BC于点M，DN平分∠PDM，交EF于点N，连接NG，若DG⊥NG，∠DBF−∠DNG=∠EDN，则∠DBF的度数是多少．【思路点拨】（1）通过证明∠DBF=∠EFG，利用同位角相等，两直线平行即可得出结论；（2）过点E作GH∥BD，交AD于点H，利用（1）的结论和平行线的性质即可得出结论；（3）设∠BDM=∠MDG=α，则∠BDG=∠EDG=∠DGB=2α，∠PDE=180°-4α，∠PDM=180°-α；利用已知条件用含α的式子表示∠PDN，∠EDN，∠GDN，∠DNG，再利用∠DBF-∠DNG=∠EDN，得到关于α的方程，解方程求得α的值，则∠B=180°-4α，结论可求．【解题过程】（1）证明：∵DG平分∠BDE，∴∠BDG=∠ADG，又∵∠BDG=∠BGD，∴∠ADG=∠DGB，∴AD//BC，∴∠DEF=∠EFG，∵∠DBF=∠DEF，∴∠DBF=∠EFG，∴BD//EF；（2）证明：过点G作GH//BD，交AD于点H，如图，由（1）可知：BD//EF，∴GH//EF，∴∠BDG=∠DGH，∠GEF=∠HGE，∵∠DGE=∠DGH+∠HGE，∴∠DGE=∠BDG+∠FEG；（3）解：设∠BDM=∠MDG=α，则∠BDG=∠EDG=∠DGB=2α，∠PDE=180°−4α，∴∠PDM=180°−α，∵DN平分∠PDM，∴∠PDN=∠MDN=90°−12α，∴∠EDN=∠PDN−∠PDE=90°−12α−(180°−4α)=72α−90°，∴∠GDN =∠MDN −∠MDG =90°−12α−α=90°−32α， ∵DG ⊥ON ，∴∠DNG =90°，∴∠DNG =90°−(90°−32α)=32α，∵DE//BF ，∴∠DBF =∠PDE =180°−4α，∵∠DBF −∠DNG =∠EDN ，∴180°−4α−32α=72α−90°，解得：α=30°，∴∠DBF =180°−4α=60°．12．（2022春·河北衡水·七年级校考期末）【发现】如图1，CE 平分∠ACD ，AE 平分∠BAC ．(1)当∠EAC ＝∠ACE ＝45°时，AB 与CD 的位置关系是______；当∠EAC ＝50°，∠ACE ＝40°时，AB 与CD 的位置关系是______；当∠EAC +∠ACE ＝90°，请判断AB 与CD 的位置关系并说明理由；(2)【探究】如图2，AB ∥CD ，M 是AE 上一点，∠AEC ＝90°保持不变，移动顶点E ，使CE 平分∠MCD ，∠BAE 与∠MCD 存在怎样的数量关系？并说明理由，(3)【拓展】如图3，AB ∥CD ，P 为线段AC 上一定点，Q 为直线CD 上一动点，且点Q 不与点C 重合．直接写出∠CPQ +∠CQP 与∠BAC 的数量关系．【思路点拨】（1）由角平分线的定义得∠BAC＝2∠EAC，∠ACD＝2∠ACE，则∠BAC+∠ACD＝180°，可得结论AB∥CD；（2）过点E作EF∥AB，利用平行线的性质可得答案；（3）利用平行线的性质和三角形内角和定理可得答案．【解题过程】（1）解：当∠EAC＝∠ACE＝45°时，AB∥CD，理由如下：∵CE平分∠ACD，AE平分∠BAC，∴∠BAC＝2∠EAC，∠ACD＝2∠ACE，∵∠EAC＝∠ACE＝45°，∴∠BAC＝∠ACD＝90°，∴∠BAC+∠ACD＝180°，∴AB∥CD，故答案为：AB∥CD；当∠EAC＝50°，∠ACE＝40°时，AB∥CD，理由如下：∵CE平分∠ACD，AE平分∠BAC，∴∠BAC＝2∠EAC，∠ACD＝2∠ACE，∵∠EAC＝50°，∠ACE＝40°∴∠BAC＝100°，∠ACD＝80°，∴∠BAC+∠ACD＝180°，∴AB∥CD，故答案为：AB∥CD；当∠EAC+∠ACE＝90°，AB∥CD，理由如下：∵CE平分∠ACD，AE平分∠BAC，∴∠BAC＝2∠EAC，∠ACD＝2∠ACE，∵∠EAC+∠ACE＝90°，∴∠BAC+∠ACD＝180°，∴AB∥CD；∠MCD＝90°，理由如下：（2）解：∠BAE+12过点E作EF∥AB，如图所示，∵AB∥CD，∴EF∥AB∥CD，∴∠BAE＝∠AEF，∠FEC＝∠DCE，∵∠AEC＝90°，∴∠AEF+∠FEC＝∠BAE+∠ECD＝90°，∵CE平分∠MCD，∴∠ECD＝1∠MCD，2∠MCD＝90°；∴∠BAE+12（3）解：分两种情况分类讨论，第一种情况如图，当点Q在射线CD上运动时，∠BAC＝∠PQC+∠QPC，理由：过点P作PE∥AB，∵AB∥CD，∴EP∥AB∥CD，∴∠BAC＝∠EPC，∠PQC＝∠EPQ，∵∠EPC＝∠EPQ+∠QPC∴∠BAC＝∠PQC+∠QPC；第二种情况如图，当点Q在射线CD的反向延长线上运动时（点C除外）∠PQC+∠QPC+∠BAC＝180°，理由：∵AB∥CD，∴∠BAC＝∠PCQ，∵∠PQC+∠QPC +∠PCQ＝180°，∴∠PQC+∠QPC+∠BAC＝180°，综上，∠BAC＝∠PQC+∠QPC或∠PQC+∠QPC+∠BAC＝180°．13．（2022春·广东深圳·七年级深圳大学附属中学校考期末）（1）如图1，点E在BC上，∠A＝∠D，∠ACB ＝∠CED．请说明AB∥CD的理由．（2）如图2，AB∥CD，BG平分∠ABE，与∠EDF的平分线交于H点，若∠DEB比∠DHB大60°．求∠DEB 的度数．（3）保持（2）中所求的∠DEB的度数不变，如图3，AB∥CD，BM平分∠EBK，DN平分∠CDE，作BP∥DN，则∠PBM的度数是否改变？若不变，请直接写出∠PBM的度数；若改变，请说明理由．【思路点拨】（1）由∠ACB=∠CED，得AC∥DF，可得∠A=∠DFB，又∠A=∠D，进而可得结论；（2）如图2，作EM∥CD，HN∥CD，根据AB∥CD，可得AB∥EM∥HN∥CD，根据平行线的性质得角之间的关系，再根据∠DEB比∠DHB大60°，列出等式即可求∠DEB的度数；（3）如图3，过点E作ES∥CD，设直线DF和直线BP相交于点G，根据平行线的性质和角平分线定义可求∠PBM的度数．【解题过程】（1）∵∠ACB=∠CED，∴AC∥DF，∵∠A =∠D ， ∴∠DFB =∠D ， ∴AB ∥CD ；（2）如图2，作EM ∥CD ，HN ∥CD ，∵AB ∥CD ，∴AB ∥EM ∥HN ∥CD ，∴∠1+∠EDF =180°，∠MEB =∠ABE ， ∵BG 平分∠ABE ， ∴∠ABG =12∠ABE ，∵AB ∥HN ， ∴∠2=∠ABG ， ∵CF ∥HN ， ∴∠2+∠β=∠3， ∴12∠ABE +∠β=∠3， ∵DH 平分∠EDF ， ∴∠3=12∠EDF ， ∴12∠ABE +∠β=12∠EDF ，∴∠β=12（∠EDF -∠ABE ），∴∠EDF -∠ABE =2∠β，设∠DEB =∠α，∵∠α=∠1+∠MEB =180°-∠EDF +∠ABE =180°-（∠EDF -∠ABE ）=180°-2∠β， ∵∠DEB 比∠DHB 大60°，∴∠α=180°-2（∠α-60°）解得∠α=100°∴∠DEB 的度数为100°；（3）∠PBM 的度数不变，理由如下：如图3，过点E 作ES ∥CD ，设直线DF 和直线BP 相交于点G ，∵BM 平分∠EBK ，DN 平分∠CDE ， ∴∠EBM =∠MBK =12∠EBK ， ∠CDN =∠EDN =12∠CDE ，∵ES ∥CD ，AB ∥CD ， ∴ES ∥AB ∥CD ，∴∠DES =∠CDE ，∠BES =∠ABE =180°-∠EBK ，∠G =∠PBK ，由（2）可知：∠DEB =100°， ∴∠CDE +180°-∠EBK =100°， ∴∠EBK -∠CDE =80°， ∵BP ∥DN ， ∴∠CDN =∠G ，∴∠PBK =∠G =∠CDN =12∠CDE ，∴∠PBM =∠MBK -∠PBK =12∠EBK -12∠CDE =12（∠EBK -∠CDE ）=12×80°=40°．14．（2022春·浙江宁波·七年级校联考期末）如图①，AB ，BC 被直线AC 所截，点D 是线段AC 上的点，过点D 作DE ∥AB ，连接AE ，∠B =∠E =60°.(1)请说明AE∥BC；(2)将线段AE沿着直线．．AC平移得到线段PQ，连接DQ．①.如图②，当DE⊥DQ时，则∠Q的度数=_____________；②.在整个运动中，当∠Q=2∠EDQ时，∠Q=_____________．【思路点拨】（1）根据平行线的性质得到∠BAE+∠E=180°，利用等量代换得到∠BAE+∠B=180°，即可证出AE∥BC；（2）①过点D作DM∥PQ，则DM∥AE，根据平行线的性质即可得到答案；②两种情况，运用类比的方法，当点P在线段AD上时，过点D作DF∥AE交AB于点F，根据平行线的性质即可得到答案；当点P在线段DA的延长线上时，过点D作DF′∥AE交AB于点F′，根据平行线的性质即可得到答案．【解题过程】（1）证明：∵DE∥AB，∴∠BAE+∠E=180°，又∵∠B=∠E，∴∠BAE+∠B=180°，∴AE∥BC．（2）解：①解：过点D作DM∥PQ，如图所示：∵AE∥PQ，∴DM∥AE，∴∠E=∠EDM，∠Q=∠MDQ，∵DE⊥DQ，∴∠EDQ=90°，∴∠E+∠Q=∠EDM+∠MDQ=90°，而∠E=60°，∴∠Q=90°−60°=30°．故答案为：30°．②当点P在线段AD上时，过点D作DF∥AE交AB于点F，如图所示：∵PQ∥AE，∴DF∥PQ，∴∠QDF=180°−∠Q，∵∠Q=2∠EDQ，∴∠EDQ=1∠Q，2∵∠E=60°，∴∠EDF=180°−60°=120°，∠Q=180°−∠Q，∴∠QDF=120°+12∴∠Q=40°；当点P在线段DA的延长线上时，过点D作DF′∥AE交AB于点F′，如图所示：∵PQ∥AE，∴DF′∥PQ，∴∠QDF′=180°−∠Q，∵∠Q=2∠EDQ，∠Q，∴∠EDQ=12∵∠E=60°，∴∠EDF′=180°−60°=120°，∴180°−∠Q+1∠Q=120°，2∴∠Q=120°；综上所述：∠Q的度数为40°或120°．故答案为：40°或120°．15．（2022春·重庆·七年级西南大学附中校考期末）对于各位数字均不为零的三位自然数m=abc，若m满足各位数字之和能被十位数字整除，则称m为“对偶数”．例如m=327，∵3+2+7=12，12÷2=6，∴327是“对偶数”；又如n=136，∵1+3+6=10，10不能被3整除，∴136不是“对偶数”．将m的百位数字放在其个位数字后得m1=bca，再将m1的百位数字放在其个位数字后得m2=cab．记F(m)=m+m1+m2．111(1)判断248，933是否是“对偶数”，并说明理由；(2)已知“对偶数”n=100a+10b+4（其中1≤a+b≤9），若18F(n)+2(a−4)能被7整除，求出所有满足条件的n．【思路点拨】（1）根据“对偶数”的定义直接判断即可；（2）先表示出F(n)，进而得出F(n)=a+b+4，即可得出18F(n)+2(a−4)=7(2a+2b+9)+6a+4b+ 1，进而得出(6a+4b+1)是7的倍数，可推导6a+4b+1=21或35或49，最后分类讨论即可求出答案．【解题过程】（1）解：248不是“对偶数”，933是“对偶数”，理由如下：∵对于248，2+4+8=14，14不能被4整除，∴248不是“对偶数”，∵对于933，9+3+3=15，15能被3整除，∴933是“对偶数”；（2）∵n=100a+10b+4，∴n1=b4a=100b+40+a，n2=4ab=400+10a+b，∴F(n)=n+n1+n2111=100a+10b+4+100b+40+a+400+10a+b111=a+b+4，∴18F(n)+2(a−4)=18(a+b+4)+2(a−4)=20a+18b+64=7(2a+2b+9)+6a+4b+1，∵18F(n)+2(a−4)能被7整除，∴(6a+4b+1)是7的倍数，∵1≤a+b≤9，且a、b为整数，∴1≤a≤8，1≤b≤8，∴11≤6a+4b+1≤53，∴6a+4b+1=14或21或28或35或42或49，∵6a+4b=2(3a+2b)，即为偶数，∴6a+4b+1是奇数，∴6a+4b+1=21或35或49，①当6a+4b+1=21时，b=5−32a，∵a、b为整数，∴a=2，b=2，∴n=224，∵2+2+4=8，8能被2整除，∴224是“对偶数”，符合题意；②当6a+4b+1=35时，b=17−3a2，∵a、b为整数，∴a=1，b=7或a=3，b=4或a=5，b=1，当a=1，b=7时，n=174，1+7+4=12，12不能被7整除，故174不是“对偶数”，不符合题意；当a=3，b=4时，n=344，3+4+4=11，11不能被4整除，故344不是“对偶数”，不符合题意；当a=5，b=1时，n=514，5+1+4=10，10能被1整除，故514是“对偶数”，符合题意；③当6a+4b+1=49时，b=12−3a，2∵a、b为整数，∴a=4，b=6或a=6，b=3，当a=4，b=6时，n=464，4+6+4=14，14不能被6整除，故464不是“对偶数”，不符合题意；当a=6，b=3时，n=634，6+3+4=13，13能被3整除，故634不是“对偶数”，不符合题意；综上所述，所以满足条件的n为224或514．16．（2022春·湖北黄石·七年级统考期末）如图，以直角△AOC的直角顶点O为原点，以OC，OA所在直线为x轴和y轴建立平面直角坐标系，点A（0，a），C（b，0）满足√a−b+2+|b−8|=0．（1）点A的坐标为________；点C的坐标为________．（2）已知坐标轴上有两动点P，Q同时出发，P点从C点出发沿x轴负方向以每秒2个单位长度的速度匀速移动，Q点从O点出发沿y轴正方向以每秒1个单位长度的速度匀速移动，点P到达O点整个运动随之结束．AC的中点D的坐标是（4，3），设运动时间为t秒．问：是否存在这样的t，使得△ODP与△ODQ 的面积相等？若存在，请求出t的值；若不存在，请说明理由．（3）在（2）的条件下，若∠DOC=∠DCO，点G是第二象限中一点，并且y轴平分∠GOD．点E是线段OA上一动点，连接接CE交OD于点H，当点E在线段OA上运动的过程中，探究∠GOA，∠OHC，∠ACE 之间的数量关系，并证明你的结论（三角形的内角和为180°可以直接使用）．【思路点拨】（1）根据算术平方根的非负性，绝对值的非负性即可求解；（2）根据运动速度得到OQ=t，OP=8-2t，根据△ODP与△ODQ的面积相等列方程求解即可；（3）由∠AOC=90°，y轴平分∠GOD证得OG∥AC，过点H作HF∥OG交x轴于F，得到∠FHC=∠ACE，∠FHO=∠GOD，从而∠GOD+∠ACE=∠FHO+∠FHC，即可证得2∠GOA+∠ACE=∠OHC．【解题过程】解：（1）∵√a−b+2+|b−8|=0，∴a-b+2=0，b-8=0，∴a=6，b=8，∴A（0，6），C（8，0）；故答案为：（0，6），（8，0）；（2）由（1）知，A（0，6），C（8，0），∴OA=6，OB=8，由运动知，OQ=t，PC=2t，∴OP=8-2t，∵D（4，3），∴S△ODQ=12OQ×|x D|=12t×4=2t，S△ODP=12OP×|y D|=12（8−2t）×3=12−3t，∵△ODP与△ODQ的面积相等，∴2t=12-3t，∴t=2.4，∴存在t=2.4时，使得△ODP与△ODQ的面积相等；（3）2∠GOA+∠ACE=∠OHC，理由如下：∵x轴⊥y轴，∴∠AOC=∠DOC+∠AOD=90°，∴∠OAC+∠ACO=90°.又∵∠DOC=∠DCO，∴∠OAC=∠AOD.∵x轴平分∠GOD，∴∠GOA=∠AOD.∴∠GOA=∠OAC.∴OG∥AC，如图，过点H作HF∥OG交x轴于F，∴HF∥AC，∴∠FHC=∠ACE.∵OG∥FH，∴∠GOD=∠FHO，∴∠GOD+∠ACE=∠FHO+∠FHC，即∠GOD+∠ACE=∠OHC，∴2∠GOA+∠ACE=∠OHC．17．（2022春·湖北武汉·七年级统考期末）在平面直角坐标系中，A(a,0)，B(1,b)，a，b满足|a+b−1|+√2a−b+10=0，连接AB交y轴于C．(1)直接写出a=______，b=______；(2)如图1，点P是y轴上一点，且三角形ABP的面积为12，求点P的坐标；(3)如图2，直线BD交x轴于D(4,0)，将直线BD平移经过点A，交y轴于E，点Q(x,y)在直线AE上，且三角形ABQ的面积不超过三角形ABD面积的13，求点Q横坐标x的取值范围．【思路点拨】（1）根据非负数的性质构建方程组，解方程组求出a，b；（2）过点B作BM⊥x轴于M，设OC=m，由三角形面积关系得出12OA⋅OC+12(OC+BM)⋅OM=12AM⋅BM，求出m=3，过点B作BN⊥y轴于N，由三角形面积关系得出12×3×CP+12CP=12，求出CP即可；（3）连接DQ，过点Q作QR⊥x轴，分点Q在第二象限，点Q在第三象限时，两种情况，分别列出方程，解之即可．【解题过程】（1）解：∵√a+b−1+|2a−b+10|=0，又∵√a +b −1⩾0，|2a −b +10|⩾0，∴ {a +b −1=02a −b +10=0 ，解得：{a =−3b =4 ，故答案为：-3，4．（2）过点B 作BM ⊥x 轴于M ，设OC =m ，∵三角形AOC 的面积+四边形OCBM 的面积=三角形ABM 的面积，∴ 12OA ⋅OC +12(OC +BM)⋅OM =12AM ⋅BM ，即12×3m +12(m +4)×1=12×4×4，解得：m =3，点C 的坐标为(0,3)，过点B 作BN ⊥y 轴于N ，∵三角形ABP 的面积=三角形ACP 的面积+三角形BCP 的面积，∴ 12OA ⋅CP +12BN ⋅CP =12，即12×3×CP +12CP =12，∴CP =6，∴点P 的坐标为(0,−3)或(0,9)．（3）点B 向左平移4个单位长度，向下平移4个单位长度到点A ，∵点D 向左平移4个单位长度后的对应点正好在y 轴上，∴点D 平移后的对应点恰好是点E(0,−4)，连接DQ ，过点Q 作QR ⊥x 轴，如图所示：∵AE ∥BD ，∴三角形ADQ 的面积=三角形ABQ 的面积，当三角形ABQ 的面积=13三角形ABD 的面积时，QR =13y B =43，当点Q 在第三象限时，∴ 12(x +3)×43+12(43+4)(−x)=12×4×3，解得：x =−2，当点Q 在第二象限时，∴ 12×3×4+12(3−x)×43=12(−x)×163，解得：x =−4，∴当三角形ABQ 的面积不超过三角形ABD 面积的13时，点Q 的横坐标x 的取值范围是−4⩽x ⩽−2，且x ≠−3．18．（2022秋·黑龙江绥化·七年级校考期末）如图①，在平面直角坐标系中，点A 、B 的坐标分别为(−1，0)、(3，0)，现同时将点A 、B 向上平移2个单位长度，再向右平移一个单位长度，得到A 、B 的对应点C 、D ，连接AC 、BD 、CD ．(1)写出点C 、D 的坐标并求出四边形ABDC 的面积；(2)在x轴上是否存在一点F，使得△DFC的面积是△DFB面积的2倍？若存在，请求出点F的坐标；若不存在，请说明理由；(3)如图②，点P是直线BD上一个动点，连接PC、PO，当点P在直线BD上运动时，请直接写出∠OPC与∠PCD、∠POB的数量关系．【思路点拨】（1）根据点的平移规律可得C，D的坐标，然后利用平行四边形的面积计算即可求出四边形ABDC的面积；（2）根据△DFC的面积是△DFB面积的2倍，得BF=12CD=2，即可求出点F的坐标；（3）当点P在线段DB延长线上运动时，当点P在线段BD的延长线上时，当点P在线段BD上运动时，作PQ∥AB，分别根据平行线的性质和平行线间的传递性求解即可．【解题过程】（1）∵点A，B的坐标分别为(−1，0)、(3，0)，将点A，B分别向上平移2个单位长度，再向右平移1个单位长度，分别得到点A，B的对应点C，D，∴点C(0，2)，点D(4，2)，AB=4，AB∥CD，AB=CD，∴OC=2，四边形ABDC是平行四边形，∴S四边形ABDC=4×2=8；（2）存在，理由：设F坐标为(m，0)，∵△DFC的面积是△DFB面积的2倍，∴12×CD×OC=2×12BF×OC，即4=2|m−3|，解得m=5或1，∴P点的坐标为(5，0)或(1，0)；（3）①当点P在线段BD上时，如图，作PE∥CD，由平移可知：CD∥AB，∴CD∥PE∥AB，∴∠DCP=∠EPC，∠BOP=∠EPO，∴∠DCP+∠BOP=∠EPC+∠EPO=∠CPO；即∠OPC=∠PCD+∠POB；②当点P在线段BD的延长线上时，如图，作PE∥CD，由平移可知：CD∥AB，∴CD∥PE∥AB，∴∠DCP=∠EPC，∠BOP=∠EPO，∴∠BOP−∠DCP=∠EPO−∠EPC=∠CPO；即∠OPC=∠POB−∠PCD；③当点P在线段DB的延长线上时，如图，作PE∥CD，由平移可知：CD∥AB，∴CD∥PE∥AB，∴∠DCP=∠EPC，∠BOP=∠EPO，∴∠DCP−∠BOP=∠EPC−∠EPO=∠CPO；即∠OPC=∠PCD−∠POB；综上，∠OPC=∠PCD+∠POB或∠OPC=∠POB−∠PCD或∠OPC=∠PCD−∠POB．19．（2022春·湖南长沙·七年级校联考期末）如图所示，在平面直角坐标系中，如图①，将线段AB平移至线段CD，点A在x轴的负半轴，点C在y轴的正半轴上，连接AC、BD．(1)若A(−3,0)、B(−2,−2)，C(0,2)，直接写出点D的坐标；(2)如图②，在平面直角坐标系中，已知一定点M(2,0)，两个动点E(a,2a+1)、F(b,−2b+3)．请你探索是否存在以两个动点E、F为端点的线段EF平行于线段OM且等于线段OM，若存在，求点E、F的坐标；若不存在，请说明理由；(3)如图③，在直线EF上有两点A、C，分别引两条射线AB、CD．∠BAF=110°，∠DCF=60°，射线AB、CD分别绕A点，C点以1度/秒和3度/秒的速度同时顺时针转动，设时间为t，在射线CD转动一周的时间内，是否存在某时刻，使得CD与AB平行？若存在，求出所有满足条件的时间t．【思路点拨】(1)根据平移变换只改变图形的位置不改变图形的形状可知对应线段平行且相等，对应点的连线平行且相等；(2) 根据EF∥OM，EF=OM，O(0,0)，M(2,0)，得出2a+1=−2b+3，|a−b|=2，解答即可．(3) 分①AB与CD在EF的两侧，分别表示出∠ACD与∠BAC，然后根据内错角相等两直线平行，列式计算即可得解；②CD旋转到与AB都在EF的右侧，分别表示出∠DCF与∠BAC，然后根据同位角相等两直线平行，列式计算即可得解；③CD旋转到与AB都在EF的左侧，分别表示出∠DCF与∠BAC，然后根据同位角相等两直线平行，列式计算即可得解.【解题过程】（1）解：设D(x,y)，∵将线段AB平移至线段CD，A(−3,0)、B(−2,−2)，C(0,2)，∴x−0=−2−(−3)，y−2=−2−0，∴x=1，y=0，∴D(1,0)；。

七年级下册数学期末压轴难题试题及答案解答

七年级下册数学期末压轴难题试题及答案解答一、选择题1．如图，下列各组角中是同位角的是（）A ．∠1和∠2B ．∠3和∠4C ．∠2和∠4D ．∠1和∠42．下列图案可以由部分图案平移得到的是（）A ．B ．C ．D ．3．点()3,5A -在平面直角坐标系中所在的象限是（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限4．下列四个命题：①两条直线相交，若对顶角互补，则这两条直线互相垂直；②两条直线被第三条直线所截，内错角相等；③如果两条直线都与第三条直线平行，那么这两条直线也互相平行；④经过直线外一点，有且只有一条直线与已知直线平行．其中是真命题的个数是（）A ．1B ．2C ．3D ．45．将一张边沿互相平行的纸条如图折叠后，若边//AD BC ，则翻折角1∠与2∠一定满足的关系是（）A ．122∠=∠B ．1290∠+∠=︒C ．1230∠-∠=︒D ．213230∠-∠=︒6．下列说法正确的是（）A ．0的立方根是0B ．0.25的算术平方根是－0.5C ．－1000的立方根是10D ．49的算术平方根是23±7．如图，已知////AB CD EF ，FC 平分AFE ∠，26C ∠=︒，则A ∠的度数是（）A ．35︒B ．45︒C ．50︒D ．52︒8．如图，一个机器人从点O 出发，向正西方向走2m 到达点1A ；再向正北方向走4m 到达点2A ，再向正东方向走6m 到达点3A ，再向正南方向走8m 到达点4A ，再向正西方向走10m 到达点5A ，…按如此规律走下去，当机器人走到点20A 时，点20A 的坐标为（）A ．(20,20)-B ．(20,20)C ．(22,20)--D ．(22,22)-二、填空题9．算术平方根等于本身的实数是__________.10．在平面直角坐标系中，已知点A 的坐标为（﹣2，5），点Q 与点A 关于y 轴对称，点P 与点Q 关于x 轴对称，则点P 的坐标是___．11．如图，已知在四边形ABCD 中，∠A =α，∠C =β，BF ，DP 为四边形ABCD 的∠ABC 、∠ADC 相邻外角的角平分线．当α、β满足条件____________时，BF ∥DP ．12．已知//AB CD ，ABE α∠=，FCD β∠=，CFE γ∠=，且BE EF ⊥，请直接写出α、β、γ的数量关系________．13．如图，将△ABC 沿直线AC 翻折得到△ADC ，连接BD 交AC 于点E ，AF 为△ACD 的中线，若BE ＝2，AE ＝3，△AFC 的面积为2，则CE=_____．14．对于三个数a ，b ，c ，用M{a ，b ，c}表示这三个数的平均数，用min{a ，b ，c}表示这三个数中最小的数．例如：M{－1，2，3}＝123433-++=，min{－1，2，3}＝－1，如果M{3，2x ＋1，4x －1}＝min{2，－x ＋3，5x}，那么x ＝_______.15．已知AB ∥x 轴，A （-2，4），AB =5，则B 点横纵坐标之和为______．16．如图，在平面直角坐标系中，点()10,0A ，点()22,1A ，点()34,2A ，点()46,3A ，，按照这样的规律下去，点2021A 的坐标为__________．三、解答题17．计算下列各题:;18．已知：215a ab +=，210b ab +=，1a b -=，求下列各式的值：（1）a b +的值；（2）22a b +的值．19．如图．已知∠1＝∠2，∠C ＝∠D ，求证：∠A ＝∠F ．（1）请把下面证明过程中序号对应的空白内容补充完整．证明：∴∠1＝∠2（已知）又∵∠1＝∠DMN （）∵∠2＝∠DMN （等量代换）∴DB ∥EC （）∴∠DBC ＋∠C ＝180°（）．∵∠C ＝∠D （已知），∴∠DBC＋（）＝180°（等量代换）∴DF∥AC（）∴∠A＝∠F（）（2）在（1）的基础上，小明进一步探究得到∠DBC＝∠DEC，请帮他写出推理过程．20．将△ABO向右平移4个单位，再向下平移1个单位，得到三角形A′B′O′（1）请画出平移后的三角形A′B′O′．（2）写出点A′、O′的坐标．21．阅读理解．23．∴11＜21的整数部分为1，12．解决问题：已知a3的整数部分，b﹣3的小数部分．（1）求a，b的值；（2）求（﹣a）3+（b+4）2）2＝17．二十二、解答题22．已知在44⨯的正方形网格中，每个小正方形的边长为1．（1）计算图①中正方形ABCD的面积与边长．（2）利用图②中的正方形网格，作出面积为8的正方形，并在此基础上建立适当的数．二十三、解答题23．已知，AB ∥DE ，点C 在AB 上方，连接BC 、CD ．（1）如图1，求证：∠BCD ＋∠CDE ＝∠ABC ；（2）如图2，过点C 作CF ⊥BC 交ED 的延长线于点F ，探究∠ABC 和∠F 之间的数量关系；（3）如图3，在（2）的条件下，∠CFD 的平分线交CD 于点G ，连接GB 并延长至点H ，若BH 平分∠ABC ，求∠BGD ﹣∠CGF 的值．24．如图1，//AB CD ，E 是AB 、CD 之间的一点．（1）判定BAE ∠，CDE ∠与AED ∠之间的数量关系，并证明你的结论；（2）如图2，若BAE ∠、CDE ∠的两条平分线交于点F ．直接写出AFD ∠与AED ∠之间的数量关系；（3）将图2中的射线DC 沿DE 翻折交AF 于点G 得图3，若AGD ∠的余角等于2E ∠的补角，求BAE ∠的大小．25．如图①，AD 平分BAC ∠，AE ⊥BC ，∠B=450,∠C=730．（1）求DAE ∠的度数；（2）如图②，若把“AE ⊥BC ”变成“点F 在DA 的延长线上，FE BC ⊥”，其它条件不变，求DFE ∠的度数；（3）如图③，若把“AE ⊥BC ”变成“AE 平分BEC ∠”，其它条件不变，DAE ∠的大小是否变化，并请说明理由．26．如图①所示，在三角形纸片ABC 中，70C ∠=︒，65B ∠=︒，将纸片的一角折叠，使点A 落在ABC 内的点A '处.（1）若140∠=︒，2∠=________.（2）如图①，若各个角度不确定，试猜想1∠，2∠，A ∠之间的数量关系，直接写出结论.②当点A 落在四边形BCDE 外部时（如图②），（1）中的猜想是否仍然成立？若成立，请说明理由，若不成立，A ∠，1∠，2∠之间又存在什么关系？请说明．（3）应用：如图③：把一个三角形的三个角向内折叠之后，且三个顶点不重合，那么图中的123456∠+∠+∠+∠+∠+∠和是________.【参考答案】一、选择题1．D解析：D【分析】根据同位角的定义分析即可，两条直线被第三条直线所截,如果两个角分别在两条直线的同侧,且在第三条直线的同旁,那么这两个角叫做同位角．【详解】A.∠1和∠2是邻补角，不符合题意；B.∠3和∠4是同旁内角，不符合题意；C.∠2和∠4没有关系，不符合题意；D.∠1和∠4是同位角，符合题意；故选D ．【点睛】本题考查了同位角的定义，理解同位角的定义是解题的关键．2．C【分析】根据平移的定义，逐一判断即可．【详解】解：、是旋转变换，不是平移，选项错误，不符合题意；、轴对称变换，不是平移，选项错误，不符合题意；、是平移，选项正确，符合题意；、图形的大解析：C【分析】根据平移的定义，逐一判断即可．【详解】解：A 、是旋转变换，不是平移，选项错误，不符合题意；B 、轴对称变换，不是平移，选项错误，不符合题意；C 、是平移，选项正确，符合题意；D 、图形的大小发生了变化，不是平移，选项错误，不符合题意．故选：C ．【点睛】本题考查平移变换，解题的关键是判断图形是否由平移得到，要把握两个“不变”，图形的形状和大小不变；一个“变”，位置改变．3．B【分析】根据坐标的特点即可求解．【详解】点()3,5A -在平面直角坐标系中所在的象限是第二象限故选B ．【点睛】此题主要考查坐标所在象限，解题的关键是熟知直角坐标系的特点．4．C【分析】根据对顶角的性质和垂直的定义判断①；根据内错角相等的判定方法判定②；根据平行线的判定对③进行判断；根据经过直线外一点，有且只有一条直线与已知直线平行判断④即可【详解】解：两条直线相交，若对顶角互补，则这两条直线互相垂直，所以①正确；两条互相平行的直线被第三条直线所截，内错角相等；，所以②错误；如果两条直线都与第三条直线平行，那么这两条直线也互相平行，所以③正确；经过直线外一点，有且只有一条直线与已知直线平行，所以④正确．故选：C ．【点睛】本题主要考查命题的真假判断，正确的命题叫真命题，错误的命题叫做假命题，熟练掌握相关性质是解题的关键．5．B【分析】根据平行可得出∠DAB +∠CBA =180°，再根据折叠和平角定义可求出1290∠+∠=︒．【详解】解：由翻折可知，∠DAE =21∠，∠CBF =22∠，∵//AD BC ,∴∠DAB +∠CBA =180°，∴∠DAE +∠CBF =180°，即2122180∠+∠=°，∴1290∠+∠=︒，故选：B ．【点睛】本题考查了平行线的性质和角平分线的性质，解题关键是熟练运用平行线的性质进行推理计算．6．A【分析】根据算术平方根以及立方根的概念逐一进行凑数即可得．【详解】A ．0的立方根是0，正确，符合题意；B ．0.25的算术平方根是0.5，故B 选项错误，不符合题意；C ．－1000的立方根是-10，故C 选项错误，不符合题意；D ．49的算术平方根是23，故D 选项错误，不符合题意，故选A ．【点睛】本题考查了算术平方根、立方根，熟练掌握相关概念以及求解方法是解题的关键．7．D【分析】由题意易得26EFC C ∠=∠=︒，则有52EFA ∠=︒，然后根据平行线的性质可求解．【详解】解：∵//CD EF ，26C ∠=︒，∴26EFC C ∠=∠=︒，∵FC 平分AFE ∠，∴26EFC CFA ∠=∠=︒，∴52EFA ∠=︒，∵//AB CD ，∴52A EFA ∠=∠=︒；故选D ．【点睛】本题主要考查平行线的性质及角平分线的定义，熟练掌握平行线的性质及角平分线的定义是解题的关键．8．A【分析】先求出A1，A2，A3，…A8，发现规律，根据规律求出A20的坐标即可．【详解】解：∵一个机器人从点出发，向正西方向走到达点，点A1在x 轴的负半轴上，∴A1（-2,0）从点A2解析：A【分析】先求出A 1，A 2，A 3，…A 8，发现规律，根据规律求出A 20的坐标即可．【详解】解：∵一个机器人从点O 出发，向正西方向走2m 到达点1A ，点A 1在x 轴的负半轴上，∴A 1（-2,0）从点A 2开始，由点1A 再向正北方向走4m 到达点2A ，A 2（-2,4），由点2A 再向正东方向走6m 到达点3A ，A 3（6-2，4）即（4，4），由点3A 再向正南方向走8m 到达点4A ，A 4（4，4-8）即（4，-4），由点A 4再向正西方向走10m 到达点5A ，A 5（4-10，-4）即（-6，-4），由点A 5再向正北方向走12m 到达点A 6，A 6（-6，12-4）即（-6，8），由点A 6再向再向正东方向走14m 到达点A 7，A 7（14-6，8）即（8，8），由点A 7再向正南方向走16m 到达点8A ，A 8（8，8-16）即（8，-8），观察图象可知，下标为偶数时在二四象限，下标为奇数时（除1外）在一三象限，下标被4整除在第四象限．且横坐标与下标相同，因为2054=⨯，所以20A 在第四象限，坐标为(20,20)-．故选择A ．【点睛】本题考查平面直角坐标系点的坐标规律问题，掌握求点的坐标方法与过程，利用下标与坐标的关系找出规律是解题关键．二、填空题9．0或1【详解】根据负数没有算术平方根，一个正数的算术平方根只有一个，1和0的算术平方根等于本身，即可得出答案．解：1和0的算术平方根等于本身.故答案为1和0“点睛”本题考查了算术平方根的知解析：0或1【详解】根据负数没有算术平方根，一个正数的算术平方根只有一个，1和0的算术平方根等于本身，即可得出答案．解：1和0的算术平方根等于本身.故答案为1和0“点睛”本题考查了算术平方根的知识，注意掌握1和0的算术平方根等于本身．10．（2，﹣5）．【分析】根据题意分析点P，先关于y轴对称，再求关于x轴对称的点即可【详解】∵点A的坐标为（﹣2，5），点Q与点A关于y轴对称，∴点Q的坐标为（2，5），∵点P与点Q关于x轴解析：（2，﹣5）．【分析】根据题意分析点P，先关于y轴对称，再求关于x轴对称的点即可【详解】∵点A的坐标为（﹣2，5），点Q与点A关于y轴对称，∴点Q的坐标为（2，5），∵点P与点Q关于x轴对称，∴点P的坐标是（2，﹣5）．故答案为：（2，﹣5）．【点睛】本题考查了平面直角坐标系的定义，轴对称，理解题意是解题的关键．11．α=β【详解】试题解析：当BF ∥DP 时，即：整理得：故答案为解析：α=β【详解】试题解析：360.ABC ADC A C ∠+∠+∠+∠= 360.ABC ADC CBM CDN ∠+∠+∠+∠= .CBM CDN A C αβ∴∠+∠=∠+∠=+当BF ∥DP 时，()1,2C PDC FBC CDN CBM ∠=∠+∠=∠+∠即：()1,2βαβ=+整理得：.αβ=故答案为.αβ=12．（上式变式都正确）【分析】过点E 作，过点F 作，可得出（根据平行于同一直线的两条直线互相平行），根据平行线的性质，可得出各个角之间的关系，利用等量代换、等式的性质即可得出答案．【详解】解：如图解析：90γαβ+=︒+（上式变式都正确）【分析】过点E 作//EM AB ，过点F 作//FN AB ，可得出//////AB EM FN CD （根据平行于同一直线的两条直线互相平行），根据平行线的性质，可得出各个角之间的关系，利用等量代换、等式的性质即可得出答案．【详解】解：如图所示，过点E 作//EM AB ，过点F 作//FN AB ，∵//AB CD ，∴//////AB EM FN CD ，∵//AB EM ，∴ABE BEM ∠=∠，∵//EM FN ，∴MEF EFN ∠=∠，∵//NF CD ，∴NFC FCD ∠=∠，∴ABE EFN NFC BEM MEF FCD ∠+∠+∠=∠+∠+∠，∴ABE EFC BEF FCD ∠+∠=∠+∠，∵ABE α∠=，FCD β∠=，CFE γ∠=，且BE EF ⊥，∴90αγβ+=︒+，故答案为：90αγβ+=︒+．【点睛】题目主要考察平行线的性质及等式的性质，作出相应的辅助线、找出相应的角的关系是解题关键．13．【分析】根据已知条件以及翻折的性质，先求得S 四边形ABCD ，根据S 四边形ABCD ，即可求得，进而求得【详解】∵AF 为△ACD 的中线，△AFC 的面积为2，∴S △ACD ＝2S △AFC ＝4，∵解析：【分析】根据已知条件以及翻折的性质，先求得S 四边形ABCD ，根据S 四边形ABCD =12AC BD ⨯⨯，即可求得AC ，进而求得CE【详解】∵AF 为△ACD 的中线，△AFC 的面积为2，∴S △ACD ＝2S △AFC ＝4，∵△ABC沿直线AC翻折得到△ADC，∴S△ABC＝S△ADC，BD⊥AC，BE＝ED，∴S四边形ABCD＝8，∴18 2AC BD⨯⨯=，∵BE＝2，AE＝3，∴BD＝4，∴AC＝4，∴CE＝AC﹣AE＝4﹣3＝1．故答案为1．【点睛】本题考查了三角形中线的性质，翻折的性质，利用四边形ABCD的等面积法求解是解题的关键．14．或【详解】【分析】根据题中的运算规则得到M{3，2x＋1，4x－1}=1+2x，然后再根据min{2，－x＋3，5x}的规则分情况讨论即可得.【详解】M{3，2x＋1，4x－1}==2x+1解析：12或13【详解】【分析】根据题中的运算规则得到M{3，2x＋1，4x－1}=1+2x，然后再根据min{2，－x＋3，5x}的规则分情况讨论即可得.【详解】M{3，2x＋1，4x－1}=321413x x+++-=2x+1，∵M{3，2x＋1，4x－1}＝min{2，－x＋3，5x}，∴有如下三种情况：①2x+1=2，x=12，此时min{2，－x＋3，5x}=min{2，52，52}=2，成立；②2x+1=-x+3，x=23，此时min{2，－x＋3，5x}=min{2，73，103}=2，不成立；③2x+1=5x，x=13，此时min{2，－x＋3，5x}=min{2，83，53}=53，成立，∴x=12或13，故答案为12或13.【点睛】本题考查了阅读理解题，一元一次方程的应用，分类讨论思想的运用等，解决问题的关键是读懂题意，依题意分情况列出一元一次方程进行求解．15．-3或7【分析】由AB ∥x 轴可知B 点的纵坐标和A 点的纵坐标相同，再根据线段AB 的长度为5，B 点在A 点的坐标或右边，分别求出B 点的坐标，即可得到答案．【详解】解：∵AB ∥x 轴，∴B 点的纵坐标解析：-3或7【分析】由AB ∥x 轴可知B 点的纵坐标和A 点的纵坐标相同，再根据线段AB 的长度为5，B 点在A 点的坐标或右边，分别求出B 点的坐标，即可得到答案．【详解】解：∵AB ∥x 轴，∴B 点的纵坐标和A 点的纵坐标相同，都是4，又∵A （-2，4），AB =5，∴当B 点在A 点左侧的时候，B （-7，4），此时B 点的横纵坐标之和是-7+4=-3，当B 点在A 点右侧的时候，B （3，4），此时B 点的横纵坐标之和是3+4=7；故答案为：-3或7．【点睛】本题考查了与坐标轴平行的线上点的坐标特征以及分情况讨论的思想，要注意根据B 点位置的不确定得出两种情况分别求解．16．【分析】观察点，点，点，点点的横坐标为，纵坐标为，据此即可求得的坐标；【详解】，，，，，故答案为：【点睛】本题考查了坐标系中点的规律，找到规律是解题的关键．解析：(4040,2020)【分析】观察点()10,0A ，点()22,1A ，点()34,2A ，点()46,3A ，，点的横坐标为22n -，纵坐标为1n -，据此即可求得2021A 的坐标；【详解】()10,0A ，()22,1A ，()34,2A ，()46,3A ，，(22,1)n A n n --，∴2021(4040,2020)A 故答案为：(4040,2020)【点睛】本题考查了坐标系中点的规律，找到规律是解题的关键．三、解答题17．(1)5;(2)-2;(3)2【解析】【分析】根据实数的性质进行化简，再求值.【详解】解:(1)==5;(2)-×=-×4=-2;(3)-++=-6+5+3=2.【点睛】此题主要解析：(1)5;(2)-2;(3)2【解析】【分析】根据实数的性质进行化简，再求值.【详解】解=-12×4=-2;【点睛】此题主要考查实数的计算，解题的关键是熟知实数的性质.18．（1）±5；（2）13【分析】（1）将已知两式相减，再利用完全平方公式得到，可得结果；（2）根据完全平方公式可得=，代入计算即可【详解】解：（1）∵①，②，①+②得：，即，∴；（2）解析：（1）±5；（2）13【分析】（1）将已知两式相减，再利用完全平方公式得到()225a b +=，可得结果；（2）根据完全平方公式可得22a b +=()()2212a b a b ⎡⎤++-⎣⎦，代入计算即可【详解】解：（1）∵215a ab +=①，210b ab +=②，①+②得：22225a b ab ++=，即()225a b +=，∴5a b +=±；（2）∵1a b -=，∴22a b +=()()2212a b a b ⎡⎤++-⎣⎦=()221512⎡⎤±+⎣⎦=13．【点睛】本题主要考查了完全平方公式的变式应用，熟练应用完全平方公式的变式进行计算是解决本题的关键．19．（1）见解析；（2）见解析【分析】（1）由对顶角相等及等量代换得到∠2=∠DMN ，由此判定DB ∥EC ，由平行线的性质及等量代换得出∠DBC+∠D=180°即可判定DF ∥AC ，再根据平行线的性质即解析：（1）见解析；（2）见解析【分析】（1）由对顶角相等及等量代换得到∠2=∠DMN ，由此判定DB ∥EC ，由平行线的性质及等量代换得出∠DBC +∠D =180°即可判定DF ∥AC ，再根据平行线的性质即可得解；（2）由平行线的性质及等量代换即可得解．【详解】解：（1）证明：∵∠1=∠2（已知），又∵∠1=∠DMN （对顶角相等），∴∠2=∠DMN （等量代换），∴DB ∥EC （同位角相等，两直线平行），∴∠DBC +∠C =180°（两直线平行，同旁内角互补），∵∠C =∠D （已知），∵∠DBC +（∠D ）=180°（等量代换），∴DF ∥AC （同旁内角互补，两直线平行），∴∠A =∠F （两直线平行，内错角相等）．（2）∵DB ∥EC ，∴∠DBC +∠C =180°，∠DEC +∠D =180°，∵∠C =∠D ，∴∠DBC =∠DEC ．【点睛】此题考查了平行线的判定与性质，熟练掌握平行线的判定定理与性质定理是解题的关键．20．（1）见解析；（2）A′，O′【分析】（1）分别作出A ，B ，O 的对应点A′，B′，O′即可．（2）根据点的位置写出坐标即可．【详解】解：（1）如图，△A′B′O′即为所求作．（2）A′（解析：（1）见解析；（2）A ′()2,1，O ′()41-,【分析】（1）分别作出A ，B ，O 的对应点A ′，B ′，O ′即可．（2）根据点的位置写出坐标即可．【详解】解：（1）如图，△A ′B ′O ′即为所求作．（2）A ′（2，1），O ′（4，−1）．【点睛】本题考查作图−平移变换，解题的关键是熟练掌握基本知识，属于中考常考题型．21．（1）a ＝1，b ＝﹣4；（2）±4．【分析】（1）根据被开饭数越大算术平方根越大，可得a，b的值，（2）根据开平方运算，可得平方根．【详解】解：（1）∴，∴4＜5，∴1＜﹣3＜2，∴解析：（1）a＝1，b4；（2）±4．【分析】（1）根据被开饭数越大算术平方根越大，可得a，b的值，（2）根据开平方运算，可得平方根．【详解】解：（1<∴4<＜5，∴1﹣3＜2，∴a＝1，b﹣4；（2）（﹣a）3+（b+4）2＝（﹣1）3+﹣4+4）2＝﹣1+17＝16，∴（﹣a）3+（b+4）2的平方根是：±4．【点睛】本题考查了估算无理数的大小，利用被开方数越大算术平方根越大得出4＜5是解题关键．二十二、解答题22．（1）正方形的面积为10，正方形的边长为；（2）见解析【分析】（1）利用正方形的面积减去4个直角三角形的面积即可求出正方形的面积，然后根据算术平方根的意义即可求出边长；（2）根据（1）的方法画解析：（1）正方形ABCD的面积为10，正方形ABCD；（2）见解析【分析】（1）利用正方形的面积减去4个直角三角形的面积即可求出正方形ABCD的面积，然后根据算术平方根的意义即可求出边长；（2）根据（1）的方法画出图形，然后建立数轴，根据算术平方根的意义即可表示出结论．【详解】解：（1）正方形ABCD的面积为4×4－4×12×3×1=10则正方形ABCD ；（2）如下图所示，正方形的面积为4×4－4×12×2×2=8，所以该正方形即为所求，如图建立数轴，以数轴的原点为圆心，正方形的边长为半径作弧，分别交数轴于两点∴弧与数轴的左边交点为【点睛】此题考查的是求网格中图形的面积和实数与数轴，掌握算术平方根的意义和利用数轴表示无理数是解题关键．二十三、解答题23．（1）证明见解析；（2）；（3）．【分析】（1）过点作，先根据平行线的性质可得，再根据平行公理推论可得，然后根据平行线的性质可得，由此即可得证；（2）过点作，同（1）的方法，先根据平行线的性质解析：（1）证明见解析；（2）90ABC F ∠-∠=︒；（3）45︒．【分析】（1）过点C 作CF AB ∥，先根据平行线的性质可得180ABC BCF ∠+∠=︒，再根据平行公理推论可得CF DE ，然后根据平行线的性质可得180CDE BCF BCD ∠+∠+∠=︒，由此即可得证；（2）过点C 作CG AB ∥，同（1）的方法，先根据平行线的性质得出180ABC BCG ∠+∠=︒，180F BCG BCF ∠+∠+∠=︒，从而可得ABC F BCF ∠-∠=∠，再根据垂直的定义可得90BCF ∠=︒，由此即可得出结论；（3）过点G 作GM AB ，延长FG 至点N ，先根据平行线的性质可得ABH MGH ∠=∠，MGN DFG ∠=∠，从而可得MGH MGN ABH DFG ∠-∠=∠-∠，再根据角平分线的定义、结合（2）的结论可得45MGH MGN ∠=-∠︒，然后根据角的和差、对顶角相等可得BGD CG MGH MGN F ∠-∠=∠-∠，由此即可得出答案．【详解】证明：（1）如图，过点C 作CF AB ∥，180ABC BCF ∴∠+∠=︒，AB DE ，CF DE ∴P ，180CDE DCF ∴∠+∠=︒，即180CDE BCF BCD ∠+∠+∠=︒，CDE BCF BCD ABC BCF ∴∠+∠+∠=∠+∠，BCD CDE ABC ∴∠+∠=∠；（2）如图，过点C 作CG AB ∥，180ABC BCG ∴∠+∠=︒，AB DE ，CG DE ∴ ，180F FCG ∴∠+∠=︒，即180F BCG BCF ∠+∠+∠=︒，F BCG BCF ABC BCG ∴∠+∠+∠=∠+∠，ABC F BCF ∴∠-∠=∠，CF BC ⊥ ，90BCF ∴∠=︒，90ABC F ∴∠-∠=︒；（3）如图，过点G 作GM AB ，延长FG 至点N ，ABH MGH ∴∠=∠，AB DE ，GM DE ∴ ，MGN DFG ∴∠=∠，BH 平分ABC ∠，FN 平分CFD ∠，11,22ABH AB D C CF DFG ∴∠=∠∠∠=，由（2）可知，90ABC CFD ∠-∠=︒，411225MGH MGN ABH DFG CF B D A C ∠-∠=∠-∠∠-==∴︒，又BGD MGH MGD CGF DGN MGN MGD ∠=∠+∠⎧⎨∠=∠=∠+∠⎩，45MGH BGD GF MGN C ∠-∠∴-==∠∠︒．【点睛】本题考查了平行线的性质、对顶角相等、角平分线的定义等知识点，熟练掌握平行线的性质是解题关键．24．（1），见解析；（2）；（3）60°【分析】（1）作EF//AB ，如图1，则EF//CD ，利用平行线的性质得∠1＝∠BAE ，∠2＝∠CDE ，从而得到∠BAE ＋∠CDE ＝∠AED ；（2）如图2，解析：（1）BAE CDE AED ∠+∠=∠，见解析；（2）12AFD AED ∠=∠；（3）60°【分析】（1）作EF //AB ，如图1，则EF //CD ，利用平行线的性质得∠1＝∠BAE ，∠2＝∠CDE ，从而得到∠BAE ＋∠CDE ＝∠AED ；（2）如图2，由（1）的结论得∠AFD ＝∠BAF ＋∠CDF ，根据角平分线的定义得到∠BAF ＝12∠BAE ，∠CDF ＝12∠CDE ，则∠AFD ＝12（∠BAE ＋∠CDE ），加上（1）的结论得到∠AFD ＝12∠AED ；（3）由（1）的结论得∠AGD ＝∠BAF ＋∠CDG ，利用折叠性质得∠CDG ＝4∠CDF ，再利用等量代换得到∠AGD ＝2∠AED －32∠BAE ，加上90°－∠AGD ＝180°－2∠AED ，从而可计算出∠BAE 的度数．【详解】解：（1）BAE CDE AED∠+∠=∠理由如下：作//EF AB ，如图1，//AB CD Q ，//EF CD ∴．1BAE ∴∠=∠，2CDE ∠=∠，BAE CDE AED ∴∠+∠=∠；（2）如图2，由（1）的结论得AFD BAF CDF ∠=∠+∠，BAE ∠ 、CDE ∠的两条平分线交于点F ，12BAF BAE ∴∠=∠，12CDF CDE ∠=∠，1()2AFD BAE CDE ∴∠=∠+∠，BAE CDE AED ∠+∠=∠ ，12AFD AED ∴∠=∠；（3）由（1）的结论得AGD BAF CDG ∠=∠+∠，而射线DC 沿DE 翻折交AF 于点G ，4CDG CDF ∴∠=∠，11422()22AGD BAF CDF BAE CDE BAE AED BAE ∴∠=∠+∠=∠+∠=∠+∠-∠=322AED BAE ∠-∠，901802AGD AED ︒-∠=︒-∠ ，390218022AED BAE AED ∴︒-∠+∠=︒-∠，60BAE ∴∠=︒．【点睛】本题考查了平行线性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．25．（1）∠DAE =14°；（2）∠DFE =14°；（3）∠DAE 的大小不变，∠DAE =14°，证明详见解析.【分析】（1）求出∠ADE 的度数，利用∠DAE=90°-∠ADE 即可求出∠DAE解析：（1）∠DAE =14°；（2）∠DFE =14°；（3）∠DAE 的大小不变，∠DAE =14°，证明详见解析.【分析】（1）求出∠ADE 的度数，利用∠DAE=90°-∠ADE 即可求出∠DAE 的度数．（2）求出∠ADE 的度数，利用∠DFE=90°-∠ADE 即可求出∠DAE 的度数．（3）利用AE 平分∠BEC ，AD 平分∠BAC ，求出∠DFE=15°即是最好的证明．【详解】（1）∵∠B=45°，∠C=73°，∴∠BAC=62°，∵AD 平分∠BAC ，∴∠BAD=∠CAD=31°，∴∠ADE=∠B+∠BAD=45°+31°=76°，∵AE ⊥BC ，∴∠AEB=90°，∴∠DAE=90°-∠ADE=14°．（2）同（1），可得，∠ADE=76°，∵FE ⊥BC ，∴∠FEB=90°，∴∠DFE=90°-∠ADE=14°．（3）DAE ∠的大小不变.DAE ∠=14°理由：∵AD 平分∠BAC ，AE 平分∠BEC∴∠BAC=2∠BAD ，∠BEC=2∠AEB∵∠BAC+∠B+∠BEC+∠C =360°∴2∠BAD+2∠AEB=360°-∠B-∠C=242°∴∠BAD+∠AEB=121°∵∠ADE=∠B+∠BAD∴∠ADE=45°+∠BAD∴∠DAE=180°-∠AEB-∠ADE=180°-∠AEB-45°-∠BAD=135°-（∠AEB+∠BAD ）=135°-121°=14°【点睛】本题考查了三角形内角和定理和三角形外角的性质，熟练掌握性质是解题的关键.26．(1)50°；(2)①见解析;②见解析;(3)360°.【分析】（1）根据题意，已知，，可结合三角形内角和定理和折叠变换的性质求解；（2）①先根据折叠得：∠ADE=∠A′DE ，∠AED=∠A′解析：(1)50°；(2)①见解析;②见解析;(3)360°.【分析】（1）根据题意，已知70C ∠=︒，65B ∠=︒，可结合三角形内角和定理和折叠变换的性质求解；（2）①先根据折叠得：∠ADE=∠A′DE ，∠AED=∠A′ED ，由两个平角∠AEB 和∠ADC 得：∠1+∠2等于360°与四个折叠角的差，化简得结果；②利用两次外角定理得出结论；（3）由折叠可知∠1+∠2+∠3+∠4+∠5+∠6等于六边形的内角和减去（∠B'GF+∠B'FG ）以及（∠C'DE+∠C'ED ）和（∠A'HL+∠A'LH ），再利用三角形的内角和定理即可求解．【详解】解：（1）∵70C ∠=︒，65B ∠=︒，∴∠A′=∠A=180°-（65°+70°）=45°，∴∠A′ED+∠A′DE =180°-∠A′=135°，∴∠2=360°-（∠C+∠B+∠1+∠A′ED+∠A′DE ）=360°-310°=50°；（2）①122A ∠+∠=∠,理由如下由折叠得：∠ADE=∠A′DE ，∠AED=∠A′ED ，∵∠AEB+∠ADC=360°，∴∠1+∠2=360°-∠ADE-∠A′DE-∠AED-∠A′ED=360°-2∠ADE-2∠AED ，∴∠1+∠2=2（180°-∠ADE-∠AED ）=2∠A ；②221A ∠=∠+∠，理由如下：∵2∠是ADF 的一个外角∴2A AFD ∠=∠+∠.∵AFD ∠是A EF '△的一个外角∴1AFD A '∠=∠+∠又∵A A '∠=∠∴221A ∠=∠+∠（3）如图由题意知，∠1+∠2+∠3+∠4+∠5+∠6=720°-（∠B'GF+∠B'FG ）-（∠C'DE+∠C'ED ）-（∠A'HL+∠A'LH ）=720°-（180°-∠B'）-（180°-C'）-（180°-A'）=180°+（∠B'+∠C'+∠A'）又∵∠B=∠B'，∠C=∠C'，∠A=∠A'，∠A+∠B+∠C=180°，∴∠1+∠2+∠3+∠4+∠5+∠6=360°．【点睛】题主要考查了折叠变换、三角形、四边形内角和定理．注意折叠前后图形全等；三角形内角和为180°；四边形内角和等于360度．。

七年级下册数学几何压轴题

七年级下册数学几何压轴题
1. 把一个长方形沿x轴正方向移动m个单位，求移动前后阴影的面积差。

2. 一个小正方体沿着x轴正方向移动，它的一面在x轴上翻转，求翻转前后阴影的面积比值。

3. 一个方形沿着y轴正方向移动，移动到一个圆的周围，求圆和方形的阴影面积比值。

4. 把一个正方形沿对角线方向移动，它最后完全重合的时候恰好覆盖了一个面积为S的等腰三角形，求三角形面积S。

5. 把一个正方形沿着y轴正方向移动，移动m个单位的时候与另外一个正方形刚好重合，求另外一个正方形的边长。

6. 一个矩形沿x轴正方向移动，移动到另外一个矩形的正上方还有b个单位，求两个矩形的阴影面积比值。

7. 把一个半圆形沿y轴正方向移动，移动到正方形的中心时，求正方形面积和半圆形面积的阴影面积比值。

8. 把一个梯形沿y轴正方向移动，移动到一个与梯形相似的大梯形上面靠着底边的位置，求阴影的面积比值。

9. 把一个正三角形沿着x轴正方向移动，相邻两次的位移满足一个等差数列，第一次移动2个单位，第三次移动8个单位，求正三角形的边长。

10. 一个椭圆形沿y轴正方向移动，移动到一个长方形上方恰好横跨长方形的两个端点，求已经移动了多少个单位。

七年级下册数学的压轴题

1.下面哪个数是 8 和 12 的最小公倍数？
A.24
B.36
C.48
D.60
2.如果 3x - 7 = 11，那么 x 的值是多少？
A. 4
B. 6
C.8
D.9
3.一个三角形的三个内角分别为 50°、60°和多少度？
A.70°
B.80°
C.90°
D.100°
4.一辆汽车以每小时 60 公里的速度行驶，4 小时后行驶了多少公里？
A.120 公里
B.180 公里
C.240 公里
D.300 公里
5.一个正方形的边长是 7 厘米，它的面积是多少平方厘米？
A.49 平方厘米
B.54 平方厘米
C.56 平方厘米
D.63 平方厘米
6.如果一个圆的半径是 5 厘米，则它的直径是多少厘米？
A. 5 厘米
B.10 厘米
C.15 厘米
D.20 厘米
7.下列哪个数是 7 的平方？
A.49
B.56
C.64
D.72
8.一个长方体的长是 8 厘米，宽是 5 厘米，高是 4 厘米，它的体积是多少立方厘米？
A.160 立方厘米
B.180 立方厘米
C.200 立方厘米
D.240 立方厘米
9.如果一个数的 25% 是 15，那么这个数是多少？
A.50
B.60
C.75
D.80。

七年级下册数学压轴题集锦

七年级下册数学压轴题集锦（一）1、如图，已知A(0，a)，B （0，b ），C （m ，b ）且（a －4）2＋|b ＋3|＝0，S △ABC ＝14. （1）求C 点坐标（2）作DE ⊥DC ，交y 轴于E 点，EF 为∠AED 的平分线，且∠DFE ＝900.求证：FD 平分∠ADO ；（3）E 在y 轴负半轴上运动时，连EC ，点P 为AC 延长线上一点，EM 平分∠AEC ，且PM ⊥EM ，PN ⊥x轴于N 点，PQ 平分∠APN ，交x 轴于Q 点，则E 在运动过程中，∠MPQ∠ECA 的大小是否发生变化，若不变，求出其值.2、如图1，AB ∥EF ，∠2＝2∠1（1）证明∠FEC ＝∠FCE ；图1（2）如图2，M 为AC 上一点，N 为FE 延长线上一点，且∠FNM ＝∠FMN ，则∠NMC 与∠CFM 有何数量关系，并证明。

图2B C B3、（1）如图，△ABC, ∠ABC 、∠ACB 的三等分线交于点E 、D ，若∠1=130°，∠2=110°，求∠A 的度数。

（2）如图，△ABC,∠ABC 的三等分线分别与∠ACB 的平分线交于点D,E 若∠1=110°，∠2=130°，求∠A 的度数。

4、如图，∠ABC+∠ADC=180°，OE 、OF 分别是角平分线，则判断OE 、OF 的位置关系为？5、已知∠A=∠C=90°.(1)如图，∠ABC 的平分线与∠ADC 的平分线交于点E ，试问BE 与DE 有何位置关系？说明你的理由。

（2）如图，试问∠ABC 的平分线BE 与∠ADC 的外角平分线DF 有何位置关系？说明你的理由。

（3）如图，若∠ABC 的外角平分线与∠ADC 的外角平分线交于点E ，试问BE 与DE 有何位置关系？说明你的理由。

BA B6、（1）如图，点E 在AC 的延长线上，∠BAC 与∠DCE 的平分线交于点F ，∠B=60°,∠F=56°,求∠BDC 的度数。

七下数学压轴题

1、若关于x的方程3x - 7 = 2x + a的解为x = 5，则a的值为：A、8B、12C、18D、20解析：将x = 5代入方程3x - 7 = 2x + a，得到35 - 7 = 25 + a，即15 - 7 = 10 + a，解得a = -2 + 15 - 10 = 35 - 25 - 7 = 8。

（答案）A2、下列说法中，正确的是：A、两个角的和一定大于每一个加角B、两个角的和一定小于每一个加角C、两个直角的和等于一个平角D、两个锐角的和一定是钝角解析：两个角的和可能大于、等于或小于每一个加角，取决于这两个角的具体度数，故A、B错误；直角是90度的角，两个直角的和就是90+90=180度，等于一个平角，故C正确；锐角是小于90度的角，两个锐角的和可能仍是锐角（如30+40=70），可能是直角（如45+45=90），也可能是钝角（如60+70=130），故D错误。

（答案）C3、若a、b、c为三角形的三边，且a = 3，b = 4，则c的取值范围是：A、1 < c < 7B、3 < c < 4C、4 < c < 7D、无法确定解析：根据三角形的性质，任意两边之和大于第三边，任意两边之差小于第三边。

所以，a + b > c，即3 + 4 > c，得c < 7；同时，b - a < c，即4 - 3 < c，得c > 1。

因此，c的取值范围是1 < c < 7。

（答案）A4、下列运算中，结果正确的是：A、3√2 + 2√3 = 5√5B、(a + b)2 = a2 + b2C、(3a)2 = 6a2D、(-2x)3 = -8x3解析：3√2和2√3不是同类项，不能合并，故A错误；(a + b)2根据平方差公式展开为a2 + 2ab + b2，与B选项给出的a2 + b2不符，故B错误；(3a)2根据乘方定义计算为9a2，与C选项给出的6a2不符，故C错误；(-2x)3根据乘方定义和乘法分配律计算为-8x3，与D选项一致，故D正确。

七年级数学版下册压轴题

七年级数学版下册压轴题第一题：分数的加减乘除运算题目要求：请计算以下数式的值，并将答案化简至最简形式。

1.（1/3） + （2/5）2.（4/7） - （1/5）3.（2/3） × （3/8）4.（5/6） ÷ （1/4）答案及解析1.（1/3） + （2/5）解法：首先最小公倍数为15，将分数的分母变为15，得到（5/15） + （6/15） = 11/15，所以答案为11/15。

2.（4/7） - （1/5）解法：首先最小公倍数为35，将分数的分母变为35，得到（20/35） - （7/35） = 13/35，所以答案为13/35。

3.（2/3） × （3/8）解法：将分数相乘得到（2×3）/（3×8） = 6/24，将6/24化简为最简形式，得到1/4，所以答案为1/4。

4.（5/6） ÷ （1/4）解法：将除法转化为乘法，得到（5/6） × （4/1）= （5×4）/（6×1） = 20/6，将20/6化简为最简形式，得到10/3，所以答案为10/3。

第二题：解一元一次方程题目要求：解下列一元一次方程。

1.2x - 3 = x + 42.3(x + 5) = 6x - 93.2(x + 3) - 4(x - 2) = 5(2x - 1)答案及解析1.2x - 3 = x + 4解法：将方程中的变量合并在一起，得到2x - x = 4 + 3，化简得到x = 7，所以方程的解为x = 7。

2.3(x + 5) = 6x - 9解法：先将方程中的括号展开，得到3x + 15 = 6x - 9，将变量合并在一起，得到3x - 6x = -9 - 15，化简得到-3x = -24，再将方程两边同时除以-3，得到x = 8，所以方程的解为x = 8。

3.2(x + 3) - 4(x - 2) = 5(2x - 1)解法：先将方程中的括号展开，得到2x + 6 - 4x + 8 = 10x - 5，将变量合并在一起，得到-2x + 14 = 10x - 5，将方程中的常数项合并在一起，得到-2x - 10x = -5 - 14，化简得到-12x = -19，再将方程两边同时除以-12，得到x =19/12，所以方程的解为x = 19/12。

七年级(下册)数学压轴题集锦

1、2a b m b a-+b+3=0=14.ABCA S如图，已知（0，），B （0，），C （，）且（4），o y =DC FD ADO ⊥∠∠∠（1）求C 点坐标（2）作DE ，交轴于E 点，EF 为AED 的平分线，且DFE 90。

求证：平分；（3）E 在y 轴负半轴上运动时.连EC.点P 为AC 延长线上一点.EM 平分∠AEC.且PM ⊥EM,PN ⊥x 轴于N 点.PQ 平分∠APN.交x 轴于Q 点.则E 在运动过程中.MPQECA∠∠的大小是否发生变化.若不变.求出其值。

2、如图1.AB//EF, ∠2=2∠1 (1)证明∠FEC=∠FCE;(2)如图2.M 为AC 上一点.N 为FE 延长线上一点.且∠FNM=∠FMN.则∠NMC 与∠CFM 有何数量关系.并证明。

图1 图2 3、（1）如图.△ABC, ∠ABC 、∠ACB 的三等分线交于点E 、D.若∠1=130°.∠B C B C2=110°.求∠A 的度数。

（2）如图.△ABC,∠ABC 的三等分线分别与∠ACB 的平分线交于点D,E 若∠1=110°.∠2=130°.求∠A 的度数。

4、如图.∠ABC+∠ADC=180°.OE 、OF 分别是角平分线.则判断OE 、OF 的位置关系为？5、已知∠A=∠C=90°.BCCFA(1)如图.∠ABC 的平分线与∠ADC 的平分线交于点E.试问BE 与DE 有何位置关系？说明你的理由。

（2）如图.试问∠ABC 的平分线BE 与∠ADC 的外角平分线DF 有何位置关系？说明你的理由。

（3）如图.若∠ABC 的外角平分线与∠ADC 的外角平分线交于点E.试问BE 与DE 有何位置关系？说明你的理由。

6．（1）如图.点E 在AC 的延长线上.∠BAC 与∠DCE 的平分线交于点F.∠B=60°,∠F=56°,求∠BDC 的度数。

(完整版)七年级下学期数学压轴题

1如图①，OP 是∠MON 的平分线，请你利用该图形画一对以OP 所在直线为对称轴的全等三角形，写出作法并证明。

（5分）请你参考这个作全等三角形的方法，解答下列问题：（1）如图②，在△ABC 中，∠ACB 是直角，∠B =60°，AD 、CE 分别是∠BAC 、∠BCA 的平分线，AD 、CE 相交于点F 。

直接写出FE 和FD 之间的数量关系；（3分）（2）如图③，在△ABC 中，如果∠ACB 不是直角，而(1)中的其它条件不变，请问，你在(1)中结论是否仍然成立？若成立，请证明；若不成立，请说明理由。

（8分）2如图12-1，点O 是线段AD 上的一点，分别以AO 和DO 为边在线段AD 的同侧作等边三角形OAB 和等边三角形OCD ，连结AC 和BD ，相交于点E ，连结BC . （1）求∠AEB 的大小；（2）如图12-2，△OAB 固定不动，保持△OCD 的形状和大小不变，将△OCD 绕着点O 旋转（△OAB 和△OCD 不能重叠），求∠AEB 的大小.O图12-1 A 图12-2 (第18题图)O P AMNEB CD FACEFBD图①图② 图③3.如图，在ABC ∆中，40,2=∠==B AC AB ，点D 在线段BC 上运动（D 不与B 、C 重合），连接AD ，作40=∠ADE ，DE 交线段AC 于E ．（1）当115=∠BDA 时，=∠EDC °,=∠DEC °；点D 从B 向C 运动时，BDA ∠逐渐变（填“大”或“小”）；（本小题3分）（2）当DC 等于多少时，ABD ∆≌DCE ∆，请说明理由；（本小题4分）（3）在点D 的运动过程中，ADE ∆的形状可以是等腰三角形吗？若可以，请直接写出BDA ∠的度数.若不可以,请说明理由。

（本小题3分）4、如果一个角的两边与另一个角的两边分别垂直，那么这两个角的关系是_______ 40、（本题满分10分）如图1，两个不全等的等腰直角三角形OAB 和OCD 叠放在一起，并且有公共的直角顶点O 。

初一下册数学压轴题

初一下册数学压轴题一、下列关于三角形的说法中，正确的是：A. 三个内角之和大于180度B. 任意两边之和等于第三边C. 直角三角形中，斜边一定是最长边D. 等腰三角形的底角一定小于90度（答案：C、D）二、在平行线的性质中，下列说法错误的是：A. 两直线平行，同位角相等B. 两直线平行，内错角相等C. 两直线平行，同旁内角互补D. 两直线平行，它们之间的任意一条横截线都与这两条直线垂直（答案：D）三、对于不等式ax + b > 0，当a < 0时，下列关于x的解集说法正确的是：A. x的解集为全体实数B. x的解集为空集C. x的解集为x < -b/aD. x的解集为x > -b/a（答案：C）四、在坐标系中，点A(3, -2)关于x轴对称的点B的坐标是：A. (-3, 2)B. (3, 2)C. (-3, -2)D. (2, 3)（答案：B）五、下列关于多边形的说法中，错误的是：A. 三角形的内角和为180度B. 四边形的外角和为360度C. 五边形的对角线数量为5条D. n边形的内角和为(n-2) * 180度（答案：C）六、在二元一次方程组中，若方程组{x + y = 5, 2x - y = m}的解满足x > y，则m的取值范围是：A. m < 5B. m > 5C. m < 15D. m > 15（答案：B）七、下列关于实数的说法中，正确的是：A. 实数包括有理数和无理数，其中有理数包括整数和分数B. 实数都可以表示为两个整数的比C. 无理数就是开方开不尽的数D. 实数轴上的点与有理数一一对应（答案：A）八、在数据的统计与分析中，下列说法错误的是：A. 中位数是将一组数据从小到大排列后，位于中间位置的数B. 众数是一组数据中出现次数最多的数C. 平均数可以反映数据的集中程度，但受极端值影响较大D. 方差用于衡量数据的波动大小，方差越大，数据越稳定（答案：D）。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

不等式与方程组部分1、定义“*”：)1)(1(++++=*B A YB A X B A ，已知321=*，432=*，求43*的值．（7分）2．阅读下列解题过程，借鉴其中一种方法解答后面给出的试题：(11分)问题：某人买13个鸡蛋，5个鸭蛋、9个鹅蛋共用去了9.25元；买2个鸡蛋，4个鸭蛋、3个鹅蛋共用去了3.20元．试问只买鸡蛋、鸭蛋、鹅蛋各一个共需多少元．分析：设买鸡蛋，鸭蛋、鹅蛋各一个分别需x 、y 、z 元，则需要求x+y+z 的值．由题意，知⎩⎨⎧----=++---=++)2(20.3342)1(25.99513z y x z y x ；视x 为常数，将上述方程组看成是关于y 、z 的二元一次方程组，化“三元”为“二元”、化“二元”为“一元”从而获解．解法1：视x 为常数，依题意得⎩⎨⎧-----=+----=+)4(220.334)3(1325.995x z y x z y解这个关于y 、z 的二元一次方程组得⎩⎨⎧-=+=x z xy 2105.0于是05.12105.0=-+++=++x x x z y x ．评注：也可以视z 为常数，将上述方程组看成是关于x 、y 的二元一次方程组，解答方法同上，你不妨试试．分析：视z y x ++为整体，由(1)、(2)恒等变形得 25.9)2(4)(5=++++z x z y x ， 20.3)2()(4=+-++z x z y x ．解法2：设a z y x =++，b z x =+2，代入(1)、(2)可以得到如下关于a 、b 的二元一次方程组⎩⎨⎧----=----=+)6(20.34)5(25.945b a b a由⑤+4×⑥，得2122.05a =， 1.05a =．代人①、②将原方程组转化为关于a 、b 的二元一次方程组从而获解．请你运用以上介绍的任意一种方法解答如下数学竞赛试题：购买五种教学用具A 1、A 2、A 3、A 4、A 5的件数和用钱总数列成下表：那么，购买每种教学用具各一件共需多少元?3、先阅读理解下面的例题，再按要求解答：例题：解一元二次不等式.解：∵，∴.由有理数的乘法法则“两数相乘，同号得正”，有（1）（2）解不等式组（1），得，解不等式组（2），得，故的解集为或，品名次数 A 1A 2A 3A 4A 5总钱数第一次购买件数 l34561992第二次购买件数l579112984即一元二次不等式的解集为或.问题：求分式不等式的解集.4若不等式0432b ＜a x b a -+-)(的解集是49x ＞，求不等式的解集是0324b ＞a x b a -+-)(。

（选讲）例5、已知a ＞b ＞c ，且a+b+c=0，则ac的取值范围是_________。

（选讲）5、阅读下列材料：我们知道|x|的几何意义是在数轴上数x 对应的点与原点的距离；即0-=x x ，也就是说，|x|表示在数轴上数x 与数0对应点之间的距离；这个结论可以推广为21x x -表示在数轴上21,x x 对应点之间的距离；例1 解方程2=x ，容易看出，在数轴下与原点距离为2点的对应数为±2，即该方程的解为x=±2例2 解不等式▏x-1▏＞2，如图，在数轴上找出▏x-1▏=2的解，即到1的距离为2的点对应的数为－1、3，则▏x-1▏＞2的解为x<－1或x>3例3 解方程521=++-x x 。

由绝对值的几何意义知，该方程表示求在数轴上与1和－2的距离之和为x 对应点在1的右边，由图可以看出x ＝2；同理，若x 对应点在－2的左边，可得x ＝－3，故原方程的解是x=2或x=－3参考阅读材料，解答下列问题：（1）方程43=+x 的解为（2）解不等式943≥++-x x ；（3）若a x x ≤++-43对任意的x 都成立，求a 的取值范围.几何题部分1、（广益实验中学）如图1，A 、B 两点同时从原点O 出发，点A 以每秒x 个单位长度沿x 轴的负方向运动，点B 以每秒y 个单位长度沿y 轴的正方向运动.（1）若∣x ＋2y －5∣＋(2x －y)2＝0，试分别求出1秒钟后，A 、B 两点的坐标.（2）如图2，设∠BAO 的邻补角和∠ABO 的邻补角的平分线相交于点P 。

问：点A 、B 在运动的过程中，∠P 的大小是否会发生变化？若不发生变化，请求出其值；若发生变化，请说明理由. （3）如图3，延长BA 至E ，在∠ABO 的内部作射线BF 交x 轴于点C ，若∠EAC 、∠FCA 、 ∠ABC 的平分线相交于点G ，过点G 作BE 的垂线，垂足为H ，试问∠AGH 和∠BGC 的大小关系如何？请写出你的结论并说明理由.图1 图2 图32、探究（14分）（1）如图①∠1＋∠2与∠B＋∠C有什么关系？为什么？（2）把图①△ABC沿DE折叠，得到图②，填空：∠1＋∠2_______∠B＋∠C(填“＞”“＜”“=”)，当∠A＝40°时，∠B＋∠C＋∠1＋∠2＝______（3）如图③，是由图①的△ABC沿DE折叠得到的，如果∠A＝30°，则x＋y＝360°－（∠B＋∠C＋∠1＋∠2）＝360°－＝, 猜想∠BDA＋∠CEA与∠A的关系为什么？3、求下列字母所示的角的和（12分）BDACECFEBAG DBAFE（1）（2）（3）KB CD E FG HIJAFDHE GCABDEFG（4）（5）（6）4.如图，在平面直角坐标系中，∠ABO=2∠BAO ，P 为x 轴正半轴上一动点，BC 平分∠ABP ，PC 平分∠APF ，OD 平分∠POE 。

（1）求∠BAO 的度数；（2）求证：∠C=15°+21∠OAP ；（3）P 在运动中，∠C+∠D 的值是否变化，若发生变化，说明理由，若不变求其值。

应用题部分1、2004年雅典运动会开幕式的门票价格为：一等票300美元，二等票200美元，三等票125美元。

某服装公司在促销活动中，组织获奖的36名顾客到希腊观看2004年雅典奥运会开幕式，除去其他费用，计划用5025美元购买两种门票。

你能设计出几种购票方案供服装公司选择？并说明理由。

2、某校组织七年级的师生去春游，如果单位租用45座客车若干辆，刚好坐满；如果单独租用60座客车，可少租1辆，且余15个座位。

（1）求参加春游的人数；（2）已知租用45座客车的日租金为每辆车250元，60座客车的日租金为每辆车300元，租用哪种客车更合算？3、某班要买一些乒乓球和乒乓球拍，现了解情况如下：甲、乙两家商店出售两种同样品牌的乒乓球和乒乓球拍。

乒乓球拍每副定价30元，乒乓球每盒定价5元，经洽谈后，甲店每买一副球拍赠一盒乒乓球，问：（1）当购买乒乓球多少盒时，两种优惠办法付款一样？（2）当购买15盒、30盒乒乓球时，请你去办这件事，你打算去哪家商店购买？为什么？4、陈老师为学校买了运动会的奖品后，回学校向后勤处王老师交账时说：“我买了两种书，共105本，单价分别为8元和12元，买书前我领了1500元，现在还剩余418元。

”王老师算了一下，说：“你肯定搞错了。

”王老师为什么说陈老师搞错了？试用方程的知识给予解释。

5、工厂生产一种产品，每件产品的出厂价为50元，成本价为25元，因为在生产过程中，平均每生产一件产品有0.5立方米的污水排出，所以为净化环境工厂计划了两种处理污水的方案：方案一：工厂污水先净化处理后再排出，每处理1立方米污水所用的费用为2元，并且每月排污设备损耗费为30000元；方案二：工厂将污水排到污水处理厂统一处理，每处理1立方米污水需付14元的排污费。

问：如果你是厂长，在不污染环境，又节约资金的前提下，你会选用哪种处理污水的方案？请通过计算加以说明。

6、某商店出售一种商品，其原价为a元，现有两种调价方案：甲种是先提价12％，然后再降价12％；乙种是先降价12％，然后再提价12％。

试问：（1）甲、乙两种方案调价的结果是否一样？为什么？个商店买10件商品你要选择哪一种调价方案？为什么？7.响应“家电下乡”的惠农政策，某商场决定从厂家购进甲、乙、丙三种不同型号的电冰箱80台，其中甲种电冰箱的台数是乙种电冰箱台数的2倍，购买三种电冰箱的总金额不超过132 000元．已知甲、乙、丙三种电冰箱的出厂价格分别为：1 200元/台、1 600元/台、2 000元/台．（1）至少购进乙种电冰箱多少台？（2）若要求甲种电冰箱的台数不超过丙种电冰箱的台数，则有哪些购买方案？8.某电脑公司经销甲种型号电脑，受经济危机影响，电脑价格不断下降．今年三月份的电脑售价比去年同期每台降价1000元，如果卖出相同数量的电脑，去年销售额为10万元，今年销售额只有8万元．（1）今年三月份甲种电脑每台售价多少元？（2）为了增加收入，电脑公司决定再经销乙种型号电脑，已知甲种电脑每台进价为3500元，乙种电脑每台进价为3000元，公司预计用不多于5万元且不少于4.8万元的资金购进这两种电脑共15台，有几种进货方案？（3）如果乙种电脑每台售价为3800元，为打开乙种电脑的销路，公司决定每售出一台乙种电脑，返还顾客现金a元，要使（2）中所有方案获利相同，a值应是多少？此时，哪种方案对公司更有利？9.小杰到学校食堂买饭，看到A、B窗口前面排队的人一样多（设为a人，a>8），就站在A窗口的队伍后面.过了2分钟后，他发现A窗口每分钟有4人买了饭离开队伍，B窗口每分钟有6人买了饭离开队伍，且B窗口队伍后面每分钟增加5人.（1）若小杰继续在A窗口排队，则他到达窗口所花的时间是多少（用含a的代数式表示）？（2）此时，若小杰迅速从A窗口队伍转移到B窗口队伍重新排队，且到达B窗口的时间比继续在A窗口队伍排队到达A窗口的时间少，求a的取值范围.（不考虑其他因素）。