初一数学压轴题及答案

合集下载

数学初一上学期数学压轴题期末复习试卷带答案

数学初一上学期数学压轴题期末复习试卷带答案一、压轴题1．如图，在数轴上的A 1，A 2，A 3，A 4，……A 20，这20个点所表示的数分别是a 1，a 2，a 3，a 4，……a 20．若A 1A 2＝A 2A 3＝……＝A 19A 20，且a 3＝20，|a 1﹣a 4|＝12．（1）线段A 3A 4的长度＝；a 2＝；（2）若|a 1﹣x |＝a 2+a 4，求x 的值；（3）线段MN 从O 点出发向右运动，当线段MN 与线段A 1A 20开始有重叠部分到完全没有重叠部分经历了9秒．若线段MN ＝5，求线段MN 的运动速度．2．如图1，已知面积为12的长方形ABCD ，一边AB 在数轴上。

点A 表示的数为—2，点B 表示的数为1，动点P 从点B 出发，以每秒1个单位长度的速度沿数轴向左匀速运动，设点P 运动时间为t （t>0）秒.（1）长方形的边AD 长为单位长度；（2）当三角形ADP 面积为3时，求P 点在数轴上表示的数是多少；（3）如图2，若动点Q 以每秒3个单位长度的速度，从点A 沿数轴向右匀速运动，与P 点出发时间相同。

那么当三角形BDQ ，三角形BPC 两者面积之差为12时，直接写出运动时间t 的值.3．东东在研究数学问题时遇到一个定义：将三个已经排好顺序数：x 1，x 2，x 3，称为数列x 1，x 2，x 3．计算|x 1|，122x x +，1233x x x ++，将这三个数的最小值称为数列x 1，x 2，x 3的最佳值．例如，对于数列2，-1，3，因为|2|=2，()212+-=12，()2133+-+=43，所以数列2，-1，3的最佳值为12．东东进一步发现：当改变这三个数的顺序时，所得到的数列都可以按照上述方法计算其相应的最佳值．如数列-1，2，3的最佳值为12；数列3，-1，2的最佳值为1；…．经过研究，东东发现，对于“2，-1，3”这三个数，按照不同的排列顺序得到的不同数列中，最佳值的最小值为12．根据以上材料，回答下列问题：（1）数列-4，-3，1的最佳值为（2）将“-4，-3，2”这三个数按照不同的顺序排列，可得到若干个数列，这些数列的最佳值的最小值为，取得最佳值最小值的数列为（写出一个即可）；（3）将2，-9，a（a＞1）这三个数按照不同的顺序排列，可得到若干个数列．若这些数列的最佳值为1，求a的值．4．如图，已知数轴上点A表示的数为8，B是数轴上位于点A左侧一点，且AB=22，动点P从A点出发，以每秒5个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＞0）秒．（1）出数轴上点B表示的数；点P表示的数（用含t的代数式表示）（2）动点Q从点B出发，以每秒3个单位长度的速度沿数轴向右匀速运动，若点P、Q同时出发，问多少秒时P、Q之间的距离恰好等于2？（3）动点Q从点B出发，以每秒3个单位长度的速度沿数轴向左匀速运动，若点P、Q同时出发，问点P运动多少秒时追上点Q？（4）若M为AP的中点，N为BP的中点，在点P运动的过程中，线段MN的长度是否发生变化？若变化，请说明理由，若不变，请你画出图形，并求出线段MN的长．5．已知数轴上两点A、B，其中A表示的数为-2，B表示的数为2，若在数轴上存在一点C，使得AC+BC=n，则称点C叫做点A、B的“n节点”．例如图1所示：若点C表示的数为0，有AC+BC=2+2=4，则称点C为点A、B的“4节点”．请根据上述规定回答下列问题：（1）若点C为点A、B的“n节点”，且点C在数轴上表示的数为-4，求n的值；（2）若点D是数轴上点A、B的“5节点”，请你直接写出点D表示的数为______；（3）若点E在数轴上（不与A、B重合），满足BE=12AE，且此时点E为点A、B的“n节点”，求n的值．6．某商场在黄金周促销期间规定：商场内所有商品按标价的50%打折出售；同时，当顾客在该商场消费打折后的金额满一定数额，还可按如下方案抵扣相应金额：说明：[)a,b 表示在范围a b ～中，可以取到a ，不能取到b ．根据上述促销方法，顾客在该商场购物可以获得双重优惠：打折优惠与抵扣优惠．例如：购买标价为900元的商品，则打折后消费金额为450元，获得的抵扣金额为30元，总优惠额为：()900150%30480⨯-+=元，实际付款420元．(购买商品得到的优惠率100%)=⨯购买商品获得的总优惠额商品的标价，请问：()1购买一件标价为500元的商品，顾客的实际付款是多少元？ ()2购买一件商品，实际付款375元，那么它的标价为多少元？()3请直接写出，当顾客购买标价为______元的商品，可以得到最高优惠率为______．7．如图，数轴上点A 表示的数为4-，点B 表示的数为16，点P 从点A 出发，以每秒3个单位长度的速度沿数轴向右匀速运动同时点Q 从点B 出发，以每秒2个单位长度的速度向左匀速运动.设运动时间为t 秒(t 0)>．()1A ，B 两点间的距离等于______，线段AB 的中点表示的数为______；()2用含t 的代数式表示：t 秒后，点P 表示的数为______，点Q 表示的数为______； ()3求当t 为何值时，1PQ AB 2=？()4若点M 为PA 的中点，点N 为PB 的中点，点P 在运动过程中，线段MN 的长度是否发生变化？若变化，请说明理由；若不变请直接写出线段MN 的长．8．已知线段30AB cm =（1）如图1，点P 沿线段AB 自点A 向点B 以2/cm s 的速度运动，同时点Q 沿线段点B 向点A 以3/cm s 的速度运动，几秒钟后，P Q 、两点相遇？（2）如图1，几秒后，点P Q 、两点相距10cm ？（3）如图2，4AO cm =，2PO cm =，当点P 在AB 的上方，且060=∠POB 时，点P绕着点O 以30度/秒的速度在圆周上逆时针旋转一周停止，同时点Q 沿直线BA 自B 点向A 点运动，假若点P Q 、两点能相遇，求点Q 的运动速度．9．对于数轴上的点P ，Q ，给出如下定义：若点P 到点Q 的距离为d(d≥0)，则称d 为点P 到点Q 的d 追随值，记作d[PQ]．例如，在数轴上点P 表示的数是2，点Q 表示的数是5，则点P 到点Q 的d 追随值为d[PQ]=3．问题解决：(1)点M ，N 都在数轴上，点M 表示的数是1，且点N 到点M 的d 追随值d[MN]=a(a≥0)，则点N 表示的数是_____(用含a 的代数式表示)；(2)如图，点C 表示的数是1，在数轴上有两个动点A ，B 都沿着正方向同时移动，其中A 点的速度为每秒3个单位，B 点的速度为每秒1个单位，点A 从点C 出发，点B 表示的数是b ，设运动时间为t(t>0)．①当b=4时，问t 为何值时，点A 到点B 的d 追随值d[AB]=2； ②若0<t≤3时，点A 到点B 的d 追随值d[AB]≤6，求b 的取值范围．10．已知∠AOB 和∠AOC 是同一个平面内的两个角,OD 是∠BOC 的平分线. (1)若∠AOB=50°,∠AOC=70°,如图(1),图(2),求∠AOD 的度数；(2)若∠AOB=m 度,∠AOC=n 度,其中090090180m n m n ＜＜，＜＜，＜+且m n ＜，求∠AOD 的度数(结果用含m n 、的代数式表示)，请画出图形，直接写出答案．11．从特殊到一般，类比等数学思想方法，在数学探究性学习中经常用到，如下是一个具体案例，请完善整个探究过程。

徐州市人教版(七年级)初一上册数学压轴题期末复习测试题及答案

徐州市人教版(七年级)初一上册数学压轴题期末复习测试题及答案一、压轴题1．阅读理解：如图①，若线段AB 在数轴上，A 、B 两点表示的数分别为a 和b (b a >），则线段AB 的长（点A 到点B 的距离）可表示为AB=b a -.请用上面材料中的知识解答下面的问题:如图②，一个点从数轴的原点开始，先向左移动2cm 到达P 点，再向右移动7cm 到达Q 点，用1个单位长度表示1cm ．（1）请你在图②的数轴上表示出P ，Q 两点的位置；（2）若将图②中的点P 向左移动x cm ，点Q 向右移动3x cm ，则移动后点P 、点Q 表示的数分别为多少？并求此时线段PQ 的长.（用含x 的代数式表示）；（3）若P 、Q 两点分别从第⑴问标出的位置开始，分别以每秒2个单位和1个单位的速度同时向数轴的正方向运动，设运动时间为t （秒），当t 为多少时PQ=2cm ？2．已知数轴上，点A 和点B 分别位于原点O 两侧，AB=14，点A 对应的数为a ，点B 对应的数为b.(1) 若b ＝－4，则a 的值为__________. (2) 若OA ＝3OB ，求a 的值.(3) 点C 为数轴上一点，对应的数为c ．若O 为AC 的中点，OB ＝3BC ，直接写出所有满足条件的c 的值.3．如图，已知数轴上有三点 A ，B ，C ，若用 AB 表示 A ，B 两点的距离，AC 表示 A ，C 两点的距离，且 BC = 2 AB ，点 A 、点C 对应的数分别是a 、c ，且| a - 20 | + | c +10 |= 0 .（1）若点 P ，Q 分别从 A ，C 两点同时出发向右运动，速度分别为 2 个单位长度/秒、5个单位长度/ 秒，则运动了多少秒时，Q 到 B 的距离与 P 到 B 的距离相等？（2）若点 P ，Q 仍然以（1）中的速度分别从 A ，C 两点同时出发向右运动，2 秒后，动点 R 从 A 点出发向左运动，点 R 的速度为1个单位长度/秒，点 M 为线段 PR 的中点，点 N 为线段 RQ 的中点，点R 运动了x 秒时恰好满足 MN + AQ = 25，请直接写出x 的值. 4．东东在研究数学问题时遇到一个定义：将三个已经排好顺序数：x 1，x 2，x 3，称为数列x 1，x 2，x 3．计算|x 1|，122x x +，1233x x x ++，将这三个数的最小值称为数列x 1，x 2，x 3的最佳值．例如，对于数列2，-1，3，因为|2|=2，()212+-=12，()2133+-+=43，所以数列2，-1，3的最佳值为12．东东进一步发现：当改变这三个数的顺序时，所得到的数列都可以按照上述方法计算其相应的最佳值．如数列-1，2，3的最佳值为12；数列3，-1，2的最佳值为1；…．经过研究，东东发现，对于“2，-1，3”这三个数，按照不同的排列顺序得到的不同数列中，最佳值的最小值为12．根据以上材料，回答下列问题：（1）数列-4，-3，1的最佳值为（2）将“-4，-3，2”这三个数按照不同的顺序排列，可得到若干个数列，这些数列的最佳值的最小值为，取得最佳值最小值的数列为（写出一个即可）；（3）将2，-9，a（a＞1）这三个数按照不同的顺序排列，可得到若干个数列．若这些数列的最佳值为1，求a的值．5．已知数轴上有A、B、C三个点对应的数分别是a、b、c，且满足|a+24|+|b+10|+（c-10）2=0；动点P从A出发，以每秒1个单位的速度向终点C移动，设移动时间为t秒．（1）求a、b、c的值；（2）若点P到A点距离是到B点距离的2倍，求点P的对应的数；（3）当点P运动到B点时，点Q从A点出发，以每秒2个单位的速度向C点运动，Q点到达C点后．再立即以同样的速度返回，运动到终点A，在点Q开始运动后第几秒时，P、Q两点之间的距离为8？请说明理由．6．如图，在平面直角坐标系中，点M的坐标为（2，8），点N的坐标为（2，6），将线段MN向右平移4个单位长度得到线段PQ（点P和点Q分别是点M和点N的对应点），连接MP、NQ，点K是线段MP的中点．（1）求点K的坐标；（2）若长方形PMNQ以每秒1个单位长度的速度向正下方运动，（点A、B、C、D、E分别是点M、N、Q、P、K的对应点），当BC与x轴重合时停止运动，连接OA、OE，设运动时间为t秒，请用含t的式子表示三角形OAE的面积S（不要求写出t的取值范围）；（3）在（2）的条件下，连接OB、OD，问是否存在某一时刻t，使三角形OBD的面积等于三角形OAE的面积？若存在，请求出t值；若不存在，请说明理由．7．如图，已知数轴上点A表示的数为8，B是数轴上位于点A左侧一点，且AB=20，动点P从A点出发，以每秒5个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＞0）秒．（1）写出数轴上点B表示的数______；点P表示的数______（用含t的代数式表示）（2）动点Q从点B出发，以每秒3个单位长度的速度沿数轴向右匀速运动，若点P、Q同时出发，问多少秒时P、Q之间的距离恰好等于2？（3）动点Q从点B出发，以每秒3个单位长度的速度沿数轴向左匀速到家动，若点P、Q 同时出发，问点P运动多少秒时追上Q？（4）若M为AP的中点，N为BP的中点，在点P运动的过程中，线段MN的长度是否发生变化？若变化，请说明理由，若不变，请你画出图形，并求出线段MN的长．8．如图，P是定长线段AB上一点，C、D两点分别从P、B出发以1cm/s、2cm/s的速度沿直线AB向左运动（C在线段AP上，D在线段BP上）（1）若C、D运动到任一时刻时，总有PD＝2AC，请说明P点在线段AB上的位置：（2）在（1）的条件下，Q是直线AB上一点，且AQ﹣BQ＝PQ，求PQAB的值．（3）在（1）的条件下，若C、D运动5秒后，恰好有1CD AB2，此时C点停止运动，D点继续运动（D点在线段PB上），M、N分别是CD、PD的中点，下列结论：①PM﹣PN的值不变；②MNAB的值不变，可以说明，只有一个结论是正确的，请你找出正确的结论并求值．9．数轴上线段的长度可以用线段端点表示的数进行减法运算得到，例如：如图①，若点A，B在数轴上分别对应的数为a，b(a<b)，则AB的长度可以表示为AB=b－a．请你用以上知识解决问题：如图②，一个点从数轴上的原点开始，先向左移动2个单位长度到达A点，再向右移动3个单位长度到达B点，然后向右移动5个单位长度到达C点．（1）请你在图②的数轴上表示出A，B，C三点的位置．（2）若点A以每秒1个单位长度的速度向左移动，同时，点B和点C分别以每秒2个单位长度和3个单位长度的速度向右移动，设移动时间为t秒．①当t=2时，求AB和AC的长度；②试探究：在移动过程中，3AC－4AB的值是否随着时间t的变化而改变？若变化，请说明理由；若不变，请求其值．10．如图，数轴上有A、B两点，且AB=12，点P从B点出发沿数轴以3个单位长度/s的速度向左运动，到达A点后立即按原速折返，回到B点后点P停止运动，点M始终为线段BP的中点(1)若AP=2时，PM=____；(2)若点A表示的数是-5，点P运动3秒时，在数轴上有一点F满足FM=2PM，请求出点F 表示的数；(3)若点P从B点出发时，点Q同时从A点出发沿数轴以2.5个单位长度/s的速度一直．．向右运动，当点Q的运动时间为多少时，满足QM=2PM.11．如图，在数轴上从左往右依次有四个点,,,A B C D，其中点,,A B C表示的数分别是0,3,10，且2CD AB=.(1)点D表示的数是；（直接写出结果）(2)线段AB以每秒2个单位长度的速度沿数轴向右运动，同时线段CD以每秒1个单位长度的速度沿数轴向左运动，设运动时间是t（秒），当两条线段重叠部分是2个单位长度时.①求t的值;②线段AB上是否存在一点P，满足3BD PA PC-=?若存在，求出点P表示的数x；若不存在，请说明理由.12．阅读下列材料，并解决有关问题：我们知道，(0)0(0)(0)x xx xx x>⎧⎪==⎨⎪-<⎩，现在我们可以用这一结论来化简含有绝对值的式子，例如化简式子|1||2|x x++-时，可令10x+=和20x-=，分别求得1x=-，2x=（称1-、2分别为|1|x+与|2|x-的零点值）．在有理数范围内，零点值1x=-和2x=可将全体有理数不重复且不遗漏地分成如下三种情况：（1）1x <-；（2）1-≤2x <；（3）x ≥2．从而化简代数式|1||2|x x ++-可分为以下3种情况：（1）当1x <-时，原式()()1221x x x =-+--=-+；（2）当1-≤2x <时，原式()()123x x =+--=；（3）当x ≥2时，原式()()1221x x x =++-=-综上所述：原式21(1)3(12)21(2)x x x x x -+<-⎧⎪=-≤<⎨⎪-≥⎩通过以上阅读，请你类比解决以下问题：（1）填空：|2|x +与|4|x -的零点值分别为；（2）化简式子324x x -++．13．如图所示，已知数轴上A ，B 两点对应的数分别为－2，4，点P 为数轴上一动点，其对应的数为x .(1)若点P 到点A ，B 的距离相等，求点P 对应的数x 的值．(2)数轴上是否存在点P ，使点P 到点A ，B 的距离之和为8？若存在，请求出x 的值；若不存在，说明理由．(3)点A ，B 分别以2个单位长度/分、1个单位长度/分的速度向右运动，同时点P 以5个单位长度/分的速度从O 点向左运动．当遇到A 时，点P 立即以同样的速度向右运动，并不停地往返于点A 与点B 之间．当点A 与点B 重合时，点P 经过的总路程是多少？ 14．如图,在数轴上点A 表示数a,点B 表示数b,AB 表示A 点和B 点之间的距离,且a,b 满足|a+2|+(b+3a)2=0. (1)求A,B 两点之间的距离;(2)若在线段AB 上存在一点C,且AC=2BC,求C 点表示的数;(3)若在原点O 处放一个挡板,一小球甲从点A 处以1个单位/秒的速度向左运动,同时,另一个小球乙从点B 处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略小球的大小,可看做一个点)以原来的速度向相反的方向运动. 设运动时间为t 秒.①甲球到原点的距离为_____,乙球到原点的距离为_________;(用含t 的代数式表示) ②求甲乙两小球到原点距离相等时经历的时间.15．如图，已知线段AB=12cm ，点C 为AB 上的一个动点，点D 、E 分别是AC 和BC 的中点．（1）若AC=4cm ，求DE 的长；（2）试利用“字母代替数”的方法，说明不论AC 取何值（不超过12cm ），DE 的长不变；（3）知识迁移：如图②，已知∠AOB=α，过点O 画射线OC ，使∠AOB:∠BOC=3:1若OD 、OE 分别平分∠AOC 和∠BOC ，试探究∠DOE 与∠AOB 的数量关系．【参考答案】***试卷处理标记，请不要删除一、压轴题1．（1）见详解；（2）2x --，53x +，47x +；（3）当运动时间为5秒或9秒时，PQ=2cm. 【解析】【分析】（1）根据数轴的特点，所以可以求出点P ，Q 的位置；（2）根据向左移动用减法，向右移动用加法，即可得到答案；（3）根据题意，可分为两种情况进行分析：①点P 在点Q 的左边时；②点P 在点Q 的右边时；分别进行列式计算，即可得到答案. 【详解】解：（1）如图所示：.（2）由（1）可知，点P 为2-，点Q 为5；∴移动后的点P 为：2x --；移动后的点Q 为：53x +； ∴线段PQ 的长为：53(2)47x x x +---=+；（3）根据题意可知，当PQ=2cm 时可分为两种情况： ①当点P 在点Q 的左边时，有(21)72t -=-，解得：5t =；②点P 在点Q 的右边时，有(21)72t-=+，解得：9t=；综上所述，当运动时间为5秒或9秒时，PQ=2cm.【点睛】本题要是把方程和数轴结合起来，既要根据条件列出方程，又要把握数轴的特点．解题的关键是熟练掌握数轴上的动点运动问题，注意分类讨论进行解题.2．(1)10；(2)212±；(3)288.5±±，【解析】【分析】(1)根据题意画出数轴，由已知条件得出AB=14,OB=4,则OA=10,得出a的值为10.(2)分两种情况,点A在原点的右侧时,设OB=m,列一元一次方程求解,进一步得出OA的长度,从而得出a的值.同理可求出当点A在原点的左侧时,a的值.(3)画数轴,结合数轴分四种情况讨论计算即可.【详解】(1)解：若b＝－4，则a的值为 10(2)解：当A在原点O的右侧时（如图）：设OB=m,列方程得：m+3m=14，解这个方程得，7m2 =，所以，OA=212，点A在原点O的右侧，a的值为212.当A在原点的左侧时（如图)，a=－21 2综上，a的值为±212.(3)解：当点A在原点的右侧，点B在点C的左侧时（如图), c=－28 5.当点A在原点的右侧，点B在点C的右侧时（如图), c=－8.当点A在原点的左侧，点B在点C的右侧时，图略，c=28 5.当点A在原点的左侧，点B在点C的左侧时,图略，c=8.综上，点c的值为：±8，±28 5.【点睛】本题考查的知识点是通过画数轴,找出数轴上各线段间的数量关系并用一元一次方程来求解,需要注意的是分情况讨论时要考虑全面,此题充分锻炼了学生动手操作能力以及利用数行结合解决问题的能力.3．（1）107秒或10秒；（2）1413或11413．【解析】【分析】（1）由绝对值的非负性可求出a，c的值，设点B对应的数为b，结合BC 2 AB，求出b 的值，当运动时间为t秒时，分别表示出点P、点Q对应的数，根据“Q到B的距离与P 到B的距离相等”列方程求解即可；（2）当点R运动了x秒时，分别表示出点P、点Q、点R对应的数为，得出AQ的长，由中点的定义表示出点M、点N对应的数，求出MN的长．根据MN+AQ=25列方程，分三种情况讨论即可．【详解】（1）∵|a-20|+|c+10|=0，∴a-20=0，c+10=0，∴a=20，c=﹣10．设点B对应的数为b．∵BC=2AB，∴b﹣（﹣10）=2（20﹣b）．解得：b=10．当运动时间为t秒时，点P对应的数为20+2t，点Q对应的数为﹣10+5t．∵Q到B的距离与P到B的距离相等，∴|﹣10+5t﹣10|=|20+2t﹣10|，即5t﹣20=10+2t或20﹣5t=10+2t，解得：t=10或t=107．答：运动了107秒或10秒时，Q到B的距离与P到B的距离相等．（2）当点R运动了x秒时，点P对应的数为20+2（x+2）=2x+24，点Q对应的数为﹣10+5（x+2）=5x，点R对应的数为20﹣x，∴AQ=|5x﹣20|．∵点M为线段PR的中点，点N为线段RQ的中点，∴点M 对应的数为224202x x ++-=442x+，点N 对应的数为2052x x-+=2x +10， ∴MN =|442x+﹣（2x +10）|=|12﹣1.5x |． ∵MN +AQ =25，∴|12﹣1.5x |+|5x ﹣20|=25．分三种情况讨论：①当0＜x ＜4时，12﹣1.5x +20﹣5x =25，解得：x =1413；当4≤x ≤8时，12﹣1.5x +5x ﹣20=25，解得：x =667＞8，不合题意，舍去；当x ＞8时，1.5x ﹣12+5x ﹣20=25，解得：x 31141=．综上所述：x 的值为1413或11413．【点睛】本题考查了一元一次方程的应用、数轴、绝对值的非负性以及两点间的距离，找准等量关系，正确列出一元一次方程是解题的关键． 4．（1）3；（2）12；-3，2，-4或2，-3，-4．（3）a=11或4或10．【解析】【分析】（1）根据上述材料给出的方法计算其相应的最佳值为即可；（2）按照三个数不同的顺序排列算出最佳值，由计算可以看出，要求得这些数列的最佳值的最小值；只有当前两个数的和的绝对值最小，最小只能为|−3＋2|＝1，由此得出答案即可；（3）分情况算出对应的数值，建立方程求得a 的数值即可．【详解】（1）因为|−4|＝4，-4-32＝3.5，-4-312+＝3，所以数列−4，−3，1的最佳值为3．故答案为：3；（2）对于数列−4，−3，2，因为|−4|＝4，432--＝72，432||2--＋＝52，所以数列−4，−3，2的最佳值为52；对于数列−4，2，−3，因为|−4|＝4，||422-＋＝1，432||2--＋＝52，所以数列−4，2，−3的最佳值为1；对于数列2，−4，−3，因为|2|＝2，224-＝1，432||2--＋＝52，所以数列2，−4，−3的最佳值为1；对于数列2，−3，−4，因为|2|＝2，223-＝12，432||2--＋＝52，所以数列2，−3，−4的最佳值为1 2∴数列的最佳值的最小值为223-＝12，数列可以为：−3，2，−4或2，−3，−4．故答案为：12，−3，2，−4或2，−3，−4．（3）当22a＋＝1，则a＝0或−4，不合题意；当92a-＋＝1，则a＝11或7；当a＝7时，数列为−9，7，2，因为|−9|＝9，972-＋＝1，9722-+＋＝0，所以数列2，−3，−4的最佳值为0，不符合题意；当972a-+＋＝1，则a＝4或10．∴a＝11或4或10．【点睛】此题考查数字的变化规律，理解新定义运算的方法是解决问题的关键．5．(1) a=-24，b=-10，c=10；(2) 点P的对应的数是-443或4；(3) 当Q点开始运动后第6、21秒时，P、Q两点之间的距离为8，理由见解析【解析】【分析】（1）根据绝对值和偶次幂具有非负性可得a+24=0，b+10=0，c-10=0，解可得a、b、c的值；（2）分两种情况讨论可求点P的对应的数；（3）分类讨论：当P点在Q点的右侧，且Q点还没追上P点时；当P在Q点左侧时，且Q点追上P点后；当Q点到达C点后，当P点在Q点左侧时；当Q点到达C点后，当P 点在Q点右侧时，根据两点间的距离是8，可得方程，根据解方程，可得答案．【详解】（1）∵|a+24|+|b+10|+（c-10）2=0，∴a+24=0，b+10=0，c-10=0，解得：a=-24，b=-10，c=10；（2）-10-（-24）=14，①点P在AB之间，AP=14×221=283，-24+283=-443，点P的对应的数是-443；②点P在AB的延长线上，AP=14×2=28，-24+28=4，点P的对应的数是4；（3）∵AB=14，BC=20，AC=34，∴t P=20÷1=20（s），即点P运动时间0≤t≤20，点Q到点C的时间t1=34÷2=17（s），点C回到终点A时间t2=68÷2=34（s），当P点在Q点的右侧，且Q点还没追上P点时，2t+8=14+t，解得t=6；当P在Q点左侧时，且Q点追上P点后，2t-8=14+t，解得t=22＞17（舍去）；当Q点到达C点后，当P点在Q点左侧时，14+t+8+2t-34=34，t=463＜17（舍去）；当Q点到达C点后，当P点在Q点右侧时，14+t-8+2t-34=34，解得t=623＞20（舍去），当点P到达终点C时，点Q到达点D，点Q继续行驶（t-20）s后与点P的距离为8，此时2（t-20）+（2×20-34）=8，解得t=21；综上所述：当Q点开始运动后第6、21秒时，P、Q两点之间的距离为8．【点睛】此题主要考查了一元一次方程的应用，关键是正确理解题意，掌握非负数的性质，再结合数轴解决问题．6．（1）（4，8）（2）S△OAE＝8﹣t（3）2秒或6秒【解析】【分析】（1）根据M和N的坐标和平移的性质可知：MN∥y轴∥PQ，根据K是PM的中点可得K 的坐标；（2）根据三角形面积公式可得三角形OAE的面积S；（3）存在两种情况：①如图2，当点B在OD上方时②如图3，当点B在OD上方时，过点B作BG⊥x轴于G，过D作DH⊥x轴于H，分别根据三角形OBD的面积等于三角形OAE的面积列方程可得结论．【详解】（1）由题意得：PM＝4，∵K是PM的中点，∴MK＝2，∵点M的坐标为（2，8），点N的坐标为（2，6），∴MN∥y轴，∴K（4，8）；（2）如图1所示，延长DA交y轴于F，则OF⊥AE，F（0，8﹣t），∴OF＝8﹣t，∴S△OAE＝12OF•AE＝12（8﹣t）×2＝8﹣t；（3）存在，有两种情况：，①如图2，当点B在OD上方时，过点B作BG⊥x轴于G，过D作DH⊥x轴于H，则B（2，6﹣t），D（6，0），∴OG＝2，GH＝4，BG＝6﹣t，DH＝8﹣t，OH＝6，S△OBD＝S△OBG+S四边形DBGH+S△ODH，＝12OG•BG+12（BG+DH）•GH﹣12OH•DH，＝12×2（6-t）+12×4（6﹣t+8﹣t）﹣12×6（8﹣t），＝10﹣2t，∵S△OBD＝S△OAE，∴10﹣2t＝8﹣t，t＝2；②如图3，当点B在OD上方时，过点B作BG⊥x轴于G，过D作DH⊥x轴于H，则B（2，6﹣t），D（6，8﹣t），∴OG＝2，GH＝4，BG＝6﹣t，DH＝8﹣t，OH＝6，S△OBD＝S△ODH﹣S四边形DBGH﹣S△OBG，＝12OH•DH﹣12（BG+DH）•GH﹣12OG•BG，＝12×2（8-t）﹣12×4（6﹣t+8﹣t）﹣12×2（6﹣t），＝2t﹣10，∵S△OBD＝S△OAE，∴2t﹣10＝8﹣t，t＝6；综上，t的值是2秒或6秒．【点睛】本题考查四边形综合题、矩形的性质、三角形的面积、一元一次方程等知识，解题关键是灵活运用所学知识解决问题，学会用分类讨论的思想思考问题．7．（1）-12,8-5t；（2）94或114；（3）10；（4）MN的长度不变，值为10.【解析】【分析】(1)根据已知可得B点表示的数为8﹣20；点P表示的数为8﹣5t；(2)运动时间为t秒，分点P、Q相遇前相距2，相遇后相距2两种情况列方程进行求解即可；(3)设点P运动x秒时追上Q，根据P、Q之间相距20，列方程求解即可；(4)分①当点P在点A、B两点之间运动时，②当点P运动到点B的左侧时，利用中点的定义和线段的和差求出MN的长即可．【详解】(1)∵点A表示的数为8，B在A点左边，AB=20，∴点B表示的数是8﹣20=﹣12，∵动点P从点A出发，以每秒5个单位长度的速度沿数轴向左匀速运动，设运动时间为t(t＞0)秒，∴点P表示的数是8﹣5t，故答案为﹣12，8﹣5t；(2)若点P、Q同时出发，设t秒时P、Q之间的距离恰好等于2；分两种情况：①点P、Q相遇之前，由题意得3t+2+5t=20，解得t=94；②点P、Q相遇之后，由题意得3t﹣2+5t=20，解得t=11 4，答：若点P、Q同时出发，94或114秒时P、Q之间的距离恰好等于2；(3)如图，设点P运动x秒时，在点C处追上点Q，则AC=5x，BC=3x，∵AC﹣BC=AB，∴5x﹣3x=20，解得：x=10，∴点P运动10秒时追上点Q；(4)线段MN的长度不发生变化，都等于10；理由如下：①当点P在点A、B两点之间运动时：MN=MP+NP=12AP+12BP=12(AP+BP)=12AB=10，②当点P运动到点B的左侧时：MN=MP﹣NP=12AP﹣12BP=12(AP﹣BP)=12AB=10，∴线段MN的长度不发生变化，其值为10．【点睛】本题考查了数轴上的动点问题，一元一次方程的应用，用到的知识点是数轴上两点之间的距离，关键是根据题意画出图形，注意分两种情况进行讨论．8．（1）点P在线段AB上的13处；（2）13；（3）②MNAB的值不变.【解析】【分析】（1）根据C、D的运动速度知BD=2PC，再由已知条件PD=2AC求得PB=2AP，所以点P在线段AB上的13处；（2）由题设画出图示，根据AQ-BQ=PQ求得AQ=PQ+BQ；然后求得AP=BQ，从而求得PQ 与AB的关系；（3）当点C停止运动时，有CD＝12AB，从而求得CM与AB的数量关系；然后求得以AB表示的PM与PN的值，所以MN＝PN−PM＝112AB．【详解】解：（1）由题意：BD=2PC∵PD=2AC，∴BD+PD=2（PC+AC），即PB=2AP.∴点P在线段AB上的13处；（2）如图：∵AQ-BQ=PQ，∴AQ=PQ+BQ，∵AQ=AP+PQ，∴AP=BQ，∴PQ=13 AB，∴13 PQ AB（3）②MNAB的值不变.理由：如图，当点C停止运动时，有CD=12 AB，∴CM=14 AB，∴PM=CM-CP=14AB-5，∵PD=23AB-10，∴PN=1223（AB-10）=13AB-5，∴MN=PN-PM=112AB，当点C停止运动，D点继续运动时，MN的值不变，所以111212ABMNAB AB==.【点睛】本题考查了比较线段的长短．利用中点性质转化线段之间的倍分关系是解题的关键，在不同的情况下灵活选用它的不同表示方法，有利于解题的简洁性．同时，灵活运用线段的和、差、倍、分转化线段之间的数量关系也是十分关键的一点．9．（1）详见解析；（2）①16；②在移动过程中，3AC﹣4AB的值不变【解析】【分析】（1）根据点的移动规律在数轴上作出对应的点即可；（2）①当t=2时，先求出A、B、C点表示的数，然后利用定义求出AB、AC的长即可；②先求出A、B、C点表示的数，然后利用定义求出AB、AC的长，代入3AC－4AB即可得到结论．【详解】（1）A，B，C三点的位置如图所示：．（2）①当t=2时，A点表示的数为－4，B点表示的数为5，C点表示的数为12，∴AB=5－(－4)=9，AC=12－(－4)=16．②3AC－4AB的值不变．当移动时间为t秒时，A点表示的数为－t－2，B点表示的数为2t＋1，C点表示的数为3t ＋6，则：AC=(3t＋6)－(－t－2)=4t＋8，AB=(2t＋1)－(－t－2)=3t＋3，∴3AC－4AB=3(4t＋8)－4(3t＋3)=12t＋24－12t－12=12．即3AC﹣4AB的值为定值12，∴在移动过程中，3AC﹣4AB的值不变．【点睛】本题考查了数轴上的动点问题．表示出对应点所表示的数是解答本题的关键．10．(1)5 ；(2)点F表示的数是11.5或者-6.5；(3)127t=或6t=.【解析】【分析】（1）由AP=2可知PB=12-2=10，再由点M 是PB 中点可知PM 长度；（2）点P 运动3秒是9个单位长度，M 为PB 的中点，则可求解出点M 表示的数是2.5，再由FM=2PM 可求解出FM=9，此时点F 可能在M 点左侧，也可能在其右侧；（3）设Q 运动的时间为t 秒，由题可知t=4秒时，点P 到达点A ，再经过4秒点P 停止运动；则分04t ≤≤和48t <≤两种情况分别计算，由题可知即可QM=2PM=BP ，据此进行解答即可.【详解】(1)5 ；(2)∵点A 表示的数是5-∴点B 表示的数是7∵点P 运动3秒是9个单位长度，M 为PB 的中点∴PM=12PB=4.5，即点M 表示的数是2.5 ∵FM=2PM∴FM=9∴点F 表示的数是11.5或者-6.5(3)设Q 运动的时间为t 秒，当04t ≤≤时，由题可知QM=2PM=BP ，故点Q 位于点P 左侧，则AB=AQ+QP+PB ，而QP=QM-PM=2PM-PM=12BP ，则可得12=2.5t+12⨯3t+3t=7t ，解得t=127；当48t <≤时，由题可知QM=2PM=BP ，故点Q 位于点B 右侧，则PB=2QB ，则可得，()()123422.512t t --=-，整理得8t=48，解得6t =.【点睛】本题结合数轴上的动点问题考查了一元一次方程的应用，第3问要根据题干条件分情况进行讨论，作出图形更易理解.11．（1）16；（2）①t 的值为3或143秒；②存在，P 表示的数为314. 【解析】【分析】（1）由数轴可知，AB=3,则CD=6,所以D 表示的数为16，（2）①当运动时间是t 秒时，在运动过程中，B 点表示的数为3+2t,A 点表示的数为2t,C 点表示的数为10-t ，D 点表示的数为16-t ，分情况讨论两条线段重叠部分是2个单位长度解答即可；②分情况讨论当t=3秒, t=143秒时，满足3BD PA PC -=的点P , 注意P 为线段AB 上的点对x 的值的限制.【详解】（1）16（2）①在运动过程中，B 点表示的数为3+2t,A 点表示的数为2t,C 点表示的数为10-t ，D 点表示的数为16-t.当BC ＝2，点B 在点C 的右边时，由题意得：32-10-2BC t t =+=（），解得：t ＝3，当AD=2，点A 在点D 的左边时，由题意得：16--22AD t t ==，解得：t ＝143．综上，t 的值为3或143秒 ②存在，理由如下:当t=3时，A 点表示的数为6，B 点表示的数为9，C 点表示的数为7，D 点表示的数为13. 则13-94-6|-7|BD PA x PC x ====，，，-3BD PA PC =，()4--6|-7|x x ∴=，解得：314x =或112，又P 点在线段AB 上，则69x ≤≤314x ∴=. 当143t =时，A 点表示的数为283，B 点表示的数为373，C 点表示的数为163，D 点表示的数为343. 则37343816-1-|-|3333BD PA x PC x ====，，， -3BD PA PC =， ∴ 28161--|-|33x x ⎛⎫= ⎪⎝⎭，解得：7912x =或176，又283733x ≤≤， x ∴无解综上，P 表示的数为314. 【点睛】本题考查了一元一次方程的应用以及数轴，解题的关键是：(1)由路程=速度×时间结合运动方向找出运动t 秒时点A 、B 、C 、D 所表示的数,(2)根据3BD PA PC -=列出关于t 的含绝对值符号的一元一次方程． 12．(1) 2x =-和4x = ;(2) 35(4)11(43)35(3)x x x x x x --<-⎧⎪+-≤<⎨⎪+≥⎩【解析】【分析】（1）令x +2=0和x -4=0,求出x 的值即可得出|x +2|和|x -4|的零点值,（2）零点值x =3和x =-4可将全体实数分成不重复且不遗漏的如下3种情况:x ＜-4、-4≤x ＜3和x ≥3．分该三种情况找出324x x -++的值即可．【详解】解：（1）2x =-和4x =,（2）由30x -=得3,x =由40x +=得4x =-,①当4x <-时,原式()()32435x x x =---+=--,②当4-≤3x <时,原式()()32411x x x =--++=+,③当x ≥3时,原式()()32435x x x =-++=+,综上所述：原式()35(4)11(43)353x x x x x x ⎧--<-⎪=+-≤<⎨⎪+≥⎩, 【点睛】本题主要考查了绝对值化简方法,解决本题的关键是要熟练掌握绝对值化简方法.13．(1)x=1;(2) x ＝－3或x ＝5;(3) 30.【解析】【分析】（1）根据题意可得4－x ＝x －（－2），解出x 的值；（2）此题分为两种情况，当点P 在B 的右边时，当点P 在B 的左边时，分别列出方程求解即可；（3）设经过x 分钟点A 与点B 重合，根据题意得：2x ＝6＋x 进而求出即可.【详解】（1）4－x ＝x －（－2），解得：x ＝1，（2）①当点P 在B 的右边时得：x －（－2）＋x －4＝8，解得：x ＝5，②当点P 在B 的左边时得：－2－x ＋4－x ＝8，解得：x ＝－3，则x ＝－3或x ＝5.（3）设经过x 分钟点A 与点B 重合，根据题意得：2x ＝6＋x ，解得：x ＝6，则5x ＝30，故答案为30个单位长度.【点睛】本题主要考查了一元二次方程的应用，解此题的要点在于根据数轴得出点的位置. 14．2+t 6-2t 或2t-6【解析】分析：(1)、先根据非负数的性质求出a 、b 的值，再根据两点间的距离公式即可求得A 、B 两点之间的距离；(2)、设BC 的长为x ，则AC=2x ，根据AB 的长度得出x 的值，从而得出点C 所表示的数；（3）①甲球到原点的距离=甲球运动的路程+OA 的长，乙球到原点的距离分两种情况：（Ⅰ）当0＜t≤3时，乙球从点B 处开始向左运动，一直到原点O ，此时OB 的长度-乙球运动的路程即为乙球到原点的距离；（Ⅱ）当t ＞3时，乙球从原点O 处开始向右运动，此时乙球运动的路程-OB 的长度即为乙球到原点的距离；②分两种情况：（Ⅰ）0＜t≤3，（Ⅱ）t ＞3，根据甲、乙两小球到原点的距离相等列出关于t 的方程，解方程即可．详解：(1)、由题意知a=-2,b=6,故AB=8.(2)、设BC 的长为x,则AC=2x, ∵BC+AC=AB,∴x+2x=8,解得x=83， ∴C 点表示的数为6-83=103． (3)①2+t;6-2t 或2t-6.②当2+t=6-2t 时,解得t=43，当2+t=2t-6时, 解得t=8. ∴t=43或8. 点睛：本题考查了非负数的性质，方程的解法，数轴，两点间的距离，有一定难度，运用分类讨论思想、方程思想及数形结合思想是解题的关键．15．(1)DE=6;(2) DE=2a ,理由见解析；（3）∠DOE=12∠AOB ，理由见解析【解析】试题分析：（1）由AC=4cm ，AB=12cm ，即可推出BC=8cm ，然后根据点D 、E 分别是AC 和BC 的中点，即可推出AD=DC=2cm ，BE=EC=4cm ，即可推出DE 的长度，（2）设AC=acm ，然后通过点D 、E 分别是AC 和BC 的中点，即可推出DE=12（AC+BC ）=12AB=2a cm ，即可推出结论，（3）分两种情况，OC 在∠AOB 内部和外部结果都是∠DOE=12∠AOB 试题解析：（1））∵AB=12cm ，∴AC=4cm ，∴BC=8cm ，∵点D、E分别是AC和BC的中点，∴CD=2cm，CE=4cm，∴DE=6cm;(2) 设AC=acm，∵点D、E分别是AC和BC的中点，∴DE=CD+CE=12（AC+BC）=12AB=6cm，∴不论AC取何值（不超过12cm），DE的长不变;(3)①当OC在∠AOB内部时，如图所示：∵OM平分∠AOC，ON平分∠BOC，∴∠NOC=12∠BOC，∠COM=12∠COA．∵∠CON+∠COM=∠MON，∴∠MON=12（∠BOC+∠AOC）=12α；②当OC在∠AOB外部时，如图所示：∵OM平分∠AOC，ON平分∠BOC，∴∠MOC=12（∠AOB+∠BOC），∠CON=12∠BOC．∵∠MON+∠CON=∠MOC，∴∠MON=∠MOC-∠CON=12（AOB+∠BOC）-12∠BOC=12∠AOB=12α．【点睛】本题主要考察角平分线和线段的中点的性质，关键在于认真的进行计算，熟练运用相关的性质定理．。

人教版(七年级)初一上册数学压轴题期末复习测试题及答案

人教版(七年级)初一上册数学压轴题期末复习测试题及答案一、压轴题1．数轴上A 、B 两点对应的数分别是﹣4、12，线段CE 在数轴上运动，点C 在点E 的左边，且CE ＝8，点F 是AE 的中点．（1）如图1，当线段CE 运动到点C 、E 均在A 、B 之间时，若CF ＝1，则AB ＝，AC ＝，BE ＝；（2）当线段CE 运动到点A 在C 、E 之间时,①设AF 长为x ，用含x 的代数式表示BE ＝（结果需化简．．．．．）； ②求BE 与CF 的数量关系；（3）当点C 运动到数轴上表示数﹣14的位置时，动点P 从点E 出发，以每秒3个单位长度的速度向右运动，抵达B 后，立即以原来一半速度返回，同时点Q 从A 出发，以每秒2个单位长度的速度向终点B 运动，设它们运动的时间为t 秒（t ≤8），求t 为何值时，P 、Q 两点间的距离为1个单位长度． 2．综合试一试（1）下列整数可写成三个非0整数的立方和：45=_____；2=______．（2）对于有理数a ，b ，规定一种运算：2a b a ab ⊗=-．如2121121⊗=-⨯=-，则计算()()532-⊗⊗-=⎡⎤⎣⎦______．（3）a 是不为1的有理数，我们把11a-称为a 的差倒数．如：2的差倒数是1112=--，1-的差倒数是()11112=--．已知12a =，2a 是1a 的差倒数，3a 是2a 的差倒数，4a 是3a 的差倒数，……，以此类推，122500a a a ++⋅⋅⋅+=______．（4）10位裁判给一位运动员打分，每个人给的分数都是整数，去掉一个最高分，再去掉一个最低分，其余得分的平均数为该运动员的得分．若用四舍五入取近似值的方法精确到十分位，该运动员得9.4分，如果精确到百分位，该运动员得分应当是_____分．（5）在数1.2.3...2019前添加“+”，“-”并依次计算，所得结果可能的最小非负数是______（6）早上8点钟，甲、乙、丙三人从东往西直行，乙在甲前400米，丙在乙前400米，甲、乙、丙三人速度分别为120米/分钟、100米/分钟、90米/分钟，问：______分钟后甲和乙、丙的距离相等.3．问题：将边长为的正三角形的三条边分别等分，连接各边对应的等分点，则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个？探究：要研究上面的问题，我们不妨先从最简单的情形入手，进而找到一般性规律.探究一：将边长为2的正三角形的三条边分别二等分，连接各边中点，则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个？如图①，连接边长为2的正三角形三条边的中点，从上往下看：边长为1的正三角形，第一层有1个，第二层有3个，共有个；边长为2的正三角形一共有1个.探究二：将边长为3的正三角形的三条边分别三等分，连接各边对应的等分点，则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个？如图②，连接边长为3的正三角形三条边的对应三等分点，从上往下看：边长为1的正三角形，第一层有1个，第二层有3个，第三层有5个，共有个；边长为2的正三角形共有个.探究三：将边长为4的正三角形的三条边分别四等分（图③），连接各边对应的等分点，则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个？（仿照上述方法，写出探究过程）结论：将边长为的正三角形的三条边分别等分，连接各边对应的等分点，则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个？（仿照上述方法，写出探究过程）应用：将一个边长为25的正三角形的三条边分别25等分，连接各边对应的等分点，则该三角形中边长为1的正三角形有______个和边长为2的正三角形有______个. 4．已知数轴上两点A 、B ，其中A 表示的数为-2，B 表示的数为2，若在数轴上存在一点C ，使得AC+BC=n ，则称点C 叫做点A 、B 的“n 节点”．例如图1所示：若点C 表示的数为0，有AC+BC=2+2=4，则称点C 为点A 、B 的“4节点”．请根据上述规定回答下列问题：（1）若点C 为点A 、B 的“n 节点”，且点C 在数轴上表示的数为-4，求n 的值；（2）若点D 是数轴上点A 、B 的“5节点”，请你直接写出点D 表示的数为______；（3）若点E 在数轴上（不与A 、B 重合），满足BE=12AE ，且此时点E 为点A 、B 的“n 节点”，求n 的值．5．如图，在平面直角坐标系中，点M 的坐标为（2，8），点N 的坐标为（2，6），将线段MN 向右平移4个单位长度得到线段PQ （点P 和点Q 分别是点M 和点N 的对应点），连接MP 、NQ ，点K 是线段MP 的中点．（1）求点K 的坐标；（2）若长方形PMNQ 以每秒1个单位长度的速度向正下方运动，（点A 、B 、C 、D 、E 分别是点M 、N 、Q 、P 、K 的对应点），当BC 与x 轴重合时停止运动，连接OA 、OE ，设运动时间为t 秒，请用含t 的式子表示三角形OAE 的面积S （不要求写出t 的取值范围）；（3）在（2）的条件下，连接OB 、OD ，问是否存在某一时刻t ，使三角形OBD 的面积等于三角形OAE 的面积？若存在，请求出t 值；若不存在，请说明理由．6．如图，数轴上有A ， B 两点，分别表示的数为a ，b ，且()225350a b ++-=．点P从A 点出发以每秒13个单位长度的速度沿数轴向右匀速运动，当它到达B 点后立即以相同的速度返回往A点运动，并持续在A，B两点间往返运动．在点P出发的同时，点Q从B点出发以每秒2个单位长度向左匀速运动，当点Q达到A点时，点P，Q停止运动．（1）填空：a=，b=；（2）求运动了多长时间后，点P，Q第一次相遇，以及相遇点所表示的数；（3）求当点P，Q停止运动时，点P所在的位置表示的数；（4）在整个运动过程中，点P和点Q一共相遇了几次．（直接写出答案）7．射线OA、OB、OC、OD、OE有公共端点O．（1）若OA与OE在同一直线上（如图1），试写出图中小于平角的角；（2）若∠AOC＝108°，∠COE＝n°（0＜n＜72），OB平分∠AOE，OD平分∠COE（如图2），求∠BOD的度数；（3）如图3，若∠AOE＝88°，∠BOD＝30°，射OC绕点O在∠AOD内部旋转（不与OA、OD重合）．探求：射线OC从OA转到OD的过程中，图中所有锐角的和的情况，并说明理由．8．在数轴上，图中点A表示－36，点B表示44，动点P、Q分别从A、B两点同时出发，相向而行，动点P、Q的运动速度比之是3∶2（速度单位：1个单位长度/秒）．12秒后，动点P到达原点O，动点Q到达点C，设运动的时间为t（t＞0）秒．（1）求OC的长；（2）经过t秒钟，P、Q两点之间相距5个单位长度，求t的值；（3）若动点P到达B点后，以原速度立即返回，当P点运动至原点时，动点Q是否到达A点，若到达，求提前到达了多少时间，若未能到达，说明理由．9．如图，直线l上有A、B两点，点O是线段AB上的一点，且OA=10cm，OB=5cm．（1）若点C是线段AB的中点，求线段CO的长．（2）若动点P、Q分别从 A、B同时出发，向右运动，点P的速度为4c m/s，点Q的速度为3c m/s，设运动时间为x秒，①当x=__________秒时，PQ=1cm；②若点M从点O以7c m/s的速度与P、Q两点同时向右运动，是否存在常数m，使得4PM +3OQ ﹣mOM 为定值，若存在请求出m 值以及这个定值；若不存在，请说明理由．（3）若有两条射线 OC 、OD 均从射线OA 同时绕点O 顺时针方向旋转，OC 旋转的速度为6度/秒，OD 旋转的速度为2度/秒.当OC 与OD 第一次重合时，OC 、OD 同时停止旋转，设旋转时间为t 秒，当t 为何值时，射线 OC ⊥OD ？10．如图①，点C 在线段AB 上，图中共有三条线段AB 、AC 和BC ，若其中有一条线段的长度是另外一条线段长度的2倍，则称点C 是段AB 的“2倍点”．（1）线段的中点__________这条线段的“2倍点”；（填“是”或“不是”）（2）若AB ＝15cm ，点C 是线段AB 的“2倍点”．求AC 的长；（3）如图②，已知AB ＝20cm ．动点P 从点A 出发，以2c m ／s 的速度沿AB 向点B 匀速移动．点Q 从点B 出发，以1c m/s 的速度沿BA 向点A 匀速移动．点P 、Q 同时出发，当其中一点到达终点时，运动停止，设移动的时间为t （s ），当t ＝_____________s 时，点Q 恰好是线段AP 的“2倍点”．（请直接写出各案）11．如图，12cm AB =，点C 是线段AB 上的一点，2BC AC =.动点P 从点A 出发，以3cm /s 的速度向右运动，到达点B 后立即返回，以3cm /s 的速度向左运动；动点Q 从点C 出发，以1cm/s 的速度向右运动. 设它们同时出发，运动时间为s t . 当点P 与点Q 第二次重合时，P Q 、两点停止运动. （1）求AC ，BC ；（2）当t 为何值时，AP PQ =；（3）当t 为何值时，P 与Q 第一次相遇；（4）当t 为何值时，1cm PQ =.12．如图，在数轴上从左往右依次有四个点,,,A B C D ，其中点,,A B C 表示的数分别是0,3,10，且2CD AB =.(1)点D 表示的数是；（直接写出结果）(2)线段AB 以每秒2个单位长度的速度沿数轴向右运动，同时线段CD 以每秒1个单位长度的速度沿数轴向左运动，设运动时间是t （秒），当两条线段重叠部分是2个单位长度时. ①求t 的值;②线段AB 上是否存在一点P ，满足3BD PA PC -=?若存在，求出点P 表示的数x ；若不存在，请说明理由.13．已知：如图，点M 是线段AB 上一定点，12AB cm =，C 、D 两点分别从M 、B 出发以1/cm s 、2/cm s 的速度沿直线BA 向左运动，运动方向如箭头所示（C 在线段AM 上，D 在线段BM 上）()1若4AM cm =，当点C 、D 运动了2s ，此时AC =________，DM =________；（直接填空）()2当点C 、D 运动了2s ，求AC MD +的值．()3若点C 、D 运动时，总有2MD AC =，则AM =________（填空）()4在()3的条件下，N 是直线AB 上一点，且AN BN MN -=，求MN AB的值．14．问题一：如图1，已知A ，C 两点之间的距离为16 cm ，甲，乙两点分别从相距3cm 的A ，B 两点同时出发到C 点，若甲的速度为8 cm/s ，乙的速度为6 cm/s ，设乙运动时间为x （s ），甲乙两点之间距离为y （cm ）． (1)当甲追上乙时，x = ． (2)请用含x 的代数式表示y ．当甲追上乙前，y = ；当甲追上乙后，甲到达C 之前，y = ；当甲到达C 之后，乙到达C 之前，y = ．问题二：如图2，若将上述线段AC 弯曲后视作钟表外围的一部分，线段AB 正好对应钟表上的弧AB （1小时的间隔），易知∠AOB=30°．(1)分针OD 指向圆周上的点的速度为每分钟转动 cm ；时针OE 指向圆周上的点的速度为每分钟转动 cm ．(2)若从4：00起计时，求几分钟后分针与时针第一次重合．15．如图所示，已知数轴上A ，B 两点对应的数分别为－2，4，点P 为数轴上一动点，其对应的数为x .(1)若点P 到点A ，B 的距离相等，求点P 对应的数x 的值．(2)数轴上是否存在点P ，使点P 到点A ，B 的距离之和为8？若存在，请求出x 的值；若不存在，说明理由．(3)点A ，B 分别以2个单位长度/分、1个单位长度/分的速度向右运动，同时点P 以5个单位长度/分的速度从O 点向左运动．当遇到A 时，点P 立即以同样的速度向右运动，并不停地往返于点A 与点B 之间．当点A 与点B 重合时，点P 经过的总路程是多少？【参考答案】***试卷处理标记，请不要删除一、压轴题1．（1）16,6,2；（2）①162x -②2BE CF =；（3）t=1或3或487或527 【解析】【分析】(1)由数轴上A 、B 两点对应的数分別是-4、12，可得AB 的长;由CE ＝8，CF ＝1，可得EF 的长，由点F 是AE 的中点，可得AF 的长，用AB 的长减去2倍的EF 的长即为BE 的长；(2)设AF ＝FE ＝x ，则CF ＝8-x ，用含x 的式子表示出BE ，即可得出答案 (3)分①当0＜t ≤6时； ②当6＜t ≤8时，两种情况讨论计算即可得解【详解】（1）数轴上A 、B 两点对应的数分别是-4、12， ∴AB=16，∵CE=8，CF=1，∴EF=7， ∵点F 是AE 的中点，∴AF=EF=7，,∴AC=AF ﹣CF=6，BE=AB ﹣AE=16﹣7×2=2，故答案为16，6，2；(2)∵点F 是AE 的中点，∴AF=EF ，设AF=EF=x,∴CF=8﹣x ， ∴BE=16﹣2x=2（8﹣x ）， ∴BE=2CF.故答案为①162x -②2BE CF =；(3) ①当0＜t ≤6时，P 对应数：-6+3t ，Q 对应数-4+2t ，=4t t =2t =1PQ ﹣＋2﹣（﹣6＋3）﹣，解得：t=1或3；②当6＜t ≤8时，P 对应数()33126t 22t ---＝21 ， Q 对应数-4+2t ， 37=4t =t 2=12t PQ -﹣＋2﹣（）25﹣21，解得：48t=7或527；故答案为t=1或3或487或527. 【点睛】本题考查了一元一次方程在数轴上的动点问题中的应用，根据题意正确列式，是解题的关健2．（1）23+(-3)3+43，73+(-5)3+(-6)3；（2）100；（3）25032；（4）9.38；（5）0；（6）24或40 【解析】【分析】（1）把45分解为2、-3、4三个整数的立方和，2分解为7、-5、-6三个整数的立方和即可的答案；（2）按照新运算法则，根据有理数混合运算法则计算即可得答案；（3）根据差倒数的定义计算出前几项的值，得出规律，计算即可得答案；（4）根据精确到十分位得9.4分可知平均分在9.35到9.44之间，可求出总分的取值范围，根据裁判打分是整数即可求出8个裁判给出的总分，再计算出平均分，精确到百分位即可；（5）由1+2-3=0，连续4个自然数通过加减运算可得0，列式计算即可得答案；（6）根据题意得要使甲和乙、甲和丙的距离相等就可以得出甲在乙、丙之间，设x 分钟后甲和乙、甲和丙的距离相等，就有甲走的路程-乙走的路程-400=丙走的路程+800-甲走的路程建立方程求出其解，就可以得出结论．当乙追上丙时，甲和乙、丙的距离相等，求出乙追上丙的时间即可.综上即可的答案. 【详解】（1）45=23+(-3)3+43，2=73+(-5)3+(-6)3，故答案为23+(-3)3+43，73+(-5)3+(-6)3 （2）∵2a b a ab ⊗=-，∴()()532-⊗⊗-=⎡⎤⎣⎦(-5)⊗[32-3×(-2)]=(-5)⊗15 =(-5)2-(-5)×15 =100. （3）∵a 1=2， ∴a 2=1112=--， a 3=11(1)--=12， 412112a ==-a 5=-1 ……∴从a 1开始，每3个数一循环， ∵2500÷3=833……1， ∴a 2500=a 1=2，∴122500a a a ++⋅⋅⋅+=833×(2-1+12)+2=25032. （4）∵10个裁判打分，去掉一个最高分，再去掉一个最低分， ∴平均分为中间8个分数的平均分， ∵平均分精确到十分位的为9.4， ∴平均分在9.35至9.44之间， 9.35×8=74.8，9.44×8=75.52，∴8个裁判所给的总分在74.8至75.52之间， ∵打分都是整数， ∴总分也是整数， ∴总分为75，∴平均分为75÷8=9.375， ∴精确到百分位是9.38. 故答案为9.38（5）2019÷4=504……3，∵1+2-3=0，4-5-6+7=0，8-9-10+11=0，…… ∴(1+2-3)+(4-5-6+7)+……+(2016-2017-2018+2019)=0 ∴所得结果可能的最小非负数是0，故答案为0（6）设x 分钟后甲和乙、丙的距离相等，∵乙在甲前400米，丙在乙前400米，速度分别为120米/分钟、100米/分钟、90米/分钟，∴120x-400-100x=90x+800-120x解得：x=24.∵当乙追上丙时，甲和乙、丙的距离相等，∴400÷(100-90)=40(分钟)∴24分钟或40分钟时甲和乙、丙的距离相等.故答案为24或40.【点睛】本题考查数字类的变化规律、有理数的混合运算、近似数及一元一次方程的应用，熟练掌握相关知识是解题关键.3．探究三：16,6；结论：n²,;应用：625，300.【解析】【分析】探究三：模仿探究一、二即可解决问题；结论：由探究一、二、三可得：将边长为的正三角形的三条边分别等分，连接各边对应的等分点，边长为1的正三角形共有个；边长为2的正三角形共有个；应用：根据结论即可解决问题.【详解】解：探究三：如图3，连接边长为4的正三角形三条边的对应四等分点，从上往下看：边长为1的正三角形，第一层有1个，第二层有3个，第三层有5个，第四层有7个，共有个；边长为2的正三角形有个.结论：连接边长为的正三角形三条边的对应等分点，从上往下看：边长为1的正三角形，第一层有1个，第二层有3个，第三层有5个，第四层有7个，……，第层有个，共有个；边长为2的正三角形，共有个.应用：边长为1的正三角形有=625（个），边长为2的正三角形有（个）.故答案为探究三：16,6；结论：n², ;应用：625，300.【点睛】本题考查规律型问题，解题的关键是理解题意，学会模仿例题解决问题．4．（1）n= 8；（2）-2.5或2.5；（3）n=4或n=12．【解析】【分析】（1）根据“n节点”的概念解答；（2）设点D表示的数为x，根据“5节点”的定义列出方程分情况，并解答；（3）需要分类讨论：①当点E在BA延长线上时，②当点E在线段AB上时，③当点E在AB延长线上时，根据BE=12AE，先求点E表示的数，再根据AC+BC=n，列方程可得结论．【详解】（1）∵A表示的数为-2，B表示的数为2，点C在数轴上表示的数为-4，∴AC=2，BC=6，∴n=AC+BC=2+6=8．（2）如图所示：∵点D是数轴上点A、B的“5节点”，∴AC+BC=5，∵AB=4，∴C在点A的左侧或在点A的右侧，设点D表示的数为x，则AC+BC=5，∴-2-x+2-x=5或x-2+x-（-2）=5，x=-2.5或2.5，∴点D表示的数为2.5或-2.5；故答案为-2.5或2.5；（3）分三种情况：①当点E在BA延长线上时，∵不能满足BE=12 AE，∴该情况不符合题意，舍去；②当点E在线段AB上时，可以满足BE=12AE，如下图，n=AE+BE=AB=4；③当点E在AB延长线上时，∵BE=12 AE，∴BE=AB=4，∴点E表示的数为6，∴n=AE+BE=8+4=12，综上所述：n=4或n=12．【点睛】本题考查数轴，一元一次方程的应用，解题的关键是掌握“n节点”的概念和运算法则，找出题中的等量关系，列出方程并解答，难度一般．5．（1）（4，8）（2）S△OAE＝8﹣t（3）2秒或6秒【解析】【分析】（1）根据M和N的坐标和平移的性质可知：MN∥y轴∥PQ，根据K是PM的中点可得K 的坐标；（2）根据三角形面积公式可得三角形OAE的面积S；（3）存在两种情况：①如图2，当点B在OD上方时②如图3，当点B在OD上方时，过点B作BG⊥x轴于G，过D作DH⊥x轴于H，分别根据三角形OBD的面积等于三角形OAE的面积列方程可得结论．【详解】（1）由题意得：PM＝4，∵K是PM的中点，∴MK＝2，∵点M的坐标为（2，8），点N的坐标为（2，6），∴MN∥y轴，∴K（4，8）；（2）如图1所示，延长DA交y轴于F，则OF⊥AE，F（0，8﹣t），∴OF＝8﹣t，∴S△OAE＝12OF•AE＝12（8﹣t）×2＝8﹣t；（3）存在，有两种情况：，①如图2，当点B在OD上方时，过点B作BG⊥x轴于G，过D作DH⊥x轴于H，则B（2，6﹣t），D（6，0），∴OG＝2，GH＝4，BG＝6﹣t，DH＝8﹣t，OH＝6，S△OBD＝S△OBG+S四边形DBGH+S△ODH，＝12OG•BG+12（BG+DH）•GH﹣12OH•DH，＝12×2（6-t）+12×4（6﹣t+8﹣t）﹣12×6（8﹣t），＝10﹣2t，∵S△OBD＝S△OAE，∴10﹣2t＝8﹣t，t＝2；②如图3，当点B在OD上方时，过点B作BG⊥x轴于G，过D作DH⊥x轴于H，则B（2，6﹣t），D（6，8﹣t），∴OG＝2，GH＝4，BG＝6﹣t，DH＝8﹣t，OH＝6，S△OBD＝S△ODH﹣S四边形DBGH﹣S△OBG，＝12OH•DH﹣12（BG+DH）•GH﹣12OG•BG，＝12×2（8-t）﹣12×4（6﹣t+8﹣t）﹣12×2（6﹣t），＝2t﹣10，∵S△OBD＝S△OAE，∴2t﹣10＝8﹣t，t＝6；综上，t的值是2秒或6秒．【点睛】本题考查四边形综合题、矩形的性质、三角形的面积、一元一次方程等知识，解题关键是灵活运用所学知识解决问题，学会用分类讨论的思想思考问题．6．（1）25-，35（2）运动时间为4秒，相遇点表示的数字为27 ；（3）5;(4) 一共相遇了7次.【解析】【分析】（1）根据0+0式的定义即可解题；（2）设运动时间为x秒,表示出P,Q的运动路程,利用路程和等于AB长即可解题；（3）根据点Q达到A点时，点P，Q停止运动求出运动时间即可解题；（4）根据第三问点P运动了6个来回后，又运动了30个单位长度即可解题.【详解】解：（1）25-，35（2）设运动时间为x秒13x2x2535+=+解得x4=352427-⨯=答：运动时间为4秒，相遇点表示的数字为27（3）运动总时间：60÷2=30（秒），13×30÷60=6…30即点P运动了6个来回后，又运动了30个单位长度,∵25305-+=，∴点P所在的位置表示的数为5 .（4）由（3）得：点P运动了6个来回后，又运动了30个单位长度,∴点P和点Q一共相遇了6+1=7次.【点睛】本题考查了一元一次方程的实际应用,数轴的应用,难度较大,熟悉路程,时间,速度之间的关系是解题关键.7．（1）图1中小于平角的角∠AOD，∠AOC，∠AOB，∠BOE，∠BOD，∠BOC，∠COE，∠COD，∠DOE；（2）∠BOD＝54°；（3）∠AOE+∠AOB+∠AOC+∠AOD+∠BOC+∠BOD+∠BOE+∠COD+∠COE+∠DOE＝412°．理由见解析. 【解析】【分析】（1）根据角的定义即可解决；（2）利用角平分线的性质即可得出∠BOD=12∠AOC+12∠COE，进而求出即可；（3）将图中所有锐角求和即可求得所有锐角的和与∠AOE、∠BOD和∠BOD的关系，即可解题．【详解】（1）如图1中小于平角的角∠AOD，∠AOC，∠AOB，∠BOE，∠BOD，∠BOC，∠COE，∠COD，∠DOE．（2）如图2，∵OB平分∠AOE，OD平分∠COE，∠AOC＝108°，∠COE＝n°（0＜n＜72），∴∠BOD＝12∠AOD﹣12∠COE+12∠COE＝12×108°＝54°；（3）如图3，∠AOE＝88°，∠BOD＝30°，图中所有锐角和为∠AOE+∠AOB+∠AOC+∠AOD+∠BOC+∠BOD+∠BOE+∠COD+∠COE+∠DOE＝4∠AOB+4∠DOE＝6∠BOC+6∠COD＝4（∠AOE﹣∠BOD）+6∠BOD＝412°．【点睛】本题考查了角的平分线的定义和角的有关计算，本题中将所有锐角的和转化成与∠AOE、∠BOD和∠BOD的关系是解题的关键，8．（1）20；（2）t=15s或17s （3）4 3 s.【解析】【分析】（1）设P、Q速度分别为3m、2m，根据12秒后，动点P到达原点O列方程，求出P、Q 的速度，由此即可得到结论．（2）分两种情况讨论：①当A、B在相遇前且相距5个单位长度时；②当A、B在相遇后且相距5个单位长度时；列方程，求解即可．（3）算出P运动到B再到原点时，所用的时间，再算出Q从B到A所需的时间，比较即可得出结论．【详解】（1）设P、Q速度分别为3m、2m，根据题意得：12×3m=36，解得：m=1，∴P、Q速度分别为3、2，∴BC=12×2=24，∴OC=OB－BC=44－24=20．（2）当A、B在相遇前且相距5个单位长度时：3t＋2t＋5=44＋36，5t=75，∴t=15（s）；当A、B在相遇后且相距5个单位长度时：3t＋2t－5=44＋36，5t=85，∴t=17（s）．综上所述：t=15s或17s．（3）P运动到原点时，t=3644443++=1243s，此时QB=2×1243=2483＞44+38=80，∴Q点已到达A点，∴Q点已到达A点的时间为：3644804022+==（s），故提前的时间为：1243－40=43（s）．【点睛】本题考查了一元一次方程的应用-行程问题以及数轴上的动点问题．解题的关键是找出等量关系，列出方程求解．9．（1）CO=2.5；（2）①14和16 ；②定值55，理由见解析；（3）t=22.5和67.5【解析】【分析】（1）先求出线段AB的长，然后根据线段中点的定义解答即可；（2）①由PQ=1，得到|15-（4x-3x）|=1，解方程即可；②先表示出PM、OQ、OM的长，代入4PM+3OQ﹣mOM得到55+（21-7m）x，要使4PM+3OQ﹣mOM为定值，则21-7m=0，解方程即可；（3）分两种情况讨论，画出图形，根据图形列出方程，解方程即可．【详解】（1）∵OA=10cm，OB=5cm，∴AB=OA+OB=15cm．∵点C是线段AB的中点，∴AC=AB=7.5cm，∴CO=AO-AC=10-7.5=2.5（cm）．（2）①∵PQ=1，∴|15-（4x-3x）|=1，∴|15-x|=1，∴15-x=±1，解得：x=14或16．②∵PM=10+7x-4x=10+3x，OQ=5+3x，OM=7x，∴4PM+3OQ﹣mOM=4（10+3x）+3（5+3x）-7mx=55+（21-7m）x，要使4PM+3OQ﹣mOM为定值，则21-7m=0，解得：m=3，此时定值为55．（3）分两种情况讨论：①如图1，根据题意得：6t-2t=90，解得：t=22.5；②如图2，根据题意得：6t+90=360+2t，解得：t=67.5．综上所述：当t =22.5秒和67.5秒时，射线 OC ⊥OD ．【点睛】本题考查了一元一次方程的应用．解题的关键是分类讨论．10．（1）是；（2）5cm 或7.5cm 或10cm ；（3）10或607．【解析】【分析】（1）根据“2倍点”的定义即可求解；（2）分点C 在中点的左边，点C 在中点，点C 在中点的右边三种情况，进行讨论求解即可；（3）根据题意画出图形，P 应在Q 的右边，分别表示出AQ 、QP 、PB ，求出t 的范围．然后根据（2）分三种情况讨论即可．【详解】（1）∵整个线段的长是较短线段长度的2倍，∴线段的中点是这条线段的“2倍点”．故答案为是；（2）∵AB ＝15cm ，点C 是线段AB 的2倍点，∴AC ＝1513⨯=5cm 或AC ＝1512⨯=7.5cm 或AC ＝1523⨯=10cm ．（3）∵点Q 是线段AP 的“2倍点”，∴点Q 在线段AP 上．如图所示：由题意得：AP =2t ，BQ =t ，∴AQ =20-t ，QP =2t -（20-t ）=3t -20，PB =20-2t ．∵PB =20-2t ≥0，∴t ≤10．∵QP =3t -20≥0，∴t ≥203，∴203≤t ≤10．分三种情况讨论：①当AQ ＝13AP 时，20-t ＝13×2t ，解得：t ＝12＞10，舍去； ②当AQ ＝12AP 时，20-t ＝12×2t ，解得：t ＝10； ③当AQ ＝23AP 时，20-t ＝23×2t ，解得：t 607=；答：t 为10或607时，点 Q 是线段AP 的“2倍点”．【点睛】本题考查了一元一次方程的解法、线段的和差等知识点，题目需根据“2倍点”的定义分类讨论，理解“2倍点”的定义是解决本题的关键．11．（1）AC=4cm, BC=8cm ；(2)当45t =时，AP PQ =；(3)当2t =时，P 与Q 第一次相遇；(4)35191cm.224t PQ =当为，，时，【解析】【分析】（1）由于AB=12cm ，点C 是线段AB 上的一点，BC=2AC ，则AC+BC=3AC=AB=12cm ，依此即可求解；（2）分别表示出AP 、PQ ，然后根据等量关系AP=PQ 列出方程求解即可；（3）当P 与Q 第一次相遇时由AP AC CQ =+得到关于t 的方程，求解即可；（4）分相遇前、相遇后以及到达B 点返回后相距1cm 四种情况列出方程求解即可．【详解】（1）AC=4cm, BC=8cm.(2) 当AP PQ =时，AP 3t,PQ AC AP CQ 43t t ==-+=-+,即3t 43t t =-+,解得4t 5=. 所以当4t 5=时，AP PQ =. (3) 当P 与Q 第一次相遇时，AP AC CQ =+,即3t 4t =+,解得t 2=.所以当t 2=时，P 与Q 第一次相遇.(4)()()P,Q 1cm,4t 3t 13t 4t 1+-=-+=因为点相距的路程为所以或，35t t 22解得或==， P B P,Q 1cm 当到达点后时立即返回，点相距的路程为，193t 4t 1122,t 4+++=⨯=则解得， 3519t PQ 1cm.224所以当为，，时，= 【点睛】此题考查一元一次方程的实际运用，掌握行程问题中的基本数量关系以及分类讨论思想是解决问题的关键．12．（1）16；（2）①t 的值为3或143秒；②存在，P 表示的数为314.【解析】【分析】（1）由数轴可知，AB=3,则CD=6,所以D 表示的数为16，（2）①当运动时间是t 秒时，在运动过程中，B 点表示的数为3+2t,A 点表示的数为2t, C 点表示的数为10-t ，D 点表示的数为16-t ，分情况讨论两条线段重叠部分是2个单位长度解答即可；②分情况讨论当t=3秒, t=143秒时，满足3BD PA PC -=的点P , 注意P 为线段AB 上的点对x 的值的限制.【详解】（1）16（2）①在运动过程中，B 点表示的数为3+2t,A 点表示的数为2t,C 点表示的数为10-t ，D 点表示的数为16-t.当BC ＝2，点B 在点C 的右边时，由题意得：32-10-2BC t t =+=（），解得：t ＝3，当AD=2，点A 在点D 的左边时，由题意得：16--22AD t t ==，解得：t ＝143．综上，t 的值为3或143秒 ②存在，理由如下:当t=3时，A 点表示的数为6，B 点表示的数为9，C 点表示的数为7，D 点表示的数为13. 则13-94-6|-7|BD PA x PC x ====，，，-3BD PA PC =，()4--6|-7|x x ∴=，解得：314x =或112，又P 点在线段AB 上，则69x ≤≤314x ∴=. 当143t =时，A 点表示的数为283，B 点表示的数为373，C 点表示的数为163，D 点表示的数为343. 则37343816-1-|-|3333BD PA x PC x ====，，， -3BD PA PC =，∴ 28161--|-|33x x ⎛⎫= ⎪⎝⎭，解得：7912x =或176，又283733x ≤≤， x ∴无解综上，P 表示的数为314. 【点睛】本题考查了一元一次方程的应用以及数轴，解题的关键是：(1)由路程=速度×时间结合运动方向找出运动t 秒时点A 、B 、C 、D 所表示的数,(2)根据3BD PA PC -=列出关于t 的含绝对值符号的一元一次方程．13．（1）2AC cm =，4DM cm =；（2）6AC MD cm +=；（3）4AM =；（4）13MN AB =或1．【解析】【详解】（1）根据题意知，CM=2cm ，BD=4cm ．∵AB=12cm ，AM=4cm ，∴BM=8cm ，∴AC=AM ﹣CM=2cm ，DM=BM ﹣BD=4cm ．故答案为2，4；（2）当点C 、D 运动了2 s 时，CM=2 cm ，BD=4 cm ．∵AB=12 cm ，CM=2 cm ，BD=4 cm ，∴AC+MD=AM ﹣CM+BM ﹣BD=AB ﹣CM ﹣BD=12﹣2﹣4=6 cm ；（3）根据C 、D 的运动速度知：BD=2MC ．∵MD=2AC ，∴BD+MD=2（MC+AC ），即MB=2AM ．∵AM+BM=AB ，∴AM+2AM=AB ，∴AM=13AB=4．故答案为4；（4）①当点N 在线段AB 上时，如图1．∵AN ﹣BN=MN ．又∵AN ﹣AM=MN ，∴BN=AM=4，∴MN=AB ﹣AM ﹣BN=12﹣4﹣4=4，∴MN AB =412=13； ②当点N 在线段AB 的延长线上时，如图2．∵AN ﹣BN=MN ．又∵AN ﹣BN=AB ，∴MN=AB=12，∴MN AB =1212=1．综上所述：MN AB =13或1．【点睛】本题考查了两点间的距离，灵活运用线段的和、差、倍、分转化线段之间的数量关系是十分关键的一点．14．问题一、(1)32；（2）3-2x ；2x -3；13-6x ；问题一、（1）35；120；24011. 【解析】【分析】问题一根据等量关系，路程=速度⨯时间，路程差=路程1-路程2，即可列出方程求解。

(完整版)初一数学上册压轴题测试卷及答案

(完整版)初一数学上册压轴题测试卷及答案一、压轴题1．已知ABC ，P 是平面内任意一点（A 、B 、C 、P 中任意三点都不在同一直线上）．连接 PB 、PC ，设∠PBA ＝s°，∠PCA ＝t°，∠BPC ＝x°，∠BAC ＝y°．（1）如图，当点 P 在ABC 内时，①若 y ＝70，s ＝10，t ＝20，则 x ＝；②探究 s 、t 、x 、y 之间的数量关系，并证明你得到的结论．（2）当点 P 在ABC 外时，直接写出 s 、t 、x 、y 之间所有可能的数量关系，并画出相应的图形．2．如图，ABC ∆在平面直角坐标系中，60BAC ∠=︒，()0,43A ，8AB =，点B 、C 在x 轴上且关于y 轴对称．（1）求点C 的坐标；（2）动点P 以每秒2个单位长度的速度从点B 出发沿x 轴正方向向终点C 运动，设运动时间为t 秒，点P 到直线AC 的距离PD 的长为d ，求d 与t 的关系式；（3）在（2）的条件下，当点P 到AC 的距离PD 为33AP ，作ACB ∠的平分线分别交PD 、PA 于点M 、N ，求MN 的长．3．已知在△ABC 中，AB ＝AC ，射线BM 、BN 在∠ABC 内部，分别交线段AC 于点G 、H ．（1）如图1，若∠ABC ＝60°，∠MBN ＝30°，作AE ⊥BN 于点D ，分别交BC 、BM 于点E 、F ．①求证：∠1＝∠2；②如图2，若BF ＝2AF ，连接CF ，求证：BF ⊥CF ；（2）如图3，点E 为BC 上一点，AE 交BM 于点F ，连接CF ，若∠BFE ＝∠BAC ＝2∠CFE ，求ABF ACF S S 的值．4．（阅读材科）小明同学发现这样一个规律：两个顶角相等的等腰三角形，如果具有公共的项角的顶点，并把它们的底角顶点连接起来则形成一组全等的三角形，小明把具有这个规律的图形称为“手拉手”图形．如图1，在“手拉手”图形中，小明发现若∠BAC =∠DAE ，AB =AC ，AD =AE ，则△ABD ≌△ACE ．（材料理解）（1）在图1中证明小明的发现．（深入探究）（2）如图2，△ABC 和△AED 是等边三角形，连接BD ，EC 交于点O ，连接AO ，下列结论：①BD =EC ；②∠BOC =60°；③∠AOE =60°；④EO =CO ，其中正确的有．(将所有正确的序号填在横线上)．（延伸应用）（3）如图3，AB =BC ，∠ABC =∠BDC =60°，试探究∠A 与∠C 的数量关系．5．问题情景：数学课上，老师布置了这样一道题目，如图1，△ABC 是等边三角形，点D 是BC 的中点，且满足∠ADE ＝60°，DE 交等边三角形外角平分线于点E ．试探究AD 与DE 的数量关系．操作发现：（1）小明同学过点D 作DF ∥AC 交AB 于F ，通过构造全等三角形经过推理论证就可以解决问题，请您按照小明同学的方法确定AD 与DE 的数量关系，并进行证明．类比探究：（2）如图2，当点D是线段BC上任意一点(除B、C外)，其他条件不变，试猜想AD与DE之间的数量关系，并证明你的结论．拓展应用：（3）当点D在线段BC的延长线上，且满足CD＝BC，在图3中补全图形，直接判断△ADE的形状(不要求证明)．6．学习了三角形全等的判定方法（即“SAS”、“ASA”、“AAS”、“SSS”）和直角三角形全等的判定方法（即“HL”）后，我们继续对“两个三角形满足两边的其中一边的对角对应相等”的情形进行研究．（初步思考）我们不妨将问题用符号语言表示为：在△DEF中，AC＝DF，BC＝EF，∠B＝∠E，然后，对∠B进行分类，可分为“∠B是直角、钝角、锐角”三种情况进行探究．（深入探究）第一种情况：当∠B是直角时，△ABC≌△DEF．（1）如图①，在△ABC和△DEF中，AC＝DF，BC＝EF，∠B＝∠E＝90°，根据______，可以知道Rt△ABC≌Rt△DEF．第二种情况：当∠B 是钝角时，△ABC ≌△DEF ．（2）如图②，在△ABC 和△DEF 中，AC ＝DF ，BC ＝EF ，∠B ＝∠E ，且∠B 、∠E 都是钝角．求证：△ABC ≌△DEF ．第三种情况：当∠B 是锐角时，△ABC 和△DEF 不一定全等．（3）在△ABC 和△DEF 中，AC ＝DF ，BC ＝EF ，∠B ＝∠E ，且∠B 、∠E 都是锐角．请你用直尺在图③中作出△DEF ，使△DEF 和△ABC 不全等，并作简要说明．7．如图，若要判定纸带两条边线a ，b 是否互相平行，我们可以采用将纸条沿AB 折叠的方式来进行探究．（1）如图1，展开后，测得12∠=∠，则可判定a//b ，请写出判定的依据_________；（2）如图2，若要使a//b ，则1∠与2∠应该满足的关系是_________；（3）如图3，纸带两条边线a ，b 互相平行，折叠后的边线b 与a 交于点C ，若将纸带沿11A B （1A ，1B 分别在边线a ，b 上）再次折叠，折叠后的边线b 与a 交于点1C ，AB//11A B ，137BB AC ==，，求出1AC 的长．8．如图，在等边ABC ∆中，线段AM 为BC 边上的中线．动点D 在直线AM 上时，以CD 为一边在CD 的下方作等边CDE ∆，连结BE ．（1）求CAM ∠的度数；（2）若点D 在线段AM 上时，求证：ADC BEC ∆≅∆；（3）当动点D 在直线AM 上时，设直线BE 与直线AM 的交点为O ，试判断AOB ∠是否为定值？并说明理由．9．在△ABC 中，∠BAC =45°，CD ⊥AB ，垂足为点D ，M 为线段DB 上一动点（不包括端点），点N 在直线AC 左上方且∠NCM =135°，CN =CM ，如图①．（1）求证：∠ACN =∠AMC ；（2）记△ANC 得面积为5，记△ABC 得面积为5．求证：12S AC S AB=；（3）延长线段AB 到点P ，使BP =BM ，如图②．探究线段AC 与线段DB 满足什么数量关系时对于满足条件的任意点M ，AN =CP 始终成立？（写出探究过程）10．如图，△ABC 是等边三角形，△ADC 与△ABC 关于直线AC 对称，AE 与CD 垂直交BC 的延长线于点E ，∠EAF ＝45°，且AF 与AB 在AE 的两侧，EF ⊥AF ．（1）依题意补全图形．（2）①在AE 上找一点P ，使点P 到点B ，点C 的距离和最短；②求证：点D 到AF ，EF 的距离相等．11．如图，以直角三角形AOC 的直角顶点O 为原点，以OC ，OA 所在直线为轴和轴建立平面直角坐标系，点A （0，a ），C （b ，0a 6b 80--=．（1）a = ；b = ；直角三角形AOC 的面积为．（2）已知坐标轴上有两动点P ，Q 同时出发，P 点从C 点出发以每秒2个单位长度的速度向点O 匀速移动，Q 点从O 点出发以每秒1个单位长度的速度向点A 匀速移动，点P 到达O 点整个运动随之结束．AC 的中点D 的坐标是（4，3），设运动时间为t 秒．问：是否存在这样的t ，使得△ODP 与△ODQ 的面积相等？若存在，请求出t 的值；若不存在，请说明理由．（3）在（2）的条件下，若∠DOC =∠D CO ，点G 是第二象限中一点，并且y 轴平分∠GOD ．点E 是线段OA 上一动点，连接接CE 交OD 于点H ，当点E 在线段OA 上运动的过程中，探究∠GOD ，∠OHC ，∠ACE 之间的数量关系，并证明你的结论(三角形的内角和为180)．12．数学活动课上，老师出了这样一个题目：“已知：MF NF ⊥于F ，点A 、C 分别在NF 和MF 上，作线段AB 和CD （如图1），使90FAB MCD ∠-∠=︒．求证：//AB CD ”．（1）聪聪同学给出一种证明问题的辅助线：如图2，过A 作//AG FM ，交CD 于G ．请你根据聪聪同学提供的辅助线（或自己添加其它辅助线），给出问题的证明．（2）若点E 在直线CD 下方，且知30BED ∠=︒，直接写出ABE ∠和CDE ∠之间的数量关系．13．在△ABC 中，AB =AC ，D 是直线BC 上一点，以AD 为一条边在AD 的右侧作△ADE ，使AE =AD ，∠DAE =∠BAC ，连接CE ．（1）如图，当点D 在BC 延长线上移动时，若∠BAC =40°，则∠ACE = ，∠DCE = ，BC 、DC 、CE 之间的数量关系为；（2）设∠BAC =α，∠DCE =β．①当点D 在BC 延长线上移动时，α与β之间有什么数量关系？请说明理由； ②当点D 在直线BC 上（不与B ，C 两点重合）移动时，α与β之间有什么数量关系？请直接写出你的结论．（3）当CE ∥AB 时，若△ABD 中最小角为15°，试探究∠ACB 的度数（直接写出结果，无需写出求解过程）．14．（1）如图1，ABC 和DCE 都是等边三角形，且B ，C ，D 三点在一条直线上，连接AD ，BE 相交于点P ，求证：BE AD =．（2）如图2，在BCD 中，若120BCD ∠<︒，分别以BC ，CD 和BD 为边在BCD 外部作等边ABC ，等边CDE △，等边BDF ，连接AD 、BE 、CF 恰交于点P ． ①求证：AD BE CF ==；②如图2，在（2）的条件下，试猜想PB ，PC ，PD 与BE 存在怎样的数量关系，并说明理由．15．探究发现：如图①，在ABC 中，内角ACB ∠的平分线与外角ABD ∠的平分线相交于点E ．（1）若80A ∠=︒，则E ∠= ；若50A ∠=︒，则E ∠= ；（2）由此猜想：A ∠与E ∠的关系为 (不必说明理由)．拓展延伸：如图②，四边形ABCD 的内角DCB ∠与外角ABE ∠的平分线相交于点F ，//BF CD ．（3）若125A ∠=︒，95D ∠=︒，求F ∠的度数，由此猜想F ∠与A ∠，D ∠之间的关系，并说明理由．16．已知//,MN GH 在Rt ABC 中，90,30ACB BAC ∠=︒∠=︒，点A 在MN 上，边BC 在GH 上，在Rt DEF △中，90,DFE ∠=︒边DE 在直线AB 上，45EDF ∠=︒；（1）如图1，求BAN ∠的度数；（2）如图2，将Rt DEF △沿射线BA 的方向平移，当点F 在M 上时，求AFE ∠度数；（3）将Rt DEF △在直线AB 上平移，当以A D F 、、为顶点的三角形是直角三角形时，直接写出FAN ∠度数．17．完全平方公式：()2222a b a ab b ±=±+适当的变形，可以解决很多的数学问题．例如：若3,1a b ab ，求22a b +的值．解：因为3,1a b ab 所以()29,22a b ab +==所以2229,22a b ab ab ++==得227a b +=．根据上面的解题思路与方法，解决下列问题：（1）若228,40x y x y +=+=，求xy 的值；（2）①若()45x x -=,则()224x x -+= ； ②若()()458x x --=则()22()45x x -+-= ；（3）如图，点C 是线段AB 上的一点，以AC BC 、为边向两边作正方形，设6AB =，两正方形的面积和1218S S +=，求图中阴影部分面积．18．（1）在等边三角形ABC 中，①如图①，D ，E 分别是边AC ，AB 上的点且AE=CD ，BD 与EC 交于点F ，则∠BFE 的度数是度；②如图②，D ，E 分别是边AC ，BA 延长线上的点且AE=CD ，BD 与EC 的延长线交于点F ，此时∠BFE 的度数是度；（2）如图③，在△ABC 中，AC=BC ，∠ACB 是锐角，点O 是AC 边的垂直平分线与BC 的交点，点D ，E 分别在AC ，OA 的延长线上，AE=CD ，BD 与EC 的延长线交于点F ，若∠ACB=α，求∠BFE 的大小．（用含α的代数式表示）．19．如图，在ABC ∆中，90,,8ACB AC BC AB cm ∠=︒==，过点C 做射线CD ，且//CD AB ，点P 从点C 出发，沿射线CD 方向均匀运动，速度为3/cm s ；同时，点Q 从点A 出发，沿AB 向点B 匀速运动，速度为1/cm s ，当点Q 停止运动时，点P 也停止运动．连接,PQ CQ ，设运动时间为()()08t s t <<．解答下列问题：（1）用含有t 的代数式表示CP 和BQ 的长度；（2）当2t =时，请说明//PQ BC ；（3）设BCQ ∆的面积为()2S cm ，求S 与t 之间的关系式． 20．在ABC ∆中，若存在一个内角角度，是另外一个内角角度的n 倍（n 为大于1的正整数），则称ABC ∆为n 倍角三角形．例如，在ABC ∆中，80A ∠=︒，75B ∠=︒，25C ∠=︒，可知3∠=∠B C ，所以ABC ∆为3倍角三角形．（1）在ABC ∆中，55A ∠=︒，25B ∠=︒，则ABC ∆为________倍角三角形；（2）若DEF ∆是3倍角三角形，且其中一个内角的度数是另外一个内角的余角的度数的13，求DEF ∆的最小内角．（3）若MNP ∆是2倍角三角形，且90M N P ∠<∠<∠<︒，请直接写出MNP ∆的最小内角的取值范围．【参考答案】***试卷处理标记，请不要删除一、压轴题1．（1）①100；②x=y+s+t；（2）见详解．【解析】【分析】（1）①利用三角形的内角和定理即可解决问题；②结论：x=y+s+t．利用三角形内角和定理即可证明；（2）分6种情形分别求解即可解决问题．【详解】解：（1）①∵∠BAC=70°，∴∠ABC+∠ACB=110°，∵∠PBA=10°，∠PCA=20°，∴∠PBC+∠PCB=80°，∴∠BPC=100°，∴x=100，故答案为：100．②结论：x=y+s+t．理由：∵∠A+∠ABC+∠ACB=∠A+∠PBA+∠PCA+∠PBC+∠PCB=180°，∠PBC+∠PCB+∠BPC=180°，∴∠A+∠PBA+∠PCA=∠BPC，∴x=y+s+t．（2）s、t、x、y之间所有可能的数量关系：如图1：s+x=t+y；如图2：s+y=t+x；如图3：y=x+s+t；如图4：x+y+s+t=360°；如图5：t=s+x+y ；如图6：s=t+x+y ；【点睛】本题考查三角形的内角和定理，三角形的外角的性质等知识，解题的关键是学会用分类讨论的思想思考问题．2．（1）C （4，0）；（2）433d t =；（3）103MN =【解析】【分析】（1）根据对称的性质知ABC ∆为等边三角形，利用直角三角形中30度角的性质即可求得答案；（2）利用面积法可求得AC PD PC OA ⋅=⋅，再利用坐标系中点的特征即可求得答案；（3）利用(2)的结论求得2BP =，利用角平分线的性质证得ABO CBQ ∆∆≌，求得43CQ AO ==，利用面积法求得437QN =，再利用直角三角形中30度角的性质即可求得答案．【详解】（1）∵点B 、C 关于y 轴对称，∴12OB OC BC ==， ∴AB AC =，∵60BAC ∠=︒，∴ABC ∆为等边三角形，∴8AB BC AC ===，∴142OC BC ==， ∴点C 的坐标为：()4,0C ；（2）连接AP ，∵1122APC S AC PD PC OA ∆=⋅=⋅， ∴AC PD PC OA ⋅=⋅，∵(0,43A ，∴43OA =∵2BP t =，∴82PC t =-，∵8AC =， ∴433PC OA PD t AC ⋅==-，即：433d t =-；（3）∵点P 到AC 的距离为33，∴43333d t =-=，∴1t =，∴2BP =，延长CN 交AB 于点Q ，过点N 作NE x ⊥轴于点E ，连接PQ 、BN ，∵CQ 为ACB ∠的角平分线，ABC ∆为等边三角形，∴1302BCQ ACB ∠=∠=︒，CQ AB ⊥， ∵1302BAO BAC ∠=∠=︒，AB BC =， ∴ABO CBQ ∆∆≌，∴43CQ AO ==设2QN a =，在Rt CNE ∆中，30QCB ∠=︒，∴11(432)2322NE CN a a ===， ∵ABP ABN BPN S S S ∆∆∆=+，∴111222BP OA AB QN BP NE ⋅=⋅+⋅，∴1112822)222a a ⨯⨯=⨯⨯+⨯⨯，∴a =∴QN =， ∵60ACB ∠=︒，90PDC ∠=︒，∴30DPC ∠=︒，∵30BCQ ∠=︒，∴PM CM =，在Rt CDM ∆中，90MDC ∠=︒，30MCD ∠=︒， ∴12MD MC =，∴12MD PM =，PD =∴PM CM ==∴MN CQ QN CM =--== 【点睛】本题是三角形综合题，涉及的知识有：含30度直角三角形的性质，全等三角形的判定与性质，外角性质，角平分线的性质，等边三角形的判定和性质，坐标与图形性质，熟练掌握性质及定理、灵活运用面积法求线段的长是解本题的关键．3．（1）①见解析；②见解析；（2）2【解析】【分析】（1）①只要证明∠2+∠BAF ＝∠1+∠BAF ＝60°即可解决问题；②只要证明△BFC ≌△ADB ，即可推出∠BFC ＝∠ADB ＝90°；（2）在BF 上截取BK ＝AF ，连接AK ．只要证明△ABK ≌CAF ，可得S △ABK ＝S △AFC ，再证明AF ＝FK ＝BK ，可得S △ABK ＝S △AFK ，即可解决问题；【详解】（1）①证明：如图1中，∵AB＝AC，∠ABC＝60°∴△ABC是等边三角形，∴∠BAC＝60°，∵AD⊥BN，∴∠ADB＝90°，∵∠MBN＝30°，∠BFD＝60°＝∠1+∠BAF＝∠2+∠BAF，∴∠1＝∠2②证明：如图2中，在Rt△BFD中，∵∠FBD＝30°，∴BF＝2DF，∵BF＝2AF，∴BF＝AD，∵∠BAE＝∠FBC，AB＝BC，∴△BFC≌△ADB，∴∠BFC＝∠ADB＝90°，∴BF⊥CF（2）在BF上截取BK＝AF，连接AK．∵∠BFE＝∠2+∠BAF，∠CFE＝∠4+∠1，∴∠CFB ＝∠2+∠4+∠BAC ，∵∠BFE ＝∠BAC ＝2∠EFC ，∴∠1+∠4＝∠2+∠4∴∠1＝∠2，∵AB ＝AC ，∴△ABK ≌CAF ，∴∠3＝∠4，S △ABK ＝S △AFC ，∵∠1+∠3＝∠2+∠3＝∠CFE ＝∠AKB ，∠BAC ＝2∠CEF ，∴∠KAF ＝∠1+∠3＝∠AKF ，∴AF ＝FK ＝BK ，∴S △ABK ＝S △AFK ， ∴ABF AFCS 2S ∆∆=．【点睛】本题考查全等三角形的判定和性质、等边三角形的性质、等腰三角形的判定和性质、直角三角形30度角性质等知识，解题的关键是能够正确添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．4．（1）证明见解析；（2）①②③；（3）∠A +∠C =180°．【解析】【分析】（1）利用等式的性质得出∠BAD=∠CAE ，即可得出结论；（2）同（1）的方法判断出△ABD ≌△ACE ，得出BD=CE ，再利用对顶角和三角形的内角和定理判断出∠BOC=60°，再判断出△BCF ≌△ACO ，得出∠AOC=120°，进而得出∠AOE=60°，再判断出BF ＜CF ，进而判断出∠OBC ＞30°，即可得出结论；（3）先判断出△BDP 是等边三角形，得出BD=BP ，∠DBP=60°，进而判断出△ABD ≌△CBP （SAS ），即可得出结论．【详解】（1）证明：∵∠BAC=∠DAE ，∴∠BAC+∠CAD=∠DAE+∠CAD ，∴∠BAD=∠CAE ，在△ABD 和△ACE 中，AB AC BAD CAE AD AE ⎧⎪∠∠⎨⎪⎩＝＝＝， ∴△ABD ≌△ACE ；（2）如图2，∵△ABC 和△ADE 是等边三角形，∴AB=AC ，AD=AE ，∠BAC=∠DAE=60°，∴∠BAD=∠CAE ，在△ABD 和△ACE 中，AB AC BAD CAE AD AE ⎧⎪∠∠⎨⎪⎩＝＝＝， ∴△ABD ≌△ACE ，∴BD=CE ，①正确，∠ADB=∠AEC ，记AD 与CE 的交点为G ，∵∠AGE=∠DGO ，∴180°-∠ADB-∠DGO=180°-∠AEC-∠AGE ，∴∠DOE=∠DAE=60°，∴∠BOC=60°，②正确，在OB 上取一点F ，使OF=OC ，∴△OCF 是等边三角形，∴CF=OC ，∠OFC=∠OCF=60°=∠ACB ，∴∠BCF=∠ACO ，∵AB=AC ，∴△BCF ≌△ACO （SAS ），∴∠AOC=∠BFC=180°-∠OFC=120°，∴∠AOE=180°-∠AOC=60°，③正确，连接AF ，要使OC=OE ，则有OC=12CE ， ∵BD=CE ，∴CF=OF=12BD ， ∴OF=BF+OD ，∴BF ＜CF ，∴∠OBC ＞∠BCF ，∵∠OBC+∠BCF=∠OFC=60°，∴∠OBC ＞30°，而没办法判断∠OBC 大于30度，所以，④不一定正确，即：正确的有①②③，故答案为①②③；（3）如图3，延长DC 至P ，使DP=DB ，∵∠BDC=60°，∴△BDP 是等边三角形，∴BD=BP ，∠DBP=60°，∵∠BAC=60°=∠DBP ，∴∠ABD=∠CBP ，∵AB=CB ，∴△ABD ≌△CBP （SAS ），∴∠BCP=∠A ，∵∠BCD+∠BCP=180°，∴∠A+∠BCD=180°．【点睛】此题考查三角形综合题，等腰三角形的性质，等边三角形的性质，全等三角形的判定和性质，构造等边三角形是解题的关键．5．（1）AD ＝DE ，见解析；（2）AD ＝DE ，见解析；（3）见解析，△ADE 是等边三角形，【解析】【分析】（1）根据题意，通过平行线的性质及等边三角形的性质证明ADF EDC ∆∆≌即可得解；（2）根据题意，通过平行线的性质及等边三角形的性质证明AFD DCE ∆∆≌即可得解；（3）根据垂直平分线的性质及等边三角形的判定定理进行证明即可.【详解】（1）如下图，数量关系：AD ＝DE .证明：∵ABC ∆是等边三角形∴AB ＝BC ，60B BAC BCA ∠∠∠︒＝＝＝∵DF ∥AC∴BFD BAC ∠∠＝，∠BDF ＝∠BCA∴60B BFD BDF ∠∠∠︒＝＝＝∴BDF ∆是等边三角形，120AFD ∠︒＝∴DF ＝BD∵点D 是BC 的中点∴BD ＝CD∴DF ＝CD∵CE 是等边ABC ∆的外角平分线∴120DCE AFD ∠︒∠＝＝ ∵ABC ∆是等边三角形，点D 是BC 的中点∴AD ⊥BC∴90ADC ∠︒＝∵60BDF ADE ∠∠︒＝＝∴30ADF EDC ∠∠︒＝＝在ADF ∆与EDC ∆中AFD ECD DF CDADF EDC ∠∠⎧⎪⎨⎪∠∠⎩＝＝＝ ∴()ADF EDC ASA ∆∆≌∴AD ＝DE ；（2）结论：AD ＝DE .证明：如下图，过点D 作DF ∥AC ，交AB 于F∵ABC ∆是等边三角形∴AB ＝BC ，60B BAC BCA ∠∠∠︒＝＝＝∵DF ∥AC∴BFD BAC BDF BCA ∠∠∠∠＝，＝∴60B BFD BDF ∠∠∠︒＝＝＝∴BDF ∆是等边三角形，120AFD ∠︒＝∴BF ＝BD∴AF ＝DC∵CE 是等边ABC ∆的外角平分线∴120DCE AFD ∠︒∠＝＝ ∵∠ADC 是ABD ∆的外角∴60ADC B FAD FAD ∠∠∠︒∠＝＋＝＋∵60ADC ADE CDE CDE ∠∠∠︒∠＝＋＝＋∴∠FAD ＝∠CDE在AFD ∆与DCE ∆中AFD DCE AF CDFAD EDC ∠∠⎧⎪⎨⎪∠∠⎩＝＝＝ ∴()AFD DCE ASA ∆∆≌∴AD ＝DE ；（3）如下图，ADE ∆是等边三角形.证明：∵BC CD =∴AC CD =∵CE 平分ACD ∠∴CE 垂直平分AD∴AE =DE∵60ADE ∠=︒∴ADE ∆是等边三角形.【点睛】本题主要考查了等边三角形的性质及判定，三角形全等的判定及性质，平行线的性质，垂直平分线的性质等相关内容，熟练掌握三角形综合解决方法是解决本题的关键.6．（1）HL ；（2）见解析；（3）如图②，见解析；△DEF 就是所求作的三角形，△DEF 和△ABC 不全等．【解析】【分析】（1）根据直角三角形全等的方法“HL”证明；（2）过点C作CG⊥AB交AB的延长线于G，过点F作FH⊥DE交DE的延长线于H，根据等角的补角相等求出∠CBG=∠FEH，再利用“角角边”证明△CBG和△FEH全等，根据全等三角形对应边相等可得CG=FH，再利用“HL”证明Rt△ACG和Rt△DFH全等，根据全等三角形对应角相等可得∠A=∠D，然后利用“角角边”证明△ABC和△DEF全等；（3）以点C为圆心，以AC长为半径画弧，与AB相交于点D，E与B重合，F与C重合，得到△DEF与△ABC不全等；（4）根据三种情况结论，∠B不小于∠A即可．【详解】（1）在直角三角形中一条斜边和一条直角边对应相等的两个直角三角形全等运用的是HL．（2）证明：如图①，分别过点C、F作对边AB、DE上的高CG、FH，其中G、H为垂足．∵∠ABC、∠DEF都是钝角∴G、H分别在AB、DE的延长线上．∵CG⊥AG，FH⊥DH，∴∠CGA＝∠FHD＝90°．∵∠CBG＝180°－∠ABC，∠FEH＝∠180°－∠DEF，∠ABC＝∠DEF，∴∠CBG＝∠FEH．在△BCG和△EFH中，∵∠CGB＝∠FHE，∠CBG＝∠FEH，BC＝EF，∴△BCG≌△EFH．∴CG＝FH．又∵AC＝DF．∴Rt△ACG≌△DFH．∴∠A＝∠D．在△ABC和△DEF中，∵∠ABC＝∠DEF，∠A＝∠D，AC＝DF，∴△ABC≌△DEF．（3）如图②，△DEF就是所求作的三角形，△DEF和△ABC不全等．【点睛】本题是三角形综合题，主要考查了全等三角形的判定与性质，应用与设计作图，熟练掌握三角形全等的判定方法是解题的关键，阅读量较大，审题要认真仔细．7．（1）内错角相等，两直线平行；（2）∠1+2∠2=180°；（3）4或10【解析】【分析】（1）根据平行线的判定定理，即可得到答案；（2）由折叠的性质得：∠3=∠4，若a ∥b ，则∠3=∠2，结合三角形内角和定理，即可得到答案；（3）分两种情况：①当B 1在B 的左侧时，如图2，当B 1在B 的右侧时，如图3，分别求出1AC 的长，即可得到答案．【详解】（1）∵12∠=∠，∴a ∥b （内错角相等，两直线平行），故答案是：内错角相等，两直线平行；（2）如图1，由折叠的性质得：∠3=∠4，若a ∥b ，则∠3=∠2，∴∠4=∠2，∵∠2+∠4+∠1=180°，∴∠1+2∠2=180°，∴要使a ∥b ，则1∠与2∠应该满足的关系是：∠1+2∠2=180°．故答案是：∠1+2∠2=180°；（3）①当B 1在B 的左侧时，如图2，∵AB//11A B ，a ∥b ，∴AA 1=BB 1=3，∴1AC =AC- AA 1=7-3=4；②当B 1在B 的右侧时，如图3，∵AB//11A B ，a ∥b ，∴AA 1=BB 1=3，∴1AC =AC+AA 1=7+3=10．综上所述：1AC =4或10．【点睛】本题主要考查平行线的判定和性质定理，折叠的性质以及三角形的内角和定理，掌握“平行线间的平行线段长度相等”是解题的关键．8．（1）30°；（2）证明见解析；（3）AOB ∠是定值，60AOB ∠=︒.【解析】【分析】（1）根据等边三角形的性质可以直接得出结论；（2）根据等边三角形的性质就可以得出AC AC =，DC EC =，，60ACB DCE ∠=∠=︒，由等式的性质就可以BCE ACD ∠=∠，根据SAS 就可以得出ADC BEC ∆≅∆；（3）分情况讨论：当点D 在线段AM 上时，如图1，由（2）可知ACD BCE ≅∆∆，就可以求出结论；当点D 在线段AM 的延长线上时，如图2，可以得出ACD BCE ≅∆∆而有30CBE CAD ∠=∠=︒而得出结论；当点D 在线段MA 的延长线上时，如图3，通过得出ACD BCE ≅∆∆同样可以得出结论．【详解】（1）ABC ∆是等边三角形，60BAC ∴∠=︒．线段AM 为BC 边上的中线，12CAM BAC ∴∠=∠， 30CAM ∴∠=︒．（2）ABC ∆与DEC ∆都是等边三角形，AC BC ∴=，CD CE =，60ACB DCE ∠=∠=︒，ACD DCB DCB BCE ∴∠+∠=∠+∠，ACD BCE ∠∠∴=．在ADC ∆和BEC ∆中AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩， ()ACD BCE SAS ∴∆≅∆；（3）AOB ∠是定值，60AOB ∠=︒，理由如下：①当点D 在线段AM 上时，如图1，由（2）可知ACD BCE ≅∆∆，则30CBE CAD ∠=∠=︒，又60ABC ∠=︒，603090CBE ABC ∴∠+∠=︒+︒=︒，ABC ∆是等边三角形，线段AM 为BC 边上的中线AM ∴平分BAC ∠，即11603022BAM BAC ∠=∠=⨯︒=︒ 903060BOA ∴∠=︒-︒=︒．②当点D 在线段AM 的延长线上时，如图2，ABC ∆与DEC ∆都是等边三角形，AC BC ∴=，CD CE =，60ACB DCE ∠=∠=︒，ACB DCB DCB DCE ∴∠+∠=∠+∠，ACD BCE ∠∠∴=，在ACD ∆和BCE ∆中AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩， ()ACD BCE SAS ∴∆≅∆，30CBE CAD ∴∠=∠=︒，同理可得：30BAM ∠=︒，903060BOA ∴∠=︒-︒=︒．③当点D 在线段MA 的延长线上时，ABC ∆与DEC ∆都是等边三角形，AC BC ∴=，CD CE =，60ACB DCE ∠=∠=︒，60ACD ACE BCE ACE ∴∠+∠=∠+∠=︒，ACD BCE ∠∠∴=，在ACD ∆和BCE ∆中AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩， ()ACD BCE SAS ∴∆≅∆，CBE CAD ∴∠=∠，同理可得：30CAM ∠=︒150CBE CAD ∴∠=∠=︒30CBO ∴∠=︒，∵30BAM ∠=︒，903060BOA ∴∠=︒-︒=︒．综上，当动点D 在直线AM 上时，AOB ∠是定值，60AOB ∠=︒．【点睛】此题考查等边三角形的性质，全等三角形的判定及性质，等边三角形三线合一的性质，解题中注意分类讨论的思想解题.9．（1）证明见解析；（2）证明见解析；（3）当AC =2BD 时，对于满足条件的任意点N ，AN =CP 始终成立，证明见解析．【解析】【分析】（1）由三角形的内角和定理可求∠ACN=∠AMC=135°-∠ACM ；（2）过点N 作NE ⊥AC 于E ，由“AAS ”可证△NEC ≌△CDM ，可得NE=CD ，由三角形面积公式可求解；（3）过点N 作NE ⊥AC 于E ，由“SAS ”可证△NEA ≌△CDP ，可得AN=CP ．【详解】（1）∵∠BAC=45°，∴∠AMC=180°﹣45°﹣∠ACM=135°﹣∠ACM ．∵∠NCM=135°，∴∠ACN=135°﹣∠ACM ，∴∠ACN=∠AMC ；（2）过点N 作NE ⊥AC 于E ，∵∠CEN=∠CDM=90°，∠ACN=∠AMC ，CM=CN ，∴△NEC ≌△CDM （AAS ），∴NE=CD ，CE=DM ；∵S 112=AC•NE ，S 212=AB•CD ， ∴12S AC S AB=；（3）当AC=2BD 时，对于满足条件的任意点N ，AN=CP 始终成立，理由如下：过点N 作NE ⊥AC 于E ，由（2）可得NE=CD ，CE=DM ．∵AC=2BD ，BP=BM ，CE=DM ，∴AC ﹣CE=BD+BD ﹣DM ，∴AE=BD+BP=DP ．∵NE=CD ，∠NEA=∠CDP=90°，AE=DP ，∴△NEA ≌△CDP （SAS ），∴AN=PC ．【点睛】本题三角形综合题，考查了全等三角形的判定和性质，三角形内角和定理，三角形面积公式等知识，添加恰当辅助线构造全等三角形是本题的关键．10．（1）详见解析；（2）①详见解析；②详见解析．【解析】【分析】（1）本题考查理解题意能力，按照题目所述依次作图即可．（2）①本题考查线段和最短问题，需要通过垂直平分线的性质将所求线段转化为其他等量线段之和，以达到求解目的．②本题考查垂直平分线的判定以及全等三角形的证明，继而利用角的平分线性质即可得出结论．【详解】（1）补全图形，如图1所示（2）①如图2，连接BD，P为BD与AE的交点∵等边△ACD，AE⊥CD∴PC=PD,PC+PB最短等价于PB+PD最短故B,D之间直线最短，点P即为所求．②证明：连接DE，DF．如图3所示∵△ABC，△ADC是等边三角形∴AC＝AD，∠ACB＝∠CAD＝60°∵AE⊥CD∴∠CAE＝12∠CAD＝30°∴∠CEA＝∠ACB﹣∠CAE＝30°∴∠CAE＝∠CEA∴CA＝CE∴CD垂直平分AE∴DA＝DE∴∠DAE＝∠DEA∵EF⊥AF，∠EAF＝45°∴∠FEA＝45°∴∠FEA＝∠EAF∴FA ＝FE ，∠FAD ＝∠FED∴△FAD ≌△FED （SAS ）∴∠AFD ＝∠EFD∴点D 到AF ，EF 的距离相等．【点睛】本题第一问作图极为重要，要求对题意有较深的理解，同时对于垂直平分线以及角平分线的定义要清楚，能通过题目文字所述转化为考点，信息转化能力需要多做题目加以提升．11．（1）6；8；24；（2）存在 2.4t =时，使得△ODP 与△ODQ 的面积相等；（3）∠GOD+∠ACE=∠OHC ，见解析【解析】【分析】（1）利用非负性即可求出a ，b 即可得出结论,即可求出△ABC 的面积；（2）先表示出OQ ，OP ，利用那个面积相等，建立方程求解即可得出结论；（3）先判断出∠OAC=∠AOD ，进而判断出OG ∥AC ，即可判断出∠FHC=∠ACE ，同理∠FHO=∠GOD ，即可得出结论．【详解】解：(1) 解：（1）∵b 80-=， ∴a-6=0，b-8=0，∴a=6，b=8，∴A （0，6），C （8，0）；∴S △ABC=6×8÷2=24,故答案为（0，6），（8，0）； 6；8；24(2) ∵114222ODQ D S OQ x t t ∆=⋅=⋅⋅= 11(82)312322ODP D S OP y t t ∆=⋅=⋅-⋅=- 由2123t t =-时, 2.4t =∴存在 2.4t =时,使得△ODP 与△ODQ 的面积相等(3) ）∴2∠GOA+∠ACE=∠OHC ，理由如下：∵x 轴⊥y 轴，∴∠AOC=∠DOC+∠AOD=90°∴∠OAC+∠ACO=90°又∵∠DOC=∠DCO∴∠OAC=∠AOD∵y 轴平分∠GOD∴∠GOA=∠AOD∴∠GOA=∠OAC∴OG ∥AC ，如图，过点H 作HF ∥OG 交x 轴于F ，∴HF ∥AC∴∠FHC=∠ACE同理∠FHO=∠GOD ，∵OG ∥FH ，∴∠GOD=∠FHO ，∴∠GOD+∠ACE=∠FHO+∠FHC即∠GOD+∠ACE=∠OHC ，∴2∠GOA+∠ACE=∠OHC ．∴∠GOD+∠ACE=∠OHC ．【点睛】此题是三角形综合题，主要考查了非负性的性质，三角形的面积公式，角平分线的定义，平行线的性质，正确作出辅助线是解本题的关键．12．（1）见解析；（2）30ABE CDE ∠-∠=︒【解析】【分析】（1）根据聪聪提供的辅助线作法进行证明，先由平行线的性质得：AGC MCD ∠=∠，90F GAF ∠+∠=︒，再证明MCD BAG ∠=∠，可得结论；（2）根据平行线的性质和三角形的外角性质可得结论．【详解】解：（1）证明：如图2，过A 作//AG FM ，交CD 于G ，AGC MCD ∴∠=∠，90F GAF ∠+∠=︒，FN FM ⊥，90F ∴∠=︒，90GAF ∴∠=︒，90FAB MCD ∠-∠=︒，FAB GAF MCD BAG ∴∠-∠=∠=∠，//AB CD ∴；（2）解：30ABE CDE ∠-∠=︒，理由如下：如图3，//AB CD ，BPD ABE ∴∠=∠，BPD CDE BED ∠=∠+∠，30BED ∠=︒，30BPD CDE ∴∠-∠=︒，∴30ABE CDE ∠-∠=︒．【点睛】本题主要考查了平行线的性质和判定以及三角形外角性质的运用，熟练掌握平行线的性质和判定是解决问题的关键．13．（1）70°，40°，BC +DC =CE ；（2）①α=β；②当点D 在BC 上移动时，α=β或α+β=180°；（3）∠ACB =60°．【解析】【分析】（1）证△BAD ≌△CAE ，推出∠B=∠ACE ，根据三角形外角性质和全等三角形的性质求出即可；（2）①证△BAD ≌△CAE ，推出∠B=∠ACE ，根据三角形外角性质求出即可；②分三种情况：（Ⅰ）当D 在线段BC 上时，证明△ABD ≌△ACE （SAS ），则∠ADB=∠AEC ，∠ABC=∠ACE ，推出∠DAE+∠DCE=180°，即α+β=180°；（Ⅱ）当点D 在线段BC 反向延长线上时，α=β，同理可证明△ABD ≌△ACE （SAS ），则∠ABD=∠ACE ，推出∠BAC=∠DCE ，即α=β；（Ⅲ）当点D 在线段BC 的延长线上时，由①得α=β；（3）当点D 在线段BC 的延长线上或在线段BC 反向延长线上移动时，α=β，由CE ∥AB ，得∠ABC=∠DCE ，推出∠ABC=∠BAC ，易证∠ABC=∠ACB=∠BAC ，则△ABC 是等边三角形，得出∠ACB=60°；当D 在线段BC 上时，α+β=180°，由CE ∥AB ，得∠ABC+∠DCE=180°，推出∠ABC=∠BAC ，易证∠ABC=∠ACB=∠BAC ，则△ABC 是等边三角形，得出∠ACB=60°．【详解】（1）如图1所示：∵∠DAE=∠BAC，∴∠DAE+∠CAD=∠BAC+∠CAD，∴∠BAD=∠CAE．在△BAD和△CAE中，AB ACBAD CAE AD AE=⎧⎪∠=∠⎨⎪=⎩，∴△BAD≌△CAE（SAS），∴∠ACE=∠B12=（180°﹣40°）=70°，BD=CE，∴BC+DC=CE．∵∠ACD=∠B+∠BAC=∠ACE+∠DCE，∴∠BAC=∠DCE．∵∠BAC=40°，∴∠DCE=40°．故答案为：70°，40°，BC+DC=CE；（2）①当点D在线段BC的延长线上移动时，α与β之间的数量关系是α=β．理由如下：∵∠DAE=∠BAC，∴∠DAE+∠CAD=∠BAC+∠CAD，∴∠BAD=∠CAE．在△BAD和△CAE中，AB ACBAD CAE AD AE=⎧⎪∠=∠⎨⎪=⎩，∴△BAD≌△CAE（SAS），∴∠B=∠ACE．∵∠ACD=∠B+∠BAC=∠ACE+∠DCE，∴∠BAC=∠DCE．∵∠BAC=α，∠DCE=β，∴α=β；②分三种情况：（Ⅰ）当D在线段BC上时，α+β=180°，如图2所示．理由如下：同理可证明：△ABD≌△ACE（SAS），∴∠ADB=∠AEC，∠ABC=∠ACE．∵∠ADC+∠ADB=180°，∴∠ADC+∠AEC=180°，∴∠DAE+∠DCE=180°．∵∠BAC=∠DAE=α，∠DCE=β，∴α+β=180°；（Ⅱ）当点D在线段BC反向延长线上时，α=β，如图3所示．理由如下：同理可证明：△ABD≌△ACE（SAS），∴∠ABD=∠ACE．∵∠ACE=∠ACD+∠DCE，∠ABD=∠ACD+∠BAC，∴∠ACD+∠DCE=∠ACD+∠BAC，∴∠BAC=∠DCE．∵∠BAC=α，∠DCE=β，∴α=β；（Ⅲ）当点D在线段BC的延长线上时，如图1所示，α=β；综上所述：当点D在BC上移动时，α=β或α+β=180°；（3）∠ACB=60°．理由如下：∵当点D在线段BC的延长线上或在线段BC反向延长线上移动时，α=β，即∠BAC=∠DCE．∵CE∥AB，∴∠ABC=∠DCE，∴∠ABC=∠BAC．∵AB =AC ，∴∠ABC =∠ACB =∠BAC ，∴△ABC 是等边三角形，∴∠ACB =60°；∵当D 在线段BC 上时，α+β=180°，即∠BAC +∠DCE =180°．∵CE ∥AB ，∴∠ABC +∠DCE =180°，∴∠ABC =∠BAC ．∵AB =AC ，∴∠ABC =∠ACB =∠BAC ，∴△ABC 是等边三角形，∴∠ACB =60°；综上所述：当CE ∥AB 时，若△ABD 中最小角为15°，∠ACB 的度数为60°．【点睛】本题是三角形综合题目，考查了全等三角形的判定与性质、等腰三角形的性质、等边三角形的判定与性质、平行线的性质、三角形的外角性质和多边形内角和等知识．本题综合性强，熟练掌握全等三角形的判定与性质是解题的关键．14．（1）详见解析；（2）①详见解析；②PB PC PD BE ++=，理由详见解析【解析】【分析】（1）根据等边三角形的性质得出BC=AC ，CE=CD ，∠ACB=∠DCE=60°，进而得出∠BCE=∠ACD ，判断出BCE ACD ≌（SAS ），即可得出结论；（2）①同（1）的方法判断出≌ACD BCE （SAS ），ABD CBF ≌（SAS ），即可得出结论； ②先判断出∠APB=60°，∠APC=60°，在PE 上取一点M ，使PM=PC ，证明CPM △是等边三角形，进而判断出PCD MCE ≌（SAS ），即可得出结论．【详解】（1）证明：∵ABC 和DCE 都是等边三角形，∴BC=AC ，CE=CD ，∠ACB=∠DCE=60°，∴∠ABC+∠ACE=∠DCE+∠ACE ，即∠BCE=∠ACD ，∴BCE ACD ≌（SAS ），∴BE=AD ；（2）①证明：∵ABC 和DCE 是等边三角形，∴AC=BC ，CD=CE ，∠ACB=∠DCE=60°，∴∠ACB+∠BCD=∠DCE+∠BCD ，即∠ACD=∠BCE ，∴≌ACD BCE （SAS ），∴AD=BE ，同理：ABD CBF≌（SAS），∴AD=CF，即AD=BE=CF；②解：结论：PB+PC+PD=BE，理由：如图2，AD与BC的交点记作点Q，则∠AQC=∠BQP，由①知，≌ACD BCE，∴∠CAD=∠CBE，在ACQ中，∠CAD+∠AQC=180°-∠ACB=120°，∴∠CBE+∠BQP=120°，在BPQ中，∠APB=180°-（∠CBE+∠BQP）=60°，∴∠DPE=60°，同理：∠APC=60°，60,CPE∴∠=︒∠CPD=120°，在PE上取一点M，使PM=PC，∴CPM△是等边三角形，∴CP CM PM==，∠PCM=∠CMP=60°，∴∠CME=120°=∠CPD，∵CDE△是等边三角形，∴CD=CE，∠DCE=60°=∠PCM，∴∠PCD=∠MCE，∴PCD MCE≌（SAS），∴PD=ME，∴BE=PB+PM+ME=PB+PC+PD．【点睛】此题是三角形综合题，主要考查了三角形的内角和定理，等边三角形的性质和判定，全等三角形的判定和性质，构造出全等三角形是解本题的关键．15．（1）40°25°；（2）12∠=∠E A(或2E∠=∠Ａ)（3）F∠=()1902A D∠+∠-︒【解析】【分析】（1）先根据两角平分线写出对应的等式关系，再分别写出两个三角形内角和的等式关系，最后联立两等式化解，将A ∠的角度带入即可求解；（2）由（1）可得，即可求解；（3）在DCB ∠与ABE ∠的平分线相交于点F ，可知1==2BCF DCF BCD ∠∠∠12EBF ABE ∠=∠，又因为//BF CD ，两直线平行内错角相等，得出F DCF ∠=∠，再根据三角形一外角等于不相邻的两个内角的和，得出+EBF F BCF ∠=∠∠，再由四边形的内角和定理得出++360ABC BCD A D ∠+∠∠∠=，最后在FBC 中：++180F FBC BCF ∠∠∠=，代入整理即可得出结论．【详解】解：（1）由题可知：BE 为DBA ∠的角平分线，CE 为BCA ∠的角平分线，∴DBA ∠=2EBA ∠=2EBD ∠，BCA ∠=2BCE ∠，∴1802ABC EBA ∠=-∠，三角形内角和等于180，∴在ABC 中：+180A ABC BCA ∠∠+∠=，即：+(1802)2180A EBA BCE ∠-∠+∠=，220A EBA BCE ∠-∠+∠=①，在EBC 中：+180E EBC BCE ∠∠+∠=，即：+180-180E EBA BCE ∠∠+∠=（），-0E EBA BCE ∠∠+∠=②，综上所述联立①②，由①-②×2可得：22-2-0A EBA BCE E EBA BCE ∠-∠+∠∠∠+∠=（），22-2+2-20A EBA BCE E EBA BCE ∠-∠+∠∠∠∠=，-20A E ∠∠=，1=2E A ∠∠，当80A =∠，则E ∠=40；当50A ∠=，则E ∠=25；故答案为40，25；（2）由（1）知：12∠=∠E A (或2A E ∠=∠)；（3）∵DCB ∠与ABE ∠的平分线相交于点F ， ∴1==2BCF DCF BCD ∠∠∠，12EBF ABE FBA ∠=∠=∠ ，又∵//BF CD ，∴F DCF ∠=∠（两直线平行，内错角相等）BCF =∠，。

人教版(七年级)初一上册数学压轴题期末复习模拟测试题及答案

人教版(七年级)初一上册数学压轴题期末复习模拟测试题及答案一、压轴题>），1．阅读理解：如图①，若线段AB在数轴上，A、B两点表示的数分别为a和b(b a-.则线段AB的长（点A到点B的距离）可表示为AB=b a请用上面材料中的知识解答下面的问题:如图②，一个点从数轴的原点开始，先向左移动2cm到达P点，再向右移动7cm到达Q点，用1个单位长度表示1cm．（1）请你在图②的数轴上表示出P，Q两点的位置；（2）若将图②中的点P向左移动x cm，点Q向右移动3x cm，则移动后点P、点Q表示的数分别为多少？并求此时线段PQ的长.（用含x的代数式表示）；（3）若P、Q两点分别从第⑴问标出的位置开始，分别以每秒2个单位和1个单位的速度同时向数轴的正方向运动，设运动时间为t（秒），当t为多少时PQ=2cm？2．数轴上A、B两点对应的数分别是﹣4、12，线段CE在数轴上运动，点C在点E的左边，且CE＝8，点F是AE的中点．（1）如图1，当线段CE运动到点C、E均在A、B之间时，若CF＝1，则AB＝，AC ＝，BE＝；（2）当线段CE运动到点A在C、E之间时,①设AF长为x，用含x的代数式表示BE＝（结果需化简．．．．．）；②求BE与CF的数量关系；（3）当点C运动到数轴上表示数﹣14的位置时，动点P从点E出发，以每秒3个单位长度的速度向右运动，抵达B后，立即以原来一半速度返回，同时点Q从A出发，以每秒2个单位长度的速度向终点B运动，设它们运动的时间为t秒（t≤8），求t为何值时，P、Q 两点间的距离为1个单位长度．3．已知数轴上，点A和点B分别位于原点O两侧，AB=14，点A对应的数为a，点B对应的数为b.(1) 若b＝－4，则a的值为__________.(2) 若OA＝3OB，求a的值.(3) 点C为数轴上一点，对应的数为c．若O为AC的中点，OB＝3BC，直接写出所有满足条件的c的值.4．已知∠AOB＝110°，∠COD＝40°，OE平分∠AOC，OF平分∠BOD．（1）如图1，当OB、OC重合时，求∠AOE﹣∠BOF的值；（2）如图2，当∠COD从图1所示位置绕点O以每秒3°的速度顺时针旋转t秒（0＜t＜10），在旋转过程中∠AOE﹣∠BOF的值是否会因t的变化而变化？若不发生变化，请求出该定值；若发生变化，请说明理由．（3）在（2）的条件下，当∠COF＝14°时，t＝秒．5．借助一副三角板，可以得到一些平面图形（1）如图1，∠AOC＝度．由射线OA，OB，OC组成的所有小于平角的和是多少度？（2）如图2，∠1的度数比∠2度数的3倍还多30°，求∠2的度数；（3）利用图3，反向延长射线OA到M，OE平分∠BOM，OF平分∠COM，请按题意补全图（3），并求出∠EOF的度数．6．如图，已知数轴上点A表示的数为8，B是数轴上位于点A左侧一点，且AB=22，动点P从A点出发，以每秒5个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＞0）秒．（1）出数轴上点B表示的数；点P表示的数（用含t的代数式表示）（2）动点Q从点B出发，以每秒3个单位长度的速度沿数轴向右匀速运动，若点P、Q同时出发，问多少秒时P、Q之间的距离恰好等于2？（3）动点Q从点B出发，以每秒3个单位长度的速度沿数轴向左匀速运动，若点P、Q同时出发，问点P运动多少秒时追上点Q？（4）若M为AP的中点，N为BP的中点，在点P运动的过程中，线段MN的长度是否发生变化？若变化，请说明理由，若不变，请你画出图形，并求出线段MN的长．7．对于数轴上的点P，Q，给出如下定义：若点P到点Q的距离为d(d≥0)，则称d为点P 到点Q的d追随值，记作d[PQ]．例如，在数轴上点P表示的数是2，点Q表示的数是5，则点P到点Q的d追随值为d[PQ]=3．问题解决：(1)点M，N都在数轴上，点M表示的数是1，且点N到点M的d追随值d[MN]=a(a≥0)，则点N表示的数是_____(用含a的代数式表示)；(2)如图，点C表示的数是1，在数轴上有两个动点A，B都沿着正方向同时移动，其中A点的速度为每秒3个单位，B点的速度为每秒1个单位，点A从点C出发，点B表示的数是b，设运动时间为t(t>0)．①当b=4时，问t为何值时，点A到点B的d追随值d[AB]=2；②若0<t≤3时，点A到点B的d追随值d[AB]≤6，求b的取值范围．8．如图1，O为直线AB上一点，过点O作射线OC，∠AOC=30°，将一直角三角尺（∠M=30°）的直角顶点放在点O处，一边ON在射线OA上，另一边OM与OC都在直线AB的上方．(1)若将图1中的三角尺绕点O以每秒5°的速度，沿顺时针方向旋转t秒，当OM恰好平分∠BOC时，如图2．①求t值；②试说明此时ON平分∠AOC；(2)将图1中的三角尺绕点O顺时针旋转，设∠AON=α，∠COM=β，当ON在∠AOC内部时，试求α与β的数量关系；(3)若将图1中的三角尺绕点O以每秒5°的速度沿顺时针方向旋转的同时，射线OC也绕点O以每秒8°的速度沿顺时针方向旋转，如图3，那么经过多长时间，射线OC第一次平分∠MON?请说明理由．9．如图①，点C在线段AB上，图中共有三条线段AB、AC和BC，若其中有一条线段的长度是另外一条线段长度的2倍，则称点C是段AB的“2倍点”．（1）线段的中点__________这条线段的“2倍点”；（填“是”或“不是”）（2）若AB＝15cm，点C是线段AB的“2倍点”．求AC的长；（3）如图②，已知AB＝20cm．动点P从点A出发，以2c m／s的速度沿AB向点B匀速移动．点Q从点B出发，以1c m/s的速度沿BA向点A匀速移动．点P、Q同时出发，当其中一点到达终点时，运动停止，设移动的时间为t（s），当t＝_____________s时，点Q 恰好是线段AP的“2倍点”．（请直接写出各案）10．如图：在数轴上A点表示数a，B点示数b，C点表示数c，b是最小的正整数，且a、c满足|a+2|+（c-7）2=0．（1）a=______，b=______，c=______；（2）若将数轴折叠，使得A点与C点重合，则点B与数______表示的点重合；（3）点A、B、C开始在数轴上运动，若点A以每秒1个单位长度的速度向左运动，同时，点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动，假设t秒钟过后，若点A与点B之间的距离表示为AB，点A与点C之间的距离表示为AC，点B与点C 之间的距离表示为BC．则AB=______，AC=______，BC=______．（用含t的代数式表示）.（4）直接写出点B为AC中点时的t的值.11．如图，在数轴上从左往右依次有四个点,,,A B C D，其中点,,A B C表示的数分别是0,3,10，且2CD AB=.(1)点D表示的数是；（直接写出结果）(2)线段AB以每秒2个单位长度的速度沿数轴向右运动，同时线段CD以每秒1个单位长度的速度沿数轴向左运动，设运动时间是t（秒），当两条线段重叠部分是2个单位长度时.①求t的值;②线段AB上是否存在一点P，满足3BD PA PC-=?若存在，求出点P表示的数x；若不存在，请说明理由.12．阅读下列材料，并解决有关问题：我们知道，(0)0(0)(0)x xx xx x>⎧⎪==⎨⎪-<⎩，现在我们可以用这一结论来化简含有绝对值的式子，例如化简式子|1||2|x x++-时，可令10x+=和20x-=，分别求得1x=-，2x=（称1-、2分别为|1|x+与|2|x-的零点值）．在有理数范围内，零点值1x=-和2x=可将全体有理数不重复且不遗漏地分成如下三种情况：（1）1x<-；（2）1-≤2x<；（3）x≥2．从而化简代数式|1||2|x x++-可分为以下3种情况：（1）当1x<-时，原式()()1221x x x=-+--=-+；（2）当1-≤2x<时，原式()()123x x=+--=；（3）当x≥2时，原式()()1221x x x=++-=-综上所述：原式21(1)3(12)21(2)x xxx x-+<-⎧⎪=-≤<⎨⎪-≥⎩通过以上阅读，请你类比解决以下问题：（1）填空：|2|x+与|4|x-的零点值分别为；（2）化简式子324x x-++．13．问题一：如图1，已知A，C两点之间的距离为16 cm，甲，乙两点分别从相距3cm的A，B两点同时出发到C点，若甲的速度为8 cm/s，乙的速度为6 cm/s，设乙运动时间为x（s），甲乙两点之间距离为y（cm）．(1)当甲追上乙时，x = ．(2)请用含x的代数式表示y．当甲追上乙前，y= ；当甲追上乙后，甲到达C之前，y= ；当甲到达C之后，乙到达C之前，y= ．问题二：如图2，若将上述线段AC弯曲后视作钟表外围的一部分，线段AB正好对应钟表上的弧AB（1小时的间隔），易知∠AOB=30°．(1)分针OD指向圆周上的点的速度为每分钟转动 cm；时针OE指向圆周上的点的速度为每分钟转动 cm．(2)若从4：00起计时，求几分钟后分针与时针第一次重合．14．如图所示，已知数轴上A，B两点对应的数分别为－2，4，点P为数轴上一动点，其对应的数为x.(1)若点P 到点A ，B 的距离相等，求点P 对应的数x 的值．(2)数轴上是否存在点P ，使点P 到点A ，B 的距离之和为8？若存在，请求出x 的值；若不存在，说明理由．(3)点A ，B 分别以2个单位长度/分、1个单位长度/分的速度向右运动，同时点P 以5个单位长度/分的速度从O 点向左运动．当遇到A 时，点P 立即以同样的速度向右运动，并不停地往返于点A 与点B 之间．当点A 与点B 重合时，点P 经过的总路程是多少？ 15．如图，已知线段AB=12cm ，点C 为AB 上的一个动点，点D 、E 分别是AC 和BC 的中点．（1）若AC=4cm ，求DE 的长；（2）试利用“字母代替数”的方法，说明不论AC 取何值（不超过12cm ），DE 的长不变；（3）知识迁移：如图②，已知∠AOB=α，过点O 画射线OC ，使∠AOB:∠BOC=3:1若OD 、OE 分别平分∠AOC 和∠BOC ，试探究∠DOE 与∠AOB 的数量关系．【参考答案】***试卷处理标记，请不要删除一、压轴题1．（1）见详解；（2）2x --，53x +，47x +；（3）当运动时间为5秒或9秒时，PQ=2cm. 【解析】【分析】（1）根据数轴的特点，所以可以求出点P ，Q 的位置；（2）根据向左移动用减法，向右移动用加法，即可得到答案；（3）根据题意，可分为两种情况进行分析：①点P 在点Q 的左边时；②点P 在点Q 的右边时；分别进行列式计算，即可得到答案. 【详解】解：（1）如图所示：.（2）由（1）可知，点P 为2-，点Q 为5；∴移动后的点P 为：2x --；移动后的点Q 为：53x +； ∴线段PQ 的长为：53(2)47x x x +---=+；（3）根据题意可知，当PQ=2cm 时可分为两种情况： ①当点P 在点Q 的左边时，有(21)72t -=-，解得：5t =；②点P 在点Q 的右边时，有(21)72t -=+，解得：9t =；综上所述，当运动时间为5秒或9秒时，PQ=2cm. 【点睛】本题要是把方程和数轴结合起来，既要根据条件列出方程，又要把握数轴的特点．解题的关键是熟练掌握数轴上的动点运动问题，注意分类讨论进行解题. 2．（1）16,6,2；（2）①162x -②2BE CF =；（3）t=1或3或487或527 【解析】【分析】(1)由数轴上A 、B 两点对应的数分別是-4、12，可得AB 的长;由CE ＝8，CF ＝1，可得EF 的长，由点F 是AE 的中点，可得AF 的长，用AB 的长减去2倍的EF 的长即为BE 的长；(2)设AF ＝FE ＝x ，则CF ＝8-x ，用含x 的式子表示出BE ，即可得出答案 (3)分①当0＜t ≤6时； ②当6＜t ≤8时，两种情况讨论计算即可得解【详解】（1）数轴上A 、B 两点对应的数分别是-4、12， ∴AB=16，∵CE=8，CF=1，∴EF=7， ∵点F 是AE 的中点，∴AF=EF=7，,∴AC=AF ﹣CF=6，BE=AB ﹣AE=16﹣7×2=2，故答案为16，6，2；(2)∵点F 是AE 的中点，∴AF=EF ，设AF=EF=x,∴CF=8﹣x ， ∴BE=16﹣2x=2（8﹣x ）， ∴BE=2CF.故答案为①162x -②2BE CF =；(3) ①当0＜t ≤6时，P 对应数：-6+3t ，Q 对应数-4+2t ，=4t t =2t =1PQ ﹣＋2﹣（﹣6＋3）﹣，解得：t=1或3；②当6＜t ≤8时，P 对应数()33126t 22t ---＝21 ， Q 对应数-4+2t ， 37=4t =t 2=12t PQ -﹣＋2﹣（）25﹣21，解得：48t=7或527；故答案为t=1或3或487或527. 【点睛】本题考查了一元一次方程在数轴上的动点问题中的应用，根据题意正确列式，是解题的关健3．(1)10；(2)212±；(3)288. 5±±，【解析】【分析】(1)根据题意画出数轴，由已知条件得出AB=14,OB=4,则OA=10,得出a 的值为10. (2)分两种情况,点A 在原点的右侧时,设OB=m,列一元一次方程求解,进一步得出OA 的长度,从而得出a 的值.同理可求出当点A 在原点的左侧时,a 的值. (3)画数轴,结合数轴分四种情况讨论计算即可. 【详解】(1)解：若b ＝－4，则a 的值为 10 (2)解：当A 在原点O 的右侧时（如图）：设OB=m,列方程得：m+3m=14，解这个方程得，7m 2=，所以，OA=212，点A 在原点O 的右侧，a 的值为212. 当A 在原点的左侧时（如图)，a=－212综上，a 的值为±212. (3)解：当点A 在原点的右侧，点B 在点C 的左侧时（如图), c=－285.当点A 在原点的右侧，点B 在点C 的右侧时（如图), c=－8.当点A 在原点的左侧，点B 在点C 的右侧时，图略，c=285. 当点A 在原点的左侧，点B 在点C 的左侧时,图略，c=8.综上，点c 的值为：±8，±285. 【点睛】本题考查的知识点是通过画数轴,找出数轴上各线段间的数量关系并用一元一次方程来求解,需要注意的是分情况讨论时要考虑全面,此题充分锻炼了学生动手操作能力以及利用数行结合解决问题的能力.4．（1）35°；（2）∠AOE ﹣∠BOF 的值是定值，理由详见解析；（3）4．【解析】【分析】（1）首先根据角平分线的定义求得∠AOE 和∠BOF 的度数，然后根据∠AOE ﹣∠BOF 求解；（2）首先由题意得∠BOC ＝3t°，再根据角平分线的定义得∠AOC ＝∠AOB+3t°，∠BOD ＝∠COD+3t°，然后由角平分线的定义解答即可；（3）根据题意得∠BOF ＝（3t+14）°，故3314202t t +=+，解方程即可求出t 的值．【详解】解：（1）∵OE 平分∠AOC ，OF 平分∠BOD ， ∴11AOE AOC 11022︒∠=∠=⨯＝55°，11AOF BOD 402022︒︒∠=∠=⨯=， ∴∠AOE ﹣∠BOF ＝55°﹣20°＝35°；（2）∠AOE ﹣∠BOF 的值是定值由题意∠BOC ＝3t°，则∠AOC ＝∠AOB+3t°＝110°+3t°，∠BOD ＝∠COD+3t°＝40°+3t°， ∵OE 平分∠AOC ，OF 平分∠BOD ，()11AOE AOC 1103t =22︒︒∴∠=∠=⨯+3552t ︒︒+ ∴()113BOF BOD 403t 20t 222︒︒︒︒∠=∠=+=+，∴33AOE BOF55t20t3522︒︒︒︒︒⎛⎫⎛⎫∠-∠=+-+=⎪ ⎪⎝⎭⎝⎭，∴∠AOE﹣∠BOF的值是定值，定值为35°；（3）根据题意得∠BOF＝（3t+14）°，∴3 314202t t +=+，解得4t=．故答案为4．【点睛】本题考查了角度的计算以及角的平分线的性质，理解角度之间的和差关系是关键．5．（1）75°，150°；（2）15°；（3）15°.【解析】【分析】（1）根据三角板的特殊性角的度数，求出∠AOC即可,把∠AOC、∠BOC、∠AOB相加即可求出射线OA，OB，OC组成的所有小于平角的和；（2）依题意设∠2＝x，列等式，解方程求出即可；（3）依据题意求出∠BOM,∠COM,再根据角平分线的性质得出∠MOE，∠MOF，即可求出∠EOF.【详解】解：（1）∵∠BOC＝30°，∠AOB＝45°，∴∠AOC＝75°，∴∠AOC+∠BOC+∠AOB＝150°；答：由射线OA，OB，OC组成的所有小于平角的和是150°；故答案为：75；（2）设∠2＝x，则∠1＝3x+30°，∵∠1+∠2＝90°，∴x+3x+30°＝90°，∴x＝15°，∴∠2＝15°，答：∠2的度数是15°；（3）如图所示，∵∠BOM＝180°﹣45°＝135°，∠COM＝180°﹣15°＝165°，∵OE为∠BOM的平分线，OF为∠COM的平分线，∴∠MOF＝12∠COM＝82.5°，∠MOE＝12∠MOB＝67.5°，∴∠EOF＝∠MOF﹣∠MOE＝15°．【点睛】本题主要考查了三角板各角的度数、角平分线的性质及列方程解方程在几何中的应用，熟记概念是解题的关键.6．（1）﹣14，8﹣5t；（2）2.5或3秒时P、Q之间的距离恰好等于2；（3）点P运动11秒时追上点Q；（4）线段MN的长度不发生变化，其值为11，见解析.【解析】【分析】（1）根据已知可得B点表示的数为8﹣22；点P表示的数为8﹣5t；（2）设t秒时P、Q 之间的距离恰好等于2．分①点P、Q相遇之前和②点P、Q相遇之后两种情况求t值即可；（3）设点P运动x秒时，在点C处追上点Q，则AC=5x，BC=3x，根据AC﹣BC=AB，列出方程求解即可；（3）分①当点P在点A、B两点之间运动时，②当点P运动到点B的左侧时，利用中点的定义和线段的和差求出MN的长即可．【详解】（1）∵点A表示的数为8，B在A点左边，AB=22，∴点B表示的数是8﹣22=﹣14，∵动点P从点A出发，以每秒5个单位长度的速度沿数轴向左匀速运动，设运动时间为t （t＞0）秒，∴点P表示的数是8﹣5t．故答案为：﹣14，8﹣5t；（2）若点P、Q同时出发，设t秒时P、Q之间的距离恰好等于2．分两种情况：①点P、Q相遇之前，由题意得3t+2+5t=22，解得t=2.5；②点P、Q相遇之后，由题意得3t﹣2+5t=22，解得t=3．答：若点P、Q同时出发，2.5或3秒时P、Q之间的距离恰好等于2；（3）设点P运动x秒时，在点C处追上点Q，则AC=5x，BC=3x，∵AC﹣BC=AB，∴5x﹣3x=22，解得：x=11，∴点P运动11秒时追上点Q；（4）线段MN的长度不发生变化，都等于11；理由如下：①当点P在点A、B两点之间运动时：MN=MP+NP=12AP+12BP=12（AP+BP）=12AB=12×22=11；②当点P运动到点B的左侧时：MN=MP﹣NP=12AP﹣12BP=12（AP﹣BP）=12AB=11，∴线段MN的长度不发生变化，其值为11．【点睛】本题考查了数轴一元一次方程的应用，用到的知识点是数轴上两点之间的距离，关键是根据题意画出图形，注意分两种情况进行讨论．7．(1)1＋a或1－a；(2)12或52；(3)1≤b≤7.【解析】【分析】(1)根据d追随值的定义，分点N在点M左侧和点N在点M右侧两种情况，直接写出答案即可；(2)①分点A在点B左侧和点A在点B右侧两种情况，类比行程问题中的追及问题，根据“追及时间=追及路程÷速度差”计算即可；②【详解】解：(1)点N在点M右侧时，点N表示的数是1+a；点N在点M左侧时，点N表示的数是1-a；(2)①b=4时，AB相距3个单位，当点A在点B左侧时，t=(3-2)÷(3-1)=12，当点A在点B右侧时，t=(3+2)÷(3-1)=52；②当点B在点A左侧或重合时，即d≤1时，随着时间的增大，d追随值会越来越大，∵0<t≤3，点A到点B的d追随值d[AB]≤6，∴1-d+3×(3-1)≤6，解得d≥1，∴d=1，当点B在点A右侧时，即d>1时，在AB重合之前，随着时间的增大，d追随值会越来越小，∵点A到点B的d追随值d[AB]≤6，∴d≤7∴1<d≤7，综合两种情况，d的取值范围是1≤d≤7.故答案为(1)1＋a或1－a；(2)①12或52；②1≤b≤7.【点睛】本题考查了数轴上两点之间的距离和动点问题.8．（1）①t=3；②见解析；（2）β=α+60°；（3）t=5时，射线OC第一次平分∠MON.【解析】【分析】（1）根据角平分线的性质以及余角补角的性质即可得出结论；（2）根据∠NOC=∠AOC－∠AON=90°－∠MOC即可得到结论；（3）分别根据转动速度关系和OC平分∠MON列方程求解即可．【详解】（1）①∵∠AOC=30°，OM平分∠BOC，∴∠BOC=2∠COM=2∠BOM=150°，∴∠COM=∠BOM=75°．∵∠MON=90°，∴∠CON=15°，∠AON+∠BOM=90°，∴∠AON=∠AOC﹣∠CON=30°﹣15°=15°，∴∠AON=∠CON，∴t=15°÷3°=5秒；②∵∠CON=15°，∠AON=15°，∴ON平分∠AOC．（2）∵∠AOC=30°，∴∠NOC=∠AOC－∠AON=90°－∠MOC，∴30°－α=90°－β，∴β=α+60°；（3）设旋转时间为t秒，∠AON=5t，∠AOC=30°+8t，∠CON=45°，∴30°+8t=5t+45°，∴t=5．即t=5时，射线OC第一次平分∠MON．【点睛】本题考查了一元一次方程的应用以及角的计算，关键是应该认真审题并仔细观察图形，找到各个量之间的关系求出角的度数是解题的关键．9．（1）是；（2）5cm或7.5cm或10cm；（3）10或607．【解析】【分析】（1）根据“2倍点”的定义即可求解；（2）分点C在中点的左边，点C在中点，点C在中点的右边三种情况，进行讨论求解即可；（3）根据题意画出图形，P应在Q的右边，分别表示出AQ、QP、PB，求出t的范围．然后根据（2）分三种情况讨论即可．【详解】（1）∵整个线段的长是较短线段长度的2倍，∴线段的中点是这条线段的“2倍点”．故答案为是；（2）∵AB ＝15cm ，点C 是线段AB 的2倍点，∴AC ＝1513⨯=5cm 或AC ＝1512⨯=7.5cm 或AC ＝1523⨯=10cm ．（3）∵点Q 是线段AP 的“2倍点”，∴点Q 在线段AP 上．如图所示：由题意得：AP =2t ，BQ =t ，∴AQ =20-t ，QP =2t -（20-t ）=3t -20，PB =20-2t ．∵PB =20-2t ≥0，∴t ≤10．∵QP =3t -20≥0，∴t ≥203，∴203≤t ≤10．分三种情况讨论：①当AQ ＝13AP 时，20-t ＝13×2t ，解得：t ＝12＞10，舍去； ②当AQ ＝12AP 时，20-t ＝12×2t ，解得：t ＝10； ③当AQ ＝23AP 时，20-t ＝23×2t ，解得：t 607=；答：t 为10或607时，点 Q 是线段AP 的“2倍点”．【点睛】本题考查了一元一次方程的解法、线段的和差等知识点，题目需根据“2倍点”的定义分类讨论，理解“2倍点”的定义是解决本题的关键．10．（1）-2；1；7；（2）4；（3）3+3t ；9+5t ；6+2t ；（4）3.【解析】【分析】（1）利用|a +2|+（c ﹣7）2＝0，得a +2＝0，c ﹣7＝0，解得a ，c 的值，由b 是最小的正整数，可得b ＝1；（2）先求出对称点，即可得出结果；（3）分别写出点A 、B 、C 表示的数为，用含t 的代数式表示出AB 、AC 、BC 即可；（4）由点B 为AC 中点，得到AB =BC ，列方程，求解即可．【详解】（1）∵|a +2|+（c ﹣7）2＝0，∴a +2＝0，c ﹣7＝0，解得：a ＝﹣2，c ＝7．∵b 是最小的正整数，∴b ＝1．故答案为﹣2，1，7．（2）（7+2）÷2＝4.5，对称点为7﹣4.5＝2.5，2.5+（2.5﹣1）＝4．故答案为4．（3）点A 表示的数为：－2－t ，点B 表示的数为：1+2t ，点C 表示的数为：7+4t ，则AB ＝t +2t +3＝3t +3，AC ＝t +4t +9＝5t +9，BC ＝2t +6．故答案为3t +3，5t +9，2t +6．（4）∵点B 为AC 中点，∴AB =BC ，∴3t +3=2t +6，解得：t =3．【点睛】本题考查了一元一次方程的应用、数轴及两点间的距离，解题的关键是利用数轴的特点能求出两点间的距离．11．（1）16；（2）①t 的值为3或143秒；②存在，P 表示的数为314. 【解析】【分析】（1）由数轴可知，AB=3,则CD=6,所以D 表示的数为16，（2）①当运动时间是t 秒时，在运动过程中，B 点表示的数为3+2t,A 点表示的数为2t, C 点表示的数为10-t ，D 点表示的数为16-t ，分情况讨论两条线段重叠部分是2个单位长度解答即可；②分情况讨论当t=3秒, t=143秒时，满足3BD PA PC -=的点P , 注意P 为线段AB 上的点对x 的值的限制.【详解】（1）16（2）①在运动过程中，B 点表示的数为3+2t,A 点表示的数为2t,C 点表示的数为10-t ，D 点表示的数为16-t.当BC ＝2，点B 在点C 的右边时，由题意得：32-10-2BC t t =+=（），解得：t ＝3，当AD=2，点A 在点D 的左边时，由题意得：16--22AD t t ==，解得：t ＝143．综上，t 的值为3或143秒 ②存在，理由如下:当t=3时，A 点表示的数为6，B 点表示的数为9，C 点表示的数为7，D 点表示的数为13. 则13-94-6|-7|BD PA x PC x ====，，，-3BD PA PC =，()4--6|-7|x x ∴=，解得：314x =或112，又P 点在线段AB 上，则69x ≤≤314x ∴=. 当143t =时，A 点表示的数为283，B 点表示的数为373，C 点表示的数为163，D 点表示的数为343. 则37343816-1-|-|3333BD PA x PC x ====，，， -3BD PA PC =， ∴ 28161--|-|33x x ⎛⎫= ⎪⎝⎭，解得：7912x =或176，又283733x ≤≤， x ∴无解综上，P 表示的数为314. 【点睛】本题考查了一元一次方程的应用以及数轴，解题的关键是：(1)由路程=速度×时间结合运动方向找出运动t 秒时点A 、B 、C 、D 所表示的数,(2)根据3BD PA PC -=列出关于t 的含绝对值符号的一元一次方程．12．(1) 2x =-和4x = ;(2) 35(4)11(43)35(3)x x x x x x --<-⎧⎪+-≤<⎨⎪+≥⎩【解析】【分析】（1）令x +2=0和x -4=0,求出x 的值即可得出|x +2|和|x -4|的零点值,（2）零点值x =3和x =-4可将全体实数分成不重复且不遗漏的如下3种情况:x ＜-4、-4≤x ＜3和x ≥3．分该三种情况找出324x x -++的值即可．【详解】解：（1）2x =-和4x =,（2）由30x -=得3,x =由40x +=得4x =-,①当4x <-时,原式()()32435x x x =---+=--,②当4-≤3x <时,原式()()32411x x x =--++=+,③当x ≥3时,原式()()32435x x x =-++=+,综上所述：原式()35(4)11(43)353x x x x x x ⎧--<-⎪=+-≤<⎨⎪+≥⎩, 【点睛】本题主要考查了绝对值化简方法,解决本题的关键是要熟练掌握绝对值化简方法.13．问题一、(1)32；（2）3-2x ；2x -3；13-6x ；问题一、（1）35；120；24011. 【解析】【分析】问题一根据等量关系，路程=速度⨯时间，路程差=路程1-路程2，即可列出方程求解。

数学人教版(七年级)初一下册数学期末复习压轴题解答题测试题及答案

（2）如图②，分别为的平分线所在直线，试探究与的数量关系；
（3）如图③，在（2）的前提下，且有，直线交于点，，请直接写出 ______________．
16．（问题背景）
（1）如图1的图形我们把它称为“8字形”，请说理证明∠A+∠B＝∠C+∠D
（简单应用）
（2）如图2，AP、CP分别平分∠BAD、∠BCD，若∠ABC＝28°，∠ADC＝20°，求∠P的度数（可直接使用问题（1）中的结论）
（2）x2（2a﹣b）﹣y2（2a﹣b）；
（3）y2﹣6y+9；
（4）x4﹣8x2y2+16y4．
4．先化简，再求值：
（1），其中；
（2），其中．
5．[知识生成]通常，用两种不同的方法计算同一个图形的面积，可以得到一个恒等式．
例如：如图①是一个长为，宽为的长方形，沿图中虚线用剪刀均分成四个小长方形，然后按图②的形状拼成一个正方形．请解答下列问题：
（1）
（2）如果，求满足条件的所有整数。
7．问题1：现有一张△ABC纸片，点D、E分别是△ABC边上两点，若沿直线DE折叠．
（1）探究1：如果折成图①的形状，使A点落在CE上，则∠1与∠A的数量关系是；
（2）探究2：如果折成图②的形状，猜想∠1+∠2和∠A的数量关系是；
（3）探究3：如果折成图③的形状，猜想∠1、∠2和∠A的数量关系，并说明理由．
数学人教版(七年级)初一下册数学期末复习压轴题解答题测试题及答案
一、解答题
1．计算：
（1）2a（a﹣2a2）；
（2）a7＋a﹣（a2）3；
（3）（3a＋2b）（2b﹣3a）；
（4）（m﹣n）2﹣2m（m﹣n）．

郑州市人教版(七年级)初一上册数学压轴题期末复习测试题及答案

郑州市人教版(七年级)初一上册数学压轴题期末复习测试题及答案一、压轴题1．小刚运用本学期的知识，设计了一个数学探究活动.如图1，数轴上的点M ，N 所表示的数分别为0，12.将一枚棋子放置在点M 处，让这枚棋子沿数轴在线段MN 上往复运动（即棋子从点M 出发沿数轴向右运动，当运动到点N 处，随即沿数轴向左运动，当运动到点M 处，随即沿数轴向右运动，如此反复⋯）.并且规定棋子按照如下的步骤运动：第1步，从点M 开始运动t 个单位长度至点1Q 处；第2步，从点1Q 继续运动2t 单位长度至点2Q 处；第3步，从点2Q 继续运动3t 个单位长度至点3Q 处…例如：当3t =时，点1Q 、2Q 、3Q 的位置如图2所示.解决如下问题：（1）如果4t =，那么线段13Q Q =______；（2）如果4t <，且点3Q 表示的数为3，那么t =______；（3）如果2t ≤，且线段242Q Q =，那么请你求出t 的值.2．东东在研究数学问题时遇到一个定义：将三个已经排好顺序数：x 1，x 2，x 3，称为数列x 1，x 2，x 3．计算|x 1|，122x x +，1233x x x ++，将这三个数的最小值称为数列x 1，x 2，x 3的最佳值．例如，对于数列2，-1，3，因为|2|=2，()212+-=12，()2133+-+=43，所以数列2，-1，3的最佳值为12．东东进一步发现：当改变这三个数的顺序时，所得到的数列都可以按照上述方法计算其相应的最佳值．如数列-1，2，3的最佳值为12；数列3，-1，2的最佳值为1；…．经过研究，东东发现，对于“2，-1，3”这三个数，按照不同的排列顺序得到的不同数列中，最佳值的最小值为12．根据以上材料，回答下列问题：（1）数列-4，-3，1的最佳值为（2）将“-4，-3，2”这三个数按照不同的顺序排列，可得到若干个数列，这些数列的最佳值的最小值为，取得最佳值最小值的数列为（写出一个即可）；（3）将2，-9，a （a ＞1）这三个数按照不同的顺序排列，可得到若干个数列．若这些数列的最佳值为1，求a 的值．3．如图，已知数轴上点A 表示的数为8，B 是数轴上位于点A 左侧一点，且AB =22，动点P 从A 点出发，以每秒5个单位长度的速度沿数轴向左匀速运动，设运动时间为t （t ＞0）秒．（1）出数轴上点B 表示的数；点P 表示的数（用含t 的代数式表示）（2）动点Q 从点B 出发，以每秒3个单位长度的速度沿数轴向右匀速运动，若点P 、Q 同时出发，问多少秒时P 、Q 之间的距离恰好等于2？（3）动点Q 从点B 出发，以每秒3个单位长度的速度沿数轴向左匀速运动，若点P 、Q 同时出发，问点P 运动多少秒时追上点Q ？（4）若M 为AP 的中点，N 为BP 的中点，在点P 运动的过程中，线段MN 的长度是否发生变化？若变化，请说明理由，若不变，请你画出图形，并求出线段MN 的长．4．已知线段30AB cm =（1）如图1，点P 沿线段AB 自点A 向点B 以2/cm s 的速度运动，同时点Q 沿线段点B 向点A 以3/cm s 的速度运动，几秒钟后，P Q 、两点相遇？（2）如图1，几秒后，点P Q 、两点相距10cm ？（3）如图2，4AO cm =，2PO cm =，当点P 在AB 的上方，且060=∠POB 时，点P 绕着点O 以30度/秒的速度在圆周上逆时针旋转一周停止，同时点Q 沿直线BA 自B 点向A 点运动，假若点P Q 、两点能相遇，求点Q 的运动速度．5．对于数轴上的点P ，Q ，给出如下定义：若点P 到点Q 的距离为d(d≥0)，则称d 为点P 到点Q 的d 追随值，记作d[PQ]．例如，在数轴上点P 表示的数是2，点Q 表示的数是5，则点P 到点Q 的d 追随值为d[PQ]=3．问题解决：(1)点M ，N 都在数轴上，点M 表示的数是1，且点N 到点M 的d 追随值d[MN]=a(a≥0)，则点N 表示的数是_____(用含a 的代数式表示)；(2)如图，点C 表示的数是1，在数轴上有两个动点A ，B 都沿着正方向同时移动，其中A 点的速度为每秒3个单位，B 点的速度为每秒1个单位，点A 从点C 出发，点B 表示的数是b ，设运动时间为t(t>0)．①当b=4时，问t 为何值时，点A 到点B 的d 追随值d[AB]=2；②若0<t≤3时，点A 到点B 的d 追随值d[AB]≤6，求b 的取值范围．6．如图，在平面直角坐标系中，点M 的坐标为（2，8），点N 的坐标为（2，6），将线段MN 向右平移4个单位长度得到线段PQ （点P 和点Q 分别是点M 和点N 的对应点），连接MP 、NQ ，点K 是线段MP 的中点．（1）求点K 的坐标；（2）若长方形PMNQ 以每秒1个单位长度的速度向正下方运动，（点A 、B 、C 、D 、E 分别是点M 、N 、Q 、P 、K 的对应点），当BC 与x 轴重合时停止运动，连接OA 、OE ，设运动时间为t 秒，请用含t 的式子表示三角形OAE 的面积S （不要求写出t 的取值范围）；（3）在（2）的条件下，连接OB 、OD ，问是否存在某一时刻t ，使三角形OBD 的面积等于三角形OAE 的面积？若存在，请求出t 值；若不存在，请说明理由．7．如图，数轴上有A ， B 两点，分别表示的数为a ，b ，且()225350a b ++-=．点P 从A 点出发以每秒13个单位长度的速度沿数轴向右匀速运动，当它到达B 点后立即以相同的速度返回往A 点运动，并持续在A ，B 两点间往返运动．在点P 出发的同时，点Q 从B 点出发以每秒2个单位长度向左匀速运动，当点Q 达到A 点时，点P ，Q 停止运动．（1）填空：a = ，b = ；（2）求运动了多长时间后，点P ，Q 第一次相遇，以及相遇点所表示的数；（3）求当点P ，Q 停止运动时，点P 所在的位置表示的数；（4）在整个运动过程中，点P 和点Q 一共相遇了几次．（直接写出答案）8．我国著名数学家华罗庚曾经说过，“数形结合百般好，隔裂分家万事非．”数形结合的思想方法在数学中应用极为广泛.观察下列按照一定规律堆砌的钢管的横截面图：用含n的式子表示第n个图的钢管总数.（分析思路）图形规律中暗含数字规律，我们可以采用分步的方法,从图形排列中找规律;把图形看成几个部分的组合,并保持结构,找到每一部分对应的数字规律,进而找到整个图形对应的数字规律．如:要解决上面问题，我们不妨先从特例入手: (统一用S表示钢管总数)（解决问题）(1)如图，如果把每个图形按照它的行来分割观察，你发现了这些钢管的堆砌规律了吗?像n=1、n=2的情形那样,在所给横线上,请用数学算式表达你发现的规律.S=1+2 S=2+3+4 _____________ ______________(2)其实，对同一个图形，我们的分析眼光可以是不同的．请你像(1)那样保持结构的、对每一个所给图形添加分割线，提供与(1)不同的分割方式;并在所给横线上，请用数学算式表达你发现的规律:_______ ____________ _______________ _______________(3)用含n的式子列式，并计算第n个图的钢管总数.9．如图，已知数轴上点A表示的数为8，B是数轴上位于点A左侧一点，且AB=20，动点P从A点出发，以每秒5个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＞0）秒．（1）写出数轴上点B表示的数______；点P表示的数______（用含t的代数式表示）（2）动点Q从点B出发，以每秒3个单位长度的速度沿数轴向右匀速运动，若点P、Q同时出发，问多少秒时P、Q之间的距离恰好等于2？（3）动点Q从点B出发，以每秒3个单位长度的速度沿数轴向左匀速到家动，若点P、Q 同时出发，问点P运动多少秒时追上Q？（4）若M为AP的中点，N为BP的中点，在点P运动的过程中，线段MN的长度是否发生变化？若变化，请说明理由，若不变，请你画出图形，并求出线段MN的长．10．如图，P是定长线段AB上一点，C、D两点分别从P、B出发以1cm/s、2cm/s的速度沿直线AB向左运动（C在线段AP上，D在线段BP上）（1）若C、D运动到任一时刻时，总有PD＝2AC，请说明P点在线段AB上的位置：（2）在（1）的条件下，Q是直线AB上一点，且AQ﹣BQ＝PQ，求PQAB的值．（3）在（1）的条件下，若C、D运动5秒后，恰好有1CD AB2=，此时C点停止运动，D点继续运动（D点在线段PB上），M、N分别是CD、PD的中点，下列结论：①PM﹣PN 的值不变；②MNAB的值不变，可以说明，只有一个结论是正确的，请你找出正确的结论并求值．11．如图，数轴上有A、B两点，且AB=12，点P从B点出发沿数轴以3个单位长度/s的速度向左运动，到达A点后立即按原速折返，回到B点后点P停止运动，点M始终为线段BP的中点(1)若AP=2时，PM=____；(2)若点A表示的数是-5，点P运动3秒时，在数轴上有一点F满足FM=2PM，请求出点F 表示的数；(3)若点P从B点出发时，点Q同时从A点出发沿数轴以2.5个单位长度/s的速度一直．．向右运动，当点Q的运动时间为多少时，满足QM=2PM.12．阅读下列材料，并解决有关问题：我们知道，(0)0(0)(0)x xx xx x>⎧⎪==⎨⎪-<⎩，现在我们可以用这一结论来化简含有绝对值的式子，例如化简式子|1||2|x x++-时，可令10x+=和20x-=，分别求得1x=-，2x=（称1-、2分别为|1|x+与|2|x-的零点值）．在有理数范围内，零点值1x=-和2x=可将全体有理数不重复且不遗漏地分成如下三种情况：（1）1x<-；（2）1-≤2x<；（3）x≥2．从而化简代数式|1||2|x x++-可分为以下3种情况：（1）当1x<-时，原式()()1221x x x=-+--=-+；（2）当1-≤2x<时，原式()()123x x=+--=；（3）当x≥2时，原式()()1221x x x=++-=-综上所述：原式21(1)3(12)21(2)x xxx x-+<-⎧⎪=-≤<⎨⎪-≥⎩通过以上阅读，请你类比解决以下问题：（1）填空：|2|x+与|4|x-的零点值分别为；（2）化简式子324x x-++．13．（阅读理解）若A，B，C为数轴上三点，若点C到A的距离是点C到B的距离的2倍，我们就称点C是（A，B）的优点．例如，如图①，点A表示的数为﹣1，点B表示的数为2．表示1的点C到点A的距离是2，到点B的距离是1，那么点C是（A，B）的优点；又如，表示0的点D到点A的距离是1，到点B的距离是2，那么点D就不是（A，B）的优点，但点D是（B，A）的优点．（知识运用）如图②，M、N为数轴上两点，点M所表示的数为﹣2，点N所表示的数为4．（1）数所表示的点是（M，N）的优点；（2）如图③，A、B为数轴上两点，点A所表示的数为﹣20，点B所表示的数为40．现有一只电子蚂蚁P从点B出发，以4个单位每秒的速度向左运动，到达点A停止．当t为何值时，P、A和B中恰有一个点为其余两点的优点？14．如图所示，已知数轴上A，B两点对应的数分别为－2，4，点P为数轴上一动点，其对应的数为x.(1)若点P到点A，B的距离相等，求点P对应的数x的值．(2)数轴上是否存在点P，使点P到点A，B的距离之和为8？若存在，请求出x的值；若不存在，说明理由．(3)点A，B分别以2个单位长度/分、1个单位长度/分的速度向右运动，同时点P以5个单位长度/分的速度从O点向左运动．当遇到A时，点P立即以同样的速度向右运动，并不停地往返于点A与点B之间．当点A与点B重合时，点P经过的总路程是多少？15．如图①，点O为直线AB上一点，过点O作射线OC，使∠AOC=120°，将一直角三角板的直角顶点放在点O处，一边OM在射线OB上，另一边ON在直线AB的下方．（1）将图①中的三角板OMN摆放成如图②所示的位置，使一边OM在∠BOC的内部，当OM平分∠BOC时，∠BO N= ；（直接写出结果）（2）在（1）的条件下，作线段NO 的延长线OP （如图③所示），试说明射线OP 是∠AOC 的平分线；（3）将图①中的三角板OMN 摆放成如图④所示的位置，请探究∠NOC 与∠AOM 之间的数量关系．（直接写出结果，不须说明理由）【参考答案】***试卷处理标记，请不要删除一、压轴题1．(1)4；(2)12或72；(3)27或2213或2 【解析】【分析】(1)根据题目得出棋子一共运动了t+2t+3t=6t 个单位长度，当t=4时，6t=24,为MN 长度的整的偶数倍，即棋子回到起点M 处，点3Q 与M 点重合，从而得出13Q Q 的长度.(2)根据棋子的运动规律可得，到3Q 点时，棋子运动运动的总的单位长度为6t,,因为t<4,由(1)知道，棋子运动的总长度为3或12+9=21，从而得出t 的值.(3)若t 2,≤则棋子运动的总长度10t 20≤,可知棋子或从M 点未运动到N 点或从N 点返回运动到2Q 的左边或从N 点返回运动到2Q 的右边三种情况可使242Q Q =【详解】解：(1)∵t+2t+3t=6t,∴当t=4时，6t=24,∵24122=⨯,∴点3Q 与M 点重合， ∴134Q Q =(2)由已知条件得出：6t=3或6t=21,解得：1t 2=或7t 2= (3)情况一：3t+4t=2, 解得：2t 7=情况二：点4Q 在点2Q 右边时：3t+4t+2=2(12-3t) 解得：22t 13= 情况三：点4Q 在点2Q 左边时：3t+4t-2=2(12-3t)解得：t=2.综上所述：t 的值为，2或27或2213. 【点睛】本题是一道探索动点的运动规律的题目，考查了学生数形结合的能力，探索规律的能力，用一元一次方程解决问题的能力.最后要注意分多种情况讨论.2．（1）3；（2）12；-3，2，-4或2，-3，-4．（3）a=11或4或10．【解析】【分析】（1）根据上述材料给出的方法计算其相应的最佳值为即可；（2）按照三个数不同的顺序排列算出最佳值，由计算可以看出，要求得这些数列的最佳值的最小值；只有当前两个数的和的绝对值最小，最小只能为|−3＋2|＝1，由此得出答案即可；（3）分情况算出对应的数值，建立方程求得a 的数值即可．【详解】（1）因为|−4|＝4，-4-32＝3.5，-4-312+＝3，所以数列−4，−3，1的最佳值为3．故答案为：3；（2）对于数列−4，−3，2，因为|−4|＝4，432--＝72，432||2--＋＝52，所以数列−4，−3，2的最佳值为52；对于数列−4，2，−3，因为|−4|＝4，||422-＋＝1，432||2--＋＝52，所以数列−4，2，−3的最佳值为1；对于数列2，−4，−3，因为|2|＝2，224-＝1，432||2--＋＝52，所以数列2，−4，−3的最佳值为1；对于数列2，−3，−4，因为|2|＝2，223-＝12，432||2--＋＝52，所以数列2，−3，−4的最佳值为12∴数列的最佳值的最小值为223-＝12，数列可以为：−3，2，−4或2，−3，−4．故答案为：12，−3，2，−4或2，−3，−4．（3）当22a＋＝1，则a＝0或−4，不合题意；当92a-＋＝1，则a＝11或7；当a＝7时，数列为−9，7，2，因为|−9|＝9，972-＋＝1，9722-+＋＝0，所以数列2，−3，−4的最佳值为0，不符合题意；当972a-+＋＝1，则a＝4或10．∴a＝11或4或10．【点睛】此题考查数字的变化规律，理解新定义运算的方法是解决问题的关键．3．（1）﹣14，8﹣5t；（2）2.5或3秒时P、Q之间的距离恰好等于2；（3）点P运动11秒时追上点Q；（4）线段MN的长度不发生变化，其值为11，见解析.【解析】【分析】（1）根据已知可得B点表示的数为8﹣22；点P表示的数为8﹣5t；（2）设t秒时P、Q 之间的距离恰好等于2．分①点P、Q相遇之前和②点P、Q相遇之后两种情况求t值即可；（3）设点P运动x秒时，在点C处追上点Q，则AC=5x，BC=3x，根据AC﹣BC=AB，列出方程求解即可；（3）分①当点P在点A、B两点之间运动时，②当点P运动到点B的左侧时，利用中点的定义和线段的和差求出MN的长即可．【详解】（1）∵点A表示的数为8，B在A点左边，AB=22，∴点B表示的数是8﹣22=﹣14，∵动点P从点A出发，以每秒5个单位长度的速度沿数轴向左匀速运动，设运动时间为t （t＞0）秒，∴点P表示的数是8﹣5t．故答案为：﹣14，8﹣5t；（2）若点P、Q同时出发，设t秒时P、Q之间的距离恰好等于2．分两种情况：①点P、Q相遇之前，由题意得3t+2+5t=22，解得t=2.5；②点P、Q相遇之后，由题意得3t﹣2+5t=22，解得t=3．答：若点P、Q同时出发，2.5或3秒时P、Q之间的距离恰好等于2；（3）设点P 运动x 秒时，在点C 处追上点Q ，则AC =5x ，BC =3x ，∵AC ﹣BC =AB ，∴5x ﹣3x =22，解得：x =11，∴点P 运动11秒时追上点Q ；（4）线段MN 的长度不发生变化，都等于11；理由如下：①当点P 在点A 、B 两点之间运动时：MN =MP +NP =12AP +12BP =12（AP +BP ）=12AB =12×22=11； ②当点P 运动到点B 的左侧时：MN =MP ﹣NP =12AP ﹣12BP =12（AP ﹣BP ）=12AB =11， ∴线段MN 的长度不发生变化，其值为11．【点睛】本题考查了数轴一元一次方程的应用，用到的知识点是数轴上两点之间的距离，关键是根据题意画出图形，注意分两种情况进行讨论．4．（1）6秒钟;（2）4秒钟或8秒钟；（3）点Q 的速度为7/cm s 或2.4/cm s ．【解析】【分析】（1）设经过ts 后，点P Q 、相遇，根据题意可得方程2330t t +=，解方程即可求得t 值；（2）设经过xs ，P Q 、两点相距10cm ，分相遇前相距10cm 和相遇后相距10cm 两种情况求解即可；（3）由题意可知点P Q 、只能在直线AB 上相遇，由此求得点Q 的速度即可.【详解】解：（1）设经过ts 后，点P Q 、相遇．依题意，有2330t t +=，解得：6t =．答：经过6秒钟后，点P Q 、相遇；（2）设经过xs ，P Q 、两点相距10cm ，由题意得231030x x ++=或231030x x +-=，解得：4x =或8x =．答：经过4秒钟或8秒钟后，P Q 、两点相距10cm ；（3）点P Q 、只能在直线AB 上相遇，则点P 旋转到直线AB 上的时间为：()120430s =或()1201801030s +=，设点Q 的速度为/ycm s ，则有4302y =-，解得：7y =；或10306y =-，解得 2.4y =，答：点Q 的速度为7/cm s 或2.4/cm s ．【点睛】本题考查了一元一次方程的综合应用解决第（2）（3）问都要分两种情况进行讨论，注意不要漏解.5．(1)1＋a 或1－a ；(2)12或52；(3)1≤b≤7. 【解析】【分析】(1)根据d 追随值的定义，分点N 在点M 左侧和点N 在点M 右侧两种情况，直接写出答案即可；(2)①分点A 在点B 左侧和点A 在点B 右侧两种情况，类比行程问题中的追及问题，根据“追及时间=追及路程÷速度差”计算即可；②【详解】解：(1)点N 在点M 右侧时，点N 表示的数是1+a ；点N 在点M 左侧时，点N 表示的数是1-a ；(2)①b=4时，AB 相距3个单位，当点A 在点B 左侧时，t=(3-2)÷(3-1)=12，当点A 在点B 右侧时，t=(3+2)÷(3-1)=52； ②当点B 在点A 左侧或重合时，即d ≤1时，随着时间的增大，d 追随值会越来越大， ∵0<t≤3，点A 到点B 的d 追随值d[AB]≤6，∴1-d+3×(3-1)≤6，解得d ≥1，∴d=1，当点B 在点A 右侧时，即d>1时，在AB 重合之前，随着时间的增大，d 追随值会越来越小，∵点A 到点B 的d 追随值d[AB]≤6，∴d ≤7∴1<d ≤7，综合两种情况，d 的取值范围是1≤d ≤7.故答案为(1)1＋a或1－a；(2)①12或52；②1≤b≤7.【点睛】本题考查了数轴上两点之间的距离和动点问题.6．（1）（4，8）（2）S△OAE＝8﹣t（3）2秒或6秒【解析】【分析】（1）根据M和N的坐标和平移的性质可知：MN∥y轴∥PQ，根据K是PM的中点可得K 的坐标；（2）根据三角形面积公式可得三角形OAE的面积S；（3）存在两种情况：①如图2，当点B在OD上方时②如图3，当点B在OD上方时，过点B作BG⊥x轴于G，过D作DH⊥x轴于H，分别根据三角形OBD的面积等于三角形OAE的面积列方程可得结论．【详解】（1）由题意得：PM＝4，∵K是PM的中点，∴MK＝2，∵点M的坐标为（2，8），点N的坐标为（2，6），∴MN∥y轴，∴K（4，8）；（2）如图1所示，延长DA交y轴于F，则OF⊥AE，F（0，8﹣t），∴OF＝8﹣t，∴S△OAE＝12O F•AE＝12（8﹣t）×2＝8﹣t；（3）存在，有两种情况：，①如图2，当点B在OD上方时，过点B作BG⊥x轴于G，过D作DH⊥x轴于H，则B（2，6﹣t），D（6，0），∴OG＝2，GH＝4，BG＝6﹣t，DH＝8﹣t，OH＝6，S△OBD＝S△OBG+S四边形DBGH+S△ODH，＝12OG•BG+12（BG+DH）•GH﹣12OH•DH，＝12×2（6-t）+12×4（6﹣t+8﹣t）﹣12×6（8﹣t），＝10﹣2t，∵S△OBD＝S△OAE，∴10﹣2t＝8﹣t，t＝2；②如图3，当点B在OD上方时，过点B作BG⊥x轴于G，过D作DH⊥x轴于H，则B（2，6﹣t），D（6，8﹣t），∴OG＝2，GH＝4，BG＝6﹣t，DH＝8﹣t，OH＝6，S△OBD＝S△ODH﹣S四边形DBGH﹣S△OBG，＝12OH•DH﹣12（BG+DH）•GH﹣12OG•BG，＝12×2（8-t）﹣12×4（6﹣t+8﹣t）﹣12×2（6﹣t），＝2t﹣10，∵S△OBD＝S△OAE，∴2t﹣10＝8﹣t，t ＝6；综上，t 的值是2秒或6秒．【点睛】本题考查四边形综合题、矩形的性质、三角形的面积、一元一次方程等知识，解题关键是灵活运用所学知识解决问题，学会用分类讨论的思想思考问题．7．（1）25- ，35 （2）运动时间为4秒，相遇点表示的数字为27 ；（3）5;(4) 一共相遇了7次.【解析】【分析】（1）根据0+0式的定义即可解题；（2）设运动时间为x 秒,表示出P ,Q 的运动路程,利用路程和等于AB 长即可解题；（3）根据点Q 达到A 点时，点P ，Q 停止运动求出运动时间即可解题；（4）根据第三问点P 运动了6个来回后，又运动了30个单位长度即可解题.【详解】解：（1）25- ，35（2）设运动时间为x 秒13x 2x 2535+=+解得 x 4=352427-⨯=答：运动时间为4秒，相遇点表示的数字为27（3）运动总时间：60÷2=30（秒），13×30÷60=6…30即点P 运动了6个来回后，又运动了30个单位长度,∵25305-+=，∴点P 所在的位置表示的数为5 .（4）由（3）得：点P 运动了6个来回后，又运动了30个单位长度,∴点P 和点Q 一共相遇了6+1=7次.【点睛】本题考查了一元一次方程的实际应用,数轴的应用,难度较大,熟悉路程,时间,速度之间的关系是解题关键.8．（1）3456;45678S S =+++=++++ ;(2) 方法不唯一，见解析；（3）方法不唯一，见解析【解析】【分析】先找出前几项的钢管数，在推出第n 项的钢管数.【详解】（1）3456;45678S S =+++=++++（2）方法不唯一，例如：12S =+ 1233S =+++ 123444S =+++++ 12345555S =+++++++ （3）方法不唯一，例如：()()12.....2S n n n n =++++++()()()()=.....12.. (1112)n n n n n n n n +++++++=+++ ()312n n =+ 【点睛】此题主要考察代数式的规律探索及求和，需要仔细分析找到规律.9．（1）-12,8-5t ；（2）94或114；（3）10；（4）MN 的长度不变，值为10. 【解析】【分析】(1)根据已知可得B 点表示的数为8﹣20；点P 表示的数为8﹣5t ；(2)运动时间为t 秒，分点P 、Q 相遇前相距2，相遇后相距2两种情况列方程进行求解即可；(3)设点P 运动x 秒时追上Q ，根据P 、Q 之间相距20，列方程求解即可；(4)分①当点P 在点A 、B 两点之间运动时，②当点P 运动到点B 的左侧时，利用中点的定义和线段的和差求出MN 的长即可．【详解】(1)∵点A 表示的数为8，B 在A 点左边，AB=20，∴点B 表示的数是8﹣20=﹣12，∵动点P 从点A 出发，以每秒5个单位长度的速度沿数轴向左匀速运动，设运动时间为t(t ＞0)秒，∴点P 表示的数是8﹣5t ，故答案为﹣12，8﹣5t ；(2)若点P 、Q 同时出发，设t 秒时P 、Q 之间的距离恰好等于2；分两种情况：①点P 、Q 相遇之前，由题意得3t+2+5t=20，解得t=94； ②点P 、Q 相遇之后，由题意得3t﹣2+5t=20，解得t=11 4，答：若点P、Q同时出发，94或114秒时P、Q之间的距离恰好等于2；(3)如图，设点P运动x秒时，在点C处追上点Q，则AC=5x，BC=3x，∵AC﹣BC=AB，∴5x﹣3x=20，解得：x=10，∴点P运动10秒时追上点Q；(4)线段MN的长度不发生变化，都等于10；理由如下：①当点P在点A、B两点之间运动时：MN=MP+NP=12AP+12BP=12(AP+BP)=12AB=10，②当点P运动到点B的左侧时：MN=MP﹣NP=12AP﹣12BP=12(AP﹣BP)=12AB=10，∴线段MN的长度不发生变化，其值为10．【点睛】本题考查了数轴上的动点问题，一元一次方程的应用，用到的知识点是数轴上两点之间的距离，关键是根据题意画出图形，注意分两种情况进行讨论．10．（1）点P在线段AB上的13处；（2）13；（3）②MNAB的值不变.【解析】【分析】（1）根据C、D的运动速度知BD=2PC，再由已知条件PD=2AC求得PB=2AP，所以点P在线段AB上的13处；（2）由题设画出图示，根据AQ-BQ=PQ求得AQ=PQ+BQ；然后求得AP=BQ，从而求得PQ 与AB的关系；（3）当点C停止运动时，有CD＝12AB，从而求得CM与AB的数量关系；然后求得以AB表示的PM与PN的值，所以MN＝PN−PM＝112AB．【详解】解：（1）由题意：BD=2PC∵PD=2AC，∴BD+PD=2（PC+AC），即PB=2AP.∴点P在线段AB上的13处；（2）如图：∵AQ-BQ=PQ，∴AQ=PQ+BQ，∵AQ=AP+PQ，∴AP=BQ，∴PQ=13 AB，∴13 PQ AB=（3）②MNAB的值不变.理由：如图，当点C停止运动时，有CD=12 AB，∴CM=14 AB，∴PM=CM-CP=14AB-5，∵PD=23AB-10，∴PN=1223（AB-10）=13AB-5，∴MN=PN-PM=112AB，当点C停止运动，D点继续运动时，MN的值不变，所以111212ABMNAB AB==.【点睛】本题考查了比较线段的长短．利用中点性质转化线段之间的倍分关系是解题的关键，在不同的情况下灵活选用它的不同表示方法，有利于解题的简洁性．同时，灵活运用线段的和、差、倍、分转化线段之间的数量关系也是十分关键的一点． 11．(1)5 ；(2)点F 表示的数是11.5或者-6.5；(3)127t =或6t =. 【解析】【分析】（1）由AP=2可知PB=12-2=10，再由点M 是PB 中点可知PM 长度；（2）点P 运动3秒是9个单位长度，M 为PB 的中点，则可求解出点M 表示的数是2.5，再由FM=2PM 可求解出FM=9，此时点F 可能在M 点左侧，也可能在其右侧；（3）设Q 运动的时间为t 秒，由题可知t=4秒时，点P 到达点A ，再经过4秒点P 停止运动；则分04t ≤≤和48t <≤两种情况分别计算，由题可知即可QM=2PM=BP ，据此进行解答即可.【详解】(1)5 ；(2)∵点A 表示的数是5-∴点B 表示的数是7∵点P 运动3秒是9个单位长度，M 为PB 的中点 ∴PM=12PB=4.5，即点M 表示的数是2.5 ∵FM=2PM∴FM=9∴点F 表示的数是11.5或者-6.5(3)设Q 运动的时间为t 秒，当04t ≤≤时，由题可知QM=2PM=BP ，故点Q 位于点P 左侧，则AB=AQ+QP+PB ，而QP=QM-PM=2PM-PM=12BP ，则可得12=2.5t+12⨯3t+3t=7t ，解得t=127；当48t <≤时，由题可知QM=2PM=BP ，故点Q 位于点B 右侧，则PB=2QB ，则可得，()()123422.512t t --=-，整理得8t=48，解得6t =.【点睛】本题结合数轴上的动点问题考查了一元一次方程的应用，第3问要根据题干条件分情况进行讨论，作出图形更易理解.12．(1) 2x =-和4x = ;(2) 35(4)11(43)35(3)x x x x x x --<-⎧⎪+-≤<⎨⎪+≥⎩【解析】【分析】（1）令x +2=0和x -4=0,求出x 的值即可得出|x +2|和|x -4|的零点值,（2）零点值x =3和x =-4可将全体实数分成不重复且不遗漏的如下3种情况:x ＜-4、-4≤x ＜3和x ≥3．分该三种情况找出324x x -++的值即可．【详解】解：（1）2x =-和4x =,（2）由30x -=得3,x =由40x +=得4x =-,①当4x <-时,原式()()32435x x x =---+=--,②当4-≤3x <时,原式()()32411x x x =--++=+,③当x ≥3时,原式()()32435x x x =-++=+,综上所述：原式()35(4)11(43)353x x x x x x ⎧--<-⎪=+-≤<⎨⎪+≥⎩, 【点睛】本题主要考查了绝对值化简方法,解决本题的关键是要熟练掌握绝对值化简方法.13．（1）2或10；（2）当t 为5秒、10秒或7.5秒时，P 、A 和B 中恰有一个点为其余两点的优点．【解析】【分析】（1）设所求数为x ，根据优点的定义分优点在M 、N 之间和优点在点N 右边，列出方程解方程即可；（2）根据优点的定义可知分三种情况：①P 为（A ，B ）的优点；②P 为（B ，A ）的优点；③B 为（A ，P ）的优点．设点P 表示的数为x ，根据优点的定义列出方程，进而得出t 的值．【详解】解：（1）设所求数为x ，当优点在M 、N 之间时，由题意得x ﹣（﹣2）=2（4﹣x ），解得x=2；当优点在点N 右边时，由题意得x ﹣（﹣2）=2（x ﹣4），解得：x=10；故答案为：2或10；（2）设点P 表示的数为x ，则PA=x+20，PB=40﹣x ，AB=40﹣（﹣20）=60，分三种情况：①P 为（A ，B ）的优点．由题意，得PA=2PB ，即x ﹣（﹣20）=2（40﹣x ），解得x=20，∴t=（40﹣20）÷4=5（秒）；②P为（B，A）的优点．由题意，得PB=2PA，即40﹣x=2（x+20），解得x=0，∴t=（40﹣0）÷4=10（秒）；③B为（A，P）的优点．由题意，得AB=2PA，即60=2（x+20）解得x=10，此时，点P为AB的中点，即A也为（B，P）的优点，∴t=30÷4=7.5（秒）；综上可知，当t为5秒、10秒或7.5秒时，P、A和B中恰有一个点为其余两点的优点．【点睛】本题考查了一元一次方程的应用及数轴，解题关键是要读懂题目的意思，理解优点的定义，找出合适的等量关系列出方程，再求解．14．(1)x=1;(2) x＝－3或x＝5;(3) 30.【解析】【分析】（1）根据题意可得4－x＝x－（－2），解出x的值；（2）此题分为两种情况，当点P在B的右边时，当点P在B的左边时，分别列出方程求解即可；（3）设经过x分钟点A与点B重合，根据题意得：2x＝6＋x进而求出即可.【详解】（1）4－x＝x－（－2），解得：x＝1，（2）①当点P在B的右边时得：x－（－2）＋x－4＝8，解得：x＝5，②当点P在B的左边时得：－2－x＋4－x＝8，解得：x＝－3，则x＝－3或x＝5.（3）设经过x分钟点A与点B重合，根据题意得：2x＝6＋x，解得：x＝6，则5x＝30，故答案为30个单位长度.【点睛】本题主要考查了一元二次方程的应用，解此题的要点在于根据数轴得出点的位置. 15．（1）60°；（2）射线OP是∠AOC的平分线；（3）30°．【解析】整体分析：(1)根据角平分线的定义与角的和差关系计算；(2)计算出∠AOP的度数，再根据角平分线的定义判断；(3)根据∠AOC，∠AON，∠NOC，∠MON，∠AOM的和差关系即可得到∠NOC 与∠AOM之间的数量关系．解：(1)如图②，∠AOC=120°，∴∠BOC=180°﹣120°=60°，又∵OM平分∠BOC，∴∠BOM=30°，又∵∠NOM=90°，∴∠BOM=90°﹣30°=60°，故答案为60°；(2)如图③，∵∠AOP=∠BOM=60°，∠AOC=120°，∴∠AOP=12∠AOC，∴射线OP是∠AOC的平分线；(3)如图④，∵∠AOC=120°，∴∠AON=120°﹣∠NOC，∵∠MON=90°，∴∠AON=90°﹣∠AOM，∴120°﹣∠NOC=90°﹣∠AOM，即∠NOC﹣∠AOM=30°．。

初一上学期数学压轴题期末复习试卷带答案

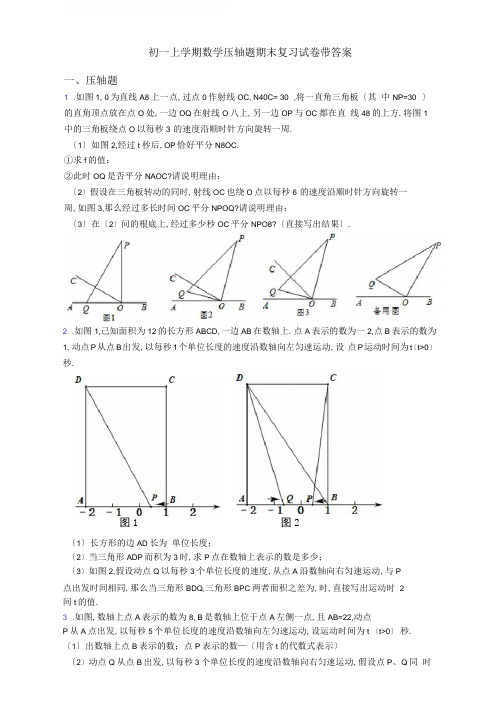
初一上学期数学压轴题期末复习试卷带答案一、压轴题1 .如图1,0为直线A8上一点,过点0作射线OC, N40C= 30° ,将一直角三角板〔其中NP=30°〕的直角顶点放在点O处,一边OQ在射线O八上,另一边OP与OC都在直线48的上方.将图1中的三角板绕点O以每秒3°的速度沿顺时针方向旋转一周.〔1〕如图2,经过t秒后,OP恰好平分N8OC.①求f的值：②此时OQ是否平分NAOC?请说明理由；〔2〕假设在三角板转动的同时,射线OC也绕O点以每秒6°的速度沿顺时针方向旋转一周,如图3,那么经过多长时间OC平分NPOQ?请说明理由：〔3〕在〔2〕问的根底上,经过多少秒OC平分NPO8?〔直接写出结果〕.2 .如图1,己知面积为12的长方形ABCD, 一边AB在数轴上.点A表示的数为一2,点B 表示的数为1,动点P从点B出发,以每秒1个单位长度的速度沿数轴向左匀速运动,设点P运动时间为t 〔t>0〕秒.图1 图2〔1〕长方形的边AD长为单位长度；〔2〕当三角形ADP而积为3时,求P点在数轴上表示的数是多少；〔3〕如图2,假设动点Q以每秒3个单位长度的速度,从点A沿数轴向右匀速运动,与P点出发时间相同.那么当三角形BDQ,三角形BPC两者面积之差为,时,直接写出运动时2间t的值.3 .如图,数轴上点A表示的数为8, B是数轴上位于点A左侧一点,且AB=22,动点P从A点出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t 〔t>0〕秒. 〔1〕出数轴上点B表示的数；点P表示的数—〔用含t的代数式表示〕〔2〕动点Q从点B出发,以每秒3个单位长度的速度沿数轴向右匀速运动,假设点P、Q同时出发,问多少秒时P、Q之间的距离恰好等于2?〔3〕动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,假设点P、Q同时出发,问点P运动多少秒时追上点Q?〔4〕假设M为AP的中点,N为BP的中点,在点P运动的过程中,线段MN的长度是否发生变化？假设变化,请说明理由,假设不变,请你画出图形,并求出线段MN的长.B O A0 84 .己知多项式3x6-2x2-4的常数项为a,次数为b.〔1〕设.与b分别对应数轴上的点4点8,请直接写出, b=,并在数轴上确定点4、点8的位置；〔2〕在〔1〕的条件下,点P以每秒2个单位长度的速度从点八向8运动,运动时间为t 秒：①假设%-P8=6,求t的值,并写出此时点P所表示的数：②假设点P从点4出发,到达点8后再以相同的速度返回点4在返回过程中,求当0P=3 时,t为何值？-8 0；85 .有理数a, b, c在数轴上对应的点分别为A, B, C,且满足〔a-1〕2+|ab+3|=0, c=-2a+b.।।।।।।।।।； ,-4-3 -2 -1 0 1 2 3 4 5-4 -3 -2 -1 0 1 2 3 4 5〔1〕分别求a, b, c的值；〔2〕假设点A和点B分别以每秒2个单位长度和每秒1个单位长度的速度在数轴上同时相向运动,设运动时间为t秒.i〕是否存在一个常数k,使得3BC-k・AB的值在一定时间范围内不随运动时间t的改变而改变？假设存在,求出k的值：假设不存在,请说明理由.ii〕假设点C以每秒3个单位长度的速度向右与点A, B同时运动,何时点C为线段AB的三等分点？请说明理由.6 .如图,数轴上点A表示的数为6, B是数轴上在A左侧的一点,且A, B两点间的距离为10.动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动.〔1〕设运动时间为t0〕秒,数轴上点B表示的数是,点P表示的数是〔用含t的代数式表示〕：〔2〕假设点P、Q 同时出发,求：①当点P运动多少秒时,点P与点Q相遇？②当点P运动多少秒时,点P与点Q 间的距离为8个单位长度？7 .如图,在平面直角坐标系中,点M的坐标为〔2, 8〕,点N的坐标为〔2, 6〕,将线段MN向右平移4个单位长度得到线段PQ 〔点P和点Q分别是点M和点N的对应点〕,连接MP、NQ,点K 是线段MP的中点.〔1〕求点K的坐标：〔2〕假设长方形PMNQ以每秒1个单位长度的速度向正下方运动,〔点A、B、C、D、E分别是点M、N、Q、P、K的对应点〕,当BC与x轴重合时停止运动,连接OA、0E,设运动时间为t 秒,请用含t的式子表示三角形OAE的面积S 〔不要求写出t的取值范围〕；〔3〕在〔2〕的条件下,连接OB、0D,问是否存在某一时刻t,使三角形OBD的面积等于三角形OAE的面积,？假设存在,请求出t值；假设不存在,请说明理由.8 .我国著名数学家华罗庚曾经说过,“数形结合百般好,隔裂分家万事非.〞数形结合的思想方法在数学中应用极为广泛.观察以下根据一定规律堆砌的钢管的横截面图：用含n的式子表示第n个图的钢管总数.〔分析思路〕图形规律中暗含数字规律,我们可以采用分步的方法,从图形排列中找规律;把图形看成几个局部的组合,并保持结构,找到每一局部对应的数字规律,进而找到整个图形对应的数字规律.如:要解决上而问题,我们不妨先从特例入手：〔统一用S表示钢管总数〕〔解决问题〕⑴如图,如果把每个图形根据它的行来分割观察,你发现了这些钢管的堆砌规律了吗?像n=l、n=2的情形那样,在所给横线上,请用数学算式表达你发现的规律.S=l+2 S=2+3+4 __________________________________⑵其实,对同一个图形,我们的分析眼光可以是不同的.请你像⑴那样保持结构的、对每一个所给图形添加分割线,提供与⑴不同的分割方式;并在所给横线上,请用数学算式表达你发现的规律：⑶用含n的式子列式,并计算第n个图的钢管总数.9 .如图,P是定长线段A8上一点,C、.两点分别从P、8出发以lcm/s、2cm/s的速度沿直线48向左运动〔C在线段AP上,.在线段8P上〕〔1〕假设C、.运动到任一时刻时,总有PD=〃C,请说明P点在线段A8上的位置：III 1 1 A CP D3〔2〕在〔1〕的条件下,Q是直线48上一点,且4Q-8Q=PQ,求丝的值.AB। ____________ । --------------------------------------------------------------- 1A P B〔3〕在〔1〕的条件下,假设C、.运动5秒后,恰好有CD =,AB.此时C点停止运动, 2.点继续运动〔.点在线段P8上〕,M、A/分别是CD、P.的中点,以下结论：①PM - PNMN的值不变；②一二的值不变,可以说明,只有一个结论是正确的,请你找出正确的结论并AB求值.111 1 1A CP D310.点A在数轴上对应的数为-3,点8对应的数为2.⑴如图1点C在数轴上对应的数为x,且x是方程2x+l二;x-5的解,在数轴上是否存在点P使PA+PB==BC+A8?假设存在,求出点P对应的数：假设不存在,说明理由：2⑵如图2,假设P点是8点右侧一点,%的中点为N为P8的三等分点且靠近于P点, 13 .问题一：如图1,4, C两点之间的距离为16 cm,甲,乙两点分别从相距3cm的A, 8两点同时出发到C点,假设甲的速度为8cm/s,乙的速度为6cm/s,设乙运动时间为x〔s〕,甲乙两点之间距离为y〔 cm〕 .⑴当甲追上乙时,x=.〔2〕请用含x的代数式表示y.当甲追上乙前,y=；当甲追上乙后,甲到达C之前,y=；当甲到达C之后,乙到达C之前,y=.R乙问题二：如图2,假设将上述线段4c弯曲后视作钟表外国的一局部,线段48正好对应钟表上的弧4B 〔1小时的间隔〕,易知/408=30..⑴分针0D指向圆周上的点的速度为每分钟转动—cm；时针0E指向圆周上的点的速度为每分钟转动cm .⑵假设从4 ：00起计时,求几分钟后分针与时针第一次重合.图214.：如图,点A、B分别是NMON的边OM、ON上两点,0C平分NMON,在NCON的内部取一点P 〔点A、P、B三点不在同一直线上〕,连接PA、PB .〔1〕探索NAPB与NMON、NPAO、NPBO之间的数量关系,并证实你的结论：〔2〕设NOAP二x.,NOBP=y.,假设NAPB的平分线PQ交0C于点Q,求NOQP的度数〔用含有x、y的代数式表示〕.15.数轴上三点A, 0, B表示的数分别为6, 0,-4,动点P从A出发,以每秒6个单位的速度沿数轴向左匀速运动.〔1〕当点P到点A的距离与点P到点B的距离相等时,点P在数轴上表示的数是(2)另一动点R从B出发,以每秒4个单位的速度沿数轴向左匀速运动,假设点P、R同时出发,问点P运动多少时间追上点R?(3)假设M为AP的中点,N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化？假设发生变化,请你说明理由；假设不变,请你画出图形,并求出线段MN的长度.【参考答案】***试卷处理标记,请不要删除一、压轴题1. (1)①5；②0Q平分NA9C,理由详见解析：(2) 5秒或65秒时0C平分NPOQ：70 ,(3) t=——秒.3【解析】【分析】(1)①由N4OC=30.得到N80c=150.,借助角平分线定义求出NPOC度数,根据角的和差关系求出NCOQ度数,再算出旋转角NAOQ度数,最后除以旋转速度3即可求出t 值：②根据NAOQ和NCOQ 度数比拟判断即可：(2)根据旋转的速度和起始位置,可知NAOQ=3t, N4OC=30° +63根据角平分线定义可知NCOQ=45°,利用乙4OQ、NAOC、NCOQ角之间的关系构造方程求出时间t；(3)先证实NAOQ与NPO8互余,从而用t表示出NPO8=90° -33根据角平分线定义再用t表示N8OC度数：同时旋转后N4OC=30' +6t,那么根据互补关系表示出N8OC度数,同理再把N8OC度数用新的式子表达出来.先后两个关于N8OC的式子相等,构造方程求解.【详解】(1) ©V ZAOC=30" ,A ZBOC= 180° - 30° =150° ,9：0P^^ZB0C,：.ZCOP=- ZBOC=75° , 2：.ZCOQ=900 - 75° =15° ,：.ZAOQ= ZAOC - ZCOQ=30° -15° =15° , t=15-？3=5；②是,理由如下：VZCOQ=15° , 4OQ=15° ,：.OQ平分NAOC：(2) 9：0C^^ZP0Q.,NCOQ=1/POQ=45° .2设NA0Q=3t, Z/AOC=300 +6t,由NAOC- N4OQ=45° ,可得30+6t - 3t=45,解得：t=5,当30+6L 3t=225,也符合条件,解得：t=65 ,,5秒或65秒时,OC平分NPOQ：(3)设经过t秒后OC平分NPO8,•「OC 平分NPO8,1；./BOC=- NBOP, 2•••/40Q+N 80P=90 ° ,A ZBOP= 90° -3t,又N8OC=180口- ZAOC= 180" -300 - 63,180 - 30 - 6t=1 ( 90- 3t),2, 70解得t= ——・3【点睛】此题主要考查一元一次方程的应用,根据角度的和差倍分关系,列出方程,是解题的关键.2. (1) 4； (2) —3.5 或一0・5： (3)1的值为口、— . U 或16 16 8 8【解析】【分析】(1)先求出A8的长,由长方形八8c .的面积为12,即可求出4)的长；(2)由三角形4DP 面积为3,求出AP 的长,然后分两种情况讨论：①点P 在点八的左边：②点P 在点4的右边.(3)分两种情况讨论：①假设Q 在8的左边,贝lj8Q=3-3t.由IS/aa-SrePck ］,解方程即可：②假设Q 在8的右边,那么8Q=3L3.由|S,,BOQ -S.田c| = ；,解方程即可.【详解】(1) AB=1- (-2) =3.・二长方形 48CD 的面枳为 12, ：.ABXAD=12, ：.AD=12^3=4.故答案为：4.(2)三角形 4DP 面积为：-AP^AD=-APX^3, 2 2解得:4P=1.5,点P 在点4的左边：-2-1.5=35, P 点在数轴上表示-3.5：点P 在点A 的右边：-2+L5=-0.5, P 点在数轴上表示-05 综上所述：P 点在数轴上表示-3.5或-0.5. (3)分两种情况讨论：①假设Q 在8的左边,贝8Q=A8 - 4Q=3-3t.S ABOQU ：8Q ・AD= )(3-31)x4 = 6-6/,S.,.BPC =；8P ・4D=；/x4 = 2l,|(6-6/)-2r| = ^-, 6-8/ = ±0.5,解得：g ■^或g ：②假设Q 在8的右边,那么8Q=4Q-A8=3t —3.S A BOQ = — BQ9AD= — (3/ -3)X4 = 6r -6, S .田C 」8P ・4D=L X 4 = 21, 2 2 22 |(6/-6)-2/| = —, 4,一6 = ±0.5,解得：仁匚或U. 28 8 综上所述：t 的值为二、二、F 或1.16 16 8 8【点睛】此题考查了数轴、一元一次方程的应用,用到的知识点是数轴上两点之间的距离公式.3. (1) - 14, 8-5t ： (2) 2.5或3秒时P 、Q 之间的距离恰好等于2： (3)点P 运动 11秒时追上点Q: (4)线段MN 的长度不发生变化,其值为11,见解析.【解析】【分析】(1)根据可得B 点表示的数为8-22：点P 表示的数为8-5t ： (2)设t 秒时P 、Q 之间的距离恰好等于2.分①点P 、Q 相遇之前和②点P 、Q 相遇之后两种情况求t 值即可：(3)设点P 运动x 秒时,在点C 处追上点Q,那么AC=5x, BC=3x,根据AC-BC 二AB, 列出方程求解即可；(3)分①当点P 在点A 、B 两点之间运动时,②当点P 运动到点B 的左侧时,利用中点的定义和线段的和差求出MN的长即可.【详解】(1)•••点A表示的数为8, B在A点左边,AB=22,,点B表示的数是8-22二-14,•二动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t (t>0)秒, ・•・点P表示的数是8-5t.故答案为：-14, 8 - 5t；(2)假设点P、Q同时出发,设t秒时P、Q之间的距离恰好等于2.分两种情况：①点P、Q相遇之前,由题意得3t+2+5t=22,解得"2. 5；②点P、Q相遇之后,由题意得3t-2+5t=22,解得13.答：假设点P、Q同时出发,2. 5或3秒时P、Q之间的距离恰好等于2：(3)设点P运动x秒时,在点C处追上点Q,c B Qd )0 6那么AC=5x, BC=3x,VAC - BC二AB....5x - 3x=22,解得：x=ll,・•.点P运动11秒时追上点Q：(4)线段MN的长度不发生变化,都等于11：理由如下：①当点P在点A、B两点之间运动时：U 01 1 1 1 1MN=MP+NP二一AP+-BP二一(AP+BP)二一AB二一X22=ll； 2 2 2 2 2②当点P运动到点B的左侧时：p N B M O A•1—110 81 1 1 1MN = MP-NP 二一AP- - BP 二一 (AP・BP)二一AB 二11, 2 2 2 2・•・线段MN的长度不发生变化,其值为11.【点睛】此题考查了数轴一元一次方程的应用,用到的知识点是数轴上两点之间的距离,关键是根据题意画出图形,注意分两种情况进行讨论.13 194. (1) -4, 6： (2)①4：②一,或一 2 2【解析】【分析】(1)根据多项式的常数项与次数的定义分别求出a, b的值,然后在数轴上表示即可：(2)①根据PA - PB = 6列出关于t的方程,解方程求出t的值,进而得到点P所表示的数：②在返回过程中,当0P = 3时,分两种情况：(I) P在原点右边；(口) P在原点左边.分别求出点P运动的路程,再除以速度即可.【详解】(1)•••多项式3x6-2x2-4的常数项为a,次数为b,.\a= - 4, b = 6.如下图：A B_I ------- _I_I ------- !~!~~! ----- !~~!•-------8 -4 0 6 8故答案为-4, 6：(2)①:3=23 AB=6- ( - 4) =10,.\PB=AB - PA=10 - 2t.VPA- PB = 6,A 2t - (10-2t ) =6,解得t=4,此时点P所表示的数为-4+2t= - 4+2x4=4：②在返回过程中,当OP=3时,分两种情况：13(I )如果P在原点右边,那么AB+BP=10+ (6 - 3) =13, t=—；219(II)如果P 在原点左边,那么AB+BP=10+ (6+3) =19, t=—.【点睛】此题考查了一元一次方程的应用,路程、速度与时间关系的应用,数轴以及多项式的有关定义,理解题意利用数形结合是解题的关键.5. (1) 1, -3, -5 (2) i)存在常数m, m=6这个不变化的值为26, ii) 11.5s【解析】【分析】(1)根据非负数的性质求得a、b、c的值即可：(2) i)根据3BC-k・AB求得k的值即可：ii)当AC=,AB时,满足条件.3【详解】(1)Ya、b 满足(a-1) 2+|ab+3|=0,Aa-l=0 且ab+3=0.解得a=l, b=-3.c=-2a+b=-5.故a, b, c的值分别为1, -3, 5(2)i)假设存在常数k,使得3BC-k・AB不随运动时间t的改变而改变.那么依题意得：AB=5+t, 2BC=4+6t.所以m・AB-2BC=m (5+t) - (4+6t) =5m+mt-4-6t 与t 的值无关,即m-6=0,解得m=6,所以存在常数m, m=6这个不变化的值为26.Ii) AC」AB,3AB=5+t, AC=-5+3t- (l+2t) =t-6,t-6=l (5+t),解得t=ll.5s.3【点睛】此题考查了一元一次方程的应用,找准等量关系,正确列出一元一次方程是解题的关键.6. (1) -4, 6-5t； (2)①当点P运动5秒时,点P与点Q相遇：②当点P运动1或9 秒时,点P与点Q 间的距离为8个单位长度.【解析】【分析】(1)根据题意可先标出点A,然后根据B在A的左侧和它们之间的距离确定点B,由点P 从点A出发向左以每秒5个单位长度匀速运动,表示出点P即可；〔2〕①由于点P和Q都是向左运动,故当P追上Q时相遇,根据P比Q多走了10个单位长度列出等式,根据等式求出t的值即可得出答案；②要分两种情况计算：第一种是点P追上点Q之前,第二种是点P追上点Q之后.【详解】解：〔1〕•・•数轴上点A表示的数为6,...OA=6,那么OB = AB - OA=4, 点B在原点左边,・•・数轴上点B所表示的数为-4：点P运动t秒的长度为53・・•动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,・2所表示的数为：6-53故答案为-4, 6-5t；〔2〕①点P运动t秒时追上点Q,根据题意得5t=10+3t,解得t=5,答：当点P运动5秒时,点P与点Q相遇：②设当点P运动a秒时,点P与点Q间的距离为8个单位长度,当P不超过Q,贝10+3a - 5a=8,解得a = L当P超过Q,那么10+3a+8 = 5a,解得a = 9：答：当点P运动1或9秒时,点P与点Q间的距离为8个单位长度.【点睛】在数轴上找出点的位置并标出,结合数轴求追赶和相遇问题是此题的考点,正确运用数形结合解决问题是解题的关键,注意不要漏解.7. 〔1〕〔4, 8〕⑵％oAE = 8-t ⑶ 2 秒或 6 秒【解析】【分析】〔1〕根据M和N的坐标和平移的性质可知：MN〃y轴〃PQ,根据K是PM的中点可得K 的坐标；〔2〕根据三角形面积公式可得三角形OAE的而积S ；〔3〕存在两种情况：①如图2,当点B在OD上方时②如图3,当点B在OD上方时,过点B作BG_Lx轴于G,过D作DHJ_x轴于H,分别根据三角形OBD的面积等于三角形OAE的面积列方程可得结论.【详解】〔1〕由题意得：PM = 4,•.•K是PM的中点,AMK = 2 ,■1点M的坐标为(2 , 8),点N的坐标为(2,6), ,MN〃y 轴,-,K (4, 8)；(2)如图1所示,延长DA交y轴于F ,,0F = 8 - t ,1 1 z/.S A OAE =— OF・AE = — ( 8 - t ) x2 = 8 - t ；2 2(3)存在,有两种情况：,①如图2,当点B在0D上方时,过点B作BG±x轴于G,过D作DH±x轴于H ,那么B ( 2 , 6 - t ) ,0(6,0), AOG = 2 , GH=4 , BG = 6 - t , DH = 8 - t , OH =6 ,S^OBD =S AOBG+S /边形DBGH+S AODH ,1 1 z、 1=-OG・BG+— ( BG+DH )・GH — -OH,DH r2 2 ' 2=—x2 ( 6-t ) + — x4 ( 6 - t+8 - t ) - - x6 ( 8 - t ), 2 2 2=10 - 2t ,V S A.OBD - S AOA E/A10 - 2t = 8 - t , t = 2 ；②如图3,当点B在OD上方时,11 , 、 =-OH>DH- - ( B G+DH )・GH - 2 21 , 、 1 , =—x2 ( 8-t ) - - x4( 6 - t+8 - t 2 2 =2t - io ,,*, S AOBD = S AOAE i.\2t - 10 = 8 - t ,t = 6 ；综上,t 的值是2秒或6秒.【点睛】此题考查四边形综合题、矩形的性质、三角形的而积、一元一次方程等知识,解题关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题.8 . ( 1) S =3 + 4 + 5 + 6;S = 4 + 5 + 6 + 7 + 8 ；(2)方法不唯一,见解析：(3 )方法不唯一,见解析【解析】【分析】先找出前几项的钢管数,在推出第n 项的钢管数.【详解】(1) S = 3 + 4 + 5 + 6;S =4 + 5 + 6 + 7+8(2)方法不唯一,例如：S = l+2 S = l + 2+3+3 S = l + 2+3+4+4+4 S = 1 + 2+3+4+5+5+5+51 一OG ・BG ,2 4鑫S A OBD = S A ODH -S 四边形 DBGH - S^OBG ,(3)方法不唯一,例如：S = 〃+(〃 +1)+(〃+ 2)+•….+ 2〃=(〃 + 〃 + + 〃) + (1 + 2 + + 〃) 23 / 八【点睛】此题主要考察代数式的规律探索及求和,需要仔细分析找到规律.9. (1)点P在线段AB上的1处：(2)1；(3)②丝的值不变. 3 3 AB【解析】【分析】(1)根据c、D的运动速度知BD=2PC,再由条件PD=2AC求得PB=2AP,所以点P在线段AB上的g 处：(2)由题设画出图示,根据AQ-BQ=PQ求得AQ=PQ+BQ：然后求得AP=BQ,从而求得PQ 与AB的关系：(3)当点C停止运动时,有CD二;AB,从而求得CM与AB的数量关系：然后求得以AB表示的PM与PN的值,所以MN = PN-PM = — AB . 12【详解】解：(1)由题意：BD=2PCVPD=2AC , ABD+PD=2 ( PC+AC),即PB=2AP.・•.点P在线段AB上的1处：(2)如图：«----------- 1------------ 1 1A P 0 EVAQ-BQ=PQ ,,AQ=PQ+BQ ,VAQ=AP+PQ ,AAP=BQ , 1 ,PQ二一AB ,.尸._1..南一3z .与MN.比T士〔3 〕②——的值不变.AB理由：如图, 当点C停止运动时,有CD=±AB,21,CM二一AB ,41APM=CM-CP=-AB-5 ,42VPD=-AB-10 ,31 z2 、 1APN=-〔-AB-10 〕 =-AB-5 , 2 3 31AMN=PN-PM= —AB ,12当点C停止运动,D点继续运动时,MN的值不变,所以MW _石1~AB~ AB _12【点睛】此题考查了比拟线段的长短.利用中点性质转化线段之间的倍分关系是解题的关键,在不同的情况下灵活选用它的不同表示方法,有利于解题的简洁性.同时,灵活运用线段的和、差、倍、分转化线段之间的数量关系也是十分关键的一点.9 7 310 . 〔1〕存在满足条件的点P,对应的数为-—和一；〔2〕正确的结论是：PM- -8N的值不 2 2 4变,且值为2.5 .【解析】【分析】〔1〕先利用数轴上两点间的距离公式确定出入8的长,然后求得方程的解,得到C表示的点,由此求得;8C+48=8设点P在数轴上对应的数是.,分①当点P在点a的左侧时〔a V-3〕、②当点P在线段八8上时〔-3AV2〕和③当点P在点8的右侧时〔a>2〕三种情况求点P所表示的数即可；〔2〕设P点所表示的数为〃,就有%;"3, P8=〃-2,根3 1 3据条件表示出PM、8/V的长,再分别代入①PM- -8/V和②7PM+ - 8N求出其值即4 2 4可解答.【详解】⑴丁点A在数轴上对应的数为-3,点8对应的数为2 ,48 = 5 .解方程2x+l=Lx - 5得x=-4. 2 所以8c =2 - ( -4)=6 .所以.设存在点P满足条件,且点P在数轴上对应的数为a , ①当点P在点.的左侧时,a < - 3 ,PA=- 3- a,P8 = 2-.,所以4P+P8 =-2a - 1 = 8 ,解得a=--y , -£< - 3满足条件：②当点P 在线段48 上时,-3<a<2 t PA = a- ( - 3 )= a+3 , PB = 2 -.,所以%+P8=a+3+2 - a=508,不满足条件：③当点P 在点8 的右侧时,a>2 , PA = a- ( -3)= a+3 , PB = a- 2 .,77所以%+P8 =.+3+.- 2=2.+1= 8,解得：a 二十,彳>2,9 7所以,存在满足条件的点P,对应的数为-手咕.⑵设P点所表示的数为.,PA = n+3 , P8 =.-2 . ,「雨的中点为M,/. PM= -PA = ^-.2 2N为PB的三等分点且靠近于P点,2 2..BA/ = -PB = -x(n-2). sJ %J3 n+3 3 2 , 、PM - - 8/V = -x—x ( n - 2 ),4 / 4 §r =77 (不变).②！PM+；8N=呼+ g 乂*(n - 2 ) = yn - (随P点的变化而变化).2 4 4 434 4・•.正确的结论是：PM-*/V的值不变,且值为2.5.【点睛】此题考查了一元一次方程的解,数轴的运用,数轴上任意两点间的距离公式的运用,去绝对值的运用,解答时了灵活运用两点间的距离公式求解是关键.11. (1) 45°； (2) 45°；(3)45°或135°.【解析】【分析】(1)由NBOC的度数求出NAOC的度数,利用角平分线定义求出NCOD与NCOE的度数, 相加即可求出NDOE的度数：〔2〕ND0E度数不变,理由为：利用角平分线定义得到/COD为/AOC的一半,NCOE为NCOB的一半,而NDOE=NCOD+NCOE,即可求出NDOE度数为45度；〔3〕分两种情况考虑,同理如图3,那么NDOE为45.：如图4,那么NDOE为135..【详解】〔1〕如图,ZAOC=90° - ZBOC=20°zVOD X OE分别平分NAOC和NBOC ,AZCOD=ZAOC=10o r NCOE」ZBOC=35°f 2AZDOE=ZCOD+ZCOE=45°；(2) NDOE的大小不变,理由是：1 1 1 z、 1ZDOE= ZCOD+ ZCOE= - ZAOC+ - ZCOB= - ( ZAOC+ZCOB ) =- ZAOB=45°； 2 2 2 2(3 ) NDOE的大小发生变化情况为：如图③,那么NDOE为45.：如图④,那么NDOE为135.,分两种情况：如图3所示,VOD. 0E分别平分NAOC和NBOC,1 1AZCOD=-ZAOC , ZCOE=- ZBOC , 2 2AZDOE=ZCOD - ZCOE=- ( ZAOC - ZBOC ) =45°； 2如图4所示,VOD S OE分别平分NAOC和NBOC ,I I,ZCOD=-ZAOC , ZCOE=- ZBOC , 2 2A ZDOE=ZCOD+ZCOE=- ( ZAOC+ZBOC ) = - x270°=135° . 2 2【点睛】此题主要考查了角平分线的性质以及角的有关计算,正确作图,熟记角的特点与角平分线的定义是解决此题的关键.12. ( 1)2或10；(2)当t为5秒、10秒或7.5秒时,P、A和B中恰有一个点为其余两点的优点. 【解析】【分析】(1)设所求数为X,根据优点的定义分优点在M、N之间和优点在点N右边,列出方程解方程即可；(2)根据优点的定义可知分三种情况：①P为(A. B)的优点；②P为(B, A)的优点：③B为(A, P)的优点.设点P表示的数为X,根据优点的定义列出方程, 进而得出t的值.【详解】解：(1)设所求数为X,当优点在M、N之间时,由题意得x - ( -2)=2 (4-x),解得x=2；当优点在点N右边时,由题意得x- ( -2)=2(x-4),解得：x=10；故答案为：2或10；(2)设点P 表示的数为x,贝lj PA=x+20 , PB=40 - x , AB=40 - ( - 20 ) =60 , 分三种情况：①P为(A , B)的优点.由题意,得PA=2PB,即x- ( - 20 ) =2 ( 40 - x ),解得x=20 ,/. t= ( 40 - 20 ) +4=5 (秒)；②P为(B , A)的优点.由题意,得PB=2PA,即40 - x=2 ( x+20 ),解得x=0 ,/. t= ( 40 - 0 ) 4-4=10 (秒)：③B为(A, P)的优点.由题意,得AB=2PA,即60=2 ( x+20 )解得x=10 ,此时,点P为AB的中点,即A也为(B, P)的优点,/. t=30M=7.5 (秒)；综上可知,当t为5秒、10秒或7.5秒时,P、A和B中恰有一个点为其余两点的优点.【点睛】此题考查了一元一次方程的应用及数轴,解题关键是要读懂题目的意思,理解优点的定义,找出适宜的等量关系列出方程,再求解.3 3 1 24013.问题一、(1)二；(2) 3-2x： 2廿3； 13-6* 问题一、(1)-；—；-—.2 5 20 11【解析】【分析】问题一根据等量关系,路程=速度x时间,路程差=路程1-路程2,即可列出方程求解.【详解】问题一：(1)当甲追上乙时,甲的路程二乙的路程+3所以,8x = 6x+32x = 33 x = —23 故答案为大.2(2)当甲追上乙前,路程差=乙所行的路程+3-甲所行的路程；所以,y = 6x + 3-8K =3-2X.当甲追上乙后,甲到达c之前,路程差二甲所行的路程-3-乙所行的路程；所以,y = 8x-3-6x = 2x-3.当甲到达C之后,乙到达C之前,路程差=总路程-3-乙所行的路程；所以,y = 16—3 - 6x = 13—6x.问题二：(1)由题意AB为钟表外围的一局部,且NAO8=30°可知,钟表外围的长度为3x12 = 360〃分针OD的速度为364-60 = -cn/nin时针OE的速度为3^60 = —203 1故OD每分钟转动,OE每分钟转动一cm . 5 20(2 ) 4点时时针与分针的路程差为4x3 = 12cm设“分钟后分针与时针第一次重合.3 1由题意得,-= u x +12解得,x = —.11240即—分钟后分针与时针第一次重合.11【点睛】此题考查了一元一次方程中的行程问题,解题的关键是要读懂题目的意思,根据题目给出的条件找出等量关系,列出方程求解即可.14 . ( 1)见解析：(2 ) ZOQP=180o+-x°-,丫°或/0(^=,乂° - -y° .2 2 2 2【解析】【试题分析】(1)分下面两种情况进行说明；①如图1,点P 在直线AB 的右侧,ZAPB+Z MON+Z PAO+Z PBO=360°f②如图2,点P在直线AB的左侧,ZAPB=Z MON+Z PAO+Z PBO ,(2)分两种情况讨论,如图3和图4.【试题解析】(1)分两种情况：①如图1,点P 在直线AB 的右侧,ZAPB+Z MON+z PAO+Z PBO=360° ,证实::四边形AOBP的内角和为(4 - 2 ) xl80°=360°r••. Z APB=3600 - Z MON - Z PAO - Z PBO ；②如图2,点P在直线AB的左侧,ZAPB=Z MON+Z PAO+Z PBO ,证实：延长AP交ON于点D,ADB是aAOD的外角,/. Z ADB=Z PAO+Z AOD ,••,N ABB是4PDB的外角,Z APB=Z PDB+Z PBO ,/. Z APB=Z MON+Z PAO+Z PBO ；(2)设NM0N=2m° , Z APB=2n°,,/ OC 平分NMON ,/. Z AOC=i-Z M0N=m° ,•「PQ 平分NAPB ,「・Z APQ二;N APB=n° ,分两种情况：第一种情况：如图 3 , N OQP=Z MOC+Z PAO+Z APQ, RPZOQP=m°+x o+n°©Z OQP+Z CON+Z OBP+Z BPQ=360°fZ OQP=360° - Z CON - Z OBP - Z BPQ,即NOQP=360° - m° - y° - n°②,①+②得2Z OQP=360°+x° - y°r04第二种情况：如图 4 f / Z OQP+Z APQ=Z MOC+Z PAO f即NOQP+n°=m°+x° ,/. 2Z OQP+2n o=2m o+2x°© ,: Z APB=Z MON+Z PAO+Z PBO , 2n o=2m°+x o+y0@ ,①-②得2Z OQP=x° - y° ,:乙 OQP=~x°-聂,综上所述,ZOQP=180o+-^x° -泰.或NOQP M*.- -1y° .15 . 〔1〕1；〔 2〕点P运动5秒时,追上点R；〔 3〕线段MN的长度不发生变化,其长度为5.【解析】试题分析：〔1〕由条件得到AB=10,由PA=PB,于是得到结论：〔2〕设点P运动x秒时,在点C处追上点R,于是得到AC=6x BC=4x, AB=10,根据RC-BC=AB,列方程即可得到结论：〔3〕线段MN的长度不发生变化,理由如下分两种情况：①当点P在A、B之间运动时②当点P运动到点B左侧时,求得线段MN的长度不发生变化.试题解析：解：〔1〕〔1〕VA, B表示的数分别为6, 4, AAB=10>VPA=PB,・••点p表示的数是1,〔2〕设点P运动x秒时,在点C处追上点R 〔如图〕那么：AC = 6x BC = 4x AB = 10VAC - BC = AB,6x - 4x = 10解得,x = 5,点P运动5秒时,追上点R.〔3〕线段MN的长度不发生变化,理由如下:分两种情况: 点P在A、B之间运动时：MN = MP + NP=^AP+^BP = j 〔 AP + BP 〕 = jAB = 5点P运动到点B左侧时：• 一•——S. _____________ S _____________________ iP N6MN = MP-NP 二：AP-；BP二;〔AP-BP〕 = |A B = 5综上所述,线段MN的长度不发生变化,其长度为5.点睛：此题主要考查了一元一次方程的应用、数轴,以及线段的计算,解决问题的关键是根据题意正确画出图形,要考虑全面各种情况,不要漏解.。

初一数学考试压轴题

1、在一个班级中，男生的人数是女生人数的2倍。

如果班级总人数是45人，那么男生有多少人？A. 15人B. 20人C. 30人（答案）D. 35人2、小明从家到学校的距离是2公里，他每天步行上学，往返一次。

一周五天上学，他总共步行多少公里？A. 10公里B. 20公里C. 30公里（答案）D. 40公里3、一个长方形的花坛，长是10米，宽是4米。

现在要在花坛周围铺一条1米宽的小路，这个小路的面积是多少平方米？A. 24平方米B. 32平方米C. 40平方米（答案）D. 48平方米4、小红和小华一起去买书，小红带了40元，小华带了50元。

他们买了一本书，共花了60元，那么他们一共节省了多少元？A. 20元B. 30元C. 40元（答案）D. 50元5、一个正方形的面积是64平方米，那么它的周长是多少米？A. 16米B. 24米C. 32米（答案）D. 40米6、小明有20本书，他送了5本书给小华，剩下的书他又分成了两份，每份有多少本书？A. 5本B. 7本C. 10本（答案）D. 15本7、一桶水重50公斤，如果倒入一个空桶中，两桶水的重量是100公斤。

如果只倒出一半的水，那么两桶水的重量是多少公斤？A. 75公斤B. 80公斤C. 90公斤D. 95公斤（答案）8、小明有5个苹果，小红有3个苹果。

小明给小红2个苹果后，小明和小红各有多少个苹果？A. 小明有3个，小红有5个（答案）B. 小明有2个，小红有6个C. 小明有4个，小红有4个D. 小明有1个，小红有7个。

初一下册数学压轴题精练答案

初一下册数学压轴题精练答案参考答案与试题解析一．解答题（共9小题）1．如图1，在平面直角坐标系中，△AOB是直角三角形，∠AOB=90°，斜边AB与y轴交于点C．（1）若∠A=∠AOC，求证：∠B=∠BOC；（2）如图2，延长AB交x轴于点E，过O作OD⊥AB，若∠DOB=∠EOB，∠A=∠E，求∠A的度数；（3）如图3，OF平分∠AOM，∠BCO的平分线交FO的延长线于点P，∠A=40°，当△ABO绕O点旋转时（斜边AB与y轴正半轴始终相交于点C），问∠P的度数是否发生变更？若不变，求其度数；若变更，请说明理由．考点：三角形内角和定理；坐标与图形性质．专题：证明题．分析：（1）由直角三角形两锐角互余及等角的余角相等即可证明；（2）由直角三角形两锐角互余、等量代换求得∠DOB=∠EOB=∠OAE=∠E；然后依据外角定理知∠DOB+∠EOB+∠OEA=90°；从而求得∠DOB=30°，即∠A=30°；（3）由角平分线的性质知∠FOM=45°﹣∠AOC ①，∠PCO=∠A+∠AOC ②，依据①②解得∠PCO+∠FOM=45°+∠A，最终依据三角形内角和定理求得旋转后的∠P的度数．解答：（1）证明：∵△AOB是直角三角形，∴∠A+∠B=90°，∠AOC+∠BOC=90°，∵∠A=∠AOC，∴∠B=∠BOC；解：（2）∵∠A+∠ABO=90°，∠DOB+∠ABO=90°，∴∠A=∠DOB，又∵∠DOB=∠EOB，∠A=∠E，∴∠DOB=∠EOB=∠OAE=∠OEA，∵∠DOB+∠EOB+∠OEA=90°，∴∠A=30°；（3）∠P的度数不变，∠P=25°．理由如下：（只答不变不得分）∵∠AOM=90°﹣∠AOC，∠BCO=∠A+∠AOC，又∵OF平分∠AOM，CP平分∠BCO，∴∠FOM=45°﹣∠AOC ①，∠PCO=∠A+∠AOC ②，①+②得：∠PCO+∠FOM=45°+∠A，∴∠P=180°﹣（∠PCO+∠FOM+90°）=180°﹣（45°+∠A+90°）=180°﹣（45°+20°+90°）=25°．点评：本题综合考察了三角形内角和定理、坐标与图形的性质．解答时，需留意，△ABO旋转后的形态与大小均无变更．2．在平面直角坐标系中，A（﹣1，0），B（0，2），点C在x轴上．（1）如图（1），若△ABC的面积为3，则点C的坐标为（2，0）或（﹣4，0）．（2）如图（2），过点B点作y轴的垂线BM，点E是射线BM上的一动点，∠AOE的平分线交直线BM于F，OG⊥OF且交直线BM于G，当点E在射线BM上滑动时，的值是否变更？若不变，恳求出其值；若变更，请说明理由．考点：三角形内角和定理；坐标与图形性质；垂线；平行线的性质；三角形的面积；三角形的外角性质．分析：（1）利用A，B点坐标，△ABC的面积为3，得出AC的长，进而得出C点坐标；（2）首先依据已知得出∠EOG=∠EOx，进而得出FM∥x轴，再利用已知得出∠BOF=∠EGO，即可得出∠BEO=2∠BOF，得出答案即可．解答：解：（1）∵A（﹣1，0），B（0，2），点C在x轴上．△ABC的面积为3，∴AC的长为3，则点C的坐标为（2，0）或（﹣4，0）；故答案为：（2，0）或（﹣4，0）；（2）∵∠AOE+∠EOx=180°，∴∠AOE+∠EOx=90°，即∠EOF+∠EOx=90°∵∠EOF+∠EOG=90°，∴∠EOG=∠EOx，∴FM∥x轴，∴∠GOx=∠EGO，∴∠EOG=∠EGO，∴∠BEO=2∠EGO，∵∠FOG=90°，∴∠EGO+∠OFG=90°，∵FM⊥y轴，∴∠BOF+∠OFG=90°，∴∠BOF=∠EGO，∴∠BEO=2∠BOF，∴=2．点评：此题主要考察了三角形内角和定理应用以及平行线的断定和三角形面积求法等学问，依据已知得出FM∥x轴以及∠BOF=∠EGO是解题关键．3．如图1，在平面直角坐标系中，A（a，0），B（b，0），C（﹣1，2），且|2a+b+1|+（a+2b ﹣4）2=0．（1）求a，b的值；（2）①在x轴的正半轴上存在一点M，使△COM的面积=△ABC的面积，求出点M的坐标；②在坐标轴的其它位置是否存在点M，使△COM的面积=△ABC的面积仍旧成立？若存在，请干脆写出符合条件的点M的坐标；（3）如图2，过点C作CD⊥y轴交y轴于点D，点P为线段CD延长线上一动点，连接OP，OE平分∠AOP，OF⊥OE．当点P运动时，的值是否会变更？若不变，求其值；若变更，说明理由．考点：三角形内角和定理；非负数的性质：肯定值；非负数的性质：偶次方；解二元一次方程组；三角形的面积；三角形的外角性质．分析：（1）依据非负数的性质即可列出关于a，b的方程组求得a，b的值；（2）①过点C做CT⊥x轴，CS⊥y轴，垂足分别为T、S，依据三角形的面积公式即可求得OM的长，则M的坐标即可求得；②依据三角形的面积公式，即可写出M的坐标；（3）利用∠BOF依据平行线的性质，以及角平分线的定义表示出∠OPD和∠DOE即可求解．解答：解：（1）∵|2a+b+1|+（a+2b﹣4）2=0，又∵|2a+b+1|≥0，（a+2b﹣4）2≥0，∴|2a+b+1|=0且（a+2b﹣4）2=0．∴∴即a=﹣2，b=3．（2）①过点C做CT⊥x轴，CS⊥y轴，垂足分别为T、S．∵A（﹣2，0），B（3，0），∴AB=5，因为C（﹣1，2），∴CT=2，CS=1，△ABC的面积=AB•CT=5，要使△COM的面积=△ABC的面积，即△COM的面积=，所以OM•CT=，∴OM=2.5．所以M的坐标为（2.5，0）．②存在．点M的坐标为（0，5）或（﹣2.5，0）或（0，﹣5）．（3）的值不变，理由如下：∵CD⊥y轴，AB⊥y轴∴∠CDO=∠DOB=90°∴AB∥CD∴∠OPD=∠POB∵OF⊥OE∴∠POF+∠POE=90°，∠BOF+∠AOE=90°∵OE平分∠AOP∴∠POE=∠AOE∴∠POF=∠BOF∴∠OPD=∠POB=2∠BOF∵∠DOE+∠DOF=∠BOF+∠DOF=90°∴∠DOE=∠BOF∴∠OPD=2∠BOF=2∠DOE∴．点评：本题考察了非负数的性质，三角形的面积公式，以及角平分线的定义，平行线的性质，求点的坐标问题常用的方法就是转化成求线段的长的问题．4．长方形OABC，O为平面直角坐标系的原点，OA=5，OC=3，点B在第三象限．（1）求点B的坐标；（2）如图1，若过点B的直线BP与长方形OABC的边交于点P，且将长方形OABC的面积分为1：4两局部，求点P的坐标；（3）如图2，M为x轴负半轴上一点，且∠CBM=∠CMB，N是x轴正半轴上一动点，∠MCN的平分线CD交BM的延长线于点D，在点N运动的过程中，的值是否变更？若不变，求出其值；若变更，请说明理由．考点：平行线的断定与性质；坐标与图形性质；三角形的面积．分析：（1）依据第三象限点的坐标性质得出答案；（2）利用长方形OABC的面积分为1：4两局部，得出等式求出AP的长，即可得出P 点坐标，再求出PC的长，即可得出OP的长，进而得出答案；（3）首先求出∠MCF=2∠CMB，即可得出∠CNM=∠NCF=∠MCF﹣∠NCM=2∠BMC﹣2∠DCM，得出答案．解答：解：（1）∵四边形OABC为长方形，OA=5，OB=3，且点B在第三象限，∴B（﹣5，﹣3）．（2）若过点B的直线BP与边OA交于点P，依题意可知：×AB×AP=×OA×OC，即×3×AP=×5×3，∴AP=2∵OA=5，∴OP=3，∴P（﹣3，0），若过点B的直线BP与边OC交于点P，依题意可知：×BC×PC=×OA×OC，即×5×PC=×5×3，∴PC=∵OC=3，∴OP=，∴P（0，﹣）．综上所述，点P的坐标为（﹣3，0）或（0，﹣）．（3）延长BC至点F，∵四边形OABC为长方形，∴OA∥BC．∴∠CBM=∠AMB，∠AMC=∠MCF．∵∠CBM=∠CMB，∴∠MCF=2∠CMB．过点M作ME∥CD交BC于点E，∴∠EMC=∠MCD．又∵CD平分∠MCN，∴∠NCM=2∠EMC．∴∠D=∠BME=∠CMB﹣∠EMC，∠CNM=∠NCF=∠MCF﹣∠NCM=2∠BMC﹣2∠DCM=2∠D，∴=．点评：此题主要考察了平行线的性质以及矩形的性质、图形面积求法等学问，利用数形结合得出的是解题关键．5．如图，直线AB∥CD．（1）在图1中，∠BME、∠E，∠END的数量关系为：∠E=∠BME+∠END ；（不需证明）在图2中，∠BMF、∠F，∠FND的数量关系为：∠BMF=∠F+∠FND ；（不需证明）（2）如图3，NE平分∠FND，MB平分∠FME，且2∠E与∠F互补，求∠FME的大小．（3）如图4中，∠BME=60°，EF平分∠MEN，NP平分∠END，EQ∥NP，则∠FEQ的大小是否发生变更？若变更，说明理由；若不变更，求∠FEQ的度数．考点：平行线的性质．分析：（1）过点E作EF∥AB，依据两直线平行，内错角相等可得∠BME=∠1，∠END=∠2，然后相加即可得解；先依据两直线平行，同位角相等求出∠3=∠FND，再依据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解；（2）设∠END=x°，∠BNE=y°，依据（1）的结论可得x+y=∠E，2x+∠F=y，然后消掉x并表示出y，再依据2∠E与∠F互补求出y，然后依据角平分线的定义求解即可；（3）依据（1）的结论表示出∠MEN，再依据角平分线的定义表示出∠FEN和∠ENP，再依据两直线平行，内错角相等可得∠NEQ=∠ENP，然后依据∠FEQ=∠FEN﹣∠NEQ整理即可得解．解答：解：（1）如图1，过点E作EF∥AB，∵AB∥CD，∴AB∥EF∥CD，∴∠BME=∠1，∠END=∠2，∴∠1+∠2=∠BME+∠END，即∠E=∠BME+∠END；如图2，∵AB∥CD，∴∠3=∠FND，∴∠BMF=∠F+∠3=∠F+∠FND，即∠BMF=∠F+∠FND；故答案为：∠E=∠BME+∠END；∠BMF=∠F+∠FND；（2）如图3，设∠END=x°，∠BNE=y°，由（1）的结论可得x+y=∠E，2x+∠F=y，消掉x得，3y=2∠E+∠F，∵2∠E与∠F互补，∴2∠E+∠F=180°，∴3y=180°，解得y=60°，∵MB平分∠FME，∴∠FME=2y=2×60°=120°；（3）由（1）的结论得，∠MEN=∠BME+∠END，∵EF平分∠MEN，NP平分∠END，∴∠FEN=∠MEN=（∠BME+∠END），∠ENP=∠END，∵EQ∥NP，∴∠NEQ=∠ENP，∴∠FEQ=∠FEN﹣∠NEQ=（∠BME+∠END）﹣∠END=∠BME，∵∠BME=60°，∴∠FEQ=×60°=30°．点评：本题考察了平行线的性质，三角形的一个外角等于与它不相邻的两个内角的和的性质，角平分线的定义，此类题目，过拐点作平行线是解题的关键，精确识图理清图中各角度之间的关系也很重要．6．在平面直角坐标系中，点B（0，4），C（﹣5，4），点A是x轴负半轴上一点，S四边形AOBC=24．（1）线段BC的长为 5 ，点A的坐标为（﹣7，0）；（2）如图1，BM平分∠CBO，CM平分∠ACB，BM交CM于点M，试给出∠CMB与∠CAO之间满意的数量关系式，并说明理由；（3）若点P是在直线CB与直线AO之间的一点，连接BP、OP，BN平分∠CBP，ON平分∠AOP，BN交ON于N，请依题意画出图形，给出∠BPO与∠BNO之间满意的数量关系式，并说明理由．考点：三角形内角和定理；坐标与图形性质；三角形的面积；三角形的外角性质．专题：分类探讨．分析：（1）依据点B、C的横坐标求出BC的长度即可；再依据四边形的面积求出OA的长度，然后依据点A在y轴的负半轴写出点A的坐标；（2）依据两直线平行，同旁内角互补用∠CAO表示出∠ACB，再依据角平分线的定义表示出∠MAB和∠MBC，然后利用三角形的内角和定理列式整理即可得解；（3）分①点P在OB的左边时，依据三角形的内角和定理表示出∠PBO+∠POB，再依据两直线平行，同旁内角互补和角平分线的定义表示出∠NBP+∠NOP，然后在△NBO中，利用三角形的内角和定理列式整理即可得解；②点P在OB的右边时，求出∠CBP+∠AOP+∠BPO=360°，再依据角平分线的定义表示出∠PBN+∠PON，然后利用四边形的内角和定理列式整理即可得解．解答：解：（1）∵点B（0，4），C（﹣5，4），∴BC=5，S四边形AOBC=（BC+OA）•OB=（5+OA）•4=24，解得OA=7，所以，点A的坐标为（﹣7，0）；（2）∵点B、C的纵坐标一样，∴BC∥OA，∴∠ACB=180°﹣∠CAO，∠CBO=90°，∵BM平分∠CBO，CM平分∠ACB，∴∠MCB=（180°﹣∠CAO）=90°﹣∠CAO，∠MBC=∠CBO=×90°=45°，在△MBC中，∠CMB+∠MCB+∠MBC=180°，即∠CMB+90°﹣∠CAO+45°=180°，解得∠CMB=45°+∠CAO；（3）①如图1，当点P在OB左侧时，∠BPO=2∠BNO．理由如下：在△BPO中，∠PBO+∠POB=180°﹣∠BPO，∵BC∥OA，BN平分∠CBP，ON平分∠AOP，∴∠NBP+∠NOP=（180°﹣∠PBO﹣∠POB），在△NOB中，∠BNO=180°﹣（∠NBP+∠NOP+∠PBO+∠POB），=180°﹣[（180°﹣∠PBO﹣∠POB）+∠PBO+∠POB]，=90°﹣（∠PBO+∠POB），=90°﹣（180°﹣∠BPO），=∠BPO，∴∠BPO=2∠BNO；②如图2，当点P在OB右侧时，∠BNO+∠BPO=180°．理由如下：∵BC∥OA，∴∠CBP+∠AOP+∠BPO=360°，∵BN平分∠CBP，ON平分∠AOP，∴∠PBN+∠PON+∠BPO=×360°=180°，∴∠PBN+∠PON=180°﹣∠BPO，在四边形BNOP中，∠BNO=360°﹣∠PBN﹣∠PON﹣∠BPO=360°﹣（180°﹣∠BPO）﹣∠BPO=180°﹣∠BPO，∴∠BNO+∠BPO=180°．点评：本题考察了三角形的内角和定理，角平分线的定义，平行线的性质，以及坐标与图形性质，精确识图理清图中各角度之间的关系是解题关键，（3）要留意分状况探讨．7．如图1，在平面直角坐标系中，四边形OBCD各个顶点的坐标分别是O（0，0），B（2，6），C（8，9），D（10，0）；（1）三角形BCD的面积= 30（2）将点C平移，平移后的坐标为C′（2，8+m）；①若S△BDC′=32，求m的值；②当C′在第四象限时，作∠C′OD的平分线OM，OM交于C′C于M，作∠C′CD的平分线CN，CN交OD于N，OM与CN相交于点P（如图2），求的值．考点：作图-平移变换；坐标与图形性质；三角形内角和定理．分析：（1）三角形BCD的面积=正方形的面积﹣3个小三角形的面积；（2）①分平移后的坐标为C′在B点的上方；在B点的下方两种状况探讨可求m的值；②利用外角以及角平分线的性质得出∠ODC+∠CC′O=2∠P，即可得出答案．解答：解：（1）三角形BCD的面积为：×6×10=30；故答案为：30；（2）①当C在x轴上方，如图1所示：∵S△BDC′=32，D到BC″的间隔为8，∴BC″=8，∵B（2，6），∴8+m=14，∴m=6，∵AB=6，BC′=8，∴C′在x轴下方，且AC′=2，∴8+m=﹣2，∴m=﹣10，即m=6或m=﹣10；②如图2，在△OC′M中，∵∠OMC是∠OMC′的外角，∴∠2+∠6=∠OMC，在△PMC中，∵∠OMC是∠CMP的外角，∴∠4+∠P=∠OMC，∴∠2+∠6=∠4+∠P，在△CND中，∵∠ONC是∠CND的外角，∴∠3+∠7=∠ONC，在△ONP中，∵∠ONC是∠ONP的外角，∴∠1+∠P=∠ONC，∴∠3+∠7=∠1+∠P，∴∠3+∠7+∠2+∠6=∠4+∠P+∠1+∠P，∵∠2=∠1，∠3=∠4，∴∠6+∠7=2∠P，∴∠ODC+∠CC′O=2∠P，∴=．点评：此题主要考察了外角的性质以及三角形面积求法和点坐标性质等学问，利用数形结合得出C′的不同位置是解题关键．8．如图，四边形ABCD中，AD∥BC，DE平分∠ADB，∠BDC=∠BCD．（1）求证：∠1+∠2=90°；（2）若∠ABD的平分线与CD的延长线交于F，且∠F=55°，求∠ABC；（3）若H是BC上一动点，F是BA延长线上一点，FH交BD于M，FG平分∠BFH，交DE于N，交BC于G．当H在BC上运动时（不与B点重合），的值是否变更？假如变更，说明理由；假如不变，试求出其值．考点：等腰三角形的性质；角平分线的定义；平行线的性质．专题：综合题．分析：本题考察了等腰三角形的性质、角平分线的性质以及平行线的性质，解决问题的关键在于熟识驾驭学问要点，并且擅长运用角与角之间的联络进展传递．（1）由AD∥BC，DE平分∠ADB，得∠ADC+∠BCD=180，∠BDC=∠BCD，得出∠1+∠2=90°；（2）由DE平分∠ADB，CD平分∠ABD，四边形ABCD中，AD∥BC，∠F=55°，得出∠ABC=∠ABD+∠DBC=∠ABD+∠ADB，即∠ABC=70°；（3）在△BMF中，依据角之间的关系∠BMF=180°﹣∠ABD﹣∠BFH，得∠GND=180°﹣∠AED﹣∠BFG，再依据角之间的关系得∠BAD=﹣∠DBC，在综上得出答案．解答：（1）证明：AD∥BC，∠ADC+∠BCD=180，∵DE平分∠ADB，∠BDC=∠BCD，∴∠ADE=∠EDB，∠BDC=∠BCD，∵∠ADC+∠BCD=180°，∴∠EDB+∠BDC=90°，∠1+∠2=90°．解：（2）∠FBD+∠BDE=90°﹣∠F=35°，∵DE平分∠ADB，BF平分∠ABD，∴∠ADB+∠ABD=2（∠FBD+∠BDE）=70°，又∵四边形ABCD中，AD∥BC，∴∠DBC=∠ADB，∴∠ABC=∠ABD+∠DBC=∠ABD+∠ADB，即∠ABC=70°；（3）的值不变．证明：在△BMF中，∠BMF=∠DMH=180°﹣∠ABD﹣∠BFH，又∵∠BAD=180°﹣（∠ABD+∠ADB），∠DMH+∠BAD=（180°﹣∠ABD﹣∠BFH）+（180°﹣∠ABD﹣∠ADB），=360﹣∠BFH﹣2∠ABD﹣∠ADB，∠DNG=∠FNE=180°﹣∠BFH﹣∠AED，=180°﹣∠BFH﹣∠ABD﹣∠ADB，=（∠DMH+∠BAD），∴=2．点评：本题考察等腰三角形的性质及三角形内角和定理；此题为探究题，比拟新奇，实际涉及的学问不多．9．如图（1）所示，一副三角板中，含45°角的一条直角边AC在y轴上，斜边AB交x轴于点G．含30°角的三角板的顶点与点A重合，直角边AE和斜边AD分别交x轴于点F、H．（1）若AB∥ED，求∠AHO的度数；（2）如图2，将三角板ADE绕点A旋转．在旋转过程中，∠AGH的平分线GM与∠AHF的平分线HM相交于点M，∠COF的平分线ON与∠OFE的平分线FN相交于点N．①当∠AHO=60°时，求∠M的度数；②试问∠N+∠M的度数是否发生变更？若变更，求出变更范围；若保持不变，请说明理由．考点：三角形内角和定理；角平分线的定义；平行线的性质；三角形的外角性质．专题：综合题．分析：（1）由AB∥ED可以得到∠BAD=∠D=60°，即∠BAC+∠CAD=60°，然后依据已知条件即可求出∠AHO；（2）①由∠AHO+∠AHF=180°，∠AHO=60°，可以求出∠AHF，而HM是∠AHF的平分线，GM是∠AGH的平分线，∠MHF=∠MGH+∠M，由此即可求出∠M；②∠N+∠M的度数不变，当∠BAC与∠DAE没有重合局部时，∠GAH﹣∠OAF=（45°+∠OAH）﹣（30°+∠OAH）=15°；当AC与AD在一条直线上时，∠GAH﹣∠OAF=45°﹣30°=15°；当∠BAC与∠DAE有重合局部时，∠GAH﹣∠OAF=（45°﹣∠OAH）﹣（30°﹣∠OAH）=15°，即∠GAH﹣∠OAF=15°．而依据已知条件∠M=∠MHF﹣∠MGH=∠AHF ﹣∠AGH=∠GAH，∠N=180°﹣（∠OFE+90°）=180°﹣（∠OAF+90°）﹣90°=90°﹣∠OAF，由此即可得到结论．解答：解：（1）∵AB∥ED∴∠BAD=∠D=60°（两直线平行，内错角相等），即∠BAC+∠CAD=60°．∵∠BAC=45°，∴∠CAD=60°﹣45°=15°，∠AHO=90°﹣∠CAD=75°；（2）①∵∠AHO+∠AHF=180°，∠AHO=60°，∴∠AHF=180°﹣60°=120°∵HM是∠AHF的平分线，∴∠MHF=∠AHF=60°（角平分线的定义）．∵GM是∠AGH的平分线，∠AGH=45°，∴∠MGH=∠AGH=22.5°，∵∠MHF=∠MGH+∠M，∴∠M=60°﹣22.5°=37.5°；②∠N+∠M的度数不变，理由是：当∠BAC与∠DAE没有重合局部时，∠GAH﹣∠OAF=（45°+∠OAH）﹣（30°+∠OAH）=15°；当AC与AD在一条直线上时，∠GAH﹣∠OAF=45°﹣30°=15°；当∠BAC与∠DAE有重合局部时，∠GAH﹣∠OAF=（45°﹣∠OAH）﹣（30°﹣∠OAH）=15°；∴∠GAH﹣∠OAF=15°．易得出∠M=∠MHF﹣∠MGH=∠AHF﹣∠AGH=∠GAH，∠N=180°﹣（∠OFE+90°）=180°﹣（∠OAF+90°）﹣90°=90°﹣∠OAF，∴∠M+∠N=∠GAH+90°﹣∠OAF=90°+×15°=97.5°（定值）．点评：此题比拟困难，考察了三角形的内角和、三角形的外角的性质、角平分线的性质、平行线的性质等多个学问，综合性比拟强，难度比拟大，学生首先心理上要信任自己，才能有信念解决问题．。

七年级上册上册数学压轴题测试卷附答案

七年级上册上册数学压轴题测试卷附答案七年级上册上册数学压轴题测试卷附答案⼀、压轴题1．如图，已知数轴上两点A ，B 表⽰的数分别为﹣2，6，⽤符号“AB ”来表⽰点A 和点B 之间的距离．（1）求AB 的值；（2）若在数轴上存在⼀点C ，使AC ＝3BC ，求点C 表⽰的数；（3）在（2）的条件下，点C 位于A 、B 两点之间．点A 以1个单位/秒的速度沿着数轴的正⽅向运动，2秒后点C 以2个单位/秒的速度也沿着数轴的正⽅向运动，到达B 点处⽴刻返回沿着数轴的负⽅向运动，直到点A 到达点B ，两个点同时停⽌运动．设点A 运动的时间为t ，在此过程中存在t 使得AC ＝3BC 仍成⽴，求t 的值．2．如图，数轴上点A ，B 表⽰的有理数分别为6-，3，点P 是射线AB 上的⼀个动点（不与点A ，B 重合），M 是线段AP 靠近点A 的三等分点，N 是线段BP 靠近点B 的三等分点．（1）若点P 表⽰的有理数是0，那么MN 的长为________；若点P 表⽰的有理数是6，那么MN 的长为________；（2）点P 在射线AB 上运动（不与点A ，B 重合）的过程中，MN 的长是否发⽣改变？若不改变，请写出求MN 的长的过程；若改变，请说明理由． 3．如图，数轴上A ，B 两点对应的数分别为4-，-1 （1）求线段AB 长度（2）若点D 在数轴上，且3DA DB =，求点D 对应的数（3）若点A 的速度为7个单位长度/秒，点B 的速度为2个单位长度/秒，点O 的速度为1个单位长度/秒，点A ，B ，O 同时向右运动，⼏秒后，3?OA OB =4．（理解新知）如图①，已知AOB ∠，在AOB ∠内部画射线OC ，得到三个⾓，分别为AOC ∠，BOC ∠，AOB ∠，若这三个⾓中有⼀个⾓是另外⼀个⾓的两倍，则称射线OC 为AOB ∠的“⼆倍⾓线”．（1）⼀个⾓的⾓平分线______这个⾓的“⼆倍⾓线”（填“是”或“不是”）（2）若60AOB ∠=?，射线OC 为AOB ∠的“⼆倍⾓线”，则AOC ∠的⼤⼩是______；（解决问题）如图②，⼰知60AOB ∠=?，射线OP 从OA 出发，以20?/秒的速度绕O 点逆时针旋转；射线OQ 从OB 出发，以10?/秒的速度绕O 点顺时针旋转，射线OP ，OQ 同时出发，当其中⼀条射线回到出发位置的时候，整个运动随之停⽌，设运动的时间为t 秒．（3）当射线OP ，OQ 旋转到同⼀条直线上时，求t 的值；（4）若OA ，OP ，OQ 三条射线中，⼀条射线恰好是以另外两条射线为边组成的⾓的“⼆倍⾓线”，直接写出t 所有可能的值______． 5．问题情境：在平⾯直⾓坐标系xOy 中有不重合的两点A （x 1，y 1）和点B （x 2，y 2），⼩明在学习中发现，若x 1=x 2，则AB ∥y 轴，且线段AB 的长度为|y 1﹣y 2|；若y 1=y 2，则AB ∥x 轴，且线段AB 的长度为|x 1﹣x 2|；（应⽤）：（1）若点A （﹣1，1）、B （2，1），则AB ∥x 轴，AB 的长度为．（2）若点C （1，0），且CD ∥y 轴，且CD=2，则点D 的坐标为．（拓展）：我们规定：平⾯直⾓坐标系中任意不重合的两点M （x 1，y 1），N （x 2，y 2）之间的折线距离为d （M ，N ）=|x 1﹣x 2|+|y 1﹣y 2|；例如：图1中，点M （﹣1，1）与点N （1，﹣2）之间的折线距离为d （M ，N ）=|﹣1﹣1|+|1﹣（﹣2）|=2+3=5．解决下列问题：（1）已知E （2，0），若F （﹣1，﹣2），求d （E ，F ）；（2）如图2，已知E （2，0），H （1，t ），若d （E ，H ）=3，求t 的值；（3）如图3，已知P （3，3），点Q 在x 轴上，且三⾓形OPQ 的⾯积为3，求d （P ，Q ）．6．定义：若90αβ-=，且90180α<<，则我们称β是α的差余⾓．例如：若110α=，则α的差余⾓20β=．（1）如图1，点O 在直线AB 上，射线OE 是BOC ∠的⾓平分线，若COE ∠是AOC ∠的差余⾓，求∠BOE 的度数．（2）如图2，点O 在直线AB 上，若BOC ∠是AOE ∠的差余⾓，那么BOC ∠与∠BOE 有什么数量关系．（3）如图3，点O 在直线AB 上，若COE ∠是AOC ∠的差余⾓，且OE 与OC 在直线AB 的同侧，请你探究AOC BOCCOE∠-∠∠是否为定值？若是，请求出定值；若不是，请说明理由．7．如图，已知150AOB ∠=，将⼀个直⾓三⾓形纸⽚(90D ∠=)的⼀个顶点放在点O 处，现将三⾓形纸⽚绕点O 任意转动，OM 平分斜边OC 与OA 的夹⾓，ON 平分BOD ∠. （1）将三⾓形纸⽚绕点O 转动(三⾓形纸⽚始终保持在AOB ∠的内部)，若30COD ∠=，则MON ∠=_______；（2）将三⾓形纸⽚绕点O 转动(三⾓形纸⽚始终保持在AOB ∠的内部)，若射线OD 恰好平分MON ∠，若8MON COD ∠=∠，求COD ∠的度数;（3）将三⾓形纸⽚绕点O 从OC 与OA 重合位置逆时针转到OD 与OA 重合的位置，猜想在转动过程中COD ∠和MON ∠的数量关系？并说明理由.8．如图，A 、B 、C 三点在数轴上，点A 表⽰的数为10-，点B 表⽰的数为14，点C 为线段AB 的中点.动点P 在数轴上，且点P 表⽰的数为x .（1）求点C 表⽰的数；（2）点P 从点A 出发，向终点B 运动.设BP 中点为M .请⽤含x 的整式表⽰线段MC 的长.（3）在（2）的条件下，当x 为何值时，2AP CM PC -=？9．如图①，已知线段30cm AB =，4cm CD =，线段CD 在线段AB 上运动，E 、F 分别是AC 、BD 的中点.（1）若8cm AC ，则EF =______cm ；（2）当线段CD 在线段AB 上运动时，试判断EF 的长度是否发⽣变化？如果不变请求出EF 的长度，如果变化，请说明理由；（3）我们发现⾓的很多规律和线段⼀样，如图②已知COD ∠在AOB ∠内部转动，OE 、OF 分别平分AOC ∠和BOD ∠，则EOF ∠、AOB ∠和COD ∠有何数量关系，请直接写出结果不需证明.10．综合与探究问题背景数学活动课上，⽼师将⼀副三⾓尺按图（1）所⽰位置摆放，分别作出∠AOC ，∠BOD 的平分线OM 、ON ，然后提出如下问题：求出∠MON 的度数．特例探究“兴趣⼩组”的同学决定从特例⼊⼿探究⽼师提出的问题，他们将三⾓尺分别按图2、图3所⽰的⽅式摆放，OM 和ON 仍然是∠AOC 和∠BOD 的⾓平分线．其中，按图2⽅式摆放时，可以看成是ON 、OD 、OB 在同⼀直线上．按图3⽅式摆放时，∠AOC 和∠BOD相等．（1）请你帮助“兴趣⼩组”进⾏计算：图2中∠MON的度数为°．图3中∠MON的度数为°．发现感悟解决完图2，图3所⽰问题后，“兴趣⼩组”⼜对图1所⽰问题进⾏了讨论：⼩明：由于图1中∠AOC和∠BOD的和为90°，所以我们容易得到∠MOC和∠NOD的和，这样就能求出∠MON的度数．⼩华：设∠BOD为x°，我们就能⽤含x的式⼦分别表⽰出∠NOD和∠MOC度数，这样也能求出∠MON的度数．（2）请你根据他们的谈话内容，求出图1中∠MON的度数．类⽐拓展受到“兴趣⼩组”的启发，“智慧⼩组”将三⾓尺按图4所⽰⽅式摆放，分别作出∠AOC、∠BOD的平分线OM、ON，他们认为也能求出∠MON的度数．（3）你同意“智慧⼩组”的看法吗？若同意，求出∠MON的度数；若不同意，请说明理由．11．如图，P是定长线段AB上⼀点，C、D两点分别从P、B出发以1cm/s、2cm/s的速度沿直线AB向左运动（C在线段AP 上，D在线段BP上）（1）若C、D运动到任⼀时刻时，总有PD＝2AC，请说明P点在线段AB上的位置：（2）在（1）的条件下，Q是直线AB上⼀点，且AQ﹣BQ＝PQ，求PQAB的值．（3）在（1）的条件下，若C、D运动5秒后，恰好有1CD AB2，此时C点停⽌运动，D点继续运动（D点在线段PB上），M、N分别是CD、PD的中点，下列结论：①PM﹣PN的值不变；②MNAB的值不变，可以说明，只有⼀个结论是正确的，请你找出正确的结论并求值．12．⼀般地，n 个相同的因数a 相乘......a a a ?，记为n a ，如322228??==，此时，3叫做以2为底8的对数，记为2log 8 (即2log 83=) ．⼀般地，若(0na b a =>且1,0)a b ≠>，则n 叫做以a 为底b 的对数，记为log a b (即log a b n =) ．如4381=，则4叫做以3为底81的对数，记为3log 81 (即3log 814=) ．（1）计算下列各对数的值：2log 4= ；2log 16= ；2log 64= ．（2）观察（1）中三数4、16、64之间满⾜怎样的关系式，222log 4,log 16,log 64之间⼜满⾜怎样的关系式；（3）由（2）的结果，你能归纳出⼀个⼀般性的结论吗?（4）根据幂的运算法则：n m n m a a a +=以及对数的含义说明上述结论．【参考答案】***试卷处理标记，请不要删除⼀、压轴题1．（1）8；（2）4或10；（3）t 的值为167和329【解析】【分析】（1）由数轴上点B 在点A 的右侧，故⽤点B 的坐标减去点A 的坐标即可得到AB 的值；（2）设点C 表⽰的数为x ，再根据AC=3BC ，列绝对值⽅程并求解即可；（3）点C 位于A ，B 两点之间，分两种情况来讨论：点C 到达B 之前，即23时，然后列⽅程并解⽅程再结合进⾏取舍即可.【详解】解：（1）∵数轴上两点A ，B 表⽰的数分别为﹣2，6 ∴AB ＝6﹣（﹣2）＝8 答：AB 的值为8．（2）设点C 表⽰的数为x ，由题意得 |x ﹣（﹣2）|＝3|x ﹣6| ∴|x +2|＝3|x ﹣6|∴x +2＝3x ﹣18或x +2＝18﹣3x ∴x ＝10或x ＝4答：点C 表⽰的数为4或10．（3）∵点C位于A，B两点之间，∴点C表⽰的数为4，点A运动t秒后所表⽰的数为﹣2+t，①点C到达B之前，即2＜t＜3时，点C表⽰的数为4+2（t﹣2）＝2t ∴AC＝t+2，BC＝6﹣2t∴t+2＝3（2t﹣6）解得t＝16 7②点C到达B之后，即t＞3时，点C表⽰的数为6﹣2（t﹣3）＝12﹣2t ∴AC＝|﹣2+t﹣（12﹣2t）|＝|3t﹣14|，BC＝6﹣（12﹣2t）＝2t﹣6∴|3t﹣14|＝3（2t﹣6）解得t＝329或t＝43，其中43＜3不符合题意舍去答：t的值为167和329【点睛】本题考查了数轴上的动点问题，列⼀元⼀次⽅程和绝对值⽅程进⾏求解，是解答本题的关键.2．（1）6；6；（2）不发⽣改变，MN为定值6，过程见解析【解析】【分析】（1）由点P表⽰的有理数可得出AP、BP的长度，根据三等分点的定义可得出MP、NP的长度，再由MN=MP+NP（或MN=MP-NP），即可求出MN的长度；（2）分-6＜a＜3及a＞3两种情况考虑，由点P表⽰的有理数可得出AP、BP的长度（⽤含字母a的代数式表⽰），根据三等分点的定义可得出MP、NP的长度（⽤含字母a的代数式表⽰），再由MN=MP+NP（或MN=MP-NP），即可求出MN=6为固定值．【详解】解：（1）若点P表⽰的有理数是0（如图1），则AP=6，BP=3．∵M是线段AP靠近点A的三等分点，N是线段BP靠近点B的三等分点．∴MP=23AP=4，NP=23BP=2，∴MN=MP+NP=6；若点P表⽰的有理数是6（如图2），则AP=12，BP=3．∵M是线段AP靠近点A的三等分点，N是线段BP靠近点B的三等分点．∴MP=23AP=8，NP=23BP=2，∴MN=MP-NP=6．故答案为：6；6．（2）MN 的长不会发⽣改变，理由如下：设点P 表⽰的有理数是a （a ＞-6且a≠3）．当-6＜a ＜3时（如图1），AP=a+6，BP=3-a ．∵M 是线段AP 靠近点A 的三等分点，N 是线段BP 靠近点B 的三等分点．∴MP=23AP=23（a+6），NP=23BP=23（3-a ），∴MN=MP+NP=6；当a ＞3时（如图2），AP=a+6，BP=a-3．∵M 是线段AP 靠近点A 的三等分点，N 是线段BP 靠近点B 的三等分点．∴MP=23AP=23（a+6），NP=23BP=23（a-3），∴MN=MP-NP=6．综上所述：点P 在射线AB 上运动（不与点A ，B 重合）的过程中，MN 的长为定值6．【点睛】本题考查了两点间的距离，解题的关键是：（1）根据三点分点的定义找出MP 、NP 的长度；（2）分-6＜a ＜3及a ＞3两种情况找出MP 、NP 的长度（⽤含字母a 的代数式表⽰）． 3．（1）3；（2）12或74-；（3）13秒或79秒【解析】【分析】（1）根据数轴上两点间距离即可求解；（2）设点D 对应的数为x ，可得⽅程314x x +=+，解之即可；（3）设t 秒后，OA=3OB ，根据题意可得47312t t t t -+-=-+-，解之即可．【详解】解：（1）∵A 、B 两点对应的数分别为-4，-1，∴线段AB 的长度为：-1-（-4）=3；（2）设点D 对应的数为x ，∵DA=3DB ，则314x x +=+，则()314x x +=+或()314x x +=--，解得：x=12或x=74-，∴点D 对应的数为12或74-；（3）设t 秒后，OA=3OB ，则有：47312t t t t -+-=-+-，则4631t t -+=-+，则()4631t t -+=-+或()4631t t -+=--+，解得：t=13或t=79，∴13秒或79秒后，OA=3OB ．【点睛】本题考查了⼀元⼀次⽅程的运⽤，数轴的运⽤和绝对值的运⽤，解题的关键是掌握数轴上两点之间距离的表⽰⽅法．4．（1）是；（2）30?或40?或20?；（3）4t =或10t =或16t =；（4）2t =或12t =. 【解析】【分析】（1）若OC 为AOB ∠的⾓平分线，由⾓平分线的定义可得2AOB AOC ∠=∠，由⼆倍⾓线的定义可知结论；（2）根据⼆倍⾓线的定义分2,2,2AOB AOC AOC BOC BOC AOC ∠=∠∠=∠∠=∠三种情况求出AOC ∠的⼤⼩即可.（3）当射线OP ，OQ 旋转到同⼀条直线上时，180POQ ?∠=，即180POA AOB BOQ ?∠+∠+∠=或180BOQ BOP ?∠+∠=，或OP 和OQ 重合时，即360POA AOB BOQ ?∠+∠+∠=，⽤含t 的式⼦表⽰出OP 、OQ 旋转的⾓度代⼊以上三种情况求解即可；（4）结合“⼆倍⾓线”的定义，根据t 的取值范围分04t <<，410t ≤<，1012t <≤，1218t <≤4种情况讨论即可. 【详解】解：（1）若OC 为AOB ∠的⾓平分线，由⾓平分线的定义可得2AOB AOC ∠=∠，由⼆倍⾓线的定义可知⼀个⾓的⾓平分线是这个⾓的“⼆倍⾓线”；（2）当射线OC 为AOB ∠的“⼆倍⾓线”时，有3种情况，①2AOB AOC ∠=∠，60,30AOB AOC∠=∴∠=；②2AOC BOC ∠=∠，360AOB AOC BOC BOC ?∠=∠+∠=∠=，20BOC ?∴∠=，40AOC ?∴∠=；③2BOC AOC ∠=∠，360AOB AOC BOC AOC ?∠=∠+∠=∠=，20AOC ?∴∠=，综合上述，AOC ∠的⼤⼩为30?或40?或20?；（3）当射线OP ，OQ 旋转到同⼀条直线上时，有以下3种情况，①如图此时180POA AOB BOQ ?∠+∠+∠=，即206010180t t ++=，解得4t =；②如图此时点P 和点Q 重合，可得360POA AOB BOQ ?∠+∠+∠=，即206010360t t ++=，解得10t =；③如图此时180BOQ BOP ?∠+∠=，即1060(36020)180t t+--=，解得16t =，综合上述，4t =或10t =或16t =；（4）由题意运动停⽌时3602018t ??=÷=，所以018t <≤，①当04t <<时，如图，此时OA 为POQ ∠的“⼆倍⾓线”，2AOQ POA ∠=∠，即6010220t t +=?，解得2t =；②当410t ≤<时，如图，此时，180,180AOQ AOP ??∠>∠>，所以不存在；③当1012t <≤时，如图此时OP 为AOQ ∠的“⼆倍⾓线”，2AOP POQ ∠=∠，即360202(201060360)t t t ?-=?++- 解得 12t =；④当1218t <≤时，如图，此时180,180AOQ AOP ??∠>∠>，所以不存在；综上所述，当2t =或12t =时，OA ，OP ，OQ 三条射线中，⼀条射线恰好是以另外两条射线为边组成的⾓的“⼆倍⾓线”. 【点睛】本题考查了⼀元⼀次⽅程的应⽤，正确理解“⼆倍⾓线”的定义，找准题中⾓之间等量关系是解题的关键.5．【应⽤】：（1）3；（2）（1，2）或（1，﹣2）；【拓展】：（1）5；（2）t =±2；（3）d （P ，Q ）的值为4或8．【解析】【分析】（1）根据若y 1=y 2，则AB ∥x 轴，且线段AB 的长度为|x 1-x 2|，代⼊数据即可得出结论；（2）由CD ∥y 轴，可设点D 的坐标为（1，m ），根据CD=2即可得出|0-m|=2，解之即可得出结论；【拓展】：（1）根据两点之间的折线距离公式，代⼊数据即可得出结论；（2）根据两点之间的折线距离公式结合d （E ，H ）=3，即可得出关于t 的含绝对值符号的⼀元⼀次⽅程，解之即可得出结论；（3）由点Q 在x 轴上，可设点Q 的坐标为（x ，0），根据三⾓形的⾯积公式结合三⾓形OPQ 的⾯积为3即可求出x 的值，再利⽤两点之间的折线距离公式即可得出结论．【详解】解：【应⽤】：（1）AB 的长度为|﹣1﹣2|=3．故答案为：3．（2）由CD ∥y 轴，可设点D 的坐标为（1，m ），∵CD=2，∴|0﹣m|=2，解得：m=±2，∴点D 的坐标为（1，2）或（1，﹣2）．【拓展】：（1）d （E ，F ）=|2﹣（﹣1）|+|0﹣（﹣2）|=5．故答案为：5．（2）∵E （2，0），H （1，t ），d （E ，H ）=3，∴|2﹣1|+|0﹣t |=3，解得：t =±2．（3）由点Q 在x 轴上，可设点Q 的坐标为（x ，0），∵三⾓形OPQ 的⾯积为3，∴12|x |×3=3，解得：x =±2．当点Q 的坐标为（2，0）时，d （P ，Q ）=|3﹣2|+|3﹣0|=4；当点Q 的坐标为（﹣2，0）时，d （P ，Q ）=|3﹣（﹣2）|+|3﹣0|=8 综上所述，d （P ，Q ）的值为4或8．【点睛】本题考查了两点间的距离公式，读懂题意并熟练运⽤两点间的距离及两点之间的折线距离公式是解题的关键．6．（1）30°；（2）BOC ∠+∠BOE =90°；（3）为定值2，理由见解析【解析】【分析】（1）根据差余⾓的定义，结合⾓平分线的性质可得∠BOE 的度数；（2）根据差余⾓的定义得到BOC ∠和AOE ∠的关系，（3）分当OE 在OC 左侧时，当OE 在OC 右侧时，根据差余⾓的定义得到COE ∠和AOC ∠的关系，再结合余⾓和补⾓的概念求出AOC BOCCOE∠-∠∠的值.【详解】解：（1）如图，∵COE ∠是AOC ∠的差余⾓∴AOC ∠-COE ∠=90°，即AOC ∠=COE ∠+90°，⼜∵OE 是BOC ∠的⾓平分线，∴∠BOE =COE ∠，则COE ∠+90°+COE ∠+COE ∠=180°，解得COE ∠=30°；（2）∵BOC ∠是AOE ∠的差余⾓，∴AOE ∠-BOC ∠=90°，∵AOE ∠=AOC ∠+COE ∠，BOC ∠=∠BOE +COE ∠，∴AOC ∠-∠BOE =90°，∵AOC ∠=180°-BOC ∠，∴180°-BOC ∠-∠BOE =90°，∴BOC ∠+∠BOE =90°；（3）当OE 在OC 左侧时，∵COE ∠是AOC ∠的差余⾓，∴AOC ∠-COE ∠=90°，∴∠AOE =∠BOE=90°，则AOC BOCCOE∠-∠∠=90COE BOCCOE ∠+?-∠∠=COE COE COE ∠+∠∠=2；当OE 在OC 右侧时，过点O 作OF ⊥AB ，∵COE ∠是AOC ∠的差余⾓，∴AOC ∠=90°+COE ∠，⼜∵AOC ∠=90°+COF ∠，∴COE ∠=COF ∠，∴AOC BOCCOE∠-∠∠=90COE BOCCOE∠+?-∠∠=9090COE COF COE∠+?-?+∠∠=COE COF COE ∠+∠∠=COE COE COE ∠+∠∠=2.综上：AOC BOCCOE∠-∠∠为定值2.【点睛】本题属于新概念题，考查了余⾓、补⾓的知识，仔细观察图形理解两个⾓的差余⾓关系、互补关系是解题的关键．7．（1）90?；（2）COD=10∠?；（3）1752MON COD ∠=∠+?，证明见解析【解析】【分析】（1）利⽤⾓平分线定义得出12AOM MOC AOC x ∠=∠=∠=，12BON DON BOD y ∠=∠=∠=，再利⽤∠AOB 的和差关系进⾏列⽅程即可求解；（2）利⽤8MON COD ∠=∠，表达出∠AOC 、∠BOD ，利⽤∠AOB 的和差关系进⾏列⽅程即可求解；（3）画出图形后利⽤⾓的和差关系进⾏计算求解即可．【详解】解：（1）∵OM 平分斜边OC 与OA 的夹⾓，ON 平分BOD ∠．∴OM 平分∠AOC, ON 平分∠BOD∴设11,22AOM MOC AOC x BON DON BOD y ∠=∠=∠=∠=∠=∠=∴2,2AOC x BOD y ∠=∠=，30MON MOC COD DON x y ∠=∠+∠+∠=+?+∵2302150AOB AOC BOD COD x y ∠=∠+∠+∠=+?+=? ∴60x y +=?∴3090MON x y ∠=+?+=? 故答案为: 90?（2）∵8MON COD ∠=∠∴设=,8COD a MON a ∠∠= ∵射线OD 恰好平⽅MON ∠∴14,2DOM DON MON a ∠=∠=∠= ∴43,COM DOM COD a a a ∠=∠-∠=-=∵OM 平分斜边OC 与OA 的夹⾓，ON 平分BOD ∠．∴OM 平分∠AOC, ON 平分∠BOD∴113,422AOM MOC AOC a BON DON BOD a ∠=∠=∠=∠=∠=∠= ∴6,8AOC a BOD a ∠=∠=∵68150AOB AOC BOD COD a a a ∠=∠+∠+∠=++=? ∴=10a ? ∴COD=10∠?(3) 1752MON AOC ∠=∠+?,证明如下：当OC 与OA 重合时，设∠COD=x,则150150BOD AOB COD COD x ∠=∠-∠=?-∠=?-∵ON 平分∠BOD∴117522DON BOD x ∠=∠=?- ∴MON COD DON ∠=∠+∠1752x x =+?-1752x =?+∴1752MON COD ∠=?+∠当OC 在OA 的左侧时设∠AOD=a ，∠AOC=b，则∠BOD=∠AOB -∠AOD=150°-a ，∠COD=∠AOD+∠AOC=a+b ∵ON 平分∠BOD ∴117522DON BOD a ∠=∠=?- ∵OM 平分∠AOC∴1122AOM COM AOC b ∠=∠=∠=∴∠MON=∠MOA+∠AOD+∠DON 117522b a a =++?- 117522b a =++? 1752COD =∠+?当OD 与OA 重合时∵ON 平分∠AOB∴1752AON AOB ∠=∠=? ∵OM 平分∠AOC∴12MON AOC ∠=∠∴MON MOD AON ∠=∠+∠1752AOC =∠+? 综上所述 1MON AOC ∠=∠+? 【点睛】本题考查了⾓平分线的动态问题，掌握⾓平分线的性质是解题的关键． 8．（1）2；（2）52x MC =+；（3）当25x =-或6x =时，有2AP CM PC -=成⽴. 【解析】【分析】（1）根据中点的定义，即可求出点C 的坐标；（2）先表⽰出点M 的数，然后利⽤线段上两点之间的距离，即可表⽰出MC 的长度；（3）分别求出AP ，MC 和PC 的长度，结合题意，分为三种情况进⾏讨论，即可求出x 的值. 【详解】解：（1）点A 表⽰的数为10-，点B 表⽰的数为14，∴线段AB=14(10)24--=，∴点C 表⽰的数为：142422-÷=；（2）根据题意，点M 表⽰的数为：142x +，∴线段MC 的长度为：142522x x+-=+；（3）根据题意，线段AP 的长度为：10x +，线段MC 的长度为：52x +，线段PC 的长度为：2x -，∵2AP CM PC -=，∴10(5)222x x x +-+=-，整理得：15242x x -=+，①当点P 在点C 的左边时，2x <，则20x ->，∴15242x x -=+，解得：25x =-；②当点P 与点C 重合时，2x =，∴15042x +=，解得：10x =-（不符合题意，舍去）；③当点P 在点C 的右边时，2x >，则20x -<，∴15242x x -=+，解得：6x =. ∴当25x =-或6x =时，有2AP CM PC -=成⽴. 【点睛】本题考查了数轴上的动点的问题，数轴上两点之间的距离，解⼀元⼀次⽅程，以及绝对值的意义，解题的关键是掌握数轴上两点之间的距离.9．（1）17cm EF =；（2）EF 的长度不变，17cm EF =；（3）2EOF AOB COD ∠=∠+∠. 【解析】【分析】（1）根据已知条件求出BD=18cm ，再利⽤E 、F 分别是AC 、BD 的中点，分别求出AE 、BF 的长度，即可得到EF ；（2）根据中点得到12EC AC =，12DF DB =，由EF EC CD DF =++推导得出EF=()12AB CD +，将AB 、CD 的值代⼊即可求出结果；（3）由OE 、OF 分别平分AOC ∠和BOD ∠得到12COE AOC ∠=∠， 12DOF BOD ∠=∠，即可列得EOF COE COD DOF ∠=∠+∠+∠，通过推导得出()12EOF AOB COD ∠=∠+∠. 【详解】（1）∵30cm AB =，4cm CD =，8cm AC ，∴308418BD AB AC CD =--=--=cm ，∵E 、F 分别是AC 、BD 的中点，∴142AE AC ==cm ， 192BF BD ==cm ，∴304917EF AB AE BF =--=--=cm ，故17cm EF =；（2）EF 的长度不变. 17cm EF = ∵E 、F 分别是AC 、BD 的中点，∴12EC AC =，12DF DB =∴EF EC CD DF =++ 1122AC CD BD =++ 1()2AC BD CD =++ ()12AB CD CD =-+ ()117cm 2AB CD =+= （3）∵OE 、OF 分别平分AOC ∠和BOD ∠，∴12COE AOC ∠=∠， 12DOF BOD ∠=∠，∴EOF COE COD DOF ∠=∠+∠+∠, 1122AOC COD BOD =∠+∠+∠, 1()2AOC BOD COD =∠+∠+∠, 1()2AOB COD COD =∠-∠+∠, ()12AOB COD =∠+∠, ∴()12EOF AOB COD ∠=∠+∠. 【点睛】此题考查线段的和差、⾓的和差计算，解题中会看图形，根据图中线段或⾓的⼤⼩关系得到和差关系，由此即可正确解题. 10．（1）135，135；（2）∠MON ＝135°；（3）同意，∠MON ＝（90°﹣12x °）+x °+。

初一下册数学压轴题精练答案

初一下册数学压轴题精练答案【1 】参考答案与试题解析一．解答题（共9小题）1．如图1,在平面直角坐标系中,△AOB是直角三角形,∠AOB=90°,斜边AB与y轴交于点C．（1）若∠A=∠AOC,求证：∠B=∠BOC;（2）如图2,延伸AB交x轴于点E,过O作OD⊥AB,若∠DOB=∠EOB,∠A=∠E,求∠A的度数;（3）如图3,OF等分∠AOM,∠BCO的等分线交FO的延伸线于点P,∠A=40°,当△ABO绕O 点扭转时（斜边AB与y轴正半轴始终订交于点C）,问∠P的度数是否产生转变？若不变,求其度数;若转变,请解释来由．考点：三角形内角和定理;坐标与图形性质．专题：证实题．剖析：（1）由直角三角形两锐角互余及等角的余角相等即可证实;（2）由直角三角形两锐角互余.等量代换求得∠DOB=∠EOB=∠OAE=∠E;然后依据外角定理知∠DOB+∠EOB+∠OEA=90°;从而求得∠DOB=30°,即∠A=30°;（3）由角等分线的性质知∠FOM=45°﹣∠AOC ①,∠PCO=∠A+∠AOC ②,依据①②解得∠PCO+∠FOM=45°+∠A,最后依据三角形内角和定理求得扭转后的∠P的度数．解答：（1）证实：∵△AOB是直角三角形,∴∠A+∠B=90°,∠AOC+∠BOC=90°,∵∠A=∠AOC,∴∠B=∠BOC;解：（2）∵∠A+∠ABO=90°,∠DOB+∠ABO=90°,∴∠A=∠DOB,又∵∠DOB=∠EOB,∠A=∠E,∴∠DOB=∠EOB=∠OAE=∠OEA,∵∠DOB+∠EOB+∠OEA=90°,∴∠A=30°;（3）∠P的度数不变,∠P=25°．来由如下：（只答不变不得分）∵∠AOM=90°﹣∠AOC,∠BCO=∠A+∠AOC,又∵OF等分∠AOM,CP等分∠BCO,∴∠FOM=45°﹣∠AOC ①,∠PCO=∠A+∠AOC ②,①+②得：∠PCO+∠FOM=45°+∠A,∴∠P=180°﹣（∠PCO+∠FOM+90°）=180°﹣（45°+∠A+90°）=180°﹣（45°+20°+90°）=25°．点评：本题分解考核了三角形内角和定理.坐标与图形的性质．解答时,需留意,△ABO扭转后的外形与大小均无变更．2．在平面直角坐标系中,A（﹣1,0）,B（0,2）,点C在x轴上．（1）如图（1）,若△ABC的面积为3,则点C的坐标为（2,0）或（﹣4,0）．（2）如图（2）,过点B点作y轴的垂线BM,点E是射线BM上的一动点,∠AOE的等分线交直线BM于F,OG⊥OF且交直线BM于G,当点E在射线BM上滑动时,的值是否变更？若不变,要求出其值;若变更,请解释来由．考点：三角形内角和定理;坐标与图形性质;垂线;平行线的性质;三角形的面积;三角形的外角性质．剖析：（1）应用A,B点坐标,△ABC的面积为3,得出AC的长,进而得出C点坐标;（2）起首依据已知得出∠EOG=∠EOx,进而得出FM∥x轴,再应用已知得出∠BOF=∠EGO,即可得出∠BEO=2∠BOF,得出答案即可．解答：解：（1）∵A（﹣1,0）,B（0,2）,点C在x轴上．△ABC的面积为3, ∴AC的长为3,则点C的坐标为（2,0）或（﹣4,0）;故答案为：（2,0）或（﹣4,0）;（2）∵∠AOE+∠EOx=180°,∴∠AOE+∠EOx=90°,即∠EOF+∠EOx=90°∵∠EOF+∠EOG=90°,∴∠EOG=∠EOx,∴FM∥x轴,∴∠GOx=∠EGO,∴∠EOG=∠EGO,∴∠BEO=2∠EGO,∵∠FOG=90°,∴∠EGO+∠OFG=90°,∵FM⊥y轴,∴∠BOF+∠OFG=90°,∴∠BOF=∠EGO,∴∠BEO=2∠BOF,∴=2．点评：此题重要考核了三角形内角和定理应用以及平行线的剖断和三角形面积求法等常识,依据已知得出FM∥x轴以及∠BOF=∠EGO是解题症结．3．如图1,在平面直角坐标系中,A（a,0）,B（b,0）,C（﹣1,2）,且|2a+b+1|+（a+2b﹣4）2=0．（1）求a,b的值;（2）①在x轴的正半轴上消失一点M,使△COM的面积=△ABC的面积,求出点M的坐标;②在坐标轴的其它地位是否消失点M,使△COM的面积=△ABC的面积仍然成立？若消失,请直接写出相符前提的点M的坐标;（3）如图2,过点C作CD⊥y轴交y轴于点D,点P为线段CD延伸线上一动点,衔接OP,OE 等分∠AOP,OF⊥OE．当点P活动时,的值是否会转变？若不变,求其值;若转变,解释来由．考点：三角形内角和定理;非负数的性质：绝对值;非负数的性质：偶次方;解二元一次方程组;三角形的面积;三角形的外角性质．剖析：（1）依据非负数的性质即可列出关于a,b的方程组求得a,b的值;（2）①过点C做CT⊥x轴,CS⊥y轴,垂足分离为T.S,依据三角形的面积公式即可求得OM的长,则M的坐标即可求得;②依据三角形的面积公式,即可写出M的坐标;（3）应用∠BOF依据平行线的性质,以及角等分线的界说暗示出∠OPD和∠DOE即可求解．解答：解：（1）∵|2a+b+1|+（a+2b﹣4）2=0,又∵|2a+b+1|≥0,（a+2b﹣4）2≥0,∴|2a+b+1|=0且（a+2b﹣4）2=0．∴∴即a=﹣2,b=3．（2）①过点C做CT⊥x轴,CS⊥y轴,垂足分离为T.S．∵A（﹣2,0）,B（3,0）,∴AB=5,因为C（﹣1,2）,∴CT=2,CS=1,△ABC的面积=AB•CT=5,要使△COM的面积=△ABC的面积,即△COM的面积=,所以OM•CT=,∴OM=2.5．所以M的坐标为（2.5,0）．②消失．点M的坐标为（0,5）或（﹣2.5,0）或（0,﹣5）．（3）的值不变,来由如下：∵CD⊥y轴,AB⊥y轴∴∠CDO=∠DOB=90°∴AB∥CD∴∠OPD=∠POB∵OF⊥OE∴∠POF+∠POE=90°,∠BOF+∠AOE=90°∵OE等分∠AOP∴∠POE=∠AOE∴∠POF=∠BOF∴∠OPD=∠POB=2∠BOF∵∠DOE+∠DOF=∠BOF+∠DOF=90°∴∠DOE=∠BOF∴∠OPD=2∠BOF=2∠DOE∴．点评：本题考核了非负数的性质,三角形的面积公式,以及角等分线的界说,平行线的性质,求点的坐标问题经常应用的办法就是转化成求线段的长的问题．4．长方形OABC,O为平面直角坐标系的原点,OA=5,OC=3,点B在第三象限．（1）求点B的坐标;（2）如图1,若过点B的直线BP与长方形OABC的边交于点P,且将长方形OABC的面积分为1：4两部分,求点P的坐标;（3）如图2,M为x轴负半轴上一点,且∠CBM=∠CMB,N是x轴正半轴上一动点,∠MCN的等分线CD交BM的延伸线于点D,在点N活动的进程中,的值是否变更？若不变,求出其值;若变更,请解释来由．考点：平行线的剖断与性质;坐标与图形性质;三角形的面积．剖析：（1）依据第三象限点的坐标性质得出答案;（2）应用长方形OABC的面积分为1：4两部分,得出等式求出AP的长,即可得出P 点坐标,再求出PC的长,即可得出OP的长,进而得出答案;（3）起首求出∠MCF=2∠CMB,即可得出∠CNM=∠NCF=∠MCF﹣∠NCM=2∠BMC ﹣2∠DCM,得出答案．解答：解：（1）∵四边形OABC为长方形,OA=5,OB=3,且点B在第三象限, ∴B（﹣5,﹣3）．（2）若过点B的直线BP与边OA交于点P,依题意可知：×AB×AP=×OA×OC, 即×3×AP=×5×3,∴AP=2∵OA=5,∴OP=3,∴P（﹣3,0）,若过点B的直线BP与边OC交于点P,依题意可知：×BC×PC=×OA×OC,即×5×PC=×5×3,∴PC=∵OC=3,∴OP=,∴P（0,﹣）．综上所述,点P的坐标为（﹣3,0）或（0,﹣）．（3）延伸BC至点F,∵四边形OABC为长方形,∴OA∥BC．∴∠CBM=∠AMB,∠AMC=∠MCF．∵∠CBM=∠CMB,∴∠MCF=2∠CMB．过点M作ME∥CD交BC于点E,∴∠EMC=∠MCD．又∵CD等分∠MCN,∴∠NCM=2∠EMC．∴∠D=∠BME=∠CMB﹣∠EMC,∠CNM=∠NCF=∠MCF﹣∠NCM=2∠BMC﹣2∠DCM=2∠D,∴=．点评：此题重要考核了平行线的性质以及矩形的性质.图形面积求法等常识,应用数形联合得出的是解题症结．5．如图,直线AB∥CD．（1）在图1中,∠BME.∠E,∠END的数目关系为：∠E=∠BME+∠END;（不需证实）在图2中,∠BMF.∠F,∠FND的数目关系为：∠BMF=∠F+∠FND;（不需证实）（2）如图3,NE等分∠FND,MB等分∠FME,且2∠E与∠F互补,求∠FME的大小．（3）如图4中,∠BME=60°,EF等分∠MEN,NP等分∠END,EQ∥NP,则∠FEQ的大小是否产生变更？若变更,解释来由;若不变更,求∠FEQ的度数．考点：平行线的性质．剖析：（1）过点E作EF∥AB,依据两直线平行,内错角相等可得∠BME=∠1,∠END=∠2,然后相加即可得解;先依据两直线平行,同位角相等求出∠3=∠FND,再依据三角形的一个外角等于与它不相邻的两个内角的和列式盘算即可得解;（2）设∠END=x°,∠BNE=y°,依据（1）的结论可得x+y=∠E,2x+∠F=y,然后消失落x 并暗示出y,再依据2∠E与∠F互补求出y,然后依据角等分线的界说求解即可;（3）依据（1）的结论暗示出∠MEN,再依据角等分线的界说暗示出∠FEN和∠ENP,再依据两直线平行,内错角相等可得∠NEQ=∠ENP,然后依据∠FEQ=∠FEN﹣∠NEQ 整顿即可得解．解答：解：（1）如图1,过点E作EF∥AB,∵AB∥CD,∴AB∥EF∥CD,∴∠BME=∠1,∠END=∠2,∴∠1+∠2=∠BME+∠END,即∠E=∠BME+∠END;如图2,∵AB∥CD,∴∠3=∠FND,∴∠BMF=∠F+∠3=∠F+∠FND,即∠BMF=∠F+∠FND;故答案为：∠E=∠BME+∠END;∠BMF=∠F+∠FND;（2）如图3,设∠END=x°,∠BNE=y°,由（1）的结论可得x+y=∠E,2x+∠F=y,消失落x得,3y=2∠E+∠F,∵2∠E与∠F互补,∴2∠E+∠F=180°,∴3y=180°,解得y=60°,∵MB等分∠FME,∴∠FME=2y=2×60°=120°;（3）由（1）的结论得,∠MEN=∠BME+∠END,∵EF等分∠MEN,NP等分∠END,∴∠FEN=∠MEN=（∠BME+∠END）,∠ENP=∠END,∵EQ∥NP,∴∠NEQ=∠ENP,∴∠FEQ=∠FEN﹣∠NEQ=（∠BME+∠END）﹣∠END=∠BME, ∵∠BME=60°,∴∠FEQ=×60°=30°．点评：本题考核了平行线的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,角等分线的界说,此类标题,过拐点作平行线是解题的症结,精确识图理清图中各角度之间的关系也很重要．6．在平面直角坐标系中,点B（0,4）,C（﹣5,4）,点A是x轴负半轴上一点,S四边形AOBC=24．（1）线段BC的长为5,点A的坐标为（﹣7,0）;（2）如图1,BM等分∠CBO,CM等分∠ACB,BM交CM于点M,试给出∠CMB与∠CAO之间知足的数目关系式,并解释来由;（3）若点P是在直线CB与直线AO之间的一点,衔接BP.OP,BN等分∠CBP,ON等分∠AOP,BN交ON于N,请依题意画出图形,给出∠BPO与∠BNO之间知足的数目关系式,并解释来由．考点：三角形内角和定理;坐标与图形性质;三角形的面积;三角形的外角性质．专题：分类评论辩论．剖析：（1）依据点B.C的横坐标求出BC的长度即可;再依据四边形的面积求出OA的长度,然后依据点A在y轴的负半轴写出点A的坐标;（2）依据两直线平行,同旁内角互补用∠CAO暗示出∠ACB,再依据角等分线的界说暗示出∠MAB和∠MBC,然后应用三角形的内角和定理列式整顿即可得解;（3）分①点P在OB的左边时,依据三角形的内角和定理暗示出∠PBO+∠POB,再依据两直线平行,同旁内角互补和角等分线的界说暗示出∠NBP+∠NOP,然后在△NBO中,应用三角形的内角和定理列式整顿即可得解;②点P在OB的右边时,求出∠CBP+∠AOP+∠BPO=360°,再依据角等分线的界说暗示出∠PBN+∠PON,然后应用四边形的内角和定理列式整顿即可得解．点评：本题考核了三角形的内角和定理,角等分线的界说,平行线的性质,以及坐标与图形性质,精确识图理清图中各角度之间的关系是解题症结,（3）要留意分情形评论辩论．7．如图1,在平面直角坐标系中,四边形OBCD各个极点的坐标分离是O（0,0）,B（2,6）,C （8,9）,D（10,0）;（1）三角形BCD的面积=30（2）将点C平移,平移后的坐标为C′（2,8+m）;①若S△BDC′=32,求m的值;②当C′在第四象限时,作∠C′OD的等分线OM,OM交于C′C于M,作∠C′CD的等分线CN,CN 交OD于N,OM与CN订交于点P（如图2）,求的值．考点：作图-平移变换;坐标与图形性质;三角形内角和定理．剖析：（1）三角形BCD的面积=正方形的面积﹣3个小三角形的面积;（2）①分平移后的坐标为C′在B点的上方;在B点的下方两种情形评论辩论可求m 的值;②应用外角以及角等分线的性质得出∠ODC+∠CC′O=2∠P,即可得出答案．点评：此题重要考核了外角的性质以及三角形面积求法和点坐标性质等常识,应用数形联合得出C′的不合地位是解题症结．8．如图,四边形ABCD中,AD∥BC,DE等分∠ADB,∠BDC=∠BCD．（1）求证：∠1+∠2=90°;（2）若∠ABD的等分线与CD的延伸线交于F,且∠F=55°,求∠ABC;（3）若H是BC上一动点,F是BA延伸线上一点,FH交BD于M,FG等分∠BFH,交DE于N,交BC于G．当H在BC上活动时（不与B点重合）,的值是否变更？假如变更,解释来由;假如不变,试求出其值．考点：等腰三角形的性质;角等分线的界说;平行线的性质．专题：分解题．剖析：本题考核了等腰三角形的性质.角等分线的性质以及平行线的性质,解决问题的症结在于熟习控制常识要点,并且擅长应用角与角之间的接洽进行传递．（1）由AD∥BC,DE等分∠ADB,得∠ADC+∠BCD=180,∠BDC=∠BCD,得出∠1+∠2=90°;（2）由DE等分∠ADB,CD等分∠ABD,四边形ABCD中,AD∥BC,∠F=55°,得出∠ABC=∠ABD+∠DBC=∠ABD+∠ADB,即∠ABC=70°;（3）在△BMF中,依据角之间的关系∠BMF=180°﹣∠ABD﹣∠BFH,得∠GND=180°﹣∠AED﹣∠BFG,再依据角之间的关系得∠BAD=﹣∠DBC,在综上得出答案．解答：（1）证实：AD∥BC,∠ADC+∠BCD=180,∵DE等分∠ADB,∠BDC=∠BCD,∴∠ADE=∠EDB,∠BDC=∠BCD,∵∠ADC+∠BCD=180°,∴∠EDB+∠BDC=90°,∠1+∠2=90°．解：（2）∠FBD+∠BDE=90°﹣∠F=35°,∵DE等分∠ADB,BF等分∠ABD,∴∠ADB+∠ABD=2（∠FBD+∠BDE）=70°,又∵四边形ABCD中,AD∥BC,∴∠DBC=∠ADB,∴∠ABC=∠ABD+∠DBC=∠ABD+∠ADB,即∠ABC=70°;（3）的值不变．证实：在△BMF中,∠BMF=∠DMH=180°﹣∠ABD﹣∠BFH,又∵∠BAD=180°﹣（∠ABD+∠ADB）,∠DMH+∠BAD=（180°﹣∠ABD﹣∠BFH）+（180°﹣∠ABD﹣∠ADB）,=360﹣∠BFH﹣2∠ABD﹣∠ADB,∠DNG=∠FNE=180°﹣∠BFH﹣∠AED,=180°﹣∠BFH﹣∠ABD﹣∠ADB,=（∠DMH+∠BAD）,∴=2．点评：本题考核等腰三角形的性质及三角形内角和定理;此题为摸索题,比较新鲜,现实涉及的常识不久不多．9．如图（1）所示,一副三角板中,含45°角的一条直角边AC在y轴上,斜边AB交x轴于点G．含30°角的三角板的极点与点A重合,直角边AE和斜边AD分离交x轴于点F.H．（1）若AB∥ED,求∠AHO的度数;（2）如图2,将三角板ADE绕点A扭转．在扭转进程中,∠AGH的等分线GM与∠AHF的等分线HM订交于点M,∠COF的等分线ON与∠OFE的等分线FN订交于点N．①当∠AHO=60°时,求∠M的度数;②试问∠N+∠M的度数是否产生变更？若转变,求出变更规模;若保持不变,请解释来由．考点：三角形内角和定理;角等分线的界说;平行线的性质;三角形的外角性质．专题：分解题．剖析：（1）由AB∥ED可以得到∠BAD=∠D=60°,即∠BAC+∠CAD=60°,然后依据已知前提即可求出∠AHO;（2）①由∠AHO+∠AHF=180°,∠AHO=60°,可以求出∠AHF,而HM是∠AHF的等分线,GM是∠AGH的等分线,∠MHF=∠MGH+∠M,由此即可求出∠M;②∠N+∠M的度数不变,当∠BAC与∠DAE没有重合部分时,∠GAH﹣∠OAF=（45°+∠OAH）﹣（30°+∠OAH）=15°;当AC与AD在一条直线上时,∠GAH﹣∠OAF=45°﹣30°=15°;当∠BAC与∠DAE有重合部分时,∠GAH﹣∠OAF=（45°﹣∠OAH）﹣（30°﹣∠OAH）=15°,即∠GAH﹣∠OAF=15°．而依据已知前提∠M=∠MHF ﹣∠MGH=∠AHF﹣∠AGH=∠GAH,∠N=180°﹣（∠OFE+90°）=180°﹣（∠OAF+90°）﹣90°=90°﹣∠OAF,由此即可得到结论．解答：解：（1）∵AB∥ED∴∠BAD=∠D=60°（两直线平行,内错角相等）,即∠BAC+∠CAD=60°．∵∠BAC=45°,∴∠CAD=60°﹣45°=15°,∠AHO=90°﹣∠CAD=75°;（2）①∵∠AHO+∠AHF=180°,∠AHO=60°,∴∠AHF=180°﹣60°=120°∵HM是∠AHF的等分线,∴∠MHF=∠AHF=60°（角等分线的界说）．∵GM是∠AGH的等分线,∠AGH=45°,∴∠MGH=∠AGH=22.5°,∵∠MHF=∠MGH+∠M,∴∠M=60°﹣22.5°=37.5°;②∠N+∠M的度数不变,来由是：当∠BAC与∠DAE没有重合部分时,∠GAH﹣∠OAF=（45°+∠OAH）﹣（30°+∠OAH）=15°;当AC与AD在一条直线上时,∠GAH﹣∠OAF=45°﹣30°=15°;当∠BAC与∠DAE有重合部分时,∠GAH﹣∠OAF=（45°﹣∠OAH）﹣（30°﹣∠OAH）=15°;∴∠GAH﹣∠OAF=15°．易得出∠M=∠MHF﹣∠MGH=∠AHF﹣∠AGH=∠GAH,∠N=180°﹣（∠OFE+90°）=180°﹣（∠OAF+90°）﹣90°=90°﹣∠OAF,∴∠M+∠N=∠GAH+90°﹣∠OAF=90°+×15°=97.5°（定值）．点评：此题比较庞杂,考核了三角形的内角和.三角形的外角的性质.角等分线的性质.平行线的性质等多个常识,分解性比较强,难度比较大,学生起首心理上要信任本身,才干有信念解决问题．。

初一数学期末复习三角函数计算压轴题难题(附答案详解)

初一数学期末复习三角函数计算压轴题难题(附答案详解)题目一已知直角三角形中一边的长为6cm，另一边的长为8cm，求另外两个角的正弦、余弦和正切值。

解答：设直角三角形中两个锐角分别为A和B。

已知边长分别为6cm 和8cm，则根据勾股定理，可得直角边的长为：c = √(a^2 + b^2)c = √(6^2 + 8^2)c = √(36 + 64)c = √100c = 10cm因此，三角形的斜边长为10cm。

对于角A：正弦值(sin) = 对边/斜边 = 6/10 = 0.6余弦值(cos) = 邻边/斜边 = 8/10 = 0.8正切值(tan) = 对边/邻边 = 6/8 = 0.75对于角B：正弦值(sin) = 8/10 = 0.8余弦值(cos) = 6/10 = 0.6正切值(tan) = 8/6 = 1.3333因此，角A的正弦值为0.6，余弦值为0.8，正切值为0.75；角B的正弦值为0.8，余弦值为0.6，正切值为1.3333。

题目二已知一条斜边为12cm的直角三角形，其中一个锐角的正切值为1.5，求另外两个角的正弦、余弦和正切值。

解答：设直角三角形中两个锐角分别为A和B。

已知斜边长为12cm，角A的正切值为1.5。

对于角A：正切值(tan) = 对边/邻边 = a/b = 1.5设对边为a，邻边为b，则可以得到以下两个方程：a^2 + b^2 = 12^2a/b = 1.5从第二个方程可以得到：a = 1.5b将a的值代入第一个方程中，得到：(1.5b)^2 + b^2 = 1442.25b^2 + b^2 = 1443.25b^2 = 144b^2 = 144/3.25b^2 = 44.3077b ≈ 6.648由于b是邻边，所以b ≈ 6.648cm，a ≈ 1.5 * 6.648 ≈ 9.972cm。

因此，三角形的对边和邻边分别为9.972cm和6.648cm。

对于角A：正弦值(sin) = 对边/斜边≈ 9.972/12 ≈ 0.831余弦值(cos) = 邻边/斜边≈ 6.648/12 ≈ 0.554正切值(tan) = 对边/邻边≈ 9.972/6.648 ≈ 1.5对于角B：正弦值(sin) = 对边/斜边≈ 6.648/12 ≈ 0.554余弦值(cos) = 邻边/斜边≈ 9.972/12 ≈ 0.831正切值(tan) = 对边/邻边≈ 6.648/9.972 ≈ 0.667因此，角A的正弦值约为0.831，余弦值约为0.554，正切值约为1.5；角B的正弦值约为0.554，余弦值约为0.831，正切值约为0.667。

初一上学期数学压轴题期末复习试卷带答案

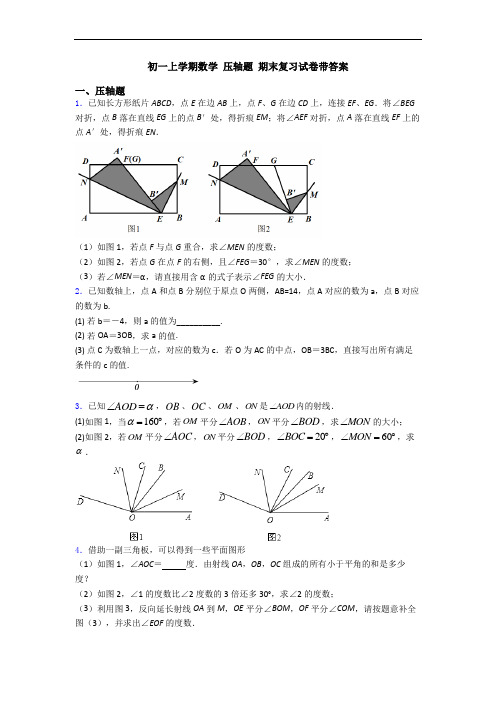
初一上学期数学压轴题期末复习试卷带答案一、压轴题1．已知长方形纸片ABCD ，点E 在边AB 上，点F 、G 在边CD 上，连接EF 、EG ．将∠BEG 对折，点B 落在直线EG 上的点B ′处，得折痕EM ；将∠AEF 对折，点A 落在直线EF 上的点A ′处，得折痕EN ．（1）如图1，若点F 与点G 重合，求∠MEN 的度数；（2）如图2，若点G 在点F 的右侧，且∠FEG ＝30°，求∠MEN 的度数；（3）若∠MEN ＝α，请直接用含α的式子表示∠FEG 的大小．2．已知数轴上，点A 和点B 分别位于原点O 两侧，AB=14，点A 对应的数为a ，点B 对应的数为b.(1) 若b ＝－4，则a 的值为__________. (2) 若OA ＝3OB ，求a 的值.(3) 点C 为数轴上一点，对应的数为c ．若O 为AC 的中点，OB ＝3BC ，直接写出所有满足条件的c 的值.3．已知AOD α∠=，OB 、OC 、OM 、ON 是AOD ∠内的射线．(1)如图1，当160α=︒，若OM 平分AOB ∠，ON 平分BOD ∠，求MON ∠的大小； (2)如图2，若OM 平分AOC ∠，ON 平分BOD ∠，20BOC ∠=︒，60MON ∠=︒，求α．4．借助一副三角板，可以得到一些平面图形（1）如图1，∠AOC ＝度．由射线OA ，OB ，OC 组成的所有小于平角的和是多少度？（2）如图2，∠1的度数比∠2度数的3倍还多30°，求∠2的度数；（3）利用图3，反向延长射线OA 到M ，OE 平分∠BOM ，OF 平分∠COM ，请按题意补全图（3），并求出∠EOF 的度数．5．综合试一试（1）下列整数可写成三个非0整数的立方和：45=_____；2=______．（2）对于有理数a ，b ，规定一种运算：2a b a ab ⊗=-．如2121121⊗=-⨯=-，则计算()()532-⊗⊗-=⎡⎤⎣⎦______．（3）a 是不为1的有理数，我们把11a-称为a 的差倒数．如：2的差倒数是1112=--，1-的差倒数是()11112=--．已知12a =，2a 是1a 的差倒数，3a 是2a 的差倒数，4a 是3a 的差倒数，……，以此类推，122500a a a ++⋅⋅⋅+=______．（4）10位裁判给一位运动员打分，每个人给的分数都是整数，去掉一个最高分，再去掉一个最低分，其余得分的平均数为该运动员的得分．若用四舍五入取近似值的方法精确到十分位，该运动员得9.4分，如果精确到百分位，该运动员得分应当是_____分．（5）在数1.2.3...2019前添加“+”，“-”并依次计算，所得结果可能的最小非负数是______（6）早上8点钟，甲、乙、丙三人从东往西直行，乙在甲前400米，丙在乙前400米，甲、乙、丙三人速度分别为120米/分钟、100米/分钟、90米/分钟，问：______分钟后甲和乙、丙的距离相等. 6．观察下列等式：111122=-⨯，1112323=-⨯，1113434=-⨯，则以上三个等式两边分别相加得：1111111131122334223344++=-+-+-=⨯⨯⨯． ()1观察发现()1n n 1=+______；()1111122334n n 1+++⋯+=⨯⨯⨯+______．()2拓展应用有一个圆，第一次用一条直径将圆周分成两个半圆(如图1)，在每个分点标上质数m ，记2个数的和为1a ；第二次再将两个半圆周都分成14圆周(如图2)，在新产生的分点标上相邻的已标的两数之和的12，记4个数的和为2a ；第三次将四个14圆周分成18圆周(如图3)，在新产生的分点标上相邻的已标的两数之和的13，记8个数的和为3a；第四次将八个18圆周分成116圆周，在新产生的分点标上相邻的已标的两个数的和的14，记16个数的和为4a；⋯⋯如此进行了n次．na=①______(用含m、n的代数式表示)；②当na6188=时，求123n1111a a a a+++⋯⋯+的值．7．已知数轴上有A、B、C三个点对应的数分别是a、b、c，且满足|a+24|+|b+10|+（c-10）2=0；动点P从A出发，以每秒1个单位的速度向终点C移动，设移动时间为t秒．（1）求a、b、c的值；（2）若点P到A点距离是到B点距离的2倍，求点P的对应的数；（3）当点P运动到B点时，点Q从A点出发，以每秒2个单位的速度向C点运动，Q点到达C点后．再立即以同样的速度返回，运动到终点A，在点Q开始运动后第几秒时，P、Q两点之间的距离为8？请说明理由．8．如图1，线段AB的长为a．（1）尺规作图：延长线段AB到C，使BC＝2AB；延长线段BA到D，使AD＝AC．（先用尺规画图，再用签字笔把笔迹涂黑．）（2）在（1）的条件下，以线段AB所在的直线画数轴，以点A为原点，若点B对应的数恰好为10，请在数轴上标出点C，D两点，并直接写出C，D两点表示的有理数，若点M 是BC的中点，点N是AD的中点，请求线段MN的长．（3）在（2）的条件下，现有甲、乙两个物体在数轴上进行匀速直线运动，甲从点D处开始，在点C，D之间进行往返运动；乙从点N开始，在N，M之间进行往返运动，甲、乙同时开始运动，当乙从M点第一次回到点N时，甲、乙同时停止运动，若甲的运动速度为每秒5个单位，乙的运动速度为每秒2个单位，请求出甲和乙在运动过程中，所有相遇点对应的有理数．9．如图，数轴上点A表示的数为4-，点B表示的数为16，点P从点A出发，以每秒3个单位长度的速度沿数轴向右匀速运动同时点Q从点B出发，以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒(t0)>．()1A ，B 两点间的距离等于______，线段AB 的中点表示的数为______；()2用含t 的代数式表示：t 秒后，点P 表示的数为______，点Q 表示的数为______； ()3求当t 为何值时，1PQ AB 2=？()4若点M 为PA 的中点，点N 为PB 的中点，点P 在运动过程中，线段MN 的长度是否发生变化？若变化，请说明理由；若不变请直接写出线段MN 的长．10．已知，如图，A 、B 、C 分别为数轴上的三点，A 点对应的数为60，B 点在A 点的左侧，并且与A 点的距离为30，C 点在B 点左侧，C 点到A 点距离是B 点到A 点距离的4倍．（1）求出数轴上B 点对应的数及AC 的距离．（2）点P 从A 点出发，以3单位/秒的速度向终点C 运动，运动时间为t 秒． ①当P 点在AB 之间运动时，则BP ＝．（用含t 的代数式表示）②P 点自A 点向C 点运动过程中，何时P ，A ，B 三点中其中一个点是另外两个点的中点？求出相应的时间t ．③当P 点运动到B 点时，另一点Q 以5单位/秒的速度从A 点出发，也向C 点运动，点Q 到达C 点后立即原速返回到A 点，那么Q 点在往返过程中与P 点相遇几次？直．接．写．出．相遇时P 点在数轴上对应的数11．如图，在平面直角坐标系中，点M 的坐标为（2，8），点N 的坐标为（2，6），将线段MN 向右平移4个单位长度得到线段PQ （点P 和点Q 分别是点M 和点N 的对应点），连接MP 、NQ ，点K 是线段MP 的中点．（1）求点K 的坐标；（2）若长方形PMNQ 以每秒1个单位长度的速度向正下方运动，（点A 、B 、C 、D 、E 分别是点M 、N 、Q 、P 、K 的对应点），当BC 与x 轴重合时停止运动，连接OA 、OE ，设运动时间为t 秒，请用含t 的式子表示三角形OAE 的面积S （不要求写出t 的取值范围）；（3）在（2）的条件下，连接OB 、OD ，问是否存在某一时刻t ，使三角形OBD 的面积等于三角形OAE 的面积？若存在，请求出t 值；若不存在，请说明理由．12．如图，在数轴上从左往右依次有四个点,,,A B C D ，其中点,,A B C 表示的数分别是0,3,10，且2CD AB =.(1)点D表示的数是；（直接写出结果）(2)线段AB以每秒2个单位长度的速度沿数轴向右运动，同时线段CD以每秒1个单位长度的速度沿数轴向左运动，设运动时间是t（秒），当两条线段重叠部分是2个单位长度时.①求t的值;②线段AB上是否存在一点P，满足3BD PA PC-=?若存在，求出点P表示的数x；若不存在，请说明理由.13．阅读下列材料，并解决有关问题：我们知道，(0)0(0)(0)x xx xx x>⎧⎪==⎨⎪-<⎩，现在我们可以用这一结论来化简含有绝对值的式子，例如化简式子|1||2|x x++-时，可令10x+=和20x-=，分别求得1x=-，2x=（称1-、2分别为|1|x+与|2|x-的零点值）．在有理数范围内，零点值1x=-和2x=可将全体有理数不重复且不遗漏地分成如下三种情况：（1）1x<-；（2）1-≤2x<；（3）x≥2．从而化简代数式|1||2|x x++-可分为以下3种情况：（1）当1x<-时，原式()()1221x x x=-+--=-+；（2）当1-≤2x<时，原式()()123x x=+--=；（3）当x≥2时，原式()()1221x x x=++-=-综上所述：原式21(1)3(12)21(2)x xxx x-+<-⎧⎪=-≤<⎨⎪-≥⎩通过以上阅读，请你类比解决以下问题：（1）填空：|2|x+与|4|x-的零点值分别为；（2）化简式子324x x-++．14．已知：∠AOB是一个直角，作射线OC，再分别作∠AOC和∠BOC的平分线OD、OE．（1）如图①，当∠BOC=70°时，求∠DOE的度数；（2）如图②，若射线OC在∠AOB内部绕O点旋转，当∠BOC=α时，求∠DOE的度数.（3）如图③，当射线OC在∠AOB外绕O点旋转时，画出图形，直接写出∠DOE的度数．15．如图①，点O为直线AB上一点，过点O作射线OC，使∠AOC=120°，将一直角三角板的直角顶点放在点O处，一边OM在射线OB上，另一边ON在直线AB的下方．（1）将图①中的三角板OMN摆放成如图②所示的位置，使一边OM在∠BOC的内部，当OM平分∠BOC时，∠BO N= ；（直接写出结果）（2）在（1）的条件下，作线段NO的延长线OP（如图③所示），试说明射线OP是∠AOC的平分线；（3）将图①中的三角板OMN摆放成如图④所示的位置，请探究∠NOC与∠AOM之间的数量关系．（直接写出结果，不须说明理由）【参考答案】***试卷处理标记，请不要删除一、压轴题1．（1）∠MEN＝90°；（2）∠MEN＝105°；（3）∠FEG＝2α﹣180°，∠FEG＝180°﹣2α．【解析】【分析】（1）根据角平分线的定义，平角的定义，角的和差定义计算即可．（2）根据∠MEN=∠NEF+∠FEG+∠MEG，求出∠NEF+∠MEG即可解决问题．（3）分两种情形分别讨论求解．【详解】（1）∵EN平分∠AEF，EM平分∠BEF∴∠NEF＝12∠AEF，∠MEF＝12∠BEF∴∠MEN＝∠NEF+∠MEF＝12∠AEF+12∠BEF＝12（∠AEF+∠BEF）＝12∠AEB∵∠AEB＝180°∴∠MEN＝12×180°＝90°（2）∵EN平分∠AEF，EM平分∠BEG∴∠NEF＝12∠AEF，∠MEG＝12∠BEG∴∠NEF+∠MEG＝12∠AEF+12∠BEG＝12（∠AEF+∠BEG）＝12（∠AEB﹣∠FEG）∵∠AEB＝180°，∠FEG＝30°∴∠NEF+∠MEG＝12（180°﹣30°）＝75°∴∠MEN＝∠NEF+∠FEG+∠MEG＝75°+30°＝105°（3）若点G在点F的右侧，∠FEG＝2α﹣180°，若点G在点F的左侧侧，∠FEG＝180°﹣2α．【点睛】考查了角的计算，翻折变换，角平分线的定义，角的和差定义等知识，解题的关键是学会用分类讨论的思想思考问题．2．(1)10；(2)212±；(3)288.5±±，【解析】【分析】(1)根据题意画出数轴，由已知条件得出AB=14,OB=4,则OA=10,得出a的值为10.(2)分两种情况,点A在原点的右侧时,设OB=m,列一元一次方程求解,进一步得出OA的长度,从而得出a的值.同理可求出当点A在原点的左侧时,a的值.(3)画数轴,结合数轴分四种情况讨论计算即可.【详解】(1)解：若b＝－4，则a的值为 10(2)解：当A在原点O的右侧时（如图）：设OB=m,列方程得：m+3m=14，解这个方程得，7m2 =，所以，OA=212，点A在原点O的右侧，a的值为212.当A在原点的左侧时（如图)，a=－21 2综上，a的值为±212.(3)解：当点A在原点的右侧，点B在点C的左侧时（如图), c=－28 5.当点A在原点的右侧，点B在点C的右侧时（如图), c=－8.当点A在原点的左侧，点B在点C的右侧时，图略，c=28 5.当点A在原点的左侧，点B在点C的左侧时,图略，c=8.综上，点c的值为：±8，±28 5.【点睛】本题考查的知识点是通过画数轴,找出数轴上各线段间的数量关系并用一元一次方程来求解,需要注意的是分情况讨论时要考虑全面,此题充分锻炼了学生动手操作能力以及利用数行结合解决问题的能力.3．（1）80°；（2）140°【解析】【分析】（1）根据角平分线的定义得∠BOM=12∠AOB，∠BON=12∠BOD，再根据角的和差得∠AOD=∠AOB+∠BOD，∠MON=∠BOM+∠BON，结合三式求解；（2）根据角平分线的定义∠MOC=12∠AOC，∠BON=12∠BOD，再根据角的和差得∠AOD=∠AOC+∠BOD-∠BOC，∠MON=∠MOC+∠BON-∠BOC结合三式求解.【详解】解：（1）∵OM平分∠AOB，ON平分∠BOD，∴∠BOM=12∠AOB，∠BON=12∠BOD，∴∠MON=∠BOM+∠BON=12∠AOB+12∠BOD=12(∠AOB+∠BOD).∵∠AOD=∠AOB+∠BOD=α=160°，∴∠MON=12×160°=80°；（2）∵OM平分∠AOC，ON平分∠BOD，∴∠MOC=12∠AOC，∠BON=12∠BOD，∵∠MON=∠MOC+∠BON-∠BOC，∴∠MON=12∠AOC+12∠BOD -∠BOC=12(∠AOC+∠BOD )-∠BOC.∵∠AOD=∠AOB+∠BOD，∠AOC=∠AOB+∠BOC,∴∠MON=12(∠AOB+∠BOC+∠BOD )-∠BOC=12(∠AOD+∠BOC )-∠BOC，∵∠AOD=α，∠MON=60°,∠BOC=20°,∴60°=12(α+20°)-20°,∴α=140°.【点睛】本题考查了角的和差计算，角平分线的定义，明确角之间的关系是解答此题的关键. 4．（1）75°，150°；（2）15°；（3）15°.【解析】【分析】（1）根据三角板的特殊性角的度数，求出∠AOC即可,把∠AOC、∠BOC、∠AOB相加即可求出射线OA，OB，OC组成的所有小于平角的和；（2）依题意设∠2＝x，列等式，解方程求出即可；（3）依据题意求出∠BOM,∠COM,再根据角平分线的性质得出∠MOE，∠MOF，即可求出∠EOF.【详解】解：（1）∵∠BOC＝30°，∠AOB＝45°，∴∠AOC＝75°，∴∠AOC+∠BOC+∠AOB＝150°；答：由射线OA，OB，OC组成的所有小于平角的和是150°；故答案为：75；（2）设∠2＝x，则∠1＝3x+30°，∵∠1+∠2＝90°，∴x+3x+30°＝90°，∴x＝15°，∴∠2＝15°，答：∠2的度数是15°；（3）如图所示，∵∠BOM ＝180°﹣45°＝135°，∠COM ＝180°﹣15°＝165°， ∵OE 为∠BOM 的平分线，OF 为∠COM 的平分线，∴∠MOF ＝12∠COM ＝82.5°，∠MOE ＝12∠MOB ＝67.5°， ∴∠EOF ＝∠MOF ﹣∠MOE ＝15°．【点睛】本题主要考查了三角板各角的度数、角平分线的性质及列方程解方程在几何中的应用，熟记概念是解题的关键.5．（1）23+(-3)3+43，73+(-5)3+(-6)3；（2）100；（3）25032；（4）9.38；（5）0；（6）24或40 【解析】【分析】（1）把45分解为2、-3、4三个整数的立方和，2分解为7、-5、-6三个整数的立方和即可的答案；（2）按照新运算法则，根据有理数混合运算法则计算即可得答案；（3）根据差倒数的定义计算出前几项的值，得出规律，计算即可得答案；（4）根据精确到十分位得9.4分可知平均分在9.35到9.44之间，可求出总分的取值范围，根据裁判打分是整数即可求出8个裁判给出的总分，再计算出平均分，精确到百分位即可；（5）由1+2-3=0，连续4个自然数通过加减运算可得0，列式计算即可得答案；（6）根据题意得要使甲和乙、甲和丙的距离相等就可以得出甲在乙、丙之间，设x 分钟后甲和乙、甲和丙的距离相等，就有甲走的路程-乙走的路程-400=丙走的路程+800-甲走的路程建立方程求出其解，就可以得出结论．当乙追上丙时，甲和乙、丙的距离相等，求出乙追上丙的时间即可.综上即可的答案. 【详解】（1）45=23+(-3)3+43，2=73+(-5)3+(-6)3，故答案为23+(-3)3+43，73+(-5)3+(-6)3 （2）∵2a b a ab ⊗=-，∴()()532-⊗⊗-=⎡⎤⎣⎦(-5)⊗[32-3×(-2)]=(-5)⊗15 =(-5)2-(-5)×15 =100. （3）∵a 1=2，∴a 2=1112=--， a 3=11(1)--=12， 412112a ==-a 5=-1…… ∴从a 1开始，每3个数一循环，∵2500÷3=833……1，∴a 2500=a 1=2，∴122500a a a ++⋅⋅⋅+=833×(2-1+12)+2=25032. （4）∵10个裁判打分，去掉一个最高分，再去掉一个最低分，∴平均分为中间8个分数的平均分，∵平均分精确到十分位的为9.4，∴平均分在9.35至9.44之间，9.35×8=74.8，9.44×8=75.52，∴8个裁判所给的总分在74.8至75.52之间，∵打分都是整数，∴总分也是整数，∴总分为75，∴平均分为75÷8=9.375，∴精确到百分位是9.38.故答案为9.38（5）2019÷4=504……3，∵1+2-3=0，4-5-6+7=0，8-9-10+11=0，……∴(1+2-3)+(4-5-6+7)+……+(2016-2017-2018+2019)=0∴所得结果可能的最小非负数是0，故答案为0（6）设x 分钟后甲和乙、丙的距离相等，∵乙在甲前400米，丙在乙前400米，速度分别为120米/分钟、100米/分钟、90米/分钟，∴120x-400-100x=90x+800-120x解得：x=24.∵当乙追上丙时，甲和乙、丙的距离相等，∴400÷(100-90)=40(分钟)∴24分钟或40分钟时甲和乙、丙的距离相等.故答案为24或40.【点睛】本题考查数字类的变化规律、有理数的混合运算、近似数及一元一次方程的应用，熟练掌握相关知识是解题关键.6．（1）11n n 1-+，n n 1+（2）①()()n 1n 2m 3++②75364 【解析】【分析】 ()1观察发现：先根据题中所给出的列子进行猜想，写出猜想结果即可；根据第一空中的猜想计算出结果；()2①由16a 2m m 3==，212a 4m m 3==，320a m 3=，430a 10m m 3==，找规律可得结论；②由()()n 1n 2m 22713173++=⨯⨯⨯⨯知()()m n 1n 22237131775152++=⨯⨯⨯⨯⨯=⨯⨯，据此可得m 7=，n 50=，再进一步求解可得．【详解】()1观察发现：()111n n 1n n 1=-++； ()1111122334n n 1+++⋯+⨯⨯⨯+， 1111111122334n n 1=-+-+-+⋯+-+， 11n 1=-+， n 11n 1+-=+， n n 1=+；故答案为11n n 1-+，n n 1+． ()2拓展应用16a 2m m 3①==，212a 4m m 3==，320a m 3=，430a 10m m 3==， ⋯⋯()()n n 1n 2a m 3++∴=，故答案为()()n 1n 2m.3++ ()()n n 1n 2a m 61883②++==，且m 为质数，对6188分解质因数可知61882271317=⨯⨯⨯⨯，()()n 1n 2m 22713173++∴=⨯⨯⨯⨯， ()()m n 1n 22237131775152∴++=⨯⨯⨯⨯⨯=⨯⨯，m 7∴=，n 50=，()()n 7a n 1n 23∴=++， ()()n 131a 7n 1n 2=⋅++， 123n1111a a a a ∴+++⋯+ ()()33336m 12m 20m n 1n 2m =+++⋯+++()()311172334n 1n 2⎡⎤=++⋯+⎢⎥⨯⨯++⎢⎥⎣⎦31131172n 27252⎛⎫⎛⎫=-=- ⎪ ⎪+⎝⎭⎝⎭ 75364=．【点睛】本题主要考查数字的变化规律，解题的关键是掌握并熟练运用所得规律：()111n n 1n n 1=-++． 7．(1) a =-24，b =-10，c =10；(2) 点P 的对应的数是-443或4；(3) 当Q 点开始运动后第6、21秒时，P 、Q 两点之间的距离为8，理由见解析【解析】【分析】（1）根据绝对值和偶次幂具有非负性可得a+24=0，b+10=0，c-10=0，解可得a 、b 、c 的值；（2）分两种情况讨论可求点P 的对应的数；（3）分类讨论：当P点在Q点的右侧，且Q点还没追上P点时；当P在Q点左侧时，且Q点追上P点后；当Q点到达C点后，当P点在Q点左侧时；当Q点到达C点后，当P 点在Q点右侧时，根据两点间的距离是8，可得方程，根据解方程，可得答案．【详解】（1）∵|a+24|+|b+10|+（c-10）2=0，∴a+24=0，b+10=0，c-10=0，解得：a=-24，b=-10，c=10；（2）-10-（-24）=14，①点P在AB之间，AP=14×221=283，-24+283=-443，点P的对应的数是-443；②点P在AB的延长线上，AP=14×2=28，-24+28=4，点P的对应的数是4；（3）∵AB=14，BC=20，AC=34，∴t P=20÷1=20（s），即点P运动时间0≤t≤20，点Q到点C的时间t1=34÷2=17（s），点C回到终点A时间t2=68÷2=34（s），当P点在Q点的右侧，且Q点还没追上P点时，2t+8=14+t，解得t=6；当P在Q点左侧时，且Q点追上P点后，2t-8=14+t，解得t=22＞17（舍去）；当Q点到达C点后，当P点在Q点左侧时，14+t+8+2t-34=34，t=463＜17（舍去）；当Q点到达C点后，当P点在Q点右侧时，14+t-8+2t-34=34，解得t=623＞20（舍去），当点P到达终点C时，点Q到达点D，点Q继续行驶（t-20）s后与点P的距离为8，此时2（t-20）+（2×20-34）=8，解得t=21；综上所述：当Q点开始运动后第6、21秒时，P、Q两点之间的距离为8．【点睛】此题主要考查了一元一次方程的应用，关键是正确理解题意，掌握非负数的性质，再结合数轴解决问题．8．（1）详见解析；（2）35；（3）﹣5、15、1123、﹣767．【解析】【分析】（1）根据尺规作图的方法按要求做出即可；（2）根据中点的定义及线段长度的计算求出；（3）认真分析甲、乙物体运行的轨迹来判断它们相遇的可能性，分情况建立一元一次方程来计算相遇的时间，然后计算出位置．【详解】解：（1）如图所示；（2）根据（1）所作图的条件，如果以点A为原点，若点B对应的数恰好为10，则有点C对应的数为30，点D对应的数为﹣30，MN＝|20﹣（﹣15）|＝35（3）设乙从M点第一次回到点N时所用时间为t，则t＝223522MN⨯=＝35（秒）那么甲在总的时间t内所运动的长度为s＝5t＝5×35＝175可见，在乙运动的时间内，甲在C，D之间运动的情况为175÷60＝2……55，也就是说甲在C，D之间运动一个来回还多出55长度单位．①设甲乙第一次相遇时的时间为t1，有5t1＝2t1+15，t1＝5（秒）而﹣30+5×5＝﹣5，﹣15+2×5＝﹣5这时甲和乙所对应的有理数为﹣5．②设甲乙第二次相遇时的时间经过的时间t2，有5t2+2t2＝25+30+5+10，t2＝10（秒）此时甲的位置：﹣15×5+60+30＝15，乙的位置15×2﹣15＝15这时甲和乙所对应的有理数为15．③设甲乙第三次相遇时的时间经过的时间t3，有5t3﹣2t3＝20，t3＝203（秒）此时甲的位置：30﹣（5×203﹣15）＝1123，乙的位置：20﹣（2×203﹣5）＝1123这时甲和乙所对应的有理数为112 3④从时间和甲运行的轨迹来看，他们可能第四次相遇．设第四次相遇时经过的时间为t4，有5t4﹣1123﹣30﹣15+2t4＝1123，t4＝91621（秒）此时甲的位置：5×91621﹣45﹣1123＝﹣767，乙的位置：1123﹣2×91621＝﹣767这时甲和乙所对应的有理数为﹣767．四次相遇所用时间为：5+10+203+91621＝3137（秒），剩余运行时间为：35﹣3137＝347（秒）当时间为35秒时，乙回到N 点停止，甲在剩余的时间运行距离为5×347＝5257⨯＝1767．位置在﹣767+1767＝10，无法再和乙相遇，故所有相遇点对应的有理数为﹣5、15、1123、﹣767．【点睛】本题考查数轴作图及线段长度计算的基础知识，重要的是两个点在数轴上做复杂运动时的运动轨迹和相遇的位置，具有比较大的难度．正确分析出可能相遇的情况并建立一元一次方程是解题的关键．9．（1）20,6；（2）43t -+，162t -；（3）t 2=或6时；（4）不变，10，理由见解析.【解析】【分析】（1）由数轴上两点距离先求得A ，B 两点间的距离，由中点公式可求线段AB 的中点表示的数；（2）点P 从点A 出发，以每秒3个单位长度的速度沿数轴向右匀速运动同时点Q 从点B 出发，向右为正，所以-4+3t ； Q 从点B 出发，以每秒2个单位长度的速度向左匀速运动，向左为负，16-2t.（3）由题意,1PQ AB 2=表示出线段长度，可列方程求t 的值；（4）由线段中点的性质可求MN 的值不变．【详解】解：()1点A 表示的数为4-，点B 表示的数为16，A ∴，B 两点间的距离等于41620--=，线段AB 的中点表示的数为41662-+= 故答案为20，6 ()2点P 从点A 出发，以每秒3个单位长度的速度沿数轴向右匀速运动，∴点P 表示的数为：43t -+，点Q 从点B 出发，以每秒2个单位长度的速度向左匀速运动，∴点Q 表示的数为：162t -，故答案为43t -+，162t -()13PQ AB 2=()43t 162t 10∴-+--=t 2∴=或6答：t 2=或6时，1PQ AB 2= ()4线段MN 的长度不会变化，点M 为PA 的中点，点N 为PB 的中点，1PM PA 2∴=，1PN PB 2= ()1MN PM PN PA PB 2∴=-=- 1MN AB 102∴== 【点睛】本题考查了一元一次方程的应用，数轴上两点之间的距离，找到正确的等量关系列出方程是本题的关键．10．（1）30，120（2）①30﹣3t②5或20③﹣15或﹣4834【解析】【分析】（1）根据A 点对应的数为60，B 点在A 点的左侧，AB ＝30求出B 点对应的数；根据AC ＝4AB 求出AC 的距离；（2）①当P 点在AB 之间运动时，根据路程＝速度×时间求出AP ＝3t ，根据BP ＝AB ﹣AP 求解；②分P 点是A 、B 两个点的中点；B 点是A 、P 两个点的中点两种情况讨论即可；③根据P 、Q 两点的运动速度与方向可知Q 点在往返过程中与P 点相遇2次．设Q 点在往返过程中经过x 秒与P 点相遇．第一次相遇是点Q 从A 点出发，向C 点运动的途中．根据AQ ﹣BP ＝AB 列出方程；第二次相遇是点Q 到达C 点后返回到A 点的途中．根据CQ+BP ＝BC 列出方程，进而求出P 点在数轴上对应的数．【详解】（1）∵A 点对应的数为60，B 点在A 点的左侧，并且与A 点的距离为30，∴B 点对应的数为60﹣30＝30；∵C 点到A 点距离是B 点到A 点距离的4倍，∴AC＝4AB ＝4×30＝120；（2）①当P 点在AB 之间运动时，∵AP＝3t ，∴BP＝AB ﹣AP ＝30﹣3t ．故答案为30﹣3t ；②当P点是A、B两个点的中点时，AP＝12AB＝15，∴3t＝15，解得t＝5；当B点是A、P两个点的中点时，AP＝2AB＝60，∴3t＝60，解得t＝20．故所求时间t的值为5或20；③相遇2次．设Q点在往返过程中经过x秒与P点相遇．第一次相遇是点Q从A点出发，向C点运动的途中．∵AQ﹣BP＝AB，∴5x﹣3x＝30，解得x＝15，此时P点在数轴上对应的数是：60﹣5×15＝﹣15；第二次相遇是点Q到达C点后返回到A点的途中．∵CQ+BP＝BC，∴5（x﹣24）+3x＝90，解得x＝1054，此时P点在数轴上对应的数是：30﹣3×1054＝﹣4834．综上，相遇时P点在数轴上对应的数为﹣15或﹣4834．【点睛】本题考查了一元一次方程的应用，行程问题相等关系的应用，线段中点的定义，进行分类讨论是解题的关键．11．（1）（4，8）（2）S△OAE＝8﹣t（3）2秒或6秒【解析】【分析】（1）根据M和N的坐标和平移的性质可知：MN∥y轴∥PQ，根据K是PM的中点可得K 的坐标；（2）根据三角形面积公式可得三角形OAE的面积S；（3）存在两种情况：①如图2，当点B在OD上方时②如图3，当点B在OD上方时，过点B作BG⊥x轴于G，过D作DH⊥x轴于H，分别根据三角形OBD的面积等于三角形OAE的面积列方程可得结论．【详解】（1）由题意得：PM＝4，∵K是PM的中点，∴MK＝2，∵点M的坐标为（2，8），点N的坐标为（2，6），∴MN∥y轴，∴K（4，8）；（2）如图1所示，延长DA交y轴于F，则OF⊥AE，F（0，8﹣t），∴OF＝8﹣t，∴S△OAE＝12OF•AE＝12（8﹣t）×2＝8﹣t；（3）存在，有两种情况：，①如图2，当点B在OD上方时，过点B作BG⊥x轴于G，过D作DH⊥x轴于H，则B（2，6﹣t），D（6，0），∴OG＝2，GH＝4，BG＝6﹣t，DH＝8﹣t，OH＝6，S△OBD＝S△OBG+S四边形DBGH+S△ODH，＝12OG•BG+12（BG+DH）•GH﹣12OH•DH，＝12×2（6-t）+12×4（6﹣t+8﹣t）﹣12×6（8﹣t），＝10﹣2t，∵S△OBD＝S△OAE，∴10﹣2t＝8﹣t，t＝2；②如图3，当点B在OD上方时，过点B作BG⊥x轴于G，过D作DH⊥x轴于H，则B （2，6﹣t ），D （6，8﹣t ），∴OG ＝2，GH ＝4，BG ＝6﹣t ，DH ＝8﹣t ，OH ＝6，S △OBD ＝S △ODH ﹣S 四边形DBGH ﹣S △OBG ，＝12OH•DH ﹣12（BG+DH ）•GH ﹣12OG•BG ，＝12×2（8-t ）﹣12×4（6﹣t+8﹣t ）﹣12×2（6﹣t ），＝2t ﹣10，∵S △OBD ＝S △OAE ，∴2t ﹣10＝8﹣t ，t ＝6；综上，t 的值是2秒或6秒．【点睛】本题考查四边形综合题、矩形的性质、三角形的面积、一元一次方程等知识，解题关键是灵活运用所学知识解决问题，学会用分类讨论的思想思考问题．12．（1）16；（2）①t 的值为3或143秒；②存在，P 表示的数为314. 【解析】【分析】（1）由数轴可知，AB=3,则CD=6,所以D 表示的数为16，（2）①当运动时间是t 秒时，在运动过程中，B 点表示的数为3+2t,A 点表示的数为2t, C 点表示的数为10-t ，D 点表示的数为16-t ，分情况讨论两条线段重叠部分是2个单位长度解答即可；②分情况讨论当t=3秒, t=143秒时，满足3BD PA PC -=的点P , 注意P 为线段AB 上的点对x 的值的限制.【详解】（1）16（2）①在运动过程中，B 点表示的数为3+2t,A 点表示的数为2t,C 点表示的数为10-t ，D 点表示的数为16-t.当BC ＝2，点B 在点C 的右边时，由题意得：32-10-2BC t t =+=（），解得：t ＝3，当AD=2，点A 在点D 的左边时，由题意得：16--22AD t t ==，解得：t ＝143．综上，t 的值为3或143秒 ②存在，理由如下:当t=3时，A 点表示的数为6，B 点表示的数为9，C 点表示的数为7，D 点表示的数为13. 则13-94-6|-7|BD PA x PC x ====，，，-3BD PA PC =，()4--6|-7|x x ∴=，解得：314x =或112，又P 点在线段AB 上，则69x ≤≤314x ∴=. 当143t =时，A 点表示的数为283，B 点表示的数为373，C 点表示的数为163，D 点表示的数为343. 则37343816-1-|-|3333BD PA x PC x ====，，， -3BD PA PC =，∴ 28161--|-|33x x ⎛⎫= ⎪⎝⎭，解得：7912x =或176，又283733x ≤≤， x ∴无解综上，P 表示的数为314. 【点睛】本题考查了一元一次方程的应用以及数轴，解题的关键是：(1)由路程=速度×时间结合运动方向找出运动t 秒时点A 、B 、C 、D 所表示的数,(2)根据3BD PA PC -=列出关于t 的含绝对值符号的一元一次方程．13．(1) 2x =-和4x = ;(2) 35(4)11(43)35(3)x x x x x x --<-⎧⎪+-≤<⎨⎪+≥⎩【解析】【分析】（1）令x +2=0和x -4=0,求出x 的值即可得出|x +2|和|x -4|的零点值,（2）零点值x =3和x =-4可将全体实数分成不重复且不遗漏的如下3种情况:x ＜-4、-4≤x ＜3和x ≥3．分该三种情况找出324x x -++的值即可．【详解】解：（1）2x =-和4x =,（2）由30x -=得3,x =由40x +=得4x =-,①当4x <-时,原式()()32435x x x =---+=--,②当4-≤3x <时,原式()()32411x x x =--++=+,③当x ≥3时,原式()()32435x x x =-++=+,综上所述：原式()35(4)11(43)353x x x x x x ⎧--<-⎪=+-≤<⎨⎪+≥⎩, 【点睛】本题主要考查了绝对值化简方法,解决本题的关键是要熟练掌握绝对值化简方法.14．（1）45°；（2）45°；（3）45°或135°.【解析】【分析】（1）由∠BOC 的度数求出∠AOC 的度数，利用角平分线定义求出∠COD 与∠COE 的度数，相加即可求出∠DOE 的度数；（2）∠DOE 度数不变，理由为：利用角平分线定义得到∠COD 为∠AOC 的一半，∠COE 为∠COB 的一半，而∠DOE=∠COD+∠COE ，即可求出∠DOE 度数为45度；（3）分两种情况考虑，同理如图3，则∠DOE 为45°；如图4，则∠DOE 为135°．【详解】（1）如图，∠AOC=90°﹣∠BOC=20°，∵OD 、OE 分别平分∠AOC 和∠BOC ，∴∠COD=∠AOC=10°，∠COE=12∠BOC=35°，∴∠DOE=∠COD+∠COE=45°；（2）∠DOE的大小不变，理由是：∠DOE=∠COD+∠COE=12∠AOC+12∠COB=12（∠AOC+∠COB）=12∠AOB=45°；（3）∠DOE的大小发生变化情况为：如图③，则∠DOE为45°；如图④，则∠DOE为135°，分两种情况：如图3所示，∵OD、OE分别平分∠AOC和∠BOC，∴∠COD=12∠AOC，∠COE=12∠BOC，∴∠DOE=∠COD﹣∠COE=12（∠AOC﹣∠BOC）=45°；如图4所示，∵OD、OE分别平分∠AOC和∠BOC，∴∠COD=12∠AOC，∠COE=12∠BOC，∴∠DOE=∠COD+∠COE=12（∠AOC+∠BOC）=12×270°=135°．【点睛】此题主要考查了角平分线的性质以及角的有关计算，正确作图，熟记角的特点与角平分线的定义是解决此题的关键．15．（1）60°；（2）射线OP是∠AOC的平分线；（3）30°．【解析】整体分析：(1)根据角平分线的定义与角的和差关系计算；(2)计算出∠AOP的度数，再根据角平分线的定义判断；(3)根据∠AOC，∠AON，∠NOC，∠MON，∠AOM的和差关系即可得到∠NOC 与∠AOM之间的数量关系．解：(1)如图②，∠AOC=120°，∴∠BOC=180°﹣120°=60°，又∵OM平分∠BOC，∴∠BOM=30°，又∵∠NOM=90°，∴∠BOM=90°﹣30°=60°，故答案为60°；(2)如图③，∵∠AOP=∠BOM=60°，∠AOC=120°，∴∠AOP=12∠AOC，∴射线OP是∠AOC的平分线；(3)如图④，∵∠AOC=120°，∴∠AON=120°﹣∠NOC，∵∠MON=90°，∴∠AON=90°﹣∠AOM，∴120°﹣∠NOC=90°﹣∠AOM，即∠NOC﹣∠AOM=30°．。

初一数学压轴题及答案

数学初一上学期数学 压轴题 期末复习试卷带答案

徐州市人教版(七年级)初一上册数学 压轴题 期末复习测试题及答案

人教版(七年级)初一上册数学 压轴题 期末复习测试题及答案

(完整版)初一数学上册压轴题测试卷及答案

人教版(七年级)初一上册数学 压轴题 期末复习模拟测试题及答案

数学人教版(七年级)初一下册数学期末复习压轴题 解答题测试题及答案

郑州市人教版(七年级)初一上册数学 压轴题 期末复习测试题及答案

初一上学期数学压轴题期末复习试卷带答案

初一数学考试压轴题

初一下册数学压轴题精练答案

七年级上册上册数学压轴题测试卷附答案

初一下册数学压轴题精练答案

初一数学期末复习三角函数计算压轴题难题(附答案详解)

初一上学期数学 压轴题 期末复习试卷带答案

数学初一上学期数学压轴题期末复习试卷带答案

徐州市人教版(七年级)初一上册数学压轴题期末复习测试题及答案

人教版(七年级)初一上册数学压轴题期末复习测试题及答案

人教版(七年级)初一上册数学压轴题期末复习模拟测试题及答案

数学人教版(七年级)初一下册数学期末复习压轴题解答题测试题及答案

郑州市人教版(七年级)初一上册数学压轴题期末复习测试题及答案

初一上学期数学压轴题期末复习试卷带答案