【水力学习题评讲】第二章
《水力学》第二章答案

第二章:水静力学 一:思考题2-1.静水压强有两种表示方法,即:相对压强和绝对压强2-2.特性(1)静水压强的方向与受压面垂直并指向手压面;(2)任意点的静水压强的大小和受压面的方位无关,或者说作用于同一点上各方向的静水压强都相等. 规律:由单位质量力所决定,作为连续介质的平衡液体内,任意点的静水压强仅是空间坐标的连续函数,而与受压面的方向无关,所以p=(x,y,z)2-3答:水头是压强的几何意义表示方法,它表示h 高的水头具有大小为ρgh 的压强。
绝对压强预想的压强是按不同的起点计算的压强,绝对压强是以0为起点,而相对压强是以当地大气压为基准测定的,所以两者相差当地大气压Pa.绝对压强小于当地大气压时就有负压,即真空。
某点负压大小等于该点的相对压强。
Pv=p'-pa2-4.在静水压强的基本方程式中C g p z =+ρ中,z 表示某点在基准面以上的高度,称为位置水头,g p ρ表示在该点接一根测压管,液体沿测压管上升的高度,称为测压管高度或压强水头,g p z ρ+称为测压管水头,即为某点的压强水头高出基准面的高度。
关系是:(测压管水头)=(位置水头)+(压强水头)。
2-5.等压面是压强相等的点连成的面。
等压面是水平面的充要条件是液体处于惯性坐标系,即相对静止或匀速直线运动的状态。
2-6。
图中A-A 是等压面,C-C,B-B 都不是等压面,因为虽然位置高都相同,但是液体密度不同,所以压强水头就不相等,则压强不相等。
2-7.两容器内各点压强增值相等,因为水有传递压强的作用,不会因位置的不同压强的传递有所改变。
当施加外力时,液面压强增大了Ap∆,水面以下同一高度的各点压强都增加Ap∆。
2-8.(1)各测压管中水面高度都相等。
(2)标注如下,位置水头z,压强水头h,测压管水头p.图2-82-9.选择A2-10.(1)图a 和图b 静水压力不相等。
因为水作用面的面积不相等,而且作用面的形心点压强大小不同。
水力学第二章课后习题答案解析

WORD 格式.分享精品.资料2.12密闭容器,测压管液面高于容器内液面h =1.8m =1.8m,液体的密度为,液体的密度为850kg/m 3,求液面压强。
p 0解:08509.807 1.8a a p p gh p r =+=+´´相对压强为:15.00kPa kPa。
绝对压强为:116.33kPa kPa。
答:液面相对压强为15.00kPa kPa,绝对压强为,绝对压强为116.33kPa kPa。
2.13密闭容器,压力表的示值为4900N/m 2,压力表中心比A 点高0.4m 0.4m,,A 点在水下1.5m 1.5m,,,求水面压强。
p 0A1.5m0.4m解:0 1.1a p p p gr =+-4900 1.110009.807a p =+-´´5.888a p =-(kPa kPa)) 相对压强为: 5.888-kPa kPa。
绝对压强为:95.437kPa kPa。
答:水面相对压强为 5.888-kPa kPa,绝对压强为,绝对压强为95.437kPa kPa。
1m3m解:(1)总压力:433353.052ZP A p g r =×=´´=(kN kN))(2)支反力:()111333R W W W W g r ==+=+´´+´´总水箱箱980728274.596W =+´=箱kN W +箱不同之原因:总压力位底面水压力与面积的乘积,为压力体g r ´。
而支座反力与水体重量及箱体重力相平衡,而水体重量为水的实际体积g r ´。
答:水箱底面上总压力是353.052kN kN,,4个支座的支座反力是274.596kN kN。
2.14 盛满水的容器,顶口装有活塞A ,直径d =0.4m =0.4m,,容器底的直径D =1.0m =1.0m,,高h =1.8m =1.8m,,如活塞上加力2520N 2520N(包括活塞自重)(包括活塞自重),求容器底的压强和总压力。
《水力学》第二章答案

第二章:水静力学 一:思考题2-1.静水压强有两种表示方法,即:相对压强和绝对压强2-2.特性(1)静水压强的方向与受压面垂直并指向手压面;(2)任意点的静水压强的大小和受压面的方位无关,或者说作用于同一点上各方向的静水压强都相等. 规律:由单位质量力所决定,作为连续介质的平衡液体内,任意点的静水压强仅是空间坐标的连续函数,而与受压面的方向无关,所以p=(x,y,z)2-3答:水头是压强的几何意义表示方法,它表示h 高的水头具有大小为ρgh 的压强。
绝对压强预想的压强是按不同的起点计算的压强,绝对压强是以0为起点,而相对压强是以当地大气压为基准测定的,所以两者相差当地大气压Pa.绝对压强小于当地大气压时就有负压,即真空。
某点负压大小等于该点的相对压强。
Pv=p'-pa2-4.在静水压强的基本方程式中C g p z =+ρ中,z 表示某点在基准面以上的高度,称为位置水头,g p ρ表示在该点接一根测压管,液体沿测压管上升的高度,称为测压管高度或压强水头,g p z ρ+称为测压管水头,即为某点的压强水头高出基准面的高度。
关系是:(测压管水头)=(位置水头)+(压强水头)。
2-5.等压面是压强相等的点连成的面。
等压面是水平面的充要条件是液体处于惯性坐标系,即相对静止或匀速直线运动的状态。
2-6。
图中A-A 是等压面,C-C,B-B 都不是等压面,因为虽然位置高都相同,但是液体密度不同,所以压强水头就不相等,则压强不相等。
2-7.两容器内各点压强增值相等,因为水有传递压强的作用,不会因位置的不同压强的传递有所改变。
当施加外力时,液面压强增大了Ap∆,水面以下同一高度的各点压强都增加Ap∆。
2-8.(1)各测压管中水面高度都相等。
(2)标注如下,位置水头z,压强水头h,测压管水头p.图2-82-9.选择A2-10.(1)图a 和图b 静水压力不相等。
因为水作用面的面积不相等,而且作用面的形心点压强大小不同。
【重庆大学出版社·肖明葵】版【水力学习题评讲】第二章

E F G 20.0 15.0 11.6 8.0 6.0 hp ρ p 2.10 4.0 ρ 1 ρ2 ρ3
ρ1 g ( H E − 11.6) = 40524 pa, H E = 12.5m
F: −17200 + ρ1 g (15.0 − 11.6) + ρ2 g (11.6 − 8.0) = ρ2 g ( H F − 8.0) 测管 测管F
A h3 4 B N N h2 2 D h1 1 D C C 3 ρp 2.12
pM = 0.3 ×1000 × 9.8
= 29.4(kN / m2 )
作等压面DD、NN、CC
pM + ρ水 g ( h3 + h1 ) = pB + ρ p gh2 − ρ0 gh1 + ρ p gh1
pB = pM + ρ水 g (h3 + h1 ) − ρp gh1 + ρ0 gh1 − ρp gh2 = −28.812(kN / m2 )
▽1=100cm, 图所示封闭水箱两测压管的液面高程为▽ 2.2 如题2.2图所示封闭水箱两测压管的液面高程为 ▽2=20cm,箱内液面高程为 1 ▽3为多少? ▽4=60cm。问 。问▽ ▽4 标高等压面有: 解:在 解:在▽
4 ρ
p 0 2 3 ρp
P 1−∇4) (1) 0 = ρ g(∇
在▽3标高等压面有:
d=1m,水平倾角 α = 60,闸门中心点位于上游水面以下 4m处,闸门重G=980N,求闸门分别当:
(1)下游无水;( 2)下游水面与门顶同高时,在E处将 )下游无水;(2 闸门吊起所需的拉力 ? 分别为多大 分别为多大? FT
吴持恭版水力学-第二章-思考题答案-精选.pdf

变流和急变流。 渐变流具有的重要性质:过水断面上的压强近似服从 图( a)表示一水闸正在提升闸门放水,图( b)表示一水管正在打开阀门 放水,若它们的上游水位均保持不变,问此时的水流是否符合 A 1V 1= AaVa 的连续方程?为什么?
否,因水流均属非恒定流
图 2.2
组成的,它们间可相互转化,但不能分割。水流总是从总机械能大的
1-1
断面流向总机械能小的 2-2 断面,其差值用来克服两断面间的总水头损失。
2.5 什么叫总水头线和测压管水头线?水力坡度和测压管坡度?均匀流的测压
管水头线和总水头线的关系怎样?
p
v2
各断面总能量值 H z
连接起来的曲线或直线称总水头线,
第二章
2.1 “恒定流与非恒定流” ,“均匀流与非均匀流” ,“渐变流与急变流”等三个
概念是如何定义的?它们之间有么联系?渐变流具有什么重要的性质?
恒定流:如果在流场中任何空间点上所有的运动要素都不随时间而改变, 这
种水流称为恒定流。
非恒定流: 如果在流场中有任何一个运动要素是随时间而改变的, 这种水流 称为非恒定流。
2
( 2)如果由动量方程式求得的力为负值说明什么问题。 ( 1)包括动水压力、粘滞力、固体边壁对水流的反作用力、重力及惯性力。 ( 2)说明假设未知力的方向与实际方向相反。
3
均匀流:当水流的流线为相互平行的直线时,该水流称为均匀流。
非均匀流:当水流的流线不是相互平行的直线,该水流称为非均匀流。
渐变流:当水流的流线虽然不是相互平行直线, 但几乎近于平行直线时称为
渐变流。
急变流:当水流的流线之间的夹角很大或流线的曲率很小, 这种水流称为急
变流。
联系:恒定流和非恒定流均可以是均匀流或非均匀流, 非均匀流中又包括渐
水力学第二章(3)

主要内容: §2-6 作用在曲面上的静水总压力
§2-7 浮体的平衡与稳定 §2-8 在重力与惯性力同时作用下 液体的相对平衡
2.6
作用在曲面上的静水总压力
在水利工程上常遇到受压面为曲面的情况,如拱坝坝面、
弧形闸墩、弧形闸门等。
A′ B′
作用在曲面上静水总 压力分解为水平分力
θ
和铅直分力分别计算,
δ
T
2 T Px p 2 r
p T r
图 2.6.4
5 3
A
r
1 . 5 10 4 10 5 10
2
1 . 2 10 ( kN/m
4
2
)
2.7
浮体的平衡与稳定
2.7.1 浮力及物体的沉浮
y
z
浸没于液体中的物体受到的x轴方向静水总压力应 为零
Px 左 = Px 右
(a)
(b)
(c)
图 2.7.2
不稳定平衡:重心C在浮心D之上,重力与浮力组 成使物体继续倾斜的力矩,这种状态下的平衡为 不稳定平衡。
随遇平衡:当重心C与浮心D重合时,潜体在液体 中的方位是任意的,称为随遇平衡。
(a)
(b)
(c)
注意:要使潜体处于稳定平衡状态,必须使其重 心位于浮心之下。
图 2.7.2
Z
图 2.6.1
静水总压力的铅直分力
作用在曲面AB上的静水总压力的铅直分力Pz
Pz
dP sin
A
hdA sin
AZ
h ( dA ) Z
A′ B′
h(dA)z是微小曲面和它在自
由水面延长面上的投影之间
(完整)水力学第二章思考题答案

(完整)水力学第二章思考题答案2.1。
恒定流:如果在流场中任何空间点上所有的运动要素都不随时间而改变.非恒定流:如果在流场中任何空间点上有任何一个运动要素是随时间而变化。
均匀流:水流的流线为相互平行的直线.非均匀流:水流的流线不是相互平行的直线。
渐变流:水流的流线虽然不是相互平行的直线,但几乎近于平行的直线.急变流:水流的流线之间夹角很大或者流线的曲率半径很小.按运动要素是否彼此平行的直线分为均匀流和非均匀流,而非均匀流按流线的不平行和弯曲程度又分为渐变流和急变流。
渐变流重要性质为:过水断面上近似服从静压分布:Z+P/y=C2.2。
此时的A₁υ₁=A₂υ₂符合连续方程.两个断面无支流,且上游水位恒定,则下游通过的流量一定,则流量保持平衡,满足该公式。
2。
3能量方程:Ζ₁+Ρ₁/ρg+α₁(μ₁)²/2g=Ζ₂+Ρ₂/ρg+α₂(μ₂)²/2g+hw’。
Ζ₁:位置水头;Ρ₁/ρg:压强水头;(μ₁)²/2g:流速水头;Ζ₂:单位位能;Ρ₂/ρg:单位压能;(μ₂)²/2g:单位动能;hw’:水头损失。
能量意义:在总流中任意选取两个过水断面,该两断面上液流所具有的总水头若为H₁和H₂,则:H₁=H₂+hw。
2.4这些说法都不对.对于理想液体来说,在无支流进去的情况下,其各断面的流量总和是相等的,根据能量方程:Ζ₁+Ρ₁/ρg+α₁(μ₁)²/2g=Ζ₂+Ρ₂/ρg+α₂(μ₂)²/2g+hw’,及连续方程:A ₁υ₁=A₂υ₂。
可以看出:只要其流量不改变,能量的总和就不会变。
则水是由流速大地方向流速小的地方流这种说法就是错误的。
总流的动量方程:ΣF=ρQ(Β₂υ₂-Β₁υ₁),也说明了这一点。
2.5总水头线:把各断面H=Ζ+Ρ/ρg+α(μ)²/2g描出的点子连接起来得到的线就是总水头线;测压管水头线:把各断面的(Ζ+Ρ/ρg)值的点子连接起来得到的线就是测压管水头线。
水力学(闻德荪)习题答案第二章

选择题(单选题)2.1 静止流体中存在:(a )(a )压应力;(b )压应力和拉应力;(c )压应力和剪应力;(d )压应力、拉应力和剪应力。
2.2 相对压强的起算基准是:(c )(a )绝对真空;(b )1个标准大气压;(c )当地大气压;(d )液面压强。
2.3 金属压力表的读值是:(b )(a )绝对压强;(b )相对压强;(c )绝对压强加当地大气压;(d )相对压强加当地大气压。
2.4 某点的真空度为65000Pa ,当地大气压为0.1MPa,该点的绝对压强为:(d )(a )65000Pa ;(b )55000Pa ;(c )35000Pa ;(d )165000Pa 。
2.5 绝对压强abs p 与相对压强p 、真空度V p 、当地大气压a p 之间的关系是:(c )(a )abs p =p +V p ;(b )p =abs p +a p ;(c )V p =a p -abs p ;(d )p =V p +V p 。
2.6 在密闭容器上装有U 形水银测压计,其中1、2、3点位于同一水平面上,其压强关系为:(c )(a )1p >2p >3p ;(b )1p =2p =3p ;(c )1p <2p <3p ;(d )2p <1p <3p 。
2.7 用U 形水银压差计测量水管内A 、B 两点的压强差,水银面高差h p =10cm, A p -B p 为:(b )(a)13.33kPa;(b)12.35kPa;(c)9.8kPa;(d)6.4kPa。
2.8露天水池,水深5 m处的相对压强为:(b)(a)5kPa;(b)49kPa;(c)147kPa;(d)205kPa。
2.9垂直放置的矩形平板挡水,水深3m,静水总压力P的作用点到水面的距离Dy为:(c)(a)1.25m;(b)1.5m;(c)2m;(d)2.5m。
2.10圆形水桶,顶部及底部用环箍紧,桶内盛满液体,顶箍与底箍所受张力之比为:(a)(a)1/2;(b)1.0;(c)2;(d)3。
水力学第二章课后习题答案
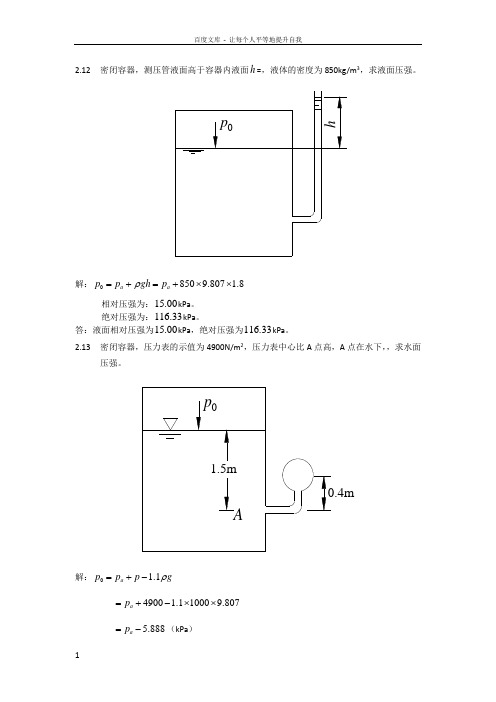
2.12 密闭容器,测压管液面高于容器内液面h =,液体的密度为850kg/m 3,求液面压强。
解:08509.807 1.8a a p p gh p ρ=+=+⨯⨯相对压强为:15.00kPa 。
绝对压强为:116.33kPa 。
答:液面相对压强为15.00kPa ,绝对压强为116.33kPa 。
2.13 密闭容器,压力表的示值为4900N/m 2,压力表中心比A 点高,A 点在水下,,求水面压强。
解:0 1.1a p p p g ρ=+-4900 1.110009.807a p =+-⨯⨯ 5.888a p =-(kPa )相对压强为: 5.888-kPa 。
绝对压强为:95.437kPa 。
答:水面相对压强为 5.888-kPa ,绝对压强为95.437kPa 。
解:(1)总压力:433353.052Z P A p g ρ=⋅=⨯⨯=(kN ) (2)支反力:()111333R W W W W g ρ==+=+⨯⨯+⨯⨯总水箱箱980728274.596W =+⨯=箱kN W +箱不同之原因:总压力位底面水压力与面积的乘积,为压力体g ρ⨯。
而支座反力与水体重量及箱体重力相平衡,而水体重量为水的实际体积g ρ⨯。
答:水箱底面上总压力是353.052kN ,4个支座的支座反力是274.596kN 。
2.14 盛满水的容器,顶口装有活塞A ,直径d =,容器底的直径D =,高h =,如活塞上加力2520N (包括活塞自重),求容器底的压强和总压力。
解:(1)容器底的压强:225209807 1.837.7064D A p p gh dρπ=+=+⨯=(kPa )(相对压强) (2)容器底的总压力:223137.7061029.61444D D D P Ap D p ππ==⋅=⨯⨯⨯=(kN )答:容器底的压强为37.706kPa ,总压力为29.614kN 。
用多管水银测压计测压,图中标高的单位为m ,试求水面的压强0p 。
水力学 第二章课后题答案

r • H • D 2[ ]
rHD 2
9.8 14000 200 2 14000000
0.98cm
2.1 盛有同种介质(密度A =B
=1200kg/m 3 )的两容器,其中心
点A、B位于同一高程,今用U形
差压计测定A、B点之压差(差
压计内盛油,密度 0=
800kg/m 3),A点还装有一水银
测压计。其它有关数据如图题1-
2所示(s=5cm,
h 1
=20cm,h=4cm)
问:
1. A、B两点之压差为多少?
解:当下游无水时: 水平分力
Px rhC 1Ax1 9.8 13 26 1 3312.4KN(水平向右)
垂直分力
Pz rV1 9.8 梯形abcd 1 9.8 0.5 (26 18) 4 1 862.04KN(竖直向下)
当下游有水时 水平分力
Px rhC 1Ax1 rhc2Ax 2 3312.4 9.8 3 6 1 3316KN(水平向右)
(1)相同,不相等 (2)减小,上升
2.5 压力体的概念是什么?如何确定压力体的范围及作用力 方向?
压力体是计算总压力垂直分力 FPZ 的概念,只是作为计算
曲面上垂直压力的一个数值当量,不是由实际水体构成。
由受压曲面本身、通过曲面的四个边缘向自由液面作的
铅垂面、自由液面或其延伸面围成的体积就是压力体。压力 体位于受压面同一侧的叫做实压力体,液体压力向下;压力 体位于受压面异侧的叫做虚压力体,液体压力向上。
2
98
1 ctg 60
2
2
P
1 2
2 sin 60
则拉力 T 139.5KN
2.8 有—直立的矩形自动 翻板闸门,门高H为5m, 如果要求水面超过门顶h 为lm时,翻板闸门即可
水力学第二章课后答案

12611 ^<4作业本2.122.13(注:书中求绝对压强丿用多管水银测压计测压,图中榇嵩的单住为m,试求水面的庄强几。
鮮:P()= “4—(3.0—1.4)Qg=几+265.00 (kPa丿答:水面的压强几= 265.00kPa。
2・12形平板闸门AB ,-側档水,己知长/=2m,宽/? = 1 m,形心点水深J?c=2m,倾角a =45。
,闸门上缘A处设有转轴,忽略闸门自重及门轴摩擦力,试求开启闸门所需拉力T。
解:fl)解析法。
P = p c A = h c pg-Z?/ = 1000x9.807x2xlx2 = 39.228 (kN 丿2-13矩形闸门嵩〃=3m,宽b =2m,上游水深h} =6m,下游水深仏=4.5m,试求:f 1J作用淮.闸门上的费水总、压力;(2)压力中心的住置。
鮮:fl)图解法。
压强分布如图所示:T P =[(人一方)一(站一方)]Qg= 14.71 (kPa)P = /^./?./? = 14.71x3x2 = 88.263 (kN)合力作用住置:亦闸门的几何中心,即距地面(1.5m.—)处。
2(2)鮮析出。
A = pA = Qg(九一 1.5)•肋= (6-1.5)x9807x3x2 = 264.789(kN丿=-L x (20.25 + 0.75) = 4.667 (m)4* • 5W = P2A = Qg仇一1.5)•肪= 3x9.807x3x2 = 176.526 (kN丿%2 = yci + = j-^ci+^ = |(32+0.75) = 3.25 (mJ合力:P = P}-P2 =88.263 (kN丿合力作用住置(对闸门与渠底接融点取矩丿:=1.499 (mJ答:(\)作用柱闸门上的静水总压力88.263 kN;(2) 压力中心的住置往闸门的几何中心,即距地面(1.5m,-)处。
22・14矩形平核闸门一側宿水,门寓/? = lm,宽b=0.8m,要求扌当水深曾超过2m时,闸门即可自动开启,试求转轴应设的住置y °鮮:当扌当水深达到片时,水压力作用住置应作用亦转轴上,当水深大于%时,水压力作用住置应作用于转轴上,使闸门开启。
【最新试题库含答案】水力学第二章课后答案

水力学第二章课后答案篇一:水力学第二章答案(吕宏兴__裴国霞等)2-1 解:(1)pA+γ水·ΔH=γH·Δh;所以pA=γH·Δh-γ水·ΔH=38.02kPa(γH=13.6γ水)(2)测压管长度:pA=γ水·h 所以h= pA/γ水=38.02×103/9.8×103=3.88m2-3 解:PA-γh=pB-γ(h1+h2+h)+γHh1所以,pA-pB=γHh1-γ(h1+h2)=13.6×9.8×0.53-9.8×(0.53+1.2) =53.68kPa2-6解:pA=γH(h1+h2)-γ(h1+h2)=13.6××9.8××0.53-9.8×(0.53+1.2)=53.68kpa2-7 解:(1)左支:绝对:pc =p0 +γh0=86.5+9.8×2=106.1kPa(2)右支:pc =pa+γ水h;h=(pc -pa)/γ水=(106.1-9.8)/9.8=0.827m2-8 解:pA=0.6pa=0.6×98=58.8kpa(1)左支:pA=γh1 h1=pA/γ=58.8/9.8=6m(2)右支:pA+γh=γHh2 h2=(pA+γh)/γH=0.456m2-10解:设管嘴内的绝对压强为p ,则p +γh= paPv=pa- p =γh=9.8×0.6=5.886kpa2-12解:(1)设容器底部面积为S,相对压强为P,对容器底部进行受力分析:由牛顿第二定律:ΣF=m·a;-(P+G)=-m·a 所以得出p·s+γ·s·h=ρ·s·h·ap=ρ·h·a -γh=γh/g·a-γh=γh(a/g-1)篇二:《水力学》第二章答案第二章:水静力学一:思考题2-1.静水压强有两种表示方法,即:相对压强和绝对压强2-2.特性(1)静水压强的方向与受压面垂直并指向手压面;(2)任意点的静水压强的大小和受压面的方位无关,或者说作用于同一点上各方向的静水压强都相等. 规律:由单位质量力所决定,作为连续介质的平衡液体内,任意点的静水压强仅是空间坐标的连续函数,而与受压面的方向无关,所以p=(x,y,z)2-3答:水头是压强的几何意义表示方法,它表示h高的水头具有大小为?gh的压强。
水力学第二章课后习题答案

2.12 密闭容器,测压管液面高于容器内液面h =1.8m ,液体的密度为850kg/m 3,求液面压强。
解:08509.807 1.8a a p p gh p ρ=+=+⨯⨯相对压强为:15.00kPa 。
绝对压强为:116.33kPa 。
答:液面相对压强为15.00kPa ,绝对压强为116.33kPa 。
2.13 密闭容器,压力表的示值为4900N/m 2,压力表中心比A 点高0.4m ,A 点在水下1.5m ,,求水面压强。
解:0 1.1a p p p g ρ=+-5.888a p =-(kPa )相对压强为: 5.888-kPa 。
绝对压强为:95.437kPa 。
答:水面相对压强为 5.888-kPa ,绝对压强为95.437kPa 。
解:(1)总压力:433353.052Z P A p g ρ=⋅=⨯⨯=(kN ) (2)支反力:()111333R W W W W g ρ==+=+⨯⨯+⨯⨯总水箱箱980728274.596W =+⨯=箱kN W +箱不同之原因:总压力位底面水压力与面积的乘积,为压力体g ρ⨯。
而支座反力与水体重量及箱体重力相平衡,而水体重量为水的实际体积g ρ⨯。
答:水箱底面上总压力是353.052kN ,4个支座的支座反力是274.596kN 。
2.14 盛满水的容器,顶口装有活塞A ,直径d =0.4m ,容器底的直径D =1.0m ,高h =1.8m ,如活塞上加力2520N (包括活塞自重),求容器底的压强和总压力。
解:(1)容器底的压强:225209807 1.837.7064D A p p gh dρπ=+=+⨯=(kPa )(相对压强) (2)容器底的总压力:223137.7061029.61444D D D P Ap D p ππ==⋅=⨯⨯⨯=(kN )答:容器底的压强为37.706kPa ,总压力为29.614kN 。
2.6用多管水银测压计测压,图中标高的单位为m ,试求水面的压强0p 。
水力学第二章课后答案

1 2 6 11 答案在作业本2.12(注:书中求绝对压强)用多管水银测压计测压,图中标高的单位为m,试求水面的压强 p0。
p0 3.0水2.52.3水1.4 1.2汞解: p0 p4 3.0 1.4gp5 2.5 1.4Hg g3.0 1.4gp a 2.3 1.2Hg g2.5 1.2g 2.5 1.4Hgg3.0 1.4 gp a 2.3 2.51.2 1.4Hg g 2.5 3.0 1.2 1.4gp a 2.3 2.51.2 1.413.6 2.5 3.0 1.2 1.4g gp a265.00 (kPa)答:水面的压强p0265.00kPa。
2-12 形平板闸门AB,一侧挡水,已知长 l =2m,宽 b =1m,形心点水深h c =2m,倾角 = 45 ,闸门上缘A处设有转轴,忽略闸门自重及门轴摩擦力,试求开启闸门所需拉力 T 。
Th c AbBlα解:( 1)解析法。
P p C A h C g bl1000 9.8072 1 239.228 (kN)I C h C bl 32222y D122 2y Csin h C sin 45o122 2.946 y C Abl12sin sin 45o2-13 矩形闸门高 h =3m,宽 b =2m,上游水深 h1 =6m,下游水深 h2 =4.5m,试求:( 1)作用在闸门上的静水总压力;(2)压力中心的位置。
h1h2h解:( 1)图解法。
压强分布如图所示:h1h2p∵p h1h h2h gh1h2g6 4.5 1000 9.80714.71( kPa)P p h b 14.71 3 288.263 (kN)合力作用位置:在闸门的几何中心,即距地面(1.5m, b) 处。
2(2)解析法。
11g 11.5 hb6 1.59807 3 2 264.789 (kN )Pp A hI Cbh 3 1h 2 yD1yC 24.5 122y C2 A 4.5 bh4.5 4.5121 20.250.754.667 (m )4.5P 2 p 2 A g h 2 1.5 hb 3 9.807 32(kN )176.526yD 2yC1I C1y C 21 I C132 0.753.25 (m )y C1 A yC1 A 3合力: PP 1 P 2 88.263 (kN )合力作用位置(对闸门与渠底接触点取矩) :y D P P 1 h 1yD1P 2 h 2yD 2P 1 h 1yD1 P 2 h 2yD 2y DP264.7896 4.667 176.5264.5 3.2588.2631.499 (m )答:( 1)作用在闸门上的静水总压力 88.263kN ;(2)压力中心的位置在闸门的几何中心,即距地面 (1.5m, b) 处。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
得:
H F = 12.2m
测管G: 17200 + ρ1 g (15.0 − 11.6) + ρ 2 g (11.6 − 8.0) + ρ3 g (8.0 − 6.0) = ρ3 gH G −
1
p1 ,板的面积为 1, 板的面积为A
p1 = ( ρ油 g × h1 / 2) A1 = 4.619kN ×
I xc1 = 0.77 m y1 = yc1 + yc1 × A1
水
h2
0 B 60
题2.19图
对于BE板部分:设此部分板的面积为 静水压力为p 对于 板部分:设此部分板的面积为A2,静水压力为 2, 板部分 p2的作用点距A为y2 的作用点距A
A p A H F1 h2 F h1 2 ρp p
B
C
ρ汞 gh2 = pB + ρ水 gh1
pB = ρ汞 gh2 − ρ水 gh1 =113.68kN / m2
D B
题2.22图
p A = pB − ρ水 gH = 84.28kN / m2 (2)箱顶压强
(3)为方便计算,可将压强分布图划分为两部分: 为方便计算,可将压强分布图划分为两部分: 矩形部分压力F 作用点为C, 矩形部分压力 1,作用点为 ,三角形部分提供的压力为 F2,作用点为 , 作用点为D,
代入数据并整理可得
FT = 28.0kN
FT a
B C E D
当下游水面与门顶同高时, 当下游水面与门顶同高时,在E处 处 将闸门吊起所需要的拉力
hD hC
θ
FP
FT ≥ 28.0kN
G d
题2.20图
2.22
高度H= ,宽度b= ,的密闭高压水箱, 高度 =3m,宽度 =1m,的密闭高压水箱,在水箱
h2
水
Hale Waihona Puke ρ gh 水B600
题2.19图
有一圆形平板闸门铰接于B,如图所示。 2.20 有一圆形平板闸门铰接于 ,如图所示。闸门的直径 d=1m,水平倾角 ,
α = 60,闸门中心点位于上游水面以下
4m处,闸门重G=980N,求闸门分别当: 处 闸门重 ,求闸门分别当: (1)下游无水;(2)下游水面与门顶同高时,在E处将 下游无水;(2 下游水面与门顶同高时, ;( 处将 闸门吊起所需的拉力 分别为多大? FT分别为多大?
1 1 h2 2 o 2 = ρ油gh1 ⋅1/ sin 60 + ρ 水 gh2 + ρ 水 gh1 ⋅1 o 2 2 sin 60
A
可以采用合力之矩定理求得, 可以采用合力之矩定理求得,
h1
油
ρ gh 油
2 F ⋅ AD = F1 ⋅ h1 / sin 60o 3 2 + F2 ⋅ h2 + h1 / sin 60o 3 1 + F3 ⋅ h2 + h1 / sin 60o 2
h 水 = 1m水柱 P 9.8 h汞 = A = = 73.6mm汞柱 ρ汞 g 133.28
图示容器中盛有三种不相混合的液体, 2.10 图示容器中盛有三种不相混合的液体,其密度分别为 ρ1 = 700kg / m3 ρ 2 = 1000kg / m3 ρ3 = 1600kg / m 3 ,在容器右侧壁上安装三根测管E、F、G,左侧壁上安装有 在容器右侧壁上安装三根测管 、 、 , U形水银测压计,容器上部压力压的读数为 − 17200 pa 形水银测压计, 形水银测压计 试求:(1 中液面的高程; 试求:(1)测压管E、F、G中液面的高程; :( (2)水银测压计的液面高差 hP (注:不计空气质量)。 不计空气质量)。 解:测管E: 测管E PE = P表 + ρ1 gh1
2.2 如题 图所示封闭水箱两测压管的液面高程为▽1=100cm, 如题2.2图所示封闭水箱两测压管的液面高程为 图所示封闭水箱两测压管的液面高程为▽ , ▽2=20cm,箱内液面高程为 , 1 为多少? ▽4=60cm。问▽3为多少? 。 为多少 标高等压面有: 解:在▽4 标高等压面有:
4 ρ
p 0
底部连接一水银测压计如图所示,测得水银柱高 底部连接一水银测压计如图所示,测得水银柱高h2=1m,水柱 , 与水平方向成45 转轴在A点 高h1=2m,矩形闸门 与水平方向成 °角,转轴在 点。试 ,矩形闸门AB与水平方向成 求为使闸门关闭所需施加在转轴上的锁紧力矩。 求为使闸门关闭所需施加在转轴上的锁紧力矩。 解:(1)求高压水箱底部压强 :(1 如图取等压面N-N,则: 如图取等压面N N,则 N,
由(1)可知: 可知:
P左
的作用点 yD1=4.632m,
FT hD hC FP
E
P右的作用点
I xc yD1 = yc + yc × A
4 hc π d / 64 = + hc sin θ ×π d 2 / 4 sin θ = 4.74m
a
B C D
θ
G d
题2.20图
根据
∑M
B
= 0 可得
G × d / 2 cos θ + p左 × BD − FT × d cos θ-p右 BD2 = 0
P = ρ g(∇1−∇4) (1) 0
在▽3标高等压面有: 标高等压面有:
2 3 ρp
P0 +ρ g (∇ 4 − ∇3)=ρ P g(∇ 2 − ∇3) (2)
由(1)、(2)两式可得: ) )两式可得:
∇3 = 13.65cm
用图示U形管量测密闭盛水容器中 点压强, 形管量测密闭盛水容器中A 2.3 用图示 形管量测密闭盛水容器中A点压强,管右端开口通 大气,如果h 点的绝对压强和相对压强, 大气,如果 1=1m ,求A点的绝对压强和相对压强,并分别用 国际单位( 水柱高度( ),水银柱高度( ),水银柱高度 国际单位(N/m2) ,水柱高度(m),水银柱高度(mm)压示。 )压示。 解:取等压面N-N,A点相对压强: 取等压面N 点相对压强: PA = ρ水 gh = 1000 × 9.8 ×1 = 9.8 kN / m2) ( 点的绝对压强: A点的绝对压强:
水A 水
h3 4 B N N h2 2 D h1 1 D C C 3
气体
pM = 0.3 ×1000 × 9.8 = 29.4(kN / m2 )
作等压面DD 作等压面 、NN、CC
pM + ρ水 g (h3 + h1 ) = pB + ρ p gh2 − ρ0 gh1 + ρ p gh1
水银 ρp 题2.12图
AC = 2.12m
F1 = p A × AB × b = 357.35kN
A p A H F1 h2 F h1 2 ρp p
B
1 F2 = ( pB − p A ) ⋅ AB ⋅ b 2 = 62.328kN
C
D B
AD = 2.83m
(4)由静水压力施加的绕A 由静水压力施加的绕A 轴的力矩
题2.22图
根据 可得
∑M
B
=0
G × d / 2 × cos θ + p × BD − FT × d cos θ = 0
FT hD hC FP
E
FT = 32.2kN
a
B C D
θ
G d
题2.20图
(2)根据解析法可得此时图形阀门上的静水总压力
P左 = pc A = 30.79kN , P右 = pc' A = 3.33kN
pB = pM + ρ水 g (h3 + h1 ) − ρp gh1 + ρ0 gh1 − ρp gh2 = −28.812(kN / m2 )
2.17如图所示容器中,两测压管的上端封闭,并为完全真空, 2.17如图所示容器中,两测压管的上端封闭,并为完全真空, 如图所示容器中 测得 z1 = 50mm ,求封闭容器中液面上的绝对压强 p0abs 及 z2 之值。 之值。 解:
M ' = F1 × AC + F2 × AD = 933.97 kN ⋅ m
一密闭盛水容器, 2.25 一密闭盛水容器,已知 h1 = 0.6m ,2 = 1m , h 水银测压计读数 hP = 0.25m 。试求半径 R = 0.5m 的球形盖AB所受总压力的水平分力和铅垂分力。 所受总压力的水平分力和铅垂分力。 解: Px = pc Az
E F G 20.0 15.0 11.6 8.0 6.0 hp ρ p 4.0
空气
ρ 1 ρ2 ρ3
H P = 0.6m
题 2.10图
2.12 图示为一测压装置,容器A中水面上压力压M的读数 为0.3个大气压,1 = 20cm , h2 = 30cm ,h3 = 50cm,该测压 h 装置中U形上部是酒精,其密度为800kg/m3,试求容器B中 气体的压强 p,ρ、ρ p、ρ 0 分别 M 酒精 ρ 0 为水、水银、酒精的密度。 解:压力压读数
2
N
h A
PAbs = Pa + PA = 98 + 9.8 = 107.8 kN / m ) (
N
A点绝对压强用水柱压示 PAbs 题2.3图 h水 = = 11m水柱 ρ水 g Pabs 107.8 = = 808.8 (mm汞柱) 用mm汞柱压示为 h汞 = 汞柱压示为 ρ汞 g 13600 × 9.8 A点相对压:用水柱压示为 点相对压: 用汞柱压示
p0 abs = ρ汞 gz1 = 13600 × 9.8 × 0.05 = 6.664kN / m
