锐角三角函数的题型及解题技巧
人教版九年级下册数学作业课件 第二十八章锐角三角函数 专题:求锐角三角函数常用的3种方法(一题多变)

∴BD=CD=k,AD=2k. ∴tanA=BADD=12.
方法总结:作垂线构造直角三角形时“不破坏”特殊 角(30°,45°,60°),如下展示部分常见构造方 法:
题型二 不含特殊角的非直角三角形 3.(1)[延长+连接线段构造直角三角形]如图,在正 方形网格中,已知△ABC 的三个顶点均在格点上, 则∠ACB 的正切值为( D )
◆类型一 构造直角三角形求解 题型一 含特殊角的非直角三角形 1.如图,在△ABC 中,∠B=45°,∠A=75°, AC=8,求 BC 和 AB 的长. 解:如图,过点 A 作 AD⊥BC,垂足为点 D. ∵在 Rt△ABD 中,∠B=45°, ∴∠BAD=45°,BD=AD,AB= 2AD. ∵∠BAC=75°,
2
2
∴AE=125x.
∴tan∠CAD=EACE=15.
◆类型三 利用等角转化求解【转化思想】 7.如图,CD 是 Rt△ABC 斜边 AB 上的高,AC=8, BC=6,则 cos∠BCD 的值是( D ) A.3 B.3 C.4 D.4
543 5
8.如图,在△ABC 中,AC=BC,过点 C 作 CD⊥AB,
(3)[利用垂径定理构造直角三角形]如图,⊙O 为△ABC
的外接圆,⊙O 的半径为 5,BC=8,则 cosA 的值为
3 5
.
10.如图,在矩形 ABCD 中,AB=2,BC=2 5,E 是 BC 的中点,将△ABE 沿直线 AE 翻折,点 B 落在点 F 处,连接 CF,求 cos∠ECF 的值.
A.2
B.2 5 5
C.
5 5
D.12
(2)如图,△ABC 的三个顶点都在正方形网格线的交 点处,将△ABC 绕着点 A 逆时针旋转得到△AB′C′. 若 A,C,B′三点共线,则 tan∠B′CB= 2 ;
解锐角三角函数的技巧

6. 三角函数的倒数关系:利用三角函数的倒数关系,将一个三角函数转化为另一个三角函 数的倒数形式。例如,tanθ=1/cotθ,cotθ=1/tanθ。
解锐角三角函数的技巧
解锐角三角函数的技巧主要包括以下几点:
1. 特殊角的数值:熟记30°、45°、60°三个特殊角的正弦、余弦和正切值。例如, sin30°=1/2,cos45°=1/√2,tan60°=√3。
2. 三角函数的性质:利用三角函数的周期性、对称性倒数关系等性质,将角度转化为在 特定范围内的等效角度。例如,sin(180°+θ)=-sinθ,cos(-θ)=cosθ,tan(θ+π)=-tanθ。
解锐角三角函数的技巧
7. 三角函数的逆函数:利用三角函数的逆函数,将一个三角函数的值转化为对应的角度。 例如,sin^(-1)(x)表示sinθ=x的解,cos^(-1)(x)表示cosθ=x的解。
通过掌握这些技巧,可以在解锐角三角函数的过程中更加灵活和高效地进行计算。同时, 多做练习和应用,加深对三角函数的理解和熟练度,也是提高解题能力的重要方法。
3. 三角函数的和差公式:利用三角函数的和差公式,将复杂的角度拆分为简单的角度的和 或差。例如,sin(A+B)=sinAcosB+cosAsinB,cos(A-B)=cosAcosB+sinAsinB。
解锐角三角函数的技巧
4. 三角函数的倍角公式:利用三角函数的倍角公式,将角度转化为两倍角度的三角函数。 例如,sin2θ=2sinθcosθ,cos2θ=cos^2θ-sin^2θ。
初中数学 函数模块3-5--锐角三角函数讲义(含答案解析)

锐角三角函数题型一:正切的概念在直角三角形ABC 中,90C ∠=︒,A ∠,B Ð,C ∠所对应的边分别是a ,b ,c ,则正弦值等于对边与邻边的比值.即tan aA b=,根据直角三角形三边关系易证,0tan A <,()090︒<∠<︒A ①角的正切值例1.1如图,点E 在正方形ABCD 的边AB 上,若1EB =,2EC =,则tan DCE ∠为()A .12B .2C D 【详解】∵四边形ABCD 是正方形,∴90B ∠=︒,//AB CD ∴DCE BEC ∠=∠,∵1EB =,2EC =,∴BC ==,∴tan tan ∠=∠==BCDCE BEC BE;故答案选D .变式1.11.如图,在直角BAD 中,延长斜边BD 到点C ,使12DC BD =,连接AC ,若tanB=53,则tan CAD ∠的值()A.3B.5C.13D.15【答案】D 【解析】【分析】延长AD ,过点C 作CE AD ⊥,垂足为E ,由5tan 3B =,即53AD AB =,设5AD x =,则3AB x =,然后可证明CDE BDA ∆∆∽,然后相似三角形的对应边成比例可得:12CE DE CD AB AD BD ===,进而可得32CE x =,52DE x =,从而可求1tan 5EC CAD AE ∠==.【详解】解:如图,延长AD ,过点C 作CE AD ⊥,垂足为E ,5tan 3B =,即53AD AB =,∴设5AD x =,则3AB x =,CDE BDA ∠=∠Q ,CED BAD ∠=∠,CDE BDA ∴∆∆∽,∴12CE DE CD AB AD BD ===,32CE x ∴=,52DE x =,152AE x ∴=,1tan 5EC CAD AE ∴∠==.故选:D .【点睛】本题考查了锐角三角函数的定义,相似三角形的判定和性质以及直角三角形的性质,是基础知识要熟练掌握,解题的关键是:正确添加辅助线,将CAD ∠放在直角三角形中.②网格图中求正切值例1.2如图,ABC 的顶点在正方形网格的格点上,则tan A 的值为________.【详解】解:如图,由格点知:AB ==,AC ∵12=⋅⋅ ABC S BC AE 1432=⨯⨯6=,12=⋅⋅ ABC S AB CD 12=⨯=,6=,∴CD =.∴AD ==.∴tan 2==CDA AD.故答案为:2.变式1.22.如图,小正方形的边长均为1,A 、B 、C 分别是小正方形的三个顶点,则sin BAC ∠的值为()A.12B.2C.1D.【答案】B 【解析】【分析】连接BC ,先根据勾股定理求得AB 、BC 、AC 的长,然后再利用勾股定理逆定理证得ABC ∆是直角三角形,最后根据正弦的定义解答即可【详解】解:如图:连接BC ,每个小正方形的边长均为1,AB ∴==BC ==AC ==,222AB BC AC += ,ABC ∆∴是直角三角形,sin2BC BAC AC ∴∠===.故答案为B .【点睛】本题主要考查了勾股定理、勾股定理逆定理以及正弦的定义,根据题意证得ABC ∆是直角三角形是解答本题的关键.③利用图形的变换求正切值例1.3如图,矩形ABCD 中,5AB =,3BC =,E 为边AB 上一点,且3BE =,DAE△沿DE 翻折得到DFE △,连接BF ,tan ∠EFB 的值为________.【详解】解:过点F 作FO AO ⊥于点O ,作FH AB ⊥于点H ,过B 作BG FE ⊥于点G ,∵折叠∴90DAE DFE ∠=∠=︒∴180︒∠=-∠ADF AEF ∵180∠=︒-∠FEB AEF ∴ADF FEB∠=∠∵90∠=∠=︒EGB DOF ,3DF AD ==,3BE =∴DF BE=∴() ≌DOF EGB AAS ∴=GB OF532AE AB BE =-=-=∵13112222=⋅==⋅=⋅= FEB S BE FH FH FE GB AE GB GB ∴32GB FH =∵四边形OAHF 中,四个内角均为90︒,∴四边形OAHF 是矩形,∴=FH AO ∵=GB FO ∴32=FO AO3=∴22(3)9+-=FO AO ∴2413=AO 或0AO =(舍去)∴241531313==-=OD EG ∴3243621313==⨯=FO GB Rt FGB V 中,363613tan 1511213GB GFB GF ∠===-∴36tan 11∠=EFB 故答案为:3611.变式1.33.如图,在菱形纸片ABCD 中,3AB =,60A ∠=︒,将菱形纸片翻折,使点A 落在CD 的中点E 处,折痕为FG ,点F ,G 分别在边AB ,AD 上,则tan EFG ∠的值为________.【答案】3【解析】【分析】连接AE 交GF 于O ,连接BE ,BD ,则△BCD 为等边三角形,设AF=x=EF ,则BF=3-x ,依据勾股定理可得Rt △BEF 中,BF 2+BE 2=EF 2,解方程(3-x )2+2=x 2,即可得到EF=218,再根据Rt △EOF 中,=即可得出tan ∠EFG=EO FO =.【详解】解:如图,连接AE 交GF 于O ,连接BE ,BD ,则△BCD 为等边三角形,∵E 是CD 的中点,∴BE ⊥CD ,∴∠EBF=∠BEC=90°,Rt △BCE 中,CE=cos60°×3=1.5,∴Rt △ABE 中,由折叠可得,AE ⊥GF ,EO=12,设AF=x=EF ,则BF=3-x ,∵Rt △BEF 中,BF 2+BE 2=EF 2,∴(3-x )2+)2=x 2,解得x=218,即EF=218,∴Rt △EOF 中,=,∴tan ∠EFG=EO FO =【点睛】本题考查了菱形的性质、解直角三角形以及折叠的性质:折叠是一种对称变换,对应边和对应角相等.解题时,常设要求的线段长为x ,然后根据折叠和轴对称的性质用含x 的代数式表示其他线段的长度,选择适当的直角三角形,运用勾股定理列出方程求出答案.题型二:正弦的概念在直角三角形ABC 中,90C ∠=︒,A ∠,B Ð,C ∠所对应的边分别是a ,b ,c ,则正弦值等于对边与斜边的比值.即sin aA c=,根据直角三角形三边关系易证,0sin 1A <<,()090︒<∠<︒A ①角的正弦值例2.1在ABC 中,90C ∠=︒,2BC =,2sin 3A =,则边AC 的长是()A B .3C .43D 【详解】解答:在Rt ABC △中,∵22sin 3===BC A AB AB ,∴3AB =,∴根据勾股定理,得AC =故选A .变式2.14.在Rt ABC ∆中,90C ∠=︒,1BC =,4AB =,则sin B 的值是()A.5B.14C.13D.4【答案】D 【解析】【分析】首先根据勾股定理求得AC 的长,然后利用正弦函数的定义即可求解.【详解】∵∠C=90°,BC=1,AB=4,∴AC ===∴4AC sinB AB ==,故选:D .【点睛】本题考查了三角函数的定义,求锐角的三角函数值的方法:利用锐角三角函数的定义,转化成直角三角形的边长的比.②网格图中求正弦值例2.2如图,ABC 的顶点是正方形网格的格点,则sin A 的值为()A .12B C .10D 【详解】解:如图所示,取格点D ,连接DC ,由网格可得出DC =,AC =,AD =,∵222+=∴222DC AD AC =+,则:90CDA ∠=︒,故sin5===DCA AC .故选:B .变式2.25.正方形网格中,∠AOB 如图放置,则sin ∠AOB 的值为()A.2B.2C.3D.1【答案】B【解析】【分析】如图,连接AD ,CD ,根据勾股定理可以得到OD=AD ,则OC 是等腰三角形底边上的中线,根据三线合一定理,可以得到△ODC 是直角三角形.根据三角函数的定义就可以求解.【详解】解:如图,连接AD ,CD ,设正方形网格的边长是1,则根据勾股定理可以得到:,,∠OCD=90°.则=∴sin ∠AOB=2CD OD ==,故选:B .【点睛】本题考查锐角三角函数的概念,注意到图中的等腰三角形是解决本题的关键.③利用图形的变换求正弦值例2.3如图,Rt ABC 中,90ACB ∠=︒,D 是AC 上一点,连接BD ,将ABC 沿BD翻折,点C 落在边AB 的点C '处,连接CC '.若15AB =,4sin 5A =,则CC '长________.【详解】如图,设BD 与CC '的交点为点O ,∵在Rt ABC 中,90ACB ∠=︒,15AB =,4sin 5A =,∴45BC AB =,即4155BC =,解得12BC =,∴9==AC ,由翻折的性质得:12'==BC BC ,C D CD '=,90'∠=∠=︒BC D ACB ,∴15123''=-=-=AC AB BC ,设AD x =,则9C D CD AC AD x '==-=-,在Rt AC D ' 中,222AC C D AD ''+=,即2223(9)x x +-=,解得5x =,∴5AD =,4CD =,在Rt BCD 中,BD ==又∵BC BC '=,C D CD '=,∴BD 是CC '的垂直平分线,∴BD CC '⊥,2'=CC OC ,∴Rt 1122=⋅=⋅ BCD S BC CD BD OC ,即1112422⨯⨯=⨯,解得5OC =,∴25'==CC OC ,故答案为:5.变式2.36.如图,将矩形ABCD 沿对角线BD 对折,点C 落在E 处,BE 与AD 相交于点F .(1)求证:BFD △是等腰三角形;(2)若4BC =,2CD =,求AFB ∠的正弦值.【答案】(1)见解析;(2)45【解析】【分析】(1)根据矩形性质和平行线的性质得∠ADB =∠CBD ,结合折叠性质得出∠ADB =∠DBF ,再根据等腰三角形的判定即可证得结论;(2)设BF=DF =x ,则AF=4﹣x ,利用勾股定理求解x 值,再根据正弦定义求解即可.【详解】解:(1)∵四边形ABCD 是矩形,∴AD ∥BC ,∴∠ADB =∠CBD ,由折叠性质得:∠DBF =∠CBD ,∴∠ADB =∠DBF ,∴BF=DF ,∴△BFD 是等腰三角形;(2)∵四边形ABCD 是矩形,∴AD=BC =4,AB=CD =2,∠A =90°,设BF=DF =x ,则AF=4﹣x ,在Rt △ABF 中,由勾股定理得:22+(4﹣x )2=x 2解得:x =52,∴sin ∠AFB =24552AB BF ==,即AFB ∠的正弦值为45.【点睛】本题考查矩形性质、折叠性质、平行线的性质、等腰三角形的判定、勾股定理、正弦定义、解一元一次方程,熟练掌握相关知识的联系与运用是解答的关键.题型三:余弦的概念在直角三角形ABC 中,90C ∠=︒,A ∠,B Ð,C ∠所对应的边分别是a ,b ,c ,则正弦值等于邻边与斜边的比值.即cos b A c=,根据直角三角形三边关系易证,0cos 1A <<,()090︒<∠<︒A 角的余弦值例3.1如图,在Rt ABC 中,90C ∠︒=,13AB =,5AC =,则cos A 的值是________.【详解】解:在Rt ABC 中,5cos 13AC A AB ==,故答案为:513.变式3.17.在Rt △ABC 中,∠C =90°,AB =10,AC =8,则cos A =_____.【答案】45【解析】【分析】根据勾股定理求出边BC 的长,利用余弦定理cos A=A A ∠∠的临边的斜边即可解得.【详解】Rt △ABC 中,∠C =90°,AB =10,AC =8,所以所以cos A =AC AB =810=45.【点睛】本题考查勾股定理以及余弦定理.②网格图中求余弦值例3.2如图,已知ABC 的三个顶点均在正方形网格的格点上,则cos A 的值为________.【详解】解:如图所示:连接BD ,可得:90CDB ∠=︒,BD =,AD =AB ,故cos5AD A AB ===..变式3.28.如图,在4×4的正方形方格图形中,小正方形的顶点称为格点,△ABC 的顶点都在格点上,则∠BAC 的余弦值是____.【答案】5【解析】【分析】先根据勾股定理的逆定理判断出△ABC 的形状,再由锐角三角函数的定义即可得出结论.【详解】解:∵AB 2=32+42=25、AC 2=22+42=20、BC 2=12+22=5,∴AC 2+BC 2=AB 2,∴△ABC 为直角三角形,且∠ACB =90°,则cos ∠BAC 5AC AB ==,.【点睛】本题考查的是锐角三角函数的定义,勾股定理及其逆定理,熟知在一个三角形中,如果两条边长的平方之和等于第三边长的平方,那么这个三角形是直角三角形是解答此题的关键.③利用图形的变换求余弦值例3.3如图,在菱形纸片ABCD 中,2AB =,60A ∠=︒,将菱形纸片翻折,使点A 落在CD 的中点E 处,折痕为FG ,点F ,G 分别在边AB ,AD 上,则cos EFG ∠的值为________.【详解】过点A 作AP CD ⊥,交CD 延长线于P ,连接AE ,交FG 于O ,∵四边形ABCD 是菱形,∴2AD AB ==,∵将菱形纸片翻折,使点A 落在CD 的中点E 处,折痕为FG ,∴∠=∠AFG EFG ,FG AE ⊥,∵//CD AB ,AP CD ⊥,∴AP AB ⊥,∴90∠+∠=︒PAE EAF ,∵90∠+∠=︒EAF AFG ,∴∠=∠PAE AFG ,∴∠=∠EFG APE ,∵//CD AB ,60DAB ∠=︒,∴60PDA ∠=︒,∴sin 6022=⋅︒=⨯=AP AD ,1cos60212=⋅︒=⨯=PD AD ,∵E 为CD 中点,∴112DE AD ==,∴2=+=PE DE PD ,∴==AE ,∴cos cos7∠=∠===AP EFG PAE AE .故答案为7变式3.39.如图,在菱形ABCD 中,4AB =,B Ð是锐角,AE BC ⊥于点E ,M 是AB 的中点,连接MD ,ME .若90EMD ∠=︒,则cos B 的值为___________.【答案】12【解析】【分析】延长DM 交CB 的延长线于点H .首先证明△ADM ≌△BHM ,得出AD=HB=4,MD=MH ,由线段垂直平分线的性质得出EH=ED ,设BE=x ,利用勾股定理构建方程求出x ,即BE ,结合AB 得出cosB 的值.【详解】解:延长DM 交CB 的延长线于点H .如图所示:∵四边形ABCD 是菱形,∴AB=BC=AD=4,AD ∥CH ,∴∠ADM=∠H ,∵M 是AB 的中点,∴AM=BM ,在△ADM 和△BHM 中,AMD BMH ADM H AM BM ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ADM ≌△BHM (AAS ),∴AD=HB=4,MD=MH ,∵∠EMD=90°,∴EM ⊥DH ,∴EH=ED ,设BE=x ,∵AE ⊥BC ,∴AE ⊥AD ,∴∠AEB=∠EAD=90°,∵AE 2=AB 2-BE 2=DE 2-AD 2,∴42-x 2=(4+x )2-42,解得:x=2-,或x=2--(舍),∴BE=2,∴cosB=2142BE AB-==.故答案为:12-.【点睛】本题考查菱形的性质、勾股定理、线段的垂直平分线的性质、全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.题型四:同角三角函数关系(拓展)1.若90A B ∠+∠=︒,则sin cos A B =,sin cos B A =,tan tan 1A B ⋅=2.平方关系:22sin cos 1A B +=3.比值关系:sin tan cos =AA A例4若α是锐角,tan tan501⋅︒=α,则α的值为()A .20︒B .30°C .40︒D .50︒【详解】解:∵tan tan501⋅︒=α∴5090+︒=︒α∴40α=︒.故选C .变式410.比较大小:sin81︒________tan 47︒;cos30︒________tan 60︒.(填“>,<或=”)【答案】①.<②.<【解析】【分析】①把sin81︒、tan 47︒分别与1进行比较,即可得到答案;②分别求出cos30︒、tan 60︒的值,然后进行比较即可.【详解】解:∵sin811︒<,tan 47tan 451︒>︒=,∴sin81tan 47︒<︒;∵cos302=°,tan 60︒=又∵2<,∴0cos30tan 6︒<︒;故答案为:<;<;【点睛】本题考查了三角函数的比较大小,解题的关键是正确的掌握三角函数的值,然后进行比较.题型五:特殊角的三角函数值①特殊角的三角函数值的混合运算例5.1计算:sin 30cos 601sin 60cos 45tan 60sin452︒︒+︒-︒︒+︒.【详解】原式1122=+,===,=;变式5.111.计算:(1)28sin 60tan 454cos30︒+︒-︒;(2)222tan 60cos 30sin 45tan 45︒+︒-︒︒.【答案】(1)7-;(2)134.【解析】【分析】(1)根据特殊锐角三角函数值代入计算即可;(2)根据特殊锐角三角函数值代入计算即可.【详解】解:(1)原式281422⎛⎫=⨯+-⨯ ⎪ ⎪⎝⎭3814=⨯+-7=-;(2)原式222122⎛⎫⎛⎫=+-⨯ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭31342=+-134=.【点睛】本题考查了特殊角的三角函数值,掌握特殊锐角的三角函数值是解决问题的关键.②由特殊角的三角函数值判断三角形的形状例5.2在ABC 中2(2cos |1tan |0-+-=A B ,则ABC 一定是()A .直角三角形B .等腰三角形C .等边三角形D .等腰直角三角形【详解】解:由2(2cos |1tan |0-+-=A B ,得2cos A =,1tan 0B -=.解得45A ∠=︒,45B ∠=︒,则ABC 一定是等腰直角三角形,故选:D .变式5.212.在ABC 中,若tanA=1,cosB=2,则下列判断最确切的是()A.ABC 是等腰三角形B.ABC 是等腰直角三角形C.ABC 是直角三角形D.ABC 是一般锐角三角形【答案】B【解析】【分析】先根据正切值、余弦值求出A ∠、B Ð的度数,再根据三角形的内角和定理可得C ∠的度数,然后根据等腰直角三角形的定义即可得.【详解】A ∠、B Ð是ABC 的内角,且tan 1A =,cos 2B =,45A ∴∠=︒,45B ∠=︒,18090C A B ∴∠=︒-∠-∠=︒,ABC ∴ 是等腰直角三角形,故选:B .【点睛】本题考查了特殊角的正切值与余弦值、三角形的内角和定理、等腰直角三角形的定义,熟记特殊角的正切值与余弦值是解题关键.③根据特殊角三角函数值求角的度数例5.3在ABC 1cos 02+-=C ,且B Ð,C ∠都是锐角,则A ∠的度数是()A .15︒B .60︒C .75︒D .30°1cos 02+-=C ,∴sin 02-=B ;1cos 02-=C .即sin 2B =;1cos 2C =.∴45B ∠=︒,60C ∠=°.∴180180456075∠=︒-∠-∠=︒-︒-︒=︒A B C .故选:C .变式5.313.已知tan tan tan()1tan tan αβαβαβ++=-⋅,22tan tan 21tan ααα=-α和β都表示角度),比如求tan105︒,可利用公式得()tan105tan 60452︒=︒+︒==-,又如求tan120︒,可利用公式得()()22tan120tan 2601︒=⨯︒==-,请你结合材料,若()tan 1203λ︒+=-(λ为锐角),则λ的度数是__________.【答案】30°【解析】【分析】设tan λx =,先根据公式可得到一个关于x 的分式方程,解方程可求出x 的值,再根据特殊角的正切函数值即可得出答案.【详解】设tan λx=由题意得:()tan120tan tan 1201tan120tan λλλ︒+︒+=-︒⋅()tan120tan ,tan 1203λx λ︒==︒+=-3=-解得3x =经检验,3x =是分式方程的根即tan 3λ=λQ 为锐角30λ∴=︒故答案为:30°.【点睛】本题考查了分式方程的解法、特殊角的正切函数值,熟记特殊角的正切函数值是解题关键.④三角函数值的大小例5.4如图所示的网格是正方形网格,则AOB ∠________COD ∠.(填“>”,“=”或“<”)【详解】解:根据题意可知tan 2AOB ∠=,tan 2∠=COD ,∴AOB COD ∠=∠,故答案为=.变式5.4.114.如果α是锐角,则下列成立的是()A.sin αcos α1+= B.sin αcos α1+> C.sin αcos α1+< D.sin αcos α1+≤【答案】B【解析】【分析】根据正弦函数是对边比斜边,余弦函数是邻边比斜边,三角形的两边之和大于第三边,可得答案.【详解】解:∵a 、b 是直角边,c 是斜边,∴sin α+cos α=a c +bc =a b c +,∵a+b>c ,∴a b c+>1,∴sin αcos α1+>.故选B.【点睛】本题考查了同角三角函数关系,利用正弦函数是对边比斜边,余弦函数是邻边比斜边是解题关键.变式5.4.215.如图,将ABC 绕点B 顺时针旋转()90αα︒<得到A BC ''△.请比较大小:sin ABA '∠______tan CBC '∠.【答案】<【解析】【分析】由旋转可得:ABA CBC α''∠=∠=<90,︒如图,构建直角三角形,ABA '且,ABA CBC ''∠=∠再利用锐角三角函数的定义可得:sin ,tan tan ,AA AA ABA CBC ABA AB A B'''''∠=∠=∠='由A B '<,AB 从而可得答案.【详解】解:由旋转可得:ABA CBC α''∠=∠=<90,︒如图,构建直角三角形,ABA '且,ABA CBC ''∠=∠由三角函数定义可得:sin ,tan tan ,AA AA ABA CBC ABA AB A B'''''∠=∠=∠='A B ' <,AB AA AB '∴<,AA A B''sin ABA '∴∠<tan .CBC '∠故答案为:<.【点睛】本题考查旋转的性质,锐角三角函数的定义,掌握以上知识是解题的关键.题型五:解直角三角形①解直角三角形1.解直角三角形的概念:在直角三角形中除直角外一共有五个元素,即三条边和两个锐角,由直角三角形中除直角外的已知元素,求出所有未知元素的过程叫做解直角三角形.2.理论依据:①三边关系:勾股定理222+=a b c ②两锐角互余:90A B ∠+∠=︒③边角之间的关系:tan a A b =,sin a A c=,cos a A c =3.常见类型:①已知两条边,先利用边角关系求出两个角,再利用勾股定理求出另一条边②已知一边一角,先求出另一角,再利用边角关系求出其余的边长例5.1已知2sin 3α=,其中α为锐角,求cos α、tan α、cot α的値.【详解】∵2sin 3α=∴设α的对边2k =,直角三角形的斜边3=k ,由勾股定理求出α的邻边=,∴cos α33k ==,tan 5α===,cot 22k α==.变式5.116.(1)在△ABC 中,∠B =45°,cosA 12=.求∠C 的度数.(2)在直角三角形ABC 中,已知sinA 45=,求tanA 的值.【答案】(1)75°;(2)43.【解析】【分析】(1)由条件根据∠A 的余弦值求得∠A 的值,再根据三角形的内角和定理求∠C 即可;(2)根据角A 的正弦设BC=4x ,AB=5x ,得AC 的长,根据三角函数的定义可得结论.【详解】解:(1)∵在△ABC 中,cosA 12=,∴∠A =60°∵∠B =45°,∴∠C =180°﹣∠B ﹣∠A =75°;(2)∵sinA 45BC AB ==,∴设BC =4x ,AB =5x ,∴AC =3x ,∴tanA 4433BC x AC x ===.【点睛】本题主要考查了锐角三角函数的知识以及三角形的内角和定理,属基础题.②构造直角三角形例5.2在ABC 中,8AB =,6BC =,B Ð为锐角且1cos 2B =.(1)求ABC 的面积;(2)求tan C .【详解】(1)如图,过点A 作AH BC ⊥于H .∵1cos 2B =,∴60B ∠=︒,∴1cos 842=⋅=⨯=BH AB B ,sin 82=⋅=⨯=AH AB B ,∴11622=⋅⋅=⨯⨯= ABC S BC AH (2)在Rt ACH 中,∵90AHC ∠=︒,AH =742=-=-=CH BC BH ,∴tan 2===AH C CH.变式5.217.如图,在△ABC ,∠A=30°.(1)求BD 和AD 的长;(2)求tan C 的值.【答案】(1)BD =3,AD =(2)tan C =2.【解析】【详解】(1)∵BD ⊥AC ,∴∠ADB =∠BDC =90°.在Rt △ADB 中,AB =6,∠A =30°,∴BD =AB·sin30°=3,∴ꞏcos30AD AB =︒=.(2)CD AC AD =-==在Rt △BDC 中,tan2BD C CD ∠===.视频题型六:解直角三角形的实际应用①方位角问题从标准方向的北端起,顺时针方向到直线的水平角,称为该直线的方位角,方位角的取值范围是0360︒-︒.例6.1如图,在A 处测得点P 在北偏东60︒方向上,在B 处测得点P 在北偏东30°方向上,若AP =千米,则点AB 两点的距离为()千米.A .4B .C .2D .6【详解】解:由题意可知,30︒∠= PAC ,60PBC ∠=︒,∵AP =,∴1sin 302PC AP =︒=⨯=cos 609AC AP =︒==,∴3tan 60PC BC ===︒,∴936AB AC BC =-=-=,故选:D .变式6.118.如图,在一条笔直的海岸线上有A ,B 两个观测站,A 在B 的正东方向.有一艘小船从A 处沿北偏西60︒方向出发,以每小时20海里速度行驶半小时到达P 处,从B 处测得小船在它的北偏东45︒的方向上.(1)求AB 的距离;(2)小船沿射线AP 的方向继续航行一段时间后,到达点C 处,此时,从B 测得小船在北偏西15︒的方向.求点C 与点B 之间的距离.(上述两小题的结果都保留根号)【答案】(1)(5AB =+海里;(2)52+海里.【解析】【分析】(1)过点P 作PD AB ⊥于点D ,利用余弦定义解出AP 、AD 的长,再由直角三角形中,30°角所对的直角边等于斜边的一半解得PD 的长,最后根据等腰直角三角形两直角边相等的性质解题即可;(2)过点B 作BF AC ⊥于点F ,根据直角三角形中30°角所对的直角边等于斜边的一半,解得BF 的长,在Rt BCF 中,由勾股定理解得BC 的长即可.【详解】解:(1)如图,过点P 作PD AB ⊥于点D ,在Rt PAD V 中,90ADP ∠=︒,906030PAD ∠=︒-︒=︒,∵cos AD PAD AP∠=,200.510AP ⨯==∴cos 102PA A D D AP =⋅=⨯=∠152PD AP ==在Rt PBD 中,90BDP ∠=︒,904545PBD ∠=︒-︒=︒,∴5BD PD ==.∴(5AB =+海里(2)如图,过点B 作BF AC ⊥于点F ,在Rt ABF 中,90AFB ∠=︒,30BAF ∠=︒,∴(11522BF AB ==+在ABC 中,18045C BAC ABC ∠=︒-∠-∠=︒.在Rt BCF 中,90BFC ∠=︒,45C ∠=︒,∴52C B ==海里.∴点C 与点B 之间的距离为52海里.【点睛】本题考查解直角三角形的应用之方向角的问题,其中涉及含30°角的直角三角形的性质、余弦、三角形内角和、勾股定理等知识,是重要考点,难度较易,正确作出辅助线,构造直角三角形、掌握相关知识是解题关键.②仰角俯角问题仰角:视线在水平线上方的角.俯角:视线在水平线下方的角.例6.2如图,护林员在离树8m 的A 处测得树顶B 的仰角为45︒,已知护林员的眼睛离地面的距离AC 为1.6m ,则树的高度BD 为()A .8mB .9.6mC . 1.6)mD . 1.6)m +【详解】解:过点C 作CE BD ⊥于E ,∵45BCE ∠=︒,∴CEB △是等腰直角三角形,∴8==CE BE ,四边形ACED 是矩形,∴ 1.6==AC DE ,∴8 1.69.6=+=BD 米,故选B .变式6.219.如图,某飞机在空中A 处探测到地平面目标B ,此时从飞机上看目标B 的俯角为α,飞行高度AC a =,则飞机到目标B 的距离AB 为()A.sin a α⋅B.sin a αC.cos a α⋅ D.cos a α【答案】B 【解析】【分析】由题意得∠ABC=α,然后根据解直角三角形,即可求出AB 的长度.【详解】解:在Rt △ABC 中,∠ABC=α,AC a =,∵sin ACABα=,∴sin a AB α=.故选:B .【点睛】本题考查了解直角三角形的应用——仰角俯角问题,解题的关键是掌握正弦的定义进行解题.③坡度与坡比问题坡面的铅直高度h 与水平宽度l 的比叫做坡度,也称之为坡比,用字母i 表示坡比.即=hi l.坡度一般写成:a b 的形式,如1:5i =等.把坡面与水平面的夹角记作α,α叫做坡角,有tan ==hi lα.例6.3我市里运河有一座人行天桥如图所示,天桥高为6米,坡面BC 的坡度为1:1,文化墙PM 在天桥底部正前方8米处(PB 的长),为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为.有关部门规定,文化墙距天桥底部小于3米时应拆除,天桥改造后,该文化墙PM 是否需要拆除?请说明理由. 1.414=,1.732=)【详解】解:该文化墙PM 不需要拆除,理由:设新坡面坡角为α,新坡面的坡度为,∴3tan α==,∴30α=︒.作CD AB ⊥于点D ,则6CD =米,∵新坡面的坡度为,∴6tanCD CAD AD AD ∠===解得,AD =BC 的坡度为1:1,6CD =米,∴6BD =米,∴6)=-=-AB AD BD 米,又∵8PB =米,∴86)14146 1.732 3.6=-=--=-≈-⨯≈PA PB AB 米3>米,∴该文化墙PM 不需要拆除.变式6.320.如图,在市区A 道路上建造一座立交桥,要求桥面的高度h 为4.8米,引桥的坡角为14°,则引桥的水平距离l 为____米(结果精确到0.1m ,参考数据:sin14°≈0.24,cos14°≈0.97,tan14°≈0.25).【答案】19.2【解析】【分析】根据题意利用正切列式进行求解即可.【详解】解:由题意可得:tan14°=4.80.24h l l=≈,解得:l =19.2,故答案为:19.2.【点睛】本题主要考查解直角三角形,熟练掌握利用三角函数进行求解问题是解题的关键.④利用三角函数测量高度例6.4如图所示,某建筑物楼顶有信号塔EF ,卓玛同学为了探究信号塔EF 的高度,从建筑物一层A 点沿直线AD 出发,到达C 点时刚好能看到信号塔的最高点F ,测得仰角60ACF ∠=︒,AC 长7米.接着卓玛再从C 点出发,继续沿AD 方向走了8米后到达B 点,此时刚好能看到信号塔的最低点E ,测得仰角30B ∠=︒.(不计卓玛同学的身高)求信号塔EF 的高度(结果保留根号).【详解】解:在Rt △ACF 中,∵60ACF ∠=︒,7AC =米,∴tan 60=⋅︒=AF AC ∵8BC =米,∴15AB =米,在Rt ABE △中,∵30B ∠=︒,∴tan30153=⋅︒=⨯=AE AB 米,∴=-=-=EF AF AE ,答:信号塔EF 的高度为变式6.421.如图,AB 和CD 是同一地面上的两座相距36米的楼房,在楼AB 的楼顶A 点测得楼CD 的楼顶C 的仰角为45°,楼底D 的俯角为30°,求楼CD 的高.【答案】楼CD 的高是(【解析】【分析】在题中两个直角三角形中,知道已知角和其邻边,只需根据正切值求出对边后相加即可.【详解】延长过点A 的水平线交CD 于点E则有AE ⊥CD ,四边形ABDE 是矩形,AE=BD=36∵∠CAE=45°∴△AEC 是等腰直角三角形∴CE=AE=36在Rt △AED 中,tan ∠EAD=EDAE∴∴答:楼CD 的高是()米.【点睛】本题考查了解直角三角形的应用-仰角俯角问题,借助俯角构造直角三角形,并结合图形利用三角函数解直角三角形是解题的关键.实战练22.在Rt △ABC 中,∠C =90°,AC =2,BC =3,那么下列各式中,正确的是()A.sin B =23B.cos B =23C.tan B =23D.tan B =32【答案】C 【解析】【详解】∵∠C =90°,AC =2,BC =3,∴,∴sinB=13AC AB ==,cosB=13BC AB ==,tanB=23AC BC =,故选C.23.如果把∠C 为直角的Rt ABC 各边的长都扩大到原来的2倍,那么锐角A 的各三角比的值()A.都扩大到原来的2倍B.都缩小到原来的一半C.都没有变化D.有些有变化【答案】C 【解析】【分析】根据正弦、余弦、正切的定义即可得.【详解】 在Rt ABC 中,90C ∠=︒,sin ,cos ,tan a b aA A A c c b ∴===,222sin ,cos ,tan 222a a b b a aA A A c c c c b b∴======,则当Rt ABC 各边的长都扩大到原来的2倍,锐角A 的各三角比的值都没有变化,故选:C .【点睛】本题考查了正弦、余弦、正切的定义,熟记定义是解题关键.24.在Rt △ABC 中,∠C =90°,BC =5,AC =12,则sinB 的值是()A.512B.125C.513D.1213【答案】D 【解析】【分析】直接利用勾股定理得出AB 的长,再利用锐角三角函数得出答案.【详解】解:如图所示:∵∠C =90°,BC =5,AC =12,∴13AB ==,∴12sin 13AC B AB ==.故选:D .【点睛】本题考查勾股定理的应用和锐角三角函数的定义,在直角三角形中,锐角的正弦为对边比斜边,解题的关键是理解三角函数的定义.25.若锐角A 、B 满足条件4590A B <<< 时,下列式子中正确的是()A.sin sin A B > B.cot cot B A> C.tan tan A B> D.cos cos A B>【答案】D 【解析】【分析】根据锐角三角函数的增减性进行判断即可.【详解】∵4590A B <<< ,∴sin sin A B <,cot cot B A <,tan tan A B <,cos cos A B >.故只有D 选项正确.故选D.【点睛】本题考查锐角三角函数的增减性,锐角的余弦值和余切值是随着角度的增大而减小,锐角的正弦值和正切值随着角度的增大而增大.26.如图,在菱形ABCD 中,∠ABC =120°,对角线AC ABCD 的周长为()A. B.20C. D.16【答案】D 【解析】【分析】连接BD 交AC 于点O ,由菱形的性质得出AB =BC =CD =AD ,AC ⊥BD ,OA =OC =12AC ,∠ABD =∠CBD =12∠ABC =60°,求出∠BAO =30°,由直角三角形的性质得OB =3OA =2,AB =2OB =4,即可得出答案.【详解】解:连接BD 交AC 于点O ,如图:∵四边形ABCD 是菱形,∴AB =BC =CD =AD ,AC ⊥BD ,OA =OC =12AC ,∠ABD =∠CBD =12∠ABC =60°,∴∠BAO =30°,∴OB =OA tan 30⋅︒=3⨯,AB =2OB =4,∴菱形ABCD 的周长=4AB =16;故选:D .【点睛】本题考查了菱形的性质,解直角三角形,含30°角的直角三角形的性质等知识;熟练掌握菱形的性质是解题的关键.27.如图,在△ABC 中,sinB=13,tanC=2,AB=3,则AC 的长为()A.B.C.D.2【答案】B 【解析】【分析】过A 点作AH ⊥BC 于H 点,先由sin ∠B 及AB=3算出AH 的长,再由tan ∠C 算出CH 的长,最后在Rt △ACH 中由勾股定理即可算出AC 的长.【详解】解:过A 点作AH ⊥BC 于H 点,如下图所示:由1sin =3∠=AH B AB ,且=3AB 可知,=1AH ,由tan =2∠=AHC CH ,且=1AH 可知,12CH =,∴在Rt ACH ∆中,由勾股定理有:2===AC .故选:B .【点睛】本题考查了解直角三角形及勾股定理等知识,如果图形中无直角三角形时,可以通过作垂线构造直角三角形进而求解.28.如图,点A ,B ,C 在正方形网格的格点上,则sin BAC ∠等于()A.3B.5C.10D.5【答案】D 【解析】【分析】连接格点CD ,根据勾股定理求出三角形的边长,再利用勾股定理的逆定理判断出直角三角形,最后由三角函数的意义求解即可.【详解】解:如图,连接格点CD ,∵AD 2=22+22=8,CD 2=12+12=2,AC 2=12+32=10,∴AD 2+CD 2=AC 2,∴∠ADC =90°,由勾股定理得,AC ,CD ,∴sin ∠BAC =CDAC 5 ,故选:D .【点睛】本题考查了三角函数的意义,勾股定理等知识,根据网格构造直角三角形和利用勾股定理求边长是解决问题的关键.29.如图,△ABC 与△DEF 都是正方形网格中的格点三角形(顶点在格点上),那么△ABC 与△DEF 的周长比为()A. B.1:2 C.1:3 D.1:4【答案】A 【解析】【分析】设正方形网格的边长为1,根据勾股定理求出△EFD 、△ABC 的边长,运用三边对应成比例,则两个三角形相似这一判定定理证明△BAC ∽△EDF ,即可解决问题.【详解】解:如图,设正方形网格的边长为1,由勾股定理得:DE 2=22+22,EF 2=22+42,∴DE =,EF =同理可求:AC ,BC ,∵DF =2,AB =2,∴BC AB AC EF DE DF ===,∴△BAC ∽△EDF ,∴C △ABC :C △DEF =1,故选A .【点睛】本题主要考查了勾股定理和相似三角形的判定及其性质定理的应用问题,熟练掌握相似三角形的判定与性质是解题的关键.30.如图,在等腰ABC ∆中,AB AC =.若BAC α∠=,AB m =,则底边BC =()A.sin m α⋅B.2sin m α⋅C.2sin2m α⋅ D.sin2m α⋅【答案】C 【解析】【分析】首先如图过点A 作AD ⊥BC 交BC 于D 点,据此接着利用等腰三角形性质可以得出∠BAD=12∠BAC=12α,BC=2BD ,然后在Rt △ABD 中,根据sin ∠=BDBAD AB求出BD ,最后利用BC=2BD 求出答案即可.【详解】如图,过点A 作AD ⊥BC 交BC 于D 点,则△ABD 是直角三角形,∵△ABC 为等腰三角形,AD ⊥BC ,∴∠BAD=12∠BAC=12α,BC=2BD ,在Rt △ABD 中,sin sin2BD BDBAD AB mα===∠,∴sin2BD m α=⋅,∴22sin 2BC BD m α==⋅⋅,故选:C .【点睛】本题主要考查了解直角三角形的综合运用,熟练掌握相关方法是解题关键.31.如图,在高楼前D 点测得楼顶A 的仰角为30°,向高楼前进60m 到达C 点,又测得楼顶A 的仰角为45°,则该高楼的高度大约为()A.82mB.160mC.52mD.30m【答案】A【解析】【分析】【详解】解:Rt△ABC中,∠ACB=45°,∴BC=AB,Rt△ABD中,∠ADB=30°,∴BD=AB÷tan AB,∴DC=BD-BC=)AB=60米,≈82米,即楼的高度约为82.0米,∴AB故选A.32.如图,河坝横断面迎水坡AB的坡比为1,坝高BC=3m,则AB的长度为()A.6mB.mC.9mD.【答案】A【解析】【分析】根据坡比的概念求出AC,根据勾股定理求出AB.【详解】解:∵迎水坡AB的坡比为1,∴BC AC =3AC =解得,AC =,由勾股定理得,AB ==6(m ),故选:A .【点睛】本题考查的是解直角三角形的应用-坡度坡角问题,掌握坡度的概念是解题的关键.33.在△ABC 中,∠C 90°,sinA 1213,BC 12,那么AC ______.【答案】5【解析】【分析】先根据正切的定义得到sinA=BC AB =1213,则可得到AB=13,然后根据勾股定理计算AC 的长.【详解】在△ABC 中,∠C=90°,∵sinA=BC AB =1213,BC=12,∴AB=13,∴.故答案为5.【点睛】本题考查锐角三角函数的定义,勾股定理.解此题的关键在于熟练掌握其知识点.34.cos45°-12tan60°=________;【答案】12-【解析】【分析】根据特殊角的三角函数值进行计算.【详解】解:原式11222=-=-.故答案是:12-.【点睛】本题考查特殊角的三角函数值,解题的关键是记住特殊角的三角函数值.35.在ABC 中,2cos (1cot )0A B +-=,则ABC ∆的形状是__________.【答案】钝角三角形【解析】【分析】根据非负数的性质得到cos =02-A ,1cot =0-B ,从而求出∠A 与∠B 的度数,即可判断△ABC 的形状.【详解】∵2cos (1cot )0A B -+-=∴cos =02-A ,1cot =0-B即cos =2A ,cot =1B ∴=30A ∠︒,=45∠︒B ∴=1803045=105∠︒-︒-︒︒C ∴ABC ∆是钝角三角形故答案为:钝角三角形【点睛】本题考查了非负数的性质,三角形的分类与特殊角度的三角函数值,熟记特殊角度的三角函数值是解题的关键.36.如图,在Rt △ABC 中,∠C =90°,b =20,c =,则∠B 的度数为_______.【答案】45°【解析】。
锐角三角函数的题型及解题技巧

锐角三角函数的题型及解题技巧锐角三角函数是三角函数的基础,它应用广泛,解题技巧性强,下面归纳出锐角三角函数的常见题型,并结合例题介绍一些解题技巧。
一、 化简或求值例1 (1)已知tan 2cot 1a a -=,且a 是锐角,求22tan cot 2a a +-的值。
(2)化简()()22sin cos cos sin a b a b a a a a ++-。
分析分析 (1)由已知可以求出tan a 的值,化简22tan cot 2a a +-可用1tan cot a a =×;(2)先把平方展开,再利用22sin cos 1a a +=化简。
化简。
解 (1)由tan 2cot 1a a -=得2tan 2tan a a -=,解关于tan a 的方程得tan 2a =或tan 1a =-。
又a 是锐角,∴tan 2a =。
∴22tan cot 2a a +-=22tan 2tan cot cot a a a a -×+=2(tan cot )a a -=tan cot a a -。
由tan 2a =,得1cot 2a =,∴22tan cot 2a a +-=tan cot a a -=13222-=。
(2)()()22sin cos cos sin a b a b a a a a ++-=2222sin 2sin cos cos a ab b a a a a +××++2222cos 2cos sin sin a ab b a a a a -××+=()()222222sin cos sin cos a b a a a a +++=22a b +。
说明说明 在化简或求值问题中,经常用到“1”的代换,即22sin cos 1a a +=,tan cot 1a a ×=等。
等。
二、已知三角函数值,求角例2 在△ABC 中,若223cos sin 022A B æö-+-=ç÷ç÷èø(),A B ÐÐ均为锐角,求C Ð的度数。
第7章锐角三角函数(题型分类全解)

第7章锐角三角函数一、知识点梳理--------锐角三角函数【考点1】如图,在Rt △ABC 中,∠C =90°, a 、b 分别是∠A 的对边和邻边,c 是斜边。
1、正切将∠A 的对边a 与邻边b 的比叫做∠A 的正切,记作:tanA . 即:baA A A =∠∠=的邻边的对边tan2、正弦将∠A 的对边a 与斜边c 的比叫做∠A 的正弦,记作:sinA 即:c aA A =∠=斜边的对边sin3、将∠A 的邻边b 与斜边c 的比叫做∠A 的余弦,记作:cosA 即cbA A =∠=斜边的邻边cos【考点2】特殊角三角函数值【考点3】解直角三角形---------构造直角三角形 1、解直角三角形-------已知元素至少有一个是边在直角三角形中,除直角外,由直角三角形中的已知元素,求出其余未知元素的过程,叫做解直角三角形。
2、方法点拨(1)涉“斜”选“弦”的策略 ( 2) 无“斜”选“切”的策略3、方位角方位角:首先确定好基准点,然后在基准点做好坐标,规定以南北方向为始边,左右旋转即可得到方位角.4、仰角和俯角5、坡度或破比通常把坡面的铅直高度h和水平宽度l的比hl叫做坡面的坡度或坡比,坡面与水平面的夹角叫做坡角,通常用α表示,即tanα=hl.显然,坡度越大,坡角越大,坡面就越陡.6、利用解直角三角形的知识解决实际问题的过程:.(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);(2)根据问题中的条件,适当选用锐角三角函数等解直角三角形;(3)得到数学问题的答案;(4)得到实际问题的答案.二、题型分类全解1、在Rt△ABC中,∠C=90°,AB=10,sin A=35,cos A=45,tan A=34,则BC的长为( )A.6B.7.5C.8D.12.52、在Rt△ABC中,∠C=90°,若∠A=60°,AC=20 m,则BC是3、如图,在Rt △ABC 中,∠C =90°,AC =2,BC =6,解这个直角三角形.3、如图,在锐角△ABC 中,AB=10,AC=32,53sin B ,求(1)C tan (2)BC 长4.在△ABC 中,若∠C =90°,sin A =12,AB =2,则△ABC 的周长为__ __.5.在Rt △ABC 中,∠C =90°,有两边长分别为3和4,则sin A 的值为__ _.6.如图28-2-8,在△ABC 中,BD ⊥AC ,AB =6,AC =5 3,∠A =30°. (1)求BD 和AD 的长; (2)求tan C 的值.7、如图,在边长为1的小正方形网格中,点A 、B 、C 、D 都在这些小正方形的顶点上,连结CD 与AB 相交于点P ,则tan∠APD 的值是( ) A .2 B .C .D .8、如图,A 、B 、C 是小正方形的顶点,且每个小正方形的边长为1,则tan ∠BAC 的值为( )A .12B .1CD9、若a ,β是一个三角形的两个锐角,且满足2sin tan 0αβ⎫-+-=⎪⎪⎝⎭,则此三角形是________.10、如图,若直线y =-3x +3与x 轴所形成的锐角为α,求α的正切值.11、如图, 在Rt △ABC 中, ∠A=90°,AB=AC,D 为AC 上的一点,AD=13AC,求tan ∠DBC 的值12、如图,将矩形ABCD沿CE 折叠,点B 恰好落在边AD 上的点F 处,如果AB BC =23.求tan ∠DCF 的值.13、如图,在半径为3的⊙O 中,直径AB 与弦CD 相交于点E ,连接AC 、BD ,若AC =2,则cosD = .14、如图,⊙O 是△ABC 的外接圆,AB 为直径,OD ∥BC 交⊙O 于点D ,交AC 于点E ,连接AD 、BD 、CD.(1)求证:AD =CD ;(2)若AB =10,cos ∠ABC =35,求tan ∠DBC 的值.15.如图,AB 是⊙O 的直径,CD 与⊙O 相切于点C ,与AB 的延长线交于点D ,DE ⊥AD 且与AC 的延长线交于点E. (1)求证:DC =DE ;(2)若tan ∠CAB =12,AB =3,求BD 的长.16、热气球的探测器显示,从热气球看一栋楼顶部的仰角为30°,看这栋楼底部的俯角为60°,热气球与楼的水平距离为120 m.这栋楼有多高?17、如图,小明想测量河对岸的一幢高楼AB的高度,在河边C处测得楼顶A的仰角是60°,在距C处60米的E处有幢楼房,小明从该楼房距离地面20米的D处测得高楼顶端A的仰角是30°(点B,C,E在同一直线上,且AB,DE均与地面BE垂直),求楼AB的高度.18、如图一水库大坝的横断面为梯形ABCD,坝顶BC宽6米,坝高20米,斜坡AB的坡度i=1∶2.5,斜坡CD的坡角为30°,求坝底AD的长度(精确到0.1米,参考数据:2≈1.414,3≈1.732).19、如图,某建筑物BC上有一旗杆AB,小明在与BC相距12 m的F处,观测到旗杆顶部A的仰角为60°,底部B的仰角为45°,小明的眼睛E与地面的距离EF为1.6 m.(1)求建筑物BC的高度;(2)求旗杆AB的高度.(结果精确到0.1 m,参考数据:2≈1.41,3≈1.73)三、才华展示1、(8分)如图,1号楼在2号楼的南侧,两楼高度均为90m,楼间距为AB.冬至日正午,太阳光线与水平面所成的角为32.3°,1号楼在2号楼墙面上的影高为CA;春分日正午,太阳光线与水平面所成的角为55.7°,1号楼在2号楼墙面上的影高为DA.已知CD=42m.(1)求楼间距AB;(2)若2号楼共30层,层高均为3m,则点C位于第几层?(参考数据:sin32.3°≈0.53,cos32.3°≈0.85,tan32.3°≈0.63,sin55.7°≈0.83,cos55.7°≈0.56,tan55.7°≈1.47)2、(3分)如图,无人机于空中A 处测得某建筑顶部B 处的仰角为45°,测得该建筑底部C 处的俯角为17°.若无人机的飞行高度AD 为62m ,则该建筑的高度BC 为 m .(参考数据:sin17°≈0.29,cos17°≈0.96,tan17°≈0.31)4、如图,梯子斜靠在与地面垂直(垂足为O )的墙上,当梯子位于AB 位置时, 它与地面所成的角∠ ABO = 60°;当梯子底端向右滑动1 m (即BD = 1m )到达CD 位置时,它与地面所成的角∠ CDO = 51°18′,求梯子的长. (参考数据:sin 51°18′ ≈ 0.780,cos 51°18′ ≈ 0.625,tan51°18′ ≈ 1.248)。
第二十八章 锐角三角函数(单元总结)-2021学年九年级数学下册(人教版)(解析版)
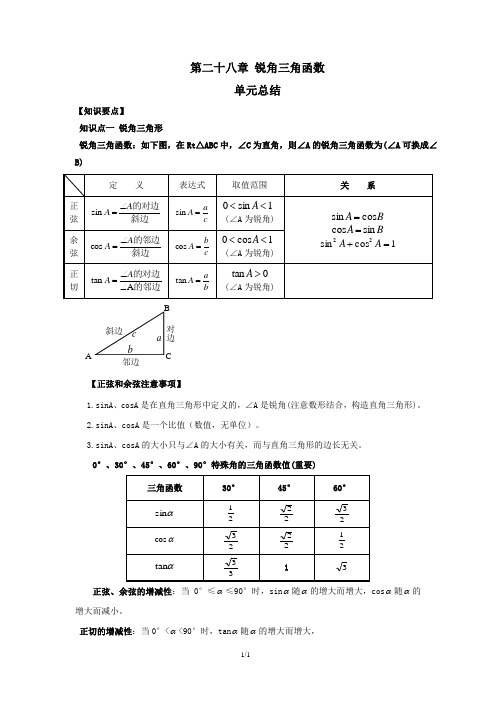
第二十八章 锐角三角函数单元总结【知识要点】 知识点一 锐角三角形锐角三角函数:如下图,在Rt △ABC 中,∠C 为直角,则∠A 的锐角三角函数为(∠A 可换成∠B)【正弦和余弦注意事项】1.sinA 、cosA 是在直角三角形中定义的,∠A 是锐角(注意数形结合,构造直角三角形)。
2.sinA 、cosA 是一个比值(数值,无单位)。
3.sinA 、cosA 的大小只与∠A 的大小有关,而与直角三角形的边长无关。
0°、30°、45°、60°、90°特殊角的三角函数值(重要)正弦、余弦的增减性:当0°≤α≤90°时,sin α随α的增大而增大,cos α随α的增大而减小。
正切的增减性:当0°<α<90°时,tan α随α的增大而增大,对边邻边C知识点二 解直角三角形一般地,直角三角形中,除直角外,共有五个元素,即三条边和两个锐角.由直角三角形中的已知元素,求出其余未知元素的过程,叫做解直角三角形. 直角三角形五元素之间的关系: 1. 勾股定理()2. ∠A+∠B=90°3. sin A==4. cos A= =5.tan A= =【考查题型】考查题型一 正弦典例1.(2020·陕西西安市·西北工业大学附属中学九年级期中)如图,在54⨯的正方形网格中,每个小正方形的边长都是1,ABC ∆的顶点都在这些小正方形的顶点上,则sin BAC ∠的值为( )A .43B .34C .35D .45【答案】D 【分析】过C 作CD AB ⊥于D ,首先根据勾股定理求出AC ,然后在Rt ACD ∆中即可求出sin BAC ∠的值.【详解】如图,过C 作CD AB ⊥于D ,则=90ADC ∠︒,∴AC =222234=+=+AC AD CD =5. ∴4sin 5CD BAC AC ∠==. 故选D . 【点睛】本题考查了勾股定理的运用以及锐角三角函数,正确作出辅助线是解题的关键.变式1-1.(2018·西城区·北京四中九年级期中)如图,在Rt ABC ∆中,90C =∠,10AB =,8AC =,则sin A 等于( )A .35B .45C .34D .43【答案】A 【解析】分析:先根据勾股定理求得BC=6,再由正弦函数的定义求解可得. 详解:在Rt △ABC 中,∵AB=10、AC=8, ∴2222=108=6AB AC --,∴sinA=63105BC AB ==. 故选:A .点睛:本题主要考查锐角三角函数的定义,解题的关键是掌握勾股定理及正弦函数的定义.变式1-2.(2019·山东淄博市·九年级期中)如图,在Rt△ABC中,∠C=90°,sin A=45,AC=6cm,则BC的长度为()A.6cm B.7cm C.8cm D.9cm 【答案】C【详解】已知sinA=45BCAB=,设BC=4x,AB=5x,又因AC2+BC2=AB2,即62+(4x)2=(5x)2,解得:x=2或x=﹣2(舍),所以BC=4x=8cm,故答案选C.考查题型二余弦典例2.(2020·福建省泉州市培元中学九年级期中)如图,△ABC的顶点都是正方形网格中的格点,则cos∠ABC等于()A 5B25C5D.23【答案】B【详解】由格点可得∠ABC所在的直角三角形的两条直角边为2,4,222425+=∴cos∠25525=.故选B .变式2-1.(2016·辽宁铁岭市·九年级期末)在ABC 中,C 90∠=,AB 6=,1cosA 3=,则AC 等于( ) A .18 B .2C .12D .118【答案】B 【分析】根据三角函数的定义,在直角三角形ABC 中,cosA =ACAB,即可求得AC 的长. 【详解】解:∵在△ABC 中,∠C =90°,∴cosA =ACAB , ∵cosA =13,AB =6,∴AC =123AB =,故答案选:B . 【点睛】本题考查了解直角三角形中三角函数的应用,解题的关键是要熟练掌握直角三角形中边角之间的关系.变式2-2.(2019·山东滨州市·九年级期末)如图,在平面直角坐标系中,点M 的坐标为M (5,2),那么cosα的值是( )A 5B .23C 25D 5【答案】D 【分析】如图,作MH⊥x轴于H.利用勾股定理求出OM,即可解决问题.【详解】解:如图,作MH⊥x轴于H.∵M(5,2),∴OH=5,MH=2,∴OM=22(5)2+=3,∴cosα=5 OHOM=,故选:D.【点睛】本题考查解直角三角形的应用,勾股定理等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.考查题型三正切典例3.(2020·广东深圳市·深圳中学八年级期中)如图,A、B、C是小正方形的顶点,且每个小正方形的边长为1,则tan∠BAC的值为()A.12B.1 C3D3【答案】B【分析】连接BC,由网格求出AB,BC,AC的长,利用勾股定理的逆定理得到△ABC为等腰直角三角形,即可求出所求. 【详解】 如图,连接BC ,由网格可得AB=BC=5,AC=10,即AB 2+BC 2=AC 2, ∴△ABC 为等腰直角三角形, ∴∠BAC=45°, 则tan ∠BAC=1, 故选B .【点睛】本题考查了锐角三角函数的定义,解直角三角形,以及勾股定理,熟练掌握勾股定理是解本题的关键.变式3-1.(2018·江苏苏州市·九年级期末)如图,在等腰Rt ABC ∆中,90C ∠=︒,6AC =,D 是AC 上一点,若1tan 5DBA ∠=,则AD 的长为( ).A .2B .3C .2D .1【答案】A 【解析】分析:本题考查等腰直角三角形的性质及解直角三角形.解题的关键是作辅助线,构造直角三角形,运用三角函数的定义建立关系式然后求解. 解析:如图,作DE ⊥AB 于E .∵tan ∠DBA==,∴BE=5DE .∵△ABC 为等腰直角三角形,∴∠A=45°,∴AE=DE .∴BE=5AE ,又∵AC=6,∴AB=6,∴AE+BE=AE+5AE=6,∴AE=,∴在等腰直角△ADE中,由勾股定理,得AD=,AE=2.故选A.变式3-2.(2020·河北唐山市·九年级期末)如图,有一斜坡AB,坡顶B离地面的高度BC为30m,斜坡的倾斜角是∠BAC,若2tan5BAC∠=,则此斜坡的水平距离AC为()A.75m B.50m C.30m D.12m 【答案】A【分析】根据BC的长度和tan BAC∠的值计算出AC的长度即可解答.【详解】解:因为2tan5BCBACAC=∠=,又BC=30,所以,3025AC=,解得:AC=75m,所以,故选A.【点睛】本题考查了正切三角函数,熟练掌握是解题的关键.考查题型四特殊角的三角函数值典例4.(2018·南昌市期末)点M(-sin60°,cos60°)关于x轴对称的点的坐标是( )A.(32,12) B.(-32,-12)C.(312) D.(-123【答案】B 【详解】∵点(-sin60°,cos60°)即为点(312),∴点(-sin60°,cos60°)关于y 3,12).变式4-1.(2019·山东淄博市·九年级期中)下列式子错误的是()A.cos40°=sin50°B.tan15°•tan75°=1C.sin225°+cos225°=1 D.sin60°=2sin30°【答案】D【详解】试题分析:选项A,sin40°=sin(90°﹣50°)=cos50°,式子正确;选项Btan15°•tan75°=tan15°•cot15°=1,式子正确;选项C,sin225°+cos225°=1正确;选项D,sin60°=3,sin30°=12,则sin60°=2sin30°错误.故答案选D.变式4-2.(2018·河北唐山市·九年级期末)如果△ABC中,sin A=cos B=22,则下列最确切的结论是()A.△ABC是直角三角形B.△ABC是等腰三角形C.△ABC是等腰直角三角形D.△ABC是锐角三角形【答案】C【解析】因为sin A=cos B 2,所以∠A=∠B=45°,所以△ABC是等腰直角三角形. 故选C.考查题型五同角的三角函数典例5.(2018·山东潍坊市·九年级期末)在Rt△ABC中,∠C =90°,sinA=45,则cosB的值等于( )A.35B.45C.34D5【答案】B 【解析】在Rt△ABC中,∠C=90°,∠A+∠B=90°,则cos B=sin A=45.故选B.点睛:本题考查了互余两角三角函数的关系.在直角三角形中,互为余角的两角的互余函数变式5-1.(2018·浙江台州市·九年级期末)在Rt △ABC 中,cosA= 12,那么sinA 的值是( )A .2B .2C .3D .12【答案】B 【分析】利用同角三角函数间的基本关系求出sinA 的值即可. 【详解】:∵Rt △ABC 中,cosA=12 ,∴ =2, 故选B . 【点睛】本题考查了同角三角函数的关系,以及特殊角的三角函数值,熟练掌握同角三角函数的关系是解题的关键.变式5-2.(2018·湖南岳阳市·九年级期末)在Rt ABC 中,C 90∠=,如果4cosA 5=,那么tanA 的值是( ) A .35B .53C .34D .43【答案】C 【分析】本题可以利用锐角三角函数的定义求解. 【详解】解:∵在Rt △ABC 中,∠C=90°,∴cosA=b c ,tanA=ab ,a 2+b 2=c 2. ∵cosA=45,设b=4x ,则c=5x ,a=3x .∴tanA=a b =3344x x =. 故选C.【点睛】利用锐角三角函数的定义,通过设参数的方法求三角函数值.考查题型六 解直角三角形典例6.(2020·东北师大附中明珠学校九年级期中)如图,两根竹竿AB 和AD 斜靠在墙CE 上,量得∠ABC=α,∠ADC=β,则竹竿AB 与AD 的长度之比为( )A .tan tan αβB .sin sin βαC .sin sin αβD .cos cos βα【答案】B【分析】在两个直角三角形中,分别求出AB 、AD 即可解决问题;【详解】在Rt △ABC 中,AB=AC sin α, 在Rt △ACD 中,AD=AC sin β, ∴AB :AD=AC sin α:AC sin β=sin sin βα, 故选B .【点睛】 本题考查解直角三角形的应用、锐角三角函数等知识,解题的关键是学会利用参数解决问题. 变式6-1.(2020·山东枣庄市·九年级期末)如图,在ABC ∆中,144CA CB cosC ==,=,则sinB 的值为( )A .10B .15C .6D .10 【答案】D【分析】过点A 作AD BC ⊥,垂足为D ,在Rt ACD ∆中可求出AD ,CD 的长,在Rt ABD ∆中,利用勾股定理可求出AB 的长,再利用正弦的定义可求出sinB 的值.【详解】解:过点A 作AD BC ⊥,垂足为D ,如图所示.在Rt ACD ∆中,1CD CA cosC ⋅==,2215AD AD CD ∴=-=;在Rt ABD ∆中,315BD CB CD AD =﹣=,=,22BD AD 26AB ∴=+=,AD 10sin AB B ∴==. 故选:D .【点睛】考查了解直角三角形以及勾股定理,通过解直角三角形及勾股定理,求出AD ,AB 的长是解题的关键.变式6-2.(2019·辽宁沈阳市·九年级期末)如图,甲乙两楼相距30米,乙楼高度为36米,自甲楼顶A 处看乙楼楼顶B 处仰角为30°,则甲楼高度为( )A.11米B.(36﹣153)米C.153米D.(36﹣103)米【答案】D【分析】分析题意可得:过点A作AE⊥BD,交BD于点E;可构造Rt△ABE,利用已知条件可求BE;而乙楼高AC=ED=BD﹣BE.【详解】解:过点A作AE⊥BD,交BD于点E,在Rt△ABE中,AE=30米,∠BAE=30°,∴BE=30×tan30°=103(米),∴AC=ED=BD﹣BE=(36﹣103)(米).∴甲楼高为(36﹣103)米.故选D.【点睛】此题主要考查三角函数的应用,解题的关键是熟知特殊角的三角函数值.考查题型七利用解直角三角形相关知识解决实际问题典例7.(2019·河南许昌市·九年级期末)如图,某消防队在一居民楼前进行演习,消防员利用云梯成功救出点B 处的求救者后,又发现点B 正上方点C 处还有一名求救者.在消防车上点A 处测得点B 和点C 的仰角分别是45°和65°,点A 距地面2.5米,点B 距地面10.5米.为救出点C 处的求救者,云梯需要继续上升的高度BC 约为多少米?(结果保留整数.参考数据:tan65°≈2.1,sin65°≈0.9,cos65°≈0.4,2≈1.4)【答案】云梯需要继续上升的高度BC 约为9米.【分析】过点A 作AM EF ⊥于点M ,AD BC ⊥于点D ,在Rt ABD ∆中,求得AD 的长;在Rt ACD ∆中,求得CD 的长,根据BC=CD-BD 即可求得BC 的长.【详解】过点A 作AM EF ⊥于点M ,AD BC ⊥于点D ,∵CN EF ⊥ ,∴90AMN MND ADN ∠=∠=∠=︒,∴四边形AMND 为矩形.∴ 2.5DN AM ==米.∴10.5 2.58BD BN DN =-=-=(米),由题意可知,45BAD ∠=︒,65CAD ∠=︒,∵AD BC ⊥,∴90ADB ∠=︒,在Rt ABD ∆中,tan BD BAD AD ∠=, ∴88tan tan45BD AD BAD ===∠︒(米). 在Rt ACD ∆中,tan CD CAD AD∠=, ∴tan 8tan658 2.116.8CD AD CAD =⋅∠=︒≈⨯=(米).∴16.888.89BC CD BD =-≈-=≈(米).答:云梯需要继续上升的高度BC 约为9米.【点睛】本题考查解直角三角形﹣仰角俯角问题,添加辅助线,构造直角三角形,建立直角三角形模型是解决问题的关键.变式7-1.(2018·江苏无锡市·九年级期末)如图,为了测量出楼房AC 的高度,从距离楼底C 处603米的点D (点D 与楼底C 在同一水平面上)出发,沿斜面坡度为i=1:3的斜坡DB 前进30米到达点B ,在点B 处测得楼顶A 的仰角为53°,求楼房AC 的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈43,计算结果用根号表示,不取近似值).【答案】153+【分析】如图作BN ⊥CD 于N ,BM ⊥AC 于M ,先在RT △BDN 中求出线段BN ,在RT △ABM 中求出AM ,再证明四边形CMBN 是矩形,得CM=BN 即可解决问题.【详解】如图作BN ⊥CD 于N ,BM ⊥AC 于M .在RT △BDN 中,BD=30,BN :ND=13,∴BN=15,DN=153,∵∠C=∠CMB=∠CNB=90°,∴四边形CMBN是矩形,∴CM=BM=15,BM=CN=603153453-=,在RT△ABM中,tan∠ABM=43 AMBM=,∴AM=603,∴AC=AM+CM=15603+.【点睛】构造适当的直角三角形,并应用锐角的三角函数,正确理解坡比的概念.变式7-2.(2018·山西晋中市期末)“高低杠”是女子体操特有的一个竞技项目,其比赛器材由高、低两根平行杠及若干支架组成,运动员可根据自己的身高和习惯在规定范围内调节高、低两杠间的距离.某兴趣小组根据高低杠器材的一种截面图编制了如下数学问题,请你解答.如图所示,底座上A,B两点间的距离为90cm.低杠上点C到直线AB的距离CE的长为155cm,高杠上点D到直线AB的距离DF的长为234cm,已知低杠的支架AC与直线AB的夹角∠CAE为82.4°,高杠的支架BD与直线AB的夹角∠DBF为80.3°.求高、低杠间的水平距离CH的长.(结果精确到1cm,参考数据sin82.4°≈0.991,cos82.4°≈0.132,tan82.4°≈7.500,sin80.3°≈0.983,cos80.3°≈0.168,tan80.3°≈5.850)【答案】高、低杠间的水平距离CH 的长为151cm .【解析】分析:利用锐角三角函数,在Rt △ACE 和Rt △DBF 中,分别求出AE 、BF 的长.计算出EF .通过矩形CEFH 得到CH 的长.详解:在Rt △ACE 中,∵tan ∠CAE=CE AE, ∴AE=()15515521tan tan82.47.5CE cm CAE =≈≈∠︒ 在Rt △DBF 中,∵tan ∠DBF=DF BF, ∴BF=()23423440tan tan80.3 5.85DF cm DBF =≈=∠︒. ∵EF=EA+AB+BF≈21+90+40=151(cm )∵CE ⊥EF ,CH ⊥DF ,DF ⊥EF∴四边形CEFH 是矩形,∴CH=EF=151(cm ).答:高、低杠间的水平距离CH 的长为151cm .点睛:本题考查了锐角三角函数解直角三角形.题目难度不大,注意精确度.。
第01讲 锐角三角函数和特殊角的三角函数(知识解读+真题+巩固)(学生版)

第01讲锐角三角函数和特殊角的三角函数1.理解锐角正弦、余弦和正切概念的意义,并会求锐角的正弦值、余弦值和正切值;2.会推算30°、45°、60°角的三角函数值,并熟练准确的记住特殊角的三角函数值;3.理解并能熟练运用“同角三角函数的关系”及“锐角三角函数值随角度变化的规律”.知识点1锐角三角函数的概念如图所示,在Rt△ABC 中,∠C=90°,∠A 所对的边BC 记为a,叫做∠A 的对边,也叫做∠B 的邻边,∠B所对的边AC 记为b,叫做∠B 的对边,也是∠A 的邻边,直角C 所对的边AB 记为c,叫做斜边.锐角A 的对边与斜边的比叫做∠A 的正弦,记作sinA,即sin A aA c ∠==的对边斜边;锐角A 的邻边与斜边的比叫做∠A 的余弦,记作cosA,即cos A bA c ∠==的邻边斜边;锐角A 的对边与邻边的比叫做∠A 的正切,记作tanA,即tan A aA A b∠==∠的对边的邻边.同理sin B b B c ∠==的对边斜边;cos B a B c ∠==的邻边斜边;tan B bB B a∠==∠的对边的邻边.注意:(1)正弦、余弦、正切函数是在直角三角形中定义的,反映了直角三角形边与角的关系,是两条线段的比值.角的度数确定时,其比值不变,角的度数变化时,比值也随之变化.(2)sinA,cosA,tanA分别是一个完整的数学符号,是一个整体,不能写成,,,不能理解成sin 与∠A,cos 与∠A,tan 与∠A 的乘积.书写时习惯上省略∠A 的角的记号“∠”,但对三个大写字母表示成的角(如∠ABC),其正切应写成“tan∠ABC”,不能写成“tanABC”;另外,、、常写成、、.ACa(3)任何一个锐角都有相应的锐角三角函数值,不因这个角不在某个三角形中而不存在.(4)由锐角三角函数的定义知:当角度在0°<∠A<90°间变化时,,,tanA>0知识点2锐角三角函数的增减性(1)在0°-90°之间,锐角的正弦值随角度的增大而增大;(2)在0°-90°之间,锐角的余弦值随角度的增大而减小;(3)在0°-90°之间,锐角的正切值随角度的增大而增大.知识点2特殊角的三角函数值锐角注意:(1)通过该表可以方便地知道30°、45°、60°角的各三角函数值,它的另一个应用就是:如果知道了一个锐角的三角函数值,就可以求出这个锐角的度数,例如:若,则锐角.(2)仔细研究表中数值的规律会发现:、、的值依次为、、,而、、的值的顺序正好相反,、、的值依次增大,其变化规律可以总结为:①正弦、正切值随锐角度数的增大(或减小)而增大(或减小);②余弦值随锐角度数的增大(或减小)而减小(或增大).知识点3锐角三角函数之间的关系如图所示,在Rt△ABC中,∠C=90°.(1)互余关系:,;(2)平方关系:;(3)倒数关系:或;(4)商数关系:.注意:锐角三角函数之间的关系式可由锐角三角函数的意义推导得出,常应用在三角函数的计算中,计算时巧用这些关系式可使运算简便.【题型1锐角三角函数的概念】【典例1】(2022秋•西岗区校级期末)在Rt△ABC中,∠C=90°,AB=5,BC=3,则tanA的值是()A.B.C.D.【变式1-1】(2022秋•金山区校级期末)在Rt△ABC中,∠C=90°,BC=1,AB=3,下列各式中,正确的是()A.sinA=B.cosA=C.tanA=D.cotA=【变式1-2】(2022秋•晋江市期末)在Rt△ABC中,∠C=90°,sinA=,BC=6,则AC=()A.10B.8C.5D.4【变式1-3】(2022秋•贵池区期末)如图,在Rt△ABC中,∠C=90°,AB=13,BC=12,下列三角函数正确的是()A.sinB=B.cosA=C.tanB=D.cosB=【题型2锐角三角函数的增减性】【典例2】(2022秋•兴隆县期中)如果∠α为锐角,且sinα=0.6,那么α的取值范围是()A.0°<α≤30°B.30°<α<45°C.45°<α<60°D.60°<α≤90°【变式2-1】(2021秋•周村区期末)已知cosα=,则锐角α的取值范围是()A.0°<α<30°B.30°<α<45°C.45°<α<60°D.60°<α<90°【变式2-2】(2022•五通桥区模拟)若锐角α满足cosα<且tanα<,则α的范围是()A.30°<α<45°B.45°<α<60°C.60°<α<90°D.30°<α<60°【变式2-3】(2022春•洪泽区校级月考)比较大小:sin80°sin50°(填“>”或“<”).【题型3特殊角三角函数值】【典例3】(2023•红桥区二模)tan30°的值等于()A.B.C.1D.【变式3-1】(2022秋•云州区期末)已知∠α为锐角,且sinα=,则∠α=()A.30°B.45°C.60°D.90°【变式3-2】(2023秋•莘县校级月考)在△ABC中,若cosA=,tanB=,这个三角形一定是()A.锐角三角形B.直角三角形C.钝角三角形D.等腰三角形【变式3-3】(2023•江都区模拟)在△ABC中,若|sinA﹣|+(﹣cosB)2=0,则∠C的度数是()A.45°B.75°C.105°D.120°【题型4同角三角函数的关系】【典例4】(2023秋•沙坪坝区校级月考)在Rt△ABC中,∠C=90°,cosA=,则tanA的值为()A.B.C.D.8【变式4-1】(2023•泉州一模)在Rt△ABC中,∠C=90°,sinA=,则cosA的值等于()A.B.C.D.【变式4-2】(2022秋•渌口区期末)在Rt△ABC中,∠C=90°,若cosA=,则sinA的值为()A.B.C.D.【变式4-3】(2022秋•石景山区校级期末)在△ABC中,∠C=90°,,则sinA的值是()A.B.C.D.【题型5互余两角三角函数的关系】【典例5】(2023秋•南岗区校级月考)在Rt△ABC中,∠C=90°,,则tanB等于()A.B.C.D.【变式5-1】(2022秋•磴口县校级期末)在Rt△ABC中,∠C=90°,sinA=,则cosB的值为()A.B.C.D.【变式5-2】(2023春•普陀区期中)在Rt△ABC中,∠C=90°,若sinA=,则cosB=()A.B.C.D.【变式5-3】(2022秋•太康县期末)在三角形ABC中,∠C为直角,sinA=,则tanB的值为()A.B.C.D.【变式5-4】(2022秋•池州期末)在Rt△ACB中,∠C=90°,,则sinB的值为()A.B.C.D.【题型6三角函数的计算】【典例6】(2023秋•聊城月考)计算:(1)2cos30°﹣tan60°+sin45°cos45°;(2)(﹣1)2023+2sin45°﹣cos30°+sin60°+tan260°.【变式6-1】(2022秋•浦东新区期末)计算:4sin45°﹣2tan30°cos30°+.【变式6-2】(2022秋•济南期末)计算:sin30°﹣tan30°•tan60°+cos245°.【变式6-3】(2023•虹口区一模)计算:cos245°﹣+cot230°.1.(2021•云南)在△ABC中,∠ABC=90°.若AC=100,sinA=,则AB的长是()A.B.C.60D.802.(2021•天津)tan30°的值等于()A.B.C.1D.23.(2019•怀化)已知∠α为锐角,且sinα=,则∠α=()A.30°B.45°C.60°D.90°4.(2022•滨州)在Rt△ABC中,若∠C=90°,AC=5,BC=12,则sinA的值为.5.(2022•广东)sin30°=.6.(2022•荆门)计算:+cos60°﹣(﹣2022)0=.7.(2022•金华)计算:(﹣2022)0﹣2tan45°+|﹣2|+.1.(2022秋•大名县校级期末)在Rt△ABC中,∠C=90°,BC=1,AC=,那么tanB的值是()A.B.C.D.2.(2022秋•泰兴市期末)在Rt△ABC中,各边都扩大5倍,则锐角A的正切函数值()A.不变B.扩大5倍C.缩小D.不能确定3.(2023•西陵区模拟)由小正方形组成的网格如图,A,B,C三点都在格点上,则∠ABC的正切值为()A.B.C.D.4.(2023•南岗区校级模拟)在Rt△ABC中,∠C=90°,AC=6,sinA=,则AB的值为()A.8B.9C.10D.125.(2022秋•阜平县期末)计算:sin60°•tan30°=()A.1B.C.D.26.(2023•偃师市模拟)计算sin45°的值等于()A.B.C.D.7.(2023•西湖区模拟)如图,在△ABC中,∠C=90°,定义:斜边与∠A的对边的比叫做∠A的余割,用“cscA”表示.如设该直角三角形的三边分别为a,b,c,则,那么下列说法正确的是()A.cscB•sinA=1B.C.cscA•cosB=1D.csc2A+csc2B=18.(2022秋•清水县校级期末)在Rt△ABC中,∠C=90°,若cosA=,则tanB的值为()A.B.C.D.9.(2022秋•蚌埠月考)在Rt△ABC中,∠C=90°,sinA=,∠B等于()A.60°B.30°C.45°D.无法确定10.(2022•滨州)下列计算结果,正确的是()A.(a2)3=a5B.=3C.=2D.cos30°=11.(2022秋•路北区校级期末)已知6cosα=3,且α是锐角,则α=()A.75°B.60°C.45°D.30°12.(2022秋•内乡县期末)在△ABC中,若|sinA﹣|+(﹣cosB)2=0,则∠C的度数是.13.(2023•新邵县二模)在Rt△ABC中,∠C=90°,若sinA=,则cosB=.14.(2022秋•离石区期末)在△ABC中,若,∠A,∠B都是锐角,则△ABC是三角形.15.(2022秋•新城区期末)计算:sin45°•cos45°﹣tan60°÷cos30°.。
用锐角三角函数概念解题的常见方法(含答案11页)

用锐角三角函数概念解题的常见方法知识要点1.锐角三角函数(1)锐角三角函数的定义我们规定:sinA=ac,cosA=bc,tanA=ab,cotA=ba.锐角的正弦、余弦、正切、余切统称为锐角的三角函数.(2)用计算器由已知角求三角函数值或由已知三角函数值求角度对于特殊角的三角函数值我们很容易计算,甚至可以背诵下来,但是对于一般的锐角又怎样求它的三角函数值呢?用计算器可以帮我们解决大问题.①已知角求三角函数值;②已知三角函数值求锐角.2αsinαcosαtanαcotα30º123233345º22221 160º3212333直角三角形中,30°的锐角所对的直角边等于斜边的一半. 3.锐角三角函数的性质(1)0<sinα<1,o<cosα<1(0°<α<90°)(2)tan α·cot α=1或tan α=1cot α; (3)tan α=sin cos αα,cot α=cos sin αα. (4)sin α=cos (90°-α),tan α=cot (90°-α).方法点拨有关锐角三角函数的问题,常用下面几种方法: 一、设参数例1. 在ABC ∆中,︒=∠90C ,如果125tan =A ,那么sinB 的值等于( ) 512.125.1312.135.D C B A 解析:如图1,要求sinB 的值,就是求AB AC 的值,而已知的125tan =A ,也就是125=AC BC 可设k AC k BC 125==, 则k k k AB 13)12()5(22=+=13121312sin ==∴k k B ,选B 二、巧代换例2. 已知3tan =α,求ααααcos sin 5cos 2sin +-的值。
解析:已知是正切值,而所求的是有关正弦、余弦的值,我们可以利用关系式3cos sin tan ==ααα,作代换ααcos 3sin =,代入即可达到约分的目的,也可以把所求的分式的分子、分母都除以αcos 。
中考《锐角三角函数》解题策略

中考《锐角三角函数》解题策略《锐角三角函数》是中考的必考点,与相似三角形等知识点结合,极具灵活性.这要求我们在理解直角三角形中五个元素的关系、运用勾股定理、直角三角形的两个锐角互余及锐角三角函数解直角三角形的基础上,会把实际问题转化为解直角三角形问题,从而会把实际问题转化为数学问题来解决.我们可以从以下几方面找到《锐角三角函数》解题策略,达到以“不变”应“万变”的功效。
一、基础知识(一)锐角三角函数的定义如下图,在Rt△ABC中,∠C=900,AB=c,AC=b,BC=a,则∠A的:1 .正弦:2.余弦:3 .正切:(二)特殊角的三角函数值注:我们很多学生在考试时因为紧张等原因,常常出现竟然把特殊锐角的有三角函数值记错了现象,因此我们只要要求学生记住右边的两个特殊直角三角形,就记住了特殊角的三角函数值了,就不会出错了。
(三)规律探索1.(1);(2)tanA=2.(1)sinA=cos(90°一 A)=cosB;(2)cosA=sin(90°一A)=sinB3.(1)0<sinA<1;0<cosA<14.三角函数值的变化规律(1)当角度在0°— 90°间变化时,正弦值随着角度的增大而增大;(2)当角度在0°—90°间变化时,余弦值随着角度的增大而减小。
(3)450的正弦值等于其余弦值。
(四)应用中的常识1 .仰角、俯角:在视线与水平线所成的锐角中,视线在水平线上方的角叫;视线在水平线下方的角叫。
(如图1示)2.坡度(坡比)、坡角:坡面的铅直高度h和水平宽度l的比叫坡度(坡比),用字母i表示;坡面与水平线的夹角a叫坡角,i=tana=。
(如图2示)3.方向角:一般指以观测者的位置为中心,将正北或正南方向作为起始方向旋转到目标方向线所成的角(一般指锐角),通常表达成北(南)偏东(西)××度。
如图,A点位于O点的北偏东300方向,B点位于O点的南偏东600方向,C点位于O点的北偏西450方向(或西北方向)。
专题11 锐角三角函数重难点题型专训(7大题型)(解析版)

专题11锐角的三角函数重难点题型专训(7大题型)【题型目录】题型一正弦、余弦与正切的概念辨析题型二求角的正弦值题型三已知正弦值求边长题型四求角的余弦值题型五已知余弦值求边长题型六求角的正切值题型七已知正切值求边长【知识梳理】知识点1:正切与余切1.正切直角三角形中一个锐角的对边与邻边的比叫做这个锐角的正切(tangent ).锐角A 的正切记作tan A .tan A BC a A A AC b锐角的对边锐角的邻边.2.余切直角三角形中一个锐角的邻边与对边的比叫做这个锐角的余切(cotangent ).锐角A 的余切记作cot A .cot A AC b A A BC a锐角的邻边锐角的对边.ac A BC b知识点2:正弦与余弦1.正弦直角三角形中一个锐角的对边与斜边的比叫做这个锐角的正弦(sine ).锐角A 的正弦记作sin A .sin A BC a A AB c锐角的对边斜边.2.余弦直角三角形中一个锐角的邻边与斜边的比叫做这个锐角的余弦(cosine ).锐角A 的余弦记作cos A .cos A AC b A AB c 锐角的邻边斜边.a c A BC b【经典例题一正弦、余弦与正切的概念辨析】1.(2023上·福建泉州·九年级校考期中)若A 是锐角,下列说法正确的是()A .tan sin A AB . 2sin 1sin 1A AC . cos tan 90A AD .sin cos 1A A 【答案】A【分析】本题考查三角函数.根据三角函数的定义和性质,逐一进行判断即可.【详解】解:如图,90C ,则:tan ,sin a a A A b c,∵b c ,∴tan sin A A ;故A 正确;∵0sin 1A ,∴ 2sin 11sin A A ;故B 错误;∵ cos ,tan 90tan b b A A B c a,∴ cos tan 90A A ;故C 错误;∵sin ,cos a b A A c c ,35BC AB ,设3BC k ,由勾股定理得:cos AC A AB 故选:C .【点睛】本题考查了锐角三角函数,勾股定理,熟练掌握锐角三角函数的定义是解题关键.3.(2021上格点上,则,得出∵CD是斜边AB∴A ACD(1)利用锐角三角函数的定义求证:(2)若tan 2 ,求sin cos sin cos 【答案】(1)见解析(2)3【经典例题二求角的正弦值】A.12【答案】B【分析】本题考查网格中求三角函数值,三角函数定义,勾股定理及其逆定理,连接设小正方形边长为22AB24A .34【答案】C【分析】本题考查圆周角定理,求角的正弦值.连接OBF ACD ,得到∵F 为弦BC 的中点,∴,OF BC BOF ∴90OBF BOF ∵CD AB ,是解题的关键.由题意知,22AC BC AB ∴222222sin sin BC AC A B AB AB 故答案为:1.4.(2023上·广西贵港·九年级统考期中)如图,在【答案】55/155【分析】本题考查正方形的性质,E 、C 、B 共线,再根据角三角形解决问题.【详解】解:如图,连接设正方形的边长为a ,由题意得∴AEC AEF ∴E 、C 、B 共线,【经典例题三已知正弦值求边长】A.2【答案】C【分析】连接OB、OC求出【点睛】本题考查了圆周角定理,等腰三角形的性质,特殊角的三角函数,解题关键是利用圆周角定理和等腰三角形的性质求出 3.(2023上·重庆万州·九年级重庆市万州第二高级中学校考期中)则cos A 的值为.【答案】215【分析】本题考查了三角函数:则5AB k ,由勾股定理可求得【详解】解:如图,∵sin 52BC A AB,∴设2BC k ,其中k 由勾股定理得AC AB =54.(2023下·九年级课时练习)在【答案】21或11【详解】如下图,过点AD AB Bsin满足的条件是两边一角,【易错点分析】条件中ABC所以对三角形的形状、大小进行确定性判断是不漏解的重要方法.5.(2023上·上海崇明·九年级校联考期中)如图,在(1)求BC的长.(2)若点D在BC边上,且在Rt ABE △中,∵3sin 5AE B AB,AB ∵:3:2BD CD ,BC ∴6BD ,4CD ,在Rt DHC △中,tan C【经典例题四求角的余弦值】则23BC AC ,23BC AC ,∴22223AB AC AC B C∵ 1,2A,【答案】2 2【分析】连接AF,由矩形的性质可得中点可得DE CE∵四边形ABCD是矩形,2AB CD,AD∵点E是CD的中点,11DE CE CD(1)求AC的长;(2)求cos OCA与tan B 的值.【答案】(1)AC的长为12(2)12cos13OCA,tan B【分析】本题考查了直角三角形中,斜边的上的中线等于斜边的一半,勾股定理,求角的余弦和正切等知识点.熟记相关几何结论是解题关键.(1)由“斜边的上的中线等于斜边的一半(2)由“斜边的上的中线等于斜边的一半定义即可求解.【详解】(1)解:ACB∵213AB CO.5BC∵,【经典例题五已知余弦值求边长】A.212B.9【答案】C【分析】根据题意得出CD边上一点,A .94B .125【答案】A【分析】根据4AC ,4cos 5A,可求出【详解】∵Rt ABC △,4AC ,cos A【点睛】本题考查了锐角三角函数,勾股定理,圆周的侧面积,熟练掌握圆锥的侧面积公式是解题关键.4.(2022秋·九年级单元测试)如图所示,在四边形2BE ,则sin DBE【答案】255/255【分析】先根据余弦的定义可得AD AB AE BE可求出x的值,从而可得(1)求证;BEA ADC∽(2)求证:··CD AD AC BE(3)若2AD 5,cos ABE 【答案】(1)见解析【经典例题六求角的正切值】A .27【答案】C【分析】证明ABE △A.13B【答案】A【分析】根据题意,先证明CDE ADE ADC,【答案】12/0.5【分析】根据折叠的性质可得Rt AED△,再利用正切函数的定义求解.【答案】1174【分析】由题意可知,90CAH ACB,可得,∵EF BC,∴AH EF∴CAH CEF ,∴BCD CEF ,ABCD (1)求证:CDE CBF △△≌;(2)求CF 的长;(3)求tan BCF 的值.【答案】(1)见解析(2)35CF∵CDE CBF △△≌,∴45FBR EDC ,∴BRF △是等腰直角三角形,RF RB ,【经典例题七已知正切值求边长】在边AD A .53B .2【答案】A【分析】连接AP ,根据折叠的性质和平行线的性质,求得DF 的长度,根据勾股定理即可求得答案.【详解】如图所示,连接AP 根据折叠的性质可知AE EF ∴1tan 3EF FBE BF .∵FP AD ∥,∴AEB EPF .∴FEB EPF .∴PF EF .∴AE EF AP PF .∵180DEF DFE D ∴DEF BFC .又D C ,∴DEF CFB △∽△.∴13EF DF BF BC .A.4033B.3340【答案】A【分析】作BH AD于H,延长∵4tan 3BH BAD AH ,∴令4BH x ,3AH x ,∴255AB BH DH x ,【答案】313【分析】点G 为求出AD ,利用正切的定义求出∵点G 为ABC ∴BD 是中线,∴132AD AC ∵1tan ABG90PQO ,∵4tan 3O ,43PQ OQ , 设4PQ x ,则3OQ x ,同理可求3OQ ,1MQ ,4OM OQ MQ ;综上所述:2OM 或4.故答案:2或4.(1)求证:四边形BCEF (2)BG CE 于点G ,连结①求CG 的长.②求平行四边形BCEF 【答案】(1)见解析BG的结论,勾股定理求得∵是CE的中点,GEC EG CG,22∵四边形BCEF是平行四边形,,EF BCFB EC设EG CG x,则FB【重难点训练】九年级校考阶段练习)如图,融创乐园彩虹滑梯的高度为A .cos h【答案】D∵90,BCA CD 是∴5CD AD BD ∴10,AB ACD ∵6BC ,A .BDBC B .BCAB 【答案】C【分析】此题主要考查了锐角三角函数的定义,得出【详解】解:∵AC BC CD AB ,∵四边形ABCD 是菱形,∴AC BD AB BC ,∴22OB AB AO∵3PC AP ,∴118422AP AC ,∴448OP AO AP ,∴3tan 8OB BPC OP,【答案】55/155【分析】题目主要考查勾股定理解三角形及其逆定理,余弦函数的定义,先根据勾股定理的逆定理判断出ABC 的形状,再由锐角三角函数的定义即可得出结论.【详解】解:∵由图可知,【答案】2【分析】本题考查了三角形内角和定理,作垂线,正弦.熟练掌握作垂线,由作图可知,CF是BD的垂直平分线,根据【答案】5 8【分析】此题主要考查了正方形性质,全等三角形的判定和性质,相似三角形的判定和性质,解直角三角形,求出BM是解本题的关键.根据正方形性质,证明(1)tan FEC(2)若15AB ,则CF【答案】377/37【答案】②③【分析】本题考查了三角形综合.交BD于点H,由2sin3D 即可求出由勾股定理即可求解,④过点在PDC中,利用三角形的三边关系即可求出∵2sin 3D ,2AD ,∴24sin 233AH AD D∴1144223ABD S BD AH △③∵2AD ,4BD ,1AD ∵90ABC ,1tan 2BAC ∴1tan tan 2DAP BAC,∴12DP AD ,【答案】菱形的边长为26cm 【分析】本题考查菱形的性质、,得出(1)以O 点为旋转中心,将ABC 逆时针方向旋转(2)画出A 关于直线1BB 的对称点D ;(3)在1AC 上画点P ,使1tan 3ACP【答案】(1)画图见解析,131C , (2)画图见解析(3)画图见解析,延长∴ 131C , ;(2)如图,D 即为所求,(3)如图,P 即为所求;【点睛】本题考查的是复杂作图,旋转的性质,轴对称的性质,全等三角形的判定与性质,平行线分线段成比例的应用,锐角三角函数的应用,掌握扎实的基础知识并应用于作图是解本题的关键.15.(2023上·安徽六安·九年级统考阶段练习)如图,于E ,点M 在AC 上,且AM AD ,连接(1)求证:2CF GE AE (2)求FM MG的值;(3)求tan CMF 的值.【答案】(1)证明见解析(2)222FM MG,再由等腰三角形的性质得。
锐角三角函数应用题的方法与技巧

锐角三角函数应用题的方法与技巧
x
《锐角三角函数应用题的方法与技巧》
一、总体思路
1、识别出三角形所涉及的三角函数,并确定三角函数的参数:根据题干里面提供的线段、角度等长度或角度来初步判断三角形的形状,并由此来计算出三个角度和三条边。
2、判断题目的性质:根据题目要求,判断出是求边长还是求角度。
3、解答:
(1)求边长:利用相应的三角函数关系(正弦定理、余弦定理、正切定理等),求出答案;
(2)求角度:利用相应的三角函数关系,求出角度的三角函数值,再用反三角函数求出角度。
二、技巧总结
1、画图法:根据题干中提供的信息,画出准确的三角形图形,便于计算和判断。
2、直角三角形快速求角度:根据对边比斜边的特点,找出角度所对应的三角函数值,再用反三角函数计算出角度。
3、正弦定理、余弦定理:正弦定理可用于计算夹角的一边的长度,余弦定理可用于求另一边的长度。
4、正切定理:正切定理可以用于求夹角的角度大小。
5、各种三角函数的关系:在计算三个角度的大小时,可以利用三个角度的和为180°;在计算三条边的长度时,可以利用三条边之和的性质。
数学九年级培优第25讲 《锐角三角函数》

第二十八章锐角三角函数第25讲锐角三角函数知识导航1.正弦、余弦、正切的概念及表示方法.2.特殊角的三角函数值.【板块一】求锐角三角函数值方法技巧1.结合图形,理解并牢记三角函数的定义.2.数形结合法熟记特殊角的三角函数值.3.求一个角的三角函数值,一般利用已有的或构造的直角三角形,也可以利用等角转化等,结合三角函数定义求解.题型一紧扣定义求三角函数值【例1】已知锐角α满足tanα=12,求sinα的值.【解析】在Rt△ABC中,∠C=90°,∠A=α,∵tanα=12BCAC=,∴设BC=x,AC=2x,∴AB,∴sinBCABα===【点评】由于三角函数的定义是基于直角三角形,所以要画出符合题意的直角三角形,结合勾股定理和三角函教的定义求解.【例2】如图,在正方形ABCD中,点M为AD的中点,点E为AB上一点,且BE=3AE,求cos∠ECM 的值.【解析】首先确定△EMC为直角三角形,设AE=x,则BE=3x,AM=MD=2x,CD=4x.∴AE MDAM CD=,又∠A=∠D=90°,∴△AEM∽△DMC,可得∠EMC=90°,由勾股定理可求CM=x,CE=5x,在Rt△CEM中,cos∠ECM=CMCE=.题型二等角转换求三角函数值【例3】如图,半径为3的⊙A经过原点O和点C(0,2),点B是y轴左侧⊙A优弧上一点,求tan∠OBC 的值.αA BCCBEA M D【解析】作直径CD,在Rt△OCD中.CD=6.OC=2.∴ODtan∠CDO=OCOD=,由圆周角定理得∠OBC=∠CDO,则tan∠OBC【点评】在圆中经常利用同弧或等弧所对的圆周角相等进行角的转换,用直径所对的圆周角去构造直角三角形.题型三构造直角求三角函数值【例4】如图,在Rt△BAD中,tan∠B=53,延长斜边BD到点C,使DC=12BD,连接AC,求tan∠CAD 的值.【解析】要求tan∠CAD,必须将∠CAD放在直角三角形中,考虑∠BAD=90°,故过点D作DE∥AB交AC于点E.则∠ADE=90°,且有△CDE∽△CBA可利用,由tan∠B=53ADAB=,设AD=5x,AB=3x,而13DE CDAB BC==,∴DE=x,∴tan∠CAD=155DE xAD x==.【点评】求一个角的三角函数值,必须将所求的角放在直角三角形中.题型四等比转化求三角函数值【例5】如图,等腰直角△ABC中,∠ACB=90°,过BC的中点D作DE⊥AB,垂足为点E,连接CE,求tan∠ACE的值.CDBACDEBAA BDEC【解析】过点E 作EH ⊥AC 于点H ,易证AH =HE ,∴tan ∠ACE =HE AH AECH CH EB==,设BE =x ,则BD =CD,∴BC =x ,AB =4x ,∴AE =AB -BE =3x ,∴tan ∠ACE =AEEB=3.【例6】如图,AB 是⊙O 的直径,且AB =10,CD 是⊙O 的弦,AD 与BC 相交于点P ,若弦CD =6,试求cos ∠APC 的值.【解析】连接AC ,∵AB 是⊙O 的直径,∴∠ACP =90°,∴cos ∠APC =PCPA,又易证△PCD ∽△P AB ,∴63105PC CD PA AB ===,∴cos ∠APC =35. 【点评】在直角三角形中,锐角的三角函数值等于两边的比值,当这个比值无法直接求解时,可利用相似三角形对应线段成比例进行转化.题型五 利用特殊角求三角函数值【例7】利用45°角的正切,求tan 22.5°的值,方法如下:解:构造Rt △ABC ,其中∠C =90°,∠B =45°,如图,延长CB 到点D ,使BD =AB ,连接AD ,则∠D =12∠ABC =22.5°,设AC =a ,AB =BDa a ,∴CD =(1)a ,∴tan 22.5°=tan ∠D=AC CD =-1.A BE DHCAACA请你依照此法求tan 15°的值.【解析】构造如图所示的∠A =15°的直角三角形,∠C =90°,并过点B 作∠ABD =15°交AC 于点D ,则∠BDC =30°,设BC =x ,则BD =AD =2x ,CD,∴AC =(2x ,∴tan 15°=BC AC=2针对练习11.如图,△ABC 的顶点是正方形网格的格点,则sin A =.2.在Rt △ABC 中,∠C =90°,sin A =513,则tan B = 125 .3.如图,将边长为2的正方形ABCD 沿 EF 和ED 折叠,使得点B ,C 两点折叠后重合于点G ,则tan ∠FEG =12.4.如图,直线MN 与⊙O 相切于点M ,ME =EF ,EF ∥MN ,则cos ∠E =12. A D CBABCDG F DCBA E5.如图,在△ABC 中,∠C =90°,BC =1,AC =tan 2A的值.解:AB=7.延长CA 到点D ,使AD =AB =7,则CD =7+tan2A=tan ∠D=7- 6.如图,AC 为⊙O 的直径,△ABD 内接于⊙O ,BD 交AC 于点F ,过点B 的切线BE ∥AD 交AC 的延长线于点E ,若CF =2,AF =8,求sin ∠E 的值.解:连接OB ,CD ,∵CF =2,AF =8,∴AC =10.∴OB =5.易证CD ⊥AD ,OB ⊥AD ,∴OB ∥CD ,∴△BOF ∽△DCF .∴32OB OF CD CF ==.CD =103.sin ∠E =sin ∠CAD =CD AC =13. 7.将一副三角尺(Rt △ABC 与Rt △BDC )按如图所示摆放在一起,连接AD ,试求∠ADB 的正切值.解:过点A 作AM ⊥DB 交DB 的延长线于点M ,易证∠MBA =45°,∴设AM =BM =x,则AB x .∴BC,BD .∴tan ∠ADB =AMDM8.如图,在△ABC 中,BC =4,AC =6,AB =5,求tan12∠BAC ·tan 12∠CBA 的值.ABCDEAAEDCBABCDM解:过点C作CH⊥AB于点H,延长BA到点D,使AD=AC,延长AB到点E,使BE=BC,设AH=x,则BH=5-x,∴42-(5-x)2=62-x2,∴x=92.∴BH=12,CH∴tan12∠BAC=tan∠D=CHDH=2962+.tan12∠CBA=tan∠E=CHHE=2142+,∴tan12∠BAC·tan12∠CBA=13.方法技巧:深刻理解三角函数的定义,画出符合题意的示意图,充分运用数形结合的思想解题.▶题型一利用已知三角函数,求其他角的三角函数值【例1】同学们,在我们进入高中以后,将会学到三角函数公式:sin2α=2sinα·cosα,则当锐角a的正切值为12时,sin2a=.【解析】如图,在Rt△ABC中.∠C=90°,∠A=α,由tanα=BCAC=12,设BC=1,AC=2,则AB.sinα=BCAB,cosα=ACAB,由公式sin2α=2sinα·cosα=2=45.【点评】紧扣定义,运用公式解题.▶题型二利用已知三角函数,求线段长【例2】如图,点D是△ABC的边AC上一点,BD=8,sin∠CBD=34,AE⊥BC于点E,若CD=2AD,求AE的长.BACEDCBA HC BADBAO OFAB CDE【解析】过点D作DF⊥BC于点F,则DF=BD·sin∠CBD=8×2=6,由AE⊥B C.DF⊥BC,∴DF∥AE.∴△CDF∽△CAE.∴CDAC=DFAE=23.∴AE=32DF=9.【点评】因三角函数的本质是线段比,故与三角函数相关的计算常与相似三角形联系在一起.▶题型三利用已知三角函数,求线段比【例3】如图,在Rt△ABC中,CD,CE分别为斜边AB上的高和中线,BC=a,AC=b(b>a),若tan∠DCE=12,求ab的值.【解析】易证△BCD∽△BAC,∴BC2=BD·BA,又BA,∴BD2,同理CD=DE=BE-BD222,又∵谈∠DCE=DECD=222b aab-=12,∴a2+ab-b2=0,∴ab▶题型四利用已知三角函数,求面积【例4】如图,在四边形ABCD中,∠BAC=90°,tan∠CAD=12,cos∠ACD,AC与BD交于点E,CDBE=2ED,求四边形ABCD的面积.【解析】过点D作DF⊥ACC于点F,则AB∥DF.∴△ABE∽△FDE.∴ABDF=AEEF=BEED=2,设EF=2a,AE=4a.∴AF=6a,在Rt△AFD中.tan∠F AD=FDAF=12,∴DF=3a,在Rt△CFD中,cos∠ACD =CFCD.∴CF=1,DF=3a=3,∴a=1,AC=7,AB=2DF=6,∴S四边形ABCD=S△ABC+S△AC=12AB·AC+12AC·DF=12×6×7+12×7×3=632.针对练习21.在△ABC中,∠A为锐角,BC=12.tan A=34.∠B=30°,则AB2.如图,点E是正方形ABCD的边CB的延长线上的一点,且tan∠DEC=34,则tan∠AED的值为EDCBAABCDEFE DCBA913.3.已知△ABC中,AB=10,AC=B=30°,则△ABC4.如图,在四边形ABCD中,BD是对角线,∠ABC=90”,tan∠ABD=34,AB=20,BC=10,AD=13,求CD的长.解:分别过点A,C作AH⊥BD于点H,CG⊥BD于点G,∵tan∠ABD=AHBH=34,∴设AH=3x,BH=4x,(3x)2+(4x)2=202,∴x=4.∴AH=12,BH=16.∴HD=5,BD=21,易证∠BCG=∠ABD,..tan∠BCG=GBGC=34,又BC=10,∴BG=6,CG=8,∴DG=BD-BG=15,∴CD==17.5.如图,在△ABC中,AB=BC=5,tan∠ABC=34.边BC的重直平分线与AB的交点为点D.求ADDB的值.解:过点D作DF⊥BC于点F,连接CD,则BD=CD,BF=CF=52,tan∠DBF=DFBF=34.∴DF =158,在Rt△BFD中,BD=258,∴AD=5-258=158,∴ADDB=35.6.如图,已知四边形ABCD的一组对边AD,BC的延长线相交于点E,∠ABC=120°,cos∠ADC=35,CD=5,AB=12,ACDE的面积为6,求四边形ABCD的面积.EDCBAAB CDGHDCBAAB CDF CBA解:过点C作CF⊥AD于点F,过点A作AG⊥EB于点G,在Rt△ACDF中,cos∠ADC=DF CD=3 5.又CD=5,DF=3,CF=4,∵S△CDE=12ED·CF=6,∴ED=3,∴EF=6,在Rt△BAG中,∠BAG=30°,AB=12,∴AG=EFC∽△EAG,得EFEG=CFAG,可求EG=BE=EG-BG=9 6.∴S四边形ABCD=S△ABE-S△CED=126)×6=75-E DCBA ABCDE FG。
初三锐角三角函数题型及解题方法

初三锐角三角函数题型及解题方法初三数学中,锐角三角函数是一个非常重要的内容。
学习锐角三角函数,不仅需要掌握其概念和公式,还需要掌握一些常见的题型及解题方法。
本文将介绍一些常见的锐角三角函数题型及解题方法,帮助初三学生更好地掌握这一内容。
一、求三角函数值求三角函数值是锐角三角函数中最基本的题型。
一般来说,题目都会给出三角函数的角度,要求求出其对应的正弦、余弦、正切等函数值。
解题方法:对于这类题目,我们需要掌握三角函数的定义和公式。
例如,正弦函数的定义是:在直角三角形中,对于一个锐角角度A,其对边长度与斜边长度的比值称为正弦值sinA。
因此,我们只需要根据这个定义和公式进行计算即可。
举个例子,题目给出角度A=30度,要求求出其正弦值sinA。
根据正弦函数的定义和公式,我们得到:sinA=对边长度/斜边长度=sqrt(3)/2因此,sinA=√3/2。
二、三角函数的基本关系式三角函数的基本关系式指的是三角函数之间的基本等式。
例如,正切函数的基本关系式是tanA=sinA/cosA。
这类题目一般要求将一个三角函数用另外一个三角函数表示出来,或者将两个三角函数相互表示。
解题方法:对于这类题目,我们需要掌握三角函数之间的基本关系式。
例如,正切函数的基本关系式是:tanA=sinA/cosA因此,如果题目给出sinA的值,要求求出tanA的值,我们只需要将sinA/cosA代入上式,即可得到:tanA=sinA/cosA=√3/3三、三角函数值的范围三角函数值的范围是指,每个三角函数的取值范围。
例如,正弦函数的取值范围是[-1,1],余弦函数的取值范围也是[-1,1]。
解题方法:对于这类题目,我们需要掌握每个三角函数的取值范围。
例如,正弦函数的取值范围是[-1,1],因此,如果题目给出sinA=-0.5,我们就可以知道sinA的值在[-1,1]范围之内。
四、三角函数的性质三角函数的性质指的是,它们在不同象限中的正负性和大小关系。
用锐角三角函数概念解题的常见方法(含答案页)

用锐角三角函数概念解题的常见方法(含答案11页)用锐角三角函数概念解题的常见方法1.锐角三角函数(1)锐角三角函数的定义我们规定:sinA=abab,cosA=,tanA=,cotA=.ccba锐角的正弦、余弦、正切、余切统称为锐角的三角函数.(2)用计算器由已知角求三角函数值或由已知三角函数值求角度对于特殊角的三角函数值我们很容易计算,甚至可以背诵下来,但是对于一般的锐角又怎样求它的三角函数值呢?用计算器可以帮我们解决大问题.①已知角求三角函数值;②已知三角函数值求锐角.2直角三角形中,30°的锐角所对的直角边等于斜边的一半.3.锐角三角函数的性质(1)0<sinα<1,o<cosα<1(0°<α<90°)1(2)tanα·cotα=1或tanα=(3)tanα=1;cot?sin?cos?,cotα=.cos?sin?(4)sinα=cos(90°-α),tanα=cot(90°-α).有关锐角三角函数的问题,常用下面几种方法:一、设参数例1. 在?ABC中,?C?90?,如果tanA?5,那么sinB的值等于()12D.12 5A.513B.1213C.512解析:如图1,要求sinB的值,就是求AC5的值,而已知的tanA?,也就是AB12BC5? AC12可设BC?5k,AC?12k则AB?(5k)2?(12k)2?13k?sinB?12k12?,选B 13k13二、巧代换例2. 已知tan??3,求sin??2cos?的值。
5sin??cos?解析:已知是正切值,而所求的是有关正弦、余弦的值,我们可以利用关系式sin??3,作代换sin??3cos?,代入即可达到约分的目的,也可以把所求的cos?分式的分子、分母都除以cos?。
tan??2sin??2sin??2cos? ?cos?sin5sin??cos?5?1cos?再把sin?1?3代入,得:原式? cos?16三、妙估计例3. 若太阳光与地面成37?角,一棵树的影长为10m,则树高h的范围是(取?1.7)A. 3?h?5B. 5?h?10C. 10?h?15D. h?15 解析:如图2,树高h?10tan37?,要确定h的范围,可根据正切函数是增函数,估计tan30??tan37??tan45?即10tan30??10tan37??10tan45??10??h?10 3?5?h?10,故选B四、善转化例4. 在?ABC中,1?A?30?,tanB?BC?,求AB的长。
锐角三角函数的增减性(详细解析考点分析名师点评)

锐角三角函数的增减性一、解答题(共5小题)1、(1)如图,锐角的正弦和余弦都随着锐角的确定而确定,也随着其变化而变化,试探索随着锐角度数的增大,它的正弦值和余弦值的变化规律;(2)根据你探索到的规律,试比较18°,34°,52°,65°,88°,这些角的正弦值的大小和余弦值的大小;(3)比较大小:(在空格处填写“<”或“>”或“=”)若∠α=45°,则sinα_________cosα;若∠α<45°,则sinα_________cosα;若∠α>45°,则sinα_________c osα;(4)利用互余的两个角的正弦和余弦的关系,比较下列正弦值和余弦值的大小:sin10°,cos30°,sin50°,cos70°.2、(1)如图中①、②,锐角的正弦值和余弦值都是随着锐角的确定而确定,变化而变化,试探索随着锐角度数的增大,它的正弦值及余弦值的变化规律;(2)根据你探索到的规律,试分别比较18°、34°、50°、62°、88°这些锐角的正弦值的大小和余弦值的大小.3、设a、b、c是直角三角形的三边,c为斜边,n为正整数,试判断a n+b n与c n的关系,并证明你的结论.4、已知,凸4n+2边形A1A2…A4n+2(n是非零自然数)各内角都是30°的整数倍,又关于x 的方程:均有实根,求这凸4n+2边形各内角的度数.5、已知:在Rt△ABC中,∠C=90°,sinA、sinB是方程x2+px+q=0的两个根.(1)求实数p、q应满足的条件;(2)若p、q满足(1)的条件,方程x2+px+q=0的两个根是否等于Rt△ABC中两锐角A、B 的正弦?二、填空题(共5小题)6、有四个命题:①若45°<a<90°,则sina>cosa;②已知两边及其中一边的对角能作出唯一一个三角形;③已知x1,x2是关于x的方程2x2+px+p+1=0的两根,则x1+x2+x1x2的值是负数;④某细菌每半小时分裂一次(每个分裂为两个),则经过2小时它由1个分裂为16个.其中正确命题的序号是_________(注:把所有正确命题的序号都填上).7、比较下列三角函数值的大小:sin40°_________cos40°(选填“>”、“=”、“<”).8、若∠A是锐角,cosA>,则∠A应满足_________.9、在tan46°,sin46°,cos46°中,最小的是_________.10、将sin20°、cos20°、cos40°、cos80°的值由小到大的顺序排列_________.三、选择题(共20小题)11、如图,已知:45°<A<90°,则下列各式成立的是()A、sinA=cosAB、sinA>cosAC、sinA>tanAD、sinA<cosA12、在Rt△ABC中,∠C=90°,若将各边长度都扩大为原来的2倍,则∠A的正弦值()A、扩大2倍B、缩小2倍C、扩大4倍D、不变13、把Rt△ABC各边的长度都扩大3倍得Rt△A′B′C′,那么锐角A、A′的余弦值的关系为()A、cosA=cosA′B、cosA=3cosA′C、3cosA=cosA′D、不能确定14、如图,梯子(长度不变)跟地面所成的锐角为A,关于∠A的三角函数值与梯子的倾斜程度之间,叙述正确的是()A、sinA的值越大,梯子越陡B、cosA的值越大,梯子越陡C、tanA的值越小,梯子越陡D、陡缓程度与∠A的函数值无关15、在Rt△ABC中,∠C是直角,各边的长度都分别扩大2倍,那么∠A的三角函数值()A、没有变化B、分别扩大2倍C、分别扩大倍D、不能确定16、已知tanα=,则锐角α的取值范围是()A、0°<α<30°B、30°<α<45°C、45°<α<60°D、60°<α<90°17、在①0<cosα<1(0°≤α≤90°),②sin78°>cos78°,③sin0°>tan45°,④sin25°=cos65°这四个式子中,正确的是()A、①、③B、②、④C、①、④D、③、④18、在Rt△ABC中,如果各边长度都扩大2倍,那么锐角A的正切值()A、不变化B、扩大2倍C、缩小2倍D、不能确定19、当锐角α>30°时,则cosα的值是()A、大于B、小于C、大于D、小于20、在Rt△ABC中,如果各边长度都扩大为原来的2倍,那么锐角A的正弦值()A、扩大2倍B、缩小2倍C、扩大4倍D、没有变化21、在Rt△ABC中,如果各边的长度都扩大两倍,那么锐角A的各三角函数()A、都扩大两倍B、都缩小一半C、没有变化D、不能确定22、在Rt△ABC中,若各边的长度同时都扩大2倍,则锐角A的正弦值与余弦值的情况()A、都扩大2倍B、都缩小2倍C、都不变D、正弦值扩大2倍,余弦值缩小2倍23、在直角三角形中,如果各边都扩大1倍,则其锐角的三角函数值()A、都扩大1倍B、都缩小为原来的一半C、都没有变化D、不能确定24、若α,β都是锐角,下列说法正确的是()A、若sinα=cosβ,则α=β=45°B、若sinα=cosβ,则α+β=90°C、若sinα>cosβ,则α>βD、若sinα<cosβ,则α<β25、已知β为锐角,cosβ≤,则β的取值范围为()A、30°≤β<90°B、0°<β≤60°C、60°≤β<90°D、30°≤β<60°26、如果∠A为锐角,sinA=,那么()A、0°<∠A<30°B、30°<∠A<45°C、45°<∠A<60°D、60°<∠A<90°27、若0°<α<90°,则下列说法不正确的是()A、sinα随α的增大而增大B、cosα随α的减小而减小C、tanα随α的增大而增大D、0<sinα<128、当锐角A>30°时,∠A的余弦值()A、小于B、大于C、大于D、小于29、若∠A为锐角,sinA=3m﹣2,则m的范围是()A、<m<1B、2<m<3C、0<m<1D、<m<30、已知α为锐角,下列结论:(1)sinα+cosα=1;(2)若α>45°,则sinα>cosα;(3)如果cosα>,则α<60°;(4)=1﹣sinα.其中正确结论的序号是()A、(1)(3)(4)B、(2)(4)C、(2)(3)(4)D、(3)(4)。
锐角三角函数的题型及解题技巧

锐角三角函数的题型及解题技巧锐角三角函数是三角函数的基础,它应用广泛,解题技巧性强,下面归纳出锐角三角函数的常见题型,并结合例题介绍一些解题技巧。
一、 化简或求值例1 (1)已知tan 2cot 1αα-=,且α是锐角,的值。
(2)化简()()22sin cos cos sin a b a b αααα++-。
分析 (1)由已知可以求出tan α1tan cot αα=⋅;(2)先把平方展开,再利用22sin cos 1αα+=化简。
解 (1)由tan 2cot 1αα-=得2tan 2tan αα-=,解关于tan α的方程得tan 2α=或tan 1α=-。
又α是锐角,∴tan 2α==tan cot αα-。
由tan 2α=,得1cot 2α==tan cot αα-=13222-=。
(2)()()22sin cos cos sin a b a b αααα++-=2222sin 2sin cos cos a ab b αααα+⋅⋅++2222cos 2cos sin sin a ab b αααα-⋅⋅+=()()222222sin cos sin cos a b αααα+++=22a b +。
说明 在化简或求值问题中,经常用到“1”的代换,即22sin cos 1αα+=,tan cot 1αα⋅=等。
二、已知三角函数值,求角例2 在△ABC 中,若2cos sin 02A B ⎛--= ⎝⎭(),A B ∠∠均为锐角,求C ∠的度数。
分析 几个非负数的和为0,则这几个数均为0。
由此可得cos A 和sin B 的值,进而求出,A B ∠∠的值,然后就可求出C ∠的值。
解由题意得cos 0,2sin 0.A B ⎧-=⎪⎪-=解得cos 2sin 3A B ⎧=⎪⎪⎨⎪=⎪⎩又∵,A B ∠∠均为锐角,∴45A ∠=,60B ∠=。
∴18075C A B ∠=-∠-∠=.说明 解这类问题首先要熟记特殊角的三角函数值,还要掌握一些化简的技巧。
专题 求锐角三角函数值的常用方法

专题 求锐角三角函数值的常用方法题型一 定义法直接根据定义求三角函数值,首先求出相应边的长度﹐然后代入三角函数公式计算即可. 类型1 直接定义法例1、如图,在Rt △ABC 中,∠C =90°,AC =12,BC =5 (1)求AB 的长.(2)求sinA ,cosA ,tanA ,sinB , cosB , tanB 的值.巩固练习1、如图,在△ABC 中,AB =15,AC =13,AD 上BC 于点D .CD =5时,求tan C 的值;2、如图,在Rt △ABC 中,∠C =90°,AB =4,AC =3,则cos B 的值为 。
类型2、网格中的三角函数例2、如图,在4×8的矩形网格中,每个小正方形的边长都是1,若△ABC 的三个顶点在图中相应的格点上,则tan ∠ACB 的值为巩固练习1、正方形网格中,∠AOB 如图放置,则cos ∠AOB 的值为2、如图所示,∠AOB 是放置在正方形网格中的一个角,则cos ∠AOB =3、如图,在5×5的正方形网格中,每个小正方形的边长均为1,点A 、B 、C 都在格点上,则 cos ∠BAC 的值为 。
类型3、构造直角三角形例3、如图,在△ABC 中,AB =AC =13,BC =10, 则tan ∠BDE 的值等于巩固练习1、如图,在四边形ABCD 中,E ,F 分别是AB ,AD 的中点,若EF =2,BC =5,CD =3,则sinC 等于2、如图,在 Rt △ABC 中,∠C =90°,∠ABC =45° ,D 是AC 的中点,则sin ∠DBA =3、如图,在 Rt △BAD 中,延长斜边BD 到点C ,使DC =13BD ,连接AC ,若tanB =74,则tan ∠CAD 的值为 。
题型二 参数法若已知两边的比值或一个三角函数值,而不能直接求出三角函数相应边的长,则可采用设参数的方法﹐先用参数表示出三角函数相应边的长,再根据三角函数公式计算它们的比值,即可得出三角函数值.例3、在Rt △ABC 中,∠C =90°,AC =6,cosA =23 求 BC 的长,sinA ,tanA巩固练习1、在△ABC 中,∠C =90 , BC :CA =8:15,那么 sinA 等于 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
锐角三角函数的题型及解题技巧
锐角三角函数是三角函数的基础,它应用广泛,解题技巧性强,下面归纳出锐角三角函数的常见题型,并结合例题介绍一些解题技巧。
一、 化简或求值
例1 (1)已知tan 2cot 1αα-=,且α是锐角,的值。
(2)化简()()22sin cos cos sin a b a b αααα++-。
分析 (1)由已知可以求出tan α1tan cot αα=⋅;
(2)先把平方展开,再利用22sin cos 1αα+=化简。
解 (1)由tan 2cot 1αα-=得2tan 2tan αα-=,解关于tan α的方程得
tan 2α=或tan 1α=-。
又α是锐角,∴tan 2α==
tan cot αα-。
由tan 2α=,
得1cot 2α==tan cot αα-=13222
-=。
(2)()()22sin cos cos sin a b a b αααα++-=
2222sin 2sin cos cos a ab b αααα+⋅⋅++2222cos 2cos sin sin a ab b αααα-⋅⋅+=()()222222sin cos sin cos a b αααα+++=22a b +。
说明 在化简或求值问题中,经常用到“1”的代换,即22sin cos 1αα+=,tan cot 1αα⋅=等。
二、已知三角函数值,求角
例2 在△ABC 中,若2
cos sin 0A B ⎛-= ⎝⎭(),A B ∠∠均为锐角,求C ∠的度数。
分析 几个非负数的和为0,则这几个数均为0。
由此可得cos A 和sin B 的值,进而求出,A B ∠∠的值,然后就可求出C ∠的值。
v1.0 可编辑可修改 解 由题意得2cos 0,23sin 0.A B ⎧-=⎪⎪⎨⎪-=⎪解得2cos ,23sin .A B ⎧=⎪⎪⎨⎪=⎪⎩又∵,A B ∠∠均为锐角,∴45A ∠=,60B ∠=。
∴18075C A B ∠=-∠-∠=.
说明 解这类问题首先要熟记特殊角的三角函数值,还要掌握一些化简的技
巧。
三、 已知锐角的一个三角函数值,求其余三角函数值
例3 已知tan 2α=,求sin cos sin cos αααα
-+的值。
分析 ∵tan 2α=,根据三角函数的定义,构造如图1的直角三角形,使
90C ∠=,AC a =,2BC a =,就可求出sin ,cos αα。
解 根据三角函数的定义,构造如图1的直角三角形,使90C ∠=,AC a =,2BC a =。
则tan 2α=,()2225AB a a a =+=。
∴2sin 55
BC AB α=
=,5cos 5AC AB α==. ∴sin cos sin cos αααα-+=21555155213
355555
-==+。
说明 构造直角三角形解题,特别是解几何问题是应用比较广泛的一种方
法。
四、比较大小
例4 若太阳光线与地面成37的角,一颗树的影长10米,取3 1.7=,则
树高h 的范围是( )
A 35h <≤
B 510h <<
C 1015h <<
D 15h >
分析 ∵10tan 37h =⋅,利用正切函数的性质估算出tan37的范围即可。
解 ∵303745<<,∴tan30tan37tan 45<<。
而10tan 37h =⋅,
∴10tan3010tan3710tan 45⋅<⋅<⋅, 1.7101013
h ⨯<<⨯,即510h <<。
故选B 。
说明 掌握三角函数函数值随自变量的变化的性质,正确估算是解此题的关键。
五、求齐次式的值
例5 已知tan 2α=,(1)求sin 3cos 2cos 5sin αααα
-+的值; (2)求222sin sin cos cos αααα-+的值。
分析 (1)可以仿造例3构造直角三角形求解。
亦可考虑sin α、
cos α及tan α的关系,在sin 3cos 2cos 5sin αααα
-+的分子、分母同时除以cos α,转化为tan α的代数式,然后求值;(2)222sin sin cos cos αααα-+的分母是1,利用22sin cos 1αα+=,仿造(1)求解。
解 (1)∵tan 2α=,
∴sin 3cos 2cos 5sin αααα-+=sin 3cos cos 2cos 5sin cos αα
αααα
-+=tan 325tan αα-+23253-=+⨯=112
-。
(2)∵tan 2α=,
∴22
2sin sin cos cos αααα-+22222sin sin cos cos sin cos αααααα-+=+222tan tan 1tan 1ααα-+=+22222121⨯-+=+75
=。
说明 如果所求代数式是关于sin α和cos α的齐次式或可转化为sin α和cos α的齐次式,可把原代数式转化成关于tan α的代数式求解。
