初中数学直角三角形斜边中线性质应用专项练习题(附答案详解)
九年级数学下册《第二十八章 解直角三角形及其应用》练习题附答案解析-人教版

九年级数学下册《第二十八章解直角三角形及其应用》练习题附答案解析-人教版班级:___________姓名:___________考号:____________一、单选题1.图,在Rt△ABC中△ACB=90°,CE是斜边AB上的中线,过点E作EF⊥AB交AC于点F,若BC=4,sin△CEF= 3,则△AEF的面积为()5A.3B.4C.5D.62.小丽在小华北偏东40°的方向,则小华在小丽的()A.南偏西50°B.北偏西50°C.南偏西40°D.北偏西40°3.如图,小明在距离地面30米的P处测得A处的俯角为15︒,B处的心角为60︒,若斜面坡度为,则斜面AB的长是()米.A.B.C.D.4.如图,某渔船正在海上P处捕鱼,先向北偏东30°的方向航行10km到A处.然后右转40°再航行到B处,在点A的正南方向,点P的正东方向的C处有一条船,也计划驶往B处,那么它的航向是()A .北偏东20°B .北偏东30°C .北偏东35°D .北偏东40°5.如图,某建筑物的顶部有一块宣传牌CD .小明在山坡的坡脚A 处测得宣传牌底部D 的仰角为60°,沿山坡向上走到B 处测得宣传牌顶部C 的仰角为45°,已知斜坡AB 的坡角为30°,10AB =米,15AE =米,则宣传牌CD 的高度是( )米A .20-B .20+C .15+D .56.如图,已知正六边形ABCDEF 内接于半径为r 的O ,随机地往O 内投一粒米,落在正六边形内的概率为( )A B C D .以上答案都不对7.如图,小明利用标杆BE 测量建筑物DC 的高度,已知标杆BE 的长为1.2米,测得AB =85米,BC =425米,则楼高CD 是( )A .6.3米B .7.5米C .8米D .68.如图,点E 是⊥ABCD 的边AB 上一点,过点E 作EF ∥BC ,交CD 于F ,点P 为EF 上一点,连接PB 、PD .下列说法不正确的是( )A .若⊥ABP =⊥CDP ,则点P 在⊥ABCD 的对角线BD 上B .若AE :EB =2:3,EP :PF =1:2,则S △BEP :S △DFP =3:4C .若S △BEP =S △DFP ,则点P 在AC 上D .若点P 在BD 上,则S △BEP =S △DFP9.如图,一棵大树被台风拦腰刮断,树根A 到刮断点P 的距离是4米,折断部分PB 与地面成40︒的夹角,那么原来这棵树的高度是( )A .44cos 40+︒⎛⎫ ⎪⎝⎭米B .44sin 40+︒⎛⎫ ⎪⎝⎭米C .()44sin 40+︒米D .()44tan 40+︒米10.如图,等腰Rt △ABC 中⊥A =90°,AB =AC ,BD 为△ABC 的角平分线,若2CD =,则AB 的长为( )A.3 B .2 C .4 D 2+二、填空题11.在Rt ABC 中90C ∠=︒,有一个锐角为60︒,6AB =若点P 在直线..AB 上(不与点A ,B 重合),且30PCB ∠=︒,则AP 的长为_______.12.如图,将扇形AOB 沿OB 方向平移,使点O 移到OB 的中点O '处,得到扇形A O B '''.若⊥O =90°,OA =2,则阴影部分的面积为______.13.如图,在一次数学实践活动中小明同学要测量一座与地面垂直的古塔AB 的高度,他从古塔底部点处前行30m 到达斜坡CE 的底部点C 处,然后沿斜坡CE 前行20m 到达最佳测量点D 处,在点D 处测得塔顶A的仰角为30︒,已知斜坡的斜面坡度i =A ,B ,C ,D ,在同一平面内,小明同学测得古塔AB 的高度是___________.14.如图,在直角坐标系中点A 的坐标为(0,点B 为x 轴的正半轴上一动点,作直线AB ,⊥ABO 与⊥ABC 关于直线AB 对称,点D ,E 分别为AO ,AB 的中点,连接DE 并延长交BC 所在直线于点F ,连接CE ,当⊥CEF 为直角时,则直线AB 的函数表达式为__.15.如图,平行四边形OABC 的顶点O 是坐标原点,A 在x 轴的正半轴上,B ,C 在第一象限,反比例函数1y x =的图象经过点C ,()0k y k x=≠的图象经过点B .若OC AC =,则k =________.16.在⊥ABC 中AB =6AC =且45B ∠=,则BC =______________.17.如图,大坝横截面的迎水坡AB 的坡比为1:2,(即BC :AC=1:2),若坡面AB 的水平宽度AC 为12米,则斜坡AB 的长为________米.18.如图,等边ABC 中115,125AOB BOC ∠=︒∠=︒,则以线段,,OA OB OC 为边构成的三角形的各角的度数分别为______________________________.三、解答题19.实验学校某班开展数学“综合与实践”测量活动.有两座垂直于水平地面且高度不一的圆柱,两座圆柱后面有一斜坡,且圆柱底部到坡脚水平线MN 的距离皆为100cm .王诗嬑观测到高度90cm 矮圆柱的影子落在地面上,其长为72cm ;而高圆柱的部分影子落在坡上,如图所示.已知落在地面上的影子皆与坡脚水平线MN 互相垂直,并视太阳光为平行光,测得斜坡坡度1:0.75i =,在不计圆柱厚度与影子宽度的情况下,请解答下列问题:(1)若王诗嬑的身高为150cm ,且此刻她的影子完全落在地面上,则影子长为多少cm ?(2)猜想:此刻高圆柱和它的影子与斜坡的某个横截面一定同在一个垂直于地面的平面内.请直接回答这个猜想是否正确?(3)若同一时间量得高圆柱落在坡面上的影子长为100cm ,则高圆柱的高度为多少cm ?20.八年级二班学生到某劳动教育实践基地开展实践活动,当天,他们先从基地门口A 处向正北方向走了450米,到达菜园B 处锄草,再从B 处沿正西方向到达果园C 处采摘水果,再向南偏东37°方向走了300米,到达手工坊D 处进行手工制作,最后从D 处回到门口A 处,手工坊在基地门口北偏西65°方向上.求菜园与果园之间的距离.(结果保留整数)参考数据:sin65°≈ 0.91,cos65°≈0.42,tan65°≈2.14,sin37°≈ 0.60,cos37°≈ 0.80,tan37°≈0.7521.如图是某水库大坝的横截面,坝高20m CD =,背水坡BC 的坡度为11:1i =.为了对水库大坝进行升级加固,降低背水坡的倾斜程度,设计人员准备把背水坡的坡度改为2i =求背水坡新起点A 与原起点B之间的距离. 1.41 1.73≈结果精确到0.1m )参考答案与解析1.C【分析】连接BF ,由已知CE AE BE ==得到A FBA ACE ==∠∠∠,再得出CEF ∠与CBF ∠的关系,由三角函数关系求得CF 、BF 的值,通过BF AF =,用三角形面积公式计算即可.【详解】解:连接BF⊥CE 是斜边AB 上的中线 ⊥12CE AE BE AB ===(直角三角形斜边上的中线等于斜边的一半)⊥A FBA ACE ==∠∠∠又⊥90BCA BEF ==︒∠∠在⊥ABC 中180902CBF ACB A ABF A =︒-∠-∠-∠=︒-∠∠在⊥AEC 中180902CEF AEF A ACE A =︒-∠-∠-∠=︒-∠∠⊥CEF CBF ∠=∠3sin sin 5CBF CEF ∴∠=∠=4BC =,设3,5CF x BF x ==则222BC CF BF +=,即()()222435x x +=解得1x =(负值舍掉)3,5CF BF ∴== ⊥EF 是AB 的垂直平分线, ⊥5BF AF ==11·541022AFB S AF BC ∴==⨯⨯=△ 152AEF ABF S S ∴==△△故选:C .【点睛】本题综合考查了垂直平分线的性质、直角三角形和等腰三角形的性质、勾股定理及三角函数等相关知识,熟练利用相关定理和性质进行计算是解决本题的关键.2.C【分析】画出示意图,确定好小丽和小华的的方向和位置即可.【详解】解:如图所示,当小丽在小华北偏东40°的方向时,则小华在小丽的南偏西40°的方向.故选:C【点睛】本题考查了方位角的知识点,确定好物体的方向和位置是解题的关键.3.B【分析】过点A 作AF BC ⊥于点F ,根据三角函数的定义得到30ABF ∠=︒,根据已知条件得到3045HPB APB ∠∠=︒=︒,求得60HBP ∠=︒,解直角三角形即可得到结论.【详解】如图所示:过点A 作AF BC ⊥于点F斜面坡度为AF tan ABF BF ∠∴=== 30ABF ∠∴=︒在P 处进行观测,测得山坡上A 处的俯角为15︒,山脚B 处的俯角为60︒3045HPB APB ∠∠∴=︒=︒,60HBP ∠∴=︒9045PBA BAP ∠∠∴=︒=︒,PB AB ∴=303060PH PH m sin PB PB =︒===,解得:)PB m =故AB =故选:B .【点睛】此题主要考查了解直角三角形的应用-仰角俯角问题,解直角三角形的应用-坡度坡角问题,正确得出PB AB =是解题关键.4.C【分析】连接BC ,由锐角三角函数定义得AC A = km ,则AC =AB ,再由等腰三角形的性质得⊥ACB =⊥ABC =35°,即可得出结论.【详解】解:如图,连接BC由题意得:⊥ACP =⊥ACD =90°,⊥P AC =30°,P A =10km ,⊥BAE =40°,AB =⊥⊥BAC =180°—⊥P AC —⊥BAE =180°—30°—40°=110°⊥cos⊥P AC =ACPA =cos30°=⊥AC =P A =×10= km⊥AC =AB⊥⊥ACB =⊥ABC =12×(180°—⊥BAC )=12×(180°—110°)=35°即B 处在C 处的北偏东35°方向故选:C .【点睛】本题考查了解直角三角形的应用—方向角问题,等腰三角形的性质,锐角三角函数定义等知识,由锐角三角函数定义求出AC 的长是解题的关键.5.A【分析】过点B 分别作AE 、DE 的垂线,垂足分别为G 、F ,在Rt ⊥ABG 中由已知可求得BG 、AG 的长,从而可易得EF 及EG 、BF 的长度,由等腰直角三角形的性质可得CF 的长度,在Rt ⊥DAE 中由正切函数关系可求得DE 的长度,从而可求得CD 的长度.【详解】过点B 分别作AE 、DE 的垂线,垂足分别为G 、F ,如图在Rt ⊥ABG 中⊥BAG =30゜⊥152BG AB ==米,cos3010AG AB =︒==⊥15)EG AG AE =+=米⊥BG ⊥AE ,BF ⊥ED ,AE ⊥ED⊥四边形BGEF 是矩形⊥EF =BG =5米,15)BF EG ==米⊥⊥CBF =45゜,BF ⊥ED⊥⊥BCF =⊥CBF =45゜⊥15)CF BF ==米在Rt ⊥DAE 中⊥DAE =60゜,AE =15米⊥tan DE AE DAE =∠=米)⊥155(20CD CF EF DE =+-=+-=-米故选:A【点睛】本题考查了解直角三角形的实际应用,理解坡角、仰角的含义,构造辅助线得到直角三角形是解题的关键.6.A【分析】连接OB ,过点O 作OH ⊥AB 于点H ,由正六边形的特点可证得⊥OAB 是等边三角形,由特殊角的三角函数值可求出OH 的长,利用三角形的面积公式即可求出⊥OAB 的面积,进而可得出正六边形ABCDEF 的面积,即可得出结果.【详解】解:如图:连接OB ,过点O 作OH ⊥AB 于点H⊥六边形ABCDEF 是正六边形⊥⊥AOB =60°⊥OA =OB =r⊥⊥OAB 是等边三角形⊥AB =OA =OB =r ,⊥OAB =60°在Rt OAH △中sin OH OA OAB r =⋅∠==⊥21122OAB S AB OH r =⋅==△⊥正六边形的面积226== ⊥⊥O 的面积=πr 2⊥米粒落在正六边形内的概率为:222rπ 故选:A .【点睛】本题考查了正多边形和圆、正六边形的性质、等边三角形的判定与性质、解直角三角形;熟练掌握正六边形的性质,通过作辅助线求出⊥OAB 的面积是解决问题的关键.7.B【分析】先判断出⊥ABE ⊥⊥ACD ,再根据相似三角形对应边成比例解答.【详解】⊥AB =85,BC =425 ⊥AC =AB +BC =10⊥BE ⊥AC ,CD ⊥AC⊥BE ⊥CD⊥AB :AC =BE :CD ⊥85:10=1.2:CD⊥CD =7.5米.故选:B .【点睛】本题只要是把实际问题抽象到相似三角形中利用相似三角形的相似比,列出方程,通过解方程求出建筑物的高度,体现了方程的思想.8.D【分析】根据平行四边形的性质和判定进行判断即可.【详解】解:A 、若⊥ABP =⊥CDP ,则点P 在⊥ABCD 的对角线BD 上,说法正确;B 、若AE :EB =2:3,EP :PF =1:2则S △BEP :S △DFP =3:4,说法正确;C 、过点P 作GH AB ∥,分别交AD ,BC 于G ,H⊥GH AB ∥ GA HB ∥⊥四边形ABHG 是平行四边形同理:四边形CDGH 、四边形BHPE ,四边形DGPE 都是平行四边形 ⊥12BEP BHPE S S =△ 12DFP DGPF S S =△又BEP DFP S S =△△⊥BEPH DGPF SS = ⊥ABHG ADFE S S =同理:BCFE CDGH S S =⊥点P 在AC 上,C 说法正确;D 、若点P 在BD 上,不能得出EP =PF ,所以S △BEP 不一定等于S △DFP ,说法错误;故选:D .【点睛】此题考查平行四边形的判定和性质,掌握平行四边形的性质是解题的关键.9.B【分析】通过解直角三角形即可求得.【详解】解:在Rt ABP △中4==sin sin 40AP BP ABP ∠︒ 故原来这棵树的高度为:4=4sin 40AP BP ⎛⎫++ ⎪︒⎝⎭(米) 故选:B .【点睛】本题考查了解直角三角形的应用,熟练掌握和运用解直角三角形的方法是解决本题的关键.10.D【分析】过点D 作DE ⊥BC 于点E ,设AB =AC =x ,则AD =x -2,根据等腰Rt △ABC 中90,A AB AC ∠=︒= 得到⊥C =45°,根据BD 为△ABC 的角平分线,⊥A =90°,DE ⊥BC ,推出DE =AD =x -2,运用⊥C 的正弦即可求得.【详解】解:过点D 作DE ⊥BC 于点E ,则⊥DEB =⊥DEC =90°设AB =AC =x ,则AD =x -2⊥等腰Rt △ABC 中,⊥A =90°,AB =AC ,⊥⊥C =(180°-⊥A )=45°⊥BD 为△ABC 的角平分线⊥DE =AD =x -2⊥sin sin 452DE C CD ︒===⊥22x -⊥2x ,即2AB =.故选D .【点睛】本题主要考查了等腰直角三角形,角平分线,解直角三角形,熟练掌握等腰直角三角形的性质,角平分线的性质,正弦的定义和45°的正弦值,是解决问题的关键.11.92或9或3 【分析】分⊥ABC =60、⊥ABC =30°两种情况,利用数形结合的方法,分别求解即可.【详解】解:当⊥ABC =60°时,则⊥BAC =30°⊥132BC AB ==⊥AC ==当点P 在线段AB 上时,如图⊥30PCB ∠=︒⊥⊥BPC =90°,即PC ⊥AB⊥9cos 2AP AC BAC =⋅∠==;当点P 在AB 的延长线上时⊥30PCB ∠=︒,⊥PBC =⊥PCB +⊥CPB⊥⊥CPB =30°⊥⊥CPB =⊥PCB⊥PB =BC =3⊥AP =AB +PB =9;当⊥ABC =30°时,则⊥BAC =60°,如图⊥132AC AB ==⊥30PCB ∠=︒⊥⊥APC =60°⊥⊥ACP =60°⊥⊥APC =⊥P AC =⊥ACP⊥⊥APC 为等边三角形⊥P A =AC =3.综上所述,AP 的长为92或9或3. 故答案为:92或9或3 【点睛】本题是解直角三角形综合题,主要考查了含30度角的直角三角形、解直角三角形,等边三角形的判定和性质等,分类求解是本题解题的关键.12.3π【分析】设A O '与扇形AOB 交于点C ,连接OC ,解Rt OCO ',求得60O C COB '=∠=︒,根据阴影部分的面积为()OCO A O B OCB S S S ''''--扇形扇形,即可求解.【详解】如图,设A O '与扇形AOB 交于点C ,连接OC ,如图O '是OB 的中点11122OO OB OA '∴===, OA =2 AOB ∠=90°,将扇形AOB 沿OB 方向平移90A O O ''∴∠=︒1cos 2OO COB OC '∴∠== 60COB ∴∠=︒sin 60O C OC '∴=︒=∴阴影部分的面积为()OCO A O B OCB S S S''''--扇形扇形 OCO AOB OCB S S S ''=-+扇形扇形22906012213603602ππ=⨯-⨯+⨯3π=故答案为:3π+【点睛】本题考查了解直角三角形,求扇形面积,平移的性质,求得60COB ∠=︒是解题的关键.13.(20m +【分析】过D 作DF ⊥BC 于F ,DH ⊥AB 于H ,设DF =x m ,CF m ,求出x =10,则BH =DF =,CF =,DH =BF ,再求出AH DH ,即可求解. 【详解】解:过D 作DF ⊥BC 于F ,DH ⊥AB 于H⊥DH =BF ,BH =DF⊥斜坡的斜面坡度i =1⊥:DF CF =设DF =x m ,CFm⊥CD 220x ==⊥x =10⊥BH =DF =10m ,CF =⊥DH =BF =(m )⊥⊥ADH =30°⊥AH 10=+m ) ⊥AB =AH +BH =20103(m )故答案为:(20m +【点睛】本题考查了解直角三角形的应用-仰角俯角问题、坡角坡度问题,正确的作出辅助线构造直角三角形是解题的关键.14.y【分析】证明⊥ABO ⊥⊥ABC ,于是可知⊥CBA =⊥ABO =30°,得出OB =3即可求出直线AB 的函数表达式.【详解】解:⊥⊥ABO 与⊥ABC 关于直线AB 对称⊥⊥ACB =⊥AOB =90°⊥点E 是AB 的中点⊥CE =BE =EA⊥⊥EAC =⊥ECA⊥⊥ECA +⊥ECF =90°,⊥ECF +⊥CFE =90°⊥⊥CFE =⊥BAC而点D ,E 分别为AO ,AB 的中点⊥DF ∥OB⊥⊥CFE =⊥CBO =2⊥CBA =2⊥ABO⊥⊥ABO 与⊥ABC 关于直线AB 对称⊥⊥ABO ⊥⊥ABC⊥⊥OAB =⊥CAB =2⊥ABO⊥⊥ABO =30°而点A 的坐标为(0,即OAAB ∴=⊥OB =3即点B 的坐标为(3,0)于是可设直线AB 的函数表达式为y =kx +b ,代入A 、B 两点坐标得30b k b ⎧=⎪⎨+=⎪⎩解得kb故答案为y【点睛】本题考查的是三角形的全等,并考查了用待定系数法求函数解析式,找到两个已知点的坐标是解决本题的关键.15.3【分析】过点C 作CD ⊥OA 于D ,过点B 作BE ⊥x 轴于E ,先证四边形CDEB 为矩形,得出CD =BE ,再证Rt △COD ⊥Rt △BAE (HL ),根据S 平行四边形OCBA =4S △OCD =2,再求S △OBA =112OCBA S =平行四边形即可. 【详解】解:过点C 作CD ⊥OA 于D ,过点B 作BE ⊥x 轴于E⊥CD ⊥BE⊥四边形ABCO 为平行四边形⊥CB OA ∥ ,即CB DE ∥,OC =AB⊥四边形CDEB 为平行四边形⊥CD ⊥OA⊥四边形CDEB 为矩形⊥CD =BE⊥在Rt △COD 和Rt △BAE 中OC AB CD EB =⎧⎨=⎩⊥Rt △COD ⊥Rt △BAE (HL )⊥S △OCD =S △ABE⊥OC =AC ,CD ⊥OA⊥OD =AD⊥反比例函数1yx=的图象经过点C⊥S△OCD=S△CAD=12⊥S平行四边形OCBA=4S△OCD=2⊥S△OBA=11 2OCBAS=平行四边形⊥S△OBE=S△OBA+S△ABE=13 122 +=⊥3232k=⨯=.故答案为3.【点睛】本题考查反比例函数k的几何意义,平行四边形的性质与判定,矩形的判定与性质,三角形全等判定与性质,掌握反比例函数k的几何意义,平行四边形的性质与判定,矩形的判定与性质,三角形全等判定与性质.16.3或3【分析】画出图形,分⊥ABC为锐角三角形和钝角三角形两种情况讨论即可.【详解】解:情况一:当⊥ABC为锐角三角形时,如图1所示:过A点作AH⊥BC于H⊥⊥B=45°⊥⊥ABH为等腰直角三角形⊥363322ABAH BH在Rt⊥ACH中由勾股定理可知:2236273CH AC AH⊥333BC BH CH.情况二:当⊥ABC为钝角三角形时,如图2所示:由情况一知:363322ABAH BH2236273CH AC AH⊥333BC BH CH .故答案为:3或3.【点睛】本题考察了等腰直角三角形的性质及勾股定理的应用,本题的关键是能将⊥ABC 分成锐角三角形或钝角三角形分类讨论.17.【分析】根据坡面AB 的坡比以及AC 的值,求出BC ,再利用勾股定理即可求出斜面AB 的长.【详解】解:⊥大坝横截面的迎水坡AB 的坡比为1:2,AC=12米⊥1212BC BC AC == ⊥BC=6⊥AB =故答案为:【点睛】本题主要考查学生对坡度坡角的掌握及三角函数的运用能力,能根据坡度求出BC 是解题关键. 18.55°,60°,65°.【分析】通过旋转AOB 至CDB △,可得BOD 是等边三角形,将,,OA OB OC 放在一个三角形中进而求出各角大小。
专题14 直角三角形斜边上的中线-2020-2021学年八年级数学下册常考题专练(人教版)(解析版)

专题14直角三角形斜边上的中线★知识归纳●直角三角形斜边上的中线的性质直角三角形斜边上的中线等于斜边的一半.要点梳理:(1)直角三角形斜边上的中线的性质是矩形性质的推论.性质的前提是直角三角形,对一般三角形不可使用.(2)学过的直角三角形主要性质有:①直角三角形两锐角互余;②直角三角形两直角边的平方和等于斜边的平方;③直角三角形中30°所对的直角边等于斜边的一半.(3)性质可以用来解决有关线段倍分的问题.★实操夯实一.选择题(共16小题)1.如图,在三角形ABC中,AB=AC,BC=6,三角形DEF的周长是7,AF⊥BC于F,BE⊥AC于E,且点D是AB的中点,则AF=()A.B.C.D.7【解答】解:∵AF⊥BC,BE⊥AC,D是AB的中点,∴DE=DF=AB,∵AB=AC,AF⊥BC,∴点F是BC的中点,∴BF=FC=3,∵BE⊥AC,∴EF=BC=3,∴△DEF的周长=DE+DF+EF=AB+3=7,∴AB=4,由勾股定理知AF==,故选:B.2.如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点,若AD=6,则CP的长为()A.3B.3.5C.4D.4.5【解答】解:∵∠ACB=90°,∠ABC=60°,∴∠A=30°,∵BD平分∠ABC,∴∠CBD=∠DBA=30°,∴BD=AD,∵AD=6,∴BD=6,∵P点是BD的中点,∴CP=BD=3.故选:A.3.如图,一根木棍斜靠在与地面(OM)垂直的墙(ON)上,设木棍中点为P,若木棍A端沿墙下滑,且B沿地面向右滑行.在此滑动过程中,点P到点O的距离()A.不变B.变小C.变大D.无法判断【解答】解:不变.连接OP,在Rt△AOB中,OP是斜边AB上的中线,那么OP=AB,由于木棍的长度不变,所以不管木棍如何滑动,OP都是一个定值.故选:A.4.如图,∠ABC=∠ADC=Rt∠,E是AC的中点,则()A.∠1>∠2B.∠1=∠2C.∠1<∠2D.∠1与∠2大小关系不能确定【解答】解:∵∠ABC=∠ADC=90°,E是AC的中点,∴DE=AC,BE=AC,∴DE=BE,∴∠1=∠2.故选:B.5.如图,在△ABC中,∠ACB=90°,AC=8,BC=6,点D为斜边AB上的中点,则CD为()A.10B.3C.5D.4【解答】解:在Rt△ABC中,AC=8,BC=6,∴AB===10,∵点D为斜边AB上的中点,∴CD=AB=×10=5,故选:C.6.已知直角三角形斜边上的中线长为3,则斜边长为()A.3B.6C.9D.12【解答】解:∵直角三角形斜边上的中线长为3,∴斜边长是6.故选:B.7.直角三角形的斜边长为6cm,则斜边上的中线长为()A.2cm B.2.5cm C.3cm D.4cm【解答】解:直角三角形的斜边长为6cm,则斜边上的中线长为3cm,故选:C.8.如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,CE为AB边上的中线,AD=2,CE=10,则CD=()A.2B.3C.4D.6【解答】解:在Rt△ABC中,∠ACB=90°,CE为AB边上的中线,CE=10,∴AE=CE=10,∵AD=2,∴DE=8,∵CD为AB边上的高,在Rt△CDE中,CD===6,故选:D.9.在Rt△ABC中,∠ACB=90°,AB=6cm,D为AB的中点,则CD等于()A.2cm B.2.5cm C.3cm D.4cm【解答】解:∵∠ACB=90°,D为AB的中点,∴CD=AB=×6=3cm.故选:C.10.如图,在△ABC中,∠BAC=90°,点D在BC延长线上,且AD=BC,若∠D=40°,则∠B=()A.10°B.20°C.30°D.40°【解答】解:取BC的中点E,连接AE,∵∠BAC=90°,点E是BC的中点,∴AE=BC=BE,∴∠B=∠EAB,∵AD=BC,∴AE=AD,∴∠AED=∠D=40°,∴∠B=20°,故选:B.11.如图,△ABC中,AB=AC=10,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则DE的长为()A.10B.6C.8D.5【解答】解:∵AB=AC=10,AD平分∠BAC,∴AD⊥BC,∵E为AC的中点,∴DE=AC=×10=5,故选:D.12.如图在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点,EF=3,BC=8,则△EFM的周长是()A.21B.15C.13D.11【解答】解:∵CF⊥AB,BE⊥AC,M为BC的中点,∴EM=FM=BC=×8=4,∴△EFM的周长=8+8+3=11.故选:D.13.如图,边长为2的等边三角形ABC,点A,B分别在y轴和x轴正半轴滑动,则原点O到C的最长距离()A.B.C.D.【解答】解:取AB的中点D,连接OD,CD,在△OCD中,OC<OD+CD,只有当O,D,C三点在一条线上时,OC=OD+CD,此时OC最大,如图所示,OC⊥AB,∵△AOB为等腰直角三角形,AB=2,∴OD=AB=1,在Rt△BCD中,BC=2,BD=1,根据勾股定理得:CD==,∴OC=+1.故选:D.14.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是()A.2.5B.C.D.2【解答】解:如图,连接AC、CF,∵正方形ABCD和正方形CEFG中,BC=1,CE=3,∴AC=,CF=3,∠ACD=∠GCF=45°,∴∠ACF=90°,由勾股定理得,AF===2,∵H是AF的中点,∴CH=AF=×2=.故选:B.15.如图,△ABC中,∠A+∠B=90°,AD=DB,CD=3,则AB的长度为()A.3B.4C.5D.6【解答】解:∵△ABC中,∠A+∠B=90°,∴∠ACB=90°.∵AD=DB,∴CD是该直角三角形斜边AB上的中线,∴AB=2CD=6.故选:D.16.如图,在△ABC中,AB=AC=3,BC=4,AE平分∠BAC交BC于点E,点D为AB的中点,连接DE,则△BDE的周长是()A.3B.4C.5D.6【解答】解:∵在△ABC中,AB=AC=3,AE平分∠BAC,∴BE=CE=BC=2,又∵D是AB中点,∴BD=AB=,∴DE是△ABC的中位线,∴DE=AC=,∴△BDE的周长为BD+DE+BE=++2=5.故选:C.二.填空题(共7小题)17.如图,BE、CF分别是△ABC的高,M为BC的中点,EF=4,BC=10,则△EFM的周长是14.【解答】解:∵BE、CF分别是△ABC的高,M为BC的中点,BC=8,∴在Rt△BCE中,EM=BC=5,在Rt△BCF中,FM=BC=5,又∵EF=4,∴△EFM的周长=EM+FM+EF=5+5+4=14.故答案是:14.18.如图,已知△ABC中,AB=AC,AD平分∠BAC,E是AC的中点,若AB=6,则DE的长为3.【解答】解:∵AB=AC,AD平分∠BAC,∴AD⊥BC,∴∠ADC=90°,∵点E为AC的中点,∴DE=AC=3.故答案为:3.19.如图所示,在△ABC中,∠C=2∠B,点D是BC上一点,AD=5,且AD⊥AB,点E是BD上的点,AE=BD,AC=6.5,则AB的长度为12.【解答】解:∵Rt△ABD中,AE=BD,∴AE=BE=DE;∴∠B=∠BAE,即∠AED=2∠B;∵∠C=2∠B,∴∠AEC=∠C,即AE=AC=6.5;∴BD=2AE=13;由勾股定理,得:AB==12.20.如图,△AEF是直角三角形,∠AEF=90°,B为AE上一点,BG⊥AE于点B,GF∥BE,且AD=BD=BF,∠BFG=60°,则∠AFG的度数是20°.【解答】解:∵四边形BEFG是长方形,∴FG∥BE,∴∠FBE=∠BFG=60°,∵AD=BD=BF,∴∠A=∠ABD,∠BDF=∠BFD,∵∠BDF=∠DFB=∠A+∠ABD=2∠A,∴∠EBF=∠A+∠AFB=3∠A=60°,∴∠A=20°,∵FG∥BE,∴∠AFG=∠A=20°,故答案为:20°.21.如图,在△ABC中,∠BAC=90°,点D是BC的中点,点E、F分别是AB、AC上的动点,∠EDF=90°,M、N分别是EF、AC的中点,连接AM、MN,若AC=6,AB=5,则AM﹣MN的最大值为.【解答】解:如图,连接DM,DN,由图可以得到M的轨迹是一条线段(AD的垂直平分线的一部分),M在AN上的时候最大(此时AM最大,MN最小),当M在AN上时,设AM=x,则MN=3﹣x,DM=AM=x,DN=AB=,在直角三角形DMN中,根据勾股定理,得DM2=DN2+MN2,∴x2=(3﹣x)2+2.52,解得x=,∴3﹣x=,此时AM﹣MN=﹣=.∴AM﹣MN的最大值为.故答案为:.22.如图,Rt△ABC中,∠ACB=90°,斜边AB=9,D为AB的中点,F为CD上一点,且CF=CD,过点B 作BE∥DC交AF的延长线于点E,则BE的长为6.【解答】解:∵Rt△ABC中,∠ACB=90°,斜边AB=9,D为AB的中点,∴CD=AB=4.5.∵CF=CD,∴DF=CD=×4.5=3.∵BE∥DC,∴DF是△ABE的中位线,∴BE=2DF=6.故答案为6.23.如图,在Rt△ABC中,∠ACB=90°,将边BC沿斜边上的中线CD折叠到CB′,若∠B=50°,则∠ACB′=10°.【解答】解:∵∠ACB=90°,∠B=50°,∴∠A=40°,∵∠ACB=90°,CD是斜边上的中线,∴CD=BD,CD=AD,∴∠BCD=∠B=50°,∠DCA=∠A=40°,由翻折变换的性质可知,∠B′CD=∠BCD=50°,∴∠ACB′=∠B′CD﹣∠DCA=10°,故答案为:10°.三.解答题(共4小题)24.如图,在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG⊥CE于G,CD=AE.(1)求证:CG=EG.(2)已知BC=13,CD=5,连接ED,求△EDC的面积.【解答】(1)证明:连接DE,在Rt△ADB中,点E是AB的中点,∴DE=AB=AE,∵CD=AE,∴DE=DC,又DG⊥CE,∴CG=EG.(2)解:作EF⊥BC于F,∵BC=13,CD=5,∴BD=13﹣5=8,∵DE=BE,EF⊥BC,∴DF=BF=4,∴EF===3,∴△EDC的面积=×CD×EF=×5×3=7.5.25.如图:BE、CF是锐角△ABC的两条高,M、N分别是BC、EF的中点,若EF=6,BC=24.(1)证明∠ABE=∠ACF;(2)判断EF与MN的位置关系,并证明你的结论;(3)求MN的长.【解答】解:(1)∵BE、CF是锐角△ABC的两条高,∴∠ABE+∠A=90°,∠ACF+∠A=90°,∴∠ABE=∠ACF;(2)MN垂直平分EF.证明:如图,连接EM、FM,∵BE、CF是锐角△ABC的两条高,M是BC的中点,∴EM=FM=BC,∵N是EF的中点,∴MN垂直平分EF;(3)∵EF=6,BC=24,∴EM=BC=×24=12,EN=EF=×6=3,由勾股定理得,MN===3.26.拓展:如图四边形ABCD中,∠ABC=∠ADC=90°,E是AC中点,EF平分∠BED交BD于点F.(1)猜想EF与BD具有怎样的关系?(2)试证明你的猜想.【解答】解:(1)EF垂直平分BD,(2)∵∠ABC=∠ADC=90°,E是AC中点,∴BE=AE=EC,ED=AE=EC,∴BE=DE,∵EF平分∠BED交BD于点F,∴EF⊥BD,BF=FD,即EF垂直平分BD.27.如图,在Rt△ABC中,∠ACB=90°,M是斜边AB的中点,AM=AN,∠N+∠CAN=180°.求证:MN=AC.【解答】证明:∵∠ACB=90°,M是斜边AB的中点,∴CM=AM,∴∠MCA=∠MAC,∵AM=AN,∴∠AMN=∠ANM,∵∠N+∠CAN=180°,∴AC∥MN,∴∠AMN=∠MAC,∴∠AMC=∠NAM,∴AN∥MC,又AC∥MN,∴四边形ACMN是平行四边形,∴MN=AC.。
直角三角形性质应用(直角 中点)(含答案)

学生做题前请先回答以下问题问题1:从边与角的角度来考虑直角三角形的性质都有哪些?问题2:遇到斜边上的中点怎么想?问题3:直角三角形斜边上的中线等于__________;如果一个三角形__________________,那么这个三角形是直角三角形.直角三角形性质应用(直角+中点)一、单选题(共7道,每道12分)1.如图,在△ABC中,∠BAC=90°,斜边BC上的高AD=5cm,斜边BC上的中线AE=8cm,那么△ABC的面积为( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:直角三角形斜边中线等于斜边一半2.如图,在Rt△ABC中,CD是斜边AB上的中线,EF过点C且平行于AB.若∠BCF=35°,则∠ACD的度数是( )A.35°B.45°C.55°D.65°答案:C解题思路:试题难度:三颗星知识点:直角三角形斜边中线等于斜边一半3.如图,在△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长为( )A.20B.14C.13D.10答案:B解题思路:试题难度:三颗星知识点:直角三角形斜边中线等于斜边一半4.如图,∠ABC=∠ADC=90°,E是AC的中点,若∠BCD=75°,则∠BDE=( )A.25°B.20°C.15°D.10°答案:C解题思路:试题难度:三颗星知识点:直角三角形斜边中线等于斜边一半5.如图,在四边形ABCD中,∠ABC=∠ADC=90°,点E,F分别是对角线AC,BD的中点,则下列结论成立的是( )A. B.C. D.答案:A解题思路:试题难度:三颗星知识点:等腰三角形三线合一性质6.如图,在正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是( )A.2.5B.C. D.2答案:B解题思路:试题难度:三颗星知识点:直角三角形斜边中线等于斜边一半7.如图,BD,BE是Rt△ABC斜边AC上的中线与高线.已知AB=4,BC=3,则AD:DE:EC等于( )A.5:3:4B.25:9:16C.25:7:18D.3:2:1答案:C解题思路:试题难度:三颗星知识点:等积公式二、填空题(共1道,每道16分)8.如图,在四边形ABCD中,BC⊥AC于点C,BE⊥AD于点E,∠BAC=60°,点G是AB的中点,已知,则GE的长是____.答案:1解题思路:试题难度:知识点:含30°的直角三角形。
专题 直角三角形斜边上的中线的运用(解析版)

八年级下册数学《第十八章 平行四边形》专题 直角三角形斜边上的中线的运用【例题1】(2022春•镇江期末)如图,在Rt △ABC 中,∠ACB =90°,点D ,E ,F 分别为AB ,AC ,BC 的中点.若CD =5,则EF 的长为 .【分析】已知CD 是Rt △ABC 斜边AB 的中线,那么AB =2CD ;EF 是△ABC 的中位线,则EF应等于AB的一半.【解答】解:∵△ABC是直角三角形,CD是斜边的中线,∴CD=12 AB,又∵EF是△ABC的中位线,∴AB=2CD=2×5=10cm,∴EF=12×10=5cm.故答案为:5.【点评】此题主要考查了三角形中位线定理以及直角三角形斜边上的中线等知识,用到的知识点为:(1)直角三角形斜边的中线等于斜边的一半;(2)三角形的中位线等于对应边的一半.【变式1-1】如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,E是AC的中点.若DE=3,则AB的长为 .【分析】根据垂线的性质推知△ADC是直角三角形;然后在直角三角形ADC中,利用直角三角形斜边上的中线是斜边的一半,求得AC=6;最后由等腰三角形ABC的两腰AB=AC,求得AB=6.【解答】解:∵在△ABC中,AD⊥BC,垂足为D,∴△ADC是直角三角形;∵E是AC的中点.∴DE=12AC(直角三角形的斜边上的中线是斜边的一半),又∵DE=3,AB=AC,∴AB=6,故答案为:6.【点评】本题主要考查了直角三角形斜边上的中线、等腰三角形的性质,熟记直角三角形斜边上的中线等于斜边的一半是解题的关键.【变式1-2】(2022秋•海口期末)如图,在△ABC中,AD平分∠BAC,BD⊥AD于点D,过点D作DE∥AC,交AB于点E,若AB=6,则DE的长为( )A.2.5B.3C.3.5D.4【分析】求出∠CAD=∠BAD=∠EDA,推出AE=DE,求出∠ABD=∠EDB,推出BE=DE,求出AE=BE,根据直角三角形斜边上中线性质求出即可.【解答】解:∵AD平分∠BAC,∴∠BAD=∠CAD,∵DE∥AC,∴∠CAD=∠ADE,∴∠BAD=∠ADE,∴AE=DE,∵AD⊥DB,∴∠ADB=90°,∴∠EAD+∠ABD=90°,∠ADE+∠BDE=∠ADB=90°.∴∠ABD=∠BDE.∴DE=BE.∵AB=6,∴DE=BE=AE=12AB=3,故选:B.【点评】该题主要考查了等腰三角形的判定与性质、直角三角形的性质、平行线的性质等几何知识点的应用问题;灵活运用有关定理来分析、判断是解题的关键.【变式1-3】如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,CE为AB边上的中线,AD=2,CE=5,则CD=( )A.2B.3C.4D.【分析】根据直角三角形的性质得出AE=CE=5,进而得出DE=3,利用勾股定理解答即可.【解答】解:∵在Rt△ABC中,∠ACB=90°,CE为AB边上的中线,CE=5,∴AE=CE=5,∵AD=2,∴DE=3,∵CD为AB边上的高,∴在Rt△CDE中,CD=4,故选:C.【点评】此题考查直角三角形的性质,关键是根据直角三角形的性质得出AE=CE=5.【变式1-4】如图,在△ABC中,D是BC上一点,AB=AD,E、F分别是AC、BD的中点,EF=2,则AC的长是( )A.3B.4C.5D.6【分析】连接AF.由AB=AD,F是BD的中点,根据等腰三角形三线合一的性质得出AF⊥BD.再根据直角三角形斜边上的中线等于斜边的一半求得AC=2EF=4.【解答】解:如图,连接AF.∵AB=AD,F是BD的中点,∴AF⊥BD.∵在Rt△ACF中,∠AFC=90°,E是AC的中点,EF=2,∴AC=2EF=4.故选:B .【点评】本题考查了直角三角形斜边上的中线的性质:在直角三角形中,斜边上的中线等于斜边的一半.利用等腰三角形三线合一的性质得出AF ⊥BD 是解题的关键.【变式1-5】(2022秋•工业园区校级期中)如图∠ADB =∠ACB =90°,E 、F 分别是AB 、CD 的中点,若AB =26,CD =24,则△DEF 的周长为( )A .12B .30C .27D .32【分析】先根据直角三角形的性质求出DF 与CF 的长,再由等腰三角形的性质求出DE 的长,根据勾股定理求出EF 的长,进而可得出结论.【解答】解:∵ADB =∠ACB =90°,F 是AB 的中点,AB =26,∴DF =CF =12AB =12×26=13,∴△CDF 是等腰三角形.∵点E 是CD 的中点,CD =24,∴EF ⊥CD ,DE =12CD =12.在Rt △DEF 中,DE =5,∴△DEF 的周长为:DF +DE +EF =13+12+5=30.故选:B .【点评】本题考查的是直角三角形斜边上的中线,熟知在直角三角形中,斜边上的中线等于斜边的一半是解题的关键.【变式1-6】(2022春•南岗区校级期中)如图,△ABC 中,∠ACB =90°,D 是AB 的中点,过点D 作AB 的垂线,交BC 于E ,连接CD ,AE ,CD =4,AE =5,则AC =( )A .3B .245C .5D .247【分析】由直角三角形斜边上的中线可求AB =8,根据线段垂直平分线的性质可得BE =AE =5,再利用勾股定理求得CE 的长,进而可求解AC 的长.【解答】解:∵∠ACB =90°,D 是AB 的中点,CD =4,∴AB =2CD =8,∵ED ⊥AB ,∴DE 垂直平分AB ,∴BE =AE =5,∵AC 2=AE 2﹣CE 2=AB 2﹣BC 2,∴52﹣CE 2=82﹣(5+CE )2,解得CE =1.4,∴AC =245.故选:B .【点评】本题主要考查直角三角形斜边上的中线,线段垂直平分线的性质与判定,勾股定理,掌握勾股定理是解题的关键.【变式1-7】(2021•饶平县校级模拟)如图,在三角形ABC 中,AB =AC ,BC =6,三角形DEF 的周长是7,AF ⊥BC 于F ,BE ⊥AC 于E ,且点D 是AB 的中点,则AF =( )A B C D.7【分析】根据直角三角形斜边上的中线等于斜边的一半可得DE=DF=12AB,EF=12BC,然后代入数据计算即可得解.【解答】解:∵AF⊥BC,BE⊥AC,D是AB的中点,∴DE=DF=12 AB,∵AB=AC,AF⊥BC,∴点F是BC的中点,∴BF=FC=3,∵BE⊥AC,∴EF=12BC=3,∴△DEF的周长=DE+DF+EF=AB+3=7,∴AB=4,由勾股定理知AF故选:B.【点评】本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形三线合一的性质,熟记各性质是解题的关键.【变式1-8】如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点,EF=7,BC=10,则△EFM的周长是( )A.17B.21C.24D.27【分析】根据CF⊥AB于F,BE⊥AC于E,M为BC的中点,利用直角三角形斜边上的中线等于斜边的一半,求出FM和ME的长,即可求解.【解答】解:∵CF⊥AB,M为BC的中点,∴MF是Rt△BFC斜边上的中线,∴FM=12BC=12×10=5,同理可得,ME=12BC=12×10=5,又∵EF=7,∴△EFM的周长=EF+ME+FM=7+5+5=17.故选:A.【点评】此题主要考查学生对直角三角形斜边上的中线这个知识点的理解和掌握,解答此题的关键是利用直角三角形斜边上的中线等于斜边的一半,求出FM和ME的长.【例题2】(2022秋•莲湖区期中)如图所示,在Rt△ABC中,∠ACB=90°,∠A=62°,CD⊥AB,垂足为D,点E是BC的中点,连接ED,则∠EDB的度数是 .【分析】先利用直角三角形的两个锐角互余可得∠B=28°,然后利用直角三角形斜边上的中线性质可得ED=EB,从而利用等腰三角形的性质即可解答.【解答】解:∵∠ACB=90°,∠A=62°,∴∠B=90°﹣∠A=28°,∵CD⊥AB,∴∠CDB=90°,∵点E是BC的中点,∴ED=EB=12 BC,∴∠EDB=∠B=28°,故答案为:28°.【点评】本题考查了直角三角形斜边上的中线,熟练掌握直角三角形斜边上的中线性质是解题的关键.【变式2-1】如图,在Rt△ABC中,∠BAC=90°,AD是BC边上的中线,ED⊥BC于D,交BA延长线于点E,若∠E=35°,则∠BDA的度数是.【分析】根据直角三角形的性质得到DA=DB,根据三角形内角和定理计算即可.【解答】解:∵∠E=35°,ED⊥BC,∴∠B=55°∵∠BAC=90°,AD是BC边上的中线,∴DA=DB,∴∠B=∠DAB=55°,∴∠BDA=180°﹣55°﹣55°=70°.故答案为:70°.【点评】本题考查的是直角三角形的性质,掌握在直角三角形中,斜边上的中线等于斜边的一半是解题的关键.【变式2-2】(2022秋•仓山区校级期末)如图,在四边形ABCD中,∠ABC=∠ADC=90°,E为对角线AC的中点,连接BE,ED,BD,若∠BAD=52°,则∠EBD= °.【分析】根据已知条件可以判断EA=EB=EC=DE,根据三角形外角定理可得到:∠DEC=∠DAE+∠ADE=2∠DAE,同理∠BEC=2∠BAE,∠DEB=2∠DAE+2∠BAE=2∠DAB=104°,在等腰三角形BED中,已知顶角,即可求出底角∠EBD的度数.【解答】解:∵∠ABC=∠ADC=90°,∴EA=EB=EC=DE,∴∠DAE=∠EDA,∠BAE=∠EBA,在△AED中,∠DEC=∠DAE+∠ADE=2∠DAE,同理可得到:∠BEC=2∠BAE,∠DEB=∠DEC+∠BEC=2∠DAE+2∠BAE=2(∠DAE+∠BAE)=2×52°=104°,在等腰三角形BED中,∠EBD=12×(180°−104°)=38°;故答案是:38.【点评】本题考查了直角三角形斜边中线定理和三角形外角定理的运用,掌握基本定理是解题的关键.【变式2-3】(2022•碑林区校级模拟)如图,△ABC中,CD⊥AB,垂足为D,E为BC边的中点,AB=4,AC=2,DE=ACD=( )A.15°B.30°C.22.5°D.45°【分析】先根据直角三角形斜边上的中线等于斜边的一半得出BC=2DE=理得出∠ACB=90°,由AB=2AC可求解∠ABC=30°,然后根据同角的余角相等即可得出∠ACD=∠ABC即可求解.【解答】解:∵CD⊥AB,E为BC边的中点,DE=∴BC=2DE=∵AB=4,AC=2,∴AC2+BC2=4+12=16=AB2,∴△ABC是直角三角形,且∠ACB=90°,且∠ABC=30°,∴∠ACD+∠BCD=90°,∵∠ABC+∠BCD=90°,∴∠ACD=∠ABC=30°.故选:B.【点评】本题考查了直角三角形斜边上的中线等于斜边的一半的性质,勾股定理的逆定理,余角的性质,证明△ABC是直角三角形是解题的关键.【变式2-4】(2021秋•潍坊期末)如图,四边形ABCD中,∠ADC=∠ABC=90°,E为对角线AC的中点,∠DAC=30°,∠CAB=40°,连结BE,DE,BD,则∠BDE= 度.【分析】根据直角三角形斜边上的中线等于斜边的一半可得AE=BE=DE=12AC,根据等腰三角形的性质以及三角形外角的性质求得∠BEC=80°,∠CED=60°,那么∠BED=140°,然后在等腰△BDE中即可求出底角∠BDE的度数.【解答】解:∵∠ADC=∠ABC=90°,E为对角线AC的中点,∴AE=BE=DE=12 AC,∴∠ABE=∠CAB=40°,∠ADE=∠DAC=30°,∴∠BEC=∠ABE+∠CAB=80°,∠CED=∠ADE+∠DAC=60°,∴∠BED=∠BEC+∠CED=140°.∵BE=DE,∴∠BDE=∠DBE=180°−∠BED2=20°.故答案为:20.【点评】本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形的性质,三角形外角的性质,三角形内角和定理,熟记各性质并准确识图是解题的关键.【变式2-5】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,E是斜边AB的中点,∠ECD是 度.【分析】先求出∠BCD和∠ACD,再根据直角三角形两锐角互余求出∠B,根据直角三角形斜边上的中线等于斜边的一半可得CE=BE,根据等边对等角可得∠BCE=∠B,再求出∠ECD=45°.【解答】解:∵∠ACB=90°,∠ACD=3∠BCD,∴∠BCD=90°×113=22.5°,∠ACD=90°×313=67.5°,∵CD⊥AB,∴∠B=90°﹣22.5°=67.5°,∵E是AB的中点,∠ACB=90°,∴CE=BE,∴∠BCE=∠B=67.5°,∴∠ECD=∠BCE﹣∠BCD=67.5°﹣22.5°=45°,故答案为:45.【点评】本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形的性质,熟记性质并准确识图,理清图中各角度之间的关系是解题的关键.【变式2-6】(2021秋•温州期中)如图,在△ABC中,∠ACB=90°,∠CAB=30°.以AB长为一边作△ABD,且AD=BD,∠ADB=90°,取AB中点E,连DE、CE、CD.则∠EDC= °.【分析】根据在直角三角形中,斜边上的中线等于斜边的一半得到EC=EA=EB=12AB,根据三角形的外角的性质求出∠CEB=60°,根据直角三角形的性质得到ED=EC,根据三角形内角和定理计算即可.【解答】解:∵∠ACB=90°,点E是AB中点,∴EC=EA=EB=12 AB,∴∠ECA=∠CAB=30°,∴∠CEB=60°,∵AD=BD,点E是AB中点,∴DE⊥AB,即∠AED=90°,∴∠DEC=180°﹣90°﹣60°=30°,∵∠ADB=90°,点E是AB中点,∴DE=12 AB,∴ED=EC,∴∠EDC=75°,故答案为:75.【点评】本题考查的是直角三角形的性质、等腰三角形的性质,掌握在直角三角形中,斜边上的中线等于斜边的一半、等腰三角形的三线合一是解题的关键.【变式2-7】如图,在四边形ABCD中,∠BCD=∠BAD=90°,AC,BD相交于点E,点G,H分别是AC,BD的中点,若∠BEC=80°,那么∠GHE等于( )A.5°B.10°C.20°D.30°【分析】连接AH,CH,根据在四边形ABCD中,∠BCD=∠BAD=90°,H是BD的中点可知AH=CH=12BD,再由点G时AC的中点可知HG是线段AC的垂直平分线,故∠EGH=90°,再由对顶角相等可知∠GEH=∠BEC=80°,由直角三角形的性质即可得出结论.【解答】解:连接AH,CH,∵在四边形ABCD中,∠BCD=∠BAD=90°,H是BD的中点,∴AH=CH=12 BD.∵点G时AC的中点,∴HG是线段AC的垂直平分线,∴∠EGH=90°.∵∠BEC=80°,∴∠GEH=∠BEC=80°,∴∠GHE=90°﹣80°=10°.故选:B.【点评】本题考查的是直角三角形斜边上的中线,熟知在直角三角形中,斜边上的中线等于斜边的一半是解答此题的关键.【变式2-8】(2022秋•市中区校级月考)如图,已知△ABC中,∠ACB=90°,O为AB的中点,点E 在BC上,且CE=AC,∠BAE=15°,求∠COE的度数.【分析】根据等腰直角三角形的性质得到∠CAE=∠AEC=45°,求得∠CAB=60°,得到∠B=30°,根据直角三角形的性质得到CO=BO=AO=12AB,得到△AOC是等边三角形,∠OCB=∠B=30°,于是得到结论.【解答】解:∵∠ACB=90°,CE=AC,∴∠CAE=∠AEC=45°,∵∠BAE=15°,∴∠CAB=60°,∴∠B=30°,∵∠ACB=90°,O为AB的中点,∴CO =BO =AO =12AB ,∴△AOC 是等边三角形,∠OCB =∠B =30°,∴AC =OC =CE ,∴∠COE =∠CEO =12×(180°﹣30°)=75°.【点评】本题考查了直角三角形斜边上的中线,等腰三角形的性质,等边三角形的判定和性质,正确的识别图形是解题的关键.【例题3】如图,在四边形ABCD 中,∠ABC =∠ADC =90°,M 、N 分别是AC 、BD 的中点,试说明:(1)MD =MB ;(2)MN ⊥BD .【分析】(1)根据直角三角形斜边上的中线等于斜边的一半,以及等边对等角的性质即可证明;(2)根据等腰三角形的三线合一证明.【解答】证明:(1)∵∠ABC =∠ADC =90°,M 是AC 的中点,∴BM =12AC ,DM =12AC ,∴DM =BM ;(2)由(1)可知DM =BM ,∵N 是BD 的中点,∴MN ⊥BD.【点评】此题主要是运用了直角三角形的性质以及等腰三角形的性质,题目难度不大.【变式3-1】(2022春•零陵区校级期中)如图,△ABC中,BE平分∠ABC,BE⊥AF于F,D为AB中点,请说明DF∥BC的理由.【分析】根据在直角三角形中斜边上的中线是斜边的一半得,BD=DF,∠DFB=∠DBF,根据角的平分线的定义知∠FBC=∠FBD,∴∠DFB=∠FBC,再根据内错角相等两直线平行得DF∥BC.【解答】解:∵在直角△AFB中,点D是斜边上的中点,∴DF=BD=12 AB,∴∠DFB=∠DBF,∵BE平分∠ABC,∴∠FBC=∠FBD,∴∠DFB=∠FBC,∴DF∥BC.【点评】本题的关键是明白在直角三角形的性质中斜边上的中线是斜边的一半,角的平分线的定义,平行线的判定中内错角相等,两直线平行.注意等边对等角的运用.【变式3-2】(2021秋•虹口区校级期末)如图,已知△ABC的高BD、CE相交于点O,M、N分别是BC、AO的中点,求证:MN垂直平分DE.【分析】连接EN、DN、EM、DM,由BD与CE为三角形ABC的两条高,可得∠AEC=∠ADB=∠BEC =∠BDC=90°,根据M,N为BC,AO的中点,利用斜边上的中线等于斜边的一半可得EN=DN,EM =DM,根据线段垂直平分线的逆定理得到M、N在线段DE的垂直平分线上,得证.【解答】证明:连接EN、DN、EM、DM,∵BD⊥AC,CE⊥AB,∴∠AEC=∠ADB=∠BEC=∠BDC=90°,∵M、N是BC、AO的中点,∴EN=12AO,DN=12AO,EM=12BC,DM=12BC,∴EN=DN,EM=DM,∴M、N在线段DE的垂直平分线上,∴MN垂直平分DE.【点评】此题考查了直角三角形斜边上中线的性质,以及线段垂直平分线的逆定理,利用了转化的思想,其中连接出如图所示的辅助线是解本题的关键.【变式3-3】如图,△ABC中,AD是边BC上的高,CF是边AB上的中线,DC=BF,点E是CF的中点.(1)求证:DE⊥CF;(2)求证:∠B=2∠BCF.【分析】(1)连接DF,根据直角三角形的性质得到DF=12AB=BF,进而证明DC=DF,根据等腰三角形的三线合一证明结论;(2)根据三角形的外角性质得到∠FDB=2∠DFC,根据等腰三角形的性质证明结论.【解答】证明:(1)连接DF,∵AD是边BC上的高,∴∠ADB=90°,∵点F是AB的中点,∴DF=12AB=BF,∵DC=BF,∴DC=DF,∵点E是CF的中点.∴DE⊥CF;(2)∵DC=DF,∴∠DFC=∠DCF,∴∠FDB=∠DFC+∠DCF=2∠DFC,∵DF=BF,∴∠FDB=∠B,∴∠B=2∠BCF.【点评】本题考查的是直角三角形的性质、等腰三角形的性质,掌握在直角三角形中,斜边上的中线等于斜边的一半是解题的关键.【变式3-4】如图,在△ABC中,∠BAC=90°,AD是中线,E是AD中点,过A作AF∥BC交BE的延长线于点F,连接CF.(1)求证:AD=AF;(2)如果AB=AC,试判断四边形ADCF的形状,并证明你的结论.【分析】(1)由E是AD的中点,AF∥BC,易证得△AEF≌△DEB,即可得AF=BD,又由在△ABC 中,∠BAC=90°,AD是中线,根据直角三角形斜边的中线等于斜边的一半,即可证得AD=BD=CD=12BC,即可证得:AD=AF;(2)当AB=AC时,四边形ADCF是矩形.由AF=BD=DC,AF∥BC,可证得:四边形ADCF是平行四边形,又由AB=AC,根据三线合一的性质,可得AD⊥BC,AD=DC,继而可得四边形ADCF是正方形.【解答】(1)证明:∵AF∥BC,∴∠EAF=∠EDB,∵E是AD的中点,∴AE=DE,在△AEF和△DEB中,∠EAF=∠EDB AE=DE∠AEF=∠DEB,∴△AEF≌△DEB(ASA),∴AF=BD,∵在△ABC中,∠BAC=90°,AD是中线,∴AD=BD=DC=12 BC,∴AD=AF;(2)当AB=AC时,四边形ADCF是正方形.∵AF=BD=DC,AF∥BC,∴四边形ADCF是平行四边形,∵AB=AC,AD是中线,∴AD⊥BC,∵AD=AF,∴四边形ADCF是正方形.【点评】此题考查了正方形的判定、平行四边形的判定与性质以及全等三角形的判定与性质.此题难度适中.【变式3-5】在Rt△ABC中,∠ABC=90°,BD为∠ABC的角平分线,F为AC的中点,AE∥BC交BD的延长线于点E,其中∠FBC=2∠FBD.(1)求∠EDC的度数.(2)求证:BF=AE.【分析】(1)由角平分线的性质可得∠ABD=∠DBC=45°,可求∠FBD=15°,∠FBC=30°,由直角三角形的性质可得∠C=∠FBC=30°,即可求解;(2)由直角三角形的性质可得BF=AB,由平行线的性质和等腰三角形的性质可得AB=AE,可证BF=AE.【解答】解:(1)∵∠ABC=90°,BD为∠ABC的角平分线,∴∠ABD=∠DBC=45°,∵∠FBC=2∠FBD.∴∠FBD=15°,∠FBC=30°,∵∠ABC=90°,点F是AC中点,∴AF=BF=CF,∴∠C=∠FBC=30°,∴∠EDC=∠C+∠DBC=75°;(2)∵∠C=30°,∠ABC=90°,∴AC=2AB,∴AB=AF=BF,∵AE∥BC,∴∠E=∠DBC=45°=∠ABD,∴AB=AE,∴AE=BF.【点评】本题考查了直角三角形的性质,角平分线的性质,平行线的性质,灵活运用这些性质是本题的关键.【变式3-6】已知,如图,在Rt△ABC中,∠C=90°,点E在AC上,AB=12DE,AD∥BC.求证:∠CBA=3∠CBE.【分析】取DE的中点F,连接AF,根据直角三角形的性质求出AF=DF=FE=12DE,推出DF=AF=AB,根据等腰三角形的性质求出∠D=∠DAF,∠AFB=∠ABF,求出∠ABF=2∠D,∠CBE=∠D,即可得出答案.【解答】证明:取DE的中点F,连接AF,∵AD∥BC,∠ACB=90°,∴∠DAE=∠ACB=90°,∴AF=DF=EF=12 DE,∵AB=12 DE,∴DF=AF=AB,∴∠D=∠DAF,∠AFB=∠ABF,∴∠AFB=∠D+∠DAF=2∠D,∴∠ABF=2∠D,∵AD∥BC,∴∠CBE=∠D,∴∠CBA=∠CBE+∠ABF=3∠CBE.【点评】本题考查了等腰三角形的性质,直角三角形的性质,平行线的性质,三角形的外角性质的应用,能正确作出辅助线是解此题的关键,难度适中.【变式3-7】如图,已知四边形ABCD中,∠ABC=∠ADC=90°,点E是AC中点,点F是BD中点.(1)求证:EF⊥BD;(2)过点D作DH⊥AC于H点,如果BD平分∠HDE,求证:BA=BC.【分析】(1)根据直角三角形和等腰三角形的性质即可得到结论;(2)设AC,BD交于点O,根据垂直的定义得到∠DHO=∠EFO=90°,根据等腰三角形的性质得到∠EDO=∠EBO,由角平分线的定义得到∠HDF=∠BDE,根据等腰三角形的判定定理即可得到结论.【解答】(1)证明:∵∠ABC=∠ADC=90°,点E是AC中点,∴DE=12AC,BE=12AC,∴DE=BE,∵点F是BD中点,∴EF⊥BD;(2)证明:设AC,BD交于点O,∵DH⊥AC,EF⊥BD,∴∠DHO=∠EFO=90°,∵∠DOH=∠BOE,∴∠HDF=∠OEF,∵DE=BE,∴∠EDO=∠EBO,∵BD平分∠HDE,∴∠HDF=∠BDE,∴∠OEF=∠OBE,∵∠OEF+∠EOF=90°,∴∠EOF+∠EBO=90°,∴∠BEO=90°,∴BE⊥AC,∴BA=BC.【点评】本题考查了直角三角形斜边上的中线,等腰三角形的判定和性质,正确的识别图形是解题的关键.【变式3-8】(2021•安顺模拟)如图,在△ABC中,点D在AB上,且CD=CB,E为BD的中点,F为AC的中点,连接EF交CD于点M,连接AM.(1)求证:EF=12 AC;(2)若EF⊥AC,求证:AM+DM=CB.【分析】(1)根据等腰三角形三线合一的性质可得CE⊥BD,再根据直角三角形斜边上的中线等于斜边的一半可得EF=12 AC;(2)根据“SAS”证明△AFM≌△CFM,可得AM=CM,进而可得结论.【解答】(1)证明:连接CE,如图,∵CD=CB,E为BD的中点,∴CE⊥BD,∵F为AC的中点,∴EF=12 AC;(2)证明:∵EF⊥AC,∴∠AFM=∠CFM,∵F为AC的中点,∴AF=CF,∵MF=MF,∴△AFM≌△CFM(SAS),∴AM=CM,∵CD=DM+MC,∴CD=DM+AM,∵BC=DC,∴AM+DM=CB.【点评】本题考查了等腰三角形的性质,直角三角形的性质,全等三角形的判定与性质,灵活应用定理是解决本题的关键.【变式3-9】(2022秋•宿城区期中)如图,在锐角三角形ABC中,CD,BE分别是AB,AC边上的高,M,N分别是线段BC,DE的中点.(1)求证:MN⊥DE.(2)连接DM,ME,猜想∠A与∠DME之间的关系,并证明你的猜想.(3)当∠BAC变为钝角时,如图②,上述(1)(2)中的结论是否都成立?若成立,直接回答,不需证明;若不成立,请说明理由.【分析】(1)连接DM,ME,根据直角三角形的性质得到DM=12BC,ME=12BC,得到DM=ME,根据等腰直角三角形的性质即可得到结论;(2)根据三角形内角和定理、等腰三角形的性质计算即可得到结论;(3)仿照(2)的计算过程解答即可得到结论.【解答】(1)证明:如图(1),连接DM,ME,∵CD、BE分别是AB、AC边上的高,M是BC的中点,∴DM=12BC,ME=12BC,∴DM=ME,又∵N为DE中点,∴MN⊥DE;(2)在△ABC中,∠ABC+∠ACB=180°﹣∠A,∵DM=ME=BM=MC,∴∠BMD+∠CME=(180°﹣2∠ABC)+(180°﹣2∠ACB)=360°﹣2(∠ABC+∠ACB)=360°﹣2(180°﹣∠A)=2∠A,∴∠DME=180°﹣2∠A;(3)结论(1)成立,结论(2)不成立,理由如下:连接DM,ME,在△ABC中,∠ABC+∠ACB=180°﹣∠BAC,∵DM=ME=BM=MC,∴∠BME+∠CMD=2∠ACB+2∠ABC=2(180°﹣∠BAC )=360°﹣2∠BAC ,∴∠DME =180°﹣(360°﹣2∠BAC )=2∠BAC ﹣180°.【点评】本题考查的是直角三角形的性质、三角形内角和定理,掌握直角三角形中,斜边上的中线等于斜边的一半是解题的关键.且AF ⊥CF ,若AC =3,BC =6,则DF 的长为( )A .1.5B .1C .0.5D .2【分析】根据三角形中位线定理求出DE ,根据直角三角形的性质求出FE ,计算即可.【解答】解:∵D 、E 分别为AB 、AC 的中点,BC =6,∴DE =12BC =3,∵AF ⊥CF ,∴∠AFC =90°,∵E 为AC 的中点,AC =3,∴FE =12AC =1.5,∴DF =DE ﹣FE =1.5,故选:A .【点评】本题考查的是三角形中位线定理、直角三角形的性质,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.【变式4-1】(2022春•南岗区校级期中)如图,在△ABC 中,D ,E 分别是AB ,AC 的中点,连接ED ,F 是ED 延长线上一点,连接AF 、CF ,若∠AFC =90°,DF =1,AC =6,则BC 的长度为( )A .2B .3C .4D .5【分析】根据直角三角形斜边上的中线的性质求出EF ,进而求出DE ,根据三角形中位线定理计算,得到答案.【解答】解:在Rt △AFC 中,∠AFC =90°,E 是AC 的中点,AC =6,则EF =12AC =3,∵DF =1,∴DE =3﹣1=2,∵D ,E 分别是AB ,AC 的中点,∴DE 是△ABC 的中位线,∴BC =2DE =4,故选:C .【点评】本题考查的是三角形中位线定理、直角三角形斜边上的中线的性质,掌握三角形中位线等于第三边的一半是解题的关键.【变式4-2】(2022•金乡县三模)如图,在△ABC 中,∠BAC =90°,AD 是BC 边上的高,E 、F 分别是AB 、AC 边的中点,若AB =8,AC =6,则△DEF 的周长为 .【分析】根据勾股定理求出BC,根据直角三角形斜边上的中线性质求出DE和DF,根据三角形的中位线性质求出EF,再求出答案即可.【解答】解:在Rt△ABC中,由勾股定理得:BC==10,∵AD⊥BC,∴∠ADB=∠ADC=90°,∵E、F分别是AB、AC边的中点,AB=8,AC=6,BC=10,∴DE=12AB=4,DF=12AC=3,EF=12BC=5,∴△DEF的周长=EF+DE+DF=5+4+3=12,故答案为:12.【点评】本题考查了勾股定理,直角三角形斜边上的中线性质,三角形的中位线性质等知识点,能熟记直角三角形斜边上的中线等于斜边的一半是解此题的关键.【变式4-3】如图,△ABC的周长为16,G、H分别为AB、AC的中点,分别以AB、AC为斜边向外作Rt △ADB和Rt△AEC,连接DG、GH、EH,则DG+GH+EH的值为( )A.6B.7C.8D.9【分析】根据直角三角形斜边上的中线等于斜边的一半可得DG=12AB,EH=12AC,三角形的中位线平行于第三边并且等于第三边的一半可得GH=12BC,然后求出DG+GH+EH的值为△ABC的一半.【解答】解:∵G、H分别为AB、AC的中点,△ADB和△AEC为直角三角形,∴DG=12AB,EH=12AC,∴GH为△ABC的中位线,∴GH=12 BC,∴DG+GH+EH=12(AB+AC+BC)=12×16=8.故选:C.【点评】本题考查了直角三角形斜边上的中线等于斜边的一半的性质,三角形的中位线平行于第三边并且等于第三边的一半,熟记性质和定理是解题的关键.【变式4-4】(2022春•大足区期末)如图,在Rt△ABC中∠ACB=90°,∠A=30°,点D,E分别是边AB,AC的中点,延长BC到点F,使CF=12BC,若EF=2,则DE的长为( )A.2B.1C D+1【分析】连接CD,根据三角形中位线定理得到DE∥BC,DE=12BC,根据平行四边形的性质求出CD,根据直角三角形斜边上的中线的性质求出AB,根据含30°角的直角三角形的性质求出BC,进而求出DE.【解答】解:连接CD,∵点D,E分别是边AB,AC的中点,∴DE是△ABC的中位线,∴DE∥BC,DE=12 BC,∵CF=12 BC,∴DE∥CF,∴四边形DEFC为平行四边形,∴CD=EF=2,在Rt △ACB 中,∠ACB =90°,点D 是边AB 的中点,则AB =2CD =4,在Rt △ACB 中,∠ACB =90°,∠A =30°,则BC =12AB =2,∴DE =12BC =1,故选:B .【点评】本题考查的是三角形中位线定理、平行四边形的判定和性质、直角三角形斜边上的中线的性质、含30°角的直角三角形的性质,灵活运用各个定理是解题的关键.【变式4-5】(2021春•赣榆区期中)如图,在△ABC 中,E 、F 分别是AB 、AC 的中点,延长EF 交△ABC 的外角∠ACD 的平分线于点G .AG 与CG 有怎样的位置关系?证明你的结论.【分析】利用三角形中位线定理推知EF ∥BC .所以利用平行线的性质、三角形角平分线的性质以及等腰三角形的判定证得FG =FC .又由AF =CF ,则FG 是△ACG 中AC 边上的中线,且FG =12AC ,则△AGC 是直角三角形.【解答】解:AG ⊥CG ,理由:∵E 、F 分别是AB 、AC 的中点,∴EF 是△ABC 的中位线,AF =CF ,∴EF ∥BC ,∴∠FGC =∠GCD .∵CG平分∠ACD,∴∠FCG=∠GCD,∴∠FCG=∠FGC,∴FG=FC.又∵AF=CF,∴FG是△ACG中AC边上的中线,且FG=12 AC,∴△AGC是直角三角形,∴AG⊥CG.【点评】本题考查了三角形中位线定理、直角三角形斜边上的中线定理.一个三角形,如果一边上的中线等于这条边的一半,那么这个三角形是以这条边为斜边的直角三角形.该定理可以用来判定直角三角形.【变式4-6】(2022春•海淀区校级期中)如图,在△ABC中,点D,点E分别是边AC,AB的中点,点F在线段DE上,AF=5,BF=12,AB=13,BC=19,求DF的长度.【分析】由三角形中位线定理求出DE,由勾股定理逆定理证得△ABF是直角三角形,根据直角三角形斜边中线定理求出EF,即可求出DF的长度.【解答】解:∵点D,点E分别是边AC,AB的中点,∴DE是△ABC的中位线,∴DE=12BC=12×19=192,在△ABF中,∵AF2+BF2=52+122=169=132,AB2=132,∴AF2+BF2=AB2,∴∠AFB=90°,∴EF=12AB=12×13=132,∴DF=DE﹣EF=192−132=3.【点评】本题主要考查了三角形中位线定理,直角三角形斜边中线定理,勾股定理逆定理,灵活运用这三个定理是解决问题的关键.【变式4-7】(2022春•徐州期中)已知:如图,在△ABC中,D、E、F分别是各边的中点,AH是高.(1)求证:DH=EF;(2)求证:∠DHF=∠DEF.【分析】(1)根据三角形中位线定理得到EF=12AB,根据直角三角形的性质得到DH=12AB,证明结论;(2)连接DF,证明△DHF≌△DEF,证明结论.【解答】证明:(1)∵E、F分别是边BC、AC的中点,∴EF=12 AB,∵AH⊥BC,D是AB的中点,∴DH=12 AB,∴DH=EF;(2)连接DF,由(1)得,DH=EF,同理DE=HF,在△DHF和△DEF中,DH=FEHF=EDDF=FD,∴△DHF≌△DEF,∴∠DHF=∠DEF.【点评】本题考查的是直角三角形的性质、全等三角形的判定和性质,掌握直角三角形中,斜边上的中线等于斜边的一半是解题的关键.【变式4-8】(2021春•罗湖区校级期末)如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.(1)求证:BM=MN;(2)若∠BAD=60°,AC平分∠BAD,AC=2,写出求BN长的思路.【分析】(1)根据直角三角形的性质得到BM=12AC,根据三角形中位线定理得到MN=12AD,根据题意证明;(2)证明△NMB是等腰直角三角形,根据勾股定理计算即可.【解答】(1)证明:∵∠ABC=90°,M为AC中点,∴BM=12 AC,∵M为AC中点,N为DC中点,∴MN=12 AD,∵AD=AC,∴BM=MN;(2)解:∵∠BAD=60°,AC平分∠BAD,∴∠DAC=∠CAB=30°,∴BM=AM=12AC=1,∴∠MAB=∠MBA=30°,∴∠CMB=60°根据三角形中位线定理得,MN∥AD,MN=12AD=1,∴∠DAC=∠NMC=30°,∴△NMB是等腰直角三角形,由勾股定理得,BN=【点评】本题考查的是直角三角形的性质、三角形中位线定理以及等腰三角形的性质,掌握直角三角形中,斜边上的中线等于斜边的一半是解题的关键.。
八上数学每日一练:直角三角形斜边上的中线练习题及答案_2020年综合题版

八上数学每日一练:直角三角形斜边上的中线练习题及答案_2020年综合题版答案解析答案解析答案解析2020年八上数学:图形的性质_三角形_直角三角形斜边上的中线练习题1.(2020东台.八上期中) 已知:如图∠ABC=∠ADC=90°,M ,N 分别是AC 、BD 的中点.(1) 试判断△BMD 的形状,并说明理由.(2) 求证: MN ⊥BD.考点: 等腰三角形的判定与性质;直角三角形斜边上的中线;2.(2020武汉.八上期末) 如图,四边形ABCD 中,AB ∥CD ,AB ⊥BC ,AB =BC ,AB >CD ,AE ⊥BD于E 交BC 于F.(1) 若AB =2CD ;①求证:BC =2BF ;②连CE ,若DE =6,CE = ,求EF 的长;(2) 若AB =6,则CE 的最小值为.考点: 全等三角形的判定与性质;直角三角形斜边上的中线;相似三角形的判定与性质;3.(2019嵊州.八上期末) 如图,在Rt △ACB 中,∠ACB=90º,点D 是AB 的中点,点E 是CD 的中点,过C 作CF ∥AB 交AE 的延长线于点F ,连BF.(1) 求证:△ADE ≌△FCE ;(2) 若∠DCF=120º,DE=2,求BC 的长.考点: 等边三角形的判定与性质;直角三角形斜边上的中线;4.(2020南浔.八上期中) 如图,在△ABC 中,AD 是△ABC 的高线,CE 是△ABC 的角平分线,它们相交于点P .(1) 若∠B =40°,∠AEC =75°,求证:AB =BC ;答案解析答案解析(2) 若∠BAC =90°,AP 为△AEC 边EC 上中线,求∠B 的度数.考点: 等腰三角形的性质;直角三角形斜边上的中线;5.(2019庆元.八上期末) 已知:如图,在△ABC 中,AD 是BC 边上的高,∠C=30°,∠ABC=45°,BE 是AC 边上的中线.(1)求证:AC=2BD ;(2) 求∠CBE 的度数;(3) 若点E 到边BC 的距离为 ,求BC 的长.考点:等腰直角三角形;含30度角的直角三角形;直角三角形斜边上的中线;2020年八上数学:图形的性质_三角形_直角三角形斜边上的中线练习题答案1.答案:2.答案:3.答案:4.答案:5.答案:。
专题12 直角三角形斜边上的中线(解析版)

专题12 直角三角形斜边上的中线【考点归纳】(1)性质:在直角三角形中,斜边上的中线等于斜边的一半.(即直角三角形的外心位于斜边的中点)(2)定理:一个三角形,如果一边上的中线等于这条边的一半,那么这个三角形是以这条边为斜边的直角三角形.该定理可一用来判定直角三角形.【好题必练】一、选择题1.(2020秋•贵阳期末)如图,在长为10的线段AB上,作如下操作:经过点B作BC⊥AB,使得BC=AB;连接AC,在CA上截取CE=CB;在AB上截取AD=AE,则AD的长为()A.5﹣5B.10﹣5C.10﹣10D.5+5【答案】A【解析】解:∵AB=10,BC=AB,∴BC=5,由勾股定理得:AC=5,∵CE=BC=5,∴AD=AE=AC﹣CE=5﹣5.故选:A.2.(2020秋•仪征市期末)A、B、C分别表示三个村庄,AB=1000米,BC=600米,AC=800米,为拟建一个文化活动中心,要求这三个村庄到活动中心的距离相等,则活动中心P的位置应在()A.AB中点B.BC中点C.AC中点D.∠C的平分线与AB的交点【答案】A.【解析】解:∵AB2=10002=1000000,BC2=6002=360000,AC2=8002640000,∴AB2=BC2+AC2,∴△ABC为以AB为斜边的直角三角形,当点P在AB的中点时,CP=AB=P A=PB,故选:A.3.(2020秋•莲湖区期末)如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开,若测得AB 的长为4.8km,则M,C两点间的距离为()A.1.2km B.2.4km C.3.6km D.4.8km【答案】B.【解析】解:∵公路AC,BC互相垂直,∴∠ACB=90°,∵M为AB的中点,∴CM=AB,∵AB=4.8km,∴CM=2.4(km),即M,C两点间的距离为2.4km,故选:B.4.(2020秋•新华区校级月考)如图所示,在△ABC中,∠ACB=90°,D是AB的中点,DE⊥BC,E为垂足,AC=AB,图中为60°的角有()A.2个B.3个C.4个D.5个【答案】D.【解析】解:在Rt△ABC中,∠ACB=90°,AC=AB,∴∠B=30°.∵D是AB的中点,∴BD=CD.∴∠DCB=∠B=30°.又∵DE⊥BC于E,∴∠BDE=∠CDE=60°.∴∠ACD=90°﹣30°=60°.∴△ACD为等边三角形.∴∠ADC=∠DAC=∠ACD=∠CDE=∠BDE=60°.故选:D.5.(2020秋•嵊州市期中)直角三角形的两条直角边为3,4,则这个直角三角形斜边上的中线长为()A.5B.2.5C.3.5D.4.5【答案】B【解析】解:由勾股定理得:直角三角形的斜边长是=5,所以=2.5,故选:B.6.(2020秋•高州市期中)如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,CE为AB边上的中线,AD=2,CE=10,则CD=()A.2B.3C.4D.6【答案】D【解析】解:在Rt△ABC中,∠ACB=90°,CE为AB边上的中线,CE=10,∴AE=CE=10,∵AD=2,∴DE=8,∵CD为AB边上的高,在Rt△CDE中,CD===6,故选:D.二、填空题7.如图,在Rt△ABC中,CD是斜边AB上的中线,若AB=20,则CD=.【答案】10【解析】解:∵∠ACB=90°,CD是斜边AB上的中线,∴CD=AB=10,故答案为:10.8.如图,直角三角形ABC中,∠ACB=90°,∠B=36°,D是AB的中点,ED⊥AB交BC于E,连接CD,则∠CDE:∠ECD=.【答案】1:2.【解析】解:∵∠ACB=90°,∠B=36°,D是AB的中点,∴CD=DB,∴∠ECD=∠B=36°,∴∠CDB=180°﹣∠ECD﹣∠B=180°﹣36°﹣36°=108°,∵ED⊥AB,∴∠EDB=90°,∠CDE=∠CDB﹣∠EDB=108°﹣90°=18°,∠CDE:∠ECD=1:2.故答案为1:2.9.(2020春•南岗区校级期中)如图,已知在△ABC中,∠C=25°,点D在边BC上,且∠DAC=90°,AB=DC.则∠BAC的度数为°.【答案】105【解析】解:取CD的中点E,连接AE,在Rt△ADC中,DE=EC,∴AE=CD=ED=EC,∴∠EAC=∠C=25°,∴∠AED=∠EAC+∠C=50°,∵AE=ED,∴∠EAD=∠EDA=65°,∵AB=DC,AE=CD,∴AB=AE,∴∠BAE=80°,∴∠BAC=∠BAE+∠EAC=105°,故答案为:105.10.在Rt△ABC中,∠ACB=90°,如果斜边AB上的中线CD=4cm,那么斜边AB=cm.【答案】8【解析】解:∵在Rt△ABC中,斜边AB上的中线CD=4cm,∴AB=2CD=8cm.故答案为:8.11.已知:如图,四边形ABCD中,∠ABC=∠ADC=90°,AC与BD相交于点O,E、F分别是AC、BD的中点.则∠EFO=.【答案】90°【解析】解:连接EB、ED,∵∠ABC=90°,E是AC的中点,∴BE=AC,同理,DE=AC,∴EB=ED,又F是BD的中点,∴EF⊥BD,∴∠EFO=90°,故答案为:90°.三、解答题12.如图,在△ABC中,AB=AC,BD平分∠ABC,AD⊥BD于点D.(1)若∠C=74°,求∠BAD的度数;(2)点E为线段AB的中点,连接DE.求证:DE∥BC.【答案】(1)解:∵AB=AC,∴∠ABC=∠C=74°,∵BD平分∠ABC,∴∠ABD=∠ABC=37°,∵AD⊥BD,∴∠BAD=90°﹣37°=53°;(2)证明:在Rt△ADB中,点E为线段AB的中点,∴ED=EB∴∠EBD=∠EDB,∵BD平分∠ABC,∴∠ABD=∠CBD,∴∠EDB=∠CBD,∴DE∥BC.【解析】(1)根据等腰三角形的性质得到∠ABC=∠C=74°,根据角平分线的定义、三角形内角和定理计算即可;(2)根据直角三角形的性质得到ED=EB根据等腰三角形的性质得到∠EBD=∠EDB,根据平行线的判定定理证明结论.13.如图,在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG⊥CE于G,CD=AE.(1)求证:CG=EG.(2)已知BC=13,CD=5,连结ED,求△EDC的面积.【答案】(1)证明:连接DE,在Rt△ADB中,点E是AB的中点,∴DE=AB=AE,∵CD=AE,∴DE=DC,又DG⊥CE,∴CG=EG.(2)解:作EF⊥BC于F,∵BC=13,CD=5,∴BD=13﹣5=8,∵DE=BE,EF⊥BC,∴DF=BF=4,∴EF===3,∴△EDC的面积=×CD×EF=×5×3=7.5.【解析】(1)连接DE,根据直角三角形的性质得到DE=AB=AE,根据等腰三角形的性质证明结论;(2)作EF⊥BC于F,根据题意求出BD,根据等腰三角形的性质求出DF,根据勾股定理求出EF,根据三角形的面积公式计算,得到答案.14.如图,在△ABC中,AD是高,CE是中线,DG垂直平分CE,连接DE.(1)求证:DC=BE;(2)若∠AEC=72°,求∠BCE的度数.【答案】(1)证明:∵DG垂直平分CE,∴DE=DC,∵AD是高,CE是中线,∴DE是Rt△ADB的斜边AB上的中线,∴DE=BE=AB,∴DC=BE;(2)∵DE=DC,∴∠DEC=∠DCE,∴∠EDB=∠DEC+∠BCE=2∠BCE∵DE=BE∴∠B=∠EDB,∴∠B=2∠BCE,∴∠AEC=3∠BCE=72°,∴∠BCE=24°.【解析】(1)根据线段垂直平分线的性质得到DE=DC,根据直角三角形斜边上的中线是斜边的一半得到DE=BE=AB,证明结论;(2)根据等腰三角形想的性质得到∠DEC=∠DCE,根据三角形的外角性质列式计算即可.15.如图.△ABC中,∠C=2∠B,D是BC上一点,且AD⊥AB,点E是BD的中点,连结AE.(1)求证:BD=2AC;(2)若AE=6.5,AD=5,那么△ABE的周长是多少?【答案】(1)证明:∵AD⊥AB,∴∠BAD=90°,又点E是BD的中点,∴EA=BD=EB,∴∠EAB=∠EBA,∴∠AEC=2∠B,又∠C=2∠B,∴∠AEC=∠C,∴AE=AC,∴BD=2AC;(2)解:∵∠BAD=90°,点E是BD的中点,∴BD=2AE=13,EA=EB=6.5,由勾股定理得,AB===12,∴△ABE的周长=AB+AE+BE=12+6.5+6.5=25.【解析】(1)根据直角三角形的性质得到EA=BD=EB,根据等腰三角形的性质和三角形的外角的性质证明;(2)根据直角三角形的性质分别求出BC和BE,根据勾股定理求出AB,根据三角形的周长公式计算.16.已知:如图,∠ABC=∠ADC=90°,M、N分别是AC、BD的中点,求证:MN⊥BD.【答案】证明:连接DM,BM,∵∠ABC=∠ADC=90°,M是AC的中点,∴DM=AC,BM=AC,∴DM=BM,又N是BD的中点,∴MN⊥BD.【解析】连接DM,BM,根据直角三角形的性质得到DM=AC,BM=AC,得到DM=BM,根据等腰三角形的三线合一证明.11/ 11。
中考数学真题解析矩形的性质与判定,直角三角形斜边上的中线等于斜边的一半(含答案)

(2012年1月最新最细)2011全国中考真题解读120考点汇编矩形的性质与判定,直角三角形斜边上的中线等于斜边的一半一、选择题1.(2011•南通)如图,在矩形纸片ABCD中,AB=2cm,点E在BC上,且AE=CE.若将纸片沿AE折叠,点B恰好与AC上的点B1重合,则AC=4cm.考点:翻折变换(折叠问题)。
分析:根据题意推出AB= A'B=2,由AE=CE推出AB1=B1C,即AC=4.解答:解:∵AB=2cm,A'B=AB,,∴A'B=2,∵矩形ABCD,AE=CE,∴∠ABE=∠AB1E=90°,∵AE=CE,∴A'B='B C,∴AC=4.故答案为4.点评:本题主要考察翻折的性质、矩形的性质、等腰三角形的性质,解题的关键在于推出AB= A'B.2.(2011江苏无锡,5,3分)菱形具有而矩形不一定具有的性质是()A.对角线互相垂直B.对角线相等C.对角线互相平分D.对角互补考点:矩形的性质;菱形的性质。
专题:推理填空题。
分析:根据菱形对角线垂直平分的性质及矩形对交线相等平分的性质对各个选项进行分析,从而得到最后的答案.解答:解:A、菱形对角线相互垂直,而矩形的对角线则不垂直;故本选项错误;B、菱形和矩形的对角线都相等;故本选项正确;C、菱形和矩形的对角线都互相平分;故本选项正确;D、菱形对角相等,但不互补;故本选项正确;故选A.点评:此题主要考查了学生对菱形及矩形的性质的理解及运用.菱形和矩形都具有平行四边形的性质,但是菱形的特性是:对角线互相垂直、平分,四条边都相等.3.(2011•宁夏,2,3分)如图,矩形ABCD 的两条对角线相交于点O ,∠AOD=60°,AD=2,则AB 的长是( )A 、2B 、4C 、23D 、43考点:矩形的性质;等边三角形的判定与性质。
分析:本题的关键是本题的关键是利用等边三角形和矩形对角线的性质即锐角三角函数关系求长度.解答:解:∵在矩形ABCD 中,AO=21AC ,DO=21BD ,AC=BD , ∴AO=DO , 又∵∠AOD=60°, ∴∠ADB=60°, ∴∠ABD=30°, ∴AB AD=tan30°, 即AB 2=33, ∴AB=23. 故选C .点评:本题考查了矩形的性质和锐角三角函数关系,具有一定的综合性,难度不大属于基础性题目.4.(2011台湾,29,4分)如图,长方形ABCD 中,E 为BC 中点,作∠AEC 的角平分线交AD 于F 点.若AB =6,AD =16,则FD 的长度为何?( )A .4B .5C .6D .8考点:矩形的性质;角平分线的性质;勾股定理。
八上数学每日一练:直角三角形斜边上的中线练习题及答案_2020年填空题版

2020年 八 上 数 学 : 图 形 的 性 质 _三 角 形 _直 角 三 角 形 斜 边 上 的 中 线 练 习 题
1. (2020苍南.八上期末) 如图,Rt△ABC中,∠ACB=90°,∠A=28°,D是AB的中点,则∠DCB=________度。
答案解析
4. (2020淮安.八上期末) 直角三角形的两条直角边长为6,8,那么斜边上的中线长是________. 考点: 直角三角形斜边上的中线;勾股定理;
答案解析
5.
(2020东台.八上期中) 若
的三边长分别是6、8、10,则最长边上的中线长为________.
考点: 直角三角形斜边上的中线;勾股定理的逆定理;
,则此直角三角形斜边上的中线长是________.
答案解析
10.
(2019秀洲.八上期末) (2018八上·宜兴期中) 若直角三角形斜边上的高和中线长分别是3cm,4cm,则它的面积是_____
___cm2 .
考点: 三角形的面积;直角三角形斜边上的中线;
答案解析
2020年 八 上 数 学 : 图 形 的 性 质 _三 角 形 _直 角 三 角 形 斜 边 上 的 中 线 练 习 题 答 案
考点: 三角形内角和定理;等腰三角形的性质;直角三角形斜边上的中线;
答案解析
2. (2020通榆.八上期末) 特例探究:如图1,已知在△ABC中,AB=CB,∠ABC=90°,D为AC边的中点,连接BD,则△ ABD是________三角形。
归纳证明:如图2,已知在△ABC中,AB=CB,∠ABC=90°,D为AC边的中点,连接BD,把Rt△DEF的直角顶点D放 在AC的中点上,DE交AB于M,DF交BC于N。证明:DM=DN。
(好题)初中数学九年级数学下册第一单元《直角三角形的边角关系》检测卷(含答案解析)

一、选择题1.在Rt ABC ∆中,90C ∠=︒,若5sin 13A =,则cos A 的值为( ) A .512 B .813 C .1312 D .12132.如图,传送带和地面所成斜坡AB 的坡度为1∶2,物体从地面沿着该斜坡前进了10米,那么物体离地面的高度为( )A .5米B .5米C .25米D .45米 3.如图,在矩形ABCD 中,点E 是CD 的中点,点F 是BC 上一点,且FC=2BF ,连接AE ,EF .若AB=2,AD=3,则cos ∠AEF 的值是( )A .12B .1C .22D .324.在Rt ABC 中,∠C =90º,下列关系式中错误的是( )A .BC =AB•sinAB .BC =AC•tanA C .AC =BC•tanBD .AC =AB•cosB 5.如图,在Rt ABC △中,90ABC ∠=︒,4AB =,8BC =,D ,E 分别为边AB ,BC 上一点,且满足:1:3AD DB =.连接DE ,将ADBE 沿DE 翻折,点B 的对应点F 恰好落在边AC 上,则CF 的长度为( )A .1952055B .275C .52055D .3156.Rt ABC 中,90C ∠=︒,2AC =,1BC =,sin A =( )A .55B .2C .32D .127.如图,直线123////l l l ,ABC 的三个顶点分别落在123,,l l l 上,AC 交2l 于点D ,设1l 与2l 的距离为12,h l 与3l 的距离为2h .若12,:1:2AB BC h h ==,则下列说法正确的是( )A .:2:3ABD ABC S S =B .:1:2ABD ABC S S =△△C .sin :sin 2:3ABD DBC ∠∠=D .sin :sin 1:2ABD DBC ∠∠= 8.在ABC 中,90,13,12C AB BC ∠=︒==,则sin B 的值为( )A .1213B .512 C .513 D .1359.在Rt ABC 中,90C ∠=︒,5AB =,4BC =,则tan A 的值为( ) A .35 B .45 C .34 D .4310.如图,在正方形ABCD 中,边长为2的等边三角形AEF 的顶点E 、F 分别在BC 和CD 上,下列结论:①CE CF =;②75AEB ∠=︒;③BE DF EF +=;④正方形对角线:13AC =+,其中正确的序号是( )A .①②④B .①②C .②③④D .①③④ 11.如图,直线y =-33x +2与x 轴、y 轴分别交于A 、B 两点,把△AOB 绕点A 顺时针旋转60°后得到△AO'B',则点B'的坐标是( ) A .(4,23)B .(23,4)C .(3,3)D .(23+2,2) 12.如图,在边长相同的小正方形组成的网格中,点A B C D 、、、都在这些小正方形的顶点上,AB CD 、相交于点P ,则tan APD ∠=( ).A .5B .3C .10D .2二、填空题13.如图,测角仪CD 竖直放在距建筑物AB 底部8m 的位置,在D 处测得建筑物顶端A 的仰角为50°.若测角仪CD 的高度是1.5m ,则建筑物AB 的高度约为_____m .(结果精确到个位,参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)14.如图,在Rt ABC 中,90B ∠=︒,2AB =,1BC =.将ABC 绕点A 按逆时针方向旋转90︒得到''AB C ,连接'B C ,则tan 'ACB ∠=__________.15.如图,在Rt ABC △中,90A ∠=︒,AB AC =,BD 是AC 边上的中线,则tan ADB ∠的值是______.16.如图,点P (m ,1)是反比例函数3y x=图象上的一点,PT ⊥x 轴于点T ,把△PTO 沿直线OP 翻折得到△PT O ',则点T '的坐标为_______________.17.ABC ∆中,67.5A ,8BC =,BE AC ⊥交AC 于E ,CF AB ⊥交AB 于F ,点D 是BC 的中点.以点F 为原点,FD 所在的直线为x 轴构造平面直角坐标系,则点E 的横坐标为________.18.如图,四边形ABCD 中,AB=BC=3,∠A=∠C=90°,∠ABC=120°,点E 是对角线BD 上的一个动点,过点E 分别作AB ,BC ,CD ,AD 的垂线,垂足分别为点F ,H ,I ,G ,连结FG 和HI ,则FG+HI 的最小值为________.19.如图所示,在四边形ABCD 中,90B ∠=︒,2AB =,8CD =.连接AC ,AC CD ⊥,若1sin 3ACB ∠=,则AD 长度是_________.20.在Rt ABC ∆中,90A ∠=︒,3AB =,4BC =则cos B =______.三、解答题21.计算:20210+|﹣3|﹣2sin60°.22.如图,根据道路管理规定,在某笔直的大道AB 上行驶的车辆,限速60千米/时,已知测速站点M 距大道AB 的距离MN 为30米,现有一辆汽车从A 向B 方向匀速行驶,测得此车从A 点行驶到B 点所用时间为6秒,已知60AMN ∠=︒,45BMN ∠=︒.(参考数据:3 1.732≈,2 1.414≈)(1)计算AB 的长度(结果保留整数);(2)试判断此车是否超速,并说明理由.23.图①是一辆登高云梯消防车的实物图,图②是其工作示意图,起重臂AC 是可伸缩的(10m 20m AC ),且起重臂AC 可绕点A 在一定范围内转动,张角为()90150CAE CAE ∠∠︒︒,转动点A 距离地面BD 的高度AE 为3.5m .(1)当起重臂AC 长度为12m ,张角CAE ∠为120︒时,求云梯消防车最高点C 距离地面的高度CF ;(2)某日、一居民家突发险情,该居民家距离地面的高度为18m ,请问该消防车能否实3 1.732≈)24.如图在平面直角坐标系xOy 中,一次函数()0y kx b k =+≠的图象与反比例函数()0m y m x=≠的图象交于第二、四象限内的A 、B 两点,与x 轴交于C 点,点B 的坐标为()6,n .线段5OA =,E 为x 轴上一点,且4sin 5AOE ∠=.(1)求该反比例函数和一次函数的解析式;(2)求AOB的面积;25.(1)解方程:22360x x--=(2)计算:12cos301tan602sin30︒--︒+︒26.为了方便市民出行,县政府决定从“七星广场”河堤到对岸修建一座便民桥.为测量河的宽度,在河的对岸取一点A,在广场河边取两点,O B测得点A在点O的北偏东60︒方向,测得点A在点B北偏东45︒方向,量得OB长为50米,求河的宽度AC(结果保留根号)【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【分析】由三角函数的定义可知sinBCAAB=,可设BC=5k,AB=13k由勾股定理可求得12AC k=,再利用余弦的定义代入计算即可.【详解】解:如图:在Rt ABC 中,sin BC A AB =,可设BC=5k ,AB=13k . 由勾股定理可求得()()222213512AC AB BC k k k =-=-=. 所以,1212cos =1313AC k A AB k ==. 故选:D .【点睛】 本题主要考查三角函数的定义,掌握正弦、余弦函数的定义是解题的关键.2.C解析:C【分析】作BC ⊥底面于点C ,根据坡度的概念、勾股定理列式计算即可;【详解】作BC ⊥底面于点C ,设BC x =,∵传送带和底面所成斜坡AB 的坡度为1∶2,∴2AC x =,由勾股定理得:222AC BC AB +=,即()222210x x +=,解得:25x =,即25BC =.故答案选C .【点睛】本题主要考查了解直角三角形的应用-坡度坡角问题,准确计算是解题的关键. 3.C解析:C【分析】连接AF ,根据题意可分别求出BF 、FC 、DE 的长,再利用勾股定理分别求出AF 、AE 、EF 的长,利用勾股定理的逆定理判断出AEF 为等腰直角三角形,再利用三角函数即可求得答案.【详解】如图:连接AF ,四边形ABCD 是矩形∴2,3AB DC AD BC ====∴∠B=∠C=∠D=90°FC=2BF∴BF=1,FC=2E 是CD 的中点∴DE=CE=1∴BF=CE=1在Rt ABF 中22222215AF AB BF =+=+=在Rt EFC 中22222215EF FC CE =+=+=在Rt ADE △中222223110AE AD DE =+=+=∴222AE EF AF =+且AF=EF∴△AEF 为等腰直角三角形∴∠AFE=90°,∠AEF=∠EAF=45°∴cos ∠AEF=cos45°=22故选:C .【点睛】本题考查了矩形的性质,勾股定理及其逆定理的运用,特殊角的三角函数值,解题关键是利用勾股定理逆定理判断出AEF 为等腰直角三角形. 4.D解析:D【分析】根据三角函数的定义即可作出判断.【详解】解:A 、∵sin BC A AB=, ∴sin BC AB A =, 故正确,不符合题意;B 、∵tanA= BC AC, ∴BC=AC•tanA ,故正确,不符合题意;C 、∵tanB=AC BC, ∴AC=BC•tanB , 故正确,不符合题意;D 、∵cos BC B AB=, ∴cos BC AB B =,故错误,符合题意;故选:D .【点睛】本题考查锐角三角函数的定义:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.5.A解析:A【分析】如图,过D 作DM AC ⊥于,M 根据已知条件先求解:,,,AD BD AC 再利用A ∠的三角函数求解,,AM DM 由对折得到:,DF 再利用勾股定理求解MF ,从而由CF AC AM MF =--可得答案.【详解】解:如图,过D 作DM AC ⊥于,M4:1:3,AB AD DB ==,13AD DB ∴==,,90ABC ∠=︒,4AB =,8BC =,22224845,AC AB BC ∴=+=+=1,AD DM AC =⊥,sin ,45DM BC A AD AC ∴=== 255DM ∴=, 同理:5cos ,545AM AB A AD AC ==== 55AM ∴=, 由对折可得:3,DF DB == 22222520535MF DF DM ⎛⎫∴=-=-= ⎪ ⎪⎝⎭,520519520545CF AC AM MF -∴=--== 故选:.A【点睛】 本题考查的是轴对称的性质,勾股定理的应用,锐角三角函数的应用,掌握以上知识是解题的关键.6.A解析:A【分析】求出斜边AB ,再求∠A 的正弦值.【详解】解:∵90C ∠=︒,2AC =,1BC =,∴2222215AB AC BC +=+= 5sin 5BC A AB ===, 故选:A .【点睛】本题考查了勾股定理和锐角的正弦函数值的求法,解题关键是求出斜边长,熟知正弦的意义.7.D解析:D【分析】作2⊥AE l ,2⊥CF l ,如图,则1AE h =,2CF h =,利用三角形面积公式可得到12::1:2ABD BCD S S h h ∆∆==,则可对A 、B 进行判断;利用正弦的定义得到1sin h ABD AB ∠=,2sin h DBC BC∠=,利用AB CB =可对C 、D 进行判断. 【详解】 解:作2⊥AE l ,2⊥CF l ,如图,则1AE h =,2CF h =,11122ABD S BD AE BD h ∆==,21122BCE S BD CF BD h ∆==, 12::1:2ABD BCD S S h h ∆∆∴==,:1:3ABD ABC S S ∆∆∴=,所以A 、B 选项错误;在Rt ABE ∆中,1sin h AE ABD AB AB ∠==, 在Rt BCF ∆中,2sin h CF DBC BC BC∠==, 而AB CB =,12sin :sin :1:2ABD DBC h h ∴∠∠==,所以C 选项错误,D 选项正确. 故选:D .【点睛】本题考查了考查了解直角三角形,也考查了平行线之间的距离和等腰直角三角形的性质,难度一般.8.C解析:C【分析】先根据勾股定理求得AC ,再根据正弦的定义求解即可;【详解】∵在ABC 中,90C ∠=︒,13AB =,12BC =,∴2213125AC =-=,∴5sin 13AC B AB ==; 故答案选C .【点睛】本题主要考查了勾股定理与解直角三角形,准确理解计算是解题的关键.9.D解析:D【分析】由勾股定理算出AC 的值,然后根据正切函数的定义即可得到解答.【详解】 解:由勾股定理可得:2222543AC AB BC =-=-=,∴tanA=43BC AC =, 故选D .【点睛】 本题考查解直角三角形,熟练掌握勾股定理及三角函数的定义是解题关键.10.A解析:A【分析】证明()Rt ABE Rt ADF HL ≅△△即可证明①正确,由①的结论得到三角形CEF 是等腰直角三角形,即可证明②正确,根据AC 垂直平分EF 可以判断③错误,利用锐角三角函数值求出AC 的长度证明④正确.【详解】解:∵四边形ABCD 是正方形,∴AB AD =,90B D ∠=∠=︒,∵AEF 是等边三角形,∴AE AF =, 在Rt ABE △和Rt ADF 中,AE AF AB AD =⎧⎨=⎩, ∴()Rt ABE Rt ADF HL ≅△△,∴BE DF =,∵BC CD =,∴BC BE CD DF -=-,即CE CF =,故①正确;∵CE CF =,90C ∠=︒,∴45CEF ∠=︒,∵60AEF ∠=︒,∴180604575AEB ∠=︒-︒-︒=︒,故②正确;如图,连接AC ,交EF 于点G ,∵AE AF =,CE CF =,∴AC 是EF 的垂直平分线,∵CAF DAF ∠≠∠,∴DF FG ≠,同理BE EG ≠,∴BE DF EF +≠,故③错误;∵AEF 是边长为2的等边三角形,ACB ACD ∠=∠,∵AC EF ⊥,EG FG =, ∴3sin 6023AG AE =⋅︒==112CG EF ==, ∴13AC AG CG =+=+,故④正确.故选:A .【点睛】本题考查四边形综合题,解题的关键是掌握正方形的性质,等边三角形的性质,解直角三角形的方法.11.B解析:B【分析】根据直线解析式求出点A 、B 的坐标,从而得到OA 、OB 的长度,再求出∠OAB =30°,利用勾股定理列式求出AB ,然后根据旋转角是60°判断出AB′⊥x 轴,再写出点B′的坐标即可.【详解】令y =0,则−3x +2=0,解得x =,令x =0,则y =2,所以,点A (0),B (0,2),所以,OA =OB =2,∵tan ∠OAB =OB OA ==, ∴∠OAB =30°,由勾股定理得,AB 4==, ∵旋转角是60°,∴∠OAB′=30°+60°=90°,∴AB′⊥x 轴,∴点B′(4).故选:B .【点睛】本题考查了坐标与图形性质−旋转,一次函数图象上点的坐标特征,勾股定理的应用,三角函数的应用,求出AB′⊥x 轴是解题的关键. 12.B解析:B【分析】设小正方形的边长为1,根据勾股定理可得AD 、AC 的值,进而可得△ADC 是等腰直角三角形,进而可得AD ⊥CD ,根据相似三角形的判定和性质可得PC =2DP ,根据等量代换和线段和差可得AD =CD =3DP ,继而即可求解.【详解】解析 设小正方形的边长为1,由图形可知,2AD DC AC ===,ADC ∴是等腰直角三角形,AD DC ∴⊥.//AC BD ,2AC CP BD DP∴==, 2PC DP ∴=,3AD DC DP ∴==,tan 3AD APD DP∴∠==.故选B.【点睛】本题考查了正方形的性质、等腰直角三角形的判定、勾股定理、相似三角形的判定及其性质以及锐角三角函数.此题难度适中,注意转化思想与数形结合思想的应用.二、填空题13.11【分析】根据题意作辅助线DE⊥AB然后根据锐角三角函数可以得到AE 的长从而可以求得AB的长本题得以解决【详解】解:作DE⊥AB于点E由题意可得DE=CD=8m∵∠ADE=50°∴AE=DE•ta解析:11【分析】根据题意,作辅助线DE⊥AB,然后根据锐角三角函数可以得到AE的长,从而可以求得AB 的长,本题得以解决.【详解】解:作DE⊥AB于点E,由题意可得,DE=CD=8m,∵∠ADE=50°,∴AE=DE•tan50°≈8×1.19=9.52(m),∵BE=CD=1.5m,∴AB=AE+BE=9.52+1.52=11.2≈11(m),故答案为:11.【点睛】本题考查了解直角三角形的应用-仰角俯角问题,解答本题的关键是明确题意,利用数形结合的思想解答.14.【分析】如图延长与的延长线交于点证明四边形为正方形再求解过作于利用等面积法求解再利用勾股定理求解从而可得答案【详解】解:如图由题意得:延长与的延长线交于点则四边形为正方形过作于故答案为:【点睛】本题解析:4 3【分析】如图,延长C B''与BC的延长线交于点,G证明四边形ABGB'为正方形,再求解,B C AC ',过A 作AM B C '⊥于M , 利用等面积法求解,AM 再利用勾股定理求解,MC 从而可得答案.【详解】解:如图,由题意得:9090BAB B AB C '''∠=︒∠=∠=︒,, 2AB AB '==, 1BC =,22215,AC ∴=+=延长C B ''与BC 的延长线交于点,G 则90AB G '∠=︒,∴ 四边形ABGB '为正方形, 2211B G BG CG BG BC '∴===-=-=,,90B GB '∠=︒, 22215,B C '∴=+=过A 作AM B C '⊥于M ,11,22AB C S AB AB B C AM '''∴== 54AM =, 4555AM ∴==, ()224355555MC ⎛⎫∴=-= ⎪⎝⎭, 4545tan '.3355AM ACB MC ∴∠=== 故答案为:4.3【点睛】本题考查的是勾股定理的应用,旋转的性质,正方形的判定与性质,锐角三角函数的应用,掌握以上知识是解题的关键. 15.2【分析】由题意得到则结合角的正切值即可得到答案【详解】解:∵是边上的中线∴∴∵∴∵在中∴;故答案为:2【点睛】本题考查了求角的正切值三角形中线的性质解题的关键是掌握三角形中线的性质正确得到解析:2【分析】由题意,得到12AD AC =,则2AC AD =,结合角的正切值tan AB ADB AD∠=,即可得到答案.【详解】 解:∵BD 是AC 边上的中线,∴12AD AC =, ∴2AC AD=, ∵AB AC =,∴2AB AD=, ∵在Rt ABD 中,90A ∠=︒, ∴tan 2AB ADB AD ∠==; 故答案为:2.【点睛】本题考查了求角的正切值,三角形中线的性质,解题的关键是掌握三角形中线的性质,正确得到2AB AD=. 16.【分析】连接过点作于点C 先根据反比例函数解析式求出点P 坐标根据的正切值得到它的度数再根据折叠的性质证明是等边三角形再解直角三角形得到OC 和的长即可求出的坐标【详解】解:如图连接过点作于点C ∵点P(m解析:33,2⎛⎫ ⎪ ⎪⎝⎭【分析】连接TT ',过点T '作T C OT '⊥于点C ,先根据反比例函数解析式求出点P 坐标,根据POT ∠的正切值得到它的度数,再根据折叠的性质证明TOT '是等边三角形,再解直角三角形得到OC 和CT '的长,即可求出T '的坐标.【详解】解:如图,连接TT ',过点T '作T C OT '⊥于点C ,∵点P (m ,1)是反比例函数y x =图象上的一点,∴1=m ,∴OT =,1PT =,∵tan 3POT ∠=, ∴30POT ∠=︒,由折叠的性质得:30,POT POT OT OT ∠=∠=︒='='∴60TOT '∠=︒,又∵OT OT '=,∴TOT '是等边三角形,∵T C OT '⊥,∴12OC OT ==,3sin 2CT OT TOT '''=⋅∠==,∴322T ⎛⎫' ⎪ ⎪⎝⎭.故答案为:322⎛⎫ ⎪⎪⎝⎭. 【点睛】本题考查反比例函数与几何,解题的关键是掌握反比例函数的性质,利用锐角三角函数值得到特殊角的度数,然后解直角三角形. 17.【分析】连接DE 过E 作EH ⊥OD 于H 求得∠EDO =45°即可得到Rt △DEH 中求得DH 进而得出OH 即可求解【详解】如图所示连接过作于于于是的中点中点的横坐标是【点睛】本题主要考查了直角三角形斜边上中 解析:4-【分析】连接DE ,过E 作EH ⊥OD 于H ,求得∠EDO =45°,即可得到Rt △DEH 中,求得DH ,进而得出OH ,即可求解.【详解】如图所示,连接DE ,过E 作EH OD ⊥于H ,BE CA ⊥于E ,CF AB ⊥于F ,D 是BC 的中点,142DE DC BC DO DB ∴=====, DCE DEC ∴∠=∠,DBO DOB ∠=∠,67.5A ∴∠=︒,112.5ACB ABC ∴∠+∠=︒,18021802()()CDE BDO DCE DBO ∴∠+∠=︒-∠+︒-∠ 3602()DCE DBO =︒-∠+∠3602112.5=︒-⨯︒135=︒,45EDO ∴∠=︒,Rt DEH ∴∆中,cos 4522DH DE =︒⨯=422OH OD DH ∴=-=-点E 的横坐标是422-【点睛】本题主要考查了直角三角形斜边上中线的性质:在直角三角形中,斜边上的中线等于斜边的一半.解决问题的关键是作辅助线构造等腰直角三角形.18.3【分析】先证明得到再证明:四边形四边形为矩形得到所以只要求的最小值即可当时最小再利用锐角三角函数可得答案【详解】解:AB=BC=3∠A=∠C=90°由过点E 分别作ABBCCDAD 的垂线垂足分别为点 解析:3【分析】先证明,Rt ABD Rt CBD ≌得到60,30,ABD CBD GDE IDE ∠=∠=︒∠=∠=︒再证明:,FG HI =四边形,AFEG 四边形CHEI 为矩形,得到AE FG =,所以只要求AE 的最小值即可,当AE BD ⊥时,AE 最小,再利用锐角三角函数可得答案.【详解】 解: AB=BC=3,∠A=∠C=90°,,120,BD BD ABC =∠=︒,Rt ABD Rt CBD ∴≌60,30,ABD CBD GDE IDE ∴∠=∠=︒∠=∠=︒由过点E 分别作AB ,BC ,CD ,AD 的垂线,垂足分别为点F ,H ,I ,G ,,,EF EH EG EI ∴== 四边形,AFEG 四边形CHEI 为矩形,90,FEG HEI ∴∠=∠=︒,FEG HEI ∴≌∴ ,FG HI =当FG 最小,则FG HI +最小,四边形AFEG 为矩形,,AE FG ∴=所以:当AE BD ⊥时,AE 最小,3,60,AB ABE =∠=︒sin 60,AE AB ∴︒= 3333,AE ∴=⨯= 所以:FG 的最小值是:33, 所以:FG HI +的最小值是:3323 3.⨯= 故答案为:3 3.【点睛】本题考查的是点到直线的距离垂线段最短,三角形全等的判定与性质,矩形的判定与性质,锐角三角函数的应用,掌握以上知识是解题的关键.19.10【分析】根据直角三角形的边角间关系先计算再在直角三角形中利用勾股定理即可求出【详解】解:在中∵∴在中故答案为:10【点睛】本题考查了解直角三角形和勾股定理利用直角三角形的边角间关系求出AC 是解决 解析:10【分析】根据直角三角形的边角间关系,先计算AC ,再在直角三角形ACD 中,利用勾股定理即可求出AD .【详解】解:在Rt ABC 中,∵12,sin3ABAB ACBAC=∠==,∴1263AC=÷=.在Rt ADC中,22AD AC CD=+2268=+10=.故答案为:10.【点睛】本题考查了解直角三角形和勾股定理,利用直角三角形的边角间关系,求出AC是解决本题的关键.20.【分析】根据题意画出图形进而得出cosB=求出即可【详解】解:∵∠A=90°AB=3BC=4则cosB==故答案为:【点睛】本题考查了锐角三角函数的定义正确把握锐角三角函数关系是解题的关键解析:3 4【分析】根据题意画出图形,进而得出cosB=ABBC求出即可.【详解】解:∵∠A=90°,AB=3,BC=4,则cosB=ABBC=34.故答案为:34.【点睛】本题考查了锐角三角函数的定义,正确把握锐角三角函数关系是解题的关键.三、解答题21.1【分析】直接利用特殊角的三角函数值以及绝对值的性质、零指数幂的性质分别化简得出答案.【详解】解:原式=12×2=1=1.【点睛】本题主要考查了实数的混合运算,结合特殊角三角函数中、零指数幂计算是解题的关键. 22.(1)82米;(2)不超速,见解析【分析】(1)已知MN=30m ,∠AMN=60°,∠BMN=45°求AB 的长度,可以转化为解直角三角形; (2)求得从A 到B 的速度,然后与60千米/时≈16.66米/秒,比较即可确定答案.【详解】解:(1)由题意可得在Rt AMN △中,30MN =米,60AMN ∠=︒, ∴tan AN MN AMN =⋅∠=在Rt BMN 中,∵45BMN ∠=︒,∴30BN MN ==(米). ∴3082AB AN BN =+=≈(米).(2)此车不超速,理由如下:由题意可得,汽车从A 到B 为匀速行驶,用时为6秒,且82AB =米,则汽车的速度为()306513.66÷=≈(米/秒).∵60千米/时≈16.67米/秒,13.6616.67<,∴此车不会超速.【点睛】本题考查了勾股定理以及解直角三角形的应用,解题的关键是从题目中抽象出直角三角形,难度不大.23.(1)9.5m ;(2)可以有效救援.【分析】(1)过点C 作CF ⊥BD ,垂足为F ,过点A 作AG ⊥CF ,垂足为G ,解直角三角形ACG 即可;(2)当起重臂最长,张角最大时,计算远臂点距离地面的最大高度,比较判断即可.【详解】(1)如图1,过点C作CF⊥BD,垂足为F,过点A作AG⊥CF,垂足为G,∵AE⊥BD,∴四边形AEFG是矩形,∴∠EAG=90°,FG=AE=3.5,∴∠CAG=30°,∵AC=12,∴CG=ACsin30°=12×1=6,2∴CF=CG+FG=6+3.5=9.5(米);(2)如图2,过点C作CF⊥BD,垂足为F,过点A作AG⊥CF,垂足为G,∵AE⊥BD,∴四边形AEFG是矩形,∴∠EAG=90°,FG=AE=3.5,∴∠CAG=60°,∵AC=20,∴CG=ACsin60°3,∴CF=CG+FG=17.32+3.5=20.82>18;∴能有效救援.【点睛】本题考查了生活实际问题中的解直角三角形,熟练把生活问题转化数学解直角三角形模型问题是解题的关键.24.(1)12y x =-,223y x =-+;(2)9 【分析】(1)过点A 作AH ⊥x 轴于H 点,由4sin 5AH ACE AO∠==,OA=5,根据正弦的定义可求出AH ,再根据勾股定理得到OH ,即得到A 点坐标(-3,4),把A (-3,4)代入y= ,确定反比例函数的解析式为y=- ;将B (6,n )代入,确定点B 点坐标,然后把A 点和B 点坐标代入y=kx+b (k≠0),求出k 和b .(2)先令y=0,求出C 点坐标,得到OC 的长,然后根据AOB BOC AOC SS S =+计算△AOB 的面积即可.【详解】解:(1)过A 作AH x ⊥轴交x 轴于H ,∴4sin 5AH ACE AO∠==,5OA =, ∴4AH =,∴223OH OA AH ,∴()3,4A -,将()3,4A -代入m y x=,得12=-m , ∴反比例函数的解析式为12y x =-, 将()6,B n 代入12y x=-,得2n =-, ∴()6,2B -, 将()3,4A -和()6,2B -分别代入()0y kx b k =+≠,得3462k b k b -+=⎧⎨+=-⎩,解得232k b ⎧=-⎪⎨⎪=⎩, ∴直线解析式:223y x =-+; (2)在直线223y x =-+中,令0y =,则有2203x -+=,解得3x =, ∴()3,0C ,即3OC =,∴13462AOC S =⨯⨯=△; 同理3BOC S =△,则9AOB BOC AOC S S S =+=△△△.【点睛】本题考查了反比例函数的综合运用.关键是作x 轴的垂线,解直角三角形求A 点坐标,用待定系数法求直线,双曲线的解析式.25.(1)134x +=,234x =;(2)5【分析】(1)用公式法解方程即可;(2)先求特殊角三角函数值,再进行实数计算.【详解】解:(1)22360x x --=, 2a =,3b =-,6c =-∴224(3)42(6)570b ac -=--⨯⨯-=>∴332224b x a -===⨯∴134x =,234x -=(2)原式)1122=-+⨯311=+5=-【点睛】本题考查了一元二次方程的解法和含有特殊角三角函数值的实数计算,解题关键是选择恰当的方法解一元二次方程和熟记特殊角三角函数值并熟练进行计算.26.河的宽度AC 为(25+米【分析】根据点A 在点B 北偏东45°方向,结合方位角的知识可证AC BC =,利用三角函数解直角三角形,列关出方程,解方程即可.【详解】根据题意,有30,45AOC ABC ∠=︒∠=︒, 又90ACB ∠=︒所以BC AC =, 在Rt AOC ∆中,tan AC AOC OC ∠=,即tan 30AC OC ︒= 设AC x =米,则BC x =米,由题意得503x x =+ 解得x =化简得25x =+∴河的宽度AC 为(25+米.【点睛】本题考查了解直角三角形的实际应用,熟记特殊角的三角函数值,灵活运用方位角的知识,规范解直角三角形是解题关键.。
八下数学每日一练:直角三角形斜边上的中线练习题及答案_2020年压轴题版

八下数学每日一练:直角三角形斜边上的中线练习题及答案_2020年压轴题版答案答案答案2020年八下数学:图形的性质_三角形_直角三角形斜边上的中线练习题~~第1题~~(2019昭通.八下期中) 如图,四边形,对角线交于点, ,点分别为 的中点,求证: 是等边三角形.考点: 直角三角形斜边上的中线;~~第2题~~(2019浏阳.八下期中) 已知:在△ABC 年,∠BAC=90°,AB=AC ,点D 为直线BC 上一动点(点D 不与B 、C 重合).以AD 为边作正方形ADEF ,连接CF.(1)如图1,当点D 在线段BC 上时,求证:①BD ⊥CF.② .(2) 如图2,当点D 在线段BC 的延长线上时,其它条件不变,请直接写出CF 、BC 、CD 三条线段之间的关系;(3) 如图3,当点D 在线段BC 的反向延长线上时,且点A 、F 分别在直线BC 的两侧,其它条件不变:①请直接写出CF 、BC 、CD 三条线段之间的关系,②若连接正方形对角线AE ,DF ,交点为0,连接OC ,探究△AOC 的形状,并说明理由.考点: 全等三角形的判定与性质;直角三角形斜边上的中线;~~第3题~~(2019来宾.八下期末) 在▱ABCD 中,对角线AC 、BD 交于点O ,将过点A 的直线l 绕点A 旋转,交射线CD 于点E ,BF ⊥l 于点F ,DG ⊥l 于点G ,连接OF ,OG .(1) 如图①当点E 与点C 重合时,请直接写出线段OF ,OG 的数量关系;(2) 如图②,当点E 在线段CD 上时,OF 与OG 有什么数量关系?请证明你的结论;(3) 如图③,当点E 在线段CD 的延长线上时,上述的结论是否仍成立?请说明理由.考点: 全等三角形的判定与性质;直角三角形斜边上的中线;平行四边形的性质;答案答案~~第4题~~(2018深圳.八下期中) 已知:正方形ABCD,E 是BC 的中点,连接AE,过点B 作射线BM 交正方形的一边于点F,交AE 于点O.(1) 若BF ⊥AE ,①求证:BF=AE ;②连接OD,确定OD 与AB 的数量关系,并证明。
八上数学每日一练:直角三角形斜边上的中线练习题及答案_2020年压轴题版

(2) 如图4,当∠CDF=30°时,AM+CKMK(填“>”或“<”);
(3) 猜想:如图1,当0°<∠CDF<60°时,AM+CKMK,试证明你的猜想.. 考点: 全等三角形的判定与性质;等腰三角形的性质川.八上期中) 如图,在等腰Rt△ABC中,∠C=90°,D是斜边上AB上任一点,AE⊥CD于E , BF⊥CD交CD 的延长线于F , CH⊥AB于H点,交AE于G .
(2) 问题2: 如图,△ABC中,∠ACB=80°, ∠BAC=40°,求画一条直线l把△ABC分成两个等腰三角形, 并在图中标注两个顶角的 度数.
(3) 问题3: 如图,△ABC中,∠ACB=120°, ∠BAC=40°,求画一条直线l把△ABC分成两个等腰三角形, 并在图中标注两个顶角的 度数.
答案解析
2. (2016平谷.八上期末) 如图1,有两个全等的直角三角形△ABC和△EDF,∠ACB=∠F=90°,∠A=∠E=30°,点D在边 AB上,且AD=BD=CD.△EDF绕着点D旋转,边DE,DF分别交边AC于点M,K.
(1) 如图2、图3,当∠CDF=0°或60°时,AM+CKMK(填“>”,“<”或“=”),你的依据是;
八上数学每日一练:直角三角形斜边上的中线练习题及答案_2020年压轴题版
2020年 八 上 数 学 : 图 形 的 性 质 _三 角 形 _直 角 三 角 形 斜 边 上 的 中 线 练 习 题
1. (2017温岭.八上期末) 动手操作题:如何能把一个三角形分成两个等腰三角形吗? 实际上,一个三角形只要具备下列三个条件之一,都可以被分成两个等腰三角形: ①一个角为90°;②一个角是另一个的2倍(第三角必须大于45°); ③一个角是另一个角的3倍.今天,我们通过作图来验证这个结论。 (1) 问题1: 如图,Rt△ABC中,求画一条直线l将△ABC分成两个等腰三角形.并说明直线l与△ABC 边上的交点D的位置.
直角三角形性质应用(直角+中点)(人教版)(含答案)

学生做题前请先回答以下问题问题1:从边与角的角度来考虑直角三角形的性质都有哪些?问题2:遇到斜边上的中点怎么想?问题3:直角三角形斜边上的中线等于__________;如果一个三角形__________________,那么这个三角形是直角三角形.以下是问题及答案,请对比参考:问题1:从边与角的角度来考虑直角三角形的性质都有哪些?答:①直角三角形两锐角互余,且任一直角边长小于斜边长.②勾股定理:直角三角形两直角边的平方和等于斜边的平方;勾股定理逆定理:如果三角形三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.问题2:遇到斜边上的中点怎么想?答:直角三角形斜边上的中线等于斜边的一半.问题3:直角三角形斜边上的中线等于;如果一个三角形,那么这个三角形是直角三角形.答:斜边的一半;一边上的中线等于这边的一半.直角三角形性质应用(直角+中点)(人教版)一、单选题(共7道,每道12分)1.如图,在△ABC中,∠BAC=90°,斜边BC上的高AD=5cm,斜边BC上的中线AE=8cm,那么△ABC的面积为( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:直角三角形斜边中线等于斜边一半2.如图,在Rt△ABC中,CD是斜边AB上的中线,EF过点C且平行于AB.若∠BCF=35°,则∠ACD的度数是( )A.35°B.45°C.55°D.65°答案:C解题思路:试题难度:三颗星知识点:直角三角形斜边中线等于斜边一半3.如图,在△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长为( )A.20B.14C.13D.10答案:B解题思路:试题难度:三颗星知识点:直角三角形斜边中线等于斜边一半4.如图,∠ABC=∠ADC=90°,E是AC的中点,若∠BCD=75°,则∠BDE=( )A.25°B.20°C.15°D.10°答案:C解题思路:试题难度:三颗星知识点:直角三角形斜边中线等于斜边一半5.如图,在四边形ABCD中,∠ABC=∠ADC=90°,点E,F分别是对角线AC,BD的中点,则( )A. B.C. D.答案:A解题思路:试题难度:三颗星知识点:等腰三角形三线合一性质6.如图,在正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是( )A.2.5B.C. D.2答案:B解题思路:试题难度:三颗星知识点:直角三角形斜边中线等于斜边一半7.如图,BD,BE是Rt△ABC斜边AC上的中线与高线.已知AB=4,BC=3,则AD:DE:EC等于( )A.5:3:4B.25:9:16C.25:7:18D.3:2:1答案:C解题思路:试题难度:三颗星知识点:等积公式二、填空题(共1道,每道16分)8.如图,在四边形ABCD中,BC⊥AC于点C,BE⊥AD于点E,∠BAC=60°,点G是AB的中点,已知,则GE的长是____.答案:1解题思路:试题难度:知识点:含30°的直角三角形。
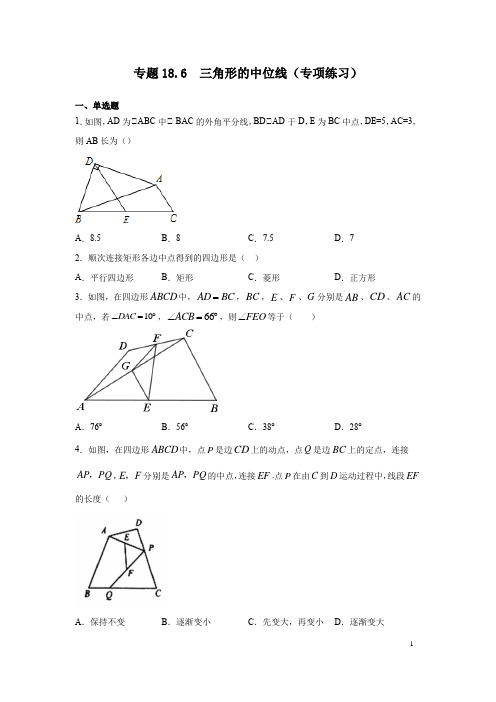
三角形的中位线(专项练习)-2020-2021学年八年级数学下册基础知识专项讲练(华东师大版)
专题18.6 三角形的中位线(专项练习)一、单选题1.如图,AD 为△ABC 中△ BAC 的外角平分线,BD△AD 于D ,E 为BC 中点,DE=5,AC=3,则AB 长为()A .8.5B .8C .7.5D .72.顺次连接矩形各边中点得到的四边形是( )A .平行四边形B .矩形C .菱形D .正方形 3.如图,在四边形ABCD 中,AD BC =,BC ,E 、F 、G 分别是AB 、CD 、AC 的中点,若10DAC ∠=︒,66ACB ∠=︒,则FEO ∠等于( )A .76°B .56°C .38°D .28° 4.如图,在四边形ABCD 中,点P 是边CD 上的动点,点Q 是边BC 上的定点,连接AP PQ ,,EF ,分别是AP PQ ,的中点,连接EF .点P 在由C 到D 运动过程中,线段EF 的长度( )A .保持不变B .逐渐变小C .先变大,再变小D .逐渐变大5.ABC 中,D 、E 分别为AB 、AC 边的中点,若BC=8cm ,则DE 为( ) A .16cm B .8cm C .4cm D .2cm6.在Rt ABC △中,90,13,5ACB AB AC ︒∠===,点D 是AB 上一动点,作//DE AC ,且2DE =,连结,BE CD P Q ,,分别是BE DC 、的中点连结PQ ,则PQ 长为( )A B .C .6 D .6.57.如图,已知△ABC 中,点M 是BC 边上的中点,AN 平分△BAC ,BN△AN 于点N ,若AB =8,MN =2,则AC 的长为( )A .12B .11C .10D .98.如图,将三角形纸片ABC 沿过,AB AC 边中点D 、E 的线段DE 折叠,点A 落在BC 边上的点F 处,下列结论中,一定正确的个数是( )△BDF 是等腰三角形 △12DE BC = △四边形ADFE 是菱形 △2BDF FEC A ∠+∠=∠A .1B .2C .3D .4二、填空题9.如图,在Rt ABC 中,90ACB ∠=︒,30A ∠=︒,点D ,E 分别是AB 和AC 边的中点,若4CD =,则DE =__________.10.如图,,,D E F 分别是ABC ∆各边的中点,AH 是高,,5AB AC ED ≠=,判断AD ________AH (大小),FHC ∆是___________(类别),四边形AEDF 是______________________(类别)11.如图,在Rt △ABC 中,△ACB =90°,点D 、E 、F 分别为AB 、AC 、AD 的中点,若AB =12,则EF 的长为__________.12.如图,CD 是ABC ∆的中线,点E 、F 分别是AC 、DC 的中点,3BD =,则EF =_________.13.如图,在ABC中,AB=AC,AM BC⊥,延长AC到点D,连接BD,取BD的中点N,连接MN.若AB=3,AD=5,则MN=_______________.14.如图,在△ABC中,D是AC边的中点,且BD△AC,ED△BC,ED交AB于点E,若AC=4,BC=6,则△ADE的周长为______.15.如图,△ABC的中位线DE=6cm,把△ABC沿DE折叠,使点A落在边BC上的点F处,若A、F两点间的距离是8cm,则△ABC的面积为_____cm2.16.如图,在ABC中,△ACB=90°,M、N分别是AB、AC的中点,延长BC至点D,使CD=13BD,连接DM、DN、MN.若AB=4,则DN=_____.17.如图,在ABC∆中,D、E分别为BC、AC的中点,且ABC的面积为16,则ADE 的面积是______.18.如图,面积为16的菱形ABCD 中,点O 为对角线的交点,点E 是边BC 的中点,过点E 作EF BD ⊥ 于点F ,EG AC ⊥于点G ,则四边形EFOG 的面积为__.19.如图,在菱形ABCD 中,45B ∠=︒,BC =E ,F 分别是边CD ,BC 上的动点,连接AE ,EF ,G ,H 分别为AE ,EF 的中点,连接GH ,则GH 的最小值为________.20.如图,有一块形状为Rt △ABC 的斜板余料,△A =90°,AB =6cm ,AC =8cm ,要把它加工成一个形状为□DEFG 的工件,使GF 在边BC 上,D 、E 两点分别在边AB 、AC 上,若点D 是边AB 的中点,则DEFG 的面积为_________2cm .21.如图,在平行四边形纸片ABCD 中,2cm AB =,将纸片沿对角线AC 对折至CF ,交AD 边于点E ,此时BCF △恰为等边三角形,则图中折叠重合部分的面积是________.22.如图,在ABC 中,点D E 、分别在边AB 、 AC 上,//DE BC ,将ADE 沿直线DE 翻折后与 FDE 重合,DF 、EF 分别与边BC 交于点M 、N ,如果 8DE =,23AD AB =,那么MN 的长是 _____ .23.如图,△ABC 是边长为1的等边三角形,取BC 边中点E ,作ED △AB ,EF △AC ,得到四边形EDAF ,它的周长记作C 1;取BE 中点E 1,作E 1D 1△FB ,E 1F 1△EF ,得到四边形E 1D 1FF 1,它的周长记作C 2.照此规律作下去,则C 2020=__.24.如图,在Rt ABC △中,90A ︒∠=,2AB =,点D 是BC 边的中点,点E 在AC 边上,若45DEC ︒∠=,那么DE 的长是__________.三、解答题25.在正方形ABCD 中,点E 是边CD 的中点,点P 是边AD 上一点(与点A 、D 不重合),射线PE 与BC 的延长线交于点Q .(1)如图,求证:PE QE =;(2)如图,连接PB ,PB PQ =,过点E 作//EF BC 交PB 于点F ,连接AF ,在不添加任何辅助线的情况下,请直接写出与线段AF 相等的所有线段.26.如图,在ABC 中,AB AC =,E ,F 分别是BC ,AC 的中点,连接EF ,以AC 为斜边作直角三角形ADC ,连接DE 、DF .(1)求证:FE FD =.(2)若24CAD CAB ∠=∠=︒,求EDF ∠的度数.27.如图,在△ABC 中,点D ,E 分别是BC ,AC 的中点,延长BA 至点F ,使得AF =12AB ,连接DE ,AD ,EF ,DF .(1)求证:四边形ADEF 是平行四边形;(2)若AB =6,AC =8,BC =10,求EF 的长.28.如图,等边ABC ∆中,D ,E 分别是AB ,AC 的中点,延长BC 到点F ,使12CF BC =,连结DE ,CD ,EF .(1)求证:四边形DCFE 是平行四边形;(2)若等边ABC ∆的边长为6,求EF 的长.29.如图,在ABC 中,D E 、分别是AB AC 、的中点,延长DE 到点,F 使得,EF BE =连接CF .若EC 平分BEF ∠.(1)求证:四边形BCFE 是菱形;(2)若8,120AC BCF =∠=︒,求菱形BCFE 的面积.参考答案1.D【分析】延长BD、CA交于点F,易证△ADF≌△ADB(ASA),则BD=DF,AB=AF,得到点D为BF中点,即DE为△BCF的中位线,再根据已知线段的长度,即可顺利求得AB的长.【详解】解:如图,分别延长BD、AC交于点F,△AD为△ABC中△BAC的外角平分线,△△FAD=△BAD,△BD△AD,△△FDA=△BDA=90°,在△BDA和△FDA中,FAD BAD AD ADFDA BDA ∠=∠⎧⎪=⎨⎪∠=∠⎩,△△BDA≌△FDA(ASA),△AB=AF,BD=FD,即D为BF的中点,△E为BC中点,△DE为△BCF的中位线,△DE=5,AC=3,△CF=2DE=2⨯5=10,△AF=CF-AC=10-3=7.△AB=AF=7.故选D.【点拨】本题考查三角形的综合,涉及的知识点有全等三角形的判定,中位线定理等,难度一般,是中考的常考知识点,正确作出辅助线并证明全等是顺利解题的关键.2.C【分析】根据三角形的中位线定理,得新四边形各边都等于原四边形的对角线的一半,进而可得连接对角线相等的四边形各边中点得到的四边形是菱形.【详解】解:如图,矩形ABCD 中,,AC BD ∴=,,,E F G H 分别为四边的中点,1//,,2EF BD EF BD ∴=1//,,2GH BD GH BD = 1,2FG AC = //,,EF GH EF GH ∴=∴ 四边形ABCD 是平行四边形, 11,,,22AC BD EF BD FG AC === ,EF FG ∴=∴ 四边形EFGH 是菱形.故选C .【点拨】本题主要考查了矩形的性质、菱形的判定,以及三角形中位线定理,关键是掌握三角形的中位线定理及菱形的判定.3.D 【分析】利用EG 、FG 分别是ABC ∆和ADC ∆两个三角形的中位线,求出EG FG =,从而得出FGC ∠和EGC ∠,再根据EG FG =,利用三角形内角和定理即可求出FEG ∠的度数.【详解】解:△E 、F 、G 分别是AB 、CD 、AC 的中点, △EG 、FG 分别是ABC ∆和ADC ∆两个三角形的中位线, △//EG BC ,//FG AD ,且22AD BCEG FG ===, △10FGC DAC ∠=∠=︒,180114EGC ACB ∠=︒-∠=︒, △124EGF FGC EGC ∠=∠+∠=︒, 又△EG FG =, △()()111801801242822FEG EGF ∠=-∠=-︒=︒︒︒. 故本题答案为:D . 【点拨】本题考查了三角形内角和定理,等腰三角形的判定与性质,三角形中位线定理.解决本题的关键是正确理解题意,熟练掌握三角形中位线定理,通过等腰三角形的性质找到相等的角. 4.A 【分析】连接AQ ,则可知EF 为△PAQ 的中位线,可知EF =12AQ ,可知EF 不变. 【详解】 如图,连接AQ ,△E 、F 分别为PA 、PQ 的中点, △EF 为△PAQ 的中位线, △EF =12AQ , △Q 为定点,△AQ 的长不变, △EF 的长不变, 故选:A .【点拨】本题主要考查三角形中位线定理,掌握三角形中位线平行第三边且等于第三边的一半是解题的关键. 5.C 【分析】先画出图形,再根据三角形的中位线定理即可得. 【详解】由题意,画出图形如下:点D 、E 分别为AB 、AC 边的中点,DE ∴是ABC 的中位线, 1184()22DE BC cm ∴==⨯=, 故选:C . 【点拨】本题考查了三角形的中位线定理,熟记三角形的中位线定理是解题关键. 6.A 【分析】由勾股定理得出,取BD 中点F ,连接PF 、QF ,证出PF 是△BDE的中位线,FQ是△BCD的中位线,由三角形中位线定理得出PF△ED,PF=12DE=1,FQ△BC,FQ=12BC=6,证出PF△FQ,再由勾股定理求出PQ即可.【详解】解:△△ACB=90°,AB=13,AC=5,,取BD中点F,连接PF、QF,如图所示:△P、Q分别是BE、DC的中点,△PF是△BDE的中位线,FQ是△BCD的中位线,△PF△ED,PF=12DE=1,FQ△BC,FQ=12BC=6,△DE△AC,AC△BC,△PF△FQ,==故选:A.【点拨】本题考查了三角形中位线定理、勾股定理、平行线的性质;熟练掌握勾股定理,由三角形中位线定理得出PF△ED,FQ△BC是解题的关键.7.A【分析】延长BN交AC于D,证明△ANB△△AND,根据全等三角形的性质、三角形中位线定理计算即可.【详解】解:延长BN交AC于D,在△ANB 和△AND 中,90NAB NAD AN ANANB AND ∠∠⎧⎪⎨⎪∠∠︒⎩====, △△ANB△△AND , △AD=AB=8,BN=ND , △M 是△ABC 的边BC 的中点, △DC=2MN=4, △AC=AD+CD=12, 故选:A . 【点拨】本题考查的是三角形中位线定理,三角形的中位线平行于第三边,并且等于第三边的一半. 8.C 【分析】根据菱形的判定和等腰三角形的判定,采用排除法,逐条分析判断. 【详解】 解:△△DE △BC ,△△ADE =△B ,△EDF =△BFD , 又△△ADE △△FDE ,△△ADE =△EDF ,AD =FD ,AE =CE , △△B =△BFD ,△△BDF 是等腰三角形,故△正确; 同理可证,△CEF 是等腰三角形, △BD =FD =AD ,CE =FE =AE , △DE 是△ABC 的中位线,△DE =12BC ,故△正确; △△B =△BFD ,△C =△CFE ,又△△A +△B +△C =180°,△B +△BFD +△BDF =180°,△C +△CFE +△CEF =180°, △△BDF +△FEC =2△A ,故△正确.而无法证明四边形ADFE 是菱形,故△错误. 所以一定正确的结论个数有3个, 故选:C . 【点拨】本题考查了菱形的判定,中位线定理,等腰三角形的判定和性质,菱形的判别方法是说明一个四边形为菱形的理论依据,常用三种方法:△定义;△四边相等;△对角线互相垂直平分.具体选择哪种方法需要根据已知条件来确定. 9.2 【分析】由直角三角形斜边上的中线等于斜边的一半可得出28AB CD ==,又因为30A ∠=︒,所以4BC =,由三角形的中位线定理可得出122DE BC ==. 【详解】解:△CD 是Rt ABC 中斜边上的中线,4CD = △28AB CD ==△90ACB ∠=︒,30A ∠=︒ △4BC =△点D ,E 分别是AB 和AC 边的中点 △122DE BC == 故答案为:2. 【点拨】本题考查的知识点是三角形的中位线定理,由直角三角形斜边上的中线等于斜边的一半可得出28AB CD ==,是解此题的关键. 10.> 等腰三角形 平行四边形 【分析】(1)连接AD 可知,在Rt ADH 中,AH 为直角边,AD 为斜边,可得AH 与AD 大小关系;(2)在Rt AHC 中,11,22HF AC FC AC ==,可得HF FC =,可得FHC 为等腰三角形;(3)根据中位线的性质,可得//,//DE AF AE DF ,可得AEDF 的形状 【详解】(1)连接AD ,在Rt ADH 中,AH 为直角边,AD 为斜边,得AD AH >; 故答案为:>(2)在Rt ADC 中,F 为AC 中点 △11,22HF AC FC AC ==, △HF FC =,△FHC 为等腰三角形; 故答案为:等腰三角形(3)△,,D E F 分别是ABC ∆各边的中点 △//,//DE AF AE DF△四边形AEDF 为平行四边形 故答案为:平行四边形 【点拨】本题考查了直角三角形的边角关系,以及中点的应用,熟知中点的作用是解题的关键. 11.3 【分析】根据直角三角形的性质求出CD ,根据三角形中位线定理计算即可. 【详解】在Rt△ABC中,△ACB=90°,D为AB的中点,△CD12=AB=6△E,F分别为AC,AD的中点,△EF12=CD=3.故答案为:3【点拨】本题考查的是三角形中位线定理、直角三角形的性质,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.12.1.5【分析】先由中线知BD=AD,求出AD,再利用三角形中位线是性质即可解答.【详解】解:△CD是ABC的中线,3BD=△AD=BD= 3△点E、F分别是AC、DC的中点,△EF是ACD的中位线,△EF=12AD=1.5,故答案为:1.5.【点拨】本题考查了三角形的中线和中位线,熟练掌握三角形中位线的性质是解答的关键.13.1【分析】由题意易得BM=MC,则有MN△CD,12MN CD=,进而可求解.【详解】解:AB=AC,AM BC⊥,∴BM=MC,BN=ND,∴MN△CD,12MN CD=,AB=3,AD=5,∴CD=2,∴MN=1;故答案为1.【点拨】本题主要考查等腰三角形的性质及三角形中位线,熟练掌握等腰三角形的性质及三角形中位线是解题的关键.14.8【分析】根据线段垂直平分线的性质得到AB=BC=6,根据三角形中位线定理求出DE,根据直角三角形的性质求出AE,根据三角形的周长公式计算,得到答案.【详解】△D是AC边的中点,BD△AC,△BD是线段AC的垂直平分线,AD12=AC=2,△AB=BC=6,△D是AC边的中点,ED△BC,△点E是AB的中点,DE12=BC=3,在Rt△ADB中,点E是AB的中点,△DE12=AB=3,△△ADE的周长=AE+DE+AD=8,故答案为:8.【点拨】本题考查的是三角形中位线定理、直角三角形的性质,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.15.48【分析】根据对称轴垂直平分对应点连线,可得AF即是△ABC的高,再由中位线的性质求出BC,继而可得△ABC的面积.【详解】解:连接AF,△DE是△ABC的中位线,△DE△BC,BC=2DE=12cm;由折叠的性质可得:AF△DE,△AF△BC,△S△ABC=12BC×AF=12×12×8=48cm2.故答案为:48.【点拨】本题考查了翻折变换的性质及三角形的中位线定理,解答本题的关键是得出AF是△ABC的高.16.2【分析】连接CM,根据直角三角形的性质求出CM,根据三角形中位线定理得到MN=12BC,MN//BC,证明四边形NDCM是平行四边形,根据平行四边形的性质解答.【详解】解:连接CM,△△ACB=90°,M是AB的中点,△CM=12AB=2,△M、N分别是AB、AC的中点,△MN=12BC,MN//BC,△CD=13 BD,△CD=12 BC,△MN=CD,又MN//BC,△四边形NDCM是平行四边形,△DN=CM=2,故答案为:2.【点拨】本题考查直角三角形斜边的中线定理、三角形中位线定理、平行四边形的判定与性质等知识,是重要考点,难度较易,掌握相关知识是解题关键.17.4【分析】先根据D点是BC的中点,E点是AC的中点,得出S△ADE=14×S△ABC,即可得出答案.【详解】△D点是BC的中点,△S△ABD=S△ADC=12S△ABC,△E点是AC的中点,△S△ADE=S△DCE=12S△ADC=14×S△ABC△S△ABC=16,△S△ADE=4,故答案为:4.【点拨】本题考查了三角形中线的性质,得出S△ADE=14×S△ABC是解题关键.18.2【分析】由菱形的性质得出OA=OC,OB=OD,AC△BD,面积=12AC×BD,证出四边形EFOG是矩形,EF//OC,EG//OB,得出EF、EG都是△OBC的中位线,则EF=12OC=14AC,EG =12OB =14BD ,由矩形面积即可得出答案. 【详解】解:△四边形ABCD 是菱形,△OA =OC ,OB =OD ,AC△BD ,面积=12AC×BD=16, △AC×BD=32△EF△BD 于F ,EG△AC 于G ,△四边形EFOG 是矩形,EF//OC ,EG//OB ,△点E 是线段BC 的中点,△EF 、EG 都是△OBC 的中位线,△EF =12OC =14AC ,EG =12OB =14BD , △矩形EFOG 的面积=EF×EG =14AC×14BD =116×32=2; 故答案为:2.【点拨】本题考查了菱形的性质、矩形的判定与性质、三角形中位线定理等知识;熟练掌握菱形的性质和矩形的性质是解题的关键.19.2【分析】连结AF ,利用中位线的性质GH=12AF ,要使GH 最小,只要AF 最小,由点F 在BC ,当AF△BC 时,AF 最小,利用菱形性质求出AB =45B ∠=︒确定△ABF 为等腰直角三角形,得出AF=BF ,由勾股定理得:22222AB BF AF AF =+=求出AF 即可.【详解】连结AF ,△G ,H 分别为AE ,EF 的中点,△GH△AF ,且GH=12AF , 要使GH 最小,只要AF 最小,由点F 在BC ,当AF△BC 时,AF 最小,在菱形ABCD 中,BC = △AB =在Rt△ABF 中,45B ∠=︒,△△ABF 为等腰直角三角形,△AF=BF ,由勾股定理得:22222AB BF AF AF =+=,△(22=2AF ,△AFGH 最小=12【点拨】本题考查动点图形中的中位线,菱形的性质,等腰直角三角形的性质,勾股定理应用问题,掌握中位线的性质,菱形性质,等腰直角三角形的性质, 点F 在BC 上,AF 最短,点A 到BC 直线的距离最短时由点A 向直线BC 作垂线,垂线段AF 为最短是解题关键. 20.12【分析】作AH BC ⊥交BC 于H 点,交DE 于I 点,根据90,6,8A AB cm AC cm 可得BC 10cm =,根据D 是边AB 的中点可知DE 是ABC 的中位线,得12AIIH AH ,利用三角形面积1122ABC S AC AB BC AH ,可得245AH =,11225IH AH ,则根据DEFG S DE IH ,计算可得结果.【详解】如图示,作AH BC ⊥交BC 于H 点,交DE 于I 点,△90,6,8A AB cm AC cm△BC 10cm =△D 是边AB 的中点,//DE BC ,△DE 是ABC 的中位线,5DE cm = △12AIIH AH , 又△1122ABCS AC AB BC AH , 即有6810AH , △245AH =, △1124122255IHAH , △2125125DEFG S DE IHcm , 故答案为:12.【点拨】本题考查了三角形中位线的应用,勾股定理,三角形的面积和平行四边形的面积,熟悉相关性质定理是解题的关键.中位线定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.212cm【分析】BCF △为等边三角形,点A 为BF 的中点,可得90BAC ∠=︒,求得12ACD S AC CD =,再证明出点E 为AD 的中点,得到12ACE ACD S S =,可求出面积. 【详解】解:ABC 折叠至ACF 处,∴AB=AF=2cm ,BC=BF=CF=4cm ,BCF △为等边三角形,AC BF ∴⊥,90BAC ∠=︒, 又四边形ABCD 为平行四边形,∴//AB CD ,90ACD ∴∠=︒,AC ==,CD=AB=2cm ,12ACD S AC CD ∴==212⨯=2cm , 点A 为BF 的中点,//AE BC ,∴AE 为BCF △的中位线,1122AE BC AD ∴==, ∴点E 为AD 的中点, 12ACE ACD S S ∴==12⨯2cm 为折叠重合部分的面积,2cm .【点拨】本题考查了折叠问题以及等边三角形和平行四边形的综合问题,还涉及勾股定理,需要有一定的推理论证能力,熟练掌握等边三角形和平行四边形的性质是解题的关键.22.4【分析】设3AB a =,从而可得2,a AD a BD ==,先根据平行线的性质可得,ADE B EDM BMD ∠=∠∠=∠,再根据翻折的性质可得,2ADE EDM DF AD a ∠=∠==,从而可得B BMD ∠=∠,然后根据等腰三角形的判定可得DM BD a ==,从而可得FM a =,最后根据三角形的中位线定理即可得.【详解】设3AB a =,则2,BD D a A a A AB D =-==,//DE BC ,,ADE B EDM BMD ∠=∠∠=∠∴,由翻折的性质得:,2ADE EDM DF AD a ∠=∠==,B BMD ∴∠=∠,DM BD a ∴==,FM DF DM a DM ∴=-==,即点M 是DF 的中点,又//DE BC ,MN ∴是FDE 的中位线,118422MN DE ∴==⨯=, 故答案为:4.【点拨】本题考查了翻折的性质、等腰三角形的判定、三角形的中位线定理等知识点,熟练掌握翻折的性质是解题关键.23.201812【分析】先计算出C 1、C 2的长,进而得到规律,最后求出C 2020的长即可.【详解】解:△E 是BC 的中点,ED △AB ,△DE 是△ABC 的中位线,△DE =12AB =12,AD =12AC =12, △EF △AC ,△四边形EDAF 是菱形,△C 1=4×12, 同理C 2=4×12×12=4×212, …C n =4×12n , △20202020201811422C =⨯=. 故答案为:201812.【点拨】本题考查了中位线的性质,菱形的判定与性质,根据题意得到规律是解题关键.24【分析】过D作DF△AC于F,得到AB△DF,求得AF=CF,根据三角形中位线定理得到DF=12 AB=1,根据等腰直角三角形的性质即可得到结论.【详解】解:过D作DF△AC于F,△△DFC=△A=90°,△AB△DF,△点D是BC边的中点,△BD=DC,△AF=CF,△DF=12AB=1,△△DEC=45°,△△DEF是等腰直角三角形,△DE DF,【点拨】本题考查了三角形的中位线定理,平行线的判定和性质,等腰直角三角形的性质,正确的作出辅助线构造等腰直角三角形是解题的关键.25.(1)见解析;(2)BF、PF、PE、QE.【分析】(1)根据正方形的性质及对顶角相等利用ASA即可证明PDE QCE≌,再利用全等三角形的性质即可得证;(2)根据三角形中位线的判定及性质定理、直角三角形斜边上的中线即可得出答案.【详解】(1)证明:如图,△四边形ABCD 是正方形△90D ECQ ∠=∠=︒,△E 是CD 的中点△DE CE =,又△DEP CEQ ∠=∠△()PDE QCE ASA ≌△△△PE QE =(2)如图,BF 、PF 、PE 、QE,//PB PQ EF BC =,PE QE =∴EF 为PBQ △的中位线PF FB PE EQ ∴===,四边形ABCD 为正方形,90BAP ∴∠=︒,∴AF 为BAP Rt △斜边的中线12AF BP BF PF ∴=== ∴与线段AF 相等的所有线段为:BF 、PF 、PE 、QE .【点拨】本题考查了正方形的性质、三角形中位线的判定及性质定理、直角三角形斜边上的中线、全等三角形的判定及性质,熟练掌握性质定理是解题的关键.26.(1)见解析;(2)54︒【分析】(1)根据三角形中位线定理推出12FE AB =,根据直角三角形斜边上的中线等于斜边的一半推出12FD AC =,即可证明FE FD =; (2)根据三角形中位线定理推出24EFC BAC ∠=∠=︒,根据直角三角形斜边上的中线的性质结合三角形的外角性质推出48DFC ∠=︒,利用(1)的结论结合三角形内角和定理即可求得EDF ∠的度数.【详解】(1)△E ,F 分别是BC ,AC 的中点, △12FE AB =, △F 是AC 的中点,90ADC ∠=︒, △12FD AC =, △AB AC =,△FE FD =;(2)△E ,F 分别是BC ,AC 的中点,△//FE AB ,△24EFC BAC ∠=∠=︒,△F 是AC 的中点,90ADC ∠=︒,△FD AF =,△24ADF CAD ︒∠=∠=,△48DFC ∠=︒,△72EFD ∠=︒,△FE FD=,△18072542FED EDF︒-︒∠=∠==︒.【点拨】本题考查了三角形中位线定理,直角三角形斜边上的中线等于斜边一半,平行线的性质,三角形的外角性质等,灵活运用有关定理来分析、判断、推理或解答是解题的关键.27.(1)见解析;(2)EF=5.【分析】(1)利用三角形的中位线的性质与等量代换得出DE=AF,DE△AF,从而得出结论.(2)先利用(1)中的结论得出EF=AD,再利用勾股定理的逆定理,求出△ABC是直角三角形,再利用直角三角形斜边上的中线等于斜边的一半求出。
三角形中与中点有关的两个性质的运用-

图1-1F EDC BA 图1-2F EDC BA三角形中与中点有关的两个性质的运用江苏省通州市刘桥中学 吴锋三角形知识是初中数学的一个重要内容,特别是两个与中点有关的性质,在三角形及四边形的有关证明中使用尤为广泛,它们是直角三角形斜边上中线性质及三角形中位线性质.两条性质有的是独立使用,也有综合运用.主要反映在下面几点。
一、单独使用斜边中线性质,利用公共斜边找相等线段例1 如图1-1,四边形ABCD 中,∠ABC=∠ADC=90°,E 为AC 中点,EF 平分∠BED.请猜想EF 与BD 的关系,并证明你的结论.分析:对于线段间关系的猜想,一般从两个角度考虑,一是大小关系,二是位置关系.就本题而言,EF 与BD 并无确定的大小关系,因而初步猜想位置关系为垂直.结合条件EF 平分∠BED ,联想到“三线合一”,可将目标转化证明BE=DE ,从而进一步明确最终猜想为EF 垂直平分BD.解:猜想:EF 垂直平分BD. 连结BE 、DE ,如图1-2 ∵∠ABC=∠ADC=90°, ∴△ABC 与△ADC 为直角三角形. ∵E 为AC 中点, ∴11,22BE AC DE AC ==, ∴BE =DE ,即△BED 是等腰三角形.PABCDEF图5-2O NM图2-2 图2-1FEDMNCB A ∵EF 平分∠BED, ∴EF 垂直平分BD.二、单独使用三角形中位线性质,将相等条件进行集中转化例2 如图2-1,已知四边形ABCD 的对角线AC 与BD 相交于点O ,且AC=BD ,M 、N 分别是AB 、CD 的中点,MN 分别交BD 、AC 于点E 、F.你能说出OE 与OF 的大小关系并加以证明吗?分析:猜想两线段大小关系时,一般结果为相等,注意到两线段处于同个三角形,此时常用“等角对等边”进行证明.题中所给条件AC=BD 在任意四边形中不便直接使用,结合AB 、CD 中点,可取BC 中点,利用中位线,将AC 、BD 的相等关系转化到同一个三角形PMN 中,易证PM=PN ,所以∠PMN=∠PNM,再将其转化为∠OEF=∠OFE,完成证明.解:取BC 中点P ,连结PM 、PN ,如图2-2, ∵M、N 分别是AB 、CD 的中点, ∴11,22PM AC PN BD ==. ∵AC=BD, ∴PM=PN∴PMN PNM ∠=∠. 又PM∥AC,PN∥BD,∴,PMN OFE PNM OEF ∠=∠∠=∠, ∴OFE OEF ∠=∠, ∴OE=OF .三、综合使用斜边中线及中位线性质,证明相等关系问题例3 如图3-1,等腰梯形ABCD 中,CD ∥AB ,对角线AC 、BD 相交于点O ,60ACD ∠=︒,点S 、P 、Q 分别是DO 、AO 、BC 的中点.求证:△SPQ 是等边三角形。
初中数学三角形专题训练50题(含答案)

初中数学三角形专题训练50题含答案(单选、填空、解答题)一、单选题1.如图,已知⊙O的半径为R,C、D是直径AB的同侧圆周上的两点,AC的度数为100°,BC=2BD,动点P在线段AB上,则PC+PD的最小值为()C D RA.R B2.如图,在⊙ABCD中,连接AC,⊙ABC=⊙CAD=45°,AB=2,则BC的长是()AB.2C.D.43.如图点P是⊙BAC内一点,PE⊙AB于点E,PF⊙AC于点F,PE=PF,则直接得到⊙PEA⊙⊙PFA的理由是()A.HL B.ASA C.AAS D.SAS【答案】A【详解】解:⊙PE⊙AB于点E,PF⊙AC于点F,⊙⊙PEA=⊙PFA=90°,⊙PE=PF,AP=AP,⊙⊙PEA⊙⊙PFA(HL);4.如图,在平面直角坐标系中,菱形ABCD 的顶点A 在y 轴上,已知B(﹣3,0)、C(2,0),则点D 的坐标为( )A .(4,5)B .(5,4)C .(5,3)D .(4,3)5.适合下列条件的ABC ∆中,是直角三角形的共有( )⊙6a =,45A ∠=︒;⊙32A ∠=,58B ∠=︒;⊙2a =,2b =,4c =;⊙7a =,24b =,25c =.A .1个B .2个C .3个D .4个【答案】B 【分析】根据构成直角三角形三边关系的条件:三角形两条边的平方和等于第三边的平方,那么这个三角形就是直角三角形,最长边所对的角为直角,判定即可.【详解】⊙6a =,45A ∠=︒,不能判定ABC ∆中是直角三角形;⊙3258A B ︒︒==∠,∠,A B ∠∠=︒+90,是直角三角形;⊙2222222a b c +=+≠,不能判定ABC ∆中是直角三角形;⊙()()22222272425a b c +=+==,是直角三角形;【点睛】此题主要考查构成直角三角形条件的判定,熟练掌握,即可解题.=,点N在CD上,且6.如图,已知四边形ABCD是矩形,点M在BC上,BM CD=与BN交于点P,则:DN CM DM,DM BN=()A2B.C D.27.如图,已知正方形的面积为25,且AB比AC大1,BC的长为()A.3B.4C.5D.6【答案】A8.如图,在Rt ABC △中,90ACB ∠=︒,30ABC ∠=︒,若ABC A B C ''△≌△,且点A '恰好落在AB 上,则ACA ∠'的度数为( )A .30°B .45°C .50°D .60° 【答案】D 【分析】根据全等三角形的性质可得A C AC '=,从而得到60AA CA ,即可求解.【详解】解:⊙90ACB ∠=︒,30ABC ∠=︒,⊙⊙A =60°,⊙ABC A B C ''△≌△,⊙A C AC '=,⊙60AA C A ,⊙60ACA '∠=︒.故选:D【点睛】本题主要考查了全等三角形的性质,等腰三角形的性质,熟练掌握全等三角形的性质,等腰三角形的性质是解题的关键.9.如图,将三角板的直角顶点放在直尺的一边上,1=30∠︒,2=50∠︒,3=∠( )度A .10B .20C .30D .50 【答案】B 【分析】根据两直线平行,同位角相等求出⊙2的同位角,再根据三角形的一个外角等于与它不相邻的两个内角的和列式进行计算即可得解.【详解】解:如图:⊙⊙2=50°,直尺的两边互相平行,⊙⊙4=⊙2=50°,⊙⊙1=30°,⊙⊙3=⊙4-⊙1=50°-30°=20°.故选:B .【点睛】本题考查了两直线平行,同位角相等的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质是解题的关键.10.在ABC 中,若90A C ∠+∠=︒,则( ).A .BC AB AC =+B .222AC AB BC =+ C .222AB AC BC =+D .222BC AB AC =+【答案】B【分析】由⊙A +⊙C =90°可得⊙B =90°,于是可确定AC 是Rt⊙ABC 的斜边,再根据勾股定理即得答案.【详解】解:⊙⊙A +⊙C =90°,⊙⊙B =90°,⊙AC 是Rt⊙ABC 的斜边,222【点睛】本题考查了勾股定理和三角形的内角和定理,由题意确定AC 是Rt ⊙ABC 的斜边是解题的关键.11.如图,直线AB CD ∥,AE CE ⊥于点E ,若140EAB ∠=︒,则ECD ∠的度数是( )A .120°B .130°C .150°D .160° 【答案】B 【分析】延长AE ,与DC 的延长线交于点F ,根据平行线的性质,求出⊙AFC 的度数,再利用外角的性质求出⊙ECF ,从而求出⊙EC D .【详解】解:延长AE ,与DC 的延长线交于点F ,⊙AB ⊙CD ,⊙⊙A +⊙AFC =180°,⊙⊙EAB =140°,⊙⊙AFC =40°,⊙AE ⊙CE ,⊙⊙AEC =90°,而⊙AEC =⊙AFC +⊙ECF ,⊙⊙ECF =⊙AEC -⊙F =50°,⊙⊙ECD =180°-50°=130°,故选:B .【点睛】本题考查平行线的性质和外角的性质,正确作出辅助线和正确利用平行线的性质是解题的关键.12.如图,在ABC 中,AB AC =,AD 是BAC ∠的平分线,DE AB ⊥,DF AC ⊥,垂足分别是E 、F ,下面给出的四个结论,其中正确的有( ).距离相等的点到DE 、DF 的距离也相等.A .1个B .2个C .3个D .4个 【答案】D 【分析】由等腰三角形“三线合一”可知AD⊙BC ,BD=DC ,得到AD 上的点到B 、C 两点的距离相等,根据角平分线性质定理可知DE=DF ,根据HL 证直角三角形全等,得到AE=AF ,从而得到AD 平分EDF ∠,即可得出答案.【详解】解:⊙AB AC =,AD 是BAC ∠的平分线,⊙AD⊙BC ,BD=DC ,⊙AD 上的点到B 、C 两点的距离相等,⊙⊙正确;⊙AD 是BAC ∠的平分线,DE AB ⊥,DF AC ⊥,⊙DE=DF ,⊙EDA=⊙FDA ,⊙AD 平分⊙EDF ,⊙⊙正确;在直角△AED 和直角△AFD 中,AD AD DE DF=⎧⎨=⎩ ⊙⊙AED⊙⊙AFD ,⊙AE=AF ,⊙AD 平分⊙BAC ,又⊙AD 是BAC ∠的平分线,⊙到AE 、AF 距离相等的点到DE 、DF 的距离也相等,⊙⊙、⊙正确,故选D .【点睛】本题考查了全等三角形的证明和性质,角平分线性质,等腰三角形的性质的应用,对条件的合理利用是解题的关键.13.如图,BO 、CO 分别平分⊙ABC 、⊙ACB ,OD ⊙BC 于点D ,OD =2,⊙ABC 的周长为28,则⊙ABC 的面积为( )A .28B .14C .21D .7在BOD 和△OEB OBE BO ∠=∠∠==BOD △≌△OE =OD =21122AB OE BC OD AC OF ++ )AB BC AC OD ++ 282⨯故选:A.【点睛】本题考查了角平分线的性质定理,求三角形的面积等知识,关键是根据条件构造适合角平分线性质定理条件的辅助线.14.如图,菱形ABCD的对角线AC与BD相交于点O,AE垂直平分CD,垂足为点E,则BAD∠=()A.100°B.120°C.135°D.150°【答案】B【分析】直接利用线段垂直平分线的性质得出AC=AD,再利用菱形的性质以及等边三角形的判定与性质得出答案.【详解】解:⊙AE垂直且平分边CD,⊙AC=AD,⊙四边形ABCD是菱形,⊙AD=DC,⊙ACB=⊙ACD,⊙⊙ACD是等边三角形,⊙⊙ACD=60︒,⊙⊙BCD=120︒.⊙⊙BAD=⊙BCD=120︒,故选:B.【点睛】此题主要考查了菱形的性质以及等边三角形的判定与性质,得出⊙ACD是等边三角形是解题关键.15.如图中字母A所代表的正方形的面积为()【详解】试题分析:根据勾股定理的几何意义解答.解:根据勾股定理以及正方形的面积公式知:以直角三角形的两条直角边为边长的正方形的面积和等于以斜边为边长的正方形的面积,所以A=289﹣225=64.故选D.16.三角形的三边长为a,b,c,且满足22-=-,则这个三角形是()()2a b c abA.等边三角形B.钝角三角形C.直角三角形D.锐角三角形【答案】C【分析】先利用完全平方公式化简已知等式,再根据勾股定理的逆定理即可得.【详解】由22a b c ab-=-得:222()2-+=-,a ab bc ab22即222a b c,+=,,a b c为三角形的三边长,∴这个三角形是直角三角形,故选:C.【点睛】本题考查了完全平方公式、勾股定理的逆定理,熟练掌握勾股定理的逆定理是解题关键.17.如图,⊙ABC的两边AB和AC的垂直平分线分别交BC于D,E,若⊙BAC+⊙DAE=150°,则⊙BAC的度数是()A.105B.110C.115D.120【答案】B【分析】根据垂直平分线性质,⊙B=⊙DAB,⊙C=⊙EAC.则有⊙B+⊙C+2⊙DAE=150°,即180°-⊙BAC+2⊙DAE=150°,再与⊙BAC+⊙DAE=150°联立解方程组即可.【详解】⊙⊙ABC的两边AB,AC的垂直平分线分别交BC于D,E,⊙DA=DB,EA=EC,⊙⊙B=⊙DAB,⊙C=⊙EAC.⊙⊙BAC+⊙DAE=150°,⊙⊙⊙B+⊙C+2⊙DAE=150°.⊙⊙B+⊙C+⊙BAC=180°,⊙180°-⊙BAC+2⊙DAE=150°,即⊙BAC-2⊙DAE=30°.⊙由⊙⊙组成的方程组150230BAC DAEBAC DAE∠+∠=︒⎧⎨∠-∠=︒⎩,解得⊙BAC=110°.故选B.【点睛】此题考查了线段的垂直平分线、等腰三角形的性质、三角形内角和定理等知识点,解题的关键是得到⊙BAC和⊙DAE的数量关系.18.如图,在平面直角坐标系中,已知A(﹣2,4)、P(﹣1,0),B为y轴上的动点,以AB为边构造⊙ABC,使点C在x轴上,⊙BAC=90°,M为BC的中点,则PM 的最小值为()A B C D【答案】C【分析】作AH⊙y轴,CE⊙AH,证明⊙AHB⊙⊙CEA,根据相似三角形的性质得到AE =2BH,求出点M的坐标,根据两点间的距离公式用x表示出PM,根据二次函数的性质解答即可.【详解】解:如图,过点A作AH⊙y轴于H,过点C作CE⊙AH于E,则四边形CEHO是矩形,⊙OH=CE=4,⊙⊙BAC=⊙AHB=⊙AEC=90°,19.如图,在ABC 和ADE 中,36CAB DAE ∠=∠=︒,AB AC =,AD AE =.连接CD ,连接BE 并延长交AC ,AD 于点F ,G .若BE 恰好平分ABC ∠,则下列结论错误的是( )A .ADC AEB ∠=∠B .//CD ABC .DE GE=D .2BF CF AC =⋅ 【答案】C 【分析】根据SAS 即可证明DAC EAB △≌△,再利用全等三角形的性质以及等腰三角形的性质,结合相似三角形的判定和性质,即可一一判断【详解】,,36AB AC AD AE CAB DAE ==∠=∠=︒DAC EAB ∴∠=∠AB AC=∴∠=ABCBE平分∴∠=ABEDAC△≌△∴∠ACD∴∠=ACDAD AE=∴∠=ADE∠=DGE∠即ADE∴≠DE GE∠=ABCCFB∴∠=∴=BC BF∴△∽△ABCBF CF∴=AB BC=AB ACBF CF∴=AC BF2=BF CF故答案选:【点睛】本题考查了全等三角形的判定和性质,等腰三角形的判定和性质,相似三角20.如图,在Rt△ABC中,⊙ACB=90°,点D是AB边的中点,过D作DE⊙BC于点E,点P是边BC上的一个动点,AP与CD相交于点Q.当AP+PD的值最小时,AQ 与PQ之间的数量关系是()A.AQ=52PQ B.AQ=3PQ C.AQ=83PQ D.AQ=4PQ⊙MN =PE ,ND =PC ,在△DNQ 和△CPQ 中,NDQ QCP NQD PQC DN PC ∠=∠⎧⎪∠=∠⎨⎪=⎩,⊙⊙DNQ ⊙⊙CPQ ,⊙NQ =PQ ,⊙AN =NP ,⊙AQ =3PQ故选:B .【点睛】本题考查轴对称最短问题、全等三角形的判定和性质、平行线分线段成比例定理等知识,解题的关键是利用对称找到点P 位置,熟练掌握平行线的性质,属于中考常考题型.解两条线段之和最小(短)类问题,一般是运用轴对称变换将处于直线同侧的点转化为直线异侧的点,从而把两条线段的位置关系转换,再根据两点之间线段最短来确定方案,使两条线段之和转化为一条线段.二、填空题21.在Rt⊙ABC 中,⊙C =90°,若a =6,b =8,则c =________.【答案】10【详解】根据勾股定理2223664100c a b =+=+=c 为三角形边长,故c=10.22.在半径为5的圆中,弧所对的圆心角为90°,则弧所对的弦长是________.【点睛】本题考查利用半径和圆心角求弦长,难度不大,掌握勾股定理是解题的关键.23.在ABC 中,AB AC =,CD 是AB 边上的高,40ACD ∠=︒,则B ∠的度数为______.【答案】65︒或25︒【分析】分两种情况:当D 在线段AB 上时,根据题意,得出90ADC ∠=︒,再根据三角形的内角和定理,得出50A ∠=︒,再根据等边对等角,得出B ACB ∠=∠,再根据三角形的内角和定理,计算即可得出B ∠的度数;当D 在线段AB 的延长线上时,根据题意,得出90ADC ∠=︒,再根据三角形的内角和定理,得出50A ∠=︒,再根据等边对等角,得出B ACB ∠=∠,再根据三角形的外角的性质,计算即可得出B ∠的度数,综合即可得出答案.【详解】解:如图,当D 在线段AB 上时,⊙CD 是AB 边上的高,⊙90ADC ∠=︒,又⊙40ACD ∠=︒,⊙180904050A ∠=︒-︒-︒=︒,⊙AB AC =,⊙B ACB ∠=∠,⊙218018050130B A ∠=︒-∠=︒-︒=︒,⊙65B ∠=︒;如图,当D 在线段BA 的延长线上时,⊙CD 是AB 边上的高,⊙90ADC ∠=︒,又⊙40ACD ∠=︒,⊙180904050DAC ∠=︒-︒-︒=︒,⊙AB AC =,⊙B ACB ∠=∠,又⊙2DAC B ACB B ∠=∠+∠=∠,⊙250B ∠=︒,⊙25B ∠=︒,综上所述,B ∠的度数为65︒或25︒.故答案为:65︒或25︒.【点睛】本题考查了三角形的内角和定理、等边对等角、三角形的外角的性质,解本题的关键在熟练掌握相关的性质定理,分类讨论.24.如图,分别以等边三角形的每个顶点为圆心,以边长为半径,在另两个顶点间作一段圆弧,三段圆弧围成的曲边三角形称为勒洛三角形.若等边三角形的边长为4,则勒洛三角形的周长为:_________.25.边长为2的等边三角形的高与它的边长的比值为___________.【详解】解:等边三角形的边长是26.在Rt⊙ABC中,⊙C=90°,⊙A=30°,BC=2,则AC=_______ .27.如图,在四边形ABCD中,90∠=︒,2A==,BC=CD=AD AB∠的度数为________.ABC28.如图,在O 中,弦2BC =,点A 是圆上一点,且30BAC ∠=︒,则O 的半径是________.【答案】2【分析】连接OB ,OC ,先由圆周角定理求出BOC ∠的度数,再由OB OC =判断出BOC 是等边三角形,故可得出结论.【详解】解:连接OB ,OC ,⊙30BAC ∠=︒,⊙260BOC BAC ∠=∠=︒,⊙OB OC =,⊙BOC 是等边三角形,⊙2OB BC ==.故答案为:2【点睛】本题考查了圆周角定理,根据题意作出辅助线,构造出圆心角是解答此题的关键.29.如果等腰三角形的两边长分别为5cm 和10cm ,那么它的周长等于___________cm .【答案】25【分析】分5cm为腰和10cm为腰,两种情况求解.【详解】解:因为等腰三角形的两边长分别为5cm和10cm,当腰长为5cm时,三边长分别为5cm,5cm,10cm,+,因为55=10所以三角形不存在;当腰长为10cm时,三边长分别为5cm,10cm,10cm,+>,因为51010所以三角形存在;++=,所以三角形的周长为5101025(cm)故答案为:25.【点睛】本题考查了等腰三角形周长的分类计算,正确进行分类和判定三角形的存在性是解题的关键.30.等腰三角形的一边长为3,周长为15,则该三角形的腰长是______.31.如图,⊙O的半径为5cm,△ABC内接于⊙O,BC=5cm,则⊙A的度数为_____°.【答案】3032.如图,AD 、AE 分别是⊙ABC 的角平分线和高,⊙B =60°,⊙C =70°,则⊙EAD =______.【答案】5︒【分析】根据角平分线的性质及三角形内角和定理进行求解.【详解】解:由题意可知,⊙B =60°,⊙C =70°,所以18013050A ∠=-=°,所以25BAD ∠=°,在三角形BAE 中,906030BAE ∠=-=°,所以⊙EAD=5°故答案为:5°.【点睛】本题属于对角平分线和角度基本知识,解题的关键是进行变换求解.33.如图,正方形ABCD的对角线AC、BD相交于点O,点E、F分别在边AB、BC 上,且⊙EOF=90°,则S四边形OEBF⊙S正方形ABCD=___.34.图1是一个闭合时的夹子,图2是该夹子的主视示意图,夹子两边为AC,BD (点A与点B重合),点O是夹子转轴位置,O E⊙AC于点E,OF⊙BD于点F,OE=OF=1cm,AC=BD=6cm,CE=DF,CE:AE=2:3.按图示方式用手指按夹子,夹子两边绕点O转动.(1)当E,F两点的距离最大值时,以点A,B,C,D为顶点的四边形的周长是_____cm.(2)当夹子的开口最大(点C与点D重合)时,A,B两点的距离为_____cm.35.如图,直线L 1、L 2、L 3分别过正方形ABCD 的三个顶点A 、D 、C ,且相互平行,若L 1、L 2的距离为1,L 2、L 3的距离为2,则正方形的边长为__________.AED DFC ≌,从而可得度.【详解】如图,过D ⊙123////L L L⊙13,EF L EF L ⊥⊥⊙AED DFC ≌1,DE CF AE DF ===22AD AE ED =+=故答案为:5.【点睛】本题考查了正方形与平行线的问题,掌握平行线的性质、全等三角形的性质以及判定定理、勾股定理是解题的关键.36.正方形ABCD 中.E 是AD 边中点.连接CE .作⊙BCE 的平分线交AB 于点F .则以下结论:⊙⊙ECD =30°.⊙⊙BCF 的外接圆经过点E ;⊙四边形AFCD 的面积是⊙BCF⊙BF AB =.其中正确的结论有 _____.(请填写所有正确结论的序号),易证BCF GCF ≅37.菱形ABCD中,AD=4,⊙DAB=60°,E、F、G、H分别是AD、AB、BC、CD上的点,且DH=FB,DE=BG,当四边形EFGH为正方形时,DH=____.38.已知菱形ABCD中,AC=6cm,BD=4cm.若以BD为边作正方形BDEF,则AF=__cm.⊙如图1,正方形BDEF在点A一侧时,延长CA交EF于点M.39.如图,正方形ABCD中,2AB=,AC,BD交于点O.若E,F分别是边AB,BC上的动点,且OE OF∆周长的最小值是__________.⊥,则OEF40.如图,在平行四边形ABCD 中,AC =3cm ,BD ,AC ⊙CD ,⊙O 是△ABD 的外接圆,则AB 的弦心距等于_____cm .【答案】116##516【分析】设AC、BD的交点为G,作圆的直径AN,连接BN,过点O作OF⊙AB于点三、解答题41.如图,AD⊙BC,⊙BAC=70°,DE⊙AC于点E,⊙D=20°.(1)求⊙B的度数,并判断⊙ABC的形状;(2)若延长线段DE恰好过点B,试说明DB是⊙ABC的平分线.【答案】(1)⊙ABC是等腰三角形,⊙B=40°;(2)见解析.【详解】分析:(1)、根据Rt⊙ADE的内角和得出⊙DAC=70°,根据平行线的性质得出⊙C=70°,从而根据有两个角相等的三角形是等腰三角形得出答案;(2)、根据等腰三角形底边上的三线合一定理得出DB为顶角的角平分线.详解:解:(1)⊙DE⊙AC于点E,⊙D=20°,⊙⊙CAD=70°,⊙AD⊙BC,⊙⊙C=⊙CAD=70°,又⊙⊙BAC=70°,⊙⊙BAC=⊙C,⊙AB=BC,⊙⊙ABC是等腰三角形,⊙⊙B=180°-⊙BAC-⊙C=180°-70°-70°=40°.(2)⊙延长线段DE恰好过点B,DE⊙AC,⊙BD⊙AC,⊙⊙ABC是等腰三角形,⊙DB是⊙ABC的平分线.点睛:本题主要考查的是等腰三角形的判定及性质,属于基础题型.明确等腰三角形底边上的三线合一定理是解决这个问题的关键.42.如图,小雪坐着轮船由点A出发沿正东方向AN航行,在点A处望湖中小岛M,测得小岛M在点A的北偏东60°,航行100米到达点B时,此时测得小岛M在点B的北偏东30°,求小岛M到航线AN的距离.Rt BDM 中,12BD MB ==2MD MB =答:小岛M 到航线【点睛】本题考查了方向角问题,勾股定理,等腰三角形的判定,含43.如图,BD 是⊙ABC 的高,AE 是⊙ABC 的角平分线,BD 交AE 于F ,若⊙BAC =44°,⊙C =80°,求⊙BEF 和⊙AFD 的度数.【答案】⊙BEF=102°;⊙AFD=68°【分析】根据BD是⊙ABC的高,AE是⊙ABC的角平分线,求得⊙ADB=90°,⊙BAE=⊙EAD=22°,根据三角形内角和定理即可求得⊙BEF和⊙AFD的度数.【详解】解:⊙BD是⊙ABC的高,AE是⊙ABC的角平分线,⊙BAC=44°,⊙C=80°,⊙⊙ADB=90°,⊙BAE=⊙EAD=22°,⊙⊙CBA=180°﹣44°﹣80°=56°,⊙⊙BEF=180°﹣22°﹣56°=102°,⊙AFD=180°﹣90°﹣22°=68°.【点睛】本题考查了三角形的高,角平分线,三角形内角和定理的应用,掌握三角形的高,角平分线的意义是解题的关键.44.(1)如图,90∠=∠=︒,O是AC的中点,求证:OB ODABC ADC=.(2)解方程:2430-+=.x x⊙()()130x x --=,即10,30x x -=-=,解得:121,3x x ==.【点睛】本题主要考查了直角三角形的性质,解一元二次方程,熟练掌握直角三角形斜边中线等于斜边的一半,一元二次方程的解法是解题的关键.45.如图,点E 在边长为10的正方形ABCD 内,6AE =,8BE =,请求出阴影部分的面积,AEB S =四边形ABCD =10ABCD ⨯AEB S =【点睛】本题主要考查了勾股定理的逆定理,熟知勾股定理的逆定理是解题的关键.46.图(a )、图(b )是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1.请在图(a )、图(b )中,分别画出符合要求的图形,所画图形各顶点必须与方格纸中的小正方形顶点重合.具体要求如下:(1)画一个底边长为4,面积为8的等腰三角形;(2)画一个面积为16的等腰直角三角形.47.如图,点A,B,C,D在同一条直线上,AB=DC,在四个论断“EA=ED,EF⊙AD,AB=DC,FB=FC”中选择二个作为已知条件,另一个作为结论,构成真命题(补充已知和求证),并进行证明.已知、如图,点A,B,C,D在同一条直线上,.求证、.证明、.【答案】见解析【分析】已知:EA=ED ,EF⊙AD ,AB=DC ,求证FB=FC .想办法证明EF 是线段BC 的垂直平分线即可.(答案不唯一)【详解】已知:如图,EA=ED ,EF⊙AD ,AB=DC ,求证FB=FC .理由:延长EF 交BC 于H .⊙EA=ED ,EF⊙AD ,⊙AH=HD ,⊙AB=DC ,⊙BH=CH ,⊙FH⊙BC ,⊙FB=FC .故答案为EA=ED ,EF⊙AD ,AB=DC ;FB=FC ;延长EF 交BC 于H .⊙EA=ED ,EF⊙AD ,⊙AH=HD ,⊙AB=DC ,⊙BH=CH ,⊙FH⊙BC ,⊙FB=FC .【点睛】此题考查等腰三角形的判定和性质,线段的垂直平分线的性质,解题的关键是理解题意,灵活运用所学知识解决问题,属于开放性题目.48.如图,已知60AOB ∠︒=,OC 平分AOB ∠,CD ⊥OA 于点D .(1)实践与操作:作OC的垂直平分线分别交OA于点E;(要求:尺规作图,保留作图痕迹,不写作法)(2)连接CE,若DE的长为1,求OC的长.(1)解:如图所示,49.正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,A(-2,3),B(-3,1),C(-1,2),现将△ABC平移先向右平移3个单位长度,再向下平移2单位长度.(1)请画出平移后的A B C '''(点B C ''、分别是B 、C 的对应点);(2)写出点A B C '''、、三点的坐标;(3)求A B C '''的面积. 【答案】(1)画图见解析 (2)A '(1,1),B '(0,-1),C '(2,0)(3)1.5【分析】(1)根据所给的平移方式作图即可;(2)根据平移方式即可求出A 、B 、C 对应点A B C '''、、三点的坐标;(3)用A B C '''所在的正方形面积减去周围三个小三角形面积即可得到答案. (1)解:如图所示,A B C '''即为所求;(2)解:⊙A B C '''是△ABC 向右平移3个单位长度,向下平移2个单位长度得到的,A (-2,3),B (-3,1),C (-1,2),⊙A '(1,1),B '(0,-1),C '(2,0);(3)50.如图1,Rt⊙ABC中,⊙ABC=90°,P是斜边AC上一个动点,以BP为直径作⊙O交BC于点D,与AC的另一个交点为E(点E在点P右侧),连结DE、BE,已知AB=3,BC=6.(1)求线段BE的长;(2)如图2,若BP平分⊙ABC,求⊙BDE的正切值;(3)是否存在点P,使得⊙BDE是等腰三角形,若存在,求出所有符合条件的CP的长;若不存在,请说明理由.。
专项6.3 三角形中位线计算(解析版)

2020—2021八年级下学期专项冲刺卷(北师大版)专项6.3三角形中位线计算姓名:___________考号:___________分数:___________(考试时间:100分钟 满分:120分)一、 选择题(本大题共12小题,每小题3分,共36分。
在每小题给出的四个选项中,只有一项是符合题目要求的)1.如图,在□ABCD 中,对角线AC ,BD 相交于点O ,E 是BC 的中点,若OE =3,则AB 的长为( )A .3B .6C .9D .12【答案】B【分析】 点O 是AC 的中点,E 是BC 的中点,则OE 是三角形ABC 的中位线,据此计算即可【详解】∵在□ABCD 中,对角线AC ,BD 相交于点O ,∴OA =OC ,∵EB =EC ,∴AB =2OE ,∵OE =3,∴AB =6,故选:B .【点睛】本题考查了平行四边形的性质,三角形的中位线定理,熟练掌握平行四边形的性质,灵活运用三角形中位线定理是解题的关键.2.如图,平行四边形ABCD 中,对角线AG ,BD 相交于点O ,10AC =,6BD =,AD BD ⊥.在边AB 上取一点E ,使AE AO =,则AEO △的面积为( )A .61313B .91313C .121313D .151313【答案】D【分析】先过O 作OF AB ⊥于F ,过D 作DG AB ⊥于G ,依据勾股定理求得AD 和AB 的长,再根据面积法即可得出DG 的长,进而得到OF 的长,再根据三角形面积公式即可得到AEO ∆的面积.【详解】解:如图所示,过O 作OF AB ⊥于F ,过D 作DG AB ⊥于G ,平行四边形ABCD 中,10AC =,6BD =,5AO ∴=,3DO =,又AD BD ⊥,Rt AOD ∴△中,2222534AD AO DO =-=-=,Rt ABD ∴中,222246213AB AD BD =+=+=,1122AD BD AB DG ⨯=⨯, 121313AD BD DG AB ⨯∴==, //DG OF ,BO DO =,1613213OF DG ∴==, 又5AE AO ==,1161551313221313AOE S AE OF ∆∴=⨯=⨯⨯=, 故选:D .【点睛】此题考查了平行四边形的性质与勾股定理的运用,三角形的中位线的性质.依据平行四边形的性质得到O 是对角线的中点是解决问题的关键.3.如图,在△ABC 中,点D 、E 、F 分别是各边的中点,若△ABC 的面积为16cm 2,则△DEF 的面积是( )cm 2.A .2B .4C .6D .8【答案】B【分析】 根据三角形中位线定理判定四边形BEFD 是平行四边形,然后可证明△BDE ≌△FED ,同理可证:△DAF ≌△FED ,△EFC ≌△FED ,从而这四个三角形彼此全等,它们的面积也相等,所以可求得△DEF 的面积.【详解】∵点D 、F 分别是AB ,AC 的中点,∴//DF BC ,DF =12BC , ∴//DF BE ,∵E 是BC 的中点,∴BE =12BC , ∴DF =BE ,∴四边形BEFD 是平行四边形,∴BD =EF ,在△BDE 和△FED 中,BE DF BD EF DE ED =⎧⎪=⎨⎪=⎩,∴△BDE ≌△FED (SSS ),同理可证△DAF ≌△FED ,△EFC ≌△FED ,即△BDE ≌△DAF ≌△EFC ≌△FED ,∴S △DEF =14S △ABC =14×16=4(cm 2), 故选:B .【点睛】本题考查了三角形的中位线定理、三角形全等的判定等知识.4.如图,AD 是ABC ∆的中线,E ,F 分别是AD 和AD 延长线上的点,且DE DF =,连结BF ,CE 下列说法中不正确的有( )A .CE AE =B .ABD ∆和ACD ∆面积相等C .//BF CED .BDF CDE ∆∆≌【答案】A【分析】 根据三角形中线的定义可得BD =CD ,然后利用“边角边”证明△BDF 和△CDE 全等,根据全等三角形对应边相等可得CE =BF ,不能得出CE =AE 全等三角形对应角相等可得∠F =∠CED ,再根据内错角相等,两直线平行可得BF //CE ,最后根据等底等高的三角形的面积相等判断ABD ∆和ACD ∆面积相等.【详解】解:∵AD 是△ABC 的中线,∴BD =CD ,在△BDF 和△CDE 中,BD CD BDF CDE DF DE ⎧⎪∠∠⎨⎪⎩===,∴△BDF ≌△CDE (SAS ),故D 选项正确,不符合题意;∴CE =BF ,∠F =∠CED ,不能得出CE =AE ,故A 说法错误,符合题意,∴BF //CE ,故C 正确,不符合题意;∵BD =CD ,点A 到BD 、CD 的距离相等,∴△ABD 和△ACD 面积相等,故B 正确,不符合题意;故选A .【点睛】本题考查了全等三角形的判定与性质,等底等高的三角形的面积相等,熟练掌握三角形全等的判定方法并准确识图是解题的关键.5.如图,在ABC 中,AB =10,BC =16,点D 、E 分别是边AB 、AC 的中点,点F 是线段DE 上的一点,连接AF 、BF ,若∠AFB =90°,则线段EF 的长为( )A .2B .3C .4D .5【答案】B【分析】 根据直角三角形的斜边的中线等于斜边的一半,得到DF =5,由三角形中位线的性质得到DE =8,最后由线段的和差解题即可.【详解】解:∵∠AFB =90°,点D 是AB 的中点,∴DF = 12AB =5, ∵BC = 16,D 、E 分别是AB ,AC 的中点, ∴DE =12BC =8, ∴EF=DE -DF =3,【点睛】本题考查了直角三角形的性质和中位线性质,掌握定理是解题的关键.6.如图,在平行四边形ABCD中,AB=10,∠BAD的平分线与DC交于点F,AF⊥BF,DG⊥AF,垂足为G,DG=4,则AF的长为()A.6 B.5 C7D.8【答案】A【分析】延长AD、BF交于点E,证明△DEF≌△CBF(AAS),得出DE=BC,EF=BF,证出DG是△AEF 的中位线,得出EF=2DG=8,即可得出答案.【详解】解:延长AD、BF交于点E,如图所示:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∴∠E=∠CBF,∠BAF+∠DAF+∠ABF+∠CBF=180°,∵AF平分∠BAD,∴∠BAF=∠DAF,∵AF⊥BF,∴∠BAF+∠ABF=90°,∴∠ABF=∠CBF,∵四边形ABCD为平行四边形,∴AB∥CD,BC=AD,∴∠CFB=∠ABF,∠BAF=∠DF A,∴∠CFB=∠CBF,∠DF A=∠DAF,∴CB=CF,DA=DF,在△DEF 和△CBF 中,E CBF DFE CFB DF CF ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△DEF ≌△CBF (AAS ),∴DE =BC ,EF =BF ,∴AD =DE ,∵AF ⊥BF ,DG ⊥AF ,∴DG ∥EF ,∴DG 是△AEF 的中位线,∴EF =2DG =2×4=8,∴BF =EF =8, 226AF AB BF =-=;故选:A .【点睛】本题考查了平行四边形的性质、全等三角形的判定与性质、三角形中位线定理等知识;熟练掌握平行四边形的性质和三角形中位线定理,证明三角形全等是解题的关键.7.如图,在四边形ABCD 中,AB =6,BC =10,∠A =130°,∠D =100°,AD =CD .若点E,F 分别是边AD ,CD 的中点,则EF 的长是( )A .3B .4C .2D .5 【答案】B【分析】 连接AC ,根据等腰三角形的性质、三角形内角和定理求出∠DAC ,结合图形求出∠BAC =90°,根据勾股定理求出AC ,根据三角形中位线定理计算,得到答案.【详解】解:连接AC ,∵DA =DC ,∠D =100°,∴∠DAC =∠DCA =40°,∴∠BAC =∠BAD ﹣∠DAC =130°﹣40°=90°,∴AC =22221068BC AB --==,∵点E ,F 分别是边AD ,CD 的中点,∴EF =12AC =4, 故选:B .【点睛】本题考查的是三角形中位线定理、勾股定理、等腰三角形的性质,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.8.如图所示,在ABC 中,D 是BC 边上任一点,,,F G E 分别是,,AD BF CF 的中点,连结GE ,若FGE △的面积为6,则ABC 的面积为( )A .32B .48C .64D .72【答案】B【分析】 过点F 作FH ⊥BC 于点H ,交GE 于点M ,由题意易得1//,2GE BC GE BC =,,ABF FBD AFC FDC SS S S ==,进而可得12GE FM ⋅=,然后可得11222422FBC S BC FH GE FM =⋅=⨯⋅=,最后问题可求解. 【详解】解:过点F 作FH ⊥BC 于点H ,交GE 于点M ,如图所示:∵点,G E 分别是,BF CF 的中点,∴1//,2GE BC GE BC =, ∴12FM FH =, ∵162FGE S GE FM =⋅=, ∴12GE FM ⋅=, ∴11222422FBC S BC FH GE FM =⋅=⨯⋅=, ∵点F 是AD 的中点,∴,ABF FBD AFC FDC SS S S ==, ∵FBC FBD FDC SS S =+, ∴248ABC FBC S S ==,故选B .【点睛】本题主要考查三角形中位线及三角形的中线,熟练掌握三角形中位线及三角形的中线是解题的关键.9.如图,在四边形ABCD 中,E ,F 分别为DC 、AB 的中点,G 是AC 的中点,则EF 与AD CB +的关系是( )A .2EF AD BC =+B .2EF AD BC >+ C .2EF AD BC ≤+ D .不确定【答案】C【分析】 由题意易得11,22GE AD GF BC ==,然后根据三角形三边关系可进行排除选项. 【详解】解:∵E ,F 分别为DC 、AB 的中点,G 是AC 的中点, ∴11,22GE AD GF BC ==, 由三角形三边关系可得:GE GF EF +>,即1122AD BC EF +>, ∴2AD BC EF +>,当四边形ABCD 是平行四边形时,则有2AD BC EF +=,∴2EF AD BC ≤+;故选C .【点睛】本题主要考查三角形中位线,熟练掌握三角形中位线是解题的关键.10.如图,已知AD 是△ABC 的高,把三角形纸片ABC 折叠,使A 点落在D 处,折痕为EF ,则下列结论中错误的是( )A .EF ⊥ADB .EF =12BC C .DF =12ACD .DF =12AB 【答案】D【分析】 如图,证明EF ⊥AD ,且平分AD ;证明EF ∥BC ,得到AF =FC ,AE =BE ,进而得到EF =12BC ;证明DF =12AC ,即可解决问题. 【详解】解:如图,由题意得:EF ⊥AD ,且平分AD ,∵BC ⊥AD ,∴EF ∥BC ,AF =FC ,AE =BE ,∴EF 为△ABC 的中位线, ∴EF =12BC ;而点F 为AC 的中点, ∴DF =12AC , 综上所述,选项A 、B 、C 均正确.故选:D .【点睛】该题主要考查了翻折变换的性质、三角形中位线定理、直角三角形的性质等几何知识点及其应用问题;应牢固掌握三角形中位线定理、直角三角形的性质等几何知识点.11.如图,在平行四边形ABCD 中,对角线,AC BD 交于点O ,2BD AD =,E ,F ,G 分别是,,OA OB CD 的中点,EG 交FD 于点H .下列结论:①ED CA ⊥;②EF EG =;③12EH EG =;成立的个数有( )A.3个B.2个C.1个D.0个【答案】A【分析】由平行四边形性质和等腰三角形“三线合一”即可得ED⊥CA,根据三角形中位线定理可得EF=12AB;由直角三角形斜边上中线等于斜边一半可得EG=12CD,即可得EF=EG;连接EG,可证四边形DEFG是平行四边形,即可得EH=12 EG.【详解】解:如图,连接FG,∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,AD=BC,AD∥BC,AB=CD,AB∥CD,∵BD=2AD,∴OD=AD,∵点E为OA中点,∴ED⊥CA,故①正确;∵E,F,G分别是OA,OB,CD的中点,∴EF∥AB,EF=12AB,∵∠CED=90°,CG=DG=12 CD,∴EG=12 CD,∴EF=EG,故②正确;∵EF∥CD,EF=DG,∴四边形DEFG是平行四边形,∴EH=HG,即EH=12EG ,故③正确; 故选:A .【点睛】本题考查了平行四边形性质和判定,三角形中位线定理,三角形面积,直角三角形斜边上中线等于斜边一半,等腰三角形性质等;熟练运用三角形中位线定理、等腰三角形“三线合一”、直角三角形斜边上中线等于斜边一半等性质是解题关键.12.如图,在ABC 中,AB AC =,90BAC ∠=︒,直角EPF ∠的顶点P 是BC 的中点,两边PE ,PF 分别交AB ,AC 于点E ,F .现给出以下四个结论:①AE CF =;②EPF 是等腰直角三角形;③EF AP =;④12ABC AEPF S S =四边形△.当EPF ∠在ABC 内绕顶点P 旋转时(点E 不与点A ,B 重合),上述结论中始终正确的是( )A .①②③B .①②④C .②③④D .①③④【答案】B【分析】 根据等腰直角三角形的性质得出∠B =∠C =∠BAP =∠CAP =45°,AP =PC =PB ,∠APC =∠EPF =90°,求出∠APE =∠CPF ,证△APE ≌△CPF ,推出AE =CF ,EP =PF ,推出S △AEP =S △CPF ,求出S 四边形AEPF =S △APC =12S △ABC ,EF 不是△ABC 的中位线,故EF ≠AP ,即可得出答案. 【详解】解:∵△ABC 中,AB =AC ,∠BAC =90°,P 是BC 中点,∴∠B =∠C =∠BAP =∠CAP =45°,AP =PC =PB ,∠APC =∠EPF =90°,∴∠EPF -∠APF =∠APC -∠APF ,∴∠APE =∠CPF ,在△APE 和△CPF 中45EAP C AP CPAPE CPF ∠∠︒⎧⎪⎨⎪∠∠⎩====, ∴△APE ≌△CPF (ASA ),∴AE =CF ,EP =PF ,∴△EPF 是等腰直角三角形,∴①正确;②正确;∵△ABC 是等腰直角三角形,P 是BC 的中点,∴AP =12BC , ∵EF 不是△ABC 的中位线,∴EF ≠AP ,故③错误;∵△APE ≌△CPF ,∴S △AEP =S △CPF ,∴S 四边形AEPF =S △AEP +S △APF =S △CPF +S △APF =S △APC =12S △ABC , ∴④正确;∴正确的有①②④,故选:B .【点睛】本题考查了等腰三角形性质,三角形中位线的性质,三角形三边关系定理,全等三角形的性质和判定的应用,主要考查学生综合运用性质进行推理的能力.二、 填空题(本大题共6小题,每小题3分,共18分)13.如图,等边ABC 中,10AB =,E 为AC 中点,F ,G 为AB 边上的动点,且5FG =,则EF CG +的最小值是__________.【答案】57【分析】作C点关于AB的对称点C',取BC的中点Q,连接C'Q,交AB于点G,此时CG+EF最小,作C'H⊥BC交BC的延长线于点H,再根据等边三角形的性质和勾股定理可得答案.【详解】解:如图,作C点关于AB的对称点C',则C'G=CG,取BC的中点Q,连接EQ,GQ,B C',∵点E是AC的中点,∴EQ=12AB=5=FG,EQ∥AB,∴四边形EFGQ是平行四边形,∴EF=GQ,∴当点C',G,Q在同−条线上时,CG+EF最小,作C'H⊥BC交BC的延长线于点H,∵BC=BC'=10,∠CBC'=120°,∠HB C'=60°,∴HC'=3HB=5,∴HQ=10,∴C'Q7510057+=∴EF+CG的最小值是57故答案为:57【点睛】本题主要考查等边三角形的性质与判定,勾股定理,轴对称最值问题,根据题意作出正确的辅助线是解题关键.14.如图,在四边形ABCD 中,CD 平分对角线AC 与BC 边延长线的夹角,AD DC ⊥,点E 为AB 中点,若3AC =,5BC =,则线段DE 的长为________.【答案】4【分析】如图,延长AD 交BC 延长线于G ,利用ASA 可证明△ACD ≌△GCD ,可得AC =CG ,AD =GD ,根据线段的和差关系可得BG 的长,根据点E 为AB 中点可得DE 为△ABG 的中位线,根据中位线的性质即可得答案.【详解】如图,延长AD 交BC 延长线于G ,∵CD 平分对角线AC 与BC 边延长线的夹角,AD DC ⊥,∴∠ACD =∠GCD ,∠ADC =∠GDC =90°,在△ACD 和△GCD 中,ACD GCD CD CD ADC GDC ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△ACD ≌△GCD ,∴AC =CG ,AD =GD ,∵3AC =,5BC =,∴BG =BC +CG =BC +AC =8,∵点E 为AB 中点,∴DE 为△ABG 的中位线,∴DE =12BG =4,故答案为:4【点睛】本题考查全等三角形的判定与性质及三角形中位线定理,三角形的中位线平行于第三边,且等于第三边的一半;熟练掌握相关定理及性质是解题关键.15.如图,在平行四边形ABCD 中,M N 、分别为CD BC 、的中点,4,2,60AM AN MAN ==∠=,则对角线BD 的长为____.【答案】43 【分析】延长AM 至E ,使得ME =AM ,过点E 作EH ⊥AN ,交AN 延长线于H 点,连接MN .证明N 点为AH 中点,则MN =12HE =12BD ,即求BD 长转化为求HE 值即可. 【详解】解:延长AM 至E ,使得ME =AM ,过点E 作EH ⊥AN ,交AN 延长线于H 点,连接MN .∴AE =2AM =8.∵∠MAN =60°,∴∠E =30°,∴AH =12AE =4,HE =2243AE AH -=. ∵AN =2,∴N 点为AH 中点.∴MN =12HE . ∵M 、N 分别为CD 、BC 的中点,∴MN =12BD . ∴BD =HE =43故答案为43.【点睛】本题主要考查了了平行四边形的性质、勾股定理、三角形中位线的性质,解决此题的关键是借助线段的中点作“倍长中线”辅助线,使得线段得以转化.16.如图,在Rt ABC 中,4AC BC ==,90ACB ∠=︒,正方形BDEF 的边长为2,将正方形BDEF 绕点B 旋转一周,连接AE ,点M 为AE 的中点,连接FM ,则线段FM 的最大值是__________.【答案】32【分析】延长EF 到G ,使FG =EF ,连接BG ,FG ,可得△BFG 是等腰直角三角形,得到BG 222BF =根据三角形中位线定理得AG =2FM ,由勾股定理求出AB ,再根据三角形三边关系可求出AG 的最大值,从而可得结论.【详解】解:延长EF 到G ,使FG =EF ,连接BG ,FG ,如图,∵四边形BDEF 是正方形,∴BF =EF ,∠BFE =90°∴∠BFG =90°∴△BFG 是等腰直角三角形,∴BG 22222BF ==在Rt △ABC 中,∠C =90°,AC =BC =4 ∴2242AB AC BC =+=∵AB BG AG AB BG -≤≤+ ∴2262AG ≤≤ 232FM ≤∴线段FM 的最大值是32故答案为:32【点睛】此题主要考查了正方形的性质、等腰直角三角形的判定与性质,三角形中位线定理,银河股定理等知识,能正确作出相关的辅助线是解决本题的关键.17.如图,在等边三角形ABC 中,6AB =,D ,E 分别为边AB 和AC 上的点,连接DE ,将ADE ∆沿DE 折叠得到FDE ∆.若点F 始终落在边BC 上,则线段DE 的取值范围为___________.≤≤【答案】333DE【分析】当A点与F点重合,D点与E点重合时,此时DE最大;当点F在BC上且DE∥BC时,此时DE 最短,结合等边三角形的性质和中位线定理求解,从而确定DE的取值范围.【详解】解:当A点与F点重合,D点与E点重合时,此时DE最大由折叠性质可得,此时DE⊥AB,∠AED=∠BED=30°AB=,∵在等边三角形ABC中,6∴BD=3,DE=333BD=当点F在BC上且DE∥BC时,此时DE最短由折叠性质可得此时DE为△ABC的中位线∴DE=3∴线段DE的取值范围为333≤≤DE故答案为:333DE≤≤.【点睛】本题考查等边三角形的性质,含30°的直角三角形性质以及三角形中位线定理,掌握相关性质定理正确推理论证是解题关键.18.如图,在边长为4的等边△ABC中,D,E分别为AB,BC的中点,EF⊥AC于点F,G为EF 的中点,连接DG,则DG的长为________【答案】19 2【分析】连接DE,根据等边三角形的性质可得∠C=60°,根据三角形的中位线的性质得DE∥AC,DE=2,再根据等边三角形的性质可得∠C=60°,利用直角三角形中30°所对的直角边是斜边的一半和勾股定理求得EG和DG即可.【详解】解:连接DE,∵△ABC是等边三角形,∴∠C=60°,AC=BC=4,∵D、E分别是AB、BC的中点,∴DE为△ABC的中位线,CE= 12BC=2,∴DE∥AC,DE= 12AC=2,∵EF⊥AC,∴∠EFC=∠DEF=90°,在Rt△EFC中,∠CEF=90°﹣∠C=30°,CE=2,∴CF= 12CE=1,EF= 2222213CE CF--=∵G为EF的中点,∴EG = 12EF = 3, 在Rt △DEG 中,由勾股定理得DG =22223192()2DE EG +=+=, 故答案为:19.【点睛】本题考查等边三角形的性质、三角形的中位线、平行线的性质、含30°角的直角三角形的性质、勾股定理,熟练掌握等边三角形的性质和三角形的中位线性质是解答的关键.三、解答题(本大题共6小题,共66分,解答应写出文字说明、演算步骤或推理过程) 19.已知:平行四边形ABCD 中,点M 为边CD 的中点,点N 为边AB 的中点,联结AM 、CN . (1)求证:AM ∥CN ;(2)过点B 作BH AM ⊥,垂足为H ,联结CH .求证:△BCH 是等腰三角形.【答案】(1)见解析;(2)见解析【分析】(1)由四边形ABCD 是平行四边形,根据平行四边形的性质,可得AB ∥CD ,AB=CD ,又由点M 为边CD 的中点,点N 为边AB 的中点,即可得CM=AN ,继而可判定四边形ANCM 是平行四边形,则可证得AM ∥CN .(2)由AM ∥CN ,BH ⊥AM ,点N 为边AB 的中点,可证得BH ⊥CN ,ME 是△BAH 的中位线,则可得CN 是BH 的垂直平分线,继而证得△BCH 是等腰三角形.【详解】解:(1)证明:∵四边形ABCD 是平行四边形,∴AB ∥CD 且AB CD =.∵点M 、N 分别是边CD 、AB 的中点, ∴12CM CD =,1AN AB 2=. ∴CM AN =.又∵AB ∥CD ,∴四边形ANCM 是平行四边形∴AM ∥CN .(2)设BH 与CN 交于点E ,∵AM ∥CN ,BH ⊥AM ,∴BH ⊥CN ,∵N 是AB 的中点,∴EN 是△BAH 的中位线,∴BE=EH ,∴CN 是BH 的垂直平分线,∴CH=CB ,∴△BCH 是等腰三角形.【点睛】此题考查了平行四边形的判定与性质、线段垂直平分线的性质以及等腰三角形的判定.此题难度适中,注意掌握数形结合思想的应用.20.在ABC 中,AC BC =,90ACB ∠=︒,点D 为AC 的中点.(1)如图1,E为线段DC上任意一点,将线段DE绕点D逆时针旋转90°得到线段DF,连结CF,过点F作FH FC,交直线AB于点H.判断FH与FC的数量关系并加以证明.(2)如图2,若E为线段DC的延长线上任意一点,(1)中的其他条件不变,你在(1)中得出的结论是否发生改变,给出证明.【答案】(1)CF=FH;理由见解析;(2)结论不变,CF=FH;理由见解析.【分析】(1)延长DF交AB于点G,根据三角形中位线的判定得出点G为AB的中点,根据中位线的性质及已知条件AC=BC,得出DC=DG,从而EC=FG,易证∠1=∠2=90°-∠DFC,∠CEF=∠FGH=135°,于是证出△CEF≌△FGH.故CF=FH.(2)类似(1)的证法证明△CEF≌△FGH,故CF=FH.【详解】解:(1)FH与FC的数量关系是:FH=FC.理由如下:如图1,延长DF交AB于点G,由题意,知∠EDF=∠ACB=90°,DE=DF,∴DG∥CB,∵点D为AC的中点,∴点G为AB的中点,且DC=12 AC,∴DG为△ABC的中位线,∴DG=12 BC.∵AC=BC,∴DC=DG,∴DC-DE=DG-DF,即EC=FG.∵∠EDF=90°,FH⊥FC,∴∠1+∠CFD=90°,∠2+∠CFD=90°,∴∠1=∠2.∵△DEF与△ADG都是等腰直角三角形,∴∠DEF=∠DGA=45°,∴∠CEF=∠FGH=135°,∴△CEF≌△FGH,∴CF=FH.(2)FH与FC仍然相等.理由如下:如图2,由题意可得出:DF=DE,∴∠DFE=∠DEF=45°,∵AC=BC,∴∠A=∠CBA=45°,∵DF∥BC,∴∠CBA=∠FGB=45°,∴∠FGH=∠CEF=45°,∵点D为AC的中点,DF∥BC,∴DG=12BC ,DC= 12AC , ∴DG=DC ,∴EC=GF ,∵∠DFC=∠FCB ,∴∠GFH=∠FCE ,在△FCE 和△HFG 中,CEF FGH EC GF ECF GFH ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△FCE ≌△HFG (ASA ),∴HF=FC .【点睛】本题考查了全等三角形的判定和性质、等腰三角形的性质、三角形中位线定理等知识,综合性强,难度较大.21.如图,在Rt ABC △中,90BAC ∠=︒,中线BD ,CE 相交于点O ,点F ,G 分别为OB ,OC 的中点.(1)求证://EF DG ,EF DG =;(2)若3AB =,4AC =,求四边形EFGD 的面积.【答案】(1)见解析;(2)2【分析】(1)利用中位线性质可得12ED BC =,//ED BC .12FG BC =,//FG BC .可证四边形EFGD 是平行四边形.由平行四边形性质可得EF DG =,//EF DG .(2)由EFGD 和OG GC =,可推得EO OG CG ==.求13462ABC S =⨯⨯=△由点D 是AC 中点,1322DEC AEC S S ==△△.由三等分可求2231332DEG DEC S S ==⨯=△△.根据平行四边形性质可得四边形DEFG 的面积22DEG S ==△.【详解】(1)证明:∵点E ,D 分别是AB ,AC 的中点, ∴12ED BC =,//ED BC . ∵点F ,G 分别是OB ,OC 的中点, ∴12FG BC =,//FG BC . ∴FG ED =,//FG ED .∴四边形EFGD 是平行四边形.∴EF DG =,//EF DG ;(2)解:∵EFGD ,∴EO OG =.又∵OG GC =,∴EO OG CG ==.∵3AB =,4AC =, ∵13462ABC S =⨯⨯=△, ∵点D 是AC 中点, ∴1322DEC AEC S S ==△△. ∴2231332DEG DEC S S ==⨯=△△. ∴四边形DEFG 的面积22DEG S ==△.【点睛】本题考查中位线性质,平行四边形的判定与性质,中线的性质,掌握中位线性质,平行四边形的判定与性质,中线的性质,注意中线与中位线的区别以及它们性质是解题关键.22.如图1,在ABC 中,点D 是边BC 的中点,点E 在ABC 内,AE 平分BAC ∠,CE AE ⊥,点F 在边AB 上,//EF BC .(1)求证:四边形BDEF 是平行四边形.(2)判断线段BF 、AB 、AC 的数量之间具有怎样的关系?证明你所得到的结论.(3)点P 是ABC 的边AB 上的一点,若DCE 的面积3DCE S =△,请直接写出DPE 的面积(不需要写出解答过程).【答案】(1)证明见解析;(2)()12BF AB AC =-,证明见解析;(3)DPE S =3. 【分析】(1)证明△AGE ≌△ACE ,根据全等三角形的性质可得到GE =EC ,再利用三角形的中位线定理证明DE ∥AB ,再加上条件EF ∥BC 可证出结论;(2)先证明BF =DE =12BG ,再证明AG =AC ,可得到BF =12(AB−AG )=12(AB−AC ); (3) 根据△DCE 中DC 边上的高与BDEF 中BD 边上的高相等,得出BDEF 的面积为6,设BDEF 中BF 边上的高为h ,由DPE BDP BDEP SS S=-梯形即可求解. 【详解】(1)延长CE 交AB 于点G ,AE CE ⊥,90AEG AEC ∴∠=∠=︒,又∵AE 平分BAC ∠,∴∠GAE=∠CAE在AEG △和AEC 中,GAE CAE AE AE AEG AEC ∠=∠⎧⎪=⎨⎪∠=∠⎩,()ASA AEG ACE ∴≌△△,GE EC ∴=,∵点D 是边BC 的中点,∴BD CD =DE ∴为CGB △的中位线,//DE AB ∴,//EF BC ,∴四边形BDEF 是平行四边形.(2)四边形BDEF 是平行四边形,BF DE ∴=, D ,E 分别是BC ,GC 的中点, 12BF DE BG ∴==, AEG AEC ≌△△,AG AC ∴=,()()1122BF AB AG AB AC ∴=-=-. (3)如图:∵BD=DC ,EF ∥BC∴△DCE 中DC 边上的高与BDEF 中BD 边上的高相等, ∴2236BDEF DCE S S ==⨯=∵BF ∥DE设BDEF 中BF 边上的高为h , 则DPE BDP BDEP S S S =-梯形=(DE+BP )×h÷2-BP×h÷2=DE×h÷2=6÷2=3.【点睛】此题主要考查了平行四边形的判定与性质,全等三角形的判定与性质,三角形中位线定理,以及等底同高的平行四边形和三角形的面积之间的关系,证明GE =EC ,再利用三角形中位线定理证明DE ∥AB 是解决问题的关键.23.已知等边ABC ,D 为边BC 中点,M 为边AC 上一点(不与A ,C 重合),连接DM .(1)如图1,点E 是边AC 的中点,当M 在线段AE 上(不与A ,E 重合)时,将DM 绕点D 逆时针旋转120︒得到线段DF ,连接BF .①依题意补全图1;②此时EM 与BF 的数量关系为: ,DBF ∠= °.(2)如图2,若2DM MC =,在边AB 上有一点N ,使得120NDM ∠=︒.直接用等式表示线段BN ,ND ,CD 之间的数量关系,并证明.【答案】(1)①见解析;②EM BF =,120;(2)12CD BN ND =+,证明见解析 【分析】(1)①根据提示画出图形即可;②连接DE ,证明△DME ≌△DFB 即可得到结论;(3)取线段AC 中点E ,连接ED .由三角形中位线定理得12DE BA =,12CE CA =,12BD CD BC ==.根据ABC 是等边三角形可证明DE BD CD CE ===,60CED EDC B ∠=∠=∠=︒,再证明EDM BDN ≅△△得BN EM =,2ND MD MC ==,进一步可得结论.【详解】 解:(1)①补全图形如图1.②线段EM 与BF 的数量关系为EM BF =;120DBF ∠=︒.连接DE ,∵D 为BC 的中点,E 为AC 的中点,∴DE 为△ABC 的中䏠线,∴DE =12AB ,DE //AB ∵ABC 是等边三角形,∴AB BC AC ==,60∠=∠=∠=︒A B C .∵D 为BC 的中点,∴12BD BC DE == ∵//DE AB∴60CDE ABC ∠=∠=︒,60CED A ∠=∠=︒∴120BDE BDM EDM ∠=︒=∠+∠∵120BDM BDF ∠+∠=︒ ,,DM DF =∴ BDF EDM ∠=∠∴△DME ≌△DFB∴EM BF =;DBF DEM ∠=∠.∵60CED ∠=︒∴120DEM ∠=︒∴120DBF ∠=︒.故答案为:EM BF =;120DBF ∠=︒.(2)证明:取线段AC 中点E ,连接ED .如图2 .∵点D 是边BC 的中点,点E 是边AC 的中点, ∴12DE BA =,12CE CA =,12BD CD BC ==. ∵ABC 是等边三角形,∴AB BC AC ==,60B C ∠=∠=︒.∴DE BD CD CE ===,60CED EDC B ∠=∠=∠=︒.∴120∠=︒BDE ,∵120NDM ∠=︒,∴EDM BDN ∠=∠.∴EDM BDN ≅△△.∴BN EM =,2ND MD MC ==,∵EC EM MC =+,∴12CD BN ND =+.【点睛】此题主要考查了全等三角形的判定与性质,等边三角形的性质以及三角形中位线定理,正确作出辅助线构造全等三角形是解答此题的关键.24.问题提出(1)如图①,在ABC 中,D 、E 分别是AB 和AC 的中点,连接DE ,则DE 与BC 的数量关系是______,位置关系是______;问题探究(2)如图②,在四边形ABCD 中,90BAC ∠=︒,42AB AC ==,4CD =,E 为AD 中点,连接BE ,求BE 的最大值;问题解决(3)如图③,某小区计划在一片足够大的空地上修建四边形的花园ABCD ,其中20BC =米,AD CD =,AD CD ⊥,//AB CD ,由于受地理位置的影响,90ABC ∠<︒.根据要求,现计划给该花园修建条笔直的绿色长廊,且绿色长廊的入口O 定为BC 的中点,出口定为点D ,为了尽可能地提高观赏体验,要求绿色长廊OD 最长,试求绿色长廊OD 最长为多少米?【答案】(1)12DE BC =,//DE BC ;(2)2102;(3)()10210米 【分析】 (1)根据中位线定理即可得出答案;(2)取AC 的中点F ,连接EF 、BF ,由图在三角形BEF 中,BF EF BE +>,可得当B 、E 、F 三点共线的时候BE 最大,此时=BE BF EF +,根据中位线可得出EF 的长度,在Rt ABF 中根据勾股定理可得BF 的长度,即可得出BE 的最大值;(3)过C 作CM AB ⊥于M 点,在AD 上截取DN 使DN BM =,连接BN ,取CN 中点P ,连接DP 、OP ,可证得ADCM 为正方形,再证明CMB CDN ≅,易证BCN △为等腰直角三角形,从而得出BN 的长度,根据中位线定理可得出OP 的长度;利用直角三角形斜边中线等于斜边的一半求出1102DP CN ==,再根据OP PD OD +>可得,当O 、P 、D 三点共线的时OD 最大,即可得出答案.【详解】解:(1)由题可知,D 、E 分别是AB 和AC 的中点,DE ∴为ABC 的中位线,//DE BC ∴且12DE BC =; 故答案为:12DE BC =,//DE BC . (2)如图,取AC 的中点F ,连接EF 、BFE 、F 分别是AD 和AC 的中点,EF ∴为ADC 的中位线,//D EF C ∴且114222EF CD ==⨯=, 在Rt ABF 中,142,222AB AF AC ===, ()()22224222210BF AB AF ∴=+=+=;如图在BEF 中,BF EF BE +>,∴当B 、E 、F 三点共线的时候BE 最大,即此时=2102BE BF EF +=+.答:BE 的最大值为2102+.(3)过C 作CM AB ⊥于M 点,在AD 上截取DN 使DN BM =,连接BN ,取CN 中点P ,连接DP 、OP ,CM AB ⊥,//AB CD ,90CMA MCD ADC ∴∠=∠=∠=︒,ADCM ∴为矩形,AD CD =,ADCM ∴为正方形,CD CM ∴=,在CMB 与CDN △中,90CM CD CMB CDN BM DN =⎧⎪∠=∠=︒⎨⎪=⎩()CMB CDN SAS ∴≅,CN CB ∴=,BCM NCD ∠=∠,90BCN MCD ∴∠=∠=︒,在Rt BCN △中,20BC CN ==,BN ∴===在Rt CDN 中,点P 为CN 中点,1102DP CN ∴==, 在Rt BCN △中,点P 、O 分别为CN 、CB 中点,OP ∴为BCN △的中位线,//OP BN ∴且12OP BN == 在OPD △中,OP PD OD +>,∴当O 、P 、D 三点共线的时OD 最大,即此时OD=OP 10PD +=,答:绿色长廊OD最长为()10米.【点睛】本题考查中位线定理的综合应用,结合三角形的全等以及三角形三边长度关系,在做此类题目时注意类比每一问之间的关系,一般下一问都会用到上一问的结论和做题思路.。
中考数学《三角形》专题训练(附答案解析)

中考数学《三角形》专题训练(附答案解析)一单选题1.下列多边形具有稳定性的是()A.B.C.D.【答案】D【解析】利用三角形具有稳定性直接得出答案.【详解】解:三角形具有稳定性四边形五边形六边形都具有不稳定性故选D.【点睛】本题考查三角形的特性牢记三角形具有稳定性是解题的关键.2.请你量一量如图ABC中BC边上的高的长度下列最接近的是()A.0.5cm B.0.7cm C.1.5cm D.2cm【答案】D【解析】作出三角形的高然后利用刻度尺量取即可.【详解】解:如图所示过点A作AO⊥BC用刻度尺直接量得AO更接近2cm故选:D.【点睛】题目主要考查利用刻度尺量取三角形高的长度作出三角形的高是解题关键.3.若等腰三角形的两边长分别是3cm和5cm 则这个等腰三角形的周长是()A.8cm B.13cm C.8cm或13cm D.11cm或13cm【答案】D【解析】题目给出等腰三角形有两条边长为3和5 而没有明确腰底分别是多少所以要进行讨论还要应用三角形的三边关系验证能否组成三角形.【详解】解:当3是腰时⊥3+3>5⊥3 3 5能组成三角形此时等腰三角形的周长为3+3+5=11(cm)当5是腰时⊥3+5>55 5 3能够组成三角形此时等腰三角形的周长为5+5+3=13(cm)则三角形的周长为11cm或13cm.故选:D【点睛】本题考查等腰三角形的性质及三角形三边关系已知没有明确腰和底边的题目一定要想到两种情况分类进行讨论还应验证各种情况是否能构成三角形进行解答这点非常重要也是解题的关键.4.下列长度的三条线段能首尾相接构成三角形的是()A.1cm2cm3cm B.3cm4cm5cmC.4cm5cm10cm D.6cm9cm2cm【答案】B【解析】根据三角形的三边关系“任意两边之和大于第三边任意两边之差小于第三边” 进行分析.【详解】解:根据三角形的三边关系知A1+2=3 不能组成三角形故选项错误不符合题意B3+4>5 能够组成三角形故选项正确符合题意C5+4<10 不能组成三角形故选项错误不符合题意D2+6<9 不能组成三角形故选项错误不符合题意故选:B.【点睛】此题考查了三角形的三边关系.解题的关键是看较小的两个数的和是否大于第三个数.5.下列长度的三条线段能组成三角形的是()A.3 4 8B.5 6 11C.5 6 10D.5 5 10【答案】C【解析】根据三角形的三边关系定理(任意两边之和大于第三边)逐项判断即可得.【详解】+=<不能组成三角形此项不符题意解:A3478B5611+=不能组成三角形此项不符题意+=>能组成三角形此项符合题意C561110D5510+=不能组成三角形此项不符题意故选:C.【点睛】本题考查了三角形的三边关系定理熟练掌握三角形的三边关系定理是解题关键.6.如图在Rt△AB C中⊥C=90° ⊥B=56° 则⊥A的度数为()A.34︒B.44︒C.124︒D.134︒【答案】A【解析】根据直角三角形的两个锐角互余即可得出⊥A的度数.【详解】解:⊥Rt△AB C中⊥C=90° ⊥B=56°⊥⊥A=90°-⊥B=90°-56°=34°故选:A.【点睛】本题考查了直角三角形的性质:直角三角形的两个锐角互余熟练掌握直角三角形的性质并能进行推理计算是解决问题的关键.7.若长度分别是a 3 5的三条线段能组成一个三角形则a的值可以是()A.1B.2C.4D.8【答案】C【解析】根据三角形的三边关系:任意两边之和大于第三边 任意两边之差小于第三边 求出a 的取值范围即可得解.【详解】根据三角形的三边关系得5353a -<<+ 即28a << 则选项中4符合题意故选:C .【点睛】本题主要考查了三角形的三边关系 熟练掌握相关不等关系是解决本题的关键.8.(2021·山东泰安)如图 直线//m n 三角尺的直角顶点在直线m 上 且三角尺的直角被直线m 平分 若160∠=︒ 则下列结论错误的是( )A .275∠=︒B .345∠=︒C .4105∠=︒D .5130∠=︒【答案】D 【解析】根据角平分线的定义求出⊥6和⊥7的度数 再利用平行线的性质以及三角形内角和求出⊥3 ⊥8 ⊥2的度数 最后利用邻补角互补求出⊥4和⊥5的度数.【详解】首先根据三角尺的直角被直线m 平分⊥⊥6=⊥7=45°A ⊥⊥1=60° ⊥6=45° ⊥⊥8=180°-⊥1-⊥6=180-60°-45°=75° m∥n ⊥⊥2=⊥8=75°结论正确 选项不合题意B ⊥⊥7=45° m ⊥n ⊥⊥3=⊥7=45° 结论正确 选项不合题意C ⊥⊥8=75° ⊥⊥4=180-⊥8=180-75°=105° 结论正确 选项不合题意D ⊥⊥7=45° ⊥⊥5=180-⊥7=180-45°=135° 结论错误 选项符合题意.故选:D .【点睛】本题考查了角平分线的定义平行线的性质三角形内角和邻补角互补解答本题的关键是掌握平行线的性质:两直线平行同位角相等内错角相等同旁内角互补.9.(2020·山东淄博)如图若⊥ABC⊥⊥ADE则下列结论中一定成立的是()A.AC=DE B.⊥BAD=⊥CAE C.AB=AE D.⊥ABC=⊥AED【答案】B【解析】根据全等三角形的性质即可得到结论.【详解】解:⊥⊥ABC⊥⊥ADE⊥AC=AE AB=AD⊥ABC=⊥ADE⊥BAC=⊥DAE⊥⊥BAC﹣⊥DAC=⊥DAE﹣⊥DAC即⊥BAD=⊥CAE.故A C D选项错误B选项正确故选:B.【点睛】本题考查了全等三角形的性质熟练掌握全等三角形的性质是解题的关键.10.(2020·广东深圳)如图已知AB=AC BC=6 尺规作图痕迹可求出BD=()A.2B.3C.4D.5【答案】B【解析】根据尺规作图的方法步骤判断即可.【详解】由作图痕迹可知AD为⊥BAC的角平分线而AB=AC由等腰三角形的三线合一知D为BC重点BD =3故选B【点睛】本题考查尺规作图-角平分线及三线合一的性质,关键在于牢记尺规作图的方法和三线合一的性质.11.(2020·福建)如图 面积为1的等边三角形ABC 中 ,,D E F 分别是AB BC CA 的中点 则DEF ∆的面积是( )A .1B .12C .13D .14【答案】D 【解析】根据题意可以判断四个小三角形是全等三角形,即可判断一个的面积是14. 【详解】⊥,,D E F 分别是AB BC CA 的中点,且⊥ABC 是等边三角形⊥⊥ADF ⊥⊥DBE ⊥⊥FEC ⊥⊥DFE ⊥⊥DEF 的面积是14. 故选D .【点睛】本题考查等边三角形的性质及全等,关键在于熟练掌握等边三角形的特殊性质.12.(2020·四川巴中)如图 在ABC 中 120BAC ∠=︒ AD 平分BAC ∠ //DE AB 3AD = 5CE = 则AC 的长为( )A .9B .8C .6D .7【答案】B 【解析】根据角平分线的性质可得到1602BAD CAD BAC ∠=∠=∠=︒ 然后由DE AB ∥可知60BAD ADE ∠=∠=︒ 从而得到60ADE EAD ∠=∠=︒ 所以ADE 是等边三角形 由AC AE CE =+ 即可得出答案.【详解】解:⊥120BAC ∠=︒ AD 平分BAC ∠ ⊥1602BAD CAD BAC ∠=∠=∠=︒ ⊥//DE AB⊥60BAD ADE ∠=∠=︒⊥60ADE EAD ∠=∠=︒⊥ADE 是等边三角形⊥3AE AD ==⊥5CE =⊥358AC AE CE =+=+=故选:B .【点睛】本题主要考查了角平分线的性质 平行线的性质 等边三角形的判定和性质 熟练掌握相应的判定定理和性质是解题的关键 属于基础综合题.13.(2020·广西贺州)如图 将两个完全相同的Rt ⊥ACB 和Rt ⊥A'C ′B ′拼在一起 其中点A ′与点B 重合 点C '在边AB 上 连接B ′C 若⊥ABC =⊥A ′B ′C ′=30° AC =A ′C ′=2 则B ′C 的长为( )A .7B .7C .3D .3【答案】A 【解析】先根据直角三角形的性质可得4,4,60AB A B B A C '''=''=∠=︒ 再根据勾股定理和角的和差可得3,90BC B BC '=∠=︒ 最后在Rt B BC '中 利用勾股定理即可得.【详解】解:⊥90,30,2ACB A C B ABC A B C AC A C ''''∠=∠''=︒∠=∠=︒=''=⊥4,4,60AB A B B A C '''=''=∠=︒ ⊥2223BC AB AC -= 90B BC ABC B A C ''''∠=∠+∠=︒则在Rt B BC '中 2222(23)427B C BC B B ''=+=+故选:A .【点睛】本题考查了含30度角的直角三角形的性质勾股定理等知识点熟练掌握含30度角的直角三角形的性质是解题关键.14.(2020·四川广安)如图在五边形ABCDE中若去掉一个30°的角后得到一个六边形BCDEMN则⊥l+⊥2的度数为()A.210°B.110°C.150°D.100°【答案】A【解析】根据三角形的内角和定理可得⊥AMN+⊥ANM=150° 根据平角的定义可得⊥1+⊥AMN=180°⊥2+⊥ANM=180° 从而求出结论.【详解】解:⊥⊥A=30°⊥⊥AMN+⊥ANM=180°-⊥A=150°⊥⊥1+⊥AMN=180° ⊥2+⊥ANM=180°⊥⊥1+⊥2=180°+180°-(⊥AMN+⊥ANM)=210°故选A.【点睛】此题考查的是三角形内角和定理的应用掌握三角形的内角和定理是解题关键.15.(2020·山东济南)如图在ABC中AB=AC分别以点A B为圆心以适当的长为半径作弧两弧分别交于E F作直线EF D为BC的中点M为直线EF上任意一点.若BC=4 ABC面积为10 则BM+MD长度的最小值为()A.52B.3C.4D.5【答案】D【解析】由基本作图得到得EF垂直平分AB则MB=MA所以BM+MD=MA+MD连接MA DA如图利用两点之间线段最短可判断MA+MD的最小值为AD再利用等腰三角形的性质得到AD⊥BC 然后利用三角形面积公式计算出AD即可.【详解】解:由作法得EF垂直平分AB⊥MB=MA⊥BM+MD=MA+MD连接MA DA如图⊥MA+MD≥AD(当且仅当M点在AD上时取等号)⊥MA+MD的最小值为AD⊥AB=AC D点为BC的中点⊥AD⊥BC⊥110,2ABCS BC AD==⊥1025,4AD⨯==⊥BM+MD长度的最小值为5.故选:D.【点睛】本题考查的是线段的垂直平分线的性质利用轴对称求线段和的最小值三角形的面积两点之间线段最短掌握以上知识是解题的关键.16.(2020·山东烟台)如图点G为ABC的重心连接CG AG并延长分别交AB BC于点E F 连接EF若AB=4.4 AC=3.4 BC=3.6 则EF的长度为()A.1.7B.1.8C.2.2D.2.4【答案】A【解析】由已知条件得EF是三角形的中位线进而根据三角形中位线定理求得EF的长度.【详解】解:⊥点G为△ABC的重心⊥AE=BE BF=CF⊥EF=12AC=1.7故选:A.【点睛】本题主要考查了三角形的重心三角形的中位线定理关键正确利用重心定义得EF为三角形的中位线.17.(2020·山东淄博)如图在⊥AB C中AD BE分别是BC AC边上的中线且AD⊥BE垂足为点F设BC=a AC=b AB=c则下列关系式中成立的是()A.a2+b2=5c2B.a2+b2=4c2C.a2+b2=3c2D.a2+b2=2c2【答案】A【解析】【详解】设EF=x DF=y根据三角形重心的性质得AF=2y BF=2EF=2x利用勾股定理得到4x2+4y2=c2 4x2+y2=b2x2+4y2=a2然后利用加减消元法消去x y得到a b c的关系.【解答】解:设EF=x DF=y⊥AD BE分别是BC AC边上的中线⊥点F为⊥ABC的重心AF=AC=b BD=a⊥AF=2DF=2y BF=2EF=2x⊥AD⊥BE⊥⊥AFB=⊥AFE=⊥BFD=90°在Rt⊥AF B中4x2+4y2=c2⊥在Rt⊥AEF中4x2+y2=b2⊥在Rt ⊥BF D 中 x 2+4y 2=a 2 ⊥⊥+⊥得5x 2+5y 2=(a 2+b 2) ⊥4x 2+4y 2=(a 2+b 2) ⊥⊥﹣⊥得c 2﹣(a 2+b 2)=0 即a 2+b 2=5c 2.故选:A .【点评】本题考查了三角形的重心:重心到顶点的距离与重心到对边中点的距离之比为2:1. 也考查了勾股定理.18.(2020·湖南益阳)如图 在ABC ∆中 AC 的垂直平分线交AB 于点D DC 平分ACB ∠ 若50A ∠= 则B 的度数为( )A .25B .30C .35D .40【答案】B 【解析】根据垂直平分线的性质和角平分线的定义求得⊥ACB 的度数 再根据三角形内角和求出⊥B 的度数.【详解】解:⊥DE 是AC 的垂直平分线⊥AD =CD ⊥ACD =⊥A =50°⊥DC 平分ACB ∠⊥⊥ACB =2⊥ACD =100°⊥⊥B =180°-100°-50°=30°故选:B .【点睛】本题考查垂直平分线的性质 角平分线的定义和三角形内角和定理 熟练掌握垂直平分线的性质和角平分线的定义是解题的关键.19.(2021·广西河池)如图 40A ∠︒= CBD ∠是ABC 的外角 120CBD ∠︒= 则C ∠的大小是( )A .90︒B .80︒C .60︒D .40︒【答案】B 【解析】根据三角形的外角性质直接求解即可.【详解】CBD ∠是ABC 的外角 40A ∠︒= 120CBD ∠︒=∴CBD A C ∠=∠+∠.1204080C CBD A ∴∠=∠-∠=︒-︒=︒.故选B .【点睛】本题考查了三角形外角的性质 掌握三角形外角性质是解题的关键.20.(2021·黑龙江哈尔滨)如图 ABC DEC ≌△△ 点A 和点D 是对应顶点 点B 和点E 是对应顶点 过点A 作AF CD ⊥ 垂足为点F 若65BCE ∠=︒ 则CAF ∠的度数为( )A .30B .25︒C .35︒D .65︒【答案】B 【解析】由题意易得65ACF BCE ∠=∠=︒ 90AFC ∠=︒ 然后问题可求解.【详解】解:⊥ABC DEC ≌△△⊥ACB DCE ∠=∠⊥ACB ACE DCE ACE ∠-∠=∠-∠ 即ACF BCE ∠=∠⊥65BCE ∠=︒⊥65ACF BCE ∠=∠=︒⊥AF CD ⊥⊥90AFC ∠=︒⊥9025CAF ACF ∠=︒-∠=︒故选B .【点睛】本题主要考查全等三角形的性质及直角三角形的性质 熟练掌握全等三角形的性质及直角三角形的性质是解题的关键.21.(2021·广西贵港)如图 在AB C 中 ⊥ABC =90° AB =8 BC =12 D 为AC 边上的一个动点 连接BD E 为BD 上的一个动点 连接AE CE 当⊥ABD =⊥BCE 时 线段AE 的最小值是( )A .3B .4C .5D .6【答案】B 【解析】如图 取BC 的中点T 连接AT ET .首先证明90CEB ∠=︒ 求出AT ET 根据AE AT ET ≥- 可得结论.【详解】解:如图 取BC 的中点T 连接AT ET .90ABC ∠=︒90ABD CBD ∴∠+∠=︒ABD BCE ∠=∠90CBD BCE ∴∠+∠=︒90CEB ∴∠=︒6CT TB ==162ET BC ∴== 22228610AT AB BT =++ AE AT ET ≥-4AE ∴≥AE ∴的最小值为4故选:B .【点睛】本题考查直角三角形斜边中线的性质 勾股定理等知识 解题的关键是求出AT ET 的长 属于中考常考题型.22.(2021·辽宁本溪)如图 在ABC 中 AB BC = 由图中的尺规作图痕迹得到的射线BD 与AC 交于点E 点F 为BC 的中点 连接EF 若2BE AC == 则CEF △的周长为( )A 31B 53C 51D .4【答案】C 【解析】根据作图可知BD 平分ABC ∠ AB BC = 由三线合一 解Rt BEC △ 即可求得.【详解】BD 平分ABC ∠,AB BC =,2BE AC ==BE AC ∴⊥,112AE EC AC === ∴2222215BC BE EC ++点F 为BC 的中点 ∴152EF BC FC === ∴CEF △的周长为:55151CE EF FC ++=+=+ 故选C .【点睛】本题考查了角平分线的概念 等腰三角形性质 勾股定理 直角三角形性质 求出BC 边是解题的关键.23.(2022·青海)如图 在Rt ABC △中 90ACB ∠=︒ D 是AB 的中点 延长CB 至点E 使BE BC = 连接DE F 为DE 中点 连接BF .若16AC = 12BC = 则BF 的长为( )A .5B .4C .6D .8【答案】A 【解析】利用勾股定理求得20AB = 然后由直角三角形斜边上的中线等于斜边的一半求得CD 的长度结合题意知线段BF 是CDE △的中位线 则12BF CD =. 【详解】 解:在Rt ABC △中 90ACB ∠=︒ 16AC = 12BC =2222161220AB AC BC ∴+=+=.又CD 为中线1102CD AB ∴==. F 为DE 中点 BE BC =即点B 是EC 的中点BF ∴是CDE △的中位线 则152BF CD ==. 故选:A .【点睛】本题主要考查了勾股定理 三角形中位线定理 直角三角形斜边上的中线 利用直角三角形的中线性质求出线段CD 的长度是解题的关键.24.(2022·辽宁大连)如图 在ABC 中 90ACB ∠=︒ 分别以点A 和点C 为圆心 大于12AC 的长为半径作弧 两弧相交于M N 两点 作直线MN 直线MN 与AB 相交于点D 连接CD 若3AB = 则CD 的长是( )A .6B .3C .1.5D .1【答案】C 【解析】由作图可得:MN 是AC 的垂直平分线 记MN 与AC 的交点为G 证明,MN BC ∥ 再证明,AD BD = 可得AD BD CD == 从而可得答案.【详解】解:由作图可得:MN 是AC 的垂直平分线 记MN 与AC 的交点为G⊥,,,AG CG MNAC AD CD⊥90ACB ∠=︒,MN BC ∥ ⊥,AGAD CG BD⊥,AD BD =3,AB = 13 1.5.22CD AB 故选C【点睛】本题考查的是线段的垂直平分线的性质 平行线分线段成比例 证明AD BD CD ==是解本题的关键. 25.(2022·湖南)如图 点O 是等边三角形ABC 内一点 2OA = 1OB = 3OC = 则AOB ∆与BOC ∆的面积之和为( )A 3B 3C 33D 3【答案】C【解析】将AOB ∆绕点B 顺时针旋转60︒得BCD ∆ 连接OD 得到BOD 是等边三角形 再利用勾股定理的逆定理可得90COD ∠=︒ 从而求解.【详解】解:将AOB ∆绕点B 顺时针旋转60︒得BCD ∆ 连接ODOB OD ∴= 60BOD ∠=︒ 2CD OA ==BOD ∴∆是等边三角形1OD OB ∴== ∵2222134OD OC +=+= 2224CD ==222OD OC CD ∴+=90DOC ∴∠=︒ AOB ∴∆与BOC ∆的面积之和为2313311342BOC BCD BOD COD S S S S +=+=+⨯= 故选:C .【点睛】本题主要考查了等边三角形的判定与性质 勾股定理的逆定理 旋转的性质等知识 利用旋转将AOB ∆与BOC ∆的面积之和转化为BOC BCD SS + 是解题的关键. 26.(2022·黑龙江)如图 ABC 中 AB AC = AD 平分BAC ∠与BC 相交于点D 点E 是AB 的中点 点F 是DC 的中点 连接EF 交AD 于点P .若ABC 的面积是24 1.5PD = 则PE 的长是( )A .2.5B .2C .3.5D .3【答案】A 【解析】连接DE 取AD 的中点G 连接EG 先由等腰三角形“三线合一“性质 证得AD ⊥BC BD =CD 再由E 是AB 的中点 G 是AD 的中点 求出S △EGD =3 然后证△EGP ⊥△FDP (AAS ) 得GP =CP =1.5 从而得DG =3 即可由三角形面积公式求出EG 长 由勾股定理即可求出PE 长.【详解】解:如图 连接DE 取AD 的中点G 连接EG⊥AB =AC AD 平分BAC ∠与BC 相交于点D⊥AD⊥BC BD=CD⊥S△ABD=112422ABCS=⨯=12⊥E是AB的中点⊥S△AED=1112 22ABDS=⨯=6⊥G是AD的中点⊥S△EGD=116 22AEDS=⨯=3⊥E是AB的中点G是AD的中点⊥EG∥BC EG=12BD=12CD⊥⊥EGP=⊥FDP=90°⊥F是CD的中点⊥DF=12CD⊥EG=DF⊥⊥EPG=⊥FPD⊥⊥EGP⊥⊥FDP(AAS)⊥GP=PD=1.5⊥GD=3⊥S△EGD=12GD EG⋅=3 即1332EG⨯=⊥EG=2在Rt⊥EGP中由勾股定理得PE22222 1.5EG GP+=+故选:A.【点睛】本题考查等腰三角形的性质 三角形面积 全等三角形判定与性质 勾股定理 熟练掌握三角形中线分三角形两部分的面积相等是解题的关键.27.(2022·四川乐山)如图 在Rt ABC 中 90C ∠=︒ 5BC = 点D 是AC 上一点 连接B D .若1tan 2A ∠= 1tan 3ABD ∠= 则CD 的长为( )A .5B .3C 5D .2【答案】C 【解析】先根据锐角三角函数值求出25AC = 再由勾股定理求出5,AB =过点D 作DE AB ⊥于点E 依据三角函数值可得11,,23DE AE DE BE ==从而得32BE AE = 再由5AE BE +=得AE =2 DE =1 由勾股定理得AD 5 从而可求出C D .【详解】解:在Rt ABC 中 90C ∠=︒ 5BC = ⊥1tan 2BC A AC ∠== ⊥225,AC BC ==由勾股定理得,2222(25)(5)5AB AC BC =++=过点D 作DE AB ⊥于点E 如图⊥1tan 2A ∠=1tan 3ABD ∠= ⊥11,,23DE DE AE BE == ⊥11,,23DE AE DE BE == ⊥1123AE BE = ⊥32BE AE =⊥5,AE BE += ⊥352AE AE += ⊥2,AE =⊥1DE =在Rt ADE ∆中,222AD AE DE =+ ⊥2222215AD AE DE ++⊥25,AD CD AC +== ⊥2555,CD AC AD =-==故选:C【点睛】本题主要考查了勾股定理 由锐角正切值求边长 正确作辅助线求出DE 的长是解答本题的关键. 28.(2022·内蒙古包头)如图 在Rt ABC 中 90,30,2ACB A BC ∠=︒∠=︒= 将ABC 绕点C 顺时针旋转得到A B C '' 其中点A '与点A 是对应点 点B '与点B 是对应点.若点B '恰好落在AB 边上 则点A 到直线A C '的距离等于( )A .33B .23C .3D .2【答案】C 【解析】如图 过A 作AQ A C 于,Q 求解4,23,AB AC 结合旋转:证明60,,90,B A B C BC B C A CB 可得BB C '△为等边三角形 求解60,A CA 再应用锐角三角函数可得答案.【详解】解:如图 过A 作AQ A C 于,Q由90,30,2ACB A BC ∠=︒∠=︒= 224,23,AB ACAB BC结合旋转: 60,,90,B A B C BC B C A CBBB C 为等边三角形60,30,BCB ACB60,A CA 3sin 6023 3.2AQ AC⊥A 到A C '的距离为3.故选C【点睛】本题考查的是旋转的性质 含30的直角三角形的性质 勾股定理的应用 等边三角形的判定与性质 锐角三角函数的应用 作出适当的辅助线构建直角三角形是解本题的关键.29.(2021·内蒙古鄂尔多斯)如图 在Rt ABC 中 90,8,6ACB AC BC ∠=︒== 将边BC 沿CN 折叠 使点B 落在AB 上的点B ′处 再将边AC 沿CM 折叠 使点A 落在CB '的延长线上的点A '处 两条折痕与斜边AB 分别交于点N M 则线段A M '的长为( )A .95B .85C .75D .65【答案】B【解析】利用勾股定理求出AB =10 利用等积法求出CN =245 从而得AN =325 再证明⊥NMC =⊥NCM =45° 进而即可得到答案.【详解】解:⊥90,8,6ACB AC BC ∠=︒==⊥AB 22226810AC BC ++⊥S △ABC =12×AB ×CN =12×AC ×BC⊥CN =245⊥AN 22222432855AC CN ⎛⎫-=-= ⎪⎝⎭⊥折叠⊥AM =A'M ⊥BCN =⊥B'CN ⊥ACM =⊥A'CM⊥⊥BCN +⊥B'CN +⊥ACM +⊥A'CM =90°⊥⊥B'CN +⊥A'CM =45°⊥⊥MCN =45° 且CN ⊥AB⊥⊥NMC =⊥NCM =45°⊥MN =CN =245⊥A'M =AM =AN −MN =325-245=85. 故选B .【点睛】本题考查了翻折变换 勾股定理 等腰直角三角形的性质 熟练运用折叠的性质是本题的关键.二 填空题30.(2022·云南)已知△ABC是等腰三角形.若⊥A=40° 则△ABC的顶角度数是____.【答案】40°或100°【解析】分⊥A为三角形顶角或底角两种情况讨论即可求解.【详解】解:当⊥A为三角形顶角时则△ABC的顶角度数是40°当⊥A为三角形底角时则△ABC的顶角度数是180°-40°-40°=100°故答案为:40°或100°.【点睛】本题考查了等腰三角形的性质此类题目难点在于要分情况讨论.31.(2022·青海西宁)如图在△AB C中⊥C=90° ⊥B=30° AB=6 将△ABC绕点A逆时针方向旋转15°得到△AB′C′ B′C′交AB于点E则B′E=________.【答案】333【解析】根据已知可以得出⊥BAC=60° 而将△ABC绕点A按逆时针方向旋转15° 可知⊥C′AE=45° 可以求出AC=AC′=EC′=3 据此即可求解.【详解】解:在Rt△AB C中⊥ACB=90° ⊥B=30° AB=6则⊥BAC=60° AC=3 BC22-363将△ABC绕点A按逆时针方向旋转15°后则⊥C′AC=15° AC= AC′=3 B′C′=BC3⊥⊥C′AE=45°而⊥AC′E=90° 故△AC′E是等腰直角三角形⊥AC=AC′=EC′=3⊥B′E= B′C′-EC33.故答案为:33.【点睛】本题考查旋转变换直角三角形30度角的性质等腰直角三角形的判定和性质勾股定理等知识解题的关键是熟练掌握基本知识.32.(2021·吉林长春)将一副三角板按如图所示的方式摆放点D在边AC上//BC EF则ADE∠的大小为_______度.【答案】75︒∠利用平角为180︒即可求解.【解析】根据两直线平行得同位角相等根据三角形外角性质求得CDG【详解】、交于点G设DF BCBC EF//∴∠=∠F DGB=∠+∠=︒C CDG45∠=︒C30CDG∴∠=︒15∴∠=︒-︒-︒=︒180901575ADE故答案为75︒.【点睛】本题考查了平行线的性质三角形的外角性质平角的概念解题的关键是构建未知量和已知量之间的关系.△的周长为13 则33.(2020·湖北)如图在ABC中DE是AC的垂直平分线.若3AE=ABDABC的周长为______.【答案】19.【解析】由线段的垂直平分线的性质可得2,AC AE AD DC == 从而可得答案.【详解】 解: DE 是AC 的垂直平分线.3AE =26,,AC AE AD DC ∴===13,AB BD AD ++=ABC ∴的周长AB BC AC AB BD AD AC =++=+++13619.=+=故答案为:19.【点睛】本题考查的是线段的垂直平分线的性质 掌握线段的垂直平分线的性质是解题的关键.34.(2020·山东日照)如图 有一个含有30°角的直角三角板 一顶点放在直尺的一条边上若⊥2=65°则⊥1的度数是_____.【答案】25°##25度【解析】延长EF 交BC 于点G 根据题意及直角三角形的性质可直接进行求解.【详解】解:如图 延长EF 交BC 于点G⊥直尺⊥AD ⊥BC⊥⊥2=⊥3=65°又⊥30°角的直角三角板⊥⊥1=90°﹣65°=25°.故答案为:25°.【点睛】本题主要考查平行线的性质及直角三角形的性质熟练掌握知识点是解题的关键.35.(2020·江苏常州)如图在ABC中BC的垂直平分线分别交BC AB于点E F.若AFC△是等边三角形则B∠=_________°.【答案】30【解析】根据垂直平分线的性质得到⊥B=⊥BCF再利用等边三角形的性质得到⊥AFC=60° 从而可得⊥B.【详解】解:⊥EF垂直平分BC⊥BF=CF⊥⊥B=⊥BCF⊥⊥ACF为等边三角形⊥⊥AFC=60°⊥⊥B=⊥BCF=30°.故答案为:30.【点睛】本题考查了垂直平分线的性质等边三角形的性质外角的性质解题的关键是利用垂直平分线的性质得到⊥B=⊥BCF.36.(2020·辽宁辽宁)如图在ABC∆中M N分别是AB和AC的中点连接MN点E是CN的BC=则CD的长为_________.中点连接ME并延长交BC的延长线于点D若4【答案】2【解析】依据三角形中位线定理 即可得到MN =12BC =2 MN //BC 依据⊥MNE ⊥⊥DCE (AAS ) 即可得到CD =MN =2.【详解】解:⊥M N 分别是AB 和AC 的中点⊥MN 是⊥ABC 的中位线⊥MN =12BC =2 MN ⊥BC⊥⊥NME =⊥D ⊥MNE =⊥DCE⊥点E 是CN 的中点⊥NE =CE⊥⊥MNE ⊥⊥DCE (AAS )⊥CD =MN =2.故答案为:2.【点睛】本题主要考查了三角形中位线定理以及全等三角形的判定与性质 全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时 关键是选择恰当的判定条件.37.(2021·新疆)如图 在ABC 中 AB AC = 70C ∠=︒ 分别以点A B 为圆心 大于12AB 的长为半径作弧 两弧相交于M N 两点 作直线MN 交AC 于点D 连接BD 则BDC ∠=__________︒.【答案】80︒【解析】由等腰三角形 “等边对等角”求出ABC ∠ 再由垂直平分线的性质得到AD DB = 最后由三角形外角求解即可.【详解】 解:AB AC =,70C ∠=︒70ABC ∴∠=︒,40A ∠=︒ MN 垂直平分ABAD DB ∴=40ABD A ∴∠=∠=︒404080BDC A ABD ∠=∠+∠=︒+︒=︒ .故答案为:80︒.【点睛】本题考查了等腰三角形性质 垂直平分线性质 三角形外角概念 能正确理解题意 找到所求的角与已知条件之间的关系是解题的关键.38.(2021·山东聊城)如图 在⊥AB C 中 AD ⊥BC CE ⊥AB 垂足分别为点D 和点E AD 与CE 交于点O 连接BO 并延长交AC 于点F 若AB =5 BC =4 AC =6 则CE :AD :BF 值为____________.【答案】12:15:10【解析】由题意得:BF ⊥AC 再根据三角形的面积公式 可得5432ABC SAD CE BF === 进而即可得到答案.【详解】解:⊥在⊥AB C 中 AD ⊥BC CE ⊥AB 垂足分别为点D 和点E AD 与CE 交于点O⊥BF ⊥AC⊥AB =5 BC =4 AC =6 ⊥111222ABC SBC AD AB CE AC BF =⋅=⋅=⋅ ⊥5432ABC S AD CE BF === ⊥CE :AD :BF =12:15:10故答案是:12:15:10.【点睛】本题主要考查三角形的高 掌握“三角形的三条高交于一点”是解题的关键.56.(2022·北京)如图 在ABC ∆中 AD 平分,.BAC DE AB ∠⊥若2,1,AC DE ==则ACD S ∆=____.【答案】1【解析】作DF AC ⊥于点F 由角平分线的性质推出1DF DE == 再利用三角形面积公式求解即可.【详解】解:如图 作DF AC ⊥于点F⊥AD 平分BAC ∠ DE AB ⊥ DF AC ⊥⊥1DF DE == ⊥1121122ACD S AC DF ∆=⋅=⨯⨯=.故答案为:1.【点睛】本题考查角平分线的性质 通过作辅助线求出三角形AC D 中AC 边的高是解题的关键. 39.(2022·山东青岛)如图 已知,,16,,ABC AB AC BC AD BC ABC ==⊥∠△的平分线交AD 于点E 且4DE =.将C ∠沿GM 折叠使点C 与点E 恰好重合.下列结论正确的有:__________(填写序号) ⊥8BD =⊥点E 到AC 的距离为3 ⊥103=EM⊥EM AC ∥【答案】①④##⊥⊥【解析】根据等腰三角形的性质即可判断⊥ 根据角平分线的性质即可判断⊥ 设DM x = 则8EM x =- Rt EDM △中 222EM DM DE =+ 4DE =.继而求得EM 设AE a = 则4,8AD AE ED a BD =+=+= 根据AE AB ED BD = 进而求得a 的值 根据20443tan 83AD C DC +===4tan 3EDEMD DM ∠== 可得C EMD ∠=∠ 即可判断⊥【详解】解:⊥,,16,,ABC AB AC BC AD BC ==⊥△ ⊥182BD DC BC === 故⊥正确 如图 过点E 作EF AB ⊥于F EH AC ⊥于H,AD BC AB AC ⊥=AE ∴平分BAC ∠EH EF ∴=BE 是ABD ∠的角平分线,ED BC EF AB ⊥⊥EF ED ∴=4EH ED ∴== 故⊥不正确 .将C ∠沿GM 折叠使点C 与点E 恰好重合 ,8EM MC DM MC DM EM CD ∴=+=+== 设DM x = 则8EM x =-Rt EDM △中 222EM DM DE =+ 4DE =. ()22284x x -=+解得3x =5EM MC ∴==故⊥不正确设AE a = 则4,8AD AE ED a BD =+=+= ()22248AB a =++11221122ABE BDE AB EF AE BD SS BD ED ED BD ⨯⨯==⨯⨯ AE AB ED BD∴= 48a AB = 2AB a =∴()2248a ++()22a = 解得203a =或4a =-(舍去) 20443tan 83AD C DC +∴=== 4tan 3ED EMD DM ∠== C EMD ∴∠=∠EM AC ∴∥ 故⊥正确故答案为:①⊥【点睛】本题考查了解直角三角形 三线合一 角平分线的性质 掌握以上知识是解题的关键.40.(2022·河南)如图 在Rt ⊥AB C 中 ⊥ACB =90° 22AC BC == 点D 为AB 的中点 点P 在AC 上 且CP =1 将CP 绕点C 在平面内旋转 点P 的对应点为点Q 连接AQ DQ .当⊥ADQ =90°时 AQ 的长为______.513135【解析】连接CD 根据题意可得当⊥ADQ =90°时 分Q 点在线段CD 上和DC 的延长线上 且1CQ CP == 勾股定理求得AQ 即可.【详解】如图 连接CD在Rt ⊥AB C 中 ⊥ACB =90° 22AC BC ==4AB ∴= CD AD ⊥122CD AB ∴== 根据题意可得 当⊥ADQ =90°时 Q 点在CD 上 且1CQ CP ==211DQ CD CQ ∴=-=-=如图 在Rt ADQ △中 2222215AQ AD DQ ++在Rt ADQ △中 2,3AD CD QD CD CQ ===+=22222313AQ AD DQ ∴=+=+513【点睛】本题考查了旋转的性质 勾股定理 直角三角形斜边上中线的性质 确定点Q 的位置是解题的关键. 41.(2022·青海西宁)矩形ABC D 中 8AB = 7AD = 点E 在AB 边上 5AE =.若点P 是矩形ABCD边上一点 且与点A E 构成以AE 为腰的等腰三角形 则等腰三角形AEP 的底边长是________. 【答案】245【解析】分情况讨论:⊥当AP =AE =5 点P 在边AD 上时 由勾股定理可求得底边PE 的长 ⊥当PE =AE =5 点P 在边BC 上时 求出BE 由勾股定理求出PB 再由勾股定理求出底边AP 即可.【详解】解:⊥矩形ABCD⊥⊥A =⊥B =90°分两种情况:当AP =AE =5 点P 在边AD 上时 如图所示:⊥⊥BAD =90°⊥PE 222255AP AE ++2当PE =AE =5 点P 在边BC 上时 如图所示:⊥BE =AB -AE =8-5=3 ⊥B =90°⊥PB 222253PE BE --⊥底边AP 22228445AB PB ++=综上 等腰三角形AEP 的底边长是5245【点睛】本题考查了矩形的性质 勾股定理 熟练掌握矩形的性质和等腰三角形的判定 进行分类讨论是解决问题的关键.42.(2022·辽宁锦州)如图 在ABC 中 ,30AB AC ABC =∠=︒ 点D 为BC 的中点 将ABC 绕点D 逆时针旋转得到A B C ''' 当点A 的对应点A '落在边AB 上时 点C '在BA 的延长线上 连接BB ' 若1AA '= 则BB D '△的面积是____________.33【解析】先证明A AD ' 是等边三角形 再证明AO BC '⊥ 再利用直角三角形30角对应的边是斜边的一般分别求出A B ''和A O ' 再利用勾股定理求出OD 从而求得BB D '△的面积.【详解】解:如下图所示 设A B ''与BD 交于点O 连接A D '和AD⊥点D 为BC 的中点 ,30AB AC ABC =∠=︒⊥AD BC ⊥,A D B C '''⊥ A D '是B A C '''∠的角平分线 AD 是BAC ∠⊥120B A C ︒'''∠= 120BAC ︒∠=⊥60BAD B A D ︒'∠'=∠=⊥A D AD '=⊥A AD ' 是等边三角形⊥1A A AD A D ''===⊥18060BA B B A C ︒︒'''''∠=-∠=⊥BA B A AD '''∠=∠⊥//A B AD ''⊥AO BC '⊥ ⊥1122A O A D ''==⊥1314OD =-=⊥22A B A D '''==⊥30A BD A DO ︒''∠=∠=⊥BO OD = ⊥13222OB '=-= 23BD OD ==⊥113333222BB DS BD B O ''=⨯⨯==. 【点睛】本题考查等腰三角形 等边三角形和直角三角形的性质 证明A AD ' 是等边三角形是解本题的关键. 43.(2022·广西贵港)如图 将ABC 绕点A 逆时针旋转角()0180αα︒<<︒得到ADE 点B 的对应点D 恰好落在BC 边上 若,25DE AC CAD ⊥∠=︒ 则旋转角α的度数是______.【答案】50︒【解析】先求出65ADE ∠=︒ 由旋转的性质 得到65∠=∠=︒B ADE AB AD = 则65ADB ∠=︒ 即可求出旋转角α的度数.【详解】解:根据题意⊥,25DE AC CAD ⊥∠=︒⊥902565ADE ∠=︒-︒=︒由旋转的性质 则65∠=∠=︒B ADE AB AD =⊥65ADB B ∠=∠=︒⊥180665550BAD ︒-∠=︒=︒-︒⊥旋转角α的度数是50°故答案为:50°.【点睛】本题考查了旋转的性质 三角形的内角和定理 解题的关键是熟练掌握旋转的性质进行计算.44.(2022·湖北十堰)【阅读材料】如图⊥ 四边形ABCD 中 AB AD = 180B D ∠+∠=︒ 点E F 分别在BC CD 上 若2BAD EAF ∠∠= 则EF BE DF =+.【解决问题】如图⊥ 在某公园的同一水平面上 四条道路围成四边形ABCD .已知100m CD CB == 60D ∠=︒ 120ABC ∠=︒ 150BCD ∠=︒ 道路AD AB 上分别有景点M N 且100m DM = )5031m BN = 若在M N 之间修一条直路 则路线M N →的长比路线M A N →→的长少_________m (结果取整数 3 1.7≈).【答案】370【解析】延长,AB DC 交于点E 根据已知条件求得90E ∠=︒,进而根据含30度角的直角三角形的性质 求得,EC EB ,AE AD 从而求得AN AM +的长 根据材料可得MN DM BN =+ 即可求解.【详解】解:如图 延长,AB DC 交于点E 连接,CM CN60D ∠=︒ 120ABC ∠=︒ 150BCD ∠=︒30A ∴∠=︒ 90E ∠=︒100DC DM ==DCM ∴是等边三角形60DCM ∴∠=︒90BCM ∴∠=︒。
2023年中考数学真题汇编几何综合压轴问题专项练习(共40题)(解析版)

几何综合压轴问题专项练习答案(40题)(1)将CDE 绕顶点C 旋转一周,请直接写出点M ,N 距离的最大值和最小值;(2)将CDE 绕顶点C 逆时针旋转120︒(如图2),求MN 【答案】(1)最大值为3,最小值为1(2)7【分析】(1)根据直角三角形斜边上的中线,得出,CM CN 解;(2)过点N 作NP MC ⊥,交MC 的延长线于点P ,根据旋转的性质求得进而可得1CP =,勾股定理解Rt ,Rt NCP MCP ,即可求解.【详解】(1)解:依题意,112CM DE ==,12CN AB =当M 在NC 的延长线上时,,M N 的距离最大,最大值为(2)解:如图所示,过点N 作NP MC ⊥,交MC 的延长线于点∵CDE 绕顶点C 逆时针旋转∴120BCE ∠=︒,∵45BCN ECM ∠=∠=︒,∴MCN BCM ECM ∠=∠-∠=∴60NCP ∠=︒,∴30CNP ∠=︒,∴112CP CN ==,在Rt CNP 中,2NP NC =-在Rt MNP △中,MP MC CP =+∴2234MN NP MP =+=+【点睛】本题考查了直角三角形斜边上的中线等于斜边的一半,勾股定理,旋转的性质,含(1)如图1,求证:DE BF =;(2)如图2,若2AD BF =,的延长线恰好经过DE 的中点【答案】(1)见解析(2)22BE =+△∵点G 是DE 的中点,∴GH 是FCD 的中位线,∴11122GH CD AD ===,设BE a =,则CH EH ==(1)如图1,求AB边上的高CH的长.''.(2)P是边AB上的一动点,点,C D同时绕点P按逆时针方向旋转90︒得点,C D①如图2,当点C'落在射线CA上时,求BP的长.△是直角三角形时,求BP的长.②当AC D''∴90C PQ PC Q '∠+∠='︒∵90C PQ CPH ∠+∠='︒∴PC Q CPH ∠=∠'.由旋转知PC PC '=,设C D ''与射线BA 的交点为作CH AB ⊥于点H .∵PC PC ⊥',∴90CPH TPC ∠'+∠=︒,∵C D AT ''⊥,∴90PC T TPC ∠'+∠='︒,【答案】(1)①见解析;②AD DF BD =+,理由见解析;【分析】(1)①证明:ABE CBD ∠=∠,再证明ABE ≅△可得DF DC =.证明AE DF =,从而可得结论;(2)如图,过点B 作BE AD ⊥于点E ,得90BED ∠=︒,证明2DE BD =,证明2AB BC =,ABE CBD ∠=∠,可得②AD DF BD=+.理由如下:∵DF和DC关于AD对称,=.∴DF DC=,∵AE CD∴AE DF=.∴AD AE DE DF BD=+=+∵DF 和DC 关于AD 对称,∴DF DC =,ADF ADC ∠=∠.∵CD BD ⊥,∴45ADF ADC ∠=∠=︒,∴45EBD ∠=︒.∴2DE BD =.∵AB AC AF ==,∴()11222HF BF BD DF ==-=,222262210BC BD CD =+=+=∴2221022AF AC BC ===⨯=25HF (2)知识应用:如图2Y是菱形;①求证:ABCD②延长BC至点E,连接OE交【答案】(1)见解析5∴1BG BO GC OD==,∴115222CG BC AD ===,∴552OF GC .处从由60PC P C PCP ''=∠=︒,,可知PCP '△为①三角形,故PP PC '=,又P A PA ''=,故PA PB PC PA PB PP A B '''++=++≥,由②可知,当B ,P ,P ',A 在同一条直线上时,PA PB PC ++取最小值,如图2,最小值为(3)如图5,设村庄A ,B ,C 的连线构成一个三角形,且已知4km 23km AC BC ==,,建一中转站P 沿直线向A ,B ,C 三个村庄铺设电缆,已知由中转站P 到村庄A ,B ,C 元/km ,a 元/km ,2a 元/km ,选取合适的P 的位置,可以使总的铺设成本最低为___________用含的式子表示)∵ACP A CP ''∠=∠,∴ACP BCP A CP BCP ∠+∠=∠+∠''又∵60PCP '∠=︒过点A '作A H BC '⊥,垂足为H ,∵60ACB ∠=︒,90ACA '∠=︒,∴30A CH '∠=︒,1猜想证明:(1)如图2,试判断四边形AEDG的形状,并说明理由.问题解决;(2)如图3,将图2中左侧折叠的三角形展开后,重新沿MN折叠,使得顶点B与点∵1122 CHGS CH HG=⋅=∴154302CG HE⋅=⨯=,①求证:PD PB =;②将线段DP 绕点P 逆时针旋转,化时,DPQ ∠的大小是否发生变化?请说明理由;③探究AQ 与OP 的数量关系,并说明理由.【答案】(1)①见解析;②不变化,(2)AQ CP =,理由见解析【分析】(1)①根据正方形的性质证明②作,PM AB PN AD ⊥⊥,垂足分别为点∵四边形ABCD 是正方形,∴45DAC BAC ∠=∠=︒,∴四边形AMPN 是矩形,∴90MPN ∠=︒,∵四边形ABCD 是正方形,∴45BAC ∠=︒,90AOB ∠=∴45AEP ∠=︒,四边形OPEF=作PM AB⊥于点M,则QM MB=,∴QA BE=.∴AQ CP(1)求BCF ∠的度数;(2)求CD 的长.深入探究:(3)若90BAC ∠<︒,将BMN 绕点B 顺时针旋转α,得到BEF △,连接AE ,CF 满足0360α︒<<︒,点,,C E F 在同一直线上时,利用所提供的备用图探究BAE ∠与ABF ∠的数量关系,并说明理由.【答案】初步尝试:(1)1MN AC =;MN AC ∥;(2)特例研讨:(1)30BCF ∠=︒;(2)CD∵MN 是BAC 的中位线,∴MN AC ∥,∴90BMN BAC ∠=∠=︒∵将BMN 绕点B 顺时针旋转α∴,BE BM BF BN ==;BEF ∠=∵点,,A E F 在同一直线上时,2∵,ADN BDE ANB BED ∠=∠∠=∠∴ADN BDE ∽,∴2222DN AN DE BE ===,设DE x =,则2DN x =,在Rt ABE △中,2,2BE AE ==在Rt ADN △中,22AD DN AN =+∵AB AC =,∴A ABC CB =∠∠,设ABC ACB θ∠=∠=,则1802BAC θ∠=︒-,∵MN 是ABC 的中位线,∴MN AC∥∴MNB MBN θ∠=∠=,∵将BMN 绕点B 顺时针旋转α,得到BEF △,∴EBF MBN ≌,MBE NBF α∠=∠=,∴EBF EFB θ∠=∠=∴1802BEF θ∠=︒-,∵点,,C E F 在同一直线上,∴2BEC θ∠=∴180BEC BAC ∠+∠=︒,∴,,,A B E C 在同一个圆上,∴EAC EBC αθ∠=∠=-∴()()1802BAE BAC EAC θαθ∠=∠-∠=︒---180αθ=︒--∵ABF αθ∠=+,∴180BAE ABF ∠∠=+︒;如图所示,当F 在EC 上时,∵,BEF BAC BC BC∠=∠=∴,,,A B E C 在同一个圆上,设ABC ACB θ∠=∠=,则1802BAC BEF θ∠=∠=︒-,将BMN 绕点B 顺时针旋转α,得到BEF △,设NBF β∠=,则EBM β∠=,则360αβ+=︒,∴ABF θβ∠=-,∵BFE EBF θ∠=∠=,EFB FBC FCB∠=∠+∠∴ECB FCB EFB FBC θβ∠=∠=∠-∠=-,∵ EBEB =∴EAB ECB θβ∠=∠=-∴BAE ∠ABF=∠综上所述,BAE ABF ∠=∠或180BAE ABF ∠∠=+︒【点睛】本题考查了圆周角定理,圆内接四边形对角互补,相似三角形的性质与判定,旋转的性质,中位线的性质与判定,等腰三角形的性质与判定,三角形内角和定理,三角形外角的性质,勾股定理,熟练掌握以上知识是解题的关键.10.(2023·湖北黄冈·统考中考真题)【问题呈现】CAB △和CDE 都是直角三角形,90,,ACB DCE CB mCA CE mCD ∠=∠=︒==,连接AD ,BE ,探究AD ,BE 的位置关系.(1)如图1,当1m =时,直接写出AD ,BE 的位置关系:____________;(2)如图2,当1m ≠时,(1)中的结论是否成立?若成立,给出证明;若不成立,说明理由.【拓展应用】(3)当3,47,4m AB DE ===时,将CDE 绕点C 旋转,使,,A D E 三点恰好在同一直线上,求(2)解:成立;理由如下:∵90DCE ACB ∠=∠=︒,∴DCA ACE ACE ∠+∠=∠+(3)解:当点E 在线段AD设AD y =,则AE AD DE =+根据解析(2)可知,DCA △∴3BE BC m AD AC===,勾股定理,解题的关键是熟练掌握三角形相似的判定方法,画出相应的图形,注意分类讨论.(1)若点P 在AB 上,求证:A P AP '=;(2)如图2.连接BD .①求CBD ∠的度数,并直接写出当180n =时,x 的值;②若点P 到BD 的距离为2,求tan A MP '∠的值;∵PM 平分A MA '∠∴90PMA ∠=︒∴PM AB∥∴DNM DBA V V ∽∴DN DM MN DB DA BA ==∵8,6,90AB DA A ==∠=︒,∴2226BD AB AD =+=+∴2103sin 3BQ BP DBA ===∠,∵90PQB CBD DAB ∠=∠=∠=︒,∴90QPB PBQ DBA ∠=︒-∠=∠,∵A MP AMP ' ≌,∴90PA M A '∠=∠=︒,(2)如图②,在矩形ABCD 的BC 边上取一点E ,将四边形ABED 沿DE 翻折,使点B '处,若24,6BC CE AB ⋅==,求BE 的值;(3)如图③,在ABC 中,45,BAC AD BC ∠=︒⊥,垂足为点,10,D AD AE ==于点F ,连接DF ,且满足2DFE DAC ∠=∠,直接写出53BD EF +的值.∵EF BC ∥,∴2CDF DFE ∠=∠=∴CDH FDH ∠=∠,又∵DH DH =,CHD ∠∴(ASA CHD FHD ≌【点睛】本题考查矩形的性质、翻折性质、勾股定理、相似三角形的判定与性质、等腰三角形的判定与性质、全等三角形的判定与性质、锐角三角函数等知识,综合性强,较难,属于中考压轴题,熟练掌握相关知识的联系与运用,添加辅助线求解是解答的关键.13.(2023·湖南郴州·=,连接点E,使CE AD(1)如图1,当点D在线段AB上时,猜测线段CF与BD的数量关系并说明理由;(2)如图2,当点D在线段AB的延长线上时,①线段CF与BD的数量关系是否仍然成立?请说明理由;②如图3,连接AE.设4AB=,若AEB DEB∠=∠,求四边形BDFC的面积.【答案】(1)1CF BD=,理由见解析∴60,ADG ABC AGD ∠=∠=︒∠=∠∴ADG △为等边三角形,∴AD AG DG ==,∵AD CE =,AD AB AG AC -=-∴DG CE =,BD CG =,于点由①知:ADG △为等边三角形,∵ABC 为等边三角形,∴4,AB AC BC BH CH =====∴2223AH AB BH =-=,(1)若正方形ABCD 的边长为2,E 是AD 的中点.①如图1,当90FEC ∠=︒时,求证:AEF DCE ∽△△;②如图2,当2tan 3FCE ∠=时,求AF 的长;(2)如图3,延长CF ,DA 交于点G ,当1,sin 3GE DE FCE =∠=时,求证:,可得结论;正方形ABCD 中,①ADC BAD ∠=∠ ∴AEF CED ∠+∠=AEF ECD ∴∠=∠,延长DA ,CF 交于点G ,作GH CE ⊥,垂足为H ,90EDC EHG ∠=∠=︒ 且∠问题探究:(1)先将问题特殊化,如图(2),当90α=︒时,直接写出GCF ∠的大小;(2)再探究一般情形,如图(1),求GCF ∠与α的数量关系.问题拓展:(3)将图(1)特殊化,如图(3),当120α=︒时,若12DG CG =,求BE CE 的值.故答案为:45︒.(2)解:在AB上截取ANABC BAE AEB∠+∠+∠=∠=∠,ABC AEF22⎝⎭(3)解:过点A作CD的垂线交CD的延长线于点【点睛】此题考查菱形性质、三角形全等、三角形相似,解题的关键是熟悉菱形性质、三角形全等、三角形相似.16.(2023·山西·统考中考真题)问题情境:“综合与实践沿对角线剪开,得到两个全等的三角形纸片,表示为∠=∠=︒∠=∠.将ABCACB DEF A D90,和DFE△(1)数学思考:谈你解答老师提出的问题;(2)深入探究:老师将图2中的DBE绕点B逆时针方向旋转,使点问题.∠①“善思小组”提出问题:如图3,当ABE②“智慧小组”提出问题:如图AH的长.请你思考此问题,直接写出结果.【答案】(1)正方形,见解析(2)①AM BE=,见解析;【分析】(1)先证明四边形形;∠(2)①由已知ABE【点睛】本题考查了旋转的性质、全等三角形的判定与性质、正方形的判定与性质、相似三角形的判定与性质、三角函数、勾股定理等知识点,适当添加的辅助线、构造相似三角形是解题的关键.17.(2023·湖北十堰·统考中考真题)过正方形E ,连接AE ,直线AE 交直线(1)如图1,若25CDP ∠=︒,则DAF ∠=___________(2)如图1,请探究线段CD ,EF ,AF 之间的数量关系,并证明你的结论;(3)在DP 绕点D 转动的过程中,设AF a =,EF 【答案】(1)20︒。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中数学直角三角形斜边中线性质应用专项练习题(附答案详解)1.如图,在ABC 中,∠B=60°,CD 为AB 边上的高,E 为AC 边的中点,点 F 在BC 边上,∠EDF=60°,若 BF=3,CF=5,则AC 边的长为 .2.如图,在矩形ABCD 中,∠BAD 的平分线交BC 于点E ,交DC 的延长线于点F .(1)若AB =2,AD =3,求EF 的长;(2)若G 是EF 的中点,连接BG 和DG ,求证:DG =BG .3.如图所示,在ABC ∆中,BD AC ⊥于D ,CE AB ⊥于E ,点M ,N 分别是BC ,DE 的中点,求证:MN DE ⊥.4.△ABC 中,AC=BC ,∠ACB=90°,CD=BD ,∠1=∠2,求证:CM ⊥AD 。
5.如图所示,ABC ∆中,90BAC ∠=︒,延长BA 到D ,使12AD AB =,点E 是AC 的中点,求证:2BC DE .6.如图所示,CDE ∆中,135CDE ∠=︒,CB DE ⊥于V ,EA CD ⊥于A ,求证:2CE AB =.7.如图所示,四边形ACBD 中,90ADB ACB ∠=∠=︒,60DBC ∠=︒,点E 是AB 的中点,求DCE ∠的度数.8.如图所示,90DBC BCE ∠=∠=︒,M 为DE 的中点,求证:MB MC =.9.如图所示,ABC ∆中,,90,AB AC BAC D =∠=为BC 延长线上一点,过D 作DE AD ⊥,且DE AD =,求DBE ∠的度数.10.如图所示,ABC ∆中,,90,AB AC BAC D =∠=是AC 的中点,,DE DF DE ⊥交BA 的延长线于点,E DF 交AC 的延长线于点F ,求证:BE AF =.11.如图所示,ABC ∆中,,90,AB AC BAC D =∠=为BC 的中点,G 为AC 上一点,AE BG ⊥于点E ,连结DE .求证:2BE AE DE -=.12.如图所示,BCD ∆和BCE ∆中,90BDC BEC ∠=∠=︒,O 为BC 的中点,BD ,CE 交于A ,120BAC ∠=︒,求证:DE OE =.13.如图所示,E ,F 分别是正方形ABCD 的边AD ,CD 上的两个动点,且AE DF =,BE 交AF 于点H ,2AB =,连DH .求线段DH 长度的最小值.14.如图所示,ABC ∆中,2B A ∠=∠,CD AB ⊥于D ,E 为AB 的中点,求证:2BC DE =.15.如图所示,四边形ACBD 中,90ADB ACB ∠=∠=︒,60DBC ∠=︒,点E 是AB 的中点,求CE CD的值.16.如图,正方形ABCD 中,对角线AC 上有一点P ,连接BP 、DP ,过点P 作PE ⊥PB 交CD 于点E ,连接BE .(1)求证:BP=EP;(2)若CE=3,BE=6,求∠CPE的度数;(3)探究AP、PC、BE之间的数量关系,并给予证明.参考答案1.【解析】【分析】如图(见解析),先根据直角三角形的性质、勾股定理得出,4D B F D ==,再根据等边三角形的判定与性质得出4,60DH BDH =∠=︒,然后根据三角形的中位线定理、平行线的性质得出60EHD BDH ∠=∠=︒,从而可得EHD B ∠=∠,BDF HDE ∠=∠,最后根据三角形全等的判定定理与性质得出DE DF ==据此根据直角三角形斜边上的中线等于斜边的一半即可得.【详解】如图,过点D 作DG BC ⊥于点G3,5BF CF ==8BC BF CF ∴=+=在Rt BCD 中,60B ∠=︒,9030BCD B ∠=︒-∠=︒142BD BC ∴== 在Rt BDG 中,60B ∠=︒,9030BDG B ∠=︒-∠=︒12,2BG BD DG ∴====1GF BF BG ∴=-=,DF ==取BC 的中点H ,连接DH 、EH142DH BH BC BD ∴==== BDH ∴是等边三角形60BDH ∴∠=︒点E 是AC 边的中点∴EH 是ABC 的中位线//EH AB ∴60EHD BDH ∴∠=∠=︒60EHD B ∴∠=∠=︒又60BDF FDH BDH ∠+∠=∠=︒,60HDE FDH EDF ∠+∠=∠=︒BDF HDE ∴∠=∠在HDE 和BDF 中,EHD B DH DB HDE BDF ∠=∠⎧⎪=⎨⎪∠=∠⎩()HDE BDF ASA ∴≅13DE DF ∴==则在Rt ACD △中,12DE AC =,即2213AC DE == 故答案为:213.【点睛】本题考查了直角三角形的性质、等边三角形的判定与性质、三角形全等的判定定理与性质、三角形的中位线定理等知识点,通过作辅助线,构造等边三角形和全等三角形是解题关键. 2.(1)EF 2;(2)见解析【解析】【分析】(1)由AE 平分∠BAD ,可得∠DAF =45°,从而∠F =45°,可证△ADF ,△ECF 都是等腰直角三角形,求出CF 的长,最后根据勾股定理即可求出EF 的长;(2)连结CG ,易证∠BEG =∠DCG =135°,根据“SAS ”可证△BEG ≌△DCG ,从而可得DG =BG .【详解】解:(1)在矩形ABCD 中∵AE 平分∠BAD ,∴∠DAF =45°, ∴∠F =45°,∴△ADF,△ECF都是等腰直角三角形,∴DF=AD=3, CF=DF-CD= 1.在Rt△CEF中,∴EF=2.(2)连结CG,∵G是EF中点,∴CG⊥EF,∠ECG=∠CEF=45°.∴∠BEG=∠DCG=135°.∴EG=12EF=CG.∵AB=BE=CD,∴BE=CD.∴△BEG≌△DCG,∴DG=BG.【点睛】本题考查了矩形的性质,角平分线的定义,等腰直角三角形的判定与性质,勾股定理,以及全等三角形的判定与性质,证明△ADF,△ECF都是等腰直角三角形是解(1)的关键,证明△BEG≌△DCG是解(2)的关键.3.见解析【解析】【分析】连接ME、MD,根据直角三角形斜边上的中线等于斜边的一半可得MD=ME=12BC,再根据等腰三角形三线合一的性质证明即可;【详解】证明:连结MD ,ME ,点M 分别是Rt EBC ∆和Rt DBC ∆斜边的中点,MD ME ∴==1BC 2,又N 是DE 的中点, MN DE ∴⊥.【点睛】本题主要考查直角三角形和等腰三角形的性质,遇到直角三角形斜边上的中点时,往往连结斜边上的中线.利用直角三角形斜边上的中线等于斜边的一半求得DM =EM 是解题的关键. 4.见解析.【解析】【分析】 过点C 作CE ⊥AB 交AB 于点E ,交AD 于点F ,AD 与CM 交于点G ,根据∠B=∠BCE=45°,CD=BD ,∠1=∠2证明△CDF ≌△BDM ,得到CF=BM ,然后再由AC=BC 及通过SAS 证明△ACF ≌△CBM ,得到∠CAF=∠BCM ,再根据角之间的等量代换可证明∠CFG+∠ECM=90°,问题得证.【详解】证明:过点C 作CE ⊥AB 交AB 于点E ,交AD 于点F ,AD 与CM 交于点G ,∵AC=BC ,∠ACB=90°,∴∠B=∠BCE=45°,在△CDF 和△BDM 中,,∴△CDF ≌△BDM (ASA ),∴CF=BM ,在△ACF 和△CBM 中,,∴△ACF ≌△CBM (SAS ),∴∠CAF=∠BCM,∵∠BCM +∠ECM =∠CAF+∠EAF=45°,∴∠ECM =∠EAF,∵∠AFE=∠CFG,且∠AFE+∠EAF=90°,∴∠CFG+∠ECM=90°,即∠CGF=90°,∴CM⊥AD.【点睛】本题主要考查等腰直角三角形的性质、全等三角形的判定和性质,正确作出辅助线,寻找合适的全等三角形是解题关键,有一定难度.5.见解析【解析】【分析】可知EF是△ABC的中位线,根据三角形中位线的性质,可得EF∥AB,EF=12AB,又由AD=12AB,即可得AD=EF,根据有一组对边平行且相等的四边形是平行四边形,可证得四边形AEFD是平行四边形.DE=AF,由在Rt△ABC中,∠BAC=90°,点E边BC的中点,根据直角三角形斜边的中线等于斜边的一半,可求得AF=12BC.所以DE=2BC.【详解】证明:取BC的中点F,连EF,AF,∵点E、F分别为边BC,AC的中点,即EF是△ABC的中位线,∴EF∥AB,EF=12 AB,即EF∥AD,∵AD=12 AB,∴EF=AD,∴四边形AEFD是平行四边形;∴AF=DE.∵在Rt△ABC中,∠BAC=90°,点E边BC的中点,∴AF=12 BC,∵四边形AFED是平行四边形,∴BC=2DE.【点睛】此题考查了平行四边形的判定与性质、三角形中位线的性质、直角三角形斜边上的中线的性质.灵活运用中点的有关性质解题是解题关键.6.见解析【解析】【分析】取CE的中点F,连接AF、BF,根据直角三角形斜边上的中线等于斜边的一半可得AF=EF=BF=CF,根据三角形的内角和等于180°求出∠ACE+∠BEC=45°,然后求出∠AEC+∠BCE=135°,再根据等腰三角形两底角相等求出∠BFC+∠AFE=90°,然后求出∠AFB=90°,从而判断出△ABF是等腰直角三角形,然后根据等腰直角三角形的直角边等于斜边的2可得AF=2AB,然后证明即可.【详解】证明:如图,取CE的中点F,连接AF、BF,∵CB⊥DE,EA⊥CD,∴AF=EF=BF=CF=12 CE,在△CDE中,∵∠CDE=135°,∴∠ACE+∠BEC=180°-135°=45°,∴∠AEC+∠BCE=(90°-∠ACE)+(90°-∠BEC)=180°-45°=135°,∴∠BFC+∠AFE=(180°-2∠BCE)+(180°-2∠AEC)=360°-2(∠AEC+∠BCE)=360°-2×135°=90°,∴∠AFB=180°-(∠BCF+∠AFE)=180°-90°=90°,∴△ABF是等腰直角三角形,∴AF=22AB,∴CE=2AF=2×22AB=2AB,即CE=2AB.【点睛】本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形两底角相等的性质,三角形的内角和定理,等腰直角三角形的判定与性质,熟记各性质是解题的关键,作出图形更形象直观.7.30【解析】【分析】连接DE,根据直角三角形的性质得到DE=12AB=BE,CE=12AB=BE,根据三角形的外角性质计算即可;【详解】证明:连接DE,∵∠ACB=∠ADB=90°,E是AB的中点,∴DE=12AB =BE ,CE =12AB =BE , ∴ED =EC ,∠EDB =∠EBD ,∠ECB =∠EBC ,∴∠DEC =∠AED +∠AEC =2∠DBC =120°,∵ED =EC ,∴∠DCE =12×(180°-120°)=30°; 【点睛】本题主要考查直角三角形和等腰三角形的性质,遇到直角三角形斜边上的中点时,往往连结斜边上的中线.利用直角三角形斜边上的中线等于斜边的一半求得DE =CE 是解题的关键. 8.见解析【解析】【分析】延长BM 交CE 于N ,易得DBM ENM ∆∆≌,BM =MN ,由直角三角形斜边中线性质可得CM =MN =BM .【详解】证明:延长BM 交CE 于N ,∵90DBC BCE ∠=∠=︒,∴CE ∥DB ,∴∠D =∠E ,在DBM ∆和ENM ∆中D=E DM=EMDMB=EMN ∠∠⎧⎪⎨⎪∠∠⎩∴DBM ENM ∆∆≌,BM MN =∴,∵∠BCE =90°,12CM BN BM ∴==. 【点睛】本题主要考查了直角三角形斜边中线的性质,解题的关键是正确作出辅助线.构造直角三角形.9.45°【解析】【分析】分别过点A 、E 分别作于AF BD ⊥于F ,EG BD ⊥于G ,由等腰直角三角形的性质可得AF BF CF ==,由同角的余角相等得FAD FDE ∠=∠,结合已知可证ADF DEG ∆∆≌ ,由全等三角形的对应边相等得DF=EG ,AF=DG ,则EG FD FG GD FG AF FG BF BG ==+=+=+= ,即△BEG 为等腰直角三角形,即可得DBE ∠的度数.【详解】解:分别过点A 、E 分别作于AF BD ⊥于F ,EG BD ⊥于G ,则AF BF CF ==,90FAD ADF ADF FDE ∠+∠=∠+∠=︒,∴FAD FDE ∠=∠,AD DE ⊥ AD DE =,ADF DEG ∴∆∆≌,DF EG ∴=,AF DG =,EG FD FG GD FG AF FG BF BG ∴==+=+=+=,∴△BEG 为等腰直角三角形,45DBE BEG ∴∠=∠=︒.故答案为45°. 【点睛】本题考查全等三角形的判定和性质、等腰直角三角形的判定和性质等知识,本题中作辅助线证出△BEG 为等腰直角三角形是解题的关键.10.详见解析【解析】【分析】连结AD ,根据等腰直角三角形的性质得AD ⊥BC ,AD=BD ,由同角的余角相等得B FAD ∠=∠ ,证明BDE ADF ∆∆≌ ,即可得出结论.【详解】证明:连结AD ,AB AC =,90BAC ∠=︒,BD DC = AD BC ∴⊥AD BD ∴=90B BAD BAD FAD ∠+∠=∠+∠=︒B FAD ∴∠=∠BDE BDA ADE ∠=∠+∠ FDA FDE ADE ∠=∠+∠ 90BDA FDE ∠=∠=︒ BDE FDA ∴∠=∠BDE ADF ∴∆∆≌BE AF ∴=.【点睛】本题考查全等三角形的判定和性质,等腰直角三角形的性质,熟练掌握全等三角形的判定与性质是解题的关键.11.详见解析【解析】【分析】连结AD ,过点D 作DF DE ⊥交BG 于点F ,由等腰直角三角形的性质可得AD BD =,AD ⊥BC ,由等角的余角相等得ADE BDF ∠=∠,DAE DBF ∠=∠,根据ASA 可证出ADE BDF ∆∆≌ ,由全等三角形的对应边相等得AE=BF ,DE=DF ,则△EDF 为等腰直角三角形,即可得BE 2EF BF BE AE DE ∴=-=-=.【详解】 证明:连结AD ,过点D 作DF DE ⊥交BG 于点F ,∵,90,AB AC BAC D =∠=为BC 的中点,∴AD BD =,AD ⊥BC ,∵DF DE ⊥,∠BAC=90°,AE BG ⊥∴ADE BDF ∠=∠,DAE DBF ∠=∠, ∴ADE BDF ∆∆≌(ASA )∴AE=BF ,DE=DF ,∵DF DE ⊥∴2EF DE =∴BE EF 2BE AE BF DE -=-==. 【点睛】本题考查全等三角形的判定和性质、等腰直角三角形的判定和性质等知识,本题中求证ADE BDF ∆∆≌是解题的关键.12.见解析【解析】【分析】连接OD.因为∠BDC=∠BEC=90°,O 为BC 的中点;所以有OE OD =OB=OC ,进而∠COD=2∠CBD ,∠BOE=2∠BCE ;又因为∠BAC=120°;所以有∠CBD+∠BCE=60°,∠COD+∠BOE=120°;所以∠DOE=60°;从而证得△DOE 是等边三角形,所以DE=OE.【详解】连OD ,∵O为BC的中点,∵OE OD=OB=OC,∴∠COD=2∠CBD,∠BOE=2∠BCE.∵∠BAC=120°,∴∠CBD+∠BCE=60°,∴∠COD+∠BOE=120°,∴∠DOE=60°,∴△DOE是等边三角形,∴DE=OE.【点睛】此题考查了等边三角形的判定和性质,直角三角形斜边的中线等于斜边的一半,等腰三角形的性质及三角形外角的性质,解答此题的关键是要掌握分析题中的各种信息条件,找到相应的知识来解决问题,然后根据以往做题经验找出解决问题的方法.13.DH51【解析】【分析】根据正方形性质可得AB=DA,∠BAD=∠ADF=90°,又根据AE=DF,利用SAS可证得△ABE≌△DAF,于是∠ABE=∠DAF;由于∠DAF+∠BAH=∠ABE+∠BAH=90°,从而∠AHB=90°,取AB的中点O,连接OH、OD,则OH=12AB=1,在Rt△AOD中,根据勾股定理计算出OD的值;根据三角形的三边关系,可得OH+DH>OD,于是当O、D、H三点共线时,DH的长度最小为OD-OH,据此解答.【详解】解:∵四边形ABCD是正方形,∴AB=DA,∠BAD=∠ADF=90°,又∵AE=DF,∴∠ABE=∠DAF.∴∠DAF+∠BAH=∠ABE+∠BAH=90°,∴∠AHB=90°,取AB的中点O,连OH、OD,∴112OH AB==,225OD OA AD=+=,在OHD∆中有DH OD OH>-,即51DH>-.故O、H、D三点共线时DH最小,∴DH最小值为51-.【点睛】本题考查了正方形的性质,全等三角形的判定与性质,直角三角形斜边的中线等于斜边的一半,勾股定理及三角形三条边的关系,确定出点H的位置是解答本题的关键.14.见解析【解析】【分析】取AC中点F,连接EF、DF,则EF为△ABC的中位线,结合条件可得到∠FEA=2∠A,结合直角三角形的性质可得到∠FDE=∠EFD,得到DE=EF,可得出结论.【详解】证明:取AC的中点F,连EF,DF,则EF为中位线,∴∠FEA=∠B=2∠A ,在直角三角形ACD 中,F 是斜边BC 的中点,∴DF=CF=AF ,∴∠FDA=∠A ,即有2∠FDA=∠FEA ,∵∠FEA=∠FDA+∠DFE ,∴∠DFE=∠FDA ,∴DE=EF ,∴BC=2DE .【点睛】本题考查了三角形中位线的判定与性质,直角三角形斜边的中线等于斜边的一半,三角形外角的性质,等腰三角形的判定等知识,正确作出辅助线是解答本题的关键.15.33CE CD = 【解析】【分析】根据直角三角形斜边上中线等于斜边的一半,可得出DE=CE=BE ,根据三角形外角的性质及等腰三角形的性质可求出30DCE ∠=︒,过E 作EM CD ⊥于M ,设1EM =,可求出CE 、CM 、CD 的值.【详解】证明:连结DE ,在Rt △ACB 和Rt △ADB 中,∵E 是AB 的中点,∴12DE AB =,12CE AB =, ∴DE CE EB ==,∴2DEA DBE ∠=∠,2AEC EBC ∠=∠,∴2120DEC DBC ∠=∠=︒,30DCE ∠=︒.过E 作EM CD ⊥于M ,设1EM =,则2CE =,CM =,∴CD =,∴CE CD =【点睛】本题考查了含30°角的直角三角形的性质,三角形外角的性质,等腰三角形的性质,勾股定理等知识,正确作出辅助线是解答本题的关键.16.(1)证明见解析;(2)∠EBC=30°;(3)BE 2=AP 2+PC 2,理由见解析.【解析】【分析】(1)利用正方形的性质得出△CBP ≌△CDP ,得出BP =DP ,利用四边形的内角和,得出EP =DP ,从而得出结论;(2)取BE 的中点F ,得出△CEF 是等边三角形,利用撒尿行内角和定理,得出∠EPC =30°; (3)过点P 作PC /⊥AC ,得出△BPC ≌△EPC /, 近而得出四边形ABEC /为平行四边形,在Rt △APC /中,利用勾股定理得出结论即可.【详解】(1)∵ 四边形ABCD 是正方形,∴CB =CD ,AC 平分∠BCD , 即 ∠BCP =∠DCP , 又CP 是公共边 所以△CBP ≌△CDP ∴ BP =DP , ∠PBC =∠PDC∵ ∠BPE -∠BCE =90°,∠BPE +∠BCE +∠PBC +∠PEC =360°∴∠PBC +∠PEC =90°∵ ∠PED +∠PEC =90°∴∠PED =∠PBC ∴∠PED =∠PDC ∴EP =DP ,∴ BP =DP .(2)取BE 的中点F ,连CF ,则CE =CF -EF =3, ∴△CEF 是等边三角形,则∠BEC =60°,∵∠BCE =90°,∴∠EBC +∠BEC =90°, ∴∠EBC =30°, ∵∠EBC +∠BCP =∠PEB +∠EPC , ∠PEB =∠BCP =45°∴∠EBC =∠EPC =30°﹒(3)过点P作PC/⊥AC,交CD的延长线于C/,得△BPC≌△EPC/, CP=C/P,BC=EC/, ∵AB=BC,∴AB=EC/∵AB∥EC/∴四边形ABEC/为平行四边形,∴AC/=BE,∵在Rt△APC/中,C/A2=AP2+C/P2∴BE2=AP2+PC2﹒。
