【重庆大学出版社·肖明葵】版【水力学习题评讲】第二章(精)

合集下载

水力学第二章课后习题答案解析

WORD 格式.分享精品.资料2.12密闭容器，测压管液面高于容器内液面h =1.8m =1.8m，液体的密度为，液体的密度为850kg/m 3，求液面压强。

p 0解：08509.807 1.8a a p p gh p r =+=+´´相对压强为：15.00kPa kPa。

绝对压强为：116.33kPa kPa。

答：液面相对压强为15.00kPa kPa，绝对压强为，绝对压强为116.33kPa kPa。

2.13密闭容器，压力表的示值为4900N/m 2，压力表中心比A 点高0.4m 0.4m，，A 点在水下1.5m 1.5m，，，求水面压强。

p 0A1.5m0.4m解：0 1.1a p p p gr =+-4900 1.110009.807a p =+-´´5.888a p =-（kPa kPa））相对压强为： 5.888-kPa kPa。

绝对压强为：95.437kPa kPa。

答：水面相对压强为 5.888-kPa kPa，绝对压强为，绝对压强为95.437kPa kPa。

1m3m解：（1）总压力：433353.052ZP A p g r =×=´´=（kN kN））（2）支反力：()111333R W W W W g r ==+=+´´+´´总水箱箱980728274.596W =+´=箱kN W +箱不同之原因：总压力位底面水压力与面积的乘积，为压力体g r ´。

而支座反力与水体重量及箱体重力相平衡，而水体重量为水的实际体积g r ´。

答：水箱底面上总压力是353.052kN kN，，4个支座的支座反力是274.596kN kN。

2.14 盛满水的容器，顶口装有活塞A ，直径d =0.4m =0.4m，，容器底的直径D =1.0m =1.0m，，高h =1.8m =1.8m，，如活塞上加力2520N 2520N（包括活塞自重）（包括活塞自重），求容器底的压强和总压力。

《水力学》第二章答案

第二章:水静力学一：思考题2-1.静水压强有两种表示方法,即:相对压强和绝对压强2-2.特性(1)静水压强的方向与受压面垂直并指向手压面;(2)任意点的静水压强的大小和受压面的方位无关,或者说作用于同一点上各方向的静水压强都相等. 规律:由单位质量力所决定,作为连续介质的平衡液体内,任意点的静水压强仅是空间坐标的连续函数,而与受压面的方向无关,所以p=(x,y,z)2-3答：水头是压强的几何意义表示方法，它表示h高的水头具有大小为p gh的压强。

绝对压强预想的压强是按不同的起点计算的压强，绝对压强是以0为起点，而相对压强是以当地大气压为基准测定的，所以两者相差当地大气压Pa.绝对压强小于当地大气压时就有负压，即真空。

某点负压大小等于该点的相对压强。

Pv=p'-pa2-4•在静水压强的基本方程式中z+〃=C中，z表示某点在基准面以上的高度，/pg称为位置水头，*表示在该点接一根测压管，液体沿测压管上升的高度，称为测p g压管高度或压强水头，z+亠称为测压管水头，即为某点的压强水头高出基准面p g的高度。

关系是：(测压管水头)=(位置水头)+(压强水头)。

2-5.等压面是压强相等的点连成的面。

等压面是水平面的充要条件是液体处于惯性坐标系，即相对静止或匀速直线运动的状态。

2-6。

图中A-A是等压面，C-C,B-B都不是等压面，因为虽然位置高都相同，但是液体密度不同，所以压强水头就不相等，则压强不相等。

2-7.两容器内各点压强增值相等，因为水有传递压强的作用，不会因位置的不同压强的传递有所改变。

当施加外力时，液面压强增大了坐，水面以下同一高度A的各点压强都增加坐。

A2-8.(1)各测压管中水面高度都相等。

(2)标注如下，位置水头z,压强水头h,测压管水头p・2-10・(1)图a和图b静水压力不相等。

因为水作用面的面积不相等，而且作用面的形心点压强大小不同。

所以静水压力Pa>Pb・(2)图c和图d静水压力大小相等。

【重庆大学出版社·肖明葵】版【水力学习题评讲】第二章

gH PghP g (H H hP ) H 2.52m
I xc yD1 yc yc A
4 hc d / 64 hc sin d 2 / 4 sin 4.74m
a
B C D
θ
G d
题2.20图
根据
M
B
0 可得
G d / 2cos p左 BD FT d cos－p右BD2 0
代入数据并整理可得
FT hD hC FP
E
FT 32.2kN
a
B C D
θ
G d
题2.20图
（2）根据解析法可得此时图形阀门上的静水总压力
' P p A 30.79 kN , P p c c A 3.33kN 左右
由（1）可知：
P左
的作用点 yD1=4.632m，
FT hD hC FP
E
P右的作用点
17200 700 9.8 3.4 1000 9.8 3.6 1600 9.8 2 1600 9.8 HG
得： HG 10.6m 求 HP
20.0 15.0 11.6 8.0 6.0 hp ρ p 4.0
E F G
2 g (HF 8.0) 2 g (8.0 4.0) p gH p
2.20 有一圆形平板闸门铰接于B，如图所示。闸门的直径
d=1m，水平倾角
60，闸门中心点位于上游水面以下
4m处，闸门重G=980N，求闸门分别当：（1）下游无水；（2）下游水面与门顶同高时，在E处将闸门吊起所需的拉力
FT分别为多大?
FT hD hC FP
E
解；根据解析法可得图形平板阀门的静水总压力

【最新试题库含答案】水力学第二章课后答案_0

水力学第二章课后答案：篇一：水力学第二章课后答案1 2 6 11答案在作业本2.12 （注：书中求绝对压强）用多管水银测压计测压，图中标高的单位为m，试求水面的压强p0。

解： p0?p4??3.0?1.4??g?p5??2.5?1.4??Hgg??3.0?1.4??g?pa??2.3?1.2??Hgg??2.5?1.2??g??2.5?1.4??Hgg??3.0?1.4??g ?pa ??2.3?2.5?1.2?1.4??Hgg??2.5?3.0?1.2?1.4??g?pa????2.3?2.5?1.2?1.4??13.6??2.5?3.0?1.2?1.4??g???g?pa?265.00（kPa）答：水面的压强p0?265.00kPa。

2-12形平板闸门AB，一侧挡水，已知长l=2m，宽b=1m，形心点水深hc=2m，倾角?=45?，闸门上缘A处设有转轴，忽略闸门自重及门轴摩擦力，试求开启闸门所需拉力T。

解：（1）解析法。

P?pC?A?hC?g?bl?1000?9.807?2?1?2?39.228（kN）bl3IChC222yD?yC???????2.946CyCAsin?sin4512?blsin45sin?2-13矩形闸门高h=3m，宽b=2m，上游水深h1=6m，下游水深h2=4.5m，试求：（1）作用在闸门上的静水总压力；（2）压力中心的位置。

解：（1）图解法。

压强分布如图所示：∵ p????h1?h???h2?h????g??h1?h2??g??6?4.5??1000?9.807?14.71（kPa）P?p?h?b?14.71?3?2?88.263（kN）b合力作用位置：在闸门的几何中心，即距地面(1.5m,)处。

2（2）解析法。

P1?p1A??g?h1?1.5??hb??6?1.5??9807?3?2?264.789（kN） bh3IC1?2h2?yD1?yC2??4.5???4.5?? yC2A4.5?bh4.5?12??1??20.25?0.75??4.667（m） 4.5P2?p2A??g?h2?1.5??hb?3?9.807?3?2?176.526（kN） yD2?yC1?IC1?2IC?12??yC1????3?0.75??3.25（m） yC1AyC1?A?3合力：P?P1?P2?88.263（kN）合力作用位置（对闸门与渠底接触点取矩）：yDP?P1?h1?yD1??P2?h2?yD2?。

【重庆大学出版社·肖明葵】版【水力学习题评讲】第四章解析

l 1 1 2 2
Hale Waihona Puke v v1 v2 Q 1 2 d 4
h
7.7 4 27.23cm / s 2 0.6
题4.11图
2 p1 1v12 p2 2v2 0 0 h f 12 g 2g g 2g
p1 p2 汞 g 油 g 9.8 13600 9.8 843 h 0.15 2.222m g g 油 g 9.8 843
已知液体的运动粘滞系数ν为0.015cm2/s。试求Q为5000cm3/s、
4000cm3/s、2000cm3/s时，管道的沿程阻力系数λ各为若干? 解：由于 Re vd 4Q

d
2000 Re1 105
4 5000 Re1 21221.29, 3.1415 20 0.015
H
选取1-1、2-2两渐变流过水断面分别在两水池液面上，并取2-2断面为基准面0-0，则写1-2的伯诺里方程有：
题4.25图
l v2 v2 H 00 000 (进 3弯阀出 ) d 2g 2g
l v2 v2 H (进 3弯阀出 ) d 2g 2g
v1d1 4v2 d 2 / 2 v2 d 2 Re1 2 2 Re 2 v v v Re1 2 所以小管径对应的断面雷诺数大， Re 2
4.4
圆管内径d =6 mm，有重油通过，密度
ρ=870.0kg/m3，运动粘性系数为ν=2.2×10–6 m2/s，管中流量Q=0.02×10-3m3/s。试判别其流态。
o A l1 d1 B d2 o 1 h1 1 2 h2 H 2
伯诺里方程，
C
题4.27图

【重庆大学出版社·肖明葵】版【水力学习题评讲】第六章

i = 0.0004 。求均匀流时的水深为多少? 求均匀流时的水深为多少?
解：
χ = b + 2 h 1 + m 2 = 5 + 2 2h
R= A
χ
=
5 + 2 2h
(5 + h) h ,
1 1/ 6 1 1/ 6 Q2 102 C= R = R , i = 2 = 70.004 = 2 n 0.02 k k
∴ b = 3m
χ = b + 2h 1 + m = 8, R =
2
A
χ
= 0.8925
1 1/ 6 n = 0.0225, C = R = 43.57, k = AC R = 293.89 n
Q2 i = 2 = 0.0012 k
。
6.2 某渠道断面为矩形，按水力最优断面设计，底宽b=8m，渠某渠道断面为矩形，按水力最优断面设计，底宽， 1 壁用石料砌成(n=0.028)，底坡 i = 壁用石料砌成，，试校核能否通过均匀 8000 3 流设计流量 Q = 20m /s . 由于为矩形断面，根据水力最优断面条件: 解：由于为矩形断面，根据水力最优断面条件: b = 2h0 h0 = 4m 断面面积 A = b ⋅ h = 8 × 4 = 32m 2
0
水力半径 R = A =
χ
32 = 2m 8+ 2×4
1 2
流量
1 Q = A ⋅ R ⋅ i = 20.28m 3 / s > 20m 3 / s n
2 3
故能通过。故能通过。
6.3 梯形断面渠道，通过流量 Q = 85m3 /s i = 0.0015，n = 0.020，梯形断面渠道，试按水力最优断面设计断面尺寸。 m = 1.0 ，试按水力最优断面设计断面尺寸。最优断面时，解：由 A = (b + mh0 )h0 = (b + h0 ) h0 ，最优断面时，R0 = h0 / 2

水力学第二章课后答案

12611 ^<4作业本2.122.13(注：书中求绝对压强丿用多管水银测压计测压，图中榇嵩的单住为m,试求水面的庄强几。

鮮：P()= “4—(3.0—1.4)Qg=几+265.00 (kPa丿答：水面的压强几= 265.00kPa。

2・12形平板闸门AB ,-側档水，己知长/=2m,宽/? = 1 m,形心点水深J?c=2m,倾角a =45。

，闸门上缘A处设有转轴，忽略闸门自重及门轴摩擦力，试求开启闸门所需拉力T。

解：fl)解析法。

P = p c A = h c pg-Z?/ = 1000x9.807x2xlx2 = 39.228 (kN 丿2-13矩形闸门嵩〃=3m,宽b =2m,上游水深h} =6m,下游水深仏=4.5m,试求：f 1J作用淮.闸门上的费水总、压力；(2)压力中心的住置。

鮮：fl)图解法。

压强分布如图所示：T P =[(人一方)一(站一方)]Qg= 14.71 (kPa)P = /^./?./? = 14.71x3x2 = 88.263 (kN)合力作用住置：亦闸门的几何中心，即距地面(1.5m.—)处。

2(2)鮮析出。

A = pA = Qg(九一 1.5)•肋= (6-1.5)x9807x3x2 = 264.789(kN丿=-L x (20.25 + 0.75) = 4.667 (m)4* • 5W = P2A = Qg仇一1.5)•肪= 3x9.807x3x2 = 176.526 (kN丿%2 = yci + = j-^ci+^ = |(32+0.75) = 3.25 (mJ合力:P = P}-P2 =88.263 (kN丿合力作用住置(对闸门与渠底接融点取矩丿：=1.499 (mJ答：(\)作用柱闸门上的静水总压力88.263 kN；(2) 压力中心的住置往闸门的几何中心，即距地面(1.5m,-)处。

22・14矩形平核闸门一側宿水，门寓/? = lm,宽b=0.8m,要求扌当水深曾超过2m时，闸门即可自动开启，试求转轴应设的住置y °鮮：当扌当水深达到片时，水压力作用住置应作用亦转轴上，当水深大于％时，水压力作用住置应作用于转轴上，使闸门开启。

水力学课后习题详解ppt课件

最新编辑ppt
91
•
最新编辑ppt
92
•
最新编辑ppt
93
•
最新编辑ppt
94
•
最新编辑ppt
95
•
最新编辑ppt
96
•
最新编辑ppt
97
•
最新编辑ppt
98
•
最新编辑ppt
99
•
最新编辑ppt
100
•
最新编辑ppt
101
76
最新编辑ppt
77
最新编辑ppt
78
最新编辑ppt
79
最新编辑ppt
80
最新编辑pHale Waihona Puke t81最新编辑ppt
82
最新编辑ppt
83
•
最新编辑ppt
84
•
最新编辑ppt
85
•
最新编辑ppt
86
•
最新编辑ppt
87
•
最新编辑ppt
88
•
最新编辑ppt
89
•
最新编辑ppt
90
•
31
最新编辑ppt
32
最新编辑ppt
33
最新编辑ppt
34
最新编辑ppt
35
最新编辑ppt
36
最新编辑ppt
37
最新编辑ppt
38
最新编辑ppt
39
最新编辑ppt
40
最新编辑ppt
41
最新编辑ppt
42
最新编辑ppt
43
最新编辑ppt
44
最新编辑ppt
45
最新编辑ppt

【重庆大学出版社·肖明葵】版【水力学习题评讲】第四章

解：雷诺数为
Qd 0.02 103 0.006 Re 1929 2000 2 6 A 0.25 (0.006) 2.2 10 vd
故管内为层流。
4.8 为了确定某圆管内径，在管中通水，温度为15℃，实测
流量为Q = 10cm3/s，长6m，水头损失hf=0.22m水柱，试求：圆管的直径d。
A A (b mh0 )h0 R x A b mh0 h0
x b 2h0 1 m 2
A m h v i b (a) A (b)A-A断面 1 h θ
题4.22图
(b mh0 )h0 A (2 1.5 1.5) 1.57 R 0.8605m 2 2 x b 2h0 1 m 2 2 1.5 1 1.5
如图所示A、B、C三个水箱由两段普通钢管相连接，
经过调节，管中为恒定流动。已知：A、C箱水面差H=10m，
l1=50m，l2 = 40 m，d1 =250mm，d2 =200mm，ζb= 0.25，
假设流动流态在阻力平方区，管壁的当量粗糙度Δ=0.2 mm，试求：（1）管中流量Q；（2）图中h1及h2。解：以2-2断面为基准面，写0-2的
0.2mm 0.4 L 1.70mm
0.316 0.316 3 1/ 4 4 0.0277 Re 16977.03
4 2000 Re2 8488.51 3.1415 20 0.015
L
32.8d 32.8 200 4.26mm Re 8488.51 0.0329
0.316 0.316 1 1/ 4 4 0.0262 Re 21221.29
32.8d 32.8 200 L 1.91mm Re 21221.29 0.02

【最新试题库含答案】水力学第二章课后答案

水力学第二章课后答案篇一：水力学第二章答案(吕宏兴__裴国霞等)2-1 解：（1）pA+γ水·ΔH=γH·Δh；所以pA=γH·Δh-γ水·ΔH=38.02kPa（γH=13.6γ水）（2）测压管长度：pA=γ水·h 所以h= pA/γ水=38.02×103/9.8×103=3.88m2-3 解：PA-γh=pB-γ(h1+h2+h)+γHh1所以，pA-pB=γHh1-γ(h1+h2)=13.6×9.8×0.53-9.8×(0.53+1.2) =53.68kPa2-6解：pA=γH(h1+h2)-γ(h1+h2)=13.6××9.8××0.53-9.8×(0.53+1.2)=53.68kpa2-7 解：（1）左支：绝对：pc =p0 +γh0=86.5+9.8×2=106.1kPa（2）右支：pc =pa+γ水h；h=（pc -pa）/γ水=（106.1-9.8）/9.8=0.827m2-8 解：pA=0.6pa=0.6×98=58.8kpa（1）左支：pA=γh1 h1=pA/γ=58.8/9.8=6m（2）右支：pA+γh=γHh2 h2=（pA+γh）/γH=0.456m2-10解：设管嘴内的绝对压强为p ,则p +γh= paPv=pa- p =γh=9.8×0.6=5.886kpa2-12解：(1)设容器底部面积为S，相对压强为P，对容器底部进行受力分析：由牛顿第二定律：ΣF=m·a；-（P+G)=-m·a 所以得出p·s+γ·s·h=ρ·s·h·ap=ρ·h·a -γh=γh/g·a-γh=γh(a/g-1)篇二：《水力学》第二章答案第二章:水静力学一：思考题2-1.静水压强有两种表示方法,即:相对压强和绝对压强2-2.特性(1)静水压强的方向与受压面垂直并指向手压面;(2)任意点的静水压强的大小和受压面的方位无关,或者说作用于同一点上各方向的静水压强都相等. 规律:由单位质量力所决定,作为连续介质的平衡液体内,任意点的静水压强仅是空间坐标的连续函数,而与受压面的方向无关,所以p=(x,y,z)2-3答：水头是压强的几何意义表示方法，它表示h高的水头具有大小为?gh的压强。

【重庆大学出版社·肖明葵】版-水力学课后习题讲解第三章

解: 以管轴线0-0为基准线，
写A→B的伯方程:
hp
pA
u
2 A
0
pa
0
0 uA A
0
g 2g
g
d
u
2 A
pa pA
2g g
(1)
题3.11图
又由水银压差计公式:
(zB
pB
g
)
(
z
A
pA )
g
pg g
g
h
在本题中: zA=zB=0，故知: pB pA p g g h
(2)
将(2)代入(1)中得:
又由连续性方程：Q1=Q2 或 v1A1=v2A2 得：
v2
A1 A2
v1
d12 d22
0.795
0.22 0.12
0.795
3.18m /
s
3.8 题3.8图所示输送海水的管道，管径d＝0.2m，进口断面
平均流速v=1m/s，若从此管中分出流量 Q1 0.012 m3 / s ，问
管中。尚余流量Q2等于多少？设海水密度为1.02×103kg/m3，求
3.17 题图示一文丘里流量计，水银压差计读数为360mm，若不计A.B 两点间的水头损失，试求管道中的流量。已知管道直径d1=300mm，喉段直径d2＝150mm，渐变段AB长为 750mm。
解: 以1-1水平面为基准面，写1-1到2-2断面的能量方程 d2=150mm
p1 1v12 0.75 p2 2v22
p1 p2 5.3m水柱
g
又令1 2 1,
代入能量方程中得:
d2=150mm
2
B2
5.3 v22 1 v22 0.75,

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2.25 一密闭盛水容器，已知 h1 0.6m ， h2 1m ，水银测压计读数 hP 0.25m 。试求半径 R 0.5m 的球形盖AB所受总压力的水平分力和铅垂分力。解： Px pc Az
，
[13600 9.8 0.25 9.8 (1 0.6)] 0.5 0.5 29.24kN , 水平向左 p
2
N
h
A
P （kN / m ） Abs P a P A 98 9.8 107.8
N
A点绝对压强用水柱表示 PAbs 题2.3图 h水 11m水柱水 g Pabs 107.8 808.8 （mm汞柱）用mm汞柱表示为 h汞汞 g 13600 9.8
A点相对压：用水柱表示为
FT 28.0kN
FT a
B C E D
当下游水面与门顶同高时，在E处将闸门吊起所需要的拉力
hD hC
FP
θ
FT 28.0kN
G d
题2.20图
2.22
高度H＝3m，宽度b＝1m，的密闭高压水箱，在水箱
底部连接一水银测压计如图所示，测得水银柱高h2=1m，水柱
高h1=2m，矩形闸门AB与水平方向成45°角，转轴在A点。试求为使闸门关闭所需施加在转轴上的锁紧力矩。解：（１）求高压水箱底部压强如图取等压面Ｎ-Ｎ，则：
由（1）、（2）两式可得：
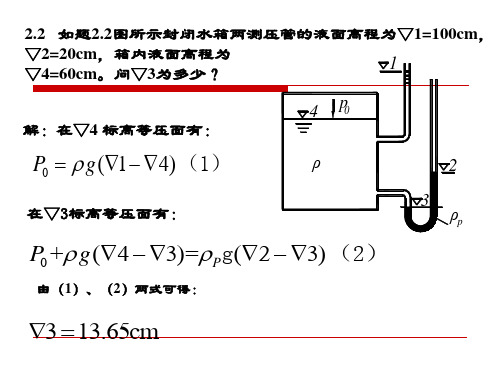
3 13.65cm
2.3 用图示U形管量测密闭盛水容器中A点压强，管右端开口通大气，如果h1=1m ，求A点的绝对压强和相对压强，并分别用国际单位(N/m2) ，水柱高度（m），水银柱高度（mm）表示。解：取等压面N-N，A点相对压强： PA 水 gh 1000 9.81 9.8 （kN / m2） A点的绝对压强：
1000 9.8 (12.2 8.0) 1000 9.8 4 13600 9.8 H p
空气
ρ 1 ρ 2 ρ 3
H P 0.6m
题2.10图
2.12 图示为一测压装置，容器A中水面上压力表M的读数为0.3个大气压， h1 20cm , h2 30cm ,h3 50cm，该测压装置中U形上部是酒精，其密度为800kg/m3，试求容器B中气体的压强 p，、 p、0 分别 M 酒精 ρ 0 为水、水银、酒精的密度。解：压力表读数
题2.17图
设一受两种液压的平板AB如图所示其倾角， 60 上部油的深度 h 1.0m ，下部水的深度 h2 2.0m ，油 2.19 的密度油 816.33kg / m3 ，求作用在AB板上（单宽）的静水总压力及其作用点的位置。解：解析法求解，由于AB板浸在两种不同的液体中，计算分为AE板和BE板 A 对于AE板部分： h1 油设此部分板上受到的静水压力为
17200 700 9.8 3.4 1000 9.8 3.6 1000 9.8 (H F 8.0)
得：
H F 12.2m
测管G： 17200 1 g (15.0 11.6) 2 g (11.6 8.0) 3 g (8.0 6.0) 3 gHG
a
B C D
p pc A 水 ghc d / 4
2
θ
G d
30.79kN
题2.20图
总压力P的作用点
I xc hc d 4 / 64 yD yc 4.632m hc yc A sin d 2 / 4 sin
根据可得
M
B
0
G d / 2 cos p BD FT d cos 0
gH PghP g (H H hP ) H 2.52m
17200 700 9.8 3.4 1000 9.8 3.6 1600 9.8 2 1600 9.8 HG
得： HG 10.6m 求 HP
20.0 15.0 11.6 8.0 6.0 hp ρ p 4.0
E F G
2 g (HF 8.0) 2 g (8.0 4.0) p gH p
2.20 有一圆形平板闸门铰接于B，如图所示。闸门的直径
d=1m，水平倾角
60，闸门中心点位于上游水面以下
4m处，闸门重G=980N，求闸门分别当：（1）下游无水；（2）下游水面与门顶同高时，在E处将闸门吊起所需的拉力
FT分别为多大?
FT hD hC FP
E
解；根据解析法可得图形平板阀门的静水总压力
17200 700 9.8 (15 11.6) pa 40524 pa
20.0 15.0 11.6 8.0 6.0 hp ρ p 4.0 E F G
空气
ρ 1 ρ 2 ρ 3
1 g ( H E 11.6) 40524 pa,
H E 12.5m
题2.10图
测管F： 17200 1g (15.0 11.6) 2 g (11.6 8.0) 2 g (H F 8.0)
I xc yD1 yc yc A
4 hc d / 64 hc sin d 2 / 4 sin 4.74m
a
B C DθBiblioteka G d题2.20图
根据
M
B
0 可得
G d / 2cos p左 BD FT d cos－p右BD2 0
代入数据并整理可得
2.17如图所示容器中，两测压管的上端封闭，并为完全真空，测得 z1 50mm ，求封闭容器中液面上的绝对压强 p0abs 及 z2 之值。解：
p0 abs 汞 gz1 13600 9.8 0.05 6.664kN / m
得z2 0.68m
2
p z1
z2
0
N
N
水
p0 abs 水 gz2 6.664kN / m2，
FT hD hC FP
E
FT 32.2kN
a
B C D
θ
G d
题2.20图
（2）根据解析法可得此时图形阀门上的静水总压力
' P p A 30.79 kN , P p c c A 3.33kN 左右
由（1）可知：
P左
的作用点 yD1=4.632m，
FT hD hC FP
E
P右的作用点
BE 3 /12 y2 ( AE BE / 2) ( AE BE / 2) BE 2.502m
h1 h2
A
油水
p p1 p2 4.619 41.107 45.725kN
0 B 60
题2.19图
pyD p1 y1 p2 y2
yD 4.619 0.77 41.107 2.502 2.327m
o
Px 水 gV 1000 9.8 2 / 3 0.5 0.5 2.57kN，铅直向下
R
h2 ρ
h1
hp ρp
题2.25图
2.28 图示一溢流坝上的弧形闸门，已知R＝10m，闸门宽b=8m， α＝30°，试求作用在该弧形闸门上的静水总压力的大小及其作用点的位置。 E C 解：
2.2 如题2.2图所示封闭水箱两测压管的液面高程为▽1=100cm， ▽2=20cm，箱内液面高程为 1 ▽4=60cm。问▽3为多少？解：在▽4 标高等压面有：
4 ρ
p 0 2 3 ρp
P0 g (1 4) （1）
在▽3标高等压面有：
P 0 + g (4 3)=Pg(2 3) （2）
H
F 水平
α
FR
B
题2.28图
2.30 图示两水池间隔墙上装有一半球形曲面堵头，已知球形曲面的半径R=0.5m，两水池下方接通一U形水银压差计，其水银液面差hp=0.2m。又H=1.5m，试求：（1）两水池液面的水位差△H；（2）曲面堵头上的静水总压力。
解:(1) 由题意，作1-1等压面
H R H
AC 2.12m
F1 pA AB b 357.35kN
H p A F1 h2 F h1 2 ρp p
B
1 F2 ( pB p A ) AB b 2 62.328kN
A C D B
AD 2.83m
（４）由静水压力施加的绕Ａ轴的力矩
'
题2.22图
M F1 AC F2 AD 933.97kN m
H 10sin 30 5m
o
4m H
F水平水 ghbH 9800 4 2.5 8 5 2548kN
F 水平
A
D R β
α
O
FR
B
F竖 gV g VABO VBDO VADCE
题2.28图
R 2 1 o 0 gb 5 10 cos 30 4 10 10 cos 30 360 2 =9800 9.88 8 774.59kN
，
H D 2.02m
采用几何法：画出压强分布图如图所示；静水总压力为
F F1 F2 F3
静水总压力合力作用线位置
1 1 h2 2 o 2 油gh1 1/ sin 60 水 gh2 水 gh1 1 o 2 2 sin 60
h1 ρ gh 油 A
h水 1m水柱
用汞柱表示
h汞
PA 9.8 73.6mm汞柱汞 g 133.28
2.10 图示容器中盛有三种不相混合的液体，其密度分别为 kg / m3 kg / m3 3 1600 1 700kg / m3 2 1000