二进制,八进制,十进制,十六进制之间的相互转换
二进制、八进制、十进制、十六进制之间转换(含小数部分)

二进制、八进制、十进制、十六进制之间转换一、十进制与二进制之间的转换(1)十进制转换为二进制,分为整数部分和小数部分①整数部分方法:除2取余法,即每次将整数部分除以2,余数为该位权上的数,而商继续除以2,余数又为上一个位权上的数,这个步骤一直持续下去,直到商为0为止,最后读数时候,从最后一个余数读起,一直到最前面的一个余数。
下面举例:例:将十进制的168转换为二进制分析:(2)例1分析:第一步,将0.125乘以2,得0.25,则整数部分为0,小数部分为0.25;第二步, 将小数部分0.25乘以2,得0.5,则整数部分为0,小数部分为0.5;第三步, 将小数部分0.5乘以2,得1.0,则整数部分为1,小数部分为0.0;第四步,读数,从第一位读起,读到最后一位,即为0.001。
例2,将0.45转换为二进制(保留到小数点第四位)大家从上面步骤可以看出,当第五次做乘法时候,得到的结果是0.4,那么小数部分继续乘以2,得0.8,0.8又乘以2的,到1.6这样一直乘下去,最后不可能得到小数部分为零,因此,这个时候只好学习十进制的方法进行四舍五入了,但是二进制只有0和1两个,于是就出现0舍1入。
这个也是计算机在转换中会产生误差,但是由于保留位数很多,精度很高,所以可以忽略不计。
那么,我们可以得出结果将0.45转换为二进制约等于0.0111上面介绍的方法是十进制转换为为二进制的方法,需要大家注意的是:1)十进制转换为二进制,需要分成整数和小数两个部分分别转换2)当转换整数时,用的除2取余法,而转换小数时候,用的是乘2取整法3)注意他们的读数方向因此,我们从上面的方法,我们可以得出十进制数168.125转换为二进制为10101000.001,或者十进制数转换为二进制数约等于10101000.0111。
(3)二进制转换为十进制不分整数和小数部分1)2)二、(1)②将二进制数1101.1转换为八进制得到结果:将1101.1转换为八进制为15.4(2)将八进制转换为二进制方法:取一分三法,即将一位八进制数分解成三位二进制数,用三位二进制按权相加去凑这位八进制数,小数点位置照旧。
二进制八进制十进制十六进制之间的进制转换

二进制八进制十进制十六进制之间的进制转换详情可参考百度百科:进制转换这个词条【主要搞懂1和2两条,其他的进制之间的转化就迎刃而解,很好懂了】1. 十进制-> 二进制:将这个十进制数连续除以2的过程,第一步除以2,得到商和余数,将商再继续除以2,得到又一个商和余数,直到商为0。
最后将所有余数倒序排列,得到的数就是转换成二进制的结果。
2. 二进制-> 十进制:二进制数第1位的权值是2的0次方,第2位的权值是2的1次方,第3位的权值是2的2次方。
(例如1258这个十进制数,实际上代表的是:1x1000+2x100+5x10+8x1=1258)那么1011这个二进制数,实际上代表的是:1x8+0x4+1x2+1x1=11(十进制数11)。
(这里的8就是2的3次方,4就是2的2次方,2就是2的1次方,1就是2的0次方)3. 十进制-> 八进制:十进制数转换成八进制的方法,和转换为二进制的方法类似,唯一变化:除数由2变成8。
4. 八进制-> 十进制和转换为二进制的方法类似,唯一变化是,底数变成8,第1位表示8的0次方,第二位表示8的一次方,第三位表示8的2次方,第四位表示8的3次方。
例如1314这个八进制数,十进制数就是1x512+3x64+1x8+4x1=716(十进制)5. 十进制-> 十六进制10进制数转换成16进制的方法,和转换为2进制的方法类似,唯一变化:除数由2变成16。
十六进制是0123456789ABCDEF这十六个字符表示。
那么单独一个A就是10,单独一个B就是11,CDEF,就分表表示12,13,14,15。
而10这个十六进制数,实际就是十进制中的16。
6. 十六进制-> 十进制和转换为二进制的方法类似,唯一变化是,底数变成16,第1位表示16的0次方,第二位表示16的一次方,第三位表示16的2次方,第四位表示16的3次方。
7. 二进制<--->八进制,之间的相互转换,更简单一些,因为8本身是2的三次方。
二进制、八进制、十进制、十六进制之间转换(含小数部分)[整理]
![二进制、八进制、十进制、十六进制之间转换(含小数部分)[整理]](https://img.taocdn.com/s3/m/9b71bc6ba36925c52cc58bd63186bceb19e8edb4.png)
二进制、八进制、十进制、十六进制之间转换一、十进制与二进制之间的转换(1)十进制转换为二进制,分为整数部分和小数部分①整数部分方法:除2取余法,即每次将整数部分除以2,余数为该位权上的数,而商继续除以2,余数又为上一个位权上的数,这个步骤一直持续下去,直到商为0为止,最后读数时候,从最后一个余数读起,一直到最前面的一个余数。
下面举例:例:将十进制的168转换为二进制得出结果将十进制的168转换为二进制,(10101000)2分析:第一步,将168除以2,商84,余数为0。
第二步,将商84除以2,商42余数为0。
第三步,将商42除以2,商21余数为0。
第四步,将商21除以2,商10余数为1。
第五步,将商10除以2,商5余数为0。
第六步,将商5除以2,商2余数为1。
第七步,将商2除以2,商1余数为0。
第八步,将商1除以2,商0余数为1。
第九步,读数,因为最后一位是经过多次除以2才得到的,因此它是最高位,读数字从最后的余数向前读,即10101000(2)小数部分方法:乘2取整法,即将小数部分乘以2,然后取整数部分,剩下的小数部分继续乘以2,然后取整数部分,剩下的小数部分又乘以2,一直取到小数部分为零为止。
如果永远不能为零,就同十进制数的四舍五入一样,按照要求保留多少位小数时,就根据后面一位是0还是1,取舍,如果是零,舍掉,如果是1,向入一位。
换句话说就是0舍1入。
读数要从前面的整数读到后面的整数,下面举例:例1:将0.125换算为二进制得出结果:将0.125换算为二进制(0.001)2分析:第一步,将0.125乘以2,得0.25,则整数部分为0,小数部分为0.25;第二步, 将小数部分0.25乘以2,得0.5,则整数部分为0,小数部分为0.5;第三步, 将小数部分0.5乘以2,得1.0,则整数部分为1,小数部分为0.0;第四步,读数,从第一位读起,读到最后一位,即为0.001。
例2,将0.45转换为二进制(保留到小数点第四位)大家从上面步骤可以看出,当第五次做乘法时候,得到的结果是0.4,那么小数部分继续乘以2,得0.8,0.8又乘以2的,到1.6这样一直乘下去,最后不可能得到小数部分为零,因此,这个时候只好学习十进制的方法进行四舍五入了,但是二进制只有0和1两个,于是就出现0舍1入。
二进制、八进制、十进制、十六进制数据之间相互转换方法

二进制、八进制、十进制、十六进制数据之
间相互转换方法
1. 二进制转十进制:将二进制数从右往左依次乘以2,每一位的乘积再相加,结果即为十进制数。
例如:1101(2)= 1×2³ + 1×2² + 0×2¹ + 1×2⁰ = 13(10)
2. 十进制转二进制:将十进制数不断除以2,余数依次排列得到的数字序列即为二进制数。
例如:13(10)= 1101(2)
3. 八进制转十进制:将八进制数从右往左依次乘以8,每一位的乘积再相加,结果即为十进制数。
例如:345(8)= 5×8⁰ + 4×8¹+ 3×8² = 229(10)
4. 十进制转八进制:将十进制数不断除以8,余数依次排列得到的数字序列即为八进制数。
例如:229(10)= 345(8)
5. 十六进制转十进制:将十六进制数从右往左依次乘以16的幂次方,每一位的乘积再相加,结果即为十进制数。
例如:2D(16)= 13×16⁰ + 2×16¹ = 45(10)
6. 十进制转十六进制:将十进制数不断除以16,余数依次排列得到的数字序列即为十六进制数,若余数为10~15,则用A~F表示。
例如:45(10)= 2D(16)。
二进制,八进制,十进制,十六进制的相互转换

⼆进制,⼋进制,⼗进制,⼗六进制的相互转换常⽤进制数:⼆进制,⼋进制,⼗进制,⼗六进制进制理解计算机中硬件之间的信息传递是由电流确定,假如⼀个半导体允许通过的电流是5A,如果电流通过的为5A,则通过,计为1,如果通过的电流⼩于5A,则不通过,计为0。
由此,出现两种情况的判断,与或⾮。
电流的传递由0或1来完成,由此引申出⼆进制数的概念,以便底层硬件有共同的“语⾔”,即机器语⾔,相互沟通和交流。
我们⽣活中⼀般数值的运算是⼗进制。
就是满10进1,个⼗百千万,依次递进。
由此,可以类⽐。
⼆进制(Binary):0,1。
基数为2,逢⼆进⼀。
表⽰:(111)2或者(111)B⼋进制(Octal number system):0,1,2,3,4,5,6,7。
基数为8,逢⼋进⼀。
表⽰:(111)8或者(111)O⼗进制(Decimal system):0,1,2,3,4,5,6,7,8,9。
基数为10,逢⼗进⼀。
表⽰:(111)10或者(111)D⼗六进制(Hexadecimal):0,1,2,3,4,5,6,7,8,9,A(10),B(11),C(12),D(13),E(14),F(15)。
基数为16,逢⼗六进⼀。
表⽰:(111)16或者(111)Hn进制:(逢n进1)个位数:n0( 0个8)⼗位数:n1( 1个8)百位数:n2( 8个8)进制转换1.⼗进制转其他进制① 除⼆取余法(整数部分):把被转换的⼗进制整数反复除以2,直⾄商为0,所得的余数(从末位读起)就是这个数的⼆进制表⽰。
② 乘⼆取整法(⼩数部分):将⼩数部分乘以2,然后取整数部分,剩下的⼩数部分继续乘以2,然后取整数部分,剩下的⼩数部分⼜乘以2,⼀直取到⼩数部分为零为⽌。
如果永远不能为零,就同⼗进制数的四舍五⼊⼀样,按照要求保留多少位⼩数时,就根据后⾯⼀位是0还是1,取舍,如果是零,舍掉,如果是1,向⼊⼀位。
换句话说就是0舍1⼊。
读数要从前⾯的整数读到后⾯的整数。
二、八、十、十六进制之间的相互转换

在计算机应用中,二进制使用后缀B表示;十进制使用后缀D表示,八进制用Q表示,十六制使用后缀H表示。
1、二、八、十六进制数转十进制各位数字分别乖以各自的基数的(N-1)次方,其和相加之和便是相应的十进制数。
个位,N=1;十位,N=2...举例:110B=1*2的2次方+1*2的1次方+0*2的0次方=0+4+2+0=6D110Q=1*8的2次方+1*8的1次方+0*8的0次方=64+8+0=72D110H=1*16的2次方+1*16的1次方+0*16的0次方=256+16+0=272D2、十进制数转二、八、十六进制数方法是相同的,即整数部分用除基取余的算法,小数部分用乘基取整的方法,然后将整数与小数部分拼接成一个数作为转换的最后结果。
要将十进制转为各进制的方式,只需除以各进制的权值,取得其余数,第一次的余数当个位数,第二次余数当十位数,其余依此类推,直到被除数小于权值,最后的被除数当最高位数。
十进制转二进制如:55转为二进制2|5527――1 个位13――1 第二位6――1 第三位3――0 第四位1――1 第五位最后被除数1为第七位,即得110111十进制转八进制如:5621转为八进制8|5621702 ――5 第一位(个位)87 ――6 第二位10 ――7 第三位1 ――2 第四位最后得八进制数:12765十进制数十六进制如:76521转为十六进制16|765214782 ――9 第一位(个位)298 ――14 第二位18 ――10 第三位1 ――2 第四位最后得12AE93、二进制数转换八、十、十六进制数二进制转八进制:从小数点位置开始,整数部分向左,小数部分向右,每三位二进制为一组用一位八进制的数字来表示,不足三位的用0补足,就是一个相应八进制数的表示。
010110.001100B=26.14Q八进制转二进制反之则可。
二进制转十进制:当前位乘以基数2的(N-1)次方计算公式:二进制数据N位数字乘以2的N-1次方的积的总和例:10101011B=( )D数据1 0 1 0 1 0 1 1N-1位7 6 5 4 3 2 1 0相应的十进制值即为:27 +25+23+21+20=128+32+8+2+1=171二进制转十六进制:从小数点位置开始,整数部分向左,小数部分向右,每四位二进制为一组用一位十六进制的数字来表示,不足四位的用0补足,就是一个相应十六进制数的表示。
(完整版)二进制、八进制、十进制、十六进制之间转换详解

二进制、八进制、十进制、十六进制之间转换一、十进制与二进制之间的转换(1)十进制转换为二进制,分为整数部分和小数部分①整数部分方法:除2取余法,即每次将整数部分除以2,余数为该位权上的数,而商继续除以2,余数又为上一个位权上的数,这个步骤一直持续下去,直到商为0为止,最后读数时候,从最后一个余数读起,一直到最前面的一个余数。
下面举例:例:将十进制的168转换为二进制得出结果将十进制的168转换为二进制,(10101000)2分析:第一步,将168除以2,商84,余数为0。
第二步,将商84除以2,商42余数为0。
第三步,将商42除以2,商21余数为0。
第四步,将商21除以2,商10余数为1。
第五步,将商10除以2,商5余数为0。
第六步,将商5除以2,商2余数为1。
第七步,将商2除以2,商1余数为0。
第八步,将商1除以2,商0余数为1。
第九步,读数,因为最后一位是经过多次除以2才得到的,因此它是最高位,读数字从最后的余数向前读,即10101000(2)小数部分方法:乘2取整法,即将小数部分乘以2,然后取整数部分,剩下的小数部分继续乘以2,然后取整数部分,剩下的小数部分又乘以2,一直取到小数部分为零为止。
如果永远不能为零,就同十进制数的四舍五入一样,按照要求保留多少位小数时,就根据后面一位是0还是1,取舍,如果是零,舍掉,如果是1,向入一位。
换句话说就是0舍1入。
读数要从前面的整数读到后面的整数,下面举例:例1:将0.125换算为二进制得出结果:将0.125换算为二进制(0.001)2分析:第一步,将0.125乘以2,得0.25,则整数部分为0,小数部分为0.25;第二步, 将小数部分0.25乘以2,得0.5,则整数部分为0,小数部分为0.5;第三步, 将小数部分0.5乘以2,得1.0,则整数部分为1,小数部分为0.0;第四步,读数,从第一位读起,读到最后一位,即为0.001。
例2,将0.45转换为二进制(保留到小数点第四位)大家从上面步骤可以看出,当第五次做乘法时候,得到的结果是0.4,那么小数部分继续乘以2,得0.8,0.8又乘以2的,到1.6这样一直乘下去,最后不可能得到小数部分为零,因此,这个时候只好学习十进制的方法进行四舍五入了,但是二进制只有0和1两个,于是就出现0舍1入。
二进制 八进制 十进制 十六进制之间的转换方法

一、十进制与二进制之间的转换(1)十进制转换为二进制,分为整数部分和小数部分①整数部分方法:除2取余法,即每次将整数部分除以2,余数为该位权上的数,而商继续除以2,余数又为上一个位权上的数,这个步骤一直持续下去,直到商为0为止,最后读数时候,从最后一个余数读起,一直到最前面的一个余数。
下面举例:例:将十进制的168转换为二进制得出结果将十进制的168转换为二进制,(10101000)2分析:第一步,将168除以2,商84,余数为0。
第二步,将商84除以2,商42余数为0。
第三步,将商42除以2,商21余数为0。
第四步,将商21除以2,商10余数为1。
第五步,将商10除以2,商5余数为0。
第六步,将商5除以2,商2余数为1。
第七步,将商2除以2,商1余数为0。
第八步,将商1除以2,商0余数为1。
第九步,读数,因为最后一位是经过多次除以2才得到的,因此它是最高位,读数字从最后的余数向前读,即10101000(2)小数部分方法:乘2取整法,即将小数部分乘以2,然后取整数部分,剩下的小数部分继续乘以2,然后取整数部分,剩下的小数部分又乘以2,一直取到小数部分为零为止。
如果永远不能为零,就同十进制数的四舍五入一样,按照要求保留多少位小数时,就根据后面一位是0还是1,取舍,如果是零,舍掉,如果是1,向入一位。
换句话说就是0舍1入。
读数要从前面的整数读到后面的整数,下面举例:例1:将0.125换算为二进制得出结果:将0.125换算为二进制(0.001)2分析:第一步,将0.125乘以2,得0.25,则整数部分为0,小数部分为0.25;第二步, 将小数部分0.25乘以2,得0.5,则整数部分为0,小数部分为0.5;第三步, 将小数部分0.5乘以2,得1.0,则整数部分为1,小数部分为0.0;第四步,读数,从第一位读起,读到最后一位,即为0.001。
例2,将0.45转换为二进制(保留到小数点第四位)大家从上面步骤可以看出,当第五次做乘法时候,得到的结果是0.4,那么小数部分继续乘以2,得0.8,0.8又乘以2的,到1.6这样一直乘下去,最后不可能得到小数部分为零,因此,这个时候只好学习十进制的方法进行四舍五入了,但是二进制只有0和1两个,于是就出现0舍1入。
二进制、十进制、八进制、十六进制四种进制之间相互的转换

二进制、十进制、八进制、十六进制四种进制之间相互的转换一.在计算机应用中,二进制使用后缀b表示;十进制使用后缀d表示八制使用后缀Q表示,十六制使用后缀H表示。
二.二进制,十六进制与十进制的计算转换1.二进制转换为十进制计算公式:二进制数据X位数字乘以2的X-1次方的积的总和例:10101011b=( )d相应的十进制值即为:27 +25+23+21+20=128+32+8+2+1=1712.十六进制转换十进制计算公式:二进制数据X位数字乘以16的X-1次方的积的总和(与二进制转换十制进同理的,将底数换为16)注意:在十六进制中,10-15依次用A,B,C,D,E,F表示例:1F3E H=()d计算:1*16的3次方+15*16的2次方+3*16的1次方+14*16的0次方=1*4096+15*256+3*16+14=7998三.十进制与二进制,十六制的计算转换1.十进制转换为二进制十进制数据数字除以2的余数的逆序组合例:404d=( )b2|404余02|202余02|101余02|50余12|25余02|12余12|6余02|3余12|1计算结果便是:1101010002.十进制转换十六进制。
与上面同理,注意的是10以上的数字用字母表示,除数是16十六进制与二进制的转换,建议通过十进制来进行中转。
带小数点的十进制转换为二进制时同理,小数店后的数位指数为负指数===================================================================== =================关于“进制之间的转换”问题的分析指导在计算机文化一书中,在其中一个章节里面详细介绍了进制之间的转换,而且在考试中进制转换也占了一定的比例,虽然分数不是很多,但是因为平时大家接触的不多,并且有点繁复,所以很多学员在做这种题目,要么选择猜答案,要么选择放弃。
笔者觉得只要掌握了方法,其实这些题目也很简单的,下面我就对进制的转换进行具体的分析和讲解,以供大家参考。
二进制、八进制、十进制、十六进制之间的转换

⼆进制、⼋进制、⼗进制、⼗六进制之间的转换⼆进制是Binary,简写为B⼋进制是Octal,简写为O⼗进制为Decimal,简写为D⼗六进制为Hexadecimal,简写为H⽅法为:⼗进制数除2取余法,即⼗进制数除2,余数为权位上的数,得到的商值继续除2,依此步骤继续向下运算直到商为0为⽌。
读数要倒叙读。
⼩数:乘2取整法,即将⼩数部分乘以2,然后取整数部分,剩下的⼩数部分继续乘以2,然后取整数部分,剩下的⼩数部分⼜乘以2,⼀直取到⼩数部分为零。
如果永远不能为零,就同⼗进制数的四舍五⼊⼀样,按照要求保留多少位⼩数时,就根据后⾯⼀位是0还是1,取舍,如果是零,舍掉,如果是1,向⼊⼀位。
换句话说就是0舍1⼊。
读数要从前⾯的整数读到后⾯的整数,即读数要顺序读。
0.125 转⼆进制第⼀步,将0.125乘以2,得0.25,则整数部分为0,⼩数部分为0.25;第⼆步, 将⼩数部分0.25乘以2,得0.5,则整数部分为0,⼩数部分为0.5;第三步, 将⼩数部分0.5乘以2,得1.0,则整数部分为1,⼩数部分为0.0;第四步,读数,从第⼀位读起,读到最后⼀位,即为0.001。
积整数部分0.125 x 2 = 0.25 00.25 x 2 = 0.5 00.5 x 2 = 1.0 1150.125 转⼆进制10010110.0010.45 转⼆进制(保留到⼩数点第四位)第⼀步,将0.45乘以2,得0.9,则整数部分为0,⼩数部分为0.9;第⼆步, 将⼩数部分0.9乘以2,得1.8,则整数部分为1,⼩数部分为0.8;第三步, 将⼩数部分0.8乘以2,得1.6,则整数部分为1,⼩数部分为0.6;第四步, 将⼩数部分0.6乘以2,得1.2,则整数部分为1,⼩数部分为0.2; 算到这⼀步就可以了,因为只需要保留四位⼩数第五步, 将⼩数部分0.2乘以2,得0.4,则整数部分为0,⼩数部分为0.4;第六步, 将⼩数部分0.4乘以2,得0.8,则整数部分为0,⼩数部分为0.8;后⾯会⼀直循环重复第七步, 将⼩数部分0.8乘以2,得1.6,则整数部分为1,⼩数部分为0.6;。
各种进制之间的转换方法

各种进制之间的转换方法进制是数学中用来表示数字的一种方法。
常见的进制包括二进制、八进制、十进制和十六进制。
不同进制之间的转换可以用以下方法实现。
一、二进制与八进制的互相转换:二进制转换为八进制:将二进制数从右到左按照三位一组进行分组,然后将每组转换为对应的八进制数即可。
从右到左分组得到:(1)(011)(101)(011)。
将每组转换为对应的八进制数:(1)(3)(5)(3)。
八进制转换为二进制:将八进制数的每个位转换为对应的三位二进制数即可。
例如:将八进制数652转换为二进制数。
将八进制数的每个位转换为对应的三位二进制数:(6)(5)(2)=(110)(101)(010)。
二、二进制与十进制的互相转换:二进制转换为十进制:将二进制数的每个位与其对应的权重相乘,再将乘积相加即可得到十进制数。
例如:将二进制数1101转换为十进制数。
将二进制数的每个位与其对应的权重相乘,并将乘积相加:1×2³+1×2²+0×2¹+1×2⁰=13因此,二进制数1101转换为十进制数为13十进制转换为二进制:将十进制数不断除以二,将余数从下到上排列即可得到二进制数。
例如:将十进制数25转换为二进制数。
将十进制数25不断除以二,将余数从下到上排列:25/2=12余1、12/2=6余0、6/2=3余0、3/2=1余1、1/2=0余1三、二进制与十六进制的互相转换:二进制转换为十六进制:将二进制数从右到左按照四位一组进行分组,然后将每组转换为对应的十六进制数即可。
从右到左分组得到:(1)(0110)(0110)。
将每组转换为对应的十六进制数:(1)(6)(6)。
十六进制转换为二进制:将十六进制数的每个位转换为对应的四位二进制数即可。
例如:将十六进制数F8转换为二进制数。
将十六进制数的每个位转换为对应的四位二进制数:F=1111、8=1000。
四、八进制与十进制的互相转换:八进制转换为十进制:将八进制数的每个位与其对应的权重相乘,再将乘积相加即可得到十进制数。
二进制、八进制、十进制、十六进制之间的转换

一、二进制数的数码为0、1共两个,进数规则为逢2进一,借一当二。
二、十进制数的数码为0-9共十个,进数规则为逢10进一,借一当十。
三、八进制数的数码为0-7共八个,进数规则为逢八进一,借一当八。
四、十六进制数的数码为0-9、A-F共十六个,其中数码A、B、C、D、E、F分别代表十进制数中的10、11、12、13、14、15,进数规则为逢16进一,借一当十六。
1、正整数的十进制转换二进制要点:除2取余,倒序排列[低位有效位——》高位有效位]解释:将一个十进制数除以二,得到的商再除以二,以此类推,直到商等于一或零时,倒取除得的余数,即换算为二进制数的结果。
【例如:(52)10 = (00110100)2】2、负整数转换为二进制要点:取反加一解释:将该负整数对应的正整数先转换成二进制,然后对其“取补”,再对取补后的结果加1即可。
【例如:(-52)10 = (11001100)2】3、小数转换为二进制要点:乘2取整,正序排列[高位有效位——》低位有效位]解释:用2乘以十进制小数,取其整数部分(0或1)作为二进制小数部分,取其小数部分,再乘以2,又取其整数部分作为二进制小数部分,然后取小数部分,再乘以2,直到小数部分为0或者已经取到了足够位数,每次取的整数部分,按先后次序排列,就构成了二进制小数的序列。
【例如:(0.2)10 = (0.0011 0011 0011 (2)4、二进制转十进制:要点:整数二进制用数值乘以2的幂次方依次相加,小数二进制用数值乘以2的负幂次方,然后依然相加。
首先二进制数补足位数,首位为0,则为正整数;首位为1,则为负整数,那么需要先取反在换算【例如:二进制110 转换为十进制后的结果为0 +2 +4 =6;11111001 =-00000110 = -6;0.110 = 0.75】5.二进制转八进制方法为:以小数点为基准,整数部分从右向左,三位一组,最高位不足三位时,左边添0补足三位;小数部分从左向右,三位一组,最低位不足三位时,右边添0补足三位。
二进制、八进制、十进制、十六进制之间转换(含小数部分)

二进制、八进制、十进制、十六进制之间转换一、十进制与二进制之间的转换(1)十进制转换为二进制,分为整数部分和小数部分①整数部分方法:除2取余法,即每次将整数部分除以2,余数为该位权上的数,而商继续除以2,余数又为上一个位权上的数,这个步骤一直持续下去,直到商为0为止,最后读数时候,从最后一个余数读起,一直到最前面的一个余数。
下面举例:例:将十进制的168转换为二进制得出结果将十进制的168转换为二进制,(10101000)2分析:第一步,将168除以2,商84,余数为0。
第二步,将商84除以2,商42余数为0。
第三步,将商42除以2,商21余数为0。
第四步,将商21除以2,商10余数为1。
第五步,将商10除以2,商5余数为0。
第六步,将商5除以2,商2余数为1。
第七步,将商2除以2,商1余数为0。
第八步,将商1除以2,商0余数为1。
第九步,读数,因为最后一位是经过多次除以2才得到的,因此它是最高位,读数字从最后的余数向前读,即10101000(2)小数部分方法:乘2取整法,即将小数部分乘以2,然后取整数部分,剩下的小数部分继续乘以2,然后取整数部分,剩下的小数部分又乘以2,一直取到小数部分为零为止。
如果永远不能为零,就同十进制数的四舍五入一样,按照要求保留多少位小数时,就根据后面一位是0还是1,取舍,如果是零,舍掉,如果是1,向入一位。
换句话说就是0舍1入。
读数要从前面的整数读到后面的整数,下面举例:例1:将0.125换算为二进制得出结果:将0.125换算为二进制(0.001)2分析:第一步,将0.125乘以2,得0.25,则整数部分为0,小数部分为0.25;第二步, 将小数部分0.25乘以2,得0.5,则整数部分为0,小数部分为0.5;第三步, 将小数部分0.5乘以2,得1.0,则整数部分为1,小数部分为0.0;第四步,读数,从第一位读起,读到最后一位,即为0.001。
例2,将0.45转换为二进制(保留到小数点第四位)大家从上面步骤可以看出,当第五次做乘法时候,得到的结果是0.4,那么小数部分继续乘以2,得0.8,0.8又乘以2的,到1.6这样一直乘下去,最后不可能得到小数部分为零,因此,这个时候只好学习十进制的方法进行四舍五入了,但是二进制只有0和1两个,于是就出现0舍1入。
二进制、八进制、十进制、十六进制的转换

在高速发展的现代社会,计算机浩浩荡荡的成为了人们生活中不可缺少的一部分,帮助人们解决通信,联络,互动等各方面的问题,今天我就给大家讲讲与计算机有关的“进制转换”问题。
我们都知道,在计算机中数值是用二进制表示的,之所以要用八进制和十六进制,是因为它们与二进制之间的互相转换很方便,而且它们比长长的一串二进制数要方便书写和记忆。
一、二进制与八进制之间的转换(1)二进制转换为八进制方法:取三合一法,即从二进制的小数点为分界点,向左(向右)每三位取成一位,接着将这三位二进制按权相加,得到的数就是一位八位二进制数,然后,按顺序进行排列,小数点的位置不变,得到的数字就是我们所求的八进制数。
如果向左(向右)取三位后,取到高(最低)位时候,如果无法凑足三位,可以在小数点最左边(最右边),即整数的最高位(最低位)添0,凑足三位。
要把二进制转换为八进制,需要用一张表。
如下:二进制八进制000 0001 1010 2011 3100 4101 5110 6111 7有了这张表,就可以方便的把二进制数转换成八进制数。
首先,将一个二进制数自右向左每三位分成一段。
然后,将每一段用表中的八进制数替换,即可例如:100101010把它分成100 101 010查表:100->4 101->5 010->2替换:452例①将二进制数101110.101转换为八进制得到结果:将101110.101转换为八进制为56.5②将二进制数1101.1转换为八进制得到结果:将1101.1转换为八进制为15.4(2)将八进制转换为二进制方法:取一分三法,即将一位八进制数分解成三位二进制数,用三位二进制按权相加去凑这位八进制数,小数点位置照旧。
例:①将八进制数67.54转换为二进制因此,将八进制数67.54转换为二进制数为110111.101100,即110111.1011大家从上面这道题可以看出,计算八进制转换为二进制首先,将八进制按照从左到右,每位展开为三位,小数点位置不变然后,按每位展开为22,21,20(即4、2、1)三位去做凑数,即a×22+ b×21 +c×20=该位上的数(a=1或者a=0,b=1或者b=0,c=1或者c=0),将abc排列就是该位的二进制数接着,将每位上转换成二进制数按顺序排列.最后,就得到了八进制转换成二进制的数字。
二进制八进制十进制十六进制之间的转换算法

二进制八进制十进制十六进制之间的转换算法
一、二进制与八进制转换
1.二进制转换为八进制
(1)确定要转换的二进制数
(2)把二进制数,从右边分为三组
(3)每组独立转换成八进制数
(4)把转换后的八进制数,组合在一起即是要转换的八进制数
分组成:101010110
将每组独立的转换成八进制数
101:101等于5
010:010等于2
110:110等于6
组合在一起:
526即是要转换的八进制数
2.八进制转换为二进制
(1)确定要转换的八进制数
(2)将八进制数,从右边分组
(3)把每组独立转换成二进制数
(4)把转换后的二进制数,组合在一起,即为要转换的二进制数
如:将256转换成二进制数
256
分组成:256
把每组独立的转换成二进制数
2:010等于2
5:101等于5
6:110等于6
把转换后的二进制数,组合在一起:
二、二进制与十六进制转换
1.二进制转换为十六进制
(1)确定要转换的二进制数
(2)把二进制数,从右到左,按4位分组
(3)把每组独立转换成十六进制数
(4)把转换后的十六进制数,组合在一起,即为要转换的十六进制数。
二进制、八进制、十进制、十六进制之间转换(含小数部分)

二进制、八进制、十进制、十六进制之间转换一、十进制与二进制之间的转换(1)十进制转换为二进制,分为整数部分和小数部分①整数部分方法:除2取余法,即每次将整数部分除以2,余数为该位权上的数,而商继续除以2,余数又为上一个位权上的数,这个步骤一直持续下去,直到商为0为止,最后读数时候,从最后一个余数读起,一直到最前面的一个余数。
下面举例:例:将十进制的168转换为二进制得出结果将十进制的168转换为二进制,(10101000)2分析:第一步,将168除以2,商84,余数为0。
第二步,将商84除以2,商42余数为0。
第三步,将商42除以2,商21余数为0。
第四步,将商21除以2,商10余数为1。
第五步,将商10除以2,商5余数为0。
第六步,将商5除以2,商2余数为1。
第七步,将商2除以2,商1余数为0。
第八步,将商1除以2,商0余数为1。
第九步,读数,因为最后一位是经过多次除以2才得到的,因此它是最高位,读数字从最后的余数向前读,即10101000(2)小数部分方法:乘2取整法,即将小数部分乘以2,然后取整数部分,剩下的小数部分继续乘以2,然后取整数部分,剩下的小数部分又乘以2,一直取到小数部分为零为止。
如果永远不能为零,就同十进制数的四舍五入一样,按照要求保留多少位小数时,就根据后面一位是0还是1,取舍,如果是零,舍掉,如果是1,向入一位。
换句话说就是0舍1入。
读数要从前面的整数读到后面的整数,下面举例:例1:将0.125换算为二进制得出结果:将0.125换算为二进制(0.001)2分析:第一步,将0.125乘以2,得0.25,则整数部分为0,小数部分为0.25;第二步, 将小数部分0.25乘以2,得0.5,则整数部分为0,小数部分为0.5;第三步, 将小数部分0.5乘以2,得1.0,则整数部分为1,小数部分为0.0;第四步,读数,从第一位读起,读到最后一位,即为0.001。
例2,将0.45转换为二进制(保留到小数点第四位)大家从上面步骤可以看出,当第五次做乘法时候,得到的结果是0.4,那么小数部分继续乘以2,得0.8,0.8又乘以2的,到1.6这样一直乘下去,最后不可能得到小数部分为零,因此,这个时候只好学习十进制的方法进行四舍五入了,但是二进制只有0和1两个,于是就出现0舍1入。
二进制、八进制、十进制、十六进制之间转换(含小数部分)

二进制、八进制、十进制、十六进制之间转换一、十进制与二进制之间的转换(1)十进制转换为二进制,分为整数部分和小数部分①整数部分方法:除2取余法,即每次将整数部分除以2,余数为该位权上的数,而商继续除以2,余数又为上一个位权上的数,这个步骤一直持续下去,直到商为0为止,最后读数时候,从最后一个余数读起,一直到最前面的一个余数。
下面举例:例:将十进制的168转换为二进制得出结果将十进制的168转换为二进制,(10101000)2分析:第一步,将168除以2,商84,余数为0。
第二步,将商84除以2,商42余数为0。
第三步,将商42除以2,商21余数为0。
第四步,将商21除以2,商10余数为1。
第五步,将商10除以2,商5余数为0。
第六步,将商5除以2,商2余数为1。
第七步,将商2除以2,商1余数为0。
第八步,将商1除以2,商0余数为1。
第九步,读数,因为最后一位是经过多次除以2才得到的,因此它是最高位,读数字从最后的余数向前读,即10101000(2)小数部分方法:乘2取整法,即将小数部分乘以2,然后取整数部分,剩下的小数部分继续乘以2,然后取整数部分,剩下的小数部分又乘以2,一直取到小数部分为零为止。
如果永远不能为零,就同十进制数的四舍五入一样,按照要求保留多少位小数时,就根据后面一位是0还是1,取舍,如果是零,舍掉,如果是1,向入一位。
换句话说就是0舍1入。
读数要从前面的整数读到后面的整数,下面举例:例1:将0.125换算为二进制得出结果:将0.125换算为二进制(0.001)2分析:第一步,将0.125乘以2,得0.25,则整数部分为0,小数部分为0.25;第二步, 将小数部分0.25乘以2,得0.5,则整数部分为0,小数部分为0.5;第三步, 将小数部分0.5乘以2,得1.0,则整数部分为1,小数部分为0.0;第四步,读数,从第一位读起,读到最后一位,即为0.001。
例2,将0.45转换为二进制(保留到小数点第四位)大家从上面步骤可以看出,当第五次做乘法时候,得到的结果是0.4,那么小数部分继续乘以2,得0.8,0.8又乘以2的,到1.6这样一直乘下去,最后不可能得到小数部分为零,因此,这个时候只好学习十进制的方法进行四舍五入了,但是二进制只有0和1两个,于是就出现0舍1入。
(完整版)二进制、八进制、十进制、十六进制之间转换详解.doc

二进制、八进制、十进制、十六进制之间转换一、十进制与二进制之间的转换(1)十进制转换为二进制,分为整数部分和小数部分① 整数部分方法:除 2 取余法,即每次将整数部分除以 2,余数为该位权上的数,而商继续除以 2,余数又为上一个位权上的数,这个步骤一直持续下去,直到商为 0 为止,最后读数时候,从最后一个余数读起,一直到最前面的一个余数。
下面举例:例:将十进制的 168 转换为二进制得出结果将十进制的 168 转换为二进制,(10101000)2分析 : 第一步,将 168 除以 2, 商 84, 余数为 0。
第二步,将商 84 除以 2,商 42 余数为 0。
第三步,将商 42 除以 2,商 21 余数为 0。
第四步,将商 21 除以 2,商 10 余数为 1。
第五步,将商 10 除以 2,商 5 余数为 0。
第六步,将商 5 除以 2,商 2 余数为 1。
第七步,将商 2 除以 2,商 1 余数为 0。
第八步,将商 1 除以 2,商 0 余数为 1。
第九步,读数,因为最后一位是经过多次除以 2 才得到的,因此它是最高位,读数字从最后的余数向前读,即 10101000(2)小数部分方法:乘 2 取整法,即将小数部分乘以2,然后取整数部分,剩下的小数部分继续乘以2,然后取整数部分,剩下的小数部分又乘以2,一直取到小数部分为零为止。
如果永远不能为零,就同十进制数的四舍五入一样,按照要求保留多少位小数时,就根据后面一位是 0 还是 1,取舍,如果是零,舍掉,如果是 1,向入一位。
换句话说就是 0 舍 1 入。
读数要从前面的整数读到后面的整数,下面举例:例 1:将 0.125 换算为二进制得出结果:将 0.125 换算为二进制( 0.001 )2分析:第一步,将0.125 乘以 2,得 0.25, 则整数部分为0, 小数部分为0.25;第二步 ,将小数部分0.25 乘以 2, 得 0.5, 则整数部分为0, 小数部分为0.5;第三步 ,将小数部分0.5乘以2,得 1.0,则整数部分为1,小数部分为0.0;第四步 , 读数 , 从第一位读起 , 读到最后一位 , 即为 0.001 。
二进制、八进制、十进制、十六进制之间转换
二进制、八进制、十进制、十六进制之间转换一、进制的概念在计算机语言中常用的进制有二进制、八进制、十进制和十六进制,十进制是最主要的表达形式。
对于进制,有两个基本的概念:基数和运算规则。
基数:基数是指一种进制中组成的基本数字,也就是不能再进行拆分的数字。
二进制是0和1;八进制是0-7;十进制是0-9;十六进制是0-9+A-F(大小写均可)。
也可以这样简单记忆,假设是n进制的话,基数就是【0,n-1】的数字,基数的个数和进制值相同,二进制有两个基数,十进制有十个基数,依次类推。
运算规则:运算规则就是进位或错位规则。
例如对于二进制来说,该规则是“满二进一,借一当二”;对于十进制来说,该规则是“满十进一,借一当十”。
其他进制也是这样。
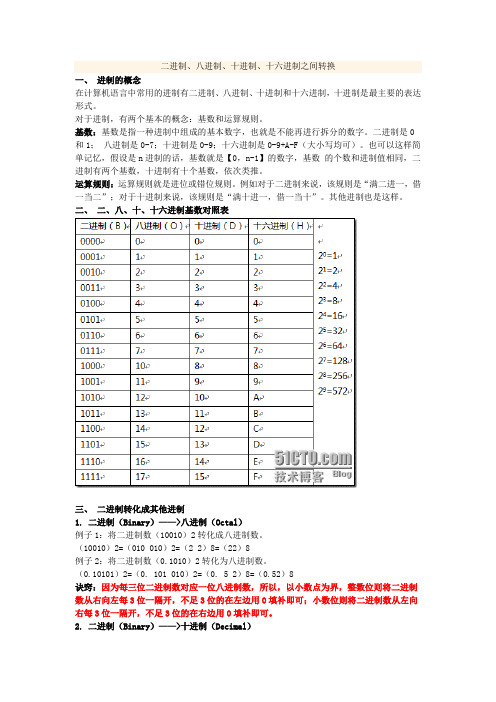
二、二、八、十、十六进制基数对照表三、二进制转化成其他进制1. 二进制(Binary)——>八进制(Octal)例子1:将二进制数(10010)2转化成八进制数。
(10010)2=(010 010)2=(2 2)8=(22)8例子2:将二进制数(0.1010)2转化为八进制数。
(0.10101)2=(0. 101 010)2=(0. 5 2)8=(0.52)8诀窍:因为每三位二进制数对应一位八进制数,所以,以小数点为界,整数位则将二进制数从右向左每3位一隔开,不足3位的在左边用0填补即可;小数位则将二进制数从左向右每3位一隔开,不足3位的在右边用0填补即可。
2. 二进制(Binary)——>十进制(Decimal)例子1:将二进制数(10010)2转化成十进制数。
(10010)2=(1x24+0x23+0x22+1x21+0x20)10=(16+0+0+2+0)10=(18) 10例子2:将二进制数(0.10101)2转化为十进制数。
(0.10101)2=(0+1x2-1+0x2-2+1x2-3+0x2-4+1x2-5)10=(0+0.5+0.25+0.125+0.0625+0.03125)10=(0.96875)10诀窍:以小数点为界,整数位从最后一位(从右向左)开始算,依次列为第0、1、2、3………n,然后将第n位的数(0或1)乘以2的n-1次方,然后相加即可得到整数位的十进制数;小数位则从左向右开始算,依次列为第1、2、3……..n,然后将第n位的数(0或1)乘以2的-n次方,然后相加即可得到小数位的十进制数(按权相加法)。
进制转换:二进制、八进制、十六进制、十进制之间的转换

将二进制、八进制、十六进制转换为十进制二进制、八进制和十六进制向十进制转换都非常容易,就是“按权相加”。
所谓“权”,也即“位权”。
假设当前数字是 N 进制,那么:•对于整数部分,从右往左看,第 i 位的位权等于N i-1•对于小数部分,恰好相反,要从左往右看,第 j 位的位权为N-j。
更加通俗的理解是,假设一个多位数(由多个数字组成的数)某位上的数字是 1,那么它所表示的数值大小就是该位的位权。
1) 整数部分例如,将八进制数字53627 转换成十进制:从右往左看,第1位的位权为 80=1,第2位的位权为 81=8,第3位的位权为 82=64,第4位的位权为 83=512,第5位的位权为84=4096 ……第n位的位权就为 8n-1。
将各个位的数字乘以位权,然后再相加,就得到了十进制形式。
注意,这里我们需要以十进制形式来表示位权。
再如,将十六进制数字 9FA8C 转换成十进制:从右往左看,第1位的位权为 160=1,第2位的位权为 161=16,第3位的位权为 162=256,第4位的位权为 163=4096,第5位的位权为164=65536 ……第n位的位权就为 16n-1。
将各个位的数字乘以位权,然后再相加,就得到了十进制形式。
将二进制数字转换成十进制也是类似的道理:从右往左看,第1位的位权为 20=1,第2位的位权为 21=2,第3位的位权为 22=4,第4位的位权为 23=8,第5位的位权为 24=16 ……第n位的位权就为 2n-1。
将各个位的数字乘以位权,然后再相加,就得到了十进制形式。
2) 小数部分例如,将八进制数字 423.5176 转换成十进制:小数部分和整数部分相反,要从左往右看,第1位的位权为 8-1=1/8,第2位的位权为 8-2=1/64,第3位的位权为 8-3=1/512,第4位的位权为 8-4=1/4096 ……第m位的位权就为 8-m。
再如,将二进制数字 1010.1101 转换成十进制:小数部分和整数部分相反,要从左往右看,第1位的位权为 2-1=1/2,第2位的位权为 2-2=1/4,第3位的位权为 2-3=1/8,第4位的位权为2-4=1/16 ……第m位的位权就为 2-m。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
16进制 0 1 2 3 4 5 6 7
2进制 1000 1001 1010 1011 1100 1101 1110 1111
16进制 8 9 a(10) b(11) c(12) d(13) e(14) f(15)
有一个公式:二进制数、八进制数、十六进制数的各位数字分别乖以各自的基数的(N-1)次方,其和相加之和便是相应的十进制数。个位,N=1;十位,N=2...举例:
110B=1*2的2次方+1*2的1次方+0*2的0次方=0+4+2+0=6D
110Q=1*8的2次方+1*8的1次方+0*8的0次方=64+8+0=72D
=(11.25)10
(2)十进制转二进制
· 十进制整数转二进制数:"除以2取余,逆序输出"
例: (89)10=(1011001)2
2 89
2 44 …… 1
2 22 …… 0
2 11 …… 0
2 5 …… 1
2 2 …… 1
2 1 …… 0
0 …… 1
2.十进制小数转换为二进制小数
十进制小数转换成二进制小数采用"乘2取整,顺序排列"法。具体做法是:用2乘十进制小数,可以得到积,将积的整数部分取出,再用2乘余下的小数部分,又得到一个积,再将积的整数部分取出,如此进行,直到积中的小数部分为零,或者达到所要求的精度为止。
然后把取出的整数部分按顺序排列起来,先取的整数作为二进制小数的高位有效位,后取的整数作为低位有效位。
例:10101011b=( )d
数据
1 0 1 0 1 0 1 1
X-1位
7 6 5 4 3 2 1 0
相应的十进制值即为:27 +25+23+21+20=128+32+8+2+1=171
2.十六进制转换十进制
计算公式:二进制数据X位数字乘以16的X-1次方的积的总和(与二进制转换十制进同理的,将底数换为16)
回答者:HackerKinsn - 试用期 一级 2-24 13:31
1.二进制与十进制的转换
(1)二进制转十进制<BR>方法:"按权展开求和"
例:
(1011.01)2 =(1×23+0×22+1×21+1×20+0×2-1+1×2-2)10
=(8+0+2+1+0+0.25)10
若要将二进制转为八进制,将二进制的位数由右向左每三位一个单位分隔,将事单位对照出八进制的值即可。
一.在计算机应用中,二进制使用后缀b表示;十进制使用后缀d表示,八进制用Q表示,十六制使用后缀H表示。
二.二进制,十六进制与十进制的计算转换
1.二进制转换为十进制
计算公式:二进制数据X位数字乘以2的X-1次方的积的总和
二进制 000 001 010 011 100 101 110 111
八进制 0 1 2 3 4 5 6 7
二进制与八进制的关系类似于二进制与十六进制的关系,以八进制的各数为0到7,以三位二进制数来表示。如要将51028 转为二进制,5为101,1为001,0为000,2为010,将这些数的二进制合并后为1010010000102,即是二进制的值。
如:55转为二进制
2|55
27――1 个位
13――1 第二位
6――1 第三位
3――0 第四位
1――1 第五位
最后被除数1为第七位,即得110111
二、十进制转八进制
如:5621转为八进制
8|5621
702 ―― 5 第一位(个位)
87 ―― 6 第二位
不足四位的用0补足,就是一个相应十六进制数的表示。
00100110.00010100B=26.14H
十进制转各进制
要将十进制转为各进制的方式,只需除以各进制的权值,取得其余数,第一次的余数当个位数,第二次余数当十位数,其余依此类推,直到被除数小于权值,最后的被除数当最高位数。
一、十进制转二进制
注意:在十六进制中,10-16依次用A,B,C,D,E,F表示
例:1F3E H=( )d
计算:1*16的3次方+16*16的2次方+3*16的1次方+15*16的0次方=1*4096+16*256+3*16+15*16=4096+4096+48+240=8480
三.十进制与二进制,十六制的计算转换
· 十进制小数转二进制数:"乘以2取整,顺序输出"
例:
(0.625)10= (0.101)2
0.625
X 2
1.25
X 2
0.5
X 2
1.0
110H=1*16的2次方+1*16的1次方+0*16的0次方=256+16+0=272D
2、十进制数转二进制数、八进制数、十六进制数
方法是相同的,即整数部分用除基取余的算法,小数部分用乘基取整的方法,然后将整数与小数部分拼接成一个数作为转换的最后结果。
3、二进制数转换成其它数据类型
10 ―― 7 第三位
1 ―― 2 第四位
最后得八进制数:127658
三、十进制数十六进制
如:765216 ――5 第一位(个位)
295 ――6 第二位
18 ――6 第三位
1 ―― 2 第四位
最后得1276516
二进制与十六进制的关系
1.十进制转换为二进制
十进制数据数字除以2的余数的逆序组合
例:404d=( )b
2|404 余0
2|202 余0
2|101 余0
2|50 余1
2|25 余0
2|12 余1
2|6 余0
2|3 余1
2|1
计算结果便是:110101000
2.十进制转换十六进制。。。与上面同理,注意的是10以上的数字用字母表示,除数是16
十六进制与二进制的转换,建议通过十进制来进行中转。
带小数点的十进制转换为二进制时同理,小数店后的数位指数为负指数
一、二进制数转换成十进制数
由二进制数转换成十进制数的基本做法是,把二进制数首先写成加权系数展开式,然后按十进制加法规则求和。这种做法称为"按权相加"法。
二、十进制数转换为二进制数
3-1二进制转八进制:从小数点位置开始,整数部分向左,小数部分向右,每三位二进制为一组用一位八进制的数字来表示,不足三位的用0补足,
就是一个相应八进制数的表示。
010110.001100B=26.14Q
八进制转二进制反之则可。
3-2二进制转十进制:见1
3-3二进制转十六进制:从小数点位置开始,整数部分向左,小数部分向右,每四位二进制为一组用一位十六进制的数字来表示,
可以用四位数的二进制数来代表一个16进制,如3A16 转为二进制为:
3为0011,A 为1010,合并起来为00111010。可以将最左边的0去掉得1110102
右要将二进制转为16进制,只需将二进制的位数由右向左每四位一个单位分隔,将各单位对照出16进制的值即可。
二进制与八进制间的关系
十进制数转换为二进制数时,由于整数和小数的转换方法不同,所以先将十进制数的整数部分和小数部分分别转换后,再加以合并。
1. 十进制整数转换为二进制整数
十进制整数转换为二进制整数采用"除2取余,逆序排列"法。具体做法是:用2去除十进制整数,可以得到一个商和余数;再用2去除商,又会得到一个商和余数,如此进行,直到商为零时为止,然后把先得到的余数作为二进制数的低位有效位,后得到的余数作为二进制数的高位有效位,依次排列起来。
