7第七章 图 (Graph)
第七章图习题答案

第七章图习题答案基础知识:7.1 在图7.23所示的各无向图中:(1)找出所有的简单环。
(2)哪些图是连通图?对非连通图给出其连通分量。
(3)哪些图是自由树(或森林)?答:(1)所有的简单环:(同一个环可以任一顶点作为起点)(a)1231(b)无(c)1231、2342、12341(d)无(2)连通图:(a)、(c)、(d)是连通图,(b)不是连通图,因为从1到2没有路径。
具体连通分量为:(3)自由树(森林):自由树是指没有确定根的树,无回路的连通图称为自由树:(a)不是自由树,因为有回路。
(b)是自由森林,其两个连通分量为两棵自由树。
(c)不是自由树。
(d)是自由树。
7.2 在图7.24(下图)所示的有向图中:(1) 该图是强连通的吗? 若不是,则给出其强连通分量。
(2) 请给出所有的简单路径及有向环。
(3) 请给出每个顶点的度,入度和出度。
(4) 请给出其邻接表、邻接矩阵及逆邻接表。
答:(1)该图是强连通的,所谓强连通是指有向图中任意顶点都存在到其他各顶点的路径。
(2)简单路径是指在一条路径上只有起点和终点可以相同的路径:有v1v2、v2v3、v3v1、v1v4、v4v3、v1v2v3、v2v3v1、v3v1v2、v1v4v3、v4v3v1、v3v1v4、另包括所有有向环,有向环如下:v1v2v3v1、v1v4v3v1(这两个有向环可以任一顶点作为起点和终点)(3)每个顶点的度、入度和出度:D(v1)=3ID(v1)=1OD(v1)=2D(v2)=2 ID(v2)=1OD(v2)=1D(v3)=3 ID(v3)=2OD(v3)=1D(v4)=2 ID(v4)=1OD(v4)=1(4)邻接表:(注意边表中邻接点域的值是顶点的序号,这里顶点的序号是顶点的下标值-1) vertex firstedge next┌─┬─┐┌─┬─┐┌─┬─┐0│v1│─→│ 1│─→│ 3│∧│├─┼─┤├─┼─┤└─┴─┘1│v2│─→│ 2│∧│├─┼─┤├─┼─┤2│v3│─→│ 0│∧│├─┼─┤├─┼─┤3│v4│─→│ 2│∧│└─┴─┘└─┴─┘逆邻接表:┌─┬─┐┌─┬─┐0│v1│─→│ 2│∧│├─┼─┤├─┼─┤1│v2│─→│ 0│∧│├─┼─┤├─┼─┤┌─┬─┐2│v3│─→│ 1│─→│ 3│∧│├─┼─┤├─┼─┤└─┴─┘3│v4│─→│ 0│∧│└─┴─┘└─┴─┘邻接矩阵:0 1 0 10 0 1 01 0 0 00 0 1 07.3 假设图的顶点是A,B...,请根据下述的邻接矩阵画出相应的无向图或有向图。
数据结构第七章-图

*
V0
V7
V6
V5
V4
V3
V2
V1
若图的存储结构为邻接表,则 访问邻接点的顺序不唯一, 深度优先序列不是唯一的
V0
V1
V3
V2
V7
V6
V5
V4
V0,V1,V3,V4,V7,V2,V5,V6,
※求图G以V0为起点的的深度优先序列(设存储结构为邻接矩阵)
void DFSAL(ALGraph G, int i) {/*从第v个顶点出发,递归地深度优先遍历图G*/ /* v是顶点的序号,假设G是用邻接表存储*/ EdgeNode *p; int w; visited[i] =1; Visit(i); /*访问第v个顶点*/ for (p=G.vertices[i].firstarc;p;p=p->nextarc) {w=p->adjvex; /*w是v的邻接顶点的序号*/ if (!visited[w]) DFSAL(G, w); /*若w尚未访问, 递归调用DFS*/ } }/*DFSAL*/
在邻接表存储结构上的广度优先搜索
*
Q
V0
V1
V2
V3
V4
V7
V5
V6
V1
V2
V3
V0
V4
V7
V5
V6
V0
V7
V6
V5
V4
V3
V2
V1
7.3 图的遍历
7
0
1
2
V0
V2
V3
V1
data
firstarc
0
1
^
^
adjvex
next
3
第七章——图及其应用

29
1
2
例
a
b
3c
d4
1a
2b
^
3c
31
4d
4 1^
12 42^
13 ^
3 4 ^^ 4 3 ^^
30
无向图的邻接多重表表示法
边结点:
mark ivex ilink jvex jlink
typedef struct node
{ int mark; // 访问标记域
int ivex, jvex; //该边依附的两个顶点在表头数组中位置
3. 图的算法应用。
3
图的定义和术语
• 图(Graph):图G是由两个集合V(G)和E(G)组成的,记为G=(V,E)。
其中:V(G)是顶点的非空有限集,E(G)是边的有限集合,边 是顶点的无序对或有序对。
• 有向图:有向图G是由两个集合V(G)和E(G)组成。
其中:V(G)是顶点的非空有限集E(G)是有向边(也称弧)的 有限集合,弧是顶点的有序对,记为<v,w>,v,w是顶点,v 为弧尾,w为弧头。
// 弧的定义
VRType adj;
// VRType是顶点关系类型。
// 对无权图,用1或0表示相邻否;对带权图,则为权值类型。
InfoType *info;
// 该弧相关信息的指针
} AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
typedef struct {
间是否有边(弧)、找顶点的邻接点等等。 邻接矩阵存储方式缺点:
n个顶点需要n*n个单元存储边(弧);空间效率为O(n2)。
20
图的邻接表存储表示
第7章图_数据结构

v4
11
2013-8-7
图的概念(3)
子图——如果图G(V,E)和图G’(V’,E’),满足:V’V,E’E 则称G’为G的子图
2 1 4 3 5 6 3 5 6 1 2
v1 v2 v4 v3 v2
v1 v3 v4
v3
2013-8-7
12
图的概念(4)
路径——是顶点的序列V={Vp,Vi1,……Vin,Vq},满足(Vp,Vi1),
2013-8-7 5
本章目录
7.1 图的定义和术语 7.2 图的存储结构
7.2.1 数组表示法 7.2.2 邻接表 ( *7.2.3 十字链表 7.3.1 深度优先搜索 7.3.2 广度优先搜索 7.4.1 图的连通分量和生成树 7.4.2 最小生成树
*7.2.4 邻接多重表 )
7.3 图的遍历
连通树或无根树
无回路的图称为树或自由树 或无根树
2013-8-7
18
图的概念(8)
有向树:只有一个顶点的入度为0,其余 顶点的入度为1的有向图。
V1 V2
有向树是弱 连通的
V3
V4
2013-8-7
19
自测题
7. 下列关于无向连通图特性的叙述中,正确的是
2013-8-7
29
图的存贮结构:邻接矩阵
若顶点只是编号信息,边上信息只是有无(边),则 数组表示法可以简化为如下的邻接矩阵表示法: typedef int AdjMatrix[MAXNODE][MAXNODE];
*有n个顶点的图G=(V,{R})的邻接矩阵为n阶方阵A,其定 义如下:
1 A[i ][ j ] 0
【北方交通大学 2001 一.24 (2分)】
第7章 图论
图
论
1
图(Graph):
可直观地表示离散对象之间的相互关系,
研究它们的共性和特性,以便解决具体问题。
图是一类相当广泛的实际问题的数学模型,
有着极其丰富的内容,是数据结构等课程的先
修内容。学习时应掌握好图论的基本概念、基
本方法、基本算法,善于把实际问题抽象为图
论的问题,然后用图论的方法解决问题。
5
G=<V(G),E(G), φG>
说明:
若把图中的边ei看作总是与两个结点 关联,则一个图G由两种实体组成,它有 一个叫做顶点(有时也叫做节点)的元素 的有限集合V={a,b,c……}和一个叫做边的 不同顶点对的有限集合E,一个图可简记 为G=<V,E>。集合V中顶点的个数n叫做图 的阶。6Fra bibliotek 2 一些概念
若边ei与结点无序偶(vj,vk)相关联,则 称该边为无向边。 若边ei与结点有序偶<vj,vk>相关联, 则称该边为有向边。其中vj称为ei的起 始结点;vk 称为ei的终止结点。 每一条边都是无向边 的图称无向图。
G=<V,E>=<{v1,v2,v3, v4,v5},{(v1,v2),(v2,v3), (v3,v4),(v2,v4)}>
16
例:图 7-1.5 所示的均为多重图。
图(a) 中结点 a 和 b 之间有两条平行边,结点 b 和 c 之间有三条平行边,在结点 b 有两个平行的 环。结点 a 的度数为 3 ,结点 c 的度数为 4 ,结 点 b 的度数为 9 。 图(b) 中,只有结点v1和v2之间有两条平行边。 这是因为该有向图中, < v1,v2 > 与 < v2 , v1 > 认为是不同的结点对。 17
数据结构课后习题答案第七章
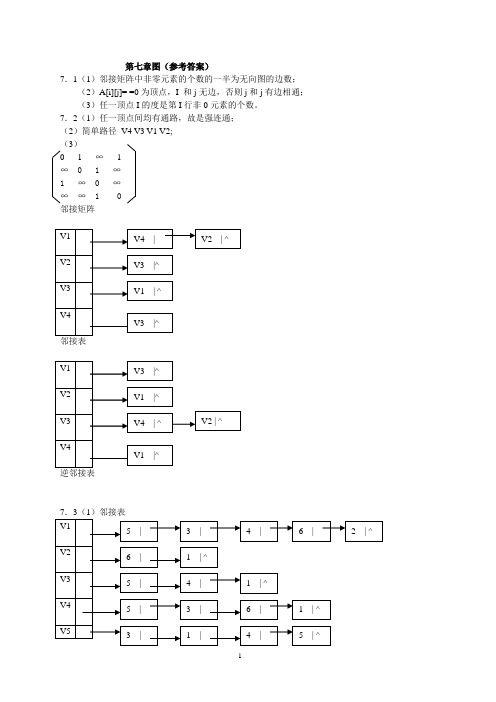
第七章图(参考答案)7.1(1)邻接矩阵中非零元素的个数的一半为无向图的边数;(2)A[i][j]= =0为顶点,I 和j无边,否则j和j有边相通;(3)任一顶点I的度是第I行非0元素的个数。
7.2(1)任一顶点间均有通路,故是强连通;(2)简单路径V4 V3 V1 V2;(3)0 1 ∞ 1∞ 0 1 ∞1 ∞ 0 ∞∞∞ 1 0邻接矩阵邻接表(2)从顶点4开始的DFS序列:V5,V3,V4,V6,V2,V1(3)从顶点4开始的BFS序列:V4,V5,V3,V6,V1,V27.4(1)①adjlisttp g; vtxptr i,j; //全程变量② void dfs(vtxptr x)//从顶点x开始深度优先遍历图g。
在遍历中若发现顶点j,则说明顶点i和j间有路径。
{ visited[x]=1; //置访问标记if (y= =j){ found=1;exit(0);}//有通路,退出else { p=g[x].firstarc;//找x的第一邻接点while (p!=null){ k=p->adjvex;if (!visited[k])dfs(k);p=p->nextarc;//下一邻接点}}③ void connect_DFS (adjlisttp g)//基于图的深度优先遍历策略,本算法判断一邻接表为存储结构的图g种,是否存在顶点i //到顶点j的路径。
设 1<=i ,j<=n,i<>j.{ visited[1..n]=0;found=0;scanf (&i,&j);dfs (i);if (found) printf (” 顶点”,i,”和顶点”,j,”有路径”);else printf (” 顶点”,i,”和顶点”,j,”无路径”);}// void connect_DFS(2)宽度优先遍历全程变量,调用函数与(1)相同,下面仅写宽度优先遍历部分。
数据结构第七章:图

例
a c G1
b d
vexdata firstarc adjvex next 1 4 ^ a 2 3 4 b c d 1 1 3 ^ ^ ^
19
7.3 图的遍历
深度优先遍历(DFS) 深度优先遍历
方法:从图的某一顶点 出发,访问此顶点; 方法:从图的某一顶点V0出发,访问此顶点;然后依 次从V 的未被访问的邻接点出发,深度优先遍历图, 次从 0的未被访问的邻接点出发,深度优先遍历图, 直至图中所有和V 相通的顶点都被访问到; 直至图中所有和 0相通的顶点都被访问到;若此时图 中尚有顶点未被访问, 中尚有顶点未被访问,则另选图中一个未被访问的顶 点作起点,重复上述过程, 点作起点,重复上述过程,直至图中所有顶点都被访 问为止。 问为止。
ω ij , 若(v i , v j )或 < v i , v j >∈ E(G) A[i, j ] = 0,其它
11
例
1 3
5
2
8 4 7 5 1 6 3 4 2
0 5 7 0 3
5 0 0 4 8
7 0 0 2 1
0 4 2 0 6
3 8 1 6 0
12
关联矩阵——表示顶点与边的关联关系的矩阵 表示顶点与边的关联关系的矩阵 关联矩阵
1
7.1 图的定义和术语
是由两个集合V(G)和E(G)组成的 组成的, 图(Graph)——图G是由两个集合 图 是由两个集合 和 组成的 记为G=(V,E) 记为
其中: 其中:V(G)是顶点的非空有限集 是顶点的非空有限集 E(G)是边的有限集合,边是顶点的无序对或有序对 是边的有限集合, 是边的有限集合
有向图——有向图 是由两个集合 有向图G是由两个集合 有向图 有向图 是由两个集合V(G)和E(G)组成的 和 组成的
北京理工大学数据结构图课件

B C D
第 5 页
E
7.1 图的定义与术语
3、无向图——无向图G是由两个集合V(G)和 E(G)组成的。 其中:V(G)是顶点的非空有限集。 E(G)是边的有限集合,边是顶点的 无序对,记为 (v,w) 或 (w,v),并且 (v,w)=(w,v)。
第 6 页
7.1 图的定义与术语
例如:
G2 = <V2,E2> V2 = { v0 ,v1,v2,v3,v4 } E2 = { (v0,v1), (v0,v3), (v1,v2), (v1,v4), (v2,v3), (v2,v4) }
V5
第 15 页
7.1 图的定义与术语
非 连 通 图
V0
V1
V2
V3
V0
V1 V3
V2
强连通分量
第 16 页
7.1 图的定义与术语
7、生成树
包含无向图 G 所有顶点的极小连通子图称为G生 成树。 极小连通子图意思是:该子图是G的连通子图, 在该子图中删除任何一条边,子图不再连通。
V0 V2 V3 V4 V3 连通图G1 V1 V0 V1 连通 所有顶点 V4 无回路
第 22 页
7.2 图的存储结构 3、有向图的逆邻接表 顶点:用一维数组存储(按编号顺序) 以同一顶点为终点的弧:用线性链表存储。
vexdata V0 V1 0 1 v0 v1 v2
v3
firstarc 3 0 0 ^ ^
V2
V3
2 3
^
^
2
章 类似于有向图的邻接表,所不同的是: 以同一顶点为终点弧:用线性链表存储
Boolean visited[MAX]; // 访问标志数组
第7章 图论 [离散数学离散数学(第四版)清华出版社]
![第7章 图论 [离散数学离散数学(第四版)清华出版社]](https://img.taocdn.com/s3/m/58b7923143323968011c9244.png)
6/27/2013 6:02 PM
第四部分:图论(授课教师:向胜军)
21
例:
a j i h c g d
1(a)
无 向 图
b
f
e
2(b)
7(j) 8(g) 9(d) 10(i)
6(e)
3(c) 4(h)
5(f)
6/27/2013 6:02 PM
第四部分:图论(授课教师:向胜军)
22
例:
1(b)
有向图
第四部分:图论(授课教师:向胜军)
6
[定义] 相邻和关联
在无向图G中,若e=(a, b)∈E,则称a与 b彼此相邻(adjacent),或边e关联 (incident) 或联结(connect) a, b。a, b称为边e的端点或 结束顶点(endpoint)。 在有向图D中,若e=<a, b>∈E,即箭头 由a到b,称a邻接到b,或a关联或联结b。a 称为e的始点(initial vertex),b称为e的终点 (terminal/end vertex)。
证明思路:将图中顶点的度分类,再利用定理1。
6/27/2013 6:02 PM 第四部分:图论(授课教师:向胜军) 9
[定理3] 设有向图D=<V, E>有n个顶点,m 条边,则G中所有顶点的入度之和等于所 有顶点的出度之和,也等于m。
即:
d ( v i ) d ( v i ) m.
i 1 i 1
n
n
证明思路:利用数学归纳法。
6/27/2013 6:02 PM
第四部分:图论(授课教师:向胜军)
10
一些特殊的简单图:
(1) 无向完全图Kn(Complete Graphs)
数据结构(C语言版)_第7章 图及其应用

实现代码详见教材P208
7.4 图的遍历
图的遍历是对具有图状结构的数据线性化的过程。从图中任 一顶点出发,访问输出图中各个顶点,并且使每个顶点仅被访 问一次,这样得到顶点的一个线性序列,这一过程叫做图的遍 历。
图的遍历是个很重要的算法,图的连通性和拓扑排序等算法 都是以图的遍历算法为基础的。
V1
V1
V2
V3
V2
V3
V4
V4
V5
图9.1(a)
图7-2 图的逻辑结构示意图
7.2.2 图的相关术语
1.有向图与无向图 2.完全图 (1)有向完全图 (2)无向完全图 3.顶点的度 4.路径、路径长度、回路、简单路径 5.子图 6.连通、连通图、连通分量 7.边的权和网 8.生成树
2. while(U≠V) { (u,v)=min(wuv;u∈U,v∈V-U); U=U+{v}; T=T+{(u,v)}; }
3.结束
7.5.1 普里姆(prim)算法
【例7-10】采用Prim方法从顶点v1出发构造图7-11中网所对 应的最小生成树。
构造过程如图7-12所示。
16
V1
V1
V2
7.4.2 广度优先遍历
【例7-9】对于图7-10所示的有向图G4,写出从顶点A出发 进行广度优先遍历的过程。
访问过程如下:首先访问起始顶点A,再访问与A相邻的未被 访问过的顶点E、F,再依次访问与E、F相邻未被访问过的顶 点D、C,最后访问与D相邻的未被访问过的顶点B。由此得到 的搜索序列AEFDCB。此时所有顶点均已访问过, 遍历过程结束。
【例7-1】有向图G1的逻辑结构为:G1=(V1,E1) V1={v1,v2,v3,v4},E1={<v1,v2>,<v2,v3>,<v2,v4>,<v3,v4>,<v4,v1>,<v4,v3>}
数据结构-第7章图答案

7.3 图的遍历 从图中某个顶点出发游历图,访遍图中其余顶点, 并且使图中的每个顶点仅被访问一次的过程。 一、深度优先搜索 从图中某个顶点V0 出发,访问此顶点,然后依次 从V0的各个未被访问的邻接点出发深度优先搜索遍 历图,直至图中所有和V0有路径相通的顶点都被访 问到,若此时图中尚有顶点未被访问,则另选图中 一个未曾被访问的顶点作起始点,重复上述过程, 直至图中所有顶点都被访问到为止。
void BFSTraverse(Graph G, Status (*Visit)(int v)) { // 按广度优先非递归遍历图G。使用辅助队列Q和访问标志数组 visited。 for (v=0; v<G.vexnum; ++v) visited[v] = FALSE; InitQueue(Q); // 置空的辅助队列Q for ( v=0; v<G.vexnum; ++v ) if ( !visited[v]) { // v尚未访问 EnQueue(Q, v); // v入队列 while (!QueueEmpty(Q)) { DeQueue(Q, u); // 队头元素出队并置为u visited[u] = TRUE; Visit(u); // 访问u for ( w=FirstAdjVex(G, u); w!=0; w=NextAdjVex(G, u, w) ) if ( ! visited[w]) EnQueue(Q, w); // u的尚未访问的邻接顶点w入队列Q
4。邻接多重表
边结点
mark ivex
顶点结点
ilink
jvex
jlink
info
data
firstedge
#define MAX_VERTEX_NUM 20 typedef emnu {unvisited, visited} VisitIf; typedef struct Ebox { VisitIf mark; // 访问标记 int ivex, jvex; // 该边依附的两个顶点的位置 struct EBox *ilink, *jlink; // 分别指向依附这两个顶点的下一条 边 InfoType *info; // 该边信息指针 } EBox; typedef struct VexBox { VertexType data; EBox *firstedge; // 指向第一条依附该顶点的边 } VexBox; typedef struct { VexBox adjmulist[MAX_VERTEX_NUM]; int vexnum, edgenum; // 无向图的当前顶点数和边数 } AMLGraph;
第七章 图

顶点结点结构
顶点值域 指针域 指针域
tailvex headvex hlink
tlink
info
弧结点结构
弧尾结点 弧头结点 指针域 指针域 弧上信息
A B
C
在十字链表中容易求 得顶点的出度和入度
0 A
0 1
∧
2 0∧∧
1 B 2 C
2 1∧
0 2∧∧
图的遍历方法有两种: 深度优先搜索和广度优先搜索
7.3.1 深度优先搜索
按照深度方向搜索 ,它类似于树的先根遍历。 深度优先算法的基本思想是: (1)从图中某个顶点v0出发,首先访问v0。 (2)找出刚访问过的顶点vi的第一个未被访问 的邻接点,然后访问该顶点。重复此步骤,直 到当前的顶点没有未被访问的邻接点为止。 (3)返回前一个访问过的顶点,找出该顶点的 下一个未被访问的邻接点,访问该顶点。转2。
一、图的数组(邻接矩阵)存储表示 二、图的邻接表存储表示
三、有向图的十字链表存储表示 四、无向图的邻接多重表存储表示
一、图的数组(邻接矩阵)表示法
所谓邻接矩阵(Adjacency Matrix)的存 储结构,就是用一维数组存储图中顶点的信息, 用矩阵表示图中各顶点之间的邻接关系。假设 图G=(V,E)有n个确定的顶点,即V= {v0,v1,…,vn-1},则表示G中各顶点相邻关系为一 个n×n的矩阵
遍 历
DFSTraverse(G, v, Visit());
//从顶点v起深度优先遍历图G,并对每 //个顶点调用函数Visit一次且仅一次。
BFSTraverse(G, v, Visit());
//从顶点v起广度优先遍历图G,并对每 //个顶点调用函数Visit一次且仅一次。
第7章图(Graphs)

7.1 图的概念及术语
v1 v3 有向边<v3, v4> V3:始点, v4: 终点 v2 v4
图的构成: • 结点集:V={v1,v2,v3,v4}, • 有向边集:E={<v1,v3>,<v1,v2>,<v3,v4>,<v4,v1>}
7.1 图的概念及术语
v1 v3 v2 v4 v1 v2
v3
为从顶点vi 到顶点 vj 的路径。 • 路径长度 –非带权图的路径长度是指此路径上的边数。 –带权图的路径长度是指路径上各边的权之和
7.1 图的概念及术语
• 简单路径 若路径上各顶点 v1,v2,...,vm 均不互相重 复, 则称这样的路径为简单路径。 • 回路 若路径上第一个顶点 v1 与最后一个顶点vm 重合, 则称这样的路径为回路或环。 • 连通图与连通分量 在无向图中, 若从顶点v1到顶 点v2有路径, 则称顶点v1与v2是连通的。 • 如果图中任意一对顶点都是连通的, 则称此图是连 通图。 • 非连通图的极大连通子图叫做连通分量.
7.1 图的概念及术语
v1
v2
v4Βιβλιοθήκη v3路径: (1) <v1, v3>, <v3, v4> (简单路径)
(2) <v1, v3>, <v3, v4>, <v4, v1> (环)
(3) <v3, v4>
7.1 图的概念及术语
• 路径: 在图 G=(V, E) 中, 若存在边的序列 (vi, vp1)、(vp1, vp2)、...、(vpm, vj) 则称顶点序列 ( vi vp1 vp2 ... vpm vj )
v4 v5
数据结构 C语言版(严蔚敏版)第7章 图

1
2
4
1
e6 2 4
2016/11/7
29
7.3 图的遍历
从已给的连通图中某一顶点出发,沿着一 些边访遍图中所有的顶点,且使每个顶点 仅被访问一次,就叫做图的遍历 ( Graph Traversal )。 图中可能存在回路,且图的任一顶点都可 能与其它顶点相通,在访问完某个顶点之 后可能会沿着某些边又回到了曾经访问过 的顶点。 为了避免重复访问,可设置一个标志顶点 是否被访问过的辅助数组 visited [ ]。
2
1 2
V2
V4
17
结论:
无向图的邻接矩阵是对称的; 有向图的邻接矩阵可能是不对称的。 在有向图中, 统计第 i 行 1 的个数可得顶点 i 的出度,统计第 j 行 1 的个数可得顶点 j 的入度。 在无向图中, 统计第 i 行 (列) 1 的个数可得 顶点i 的度。
2016/11/7
18
2
邻接表 (出度表)
adjvex nextarc
data firstarc
0 A 1 B 2 C
2016/11/7
1 0 1
逆邻接表 (入度表)
21
网络 (带权图) 的邻接表
6 9 0 2 1 C 2 8 3 D
data firstarc Adjvex info nextarc
2016/11/7
9
路径长度 非带权图的路径长度是指此路径 上边的条数。带权图的路径长度是指路径 上各边的权之和。 简单路径 若路径上各顶点 v1,v2,...,vm 均不 互相重复, 则称这样的路径为简单路径。 回路 若路径上第一个顶点 v1 与最后一个 顶点vm 重合, 则称这样的路径为回路或环。
运筹学第7章图与网络优化

1
链,圈,初等链,初等圈,简单链(圈)
2
相邻节点的序列 {v1 ,v2 ,…, vn} 构成一条链(link)p178;
3
在无向图中,节点不重复出现的链称为初等链;
4
首尾相连的链称为圈(loop) ;首尾相连的初等链称为初等圈;
5
边不重复出现的链(圈)称为简单链(圈)
01
02
子图,部分图;连通图,成分
(1).与v3相连的临时标号有v5
第五步:
T(v5)=min{T(v5),P(v3)+d35}=min{9,7+3}=9
(2).P(v5)=9
最短路线:
vs→v1→v4→ v5 vs→v2→v4→ v5
vS
v2
v3
v4
v5
1
2
2
2
3
3
3
4
4
0
4
5
3
7
9
*
也可以用表格的形式求解。p190
斯坦纳树问题
假设我们在北京、上海、西安三城市之间架设电话线,一种办法是分别联通北京--上海和北京--西安。另一种办法是选第四个点,假设郑州。由此分别向三城市架线,可能你不会想到第二种办法所用的电话线只是第一种办法的86.6%,即可取得比第一种办法节约13%的显著经济效益。这就是离散数学界30年代提出的著名的斯坦纳树问题,但一直未能得到证明。
平面图(planar graph),若在平面上可以画出该图而没有任何边相交
*
7基础图,路,回路,欧拉回路
在有向图D(V,A)中去掉箭头,称为D的基础图,G(D)
01
在有向图中,链 路
02
圈 回路
03
图(Graph)是一种比线性表和树更为复杂的数据结构在图形....ppt

第七章
12
权、网、子图
在图的边或弧中给出相关的数,称
15 A 9
为权。 权可以代表一个顶点到另一个顶
11
点的距离、耗费等。带权的图通常称作 B 7 21
E
网。
3 C2F
假设有两个图G=(V,{VR}) 和 图 G=(V,{VR}), 如果 VV且 VRVR, 则称 G 为 G 的子图。
B B
C
A E
第七章
11
完全图、稀疏图、稠密图
假设图中有 n 个顶点,e 条边,则: ❖ 含有 n(n-1)/2 条边的无向图称作完全图; (无向图中边的取 值范围为0~n(n-1)/2) ❖ 含有 n(n-1) 条弧的有向图称作 有向完全图; (有向图中边 的取值范围为0~n(n-1))
❖ 若边或弧的个数 e<n*logn,则称作稀疏图,否则称作稠密 图。(当n很大时,n2>> n*log n)
❖ 生成树是对连通图而言的; ❖ 是连通图的极小连通子图; ❖ 包含图中的所有顶点; ❖ 有且仅有n-1条边。
B A
F
C D
E
第七章
19
7.2 图的存储结构
一、数组表示法(邻接矩阵) 二、邻接表存储表示 三、有向图的十字链表存储表示 四、无向图的邻接多重表存储表示
第七章
20
一、数组表示法(邻接矩阵)
由顶点集和边集构成的图称作无向图(Undigraph)。
例如: G2=(V2, {R2})
B
C
V2={A, B, C, D, E, F} R2={(A,B), (A,E),
(B,E), (B,F),
(C,D), (C,F) ,
A
D
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
V2
V3
V2
V3
连通分图(有向图中为强连通分量)
无向图G 的极大连通子图称为G的连通分量
极大连通子图意思是:该子图是 G 连通子图
,将G 的任何不在该子图中的顶点加入,子 图不再连通;
连通分图
非 连 通 图 V0 V3 V1 V2 V4 V5
有向图D 的极大强连通子图称为D 的强连通分量
3 2 3 2 2
4
4
邻接结点 指向下一邻 数据 接点的指针
2.有向图的邻接表和逆邻接表 1)有向图的邻接表(出边表) 顶点:用一维数组存储(按编号顺序) 以同一顶点为起点的弧:用线性链表存储
下标 编号 0 1 2 3 link
V0 V1 V2 V3
1
2
V0
V1
3 0
V2
V3
m-1
2)有向图的逆邻接表(入边表) 顶点:用一维数组存储(按编号顺序) 以同一顶点为终点的弧:用线性链表存储
接的有向图。
V0 V2 V3
在一个含有n个顶点的有向完全图中,有n(n-1)条弧。
V1
V0
V1
V4
V2
V3
邻接点:边的两个顶点 关联边:若边e= (v, u), 则称顶点v、u 关联边 顶点的度 在无向图中,顶点V的度 = 与V相关联的 边的数目,记作TD(V) 在有向图中,顶点V的度= V的出度+V的入 度 顶点V的出度=以V为起点有向边数 顶点V的入度=以V为终点有向边数
V0 V1 V2 V3 V4
0 1 0 1 0 1 0 1 0 1 0 1 0 1 1 1 0 1 0 0 0 1 1 0 0
V0
V1
V0 V1 V2 V3
V2
V3
0 0 0 1
1 0 0 0
1 0 0 0
0 0 1 0
4.邻接矩阵的C语言描述
#define N 5/*顶点数*/ #define M 6 /*边数*/ typedef char vextype; /*顶点类型*/ typedef sturct{ vextype vexs[N]; /*存顶点的数组*/ adjtype edge[N][M];/*存边信息的矩阵 */ V0 V1 V2 V3 V4 0 1 0 1 0 }
V0 V1 V2 V3 V4
V0 V2 V3
V1
V4
0 1 0 1 0 1 0 1 0 1 0 1 0 1 1 1 0 1 0 0 0 1 1 0 0
V0
V1
V0 V1 V2 V3
V2
V3
0 0 0 1
1 0 0 0
1 0 0 0
0 0 1 0
邻接矩阵存储下图的有关操作
1)求顶点v的度:等于二维数组对应行(或列)中1的个数; 2)判断两顶点是否邻接:只需判二维数组对应分量是否为1; 3)在图中增加、删除边:只需对二维数组对应分量赋值1或清0; 4)检测图中的总边数:扫描整个数组A,统计出数组中非0元素的 个数。无向图的总边数为非0元素个数的一半,而有向图的总弧 数为非0元素个数; V0 V2 V3 V4 V1
0 1 2 3 4 m-1 V0 V1 V2 V3 V4 1 0 1
0
3 2 3 2 2
邻接表的空间代价 与图的边及顶点数均有关
V0
V1
4
V2
V3 V4
4
1
4. 邻接表在C语言中的类型定义 typedef struct node //定义 边结点的类型 { char adjver; //边的邻接点的数据 struct node *next; //指向本边下一邻接点的指针 }edgenode; typedef struct { //定义 顶点的类型 char vertex; //顶点的数据 edgenode *link; //指向本边邻接表 }vernode;
极大强连通子图意思是:该子图是D强连通子图
,将D的任何不在该子图中的顶点加入,子图不 再是强连通的;
强连通分量 V0 V1 V0 V1
V2
V3
V2
V3
生成树 包含无向图G 所有顶点的的极小连通子图称为G 的生成树 极小连通子图意思是:该子图是G 的连通子图,在该子图中删除任何一 条边,子图不再连通, 若T是G 的生成树当且仅当T 满足如下条件 T是G 的连通子图 T包含G 的所有顶点 T中无回路
0 1 2 3
V0 V1 V2 V3
3 0 0 2
V0
V1
V2
V3
m-1
3.邻接表存储下图的有关操作
1)求顶点v的度: 2)判断两顶点是否邻接: 3)在图中增加、删除边: 4)检测图中的总边数:
V0 V2 V3 V4 V1 0 1 2 3 4 m-1 V0 V1 V2 V3 V4 1 3
0 1
0
1
V0 V1 V2 V3 V4
V1
V0 V2 V3
V1
V4
0 1 0 1 0
1 0 1 0 1
0 1 0 1 1
1 0 1 0 0
0 1 1 0 0
V2
0 0 0 1 1 0 0 0
V3
1 0 0 0 0 1 0 0
V0 V1 V2 V3
2.无向图邻接矩阵表示的特点: 1)无向图邻接矩阵是对称矩阵,可考虑矩阵的压缩 存储 2)G占用存储空间只与它的顶点数有关,与边数无 关;适用于边稠密的图;
V0
V2 V3
V1
V0
V1
V4
V2
V3
图的存储结构要保存两类信息: 1)顶点的数据 V0 V1 V2 V3 2)顶点间的关系
V4
邻接矩阵表示法
邻接表表示法
7.2.1. 邻接矩阵(数组)表示
1.图的邻接矩阵 图G的邻接矩阵是满足如下条件:
A[i][j]= 1 0 若(vi,vi+1)E 或 <vi,vi+1>E V0 否则
0 1 2 3 4 m-1
V0 V1 V2 V3 V4
1 0 1
3 2 3 2 2 4 4
0 1
函数:
int create(link_graph *ga ) { NODE *p;
int n, e, i;char v1, v2;
scanf(“%d%d\n”, &n,&e); //读入顶点数、边数 ga->n=n, ga->e=e; for(i=0; i<n; i++) //建立顶点数组 { scanf(“%c”, &ga->adjlist[i].vertex); //读入顶点数据
,
时间复杂度O(n+e)
typedef struct node //定义 边结点 { char adjver struct node *next; }edgenode; typedef struct { //定义 顶点 char vertex; edgenode *link; }vernode; typedef struct {//定义 图 vernode adjlist[MAX]; int n,e; //n-顶点数,e-边数 }link_graph; link_graph *ga;
V0 V1 V2 V3 V4
V0 V2
V1
V3
V4
0 1 0 1 0
1 0 1 0 1
0 1 0 1 0 1 0 1 1 1 0 0 1 0 0
邻接矩阵表示法的空间代价 只与图的顶点数有关
3.邻接矩阵下图的有关操作
1)求顶点v的度: 2)判断两顶点是否邻接: 3)在图中增加、删除边: 4)检测图中的总边数:
(b)
连通图、强连通图
在无(有)向图G=< V, E >中,若对任何两个顶
点 v、u 都存在从v 到 u 的路径,则称G是连通 图 对有向图而言,称强连通图
连 通 图 V0 V1
V0
V1 V4
V2 V5 V1
V2
V3
V0
V4
V1
V3 V0
非 连 通 图 非 强 连 通 图
强 连 通 图
V1
V2
V3 V4 V2 V3
子图
设有两个图G=(V,E)、G1=(V1,E1)
,若V1 V,E1 E,E1关联的顶点都在 V1中,则称 G1是G的子图;
(b)、(c) 是 (a) 的子图
V0 V1 V0 V2 V4 V3 V4 V3 (c) V1 V0 V1
例
V2
V3
V2
V4
(a)
V0 V1
V2
V3 V4
G1=<V1,E1> V1={v0 ,v1,v2,v3,v4} E1={(v0,v1),(v0,v3),(v1,v2),(v1,v4),(v2,v3)(v2,v4)}
图的应用举例:
例1 交通图(公路、铁路) 顶点:地点 边:连接地点的公路 交通图中的有单行道双行道,分别用有向边、无向边表示; 例2 电路图 顶点:元件 边:连接元件之间的线路 例3 通讯线路图 顶点:地点 边:地点间的连线 例4 各种流程图 如产品的生产流程图 顶点:工序 边:各道工序之间的顺序关系
2 3 2 2
4 4
1)求顶点v的度:等于v对应线性链表的长度; 2)判断两顶点是否邻接:要看v对应线性链表中 有无对应的结点 3)在图中增加、删除边:在相应的顶点的链表 中插入、删除结点 4)检测图中的总边数:
无向图的邻接表的特点
1)在G邻接表中,同一条边对应两个结点; 2)设存储顶点的一维数组大小为m(m图的顶点数n), 图 的边数为e,G占用存储空间为:m+2*e。G占用存储空间 与 G 的顶点数、边数均有关;适用于边稀疏的图
