2010年中考数学压轴题100题精选(91-100题)答案巩固基础

合集下载

2010年中考数学压轴题100题精选(81-90题)答案

合并自： (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、、等站 E 度教育网2010年中考数学压轴题100题精选（81-90题）答案【081】解：（1）（0，－3），b ＝－94，c ＝－3． ···································································· 3分（2）由（1），得y ＝34x 2－94x －3，它与x 轴交于A ，B 两点，得B （4，0）．∴OB ＝4，又∵OC ＝3，∴BC ＝5．由题意，得△BHP ∽△BOC ， ∵OC ∶OB ∶BC ＝3∶4∶5，∴HP ∶HB ∶BP ＝3∶4∶5，∵PB ＝5t ，∴HB ＝4t ，HP ＝3t ．∴OH ＝OB －HB ＝4－4t ．由y ＝34tx －3与x 轴交于点Q ，得Q （4t ，0）．∴OQ ＝4t ． ······································································································· 4分 ①当H 在Q 、B 之间时， QH ＝OH －OQ＝（4－4t ）－4t ＝4－8t ． ········································································ 5分 ②当H 在O 、Q 之间时， QH ＝OQ －OH＝4t －（4－4t ）＝8t －4． ········································································ 6分综合①，②得QH ＝｜4－8t ｜； ········································································ 6分（3）存在t 的值，使以P 、H 、Q 为顶点的三角形与△COQ 相似． ······················· 7分①当H 在Q 、B 之间时，QH ＝4－8t ，若△QHP ∽△COQ ，则QH ∶CO ＝HP ∶OQ ，得483t -＝34tt，∴t ＝732． ········································································································ 7分若△PHQ ∽△COQ ，则PH ∶CO ＝HQ ∶OQ ，得33t ＝484tt -，即t 2＋2t －1＝0．∴t 11，t 21（舍去）． ······················································· 8分 ②当H 在O 、Q 之间时，QH ＝8t －4．若△QHP ∽△COQ ，则QH ∶CO ＝HP ∶OQ ，得843t -＝34tt，∴t ＝2532． ········································································································ 9分若△PHQ ∽△COQ ，则PH ∶CO ＝HQ ∶OQ ，得33t ＝844t t -，即t 2－2t ＋1＝0． ∴t 1＝t 2＝1（舍去）． ···················································································· 10分综上所述，存在t 的值，t 11，t 2＝732，t 3＝2532． ··························· 10分附加题：解：（1）8； ·················································································································· 5分（2）2．················································································································ 10分合并自： (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、、等站 E 度教育网【082】（09上海）略【083】. 解：（1）B （1（2）设抛物线的解析式为y =ax (x+a )，代入点B （1,，得a =，因此2y x =+ （3）如图，抛物线的对称轴是直线x =—1，当点C 位于对称轴与线段AB 的交点时，△BOC的周长最小.设直线AB 为y =kx +b .所以20.k k b k b b ⎧⎪⎧+=⎪⎪⎨⎨-+=⎪⎩⎪⎪⎩解得因此直线AB 为y x =+ 当x =－1时，y =，因此点C 的坐标为（－1.（4）如图，过P 作y 轴的平行线交AB 于D .2221()()213212PAB PAD PBD D P B A S S S y y x x x ∆∆∆=+=--⎡⎤⎫=+-⨯⎢⎥⎪⎪⎢⎥⎝⎭⎝⎭⎣⎦=⎫=+⎪⎝⎭当x =－12时，△PAB ，此时1,2P ⎛- ⎝⎭. 【084】解：（1）⊙P 与x 轴相切.∵直线y =－2x －8与x 轴交于A （4，0），与y 轴交于B （0，－8），∴OA =4，OB =8.由题意，OP =－k ，∴PB =PA =8+k . 在Rt △AOP 中，k 2+42=(8+k )2， ∴k =－3，∴OP 等于⊙P 的半径， ∴⊙P 与x 轴相切.（2）设⊙P 与直线l 交于C ，D 两点，连结PC ，PD 当圆心P 在线段OB 上时,作PE ⊥CD 于E .合并自： (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、、等站 E 度教育网∵△PCD 为正三角形，∴DE =12CD =32，PD =3， ∴PE. ∵∠AOB =∠PEB =90°， ∠ABO =∠PBE ，∴△AOB ∽△PEB ，∴2,AO PE AB PB PB=，∴PB =∴8PO BO PB =-=，∴8)P -，∴8k =-. 当圆心P 在线段OB 延长线上时,同理可得P (0,8)， ∴k =8，∴当k8或k =8时，以⊙P 与直线l 的两个交点和圆心P 为顶点的三角形是正三角形.【085】解: (1)由题知: ⎩⎨⎧=+-=++033903b a b a ……………………………………1 分解得: ⎩⎨⎧-=-=21b a ……………………………………………………………2分∴ 所求抛物线解析式为: 322+=x －－x y ……………………………3分(2) 存在符合条件的点P , 其坐标为P (－1, 10)或P(－1,－ 10)或P (－1, 6) 或P (－1, 35)………………………………………………………7分 (3)解法①：过点E 作EF ⊥x 轴于点F , 设E ( a ,-2a -2a ＋3 )( －3< a < 0 ) ∴EF =-2a -2a ＋3，BF =a ＋3，OF =－a ………………………………………………8 分∴S 四边形BOCE =21BF ·EF + 21(OC +EF )·OF =21( a ＋3 )·(－2a －2a ＋3) + 21(－2a －2a ＋6)·（－a ）……………………………9 分合并自： (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、、等站 E 度教育网=2929232+--a a ………………………………………………………………………10 分 =－232)23(+a +863∴ 当a =－23时，S 四边形BOCE 最大, 且最大值为 863．……………………………11 分此时，点E 坐标为 (－23，415)……………………………………………………12分解法②：过点E 作EF ⊥x 轴于点F ，设E ( x , y ) ( －3< x < 0 ) …………………………8分则S 四边形BOCE =21(3 + y )·(－x ) + 21( 3 + x )·y ………………………………………9分 = 23( y －x )= 23(332+x －－x ) …………………………………10 分= －232)23(+x + 863∴ 当x =－23时，S 四边形BOCE 最大，且最大值为 863． …………………………11分此时，点E 坐标为 (－23，415) ……………………………………………………12分【086】⑴证明：∵BC 是⊙O 的直径∴∠BAC=90o又∵EM ⊥BC ，BM 平分∠ABC ， ∴AM=ME ，∠AMN=EMN 又∵MN=MN ， ∴△ANM ≌△ENM⑵∵AB 2=A F ·AC ∴ABAF AC AB =又∵∠BAC=∠FAB=90o ∴△ABF ∽△ACB ∴∠ABF=∠C又∵∠FBC=∠ABC+∠FBA=90o ∴FB 是⊙O 的切线合并自： (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、、等站 E 度教育网⑶由⑴得AN=EN ，AM=EM ，∠AMN=EMN ，又∵AN ∥ME ，∴∠ANM=∠EMN ， ∴∠AMN=∠ANM ，∴AN=AM ， ∴AM=ME=EN=AN ∴四边形AMEN 是菱形 ∵cos ∠ABD=53，∠ADB=90o∴53=AB BD 设BD=3x ，则AB=5x ，，由勾股定理()()x x －x AD 43522==而AD=12，∴x=3 ∴BD=9，AB=15∵MB 平分∠AME ，∴BE=AB=15 ∴DE=BE-BD=6∵ND ∥ME ，∴∠BND=∠BME ，又∵∠NBD=∠MBE ∴△BND ∽△BME ，则BEBD ME ND =设ME=x ，则ND=12-x ，15912=-x x ，解得x=215∴S=M E ·DE=215×6=45【087】（天门）略合并自： (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、、等站 E 度教育网【088】解：（1）法一：由图象可知：抛物线经过原点，设抛物线解析式为2(0)y ax bx a =+≠．把(11)A ，，(31)B ，代入上式得： ································································································ 1分 11931a b a b =+⎧⎨=++⎩解得1343a b ⎧=-⎪⎪⎨⎪=⎪⎩··································································································· 3分 ∴所求抛物线解析式为21433y x x =-+··················································································· 4分法二：∵(11)A ，，(31)B ，，∴抛物线的对称轴是直线2x =．设抛物线解析式为2(2)y a x h =-+（0a ≠） ······································································ 1分把(00)O ，，(11)A ，代入得 220(02)1(12)a h a h ⎧=-+⎪⎨=-+⎪⎩ 解得1343a h ⎧=-⎪⎪⎨⎪=⎪⎩······················································································ 3分 ∴所求抛物线解析式为214(2)33y x x =--+． ····································································· 4分合并自： (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、、等站 E 度教育网（2）分三种情况：①当02t <≤，重叠部分的面积是OPQ S △，过点A 作AF x ⊥轴于点F ， ∵(11)A ，，在Rt OAF △中，1AF OF ==，45AOF ∠=°在Rt OPQ △中，OP t =，45OPQ QOP ∠=∠=°，∴cos 452PQ OQ t ===°， ∴2211224S t ⎛⎫== ⎪ ⎪⎝⎭． ····················································· 6分 ②当23t <≤，设PQ 交AB 于点G ，作GH x ⊥轴于点H 45OPQ QOP ∠=∠=°，则四边形OAGP 是等腰梯形，重叠部分的面积是OAGP S 梯形． ∴2AG FH t ==-， ∴11()(2)1122S AG OP AF t t t =+=+-⨯=-． ············ 8分 ③当34t <<，设PQ 与AB 交于点M ，交BC 于点N ，重叠部分的面积是OAMNC S 五边形．因为P N C △和BMN △都是等腰直角三角形，所以重叠部分的面积是OA M NS 五边形B M NOA B C S S=-△梯形． ∵(31)B ，，OP t =， ∴3PC CN t ==-，∴1(3)4BM BN t t ==--=-，∴211(23)1(4)22S t =+⨯--2111422S t t =-+-． ······················································· 10分（3）存在 11t = ·················································································································· 12分 22t = ················································································································ 14分合并自： (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、、等站 E 度教育网【089】解：（1）圆心O 在坐标原点，圆O 的半径为1，∴点A B C D 、、、的坐标分别为(10)(01)(10)(01)A B C D --，、，、，、，抛物线与直线y x =交于点M N 、，且MA NC 、分别与圆O 相切于点A 和点C ，∴(11)(11)M N --，、，． ············································································································ 2分点D M N 、、在抛物线上，将(01)(11)(11)D M N --，、，、，的坐标代入 2y ax bx c =++，得：111c a b c a b c =⎧⎪-=-+⎨⎪=++⎩ 解之，得：111a b c =-⎧⎪=⎨⎪=⎩∴抛物线的解析式为：21y x x =-++． ················································································ 4分（2）2215124y x x x ⎛⎫=-++=--+ ⎪⎝⎭∴抛物线的对称轴为12x =，12OE DE ∴===，． ······················· 6分连结90BF BFD ∠=，°，BFD EOD ∴△∽△，DE ODDB FD∴=，又12DE OD DB ===，，5FD ∴=，5210EF FD DE ∴=-=-=． ··············································································· 8分（3）点P 在抛物线上． ············································································································· 9分设过D C 、点的直线为：y kx b =+，将点(10)(01)C D ，、，的坐标代入y kx b =+，得：11k b =-=，，合并自： (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、、等站 E 度教育网∴直线DC 为：1y x =-+． ·································································································· 10分过点B 作圆O 的切线BP 与x 轴平行，P 点的纵坐标为1y =-，将1y =-代入1y x =-+，得：2x =．∴P 点的坐标为(21)-，， ········································································································ 11分当2x =时，2212211y x x =-++=-++=-，所以，P 点在抛物线21y x x =-++上． ·············································································· 12分说明：解答题各小题中只给出了1种解法，其它解法只要步骤合理、解答正确均应得到相应的分数．合并自： (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、、等站 E 度教育网【090】（1）解：把A （1-，0），C （3，2-）代入抛物线 23y ax ax b =-+ 得⎩⎨⎧-=+-=+-⨯--2990)1(3)1(2b a a b a a ···························································································· 1分整理得 ⎩⎨⎧-==+204b b a ·················· ……………… 2分解得⎪⎩⎪⎨⎧-==221b a ………………3分∴抛物线的解析式为 223212--=x x y ············································································ 4分（2）令0223212=--x x 解得 1214x x =-=，∴ B 点坐标为（4，0）又∵D 点坐标为（0，2-） ∴AB ∥CD ∴四边形ABCD 是梯形． ∴S 梯形ABCD ＝82)35(21=⨯+ ································ 5分设直线)0(1≠+=k kx y 与x 轴的交点为H ，与CD 的交点为T ，则H （k 1-，0）， T （k3-，2-） ····················· 6分∵直线)0(1≠+=k kx y 将四边形ABCD 面积二等分∴S 梯形AHTD ＝21S 梯形ABCD ＝４∴42)311(21=⨯-+-kk ·········································· 7分 ∴34-=k ···································································· 8分（3）∵MG ⊥x 轴于点G ，线段MG ︰AG ＝1︰2∴设M （m ，21+-m ）， (9)∵点M 在抛物线上 ∴22321212--=+-m m m 解得1231m m ==-，（舍去） ······························· 10分∴M 点坐标为（3，2-） ································································································ 11分根据中心对称图形性质知，MQ ∥AF ，MQ ＝AF ，NQ ＝EF ，∴N 点坐标为（1，3-） ······························································································· 12分图(9) -2图(9) -1。

2010年数学中考压轴题精选

EF 将△ ABC 的周长和面积同时平分？若存在直线
EF，求出 x 的值；若不存在直线 EF ，请说明理由． C
A
D
B
C
A
D
B
备用图
2010 年苏州市
5.如图，以 A 为顶点的抛物线与 y 轴交于点 B．已知 A 、 B 两点的坐标分别为 (3， 0)、 (0 ，4)．
(1) 求抛物线的解析式；
(2)设 M(m ， n)是抛物线上的一点 (m 、 n 为正整数 ) ，且它位于对称轴的右侧．若以 M 、 B、 O、 A 为顶
t，
使面积 y 最小？若存在，求出 y 的最小值；若不存在，说明理由．
（ 3）是否存在某一时刻 t ，使 P、Q、 F 三点在同一条直线上？若存在，求出此时
t 的值；若不存在，
说明理由．（图（ 3）供同学们做题使用）
A
A
D
B
C（ E）
F
图（ 1）
解：（ 1）（2）（3）
D P
Q
B
EC
F
图（ 2）
点的四边形四条边的长度是四个连续的正整数，求点 (3) 在(2) 的条件下，试问：对于抛物线对称轴上的任意一点
否总成立 ?请说明理由．
M 的坐标； P， PA2+PB2+PM 2＞ 28 是
大连市 2010
6.如图 17，抛物线 F：y ax2 bx c(a 0) 与 y 轴相交于点 C，直线 L1 经过点 C 且平行于 x 轴，
（ 2）若 CE=2 ，BD=BC ，求∠ BPD 的正切值；
（ 3）若 tan BPD
1
，设 CE=x ，△ ABC 的周长为 y，求 y 关于 x 的函数关系式 .

【中考分类】2010年中考数学压轴题精选

2010年各地中考数学压轴题精选1（北京）问题：已知△ABC中，∠BAC=2∠ACB，点D是△ABC内的一点，且AD=CD，BD=BA。

探究∠DBC与∠ABC度数的比值。

请你完成下列探究过程：先将图形特殊化，得出猜想，再对一般情况进行分析并加以证明。

(1) 当∠BAC=90︒时，依问题中的条件补全右图。

观察图形，AB与AC的数量关系为；可得到∠DBC与∠ABC度数的比值为；(2) 当∠BAC≠90︒时，请你画出图形，研究∠DBC与∠ABC度数的比值是否与(1)中的结论相同，写出你的猜想并加以证明。

2（盐城）已知：函数y=ax2+x+1的图象与x轴只有一个公共点．（1）求这个函数关系式；（2）如图所示，设二次．．函数y=ax2+x+1图象的顶点为B，与y轴的交点为A，P为图象上的一点，若以线段PB为直径的圆与直线AB相切于点B，求P点的坐标；（3）在(2)中，若圆与x轴另一交点关于直线PB的对称点为M，试探索点M是否在抛物线y=ax2+x+1上，若在抛物线上，求出M点的坐标；若不在，请说明理由．3.（广州）如图所示，四边形OABC 是矩形，点A 、C 的坐标分别为（3，0），（0，1），点D是线段BC 上的动点（与端点B 、C 不重合），过点D 作直线y ＝－12x ＋b 交折线OAB 于点E ．（1）记△ODE 的面积为S ，求S 与b 的函数关系式；（2）当点E 在线段OA 上时，若矩形OABC 关于直线DE 的对称图形为四边形OA 1B 1C 1，试探究OA 1B 1C 1与矩形OABC 的重叠部分的面积是否发生变化，若不变，求出该重叠部分的面积；若改变，请说明理由.4.（南平）如图1，已知点B （1，3）、C （1，0），直线y=x +k 经过点B ，且与x 轴交于点A ，将△ABC 沿直线AB 折叠得到△ABD. （1）填空：A 点坐标为（____，____），D 点坐标为（____，____）；（2）若抛物线y= 13x 2+b x +c 经过C 、D 两点，求抛物线的解析式；（3）将（2）中的抛物线沿y 轴向上平移，设平移后所得抛物线与y 轴交点为E ，点M 是平移后的抛物线与直线AB 的公共点，在抛物线平移过程中是否存在某一位置使得直线EM ∥x 轴.若存在，此时抛物线向上平移了几个单位？若不存在，请说明理由.（提示：抛物线y=ax 2+b x +c(a ≠0)的对称轴是x =－b 2a ，顶点坐标是（－b 2a ，4a c －b24a）.图1备用图5（大连）如图17，抛物线F ：2(0)y ax bx c a =++>与y 轴相交于点C ，直线1L 经过点C 且平行于x 轴，将1L 向上平移t 个单位得到直线2L ，设1L 与抛物线F 的交点为C 、D ，2L 与抛物线F 的交点为A 、B ，连接AC 、BC （1）当12a =，32b =-，1c =，2t =时，探究△ABC 的形状，并说明理由；（2）若△ABC 为直角三角形，求t 的值（用含a 的式子表示）；（3）在（2）的条件下，若点A 关于y 轴的对称点A ’恰好在抛物线F 的对称轴上，连接A ’C ，BD ，求四边形A ’CDB 的面积（用含a 的式子表示）6.（宿迁）已知抛物线c bx x y ++=2交x 轴于)0,1(A 、)0,3(B ，交y轴于点C ，其顶点为D ．（1）求b 、c 的值并写出抛物线的对称轴；（2）连接BC ，过点O 作直线BC OE ⊥交抛物线的对称轴于点E ．求证：四边形ODBE 是等腰梯形；（3）问Q 抛物线上是否存在点Q ，使得△OBQ的面积等于四边形ODBE 的面积的31？若存在，求出点Q 的坐标；若不存在，请说明理由．（第28题）（第28题2）7.（烟台）如图，已知抛物线y=x2+bx-3a过点A（1,0），B(0,-3),与x轴交于另一点C。

2010年部分地区中考数学试题压轴题解答及点评(全国通用)

2010 年部分地区中考数学试题压轴题解答及点评(全
国通用)
2010 年部分地区中考数学试题压轴题解答及点评
1.（2010 广东肇庆）已知二次函数的图象过点P（2，1）．
（1）求证：；
（2）求的最大值；
（3）若二次函数的图象与轴交于点A（，0）、B（，0），△ABP 的面积是，求的值．
【答案】（1）证明：将点P（2，1）代入得：（1 分）
整理得：（2 分）
（2）解：∵∴= （4 分）
∵-2?0 ∴当= -1 时，有最大值2；（5 分）
（3）解：由题意得：，
∴=︱-︱=，即︱-︱= （6 分）
亦即（7 分）
由根与系数关系得：，（8 分）
代入得：，
整理得：（9 分）
解得：，经检验均合题意．（10 分）
【点评】本题以二次函数为载体，重点考查根与系数关系及简单的代数证明，尤其第一问的证明很特别。

但难度低，区分度小。

2.（2010 广东广州）如图所示，四边形OABC 是矩形，点A、C 的坐标分别为（3，0），（0，1），点D 是线段BC 上的动点（与端点B、C 不重合），。

2010年全国中考数学经典压轴题100题(三)答案

2010全国中考数学经典压轴题100题（三)答案【021】解：（1）21k k −；………………………………3分（2）①EF ∥AB ．……………………………………4分证明：如图，由题意可得A （–4，0），B （0，3），2(4,)4k E −−，2(,3)3k F ．∴PA=3，PE=234k +，PB=4，PF=243k +．∴223121234PA k PEk ==++，224121243PB k PFk ==++∴∴7分②过轴于点N ，两线交由上知M （0，24−），N （23，0），Q （23，24k −）．…8分而S △EFQ=S △PEF ，∴S2＝S △PEF －S △OEF ＝S △EFQ －S △OEF ＝S △EOM ＋S △FON ＋S 矩形OMQN ＝4321212222kk k k ⋅++＝222112k k+=221(6)312k+−．…………………………10分当26k>−时，S2的值随k2的增大而增大，而0＜k2＜12．……………11分∴0＜S2＜24，s2没有最小值．………12分说明：1．证明AB∥EF时，还可利用以下三种方法．方法一：分别求出经过A、B两点和经过E、F两点的直线解析式，利用这两个解析式中x的系数相等来证明AB∥EF；方法二：利用tan PAB∠＝tan PEF∠来证明AB∥EF；方法三：连接AF、BE，利用S△AEF＝S△BFE得到点A、点B到直线EF 的距离相等，再由A、B两点在直线EF同侧可得到AB∥EF．2．求S2的值时，还可进行如下变形：S2＝S△PEF－S△OEF＝S△PEF－（S四边形PEOF－S△PEF）＝2S△PEF－S四边形PEOF，再利用第（1）题中的结论．【022】解：(1)设抛物线的解析式为：y＝a(x－m＋2)(x－m －2)＝a(x－m)2－4a．……2分∵AC⊥BC，由抛物线的对称性可知：△ACB是等腰直角三角形，又AB＝4，∴C(m，－2)代入得a＝12．∴解析式为：y＝12(x－m)2－2．………………………5分(亦可求C点，设顶点式)(2)∵m为小于零的常数，∴只需将抛物线向右平移－m个单位，再向上平移2个单位，可以使抛物线y ＝12(x －m)2－2顶点在坐标原点．……………………………………7分(3)由(1)得D(0，12m2－2)，设存在实数m ，使得△BOD 为等腰三角形．∵△BOD 为直角三角形，∴只能OD ＝OB ．……………9分∴12m2－2＝|m ＋2|，当m ＋2＞0时，解得m ＝4或m ＝－2(舍)．当m ＋2＜0时，解得m ＝0(舍)或m ＝－2(舍)；当m ＋2＝0时，即m ＝－2时，B 、O 、D 三点重合(不合题意，舍)综上所述：存在实数m ＝4，使得△BOD 为等腰三角形．……………………………12分【023】（1）证明：∵MBC △是等边三角形∴60MB MC MBC MCB ===°，∠∠∵M 是AD 中点∴AM MD =∵AD BC∥∴60AMB MBC ==°∠∠，60DMC MCB ==°∠∠∴AMB DMC △≌△∴AB DC =∴梯形ABCD 是等腰梯形．（2）解：在等边MBC △中，4MB MC BC ===，60MBC MCB ==°∠∠，60MPQ =°∠∴120BMP BPM BPM QPC +=+=°∠∠∠∠∴BMP QPC =∠∠∴BMP CQP △∽△∴PC CQBM BP =5分∵PC x MQ y ==，∴44BP x QC y =−=−，6分ADCBPMQ60°∴444x y x−=−∴2144y x x =−+7分（3）解：①当1BP =时，则有BP BP MD ∥∥，则四边形ABPM和四边形MBPD均为平行四边形∴211333444MQ y ==×−+=当3BP =时，则有PC AM PC MD ∥∥，，则四边形MPCD和四边形APCM均为平行四边形∴11311444MQ y ==×−+=∴当1314BP MQ ==，或1334BP MQ ==，时，以P 、M 和A 、B 、C 、D△y 取最小值时，x =∴P°，∴30CPQ =°∠，∴∠【ABC 为等腰直∴3,0m −）.（2）∵45ODA OAD ∠=∠=°∴3OD OA m ==−，则点D 的坐标是（0,3m −）.又抛物线顶点为(1,0)P ，且过点B 、D ，所以可设抛物线的解析式为：2(1)y a x =−，得：22(31)(01)3a m a m ⎧−=⎪⎨−=−⎪⎩解得14a m =⎧⎨=⎩∴抛物线的解析式为221y x x =−+………7分（3）过点Q 作QM AC ⊥于点M ，过点Q 作QN BC ⊥于点N ，设点Q 的坐标是2(,21)x x x −+，则2(1)QM CN x ==−，3MC QN x ==−.∵//QM CE ∴PQM ∆∽PEC∆∴QM PMEC PC =即2(1)12x x EC −−=，得2(1)EC x =−∵//QN FC∴BQN∆∽BFC∆∴QN BNFC BC=即234(1)4x x FC −−−=，得41FC x =+又∵4AC =∴2(1)8x +=即【M 的纵坐标为－x ∣＝x ；∴C x+4+x ）＝8的周长不发生变（2）根据题意得：S 四边形OCMD ＝MC ·MD ＝（－x+4）·x ＝－x2+4x ＝－(x-2)2+4∴四边形OCMD 的面积是关于点M 的横坐标x （0<x<4）的二次函数，并且当x ＝2，即当点M 运动到线段AB 的中点时，四边形OCMD 的面积最大且最大面积为4；（3）如图10（2），当20≤<a时，42121422+−=−=aaS；如图10（3），当42<≤a时，22)4(21)4(21−=−=aaS；∴S与a的函数的图象如下图所示：的))4<≤a【026】解：（1）∵AH∶AC=2∶3，AC=6 ∴AH=23AC=23×ACB………1分 ∴2分 ∴3分（4分∵′H为平行四边5分又∴当CD=CH=2时，四边形CDH′H为正方形此时可得t=2秒时，四边形CDH′H为正方形………6分 ②（Ⅰ）∵∠DEF=∠ABC，∴EF∥AB∴当t=4秒时，直角梯形的腰EF与BA重合.当0≤t≤4时，重叠部分的面积为直角梯形DEFH′的面积.…………7分过F 作FM ⊥DE 于M ，F M M E=tan ∠DEF=tan ∠ABC=A CB C=68=34∴ME=43FM=43×2=83，HF=DM=DE-ME=4-83=43∴直角梯形DEFH ′的面积为12（4+43）×2=163∴y=163（Ⅱ）∵当4＜t ≤513时，重叠部分的面积为四边形CBGH的面积-矩形CDH ′H 的面积. 而S 边形CBGH=S △ABC-S△AHG=12×8×6-323=403S 矩形CDH ′H =2t ∴y=403-2tAB 于P. BD=8-t∴y=S ,△8-t ）2=38t2-6t+24y=40338t2-6t+24（513＜t ≤8）【027】解：(1)设抛物线的解析式为：4)1(21+−=x a y ,把A （3,0）代入解析式求得1−=a所以324)1(221++−=+−−=x x x y ，设直线AB 的解析式为：bkx y +=2由3221++−=x x y 求得B 点的坐标为)3,0(把)0,3(A ，)3,0(B 代入b kx y +=2中解得：3,1=−=b k 所以32+−=x y 6分(2)因为C 点坐标为(１,4)，所以当x ＝１时，y1＝4，y2＝2所以CD ＝4-2＝28分32321=××=∆CAB S (平方单位)(3)假设存在符合条件的点P ，设P 点的横坐标为x ，△PABx x x 3)32+−=+−，由S △389×，化简得：42−x 322++x x 中，解得P【0，3），)根据题意，得⎩⎨=++0339b a ，解得⎩⎨=2b ∴抛物线的解析式为322++−=x x y (5′)(2)(5′)由顶点坐标公式得顶点坐标为（1，4）（2′)设对称轴与x 轴的交点为F∴四边形ABDE 的面积=ABO DFEBOFD S S S ∆∆++梯形=111()222AO BO BO DF OF EF DF⋅++⋅+⋅=11113(34)124222××++×+××=9（5′）（3）(2′)相似如图，BD===；∴====∴2220BDBE +=,220DE =即：222BD BE DE +=,所以BDE ∆是直角三角形∴∠∴∆(2′)【04>所x 轴总有两个交（2a x x −=+21，1•x x 是13，所以|1−x 即：13)(221=−x x 变形为：134)(21221=•−+x x x x ……………………（5分）所以：13)2(4)(2=−−−a a ，整理得：0)1)(5(=+−a a 解方程得：15−=或a ，又因为：a<0，所以：a=－1所以：此二次函数的解析式为32−−=x xy ………………（6分）（3）设点P 的坐标为),(0y x o ，因为函数图象与x 轴的两个交点间的距离等于13，所以：AB=13，所以：S △PAB=213||210=•y AB 所以：2132||130=y 即：3||0=y ，则30±=y 当30=y 时，3320=−−o x x ，即0)2)(3(0=+−o x x 解此方程得：x =－2或3，当30−=y 时，3320−=−−o x x ，即)1(0=−o x x 解此方程得：0x =0或1(－2,3),(3,3),(0,－3)【2分）（2A 到点D 并随⊙有5，垂足为F ，则由∠得CDF EDO △∽△，则3(5)45CF t −−=．解得485t CF −=．由12CF ≤t ，即48152t t −≤，解得163t ≤．∴当C ⊙与射线DE 有公共点时，t 的取值范围为41633t ≤≤．11（5分）②当PA AB =时，过P 作PQ x ⊥轴，垂足为Q ，有222PA PQ AQ =+221633532525t t t ⎛⎞=+−−+⎜⎟⎝⎠．2229184205t t t ∴−+=，即2972800t t −+=．解得1242033t t ==．（7分）当PA PB =时，有PC AB ⊥，3535t t ∴−=−．解得35t =．（9分）当PB AB =时，有2222216132525PB ⎛⎞1320t ∴11分）∴当5t =，或203t =．。

2010年中考数学压轴题100题精选(61-70题)答案

2010年中考数学压轴题100题精选（61-70题）答案【061】解（1）A （4-，0），B （0，3） ············································· 2分（每对一个给1分）（2）满分3分．其中过F 作出垂线1分，作出BF 中垂线1分，找出圆心并画出⊙P 给1分．（注：画垂线PF 不用尺规作图的不扣分）（3）过点P 作PD ⊥y 轴于D ，则PD =x ，BD =3y -， ··············· 6分 PB =PF =y ，∵△BDP 为直角三形，∴ 2PB =∴222BP PD BD =+，即223y x =+-即222(3)y x y =+-∴y 与x 的函数关系为y =（4）存在解法1：∵⊙P 与x 轴相切于点F ，且与直线l ∴AB AF =，∵22225AB OA OB =+=，∴∵AF =4x + ， ∴22(4)5x +=，∴19x x ==-或 11分把19x x ==-或代入21362y x =+，得5153y y ==或 ∴点P 的坐标为（1，53）或（-9，15）12分【062】解：实践应用（1）2；l c．16；13．（2）54．拓展联想（1）∵△ABC 的周长为l ，∴⊙O 在三边上自转了lc周．又∵三角形的外角和是360°，∴在三个顶点处，⊙O 自转了3601360=（周）．∴⊙O 共自转了（lc +1）周．（2）lc+1．【063】（1）① 对称轴422x =-=- ················································································ （2分） ② 当0y =时，有2430x x ++=，解之，得 11x =-，23x =-∴ 点A 的坐标为（3-，0）．············································································ （4分）（2）满足条件的点P 有3个，分别为（2-，3），（2，3），（4-，3-）． ········ （7分）（3）存在．当0x =时，2433y x x =++= ∴ 点C 的坐标为（0，3）∵ DE ∥y 轴，AO =3，EO =2，AE =1，CO =3∴ AED △∽AOC △ ∴ AE DE AO CO = 即 133DE= ∴ DE =1 ············· （9分） ∴ DEOC S =梯形1(13)22⨯+⨯=4 在OE 上找点F ，使OF =43，此时COF S =△14323⨯⨯=2，直线CF 把四边形DEOC分成面积相等的两部分，交抛物线于点M ． ································································ （10分）设直线CM 的解析式为3y kx =+，它经过点403F ⎛⎫- ⎪⎝⎭，．则4303k -+= · （11分）解之，得 94k =∴ 直线CM 的解析式为 934y x =+ ······························ （12分）【064】解：（1）抛物线2124y x x =--+与y∴B （0，2）∵22112(2)344y x x x =--+=-++ ∴A （—2（2）当点P 是 AB 的延长线与x 轴交点时，AB PB PA =-．当点P 在x 轴上又异于AB 的延长线与x 在点P 、A 、B 构成的三角形中，PB PA -综合上述：PA PB AB -≤（3）作直线AB 交x 轴于点P ，由（2）可知：当PA —PB 最大时，点P 是所求的点 ······· 8分作AH ⊥OP 于H ．∵BO ⊥OP ，∴△BOP ∽△AHP∴AH HPBO OP=由（1）可知：AH=3、OH=2、OB=2，∴OP=4，故P （4，0）【065】解：（1）∵AB 是⊙O 的直径（已知） ∴∠ACB ＝90º（直径所对的圆周角是直角） ∵∠ABC ＝60º（已知） ∴∠BAC ＝180º－∠ACB －∠ABC ＝ 30º（三角形的内角和等于180º） ∴AB ＝2BC ＝4cm （直角三角形中，30º锐角所对的直角边等于斜边的一半）即⊙O 的直径为4cm ．（2）如图10（1）CD 切⊙O 于点C ，连结OC ，则OC ＝OB ＝1/2·AB ＝2cm ． ∴CD ⊥CO （圆的切线垂直于经过切点的半径） ∴∠OCD ＝90º（垂直的定义） ∵∠BAC ＝ 30º（已求）∴∠COD ＝2∠BAC ＝ 60º ∴∠D ＝180º－∠COD －∠OCD ＝ 30º∴OD ＝2OC ＝4cm ∴BD ＝OD －OB ＝4－2＝2（cm ） ∴当BD 长为2cm ，CD 与⊙O 相切．（3）根据题意得：BE ＝（4－2t ）cm ，BF ＝tcm ；如图10（2）当EF ⊥BC 时，△BEF 为直角三角形，此时△BEF ∽△BAC ∴BE ：BA ＝BF ：BC 即：（4－2t ）：4＝t ：2解得：t ＝1如图10（3）当EF ⊥BA 时，△BEF 为直角三角形，此时△BEF ∽△BCA ∴BE ：BC ＝BF ：BA 即：（4－2t ）：2＝t ：4解得：t ＝1.6 ∴当t ＝1s 或t ＝1.6s 时，△BEF 为直角三角形．第28题图【066】（1）由112C ⎛⎫⎪⎝⎭，得(12)A ，，代入反比例函数my x=中，得2m = ∴反比例函数解析式为：2(0)y x x=> ·························································································· 2分解方程组15222y x y x ⎧=-+⎪⎪⎨⎪=⎪⎩由15222x x -+=化简得：2540x x -+=(4)(1)0x x --=，1241x x ==，所以142B ⎛⎫⎪⎝⎭， ·········································································· 5分（2）无论P 点在AB 之间怎样滑动，PMN △与CAB △总能相似．因为B C 、两点纵坐标相等，所以BC x ∥轴．又因为AC y ∥轴，所以CAB △为直角三角形．同时PMN △也是直角三角形，AC PM BC PN ∥，∥．∴PMN CAB △∽△．········································································································· 8分（在理由中只要能说出BC x ∥轴，90ACB ∠=°即可得分．）【067】（1）解：∵直角梯形ABCD ，AD BC ∥ PD QC ∴∥∴当PD QC =时，四边形PQCD为平行四边形．由题意可知：2AP t CQ t ==，82t t ∴-=38t = 83t =∴当83t s =时，四边形PQCD 为平行四边形． ·········································································· 3分（2）解：设PQ 与O ⊙相切于点H ，过点P 作PE BC ⊥，垂足为E 直角梯形ABCD AD BC ，∥PE AB ∴=由题意可知：2AP BE t CQ t ===，222BQ BC CQ t ∴=-=-222223EQ BQ BE t t t =-=--=-BQBQEAB 为O ⊙的直径，90ABC DAB ∠=∠=°AD BC ∴、为O ⊙的切线AP PH HQ BQ ∴==，22222PQ PH HQ AP BQ t t t ∴=+=+=+-=- ···························································· 5分在Rt PEQ △中，222PE EQ PQ +=，22212(223)(22)t t ∴+-=- 即：28881440t t -+=，211180t t -+=，(2)(9)0t t --=1229t t ∴==，，因为P 在AD 边运动的时间为8811AD ==秒而98t =>，9t ∴=（舍去），∴当2t =秒时，PQ 与O ⊙相切． ··································· 8分【068】解：（1）如图4，过B 作BG OA G ⊥于，则13AB ====过Q 作，于H OA QH ⊥则QP === ····································································································· （2分）要使四边形PABQ 是等腰梯形，则AB QP =，即,13)310(1442=-+tt ∴53=或5t =（此时PABQ 是平行四边形，不合题意，舍去） ····························· （3分）（2）当2=t 时，410282OP CQ QB ==-==，，。

2010年中考数学压轴题100题精选(51-60题)答案巩固基础

2010年中考数学压轴题100题精选（51-60题）答案【051】解：（1）3k =-，（-1，0），B （3，0）． ······················· 3分（2）如图14（1），抛物线的顶点为M （1，-4），连结OM ．则 △AOC 的面积=23，△MOC 的面积=23，△MOB 的面积=6，∴ 四边形 ABMC 的面积=△AOC 的面积+△MOC 的面积+△MOB 的面积=9． ·································· 6分说明：也可过点M 作抛物线的对称轴，将四边形ABMC 的面积转化为求1个梯形与2个直角三角形面积的和．（3）如图14（2），设D （m ，322--m m ），连结OD ．则 0＜m ＜3，322--m m ＜0．且 △AOC 的面积=23，△DOC 的面积=m 23， △DOB 的面积=-23（322--m m ）， ∴ 四边形 ABDC 的面积=△AOC 的面积+△DOC 的面积+△DOB 的面积=629232++-m m =875)23(232+--m ． ∴ 存在点D 315()24-，，使四边形ABDC 的面积最大为875．（4）有两种情况：如图14（3），过点B 作BQ 1⊥BC ，交抛物线于点Q 1、交y 轴于点E ，连接Q 1C ． ∵ ∠CBO =45°，∴∠EBO =45°，BO =OE =3． ∴ 点E 的坐标为（0，3）． ∴ 直线BE 的解析式为3y x =-+． ···························· 12分由2323y x y x x =-+⎧⎨=--⎩，解得1125x y ，；2230.x y ，∴ 点Q 1的坐标为（-2，5）． ········· 13分如图14（4），过点C 作CF ⊥CB ，交抛物线于点Q 2、交x 轴于点F ，连接BQ 2．∵ ∠CBO =45°，∴∠CFB =45°，OF =OC =3． ∴ 点F 的坐标为（-3，0）．∴ 直线CF 的解析式为3y x =--．····························· 14分由2323y x y x x =--⎧⎨=--⎩，解得1103x y ，；2214x y ，．∴点Q 2的坐标为（1，-4）．综上，在抛物线上存在点Q 1（-2，5）、Q 2（1，-4），使△BCQ 1、△BCQ 2是以BC 为直角边的直角三角形．【052】解：（1）根据题意，得04202.a b c a b c c ++=⎧⎪++=⎨⎪=-⎩，，图14（2）图14（3）图14（4）yxOBA DE 1 (E 2)解得132a b c =-==-，，．232y x x ∴=-+-．（2分）（2）当EDB AOC △∽△时，得AO CO ED BD =或AO COBD ED=， ∵122AO CO BD m ===-，，，当AO CO ED BD =时，得122ED m =-， ∴22m ED -=，∵点E 在第四象限，∴122m E m -⎛⎫⎪⎝⎭，． ··········································· （4分）当AO CO BD ED =时，得122m ED=-，∴24ED m =-， ∵点E 在第四象限，∴2(42)E m m -，． ········································································· （6分）（3）假设抛物线上存在一点F ，使得四边形ABEF 为平行四边形，则 1EF AB ==，点F 的横坐标为1m -，当点1E 的坐标为22m m -⎛⎫ ⎪⎝⎭，时，点1F 的坐标为212m m -⎛⎫- ⎪⎝⎭，，∵点1F 在抛物线的图象上，∴22(1)3(1)22mm m -=--+--，∴2211140m m -+=， ∴(27)(2)0m m --=，∴722m m ==，（舍去），∴15324F ⎛⎫- ⎪⎝⎭，， ∴33144ABEFS=⨯=． ····································································································· （9分）当点2E 的坐标为(42)m m -，时，点2F 的坐标为(142)m m --，， ∵点2F 在抛物线的图象上，∴242(1)3(1)2m m m -=--+--，∴27100m m -+=，∴(2)(5)0m m --=，∴2m =（舍去），5m =，∴2(46)F -，，∴166ABEFS =⨯=．【053】解：（1）设(1)(3)y a x x =+-，把(03)C ，代入，得1a =-， ······························ 2分∴抛物线的解析式为：223y x x =-++．顶点D 的坐标为(14)，． ··································· 5分（2）设直线BD 解析式为：y kx b =+（0k ≠），把B D 、两点坐标代入，得304.k b k b +=⎧⎨+=⎩，解得26k b =-=，．∴直线AD 解析式为26y x =-+． ························· 7分2111(26)3222s PE OE xy x x x x ===-+=-+，∴23(13)s x x x =-+<< ·················· 9分 22993934424s x x x ⎛⎫⎛⎫=--++=--+ ⎪ ⎪⎝⎭⎝⎭． ····································································· 10分∴当32x =时，s 取得最大值，最大值为94． ······································································ 11分（3）当s 取得最大值，32x =，3y =，∴332P ⎛⎫⎪⎝⎭，．∴四边形PEOF 是矩形．作点P 关于直线EF 的对称点P '，连接P E P F ''、．法一：过P '作P H y '⊥轴于H ，P F '交y 轴于点M设MC m =，则332MF m P M m P E ''==-=，，．在Rt P MC '△中，由勾股定理，223(3)2m m ⎛⎫+-= ⎪⎝⎭解得158m =．∵CM P H P M PE '''=，∴910P H '=．由EHP EP M ''△∽△，可得EH EP EP EM '='，65EH =．∴69355OH =-=． ∴P '坐标99105⎛⎫-⎪⎝⎭，． ·············································································································· 13分法二：连接PP '，交CF 于点H ，分别过点H P '、作PC 的垂线，垂足为M N 、．易证CMH HMP △∽△．∴12CM MH MH PM ==．设CM k =，则24MH k PM k ==，．∴5PC =由三角形中位线定理，12845PN k P N k '====，∴12395210CN PN PC =-=-=，即910x =-． 69355y PF P N '=-=-=∴P '坐标99105⎛⎫- ⎪⎝⎭，． ··把P '坐标99105⎛⎫-⎪⎝⎭，代入抛物线解析式，不成立，所以P '不在抛物线上． ····················· 14分【054】（1）由抛物线经过点A (0，1)，C (2，4)，得21,122 4.4c b c =⎧⎪⎨-⨯++=⎪⎩解得2,1.b c =⎧⎨=⎩ ∴抛物线对应的函数关系式为：21214y x x =-++． ··································· （2分）（2）当1t =时，P 点坐标为(1，1)，∴Q 点坐标为(2，0)．当4t =时，P 点坐标为(2，3)，∴Q 点坐标为(5，0)． ································ （5分）（3）当0t <≤2时，211(211)124S t t =-++-⨯．S 218t t =-+．当2t <≤5时，1(5)(2212)2S t t =-+-+-．S 215322t t =-+-．（8分）当3t =时，S 的最大值为2． ································【055】（1）过点B 作BD x ⊥轴，垂足为D ， 9090BCD ACO ACO CAO ∠+∠=∠+∠=°，°BCD CAO ∴∠=∠；又90BDC COA CB AC ∠=∠==°；， BCD CAO ∴△≌△，12BD OC CD OA ∴====，∴点B 的坐标为(31)-，； ·················································· 4（2）抛物线22y ax ax =+-经过点(31)B -，，则得到1932a a =--， ··························· 5分解得12a =，所以抛物线的解析式为211222y x x =+-； ···················································· 7分（3）假设存在点P ，使得ACP △仍然是以AC 为直角边的等腰直角三角形：①若以点C 为直角顶点；则延长BC 至点1P ，使得1PC BC =，得到等腰直角三角形1ACP △， ······························ 8分过点1P 作1PM x ⊥轴，11190CP BC MCP BCD PMC BDC =∠=∠∠=∠=，，°； 1MPC DBC ∴△≌△121CM CD PM BD ∴====，，可求得点1P (1，-1)； ·········· 11分 ②若以点A 为直角顶点；则过点A 作2AP CA ⊥，且使得2AP AC =，得到等腰直角三角形2ACP △， ················ 12分过点2P 作2P N y ⊥轴，同理可证2AP N CAO △≌△； ····················································· 13分221NP OA AN OC ∴====，，可求得点2(21)P ，； ······················································· 14分经检验，点1(11)P -，与点2(21)P ，都在抛物线211222y x x =+-上． ································ 16分【056】解：（1） C （3，0）；（2）①抛物线c bx ax y ++=2，令x =0，则y =c ， ∴A 点坐标（0，c ）．∵ac b 22=，∴ 242424442c a ac a ac ac a b ac ==-=-，∴点P 的坐标为（2,2ca b -）． ∵PD ⊥x 轴于D ，∴点D 的坐标为（0,2ab-）． ……………………………………5分根据题意，得a=a ′，c= c ′，∴抛物线F ′的解析式为c x b ax y ++='2．又∵抛物线F ′经过点D （0,2a b-），∴c a b b ab a +-+⨯=)2('4022．……………6分 ∴ac bb b 4'202+-=．又∵ac b 22=，∴'2302bb b -=．∴b :b ′=32． ②由①得，抛物线F ′为c bx ax y ++=232．令y=0，则0232=++c bx ax ． ∴abx a b x -=-=21,2．∵点D 的横坐标为,2a b -∴点C 的坐标为（0,ab-）．设直线OP 的解析式为kx y =．∵点P 的坐标为（2,2ca b -）， ∴k a b c 22-=，∴22222b b b b ac b ac k -=-=-=-=，∴x by 2-=． ∵点B 是抛物线F 与直线OP 的交点，∴x b c bx ax 22-=++．∴abx a b x -=-=21,2．∵点P 的横坐标为a b 2-，∴点B 的横坐标为ab-．把a b x -=代入x by 2-=，得c a ac a b a b b y ===--=222)(22．∴点B 的坐标为),(c ab-．∴BC ∥OA ，AB ∥OC ．（或BC ∥OA ，BC =OA ），∴四边形OABC 是平行四边形．又∵∠AOC =90°，∴四边形OABC 【057】(1) )6,0(),0,8(B A(2)∵8=OA ，6=OB ，∴AB 当点P 在OB 上运动时，t OP =1t t OP OA S 4821211=⨯⨯=⨯=；当点P 在BA 上运动时，作D P ⊥2有AB AP BO D P 22=∵t AP -+=1062∴51925125348821212+-=-⨯⨯=⨯⨯=t t D P OA S （3）当124=t 时，3=t ，)3,0(1P ，此时，过AOP ∆各顶点作对边的平行线，与坐标轴无第二个交点，所以点M 不存在；当125192512=+-t 时，11=t ，)3,4(2P ，此时，)3,0(1M 、)6,0(2-M 【058】解：（1）令0y =，得210x -= 解得1x =±，令0x =，得1y =-∴ A (1,0)- B (1,0) C (0,1)- ·············（2）∵O A =O B =O C =1 ∴∠BAC =∠AC O=∠BC O=45 ∵A P ∥CB ，∴∠P AB =45，过点P 作P E ⊥x 轴于E ，则∆A P E 为等腰直角三角形令O E =a ，则P E =1a + ∴P (,1)a a +∵点P 在抛物线21y x =-上 ∴211a a +=-解得12a =，21a =-（不合题意，舍去） ∴P E =3 · 4分 ∴四边形ACB P 的面积S =12AB •O C +12AB •P E =112123422⨯⨯+⨯⨯= ································ 5分 (3)．假设存在∵∠P AB =∠BAC =45 ∴P A ⊥AC∵MG ⊥x 轴于点G ， ∴∠MG A =∠P AC =90在Rt △A O C 中，O A =O C =1 ∴AC ，在Rt △P AE 中，AE =P E =3 ∴A P= ······· 6分设M 点的横坐标为m ，则M 2(,1)m m - ①点M 在y 轴左侧时，则1m <- (ⅰ) 当∆A MG ∽∆P CA 时，有AG PA =MGCA∵A G=1m --MG=21m -2= 解得11m =-（舍去） 223m =（舍去）………7分 (ⅱ) 当∆M A G ∽∆P CA 时有AG CA =MGPA即 2=，解得：1m =-（舍去） 22m =-∴M (2,3)- ························································ 8分② 点M 在y 轴右侧时，则1m >(ⅰ) 当∆A MG ∽∆P CA 时有AG PA =MGCA∵A G=1m +，MG=21m -∴2= 解得11m =-（舍去） 243m = ∴M 47(,)39(ⅱ) 当∆M A G ∽∆P CA 时有AG CA =MGPA 即2=解得：11m =-（舍去） 24m = ∴M (4,15) ∴存在点M ，使以A 、M 、G 三点为顶点的三角形与∆P CA 相似，M 点的坐标为(2,3)-，47(,)39，(4,15)【059】解：（1）∵四边形ABCD 和四边形AEFG 是正方形 ∴AB =AD ，AE =AG ，∠BAD ＝∠EAG ＝90º∴∠BAE ＋∠EAD ＝∠DAG ＋∠EAD ∴∠BAE ＝∠DAG∴△ BAE ≌△DAG …………4分（2）∠FCN ＝45º …………5分理由是：作FH ⊥MN 于H∵∠AEF ＝∠ABE ＝90º∴∠BAE +∠AEB ＝90º，∠FEH +∠AEB ＝90º∴∠FEH ＝∠BAE 又∵AE =EF ，∠EHF ＝∠EBA ＝90º∴△EFH ≌△ABE …………7分 ∴FH ＝BE ，EH ＝AB ＝BC ，∴CH ＝BE ＝FH∵∠FHC ＝90º，∴∠FCH ＝45º …………8分（3）当点E 由B 向C 运动时，∠FCN的大小总保持不变，…………9分理由是：作FH ⊥MN 于H由已知可得∠EAG ＝∠BAD ＝∠AEF ＝90º 结合（1）（2）得∠FEH ＝∠BAE ＝∠DAG又∵G 在射线CD 上，∠GDA ＝∠EHF ＝∠EBA ＝90º ∴△EFH ≌△GAD ，△EFH ∽△ABE ……11分 ∴EH ＝AD ＝BC ＝b ，∴CH ＝BE ，∴EH AB ＝FH BE ＝FHCH∴在Rt △FEH 中，tan ∠FCN ＝FH CH ＝EH AB ＝b a∴当点E 由B 向C 运动时，∠FCN ＝ba【060】解：（1）根据题意，得 4203660a c a c -+=⎧⎨++=⎩，解得143a c ⎧=-⎪⎨⎪=⎩ ∴抛物线的解析式为2134y x x =-++，顶点坐标是（2，4）（2）(43)D ，，设直线AD 的解析式为(0)y kx b k =+≠ 直线经过点(20)A -，、点(43)D ，2043k b k b -+=⎧∴⎨+=⎩121k b ⎧=⎪∴⎨⎪=⎩ 112y x ∴=+（3）存在．120)Q ，，2(2)Q -，0，3(6Q -，4(6Q +M B E AC ND F G 图（2） HM B E A C ND F G图（1）H第26题图。

【配套K12】2010年各地中考数学压轴题精选

2010中考数学压轴题精选（一）★★1、（2010北京）在平面直角坐标系xOy 中，抛物线y = -41-m x 2+45mx +m 2-3m +2 与x 轴的交点分别为原点O 和点A ，点B (2，n )在这条抛物线上。

（1）求点B 的坐标；（2）点P 在线段OA 上，从O 点出发向点运动，过P 点作x 轴的垂线，与直线OB 交于点E 。

延长PE 到点D ，使得ED =PE ，以PD 为斜边在PD 右侧作等腰直角三角形PCD （当P 点运动时，C 点、D 点也随之运动）当等腰直角三角形PCD 的顶点C 落在此抛物线上时，求OP 的长；若P 点从O 点出发向A 点作匀速运动，速度为每秒1个单位，同时线段OA 上另一点Q 从A 点出发向O 点作匀速运动，速度为每秒2个单位(当Q 点到达O 点时停止运动，P 点也同时停止运动)。

过Q 点作x 轴的垂线，与直线AB 交于点F 。

延长QF 到点M ，使得FM =QF ，以QM 为斜边，在QM 的左侧作等腰直角三角形QMN (当Q 点运动时，M 点，N 点也随之运动)。

若P 点运动到t 秒时，两个等腰直角三角形分别有一条直角边恰好落在同一条直线上，求此刻t 的值。

★★2、（2010北京）问题：已知△ABC 中，∠BAC =2∠ACB ，点D 是△ABC 内的一点，且AD =CD ，BD =BA 。

探究∠DBC 与∠ABC 度数的比值。

请你完成下列探究过程：先将图形特殊化，得出猜想，再对一般情况进行分析并加以证明。

(1) 当∠BAC =90︒时，依问题中的条件补全右图。

观察图形，AB 与AC 的数量关系为；当推出∠DAC =15︒时，可进一步推出∠DBC 的度数为；可得到∠DBC 与∠ABC 度数的比值为；(2) 当∠BAC ≠90︒时，请你画出图形，研究∠DBC 与∠ABC 度数的比值是否与(1)中的结论相同，写出你的猜想并加以证明。

★★3、（2010郴州）如图（1），抛物线42y x x =+-与y 轴交于点A ，E （0，b ）为y A C B轴上一动点，过点E 的直线y x b =+与抛物线交于点B 、C .（1）求点A 的坐标；（2)当b =0时（如图（2）），ABE 与ACE 的面积大小关系如何？当4b >-时，上述BOC 是以b ；若★★4、（2010滨州）如图，四边形ABCD 是菱形，点D的坐标是（0，3），以点C 为顶点的抛物线c bx ax y ++=2恰好经过x 轴上A 、B 两点．（1）求A 、B 、C 三点的坐标；（2）求过A 、B 、C 三点的抛物线的解析式；（3）若将上述抛物线沿其对称轴向上平移后恰好过D 点，求平移后抛物线的解析式，并指出平移了多少个单位?★★5、（2010长沙）已知：二次函数22y ax bx =+-的图象经过点（1，0），一次函数图象经过原点和点（1，－b ），其中0a b >>且a 、b 为实数．（1）求一次函数的表达式（用含b 的式子表示）；（2）试说明：这两个函数的图象交于不同的两点；（3）设（2）中的两个交点的横坐标分别为x1、x2，求| x1－x2 |的范围．★★6、（2010长沙）如图，在平面直角坐标系中，矩形OABC的两边分别在x轴和y轴上，OA ， OC=8cm，现有两动点P、Q分别从O、C同时出发，P在线段OA上沿OA cm的速度匀速运动，Q在线段CO上沿CO方向以每秒1cm的速度匀速运动．设运动时间为t秒．（1）用t 的式子表示△OPQ 的面积S ；（2）求证：四边形OPBQ 的面积是一个定值，并求出这个定值；（3）当△OPQ 与△PAB 和△QPB 相似时，抛物线214y x bx c =++经过B 、P 两点，过线段BP 上一动点M 作y 轴的平行线交抛物线于N ，当线段MN 的长取最大值时，求直线MN 把四边形OPBQ 分成两部分的面积之比．★★7、（2010常德）如图9，已知抛物线212y x bx c x =++与轴交于点A （-4，0）和B （1，0）两点，与y 轴交于C 点. （1）求此抛物线的解析式；第26题图（2）设E 是线段AB 上的动点，作EF∥AC 交BC 于F ，连接CE ，当C E F 的面积是BEF 面积的2倍时，求E 点的坐标；（3）若P 为抛物线上A 、C 两点间的一个动点，过P 作y 轴的平行线，交AC 于Q ，当P 点运动到什么位置时，线段PQ 的值最大，并求此时P 点的坐标.★★8、（2010常德）如图10，若四边形ABCD 、四边形CFED 都是正方形，显然图中有AG=CE ，AG⊥CE.（1）当正方形GFED 绕D 旋转到如图11的位置时，AG=CE 是否成立？若成立，请给出证明；图9x若不成立，请说明理由.（2）当正方形GFED 绕D 旋转到如图12的位置时，延长CE 交AG 于H ，交AD 于M. ①求证：AG⊥CH;②当AD=4，CH 的长。

2010年中考数学压轴题100题精选(5160题)答案

2010 年中考数学压轴题100 题优选（ 5160 题）答案2010 年中考数学压轴题100 题优选（ 51-60 题）【051】如图 14（ 1），抛物线与x轴交于A、B两点，与y 轴交于点 C（ 0，）．［图 14（ 2）、图 14（ 3）为解答备用图］（1），点A的坐标为，点B的坐标为；（2）设抛物线的极点为 M ，求四边形 ABMC 的面积；（3）在x 轴下方的抛物线上能否存在一点 D ，使四边形 ABDC 的面积最大？若存在，恳求出点 D 的坐标；若不存在，请说明原因；（4）在抛物线角三角形．图上求点14（ 1）Q，使△BCQ是以 BC 为直角边的直图 14（ 2）图 14（3）【052】已知二次函数（）的图象经过点，，，直线（）与轴交于点．（1）求二次函数的分析式；（2）在直线（）上有一点（点在第四象限），使得为极点的三角形与以为极点的三角形相像，求点坐标（用含的代数式表示）；（3）在（ 2）建立的条件下，抛物线上能否存在一点，使得四边形为平行四边形？若存在，恳求出的值及四边形的面积；若不存在，请说明原因．yxO【053】如下图，在平面直角坐标系中，抛物线（）经过，，三点，其极点为，连结，点是线段上一个动点（不与重合），过点作轴的垂线，垂足为，连结．（1）求抛物线的分析式，并写出极点的坐标；（2）假如点的坐标为，的面积为，求与的函数关系式，写出自变量的取值范围，并求出的最大值；12331DyCBAP2ExO （ 3）在（ 2）的条件下，当获得最大值时，过点作的垂线，垂足为，连结，把沿直线折叠，点的对应点为，请直接写出点坐标，并判断点能否在该抛物线上．【054】如图，在直角坐标系中，矩形ABCD 的边 AD 在 y轴正半轴上，点 A 、 C 的坐标分别为（ 0，1）、（ 2，4）．点 P 从点 A 出发，沿 A → B → C 以每秒 1 个单位的速度运动，到点C 停止；点 Q 在 x 轴上，横坐标为点 P 的横、纵坐标之和．抛物线经过 A 、C 两点．过点 P 作 x 轴的垂线，垂足为 M ，交抛物线于点 R．设点 P 的运动时间为 t（秒），△ PQR 的面积为 S （平方单位）．（1）求抛物线对应的函数关系式．（2）分别求 t=1 和 t=4 时，点 Q 的坐标．（3）当 0＜≤ 5 时，求 S 与 t 之间的函数关系式，并直接写出S 的最大值．【055】在平面直角坐标系中，现将一块等腰直角三角板放在第二象限，斜靠在两坐标轴上，且点，点，如下图：抛物线经过点．（1）求点的坐标；（2）求抛物线的分析式；（3）在抛物线上能否还存在点（点除外），使仍旧是以为直角边的等腰直角三角形？若存在，求全部点的坐标；若不存在，请说明原因． BACxy （ 0，2）（－ 1， 0）（第 25 题）【056】如图 18，抛物线 F：的极点为 P，抛物线：与 y 轴交于点 A ，与直线 OP 交于点 B．过点 P 作 PD⊥ x 轴于点 D ，平移抛物线 F 使其经过点 A 、D 获得抛物线 F′：，抛物线F′与 x 轴的另一个交点为C．⑴当 a = 1，b=－ 2，c = 3 时，求点 C 的坐标 (直接写出答案 )；⑵若 a、 b、c 知足了①求 b： b′的值；②研究四边形OABC 的形状，并说明原因．图18【057】直线与坐标轴分别交于、两点，、的长分别是方程的两根（），动点从点出发，沿路线→ → 以每秒1 个单位长度的速度运动，抵达点时运动停止．（1）直接写出、两点的坐标；（2）设点的运动时间为 (秒 )，的面积为，求与之间的函数关系式（不用写出自变量的取值范围）；（3）当时，直接写出点的坐标，此时，在座标轴上能否存在点，使以、、、为极点的四边形是梯形？若存在，请直接写出点的坐标；若不存在，请说明原因．【058】如图，已知抛物线与轴交于A、B两点，与轴交于点 C．（1）求 A 、 B、 C 三点的坐标．（2）过点 A 作 AP ∥CB 交抛物线于点 P，求四边形 ACBP的面积．CPByA （3）在轴上方的抛物线上能否存在一点M ，过 M 作 MG 轴于点 G，使以 A 、M 、G 三点为极点的三角形与 PCA 相像．若存在，恳求出 M 点的坐标；不然，请说明原因．【059】如图（ 1），已知正方形 ABCD 在直线 MN 的上方， BC 在直线 MN 上， E 是 BC 上一点，以 AE 为边在直线 MN的上方作正方形AEFG ．（1）连结 GD ，求证：△ ADG ≌△ ABE ；(4 分 )（2）连结 FC，察看并猜想∠ FCN 的度数，并说明原因； (4分)（3）如图（2），将图（1）中正方形 ABCD 改为矩形 ABCD ，AB=a ，BC=b（ a、b 为常数），E 是线段 BC 上一动点（不含端点 B、 C），以 AE 为边在直线 MN 的上方作矩形 AEFG ，使极点G 恰巧落在射线CD上．判断当点 E 由B 向C 运动时，∠FCN的大小能否总保持不变，若∠FCN的大小不变，请用含 a、b 的代数式表示tan∠FCN 的值；若∠ FCN 的大小发生改变，请举例说明．(5 分 )图（ 2） MBEACDFG NNMBE CDFG图（ 1）【060】已知：如下图，对于的抛物线与轴交于点、点，与轴交于点．（1）求出此抛物线的分析式，并写出极点坐标；（2）在抛物线上有一点，使四边形为等腰梯形，写出点的坐标，并求出直线的分析式； BAOCyx （第 26 题图）（ 3）在（ 2）中的直线交抛物线的对称轴于点，抛物线上有一动点，轴上有一动点．能否存在以为极点的平行四边形？假如存在，请直接写出点的坐标；假如不存在，请说明原因．2010 年中考数学压轴题100 题优选（ 51-60 题）答案【051】解：（ 1），（ -1，0），B（3，0）． (3)分（2）如图 14（1），抛物线的极点为M （1，-4），连结 OM ．则△AOC 的面积 = ，△ MOC 的面积 = ，△ MOB 的面积=6，∴ 四边形 ABMC 的面积 =△ AOC 的面积 +△ MOC 的面积+△ MOB 的面积=9．···················································6分图 14（ 2）说明：也可过点 M 作抛物线的对称轴，将四边形ABMC 的面积转变为求 1 个梯形与 2 个直角三角形面积的和．（3）如图 14（ 2），设 D（ m，），连结OD ．则 0＜ m＜ 3，＜ 0．且△ AOC 的面积 = ，△ DOC 的面积= ，△DOB 的面积 =- （），∴四边形 ABDC 的面积 =△AOC 的面积 +△DOC 的面积 +△DOB的面积= =．图14（3）图 14（4）∴存在点D ，使四边形ABDC（4）有两种状况：的面积最大为．如图 14（ 3），过点 B 作 BQ1⊥ BC，交抛物线于点轴于点 E，连结 Q1C．∵ ∠ CBO=45 °，∴∠ EBO=45 °， BO=OE=3 ．∴点 E 的坐标为（ 0， 3）．∴直线 BE 的分析式为．···················· 12 分由解得∴ 点Q1的坐标为（-2，5）．······Q1、交13 分y如图 14（ 4），过点 C 作 CF⊥ CB，交抛物线于点 Q2、交 x轴于点 F，连结 BQ2．∵ ∠ CBO=45 °，∴∠ CFB=45 °，OF=OC=3 ．∴点 F 的坐标为（ -3，0）．∴ 直线CF 的分析式为． (14)分由解得∴点 Q2 的坐标为（ 1，-4）．综上，在抛物线上存在点 Q1（-2 ，5）、 Q2（ 1，-4），使△ BCQ1 、△ BCQ2 是以 BC 为直角边的直角三角形． yxOBADC(x=m)(F2)F1E1 (E2) 【 052】解：（1）依据题意，得解得．．（2分）（2）当时，得或，∵ ，当时，得，∴ ，∵点在第四象限，∴ ．······························（4 分）当时，得，∴ ，∵点在第四象限，∴ ．···················································（ 6 分）（3）假定抛物线上存在一点，使得四边形为平行四边形，则，点的横坐标为，当点的坐标为时，点的坐标为，∵点在抛物线的图象上，∴ ，∴ ，∴ ，∴（舍去），∴ ，∴ ．·······································································（9 分）当点的坐标为时，点的坐标为，∵点在抛物线的图象上，∴ ，∴ ，∴ ，∴ （舍去），，∴ ，∴ ．【053】解：（1）设，把代入，得， (2)分∴抛物线的分析式为：．极点的坐标为． (5)分（2）设直线分析式为：（），把两点坐标代入，得解得．∴直线分析式为．················· 7分，∴············ 9分．················································10 分∴当时，获得最大值，最大值为．·················································11 分 (E)12331DyCBAP2xOFMH （ 3）当获得最大值，，，∴ ．∴四边形是矩形．作点对于直线的对称点，连结．法一：过作轴于，交轴于点．设，则．在中，由勾股定理，．解得．∵，∴．由，可得，．∴．∴ 坐标．············································································· 13 分法二：连结，交于点，分别过点作的垂线，垂足为．易证．(E)12331DyCBAP2xOFMHNM∴ ．设，则．∴，．由三角形中位线定理，．∴ ，即．∴ 坐标． (13)分把坐标代入抛物线分析式，不建立，因此不在抛物线上．·············· 14 分【054】（1）由抛物线经过点 A(0 ， 1)，C(2， 4)，得解得∴抛物线对应的函数关系式为：．························· （2分）（2）当时， P 点坐标为 (1，1)，∴ Q 点坐标为 (2， 0)．当时， P 点坐标为 (2， 3)，∴ Q 点坐标为 (5，0)．·······················（ 5 分）（3）当≤ 2 时，． S ．BADCOMNxyP1P2当≤ 5 时，．S．（8分）当时， S 的最大值为2．···················································（10 分）【055】（1）过点作轴，垂足为，；又，，点的坐标为； (4)分（2）抛物线经过点，则获得， (5)分解得，因此抛物线的分析式为；···································· 7 分（3）假定存在点，使得仍旧是以为直角边的等腰直角三角形：若以点直角点；延至点，使得，获得等腰直角三角形，····················· 8 分点作，；，可求得点；······· 11 分若以点直角点；点作，且使得，获得等腰直角三角形，··········· 12 分点作，同理可；····································· 13 分，可求得点；······································· 14 分，点与点都在抛物上．······················ 16 分【056】解：（ 1） C（ 3， 0）；（2）①抛物，令 =0， = ，∴A 点坐（ 0， c）．∵，∴ ，∴点 P的坐（）．∵PD⊥于 D ，∴点 D 的坐（）．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 5 分依据意，得 a=a′， c= c′，∴抛物 F′的分析式．又∵抛物 F′ 点 D（），∴．⋯⋯⋯⋯⋯ 6 分∴ ．又∵，∴．∴ b:b′ = ．②由①得，抛物线F′为．令 y=0 ，则．∴ ．∵点 D 的横坐标为∴点C的坐标为（）．设直线 OP 的分析式为．∵点P的坐标为（），∴ ，∴，∴．∵点 B 是抛物线 F 与直线 OP 的交点，∴．∴．∵点 P 的横坐标为，∴点B的横坐标为．把代入，得．∴点 B 的坐标为．∴ BC∥ OA，AB∥ OC．（或BC∥ OA，BC =OA ），∴四边形 OABC 是平行四边形．又∵∠ AOC=90 °，∴四边形OABC 是矩形．【057】(1)(2)∵，，∴当点在上运动时，，；当点在上运动时，作于点，有∵ ，∴∴（3）当时，，，此时，过各极点作对边的平行线，与坐标轴无第二个交点，因此点不存在；当，，，此，、【058】解：（ 1）令，得解得，令，得ECB yPA∴A B C ········· 3 分（2）∵ OA=OB=OC=∴ BAC= ACO= BCO=∵A P∥ CB，∴ PAB= ，点 P 作 PE 于 E，APE 等腰直角三角形令OE=，PE=∴ P∵点P 在抛物上∴解得，（不合意，舍去）∴PE= ······································· 4 分∴四形 ACBP 的面= AB?OC+AB?PE=····················· 5 分(3)．假存在∵PAB= BAC =∴PA AC∵MG于点G，∴MGA= PAC =在 Rt△ AOC中，OA=OC=∴ AC=，在Rt△ PAE中，AE=PE=∴ AP=·· 6 分GM CB yPA M点的横坐， M①点 M 在左，(ⅰ ) 当 AMG PCA ，有= ∵ AG= ，MG=即解得（舍去）（舍去）⋯⋯⋯7 分(ⅱ ) 当 MAG PCA 有= GM CB yPA 即，解得：（舍去）∴M··············································································· 8 分②点 M 在右，(ⅰ ) 当 AMG PCA 有=∵AG=， MG=∴解得（舍去）∴ M(ⅱ )当MAG PCA有=即解得：（舍去）∴ M∴存在点M ，使以 A 、M 、G 三点点的三角形与MBEACNDFG（1）H PCA 相像， M 点的坐【 059】解：（ 1）∵四形，，ABCD和四形AEFG是正方形∴A B=AD ， AE=AG ，∠ BAD ＝∠ EAG ＝ 90o ∴∠ BAE ＋∠ EAD ＝∠ DAG ＋∠ EAD∴∠ BAE ＝∠DAG∴△BAE ≌△ DAG （2）∠ FCN ＝ 45o ⋯⋯⋯⋯ 4 分⋯⋯⋯⋯ 5 分原因是：作FH ⊥MN于H∵∠ AEF ＝∠ ABE ＝ 90o∴∠ BAE + ∠ AEB ＝ 90o，∠ FEH+ ∠AEB ＝ 90o∴∠ FEH ＝∠ BAE又∵ AE=EF，∠ EHF＝∠ EBA ＝90o∴△ EFH ≌△ ABE⋯⋯⋯⋯7分∴F H ＝ BE， EH＝ AB ＝ BC ，∴ CH ＝BE＝ FH∵∠ FHC ＝ 90o，∴∠FCH ＝ 45o⋯⋯⋯⋯ 8 分MBEACNDFG（ 2）H（3）当点 E 由B 向C运，∠FCN的大小保持不，⋯⋯⋯⋯9 分原因是：作FH ⊥MN于H由已知可得∠ EAG ＝∠ BAD ＝∠ AEF ＝ 90o合（ 1）（ 2）得∠ FEH＝∠ BAE ＝∠ DAG又∵ G 在射 CD 上，∠ GDA ＝∠ EHF ＝∠ EBA ＝ 90o ∴△ EFH ≌△ GAD ，△ EFH ∽△ ABE⋯⋯11分∴E H＝ AD ＝BC ＝b，∴ CH＝ BE，∴＝＝∴在 Rt△ FEH 中， tan∠ FCN＝＝＝BAOCyx 第 26Q4Q3Q1Q2P3P1P2DCP4 ∴当点 E 由 B 向 C 运，∠ FCN 的大小保持不， tan∠ FCN＝【060】解：（ 1）依据意，得，解得抛物的分析式，点坐是（ 2，4）（2），直的分析式直点点（3）存在．，，，。

完整word版,2010年全国各地中考数学压轴题专集答案1

2010年全国各地中考数学压轴题专辑参考答案及评分标准（一）1 •解：(1)V 抛物线 y = — m Jx2 + 5m x + m 2-3m + 2 经过原点4 4m 2 — 3m + 2= 0，解得 m i = 1, m 2= 2 由题意知m 1M 1,.・.m = 2 •••抛物线的解析式为 y = — 1 x 2+ 5 x 4 2•.•点 B (2, n )在抛物线 y = — 1 x 2+ 5 x 上，• n = 4 4 2 •••点B 的坐标为(2, 4).......................... 2分(2)①设直线0B 的解析式为y = k 1x 求得直线OB 的解析式为y = 2x •/ A 点是抛物线与x 轴的一个交点，可求得 A 点的坐标为（10, 0）设P 点的坐标为（a , 0）,则E 点的坐标为（a , 2a ）根据题意作等腰直角三角形PCD ，如图1可求得点C 的坐标为（3a , 2a ）由C 点在抛物线上，得 2a = — 1 x （3a ）2+ - x 3a4 2 92 11 22即—a — — a = 0，解得 a 1 = — , a 2= 0 （舍去） ②依题意作等腰直角三角形 QMN 设直线AB 的解析式为y = k 2x + b1由点A （10, 0）,点B （2, 4），求得直线 AB 的解析式为y = — - x + 52 当P 点运动到t 秒时，两个等腰直角三角形分别有一条边恰好落在同一条直线上, 有以下三种情况：第一种情况：CD 与NQ 在同一条直线上，如图 2所示可证△ DPQ 为等腰直角三角形此时OP 、DP 、AQ 的长可依次表示为 t 、4t 、2t 个单位 • PQ = DP = 4t , • t + 4t + 2t = 10• t =卫7第二种情况：PC 与MN 在同一条直线上，如图 3所示可证△ PQM 为等腰直角三角形42—22• OP = 2 .......................................................................... 4 分— y J ')MN1AQx1 P图3此时OP 、AQ 的长可依次表示为t 、2t 个单位 ••• OQ = 10-2t•/ F 点在直线 AB 上，• FQ = t ,• MQ = 2t • - PQ = MQ = CQ = 2t , • t + 2t + 2t = 10 • t = 2第三种情况：点 P 、Q 重合时，PD 与QM 在同一条直线上, 如图4 所示此时OP 、AQ 的长可依次表示为t 、2t 个单位 • t + 2t = 10 • t =巴3综上，符合题意的t 值分别为, 2, 1° ........................................ 7 3 2•解：（I ）如图1，作点D 关于x 轴的对称点D ，连接CD 与x 轴交于点E ,连接DE若在边OA 上任取点E'（与点E 不重合），连接 CE'、DE'、D E（n ）如图2,作点D 关于x 轴的对称点 D ；在CB 边上截取 CG = 2，连接D G 与x 轴交于点E ,在EA 上截取EF = 2，则四边形GEFC 为平行四边形，得 GE = C y•抛物线顶点E 的坐标为（1 , 4）由 DE + CE '= D E + CE '> CD ' = D E + CE = DE + CE 可知△ CDE 的周长最小•••在矩形OACB 中, OA = 3, OB = 4, D 为边OB 的中点 • BC = 3, D O = DO = 2, D B = 6T OE // BC ,「. Rt △ D OE s Rt △ D BC , OE BC• OE =• BC = - x 3 = 1D B6•点E 的坐标为(1, 0) ............................................. 6分yJBC/ // D K //is/ :uO /E 隹'A x* 声D图1又DC 、EF 的长为定值，•此时得到的点 E 、F 使四边形CDEF 的周长最小 OE // BC ,「. Rt △ D OE s Rt △ D BG ,OE BGOE = DO • BG =D O •2 1 (BC — CG) = x 1 =-D B D B 6 3OF = OE + EF = -+ 2 = 73 3点E 的坐标为（ -,0) ，点F 的坐标为（-,0） .......... (10)分3 3C(H)将(I)中的抛物线向下平移，则顶点E在对称轴x= 1上，又b = 2•••抛物线的解析式为y=—x2+ 2x + c (a>0)•••此时抛物线与y轴的交点为C (0, c),顶点为E (1,1 + c)•••方程—X2+ 2X+ C= 0 的两个根为X1= 1—一1 C , X2 = 1+ 1 c•此时抛物线与x轴的交点为A (1 —1 c , 0), B (1 + , 1 c , 0)如图，过点E作EF // CB与x轴交于点F，连接CF，贝U S^BCE = S^BCFS^BCE = S^ABC, • S^ BCF = S^ABCBF = AB= 2 1 c设对称轴x= 1与x轴交于点D ,1 ,______________则DF = - AB + BF = 3 1 c2由EF // CB 得/ EFD = / CBO • Rt △EDF s Rt △COB,.史=C° DF OB即3.1 ——c，结合题意，解得1 1 c5c=—4•••点C设直线(0,BC的解析式为y= mx + n,贝U 5 =n 4c 5 ,0 = m+ n2 解得1m =25n =-1 5y= —一x+ ..........................2 4(川)根据题意，设抛物线的顶点为 E (h, k),( h>0, k>0)则抛物线的解析式为y= —(x—h)2+ k 此时抛物线与y轴的交点为C (0, —h2+ k),与x轴的交点为 A (h—k , 0), B ( h+ ... k , 0).( ,k >h>0)•直线BC的解析式为过点E作EF // CB与x轴交于点F，连接CF，贝U S^BCE = S MCFS^BCE = 29AOC,• S^BCF = 2S S OC• BF = 2AO = 2( ■. k —h)设该抛物线的对称轴与x轴交于点D,则DF = ^AB + BF = 3 k —2h2由Rt△ EDF s Rt△ COB，得■E D =DF OBh2 k h k ,即2h2—5、k h+ 2k= 0x结合题意，解得h =2①•••点 E ( h , k )在直线 y =— 4x + 3上， k = — 4h + 3②由①②，并结合题意，解得 ,k = 1.k = 1，h =丄2.抛物线的解析式为 y =— x 2+ x + 3 .................................................................................... 10分44.解：（1）vZ B = 30° / ACB = 90° BAC = 60°T AD = AE ，./ AED = 60°=/ CEP •••/ EPC = 30°................................................................................................................... 1 分•••△ BDP 为等腰三角形•/△ AEPBDP , •/ EAP = / EPA = / DBP = / DPB = 30° AE = EP = 1•// ACB = 90° ADQ ABC.AD = AQ AB = AC 'x 2 2x 8 ..DQ = AD BC = AB ' • tan / BPD =匹=-=丄 ........................... 9 分CP 4 2 (3)如图3，过D 点作DQ 丄AC 于点0,则厶DQE PCE•••在 RT △ ECP 中, (2)如图2，过点 1 1EC =丄 EP = 1 ........... 2 2 D 作DQ 丄AC 于点Q , 且设AQ = a , BD = x •/ AE = 1 , EC = 2, • QC = 3 — a •••在 RT △ ADQ中，DQ = , AD 2 — AQ 2 x 2 2x 8x 1解得x = 4,即卩BD = 4过点 C 作 CF//DP ，则△ ADE AFCAE ACADAF• AF = AC ，即 DF = EC = 2BF = DF = 2•/△ BFCBDP , BF BDBC BP即 BC = CP = 46分设 AQ = a ,贝V QE = 1 — a...Q E = DQ 且 tan / BPD = - , DQ = 3( 1 — a)EC CP 3在Rt △ ADQ 中，由勾股定理得： AD 2= AQ 2+ DQ 2即 12= a 2+ [3(1 — a)] 2,解得 a = 1 (舍去)或 a = — , . DQ = — .............. 10 分5 54•/△ ADQABC ，二 AD = DH =竺=—^ =——AB BC AC 1 x 5 5x...AB = 5 5x , BC = 3 3x ......................................................................................................... 12 分•/ OC = AC ，/ ACO = 120° •/AOC = / OAC = 30° •/ OC = AC , CD 丄 OA ,. OD = DA = 1在 Rt △ ODC 中，OC = 一OD 一 = 一1一 =兰迢 .............. 1 分 cos AOC cos 30 32(i)当 0 V t v 时，OQ = t , AP = 3t , OP = 2— 3t31过点Q 作QE 丄OA 于点E ,贝U EQ = 1 t2••• OPQ = 1 OP • EQ = 1 (2— 3t) • 1 t = — - t 2+ 丄 t2 2 2 4 2即 S = — 3t 2+ ^t ........................................................................ 3 分4 2(ii)当 2 v t < ◎时，如图②，OQ = t , OP = 3t —233•// BOA = 60° / AOC = 30° •/ POQ = 90° 1 1 3 2• S ^OPQ = OQ • OP = -1 • (3t — 2) = t — t2 2 2即 S = 3t 2—t2故当0v t v - 时,S =— 3t 2+丄仁当 2 — 2.3 时，S = -12— t 3 4 2 3 3 2(2) D (三 ,1）或（空,0 ）或 2 (—,0)或( 4 2 3 /3 3 3 3 3(3) BMN 的周长不发生变化如图③，延长 BA 至点F ，使AF = OM ,连结CF•// MOC = / FAC = 90° OC = AC ,.A MOC FAC4 4•••三角形 ABC 的周长 y = AB + BC + AC =+ 丄仝 + 1 + x = 3 + 3x 44即 y = 3+ 3 (x >0) ............................................................. 14 分5.解：（1）如图①，过点C 作CD 丄E O图①A x•该抛物线的解析式为y =丄x 2 — - x — 6164在 Rt △ AOC 中，AC = . 82 + 62 = 10 = AD •点D 在对称轴上，连结 DQ ,显然Z PDC = Z QDC 由已知Z PDC = Z ACD• Z QDC = Z ACD , • DQ // ACDB = AB — AD = 20— 10= 10 1• DQ ABC 的中位线，• DQ = 1 AC = 5 ............................................................................... •分2 AP = AD — PD = AD — DQ = 10— 5= 5, • t = 5— 1 = 5 (秒)•存在t = 5秒时，线段 PQ 被直线CD 垂直平分 .................................... •分在 Rt △ BOC 中，BC = - 122 + 62 = 6、、5 , • CQ = 3.5••• MC = CF ，/ MCO = / FCA ....................... ••• FCN = / FCA + / NCA = / MCO + / NCA10分 =/ OCA - Z MCN = 60° • FCN = Z MCN又••• MC = CF , CN = CNMCN ◎△ FCN• MN = NF ......................................................................................................................... 11 分 • BM + MN + BN = BM + NF + BN = BO — OM + BA + AF = BA + BO = 4• BMN 的周长不变，其周长为 412分6•解：（1）方法2•••抛物线过 C (0, — 6) ,• c = — 6，即 y = ax + bx — 62a144a +12b — 6 = 0解得 a = — , b =——16 416•该抛物线的解析式为1y = — (x + 8)( x — 12) 16方法二：••• A 、B 关于 x = 2 对称，• A ( — 8, 0) 设y = a(x + 8)( x — 12) , v C ( 0, — 6)在抛物线上1 • — 6= a(0+ 8)( 0 —12), • a =(2)存在，设直线 CD 垂直平分PQ3分4分•点Q的运动速度为每秒？亦单位长度............................................ •分5(3)存在过点Q作QH丄x轴于H，则QH = 3, PH = 9在Rt△ PQH 中，PQ = V92+ 32= ^'10 .............................................................................. •分①当MP = MQ ，即M 为顶点时设直线CD 的解析式为y = kx + m (k z 0)则:-6 = mk = 3 0 = 2k + m解得• y = 3x -6m = - 6当 x = 1 时，y = -3,••• M i (1, -3)......................................... 10 分② 当PQ 为等腰△ MPQ 的腰且P 为顶点时设直线x = 1上存在点M (1,y )，由勾股定理得： 42 + y 2= (3、、10)2,.，. y = ± ,74 • M 2 (1 , v'74 ), M 3 (1, - V?4 )......................................... 11 分③ 当PQ 为等腰△ MPQ 的腰且Q 为顶点时过点Q 作QE 丄y 轴于E ,交直线x = 1于F ，则F ( 1, -3) 设直线x = 1上存在点M (1,y )，由勾股定理得：52 + ( y + 3)2= (3J0)2,： y =- 3 ± ,65 •- M 4 (1 , - 3+ \65 ), M 5 ( 1, -3- .65 ).................................. 12 分综上所述，存在点 M ，使△ MPQ 为等腰三角形，点 M 的坐标为：M 1 (1 , - 3), M 2 (1，-. 74 ), M 3 ( 1, - ： 74 ), M 4 (1 , - 3+ .65 ), M 5 (1, - 3 -.65 )7•解：2(1) 把 A ( - 1, 0), B (1, 0)代入 y = ax + bx + 1 得：a -b + 1 = 0 a = - 1解得a +b + 1 = 0b = 0• ............................................................................................................................... •抛物线的解析式为 y = - x + 1 ............................................................................................... •分 (2) .................................................................................................................................... 令 x = 0,得 y — 1 ,• C (0, 1) ................................................... •分OA — OB — OC — 1，•/ BAC — / ACO — / BCO — / ABC — 45° •/ BD // CA ，•/ ABD — / BAC — 45°如图1,过点D 作DE 丄x 轴于丘，则厶EDB 为等腰直角三角形设 EO — x ,贝U ED — x + 1,. D ( -x , - x -1) •••点 D 在抛物线 y =- x 2 + 1 上，• - x - 1=-( - x)2+ 1 解得X 1= 2, X 2 =- 1 (不合题意，舍去)也可)1 1• S 四边形 ACBD — AB - OC + 一 AB - ED2 21 1= J.x 2 x 1 + x 2x 3 22=4 ....................................................................................................... •分（说明：也可直接求直角梯形ACBD的面积为4）（3）存在.................................................................. 8分•••/ ABC = / ABD = 45°,DBC = 90°•/ MN 丄x 轴，•••/ MNA = Z DBC = 90°BC = OB2+ OC2= 2 , BD = .. ED2+ EB2= 3、. 2 设M点的横坐标为m,则M （m, - m2+ 1）①当点M在y轴左侧时，如图2,则m< - 1i ）若厶NMA BCD，则MNNA BC BD即m - 1= _2，整理得3m2+ m-2 = 0—m —1 3,2解得m1 = —1 （舍去），m2=—（舍去）3.............................................................. 9分ii ）若厶NAM BCD，则■MN= BD NA BCm2- 1 3j2—m —1 . 2整理得m2+ 3m+ 2 = 0解得m1= - 1 （舍去），m2= -2- m2+ 1 = - （-2）2+ 1= - 3•- M1 （-2, - 3）10分②当点M在y轴右侧时，如图2,则m> 1i ）若厶NMA BCD，则■MN=匹AN BD即必1= _2，整理得3m2- m- 4= 0m + 1 3・2解得m1= - 1 （舍去），m2=-3•—m2+ 1 = —（—）2+ 1 =——3 94 7•M 2 （—,—-）.........................3 9i ）若NAM BCD，则MNAN BD BCm2-1 m+ 13、-2=2，整理得m2- 3m-4 = 0解得m i= —1 (舍去)，m2 = 4 /• —m2+ 1 = —42+ 1 = —15• M3 （4, —15）•存在点M,使以A、M、N为顶点的三角形与△ BCD相似，M点的坐标分别为： 4 7M1 (—2, —3), M2(_,—_), M3 (4, —15) (12)分3 9&解：（1）：抛物线y= 1x2+ bx+ c 经过点 A ( 2, 0), C (0, —1) 2.2+ 2b + c= 0c = —1解得：b =—丄,2c= —1 .................................................................................... (2)分•抛物线的解析式为1 2 1 ‘y= x —x—1 ............................................................ (3)分2 2(2)设点D 的坐标为(m, 0)( 0v m v 2)，贝U OD = m, AD = 2 —m由厶ADEAOC得，竺=匹......................................................... •分AO OC...2 m = DE_2 = 1••• DE = .................................................................................................................... 5分2DCE 的面积=—x 2——m x m =—丄m2+ 1 m = —— ( m—1) 2+ —2 2 4 2 4 4当m= 1时，△ DCE的面积最大•••点D的坐标为（1, 0）(3)存在12 1 12 1在y= x —x—1 中，令y = 0,得—x —x—1= 02 2 2 2解得X1= —1 , x2= 2，•点B的坐标为（—1 , 0）设直线BC的解析式为y= kx+ b一k + b = 0则 b =—1 解得k=—1, b=- 1•直线BC的解析式为y=—x—1AC = 、、OA2+ OC2= 5在Rt△ AOC中，由勾股定理得:•••点B ( —1, 0),点C (0, ①当以C为顶点且PC = AC = —1),. OB = OC / BCO = 45.5时，如图1ACHP1OB Oj y9/图1设P (n , -n - 1)，过点P 作PH 丄y 轴于H 则/ HCP = Z BCO = 45° CH = PH = | n|在 Rt △ PCH 中，n 2+ n 2= ( 5)2，解得 n i = -I 0 , &= -—°22••• P i (兰，-』-1),卩2(-丄，210 -1) 2 2 2 2........................................................... -10 分②当以A 为顶点且AC = AP = ,5时，如图2 设P ( t ，-1 - 1)，过点P 作PG 丄x 轴于G 则 AG = | 2 -1| , GP = | -1- 1| 在 Rt △ APG 中，T AG 2+ PG 2= AP 2•••(2-t)2+ ( -1- 1)2 = 5,解得：t 1= 1, t 2= 0 (舍去)二 P 3 (1 , - 2) ................................ -11 分 ③当以P 为顶点时，PC = PA ,如图3设P (x , - X - 1),过点P 作PM 丄y 轴于M , PN 丄x 轴于N 则 N (x , 0)•/△ C 为等腰直角三角形，• PM = CM = x , PA = PC =2 x• AN = | x - 2| , PN = | -x -1| 在 Rt △ PAN 中，T AN 2+ PN 2= PA 2 •••(x -2) 2+ (x + 1)2= ( , 2 x) 2,解得：x=-212分BC 上存在点卩，使厶ACP 为等腰三角形，点 P的坐标为：八 r 顶怖八 r 57、―1 ) , P 2 ( -,― 1), P 3 ( 1 , - 2), P 4 (,)2 2 2 2 2a9.( 1)证：T △ ABC s^ A 1B 1C 1，且相似比为 k (k > 1),.••旦=k ,「. a = ka 1a 1又T c = a 1, • a = kc ............................................................................................................. •分 (2)解：取 a = 8, b = 6, c = 4,冋时取 a 1 = 4, b 1 = 3, C 1 = 2 ............................................. •分此时—=—=—=2, • △ ABCA 1B 1C 1 且 c = a 1 ............................................................................................................ 10 分a 1b 1 C 1 注：本题也是开放型的，只要给出的 △ ABC 和厶A 1B 1C 1符合要求就相应赋分.(3)解：不存在这样的 △ ABC 和厶A 1B 1C 1 .理由如下：若 k = 2,贝V a = 2a 1, b = 2b 1, c = 2c 1综上所述，在直线 P 1 (于，又T b= a1, c= b1,. a= 2a1 = 2b= 4b1 = 4c•- b= 2c ................................................................................................................................ 12 分••• b + c = 2c + c = 3c v 4c = a ，而 b + c > a 故不存在这样的 △ ABC 和厶A I B I C I ，使得k = 2..................................注：本题不要求学生严格按反证法的证明格式推理，只要能说明在题设要求下情况不可能即可.10. ( 1)猜想：OG 丄 CD .证明：如图，连结 OC 、OD ，贝y OC = OD .••• G 是CD 的中点 •由等腰三角形的性质，有 OG 丄CD . 2分(2)证明：T AB 是O O 的直径，•/ ACB = 90°.而/ CAE = Z CBF (同弧所对的圆周角相等). 在 Rt △ ACE 和 Rt △ BCF 中vZ ACE = Z BCF = 90° AC = BC ,Z CAE = Z CBF• Rt △ ACE 也 Rt △ BCF . ( ASA )• AE = BF . ........................................................ •分(3)解：如图，过点 O 作BD 的垂线，垂足为 H ，贝U H 为BD 的中点.1• OH = - AD ，即 AD = 2OH .2又Z CAD = Z BAD , • CD = Z BD , • OH = OG . 在 Rt △ BDE 和 Rt △ ADB 中vZ DBE = Z DAC = Z BAD , • Rt △ BDE s Rt △ ADB .• BD =匹，即 BD 2= AD - DE .AD DB• BD 2= AD - DE = 2OG - DE = 6(2 -屁). ................................................ •分又 BD = FD , • BF = 2BD .• BF 2= 4BD 2= 24(2-近) ............................... ①. .... •分设 AC = x ,贝V BC = x , AB = . 2 x .v AD 是Z BAC 的平分线，•/ FAD = Z BAD .在 Rt △ ABD 和 Rt △ AFD 中vZ ADB = Z ADF = 90°, AD = AD , Z FAD = Z BAD• Rt △ ABD 也 Rt △ AFD . ( ASA ) • AF = AB = . 2x , BD = FD . • CF = AF — AC = 2x -x = (2 — 1)x .在Rt △ BCF 中，由勾股定理，得BF 2= BC 2+ CF 2= x 2+ [(血—1)x]2= 2(2—V2)X 2. ............... ②.••…10 分••••14 分 k = 2的由①、②，得2(2 —、、2)x2= 24( 2—.2 ).••• x 2= 12,.・.x = 2.3 或—2. 3 (舍去) AB = 2x =2 • 2.3 = 2.6.•••o O 的半径长为J6 . ....................................................................................... 11分 •• S o o = n •( 6)2= 6 n........................................................................................................................ 12 分11. 解：(1 )由题意得2 4解得 a = — , b = — , c = — 2.3 3 •这条抛物线的函数表达式为y = — x 2+ — x — 233(2)如图，连结 AC 、BC .A ,AC 与对称轴x = — 1的交点即为所求的点 P .设直线AC 的表达式为y = kx + b ,则—3k + b = 0b = —2解得 k =— 2 , b = — 2.3•直线AC 的表达式为y = — -x — 2 ......................3 把x = — 1代入上式，得y = — 2 X ( — 1)— 2= 3•/ DE // PC ,即卩 DE // AC ,.A OEDOAC . 3 3 3 -,• OE = 3— -m , • AE = - m .222方法连结OPS = S ^POE + S A POD —S A OED=—X( 3—— m) X - + 丄 X( 2—m) X1—— X(3 — — m) X ( 2 — m)2 23 2 2 23 2 3= --- m + 一 m ................................................................................................. 10 分— 2由于BC 的长度一定，要使△ PBC 的周长最小，必须使PB + PC 最小.••点 P 的坐标为(—1,—-)3(3) S 存在最大值，理由如下：OE = OA ，即 _0EOD 0C 2— m点B 关于对称轴的对称点是点 2a9a — 3b + c =08分••• — - v 0,. S存在最大值. ............................................ 11分—s = — 3 m + — m = - 3( m_ 1) 2 2 3 4 5 6+ 34 2 44•••当m = 1时，S 最大=-.......................................... 12分4 方法二：S = S ^OAC — S ^OED — S^ PAE — S^ PCD11 3 13 4 1=—x 3 x 2 — x ( 3— m) x ( 2— m) 一 x — m x — — — x m x 1 2 2 2 2 2 3 23 2 3 =—一 m H ——m ................................................................................................. 10 分4 2 以下同方法一.12. ......................................................................................... ( 1)证明：连接0M ......................................................................... 1分•/ MP 是O O 的切线，• 0M 丄MP•••/ OMD + / DMP = 90° •/ 0A 丄 0B ,「./ OND + Z ODM= 90°又•••/ MNP = Z OND , Z ODM = Z OMD• Z DMP = Z MNP ,• PM = PN ........................ •分 1 (2)解：设 BC 交 OM 于点 E ,v BD = 4, • OA = OB = BD = 2 23•- PA = - AO = 3,「. PO = 5 ....................................................................................... •分2• tan Z EFO = .3，直线EF 的倾斜角为 60° •直线EF 的解析式为：y —= tan60 ° x — ( — , 3 )] 化简得：y = 13 x + 4. .................................................................................................... •分(2)设矩形沿直线 EF 向右下方翻折后，B 、C 的对应点为B (X 1, y 1), C (X 2, y 2) 过B '作B 'A '丄AE 交AE 所在直线于 A '点2•/ BC // MP , OM 丄 MP ,• OM 丄 BC ,• BE = BC .................................................. 7 分 vZ BOM + Z MOP = 90°,在 Rt △ OMP 中，Z MPO + Z MOP = 90° • Z BOM = Z MPO ，又 vZ BEO = Z OMP = 90° •••△ OMPBEO ,「. 9^ =匹 ................................................ 10 分OP BO13.解: 得: = BE ，• BE = - , • • BC = 8 .................................................................... 12分 5 2 5 51)由于折痕所在直线 EF0) P过 E(— ■ 3 , 1 )、v B 'E= BE= 2、、3 , Z B EF = Z BEF = 60 °•••/ B'EA'= 60° A A E = J3 , B A = 3二 A 与 A '重合,B '在 y 轴上，••• X 1= 0, y i = -2，即 B '( 0, - 2) 【此时需说明B ' （x i , y i ）在y 轴上】设二次函数的解析式为： y = ax 2 + bx + c抛物线经过 B （- 3. 3，1）、E （- . 3，1）•••该二次函数解析式为：y =- ^x 2- -/3x -2 ....................................................................... •分33（3）能，可以在直线 EF 上找到P 点，连接B 'C 交EF 于P 点，再连接BP由于B 'p = BP ，此时点 P 与C 、B '在一条直线上，故 BP + PC = B P + PC 的和最小由于为BC 定长所以满足 △ PBC 周长最小. ............................................ 10分设直线B C 的解析式为：y = kx + b•••点P 的坐标为( -18 3 ,-巴) 11 111）设线段AB 所对应的函数关系式为 y = kx + b•线段AB 所对应的函数关系式为 y 甲=-80X + 540 .................................................自变量x 的取值范围是3< x < -27 （或3< x < 旦，下同） .................... •分4 427a — 3 3 b + c = 1 3a — v'3 b + c = 1c = - 2a =--3解得b = - — V33c = — 2B ' ( 0, - 2)-2 = b则0 =-3、、3k + b解得k =-92 ；3••直线B C 的解析式为：y =- ' x -29 又•••点P 为直线B C 与直线EF 的交点解得y = 3x + 410 y =-石14分14.解:把(3, 300),(27 , 0)代入得 300 = 3k + b27 0= k + b4k = - 80 解得b = 540C(2)••• x=-在3<x w 27中，.••把x=-代入y 甲=—80x+ 540 中得y 甲=1802 4 2(3)①若直线经过顶点，则 AC 边上的中垂线即为所求线段 ....................... 8分②若直线不过顶点，可分以下三种情况： (a)直线与BC 、AC 分别交于E 、F ，如图2所示过点E 作EH 丄AC 于点H ，过点B 作BG 丄AC 于点G 易求得 BG = 4， AG = CG = 3 设 CF = X ，贝U CE = 8—x4 由厶 CEHCBG ，可得 EH = - (8 — x)5根据面积相等，可得丄• x • — ( 8— x) = 6 ......................... 10分2 5 •- x =3 (舍去，即为①)或 x = 5• CF = 5， CE = 3，直线EF 即为所求直线 ................ .乙车的速度为—=40 (km/h ) 12分(3)由题意知有两次相遇方法一:15①当 0W x < 3 时，100x + 40x = 300，解得：x =716分 ②当 3v x w 27 时，(540 — 80x) + 40x = 300,解得：x = 64 20分综上所述，当它们行驶了15小时或6小时时，两车相遇 7方法二：设经过X 1小时两车首次相遇 15则 40X 1 + 100x 1= 300，解得：x 1 =..............716分设经过X 小时则 80(X 2 — 3) = 40X 2，解得:X 2= 620分15.解：(1)图(2)不能如图1,若直线CD 平分△ ABC 的面积那么 S\ ADC = S^ DBC 1 1•——AD • CE = BD • CE 2 2• - AD = BD ............................................... 5 分 •/ AC 丰 BC ,「. AD + AC 丰 BD + BC •过点C 不能画出一条“等分积周线” ............ 7分图1(b) 直线与AB、AC分别交于M、N，如图3 所示图212分由（a ）可得AM = 3, AN = 5,直线MN 即为所求直线（仿照上面给分） ................................. 15分（c ）直线与AB 、BC 分别交于P 、Q ,如图4所示过点A 作AY 丄BC 于点Y ,过点P 作PX 丄BC 于点XAY = 245BQ = 8 —xPC CQ 16•解：（1）①如图1，当PQ // AB 时，有 =...... 2分AC CB3 3t-，解得：t = 24.•.当 t = 2 秒时，PQ // AB②解法1:如图2，当t = 2秒时，PQ // AB ,此时PQ 为 5△ ACB 的中位线，PQ = 5 ............................................ 6分2 取PQ 的中点M ，则以PQ 为直径的圆的圆心为 M , 1半径为丄PQ ................................................................. 8分2 过点M 、C 向AB 作垂线，垂足分别为 N 、H12 1 6贝U CH = 一 , MN = — CH = 一 ................ 10 分5 2 5 1••• MN v— PQ ,.直线AB 与以PQ 为直径的圆相交2.......................................................... 12分解法2:如图3,当t = 2秒时，PQ // AB ,此时PQ 为 △ ACB 的中位线，取 PQ 的中点M ，分别过点 M 、C 向由面积法可得（注：若直接按与两边相交的情况分类, 也相应给分）设BP = x ,则C综上所述，符合条件的直线共有三条 20分图1AB作垂线，垂足分别为N、H , CH交PQ于点G,连接CM1••• MN = _ CH ，即 MN = GH = CG2 在 Rt △ CGM 中，GC V MC ,「. MN V MC•••直线AB 与以PQ 为直径的圆相交 .............. 12分解法3:如图4,当t = 2秒时，PQ // AB ,此时PQ 为仏ACB 的中位线，过点Q 向AB 作垂线，垂足为N ,则 Rt △ BNQ s Rt △ BCA , • =竺，即-=竺,AB AC 5 3• NQ = 65•直线AB 与以PQ 为直径的圆相交(2) 解法1:如图5，取PQ 的中点 M ，作MN 丄AB 、PG 丄AB 、QH丄AB ,垂足分别为N 、G 、H则由 Rt △ APG s Rt △ ABC ，得 PG = 4t ................... 14 分5 3由 Rt △ BHQ s Rg BCA ，得 HQ = - (4 -1) ................ 16 分此时MN 是梯形PGHQ 的中位线，• MN = 6 + _L510.......................................................... 20分当PQ 2= 4MN 2时，以PQ 为直径的圆与直线 AB 相切即(3 — t) 2+ t 2= 4( 6 + —)2 ........................................ 26 分5 10G 、N连接 AM 、BM 、CM由 S A ABC = S^ ACM + S^ BCM + S ^ ABM 可得： 1 t 1 1 1 1 x 3 x + —x 4 x ( 3—t) + x 5x MH =—x 3 x 4 22 2 2 2 2解得：MH = 6 + —5 10当PQ 2= 4MN 2时，以PQ 为直径的圆与直线 AB 相切即(3 — t) 2+ t 2= 4( 6 + — ) 2 ........................................ 26 分5 10 解得：t 1 = 3, t 2= 27 ...................................................... 30 分由平行线间的距离处处相等可知，点 M 到AB 的距离为-，小于-PQ5 212分解得:t1= 3, t2= £ 30分解法2:如图6,取PQ 的中点M ，作MH 丄AB 、MG 丄AC 、垂足分别为H 、N ,图4MN 丄BC ,垂足分别为H 、图649解法3:如图7,取PQ的中点M ,作MH丄AB、MN丄BC,延长 NM 交 AB 于点 G ,贝U MN = - PC = -（3-t ） , NQ = - CQ=-,2 2 2 2由 Rt △ BGN s Rt △ BAC ,得 GN = 3 - ?t , • GM = 3-- t -丄（3-1）=8 - -又••• Rt A GMH s Rt △ ABC ,：些 BC解得：MH = 6 +丄5 10当PQ 2= 4MN 2时，以PQ 为直径的圆与直线 AB 相切即（3-1）2+ t 2= 4（ 6 + — ）25 10 解得：&= 3, t 2= 27 ..................492.5 （小时）17.解：（1）若二分队应在营地不休息, 则 a = 0,速度为4千米/时,一 10行至塌方处需一4因为一分队到塌方处并打通道路需要 10+ 1 （小时） b所以要使二分队在最短时间内赶到A 镇，则有：10 + 1 <2.5,• b >迴（千米/时）b 3故一分队的行进速度至少为20千米/时3分3（2）若b = 4千米/时，则一分队到塌方处并打通道路需要 10+ 1= 3.5 （小时） 4一分队赶到A 镇共需30 + 1 = & 5 （小时）4（I ）若二分队在营地不休息,且在塌方处需停留，则后 20千米与一分队同行，二分队和一分队可同时赶到 A 镇;10分（n ）若二分队在营地休息，则a > 0，二分队的行进速度为 4+ a > 4千米/时①若二分队在塌方处需停留，则当一分队打通道路后，二分队将先赶到A 镇，不符合题意，舍去; .................................................................................................................. 11分②若二分队在塌方处不停留，要使二分队和一分队同时赶到 A 镇，则有： 30 2a + = & 5,即 a 2-4. 5a — 4= 04 a••• NB =GM 即 MH AB ' 4AH26分M30分4.536.254.536.25 4 6解得a i =v 0 (舍去)，a 2= > > 3 (舍去)22 2.................................................................................................................. 13分综上所述，要使二分队和一分队同时赶到 A 镇，二分队应在营地不休息 14分(1) 如图4，由一于AD = BD ，将△ AED 绕点D 旋转180 °得厶BE 贝V AE = BE ； ED = E'D ,连接 E F•••/ FBE = / ABC + / ABE = / ABC + / CAB = 90°•••在 Rt △ BE ；F 中有 BE ' 2+ BF 2= E F 2 又••• FD 垂直平分 EE ；••• EF = E 'F • AE 2+ BF 2= EF 2(2) 如图5,由于AC = BC ,将厶AEC 绕点C 旋转90°得厶BE C 贝U AE = BE , CE = CE '，连接 E F•••/ FBE '= / ABC + / CBE '= / ABC + / CAB = 90•••在 Rt △ BE 'F 中有 BE ' 2+ BF 2= E F 2•••/ E CF = Z E CB + / BCF = Z ACE + / BCF=90° — Z ECF = 90° — 45°= 45°= Z ECFCE = CE ', CF = CF• △ CEF 也厶 CE 'F ,••• EF = E F2 2 2• AE 2+ BF 2= EF 2(3) 将厶ADF 绕点A 顺时针旋转 90°得厶ABG ，且FD = GB , AF = AG 因为△ CEF 的周长等于正方形 ABCD 的周长的一半，所以 CE + EF + CF = CD + CB = CF + FD + CE + BE EF = FD + BE = GB + BE = GE 从而可得厶 AEG ^A AEF ,.Z EAG = Z EAF 又•••/ EAG = Z EAB + Z BAG ,Z BAG = Z DAF• Z EAF = Z EAB + Z DAF ，而Z EAB + Z EAF + Z DAF = 90° • Z EAF = 45°由(2)知 BM 2 + DN 2= MN 2•••由勾股定理的逆定理知：线段 BM 、MN 、DN 能构成直角三角形 ................ 18分19.解: (1)由题意知：k 2= 1x 6 = 6 ........................................................................................... 1分•••反比例函数的解析式为 y = 6x18.12分/DD 图4D FA又 B (a, 3)在y= 6的图象上，• a = 2,二B ( 2, 3)x231•••直线 y = k i x + b 过 A (1, 6), B (2, 3)两点(2) x 的取值范围为1 v x v 2(3) ..................................................................................................................................... 当 S 梯形 OBCD = 12 时，PC = PE ................................................................................................. •分设点 P 的坐标为(m , n ),T BC // OD , CE 丄OD , OB = CD , B ( 2, 3) C (m , 3) , CE = 3, BC = m — 2, OD = m + 21iS 梯形 OBCD =CE ,即卩 12=丄 x (m — 2 + m + 2) x 322• m = 4, mn = 6,「. n = 3，即 PE = 1 CE2 2• PC = PE ......................................................................................................................... 10 分20. 解：(1)同意.连接 EF ，则/ EGF = Z D = 90 ° EG = AE = ED , EF = EF• Rt △ EGF 也 Rt △ EDF , • GF = DF ........................................................................... •分 (2) 由(1 )知 GF = DF ，设 DF = x , BC = y ,则有 GF = x , AD = y •/ DC = 2DF , • CF = x , DC = AB = BG = 2x • BF = BG + GF = 3x在 Rt △ BCF 中，BC 2+ CF 2= BF 2,即即 y 2+ x 2= (3x)2• y = 2^2 x ,「. -AD = — =、、2 ................................................. 6 分AB 2x (3) 由(1 )知 GF = DF ，设 DF = x , BC = y ,则有 GF = x , AD = yT DC = n ■ DF , • DC = AB = BG = nx• CF = (n — 1)x , BF = BG + GF = (n + 1)x在 Rt △ BCF 中，BC 2+ CF 2= BF 2,即卩 y 2+ [( n — 1)x]2 = [( n + 1)x]2 • y = 2jn x ,「. -AD = — = (或鼻)................................ 10 分AB nx nJ n21.解：(1)设抛物线的解析式为 y = ax 2 + bx + c (0),则有=1 16a — 4b + c = 0 a= 2c = — 4 解得 b = 14a + 2b + c = 0c = —4•抛物线的解析式为 y =丄x 2 + x — 4k , + b = 6 2k i + b = 3解得：爲3(2)过点M 作MD 丄x 轴于点D ，设M 点的坐标为(m , - m 2+ m — 4)2232则AD = m + 4, MD = —— m2—m + 42S = S^AMD + S 梯形DMBO ——S^ABO1 12 1 1 2—=-(m+ 4)( —-m2—m+ 4) + — ( —— m2—m+ 4+ 4)( —m)—丄x 4x 42 2 2 2 2=—m2—4m ( —4v mv 0) ................................................... •分即S= —m2—4m = —(m+ 2) 2+ 4.S最大值=4 .............................................................................................................................. 7分(3)满足题意的Q点的坐标有四个，分别是：( —4, 4),( 4, —4)(—2 + 2,5 , 2—2...5 ),( —2—2. 5 , 2 + 2、、5 ) ......................... 11 分22. 解：(1)设直线DE的解析式为y= kx+ b3= b k = —1•••点D , E的坐标为(0, 3)、( 6, 0),. 解得 20= 6k + bb = 3直线DE 的解析式为y= —1 x+ 3 ..................................................................................... 1分2•••点M在AB边上，B (4, 2)，而四边形OABC是矩形，.••点M的纵坐标为2一11又•••点M 在直线y=—— x+ 3 上，.2= —— x+ 3,. x = 2 2 2.M (2, 2) ................................................................. •分(2)V y= m( x> 0)经过点M (2, 2),. m = 4,. y= - ............................. •分x x又•••点N在BC边上，B (4, 2),.点N的横坐标为4, ,,, 1•••点N 在直线y= —-x+ 3 上，.y = 12.N (4, 1) ............................................................... •分4 4•.•当x= 4时，y= — = 1,.点N在函数y=-的图象上 .............................. •分x x(3) 4< mW 8 .................................................................................................................... •分23•解：(1) y= 2t；(2)当BP = 1时，有两种情形:1①如图1,若点P从点M向点B运动，有MB = -BC = 4,2.PQ = 6 •连接EM ,•••△ EPQ是等边三角形，. EM丄PQ,. EM = 3.3•/ AB = 3.3 ,•.点E 在AD 上•••△ EPQ与梯形ABCD重叠部分为△ EPQ，其面积为：33。

2010年全国压轴题精选

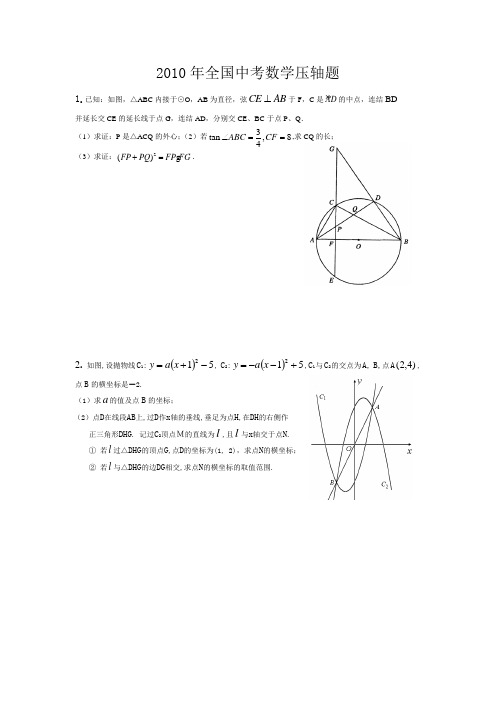
2010年全国中考数学压轴题1.已知：如图，△ABC 内接于⊙O ，AB 为直径，弦CE AB ⊥于F ，C 是 AD 的中点，连结BD并延长交CE 的延长线于点G ，连结AD ，分别交CE 、BC 于点P 、Q ．（1）求证：P 是△ACQ 的外心；（2）若3tan ,84ABC CF ∠==,求CQ 的长；（3）求证：2()FP PQ FP FG += ．2. 如图,设抛物线C 1:()512-+=x a y , C 2:()512+--=x a y ,C 1与C 2的交点为A, B,点A )4,2(,点B 的横坐标是－2.（1）求a 的值及点B 的坐标；（2）点D 在线段AB 上,过D 作x 轴的垂线,垂足为点H ,在DH 的右侧作正三角形DHG . 记过C 2顶点Ｍ的直线为l ,且l 与x 轴交于点N . ① 若l 过△DHG 的顶点G ,点D 的坐标为(1, 2)，求点N 的横坐标； ② 若l 与△DHG 的边DG 相交,求点N 的横坐标的取值范围.3.如图，二次函数k m x y ++=2)(的图象，其顶点坐标为M(1,-4).（1）求出图象与x 轴的交点A,B 的坐标；（2）二次函数的图象上是否存在点P ，使M A B P A BS S ∆∆=45,若存在，求P 点的坐标；若不存在，请说明；（3）将二次函数的图象在x 轴下方的部分沿x 轴翻折，图象的其余部分保持不变，得到一个新的图象，请你结合这个新的图象回答：当直线)1(<+=b b x y 与此图象有两个公共点时，b 的取值范围.4.已知：函数y=ax 2+x+1的图象与x 轴只有一个公共点．（1）求这个函数关系式；（2）如图所示，设二次．．函数y=ax 2+x+1图象的顶点为B ，与y 轴的交点为A ，P 为图象上的一点，若以线段PB 为直径的圆与直线AB 相切于点B ，求P 点的坐标；（3）在(2)中，若圆与x 轴另一交点关于直线PB 的对称点为M ，试探索点M 是否在抛物线y=ax 2+x+1上，若在抛物线上，求出M 点的坐标；若不在，请说明理由．A xyOB5.如图，在平面直角坐标系中，顶点为（4，1-）的抛物线y 轴于A 点，交x 轴于B ，C 两点（点B在点C 的左侧）. 已知A 点坐标为（0，3）. （1）求此抛物线的解析式；（2）过点B 作线段AB 的垂线交抛物线于点D ，如果以点C 为圆心的圆与直线BD 相切，请判断抛物线的对称轴l 与⊙C 有怎样的位置关系，并给出证明；（3）已知点P 是抛物线上的一个动点，且位于A ，C 两点之间，问：当点P 运动到什么位置时，PAC∆的面积最大？并求出此时P 点的坐标和PAC ∆的最大面积.6.在直角梯形OABC 中，CB//OA ，∠COA=90︒，CB=3，OA=6，BA=3分别以OA 、OC 边所在直线为x 轴、y 轴建立如图所示的平面直角坐标系。

2010年中考数学压轴100题精选湘教版

2010年中考数学压轴题100题精选【001】如图，已知抛物线2(1)y a x =-+a ≠0）经过点(2)A -，0，抛物线的顶点为D ，过O 作射线OM AD ∥．过顶点D 平行于x 轴的直线交射线OM 于点C ，B 在x 轴正半轴上，连结BC ．（1）求该抛物线的解析式；（2）若动点P 从点O 出发，以每秒1个长度单位的速度沿射线OM 运动，设点P 运动的时间为()t s ．问当t 为何值时，四边形DAOP 分别为平行四边形？直角梯形？等腰梯形？（3）若OC OB =，动点P 和动点Q 分别从点O 和点B 同时出发，分别以每秒1个长度单位和2个长度单位的速度沿OC 和BO 运动，当其中一个点停止运动时另一个点也随之停止运动．设它们的运动的时间为t ()s ，连接PQ ，当t 为何值时，四边形BCPQ 的面积最小？并求出最小值及此时PQ 的长．【002】如图16，在Rt △ABC 中，∠C =90°，AC = 3，AB = 5．点P 从点C 出发沿CA 以每秒1个单位长的速度向点A 匀速运动，到达点A 后立刻以原来的速度沿AC 返回；点Q 从点A 出发沿AB 以每秒1个单位长的速度向点B 匀速运动．伴随着P 、Q 的运动，DE 保持垂直平分PQ ，且交PQ 于点D ，交折线QB -BC -CP 于点E ．点P 、Q 同时出发，当点Q 到达点B 时停止运动，点P 也随之停止．设点P 、Q 运动的时间是t 秒（t ＞0）．（1）当t = 2时，AP = ，点Q 到AC 的距离是；（2）在点P 从C 向A 运动的过程中，求△APQ 的面积S 与t 的函数关系式；（不必写出t 的取值范围）（3）在点E 从B 向C 运动的过程中，四边形QBED 能否成为直角梯形？若能，求t 的值．若不能，请说明理由；（4）当DE 经过点C 时，请直接．．写出t 的值．图16【003】如图，在平面直角坐标系中，已知矩形ABCD 的三个顶点B （4，0）、C （8，0）、D （8，8）.抛物线y=ax 2+bx 过A 、C 两点.(1)直接写出点A 的坐标，并求出抛物线的解析式；(2)动点P 从点A 出发．沿线段AB 向终点B 运动，同时点Q 从点C 出发，沿线段CD向终点D 运动．速度均为每秒1个单位长度，运动时间为t 秒.过点P 作PE ⊥AB 交AC 于点E ，①过点E 作EF ⊥AD 于点F ，交抛物线于点G.当t 为何值时，线段EG 最长?②连接EQ ．在点P 、Q 运动的过程中，判断有几个时刻使得△CEQ 是等腰三角形? 请直接写出相应的t 值。

2010年中考数学压轴题100题精选(81-90题)巩固基础

2010年中考数学压轴题100题精选（81-90题）【081】如图，已知抛物线y ＝34x 2＋bx ＋c 与坐标轴交于A 、B 、C 三点， A 点的坐标为（－1，0），过点C 的直线y ＝34tx －3与x 轴交于点Q ，点P 是线段BC 上的一个动点，过P 作PH ⊥OB 于点H ．若PB ＝5t ，且0＜t ＜1．（1）填空：点C 的坐标是_▲_，b ＝_▲_，c ＝_▲_；（2）求线段QH 的长（用含t 的式子表示）；（3）依点P 的变化，是否存在t 的值，使以P 、H 、Q 为顶点的三角形与△COQ 相似？若存在，求出所有t 的值；若不存在，说明理由．【082】（09上海）在直角坐标平面内，O 为原点，点A 的坐标为(10)，，点C 的坐标为(04)，，直线CM x ∥轴（如图7所示）．点B 与点A 关于原点对b=+（b为常数）经过点B，且与直线CM相交于点D，联结OD．称，直线y x b（1）求b的值和点D的坐标；△是等腰三角形，求点P的坐标；（2）设点P在x轴的正半轴上，若POD（3）在（2）的条件下，如果以PD为半径的圆P与圆O外切，求圆O的半径．【083】如图，在直角坐标系中，点A的坐标为（－2，0），连结OA，将线段OA绕原点O顺时针旋转120°，得到线段OB.（1）求点B的坐标；（2）求经过A、O、B三点的抛物线的解析式；（3）在（2）中抛物线的对称轴上是否存在点C，使△BOC的周长最小？若存在，求出点C的坐标；若不存在，请说明理由.（4）如果点P是（2）中的抛物线上的动点，且在x轴的下方，那么△PAB是否有最大面积？若有，求出此时P点的坐标及△PAB的最大面积；若没有，请说明理由.【084】如图，在平面直角坐标系中，直线l：y=－2x－8分别与x轴，y轴相交于A，B两点，点P （0，k）是y轴的负半轴上的一个动点，以P为圆心，3为半径作⊙P.（1）连结PA，若PA=PB，试判断⊙P与x轴的位置关系，并说明理由；（2）当k为何值时，以⊙P与直线l的两个交点和圆心P为顶点的三角形是正三角形？BAOyx【085】如图①，已知抛物线32++=bx ax y （a ≠0）与x 轴交于点A (1，0)和点B (－3，0)，与y 轴交于点C ．(1) 求抛物线的解析式；(2) 设抛物线的对称轴与x 轴交于点M ，问在对称轴上是否存在点P ，使△CMP 为等腰三角形？若存在，请直接写出所有符合条件的点P 的坐标；若不存在，请说明理由．(3) 如图②，若点E 为第二象限抛物线上一动点，连接BE 、CE ，求四边形BOCE 面积的最大值，并求此时E 点的坐标．【086】如图，以BC为直径的⊙O交△CFB的边CF于点A，BM平分3，∠ABC交AC于点M，AD⊥BC于点D，AD交BM于点N，ME⊥BC于点E，AB2=AF·AC，cos∠ABD=5 AD=12．⑴求证：△ANM≌△ENM；⑵求证：FB是⊙O的切线；⑶证明四边形AMEN是菱形，并求该菱形的面积S．【087】如图，已知抛物线y ＝x 2＋bx ＋c 经过矩形ABCD 的两个顶点A 、B ，AB 平行于x 轴，对角线BD 与抛物线交于点P ，点A 的坐标为(0，2)，AB ＝4． (1)求抛物线的解析式；(2)若S △APO ＝23，求矩形ABCD 的面积．【088】如图所示，已知在直角梯形OABC 中，AB OC BC x ∥，⊥轴于点(11)(31)C A B ，，、，．动点P 从O 点出发，沿x 轴正方向以每秒1个单位长度的速度移动．过P 点作PQ 垂直于直线．．OA ，垂足为Q ．设P 点移动的时间为t 秒（04t <<），OPQ △与直角梯形OABC 重叠部分的面积为S ．（1）求经过O A B 、、三点的抛物线解析式；（2）求S 与t 的函数关系式；（3）将OPQ △绕着点P 顺时针旋转90°，是否存在t ，使得OPQ △的顶点O 或Q 在抛物线上？若存在，直接写出t 的值；若不存在，请说明理由．【089】如图，在平面直角坐标系xOy 中，半径为1的圆的圆心O 在坐标原点，且与两坐标轴分别交于A B C D 、、、四点．抛物线2y ax bx c =++与y 轴交于点D ，与直线y x =交于点M N 、，且MA NC 、分别与圆O 相切于点A 和点C ．（1）求抛物线的解析式；（2）抛物线的对称轴交x 轴于点E ，连结DE ，并延长DE 交圆O 于F ，求EF 的长．（3）过点B 作圆O 的切线交DC 的延长线于点P ，判断点P 是否在抛物线上，说明理由．【090】如图（9）-1，抛物线23y ax ax b =-+经过A （1-，0），C （3，2-）两点，与y 轴交于点D ，与x 轴交于另一点B ．（1）求此抛物线的解析式；（2）若直线)0(1≠+=k kx y 将四边形ABCD 面积二等分，求k 的值；（3）如图（9）-2，过点E （1，1）作EF ⊥x 轴于点F ，将△AEF 绕平面内某点旋转180°得△MNQ （点M 、N 、Q 分别与点A 、E 、F 对应），使点M 、N 在抛物线上，作MG ⊥x 轴于点G ，若线段MG ︰AG ＝1︰2，求点M ，N 的坐标．y=kx +1图（9）-1图（9）-2。

中考数学压轴题100题精选(91-100题)含答案2010

合并自： (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、、等站 E 度教育网2010年中考数学压轴题（91-100题）【091】已知二次函数y ＝x 2－x ＋c ．(1)若点A (－1，a )、B (2，2n －1)在二次函数y ＝x 2－x ＋c 的图象上，求此二次函数的最小值； (2)若点D (x 1，y 1)、E (x 2，y 2)、P (m ，n )(m ＞n )在二次函数y ＝x 2－x ＋c 的图象上，且D 、E两点关于坐标原点成中心对称，连接OP ．当22≤OP ≤2＋2时，试判断直线DE 与抛物线y ＝x 2－x ＋c ＋ 38的交点个数，并说明理由．合并自： (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、、等站 E 度教育网【092】已知：直角梯形OABC 的四个顶点是O (0，0)，A (32，1)， B (s ，t )，C (72，0)，抛物线y =x 2＋mx －m 的顶点P 是直角梯形OABC 内部或边上的一个动点，m 为常数． (1)求s 与t 的值，并在直角坐标系中画出．．直角梯形OABC ； (2)当抛物线y =x 2＋mx －m 与直角梯形OABC 的边AB 相交时，求m 的取值范围．（第24题）合并自： (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、、等站 E 度教育网【093】已知在平面直角坐标系中，四边形OABC 是矩形，点A 、C 的坐标分别为()3A 0，、()04C ，，点D 的坐标为()D 5-0，，点P 是直线AC 上的一动点，直线DP 与y 轴交于点M ．问：（1）当点P 运动到何位置时，直线DP 平分矩形OABC 的面积，请简要说明理由，并求出此时直线DP 的函数解析式；（2）当点P 沿直线AC 移动时，是否存在使D O M △与A B C △相似的点M ，若存在，请求出点M的坐标；若不存在，请说明理由；（3）当点P 沿直线AC 移动时，以点P 为圆心、半径长为R （R ＞0）画圆，所得到的圆称为动圆P ．若设动圆P 的直径长为AC ，过点D 作动圆P 的两条切线，切点分别为点E 、F ．请探求是否存在四边形DEPF 的最小面积S ，若存在，请求出S 的值；若不存在，请说明理由．注：第（3）问请用备用图解答．备用图合并自： (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、、等站 E 度教育网【094】在平面直角坐标系中，已知(40)A -，，(10)B ，，且以A B 为直径的圆交y 轴的正半轴于点(02)C ，，过点C 作圆的切线交x 轴于点D ．（1）求过A B C ，，三点的抛物线的解析式（2）求点D 的坐标（3）设平行于x 轴的直线交抛物线于E F ，两点，问：是否存在以线段E F 为直径的圆，恰好与x合并自： (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、、等站 E 度教育网【095】）如图1，已知：抛物线212y x b x c =++与x 轴交于A B 、两点，与y 轴交于点C ，经过B C 、两点的直线是122y x =-，连结A C ．（1）B C 、两点坐标分别为B （_____，_____）、C （_____，_____），抛物线的函数关系式为______________；（2）判断A B C △的形状，并说明理由；（3）若A B C △内部能否截出面积最大的矩形D E F C （顶点D E F 、、、G 在A B C △各边上）？若能，求出在A B 边上的矩形顶点的坐标；若不能，请说明理由．[抛物线2y ax bx c =++的顶点坐标是24,24b a c b a a ⎛⎫-- ⎪⎝⎭]图1图2(备用)（第26题）合并自： (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、、等站 E 度教育网【096】如图12，已知抛物线经过坐标原点O 和x 轴上另一点E ，顶点M 的坐标为 (2,4)；矩形ABCD 的顶点A 与点O 重合，AD 、AB 分别在x 轴、y 轴上，且AD=2，AB=3. （1）求该抛物线所对应的函数关系式；（2）将矩形ABCD 以每秒1个单位长度的速度从图12所示的位置沿x 轴的正方向匀速平行移动，同时一动点P 也以相同的速度．．．．．从点A 出发向B 匀速移动，设它们运动的时间为t 秒（0≤t ≤3），直线AB 与该抛物线的交点为N （如图13所示）. ① 当t=25时，判断点P 是否在直线ME 上，并说明理由；② 设以P 、N 、C 、D 为顶点的多边形面积为S ，试问S 是否存在最大值？若存在，求出这个最大值；若不存在，请说明理由．合并自： (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、、等站 E 度教育网【097】矩形O A B C 在平面直角坐标系中位置如图13所示，A C 、两点的坐标分别为(60)A ，，(03)C -，，直线34y x =-与B C 边相交于D 点．（1）求点D 的坐标；（2）若抛物线294y a x x =-经过点A ，试确定此抛物线的表达式；（3）设（2）中的抛物线的对称轴与直线O D 交于点M ，点P 为对称轴上一动点，以P O M、、为顶点的三角形与O C D △相似，求符合条件的点P 的坐标．合并自： (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、、等站 E 度教育网【098】如图，在平面直角坐标系中，点A （0，6），点B 是x 轴上的一个动点，连结AB ，取AB 的中点M ，将线段MB 绕着点B 按顺时针方向旋转90o ，得到线段BC .过点B 作x 轴的垂线交直线AC 于点D .设点B 坐标是（t ，0）.（1）当t =4时，求直线AB 的解析式；（2）当t >0时，用含t 的代数式表示点C 的坐标及△ABC 的面积；（3）是否存在点B ,使△ABD 为等腰三角形?若存在，请求出所有符合条件的点B 的坐标；若不存在，请说明理由.· yOA x备用图合并自： (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、、等站 E 度教育网【099】我们所学的几何知识可以理解为对“构图”的研究：根据给定的（或构造的）几何图形提．．．．．．．．．．．．．．．．出相关的概念和问题（或者根据问题构造图形），并加以研究．．．．．．．．．．．．．．．．．．．．．．．．．．．. 例如：在平面上根据两条直线的各种构图，可以提出“两条直线平行”、“两条直线相交”的概念；若增加第三条直线，则可以提出并研究“两条直线平行的判定和性质”等问题（包括研究的思想和方法）.请你用上面的思想和方法对下面关于圆的问题进行研究：(1) 如图1，在圆O 所在平面上，放置一条．．直线m （m 和圆O 分别交于点A 、B ），根据这个图形可以提出的概念或问题有哪些（直接写出两个即可）？(2) 如图2，在圆O 所在平面上，请你放置与圆O 都相交且不同时经过圆心．．．．．．．的两条．．直线m 和n （m 与圆O 分别交于点A 、B ，n 与圆O 分别交于点C 、D ）. 请你根据所构造的图形提出一个结论，并证明之. (3) 如图3，其中AB 是圆O 的直径，AC 是弦，D 是的中点，弦DE ⊥AB 于点F . 请找出点C 和点E 重合的条件，并说明理由.ABC 第25题图1第25题图2AB第25题图3合并自： (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、、等站 E 度教育网【100】抛物线)0(2≠++=a c bx axy 的顶点为M ，与x 轴的交点为A 、B （点B 在点A 的右侧），△ABM 的三个内角∠M 、∠A 、∠B 所对的边分别为m 、a 、b 。

2010年中考数学压轴题100题精选(71-80题)含答案

合并自： (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、、等站 E 度教育网2010年中考数学压轴题100题精选（71-80题）【071】已知：抛物线()20y ax bx c a =++≠的对称轴为1x =-，与x 轴交于A B ，两点，与y 轴交于点C ，其中()30A -，、()02C -，．（1）求这条抛物线的函数表达式．（2）已知在对称轴上存在一点P ，使得PBC △的周长最小．请求出点P 的坐标．（3）若点D 是线段OC 上的一个动点（不与点O 、点C 重合）．过点D 作DE PC ∥交x 轴于点E ．连接PD 、PE ．设CD 的长为m ，PDE △的面积为S ．求S 与m 之间的函数关系式．试说明S 是否存在最大值，若存在，请求出最大值；若不存在，请说明理由．（第24题图）合并自： (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、、等站 E 度教育网【072】如图1所示，直角梯形OABC 的顶点A 、C 分别在y 轴正半轴与x 轴负半轴上.过点B 、C 作直线l ．将直线l 平移，平移后的直线l 与x 轴交于点D ，与y 轴交于点E ．（1）将直线l 向右平移，设平移距离CD 为t (t ≥0)，直角梯形OABC 被直线l 扫过的面积（图中阴影部份）为s ，s 关于t 的函数图象如图2所示， OM 为线段，MN 为抛物线的一部分，NQ 为射线，N 点横坐标为4．①求梯形上底AB 的长及直角梯形OABC 的面积； ②当42<<t 时，求S 关于t 的函数解析式；（2）在第（1）题的条件下，当直线l 向左或向右平移时（包括l 与直线BC 重合），在直线．．AB ．．上是否存在点P ，使PD E ∆为等腰直角三角形?若存在，请直接写出所有满足条件的点P 的坐标;若不存在，请说明理由．【073】)如图，半径为O 内有互相垂直的两条弦AB 、CD 相交于P 点．合并自： (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、、等站 E 度教育网(1)求证：PA ·PB =PC ·PD ；(2)设BC 的中点为F ，连结FP 并延长交AD 于E ，求证：EF ⊥AD ： (3)若AB =8，CD =6，求OP 的长．【074】如图，在平面直角坐标系中，点1O 的坐标为(40) ，，以点1O 为圆心，8为半径的圆与x 轴交于A B ，两点，过A 作直线l 与x 轴负方向相交成60°的角，且交y 轴于C 点，以点2(135)O ，为第23题图合并自： (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、、等站 E 度教育网圆心的圆与x 轴相切于点D ．（1）求直线l 的解析式；（2）将2O ⊙以每秒1个单位的速度沿x 轴向左平移，当2O ⊙第一次与1O ⊙外切时，求2O ⊙平移的时间．【075】如图11，已知抛物线b ax ax y --=22（0>a ）与x 轴的一个交点为(10)B -，，与y 轴的负半轴交于点C ，顶点为D ．（1）直接写出抛物线的对称轴，及抛物线与x 轴的另一个交点A 的坐标；（2）以AD 为直径的圆经过点C ． ①求抛物线的解析式；合并自： (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、、等站 E 度教育网②点E 在抛物线的对称轴上，点F 在抛物线上，且以E F A B ，，，四点为顶点的四边形为平行四边形，求点F 的坐标．【076】如图，抛物线n mx x y ++=221与x 轴交于A 、B 两点，与y 轴交于C 点，四边形OBHC 为矩形，CH 的延长线交抛物线于点D （5，2），连结BC 、AD . （1）求C 点的坐标及抛物线的解析式；（2）将△BCH 绕点B 按顺时针旋转90°后再沿x 轴对折得到△BEF （点C 与点E 对应），判断点E 是否落在抛物线上，并说明理由；（3）设过点E 的直线交AB 边于点P ，交CD 边于点Q . 问是否存在点P ，使直线PQ 分梯形ABCD的面积为1∶3两部分？若存在，求出P 点坐标；若不存在，请说明理由.图11合并自： (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、、等站 E 度教育网【077】已知直线m x y +-=43与x 轴y 轴分别交于点A 和点B ，点B 的坐标为（0，6）（1）求的m 值和点A 的坐标；（2）在矩形OACB 中，点P 是线段BC 上的一动点，直线PD ⊥AB 于点D ，与x 轴交于点E ，设BP=a ，梯形PEAC 的面积为s 。

2010年中考数学压轴题及答案

1、如图，⊙O 的半径为1，等腰直角三角形ABC 的顶点B 的坐标为（2，0），∠CAB=90°，AC =AB ，顶点A 在⊙O 上运动．（1）当点A 在x 轴上时，求点C 的坐标；（2）当点A 运动到x 轴的负半轴上时，试判断直线BC 与⊙O 位置关系，并说明理由；（3）设点A 的横坐标为x ，△ABC 的面积为S ，求S 与x 之间的函数关系式，并求出S 的最大值与最小值；（4）当直线AB 与⊙O 相切时，求AB 所在直线对应的函数关系式．10当点A 的坐标为（－1，0）时，AB=AC=2＋1，点C 的坐标为（－1，2＋1）；（2）直线BC 与⊙O 相切，过点O 作OM ⊥BC 于点M ，∴∠OBM ＝∠BOM =45°, ∴OM=OB ·sin45°=1，∴直线BC 与⊙O 相切（3）过点A 作AE ⊥OB 于点E 在Rt △OAE 中，AE 2=OA 2－OE 2=1－x 2，在Rt △BAE 中，AB 2=AE 2+BE 2=(1-x 2) +（2-x ）2=3-22x∴S=21AB ·AC=21 AB 2=21(3-22x)=x 223- 其中－1≤x ≤1，当x=－1时，S 的最大值为223+，当x=1时，S 的最小值为223-．（4）①当点A 位于第一象限时(如右图)：连接OA ，并过点A 作AE ⊥OB 于点E ∵直线AB 与⊙O 相切，∴∠OAB=90°，又∵∠CAB=90°，∴∠CAB +∠OAB=180°，∴点O 、A 、C 在同一条直线上，∴∠AOB =∠C=45°，在Rt △OAE 中，OE=AE=22．点A 的坐标为（22，22）过A 、B 两点的直线为y=－x+2．②当点A 位于第四象限时(如右图)点A 的坐标为（22，－22），过A 、B 两点的直线为y=x －2．2、如图，已知抛物线与x 轴交于点A (-2,0),B(4,0)，与y 轴交于点C(0,8)．（1）求抛物线的解析式及其顶点D 的坐标；（2）设直线CD 交x 轴于点E ．在线段OB 的垂直平分线上是否存在点P ，使得点P 到直线CD 的距离等于点P 到原点O 的距离？如果存在，求出点P 的坐标；如果不存在，请说明理由；（3）过点B 作x 轴的垂线，交直线CD 于点F ，将抛物线沿其对称轴平移，使抛物线与线段EF 总有公共点．试探究：抛物线向上最多可平移多少个单位长度？向下最多可平移多少个单位长度？用图2解：（1）设抛物线解析式为(2)(4)y a x x =+-，把(08)C ，代入得1a =-．228y x x ∴=-++2(1)9x =--+，顶点(19)D ，（2）假设满足条件的点P 存在，依题意设(2)P t ，，由(08)(19)C D ，，，求得直线CD 的解析式为8y x =+，它与x 轴的夹角为45，设OB 的中垂线交CD 于H ，则(210)H ，．则10PHt =-，点P 到CD的距离为d PH t ==-．又PO =．t =-．平方并整理得：220920t t +-=，10t =-±∴存在满足条件的点P ，P的坐标为(210-±，．（3）由上求得(80)(412)E F -，，，． ①若抛物线向上平移，可设解析式为228(0)y x x m m =-+++>当8x =-时，72y m =-+．当4x=时，y m =．720m ∴-+≤或12m ≤．072m ∴<≤．②若抛物线向下移，可设解析式为228(0)y x x m m =-++->．由2288y x x m y x ⎧=-++-⎨=+⎩，有20xx m -+=．140m ∴=-≥△，104m ∴<≤． ∴向上最多可平移72个单位长，向下最多可平移14个单位长．3、如图，直线443y x =-+与X 轴Y 轴分别交于点M,N（1）求M,N 两点的坐标。

中考数学压轴题100题精选及答案全3篇

中考数学压轴题100题精选及答案全第一篇：数与代数1.下列各组数中，哪一组数最大？A. \frac{1}{2} ,\frac{2}{3},\frac{3}{4},\frac{4}{5}B. 0.99,0.999,0.9999,0.99999C. \sqrt{2},\sqrt{3},\sqrt{5},\sqrt{7}D. 1,10^2,10^3,10^42. 一个整数，十位数与各位数的和为9，再去掉该整数中的各位数，十位数与剩下的数字的和为40，该整数为__________。

A. 45B. 54C. 63D. 723. 已知 a+b=2, ab=-1，求a^2+b^2的值。

A. 3B. 5C. 7D. 94. 解方程 2x-5=3x+1。

A. x=-3.5B. x=-2C. x=2D. x=3.55. 有两个数，各位数字相同，但顺序颠倒，若它们的和为110，这两个数分别是多少？A. 47,74B. 49,94C. 56,65D. 59,956. 若x-3y=-7，x+4y=1，则y的值为__________。

A. -2B. -1C. 0D. 17. 16÷(a-2)=4，则 a 的值为__________。

A. 6B. 8C. 10D. 128. 若a:b=5:3，b:c=7:4，则a∶b∶c=__________。

A. 35:21:12B. 25:15:12C. 25:21:16D. 35:15:169. 若a+3b=5，3a-5b=7，则 a 的值为__________。

A. -2B. -1C. 0D. 110. 已知x+y=3，xy=2，则y的值为__________。

A. 1B. 2C. 3D. 4第二篇：几何图形11. 已知正方形 ABCD 的边长为6，以 BC 为边，画一个正三角形 BCE，连接 AE，AD，请问△ADE 和正方形 ABCD 的面积之比是多少？A. \frac{2}{9}B. \frac{1}{2}C. \frac{4}{9}D.\frac{5}{6}12. 把一张纸平整地放在桌上，在纸的中央画一个圆形，请问可以用多少个直径为5 厘米的圆去覆盖这个圆形（圆覆盖圆）？A. 1B. 2C. 3D. 413. 已知△ABC 是等腰三角形，AB=AC，E是BC中点，DE∥AC，AE=CD=2，求△ABC 的面积。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2010年中考数学压轴题100题精选（91-100题）答案【091】(1)解：法1：由题意得⎩⎨⎧n ＝2＋c ，2n －1＝2＋c . ……1分解得⎩⎨⎧n ＝1，c ＝－1.……2分法2：∵ 抛物线y ＝x 2－x ＋c 的对称轴是x ＝12，且 12－(－1) ＝2－12，∴ A 、B 两点关于对称轴对称. ∴ n ＝2n －1 ……1分 ∴ n ＝1，c ＝－1. ……2分 ∴ 有 y ＝x 2－x －1 ……3分＝(x －12)2－54.∴ 二次函数y ＝x 2－x －1的最小值是－54. ……4分 (2)解：∵ 点P (m ，m )(m ＞0)，∴ PO ＝2m .∴ 22≤2m ≤2＋2.∴ 2≤m ≤1＋2. ……5分法1： ∵ 点P (m ，m )(m ＞0)在二次函数y ＝x 2－x ＋c 的图象上， ∴ m ＝m 2－m ＋c ，即c ＝－m 2＋2m . ∵ 开口向下，且对称轴m ＝1，∴ 当2≤m ≤1＋2 时，有－1≤c ≤0. ……6分法2：∵ 2≤m ≤1＋2， ∴ 1≤m －1≤2. ∴ 1≤(m －1)2≤2.∵ 点P (m ，m )(m ＞0)在二次函数y ＝x 2－x ＋c 的图象上， ∴ m ＝m 2－m ＋c ，即1－c ＝(m －1)2. ∴ 1≤1－c ≤2.∴ －1≤c ≤0. ……6分 ∵ 点D 、E 关于原点成中心对称，法1： ∴ x 2＝－x 1，y 2＝－y 1.∴ ⎩⎨⎧y 1＝x 12－x 1＋c ，－y 1＝x 12＋x 1＋c .∴ 2y 1＝－2x 1， y 1＝－x 1. 设直线DE ：y ＝kx . 有－x 1＝kx 1.由题意，存在x 1≠x 2.∴ 存在x 1，使x 1≠0. ……7分∴ k ＝－1.∴ 直线DE ： y ＝－x . ……8分法2：设直线DE ：y ＝kx .则根据题意有 kx ＝x 2－x ＋c ，即x 2－(k ＋1) x ＋c ＝0. ∵ －1≤c ≤0，∴ (k ＋1)2－4c ≥0.∴ 方程x 2－(k ＋1) x ＋c ＝0有实数根. ……7分 ∵ x 1＋x 2＝0， ∴ k ＋1＝0. ∴ k ＝－1.∴ 直线DE ： y ＝－x . ……8分若 ⎩⎪⎨⎪⎧y ＝－x ，y ＝x 2－x ＋c ＋38.则有 x 2＋c ＋38＝0.即 x 2＝－c －38. ① 当－c －38＝0时，即c ＝－38时，方程x 2＝－c －38有相同的实数根，即直线y ＝－x 与抛物线y ＝x 2－x ＋c ＋38有唯一交点. ……9分 ② 当－c －38＞0时，即c ＜－38时，即－1≤c ＜－38时，方程x 2＝－c －38有两个不同实数根，即直线y ＝－x 与抛物线y ＝x 2－x ＋c ＋38有两个不同的交点. ……10分 ③ 当－c －38＜0时，即c ＞－38时，即－38＜c ≤0时，方程x 2＝－c －38没有实数根，即直线y ＝－x 与抛物线y ＝x 2－x ＋c ＋38没有交点. ……11分【092】解：（1）如图，在坐标系中标出O ，A ，C∵∠AO C≠90°， ∴∠ABC =90°，故BC ⊥OC ， BC ⊥AB ，∴B （72，1）．（1分，）即s =72，t =1．直角梯形如图所画．（2分）（大致说清理由即可）（2）由题意，y =x 2+mx －m 与 y =1（线段AB ）相交，得，12y =x mx m,y =.+-⎧⎨⎩ （3分）∴1＝x 2+mx －m ，由 (x －1)(x +1+m )=0，得121,1x x m ==--．∵1x =1<32，不合题意，舍去．（4分）∴抛物线y =x 2+mx -m 与AB 边只能相交于（2x ，1）， ∴32≤－m －1≤72，∴9252m --≤≤ ． ①（5分）又∵顶点P (2424,m m m +--)是直角梯形OABC 的内部和其边上的一个动点，∴7022m ≤-≤，即70m -≤≤ ． ② （6分）∵2224(2)4(1)44211m m m m ++-+-=-=-+≤，（或者抛物线y =x 2+mx －m 顶点的纵坐标最大值是1）∴点P 一定在线段AB 的下方．（7分）又∵点P 在x 轴的上方， ∴2440m m +-≥，(4)0,m m +≤∴0,0,4040m m m m ≤≥+≥+≤⎧⎧⎨⎨⎩⎩或者．（*8分）4(9)0. m ∴-≤≤分③（9分）又∵点P 在直线y =23x 的下方，∴242()432m m m +-≤⨯-，（10分）即(38)0.m m +≥0,0,380380.m m m m ≤≥+≤+≥⎧⎧⎨⎨⎩⎩或者（*8分处评分后，此处不重复评分） 80.3m m ∴≤-≥(11分)，或 ④由①②③④ ，得4-≤83m ≤-．（12分）说明：解答过程，全部不等式漏写等号的扣1分，个别漏写的酌情处理．【093】解：（1）连结BO 与AC 交于点H ，则当点P 运动到点H 时，直线DP 平分矩形OABC 的面积．理由如下：∵矩形是中心对称图形，且点H 为矩形的对称中心．又据经过中心对称图形对称中心的任一直线平分此中心对称图形的面积，因为直线DP 过矩形OABC 的对称中心点H ，所以直线DP 平分矩形OABC 的面积．…………2分由已知可得此时点P 的坐标为3(2)2P ，．设直线DP 的函数解析式为y kx b =+．则有503 2.2k b k b -+=⎧⎪⎨+=⎪⎩，解得413k =，2013b =．所以，直线DP 的函数解析式为：4201313y x =+． ·························································· 5分（2）存在点M 使得DOM △与ABC △相似．如图，不妨设直线DP 与y 轴的正半轴交于点(0)m M y ，．因为DOM ABC ∠=∠，若△DOM 与△ABC 相似，则有OM BC OD AB =或OM ABOD BC=．当OM BC OD AB =时，即354m y =，解得154m y =．所以点115(0)4M ，满足条件．当OM AB OD BC =时，即453m y =，解得203m y =．所以点220(0)3M ，满足条件．由对称性知，点315(0)4M -，也满足条件．综上所述，满足使DOM △与ABC △相似的点M 有3个，分别为115(0)4M ，、220(0)3M ，、315(0)4M -，． ······························································································································ 9分（3）如图，过D 作DP ⊥AC 于点P ，以P 为圆心，半径长为52画圆，过点D 分别作P 的切线DE 、DF ，点E 、F 是切点．除P 点外在直线AC 上任取一点P 1，半径长为52画圆，过点D 分别作P 的切线DE 1、DF 1，点E 1、F 1是切点．在△DEP 和△DFP 中，∠PED ＝∠PFD ，PF ＝PE ，PD ＝PD ，∴△DPE ≌△DPF ．∴Ｓ四边形DEPF ＝2Ｓ△DPE ＝2×1522DE PE DE PE DE ⨯⋅=⋅=．∴当DE 取最小值时，Ｓ四边形DEPF 的值最小．∵222DE DP PE =-，2221111DE DP PE =-，∴222211DE DE DP DP -=-．∵1DP DP >，∴2210DE DE ->．∴1DE DE >．由1P 点的任意性知：DE 是D 点与切点所连线段长的最小值．……12分在△ADP 与△AOC 中，∠DPA ＝∠AOC ， ∠DAP ＝∠CAO ， ∴△ADP ∽△AOC ．x∴DP CO DA CA =，即485DP =．∴325DP =．∴DE == ∴Ｓ四边形ＤＥＰＦ·············································································· 14分（注：本卷中所有题目，若由其它方法得出正确结论，请参照标准给分．）【094】解：（1）令二次函数2y ax bx c =++，则164002a b c a b c c -+=⎧⎪++=⎨⎪=⎩························································································································ 1分 12322a b c ⎧=-⎪⎪⎪∴=-⎨⎪=⎪⎪⎩··································································································································· 2分 ∴过A B C ，，三点的抛物线的解析式为213222y x x =--+ ············································· 4分（2）以AB 为直径的圆圆心坐标为302O ⎛⎫' ⎪⎝⎭，52O C '∴=32O O '= ··············································································································· 5分 CD 为圆O '切线 OC CD '∴⊥ ··························································································· 6分 90O CD DCO '∴∠+∠=°90CO O O CO ''∠+∠=° CO O DCO '∴∠=∠O CO CDO '∴△∽△ //O O OC OC OD '= ······································································· 8分 3/22/2OD = 83OD ∴= D ∴坐标为803⎛⎫⎪⎝⎭， ······················································································································ 9分（3）存在 ···································································································································· 10分抛物线对称轴为32X =-设满足条件的圆的半径为r ，则E 的坐标为3()2r r -+，或3()2F r r --，而E 点在抛物线213222y x x =--+上 21333()()22222r r r ∴=--+--++11r ∴=-+21r =-故在以EF 为直径的圆，恰好与x轴相切，该圆的半径为12-+，12+ ············ 12分注：解答题只要方法合理均可酌情给分【095】（1）B （4，0），(02)C -，． ······················································································ 2分 213222y x x =--． ··················································································································· 4分（2）ABC △是直角三角形． ··································································································· 5分证明：令0y =，则2132022x x --=．1214x x ∴=-=，．(10)A ∴-，． ································································································································· 6分解法一：5AB AC BC ∴===，． ······································································· 7分22252025AC BC AB ∴+=+==．ABC ∴△是直角三角形． ·········································································································· 8分解法二：11242CO AO AO CO BO BO OC ===∴==，，，90AOC COB ∠=∠=°，AOC COB ∴△∽△． ··············································································································· 7分 ACO CBO ∴∠=∠．90CBO BCO ∠+∠=°，90ACO BCO ∴∠+∠=°．即90ACB ∠=°．ABC ∴△是直角三角形． ·········································································································· 8分（3）能．①当矩形两个顶点在AB 上时，如图1，CO 交GF 于H ．GF AB ∥，CGF CAB ∴△∽△． GF CHAB CO∴=． ······························································· 9分解法一：设GF x =，则DE x =，25CH x =，225DG OH OC CH x ==-=-．2222255DEFG S x x x x ⎛⎫∴=-=-+ ⎪⎝⎭矩形·图1=2255522x ⎛⎫--+ ⎪⎝⎭． ················································································································· 10分当52x =时，S 最大． 512DE DG ∴==，．ADG AOC △∽△， 11222AD DG AD OD OE AO OC ∴=∴=∴==，，，． 102D ⎛⎫∴- ⎪⎝⎭，，(20)E ，． ········································································································· 11分解法二：设DG x =，则1052xDE GF -==． 221055555(1)2222DEFG x S x x x x -∴==-+=--+矩形·．················································· 10分 ∴当1x =时，S 最大．512DG DE ∴==，．ADG AOC △∽△， 11222AD DG AD OD OE AO OC ∴=∴=∴==，，，． 102D ⎛⎫∴- ⎪⎝⎭，，(20)E ，． ········································································································· 11分 ②当矩形一个顶点在AB 上时，F 与C 重合，如图2，DG BC ∥， AGD ACB ∴△∽△． GD AGBC AF∴=．解法一：设GD x =，AC BC ∴==2xGF AC AG ∴=-=．∴2122DEFG x S xx ⎫==-⎪⎭矩形·=(21522x --+． ··············································································································· 12分当x =S 最大．GD AG ∴==，52AD ∴==．32OD ∴=图2302D ⎛⎫∴ ⎪⎝⎭， ································································································································· 13分解法二：设DE x =，5AC =BC =GC x ∴=，AG x =．2GD x ∴=．()222DEFG S x x x ∴==-+矩形·=25222x ⎛--+ ⎝⎭ ··················································································································· 12分∴当x =S 最大，GD AG ∴==．52AD ∴==．3.2OD ∴= ∴302D ⎛⎫⎪⎝⎭， ································································································································· 13分综上所述：当矩形两个顶点在AB 上时，坐标分别为102⎛⎫- ⎪⎝⎭，，（2，0）；当矩形一个顶点在AB 上时，坐标为302⎛⎫ ⎪⎝⎭， ·········································································· 14分【096】（1）因所求抛物线的顶点M 的坐标为(2,4)，故可设其关系式为()224y a x =-+ ………………(1分) 又抛物线经过O (0,0)，于是得()20240a -+=， ………………(2分) 解得 a=-1 ………………(3分) ∴ 所求函数关系式为()224y x =--+，即24y x x =-+. ……………(4分)（2）① 点P 不在直线ME 上. ………………(5分)根据抛物线的对称性可知E 点的坐标为(4,0)，又M 的坐标为(2,4)，设直线ME 的关系式为y=kx +b .于是得⎩⎨⎧=+=+4204b k b k ，解得⎩⎨⎧=-=82b k所以直线ME 的关系式为y=-2x +8. ……(6分)由已知条件易得，当t 25=时，OA=AP 25=，⎪⎭⎫⎝⎛∴25,25P ……………(7分)∵ P 点的坐标不满足直线ME 的关系式y=-2x +8.∴ 当t 25=时，点P 不在直线ME 上. ………………(8分)② S 存在最大值. 理由如下： ………………(9分) ∵ 点A 在x 轴的非负半轴上，且N 在抛物线上， ∴ OA=AP=t .∴ 点P ，N 的坐标分别为(t ,t )、(t ,-t 2+4t ) ∴ AN=-t 2+4t (0≤t ≤3) , ∴ AN -AP=(-t 2+4 t )- t=-t 2+3 t=t (3-t )≥0 , ∴ PN=-t 2+3 t …(10分)（ⅰ）当PN=0，即t=0或t =3时，以点P ，N ，C ，D 为顶点的多边形是三角形，此三角形的高为AD ，∴ S=21DC ·AD=21×3×2=3. ………………(11分)（ⅱ）当PN ≠0时，以点P ，N ，C ，D 为顶点的多边形是四边形∵ PN ∥CD ，AD ⊥CD ，∴ S=21(CD+PN )·AD=21[3+(-t 2+3 t )]×2=-t 2+3 t +3=421232+⎪⎭⎫ ⎝⎛--t 其中(0＜t ＜3)，由a=-1，0＜23＜3，此时421=最大S . …………(12分)综上所述，当t 23=时，以点P ，N ，C ，D 为顶点的多边形面积有最大值，这个最大值为421. ………………(13分) 说明：（ⅱ）中的关系式，当t=0和t=3时也适合.【097】解：（1）点D 的坐标为(43)-，． ······································································· （2分）（2）抛物线的表达式为23984y x x =-． ········································································ （4分）（3）抛物线的对称轴与x 轴的交点1P 符合条件． ∵OA CB ∥，∴1POM CDO ∠=∠． ∵190OPM DCO ∠=∠=°， ∴1Rt Rt POM CDO △∽△． ······························ （6∵抛物线的对称轴3x =，∴点1P 的坐标为1(30)P ，． ································································································ （7分）过点O 作OD 的垂线交抛物线的对称轴于点2P ． ∵对称轴平行于y 轴， ∴2P MO DOC ∠=∠． ∵290P OM DCO ∠=∠=°，∴21Rt Rt P M O DOC △∽△． ························································································ （8分） ∴点2P 也符合条件，2OP M ODC ∠=∠．∴121390PO CO P PO DCO ==∠=∠=，°， ∴21Rt Rt P PO DCO △≌△． ·························································································· （9分） ∴124PP CD ==． ∵点2P 在第一象限， ∴点2P 的坐标为2P (34)，，∴符合条件的点P 有两个，分别是1(30)P ，，2P (34)，． ············································· （11分）【098】解：（1）当t =4时，B (4,0) 设直线AB 的解析式为y = kx +b . 把 A (0,6)，B (4,0) 代入得：⎩⎨⎧b =64k +b =0 , 解得：⎩⎪⎨⎪⎧k =－32b =6, ∴直线AB 的解析式为：y =－32x +6.………………………………………4分 (2) 过点C 作CE ⊥x 轴于点E由∠AOB =∠CEB =90°，∠ABO =∠BCE ，得△AOB ∽△BEC . ∴12BE CE BC AO BO AB ===， ∴BE = 12AO =3，CE = 12OB = t2，∴点C 的坐标为(t +3，t2).…………………………………………………………2分方法一：S 梯形AOEC = 12O E ·(AO +EC )= 12(t +3)(6+t 2)=14t 2+154t +9， S △ AOB = 12AO ·OB = 12×6·t =3t ， S △ BEC = 12BE ·CE = 12×3×t 2= 34t ， ∴S △ ABC = S 梯形AOEC － S △ AOB －S △ BEC= 14t 2+154t +9－3t －34t = 14t 2+9. 方法二：∵AB ⊥BC ，AB =2BC ，∴S △ ABC = 12AB ·BC = BC 2. 在R t △ABC 中，BC 2= CE 2+ BE 2 = 14t 2+9，即S △ ABC = 14t 2+9.…………………………………………………………2分。