(完整word版)解直角三角形的应用中考练习题
专题28 解直角三角形(58题)(原卷版)--2024年中考数学真题分类汇编

专题28解直角三角形(58题)一、单选题1.(2024·吉林长春·中考真题)2024年5月29日16时12分,“长春净月一号”卫星搭乘谷神星一号火箭在黄海海域成功发射.当火箭上升到点A 时,位于海平面R 处的雷达测得点R 到点A 的距离为a 千米,仰角为θ,则此时火箭距海平面的高度AL 为()A .sin a θ千米B .sin aθ千米C .cos a θ千米D .cos aθ千米2.(2024·天津·2cos451- 的值等于()A .0B .1C .212-D 213.(2024·甘肃临夏·中考真题)如图,在ABC 中,5AB AC ==,4sin 5B =,则BC 的长是()A .3B .6C .8D .94.(2024·四川自贡·中考真题)如图,等边ABC 钢架的立柱CD AB ⊥于点D ,AB 长12m .现将钢架立柱缩短成DE ,60BED ∠=︒.则新钢架减少用钢()A .(243m-B .(243m-C .(2463m-D .(243m-5.(2024·四川德阳·中考真题)某校学生开展综合实践活动,测量一建筑物CD 的高度,在建筑物旁边有一高度为10米的小楼房AB ,小李同学在小楼房楼底B 处测得C 处的仰角为60︒,在小楼房楼顶A 处测得C 处的仰角为30︒.(AB CD 、在同一平面内,B D 、在同一水平面上),则建筑物CD 的高为()米A .20B .15C .12D .10+6.(2024·广东深圳·中考真题)如图,为了测量某电子厂的高度,小明用高1.8m 的测量仪EF 测得的仰角为45︒,小军在小明的前面5m 处用高1.5m 的测量仪CD 测得的仰角为53︒,则电子厂AB 的高度为()(参考数据:sin 5345︒≈,cos5335︒≈,tan 5343︒≈)A .22.7mB .22.4mC .21.2mD .23.0m7.(2024·内蒙古包头·中考真题)如图,在矩形ABCD 中,,E F 是边BC 上两点,且BE EF FC ==,连接,,DE AF DE 与AF 相交于点G ,连接BG .若4AB =,6BC =,则sin GBF ∠的值为()A .10B .10C .13D .238.(2024·黑龙江大兴安岭地·中考真题)如图,菱形ABCD 中,点O 是BD 的中点,AM BC ⊥,垂足为M ,AM 交BD 于点N ,2OM =,8BD =,则MN 的长为()A 5B 455C 355D 259.(2024·四川乐山·中考真题)如图,在菱形ABCD 中,60ABC ∠=︒,1AB =,点P 是BC 边上一个动点,在BC 延长线上找一点Q ,使得点P 和点Q 关于点C 对称,连接DP AQ 、交于点M .当点P 从B 点运动到C 点时,点M 的运动路径长为()A .36B 33C 32D 310.(2024·山东泰安·中考真题)如图,菱形ABCD 中,=60B ∠︒,点E 是AB 边上的点,4AE =,8BE =,点F 是BC 上的一点,EGF △是以点G 为直角顶点,EFG ∠为30︒角的直角三角形,连结AG .当点F 在直线BC 上运动时,线段AG 的最小值是()A .2B .432-C .23D .411.(2024·四川泸州·512-的美感.如图,把黄金矩形ABCD 沿对角线AC 翻折,点B 落在点B '处,AB '交CD 于点E ,则sin DAE ∠的值为()A 55B .12C .35D 25512.(2024·黑龙江大兴安岭地·中考真题)如图,在正方形ABCD 中,点H 在AD 边上(不与点A 、D 重合),90BHF ∠=︒,HF 交正方形外角的平分线DF 于点F ,连接AC 交BH 于点M ,连接BF 交AC 于点G ,交CD 于点N ,连接BD .则下列结论:①45HBF ∠=︒;②点G 是BF 的中点;③若点H 是AD 的中点,则sinNBC ∠BN =;⑤若12AH D H =,则112BND AHM S S =△△,其中正确的结论是()A .①②③④B .①③⑤C .①②④⑤D .①②③④⑤二、填空题13.(2024·黑龙江绥化·中考真题)如图,用热气球的探测器测一栋楼的高度,从热气球上的点A 测得该楼顶部点C 的仰角为60︒,测得底部点B 的俯角为45︒,点A 与楼BC 的水平距离50m AD =,则这栋楼的高度为m (结果保留根号).14.(2024·内蒙古赤峰·中考真题)综合实践课上,航模小组用无人机测量古树AB 的高度.如图,点C 处与古树底部A 处在同一水平面上,且10AC =米,无人机从C 处竖直上升到达D 处,测得古树顶部B 的俯角为45︒,古树底部A 的俯角为65︒,则古树AB 的高度约为米(结果精确到0.1米;参考数据:sin 650.906︒≈,cos 650.423︒≈,tan 65 2.145︒≈).15.(2024·湖北武汉·中考真题)黄鹤楼是武汉市著名的旅游景点,享有“天下江山第一楼”的美誉.在一次综合实践活动中,某数学小组用无人机测量黄鹤楼AB 的高度,具体过程如下:如图,将无人机垂直上升至距水平地面102m 的C 处,测得黄鹤楼顶端A 的俯角为45︒,底端B 的俯角为63︒,则测得黄鹤楼的高度是m .(参考数据:tan632︒≈)16.(2024·四川内江·中考真题)如图,在矩形ABCD 中,3AB =,5AD =,点E 在DC 上,将矩形ABCD 沿AE 折叠,点D 恰好落在BC 边上的点F 处,那么tan ∠=EFC .17.(2024·江苏盐城·中考真题)如图,小明用无人机测量教学楼的高度,将无人机垂直上升距地面30m 的点P 处,测得教学楼底端点A 的俯角为37︒,再将无人机沿教学楼方向水平飞行26.6m 至点Q 处,测得教学楼顶端点B 的俯角为45︒,则教学楼AB 的高度约为m .(精确到1m ,参考数据:sin370.60︒≈,cos370.80︒≈,tan370.75︒≈)18.(2024·北京·中考真题)如图,在正方形ABCD 中,点E 在AB 上,AF D E ⊥于点F ,CG DE ⊥于点G .若5AD =,CG 4=,则AEF △的面积为.19.(2024·甘肃临夏·中考真题)如图,对折边长为2的正方形纸片ABCD ,OM 为折痕,以点O 为圆心,OM 为半径作弧,分别交AD ,BC 于E ,F 两点,则 EF的长度为(结果保留π).20.(2024·黑龙江齐齐哈尔·中考真题)如图,数学活动小组在用几何画板绘制几何图形时,发现了如“花朵”形的美丽图案,他们将等腰三角形OBC 置于平面直角坐标系中,点O 的坐标为(00),,点B 的坐标为(1)0,,点C 在第一象限,120OBC ∠=︒.将OBC △沿x 轴正方向作无滑动滚动,使它的三边依次与x 轴重合,第一次滚动后,点O 的对应点为O ',点C 的对应点为C ',OC 与O C ''的交点为1A ,称点1A 为第一个“花朵”的花心,点2A 为第二个“花朵”的花心;……;按此规律,OBC △滚动2024次后停止滚动,则最后一个“花朵”的花心的坐标为.21.(2024·黑龙江大兴安岭地·中考真题)矩形ABCD 中,3AB =,4BC =,将AB 沿过点A 的一条直线折叠,折痕交直线BC 于点P (点P 不与点B 重合),点B 的对称点落在矩形对角线所在的直线上,则PC 长为.22.(2024·山东泰安·中考真题)在综合实践课上,数学兴趣小组用所学数学知识测量大汶河某河段的宽度,他们在河岸一侧的瞭望台上放飞一只无人机,如图,无人机在河上方距水面高60米的点P 处测得瞭望台正对岸A 处的俯角为50︒,测得瞭望台顶端C 处的俯角为63.6︒,已知瞭望台BC 高12米(图中点A ,B ,C ,P 在同一平面内),那么大汶河此河段的宽AB 为米.(参考数据:3sin 405︒≈,9sin 63.610︒≈,6tan 505︒≈,tan 63.62︒≈)23.(2024·四川达州·中考真题)如图,在Rt ABC △中,90C ∠=︒.点D 在线段BC 上,45BAD ∠=︒.若4AC =,1CD =,则ABC 的面积是.24.(2024·贵州·中考真题)如图,在菱形ABCD 中,点E ,F 分别是BC ,CD 的中点,连接AE ,AF .若4sin 5EAF ∠=,5AE =,则AB 的长为.25.(2024·广东深圳·中考真题)如图,在ABC 中,AB BC =,5tan 12B ∠=,D 为BC 上一点,且满足85BD CD =,过D 作DE AD ⊥交AC 延长线于点E ,则CEAC=.26.(2024·黑龙江绥化·中考真题)在矩形ABCD 中,4cm AB =,8cm BC =,点E 在直线AD 上,且2cm DE =,则点E 到矩形对角线所在直线的距离是cm .三、解答题27.(2024·内蒙古通辽·0322sin60(π)-+︒--.28.(2024·四川甘孜·中考真题)如图,一艘海轮位于灯塔P 的北偏东37︒方向,距离灯塔100海里的A 处,它沿正南方向航行一段时间后,到达位于灯塔P 的南偏东45︒方向上的B 处.这时,B 处距离A 处有多远?(参考数据:sin 370.60︒≈,cos370.80︒≈,tan 370.75︒≈)29.(2024·北京·中考真题)计算:()0582sin 302π-︒+-30.(2024·湖南长沙·中考真题)计算:()011(32cos 30π 6.84-+-︒-.31.(2024·广东深圳·中考真题)计算:()112cos 45 3.14124π-⎛⎫-⋅︒+-++ ⎪⎝⎭.32.(2024·黑龙江大兴安岭地·中考真题)先化简,再求值:22222111m m m m m m ⎛⎫-+÷- ⎪-+⎝⎭,其中cos60m =︒.33.(2024·吉林·中考真题)图①中的吉林省广播电视塔,又称“吉塔”.某直升飞机于空中A 处探测到吉塔,此时飞行高度873m AB =,如图②,从直升飞机上看塔尖C 的俯角37EAC ∠=︒,看塔底D 的俯角45EAD ∠=︒,求吉塔的高度CD (结果精确到0.1m ).(参考数据:sin 370.60︒=,cos370.80︒=,tan 370.75︒=)34.(2024·青海·018tan 452π︒+--.35.(2024·内蒙古呼伦贝尔·中考真题)计算:301tan6032(π2024)2-⎛⎫--+︒-+- ⎪⎝⎭.36.(2024·内蒙古呼伦贝尔·中考真题)综合实践活动中,数学兴趣小组利用无人机测量大楼的高度.如图,无人机在离地面40米的D 处,测得操控者A 的俯角为30︒,测得楼BC 楼顶C 处的俯角为45︒,又经过人工测量得到操控者A 和大楼BC 之间的水平距离是80米,则楼BC 的高度是多少米?(点A B C D ,,,都3 1.7≈)37.(2024·内蒙古通辽·中考真题)在“综合与实践”活动课上,活动小组测量一棵杨树的高度.如图,从C 点测得杨树底端B 点的仰角是30︒,BC 长6米,在距离C 点4米处的D 点测得杨树顶端A 点的仰角为45︒,求杨树AB 的高度(精确到0.1米,AB ,BC ,CD 在同一平面内,点C ,D 在同一水平线上.参考数据:3 1.73)≈.38.(2024·湖南·中考真题)某数学研究性学习小组在老师的指导下,利用课余时间进行测量活动.活动主题测算某水池中雕塑底座的底面积测量工具皮尺、测角仪、计算器等活动过程模型抽象某休闲广场的水池中有一雕塑,其底座的底面为矩形ABCD ,其示意图如下:测绘过程与数据信息①在水池外取一点E ,使得点C ,B ,E 在同一条直线上;②过点E 作GH CE ⊥,并沿EH 方向前进到点F ,用皮尺测得EF 的长为4米;③在点F 处用测角仪测得60.3CFG ∠=︒,45BFG ∠=︒,21.8AFG ∠=︒;④用计算器计算得:sin60.30.87︒≈,cos60.30.50︒≈,tan60.3 1.75︒≈.sin21.80.37︒≈,cos21.80.93︒≈,tan21.80.40︒≈.请根据表格中提供的信息,解决下列问题(结果保留整数):(1)求线段CE 和BC 的长度:(2)求底座的底面ABCD 的面积.39.(2024·贵州·中考真题)综合与实践:小星学习解直角三角形知识后,结合光的折射规律进行了如下综合性学习.【实验操作】第一步:将长方体空水槽放置在水平桌面上,一束光线从水槽边沿A 处投射到底部B 处,入射光线与水槽内壁AC 的夹角为A ∠;第二步:向水槽注水,水面上升到AC 的中点E 处时,停止注水.(直线NN '为法线,AO 为入射光线,OD 为折射光线.)【测量数据】如图,点A ,B ,C ,D ,E ,F ,O ,N ,N '在同一平面内,测得20cm AC =,45A ∠=︒,折射角32DON ∠=︒.【问题解决】根据以上实验操作和测量的数据,解答下列问题:(1)求BC 的长;(2)求B ,D 之间的距离(结果精确到0.1cm ).(参考数据:sin 320.52︒≈,cos320.84︒≈,tan 320.62︒≈)40.(2024·河南·中考真题)如图1,塑像AB 在底座BC 上,点D 是人眼所在的位置.当点B 高于人的水平视线DE 时,由远及近看塑像,会在某处感觉看到的塑像最大,此时视角最大.数学家研究发现:当经过A ,B 两点的圆与水平视线DE 相切时(如图2),在切点P 处感觉看到的塑像最大,此时APB ∠为最大视角.(1)请仅就图2的情形证明APB ADB ∠>∠.(2)经测量,最大视角APB ∠为30︒,在点P 处看塑像顶部点A 的仰角APE ∠为60︒,点P 到塑像的水平距离PH 为6m .求塑像AB 的高(结果精确到0.1m 3 1.73≈).41.(2024·天津·中考真题)综合与实践活动中,要用测角仪测量天津海河上一座桥的桥塔AB 的高度(如图①).某学习小组设计了一个方案:如图②,点,,C D E 依次在同一条水平直线上,36m,DE EC AB =⊥,垂足为C .在D 处测得桥塔顶部B 的仰角(CDB ∠)为45︒,测得桥塔底部A 的俯角(CDA ∠)为6︒,又在E 处测得桥塔顶部B 的仰角(CEB ∠)为31︒.(1)求线段CD 的长(结果取整数);(2)求桥塔AB 的高度(结果取整数).参考数据:tan310.6,tan60.1︒≈︒≈.42.(2024·四川乐山·中考真题)我国明朝数学家程大位写过一本数学著作《直指算法统宗》,其中有一道与荡秋千有关的数学问题是使用《西江月》词牌写的:平地秋千未起,踏板一尺离地.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几?词写得很优美,翻译成现代汉语的大意是:有一架秋千,当它静止时,踏板离地1尺,将它往前推进10尺(5尺为一步),秋千的踏板就和某人一样高,这个人的身高为5尺.(假设秋千的绳索拉的很直)(1)如图1,请你根据词意计算秋千绳索OA 的长度;(2)如图2,将秋千从与竖直方向夹角为α的位置OA '释放,秋千摆动到另一侧与竖直方向夹角为β的地方OA '',两次位置的高度差PQ h =.根据上述条件能否求出秋千绳索OA 的长度?如果能,请用含α、β和h 的式子表示;如果不能,请说明理由.43.(2024·山东·中考真题)【实践课题】测量湖边观测点A 和湖心岛上鸟类栖息点P 之间的距离【实践工具】皮尺、测角仪等测量工具【实践活动】某班甲小组根据湖岸地形状况,在岸边选取合适的点B .测量A ,B 两点间的距离以及∠PAB 和PBA ∠,测量三次取平均值,得到数据:60AB =米,79PAB ∠=︒,64PBA ∠=︒.画出示意图,如图【问题解决】(1)计算A ,P 两点间的距离.(参考数据:sin640.90︒≈,sin790.98︒≈,cos790.19︒≈,sin370.60︒≈,tan370.75︒≈)【交流研讨】甲小组回班汇报后,乙小组提出了另一种方案:如图2,选择合适的点D ,E ,F ,使得A ,D ,E 在同一条直线上,且AD DE =,DEF DAP ∠=∠,当F ,D ,P 在同一条直线上时,只需测量EF 即可.(2)乙小组的方案用到了________.(填写正确答案的序号)①解直角三角形②三角形全等【教师评价】甲、乙两小组的方案都很好,对于实际测量,要根据现场地形状况选择可实施的方案.44.(2024·北京·中考真题)如图,在四边形ABCD 中,E 是AB 的中点,DB ,CE 交于点F ,DF FB =,AF DC .(1)求证:四边形AFCD 为平行四边形;(2)若90EFB ∠=︒,tan 3FEB ∠=,1EF =,求BC 的长.45.(2024·甘肃临夏·中考真题)乾元塔(图1)位于临夏州临夏市的北山公园内,共九级,为砼框架式结构,造型独特别致,远可眺太子山露骨风月,近可收临夏市城建全貌,巍巍峨峨,傲立苍穹.某校数学兴趣小组在学习了“解直角三角形”之后,开展了测量乾元塔高度AB 的实践活动.A 为乾元塔的顶端,AB BC ⊥,点C ,D 在点B 的正东方向,在C 点用高度为1.6米的测角仪(即 1.6CE =米)测得A 点仰角为37︒,向西平移14.5米至点D ,测得A 点仰角为45︒,请根据测量数据,求乾元塔的高度AB .(结果保留整数,参考数据:sin370.60︒≈,cos370.80︒≈,tan370.75︒≈)46.(2024·安徽·中考真题)科技社团选择学校游泳池进行一次光的折射实验,如图,光线自点B 处发出,经水面点E 折射到池底点A 处.已知BE 与水平线的夹角36.9α=︒,点B 到水面的距离 1.20BC =m ,点A 处水深为1.20m ,到池壁的水平距离 2.50m AD =,点B C D ,,在同一条竖直线上,所有点都在同一竖直平面内.记入射角为β,折射角为γ,求sin sin βγ的值(精确到0.1,参考数据:sin 36.90.60︒≈,cos36.90.80︒≈,tan 36.90.75︒≈).47.(2024·浙江·中考真题)如图,在ABC 中,AD BC ⊥,AE 是BC 边上的中线,10,6,tan 1AB AD ACB ==∠=.(1)求BC 的长;(2)求sin DAE ∠的值.48.(2024·甘肃·中考真题)习近平总书记于2021年指出,中国将力争2030年前实现碳达峰、2060年前实现碳中和.甘肃省风能资源丰富,风力发电发展迅速.某学习小组成员查阅资料得知,在风力发电机组中,“风电塔筒”非常重要,它的高度是一个重要的设计参数.于是小组成员开展了“测量风电塔筒高度”的实践活动.如图,已知一风电塔筒AH 垂直于地面,测角仪CD ,EF 在AH 两侧, 1.6m CD EF ==,点C 与点E 相距182m (点C ,H ,E 在同一条直线上),在D 处测得简尖顶点A 的仰角为45︒,在F 处测得筒尖顶点A 的仰角为53︒.求风电塔筒AH 的高度.(参考数据:sin 5345︒≈,cos5335︒≈,tan 5343︒≈.)49.(2024·河北·中考真题)中国的探月工程激发了同学们对太空的兴趣.某晚,淇淇在家透过窗户的最高点P 恰好看到一颗星星,此时淇淇距窗户的水平距离4m BQ =,仰角为α;淇淇向前走了3m 后到达点D ,透过点P 恰好看到月亮,仰角为β,如图是示意图.已知,淇淇的眼睛与水平地面BQ 的距离 1.6m ==AB CD ,点P 到BQ 的距离 2.6m PQ =,AC 的延长线交PQ 于点E .(注:图中所有点均在同一平面)(1)求β的大小及tan α的值;(2)求CP 的长及sin APC ∠的值.50.(2024·四川广元·中考真题)计算:()2012024π32tan 602-⎛⎫-++︒- ⎪⎝⎭.51.(2024·四川广元·中考真题)小明从科普读物中了解到,光从真空射入介质发生折射时,入射角α的正弦值与折射角β的正弦值的比值sin sin αβ叫做介质的“绝对折射率”,简称“折射率”.它表示光在介质中传播时,介质对光作用的一种特征.(1)若光从真空射入某介质,入射角为α,折射角为β,且7cos 4α=30β=︒,求该介质的折射率;(2)现有一块与(1)中折射率相同的长方体介质,如图①所示,点A ,B ,C ,D 分别是长方体棱的中点,若光线经真空从矩形2121A D D A 对角线交点O 处射入,其折射光线恰好从点C 处射出.如图②,已知60α=︒,10cm CD =,求截面ABCD 的面积.52.(2024·内蒙古包头·中考真题)如图,学校数学兴趣小组开展“实地测量教学楼AB 的高度”的实践活动.教学楼周围是开阔平整的地面,可供使用的测量工具有皮尺、测角仪(皮尺的功能是直接测量任意可到达的两点间的距离;测角仪的功能是测量角的大小).(1)请你设计测量教学楼AB 的高度的方案,方案包括画出测量平面图,把应测数据标记在所画的图形上(测出的距离用,m n 等表示,测出的角用,αβ等表示),并对设计进行说明;(2)根据你测量的数据,计算教学楼AB 的高度(用字母表示).53.(2024·甘肃·中考真题)马家窑文化以发达的彩陶著称于世,其陶质坚固,器表细腻,红、黑、白彩共用,彩绘线条流畅细致,图案繁缛多变,形成了绚丽典雅的艺术风格,创造了一大批令人惊叹的彩陶艺术精品,体现了古代劳动人民的智慧.如图1的彩陶纹样呈现的是三等分圆周,古人用等边三角形三点定位的方法确定圆周的三等分点,这种方法和下面三等分圆周的方法相通.如图2,已知O 和圆上一点M .作法如下:①以点M 为圆心,OM 长为半径,作弧交O 于A ,B 两点;②延长MO 交O 于点C ;即点A ,B ,C 将O 的圆周三等分.(1)请你依据以上步骤,用不带刻度的直尺和圆规在图2中将O 的圆周三等分(保留作图痕迹,不写作法);(2)根据(1)画出的图形,连接AB ,AC ,BC ,若O 的半径为2cm ,则ABC 的周长为______cm .54.(2024·黑龙江牡丹江·中考真题)如图,某数学活动小组用高度为1.5米的测角仪BC ,对垂直于地面CD 的建筑物AD 的高度进行测量,BC CD ⊥于点C .在B 处测得A 的仰角=45ABE ∠︒,然后将测角仪向建筑物方向水平移动6米至FG 处,FG CD ⊥于点G ,测得A 的仰角58AFE ∠=︒,BF 的延长线交AD 于点E ,求建筑物AD 的高度(结果保留小数点后一位).(参考数据:sin580.85,cos580.53,tan58 1.60︒≈︒≈︒≈)55.(2024·广东·中考真题)中国新能源汽车为全球应对气候变化和绿色低碳转型作出了巨大贡献.为满足新能源汽车的充电需求,某小区增设了充电站,如图是矩形PQMN 充电站的平面示意图,矩形ABCD 是其中一个停车位.经测量,60ABQ ∠=︒, 5.4m AB =, 1.6m CE =,GH CD ⊥,GH 是另一个车位的宽,所有车位的长宽相同,按图示并列划定.根据以上信息回答下列问题:(结果精确到0.1m 3 1.73≈)(1)求PQ 的长;(2)该充电站有20个停车位,求PN 的长.56.(2024·广东广州·中考真题)2024年6月2日,嫦娥六号着陆器和上升器组合体(简称为“着上组合体”)成功着陆在月球背面.某校综合实践小组制作了一个“着上组合体”的模拟装置,在一次试验中,如图,该模拟装置在缓速下降阶段从A 点垂直下降到B 点,再垂直下降到着陆点C ,从B 点测得地面D 点的俯角为36.87︒,17AD =米,10BD =米.(1)求CD 的长;(2)若模拟装置从A 点以每秒2米的速度匀速下降到B 点,求模拟装置从A 点下降到B 点的时间.(参考数据:sin 36.870.60︒≈,cos36.870.80︒≈,tan 36.870.75︒≈)57.(2024·青海·中考真题)如图,某种摄像头识别到最远点A 的俯角α是17︒,识别到最近点B 的俯角β是45︒,该摄像头安装在距地面5m 的点C 处,求最远点与最近点之间的距离AB (结果取整数,参考数据:sin170.29︒≈,cos170.96︒≈,tan170.31︒≈).58.(2024·陕西·中考真题)问题提出(1)如图1,在ABC 中,15AB =,30C ∠=︒,作ABC 的外接圆O .则 ACB 的长为________;(结果保留π)问题解决(2)如图2所示,道路AB 的一侧是湿地.某生态研究所在湿地上建有观测点D ,E ,C ,线段AD AC ,和BC 为观测步道,其中点A 和点B 为观测步道出入口,已知点E 在AC 上,且AE EC =,60DAB ∠=︒,120ABC ∠=︒,1200m AB =,900m AD BC ==,现要在湿地上修建一个新观测点P ,使60DPC ∠=︒.再在线段AB 上选一个新的步道出入口点F ,并修通三条新步道PF PD PC ,,,使新步道PF 经过观测点E ,并将五边形ABCPD 的面积平分.请问:是否存在满足要求的点P 和点F ?若存在,求此时PF 的长;若不存在,请说明理由.(点A ,B ,C ,P ,D 在同一平面内,道路AB 与观测步道的宽、观测点及出入口的大小均忽略不计,结果保留根号)。
初三解直角三角形经典习题.docx

1.如图,港口A在观测站0的正东方向,0A=4km,某船从港口A出发,沿北偏东15。
方向航行一段距离后到达B处,此时从观测站0处测得该船位于北偏东60。
的方向,则该船航行的距离(即AB的长)为・北2.已知点A(VI,3)在抛物线y=--|x2+l^x的图象上,设点A关于抛物线对称轴对称的点为B.(1)求点B的他标;3,娄底)2013年3月,某煤矿发住瓦斯爆炸,该地救援队立即赶赴现场进行救援,救援队利用生命探测仪在地面A、B两个探测点探测到C处冇生命迹彖.己知A、B两点相距4 米,探测线与地而的夹角分别是30。
和45。
,试确定生命所在点C的深度.(精确到0」米,参考数据:、任u 1.41, V3 «1.73)4、(2013・益阳)如图,益阳市梓山湖中有一孤立小岛,湖边有一条笔直的观光小道AB, 现决定从小岛架一座与观光小道垂胃的小桥PD,小张在小道上测得如下数据:ABF0.0米,ZPAB=38.5°, ZPBA=26.5.请帮助小张求出小桥PD的长并确定小桥在小道上的位置.(以A, B为参照点,结杲精确到0.1米)(参考数据:sin38.5°=0.62, cos38.5°=0.78, tan38.5°=0.80, sin26.5°=0.45, cos26.5°=0.89,tan26.5°=0.50)D5、(2013•广安)如图,广安市防洪指挥部发现渠江边一处长400米,高8米,背水坡的坡角为45。
的防洪大堤(横截而为梯形ABCD)急需加固.经调査论证,防洪指挥部专家组制定的加固方案是:背水坡面用土石进行加固,并使上底加宽2米,加固后,背水坡EF的坡比i=l: 2.(1)求加固后坝底增加的宽度AF的长;(2)求完成这项工程需要土石多少立方米?6、(2013-乐山)如鹵11,山顶有一铁塔AB的高度为20米,为测量山的高度BC, 在山脚点D处测得塔顶A和塔基B的仰角分别为60。
中考数学分类(含答案)解直角三角形的应用

中考数学分类(含答案)解直角三角形应用一、选择题 1.(2010辽宁丹东市)如图,小颖利用有一个锐角是30°的三角板测量一棵树 的高度,已知她与树之间的水平距离BE 为5m ,AB 为1.5m 二、填空题1.(2010山东济宁)如图,是一张宽m 的矩形台球桌ABCD ,一球从点M (点M 在长边CD 上)出发沿虚线MN 射向边BC ,然后反弹到边AB 上的P 点. 如果MC n =,CMN α∠=.那么P 点与B 点的距离为 .【答案】tan tan m n αα-⋅2.(2010重庆市潼南县)如图所示,小明在家里楼顶上的点A 处,测量建在与小明家楼房同一水平线上相邻的电梯楼的高,在点A 处看电梯楼顶部点B 处的仰角为60°,在点A 处看这栋电梯楼底部点C 处的俯角为45°,两栋楼之间的距离为30m ,则电梯楼的高BC 为 米(精确到0.1).(参考数据:414.12≈732.13≈)【答案】82.0 3.(2010江西)如图,从点C 测得树的顶角为33º,BC =20米,则树高AB = 米(用计算器计算,结果精确到0.1米)(第15题)13【答案】0.4.(2010 湖北孝感)如图,一艘船向正北航行,在A处看到灯塔S在船的北偏东30°的方向上,航行12海里到达B点,在B处看到灯塔S在船的北偏东60°的方向上,此船继续沿正北方向航行过程中距灯塔S的最近距离是海里(不作近似计算)。
6【答案】35.(2010广东深圳)如图5,某渔船在海面上朝正方方向匀速航行,在A处观测到灯塔M 在北偏东60°方向上,航行半小时后到达B处,此时观测到灯塔M在北偏东30°方向上,那么该船继续航行分钟可使渔船到达离灯塔距离最近的位置。
【答案】156.(2010广东佛山)如图,AB是伸缩式的遮阳棚,CD是窗户,要想在夏至的政务时刻阳光刚好不能射入窗户,则AB的长度是米。
中考数学复习《解直角三角形的应用》专项检测卷(附带答案)

中考数学复习《解直角三角形的应用》专项检测卷(附带答案)学校:___________班级:___________姓名:___________考号:___________1.如图,ABC 中4C ABC A ∠=∠=∠,BD 是AC 边上的高,求DBC ∠的度数.2.如图所示,ABC 是边长为6的等边三角形,P 是AC 边上一动点,由点A 向点C 运动(P 不与A ,C 重合),Q 是CB 延长线上一点,与点P 同时以相同的速度由点B 向CB 延长线方向运动(Q 不与B 重合).连接PQ 交AB 于点D .当30BQD ∠=︒时,求AP 的长.3.如图所示,已知Rt Rt ABC CDE ≌△△,且点B ,C ,D 在同一条直线上,试判断AC 与CE 的位置关系,并给予证明.4.如图,在ABC 中90ACB ∠=︒,O 是AB 的中点, 6.5CO =,BC=55BC =.(1)求AC 的长;(2)求cos OCA ∠与tan B ∠的值.5.如图,在ACB △中90ACB ∠=︒,CD AB ⊥于D .(1)求证:ACD B ∠=∠;(2)若AF 平分CAB ∠分别交CD 、BC 于E 、F ,求证:CEF CFE ∠=∠.6.如图,在ABC 中,AD 是BC 边上的高,E 是AB 边上一点,CE 交AD 于点M ,且DCM MAE ∠∠=.求证:AEM △是直角三角形.7.如图,在ABC 中9030ACB A ∠=︒∠=︒,,AB 的垂直平分线分别交AB 和AC 于点D ,E .(1)求证:2AE CE =;(2)连接CD ,请判断BCD △的形状,并说明理由.8.已知:如图,在ABC 中120AB AC A AB =∠=︒,,的垂直平分线MN 分别交BC ,AB 于点M N ,,求证2CM BM =:.9.如图所示,ABC 中,120AB AC BAC =∠=︒,AC 的垂直平分线EF 交AC 于点E ,交BC 于点F .求证:2BF CF =.10.如图,在四边形ABCD 中AD BC ∥,E 是BC 的中点,CA 平分BCD ∠,且AC AB ⊥,连接DE ,交AC 于F .(1)求证:AD EC =;(2)若60B ∠=︒,试确定四边形ABED 是什么特殊四边形?请说明理由.11.已知:如图所示90ACB ∠=,AC=BC ,CD 是经过点C 的一条直线,过点A ,B 分别作AE CD ⊥,BF CD ⊥垂足分别为E ,F ,猜想AE ,BF ,EF 三者之间的数量关系,并予以证明.12.如图①,直角三角形DEF 与直角三角形ABC 的斜边在同一直线上90ACB E ∠=∠=︒ 36EDF ∠=︒40ABC ∠=︒,CD 平分ACB ∠,将三角形DEF 绕点D 按逆时针方向旋转,如图①,记ADF ∠为()0180αα︒<<︒,在旋转的过程中:(1)当α为多少度时DE BC ∥?(2)直接写出当α为多少度时DE BC ⊥?13.如图,四边形ABCD 中90A C ∠=∠=︒,BE ,DF 分别是ABC ∠,ADC ∠的平分线(1)1∠与2∠有什么关系,为什么?(2)BE 与DF 有什么位置关系?请说明理由.14.如图,在Rt ABC △中90ACB ∠=︒,过点C 的直线MN AB ∥,D 在AB 边上一点.过点D 作DE BC ⊥,交直线MN 于E ,垂足为F ,连接CD 、BE .(1)求证:CE AD =;(2)当点D 在AB 中点时,四边形BECD 是什么特殊四边形?说明你的理由.15.综合与实践问题情境:如图1,在Rt ABC △中90ACB ∠=︒,点D 是AB 的中点,连接CD ,将BCD △沿直线CD 折叠,点B 落在点E 处,连接AE .独立思考:(1)在图1中,若2, 2.5BC CD ==,则AC 的长为__________. 实践探究:(2)在图1中,请你判断AE 与DC 的位置关系,并说明理由; 问题解决:(3)如图2,在Rt ABC △中90,60ACB B ∠=︒∠=︒,点D 是AB 的中点,连接CD ,将BCD 沿直线CD 折叠,点B 落在点E 处,连接AE .请判断四边形CDAE 的形状,并说明理由.参考答案:1.10DBC ∠=︒2.23.AC CE ⊥4.(1)AC 的长为12 (2)12cos 13OCA ∠= 12tan 5B ∠= 7.(2)BCD △是等边三角形(2)菱形11.AE BF EF =+ 12.(1)4α=︒(2)94α=︒时 DE BC ⊥13.(1)1290∠+∠=︒(2)BE DF ∥14.(2)四边形BECD 是菱形15.(121(2)CD AE (3)四边形CDAE 是菱形。
中考数学复习《解直角三角形的实际应用 》专项检测卷(附带答案)
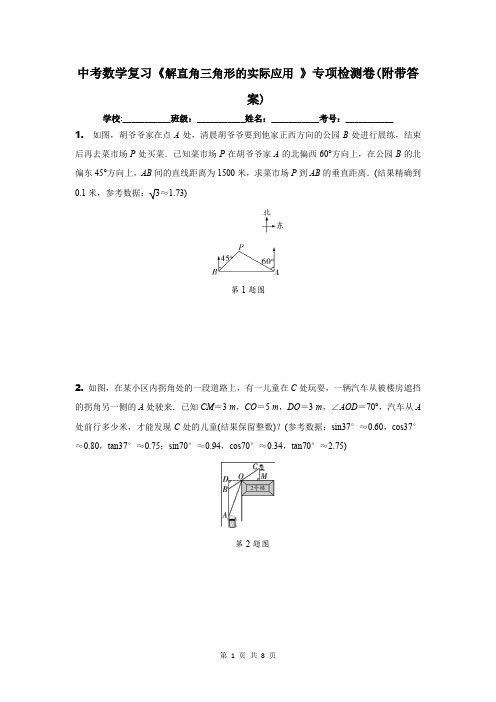
中考数学复习《解直角三角形的实际应用》专项检测卷(附带答案)学校:___________班级:___________姓名:___________考号:___________1.如图,胡爷爷家在点A处,清晨胡爷爷要到他家正西方向的公园B处进行晨练,结束后再去菜市场P处买菜.已知菜市场P在胡爷爷家A的北偏西60°方向上,在公园B的北偏东45°方向上,AB间的直线距离为1500米,求菜市场P到AB的垂直距离.(结果精确到0.1米,参考数据:3≈1.73)第1题图2.如图,在某小区内拐角处的一段道路上,有一儿童在C处玩耍,一辆汽车从被楼房遮挡的拐角另一侧的A处驶来.已知CM=3 m,CO=5 m,DO=3 m,∠AOD=70°,汽车从A 处前行多少米,才能发现C处的儿童(结果保留整数)?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75;sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)第2题图3.如图,在数学综合实践活动课上,九年级(1)班数学兴趣小组的同学们利用所学的数学知识测量建筑物CD的遮光板DE的长度,先测得建筑物CD的高为10 m,然后在A处测得建筑物CD的遮光板外沿E的仰角为30°,向正前方走9 m到达B处后测得遮光板内沿D的仰角为45°,求遮光板DE的长.(点A、B、C在一条直线上,DE∥AC,结果保留根号)第3题图4.小明周末与父母一起到遂宁湿地公园进行数学实践活动,在A处看到B、C处各有一棵被湖水隔开的银杏树,他在A处测得B在北偏西45°方向,C在北偏东30°方向,他从A 处走了20米到达B处,又在B处测得C在北偏东60°方向.(1)求∠C的度数;(2)求两棵银杏树B、C之间的距离(结果保留根号).第4题图5.王刚同学在学习了解直角三角形及其应用的知识后,尝试利用所学知识测量河对岸大树AB的高度,他在点C处测得大树顶端A的仰角为45°,再从C点出发沿斜坡走210米到达斜坡上D点,在点D处测得树顶端A的仰角为30°,若斜坡CF的坡比为i=1∶3(点E、C、B在同一水平线上).(1)求王刚同学从点C到点D的过程中上升的高度;(2)求大树AB的高度(结果保留根号).第5题图6.拓展小组研制的智能操作机器人,如图①,水平操作台为l,底座AB固定,高AB为50 cm,连杆BC长度为70 cm,手臂CD长度为60 cm,点B,C是转动点,且AB,BC与CD始终在同一平面内.(1)转动连杆BC,手臂CD,使∠ABC=143°,CD∥l,如图②,求手臂端点D离操作台l的高度DE的长(精确到1 cm,参考数据:sin53°≈0.8,cos53°≈0.6);(2)物品在操作台l上,距离底座A端110 cm的点M处,转动连杆BC,手臂CD,手臂端点D能否碰到点M?请说明理由.第6题图创新题7.白塔市位于呼和浩特市东临17公里的白塔村,原为辽代丰州古城内一座佛教寺院中的藏经塔.某数学活动小组在学习完“锐角三角函数”之后,决定测量白塔的高度.为了减小误差,该数学活动小组在测量仰角的度数及两个测量点之间的距离时,都分别测量了两次并取他们的平均值作为测量结果,测量数据如下表(不完整):活动课题测量白塔的高度活动工具测角仪和皮尺测量示意图第7题图说明:如图,他们先在点C处测得古塔顶端A的仰角为∠ACB,再在点D处测得古塔顶端A的仰角为∠ADB,且B、C、D在同一条直线上测量数据测量项目第一次第二次平均值∠ACB40.5°39.5°40°∠ADB30.2°29.8°30°C、D之间的距离29.6 m29.4 m……(1)两次测量C、D之间的距离的平均值是_____________________________________m;(2)根据以上测量结果,请你帮助该数学活动小组计算白塔AB的高度.(结果精确到1 m,参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,3≈1.73)参考答案1.解:如解图,过点P作PD⊥AB于点D第1题解图则∠PDB =∠PDA =90°由题意,得∠BPD =45°,∠APD =60°,AB =1500 设菜市场P 到AB 的垂直距离PD 为x ∴AD =PD ·tan60°=3x ,BD =PD =x ∴AB =AD +BD =3x +x =1500 解得x ≈547.5.答:菜市场P 到AB 的垂直距离约为547.5米. 2. 解:∵CM =3,CO =5,∠CMO =90° ∴在Rt △CMO 中,MO =52-32=4. ∵∠BOD =∠COM ,∠BDO =∠CMO =90° ∴△BDO ∽△CMO ∴BD CM =DO MO即BD 3=34,∴BD =2.25. 在Rt △ADO 中,tan ∠AOD =ADOD∴tan70°=AD3∴AD ≈3×2.75=8.25∴AB =AD -BD =8.25-2.25=6(m ).答:汽车从A 处前行约6 m ,才能发现C 处的儿童.3. 解:如解图,过点E 作EF ⊥AC 于点F ,可得四边形EFCD 是矩形第3题解图由题意得∠EAC =30°,∠DBC =45°,AB =9,CD =10∴EF =CD =10,DE =CF .在Rt △AEF 中,AF =EFtan30°=103在Rt △BCD 中,BC =CDtan45°=10∴CF =AC -AF =AB +BC -AF =19-103 ∴DE =CF =19-103答:遮光板DE 的长为(19-103)m . 4. 解:(1)由题意知,BE ∥AD ,∠EBD =60° ∴∠BDA =∠EBD =60°.∵∠BDA =∠C +∠CAD ,∠CAD =30° ∴∠C =∠BDA -∠CAD =30°; (2)如解图,过点B 作BG ⊥AD 于点G . ∴∠AGB =∠BGD =90°.在Rt △AGB 中,AB =20,∠BAG =45° ∴AG =BG =20×sin45°=10 2. 在Rt △BGD 中,∠BDA =60° ∴BD =BG sin60°=2063,DG =BG tan60°=1063.∵∠C =∠CAD =30°∴CD =AD =AG +DG =102+1063∴BC =BD +CD =102+106=10(2+6)米. 答:两棵银杏树B 、C 之间的距离为10(2+6)米.第4题解图5. 解:(1)如解图,过点D 作DH ⊥CE 于点H 在Rt △CDH 中,i =DH CH =13∴CH =3DH .∵CH2+DH2=CD2∴(3DH)2+DH2=(210)2解得DH=2或-2(舍去)∴王刚同学从点C到点D的过程中上升的高度为2米;(2)如解图,延长AD交CE于点G由题意,得∠AGC=30°∴GH=DHtan∠AGC=233=2 3.∵CH=3DH=6∴GC=GH+CH=23+6.在Rt△BAC中,∠ACB=45°∴AB=BC∴tan∠AGB=ABBG=ABBC+CG=ABAB+23+6=33解得AB=6+43答:大树AB的高度为(6+43)米.第5题解图6.解:(1)如解图①,过点C作CP⊥AE于点P,过点B作BQ⊥CP于点Q第6题解图①由题意,得∠ABC=143°,∠ABQ=90°∴∠CBQ=53°∴在Rt△BCQ中,CQ=BC·sin53°≈70×0.8=56.∵CD∥l,PQ=AB=50∴DE=CP=CQ+PQ=56+50=106答:手臂端点D离操作台l的高度DE长为106 cm;(2)能.理由如下:如解图②,当点B,C,D共线时第6题解图②BD=60+70=130,AB=50在Rt△ABD中,AD=BD2-AB2=1302-502=120.∵120>110∴手臂端点D能碰到点M.7.解:(1)29.5;(2)由题意,设白塔AB的高度为x m在Rt△ABC中,∠ACB=40°,tan∠ACB=xBC∴BC=xtan40°.在Rt△ABD中,∠ADB=30°,tan∠ADB=x BD∴BD=x tan30°.∵BD-BC=29.5∴xtan30°-xtan40°=29.5解得x≈55.答:白塔AB的高度约为55 m.。
中考数学复习《解直角三角形的应用》专项检测卷-附带答案

中考数学复习《解直角三角形的应用》专项检测卷-附带答案学校:___________班级:___________姓名:___________考号:___________1.小王同学学习了锐角三角函数后,通过观察广场的台阶与信号塔之间的相对位置,他认为利用台阶的可测数据与在点A,B处测出点D的仰角度数,可以求出信号塔DE的高.如图,AB的长为5m,高BC为3m.他在点A处测得点D的仰角为45°,在点B处测得点D的仰角为38.7°.A,B,C,D,E在同一平面内.你认为小王同学能求出信号塔DE的高吗?若能,请求出信号塔DE的高;若不能,请说明理由.(参考数据:sin38.7°≈0.625,cos38.7°≈0.780,tan38.7°≈0.80,结果保留整数)2.如图,太阳能电池板宽为AB,点O是AB的中点,OC是灯杆,地面上三点D,E与C在一条直线上,DE=10.5m,EC=5m.在D处测得电池板边缘点B的仰角为37°,在E处测得电池板边缘点B的仰角为45°.此时点A、B与E在一条直线上,求太阳能电池板宽AB的长度.(结果精确到0.1m.参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,√2≈1.41,√3≈1.73)3.为积极响应绿色出行的号召,骑车出行已经成为人们的新风尚.图①是某品牌自行车放在水平地面上的实物图,图②是其示意图,其中AB∥CD∥l,车轮半径为32cm,∠ABC=64°,BC=60cm,坐垫E与点B的距离BE为10cm.(1)求坐垫E到地面的距离;(2)根据经验,当坐垫E到CD的距离调整为人体腿长的0.8时,坐骑比较舒适.小明的腿长约为84cm,现将坐垫E调整至坐骑舒适高度位置E′,求EE′的长.(结果精确到0.lcm.参考数据:sin64°≈0.90,cos64°≈0.44,tan64°≈2.05)4.在学校的数学学科周上,李老师指导学生测量学校旗杆AB的高度.在旗杆附近有一个斜坡,坡长CD=10米,坡度i=3:4,小华在C处测得旗杆顶端A的仰角为60°,在D处测得旗杆顶端A的仰角为45°.求旗杆AB的高度.(点A,B,C,D在同一平面内,B,C在同一水平线上,结果保留根号)5.如图1是某商场的入口,它是由立柱、斜杆、支撑杆组成的支架撑起的,如图2是它的示意图,点P、A、C在同一水平线上,经过测量,支架的立柱BC与地面PC垂直(∠ACB=90°),BC=3米,支撑杆DE⊥AB于点E,∠BDE=α且sinα=25,从点B观测点D的仰角为45°,又测得BE =4米.(1)求该支架的边BD的长;(2)求支架的边BD的顶端点D到地面PC的距离DF.(结果保留根号)6.桔槔俗称“吊杆”“称杆”(如图1),是我国古代农用工具,始见于《墨子•备城门》,是一种利用杠杆原理的取水机械.如图2所示的是桔槔示意图,OM是垂直于水平地面的支撑杆,OM=3米,AB是杠杆,且AB=6米,OA:OB=2:1.当点A位于最高点时,∠AOM=127°.(1)求点A位于最高点时到地面的距离;(2)当点A从最高点逆时针旋转54.5°到达最低点A1时,求此时水桶B上升的高度.(参考数据:sin37°≈0.6,sin17.5°≈0.3,tan37°≈0.8)7.某班同学在一次综合实践课上,测量校园内一棵树的高度.如图,测量仪在A处测得树顶D的仰角为45°,在C处测得树顶D的仰角为37°(点A、B、C在同一条水平直线上).已知测量仪高度AE=CF=1.65米,AC=28米,求树BD的高度.(结果精确到0.1米)【参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75】8.如图,某工厂坐落在东西方向公路MN的北侧,H,E分别是矩形生产车间ABCD的入口和出口(AD∥MN,HE⊥BC),车间宽度EH=80m,生产出来的产品沿北偏西53°的厂内道路EF运送到库房F存放,EF=500m,工厂大门G在库房F南偏西26.6°的方向,求大门与车间入口之间的距离GH的长.(点G,B,H,C在直线MN上.参考数据:sin26.6°≈0.45,cos26.6°≈0.89,tan26.6°≈0.5,sin53°≈45,cos53°≈35,tan53°≈43)9.数学兴趣小组测量某楼房的高度.如图所示,楼房剖面和台阶的剖面在同一平面,在台阶底部点A处测得楼顶端点E的仰角∠GAE=50.2°,台阶AB长39米,台阶坡面AB的坡度i=5:12,然后在点B处测得楼顶端点E的仰角∠EBF=63.4°,则楼顶到地面的高度EF约为多少米.(参考数据:tan50.2°≈1.20,tan63.4°≈2.00,sin50.2°≈0.77,sin63.4°≈0.89)10.“工欲善其事,必先利其器”,如图为钓鱼爱好者购买的神器“晴雨伞”,其截面示意图是轴对称图形,对称轴是垂直于地面的支杆AD,用绳子拉直AC后系在树干PQ上的点E处,使得A,C,E在一条直线上,AB=AC=2m,DQ=3m.(1)垂钓时打开“晴雨伞”,若∠α=60°,求遮蔽宽度BC(结果精确到0.01m);(2)若由(1)中的位置收合“晴雨伞”,使得∠BAC=106°,求点E下降的高度(结果精确到0.1m).(参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33,√3≈1.73)参考答案1.解:能,过B作BF⊥DE于F则EF=BC=3m,BF=CE在Rt△ABC中,∵AB=5m,BC=3m∴AC=√AB2−BC2=4(m)在Rt△ADE中,∵∠DAE=45°∴AE=DE设AE=DE=x m∴BF=(4+x)m,DF=(x﹣3)m在Rt△BDF中,tan38.7°=DFBF =x−34+x≈0.80解得x=31∴DE=31m答:信号塔DE的高为31m.2.解:过B作BM⊥ED于M,BN⊥CO于N ∴∠DMB=90°,∠ONB=90°∵∠BEM=45,∠BDE=37°,∠OCE=90°∴△OEC,OBN是等腰直角三角形设BN=MC=x m∴ME=(5﹣x)m,MD=(5.5﹣x)m在Rt△BMD中,∠DMB=90°∴tan∠BDM=BMDM =5−x5.5−x=0.75∴x=0.5∵∠BEM=45°,∠ECO=90°∴OB=√22∴AB=2OB=√2≈1.4(m)答:太阳能电池板宽AB的长度约为1.4m.3.解:过点E作EG⊥CD于点G∴∠EGC=90°.∵BC=60cm,坐垫E与点B的距离BE为10cm ∴CE=70(cm).∵∠ABC=64°,AB∥CD∴∠ECD=64°.∴EG=EC•sin64°≈70×0.90=63(cm).∵CD∥l,CF⊥l,l与⊙D相切,车轮半径为32cm ∴CF=32(cm).∴坐垫E到地面的距离为:63+32=95(cm).答:坐垫E到地面的距离为95cm;(2)过点E′作E′G′⊥CD于点G′∴∠E′G′C=90°.∵小明的腿长约为84cm∴E′G′=84×0.8=67.2(cm).∵∠ECD=64°∴CE′=67.2sin64°=67.20.90≈74.67(cm).∴EE′=CE′﹣CE=74.67﹣70=4.67≈4.7(cm).答:EE′长4.7cm.4.解:过点D作DE⊥BC,垂足为E,过点D作DF⊥AB,垂足为F由题意得:DF=BE,BF=DE∵坡长CD=10米,坡度i=3:4∴DECE=34∴设DE=3x米,则CE=4x米在Rt△CDE中,CD=√CE2+DE2=√(4x)2+(3x)2=5x(米)∴5x=10解得:x=2∴CE=8米,DE=BF=6米设BC=y米∴DF=BE=BC+CE=(y+8)米在Rt△ABC中,∠ACB=60°∴AB=BC•tan60°=√3y(米)在Rt△ADF中,∠ADF=45°∴AF=DF•tan45°=(y+8)米∵AB=AF+BF∴√3y=y+8+6解得:y=7√3+7∴AB=√3y=(21+7√3)米∴旗杆AB的高度为(21+7√3)米.5.解:(1)∵DE⊥AB∴△DBE是直角三角形在Rt△DBE中,sinα=BEDB=25∵BE=4∴BD=10即该支架的边BD的长为10米;(2)根据已知可得,在Rt△DBG中∠DBG=45°,且BD=10∴sin∠DBG=sin45°=DGDB即DG10=√22解得:DG=5√2在矩形GFCB中,GF=BC=3∴DF=DG+GF=(5√2+3)米.6.解:(1)过O作EF⊥OM于O,过A作AG⊥EF于G ∵AB=6米,OA:OB=2:1∴OA=4米,OB=2米∵∠AOM=127°,∠EOM=90°∴∠AOE=127°﹣90°=37°在Rt△AOG中,AG=AO×sin37°≈4×0.6=2.4(米)点A位于最高点时到地面的距离为2.4+3=5.4(米)答:点A位于最高点时到地面的距离为5.4米;(2)过O作EF⊥OM,过B作BC⊥EF于C,过B1作B1D⊥EF于D ∵∠AOE=37°∴∠BOC=∠AOE=37°,∠B1OD=∠A1OE=17.5°∵OB1=OB=2(米)在Rt△OBC中,BC=sin∠OCB×OB=sin37°×OB≈0.6×2=1.2(米)在Rt△OB1D中,B1D=sin17.5°×OB1≈0.3×2=0.6(米)∴BC+B1D=1.2+0.6=1.8(米)∴此时水桶B上升的高度为1.8米.7.解:连接EF交树BD于点G.由题意知;AE⊥AC,CF⊥AC,BD⊥AC又∵AE=CF=1.65米∴四边形EAGB、CFGB是矩形.∴BG=AE=1.65米.∠DGE=∠DGF=90°AB=EG,BC=GF.在Rt△EGD中∵∠DEG=45°∴AB=DG=EG=(DB﹣1.65)米.在Rt△FGD中∵tan∠DFG=DGGF∴BC=GF=DGtan∠DFG ≈DB−1.650.75米.∵AB+BC=AC=28∴DB﹣1.65+DB−1.65=280.75∴DB=13.65≈13.7(米).答:树BD的高度为13.7米.8.解:过F作FP⊥BG于P,延长EA交FP于Q则四边形PHEQ是矩形∴PQ=EH=80m,EQ=PH在Rt△EFQ中,∠FQE=90°,∠EFQ=53°,EF=500m∴FQ=EF•cos53°≈500×3=300(m),EQ=EF•sin53°≈500×45=400(m)5∴PH=EQ=400m,PF=FQ+PQ=300+80=380(m)在Rt△PFG中,∠FPG=90°,∠PFG=26.6°∴PG=PF•tan26.6°≈380×0.5=190(m)∴GH=PG+PH=190+400=590(m)答:大门与车间入口之间的距离GH的长约为590m.9.解:如图,延长EF交AG于点H,则EH⊥AG,作BP⊥AG于点P,则四边形BFHP是矩形∴FB=PH,FH=PB由i=5:12,可以假设BP=5x,AP=12x∵PB2+P A2=AB2∴(5x)2+(12x)2=392∴x=3或﹣3(舍去)∴PB=FH=15,AP=36设EF=a米,BF=b米∵tan∠EBF=EFBF∴ab≈2∴a≈2b①∵tan∠EAH=EHAH =EF+HFAP+PH=EF+BPAP+BF∴a+1536+b≈1.2②由①②得a≈70.5,b≈35.25答:塔顶到地面的高度EF约为70.5米.10.解:(1)∵AB=AC=2m,AO⊥BC ∴BC=2OC在Rt△AOC中,∠α=60°∴OC=AC•sin60°=2×√32=√3(m)∴BC=2OC=2√3≈3.46(m)∴遮蔽宽度BC约为3.46m;(2)过点E作EF⊥AD,垂足为F由题意得:EF=DQ=3m当∠α=60°时在Rt△AFE中,AF=EFtan60°=√3=√3(m)当∠BAC=106°时∵AB=AC,AO⊥BC∴∠EAF=12∠BAC=53°在Rt△AFE中,AF=EFtan53°≈31.33≈2.26(m)∴点E下降的高度=2.26﹣1.73≈0.5(m)∴点E下降的高度约为0.5m.第11页共11页。
(完整word版)解直角三角形的应用中考练习题

解直角三角形的应用练习题一.选择题(共5小题)1.(2012•襄阳)在一次数学活动中,李明利用一根栓有小锤的细线和一个半圆形量角器制作了一个测角仪,去测量学校内一座假山的高度CD.如图,已知小明距假山的水平距离BD为12m,他的眼镜距地面的高度为1.6m,李明的视线经过量角器零刻度线OA和假山的最高点C,此时,铅垂线OE经过量角器的60°刻度线,则假山的高度为()A.(4+1.6)m B.(12+1.6)m C.(4+1.6)m D.4m2.(2014•随州)如图,要测量B点到河岸AD的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=100米,则B点到河岸AD的距离为()D.50米A.100米B.50米C.米3.(2014•衡阳)如图,一河坝的横断面为等腰梯形ABCD,坝顶宽10米,坝高12米,斜坡AB的坡度i=1:1.5,则坝底AD的长度为()A.26米B.28米C.30米D.46米4.(2014•西宁)如图1,某超市从一楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的坡度为1:2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角为42°,则二楼的层高BC约为(精确到0.1米,sin42°≈0.67,tan42°≈0.90)()A.10.8米B.8.9米C.8.0米D.5.8米5.(2014•临沂)如图,在某监测点B处望见一艘正在作业的渔船在南偏西15°方向的A处,若渔船沿北偏西75°方向以40海里/小时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东60°方向上,则B、C之间的距离为A.20海里B.10海里C.20海里D.30海里()二.填空题6.(2009•仙桃)如图所示,小华同学在距离某建筑物6米的点A处测得广告牌B点、C点的仰角分别为52°、35°,则广告牌的高度BC为_________米(精确到0.1米).(sin35°≈0.57,cos35°≈0.82,tan35°≈0.70;sin52°≈0.79,cos52°≈0.62,tan52°≈1.28)7.(2009•安徽)长为4m的梯子搭在墙上与地面成45°角,作业时调整为60°角(如图所示),则梯子的顶端沿墙面升高了_________m.8.(2014•宁波)为解决停车难的问题,在如图一段长56米的路段开辟停车位,每个车位是长5米宽2.2米的矩形,矩形的边与路的边缘成45°角,那么这个路段最多可以划出_________个这样的停车位.(≈1.4)9.(2014•十堰)如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是_________海里.(结果精确到个位,参考数据:≈1.4,≈1.7,≈2.4)10.(2014•抚顺)如图,河流两岸a、b互相平行,点A、B是河岸a上的两座建筑物,点C、D是河岸b上的两点,A、B的距离约为200米.某人在河岸b上的点P处测得∠APC=75°,∠BPD=30°,则河流的宽度约为_________米.三.解答题(共5小题)11.(2014•南昌)图1中的中国结挂件是由四个相同的菱形在顶点处依次串联而成,每相邻两个菱形均成30°的夹角,示意图如图2.在图2中,每个菱形的边长为10cm,锐角为60°.(1)连接CD,EB,猜想它们的位置关系并加以证明;(2)求A,B两点之间的距离(结果取整数,可以使用计算器)(参考数据:≈1.41,≈1.73,≈2.45)12.(2014•铁岭)如图,小丽假期在娱乐场游玩时,想要利用所学的数学知识测量某个娱乐场地所在山坡AE的长度.她先在山脚下点E处测得山顶A的仰角是30°,然后,她沿着坡度是i=1:1(即tan∠CED=1)的斜坡步行15分钟抵达C处,此时,测得A点的俯角是15°.已知小丽的步行速度是18米/分,图中点A、B、E、D、C在同一平面内,且点D、E、B在同一水平直线上.求出娱乐场地所在山坡AE的长度.(参考数据:≈1.41,结果精确到0.1米)13.(2014•抚州)如图1所示的晾衣架,支架主视图的基本图形是菱形,其示意图如图2,晾衣架伸缩时,点G在射线DP上滑动,∠CED的大小也随之发生变化,已知每个菱形边长均等于20cm,且AH=DE=EG=20cm.(1)当∠CED=60°时,求C、D两点间的距离;(2)当∠CED由60°变为120°时,点A向左移动了多少cm?(结果精确到0.1cm)(3)设DG=xcm,当∠CED的变化范围为60°~120°(包括端点值)时,求x的取值范围.(结果精确到0.1cm)(参考数据≈1.732,可使用科学计算器)14.(2014•宿迁)如图是某通道的侧面示意图,已知AB∥CD∥EF,AM∥BC∥DE,AB=CD=EF,∠AMF=90°,∠BAM=30°,AB=6m.(1)求FM的长;(2)连接AF,若sin∠FAM=,求AM的长.15.(2014•邵阳)一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里每小时的速度前往救援,求海警船到大事故船C处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)解直角三角形的应用练习题参考答案与试题解析一.选择题(共5小题)1.(2012•襄阳)在一次数学活动中,李明利用一根栓有小锤的细线和一个半圆形量角器制作了一个测角仪,去测量学校内一座假山的高度CD.如图,已知小明距假山的水平距离BD为12m,他的眼镜距地面的高度为1.6m,李明的视线经过量角器零刻度线OA和假山的最高点C,此时,铅垂线OE经过量角器的60°刻度线,则假山的高度为()A.(4+1.6)m B.(12+1.6)m C.(4+1.6)m D.4m考点:解直角三角形的应用.分析:根据已知得出AK=BD=12m,再利用tan30°==,进而得出CD的长.解答:解:∵BD=12米,李明的眼睛高AB=1.6米,∠AOE=60°,∴DB=AK,AB=KD=1.6米,∠CAK=30°,∴tan30°==,解得CK=4(米),即CD=CK+DK=4+1.6=(4+1.6)米.故选:A.点评:本题考查的是解直角三角形的应用,根据题意得出tan30°==解答是解答此题的关键.2.(2014•随州)如图,要测量B点到河岸AD的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=100米,则B点到河岸AD的距离为()A.100米B.50米C.D.50米米考点:解直角三角形的应用.专题:几何图形问题.分析:过B作BM⊥AD,根据三角形内角与外角的关系可得∠ABC=30°,再根据等角对等边可得BC=AC,然后再计算出∠CBM的度数,进而得到CM长,最后利用勾股定理可得答案.解答:解:过B作BM⊥AD,∵∠BAD=30°,∠BCD=60°,∴∠ABC=30°,∴AC=CB=100米,∵BM⊥AD,∴∠BMC=90°,∴∠CBM=30°,∴CM=BC=50米,∴BM=CM=50米,故选:B.点评:此题主要考查了解直角三角形的应用,关键是证明AC=BC,掌握直角三角形的性质:30°角所对直角边等于斜边的一半.3.(2014•衡阳)如图,一河坝的横断面为等腰梯形ABCD,坝顶宽10米,坝高12米,斜坡AB的坡度i=1:1.5,则坝底AD的长度为()A.26米B.28米C.30米D.46米考点:解直角三角形的应用-坡度坡角问题.专题:几何图形问题.分析:先根据坡比求得AE的长,已知CB=10m,即可求得AD.解答:解:∵坝高12米,斜坡AB的坡度i=1:1.5,∴AE=1.5BE=18米,∵BC=10米,∴AD=2AE+BC=2×18+10=46米,故选:D.点评:此题考查了解直角三角形的应用中的坡度坡角的问题及等腰梯形的性质的掌握情况,将相关的知识点相结合更利于解题.4.(2014•西宁)如图1,某超市从一楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的坡度为1:2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角为42°,则二楼的层高BC约为(精确到0.1米,sin42°≈0.67,tan42°≈0.90)()A.10.8米B.8.9米C.8.0米D.5.8米考点:解直角三角形的应用-仰角俯角问题;解直角三角形的应用-坡度坡角问题.专题:几何图形问题.分析:延长CB交PQ于点D,根据坡度的定义即可求得BD的长,然后在直角△CDA中利用三角函数即可求得CD的长,则BC即可得到.解答:解:延长CB交PQ于点D.∵MN∥PQ,BC⊥MN,∴BC⊥PQ.∵自动扶梯AB的坡度为1:2.4,∴==.设BD=5k米,AD=12k米,则AB=13k米.∵AB=13米,∴k=1,∴BD=5米,AD=12米.在Rt△CDA中,∠CDA=90゜,∠CAD=42°,∴CD=AD•tan∠CAD≈12×0.90≈10.8米,∴BC≈5.8米.故选:D.点评:本题考查仰角和坡度的定义,要求学生能借助仰角构造直角三角形并解直角三角形.5.(2014•临沂)如图,在某监测点B处望见一艘正在作业的渔船在南偏西15°方向的A处,若渔船沿北偏西75°方向以40海里/小时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东60°方向上,则B、C之间的距离为()A.20海里B.10海里C.20海里D.30海里考点:解直角三角形的应用-方向角问题.专题:几何图形问题.分析:如图,根据题意易求△ABC是等腰直角三角形,通过解该直角三角形来求BC的长度.解答:解:如图,∵∠ABE=15°,∠DAB=∠ABE,∴∠DAB=15°,∴∠CAB=∠CAD+∠DAB=90°.又∵∠FCB=60°,∠CBE=∠FCB,∠CBA+∠ABE=∠CBE,∴∠CBA=45°.∴在直角△ABC中,sin∠ABC===,∴BC=20海里.故选:C.点评:本题考查了解直角三角形的应用﹣方向角问题.解题的难点是推知△ABC是等腰直角三角形.二.填空题(共5小题)6.(2009•仙桃)如图所示,小华同学在距离某建筑物6米的点A处测得广告牌B点、C点的仰角分别为52°、35°,则广告牌的高度BC为 3.5米(精确到0.1米).(sin35°≈0.57,cos35°≈0.82,tan35°≈0.70;sin52°≈0.79,cos52°≈0.62,tan52°≈1.28)考点:解直角三角形的应用-仰角俯角问题.专题:应用题;压轴题.分析:图中有两个直角三角形△ABD、△ACD,可根据两个已知角度,利用正切函数定义,分别求出BD和CD,求差即可.解答:解:根据题意:在Rt△ABD中,有BD=AD•tan52°.在Rt△ADC中,有DC=AD•tan35°.则有BC=BD﹣CD=6(1.28﹣0.70)=3.5(米).点评:本题考查仰角的定义,要求学生能借助仰角构造直角三角形并解直角三角形.7.(2009•安徽)长为4m的梯子搭在墙上与地面成45°角,作业时调整为60°角(如图所示),则梯子的顶端沿墙面升高了2()m.考点:解直角三角形的应用-坡度坡角问题.专题:压轴题.分析:利用所给角的正弦函数求两次的高度,相减即可.解答:解:由题意知:平滑前梯高为4•sin45°=4•=.平滑后高为4•sin60°=4•=.∴升高了2()m.点评:本题重点考查了三角函数定义的应用.8.(2014•宁波)为解决停车难的问题,在如图一段长56米的路段开辟停车位,每个车位是长5米宽2.2米的矩形,矩形的边与路的边缘成45°角,那么这个路段最多可以划出17个这样的停车位.(≈1.4)考点:解直角三角形的应用.专题:调配问题.分析:如图,根据三角函数可求BC,CE,由BE=BC+CE可求BE,再根据三角函数可求EF,再根据停车位的个数=(56﹣BE)÷EF+1,列式计算即可求解.解答:解:如图,BC=2.2×sin45°=2.2×≈1.54米,CE=5×sin45°=5×≈3.5米,BE=BC+CE≈5.04,EF=2.2÷sin45°=2.2÷≈3.14米,(56﹣5.04)÷3.14+1=50.96÷3.14+1≈16+1=17(个).故这个路段最多可以划出17个这样的停车位.故答案为:17.点评:考查了解直角三角形的应用,主要是三角函数及运算,关键把实际问题转化为数学问题加以计算.9.(2014•十堰)如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是24海里.(结果精确到个位,参考数据:≈1.4,≈1.7,≈2.4)考点:解直角三角形的应用-方向角问题.专题:几何图形问题.分析:作BD⊥AC于点D,在直角△ABD中,利用三角函数求得BD的长,然后在直角△BCD中,利用三角函数即可求得BC的长.解答:解:∠CBA=25°+50°=75°.作BD⊥AC于点D.则∠CAB=(90°﹣70°)+(90°﹣50°)=20°+40°=60°,∠ABD=30°,∴∠CBD=75°﹣30°=45°.在直角△ABD中,BD=AB•sin∠CAB=20×sin60°=20×=10.在直角△BCD中,∠CBD=45°,则BC=BD=10×=10≈10×2.4=24(海里).故答案是:24.点评:本题主要考查了方向角含义,正确求得∠CBD以及∠CAB的度数是解决本题的关键.10.(2014•抚顺)如图,河流两岸a、b互相平行,点A、B是河岸a上的两座建筑物,点C、D是河岸b上的两点,A、B的距离约为200米.某人在河岸b上的点P处测得∠APC=75°,∠BPD=30°,则河流的宽度约为100米.考点:解直角三角形的应用.专题:几何图形问题.分析:过点P作PE⊥AB于点E,先求出∠APE及∠BPE、∠ABP的度数,由锐角三角函数的定义即可得出结论.解答:解:过点P作PE⊥AB于点E,∵∠APC=75°,∠BPD=30°,∴∠APB=75°,∵∠BAP=∠APC=75°,∴∠APB=∠BAP,∴AB=PB=200m,∵∠ABP=30°,∴PE=PB=100m.故答案为:100.点评:本题考查的是解直角三角形的应用,熟知锐角三角函数的定义是解答此题的关键.三.解答题(共5小题)11.(2014•南昌)图1中的中国结挂件是由四个相同的菱形在顶点处依次串联而成,每相邻两个菱形均成30°的夹角,示意图如图2.在图2中,每个菱形的边长为10cm,锐角为60°.(1)连接CD,EB,猜想它们的位置关系并加以证明;(2)求A,B两点之间的距离(结果取整数,可以使用计算器)(参考数据:≈1.41,≈1.73,≈2.45)考点:解直角三角形的应用.分析:(1)连接DE.根据菱形的性质和角的和差关系可得∠CDE=∠BED=90°,再根据平行线的判定可得CD,EB的位置关系;(2)根据菱形的性质可得BE,DE,再根据三角函数可得BD,AD,根据AB=BD+AD,即可求解.解答:解:(1)猜想CD∥EB.证明:连接DE.∵中国结挂件是四个相同的菱形,每相邻两个菱形均成30°的夹角,菱形的锐角为60°∴∠CDE=60°÷2×2+30°=90°,∴∠BED=60°÷2×2+30°=90°,∴∠CDE=∠BED,∴CD∥EB.(2)BE=2OE=2×10×cos30°=10cm,同理可得,DE=10cm,则BD=10cm,同理可得,AD=10cm,AB=BD+AD=20≈49cm.答:A,B两点之间的距离大约为49cm.点评:此题考查了解直角三角形的应用,菱形的性质和平行线的判定,主要是三角函数的基本概念及运算,关键是运用数学知识解决实际问题.12.(2014•铁岭)如图,小丽假期在娱乐场游玩时,想要利用所学的数学知识测量某个娱乐场地所在山坡AE的长度.她先在山脚下点E处测得山顶A的仰角是30°,然后,她沿着坡度是i=1:1(即tan∠CED=1)的斜坡步行15分钟抵达C处,此时,测得A点的俯角是15°.已知小丽的步行速度是18米/分,图中点A、B、E、D、C在同一平面内,且点D、E、B在同一水平直线上.求出娱乐场地所在山坡AE的长度.(参考数据:≈1.41,结果精确到0.1米)考点:解直角三角形的应用-仰角俯角问题;解直角三角形的应用-坡度坡角问题.分析:根据速度乘以时间得出CE的长度,通过坡度得到∠ECF=30°,作辅助线EF⊥AC,通过平角减去其他角从而得到∠AEF=45°即可求出AE的长度.解答:解:作EF⊥AC,根据题意,CE=18×15=270米,∵tan∠CED=1,∴∠CED=∠DCE=45°,∵∠ECF=90°﹣45°﹣15°=30°,∴EF=CE=135米,∵∠CEF=60°,∠AEB=30°,∴∠AEF=180°﹣45°﹣60°﹣30°=45°,∴AE=135≈190.35米点评:本题考查了解直角三角形的应用,解答本题的关键是作辅助线EF⊥AC,以及坡度和坡角的关系.13.(2014•抚州)如图1所示的晾衣架,支架主视图的基本图形是菱形,其示意图如图2,晾衣架伸缩时,点G在射线DP上滑动,∠CED的大小也随之发生变化,已知每个菱形边长均等于20cm,且AH=DE=EG=20cm.(1)当∠CED=60°时,求C、D两点间的距离;(2)当∠CED由60°变为120°时,点A向左移动了多少cm?(结果精确到0.1cm)(3)设DG=xcm,当∠CED的变化范围为60°~120°(包括端点值)时,求x的取值范围.(结果精确到0.1cm)(参考数据≈1.732,可使用科学计算器)考点:解直角三角形的应用;菱形的性质.分析:(1)证明△CED是等边三角形,即可求解;(2)分别求得当∠CED是60°和120°,两种情况下AD的长,求差即可;(3)分别求得当∠CED是60°和120°,两种情况下DG的长度,即可求得x的范围.解答:解:(1)连接CD(图1).∵CE=DE,∠CED=60°,∴△CED是等边三角形,∴CD=DE=20cm;(2)根据题意得:AB=BC=CD,当∠CED=60°时,AD=3CD=60cm,当∠CED=120°时,过点E作EH⊥CD于H(图2),则∠CEH=60°,CH=HD.在直角△CHE中,sin∠CEH=,∴CH=20•sin60°=20×=10(cm),∴CD=20cm,∴AD=3×20=60≈103.9(cm).∴103.9﹣60=43.9(cm).即点A向左移动了43.9cm;(3)当∠CED=120°时,∠DEG=60°,∵DE=EG,∴△DEG是等边三角形.∴DG=DE=20cm,当∠CED=60°时(图3),则有∠DEG=120°,过点E作EI⊥DG于点I.∴∠DEI=∠GEI=60°,DI=IG,在直角△DIE中,sin∠DEI=,∴DI=DE•sin∠DEI=20×sin60°=20×=10cm.∴DG=2DI=20≈34.6cm.则x的范围是:20cm≤x≤34.6cm.点评:本题考查了菱形的性质,当菱形的一个角是120°或60°时,连接菱形的较短的对角线,即可把菱形分成两个等边三角形.14.(2014•宿迁)如图是某通道的侧面示意图,已知AB∥CD∥EF,AM∥BC∥DE,AB=CD=EF,∠AMF=90°,∠BAM=30°,AB=6m.(1)求FM的长;(2)连接AF,若sin∠FAM=,求AM的长.考点:解直角三角形的应用-坡度坡角问题.专题:几何图形问题.分析:(1)分别过点B、D、F作BN⊥AM于点N,DG⊥BC延长线于点G,FH⊥DE延长线于点H,根据AB∥CD∥EF,AM∥BC∥DE,分别解Rt△ABN、Rt△DCG、Rt△FEH,求出BN、DG、FH的长度,继而可求出FM的长度;(2)在Rt△FAM中,根据sin∠FAM=,求出AF的长度,然后利用勾股定理求出AM的长度.解答:解:(1)分别过点B、D、F作BN⊥AM于点N,DG⊥BC延长线于点G,FH⊥DE延长在Rt△ABN中,∵AB=6m,∠BAM=30°,∴BN=ABsin∠BAN=6×=3m,∵AB∥CD∥EF,AM∥BC∥DE,同理可得:DG=FH=3m,∴FM=FH+DG+BN=9m;(2)在Rt△FAM中,∵FM=9m,sin∠FAM=,∴AF=27m,∴AM==18(m).即AM的长为18m.点评:本题考查了解直角三角形的应用,解答本题的关键是根据坡角构造直角三角形,利用三角函数解直角三角形,注意勾股定理的应用.15.(2014•邵阳)一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里每小时的速度前往救援,求海警船到大事故船C处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)考点:解直角三角形的应用-方向角问题.专题:几何图形问题.分析:过点C作CD⊥AB交AB延长线于D.先解Rt△ACD得出CD=AC=40海里,再解Rt△CBD中,得出BC=≈50,然后根据时间=路程÷速度即可求出海警船到大事故船C处所需的时间.解答:解:如图,过点C作CD⊥AB交AB延长线于D.在Rt△ACD中,∵∠ADC=90°,∠CAD=30°,AC=80海里,∴CD=AC=40海里.在Rt△CBD中,∵∠CDB=90°,∠CBD=90°﹣37°=53°,∴BC=≈=50(海里),∴海警船到大事故船C处所需的时间大约为:50÷40=(小时).点评:本题考查了解直角三角形的应用﹣方向角问题,难度适中,作出辅助线构造直角三角形是解题的关键.。
中考数学解直角三角形练习

中考数学解直角三角形练习第一课时(锐角三角函数)课标要求1、 通过实例认识直角三角形的边角关系:即锐角三角函数(sinA 、cosA 、tanA 、cotA )2、 熟知300、450、600角的三角函数值3、 会用计算器求锐角的三角函数值:以及由已知的三角函数值求相应的锐角。
4、 通过特殊角三角函数值:知道互余两角的三角函数的关系。
5、 了解同角三角函数的平方关系。
sin 2α+cos 2α=1:倒数关系tan α·cot α=1.6、 熟知直角三角形中:300角的性质。
中招考点1、 锐角三角函数的概念:锐角三角函数的性质。
2、 300、450、600角的三角函数值及计算代数式的值。
3、 运用计算器求的三角函数值或由锐角三角函数值求角度。
典型例题[例题1] 选择题(四选一)1、如图19-1:在Rt △ABC 中:CD 是斜边AB 上的高:则下列线段比中不等于sinA 的是( )A. AC CDB. CB BDC.AB CBD.CBCD分析:sinA=AC CD ; sinA=sin ∠BCD=BC BD ;sinA= ABBC;从而判断D 不正确。
故应选D.。
2、在Rt △ABC 中:∠C =900:∠A =∠B :则cosA 的值是( ) A.21B. 22 C.23 D.1分析:先求出∠A 的度数:因为∠C =900:∠A =∠B :故∠A =∠B =450:再由特殊角的三角函数值可得:cosA=cos450=22故选B.。
3、在△ABC 中:∠C =900:sinA=23 ;则cosB 的值为( )A. 21B. 22C.23D.33分析:方法一:因为sinA=23;故锐角A =600。
因为∠C =900:所以∠B =300.cosB=23.故选C.方法二:因为 ∠C =900:故 ∠A 与 ∠B 互余.所以cosB=sin A =23.故选C..4、如图19-2:在△ABC 中:∠C =900:sinA=53.则BC :AC 等于( )A C图19-1A. 3:4B. 4:3C.3:5D.4:5 分析: 因为∠C =900:sinA =53 ;又sinA=AB BC .所以AB BC =53; 不妨设BC =3k ;AB=5k ;由勾股定理可得AC =22BC AB -=4k ;所以BC :AC =3k:4k=3:4故选A.。
(完整word)中考数学专题练习:锐角三角函数与解直角三角形(含答案),推荐文档

锐角三角函数与解直角三角形一、选择题1. (2018·柳州)如图,在Rt ABC ∆中,90C ∠=︒,4,3BC AC ==,sin B 的值为( )A.35 B. 45 C. 37 D. 342. (2018·孝感)在Rt ABC ∆中,90C ∠=︒,10,8AB AC ==,则sin A 的值为( ) A.35 B. 45 C. 34 D. 433. (2018·云南)在Rt ABC ∆中,90C ∠=︒,1,3AC BC ==,则A ∠的正切值为( )A. 3B.13C. 10D. 104. (2018·大庆)2cos60︒的值为( )A. 1B.C. D.125. (2018·天津) cos30︒的值为( )A.B. C. 1 D. 6. ( 2018·日照)计算11()tan 30sin 602-+︒︒g 的结果为( ) A. 32-B. 2C. 52D. 727. ( 2018·烟台)利用计算器求值时,小明将按键顺序为(sin 30)()4xy-=的显示结果记为a ,26/3x ab c =的显示结果记为b 。
则,a b 的大小关系为( )A. a b <B. a b > C . a b = D.不能比较8. (2018·葫芦岛)如图,AB 是⊙O 的直径,,C D 是⊙O 上AB 两侧的点.若30D ∠=︒,则tan ABC ∠的值为( )A.12B. C. D.9. (2018·贺州)如图,AB 是⊙O 的直径,且经过弦CD 的中点H ,已知3sin 5CDB ∠=,5BD =,则AH 的长为( )A. 253B. 163C. 256D. 16610. (2018·自贡)如图,若ABC ∆内接于半径为R 的⊙O ,且60A ∠=︒,连接,OB OC ,则边BC 的长为( )A.B.2R C. 2R D.11.(2018·娄底)如图,由四个全等的直角三角形围成的大正方形的面积是169,小正方形的面积为49,则sin cos αα-的值为( )A. 513B. 513-C. 713D. 713- 12. (2018·枣庄)如图,在矩形ABCD 中,E 是边BC 的中点,AE BD ⊥,垂足为F ,则tan BDE ∠的值是( )A.B. 14C. 13D.13. (2018·无锡)如图,E 是矩形ABCD 的对角线AC 上一动点,正方形EFGH 的顶点,G H 都在边AD 上.若3,4AB BC ==,则tan AFE ∠的值( )A.等于37B.等于3C.等于34D.随点E 位置的变化而变化 14. (2018·贵阳)如图,,,A B C 是小正方形的顶点,且每个小正方形的边长为1,则tan BAC ∠的值为( )15. (2018·常州)某数学研究性学习小组制作了如图所示的三角函数计算图尺:在半径为1的半圆形量角器中,画一个直径为1的圆,把刻度尺CA 的0刻度固定在半圆的圆心O 处,刻度尺可以绕点O 转,从图中所示的图尺可读出sin AOB ∠的值是( ) A.58 B. 78 C. 710 D. 4516. (2018·荆州)如图,在平面直角坐标系中,⊙P 经过三点(8,0)A ,(0,0)O ,(0,6)B ,D 是⊙P 上的一动点.当点D D 到弦OB 的距离最大时,tan BOD ∠的值是( )A. 2B. 3C. 4D. 517. (2018·陕西)如图。
(完整word版)初三数学解直角三角形训练题
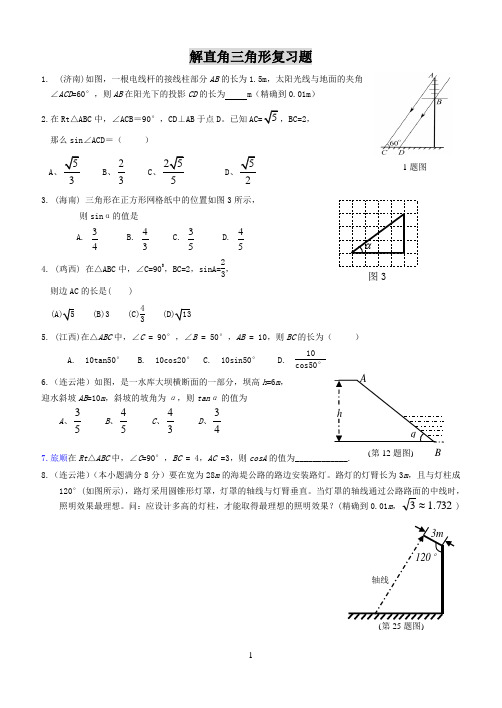
解直角三角形复习题1. (济南)如图,一根电线杆的接线柱部分AB 的长为1.5m ,太阳光线与地面的夹角 ∠ACD =60°,则AB 在阳光下的投影CD 的长为 m (精确到0.01m )2.在Rt △ABC 中,∠ACB =90°,CD ⊥AB 于点D 。
已知AC=5,BC=2,那么sin ∠ACD =( )A 、5 B 、23C 、25D 、53. (海南) 三角形在正方形网格纸中的位置如图3所示,则sin α的值是A.43 B. 34 C. 53 D. 544. (鸡西) 在△ABC 中,∠C=900,BC=2,sinA=23,则边AC 的长是( )(A) 5 (B)3 (C)43(D)135. (江西)在△ABC 中,∠C = 90°,∠B = 50°,AB = 10,则BC 的长为( )A. 10tan50°B. 10cos20°C. 10sin50°D. 10cos50°6.(连云港)如图,是一水库大坝横断面的一部分,坝高h =6m , 迎水斜坡AB =10m ,斜坡的坡角为α,则tan α的值为A 、53 B 、54 C 、34 D 、437.旅顺在Rt △ABC 中,∠C =90°,BC = 4,AC =3,则cosA 的值为____________.8.(连云港)(本小题满分8分)要在宽为28m 的海堤公路的路边安装路灯。
路灯的灯臂长为3m ,且与灯柱成120°(如图所示),路灯采用圆锥形灯罩,灯罩的轴线与灯臂垂直。
当灯罩的轴线通过公路路面的中线时,照明效果最理想。
问:应设计多高的灯柱,才能取得最理想的照明效果?(精确到0.01m ,732.13≈)1题图图3αA Bqh(第12题图)(第25题图) 3m 120°轴线9.南平如图,秋千拉绳OB 的长为3米,静止时,踏板到地面的距离BE 长时0.6米(踏板的厚度忽略不计),小亮荡该秋千时,当秋千拉绳有OB 运动到OA 时,拉绳OA 与铅垂线OE 的夹角为55°,请你计算此时该秋千踏板离地面的高度AD 是多少米?(精确到0.1米)10. 已知:如图,在山脚的C 处测得山顶A 的仰角为︒45, 沿着坡度为︒30的斜坡前进400米到D 处(即米400,30=︒=∠CD DCB ),测得A 的仰角为︒60,求山的高度AB 。
中考数学专题复习(有答案) 解直角三角形的应用

第7节解直角三角形的应用A组1.某水库大坝的横断面是梯形,坝内一斜坡的坡度i=1∶3,则这个斜坡坡角为(A) A.30°B.45°C.60°D.90°2.(2020南通)测高仪CD距离建筑物AB底部5 m,测高仪D处观测建筑物顶端的仰角为50°,测高仪高度为1.5 m,则建筑物AB的高度为7.5 m.(精确到0.1 m,sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)第2题图第3题图3.如图,传送带和地面所成斜坡AB的坡度为1∶2,物体从地面沿着该斜坡前进了10米,那么物体离地面的高度为(C)A.5米B.53米C.25米D.45米4.(2020永州)一艘渔船从位于A海岛北偏东60°方向,距A海岛60海里的B处出发,以每小时30海里的速度沿正南方向航行.已知在A海岛周围50海里水域内有暗礁.(参考数据:3≈1.73,5≈2.24,7≈2.65)(1)这艘渔船在航行过程中是否有触礁的危险?请说明理由.(2)渔船航行3小时后到达C处,求A,C之间的距离.解:(1)过A点作AD⊥BC于点D,∴∠ADB=∠ADC=90°.由题意可得∠B=60°,∴在Rt△ABD中,AD=AB·sin60°=60×32=303≈51.9>50.∴渔船在航行过程中没有触礁的危险.(2)在Rt△ABD中,BD=AB·cos60°=30.∵BC =3×30=90.∴DC =90-30=60.在Rt △ADC 中,由勾股定理,得AC =AD 2+CD 2=(303)2+602=307≈79.50. 答:A ,C 之间的距离为79.50海里.B 组5.(2020恩施州)如图,一艘轮船以每小时30海里的速度自东向西航行,在A 处测得小岛P 位于其西北方向(北偏西45°方向),2小时后轮船到达B 处,在B 处测得小岛P 位于其北偏东60°方向.求此时船与小岛P 的距离.(结果保留整数,参考数据:2≈1.414,3≈1.732)解:如图,过点P 作PH ⊥AB 于点H .由题意,得AB =30×2=60(海里),∠PBH =90°-60°=30°,∠P AH =90°-45°=45°,∴△PHA 是等腰直角三角形.∴AH =PH .在Rt △PHA 中,设AH =PH =x .在Rt △PBH 中,PB =2PH =2x ,BH =AB -AH =60-x ,∴tan ∠PBH =tan30°=PH BH =33. ∴33=x 60-x,解得x =30(3-1), ∴PB =2x =60(3-1)≈44.答:此时船与小岛P 的距离约为44海里.C 组6.(2020遂宁)在数学实践与综合课上,某兴趣小组同学用航拍无人机对某居民小区的1、2号楼进行测高实践,如图为实践时绘制的截面图.无人机从地面点B 垂直起飞到达点A 处,测得1号楼顶部E 的俯角为67°,测得2号楼顶部F 的俯角为40°,此时航拍无人机的高度为60米,已知1号楼的高度为20米,且EC 和FD 分别垂直地面于点C 和D ,点B 为CD 的中点,求2号楼的高度.(结果精确到0.1)(参考数据sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin67°≈0.92,cos67°≈0.39,tan67°≈2.36)解:过点E ,F 分别作EM ⊥AB ,FN ⊥AB ,垂足分别为M ,N .由题意,得EC =20,∠AEM =67°,∠AFN =40°,CB =DB =EM =FN ,AB =60, ∴AM =AB -MB =60-20=40.在Rt △AEM 中,∠AEM =67°.∵tan ∠AEM =AM EM, ∴EM =AM tan ∠AEM =40tan67°≈16.9. 在Rt △AFN 中,∠AFN =40°.∵tan ∠AFN =AN FN, ∴AN =tan40°×16.9≈14.2.∴FD =NB =AB -AN =60-14.2=45.8.答:2号楼的高度约为45.8米.。
解直角三角形应用Microsoft Word 文档

中考19题19.(本小题满分6分)(10)小明家所在居民楼的对面有一座大厦AB ,AB =80米.为测量这座居民楼与大厦之间的距离,小明从自己家的窗户C 处测得大厦顶部A 的仰角为37°,大厦底部B 的俯角为48°.求小明家所在居民楼与大厦的距离CD 的长度.(结果保留整数)(参考数据:o o o o 337sin37tan37sin 48tan485410≈≈≈≈,,,解:19.(本小题满分6分)(09)在一次数学活动课上,老师带领同学们去测量一座古塔CD 的高度.他们首先从A 处安置测倾器,测得塔顶C 的仰角21CFE ∠=°,然后往塔的方向前进50米到达B 处,此时测得仰角37CGE ∠=°,已知测倾器高1.5米,请你根据以上数据计算出古塔CD 的高度.(参考数据:3sin 375°≈,3tan 374°≈,9sin 2125°≈,3tan 218°≈)CGEDB AF 第19题图第19题图19.(本小题满分6分)(08)在一次课题学习课上,同学们为教室窗户设计一个遮阳蓬,小明同学绘制的设计图如图所示,其中,AB 表示窗户,且2AB =米,BCD 表示直角遮阳蓬,已知当地一年中在午时的太阳光与水平线CD 的最小夹角α为18.6,最大夹角β为64.5.请你根据以上数据,帮助小明同学计算出遮阳蓬中CD 的长是多少米?(结果保留两个有效数字)(参考数据:sin18.60.32=,tan18.60.34=,sin 64.50.90=,tan 64.5 2.1=)19.(本小题满分6分)(07)一艘轮船自西向东航行,在A 处测得东偏北21.3°方向有一座小岛C ,继续向东航行60海里到达B 处,测得小岛C 此时在轮船的东偏北63.5°方向上.之后,轮船继续向东航行多少海里,距离小岛C 最近?(参考数据:sin21.3°≈925,tan21.3°≈25, sin63.5°≈910,tan63.5°≈2)A BC北东练习:1. 如图,在青岛市某广场上空飘着一只汽球P ,A 、B 是地面上相距90米的两点,它们分别在汽球的正西和正东,测得仰角∠PAB=45o , 仰角∠PBA=30o ,求汽球P 的高度(精确到0.1米,3=1.732)2. 如图,斜坡AC 的坡度(坡比)为1:3,AC =10米.坡顶有一旗杆BC ,旗杆顶端B 点与A 点有一条彩带AB 相连,AB =14米.试求旗杆BC 的高度.3. (2009成都)某中学九年级学生在学习“直角三角形的边角关系”一章时,开展测量物体高度的实践活动,他们要测量学校一幢教学楼的高度.如图,他们先在点C 测得教学楼AB 的顶点A 的仰角为30°,然后向教学楼前进60米到达点D ,又测得点A 的仰角为45°。
【精编版】数学中考专题训练——解直角三角形的应用

中考专题训练——解直角三角形的应用1.图1是一种淋浴喷头,图2是图1的示意图,若用支架把喷头固定在点A处,手柄长AB =20cm,AB与墙壁AD的夹角∠α=30°,喷出的水流BC与AB形成的夹角∠ABC=80°.现在住户要求:当人站在E处淋浴时,水流正好喷洒在人体的C处,且使DE=50cm,CE=150cm.问:安装师傅应将支架固定在离地面多高的位置?(结果精确到1cm,参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,≈1.73,≈1.41).2.为了完成“综合与实践”作业任务,小明和小华利用周末时间邀约一起去郊外一处空旷平坦的草地上放风筝,小明负责放风筝,小华负责测量相关数据.如图,当小明把风筝放飞到空中点P处时,小华分别在地面的点A、B处测得∠P AB=45°,∠PBA=30°,AB=200米,请你求出风筝的高度PC(点C在点P的正下方,A、B、C在地面的同一条直线上)(参考数据:≈1.414,≈1.732)3.如图1所示是一种手机平板支架,由托板、支撑板和底座构成.图2是其侧面结构示意图,支撑板CD=40mm,托板AB固定在支撑板顶点C处,且CB=40mm,托板AB 可绕点C转动,支撑板CD可绕点D转动.(1)如图2,当∠CDE=60°时,求点C到直线DE的距离;(2)如图3,当∠DCB=90°时,再将CD绕点D转动,使点B落在DE上,求此时∠CDB的度数.4.火灾是生活中最常见、最突出的一种灾难,消防车是救援火灾的主要装备.图1是一辆登高云梯消防车的实物图,图2是其工作示意图,起重臂AC(10m≤AC≤20m)是可伸缩的,且起重臂AC可绕点A在一定范围内上下转动,张角∠CAE(90°≤∠CAE≤150°),转动点A距离地面的高度AE=3.5m.(1)当起重臂AC的长度为12m,张角∠CAE=120°,求云梯消防车最高点C距离地面的高度CF.(2)某日一居民家突发火灾,该居民家距离地面的高度为180m,该消防车能否实施有效救援?(参考数据:≈1.732)5.如图,是放在水平桌面上的台灯的几何图,已知台灯底座高度为2cm,固定支点O到水平桌面的距离为7.5cm,当支架OA、AB拉直时所形成的线段与点M共线且与底座垂直,此时测得B到底座的距离为31.64cm(线段AB,AO,OM的和),经调试发现,当∠OAB =115°,∠AOM=160°时,台灯所投射的光线最适合写作业,测量得A到B的水平距离(线段AC)为10cm.求:(1)∠BAC=°,OM=;(2)此时点B到桌面的距离.(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,≈1.414)6.如图1的风力发电机,风轮的三个叶片均匀分布,当风轮的叶片在风力作用下旋转时,最高点距地面145m,最低点距地面55m.如图2是该风力发电机的示意图,发电机的塔身OD垂直于水平地面MN(点O,A,B,C,D,M,N在同一平面内).(1)求风轮叶片OA的长度;(2)如图2,点A在OD右侧,且α=14.4°.求此时风叶OB的端点B距地面的高度.(参考数据:sin44.4°≈0.70,tan44.4°≈0.98)7.如图1,是某品牌的可伸缩篮球架,其侧面可抽象成图2,结点F,G,H,M,N可随着伸缩杆EF的伸缩转动,从而控制篮球圈ON离地面AB的高度,ON∥AB,主杆AH⊥AB,G,C,D均在主干AH上,结点N,G,F共线,DE∥AB,经测量,AD=150cm,DC=CG=GH=MN=GF=50cm,MH=NG=GD,∠NGD=33°,此时,EF∥AH.(结果保留小数点后一位)(1)①∠M=°,EF与AB的位置关系;②求EF的长度.(2)在图1的基础上,调节伸缩杆EF,得到图3,图4是图3的示意图,经测量,此时,篮球圈ON离地面AB的高度刚好达到国际标准305cm,求NF绕着G点顺时针旋转的度数.(参考数据:sin57°≈0.84,cos57°≈0.55,tan57°≈1.54)8.已知图1是超市购物车,图2是超市购物车侧面示意图,测得支架AC=80cm,BC=60cm,AB,DO均与地面平行.(1)若支架AC与BC之间的夹角∠ACB=90°,求两轮轮轴A,B之间的距离;(2)若OF的长度为60cm,∠FOD=120°,求点F到AB所在直线的距离.(结果精确到0.1)(参考数据:≈1.414,≈1.732)9.为应对新冠疫情,学校购进一批酒精消毒瓶(如图1),AB为喷嘴,△BCD为按压柄,CE为伸缩连杆,BE和EF为导管,其示意图如图2,∠DBE=∠BEF=108°,BD=8cm,BE=6cm,当按压柄△BCD按压到底时,BD转动到BD′,此BD′∥EF(如图3).(1)求点D转动到点D′的路径长;(2)求点D到直线EF的距离(结果精确到0.1cm).(参考数据sin36°≈0.59,cos36°≈0.81,tan30°≈0.73,sin72°≈0.95,cos72°≈0.31,tan72°≈3.08)10.如图1是学生常用的一种圆规,其手柄AB=8mm,两脚BC=BD=56mm,如图2所示,当∠CBD=74°时.(1)求A离纸面CD的距离.(2)用该圆规作如图3所示正六边形,求该正六边形的周长.(参考数据:sin37°≈0.60,cos37°≈0.80,sin74°≈0.96,cos74°≈0.28,结果精确到0.1)11.住宅的采光是建楼和购房时人们所关心的问题之一.如图,住宅小区南、北两栋楼房的高度均为16.8m.已知当地冬至这天中午12时太阳光线与地面所成的角是35°.(参考数据:sin35°≈0.57;cos35°≈0.81;tan35°≈0.70)(1)要使这时南楼的影子恰好落在北楼的墙脚,两楼间的距离应为多少米(精确到0.1m)?(2)如果两栋楼房之间的距离为20m,那么这时南楼的影子是否会影响北楼一楼的采光?12.某小区门口安装了汽车出入道闸.道闸关闭时,如图①,四边形ABCD为矩形,AB长6米,AD长2米,点D距地面为0.4米.道闸打开的过程中,边AD固定,连杆AB,CD分别绕点A,D转动,且边BC始终与边AD平行.(1)如图②,当道闸打开至∠ADC=60°时,边CD上一点P到地面的距离PE为2.4米,求点P到MN的距离PF的长;(2)一辆载满货物的货车过道闸,已知货车宽2.1米,高3.2米.当道闸打开至∠ADC =53°时,货车能否驶入小区?请说明理由.(参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)13.如图①是某中型挖掘机,该挖掘机是由基座、主臂和伸展臂构成,图②是共侧面结构示意图(MN是基座,AB是主臂,BC是伸展臂),若主臂AB长为4米,主臂伸展角∠MAB的范围是:30°≤∠MAB≤60°,伸展臂伸展角∠ABC的范围是:45°≤∠ABC≤105°.(1)如图③,当∠MAB=45°,伸展臂BC恰好垂直并接触地面时,求伸展臂BC的长(结果保留根号);(2)若(1)中BC长度不变,当∠MAB=30°时,求该挖掘机最远(即伸展臂伸展角∠ABC最大时)能挖掘到距A水平正前方多少米的土石.(结果保留根号)14.激光电视的光源是激光,它运用反射成像原理,屏幕不通电无辐射,降低了对消费者眼睛的伤害.根据THX观影标准,当观影水平视场角“θ”的度数处于33°到40°之间时(如图1),双眼肌肉处于放松状态,是最佳的感官体验的观影位.(1)小丽家决定要买一个激光电视,她家客厅的观影距离(人坐在沙发上眼睛到屏幕的距离)为3.5米,小佳家要选择电视屏幕宽(图2中的BC的长)在什么范围内的激光电视就能享受黄金观看体验?(结果精确到0.1m,参考数据:sin33°≈0.54,tan33°≈0.65,sin40°≈0.64,tan40°≈0.84,sin16.5°≈0.28,tan16.5°≈0.30,sin20°≈0.34,tan20°≈0.36)(2)由于技术革新和成本降低,激光电视的价格逐渐下降,某电器商行经营的某款激光电视今年每台销售价比去年降低4000元,在销售量相同的情况下,今年销售额在去年销售总额100万元的基础上减少20%,今年这款激光电视每台的售价是多少元?15.图1是疫情期间测温员用“额温枪”对学生测温时的实景图,图2是其侧面示意图,其中枪柄BC与手臂MC始终在同一直线上,枪身BA与额头保持垂直,量得胳膊MN=30cm,MB=44cm,肘关节M与枪身端点A之间的水平宽度为26.1cm(即MP的长度),∠ABM=113.6°.(1)求枪身BA的长度;(2)测温时规定枪身端点A与额头距离范围为3cm~5cm.在图2中,若测得∠BMN=68.6°,学生与测温员之间距离为50cm.问此时枪身端点A与学生额头的距离是否在规定范围内?并说明理由.(结果保留小数点后一位)(参考数据sin66.4°≈0.92,cos66.4°≈0.4,tan66.4°≈2.29,)16.如图1是十五中行政楼的推拉门,已知门的宽度AD=2米,且两扇门的大小相同(即AB=CD),将左边的门ABB1A1绕门轴AA1向里面旋转35°,将右边的门CDD1C1绕门轴DD1向外面旋转45°,其示意图如图2.(参考数据:sin35°≈0.6,cos35°≈0.8,≈1.4)(1)求开门过程中B与C走过的路径之和;(2)此时B与C之间的距离为多少?(结果保留一位小数)17.为解决群众“健身去哪儿”问题,某区2021年新建、改建90个市民益智健身苑点,图1是某益智健身苑点中的“侧摆器”.锻炼方法:面对器械,双手紧握扶手,双脚站立于踏板上,腰部发力带动下肢做左右摆式运动.(1)如图2是侧摆器的抽象图,已知摆臂OA的长度为80厘米,在侧摆运动过程中,点A为踏板中心在侧摆运动过程中的最低点位置,点B为踏板中心在侧摆运动过程中的最高点位置,∠BOA=25°,求踏板中心点在最高位置与最低位置时的高度差.(精确到0.1厘米)(sin25°≈0.423,cos25°≈0.906,tan25°≈0.466)(2)小杰在侧摆器上进行锻炼,原计划消耗400大卡的能量,由于小杰加快了运动频率,每小时能量消耗比原计划增加了100大卡,结果比原计划提早12分钟完成任务,求小杰原计划完成锻炼需多少小时?18.某超市大门口的台阶通道侧面如图所示,共有4级台阶,每级台阶高度都是0.25米.根据部分顾客的需要,超市计划做一个扶手AD,AB、DC是两根与地平线MN都垂直的支撑杆(支撑杆底端分别为点B、C).(1)求点B与点C离地面的高度差BH的长度;(2)如果支撑杆AB、DC的长度相等,且∠DAB=66°.求扶手AD的长度.(参考数据:sin66°≈0.9,cos66°≈0.4,tan66°≈2.25,cot66°≈0.44)19.“荡秋千”一直以来都是人们喜闻乐见的休闲方式之一,某天,小鹏和小运两人玩荡秋千.左图为实际图,右图为侧面几何图.静止时秋千位于铅垂线AB上,转轴A到地面的距离AB为3m,荡秋千的起始位置为C,终点为D,点C距离地面为1.16米,安全链AC为2.3m.需要解决问题如下:(1)秋千位于起始位置点C时,安全链AC与铅垂线AB夹角(即∠CAB)的度数;(2)如果我们把荡秋千的最高点与起始点的铅直高度之差记作H,起始点至最高点的路径长记作L,H与L的比值记作P(愉悦度),据科学研究表明,当0.20<P<0.22时,可使人愉悦感最强.当小鹏用力将小运从点C推出后可达到最高点D处,此时∠CAD=100°.请问这个过程能否实现愉悦感最强?说明理由.(结果精确到0.01,参考数据:sin37°=0.6,cos37°=0.8,sin27°=0.452,π=3)20.如图①是大家熟悉的柜式空调,关闭时叶片竖直向下.如图②,当启动时,出风口叶片会同步开始逆时针旋转到最大旋转角90°时返回,旋转速度是每秒10°,同时空调风从叶片口直线吹出.AB由5个叶片组成的出风口,经过测量,A点、B点距地面高度分别是170cm、145cm在空调正前方100cm处站着一个高70cm的小朋友(线段EF表示).(1)从启动开始,多长时间小朋友头顶E处感受到空调风;(2)若叶片从闭合旋转到最大角度的过程中,小朋友的头顶E处有多长时间感受到空调风;(3)当选择上下扫风模式时,叶片会旋转到最大角度后原速返回.从启动到第一次返回起始位的过程中,该小朋友头顶E处从第一次感受到空调风到再次感受到空调风中间间隔了多长时间.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75).参考答案与试题解析1.图1是一种淋浴喷头,图2是图1的示意图,若用支架把喷头固定在点A处,手柄长AB =20cm,AB与墙壁AD的夹角∠α=30°,喷出的水流BC与AB形成的夹角∠ABC=80°.现在住户要求:当人站在E处淋浴时,水流正好喷洒在人体的C处,且使DE=50cm,CE=150cm.问:安装师傅应将支架固定在离地面多高的位置?(结果精确到1cm,参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,≈1.73,≈1.41).【分析】过点B作BG⊥D'D,垂足为G,延长EC、GB交于点F.在△GAB中先求出GB、GA,再在△F AB中求出CF,最后利用线段的和差关系求出AD.【解答】解:如图,过点B作BG⊥D'D,垂足为G,延长EC、GB交于点F.在Rt△ABG中,∠BAG=∠a=30°,AB=20cm,∴GB=AB=10cm,.在Rt△BCF中,∠FBC=180°﹣60°﹣80°=40°,BF=DE﹣BG=40(cm),∴CF=BF•tan∠FBC=40tan40°≈33.6(cm),∴AD=CE+CF﹣AG=150+33.6﹣17.3≈166(cm).答:安装师傅应将支架固定在离地面166cm的位置.2.为了完成“综合与实践”作业任务,小明和小华利用周末时间邀约一起去郊外一处空旷平坦的草地上放风筝,小明负责放风筝,小华负责测量相关数据.如图,当小明把风筝放飞到空中点P处时,小华分别在地面的点A、B处测得∠P AB=45°,∠PBA=30°,AB=200米,请你求出风筝的高度PC(点C在点P的正下方,A、B、C在地面的同一条直线上)(参考数据:≈1.414,≈1.732)【分析】设PC=x米,根据等腰直角三角形的性质用x表示出AC,根据正切的定义列出方程,解方程求出x,得到CD的长,结合图形计算,得到答案.【解答】解:设PC=x米,在Rt△ACP中,∠P AC=45°,∴AC=PC=x,∴BC=200﹣x,在Rt△BCP中,∠PBA=30°,∴tan∠PBA=,∴=,解得x=100﹣100≈100×1.732﹣100=73.2,即PC=73.2米,答:风筝的高度PC约是73.2米.3.如图1所示是一种手机平板支架,由托板、支撑板和底座构成.图2是其侧面结构示意图,支撑板CD=40mm,托板AB固定在支撑板顶点C处,且CB=40mm,托板AB 可绕点C转动,支撑板CD可绕点D转动.(1)如图2,当∠CDE=60°时,求点C到直线DE的距离;(2)如图3,当∠DCB=90°时,再将CD绕点D转动,使点B落在DE上,求此时∠CDB的度数.【分析】(1)过点C作CF⊥DE,垂足为F,在Rt△CDF中,利用锐角三角函数的定义求出CF的长,即可解答;(2)在Rt△DCB中,利用锐角三角函数的定义进行计算即可解答.【解答】解:(1)过点C作CF⊥DE,垂足为F,在Rt△CDF中,∠CDE=60°,CD=40mm,∴CF=CD•sin60°=40×=60(mm),∴点C到直线DE的距离为60mm;(2)在Rt△DCB中,CD=40mm,CB=40mm,∴tan∠CDB===,∴∠CDB=30°,∴此时∠CDB的度数为30°.4.火灾是生活中最常见、最突出的一种灾难,消防车是救援火灾的主要装备.图1是一辆登高云梯消防车的实物图,图2是其工作示意图,起重臂AC(10m≤AC≤20m)是可伸缩的,且起重臂AC可绕点A在一定范围内上下转动,张角∠CAE(90°≤∠CAE≤150°),转动点A距离地面的高度AE=3.5m.(1)当起重臂AC的长度为12m,张角∠CAE=120°,求云梯消防车最高点C距离地面的高度CF.(2)某日一居民家突发火灾,该居民家距离地面的高度为180m,该消防车能否实施有效救援?(参考数据:≈1.732)【分析】(1)过点A作AG⊥CF,垂足为F.先在Rt△AGC中求出CG,再利用直角三角形的边角间关系求出CF;(2)先计算当AC长20m、∠CAE=150°时救援的高度,再判断该消防车能否实施有效救援.【解答】解:(1)过点A作AG⊥CF,垂足为F.由题意知:四边形AEFG是矩形.∴FG=AE=3.5m,∠EAG=∠AGC=∠AGF=90°.∵∠CAE=120°,∴∠CAG=∠CAE﹣∠EAG=30°.在Rt△AGC中,∵sin∠CAG=,∴CG=AC×sin30°=12×=6(m).∴CF=CG+GF=3.5+6=9.5(m).答:云梯消防车最高点C距离地面的高度CF为9.5m.(2)过点C作CH⊥AE,交EA的延长线于点H.当AC=20m,∠CAE=150°时,∠HAC=30°.在Rt△AHC中,∵cos∠HAC=,∴AH=cos∠HAC×AC=cos30°×20=×20=10≈1.732×10=17.32(m).∴HE=AH+AE=3.5+17.32=20.82(m).由题意知,四边形HEFC是矩形,∴CF=HE=20.82m.∵20.82<180,∴该消防车不能实施有效救援.5.如图,是放在水平桌面上的台灯的几何图,已知台灯底座高度为2cm,固定支点O到水平桌面的距离为7.5cm,当支架OA、AB拉直时所形成的线段与点M共线且与底座垂直,此时测得B到底座的距离为31.64cm(线段AB,AO,OM的和),经调试发现,当∠OAB =115°,∠AOM=160°时,台灯所投射的光线最适合写作业,测量得A到B的水平距离(线段AC)为10cm.求:(1)∠BAC=45°,OM= 5.5cm;(2)此时点B到桌面的距离.(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,≈1.414)【分析】(1)延长MO交AC于点D,则∠ADO=90°,先利用平角定义求出∠AOD=20°,然后利用直角三角形的两个锐角互余可得∠DAO=70°,再利用角的和差关系可求出∠BAC,最后根据题意利用支点O到水平桌面的距离减去台灯底座高度即可求出OM的长;(2)先在Rt△ABC中,利用锐角三角函数的定义求出BC,AB的长,从而求出AO的长,然后在Rt△ADO中,利用锐角三角函数的定义求出OD的长,进行计算即可解答.【解答】解:(1)延长MO交AC于点D,则∠ADO=90°,∵∠AOM=160°,∴∠AOD=180°﹣∠AOM=20°,∴∠DAO=90°﹣∠AOD=70°,∵∠OAB=115°,∴∠BAC=∠OAB﹣∠DAO=45°,由题意得:OM=7.5﹣2=5.5(cm),故答案为:45;5.5cm;(2)在Rt△ABC中,∠BAC=45°,AC=10cm,∴BC=AC•tan45°=10(cm),AB=AC=10≈14.14(cm),由题意得:AO=31.64﹣AB﹣OM=12(cm),在Rt△ADO中,∠AOD=20°,∴OD=AO•cos20°≈12×0.94=11.28(cm),∴BC+OD+7.5=28.78(cm),∴此时点B到桌面的距离约为28.78cm.6.如图1的风力发电机,风轮的三个叶片均匀分布,当风轮的叶片在风力作用下旋转时,最高点距地面145m,最低点距地面55m.如图2是该风力发电机的示意图,发电机的塔身OD垂直于水平地面MN(点O,A,B,C,D,M,N在同一平面内).(1)求风轮叶片OA的长度;(2)如图2,点A在OD右侧,且α=14.4°.求此时风叶OB的端点B距地面的高度.(参考数据:sin44.4°≈0.70,tan44.4°≈0.98)【分析】(1)以点O为圆心,OA的长为半径作圆,延长DO交⊙O于点P,设直线DO 与⊙O交于点Q,根据题意可得PD=145m,DQ=55m,从而求出PQ的长,进而可得OA=OP=PQ,进行计算即可解答;(2)过点B作BE⊥MN,垂足为E,过点O作OF⊥BE,垂足为F,从而得∠DOF=90°,EF=OD,进而求出∠BOF=44.4°,然后在Rt△BOF中求出BF,进行计算即可解答.【解答】解:如图,以点O为圆心,OA的长为半径作圆,延长DO交⊙O于点P,设直线DO与⊙O交于点Q,由题意得:PD=145m,DQ=55m,∴PQ=PD﹣DQ=145﹣55=90(m),∴OA=OP=PQ=45(m),∴风轮叶片OA的长度为45m;(2)如图,过点B作BE⊥MN,垂足为E,过点O作OF⊥BE,垂足为F,则四边形ODEF是矩形,∴∠DOF=90°,EF=OD,由题意得:∠AOB=120°,AOD=14.4°,∴∠BOF=∠AOB+∠AOD﹣∠DOF=44.4°,∴BF=OB sin44.4°≈45×0.70=31.5(m),∵OD=PD﹣OP=145﹣45=100(m),∴EF=OD=100m,∴BE=BF+EF=131.5(m),∴此时风叶OB的端点B距地面的高度为131.5m.7.如图1,是某品牌的可伸缩篮球架,其侧面可抽象成图2,结点F,G,H,M,N可随着伸缩杆EF的伸缩转动,从而控制篮球圈ON离地面AB的高度,ON∥AB,主杆AH⊥AB,G,C,D均在主干AH上,结点N,G,F共线,DE∥AB,经测量,AD=150cm,DC=CG=GH=MN=GF=50cm,MH=NG=GD,∠NGD=33°,此时,EF∥AH.(结果保留小数点后一位)(1)①∠M=147°,EF与AB的位置关系垂直;②求EF的长度.(2)在图1的基础上,调节伸缩杆EF,得到图3,图4是图3的示意图,经测量,此时,篮球圈ON离地面AB的高度刚好达到国际标准305cm,求NF绕着G点顺时针旋转的度数.(参考数据:sin57°≈0.84,cos57°≈0.55,tan57°≈1.54)【分析】(1)①根据平行四边形的判定定理可知四边形GHMN是平行四边形,可得∠M =∠HGN=147°;由AH⊥AB,EF∥AH,可知EF⊥AB;②过G作GP⊥EF,可求FP =GF•sin57°≈50×0.84=42.0cm,由四边形GDEP为平行四边形可得GD=PE,即可求解;(2)过点G作AB的平行线PG,再过点N作PG的垂线交PG于点P,由cos∠GNP===0.55,可求∠GNP≈57°,可得∠NGP≈33°,∠NGD≈123°,即可求得∠PGD的值.【解答】解:(1)①∵GH=MN,MH=NG,∴四边形GHMN是平行四边形,∵∠NGD=33°,∴∠M=∠HGN=147°,∵AH⊥AB,EF∥AH,∴EF⊥AB,故答案为:147,垂直;②过G作GP⊥EF,垂足为P,∵∠NGD=33°,∴∠FGP=57°,∴FP=GF•sin57°≈50×0.84=42.0cm,∵GP⊥EF,EF⊥AB,∴GP∥AB,又∵DE∥AB,∴GP∥DE,∵EF∥AH,∴四边形GDEP为平行四边形,∴GD=PE,∴EF=DG+PF=50+50+42≈142.0cm;(2)过点G作AB的平行线PG,再过点N作PG的垂线交PG于点P.∴NP=305﹣50﹣50﹣150=55cm,∵NG=GD=100cm,∴cos∠GNP===0.55,∴∠GNP≈57°,∴∠NGP≈33°,∴∠NGD≈123°,∴∠PGD≈123°﹣33°=90°,故NF绕着G点顺时针旋转了90°.8.已知图1是超市购物车,图2是超市购物车侧面示意图,测得支架AC=80cm,BC=60cm,AB,DO均与地面平行.(1)若支架AC与BC之间的夹角∠ACB=90°,求两轮轮轴A,B之间的距离;(2)若OF的长度为60cm,∠FOD=120°,求点F到AB所在直线的距离.(结果精确到0.1)(参考数据:≈1.414,≈1.732)【分析】(1)根据勾股定理求出AB的长度即可;(2)作辅助线,分别求出C点到AB的距离,F点到直线DO的距离,求和即可.【解答】解:(1)∵支架AC与BC之间的夹角(∠ACB)为90°,∴AB===100(cm),即两轮轮轴A,B之间的距离为100cm;(2)过C点作CH⊥AB于H,过F点作FG⊥DO延长线与G,则扶手F到AB所在直线的距离为FG+CH,∵OF的长度为60cm,∠FOD=120°,∴∠FOG=180°﹣120°=60°,∵∠G=90°,∴∠F=30°,∴OG=OF=30,∴FG=30,由(1)知AB=100,AC=80,BC=60,∴S△ABC=AC•BC=AB•CH,即×100×CH=×60×80,解得CH=48,∴FG+CH=48+30≈48+30×1.732≈100.0cm,即扶手F到AB所在直线的距离为100.0cm.9.为应对新冠疫情,学校购进一批酒精消毒瓶(如图1),AB为喷嘴,△BCD为按压柄,CE为伸缩连杆,BE和EF为导管,其示意图如图2,∠DBE=∠BEF=108°,BD=8cm,BE=6cm,当按压柄△BCD按压到底时,BD转动到BD′,此BD′∥EF(如图3).(1)求点D转动到点D′的路径长;(2)求点D到直线EF的距离(结果精确到0.1cm).(参考数据sin36°≈0.59,cos36°≈0.81,tan30°≈0.73,sin72°≈0.95,cos72°≈0.31,tan72°≈3.08)【分析】(1)由平行线的性质可求得∠D'BE=72°,从而可求得∠DBD'=36°,利用弧长公式即可求解;(2)过点D作DG⊥BD'于点G,过E作EH⊥BD'于点H,可求得DG=4.72cm,HE=5.7cm,利用平行线的性质可求解.【解答】解:(1)∵BD′∥EF,∠DBE=∠BEF=108°,∴∠D'BE=180°﹣∠BEF=72°,∴∠DBD'=∠DBE﹣∠D'BE=36°,∵BD=8cm,∴点D转动到点D′的路径长为:(cm);(2)过点D作DG⊥BD'于点G,过E作EH⊥BD'于点H,如图,Rt△BDG中,DG=BD•sin36°≈8×0.59=4.72(cm),Rt△BEH中,HE=BE•sin72°=6×0.95=5.7(cm),∴DG+HE=10.42cm,∵BD'∥EF,∴点D到直线EF的距离约为10.42cm.10.如图1是学生常用的一种圆规,其手柄AB=8mm,两脚BC=BD=56mm,如图2所示,当∠CBD=74°时.(1)求A离纸面CD的距离.(2)用该圆规作如图3所示正六边形,求该正六边形的周长.(参考数据:sin37°≈0.60,cos37°≈0.80,sin74°≈0.96,cos74°≈0.28,结果精确到0.1)【分析】(1)连接CD,延长AB交CD于点E,则AE⊥CD,利用等腰三角形的三线合一性质可得∠CBE=37°,CD=2CE,然后在Rt△BCE中,利用锐角三角函数的定义求出BE的长,最后进行计算即可解答;(2)在Rt△BCE中,利用锐角三角函数的定义求出CE的长,从而求出CD的长,进而求出正六边形的边长,然后进行计算即可解答.【解答】解:(1)连接CD,延长AB交CD于点E,则AE⊥CD,∵BC=BD=56mm,∴∠CBE=∠CBD=37°,CD=2CE,在Rt△BCE中,BE=BC•cos37°≈56×0.8=44.8(mm),∵AB=8mm,∴AE=AB+BE=8+44.8=52.8(mm),∴A离纸面CD的距离约为52.8mm;(2)在Rt△BCE中,∠CBE=37°,BC=56mm,∴CE=BC•sin37°≈56×0.6=33.6(mm),∴CD=2CE=67.2(mm),∴正六边形的边长为67.2mm,∴正六边形的周长=6×67.2=403.2(mm),∴正六边形的周长约为403.2mm.11.住宅的采光是建楼和购房时人们所关心的问题之一.如图,住宅小区南、北两栋楼房的高度均为16.8m.已知当地冬至这天中午12时太阳光线与地面所成的角是35°.(参考数据:sin35°≈0.57;cos35°≈0.81;tan35°≈0.70)(1)要使这时南楼的影子恰好落在北楼的墙脚,两楼间的距离应为多少米(精确到0.1m)?(2)如果两栋楼房之间的距离为20m,那么这时南楼的影子是否会影响北楼一楼的采光?【分析】(1)根据直角三角形的边角关系进行计算即可;(2)根据直角三角形的边角关系计算出AN即可.【解答】解:(1)如图1,由题意可知,AB=CD=16.8m,∠ADB=35°∵tan∠ADB=,∴≈0.7,∴BD≈24.0米,答:两楼间的距离应为24.0m;(2)如图2,过点M作MN∥BD,在Rt△AMN中,BD=20m=MN,∠AMN=35°,∴AN=tan35°×MN≈14.0(m),∴MD=AB﹣AN=16.8﹣14.0=2.8(m),答:这时南楼的影子会影响北楼一楼的采光,且影子在CD的高度为2.8 m.12.某小区门口安装了汽车出入道闸.道闸关闭时,如图①,四边形ABCD为矩形,AB长6米,AD长2米,点D距地面为0.4米.道闸打开的过程中,边AD固定,连杆AB,CD分别绕点A,D转动,且边BC始终与边AD平行.(1)如图②,当道闸打开至∠ADC=60°时,边CD上一点P到地面的距离PE为2.4米,求点P到MN的距离PF的长;(2)一辆载满货物的货车过道闸,已知货车宽2.1米,高3.2米.当道闸打开至∠ADC=53°时,货车能否驶入小区?请说明理由.(参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)【分析】(1)在Rt△PDQ中,由∠PDQ=30°得出DQ=2,进而求出FP即可;(2)当∠ADC=53°,PE=3.2米时,求出PF,与2.1米比较即可得出答案.【解答】解:(1)如图,过点D作DQ⊥PE,垂足为Q,由题意可知,∠ADC=60°,PE=2.4米,QE=0.4米,在Rt△PDQ中,∠PDQ=30°,PQ=2.4﹣0.4=2(米),∴tan30°=,∴DQ==2(米),∴PF=AB﹣DQ=(6﹣2)(米),(2)当∠ADC=53°,PE=3.2米时,则∠DPQ=53°,PQ=3.2﹣0.4=2.8(米),∴DQ=PQ•tan53°≈2.8×1.33=3.724(米),∴PF=6﹣3.724≈2.276(米),∵2.276>2.1,∴能通过.13.如图①是某中型挖掘机,该挖掘机是由基座、主臂和伸展臂构成,图②是共侧面结构示意图(MN是基座,AB是主臂,BC是伸展臂),若主臂AB长为4米,主臂伸展角∠MAB的范围是:30°≤∠MAB≤60°,伸展臂伸展角∠ABC的范围是:45°≤∠ABC≤105°.(1)如图③,当∠MAB=45°,伸展臂BC恰好垂直并接触地面时,求伸展臂BC的长(结果保留根号);(2)若(1)中BC长度不变,当∠MAB=30°时,求该挖掘机最远(即伸展臂伸展角∠ABC最大时)能挖掘到距A水平正前方多少米的土石.(结果保留根号)【分析】(1)根据题意可得:∠BCA=90°,然后在Rt△ABC中,利用锐角三角函数的定义求出BC的长,即可解答;(2)过点B作BD⊥AC,垂足为D,根据题意可得:∠MAB=30°,∠ABC=105°时,伸展臂伸展的最远,从而利用三角形内角和定理求出∠ACD=45°,然后在RtABD中,利用锐角三角函数定义求出AD的长,再在Rt△BCD中,利用锐角三角函数的定义求出CD的长,进行计算即可解答.【解答】解:(1)如图:由题意得:∠BCA=90°,在Rt△ABC中,∠MAB=45°,AB=4米,∴BC=AB•sin45°=4×=2(米),∴伸展臂BC的长为2米;(2)过点B作BD⊥AC,垂足为D,由题意得:∠MAB=30°,∠ABC=105°时,伸展臂伸展的最远,∴∠ACB=180°﹣∠ABC﹣∠MAB=45°,在RtABD中,AB=4米,∴AD=AB•cos30°=4×=2(米),在Rt△BCD中,BC=2米,CD=BC•cos45°=2×=2(米),∴AC=AD+CD=(2+2)米,∴该挖掘机最远能挖掘到距A水平正前方(2+2)米的土石.14.激光电视的光源是激光,它运用反射成像原理,屏幕不通电无辐射,降低了对消费者眼睛的伤害.根据THX观影标准,当观影水平视场角“θ”的度数处于33°到40°之间时(如图1),双眼肌肉处于放松状态,是最佳的感官体验的观影位.(1)小丽家决定要买一个激光电视,她家客厅的观影距离(人坐在沙发上眼睛到屏幕的距离)为3.5米,小佳家要选择电视屏幕宽(图2中的BC的长)在什么范围内的激光电视就能享受黄金观看体验?(结果精确到0.1m,参考数据:sin33°≈0.54,tan33°≈0.65,sin40°≈0.64,tan40°≈0.84,sin16.5°≈0.28,tan16.5°≈0.30,sin20°≈0.34,tan20°≈0.36)(2)由于技术革新和成本降低,激光电视的价格逐渐下降,某电器商行经营的某款激光电视今年每台销售价比去年降低4000元,在销售量相同的情况下,今年销售额在去年销售总额100万元的基础上减少20%,今年这款激光电视每台的售价是多少元?【分析】(1)过点A作AD⊥BC于点D,根据题意可得AB=AC,当∠BAC=33°时,当∠BAC=40°时,利用锐角三角函数即可解决问题;(2)设今年这款激光电视每台的售价是x元,则去年每台的售价为(x+4000)元.由题意列出方程即可解决问题.【解答】解:(1)如图,过点A作AD⊥BC于点D,根据题意可知:AB=AC,AD⊥BC,∴BC=2BD,∠BAD=∠CAD=∠BAC,当∠BAC=33°时,∠BAD=∠CAD=16.5°,在△ABD中,BD=AD×tan16.5°≈3.5×0.30=1.05(m),∴BC=2BD=2.10(m),当∠BAC=40°时,∠BAD=∠CAD=20°,在△ABD中,BD=AD×tan20°≈3.5×0.36=1.26(m),∴BC=2BD=2.52m,答:小佳家要选择电视屏幕宽为2.10m﹣2.52m之间的激光电视就能享受黄金观看体验;(2)设今年这款激光电视每台的售价是x元,则去年每台的售价为(x+4000)元.由题意可得:=,解得:x=16000,经检验x=16000是原方程的解,符合题意,答:今年这款激光电视每台的售价是16000元.15.图1是疫情期间测温员用“额温枪”对学生测温时的实景图,图2是其侧面示意图,其中枪柄BC与手臂MC始终在同一直线上,枪身BA与额头保持垂直,量得胳膊MN=30cm,MB=44cm,肘关节M与枪身端点A之间的水平宽度为26.1cm(即MP的长度),∠ABM=113.6°.(1)求枪身BA的长度;(2)测温时规定枪身端点A与额头距离范围为3cm~5cm.在图2中,若测得∠BMN=68.6°,学生与测温员之间距离为50cm.问此时枪身端点A与学生额头的距离是否在规定范围内?并说明理由.(结果保留小数点后一位)(参考数据sin66.4°≈0.92,cos66.4°≈0.4,tan66.4°≈2.29,)【分析】(1)过点B作BH⊥MQ,垂足为H,则BA=HP,AB∥MQ,利用平行线的性质可得∠BMH=66.4°,然后在Rt△BMH中,利用锐角三角函数的定义求出MH的长,从而求出HP的长,即可解答;(2)延长QM交FG于点K,则KQ=50cm,∠NKM=90°,利用平角定义先求出∠NMK 的度数,再在Rt△NMK中,利用锐角三角函数的定义求出KM的长,从而求出PQ的长,进行比较即可解答.【解答】解:(1)过点B作BH⊥MQ,垂足为H,则BA=HP,AB∥MQ,∵∠ABM=113.6°,∴∠BMH=180°﹣∠ABM=66.4°,在Rt△BMH中,∠BMH=66.4°,BM=44cm,∴MH=BM•cos66.4°≈44×0.4=17.6(cm),∵MP=26.1cm,∴BA=HP=MP﹣MH=26.1﹣17.6=8.5(cm),∴枪身BA的长度约为8.5cm;(2)此时枪身端点A与学生额头的距离不在规定范围内,理由:延长QM交FG于点K,则KQ=50cm,∠NKM=90°,∵∠BMN=68.6°,∠BMH=66.4°,∴∠NMK=180°﹣∠BMN﹣∠BMH=45°,在Rt△MNK中,MN=30cm,∴KM=MN•cos45°=30×=15(cm),∵KQ=50cm,∴PQ=KQ﹣KM﹣MP=50﹣15﹣26.1≈2.7(cm),。
中考数学总复习《解直角三角形的应用题》专题测试卷(附答案)

中考数学总复习《解直角三角形的应用题》专题测试卷(附答案)1.如图,小明为了测量学校旗杆CD的高度,在地面离旗杆底部C处22米的A处放置高度为1.5米的测角仪AB,测得旗杆顶端D的仰角为32°,求旗杆的高度CD.(结果精确到0.1米)【参考数据:sin32°=0.53,cos32°=0.85,tan32°=0.62】2.如图,在一次数学实践活动中,小明同学为了测量学校旗杆EF的高度,在观测点A处观测旗杆顶点E的仰角为45°,接着小明朝旗杆方向前进了7m到达C点,此时,在观测点D处观测旗杆顶点E的仰角为60°.假设小明的身高为1.68m,求旗杆EF的高度.(结果保留一位小数.参考数据:√2≈1.414,√3≈ 1.732)3.如图,在徐州云龙湖旅游景区,点A为“彭城风华”观演场地,点B为“水族展览馆”,点C为“徐州汉画像石艺术馆”.已知∠BAC=60°,∠BCA=45°,AC=1640m.求“彭城风华”观演场地与“水族展览馆”之间的距离AB(精确到1m).(参考数据:√2≈1.41,√3≈1.73)4.大连作为沿海城市,我们常常可以在海边看到有人海钓.小华陪爷爷周末去东港海钓,爷爷将鱼竿AB摆成如图所示.已知AB=2.4m,在有鱼上钩时,鱼竿与地面的夹角∠BAD=45°.此时鱼线被拉直,鱼线BO= 3m.点O恰好位于海面,鱼线BO与海面OH的夹角∠BOH=60°.求海面OH与地面AD之间的距离DH的长.(结果保留一位小数,参考数据:√2=1.414,√3=1.73)5.让运动挥洒汗水,让青春闪耀光芒.重庆某中学倡议全校师生“每天运动一小时,快乐学习每一天”,响应学校号召,小明决定早睡早起,每天步行上学.如图,小明家在A处,学校在C处,从家到学校有两条线路,他可以从点A经过点B到点C,也可以从点A经过点D到点C.经测量,点B在点A的正北方向,AB=300米.点C在点B的北偏东45°;点D在点A的正东方向,点C在点D的北偏东30°方向CD=2900米.(1)求BC的长度(精确到个位);(2)小明每天步行上学都要从点A到点C,路线一;从点A经过点B到点C,路线二;从点A经过点D到点C,请计算说明他走哪一条路线较近?(参考数据:√2≈1.414,√3≈1.732,√6≈2.449)6.拉杆箱是外出旅行常用工具.某种拉杆箱示意图如图所示(滚轮忽略不计),箱体截面是矩形BCDE,BC 的长度为60cm,两节可调节的拉杆长度相等,且与BC在同一条直线上.如图1,当拉杆伸出一节(AB)时,AC与地面夹角∠ACG=53°;如图2,当拉杆伸出两节(AM、MB)时,AC与地面夹角∠ACG=37°,两种情况下拉杆把手A点距离地面高度相同.求每节拉杆的长度.(参考数据:sin53°≈45,sin37°≈35,tan53°≈4 3,tan37°≈34)7.某中学凤栖堂前一尊孔子雕像矗立于萋萋芳草间,小刚站在雕像前,自C处测得雕像顶A的仰角为53°,小强站凤栖堂门前的台阶上,自D处测得雕像顶A的仰角为45°,此时,两人的水平距离EC为0.45m,已知凤栖堂门前台阶斜坡CD的坡比为i=1:3.(参考数据:sin53°≈45,cos53°≈35,tan53°≈43)(1)计算台阶DE的高度;(2)求孔子雕像AB的高度.8.如图为某景区平面示意图,C为景区大门,A,B,D分别为三个风景点.经测量,A,B,C在同一直线上,且A,B在C的正北方向,AB=240米,点D在点B的南偏东75∘方向,在点A的东南方向.(参考数据:√2≈1.414,√3≈1.732)(1)求B,D两地的距离;(结果精确到0.1米)(2)大门C在风景点D的南偏西60∘方向,景区管理部门决定重新翻修CD之间的步道,求CD间的距离.9.小明和小玲游览一处景点,如图,两人同时从景区大门A出发,小明沿正东方向步行60米到一处小山B处,再沿着BC前往寺庙C处,在B处测得亭台D在北偏东15°方向上,而寺庙C在B的北偏东30°方向上,小玲沿着A的东北方向上步行一段时间到达亭台D处,再步行至正东方向的寺庙C处.(1)求小山B与亭台D之间的距离;(结果保留根号)(2)若两人步行速度一样,则谁先到达寺庙C处.(结果精确到个位,参考数据:√2≈1.41,√3≈1.73,√6≈2.45)10.研学实践:为重温解放军东渡黄河“红色记忆”,学校组织研学活动,同学们来到毛主席东渡黄河纪念碑所在地,在了解相关历史背景后,利用航模搭载的3D扫描仪采集纪念碑的相关数据.数据采集:如图,点A是纪念碑顶部一点,AB的长表示点A到水平地面的距离.航模从纪念碑前水平地面的点M处竖直上升,飞行至距离地面20米的点C处时,测得点A的仰角∠ACD=18.4°;然后沿CN方向继续飞行,飞行方向与水平线的夹角∠NCD=37°,当到达点A正上方的点E处时,测得AE=9米数据应用:已知图中各点均在同一竖直平面内,E,A,B三点在同一直线上.请根据上述数据,计算纪念碑顶部点A到地面的距离AB的长.(结果精确到1米.参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin18.4°≈0.32,cos18.4°≈0.95,tan18.4°≈0.33)11.【综合与实践】如图1,光线从空气射入水中会发生折射现象,其中α代表入射角,β代表折射角.学习小组查阅资料了解到,若n=sinαsinβ,则把n称为折射率.(参考数据:sin53°≈45,cos53°≈35,tan53°≈43)【实践操作】如图2,为了进一步研究光的折射现象,学习小组设计了如下实验:将激光笔固定在MN处,光线可沿PD照射到空容器底部B处,将水加至D处,且BF=12cm时,光点移动到C处,此时测得DF=16cm,BC=7cm四边形ABFE是矩形,GH是法线.【问题解决】(1)求入射角∠PDG的度数;(2)请求出光线从空气射入水中的折射率n.12.数学兴趣小组设计了一款含杯盖的奶茶纸杯(如图1),图2为该纸杯的透视效果图,在图3的设计草图中,由AF、线段EF和ED构成的图形为杯盖部分,其中AF、与ED均在以AD为直径的⊙O上,且AF= ED,G为EF的中点,点G是吸管插孔处(忽略插孔直径和吸管直径),由点A,B,C,D构成的图形(杯身部分)为等腰梯形,已知杯壁AB=13.6cm,杯底直径BC=5.8cm,杯壁与直线l的夹角为84°.(1)求杯口半径OD的长;(2)若杯盖顶FE=3.2cm,吸管BH=22cm,当吸管斜插,即吸管的一端与杯底点B重合时,求吸管漏出杯盖部分GH的长.(参考数据:sin84∘≈0.995,cos84∘≈0.105,tan84∘≈9.514,√15.93≈3.99,17.5222≈307.02,√315.43≈17.76,结果精确到0.1cm).13.为了保护小吉的视力,妈妈为他购买了可升降夹书阅读架(如图1),将其放置在水平桌面上的侧面示意图(如图2),测得底座高AB为2cm,∠ABC=150°,支架BC为18cm,面板长DE为24cm,CD为6cm.(厚度忽略不计)(1)求支点C离桌面l的高度:(计算结果保留根号)(2)小吉通过查阅资料,当面板DE绕点C转动时,面板与桌面的夹角α满足30°≤α≤70°时,能保护视力.当α从30°变化到70°的过程中,问面板上端E离桌面l的高度是增加了还是减少了?增加或减少了多少?(精确到0.1cm,参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)14.如图,四边形ABCD是某公园的游览步道(步道可以骑行),把四个景点连接起来,为了方便,在景点C的正东方设置了休息区K,其中休息区K在景点A的南偏西30°方向800√2米处,景点A在景点B的北偏东75°方向,景点B和休息区K两地相距400√5米(∠ABK<90°),景点D分别在休息区K、景点A的正东方向和正南方向.(参考数据:√2≈1.41,√5≈2.24,√6≈2.45)(1)求步道AB的长度;(2)周末小明和小宏相约一起去公园游玩,他们在景点C一起向正东出发,不久到达休息区K,他们发现有两条路线到达景点A,于是小宏想比赛看谁先到达景点A.他们分别租了一辆共享单车,两人同时在K点出发,小明选择①K−B−A路线,速度为每分钟320米;小宏选择②K−D−A路线,速度为每分钟240米,其中两人在各个景点停留的时间不计.请你通过计算说明,小明和小宏谁先到达景点A呢?15.某公园里有一座凉亭,亭盖呈圆锥状,如图所示,凉亭的顶点为O,点O在圆锥底面、地面上的正投影分别为点O1,O2,点P为圆锥底面的圆上一点,数据显示,该圆锥的底面半径为2米(即O1P=2米),圆锥底面离地面的高度为3米(即O1O2=3米).(1)若OO1=2米,求圆锥的侧面积;(2)现计划对亭盖的外部进行喷漆作业,需测算亭盖的外部面积(即圆锥的侧面积).因凉亭内堆积建筑材料,导致无法直接测量OO2的高度,工人先在水平地面上选取观测点A,B(A,B,O2在同一直线上),利用测角仪分别测得点O的仰角为α,β,其中tanα=12,tanβ=25,再测得A,B两点间的距离为m米(即AB=MN=m米),已知测角仪的高为1米(即MA=NB=QO2=1米),求亭盖的外部面积(用含m的代数式表示).16.赤水河畔的“美酒河”三个大字,是世界上最大的摩崖石刻汉字.小茜想测量绝壁上“美”字AG的高度,根据平面镜反射原理可推出入射光线与镜面的夹角等于反射光线与镜面的夹角(如图中∠DEC=∠AEB,∠DFC=∠GFB),具体操作如下:将平面镜水平放置于E处,小茜站在C处观测,俯角∠MDE=45°时,恰好通过平面镜看到“美”字顶端A处(CD为小茜眼睛到地面的高度),再将平面镜水平放置于F处观测,俯角∠MDF=36.9°时,恰好通过平面镜看到“美”字底端G处.测得BE=163.3m,CE=1.5m,点C,E,F,B在同一水平线上,点A,G,B在同一铅垂线上.(参考数据:sin36.9°≈0.60,cos36.9°≈0.80,tan36.9°≈0.75)(1)CD的高度为__________m,CF的长为__________m;(2)求“美”字AG的高度.17.风能是一种清洁无公害的可再生能源,利用风力发电非常环保.如图1所示,是一种风力发电装置;如图2为简化图,塔座OD建在山坡DF上(坡比i=3:4,DE垂直于水平地面EF,O,D,E三点共线),坡面DF长10m,三个相同长度的风轮叶片OA,OB,OC可绕点O转动,每两个叶片之间的夹角为120°;当叶片静止,OA与OD重合时,在坡底F处向前走25米至点M处,测得点O处的仰角为53°,又向前走23.5米至点N处,测得点A处的仰角为30°(点E,F,M,N在同一水平线上).(1)求叶片OA的长;(2)在图2状态下,当叶片绕点O顺时针转动90°时(如图3),求叶片OC顶端C离水平地面EF的距离.(参考数据:sin53°≈45,cos53°≈35,tan53°≈43,√3≈1.7,结果保留整数)18.贵州旅游资源丰富.某景区为给游客提供更好的游览体验,拟在如图①景区内修建观光索道.设计示意图如图②所示,以山脚A为起点,沿途修建AB,CD两段长度相等的观光索道,最终到达山顶D处,中途设计了一段与AF平行的观光平台BC为50m.索道AB与AF的夹角为15°,CD与水平线的夹角为45°,A,B 两处的水平距离AE为576m,DF⊥AF,垂足为点F.(图中所有点都在同一平面内,点A,E,F在同一水平线上)(1)求索道AB的长(结果精确到1m);(2)求水平距离AF的长(结果精确到1m).(参考数据:sin15°≈0.26cos15°≈0.97tan15°≈0.27√2≈1.41)19.春天是踏青的好季节小明和小华决定去公园出游踏青.如图已知A为公园入口景点B位于A点东北方向400√2米处景点E位于A点南偏东30°方向景点B在景点E的正北方向景点C既位于景点B正东方向310米处又位于景点D的北偏西37.5°方向.景点F既位于景点E的正东方向又位于景点D的正南方向.DF=400米.(参考数据:√2≈1.41,√3≈1.73,sin37.5°≈35,cos37.5°≈45,tan37.5°≈34)(1)求BE的长;(精确到个位)(2)小明选择了游览路线①:A−B−C−D小明行驶的平均速度是72米/分小明在景点B、C处各停留了10分钟、5分钟.小华选择了游览路线②:A−E−F−D小华行驶的平均速度为96米/分.小华在景点E、F处各停留了9分钟、8分钟.请通过计算说明:小明和小华谁先到达景点D处.20.如图是一种家用健身卷腹机由圆弧形滑轨⌒AB可伸缩支撑杆AC和手柄AD构成.图①是其侧面简化示意图.滑轨⌒AB支撑杆AC与手柄AD在点A处连接其中D A B三点在一条直线上.(1)如图① 固定∠DAC=120°,若BC=30√6cm,AC=60cm,求∠ABC的度数;(2)如图② 固定∠DAC=100°若AC=50cm,∠ABC=30°时圆弧形滑轨AB所在的圆恰好与直线BC 相切于点B求滑轨⌒AB的长度.(结果精确到0.1 参考数据:π取3.14 sin70°≈0.940)参考答案:1.解:由题意得BE⊥CD于EBE=AC=22米∠DBE=32°在Rt△DBE中DE=BE⋅tan∠DBE=22×0.62≈13.64(米)CD=CE+DE=1.5+13.64≈15.14(米)答:旗杆的高CD约为15.14米.2.解:延长AD交EF于点G设EG=x∵AD∥BF,EF⊥BF∵AG⊥EF∵∠B=∠F=∠AGF=90°∵四边形ABFG是矩形∠AGE=90°∵∠EAG=45°∵∠AEG=90°−∠EAG=45°∵AG=EG=x∵AD=7∵DG=x−7∵∠EDG=60°=√3∵tan∠EDG=EGDG=√3∵xx−7∵x=7(3+√3)2∵EG=7(3+√3)2∵GF=AB=1.68∵EF=EG+GF=7(3+√3)2+1.68≈7(3+1.732)2+1.68 =16.562+1.68=18.242≈18.2.故旗杆EF的高度约18.2m.3.解:过B作BH⊥AC于H设AH=xm∵∠BAC=60°∵∠ABH=90°−60°=30°∵AB=2AH=2xm∵tanA=tan60°=BHAH=√3∵BH=√3xm∵∠BCA=45°∠BHC=90°∵△BHC是等腰直角三角形∵CH=BH=√3xm∵AH+CH=√3x+x=AC=1640≈600.7∵x=√3+1∵AB=2x≈1201(m).答:“彭城风华”观演场地与“水族展览馆”之间的距离AB约是1201m.4.解:过点B作BC⊥OH交OH于点C延长AD交BC于点E∵四边形DECH是矩形∵DH=CE.根据题意可知∠BAD=45°,∠BOH=60°在Rt△ABE中AB=2.4m∵sin∠BAE=BEAB即sin45°=BE2.4=1.2×1.41=1.692.解得BE=2.4×√22在Rt△BOC中BO=3m∵sin∠BOC=BCBO即sin60°=BC3=1.5×1.73=2.595解得BC=3×√32∵DH=CE=BC−BE=0.903≈0.9(m).所以海面OH与地面AD之间得距离DH的长0.9m.5.(1)解:过点C作CM⊥AD交AD的延长线于点M过点B作BN⊥AM交AM于点N过点D作DH⊥BN 交BN于点H.由题可知:∠CBN=45°∠A=90°∠CDM=60°.∵四边形ABNM、四边形ABHD、四边形DMNH都是矩形△BCN是等腰直角三角形.在Rt△CMD中∵∠CDM=60°CD=2900米∵DM=12DC=1450米CM=√3DM=1450√3米∵AB=MN=300米∵CN=CM−MN=(1450√3−300)米在Rt△CBN中∠CBN=45°∵CB=√2CN=(1450√6−300√2)米≈3127米答:BC的长度为3127米.(2)解:路线一:AB+BC=(300+1450√6−300√2)米≈3427米∵AM=BN=CN=(1450√3−300)米∵AD=AM−DM=(1450√3−1750)米∵路线二:AD+CD=(1450√3+1150)米≈3361米∵3427<3361∵路线二较近.6.解:如图1 作AF⊥CG垂足为F设AB=xcm则AC=60+x∵sin53°=AFAC =AF60+x∴AF=(60+x)⋅sin53°如图2 作AH⊥CG垂足为H则AC=60+2x∴AH=(60+2x)⋅sin37°∵AF=AH∴(60+x)⋅sin53°=(60+2x)⋅sin37°∴4(60+x)5=3(60+2x)5解得:x=30.答:每节拉杆的长度为30cm.7.(1)解:∵凤栖堂门前台阶斜坡CD的坡比为i=1:3EC为0.45m∵DE EC =13∴DE=EC3=0.15m即台阶DE的高度为0.15m;(2)解:如图所示设AB的对边为MN作DF⊥MN于F∵由题意得四边形NFDE是矩形∵FN=DE=0.15m DF=NE设MN=xm则MF=(x−0.15)m在Rt△MFD中∠MDF=45°∵FD=MF=(x−0.15)m∵NC=NE−EC=(x−0.15)−0.45=(x−0.6)m∵tan53°=MNNC ≈43即xx−0.6=43解得x=2.4经检验x=2.4是原方程的解答:孔子雕像AB的高度约2.4m.8.(1)解:过点B作BP⊥AD于点P由题意知∠BAD=45∘∠CBD=75∘∴∠ADB=30∘∠ABP=45∘=∠A∴BD=2BP AP=BP在Rt△ABP中AB=240米∴AP=BP=AB=120√2(米)sin45∘∴BD=2BP=240√2≈339.4(米).答:B、D两地的距离约为339.4米;(2)解:过点B作BM⊥CD于点M由(1)得BD=2BP=240√2(米)∵∠CDB=180∘−60∘−75∘=45∘∠CBD=75∘∠DCB=60∘∴∠DBM=45∘=∠CDB∴BM=DM在Rt△BDM中BD=240√2sin45∘=BMBD∴BM=DM=BD⋅sin45∘=240√2×√2=240(米)2在Rt△BCM中∠CBM=75∘−45∘=30∘∴CM=BM⋅tan30∘=80√3(米)∴DC=DM+CM=240+80√3(米).9.解:(1)作BE⊥AD于点E由题意知AB=60∠A=45°∠ABD=90°+15°=105°∠CBA=90°+30°=120°在Rt△ABE中在Rt△BDE中ED=√3BE=30√6BD=2BE=60√2∴小山B与亭台D之间的距离60√2米(2)延长AB作DF⊥BA于点F作CG⊥BA于点G则∠CBG=180°−∠CBA=60°由题意知CD∥AB∵四边形CDFG是矩形∵CG=DF,CD=FG.∵AE=30√2ED=30√6∴AD=30√2+30√6在Rt△AFD中DF=AF=√2=30+30√3CG=DF=30+30√3米在Rt△BCG中BG=√3=10√3+30∴CD=FG=AB+BG−AF=60−20√3∴S玲=AD+CD=30√2+30√6+60−20√3≈141.2米S明=AB+BC=60+60+20√3≈154.6米∵141.2<154.6且两人速度一致∴小玲先到.答:小玲先到达寺庙C处.10.解:如图:延长CD交AB于点H则四边形CMBH为矩形∴CM=HB=20在Rt△ACH中∠AHC=90°∠ACH=18.4°∴tan∠ACH=AH CH∴CH=AHtan∠ACH=AHtan18.4°≈AH0.33在Rt△ECH中∠EHC=90°∠ECH=37°∴tan∠ECH=EH CH∴CH=EHtan∠ECH=EHtan37°≈EH0.75设AH=x.∵AE=9∴EH=x+9∴x0.33=x+90.75解得x≈7.1∴AB=AH+HB≈7.1+20=27.1≈27(米).答:点A到地面的距离AB的长约为27米.11.(1)解:如图1 ∵GH∥FB∴∠DBF=∠PDG,∵BF=12cm,DF=16cm,∴tan∠DBF=DFBF=1612=43,∵tan53°≈4 3∴入射角∠PDG约为53°.(2)解:如图2 作DM⊥AB于点T在Rt△BDF中BF=12cm,DF=16cm∴BD=√DF2+BF2=20cm,在Rt△DTC中TC=DF−BC=16−7=9cm,DT=BF=12cm∴CD=√DT2+TC2=√122+92=15cm,∴光线从空气射入水中的折射率∴光线从空气射入水中的折射率n=43.12.(1)解:过点B作BP⊥AD于点D过点C作CQ⊥AD于点Q延长BC到点R ∵四边形BCQP是矩形∵BC=QP BP=CQ∵AB=13.6cm杯底直径BC=5.8cm杯壁与直线l的夹角为84°点A B C D构成的图形(杯身部分)为等腰梯形∵AD∥BC CD=AB=13.6cm QP=BC=5.8cm∵∠A=∠D=∠DCR=84°∵BP=CQ CD=AB∵Rt△ABP≌Rt△DCQ(HL)∵AP=DQ∵AP=DQ=CDcosD=13.6×0.105=1.428(cm)CQ=CDsinD=13.6×0.995=13.532(cm)∵AD=2AP+PQ=DQ=2×1.428+5.8=8.656(cm)AD=4.328≈4.3(cm)∵OD=12故杯口半径OD的长为4.3cm.(2)解:连接GO并延长交BC于点N∵G为EF的中点EF=1.6(cm)∵GO⊥EF,EG=FG=12连接FD∵ AF=ED,∵∠EFD=∠ADF,∵AD∥EF∵GO⊥AD∵ AD∥BC∵GO⊥BC∵NO=13.532(cm)∵GO=√(4.3)2−(1.6)2≈4.0(cm)∵GN≈17.532(cm)∵GB=√(17.532)2+(2.9)2≈17.77(cm)∵GH=BH−GB=22−17.77≈4.2(cm)13.(1)解:过点C作CF⊥l于点F过点B作BM⊥CF于点M∴∠CFA=∠BMC=∠BMF=90°.由题意得:∠BAF=90°∴四边形ABMF为矩形∴MF=AB=2cm∠ABM=90°.∵∠ABC=150°∴∠MBC=60°.∵BC=18cm∴CM=BC⋅sin60°=18×√32=9√3(cm).∴CF=CM+MF=(9√3+2)cm.答:支点C离桌面l的高度为(9√3+2)cm;(2)解:过点C作CN∥l过点E作EH⊥CN于点H∴∠EHC=90°.∵DE=24cm CD=6cm∴CE=18cm.当∠ECH=30°时EH=CE⋅sin30°=18×12=9(cm);当∠ECH=70°时EH=CE⋅sin70°≈18×0.94=16.92(cm);∴16.92−9=7.92≈7.9(cm)∴当α从30°变化到70°的过程中面板上端E离桌面l的高度是增加了增加了约7.9cm.14.(1)解:由题意得∠DAK=30°∠BAD=75°∠D=90°AK=800√2米BK=400√5米∵∠BAK=∠BAD−∠DAK=75°−30°=45°过点K作KH⊥AB于H则∠AHK=∠BHK=90°∵△AHK为等腰直角三角形∵AH=KH=√22AK=√22×800√2=800米∵BH=√BK2−KH2=√(400√5)2−8002=400米∵AB=AH+BH=800+400=1200米;(2)解:∵AK=800√2∠DAK=30°∠D=90°∵DK=12AK=400√2米AD=AK·cos30°=800√2×√32=400√6米∵路线②K−D−A的路程为KD+AD=400√2+400√6≈1544米∵小宏到达景点A的时间为1544÷240≈6.43分钟∵路线①K−B−A的路程为KB+BA=400√5+1200≈2096米∵小明到达景点A的时间为2096÷320≈6.55分钟∵6.43<6.55∵小宏先到达景点A.15.(1)解:由题意得:∠OO1P=90°.∵OO1=2米O1P=2米∴OP=2√2(米).∴圆锥的侧面积=π×2√2×2=4√2π(米2).答:圆锥的侧面积为4√2π平方米;(2)解:由题意得:∠OQM=90°.设OQ长x米.∵tanα=1 2∴MQ=2x米.∵MN=m米∴NQ=(m+2x)米.∵tanβ=2 5∴xm+2x =25.解得:x=2m.∵O1O2=3米QO2=1米∴OO1=2m+1−3=(2m−2)米.∵O1P=2米∠OO1P=90°.∴OP=√22+(2m−2)2=√4m2−8m+8=2√m2−2m+2(米).∴圆锥的侧面积=π×2√m2−2m+2×2=4π√m2−2m+2(米2).答:亭盖的外部面积为4π√m2−2m+2平方米.16.(1)解:∵∠MDE=45°∴∠DEC=45°∵DC⊥BC∴△DCE是等腰直角三角形∴DC=CE=1.5m 在Rt△DCF中∠DFC=36.9°DC=1.5m∴DF=DCsin36.9°=1.50.60=2.5(m)∴CF=√DF2−DC2=√2⋅52−1⋅52=2(m);故答案为:1.52;(2)∵∠DEC=45°∴∠AEB=45°∴∠BAE=45°∴AB=BE=163.3m由题意可知∠MDF=36.9°∴∠GFB=∠DFC=∠MDF=36.9°∵EF=CF−CE=2−1.5=0.5(m)∴BF=163.3−0.5=162.8(m)在Rt△BFG中BG=tan∠GFB⋅BF≈0.75×162.8=122.1(m)∴AG=163.3−122.1=41.2(m)即“美”字的高度AG约为41.2m.17.(1)解:∵DE垂直于水平地面EF∵∠E=90°∵坡比i=3:4∵DE EF =34设DE=3xm则EF=4xm ∵坡面DF长10m∵(3x)2+(4x)2=102解得:x=2(负值舍去)∵DE=6m EF=8m∵MF=25m∵ME=MF+EF=33m由题意得:∠OME=53°=44m∵OE=ME⋅tan53°≈33×43∵MN=23.5m∵NE=ME+MN=56.5m.由题意得:∠N=30°≈32m∵AE=NE⋅tan30°=56.5×√33∵OA=OE−AE=44−32=12m.(2)如图过点C作CH⊥OE于点M CG⊥NE于G∵∠CHE=∠HEG=∠CGE=∠CHO=90°∵四边形HEGC是矩形∵EH=CG∵叶片绕点O顺时针转动90°∵∠AOE=90°∵∠AOC=120°∵∠COH=30°由题意得:OC=OA=12m=6√3m∵OH=OCcos∠COH=12×√32∵CG=HE=OE−OH=44−6√3≈34m.∵叶片OC顶端C离水平地面EF的距离为34m.18.(1)解:在Rt△ABE中∠AEB=90°∠A=15°AE=576m∴AB=AEcosA =576cos15°≈594(m).答:索道AB的长约为594m.(2)延长BC交DF于点G∵BC∥AF DF⊥AF∴DG⊥CG.∵四边形BEFG为矩形.∴EF=BG.∵CD=AB≈594m∠DCG=45°∴CG=CD·cos∠DCG≈594×cos45°=297√2(m).∴AF=AE+EF=AE+BG=AE+BC+CG≈576+50+297√2≈1045(m).答:水平距离AF的长约为1045m19.(1)解:如图所示过点A作AH⊥BE于点H∵∠BAH=45°,AB=400√2米∴AH=BH=√22AB=400米∵∠AEB=30°∴HE=√3AH=400√3米AE=2AH=800米∴BE=400+400√3≈1092(米).∴BE长约1092米.(2)解:小华先到达景点D处理由如下:如图过点C作CN⊥EF于点N过点D作DM⊥BE于点M交CN于点G则四边形BCNE和四边形DFNG都是矩形∴BC=EN BE=CN=(400+400√3)米GN=DF=400米DG=NF∴CG=CN−GN=400√3米∵景点C既位于景点B正东方向310米处又位于景点D的北偏西37.5°方向.∴BC=310(米)∠DCN=37.5°在Rt△CGD中cos∠DCN=CGCD tan∠DCN=DGCG∴CD=CGcos37.5°=400√345≈865(米)DG=CG⋅tan37.5°=400√3×34≈519(米)∴EF=EN+NF=BC+DG≈829(米)∵小明选择了游览路线①:A−B−C−D小明行驶的平均速度是72米/秒.小明在景点B、C处各停留了10分钟、5分钟∴小明的游览时间为400√2+310+86572+10+5≈39(分钟)在Rt△AEH中AH=400米∠EAH=60°∴AE=AHcos60°=40012=800(米)∵小华选择了游览路线②:A−E−F−D小华行驶的平均速度为96米/秒.小华在景点E、F处各停留了9分钟、8分钟∴小华的游览时间为800+829+40096+9+8≈38(分钟)∴小华的游览时间更短先到达景点D处.20.(1)解:如图过点C作CE⊥AB垂足为E∵∠DAC=120°∴∠EAC=180°−∠DAC=60°在Rt△AEC中AC=60cm∴CE=AC⋅sin60°=60×√32=30√3(cm)在Rt△BEC中BC=30√6cm∴sin∠EBC=ECBC=√330√6=√22∴∠ABC=45°∴∠ABC的度数约为45°;(2)解:如图过点A作AF⊥BC垂足为F∵圆弧形滑轨⌒AB所在的圆恰好与直线BC相切于点B ∴过点B作HB⊥BC作AB的垂直平分线MG交HB于点O连接OA∴OB=OA∴圆弧形滑轨⌒AB所在的圆的圆心为O∵∠DAC=100°∠ABC=30°∴∠ACF=∠DAC−∠ABC=100°−30=70°在Rt△AFC中AC=50cm∴AF=AC⋅sin70°≈50×0.940=47(cm)在Rt△AFB中∠ABC=30°∴AB=2AF=2×47=94(cm)∵OB⊥BC∴∠OBC=90°∴∠OBA=∠OBC−∠ABC=60°∴△OBA为等边三角形∴OB=AB=94cm∠BOA=60°∴滑轨⌒AB的长度=60π×94180≈98.4(cm)∴滑轨AB⌒AB的长度约为98.4cm.。
中考数学三角函数和解直角三角形精选练习(附答案).docx

2013屮考数学三角函数和解直角三角形精选练习(附答案)2013中考三角函数和解直角三角形精选题适合培优1.下图表示一个时钟的钟面垂直固定于水平桌面上,其中分针上有一点A,且当钟面显示3点30分时,分针垂直于桌面,A点距桌面的高度为10公分。
如图(十七),若此钟面显示3点45分时,A点距桌面的高度为16公分,则钟面显示3点50分时,A点距桌面的高度为多少公分?A. 22-3B. 16+ . 18 D. 19【答案】D2、RtAABC «|>, ZC=90°, a、b、c 分别是ZA、ZB、ZC 的对边,那么c等于()答案:B3.(2011河南三门峡模拟一)某人乘雪橇沿如图所示的斜坡笔直滑下,滑下的路S (米)与时间t (秒)间的关系式为S=10t + t2,若滑到坡底的时间为2秒,则此人下滑的高度为()A.24 米B.12 米D.11 米答案:B4、(2012年浙江省杭州市一模)如图,在RtAABC中,AB=CB, BO丄AC,把AABC折叠,使AB落在AC±,点B与AC ±的点E重合,展开后,折痕AD交BO于点F,连接DE、EF.下列结论:①lanZADB=2;②图小有4对全等三角形;③若将ADEF沿EF折叠,则点D不一定落在AC上;④BD二BF;⑤S四边形,上述结论屮正确的个数是()A. 4个B. 3个C. 2个D. 1个第1题答案:B5.若AABC 屮,锐角A 满足丨sinA- I +cos2C=0.则AABC 是()。
A.等腰直角三角形B.等腰三角形C.直角三角形D.锐角三角形6.等腰三角形的而积为40,底边长4,则底角的正切值为()。
A. 10B. 20C.D.7.如图,是一张宽m的矩形台球桌ABCD, 一球从点M (点M在长边CD±)出发沿虚线MN射向边BC,然后反弹到边AB上的P点.如果,那么P点与B 点的距离为【答案】(第15题8.长为4m的梯子搭在墙上与地面成45。
2022年中考数学专题复习:解直角三角形的应用题 精选(word版、无答案)

解直角三角形应用分类中考试题精选类型一俯仰角问题1.如图,某数学兴趣小组要测量一栋五层居民楼CD的高度.该楼底层为车库,高2.5米;上面五层居住,每层高度相等.测角仪支架离地1.5米,在A处测得五楼顶部点D的仰角为60°,在B处测得四楼顶点E的仰角为30°,AB=14米.求居民楼的高度(精确到0.1米,参考数据:≈1.73)2.如图所示,某工程队准备在山坡(山坡视为直线l)上修一条路,需要测量山坡的坡度,即tanα的值.测量员在山坡P处(不计此人身高)观察对面山顶上的一座铁塔,测得塔尖C的仰角为37°,塔底B的仰角为26.6°.已知塔高BC=80米,塔所在的山高OB=220米,OA=200米,图中的点O、B、C、A、P在同一平面内,求山坡的坡度.(参考数据sin26.6°≈0.45,tan26.6°≈0.50;sin37°≈0.60,tan37°≈0.75)3.如图,一只猫头鹰蹲在一棵树AC的B(点B在AC上)处,发现一只老鼠躲进短墙DF的另一侧,猫头鹰的视线被短墙遮住,为了寻找这只老鼠,它又飞至树顶C处,已知短墙高DF=4米,短墙底部D与树的底部A的距离为2.7米,猫头鹰从C点观测F点的俯角为53°,老鼠躲藏处M(点M在DE上)距D点3米.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)(1)猫头鹰飞至C处后,能否看到这只老鼠?为什么?(2)要捕捉到这只老鼠,猫头鹰至少要飞多少米(精确到0.1米)?类型二方位角问题4、在东西方向的海岸线l上有一长为1km的码头MN(如图),在码头西端M的正西19.5km处有一观察站A.某时刻测得一艘匀速直线航行的轮船位于A的北偏西30°,且与A相距40km的B处;经过1小时20分钟,又测得该轮船位于A的北偏东60°,且与A 相距km的C处.(1)求该轮船航行的速度(保留精确结果);(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN靠岸?请说明理由.5.(如图,在海面上生产了一股强台风,台风中心(记为点M)位于海滨城市(记作点A)的南偏西15°,距离为612千米,且位于临海市(记作点B)正西方向60 3千米处,台风中心正以72千米/时的速度沿北偏东60°的方向移动(假设台风在移动过程中的风力保持不变),距离台风中心60千米的圆形区域内均会受到此次强台风的侵袭.(1)滨海市、临海市是否会受到此次台风的侵袭请说明理由;(2)若受到此次台风侵袭,该城市受到台风侵袭的持续时间有多少小时?6.如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船C 的求救信号.已知A、B两船相距100(+1)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.(1)分别求出A与C,A与D之间的距离AC和AD(如果运算结果有根号,请保留根号).(2)已知距观测点D处100海里范围内有暗礁.若巡逻船A沿直线AC去营救船C ,在去营救的途中有无触暗礁危险?(参考数据:≈1.41,≈1.73)7、钓鱼岛历来是中国领土,以它为圆心在周围12海里范围内均属于禁区,不允许它国船支进入.如图7,今有一中国海监船在位于钓鱼岛A正南方向距岛60海里的B处海域巡逻,值班人员发现在钓鱼岛的正西方向52海里的C处有一艘日本渔船,正以9节的速度沿正东方向驶向钓鱼岛,中方立即向日本渔船发出警告,并沿北偏西30°的方向以12节的速度前往拦截,其间多次发出警告,2小时后海监船到达D处,与此同时日本渔船到达E处,此时海监船再次发出严重警告.(1)当日本渔船收到严重警告信号后,必须沿北偏东转向多少度航行,才能恰好避免进入钓鱼岛12海里禁区?(4分)(2)当日本渔船不听严重警告信号,仍按原速度、原方向继续前进,那么海监船必须尽快到达距岛12海里,且位于线段AC上的F处强制拦截渔船,问海监船能否比日本渔船先到达F处?(5分)(注:①中国海监船的最大航速为18节,1节=1海里/时;②参考数据:sin26.3°≈0.44,sin20.5°≈0.35,sin18.1°≈0.3121.431.7)类型三坡度坡角问题8.(如图,点A、B、C表示某旅游景区三个缆车站的位置,线段AB、BC表示连接缆车站的钢缆,已知A、B、C三点在同一铅直平面内,它们的海拔高度AA′,BB′,CC′分别为110米、310米、710米,钢缆AB的坡度i1=1:2,钢缆BC的坡度i2=1:1,景区因改造缆车线路,需要从A到C直线架设一条钢缆,那么钢缆AC的长度是多少米?(注:坡度:是指坡面的铅直高度与水平宽度的比)9.如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:3,AB=10米,AE=15米.(i=1:3是指坡面的铅直高度BH与水平宽度AH的比)(1)求点B距水平面AE的高度BH;(2)求广告牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:2≈1.414,3≈1.732)10.校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD的长等于21米,在l上点D的同侧取点A、B,使∠CAD=30°,∠CBD=60°.(1)求AB的长(精确到0.1米,参考数据:3=1.73,2=1.41);(2)已知本路段对校车限速为40千米/小时,若测得某辆校车从A到B用时2秒,这辆校车是否超速?说明理由.类型四生活中问题11.如图,伞不论张开还是收紧,伞柄AP始终平分同一平面内两条伞架所成的角∠BAC,当伞收紧时,结点D与点M重合,且点A、E、D在同一条直线上,已知部分伞架的长度如下:单位:cm伞架DE DF AE AF AB AC长度36 36 36 36 86 86(1)求AM的长.(2)当∠BAC=104°时,求AD的长(精确到1cm).备用数据:sin52°=0.788,cos52°=0.6157,tan52°=1.2799.12.如图1,滨海广场装有风能、太阳能发电的风光互补环保路灯,灯杆顶端装有风力发电机,中间装有太阳能板,下端装有路灯.该系统工作过程中某一时刻的截面图如图2,已知太阳能板的支架BC垂直于灯杆OF,路灯顶端E距离地面6米,DE=1.8米,∠CDE=60°.且根据我市的地理位置设定太阳能板AB的倾斜角为43°.AB=1.5米,CD=1米,为保证长为1米的风力发电机叶片无障碍安全旋转,对叶片与太阳能板顶端A的最近距离不得少于0.5米,求灯杆OF至少要多高?(利用科学计算器可求得sin43°≈0.6820,cos43°≈0.7314,tan43°≈0.9325,结果保留两位小数)13.小明坐于堤边垂钓,如图,河堤AC的坡角为30°,AC 长米,钓竿AO的倾斜角是60°,其长为3米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离.。
中考数学专题训练:解直角三角形及其应用(附参考答案)

中考数学专题训练:解直角三角形及其应用(附参考答案)1.如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论不正确的是( )A.sin B=ADAB B.sin B=ACBCC.sin B=ADAC D.sin B=CDAC2.如图,在由边长为1的小正方形组成的网格中,点A,B,C,D都在这些小正方形的格点上,AB,CD相交于点E,则sin ∠AEC=( )A.2√55B.√55C.12D.√1043.计算sin 30°·tan 45°的结果是( )A.12B.√32C.√36D.√244.已知在Rt△ABC中,∠C=90°,∠A=60°,则tan B的值为( ) A.√33B.1C.√3D.25.如图,在△ABC中,∠C=90°,∠A=30°,则cos B的值为( )A.13B.12C.√22D.√326.如图,AD是△ABC的高.若BD=2CD=6,tan C=2,则边AB的长为( )A.3√2B.3√5C.3√7D.6√27.已知α为锐角,且2sin (α-10°)=√3,则α等于( )A.50°B.60°C.70°D.80°8.如图,在点F处看建筑物顶端D的仰角为32°,向前走了15米到达点E,即EF=15米,在点E处看点D的仰角为64°,则CD的长用三角函数表示为( )A.15sin 32°B.15tan 64°C.15sin 64°D.15tan 32°9.如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,E为BD上一点,使得AE =AC.若BE=3ED,则sin ∠BAE=( )A.12B.15C.35D.3410.如图,河对岸有铁塔AB,C,D,B三点共线,在C处测得塔顶A的仰角为30°,向铁塔方向水平前进14 m到达D处,在D处测得A的仰角为45°,塔高AB为( )A.4(4√3-1)m B.7(√3+1)mC.(16√3+7)m D.(10√3+7)m11.如图,在一次数学实践活动中,小明同学要测量一座与地面垂直的塔AB的高度,他从塔底部点B处前行30 m到达斜坡CE的底部点C处,然后沿斜坡CE前行20 m到达最佳测量点D处,在点D处测得塔顶A的仰角为30°,已知斜坡的斜面坡度i=1∶√3,且点A,B,C,D,E在同一平面内,小明同学测得塔AB的高度是( )A.(10√3+20)m B.(10√3+10)mC.20√3 m D.40 m12.如图,已知在Rt△ABC中,∠ACB=90°,AC=1,AB=2,则sin B的值是______.13.在△ABC中,∠A=45°,AB=4√2,BC=5,则△ABC的面积为_________.14.如图,在平面直角坐标系中,已知点A(1,0),点B(0,-3),点C在x轴上,,则点C的坐标为______.且点C在点A右方,连接AB,BC.若tan ∠ABC=1315.如图,在杭州西湖风景区游船处,在离水面高度为5 m的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为13 m,此人以0.5 m/s的速度收绳,10 s后船移动到点D的位置,则船向岸边移动了______________m.(假设绳子是直的,结果保留根号)16.某港口P位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里,它们离开港口一个半小时后相距30海里.如果知道“远航”号沿北偏东45°方向航行,那么“海天”号沿______________方向航行.17.湖中小岛上码头C处一名游客突发疾病,需要救援.位于湖面B点处的快艇和湖岸A处的救援船接到通知后立刻同时出发前往救援.计划由快艇赶到码头C 接该游客,再沿CA方向行驶,与救援船相遇后将该游客转运到救援船上.已知C在A的北偏东30°方向上,B在A的北偏东60°方向上,且B在C的正南方向900米处.(1)求湖岸A与码头C的距离;(结果精确到1米,参考数据:√3≈1.732)(2)救援船的平均速度为150米/分,快艇的平均速度为400米/分,在接到通知后,快艇能否在5分钟内将该游客送上救援船?请说明理由.(接送游客上下船的时间忽略不计)18.如图,已知正方形ABCD和正方形BEFG,点G在AD上,GF与CD交于点H,tan ∠ABG=1,正方形ABCD的边长为8,求BH的长.219.小华将一张纸对折后做成的纸飞机如图1,纸飞机机尾的横截面是一个轴对称图形,其示意图如图2.已知AD=BE=10 cm,CD=CE=5 cm,AD⊥CD,BE⊥CE,∠DCE=40°.(结果精确到0.1 cm,参考数据:sin 20°≈0.34,cos 20°≈0.94,tan 20°≈0.36,sin 40°≈0.64,cos 40°≈0.77,tan 40°≈0.84)(1)连接DE,求线段DE的长;(2)求点A,B之间的距离.参考答案1.C 2.A 3.A 4.A 5.B 6.D 7.C 8.C 9.C 10.B 11.A 12.12,0) 15.(12-√39) 16.北偏西45°13. 2或14 14.(9417.(1)湖岸A与码头C的距离约为1 559米(2)在接到通知后,快艇能在5分钟内将该游客送上救援船,理由略18.BH=1019.(1)DE的长为3.4 cm (2)点A,B之间的距离为22.2 cm。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解直角三角形的应用练习题一.选择题(共5小题)1.(2012•襄阳)在一次数学活动中,李明利用一根栓有小锤的细线和一个半圆形量角器制作了一个测角仪,去测量学校内一座假山的高度CD.如图,已知小明距假山的水平距离BD为12m,他的眼镜距地面的高度为1.6m,李明的视线经过量角器零刻度线OA和假山的最高点C,此时,铅垂线OE经过量角器的60°刻度线,则假山的高度为()A.(4+1.6)m B.(12+1.6)m C.(4+1.6)m D.4m2.(2014•随州)如图,要测量B点到河岸AD的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=100米,则B点到河岸AD的距离为()D.50米A.100米B.50米C.米3.(2014•衡阳)如图,一河坝的横断面为等腰梯形ABCD,坝顶宽10米,坝高12米,斜坡AB的坡度i=1:1.5,则坝底AD的长度为()A.26米B.28米C.30米D.46米4.(2014•西宁)如图1,某超市从一楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的坡度为1:2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角为42°,则二楼的层高BC约为(精确到0.1米,sin42°≈0.67,tan42°≈0.90)()A.10.8米B.8.9米C.8.0米D.5.8米5.(2014•临沂)如图,在某监测点B处望见一艘正在作业的渔船在南偏西15°方向的A处,若渔船沿北偏西75°方向以40海里/小时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东60°方向上,则B、C之间的距离为A.20海里B.10海里C.20海里D.30海里()二.填空题6.(2009•仙桃)如图所示,小华同学在距离某建筑物6米的点A处测得广告牌B点、C点的仰角分别为52°、35°,则广告牌的高度BC为_________米(精确到0.1米).(sin35°≈0.57,cos35°≈0.82,tan35°≈0.70;sin52°≈0.79,cos52°≈0.62,tan52°≈1.28)7.(2009•安徽)长为4m的梯子搭在墙上与地面成45°角,作业时调整为60°角(如图所示),则梯子的顶端沿墙面升高了_________m.8.(2014•宁波)为解决停车难的问题,在如图一段长56米的路段开辟停车位,每个车位是长5米宽2.2米的矩形,矩形的边与路的边缘成45°角,那么这个路段最多可以划出_________个这样的停车位.(≈1.4)9.(2014•十堰)如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是_________海里.(结果精确到个位,参考数据:≈1.4,≈1.7,≈2.4)10.(2014•抚顺)如图,河流两岸a、b互相平行,点A、B是河岸a上的两座建筑物,点C、D是河岸b上的两点,A、B的距离约为200米.某人在河岸b上的点P处测得∠APC=75°,∠BPD=30°,则河流的宽度约为_________米.三.解答题(共5小题)11.(2014•南昌)图1中的中国结挂件是由四个相同的菱形在顶点处依次串联而成,每相邻两个菱形均成30°的夹角,示意图如图2.在图2中,每个菱形的边长为10cm,锐角为60°.(1)连接CD,EB,猜想它们的位置关系并加以证明;(2)求A,B两点之间的距离(结果取整数,可以使用计算器)(参考数据:≈1.41,≈1.73,≈2.45)12.(2014•铁岭)如图,小丽假期在娱乐场游玩时,想要利用所学的数学知识测量某个娱乐场地所在山坡AE的长度.她先在山脚下点E处测得山顶A的仰角是30°,然后,她沿着坡度是i=1:1(即tan∠CED=1)的斜坡步行15分钟抵达C处,此时,测得A点的俯角是15°.已知小丽的步行速度是18米/分,图中点A、B、E、D、C在同一平面内,且点D、E、B在同一水平直线上.求出娱乐场地所在山坡AE的长度.(参考数据:≈1.41,结果精确到0.1米)13.(2014•抚州)如图1所示的晾衣架,支架主视图的基本图形是菱形,其示意图如图2,晾衣架伸缩时,点G在射线DP上滑动,∠CED的大小也随之发生变化,已知每个菱形边长均等于20cm,且AH=DE=EG=20cm.(1)当∠CED=60°时,求C、D两点间的距离;(2)当∠CED由60°变为120°时,点A向左移动了多少cm?(结果精确到0.1cm)(3)设DG=xcm,当∠CED的变化范围为60°~120°(包括端点值)时,求x的取值范围.(结果精确到0.1cm)(参考数据≈1.732,可使用科学计算器)14.(2014•宿迁)如图是某通道的侧面示意图,已知AB∥CD∥EF,AM∥BC∥DE,AB=CD=EF,∠AMF=90°,∠BAM=30°,AB=6m.(1)求FM的长;(2)连接AF,若sin∠FAM=,求AM的长.15.(2014•邵阳)一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里每小时的速度前往救援,求海警船到大事故船C处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)解直角三角形的应用练习题参考答案与试题解析一.选择题(共5小题)1.(2012•襄阳)在一次数学活动中,李明利用一根栓有小锤的细线和一个半圆形量角器制作了一个测角仪,去测量学校内一座假山的高度CD.如图,已知小明距假山的水平距离BD为12m,他的眼镜距地面的高度为1.6m,李明的视线经过量角器零刻度线OA和假山的最高点C,此时,铅垂线OE经过量角器的60°刻度线,则假山的高度为()A.(4+1.6)m B.(12+1.6)m C.(4+1.6)m D.4m考点:解直角三角形的应用.分析:根据已知得出AK=BD=12m,再利用tan30°==,进而得出CD的长.解答:解:∵BD=12米,李明的眼睛高AB=1.6米,∠AOE=60°,∴DB=AK,AB=KD=1.6米,∠CAK=30°,∴tan30°==,解得CK=4(米),即CD=CK+DK=4+1.6=(4+1.6)米.故选:A.点评:本题考查的是解直角三角形的应用,根据题意得出tan30°==解答是解答此题的关键.2.(2014•随州)如图,要测量B点到河岸AD的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=100米,则B点到河岸AD的距离为()A.100米B.50米C.D.50米米考点:解直角三角形的应用.专题:几何图形问题.分析:过B作BM⊥AD,根据三角形内角与外角的关系可得∠ABC=30°,再根据等角对等边可得BC=AC,然后再计算出∠CBM的度数,进而得到CM长,最后利用勾股定理可得答案.解答:解:过B作BM⊥AD,∵∠BAD=30°,∠BCD=60°,∴∠ABC=30°,∴AC=CB=100米,∵BM⊥AD,∴∠BMC=90°,∴∠CBM=30°,∴CM=BC=50米,∴BM=CM=50米,故选:B.点评:此题主要考查了解直角三角形的应用,关键是证明AC=BC,掌握直角三角形的性质:30°角所对直角边等于斜边的一半.3.(2014•衡阳)如图,一河坝的横断面为等腰梯形ABCD,坝顶宽10米,坝高12米,斜坡AB的坡度i=1:1.5,则坝底AD的长度为()A.26米B.28米C.30米D.46米考点:解直角三角形的应用-坡度坡角问题.专题:几何图形问题.分析:先根据坡比求得AE的长,已知CB=10m,即可求得AD.解答:解:∵坝高12米,斜坡AB的坡度i=1:1.5,∴AE=1.5BE=18米,∵BC=10米,∴AD=2AE+BC=2×18+10=46米,故选:D.点评:此题考查了解直角三角形的应用中的坡度坡角的问题及等腰梯形的性质的掌握情况,将相关的知识点相结合更利于解题.4.(2014•西宁)如图1,某超市从一楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的坡度为1:2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角为42°,则二楼的层高BC约为(精确到0.1米,sin42°≈0.67,tan42°≈0.90)()A.10.8米B.8.9米C.8.0米D.5.8米考点:解直角三角形的应用-仰角俯角问题;解直角三角形的应用-坡度坡角问题.专题:几何图形问题.分析:延长CB交PQ于点D,根据坡度的定义即可求得BD的长,然后在直角△CDA中利用三角函数即可求得CD的长,则BC即可得到.解答:解:延长CB交PQ于点D.∵MN∥PQ,BC⊥MN,∴BC⊥PQ.∵自动扶梯AB的坡度为1:2.4,∴==.设BD=5k米,AD=12k米,则AB=13k米.∵AB=13米,∴k=1,∴BD=5米,AD=12米.在Rt△CDA中,∠CDA=90゜,∠CAD=42°,∴CD=AD•tan∠CAD≈12×0.90≈10.8米,∴BC≈5.8米.故选:D.点评:本题考查仰角和坡度的定义,要求学生能借助仰角构造直角三角形并解直角三角形.5.(2014•临沂)如图,在某监测点B处望见一艘正在作业的渔船在南偏西15°方向的A处,若渔船沿北偏西75°方向以40海里/小时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东60°方向上,则B、C之间的距离为()A.20海里B.10海里C.20海里D.30海里考点:解直角三角形的应用-方向角问题.专题:几何图形问题.分析:如图,根据题意易求△ABC是等腰直角三角形,通过解该直角三角形来求BC的长度.解答:解:如图,∵∠ABE=15°,∠DAB=∠ABE,∴∠DAB=15°,∴∠CAB=∠CAD+∠DAB=90°.又∵∠FCB=60°,∠CBE=∠FCB,∠CBA+∠ABE=∠CBE,∴∠CBA=45°.∴在直角△ABC中,sin∠ABC===,∴BC=20海里.故选:C.点评:本题考查了解直角三角形的应用﹣方向角问题.解题的难点是推知△ABC是等腰直角三角形.二.填空题(共5小题)6.(2009•仙桃)如图所示,小华同学在距离某建筑物6米的点A处测得广告牌B点、C点的仰角分别为52°、35°,则广告牌的高度BC为 3.5米(精确到0.1米).(sin35°≈0.57,cos35°≈0.82,tan35°≈0.70;sin52°≈0.79,cos52°≈0.62,tan52°≈1.28)考点:解直角三角形的应用-仰角俯角问题.专题:应用题;压轴题.分析:图中有两个直角三角形△ABD、△ACD,可根据两个已知角度,利用正切函数定义,分别求出BD和CD,求差即可.解答:解:根据题意:在Rt△ABD中,有BD=AD•tan52°.在Rt△ADC中,有DC=AD•tan35°.则有BC=BD﹣CD=6(1.28﹣0.70)=3.5(米).点评:本题考查仰角的定义,要求学生能借助仰角构造直角三角形并解直角三角形.7.(2009•安徽)长为4m的梯子搭在墙上与地面成45°角,作业时调整为60°角(如图所示),则梯子的顶端沿墙面升高了2()m.考点:解直角三角形的应用-坡度坡角问题.专题:压轴题.分析:利用所给角的正弦函数求两次的高度,相减即可.解答:解:由题意知:平滑前梯高为4•sin45°=4•=.平滑后高为4•sin60°=4•=.∴升高了2()m.点评:本题重点考查了三角函数定义的应用.8.(2014•宁波)为解决停车难的问题,在如图一段长56米的路段开辟停车位,每个车位是长5米宽2.2米的矩形,矩形的边与路的边缘成45°角,那么这个路段最多可以划出17个这样的停车位.(≈1.4)考点:解直角三角形的应用.专题:调配问题.分析:如图,根据三角函数可求BC,CE,由BE=BC+CE可求BE,再根据三角函数可求EF,再根据停车位的个数=(56﹣BE)÷EF+1,列式计算即可求解.解答:解:如图,BC=2.2×sin45°=2.2×≈1.54米,CE=5×sin45°=5×≈3.5米,BE=BC+CE≈5.04,EF=2.2÷sin45°=2.2÷≈3.14米,(56﹣5.04)÷3.14+1=50.96÷3.14+1≈16+1=17(个).故这个路段最多可以划出17个这样的停车位.故答案为:17.点评:考查了解直角三角形的应用,主要是三角函数及运算,关键把实际问题转化为数学问题加以计算.9.(2014•十堰)如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是24海里.(结果精确到个位,参考数据:≈1.4,≈1.7,≈2.4)考点:解直角三角形的应用-方向角问题.专题:几何图形问题.分析:作BD⊥AC于点D,在直角△ABD中,利用三角函数求得BD的长,然后在直角△BCD中,利用三角函数即可求得BC的长.解答:解:∠CBA=25°+50°=75°.作BD⊥AC于点D.则∠CAB=(90°﹣70°)+(90°﹣50°)=20°+40°=60°,∠ABD=30°,∴∠CBD=75°﹣30°=45°.在直角△ABD中,BD=AB•sin∠CAB=20×sin60°=20×=10.在直角△BCD中,∠CBD=45°,则BC=BD=10×=10≈10×2.4=24(海里).故答案是:24.点评:本题主要考查了方向角含义,正确求得∠CBD以及∠CAB的度数是解决本题的关键.10.(2014•抚顺)如图,河流两岸a、b互相平行,点A、B是河岸a上的两座建筑物,点C、D是河岸b上的两点,A、B的距离约为200米.某人在河岸b上的点P处测得∠APC=75°,∠BPD=30°,则河流的宽度约为100米.考点:解直角三角形的应用.专题:几何图形问题.分析:过点P作PE⊥AB于点E,先求出∠APE及∠BPE、∠ABP的度数,由锐角三角函数的定义即可得出结论.解答:解:过点P作PE⊥AB于点E,∵∠APC=75°,∠BPD=30°,∴∠APB=75°,∵∠BAP=∠APC=75°,∴∠APB=∠BAP,∴AB=PB=200m,∵∠ABP=30°,∴PE=PB=100m.故答案为:100.点评:本题考查的是解直角三角形的应用,熟知锐角三角函数的定义是解答此题的关键.三.解答题(共5小题)11.(2014•南昌)图1中的中国结挂件是由四个相同的菱形在顶点处依次串联而成,每相邻两个菱形均成30°的夹角,示意图如图2.在图2中,每个菱形的边长为10cm,锐角为60°.(1)连接CD,EB,猜想它们的位置关系并加以证明;(2)求A,B两点之间的距离(结果取整数,可以使用计算器)(参考数据:≈1.41,≈1.73,≈2.45)考点:解直角三角形的应用.分析:(1)连接DE.根据菱形的性质和角的和差关系可得∠CDE=∠BED=90°,再根据平行线的判定可得CD,EB的位置关系;(2)根据菱形的性质可得BE,DE,再根据三角函数可得BD,AD,根据AB=BD+AD,即可求解.解答:解:(1)猜想CD∥EB.证明:连接DE.∵中国结挂件是四个相同的菱形,每相邻两个菱形均成30°的夹角,菱形的锐角为60°∴∠CDE=60°÷2×2+30°=90°,∴∠BED=60°÷2×2+30°=90°,∴∠CDE=∠BED,∴CD∥EB.(2)BE=2OE=2×10×cos30°=10cm,同理可得,DE=10cm,则BD=10cm,同理可得,AD=10cm,AB=BD+AD=20≈49cm.答:A,B两点之间的距离大约为49cm.点评:此题考查了解直角三角形的应用,菱形的性质和平行线的判定,主要是三角函数的基本概念及运算,关键是运用数学知识解决实际问题.12.(2014•铁岭)如图,小丽假期在娱乐场游玩时,想要利用所学的数学知识测量某个娱乐场地所在山坡AE的长度.她先在山脚下点E处测得山顶A的仰角是30°,然后,她沿着坡度是i=1:1(即tan∠CED=1)的斜坡步行15分钟抵达C处,此时,测得A点的俯角是15°.已知小丽的步行速度是18米/分,图中点A、B、E、D、C在同一平面内,且点D、E、B在同一水平直线上.求出娱乐场地所在山坡AE的长度.(参考数据:≈1.41,结果精确到0.1米)考点:解直角三角形的应用-仰角俯角问题;解直角三角形的应用-坡度坡角问题.分析:根据速度乘以时间得出CE的长度,通过坡度得到∠ECF=30°,作辅助线EF⊥AC,通过平角减去其他角从而得到∠AEF=45°即可求出AE的长度.解答:解:作EF⊥AC,根据题意,CE=18×15=270米,∵tan∠CED=1,∴∠CED=∠DCE=45°,∵∠ECF=90°﹣45°﹣15°=30°,∴EF=CE=135米,∵∠CEF=60°,∠AEB=30°,∴∠AEF=180°﹣45°﹣60°﹣30°=45°,∴AE=135≈190.35米点评:本题考查了解直角三角形的应用,解答本题的关键是作辅助线EF⊥AC,以及坡度和坡角的关系.13.(2014•抚州)如图1所示的晾衣架,支架主视图的基本图形是菱形,其示意图如图2,晾衣架伸缩时,点G在射线DP上滑动,∠CED的大小也随之发生变化,已知每个菱形边长均等于20cm,且AH=DE=EG=20cm.(1)当∠CED=60°时,求C、D两点间的距离;(2)当∠CED由60°变为120°时,点A向左移动了多少cm?(结果精确到0.1cm)(3)设DG=xcm,当∠CED的变化范围为60°~120°(包括端点值)时,求x的取值范围.(结果精确到0.1cm)(参考数据≈1.732,可使用科学计算器)考点:解直角三角形的应用;菱形的性质.分析:(1)证明△CED是等边三角形,即可求解;(2)分别求得当∠CED是60°和120°,两种情况下AD的长,求差即可;(3)分别求得当∠CED是60°和120°,两种情况下DG的长度,即可求得x的范围.解答:解:(1)连接CD(图1).∵CE=DE,∠CED=60°,∴△CED是等边三角形,∴CD=DE=20cm;(2)根据题意得:AB=BC=CD,当∠CED=60°时,AD=3CD=60cm,当∠CED=120°时,过点E作EH⊥CD于H(图2),则∠CEH=60°,CH=HD.在直角△CHE中,sin∠CEH=,∴CH=20•sin60°=20×=10(cm),∴CD=20cm,∴AD=3×20=60≈103.9(cm).∴103.9﹣60=43.9(cm).即点A向左移动了43.9cm;(3)当∠CED=120°时,∠DEG=60°,∵DE=EG,∴△DEG是等边三角形.∴DG=DE=20cm,当∠CED=60°时(图3),则有∠DEG=120°,过点E作EI⊥DG于点I.∴∠DEI=∠GEI=60°,DI=IG,在直角△DIE中,sin∠DEI=,∴DI=DE•sin∠DEI=20×sin60°=20×=10cm.∴DG=2DI=20≈34.6cm.则x的范围是:20cm≤x≤34.6cm.点评:本题考查了菱形的性质,当菱形的一个角是120°或60°时,连接菱形的较短的对角线,即可把菱形分成两个等边三角形.14.(2014•宿迁)如图是某通道的侧面示意图,已知AB∥CD∥EF,AM∥BC∥DE,AB=CD=EF,∠AMF=90°,∠BAM=30°,AB=6m.(1)求FM的长;(2)连接AF,若sin∠FAM=,求AM的长.考点:解直角三角形的应用-坡度坡角问题.专题:几何图形问题.分析:(1)分别过点B、D、F作BN⊥AM于点N,DG⊥BC延长线于点G,FH⊥DE延长线于点H,根据AB∥CD∥EF,AM∥BC∥DE,分别解Rt△ABN、Rt△DCG、Rt△FEH,求出BN、DG、FH的长度,继而可求出FM的长度;(2)在Rt△FAM中,根据sin∠FAM=,求出AF的长度,然后利用勾股定理求出AM的长度.解答:解:(1)分别过点B、D、F作BN⊥AM于点N,DG⊥BC延长线于点G,FH⊥DE延长在Rt△ABN中,∵AB=6m,∠BAM=30°,∴BN=ABsin∠BAN=6×=3m,∵AB∥CD∥EF,AM∥BC∥DE,同理可得:DG=FH=3m,∴FM=FH+DG+BN=9m;(2)在Rt△FAM中,∵FM=9m,sin∠FAM=,∴AF=27m,∴AM==18(m).即AM的长为18m.点评:本题考查了解直角三角形的应用,解答本题的关键是根据坡角构造直角三角形,利用三角函数解直角三角形,注意勾股定理的应用.15.(2014•邵阳)一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里每小时的速度前往救援,求海警船到大事故船C处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)考点:解直角三角形的应用-方向角问题.专题:几何图形问题.分析:过点C作CD⊥AB交AB延长线于D.先解Rt△ACD得出CD=AC=40海里,再解Rt△CBD中,得出BC=≈50,然后根据时间=路程÷速度即可求出海警船到大事故船C处所需的时间.解答:解:如图,过点C作CD⊥AB交AB延长线于D.在Rt△ACD中,∵∠ADC=90°,∠CAD=30°,AC=80海里,∴CD=AC=40海里.在Rt△CBD中,∵∠CDB=90°,∠CBD=90°﹣37°=53°,∴BC=≈=50(海里),∴海警船到大事故船C处所需的时间大约为:50÷40=(小时).点评:本题考查了解直角三角形的应用﹣方向角问题,难度适中,作出辅助线构造直角三角形是解题的关键.。
