空间域滤波和频域滤波
空域滤波和频域滤波的实现及比较

里仁学院课程设计说明书题目:空域滤波和频域滤波的实现及比较学院(系):里仁学院年级专业:09工业自动化仪表2班学号: 09学生姓名:苏胜指导教师:赵彦涛、程淑红教师职称:讲师、副教授燕山大学课程设计(论文)任务书学号0120 学生姓名苏胜专业(班级)09工业自动化仪表2班设计题目5空域滤波和频域滤波的实现及比较设计技术参数要求用不同的滤波器分别实现图像的空域和频域滤波,然后比较结果。
设计要求数字信号处理中,图像的空域滤波和频域滤波可以实现相同的目的,用不同的滤波器实现其空域和频域滤波,然后比较其结果。
要求用不同的滤波器同时实现图像的空域和频域滤波。
设计中应具有自己的设计思想、设计体会。
工作量1周工作计划周一:分析题目,查阅相关资料,熟悉MATLAB程序设计方法。
周二至周三:方案设计周四:编写程序代码、调试、运行周五:答辩考核参考资料1.数字图像处理学电子工业出版社贾永红 20032.数字图像处理(Matlab版)电子工业出版社冈萨雷斯 20063.其他数字图像处理和matlab编程方面的书籍及相关学习资料指导教师签字基层教学单位主任签字说明:此表一式四份,学生、指导教师、基层教学单位、系部各一份。
2012年6 月29日燕山大学课程设计评审意见表指导教师评语:成绩:指导教师:2012年6月29 日答辩小组评语:成绩:评阅人:2012年6月29 日课程设计总成绩:答辩小组成员签字:2012年6月29 日目录第一章摘要 (1)第二章引言 (2)第三章空域滤波和频域滤波 (3)3.1 空域滤波器的设计 (3)3.1.1 空域低通滤波器 (3)3.1.2 空域高通滤波器 (5)3.2 时域滤波器的设计 (5)3.2.1 时域低通滤波器 (6)3.2.2 时域高通滤波器 (6)3.3空域与时域滤波的比较 (12)第四章心得体会 (15)第五章参考文献 (16)一、摘要此次课程设计是在MATLAB软件下进行数字滤波技术的仿真分析,有助于我对数字图像处理技术的分析和理解。
空间域滤波和频率域处理的特点

空间域滤波和频率域处理的特点1.引言空间域滤波和频率域处理是数字图像处理中常用的两种图像增强技术。
它们通过对图像进行数学变换和滤波操作来改善图像质量。
本文将介绍空间域滤波和频率域处理的特点,并比较它们之间的异同。
2.空间域滤波空间域滤波是一种直接在空间域内对图像像素进行处理的方法。
它基于图像的局部像素值来进行滤波操作,常见的空间域滤波器包括均值滤波器、中值滤波器和高斯滤波器等。
2.1均值滤波器均值滤波器是最简单的空间域滤波器之一。
它通过计算像素周围邻域的平均值来实现滤波操作。
均值滤波器能够有效地去除图像中的噪声,但对图像细节和边缘保留较差。
2.2中值滤波器中值滤波器是一种非线性的空间域滤波器。
它通过计算像素周围邻域的中值来实现滤波操作。
中值滤波器能够在去除噪声的同时保持图像细节和边缘,对于椒盐噪声有较好的效果。
2.3高斯滤波器高斯滤波器是一种线性的空间域滤波器。
它通过对像素周围邻域进行加权平均来实现滤波操作。
高斯滤波器能够平滑图像并保留图像细节,它的滤波核可以通过调整方差来控制滤波效果。
3.频率域处理频率域处理是一种将图像从空间域转换到频率域进行处理的方法。
它通过对图像进行傅里叶变换或小波变换等操作,将图像表示为频率分量的集合,然后对频率分量进行处理。
3.1傅里叶变换傅里叶变换是一种将信号从时域转换到频域的数学变换。
在图像处理中,可以应用二维傅里叶变换将图像从空间域转换到频率域。
在频率域中,图像的低频分量对应于图像的整体结构,高频分量对应于图像的细节和边缘。
3.2小波变换小波变换是一种基于小波函数的时频分析方法。
它能够在频率和时间上同时提供图像的信息,对于图像的边缘和纹理特征有较好的表达能力。
小波变换在图像压缩和特征提取等方面具有广泛应用。
4.空间域滤波与频率域处理的对比空间域滤波和频率域处理都可以用来改善图像质量,但它们有着不同的特点和适用场景。
4.1处理方式空间域滤波是直接对图像像素进行处理,操作简单直接,适用于小规模图像的处理。
空域滤波和频域滤波的关系

空域滤波和频域滤波的关系空域滤波是一种基于像素级别的滤波方法,它通过直接处理图像中的像素值来实现滤波效果。
具体而言,空域滤波是基于图像的空间域进行操作,通过对图像中的像素进行加权平均或非线性处理,改变像素之间的关系来达到滤波的目的。
常见的空域滤波方法包括均值滤波、中值滤波和高斯滤波等。
频域滤波则是一种基于图像的频域进行操作的滤波方法,它通过对图像进行傅里叶变换,将图像从空域转换到频域,然后在频域中对图像进行滤波操作,最后再通过傅里叶反变换将图像转换回空域。
频域滤波方法主要利用了傅里叶变换的性质,通过滤波器的频率响应对图像的频谱进行调整,达到滤波的效果。
常见的频域滤波方法包括低通滤波、高通滤波和带通滤波等。
空域滤波和频域滤波有着密切的关系。
事实上,它们本质上是同一种滤波方法的不同表现形式。
在空域滤波中,滤波器直接作用于图像的像素值,通过对像素值进行处理来实现滤波效果;而在频域滤波中,滤波器则直接作用于图像的频谱,通过调整频谱的幅度和相位来实现滤波效果。
从这个角度来看,频域滤波可以看作是空域滤波在频域中的表现。
空域滤波和频域滤波各有其优点和适用场景。
空域滤波方法简单直观,易于理解和实现,适用于对图像的局部特征进行处理,例如去除噪声、平滑边缘等。
而频域滤波方法则适用于对图像的全局特征进行处理,例如图像增强、频谱分析等。
频域滤波方法通过傅里叶变换将图像转换到频域,可以更好地分析和处理图像的频域信息,对于频谱特征较为明显的图像处理问题具有较好的效果。
尽管空域滤波和频域滤波在原理和应用上有所差异,但它们并不是对立的关系。
事实上,这两种滤波方法常常结合使用,相互补充,以实现更好的滤波效果。
比如,在图像处理中,可以先使用空域滤波方法去除图像中的噪声和干扰,然后再将处理后的图像转换到频域进行进一步的滤波和增强。
这样的组合使用可以充分发挥两种滤波方法的优势,提高图像处理的效果和质量。
空域滤波和频域滤波是图像处理中常用的两种滤波方法。
频域滤波——精选推荐

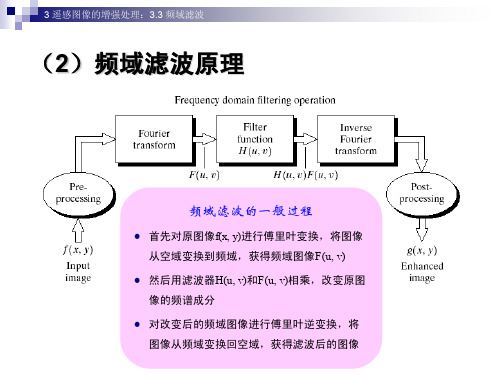
频域滤波1 频域滤波基础对⼀幅数字图像,基本的频率滤波操作包括:1)将图像变换到频率域;2)根据需要修改频率域数值;3)反变换到图像域。
使⽤公式表达为,H(u,v) 为滤波器(滤波传递函数),F(u,v) 为图像函数的傅⾥叶变换。
在将图像变换到频率域之前,对其中⼼化处理可使变换后结果更利于观察与分析,因此,乘以以实现中⼼化。
在反变换到图像域后,得到的图像是,将其乘以使图像平移还原,因此,乘以还原平移。
在对数字图像进⾏频移滤波时,需要关注卷积缠绕和振铃现象,这是在设计滤波函数时需要尽⼒避免的。
1)卷积缠绕给定⾮周期信号,对其进⾏离散傅⾥叶变换或者反变换后得到周期信号,⽽周期信号卷积操作可能产⽣缠绕。
卷积操作是对两个信号滑动乘积进⾏累加,当累加区间⼤于任意信号周期,就可能对⼀个信号周期外的值进⾏重复累加。
解决卷积缠绕的⽅法就是在傅⾥叶变换(或反变换前)进⾏0填充处理,0填充使得信号周期不⼩于卷积区间,从⽽避免了卷积缠绕。
2)振铃使⽤0填充可以避免卷积缠绕,但可能产⽣振铃现象。
公式使⽤频域乘积进⾏滤波处理,其等价操作为空间域的卷积。
当 H(u,v) 为理想低通滤波器(盒函数),其反傅⾥叶变换 h(x,y) 包含⽆限震荡频率,⽆限震荡频率使得在卷积时必然产⽣振铃现象。
如果对其进⾏0填充以避免卷积缠绕,必然对 f(x,y)信号截断,对截断后的 f(x,y) 变换到频率域,发现之前的盒函数在边缘上出现了震荡,使振铃现象更加严重。
综上描述,对于理想低通滤波器,振铃现象不可避免,如果0填充以避免卷积缠绕将使得振铃现象更加明显。
⼀个折中⽅案就是对图像进⾏0填充,但不对滤波器进⾏填充,由于图像0填充在⼀定程度降低了卷积缠绕的影响,同时由于图像0填充使得理想低通滤波器引起的振铃现象减弱,从⽽得到相对理想的结果。
⼀个更好的⽅案是使⽤⾼斯低通滤波器,由于⾼斯函数的傅⾥叶变换(或反傅⾥叶变换)均为⾼斯函数,⾼斯函数没有震荡周期,故天然没有振铃现象。
频域滤波原理
cut-off=14, power=99.85%
cut-off=12, power=99.84%
cut-off=10, power=99.82%
用不同的功率百分比恢复的水田图像 Paddy (泗洪)
3 遥感图像的增强处理:3.3 频域滤波
power=100% cut-off=40, power=99.98% cut-off=38, power=99.98% cut-off=36, power=99.98% cut-off=34, power=99.98%
cut-off=49, power=99.18%
cut-off=45, power=99.04%
cut-off=41, power=98.88%
cut-off=37, power=98.67%
cut-off=33, power=98.41%
cut-off=29, power=98.06%
cut-off=25, power=97.6
Smoothing with a Gaussian
3 遥感图像的增强处理:3.3 频域滤波
The Gaussian pyramid
3 遥感图像的增强处理:3.3 频域滤波
Character recognition
using a GLPF with D0 80
• Although humans fill these gaps visually without difficulty, • A machine recognition system has real difficulties reading broken characters.
3 遥感图像的增强处理:3.3 频域滤波
the average value of the resulting image will be zero make prominent edges stand out pixels which have negative values will be produced
空间域滤波——精选推荐

空间域滤波空间域滤波基础 某些邻域处理⼯作是操作邻域的图像像素值以及相应的与邻域有相同维数的⼦图像的值。
这些⼦图像可以被称为滤波器、掩模、核、模板或窗⼝,其中前三个词是更为普遍的术语。
在滤波器⼦图像中的值是系数值,⽽不是像素值。
空间滤波就是在待处理图像中逐点地移动掩模。
在每⼀点 (x, y) 处,滤波器在该点的响应通过事先定义的关系来计算。
对于线性空间滤波,其响应由滤波器系数与滤波掩模扫过区域的相应像素值的乘积之和给出。
对于⼀个尺⼨为 m×n 的掩模,我们假设 m=2a+1 且 n=2b+1,这⾥的 a、b 为⾮负整数。
在后续的讨论中,处理的掩模的长与宽都为奇数。
⼀般来说,在 M×N 的图像 f 上,⽤ m×n ⼤⼩的滤波器掩模进⾏线性滤波由下式给出: 这⾥,a=(m-1)/2 且 b=(n-1)/2。
为了得到⼀幅完整的经过滤波处理的图像,必须对 x=0, 1, 2, …, M-1 和 y=0, 1, 2, …, N-1 依次应⽤公式。
这样,就保证了对图像中的所有像素进⾏了处理。
式中的线性滤波处理与频率域中卷积处理的概念很相似。
因此,线性空间滤波处理经常被称为“掩模与图像的卷积”。
类似地,滤波掩模有时也可以称为“卷积模板”或“卷积核”。
当滤波中⼼靠近图像轮廓时发⽣的情况 考虑⼀个简单的⼤⼩为 n×n 的⽅形掩模,当掩模中⼼距离图像边缘为 (n-1)/2 个像素时,该掩模⾄少有⼀条边与图像轮廓相重合。
如果掩模的中⼼继续向图像边缘靠近,那么掩模的⾏或列就会处于图像平⾯之外。
⽅法⼀:最简单的⽅法就是将掩模中⼼点的移动范围限制在距离图像边缘不⼩于 (n-1)/2 个像素处。
如果要保持与原图像⼀样⼤⼩,可以直接将未处理的图像边缘像素直接复制到结果图像,或者⽤全部包含于图像中的掩模部分滤波所有像素。
通过这种⽅法,图像靠近边缘部分的像素带将⽤部分滤波掩模来处理。
⽅法⼆:在图像边缘以外再补上 (n-1)/2 ⾏和 (n-1)/2 列灰度值为0(也可为其它常值)的像素点,或者将边缘复制补在图像之外。
16、频率域滤波

16、频率域滤波1、频率域与空间域之间的关系 在中,我们已经知道了如何将图像转换到频率域,以及如何将频率域图像通过傅⾥叶逆变换转换回图像,这样⼀来,可以利⽤空域图像与频谱之间的对应关系,尝试将空域卷积滤波变换为频域滤波,⽽后再将频域滤波处理后的图像反变换回空间域,从⽽达到图像增强的⽬的,这样做的⼀个最主要的吸引⼒再域频率域滤波具有直观性的特点。
根据著名的卷积定律,两个⼆维连续函数再空间域的卷积可由其相应的两个傅⾥叶变换乘积的反变换⽽得到,反之,在频率域中的卷积可由在空间域中乘积的傅⾥叶变换⽽得到。
即f1(t)↔F1(ω),f2(t)↔F2(ω)f1(t)∗f2(t)↔F1(ω)⋅F2(ω)2、频率域滤波的基本步骤 本⽂重点就来讲⼀讲如何通过频率域滤波来实现图像的平滑和锐化。
⾸先将频率域滤波的步骤来做⼀个⼩结如下:给定⼀幅⼤⼩为MXN的输⼊图像f(x,y),选择填充参数P=2M.Q=2N.对f(x,y)添加必要数量的0,形成⼤⼩为PXQ的填充图像f p(x,y)。
⽤(−1)x+y乘以f p(x,y),移到其变换中⼼。
计算上图的DFT,得到F(u,v).⽣成⼀个实的,对称的滤波函数H(u,v),其⼤⼩为PXQ,中⼼在(P/2,Q/2)处。
⽤阵列相乘得到乘积G(u,v)=H(u,v)F(u,v);即G(i,k)=H(i,k)F(i,k)得到处理后的图像:g p(x,y)=real J−1[G(u,v)](−1)x+y其中,为忽略由于计算不准确导致的寄⽣复成分,选择实部,下标p指出我们处理的是填充后的图像。
从g p(x,y)的左上象限提取MXN区域,得到最终处理结果g(x,y) 由上述叙述可知,滤波的关键取决于滤波函数H(u,v),常常称为滤波器,或滤波器传递函数,因为它在滤波中抑制或除去了频谱中的某些分量,⽽保留其他的⼀些频率不受影响,从⽽达到滤波的⽬的。
⽽本节将讲解⼀些常⽤的滤波器。
3、使⽤频率域滤波平滑图像 在空间域我们已经讲过图像平滑的⽬的及空间域平滑滤波,现在在频率域滤波中我们⾸先讲解三种频率平滑滤波器:理想滤波器、巴特沃斯滤波器、⾼斯滤波器。
简述空域处理方法和频域处理方法的区别

空域处理方法和频域处理方法是数字图像处理中常见的两种基本处理方法,它们在处理图像时有着不同的特点和适用范围。
下面将从原理、应用和效果等方面对两种处理方法进行简要介绍,并对它们的区别进行分析。
一、空域处理方法1. 原理:空域处理是直接对图像的像素进行操作,常见的空域处理包括图像增强、平滑、锐化、边缘检测等。
这些处理方法直接针对图像的原始像素进行操作,通过像素之间的关系来改变图像的外观和质量。
2. 应用:空域处理方法广泛应用于图像的预处理和后期处理中,能够有效改善图像的质量,增强图像的细节和对比度,以及减轻图像的噪声。
3. 效果:空域处理方法对图像的局部特征和细节有很好的保护和增强作用,能够有效地改善图像的视觉效果,提升图像的清晰度和质量。
二、频域处理方法1. 原理:频域处理是通过对图像的频率分量进行操作,常见的频域处理包括傅立叶变换、滤波、频域增强等。
这些处理方法将图像从空间域转换到频率域进行处理,再通过逆变换得到处理后的图像。
2. 应用:频域处理方法常用于图像的信号处理、模糊去除、图像压缩等方面,能够有效处理图像中的周期性信息和干扰信号。
3. 效果:频域处理方法能够在频率域对图像进行精细化处理,提高图像的清晰度和对比度,对于一些特定的图像处理任务有着独特的优势。
三、空域处理方法和频域处理方法的区别1. 原理不同:空域处理方法直接对图像像素进行操作,而频域处理方法是通过对图像进行频率分析和变换来实现图像的处理。
2. 应用范围不同:空域处理方法适用于对图像的局部特征和细节进行处理,而频域处理方法适用于信号处理和频率信息的分析。
3. 效果特点不同:空域处理方法能更好地保护和增强图像的细节和对比度,频域处理方法能更好地处理图像中的周期性信息和干扰信号。
空域处理方法和频域处理方法是数字图像处理中常用的两种处理方法,它们在原理、应用和效果等方面有着不同的特点和适用范围。
在实际应用中,可以根据图像的特点和处理需求选择合适的方法,以获得更好的处理效果。
