河北衡水中学2020届高三第八次调研考试理科数学(含答案解析)

合集下载

2020届河北省衡水中学高三下学期第八次调研数学(文)试题(解析版)

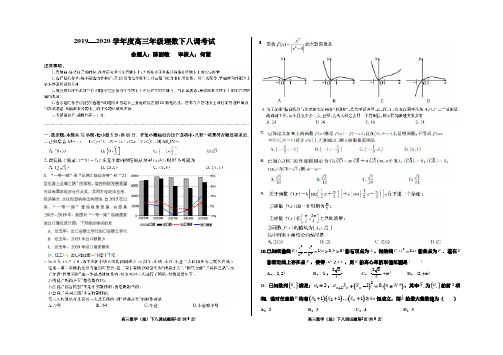
2020届河北省衡水中学高三下学期第八次调研数学（文）试题一、单选题1．设全集为R ，集合{}2|20A x x x =-<，集合{}|1B x x =<，则A B =I （） A ．()1,1- B ．()1,2- C ．()0,1 D ．()0,2【答案】C【解析】化简集合,A B ，根据交集的定义，即可求解. 【详解】()0,2A =，()1,1B =-，所以()0,1A B =I ，故选：C. 【点睛】本题考查集合的运算，属于基础题. 2．已知复数()20201z i i =⋅+，则z 的模z =（）A ．1 BC D ．4【答案】B 【解析】由20201,1i z i ==+，根据模长公式，即可求解.【详解】已知()111z i i =⋅+=+，所以z =故选：B 【点睛】本题考查虚数的定义，以及复数的模长，属于基础题.3．在2019年的国庆假期中，重庆再次展现“网红城市”的魅力，吸引了3000多万人次的客流.北京游客小李慕名而来，第一天打算游览“洪崖洞”，“解放碑”，“朝天门”.如果随机安排三个景点的游览顺序，则最后游览“朝天门”的概率为（）A ．16B ．56 C ．13D ．23【答案】C【解析】“洪崖洞”，“解放碑”，“朝天门”分别记为,,A B C ，列出游览三个景点的所有安排顺序，确定最后游览“朝天门”安排个数，根据古典概型的概率即可求解. 【详解】“洪崖洞”，“解放碑”，“朝天门”分别记为,,A B C ，随机安排三个景点的游览顺序，有以下安排方法：{,,},{,,},{,,},{,,}A B C A C B B A C B C A ， {,,},{,,}C B A C A B 共有6种安排方法，其中最后游览“朝天门”由2种安排方法其概率为2163P ==. 故选：C 【点睛】本题考查古典概型的概率，属于基础题.4．已知非零向量a v ，b v 满足：()1,1a =v，1b =v ，()a b b -⊥v v v ，则向量a v ，b v 的夹角大小为（） A ．6πB ．4π C ．3π D ．2π 【答案】B【解析】由()a b b -⊥r r r ，()1,1a =r ，1b =r ，求出a b ⋅r r，再由向量的夹角公式，即可求解. 【详解】由()a b b -⊥r r r ，有20a b b ⋅-=r r r ，则2cos a b b θ=r r r ，有2cos ,0,24b a bπθθπθ===≤≤=r r r . 故选：B【点睛】本题考查向量的数量积运算，考查向量的夹角，属于基础题.5．已知正方体1111ABCD A B C D -的棱长为1，其内切球与外接球的表面积分别为1S ，2S ，则12S S =（） A ．1 B ．12 C ．13D ．14【答案】C【解析】根据正方体的内切球的直径为正方体的棱，求出其半径，外接球的直径为正方体的对角线，求出半径，由球的表面积公式，即可求解. 【详解】内切球的半径112r =，外接球的半径2r = 所以表面积之比为2112213S r S r ⎛⎫== ⎪⎝⎭.故选：C. 【点睛】本题考查正方体的内切球和外接球的表面积，属于基础题. 6．已知tan 2θ=-，则sin sin 2πθθ⎛⎫+ ⎪⎝⎭的值为（） A ．25B ．25-C ．35D ．45【答案】B【解析】首先利用诱导公式化简函数解析式，之后利用正余弦平方和等于1，得到关于弦的分式型二次齐次式，之后化成切的式子，代入求解得结果. 【详解】222cos sin tan 22sin sin cos sin 2cos sin 1tan 145πθθθθθθθθθθ-⎛⎫+=⋅====- ⎪+++⎝⎭，故选：B. 【点睛】该题考查的是有关三角函数化简求值的问题，涉及到的知识点有诱导公式，同角三角函数关系式，属于简单题目.7．如图所示的一个算法的程序框图，则输出d 的最大值为（）A ．2B ．2C ．12+D ．122+【答案】C 【解析】【详解】模拟程序的运行，可得程序框图的功能是求半圆y ＝上的点到直线x ﹣y ﹣2＝0的距离的最大值，如图：可得：d 的最大值为OP +r ＝+1．故选：C ．8．已知()f x 是定义在[)0,+∞的函数，满足()()3f x f x +=-，当[)0,3x ∈时，()2x f x =，则()2log 192f =（）A ．12B ．13C ．2D ．3【答案】D【解析】根据条件确定函数的周期为6，利用函数周期性进行转化即可. 【详解】()()()()36f x f x f x f x +=-⇒+=，6T =，()()22log 192log 643f f =⨯()()2log 3226log 3log 323f f =+===，故选：D. 【点睛】该题考查的是有关函数值的求解问题，涉及到的知识点有函数的周期性，对数式的运算法则，属于简单题目.9．如图，网格纸上小正方形的边长为1，粗线画出的是某三棱锥的三视图，则该三棱锥的外接球的体积为（）A ．1122πB ．4411πC ．4411πD ．1122π【答案】B【解析】借助长方体作出棱锥，利用球心到顶点的距离相等确定O 的位置，利用球的性质求出半径，即可计算. 【详解】由三视图可知该几何体是如图所示的三棱锥A BCD -，F 为BD 的中点，外接球球心O 在过CD 的中点E 且垂直于平面BCD 的直线l 上，又点O 到,,A B D 的距离相等，所以O 又在过左边正方体一对棱的中点,M N 所在直线上，在OEN ∆中，由NF MF NE OE =，即223OE=，得3OE =，所以三棱锥A BCD -外接球的球半径22223(2)11R OE BE =+=+=，44113V π=.【点睛】本题主要考查了三视图，棱锥的外接球，球的体积，属于中档题.10．已知函数(2),1()1,11f x x f x x x ->⎧=⎨--≤≤⎩，关于x 的方程()log (1)a f x x =+恰有5个解，则a 的取值范围为（） A ．1175a ≤< B ．1175a << C ．1164a << D ．1164a ≤< 【答案】B【解析】根据()f x 求出()f x 有表达式，可用图象来分析，再由()f x 的图象与()log (1)a g x x =+有5个交点可得a 的范围．【详解】由题意函数()y f x =的图象与log (1)a y x =+的图象有5个交点．作出()f x 的图象，根据函数解析式，其图象在区间[21,21]n n -+（*n N ∈）上的图象与[1,1]-上相同，如图，若1a >，则log (1)a y x =+是增函数，它与()f x 的图象只有一个交点，不合题意，当01a <<时log (1)a y x =+是减函数，要有5个交点，，因此有log (41)1log (61)1a a +>-⎧⎨+<-⎩，解得1175a <<．故选：B. 【点睛】本题考查方程解的个数与函数零点问题．解题时转化为函数图象交点个数，通过数形结合思想求解．11．已知抛物线24x y =的焦点为F ,过直线2y x =-上任一点引抛物线的两条切线,切点为A ,B ,则点F 到直线AB 的距离( ) A ．无最小值B ．无最大值C ．有最小值,最小值为1D ．有最大值,【答案】D【解析】设()11,A x y ,()22,B x y ,可得2114x y =,2224x y =,即可求得A 为切点的切线方程1l 和以B 为切点的切线方程2l ,设过直线2y x =-上任一点为()00,P x y ,将()00,P x y 代入1l 和2l ,即可求得直线AB 的方程,进而求得点F 到直线AB 的距离.【详解】设()11,A x y ,()22,B x y ,可得2114x y =,2224x y =Q 以A 为切点的切线方程为1l :()1112x y y x x -=-,即112xy x y =-——① 同理可得,以B 为切点的切线方程为2l :222xy x y =- ——②设过直线2y x =-上任一点为()00,P x y∴ ()00,P x y 代入①②得10012002,2,2x y x y x y x y ⎧=-⎪⎪⎨⎪=-⎪⎩所以直线AB 的方程为002xy x y =-,即002x y x y =-, 又Q 002y x =-,即0122x y x ⎛⎫=-+⎪⎝⎭Q AB 过定点()2,2P ,∴ 当PF AB ⊥时,()0,1F 到l 的距离的最大值为=当AB 过点F 时,距离的最小值为0 故选:D . 【点睛】本题主要考查直线与圆锥曲线的综合应用能力,综合性强,本题涉及到轨迹方程的求法及直线与抛物线的相关知识,解题时要注意合理地进行等价转化.12．已知函数()()()()()22213122x x f x a a e a x e x =---+++有4个不同的零点，则实数a 的取值范围为( ) A ．1,2e ⎛⎫⎪⎝⎭B ．11,22e +⎛⎫⎪⎝⎭C ．()1,11,2e ⎛⎫⎪⎝⎭UD ．11,11,22e +⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭U 【答案】D【解析】因为()0f x =,故()()()()222131220x x a a e a x e x ---+++=,化简为:()()()e 221e 20xxa x a x ⎡⎤⎡⎤-+--+=⎣⎦⎣⎦,即2e x x a +=,221e xx a +-=,构造函数()2ex x g x +=,求其最值即可求得实数a 的取值范围. 【详解】Q 由()0f x =,()()()()222131220x x a a e a x e x ---+++=∴ 得()()()e 221e 20x xa x a x ⎡⎤⎡⎤-+--+=⎣⎦⎣⎦,可得:2e x x a +=,221ex x a +-=, 设()2e x x g x +=,则()()1ex x g x -+'=, Q 当()0g x '>时,1x <-当()<0g x '时,1x >-∴ ()g x 在(),1-∞-上单调递增,在()1,-+∞上单调递减,故()20g -=,()()max 1e g x g =-=,当2x >-,()0g x >.Q x →-∞,()g x →-∞,x →+∞,()0g x +→.要使方程有4个不同的零点,则0e021e 21a a a a<<⎧⎪<-<⎨⎪-≠⎩,可得11e 22a +<<,1a ≠, 故选:D. 【点睛】本题考查了函数零点问题,要将函数的求零点问题转化为求方程根的问题,就自变量取不同范围进行讨论求解这是解题关键.二、填空题13．设x ，y 满足约束条件3403400x y x y x y -+≥⎧⎪--≤⎨⎪+≥⎩，则2x y -的最小值是______.【答案】-3【解析】设2z x y =-，根据约束条件画出可行域，可知z 取最小值时，2y x z =-在y 轴截距最大；由图象可知当2y x z =-过A 时截距最大，求出A 点坐标，代入可得结果. 【详解】设2z x y =-，由约束条件可得可行域如下图阴影部分所示：则z 取最小值时，2y x z =-在y 轴截距最大由图象可知，当2y x z =-过A 时，截距最大由3400x y x y -+=⎧⎨+=⎩得：()1,1A -min 213z ∴=--=-，即()min 23x y -=-本题正确结果：3- 【点睛】本题考查线性规划中最值问题的求解，关键是能够将问题转化为在y 轴截距的最值求解问题，根据图象平移求得结果.14．对于三次函数()()320ax bx d a f x cx =+++≠，定义：设()f x ''是()f x '的导数，若方程()0f x ''=有实数解0x ，则称()()00,x f x 为函数()f x 的拐点.某同学经过探索发现任何一个三次函数都有“拐点”；任何一个三次函数都有对称中心，且“拐点”就是对称中心.设函数()3211533212g x x x x =-+-，则122020202120212021g g g ⎛⎫⎛⎫⎛⎫++⋅⋅⋅+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭______；()20201112021i i i g -=⎛⎫'= ⎝-⎪⎭∑______. 【答案】2020 0【解析】利用二阶导数求出三次函数()y g x =的拐点，进而可得出三次函数()y g x =图象的对称中心坐标，由此可计算出122020202120212021g g g ⎛⎫⎛⎫⎛⎫++⋅⋅⋅+⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭以及()20201120211i i i g -=⎛⎫' ⎪⎝-⎭∑的值. 【详解】()3211533212g x x x x =-+-Q ，()23g x x x '∴=-+，()21g x x ''=-，令()0g x ''=，得12x =，又112g ⎛⎫= ⎪⎝⎭，所以，三次函数()y g x =图象的对称中心坐标为1,12⎛⎫⎪⎝⎭，即()()12g x g x +-=，所以，122020101022020202120212021g g g ⎛⎫⎛⎫⎛⎫++⋅⋅⋅+=⨯=⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，()()2221212212112021202120212021n n n n n n g g g g ----⎛⎫⎛⎫⎛⎫⎛⎫''''-+-=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭Q 222212122202243320212021202120212021n n n n n ⎡⎤---⎛⎫⎛⎫=-+--+=⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦，因此，()()()202010102211121212111202120220211n n i i n g n n g i g =--=--⎛⎫⎛⎫''-⎡-+-⎢ ⎤⎪ ⎪⎝⎭⎭⎝⎭⎛⎫'= ⎪⎥⎝⎣⎦∑∑()1010221101011010202210104202242020212021n n=⨯+⨯-⨯-===∑. 故答案为：2020；0. 【点睛】本题考查新定义“拐点”的应用，涉及三次函数的对称中心以及等差数列求和问题，考查计算能力，属于难题.15．已知双曲线C :22221x y a b-=(0a >,0b >)的左,右焦点为1F ,2F ,以12F F 为直径的圆与双曲线C 的渐近线在第一象限交于点P ,线段2PF 与双曲线的交点M 为2PF 的中点,则双曲线C 的离心率为______.1【解析】因为以12F F 为直径的圆与双曲线C 的渐近线在第一象限交于点P ,故222x y c b y xa ⎧+=⎪⎨=⎪⎩解得,,x a y b =⎧⎨=⎩,求得(),P a b ,由中点坐标公式解得,22a c b M +⎛⎫⎪⎝⎭,将其代入22221x y a b-=,即可求得双曲线C 的离心率. 【详解】Q 以12F F 为直径的圆与双曲线C 的渐近线在第一象限交于点P ,∴ 222x y c by xa ⎧+=⎪⎨=⎪⎩解得:,,x a y b =⎧⎨=⎩ 故(),P a b , 又Q ()2,0F c ,∴,22a c b M +⎛⎫⎪⎝⎭,代入双曲线方程22221x y a b-= 可得:22240c ac a +-=,化简可得2240e e +-=∴1e =-,又1e >,∴1e =.故答案为1. 【点睛】本题考查了求双曲线离心率的问题,解题关键双曲线的几何性质及离心率的求法,数形结合是本题的关键,查分析能力和计算能力,属于中档题. 16．已知数列{}n a ,满足()()*112n n na n a n +--=∈N,{}na 的前n 项和为nS,对任意的*n ∈N ,当5n ≠时,都有5n S S <,则5S 的取值范围为______.【答案】()5,6【解析】由()112n n na n a +--=,当1n =,得12a =.由()()1121212n n n n na n a n a na +++⎧--=⎪⎨+-=⎪⎩ 可得212n n n a a a +++=,即可求得{}n a 为等差数列,结合当5n ≠时,都有5n S S <,即可求得5S 的取值范围. 【详解】Q 由()112n n na n a +--=,∴ 当1n =,得12a =.Q ()112n n na n a +--=——①可得()1212n n n a na +++-=——②∴ 由①②得:212n n n a a a +++=,故{}n a 为等差数列.又Q 120a =>,5S 最大,则0d <,50a >,60a <, 即240,250d d +>⎧⎨+<⎩1225d ⇒-<<-,又51010S d =+,可得()55,6S ∈ 故答案为:()5,6. 【点睛】本题解题关键是根据已知条件判断出数量是等差数列,掌握数列单调性是解本题的关键,考查了分析能力和计算能力,属于基础题.三、解答题17．已知数列{}n a ,是一个等差数列,且22a =,145a a +=,数列{}n b 是各项均为正数的等比数列,且满足:112b =,24164b b ⋅=. （1）求数列{}n a 与{}n b 的通项公式; （2）求证:11222n n a b a b a b ++⋅⋅⋅+<.【答案】（1）n a n =，12nn b ⎛⎫= ⎪⎝⎭（2）证明见解析【解析】（1）因为{}n a 为等差数列,设公差为d ,则1112,35,a d a a d +=⎧⎨++=⎩即可求得首项和公差,即可求得{}n a .因为{}n b 为等比数列,2243164b b b ⋅==,23118b b q ==,即可求得公比,进而求得{}n b .（2）因为n a n =,12nn b ⎛⎫= ⎪⎝⎭,所以()23111111123122222n nn T n n -⎛⎫⎛⎫⎛⎫⎛⎫=⨯+⨯+⨯+⋅⋅⋅+-⨯+⨯ ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭,根据数列求和错位相减法,即可求得n T ,进而求得答案. 【详解】（1）Q {}n a 为等差数列,设公差为d ,∴1112,35,a d a a d +=⎧⎨++=⎩∴11,1,a d =⎧⎨=⎩∴()11n a a n d n =+-=.Q {}n b 为等比数列,0n b >,设公比为q ,则0q >,∴2243164b b b ⋅==,23118b b q ==, ∴12q =,1111222n nn b -⎛⎫⎛⎫=⋅= ⎪ ⎪⎝⎭⎝⎭. （2）令112233n n n T a b a b a b a b =+++⋅⋅⋅+,∴ ()23111111123122222n nn T n n -⎛⎫⎛⎫⎛⎫⎛⎫=⨯+⨯+⨯+⋅⋅⋅+-⨯+⨯ ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭——①可得:()2311111112122222nn n T n n +⎛⎫⎛⎫⎛⎫⎛⎫=⨯+⨯+⋅⋅⋅+-⨯+⨯ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭——②∴由①-②得:23111112211111111222222212nn n n n T n n ++⎛⎫⎛⎫- ⎪ ⎪ ⎪⎝⎭⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎝⎭=+++⋅⋅⋅+-⨯=-⨯ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭-,∴1112222n nn T n -⎛⎫⎛⎫=--⨯< ⎪ ⎪⎝⎭⎝⎭.故11222n n a b a b a b ++⋅⋅⋅+<. 【点睛】本题考查求等差数列通项公式和数列求和.错位相减法求数列和,适用于通项公式为等差的一次函数乘以等比的数列形式,考查了学生的计算能力,属于基础题型.18．如图，已知在四棱锥P ABCD -中，底面ABCD 为正方形，PD PA =，E 点为AD 的中点，PE CD ⊥.（1）求证：平面PAD ⊥平面ABCD ；（2）若正方形的边长为4，求D 点到平面PEC 的距离. 【答案】（1）见解析；（2）455DH =【解析】（1）PD PA =，E 点为AD 的中点，可知PE AD ⊥，再由已知条件PE CD ⊥，可证PE ⊥平面ABCD ，即可证明结论；（2）连CE ，由（1）可得平面PEC ⊥平面ABCD ，过D 作DH CE ⊥与H ，根据面面垂直的性质定理，可得DH ⊥平面PCE ，即DH 为所求，且DH 为Rt CDE ∆斜边上的高，可得出结论【详解】（1）证明：由PD PA =，E 点为AD 的中点，可知PE AD ⊥，再已知PE CD ⊥，且AD ，CD 相交于D ，则PE ⊥平面ABCD . 又PE ⊂平面ADP ，所以平面PAD ⊥平面ABCD . （2）解：由（1）知PE ⊥平面ABCD ，则平面PEC ⊥平面ABCD ，相交于EC .作DH EC ⊥，可知DH 为D 点到平面PEC 的距离，且2245524DH ==+ 【点睛】本题考查面面垂直的证明以及面面垂直性质的应用，考查空间垂直的转化，属于基础题. 19．2019年双十一落下帷幕，天猫交易额定格在268（单位：十亿元）人民币（下同），再创新高，比去年218（十亿元）多了50（十亿元），这些数字的背后，除了是消费者买买买的表现，更是购物车里中国新消费的奇迹，为了研究历年销售额的变化趋势，一机构统计了2010年到2019年天猫双十一的销售额数据y （单位：十亿元），绘制如下表1：表1 年份 2010 2011 2012 2013 2014 2015 2016 2017 2018 2019 编号x 1 2 3 4 5 6 7 8 9 10 销售额y 0.98.722.4416594132.5172.5218268根据以上数据绘制散点图，如图所示．（1）把销售额超过100（十亿元）的年份叫“畅销年”，把销售额超过200（十亿元）的年份叫“狂欢年”，从2010年到2019年这十年的“畅销年”中任取2个，求至少取到一个“狂欢年”的概率；（2）根据散点图判断，y a bx =+与2y cx d =+哪一个适宜作为销售额y 关于x 的回归方程类型？（给出判断即可，不必说明理由）；（3）根据（2）的判断结果及下表中的数据，建立y 关于x 的回归方程，并预测2020年天猫双十一的销售额．（注：数据保留小数点后一位）参考数据：2i i t x =，参考公式：对于一组数据(),i i u v ，()22,u v ，…，(),n n u v ，其回归直线µµvu αβ=+$的斜率和截距的最小二乘估计公式分别为µ1221ni i i nii u v nuvunuβ==-=-∑∑，µµv u αβ=-．【答案】（1）56（2）2y cx d =+更适宜．（3）22.7 2.0y x =-$，324.7十亿元．【解析】（1）由表中数据可记畅销年中不是狂欢年为,a b ，狂欢年为,A B ，列举出基本事件个数，根据古典概型的概率计算公式即可求解. （2）由散点图可得出回归方程类型.（3）根据公式代入数据，求出b$、$a ，得出回归方程，从而可求解. 【详解】解：（1）畅销年个数：4，其中的狂欢年个数：2，记畅销年中不是狂欢年为,a b ；狂欢年为,A B ，则总共有(,)a b ，(,)a A ，(,)b A ，(,)a B ，(,)b B ，(,)A B 则5()6P A =（2）由题意2y cx d =+更适宜．（3）1011022110677701038.5102285005702.725380148301055021110i ii i i t y t ybt t==--⨯⨯====≈--∑∑$，$102 2.738.5 2.0ay bt =-=-⨯≈-$， $22.7 2.0y x ∴=-，当11x =时，$324.7y =（十亿元）， ∴预测2020年双十一的销售额为324.7十亿元．【点睛】本题考查了古典概型的概率计算公式、回归方程的求法，考查了学生的数据分析与处理能力，属于中档题.20．已知椭圆C ：22221x y a b+=()0a b >>的两个焦点为1F ,2F ,焦距为直线l :1y x =-与椭圆C 相交于A ,B 两点,31,44P ⎛⎫-⎪⎝⎭为弦AB 的中点. （1）求椭圆的标准方程;（2）若直线l :y kx m =+与椭圆C 相交于不同的两点M ,N ,()0,Q m ,若3OM ON OQ λ+=u u u u v u u u v u u u v（O 为坐标原点）,求m 的取值范围.【答案】（1）2213x y +=（2）113m <<或113m -<<-【解析】（1）因为31,44P ⎛⎫-⎪⎝⎭为弦AB 的中点,设()11,A x y ,()22,B x y ,将其代入22221x y a b+=利用点差法,即可求得答案. （2）因为M ,Q ,N 三点共线,133OQ OM ON λ=+u u u r u u u u r u u u r, 根据三点共线性质可得:1133λ+=,则2λ=,将直线l 和椭圆C 联立方程22,33y kx m x y =+⎧⎨+=⎩消掉y ,结合已知,利用韦达定理即可求得答案. 【详解】（1）Q焦距为则c =设()11,A x y ,()22,B x y ,Q 31,44P ⎛⎫- ⎪⎝⎭为弦AB 的中点,根据中点坐标公式可得:1232x x +=,1212y y +=-,又Q 将其()11,A x y ,()22,B x y 代入椭圆C :22221x ya b+=∴ 2222221122222222b x a y a b b x a y a b⎧+=⎨+=⎩ ∴ 将两式作差可得:()()()()22121212120b x x x x a y y y y +-++-=,∴()()22121222121231ABb x x y y b k x x a y y a+-==-==-+, ∴223a b =——①. Q 222a c b -=——②由①②得: 2231a b ⎧=⎨=⎩ ∴椭圆的标准方程为2213x y +=.（2）Q M ,Q ,N 三点共线,133OQ OM ON λ=+u u u ru u u ur u u u r∴ 根据三点共线性质可得:1133λ+=,则2λ= 设()11,M x y ,()22,N x y ,则1212033x x +=,∴122x x =-.将直线l 和椭圆C 联立方程22,33y kx m x y =+⎧⎨+=⎩消掉y . 可得:()222136330kxkmx m +++-=.220310k m ∆>⇒-+>——①,根据韦达定理:122613km x x k +=-+,21223313m x x k-=+, 代入122x x =-,可得:22613km x k =+,222233213m x k--=+, ∴ ()222222363321313k m m kk --⨯=++,即()2229131m k m -⋅=-. Q 2910m -≠,219m ≠, ∴22213091m k m -=≥-——②, 代入①式得22211091m m m --+>-,即()22211091m m m -+->-, ∴()()2221910m m m --<,∴2119m <<满足②式, ∴113m <<或113m -<<-.【点睛】本题主要考查直线与圆锥曲线位置关系,所使用方法为韦达定理法:因直线的方程是一次的,圆锥曲线的方程是二次的,故直线与圆锥曲线的问题常转化为方程组关系问题,最终转化为一元二次方程问题,故用韦达定理及判别式是解决圆锥曲线问题的重点方法之一,尤其是弦中点问题,弦长问题,可用韦达定理解决. 21．已知函数()x f x e ax =-.（1）若函数()f x 在1(,2)2x ∈上有2个零点，求实数a 的取值范围.（注319e >）（2）设2()()g x f x ax =-，若函数()g x 恰有两个不同的极值点1x ，2x ，证明：12ln(2)2x x a +<. 【答案】（1）(,a e ∈（2）见证明【解析】（1）将a 分离，构造函数()x e h x x=，利用导数研究()h x 的图像，得到a 的范围.（2）由已知()g x ，求其导函数，由x 1，x 2是g （x ）的两个不同极值点，可得a ＞0，结合g ′（x 1）＝0，g ′（x 2）＝0得到1120x e ax a --=，2220xe ax a --=进一步得到12122x x e e a x x -=-，把问题转化为证明1212212x x x x e e e x x +--＜，将其变形后整体换元构造函数()t ϕ．再利用导数证明()t ϕ＞0得答案．【详解】（1）1,22x ⎡⎤∈⎢⎥⎣⎦时，由()0f x =得xea x=，令()()()21x xe x e h x h x x x ='-=⇒ ∴112x ≤<时，()0h x '<， 12x <≤时，()0h x '>，∴()h x 在1,12⎡⎤⎢⎥⎣⎦上是减函数，在()1,2上是增函数.又122h e ⎛⎫= ⎪⎝⎭，()222e h =，()1h e =()344161640444e e e e e e ---==>， ∴()122h h ⎛⎫>⎪⎝⎭，∴h （x ）的大致图像：利用()y h x =与y a =的图像知(,2a e e ∈.（2）由已知()2xg x e ax ax =--，∴()2xg x e ax a =--'，因为1x ，2x 是函数()g x 的两个不同极值点（不妨设12x x <），易知0a >（若0a ≤，则函数()f x 没有或只有一个极值点，与已知矛盾），且()10g x '=，()20g x '=.所以1120x e ax a --=，2220xe ax a --=.两式相减得12122x x e e a x x -=-，于是要证明()12ln 22x x a +<，即证明1212212x xx x e e e x x +-<-，两边同除以2x e ，即证12122121x x x x e ex x ---<-，即证()12122121x x x x x x e e --->-，即证()121221210x x x x x x ee ----+>，令12x x t -=，0t <.即证不等式210tt te e -+>，当0t <时恒成立. 设()21tt t te e ϕ=-+，则()2212t t tt te t e e ϕ=+⋅⋅-'=22211]22t t t t t t e e e e ⎡⎫⎛⎫+-=--+⎪⎢ ⎪⎝⎭⎣⎭. 设()212t t h t e =--，则()221111222t t h t e e ⎛⎫=-=- ⎪⎝⎭'，当0t <时，()0h t '<，()h t 单调递减，所以()()00h t h >=，即2102t t e ⎛⎫-+> ⎪⎝⎭，所以()0t ϕ'<，所以()t ϕ在0t <时是减函数.故()t ϕ在0t =处取得最小值()00ϕ=.所以()0t ϕ>得证.所以()12ln 22x x a +<. 【点睛】本题考查利用导数研究函数的零点问题，考查了导数在解决不等式证明问题中的应用，考查了数学转化思想方法和函数构造法，属于难题． 22．在直角坐标系xOy 中,曲线1C :22cos ,2sin ,x y θθ=+⎧⎨=⎩(θ为参数),以原点O 为极点,x 轴的正半轴为极轴建立极坐标系,曲线2C :24sin 3ρρθ=-,曲线1C 与曲线2C 相交于M ,N两点.（1）求曲线2C 的直角坐标方程与直线MN 的一般方;（2）点3,04P ⎛⎫- ⎪⎝⎭,求PM PN +. 【答案】（1）2C ：2243x y y +=-，直线MN ：4430x y -+=（2【解析】（1）将曲线1C :22cos 2sin x y θθ=+⎧⎨=⎩化简为:2cos 2sin 2x y θθ-⎧=⎪⎪⎨⎪=⎪⎩,根据22sin cos 1θθ+=消参,即可得到2C 的直角坐标方程,将1C 和2C 直角坐标方程作差,即可求得直线MN 的一般方程.（2）将MN l :34y x =+方程,改写成直线参数方程: 3422x y ⎧=-+⎪⎪⎨⎪=⎪⎩（t 为参数）,将其代入1C ,即可求得PM PN +.【详解】（1）1C :()2224x y -+=即2240x x y -+=. ——① 2C :2243x y y +=-——②将①-②得: MN l :4430x y -+-=,∴ 曲线2C 的直角坐标方程: 2243x y y +=-,直线MN 的一般方程为:4430x y -+=.（2）MN l :34y x =+, ∴ 3,04P ⎛⎫- ⎪⎝⎭在MN l 上, 直线MN 的参数方程为:34x y ⎧=-+⎪⎪⎨⎪=⎪⎩（t 为参数）,代入1C :()2224x y -+=,整理得2570416t t -+=, 根据韦达定理: 124t t +=,125716t t =⋅, ∴10t >,20t >.故:124PM PN t t +=+=. 【点睛】本题考查了极坐标和直角坐标方程.解题关键是掌握直线的标准参数方程,结合韦达定理来求线段和,意在考查学生的转化能力和计算求解能力,属于基础题.23．已知函数()122f x x x a =-++.（1）若1a =,求不等式()4f x ≥的解集;（2）证明:对任意x ∈R ,()22f x a a ≥+-.【答案】（1）[)5,1,3x ⎛⎤∈-∞-+∞ ⎥⎝⎦U （2）证明见解析【解析】（1）当1a =时,()122f x x x =-++,分别讨论1x ≤-,11x -<<和1x ≥时求解()4f x ≥,即可求得答案;（2）因为()()221f x x x a x a =-++++,根据||||||||||a b a b a b -≤+≤+即可求得答案.【详解】（1）当1a =时,()122f x x x =-++①当1x ≤-时,()1224f x x x =---≥,得53x ≤-；②当11x -<<时,()12234f x x x x =-++=+≥,得1x ≥,∴x ∈∅③当1x ≥时,()122314f x x x x =-++=+≥,得1x ≥, ∴[)5,1,3x ⎛⎤∈-∞-+∞ ⎥⎝⎦U . （2）Q ()()()22121f x x x a x a x x a x a =-++++≥---++ ()2121222a x a a a a a =+++≥+=+≥+-.∴ 对任意x ∈R ,()22f x a a ≥+-.【点睛】本题主要考查了含绝对值不等式的求解,其中解答中合理分类讨论去掉绝对值,转化为等价不等式求解是解答的关键,着重考查了分类讨论思想,以及推理与运算能力,属于中档试题.。

衡水中学2020届高三第八次调研考试数学理数

5
高三数学（理）下八调试题第2页(共 6 页)
18．（12 分）
16
已知双曲线 C :
x2 a2
y2 b2
1(a
0, b
0) 的左、右焦点分别为 F1, F2, 直线 l 是双曲线 C 过第一、
第三象限的渐近线，记直线 l
的倾斜角为
，直线 l1
:
y
tan 2
x, F2M
l1,
垂足为
M，若
M
在
双曲线 C 上，则双曲线 C 的离心率为
.
高三数学（理）下八调试题第3页(共 6 页)
高三数学（理）下八调试题第4页(共 6 页)
高三数学（理）下八调试题第5页(共 6 页)
高三数学（理）下八调试题第6页(共 6 页)
A． (1, 2)
B． (1 ， 3 2 ] 4
C．[3 2 , ) 4
D． (2, )
11. 已知数列an 满足： a1 2 ， an1Sn Sn 12 0,n N * ，其中 Sn 为an 的前 n 项
和．若对任意的 n 均有 S1 1S2 1Sn 1 kn 恒成立，则 k 的最大整数值为（）
2019—2020 学年度高三年级理数下八调考试
5
命题人：陈丽敏审核人：何慧
高三数学（理）下八调试题第1页(共 6 页)
7. 8. 9.
10.已知双曲线 E : x2 y2 1(a 0,b 0) 的右顶点为 A ，抛物线 C : y2 8ax 的焦点为 F ．若在 E a2 b2
的渐近线上存在点 P ，使得 AP FP ，则 E 的离心率的取值范围是 ( )

衡水中学2020届高三数学第八次调研考试试卷(文科)4月5日-答案

因为 x1 ， x2 是函数 g x 的两个不同极值点（不妨设 x1 x2 ），易知 a 0 （若 a 0 ，则函数 f x 没有或只有一个极值点，与已知矛盾），
且 g x1 0 ， g x2 0 .所以 ex1 2ax1 a 0 ， ex2 2ax2 a 0 .
两式相减得 2a ex1 ex2 ， x1 x2
1
，
32
12
2
又
g
1 2
1 ，所以，三次函数
y
g
x
图象的对称中心坐标为
1 2
,1
，即
g
x
g
1
x
2，
所以，
g
1 2021
g
2 2021
g
2020 2021
1010
2
2020
，
1
12n2
g
2n 1 2021
1 2n1
g
2n 2021
g
2n 1 2021
g
2n 2021
ht
h0
0
，即
t
e2
t 2
1
0
，所以t
0
，
所以 t 在 t 0 时是减函数.故 t 在 t 0 处取得最小值 0 0 .
所以 t 0 得证.所以 x1 x2 ln 2a .………………………………………………12 分
2
4
2n 12 2021
2n 1 2021
3
2n 2 2021
2n 2021
3
2022 4n 20212
，
因此，
2020
i 1
1 i1
g
i 2021

2020河北衡水中学高三数学数学押题卷8(附参考答案及详细解析)

绝密★启用前2020年普通高等学校招生全国统一考试理科数学注意事项：1．答题前填写好自己的姓名、班级、考号等信息2．请将答案正确填写在答题卡上第Ⅰ卷（选择题60分）一．选择题：本题共12小题，每小题5分，共60分。

在每小题给出的4个选项中，只有一项是符合题目要求的。

1.复数在复平面内对应的点位于A. 第一象限B. 第二象限C. 第三象限D. 第四象限2.已知全集U=R ，则A. B.C. D.3.某地某所高中2018年的高考考生人数是2015年高考考生人数的1.5倍，为了更好地对比该校考生的升学情况，统计了该校2015年和2018年的高考情况，得到如下柱状图：2015年高考数据统计 2018年高考数据统计则下列结论正确的是A. 与2015年相比，2018年一本达线人数减少B. 与2015年相比，2018年二本达线人数增加了0.5倍C. 与2015年相比，2018年艺体达线人数相同D. 与2015年相比，2018年不上线的人数有所增加4.已知等差数列的公差为2，前项和为，且，则的值为A. 11B. 12C. 13D. 145.已知是定义在上的奇函数，若时，，则时，A. B. C. D.6.已知椭圆和直线，若过的左焦点和下顶点的直线与平行，则椭圆的离心率为A. B. C. D.7.如图，在平行四边形中，对角线与交于点，且，则A. B.C. D.8.某几何体的三视图如图所示，则此几何体( )A. 有四个两两全等的面B. 有两对相互全等的面C. 只有一对相互全等的面D. 所有面均不全等9.赵爽是我国古代数学家、天文学家，大约在公元年，赵爽为《周碑算经》一书作序时，介绍了“勾股圆方图”，亦称“赵爽弦图”（以弦为边长得到的正方形是由4个全等的直角三角形再加上中间的一个小正方形组成的）．类比“赵爽弦图”，可类似地构造如图所示的图形，它是由个全等的三角形与中间的一个小等边三角形拼成的一个大等边三角形，设，若在大等边三角形内部（含边界）随机取一点，则此点取自小等边三角形（阴影部分）的概率是（）A. B. C. D.10.已知函数（为自然对数的底数），若关于的方程有两个不相等的实根，则的取值范围是A. B. C. D.11.已知双曲线的左、右焦点分别为，，过作圆的切线，交双曲线右支于点，若，则双曲线的渐近线方程为A. B. C. D.12.如图，在正方体中，点，分别为棱，的中点，点为上底面的中心，过，，三点的平面把正方体分为两部分，其中含的部分为，不含的部分为，连结和的任一点，设与平面所成角为，则的最大值为A. B.C. D.第Ⅱ卷（非选择题90分）二．填空题：本大题共4小题，每小题5分，共20分13.已知实数，满足约束条件，则的最小值为________.14.已知数列，若数列的前项和，则的值为________.15.由数字0，1组成的一串数字代码，其中恰好有7个1，3个0，则这样的不同数字代码共有____________个.16.已知函数的图像关于直线对称，当时，的最大值为____________.三．解答题：共70分。

2020届河北衡水中学高三理科数学试卷及答案

2020届河北衡水中学高三年级期中考试理科数学试卷本试卷分为第I卷（选择题）和第II卷（非选择题）两部分.满分150分.考试时间120分钟.第Ⅰ卷（选择题共60分）一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.)1．已知集合S={1，2}，T={x|x2＜4x﹣3}，则S∩T=（）A．{1} B．{2} C．1 D．22．已知复数z1，z2满足|z1|=|z2|=1，|z1﹣z2|=，则|z1+z2|等于（）A．2 B． C．1 D．33．设正数x，y满足x+y=1，若不等式对任意的x，y成立，则正实数a的取值范围是（）A．a≥4 B．a＞1 C．a≥1 D．a＞44．如图，在正方体ABCD﹣A1B1C1D1中，O是底面ABCD的中心，E为CC1的中点，那么异面直线OE与AD1所成角的余弦值等于（）A． B．C．D．5．给出计算的值的一个程序框图如图，其中判断框内应填入的条件是（）A．i＞10 B．i＜10 C．i＞20 D．i＜206．如图，在Rt△ABC中，AC=1，BC=x，D是斜边AB的中点，将△BCD沿直线CD翻折，若在翻折过程中存在某个位置，使得CB⊥AD，则x的取值范围是（）A．（0，] B．（，2]C．（，2] D．（2，4]7．数列{a n}中，对任意n∈N*，a1+a2+…+a n=2n﹣1，则a12+a22+…+a n2等于（）A．（2n﹣1）2 B． C．4n﹣1 D．8．已知一个几何体的三视图及有关数据如图所示，则该几何体的体积为（）A．2 B． C． D．9．设函数f（x）=Asin（ωx+φ）（A，ω，φ是常数，A＞0，ω＞0），且函数f（x）的部分图象如图所示，则有（）A．f（﹣）＜f（）＜f（）B．f（﹣）＜f（）＜f（）C．f（）＜f（）＜f（﹣）D．f（）＜f（﹣）＜f（）10．若圆C：x2+y2+2x﹣4y+3=0关于直线2ax+by+6=0对称，则由点（a，b）向圆C所作切线长的最小值是（）A．2 B．3 C．4 D．611．若函数f（x）=x3﹣3x在（a，6﹣a2）上有最大值，则实数a的取值范围是（）A．（﹣，﹣1）B．（﹣，﹣1] C．（﹣，﹣2）D．（﹣，﹣2]12．已知f′（x）为函数f（x）的导函数，且f（x）=x2﹣f（0）x+f′（1）e x﹣1，若g（x）=f（x）﹣x2+x，则方程g（﹣x）﹣x=0有且仅有一个根时，a的取值范围是（）A．（﹣∞，0）∪{1} B．（﹣∞，1] C．（0，1] D．[1，+∞）第Ⅱ卷非选择题（共90分）二、填空题（本大题共4小题，每小题5分，共20分．）13．设变量x，y满足约束条件，则z=x﹣3y的最小值．14．设数列{a n}的n项和为S n，且a1=a2=1，{nS n+（n+2）a n}为等差数列，则{a n}的通项公式a n= ．15．已知函数f（x）的定义域为[﹣2，+∞），部分对应值如下表．f′（x）为f（x）的导函数，函数y=f′（x）的图象如下图所示．若两正数a，b满足f（2a+b）＜1，则的取值范围是．X ﹣2 0 4f（x） 1 ﹣1 116. 已知正三棱锥S﹣ABC内接于半径为6的球，过侧棱SA及球心O的平面截三棱锥及球面所得截面如右图，则此三棱锥的侧面积为．三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17．（本小题满分12分）△ABC中，已知，记角A，B，C 的对边依次为a，b，c．（1）求∠C的大小；（2）若c=2，且△ABC是锐角三角形，求a2+b2的取值范围．18. （本小题满分12分）已知数列{a n}的前n项和为S n，且S n=n（n+1）（n∈N*）．（Ⅰ）求数列{a n}的通项公式；（Ⅱ）若数列{b n}满足：，求数列{b n}的通项公式；（Ⅲ）令（n∈N*），求数列{c n}的前n项和T n．19. （本小题满分12分）已知圆C：x2+y2+2x﹣4y+3=0．（1）若圆C的切线在x轴和y轴上的截距相等，求此切线的方程；（2）从圆C外一点P（x1，y1）向该圆引一条切线，切点为M，O为坐标原点，且有|PM|=|PO|，求使得|PM|取得最小值的点P的坐标．20. （本小题满分12分）如图，ABCD是边长为3的正方形，DE⊥平面ABCD，AF∥DE，DE=3AF，BE与平面ABCD所成角为60°．（Ⅰ）求证：AC⊥平面BDE；（Ⅱ）求二面角F﹣BE﹣D的余弦值；（Ⅲ）设点M是线段BD上一个动点，试确定点M的位置，使得AM∥平面BEF，并证明你的结论．21. （本小题满分12分）已知函数f（x）=alnx+x2（a为实常数）．（1）若a=﹣2，求证：函数f（x）在（1，+∞）上是增函数；（2）求函数f（x）在[1，e]上的最小值及相应的x值；（3）若存在x∈[1，e]，使得f（x）≤（a+2）x成立，求实数a的取值范围．请考生在第22、23两题中任选一题作答，如果多做，则按所做的第一题记分.解答时请写清题号.22. （本小题满分10分）选修4-4：坐标系与参数方程在直角坐标系中，圆C的方程是x2+y2﹣4x=0，圆心为C，在以坐标原点为极点，以x轴的非负半轴为极轴建立的极坐标系中，曲线C1：ρ=﹣4sinθ与圆C相交于A，B两点．（1）求直线AB的极坐标方程；（2）若过点C（2，0）的直线C2：（t是参数）交直线AB于点D，交y轴于点E，求|CD|：|CE|的值．23. （本小题满分10分）选修4-5：不等式选讲已知函数f（x）=m﹣|x﹣3|，不等式f（x）＞2的解集为（2，4）．（1）求实数m的值；（2）若关于x的不等式|x﹣a|≥f（x）恒成立，求实数a的取值范围．理科数学参考答案一．选择题1-5 B C C DA 6-10 A D B D C 11-12 D A．二．填空题13．﹣8 14.．16.．三．解答题17．解：（1）依题意：，即，又0＜A+B＜π，∴，∴，................4分（2）由三角形是锐角三角形可得，即由正弦定理得∴，，，======，∵，∴，∴，即...............12分18. ．解：（Ⅰ）当n=1时，a1=S1=2，当n≥2时，a n=S n﹣S n﹣1=n（n+1）﹣（n﹣1）n=2n，知a1=2满足该式，∴数列{a n}的通项公式为a n=2n．（2分）（Ⅱ）∵（n≥1）①∴②（4分）②﹣①得：，b n+1=2（3n+1+1），故b n=2（3n+1）（n∈N*）．（6分）（Ⅲ）=n（3n+1）=n•3n+n，∴T n=c1+c2+c3+…+c n=（1×3+2×32+3×33+…+n×3n）+（1+2+…+n）（8分）令H n=1×3+2×32+3×33+…+n×3n，①则3H n=1×32+2×33+3×34+…+n×3n+1②①﹣②得：﹣2H n=3+32+33+…+3n﹣n×3n+1=∴，…（10分）∴数列{c n}的前n项和…（12分）19.解：（1）∵切线在两坐标轴上的截距相等，∴当截距不为零时，设切线方程为x+y=a，又∵圆C：（x+1）2+（y﹣2）2=2，∴圆心C（﹣1，2）到切线的距离等于圆的半径，即，解得：a=﹣1或a=3，当截距为零时，设y=kx，同理可得或，则所求切线的方程为x+y+1=0或x+y﹣3=0或或．-- -------6分（2）∵切线PM与半径CM垂直，∴|PM|2=|PC|2﹣|CM|2．∴（x1+1）2+（y1﹣2）2﹣2=x12+y12．∴2x1﹣4y1+3=0．∴动点P的轨迹是直线2x﹣4y+3=0．∴|PM|的最小值就是|PO|的最小值．而|PO|的最小值为原点O到直线2x﹣4y+3=0的距离，∴由，可得故所求点P的坐标为．--12分20.证明：（Ⅰ）因为DE⊥平面ABCD，所以DE⊥AC．因为ABCD是正方形，所以AC⊥BD，从而AC⊥平面BDE．…........................................（4分）解：（Ⅱ）因为DA，DC，DE两两垂直，所以建立空间直角坐标系D﹣xyz如图所示．因为BE与平面ABCD所成角为600，即∠DBE=60°，所以．由AD=3，可知，．则A（3，0，0），，，B（3，3，0），C（0，3，0），所以，．设平面BEF的法向量为=（x，y，z），则，即．令，则=．因为AC⊥平面BDE，所以为平面BDE的法向量，．所以cos．因为二面角为锐角，所以二面角F﹣BE﹣D的余弦值为．…（8分）（Ⅲ）点M是线段BD上一个动点，设M（t，t，0）．则．因为AM∥平面BEF，所以=0，即4（t﹣3）+2t=0，解得t=2．此时，点M坐标为（2，2，0），即当时，AM∥平面BEF．…（12分）21.解：（1）当a=﹣2时，f（x）=x2﹣2lnx，当x∈（1，+∞），，所以函数f（x）在（1，+∞）上是增函数；.........2分（2），当x∈[1，e]，2x2+a∈[a+2，a+2e2]．若a≥﹣2，f'（x）在[1，e]上非负（仅当a=﹣2，x=1时，f'（x）=0），故函数f（x）在[1，e]上是增函数，此时[f（x）]min=f（1）=1．若﹣2e2＜a＜﹣2，当时，f'（x）=0；当时，f'（x）＜0，此时f（x）是减函数；当时，f'（x）＞0，此时f（x）是增函数．故[f（x）]min==．若a≤﹣2e2，f'（x）在[1，e]上非正（仅当a=﹣2e2，x=e时，f'（x）=0），故函数f（x）在[1，e]上是减函数，此时[f（x）]min=f（e）=a+e2．综上可知，当a≥﹣2时，f（x）的最小值为1，相应的x值为1；当﹣2e2＜a＜﹣2时，f（x）的最小值为，相应的x值为；当a≤﹣2e2时，f（x）的最小值为a+e2，相应的x值为e．......................7分（3）不等式f（x）≤（a+2）x，可化为a（x﹣lnx）≥x2﹣2x．∵x∈[1，e]，∴lnx≤1≤x且等号不能同时取，所以lnx＜x，即x﹣lnx＞0，因而（x∈[1，e]）令（x ∈[1，e]），又，当x ∈[1，e]时，x ﹣1≥0，lnx ≤1，x+2﹣2lnx ＞0，从而g'（x ）≥0（仅当x=1时取等号），所以g （x ）在[1，e]上为增函数，故g （x ）的最小值为g （1）=﹣1，所以a 的取值范围是[﹣1，+∞）．.......12分22.解：（1）在以坐标原点为极点，x 轴的非负半轴为极轴，建立极坐标系，极坐标与直角坐标有如下关系 x=ρcosθ，y=ρsinθ，曲线C 1：ρ=﹣sinθ，∴ρ2=﹣4ρsinθ，∴x 2+y 2=﹣4y ， ∴曲线C 1：x 2+y 2+y=0，∴直线AB 的普通方程为：（x 2+y 2﹣4x ）﹣（x 2+y 2+4y ）=0， ∴y=﹣x ，∴ρsinθ=﹣ρcosθ，∴tanθ=﹣， ∴直线AB 极坐标方程为：)(61R ∈-=ρθ．.............5分（2）根据（1）知，直线AB 的直角坐标方程为y=﹣x ，根据题意可以令D （x 1，y 1），则，又点D 在直线AB 上，所以t 1=﹣（2+t 1），解得 t 1=﹣，根据参数方程的定义，得|CD|=|t 1|=，同理，令交点E （x 2，y 2），则有，又点E 在直线x=0上，令2+t 2=0，∴t 2=﹣，∴|CE|=|t 2|=，∴|CD|：|CE|=1：2．............................10分23.解：（1）∵f （x ）=m ﹣|x ﹣3|，∴不等式f （x ）＞2，即m ﹣|x ﹣3|＞2，∴5﹣m ＜x ＜m+1，而不等式f （x ）＞2的解集为（2，4），∴5﹣m=2且m+1=4，解得：m=3；........5分（2）关于x 的不等式|x ﹣a|≥f （x ）恒成立⇔关于x 的不等式|x ﹣a|≥3﹣|x ﹣3|恒成立 ⇔|x ﹣a|+|x ﹣3|≥3恒成立⇔|a ﹣3|≥3恒成立，由a ﹣3≥3或a ﹣3≤﹣3，解得：a ≥6或a ≤0．..............10分。

河北衡水2020届高三调研考试理数试题

3 3河北衡水2020届高三调研考试理数试题一、选择题（每小题5分，共60分。

下列每小题所给选项只有一项符合题意，请将正确答案的序号填涂在答题卡上）1．已知集合 A ＝{x ∈R|x +1＞0}，B ＝{x ∈Z|x ≤1}，则 A ∩B ＝A ．{x |0≤x ≤1}B ．{x |﹣1＜x ≤1}C ．{0，1}D ．{1}6.已知某算法的程序框图如图所示,则该算法的功能是A ．求首项为 1,公比为 2 的等比数列的前 2017 项的和B ．求首项为 1,公比为 2 的等比数列的前 2018 项的和C ．求首项为 1,公比为 4 的等比数列的前 1009 项的和D ．求首项为 1,公比为 4 的等比数列的前 1010 项的和2．复数 1+ i 1+ 2i 2 A ． 110C ． 3 10的共轭复数的虚部为B ． - 1 10 D ． - 310 7．如图 1，已知正方体 ABCD-A 1B 1C 1D 1 的棱长为 2，M ，N ，Q 分别是线段 AD 1，B 1C ，C 1D 1 上的动点，当三棱锥 Q-BMN 的正视图如图 2 所示时，三棱锥俯视图的面积为3．有一散点图如图所示，在 5 个（x ，y ）数据中去掉 D （3，10）后，下列说法正确的是 A ．残差平方和变小 B ．相关系数 r 变小 C ．相关指数 R 2变小D ．解释变量 x 与预报变量 y 的相关性变弱35A ．2B ．1C ．D ．2 2⎛ π ⎫ ⎛ π ⎫x 2 y 28．如图直角坐标系中，角α 0 < α < 2 ⎪ 、角 β - 2 < β < 0⎪4. 已知双曲线 C : - = 1 12 4，O 为坐标原点，F 为 C 的右焦点，过F 的直线与 C 的两条 ⎝ ⎭ ⎝ ⎭5渐近线的交点分别为 P ，Q ，若△POQ 为直角三角形，则|PQ |＝ A ．2B ．4C ．6D ．8的终边分别交单位圆于 A 、B 两点，若 B 点的纵坐标为 - ，13α ⎛ α α ⎫ 15．一个袋中放有大小、形状均相同的小球，其中红球 1 个、黑球 2 个，现随机等可能取出小且满足 S= ，则 sin cos -sin ⎪ + 的值球．当有放回依次取出两个小球时，记取出的红球数为 ξ1；当无放回依次取出两个小球时， ∆AOB 45 122 ⎝ 2 2 ⎭ 2 12 5 记取出的红球数为 ξ2，则（）A ．E ξ1＜E ξ2，D ξ1＜D ξ2B ．E ξ1＝E ξ2，D ξ1＞D ξ2C ．E ξ1＝E ξ2，D ξ1＜D ξ2D ．E ξ1＞E ξ2，D ξ1＞D ξ2A ． - 13B ．C ． -D ．13 13 13⎛ 2 3x ( 9. 已知函数 f (x ) = sin ωx - cos ωx (ω > 0) ，若集合{x ∈(0 ， π ) | f (x ) = -1} 含有 4 个元素，二、填空题（共 4 题，每题 5 分）n则实数 ω 的取值范围是 ⎛ 13. 已知二项式 2x - 1 ⎫ ⎪ 的展开式中第2 项与第3 项的二项式系数之比是 2︰5，则 x 3 的系 A ． [ 3 , 5)2 2B ． ( 3 , 5]2 2C ． [7 , 25)2 6D ． (7 , 25]2 6⎝⎭ 数为10．已知抛物线 y 2 = 4x 上有三点 A ，B ，C ，AB ，BC ，CA 的斜率分别为 3，6，-2 ，则的重心坐标为 ∆ABC 14. 数学老师给出一个定义在 R 上的函数 f （x ），甲、乙、丙、丁四位同学各说出了这个函数的一条性质：14( ,1) 9B ． 14 ,0)9C ． (14 , 0)27D ． (14 ,1)27甲：在（﹣∞，0]上函数单调递减；乙：在[0，+∞）上函数单调递增；丙：函数 f （x ）的图象关于直线 x ＝1 对称；丁：f （0）不是函数的最小值． 11．在棱长为 2 的正方体 ABCD - A 1B 1C 1D 1 中，点 M 是对角线 AC 1 上的点（点 M 与 A、C 1 不重合），则下列结论正确的个数为（）老师说：你们四个同学中恰好有三个人说的正确，那么，你认为说法错误的同学是15. 已知△ABC 的一内角 A = π3, AB = 10, AC = 6 ，O 为△ABC 所在平面上一点，满足|OA |＝|OB |＝|OC |，设 AO = m AB + n AC ，则 m +3n 的值为16．已知 ∆ABC 的内角 A 、B 、C 的对边分别为 a 、b 、c ，若 A = 2B ，则 c +2b 的取值ba①存在点 M ，使得平面 A 1DM ⊥ 平面 BC 1D ； ②存在点 M ，使得DM // 平面 B 1CD 1 ；范围为．三、解答题：（本大题共 5 小题，共 70 分，解答应写出文字说明，证明过程或演算步骤。

衡水中学2020届高三第八次调研考试数学理数+参考答案

，
9.
高三数学（理）下八调答案第1页(共 8 页)
高三数学（理）下八调答案第2页(共 8 页)
依题只须
k
≤
( ( S1
+ 1) ( S2
+ 1)L( Sn
n
+1)
)min
，令
f
(n)
=
( S1
+ 1) ( S2
+ 1)L ( Sn
n
+1)
，则Biblioteka f(n +1) f (n)
=
n ( Sn+1 +1)
n +1
=
n (2n + 3) (n +1)2
> 1 ，所以
f
( )n 为单调递增数列，
故
f (n)nin
=
f
(1) =
S1 + 1
1
=
3
，∴
kmax
=3，
故选：B．
高三数学（理）下八调答案第3页(共 8 页)
高三数学（理）下八调答案第4页(共 8 页)
高三数学（理）下八调答案第5页(共 8 页)
高三数学（理）下八调答案第6页(共 8 页)
高三数学（理）下八调答案第7页(共 8 页)
高三数学（理）下八调答案第8页(共 8 页)
k
A2
B3
C4
D5
2( 6 )
18 12
x2 y2
16
C : a2 b2 1(a 0,b 0)
F1, F2, l
l
C
C
l1 : y
tan 2
x, F2M
l1,
.

2020届河北省衡水中学高三上学期八模考试数学(理)试题

2018届河北省衡水中学高三上学期八模考试数学（理）试题第Ⅰ卷（选择题共60分）一、选择题（每小题5分，共60分。

下列每小题所给选项只有一项是符合题意，请将正确答案的序号填涂在答题卡上）1．若复数z 满足232z z i +=-，其中i 为虚数单位，则z =（） A ．12i + B ．12i - C ．12i -+ D ．12i --2．已知等差数列{}n a 的前n 项和为n S ，且639S =，则34a a +=（） A ．31 B ．12 C ．13 D ．523．某班数学课代表给全班同学出了一道证明题，以下四人中只有一人说了真话，只有一人会证明此题：甲：我不会证明乙：丙会证明丙：丁会证明丁：我不会证明根据以上条件，可以判定会证明此题的人是（） A ．甲 B ．乙 C ．丙 D ．丁4．在下列各图中，每个图的两个变量具有相关关系的图是（） A ．⑴⑵ B ．⑴⑶ C ． ⑵⑷ D ．⑵⑶5．已知抛物线212y x =的焦点与2212y x m +=的一个焦点重合，则m =（）A ．74B ．12764C ．94D ．129646．如图是一个几何体的三视图，则该几何体的表面积为（）A ．83B ．43C ．4D ．6 7．已知Rt ABC ∆，点D 为斜边BC 的中点，||63AB =||6AC =，12AE ED =，则AE EB ⋅等于（） A ．-14 B ．-9 C ．9 D ．148．已知函数()(0,1)x f x a b a a =+>≠的图象经过点(1,3)P ，(2,5)Q ．当n N *∈时，()1()(1)n f n a f n f n -=⋅+，记数列{}n a 的前n 项和为n S ，当1033n S =时，n 的值为（） A ．7 B ．6 C ．5 D ．49．若下图程序框图在输入1a =时运行的结果为p ，点M 为抛物线22y px =-上的一个动点，设点M 到此抛物线的准线的距离为1d ，到直线40x y +-=的距离为2d ，则12d d +的最小值是（）A ．52B．2 C ．2 D10．太极图是以黑白两个鱼形纹组成的图形图案，它形象化地表达了阴阳轮转，相反相成是万物生成变化根源的哲理，展现了一种相互转化，相对统一的形式美．按照太极图的构图方法，在平面直角坐标系中，圆O 被3sin6y x π=的图象分割为两个对称的鱼形图案，其中小圆的半径均为1，现在大圆内随机取一点，则此点取自阴影部分的概率为（）A ．136B ．118C ．112D ．1911．长方体1111ABCD A B C D -中，18DC CC +=，4CB =，AM MB =，点N 是平面1111A B C D 上的点，且满足1C N =，当长方体1111ABCD A B C D -的体积最大时，线段MN 的最小值是（） A．．8 D．12．已知实数0a >，函数()f x =112,02(1),022x x ae x a a e x a x x --⎧+<⎪⎪⎨⎪+-++≥⎪⎩，若关于x 的方程[()]2a a f f x e --=+有三个不等的实根，则实数a 的取值范围是（）A ．2(1,2)e + B ．2(2,2)e + C ．1(1,1)e + D ．1(2,2)e+第Ⅱ卷（共90分）二、填空题：（本大题共4小题，每题5分共20分）13．计算定积分21-= ．14．设变量,x y 满足不等式组403301x y x y x +-≤⎧⎪-+≤⎨⎪≥⎩，则z 的取值范围是．15．已知椭圆22221(0)x y a b a b +=>>的左、右焦点分别为1(,0)F c -，2(,0)F c ，若椭圆上存在点p 使1221sin sin a c PF F PF F =∠∠成立，则该椭圆的离心率的取值范围为．16．用()g n 表示自然数n 的所有因数中最大的那个奇数，例如：9的因数有1，3，9，(9)9g =，10的因数有1，2，5，10，(10)5g =，那么2015(1)(2)(3)(21)g g g g ++++-= ．三、解答题（本大题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤．）17．函数()sin()(0,||)2f x x πωϕωϕ=+><的部分图像如图所示，将()y f x =的图象向右平移4π个单位长度后得到函数()y g x =的图象．（1）求函数()y g x =的解折式；（2）在ABC ∆中，角,,A B C 满足22sin ()123A B g C π+=++，且其外接圆的半径2R =，求ABC ∆的面积的最大值．18．如图所示，该几何体是由一个直三棱柱ADE BCF -和一个正四棱锥P ABCD -组合而成，AD AF ⊥，2AE AD ==．（Ⅰ）证明：平面PAD ⊥平面ABFE ；（Ⅱ）求正四棱锥P ABCD -的高h ，使得二面角C AF P --． 19．某市政府为了引导居民合理用水，决定全面实施阶梯水价，阶梯水价原则上以住宅（一套住宅为一户）的月用水量为基准定价：若用水量不超过12吨时，按4元/吨计算水费；若用水量超过12吨且不超过14吨时，超过12吨部分按6.60元/吨计算水费；若用水量超过14吨时，超过14吨部分按7.8元/吨计算水费．为了了解全市居民月用水量的分布情况，通过抽样，获得了100户居民的月用水量（单位：吨），将数据按照[0,2],(2,4],,(14,16]分成8组，制成了如图1所示的频率分布直方图．（Ⅰ）假设用抽到的100户居民月用水量作为样本估计全市的居民用水情况．（ⅰ）现从全市居民中依次随机抽取5户，求这5户居民恰好3户居民的月用水量都超过12吨的概率；（ⅱ）试估计全市居民用水价格的期望（精确到0.01）；（Ⅱ）如图2是该市居民李某2016年1～6月份的月用水费y （元）与月份x 的散点图，其拟合的线性回归方程是233y x ∧=+．若李某2016年1～7月份水费总支出为294.6元，试估计李某7月份的用水吨数．20．已知椭圆2222:1(0)x y C a b a b+=>>的四个项点组成的四边形的面积为2．（1）求椭圆C 的方程；（2）若椭圆C 的下顶点为P ，如图所示，点M 为直线2x =上的一个动点，过椭圆C 的右焦点F 的直线l 垂直于OM ，且与C 交于,A B 两点，与OM 交于点N ，四边形AMBO 和ONP ∆的面积分别为1S ，2S ，求12S S 的最大值．21．已知函数()()ln()x f x e x a x a x =-+++，a R ∈．（1）当1a =时，求函数()f x 的图象在0x =处的切线方程；（2）若函数()f x 在定义域上为单调增函数． ①求a 最大整数值；②证明：23341ln 2(ln )(ln )(ln)231n n en e +++++<-．请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分．22.选修4-4：坐标系与参数方程在直角坐标系xOy 中，直线l 过(2,0)M ，倾斜角为(0)αα≠．以O 为极点，x 轴非负半轴为极轴，建立极坐标系，曲线C 的极坐标方程为2sin 4cos ρθθ=．（Ⅰ）求直线l 的参数方程和曲线C 的直角坐标方程；（Ⅱ）已知直线l 与曲线C 交于A 、B 两点，且||2||MA MB =，求直线l 的斜率k ． 23．选修4-5：不等式选讲已知函数()|21|f x x =-．（1）若不等式1()21(0)2f x m m +≤+>的解集为[2,2]-，求实数m 的值；（2）若不等式()2|23|2y yaf x x ≤+++，对任意的实数,x y R ∈恒成立，求实数a 的最小值．试卷答案一、选择题1-5:BCADC 6-10:DDDBB 11、12：BB二、填空题1343π 14． 15．1,1) 16．2015413- 三、解答题17．试题解析：（Ⅰ）由图知24()126πππω=+，解得2ω=∵()sin(2)11212f ππϕ=⋅+=∴2()62k k Z ππϕπ+=+∈，即2k ()3k Z πϕπ=+∈由于22ππϕ-<<，因此3πϕ=∴()sin(2)3f x x π=+∴()sin[2()]443f x x πππ-=-+sin(2)6x π=-即函数()y g x =的解析式为()sin(2)6g x x π=-（Ⅱ）∵22sin ()123A B g C π+=++ ∴1cos()1sin(2)2A B C π-+=++∵cos()cos A B C +=-，sin(2)cos22C C π+=cos cos2C C =，即2cos 2cos 1C C =-，所以1cos 2C =-或1（舍），23C π=由正弦定理得24sin cR C==，解得c =由余弦定理得2221cos 22a b c C ab+-=-=∴22122a b ab ab +=-≥，4ab ≤（当且仅当a b =等号成立）∴1sin 24ABC S ab C ∆==≤ ∴ABC ∆18．（Ⅰ）证明：正三棱柱ADE BCF -中，AB ⊥平面ADE ，所以AB AD ⊥，又AD AF ⊥，ABAF A =，所以AD ⊥平面ABFE ，AD ⊂平面PAD ，所以平面PAD ⊥平面ABFE ．（Ⅱ）由（Ⅰ）知AD ⊥平面ABFE ，以A 为原点，AB ，AE ，AD 方向为,,x y z 轴建立空间直角坐标系-A xyz ，设正四棱锥-P ABCD 的高为h ，2AE AD ==，则(0,0,0)A ，(2,2,0)F ，(2,0,2)C ，(1,,1)P h -，(2,2,0)AF =，(2,0,2)AC =，(1,,1)AP h =-．设平面ACF 的一个法向量111(,,)m x y z =，则1111220220m AF x y m AC x z ⎧⋅=+=⎪⎨⋅=+=⎪⎩，取11x =，则111y z ==-，所以(1,1,1)m =--．设平面AFP 的一个法向量222(,,)n x y z =，则222222200n AF x y n AP x hy z ⎧⋅=+=⎪⎨⋅=-+=⎪⎩，取21x =，则21y =-，21z h =--，所以(1,1,1)n h =---．二面角C AF P --的余弦值是3，所以cos ,||||m n m n m n ⋅<>=⋅3==解得1h =．19．【答案】解：（Ⅰ）（ⅰ）由题意，从全市居民中依次随机抽取5户，每户居民月用水量超过12吨的概率为110，因此这5户居民恰好3户居民的月用水量都超过12吨的概率为33251981()()101010000P C ==．（ⅱ）由题设条件及月均用水量的频率分布直方图，可得居民每月的水费数据分组与概率分布表如下：所以全市居民用水价格的期望()40.9 4.20.06 4.60.04 4.04E X =⨯+⨯+⨯≈吨．（Ⅱ）设李某2016年1～6月份的月用水费y （元）与月份x 的对应点为(,)(1,2,3,4,5,6)i i x y i =，它们的平均值分别为x ，y ，则126216x x x x +++==，又点(,)x y 在直线233y x ∧=+上，所以40y =，因此126240y y y ++=，所以7月份的水费为294.624054.6-=元．设居民月用水量为t 吨，相应的水费为()f t 元，则4,012()48(12) 6.6,121461.2(14)7.8,1416t t f t t t t t <≤⎧⎪=+-⨯<≤⎨⎪+-⨯<≤⎩，即：当13t =时，() 6.61331.254.6f t =⨯-=，所以李某7月份的用水吨数约为13吨． 20．（1）因为在椭圆C 上，所以221112a b+=，又因为椭圆四个顶点组成的四边形的面积为1222a b ⨯⨯=ab ，解得22a =，21b =，所以椭圆C 的方程为2212x y +=（2）由（1）可知(1,0)F ，设(2,)M t ，11(,)A x y ，22(,)B x y ，则当0t ≠时，:2t OM y x =，所以2AB k t =-，直线AB 的方程为2(1)y x t=--，即220(0)x ty t +-=≠，由222(1)220y x tx y ⎧=--⎪⎨⎪+-=⎩得222(8)16820t x x t +-+-=，则22242(16)4(8)(82)8(4)0t t t t ∆=--+-=+>，122168x x t +=+，2122828t x x t -=+，AB ==，又OM =112S OM AB =⨯224)8t t +=+，由2(1)2y x t t y x⎧=--⎪⎪⎨⎪=⎪⎩，得244N X t =+，所以2221421244S t t =⨯⨯=++，所以12224S S t =+2482t ==<+，当0t =，直线:1l x =，AB =1122S ==2111122S =⨯⨯=，12S S =，所以当0t =时，12max ()S S ． 21．【解析】（1）当1a =时，()(1)ln(1)x f x e x x x =-+++，∴(0)1f =，又'()ln(1)x f x e x =-+，∴'(0)1f =，则所求切线方程为1y x -=，即10x y -+=．（2）由题意知，'()ln()x f x e x a =-+，若函数()f x 在定义域上为单调增函数，则'()0f x ≥恒成立． ①先证明1x e x ≥+．设()1x g x e x =--，则'()1x g x e =-，则函数()g x 在(,0)-∞上单调递减，在(0,)+∞上单调递增， ∴()(0)0g x g ≥=，即1x e x ≥+．同理可证ln 1x x ≤-，∴ln(2)1x x +≤+，∴1ln(2)x e x x ≥+≥+．当2a ≤时，'()0f x >恒成立．当3a ≥时，'(0)1ln 0f a =-<，即'()ln()0x f x e x a =-+≥不恒成立．综上所述，a 的最大整数值为2． ②由①知，ln(2)x e x ≥+，令1t x t-+=， ∴111ln(2)ln()t tt t et t -+-++≥+=，∴11(ln )t tt e t-++≥．由此可知，当1t =时，0ln 2e >．当2t =时，123(ln )2e ->，当3t =时，234(ln )3e ->，，当t n =时，11(ln )n nn e n-++≥．累加得0121n e e e e ---+++++>23341ln 2(ln )(ln )(ln )23nn n+++++．又0121n e e e e ---+++++=11()111111ne n e e e-<=---， ∴2334ln 2(ln )(ln )23++1(ln)1n n en e +++<-．22．解：（Ⅰ）直线l 的参数方程为2cos sin x t y t αα=+⎧⎨=⎩（t 为参数），由2sin 4cos ρθθ=得22sin 4cos ρθρθ=，∴曲线C 的直角坐标方程为24y x =．（Ⅱ）把2cos x t α=+，sin y t α=代入24y x =得22(sin )(4cos )80t t αα--=．设,A B 两点对应的参数分别为1t 与2t ，则1224cos sin t t αα+=，1228sin t t α=-，易知1t 与2t 异号，又∵||2||MA MB =，∴122t t =-．消去1t 与2t 得tan 2α=±，即2k =± 23．【解析】（1）由题意，知不等式|2|21(0)x m m ≤+>解集为[2,2]-由|2|21x m ≤+，得1122m x m --≤≤+，所以，由122m +=，解得32m =．（2）不等式()2|23|2y y a f x x ≤+++等价于|21||23|22y y ax x --+≤+，由题意知max (|2x 1||2x 3|)22y y a--+≤+．因为|21||23||(21)(23)|4x x x x --+≤--+=，所以242y y a+≥，即[2(42)]y y a ≥-对任意y R ∈都成立，则max [2(42)]y y a ≥-．而22(42)2(42)[]42y y y y+--≤=，当且仅当242y y =-，即1y =时等号成立，故4a ≥，所以实数a 的最小值为4．。

衡水中学2020届高三第八次调研考试理科数学4月5日答案

2019—2020学年度高三年级理数下八调答案3.D5.B7.8.9.10.B.11. B根据所给条件，结合11n n na S S++=-，代入后展开化简，构造数列11nS⎧⎫⎨⎬-⎩⎭，由等差数列性质可知11nS⎧⎫⎨⎬-⎩⎭为等差数列，进而由首项与公差求得nS.将不等式化简可得，()()()12111()nminS S Skn+++≤L，代入后构造函数()()()()12111nS S Sf nn+++=L，并求得()()1f nf n+后可证明函数()f n为单调递增数列，求得()minf n，即可确定k的最大整数值.【详解】当1n≥时，由条件()()2110,*n n na S S n N+-∈=+，可得21(1)nn nnSS SS+--=-，整理得221(21)n n n n nS S S S S+-=--+，化简得：121n n nS S S+=-，从而111nnnSSS+--=-，故111111n nS S+-=--，由于1111S=-，所以数列11nS⎧⎫⎨⎬-⎩⎭是以1111S=-为首项，1为公差的等差数列，则11nnS=-，整理得1nnSn+=，高三数学（理）下八调答案第1页(共8页) 高三数学（理）下八调答案第2页(共8页)。

河北省衡水中学2020届高三年级八调考试数学(文)试题及答案

河北省衡水中学2020届高三年级八调考试数学试卷（文）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分．考试时间120分钟．第Ⅰ卷（选择题共60分）注意事项：1．答卷Ⅰ前，考生将自己的姓名、准考证号、考试科目涂写在答题卡上． 2．答卷Ⅰ时，每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑．一、选择题（每小题5分，共60分．下列每小题所给选项只有一项符合题意，请将正确答案的序号填涂在答题卡上）1．设全集为R ，集合{}2|20A x x x =-<，集合{|||1}B x x =<，则A B =I （） A ．(1,1)-B ．(1,2)-C ．(0,1)D ．(0,2) 2．已知复数2000(1)z ii =⋅+，则z 的模||z =（）A ．1B．43．在2019年的国庆假期中，重庆再次展现“网红城市”的魅力，吸引了3000多万人次的客流．北京游客小李慕名而来，第一天打算游览“洪崖洞”，“解放碑”，“朝天门”．如果随机安排三个景点的游览顺序，则最后游览“朝天门”的概率为（）A ．16B ．56C ．13D ．234．已知非零向量,a b r r 满足：(1,1)a =r ，||1b =r ，()a b b -⊥r r r ，则向量,a b r r的夹角大小为（）A ．6πB ．4πC ．3πD ．2π 5．已知正方体1111ABCD A B C D -的棱长为1，其内切球与外接球的表面积分别为12,S S ，则12S S =（） A ．1 B ．12C ．13D ．146．已知tan 2θ=-，则sin sin 2πθθ⎛⎫+ ⎪⎝⎭的值为（） A ．25B ．25-C ．35D ．457．如图所示的一个算法的程序框图，则输出d 的最大值为（）A ．2B ．2C ．12+D ．122+8．已知()f x 是定义在[0,)+∞的函数，满足(3)()f x f x +=-，当[0,3)x ∈时，()2xf x =，则()2log 192f =（）A ．12B ．13C ．2D ．39．如图，网格纸上小正方形的边长为1，粗线画出的是某三棱锥的三视图，则该三棱锥的外接球的体积为（）A ．11223πB ．44113πC ．4411πD ．1122π 10．已知函数(2),1,()||1,11,f x x f x x x ->⎧=⎨--<⎩„关于x 的方程()log (1)a f x x =+恰有5个解，则a 的取值范围为（） A ．1175a <„B ．1175a <<C ．1164a <<D ．1164a <„11．已知抛物线24x y =的焦点为F ，过直线2y x =-上任一点引抛物线的两条切线，切点为,A B ，则点F 到直线AB 的距离（）A ．无最小值B ．无最大值C ．有最小值，最小值为1D 5 12．已知函数22()(21)(31)(2)(2)xx f x a a e a x e x =---+++有4个不同的零点，则实数a 的取值范围为（）A ．1,2e ⎛⎫ ⎪⎝⎭B ．11,22e +⎛⎫⎪⎝⎭C ．1,1(1,)2e ⎛⎫⋃ ⎪⎝⎭D ．11,11,22e +⎛⎫⎛⎫⋃ ⎪ ⎪⎝⎭⎝⎭第Ⅱ卷本卷包括必考题和选考题两部分．第13题~第21题为必考题，每个试题考生都必须做答．第22题~第24题为选考题，考生根据要求做答．二、填空题：本大题共4小题，每小题5分．13．设,x y 满足约束条件3403400x y x y x y -+≥⎧⎪--≤⎨⎪+≥⎩，则2x y -的最小值是______．14．对于三次函数32()(0)f x ax bx cx d a =+++≠，定义：设()f x ''是()f x '的导数，若方程()0f x ''=有实数解0x ，则称()()00,x f x 为函数()f x 的拐点．某同学经过探索发现任何一个三次函数都有“拐点”；任何一个三次函数都有对称中心，且“拐点”就是对称中心设函数32115()33212g x x x x =-+-，则122020202120212021g g g ⎛⎫⎛⎫⎛⎫+++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭L ______；202011(1)2021i i i g -'=⎛⎫-= ⎪⎝⎭∑_______．（第一空2分，第二空3分）15．已知双曲线2222:1(0,0)x y C a b a b-=>>的左、右焦点为12,F F ，以12F F 为直径的圆与双曲线C 的渐近线在第一象限交于点P ，线段2PF 与双曲线的交点M 为2PF 的中点，则双曲线C 的离心率为______． 16．已知数列{}n a 满足()*1(1)2n n na n a n N +--=∈，{}n a 的前n 项和为n S ，对任意的*n N ∈，当5n ≠时，都有5n S S <，则5S 的取值范围为_____．三、解答题（共6个小题，共70分．解答题应写出文字说明、证明过程或演算步骤） 17．（本小题满分12分）已知数列{}n a 是一个等差数列，且22a =，145a a +=，数列{}n b 是各项均为正数的等比数列，且满足：112b =，24164b b ⋅=．（1）求数列{}n a 与{}n b 的通项公式；（2）求证：11222n n b a b a a b ++⋯+<． 18．（本小题满分12分）如图，已知在四棱锥P ABCD -中，底面ABCD 为正方形，PD PA =，E 点为AD 的中点，PE CD ⊥．（1）求证：平面PAD ⊥平面ABCD ；（2）若正方形的边长为4，求D 点到平面PEC 的距离． 19．（本小题满分12分）2019年双十一落下帷幕，天猫交易额定格在268（单位：十亿元）人民币（下同），再创新高，比去年218（十亿元）多了50（十亿元），这些数字的背后，除了是消费者买买买的表现，更是购物车里中国新消费的奇迹，为了研究历年销售额的变化趋势，一机构统计了2010年到2019年天猫双十一的销售额数据y （单位：十亿元），绘制如下表1：表1年份 2010 2011 2012 2013 2014 2015 2016 2017 2018 2019 编号x 1 2 3 4 5 6 7 8 9 10 销售额y0.98.722.4416594132.5172.5218268根据以上数据绘制散点图，如图所示．（1）把销售额超过100（十亿元）的年份叫“畅销年”，把销售额超过200（十亿元）的年份叫“狂欢年”，从2010年到2019年这十年的“畅销年”中任取2个，求至少取到一个“狂欢年”的概率；（2）根据散点图判断，y a bx =+与2y cx d =+哪一个适宜作为销售额y 关于x 的回归方程类型？（给出判断即可，不必说明理由）；（3）根据（2）的判断结果及下表中的数据，建立y 关于x 的回归方程，并预测2020年天猫双十一的销售额．（注：数据保留小数点后一位）参考数据：2i i t x =，参考公式：对于一组数据(),i i u v ，()22,u v，…，(),n n u v ，其回归直线µµvu αβ=+$的斜率和截距的最小二乘估计公式分别为µ1221ni ii n i i u vnuvu nuβ==-=-∑∑，µµv u αβ=-． 20．（本小题满分12分）已知椭圆2222:1(0)x y C a b a b +=>>的两个焦点为12,F F ，焦距为:1l y x =-与椭圆C 相交于,A B 两点，31,44P ⎛⎫- ⎪⎝⎭为弦AB 的中点．（1）求椭圆的标准方程；（2）若直线:l y kx m =+与椭圆C 相交于不同的两点,M N ，(0,)Q m ，若3OM ON OQ λ+=u u u u r u u u r u u u r（O 为坐标原点），求m 的取值范围．21．（本题满分12分）已知函数()xf x e ax =-．（1）若函数()f x 在1,22x ⎛⎫∈ ⎪⎝⎭上有2个零点，求实数a 的取值范围．（注319e >）（2）设2()()g x f x ax =-，若函数()g x 恰有两个不同的极值点12,x x ，证明：12ln(2)2x x a +<．请考生在第22、23题中任选择一题作答，如果多做，则按所做的第一部分，做答时请写清题号． 22．（本小题满分10分）【选修4-4：坐标系与参数方程】在直角坐标系xOy 中，曲线122cos ,:2sin ,x C y θθ=+⎧⎨=⎩（θ为参数），以原点O 为极点，x 轴的正半轴为极轴建立极坐标系，曲线22:4sin 3C ρρθ=-，曲线1C 与曲线2C 相交于,M N 两点．（1）求曲线2C 的直角坐标方程与直线MN 的一般方程；（2）点3,04P ⎛⎫-⎪⎝⎭，求||||PM PN +． 23．（本小题满分10分）【选修4-5：不等式选讲】已知函数()|1||22|f x x x a =-++. （1）若1a =，求不等式()4f x …的解集；（2）证明：对任意x ∈R ，2()|2|||f x a a +-…．文科数学八调参考答案1．(0,2)A =，(1,1)B =-，所以(0,1)A B =I ，故选C ． 2．已知1(1)1z i i =⋅+=+，所以||2z =，故选B ．3．2163P ==，故选C ． 4．由（()a b b -⊥r r r ，有20ab b -=r r r ，则2||||cos a b b θ=r r r ，有2cos ||2b a b θ==r r r ‖，故选B ．5．内切球的半径112r =，外接球的半径232r =，所以表面积之比为2112213S r S r ⎛⎫== ⎪⎝⎭，故选C ．6．222cos sin tan 22sin sin cos sin 2cos sin 1tan 145πθθθθθθθθθθ-⎛⎫+=⋅====- ⎪+++⎝⎭，故选B ． 7．C 8．(3)()(6)()f x f x f x f x +=-⇒+=，6T =，()()22log 192log 643f f =⨯()26log 3f =+()2log 32log 323f ===，故选D ．9．B 由三视图可知该几何体是如图所示的三棱锥A BCD -，F 为BD 的中点，外接球球心O 在过CD 的中点E 且垂直于平面BCD 的直线l 上，又点O 到,,A B D 的距离相等，所以O 又在过左边正方体一对棱的中点,M N 所在直线上，在OEN V 中，由NF MF NE OE =，即223OE=，得3OE =，所以三棱锥A BCD -外接球的球半径22223(2)11R OE BE =+=+=，44113V π=．10．B1l ．设()11,A x y ，()22,B x y ，则以A 为切点的切线方程为()1112x y y x x -=-，即112xy x y =-①；同理，以B 为切点的切线方程为222x y x y =-②，()00,P x y 代入①，②得100120022,2,x y x y x y x y ⎧=-⎪⎪⎨⎪=-⎪⎩所以直线AB 的方程为002x y x y =-，即002x y x y =-，又002y x =-，即0122x y x ⎛⎫=-+ ⎪⎝⎭，AB 过定点(2,2)P ，当PF AB ⊥时，(0,1)F ∴到l=AB 过点F 时，距离的最小值为0，故选D ．12．由()0f x =，得e (2)(21)e (2)0x xa x a x ⎡⎤⎡⎤-+--+=⎣⎦⎣⎦，即2e xx a +=，221e xx a +-=，2()e x x g x +=，(1)()ex x g x '-+=，()01g x x '>⇒<-，()01g x x '>⇒>-，()g x 在(,1)-∞-上单调递增，在(1,)-+∞上单调递减．(2)0g -=，max ()(1)g x g e =-=，当2x >-，()0g x >．x →-∞，()g x →-∞，x →+∞，()0g x +→．要使方程有4个不同的零点，则0e,11e 021e,2221a a a a a<<⎧+⎪<-<⇒<<⎨⎪-≠⎩，1a ≠，故选D ．13．3- 14．2020 032115()33212g x x x x =-+-Q ，2()3g x x x '∴=-+，()21g x x ''=-，令()0g x ''=，得12x =，又112g ⎛⎫= ⎪⎝⎭，所以，三次函数()y g x =图象的对称中心坐标为1,12⎛⎫⎪⎝⎭，即()(1)2g x g x +-=，所以，122020101022020202120212021g g g ⎛⎫⎛⎫⎛⎫+++=⨯= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭L ， 2221212212(1)(1)2021202120212021n n n n n n g g g g -'-'''--⎛⎫⎛⎫⎛⎫⎛⎫-+-=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭Q222212122202243320212021202120212021n n n n n ⎡⎤---⎛⎫⎛⎫=-+--+=⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦，因此，202010101222111212(1)(1)(1)202120212021i n n i n i n n g g g -'-'-'==-⎡⎤⎛⎫⎛⎫⎛⎫-=-+- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦∑∑10102211010(11010)202210104202242020212021n n=⨯+⨯-⨯-===∑． 15．222,,,,x y c x a b y b y x a ⎧+==⎧⎪⇒⎨⎨==⎩⎪⎩(,)P a b ∴，2(,0)F c ，,22a c b M +⎛⎫∴ ⎪⎝⎭，代入双曲线方程得222240240c ac a e e +-=⇒+-=，1e =-±1e >，所以1e =．16．由1(1)2n n na n a +--=，令1n =，得12a =．由1(1)2n n na n a +--=①，得12(1)2n n n a na +++-=②，①-②得212n n n a a a +++=，{}n a 为等差数列．又120a =>，5S 最大，则只0d <，50a >，60a <，即240,1225025d d d +>⎧⇒-<<-⎨+<⎩，又51010(5,6)S d =+∈． 17．（本小题满分12分）（1）解：{}n a Q 为等差数列，设公差为d ，1112,35,a d a a d +=⎧∴⎨++=⎩11,1,a d =⎧∴⎨=⎩ 1(1)n a a n d n ∴=+-=．3分{}n b Q 为等比数列，0n b >，设公比为q ，则0q >，2243164b b b ∴⋅==，23118b b q ==， 12q ∴=，1111222n nn b -⎛⎫⎛⎫=⋅= ⎪⎪⎝⎭⎝⎭． 6分（2）证明：令112233n n n T a b a b a b a b =++++L ，23111111123(1)22222n nn T n n -⎛⎫⎛⎫⎛⎫⎛⎫=⨯+⨯+⨯++-⨯+⨯ ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭L ，2311111112(1)22222nn n T n n +⎛⎫⎛⎫⎛⎫⎛⎫=⨯+⨯++-⨯+⨯ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭L ， 9分23111112211111111222222212nn n n n T n n ++⎛⎫⎛⎫- ⎪ ⎪ ⎪⎝⎭⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎝⎭∴=++++-⨯=-⨯ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭-L ，1112222n nn T n -⎛⎫⎛⎫∴=--⨯< ⎪⎪⎝⎭⎝⎭． 12分18．（本小题满分12分）（1）证明：由PD PA =，E 点为AD 的中点，可知PE AD ⊥，再已知PE CD ⊥，且,AD CD 相交于D ，则PE ⊥平面ABCD ．又PE ⊂平面ADP ，所以平面PAD ⊥平面ABCD ． 6分（2）解：由（1）知PE ⊥平面ABCD ，则平面PEC ⊥平面ABCD ，相交于EC ．作DH EC ⊥，可知DH 为D 点到平面PEC 的距离，且5DH ==． 19．（本小题满分12分）解：（1）畅销年个数：4，其中的狂欢年个数：2，记畅销年中不是狂欢年为,a b ；狂欢年为,A B ，则总共有(,)a b ，(,)a A ，(,)b A ，(,)a B ，(,)b B ，(,)A B 则5()6P A =． 4分（2）由题意2y cx d =+更适宜． 6分（3）1011022110677701038.5102285005702.725380148301055021110i ii i t yt ybt t==--⨯⨯====≈--∑∑$， 8分$102 2.738.5 2.0ay bt =-=-⨯≈-$， 10分 $22.7 2.0y x ∴=-，当11x =时，$324.7y =（十亿元）， ∴预测2020年双十一的销售额为324.7十亿元． 12分20．（本小题满分12分）解：（1）c =，设()11,A x y ，()22,B x y ，1232x x +=，1212y y +=-， 2222221122222222,,b x a y a b b x a y a b ⎧+=⎨+=⎩()()()()22121212120b x x x x a y y y y ∴+-++-=， 2分()()22121222121231AB b x x y y b k x x a y y a+-∴==-==-+，223a b ∴=． 4分222a b c -=Q ，223,1,a b ⎧=∴⎨=⎩∴椭圆的标准方程为2213x y +=． 5分（2）,,M Q N Q 三点共线，133OQ OM ON λ=+u u u r u u u u r u u u r，1133λ∴+=，2λ=．设()11,M x y ，()22,N x y ，则1212033x x +=，122x x ∴=-． 7分()22222,13633033y kx m k x kmx m x y =+⎧⇒+++-=⎨+=⎩，220310k m ∆>⇒-+>①，122613kmx x k +=-+，21223313m x x k -=+．代入122x x =-，22613km x k ∴=+，222233213m x k --=+，()222222363321313k mm k k -∴-⨯=++，即()2229131m k m -⋅=-．9分 2910m -≠Q ，219m ≠，22213091m k m -∴=-…②，代入①式得22211091m m m --+>-，即()22211091m m m -+->-，()()2221910m m m ∴--<，11分2119m ∴<<满足②式，113m ∴<<或113m -<<-． 12分 21．（1）1,22x ⎡⎤∈⎢⎥⎣⎦时，由()0f x =得x e a x =，令2(1)()()x x e e x h x h x x x '-=⇒= 112x ∴≤<时，()0h x '<，12x <≤时，()0h x '>， ()h x ∴在1,12⎡⎤⎢⎥⎣⎦上是减函数，在(1,2)上是增函数．又122h e ⎛⎫= ⎪⎝⎭，2(2)2e h =，(1)h e =()344161640444e e e e e e ---==>， 1(2)2h h ⎛⎫∴> ⎪⎝⎭，()h x ∴的大致图像：利用()y h x =与y a =的图像知()a e e ∈． 4分（2）由已知2()x g x e ax ax =--，()2x g x e ax a '∴=--，因为12,x x 是函数()g x 的两个不同极值点（不妨设12x x <），易知0a >（若0a ≤，则函数()f x 没有或只有一个极值点，与已知矛盾），且()10g x '=，()20g x '=．所以1120x e ax a --=，2220xe ax a --=．两式相减得31122x x e e a x x -=-， 7分于是要证明12ln(2)2x x a +<，即证明1212212x x x x e e e x x +-<-，两边同除以2x e ，即证12122121x x x x e e x x ---<-，即证()12122121x x x x x x e e --->-，即证()121221210x x x x x x e e ----+>，令12x x t -=，0t <．即证不等式210tt te e -+>，当0t <时恒成立．设2()1t t t te e ϕ=-+，则222221()11222t t t t t t t t t t te t e e e e e e ϕ'⎤⎡⎫⎛⎫=+⋅⋅-=+-=--+⎥⎪ ⎪⎢⎝⎭⎣⎭⎦．设2()12t t h t e =--，则22111()1222t t h t e e '⎛⎫=-=- ⎪⎝⎭，当0t <时，()0h t '<，()h t 单调递减，所以()(0)0h t h >=，即2102tt e ⎛⎫-+> ⎪⎝⎭，所以()0t ϕ'<，所以()t ϕ在0t <时是减函数．故()t ϕ在0t =处取得最小值(0)0ϕ=．所以()0t ϕ>得证．所以12ln(2)2x x a +<． 12分22．（本小题满分10分）【选修4-4：坐标系与参数方程】解：（1）221:(2)4C x y -+=，2240x x y -+=． 2分222:43C x y y +=-， 4分:4430MN l x y ∴-+-=，4430x y ∴-+=． 5分（2）3:4MN l y x =+，3,04P ⎛⎫∴- ⎪⎝⎭在MN l 上，直线MN的参数方程为3,42x y ⎧=-+⎪⎪⎨⎪=⎪⎩（t 为参数），代入221:(2)4C x y -+=，7分整理得257016t -+=，12t t ∴+=，125716t t =，10t ∴>，20t >， 9分12||||4PM PN t t +=+=． 10分23．（本小题满分10分）【选修4-5：不等式选讲】（1）解：当1a =时，()|1||22|f x x x =-++；①当1x -„时，()1224f x x x =---…，得53x -„；②当11x -<<时，()12234f x x x x =-++=+…，得1x …，x ∴∈∅；③当1x ≥时，()122314f x x x x =-++=+…，得1x …， 5,[1,)3x ⎛⎤∴∈-∞-⋃+∞ ⎥⎝⎦． 5分（2）证明：2()2(|1|||||)2(|1|||)2(|1|||)f x x x a x a x x a x a a x a =-++++---++=+++… 2|1||22||2|||a a a a +=++-厖． 10分。

2020届河北省衡水中学高三下学期一调考试数学理科试题(解析word版)

2019-2020学年度高三年级下学期一调考试数学（理科）试卷一、选择题（本大题共12小题，每题5分，共60分,下列每小题所给选项只有一项符合题意，请将正确答案的序号填涂在答题卡上）1. 已知全集U =R ，集合{}2|2A y y x x R ==+∈，，集合(){}lg 1B x y x ==-，则阴影部分所示集合为A. []12，B. ()12，C. (12]，D. [12)，【答案】B 【解析】【详解】试题分析：由函数,得到,由函数,得到,即,；全集,则.所以B 选项是正确的．考点：集合的运算.【易错点晴】集合的三要素是：确定性、互异性和无序性.研究一个集合，我们首先要看清楚它的研究对象，是实数还是点的坐标还是其它的一些元素，这是很关键的一步.第二步常常是解一元二次不等式，我们首先用十字相乘法分解因式，求得不等式的解集.在解分式不等式的过程中，要注意分母不能为零.元素与集合之间是属于和不属于的关系，集合与集合间有包含关系. 在求交集时注意区间端点的取舍. 熟练画数轴来解交集、并集和补集的题目. 2. 复数3a iz a i+=+-(其中a R ∈，i 为虚数单位)，若复数z 的共轭复数的虚部为12-，则复数z 在复平面内对应的点位于 A. 第一象限 B. 第二象限C. 第三象限D. 第四象限【答案】A 【解析】【分析】先化简复数z ，再求得其共轭复数，令其虚部为12-，解得2a =，代入求解即可. 【详解】由题意得()()()()()331313331010a i i a i a ia z a a i i i ++++-=+=+=+--+， ∴()31311010a ia z +-=-，又复数z 的共轭复数的虚部为12-， ∴31102a +=，解得2a =. ∴5122z i =+，∴复数z 在复平面内对应的点位于第一象限. 故选A.【点睛】本题考查了复数的乘法运算，考查了复数的基本概念及复数的几何意义，属于基础题. 3. 若2,,aa a ab ac a π-===，则,,a b c 的大小关系为A. c b a >>B. b c a >>C. b a c >>D. a b c >>【答案】B 【解析】【详解】分析：首先确定a 的范围，然后结合指数函数的单调性整理计算即可求得最终结果. 详解：由题意可知：()2210,1a ππ-==∈，即1a <函数()xf x a =单调递减，则1a a a >，即a a a >，由于a a a >，结合函数的单调性可得：aa a a a <，即bc >，由于01a <<，故1a a <，结合函数的单调性可得：1aa a a >，即c a >，综上可得：,,a b c 的大小关系为b c a >> . 本题选择B 选项.点睛：对于指数幂的大小的比较，我们通常都是运用指数函数的单调性，但很多时候，因幂的底数或指数不相同，不能直接利用函数的单调性进行比较．这就必须掌握一些特殊方法．在进行指数幂的大小比较时，若底数不同，则首先考虑将其转化成同底数，然后再根据指数函数的单调性进行判断．对于不同底而同指数的指数幂的大小的比较，利用图象法求解，既快捷，又准确． 4. 函数()21cos 1xf x x e ⎛⎫=-⎪+⎝⎭图象的大致形状是（）A. B. C. D.【答案】B 【解析】【分析】利用奇偶性可排除A 、C ；再由(1)f 的正负可排除D.【详解】()21e 1cos cos 1e 1e x x x f x x x -⎛⎫=-= ⎪++⎝⎭，()1e cos()1e x xf x x ----=-=+e 1cos e 1x x x -+ ()f x =-，故()f x 为奇函数，排除选项A 、C ；又1e(1)cos101ef -=<+，排除D ，选B. 故选：B.【点睛】本题考查根据解析式选择图象问题，在做这类题时，一般要结合函数的奇偶性、单调性、对称性以及特殊点函数值来判断，是一道基础题.5. 吸烟有害健康，小明为了帮助爸爸戒烟，在爸爸包里放一个小盒子，里面随机摆放三支香烟和三支跟香烟外形完全一样的“戒烟口香糖”，并且和爸爸约定，每次想吸烟时，从盒子里任取一支，若取到口香糖则吃一支口香糖，不吸烟；若取到香烟，则吸一支烟，不吃口香糖，假设每次香烟和口香糖被取到的可能性相同，则“口香糖吃完时还剩2支香烟”的概率为（） A. 15B. 815C.35D.320【答案】D 【解析】【分析】“口香糖吃完时还剩2支香烟”即第四次取到的是口香糖且前三次有两次口香糖一次香烟，根据古典概型计算出其概率即可.【详解】由题：“口香糖吃完时还剩2支香烟”说明：第四次取到的是口香糖，前三次中恰有两次口香糖一次香烟，记香烟为123,,A A A ，口香糖为123,,B B B ，进行四次取物，基本事件总数：6543360⨯⨯⨯=种事件“口香糖吃完时还剩2支香烟”前四次取物顺序分为以下三种情况：烟、糖、糖、糖：332118⨯⨯⨯=种糖、烟、糖、糖： 332118⨯⨯⨯=种糖、糖、烟、糖：323118⨯⨯⨯=种包含的基本事件个数为：54，所以，其概率为54336020= 故选：D【点睛】此题考查古典概型，解题关键在于弄清基本事件总数，和某一事件包含的基本事件个数，其本质在于计数原理的应用.6. 已知△ABC 外接圆的圆心为O ，若AB=3，AC=5，则AO BC ⋅的值是（） A. 2 B. 4C. 8D. 16【答案】C 【解析】【分析】可画出图形，并将O 和AC 中点D 相连，O 和AB 的中点E 相连，从而得到,ODAC OE AB ，根据数量积的计算公式及条件可得出259·,?22AO AC AO AB ==，而()AO BC AO AC AB ⋅=⋅-，即可得出AO BC ⋅的值．【详解】如图，取AC 中点D,AB 中点E,并连接OD,OE, 则,ODAC OE AB ；∴ 2212519·,?2222AO AC AC AO AB AB ==== ∴ ()259822AO BC AO AC AB AO AC AO AB ⋅=⋅-=⋅-⋅=-= 故选C.【点睛】解题的关键是要熟练的运用数量积的公式cos a b a b θ⋅=以及三角形法则．7. 给出下列五个命题：①若p q ∨为真命题，则p q ∧为真命题；②命题“0x ∀＞，有1x e ≥”的否定为“00x ∃≤，有01x e ＜”； ③“平面向量a 与b 的夹角为钝角”的充分不必要条件是“•0a b <”； ④在锐角三角形ABC 中，必有sin sin cos cos A B A B +>+；⑤{}n a 为等差数列，若()*,,,m n p q a a a a m n p q N +=+∈，则m n p q +=+其中正确命题的个数为 A. 1 B. 2C. 3D. 4【答案】A 【解析】【分析】根据或命题与且命题的性质判断①；根据全称命题否定的定义判断②；根据“ •0a b <，夹角有可能为π判断③；由2A B π+>，利用正弦函数的单调性判断④；根据特例法判断⑤.【详解】对于①，若p q ∨为真命题，则p 与 q 中至少有一个为真命题， p q ∧ 不一定为真命题，故错误.对于②，命题“:0p x ∀＞，有1x e ≥”,则p ⌝为00x ∃>，有01x e ＜ ,故错误. 对于③，若 •0a b < 平面向量a ，b 的夹角为可能为π，故错误. 对于④，在锐角三角形ABC 中，必有02A B π<+<,即,22A B B A ππ>->-，所以sin cos sin cos A B B A ，>>，所以sin sin cos cos A B A B +>+，故正确；对于⑤，在等差数列{}n a 中，若,n a t t =为常数，则1234a a a a +=+满足，()*,,,m n p q a a a a m n p q N +=+∈，但是1234+=+不成立，即m n p q +=+ 不成立，故错误，故选A.【点睛】本题通过对多个命题真假的判断，综合考查逻辑联接词的应用、全称命题的否定、向量的数量积、正弦函数的单调性以及等差数列的性质，属于中档题.这种题型综合性较强，也是高考的命题热点，同学们往往因为某一处知识点掌握不好而导致“全盘皆输”，因此做这类题目更要细心、多读题，尽量挖掘出题目中的隐含条件，另外，要注意从简单的自己已经掌握的知识点入手，然后集中精力突破较难的命题. 8. 已知定义在()0,∞+上的函数()f x ，恒为正数的()f x 符合()()()'2f x f x f x <<，则()()1:2f f 的取值范围为 A. (),2e e B. 11,2e e ⎛⎫⎪⎝⎭C. ()3,e eD. 211,e e ⎛⎫⎪⎝⎭【答案】D 【解析】【详解】令()()()()2,xxf x f xg xh x ee==，则()()()2'2'0xf x f x h x e-=<，()()()''0xf x f xg x e-=>，()()()()12,12g g h h ∴，()()()()()()22421212111,,2f f f f f e e e e e f e∴∴<<，选D ．【方法点睛】利用导数研究函数的单调性、构造函数比较大小,属于难题.联系已知条件和结论，构造辅助函数是高中数学中一种常用的方法，解题中若遇到有关不等式、方程及最值之类问题，设法建立起目标函数，并确定变量的限制条件，通过研究函数的单调性、最值等问题，常可使问题变得明了，准确构造出符合题意的函数是解题的关键；解这类不等式的关键点也是难点就是构造合适的函数，构造函数时往往从两方面着手：①根据导函数的“形状”变换不等式“形状”；②若是选择题，可根据选项的共性归纳构造恰当的函数.9. 已知点A (2,0)，抛物线C ：24x y =的焦点F ．射线FA 与抛物线C 相交于点M ，与其准线相交于点N ，则:FM MN =（）A. 2B. 1:2C. D. 1:3【答案】C 【解析】【详解】抛物线C ：x 2=4y 的焦点为F （0，1），定点A （2，0）， ∴抛物线C 的准线方程为y=-1.设准线与y 轴的交点P ，则FM ：MN =FP ：FN ，又F （0，1），A （2，0）， ∴直线FA 为：x +2y-2=0，当y=-1时，x=4，即N （4，-1），FP FN ∴==， :FM MN=1:10. 定义12nn p p p +++为n 个正数1p 、2p 、…、n p 的“均倒数”，若已知正整数列{}n a 的前n 项的“均倒数”为121n +，又14n n a b +=，则12231011111b b b b b b ++⋅⋅⋅+=（） A.111 B.112C.1011D.1112【答案】C 【解析】【分析】由已知得()1221n n a a a n n S +++=+=，求出n S 后，利用当2n ≥时，1n n n a S S -=-即可求得通项n a ，最后利用裂项法即可求和. 【详解】由已知得12121nn a a n a =++++， ∴()1221n n a a a n n S +++=+=，当2n ≥时，141n n n a S S n -=-=-，验证知当1n =时也成立，14n n a b n +∴==， 11111n n b b n n +∴=-⋅+，12231011111111111110122334101111b b b b b b ⎛⎫⎛⎫⎛⎫⎛⎫++⋅⋅⋅+=-+-+-+-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭∴故选：C【点睛】本题是数列中的新定义，考查了n S 与n a 的关系、裂项求和，属于中档题. 11. 对于任意的实数[1,e]x ∈，总存在三个不同的实数[1,5]y ∈-，使得21ln 0yy xeax x ---=成立，则实数a 的取值范围是 A. 24251(,]e e e- B. 4253[,)e eC. 425(0,]eD. 24253[,)e e e- 【答案】B 【解析】【分析】原方程化为21ln yx y e a x -=+，令()[]ln ,1,xf x a x e x=+∈，令()[]21,1,5y g y y e y -=∈-，可得()1,f x a a e ⎡⎤∈+⎢⎥⎣⎦，利用导数研究函数()g y 的单调性，利用数形结合可得41254,,a a e e e ⎡⎤⎡⎤+⊆⎢⎥⎢⎥⎣⎦⎣⎦，得到关于a 不等式组，解出即可.【详解】0x ≠，∴原式可化为21ln y xy e a x-=+，令()[]ln ,1,x f x a x e x =+∈时()()1ln '0,xf x f x x -=≥递增，故()1,f x a a e⎡⎤∈+⎢⎥⎣⎦，令()[]21,1,5yg y y e y -=∈-，故()()1211'22yy y g y y ey e y y e ---=⋅-=-，故()g y 在()1,0-上递减，在()0,2上递增，在()2,5上递减，而()()()()244251,00,2,5g e g g g e e-====，要使总存在三个不同的实数[]1,5y ∈-，使得21ln 0y y xe ax x ---=成立，即41254,,a a e e e ⎡⎤⎡⎤+⊆⎢⎥⎢⎥⎣⎦⎣⎦，故42514a e a e e ⎧≥⎪⎪⎨⎪+<⎪⎩，故4253a e e ≤<，实数a 的取值范围是4253,e e ⎡⎫⎪⎢⎣⎭，故选B.【点睛】本题考查了函数单调性、最值问题，考查导数的应用以及转化思想,是一道综合题. 转化与划归思想解决高中数学问题的一种重要思想方法，运用这种方法的关键是将题设条件研究透，这样才能快速找准突破点.以便将问题转化为我们所熟悉的知识领域，进而顺利解答，希望同学们能够熟练掌握并应用于解题当中.解答本题的关键是将问题转化为41254,,a a e e e⎡⎤⎡⎤+⊆⎢⎥⎢⎥⎣⎦⎣⎦.12. 如图，在正方体1111ABCDA B C D ﹣中，1A H ⊥平面11AB D ，垂足为H ，给出下面结论： ①直线1A H 与该正方体各棱所成角相等； ②直线1A H 与该正方体各面所成角相等；③过直线1A H 的平面截该正方体所得截面为平行四边形； ④垂直于直线1A H 的平面截该正方体，所得截面可能为五边形，其中正确结论的序号为（）A. ①③B. ②④C. ①②④D. ①②③【答案】D 【解析】【分析】由A 1C ⊥平面AB 1D 1，直线A 1H 与直线A 1C 重合，结合线线角和线面角的定义，可判断①②；由四边形A 1ACC 1为矩形，可判断③；由垂直于直线A 1H 的平面与平面AB 1D 1平行，可判断④．【详解】如图，在正方体ABCD ﹣A 1B 1C 1D 1中，A 1H ⊥平面AB 1D 1，垂足为H ，连接A 1C ，可得A 1C ⊥AB 1，A 1C ⊥AD 1，即有A 1C ⊥平面AB 1D 1，直线A 1H 与直线A 1C 重合，直线A 1H 与该正方体各棱所成角相等，均为2直线A 1H 与该正方体各面所成角相等，均为arctan2，故②正确；过直线A 1H 的平面截该正方体所得截面为A 1ACC 1为平行四边形，故③正确；垂直于直线A 1H 的平面与平面AB 1D 1平行，截该正方体，所得截面为三角形或六边形，不可能为五边形．故④错误．故选D ．【点睛】本题考查线线角和线面角的求法，以及正方体的截面的形状，考查数形结合思想和空间想象能力，属于中档题．二、填空题：（本大题共4小题，每题5分，共20分）13. 有一个底面圆的半径为1，高为2的圆柱，点12,O O 分别为这个圆柱上底面和下底面的圆心，在这个圆柱内随机取一点P ，则点P 到点12,O O 的距离都大于1的概率为___．【答案】13【解析】【详解】到点12,O O 距离为1的点是半径为1的球面，所以所求概率为431=1-23=1V P V ππ=-球柱14. 在数列{a n }中，若函数f （x ）＝sin 2x2x 的最大值是a 1，且a n ＝（a n +1﹣a n ﹣2）n ﹣2n 2，则a n ＝_____．【答案】a n ＝2n 2+n 【解析】【分析】()sin 23sin(2)f x x x x ϕ=+=+，可得13a =．由已知条件推出121n na a n n+-=+，然后求解数列的通项公式．【详解】解：()sin 23sin(2)f x x x x ϕ=+=+，当222x k πϕπ+=+，k Z ∈，()f x 取得最大值3，13a ∴=．21(2)2n n n a a a n n +=---，21(1)22n n na n a n n +∴=+++，121n na a n n+-=+， n a n ⎧⎫∴⎨⎬⎩⎭是以131a =为首项，2为公差的等差数列，()321na n n∴=+- 2[32(1)]2n a n n n n ∴=+-=+，故答案为：22n n +．【点睛】本题考查了数列递推关系、三角函数求值、法则求积，考查了推理能力与计算能力，属于中档题． 15. 秦九韶是我国南宋著名数学家，在他的著作数书九章》中有已知三边求三角形面积的方法:“以小斜幂并大斜幂减中斜幂余半之，自乘于上以小斜幂乘大斜幂减上，余四约之为实一为从隅，开平方得积”如果把以上这段文字写成公式就是S =，共中a 、b 、c 是△ABC 的内角A ，B ，C 的对边．若sin 2sin cos C A B =，且2b ，2，2c 成等差数列，则ABC 面积S 的最大值为____【解析】【分析】运用正弦定理和余弦定理可得a b =，再由等差数列中项性质可得2224a b c ==-，代入三角形的面积公式，配方，结合二次函数的最值求法，可得所求最大值．【详解】sin 2sin cos C A B =，∴2cos c a B =，因此2222,2a c b c a a b ac+-=⨯=∵2b ，2，2c 成等差数列，∴224b c +=，因此S ===，当285c =，即c =时，S 取得最大值12=，即ABC 面积S . 【点睛】本题考查三角形的正弦定理、余弦定理和面积公式，以及等差数列中项性质，转化为求二次函数的最值是解题的关键，属于中档题．16. 过曲线22122:1(0,0)x y C a b a b-=>>的左焦点1F 作曲线2222:C x y a +=的切线，设切点为M ，延长1F M 交曲线23:2(0)C y px p =>于点N ，其中1,C 3C 有一个共同的焦点，若10MF MN +=，则曲线1C 的离心率为________．【答案】51+ 【解析】【分析】设双曲线的右焦点为2F ，根据曲线1C 与3C 有一个共同的焦点，得到抛物线方程，再根据O 为12F F 的中点，M 为1F N 的中点，利用中位线定理，可得，2//OM NF ，22NF a =，21NF NF ⊥， 12NF b =.设(),N x y ，根据抛物线的定义可得2,2x c a x a c +=∴=-，过1F 点作x 轴的垂线，点(),N x y 到该垂线的距离为2a ，然后在1ANF ∆中，利用勾股定理求解. 【详解】如图所示：设双曲线的右焦点为2F ，则2F 的坐标为(),0c ，因为曲线1C 与3C 有一个共同的焦点，所以24y cx =，因为O 为12F F 的中点，M 为1F N 的中点，所以OM 为12NF F ∆的中位线，所以2//OM NF ，因OM a =，所以22NF a =又21NF NF ⊥，22,FF c = 所以12NF b =.设(),N x y ，则由抛物线定义可得2,2x c a x a c +=∴=-，过1F 点作x 轴的垂线，点(),N x y 到该垂线的距离为2NA a =，在1ANF ∆中，由勾股定理即得22244y a b +=，即()()2224244c a c a c a-+=-，即210e e --=，解得51e +=. 故答案为：51+ 【点睛】本题主要考查双曲线和抛物线的几何性质，还考查了数形结合的思想和运算求解的能力，属于中档题.三、解答题：（本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤．）17. 如图，在ABC ∆中，内角A ，B ，C 的对边分别为a ，b ，c ，已知4c =，2b =，2cos c C b =，D ，E 分别为线段BC 上的点，且BD CD =，BAE CAE ∠=∠．（1）求线段AD 的长；（2）求ADE ∆的面积．【答案】（1）6AD =215【解析】【详解】试题分析：（I ）在△ABC 中，利用余弦定理计算BC ，再在△ACD 中利用余弦定理计算AD ；（II ）根据角平分线性质得到2ABE ACE S AB S AC ∆∆==，又ABE ACE S BE S EC ∆∆=，所以2BE EC =，所以1433CE BC ==，42233DE =-=，再利用正弦形式的面积公式即可得到结果. 试题解析：（1）因为4c =，2b =，所以1cos 24b Cc ==．由余弦定理得22224161 cos244a b c aCab a+-+-===，所以4a=，即4BC=，在ACD∆中，2CD=，2AC=，所以2222cos6AD AC CD AC CD ACD=+-⋅⋅∠=，所以6AD=．（2）因为AE是BAC∠的平分线，所以1sin221sin2ABEACEAB AE BAES ABS ACAC AE CAE∆∆⋅⋅∠===⋅⋅∠，又ABEACES BES EC∆∆=，所以2BEEC=，所以1433CE BC==，42233DE=-=，又因为1cos4C=，所以215sin1cosC C=-=，所以115sin2ADES DE AC C∆=⨯⨯⨯=．18. 如图，在四棱锥P ABCD-中，底面ABCD是边长为2的菱形，60,90DAB ADP∠=︒∠=︒，平面ADP⊥平面ABCD，点F为棱PD的中点．（Ⅰ）在棱AB上是否存在一点E，使得AF平面PCE，并说明理由；（Ⅱ）当二面角D FC B--的余弦值为24时，求直线PB与平面ABCD所成的角．【答案】（1）见解析（2）60︒【解析】【分析】（Ⅰ）取PC 的中点Q ，连结EQ 、FQ ，得到故//AE FQ 且AE FQ =，进而得到//AF EQ ，利用线面平行的判定定理，即可证得//AF 平面PEC .（Ⅱ）以D 为坐标原点建立如图空间直角坐标系，设FD a =，求得平面FBC 的法向量为m ，和平面DFC 的法向量n ，利用向量的夹角公式，求得3a=，进而得到PBD ∠为直线PB 与平面ABCD 所成的角，即可求解.【详解】（Ⅰ）在棱AB 上存在点E ，使得//AF 平面PCE ，点E 为棱AB 的中点．理由如下：取PC 的中点Q ，连结EQ 、FQ ，由题意，//FQ DC 且12FQ CD =， //AE CD 且12AE CD =，故//AE FQ 且AE FQ =.所以，四边形AEQF 为平行四边形.所以，//AF EQ ，又EQ ⊥平面PEC ，AF ⊥平面PEC ，所以，//AF 平面PEC . （Ⅱ）由题意知ABD ∆为正三角形，所以ED AB ⊥，亦即ED CD ⊥，又90ADP ∠=︒，所以PD AD ⊥，且平面ADP ⊥平面ABCD ，平面ADP ⋂平面ABCD AD =，所以PD ⊥平面ABCD ，故以D 为坐标原点建立如图空间直角坐标系，设FD a =，则由题意知()0,0,0D ，()0,0,F a ，()0,2,0C ，)3,1,0B，()0,2,FC a =-，()3,1,0CB =-，设平面FBC 的法向量为(),,m x y z =，则由00m FC m CB ⎧⋅=⎨⋅=⎩得2030y az x y -=⎧⎪⎨-=⎪⎩，令1x =，则3y =23z =所以取231,3,m ⎛= ⎝⎭，显然可取平面DFC 的法向量()1,0,0n =，由题意：22cos ,41213m n a ==++，所以3a =. 由于PD ⊥平面ABCD ，所以PB 在平面ABCD 内的射影为BD ，所以PBD ∠为直线PB 与平面ABCD 所成的角，易知在Rt PBD ∆中，tan 3PDPBD a BD∠===，从而60PBD ∠=︒，所以直线PB 与平面ABCD 所成的角为60︒.【点睛】本题考查了立体几何中的面面垂直的判定和直线与平面所成角的求解问题，意在考查学生的空间想象能力和逻辑推理能力；解答本题关键在于能利用直线与直线、直线与平面、平面与平面关系的相互转化，通过严密推理，明确角的构成，着重考查了分析问题和解答问题的能力.19. 如图，A 为椭圆22142x y +=的左顶点，过A 的直线l 交抛物线()220y px p =>于B 、C 两点，C 是AB 的中点.（1）求证：点C 的横坐标是定值，并求出该定值；（2）若直线m 过C 点，且倾斜角和直线l 的倾斜角互补，交椭圆于M 、N 两点，求p 的值，使得BMN ∆的面积最大.【答案】(1)证明见解析，定值1. (2) 928p = 【解析】【分析】（1）由题意可求()2,0A -，设()11,B x y 、()22,C x y ，l ：2x my =-，联立直线与抛物线，利用C 是AB 的中点得122y y =，计算可得点C 的横坐标是定值；（2）由题意设直线m 的方程为213pm x m y ⎛⎫=--+ ⎪⎝⎭，联立方程，利用C 是AB 的中点，可得BMN AMN S S ∆∆=，根据三角形的面积公式以及基本不等式可求BMN ∆的面积最大值，由取等条件解得p 的值.【详解】（1）()2,0A -，过A 的直线l 和抛物线交于两点，所以l 的斜率存在且不为0，设l ：2x my =-，其中m 是斜率的倒数，设()11,B x y 、()22,C x y ，满足222x my y px=-⎧⎨=⎩，即2240y pmy p -+=，0∆>且121224y y pm y y p+=⎧⎨=⎩，因为C 是AB 中点，所以122y y =，所以223pm y =，292m p =，所以222222133pm p x m m =⋅-=-=，即C 点的横坐标为定值1. （2）直线m 的倾斜角和直线l 的倾斜角互补，所以m 的斜率和l 的斜率互为相反数.设直线m 为213pm x m y ⎛⎫=--+ ⎪⎝⎭，即4x my =-+，联列方程224240x my x y =-+⎧⎨+-=⎩得()2228120m y my +-+=， ()()222848216960m m m ∆=-+=->，所以26m >；且12212282122m y y m y y m ⎧+=⎪⎪+⎨⎪=⎪+⎩，∵点C 是AB 中点，∴BMN AMN S S ∆∆=，设()2,0A -到MN的距离d =12MN y =-，12132AMNS MN d y y ∆=⋅⋅=-=26t m =-，AMN S ∆==≤=当且仅当8t =，214m =时取到，所以9142p =，928p =. 法二：因为B 点在抛物线()220y px p =>上，不妨设2,2t B t p ⎛⎫⎪⎝⎭，又C 是AB 中点，则24,42t p t C p ⎛⎫- ⎪⎝⎭，代入抛物线方程得：224224t t p p p -⎛⎫=⋅ ⎪⎝⎭，得：28t p =，∴8414C p p x p -==为定值. （2）∵直线l 的斜率()02126tt k -==--，直线m 斜率'6t k =-， ∴直线m 的方程：()126t t y x -=--，即64x y t =-+，令6m t=代入椭圆方程整理得： ()2228120my my +-+=，设()11,B x y 、()22,C x y ，下同法一.【点睛】本题考查直线的方程和抛物线方程联立，注意运用椭圆的顶点坐标，运用韦达定理以及点到直线的距离公式，考查三角形的面积的最值求法，化简整理的运算能力，属于中档题．20. 某共享单车经营企业欲向甲市投放单车，为制定适宜的经营策略，该企业首先在已投放单车的乙市进行单车使用情况调查.调查过程分随机问卷、整理分析及开座谈会三个阶段.在随机问卷阶段，A，B两个调查小组分赴全市不同区域发放问卷并及时收回；在整理分析阶段，两个调查小组从所获取的有效问卷中，针对15至45岁的人群，按比例随机抽取了300份，进行了数据统计，具体情况如下表：（1）先用分层抽样的方法从上述300人中按“年龄是否达到35岁”抽出一个容量为60人的样本，再用分层抽样的方法将“年龄达到35岁”的被抽个体数分配到“经常使用单车”和“偶尔使用单车”中去.①求这60人中“年龄达到35岁且偶尔使用单车”的人数；②为听取对发展共享单车的建议，调查组专门组织所抽取的“年龄达到35岁且偶尔使用单车”的人员召开座谈会.会后共有3份礼品赠送给其中3人，每人1份（其余人员仅赠送骑行优惠券）.已知参加座谈会的人员中有且只有4人来自A组，求A组这4人中得到礼品的人数X的分布列和数学期望；（2）从统计数据可直观得出“是否经常使用共享单车与年龄（记作m岁）有关”的结论.在用独立性检验的方法说明该结论成立时，为使犯错误的概率尽可能小，年龄m应取25还是35？请通过比较2K的观测值的大小加以说明.参考公式：22()()()()()n ad bcKa b c d a c b d-=++++，其中n a b c d=+++.【答案】(1) ①9人②见解析；(2) 25m=【解析】【分析】（1）①根据分层抽样要求，先求从300人中抽取60人，其中“年龄达到35岁”的人数60 100300⋅，再求“年龄达到35岁” 中偶尔使用单车的人数45 20100⋅；②确定随机变量X的取值，计算X各个取值的概率，得分布列及数学期望.(2)对年龄m 是否达到35,m 是否达到25对数据重新整理（2⨯2联表），根据公式计算相应的2K ，比较大小确定.【详解】（1）①从300人中抽取60人，其中“年龄达到35岁”的有6010020300⨯=人，再将这20人用分层抽样法按“是否经常使用单车”进行名额划分，其中“年龄达到35岁且偶尔使用单车”的人数为45209100⨯=. ②A 组这4人中得到礼品的人数X 的可能取值为0，1，2，3，相应概率为：()35395042C P X C ===，()12453910121C C P X C ===， ()2145395214C C P X C ===，()34391321C P X C ===. 故其分布列为∴()5105140123422114213E X =⨯+⨯+⨯+⨯=. （2）按“年龄是否达到35岁”对数据进行整理，得到如下列联表：35m =时，由（1）中的列联表，可求得2K 的观测值()22130012545755530015002520010018012020010018012016k ⨯⨯-⨯⨯===⨯⨯⨯⨯⨯⨯.25m =时，按“年龄是否达到25岁”对数据进行整理，得到如下列联表：可求得2K 的观测值()22230067871133330021004920010018012020010018012016k ⨯⨯-⨯⨯===⨯⨯⨯⨯⨯⨯. ∴21k k >，欲使犯错误的概率尽可能小，需取25m =.【点睛】本题考查分层抽样和独立性检验，随机变量的分布列及数学期望，考查统计知识理解掌握水平、对数据的处理能力及分析推理解决实际问题的能力.21. 已知函数2()1xf x e ax bx =---，其中,a b R ∈， 2.71828e =为自然对数的底数.（Ⅰ）设()g x 是函数()f x 的导函数，求函数()g x 在区间[0,1]上的最小值；（Ⅱ）若(1)0f =，函数()f x 在区间(0,1)内有零点，求a 的取值范围【答案】（Ⅰ）当12a ≤时， ()(0)1g x g b ≥=-；当 122e a <≤时， ()22ln(2)g x a a a b ≥--；当2ea >时， ()2g x e a b ≥--.（Ⅱ） a 的范围为()2,1e -. 【解析】【详解】试题分析：（Ⅰ）易得()2,()2x x g x e ax b g x e a -='=--，再对分a 情况确定()g x 的单调区间，根据()g x 在[0,1]上的单调性即可得()g x 在[0,1]上的最小值.（Ⅱ）设0x 为()f x 在区间(0,1)内的一个零点，注意到(0)0,(1)0f f ==.联系到函数的图象可知，导函数()g x 在区间0(0,)x 内存在零点1x ，()g x 在区间0(),1x 内存在零点2x ，即()g x 在区间(0,1)内至少有两个零点. 由（Ⅰ）可知，当12a ≤及2ea ≥时，()g x 在(0,1)内都不可能有两个零点.所以122ea <<.此时，()g x 在[0,ln 2]a 上单调递减，在[ln 2,1]a 上单调递增，因此12(0,ln(2)],(ln(2),1)x a x a ∈∈，且必有(0)10,(1)20gb g e a b =->=-->.由(1)10f e a b =---=得：1b e a =--，代入这两个不等式即可得a 的取值范围.试题解答：（Ⅰ）()2,()2x x g x e ax b g x e a -='=--①当0a ≤时，()20xg x e a -'=>，所以()(0)1g x g b ≥=-. ②当0a >时，由()20x g x e a -'=>得2,ln(2)x e a x a >>. 若12a >，则ln(2)0a >；若2e a >，则ln(2)1a >. 所以当102a <≤时，()g x 在[0,1]上单调递增，所以()(0)1g x gb ≥=-. 当122e a <≤时，()g x 在[0,ln 2]a 上单调递减，在[ln 2,1]a 上单调递增，所以()(ln 2)22ln 2g x g a a a a b ≥=--. 当2e a >时，()g x 在[0,1]上单调递减，所以()(1)2g x g e a b ≥=--. （Ⅱ）设0x 为()f x 在区间(0,1)内的一个零点，则由0(0)()0f f x ==可知，()f x 在区间0(0,)x 上不可能单调递增，也不可能单调递减.则()g x 不可能恒为正，也不可能恒为负.故()g x 在区间0(0,)x 内存在零点1x .同理()g x 在区间0(),1x 内存在零点2x .所以()g x 在区间(0,1)内至少有两个零点.由（Ⅰ）知，当12a ≤时，()g x 在[0,1]上单调递增，故()g x 在(0,1)内至多有一个零点. 当2e a ≥时，()g x 在[0,1]上单调递减，故()g x 在(0,1)内至多有一个零点. 所以122e a <<. 此时，()g x 在[0,ln 2]a 上单调递减，在[ln 2,1]a 上单调递增，因此12(0,ln(2)],(ln(2),1)x a x a ∈∈，必有(0)10,(1)20g b g e a b =->=-->.由(1)10f e a b =---=得：12a b e +=-<，有(0)120,(1)210g b a e g e a b a =-=-+>=--=->.解得21e a -<<.当21e a -<<时，()g x 在区间[0,1]内有最小值(ln(2))g a .若(ln(2))0g a ≥，则()0([0,1])g x x ≥∈，从而()f x 在区间[0,1]上单调递增，这与(0)(1)0f f ==矛盾，所以(ln(2))0g a <.又(0)20,(1)10g a e g a =-+>=->，故此时()g x 在(0,ln(2))a 和(ln(2),1)a 内各只有一个零点1x 和2x .由此可知()f x 在1[0,]x 上单调递增，在1(,x 2)x 上单调递减，在2[,1]x 上单调递增.所以1()(0)0f x f >=，2()(1)0f x f <=，故()f x 在1(,x 2)x 内有零点.综上可知，a 的取值范围是(2,1)e -.【考点定位】导数的应用及函数的零点.（二）选考题，满分共10分，请考生在22，23题中任选一题作答，如果多做，则按所做的第一题计分．答时用2B 铅笔在答题卡上把所选题目的题号涂黑22. 选修4-4：坐标系与参数方程在平面直角坐标系xOy 中，直线1l 过原点且倾斜角为02παα⎛⎫< ⎪⎝⎭.以坐标原点O 为极点，x 轴正半轴为极轴建立坐标系，曲线2C 的极坐标方程为2cos ρθ=.在平面直角坐标系xOy 中，曲线2C 与曲线1C 关于直线y x =对称.（Ⅰ）求曲线2C 的极坐标方程；（Ⅱ）若直线2l 过原点且倾斜角为3πα+，设直线1l 与曲线1C 相交于O ，A 两点，直线2l 与曲线2C 相交于O ，B 两点，当α变化时，求AOB 面积的最大值.【答案】(Ⅰ) 2sin ρθ= 34【解析】【分析】(Ⅰ)法一：将1C 化为直角坐标方程，根据对称关系用2C 上的点表示出1C 上点的坐标，代入1C 方程得到2C 的直角坐标方程，再化为极坐标方程；法二：将y x =化为极坐标方程，根据对称关系将1C 上的点用2C 上的点坐标表示出来，代入1C 极坐标方程即可得到结果；(Ⅱ)利用1l 和2l 的极坐标方程与12,C C 的极坐标方程经,A B 坐标用α表示，将所求面积表示为与α有关的三角函数解析式，通过三角函数值域求解方法求出所求最值.【详解】(Ⅰ)法一：由题可知，1C 的直角坐标方程为：2220x y x +-=，设曲线2C 上任意一点(),x y 关于直线y x =对称点为()00,x y ，所以00x y y x =⎧⎨=⎩ 又因为2200020x y x +-=，即2220x y y +-=，所以曲线2C 的极坐标方程为：2sin ρθ=法二：由题可知，y x =的极坐标方程为：4πθ=()R ρ∈，设曲线2C 上一点(),ρθ关于4πθ= ()R ρ∈的对称点为()00,ρθ，所以0024ρρθθπ=⎧⎪⎨+=⎪⎩ 又因为002cos ρθ=，即2cos 2sin 2πρθθ⎛⎫=-= ⎪⎝⎭，所以曲线2C 的极坐标方程为：2sin ρθ=(Ⅱ)直线1l 的极坐标方程为：θα=，直线2l 的极坐标方程为：3πθα=+设()11,A ρθ，(),B ρθ22 所以2cos θαρθ=⎧⎨=⎩解得12cos ρα=，32sin πθαρθ⎧=+⎪⎨⎪=⎩解得22sin 3πρα⎛⎫=+ ⎪⎝⎭1211sin sin sin 2332AOB S ππρρααααα∆⎛⎫⎛⎫∴=⋅=⋅+=⋅+ ⎪ ⎪ ⎪⎝⎭⎝⎭223πααα⎛⎫=+=++ ⎪⎝⎭因为：02πα≤<，所以42333πππα≤+< 当232ππα+=即12πα=时，sin 213πα⎛⎫+= ⎪⎝⎭，AOB S ∆+34【点睛】本题考查轨迹方程的求解、三角形面积最值问题的求解，涉及到三角函数的化简、求值问题.求解面积的关键是能够明确极坐标中ρ的几何意义，从而将问题转化为三角函数最值的求解.23. 已知函数()121f x ax x =++-（1）当1a =时，求不等式()3f x >的解集；（2）若02a <<，且对任意x ∈R ，3()2f x a ≥恒成立，求a 的最小值．【答案】（1）(,1)(1,)-∞-+∞；（2）1．【解析】【分析】(1) 当1a =时，求出分段函数()3,112,1213,2x x f x x x x x ⎧⎪-<-⎪⎪=-+-≤≤⎨⎪⎪>⎪⎩，然后可以选择数形结合求解或选择解不等式组；(2)当02a <<时，化简分段函数得()()()()12,,11 12122,,212,2a x x a f x ax x a x x a a x x ⎧-+<-⎪⎪⎪=++-=-+-≤≤⎨⎪⎪+>⎪⎩可以得到函数()f x 在1,a ⎛⎫-∞- ⎪⎝⎭上单调递减，在11,2a ⎡⎤-⎢⎥⎣⎦上单调递减，在1,2⎛⎫+∞ ⎪⎝⎭上单调递增，然后利用最值分析法，即可求出参数a 的最小值.【详解】（1）当1a =时，()121f x x x =++-，即()3,112,1213,2x x f x x x x x ⎧⎪-<-⎪⎪=-+-≤≤⎨⎪⎪>⎪⎩，解法一：作函数()121f x x x =++-的图象，它与直线3y =的交点为()()1,3,1,3A B -，所以，()3f x >的解集的解集为()(),11,-∞-⋃+∞．解法2：原不等式()3f x >等价于133x x <-⎧⎨->⎩ 或11223x x ⎧-≤≤⎪⎨⎪-+>⎩ 或1233x x ⎧>⎪⎨⎪>⎩，解得：1x <-或无解或1x >，所以，()3f x >的解集为()(),11,-∞-⋃+∞．（2）1102,,20,202a a a a <<∴-+-<．则()()()()12,,1112122,,212,2a x x a f x ax x a x x a a x x ⎧-+<-⎪⎪⎪=++-=-+-≤≤⎨⎪⎪+>⎪⎩ 所以函数()f x 在1,a ⎛⎫-∞- ⎪⎝⎭上单调递减，在11,2a ⎡⎤-⎢⎥⎣⎦上单调递减，在1,2⎛⎫+∞ ⎪⎝⎭上单调递增．所以当12x =时，()f x 取得最小值，()min 1122a f x f ⎛⎫==+ ⎪⎝⎭．因为对x R ∀∈，()32f x a ≥恒成立，所以()min 3122a f x a=+≥．又因为0a >，所以2230a a +-≥，解得1a ≥ （3a ≤-不合题意）．所以a 的最小值为1．【点睛】本题第一问考查通过利用绝对值不等式的关系转化成分段函数进行求解的题目，求解的过程既可用数形结合，也可以用不等式组求解，属于简单题；第二问考查含参绝对值不等式求解参数的最值问题，因为本题的参数不容易分离，所以，选择最值分析法进行讨论求解，难度属于中等.。

2020年河北衡水中学理科数学高考模拟试卷(含答案)

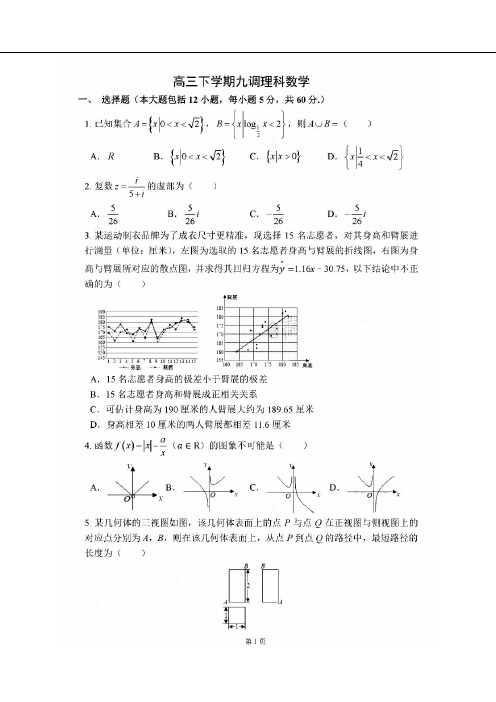
2 2✓)20如图，椭圆吓兰+.L = l (a > h > 0)的左右焦点分别为八，九，离心率为—,a b 2 2 7 过抛物线C 2:x 1 =4b y 住点J,的直线交抛物线千M,N两点，当I M们＝－时，M 4点在x轴上的射影为F;。

连接NO,MO并延长分别交c l 于A,B两点，连接AB,� LlOMN与Ll OAR的曲积分别记为S"a,,JN禾11S !,OAB '设/4=兰罕兰s!,OAB (l)求椭圆(_'\和抛物线C \的方程；(2)求入的取值范围x7 解：(1)由抛物线定义可得M (-c,--h),:. 点M在抛物线2=4by J:,47 :.c 1 =4b(--b), 即c 2=7h-4h�(D 4心一又由.:.=—，得c 2= 3b 2, 将上式代入＠，得7b:=7b,解得b = I , .". c =✓3,a 2:. a= 2,X 2 所以仙线c l 的方程为—+y 2 = 1, 曲线c 2的方程为x 2=4y 4 (2)设直线M N的方程为y =kx+I,由｛y =kx + 1 消去Y挔理得x 2-4kx—4= 0, x -= 4y 设M(x 1,y 1),N(x 2,y 2),则X 1X 2=-4,V, y 1 I 1 1 设从=m,k 。

�1= n 1', 则mm'=.:....=.—=—X1X 2=--, 所以n1'=-—-, ®x 2 x 1 164 4m 设直线ON 的方程为y =mx (m>O),叶y,=mx , 解得x 0=4m, 所以jO N!=✓一x -=4y l+m lx N l =4m五言了，1 I 山＠可知，用—一代替m ,可得IOMI=上✓l+(-上)2 I X ,11 = - 1 + '1 4m m 4m m厂二第14页由｛勹'�I '解得x ,:J.;, 气，所以iOA i :汇伈I :2汇4五＇用-i,;;代替m,可行1081:三1,./j三1 4m✓I 言�-I+ 1 m 言s 所以A,=�竺=I ON I I OM 仁1S !!.O忠I OAIIOBI 2�_2厂二=�言归丿二厂41111 1 1 4nt 2 + 2+—=2m+—:2: 2'当目仅当m=1时等号成立4m 2 2m 所以入的取伯范围为[2,+吩21已知函数f(x)= x 2 -a e x -1.(1)若f(x)有两个不同的极值点X 1,X 2, 求实数a 的取值范围；4 (2)在(l)的条件下，求证：e -''+e·'0 >一雇(1)函数f (x ) =x 2 -ae 入-1' ．寸(x)=2x -ae 入，守(x)有两个不同的极值点X1,X2, 习(x)=2.x -ae 入'=O有两个根，即a =尘，e x 即y=a与y=g (x ) =坠－有两个交点，e x :.g '(x) = 2 (1-x) X ' ea 当x<I时，g'(x)>O, 函数g (x)单调递增，当x>l H寸，g'(x)<O, 函数g (x )单调递减，: .g (x) mcu•=g (1) =乌当X ---->一动时，g Cx) ---->十心，当X---->十心时，g (x)一O ,第15页。

2020年衡水中学高三冲刺联考理科数学试题(含答案和解析)

2020 届高三冲刺联考理数试卷本试卷共4页忆3题（含选考题）。

全卷满分150分α考试用时120分钟。

注章事项：1.答题前，先将自己的姓名、考号等填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置.2.选择题的作答：每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑A写在试题卷、草鵠纸和答題卡上的非答题区域均无效。

3.填空题和解答題的作答：用签字笔直按写在答题卡上对应的答题区域内。

写柱试翹卷、草犒维和咎题卡上的非答题区域均无效。

4.选考题的作答;先把所选题目的题号在答题卡上指定的位置用2B铅笔涂黑。

答案写在答题卡上对应的答题区域内•写在试题卷、草稿纸和答题卡上的非答题区域均无效。

5.考试结束后，请将本试题卷和答题卡一并上交©第I卷一•选择题；本题共12小题■每小题5分■在毎小题给出的四个选项中■只有一项是符合题目要求的O1∙设集合A={^∣r x-62r-7<0）,B=⅛∣∣Λ~l∣>2）,ra⅛合AnB=A. {工13VGV7} E —7VzV — 1} C. {玄| —IVHV3} D. {□r∣—3V工V1}2.设复数上满足^ = i（L为虚数单位），则∕z =A. i B< —i C. 1 D e-L3.平行四边形ABCD中，E是AE的中点tBF=2FC,若E?=M AB+nAD，则w + n=A∙⅜κτc⅜D-I4.法国数学家加斯帕尔•蒙日发现占椭圆≤÷^ = 1G>6>O）相切的两条垂直切线的交点轨迹为r2+√ = d z÷6≡,这个阿亦被称为蒙日@1.现将质点F随机投人椭RC≡y + y= 1所对应的蒙日岡内’则质点落在椭圆外部的概率为（附:椭圆£+石=1的面积公式为S=如A嫗 B — C 1 —呃 D 1 —嫗A. §比3 J 丄9 U'1 35・已知斜三角形AliC中，角A、F、C所对的边分别为a、b、_若α = 4,C=60°,6GN∙,且b满足e fi+ δ-10<0（e=2,7L828-）,Irl C=A. 2√3B. √13C.2√2 或庾D.√56•如图，已⅛ΘO^z÷y=2与工轴的正半轴交于点A,与曲线CQ=辰交于第一象限的点B, 则阴影部分的面积为离三大联考•理数第1页（共4页）D∙τ÷τS 1 已知一5CGS (X +^9) = 3Sin Λ*+4COS Jr ■对 xζ R 恒成立'则 SinA 4 + 3^3" r > 3^3—4八 4—3T -I _ 4 + 3^3"A ∙F ~,B ・F -Cp-D• ~10.过双曲线y-√ = 1的右焦点F,作倾斜角为砒的直线Z,交双曲线的渐近线于点A 、B(其中A 在第一象限)，0为坐标原点，则笑竺=-5ΔΛΛftA 丄B 逕C 丄D 丄入 4 D 3 J 2 U3 11■.如图•正方体ABCD- A l B l C l D I 中，E 是棱AAJ 的中点，若三棱锥⅛E-BBlD 外按球的半径R 等于晋，则正方体ABCD-A l B I C I D l 勺的棱长为A,l C. 2√21/定义矩阵的运算如下：R ,总存在非零常数T ■使得OQ+Q=卩③若存在直线V=M 与力Q)的图象无公共点,且使的图象位于直线两側，此直线即称为函数力⑺〉的分界编则八工)的分界线的斜率的取值范围是(e z ,+oo)5④函数ra)=fCr) — SinM 的零点有无数个• A.①③④ B ①②④ C∙②③ D.①④第］!卷本卷包括必考题和选考題两部分。

2020年河北省衡水中学高考联考数学试题(附答案解析)

2020年河北省衡水中学高考联考数学试题一、单选题1．函数()log (1)1a f x x =-+（0a >，且1a ≠）的图象恒过点（） A ．(1,1)B ．(2,1)C ．(1,2)D ．(2,2)2．已知复数z 在复平面上对应的点为()1,m ，若iz 为纯虚数，则实数m 的值为（） A ．1-B ．0C ．1D ．1或1-3．若函数f (x )＝sin(ωx －3π)(ω>0)在(－2π，0)上单调递增，则ω的最大值为( )A ．13B ．12C ．1D ．24．已知双曲线C ：()222210,0x y a b a b-=>>的两个焦点为1F ，2F ，过1F 且与x 轴垂直的直线交C 的渐近线于A ，B 两点.若2ABF ∆为直角三角形，则双曲线C 的离心率为（）A BCD 5．国际上通常用年龄中位数指标作为划分国家或地区人口年龄构成的标准：年龄中位数在20岁以下为“年轻型”人口；年龄中位数在20～30岁为“成年型”人口；年龄中位数在30岁以上为“老龄型”人口．如图反映了我国全面放开二孩政策对我国人口年龄中位数的影响．据此，对我国人口年龄构成的类型做出如下判断：①建国以来直至2000年为“成年型”人口；②从2010年至2020年为“老龄型”人口；③放开二孩政策之后我国仍为“老龄型”人口．其中正确的是（） A ．②③B ．①③C ．②D ．①②6．等差数列{a n }中，a m =1k ,a k =1m (m ≠k )，则该数列前mk 项之和为（）A ．mk 2−1 B ．mk 2C ．mk+12D ．mk 2+17．已知tan （α+β）=35，tanβ=13，则tanα=（） A ．29B ．13C ．79D ．768．执行如图所示的程序框图，若输入如下四个函数：①f（x ）＝sinx ②f（x ）＝cosx ③1()f x x= ④f（x ）＝x 2则输出的函数是（） A ．f （x ）＝sinxB ．f （x ）＝cosxC ．1()f x x= D ．f （x ）＝x 29．已知,,a b c R ∈，满足，则下列不等式成立的是 A ．B ．C ．D ．10．当x A ∈时，若1x A -∉，且1x A +∉，则称x 为A 的一个“孤立元素”，由A 的所有孤立元素组成的集合称为A 的“孤星集”，若集合{}0,1,3M =的孤星集为M '，集合{}0,3,4N =的孤星集为N '，则M N '⋃'=( )A ．{}0134，，，B ．{}14，C ．{}13，D ．{}03，11．ABC 中，ACB 90∠=，AC 3=，BC 4=，CD AB ⊥，垂足为D ，则CD (= )A ．43CA CB 77+ B ．34CA CB 77+ C ．169CA CB 2525+ D ．916CA CB 2525+ 12．若函数()y f x =的定义域为R ，对于x R ∀∈，()()f x f x '<，且(1)f x +为偶函数，(2)1f =，则不等式()xf x e <的解集为（）A ．()2,+∞B ．(0,)+∞C ．(),0-∞D ．(),2-∞二、填空题13．由球O 的球面上一点P 作球的两两垂直的三条弦PA ，PB ，PC ，且PA =PBPC =则球O 的半径R =________．14．等比数列{}n a 的前n 项和为n S ，112a =，若6378S S =，则24a a ⋅=______. 15．在区间[]0,π上，关于α的方程5sin 45cos 2αα+=+解的个数为． 16．（2018届四川省南充高级中学高三1月检测）已知抛物线2:4C y x =的焦点为F ，()()1122,,,M x y N x y 是抛物线C 上的两个动点，若1222x x MN ++=，则MFN ∠的最大值为__________．三、解答题17．某工厂有两台不同机器A 和B 生产同一种产品各10万件，现从各自生产的产品中分别随机抽取20件，进行品质鉴定，鉴定成绩的茎叶图如图所示：该产品的质量评价标准规定：鉴定成绩达到()90,100的产品，质量等级为优秀；鉴定成绩达到()80,90的产品，质量等级为良好；鉴定成绩达到()60,80的产品，质量等级为合格.将这组数据的频率视为整批产品的概率.（1）完成下列22⨯列联表，以产品等级是否达到良好以上（含良好）为判断依据，判断能不能在误差不超过0.05的情况下，认为B 机器生产的产品比A 机器生产的产品好；（2）根据所给数据，以事件发生的频率作为相应事件发生的概率，从两台不同机器A 和B 生产的产品中各随机抽取2件，求4件产品中A 机器生产的优等品的数量多于B 机器生产的优等品的数量的概率；（3）已知优秀等级产品的利润为12元/件，良好等级产品的利润为10元/件，合格等级产品的利润为5元/件，A 机器每生产10万件的成本为20万元，B 机器每生产10万件的成本为30万元；该工厂决定：按样本数据测算，若收益之差不超过5万元，则仍然保留原来的两台机器.你认为该工厂会仍然保留原来的两台机器吗？附：1.独立性检验计算公式：()()()()()22n ad bc K a b c d a c b d -=++++. 2.临界值表：18．在极坐标系中，已知两点O (0，0)，B ，4π)．(1)求以OB 为直径的圆C 的极坐标方程，然后化成直角坐标方程；（2）以极点O 为坐标原点，极轴为x 轴的正半轴建立平面直角坐标系，直线l 的参数方程为,{12,x t y t ＝＝＋（t 为参数）．若直线l 与圆C 相交于M ，N 两点，圆C 的圆心为C ，求三角形MNC 的面积． 19．已知函数f(x)=|2x −1|−|x +2|. （1）求不等式f(x)≥3的解集；（2）若关于x 的不等式f(x)≥t 2−3t 在[0,1]上无解，求实数t 的取值范围.20．如图，在Rt ABC 中，AB BC ⊥，2AB BC ==，点P 为AB 的中点，//PD BC 交AC 于点D ，现将PDA 沿PD 翻折至1PDA ，使得平面1PDA ⊥平面PBCD .（1）若Q 为线段1A B 的中点，求证：PQ ⊥平面1A BC ；（2）若E 是线段1A C 的中点，求四棱锥E PBCD -的体积.21．已知1F ，2F 是椭圆()2222:10y x M a b a b +=>>的两个焦点，椭圆M ，()00,P x y 是M 上异于上下顶点的任意一点，且12PF F ∆面积的最大值为（1）求椭圆M 的方程；（2）若过点()0,1C 的直线l 与椭圆C 交于A ，B 两点，2AC CB =，求直线l 的方程. 22．已知函数()()ln =-+xf x xe a x x .（1）若0a =，求函数()f x 在1x =处的切线方程；（2）讨论()f x 极值点的个数；（3）若0x 是()f x 的一个极小值点，且()00f x >，证明：()()30002f x x x >-.23．（本小题满分12分）在三角形ABC 中，内角A 、B 、C 的对边分别是a 、b 、c ，且asinAsin(A +B)+ccos2A=√2b（1）求cb 的值；（2）若ΔABC的面积为b22，求a的值（用b表示）【答案与解析】1．B令真数为1，则可得到定点坐标.真数为1时，对数为0，所以令x=2，则f （x ）=1，所以函数()f x 的图象过定点()2,1. 本题主要考查了对数函数恒过定点问题，属于基础题. 2．B由题意易得1z mi =+，计算出iz ，结合纯虚数的概念即可得出结果. 因为复数z 在复平面上对应的点为()1,m ，1z mi =+，因为()1iz i mi m i =+=-+为实数，得0m =. 故选：B.本题主要考查了复数的几何意义，已知复数的类型求参数的值，属于基础题. 3．A,02x π⎛⎫∈- ⎪⎝⎭，则,3233x ππππωω⎛⎫-∈--- ⎪⎝⎭，因为单调递增，则232πππω--≥-，所以13ω≤，则ω的最大值为13，故选A 。

衡水中学2020届高三第八次调研考试数学理数答案

素材来源于网络，林老师搜集编辑整理2019—2020学年度高三年级理数下八调答案3.D5.B7.8.9. 10.B.11. B根据所给条件，结合11n n na S S++=-，代入后展开化简，构造数列11nS⎧⎫⎨⎬-⎩⎭，由等差数列性质可知11nS⎧⎫⎨⎬-⎩⎭为等差数列，进而由首项与公差求得nS.将不等式化简可得，()()()12111()nminS S Skn+++≤L，代入后构造函数()()()()12111nS S Sf nn+++=L，并求得()()1f nf n+后可证明函数()f n为单调递增数列，求得()minf n，即可确定k的最大整数值.【详解】当1n≥时，由条件()()2110,*n n na S S n N+-∈=+，可得21(1)nn nnSS SS+--=-，整理得221(21)n n n n nS S S S S+-=--+，化简得：121n n nS S S+=-，从而111nnnSSS+--=-，故111111n nS S+-=--，由于1111S=-，所以数列11nS⎧⎫⎨⎬-⎩⎭是以1111S=-为首项，1为公差的等差数列，则11nnS=-，整理得1nnSn+=，素材来源于网络，林老师搜集编辑整理依题只须()()()12111()nminS S Skn+++≤L，令()()()()12111nS S Sf nn+++=L，则()()()()()121123111nf n n S n nf n n n++++==>++，所以()f n为单调递增数列，故()11()131ninSf n f+===，∴3maxk=，故选：B．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

l1,
垂足为
M，若
M
在
双曲线 C 上，则双曲线 C 的离心率为
.
高三数学（理）下八调试题第3页(共 6 页)
高三数学（理）下八调试题第4页(共 6 页)
高三数学（理）下八调试题第5页(共 6 页)
高三数学（理）下八调试题第6页(共 6 页)
2019—2020 学年度高三年级理数下八调答案
3.D
10.B.
A． (1, 2)
B． (1 ， 3 2 ] 4
C．[3 2 , ) 4
D． (2, )
11. 已知数列an 满足： a1 2 ， an1Sn Sn 12 0,n N * ，其中 Sn 为an 的前 n 项
和．若对任意的 n 均有 S1 1S2 1Sn 1 kn 恒成立，则 k 的最大整数值为（）
2019—2020 学年度高三年级理数下八调考试
5
高三数学（理）下八调试题第1页(共 6 页)
7. 8. 9.
10.已知双曲线 E : x2 y2 1(a 0,b 0) 的右顶点为 A ，抛物线 C : y2 8ax 的焦点为 F ．若在 E a2 b2
的渐近线上存在点 P ，使得 AP FP ，则 E 的离心率的取值范围是 ( )
=
n +1 n
，
9.
高三数学（理）下八调答案第1页(共 8 页)
高三数学（理）下八调答案第2页(共 8 页)
依题只须 k ((S1 +1)(S2 +1)
n
(Sn
+1)
)min
，令
f
(n)
=
( S1
+ 1) ( S2
+1)
n
则
f
(n +1) f (n)
=
n (Sn+1 +1)
n +1
=
n(2n + 3) (n +1)2
11.
B
根据所给条件，结合
an+1
=
Sn+1
−
Sn
，代入后展开化简，构造数列
1 Sn −1
，由等差数列性质可知
1 Sn −
1
为等差数列，进而由首项与公差求得
Sn
.将不等式化简可得，
5.B
k
(
(
S1
+
1)
(
S2
+
1)
n
(Sn
+1)
)min
，代入后构造函数ຫໍສະໝຸດ f(n)=
( S1
+ 1) ( S2
+1)
A．2
B．3
C．4
D．5
高三数学（理）下八调试题第2页(共 6 页)
18．（12 分）
16
已知双曲线 C :
x2 a2
y2 b2
1(a
0, b
0) 的左、右焦点分别为 F1, F2, 直线 l 是双曲线 C 过第一、
第三象限的渐近线，记直线 l
的倾斜角为
，直线 l1
:
y
tan 2
x, F2M
− Sn2
=
−(Sn2
− 2Sn
+1) ，
化简得： SnSn+1 = 2Sn −1，
从而
Sn+1
−1
=
−
Sn −1 Sn
，故
1 Sn+1 −1
−
1 Sn −1
=
1，
由于
1 S1 −1
=
1 ，所以数列
1 Sn −1
是以
1 S1 −1
=
1 为首项，1
为公差的等差数列，
则
1 Sn −1
=
n
，整理得
Sn
n
( Sn +1) ，并求得
f
(n +1) f (n)
后可证明函数
f
(n)
为单调递增数列，求得
f
(n) min
，即可确定 k
的最大整数值.
7.
【详解】
当 n 1时，由条件 an+1Sn + (Sn −1)2 = 0,(n N *) ，
8.
可得 Sn+1 − Sn
= − (Sn −1)2 Sn
，整理得 Sn+1Sn
1 ，所以
f
( )n 为单调递增数列，
(Sn +1) ，
故
f
(n)nin
=
f
(1) =
S1 + 1
1
=
3
，∴
kmax
= 3，
故选：B．
高三数学（理）下八调答案第3页(共 8 页)
高三数学（理）下八调答案第4页(共 8 页)
高三数学（理）下八调答案第5页(共 8 页)
高三数学（理）下八调答案第6页(共 8 页)
高三数学（理）下八调答案第7页(共 8 页)
高三数学（理）下八调答案第8页(共 8 页)