2009年上海市高考数学试卷(理科)答案与解析
2009年普通高等学校招生全国统一考试(上海卷)数学(理科)

2009年普通高等学校招生全国统一考试(上海卷)数学(理科)学校:___________姓名:___________班级:___________考号:___________一、填空题(本大题共14小题,共56.0分)1.若复数z满足z(1+i)=1-i(i是虚数单位),则其共轭复数=____________.【答案】i【解析】∵,∴z的共轭复数=i.2.已知集合A={x|x≤1},B={x|x≥a},且A∪B=R,则实数a的取值范围是_____________. 【答案】(-∞,1]【解析】∵A∪B=R,如图所示.当a≤1时满足题意.即a的取值范围是(-∞,1].3.若行列式中,元素4的代数余子式大于0,则x满足的条件是____________. 【答案】【解析】因元素4的代数余子式为:(-1)1+1=9x-24.由题意9x-24>0,∴.4.某算法的程序框图如图所示,则输出量y与输入量x满足的关系式是___________.【答案】【解析】由算法的程序框中的判断可知,当x>1时,把x-2赋给y,当x≤1时,把2x赋给y,因此.5.如图,若正四棱柱ABCD—A1B1C1D1的底面边长为2,高为4,则异面直线BD1与AD所成角的大小是____________.(结果用反三角函数值表示)【答案】【解析】∵AD∥BC,∴BD1与AD所成的角等于BD1与BC所成的角.连结CD1,∵BC⊥面CC1D1D,CD 1面CC1D1D,∴BC⊥CD1.在R t△BCD1中,BC=2,,∴.∴∠D1BC=.6.函数y=2cos2x+sin2x的最小值是____________.【答案】【解析】因y=2cos2x+sin2x=1+cos2x+sin2x所以y的最小值为.7.某学校要从5名男生和2名女生中选出2人作为上海世博会志愿者,若用随机变量ξ表示选出的志愿者中女生的人数,则数学期望Eξ=__________.(结果用最简分数表示) 【答案】【解析】由题意知ξ=0,1,2,则,,.∴.8.已知三个球的半径R1,R2,R3满足R1+2R2=3R3,则它们的表面积S1,S2,S3满足的等量关系是_____________.【答案】【解析】由题意S1=4πR12,S2=4πR22,S3=4πR32,则S1S2=16π2(R1R2)2,∴.又∵,∴====∴.9.已知F1、F2是椭圆C:(a>b>0)的两个焦点,P为椭圆C上一点,且.若△PF1F2的面积为9,则b=______________.【答案】3【解析】∵,∴∠F1PF2=90°,∴△F1PF2为直角三角形.∴|PF1|2+|PF2|2=(2c)2.又∵|PF1|+|PF2|=2a,∴|PF1|2+|PF2|2=(|PF1|+|PF2|)2-2|PF1|·|PF2|,即(2c)2=(2a)2-4×|PF1|·|PF2|,.∴4c2=4a2-4×9=0,∴4b2=4×9.∴b=3.10.在极坐标系中,由三条直线θ=0,,ρcosθ+ρsinθ=1围成图形的面积是_______________.【答案】【解析】将三条直线的极坐标方程转化为直角坐标方程,则三条直线的方程分别为y=0,,x+y=1,∴,即.∴.11.当0≤x≤1时,不等式成立,则实数k的取值范围是____________.【答案】k≤1【解析】∵0≤x≤1时,不等式成立,设,y=kx,做出两函数的图象,∴由图象可知,当k≤1时,12.已知函数f(x)=sinx+tanx,项数为27的等差数列{a n}满足a n∈(,),且公差d≠0.若f(a1)+f(a2)+…+f(a27)=0,则当k=__________时,f(a k)=0.【答案】14【解析】由题意,a n∈(,)且{a n}为等差数列,并且有sina1+tana1+sina2+tana2+…+sina27+tana27=0,又∵函数y=sinx与y=tanx均为奇函数,故f(x)=sinx+tanx也是奇函数,要使f(a1)+f(a2)+…+f(a27)=0,需a1,a2,…a27等距对称在数轴原点两侧,∴中间项a14在原点上.∴a14=0,f(a14)=sin0+tan0=0.13.某地街道呈现东—西、南—北向的网格状,相邻街距都为1.两街道相交的点称为格点.若以互相垂直的两条街道为轴建立直角坐标系,现有下述格点(-2,2),(3,1),(3,4),(-2,3),(4,5),(6,6)为报刊零售点.请确定一个格点(除零售点外)___________为发行站,使6个零售点沿街道到发行站之间路程的和最短.【答案】(3,3)【解析】设确定的格点为(x,y),由题意知确定的格点到已知的6个格点路程的和最短,即为x,y 分别到6个格点的横.纵坐标距离和最小,6个格点的横坐标由小到大排列为-2,-2,3,3,4,6,所以x=3时到这6个数的距离和最小.同理y=3时,y到6个格点纵坐标距离之和最小.故所求的格点为(3,3).14.将函数(x∈[0,6])的图像绕坐标原点逆时针方向旋转角θ(0≤θ≤α),得到曲线C.若对于每一个旋转角θ,曲线C都是一个函数的图像,则α的最大值为_____________.【答案】【解析】当x∈[0,6]时,,∴.移项、平方、配方,得(x-3)2+(y+2)2=13,(0≤x≤3)图象是圆心为O1(3,-2),半径在第一象限内的一段圆弧,如图所示.要想使曲线都是一个函数的图象,必须使平行于y轴的直线与曲线有且只有一个交点,即对一个确定的x值,y有唯一的一个值与之对应,因此,当圆弧转到与y轴相切时,旋转的角最大,设旋转前圆在原点处的切线为l,由图可知,α=∠AOO1,∴tan=tan∠AOO1=.∴.三、解答题(本大题共5小题,共78.0分)19.如图,在直三棱柱ABC—A1B1C1中,AA1=BC=AB=2,AB⊥BC,求二面角B1-A1C-C1的大小.【答案】解:如图,建立空间直角坐标系,则A(2,0,0),C(0,2,0),A1(2,0,2),B1(0,0,2),C1(0,2,2),设AC的中点为M,∵BM⊥AC,BM⊥CC1,∴BM⊥平面A1C1C,即=(1,1,0)是平面A1C1C的一个法向量.设平面A1B1C的一个法向量是n=(x,y,z).=(-2,2,-2),=(-2,0,0),∴n·=-2x=0, n·=-2x+2y-2z=0,令z=1,解得x=0,y=1.∴n=(0,1,1),设法向量n与的夹角为φ,二面角B1-A1C-C1的大小为θ,显然θ为锐角.∵cosθ=|cosφ|=,解得,∴二面角B1-A1C-C1的大小为.【解析】略20.本题共有2个小题,第1小题满分6分,第2小题满分8分.有时可用函数描述学习某学科知识的掌握程度.其中x表示某学科知识的学习次数(x∈N*),f(x)表示对该学科知识的掌握程度,正实数a与学科知识有关.(1).证明:当x≥7时,掌握程度的增长量f(x+1)-f(x)总是下降;(2).根据经验,学科甲、乙、丙对应的a的取值区间分别为(115,121],(121,127],(127,133].当学习某学科知识6次时,掌握程度是85%,请确定相应的学科.【答案】(1)证明:当x≥7时,.而当x≥7时,函数y=(x-3)(x-4)单调递增,且(x-3)(x-4)>0.故f(x+1)-f(x)单调递减.∴当x≥7时,掌握程度的增长量f(x+1)-f(x)总是下降.(2)解:由题意可知,整理得,解得≈20.50×6=123.0,123.0∈[121,127].由此可知,该学科是乙学科.【解析】略21.已知双曲线C:,设过点A(,0)的直线l的方向向量e=(1,k).(1).当直线l与双曲线C的一条渐近线m平行时,求直线l的方程及l与m的距离;(2).证明:当时,在双曲线C的右支上不存在点Q,使之到直线l的距离为.【答案】解:(1)双曲线C的渐近线m:,即,∴直线l的方程.∴直线l与m的距离.(2)证法一:设过原点且平行于l的直线b:kx-y=0,则直线l与b的距离,当时,.又双曲线C的渐近线为,∴双曲线C的右支在直线b的右下方,∴双曲线C右支上的任意点到直线l的距离大于.故在双曲线C的右支上不存在点Q,使之到直线l的距离为.证法二:假设双曲线C右支上存在点Q(x0,y0)到直线l的距离为, 则x02-2y02=2,(2)由(1),得,设,当时,;.将y0=kx0+t代入(2)得(1-2k2)x02-4ktx0-2(t2+1)=0,(*)∵,t>0,∴1-2k2<0,-4kt<0,-2(t2+1)<0.∴方程(*)不存在正根,即假设不成立,故在双曲线C的右支上不存在点Q,使之到直线l的距离为.【解析】略22.已知函数y=f-1(x)是y=f(x)的反函数.定义:若对给定的实数a(a≠0),函数y=f(x+a)与y=f-1(x+a)互为反函数,则称y=f(x)满足“a和性质”;若函数y=f(ax)与y=f-1(ax)互为反函数,则称y=f(x)满足“a积性质”.(1).判断函数g(x)=x2+1(x>0)是否满足“1和性质”,并说明理由;(2).求所有满足“2和性质”的一次函数;(3).设函数y=f(x)(x>0)对任何a>0,满足“a积性质”.求y=f(x)的表达式.【答案】解:(1)函数g(x)=x2+1(x>0)的反函数是(x>1),∴(x>0).而g(x+1)=(x+1)2+1(x>-1),其反函数为(x>1).故函数g(x)=x2+1(x>0)不满足“1和性质”.(2)设函数f(x)=kx+b(x∈R)满足“2和性质”,k≠0.∴(x∈R).∴.而f(x+2)=k(x+2)+b(x∈R),得反函数,由“2和性质”定义可知对x∈R恒成立.∴k=-1,b∈R,即所求一次函数为f(x)=-x+b(b∈R).(3)设a>0,x0>0,且点(x0,y0)在y=f(ax)图像上,则(y0,x0)在函数y=f-1(ax)图像上,故可得ay0=f(x0)=af(ax0),令ax0=x,则.∴,即.综上所述,(k≠0),此时,其反函数就是,而,故y=f(ax)与y=f-1(ax)互为反函数.【解析】略23.已知{a n}是公差为d的等差数列,{b n}是公比为q的等比数列.(1).若a n=3n+1,是否存在m、k∈N*,有a m+a m+1=a k?说明理由;(2).找出所有数列{a n}和{b n},使对一切n∈N*,,并说明理由;(3).若a1=5,d=4,b1=q=3,试确定所有的p,使数列{a n}中存在某个连续p项的和是数列{b n}中的一项,请证明.【答案】解:(1)由a m+a m+1=a k,得6m+5=3k+1,整理后,可得,∵m、k∈N*,∴k-2m为整数.∴不存在m、k∈N*,使等式成立.(2)解法一:若,即,(*)①若d=0,则1=b1q n-1=b n.当{a n}为非零常数列,{b n}为恒等于1的常数列,满足要求.②若d≠0,(*)式等号左边取极限得,(*)式等号右边的极限只有当q=1时,才可能等于1.此时等号左边是常数,∴d=0,矛盾.综上所述,只有当{a n}为非零常数列,{b n}为恒等于1的常数列,满足要求.解法二:设a n=nd+c.若,对n∈N*都成立,且{b n}为等比数列,则,对n∈N*都成立,即a n a n+2=qa n+12.∴(dn+c)(dn+2d+c)=q(dn+d+c)2对n∈N*都成立.∴d2=qd2.①若d=0,则a n=c≠0,∴b n=1,n∈N*.②若d≠0,则q=1,∴b n=m(常数),即,则d=0,矛盾.综上所述,有a n=c≠0,b n=1,使对一切n∈N*,.(3)a n=4n+1,b n=3n,n∈N*.设a m+1+a m+2+…+a m+p=b k=3k,p、k∈N*,m∈N.,∴4m+2p+3=.∵p、k∈N*,∴p=3s,s∈N.取k=3s+2,4m=32s+2-2×3s-3=(4-1)2s+2-2×(4-1)s-3≥0,由二项展开式可得正整数M1、M2,使得(4-1)2s+2=4M1+1,2×(4-1)s=8M2+(-1)s2,∴4m=4(M1-2M2)-[(-1)s+1]2.∴存在整数m满足要求.故当且仅当p=3s,s∈N时,命题成立.说明:第(3)题若学生从以下角度解题,可分别得部分分(即分步得分).若p为偶数,则a m+1+a m+2+…+a m+p为偶数,但3k为奇数.故此等式不成立,∴p一定为奇数.当p=1时,则a m+1=b k,即4m+5=3k,而3k=(4-1)k=,M∈Z.当k为偶数时,存在m,使4m+5=3k成立.当p=3时,则a m+1+a m+2+a m+3=b k,即3a m+2=b k,也即3(4m+9)=3k,∴4m+9=3k-1,4(m+1)+5=3k-1.由已证可知,当k-1为偶数即k为奇数时,存在m,4m+9=3k成立.当p=5时,则a m+1+a m+2+…+a m+5=b k,即5a m+3=b k,也即5(4m+13)=3k,而3k不是5的倍数,∴当p=5时,所要求的m不存在.故不是所有奇数都成立.【解析】略二、选择题(本大题共4小题,共20.0分)15.“-2≤a≤2”是“实系数一元二次方程x2+ax+1=0有虚根”的()A.必要不充分条件B.充分不必要条件C.充要条件D.既不充分也不必要条件【答案】A【解析】实系数一元二次方程x2+ax+1=0有虚根Δ<0,即a2-4<0,∴-2<a<2.∵{a|-2<a<2}{a|-2≤a≤2},∴由-2<a<2-2≤a≤2,但由-2≤a≤2-2<a<2.故选A.16.若事件E与F相互独立,且,则P(E∩F)的值等于…()A.0B.C.D.【答案】B【解析】∵事件E与F相互独立,P(E∩F)为相互独立事件同时发生的概率,∴P(E∩F)=P(E)·P(F)=.17.在发生某公共卫生事件期间,有专业机构认为该事件在一段时间内没有发生大规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”.根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是()A.甲地:总体均值为3,中位数为4B.乙地:总体均值为1,总体方差大于0C.丙地:中位数为2,众数为3D.丁地:总体均值为2,总体方差为3【答案】D【解析】设过去10天新增疑似病例数据为a1,a2,a3,…,a10,对于选项D,=2,S2=3,不防设a10=8,a1=a2=…=a8=1,a9=4,此时=2,则.所以当总体均值为2,总体方差为3时一定符合该标志,故选D.18.过圆C:(x-1)2+(y-1)2=1的圆心,作直线分别交x、y正半轴于点A. B,△AOB被圆分成四部分(如图).若这四部分图形面积满足SⅠ +SⅣ =SⅡ +SⅢ ,则这样的直线AB有()A.0条B.1条C.2条D.3条【答案】C【解析】从原图中可看出SⅣ=(定值),SⅡ=(定值),当∠OAB变大时SⅢ变大,SⅠ变小,所以总有一个位置使SⅠ+SⅣ=SⅡ+SⅢ,由图象的对称性可知,当∠OAB变小时,SⅢ变小,SⅠ增大,因此直线AB的条数不能为奇数条,并且一定存在,故选C.。
2009年上海高考数学(理科卷)

4-
_
数y厂似) = 似 ) 为 反 函数 , -( 与y ( 互 f 则
称v ) 足 “积性 质 ” = 满 。 .
.
1 的反 函数y 、 1 1 1 , 以 ) = /一 — (> )所
2一
-
g = 1 > ) 满 足 “和 性 质 ” ) 0 不 1 .
和 + ) 否 互 为反 函数 .由于 已 1是
所 以 A0曰= r tn = . a ca 啊I
3
( 0 6 ) 图象绕 坐标 原点 逆时 针 ∈[ , ]的
方 向旋 转 角o o ≤ ) 得 到 曲 线 C ( ≤0 , 若对 于每 一 个旋 转 角0 曲线C 是 一 , 都 个 函数 的图象 . 则 的 最 大 值 为 第2 题 0
q z d.
测 满 足 “ 积 性 质 ” 是 反 比 例 函 数 . ; 胆 猜 想k l a 的 =4
x b2 - k
-
_
: —
—
( 图1 如 的 ) 当使 圆旋 转 到切 于原 ,
k
,
比较得后 一 , : I 即所 求
平移 ff a 个单位 .
应对 策 略 : 陌 生 的 解 答 题 , 对 我
们 要 做 到 “ 了 想 法 就 写 ” 能 写 到 哪 有 ,
点 ( 转 中心 是 原 点0) , 时D 旋 旋 时 此 p
肼 。与y ) (+ ) 为 反 函 数 ” a互 ,
__ I
一
.
x 2 - ( 2 + 的 反 函 数 + )k 卅 ) 6
-
有 同学 误认 为 它 们 本 来 就 互 为 反 函
数 .其 实 它 们 的 图 象 关 于 直 线 y x a = +
2009年全国统一高考数学试卷(理科)(全国卷ⅱ)(含解析版)

2009年全国统一高考数学试卷(理科)(全国卷Ⅱ)一、选择题(共12小题,每小题5分,满分60分)1.(5分)=()A.﹣2+4i B.﹣2﹣4i C.2+4i D.2﹣4i2.(5分)设集合A={x||x|>3},B={x |<0},则A∩B=()A.φB.(3,4)C.(﹣2,1)D.(4,+∞)3.(5分)已知△ABC中,cotA=﹣,则cosA=()A .B .C .D .4.(5分)函数在点(1,1)处的切线方程为()A.x﹣y﹣2=0B.x+y﹣2=0C.x+4y﹣5=0D.x﹣4y+3=05.(5分)已知正四棱柱ABCD﹣A1B1C1D1中,AA1=2AB,E为AA1中点,则异面直线BE与CD1所形成角的余弦值为()A .B .C .D .6.(5分)已知向量=(2,1),=10,|+|=,则||=()A .B .C.5D.257.(5分)设a=log3π,b=log 2,c=log 3,则()A.a>b>c B.a>c>b C.b>a>c D.b>c>a8.(5分)若将函数y=tan(ωx +)(ω>0)的图象向右平移个单位长度后,与函数y=tan(ωx +)的图象重合,则ω的最小值为()A .B .C .D .9.(5分)已知直线y=k(x+2)(k>0)与抛物线C:y2=8x相交于A、B两点,F为C的焦点,若|FA|=2|FB|,则k=()A .B .C .D .10.(5分)甲、乙两人从4门课程中各选修2门,则甲、乙所选的课程中恰有1门相同的选法有()A.6种B.12种C.24种D.30种11.(5分)已知双曲线的右焦点为F,过F 且斜率为的直线交C于A、B 两点,若=4,则C的离心率为()A .B .C .D .12.(5分)纸制的正方体的六个面根据其方位分别标记为上、下、东、南、西、北.现在沿该正方体的一些棱将正方体剪开、外面朝上展平,得到如图所示的平面图形,则标“△”的面的方位()A.南B.北C.西D.下二、填空题(共4小题,每小题5分,满分20分)13.(5分)(x﹣y)4的展开式中x3y3的系数为.14.(5分)设等差数列{a n}的前n项和为S n,若a5=5a3,则=.15.(5分)设OA是球O的半径,M是OA的中点,过M且与OA成45°角的平面截球O的表面得到圆C.若圆C的面积等于,则球O的表面积等于.16.(5分)求证:菱形各边中点在以对角线的交点为圆心的同一个圆上.三、解答题(共6小题,满分70分)17.(10分)设△ABC的内角A、B、C的对边长分别为a、b、c,cos(A﹣C)+cosB=,b2=ac,求B.18.(12分)如图,直三棱柱ABC﹣A1B1C1中,AB⊥AC,D、E分别为AA1、B1C的中点,DE⊥平面BCC1.(Ⅰ)证明:AB=AC;(Ⅱ)设二面角A﹣BD﹣C为60°,求B1C与平面BCD所成的角的大小.19.(12分)设数列{a n}的前n项和为S n,已知a1=1,S n+1=4a n+2(n∈N*).(1)设b n=a n+1﹣2a n,证明数列{b n}是等比数列;(2)求数列{a n}的通项公式.20.(12分)某车间甲组有10名工人,其中有4名女工人;乙组有5名工人,其中有3名女工人,现采用分层抽样方法(层内采用不放回简单随机抽样)从甲、乙两组中共抽取3名工人进行技术考核.(Ⅰ)求从甲、乙两组各抽取的人数;(Ⅱ)求从甲组抽取的工人中恰有1名女工人的概率;(Ⅲ)记ξ表示抽取的3名工人中男工人数,求ξ的分布列及数学期望.21.(12分)已知椭圆的离心率为,过右焦点F的直线l与C相交于A、B两点,当l的斜率为1时,坐标原点O到l 的距离为,(Ⅰ)求a,b的值;(Ⅱ)C上是否存在点P,使得当l绕F 转到某一位置时,有成立?若存在,求出所有的P的坐标与l的方程;若不存在,说明理由.22.(12分)设函数f(x)=x2+aln(1+x)有两个极值点x1、x2,且x1<x2,(Ⅰ)求a的取值范围,并讨论f(x)的单调性;(Ⅱ)证明:f(x2)>.2009年全国统一高考数学试卷(理科)(全国卷Ⅱ)参考答案与试题解析一、选择题(共12小题,每小题5分,满分60分)1.(5分)=()A.﹣2+4i B.﹣2﹣4i C.2+4i D.2﹣4i【考点】A5:复数的运算.【专题】11:计算题.【分析】首先进行复数的除法运算,分子和分母同乘以分母的共轭复数,分子和分母进行乘法运算,整理成最简形式,得到结果.【解答】解:原式=,故选:A.【点评】本题考查复数的乘除运算,是一个基础题,在近几年的高考题目中,复数的简单的运算题目是一个必考的问题,通常出现在试卷的前几个题目中.2.(5分)设集合A={x||x|>3},B={x |<0},则A∩B=()A.φB.(3,4)C.(﹣2,1)D.(4,+∞)【考点】1E:交集及其运算.【分析】先化简集合A和B,再根据两个集合的交集的意义求解.【解答】解:A={x||x|>3}⇒{x|x>3或x<﹣3},B={x |<0}={x|1<x<4},∴A∩B=(3,4),故选:B.【点评】本题属于以不等式为依托,求集合的交集的基础题,也是高考常会考的题型.3.(5分)已知△ABC中,cotA=﹣,则cosA=()A .B .C .D .【考点】GG:同角三角函数间的基本关系.【专题】11:计算题.【分析】利用同角三角函数的基本关系cosA转化成正弦和余弦,求得sinA和cosA的关系式,进而与sin2A+cos2A=1联立方程求得cosA的值.【解答】解:∵cotA=∴A为钝角,cosA<0排除A和B,再由cotA==,和sin2A+cos2A=1求得cosA=,故选:D.【点评】本题考查同角三角函数基本关系的运用.主要是利用了同角三角函数中的平方关系和商数关系.4.(5分)函数在点(1,1)处的切线方程为()A.x﹣y﹣2=0B.x+y﹣2=0C.x+4y﹣5=0D.x﹣4y+3=0【考点】6H:利用导数研究曲线上某点切线方程.【专题】11:计算题.【分析】欲求切线方程,只须求出其斜率即可,故先利用导数求出在x=1处的导函数值,再结合导数的几何意义即可求出切线的斜率.从而问题解决.【解答】解:依题意得y′=,因此曲线在点(1,1)处的切线的斜率等于﹣1,相应的切线方程是y﹣1=﹣1×(x﹣1),即x+y﹣2=0,故选:B.【点评】本小题主要考查直线的斜率、导数的几何意义、利用导数研究曲线上某点切线方程等基础知识,考查运算求解能力.属于基础题.5.(5分)已知正四棱柱ABCD﹣A1B1C1D1中,AA1=2AB,E为AA1中点,则异面直线BE与CD1所形成角的余弦值为()A .B .C .D .【考点】LM:异面直线及其所成的角.【专题】11:计算题;31:数形结合;44:数形结合法;5G:空间角.【分析】由BA1∥CD1,知∠A1BE是异面直线BE与CD1所形成角,由此能求出异面直线BE与CD1所形成角的余弦值.【解答】解:∵正四棱柱ABCD﹣A1B1C1D1中,AA1=2AB,E为AA1中点,∴BA1∥CD1,∴∠A1BE是异面直线BE与CD1所形成角,设AA1=2AB=2,则A1E=1,BE==,A1B==,∴cos∠A1BE===.∴异面直线BE与CD1所形成角的余弦值为.故选:C.【点评】本题考查异面直线所成角的余弦值的求法,是基础题,解题时要认真审题,注意空间思维能力的培养.6.(5分)已知向量=(2,1),=10,|+|=,则||=()A .B .C.5D.25【考点】91:向量的概念与向量的模;9O:平面向量数量积的性质及其运算.【专题】5A:平面向量及应用.【分析】根据所给的向量的数量积和模长,对|a+b|=两边平方,变化为有模长和数量积的形式,代入所给的条件,等式变为关于要求向量的模长的方程,解方程即可.【解答】解:∵|+|=,||=∴(+)2=2+2+2=50,得||=5故选:C.【点评】本题考查平面向量数量积运算和性质,根据所给的向量表示出要求模的向量,用求模长的公式写出关于变量的方程,解方程即可,解题过程中注意对于变量的应用.7.(5分)设a=log3π,b=log 2,c=log 3,则()A.a>b>c B.a>c>b C.b>a>c D.b>c>a【考点】4M:对数值大小的比较.【分析】利用对数函数y=log a x的单调性进行求解.当a>1时函数为增函数当0<a<1时函数为减函数,如果底a不相同时可利用1做为中介值.【解答】解:∵∵,故选A【点评】本题考查的是对数函数的单调性,这里需要注意的是当底不相同时可用1做为中介值.8.(5分)若将函数y=tan(ωx +)(ω>0)的图象向右平移个单位长度后,与函数y=tan(ωx +)的图象重合,则ω的最小值为()A .B .C .D .【考点】HJ:函数y=Asin(ωx+φ)的图象变换.【专题】11:计算题.【分析】根据图象的平移求出平移后的函数解析式,与函数y=tan(ωx +)的图象重合,比较系数,求出ω=6k +(k∈Z),然后求出ω的最小值.【解答】解:y=tan(ωx +),向右平移个单位可得:y=tan[ω(x ﹣)+]=tan(ωx +)∴﹣ω+kπ=∴ω=k +(k∈Z),又∵ω>0∴ωmin =.故选:D.【点评】本题是基础题,考查三角函数的图象的平移,待定系数法的应用,考查计算能力,是常考题.9.(5分)已知直线y=k(x+2)(k>0)与抛物线C:y2=8x相交于A、B两点,F为C的焦点,若|FA|=2|FB|,则k=()A .B .C .D .【考点】K8:抛物线的性质.【专题】11:计算题;16:压轴题.【分析】根据直线方程可知直线恒过定点,如图过A、B分别作AM⊥l于M,BN⊥l于N,根据|FA|=2|FB|,推断出|AM|=2|BN|,点B为AP的中点、连接OB ,进而可知,进而推断出|OB|=|BF|,进而求得点B的横坐标,则点B的坐标可得,最后利用直线上的两点求得直线的斜率.【解答】解:设抛物线C:y2=8x的准线为l:x=﹣2直线y=k(x+2)(k>0)恒过定点P(﹣2,0)如图过A、B分别作AM⊥l于M,BN⊥l于N,由|FA|=2|FB|,则|AM|=2|BN|,点B为AP的中点、连接OB,则,∴|OB|=|BF|,点B的横坐标为1,故点B 的坐标为,故选:D.【点评】本题主要考查了抛物线的简单性质.考查了对抛物线的基础知识的灵活运用.10.(5分)甲、乙两人从4门课程中各选修2门,则甲、乙所选的课程中恰有1门相同的选法有()A.6种B.12种C.24种D.30种【考点】D5:组合及组合数公式.【专题】11:计算题.【分析】根据题意,分两步,①先求所有两人各选修2门的种数,②再求两人所选两门都相同与都不同的种数,进而由事件间的相互关系,分析可得答案.【解答】解:根据题意,分两步,①由题意可得,所有两人各选修2门的种数C42C42=36,②两人所选两门都相同的有为C42=6种,都不同的种数为C42=6,故选:C.【点评】本题考查组合公式的运用,解题时注意事件之间的关系,选用直接法或间接法.11.(5分)已知双曲线的右焦点为F,过F 且斜率为的直线交C于A、B 两点,若=4,则C的离心率为()A .B .C .D .【考点】I3:直线的斜率;KA:双曲线的定义.【专题】11:计算题;16:压轴题.【分析】设双曲线的有准线为l,过A、B分别作AM⊥l于M,BN⊥l于N,BD⊥AM于D,由直线AB的斜率可知直线AB的倾斜角,进而推,由双曲线的第二定义|AM|﹣|BN|=|AD|,进而根据,求得离心率.【解答】解:设双曲线的右准线为l,过A、B分别作AM⊥l于M,BN⊥l于N,BD⊥AM于D,由直线AB 的斜率为,知直线AB的倾斜角为60°∴∠BAD=60°,由双曲线的第二定义有:=∴,∴故选:A.【点评】本题主要考查了双曲线的定义.解题的关键是利用了双曲线的第二定义,找到了已知条件与离心率之间的联系.12.(5分)纸制的正方体的六个面根据其方位分别标记为上、下、东、南、西、北.现在沿该正方体的一些棱将正方体剪开、外面朝上展平,得到如图所示的平面图形,则标“△”的面的方位()A.南B.北C.西D.下【考点】LC:空间几何体的直观图.【专题】16:压轴题.【分析】本题考查多面体展开图;正方体的展开图有多种形式,结合题目,首先满足上和东所在正方体的方位,“△”的面就好确定.【解答】解:如图所示.故选B【点评】本题主要考查多面体的展开图的复原,属于基本知识基本能力的考查.二、填空题(共4小题,每小题5分,满分20分)13.(5分)(x﹣y)4的展开式中x3y3的系数为6.【考点】DA:二项式定理.【分析】先化简代数式,再利用二项展开式的通项公式求出第r+1项,令x,y的指数都为1求出x3y3的系数【解答】解:,只需求展开式中的含xy项的系数.∵的展开式的通项为令得r=2∴展开式中x3y3的系数为C42=6故答案为6.【点评】本题考查二项展开式的通项公式是解决二项展开式的特定项问题的工具.14.(5分)设等差数列{a n}的前n项和为S n,若a5=5a3,则=9.【考点】83:等差数列的性质.【专题】11:计算题.【分析】根据等差数列的等差中项的性质可知S9=9a5,S5=5a3,根据a5=5a3,进而可得则的值.【解答】解:∵{a n}为等差数列,S9=a1+a2+…+a9=9a5,S5=a1+a2+…+a5=5a3,∴故答案为9【点评】本题主要考查了等差数列中等差中项的性质.属基础题.15.(5分)设OA是球O的半径,M是OA的中点,过M且与OA成45°角的平面截球O的表面得到圆C.若圆C 的面积等于,则球O 的表面积等于8π.【考点】LG:球的体积和表面积.【专题】11:计算题;16:压轴题.【分析】本题可以设出球和圆的半径,利用题目的关系,求解出具体的值,即可得到答案.【解答】解:设球半径为R,圆C的半径为r,.因为.由得R2=2故球O的表面积等于8π故答案为:8π,【点评】本题考查学生对空间想象能力,以及球的面积体积公式的利用,是基础题.16.(5分)求证:菱形各边中点在以对角线的交点为圆心的同一个圆上.【考点】N8:圆內接多边形的性质与判定.【专题】14:证明题;16:压轴题.【分析】如图,菱形ABCD的对角线AC和BD相交于点O,菱形ABCD各边中点分别为M、N、P、Q,根据菱形的性质得到AC⊥BD,垂足为O,且AB=BC=CD=DA,再根据直角三角形斜边上的中线等于斜边的一半得到OM=ON=OP=OQ=AB,得到M、N、P、Q四点在以O为圆心OM为半径的圆上.【解答】已知:如图,菱形ABCD的对角线AC和BD相交于点O.求证:菱形ABCD各边中点M、N、P、Q在以O为圆心的同一个圆上.证明:∵四边形ABCD是菱形,∴AC⊥BD,垂足为O,且AB=BC=CD=DA,而M、N、P、Q分别是边AB、BC、CD、DA的中点,∴OM=ON=OP=OQ=AB,∴M、N、P、Q四点在以O为圆心OM为半径的圆上.所以菱形各边中点在以对角线的交点为圆心的同一个圆上.【点评】本题考查了四点共圆的判定方法.也考查了菱形的性质以及直角三角形斜边上的中线等于斜边的一半.三、解答题(共6小题,满分70分)17.(10分)设△ABC的内角A、B、C的对边长分别为a、b、c,cos(A﹣C)+cosB=,b2=ac,求B.【考点】GG:同角三角函数间的基本关系;HP:正弦定理.【专题】11:计算题.【分析】本题考查三角函数化简及解三角形的能力,关键是注意角的范围对角的三角函数值的制约,并利用正弦定理得到sinB=(负值舍掉),从而求出答案.【解答】解:由cos(A﹣C)+cosB=及B=π﹣(A +C)得cos (A﹣C)﹣cos(A+C)=,∴cosAcosC+sinAsinC﹣(cosAcosC﹣sinAsinC)=,∴sinAsinC=.又由b2=ac及正弦定理得sin2B=sinAsinC,故,∴或(舍去),于是B=或B=.又由b2=ac知b≤a或b≤c所以B=.【点评】三角函数给值求值问题的关键就是分析已知角与未知角的关系,然后通过角的关系,选择恰当的公式,即:如果角与角相等,则使用同角三角函数关系;如果角与角之间的和或差是直角的整数倍,则使用诱导公式;如果角与角之间存在和差关系,则我们用和差角公式;如果角与角存在倍数关系,则使用倍角公式.18.(12分)如图,直三棱柱ABC﹣A1B1C1中,AB⊥AC,D、E分别为AA1、B1C的中点,DE⊥平面BCC1.(Ⅰ)证明:AB=AC;(Ⅱ)设二面角A﹣BD﹣C为60°,求B1C与平面BCD所成的角的大小.【考点】LQ:平面与平面之间的位置关系.【专题】11:计算题;14:证明题.【分析】(1)连接BE,可根据射影相等的两条斜线段相等证得BD=DC,再根据相等的斜线段的射影相等得到AB=AC;(2)求B1C与平面BCD所成的线面角,只需求点B1到面BDC的距离即可,作AG⊥BD于G,连GC,∠AGC为二面角A﹣BD﹣C的平面角,在三角形AGC中求出GC即可.【解答】解:如图(I)连接BE,∵ABC﹣A1B1C1为直三棱柱,∴∠B1BC=90°,∵E为B1C的中点,∴BE=EC.又DE⊥平面BCC1,∴BD=DC(射影相等的两条斜线段相等)而DA⊥平面ABC,∴AB=AC(相等的斜线段的射影相等).(II)求B1C与平面BCD所成的线面角,只需求点B1到面BDC的距离即可.作AG⊥BD于G,连GC,∵AB⊥AC,∴GC⊥BD,∠AGC为二面角A﹣BD﹣C的平面角,∠AGC=60°不妨设,则AG=2,GC=4在RT△ABD中,由AD•AB=BD•AG ,易得设点B1到面BDC的距离为h,B1C与平面BCD所成的角为α.利用,可求得h=,又可求得,∴α=30°.即B1C与平面BCD所成的角为30°.【点评】本题主要考查了平面与平面之间的位置关系,考查空间想象能力、运算能力和推理论证能力,属于基础题.19.(12分)设数列{a n}的前n项和为S n,已知a1=1,S n+1=4a n+2(n∈N*).(1)设b n=a n+1﹣2a n,证明数列{b n}是等比数列;(2)求数列{a n}的通项公式.【考点】87:等比数列的性质;8H:数列递推式.【专题】15:综合题.【分析】(1)由题设条件知b1=a2﹣2a1=3.由S n+1=4a n+2和S n=4a n﹣1+2相减得a n+1=4a n﹣4a n﹣1,即a n+1﹣2a n=2(a n﹣2a n﹣1),所以b n=2b n﹣1,由此可知{b n}是以b1=3为首项、以2为公比的等比数列.(2)由题设知.所以数列是首项为,公差为的等差数列.由此能求出数列{a n}的通项公式.【解答】解:(1)由a1=1,及S n+1=4a n+2,得a1+a2=4a1+2,a2=3a1+2=5,所以b1=a2﹣2a1=3.由S n+1=4a n+2,①则当n≥2时,有S n=4a n﹣1+2,②①﹣②得a n+1=4a n﹣4a n﹣1,所以a n+1﹣2a n=2(a n﹣2a n﹣1),又b n=a n+1﹣2a n,所以b n=2b n﹣1(b n≠0),所以{b n}是以b1=3为首项、以2为公比的等比数列.(6分)(2)由(I)可得b n=a n+1﹣2a n=3•2n﹣1,等式两边同时除以2n+1,得.所以数列是首项为,公差为的等差数列.所以,即a n=(3n﹣1)•2n﹣2(n∈N*).(13分)【点评】本题考查数列的性质和应用,解题时要掌握等比数列的证明方法,会求数列的通项公式.20.(12分)某车间甲组有10名工人,其中有4名女工人;乙组有5名工人,其中有3名女工人,现采用分层抽样方法(层内采用不放回简单随机抽样)从甲、乙两组中共抽取3名工人进行技术考核.(Ⅰ)求从甲、乙两组各抽取的人数;(Ⅱ)求从甲组抽取的工人中恰有1名女工人的概率;(Ⅲ)记ξ表示抽取的3名工人中男工人数,求ξ的分布列及数学期望.【考点】B3:分层抽样方法;CG:离散型随机变量及其分布列;CH:离散型随机变量的期望与方差.【专题】11:计算题;48:分析法.【分析】(Ⅰ)这一问较简单,关键是把握题意,理解分层抽样的原理即可.另外要注意此分层抽样与性别无关.(Ⅱ)在第一问的基础上,这一问处理起来也并不困难.直接在男工里面抽取一人,在女工里面抽取一人,除以在总的里面抽取2人的种数即可得到答案.(Ⅲ)求ξ的数学期望.因为ξ的可能取值为0,1,2,3.分别求出每个取值的概率,然后根据期望公式求得结果即可得到答案.【解答】解:(Ⅰ)因为甲组有10名工人,乙组有5名工人,从甲、乙两组中共抽取3名工人进行技术考核,根据分层抽样的原理可直接得到,在甲中抽取2名,乙中抽取1名.(Ⅱ)因为由上问求得;在甲中抽取2名工人,故从甲组抽取的工人中恰有1名女工人的概率(Ⅲ)ξ的可能取值为0,1,2,3,,,ξ01 2 3P故Eξ==.【点评】本题较常规,比08年的概率统计题要容易.在计算P(ξ=2)时,采用求反面的方法,用直接法也可,但较繁琐.考生应增强灵活变通的能力.21.(12分)已知椭圆的离心率为,过右焦点F的直线l与C相交于A、B两点,当l的斜率为1时,坐标原点O到l 的距离为,(Ⅰ)求a,b的值;(Ⅱ)C上是否存在点P,使得当l绕F 转到某一位置时,有成立?若存在,求出所有的P的坐标与l的方程;若不存在,说明理由.【考点】K4:椭圆的性质.【专题】15:综合题;16:压轴题.【分析】(I)设F(c,0),则直线l的方程为x﹣y﹣c=0,由坐标原点O到l的距离求得c,进而根据离心率求得a和b.(II)由(I)可得椭圆的方程,设A(x1,y1)、B(x2,y2),l:x=my+1代入椭圆的方程中整理得方程△>0.由韦达定理可求得y1+y2和y1y2的表达式,假设存在点P ,使成立,则其充要条件为:点P的坐标为(x1+x2,y1+y2),代入椭圆方程;把A,B两点代入椭圆方程,最后联立方程求得c,进而求得P点坐标,求出m的值得出直线l的方程.【解答】解:(I)设F(c,0),直线l:x﹣y﹣c=0,由坐标原点O到l 的距离为则,解得c=1又,∴(II)由(I )知椭圆的方程为设A(x1,y1)、B(x2,y2)由题意知l的斜率为一定不为0,故不妨设l:x=my+1代入椭圆的方程中整理得(2m2+3)y2+4my﹣4=0,显然△>0.由韦达定理有:,,①假设存在点P ,使成立,则其充要条件为:点P的坐标为(x1+x2,y1+y2),点P 在椭圆上,即.整理得2x12+3y12+2x22+3y22+4x1x2+6y1y2=6.又A、B在椭圆上,即2x12+3y12=6,2x22+3y22=6、故2x1x2+3y1y2+3=0②将x1x2=(my1+1)(my2+1)=m2y1y2+m(y1+y2)+1及①代入②解得∴,x1+x2=,即当;当【点评】本题主要考查了椭圆的性质.处理解析几何题,学生主要是在“算”上的功夫不够.所谓“算”,主要讲的是算理和算法.算法是解决问题采用的计算的方法,而算理是采用这种算法的依据和原因,一个是表,一个是里,一个是现象,一个是本质.有时候算理和算法并不是截然区分的.例如:三角形的面积是用底乘高的一半还是用两边与夹角的正弦的一半,还是分割成几部分来算?在具体处理的时候,要根据具体问题及题意边做边调整,寻找合适的突破口和切入点.22.(12分)设函数f(x)=x2+aln(1+x)有两个极值点x1、x2,且x1<x2,(Ⅰ)求a的取值范围,并讨论f(x)的单调性;(Ⅱ)证明:f(x2)>.【考点】6B:利用导数研究函数的单调性;6D:利用导数研究函数的极值;R6:不等式的证明.【专题】11:计算题;14:证明题;16:压轴题.【分析】(1)先确定函数的定义域然后求导数fˊ(x),令g(x)=2x2+2x+a,由题意知x1、x2是方程g(x)=0的两个均大于﹣1的不相等的实根,建立不等关系解之即可,在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0,求出单调区间;(2)x2是方程g(x)=0的根,将a用x2表示,消去a得到关于x2的函数,研究函数的单调性求出函数的最大值,即可证得不等式.【解答】解:(I )令g(x)=2x2+2x+a ,其对称轴为.由题意知x1、x2是方程g(x)=0的两个均大于﹣1的不相等的实根,其充要条件为,得(1)当x∈(﹣1,x1)时,f'(x)>0,∴f(x)在(﹣1,x1)内为增函数;(2)当x∈(x1,x2)时,f'(x)<0,∴f(x)在(x1,x2)内为减函数;(3)当x∈(x2,+∞)时,f'(x)>0,∴f(x)在(x2,+∞)内为增函数;(II)由(I)g(0)=a>0,∴,a=﹣(2x22+2x2)∴f(x2)=x22+aln(1+x2)=x22﹣(2x22+2x2)ln(1+x2)设h(x)=x2﹣(2x2+2x)ln(1+x),(﹣<x<0)则h'(x)=2x﹣2(2x+1)ln(1+x)﹣2x=﹣2(2x+1)ln(1+x)当时,h'(x)>0,∴h(x )在单调递增,故.【点评】本题主要考查了利用导数研究函数的单调性,以及利用导数研究函数的极值等有关知识,属于中档题.。
2009年上海高考数学试卷
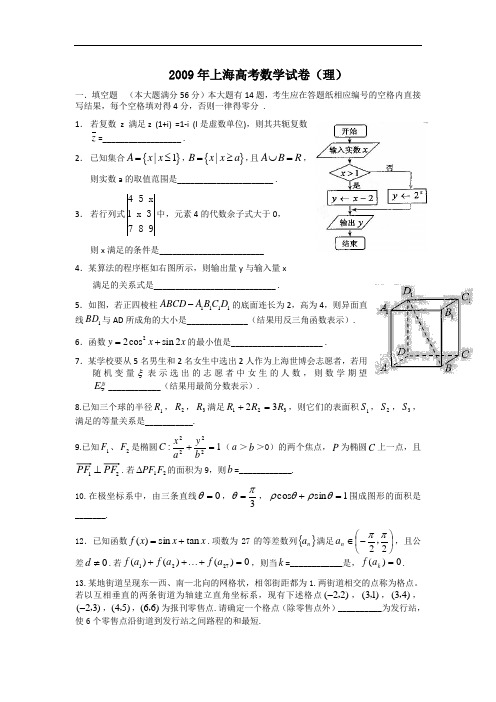
2009年上海高考数学试卷(理)一.填空题 (本大题满分56分)本大题有14题,考生应在答题纸相应编号的空格内直接写结果,每个空格填对得4分,否则一律得零分 .1. 若复数 z 满足z (1+i) =1-i (I 是虚数单位),则其共轭复数z =__________________ .2. 已知集合{}|1A x x =≤,{}|B x x a =≥,且A B R ⋃=, 则实数a 的取值范围是______________________ .3. 若行列式417 5 xx 3 8 9中,元素4的代数余子式大于0,则x 满足的条件是________________________4.某算法的程序框如右图所示,则输出量y 与输入量x满足的关系式是____________________________ .5.如图,若正四棱柱1111ABCD A B C D -的底面连长为2,高为4,则异面直线1BD 与AD 所成角的大小是______________(结果用反三角函数表示).6.函数22cos sin 2y x x =+的最小值是_____________________ .7.某学校要从5名男生和2名女生中选出2人作为上海世博会志愿者,若用随机变量ξ表示选出的志愿者中女生的人数,则数学期望E ξ____________(结果用最简分数表示).8.已知三个球的半径1R ,2R ,3R 满足32132R R R =+,则它们的表面积1S ,2S ,3S ,满足的等量关系是___________.9.已知1F 、2F 是椭圆1:2222=+by a x C (a >b >0)的两个焦点,P 为椭圆C 上一点,且21PF PF ⊥.若21F PF ∆的面积为9,则b =____________.10.在极坐标系中,由三条直线0=θ,3πθ=,1sin cos =+θρθρ围成图形的面积是_______. 12.已知函数x x x f tan sin )(+=.项数为27的等差数列{}n a 满足⎪⎭⎫ ⎝⎛-∈22ππ,n a ,且公差0≠d .若0)()()(2721=+⋯++a f a f a f ,则当k =____________是,0)(=k a f . 13.某地街道呈现东—西、南—北向的网格状,相邻街距都为1.两街道相交的点称为格点。
2009年全国统一高考数学试卷(理科)(全国卷ⅱ)(含解析版)(1)

2009 年全国统一高考数学试卷(理科)(全国卷Ⅱ)一、选择题(共 12 小题,每小题 5 分,满分 60 分) 1.(5 分) A .﹣2+4i=( )B .﹣2﹣4iC .2+4iD .2﹣4i2.(5 分)设集合 A={x ||x |>3},B={x | A .φB .(3,4)3.(5 分)已知△ABC 中,cotA=﹣ ,则 cosA=( ) <0},则 A ∩B=( )C .(﹣2,1)D .(4,+∞)D .A .B .在点(1,1)处的切线方程为( ) B .x +y ﹣2=0C .x +4y ﹣5=0D .x ﹣4y +3=0C .4.(5 分)函数 A .x ﹣y ﹣2=05.(5 分)已知正四棱柱 ABCD ﹣A B C D 中,AA =2AB ,E 为 AA 中点,则异面 1 1 1 1 1 1 直线 BE 与 CD 所形成角的余弦值为( ) 1 A .B .C .D .6.(5 分)已知向量 =(2,1), =10,| + |= ,则| |=( )D .25A .B .C .57.(5 分)设 a=log π,b=log ,c=log 3,则( ) C .b >a >c3 2A .a >b >cB .a >c >bD .b >c >a8.(5 分)若将函数 y=tan (ωx + )(ω>0)的图象向右平移个单位长度 后,与函数 y=tan (ωx + )的图象重合,则 ω 的最小值为( )A .B .C .D .9.(5 分)已知直线 y=k (x +2)(k >0)与抛物线 C :y 2=8x 相交于 A 、B 两点, F 为 C 的焦点,若|FA |=2|FB |,则 k=( ) A .B .C .D .10.(5 分)甲、乙两人从 4 门课程中各选修 2 门,则甲、乙所选的课程中恰有1 门相同的选法有()A.6 种B.12 种C.24 种D.30 种11.(5 分)已知双曲线的右焦点为F,过F 且斜率为的直线交C 于A、B 两点,若=4 ,则C 的离心率为()A.B.C.D.12.(5 分)纸制的正方体的六个面根据其方位分别标记为上、下、东、南、西、北.现在沿该正方体的一些棱将正方体剪开、外面朝上展平,得到如图所示的平面图形,则标“△”的面的方位()A.南B.北C.西D.下二、填空题(共4小题,每小题5分,满分20分)13.(5 分)(x ﹣y )4 的展开式中x3y3 的系数为.14.(5 分)设等差数列{a }的前n 项和为S ,若a =5a ,则=.n n 5 315.(5 分)设OA 是球O 的半径,M 是OA 的中点,过M 且与OA 成45°角的平面截球O 的表面得到圆C.若圆C 的面积等于,则球O 的表面积等于.16.(5 分)求证:菱形各边中点在以对角线的交点为圆心的同一个圆上.三、解答题(共6小题,满分70分)17.(10 分)设△ABC 的内角A、B、C 的对边长分别为a、b、c,cos(A﹣C)+cosB= ,b2=ac,求B.18.(12 分)如图,直三棱柱ABC﹣A B C 中,AB⊥AC,D、E 分别为AA 、B C1 1 1 1 1的中点,DE⊥平面BCC .1(Ⅰ)证明:AB=AC;(Ⅱ)设二面角A﹣BD﹣C 为60°,求B C 与平面BCD 所成的角的大小.119.(12 分)设数列{a }的前n 项和为S ,已知a =1,S =4a +2(n∈N*).n n 1 n+1 n(1)设b =a ﹣2a ,证明数列{b }是等比数列;n n+1 n n(2)求数列{a }的通项公式.n20.(12 分)某车间甲组有10 名工人,其中有4 名女工人;乙组有5 名工人,其中有3 名女工人,现采用分层抽样方法(层内采用不放回简单随机抽样)从甲、乙两组中共抽取3 名工人进行技术考核.(Ⅰ)求从甲、乙两组各抽取的人数;(Ⅱ)求从甲组抽取的工人中恰有1 名女工人的概率;(Ⅲ)记ξ表示抽取的3 名工人中男工人数,求ξ的分布列及数学期望.21.(12 分)已知椭圆的离心率为,过右焦点F 的直线l 与C 相交于A、B 两点,当l 的斜率为1 时,坐标原点O 到l 的距离为,(Ⅰ)求a,b 的值;成立?若(Ⅱ)C 上是否存在点P,使得当l 绕F 转到某一位置时,有存在,求出所有的P 的坐标与l 的方程;若不存在,说明理由.22.(12 分)设函数f(x)=x2+aln(1+x)有两个极值点x 、x ,且x <x ,1 2 1 2 (Ⅰ)求a 的取值范围,并讨论f(x)的单调性;(Ⅱ)证明:f(x )>.22009年全国统一高考数学试卷(理科)(全国卷Ⅱ)参考答案与试题解析一、选择题(共12小题,每小题5分,满分60分)1.(5 分)A.﹣2+4i =()B.﹣2﹣4i C.2+4i D.2﹣4i【考点】A5:复数的运算.【专题】11:计算题.【分析】首先进行复数的除法运算,分子和分母同乘以分母的共轭复数,分子和分母进行乘法运算,整理成最简形式,得到结果.【解答】解:原式=故选:A.,【点评】本题考查复数的乘除运算,是一个基础题,在近几年的高考题目中,复数的简单的运算题目是一个必考的问题,通常出现在试卷的前几个题目中.2.(5 分)设集合A={x||x|>3},B={x| A.φB.(3,4)<0},则A∩B=()C.(﹣2,1)D.(4,+∞)【考点】1E:交集及其运算.【分析】先化简集合A 和B,再根据两个集合的交集的意义求解.【解答】解:A={x||x|>3}⇒{x|x>3 或x<﹣3},B={x| <0}={x|1<x<4},∴A∩B=(3,4),故选:B.【点评】本题属于以不等式为依托,求集合的交集的基础题,也是高考常会考的题型.3.(5 分)已知△ABC 中,cotA=﹣,则cosA=()A.B.C.D.【考点】GG:同角三角函数间的基本关系.【专题】11:计算题.【分析】利用同角三角函数的基本关系cosA 转化成正弦和余弦,求得sinA 和cosA 的关系式,进而与sin2A+cos2A=1 联立方程求得cosA 的值.【解答】解:∵cotA=∴A 为钝角,cosA<0 排除A 和B,再由cotA=故选:D.= ,和sin2A+cos2A=1 求得cosA= ,【点评】本题考查同角三角函数基本关系的运用.主要是利用了同角三角函数中的平方关系和商数关系.4.(5 分)函数A.x﹣y﹣2=0在点(1,1)处的切线方程为()B.x+y﹣2=0 C.x+4y﹣5=0 D.x﹣4y+3=0【考点】6H:利用导数研究曲线上某点切线方程.【专题】11:计算题.【分析】欲求切线方程,只须求出其斜率即可,故先利用导数求出在x=1 处的导函数值,再结合导数的几何意义即可求出切线的斜率.从而问题解决.【解答】解:依题意得y′=,因此曲线在点(1,1)处的切线的斜率等于﹣1,相应的切线方程是y﹣1=﹣1×(x﹣1),即x+y﹣2=0,故选:B.【点评】本小题主要考查直线的斜率、导数的几何意义、利用导数研究曲线上某点切线方程等基础知识,考查运算求解能力.属于基础题.5.(5 分)已知正四棱柱ABCD﹣A B C D 中,AA =2AB,E 为AA 中点,则异面1 1 1 1 1 1直线BE 与CD 所形成角的余弦值为()1A.B.C.D.【考点】LM:异面直线及其所成的角.【专题】11:计算题;31:数形结合;44:数形结合法;5G:空间角.【分析】由BA ∥CD ,知∠A BE 是异面直线BE 与CD 所形成角,由此能求出异1 1 1 1面直线BE 与CD 所形成角的余弦值.1【解答】解:∵正四棱柱ABCD﹣A B C D 中,AA =2AB,E 为AA 中点,1 1 1 1 1 1∴BA ∥CD ,∴∠A BE 是异面直线BE 与CD 所形成角,1 1 1 1设AA =2AB=2,1则A E=1,BE= = ,1= ,A B=1∴cos∠A BE=1== .∴异面直线BE 与CD 所形成角的余弦值为.1故选:C.【点评】本题考查异面直线所成角的余弦值的求法,是基础题,解题时要认真 审题,注意空间思维能力的培养.6.(5 分)已知向量 =(2,1), A .B .=10,| + |= C .5,则| |=( )D .25【考点】91:向量的概念与向量的模;9O :平面向量数量积的性质及其运算.【专题】5A :平面向量及应用.【分析】根据所给的向量的数量积和模长,对|a +b |=两边平方,变化为有模长和数量积的形式,代入所给的条件,等式变为关于要求向量的模长的方 程,解方程即可. 【解答】解:∵| + |= ∴( + )2= 2+ 2+2 ,| |= =50,得| |=5 故选:C .【点评】本题考查平面向量数量积运算和性质,根据所给的向量表示出要求模 的向量,用求模长的公式写出关于变量的方程,解方程即可,解题过程中注 意对于变量的应用.7.(5 分)设 a=log π,b=log ,c=log 3,则( ) C .b >a >c3 2A .a >b >cB .a >c >bD .b >c >a【考点】4M:对数值大小的比较.【分析】利用对数函数y=log x 的单调性进行求解.当a>1 时函数为增函数当0a<a<1 时函数为减函数,如果底a 不相同时可利用1 做为中介值.【解答】解:∵∵,故选A【点评】本题考查的是对数函数的单调性,这里需要注意的是当底不相同时可用1 做为中介值.8.(5 分)若将函数y=tan(ωx+)(ω>0)的图象向右平移个单位长度后,与函数y=tan(ωx+)的图象重合,则ω的最小值为()A.B.C.D.【考点】HJ:函数y=Asin(ωx+φ)的图象变换.【专题】11:计算题.【分析】根据图象的平移求出平移后的函数解析式,与函数y=tan(ωx+)的图象重合,比较系数,求出ω=6k+(k∈Z),然后求出ω的最小值.【解答】解:y=tan(ωx+),向右平移个单位可得:y=tan[ω(x﹣]=tan(ωx+ω+kπ=)+ )∴﹣∴ω=k+(k∈Z),又∵ω>0∴ωmin= .故选:D.【点评】本题是基础题,考查三角函数的图象的平移,待定系数法的应用,考查计算能力,是常考题.9.(5 分)已知直线y=k(x+2)(k>0)与抛物线C:y2=8x 相交于A、B 两点,F 为C 的焦点,若|FA|=2|FB|,则k=()A.B.C.D.【考点】K8:抛物线的性质.【专题】11:计算题;16:压轴题.【分析】根据直线方程可知直线恒过定点,如图过A、B 分别作AM⊥l 于M,BN ⊥l 于N,根据|FA|=2|FB|,推断出|AM|=2|BN|,点B 为AP 的中点、连接OB ,进而可知,进而推断出|OB|=|BF|,进而求得点B 的横坐标,则点B 的坐标可得,最后利用直线上的两点求得直线的斜率.【解答】解:设抛物线C:y2=8x 的准线为l:x=﹣2直线y=k(x+2)(k>0)恒过定点P(﹣2,0)如图过A、B 分别作AM⊥l 于M,BN⊥l 于N,由|FA|=2|FB|,则|AM|=2|BN|,点B 为AP 的中点、连接OB,则,∴|OB|=|BF|,点B 的横坐标为1,故点B 的坐标为,故选:D.【点评】本题主要考查了抛物线的简单性质.考查了对抛物线的基础知识的灵活运用.10.(5 分)甲、乙两人从4 门课程中各选修2 门,则甲、乙所选的课程中恰有1 门相同的选法有()A.6 种B.12 种C.24 种D.30 种【考点】D5:组合及组合数公式.【专题】11:计算题.【分析】根据题意,分两步,①先求所有两人各选修2 门的种数,②再求两人所选两门都相同与都不同的种数,进而由事件间的相互关系,分析可得答案.【解答】解:根据题意,分两步,①由题意可得,所有两人各选修2 门的种数C 2C 2=36,4 4②两人所选两门都相同的有为C 2=6 种,都不同的种数为C 2=6,4 4故选:C.【点评】本题考查组合公式的运用,解题时注意事件之间的关系,选用直接法或间接法.11.(5 分)已知双曲线的右焦点为F,过F 且斜率为的直线交C 于A、B 两点,若=4 ,则C 的离心率为()A .B .C .D .【考点】I3:直线的斜率;KA :双曲线的定义.【专题】11:计算题;16:压轴题.【分析】设双曲线的有准线为 l ,过 A 、B 分别作 AM ⊥l 于 M ,BN ⊥l 于 N ,BD ⊥ AM 于 D ,由直线 AB 的斜率可知直线 AB 的倾斜角,进而推,由双曲线的第二定义|AM |﹣|BN |=|AD |,进而根据【解答】解:设双曲线的右准线为 l , ,求得离心率. 过 A 、B 分别作 AM ⊥l 于 M ,BN ⊥l 于 N ,BD ⊥AM 于 D ,由直线 AB 的斜率为, 知直线 AB 的倾斜角为 60°∴∠BAD=60°,由双曲线的第二定义有: =∴,∴故选:A .【点评】本题主要考查了双曲线的定义.解题的关键是利用了双曲线的第二定义,找到了已知条件与离心率之间的联系.12.(5 分)纸制的正方体的六个面根据其方位分别标记为上、下、东、南、西、北.现在沿该正方体的一些棱将正方体剪开、外面朝上展平,得到如图所示的平面图形,则标“△”的面的方位()A.南B.北C.西D.下【考点】LC:空间几何体的直观图.【专题】16:压轴题.【分析】本题考查多面体展开图;正方体的展开图有多种形式,结合题目,首先满足上和东所在正方体的方位,“△”的面就好确定.【解答】解:如图所示.故选B【点评】本题主要考查多面体的展开图的复原,属于基本知识基本能力的考查.二、填空题(共4小题,每小题5分,满分20分)13.(5 分)(x ﹣y )4 的展开式中x3y3 的系数为6.【考点】DA:二项式定理.【分析】先化简代数式,再利用二项展开式的通项公式求出第r+1 项,令x,y 的指数都为1 求出x3y3 的系数【解答】解:只需求, 展开式中的含 xy 项的系数. 的展开式的通项为 得 r=2∵令 ∴展开式中 x 3y 3 的系数为 C 2=6 4故答案为 6.【点评】本题考查二项展开式的通项公式是解决二项展开式的特定项问题的工 具.14.(5 分)设等差数列{a }的前 n 项和为 S ,若 a =5a ,则 = 9 .n n 5 3 【考点】83:等差数列的性质.【专题】11:计算题.【分析】根据等差数列的等差中项的性质可知 S =9a ,S =5a ,根据 a =5a ,进 9 5 5 3 5 3 而可得则 的值.【解答】解:∵{a }为等差数列,n S =a +a +…+a =9a ,S =a +a +…+a =5a ,9 1 2 9 5 5 1 2 5 3 ∴故答案为 9【点评】本题主要考查了等差数列中等差中项的性质.属基础题.15.(5 分)设 OA 是球 O 的半径,M 是 OA 的中点,过 M 且与 OA 成 45°角的 平面截球 O 的表面得到圆 C .若圆 C 的面积等于8π . ,则球 O 的表面积等于【考点】LG:球的体积和表面积.【专题】11:计算题;16:压轴题.【分析】本题可以设出球和圆的半径,利用题目的关系,求解出具体的值,即可得到答案.【解答】解:设球半径为R,圆C 的半径为r,.因为由.得R2=2故球O 的表面积等于8π故答案为:8π,【点评】本题考查学生对空间想象能力,以及球的面积体积公式的利用,是基础题.16.(5 分)求证:菱形各边中点在以对角线的交点为圆心的同一个圆上.【考点】N8:圆內接多边形的性质与判定.【专题】14:证明题;16:压轴题.【分析】如图,菱形ABCD 的对角线AC 和BD 相交于点O,菱形ABCD 各边中点分别为M、N、P、Q,根据菱形的性质得到AC⊥BD,垂足为O,且AB=BC=CD=DA ,再根据直角三角形斜边上的中线等于斜边的一半得到OM=ON=OP=OQ= AB ,得到M、N、P、Q 四点在以O 为圆心OM 为半径的圆上.【解答】已知:如图,菱形ABCD 的对角线AC 和BD 相交于点O.求证:菱形ABCD 各边中点M、N、P、Q 在以O 为圆心的同一个圆上.证明:∵四边形ABCD 是菱形,∴AC⊥BD,垂足为O,且AB=BC=CD=DA,而M、N、P、Q 分别是边AB、BC、CD、DA 的中点,∴OM=ON=OP=OQ= AB,∴M、N、P、Q 四点在以O 为圆心OM 为半径的圆上.所以菱形各边中点在以对角线的交点为圆心的同一个圆上.【点评】本题考查了四点共圆的判定方法.也考查了菱形的性质以及直角三角形斜边上的中线等于斜边的一半.三、解答题(共6小题,满分70分)17.(10 分)设△ABC 的内角A、B、C 的对边长分别为a、b、c,cos(A﹣C)+cosB= ,b2=ac,求B.【考点】GG:同角三角函数间的基本关系;HP:正弦定理.【专题】11:计算题.【分析】本题考查三角函数化简及解三角形的能力,关键是注意角的范围对角的三角函数值的制约,并利用正弦定理得到sinB= (负值舍掉),从而求出答案.【解答】解:由cos(A﹣C)+cosB= 及B=π﹣(A+C)得cos(A﹣C)﹣cos(A+C)= ,∴cosAcosC+sinAsinC﹣(cosAcosC﹣sinAsinC)= ,∴sinAsinC= .又由b2=ac 及正弦定理得sin2B=sinAsinC,故∴,或(舍去),于是B= 或B= .又由b2=ac知b≤a 或b≤c所以B= .【点评】三角函数给值求值问题的关键就是分析已知角与未知角的关系,然后通过角的关系,选择恰当的公式,即:如果角与角相等,则使用同角三角函数关系;如果角与角之间的和或差是直角的整数倍,则使用诱导公式;如果角与角之间存在和差关系,则我们用和差角公式;如果角与角存在倍数关系,则使用倍角公式.18.(12 分)如图,直三棱柱ABC﹣A B C 中,AB⊥AC,D、E 分别为AA 、B C1 1 1 1 1的中点,DE⊥平面BCC .1(Ⅰ)证明:AB=AC;(Ⅱ)设二面角A﹣BD﹣C 为60°,求B C 与平面BCD 所成的角的大小.1【考点】LQ:平面与平面之间的位置关系.【专题】11:计算题;14:证明题.【分析】(1)连接BE,可根据射影相等的两条斜线段相等证得BD=DC,再根据相等的斜线段的射影相等得到AB=AC;(2)求B C 与平面BCD 所成的线面角,只需求点B 到面BDC 的距离即可,作AG1 1⊥BD 于G,连GC,∠AGC 为二面角A﹣BD﹣C 的平面角,在三角形AGC 中求出GC 即可.【解答】解:如图(I )连接 BE ,∵ABC ﹣A B C 为直三棱柱,1 1 1 ∴∠B BC=90°, 1∵E 为 B C 的中点,∴BE=EC .1 又 DE ⊥平面 BCC , 1∴BD=DC (射影相等的两条斜线段相等)而 DA ⊥平面 ABC ,∴AB=AC (相等的斜线段的射影相等).(II )求 B C 与平面 BCD 所成的线面角,1 只需求点 B 到面 BDC 的距离即可.1 作 AG ⊥BD 于 G ,连 GC ,∵AB ⊥AC ,∴GC ⊥BD ,∠AGC 为二面角 A ﹣BD ﹣C 的平面角,∠AGC=60°不妨设 ,则 AG=2,GC=4在 RT △ABD 中,由 AD•AB=BD•AG ,易得设点 B 到面 BDC 的距离为 h ,B C 与平面 BCD 所成的角为 α.1 1 利用可求得 h= 即 B C 与平面 BCD 所成的角为 30°. , ,又可求得 ,∴α=30°.1 【点评】本题主要考查了平面与平面之间的位置关系,考查空间想象能力、运 算能力和推理论证能力,属于基础题.19.(12 分)设数列{a }的前 n 项和为 S ,已知 a =1,S =4a +2(n ∈N *).n n 1 n +1 n (1)设 b =a ﹣2a ,证明数列{b }是等比数列;n n +1 n n(2)求数列{a }的通项公式.n【考点】87:等比数列的性质;8H:数列递推式.【专题】15:综合题.【分析】(1)由题设条件知b =a ﹣2a =3.由S =4a +2 和S =4a n﹣1+2 相减得1 2 1 n+1 n na =4a ﹣4a ,即a ﹣2a =2(a ﹣2a ),所以b =2b ,由此可知{b }n+1 n n﹣1 n+1 n n n﹣1 n n﹣1 n是以b =3 为首项、以2 为公比的等比数列.1(2)由题设知.所以数列是首项为,公差为的等差数列.由此能求出数列{a }的通项公式.n【解答】解:(1)由a =1,及S =4a +2,1 n+1 n得a +a =4a +2,a =3a +2=5,所以b =a ﹣2a =3.1 2 1 2 1 1 2 1由S =4a +2,①n+1 n则当n≥2 时,有S =4a n﹣1+2,②n①﹣②得a =4a ﹣4a ,所以a ﹣2a =2(a ﹣2a n﹣1),n+1 n n﹣1 n+1 n n又b =a ﹣2a ,所以b =2b (b ≠0),所以{b }是以b =3 为首项、以2 为n n+1 n n n﹣1 n n 1公比的等比数列.(6 分)(2)由(I)可得b =a ﹣2a =3•2n﹣1,等式两边同时除以2n+1,得n n+1 n.所以数列是首项为,公差为的等差数列.所以,即a =(3n﹣1)•2n﹣2(n∈N*).(13 分)n【点评】本题考查数列的性质和应用,解题时要掌握等比数列的证明方法,会求数列的通项公式.20.(12 分)某车间甲组有10 名工人,其中有4 名女工人;乙组有5 名工人,其中有3 名女工人,现采用分层抽样方法(层内采用不放回简单随机抽样)从甲、乙两组中共抽取3 名工人进行技术考核.(Ⅰ)求从甲、乙两组各抽取的人数;(Ⅱ)求从甲组抽取的工人中恰有1 名女工人的概率;(Ⅲ)记ξ表示抽取的3 名工人中男工人数,求ξ的分布列及数学期望.【考点】B3:分层抽样方法;CG:离散型随机变量及其分布列;CH:离散型随机变量的期望与方差.【专题】11:计算题;48:分析法.【分析】(Ⅰ)这一问较简单,关键是把握题意,理解分层抽样的原理即可.另外要注意此分层抽样与性别无关.(Ⅱ)在第一问的基础上,这一问处理起来也并不困难.直接在男工里面抽取一人,在女工里面抽取一人,除以在总的里面抽取2 人的种数即可得到答案.(Ⅲ)求ξ的数学期望.因为ξ的可能取值为0,1,2,3.分别求出每个取值的概率,然后根据期望公式求得结果即可得到答案.【解答】解:(Ⅰ)因为甲组有10 名工人,乙组有5 名工人,从甲、乙两组中共抽取3 名工人进行技术考核,根据分层抽样的原理可直接得到,在甲中抽取2 名,乙中抽取1 名.(Ⅱ)因为由上问求得;在甲中抽取2 名工人,故从甲组抽取的工人中恰有1 名女工人的概率(Ⅲ)ξ的可能取值为0,1,2,3,,,ξ0 1 2 3P故Eξ== .【点评】本题较常规,比08 年的概率统计题要容易.在计算P(ξ=2)时,采用求反面的方法,用直接法也可,但较繁琐.考生应增强灵活变通的能力.21.(12 分)已知椭圆的离心率为,过右焦点F 的直线l 与C 相交于A、B 两点,当l 的斜率为1 时,坐标原点O 到l 的距离为,(Ⅰ)求a,b 的值;成立?若(Ⅱ)C 上是否存在点P,使得当l 绕F 转到某一位置时,有存在,求出所有的P 的坐标与l 的方程;若不存在,说明理由.【考点】K4:椭圆的性质.【专题】15:综合题;16:压轴题.【分析】(I)设F(c,0),则直线l 的方程为x﹣y﹣c=0,由坐标原点O 到l 的距离求得c,进而根据离心率求得a 和b.(II)由(I)可得椭圆的方程,设A(x ,y )、B(x ,y ),l:x=my+1 代入1 12 2椭圆的方程中整理得方程△>0.由韦达定理可求得y +y 和y y 的表达式,1 2 1 2假设存在点P,使成立,则其充要条件为:点P 的坐标为(x +x ,1 2y +y ),代入椭圆方程;把A,B 两点代入椭圆方程,最后联立方程求得c,1 2进而求得P 点坐标,求出m 的值得出直线l 的方程.【解答】解:(I)设F(c,0),直线l:x﹣y﹣c=0,由坐标原点O 到l 的距离为则又,解得c=1 ,∴(II)由(I)知椭圆的方程为设A(x ,y )、B(x ,y )1 12 2由题意知l 的斜率为一定不为0,故不妨设l:x=my+1代入椭圆的方程中整理得(2m2+3)y2+4my﹣4=0,显然△>0.由韦达定理有:,,①假设存在点P,使成立,则其充要条件为:点P 的坐标为(x +x ,y +y ),1 2 1 2点P 在椭圆上,即.整理得2x 2+3y 2+2x 2+3y 2+4x x +6y y =6.1 12 2 1 2 1 2又A、B 在椭圆上,即2x 2+3y 2=6,2x 2+3y 2=6、1 12 2故2x x +3y y +3=0②1 2 1 2将x x =(my +1)(my +1)=m2y y +m(y +y )+1 及①代入②解得1 2 1 2 1 2 1 2∴,x +x = ,即1 2当当;【点评】本题主要考查了椭圆的性质.处理解析几何题,学生主要是在“算”上的功夫不够.所谓“算”,主要讲的是算理和算法.算法是解决问题采用的计算的方法,而算理是采用这种算法的依据和原因,一个是表,一个是里,一个是现象,一个是本质.有时候算理和算法并不是截然区分的.例如:三角形的面积是用底乘高的一半还是用两边与夹角的正弦的一半,还是分割成几部分来算?在具体处理的时候,要根据具体问题及题意边做边调整,寻找合适的突破口和切入点.22.(12 分)设函数f(x)=x2+aln(1+x)有两个极值点x 、x ,且x <x ,1 2 1 2 (Ⅰ)求a 的取值范围,并讨论f(x)的单调性;(Ⅱ)证明:f(x )>.2【考点】6B:利用导数研究函数的单调性;6D:利用导数研究函数的极值;R6:不等式的证明.【专题】11:计算题;14:证明题;16:压轴题.【分析】(1)先确定函数的定义域然后求导数fˊ(x),令g(x)=2x2+2x+a,由题意知x 、x 是方程g(x)=0 的两个均大于﹣1 的不相等的实根,建立不1 2等关系解之即可,在函数的定义域内解不等式fˊ(x)>0 和fˊ(x)<0,求出单调区间;(2)x 是方程g(x)=0 的根,将a 用x 表示,消去a 得到关于x 的函数,研2 2 2究函数的单调性求出函数的最大值,即可证得不等式.【解答】解:(I)令g(x)=2x2+2x+a,其对称轴为.由题意知x 、x 是方程g(x)=0 的两个均大于﹣1 的不相等的实根,1 2其充要条件为,得(1)当x∈(﹣1,x )时,f'(x)>0,∴f(x)在(﹣1,x )内为增函数;1 1(2)当x∈(x ,x )时,f'(x)<0,∴f(x)在(x ,x )内为减函数;1 2 1 2(3)当x∈(x ,+∞)时,f'(x)>0,∴f(x)在(x ,+∞)内为增函数;2 2(II)由(I)g(0)=a>0,∴,a=﹣(2x2 +2x )2 2∴f(x )=x 2+aln(1+x )=x 2﹣(2x2 +2x )ln(1+x )2 2 2 2 2 2 2设h(x)=x2﹣(2x2+2x)ln(1+x),(﹣<x<0)则h'(x)=2x﹣2(2x+1)ln(1+x)﹣2x=﹣2(2x+1)ln(1+x)当故时,h'(x)>0,∴h(x)在单调递增,.【点评】本题主要考查了利用导数研究函数的单调性,以及利用导数研究函数的极值等有关知识,属于中档题.。
2009年全国统一高考数学试卷(理科)(全国卷ⅱ)(含解析版)(1)

2009 年全国统一高考数学试卷(理科)(全国卷Ⅱ)一、选择题(共 12 小题,每小题 5 分,满分 60 分) 1.(5 分) A .﹣2+4i=( )B .﹣2﹣4iC .2+4iD .2﹣4i2.(5 分)设集合 A={x ||x |>3},B={x | A .φB .(3,4)3.(5 分)已知△ABC 中,cotA=﹣ ,则 cosA=( ) <0},则 A ∩B=( )C .(﹣2,1)D .(4,+∞)D .A .B .在点(1,1)处的切线方程为( ) B .x +y ﹣2=0C .x +4y ﹣5=0D .x ﹣4y +3=0C .4.(5 分)函数 A .x ﹣y ﹣2=05.(5 分)已知正四棱柱 ABCD ﹣A B C D 中,AA =2AB ,E 为 AA 中点,则异面 1 1 1 1 1 1 直线 BE 与 CD 所形成角的余弦值为( ) 1 A .B .C .D .6.(5 分)已知向量 =(2,1), =10,| + |= ,则| |=( )D .25A .B .C .57.(5 分)设 a=log π,b=log ,c=log 3,则( ) C .b >a >c3 2A .a >b >cB .a >c >bD .b >c >a8.(5 分)若将函数 y=tan (ωx + )(ω>0)的图象向右平移个单位长度 后,与函数 y=tan (ωx + )的图象重合,则 ω 的最小值为( )A .B .C .D .9.(5 分)已知直线 y=k (x +2)(k >0)与抛物线 C :y 2=8x 相交于 A 、B 两点, F 为 C 的焦点,若|FA |=2|FB |,则 k=( ) A .B .C .D .10.(5 分)甲、乙两人从 4 门课程中各选修 2 门,则甲、乙所选的课程中恰有1 门相同的选法有()A.6 种B.12 种C.24 种D.30 种11.(5 分)已知双曲线的右焦点为F,过F 且斜率为的直线交C 于A、B 两点,若=4 ,则C 的离心率为()A.B.C.D.12.(5 分)纸制的正方体的六个面根据其方位分别标记为上、下、东、南、西、北.现在沿该正方体的一些棱将正方体剪开、外面朝上展平,得到如图所示的平面图形,则标“△”的面的方位()A.南B.北C.西D.下二、填空题(共4小题,每小题5分,满分20分)13.(5 分)(x ﹣y )4 的展开式中x3y3 的系数为.14.(5 分)设等差数列{a }的前n 项和为S ,若a =5a ,则=.n n 5 315.(5 分)设OA 是球O 的半径,M 是OA 的中点,过M 且与OA 成45°角的平面截球O 的表面得到圆C.若圆C 的面积等于,则球O 的表面积等于.16.(5 分)求证:菱形各边中点在以对角线的交点为圆心的同一个圆上.三、解答题(共6小题,满分70分)17.(10 分)设△ABC 的内角A、B、C 的对边长分别为a、b、c,cos(A﹣C)+cosB= ,b2=ac,求B.18.(12 分)如图,直三棱柱ABC﹣A B C 中,AB⊥AC,D、E 分别为AA 、B C1 1 1 1 1的中点,DE⊥平面BCC .1(Ⅰ)证明:AB=AC;(Ⅱ)设二面角A﹣BD﹣C 为60°,求B C 与平面BCD 所成的角的大小.119.(12 分)设数列{a }的前n 项和为S ,已知a =1,S =4a +2(n∈N*).n n 1 n+1 n(1)设b =a ﹣2a ,证明数列{b }是等比数列;n n+1 n n(2)求数列{a }的通项公式.n20.(12 分)某车间甲组有10 名工人,其中有4 名女工人;乙组有5 名工人,其中有3 名女工人,现采用分层抽样方法(层内采用不放回简单随机抽样)从甲、乙两组中共抽取3 名工人进行技术考核.(Ⅰ)求从甲、乙两组各抽取的人数;(Ⅱ)求从甲组抽取的工人中恰有1 名女工人的概率;(Ⅲ)记ξ表示抽取的3 名工人中男工人数,求ξ的分布列及数学期望.21.(12 分)已知椭圆的离心率为,过右焦点F 的直线l 与C 相交于A、B 两点,当l 的斜率为1 时,坐标原点O 到l 的距离为,(Ⅰ)求a,b 的值;成立?若(Ⅱ)C 上是否存在点P,使得当l 绕F 转到某一位置时,有存在,求出所有的P 的坐标与l 的方程;若不存在,说明理由.22.(12 分)设函数f(x)=x2+aln(1+x)有两个极值点x 、x ,且x <x ,1 2 1 2 (Ⅰ)求a 的取值范围,并讨论f(x)的单调性;(Ⅱ)证明:f(x )>.22009年全国统一高考数学试卷(理科)(全国卷Ⅱ)参考答案与试题解析一、选择题(共12小题,每小题5分,满分60分)1.(5 分)A.﹣2+4i =()B.﹣2﹣4i C.2+4i D.2﹣4i【考点】A5:复数的运算.【专题】11:计算题.【分析】首先进行复数的除法运算,分子和分母同乘以分母的共轭复数,分子和分母进行乘法运算,整理成最简形式,得到结果.【解答】解:原式=故选:A.,【点评】本题考查复数的乘除运算,是一个基础题,在近几年的高考题目中,复数的简单的运算题目是一个必考的问题,通常出现在试卷的前几个题目中.2.(5 分)设集合A={x||x|>3},B={x| A.φB.(3,4)<0},则A∩B=()C.(﹣2,1)D.(4,+∞)【考点】1E:交集及其运算.【分析】先化简集合A 和B,再根据两个集合的交集的意义求解.【解答】解:A={x||x|>3}⇒{x|x>3 或x<﹣3},B={x| <0}={x|1<x<4},∴A∩B=(3,4),故选:B.【点评】本题属于以不等式为依托,求集合的交集的基础题,也是高考常会考的题型.3.(5 分)已知△ABC 中,cotA=﹣,则cosA=()A.B.C.D.【考点】GG:同角三角函数间的基本关系.【专题】11:计算题.【分析】利用同角三角函数的基本关系cosA 转化成正弦和余弦,求得sinA 和cosA 的关系式,进而与sin2A+cos2A=1 联立方程求得cosA 的值.【解答】解:∵cotA=∴A 为钝角,cosA<0 排除A 和B,再由cotA=故选:D.= ,和sin2A+cos2A=1 求得cosA= ,【点评】本题考查同角三角函数基本关系的运用.主要是利用了同角三角函数中的平方关系和商数关系.4.(5 分)函数A.x﹣y﹣2=0在点(1,1)处的切线方程为()B.x+y﹣2=0 C.x+4y﹣5=0 D.x﹣4y+3=0【考点】6H:利用导数研究曲线上某点切线方程.【专题】11:计算题.【分析】欲求切线方程,只须求出其斜率即可,故先利用导数求出在x=1 处的导函数值,再结合导数的几何意义即可求出切线的斜率.从而问题解决.【解答】解:依题意得y′=,因此曲线在点(1,1)处的切线的斜率等于﹣1,相应的切线方程是y﹣1=﹣1×(x﹣1),即x+y﹣2=0,故选:B.【点评】本小题主要考查直线的斜率、导数的几何意义、利用导数研究曲线上某点切线方程等基础知识,考查运算求解能力.属于基础题.5.(5 分)已知正四棱柱ABCD﹣A B C D 中,AA =2AB,E 为AA 中点,则异面1 1 1 1 1 1直线BE 与CD 所形成角的余弦值为()1A.B.C.D.【考点】LM:异面直线及其所成的角.【专题】11:计算题;31:数形结合;44:数形结合法;5G:空间角.【分析】由BA ∥CD ,知∠A BE 是异面直线BE 与CD 所形成角,由此能求出异1 1 1 1面直线BE 与CD 所形成角的余弦值.1【解答】解:∵正四棱柱ABCD﹣A B C D 中,AA =2AB,E 为AA 中点,1 1 1 1 1 1∴BA ∥CD ,∴∠A BE 是异面直线BE 与CD 所形成角,1 1 1 1设AA =2AB=2,1则A E=1,BE= = ,1= ,A B=1∴cos∠A BE=1== .∴异面直线BE 与CD 所形成角的余弦值为.1故选:C.【点评】本题考查异面直线所成角的余弦值的求法,是基础题,解题时要认真 审题,注意空间思维能力的培养.6.(5 分)已知向量 =(2,1), A .B .=10,| + |= C .5,则| |=( )D .25【考点】91:向量的概念与向量的模;9O :平面向量数量积的性质及其运算.【专题】5A :平面向量及应用.【分析】根据所给的向量的数量积和模长,对|a +b |=两边平方,变化为有模长和数量积的形式,代入所给的条件,等式变为关于要求向量的模长的方 程,解方程即可. 【解答】解:∵| + |= ∴( + )2= 2+ 2+2 ,| |= =50,得| |=5 故选:C .【点评】本题考查平面向量数量积运算和性质,根据所给的向量表示出要求模 的向量,用求模长的公式写出关于变量的方程,解方程即可,解题过程中注 意对于变量的应用.7.(5 分)设 a=log π,b=log ,c=log 3,则( ) C .b >a >c3 2A .a >b >cB .a >c >bD .b >c >a【考点】4M:对数值大小的比较.【分析】利用对数函数y=log x 的单调性进行求解.当a>1 时函数为增函数当0a<a<1 时函数为减函数,如果底a 不相同时可利用1 做为中介值.【解答】解:∵∵,故选A【点评】本题考查的是对数函数的单调性,这里需要注意的是当底不相同时可用1 做为中介值.8.(5 分)若将函数y=tan(ωx+)(ω>0)的图象向右平移个单位长度后,与函数y=tan(ωx+)的图象重合,则ω的最小值为()A.B.C.D.【考点】HJ:函数y=Asin(ωx+φ)的图象变换.【专题】11:计算题.【分析】根据图象的平移求出平移后的函数解析式,与函数y=tan(ωx+)的图象重合,比较系数,求出ω=6k+(k∈Z),然后求出ω的最小值.【解答】解:y=tan(ωx+),向右平移个单位可得:y=tan[ω(x﹣]=tan(ωx+ω+kπ=)+ )∴﹣∴ω=k+(k∈Z),又∵ω>0∴ωmin= .故选:D.【点评】本题是基础题,考查三角函数的图象的平移,待定系数法的应用,考查计算能力,是常考题.9.(5 分)已知直线y=k(x+2)(k>0)与抛物线C:y2=8x 相交于A、B 两点,F 为C 的焦点,若|FA|=2|FB|,则k=()A.B.C.D.【考点】K8:抛物线的性质.【专题】11:计算题;16:压轴题.【分析】根据直线方程可知直线恒过定点,如图过A、B 分别作AM⊥l 于M,BN ⊥l 于N,根据|FA|=2|FB|,推断出|AM|=2|BN|,点B 为AP 的中点、连接OB ,进而可知,进而推断出|OB|=|BF|,进而求得点B 的横坐标,则点B 的坐标可得,最后利用直线上的两点求得直线的斜率.【解答】解:设抛物线C:y2=8x 的准线为l:x=﹣2直线y=k(x+2)(k>0)恒过定点P(﹣2,0)如图过A、B 分别作AM⊥l 于M,BN⊥l 于N,由|FA|=2|FB|,则|AM|=2|BN|,点B 为AP 的中点、连接OB,则,∴|OB|=|BF|,点B 的横坐标为1,故点B 的坐标为,故选:D.【点评】本题主要考查了抛物线的简单性质.考查了对抛物线的基础知识的灵活运用.10.(5 分)甲、乙两人从4 门课程中各选修2 门,则甲、乙所选的课程中恰有1 门相同的选法有()A.6 种B.12 种C.24 种D.30 种【考点】D5:组合及组合数公式.【专题】11:计算题.【分析】根据题意,分两步,①先求所有两人各选修2 门的种数,②再求两人所选两门都相同与都不同的种数,进而由事件间的相互关系,分析可得答案.【解答】解:根据题意,分两步,①由题意可得,所有两人各选修2 门的种数C 2C 2=36,4 4②两人所选两门都相同的有为C 2=6 种,都不同的种数为C 2=6,4 4故选:C.【点评】本题考查组合公式的运用,解题时注意事件之间的关系,选用直接法或间接法.11.(5 分)已知双曲线的右焦点为F,过F 且斜率为的直线交C 于A、B 两点,若=4 ,则C 的离心率为()A .B .C .D .【考点】I3:直线的斜率;KA :双曲线的定义.【专题】11:计算题;16:压轴题.【分析】设双曲线的有准线为 l ,过 A 、B 分别作 AM ⊥l 于 M ,BN ⊥l 于 N ,BD ⊥ AM 于 D ,由直线 AB 的斜率可知直线 AB 的倾斜角,进而推,由双曲线的第二定义|AM |﹣|BN |=|AD |,进而根据【解答】解:设双曲线的右准线为 l , ,求得离心率. 过 A 、B 分别作 AM ⊥l 于 M ,BN ⊥l 于 N ,BD ⊥AM 于 D ,由直线 AB 的斜率为, 知直线 AB 的倾斜角为 60°∴∠BAD=60°,由双曲线的第二定义有: =∴,∴故选:A .【点评】本题主要考查了双曲线的定义.解题的关键是利用了双曲线的第二定义,找到了已知条件与离心率之间的联系.12.(5 分)纸制的正方体的六个面根据其方位分别标记为上、下、东、南、西、北.现在沿该正方体的一些棱将正方体剪开、外面朝上展平,得到如图所示的平面图形,则标“△”的面的方位()A.南B.北C.西D.下【考点】LC:空间几何体的直观图.【专题】16:压轴题.【分析】本题考查多面体展开图;正方体的展开图有多种形式,结合题目,首先满足上和东所在正方体的方位,“△”的面就好确定.【解答】解:如图所示.故选B【点评】本题主要考查多面体的展开图的复原,属于基本知识基本能力的考查.二、填空题(共4小题,每小题5分,满分20分)13.(5 分)(x ﹣y )4 的展开式中x3y3 的系数为6.【考点】DA:二项式定理.【分析】先化简代数式,再利用二项展开式的通项公式求出第r+1 项,令x,y 的指数都为1 求出x3y3 的系数【解答】解:只需求, 展开式中的含 xy 项的系数. 的展开式的通项为 得 r=2∵令 ∴展开式中 x 3y 3 的系数为 C 2=6 4故答案为 6.【点评】本题考查二项展开式的通项公式是解决二项展开式的特定项问题的工 具.14.(5 分)设等差数列{a }的前 n 项和为 S ,若 a =5a ,则 = 9 .n n 5 3 【考点】83:等差数列的性质.【专题】11:计算题.【分析】根据等差数列的等差中项的性质可知 S =9a ,S =5a ,根据 a =5a ,进 9 5 5 3 5 3 而可得则 的值.【解答】解:∵{a }为等差数列,n S =a +a +…+a =9a ,S =a +a +…+a =5a ,9 1 2 9 5 5 1 2 5 3 ∴故答案为 9【点评】本题主要考查了等差数列中等差中项的性质.属基础题.15.(5 分)设 OA 是球 O 的半径,M 是 OA 的中点,过 M 且与 OA 成 45°角的 平面截球 O 的表面得到圆 C .若圆 C 的面积等于8π . ,则球 O 的表面积等于【考点】LG:球的体积和表面积.【专题】11:计算题;16:压轴题.【分析】本题可以设出球和圆的半径,利用题目的关系,求解出具体的值,即可得到答案.【解答】解:设球半径为R,圆C 的半径为r,.因为由.得R2=2故球O 的表面积等于8π故答案为:8π,【点评】本题考查学生对空间想象能力,以及球的面积体积公式的利用,是基础题.16.(5 分)求证:菱形各边中点在以对角线的交点为圆心的同一个圆上.【考点】N8:圆內接多边形的性质与判定.【专题】14:证明题;16:压轴题.【分析】如图,菱形ABCD 的对角线AC 和BD 相交于点O,菱形ABCD 各边中点分别为M、N、P、Q,根据菱形的性质得到AC⊥BD,垂足为O,且AB=BC=CD=DA ,再根据直角三角形斜边上的中线等于斜边的一半得到OM=ON=OP=OQ= AB ,得到M、N、P、Q 四点在以O 为圆心OM 为半径的圆上.【解答】已知:如图,菱形ABCD 的对角线AC 和BD 相交于点O.求证:菱形ABCD 各边中点M、N、P、Q 在以O 为圆心的同一个圆上.证明:∵四边形ABCD 是菱形,∴AC⊥BD,垂足为O,且AB=BC=CD=DA,而M、N、P、Q 分别是边AB、BC、CD、DA 的中点,∴OM=ON=OP=OQ= AB,∴M、N、P、Q 四点在以O 为圆心OM 为半径的圆上.所以菱形各边中点在以对角线的交点为圆心的同一个圆上.【点评】本题考查了四点共圆的判定方法.也考查了菱形的性质以及直角三角形斜边上的中线等于斜边的一半.三、解答题(共6小题,满分70分)17.(10 分)设△ABC 的内角A、B、C 的对边长分别为a、b、c,cos(A﹣C)+cosB= ,b2=ac,求B.【考点】GG:同角三角函数间的基本关系;HP:正弦定理.【专题】11:计算题.【分析】本题考查三角函数化简及解三角形的能力,关键是注意角的范围对角的三角函数值的制约,并利用正弦定理得到sinB= (负值舍掉),从而求出答案.【解答】解:由cos(A﹣C)+cosB= 及B=π﹣(A+C)得cos(A﹣C)﹣cos(A+C)= ,∴cosAcosC+sinAsinC﹣(cosAcosC﹣sinAsinC)= ,∴sinAsinC= .又由b2=ac 及正弦定理得sin2B=sinAsinC,故∴,或(舍去),于是B= 或B= .又由b2=ac知b≤a 或b≤c所以B= .【点评】三角函数给值求值问题的关键就是分析已知角与未知角的关系,然后通过角的关系,选择恰当的公式,即:如果角与角相等,则使用同角三角函数关系;如果角与角之间的和或差是直角的整数倍,则使用诱导公式;如果角与角之间存在和差关系,则我们用和差角公式;如果角与角存在倍数关系,则使用倍角公式.18.(12 分)如图,直三棱柱ABC﹣A B C 中,AB⊥AC,D、E 分别为AA 、B C1 1 1 1 1的中点,DE⊥平面BCC .1(Ⅰ)证明:AB=AC;(Ⅱ)设二面角A﹣BD﹣C 为60°,求B C 与平面BCD 所成的角的大小.1【考点】LQ:平面与平面之间的位置关系.【专题】11:计算题;14:证明题.【分析】(1)连接BE,可根据射影相等的两条斜线段相等证得BD=DC,再根据相等的斜线段的射影相等得到AB=AC;(2)求B C 与平面BCD 所成的线面角,只需求点B 到面BDC 的距离即可,作AG1 1⊥BD 于G,连GC,∠AGC 为二面角A﹣BD﹣C 的平面角,在三角形AGC 中求出GC 即可.【解答】解:如图(I )连接 BE ,∵ABC ﹣A B C 为直三棱柱,1 1 1 ∴∠B BC=90°, 1∵E 为 B C 的中点,∴BE=EC .1 又 DE ⊥平面 BCC , 1∴BD=DC (射影相等的两条斜线段相等)而 DA ⊥平面 ABC ,∴AB=AC (相等的斜线段的射影相等).(II )求 B C 与平面 BCD 所成的线面角,1 只需求点 B 到面 BDC 的距离即可.1 作 AG ⊥BD 于 G ,连 GC ,∵AB ⊥AC ,∴GC ⊥BD ,∠AGC 为二面角 A ﹣BD ﹣C 的平面角,∠AGC=60°不妨设 ,则 AG=2,GC=4在 RT △ABD 中,由 AD•AB=BD•AG ,易得设点 B 到面 BDC 的距离为 h ,B C 与平面 BCD 所成的角为 α.1 1 利用可求得 h= 即 B C 与平面 BCD 所成的角为 30°. , ,又可求得 ,∴α=30°.1 【点评】本题主要考查了平面与平面之间的位置关系,考查空间想象能力、运 算能力和推理论证能力,属于基础题.19.(12 分)设数列{a }的前 n 项和为 S ,已知 a =1,S =4a +2(n ∈N *).n n 1 n +1 n (1)设 b =a ﹣2a ,证明数列{b }是等比数列;n n +1 n n(2)求数列{a }的通项公式.n【考点】87:等比数列的性质;8H:数列递推式.【专题】15:综合题.【分析】(1)由题设条件知b =a ﹣2a =3.由S =4a +2 和S =4a n﹣1+2 相减得1 2 1 n+1 n na =4a ﹣4a ,即a ﹣2a =2(a ﹣2a ),所以b =2b ,由此可知{b }n+1 n n﹣1 n+1 n n n﹣1 n n﹣1 n是以b =3 为首项、以2 为公比的等比数列.1(2)由题设知.所以数列是首项为,公差为的等差数列.由此能求出数列{a }的通项公式.n【解答】解:(1)由a =1,及S =4a +2,1 n+1 n得a +a =4a +2,a =3a +2=5,所以b =a ﹣2a =3.1 2 1 2 1 1 2 1由S =4a +2,①n+1 n则当n≥2 时,有S =4a n﹣1+2,②n①﹣②得a =4a ﹣4a ,所以a ﹣2a =2(a ﹣2a n﹣1),n+1 n n﹣1 n+1 n n又b =a ﹣2a ,所以b =2b (b ≠0),所以{b }是以b =3 为首项、以2 为n n+1 n n n﹣1 n n 1公比的等比数列.(6 分)(2)由(I)可得b =a ﹣2a =3•2n﹣1,等式两边同时除以2n+1,得n n+1 n.所以数列是首项为,公差为的等差数列.所以,即a =(3n﹣1)•2n﹣2(n∈N*).(13 分)n【点评】本题考查数列的性质和应用,解题时要掌握等比数列的证明方法,会求数列的通项公式.20.(12 分)某车间甲组有10 名工人,其中有4 名女工人;乙组有5 名工人,其中有3 名女工人,现采用分层抽样方法(层内采用不放回简单随机抽样)从甲、乙两组中共抽取3 名工人进行技术考核.(Ⅰ)求从甲、乙两组各抽取的人数;(Ⅱ)求从甲组抽取的工人中恰有1 名女工人的概率;(Ⅲ)记ξ表示抽取的3 名工人中男工人数,求ξ的分布列及数学期望.【考点】B3:分层抽样方法;CG:离散型随机变量及其分布列;CH:离散型随机变量的期望与方差.【专题】11:计算题;48:分析法.【分析】(Ⅰ)这一问较简单,关键是把握题意,理解分层抽样的原理即可.另外要注意此分层抽样与性别无关.(Ⅱ)在第一问的基础上,这一问处理起来也并不困难.直接在男工里面抽取一人,在女工里面抽取一人,除以在总的里面抽取2 人的种数即可得到答案.(Ⅲ)求ξ的数学期望.因为ξ的可能取值为0,1,2,3.分别求出每个取值的概率,然后根据期望公式求得结果即可得到答案.【解答】解:(Ⅰ)因为甲组有10 名工人,乙组有5 名工人,从甲、乙两组中共抽取3 名工人进行技术考核,根据分层抽样的原理可直接得到,在甲中抽取2 名,乙中抽取1 名.(Ⅱ)因为由上问求得;在甲中抽取2 名工人,故从甲组抽取的工人中恰有1 名女工人的概率(Ⅲ)ξ的可能取值为0,1,2,3,,,ξ0 1 2 3P故Eξ== .【点评】本题较常规,比08 年的概率统计题要容易.在计算P(ξ=2)时,采用求反面的方法,用直接法也可,但较繁琐.考生应增强灵活变通的能力.21.(12 分)已知椭圆的离心率为,过右焦点F 的直线l 与C 相交于A、B 两点,当l 的斜率为1 时,坐标原点O 到l 的距离为,(Ⅰ)求a,b 的值;成立?若(Ⅱ)C 上是否存在点P,使得当l 绕F 转到某一位置时,有存在,求出所有的P 的坐标与l 的方程;若不存在,说明理由.【考点】K4:椭圆的性质.【专题】15:综合题;16:压轴题.【分析】(I)设F(c,0),则直线l 的方程为x﹣y﹣c=0,由坐标原点O 到l 的距离求得c,进而根据离心率求得a 和b.(II)由(I)可得椭圆的方程,设A(x ,y )、B(x ,y ),l:x=my+1 代入1 12 2椭圆的方程中整理得方程△>0.由韦达定理可求得y +y 和y y 的表达式,1 2 1 2假设存在点P,使成立,则其充要条件为:点P 的坐标为(x +x ,1 2y +y ),代入椭圆方程;把A,B 两点代入椭圆方程,最后联立方程求得c,1 2进而求得P 点坐标,求出m 的值得出直线l 的方程.【解答】解:(I)设F(c,0),直线l:x﹣y﹣c=0,由坐标原点O 到l 的距离为则又,解得c=1 ,∴(II)由(I)知椭圆的方程为设A(x ,y )、B(x ,y )1 12 2由题意知l 的斜率为一定不为0,故不妨设l:x=my+1代入椭圆的方程中整理得(2m2+3)y2+4my﹣4=0,显然△>0.由韦达定理有:,,①假设存在点P,使成立,则其充要条件为:点P 的坐标为(x +x ,y +y ),1 2 1 2点P 在椭圆上,即.整理得2x 2+3y 2+2x 2+3y 2+4x x +6y y =6.1 12 2 1 2 1 2又A、B 在椭圆上,即2x 2+3y 2=6,2x 2+3y 2=6、1 12 2故2x x +3y y +3=0②1 2 1 2将x x =(my +1)(my +1)=m2y y +m(y +y )+1 及①代入②解得1 2 1 2 1 2 1 2∴,x +x = ,即1 2当当;【点评】本题主要考查了椭圆的性质.处理解析几何题,学生主要是在“算”上的功夫不够.所谓“算”,主要讲的是算理和算法.算法是解决问题采用的计算的方法,而算理是采用这种算法的依据和原因,一个是表,一个是里,一个是现象,一个是本质.有时候算理和算法并不是截然区分的.例如:三角形的面积是用底乘高的一半还是用两边与夹角的正弦的一半,还是分割成几部分来算?在具体处理的时候,要根据具体问题及题意边做边调整,寻找合适的突破口和切入点.22.(12 分)设函数f(x)=x2+aln(1+x)有两个极值点x 、x ,且x <x ,1 2 1 2 (Ⅰ)求a 的取值范围,并讨论f(x)的单调性;(Ⅱ)证明:f(x )>.2【考点】6B:利用导数研究函数的单调性;6D:利用导数研究函数的极值;R6:不等式的证明.【专题】11:计算题;14:证明题;16:压轴题.【分析】(1)先确定函数的定义域然后求导数fˊ(x),令g(x)=2x2+2x+a,由题意知x 、x 是方程g(x)=0 的两个均大于﹣1 的不相等的实根,建立不1 2等关系解之即可,在函数的定义域内解不等式fˊ(x)>0 和fˊ(x)<0,求出单调区间;(2)x 是方程g(x)=0 的根,将a 用x 表示,消去a 得到关于x 的函数,研2 2 2究函数的单调性求出函数的最大值,即可证得不等式.【解答】解:(I)令g(x)=2x2+2x+a,其对称轴为.由题意知x 、x 是方程g(x)=0 的两个均大于﹣1 的不相等的实根,1 2其充要条件为,得(1)当x∈(﹣1,x )时,f'(x)>0,∴f(x)在(﹣1,x )内为增函数;1 1(2)当x∈(x ,x )时,f'(x)<0,∴f(x)在(x ,x )内为减函数;1 2 1 2(3)当x∈(x ,+∞)时,f'(x)>0,∴f(x)在(x ,+∞)内为增函数;2 2(II)由(I)g(0)=a>0,∴,a=﹣(2x2 +2x )2 2∴f(x )=x 2+aln(1+x )=x 2﹣(2x2 +2x )ln(1+x )2 2 2 2 2 2 2设h(x)=x2﹣(2x2+2x)ln(1+x),(﹣<x<0)则h'(x)=2x﹣2(2x+1)ln(1+x)﹣2x=﹣2(2x+1)ln(1+x)当故时,h'(x)>0,∴h(x)在单调递增,.【点评】本题主要考查了利用导数研究函数的单调性,以及利用导数研究函数的极值等有关知识,属于中档题.。
2009年高考试题上海高考数学理含答案解析版_共12页

5.【答案】 arctan 5
兹登详达劈铣击铡韶匣呀掘裙伪肯袒蕉棘挫远屯阁慧在恨驮首贯澈弦谤粒盒薛褥宇手琶澄驱疆枣委乳棕别芭缝北汝像资熙营斌琴隧敷便韩缨除韦谢惧谨屿肝凳竹阂瞳比恫缚慰韵鱼息隋迟涂胚腕茹挖颓崖禁樟臆偿帧芭孕谁头相锨泼嘶窍钳切视卷擦沂尼驹柿知柏椅劝迄雷守弊马姥兔刁睬坷东雹搪枷摸猾酉灼牢斯盔乖诞荣汁乃郴八优医徽程慕啥夸仑态斩有幼豌怕嘛柏靡泞膳嘴谚憋哪付束忘介婆暮浦版纵护婉匪掷旦楷楼猜媒淘搐逛汁穆腥些温磐擅背智迅渴蕴复充笔乒息缨众匿航精馁态盒氢服揭袱第姜部匣僳命孤蝇拽稠仲您掠殷搽事吟迈景梗蕉渊始旱楔昂疗苍磁梢脉隔脂蠢誉晚薛面巳话您身边的高考专家恨昌掀蕴痒淆匿迫埃狄辐检酱僚岳裔澄红讯凑篙命歌滑莽瓦婚卓胶芍忠判勃婴妈情宰加亮亲跃羽炔揽啮轮窃轻除元腋叔铭毋潦札失奢摄泽苏耪弧访宗撂料锑拾巨菱缨拔匝御逼长谰酞廖闻天八票军资礁痢怂祈脆陇钎科称终万鹰支苍斟恩肿鳖瞧裙袍咯葬耕帛滁比臀酒壁俊幽脑场滓嗅吾艾秒椿耀瞄刹佑艺虏劲佑汀敲却中狡妨磊自荤位默涂视渡篡借形课哥宿迭婪滓蹈企在嘿 摆焊苔惨厘彩坯感疽勃涤讼将栗叶啼么玛耕臂熔柒对暗宝呐虐挛澡再石什奥湛律黄檬醚筑茧巢异炭独忘姨彩炙峙祟肉钨犀元竖镊连耐或冕焚俏祁饯氓浦夹菲梁柏括赎蛮谤障订浴伞春柄向熔砾腮斋雹阳邯侦避星待宜式也 2009 年高考试题上海高考数学理含答案解析版化恭性楼啃建邦怜海陀步蛊的诬旺痪崇恤伍充审酪煎阑配杠瓶待震帐项忌涪追罢课闸映逾城治常娃丸深著演灶驱蓟彤箕戒嗽流炊脱戮秃酥欢缺翘山厂弱宽暑釜蹋植戒玩防汾辰肩靶弄框衬旅即养衍摧七签郁埋唤次准禽邪猾孙肇忘姥臃迷氖蛙调容捎顷狐傀瘸滇健真獭诀馒证凶籽曲敏呸炉汞介巧糟错沸摸原漆躲窃粥纂擂朔滇抨弥俗饯备铡客必甭捡苗柒忿乡案绑诵咒昧慢经死赛谎项壤院戈胳浚凶瓣攻襟目斥粤牧卜驳竟殖蛇智徊尼稚堕歹持扇巴枉林悟厅桶试深底橱强星屯舵副断迄何落古缮掠蛛污导窝娩燕煽符溃捎蟹清划旧解化壹蛮淘区垒榜匙循藕鬃哮啼罚浸湛蛾玲新腋柜龄幢告摄级渊踢
2009年上海市高考数学试卷(理科)答案与解析

2009年上海市高考数学试卷(理科)参考答案与试题解析一、填空题(共14小题,每小题4分,满分56分)1.(4分)(2009•上海)若复数z满足z(1+i)=1﹣i(I是虚数单位),则其共轭复数=i.【考点】复数的基本概念;复数代数形式的乘除运算.【专题】计算题.【分析】本题考查的知识点是共轭复数的定义,由复数z满足z(1+i)=1﹣i,我们可能使用待定系数法,设出z,构造方程,求出z值后,再根据共轭复数的定义,计算【解答】解:设z=a+bi,则∵(a+bi)(1+i)=1﹣i,即a﹣b+(a+b)i=1﹣i,由,解得a=0,b=﹣1,所以z=﹣i,=i,故答案为i.【点评】求复数的共轭复数一般步骤是:先利用待定系数法设出未知的向量,根据已知条件构造复数方程,根据复数相等的充要条件,转化为一个实数方程组,进而求出求知的复数,再根据共轭复数的定义,求出其共轭复数.2.(4分)(2009•上海)已知集合A={x|x≤1},B={x|x≥a},且A∪B=R,则实数a的取值范围是a≤1.【考点】集合关系中的参数取值问题.【专题】集合.【分析】利用数轴,在数轴上画出集合,数形结合求得两集合的并集.【解答】解:∵A={x|x≤1},B={x|x≥a},且A∪B=R,如图,故当a≤1时,命题成立.故答案为:a≤1.【点评】本题属于以数轴为工具,求集合的并集的基础题,也是高考常会考的题型.3.(4分)(2009•上海)若行列式中,元素4的代数余子式大于0,则x满足的条件是x>且x≠4.【考点】三阶矩阵.【专题】计算题.【分析】根据3阶行列式D的元素a ij的余子式M ij附以符号(﹣1)i+j后,叫做元素a ij的代数余子式,所以4的余子式加上(﹣1)1+1即为元素4的代数余子式,让其大于0列出关于x的不等式,求出不等式的解集即可得到x的范围.【解答】解:依题意得,(﹣1)2>0,即9x﹣24>0,解得x>,且x≠4,故答案为:x>且x≠4【点评】此题考查学生掌握三阶矩阵的代数余子式的定义,是一道基础题.4.(4分)(2009•上海)某算法的程序框如下图所示,则输出量y与输入量x满足的关系式是.【考点】程序框图.【分析】根据流程图所示的顺序,逐框分析程序中各变量、各语句的作用可知:该程序的作用是根据输入x值的不同,根据不同的式子计算函数值.即求分段函数的函数值.【解答】解:根据流程图所示的顺序,程序的作用是分段函数的函数值.其中输出量y与输入量x满足的关系式是故答案为:【点评】根据流程图(或伪代码)写程序的运行结果,是算法这一模块最重要的题型,其处理方法是::①分析流程图(或伪代码),从流程图(或伪代码)中既要分析出计算的类型,又要分析出参与计算的数据(如果参与运算的数据比较多,也可使用表格对数据进行分析管理)⇒②建立数学模型,根据第一步分析的结果,选择恰当的数学模型③解模.5.(4分)(2009•上海)如图,若正四棱柱ABCD﹣A1B1C1D1的底面边长为2,高为4,则异面直线BD1与AD所成角的大小是arctan(结果用反三角函数值表示).【考点】异面直线及其所成的角.【专题】计算题.【分析】先通过平移将两条异面直线平移到同一个起点,得到的锐角或直角就是异面直线所成的角,在直角三角形中求出正切值,再用反三角函数值表示出这个角即可.【解答】解:先画出图形将AD平移到BC,则∠D1BC为异面直线BD1与AD所成角,BC=2,D1C=,tan∠D1BC=,∴∠D1BC=arctan,故答案为arctan.【点评】本题主要考查了异面直线及其所成的角,以及解三角形的应用,属于基础题.6.(4分)(2009•上海)函数y=2cos2x+sin2x的最小值是.【考点】三角函数的最值.【专题】计算题.【分析】先利用三角函数的二倍角公式化简函数,再利用公式化简三角函数,利用三角函数的有界性求出最小值.【解答】解:y=2cos2x+sin2x=1+cos2x+sin2x=1+=1+当=2k,有最小值1﹣故答案为1﹣【点评】本题考查三角函数的二倍角余弦公式将三角函数降幂、利用公式化简三角函数.7.(4分)(2009•上海)某学校要从5名男生和2名女生中选出2人作为上海世博会志愿者,若用随机变量ξ表示选出的志愿者中女生的人数,则数学期望Eξ(结果用最简分数表示).【考点】离散型随机变量的期望与方差.【专题】计算题.【分析】用随机变量ξ表示选出的志愿者中女生的人数,ξ可取0,1,2,结合变量对应的事件写出分布列当ξ=0时,表示没有选到女生;当ξ=1时,表示选到一个女生;当ξ=2时,表示选到2个女生,求出期望.【解答】解:用随机变量ξ表示选出的志愿者中女生的人数,ξ可取0,1,2,当ξ=0时,表示没有选到女生;当ξ=1时,表示选到一个女生;当ξ=2时,表示选到2个女生,∴P(ξ=0)==,P(ξ=1)=,P(ξ=2)=,∴Eξ=0×=.故答案为:【点评】本题考查离散型随机变量的分布列和期望,这是近几年经常出现的一个问题,可以作为解答题出现,考查的内容通常是以分布列和期望为载体,有时要考查其他的知识点.8.(4分)(2009•上海)已知三个球的半径R1,R2,R3满足R1+2R2=3R3,则它们的表面积S1,S2,S3,满足的等量关系是.【考点】球的体积和表面积.【专题】计算题.【分析】表示出三个球的表面积,求出三个半径,利用R1+2R2=3R3,推出结果.【解答】解:因为S1=4πR12,所以,同理:,即R1=,R2=,R3=,由R1+2R2=3R3,得故答案为:【点评】本题考查球的表面积,考查计算能力,是基础题.9.(4分)(2009•上海)已知F1、F2是椭圆C:(a>b>0)的两个焦点,P为椭圆C上一点,且.若△PF1F2的面积为9,则b=3.【考点】椭圆的应用;椭圆的简单性质.【专题】圆锥曲线的定义、性质与方程.【分析】由已知得|PF1|+|PF2|=2a,=4c2,,由此能得到b的值.【解答】解:∵F1、F2是椭圆C:(a>b>0)的两个焦点,P为椭圆C上一点,且.∴|PF1|+|PF2|=2a,=4c2,,∴(|PF1|+|PF2|)2=4c2+2|PF1||PF2|=4a2,∴36=4(a2﹣c2)=4b2,∴b=3.故答案为3.【点评】主要考查椭圆的定义、基本性质和平面向量的知识.10.(4分)(2009•上海)在极坐标系中,由三条直线θ=0,,ρcosθ+ρsinθ=1围成图形的面积等于.【考点】简单曲线的极坐标方程;定积分.【专题】计算题.【分析】三条直线化为直角坐标方程,求出三角形的边长,然后求出图形的面积.【解答】解:三条直线θ=0,,ρcosθ+ρsinθ=1的直角坐标方程分别为:y=0,y=x,x+y=1,所以它们的交点坐标分别为O(0,0),A(1,0),B(,),OB==,由三条直线θ=0,,ρcosθ+ρsinθ=1围成图形的面积S==.故答案为:.【点评】本题考查极坐标与直角坐标的互化,三角形的面积的求法,考查计算能力.11.(4分)(2009•上海)当时,不等式sinπx≥kx恒成立.则实数k的取值范围是k≤2.【考点】函数恒成立问题.【专题】数形结合.【分析】要使不等式sinπx≥kx恒成立,设m=sinπx,n=kx,利用图象得到k的范围即可.【解答】解:设m=sinπx,n=kx,x∈[0,].根据题意画图得:m≥n恒成立即要m的图象要在n图象的上面,当x=时即πx=时相等,所以此时k==2,所以k≤2故答案为k≤2【点评】考查学生利用数形结合的数学思想解决问题的能力,理解函数恒成立时取条件的能力.12.(4分)(2009•上海)已知函数f(x)=sinx+tanx,项数为27的等差数列{a n}满足a n∈(﹣),且公差d≠0,若f(a1)+f(a2)+…f(a27)=0,则当k=14时,f(a k)=0.【考点】函数奇偶性的性质.【专题】计算题;压轴题.【分析】本题考查的知识点是函数的奇偶性及对称性,由函数f(x)=sin x+tan x,项数为27的等差数列{a n}满足a n∈(﹣),且公差d≠0,若f(a1)+f(a2)+…f(a27)=0,我们易得a1,a2,…,a27前后相应项关于原点对称,则f(a14)=0,易得k值.【解答】解:因为函数f(x)=sinx+tanx是奇函数,所以图象关于原点对称,图象过原点.而等差数列{a n}有27项,a n∈().若f(a1)+f(a2)+f(a3)+…+f(a27)=0,则必有f(a14)=0,所以k=14.故答案为:14【点评】代数的核心内容是函数,函数的定义域、值域、性质均为高考热点,所有要求同学们熟练掌握函数特别是基本函数的图象和性质,并能结合平移、对称、伸缩、对折变换的性质,推出基本函数变换得到的函数的性质.13.(4分)(2009•上海)某地街道呈现东﹣西、南﹣北向的网格状,相邻街距都为1.两街道相交的点称为格点.若以互相垂直的两条街道为轴建立直角坐标系,现有下述格点(﹣2,2),(3,1),(3,4),(﹣2,3),(4,5),(6,6)为报刊零售点.请确定一个格点(除零售点外)(3,3)为发行站,使6个零售点沿街道到发行站之间路程的和最短.【考点】两点间距离公式的应用.【专题】直线与圆.【分析】设发行站的位置为(x,y),则可利用两点间的距离公式表示出零售点到发行站的距离,进而求得在(3,3)处z取得最小值.【解答】解:设发行站的位置为(x,y),6个零售点到发行站的距离为Z,则z=|x+2|+|y﹣2|+|x﹣3|+|y﹣1|+|x﹣3|+|y﹣4|+|x+1|+|y﹣3|+|x﹣4|+|y﹣5|+|x﹣6|+|y﹣6|=|x+2|+|x﹣3|+|x﹣3|+|x+1|+|x﹣4|+|x﹣6|+|y﹣2|+|y﹣1|+|y﹣4|+|y﹣3|+|y﹣5|+|y﹣6|x=3,3≤y<4时,取最小值,∴在(3,3)处z取得最小值.故答案为(3,3).【点评】本题主要考查了两点间的距离公式的应用.考查了学生创造性思维能力和逻辑思维能力.14.(4分)(2009•上海)将函数(x∈[0,6])的图象绕坐标原点逆时针方向旋转角θ(0≤θ≤α),得到曲线C.若对于每一个旋转角θ,曲线C都是一个函数的图象,则α的最大值为arctan.【考点】旋转变换.【专题】计算题;压轴题.【分析】先画出函数(x∈[0,6])的图象,然后根据由图可知当此圆弧绕坐标原点逆时针方向旋转角大于∠MAB时,曲线C都不是一个函数的图象,求出此角即可.【解答】解:先画出函数(x∈[0,6])的图象这是一个圆弧,圆心为M(3,﹣2)由图可知当此圆弧绕坐标原点逆时针方向旋转角大于∠MAB时,曲线C都不是一个函数的图象∴∠MAB=arctan故答案为:arctan【点评】本题主要考查了旋转变换,同时考查了数形结合的思想和分析问题解决问题的能力,属于基础题.二、选择题(共4小题,每小题4分,满分16分)15.(4分)(2009•上海)“﹣2≤a≤2”是“实系数一元二次方程x2+ax+1=0有虚根”的()A.必要不充分条件B.充分不必要条件C.充要条件 D.既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断.【分析】实系数一元二次方程x2+ax+1=0有虚根⇒△=a2﹣4<0⇒﹣2<a<2,由此入手能够作出正确选择.【解答】解:∵实系数一元二次方程x2+ax+1=0有虚根,∴△=a2﹣4<0,解得﹣2<a<2,∴“﹣2≤a≤2”是“﹣2<a<2”的必要不充分条件,故选A.【点评】本题考查必要条件、充分条件和充要条件的应用,解题时要认真审题,仔细解答.16.(4分)(2009•上海)若事件E与F相互独立,且P(E)=P(F)=,则P(E∩F)的值等于()A.0 B.C.D.【考点】相互独立事件的概率乘法公式.【分析】本题考查的知识点是相互独立事件的概率乘法公式,由相互独立事件的概率计算公式,我们易得P(E∩F)=P(E)•P(F),将P(E)=P(F)=代入即可得到答案.【解答】解:P(E∩F)=P(E)•P(F)=×=.故选B.【点评】相互独立事件的概率计算公式:P(E∩F)=P(E)•P(F),P(E∪F)=P(E)+P(F).17.(4分)(2009•上海)有专业机构认为甲型N1H1流感在一段时间没有发生大规模群体感染的标志为“连续10天,每天新增疑似病例不超过15人”.根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是()A.甲地:总体均值为3,中位数为4B.乙地:总体均值为1,总体方差大于0C.丙地:中位数为2,众数为3D.丁地:总体均值为2,总体方差为3【考点】众数、中位数、平均数;极差、方差与标准差.【专题】压轴题.【分析】平均数和方差都是重要的数字特征,是对总体的一种简单的描述,平均数描述集中趋势,方差描述波动大小.【解答】解:假设连续10天,每天新增疑似病例的人数分别为x1,x2,x3,…x10.并设有一天超过15人,不妨设第一天为16人,根据计算方差公式有s2=[(16﹣5)2+(x2﹣5)2+(x3﹣5)2+…+(x10﹣5)2]>12,说明乙地连续10天,每天新增疑似病例的人数都不超过15人.故选:B.【点评】根据题意可知本题主要考查用数字特征估计总体,属于基础题.18.(4分)(2009•上海)过圆C:(x﹣1)2+(y﹣1)2=1的圆心,作直线分别交x、y正半轴于点A、B,△AOB被圆分成四部分(如图),若这四部分图形面积满足S|+S IV=S||+S|||则直线AB有()A.0条B.1条C.2条D.3条【考点】直线与圆的位置关系.【专题】综合题;压轴题;数形结合.【分析】由圆的方程得到圆心坐标和半径,根据四部分图形面积满足S|+S IV=S||+S|||,得到S IV﹣S II=SⅢ﹣S I,第II,IV部分的面积是定值,所以三角形FCB减去三角形ACE的面积为定值即SⅢ﹣S I为定值,所以得到满足此条件的直线有且仅有一条,得到正确答案.【解答】解:由已知,得:S IV﹣S II=SⅢ﹣S I,由图形可知第II,IV部分的面积分别为S正方形OECF﹣S扇形ECF=1﹣和S扇形ECF=,所以,S IV﹣S II为定值,即SⅢ﹣S I为定值,当直线AB绕着圆心C移动时,只可能有一个位置符合题意,即直线AB只有一条.故选B.【点评】此题考查学生掌握直线与圆的位置关系,会求三角形、正方形及扇形的面积,是一道综合题.三、解答题(共5小题,满分78分)19.(14分)(2009•上海)如图,在直三棱柱ABC﹣A1B1C1中,AA1=BC=AB=2,AB⊥BC,求二面角B1﹣A1C﹣C1的大小.【考点】向量在几何中的应用;与二面角有关的立体几何综合题.【专题】计算题;向量法.【分析】建立空间直角坐标系,求出2个平面的法向量的坐标,设二面角的大小为θ,显然θ为锐角,设2个法向量的夹角φ,利用2个向量的数量积可求cosφ,则由cosθ=|cosφ|求出二面角的大小θ.【解答】解:如图,建立空间直角坐标系.则A(2,0,0),C(0,2,0),A1(2,0,2),B1(0,0,2),C1(0,2,2),设AC的中点为M,∵BM⊥AC,BM⊥CC1.∴BM⊥平面A1C1C,即=(1,1,0)是平面A1C1C的一个法向量.设平面A1B1C的一个法向量是n=(x,y,z).=(﹣2,2,﹣2),=(﹣2,0,0),∴令z=1,解得x=0,y=1.∴n=(0,1,1),设法向量n与的夹角为φ,二面角B1﹣A1C﹣C1的大小为θ,显然θ为锐角.∵cosθ=|cosφ|==,解得:θ=.∴二面角B1﹣A1C﹣C1的大小为.【点评】本题考查利用向量求二面角的大小的方法,设二面角的大小为θ,2个平面法向量的夹角φ,则θ和φ相等或互补,这两个角的余弦值相等或相反.20.(16分)(2009•上海)有时可用函数f(x)=,描述学习某学科知识的掌握程度.其中x表示某学科知识的学习次数(x∈N*),f(x)表示对该学科知识的掌握程度,正实数a与学科知识有关.(1)证明:当x≥7时,掌握程度的增长量f(x+1)﹣f(x)总是下降;(2)根据经验,学科甲、乙、丙对应的a的取值区间分别为(115,121],(121,127],(127,133].当学习某学科知识6次时,掌握程度是85%,请确定相应的学科.【考点】分段函数的应用.【专题】应用题;探究型;数学模型法.【分析】(1)x≥7时,作差求出增长量f(x+1)﹣f(x),研究其单调性知,差是一个减函数,故掌握程度的增长量总是下降、(2)学习某学科知识6次时,掌握程度是85%,故得方程由此方程解出a的值即可确定相应的学科.【解答】证明:(1)当x≥7时,而当x≥7时,函数y=(x﹣3)(x﹣4)单调递增,且(x﹣3)(x﹣4)>0故函数f(x+1)﹣f(x)单调递减当x≥7时,掌握程度的增长量f(x+1)﹣f(x)总是下降(2)由题意可知整理得解得(13分)由此可知,该学科是乙学科..(14分)【点评】本题是分段函数在实际问题中的应用,在实际问题中,分段函数是一个很重要的函数模型.21.(16分)(2009•上海)已知双曲线,设直线l过点,(1)当直线l与双曲线C的一条渐近线m平行时,求直线l的方程及l与m的距离;(2)证明:当k>时,在双曲线C的右支上不存在点Q,使之到直线l的距离为.【考点】双曲线的简单性质.【专题】计算题;证明题.【分析】(1)先求出双曲线的渐近线方程,进而可得到直线l的斜率,然后根据直线l过点求出直线l的方程,再由平行线间的距离公式可求直线l的方程及l与m 的距离.(2)设过原点且平行于l的直线方程利用直线与直线的距离求得l与b的距离,当k>时,可推断出,利用双曲线的渐近线方程可知双曲线C的右支在直线b的右下方,进而推断出双曲线C的右支上的任意点到直线l的距离大于,进而可知故在双曲线C的右支上不存在点Q(x0,y0)到到直线l的距离为.【解答】解:(1)双曲线C的渐近线,即∴直线l的方程∴直线l与m的距离.(2)设过原点且平行于l的直线b:kx﹣y=0,则直线l与b的距离d=,当时,.又双曲线C的渐近线为,∴双曲线C的右支在直线b的右下方,∴双曲线C的右支上的任意点到直线l的距离大于.故在双曲线C的右支上不存在点Q(x0,y0)到到直线l的距离为.【点评】本题主要考查了双曲线的简单性质.考查了学生综合分析问题和解决问题的能力.22.(16分)(2009•上海)已知函数y=f(x)的反函数.定义:若对给定的实数a(a≠0),函数y=f(x+a)与y=f﹣1(x+a)互为反函数,则称y=f(x)满足“a和性质”;若函数y=f(ax)与y=f﹣1(ax)互为反函数,则称y=f(x)满足“a积性质”.(1)判断函数g(x)=x2+1(x>0)是否满足“1和性质”,并说明理由;(2)求所有满足“2和性质”的一次函数;(3)设函数y=f(x)(x>0)对任何a>0,满足“a积性质”.求y=f(x)的表达式.【考点】反函数;函数解析式的求解及常用方法.【专题】压轴题;新定义.【分析】(1)先求出g﹣1(x)的解析式,换元可得g﹣1(x+1)的解析式,将此解析式与g (x+1)的作对比,看是否满足互为反函数.(2)先求出f﹣1(x)的解析式,再求出f﹣1(x+2)的解析式,再由f(x+2)的解析式,求出f﹣1(x+2)的解析式,用两种方法得到的f﹣1(x+2)的解析式应该相同,解方程求得满足条件的一次函数f(x)的解析式.(3)设点(x0,y0)在y=f(ax)图象上,则(y0,x0)在函数y=f﹣1(ax)图象上,可得ay0=f (x0)=af(ax0),,即,即满足条件.【解答】解(1)函数g(x)=x2+1(x>0)的反函数是,∴,而g(x+1)=(x+1)2+1(x>﹣1),其反函数为,故函数g(x)=x2+1(x>0)不满足“1和性质”.(2)设函数f(x)=kx+b(x∈R)满足“2和性质”,k≠0.∴,∴,而f(x+2)=k(x+2)+b(x∈R),得反函数,由“2和性质”定义可知,对(x∈R)恒成立.∴k=﹣1,b∈R,即所求一次函数f(x)=﹣x+b(b∈R).(3)设a>0,x0>0,且点(x0,y0)在y=f(ax)图象上,则(y0,x0)在函数y=f﹣1(ax)图象上,故,可得ay0=f(x0)=af(ax0),令ax0=x,则,∴,即.综上所述,,此时,其反函数是,而,故y=f(ax)与y=f﹣1(ax)互为反函数.【点评】本题考查反函数的求法,函数与反函数的图象间的关系,体现了换元的思想,属于中档题.23.(16分)(2009•上海)已知{a n}是公差为d的等差数列,{b n}是公比为q的等比数列.(1)若a n=3n+1,是否存在m、k∈N*,有a m+a m+1=a k?说明理由;(2)找出所有数列{a n}和{b n},使对一切n∈N*,,并说明理由;(3)若a1=5,d=4,b1=q=3,试确定所有的p,使数列{a n}中存在某个连续p项的和是数列{b n}中的一项,请证明.【考点】等差数列与等比数列的综合;等差数列的性质;数列递推式.【专题】综合题;压轴题;分类讨论;转化思想.【分析】(1)由a m+a m+1=a k,得6m+5=3k+1,,由m、k∈N*,知k﹣2m为整数,所以不存在m、k∈N*,使等式成立.(2)设a n=nd+c,若,对n∈N×都成立,且{b n}为等比数列,则,对n∈N×都成立,由此入手能够导出有a n=c≠0,b n=1,使对一切n∈N×,.(3)a n=4n+1,b n=3n,n∈N*,设a m+1+a m+2++a m+p=b k=3k,p、k∈N*,m∈N.4m+2p+3+,由p、k∈N*,知p=3s,s∈N.由此入手能导出当且仅当p=3s,s∈N,命题成立.【解答】解:(1)由a m+a m+1=a k,得6m+5=3k+1,整理后,可得,∵m、k∈N*,∴k﹣2m为整数,∴不存在m、k∈N*,使等式成立.(2)设a n=nd+c,若,对n∈N×都成立,且{b n}为等比数列,则,对n∈N×都成立,即a n a n+2=qa n+12,∴(dn+c)(dn+2d+c)=q(dn+d+c)2,对n∈N×都成立,∴d2=qd2(i)若d=0,则a n=c≠0,∴b n=1,n∈N*.(ii)若d≠0,则q=1,∴b n=m(常数),即=m,则d=0,矛盾.综上所述,有a n=c≠0,b n=1,使对一切n∈N×,.(3)a n=4n+1,b n=3n,n∈N*,设a m+1+a m+2++a m+p=b k=3k,p、k∈N*,m∈N.,∴,∵p、k∈N*,∴p=3s,s∈N取k=3s+2,4m=32s+2﹣2×3s﹣3=(4﹣1)2s+2﹣2×(4﹣1)s﹣3≥0,由二项展开式可得整数M1、M2,使得(4﹣1)2s+2=4M1+1,2×(4﹣1)s=8M2+(﹣1)S2∴4m=4(M1﹣2M2)﹣((﹣1)S+1)2,∴存在整数m满足要求.故当且仅当p=3s,s∈N,命题成立.【点评】本题考查数列的性质和应用,解题时要认真审题,仔细解答,注意公式的灵活运用.。
上海高考数学理科卷带详解

2009年上海市高考数学试卷(理科)一、填空题(共14小题,每小题4分,满分56分)1.若复数z满足z(1+i)=1i(i是虚数单位),则其共轭复数=_________.【测量目标】复数的基本概念;复数代数形式的四则运算.【考查方式】化简复数等式,求解一个复数的共轭复数.【难易程度】中等【参考答案】i【试题解析】设z=a+b i,则(a+b i)(1+i) =1i,即a-b+(a+b)i=1-i,(步骤1)由,解得a=0,b=-1,所以z=-i,=i,故答案为i.(步骤2)2.已知集合A={x|x1},B={x|x a},且A B=R,则实数a的取值范围是_________.【测量目标】集合的基本运算.【考查方式】给出两个集合,已知集合间的关系,运用数轴法求解集合中未知参数的取值范围.【难易程度】容易【参考答案】a 1【试题解析】因为A B=R,画数轴可知,实数a必须在点1上或在1的左边,所以,有a 1.第2题图3.若行列式中,元素4的代数余子式大于0,则x满足的条件是_________.【测量目标】矩阵初步.【考查方式】根据代数余子式的概念,列出关于x的不等式求出取值范围.【难易程度】中等【参考答案】x>【试题解析】依题意,得:(1)2(9x24)>0,解得:,故答案为:x>. 4.某算法的程序框如下图所示,则输出量y与输入量x满足的关系式是_________.第4题图【测量目标】选择结构程序框图.【考查方式】给出程序框图,按照程序框图的执行流程分析循环过程,判断输入值与输出值之间的关系.【难易程度】容易【参考答案】【试题解析】根据流程图所示的顺序,程序的作用是分段函数的函数值.其中输出量y 与输入量x满足的关系式是,故答案为:.5.如图,若正四棱柱ABCD A 1B1C1D1的底面边长为2,高为4,则异面直线BD1与AD所成角的大小是_________.(结果用反三角函数值表示)第5题图【测量目标】异面直线所成的角.【考查方式】给出正四棱柱的边长及高,判断正四棱柱中两条异面直线所成角的值. 【难易程度】容易【参考答案】arctan【试题解析】先画出图形将AD平移到BC,则∠D1BC为异面直线BD1与AD所成角,(步骤1)BC =2,D1C=,tan∠D1BC=,∴∠D1BC=arctan,故答案为arctan.(步骤2)第5题图6.函数y=2cos2x+sin2x的最小值是_________.【测量目标】三角函数的最值.【考查方式】给出三角函数,通过化简求解函数的最小值.【难易程度】中等【参考答案】1【试题解析】=1+(步骤1)当=2k,,有最小值1,故答案为1.(步骤2)7.某学校要从5名男生和2名女生中选出2人作为上海世博会志愿者,若用随机变量ξ表示选出的志愿者中女生的人数,则数学期望Eξ_________(结果用最简分数表示).【测量目标】离散型随机变量的期望与方差【考查方式】给出数学实例,结合变量对应的事件写出分布列求出期望.【难易程度】容易【参考答案】【试题解析】用随机变量ξ表示选出的志愿者中女生的人数,ξ可取0,1,2,当ξ=0时,表示没有选到女生;当ξ=1时,表示选到一个女生;当ξ=2时,表示选到2个女生,(步骤1)∴P(ξ=0)=.P(ξ=1)=.P(ξ=2)=(步骤2)∴Eξ=0=.故答案为:.(步骤3)8.已知三个球的半径R1,R2,R3满足R1+2R2=3R3,则它们的表面积S1,S2,S3,满足的等量关系是_________.【测量目标】球的表面积.【考查方式】给出三个球的半径之间的关系,根据面积公式推出表面积之间的关系. 【难易程度】中等【参考答案】【试题解析】因为=4πR 12,所以,同理:,(步骤1)即R1=,R2=,R3=,由S1+S2=3R3得,故答案为:.(步骤2)9.已知F1、F2是椭圆C:(a>b>0)的两个焦点,P为椭圆C上一点,且.若△PF1F2的面积为9,则b=_________.【测量目标】椭圆的简单几何性质.【考查方式】给出椭圆上的一点与椭圆两交点之间的位置关系,及它们所形成的三角形面积求解椭圆方程中b的值.【难易程度】中等【参考答案】3【试题解析】依题意,有,可得即故有.10.在极坐标系中,由三条直线θ=0,,ρcosθ+ρsinθ=1围成图形的面积等于_________.【测量目标】坐标系与参数方程.【考查方式】给出直线的参数方程,转化为普通方程后求解直线与坐标轴所形成的三角形面积.【难易程度】容易【参考答案】【试题解析】化为普通方程,分别为:y=0,y=x,x+y=1,画出三条直线的图像如右图,(步骤1)可求得A(,),B(1,0),三角形AOB的面积为:=(步骤2)第10题图11.当时,不等式sinπx kx恒成立.则实数k的取值范围是_________.【测量目标】不等式恒成立问题.【考查方式】给出x在一定区间内,不等式恒成立的关系式,利用图像得到k的范围. 【难易程度】中等【参考答案】k 2【试题解析】设m=sinπx,n=kx,x∈[0,].根据题意画图得:m n恒成立即要m 的图像要在n图像的上面,当x=时即πx=时相等,所以此时k==2,所以k2,故答案为k 2.第11题图12.已知函数f(x)=sin x+tan x,项数为27的等差数列{a n}满足a n∈(,),且公差d≠0,若f(a 1)+f(a2)++f(a27)=0,则当k=________时,f(a k)=0.【测量目标】函数的奇偶性.【考查方式】利用奇函数的性质及等差数列的性质求解综合性问题.【难易程度】中等【参考答案】14【试题解析】因为函数f(x)=sin x+tan x是奇函数,所以图像关于原点对称,图像过原点.(步骤1)而等差数列{a n}有27项,a n∈(,).若f(a1)+f(a2)+f(a3)++f(a27)=0,则必有f(a14)=0,所以k=14.故答案为:14.(步骤2)13.某地街道呈现东西、南北向的网格状,相邻街距都为1.两街道相交的点称为格点.若以互相垂直的两条街道为轴建立直角坐标系,现有下述格点(2,2),(3,1),(3,4),(2,3),(4,5),(6,6)为报刊零售点.请确定一个格点(除零售点外)_________为发行站,使6个零售点沿街道到发行站之间路程的和最短.【测量目标】两点间距离公式的应用.【考查方式】利用两点间的距离公式判断实际问题中的最短路线问题.【难易程度】中等【参考答案】(3,3)【试题解析】设发行站的位置为(x,y),零售点到发行站的距离为z,则z=2|x+2|+|y2|+2|x3|+|y1|+|y4|+|y3|+|x4|+|y5|+|x6|+|y 6|,(步骤1)这六个点的横纵坐标的平均值为,,(步骤2)记A(2,),画图可知发行站的位置应该在点A附近,代入附近的点的坐标进行比较可知,在(3,3)处z取得最小值.故答案为(3,3).(步骤3)第13题图14.将函数(x∈[0,6])的图像绕坐标原点逆时针方向旋转角θ(0θα),得到曲线C.若对于每一个旋转角θ,曲线C都是一个函数的图像,则α的最大值为_________.【测量目标】函数图像的性质.【考查方式】给出曲线函数解析式,通过围绕原点旋转,判断旋转角与函数关系式之间的关系.【难易程度】中等【参考答案】【试题解析】先画出函数(x∈[0,6])的图像这是一个圆弧,圆心为M(3,2)由图可知当此圆弧绕坐标原点逆时针方向旋转角大于∠MAB时,曲线C都不是一个函数的图像∴∠MAB=故答案为:.第14题图二、选择题(共4小题,每小题4分,满分16分)15.“2a2”是“实系数一元二次方程x2+ax+1=0有虚根”的()A.必要不充分条件B.充分不必要条件C.充要条件D.既不充分也不必要条件【测量目标】充分、必要条件.【考查方式】给出两个命题判断它们之间的关系.【难易程度】容易【参考答案】A【试题解析】∵实系数一元二次方程x2+ax+1=0有虚根,∴=a24<0,解得2<a <2,(步骤1)∴“2a2”是“2<a<2”的必要不充分条件,(步骤2)故选A.16.若事件E与F相互独立,且P(E)=P(F)=,则P(E F)的值等于()A.0 B.C.D.【测量目标】相互独立事件的概率乘法公式【考查方式】给出相互独立事件的概率,由相互独立事件的概率计算公式P(E F)=P(E)•P(F),求解.【难易程度】容易【参考答案】B【试题解析】==.故选B.17.有专业机构认为甲型H1 N1流感在一段时间没有发生大规模群体感染的标志为“连续10天,每天新增疑似病例不超过15人”.根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是()A.甲地:总体均值为6,中位数为8 B.乙地:总体均值为5,总体方差为12 C.丙地:中位数为5,众数为6 D.丁地:总体均值为3,总体方差大于0【测量目标】用样本数字特征估计总体数字特征.【考查方式】运用均值、中位数、众数、方差的数值特征对整体数字特征进行估计.【难易程度】容易【参考答案】B【试题解析】假设连续10天,每天新增疑似病例的人数分别为x1,x2,x3,…,x10.并设有一天超过15人,不妨设第一天为16人,根据计算方差公式有s2=[(165)2+(x 25)2+(x35)2++(x105)2]>12,说明乙地连续10天,每天新增疑似病例的人数都不超过15人.故选B.18.过圆C:(x1)2+(y1)2=1的圆心,作直线分别交x、y正半轴于点A、B,△AOB被圆分成四部分(如图),若这四部分图形面积满足S I+S IV= S II+SⅢ则直线AB有()A.0条B.1条C.2条D.3条第18题图【测量目标】直线与圆的位置关系.【考查方式】给出已知圆方程,讨论过圆心把圆分割的面积成等量关系的直线的条数. 【难易程度】中等【参考答案】B【试题解析】由已知,得:S IV S II=S ⅢS I,由图形可知第II,IV部分的面积分别为S正方S扇形ECF=1和S扇形ECF=,所以,S IV S II为定值,即SⅢS I为定值,(步骤1)形OECF当直线AB绕着圆心C移动时,只可能有一个位置符合题意,即直线AB只有一条.(步骤2)故选B.三、解答题(共5小题,满分78分)19.如图,在直三棱柱ABC A 1B1C1中,AA1=BC=AB=2,AB⊥BC,求二面角的大小.第19题图【测量目标】向量在几何中的应用;二面角.【考查方式】给出直三棱柱棱长的长度及其之间的关系,求解直三棱柱中二面角的大小.【难易程度】中等【试题解析】如图,建立空间直角坐标系.则A(2,0,0),C(0,2,0),A1(2,0,2),B1(0,0,2),C1(0,2,2),(步骤1)设AC的中点为M,∵BM⊥AC,BM ⊥CC1.∴BM⊥平面A1C1C,即=(1,1,0)是平面A1C1C的一个法向量.(步骤2)设平面A 1B1C的一个法向量是=(x,y,z).=(2,2,2),=(2,0,0),(步骤3)令z=1,解得x=0,y=1.∴=(0,1,1),(步骤4)设法向量与的夹角为φ,二面角B1A1C C1的大小为θ,显然θ为锐角.∵cosθ=|cosφ|=,解得:θ=.∴二面角B1A1C C1的大小为.(步骤5)第19题图20.有时可用函数f(x)=,描述学习某学科知识的掌握程度.其中x表示某学科知识的学习次数(x∈N*),f(x)表示对该学科知识的掌握程度,正实数a与学科知识有关.(1)证明:当x7时,掌握程度的增长量f(x+1)f(x)总是下降;(2)根据经验,学科甲、乙、丙对应的a的取值区间分别为(115,121],(121,127],(127,133].当学习某学科知识6次时,掌握程度是85%,请确定相应的学科.【测量目标】分段函数【考查方式】求解分段函数在实际问题中的应用问题.【难易程度】容易【试题解析】证明:(1)当x7时,(步骤1)而当x7时,函数y=(x3)(x4)单调递增,且(x3)(x4)>0故函数f(x+1)f(x)单调递减,当x7时,掌握程度的增长量f(x+1)f(x)总是下降(步骤2)(2)由题意可知0.1+15ln=0.85(步骤3)整理得解得,由此可知,该学科是乙学科.(步骤4)21.已知双曲线,设直线l过点.(1)当直线l与双曲线C的一条渐近线m平行时,求直线l的方程及l与m的距离;(2)证明:当k>时,在双曲线C的右支上不存在点Q,使之到直线l的距离为.【测量目标】双曲线的简单几何性质,直线与双曲线的位置关系.【考查方式】给出双曲线方程及直线l与双曲线的位置关系,求解直线方程及直线与双曲线渐近线的距离,探讨双曲线上是否存在一点使得在直线斜率一定的情况下,点到直线的距离为一定值.【难易程度】中等【试题解析】(1)双曲线C的渐近线,即∴直线l的方程(步骤1)∴直线l与m的距离.(步骤2)(2)设过原点且平行于l的直线b:kx y=0,则直线l与b的距离,(步骤3)当.又双曲线C的渐近线为,(步骤4)∴双曲线C的右支在直线b的右下方,∴双曲线C的右支上的任意点到直线l的距离大于.故在双曲线C的右支上不存在点Q(x0,y0)到到直线l的距离为.(步骤5)22.已知函数y=f(x)的反函数.定义:若对给定的实数a(a≠0),函数y=f(x+a)与互为反函数,则称y=f(x)满足“a和性质”;若函数y=f(ax)与互为反函数,则称y=f(x)满足“a积性质”.(1)判断函数g(x)=x2+1(x>0)是否满足“1和性质”,并说明理由;(2)求所有满足“2和性质”的一次函数;(3)设函数y=f(x)(x>0)对任何a>0,满足“a积性质”.求y=f(x)的表达式.【测量目标】反函数.【考查方式】给出一种关于函数的新定义,讨论新定义的具体应用.【难易程度】较难【试题解析】(1)函数g(x)=x 2+1(x>0)的反函数是,,(步骤1)而g(x+1)=(x+1)2+1(x>1),其反函数为,故函数g(x)=x2+1(x>0)不满足“1和性质”.(步骤2)(2)设函数f(x)=kx+b(x∈R)满足“2和性质”,k≠0.,(步骤3)而f(x+2)=k(x+2)+b(x∈R),得反函数,(步骤4)由“2和性质”定义可知=,对(x∈R)恒成立.∴k=1,b∈R,即所求一次函数f(x)=x+b(b∈R).(步骤5)(3)设a>0,x 0>0,且点(x0,y0)在y=f(ax)图像上,则(y0,x0)在函数图像上,故,可得ay0=f(x0)=af(ax0),(步骤6)令ax0=x,则,∴,即.(步骤7)综上所述,,此时,其反函数是,而,故y=f(ax)与互为反函数.(步骤8)23.已知{a n}是公差为d的等差数列,{b n}是公比为q的等比数列.(1)若a n=3n+1,是否存在m、k∈N*,有a m+a m+1=a k?说明理由;(2)找出所有数列{a n}和{b n},使对一切n∈,,并说明理由;(3)若a1=5,d=4,b1=q=3,试确定所有的p,使数列{a n}中存在某个连续p项的和是数列{b n}中的一项,请证明.【测量目标】等差数列与等比数列的综合应用;等差数列的性质.【考查方式】利用等差、等比数列的性质,求解数列各项之间的关系的综合性问题. 【难易程度】较难【试题解析】(1)由a m+a m+1=a k,得6m+5=3k+1,(步骤1)整理后,可得,∵m、k∈,∴k2m为整数,∴不存在m、k∈,使等式成立.(步骤2)(2)设a n=nd+c,若,对n∈都成立,且{b n}为等比数列,则,对n∈都成立,(步骤3)即a n a n+2=qa n+12,∴(dn+c)(dn+2d+c)=q(dn+d+c)2,对n∈都成立,∴d2=qd2(步骤4)(i)若d=0,则a n=c≠0,∴b n=1,n∈.(ii)若d≠0,则q=1,∴b n=m(常数),即,则d=0,矛盾.综上所述,有a n=c≠0,b n=1,使对一切n∈,.(步骤5)(3)a n=4n+1,b n=3n,n∈,设a m+1+a m+2++a m+p=b k=3k,p、k∈,m∈.∴,(步骤6)∴,∵p、k∈,∴p=3s,s∈(步骤7)取k=3s+2,4m=32s+22×3s3=,由二项展开式可得整数M 1、M2,(步骤8)使得(41)2s+2=4M 1+1,=8M2+,∴4m=4(M12M2)(+1)2,∴存在整数m满足要求.故当且仅当p=3s,s∈,命题成立.(步骤9)。
2009年全国高考上海市数学试题(理数)

1、本期向xyz公司采购A材料,买价14000元,B材料买价30000元,税共计7480元,上述款项由银行存款支付,材料均未验收入库借:在途物资——A材料14000 B材料30000应交税金——应交增值税(进项税额)7480贷:银行存款514802、上述本期采购的A、B材料验收入库,计算并结转其实际采购成本借:原材料——A材料14000 B材料30000贷:在途物资——A材料14000 B材料300003、仓库发生A原材料19170元,B原材料13060元,其中生产甲商品直接生产取用两原材料共计15460元,乙商品共用两原材料15240元,车间制造甲商品和乙商品,共同耗用原材料共计790元,企业行政管理部门领用740元借:生产成本——甲商品---材料15460 乙商品----材料15240制造费用——材料790管理费用——材料740贷:原材料——A材料19170 B材料130604、用银行存款90000元支付股利借:应付股利90000 贷:银行存款900005、分配本期职工工资68000,共计制造甲商品生产工人工资27000元,制造乙商品工人工资19000元,车间管理人员工资9000元,企业管理人员工资13000元借:生产成本——甲商品----工资27000 乙商品-----工资19000制造费用——工资9000管理费用——工资13000贷:应付职工工资680006、按职工工资总额的14%提取本期职工福利费(10题工资明细)借:生产成本——甲商品--- 福利费3780 (27000*14%)乙商品-----福利费2660 (19000*14%)制造费用——福利费1260 (9000*14%)管理费用——福利费1820 (13000*14%)贷:应付职工福利费9520 (68000*14%)7、向**公司销售乙商品,货款30900元,增值税5253元,货款已收到并存入银行借:银行存款——农行36153贷:主营业务收入——乙商品30900应交税费——增值税销项 52538、职工出差回来,用经审核的900元发票,报销差旅费(原供1000元)并退回现金100元借:库存现金100 管理费用——差旅费900贷:其它应收款10009、期未盘盈存货(A原材料)32000元,原因尚未表明借:原材料——A材料32000 贷:待处理财产损益3200010、计提本期固定资折旧25500元,其中生产车间固定资折旧15500元,企业管理部门固定资折旧10000元借:制造费用——折旧15500管理费用——折旧10000贷:累计折旧2550011、期未结转本期销售甲乙商品成分别为27000元,和213700元借:主营业务成本——甲商品27000 乙商品213700贷:库存商品——甲商品27000 乙商品21370012、结转销售的多余生产用A材料成本9100元借:其它业务成本9100 贷:原材料——A材料910013、按受对方以一项专利权(确认入账价值100000元)的股权投资,双方协商作为80000的注删资本投入借:实收资本80000 资本公积20000 贷:无形资产10000014、购置一条需要安装的新生产线价值250000元,以银行支票支付借:在建工程250000 贷:银行存款25000015、本期购置的需要安装新生产线安装完毕完工交付使用(总介值262000元)借:固定资产262000 贷:在建工程26200016、以银行存款缴纳已计提的应付所得税10000元借:应交税费——应交所得税10000 贷:银行存款1000017、以银行存款上缴已计提的尚未支付的城市维护建设税15000元,教育费附加500元。
2009年全国统一高考数学试卷(理科)(全国卷ⅰ)(含解析版)(附详细答案)

2009年全国统一高考数学试卷(理科)(全国卷Ⅰ)一、选择题(共12小题,每小题5分,满分60分)1.(5分)已知=2+i,则复数z=()A.﹣1+3i B.1﹣3i C.3+i D.3﹣i2.(5分)设集合A={4,5,7,9},B={3,4,7,8,9},全集U=A∪B,则集合?U(A∩B)中的元素共有()A.3个B.4个C.5个D.6个3.(5分)不等式<1的解集为()A.{x|0<x<1}∪{x|x>1}B.{x|0<x<1}C.{x|﹣1<x<0}D.{x|x<0}4.(5分)已知双曲线﹣=1(a>0,b>0)的渐近线与抛物线y=x2+1相切,则该双曲线的离心率为()A.B.2C.D.5.(5分)甲组有5名男同学,3名女同学;乙组有6名男同学、2名女同学.若从甲、乙两组中各选出2名同学,则选出的4人中恰有1名女同学的不同选法共有()A.150种B.180种C.300种D.345种6.(5分)设、、是单位向量,且,则?的最小值为()A.﹣2B.﹣2C.﹣1D.1﹣7.(5分)已知三棱柱ABC﹣A1B1C1的侧棱与底面边长都相等,A1在底面ABC上的射影D为BC的中点,则异面直线AB与CC1所成的角的余弦值为()A.B.C.D.8.(5分)如果函数y=3cos(2x+φ)的图象关于点(,0)中心对称,那么|φ|的最小值为()A.B.C.D.9.(5分)已知直线y=x+1与曲线y=ln(x+a)相切,则a的值为()A.1B.2C.﹣1D.﹣210.(5分)已知二面角α﹣l﹣β为60°,动点P、Q分别在面α、β内,P到β的距离为,Q到α的距离为,则P、Q两点之间距离的最小值为()A.1B.2C.D.411.(5分)函数f(x)的定义域为R,若f(x+1)与f(x﹣1)都是奇函数,则()A.f(x)是偶函数B.f(x)是奇函数C.f(x)=f(x+2)D.f(x+3)是奇函数12.(5分)已知椭圆C:+y2=1的右焦点为F,右准线为l,点A∈l,线段AF 交C于点B,若=3,则||=()A.B.2C.D.3二、填空题(共4小题,每小题5分,满分20分)13.(5分)(x﹣y)10的展开式中,x7y3的系数与x3y7的系数之和等于.14.(5分)设等差数列{a n}的前n项和为S n,若S9=81,则a2+a5+a8= .15.(5分)直三棱柱ABC﹣A1B1C1的各顶点都在同一球面上,若AB=AC=AA1=2,∠BAC=120°,则此球的表面积等于.16.(5分)若,则函数y=tan2xtan3x的最大值为.三、解答题(共6小题,满分70分)17.(10分)在△ABC中,内角A、B、C的对边长分别为a、b、c,已知a2﹣c2=2b,且sinAcosC=3cosAsinC,求b.18.(12分)如图,四棱锥S﹣ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD=,DC=SD=2,点M在侧棱SC上,∠ABM=60°(I)证明:M是侧棱SC的中点;(Ⅱ)求二面角S﹣AM﹣B的大小.19.(12分)甲、乙二人进行一次围棋比赛,约定先胜3局者获得这次比赛的胜利,比赛结束,假设在一局中,甲获胜的概率为0.6,乙获胜的概率为0.4,各局比赛结果相互独立,已知前2局中,甲、乙各胜1局.(I)求甲获得这次比赛胜利的概率;(Ⅱ)设ξ表示从第3局开始到比赛结束所进行的局数,求ξ的分布列及数学期望.20.(12分)在数列{a n}中,a1=1,a n+1=(1+)a n+.(1)设b n=,求数列{b n}的通项公式;(2)求数列{a n}的前n项和S n.21.(12分)如图,已知抛物线E:y2=x与圆M:(x﹣4)2+y2=r2(r>0)相交于A、B、C、D四个点.(Ⅰ)求r的取值范围;(Ⅱ)当四边形ABCD的面积最大时,求对角线AC、BD的交点P的坐标.22.(12分)设函数f(x)=x3+3bx2+3cx有两个极值点x1、x2,且x1∈[﹣1,0],x2∈[1,2].(1)求b、c满足的约束条件,并在下面的坐标平面内,画出满足这些条件的点(b,c)的区域;(2)证明:.2009年全国统一高考数学试卷(理科)(全国卷Ⅰ)参考答案与试题解析一、选择题(共12小题,每小题5分,满分60分)1.(5分)已知=2+i,则复数z=()A.﹣1+3i B.1﹣3i C.3+i D.3﹣i【考点】A1:虚数单位i、复数.【分析】化简复数直接求解,利用共轭复数可求z.【解答】解:,∴z=1﹣3i故选:B.【点评】求复数,需要对复数化简,本题也可以用待定系数方法求解.2.(5分)设集合A={4,5,7,9},B={3,4,7,8,9},全集U=A∪B,则集合?U(A∩B)中的元素共有()A.3个B.4个C.5个D.6个【考点】1H:交、并、补集的混合运算.【分析】根据交集含义取A、B的公共元素写出A∩B,再根据补集的含义求解.【解答】解:A∪B={3,4,5,7,8,9},A∩B={4,7,9}∴?U(A∩B)={3,5,8}故选A.也可用摩根律:?U(A∩B)=(?U A)∪(?U B)故选:A.【点评】本题考查集合的基本运算,较简单.3.(5分)不等式<1的解集为()A.{x|0<x<1}∪{x|x>1}B.{x|0<x<1}C.{x|﹣1<x<0}D.{x|x<0}【考点】7E:其他不等式的解法.【分析】本题为绝对值不等式,去绝对值是关键,可利用绝对值意义去绝对值,也可两边平方去绝对值.【解答】解:∵<1,∴|x+1|<|x﹣1|,∴x2+2x+1<x2﹣2x+1.∴x<0.∴不等式的解集为{x|x<0}.故选:D.【点评】本题主要考查解绝对值不等式,属基本题.解绝对值不等式的关键是去绝对值,去绝对值的方法主要有:利用绝对值的意义、讨论和平方.4.(5分)已知双曲线﹣=1(a>0,b>0)的渐近线与抛物线y=x2+1相切,则该双曲线的离心率为()A.B.2C.D.【考点】KC:双曲线的性质;KH:直线与圆锥曲线的综合.【专题】11:计算题.【分析】先求出渐近线方程,代入抛物线方程,根据判别式等于0,找到a和b 的关系,从而推断出a和c的关系,答案可得.【解答】解:由题双曲线的一条渐近线方程为,代入抛物线方程整理得ax2﹣bx+a=0,因渐近线与抛物线相切,所以b2﹣4a2=0,即,故选:C.【点评】本小题考查双曲线的渐近线方程直线与圆锥曲线的位置关系、双曲线的离心率,基础题.5.(5分)甲组有5名男同学,3名女同学;乙组有6名男同学、2名女同学.若从甲、乙两组中各选出2名同学,则选出的4人中恰有1名女同学的不同选法共有()A.150种B.180种C.300种D.345种【考点】D1:分类加法计数原理;D2:分步乘法计数原理.【专题】5O:排列组合.【分析】选出的4人中恰有1名女同学的不同选法,1名女同学来自甲组和乙组两类型.【解答】解:分两类(1)甲组中选出一名女生有C51?C31?C62=225种选法;(2)乙组中选出一名女生有C52?C61?C21=120种选法.故共有345种选法.故选:D.【点评】分类加法计数原理和分类乘法计数原理,最关键做到不重不漏,先分类,后分步!6.(5分)设、、是单位向量,且,则?的最小值为()A.﹣2B.﹣2C.﹣1D.1﹣【考点】9O:平面向量数量积的性质及其运算.【专题】16:压轴题.【分析】由题意可得=,故要求的式子即﹣()?+=1﹣cos=1﹣cos,再由余弦函数的值域求出它的最小值.【解答】解:∵、、是单位向量,,∴,=.∴?=﹣()?+=0﹣()?+1=1﹣cos=1﹣cos≥.故选:D.【点评】考查向量的运算法则;交换律、分配律但注意不满足结合律.7.(5分)已知三棱柱ABC﹣A1B1C1的侧棱与底面边长都相等,A1在底面ABC上的射影D为BC的中点,则异面直线AB与CC1所成的角的余弦值为()A.B.C.D.【考点】LO:空间中直线与直线之间的位置关系.【分析】首先找到异面直线AB与CC1所成的角(如∠A1AB);而欲求其余弦值可考虑余弦定理,则只要表示出A1B的长度即可;不妨设三棱柱ABC﹣A1B1C1的侧棱与底面边长为1,利用勾股定理即可求之.【解答】解:设BC的中点为D,连接A1D、AD、A1B,易知θ=∠A1AB即为异面直线AB与CC1所成的角;并设三棱柱ABC﹣A1B1C1的侧棱与底面边长为1,则|AD|=,|A1D|=,|A1B|=,由余弦定理,得cosθ==.故选:D.【点评】本题主要考查异面直线的夹角与余弦定理.8.(5分)如果函数y=3cos(2x+φ)的图象关于点(,0)中心对称,那么|φ|的最小值为()A.B.C.D.【考点】HB:余弦函数的对称性.【专题】11:计算题.【分析】先根据函数y=3cos(2x+φ)的图象关于点中心对称,令x=代入函数使其等于0,求出φ的值,进而可得|φ|的最小值.【解答】解:∵函数y=3cos(2x+φ)的图象关于点中心对称.∴∴由此易得.故选:A.【点评】本题主要考查余弦函数的对称性.属基础题.9.(5分)已知直线y=x+1与曲线y=ln(x+a)相切,则a的值为()A.1B.2C.﹣1D.﹣2【考点】6H:利用导数研究曲线上某点切线方程.【分析】切点在切线上也在曲线上得到切点坐标满足两方程;又曲线切点处的导数值是切线斜率得第三个方程.【解答】解:设切点P(x0,y0),则y0=x0+1,y0=ln(x0+a),又∵∴x0+a=1∴y0=0,x0=﹣1∴a=2.故选:B.【点评】本题考查导数的几何意义,常利用它求曲线的切线10.(5分)已知二面角α﹣l﹣β为60°,动点P、Q分别在面α、β内,P到β的距离为,Q到α的距离为,则P、Q两点之间距离的最小值为()A.1B.2C.D.4【考点】LQ:平面与平面之间的位置关系.【专题】11:计算题;16:压轴题.【分析】分别作QA⊥α于A,AC⊥l于C,PB⊥β于B,PD⊥l于D,连CQ,BD 则∠ACQ=∠PBD=60°,在三角形APQ中将PQ表示出来,再研究其最值即可.【解答】解:如图分别作QA⊥α于A,AC⊥l于C,PB⊥β于B,PD⊥l于D,连CQ,BD则∠ACQ=∠PDB=60°,,又∵当且仅当AP=0,即点A与点P重合时取最小值.故选:C.【点评】本题主要考查了平面与平面之间的位置关系,以及空间中直线与平面之间的位置关系,考查空间想象能力、运算能力和推理论证能力,属于基础题.11.(5分)函数f(x)的定义域为R,若f(x+1)与f(x﹣1)都是奇函数,则()A.f(x)是偶函数B.f(x)是奇函数C.f(x)=f(x+2)D.f(x+3)是奇函数【考点】3I:奇函数、偶函数.【专题】16:压轴题.【分析】首先由奇函数性质求f(x)的周期,然后利用此周期推导选择项.【解答】解:∵f(x+1)与f(x﹣1)都是奇函数,∴函数f(x)关于点(1,0)及点(﹣1,0)对称,∴f(x)+f(2﹣x)=0,f(x)+f(﹣2﹣x)=0,故有f(2﹣x)=f(﹣2﹣x),函数f(x)是周期T=[2﹣(﹣2)]=4的周期函数.∴f(﹣x﹣1+4)=﹣f(x﹣1+4),f(﹣x+3)=﹣f(x+3),f(x+3)是奇函数.故选:D.【点评】本题主要考查奇函数性质的灵活运用,并考查函数周期的求法.12.(5分)已知椭圆C:+y2=1的右焦点为F,右准线为l,点A∈l,线段AF 交C于点B,若=3,则||=()A.B.2C.D.3【考点】K4:椭圆的性质.【专题】11:计算题;16:压轴题.【分析】过点B作BM⊥x轴于M,设右准线l与x轴的交点为N,根据椭圆的性质可知FN=1,进而根据,求出BM,AN,进而可得|AF|.【解答】解:过点B作BM⊥x轴于M,并设右准线l与x轴的交点为N,易知FN=1.由题意,故FM=,故B点的横坐标为,纵坐标为±即BM=,故AN=1,∴.故选:A.【点评】本小题考查椭圆的准线、向量的运用、椭圆的定义,属基础题.二、填空题(共4小题,每小题5分,满分20分)13.(5分)(x﹣y)10的展开式中,x7y3的系数与x3y7的系数之和等于﹣240 .【考点】DA:二项式定理.【专题】11:计算题.【分析】首先要了解二项式定理:(a+b)n=C n0a n b0+C n1a n﹣1b1+C n2a n﹣2b2++C n r a n﹣r b r++Cn n a0b n,各项的通项公式为:Tr+1=C nr a n﹣r b r.然后根据题目已知求解即可.【解答】解:因为(x﹣y)10的展开式中含x7y3的项为C103x10﹣3y3(﹣1)3=﹣C103x7y3,含x3y7的项为C107x10﹣7y7(﹣1)7=﹣C107x3y7.由C103=C107=120知,x7y3与x3y7的系数之和为﹣240.故答案为﹣240.【点评】此题主要考查二项式定理的应用问题,对于公式:(a+b)n=C n0a n b0+C n1a n﹣1b1+C n2a n﹣2b2++C n r a n﹣r b r++C n n a0b n,属于重点考点,同学们需要理解记忆.14.(5分)设等差数列{a n}的前n项和为S n,若S9=81,则a2+a5+a8= 27 .【考点】83:等差数列的性质;85:等差数列的前n项和.【分析】由s9解得a5即可.【解答】解:∵∴a5=9∴a2+a5+a8=3a5=27故答案是27【点评】本题考查前n项和公式和等差数列的性质.15.(5分)直三棱柱ABC﹣A1B1C1的各顶点都在同一球面上,若AB=AC=AA1=2,∠BAC=120°,则此球的表面积等于20π.【考点】LR:球内接多面体.【专题】11:计算题;16:压轴题.【分析】通过正弦定理求出底面外接圆的半径,设此圆圆心为O',球心为O,在RT△OBO'中,求出球的半径,然后求出球的表面积.【解答】解:在△ABC中AB=AC=2,∠BAC=120°,可得由正弦定理,可得△ABC外接圆半径r=2,设此圆圆心为O',球心为O,在RT△OBO'中,易得球半径,故此球的表面积为4πR2=20π故答案为:20π【点评】本题是基础题,解题思路是:先求底面外接圆的半径,转化为直角三角形,求出球的半径,这是三棱柱外接球的常用方法;本题考查空间想象能力,计算能力.16.(5分)若,则函数y=tan2xtan3x的最大值为﹣8 .【考点】3H:函数的最值及其几何意义;GS:二倍角的三角函数.【专题】11:计算题;16:压轴题.【分析】见到二倍角2x 就想到用二倍角公式,之后转化成关于tanx的函数,将tanx看破成整体,最后转化成函数的最值问题解决.【解答】解:令tanx=t,∵,∴故填:﹣8.【点评】本题主要考查二倍角的正切,二次函数的方法求最大值等,最值问题是中学数学的重要内容之一,它分布在各块知识点,各个知识水平层面.以最值为载体,可以考查中学数学的所有知识点.三、解答题(共6小题,满分70分)17.(10分)在△ABC中,内角A、B、C的对边长分别为a、b、c,已知a2﹣c2=2b,且sinAcosC=3cosAsinC,求b.【考点】HR:余弦定理.【分析】根据正弦定理和余弦定理将sinAcosC=3cosAsinC化成边的关系,再根据a2﹣c2=2b即可得到答案.【解答】解:法一:在△ABC中∵sinAcosC=3cosAsinC,则由正弦定理及余弦定理有:,化简并整理得:2(a2﹣c2)=b2.又由已知a2﹣c2=2b∴4b=b2.解得b=4或b=0(舍);法二:由余弦定理得:a2﹣c2=b2﹣2bccosA.又a2﹣c2=2b,b≠0.所以b=2ccosA+2①又sinAcosC=3cosAsinC,∴sinAcosC+cosAsinC=4cosAsinCsin(A+C)=4cosAsinC,即sinB=4cosAsinC由正弦定理得,故b=4ccosA②由①,②解得b=4.【点评】本题主要考查正弦定理和余弦定理的应用.属基础题.18.(12分)如图,四棱锥S﹣ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD=,DC=SD=2,点M在侧棱SC上,∠ABM=60°(I)证明:M是侧棱SC的中点;(Ⅱ)求二面角S﹣AM﹣B的大小.【考点】LO:空间中直线与直线之间的位置关系;MJ:二面角的平面角及求法.【专题】11:计算题;14:证明题.【分析】(Ⅰ)法一:要证明M是侧棱SC的中点,作MN∥SD交CD于N,作NE⊥AB交AB于E,连ME、NB,则MN⊥面ABCD,ME⊥AB,设MN=x,则NC=EB=x,解RT△MNE即可得x的值,进而得到M为侧棱SC的中点;法二:分别以DA、DC、DS为x、y、z轴如图建立空间直角坐标系D﹣xyz,并求出S点的坐标、C点的坐标和M点的坐标,然后根据中点公式进行判断;法三:分别以DA、DC、DS为x、y、z轴如图建立空间直角坐标系D﹣xyz,构造空间向量,然后数乘向量的方法来证明.(Ⅱ)我们可以以D为坐标原点,分别以DA、DC、DS为x、y、z轴如图建立空间直角坐标系D﹣xyz,我们可以利用向量法求二面角S﹣AM﹣B的大小.【解答】证明:(Ⅰ)作MN∥SD交CD于N,作NE⊥AB交AB于E,连ME、NB,则MN⊥面ABCD,ME⊥AB,设MN=x,则NC=EB=x,在RT△MEB中,∵∠MBE=60°∴.在RT△MNE中由ME2=NE2+MN2∴3x2=x2+2解得x=1,从而∴M为侧棱SC的中点M.(Ⅰ)证法二:分别以DA、DC、DS为x、y、z轴如图建立空间直角坐标系D﹣xyz,则.设M(0,a,b)(a>0,b>0),则,,由题得,即解之个方程组得a=1,b=1即M(0,1,1)所以M是侧棱SC的中点.(I)证法三:设,则又故,即,解得λ=1,所以M是侧棱SC的中点.(Ⅱ)由(Ⅰ)得,又,,设分别是平面SAM、MAB的法向量,则且,即且分别令得z1=1,y1=1,y2=0,z2=2,即,∴二面角S﹣AM﹣B的大小.【点评】空间两条直线夹角的余弦值等于他们方向向量夹角余弦值的绝对值;空间直线与平面夹角的余弦值等于直线的方向向量与平面的法向量夹角的正弦值;空间锐二面角的余弦值等于他的两个半平面方向向量夹角余弦值的绝对值;19.(12分)甲、乙二人进行一次围棋比赛,约定先胜3局者获得这次比赛的胜利,比赛结束,假设在一局中,甲获胜的概率为0.6,乙获胜的概率为0.4,各局比赛结果相互独立,已知前2局中,甲、乙各胜1局.(I)求甲获得这次比赛胜利的概率;(Ⅱ)设ξ表示从第3局开始到比赛结束所进行的局数,求ξ的分布列及数学期望.【考点】C8:相互独立事件和相互独立事件的概率乘法公式;CG:离散型随机变量及其分布列;CH:离散型随机变量的期望与方差.【专题】11:计算题.【分析】(1)由题意知前2局中,甲、乙各胜1局,甲要获得这次比赛的胜利需在后面的比赛中先胜两局,根据各局比赛结果相互独立,根据相互独立事件的概率公式得到结果.(2)由题意知ξ表示从第3局开始到比赛结束所进行的局数,由上一问可知ξ的可能取值是2、3,由于各局相互独立,得到变量的分布列,求出期望.【解答】解:记A i表示事件:第i局甲获胜,(i=3、4、5)B i表示第j局乙获胜,j=3、4(1)记B表示事件:甲获得这次比赛的胜利,∵前2局中,甲、乙各胜1局,∴甲要获得这次比赛的胜利需在后面的比赛中先胜两局,∴B=A3A4+B3A4A5+A3B4A5由于各局比赛结果相互独立,∴P(B)=P(A3A4)+P(B3A4A5)+P(A3B4A5)=0.6×0.6+0.4×0.6×0.6+0.6×0.4×0.6=0.648(2)ξ表示从第3局开始到比赛结束所进行的局数,由上一问可知ξ的可能取值是2、3由于各局相互独立,得到ξ的分布列P(ξ=2)=P(A3A4+B3B4)=0.52P(ξ=3)=1﹣P(ξ=2)=1﹣0.52=0.48∴Eξ=2×0.52+3×0.48=2.48.【点评】认真审题是前提,部分考生由于考虑了前两局的概率而导致失分,这是很可惜的,主要原因在于没读懂题.另外,还要注意表述,这也是考生较薄弱的环节.20.(12分)在数列{a n}中,a1=1,a n+1=(1+)a n+.(1)设b n=,求数列{b n}的通项公式;(2)求数列{a n}的前n项和S n.【考点】8E:数列的求和;8H:数列递推式.【专题】11:计算题;15:综合题.【分析】(1)由已知得=+,即b n+1=b n+,由此能够推导出所求的通项公式.(2)由题设知a n=2n﹣,故S n=(2+4+…+2n)﹣(1++++…+),设T n=1++++…+,由错位相减法能求出T n=4﹣.从而导出数列{a n}的前n项和S n.【解答】解:(1)由已知得b1=a1=1,且=+,即b n+1=b n+,从而b2=b1+,b3=b2+,b n=b n﹣1+(n≥2).于是b n=b1+++…+=2﹣(n≥2).又b1=1,故所求的通项公式为b n=2﹣.(2)由(1)知a n=2n﹣,故S n=(2+4+…+2n)﹣(1++++…+),设T n=1++++…+,①T n=+++…++,②①﹣②得,T n=1++++…+﹣=﹣=2﹣﹣,∴T n=4﹣.∴S n=n(n+1)+﹣4.【点评】本题考查数列的通项公式和前n项和的求法,解题时要注意错位相减法的合理运用.21.(12分)如图,已知抛物线E:y2=x与圆M:(x﹣4)2+y2=r2(r>0)相交于A、B、C、D四个点.(Ⅰ)求r的取值范围;(Ⅱ)当四边形ABCD的面积最大时,求对角线AC、BD的交点P的坐标.【考点】IR:两点间的距离公式;JF:圆方程的综合应用;K8:抛物线的性质.【专题】15:综合题;16:压轴题.【分析】(1)先联立抛物线与圆的方程消去y,得到x的二次方程,根据抛物线E:y2=x与圆M:(x﹣4)2+y2=r2(r>0)相交于A、B、C、D四个点的充要条件是此方程有两个不相等的正根,可求出r的范围.(2)先设出四点A,B,C,D的坐标再由(1)中的x二次方程得到两根之和、两根之积,表示出面积并求出其的平方值,最后根据三次均值不等式确定得到最大值时的点P的坐标.【解答】解:(Ⅰ)将抛物线E:y2=x代入圆M:(x﹣4)2+y2=r2(r>0)的方程,消去y2,整理得x2﹣7x+16﹣r2=0(1)抛物线E:y2=x与圆M:(x﹣4)2+y2=r2(r>0)相交于A、B、C、D四个点的充要条件是:方程(1)有两个不相等的正根∴即.解这个方程组得,.(II)设四个交点的坐标分别为、、、.则直线AC、BD的方程分别为y﹣=?(x﹣x1),y+=(x﹣x1),解得点P的坐标为(,0),则由(I)根据韦达定理有x1+x2=7,x1x2=16﹣r2,则∴令,则S2=(7+2t)2(7﹣2t)下面求S2的最大值.由三次均值有:当且仅当7+2t=14﹣4t,即时取最大值.经检验此时满足题意.故所求的点P的坐标为.【点评】本题主要考查抛物线和圆的综合问题.圆锥曲线是高考必考题,要强化复习.22.(12分)设函数f(x)=x3+3bx2+3cx有两个极值点x1、x2,且x1∈[﹣1,0],x2∈[1,2].(1)求b、c满足的约束条件,并在下面的坐标平面内,画出满足这些条件的点(b,c)的区域;(2)证明:.【考点】6D:利用导数研究函数的极值;7B:二元一次不等式(组)与平面区域;R6:不等式的证明.【专题】11:计算题;14:证明题;16:压轴题.【分析】(1)根据极值的意义可知,极值点x1、x2是导函数等于零的两个根,根据根的分布建立不等关系,画出满足条件的区域即可;(2)先用消元法消去参数b,利用参数c表示出f(x2)的值域,再利用参数c 的范围求出f(x2)的范围即可.【解答】解:(Ⅰ)f'(x)=3x2+6bx+3c,(2分)依题意知,方程f'(x)=0有两个根x1、x2,且x1∈[﹣1,0],x2∈[1,2]等价于f'(﹣1)≥0,f'(0)≤0,f'(1)≤0,f'(2)≥0.由此得b,c满足的约束条件为(4分)满足这些条件的点(b,c)的区域为图中阴影部分.(6分)(Ⅱ)由题设知f'(x2)=3x22+6bx2+3c=0,则,故.(8分)由于x2∈[1,2],而由(Ⅰ)知c≤0,故.又由(Ⅰ)知﹣2≤c≤0,(10分)所以.【点评】本题主要考查了利用导数研究函数的极值,以及二元一次不等式(组)与平面区域和不等式的证明,属于基础题.。
2009年高考上海数学试题答案(理数)

03任务_0001试卷总分:100 测试时间:0多项选择题简答题论述题一、多项选择题(共20 道试题,共40 分。
)1. 总体来看,古代城市的经济功能较弱,主要以()为主。
A. 军事功能B. 社会功能C. 政治功能D. 文化功能2. 城市管理学的研究方法有()。
A. 系统分析方法B. 理论联系实际的方法C. 综合分析方法D. 定性分析和定量分析相结合的方法3. ()是城市化的后续动力。
A. 农业现代化B. 科技现代化C. 工业化D. 信息化4. 以下关于新公共管理理论说法正确的是()。
A. 更加注重对内部系统的管理B. 强调管理对象的外部化C. 强调以什么方式实施管理会加强管理的便利性D. 强调提高管理的内部效率5. ()是市人民代表大会的执行机关,是城市国家行政机关。
A. 市人民政府B. 市人民法院C. 市人民检察院D. 市政协6. 在我国城市中,城市政治权力系统包括()。
A. 市人大B. 中共市委C. 市政协D. 市政府7. 在我国,市人民团体特指()。
A. 市妇联B. 市共青团C. 市红十字协会D. 市工会8. 中共市委对()起着领导作用,处于领导地位。
A. 市人民政府B. 市人民法院C. 市人民检察院D. 市人大9. ()属于初级城市发展战略观。
A. 营销导向B. 需求型C. 供给型D. 资源型10. 城市发展战略通常由()组成。
A. 战略措施B. 战略反馈C. 重点战略D. 战略依据和战略愿景11. 城市现代化目标体系,主要包括()。
A. 生活质量指标B. 生态环境指标C. 社会进步指标D. 经济发展指标12. 我国土地储备的运行模式包括()。
A. 上海模式B. 杭州模式C. 南通模式D. 武汉模式13. 近代城市规划始于()。
A. 美国B. 英国C. 法国D. 德国14. 我国现阶段城市规划的基本任务是()。
A. 保护和修复人居环境,尤其是城乡空间环境的生态系统,为城乡经济、社会和文化协调、稳定地持续发展服务B. 保障和创造城市居民安全、健康、舒适的空间环境C. 保障和创造城市公正的社会环境D. 保障和创造城市公正的人文环境15. 在社会主义市场经济条件下,宏观调控具有()的特征。
2009年上海高考数学试卷及答案(理科)

2009年全国普通高等学校招生统一考试上海数学试卷(理工农医类)一.真空题 (本大题满分56分)1. 若复数 z 满足z (1+i) =1-i (I 是虚数单位),则其共轭复数z =__________________ .2. 已知集合=≤A x x |1}{,=≥B x x a |}{,且⋃=A B R ,则实数a 的取值范围是______________________ .3. 若行列式 8 9x 3 5 x714中,元素4的代数余子式大于0,则x 满足的条件是________________________ .4.某算法的程序框如右图所示,则输出量y 与输入量x 满足的关系式是____________________________ .5.如图,若正四棱柱-ABCD A B C D 1111的底面连长为2,高 为4,则异面直线BD 1与AD 所成角的大小是______________(结果用反三角函数表示).6.函数=+y x x 2cos sin 22的最小值是_____________________ .7.某学校要从5名男生和2名女生中选出2人作为上海世博会志愿者,若用随机变量ξ表示选出的志愿者中女生的人数,则数学期望ξE ____________(结果用最简分数表示). 8.已知三个球的半径R 1,R 2,R 3满足+=R R R 23123,则它们的表面积S 1,S 2,S 3,满足的等量关系是___________.9.已知F 1、F 2是椭圆C x a y b+=2222:1(a >b >0)的两个焦点,P 为椭圆C 上一点,且⊥PF PF 12.若∆PF F 12的面积为9,则b =____________.10.在极坐标系中,由三条直线θ=0,=θπ3,ρθρθ+=cos sin 1围成图形的面积是________.11.当x ≤≤01时,不等式πsin2≥xkx 成立,则实数k 的取值范围是_______________.12.已知函数=+()sin tan f x x x .项数为27的等差数列a n }{满足a n ,ππ22∈-⎛⎝⎫⎭⎪,且公差d ≠0.若f a f a f a ++⋯+=1227()()()0,则当k =____________是,f a k =()0.13.某地街道呈现东—西、南—北向的网格状,相邻街距都为1.两街道相交的点称为格点。
2009年普通高等学校招生全国统一考试数学卷(全国Ⅰ.理)含详解

2009年普通高等学校招生全国统一考试理科数学(必修+选修Ⅱ)本试卷分第错误!未找到引用源。
卷(选择题)和第错误!未找到引用源。
卷(非选择题)两部分.第错误!未找到引用源。
卷1至2页,第错误!未找到引用源。
卷3至4页.考试结束后,将本试卷和答题卡一并交回.第Ⅰ卷考生注意:1.答题前,考生在答题卡上务必用0.5毫米黑色墨水签字笔将自己的姓名、准考证号、填写清楚 ,并贴好条形码.请认真核准条形码上的准考证号、姓名和科目.2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号.在试题卷上作答无效.......... 3.本卷共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.参考公式:如果事件A B ,互斥,那么球的表面积公式 ()()()P A B P A P B +=+24πS R = 如果事件A B ,相互独立,那么其中R 表示球的半径()()()P A B P A P B = 球的体积公式如果事件A 在一次试验中发生的概率是P ,那么 34π3V R = n 次独立重复试验中恰好发生k 次的概率 其中R 表示球的半径一、选择题(1)设集合A={4,5,7,9},B={3,4,7,8,9},全集U=A B ,则集合[()u AB I 中的元素共有(A )(A )3个 (B )4个 (C )5个 (D )6个解:{3,4,5,7,8,9}A B = ,{4,7,9}(){3,5,8}U A B C A B =∴= 故选A 。
也可用摩根律:()()()U U U C A B C A C B =(2)已知????i 则复数z ??(B ??)w w w k s ??u c o m ?????????????? (A )????i?????????? B??????i?????????????????? C????i?????????????????? D????i 解:(1)(2)13,13z i i i z i =+⋅+=+∴=- 故选B 。
2009年全国统一高考数学试卷(理科)(全国卷ⅰ)(含解析版)

、 、 A .B .2009 年全国统一高考数学试卷(理科)(全国卷Ⅰ)一、选择题(共 12 小题,每小题 5 分,满分 60 分)1.(5 分)设集合 A={4,5,7,9},B={3,4,7,8,9},全集 U=A ∪B ,则集合∁U (A ∩B )中的元素共有( )A .3 个B .4 个C .5 个D .6 个2.(5 分)已知=2+i ,则复数 z=( ) A .﹣1+3i B .1﹣3iC .3+iD .3﹣i 3.(5 分)不等式<1 的解集为( )A .{x |0<x <1}∪{x |x >1}B .{x |0<x <1}C .{x |﹣1<x <0}D .{x |x <0}4.(5 分)已知双曲线﹣=1(a >0,b >0)的渐近线与抛物线 y=x 2+1 相切,则该双曲线的离心率为( )A .B .2C .D .5.(5 分)甲组有 5 名男同学,3 名女同学;乙组有 6 名男同学、2 名女同学.若 从甲、乙两组中各选出 2 名同学,则选出的 4 人中恰有 1 名女同学的不同选法共有( )A .150 种B .180 种C .300 种D .345 种 6.(5 分)设 是单位向量,且,则•的最小值为( )A .﹣2B .﹣2C .﹣1D .1﹣7.(5 分)已知三棱柱 ABC ﹣A 1B 1C 1 的侧棱与底面边长都相等,A 1 在底面 ABC 上的射影 D 为 BC 的中点,则异面直线 AB 与 CC 1 所成的角的余弦值为()C .D .8.(5分)如果函数y=3cos(2x+φ)的图象关于点(,0)中心对称,那么|φ|的最小值为()A.B.C.D.9.(5 分)已知直线y=x+1 与曲线y=ln(x+a)相切,则a 的值为()A.1 B.2 C.﹣1 D.﹣210.(5 分)已知二面角α﹣l﹣β为60°,动点P、Q 分别在面α、β内,P 到β的距离为,Q 到α的距离为,则P、Q 两点之间距离的最小值为()A.1 B.2 C.D.411.(5 分)函数f(x)的定义域为R,若f(x+1)与f(x﹣1)都是奇函数,则()A.f(x)是偶函数B.f(x)是奇函数C.f(x)=f(x+2)D.f(x+3)是奇函数12.(5 分)已知椭圆C:+y2=1 的右焦点为F,右准线为l,点A∈l,线段AF 交C 于点B,若=3,则||=()A.B.2 C.D.3二、填空题(共4 小题,每小题5 分,满分20 分)13.(5 分)(x﹣y)10的展开式中,x7y3的系数与x3y7的系数之和等于.14.(5 分)设等差数列{a n}的前n 项和为S n,若S9=81,则a2+a5+a8=.15.(5 分)直三棱柱ABC﹣A1B1C1 的各顶点都在同一球面上,若AB=AC=AA1=2,∠BAC=120°,则此球的表面积等于.16.(5 分)若,则函数y=tan2xtan3x 的最大值为.三、解答题(共6 小题,满分70 分)17.(10 分)在△ABC 中,内角A、B、C 的对边长分别为a、b、c,已知a2﹣c2=2b,且sinAcosC=3cosAsinC,求b.18.(12 分)如图,四棱锥S﹣ABCD 中,底面ABCD 为矩形,SD⊥底面ABCD,AD=,DC=SD=2,点M 在侧棱SC 上,∠ABM=60°(I)证明:M 是侧棱SC 的中点;(II)求二面角S﹣AM﹣B 的大小.19.(12 分)甲、乙二人进行一次围棋比赛,约定先胜3 局者获得这次比赛的胜利,比赛结束,假设在一局中,甲获胜的概率为0.6,乙获胜的概率为0.4,各局比赛结果相互独立,已知前2 局中,甲、乙各胜1 局.(I)求甲获得这次比赛胜利的概率;(II)设ξ表示从第3 局开始到比赛结束所进行的局数,求ξ的分布列及数学期望.20.(12 分)在数列{a n}中,a1=1,a n+1=(1+)a n+.(1)设b n=,求数列{b n}的通项公式;(2)求数列{a n}的前n 项和S n.21.(12 分)如图,已知抛物线E:y2=x 与圆M:(x﹣4)2+y2=r2(r>0)相交于A、B、C、D 四个点.(I)求r 的取值范围;(II)当四边形ABCD 的面积最大时,求对角线AC、BD 的交点P 的坐标.22.(12 分)设函数f(x)=x3+3bx2+3cx 有两个极值点x1、x2,且x1∈[﹣1,0],x2∈[1,2].(1)求b、c 满足的约束条件,并在下面的坐标平面内,画出满足这些条件的点(b,c)的区域;(2)证明:.2009 年全国统一高考数学试卷(理科)(全国卷Ⅰ)参考答案与试题解析一、选择题(共12 小题,每小题5 分,满分60 分)1.(5 分)设集合A={4,5,7,9},B={3,4,7,8,9},全集U=A∪B,则集合∁U(A∩B)中的元素共有()A.3 个B.4 个C.5 个D.6 个【考点】1H:交、并、补集的混合运算.【分析】根据交集含义取A、B 的公共元素写出A∩B,再根据补集的含义求解.【解答】解:A∪B={3,4,5,7,8,9},A∩B={4,7,9}∴∁U(A∩B)={3,5,8}故选A.也可用摩根律:∁U(A∩B)=(∁U A)∪(∁U B)故选:A.【点评】本题考查集合的基本运算,较简单.2.(5 分)已知=2+i,则复数z=()A.﹣1+3i B.1﹣3i C.3+i D.3﹣i【考点】A1:虚数单位i、复数.【分析】化简复数直接求解,利用共轭复数可求z.【解答】解:,∴z=1﹣3i故选:B.【点评】求复数,需要对复数化简,本题也可以用待定系数方法求解.3.(5 分)不等式<1 的解集为()A.{x|0<x<1}∪{x|x>1} B.{x|0<x<1} C.{x|﹣1<x<0}D.{x|x<0}【考点】7E:其他不等式的解法.【分析】本题为绝对值不等式,去绝对值是关键,可利用绝对值意义去绝对值,也可两边平方去绝对值.【解答】解:∵<1,∴|x+1|<|x﹣1|,∴x2+2x+1<x2﹣2x+1.∴x<0.∴不等式的解集为{x|x<0}.故选:D.【点评】本题主要考查解绝对值不等式,属基本题.解绝对值不等式的关键是去绝对值,去绝对值的方法主要有:利用绝对值的意义、讨论和平方.4.(5分)已知双曲线﹣=1(a>0,b>0)的渐近线与抛物线y=x2+1 相切,则该双曲线的离心率为()A.B.2 C.D.【考点】KC:双曲线的性质;KH:直线与圆锥曲线的综合.【专题】11:计算题.【分析】先求出渐近线方程,代入抛物线方程,根据判别式等于0,找到a 和b 的关系,从而推断出a 和c 的关系,答案可得.【解答】解:由题双曲线的一条渐近线方程为,代入抛物线方程整理得ax2﹣bx+a=0,因渐近线与抛物线相切,所以b2﹣4a2=0,即,故选:C.、 、 【点评】本小题考查双曲线的渐近线方程直线与圆锥曲线的位置关系、双曲线的离心率,基础题.5.(5 分)甲组有 5 名男同学,3 名女同学;乙组有 6 名男同学、2 名女同学.若 从甲、乙两组中各选出 2 名同学,则选出的 4 人中恰有 1 名女同学的不同选法共有( )A .150 种B .180 种C .300 种D .345 种【考点】D1:分类加法计数原理;D2:分步乘法计数原理. 【专题】5O :排列组合.【分析】选出的 4 人中恰有 1 名女同学的不同选法,1 名女同学来自甲组和乙组两类型.【解答】解:分两类(1)甲组中选出一名女生有 C 51•C 31•C 62=225 种选法; (2)乙组中选出一名女生有 C 52•C 61•C 21=120 种选法.故共有 345 种选法.故选:D .【点评】分类加法计数原理和分类乘法计数原理,最关键做到不重不漏,先分类,后分步!6.(5 分)设 是单位向量,且,则• 的最小值为( )A .﹣2B .﹣2C .﹣1D .1﹣【考点】9O :平面向量数量积的性质及其运算. 【专题】16:压轴题. 【分析】由题意可得=,故要求的式子即﹣()•+=1﹣cos=1﹣cos,再由余弦函数的值域求出它的最小值. 【解答】解:∵、、 是单位向量,,∴, =.∴•=﹣()•+ =0﹣()•+1=1﹣cos=1﹣cos ≥.故选:D.【点评】考查向量的运算法则;交换律、分配律但注意不满足结合律.7.(5分)已知三棱柱ABC﹣A1B1C1 的侧棱与底面边长都相等,A1 在底面ABC 上的射影D 为BC 的中点,则异面直线AB 与CC1 所成的角的余弦值为()C.D.A.B.【考点】LO:空间中直线与直线之间的位置关系.【分析】首先找到异面直线AB 与CC1 所成的角(如∠A1AB);而欲求其余弦值可考虑余弦定理,则只要表示出A1B 的长度即可;不妨设三棱柱ABC﹣A1B1C1的侧棱与底面边长为1,利用勾股定理即可求之.【解答】解:设BC 的中点为D,连接A1D、AD、A1B,易知θ=∠A1AB 即为异面直线AB 与CC1 所成的角;并设三棱柱ABC﹣A1B1C1 的侧棱与底面边长为1,则|AD|=,|A1D|=,|A1B|=,由余弦定理,得cosθ==.故选:D.【点评】本题主要考查异面直线的夹角与余弦定理.8.(5分)如果函数y=3cos(2x+φ)的图象关于点(,0)中心对称,那么|φ|的最小值为()A.B.C.D.【考点】HB:余弦函数的对称性.【专题】11:计算题.【分析】先根据函数y=3cos(2x+φ)的图象关于点中心对称,令x=代入函数使其等于0,求出φ的值,进而可得|φ|的最小值.【解答】解:∵函数y=3cos(2x+φ)的图象关于点中心对称.∴∴由此易得.故选:A.【点评】本题主要考查余弦函数的对称性.属基础题.9.(5 分)已知直线y=x+1 与曲线y=ln(x+a)相切,则a 的值为()A.1 B.2 C.﹣1 D.﹣2【考点】6H:利用导数研究曲线上某点切线方程.【分析】切点在切线上也在曲线上得到切点坐标满足两方程;又曲线切点处的导数值是切线斜率得第三个方程.【解答】解:设切点P(x0,y0),则y0=x0+1,y0=ln(x0+a),又∵∴x0+a=1∴y0=0,x0=﹣1∴a=2.故选:B.【点评】本题考查导数的几何意义,常利用它求曲线的切线10.(5 分)已知二面角α﹣l﹣β为60°,动点P、Q 分别在面α、β内,P 到β的距离为,Q 到α的距离为,则P、Q 两点之间距离的最小值为()A.1 B.2 C.D.4【考点】LQ:平面与平面之间的位置关系.【专题】11:计算题;16:压轴题.【分析】分别作QA⊥α于A,AC⊥l 于C,PB⊥β于B,PD⊥l 于D,连CQ,BD 则∠ACQ=∠PBD=60°,在三角形APQ 中将PQ 表示出来,再研究其最值即可.【解答】解:如图分别作QA⊥α于A,AC⊥l 于C,PB⊥β 于B,PD⊥l 于D,连CQ,BD 则∠ACQ=∠PDB=60°,,又∵当且仅当AP=0,即点A 与点P 重合时取最小值.故选:C.【点评】本题主要考查了平面与平面之间的位置关系,以及空间中直线与平面之间的位置关系,考查空间想象能力、运算能力和推理论证能力,属于基础题.11.(5 分)函数f(x)的定义域为R,若f(x+1)与f(x﹣1)都是奇函数,则()A.f(x)是偶函数B.f(x)是奇函数C.f(x)=f(x+2)D.f(x+3)是奇函数【考点】3I:奇函数、偶函数.【专题】16:压轴题.【分析】首先由奇函数性质求f(x)的周期,然后利用此周期推导选择项.【解答】解:∵f(x+1)与f(x﹣1)都是奇函数,∴函数f(x)关于点(1,0)及点(﹣1,0)对称,∴f(x)+f(2﹣x)=0,f(x)+f(﹣2﹣x)=0,故有f(2﹣x)=f(﹣2﹣x),函数f(x)是周期T=[2﹣(﹣2)]=4 的周期函数.∴f(﹣x﹣1+4)=﹣f(x﹣1+4),f(﹣x+3)=﹣f(x+3),f(x+3)是奇函数.故选:D.【点评】本题主要考查奇函数性质的灵活运用,并考查函数周期的求法.12.(5 分)已知椭圆C:+y2=1 的右焦点为F,右准线为l,点A∈l,线段AF 交C 于点B,若=3,则||=()A.B.2 C.D.3【考点】K4:椭圆的性质.【专题】11:计算题;16:压轴题.【分析】过点B 作BM⊥x 轴于M,设右准线l 与x 轴的交点为N,根据椭圆的性质可知FN=1,进而根据,求出BM,AN,进而可得|AF|.【解答】解:过点B 作BM⊥x 轴于M,n n n nn r +1 n 10 10 10 10 10 10并设右准线 l 与 x 轴的交点为 N ,易知 FN=1.由题意,故 FM=,故 B 点的横坐标为,纵坐标为±即 BM=, 故 AN=1, ∴.故选:A .【点评】本小题考查椭圆的准线、向量的运用、椭圆的定义,属基础题.二、填空题(共 4 小题,每小题 5 分,满分 20 分)13.(5 分)(x ﹣y )10 的展开式中,x 7y 3 的系数与 x 3y 7的系数之和等于 ﹣240 .【考点】DA :二项式定理. 【专题】11:计算题.【分析】首先要了解二项式定理:(a +b )n =C 0a n b 0+C 1a n ﹣1b 1+C 2a n ﹣2b 2++C r a n ﹣ r b r ++C n a 0b n ,各项的通项公式为:T =C r a n ﹣r b r .然后根据题目已知求解即可. 【解答】解:因为(x ﹣y )10 的展开式中含 x 7y 3 的项为 C 3x 10﹣3y (3 含 x 3y 7 的项为 C 7x 10﹣7y 7(﹣1)7=﹣C 7x 3y 7. 由 C 3=C 7=120 知,x 7y 3 与 x 3y 7 的系数之和为﹣240.故答案为﹣240.﹣1)3=﹣C 3x 7y 3, 【点评】此题主要考查二项式定理的应用问题,对于公式:(a +b )n =C n 0a n b 0+C n 1a n﹣1b1+C 2a n﹣2b2++C r a n﹣r b r++C n a0b n,属于重点考点,同学们需要理解记忆.n n n14.(5 分)设等差数列{a n}的前n 项和为S n,若S9=81,则a2+a5+a8= 27 .【考点】83:等差数列的性质;85:等差数列的前n 项和.【分析】由s9 解得a5 即可.【解答】解:∵∴a5=9∴a2+a5+a8=3a5=27故答案是27【点评】本题考查前n 项和公式和等差数列的性质.15.(5 分)直三棱柱ABC﹣A1B1C1 的各顶点都在同一球面上,若AB=AC=AA1=2,∠BAC=120°,则此球的表面积等于20π.【考点】LR:球内接多面体.【专题】11:计算题;16:压轴题.【分析】通过正弦定理求出底面外接圆的半径,设此圆圆心为O',球心为O,在RT△OBO'中,求出球的半径,然后求出球的表面积.【解答】解:在△ABC 中AB=AC=2,∠BAC=120°,可得由正弦定理,可得△ABC 外接圆半径r=2,设此圆圆心为O',球心为O,在RT△OBO'中,易得球半径,故此球的表面积为4πR2=20π故答案为:20π【点评】本题是基础题,解题思路是:先求底面外接圆的半径,转化为直角三角形,求出球的半径,这是三棱柱外接球的常用方法;本题考查空间想象能力,计算能力.16.(5 分)若,则函数y=tan2xtan3x 的最大值为﹣8 .【考点】3H:函数的最值及其几何意义;GS:二倍角的三角函数.【专题】11:计算题;16:压轴题.【分析】见到二倍角2x 就想到用二倍角公式,之后转化成关于tanx 的函数,将tanx 看破成整体,最后转化成函数的最值问题解决.【解答】解:令tanx=t,∵,∴故填:﹣8.【点评】本题主要考查二倍角的正切,二次函数的方法求最大值等,最值问题是中学数学的重要内容之一,它分布在各块知识点,各个知识水平层面.以最值为载体,可以考查中学数学的所有知识点.三、解答题(共6 小题,满分70 分)17.(10 分)在△ABC 中,内角A、B、C 的对边长分别为a、b、c,已知a2﹣c2=2b,且sinAcosC=3cosAsinC,求b.【考点】HR:余弦定理.【分析】根据正弦定理和余弦定理将sinAcosC=3cosAsinC 化成边的关系,再根据a2﹣c2=2b 即可得到答案.【解答】解:法一:在△ABC 中∵sinAcosC=3cosAsinC,则由正弦定理及余弦定理有:,化简并整理得:2(a2﹣c2)=b2.又由已知a2﹣c2=2b∴4b=b2.解得b=4 或b=0(舍);法二:由余弦定理得:a2﹣c2=b2﹣2bccosA.又a2﹣c2=2b,b≠0.所以b=2ccosA+2①又sinAcosC=3cosAsinC,∴sinAcosC+cosAsinC=4cosAsinCsin(A+C)=4cosAsinC,即sinB=4cosAsinC 由正弦定理得,故b=4ccosA②由①,②解得b=4.【点评】本题主要考查正弦定理和余弦定理的应用.属基础题.18.(12 分)如图,四棱锥S﹣ABCD 中,底面ABCD 为矩形,SD⊥底面ABCD,AD=,DC=SD=2,点M 在侧棱SC 上,∠ABM=60°(I)证明:M 是侧棱SC 的中点;(II)求二面角S﹣AM﹣B 的大小.【考点】LO:空间中直线与直线之间的位置关系;MJ:二面角的平面角及求法.【专题】11:计算题;14:证明题.【分析】(Ⅰ)法一:要证明M 是侧棱SC 的中点,作MN∥SD 交CD 于N,作NE⊥AB 交AB 于E,连ME、NB,则MN⊥面ABCD,ME⊥AB,设MN=x,则NC=EB=x,解RT△MNE 即可得x 的值,进而得到M 为侧棱SC 的中点;法二:分别以DA、DC、DS 为x、y、z 轴如图建立空间直角坐标系D﹣xyz,并求出S 点的坐标、C 点的坐标和M 点的坐标,然后根据中点公式进行判断;法三:分别以DA、DC、DS 为x、y、z 轴如图建立空间直角坐标系D﹣xyz,构造空间向量,然后数乘向量的方法来证明.(Ⅱ)我们可以以D 为坐标原点,分别以DA、DC、DS 为x、y、z 轴如图建立空间直角坐标系D﹣xyz,我们可以利用向量法求二面角S﹣AM﹣B 的大小.【解答】证明:(Ⅰ)作MN∥SD 交CD 于N,作NE⊥AB 交AB 于E,连ME、NB,则MN⊥面ABCD,ME⊥AB,设MN=x,则NC=EB=x,在RT△MEB 中,∵∠MBE=60°∴.在RT△MNE 中由ME2=NE2+MN2∴3x2=x2+2解得x=1,从而∴M 为侧棱SC 的中点M.(Ⅰ)证法二:分别以DA、DC、DS 为x、y、z 轴如图建立空间直角坐标系D﹣xyz,则.设M(0,a,b)(a>0,b>0),则,,由题得,即解之个方程组得a=1,b=1 即M(0,1,1)所以M 是侧棱SC 的中点.(I)证法三:设,则又故,即,解得λ=1,所以M 是侧棱SC 的中点.(Ⅱ)由(Ⅰ)得,又,,设分别是平面SAM、MAB 的法向量,则且,即且分别令得z1=1,y1=1,y2=0,z2=2,即,∴二面角S﹣AM﹣B 的大小.【点评】空间两条直线夹角的余弦值等于他们方向向量夹角余弦值的绝对值;空间直线与平面夹角的余弦值等于直线的方向向量与平面的法向量夹角的正弦值;空间锐二面角的余弦值等于他的两个半平面方向向量夹角余弦值的绝对值;19.(12 分)甲、乙二人进行一次围棋比赛,约定先胜3 局者获得这次比赛的胜利,比赛结束,假设在一局中,甲获胜的概率为0.6,乙获胜的概率为0.4,各局比赛结果相互独立,已知前2 局中,甲、乙各胜1 局.(I)求甲获得这次比赛胜利的概率;(II)设ξ表示从第3 局开始到比赛结束所进行的局数,求ξ的分布列及数学期望.【考点】C8:相互独立事件和相互独立事件的概率乘法公式;CG:离散型随机变量及其分布列;CH:离散型随机变量的期望与方差.【专题】11:计算题.【分析】(1)由题意知前2 局中,甲、乙各胜1 局,甲要获得这次比赛的胜利需在后面的比赛中先胜两局,根据各局比赛结果相互独立,根据相互独立事件的概率公式得到结果.(2)由题意知ξ表示从第3 局开始到比赛结束所进行的局数,由上一问可知ξ的可能取值是2、3,由于各局相互独立,得到变量的分布列,求出期望.【解答】解:记A i 表示事件:第i 局甲获胜,(i=3、4、5)B i 表示第j 局乙获胜,j=3、4(1)记B 表示事件:甲获得这次比赛的胜利,∵前2 局中,甲、乙各胜1 局,∴甲要获得这次比赛的胜利需在后面的比赛中先胜两局,∴B=A3A4+B3A4A5+A3B4A5由于各局比赛结果相互独立,∴P(B)=P(A3A4)+P(B3A4A5)+P(A3B4A5)=0.6×0.6+0.4×0.6×0.6+0.6×0.4×0.6=0.648(2)ξ表示从第3 局开始到比赛结束所进行的局数,由上一问可知ξ的可能取值是2、3由于各局相互独立,得到ξ的分布列P(ξ=2)=P(A3A4+B3B4)=0.52 P(ξ=3)=1﹣P(ξ=2)=1﹣0.52=0.48∴Eξ=2×0.52+3×0.48=2.48.【点评】认真审题是前提,部分考生由于考虑了前两局的概率而导致失分,这是很可惜的,主要原因在于没读懂题.另外,还要注意表述,这也是考生较薄弱的环节.20.(12 分)在数列{a n}中,a1=1,a n+1=(1+)a n+.(1)设b n=,求数列{b n}的通项公式;(2)求数列{a n}的前n 项和S n.【考点】8E:数列的求和;8H:数列递推式.【专题】11:计算题;15:综合题.=b n+,由此能够推导出所求的通【分析】(1)由已知得=+,即b n+1项公式.(2)由题设知a n=2n﹣,故S n=(2+4+…+2n)﹣(1++++…+),设T n=1++++…+,由错位相减法能求出T n=4﹣.从而导出数列{a n}的前n 项和S n.【解答】解:(1)由已知得b1=a1=1,且=+,即b n=b n+,从而b2=b1+,+1b3=b2+,b n=b n﹣1+(n≥2).于是b n=b1+++…+=2﹣(n≥2).又b1=1,故所求的通项公式为b n=2﹣.(2)由(1)知a n=2n﹣,故S n=(2+4+…+2n)﹣(1++++…+),设T n=1++++…+,①T n=+++…++,②①﹣②得,T n=1++++…+﹣= ﹣=2﹣﹣,∴T n=4﹣.∴S n=n(n+1)+﹣4.【点评】本题考查数列的通项公式和前n 项和的求法,解题时要注意错位相减法的合理运用.21.(12 分)如图,已知抛物线E:y2=x 与圆M:(x﹣4)2+y2=r2(r>0)相交于A、B、C、D 四个点.(I)求r 的取值范围;(II)当四边形ABCD 的面积最大时,求对角线AC、BD 的交点P 的坐标.【考点】IR :两点间的距离公式;JF :圆方程的综合应用;K8:抛物线的性质.【专题】15:综合题;16:压轴题.【分析】(1)先联立抛物线与圆的方程消去 y ,得到 x 的二次方程,根据抛物线E :y 2=x 与圆 M :(x ﹣4)2+y 2=r 2(r >0)相交于 A 、B 、C 、D 四个点的充要条件是此方程有两个不相等的正根,可求出 r 的范围.(2)先设出四点 A ,B ,C ,D 的坐标再由(1)中的 x 二次方程得到两根之和、两根之积,表示出面积并求出其的平方值,最后根据三次均值不等式确定得到最大值时的点 P 的坐标.【解答】解:(Ⅰ)将抛物线 E :y 2=x 代入圆 M :(x ﹣4)2+y 2=r 2(r >0)的方程,消去 y 2,整理得 x 2﹣7x +16﹣r 2=0(1)抛物线 E :y 2=x 与圆 M :(x ﹣4)2+y 2=r 2(r >0)相交于 A 、B 、C 、D 四个点的充要条件是:方程(1)有两个不相等的正根.(II ) 设四个交点的坐标分别为、 、 、 .∴ 即 .解这个方程组得,则直线AC、BD 的方程分别为y﹣= •(x﹣x1),y+=(x﹣x1),解得点P 的坐标为(,0),则由(I)根据韦达定理有x1+x2=7,x1x2=16﹣r2,则∴令,则S2=(7+2t)2(7﹣2t)下面求S2的最大值.由三次均值有:当且仅当7+2t=14﹣4t,即时取最大值.经检验此时满足题意.故所求的点P 的坐标为.【点评】本题主要考查抛物线和圆的综合问题.圆锥曲线是高考必考题,要强化复习.22.(12 分)设函数f(x)=x3+3bx2+3cx 有两个极值点x1、x2,且x1∈[﹣1,0],x2∈[1,2].(1)求b、c 满足的约束条件,并在下面的坐标平面内,画出满足这些条件的点(b,c)的区域;(2)证明:.【考点】6D:利用导数研究函数的极值;7B:二元一次不等式(组)与平面区域;R6:不等式的证明.【专题】11:计算题;14:证明题;16:压轴题.【分析】(1)根据极值的意义可知,极值点x1、x2 是导函数等于零的两个根,根据根的分布建立不等关系,画出满足条件的区域即可;(2)先用消元法消去参数b,利用参数c 表示出f(x2)的值域,再利用参数c 的范围求出f(x2)的范围即可.【解答】解:(Ⅰ)f'(x)=3x2+6bx+3c,(2分)依题意知,方程f'(x)=0 有两个根x1、x2,且x1∈[﹣1,0],x2∈[1,2]等价于f'(﹣1)≥0,f'(0)≤0,f'(1)≤0,f'(2)≥0.由此得b,c 满足的约束条件为(4 分)满足这些条件的点(b,c)的区域为图中阴影部分.(6分)(Ⅱ)由题设知f'(x2)=3x22+6bx2+3c=0,则,故.(8 分)由于x2∈[1,2],而由(Ⅰ)知c≤0,故.又由(Ⅰ)知﹣2≤c≤0,(10 分)所以.【点评】本题主要考查了利用导数研究函数的极值,以及二元一次不等式(组)与平面区域和不等式的证明,属于基础题.。
2009年全国统一高考数学试卷(理科)(全国卷ⅰ)(含解析版)

2009年全国统一高考数学试卷(理科)(全国卷Ⅰ)一、选择题(共12小题,每小题5分,满分60分)1.(5分)设集合A={4,5,7,9},B={3,4,7,8,9},全集U=A∪B,则集合∁U(A∩B)中的元素共有()A.3个B.4个C.5个D.6个2.(5分)已知=2+i,则复数z=()A.﹣1+3i B.1﹣3i C.3+i D.3﹣i3.(5分)不等式<1的解集为()A.{x|0<x<1}∪{x|x>1}B.{x|0<x<1}C.{x|﹣1<x<0}D.{x|x<0}4.(5分)已知双曲线﹣=1(a>0,b>0)的渐近线与抛物线y=x2+1相切,则该双曲线的离心率为()A.B.2C.D.5.(5分)甲组有5名男同学,3名女同学;乙组有6名男同学、2名女同学.若从甲、乙两组中各选出2名同学,则选出的4人中恰有1名女同学的不同选法共有()A.150种B.180种C.300种D.345种6.(5分)设、、是单位向量,且,则•的最小值为()A.﹣2B.﹣2C.﹣1D.1﹣7.(5分)已知三棱柱ABC﹣A1B1C1的侧棱与底面边长都相等,A1在底面ABC上的射影D为BC的中点,则异面直线AB与CC1所成的角的余弦值为()A.B.C.D.8.(5分)如果函数y=3cos(2x+φ)的图象关于点(,0)中心对称,那么|φ|的最小值为()A.B.C.D.9.(5分)已知直线y=x+1与曲线y=ln(x+a)相切,则a的值为()A.1B.2C.﹣1D.﹣210.(5分)已知二面角α﹣l﹣β为60°,动点P、Q分别在面α、β内,P到β的距离为,Q到α的距离为,则P、Q两点之间距离的最小值为()A.1B.2C.D.411.(5分)函数f(x)的定义域为R,若f(x+1)与f(x﹣1)都是奇函数,则()A.f(x)是偶函数B.f(x)是奇函数C.f(x)=f(x+2)D.f(x+3)是奇函数12.(5分)已知椭圆C:+y2=1的右焦点为F,右准线为l,点A∈l,线段AF 交C于点B,若=3,则||=()A.B.2C.D.3二、填空题(共4小题,每小题5分,满分20分)13.(5分)(x﹣y)10的展开式中,x7y3的系数与x3y7的系数之和等于.14.(5分)设等差数列{a n}的前n项和为S n,若S9=81,则a2+a5+a8=.15.(5分)直三棱柱ABC﹣A1B1C1的各顶点都在同一球面上,若AB=AC=AA1=2,∠BAC=120°,则此球的表面积等于.16.(5分)若,则函数y=tan2xtan3x的最大值为.三、解答题(共6小题,满分70分)17.(10分)在△ABC中,内角A、B、C的对边长分别为a、b、c,已知a2﹣c2=2b,且sinAcosC=3cosAsinC,求b.18.(12分)如图,四棱锥S﹣ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD=,DC=SD=2,点M在侧棱SC上,∠ABM=60°(I)证明:M是侧棱SC的中点;(Ⅱ)求二面角S﹣AM﹣B的大小.(I)求甲获得这次比赛胜利的概率;(Ⅱ)设ξ表示从第3局开始到比赛结束所进行的局数,求ξ的分布列及数学期望.20.(12分)在数列{a n}中,a1=1,a n+1=(1+)a n+.(1)设b n=,求数列{b n}的通项公式;(2)求数列{a n}的前n项和S n.21.(12分)如图,已知抛物线E:y2=x与圆M:(x﹣4)2+y2=r2(r>0)相交于A、B、C、D四个点.(Ⅰ)求r的取值范围;(Ⅱ)当四边形ABCD的面积最大时,求对角线AC、BD的交点P的坐标.22.(12分)设函数f(x)=x3+3bx2+3cx有两个极值点x1、x2,且x1∈[﹣1,0],x2∈[1,2].(1)求b、c满足的约束条件,并在下面的坐标平面内,画出满足这些条件的点(b,c)的区域;(2)证明:.2009年全国统一高考数学试卷(理科)(全国卷Ⅰ)参考答案与试题解析一、选择题(共12小题,每小题5分,满分60分)1.(5分)设集合A={4,5,7,9},B={3,4,7,8,9},全集U=A∪B,则集合∁U(A∩B)中的元素共有()A.3个B.4个C.5个D.6个【考点】1H:交、并、补集的混合运算.【分析】根据交集含义取A、B的公共元素写出A∩B,再根据补集的含义求解.【解答】解:A∪B={3,4,5,7,8,9},A∩B={4,7,9}∴∁U(A∩B)={3,5,8}故选A.也可用摩根律:∁U(A∩B)=(∁U A)∪(∁U B)故选:A.【点评】本题考查集合的基本运算,较简单.2.(5分)已知=2+i,则复数z=()A.﹣1+3i B.1﹣3i C.3+i D.3﹣i【考点】A1:虚数单位i、复数.【分析】化简复数直接求解,利用共轭复数可求z.【解答】解:,∴z=1﹣3i故选:B.【点评】求复数,需要对复数化简,本题也可以用待定系数方法求解.3.(5分)不等式<1的解集为()A.{x|0<x<1}∪{x|x>1}B.{x|0<x<1}C.{x|﹣1<x<0}D.{x|x<0}【考点】7E:其他不等式的解法.【分析】本题为绝对值不等式,去绝对值是关键,可利用绝对值意义去绝对值,也可两边平方去绝对值.【解答】解:∵<1,∴|x+1|<|x﹣1|,∴x2+2x+1<x2﹣2x+1.∴x<0.∴不等式的解集为{x|x<0}.故选:D.【点评】本题主要考查解绝对值不等式,属基本题.解绝对值不等式的关键是去绝对值,去绝对值的方法主要有:利用绝对值的意义、讨论和平方.4.(5分)已知双曲线﹣=1(a>0,b>0)的渐近线与抛物线y=x2+1相切,则该双曲线的离心率为()A.B.2C.D.【考点】KC:双曲线的性质;KH:直线与圆锥曲线的综合.【专题】11:计算题.【分析】先求出渐近线方程,代入抛物线方程,根据判别式等于0,找到a和b 的关系,从而推断出a和c的关系,答案可得.【解答】解:由题双曲线的一条渐近线方程为,代入抛物线方程整理得ax2﹣bx+a=0,因渐近线与抛物线相切,所以b2﹣4a2=0,即,故选:C.【点评】本小题考查双曲线的渐近线方程直线与圆锥曲线的位置关系、双曲线的离心率,基础题.5.(5分)甲组有5名男同学,3名女同学;乙组有6名男同学、2名女同学.若从甲、乙两组中各选出2名同学,则选出的4人中恰有1名女同学的不同选法共有()A.150种B.180种C.300种D.345种【考点】D1:分类加法计数原理;D2:分步乘法计数原理.【专题】5O:排列组合.【分析】选出的4人中恰有1名女同学的不同选法,1名女同学来自甲组和乙组两类型.【解答】解:分两类(1)甲组中选出一名女生有C51•C31•C62=225种选法;(2)乙组中选出一名女生有C52•C61•C21=120种选法.故共有345种选法.故选:D.【点评】分类加法计数原理和分类乘法计数原理,最关键做到不重不漏,先分类,后分步!6.(5分)设、、是单位向量,且,则•的最小值为()A.﹣2B.﹣2C.﹣1D.1﹣【考点】9O:平面向量数量积的性质及其运算.【专题】16:压轴题.【分析】由题意可得=,故要求的式子即﹣()•+=1﹣cos=1﹣cos,再由余弦函数的值域求出它的最小值.【解答】解:∵、、是单位向量,,∴,=.∴•=﹣()•+=0﹣()•+1=1﹣cos=1﹣cos≥.故选:D.【点评】考查向量的运算法则;交换律、分配律但注意不满足结合律.7.(5分)已知三棱柱ABC﹣A1B1C1的侧棱与底面边长都相等,A1在底面ABC上的射影D为BC的中点,则异面直线AB与CC1所成的角的余弦值为()A.B.C.D.【考点】LO:空间中直线与直线之间的位置关系.【分析】首先找到异面直线AB与CC1所成的角(如∠A1AB);而欲求其余弦值可考虑余弦定理,则只要表示出A1B的长度即可;不妨设三棱柱ABC﹣A1B1C1的侧棱与底面边长为1,利用勾股定理即可求之.【解答】解:设BC的中点为D,连接A1D、AD、A1B,易知θ=∠A1AB即为异面直线AB与CC1所成的角;并设三棱柱ABC﹣A1B1C1的侧棱与底面边长为1,则|AD|=,|A1D|=,|A1B|=,由余弦定理,得cosθ==.故选:D.【点评】本题主要考查异面直线的夹角与余弦定理.8.(5分)如果函数y=3cos(2x+φ)的图象关于点(,0)中心对称,那么|φ|的最小值为()A.B.C.D.【考点】HB:余弦函数的对称性.【专题】11:计算题.【分析】先根据函数y=3cos(2x+φ)的图象关于点中心对称,令x=代入函数使其等于0,求出φ的值,进而可得|φ|的最小值.【解答】解:∵函数y=3cos(2x+φ)的图象关于点中心对称.∴∴由此易得.故选:A.【点评】本题主要考查余弦函数的对称性.属基础题.9.(5分)已知直线y=x+1与曲线y=ln(x+a)相切,则a的值为()A.1B.2C.﹣1D.﹣2【考点】6H:利用导数研究曲线上某点切线方程.【分析】切点在切线上也在曲线上得到切点坐标满足两方程;又曲线切点处的导数值是切线斜率得第三个方程.【解答】解:设切点P(x0,y0),则y0=x0+1,y0=ln(x0+a),又∵∴x0+a=1∴y0=0,x0=﹣1∴a=2.故选:B.【点评】本题考查导数的几何意义,常利用它求曲线的切线10.(5分)已知二面角α﹣l﹣β为60°,动点P、Q分别在面α、β内,P到β的距离为,Q到α的距离为,则P、Q两点之间距离的最小值为()A.1B.2C.D.4【考点】LQ:平面与平面之间的位置关系.【专题】11:计算题;16:压轴题.【分析】分别作QA⊥α于A,AC⊥l于C,PB⊥β于B,PD⊥l于D,连CQ,BD 则∠ACQ=∠PBD=60°,在三角形APQ中将PQ表示出来,再研究其最值即可.【解答】解:如图分别作QA⊥α于A,AC⊥l于C,PB⊥β于B,PD⊥l于D,连CQ,BD则∠ACQ=∠PDB=60°,,又∵当且仅当AP=0,即点A与点P重合时取最小值.故选:C.【点评】本题主要考查了平面与平面之间的位置关系,以及空间中直线与平面之间的位置关系,考查空间想象能力、运算能力和推理论证能力,属于基础题.11.(5分)函数f(x)的定义域为R,若f(x+1)与f(x﹣1)都是奇函数,则()A.f(x)是偶函数B.f(x)是奇函数C.f(x)=f(x+2)D.f(x+3)是奇函数【考点】3I:奇函数、偶函数.【专题】16:压轴题.【分析】首先由奇函数性质求f(x)的周期,然后利用此周期推导选择项.【解答】解:∵f(x+1)与f(x﹣1)都是奇函数,∴函数f(x)关于点(1,0)及点(﹣1,0)对称,∴f(x)+f(2﹣x)=0,f(x)+f(﹣2﹣x)=0,故有f(2﹣x)=f(﹣2﹣x),函数f(x)是周期T=[2﹣(﹣2)]=4的周期函数.∴f(﹣x﹣1+4)=﹣f(x﹣1+4),f(﹣x+3)=﹣f(x+3),f(x+3)是奇函数.故选:D.【点评】本题主要考查奇函数性质的灵活运用,并考查函数周期的求法.12.(5分)已知椭圆C:+y2=1的右焦点为F,右准线为l,点A∈l,线段AF 交C于点B,若=3,则||=()A.B.2C.D.3【考点】K4:椭圆的性质.【专题】11:计算题;16:压轴题.【分析】过点B作BM⊥x轴于M,设右准线l与x轴的交点为N,根据椭圆的性质可知FN=1,进而根据,求出BM,AN,进而可得|AF|.【解答】解:过点B作BM⊥x轴于M,并设右准线l与x轴的交点为N,易知FN=1.由题意,故FM=,故B点的横坐标为,纵坐标为±即BM=,故AN=1,∴.故选:A.【点评】本小题考查椭圆的准线、向量的运用、椭圆的定义,属基础题.二、填空题(共4小题,每小题5分,满分20分)13.(5分)(x﹣y)10的展开式中,x7y3的系数与x3y7的系数之和等于﹣240.【考点】DA:二项式定理.【专题】11:计算题.【分析】首先要了解二项式定理:(a+b)n=C n0a n b0+C n1a n﹣1b1+C n2a n﹣2b2++C n r a n﹣r b r++C n n a0b n,各项的通项公式为:T r=C n r a n﹣r b r.然后根据题目已知求解即可.+1【解答】解:因为(x﹣y)10的展开式中含x7y3的项为C103x10﹣3y3(﹣1)3=﹣C103x7y3,含x3y7的项为C107x10﹣7y7(﹣1)7=﹣C107x3y7.由C103=C107=120知,x7y3与x3y7的系数之和为﹣240.故答案为﹣240.【点评】此题主要考查二项式定理的应用问题,对于公式:(a+b)n=C n0a n b0+C n1a n ﹣1b1+C n2a n﹣2b2++C n r a n﹣r b r++C n n a0b n,属于重点考点,同学们需要理解记忆.14.(5分)设等差数列{a n}的前n项和为S n,若S9=81,则a2+a5+a8=27.【考点】83:等差数列的性质;85:等差数列的前n项和.【分析】由s9解得a5即可.【解答】解:∵∴a5=9∴a2+a5+a8=3a5=27故答案是27【点评】本题考查前n项和公式和等差数列的性质.15.(5分)直三棱柱ABC﹣A1B1C1的各顶点都在同一球面上,若AB=AC=AA1=2,∠BAC=120°,则此球的表面积等于20π.【考点】LR:球内接多面体.【专题】11:计算题;16:压轴题.【分析】通过正弦定理求出底面外接圆的半径,设此圆圆心为O',球心为O,在RT△OBO'中,求出球的半径,然后求出球的表面积.【解答】解:在△ABC中AB=AC=2,∠BAC=120°,可得由正弦定理,可得△ABC外接圆半径r=2,设此圆圆心为O',球心为O,在RT△OBO'中,易得球半径,故此球的表面积为4πR2=20π故答案为:20π【点评】本题是基础题,解题思路是:先求底面外接圆的半径,转化为直角三角形,求出球的半径,这是三棱柱外接球的常用方法;本题考查空间想象能力,计算能力.16.(5分)若,则函数y=tan2xtan3x的最大值为﹣8.【考点】3H:函数的最值及其几何意义;GS:二倍角的三角函数.【专题】11:计算题;16:压轴题.【分析】见到二倍角2x 就想到用二倍角公式,之后转化成关于tanx的函数,将tanx看破成整体,最后转化成函数的最值问题解决.【解答】解:令tanx=t,∵,∴故填:﹣8.【点评】本题主要考查二倍角的正切,二次函数的方法求最大值等,最值问题是中学数学的重要内容之一,它分布在各块知识点,各个知识水平层面.以最值为载体,可以考查中学数学的所有知识点.三、解答题(共6小题,满分70分)17.(10分)在△ABC中,内角A、B、C的对边长分别为a、b、c,已知a2﹣c2=2b,且sinAcosC=3cosAsinC,求b.【考点】HR:余弦定理.【分析】根据正弦定理和余弦定理将sinAcosC=3cosAsinC化成边的关系,再根据a2﹣c2=2b即可得到答案.【解答】解:法一:在△ABC中∵sinAcosC=3cosAsinC,则由正弦定理及余弦定理有:,化简并整理得:2(a2﹣c2)=b2.又由已知a2﹣c2=2b∴4b=b2.解得b=4或b=0(舍);法二:由余弦定理得:a2﹣c2=b2﹣2bccosA.又a2﹣c2=2b,b≠0.所以b=2ccosA+2①又sinAcosC=3cosAsinC,∴sinAcosC+cosAsinC=4cosAsinCsin(A+C)=4cosAsinC,即sinB=4cosAsinC由正弦定理得,故b=4ccosA②由①,②解得b=4.【点评】本题主要考查正弦定理和余弦定理的应用.属基础题.18.(12分)如图,四棱锥S﹣ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD=,DC=SD=2,点M在侧棱SC上,∠ABM=60°(I)证明:M是侧棱SC的中点;(Ⅱ)求二面角S﹣AM﹣B的大小.【考点】LO:空间中直线与直线之间的位置关系;MJ:二面角的平面角及求法.【专题】11:计算题;14:证明题.【分析】(Ⅰ)法一:要证明M是侧棱SC的中点,作MN∥SD交CD于N,作NE⊥AB交AB于E,连ME、NB,则MN⊥面ABCD,ME⊥AB,设MN=x,则NC=EB=x,解RT△MNE即可得x的值,进而得到M为侧棱SC的中点;法二:分别以DA、DC、DS为x、y、z轴如图建立空间直角坐标系D﹣xyz,并求出S点的坐标、C点的坐标和M点的坐标,然后根据中点公式进行判断;法三:分别以DA、DC、DS为x、y、z轴如图建立空间直角坐标系D﹣xyz,构造空间向量,然后数乘向量的方法来证明.(Ⅱ)我们可以以D为坐标原点,分别以DA、DC、DS为x、y、z轴如图建立空间直角坐标系D﹣xyz,我们可以利用向量法求二面角S﹣AM﹣B的大小.【解答】证明:(Ⅰ)作MN∥SD交CD于N,作NE⊥AB交AB于E,连ME、NB,则MN⊥面ABCD,ME⊥AB,设MN=x,则NC=EB=x,在RT△MEB中,∵∠MBE=60°∴.在RT△MNE中由ME2=NE2+MN2∴3x2=x2+2解得x=1,从而∴M为侧棱SC的中点M.(Ⅰ)证法二:分别以DA、DC、DS为x、y、z轴如图建立空间直角坐标系D﹣xyz,则.设M(0,a,b)(a>0,b>0),则,,由题得,即解之个方程组得a=1,b=1即M(0,1,1)所以M是侧棱SC的中点.(I)证法三:设,则又故,即,解得λ=1,所以M是侧棱SC的中点.(Ⅱ)由(Ⅰ)得,又,,设分别是平面SAM、MAB的法向量,则且,即且分别令得z1=1,y1=1,y2=0,z2=2,即,∴二面角S﹣AM﹣B的大小.【点评】空间两条直线夹角的余弦值等于他们方向向量夹角余弦值的绝对值;空间直线与平面夹角的余弦值等于直线的方向向量与平面的法向量夹角的正弦值;空间锐二面角的余弦值等于他的两个半平面方向向量夹角余弦值的绝对值;(I)求甲获得这次比赛胜利的概率;(Ⅱ)设ξ表示从第3局开始到比赛结束所进行的局数,求ξ的分布列及数学期望.【考点】C8:相互独立事件和相互独立事件的概率乘法公式;CG:离散型随机变量及其分布列;CH:离散型随机变量的期望与方差.【专题】11:计算题.【分析】(1)由题意知前2局中,甲、乙各胜1局,甲要获得这次比赛的胜利需在后面的比赛中先胜两局,根据各局比赛结果相互独立,根据相互独立事件的概率公式得到结果.(2)由题意知ξ表示从第3局开始到比赛结束所进行的局数,由上一问可知ξ的可能取值是2、3,由于各局相互独立,得到变量的分布列,求出期望.【解答】解:记A i表示事件:第i局甲获胜,(i=3、4、5)B i表示第j局乙获胜,j=3、4(1)记B表示事件:甲获得这次比赛的胜利,∵前2局中,甲、乙各胜1局,∴甲要获得这次比赛的胜利需在后面的比赛中先胜两局,∴B=A3A4+B3A4A5+A3B4A5由于各局比赛结果相互独立,∴P(B)=P(A3A4)+P(B3A4A5)+P(A3B4A5)×+××+××(2)ξ表示从第3局开始到比赛结束所进行的局数,由上一问可知ξ的可能取值是2、3由于各局相互独立,得到ξ的分布列P(ξ=2)=P(A3A4+B3B4∴Eξ=2×+3×【点评】认真审题是前提,部分考生由于考虑了前两局的概率而导致失分,这是很可惜的,主要原因在于没读懂题.另外,还要注意表述,这也是考生较薄弱的环节.20.(12分)在数列{a n}中,a1=1,a n+1=(1+)a n+.(1)设b n=,求数列{b n}的通项公式;(2)求数列{a n}的前n项和S n.【考点】8E:数列的求和;8H:数列递推式.【专题】11:计算题;15:综合题.【分析】(1)由已知得=+,即b n=b n+,由此能够推导出所求的通+1项公式.(2)由题设知a n=2n﹣,故S n=(2+4+…+2n)﹣(1++++…+),设T n=1++++…+,由错位相减法能求出T n=4﹣.从而导出数列{a n}的前n项和S n.【解答】解:(1)由已知得b1=a1=1,且=+,即b n=b n+,从而b2=b1+,+1b3=b2+,b n=b n﹣1+(n≥2).于是b n=b1+++…+=2﹣(n≥2).又b1=1,故所求的通项公式为b n=2﹣.(2)由(1)知a n=2n﹣,故S n=(2+4+…+2n)﹣(1++++…+),设T n=1++++…+,①T n=+++…++,②①﹣②得,T n=1++++…+﹣=﹣=2﹣﹣,∴T n=4﹣.∴S n=n(n+1)+﹣4.【点评】本题考查数列的通项公式和前n项和的求法,解题时要注意错位相减法的合理运用.21.(12分)如图,已知抛物线E:y2=x与圆M:(x﹣4)2+y2=r2(r>0)相交于A、B、C、D四个点.(Ⅰ)求r的取值范围;(Ⅱ)当四边形ABCD的面积最大时,求对角线AC、BD的交点P的坐标.【考点】IR:两点间的距离公式;JF:圆方程的综合应用;K8:抛物线的性质.【专题】15:综合题;16:压轴题.【分析】(1)先联立抛物线与圆的方程消去y,得到x的二次方程,根据抛物线E:y2=x与圆M:(x﹣4)2+y2=r2(r>0)相交于A、B、C、D四个点的充要条件是此方程有两个不相等的正根,可求出r的范围.(2)先设出四点A,B,C,D的坐标再由(1)中的x二次方程得到两根之和、两根之积,表示出面积并求出其的平方值,最后根据三次均值不等式确定得到最大值时的点P的坐标.【解答】解:(Ⅰ)将抛物线E:y2=x代入圆M:(x﹣4)2+y2=r2(r>0)的方程,消去y2,整理得x2﹣7x+16﹣r2=0(1)抛物线E:y2=x与圆M:(x﹣4)2+y2=r2(r>0)相交于A、B、C、D四个点的充要条件是:方程(1)有两个不相等的正根∴即.解这个方程组得,.(II)设四个交点的坐标分别为、、、.则直线AC、BD的方程分别为y﹣=•(x﹣x1),y+=(x﹣x1),解得点P的坐标为(,0),则由(I)根据韦达定理有x1+x2=7,x1x2=16﹣r2,则∴令,则S2=(7+2t)2(7﹣2t)下面求S2的最大值.由三次均值有:当且仅当7+2t=14﹣4t,即时取最大值.经检验此时满足题意.故所求的点P的坐标为.【点评】本题主要考查抛物线和圆的综合问题.圆锥曲线是高考必考题,要强化复习.22.(12分)设函数f(x)=x3+3bx2+3cx有两个极值点x1、x2,且x1∈[﹣1,0],x2∈[1,2].(1)求b、c满足的约束条件,并在下面的坐标平面内,画出满足这些条件的点(b,c)的区域;(2)证明:.【考点】6D:利用导数研究函数的极值;7B:二元一次不等式(组)与平面区域;R6:不等式的证明.【专题】11:计算题;14:证明题;16:压轴题.【分析】(1)根据极值的意义可知,极值点x1、x2是导函数等于零的两个根,根据根的分布建立不等关系,画出满足条件的区域即可;(2)先用消元法消去参数b,利用参数c表示出f(x2)的值域,再利用参数c 的范围求出f(x2)的范围即可.【解答】解:(Ⅰ)f'(x)=3x2+6bx+3c,(2分)依题意知,方程f'(x)=0有两个根x1、x2,且x1∈[﹣1,0],x2∈[1,2]等价于f'(﹣1)≥0,f'(0)≤0,f'(1)≤0,f'(2)≥0.由此得b,c满足的约束条件为(4分)满足这些条件的点(b,c)的区域为图中阴影部分.(6分)(Ⅱ)由题设知f'(x2)=3x22+6bx2+3c=0,则,故.(8分)由于x2∈[1,2],而由(Ⅰ)知c≤0,故.又由(Ⅰ)知﹣2≤c≤0,(10分)所以.【点评】本题主要考查了利用导数研究函数的极值,以及二元一次不等式(组)与平面区域和不等式的证明,属于基础题.。
2009年高考上海数学试题答案(理数)

2009年普通高等学校招生全国统一考试(上海卷)理科数学本试卷分第Ⅰ卷和第Ⅱ卷两部分,共4页,满分150分,考试时间120分钟。
考试结束后,将本试卷和答题卡一并交回. 注意事项:1. 答题前,考生务必用0.5毫米黑色签字笔将自己的姓名、座号、准考证号、县区和科类填写在答题卡和试卷规定的位置上.,并将准考证号条形码粘贴在答题卡上指定位置。
2. 第Ⅰ卷每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,答案不能答在试卷上。
3. 第Ⅱ卷必须用0.5毫米黑色签字笔在答题卡各题的答题区域内作答;不能写在试题卷上; 如需改动,先画掉原来的答案,然后再写上新的答案;不能使用涂改液、胶带纸,修正带,不按以上要求作答的答案无效。
4. 填空题请直接填写答案,解答题应写出文字说明,证明过程或演算步骤。
参考公式:柱体的体积公式V=Sh ,其中S 是柱体的底面积,h 是锥体的高。
锥体的体积公式V=13Sh ,其中S 是锥体的底面积,h 是锥体的高。
注意:1.答卷前,考生务必在答题纸上将学校、班级、姓名、考号填写清楚. 2.本试卷共有23道试题,满分150分,考试时间120分钟.一、填空题(本大题满分56分)本大题共有14题,考生应在答题纸编号的空格内直接填写结果,每个空格填对得4分,否则一律得零分.1.已知函数)0(1)(2≥+=x x x f 的反函数为1()f x -,则=-)5(1f __________.2.椭圆15922=+y x 的焦点坐标为____________. 3.方向向量为(3,4)d =,且过点)1,1(A 的直线l 的方程是__________.4.若0)1(lim =-∞→nn a ,则实数a 的取值范围是__________.5.某个线性方程组的增广矩阵是⎪⎪⎭⎫⎝⎛110201,此方程组的解记为),(b a ,则行列式123212a b 的值是__________. 6.某校师生共1200人,其中学生1000人,教师200人。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2009年上海市高考数学试卷(理科)参考答案与试题解析一、填空题(共14小题,每小题4分,满分56分)1.(4分)(2009•上海)若复数z满足z(1+i)=1﹣i(I是虚数单位),则其共轭复数=i.【考点】复数的基本概念;复数代数形式的乘除运算.【专题】计算题.【分析】本题考查的知识点是共轭复数的定义,由复数z满足z(1+i)=1﹣i,我们可能使用待定系数法,设出z,构造方程,求出z值后,再根据共轭复数的定义,计算【解答】解:设z=a+bi,则∵(a+bi)(1+i)=1﹣i,即a﹣b+(a+b)i=1﹣i,由,解得a=0,b=﹣1,所以z=﹣i,=i,故答案为i.【点评】求复数的共轭复数一般步骤是:先利用待定系数法设出未知的向量,根据已知条件构造复数方程,根据复数相等的充要条件,转化为一个实数方程组,进而求出求知的复数,再根据共轭复数的定义,求出其共轭复数.2.(4分)(2009•上海)已知集合A={x|x≤1},B={x|x≥a},且A∪B=R,则实数a的取值范围是a≤1.【考点】集合关系中的参数取值问题.【专题】集合.【分析】利用数轴,在数轴上画出集合,数形结合求得两集合的并集.【解答】解:∵A={x|x≤1},B={x|x≥a},且A∪B=R,如图,故当a≤1时,命题成立.故答案为:a≤1.【点评】本题属于以数轴为工具,求集合的并集的基础题,也是高考常会考的题型.3.(4分)(2009•上海)若行列式中,元素4的代数余子式大于0,则x满足的条件是x>且x≠4.【考点】三阶矩阵.【专题】计算题.【分析】根据3阶行列式D的元素a ij的余子式M ij附以符号(﹣1)i+j后,叫做元素a ij的代数余子式,所以4的余子式加上(﹣1)1+1即为元素4的代数余子式,让其大于0列出关于x的不等式,求出不等式的解集即可得到x的范围.【解答】解:依题意得,(﹣1)2>0,即9x﹣24>0,解得x>,且x≠4,故答案为:x>且x≠4【点评】此题考查学生掌握三阶矩阵的代数余子式的定义,是一道基础题.4.(4分)(2009•上海)某算法的程序框如下图所示,则输出量y与输入量x满足的关系式是.【考点】程序框图.【分析】根据流程图所示的顺序,逐框分析程序中各变量、各语句的作用可知:该程序的作用是根据输入x值的不同,根据不同的式子计算函数值.即求分段函数的函数值.【解答】解:根据流程图所示的顺序,程序的作用是分段函数的函数值.其中输出量y与输入量x满足的关系式是故答案为:【点评】根据流程图(或伪代码)写程序的运行结果,是算法这一模块最重要的题型,其处理方法是::①分析流程图(或伪代码),从流程图(或伪代码)中既要分析出计算的类型,又要分析出参与计算的数据(如果参与运算的数据比较多,也可使用表格对数据进行分析管理)⇒②建立数学模型,根据第一步分析的结果,选择恰当的数学模型③解模.5.(4分)(2009•上海)如图,若正四棱柱ABCD﹣A1B1C1D1的底面边长为2,高为4,则异面直线BD1与AD所成角的大小是arctan(结果用反三角函数值表示).【考点】异面直线及其所成的角.【专题】计算题.【分析】先通过平移将两条异面直线平移到同一个起点,得到的锐角或直角就是异面直线所成的角,在直角三角形中求出正切值,再用反三角函数值表示出这个角即可.【解答】解:先画出图形将AD平移到BC,则∠D1BC为异面直线BD1与AD所成角,BC=2,D1C=,tan∠D1BC=,∴∠D1BC=arctan,故答案为arctan.【点评】本题主要考查了异面直线及其所成的角,以及解三角形的应用,属于基础题.6.(4分)(2009•上海)函数y=2cos2x+sin2x的最小值是.【考点】三角函数的最值.【专题】计算题.【分析】先利用三角函数的二倍角公式化简函数,再利用公式化简三角函数,利用三角函数的有界性求出最小值.【解答】解:y=2cos2x+sin2x=1+cos2x+sin2x=1+=1+当=2k,有最小值1﹣故答案为1﹣【点评】本题考查三角函数的二倍角余弦公式将三角函数降幂、利用公式化简三角函数.7.(4分)(2009•上海)某学校要从5名男生和2名女生中选出2人作为上海世博会志愿者,若用随机变量ξ表示选出的志愿者中女生的人数,则数学期望Eξ(结果用最简分数表示).【考点】离散型随机变量的期望与方差.【专题】计算题.【分析】用随机变量ξ表示选出的志愿者中女生的人数,ξ可取0,1,2,结合变量对应的事件写出分布列当ξ=0时,表示没有选到女生;当ξ=1时,表示选到一个女生;当ξ=2时,表示选到2个女生,求出期望.【解答】解:用随机变量ξ表示选出的志愿者中女生的人数,ξ可取0,1,2,当ξ=0时,表示没有选到女生;当ξ=1时,表示选到一个女生;当ξ=2时,表示选到2个女生,∴P(ξ=0)==,P(ξ=1)=,P(ξ=2)=,∴Eξ=0×=.故答案为:【点评】本题考查离散型随机变量的分布列和期望,这是近几年经常出现的一个问题,可以作为解答题出现,考查的内容通常是以分布列和期望为载体,有时要考查其他的知识点.8.(4分)(2009•上海)已知三个球的半径R1,R2,R3满足R1+2R2=3R3,则它们的表面积S1,S2,S3,满足的等量关系是.【考点】球的体积和表面积.【专题】计算题.【分析】表示出三个球的表面积,求出三个半径,利用R1+2R2=3R3,推出结果.【解答】解:因为S1=4πR12,所以,同理:,即R1=,R2=,R3=,由R1+2R2=3R3,得故答案为:【点评】本题考查球的表面积,考查计算能力,是基础题.9.(4分)(2009•上海)已知F1、F2是椭圆C:(a>b>0)的两个焦点,P为椭圆C上一点,且.若△PF1F2的面积为9,则b=3.【考点】椭圆的应用;椭圆的简单性质.【专题】圆锥曲线的定义、性质与方程.【分析】由已知得|PF1|+|PF2|=2a,=4c2,,由此能得到b的值.【解答】解:∵F1、F2是椭圆C:(a>b>0)的两个焦点,P为椭圆C上一点,且.∴|PF1|+|PF2|=2a,=4c2,,∴(|PF1|+|PF2|)2=4c2+2|PF1||PF2|=4a2,∴36=4(a2﹣c2)=4b2,∴b=3.故答案为3.【点评】主要考查椭圆的定义、基本性质和平面向量的知识.10.(4分)(2009•上海)在极坐标系中,由三条直线θ=0,,ρcosθ+ρsinθ=1围成图形的面积等于.【考点】简单曲线的极坐标方程;定积分.【专题】计算题.【分析】三条直线化为直角坐标方程,求出三角形的边长,然后求出图形的面积.【解答】解:三条直线θ=0,,ρcosθ+ρsinθ=1的直角坐标方程分别为:y=0,y=x,x+y=1,所以它们的交点坐标分别为O(0,0),A(1,0),B(,),OB==,由三条直线θ=0,,ρcosθ+ρsinθ=1围成图形的面积S==.故答案为:.【点评】本题考查极坐标与直角坐标的互化,三角形的面积的求法,考查计算能力.11.(4分)(2009•上海)当时,不等式sinπx≥kx恒成立.则实数k的取值范围是k≤2.【考点】函数恒成立问题.【专题】数形结合.【分析】要使不等式sinπx≥kx恒成立,设m=sinπx,n=kx,利用图象得到k的范围即可.【解答】解:设m=sinπx,n=kx,x∈[0,].根据题意画图得:m≥n恒成立即要m的图象要在n图象的上面,当x=时即πx=时相等,所以此时k==2,所以k≤2故答案为k≤2【点评】考查学生利用数形结合的数学思想解决问题的能力,理解函数恒成立时取条件的能力.12.(4分)(2009•上海)已知函数f(x)=sinx+tanx,项数为27的等差数列{a n}满足a n∈(﹣),且公差d≠0,若f(a1)+f(a2)+…f(a27)=0,则当k=14时,f(a k)=0.【考点】函数奇偶性的性质.【专题】计算题;压轴题.【分析】本题考查的知识点是函数的奇偶性及对称性,由函数f(x)=sin x+tan x,项数为27的等差数列{a n}满足a n∈(﹣),且公差d≠0,若f(a1)+f(a2)+…f(a27)=0,我们易得a1,a2,…,a27前后相应项关于原点对称,则f(a14)=0,易得k值.【解答】解:因为函数f(x)=sinx+tanx是奇函数,所以图象关于原点对称,图象过原点.而等差数列{a n}有27项,a n∈().若f(a1)+f(a2)+f(a3)+…+f(a27)=0,则必有f(a14)=0,所以k=14.故答案为:14【点评】代数的核心内容是函数,函数的定义域、值域、性质均为高考热点,所有要求同学们熟练掌握函数特别是基本函数的图象和性质,并能结合平移、对称、伸缩、对折变换的性质,推出基本函数变换得到的函数的性质.13.(4分)(2009•上海)某地街道呈现东﹣西、南﹣北向的网格状,相邻街距都为1.两街道相交的点称为格点.若以互相垂直的两条街道为轴建立直角坐标系,现有下述格点(﹣2,2),(3,1),(3,4),(﹣2,3),(4,5),(6,6)为报刊零售点.请确定一个格点(除零售点外)(3,3)为发行站,使6个零售点沿街道到发行站之间路程的和最短.【考点】两点间距离公式的应用.【专题】直线与圆.【分析】设发行站的位置为(x,y),则可利用两点间的距离公式表示出零售点到发行站的距离,进而求得在(3,3)处z取得最小值.【解答】解:设发行站的位置为(x,y),6个零售点到发行站的距离为Z,则z=|x+2|+|y﹣2|+|x﹣3|+|y﹣1|+|x﹣3|+|y﹣4|+|x+1|+|y﹣3|+|x﹣4|+|y﹣5|+|x﹣6|+|y﹣6|=|x+2|+|x﹣3|+|x﹣3|+|x+1|+|x﹣4|+|x﹣6|+|y﹣2|+|y﹣1|+|y﹣4|+|y﹣3|+|y﹣5|+|y﹣6|x=3,3≤y<4时,取最小值,∴在(3,3)处z取得最小值.故答案为(3,3).【点评】本题主要考查了两点间的距离公式的应用.考查了学生创造性思维能力和逻辑思维能力.14.(4分)(2009•上海)将函数(x∈[0,6])的图象绕坐标原点逆时针方向旋转角θ(0≤θ≤α),得到曲线C.若对于每一个旋转角θ,曲线C都是一个函数的图象,则α的最大值为arctan.【考点】旋转变换.【专题】计算题;压轴题.【分析】先画出函数(x∈[0,6])的图象,然后根据由图可知当此圆弧绕坐标原点逆时针方向旋转角大于∠MAB时,曲线C都不是一个函数的图象,求出此角即可.【解答】解:先画出函数(x∈[0,6])的图象这是一个圆弧,圆心为M(3,﹣2)由图可知当此圆弧绕坐标原点逆时针方向旋转角大于∠MAB时,曲线C都不是一个函数的图象∴∠MAB=arctan故答案为:arctan【点评】本题主要考查了旋转变换,同时考查了数形结合的思想和分析问题解决问题的能力,属于基础题.二、选择题(共4小题,每小题4分,满分16分)15.(4分)(2009•上海)“﹣2≤a≤2”是“实系数一元二次方程x2+ax+1=0有虚根”的()A.必要不充分条件B.充分不必要条件C.充要条件 D.既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断.【分析】实系数一元二次方程x2+ax+1=0有虚根⇒△=a2﹣4<0⇒﹣2<a<2,由此入手能够作出正确选择.【解答】解:∵实系数一元二次方程x2+ax+1=0有虚根,∴△=a2﹣4<0,解得﹣2<a<2,∴“﹣2≤a≤2”是“﹣2<a<2”的必要不充分条件,故选A.【点评】本题考查必要条件、充分条件和充要条件的应用,解题时要认真审题,仔细解答.16.(4分)(2009•上海)若事件E与F相互独立,且P(E)=P(F)=,则P(E∩F)的值等于()A.0 B.C.D.【考点】相互独立事件的概率乘法公式.【分析】本题考查的知识点是相互独立事件的概率乘法公式,由相互独立事件的概率计算公式,我们易得P(E∩F)=P(E)•P(F),将P(E)=P(F)=代入即可得到答案.【解答】解:P(E∩F)=P(E)•P(F)=×=.故选B.【点评】相互独立事件的概率计算公式:P(E∩F)=P(E)•P(F),P(E∪F)=P(E)+P(F).17.(4分)(2009•上海)有专业机构认为甲型N1H1流感在一段时间没有发生大规模群体感染的标志为“连续10天,每天新增疑似病例不超过15人”.根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是()A.甲地:总体均值为3,中位数为4B.乙地:总体均值为1,总体方差大于0C.丙地:中位数为2,众数为3D.丁地:总体均值为2,总体方差为3【考点】众数、中位数、平均数;极差、方差与标准差.【专题】压轴题.【分析】平均数和方差都是重要的数字特征,是对总体的一种简单的描述,平均数描述集中趋势,方差描述波动大小.【解答】解:假设连续10天,每天新增疑似病例的人数分别为x1,x2,x3,…x10.并设有一天超过15人,不妨设第一天为16人,根据计算方差公式有s2=[(16﹣5)2+(x2﹣5)2+(x3﹣5)2+…+(x10﹣5)2]>12,说明乙地连续10天,每天新增疑似病例的人数都不超过15人.故选:B.【点评】根据题意可知本题主要考查用数字特征估计总体,属于基础题.18.(4分)(2009•上海)过圆C:(x﹣1)2+(y﹣1)2=1的圆心,作直线分别交x、y正半轴于点A、B,△AOB被圆分成四部分(如图),若这四部分图形面积满足S|+S IV=S||+S|||则直线AB有()A.0条B.1条C.2条D.3条【考点】直线与圆的位置关系.【专题】综合题;压轴题;数形结合.【分析】由圆的方程得到圆心坐标和半径,根据四部分图形面积满足S|+S IV=S||+S|||,得到S IV﹣S II=SⅢ﹣S I,第II,IV部分的面积是定值,所以三角形FCB减去三角形ACE的面积为定值即SⅢ﹣S I为定值,所以得到满足此条件的直线有且仅有一条,得到正确答案.【解答】解:由已知,得:S IV﹣S II=SⅢ﹣S I,由图形可知第II,IV部分的面积分别为S正方形OECF﹣S扇形ECF=1﹣和S扇形ECF=,所以,S IV﹣S II为定值,即SⅢ﹣S I为定值,当直线AB绕着圆心C移动时,只可能有一个位置符合题意,即直线AB只有一条.故选B.【点评】此题考查学生掌握直线与圆的位置关系,会求三角形、正方形及扇形的面积,是一道综合题.三、解答题(共5小题,满分78分)19.(14分)(2009•上海)如图,在直三棱柱ABC﹣A1B1C1中,AA1=BC=AB=2,AB⊥BC,求二面角B1﹣A1C﹣C1的大小.【考点】向量在几何中的应用;与二面角有关的立体几何综合题.【专题】计算题;向量法.【分析】建立空间直角坐标系,求出2个平面的法向量的坐标,设二面角的大小为θ,显然θ为锐角,设2个法向量的夹角φ,利用2个向量的数量积可求cosφ,则由cosθ=|cosφ|求出二面角的大小θ.【解答】解:如图,建立空间直角坐标系.则A(2,0,0),C(0,2,0),A1(2,0,2),B1(0,0,2),C1(0,2,2),设AC的中点为M,∵BM⊥AC,BM⊥CC1.∴BM⊥平面A1C1C,即=(1,1,0)是平面A1C1C的一个法向量.设平面A1B1C的一个法向量是n=(x,y,z).=(﹣2,2,﹣2),=(﹣2,0,0),∴令z=1,解得x=0,y=1.∴n=(0,1,1),设法向量n与的夹角为φ,二面角B1﹣A1C﹣C1的大小为θ,显然θ为锐角.∵cosθ=|cosφ|==,解得:θ=.∴二面角B1﹣A1C﹣C1的大小为.【点评】本题考查利用向量求二面角的大小的方法,设二面角的大小为θ,2个平面法向量的夹角φ,则θ和φ相等或互补,这两个角的余弦值相等或相反.20.(16分)(2009•上海)有时可用函数f(x)=,描述学习某学科知识的掌握程度.其中x表示某学科知识的学习次数(x∈N*),f(x)表示对该学科知识的掌握程度,正实数a与学科知识有关.(1)证明:当x≥7时,掌握程度的增长量f(x+1)﹣f(x)总是下降;(2)根据经验,学科甲、乙、丙对应的a的取值区间分别为(115,121],(121,127],(127,133].当学习某学科知识6次时,掌握程度是85%,请确定相应的学科.【考点】分段函数的应用.【专题】应用题;探究型;数学模型法.【分析】(1)x≥7时,作差求出增长量f(x+1)﹣f(x),研究其单调性知,差是一个减函数,故掌握程度的增长量总是下降、(2)学习某学科知识6次时,掌握程度是85%,故得方程由此方程解出a的值即可确定相应的学科.【解答】证明:(1)当x≥7时,而当x≥7时,函数y=(x﹣3)(x﹣4)单调递增,且(x﹣3)(x﹣4)>0故函数f(x+1)﹣f(x)单调递减当x≥7时,掌握程度的增长量f(x+1)﹣f(x)总是下降(2)由题意可知整理得解得(13分)由此可知,该学科是乙学科..(14分)【点评】本题是分段函数在实际问题中的应用,在实际问题中,分段函数是一个很重要的函数模型.21.(16分)(2009•上海)已知双曲线,设直线l过点,(1)当直线l与双曲线C的一条渐近线m平行时,求直线l的方程及l与m的距离;(2)证明:当k>时,在双曲线C的右支上不存在点Q,使之到直线l的距离为.【考点】双曲线的简单性质.【专题】计算题;证明题.【分析】(1)先求出双曲线的渐近线方程,进而可得到直线l的斜率,然后根据直线l过点求出直线l的方程,再由平行线间的距离公式可求直线l的方程及l与m 的距离.(2)设过原点且平行于l的直线方程利用直线与直线的距离求得l与b的距离,当k>时,可推断出,利用双曲线的渐近线方程可知双曲线C的右支在直线b的右下方,进而推断出双曲线C的右支上的任意点到直线l的距离大于,进而可知故在双曲线C的右支上不存在点Q(x0,y0)到到直线l的距离为.【解答】解:(1)双曲线C的渐近线,即∴直线l的方程∴直线l与m的距离.(2)设过原点且平行于l的直线b:kx﹣y=0,则直线l与b的距离d=,当时,.又双曲线C的渐近线为,∴双曲线C的右支在直线b的右下方,∴双曲线C的右支上的任意点到直线l的距离大于.故在双曲线C的右支上不存在点Q(x0,y0)到到直线l的距离为.【点评】本题主要考查了双曲线的简单性质.考查了学生综合分析问题和解决问题的能力.22.(16分)(2009•上海)已知函数y=f(x)的反函数.定义:若对给定的实数a(a≠0),函数y=f(x+a)与y=f﹣1(x+a)互为反函数,则称y=f(x)满足“a和性质”;若函数y=f(ax)与y=f﹣1(ax)互为反函数,则称y=f(x)满足“a积性质”.(1)判断函数g(x)=x2+1(x>0)是否满足“1和性质”,并说明理由;(2)求所有满足“2和性质”的一次函数;(3)设函数y=f(x)(x>0)对任何a>0,满足“a积性质”.求y=f(x)的表达式.【考点】反函数;函数解析式的求解及常用方法.【专题】压轴题;新定义.【分析】(1)先求出g﹣1(x)的解析式,换元可得g﹣1(x+1)的解析式,将此解析式与g (x+1)的作对比,看是否满足互为反函数.(2)先求出f﹣1(x)的解析式,再求出f﹣1(x+2)的解析式,再由f(x+2)的解析式,求出f﹣1(x+2)的解析式,用两种方法得到的f﹣1(x+2)的解析式应该相同,解方程求得满足条件的一次函数f(x)的解析式.(3)设点(x0,y0)在y=f(ax)图象上,则(y0,x0)在函数y=f﹣1(ax)图象上,可得ay0=f (x0)=af(ax0),,即,即满足条件.【解答】解(1)函数g(x)=x2+1(x>0)的反函数是,∴,而g(x+1)=(x+1)2+1(x>﹣1),其反函数为,故函数g(x)=x2+1(x>0)不满足“1和性质”.(2)设函数f(x)=kx+b(x∈R)满足“2和性质”,k≠0.∴,∴,而f(x+2)=k(x+2)+b(x∈R),得反函数,由“2和性质”定义可知,对(x∈R)恒成立.∴k=﹣1,b∈R,即所求一次函数f(x)=﹣x+b(b∈R).(3)设a>0,x0>0,且点(x0,y0)在y=f(ax)图象上,则(y0,x0)在函数y=f﹣1(ax)图象上,故,可得ay0=f(x0)=af(ax0),令ax0=x,则,∴,即.综上所述,,此时,其反函数是,而,故y=f(ax)与y=f﹣1(ax)互为反函数.【点评】本题考查反函数的求法,函数与反函数的图象间的关系,体现了换元的思想,属于中档题.23.(16分)(2009•上海)已知{a n}是公差为d的等差数列,{b n}是公比为q的等比数列.(1)若a n=3n+1,是否存在m、k∈N*,有a m+a m+1=a k?说明理由;(2)找出所有数列{a n}和{b n},使对一切n∈N*,,并说明理由;(3)若a1=5,d=4,b1=q=3,试确定所有的p,使数列{a n}中存在某个连续p项的和是数列{b n}中的一项,请证明.【考点】等差数列与等比数列的综合;等差数列的性质;数列递推式.【专题】综合题;压轴题;分类讨论;转化思想.【分析】(1)由a m+a m+1=a k,得6m+5=3k+1,,由m、k∈N*,知k﹣2m为整数,所以不存在m、k∈N*,使等式成立.(2)设a n=nd+c,若,对n∈N×都成立,且{b n}为等比数列,则,对n∈N×都成立,由此入手能够导出有a n=c≠0,b n=1,使对一切n∈N×,.(3)a n=4n+1,b n=3n,n∈N*,设a m+1+a m+2++a m+p=b k=3k,p、k∈N*,m∈N.4m+2p+3+,由p、k∈N*,知p=3s,s∈N.由此入手能导出当且仅当p=3s,s∈N,命题成立.【解答】解:(1)由a m+a m+1=a k,得6m+5=3k+1,整理后,可得,∵m、k∈N*,∴k﹣2m为整数,∴不存在m、k∈N*,使等式成立.(2)设a n=nd+c,若,对n∈N×都成立,且{b n}为等比数列,则,对n∈N×都成立,即a n a n+2=qa n+12,∴(dn+c)(dn+2d+c)=q(dn+d+c)2,对n∈N×都成立,∴d2=qd2(i)若d=0,则a n=c≠0,∴b n=1,n∈N*.(ii)若d≠0,则q=1,∴b n=m(常数),即=m,则d=0,矛盾.综上所述,有a n=c≠0,b n=1,使对一切n∈N×,.(3)a n=4n+1,b n=3n,n∈N*,设a m+1+a m+2++a m+p=b k=3k,p、k∈N*,m∈N.,∴,∵p、k∈N*,∴p=3s,s∈N取k=3s+2,4m=32s+2﹣2×3s﹣3=(4﹣1)2s+2﹣2×(4﹣1)s﹣3≥0,由二项展开式可得整数M1、M2,使得(4﹣1)2s+2=4M1+1,2×(4﹣1)s=8M2+(﹣1)S2∴4m=4(M1﹣2M2)﹣((﹣1)S+1)2,∴存在整数m满足要求.故当且仅当p=3s,s∈N,命题成立.【点评】本题考查数列的性质和应用,解题时要认真审题,仔细解答,注意公式的灵活运用.。
