微积分定积分练习题(有答案)

合集下载

微积分练习题(含答案)

练习题第六章定积分1．1()(2(0)xF x dt x =->⎰的单调增加区间为_____. 1(,)4+∞2．函数0()xt F x te dt -=⎰在点x =____处有极值. 03．设sin 201()sin ,()sin 2x f x t dt g x x x ==-⎰，则当0x →时有( A ). (A) ()~()f x g x (B) ()f x 与()g x 同阶，但()f x 不等价于()g x (C) ()(())f x o g x = (D) ()(())g x o f x =4．计算3523220sin sin 2sin cos . []3515x x x xdx ππ⋅-=⎰5．计算21e ⎰1)6.求函数dt t t x x I )ln 1(1)(-=⎰在],1[e 上的最大值与最小值. 最大值()3412-e ，最小值07.设函数⎪⎩⎪⎨⎧≥=<<-+01 2cos 110 )(2x xx xe x f x ，计算⎰-41)2(dx x f .()11tan 214-+e 8.2sin ()xt dt tπ'=⎰( C ) (其中2x π>).(A)sin x x (B)sin xC x+ (C)sin 2x x π- (D) sin 2x C x π-+ 9. 设()f x 是连续函数,且3()x f t dt x =⎰,则(8)f =_____.11210. xdt t x x cos 1)sin 1ln(lim-+⎰→=___1__ ；)1ln(cos lim202x tdtx x +⎰→=__1__ .11. 设()()()bad d I f x dx f x dx f x dx dx dx '=+-⎰⎰⎰存在,则(C ). (A) ()I f x = (B) ()I f x C =+ (C) I C = (D) 0I =12. 已知1(2),(2)02f f '==，及20()1f x dx =⎰，则120(2)x f x dx ''⎰ = 0__ .13. 若sin 0()cos xf t dt x x =+⎰(0)2x π<<，则()f x ___.第五章不定积分1. 若()()F u f u '=,则(sin )cos f x xdx =⎰__ _. (sin )F x C +2. 若()sin 2,f x dx x C =+⎰则()f x =__ _. 2cos 2x3.2()1xf x dx C x =+-⎰,则sin (cos )xf x dx =⎰_ __. 2cos sin x C x-+ 4. 若()()f u du F u C =+⎰.则211()f dx x x⋅=⎰__ _. 1()F C x -+5.求sin cos sin cos x xdx x x -=+⎰_____. ln sin cos x x C -++6. 求ln(ln )x dx x ⎰. ln (ln ln 1)x x C -+7. 已知()f x 的一个原函数为xe -,求(2)xf x dx '⎰. 211()22x e x C--++8.计算⎰+dx xx2cos 12. tan ln cos x x x C ++9.求dx ex⎰-11. ln 1xx e C --+10.计算⎰+dx x xe x2)1(. 1xx xe e C x -+++ 11.计算 ⎰++dx x xx )1(21222. 1arctan x C x-++ 12.求⎰dx x x 2sin 2cos 2. 12sin 2Cx -+13.求ln(x x C -+第四章导数应用1.计算极限（1）0ln lim ln sin x xx+→=___1___. （2） cot20lim(1)xx x →+ =___2e ___(3) 01lim(ln )xx x +→=___1___ (4) sin 0lim(cot)x x +→ =__1__(5) +1ln(1)lim arccot x x x →∞+=___1___2. 函数()(1)(2)(3)(4)f x x x x x x =----的二阶导函数有_____个零点. 33. 下列极限计算中,不能使用罗必塔法则的是( B ). (A) 111lim xx x-→ (B)201sinlimsin x x x x→(C) limx lim ln x x ax x a→+∞-+4. 设()y f x =满足方程sin 0xy y e'''+-=,且0()0f x '=,则()f x 在( A ).(A) 0x 处取得极小值 (B) 0x 处取得极大值 (C) 0x 的某个邻域内单调增加 (D) 0x 的某个邻域内单调减少 5. 若()f x 与()g x 可导，lim ()lim ()0x ax af xg x →→==，且()lim()x af x Ag x →=，则( C ). (A)必有()lim()x af x Bg x →'='存在，且A B = (B) 必有()lim()x af x Bg x →'='存在，且A B ≠ (C) 如果()lim()x af x Bg x →'='存在，则A B = (D) 如果()lim()x af x Bg x →'='存在，不一定有A B = 6. 设偶函数()f x 具有连续的二阶导数，且()0f x ''≠，则0x =( B ). (A) 不是函数()f x 的驻点(B) 一定是函数()f x 的极值点(C) 一定不是函数()f x 的极值点 (D) 是否为函数()f x 的极值点还不能确定7.求曲线22x y -=的单调区间、极值、拐点并研究图形的凹向.8.求函数32)1()4()(+⋅-=x x x f 的极值和拐点并讨论函数图形的单调性与凹向.9. 证明不等式：13(0)x x≥->.10. 证明方程5510x x -+=在(0,1)内有且仅有一个实根. (提示：设5()51f x x x =-+,利用零点存在定理和罗尔中值定理.) 11. 证明不等式：ln(1)1xx x x<+<+ (0x >). (提示：对()ln(1)f t t =+在[0,]x 上使用拉格朗日中值定理.)第三章导数1．设函数()f x 依次是,,sin x ne x x ,则()()n fx =____ ,!,sin()2x ne n x π+.2．若直线12y x b =+是抛物线2y x =在某点处的法线,则b =_____.32 3．设)(x f 是可导函数，则220()()limx f x x f x x∆→+∆-=∆( D ).(A) 0 (B) 2()f x (C) 2()f x ' (D) 2()()f x f x '4．若0()sin 20ax e x f x b x x ⎧<=⎨+≥⎩ 在0x = 处可导,则,a b 值应为( A ).(A) 2,1a b == (B) 1,2a b == (C) 2,1a b =-= (D) 1,2a b ==- 5.设函数()y f x =有01()3f x '=,则0x ∆→ 时,该函数在0x x =的微分dy 是( B ).(A) 与x ∆等价的无穷小(B) 与x ∆同价的无穷小,但不是等价无穷小 (C) 比x ∆低阶的无穷小 (D) 比x ∆高阶的无穷小6.曲线21y ax =+在点1x =处的切线与直线112y x =+垂直,则a =__ _. -1 7.设()2xf x =,则0()(0)limx f x f x→''-=____. 2ln 28.)(x f =21sin00x x xx ⎧≠⎪⎨⎪=⎩ 在点x=0处 D .A.连续且可导B.连续，不可导C.不连续D .可导，但导函数不连续9.设()f x ''存在，求函数()f x y e-=的二阶导数. ()2[(())()]f x y ef x f x -'''''=-10.2ln(1)x y e =+，求dy . 2222ln(1)1x xx e x dy e dx dx e⋅'=+=+.11.arctanyxe =确定y 是x 的函数，求导数x y '.第一、二章函数极限与连续1. )(x f 定义域是[2，3]，则)9(2x f -的定义域是___. ]5,5[-2. 设x x g -=2)(，当1≠x 时，[]1)(-=x xx g f ，则=)23(f _ _. -13. 设函数)(x f 和)(x g ，其中一个是偶函数，一个是奇函数，则必有( D ). (A))()()()(x g x f x g x f -=-+- (B) )()()()(x g x f x g x f +-=-+-(C) )()()()(x g x f x g x f ⋅=-⋅- (D) )()()()(x g x f x g x f ⋅-=-⋅-4．()()()10201521213lim16x x x x →∞+++. 53()25．()()111lim 13352121n n n →∞⎛⎫+++⎪ ⎪••-+⎝⎭. 12 6. 231sin 53limxx x x -∞→. 37. 设⎪⎪⎪⎩⎪⎪⎪⎨⎧>=<+=0sin01)1()(1x e x x x x x x f x ，求)(lim 0x f x →. e8. 0x →512。

数学必修二：微积分中的定积分习题答案

数学必修二：微积分中的定积分习题答案在微积分学习的过程中，掌握定积分的概念和求解方法是非常重要的。

本文将提供一些关于定积分的习题，并给出详细的解答，帮助读者更好地理解和掌握定积分的应用。

一、基础习题1. 求函数f(x)=2x的定积分∫[1, 3] 2x dx的值。

解答：利用定积分的定义，首先求出原函数F(x) = x^2，在[1, 3]范围内，F(3) - F(1)即为所求的定积分的值。

F(x) = x^2∫[1, 3] 2x dx = [x^2]1^3 = 3^2 - 1^2 = 8。

2. 计算定积分∫[-2, 2] |x| dx。

解答：分段函数|x|的定义为：当x≥0时，|x| = x；当x<0时，|x| = -x。

所以在[-2, 2]范围内，|x|可分为两个部分，负值和正值。

∫[-2, 2] |x| dx = ∫[-2, 0] -x dx + ∫[0, 2] x dx。

根据定积分的性质，负号可以提出定积分符号外，所以上式等于：= -∫[-2, 0] x dx + ∫[0, 2] x dx。

根据定积分的定义，∫[-2, 0] x dx = [x^2/2]_(-2)^0 = (0^2/2) - ((-2)^2/2) = 2。

同样，∫[0, 2] x dx = [x^2/2]_0^2 = 2^2/2 - 0^2/2 = 2。

将上述结果代入原式得：-∫[-2, 0] x dx + ∫[0, 2] x dx = -2 + 2 = 0。

二、综合习题1. 求函数f(x) = x^3 - 2x在[-1, 2]上的定积分。

解答：首先求出原函数F(x)，F(x) = （x^4/4） - (x^2)。

∫[-1, 2] (x^3 - 2x)dx = [（x^4/4） - (x^2)]_(-1)^2。

将x代入方程得：= （2^4/4） - (2^2) - [(-1)^4/4] - [(-1)^2] = 8/4 - 4 - 1/4 - 1。

微积分练习题及答案

微积分练习题及答案微积分练习题及答案微积分是数学中的一门重要学科，它研究的是函数的变化规律和求解各种问题的方法。

在学习微积分的过程中，练习题是非常重要的，它能够帮助我们巩固知识、提高技能。

下面，我将为大家提供一些微积分的练习题及其答案，希望能够对大家的学习有所帮助。

一、求导练习题1. 求函数f(x) = x^3 + 2x^2 - 3x + 1的导数。

答案：f'(x) = 3x^2 + 4x - 32. 求函数g(x) = e^x * sin(x)的导数。

答案：g'(x) = e^x * sin(x) + e^x * cos(x)3. 求函数h(x) = ln(x^2 + 1)的导数。

答案：h'(x) = (2x) / (x^2 + 1)二、定积分练习题1. 计算定积分∫[0, 1] (x^2 + 1) dx。

答案：∫[0, 1] (x^2 + 1) dx = (1/3)x^3 + x ∣[0, 1] = (1/3) + 1 - 0 = 4/32. 计算定积分∫[1, 2] (2x + 1) dx。

答案：∫[1, 2] (2x + 1) dx = x^2 + x ∣[1, 2] = 4 + 2 - 1 - 1 = 43. 计算定积分∫[0, π/2] sin(x) dx。

答案：∫[0, π/2] sin(x) dx = -cos(x) ∣[0, π/2] = -cos(π/2) + cos(0) = 1三、微分方程练习题1. 求解微分方程dy/dx = 2x。

答案：对方程两边同时积分，得到y = x^2 + C，其中C为常数。

2. 求解微分方程dy/dx = e^x。

答案：对方程两边同时积分，得到y = e^x + C，其中C为常数。

3. 求解微分方程d^2y/dx^2 + 2dy/dx + y = 0。

答案：设y = e^(mx)，代入方程得到m^2 + 2m + 1 = 0，解得m = -1。

定积分与微积分练习题及答案

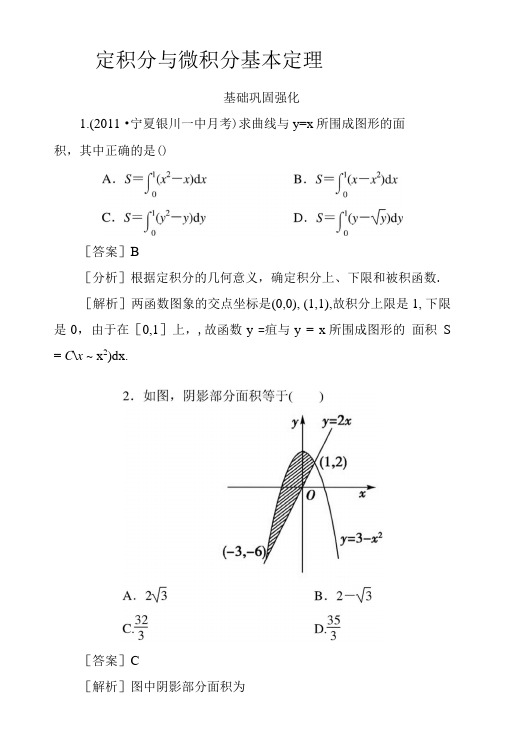
定积分与微积分练习题及答案一、选择题：1如图，阴影部分面积等于( )A ．2 3B ．2－ 3 C.323 D.353[答案] C[解析] 图中阴影部分面积为S ＝⎠⎛-31 (3－x2－2x)dx ＝(3x －13x3－x2)|1－3＝323.2.⎠⎛024－x2dx ＝( )A ．4πB ．2πC ．πD.π2[答案] C[解析] 令y ＝4－x2，则x2＋y2＝4(y≥0)，由定积分的几何意义知所求积分为图中阴影部分的面积，∴S ＝14×π×22＝π.3．(2012·山东日照模拟)向平面区域Ω＝{(x ，y)|－π4≤x≤π4，0≤y≤1}内随机投掷一点，该点落在曲线y ＝cos2x 下方的概率是( )A.π4B.12C.π2－1D.2π[答案] D[解析] 平面区域Ω是矩形区域，其面积是π2，在这个区4．设f(x)＝⎩⎪⎨⎪⎧x2， x ∈[0，1]，2－x ，x ∈[1，2]，则2⎰f(x)dx 等于 ( )A.34B.45C.56 D ．不存在解析：数形结合，2⎰f(x)dx=1⎰x2dx+21⎰(2-x)dx=321211(2)3021x x x +-=3115(422)326x +--+=.答案：C 5．如图，函数y ＝－x2＋2x ＋1与y ＝1相交形成一个闭合图形(图中的阴影部分)，则该闭合图形的面积是 ( ) A ．1 B.43C. 3 D ．2解析：函数y ＝－x2＋2x ＋1与y ＝1的两个交点为(0,1)和(2,1)，所以闭合图形的面积等于2⎰(－x2＋2x ＋1－1)dx ＝2⎰(－x2＋2x)dx ＝43.答案：B6.(2010·烟台模拟)若y ＝x⎰(sint ＋costsint)dt ，则y 的最大值是 ( )A ．1B ．2C ．－72 D ．0解析：y ＝x⎰(sint ＋costsint)dt ＝x⎰(sint ＋12sin2t)dt＝(－cost －14cos2t)0x＝－cosx －14cos2x ＋54＝－cosx －14(2cos2x －1)＋54＝－12cos2x －cosx ＋32＝－12(cosx ＋1)2＋2≤2. 答案：B7．(2010·惠州模拟)⎠⎛02(2－|1－x|)dx ＝________.[答案] 3[解析] ∵y ＝⎩⎪⎨⎪⎧1＋x 0≤x≤13－x 1<x≤2，∴⎠⎛02(2－|1－x|)dx ＝⎠⎛01(1＋x)dx ＋⎠⎛12(3－x)dx＝(x ＋12x2)|10＋(3x －12x2)|21＝32＋32＝3.8．(2012·太原模拟)已知(xlnx)′＝lnx ＋1，则⎠⎛1e lnxdx ＝( )A ．1B ．eC ．e －1D ．e ＋1[答案] A[解析] 由(xlnx)′＝lnx ＋1，联想到(xlnx －x)′＝(lnx ＋1)－1＝lnx ，于是⎠⎛1elnxdx ＝(xlnx －x)|e 1＝(elne －e)－(1×ln1－1)＝1.9．若函数f(x)＝⎩⎪⎨⎪⎧－x －1 －，π2，的图象与坐标轴所围成的封闭图形的面积为a ，则a 的值为( )A.2＋π4B.12C ．1 D.32[答案] D[解析] 由图可知a ＝12＋⎠⎜⎛0 π2cosxdx ＝12＋sinx|π20＝32.二、填空题：1．已知函数y ＝x2与y ＝kx(k ＞0)的图象所围成的阴影部分 (如图所示)的面积为43，则k ＝________.解析：直线方程与抛物线方程联立先求出积分区间为[0，k]，再由k⎰(kx －x2)dx ＝(kx22－x33)0k＝k36＝43求得k ＝2.答案：22．如图，设点P 从原点沿曲线y ＝x2向点A(2,4)移动，记直线OP 、曲线y ＝x2及直线x ＝2所围成的面积分别记为S1，S2，若S1＝S2，则点P 的坐标为________．解析：设直线OP 的方程为y ＝kx, P 点的坐标为(x ，y)，则x⎰(kx －x2)dx ＝2x⎰(x2－kx)dx ，即(12kx2－13x3)0x ＝(13x3－12kx2)2x ，解得12kx2－13x3＝83－2k －(13x3－12kx2)，解得k ＝43，即直线OP 的方程为y ＝43x ，所以点P 的坐标为(43，169)．答案：(43，169)3．一辆汽车的速度—时间曲线如图所示，则该汽车在这一分钟内行驶的路程为_______米．解析：据题意，v 与t 的函数关系式如下：v ＝v(t)＝⎩⎪⎨⎪⎧32t ，0≤t ＜20，50－t ，20≤t ＜40，10，40≤t≤60.所以该汽车在这一分钟内所行驶的路程为s ＝60()d v t t⎰＝203d 2t t ⎰＋4020(50)d t t -⎰＋604010d t ⎰＝34t2200＋(50t －12t2)4020＋10t4020＝900米．答案：9004.已知函数f(x)＝3x2＋2x ＋1，若⎠⎛-11f(x)dx ＝2f(a)成立，则a ＝________.解析：⎠⎛-11 (3x2＋2x ＋1)dx ＝(x3＋x2＋x)| 1-1＝4，所以2(3a2＋2a ＋1)＝4，即3a2＋2a －1＝0，解得a ＝－1或a ＝13.答案：－1或135．(2010·温州模拟)若f(x)是一次函数，且1⎰f(x)dx ＝5，1⎰xf(x)dx ＝176，那么21⎰f(x)xdx 的值是________．解析：∵f(x)是一次函数，∴设f(x)＝ax ＋b(a≠0)，由1⎰(ax ＋b)dx ＝5得(12ax2＋bx)10＝12a ＋b ＝5， ①由1⎰xf(x)dx ＝176得1⎰(ax2＋bx)dx ＝176，即 (13ax3＋12bx2) 10＝176，∴13a ＋12b ＝176，②解①②得a ＝4，b ＝3，∴f(x)＝4x ＋3，于是21⎰f(x)xdx ＝21⎰4x ＋3xdx ＝21⎰(4＋3x)dx ＝(4x ＋3lnx)21＝8＋3ln2－4＝4＋3ln2. 答案：4＋3ln26．抛物线y2＝2x 与直线y ＝4－x 围成的平面图形的面积为________． [答案] 18[解析] 由方程组⎩⎪⎨⎪⎧y2＝2x ，y ＝4－x ，解得两交点A(2,2)、B(8，－4)，选y 作为积分变量x ＝y22、x ＝4－y ，∴S ＝⎠⎛-42 [(4－y)－y22]dy ＝(4y －y22－y36)|2－4＝18.7．如果⎠⎛01f(x)dx ＝1，⎠⎛02f(x)dx ＝－1，则⎠⎛12f(x)dx ＝________.解析：∵⎠⎛02f(x)dx ＝⎠⎛01f(x)dx ＋⎠⎛12f(x)dx ， ∴⎠⎛12f(x)dx ＝⎠⎛02f(x)dx －⎠⎛01f(x)dx ＝－1－1＝－2.答案：－2 8．设函数f(x)＝ax2＋c(a≠0)，若⎠⎛01f(x)dx ＝f(x0)，0≤x0≤1，则x0的值为________．[答案]33[解析] ⎠⎛01f(x)dx ＝⎠⎛01(ax2＋c)dx ＝(ax33＋cx)|10＝a 3＋c ，故a 3＋c ＝ax20＋c ，即ax20＝a3，又a≠0，所以x20＝13，又0≤x0≤1，所以x0＝33.故填33.9．(2010·安徽合肥质检)抛物线y2＝ax(a>0)与直线x ＝1围成的封闭图形的面积为43，若直线l 与抛物线相切且平行于直线2x －y ＋6＝0，则l 的方程为______．[答案] 16x －8y ＋1＝0[解析] 由题意知⎠⎛01axdx ＝23，∴a ＝1，设l ：y ＝2x ＋b 代入y2＝x 中，消去y 得， 4x2＋(4b －1)x ＋b2＝0，由Δ＝0得，b ＝18，∴l 方程为16x －8y ＋1＝0.10．设n ＝⎠⎛12(3x2－2)dx ，则(x －2x )n 展开式中含x2项的系数是________．[答案] 40[解析] ∵(x3－2x)′＝3x2－2，∴n ＝⎠⎛12(3x2－2)dx ＝(x3－2x)|21 ＝(23－2×2)－(1－2)＝5.∴(x －2x )5的通项公式为Tr ＋1＝Cr 5x5－r(－2x)r ＝(－2)rCr 5x5－3r2 ，令5－3r2＝2，得r ＝2，∴x2项的系数是(－2)2C25＝40. 三、解答题： 1．计算以下定积分： (1) 21⎰(2x2－1x)dx ；(2)32⎰(x ＋1x)2dx ；(3)30π⎰(sinx －sin2x)dx ；(4)11-⎰|x|dx; (5)⎠⎛0πcos2x2dx ；解：(1)21⎰(2x2－1x )dx ＝(23x3－lnx)21 ＝163－ln 2－23＝143－ln 2.(2)32⎰(x ＋1x)2dx ＝32⎰(x ＋1x＋2)dx＝(12x2＋lnx ＋2x)32＝(92＋ln 3＋6)－(2＋ln 2＋4)＝ln 32＋92. (3) 3π⎰(sinx －sin2x)dx ＝(－cosx ＋12cos2x)30π＝(－12－14)－(－1＋12)＝－14.(4)⎠⎛1－1|x|dx ＝2⎠⎛01xdx ＝2×12x2|10＝1.(5)⎠⎛0πcos2x 2dx ＝⎠⎛0π1＋cosx 2dx ＝12x|π0＋12sinx|π0＝π22．设y ＝f(x)是二次函数，方程f(x)＝0有两个相等的实根，且f′(x)＝2x －2. (1)求y ＝f(x)的表达式；(2)求y ＝f(x)的图象与两坐标轴所围成图形的面积．解：(1)设f(x)＝ax2＋bx ＋c(a≠0)，则f′(x)＝2ax ＋b.又f′(x)＝2x －2，所以a ＝1，b ＝－2，即f(x)＝x2－2x ＋c.又方程f(x)＝0有两个相等实根，所以Δ＝4－4c ＝0，即c ＝1.故f(x)＝x2－2x ＋1. (2)依题意，所求面积为S ＝⎠⎛01(x2－2x ＋1)dx ＝(13x3－x2＋x)|10＝13.3．已知f(x)为二次函数，且f(－1)＝2，f′(0)＝0，⎠⎛01f(x)dx ＝－2.(1)求f(x)的解析式；(2)求f(x)在[－1,1]上的最大值与最小值．解：(1)设f(x)＝ax2＋bx ＋c(a≠0)，则f′(x)＝2ax ＋b.由f(－1)＝2，f′(0)＝0，得⎩⎪⎨⎪⎧ a －b ＋c ＝2b ＝0，即⎩⎪⎨⎪⎧c ＝2－a b ＝0. ∴f(x)＝ax2＋(2－a)．又⎠⎛01f(x)dx ＝⎠⎛01 [ax2＋(2－a)]dx＝[13ax3＋(2－a)x]|10＝2－23a ＝－2.∴a ＝6，∴c ＝－4.从而f(x)＝6x2－4. (2)∵f(x)＝6x2－4，x ∈[－1,1]，所以当x ＝0时，f(x)min ＝－4；当x ＝±1时，f(x)max ＝2. 4．设f(x)＝1⎰|x2－a2|dx.(1)当0≤a≤1与a ＞1时，分别求f(a)； (2)当a≥0时，求f(a)的最小值．解：(1)0≤a≤1时， f(a)＝1⎰|x2－a2|dx ＝a⎰(a2－x2)dx ＋1a⎰(x2－a2)dx＝(a2x －13x3)0a ＋(x33－a2x)1a ＝a3－13a3－0＋0＋13－a2－a33＋a3＝43a3－a2＋13. 当a ＞1时，f(a)＝1⎰(a2－x2)dx ＝(a2x －13x3)10＝a2－13.∴f(a)＝32241(0),331(>311).a a a a a ⎧-+⎪⎪⎨⎪-⎪⎩≤≤(2)当a ＞1时，由于a2－13在[1，＋∞)上是增函数，故f(a)在[1，＋∞)上的最小值是f(1)＝1－13＝23.当a ∈[0,1]时，f′(a)＝4a2－2a ＝2a(2a －1)，由f′(a)＞0知：a ＞12或a ＜0，故在[0，12]上递减，在[12，1]上递增．因此在[0,1]上，f(a)的最小值为f(12)＝14.综上可知，f(x)在[0，＋∞)上的最小值为14.5．有一条直线与抛物线y ＝x2相交于A 、B 两点，线段AB 与抛物线所围成图形的面积恒等于43，求线段AB 的中点P 的轨迹方程．[解析] 设直线与抛物线的两个交点分别为A(a ，a2)，B(b ，b2)，不妨设a<b ，则直线AB 的方程为y －a2＝b2－a2b －a(x －a)，即y ＝(a ＋b)x －ab.则直线AB 与抛物线围成图形的面积为S ＝⎠⎛a b [(a ＋b)x －ab －x2]dx ＝(a ＋b2x2－abx －x33)|b a ＝16(b －a)3，∴16(b －a)3＝43，解得b －a ＝2.设线段AB 的中点坐标为P(x ，y)，其中⎩⎨⎧x ＝a ＋b2，y ＝a2＋b22.将b －a ＝2代入得⎩⎪⎨⎪⎧x ＝a ＋1，y ＝a2＋2a ＋2.消去a 得y ＝x2＋1.∴线段AB 的中点P 的轨迹方程为y ＝x2＋1.6．如图所示，在区间[0,1]上给定曲线y ＝x2，试在此区间内确定t 的值，使图中阴影部分的面积S1＋S2最小．[解析] 由题意得S1＝t·t2－⎠⎛0t x2dx ＝23t3，S2＝⎠⎛t 1x2dx －t2(1－t)＝23t3－t2＋13，所以S ＝S1＋S2＝43t3－t2＋13(0≤t≤1)．又S′(t)＝4t2－2t ＝4t ⎝⎛⎭⎫t －12，令S′(t)＝0，得t ＝12或t ＝0.因为当0<t<12时，S′(t)<0；当12<t≤1时，S′(t)>0.所以S(t)在区间⎣⎡⎦⎤0，12上单调递减，在区间⎣⎡⎦⎤12，1上单调递增．所以，当t ＝12时，Smin ＝14.。

定积分及微积分基本定理练习题及答案

1.4定积分与微积分基本定理练习题及答案1.(2011·一中月考)求曲线y ＝x2与y ＝x 所围成图形的面积，其中正确的是( ) A ．S ＝⎠⎛01(x2－x)dx B ．S ＝⎠⎛01(x －x2)dxC ．S ＝⎠⎛01(y2－y)dyD ．S ＝⎠⎛01(y －y)dy [答案] B[分析] 根据定积分的几何意义，确定积分上、下限和被积函数．[解读] 两函数图象的交点坐标是(0,0)，(1,1)，故积分上限是1，下限是0，由于在[0,1]上，x ≥x2，故函数y ＝x2与y ＝x 所围成图形的面积S ＝⎠⎛01(x －x2)dx.2．(2010·日照模考)a ＝⎠⎛02xdx ，b ＝⎠⎛02exdx ，c ＝⎠⎛02sinxdx ，则a 、b 、c 的大小关系是( )A ．a<c<bB ．a<b<cC ．c<b<aD ．c<a<b [答案] D[解读] a ＝⎠⎛02xdx ＝12x2|02＝2，b ＝⎠⎛02exdx ＝ex|02＝e2－1>2，c ＝⎠⎛02sinxdx ＝－cosx|02＝1－cos2∈(1,2)，∴c<a<b.3．(2010·理，7)由曲线y ＝x2，y ＝x3围成的封闭图形面积为( ) A.112B.14C.13D.712 [答案] A[解读] 由⎩⎪⎨⎪⎧y ＝x2y ＝x3得交点为(0,0)，(1,1)．∴S ＝⎠⎛01(x2－x3)dx ＝⎪⎪⎪⎝ ⎛⎭⎪⎫13x3－14x401＝112.[点评] 图形是由两条曲线围成的时，其面积是上方曲线对应函数表达式减去下方曲线对应函数表达式的积分，请再做下题：(2010·师大附中)设点P 在曲线y ＝x2上从原点到A(2,4)移动，如果把由直线OP ，直线y ＝x2及直线x ＝2所围成的面积分别记作S1，S2.如图所示，当S1＝S2时，点P 的坐标是( )A.⎝ ⎛⎭⎪⎫43，169B.⎝ ⎛⎭⎪⎫45，169 C.⎝ ⎛⎭⎪⎫43，157 D.⎝ ⎛⎭⎪⎫45，137 [答案] A[解读] 设P(t ，t2)(0≤t ≤2)，则直线OP ：y ＝tx ，∴S1＝⎠⎛0t (tx －x2)dx ＝t36；S2＝⎠⎛t 2(x2－tx)dx ＝83－2t ＋t36，若S1＝S2，则t ＝43，∴P ⎝ ⎛⎭⎪⎫43，169.4．由三条直线x ＝0、x ＝2、y ＝0和曲线y ＝x3所围成的图形的面积为( ) A ．4 B.43C.185D ．6[答案] A[解读] S ＝⎠⎛02x3dx ＝⎪⎪⎪x4402＝4. 5．(2010·省考试院调研)⎠⎛1－1(sinx ＋1)dx 的值为( )A ．0B ．2C ．2＋2cos1D ．2－2cos1 [答案] B[解读] ⎠⎛1－1(sinx ＋1)dx ＝(－cosx ＋x)|－11＝(－cos1＋1)－(－cos(－1)－1)＝2.6．曲线y ＝cosx(0≤x ≤2π)与直线y ＝1所围成的图形面积是( ) A ．2π B ．3π C.3π2D ．π [答案] A [解读] 如右图， S ＝∫02π(1－cosx)dx ＝(x －sinx)|02π＝2π.[点评] 此题可利用余弦函数的对称性①②③④面积相等解决，但若把积分区间改为⎝ ⎛⎭⎪⎫π6，π，则对称性就无能为力了． 7．函数F(x)＝⎠⎛0xt(t －4)dt 在[－1,5]上( )A ．有最大值0，无最小值B ．有最大值0和最小值－323C ．有最小值－323，无最大值D ．既无最大值也无最小值 [答案] B[解读] F ′(x)＝x(x －4)，令F ′(x)＝0，得x1＝0，x2＝4， ∵F(－1)＝－73，F(0)＝0，F(4)＝－323，F(5)＝－253.∴最大值为0，最小值为－323. [点评] 一般地，F(x)＝⎠⎛0x φ(t)dt 的导数F ′(x)＝φ(x)．8．已知等差数列{an}的前n 项和Sn ＝2n2＋n ，函数f(x)＝⎠⎛1x 1t dt ，若f(x)<a3，则x的取值围是( )A.⎝⎛⎭⎪⎫36，＋∞B ．(0，e21) C ．(e －11，e) D ．(0，e11) [答案] D[解读] f(x)＝⎠⎛1x 1t dt ＝lnt|1x ＝lnx ，a3＝S3－S2＝21－10＝11，由lnx<11得，0<x<e11.9．(2010·一中)如图所示，在一个长为π，宽为2的矩形OABC ，曲线y ＝sinx(0≤x ≤π)与x 轴围成如图所示的阴影部分，向矩形OABC 随机投一点(该点落在矩形OABC 任何一点是等可能的)，则所投的点落在阴影部分的概率是( )A.1πB.2πC.3πD.π4 [答案] A[解读] 由图可知阴影部分是曲边图形，考虑用定积分求出其面积．由题意得S ＝⎠⎛0πsinxdx ＝－cosx|0π＝－(cos π－cos0)＝2，再根据几何概型的算法易知所求概率P ＝S S 矩形OABC ＝22π＝1π.10．(2010·质检)函数f(x)＝⎩⎪⎨⎪⎧x ＋2－2≤x<02cosx 0≤x ≤π2的图象与x 轴所围成的图形面积S为( )A.32B ．1 C ．4 D.12 [答案] C[解读] 面积S ＝∫π2－2f(x)dx ＝⎠⎛0－2(x ＋2)dx ＋∫π202cosxdx ＝2＋2＝4.11．(2010·二十中)设函数f(x)＝x －[x]，其中[x]表示不超过x 的最大整数，如[－1.2]＝－2，[1.2]＝1，[1]＝1.又函数g(x)＝－x3，f(x)在区间(0,2)上零点的个数记为m ，f(x)与g(x)的图象交点的个数记为n ，则⎠⎛mn g(x)dx 的值是( )A ．－52B ．－43C ．－54D ．－76[答案] A[解读] 由题意可得，当0<x<1时，[x]＝0，f(x)＝x ，当1≤x<2时，[x]＝1，f(x)＝x －1，所以当x ∈(0,2)时，函数f(x)有一个零点，由函数f(x)与g(x)的图象可知两个函数有4个交点，所以m ＝1，n ＝4，则⎠⎛m n g(x)dx ＝⎠⎛14⎝ ⎛⎭⎪⎫－x 3dx ＝⎪⎪⎪－x2614＝－52.11．(2010·调研)甲、乙两人进行一项游戏比赛，比赛规则如下：甲从区间[0,1]上随机等可能地抽取一个实数记为b ，乙从区间[0,1]上随机等可能地抽取一个实数记为c(b 、c 可以相等)，若关于x 的方程x2＋2bx ＋c ＝0有实根，则甲获胜，否则乙获胜，则在一场比赛中甲获胜的概率为( )A.13B.23C.12D.34 [答案] A[解读] 方程x2＋2bx ＋c ＝0有实根的充要条件为Δ＝4b2－4c ≥0，即b2≥c ，由题意知，每场比赛中甲获胜的概率为p ＝⎠⎛01b2db 1×1＝13.12．(2010·省调研)已知正方形四个顶点分别为O(0,0)，A(1,0)，B(1,1)，C(0,1)，曲线y ＝x2(x ≥0)与x 轴，直线x ＝1构成区域M ，现将一个质点随机地投入正方形中，则质点落在区域M 的概率是( )A.12B.14C.13D.25 [答案] C[解读] 如图，正方形面积1，区域M 的面积为S ＝⎠⎛01x2dx＝13x3|01＝13，故所求概率p ＝13.2．如图，阴影部分面积等于( )A ．23B ．2－ 3 C.323D.353 [答案] C[解读] 图中阴影部分面积为S ＝⎠⎛-31 (3－x2－2x)dx ＝(3x －13x3－x2)|1－3＝323.3.⎠⎛024－x2dx ＝( )A ．4πB ．2πC ．π D.π2[答案] C[解读] 令y＝4－x2，则x2＋y2＝4(y≥0)，由定积分的几何意义知所求积分为图中阴影部分的面积，∴S＝14×π×22＝π.4.已知甲、乙两车由同一起点同时出发，并沿同一路线(假定为直线)行驶．甲车、乙车的速度曲线分别为v甲和v乙(如图所示)．那么对于图中给定的t0和t1，下列判断中一定正确的是( )A．在t1时刻，甲车在乙车前面B．在t1时刻，甲车在乙车后面C．在t0时刻，两车的位置相同D．t0时刻后，乙车在甲车前面[答案] A[解读] 判断甲、乙两车谁在前，谁在后的问题，实际上是判断在t0，t1时刻，甲、乙两车行驶路程的大小问题．根据定积分的几何意义知：车在某段时间行驶的路程就是该时间段速度函数的定积分，即速度函数v(t)的图象与t轴以及时间段围成区域的面积．从图象知：在t0时刻，v 甲的图象与t 轴和t ＝0，t ＝t0围成区域的面积大于v 乙的图象与t 轴和t ＝0，t ＝t0围成区域的面积，因此，在t0时刻，甲车在乙车的前面，而且此时乙车的速度刚刚赶上甲车的速度，所以选项C ，D 错误；同样，在t1时刻，v 甲的图象与t 轴和t ＝t1围成区域的面积，仍然大于v 乙的图象与t 轴和t ＝t1围成区域的面积，所以，可以断定：在t1时刻，甲车还是在乙车的前面．所以选A.5．(2012·日照模拟)向平面区域Ω＝{(x ，y)|－π4≤x ≤π4，0≤y ≤1}随机投掷一点，该点落在曲线y ＝cos2x 下方的概率是( )A.π4B.12 C.π2－1 D.2π [答案] D [解读]平面区域Ω是矩形区域，其面积是π2，在这个区6． (sinx －cosx)dx 的值是( )A ．0 B.π4 C ．2 D ．－2[答案] D[解读] (sinx －cosx)dx ＝(－cosx －sinx) ＝－2.7．(2010·模拟)⎠⎛02(2－|1－x|)dx ＝________.[答案] 3[解读] ∵y ＝⎩⎪⎨⎪⎧1＋x 0≤x ≤13－x 1<x ≤2，∴⎠⎛02(2－|1－x|)dx ＝⎠⎛01(1＋x)dx ＋⎠⎛12(3－x)dx＝(x ＋12x2)|10＋(3x －12x2)|21＝32＋32＝3.8．(2010·十二中)已知函数f(x)＝3x2＋2x ＋1，若⎠⎛1－1f(x)dx ＝2f(a)成立，则a ＝________.[答案] －1或13[解读] ∵⎠⎛1－1f(x)dx ＝⎠⎛1－1(3x2＋2x ＋1)dx ＝(x3＋x2＋x)|1－1＝4，⎠⎛1－1f(x)dx ＝2f(a)，∴6a2＋4a ＋2＝4，∴a ＝－1或13.9．已知a ＝∫π20(sinx ＋cosx)dx ，则二项式(a x －1x )6的展开式中含x2项的系数是________．[答案] －192[解读] 由已知得a ＝∫π20(sinx ＋cosx)dx ＝(－cosx ＋sinx)|π20＝(sin π2－cos π2)－(sin0－cos0)＝2，(2x －1x)6的展开式中第r ＋1项是Tr ＋1＝(－1)r ×Cr 6×26－r ×x3－r ，令3－r ＝2得，r ＝1，故其系数为(－1)1×C16×25＝－192.10．有一条直线与抛物线y ＝x2相交于A 、B 两点，线段AB 与抛物线所围成图形的面积恒等于43，求线段AB 的中点P 的轨迹方程．[解读] 设直线与抛物线的两个交点分别为A(a ，a2)，B(b ，b2)，不妨设a<b ，则直线AB 的方程为y －a2＝b2－a2b －a(x －a)，即y ＝(a ＋b)x －ab.则直线AB 与抛物线围成图形的面积为S ＝⎠⎛a b[(a ＋b)x －ab －x2]dx ＝(a ＋b2x2－abx －x33)|b a ＝16(b －a)3，∴16(b －a)3＝43，解得b －a ＝2.设线段AB 的中点坐标为P(x ，y)，其中⎩⎪⎨⎪⎧x ＝a ＋b 2，y ＝a2＋b22.将b －a ＝2代入得⎩⎪⎨⎪⎧x ＝a ＋1，y ＝a2＋2a ＋2.消去a 得y ＝x2＋1.∴线段AB 的中点P 的轨迹方程为y ＝x2＋1.能力拓展提升11.(2012·二测)等比数列{an}中，a3＝6，前三项和S3＝⎠⎛034xdx ，则公比q 的值为( )A ．1B ．－12C ．1或－12D ．－1或－12[答案] C[解读] 因为S3＝⎠⎛034xdx ＝2x2|30＝18，所以6q ＋6q2＋6＝18，化简得2q2－q －1＝0，解得q ＝1或q ＝－12，故选C.12．(2012·模拟)已知(xlnx)′＝lnx ＋1，则⎠⎛1elnxdx ＝( )A ．1B ．eC ．e －1D ．e ＋1 [答案] A[解读] 由(xlnx)′＝lnx ＋1，联想到(xlnx －x)′＝(lnx ＋1)－1＝lnx ，于是⎠⎛1elnxdx ＝(xlnx －x)|e 1＝(elne －e)－(1×ln1－1)＝1.13．抛物线y2＝2x 与直线y ＝4－x 围成的平面图形的面积为________． [答案] 18[解读] 由方程组⎩⎪⎨⎪⎧y2＝2x ，y ＝4－x ，解得两交点A(2,2)、B(8，－4)，选y 作为积分变量x ＝y22、x ＝4－y ，∴S ＝⎠⎛-42 [(4－y)－y22]dy ＝(4y －y22－y36)|2－4＝18.14.已知函数f(x)＝ex －1，直线l1：x ＝1，l2：y ＝et －1(t 为常数，且0≤t ≤1)．直线l1，l2与函数f(x)的图象围成的封闭图形如图中区域Ⅱ所示，其面积用S2表示．直线l2，y 轴与函数f(x)的图象围成的封闭图形如图中区域Ⅰ所示，其面积用S1表示．当t 变化时，阴影部分的面积的最小值为________．[答案] (e －1)2[解读] 由题意得S1＋S2＝⎠⎛0t (et －1－ex ＋1)dx ＋⎠⎛t 1(ex －1－et ＋1)dx ＝⎠⎛0t (et －ex)dx＋⎠⎛t 1(ex －et)dx ＝(xet －ex)|t 0＋(ex －xet)|1t ＝(2t －3)et ＋e ＋1，令g(t)＝(2t －3)et ＋e ＋1(0≤t ≤1)，则g ′(t)＝2et ＋(2t －3)et ＝(2t －1)et ，令g ′(t)＝0，得t ＝12，∴当t ∈[0，12)时，g ′(t)<0，g(t)是减函数，当t ∈(12，1]时，g ′(t)>0，g(t)是增函数，因此g(t)的最小值为g(12)＝e ＋1－2e 12＝(e －1)2.故阴影部分的面积的最小值为(e －1)2. 15．求下列定积分．(1)⎠⎛1－1|x|dx 。

定积分及微积分基本定理练习题（附答案）

1.4定积分与微积分基本定理练习题及答案1.(2011·一中月考)求曲线y ＝x2与y ＝x 所围成图形的面积，其中正确的是()A ．S ＝1(x2－x)dx B ．S ＝01(x －x2)dx C ．S ＝01(y2－y)dy D ．S ＝01(y －y)dy[答案] B[分析] 根据定积分的几何意义，确定积分上、下限和被积函数．[解读]两函数图象的交点坐标是(0,0)，(1,1)，故积分上限是1，下限是0，由于在[0,1]上，x ≥x2，故函数y ＝x2与y ＝x 所围成图形的面积S ＝1(x －x2)dx. 2．(2010·日照模考)a ＝02xdx ，b ＝02exdx ，c ＝02sinxdx ，则a 、b 、c 的大小关系是()A ．a<c<bB ．a<b<cC ．c<b<aD ．c<a<b [答案] D [解读]a ＝2xdx ＝12x2|02＝2，b ＝02exdx ＝ex|02＝e2－1>2，c ＝02sinxdx ＝－cosx|02＝1－cos2∈(1,2)，∴c<a<b.3．(2010·理，7)由曲线y ＝x2，y ＝x3围成的封闭图形面积为()A.112B.14C.13D.712[答案] A[解读]由y ＝x2y ＝x3得交点为(0,0)，(1,1)．∴S ＝01(x2－x3)dx ＝13x3－14x401＝112.[点评]图形是由两条曲线围成的时，其面积是上方曲线对应函数表达式减去下方曲线对应函数表达式的积分，请再做下题：(2010·师大附中)设点P 在曲线y ＝x2上从原点到A(2,4)移动，如果把由直线OP ，直线y ＝x2及直线x ＝2所围成的面积分别记作S1，S2.如图所示，当S1＝S2时，点P 的坐标是( )A.43，169B.45，169C.43，157 D.45，137[答案] A[解读]设P(t ，t2)(0≤t ≤2)，则直线OP ：y ＝tx ，∴S1＝t(tx －x2)dx ＝t36；S2＝t2(x2－tx)dx ＝83－2t ＋t36，若S1＝S2，则t ＝43，∴P 43，169.4．由三条直线x ＝0、x ＝2、y ＝0和曲线y ＝x3所围成的图形的面积为()A ．4 B.43C.185D ．6[答案] A [解读]S ＝2x3dx ＝x4402＝4.5．(2010·省考试院调研)1－1(sinx ＋1)dx 的值为()A ．0B ．2C ．2＋2cos1D ．2－2cos1 [答案] B[解读] 1－1(sinx ＋1)dx ＝(－cosx ＋x)|－11＝(－cos1＋1)－(－cos(－1)－1)＝2.6．曲线y ＝cosx(0≤x ≤2π)与直线y ＝1所围成的图形面积是()A ．2πB ．3πC.3π2D ．π[答案] A [解读]如右图，S ＝∫02π(1－cosx)dx ＝(x －sinx)|02π＝2π．[点评] 此题可利用余弦函数的对称性①②③④面积相等解决，但若把积分区间改为π6，π，则对称性就无能为力了．7．函数F(x)＝xt(t －4)dt 在[－1,5]上( )A ．有最大值0，无最小值B ．有最大值0和最小值－323C ．有最小值－323，无最大值D ．既无最大值也无最小值[答案] B[解读]F ′(x)＝x(x －4)，令F ′(x)＝0，得x1＝0，x2＝4，∵F(－1)＝－73，F(0)＝0，F(4)＝－323，F(5)＝－253.∴最大值为0，最小值为－323.[点评]一般地，F(x)＝x φ(t)dt 的导数F ′(x)＝φ(x)．8．已知等差数列{an}的前n 项和Sn ＝2n2＋n ，函数f(x)＝1x 1t dt ，若f(x)<a3，则x 的取值围是()A.36，＋∞B ．(0，e21) C ．(e －11，e) D ．(0，e11) [答案] D [解读]f(x)＝1x 1t dt ＝lnt|1x ＝lnx ，a3＝S3－S2＝21－10＝11，由lnx<11得，0<x<e11.9．(2010·一中)如图所示，在一个长为π，宽为2的矩形OABC ，曲线y ＝sinx(0≤x ≤π）与x 轴围成如图所示的阴影部分，向矩形OABC 随机投一点(该点落在矩形OABC 任何一点是等可能的)，则所投的点落在阴影部分的概率是()A.1πB.2πC.3πD.π4[答案] A[解读]由图可知阴影部分是曲边图形，考虑用定积分求出其面积．由题意得S ＝0πsinxdx ＝－cosx|0π＝－(cos π－cos0)＝2，再根据几何概型的算法易知所求概率P ＝S S 矩形OABC ＝22π＝1π.10．(2010·质检)函数f(x)＝x ＋2－2≤x<02cosx0≤x ≤π2的图象与x 轴所围成的图形面积S 为( )A.32B ．1 C ．4 D.12[答案] C[解读]面积S ＝∫π2－2f(x)dx ＝0－2(x ＋2)dx ＋∫π202cosxdx ＝2＋2＝4.11．(2010·二十中)设函数f(x)＝x －[x]，其中[x]表示不超过x 的最大整数，如[－1.2]＝－2，[1.2]＝1，[1]＝1.又函数g(x)＝－x3，f(x)在区间(0,2)上零点的个数记为m ，f(x)与g(x)的图象交点的个数记为n ，则mng(x)dx 的值是()A ．－52B ．－43C ．－54D ．－76[答案] A[解读]由题意可得，当0<x<1时，[x]＝0，f(x)＝x ，当1≤x<2时，[x]＝1，f(x)＝x －1，所以当x ∈(0,2)时，函数f(x)有一个零点，由函数f(x)与g(x)的图象可知两个函数有4个交点，所以m ＝1，n ＝4，则mng(x)dx ＝14－x3dx ＝－x2614＝－52. 11．(2010·调研)甲、乙两人进行一项游戏比赛，比赛规则如下：甲从区间[0,1]上随机等可能地抽取一个实数记为b ，乙从区间[0,1]上随机等可能地抽取一个实数记为c(b 、c 可以相等)，若关于x 的方程x2＋2bx ＋c ＝0有实根，则甲获胜，否则乙获胜，则在一场比赛中甲获胜的概率为()A.13B.23C.12D.34[答案] A[解读]方程x2＋2bx ＋c ＝0有实根的充要条件为Δ＝4b2－4c ≥0，即b2≥c ，由题意知，每场比赛中甲获胜的概率为p ＝01b2db 1×１＝13. 12．(2010·省调研)已知正方形四个顶点分别为O(0,0)，A(1,0)，B(1,1)，C(0,1)，曲线y＝x2(x≥0)与x轴，直线x＝1构成区域M，现将一个质点随机地投入正方形中，则质点落在区域M的概率是( )A.12 B.14C.13 D.25[答案] C[解读] 如图，正方形面积1，区域M的面积为S＝1x2dx＝13x3|01＝13，故所求概率p＝13.2．如图，阴影部分面积等于( )A．23B．2－ 3C.323D.353[答案] C[解读] 图中阴影部分面积为S＝-31 (3－x2－2x)dx＝(3x－13x3－x2)|1－3＝323.3.24－x2dx＝( )A．4π B．2πC．π D.π2[答案] C[解读] 令y＝4－x2，则x2＋y2＝4(y≥0)，由定积分的几何意义知所求积分为图中阴影部分的面积，∴S＝14×π×22＝π．4.已知甲、乙两车由同一起点同时出发，并沿同一路线(假定为直线)行驶．甲车、乙车的速度曲线分别为v甲和v乙(如图所示)．那么对于图中给定的t0和t1，下列判断中一定正确的是( )A．在t1时刻，甲车在乙车前面B．在t1时刻，甲车在乙车后面C．在t0时刻，两车的位置相同D．t0时刻后，乙车在甲车前面[答案] A[解读] 判断甲、乙两车谁在前，谁在后的问题，实际上是判断在t0，t1时刻，甲、乙两车行驶路程的大小问题．根据定积分的几何意义知：车在某段时间行驶的路程就是该时间段速度函数的定积分，即速度函数v(t)的图象与t轴以及时间段围成区域的面积．从图象知：在t0时刻，v甲的图象与t轴和t＝0，t＝t0围成区域的面积大于v乙的图象与t轴和t＝0，t＝t0围成区域的面积，因此，在t0时刻，甲车在乙车的前面，而且此时乙车的速度刚刚赶上甲车的速度，所以选项C，D错误；同样，在t1时刻，v甲的图象与t轴和t＝t1围成区域的面积，仍然大于v乙的图象与t轴和t＝t1围成区域的面积，所以，可以断定：在t1时刻，甲车还是在乙车的前面．所以选 A.5．(2012·日照模拟)向平面区域Ω＝{(x，y)|－π4≤x≤π4，0≤y≤1}随机投掷一点，该点落在曲线y＝cos2x下方的概率是( )A.π4B.12C.π2－1 D.2π[答案] D[解读]平面区域Ω是矩形区域，其面积是π2，在这个区6． (sinx－cosx)dx的值是( )A．0 B.π4C．2 D．－2[答案] D[解读] (sinx－cosx)dx＝(－cosx－sinx) ＝－2. 7．(2010·模拟)2(2－|1－x|)dx＝________.[答案] 3[解读] ∵y＝1＋x 0≤x≤13－x 1<x≤2，∴02(2－|1－x|)dx ＝01(1＋x)dx ＋12(3－x)dx ＝(x ＋12x2)|10＋(3x －12x2)|21＝32＋32＝3.8．(2010·十二中)已知函数f(x)＝3x2＋2x ＋1，若1－1f(x)dx ＝2f(a)成立，则a ＝________.[答案] －1或13[解读]∵1－1f(x)dx＝1－1(3x2＋2x ＋1)dx ＝(x3＋x2＋x)|1－1＝4，1－1f(x)dx ＝2f(a)，∴6a2＋4a ＋2＝4，∴a ＝－1或13.9．已知a ＝∫π20(sinx ＋cosx)dx ，则二项式(ax －1x)6的展开式中含x2项的系数是________．[答案] －192 [解读]由已知得a ＝∫π20(sinx ＋cosx)dx ＝(－cosx ＋sinx)|π20＝(sin π2－cos π2)－(sin0－cos0)＝2，(2x －1x)6的展开式中第r ＋1项是Tr ＋1＝(－1)r ×Ｃr 6×26－r ×x3－r ，令3－r ＝2得，r ＝1，故其系数为(－1)1×Ｃ16×25＝－192. 10．有一条直线与抛物线y ＝x2相交于A 、B 两点，线段AB 与抛物线所围成图形的面积恒等于43，求线段AB 的中点P 的轨迹方程．[解读]设直线与抛物线的两个交点分别为A(a ，a2)，B(b ，b2)，不妨设a<b ，则直线AB 的方程为y －a2＝b2－a2b －a (x －a)，即y ＝(a ＋b)x －ab.则直线AB 与抛物线围成图形的面积为S ＝ab[(a ＋b)x －ab －x2]dx ＝(a ＋b 2x2－abx －x33)|ba ＝16(b －a)3，∴16(b －a)3＝43，解得b －a ＝2.设线段AB 的中点坐标为P(x ，y)，其中x ＝a ＋b 2，y ＝a2＋b22.将b －a ＝2代入得x ＝a ＋1，y ＝a2＋2a ＋2.消去a 得y ＝x2＋1.∴线段AB 的中点P 的轨迹方程为y ＝x2＋1. 能力拓展提升11.(2012·二测)等比数列{an}中，a3＝6，前三项和S3＝034xdx ，则公比q 的值为( )A ．1B ．－12C ．1或－12D ．－1或－12[答案] C [解读]因为S3＝34xdx ＝2x2|30＝18，所以6q ＋6q2＋6＝18，化简得2q2－q －1＝0，解得q ＝1或q ＝－12，故选 C.12．(2012·模拟)已知(xlnx)′＝lnx ＋1，则1elnxdx ＝( )A ．1B ．eC ．e －1D ．e ＋1 [答案] A[解读]由(xlnx)′＝lnx ＋1，联想到(xlnx －x)′＝(lnx ＋1)－1＝lnx ，于是1elnxdx＝(xlnx －x)|e1＝(elne －e)－(1×ln1－1)＝1.13．抛物线y2＝2x 与直线y ＝4－x 围成的平面图形的面积为________．[答案] 18 [解读]由方程组y2＝2x ，y ＝4－x ，解得两交点A(2,2)、B(8，－4)，选y 作为积分变量x＝y22、x ＝4－y ，∴S ＝-42 [(4－y)－y22]dy ＝(4y －y22－y36)|2－4＝18.14.已知函数f(x)＝ex －1，直线l1：x ＝1，l2：y ＝et －1(t 为常数，且0≤t ≤1)．直线l1，l2与函数f(x)的图象围成的封闭图形如图中区域Ⅱ所示，其面积用S2表示．直线l2，y 轴与函数f(x)的图象围成的封闭图形如图中区域Ⅰ所示，其面积用S1表示．当t 变化时，阴影部分的面积的最小值为________．[答案] (e －1)2[解读] 由题意得S1＋S2＝t(et －1－ex ＋1)dx ＋t1(ex －1－et ＋1)dx ＝0t(et －ex)dx ＋t1(ex －et)dx ＝(xet －ex)|t 0＋(ex －xet)|1t ＝(2t －3)et ＋e ＋1，令g(t)＝(2t －3)et ＋e ＋1(0≤t ≤1)，则g ′(t)＝2et ＋(2t －3)et ＝(2t －1)et ，令g ′(t)＝0，得t ＝12，∴当t ∈[0，12)时，g ′(t)<0，g(t)是减函数，当t ∈(12，1]时，g ′(t)>0，g(t)是增函数，因此g(t)的最小值为g(12)＝e ＋1－2e 12＝(e －1)2.故阴影部分的面积的最小值为(e －1)2.15．求下列定积分．(1)1－1|x|dx 。

微积分习题答案第七章定积分

4
cos
3 2
3
x
2 0
4 3
(12)
2 dx 1 x x3
21 ( 1x
x
x2
)dx 1
[ln
x
1 2
ln(1
x2 )]
2 1
1 2
ln
8 5
4 dx t
2. (1) 1 1 x
x
2 1 2tdt 1 1t
2
2
(1
1
)dt
1 1t
2[t ln(t 1)]
2 1
2(1 ln 2) 3
0
1
(x 2
0
1 0
f (t)dt) 0
1
xdx 2
0
1
f (t)dt
0
1
dx
0
1 x2 2
1 0
2
1
f (x)dx
0
.
1 f (x)dx 1x2
0
2
1 0
1 2
1
f (t)dt
0
练习 7.4
1
f (x) x 2 2 f (t)dt x 1. 0
1．（1）
2 cos5 x sin2 xdx 2 (1 sin2 )4 sin2 xd sin x
22 3 3
1 x2
0 (1 x 2 )2
dx
4 0
tan 2 sec4
t t
sec2
tdt
4 sin 2 tdt
0
4 0
1
cos 2t 2
dt
1 2
(t
1 2
sin t)
4 0
1 ( 2) 8
(8)

2024届高考数学复习：精选历年真题、好题专项(定积分与微积分基本定理)练习(附答案)

2024届高考数学复习：精选历年真题、好题专项（定积分与微积分基本定理）练习一、基础小题练透篇1．若a ＝⎠⎛02 x 2d x ，b ＝⎠⎛02 x 3d x ，c ＝⎠⎛02 sin x d x ，则a ，b ，c 的大小关系是( )A ．a<c<bB ．a<b<cC ．c<b<aD ．c<a<b2．由曲线xy ＝1，直线y ＝x ，y ＝3所围成的平面图形的面积为( )A ．329 B ．2－ln 3 C ．4＋ln 3 D ．4－ln 33．[2023ꞏ甘肃省兰州市第一次月考]求由抛物线y ＝2x 2与直线x ＝0，x ＝t(t ＞0)，y ＝0所围成的曲边梯形的面积时，将区间[0，t]等分成n 个小区间，则第i －1个区间为( )A ．⎣⎡⎦⎤i －1n ，i nB ．⎣⎡⎦⎤i n ，i ＋1n C ．⎣⎡t （i －1）n ，ti n D ．⎣⎡t （i －2）n ，t （i －1）n4．若数列{a n }是公比不为1的等比数列，且a 2 018＋a 2 020＝⎠⎛024－x 2 d x ，则a 2 017(a 2 019＋2a 2 021＋a 2 023)＝( )A ．4π2B ．2π2C ．π2D ．3π25．一辆汽车在高速公路上行驶，由于遇到紧急情况而刹车，以速度v(t)＝7－3t ＋251＋t(t 的单位：s ，v 的单位：m /s )行驶至停止. 在此期间汽车继续行驶的距离(单位：m )是( )A ．1＋25ln 5B ．8＋25ln 113 C ．4＋25ln 5 D ．4＋50ln 26．已知分段函数f(x)＝⎩⎪⎨⎪⎧1＋x 2，x ≤0，e －x，x>0，则⎠⎛13 f(x －2)d x ＝( ) A ．3＋1e B ．2－e C ．73 －1e D ．2－1e7．设函数f(x)＝ax 2＋b(a ≠0)，若⎠⎛03 f(x)d x ＝3f(x 0)，x 0>0，则x 0＝________．8．[2023ꞏ河南省信阳考试]⎠⎛12 (1x ＋1－（x －2）2 )d x ＝________．二、能力小题提升篇1．[2023ꞏ兰州检测]曲线y ＝x 2和直线x ＝0，x ＝1，y ＝14 所围成的图形(如图中阴影部分所示)的面积为( )A ．23B ．13C ．12D ．142．[2023ꞏ河北唐山联考]曲线y ＝x －1x ＋1与其在点(0，－1)处的切线及直线x ＝1所围成的封闭图形的面积为( )A ．1－ln 2B ．2－2ln 2C ．2ln 2－1D ．ln 23．[2023ꞏ河南商丘检测]已知不等式1－3x ＋a <0的解集为(－1，2)，则⎠⎛0a (2e 2x ＋x)d x＝( )A ．e ＋12B ．e －12 C ．e 2＋12 D ．e 2－124．[2023ꞏ河南省洛阳市考试]由抛物线y ＝－x 2＋4x －3及其在点M(0，－3)和点N(3，0)处的两条切线所围成的图形的面积为( )A ．94B ．92C ．74 D ．25．[2023ꞏ江西省新余市第一中学考试]函数的图象f(x)＝⎩⎪⎨⎪⎧x ＋4，－4≤x<0，4cos x ，0≤x ≤π2 与x 轴所围成的封闭图形的面积为________．6．[2023ꞏ吉林省东北师范大学模拟]设y ＝f(x)为区间[0，1]上的连续函数，且恒有0≤f(x)≤1，可以用随机模拟方法近似计算积分⎠⎛01 f(x)d x ，先产生两组(每组n 个)区间[0，1]上的均匀随机数x 1，x 2，…，x n 和y 1，y 2，…，y n ，由此得到n 个点(x i ，y i )(i ＝1，2，…，n)，再数出其中满足y i >f(x i )(i ＝1，2，…，n)的点有m 个，那么由随机模拟方法可得积分⎠⎛01f(x)d x 的近似值为________．7．[2023ꞏ吉林省实验中学检测]若f(x)＝⎩⎪⎨⎪⎧f （x －4），x>0，2x＋∫π60cos 3x d x ，x ≤0，则f(2 018)＝________．三、高考小题重现篇1.[湖南卷]由直线x ＝－π3 ，x ＝π3 ，y ＝0与曲线y ＝cos x 所围成的封闭图形的面积为( )A ．12B ．1C ．32 D ．32．[湖北卷]若函数f (x )，g (x )满足⎠⎛－11f （x ）g （x ）d x ＝0，则称f(x)，g(x)为区间[－1，1]上的一组正交函数．给出三组函数：①f(x)＝sin 12 x ，g(x)＝cos 12 x ②f(x)＝x ＋1，g(x)＝x －1 ③f(x)＝x ，g(x)＝x 2. 其中为区间[－1，1]上的正交函数的组数是( ) A ．0 B ．1 C ．2 D ．33．[江西卷]若f(x)＝x 2＋2⎠⎛01 f(x)d x ，则⎠⎛01 f(x)d x ＝( )A ．－1B ．－13C ．13 D ．14．[湖北卷]已知二次函数y ＝f(x)的图象如图所示，则它与x 轴所围图形的面积为( )A ．2π5 B ．43 C ．32 D ．π2 5．[湖南卷]⎠⎛02 (x －1)d x ＝________．6．[福建卷]如图，在边长为e (e 为自然对数的底数)的正方形中随机撒一粒黄豆，则它落到阴影部分的概率为________.四、经典大题强化篇1.[2023ꞏ四川绵阳模拟]A ，B 两站相距7.2 km ，一辆电车从A 站开往B 站，电车开出t s 后到达途中C 点，这一段的速度为1.2t m/s ，到C 点的速度为24 m/s ，从C 点到B 站前的D 点以等速行驶，从D 点开始刹车，经t s 后，速度为(24－1.2t ) m/s ，在B 站恰好停车，试求：(1)A ，C 间的距离； (2)B ，D 间的距离．2．[2023ꞏ江西省赣州市赣县月考]已知函数f (x )＝ax ＋ln x (a ∈R ).(1)若a ＝2，求导函数曲线y ＝f ′(x )与直线x ＝1，x ＝e 及x 轴所围成的面积； (2)求f (x )的单调区间．参考答案一基础小题练透篇1．答案：D答案解析：a ＝⎠⎛02x 2d x ＝⎝ ⎛⎭⎪⎫13x 3 ⎪⎪ 2 0＝83 ，b＝⎠⎛02 x 3d x＝⎝ ⎛⎭⎪⎫14x 4 ⎪⎪20＝4，c ＝⎠⎛02 sin x d x ＝（－cos x ）⎪⎪20＝1－cos 2.∵cos 2∈[－1，1]，∴1－cos 2∈[0，2]，∴1－cos 2<83<4，故c<a<b.2．答案：D答案解析：S ＝＝4－ln 3. 3．答案：D答案解析：在[0，t]上等间隔插入（n －1）个分点，把区间[0，t]等分成n 个小区间，每个小区间长度均为t n ，故第i －1个区间为⎣⎢⎡⎦⎥⎤t ()i －2n ，t ()i －1n .本题选择D 选项． 4．答案：C答案解析：根据定积分的几何意义，⎠⎛02 4－x 2d x 表示以原点为圆心，以2为半径的四分之一圆的面积，所以⎠⎛02 4－x 2d x ＝π.所以a 2 018＋a 2 020＝π，设a 2 018＝a ，公比为q ，则a ＋aq 2＝π，所以a 2 017（a 2 019＋2a 2 021＋a 2 023）＝a q（aq ＋2aq 3＋aq 5）＝a 2（1＋2q 2＋q 4）＝a 2（1＋q 2）2＝[a （1＋q 2）]2＝π2.5．答案：C答案解析：令v （t ）＝7－3t ＋251＋t ＝0，又t>0，则t ＝4，汽车刹车的距离是⎠⎛04 ⎝ ⎛⎭⎪⎫7－3t ＋251＋t d t ＝4＋25ln 5.6．答案：C答案解析：⎠⎛13 f （x －2）d x ＝⎠⎛12 f （x －2）d x ＋⎠⎛23 f （x －2）d x ＝⎠⎛12 （x 2－4x ＋5）d x＋⎠⎛23 e－x ＋2d x＝⎝ ⎛⎭⎪⎫13x 3－2x 2＋5x ⎪⎪21＋（－e －x ＋2）⎪⎪ 32＝[⎝ ⎛⎭⎪⎫13×23－2×22＋5×2 －⎝ ⎛⎭⎪⎫13×13－2×12＋5×1 ]＋[（－e －3＋2）－（－e －2＋2）]＝73 －1e.7．答案： 3答案解析：依题意得⎝ ⎛⎭⎪⎫a 3x 3＋bx ⎪⎪⎪3＝3（ax 20 ＋b ），即3ax 20 ＝9a （a≠0），x 20 ＝3（x 0>0），由此解得x 0＝ 3 .8．答案：ln 2＋π4答案解析：由题意得，⎠⎛12 ⎝ ⎛⎭⎪⎫1x ＋1－（x －2）2 d x ＝⎠⎛12 1x d x ＋⎠⎛12 1－（x －2）2 d x＝ln x|21 ＋⎠⎛12 1－（x －2）2 d x ＝ln 2＋⎠⎛12 1－（x －2）2d x .根据定积分的几何意义可知，⎠⎛121－（x －2）2 d x 表示圆（x －2）2＋y 2＝1满足1≤x≤2，y≥0的这一部分面积，即圆面积的14 ，故⎠⎛12 1－（x －2）2d x ＝π4 .因此⎠⎛12 ⎝ ⎛⎭⎪⎫1x ＋1－（x －2）2 d x ＝ln 2＋⎠⎛12 1－（x －2）2 d x ＝ln 2＋π4 .二能力小题提升篇1．答案：D答案解析：令x 2＝14 ，得x ＝12 或x ＝－12 （舍去），所以所求的阴影部分的面积为∫120⎝ ⎛⎭⎪⎫14－x 2 d x ＋∫112⎝ ⎛⎭⎪⎫x 2－14 d x ＝⎝ ⎛⎭⎪⎫14x －x 33 ⎪⎪⎪120 ＋⎝ ⎛⎭⎪⎫x 33－14x ⎪⎪⎪112 ＝14 .2．答案：C答案解析：因为y ＝x －1x ＋1 ，所以y′＝⎝ ⎛⎭⎪⎫x －1x ＋1 ′＝2（x ＋1）2 ，则曲线y ＝x －1x ＋1 在（0，－1）处的切线的斜率k ＝2，切线方程为y ＝2x －1，则曲线y ＝x －1x ＋1 与其在点（0，－1）处的切线及直线x ＝1所围成的封闭图形的面积S ＝⎠⎛01 ⎝ ⎛⎭⎪⎫2x －1－x －1x ＋1 d x ＝⎠⎛01 （2x －1－1＋2x ＋1 ）d x ＝[x 2－2x ＋2ln （x ＋1）]⎪⎪⎪1＝2ln 2－1. 3．答案：D答案解析：∵不等式1－3x ＋a <0，∴x ＋a －3x ＋a<0，∴（x ＋a ）（x ＋a －3）<0，∴－a<x<－a ＋3，由于1－3x ＋a <0的解集为（－1，2），∴⎩⎪⎨⎪⎧－a ＝－1－a ＋3＝2，解得a ＝1，∴⎠⎛0a（2e 2x＋x ）d x ＝⎠⎛01（2e 2x＋x ）d x ＝⎝ ⎛⎭⎪⎫e 2x ＋x 22 ⎪⎪⎪10 ＝e 2－12 .4．答案：A答案解析：∵y ＝－x 2＋4x －3，则y′＝－2x ＋4，在点M （0，－3）的切线斜率k 1＝y′|x ＝0＝4，切线方程y ＝4x －3，在点N （3，0）的切线斜率k 2＝y′|x ＝3＝－2，切线方程y ＝－2()x －3 ，联立方程⎩⎨⎧y ＝4x －3y ＝－2()x －3 ，解得⎩⎪⎨⎪⎧x ＝32y ＝3，即两切线的交点坐标为⎝ ⎛⎭⎪⎫32，3 ，所围成的图形的面积为S ＝∫32[]()4x －3－()－x 2＋4x －3 d x ＋∫332[]－2()x －3－()－x 2＋4x －3 d x＝∫320x 2d x ＋∫332 ()x 2－6x ＋9 d x ＝13 x 3|32 0＋（13 x 3－3x 2＋9x ）|332＝94 .故选A .5．答案：12答案解析：由题意可得：围成的封闭图形的面积为：S ＝⎠⎛－4（x ＋4）d x ＋∫π2 04cos x d x ＝（12 x 2＋4x ）|0－4 ＋4sin x|π2 0＝0－()8－16 ＋4sin π2－0＝12.6．答案：1－mn答案解析：由题意得满足y i ≤f （x i ）（i ＝1，2，…，n ）的点有n －m 个，故n －m n ≈⎠⎛01f （x ）d x 1 ，即⎠⎛01 f （x ）d x≈1－mn ，故积分⎠⎛01 f （x ）d x 的近似值为1－mn .7．答案：712答案解析：当x≤0时，f （x ）＝2x＋∫π60cos 3x d x ＝2x＋sin 3x 3⎪⎪⎪π6＝2x＋13，所以f （2 018）＝f （2）＝f （－2）＝14 ＋13 ＝712.三高考小题重现篇1．答案：D答案解析：如图可得，∫π3－π3 cos x d x ＝sin x|π3 －π3＝2sin π3 ＝ 3 .2．答案：C答案解析：由题意，要满足f （x ），g （x ）是区间[－1，1]上的一组正交函数，即需满足⎠⎛－11 f （x ）g （x ）d x ＝0.①⎠⎛－11 f （x ）g （x ）d x ＝⎠⎛－11 sin 12 x cos 12 x d x ＝12 ⎠⎛－11 sin x d x＝⎝ ⎛⎭⎪⎫－12cos x |1－1 ＝0，故第①组是区间[－1，1]上的正交函数；②⎠⎛－11 f （x ）·g （x ）d x ＝⎠⎛－11（x ＋1）（x －1）d x ＝ ⎠⎛－11（x 2－1）d x ＝⎝ ⎛⎭⎪⎫x 33－x |1－1 ＝－43 ≠0，故第②组不是区间[－1，1]上的正交函数；③⎠⎛－11 f （x ）g （x ）d x ＝⎠⎛－11 x·x 2d x ＝⎠⎛－11 x 3d x ＝x 44 |1－1 ＝0，故第③组是区间[－1，1]上的正交函数．综上，其中为区间[－1，1]上的正交函数的组数是2.3．答案：B答案解析：不妨设⎠⎛01 f （x ）d x ＝k ，则f （x ）＝x 2＋2⎠⎛01 f （x ）d x ＝x 2＋2k ，所以⎠⎛01 f（x ）d x ＝⎠⎛01 （x 2＋2k ）d x ＝⎝ ⎛⎭⎪⎫13x 3＋2kx |10 ＝13 ＋2k ＝k ，得k ＝－13 ，即⎠⎛01 f （x ）d x ＝－13. 4．答案：B答案解析：容易求得二次函数的答案解析式为f （x ）＝1－x 2，所以S ＝⎠⎛－11 （1－x 2）d x ＝⎝ ⎛⎭⎪⎫x －x 33 |1－1 ＝43 .5．答案：0答案解析：⎠⎛02 （x －1）d x ＝⎝ ⎛⎭⎪⎫12x 2－x |20 ＝12 ×22－2＝0.6．答案：2e2答案解析：联立⎩⎪⎨⎪⎧y ＝e x，y ＝e ，解得x ＝1，因为y ＝e x与y ＝ln x 互为反函数，故所求阴影部分面积S ＝2⎠⎛01 （e －e x）d x ＝2，故所求概率P ＝2e2 .四经典大题强化篇1．答案解析：（1）设A 到C 的时间为t 1 s ，则1.2t 1＝24，解得：t 1＝20，则AC ＝⎠⎛0201.2t d t ＝0.6t 2|200 ＝240（m ）.即A 、C 间的距离为240 m ．（2）设D 到B 的时间为t 2 s ，则24－1.2t 2＝0，解得t 2＝20，则BD ＝⎠⎛020 （24－1.2t ）d t ＝（24t －0.6t 2）|200 ＝240（m ），即B 、D 间的距离为240 m ． 2．答案解析：（1）由已知，当a ＝2时，f （x ）＝2x ＋ln x ， ∴导函数曲线y ＝f′（x ）与直线x ＝1，x ＝e 及坐标轴所围成的面积为：S ＝⎠⎛1e f′（x ）d x ＝()2x ＋ln x |e1 ＝2e －1.（2）由题得f′（x ）＝a ＋1x＝ax ＋1x （x>0）， ①当a≥0时，由于x>0，则ax ＋1>0恒成立，即f′（x ）>0当x>0时恒成立，∴函数f （x ）的单调递增区间为（0，＋∞）；②当a<0时，令f′（x ）＝0可得x ＝－1a>0，当x∈⎝ ⎛⎭⎪⎫0，－1a 时，f′（x ）>0；当x∈⎝ ⎛⎭⎪⎫－1a ，＋∞ 时，f′（x ）<0， ∴函数f （x ）的单调递增区间为⎝ ⎛⎭⎪⎫0，－1a ，单调递减区间为⎝ ⎛⎭⎪⎫－1a ，＋∞ . 综上，当a≥0时，函数f （x ）的单调递增区间为()0，＋∞ ；当a<0时，函数f （x ）的单调递增区间为⎝ ⎛⎭⎪⎫0，－1a ，单调递减区间为⎝ ⎛⎭⎪⎫－1a ，＋∞ .。

定积分与微积分含答案

定积分与微积分基本定理基础热身1．已知f (x )为偶函数，且⎠⎜⎛06f(x)d x ＝8，则⎠⎛6－6f(x)d x ＝( ) A ．0 B ．4 C ．8 D ．162．设f(x)＝⎩⎪⎨⎪⎧x 2，x∈[0，1]，1x，x∈1，e ](其中e 为自然对数的底数)，则⎠⎜⎛ef(x)d x 的值为( )B ．2C ．13．若a ＝⎠⎜⎛02x 2d x ，b ＝⎠⎜⎛02x 3d x ，c ＝⎠⎜⎛02sin x d x ，则a 、b 、c 的大小关系是( )A ．a<c<bB ．a<b<cC ．c<b<aD ．c<a<b4．如图K 15－1，阴影部分的面积是( )图15－1A ．2 3B ．2－ 3能力提升5．设函数f(x)＝ax 2＋1，若⎠⎜⎛1f(x)d x ＝2，则a ＝( )A ．1B ．2C ．3D ．46．由直线x ＝－π3，x ＝π3，y ＝0与曲线y ＝cos x 所围成的封闭图形的面积为( )B ．17．一物体以v ＝＋(单位：m /s )的速度自由下落，则下落后第二个4 s 内经过的路程是( )A ．260 mB ．258 mC ．259 mD ． m8．若⎠⎜⎛0k(2x －3x 2)d x ＝0，则k 等于( ) A ．0 B ．1C ．0或1D ．以上均不对9．如果10 N 的力能使弹簧压缩10 cm ，为在弹性限度内将弹簧拉长6 cm ，则力所做的功为( )A ． JB ． JC ． JD ． J10．设函数y ＝f(x)的定义域为R ＋，若对于给定的正数K ，定义函数f K (x )＝⎩⎪⎨⎪⎧K ，f x ≤K ，f x ，f x >K ，则当函数f (x )＝1x ，K ＝1时，定积分⎠⎛214f K (x)d x 的值为________．(x －x 2)d x ＝________.12． ∫π20(sin x ＋a cos x)d x ＝2，则实数a ＝________.13．由抛物线y 2＝2x 与直线x ＝12及x 轴所围成的图形绕x 轴旋转一周所得旋转体的体积为________．14．(10分)已知函数f(x)＝x 3＋ax 2＋bx ＋c 的图象如图K 15－2所示，直线y ＝0在原点处与函数图象相切，且此切线与函数图象所围成的区域(阴影)面积为274，求f(x)的解析式．图K 15－215．(13分)如图K 15－3所示，已知曲线C 1：y ＝x 2与曲线C 2：y ＝－x 2＋2ax(a>1)交于点O 、A ，直线x ＝t(0<t≤1)与曲线C 1、C 2分别相交于点D 、B ，连接OD 、DA 、AB.(1)写出曲边四边形ABOD(阴影部分)的面积S 与t 的函数关系式S ＝f(t)；(2)求函数S ＝f(t)在区间(0,1]上的最大值．图K 15－3难点突破16．(12分)已知点P 在曲线y ＝x 2－1上，它的横坐标为a(a>0)，由点P 作曲线y ＝x 2的切线PQ(Q 为切点)．(1)求切线PQ 的方程；(2)求证：由上述切线与y ＝x 2所围成图形的面积S 与a 无关．参考答案：【基础热身】1．D [解析] ⎠⎛6－6f(x)d x ＝2⎠⎜⎛6f(x)d x ＝2×8＝16.2．A [解析] 根据积分的运算法则，可知∫e0f(x)d x 可以分为两段，即∫e 0f(x)d x ＝⎠⎜⎛01x 2d x ＋∫e 11x d x ＝13x 3⎪⎪⎪⎪⎪⎪10＋ln x e 1＝13＋1＝43，所以选A .3．D [解析] a ＝⎠⎜⎛2x 2d x ＝13x 3⎪⎪⎪20＝83，b ＝⎠⎜⎛02x 3d x ＝14x 4⎪⎪⎪ 20＝4，c ＝⎠⎜⎛2sin x d x ＝－cos x ⎪⎪⎪ 20＝1－cos 2<2，∴c<a<b.4．C [解析] ⎠⎛1－3(3－x 2－2x)d x ＝⎝ ⎛⎭⎪⎫3x －13x 3－x 2⎪⎪⎪1－3＝323. 【能力提升】5．C [解析] ⎠⎜⎛1f(x)d x ＝⎠⎜⎛01(ax 2＋1)d x ＝ax 33＋x ⎪⎪⎪10＝a3＋1＝2，解得a ＝3.6．D [解析] 根据定积分的相关知识可得到：由直线x ＝－π3，x ＝π3，y ＝0与曲线y ＝cos x 所围成的封闭图形的面积为：⎪⎪⎪S ＝∫π3－π3cos x d x ＝sin x π3－π3＝sin π3－sin ⎝ ⎛⎭⎪⎫－π3＝3，故选D .7．D [解析] ⎠⎜⎛48＋d t ＝＋⎪⎪⎪ 84＝×64＋×8－×16－×4＝＋52－－26＝.8．C [解析] ⎠⎜⎛0k (2x －3x 2)d x ＝⎠⎜⎛0k2x d x －⎠⎜⎛0k3x 2d x ＝x 2⎪⎪⎪⎪⎪⎪k 0－x 3k＝k 2－k 3＝0，∴k＝0或k ＝1.9．D [解析] 由F(x)＝kx ，得k ＝100，F(x)＝100x ，错误!100x d x ＝(J )．10．2ln 2＋1 [解析] 由题设f 1(x)＝⎩⎪⎨⎪⎧1，1x≤1，1x ，1x >1，于是定积分⎠⎛214f 1(x )d x ＝⎠⎛1141x d x ＋⎠⎜⎛121d x ＝ln x⎪⎪⎪114＋x⎪⎪⎪ 21＝2ln 2＋1.[解析] ⎠⎜⎛1(x －x 2)d x ＝⎪⎪⎪⎝ ⎛⎭⎪⎫23x 32－13x 310＝13. 12．1 [解析] ∫π20(sin x ＋a cos x)d x ＝(a sin x －cos x)错误!＝⎝⎛⎭⎪⎫a sin π2－cos π2－a sin 0＋cos 0＝a ＋1＝2，∴a＝1.[解析] 如图所示，因为y 2＝2x ，x∈⎣⎢⎡⎦⎥⎤0，12，⎪⎪⎪所以V ＝π∫1202x d x ＝πx 2120＝π4.14．[解答] y ＝0在原点处相切知b ＝0，则有f (x )＝x 3＋ax 2，令f (x )＝0，得x 3＋ax 2＝0，可得x ＝0或x ＝－a (－a >0，即a <0)．可以得到图象与x 轴交点为(0,0)，(－a,0)，故∫－a 0－f (x )d x ＝⎪⎪⎪⎝ ⎛⎭⎪⎫－x 44－ax 33－a 0＝－a 44＋a 43＝a 412＝274，a＝－3，所以f (x )＝x 3－3x 2.15．[解答] (1)由⎩⎪⎨⎪⎧y ＝x 2，y ＝－x 2＋2ax ，解得⎩⎪⎨⎪⎧x ＝0，y ＝0或⎩⎪⎨⎪⎧x ＝a ，y ＝a 2.∴O (0,0)，A (a ，a 2)．又由已知得B (t ，－t 2＋2at )，D (t ，t 2)，∴S ＝⎠⎜⎛0t(－x 2＋2ax )d x －12t ×t 2＋12(－t 2＋2at －t 2)×(a －t ) ＝⎝ ⎛⎭⎪⎫－13x 3＋ax 2⎪⎪⎪t－12t 3＋(－t 2＋at )×(a －t ) ＝－13t 3＋at 2－12t 3＋t 3－2at 2＋a 2t ＝16t 3－at 2＋a 2t .故S ＝f (t )＝16t 3－at 2＋a 2t (0<t ≤1)．(2)f ′(t )＝12t 2－2at ＋a 2，令f ′(t )＝0，即12t 2－2at ＋a 2＝0，解得t ＝(2－2)a 或t ＝(2＋2)a .∵0<t ≤1，a >1，∴t ＝(2＋2)a 应舍去．①若(2－2)a ≥1，即a ≥12－2＝2＋22，∵0<t ≤1，∴f ′(t )≥0.∴f (t )在区间(0,1]上单调递增，S 的最大值是f (1)＝a 2－a ＋16.②若(2－2)a <1，即1<a <2＋22，(i)当0<t <(2－2)a 时，f ′(t )>0， (ii)当(2－2)a <t ≤1时，f ′(t )<0.∴f (t )在区间(0，(2－2)a )上单调递增，在区间[(2－2)a ，1]上单调递减．∴f (t )的最大值是f ((2－2)a )＝16[(2－2)a ]3－a [(2－2)a ]2＋a 2(2－2)a ＝22－23a 3.综上所述f (t )max＝⎩⎪⎨⎪⎧a 2－a ＋16⎝ ⎛⎭⎪⎪⎫a ≥2＋22，22－23a 3⎝ ⎛⎭⎪⎪⎫1<a <2＋22.【难点突破】16．[解答] (1)设点P 的坐标为(a ，a 2－1)，又设切点Q 的坐标为(x ，x 2)．则k PQ ＝a 2－1－x 2a －x ，由y ′＝2x 知a 2－1－x 2a －x＝2x ，解得：x ＝a ＋1或x ＝a －1.所以所求的切线方程为2(a ＋1)x －y －(a ＋1)2＝0或2(a －1)x －y －(a －1)2＝0.(2)证明：S ＝⎠⎛a a －1[x 2－2(a －1)x ＋(a －1)2]d x ＋∫a ＋1a[x 2－2(a ＋1)x ＋(a ＋1)2]d x ＝23.故所围成的图形面积S ＝23，此为与a 无关的一个常数．。

微积分考试试题及答案

微积分考试试题及答案一、选择题（每题5分，共20分）1. 函数 $ f(x) = x^2 $ 在 $ x = 1 $ 处的导数是：A. 1B. 2C. 3D. 42. 定积分 $ \int_{0}^{1} x^2 dx $ 的值是：A. 1/3B. 1/2C. 2/3D. 13. 曲线 $ y = x^3 $ 与 $ x $ 轴围成的面积是：A. 1/4B. 1/3C. 1/2D. 2/34. 函数 $ y = \sin(x) $ 的不定积分是：A. $ -\cos(x) $B. $ \cos(x) $C. $ \sin(x) $D. $ \ln(\sin(x)) $二、填空题（每题5分，共20分）5. 如果 $ f'(x) = 6x $，则 $ f(x) = _______ + C $。

6. 函数 $ y = \ln(x) $ 的导数是 _______。

7. 定积分 $ \int_{1}^{e} e^x dx $ 的值是 _______。

8. 曲线 $ y = e^x $ 与 $ x $ 轴围成的面积在 $ x = 0 $ 到 $ x = 1 $ 之间的值是 _______。

三、解答题（每题10分，共60分）9. 求函数 $ f(x) = x^3 - 3x $ 的导数。

10. 计算定积分 $ \int_{0}^{2} (2x + 1) dx $。

11. 求曲线 $ y = x^2 $ 与直线 $ y = 4x $ 相交的点。

12. 求函数 $ y = \ln(x) $ 在 $ x = e $ 处的切线方程。

四、答案一、选择题答案1. B2. B3. B4. B二、填空题答案5. $ 3x^2 + C $6. $ 1/x $7. $ e^e - 1 $8. $ e - 1 $三、解答题答案9. $ f'(x) = 3x^2 - 3 $10. $ \int_{0}^{2} (2x + 1) dx = x^2 + x \bigg|_{0}^{2} = 4 + 2 = 6 $11. 令 $ x^2 = 4x $，解得 $ x = 0 $ 或 $ x = 4 $，所以交点为 $ (0, 0) $ 和 $ (4, 16) $。

微积分试卷及标准答案6套

微积分试题 (A 卷)一. 填空题 (每空2分,共20分)1.已知则对于，总存在δ>0，使得当,)(lim 1A x f x =+→0>∀ε时，恒有│ƒ(x )─A│< ε。

2.已知，则a = ，b =2235lim 2=-++∞→n bn an n 。

3.若当时，α与β 是等价无穷小量，则。

0x x →=-→ββα0limx x 4.若f (x )在点x = a 处连续，则。

=→)(lim x f ax 5.的连续区间是。

)ln(arcsin )(x x f =6.设函数y =ƒ(x )在x 0点可导，则______________。

=-+→hx f h x f h )()3(lim0007.曲线y = x 2＋2x －5上点M 处的切线斜率为6，则点M 的坐标为。

8. 。

='⎰))((dx x f x d 9.设总收益函数和总成本函数分别为，，则当利润最大时产2224Q Q R -=52+=Q C 量是。

Q 二. 单项选择题 (每小题2分,共18分)1.若数列{x n }在a 的ε 邻域（a -ε,a +ε）内有无穷多个点，则（）。

(A) 数列{x n }必有极限，但不一定等于a (B) 数列{x n }极限存在，且一定等于a(C) 数列{x n }的极限不一定存在 (D) 数列{x n }的极限一定不存在2.设则为函数的（）。

11)(-=x arctg x f 1=x )(x f(A) 可去间断点(B) 跳跃间断点 (C) 无穷型间断点(D) 连续点3.（）。

=+-∞→13)11(lim x x x(A) 1 (B) ∞(C)(D) 2e 3e4.对需求函数，需求价格弹性。

当价格（）时，5p eQ -=5pE d -==p 需求量减少的幅度小于价格提高的幅度。

(A) 3 (B) 5 (C) 6(D) 105.假设在点的某邻域内(可以除外)存)(),(0)(lim ,0)(lim 0x g x f x g x f x x x x ''==→→得0x 0x 在，又a 是常数，则下列结论正确的是（）。

微积分综合练习题及参考答案精选全文完整版

可编辑修改精选全文完整版综合练习题1（函数、极限与连续部分）1．填空题（1）函数)2ln(1)(-=x x f 的定义域是．答案：2>x 且3≠x .（2）函数24)2ln(1)(x x x f -++=的定义域是．答案：]2,1()1,2(-⋃--（3）函数74)2(2++=+x x x f ，则=)(x f．答案：3)(2+=x x f（4）若函数⎪⎩⎪⎨⎧≥<+=0,0,13sin )(x k x xx x f 在0=x 处连续，则=k ．答案：1=k （5）函数x x x f 2)1(2-=-，则=)(x f ．答案：1)(2-=x x f（6）函数1322+--=x x x y 的间断点是．答案：1-=x（7）=∞→xx x 1sin lim ．答案：1（8）若2sin 4sin lim 0=→kxxx ，则=k ．答案：2=k2．单项选择题（1）设函数2e e xx y +=-，则该函数是（）．A ．奇函数B ．偶函数C ．非奇非偶函数D ．既奇又偶函数答案：B（2）下列函数中为奇函数是（）．A ．x x sinB ．2e e x x +- C ．)1ln(2x x ++ D ．2x x +答案：C（3）函数)5ln(4+++=x x xy 的定义域为（）． A ．5->x B ．4-≠x C ．5->x 且0≠x D ．5->x 且4-≠x答案：D（4）设1)1(2-=+x x f ，则=)(x f （）A ．)1(+x xB ．2x C ．)2(-x x D ．)1)(2(-+x x 答案：C（5）当=k （）时，函数⎩⎨⎧=≠+=0,0,2)(x k x e x f x 在0=x 处连续.A ．0B ．1C ．2D ．3 答案：D（6）当=k （）时，函数⎩⎨⎧=≠+=0,0,1)(2x k x x x f ，在0=x 处连续.A ．0B ．1C ．2D ．1- 答案：B （7）函数233)(2+--=x x x x f 的间断点是（） A ．2,1==x xB ．3=xC ．3,2,1===x x xD ．无间断点答案：A 3．计算题（1）423lim 222-+-→x x x x ．解：4121lim )2)(2()1)(2(lim 423lim 22222=+-=+---=-+-→→→x x x x x x x x x x x x （2）329lim 223---→x x x x解：234613lim )1)(3()3)(3(lim 329lim 33223==++=+-+-=---→→→x x x x x x x x x x x x （3）4586lim 224+-+-→x x x x x解：3212lim )1)(4()2)(4(lim 4586lim 44224=--=----=+-+-→→→x x x x x x x x x x x x x综合练习题2（导数与微分部分）1．填空题（1）曲线1)(+=x x f 在)2,1(点的切斜率是．答案：21 （2）曲线xx f e )(=在)1,0(点的切线方程是．答案：1+=x y（3）已知xx x f 3)(3+=，则)3(f '= ．答案：3ln 33)(2x x x f +=')3(f '=27（)3ln 1+（4）已知x x f ln )(=，则)(x f ''= ．答案：x x f 1)(='，)(x f ''=21x- （5）若xx x f -=e )(，则='')0(f．答案：x xx x f --+-=''e e 2)(='')0(f 2-2.单项选择题（1）若x x f xcos e)(-=，则)0(f '=（）．A. 2B. 1C. -1D. -2 因)(cos e cos )e ()cos e()('+'='='---x x x x f x x x)sin (cos e sin e cos e x x x x x x x +-=--=---所以)0(f '1)0sin 0(cos e 0-=+-=- 答案：C （2）设，则（）． A ． B ．C ．D ．答案：B（3）设)(x f y =是可微函数，则=)2(cos d x f （）．A ．x x f d )2(cos 2'B ．x x x f d22sin )2(cos 'C ．x x x f d 2sin )2(cos 2'D ．x x x f d22sin )2(cos '- 答案：D（4）若3sin )(a x x f +=，其中a 是常数，则='')(x f （）．A ．23cos a x + B ．a x 6sin + C ．x sin - D ．x cos 答案：C3．计算题（1）设xx y 12e =，求y '．解： )1(e e 22121xx x y xx -+=')12(e 1-=x x（2）设x x y 3cos 4sin +=，求y '.解：)sin (cos 34cos 42x x x y -+='x x x 2cos sin 34cos 4-=（3）设xy x 2e 1+=+，求y '. 解：2121(21exx y x -+='+ （4）设x x x y cos ln +=，求y '.解：)sin (cos 12321x x x y -+=' x x tan 2321-= 综合练习题3（导数应用部分）1．填空题（1）函数的单调增加区间是．答案：),1(+∞（2）函数1)(2+=ax x f 在区间),0(∞+内单调增加，则a 应满足．答案：0>a2．单项选择题（1）函数2)1(+=x y 在区间)2,2(-是（） A ．单调增加 B ．单调减少 C ．先增后减 D ．先减后增答案：D（2）满足方程0)(='x f 的点一定是函数)(x f y =的（）. A ．极值点 B ．最值点 C ．驻点 D ．间断点答案：C（3）下列结论中（）不正确． A ．)(x f 在0x x =处连续，则一定在0x 处可微. B ．)(x f 在0x x =处不连续，则一定在0x 处不可导. C ．可导函数的极值点一定发生在其驻点上.D ．函数的极值点一定发生在不可导点上. 答案： B（4）下列函数在指定区间上单调增加的是（）．A ．x sinB ．xe C ．2x D ．x -3答案：B3．应用题（以几何应用为主）（1）欲做一个底为正方形，容积为108m 3的长方体开口容器，怎样做法用料最省？解：设底边的边长为x m ，高为h m ，容器的表面积为y m 2。

微积分考试题目及答案

微积分考试题目及答案一、选择题（每题5分，共30分）1. 函数f(x)=x^2+3x-4的导数是：A. 2x+3B. x^2+3C. 2x^2+3xD. x^2+6x-4答案：A2. 曲线y=x^3-2x+1在x=1处的切线斜率是：A. 1B. 2C. 3D. 4答案：B3. 微分方程dy/dx=2x的通解是：A. y=x^2+CB. y=2x+CC. y=x^2+2x+CD. y=2x^2+C答案：A4. 定积分∫(0,1) x^2 dx的值是：A. 1/3B. 1/2C. 1D. 2答案：A5. 函数y=e^x的不定积分是：A. e^x+CB. e^xC. 1/e^x+CD. ln(e^x)+C答案：A6. 函数y=ln(x)的导数是：A. 1/xB. xC. ln(x)D. 1答案：A二、填空题（每题5分，共20分）1. 函数f(x)=sin(x)的原函数是_________。

答案：-cos(x)+C2. 曲线y=x^2在x=2处的切线方程是_________。

答案：y-4=4(x-2) 或 y=4x-43. 函数y=x^3的二阶导数是_________。

答案：6x4. 定积分∫(0,π) sin(x) dx的值是_________。

答案：2三、解答题（每题20分，共50分）1. 求函数f(x)=x^3-3x^2+2x的极值点。

答案：首先求导数f'(x)=3x^2-6x+2，令f'(x)=0，解得x=1和x=2/3。

然后求二阶导数f''(x)=6x-6，代入x=1和x=2/3，得到f''(1)=0，f''(2/3)=-2，因此x=1是拐点，x=2/3是极大值点。

2. 求曲线y=x^2-4x+3与x轴的交点。

答案：令y=0，解方程x^2-4x+3=0，得到x=1和x=3，因此交点为(1,0)和(3,0)。

3. 求定积分∫(0,2) (x^2-2x+1) dx。

定积分及微积分基本定理练习试题包括答案.docx

1.4 定积分与微积分基本定理练习题及答案1.(2011·宁夏银川一中月考) 求曲线y＝ x2与y＝ x所围成图形的面积，其中正确的是()A． S＝1(x2 － x)dx0B． S＝1(x －x2)dxC． S＝1(y2 － y)dy D0． S＝1(y －y)dy[0,1][ 答案 ]B[ 分析 ]根据定积分的几何意义，确定积分上、下限和被积函数．[ 解读 ]两函数图象的交点坐标是(0,0) ， (1,1) ，故积分上限是上， x≥ x2，故函数y＝x2 与 y＝x 所围成图形的面积S＝1(x1，下限是－x2)dx.0，由于在2．(2010 ·山东日照模考)a ＝2xdx，b＝2exdx ，c＝2sinxdx，则a、 b、c的大小关系是 ()A． a<c<bB． a<b<cC． c<b<aD． c<a<b[ 答案 ]D1[ 解读] a ＝2xdx ＝2x2|02 0＝ 2 ， b ＝2exdx ＝ex|02 0＝ e2－ 1>2， c＝2sinxdx＝－cosx|02 ＝ 1－ cos2 ∈(1,2)，∴c<a<b.3．(2010 ·山东理， 7) 由曲线 y＝ x2， y＝ x3 围成的封闭图形面积为() 1117A. 12B. 4C. 3D. 12[ 答案 ]Ay＝ x2[ 解读 ]由得交点为 (0,0)， (1,1) ．y＝ x3111∴ S＝1(x2 － x3)dx ＝3x3 －4x401＝12.[ 点评 ]图形是由两条曲线围成的时，其面积是上方曲线对应函数表达式减去下方曲线对应函数表达式的积分，请再做下题：(2010 ·湖南师大附中 ) 设点 P 在曲线 y＝ x2 上从原点到A(2,4) 移动，如果把由直线OP，直线 y＝ x2及直线 x＝ 2 所围成的面积分别记作S1，S2. 如图所示，当S1＝S2 时，点 P 的坐标是 ()A.416B.416 3，95，9C.415D.413 3，75，7[ 答案 ]At3 [ 解读 ]设 P(t ， t2)(0≤t ≤ 2) ，则直线 OP：y＝ tx ，∴ S1＝ t(tx－ x2)dx ＝6；S2＝8t344162(x2 － tx)dx＝3－ 2t ＋6，若 S1＝ S2，则 t ＝3，∴ P 3，9 .t4．由三条直线 x＝ 0、 x＝2、 y＝ 0 和曲线 y＝ x3所围成的图形的面积为 () 418A． 4 B.3C. 5 D．6[ 答案 ]Ax4[ 解读 ]S＝2x3dx ＝4 02＝ 4.5．(2010 ·湖南省考试院调研)1－1(sinx＋1)dx的值为()A． 0 B ． 2C． 2＋2cos1 D ． 2－ 2cos1[ 答案 ]B[ 解读 ]1－1(sinx＋1)dx＝(－cosx＋x)|－11＝(－cos1＋1)－(－cos(－1)－1)＝2.6．曲线 y＝ cosx(0 ≤ x≤2π) 与直线y＝ 1 所围成的图形面积是()A．2π B ．3π3πC. 2 D．π[ 答案 ]A[ 解读 ]如右图，S＝∫ 02π(1 － cosx)dx＝(x －sinx)|02 π＝ 2π.[ 点评 ]此题可利用余弦函数的对称性①②③④ 面积相等解决，但若把积分区间改为π6 ，π ，则对称性就无能为力了．7．函数 F(x) ＝xt(t－4)dt在[－1,5]上()A．有最大值0，无最小值32B．有最大值0 和最小值－332C．有最小值－ 3 ，无最大值D．既无最大值也无最小值[ 答案 ]B[ 解读 ] F′(x) ＝ x(x － 4) ，令 F′(x) ＝ 0，得 x1＝ 0， x2＝ 4，73225∵F( －1) ＝－3， F(0) ＝ 0， F(4) ＝－3， F(5) ＝－3 .32∴最大值为 0，最小值为－3 .[ 点评 ] 一般地， F(x) ＝ xφ(t)dt的导数 F′(x) ＝φ (x) ．18．已知等差数列 {an} 的前 n 项和 Sn＝ 2n2＋ n，函数 f(x) ＝x t dt ，若 f(x)<a3，则 x1的取值范围是 ()3A.6，＋∞ B． (0 ， e21)C． (e － 11， e) D ． (0 ，e11)[ 答案 ] D1[ 解读 ]f(x)＝x dt ＝ lnt|1x＝lnx，a3＝S3－S2＝21－10＝11，由lnx<11得，t10<x<e11.9．(2010 ·福建厦门一中 ) 如图所示，在一个长为π，宽为 2 的矩形 OABC内，曲线y＝sinx(0 ≤ x≤ π) 与 x 轴围成如图所示的阴影部分，向矩形OABC内随机投一点( 该点落在矩形OABC内任何一点是等可能的) ，则所投的点落在阴影部分的概率是()123πA. πB. πC. πD. 4[ 答案 ]A—[ 解读 ]由图可知阴影部分是曲边图形，考虑用定积分求出其面积．由题意得S ＝ πsinxdx ＝－ cosx|0 π＝－ (cos π－ cos0) ＝ 2 ，再根据几何概型的算法易知所求概率P ＝S 2＝1 .＝πS 矩形 OABC 2πx ＋ 2 －2≤ x<010．(2010 ·吉林质检 ) 函数 f(x) ＝ π的图象与 x 轴所围成的图形2cosx 0≤ x ≤ 2面积 S 为 ()31A. 2B ． 1 C ． 4 D. 2 [ 答案 ] C[ 解读 ]面积 S ＝∫ π－ 2f(x)dx ＝－2(x ＋ 2)dx ＋∫π02cosxdx ＝ 2＋ 2＝ 4.2 211．(2010 ·沈阳二十中 ) 设函数 f(x) ＝ x －[x] ，其中 [x] 表示不超过 x 的最大整数，如 [ －x1.2] ＝－ 2， [1.2] ＝1， [1]＝1. 又函数 g(x) ＝－ 3， f(x) 在区间 (0,2) 上零点的个数记为 m ，f(x) 与 g(x) 的图象交点的个数记为n ，则 ng(x)dx 的值是 ()m54A ．－ 2B ．－ 357C ．－ 4D ．－ 6[ 答案 ]A[ 解读 ]由题意可得，当 0<x<1 时， [x] ＝ 0， f(x) ＝ x ，当 1≤ x<2 时， [x] ＝ 1，f(x)＝x － 1，所以当 x ∈ (0,2) 时，函数 f(x) 有一个零点，由函数 f(x)与 g(x) 的图象可知两个函xx25数有 4 个交点，所以 m ＝ 1， n ＝ 4，则 ng(x)dx ＝4 － 3 dx ＝－ 614＝－ 2.m111．(2010 ·江苏盐城调研 ) 甲、乙两人进行一项游戏比赛，比赛规则如下：甲从区间 [0,1]上随机等可能地抽取一个实数记为b ，乙从区间 [0,1] 上随机等可能地抽取一个实数记为c(b 、c 可以相等 ) ，若关于 x 的方程 x2＋ 2bx ＋c ＝ 0 有实根，则甲获胜，否则乙获胜，则在一场比赛中甲获胜的概率为( )1 2 13A. 3B. 3C. 2D. 4[ 答案 ]A[ 解读 ] 方程 x2＋ 2bx ＋c ＝ 0 有实根的充要条件为＝ 4b2－ 4c ≥ 0，即 b2≥ c ，1b2db01由题意知，每场比赛中甲获胜的概率为p＝1×1＝3.12．(2010 ·吉林省调研 ) 已知正方形四个顶点分别为O(0,0) ，A(1,0) ，B(1,1) ，C(0,1) ，曲线 y＝ x2(x ≥ 0) 与 x 轴，直线 x＝1 构成区域 M，现将一个质点随机地投入正方形中，则质点落在区域 M内的概率是 ()11A. 2B. 412C. 3D.5[ 答案 ]C[ 解读 ]如图，正方形面积1，区域 M的面积为 S＝ 1x2dx111＝3x3|01 ＝3，故所求概率 p＝3.2．如图，阴影部分面积等于()A． 2 3B． 2－33235C. 3D. 3[ 答案 ]C[ 解读 ]图中阴影部分面积为132.S＝ 1(3 － x2－ 2x)dx ＝ (3x －3x3－ x2)|1－ 3＝ 3-33. 24－ x2dx ＝ ()A．4π B ．2ππC．π D.2[ 答案 ]C[ 解读 ]令 y＝4－ x2，则 x2＋y2＝ 4(y ≥0) ，由定积分的几何意义知所求积分为图中阴影部分的面积，1∴ S＝4×π× 22＝π.4.已知甲、乙两车由同一起点同时出发，并沿同一路线( 假定为直线 ) 行驶．甲车、乙车的速度曲线分别为v 甲和 v 乙 ( 如图所示 ) ．那么对于图中给定的t0 和 t1 ，下列判断中一定正确的是 ()A．在 t1 时刻，甲车在乙车前面B．在 t1 时刻，甲车在乙车后面C．在 t0 时刻，两车的位置相同D． t0 时刻后，乙车在甲车前面[ 答案 ]A[ 解读 ]判断甲、乙两车谁在前，谁在后的问题，实际上是判断在t0 ， t1 时刻，甲、乙两车行驶路程的大小问题．根据定积分的几何意义知：车在某段时间内行驶的路程就是该时间段内速度函数的定积分，即速度函数 v(t)的图象与t 轴以及时间段围成区域的面积．从图象知：在 t0时刻， v 甲的图象与 t轴和 t ＝ 0，t ＝ t0围成区域的面积大于 v 乙的图象与 t 轴和 t ＝ 0， t ＝ t0围成区域的面积，因此，在t0时刻，甲车在乙车的前面，而且此时乙车的速度刚刚赶上甲车的速度，所以选项C，D 错误；同样，在t1 时刻， v 甲的图象与 t 轴和t ＝ t1 围成区域的面积，仍然大于v 乙的图象与 t 轴和 t ＝t1围成区域的面积，所以，可以断定：在 t1 时刻，甲车还是在乙车的前面．所以选 A.ππ5．(2012 ·山东日照模拟 ) 向平面区域Ω＝ {(x ，y)| －4≤ x≤4，0≤ y≤1} 内随机投掷一点，该点落在曲线y＝ cos2x 下方的概率是 ()π 1A. 4B. 2π2C. 2－ 1D. π[ 答案 ]D[ 解读 ]π平面区域Ω 是矩形区域，其面积是2，在这个区6．(sinx－ cosx)dx的值是 ()πA． 0 B. 4C． 2D．－ 2[ 答案 ]D[ 解读 ](sinx－cosx)dx＝(－cosx－sinx)＝－2.7．(2010 ·惠州模拟 )2(2 － |1 － x|)dx ＝ ________.[ 答案 ]3[ 解读 ]1＋ x 0≤ x≤ 1∵ y＝，3－ x 1<x ≤ 2∴ 2(2 － |1 － x|)dx ＝1(1 ＋ x)dx ＋ 2(3 － x)dx0011133＝(x ＋2x2)|10＋ (3x －2x2)|21＝2＋2＝ 3.8．(2010·芜湖十二中 ) 已知函数 f(x) ＝3x2 ＋ 2x＋ 1，若1－1f(x)dx ＝2f(a) 成立，则a＝ ________.1[ 答案 ]－ 1 或3[ 解读 ]∵1－ 1f(x)dx ＝1－ 1(3x2 ＋ 2x ＋ 1)dx ＝ (x3 ＋ x2 ＋ x)|1 － 1 ＝ 4 ，1－1f(x)dx＝2f(a)，∴ 6a2＋4a＋2＝4，1∴ a＝－ 1 或3.π19．已知a＝∫2 0(sinx＋cosx)dx，则二项式(a x－x)6 的展开式中含x2项的系数是________．[ 答案 ]－192ππππ[ 解读 ]由已知得a＝∫2 0(sinx＋cosx)dx＝(－cosx＋sinx)| 2 0＝(sin2－cos2)－(sin0 － cos0) ＝ 2，1(2 x－ )6 的展开式中第 r ＋ 1 项是 Tr ＋ 1＝ ( －1)r ×C6r×26－r ×x3－r，令 3－ r ＝ 2 得，xr ＝ 1，故其系数为( －1)1 ×C16×25＝－192.10．有一条直线与抛物线y＝ x2 相交于 A、B 两点，线段 AB 与抛物线所围成图形的面积4恒等于3，求线段AB的中点 P 的轨迹方程．[ 解读 ]设直线与抛物线的两个交点分别为A(a， a2) ， B(b ， b2) ，不妨设a<b，b2－ a2则直线 AB 的方程为y－ a2＝b－a (x － a) ，即y＝(a ＋ b)x － ab.a＋ b 则直线AB 与抛物线围成图形的面积为S＝b[(a ＋b)x － ab－x2]dx ＝(2x2－abx －ax313 )|ba＝6(b －a)3 ，14∴6(b － a)3 ＝3，解得 b－ a＝ 2. 设线段 AB的中点坐标为 P(x ，y) ，a＋ b其中x＝2，将 b－a＝ 2 代入得x＝a＋ 1，y＝ a2＋ b2.y＝ a2＋ 2a＋ 2.2消去 a 得 y＝ x2＋ 1.∴线段 AB 的中点 P 的轨迹方程为 y＝ x2＋ 1.能力拓展提升11.(2012 ·郑州二测 ) 等比数列 {an} 中，a3＝ 6，前三项和 S3＝34xdx ，则公比 q 的值为()1A． 1 B ．－211C． 1 或－2D．－ 1 或－2[ 答案 ]C66[ 解读 ]因为 S3＝34xdx ＝ 2x2|30＝ 18，所以q＋q2＋ 6＝ 18，化简得 2q2－ q－1＝ 0，1解得 q＝ 1 或 q＝－2，故选 C.12． (20 12·太原模拟 ) 已知 (xlnx) ′＝ lnx ＋1，则elnxdx＝ ()1A． 1 B ． e C ． e－ 1 D ． e＋ 1[ 答案 ]A[ 解读 ]由(xlnx)′＝ lnx ＋ 1，联想到 (xlnx－x) ′＝ (lnx＋ 1) －1＝ lnx ，于是 elnxdx1＝(xlnx － x)|e1＝ (elne－ e) －(1 ×ln1 －1) ＝ 1.13．抛物线 y2＝ 2x与直线 y＝ 4－ x 围成的平面图形的面积为 ________．[ 答案 ]18[ 解读 ]y2＝ 2x，A(2,2) 、B(8 ，－4) ，选 y 作为积分变量 x 由方程组解得两交点y＝ 4－ x，y2＝2、 x＝ 4－y，2 [(4 － y) －y2y2y3∴ S＝2 ]dy ＝ (4y －2－6 )|2－ 4＝ 18.-414.已知函数 f(x)＝ ex－ 1，直线 l1 ： x＝ 1， l2 ： y＝et － 1(t 为常数，且 0≤ t ≤ 1) ．直线l1 ， l2 与函数 f(x)的图象围成的封闭图形如图中区域Ⅱ所示，其面积用S2 表示．直线 l2 ，y 轴与函数 f(x) 的图象围成的封闭图形如图中区域Ⅰ所示，其面积用S1 表示．当 t 变化时，阴影部分的面积的最小值为________．[ 答案 ]( e－ 1)2[ 解读 ]由题意得S1＋ S2＝ t(et － 1－ ex ＋ 1)dx ＋1(ex － 1－ et ＋ 1)dx ＝ t(et－0t0ex)dx ＋ 1(ex － et)dx ＝ (xet － ex)|t 0 ＋ (ex － xet)|1 t ＝ (2t－ 3)et＋ e＋ 1，令 g(t) ＝ (2t－t3)et ＋ e＋ 1(0 ≤ t ≤ 1) ，则 g′(t) ＝ 2et ＋ (2t －3)et ＝ (2t－ 1)et，令 g′(t) ＝ 0，得 t ＝1 2，11∴当 t ∈ [0 ，2) 时， g ′(t)<0 ， g(t) 是减函数，当 t ∈ ( 2，1] 时， g ′(t)>0 ， g(t)是增函数，1 1因此 g(t) 的最小值为g( 2) ＝ e ＋ 1－ 2e 2＝ ( e － 1)2. 故阴影部分的面积的最小值为( e －1)2.15．求下列定积分．(1)－ 1|x|dx 。

微积分基础试题及答案

微积分基础试题及答案一、单项选择题（每题3分，共30分）1. 函数f(x)=x^2的导数是：A. 2xB. x^2C. 2D. 0答案：A2. 定积分∫(0,1) x dx的值是：A. 0B. 1C. 0.5D. 2答案：C3. 曲线y=e^x在点x=0处的切线斜率是：A. 1B. eC. 0D. -1答案：A4. 函数f(x)=sin(x)的不定积分是：A. cos(x)B. sin(x)C. -cos(x)D. ln(x)答案：A5. 函数f(x)=ln(x)的导数是：A. 1/xB. xC. ln(x)D. x^2答案：A6. 曲线y=x^3-3x^2+2x在x=1处的切线方程是：A. y=-2x+1B. y=2x-1C. y=-x+2D. y=x-1答案：A7. 函数f(x)=x^3的二阶导数是：A. 3x^2B. 6xC. 6D. 9x^2答案：B8. 函数f(x)=x^2+2x+1的极值点是：A. x=-1B. x=1C. x=0D. x=2答案：A9. 曲线y=x^2在x=2处的法线方程是：A. y=-x/4+9/2B. y=x/4+9/2C. y=-x/2+9/2D. y=x/2+9/2答案：A10. 函数f(x)=x^3-3x^2+2x的拐点是：A. x=0B. x=1C. x=2D. x=3答案：B二、填空题（每题4分，共20分）1. 函数f(x)=x^3的一阶导数是________。

答案：3x^22. 定积分∫(0,π) sin(x) dx的值是________。

答案：23. 曲线y=ln(x)在x=e处的切线斜率是________。

答案：1/e4. 曲线y=x^2-4x+4在x=2处的切线方程是________。

答案：y=-4x+85. 函数f(x)=cos(x)的不定积分是________。

答案：sin(x)三、计算题（每题10分，共50分）1. 求函数f(x)=x^2-4x+3在区间[1,3]上的定积分。

微积分定积分练习题(有答案)

微积分定积分练习题(有答案)1利用定积分的几何意义计算1－x 2d x . 2.计算定积分⎠⎛12(x ＋1)d x . 3.定积分⎠⎛a b f (x )d x 的大小 ( )A ．与f (x )和积分区间[a ，b ]有关，与ξi 的取法无关B ．与f (x )有关，与区间[a ，b ]以及ξi 的取法无关C ．与f (x )以及ξi 的取法有关，与区间[a ，b ]无关D ．与f (x )、区间[a ，b ]和ξi 的取法都有关4．在求由x ＝a ，x ＝b (a <b )，y ＝0及y ＝f (x )(f (x )≥0)围成的曲边梯形的面积S 时，在区间[a ，b ]上等间隔地插入n －1个分点，分别过这些分点作x 轴的垂线，把曲边梯形分成n 个小曲边梯形，下列结论中正确的个数是 ( )①n 个小曲边梯形的面积和等于S ；②n 个小曲边梯形的面积和小于S ；③n 个小曲边梯形的面积和大小S ；④n 个小曲边梯形的面积和与S 之间的大小关系不确定A ．1 B ．2 C ．3 D ．45．求由曲线y ＝e x ，直线x ＝2，y ＝1围成的曲边梯形的面积时，若选择x 为积分变量，则积分区间为 ( )A ．[0，e2]B ．[0,2]C ．[1,2]D ．[0,1]6.⎠⎛011d x 的值为( )A ．0 B ．1 C.12 D ．2 7.lim n →＋∞ ⎝ ⎛⎭⎪⎫1n ＋2n ＋…＋n ＋1n ·1n写成定积分是________． 8．已知⎠⎛02f (x )d x ＝3，则⎠⎛02[f (x )＋6]d x ＝________. 9．利用定积分的几何意义求⎠⎛069－(x －3)2d x . 10 求下列定积分：(1)⎠⎛12(x 2＋2x ＋1)d x ； (2)⎠⎛0π(sin x －cos x )d x ； (3)⎠⎛12⎝ ⎛⎭⎪⎫x －x 2＋1x d x ；(4)⎠⎛0－π(cos x ＋e x )d x . (5)⎠⎛01x 2d x (6)⎠⎛01(2x ＋1)d x ； (7)⎠⎛12⎝ ⎛⎭⎪⎫2x ＋1x d x (7)⎠⎛121x d x ； (8)⎠⎛01x 3d x ； (9)⎠⎛1－1e x d x .11 求y ＝－x 2与y ＝x －2围成图形的面积S.12．由直线x ＝12，x ＝2，曲线y ＝1x 及x 轴所围图形的面积为( )A.154B.174C.12ln2 D ．2ln213.已知⎠⎛1－1(x 3＋ax ＋3a －b )d x ＝2a ＋6且f (t )＝⎠⎛0t (x 3＋ax ＋3a －b )d x 为偶函数，求a ，b . 14.已知函数f (x )＝⎠⎛0x (at 2＋bt ＋1)d t 为奇函数，且f (1)－f (－1)＝13，求a ，b 的值． 15. 求正弦曲线y ＝sin x 在[0,2π]上围成的图形的面积________16． (sin x ＋cos x )d x 的值是 ( )A ．0 B.π4 C ．2 D ．417．下列各式中，正确的是( ) A.⎠⎛a b f ′(x )d x ＝f ′(b )－f ′(a ) B.⎠⎛ab f ′(x )d x ＝f ′(a )－f ′(b ) C.⎠⎛a b f ′(x )d x ＝f (b )－f (a ) D.⎠⎛ab f ′(x )d x ＝f (a )－f (b ) 18．已知自由落体的运动速度v ＝gt (g 为常数)，则当t ∈[1,2]时，物体下落的距离为( )A.12g B ．g C.32g D ．2g19．如图中阴影部分面积用定积分表示为________．20e 2x d x ＝________.答案1. π2。

定积分与微积分基本定理随堂练习(含答案).doc

定积分与微积分基本定理基础巩固强化1.(2011 •宁夏银川一中月考)求曲线与y=x所围成图形的面积，其中正确的是()［答案］B［分析］根据定积分的几何意义，确定积分上、下限和被积函数.［解析］两函数图象的交点坐标是(0,0), (1,1),故积分上限是1, 下限是0，由于在［0,1］上，,故函数y =疽与y = x所围成图形的面积S = C\x ~ x2)dx.［答案］C［解析］图中阴影部分面积为S =「(3 - x2 - 2x)dx = (3x %2)l-3 = ~3~- J-33.J2A/4—x2dx=( )A.4TT B. 2TIC.71 D.T［答案］c［解析］令y = .4 _ x2,则x2 + y2 = 4(y^0),由定积分的几何意义知所求积分为图中阴影部分的面积，.*.S=^X K X22= 7t.Cz ，乙 Rt4.00"1已知甲、乙两车由同一起点同时出发，并沿同一路线（假定为直线）行驶.甲车、乙车的速度曲线分别为”甲和”乙（如图所示）.那么对于图中给定的姑和S下列判断中一定正确的是（）A.在h时刻，甲车在乙车前面B.在4 口寸刻，甲车在乙车后面C.在而时刻，两车的位置相同D.t.时刻后，乙车在甲车前面［答案］A［解析］判断甲、乙两车谁在前，谁在后的问题，实际上是判断在如4时刻，甲、乙两车行驶路程的大小问题.根据定积分的几何意义知：车在某段时间内行驶的路程就是该时间段内速度函数的定积分，即速度函数NO的图象与，轴以及时间段围成区域的面积.从图象知：在「0时刻，"甲的图象与♦轴和t = 0, t=t Q围成区域的面积大于华的图象与♦轴和f = 0, 围成区域的面积，因此，在£。

时刻，甲车在乙车的前面，而且此时乙车的速度刚刚赶上甲车的速度，所以选项C, D错误；同样，在》时刻，"甲的图象与£轴和t=t｛围成区域的面积，仍然大于"乙的图象与F轴和t=t x围成区域的面积，所以，可以断定：在4时刻，甲车还是在乙车的前面.所以选A.__ _IT 7T5.（2012-山东日照模拟）向平面区域Q=｛（x, y）|—云, OW）W1｝内随机投掷一点，该点落在曲线y = cos2x下方的概率是B.?A-A 714D.271［答案］D［解析］平面区域。

微积分练习100题及其解答

《微积分》练习100题及其解答1．求极限：．⎪⎭⎫ ⎝⎛--→x e x x 111lim 0解：∵，)0(~1→-x xe x ∴．()2121lim 1lim 11lim 111lim 02000-=-=+-=-+-=⎪⎭⎫ ⎝⎛--→→→→x e x e x e x e x x e x x x x x x x x x 2．求极限：．xx e e x x x sin lim sin 0--→解：∵，∴．)0(~1→-x xe x1sin 1lim sin lim sin sin 0sin 0=--⋅=---→→xx e e x x e e xx x x x x x 或者：记，则当时，在之间满足Lagrange 定理的条件，存x e x f =)(0≠x )(x f x x sin ,在（介于与之间），使得，从而ξξx x sin )(sin sin ξf x x e e xx '=--，所以，．1)0()(lim sin lim 0sin 0='='=--→→f f x x e e x x x x ξ1sin lim sin 0=--→xx e e x x x 3．求极限：．()x xx x e1lim+→解：；()11200lim lim 1xxe e xx xx x x x e xe e e →→⎡⎤⎛⎫⎢⎥+=⋅+= ⎪⎢⎥⎝⎭⎣⎦或者．()()12000ln 1limlim 2lim x x xx x x x x e x e e x e xe x →→→++==⇒+=+4．求极限：．01lim 1xx x +→⎛⎫+ ⎪⎝⎭解：，而，所以，．01lim ln 101lim 1x xx x x e x +→+⎛⎫+ ⎪⎝⎭→⎛⎫+= ⎪⎝⎭0ln(1)1lim ln 1lim0t x t x t x +→+∞→⎛⎫++== ⎪⎝⎭01lim 11xx x +→⎛⎫+= ⎪⎝⎭5．求极限：．())0,0,0(3ln ln lim0>>>-++→c b a xc b a x x x x解：．()00ln ln 3ln ln ln ln limlim 3x x x x x x x x x x x a b c a a b b c c abc xa b c →→++-++==++6．求极限：．()00x αα→>解：．()()112110001101lim lim 10111x x x x x x x αααααααααα--→→→->⎧==-=⎨∞<≤⎩-++7．求极限：．lim(0)x αα→>解：．()()22211000112202limlim022211x x x x x x x αααααααααα--→→→->⎧==-=⎨∞<≤⎩-++8．求极限：．(0)x αα→>解：．012x α→=-9．设函数在内，讨论的单调性．)(x f ()∞+∞-,0)0(,0)(≤>''f x f xx f y )(=解：，，⎥⎦⎤⎢⎣⎡-'=-'='⎪⎭⎫ ⎝⎛='x x f x f x x x f x f x x x f y )()(1)()()(20)0()()(--≤x f x f x x f 当时，，而，则，即，从而此时0>x )0()(f xx f '≤0)(>''x f )0()(f x f '≥'0>'y 递增；同理，当时，递增．x x f y )(=0<x xx f y )(=所以，在内单调增加．xx f y )(=()∞+∞-,10．设函数，求：（1）的极大值；（2）()220()2(0)xf x a ta dta =-+->⎰)(x f M 求极小时的值．M a 解：（1），而，所以xx f a x x f 2)(0)(=''±=⇒='0>a ；a a a f M 232)(3-=-=（2）时，，此时，0>a 102223223=⇒=-='⎪⎭⎫ ⎝⎛-='a a a a M a04>=''a M的极小值为．M 34)1(-=M 11．求极限：．22011lim sin x x x →⎛⎫-⎪⎝⎭解：()()2222224000sin sin 11sin lim lim lim sin sin x x x x x x x x x x x x xx →→→-+-⎛⎫-== ⎪⎝⎭．320000sin sin 1cos sin 1limlim 2lim 2lim 363x x x x x x x x x x x x x x →→→→-+-====12．求极限：．⎪⎭⎫ ⎝⎛-→x x x 220sin 11lim 解：2222222200011sin sin 22lim lim lim sin sin 2sin sin 2x x x x x x x x x x xx x x x →→→--⎛⎫-== ⎪+⎝⎭；222000cos 212sin 2limlimsin 2sin 2cos 22sin 26cos 22sin 22sin 212lim 2sin 234cos 2sin 22x x x x xx x x x x x x x x xx x x x x x x →→→--==+++--==-+-13．求极限：．⎪⎭⎫⎝⎛--→x x x ln 111lim 1解：；211ln 11lim ln 11lim ln 111lim ln )1(1ln lim ln 111lim 11111-=---=--+=--+=-+-=⎪⎭⎫ ⎝⎛--→→→→→x x x x x x xx xx x x x x x x x x x x 14．求极限：．1lim arcsin xx e x +→解：∵，∴．arcsin ~(0)x x x →11100lim arcsin lim lim t t xx x t x x ee x xe t ++=→+∞→→=====+∞15．求极限：．⎪⎭⎫⎝⎛-+∞→x x x arctan 2lim解：．22221arctan 21lim arctan lim lim lim 11121x x x x x x x x x x xxππ→+∞→+∞→+∞→+∞⎛⎫-- ⎪⎛⎫⎝⎭+-==== ⎪+⎝⎭-16．求极限：．2120lim x x x e→解：．22112lim lim t tx x x t e x et=→→+∞====+∞17．求极限：．lim sin ln x x x +→解：．00001ln tan sin lim sin ln lim lim lim 0csc csc cot x x x x x x x x x x x x x x++++→→→→===-=-18．求极限：．1lim x -→解：11lim x x -→→=112sec 24x x ππ--→→===19．求极限：．xx xx x sin tan lim 20-→解：．22232200000tan tan sec 11cos sin21lim lim lim lim lim sin 3363x x x x x x x x x x x x x x x x x x →→→→→----=====20．求极限：．()ln 1ln limcot x x xarc x→+∞+-解：()222222111ln 111lim lim lim 1lim 1.111cot 1111x x x x x x x x x x arc x x xx x x →+∞→+∞→+∞→+∞⎛⎫+-- ⎪+⎝⎭==+==-+⎛⎫⎛⎫++ ⎪ ⎪+⎝⎭⎝⎭21．求极限：．()2lim sec tan x x x π→-解：．()2221sin cos lim sec tan limlim 0cos sin x x x x xx x x x πππ→→→--===-22．求积分：．cos sin 1sin 2x xdx x --⎰解：()2cos sin cos sin 11sin 2cos sin cos sin x x x x dx dx dx x x x x x --==---⎰⎰⎰．1ln csc cot 2244sin 4dx x x C x πππ⎛⎫⎛⎫=-=---+ ⎪ ⎪⎛⎫⎝⎭⎝⎭- ⎪⎝⎭⎰23．求积分：．cos sin 1sin 2x xdx x -+⎰解：．()()()22cos sin 11cos sin cos sin sin cos sin cos x xdx d x x C x xx x x x -=+=-++++⎰⎰24．求积分：．cos sin 1cos 2x xdx x -+⎰解：()2cos sin cos sin 1sec tan sec 1cos22cos 2x x x x dx dx xdx xdxx x --==-+⎰⎰⎰⎰．()1sec ln sec tan 2x x x C =--++25．求积分：．dx xxx ⎰--2cos 1sin cos 解：()2cos sin cos sin 1csc cot csc 1cos 22sin 2x x x x dx dx x xdx xdxx x --==--⎰⎰⎰⎰．()1csc ln csc cot 2x x x C =-+-+26．求积分：．cos sin 1cos 2x xdx x +-⎰解：()2cos sin cos sin 1csc cot csc 1cos 22sin 2x x x x dx dx x xdx xdxx x ++==+-⎰⎰⎰⎰．()1csc ln csc cot 2x x x C =---+27．求积分：．1sin 1cos2xdx x--⎰解：()221sin 1sin 1csc csc 1cos 22sin 2x x dx dx xdx xdx x x --==--⎰⎰⎰⎰．()1cot ln csc cot 2x x x C =-+-+28．求积分：．1sin 1cos2xdx x -+⎰解：()221sin 1sin 1sec sec tan 1cos 22cos 2x x dx dx xdx x xdx x x --==-+⎰⎰⎰⎰．()1tan sec 2x x C =-+29．求积分：．1cos 1cos2xdx x-+⎰解：()221cos 1cos 1sec sec 1cos22cos 2x x dx dx xdx xdx x x --==-+⎰⎰⎰⎰．()1tan ln sec tan 2x x x C =-++30．求积分：．1cos 1cos2xdx x--⎰解：．()()221sin 1sin 1csc csc 1cos22sin 211cot ln tan cot ln csc cot 222x x dx dx xdx xdxx x x x C or x x x C--==--⎛⎫=-++-+-+ ⎪⎝⎭⎰⎰⎰⎰31．求积分：．1arctan21xedx x +⎰解：．1arctan11arctan arctan 21arctan 1xx x e dx e d e C x x=-=-++⎰⎰32．求积分：．2x dx解：222211222xe t x x e dx =⎛⎫==== ⎪⎝⎭．(2211ln ln 222x x e c e C ⎛ '=++=++ ⎝33．求积分：．211x dx e +⎰解：⎰+dx e x 211⎰⎰----++-=+=)1(112112222xx x x e d e dx e e C e x ++-=-)1ln(212或者：⎰⎰+=+=xxx x x x de e e dx e e e 222222)1(121)1(．[]C e x de e de e xx x x x ++-=⎥⎦⎤⎢⎣⎡+-=⎰⎰)1ln(221111212222234．求积分：．()21xxe dx x +⎰解：()()()2211(1)11111xxx xxxe xe xe dx d x xe d d xe x x x x x ⎛⎫=+=-=-+ ⎪+++⎝⎭++⎰⎰⎰⎰．11x x xxe e e dx C x x=-+=+++⎰35．求积分：．211dx x x -+⎰解：2221141133111422dx dx dxx x x x ==-+⎛⎫⎤⎫+-+- ⎪⎪⎥⎝⎭⎭⎦⎰⎰⎰．211122112d x x C x ⎤⎤⎫⎫=--+⎪⎪⎥⎥⎭⎭⎦⎦⎤⎫+-⎪⎥⎭⎦⎰36．求积分：．2141dx x x -+⎰解：()2221111413231dx dx dxx x x ==-+---⎰⎰⎰．21ln ln 3661d C C ⎫==+=⎪⎭⎫-⎪⎭⎰37．求积分：．dx解：22111ln 1111u u du du C u u u u -⎛⎫⎛⎫=-=+ ⎪ ⎪--++⎝⎭⎝⎭⎰⎰．))ln 2ln12ln1Cor x C or x C ⎛⎫=+-+-+ ⎝38．求积分：．解：设，则，，x e u +=1)1ln(2-=u x du u udx 122-=222112111u du du u u u ⎛⎫==+- ⎪--+⎝⎭⎰⎰12ln ln 1u u C C u ⎛⎫-⎛⎫=++=+ ⎪+⎝⎭．)2ln1orx C -+39．求积分：．21443dx x x +-⎰解：．21121ln 443823x dx C x x x -=++-+⎰40．求积分：．23222x dx x x --+⎰解：222323*********(1)x x dx dx x x x x x ⎡⎤--=+⎢⎥-+-+++⎣⎦⎰⎰．()23ln 22arctan(1)2x x x C =-++++41．求积分：．2dx x⎰解：设，则，，t x sin 2=t x cos 242=-tdt dx cos 2=．()222cot csc 1cot arcsin 2x dx tdt t dt t t C C x x ==-=--+=--+⎰⎰⎰42．求积分：．2dx x ⎰解：设，则，，θtan 2=x 2sec θ=θθd dx 2sec 2=．()Cxx x x C x x x x x x C d d d dx x x ++-++=++++--+-=++---=⎪⎭⎫⎝⎛-+=-==+⎰⎰⎰⎰22222222222244ln 44ln 2141sin 1sin ln 21csc sin sin 11sin 1sin sin )sin 1(1sin cos 14θθθθθθθθθθθθ43．求积分：．⎰++dx x x 1)2(1解：消去根号，记，t =122122+=+=-=t x tdtdx t x．()222arctan 21tdtt C C t t ==+=++⎰44．求积分：．⎰-+dx x x x21解：记，3122222+=+=+=⇒-=t x tdtdx t x x t ()()⎰⎰⎰⎰++=⎪⎭⎫ ⎝⎛++=++=-+dt t t dt t t t dt t t dx x x x 21222112232212222．C x x C tt +-+-=++=22arctan 2222arctan2245．求积分：．⎰++dx x x x21解：记，1122222-=+=-=⇒+=t x tdtdx t x x t ()()⎰⎰⎰⎰-+=⎪⎭⎫ ⎝⎛-+=--=++dt t t dt t t t dt t t dx x x x 21222112212212222．C x x x C t t t +++-+++=++-+=2222ln 222222ln 22246．求积分：．2dx x -⎰解：记，2213222t t t x dx tdt x +-=⇒==-=，．2222312212623332t dx dt dt t dt x t t t t C C⎛⎫==+=+ ⎪----⎝⎭=+=+⎰⎰⎰⎰47．求积分：．解：记，232212122+=+=-=⇒+=t x tdtdx t x x t ．Cxx C t t dt t t dt t dt t t dx x x ++-+=+-=+-=⎪⎭⎫ ⎝⎛+-=+=++⎰⎰⎰⎰321arctan 322123arctan3223162331232221222248．求积分：．⎰++dx x 3111解：记，dt t dx t x x t 23323,211=-=⇒+=．22233313331ln 1212142233(1)ln 142t dx dt t dt t t t C t t x C ⎛⎫==-+=-+++ ⎪++⎝⎭=+-+++⎰⎰49．求积分：．()⎰-dx x xx 2321arcsin 解：设：，则x u arcsin =；()332222arcsin sin sin sin sec cos cos 1sec sec sec ln sec tan 1lnln 1ln 12x xu u u udx d u du ud uu u x u u udu u u u u C C x x C ===-=-=-++==-++-+⎰⎰⎰⎰⎰50．求积分：．()()2213xdx xx ++⎰解：．()()()222222211111ln 4134313xx dx d x C x x x x x ⎛⎫+⎛⎫=-=+ ⎪ ⎪+++++⎝⎭⎝⎭⎰⎰51．假设某种商品的需求量，商品的总成本是，每1200080Q P =-2500050C Q =+单位商品需要纳税2元，试求使销售利润最大时商品单价（单位：元）和最大利润额．P 解：收入，28012000)8012000(P P P P PQ R -=-==总成本，P Q C 40006250005025000-=+=总利润，649000161608022-+-=--=P P Q C R L 边际利润，16160160+-='-'='P C R L 令，得，此时，有最大利润（元）．0='L 101=P 0160<-=''L 167080=Max L 52．一商家销售某种商品的价格（万元/吨），为销售量，商品的成本函数x P 2.07-=x 是（万元）．（1）若每销售1吨商品，政府征税t （万元），求商家获取最大利润时13-=x C 的销售量；（2）t 为何值时，政府税收最大？解：（1）收入，总成本，22.07)2.07(x x x x Px R -=-==13-=x C 税收，总利润，tx T =1)4(2.02+-+-=--=x t x T C R L 边际利润；令，得，此时，有最t x L -+-='44.00='L t x 5.210-=04.0<-=''L 大利润；（2），，令，得，所以当时政府税25.210t t tx T -==t T 510-='0='T 2=t 2=t 收最大．53．求积分：．()322arcsin 1x xdx x -⎰解：设，则x u arcsin =；()332222arcsin sin sin sin sec cos cos 1sec sec sec ln sec tan 1ln 1ln 1.2x xu u u udx d u du ud u u ux u u udu u u u u C Cx x C ===-=-=-++==++-+⎰⎰⎰⎰⎰54．已知的一个原函数为，求积分：．()f x ()1sin ln x x +()xf x dx '⎰解：∵，()1sin ()1sin ln cos ln xf x x x x x x'+=+=+⎡⎤⎣⎦∴()()()()xf x dx xdf x xf x f x dx'==-⎰⎰⎰．()1sin cos ln 1sin ln x x x x x x C =++-++55．设是三阶可导函数，，而．求．()f t ()0f t ''≠()()()x f t y tf t f t '=⎧⎨'=-⎩33d y dx解：由已知，，，，从而；()dx f t dt ''=()dy tf t dt ''=dy dy dt t dx dx dt ==1d dy dt dx ⎛⎫= ⎪⎝⎭，．()221d y d dy dx dt dx dt dx f t ⎛⎫== ⎪''⎝⎭()()()323321()d f t d y d d y f t dx dx dx d f t f t ⎡⎤⎢'''''⎛⎫⎣⎦===- ⎪'⎡⎤''⎡⎤⎝⎭⎣⎦⎣⎦56．设，求．()22tan()sec x yx x y tdt x y ---=≠⎰22d ydx解：对等式两边求导．得，()()()()222sec 1sec 1x y y x y y ''---=--整理，得，2sin ()y x y '=-()()()222sin cos 1d yx y x y y dx '∴=---．()()()21sin 2()cos sin 22y x y x y x y '=--=--57．已知，其中二阶可微，求．()y f x y =+()f u 22d ydx 解：，．()()1y f x y y '''=++()'1()f x y y f x y '+∴='-+对两边再求导，()()1y f x y y '''=++，()()()21y f x y y y f x y ''''''''=++++．()()()211y f x y y f x y '''++''∴='-+3"()[1'()]f x y f x y +=-+58．已知，求．0sin ()xtf x dt t p =-ò0()f t dt p ò解：由已知，，或sin ()xf x xp ¢=-sin ()()x f x xf x p ¢¢=-01cos sin ()()t t tt xdx f x dx xf x dxp ¢¢-==-òòò，()(0)()()()()()t tt f t f xf x f x dx f t tf t f x dx p p p =--+=-+òò取，有，t p =021cos ()()()f f f x dx pp p p p p =-=-+ò．()2f t dt p\=ò59．求积分：．121211x x x e x +æö÷ç+-÷ç÷çèøò解：1111122222111112222221111x x x x x x x x x x I x e dx e dx x e dx e dx xd e x x +++++æöæöæö÷ç÷÷çç÷=+-=+-=+ç÷÷çç÷÷÷ççç÷çèøèøèøòòòòò．21521232x x xee +==60．求极限：．2240sin lim x x xx®-解：224300sin sin sin lim lim x x x x x x x x x x x ®®-+-=×302sin cos 222lim x x xx x®-=．3022sin cos 2lim 8t t t t t ®-=2011cos lim 2t t t ®-=2202sin 12lim 2t t t ®=20sin 12lim 42t t t ®æö÷ç÷ç÷çç=çç÷ç÷÷çèø14=而，22223200000sin sin sin 1cos 1sin 1lim lim lim 2lim 2lim sin 3323x x x x x x x x x x x x x x x x x x x ®®®®®-+--=×==´=请问以上方法错在哪里？61．计算．x ò解：记，代入，得()221ln 1x u e u x u ==+=+原式()()222ln 1121u u uduu u ++=+ò()()22222ln 12ln 121u u du u u duu =+=+-+òò．()22ln 12222u u u arctgu c c =+-++=-++62．求积分：．()12ln 11x dx x++ò解：令，，，，11t x t -=+211x t +=+()221dt dx t =-+()()22222111111t t x t t +æö-ç+=+=ççè++代入，则()12ln 11x I dx x +=+ò()()()()21122200ln 1122ln 11211x t I dx dt x t t t ++==×++++òò()()1112220001120ln 2ln 1ln 1ln 211112ln 2ln 214t x dt dt dx t t xI dt t p-++==-+++\==+òòòò．112011ln 221I dx x \=×+òln 28p =63．求积分：1ò解：记212t x t dx tdt==-=-当时，；当时，，则0x =t 1=1x =0t =原式．110202212dt arctgtt p ===-ò64．设在内有意义，且（1）可导；（2）有反函数；（3）()F x ()0,+¥()x j ．求．()()5322115F x t dt x x j æö÷ç÷=-ç÷ç÷èøò()F x 解：由（3）可知，时，，0x =()()010F t dt j =ò()01F =记，则为其反函数()x F y =()y x j =且或()()F y y j =()()F x xj =对（3）的式子两边求导，有，即．()()()23321123F x F x x x j ¢=- ()23321123x F x x x ¢×=-化简有()F x ¢=()23321132F x dx x x c æö\==-+ò而，故．()01F =()233211132F x x x =-+65．求积分：1ò解：11I -==òò．112-==òò12arcsin tp ==66．求积分：1ò解：令sin 02x t t p =<<．()22202200sin cos cos 1cos 1cos 4t d t I dt arctg t tt p pp p==-=-=++òò67．证明：．()4011212n tg xdx n np<<+ò证明：记，则．14201n nn t I tg xdx dt t p==+òò()11212n I n n<<+68．求积分：．244sin 1xxdx ep p --+ò解：．224404sin 11sin 111x x x x dx xdx e e e pp p ---æö÷ç=+÷ç÷çèø+++òò2402sin 8xdx p p -==ò69．设，且，则方程0在()[],f x C a b Î()0f x >()()1xxabf x dx dx f x +=òò(),a b内有几个根．解：记，，()()()1xxabF x f t dt dt f t =+òò()()()110abbaF a dt dt f t f t ==-<òò，而．；()()0baF b f x dx =>ò()0f x >[],x a b Î()()()10F x f x f x ¢=+>在内严格单调增加．因此，在内只有一个根．()F x \(),a b ()F x (),a b 70．在上连续可微，且满足．试证存在一点．使()f x [)0,1()()1212f xf x dx =ò()0,1x Î．()()0f f x x x ¢+=证：设．则，()()F x xf x =()()0000F f =´=．()()()()112211122F f xf x dx F x dx =´==´òò由于在上可微，由积分中值定理，必存在一点，使得()F x []0,110,2h æö÷çÎ÷ç÷çèø，在上，满足Rolle 定理的三个条件，固而存在()()()1122F F F h h =´´=[],1h ()F x ，使得．即．x (),1h Î()0,1Ì()0F x ¢=()()0f f x x x ¢+=71．设求，．()11010x x xe x f x e x ìïïïï¹ï=íï+ïïï=ïî()0f -¢()0f +¢解：由知()()()000limx x f x f x f x x x ®-¢=-()0f -¢()()11000lim lim lim 0011txt t x x x f x f e e x e e --®-¥®®-====-++()0f +¢()()11000lim lim lim 1011txt t x x xf x f e e x ee ++®+¥®®-====-++另，时0x ¹()1121111xx x e e x f x e æö÷ç÷-+ç÷ç÷èø¢=æö÷ç÷+ç÷ç÷èø；()0f -¢()1121011lim lim 1xx x x xe e xf x e --®®æö÷ç÷-+ç÷ç÷èø¢==æö÷ç÷+ç÷ç÷èø()()121lim01u u u xu u e u e e =®-¥-+¾¾¾®=+()0f +¢()1121011lim lim 1xx x x xe e xf x e ++®®æö÷ç÷-+ç÷ç÷èø¢==æö÷ç÷+ç÷ç÷èø()()21lim1u u u u e u e e ®+¥-+=+()()()11lim21u u u u u uu e u e e e e e ®+¥-++-=+()22lim21u uu uu e ue e e ®+¥-=+．()221lim lim 1221u u u u u u e u e e e ®+¥®+¥--===+72．设在上连续，且，证明：必存在，使()f x []0,n ()()()0f f n n N =Î()0,n x Î．()()1f f x x +=证明：记，则在上连续，因而有最大（小）值()()()1x f x f x j =+-()x j []0,1n -，，；()M m ()m x M j ££[]0,1x n Î-而，，…，；()()()010f f j =-()()()121f f j =-()()()11n f n f n j -=--从而，()()()1110n n k k k f k f k m M nnj --==éù+-ëû£==£åå故而，必存在，使，即()0,n x Î()0j x =．()()1f f x x +=73．证明：函数在上一致连续．3)(x x f =[]1,0证明：任取两点，，不妨设，则，考虑到1x []1,02∈x 21x x ≠03231≠-x x ()321232312132232132121323121)()(x x x x x x x x x x x x x x x f x f +--≤++-=-=-；()2323121323121)()(x x x x x x x f x f --≤-=-即；2133231321)()(x x x x x f x f -≤-=-所以，对于任意小的正数，取，当时，必有0>ε3εη=η<-21x x 成立，ε<-≤-=-321323121)()(x x x x x f x f 故而函数在上一致连续．3)(x x f =[]1,074．函数在上有定义，且（1），（2）对于在，)(x f ()∞,0)1()(lim 1f x f x =→0>∀x ，则（为常数）．)()(2x f x f =C x f ≡)(C 证明：任取，记，，，…，()∞+∈,0x x x =1x x x ==124123xx x x ===，…．则1211-==-n x x x n n 由可知，，即)()(2x f x f =)()(x f x f =；)()()()()(321n x f x f x f x f x f ===== 而注意到，故)0(1lim >=+∞→x x n n ；)0(1lim lim 121>==-+∞→+∞→x x x n n n n 而，从而)1()(lim 1f x f x =→；)1()lim ()(lim )(11f x f x f x f n x n x ===→→所以，（为常数）．C x f ≡)()1(f C =75．求极限：．21n n n tan n lim ⎪⎭⎫ ⎝⎛∞→解：注意到⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛⋅=⎪⎭⎫ ⎝⎛n tan n ln n exp n tan n n 1122，⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧-⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+⋅⎪⎭⎫ ⎝⎛-⋅=11111112n tan n n tan n ln n tan n n exp 且，111111=-⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+∞→ntan n n tan n ln lim n 而22111tan lim 11tan lim n n n n n n n n -=⎪⎭⎫ ⎝⎛-∞→∞→30201tan lim1tan lim y y y y y y y y ny -=-=→→=.yy tan lim y y sec lim y y 31331220220==-=→→故.e n tan n lim n n 3121=⎪⎭⎫⎝⎛∞→76．已知，，求．12a =()11112n n n a a n a +⎛⎫=+> ⎪⎝⎭lim n n a →∞解：很明显，，，，，12a =0n a >11112n n n a a a +⎛⎫=+≥ ⎪⎝⎭()12111122n n n a n a a +⎛⎫=+≤>⎪⎝⎭所以，，单调有界，存在；1212n n a a a +≤≤≤≤= {}n a lim n n a →∞记,则由得，注意到，解得．lim n n a l →∞=1112n n n a a a +⎛⎫=+ ⎪⎝⎭112l l l ⎛⎫=+ ⎪⎝⎭21≤≤l 1l =77．设函数，求．xx y +=12()n y 解：，，11112++-=+=x x x x y 2111111⎪⎭⎫⎝⎛+-='⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++-='x x x y ，()()322121111+-='⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛+-=''x x y 由数学归纳法可得：．()()())1(1!11>+-=+n x n yn n n 78．设函数在区间上连续，在内可导，且，()x f []0,1()0,1()()010==f f ．试证：121=⎪⎭⎫ ⎝⎛f (1)存在，使；1,12η⎛⎫∈⎪⎝⎭()ηη=f (2)对任意实数，必存在，使得．λ()0,ξη∈()()1f f ξλξξ'--=⎡⎤⎣⎦证明：（1）设，则在区间上连续，在内可导，且()()h x x f x =-()h x []0,1()0,1，，，则存在，，即()00h =()11h =11022h ⎛⎫=-< ⎪⎝⎭1,12η⎛⎫∈ ⎪⎝⎭()()0h f ηηη=-=．()ηη=f （2）记，在区间上连续，在内可导，且，()()xF x f x x e λ-=-⎡⎤⎣⎦[]0,1()0,1()00F =，则由定理，必存在，使得，即()0F η=Rolle ()0,ξη∈()0F ξ'=．()()1f f ξλξξ'--=⎡⎤⎣⎦79．判断级数的敛散性．11nn ¥=åò提示：．220001122n xdx n n>=®<òòò80．证明：当时，.0>x ()x x xx<+<+1ln 1证明：记，则在上连续因而可积.tt f +=11)()(t f []x 0由积分第一中值定理，比存在一点，使得：()x 0∈ξ，()()x f dt t x x⋅=+=+⎰ξ0111ln 即.()x x ξ+=+111ln 而，，x <<ξ011111<+<+ξx ∴，)0(11><+<+x x x x x ξ即.()x x x x<+<+1ln 181．求在条件下，()22212312323,,2334f x x x x x x x x =+++2221231x x x ++=()123,,f x x x 的最大值和最大值点．解：利用拉格朗日乘数法，设，()()22222212312323123,,,23341L x x x x x x x x x x x λλ=++++++-，则123112233322221234206240624010x x x L x x L x x x L x x x L x x x λλλλ'=+=⎧⎪'=++=⎪⎨'=++=⎪⎪'=++-=⎩．1231222312323(1)020121(2)05x x x x Maxf x x x x x Maxf x x λ≠⇒=-⇒==→=±⇒=⎧+=⎪=⇒⇒==⇒=⎨=⎪⎩82．设随机变量，问：当取何值时，落入区间的概率最大？()2~,X N μσσX ()1,3解：因为，()212~x X f x σ⎛⎫- ⎝⎭=，{}133113()X P X P g σσσσσσ∆⎧⎫⎛⎫⎛⎫<<=<<=Φ-Φ=⎨⎬ ⎪ ⎪⎩⎭⎝⎭⎝⎭利用微积分中求极值的方法，有223311()g σσσσσ⎛⎫⎛⎫⎛⎫'''=-Φ+Φ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭；222222221311111422231111130e e σσσσ⎛⎫⎛⎫⎛⎫⎛⎫---- ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎡⎤⎢⎥==-=⎢⎥⎣⎦令得，则；又，故．404ln 3σ=0σ=0()0g σ''<0σ=故当落入区间的概率最大．σ=X ()1,383．设，讨论方程的实数根．x e x f x λ-=)(0=-x e x λ解：（1）显然，当时，方程没有实根；0λ=0=-x e x λ（2）当时，方程有唯一实根；0λ<0=-x e xλ（3）当时，；曲线为下凸的，0>λ0)(,)(>=''-='x x e x f e x f λx e x f x λ-=)(呈∪型；由可知，驻点，极小值，0)(=-='λx e x f λln 0=x )ln 1()(0λλ-=x f 由此可知，当时，方程没有实根；e <<λ00=-x e x λ当，极小值，方程只有一个实根；e =λ0)ln 1()(0=-=λλxf 0=-x e x λλln 0=x 当，极小值，方程有2个实根．e >λ0)ln 1()(0<-=λλxf 0=-x e xλ84．函数的单调增减区间、凹凸区间与极值．()()()211f x x x =-+解：，()()()()()()()()()22111211131f x x x ,f x x x x x x '=-+=++-+=+-由得驻点：；()0f x '=113x ,=-由上可知，函数在与内单调递增，在内递减；极()f x ()1,-∞-13,⎛⎫+∞ ⎪⎝⎭113,⎛⎫- ⎪⎝⎭大值，极小值；()10f -=132327f ⎛⎫=-⎪⎝⎭由可得，因而函数曲线在内()()()211f x x x =-+()62f x x ''=+13,⎛⎫-∞- ⎪⎝⎭，函数曲线上凸；在内下凸，如下图．()0f x ''<13,⎛⎫-+∞ ⎪⎝⎭85．已知收益函数为，其中为价格，为需求量，求需求弹性时260R=Q Q -P Q 2d ε=-的边际收益．MR 解：因为，所以需求函数，边际收益函数为，且260R=Q Q -60P Q =-602R =Q '-需求弹性函数为；60601d P dQ Q Q dP Q Qε-==-=-当需求弹性时，，此时的边际收益．2d ε=-20Q =()20604020MR R '==-=86．设函数，求其渐近线．xx exe x f y 111)(+==解：首先考虑其水平渐近线和垂直渐近线：x()1,-∞-1-113,⎛⎫- ⎪⎝⎭1313,⎛⎫+∞ ⎪⎝⎭()f x '+0-0+()f x 增加极大值递减极小值递增因为，，，所以，1lim 1=∞→x x e +∞=+→x x e 100lim 0lim 100=-→xx e ；11011lim lim lim 0(1)(1)1t x t t t t x xxee t t e t e x e+-→+∞→+∞→⎛⎫==== ⎪++⎝⎭+；11011lim lim lim 0(1)(1)1t x t t t t x xxee t t e t e x e--→-∞→-∞→⎛⎫==== ⎪++⎝⎭+；110011limlim lim (1)(1)1t x t t x t t xxee t t e t e x e-→∞→→⎛⎫===∞=⎪++⎝⎭+故而没有水平渐近线和垂直渐近线；xx exex f y 111)(+==由于，()111limlim 21xx x xf x e a x e →∞→∞===+()1111111211lim lim lim 2211x x x x x x x x xe x e xe b fx x x e e →∞→∞→∞⎡⎤⎛⎫-+⎢⎥⎡⎤ ⎪⎡⎤⎝⎭⎢⎥⎢⎥=-=-=⎢⎥⎢⎢⎥⎣⎦++⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦，11011111122lim lim 2(1)41x t t x t xx xe e t t e x e→∞→-+-⎛⎫==== ⎪+⎝⎭+故而有斜渐近线：．xx exe x f y 111)(+==4121+=x y 87．求函数曲线的渐近线．()1ln 1x y e x=++解：显然，，为其垂直渐近线；()01lim ln 1x x e x→⎡⎤++=∞⎢⎥⎣⎦0x =，为其水平渐近线；()()1lim ln 1lim ln 10x xx x e e x →-∞→-∞⎡⎤++=+=⎢⎥⎣⎦0y =又，，，因而()()11ln 1ln 1x x y e x e x x -=++=+++()1lim ln 10x x e x -→+∞⎡⎤++=⎢⎥⎣⎦为其一条斜渐近线．y x=88．若，试证明：与具有相同的敛散性．lim (0)n n a a a →∞=≠∑∞=+-11n n n a a ∑∞=+-1111n nn a a 证明：问题为讨论两个正项级数的敛散性，可以用比较法的极限形式，因为不是具体的级数形式．记，则,111nn n a a V -=+0,0>>n n V U ==n n n V U ∞→limnn nn n a a a a 11lim11--=++∞→1.lim +∞→n n n a a )0(2≠a 可见，与具有相同的敛散性．∑∞=+-11n n n a a∑∞=+-1111n nn a a 89．讨论下列级数的敛散性：（1）2）；（3）；（4）1n ∞=11tan 2n n n ∞+=∑()3113nnn n n ∞=⎤+-⎣⎦∑()∑∞=+-+121211n n n n n（5）；（6）；（7）．()()1111ln 1n n n ∞+=-+∑()211nn n n ∞=-+∑()()1111ln n n nn e e ∞+-=-+∑解：（1）当充分大时，比如时，有，从而n 3>n ()n n <+<1ln 1,而当时，，()n n n n <+<1ln 1∞→n 1→n n由极限的夹逼性定理知，当时，，所以，∞→n 1→1n ∞=（2）注意到，这是正项级数，当时，(等价无穷小)，0→x x x ~tan 所以，而后者收敛,所以收敛．11tan ~2n n n π∞+=∑112n n n π∞+=∑11tan 2n nn π∞+=∑（3）利用柯西判别法：也是正项级数，,可见原()33113n+-=<→级数收敛；事实上，，，)())333111333nnnn nnnn nn ⎤+-+⎣⎦<<3113nnn n ∞=⎤⎣⎦∑都收敛，且同为正项级数，因而原级数收敛．3113nn n n ∞=⎤⎣⎦∑（4）因为，()()111111122221212112121→+⋅+⋅=+=+=+-+-nn nnnn n n n n n n nnnnnu 改用比较判别法：取，则21nv n =；()11lim 1lim lim 122121=⎪⎪⎭⎫⎝⎛+=+=+∞→++∞→∞→n n n n n nn n n n n nv u其中()(){}1122222lim lim exp lim 12ln ln 111n x n x x n x x x x n x ++→∞→+∞→+∞⎛⎫⎛⎫⎡⎤==+-+ ⎪ ⎪⎣⎦++⎝⎭⎝⎭，()()()()()22222222ln ln 1211exp lim exp lim exp lim 111111x x x x x x x x x x x x x →+∞→+∞→+∞⎧⎫⎧⎫⎪⎪-⎪⎪⎧⎫-++⎪⎪⎪⎪⎪⎪+===-=⎨⎬⎨⎬⎨⎬+⎪⎪⎪⎪⎪⎪-⎩⎭+⎪⎪⎪⎪+⎩⎭⎩⎭所以，与同时收敛．()∑∞=+-+121211n n n nn ∑∞=121n n（5）条件收敛．（6），发散．()()22111111nnn n n nn n n∞∞∞===-+-=+∑∑∑（7）=,()()1111ln n n n n e e ∞+-=-+∑()()12111ln 1n n n e n∞+=-+-∑,()222ln 1n n n e n e n e +-<-<()()()22222lim lim lim ln 1ln 1ln n x xn x x x n x x e e e e n e x e e -→∞→+∞→+∞==+-+-+==∞．()=+-=--+∞→x x x x xx e e e e e 22lim ()22221lim 1x x x x e e e →+∞+-x xx x ee e 2532106lim ++∞→另一方面，==,；()x x e e -+ln 1()xe x 21ln 1-++()x e xx x 1~1ln 11112-++()+∞→x 可见，原级数非绝对收敛；但是单调减少且趋于0，所以，原级数条件收敛．()x x e e -+ln 190．若正项级数与都发散，讨论与的敛散性．1nn v∞=∑1nn u∞=∑{}1max ,nnn u v ∞=∑{}1min ,nnn u v ∞=∑解：，，{}{}1max ,2n n n n n n u v u v u v =++-{}{}1min ,2n n n n n n u v u v u v =+--（1）显然，，或者，故而{}{}1max ,2n n n n n n n u v u v u v u =++-≥{}max ,n n n u v v ≥发散；{}1max ,nnn u v ∞=∑（2）而的敛散性未定．{}1min ,nnn u v ∞=∑例如，若，()222211111111123456212n n u n n ∞==+++++++++-∑ ，()222=11111111123456221n n v n n ∞=+++++++++-∑。

定积分及微积分基本定理练习题及答案

1.4定积分与微积分基本定理练习题及答案1.（2011 •宁夏银川一中月考）求曲线y = x2与y = x 所围成图形的面积，其中正确的是( )A. S = 1(x2 — x)dxB . S = 1(x — x2)dxC. S = 1(y2 — y)dy D -S = 1(y — 'y)dy0 0［答案］B［分析］根据定积分的几何意义，确定积分上、下限和被积函数.［解读］两函数图象的交点坐标是（0,0） , （1,1），故积分上限是1，下限是0,由于在［0,1］上，x >x2，故函数y = x2与y = x 所围成图形的面积 S = 1（x — x2）dx. 02xdx , b = 2exdx , c = 2sinxdx ，贝U a 、b 、c 的大小关 0 0 0 玄阜系是A. a<c<bB . a<b<c C. c<b<aD. c<a<b ［答案］D1［解读］ a = 2xdx = rx2|02 = 2 , b = 2exdx = ex|02 = e2 — 1>2, c = 2sinxdx =—0 0 0 cosx|02 = 1 — cos2 € (1,2),c<a<b.3. (2010 •山东理，7)由曲线y = x2, y = x3围成的封闭图形面积为( )［答案］Ay = x2［解读］由得交点为(0,0) , (1,1)y = x3（2010 •湖南师大附中）设点P 在曲线y = x2上从原点到A （2,4）移动，如果把由直线OR2. （2010 •山东日照模考）a = 1117A讲.产于壬S = 1(x2 — x3)dx =1 1 1 3x3 —4x4 01 =［点评］图形是由两条曲线围成的时，其面积是上方曲线对应函数表达式减去下方曲线对应函数表达式的积分，请再做下题:直线y = x2及直线x = 2所围成的面积分别记作 S1, S2.如图所示，当S1 = S2时，点P 的坐标是()4 164 16A. 3， 9B. 5， 94 154 13 C. 3， 7 D. 5， 7 ［答案］A4. 由三条直线x = 0、x = 2、y = 0和曲线y = x3所围成的图形的面积为( )4 18A. 4B.C. wD. 63 5 ［答案］Ax4［解读］ S = 2x3dx =— 02= 4.0 5.(2010 •湖南省考试院调研)1 — 1(sinx + 1)dx 的值为()A. 0 B . 2C. 2 + 2cos1 D . 2— 2cos1 ［答案］B［解读］ 1 — 1(sinx + 1)dx = ( — cosx + x)| — 11 = ( — cos1 + 1) — ( — cos( — 1) — 1)= 2.6.曲线y = cosx(0 wx < 2n )与直线y = 1所围成的图形面积是()A. 2 n B . 3 n7t［答案］A ［解读］如右图， S =/ 02 n (1 — cosx)dx=(x — sinx)|02 n= 2 n.［点评］此题可利用余弦函数的对称性［解读］设 P(t ,⑵(0 < t < 2)，则直线 OP y = tx ,••• S1 =t(tx 0t3—x2)dx =~6; S2 =8t3 卄 , 2(x2 — tx)dx t =3― 2t + 百，若 S1= S2,则 t4 16 …P 3， 9①②③④ 面积相等解决，但若把积分区间改为4 3，n—,n ，则对称性就无能为力了.7. 函数F(x) = xt(t —4)dt 在［—1,5］上( )A. 有最大值0,无最小值32B. 有最大值0和最小值-㊁c.有最小值- 3，无最大值D.既无最大值也无最小值［答案］B［解读］F' (x) = x(x —4)，令F' (x) = 0，得x1 = 0, x2 = 4,•- F( —1) =—3, F(0) = 0, F(4) = —32, F(5)=—学的取值范围是()C. (e —11, e) D . (0 , e11)［答案］D［解读］1f(x) = x-dt = Int|1x = Inx , a3 = S3—S2= 21 —10= 11,由Inx<11 得, 1t0<x<e11.9. (2010 •福建厦门一中)如图所示，在一个长为n,宽为2的矩形OABC内，曲线y =sinx(0 w x< n )与x轴围成如图所示的阴影部分，向矩形OAB(内随机投一点(该点落在矩形OABC内任何一点是等可能的)，则所投的点落在阴影部分的概率是()1 2 3 nA. B.—C. —D.二n n n 4［答案］A•••最大值为0,最小值为—32［点评］一般地，F(x) x $ (t)dt 的导数F' (x) (x).&已知等差数列{an}的前n项和Sn= 2n2 + n,函数f(x) *dt，若f(x)<a3 ，则xA. -pmB. (0 , e21)［解读］由图可知阴影部分是曲边图形，考虑用定积分求出其面积•由题意得S = nsinxdx = — cosx|0 n=— (cos n — cosO) = 2，再根据几何概型的算法易知所求概率 P =S 2 1S 矩形 OAB CT 27=V .x + 2— 2 w x<010.(2010 •吉林质检)函数f(x) = n 的图象与x 轴所围成的图形2cosx 0w x w —面积S 为( )3 1 A. gB . 1 C .4 D. q ［答案］Cnn［解读］面积 S =/ — — 2f(x)dx =0 — 2(x + 2)dx + / —02cosxdx = 2 + 2= 4.11. (2010 •沈阳二十中)设函数f(x) = x — ［x ］，其中［x ］表示不超过x 的最大整数，女口［—x1.2］ =— 2, ［1.2］ = 1, ［1］ = 1.又函数g(x) = — 3, f(x)在区间(0,2)上零点的个数记为 m,f(x)与g(x)的图象交点的个数记为n ,贝U ng(x)dx 的值是()m5 4 A.—尹.—3C — 5D . — 74 6［答案］ A［解读］由题意可得，当 0<x<1 时，[x] = 0, f(x) = x ，当 1w x<2 时，[x] = 1, f(x)=x — 1,所以当x € (0,2)时，函数f(x)有一个零点，由函数f(x)与g(x)的图象可知两个函11. (2010 •江苏盐城调研)甲、乙两人进行一项游戏比赛，比赛规则如下：甲从区间［0,1］上随机等可能地抽取一个实数记为b ,乙从区间［0,1］上随机等可能地抽取一个实数记为c(b 、c 可以相等)，若关于x 的方程x2 + 2bx + c = 0有实根，则甲获胜，否则乙获胜，则在一场比赛中甲获胜的概率为( )1213［答案］A数有4个交点，所以 m = 1, n = 4，贝U ng(x)dx =mx —3 dx =x2 6 14= — 52.［解读］方程x2+ 2bx + c= 0有实根的充要条件为△ = 4b2 —40 0,即卩b2> c,1b2db 由题意知，每场比赛中甲获胜的概率为p = 0X1 =!12. (2010 •吉林省调研)已知正方形四个顶点分别为0(0,0) , A(1,0) , B(1,1), 曲线y= x2(x > 0)与x轴，直线x = 1构成区域M现将一个质点随机地投入正方形中，点落在区域M内的概率是()A.2B.4C.3D.5［答案］C［解读］如图，正方形面积1，区域M的面积为S= 1x2dx2•如图，阴影部分面积等于()A. 2 '3B. 2 —：3［答案］C［解读］图中阴影部分面积为1 32S= 1 (3 —x2 —2x)dx = (3x —3x3 —x2)|1 —3=石.-3 3 33. 2 ;4 —x2dx =( )A. 4 n B . 2 nnC.nD. 2 C(0,1),则质= 3x3|01 = g,故所求概率p= 332 35C.yD.y［答案］C［解读］令y= .'4 —x2,则x2 + y2 = 4（y >0）,由定积分的几何意义知所求积分为图中阴影部分的面积，1S=〒XnX 22=n.4—% •；0!2 xft电Jf XS*J F*4.已知甲、乙两车由同一起点同时出发，并沿同一路线（假定为直线）行驶•甲车、乙车的速度曲线分别为v甲和v乙（如图所示）•那么对于图中给定的tO和t1，下列判断中一定正确的是（）A. 在t1时刻，甲车在乙车前面B. 在t1时刻，甲车在乙车后面C. 在tO时刻，两车的位置相同D. tO时刻后，乙车在甲车前面［答案］A［解读］判断甲、乙两车谁在前，谁在后的问题，实际上是判断在to, t1时刻，甲、乙两车行驶路程的大小问题. 根据定积分的几何意义知：车在某段时间内行驶的路程就是该时间段内速度函数的定积分，即速度函数v(t)的图象与t轴以及时间段围成区域的面积.从图象知：在t0时刻，v甲的图象与t轴和t = 0, t = t0围成区域的面积大于v乙的图象与t轴和t = 0, t = t0围成区域的面积，因此，在t0时刻，甲车在乙车的前面，而且此时乙车的速度刚刚赶上甲车的速度，所以选项C, D错误；同样，在域中曲线COS2T下方区域的面积長J* cos2xd.T ［答案］t1时刻，v甲的图象与t轴和t = t1围成区域的面积，仍然大于v乙的图象与t轴和t = t1 围成区域的面积，所以，可以断定：在t1时刻，甲车还是在乙车的前面•所以选 A.5. (2012 •山东日照模拟)向平面区域Q= {(x,y)l 7t—才w x w —, 0 w y w 1｝内随机投掷一点，该点落在曲线y= cos2x下方的概率是(D.［答案］平面区域Q 是矩形区域n 其面积是—,在这个区2,1 o4COS2^.T1T—2( 1.故所求的概率是丄7T6.A. 0 Ji 7T(sinx —cosx)dx 的值是(C. 2D.—2［解读］(si nx —cosx)dx = ( —cosx —sinx) =—2.7. (2010 •惠州模拟) 2(2 —|1 —x|)dx =••• 2(2 — |1 — x|)dx = 1(1 + x)dx +2(3 — x)dx0 0 1 1 1 3 3=(x + 2X2)|1O + (3x —严)|21 = + 2= 3.& (2010 •芜湖十二中)已知函数 f(x) = 3x2 + 2x + 1,若 1 — 1f(x)dx = 2f(a)成立，则［答案］—1则直线AB 的方程为y — a2=学—乎(x — a), 即 y = (a + b)x — ab.则直线AB 与抛物线围成图形的面积为 S =a + bb[(a + b)x — ab — x2]dx = (—^ x2 — abx — a［答案］3［解读］3-x 1<xa =［解读］1 — 1f(x)dx1 — 1(3x2 + 2x + 1)dx = (x3 + x2 + x)|1 — 1 =4 ,1 —1f(x)dx = 2f(a),• 6a2 + 4a + 2= 4,• • a =— 1 1或3.9.已知 n —1a =/ y0(sinx + cosx)dx ，则二项式 (a x —)6 的展开式中含x2项的系数［答案］ —192［解读］ ,「.n n n n由已知得 a =/ —0(sinx + cosx)dx = ( — cosx + sinx)| —0= (sin — — cos-^) —(si n0 — cosO) = 2,(2 .x -的展开式中第 r + 1 项是 Tr + 1= ( — 1)r x (C x 26— r x x3 —，令 3— r = 2 得,r = 1，故其系数为(—1)1 XCX 25=—192.10. 有一条直线与抛物线 y = x2相交于A B 两点，线段AB 与抛物线所围成图形的面积恒等于4,求线段AB 的中点P 的轨迹方程.［解读］设直线与抛物线的两个交点分别为A(a , a2), B(b , b2)，不妨设 a<b ,1 4 ••• 6(b - a)3 = 3，解得b - a = 2.设线段AB 的中点坐标为P(x , y),a + b消去a 得y = x2 + 1.•线段AB 的中点P 的轨迹方程为y = x2 + 1. 能力拓展提升11. (2012 •郑州二测)等比数列｛an ｝中,a3= 6,前三项和S3= 34xdx ,则公比q 的值为0 ( )1A. 1 B •-、1 、 1c. 1 或—•— 1 或—2 ［答案］C6 6［解读］因为 S3= 34xdx = 2x2|30= 18,所以-+ 迈 + 6= 18,化简得 2q2- q - 1 = 0, 1解得q = 1或q =— 2，故选C. 12.(2012 •太原模拟)已知(xlnx) ' = lnx + 1，贝U elnxdx =()1A. 1 B . e C . e — 1 D . e + 1 ［答案］A［解读］由(xlnx) ' = lnx + 1,联想到(xlnx — x) '= (lnx + 1) — 1 = lnx ，于是 elnxdx1=(xlnx — x)|e1 = (elne — e) — (1 x ln1 —1) = 1.13. _________________________________________________________ 抛物线y2= 2x 与直线y = 4— x 围成的平面图形的面积为 ___________________________________ .［答案］18y2= 2x ，［解读］由方程组解得两交点A(2,2)、B(8，— 4)，选y 作为积分变量xy = 4 — x ，x = 4 — y ，其中x =a2 + b2 2将b - a = 2代入得x =a + 1, y = a2+ 2a + 2.已知函数f(x) = ex — 1，直线11 : x = 1, 12 : y = et — 1(t 为常数，且 O w t < 1).直线11 ,12与函数f(x)的图象围成的封闭图形如图中区域H 所示，其面积用 S2表示•直线12 ,y 轴与函数f(x)的图象围成的封闭图形如图中区域I 所示，其面积用S1表示.当t 变化时，阴影部分的面积的最小值为 _________ .［答案］(,e — 1)2［解读］由题意得 S1 + S2= t(et — 1 — ex + 1)dx + 1(ex — 1 — et + 1)dx = t(et — 0 t0 ex)dx + 1(ex — et)dx = (xet — ex)|t 0 + (ex — xet)|1 t = (2t — 3)et + e + 1,令 g(t) = (2t — t13)et + e + 1(0 w t w 1)，则 g ' (t) = 2et + (2t — 3)et = (2t — 1)et ，令 g ' (t) = 0,得 t = ?,s = 2 [(4 -414.=(4y - y2罟)|2— 4= 18.—y)—(t)<0 , g(t)是减函数，当 t € (2, 1]时，g ' (t)>0 , g(t)是增函数,1 1g （2）= e + 1 — 2e^ = （：e — 1）2.故阴影部分的面积的最小值为（，:e[解读]f ' (x) =— 3x2+ 2ax + b , v f ' (0) = 0 b = 0, ••• f(x) =— x3 + ax2，令 f(x) = 0，得 x = 0 或 x = a(a<0).••• S 阴影= 0[0 — ( — x3 + ax2)]dxa1 1 1 1 =(4x4 — §ax3)|0a = ^a4=匸, -a<0,. • a = — 1.1. （2011 •龙岩质检）已知函数f （x ） = sin5x + 1,根据函数的性质、积分的性质和积分1 ••当 t € [0 , 2)时，g '因此g （t ）的最小值为 1)2.15.求下列定积分. (1)1 — 1|x|dx 。

高考数学微积分(附答案解析

定积分与微积分基本定理【考点导读】1．了解定积分的实际背景，初步掌握定积分的相关概念，体会定积分的基本方法。

2．了解微积分基本定理的含义，能利用微积分基本定理计算简单的定积分，解决一些简单的几何和物理问题。

【基础练习】1．下列等于1的积分是（3）。

（1）dx x ⎰10 （2）dx x ⎰+10)1( （3）dx ⎰101 （4）dx ⎰10212.曲线3cos (0)2y x x π=≤≤与坐标轴围成的面积是 52。

3．已知自由落体运动的速率v gt =，则落体运动从0t =到0t t =所走的路程为 220gt。

4．如果10N 的力能使弹簧压缩10cm ，为在弹性限度内将弹簧拉长6cm ，则力所做的功为 0.18J 。

5．220(3)10,x k dx k +==⎰则1 , 8-=⎰__454 。

【范例导析】例1．计算下列定积分的值：（1）⎰--312)4(dx x x ；（2）⎰-215)1(dx x ；（3）dx x x ⎰+20)sin (π；（4）dx x ⎰-222cos ππ；分析：求函数()f x 在某一区间上的定积分，常用的方法有两种：一是利用定积分的几何意义，转化为曲边梯形的面积来处理；二是应用微积分基本定理，关键在于找到()F x ，使()()F x f x '=。

解：（1）3223311120(4)(2)|33x x dx x x ---=-=⎰ （2）因为56)1(])1(61[-='-x x ，所以61|)1(61)1(216215=-=-⎰x dx x ；（3）222200(sin )(cos )|128x x x dx x πππ+=-=+⎰ （4）22222221cos 2sin 2cos |2242x x x xdx dx πππππππ---+==+=⎰⎰dx x ⎰-222cos ππ点评：除了题目有明确要求之外，在求定积分的两种方法中我们基本上选用微积分基本定理解决问题，避免每次都要进行“分割、以直代曲、作和、逼近”的操作，不过有时候我们不容易找到比较()F x ，这时候用定义或者其几何意义就显得方便了。

微积分定积分练习题(有答案)

微积分练习题(含答案)

数学必修二：微积分中的定积分习题答案

微积分练习题及答案

定积分与微积分练习题及答案

定积分及微积分基本定理练习题及答案

定积分及微积分基本定理练习题（附答案）

微积分习题答案第七章定积分

2024届高考数学复习：精选历年真题、好题专项(定积分与微积分基本定理)练习(附答案)

定积分与微积分含答案

微积分考试试题及答案

微积分试卷及标准答案6套

微积分综合练习题及参考答案精选全文完整版

微积分考试题目及答案

定积分及微积分基本定理练习试题包括答案.docx

微积分基础试题及答案

微积分 定积分 练习题(有答案)

定积分与微积分基本定理随堂练习(含答案).doc

微积分练习100题及其解答

定积分及微积分基本定理练习题及答案

高考数学微积分(附答案解析

微积分定积分练习题(有答案)