matlab作业
matlb课程设计作业

matlb课程设计作业一、教学目标本课程的教学目标是使学生掌握MATLAB基本语法、编程技巧以及应用方法,培养学生解决实际问题的能力。
具体目标如下:1.知识目标:(1)理解MATLAB的基本概念,如变量、数据类型、运算符等。
(2)掌握MATLAB编程的基本语法,如矩阵操作、函数定义与调用、循环结构、条件语句等。
(3)熟悉MATLAB与其他软件(如Mathematica、Python等)的接口转换。
(4)了解MATLAB在工程领域中的应用,如信号处理、控制系统、图像处理等。
2.技能目标:(1)能够运用MATLAB进行简单的数学计算、数据分析及图形绘制。
(2)具备编写MATLAB脚本文件和函数文件的能力。
(3)学会使用MATLAB解决实际问题,如编写程序实现线性方程组求解、最优化问题求解等。
(4)掌握MATLAB在实验数据处理、仿真实验等方面的应用。
3.情感态度价值观目标:(1)培养学生对科学探究的兴趣,提高其创新意识。
(2)培养学生团队协作、沟通交流的能力。
(3)培养学生具备良好的编程习惯和职业道德。
二、教学内容本课程的教学内容主要包括以下几个部分:1.MATLAB基本概念:变量、数据类型、运算符等。
2.MATLAB编程语法:矩阵操作、函数定义与调用、循环结构、条件语句等。
3.MATLAB高级应用:数组运算、图像处理、控制系统、信号处理等。
4.MATLAB与其他软件的接口转换。
5.实践项目:利用MATLAB解决实际问题,如线性方程组求解、最优化问题求解等。
三、教学方法本课程采用讲授法、案例分析法、实验法等多种教学方法相结合,以提高学生的学习兴趣和主动性。
1.讲授法:用于讲解MATLAB基本概念、语法和应用。
2.案例分析法:通过分析实际案例,使学生掌握MATLAB在各个领域的应用。
3.实验法:让学生亲自动手实践,培养其运用MATLAB解决实际问题的能力。
四、教学资源1.教材:选用《MATLAB教程》作为主要教材,辅助以相关参考书籍。
matlab整理

作业一:P55:1.在一个MATLAB命令中,6+7i和6+7*i有何区别?i和I有何区别?解:在MATLAB中6+7i是一个复数常量,6+7*i则是一个表达式。
i是虚数单位,而I是单位向量。
4.要产生均值为3,方差为1的500个正态分布的随机序列,写出相应的表达式。
解:y=3+sqrt(1)*randn(500)5.求下列矩阵的对角线元素、上三角矩阵、逆矩阵、行列式的值、秩、迹。
(1) A =1 -12 35 1 -4 23 0 5 211 15 0 9(2) B =0.43 43 2-8.9 4 21解:(1)A=[1,-1,2,3;5,1,-4,2;3,0,5,2;11,15,0,9]主对角元素:D=diag(A)上三角矩阵:B=triu(A)下三角矩阵:C=tril(A)逆矩阵:X=inv(A)行列式的值:E=det(A)秩:F=rank(A)逆:G=trace(A)运行结果:A =1 -12 35 1 -4 23 0 5 211 15 0 9主对角元素:D =1159上三角矩阵:B =1 -12 30 1 -4 20 0 5 20 0 0 9下三角矩阵:C =1 0 0 05 1 0 03 0 5 011 15 0 9逆矩阵:X =-0.1758 0.1641 0.2016 -0.0227 -0.1055 -0.1016 -0.0391 0.0664 -0.0508 -0.0859 0.1516 0.0023 0.3906 -0.0313 -0.1813 0.0281 行列式的值:E =1280秩:F =4逆:G =16(2)B = [0.43,43,2;-8.9,4,21]主对角元素:D=diag(B)上三角矩阵:Y=triu(B)下三角矩阵:C=tril(B)逆矩阵:X=pinv(B)行列式的值:E=det(B)秩:F=rank(B)迹:G= trace(B)运行结果:B =0.4300 43.0000 2.0000-8.9000 4.0000 21.0000主对角元素:D =0.43004.0000上三角矩阵:Y =0.4300 43.0000 2.00000 4.0000 21.0000下三角矩阵:C =0.4300 0 0-8.9000 4.0000 0逆矩阵:X =0.0022 -0.01750.0234 -0.0017-0.0035 0.0405行列式的值:E = 1.2526e+003秩:F=3迹:G =5.43006. 当A=[34,NaN,Inf,-Inf,-pi,eps,0]时,求函数all(A)、any(A)、isnan(A)、isinf(A)、isfinite(A)的值。
MATLB实验作业

实验一MATLAB运算基础1、用逻辑表达式求下列分段函数的值。
t=0:0.5:2.5y=t.^2.*((t>=0)&(t<1))+(t.^2-1).*(( t>=1)&(t<2))+(t.^2-2*t+1).*((t>=2 )&(t<3))2、求[100,999]之间能被21整除的数的个数。
p=rem([100:999],21)==0;sum(p)3、建立一个字符串向量,删除其中的大写字母。
ch='KdDdfKaWdsfCI',k=find(ch>=' A'&ch<='Z'),ch(k)=[]4、输入矩阵,并找出A中大于或等于5的元素。
A=[1 2 3;4 5 6;7 8 9],[m,n]=find(A>=5),for j=1:length(m)x(j)=A(m(j),n(j))xend5、求矩阵的行列式值、逆和特征根。
a11=input('a11='),a12=input('a12 ='),a21=input('a21='),a22=input('a22 ='),A=[a11,a12;a21,a22],DA=det(A),IA=inv(A),EA=eig(A) 6、不采用循环的形式求出和式的数值解。
sum(2.^[0:63])实验二1、1行100列的Fibonacc数组a,a(1)=a(2)=1,a(i)=a(i-1)+a(i-2),用for循环指令来寻求该数组中第一个大于10000的元素,并指出其位置i。
n=100;a=ones(1,n);for i=3:na(i)=a(i-1)+a(i-2);if a(i)>10000a(i),break;end;end,i2、编写M脚本文件,定义下列分段函数,并分别求出当()、()和()时的函数值。
MATLAB与控制系统仿真大作业

>> G1=tf(num,den);
>> G1=zpk(G1)
G1 =
5 (s+0.6) ----------------(s+3) (s+2) (s+1)
>> num=[2 1]; den=[1 2.9 1]; G2=tf(num,den); >> G2=zpk(G2)
G2 =
2 (s+0.5)
>> xlabel('x') ylabel('exp(-2.*x)')
三、simulink 建模(每题 10 分,共 20 分)
1、已知单位负反馈的开环传递函数为 G(s) =
2 s2 + 4s
,试利用
simulink
建立系在单位阶跃输入作用下的模型。
要求答案包括:(1)simulink 建模结构图;
(2)在同一个坐标中的阶跃信号和响应曲线图。
2、已知系统的开环传递函数为
G1(s)
=
2s2 + 5s + 6 s2 + 2s + 3
、G2 (s)
=
s2
s+6 + 7s +1
,H
(s)
=
5(s + 2) s +10
求:建立 Simulink 仿真模型,并求出其系统在单位阶跃响应;
要求答案包括:(1)simulink 建模结构图;
x=
-2.9709
0.5491
3.6000
0.0509
2. 已知下列矩阵
2 3 1
−1 3 5
A
=
MATLAB平时作业(图文版)

MATLAB 平时作业第一章 习题16. 以下两种说法对吗?(1)“MATLAB 的数值表达精度与其指令窗中的数据显示精度相同。
”答:此种说法错误。
MATLAB 提供了控制数据显示格式的控制指format ,该指令并不改变MATLAB 内存中变量的精度,只是改变其显示精度。
(2)“MATLAB 指令窗中显示的数值有效位数不超过7位。
”答:此种说法错误。
当变量小于1000时,使用format 或format short 后,或者默认情况下,变量的显示精度最多不超过7位,但显示精度不等于变量的精度。
7. 想要在MATLAB 中产生二维数组⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=987654321S ,下面哪些指令能实现目的? S=[1,2,3;4,5,6;7,8;9]S=[1 2 3;4 5 6;7 8 9]S=[1,2,3;4,5,6;7,8,9] %整个指令在中文状态下输入 答:操作如图:第1、2条指令可以实现,第3条指令不可实现。
第三章 习题31.在MATLAB 中,先运行指令A=magic(3), B=[1,2,1;3,4,3;5,6,7], C=reshape(1:6,3,2)生成阵列33⨯A ,23⨯B ,23⨯C ,然后根据运行结果回答以下问题:运行结果如图:(1)计算A*B, B*A ,这两个乘积相同吗? 计算结果如图:答:不同。
(2)计算A\B, B/A ,左除、右除结果相同吗?计算结果如图:答:不同。
(3)计算B( : ,[1,2]).*C和C.*B( : , [1,2]),这两个乘积相同吗?计算结果如图答:相同。
(4)计算A\A和A.\A,这两个计算结果相同吗?计算结果如图:答:相同。
(5)计算A\eye(3)和inv(A),这两个计算结果相同吗?计算结果如图:答:不同。
(提示:根据对计算结果的目测回答问题)2.在MATLAB中,先运行A=[1, 2; 3, 4],b=0.5,C=[4, 2; 1, 0.5], 然后根据计算结果回答以下问题:创建数据步骤略(1)计算A^b和A.^b, 这两个计算结果相同吗?答:不同。
Matlab习题及答案
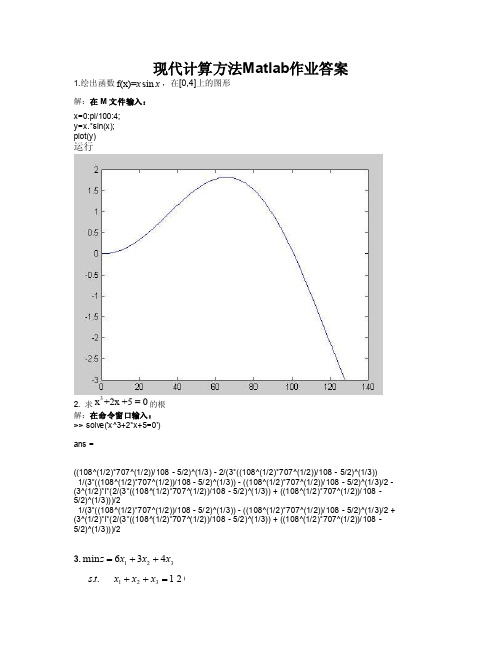
现代计算方法Matlab 作业答案1.绘出函数f(x)=sin x x ,在[0,4]上的图形解:在M 文件输入:x=0:pi/100:4;y=x.*sin(x);plot(y)运行2. 求3x +2x +5 = 0的根解:在命令窗口输入:>> solve('x^3+2*x+5=0')ans =((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3) - 2/(3*((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3))1/(3*((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)) - ((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)/2 -(3^(1/2)*i*(2/(3*((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)) + ((108^(1/2)*707^(1/2))/108 -5/2)^(1/3)))/21/(3*((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)) - ((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)/2 +(3^(1/2)*i*(2/(3*((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)) + ((108^(1/2)*707^(1/2))/108 -5/2)^(1/3)))/23.321436min x x x z ++=120..321=++x x x t s301≥x5002≤≤x203≥x解:运用单纯形法计算此题,首先把约束条件化成标准形式:,,,,,205030120654321635241321≥=-=+=-=++x x x x x x x x x x x x x x x(1)在M 文件输入SimpleMthd 函数:function [x,minf] = SimpleMthd(A,c,b,baseVector)sz = size(A);nVia = sz(2);n = sz(1);xx = 1:nVia;nobase = zeros(1,1);m = 1;for i=1:nViaif (isempty(find(baseVector == xx(i),1)))nobase(m) = i;m = m + 1;else;endendbCon = 1;M = 0;while bConnB = A(:,nobase);ncb = c(nobase);B = A(:,baseVector);cb = c(baseVector);xb = inv(B)*b;f = cb*xb;w = cb*inv(B);for i=1:length(nobase)sigma(i) = w*nB(:,i)-ncb(i);end[maxs,ind] = max(sigma);if maxs <= 0minf = cb*xb;vr = find(c~=0 ,1,'last');for l=1:vrele = find(baseVector == l,1);if (isempty(ele))x(l) = 0;elsex(l)=xb(ele);endendbCon = 0;elsey = inv(B)*A(:,nobase(ind));if y <= 0disp('不存在最优解!');x = NaN;minf = NaN;return;elseminb = inf;chagB = 0;for j=1:length(y)if y(j)>0bz = xb(j)/y(j);if bz<minbminb = bz;chagB = j;endendendtmp = baseVector(chagB);baseVector(chagB) = nobase(ind);nobase(ind) = tmp;endendM = M + 1;if (M == 1000000)disp('找不到最优解!');x = NaN;minf = NaN;return;endend(2)在命令窗口输入:clear allA=[1 1 1 0 0 0;1 0 0 -1 0 0;0 1 0 0 1 0;0 0 1 0 0 -1];c=[6 3 4 0 0 0];b=[120;30;50;20];[xm,mf]=SimpleMthd(A,c,b,[3 4 5 6])xm =0 50 70mf =4304.计算下面函数在区间(0,1)内的最小值。
matlab作业

matlab作业第一次作业[实验目的]1。
了解并熟悉Matlab,并在此基础上学习基本操作2.掌握Matlab 的基本操作和常用命令3。
了解Matlab常用的函数、运算符和表达式4.掌握Matlab的工作方法和M文件的相关知识5.在Matlab中学习矩阵和数组的运算1,[实验任务]1。
P11:例1_4写一个函数,求方程AX 2+Bx+C = 0的解2.P16: 1。
计算表达式e 12+23 3log25/tan 21.3。
写m命令文件找到?k +?1/k的值是k?1k?15010 4.编写函数文件并计算?k!并找出k=20时表达式的值k?1n3。
例2_2使用函数生成矩阵A =100020003,B = 00200000000104。
例2_3 (1)生成三阶魔方矩阵A;(2)生成一个四阶单位矩阵B 5。
示例2_10数组操作示例6。
例2_11计算sin(k?/2)(k=?2,?1,0)值7。
P27:2。
矩阵A=456,B=556,计算A*B,A.*B,并比较差值789123468323。
已知矩阵A=5,212,B=,计算A>B,A==B,A2)12,【实验步骤和结果】例1 _ 4函数y =洁(A,B,c)如果(绝对值(A)>洁(1,2,2) 9有复数根: >洁(A,B,c)(exp(1)12)+(23 3)* log2(5)/tan(21) ans =21.4426 e+0053。
函数s = J(m)s = 0;k = 1;而k v=[1 2 3] A=diag(v,0) B=diag(v,1)v =1 2 33A =1 0 02 0 03 B =100 000 200 000 300 000A =魔法(3)A =8 1 6 3 5 7 4 9 2> > B =眼睛(4)B =1 0 0 0 0 0 0 0 0 0 0 1例2-11。
a = 1:5 a =1 2 3 4 5> > b = 3:2:11 b =43 5 7 9 11> > a.ans =1 4 9 16 25> > a . * b94 5 6;7 8 9]A =1 2 3 4 5 6 7 8 9> > B =[4 6 8;5 5 6;3 2 2]B = 4 6 8 5 5 6 3 2> > A * Bans =23 22 26 59 61 74 95 100 122> > A . * Bans =4 12 245。
matlab综合大作业(附详细答案)

m a t l a b综合大作业(附详细答案)-标准化文件发布号:(9456-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII《MATLAB语言及应用》期末大作业报告1.数组的创建和访问(20分,每小题2分):1)利用randn函数生成均值为1,方差为4的5*5矩阵A;实验程序:A=1+sqrt(4)*randn(5)实验结果:A =0.1349 3.3818 0.6266 1.2279 1.5888-2.3312 3.3783 2.4516 3.1335 -1.67241.2507 0.9247 -0.1766 1.11862.42861.5754 1.6546 5.3664 0.8087 4.2471-1.2929 1.3493 0.7272 -0.6647 -0.38362)将矩阵A按列拉长得到矩阵B;实验程序:B=A(:)实验结果:B =0.1349-2.33121.25071.5754-1.29293.38183.37830.92471.65461.34930.62662.4516-0.17665.36640.72721.22793.13351.11860.8087-0.66471.5888-1.67242.42864.2471-0.38363)提取矩阵A的第2行、第3行、第2列和第4列元素组成2*2的矩阵C;实验程序:C=[A(2,2),A(2,4);A(3,2),A(3,4)]实验结果:C =3.3783 3.13350.9247 1.11864)寻找矩阵A中大于0的元素;]实验程序:G=A(find(A>0))实验结果:G =0.13491.25071.57543.38183.37830.92471.65461.34930.62662.45165.36640.72721.22793.13351.11860.80871.58882.42864.24715)求矩阵A的转置矩阵D;实验程序:D=A'实验结果:D =0.1349 -2.3312 1.2507 1.5754 -1.29293.3818 3.3783 0.9247 1.6546 1.34930.6266 2.4516 -0.1766 5.3664 0.72721.2279 3.1335 1.1186 0.8087 -0.66471.5888 -1.67242.4286 4.2471 -0.38366)对矩阵A进行上下对称交换后进行左右对称交换得到矩阵E;实验程序:E=flipud(fliplr(A))实验结果:E =-0.3836 -0.6647 0.7272 1.3493 -1.29294.2471 0.80875.3664 1.6546 1.57542.4286 1.1186 -0.1766 0.9247 1.2507-1.6724 3.1335 2.4516 3.3783 -2.33121.5888 1.2279 0.6266 3.3818 0.13497)删除矩阵A的第2列和第4列得到矩阵F;实验程序:F=A;F(:,[2,4])=[]实验结果:F =0.1349 0.6266 1.5888-2.3312 2.4516 -1.67241.2507 -0.17662.42861.5754 5.3664 4.2471-1.2929 0.7272 -0.38368)求矩阵A的特征值和特征向量;实验程序:[Av,Ad]=eig(A)实验结果:特征向量Av =-0.4777 0.1090 + 0.3829i 0.1090 - 0.3829i -0.7900 -0.2579 -0.5651 -0.5944 -0.5944 -0.3439 -0.1272-0.2862 0.2779 + 0.0196i 0.2779 - 0.0196i -0.0612 -0.5682 -0.6087 0.5042 - 0.2283i 0.5042 + 0.2283i 0.0343 0.6786 0.0080 -0.1028 + 0.3059i -0.1028 - 0.3059i 0.5026 0.3660 特征值Ad =6.0481 0 0 0 00 -0.2877 + 3.4850i 0 0 00 0 -0.2877 - 3.4850i 0 00 0 0 0.5915 00 0 0 0 -2.30249)求矩阵A的每一列的和值;实验程序:lieSUM=sum(A)实验结果:lieSUM =-0.6632 10.6888 8.9951 5.6240 6.208710)求矩阵A的每一列的平均值;实验程序:average=mean(A)实验结果:average =-0.1326 2.1378 1.7990 1.1248 1.24172.符号计算(10分,每小题5分):1)求方程组20,0++=++=关于,y z的解;uy vz w y z w实验程序:S = solve('u*y^2 + v*z+w=0', 'y+z+w=0','y,z');y= S. y, z=S. z实验结果:y =[ -1/2/u*(-2*u*w-v+(4*u*w*v+v^2-4*u*w)^(1/2))-w] [ -1/2/u*(-2*u*w-v-(4*u*w*v+v^2-4*u*w)^(1/2))-w] z =[ 1/2/u*(-2*u*w-v+(4*u*w*v+v^2-4*u*w)^(1/2))] [ 1/2/u*(-2*u*w-v-(4*u*w*v+v^2-4*u*w)^(1/2))]2)利用dsolve 求解偏微分方程,dx dyy x dt dt==-的解; 实验程序:[x,y]=dsolve('Dx=y','Dy=-x')实验结果:x =-C1*cos(t)+C2*sin(t)y = C1*sin(t)+C2*cos(t)3.数据和函数的可视化(20分,每小题5分):1)二维图形绘制:绘制方程2222125x y a a +=-表示的一组椭圆,其中0.5:0.5:4.5a =;实验程序:t=0:0.01*pi:2*pi; for a=0.5:0.5:4.5; x=a*cos(t); y=sqrt(25-a^2)*sin(t); plot(x,y) hold on end实验结果:2) 利用plotyy 指令在同一张图上绘制sin y x =和10x y =在[0,4]x ∈上的曲线;实验程序:x=0:0.1:4; y1=sin(x); y2=10.^x;[ax,h1,h2]=plotyy(x,y1,x,y2); set(h1,'LineStyle','.','color','r'); set(h2,'LineStyle','-','color','g'); legend([h1,h2],{'y=sinx';'y=10^x'});实验结果:3)用曲面图表示函数22z x y =+;实验程序:x=-3:0.1:3; y=-3:0.1:3; [X,Y]=meshgrid(x,y); Z=X.^2+Y.^2; surf(X,Y,Z)实验结果:4)用stem 函数绘制对函数cos 4y t π=的采样序列;实验程序:t=-8:0.1:8;y=cos(pi.*t/4); stem(y)实验结果:4. 设采样频率为Fs = 1000 Hz ,已知原始信号为)150π2sin(2)80π2sin(t t x ⨯+⨯=,由于某一原因,原始信号被白噪声污染,实际获得的信号为))((ˆt size randn x x+=,要求设计出一个FIR 滤波器恢复出原始信号。
MATLAB大作业题目

一、 程序分析题1、命令窗口中输入如下命令,在%号后写出每行命令的功能。
(不用写出运算结果) A=1; f0=4; phi=pi/3; w0=2*pi*f0;t=0:0.01:1; %__________________________________________ y=A*cos(w0*t+phi) ;axis off %__________________________________________ PT=plot(t,y); %__________________________________________ set(PT,’LineWidth ’,[5]); %__________________________________________ AX=gca; %__________________________________________ set(AX,’FontSize ’,14); %__________________________________________ axis square %__________________________________________ xlabel(‘时间[s]’); %__________________________________________ T=title(‘余弦波’) %__________________________________________ set(T,’FontSize ’,’16’); %__________________________________________ legend(‘cos ’); %__________________________________________ grid on %__________________________________________二、 程序设计题2、已知两个矩阵:3765213100132610A ---⎡⎤⎢⎥---⎢⎥=⎢⎥-⎢⎥-⎣⎦,1468237021570010B ⎡⎤⎢⎥⎢⎥=⎢⎥--⎢⎥-⎣⎦将矩阵A 中所有等于-1的元素改为3,将矩阵B 中等于0的元素值改为新的矩阵A 中相应位置元素的值,最后将新的矩阵A 的第三、四列的元素全改为-1,编写相应的程序。
MATLAB编程作业

《Matlab编程训练》作业专业学生姓名班级学号指导教师完成日期实训一 MATLAB 语言介绍和数值计算1.先求下列表达式的值,然后显示MATLAB 工作空间的使用情况并保存变量。
122sin 851z e =+.2. 已知 1234413134787,2033657327A B --⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦,求下列表达式的值:(1) A+6*B 和A-B+I (其中I 为单位矩阵) A+6*B:A-B+I:(2)A*B和A.*BA*B程序:A=[12 34 -4;34 7 87;3 65 7]B=[1 3 -1;2 0 3;3 -2 7]c=A*B结果:A.*B程序:A=[12 34 -4;34 7 87;3 65 7]B=[1 3 -1;2 0 3;3 -2 7]D=A.*B结果:(3)A^3和A.^3A^3程序:A=[12 34 -4;34 7 87;3 65 7]E=A^3结果:A.^3程序:A=[12 34 -4;34 7 87;3 65 7]C=A.^3(4)A/B及B\AA/B程序:A=[12 34 -4;34 7 87;3 65 7]B=[1 3 -1;2 0 3;3 -2 7]C=A/B结果:B\A程序:A=[12 34 -4;34 7 87;3 65 7]B=[1 3 -1;2 0 3;3 -2 7]D=B\A结果:(5)将矩阵C=B\A的右下角2*2子矩阵赋给D, 并(3)保存变量(mat文件)程序:A=[12 34 -4;34 7 87;3 65 7];B=[1 3 -1;2 0 3;3 -2 7];C=B*inv(A);D=C(2:3,2:3)结果:3. 求得矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=34157864653434533145A 的每行最大元素所在的位置?(至少两种方法) 第一种:A=[5 14 33;45 43 3;65 4 6;78 15 34][RowMax Order]=max(A')结果:第二种:A=[5 14 33;45 43 3;65 4 6;78 15 34][Max_num,index]=max(A,[],2)结果:实训二 MATLAB 编程基础1. 求[25,1258]之间能被15整除的数的个数。
matlab期末大作业题目及答案

matlab 期末大作业(30分,每题6分)1. 积分运算(第四数值和五章符号)(1)定积分运算:分别采用数值法(quad ,dblquad )和符号运算(syms, int )一重定积分π⎰1. 数值法(quad )a) 运行代码:b) 运行结果:2. 符号运算(syms )a) 运行代码:b) 运行结果:二重定积分112200()x y dxdy+⎰⎰1.数值法(dblquad):a)运行代码:b)运行结果:2.符号运算(syms):a)运行代码:b)运行结果:(2) 不定积分运算sin dxdy ⎰⎰((x/a)+b/y) i.运行代码:ii.运行结果:2. 用符号法和数值法求解线性代数方程 (第五章和第二章)⎩⎨⎧=+=+12*22x *213*12x *a11y a a y a (1) 用syms 定义待解符号变量x,y 和符号参数a11,a12,a21,a22,用符号solve 求x,y 通解 1. 运行代码:2. 运行结果:(2) 用subs 带入a11=2,a12=4,a21=6,a22=8,求x 和y 特解,用vpa 输出有效数值4位的结果 1. 运行代码:2. 运行结果:(3) 采用左除(\)和逆乘法求解符号参数赋值后的方程 ⎩⎨⎧=+=+12*8x *63*4x *2y y1. 运行代码:2. 运行结果:3.数值法和符号法求解非线性方程组(第四数值和五章符号 )(1)采用数值法(fsolve )求解初始估计值为x0 = [-5; -5]的数值解1. 运行代码:2. 运行结果:21x 21x 21e x 2x e x x 2--=+-=-(2)符号法(solve )的符号结果用eval 或double 转化为数值结果.1. 运行代码:2. 运行结果:4. 解二阶微分方程 (第四数值和五章符号 )⎪⎩⎪⎨⎧===++6)0(',0)0(09322y y y dx dy dx y d(1)数值ode 求特解,用plot (x,y) 画t 在[0,10]范围内(x ,y )数值曲线 1. 运行代码:2. 运行结果:(2)符号运算dsolve求通解,用ezplot画t在[0,10]范围内(x,y)符号曲线1. 运行代码:2. 运行结果:5. 三维绘图(第六章)已知:x和y都在[-8,8]范围内,采用subplot(3,1,x)绘制三个子图,它们分别是用meshgrid和mesh绘制网格图、用c=contour 绘制等位线和用surf 绘制曲面图1.运行代码:2.运行结果:。
MATLAB第一章作业答案

第一章M A T L A B概况与基本操作1.选择题:(1)最初的MATLAB核心程序是采用A语言编写的。
(2)即将于2011年9月发布的MATLAB新版本的编号为D。
2011Ra 2011Rb R2011a R2011b(3)在默认设置中,MATLAB中的注释语句显示的颜色是D。
A.黑色B.蓝色C.红色D.绿色(4)如果要以科学计数法显示15位有效数字,使用的命令是B。
long long e long g long d(5)在命令窗口新建变量a、b,如果只查看变量a的详细信息,使用的命令为B。
a a(6)如果要清除工作空间的所有变量,使用的命令为 C 。
all C.两者都可 D.两者都不可(7)在创建变量时,如果不想立即在命令窗口中输出结果,可以在命令后加上D。
A.冒号B.逗号C.空格D.分号(8)如果要重新执行以前输入的命令,可以使用B键。
A.下箭头↓B.上箭头↑C.左箭头←D.右箭头→(9)如果要查询函数inv的相关信息,并显示在命令窗口,应使用命令A。
D.三者均可(10)如果要启动Notebook文档,下列D操作是可行的。
A.在命令窗口输入notebook命令B.在命令窗口输入notebook filename命令C.在Word中启动M-book文档D.三者均可2.填空题:(1)MATLAB是MATrix和LABoratory两个单词前三个字母的组合,意为“矩阵实验室”,它的创始人是Cleve Moler和Jack Little。
(2)在MATLAB的默认设置中,关键字显示的字体为蓝色,命令、表达式、计算结果显示的字体为黑色,字符串显示的字体为紫色,注释显示的字体为绿色,错误信息显示的字体为红色。
(3)在命令窗口中,输出结果显示为各行之间添加空行的命令为format compact,各行之间不添加空行的命令为format compact。
备注:本题布置给大家时有一点小错误,现在予以更正。
离散卷积MATLAB编程作业

一、离散卷积MATLAB编程作业(1)请编程实现一维卷积功能,即自己编写MATLAB中的CONV函数,自己写出一个CONV_NEW函数。
要求,请自己学习MATLAB向量运算操作,基于学习到的内容,用尽量少的代码实现CONV_NEW。
(a)请用例子检查你写的CONV_NEW是否与CONV的输出是否一致。
(b)请用两个10000维数组检测对比你写的CONV_NEW和CONV的时间复杂度。
请查资料大致回答,为什么MATLAB自带的CONV更快一些?(2)请查询自学二维卷积的知识(a)请写一个函数CONV2_NEW实现MATLAB中的二维卷积函数CONV2功能,请用例子检查你写的CONV2_NEW与CONV2的输出是否一致(b)请用此函数,做以下两个卷积核与附件图片lenna.jpg的卷积,将卷积结果打印出来。
并想一下为什么是这样。
(请查阅imread和imwrite函数)两点提示:由于imread和imwrite函数读入和写出的数值范围都是0到255,因此需要将结果归一化。
请参考一下函数程序读入写出例程。
A = imread(‘lenna.jpg’);B = double(A);Imwrite(uint8(B),’test.bmp’);(3)请编写MATLAB程序H = DECONV(X, Y)要求输入序列X和Y,输出序列H,使Y=X*H,若没有H满足要求,则输出错误信息”No sequence satisfies this condition.”二、傅里叶变换编程题对于卷积公式:x(t)*h(t) = y(t),则根据傅里叶变换和卷积性质,在已知x(t)和y(t)的情况下,h(t)可以写成:ℎ(t)=12π∫Y(jω)X(jω)e jωt dω+∞−∞(1)若x(t)和y(t)分别是如下函数,求h(t)。
(2)请用MATLAB画出h(t)在t=[-50,50]的函数图像。
(提示:用分成小段求矩形面积的形式近似求积分,注意规避分母等于0时候的情况)。
MATLAB大作业

M A T L A B大作业(总15页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--MATLAB大作业作业要求:(1)编写程序并上机实现,提交作业文档,包括打印稿(不含源程序)和电子稿(包含源程序),以班为单位交,作业提交截止时间6月24日。
(2)作业文档内容:问题描述、问题求解算法(方案)、MATLAB程序、结果分析、本课程学习体会、列出主要的参考文献。
打印稿不要求MATLAB程序,但电子稿要包含MATLAB程序。
(3)作业文档字数不限,但要求写实,写出自己的理解、收获和体会,有话则长,无话则短。
不要抄袭复制,可以参考网上、文献资料的内容,但要理解,要变成自己的语言,按自己的思路组织内容。
(4)从给出的问题中至少选择一题(多做不限,但必须独立完成,严禁抄袭)。
(5)大作业占过程考核的20%,从完成情况、工作量、作业文档方面评分。
第一类:绘制图形。
(B级)问题一:斐波那契(Fibonacci)螺旋线,也称黄金螺旋线(Golden spiral),是根据斐波那契数列画出来的螺旋曲线,自然界中存在许多斐波那契螺旋线的图案,是自然界最完美的经典黄金比例。
斐波那契螺旋线,以斐波那契数为边的正方形拼成的长方形,然后在正方形里面画一个90度的扇形,连起来的弧线就是斐波那契螺旋线,如图所示。
问题二:绘制谢尔宾斯基三角形(Sierpinskitriangle)是一种分形,由波兰数学家谢尔宾斯基在1915年提出,它是一种典型的自相似集。
其生成过程为:取一个实心的三角形(通常使用等边三角形),沿三边中点的连线,将它分成四个小三角形,然后去掉中间的那一个小三角形。
接下来对其余三个小三角形重复上述操作,如图所示。
问题三:其他分形曲线或图形。
分形曲线还有很多,教材介绍了科赫曲线,其他还有皮亚诺曲线、分形树、康托(G. Cantor)三分集、Julia集、曼德布罗集合(Mandelbrot set),等等。
matlab作业练习及答案(有程序和截图)

1. 给出如下方程组:16323313915111081697612534141543s u p w s u p w s u p w s u p w +++=+++=+++=+++=求s ,u ,p ,w 的值,并求出系数行列式。
[答案:s =-0.1258,u =-8.7133,p =11.2875,w =-0.0500。
行列式=7680。
]>> A=[16 32 33 13;5 11 10 8;9 7 6 12;34 14 15 1];>> B=[91 16 5 43]';>> C=A\B2. 求矩阵H1()H X X X X -''=其中1731565419289121110X ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦〔答案:H =〔0.7294,0.9041,0.4477,0.9188〕'〕>> X=[17 31 5;6 5 4;19 28 9;12 11 10]; >> H=X/(X'*X)*X'>> X=[17 31 5;6 5 4;19 28 9;12 11 10]; >> H=X*inv((X'*X))*X'3.用MA TLAB语言实现下面的分段函数,()/,||,h x Dy f x h Dx x Dh x D>⎧⎪==≤⎨⎪-<-⎩。
y=h*(x>D)+h/D*x.x>=-D&x<=D)-h*(x<-D)4.636263 0S=2124822 ii==++++++∑①试不采用循环的形式,用数值方法求出上式的解。
②由于数值方法采用double形式进行计算,难以保证有效数字,试采用符号运算的方法求该式的精确解。
并给出保留16位有效数字的结果。
>> sum(2.^[1:63])>> sum(sym(2).^[1:63])5.编写一个矩阵相加函数mat_add(),使其具体的调用格式为,要求该函数能接受任意多个矩阵进行加法运算。
4个Matlab实验的作业

现给出bpsk、qpsk及“书上习题”的调制解调程序,理解各程序,完成以下习题。
将程序运行结果及各题目的解答写入word中:1.用matlab运行书上习题中的“bpskqpsk125.m”(a)说明bpsk、qpsk解调判决方法(b)误比特率为1e-2、1e-3及1e-4时的Eb/N0分别是多少?(c)从物理意义上说明为什么bpsk、qpsk误比特率曲线是重叠的(d)当samples减少为100000,10000,1000时观察误比特率曲线的变化,你得出什么结论。
2.用matlab运行“bpsk.m”、“qpsk.m”(a)在各程序中标注“注释”处加上注释(英文或中文)(b)说明加性高斯白噪声的产生方法,请再给出一种加性高斯白噪声的产生方法,并验证其正确性。
(c)参考“bpskqpsk125.m”的画图功能,给出Eb/N0---误比特率曲线和高斯信道下的理论误比特率曲线。
(d)观察nd及nloop参数变化时,曲线的现象,并说明原因。
(e)画出不同信噪比条件下的的星座图,解释其对误码率的影响。
(f)通过程序画出QPSK和BPSK的Eb/N0---误比特率曲线,观察曲线的现象,能得出什么结论。
3.若信源是你的学号,结合程序说明其在qpsk (调制mod)和(解调demod)子程序中的具体实现过程。
4.针对题目2中的BPSK、QPSK,(a)若信道使信号幅度呈瑞利衰落,画出Eb/N0---误比特率曲线和瑞利衰落下的理论误比特率曲线,说明与题目2观察结果的异同,并说明原因。
(b)若信道使信号幅度呈莱斯衰落,更改K值的大小,画出Eb/N0---误比特率曲线、瑞利衰落下的理论误比特率曲线和高斯信道下的理论误比特率曲线,观察曲线的现象,能得出什么结论。
现给出循环码及卷积码的编解码程序,理解各程序,完成以下习题。
将程序运行结果及各题目的解答写入word中:1.用matlab运行书上习题中的“clockcode.m”(a)说明(7,4)码的纠错检错方法(b)在程序中标注“注释”处加上注释(英文或中文)(c)对于编码和未编码的情况,误比特率为1e-2、1e-3及1e-4时的Eb/N0分别是多少?(d)从物理意义上说明编码增益问题(e)当采用(15,11)码时,观察与(7,4)码相比编码增益的变化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电子与通信工程学院
通信系统仿真实验报告
2013 ~ 2014 学年第1学期调频(FM)系统调制解调仿真专业:通信工程
班级:通信111 班
学号:
姓名:
指导教师姓名:陈多瑜
2013年 11 月日
1.频率调制或调频(FM )
(1)设调制信号为m(t),调频信号的数学表达式为
ττϕd m K t f ⎰=)()(
例如:m (t )的时域波形为
m (t
) 1
0 0.5 1 t -1
FM 调频波如下:
FM 信号
(2) FM 调制模型的建立
图1 FM 调制模型
其中,()m t 为基带调制信号,设调制信号为
()cos(2)m m t A f t π=
设正弦载波为
()cos(2)c c t f t π=
可得到已调调频信号为
dt t m k t f A t s FM c c FM ⎰+=)(22cos[)(ππ
(3)原理
所谓频率调制(FM ),是指瞬时频率偏移随调制信号m(t)成比例变化,即
()
()f d t K m t dt
ϕ=
式中K f 为调频灵敏度(rad/(s ·V))。
这时相位偏移为 ()()f t K m d ϕττ
=⎰
则可得到公式
()cos ()FM c f s t A t K m d ωττ⎡⎤
=
+⎣⎦
⎰
假设信号传输信道为高斯白噪声信道,其功率为2
σ。
①FM 信号的仿真
下面给出一个用MATLAB 仿真FM 信号的示例。
已知:消息信号是[-3,3]均匀分布的随机整数,产生的时间间隔为1/10s ,用FM 方法调制载波t f c πcos2。
假设调频器灵敏度50=f k ,250=c f ,100≤≤t ,消息信号的带宽W=50Hz ,试求:
(1)画出消息信号和解调信号;
(2)已调信号的功率、消息信号的功率、调制指数及调制信号的带宽; (3)用鉴频法解调该信号,画出原始信号和解调信号;
(4)假设调制信号通过AWGN 信道,信噪比为20dB ,显示解调后的信号与
原始信号。
②FM调制Simulink系统仿真
Simulink中提供了调频模块(FM Modulator Passband),它位于“Communication Blockset→Modulation→Analog Passband Modulation”模块库中。
它的参数设置对话框如图所示。
对话框中有如下两个参数:
(1)Carrier frequency(Hz):调频信号的载波频率;
(2)Initial phanse(rad):信号载波的初始相位。
(3)Frequency deviation(Hz):调频信号的频偏。
用Simulink重新仿真上例,系统模型如ex1.mdl文件给出,系统模型框图如图所示。
(1)随机整数产生器模块(Random Integer Generator),用它来产生消息信号,它的参数设置:M-ary number设为7,Initial seed设为1234,Sample time设为1/10,Fram-based outputs不选中。
(2)减法器模块(Subtract、Subtract1),因为消息信号产生的信号范围是[0,6],所以用Subtract减去3,将信号范围转换为[-3,3]。
与Subtract减法端口相连的常数模块(Constant)位于“Simulink→Commonly Used Blocks”模块库中,其值设为3。
Subtract1用来求已调信号中的消息信号功率,与Subtract1减法端口相连的常数模块(Constant1)设为8(载波功率)。
(3)调幅模块(FM Modulator Passband),它的参数设置为Frequency deviation设为50,其他参数采用默认值。
(4)量化器模块(Quantizer、Quantizer1)。
量化器模块位于“Simulink →Commonly Used Blocks”模块库中。
因为要观察消息信号和已调信号的频谱,而频谱分析器要求的输入是离散量,所以需要量化器把连续信号转换为离散信号。
两个量化器的参数设置是相同的,其中Quantization interval设为0.001,Sample time设为0.001.
(5)频谱分析器(msg signal spectrum、Modulated Signal Specturm)
位于“Signal Processing Blockset→DSP Sinks”模块中,原始名字为Spctrum Scope。
他们的参数设置分别是:在“Scopes Properties”选项中,Buffer input 选中,Buffer size设为512,Buffer overlap设为256;Spectify FFT length 选中,FFT length设为512。
在“Axis Properties”选项中,Frequency range 选为[-Fs/2…Fs/2]。
Minimum Y-limit设为-50,Maximum Y-limit设为50。
(6)数学函数模块(Math Function),用它来计算已调信号振幅的平方。
在它的参数设置中,Function要选为magnitude^2。
(7)求均值模块(Mean),它位于“Signal Processing Blockset→Statistics”模块库中,它用来求已调信号的均值。
在它的参数设置中要选中Running mean,这样它输出的是整个仿真时间内得到的功率均值。
(8)除法器模块(Divide),它用来计算调制效率。
在参数设置中,把Number of inputs设为/*。
(9)显示模块,包括显示消息信号时域波形(Scope1),已调信号时域波形(Scope),已调信号功率值(Display),消息信号在已调信号中的功率(Display1)和调制效率(Display2)。
模型建好后,设置好各个模块的参数,在仿真参数设置中把Max step size 设为0.001,Stop time设为10。
调制模块的仿真波形如下:
原信号波形
已调信号
源信号频谱图
已调信号频谱图③FM信号的解调
Simulink模型如ex2.mdl所示。
(1)在Random Integer Generator模块中,把Sample time设为1/2,在两个调幅信号解调模块中把Offset factor设为4,其他采用默认值。
(2)由于要根据调制信号的功率添加高斯白噪声,因此需要计算调制信号的功率,计算出调制信号的功率后,根据信噪比计算出噪声的功率,把噪声的功率输入AWGN信道模块中,在AWGN信道模块参数设置中,Mode要设为Variance from port。
(3)在解调出信号后,需要进行低通滤波滤除信号的高斯噪声分量,这里采用Bessel低通滤波器,在参数设置中,把Design method设为Bessel,Filter type设为Lowpass,Filter order设为8,Passband edge frequency(rad/sec)设为2*pi*100。
(4)4个示波器分别观察各点波形,模型建好后,各个模块参数设置好后,在仿真参数设置中把Max step size设为0.001,Stop time设为5。
解调模块的仿真波形如下:
原信号波形
已调信号
解调后的信号
2.结论
通过这次通信原理课程设计,可得调制在通信系统中的重要性,还有懂得了为什么现有的收音机要用AM调制而不用其它的调制类型。
由此也可得调幅波在波形上,幅度随基带信号的规律而呈正比的变化;在频谱结构上,它的频谱完全是基带信号频谱在频域内的简单搬移(精确到常数因子)由于这种搬移是线性的,因此,幅度调制通常又称为线性调制。
在仿真的过程中由于没有学过相关的仿真软件,所以一切都是自学,从头开始,所以这其中遇到了许多困难。
但同时也感受到了学习的快乐。
在此过程中能把学到的东西运用到实践中来变成自己的实验结果,即验证了课本知识的正确性,又巩固了所学知识。
所以这是一次有意义的课程设计。
我将在以后的学习中继续努力,学习matlab软件知识,提高自己的水平,同时也感谢老师的栽培,同学的帮助。
