人教版2012年中考数学压轴题精选
2012全国各地中考数学压轴题精选(21-30)解析版

2012年各地中考数学压轴题精选21~30_解析版【21.2012上海】24.如图,在平面直角坐标系中,二次函数y=ax2+6x+c的图象经过点A(4,0)、B(﹣1,0),与y轴交于点C,点D在线段OC上,OD=t,点E在第二象限,∠ADE=90°,tan∠DAE=,EF⊥OD,垂足为F.(1)求这个二次函数的解析式;(2)求线段EF、OF的长(用含t的代数式表示);(3)当∠ECA=∠OAC时,求t的值.考点:相似三角形的判定与性质;待定系数法求二次函数解析式;全等三角形的判定与性质;勾股定理。
解答:解:(1)二次函数y=ax2+6x+c的图象经过点A(4,0)、B(﹣1,0),∴,解得,∴这个二次函数的解析式为:y=﹣2x2+6x+8;(2)∵∠EFD=∠EDA=90°∴∠DEF+∠EDF=90°,∠EDF+∠ODA=90°,∴∠DEF=∠ODA∴△EDF∽△DAO∴.∵,∴=,∴,∴EF=t.同理,∴DF=2,∴OF=t﹣2.(3)∵抛物线的解析式为:y=﹣2x2+6x+8,∴C(0,8),OC=8.如图,连接EC、AC,过A作EC的垂线交CE于G点.∵∠ECA=∠OAC,∴∠OAC=∠GCA(等角的余角相等);在△CAG与△OCA中,,∴△CAG≌△OCA,∴CG=4,AG=OC=8.如图,过E点作EM⊥x轴于点M,则在Rt△AEM中,∴EM=OF=t﹣2,AM=OA+AM=OA+EF=4+t,由勾股定理得:∵AE2=AM2+EM2=;在Rt△AEG中,由勾股定理得:∴EG===∵在Rt△ECF中,EF=t,CF=OC﹣OF=10﹣t,CE=CG+EG=+4由勾股定理得:EF2+CF2=CE2,即,解得t1=10(不合题意,舍去),t2=6,∴t=6.【22. 2012广东】22.如图,抛物线y=x2﹣x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.(1)求AB和OC的长;(2)点E从点A出发,沿x轴向点B运动(点E与点A、B不重合),过点E作直线l平行BC,交AC于点D.设AE的长为m,△ADE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;(3)在(2)的条件下,连接CE,求△CDE面积的最大值;此时,求出以点E为圆心,与BC相切的圆的面积(结果保留π).考点:二次函数综合题。
2012年中考数学压轴题100题精选(71-80题)答案

2012年中考数学压轴题100题精选(71-80题)答案2 ba【071】解:(1)由题意得,解得13 2a 4 9a 3b c 0∴此抛物线的解析式为3b 3c 2 c 2 242分 y x 2x 33(2)连结、.因为的长度一定,所以周长最小,就是使最ACBCBC△PBCPC PB小.点关于对称轴的对称点是点,与对称轴的交点即为所求的点. ACx 1BAP y 设直线的表达式为ACy kx b E,k A O B x 则解得3 D2 3k b 0∴此直线的表达式为……5分b 2 b 2 P 2 C.344 (第24题图)把代入得∴点的坐标y x 2, 33 (3)为······································ 6分 ·x 1y P 1存在最大值·························································································7分S理由:∵即DE∥PC,DE∥AC.ODOE2 mOE∴∴即△OED∽△OAC. , .OCOA2333∴OE 3 mm,AE 3,OE 22方法一:OP连结△OED△POE△POD△OED四边形S S S S S SPDOE134113= 3 m 2 m 1 3 m 2 m·················································223222 332= ···········································8分m m423333m 1∵,∴当最大4424时, ·········································· 9分 0S方法二:S S S S S△OAC△OED△AEP△PCD1131341 =13 2 3 m 2 m m m2222232 33332 2= (8)分 m m m 1 424433∵,∴当时,··························································9分m 1 0S 最大448【072】解:(1)①,,,S=12 OC 4OA 4AB 2OABC梯形2②当时,直角梯形OABC被直线扫过的面积=直角梯形OABC面积-直角三角开DOE面积2 t 4l1228 (2)存S 12 (4 t) 2( 4t )t t8 4在,,4),P(4,4),P(8,4)P( 12,4),P( 4,4),P( 451233对于第(2)题我们提供如下详细解答(评分无此要求).下面提供参考解法二:① 以点D为直角顶点,作轴PP x1 设.(图示阴影), 在Rt OD E中,OE 2OD, OD b,OE 2bRt ODE Rt PPD1,在上面二图中分别可得到点的生标为P(-12,4)、P(-4,4)E点在0点 b ,2b 8P与A点之间不可能;② 以点E为直角顶点8同理在②二图中分别可得点的生标为P(-,4)、P(8,4)E点在0点下方不可能. P3③ 以点P为直角顶点同理在③二图中分别可得点的生标为P(-4,4)(与①情形二重合舍去)、P(4,4),PE点在A点下方不可能. 8综上可得点的生标共5个解,分别为P(-12,4)、P(-4,4)、P(-,4)、P3P(8,4)、P (4,4).下面提供参考解法二:以直角进行分类进行讨论(分三类):第一类如上解法⑴中所示图此时D(-b,o),E(O,2b) P为直角:设直线DE:y 2x 2b,b1b3b,直线的中垂线方程:,令得.由的中点坐标为(-,b)y b (x )P( 8,4)DEy 4 2222 3 222222 (b 8) (4 2b) b 4b 已知可得即化简得解2PE DE3b 32b 64 0283b 得 ; P( 4,4)b 8,b 将之代入P (-8,4) P (4,4)、 121232 第二类如上解法②中所示图此时D (-b,o),E(O,2b) E 为直角:设直线DE :y 2x 2b ,1,直线的方程:,令得.由已知可得即y x 2bPEPE DEP(4b 8,4)y 4 2 222222化简得解之得 ,(4b 8) (4 2b) b 4bb (2b 8)48 b 4,b ,4)将之代入P (4b-8,4) P (8,4)、P( 123433 第三类如上解法③中所示图此时D (-b,o),E(O,2b) D 为直角:设直线DE :y 2x 2b ,1,直线的方程:,令得.由已知可得即y (x b)PDPD DEP( b 8,4)y 4 2 2222 解得8 4 b 4b (-b-8,4) P (-12,4)、b 4,b 4将之代入P512. (与重合舍去)P( 4,4)P( 4,4)P6628综上可得点的生标共5个解,分别为P (-12,4)、P (-4,4)、P (-,4)、 P 3P (8,4)、P (4,4). 事实上,我们可以得到更一般的结论: b a 如果得出设,则P 点的情形如下 AB a 、OC b 、OA h 、k h 直角分类情形 k 1k 1 P(h,h)1 P( h,h) P 为直角1 P( h,h)2hk P( ,h)3h1 k P( ,h) E 为直角2hk2 P(,h)4k 1 P( h(k 1),h)P(0,h)53 D 为直角 P( 2h,h)P( h(k 1),h)46 【073】(1)∵∠A 、∠C 所对的圆弧相同,∴∠A =∠C . APPD ∴Rt △APD ∽Rt △CPB ,∴,∴PA·PB =PC·PD ;………………………3分 CPPB(2)∵F 为BC 的中点,△BPC 为Rt △,∴FP=FC,∴∠C=∠CPF.又∠C=∠A,∠DPE=∠CPF,∴∠A=∠DPE.∵∠A+∠D=90°,∴∠DPE+∠D=90°.∴EF⊥AD.(3)作OM⊥AB于M,ON⊥CD于N,同垂径定理:222222∴OM=(2)-4=4,ON=(2)-3=11 55 y 又易证四边形MONP是矩形, O l 3O P 2O 2260°∴OP= OM ON 151 B D D x O A 1 C (第22题答图)点坐标为.在中,,Rt△AOC OAC 60° A ( 12,【074】(1)解:由题意得,OA | 4| |8| 12设直线的解析式为,由过两点的坐标为. C(0, 123) 123 b0) OC OAtan OAC 12 tan60° 123b 123 解得直线的解析式为:. ly 3x 123 k 3 点,得 A、Clly kx b 0 12k b(2)如图,设平移秒后到处与第一次外切于点,⊙O⊙O⊙O t P231与轴相切于点,连接.则x OO OP PO 8 5 13在⊙ODOO,OD1313113313轴,, OD⊥x OD 531312222OD OO OD 13 5 12中,.····································6分Rt△OOD111331131,,(秒)平移的时间为5OD OO OD 4 13 17 DD OD OD 17 12 51111115秒. ····························································· 8分 ⊙O t 521【075】解:(1)对称轴是直线:, x 1点A的坐标是(3,0).···························································· 2分(说明:每写对1个给1分,“直线”两字没写不扣分)(2)如∵点ADC的坐标分别图11,连接AC、AD,过D作于点M,DM y 轴△AOC∽△CMD解法一:利用、、、, a b b是 A (3,0),D(1,)C(0),AOOC3b3 ab 0∴AO=3,MD=1.由得∴·············································3分∴函数解析式0 2CMMDa13 ab 0a 1 2又∵∴由得0 a ( 1) 2a ( 1) b b 33a b为: ·········································································· 6分 y x 2x 3解法二:利用以AD为直径的圆经过点C ∵点A、D的坐标分别是A (3,0)、D(1,)、C(0,), a b b222222∴,,∵∴…① 又AC 9 bCD 1 aAD 4 ( a b)AC CD AD2∵…②···········································4分由①、②得∴函数解析式3 ab 00 a ( 1) 2a ( 1) b2为:·······························6分a 1,b 3y x 2x 3(3)如图所示,当BAFE为平行四边形时,则∥,并且=. BAEFBAEF ∵=4,∴=4 ,由于对称为,∴点F的横坐标为5. ·························· 7分 x 1BAEF2 E 将根据抛物线的对称代入得,∴F(5,12). F x 5y x 2x 3y 12 y性可知,在对称轴的左侧抛物线上也存在点F,使得四边形BAEF是平行四边形,此时点F坐标为(,12). 3当四边形BEAF是平行四边形时,点F即为点D,此时点F的坐标为(1,). 4综上所述,点F的坐标为(5,12), O A B x (,12)或(1,). 3 4【076】解:(1)∵四边形OBHC为矩形,∴CD∥AB, C 又D(5,2),∴C(0,2),OC=2 .图11 ∴解得 2 1 2 5 5 m n 2 D 5n 2 mn 22 152 ∴抛物线的解析式为:…… 4分y x x 222(2)点E落在抛物线上. 理由如下:……… 5分152由y = 0,得. 解得x=1,x=4.∴A(4,0),B(1,0). x x 2 01222 ∴OA=4,OB=1. 由矩形性质知:CH=OB=1,BH=OC=2,∠BHC=90°,由旋转、轴对称性质知:EF=1,BF=2,∠EFB=90°,∴点E的坐标为(3,-1). 151522把x=3代入,得,2222(3)法一:∴点E在抛物线上. y x x 2y 3 3 2 1存在点P(a,0),延长EF交CD于点G,易求OF=CG=3,PB=a-1. S=5,S= 3,记S= S,S= S, BCGF ADGF BCQP 1ADQP 2梯形梯形梯形梯形1 下面分两种情形:①当S∶S=1∶3时,,S (5 3)2 512 14PFEF1此时点P在点F(3,0)的左侧,则PF = 3-a,由△EPF∽△EQG,得,则QG=9 QGEG319-3a,∴CQ=3-(9-3a) =3a -6,由S=2,得,解得;(3a 6 a 1) 2 2a 1243②当S∶S=3∶1时,此时点P在点F(3,0)的右侧,则PF = a-S (5 3) 6 51214,3,由△EPF∽△EQG,得QG = 3a-9,∴CQ = 3 +(3 a-9)= 3 a-6,913113由S= 6,得,解得,综上所述:所求点P的坐标为24440)……… 14分(,0)或(,(3a 6 a 1) 2 6a 1法二:存在点P(a,0). 记S= S,S= S,易求S= 8. BCQP 1ADQP 2ABCD 梯形梯形梯形当PQ经过点F(3,0)时,易求S=5,S= 3,此时S∶S不符合条件,故a≠3. 12 121 k,则,解得设直线PQ的解3k b 1 a 3k≠0 y = kx+b()析式为, aak b 0 b∴. 由y = 2得xa 3 1a= 3a-6,∴Q(3a-6,2)……… 10分 y x a 3a 31∴CQ1211= 2;= 3a-6,BP = a-1,. (3a 6 a 1) 2 4a 7S下面分两种情形:①当S∶S= 1∶3时,S 8S 12 1梯形ABCD449-∴4a7 = 2,解得; (12)分a 43313-②当S∶S= 3∶1时,;∴4a7 = 6,解得;1梯形ABCD444913,0)………… 14分综上S 8 6S a 12所述:所求点P的坐标为(,0)或(44913[说明:对于第(3)小题,只要考生能求出或两个答案,就给6分. ] a a 443【077】解:(1)把B(0,6)代入,得=6 (1)分my m43 把=0代入,得=8 xy 6y4∴点A 的坐标为(8,0)…………… 3分 B'PCP(2)在矩形OACB中,AC =OB=6,BC=OA=8,∠C=90°GDQ∴AB=FIE'JM∵PD⊥AB∴∠PDB=∠C=2222AC BC 6 8 1090° OMEABDBD8BC,∴∴cos CBA BPa10BA 44∴BD aAD 10 a55又∵BC∥AE,∴△PBD∽△EAD4a10 AEAEAD54a5∴,即,∴ AE (10 ) 12.5 a 4aaBPBD45511∵,∴梯形PEAC22S (PC AE)ACs (8 a 12.5 a)6 6a 61.5()……………………………7分(注:写成不扣分) o a 8o a 8② ⊙Q是△OAB的内切圆,可设⊙Q的半径为r 11∵,解得OAB22、、r=2.………………………………………8分 S (6 8 10)r 6 8设⊙Q与OBABOA分别切于点F、G、H 可知,OF=2∴BF=BG=OB-OF=6-2=4,设直线PD与⊙Q交于点I、J ,过Q作QM⊥IJ于点1M,连结IQ、QG,∵QI=2, IM IJ 1.2222 ∴∴在∴BD=矩形GQMD中,GD=QM=1.6 QM QI IM 1.6BDBC85BG+GD=4+1.6=5.6,由,得 cos CBA BP BD 7 BPBA104∴点P的坐标为(7,6)…………………………………………………………………11分当PE在圆心Q的另一侧时,同理可求点P的坐标为(3,6)………………………12分综上,P点的坐标为(7,6)或(3,6).………………………………………………13分。
2012中考数学压轴题29例及答案

2012中考数学压轴题及答案1.(2011年四川省宜宾市)已知:如图,抛物线y=-x 2+bx+c 与x 轴、y 轴分别相交于点A (-1,0)、B (0,3)两点,其顶点为D.(1) 求该抛物线的解析式;(2) 若该抛物线与x 轴的另一个交点为E. 求四边形ABDE 的面积;(3) △AOB 与△BDE 是否相似?如果相似,请予以证明;如果不相似,请说明理由.(注:抛物线y=ax 2+bx+c(a ≠0)的顶点坐标为⎪⎪⎭⎫ ⎝⎛--a b ac a b 44,22) 2. (11浙江衢州)已知直角梯形纸片OABC 在平面直角坐标系中的位置如图所示,四个顶点的坐标分别为O(0,0),A(10,0),B(8,32),C(0,32),点T 在线段OA 上(不与线段端点重合),将纸片折叠,使点A 落在射线AB 上(记为点A ′),折痕经过点T ,折痕TP 与射线AB 交于点P ,设点T 的横坐标为t ,折叠后纸片重叠部分(图中的阴影部分)的面积为S ;(1)求∠OAB 的度数,并求当点A ′在线段AB 上时,S 关于t 的函数关系式;(2)当纸片重叠部分的图形是四边形时,求t 的取值范围;(3)S 存在最大值吗?若存在,求出这个最大值,并求此时t 的值;若不存在,请说明理由.3. (11浙江温州)如图,在Rt ABC △中,90A ∠=,6AB =,8AC =,D E ,分别是边AB AC ,的中点,点P 从点D 出发沿DE 方向运动,过点P 作PQ BC ⊥于Q ,过点Q 作QR BA ∥交AC 于R ,当点Q 与点C 重合时,点P 停止运动.设BQ x =,QR y =.(1)求点D 到BC 的距离DH 的长;(2)求y 关于x 的函数关系式(不要求写出自变量的取值范围);(3)是否存在点P ,使PQR △为等腰三角形?若存在,请求出所有满足要求的x 的值;若不存在,请说明理由.4.(11山东省日照市)在△ABC 中,∠A =90°,AB =4,AC =3,M 是AB 上的动点(不与A ,B 重合),过M 点作MN ∥BC 交AC 于点N .以MN 为直径作⊙O ,并在⊙O 内作内接矩形AMPN .令AM =x .(1)用含x 的代数式表示△MNP 的面积S ;(2)当x 为何值时,⊙O 与直线BC 相切?(3)在动点M 的运动过程中,记△MNP 与梯形BCNM 重合的面积为y ,试求y 关于x 的函数表达式,并求x 为何值时,y 的值最大,最大值是多少?5、(2007浙江金华)如图1,已知双曲线y=xk (k>0)与直线y=k ′x 交于A ,B 两点,点A 在第一象限.试解答下列问题:(1)若点A 的坐标为(4,2).则点B 的坐标为 ;若点A 的横坐标为m ,则点B 的坐标可表示为 ;(2)如图2,过原点O 作另一条直线l ,交双曲线y=xk (k>0)于P ,Q 两点,点P 在第一象限.①说明四边形APBQ 一定是平行四边形;②设点A.P 的横坐标分别为m ,n ,四边形APBQ 可能是矩形吗?可能是正方形吗?若可能,直接写出mn 应满足的条件;若不可能,请说明理由.6. (2011浙江金华)如图1,在平面直角坐标系中,己知ΔAOB 是等边三角形,点A 的坐标是(0,4),点B 在第一象限,点P 是x 轴上的一个动点,连结AP ,并把ΔAOP 绕着点A 按逆时针方向旋转.使边AO 与AB 重合.得到ΔABD.(1)求直线AB 的解析式;(2)当点P 运动到点(3,0)时,求此时DP 的长及点D 的坐标;(3)是否存在点P ,使ΔOPD 的面积等于43,若存在,请求出符合条件的点P 的坐标;若不存在,请说明理由. 7.(2011浙江义乌)如图1,四边形ABCD 是正方形,G 是CD 边上的一个动点(点G 与C 、D 不重合),以CG 为一边在正方形ABCD 外作正方形CEFG ,连结BG ,DE .我们探究下列图中线段BG 、线段DE 的长度关系及所在直线的位置关系:(1)①猜想如图1中线段BG 、线段DE 的长度关系及所在直线的位置关系;②将图1中的正方形CEFG 绕着点C 按顺时针(或逆时针)方向旋转任意角度α,得到如图2、如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断.(2)将原题中正方形改为矩形(如图4—6),且AB=a ,BC=b ,CE=ka , CG=kb (a ≠b ,k >0),第(1)题①中得到的结论哪些成立,哪些不成立?若成立,以图5为例简要说明理由.(3)在第(2)题图5中,连结DG 、BE ,且a =3,b =2,k =12,求22BE DG +的值. 8. (2011浙江义乌)如图1所示,直角梯形OABC 的顶点A 、C 分别在y 轴正半轴与x 轴负半轴上.过点B 、C 作直线l .将直线l 平移,平移后的直线l 与x 轴交于点D ,与y 轴交于点E .(1)将直线l 向右平移,设平移距离CD 为t (t ≥0),直角梯形OABC 被直线l 扫过的面积(图中阴影部份)为s ,s 关于t 的函数图象如图2所示, OM 为线段,MN 为抛物线的一部分,NQ 为射线,N 点横坐标为4.①求梯形上底AB 的长及直角梯形OABC 的面积;②当42<<t 时,求S 关于t 的函数解析式;(2)在第(1)题的条件下,当直线l 向左或向右平移时(包括l 与直线BC 重合),在直线..AB ..上是否存在点P ,使PDE ∆为等腰直角三角形?若存在,请直接写出所有满足条件的点P 的坐标;若不存在,请说明理由.9.(2011山东烟台)如图,菱形ABCD 的边长为2,BD=2,E 、F 分别是边AD ,CD 上的两个动点,且满足AE+CF=2.(1)求证:△BDE ≌△BCF ;(2)判断△BEF 的形状,并说明理由;(3)设△BEF 的面积为S ,求S 的取值范围.10.(2011山东烟台)如图,抛物线21:23L y x x =--+交x 轴于A 、B 两点,交y 轴于M 点.抛物线1L 向右平移2个单位后得到抛物线2L ,2L 交x 轴于C 、D 两点.(1)求抛物线2L 对应的函数表达式;(2)抛物线1L 或2L 在x 轴上方的部分是否存在点N ,使以A ,C ,M ,N 为顶点的四边形是平行四边形.若存在,求出点N 的坐标;若不存在,请说明理由;(3)若点P 是抛物线1L 上的一个动点(P 不与点A 、B 重合),那么点P 关于原点的对称点Q 是否在抛物线2L 上,请说明理由.11.2011淅江宁波)2011年5月1日,目前世界上最长的跨海大桥——杭州湾跨海大桥通车了.通车后,苏南A 地到宁波港的路程比原来缩短了120千米.已知运输车速度不变时,行驶时间将从原来的3时20分缩短到2时.(1)求A 地经杭州湾跨海大桥到宁波港的路程.(2)若货物运输费用包括运输成本和时间成本,已知某车货物从A 地到宁波港的运输成本是每千米1.8元,时间成本是每时28元,那么该车货物从A 地经杭州湾跨海大桥到宁波港的运输费用是多少元?(3)A 地准备开辟宁波方向的外运路线,即货物从A 地经杭州湾跨海大桥到宁波港,再从宁波港运到B 地.若有一批货物(不超过10车)从A 地按外运路线运到B 地的运费需8320元,其中从A 地经杭州湾跨海大桥到宁波港的每车运输费用与(2)中相同,从宁波港到B 地的海上运费对一批不超过10车的货物计费方式是:一车800元,当货物每增加1车时,每车的海上运费就减少20元,问这批货物有几车?12.(2011淅江宁波)如图1,把一张标准纸一次又一次对开,得到“2的短开”纸、“4开”纸、“8开”纸、“16开”纸….已知标准纸...边长为a . (1)如图2,把这张标准纸对开得到的“16开”张纸按如下步骤折叠:第一步 将矩形的短边AB 与长边AD 对齐折叠,点B 落在AD 上的点B '处,铺平后得折痕AE ; 第二步 将长边AD 与折痕AE 对齐折叠,点D 正好与点E 重合,铺平后得折痕AF .则:AD AB 的值是 ,AD AB ,的长分别是 , .(2)“2开”纸、“4开”纸、“8开”纸的长与宽之比是否都相等?若相等,直接写出这个比值;若不相等,请分别计算它们的比值.(3)如图3,由8个大小相等的小正方形构成“L ”型图案,它的四个顶点E F G H ,,,分别在“16开”纸的边AB BC CD DA ,,,上,求DG 的长.(4)已知梯形MNPQ 中,MN PQ ∥,90M =∠,2MN MQ PQ ==,且四个顶点M N P Q ,,,都在“4开”纸的边上,请直接写出2个符合条件且大小不同的直角梯形的面积.13.(2011山东威海)如图,在梯形ABCD 中,AB ∥CD ,AB =7,CD =1,AD =BC =5.点M ,N 分别在边AD ,BC 上运动,并保持MN ∥AB ,ME ⊥AB ,NF ⊥AB ,垂足分别为E ,F .(1)求梯形ABCD 的面积;(2)求四边形MEFN 面积的最大值.(3)试判断四边形MEFN 能否为正方形,若能,求出正方形MEFN 的面积;若不能,请说明理由.①标准纸“2开”纸、“4开”纸、“8开”纸、“16开”纸……都是矩形. ②本题中所求边长或面积都用含a 的代数式表示.14.(2011山东威海)如图,点A (m ,m +1),B (m +3,m -1)都在反比例函数xk y的图象上. (1)求m ,k 的值;(2)如果M 为x 轴上一点,N 为y 轴上一点,以点A ,B ,M ,N 为顶点的四边形是平行四边形,试求直线MN 的函数表达式.(3)选做题:在平面直角坐标系中,点P 的坐标为(5,0),点Q 的坐标为(0,3),把线段PQ 向右平移4个单位,然后再向上平移2个单位,得到线段P 1Q 1,则点P 1的坐标为 ,点Q 1的坐标为 . 15.(2011湖南益阳)我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图12,点A 、B 、C 、D 分别是“蛋圆”与坐标轴的交点,已知点D 的坐标为(0,-3),AB 为半圆的直径,半圆圆心M 的坐标为(1,0),半圆半径为2.(1) 请你求出“蛋圆”抛物线部分的解析式,并写出自变量的取值范围;(2)你能求出经过点C 的“蛋圆”切线的解析式吗?试试看;(3)开动脑筋想一想,相信你能求出经过点D 的“蛋圆”切线的解析式.16.(2011年浙江省绍兴市)将一矩形纸片OABC 放在平面直角坐标系中,(00)O ,,(60)A ,,(03)C ,.动点Q 从点O 出发以每秒1个单位长的速度沿OC 向终点C 运动,运动23秒时,动点P 从点A 出发以相等的速度沿AO 向终点O 运动.当其中一点到达终点时,另一点也停止运动.设点P 的运动时间为t (秒).(1)用含t 的代数式表示OP OQ ,;(2)当1t =时,如图1,将OPQ △沿PQ 翻折,点O 恰好落在CB 边上的点D 处,求点D 的坐标;(4) 连结AC ,将OPQ △沿PQ 翻折,得到EPQ △,如图2.问:PQ 与AC 能否平行?PE 与AC 能否垂直?若能,求出相应的t 值;若不能,说明理由.17.(2011年辽宁省十二市)如图16,在平面直角坐标系中,直线33y x =--与x 轴交于点A ,与y 轴交于点C ,抛物线223(0)3y ax x c a =-+≠经过A B C ,,三点. (1)求过A B C ,,三点抛物线的解析式并求出顶点F 的坐标;(2)在抛物线上是否存在点P ,使ABP △为直角三角形,若存在,直接写出P 点坐标;若不存在,请说明理由;(3)试探究在直线AC 上是否存在一点M ,使得MBF △的周长最小,若存在,求出M 点的坐标;若不存在,请说明理由.18.(2011年沈阳市)如图所示,在平面直角坐标系中,矩形ABOC 的边BO 在x 轴的负半轴上,边OC 在y 轴的正半轴上,且1AB =,3OB =,矩形ABOC 绕点O 按顺时针方向旋转60后得到矩形EFOD .点A 的对应点为点E ,点B 的对应点为点F ,点C 的对应点为点D ,抛物线2y ax bx c =++过点A E D ,,.(1)判断点E 是否在y 轴上,并说明理由;(2)求抛物线的函数表达式;(3)在x 轴的上方是否存在点P ,点Q ,使以点O B P Q ,,,为顶点的平行四边形的面积是矩形ABOC 面积的2倍,且点P 在抛物线上,若存在,请求出点P ,点Q 的坐标;若不存在,请说明理由.19.(2011年四川省巴中市) 已知:如图14,抛物线2334y x =-+与x 轴交于点A ,点B ,与直线34y x b =-+相交于点B ,点C ,直线34y x b =-+与y 轴交于点E . (1)写出直线BC 的解析式.(2)求ABC △的面积.(3)若点M 在线段AB 上以每秒1个单位长度的速度从A 向B 运动(不与A B ,重合),同时,点N 在射线BC 上以每秒2个单位长度的速度从B 向C 运动.设运动时间为t 秒,请写出MNB △的面积S 与t 的函数关系式,并求出点M 运动多少时间时,MNB △的面积最大,最大面积是多少?20.(2011年成都市)如图,在平面直角坐标系xOy 中,△OAB 的顶点A的坐标为(10,0),顶点B 在第一象限内,且AB =35,sin ∠OAB=55. (1)若点C 是点B 关于x 轴的对称点,求经过O 、C 、A 三点的抛物线的函数表达式;(2)在(1)中,抛物线上是否存在一点P ,使以P 、O 、C 、A 为顶点的四边形为梯形?若存在,求出点P 的坐标;若不存在,请说明理由;(3)若将点O 、点A 分别变换为点Q ( -2k ,0)、点R (5k ,0)(k>1的常数),设过Q 、R 两点,且以QR 的垂直平分线为对称轴的抛物线与y 轴的交点为N ,其顶点为M ,记△QNM 的面积为QMN S ∆,△QNR 的面积QNR S ∆,求QMN S ∆∶QNR S ∆的值.21.(2011年乐山市)在平面直角坐标系中△ABC 的边AB 在x 轴上,且OA>OB,以AB 为直径的圆过点C 若C 的坐标为(0,2),AB=5, A,B 两点的横坐标X A ,X B 是关于X 的方程2(2)10x m x n -++-=的两根:(1) 求m ,n 的值(2) 若∠ACB 的平分线所在的直线l 交x 轴于点D ,试求直线l 对应的一次函数的解析式(3) 过点D 任作一直线`l 分别交射线CA ,CB (点C 除外)于点M ,N ,则11CM CN+的值是否为定值,若是,求出定值,若不是,请说明理由 22.(2011年四川省宜宾市)已知:如图,抛物线y=-x 2+bx+c 与x 轴、y 轴分别相交于点A (-1,0)、B (0,3)两点,其顶点为D.(1)求该抛物线的解析式;(2)若该抛物线与x 轴的另一个交点为E. 求四边形ABDE 的面积;(3)△AOB 与△BDE 是否相似?如果相似,请予以证明;如果不相似,请说明理由.(注:抛物线y=ax 2+bx+c(a ≠0)的顶点坐标为⎪⎪⎭⎫ ⎝⎛--a b ac a b 44,22) 23.(天津市2011年)已知抛物线c bx ax y ++=232,(Ⅰ)若1==b a ,1-=c ,求该抛物线与x 轴公共点的坐标;(Ⅱ)若1==b a ,且当11<<-x 时,抛物线与x 轴有且只有一个公共点,求c 的取值范围;(Ⅲ)若0=++c b a ,且01=x 时,对应的01>y ;12=x 时,对应的02>y ,试判断当10<<x 时,抛物线与x 轴是否有公共点?若有,请证明你的结论;若没有,阐述理由.24.(2011年大庆市)如图①,四边形AEFG 和ABCD 都是正方形,它们的边长分别为a b ,(2b a ≥),且点F 在AD 上(以下问题的结果均可用a b ,的代数式表示).(1)求DBF S △;(2)把正方形AEFG 绕点A 按逆时针方向旋转45°得图②,求图②中的DBF S △;(3)把正方形AEFG 绕点A 旋转一周,在旋转的过程中,DBF S △是否存在最大值、最小值?如果存在,直接写出最大值、最小值;如果不存在,请说明理由.25. (2011年上海市)已知24AB AD ==,,90DAB ∠=,AD BC ∥(如图13).E 是射线BC 上的动点(点E 与点B 不重合),M 是线段DE 的中点.(1)设BE x =,ABM △的面积为y ,求y 关于x 的函数解析式,并写出函数的定义域;(2)如果以线段AB 为直径的圆与以线段DE 为直径的圆外切,求线段BE 的长;(3)联结BD ,交线段AM 于点N ,如果以A N D ,,为顶点的三角形与BME △相似,求线段BE 的长.26. (2011年陕西省)某县社会主义新农村建设办公室,为了解决该县甲、乙两村和一所中学长期存在的饮水困难问题,想在这三个地方的其中一处建一所供水站.由供水站直接铺设管道到另外两处.如图,甲,乙两村坐落在夹角为30的两条公路的AB 段和CD 段(村子和公路的宽均不计),点M 表示这所中学.点B 在点M 的北偏西30的3km 处,点A 在点M 的正西方向,点D 在点M 的南偏西60的23km 处.为使供水站铺设到另两处的管道长度之和最短,现有如下三种方案:方案一:供水站建在点M 处,请你求出铺设到甲村某处和乙村某处的管道长度之和的最小值;方案二:供水站建在乙村(线段CD 某处),甲村要求管道建设到A 处,请你在图①中,画出铺设到点A 和点M 处的管道长度之和最小的线路图,并求其最小值;方案三:供水站建在甲村(线段AB 某处),请你在图②中,画出铺设到乙村某处和点M 处的管道长度之和最小的线路图,并求其最小值.综上,你认为把供水站建在何处,所需铺设的管道最短?27. (2011年山东省青岛市)已知:如图①,在Rt △ACB 中,∠C =90°,AC =4cm ,BC =3cm ,点P 由B 出发沿BA 方向向点A 匀速运动,速度为1cm/s ;点Q 由A 出发沿AC 方向向点C 匀速运动,速度为2cm/s ;连接PQ .若设运动的时间为t (s )(0<t <2),解答下列问题:(1)当t 为何值时,PQ ∥BC ?(2)设△AQP 的面积为y (2cm ),求y 与t 之间的函数关系式;(3)是否存在某一时刻t ,使线段PQ 恰好把Rt △ACB 的周长和面积同时平分?若存在,求出此时t 的值;若不存在,说明理由;(4)如图②,连接PC ,并把△PQC 沿QC 翻折,得到四边形PQP ′C ,那么是否存在某一时刻t ,使四边形PQP ′C 为菱形?若存在,求出此时菱形的边长;若不存在,说明理由.28. (2011年江苏省南通市)已知双曲线k y x =与直线14y x =相交于A 、B 两点.第一象限上的点M (m ,n )(在A 点左侧)是双曲线k y x =上的动点.过点B 作BD ∥y 轴于点D.过N (0,-n )作NC ∥x 轴交双曲线k y x =于点E ,交BD 于点C.(1)若点D 坐标是(-8,0),求A 、B 两点坐标及k 的值.(2)若B 是CD 的中点,四边形OBCE 的面积为4,求直线CM 的解析式.(3)设直线AM、BM分别与y轴相交于P、Q两点,且MA=pMP,MB=qMQ,求p-q的值.29.(2011年江苏省无锡市)一种电讯信号转发装置的发射直径为31km.现要求:在一边长为30km的正方形城区选择若干个安装点,每个点安装一个这种转发装置,使这些装置转发的信号能完全覆盖这个城市.问:(1)能否找到这样的4个安装点,使得这些点安装了这种转发装置后能达到预设的要求?(2)至少需要选择多少个安装点,才能使这些点安装了这种转发装置后达到预设的要求?答题要求:请你在解答时,画出必要的示意图,并用必要的计算、推理和文字来说明你的理由.(下面给出了几个边长为30km的正方形城区示意图,供解题时选用)压轴题答案1.解:(1)由已知得:310cb c=⎧⎨--+=⎩解得c=3,b=2∴抛物线的线的解析式为223y x x=-++(2)由顶点坐标公式得顶点坐标为(1,4)所以对称轴为x=1,A,E 关于x=1对称,所以E(3,0)设对称轴与x 轴的交点为F所以四边形ABDE 的面积=ABO DFE BOFD S S S ∆∆++梯形 =111()222AO BO BO DF OF EF DF ⋅++⋅+⋅ =11113(34)124222⨯⨯++⨯+⨯⨯ =9(3)相似如图,BD=2222112BG DG +=+= BE=22223332BO OE +=+= DE=22222425DF EF +=+=所以2220BD BE +=, 220DE =即: 222BD BE DE +=,所以BDE ∆是直角三角形所以90AOB DBE ∠=∠=︒,且22AO BO BD BE ==, 所以AOB DBE ∆∆.2. (1) ∵A ,B 两点的坐标分别是A(10,0)和B(8,32),∴381032OAB tan =-=∠, ∴︒=∠60OAB当点A ´在线段AB 上时,∵︒=∠60OAB ,TA=TA ´,∴△A ´TA 是等边三角形,且A T TP '⊥,∴)t 10(2360sin )t 10(TP -=︒-=,)t 10(21AT 21AP P A -===', ○2当6t 2<≤时,由图○1,重叠部分的面积EB A TP A S S S '∆'∆-=∵△A ´EB 的高是︒'60sin B A , ∴23)4t 10(21)t 10(83S 22⨯----= 当t=2时,S 的值最大是34;○3当2t 0<<,即当点A ´和点P 都在线段AB 的延长线是(如图○2,其中E 是TA ´与CB 的交点,F 是TP 与CB 的交点),∵ETF FTP EFT ∠=∠=∠,四边形ETAB 是等腰形,∴EF=ET=AB=4, ∴3432421OC EF 21S =⨯⨯=⋅= 综上所述,S 的最大值是34,此时t 的值是2t 0≤<.3. 解:(1)Rt A ∠=∠,6AB =,8AC =,10BC ∴=.点D 为AB 中点,132BD AB ∴==. 90DHB A ∠=∠=,B B ∠=∠.BHD BAC ∴△∽△,DH BD AC BC ∴=,3128105BD DH AC BC ∴==⨯=.(2)QR AB ∥,90QRC A ∴∠=∠=.C C ∠=∠,RQC ABC ∴△∽△, RQ QC AB BC ∴=,10610y x -∴=, 即y 关于x 的函数关系式为:365y x =-+.(3)存在,分三种情况: ①当PQ PR =时,过点P 作PM QR ⊥于M ,则QM RM =.1290∠+∠=,290C ∠+∠=,1C ∴∠=∠.84cos 1cos 105C ∴∠===,45QM QP ∴=, 1364251255x ⎛⎫-+ ⎪⎝⎭∴=,185x ∴=. ②当PQ RQ =时,312655x -+=, 6x ∴=.③当PR QR =时,则R 为PQ 中垂线上的点,于是点R 为EC 的中点,11224CR CE AC ∴===. tan QR BA C CR CA==,366528x -+∴=,152x ∴=. 综上所述,当x 为185或6或152时,PQR △为等腰三角形.4.解:(1)∵MN ∥BC ,∴∠AMN =∠B ,∠ANM =∠C .∴ △AMN ∽ △ABC . ∴ AM AN AB AC =,即43x AN =. ∴ AN =43x . ……………2分 ∴ S =2133248MNP AMN S S x x x ∆∆==⋅⋅=.(0<x <4) ……………3分 (2)如图2,设直线BC 与⊙O 相切于点D ,连结AO ,OD ,则AO =OD =21MN . 在Rt △ABC 中,BC =22AB AC +=5.由(1)知 △AMN ∽ △ABC . ∴ AM MN AB BC =,即45x MN =. ∴ 54MN x =, ∴ 58OD x =. …………………5分 过M 点作MQ ⊥BC 于Q ,则58MQ OD x ==.在Rt△BMQ 与Rt△BCA 中,∠B 是公共角,∴ △BMQ ∽△BCA . ∴ BM QM BC AC=. ∴ 55258324x BM x ⨯==,25424AB BM MA x x =+=+=. ∴ x =4996. ∴ 当x =4996时,⊙O 与直线B C 相切.…………………………………7分 故以下分两种情况讨论:① 当0<x ≤2时,2Δ83x S y PMN ==. ∴ 当x =2时,2332.82y =⨯=最大 ……………………………………8分 ② 当2<x <4时,设PM ,PN 分别交BC 于E ,F .∵ 四边形AMPN 是矩形,∴ PN ∥AM ,PN =AM =x .又∵ MN ∥BC ,∴ 四边形MBFN 是平行四边形.∴ FN =BM =4-x .∴ ()424PF x x x =--=-.又△PEF ∽ △ACB .∴ 2PEF ABC S PF AB S ∆∆⎛⎫= ⎪⎝⎭. ∴ ()2322PEF S x ∆=-. ……………………………………………… 9分 MNP PEF y S S ∆∆=-=()222339266828x x x x --=-+-.……………………10分 当2<x <4时,29668y x x =-+-298283x ⎛⎫=--+ ⎪⎝⎭. ∴ 当83x =时,满足2<x <4,2y =最大. ……………………11分 综上所述,当83x =时,y 值最大,最大值是2. …………………………12分 5. 解:(1)(-4,-2);(-m,-k m) (2) ①由于双曲线是关于原点成中心对称的,所以OP=OQ,OA=OB,所以四边形APBQ 一定是平行四边形②可能是矩形,mn=k 即可不可能是正方形,因为Op 不能与OA 垂直.解:(1)作BE ⊥OA ,∴ΔAOB 是等边三角形∴BE=OB ·sin60o =23,∴B(23,2)∵A(0,4),设AB 的解析式为4y kx =+,所以2342k +=,解得33k =-,的以直线AB 的解析式为 (2)由旋转知,AP=AD, ∠PAD=60o, ∴ΔAPD 是等边三角形,PD=PA=2219AO OP +=6. 解:(1)作BE ⊥OA ,∴ΔAOB 是等边三角形∴BE=OB ·sin60o =23,∴B(23,2)∵A(0,4),设AB 的解析式为4y kx =+,所以2342k +=,解得33k =-, 以直线AB 的解析式为343y x =-+ (2)由旋转知,AP=AD, ∠PAD=60o ,∴ΔAPD 是等边三角形,PD=PA=2219AO OP +=6. 解:(1)作BE ⊥OA ,∴ΔAOB 是等边三角形∴BE=OB ·sin60o =23,∴B(23,2) ∵A(0,4),设AB 的解析式为4y kx =+,所以2342k +=,解得33k =-, 以直线AB 的解析式为343y x =-+ (2)由旋转知,AP=AD, ∠PAD=60o ,∴ΔAPD 是等边三角形,PD=PA=2219AO OP +=如图,作B E ⊥AO,DH ⊥OA,GB ⊥DH,显然ΔGBD 中∠GBD=30°∴GD=12BD=32,DH=GH+GD=32+23=532, ∴GB=32BD=32,OH=OE+HE=OE+BG=37222+= ∴D(532,72) (3)设OP=x,则由(2)可得D(323,22x x ++)若ΔOPD 的面积为:133(2)224x x += 解得:23213x -±=所以P(23213-±,0)(1)①,BG DE BG DE =⊥ ………………………………………………………………2分②,BG DE BG DE =⊥仍然成立 ……………………………………………………1分在图(2)中证明如下∵四边形ABCD 、四边形ABCD 都是正方形∴ BC CD =,CG CE =, 090BCD ECG ∠=∠=∴BCG DCE ∠=∠…………………………………………………………………1分∴BCG DCE ∆≅∆ (SAS )………………………………………………………1分∴BG DE = C B G C D E∠=∠ 又∵BHC DHO ∠=∠ 090CBG BHC ∠+∠=∴090CDE DHO ∠+∠= ∴090DOH ∠=∴BG DE ⊥ …………………………………………………………………………1分(2)BG DE ⊥成立,BG DE =不成立 …………………………………………………2分简要说明如下∵四边形ABCD 、四边形CEFG 都是矩形,且AB a =,BC b =,CG kb =,CE ka =(a b ≠,0k >)∴ BC CG b DC CE a==,090BCD ECG ∠=∠= ∴BCG DCE ∠=∠∴BCG DCE ∆∆………………………………………………………………………1分∴CBG CDE ∠=∠又∵BHC DHO ∠=∠ 090CBG BHC ∠+∠= ∴090CDE DHO ∠+∠= ∴090DOH ∠=∴BG DE ⊥ ……………………………………………………………………………1分(3)∵BG DE ⊥ ∴22222222BE DG OB OE OG OD BD GE +=+++=+ 又∵3a =,2b =,k =12∴ 222222365231()24BD GE +=+++= ………………………………………………1分 ∴22654BE DG +=………………………………………………………………………1分 (1)①2AB = ……………………………………………………………………………2分842OA ==,4OC =,S 梯形OABC =12……………………………………………2分 ②当42<<t 时,直角梯形OABC 被直线l 扫过的面积=直角梯形OABC 面积-直角三角开DOE 面积2112(4)2(4)842S t t t t =--⨯-=-+-…………………………………………4分 (2) 存在 ……………………………………………………………………………………1分123458(12,4),(4,4),(,4),(4,4),(8,4)3P P P P P --- …(每个点对各得1分)……5分 对于第(2)题我们提供如下详细解答(评分无此要求).下面提供参考解法二: ① 以点D 为直角顶点,作1PP x ⊥轴同理在③二图中分别可得P 点的生标为P (-4,4)(与①情形二重合舍去)、P (4,4),E 点在A 点下方不可能.综上可得P 点的生标共5个解,分别为P (-12,4)、P (-4,4)、P (-83,4)、 P (8,4)、P (4,4).下面提供参考解法二:以直角进行分类进行讨论(分三类):第一类如上解法⑴中所示图22P DE y x b ∠=+为直角:设直线:,D 此时(-b,o),E(O,2b) 的中点坐标为b (-,b)2,直线DE 的中垂线方程:1()22b y b x -=-+,令4y =得3(8,4)2bP -.由已知可得2PE DE =即222232(8)(42)42b b b b ⨯-+-=+化简得2332640b b -+=解得121883b b P P ==∴=3b,将之代入(-8,4)(4,4)、22(4,4)P -; 第二类如上解法②中所示图22E DE y x b ∠=+为直角:设直线:,D 此时(-b,o),E(O,2b) ,直线PE 的方程:122y x b =-+,令4y =得(48,4)P b -.由已知可得PE DE =即2222(48)(42)4b b b b -+-=+化简得22(28)b b =-解之得 ,123443b b P P ==∴=,将之代入(4b-8,4)(8,4)、48(,4)3P - 第三类如上解法③中所示图22D DE y x b ∠=+为直角:设直线:,D 此时(-b,o),E(O,2b) ,直线PD 的方程:1()2y x b =-+,令4y =得(8,4)P b --.由已知可得PD DE =即2222844b b +=+解得12544b b P P ==-∴=,将之代入(-b-8,4)(-12,4)、6(4,4)P -(6(4,4)P -与2P 重合舍去).综上可得P 点的生标共5个解,分别为P (-12,4)、P (-4,4)、P (-83,4)、P (8,4)、P (4,4).事实上,我们可以得到更一般的结论: 如果得出AB a OC b ==、、OA h =、设b ak h-=,则P 点的情形如下 11. 解:(1)设A 地经杭州湾跨海大桥到宁波港的路程为x 千米, 由题意得1201023x x+=, ··········································································································· 2分 解得180x =.A ∴地经杭州湾跨海大桥到宁波港的路程为180千米. ·················································· 4分 (2)1.8180282380⨯+⨯=(元),∴该车货物从A 地经杭州湾跨海大桥到宁波港的运输费用为380元. ························ 6分(3)设这批货物有y 车,由题意得[80020(1)]3808320y y y -⨯-+=, ·································································· 8分 整理得2604160y y -+=,解得18y =,252y =(不合题意,舍去), ······································································ 9分∴这批货物有8车. ···············································································································10分12. 解:(1)21244a a ,,. ······························································································ 3分 (2)相等,比值为2. ··········· 5分(无“相等”不扣分有“相等”,比值错给1分) (3)设DG x =,在矩形ABCD 中,90B C D ∠=∠=∠=,90HGF ∠=,90DHG CGF DGH ∴∠=∠=-∠,HDG GCF ∴△∽△,12DG HG CF GF ∴==, 22CF DG x ∴==. ················································································································ 6分同理BEF CFG ∠=∠.EF FG =, FBE GCF ∴△≌△,14BF CG a x ∴==-. ··········································································································· 7分CF BF BC +=,12244x a x a ∴+-=, ················································································· 8分解得214x a -=. 即214DG a -=. ··················································································································· 9分 (4)2316a , ···························································································································10分 2271828a -. 12分∴ 6494738)2(7342+⎪⎭⎫ ⎝⎛--=-=⋅=x x x EF ME S MEFN矩形. ……………………8分 当x =47时,ME =37<4,∴四边形MEFN 面积的最大值为649.……………9分(3)能. ……………………………………………………………………10分 由(2)可知,设AE =x ,则EF =7-2x ,ME =x 34. 若四边形MEFN 为正方形,则ME =EF . 即=34x 7-2x .解,得 1021=x . ……………………………………………11分∴ EF =21147272105x -=-⨯=<4. ∴ 四边形MEFN 能为正方形,其面积为251965142=⎪⎭⎫⎝⎛=MEFNS 正方形. ∴ 6494738)2(7342+⎪⎭⎫ ⎝⎛--=-=⋅=x x x EF ME S MEFN矩形. ……………………8分 当x =47时,ME =37<4,∴四边形MEFN 面积的最大值为649.……………9分(3)能. ……………………………………………………………………10分 由(2)可知,设AE =x ,则EF =7-2x ,ME =x 34. 若四边形MEFN 为正方形,则ME =EF . 即=34x 7-2x .解,得 1021=x . ……………………………………………11分∴ EF =21147272105x -=-⨯=<4. ∴ 四边形MEFN 能为正方形,其面积为251965142=⎪⎭⎫⎝⎛=MEFNS 正方形.14.解:(1)由题意可知,()()()131-+=+m m m m .解,得 m =3. ………………………………3分∴ A (3,4),B (6,2);∴ k =4×3=12. ……………………………4分 (2)存在两种情况,如图:①当M 点在x 轴的正半轴上,N 点在y 轴的正半轴 上时,设M 1点坐标为(x 1,0),N 1点坐标为(0,y 1).∵ 四边形AN 1M 1B 为平行四边形,∴ 线段N 1M 1可看作由线段AB 向左平移3个单位,再向下平移2个单位得到的(也可看作向下平移2个单位,再向左平移3个单位得到的).由(1)知A 点坐标为(3,4),B 点坐标为(6,2),∴ N 1点坐标为(0,4-2),即N 1(0,2); ………………………………5分M 1点坐标为(6-3,0),即M 1(3,0). ………………………………6分设直线M 1N 1的函数表达式为21+=x k y ,把x =3,y =0代入,解得321-=k .∴ 直线M 1N 1的函数表达式为232+-=x y . ……………………………………8分②当M 点在x 轴的负半轴上,N 点在y 轴的负半轴上时,设M 2点坐标为(x 2,0),N 2点坐标为(0,y 2).∵ AB ∥N 1M 1,AB ∥M 2N 2,AB =N 1M 1,AB =M 2N 2, ∴ N 1M 1∥M 2N 2,N 1M 1=M 2N 2.∴ 线段M 2N 2与线段N 1M 1关于原点O 成中心对称.∴ M 2点坐标为(-3,0),N 2点坐标为(0,-2). ………………………9分设直线M 2N 2的函数表达式为22-=x k y ,把x =-3,y =0代入,解得322-=k ,∴ 直线M 2N 2的函数表达式为232--=x y .所以,直线MN 的函数表达式为232+-=x y 或232--=x y . ………………11分(3)选做题:(9,2),(4,5). ………………………………………………2分 15. 解:(1)解法1:根据题意可得:A (-1,0),B (3,0);则设抛物线的解析式为)3)(1(-+=x x a y (a ≠0)又点D (0,-3)在抛物线上,∴a (0+1)(0-3)=-3,解之得:a =1∴y =x 2-2x -3 ··············································································································· 3分 自变量范围:-1≤x ≤3 ······························································································ 4分解法2:设抛物线的解析式为c bx ax y ++=2(a ≠0)根据题意可知,A (-1,0),B (3,0),D (0,-3)三点都在抛物线上∴⎪⎩⎪⎨⎧-==++=+-30390c c b a c b a ,解之得:⎪⎩⎪⎨⎧-=-==321c b a∴y =x 2-2x -3 ······················································································ 3分 自变量范围:-1≤x ≤3 ··································································· 4分(2)设经过点C “蛋圆”的切线CE 交x 轴于点E ,连结CM ,在Rt △MOC 中,∵OM =1,CM =2,∴∠CMO =60°,OC =3 在Rt △MCE 中,∵OC =2,∠CMO =60°,∴ME =4∴点C 、E 的坐标分别为(0,3),(-3,0) ····················································· 6分∴切线CE 的解析式为3x 33y +=································································· 8分 (3)设过点D (0,-3),“蛋圆”切线的解析式为:y =kx -3(k ≠0) ··················· 9分由题意可知方程组⎪⎩⎪⎨⎧--=-=3232x x y kx y 只有一组解 即3232--=-x x kx 有两个相等实根,∴k =-2 ··············································· 11分∴过点D “蛋圆”切线的解析式y =-2x -3 ···················································· 12分(2)当1t =时,过D 点作1DD OA ⊥,交OA 于1D ,如图1, 则53DQ QO ==,43QC =, 1CD ∴=,(13)D ∴,. (3)①PQ 能与AC 平行.若PQ AC ∥,如图2,则OP OAOQ OC=, 即66233t t -=+,149t ∴=,而703t ≤≤, 149t ∴=. ②PE 不能与AC 垂直.若PE AC ⊥,延长QE 交OA 于F ,如图3,。
2012年中考数学压轴题100题精选(21-30题)答案

2012年中考数学压轴题100题精选(21-30题)答案【021】解:(1);… ………………………………3分21(2)①EF∥AB.……………………………………4分,.证明:如图,由题意可得A(–4,0),B(0,3),34kk∴PA=3,PE=,PB=4,PF=.34PA312PB412∴,k∴.………………………… 6分PEPF又∵∠APB=∠EPF.∴△APB ∽△EPF,∴∠PAB=∠PEF.∴EF∥AB.…………………………… 7分②S没有最小值,理由如下:2过E作EM⊥y轴于点M,过F作FN⊥x轴于点N,两线交于点Q.由上知M(0,),N(,0),Q(,).……………… 8分4334-而S= S,∴S=SS=S-S=S+S+SEFQPEF2PEFOEFEFQOEFEOMFONOMQN △△△△△△△△矩形==2222.………………………… 10分6当时,S的值随k的增大而增大,而0<k<12.…………… 11分 2222∴0<S<24,s没有最小值.…………………………… 12分 22、说明:1.证明AB∥EF时,还可利用以下三种方法.方法一:分别求出经过AB两点和经过、EF两点的直线解析式,利用这两个解析式中x的系数相等来证明AB∥EF;方法二:tantan、,PAB利用=来证明AB∥EF;方法三:连接AFBE利用S=SAEFBFE△△、、得到点A点B到直线EF的距离相等,再由AB两点在直线EF同侧可得到AB∥EF.2.求S的值时,还可进行如下变形:2S=S-S=S-(S-S)=2 S-S,再利用第(1)2PEFOEFPEFPEOFPEFPEFPEOF△△△四边形△△四边形题中的结论.2【022】解:(1)设抛物线的解析式为:y=a(x-m+2)(x-m-2)=a(x-m)-4a.……2分∵AC⊥BC,由抛物线的对称性可知:△ACB是等腰直角三角形,又AB=4,112∴C(m,-2)代入得a=.∴解析式为:y=(x-m)-2.………………………5分22(亦可求C点,设顶点式)(2)∵m为小于零的常数,∴只需将抛物线向右平移-m个单位,再向上平移2个单位,可以使抛12物线y=(x-m)-2顶点在坐标原点. (7)分212m-2),设存在实数m,使得△BOD为等腰三角形.(3)由(1)得D(0,2∵△BOD为直角三角形,∴只能OD=OB.……………………………………………9分12∴m-2=|m +2|,当m+2>0时,解得m=4或m=-2(舍).2当m +2<0时,解得m=0(舍)或m=-2(舍);当m+2=0时,即m=-2时,B、O、D三点重合(不合题意,舍) 综上所述:存在实数m=4,使得△BOD为等腰三角形.……………………………12分△MBC【023】(1)证明:∵是等边三角形,∠∠D ∴∥BC∵是中点∴∵∠∠∠∠,∴△AMB≌△∴∴∴梯形是等腰梯形.△MBC(2)解:在等边中,60°Q,∠∠, B C P∠∠∠∠∠∴∠∠QPC△BMP∽△CQP∴∴∴··································5分,,∵∴················································6分∴∴ (7)分,BPMDBP∥∥(3)解:①当时,则有则四边形和四边形均为平行四边形∴,PCMDPC∥∥当时,则有,则四边形和四边形均为平行四边形∴441313,,、、、、∴当或时,以PM和ABC D中的两个点为顶点的四44边形是平行四边形.此时平行四边形有4个.△PQCy∴当取最小值时,为直角三角形∵4PB,∠,∠,∠∴是的中点,而∴∴BC【024】(1)由可知,,又△ABC为等腰直角三角形,∴,,所以点A的坐标是().D(2)∵∴,则点的坐标是().又抛物线顶点为,且过点、,所以可设抛物线的解析式为:,得:解得∴抛物线的解析式为………7分M(3)过点作于点,过点作于点,设点的坐标是,则,.PQM∵∴∽∴即,得∵BQN∴∽∴即,得又∵∴即为定值8. 【025】解:(1)设点M的横坐标为x,则点M的纵坐标为-x+4(0<x<4,x>0,-x+4>0);则:MC=∣-x+4∣=-x+4,MD=∣x∣=x;∴C=2(MC+MD)=2(-x+4+x)=8 OCMD四边形∴当点M在AB上运动时,四边形OCMD的周长不发生变化,总是等于8;22(2)根据题意得:S=MC·MD=(-x+4)·x=-x+4x=-(x-2)+4 OCMD四边形∴四边形OCMD的面积是关于点M的横坐标x(0<x<4)的二次函数,并且当x=2,即当点M运动到线段AB的中点时,四边形OCMD的面积最大且最大面积为4;(3)如图10(2),当时,;如图10(3),当时,;22a∴S与的函数的图象如下图所示: S 14·2(2·12(·a0 2 4 22【026】解:(1)∵AH∶AC=2∶3,AC=6∴AH=AC=×6=433又∵HF∥DE,∴HG∥CB,∴△AHG∽△ACB…………………………1分AHHG4HG16∴=,即=,∴HG=…………………………………2分63ACBC8111632...........................................∴S=AHHG=×4×=3分△AHG2233(2)①能为正方形...........................................................................4分′′∵HH′∥CD,HC∥HD,∴四边形CDHH为平行四边形′又∠C=90°,∴四边形CDHH为矩形.......................................5分又CH=AC-AH=6-4=2′∴当CD=CH=2时,四边形CDHH为正方形′此时可得t=2秒时,四边形CDHH为正方形 (6)分②(Ⅰ)∵∠DEF=∠ABC,∴EF∥∴当t=4秒时,直角梯形的腰EF与BA重合.′当0≤t≤4时,重叠部分的面积为直角梯形DEFH的面积.…………7分FMAC63过F作FM⊥DE于M,=tan∠DEF=tan∠ABC=== BC84ME44884FM=×2=,HF=DM=DE-ME=4-=∴ME= 33333141616∴直角梯形DEFH′的面积为(4+)×2=∴y= 23331′(Ⅱ)∵当4<t≤5时,重叠部分的面积为四边形CBGH的面积-矩形CDHH的面积.而S边形31324040×8×6-==2t∴y=-=S-S=矩形′△△CDHHCBGHABCAHG233331PD′(Ⅲ)当5<t≤8时,如图,设HD交AB于P.=8-又=tan∠ABC=43DB33∴PD=DB=(8-t)∴重叠部分的面积y=S , 443331122·PDDB=·(8-t)(8-t)=(8-t)=t-△PDB=48822∴重叠部分面积y与t的函数关系式:3(0≤t≤4)16401 -2t(4<t≤5)33312t-6t+24(5<t≤8)【027】解:(1)设抛物线的解析式为:, 把A(3,0)代入解析式求得所以,设直线AB的解析式为:由求得B点的坐标为把,代入中解得:所以 6分2(2)因为C点坐标为(1,4) ,所以当x=1时,y=4,y=2所以CD=4-2=2 8分平方单位) 假设存在符合条件的点P,设P点的横坐标为x,△PAB的铅垂高为h,则,由S=CABPAB△△12819322得:,化简得:解得,将代入中,解得P点坐标为1224y【028】解:(1)(5′) ∵抛物线与轴交于点(0,3),∴设抛物线解析式为(1′) 根据题意,得,解得∴抛物线的解析式为(5′) (2)(5′)由顶点坐标公式得顶点坐标为(1,4)(2′) 设对称轴与x轴的交点为∴四边形ABDE的面积梯形(5′)222(3)(2′)相似如图,BD=∴BE= ;∴即: ,所以是直角三角形∴,且, ∴∽′【029】解(1)因为△= 所以不论a为何实数,此函数图象与x轴总有两个交点。
2012中考数学压轴题精选精析(11-20例)

2012中考数学压轴题精选精析(11-20例)11.(2011•江苏盐城)(本题满分12分)如图,已知一次函数y = - x +7与正比例函数y = 43x 的图象交于点A , 且与x 轴交于点B .(1)求点A 和点B 的坐标;(2)过点A 作AC ⊥y 轴于点C ,过点B 作直线l ∥y轴.动点P 从点O 出发,以每秒1个单位长的速度,沿O —C —A 的路线向点A 运动;同时直线l 从点B 出发,以相同速度向左平移,在平移过程中,直线l 交x 轴于点R ,交线段BA 或线段AO 于点Q .当点P 到达点A 时,点P 和直线l 都停止运动.在运动过程中,设动点P 运动的时间为t 秒.①当t 为何值时,以A 、P 、R 为顶点的三角形的面积为8?②是否存在以A 、P 、Q 为顶点的三角形是等腰三角形?若存在,求t 的值;若不存在,请说明理由.【答案】(1)根据题意,得⎩⎪⎨⎪⎧y =-x +7y=43x ,解得 ⎩⎨⎧x =3y =4,∴A (3,4) . 令y =-x +7=0,得x =7.∴B (7,0).(2)①当P 在OC 上运动时,0≤t <4.由S △APR =S 梯形COBA -S △ACP -S △P OR -S △ARB =8,得12(3+7)×4-12×3×(4-t )- 12t(7-t )- 12t ×4=8 整理,得t 2-8t +12=0, 解之得t 1=2,t 2=6(舍)l y A C P l R P C A B O yx当P在CA上运动,4≤t<7.由S△APR= 12×(7-t) ×4=8,得t=3(舍)∴当t=2时,以A、P、R为顶点的三角形的面积为8.②当P在OC上运动时,0≤t<4. 此时直线l交AB于Q。
∴AP=(4-t)2+32,AQ=2t,PQ=7-t当AP =AQ时,(4-t)2+32=2(4-t)2, 整理得,t2-8t+7=0. ∴t=1, t=7(舍) 当AP=PQ时,(4-t)2+32=(7-t)2,整理得,6t=24. ∴t=4(舍去)当AQ=PQ时,2(4-t)2=(7-t)2整理得,t2-2t-17=0 ∴t=1±3 2 (舍)当P在CA上运动时,4≤t<7. 此时直线l交AO于Q。
2012年中考数学压轴题100题精选(11-20题)答案

2012 年中考数学压轴题100题优选(11-20题)答案【011】解:(1)证明:在Rt△FCD中,∵G为D F 的中点,∴CG= FD.⋯⋯⋯ 1分同理,在Rt△DEF 中,EG= FD .⋯⋯⋯⋯ 2分∴CG=EG.⋯⋯⋯⋯⋯⋯⋯ 3分(2 )(1 )中结论仍然成立,即EG=CG.⋯⋯⋯⋯⋯⋯⋯⋯⋯分⋯4证法一:连结AG,过G点作MN⊥AD 于M ,与EF 的延伸线交于N 点.在△DAG 与△DCG 中,∵AD=CD,∠ADG=∠CDG ,DG=DG ,∴△DAG≌△DCG .∴AG=CG.⋯⋯⋯⋯⋯⋯⋯⋯分⋯5在△DMG 与△FNG中,∵∠DGM=∠FGN,FG=DG,∠MDG=∠NFG,∴△DMG≌△FNG.∴MG=NG 在矩形AENM 中,AM=EN.⋯⋯⋯⋯⋯分6在R t△AMG 与Rt△ENG 中,∵AM=EN,MG=NG ,∴△AMG≌△ENG .∴AG=EG .∴EG=CG.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯分⋯证8法二:延伸CG至M,使MG=CG,连结MF,ME,E C,⋯⋯⋯⋯⋯⋯⋯⋯分4在△DCG 与△FMG 中,∵FG=DG,∠MGF=∠CGD,MG=CG,∴△DCG ≌△FMG.∴MF=CD,∠FMG=∠DCG.∴MF∥CD∥AB.⋯⋯⋯⋯⋯⋯⋯⋯分⋯∴5在Rt△MFE与Rt△CBE 中,∵MF=CB,EF=BE,∴△MFE ≌△CBE.∴∠MEC=∠MEF+∠FEC=∠CEB+∠CEF=90°.∴△MEC为直角三角形.∵MG = CG,∴EG= MC.⋯⋯⋯ 8分(3)(1)中的结论仍旧建立,即EG=CG.其余的结论还有:EG⊥CG.⋯⋯10分OO【012】解:(1)圆心在座标原点,圆的半径为1,A、B、C、D0)B(0,1、) C(1,、0)D(0,1)A( 1,、点的坐标分别为AM、NMA、NCOC y 抛x 物线与直线交于点,且分别与圆相切于点和点,、DM 、N 1、) N(11),D(01),、M( 1,1、) N(11),M( 1 ,.点在抛物线上,将的坐标代入c 1a 1 2 1 a b cb 1,y 得:ax b解x之,c得:1 a b cc 12 y x x1·············:.·····································4 分抛物线的分析式为215 2y x x 1 x( 2 )24 1x 抛物线的对称轴为, 2115 OE ,DE 1.······················6 分242 yBF ,BFD 90连°结, D NDEOD △BFD∽△EOD,,DBFD E A O x C5 F DE ,OD ,1DB 2又,P M 2 B45 FD , 545535 EF FD DE .···············································································8 分5210P(3)点在抛物线上.·············································································b过点的直································9 分D、Cy kx设线为:,k ,1b ,1、0)D(01),y kx bC的(1坐标代入,得:,将点DCy x 1·························································10 分直线为:.·xBBPPOy过1点作圆的切线与轴平行,点的纵坐标为,x 2y 1y x将代1 入,得:.22 Px 2y x x 1 2 2 1 1 (2,,当时,,点的坐标为2Py x x 因此1 ,点在抛物线上.·············································································0该抛物线·12 分 2 y ax bx 2 ,,2)可C(设的分析式为.【013】解:(1)该抛物线过点0)B(1,0)A(4,,代入,将1 a ,16a 4b2 ,0 2得解得5a b 2.0 b .2152y x x 2 ······························(3 分)此抛物线的分析式为.·22(2)存在.··························································································································(4 分)m P 如图,设点的横坐标为,152 m m则2P点的纵坐标为,22 y1 m 4 当时,P D152PM m m 2AM ,4.m A B 22 M 1 xO 4 COA PMA 又9,0 ° E AMAO2 2时,①当 C PMOC1(第26题图)△APM∽△ACO ,15 24 m 2 m m 2 即.22 m ,2m 41) P (,2.·解得,····································································(6 分)(舍去)12AMOC1152 2(4 m) m △mA PM2∽△CAO②当时,,即.PMOA222m 4m 解5 得,(均不合题意,舍去)12 1 m 41),P.(2 ······················································,·······································(7 分)当时m 4 2)P(5,.·近似地可求出当时,·········································································(8 分)m 1 14)P( ,.3 当时,P1) 14)( ,3(2,(5,2)或.·或综上所述,符合条件的点为·································(9 分)152t t 2 DDt(0 t.(4) 3)如图,设点的横坐标为,则点的纵坐标为221y x 2DEACAC过y作轴的平行线交于.由题意可求得直线的分析式为.(10 分)215111 22 Et ,t 2 DE t t 2 t 2 点t 的2 t坐标为..·(11 分)2222211 222 S t 2t 4 t 4t .(t 2) 422 t 2△DAC1) D(2,···············································△DAC,面积最大.045AOAy x【014】(1)···········(13 分).·当时解:∵点第一次落在直线上时停止旋转,∴旋转了.2 45 2O A. ⋯⋯⋯⋯⋯分4∴在旋转过程中所扫过的面积为3602MNAC BMN BAC 45 BNM B C(A 2 4)5解:∵∥,∴,. BMN BNMBM BNBA BCAM∴.∴又∵,∴.OAOC OAM OCN OAM A O O C M N CON 又∵,,∴.∴.∴1 AOM (90 45 OABC. MNAC 过程中,当和平行时,正方形旋转的度∴旋转245 数为.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯分⋯⋯0⋯ 8AOE 45 AOMBAEpy(3 )答:值无变化.证明:延伸交轴于点,则,000 AOE CON 90 45 AOM 45 AO M ,∴. 又∵,000 OAE 180 90 90 OCN OAE OCNOE ON,AE CN.∴.∴. 0OM OM OME OMN MOE MO y N又45 ∵,, ∴. y x E MN ME AM AEMN AM ∴.∴C N, AM p MN BN BM AM CN BN BM AB∴. B C B 4 OABCp∴在旋转正方形的过程中,值无变化. ⋯⋯⋯⋯⋯分12 xN O C (第26题)72【015】⑴设二次函数的分析式为:y=a(x-h)+k∵极点C 的横坐标为4 ,且过点(0 ,)3972∴y=a(x-4)+k ⋯⋯⋯⋯⋯3⋯①16a k又9 ∵对称轴为直线x=4,图象在x轴上截得的线段长为6 ∴A(1,0),B(7,0)332 ∴0=9a+k ⋯⋯⋯⋯⋯⋯②由①②解得a=,k=∴二次函数的分析式为:y=(x-4)--33 99⑵∵点A、B 对于直线x=4对称∴PA=PB∴PA+PD=PB+PD≥ D B∴当点P 在线段DB上时P A+PD获得最小值∴DB与对称轴的交点即为所求点P设直线x=4 与x轴交于点M∵PM∥OD ,∴∠BPM=∠BDO ,又∠PBM=∠DBO 73 3 PMBM339∴点P 的坐标为(4 ,)∴△BPM∽△BDO∴∴PM DOBO373 3 ⑶由⑴知点C(4,) ,又∵AM=3 ,∴在Rt△AMC 中,cot∠ACM= , 3 3oo∴∠ACM=60 ,∵AC=BC,Q作QN⊥x,过∴∠ACB=120 ①当点Q 在x轴上方时轴于N 假如AB=BQ,由△ABC∽△ABQ有oo BQ=6,∠QBN=60∴QN=3,BN=3,ON=10,此∠ABQ=120,则时点Q(10,),333 假如AB=AQ,由对称性知Q(-2,)33 ②当点Q 在x轴下方时,△QAB就是△ACB,此时点Q 的坐标是( 4,),3经查验,点(10,)与(-2,)都在抛物线上3333综上所述,存在这样的点Q,使为(10,)或(-2,)或△QAB∽△ABC 点Q 的坐标(4,).3333 3 y kx(k 【0)016】解:(1)设正比例函数的分析式为,11k 1y kx3 3k3),A,(3因此,解得.由于的图象过点111y x这个正比率函数的分析式为.·················································································(1 分)kk22y (k 0)y ,A(3)设反比率函数的分析式为.由于的图象过点,因此2xxk923 y k ,解9得.这个反比例函数的解析式为.········································(2 分)23x9933 y m ,B m(6)B6,(2 )由于点在的图象上,所以,则点.········(3 分)x622 y kx b(k 0)y kx设b一y次函x数分析式为.因为的图象是由平移获得的,3333 k 1y x by x,因此bB,6即.又由于的图象过点,所以32 399 6 bb y ,x 解得,一次函数的解析式为.·································(4 分)22299 y x ,DD0 (y3)由于的图象交轴于点,所以的坐标为.22 2y ax bx c(a设二0)次函数的解析式为.39 2Dy ax bx ,c 3B)6A,(3 0 ,、、和由于的图象过点,22 1 9a 3b,a c3, 2 3 b ,436a 6b c ,所以·····················(5 分)解得 2 99 c. c .2 2192y x这4x个二次函数的分析式为.····························································(6 分)2299 x y x CC,0(4)交轴于点,点的坐标是,22 151131 y6 6 6 3 3 如图3所S示,22222 A 99 3 45 18 B E4281 .O 6 3 C x 4281227 S S ,E y()x假定存在点,使.1003432 Dy x0 ECDOE,四边形的极点只能在轴上方,019919819 y y .S S001S△OCD△OCE2222284819273 y y E(x ,y) ,.在二次函数的图象上,000084221932 x 4x x .2解x 得或6.00002223 x 6x 6BCD,O E当E时6,点与点重合,这时不是四边形,故舍去,002 3 ,点E的2坐标为.(8 分)2 2y b x x c,,0)B(0 ,2)A(1 ,【017 】解:(1 )已知抛物线经过0 1 b cb 3 解得2 0 0 cc 2 2 y x 3x2··················分··所····2·······求抛物线的分析式为.·OA ,1OB 2,0)B(0,2) A(1,,(2)C(31),可得旋转后点的坐标为·································································································3 分·2x 3y x 3x 2y 2当时,由得,2y x 3x 22,)(3 可知抛物线过点Cy将原抛物线沿轴向下平移 1 个单位后过点. 2 y x 3x 1·····················分·5·平·移·后·的·抛·物·线·解·析·式············为:.·22 NNy x3x 1(x,x 3x 1() 3 )点在上,可设点坐标为0002335 2x y x 3x 1y将配x方得,其对称轴为.··································6 分224 3 y 0 x ①当时,如图①,02 S 2S △NBB△NDD B11113 1 x 2 1 00 A 222 1 O x D N D 1图①x 1 02x 3x 1 此时1 00 N(1,1) 点的坐标为·········································································································8 分.·y 3x ②当时,如图②02113 B 1 x 2 同理x 可得00222 N B C 1 A x 3 O x D 0D12x 3x 1 此1时00图②N,(31).点的坐标为N,1)(1(31) ,或综上,点的坐标为 (10)分.·2 y ax bx ,40a)C(0,4)A( 1,两点,【018】解:(1)抛物线经过a b 4a ,0a,1解得4a 3. 2 y x 3x 抛物线的分析式为. 2 m 1 m 3m 4,D(mm 1)( 2 )点在抛物线上,,y2 m 1m 3m 2m 即3,或0. D CDD 4)(,3 .点在第一象限,点的坐标为CBA 45°O A,.O B由(1)知 E DEBC设点对于直线的对称点为点. A B x C∥D ABCD 3 C,(04) O ,,且,ECB DCB,45°ECE CD 3y点在轴上,且.OE 1 ,E(10),.DBC即点对于直线对称的点的坐标为(0,1).PF⊥ABFEDE⊥BC(3 )方法一:作于,于.y OBC 4 5°OB OC,,4由(1)有:DBP 45,°CBD P.BA D C∥D OBCD 3 C,(,0 4)D(3,4) C ,且.P EDCE CBO,4 53°2 A B DE CE.xF O 2 52 BC 42 OB OC 4 C B E C E B,,,2DE3 tan PBF tan C.BD BE5PF 3tBF 5tOF 5t设4,则,,P( 5t ,43t).P点在抛物线上, 2 3t ( 5t 4) 3( 5t ,4) 4 22266 t t 0 ,(P 舍去)或,.25525 DBDPBD⊥D HxHQG⊥DHQQ 方法二:过点作的垂线交直线于点,过点作轴于.过点作G 于.yPBD ,45°QD D.B 90°QDG ,BDHD C Q G P DQG QDG 90°DQG BDH 又,. A BDG BH 1△QDG≌△DBH QG DH ,,4.x OH 4) Q( 1,3)D(3 ,,.由( 2 )知312y x BP ,0B)(,4直线的分析式为.552 2 x ,y x 3x ,4 x 4,2 5解1方程组得312y;606y x,1y 55. 2 25 266 P ,点的坐标为.525 【019】(1)EO>EC,原因以下:由折叠知,EO=EF,在Rt△EFC中,EF为斜边,∴EF>EC,故EO>EC ⋯ 2 分(2 )m为定值22222∵S=CF=EF -EC=EO -EC=(EO+EC)(EO―EC)=CO·(EO―E C C F)G H四边形S=CM·CO=|CE―EO|·CO=(EO―E·C C)O C M N O四边形S四边形CFGHm ∴1⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯分⋯⋯⋯ 4 S 四边形CMNO12121 QFC,E QF∴EF=EO= ( 3 )∵CO=1 ,33331∴cos∠FEC=∴∠FEC=60°, 2180 60 60 ,O E E A A O30 FEA三角等边∴22EQ ∴△EFQ为形,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯分⋯5 31133EQ EQ 作QI⊥EO 于I,EI=,IQ= 2323 21131 ∴(,)IO=∴Q 点坐标为⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯分⋯⋯336333 312(,)∵抛物线y=mx+bx+c过点C(0,1),Q,m=1 33b ∴3可求得,c=1 2y x 3x ∴抛1 物线分析式为⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯分⋯⋯ 7 2 AO 3EO 3 (4)由(3),3 2221 2x 3y (3) 3 3 当1时,<AB 3333231(,)∴P 点坐标为⋯⋯⋯⋯⋯⋯⋯分833121 ∴BP=AO 33 方法1:若△PBK 与△AEF相像,而△AEF≌△AEO,则分状况以下: 2 234383 B K BK (,1)(,1)时①,∴K点坐标为或 3 999 223 332 2343BK (,1)(0,1) BK②时,∴K 点坐标为或⋯⋯⋯⋯1分0 333 223 3 3 故直线K P 与y轴交点T 的坐标为571(0, 或) (0,)或(0, 或)(0,1) ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯分⋯⋯333 12 方法2:若△BPK与△AEF相像,由(3)得:P作PR⊥y轴于R,则∠RTP=60°或30°23 RT 3 2当①∠RTP=30°∠BPK=3°0或60°,过时, 3 232 3 RT 当②∠RTP=60°时,33 175T(0,),T(0, ,) T(0, ,)T(0,1) ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯分⋯∴112234333【020】解:(1)①CF⊥BD,CF=BD ②建立,理由以下:∵∠FAD=∠BAC=9°0∴∠BAD=∠CAF又BA=CA ,AD=AF ∴△BAD≌△CAF∴CF=BD∠ACF=∠ACB=4°5∴∠BCF=90°∴CF⊥BD (1 分)(⋯2⋯)当∠ACB=4°5时可得CF⊥BC,原因以下:如图:过点 A 作AC 的垂线与CB 所在直线交于G则∵∠ACB=4°5∴AG=AC ∠AGC=∠ACG=4°5 ∵AG=AC AD=AF ⋯(⋯1⋯分)∴△GAD≌△CAF(SAS)∴∠ACF=∠AGD=4°5 ∴∠GCF=∠GCA+∠ACF=90°∴CF⊥BC ⋯(⋯⋯2分⋯)(3)如图:作AQBC 于Q ∵∠ACB=4°5AC=4 ∴CQ=AQ=4 2∵∠PCD=∠ADP=90°∴∠ADQ+∠CDP=∠CDP+∠CPD=90°∴△ADQ∽△DPC ⋯(1 分)PCCD∴= DQAQ 设CD为x(0 <x < 3 )则D Q=CQ -CD=4 -x 则xPC= ⋯⋯⋯⋯(1 分)44 x1212∴PC=(-x+4x)=-(x-2)+1≥1 44 当x=2时,PC最长,此时P C=1 ⋯⋯⋯(1 分)。
2012中考数学压轴题真题(含答案)
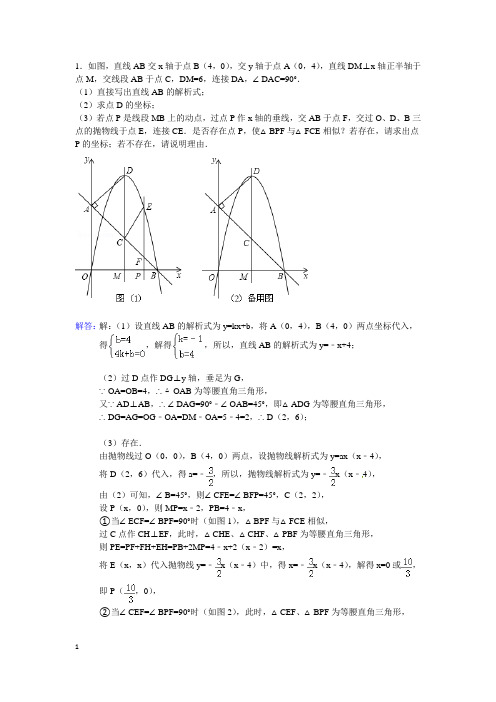
1.如图,直线AB交x轴于点B(4,0),交y轴于点A(0,4),直线DM⊥x轴正半轴于点M,交线段AB于点C,DM=6,连接DA,∠DAC=90°.(1)直接写出直线AB的解析式;(2)求点D的坐标;(3)若点P是线段MB上的动点,过点P作x轴的垂线,交AB于点F,交过O、D、B三点的抛物线于点E,连接CE.是否存在点P,使△BPF与△FCE相似?若存在,请求出点P 的坐标;若不存在,请说明理由.得,解得﹣,所以,抛物线解析式为﹣﹣﹣﹣或(﹣﹣x=(()或(2、.已知抛物线 与y 轴交于C 点,与x 轴交于A 、B 两点,点A 的坐标是(-1,0),O 是坐标原点,且OA OC 3=. (1)求抛物线的函数表达式; (2)直接写出直线BC 的函数表达式;(3)如图1,D 为y 轴的负半轴上的一点,且OD =2,以OD 为边作正方形ODEF .将正方形ODEF 以每秒1个单位的速度沿x 轴的正方向移动,在运动过程中,设正方形ODEF 与△OBC 重叠部分的面积为s ,运动的时间为t 秒(0<t ≤2). 求:①s 与t 之间的函数关系式;②在运动过程中,s 是否存在最大值?如果存在,直接写出这个最大值;如果不存在,请说明理由.(4)如图2,点P (1,k )在直线BC 上,点M 在x 轴上,点N 在抛物线上,是否存在以A 、M 、N 、P 为顶点的平行四边形?若存在,请直接写出M 点坐标;若不存在,请说明理由.c ax ax y +-=222.解答:(1)∵ A (-1,0), OA OC 3= ∴C (0,-3) ………1′∵抛物线经过A (-1,0), C (0,-3) ∴)()⎩⎨⎧=+-⨯-⨯--=012132c a a c∴⎨⎧-==31c a ∴y=x 2-2x -3 (3)(2)直线BC 的函数表达式为y=x -3(3)当正方形ODEF 的顶点D 运动到直线BC 上时,设D 点的坐标为(m ,-2), 根据题意得: -2=m-3,∴m=1 …………………6′①当0<t ≤1时S 1=2t …………………7′ 当1<t ≤2时S 2=OO DDS 11矩形-HGDS 1∆ =2t -()2121-⨯t=-213212-+t t …………………9′②当t =2秒时,S 有最大值,最大值为 ……………10′(4)M 1(-12-,0) M 2(12-,0) M 3(63-,0) M 4(63+,0 )………………14′3如图,抛物线32-+=bx ax y 交y 轴于点C ,直线 l 为抛物线的对称轴,点P 在第图1 图227三象限且为抛物线的顶点.P 到x 轴的距离为310,到y 轴的距离为1.点C 关于直线l 的对称点为A ,连接AC 交直线 l 于B. (1)求抛物线的表达式;(2)直线m x y +=43与抛物线在第一象限内交于点D ,与y 轴交于点F,连接BD 交y 轴于点E ,且DE:BE=4:1.求直线m x y +=43的表达式;(3)若N 为平面直角坐标系内的点,在直线m x y +=43上是否存在点M ,使得以点O 、F 、M 、N 为顶点的四边形是菱形?若存在,直接写出点M 的坐标;若不存在,请说明理由.3.解答:(1)∵抛物线32-+=bx axy 交y 轴于点C∴ C (0,-3)则 OC=3 ……………1分 ∵P 到x 轴的距离为310,P 到y 轴的距离是1且在第三象限 ∴P (-1,-310) ……………2分∵C 关于直线l 的对称点为A∴A (-2,-3) ……………3分 将点A (-2,-3),P (-1,-310)代入32-+=bx axy有⎪⎩⎪⎨⎧-=---=--31033324b a b a 解得⎪⎪⎩⎪⎪⎨⎧==3231b a ………………………5分 第26题图∴抛物线的表达式为 332312-+=x x y ………………………6分(2)过点D 做DG ⊥y 轴于G ,则∠DGE=∠BCE=90°∵∠DEG=∠BEC ∴△DEG ∽△BEC∵DE:BE=4:1 ∴14==BEDE BCDG 则DG=4 ………………………7分将x=4代入332312-+=x x y ,得y=5则 D (4,5) ………………………8分 ∵m x y +=43过点D (4,5)∴m +⨯=4435 则 m =2 ………………………9分∴所求直线的表达式为 243+=x y (10)分(3)存在 M 1516,58( M 254,58(-M 3)1,34(- M 42514,2548(-………………………14分4.在平面直角坐标系中,已知抛物线c bx ax y ++=2经过点A 3(-,0)、B(0,3)、C (1,0)三点.(1) 求抛物线的解析式和顶点D 的坐标;(2) 如图1,将抛物线的对称轴绕抛物线的顶点D 顺时针旋转 60,与直线x y -=交于点N .在直线DN 上是否存在点M ,使得∠MON= 75.若存在,求出点M 的坐标;若不存在,请说明理由;(3) 点P 、Q 分别是抛物线c bx ax y ++=2和直线x y -=上的点,当四边形OBPQ 是直角梯形时,求出点Q 的坐标.4解答.(1)解:由题意把A(-3,0)、B(0,3)、C(1,0)代入c bx ax y ++=2列方程组得⎪⎩⎪⎨⎧=++==+-03039c b a c c b a ,解得 ⎪⎩⎪⎨⎧=-=-=321c b a .……1分 ∴抛物线的解析式是322+--=x x y . ……2分 ∵4)1(3222++-=+--=x x x y ,∴抛物线的顶点D 的坐标为(-1,4).…… 3分(2)存在.理由:方法(一):由旋转得∠EDF=60°, 在Rt △DEF ∴EF=DE×tan60°=43.∴OF=OE+EF=1+4 ∴F 点的坐标为(341--,0).……1 设过点D 、F 的直线解析式是b x y +=κ 把D (-1,4),F (341--,0)代入求得 33433++=x y .……2分分两种情况:①当点M 在射线ND 上时, ∵∠MON=75°,∠BON=45°,∴∠MOB=∠MON ﹣∠BON=30°.∴∠MOC=60°.∴直线OM 的解析式为y =3x .……3分 ∴点M 的坐标为方程组.⎪⎩⎪⎨⎧=++=x y x y 333433的解,解方程组得,⎪⎪⎩⎪⎪⎨⎧+=+=2362132y x . ∴点M 的坐标为(2132+,236+).……4分②当点M 在射线NF 上时,不存在点M 使得∠MON=75°理由:∵∠MON=75°,∠FON=45°, ∴∠FOM=∠MON -∠FON=30°. ∵∠DFE=30°,∴∠FOM=∠DFE .∴OM ∥FN .∴不存在……5分 综上所述,存在点M ,且点M 的坐标为(2132+,236+).方法(二)①M 在射线ND 上,过点M 作MP ⊥x 轴于点P , 由旋转得∠EDF=60°, 在Rt △DEF 中,∵∠EDF=60°,DE=4 ∴EF=DE×tan60°=43.∴OF=OE ﹢EF=1+43.……2分 ∵∠MON=75°,∠BON=45°,∴∠∴∠MOC=60°.在Rt △MOP 中,∴ 在Rt △MPF 中,∵tan ∠MFP=PFMP ,∴=++3413OP OP 33.……3分∴OP=23﹢21.∴MP=6﹢23.∴M 点坐标为(23﹢21、6﹢23).……4分②M 在射线NF 上,,不存在点M 使得∠MON=75°理由:∵∠MON=75°,∠FON=45°,∴∠FOM=∠MON ﹣∠FON=30°. ∵∠DFE=30°.∴∠FOM=∠DFE .∴OM ∥DN . ∴不存在.……5分 综上所述,存在点M ,且点M 的坐标为(2132+,36(3)有两种情况①直角梯形OBPQ 中,PQ ∥OB ,∠如图3,∵∠OBP=∠AOB=90°,∴PB ∥OA . 所以点P 、B 的纵坐标相同都是3.……1分 因为点P 在抛物线322+--=x x y 上,把=y 3代入抛物线的解析式中得x 1=0(舍去) , x 2=﹣2.由PQ ∥OB 得到点P 、Q 的横坐标相同, 都等于-2.把x =﹣2代入=y ﹣x 得y =2.所以Q 点的坐标为(-2,2).……3分②在直角梯形OBPQ 中,PB ∥OQ ,∠BPQ=90°. 如图4,∵D(-1,4),B(0,3) ,∴DB ∥OQ .∵PB ∥OQ , 点P 在抛物线上,∴点P 、D 重合.……1分 ∴∠EDF=∠EFD=45°.∴EF=ED=4. ∴OF=OE+EF=5.……2分作QH ⊥x 轴于H ,∵∠QOF=∠QFO=45°, ∴OQ=FQ .∴OH=21OF=25.∴Q 点的横坐标﹣25.∵Q 点在=y ﹣x 上,∴把x =﹣25代入=y ﹣x 得=y 25.∴Q 点的坐标为(﹣25,25).…… 3分综上,符合条件的点Q 有两个,坐标分别为:(-2,2),(-25,25).※ 试题其他方法参照给分5.如图,已知抛物线经过原点O 和 轴上一点A (4,0),抛物线顶点为E ,它的对称轴与 轴交于点D.直线 经过抛物线上一点B (-2,m )且与轴交于点C , 与抛物线的对称轴交于点F.(1)求m 的值及该抛物线对应的解析式;(2)P 是抛物线上的一点,若S △ADP =S △ADC ,求出所有符合条件的点P 的坐标; (3)点Q 是平面内任意一点,点M 从点F 出发,沿对称轴向上以每秒1个单位长度的速度匀速运动,设点M 的运动时间为t 秒,是否能使以Q 、A 、E 、M 四点为顶点的四边形是菱形.若能,请直接写出点M 的运动时间t 的值;若不能,请说明理由.第26题图 备用图5.解答:(1)∵点B(-2,m)在直线12--=x y 上∴m=3 即B (-2,3)┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅ 1分 又∵抛物线经过原点O∴设抛物线的解析式为bx ax y +=2∵点B (-2,3),A (4,0)在抛物线上∴⎩⎨⎧=+=-0416324b a b a 解得:⎪⎩⎪⎨⎧-==141b a∴设抛物线的解析式为x x y -=241 ┅┅┅┅┅┅┅┅┅┅┅┅┅ 4分x 12--=x y y ),(yx(2)∵),(y x P 是抛物线上的一点 ∴)41,(2x x x P -若ADC ADP S S ∆∆= ∵OC AD S ADC ⋅=∆21 y AD S ADP ⋅=∆21 ┅┅┅┅┅┅┅┅ 6分又∵点C 是直线12--=x y 与y 轴交点 ∴C(0,1) ∴OC=1 ∴1412=-x x , 即1412=-x x 或1412-=-x x解得:2,222,2224321==-=+=x x x x∴点P 的坐标为 )1,2(),1,222(),1,222(321--+P P P ┅┅┅ 10分 (3)存在: ,541-=t ,62=t,543+=t ,2134=t ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅。
2012年中考数学压轴题1(含答案)

1、如图,已知抛物线2(1)y a x =-+a ≠0)经过点(2)A -,0,抛物线的顶点为D ,过O 作射线OM AD ∥.过顶点D 平行于x 轴的直线交射线OM 于点C ,B 在x 轴正半轴上,连结BC .(1)求该抛物线的解析式;(2)若动点P 从点O 出发,以每秒1个长度单位的速度沿射线OM 运动,设点P 运动的时间为()t s .问当t 为何值时,四边形DAOP 分别为平行四边形?直角梯形?等腰梯形? (3)若OC OB =,动点P 和动点Q 分别从点O 和点B 同时出发,分别以每秒1个长度单位和2个长度单位的速度沿OC 和BO 运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为t ()s ,连接PQ ,当t 为何值时,四边形BCPQ 的面积最小?并求出最小值及此时PQ 的长. 1、解:(1)抛物线2(1)0)y a x a =-+≠经过点(20)A -,09a a ∴=+= ∴二次函数的解析式为:2y x x =++ (2)D为抛物线的顶点(1D ∴过D 作DN OB ⊥于N,则DN =,3660AN AD DAO =∴==∴∠=,°OM AD ∥①当AD OP =时,四边形DAOP 是平行四边形66(s)OP t ∴=∴=②当DP OM ⊥时,四边形DAOP 是直角梯形过O 作OH AD ⊥于H ,2AO =,则1AH = (如果没求出60DAO ∠=°可由Rt Rt OHA DNA △∽△求AH 55(s)OP DH t ∴===③当PD OA =时,四边形DAOP 是等腰梯形26244(s)OP AD AH t ∴=-=-=∴=综上所述:当6t =、5、4时,对应四边形分别是平行四边形、直角梯形、等腰梯形. · 7分 (3)由(2)及已知,60COB OC OB OCB ∠==°,,△是等边三角形则6262(03)OB OC AD OP t BQ t OQ t t =====∴=-<<,,,过P 作PE OQ ⊥于E ,则3PE =113633(62)222BCPQS t t ∴=⨯⨯⨯-⨯23363328t ⎫-⎪⎝⎭当32t =时,BCPQ S 6338∴此时3339333324444OQ OP OE QE PE ==∴=-==,=, 22223393344PQ PE QE ⎛⎫⎛⎫∴=+=+= ⎪ ⎪ ⎪⎝⎭⎝⎭2、如图,在平面直角坐标系中,已知矩形ABCD 的三个顶点B (4,0)、C (8,0)、D (8,8).抛物线y=ax 2+bx 过A 、C 两点.(1)直接写出点A 的坐标,并求出抛物线的解析式;(2)动点P 从点A 出发.沿线段AB 向终点B 运动,同时点Q 从点C 出发,沿线段CD 向终点D 运动.速度均为每秒1个单位长度,运动时间为t 秒.过点P 作PE ⊥AB 交AC 于点E ,①过点E 作EF ⊥AD 于点F ,交抛物线于点G.当t 为何值时,线段EG 最长?②连接EQ .在点P 、Q 运动的过程中,判断有几个时刻使得△CEQ 是等腰三角形? 请直接写出相应的t 值2、解.(1)点A 的坐标为(4,8) 将A (4,8)、C (8,0)两点坐标分别代入y=ax2+bx 8=16a+4b得0=64a+8b得a=-12,b=4解∴抛物线的解析式为:y=-12x2+4x …………………3分 (2)①在Rt △APE 和Rt △ABC 中,tan ∠PAE=PE AP =BC AB ,即PE AP =48 ∴PE=12AP=12t .PB=8-t .(第4题)∴点E的坐标为(4+12t ,8-t ).∴点G 的纵坐标为:-12(4+12t )2+4(4+12t )=-18t2+8. ∴EG=-18t2+8-(8-t) =-18t2+t.∵-18<0,∴当t=4时,线段EG 最长为2.②共有三个时刻.t1=163, t2=4013,t3= .3、如图,已知直线128:33l y x =+与直线2:216l y x =-+相交于点C l l 12,、分别交x 轴于A B 、两点.矩形DEFG 的顶点D E 、分别在直线12l l 、上,顶点F G 、都在x 轴上,且点G 与点B 重合.(1)求ABC △的面积;(2)求矩形DEFG 的边DE 与EF 的长;(3)若矩形DEFG 从原点出发,沿x 轴的反方向以每秒1个单位长度的速度平移, 设移动时间为(012)t t ≤≤秒,矩形DEFG 与ABC △重叠部分的面积为S ,求S 关t 的函数关系式,并写出相应的t 的取值范围.3、(1)解:由28033x +=,得4x A =-∴.点坐标为()40-,.由2160x -+=,得8x B =∴.点坐标为()80,.∴()8412AB =--=由2833216y x y x ⎧=+⎪⎨⎪=-+⎩,.解得56x y =⎧⎨=⎩,.∴C 点的坐标为()56,. ∴111263622ABC C S AB y ==⨯⨯=△·.(2)解:∵点D 在1l 上且2888833D B D x x y ==∴=⨯+=,.∴D 点坐标为()88,.又∵点E 在2l上且821684E D E E y y x x ==∴-+=∴=,..∴E 点坐标为()48,.∴8448OE EF =-==,.(3)①当03t <≤时,如图1,矩形DEFG 与ABC △重叠部分为五边形CHFGR (0t =时,为四边形CHFG ).过C 作CM AB ⊥于M ,则Rt Rt RGB CMB △∽△.∴BG RG BM CM =,即36t RG=,∴2RG t =.Rt Rt AFH AMC △∽△, ∴()()11236288223ABC BRG AFH S S S S t t t t =--=-⨯⨯--⨯-△△△.即241644333S t t =-++.4、如图13,二次函数)0(2<++=p q px x y 的图象与x 轴交于A 、B 两点,与y 轴交于点C (0,-1),ΔABC 的面积为45。
2012年中考数学压轴题及解析分类汇编

中考数学压轴题:函数相似三角形问题(一)例1直线113y x =-+分别交x 轴、y 轴于A 、B 两点,△AOB 绕点O 按逆时针方向旋转90°后得到△COD ,抛物线y =ax 2+bx +c 经过A 、C 、D 三点.(1) 写出点A 、B 、C 、D 的坐标;(2) 求经过A 、C 、D 三点的抛物线表达式,并求抛物线顶点G 的坐标;(3) 在直线BG 上是否存在点Q ,使得以点A 、B 、Q 为顶点的三角形与△COD 相似?若存在,请求出点Q 的坐标;若不存在,请说明理由.例2 Rt △ABC 在直角坐标系内的位置如图1所示,反比例函数(0)ky k x=≠在第一象限内的图像与BC 边交于点D (4,m ),与AB 边交于点E (2,n ),△BDE 的面积为2.(1)求m 与n 的数量关系; (2)当tan ∠A =12时,求反比例函数的解析式和直线AB 的表达式; (3)设直线AB 与y 轴交于点F ,点P 在射线FD 上,在(2)的条件下,如果△AEO 与△EFP 相似,求点P 的坐标.图12012中考数学压轴题函数相似三角形问题(二)例3 如图1,已知梯形OABC,抛物线分别过点O(0,0)、A(2,0)、B(6,3).(1)直接写出抛物线的对称轴、解析式及顶点M的坐标;(2)将图1中梯形OABC的上下底边所在的直线OA、CB以相同的速度同时向上平移,分别交抛物线于点O1、A1、C1、B1,得到如图2的梯形O1A1B1C1.设梯形O1A1B1C1的面积为S,A1、B1的坐标分别为(x1,y1)、(x2,y2).用含S的代数式表示x2-x1,并求出当S=36时点A1的坐标;(3)在图1中,设点D的坐标为(1,3),动点P从点B出发,以每秒1个单位长度的速度沿着线段BC运动,动点Q从点D出发,以与点P相同的速度沿着线段DM运动.P、Q两点同时出发,当点Q到达点M时,P、Q两点同时停止运动.设P、Q两点的运动时间为t,是否存在某一时刻t,使得直线PQ、直线AB、x轴围成的三角形与直线PQ、直线AB、抛物线的对称轴围成的三角形相似?若存在,请求出t的值;若不存在,请说明理由.图1 图2例4 如图1,已知点A (-2,4) 和点B (1,0)都在抛物线22=++上.y mx mx n (1)求m、n;(2)向右平移上述抛物线,记平移后点A的对应点为A′,点B的对应点为B′,若四边形A A′B′B为菱形,求平移后抛物线的表达式;(3)记平移后抛物线的对称轴与直线AB′的交点为C,试在x轴上找一个点D,使得以点B′、C、D为顶点的三角形与△ABC相似.图12012中考数学压轴题函数相似三角形问题(三) 例5 如图1,抛物线经过点A(4,0)、B(1,0)、C(0,-2)三点.(1)求此抛物线的解析式;(2)P是抛物线上的一个动点,过P作PM⊥x轴,垂足为M,是否存在点P,使得以A、P、M为顶点的三角形与△OAC相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;(3)在直线AC上方的抛物线是有一点D,使得△DCA的面积最大,求出点D的坐标.,图1例6 如图1,△ABC 中,AB =5,AC =3,cos A =310.D 为射线BA 上的点(点D 不与点B 重合),作DE //BC 交射线CA 于点E ..(1) 若CE =x ,BD =y ,求y 与x 的函数关系式,并写出函数的定义域; (2) 当分别以线段BD ,CE 为直径的两圆相切时,求DE 的长度;(3) 当点D 在AB 边上时,BC 边上是否存在点F ,使△ABC 与△DEF 相似?若存在,请求出线段BF 的长;若不存在,请说明理由.图1 备用图 备用图例 7 如图1,在直角坐标系xOy 中,设点A (0,t ),点Q (t ,b ).平移二次函数2tx y -=的图象,得到的抛物线F 满足两个条件:①顶点为Q ;②与x 轴相交于B 、C 两点(∣OB ∣<∣OC ∣),连结A ,B .(1)是否存在这样的抛物线F ,使得OC OB OA ⋅=2?请你作出判断,并说明理由;(2)如果AQ ∥BC ,且tan ∠ABO =23,求抛物线F 对应的二次函数的解析式.图12012中考数学压轴题函数等腰三角形问题(一)例1 如图1,已知正方形OABC 的边长为2,顶点A 、C 分别在x 、y 轴的正半轴上,M 是BC 的中点.P (0,m )是线段OC 上一动点(C 点除外),直线PM 交AB 的延长线于点D .(1)求点D 的坐标(用含m 的代数式表示); (2)当△APD 是等腰三角形时,求m 的值;(3)设过P 、M 、B 三点的抛物线与x 轴正半轴交于点E ,过点O 作直线ME 的垂线,垂足为H (如图2).当点P 从O 向C 运动时,点H 也随之运动.请直接写出点H 所经过的路长(不必写解答过程).图1 图2例2 如图1,已知一次函数y =-x +7与正比例函数43y x 的图象交于点A ,且与x 轴交于点B .(1)求点A 和点B 的坐标;(2)过点A作AC⊥y轴于点C,过点B作直线l//y轴.动点P从点O出发,以每秒1个单位长的速度,沿O—C—A的路线向点A运动;同时直线l从点B出发,以相同速度向左平移,在平移过程中,直线l交x轴于点R,交线段BA或线段AO于点Q.当点P到达点A时,点P和直线l都停止运动.在运动过程中,设动点P运动的时间为t秒.①当t为何值时,以A、P、R为顶点的三角形的面积为8?②是否存在以A、P、Q为顶点的三角形是等腰三角形?若存在,求t的值;若不存在,请说明理由.图12012中考数学压轴题函数等腰三角形问题(二)例3 如图1,在直角坐标平面内有点A(6, 0),B(0, 8),C(-4, 0),点M、N 分别为线段AC和射线AB上的动点,点M以2个单位长度/秒的速度自C向A方向作匀速运动,点N以5个单位长度/秒的速度自A向B方向作匀速运动,MN交OB于点P.(1)求证:MN∶NP为定值;(2)若△BNP与△MNA相似,求CM的长;(3)若△BNP是等腰三角形,求CM的长.图1例4 如图1,在矩形ABCD 中,AB =m (m 是大于0的常数),BC =8,E 为线段BC 上的动点(不与B 、C 重合).连结DE ,作EF ⊥DE ,EF 与射线BA 交于点F ,设CE =x ,BF =y .(1)求y 关于x 的函数关系式;(2)若m =8,求x 为何值时,y 的值最大,最大值是多少? (3)若12y m,要使△DEF 为等腰三角形,m 的值应为多少?图12012中考数学压轴题函数相似三角形问题(三)例5 已知:如图1,在平面直角坐标系xOy 中,矩形OABC 的边OA 在y 轴的正半轴上,OC 在x 轴的正半轴上,OA =2,OC =3,过原点O 作∠AOC 的平分线交AB 于点D ,连接DC ,过点D 作DE ⊥DC ,交OA 于点E .(1)求过点E 、D 、C 的抛物线的解析式;(2)将∠EDC 绕点D 按顺时针方向旋转后,角的一边与y 轴的正半轴交于点F ,另一边与线段OC 交于点G .如果DF 与(1)中的抛物线交于另一点M ,点M 的横坐标为56,那么EF =2GO 是否成立?若成立,请给予证明;若不成立,请说明理由; (3)对于(2)中的点G ,在位于第一象限内的该抛物线上是否存在点Q ,使得直线GQ 与AB 的交点P 与点C 、G 构成的△PCG 是等腰三角形?若存在,请求出点Q 的坐标;若不存在成立,请说明理由.图1例6 在平面直角坐标系内,O为原点,点A的坐标为(1,0),点C的坐标为(0,4),直线CM//x轴(如图1所示).点B与点A关于原点对称,直线y=x+b(b为常数)经过点B,且与直线CM相交于点D,联结OD.(1)求b的值和点D的坐标;(2)设点P在x轴的正半轴上,若△POD是等腰三角形,求点P的坐标;(3)在(2)的条件下,如果以PD为半径的圆与圆O外切,求圆O的半径.图12012中考数学压轴题函数直角三角形问题(一)例1 如图1,已知抛物线y=x2+bx+c与x轴交于A、B两点(点A在点B 左侧),与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.(1)求抛物线的函数表达式;(2)求直线BC的函数表达式;(3)点E为y轴上一动点,CE的垂直平分线交CE于点F,交抛物线于P、Q两点,且点P在第三象限.①当线段34PQ AB =时,求tan ∠CED 的值;②当以C 、D 、E 为顶点的三角形是直角三角形时,请直接写出点P 的坐标. 温馨提示:考生可以根据第(3)问的题意,在图中补出图形,以便作答.图1例2 设直线l 1:y =k 1x +b 1与l 2:y =k 2x +b 2,若l 1⊥l 2,垂足为H ,则称直线l 1与l 2是点H 的直角线.(1)已知直线①122y x =-+;②2y x =+;③22y x =+;④24y x =+和点C (0,2),则直线_______和_______是点C 的直角线(填序号即可);(2)如图,在平面直角坐标系中,直角梯形OABC 的顶点A (3,0)、B (2,7)、C (0,7),P 为线段OC 上一点,设过B 、P 两点的直线为l 1,过A 、P 两点的直线为l 2,若l 1与l 2是点P 的直角线,求直线l 1与l 2的解析式.图12012中考数学压轴题函数直角三角形问题(三)例 5 如图1,直线434+-=x y 和x 轴、y 轴的交点分别为B 、C ,点A 的坐标是(-2,0).(1)试说明△ABC 是等腰三角形;(2)动点M 从A 出发沿x 轴向点B 运动,同时动点N 从点B 出发沿线段BC 向点C 运动,运动的速度均为每秒1个单位长度.当其中一个动点到达终点时,他们都停止运动.设M 运动t 秒时,△MON 的面积为S .① 求S 与t 的函数关系式;② 设点M 在线段OB 上运动时,是否存在S =4的情形?若存在,求出对应的t 值;若不存在请说明理由;③在运动过程中,当△MON 为直角三角形时,求t 的值.图1例6 已知Rt △ABC 中,︒=∠90ACB ,CB CA =,有一个圆心角为︒45,半径的长等于CA 的扇形CEF 绕点C 旋转,且直线CE ,CF 分别与直线AB 交于点M ,N .(1)当扇形CEF 绕点C 在ACB ∠的内部旋转时,如图1,求证:222BN AM MN +=;思路点拨:考虑222BN AM MN +=符合勾股定理的形式,需转化为在直角三角形中解决.可将△ACM 沿直线CE 对折,得△DCM ,连DN ,只需证BN DN =,︒=∠90MDN 就可以了.请你完成证明过程.(2)当扇形CEF 绕点C 旋转至图2的位置时,关系式222BN AM MN +=是否仍然成立?若成立,请证明;若不成立,请说明理由.图1 图2图5 图6 图72012中考数学压轴题函数平行四边形问题(一)例 1 已知平面直角坐标系xOy (如图1),一次函数334y x =+的图像与y 轴交于点A ,点M 在正比例函数32y x =的图像上,且MO =MA .二次函数y =x 2+bx +c 的图像经过点A 、M .(1)求线段AM 的长;(2)求这个二次函数的解析式;(3)如果点B 在y 轴上,且位于点A 下方,点C 在上述二次函数的图像上,点D 在一次函数334y x =+的图像上,且四边形ABCD 是菱形,求点C 的坐标.图1例2将抛物线c 1:2y =x 轴翻折,得到抛物线c 2,如图1所示.(1)请直接写出抛物线c 2的表达式;(2)现将抛物线c1向左平移m个单位长度,平移后得到新抛物线的顶点为M,与x轴的交点从左到右依次为A、B;将抛物线c2向右也平移m个单位长度,平移后得到新抛物线的顶点为N,与x轴的交点从左到右依次为D、E.①当B、D是线段AE的三等分点时,求m的值;②在平移过程中,是否存在以点A、N、E、M为顶点的四边形是矩形的情形?若存在,请求出此时m的值;若不存在,请说明理由.图12012中考数学压轴题函数平行四边形问题(二)例3 如图1,在平面直角坐标系中,已知抛物线经过A(-4,0)、B(0,-4)、C(2,0)三点.(1)求抛物线的解析式;(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△MAB的面积为S,求S关于m的函数关系式,并求出S的最大值;(3)若点P是抛物线上的动点,点Q是直线y=-x上的动点,判断有几个位置能使以点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.图1 图2例4在直角梯形OABC中,CB//OA,∠COA=90°,CB=3,OA=6,BA=别以OA、OC边所在直线为x轴、y轴建立如图1所示的平面直角坐标系.(1)求点B的坐标;(2)已知D、E分别为线段OC、OB上的点,OD=5,OE=2EB,直线DE交x轴于点F.求直线DE的解析式;(3)点M是(2)中直线DE上的一个动点,在x轴上方的平面内是否存在另一点N,使以O、D、M、N为顶点的四边形是菱形?若存在,请求出点N的坐标;若不存在,请说明理由.图1 图22012中考数学压轴题函数平行四边形问题(三)例 5 如图1,等边△ABC的边长为4,E是边BC上的动点,EH⊥AC于H,过E作EF∥AC,交线段AB于点F,在线段AC上取点P,使PE=EB.设EC=x(0<x≤2).(1)请直接写出图中与线段EF相等的两条线段(不再另外添加辅助线);(2)Q是线段AC上的动点,当四边形EFPQ是平行四边形时,求平行四边形EFPQ 的面积(用含x的代数式表示);(3)当(2)中的平行四边形EFPQ面积最大值时,以E为圆心,r为半径作圆,根据⊙E与此时平行四边形EFPQ四条边交点的总个数,求相应的r的取值范围.图1例6 如图1,抛物线322++-=x x y 与x 轴相交于A 、B 两点(点A 在点B 的左侧),与y 轴相交于点C ,顶点为D .(1)直接写出A 、B 、C 三点的坐标和抛物线的对称轴;(2)连结BC ,与抛物线的对称轴交于点E ,点P 为线段BC 上的一个动点,过点P 作PF //DE 交抛物线于点F ,设点P 的横坐标为m .①用含m 的代数式表示线段PF 的长,并求出当m 为何值时,四边形PEDF 为平行四边形?②设△BCF 的面积为S ,求S 与m 的函数关系.图1例 7 如图,在平面直角坐标系xOy 中,直线1y x =+与334y x =-+交于点A ,分别交x 轴于点B 和点C ,点D 是直线AC 上的一个动点.(1)求点A 、B 、C 的坐标.(2)当△CBD 为等腰三角形时,求点D 的坐标.(3)在直线AB上是否存在点E,使得以点E、D、O、A为顶点的四边形是平行四边形?如果存在,直接写出BECD的值;如果不存在,请说明理由.图12012中考数学压轴题函数梯形问题(一)例1 已知平面直角坐标系xOy中,抛物线y=ax2-(a+1)x与直线y=kx的一个公共点为A(4,8).(1)求此抛物线和直线的解析式;(2)若点P在线段OA上,过点P作y轴的平行线交(1)中抛物线于点Q,求线段PQ长度的最大值;(3)记(1)中抛物线的顶点为M,点N在此抛物线上,若四边形AOMN恰好是梯形,求点N的坐标及梯形AOMN的面积.备用图图1 图2例 2 已知二次函数的图象经过A (2,0)、C (0,12) 两点,且对称轴为直线x =4,设顶点为点P ,与x 轴的另一交点为点B .(1)求二次函数的解析式及顶点P 的坐标;(2)如图1,在直线 y =2x 上是否存在点D ,使四边形OPBD 为等腰梯形?若存在,求出点D 的坐标;若不存在,请说明理由;(3)如图2,点M 是线段OP 上的一个动点(O 、P 两点除外),以每秒2个单位长度的速度由点P 向点O 运动,过点M 作直线MN //x 轴,交PB 于点N . 将△PMN 沿直线MN 对折,得到△P 1MN . 在动点M 的运动过程中,设△P 1MN 与梯形OMNB 的重叠部分的面积为S ,运动时间为t 秒,求S 关于t 的函数关系式.图1 图22012中考数学压轴题函数梯形问题(二)例3 如图1,在平面直角坐标系xOy 中,抛物线的解析式是y =2114x ,点C 的坐标为(–4,0),平行四边形OABC 的顶点A ,B 在抛物线上,AB 与y 轴交于点M ,已知点Q (x ,y )在抛物线上,点P (t ,0)在x 轴上.(1) 写出点M 的坐标;(2) 当四边形CMQP 是以MQ ,PC 为腰的梯形时.① 求t 关于x 的函数解析式和自变量x 的取值范围;② 当梯形CMQP 的两底的长度之比为1∶2时,求t 的值.图1例 4 已知,矩形OABC 在平面直角坐标系中位置如图1所示,点A 的坐标为(4,0),点C 的坐标为)20(-,,直线x y 32-=与边BC 相交于点D . (1)求点D 的坐标;(2)抛物线c bx ax y ++=2经过点A 、D 、O ,求此抛物线的表达式;(3)在这个抛物线上是否存在点M ,使O 、D 、A 、M 为顶点的四边形是梯形?若存在,请求出所有符合条件的点M 的坐标;若不存在,请说明理由.图12012中考数学压轴题函数平行四边形问题(三)例 5 如图1,等边△ABC 的边长为4,E 是边BC 上的动点,EH ⊥AC 于H ,过E 作EF ∥AC ,交线段AB 于点F ,在线段AC 上取点P ,使PE =EB .设EC =x (0<x ≤2).(1)请直接写出图中与线段EF 相等的两条线段(不再另外添加辅助线);(2)Q 是线段AC 上的动点,当四边形EFPQ 是平行四边形时,求平行四边形EFPQ 的面积(用含x 的代数式表示);(3)当(2)中 的平行四边形EFPQ 面积最大值时,以E 为圆心,r 为半径作圆,根据⊙E 与此时平行四边形EFPQ 四条边交点的总个数,求相应的r 的取值范围.图1例6 如图1,抛物线322++-=x x y 与x 轴相交于A 、B 两点(点A 在点B 的左侧),与y 轴相交于点C ,顶点为D .(1)直接写出A 、B 、C 三点的坐标和抛物线的对称轴;(2)连结BC ,与抛物线的对称轴交于点E ,点P 为线段BC 上的一个动点,过点P 作PF //DE 交抛物线于点F ,设点P 的横坐标为m .①用含m 的代数式表示线段PF 的长,并求出当m 为何值时,四边形PEDF 为平行四边形?②设△BCF 的面积为S ,求S 与m 的函数关系.图1例 7 如图,在平面直角坐标系xOy 中,直线1y x =+与334y x =-+交于点A ,分别交x 轴于点B 和点C ,点D 是直线AC 上的一个动点.(1)求点A 、B 、C 的坐标.(2)当△CBD 为等腰三角形时,求点D 的坐标.(3)在直线AB 上是否存在点E ,使得以点E 、D 、O 、A 为顶点的四边形是平行四边形?如果存在,直接写出BE CD的值;如果不存在,请说明理由.图12012中考数学压轴题函数面积问题(一)例 1 如图1,直线l 经过点A (1,0),且与双曲线m y x=(x >0)交于点B (2,1).过点(,1)P p p -(p >1)作x 轴的平行线分别交曲线m y x =(x >0)和m y x=-(x <0)于M 、N 两点.(1)求m 的值及直线l 的解析式;(2)若点P 在直线y =2上,求证:△PMB ∽△PNA ;(3)是否存在实数p ,使得S △AMN =4S △AMP ?若存在,请求出所有满足条件的p 的值;若不存在,请说明理由.图1例2 如图1,在平面直角坐标系xOy 中,直角梯形OABC 的顶点O 为坐标原点,顶点A 、C 分别在x 轴、y 轴的正半轴上,CB ∥OA ,OC =4,BC =3,OA =5,点D 在边OC 上,CD =3,过点D 作DB 的垂线DE ,交x 轴于点E .(1)求点E的坐标;(2)二次函数y=-x2+bx+c的图像经过点B和点E.①求二次函数的解析式和它的对称轴;②如果点M在它的对称轴上且位于x轴上方,满足S△CEM=2S△ABM,求点M的坐标.图12012中考数学压轴题函数面积问题(二)例3 如图1,四边形OABC是矩形,点A、C的坐标分别为(3,0),(0,1).点D是线段BC上的动点(与端点B、C不重合),过点D作直线12y x b=-+交折线OAB于点E.(1)记△ODE的面积为S,求S与b的函数关系式;(2)当点E在线段OA上时,若矩形OABC关于直线DE的对称图形为四边形O1A1B1C1,试探究四边形O1A1B1C1与矩形OABC的重叠部分的面积是否发生变化?若不变,求出重叠部分的面积;若改变,请说明理由.例 4 如图1,在△ABC中,∠C=90°,A C=3,BC=4,CD是斜边AB上的高,点E在斜边AB上,过点E作直线与△ABC的直角边相交于点F,设AE=x,△AEF的面积为y.(1)求线段AD的长;(2)若EF⊥AB,当点E在斜边AB上移动时,①求y与x的函数关系式(写出自变量x的取值范围);②当x取何值时,y有最大值?并求出最大值.(3)若点F在直角边AC上(点F与A、C不重合),点E在斜边AB上移动,试问,是否存在直线EF将△ABC的周长和面积同时平分?若存在直线EF,求出x的值;若不存在直线EF,请说明理由.图1 备用图2012中考数学压轴题函数面积问题(三)例5 如图1,正方形ABCD中,点A、B的坐标分别为(0,10),(8,4),点C在第一象限.动点P在正方形ABCD的边上,从点A出发沿A→B→C→D匀速运动,同时动点Q以相同速度在x轴上运动,当P点到D点时,两点同时停止运动,设运动的时间为t秒.(1)当P点在边AB上运动时,点Q的横坐标x(长度单位)关于运动时间t(秒)的函数图象如图2所示,请写出点Q开始运动时的坐标及点P运动速度;(2)求正方形边长及顶点C的坐标;(3)在(1)中当t为何值时,△OPQ的面积最大,并求此时P点的坐标.(4)如果点P、Q保持原速度速度不变,当点P沿A→B→C→D匀速运动时,OP 与PQ能否相等,若能,写出所有符合条件的t的值;若不能,请说明理由.图1 图2例6 在直角坐标系中,抛物线c=2经过点(0,10)和点(4,2).+y+xbx(1)求这条抛物线的解析式.(2)如图1,在边长一定的矩形ABCD中,CD=1,点C在y轴右侧沿抛物线=2滑动,在滑动过程中CD∥x轴,AB在CD的下方.当点D在y轴上时,y++cbxxAB落在x轴上.①求边BC的长.②当矩形ABCD在滑动过程中被x轴分成两部分的面积比为1:4时,求点C的坐标.。
2012中考数学压轴题及答案40例(2)

2012中考数学压轴题及答案40例(2)5.如图,在直角坐标系xOy 中,点P 为函数214y x =在第一象限内的图象上的任一点,点A 的坐标为(01),,直线l 过(01)B -,且与x 轴平行,过P 作y 轴的平行线分别交x 轴,l 于C Q ,,连结AQ 交x 轴于H ,直线PH 交y 轴于R .(1)求证:H 点为线段AQ 的中点; (2)求证:①四边形APQR 为平行四边形;②平行四边形APQR 为菱形;(3)除P 点外,直线PH 与抛物线214y x =有无其它公共点?并说明理由. (08江苏镇江28题解析)(1)法一:由题可知1AO CQ ==.90AOH QCH ∠=∠=,AHO QHC ∠=∠,AOH QCH ∴△≌△. ····················································································· (1分)OH CH ∴=,即H 为AQ 的中点. ································································· (2分) 法二:(01)A ,,(01)B -,,OA OB ∴=. ······················································ (1分)又BQ x ∥轴,HA HQ ∴=. ·········································································· (2分) (2)①由(1)可知AH QH =,AHR QHP ∠=∠,AR PQ ∥,RAH PQH ∴∠=∠,RAH PQH ∴△≌△. ····················································································· (3分) AR PQ ∴=,又AR PQ ∥,∴四边形APQR 为平行四边形. ··············································· (4分)②设214P m m ⎛⎫ ⎪⎝⎭,,PQ y ∥轴,则(1)Q m -,,则2114PQ m =+.过P 作PG y ⊥轴,垂足为G ,在Rt APG △中,22222222111111444AP AG PG m m m m PQ ⎛⎫⎛⎫=+=-+=+=+= ⎪ ⎪⎝⎭⎝⎭.∴平行四边形APQR 为菱形. ·········································································· (6分)(3)设直线PR 为y kx b =+,由OH CH =,得22m H ⎛⎫⎪⎝⎭,,214P m m ⎛⎫ ⎪⎝⎭,代入得: 2021.4m k b km b m ⎧+=⎪⎪⎨⎪+=⎪⎩, 221.4m k b m ⎧=⎪⎪∴⎨⎪=-⎪⎩,∴直线PR 为2124m y x m =-. ······················ (7分) 设直线PR 与抛物线的公共点为214x x ⎛⎫ ⎪⎝⎭,,代入直线PR 关系式得:22110424m x x m -+=,21()04x m -=,解得x m =.得公共点为214m m ⎛⎫ ⎪⎝⎭,. 所以直线PH 与抛物线214y x =只有一个公共点P . ········································ (8分) 6.如图13,已知抛物线经过原点O 和x 轴上另一点A ,它的对称轴x =2 与x 轴交于点C ,直线y =-2x -1经过抛物线上一点B (-2,m ),且与y 轴、直线x =2分别交于点D 、E . (1)求m 的值及该抛物线对应的函数关系式; (2)求证:① CB =CE ;② D 是BE 的中点;(3)若P (x ,y )是该抛物线上的一个动点,是否存在这样的点P ,使得PB =PE ,若存在,试求出所有符合条件的点P 的坐标;若不存在,请说明理由.(1)∵ 点B (-2,m )在直线y =-2x -1上,∴ m =-2×(-2)-1=3. ………………………………(2分) ∴ B (-2,3)∵ 抛物线经过原点O 和点A ,对称轴为x =2, ∴ 点A 的坐标为(4,0) .设所求的抛物线对应函数关系式为y =a (x -0)(x -4). ……………………(3分) 将点B (-2,3)代入上式,得3=a (-2-0)(-2-4),∴ 41=a . ∴ 所求的抛物线对应的函数关系式为)4(41-=x x y ,即x x y -=241. (6分)(2)①直线y =-2x -1与y 轴、直线x =2的交点坐标分别为D (0,-1) E (2,-5). 过点B 作BG ∥x 轴,与y 轴交于F 、直线x =2交于G , 则BG ⊥直线x =2,BG =4.在Rt △BGC 中,BC =522=+BG CG .∵ CE =5,∴ CB =CE =5. ……………………(9分) ②过点E 作EH ∥x 轴,交y 轴于H , 则点H 的坐标为H (0,-5).又点F 、D 的坐标为F (0,3)、D (0,-1), ∴ FD =DH =4,BF =EH =2,∠BFD =∠EHD =90°.∴ △DFB ≌△DHE (SAS ),∴ BD =DE .即D 是BE 的中点. ………………………………(11分)(3) 存在. ………………………………(12分) 由于PB =PE ,∴ 点P 在直线CD 上,∴ 符合条件的点P 是直线CD 与该抛物线的交点.设直线CD 对应的函数关系式为y =kx +b .将D (0,-1) C (2,0)代入,得⎩⎨⎧=+-=021b k b . 解得 1,21-==b k . A BCODExy x =2 G FH∴ 直线CD 对应的函数关系式为y =21x -1.∵ 动点P 的坐标为(x ,x x -241),∴21x -1=x x -241. ………………………………(13分) 解得 531+=x ,532-=x . ∴ 2511+=y ,2511-=y . ∴ 符合条件的点P 的坐标为(53+,251+)或(53-,251-).…(14分) (注:用其它方法求解参照以上标准给分.)7.如图,在平面直角坐标系中,抛物线y =-32x 2+b x +c 经过A (0,-4)、B (x 1,0)、 C (x 2,0)三点,且x 2-x 1=5. (1)求b 、c 的值;(4分)(2)在抛物线上求一点D ,使得四边形BDCE 是以BC 为对 角线的菱形;(3分)(3)在抛物线上是否存在一点P ,使得四边形B P O H 是以OB 为对角线的菱形?若存在,求出点P 的坐标,并判断这个菱形是否为正方形?若不存在,请说明理由.(3分)解: (解析)解:(1)解法一: ∵抛物线y =-32x 2+b x +c 经过点A (0,-4),∴c =-4 ……1分又由题意可知,x 1、x 2是方程-32x 2+b x +c =0的两个根, ∴x 1+x 2=23b , x 1x 2=-23c =6 ······························································· 2分 由已知得(x 2-x 1)2=25 又(x 2-x 1)2=(x 2+x 1)2-4x 1x 2=49b 2-24 ∴49b 2-24=25 解得b =±314 ····································································································· 3分 当b =314时,抛物线与x 轴的交点在x 轴的正半轴上,不合题意,舍去. ∴b =-314. ···································································································· 4分解法二:∵x 1、x 2是方程-32x 2+b x +c=0的两个根, 即方程2x 2-3b x +12=0的两个根. ∴x =4969b 32-±b , ······································································· 2分∴x 2-x 1=2969b 2-=5,解得 b =±314 ·························································································· 3分 (以下与解法一相同.)(2)∵四边形BDCE 是以BC 为对角线的菱形,根据菱形的性质,点D 必在抛物线的对称轴上, ························································································· 5分 又∵y =-32x 2-314x -4=-32(x +27)2+625····························· 6分∴抛物线的顶点(-27,625)即为所求的点D . ································· 7分 (3)∵四边形BPOH 是以OB 为对角线的菱形,点B 的坐标为(-6,0),根据菱形的性质,点P 必是直线x =-3与 抛物线y =-32x 2-314x -4的交点, ······················································· 8分∴当x =-3时,y =-32×(-3)2-314×(-3)-4=4, ∴在抛物线上存在一点P (-3,4),使得四边形BPOH 为菱形. ·········· 9分 四边形BPOH 不能成为正方形,因为如果四边形BPOH 为正方形,点P 的坐标只能是(-3,3),但这一点不在抛物线上. ········································· 10分8.已知:如图14,抛物线2334y x =-+与x 轴交于点A ,点B ,与直线34y x b =-+相交于点B ,点C ,直线34y x b =-+与y 轴交于点E . (1)写出直线BC 的解析式. (2)求ABC △的面积.(3)若点M 在线段AB 上以每秒1个单位长度的速度从A 向B 运动(不与A B ,重合),同时,点N 在射线BC 上以每秒2个单位长度的速度从B 向C 运动.设运动时间为t 秒,请写出MNB △的面积S 与t 的函数关系式,并求出点M 运动多少时间时,MNB △的面积最大,最大面积是多少?(解析)解:(1)在2334y x =-+中,令0y = 23304x ∴-+=12x ∴=,22x =-(20)A ∴-,,(20)B ,············································· 1分又点B 在34y x b =-+上 302b ∴=-+32b =BC ∴的解析式为3342y x =-+ ·········································································· 2分 (2)由23343342y x y x ⎧=-+⎪⎪⎨⎪=-+⎪⎩,得11194x y =-⎧⎪⎨=⎪⎩ 2220x y =⎧⎨=⎩················································· 4分 914C ⎛⎫∴- ⎪⎝⎭,,(20)B ,4AB ∴=,94CD =·························································································· 5分 1994242ABC S ∴=⨯⨯=△ ····················································································· 6分 (3)过点N 作NP MB ⊥于点PEO MB ⊥ NP EO ∴∥BNP BEO ∴△∽△ ··························································································· 7分 BN NP BE EO∴=····································································································· 8分 由直线3342y x =-+可得:302E ⎛⎫ ⎪⎝⎭, ∴在BEO △中,2BO =,32EO =,则52BE = 25322t NP∴=,65NP t ∴= ··················································································· 9分 16(4)25S t t ∴=- 2312(04)55S t t t =-+<< ················································································ 10分2312(2)55S t =--+ ························································································· 11分 此抛物线开口向下,∴当2t =时,125S =最大 ∴当点M 运动2秒时,MNB △的面积达到最大,最大为125. ······················ 12分。
2012中考数学压轴题及答案40例

2012中考数学压轴题及答案40例(1)1.如图:抛物线经过A (-3,0)、B (0,4)、C (4,0)三点. (1) 求抛物线的解析式.(2)已知AD = AB (D 在线段AC 上),有一动点P 从点A 沿线段AC 以每秒1个单位长度的速度移动;同时另一个动点Q 以某一速度从点B 沿线段BC 移动,经过t 秒的移动,线段PQ 被BD 垂直平分,求t 的值;(3)在(2)的情况下,抛物线的对称轴上是否存在一点M ,使MQ+MC 的值最小?若存在,请求出点M 的坐标;若不存在,请说明理由。
(注:抛物线2y ax bx c =++的对称轴为2b x a=-)解:设抛物线的解析式为2(0)y ax bx c a =++≠,依题意得:c=4且934016440a b a b -+=⎧⎨++=⎩ 解得1313a b ⎧=-⎪⎪⎨⎪=⎪⎩所以 所求的抛物线的解析式为211433y x x =-++(2)连接DQ ,在Rt △AOB 中,2222345AB AO BO=+=+=所以AD=AB= 5,AC=AD+CD=3 + 4 = 7,CD = AC - AD = 7 – 5 = 2 因为BD 垂直平分PQ ,所以PD=QD ,PQ ⊥BD ,所以∠PDB=∠QDB 因为AD=AB ,所以∠ABD=∠ADB ,∠ABD=∠QDB ,所以DQ ∥AB 所以∠CQD=∠CBA 。
∠CDQ=∠CAB ,所以△CDQ ∽ △CABD Q C D A BC A= 即210,577D Q D Q ==所以AP=AD – DP = AD – DQ=5 –107=257,2525177t =÷=所以t 的值是257(3)答对称轴上存在一点M ,使MQ+MC 的值最小 理由:因为抛物线的对称轴为122b x a =-=所以A (- 3,0),C (4,0)两点关于直线12x =对称连接AQ 交直线12x =于点M ,则MQ+MC 的值最小过点Q 作QE ⊥x轴,于E ,所以∠QED=∠BOA=90 DQ ∥AB ,∠ BAO=∠QDE , △DQE ∽△ABOQ E D QD E B OA BA O== 即107453Q E D E ==所以QE=87,DE=67,所以OE =OD + DE=2+67=207,所以Q (207,87)设直线AQ 的解析式为(0)y kx m k =+≠则2087730k m k m ⎧+=⎪⎨⎪-+=⎩由此得8412441k m ⎧=⎪⎪⎨⎪=⎪⎩ 所以直线AQ 的解析式为8244141y x =+ 联立128244141x y x ⎧=⎪⎪⎨⎪=+⎪⎩ 由此得128244141x y x ⎧=⎪⎪⎨⎪=+⎪⎩ 所以M 128(,)241则:在对称轴上存在点M 128(,)241,使MQ+MC的值最小。
2012年中考数学最后一题--压轴题
中正教育中考研究组奉献
临沂 2006--2012 年中考数学 (几何 )高频考点透 年中考数学( 几何)
二次函数压轴题透析
内容子维度
抛物线解析式 与平行四边形 (平行四边形、矩形、 菱形、正方形)结合 与等腰梯形挂钩、 等腰三角形挂钩、 与等边三角形结合 与直角梯形结合
O B1
−2
4A
x
C (2008 年临沂中考真题) 26. (本小题满分 13 分) (第 26 题图) 如图,已知抛物线与 x 轴交于 A(-1,0) 、B(3,0)两点,与 y 轴交于点 C(0,3) 。 ⑴求抛物线的解析式; ⑵设抛物线的顶点为 D,在其对称轴的右侧的抛物线上是否存在点 P,使得△PDC 是等腰三角形?若存在,求出 符合条件的点 P 的坐标;若不存在,请说明理由; y ⑶若点 M 是抛物线上一点, D 以 B、C、D、M 为顶点的四边形是直角梯形,试求出点 M 的坐标。
了解
√
理解
√
掌握
√
能 力 维 度 真题对照 灵活运用 灵活运用真题对照
2011 年第(1)题、2010 年第(1)题、 2009 年第(1)题、2008 年第(1)题、 2007 年第(1)题、2005 年第(1)题、 2011 年第(2)题 2007 年第(2)题 2010 年第(2)题 2008 年第(2)题 2010 年第(3)题 2008 年第(3)题 2011 年第(3)题 2009 年第(2)题 2007 年第(3)题 2005 年第(3)题 2009 年第(3)题 2010 年第(1)题 2005 年第(2oring Service Inc.
2012中考数学压轴题及答案40例(7)

∴yB=a()2= 5分 设抛物线F2的对称轴与x轴交于点P,如图1. ∵a>0,∴BP=. ∵顶点N(,-),∴NP=|-|=. ∴BP=NP. 6分 ∵抛物线是轴对称图形,∴OP=AP. ∴四边形ABMN是平行四边形. 7分 ∵BN是抛物线F2的对称轴,∴BN⊥OA. ∴四边形ABMN是菱形. 8分 ∵BN=BP+NP,∴BN=. ∵四边形ABMN的面积为×OA·BN=×|m|× ∴当m>0时,四边形ABMN的面积为×m×=. 9分 当m<0时,四边形ABMN的面积为×(-m)×=-. 10 分 (3)点C的坐标为(0,+c)(参考图2).
=(yD-yP)(xB-xA) =[(x+)-(x 2+x)](1+2) =-x 2-x+ =-(x+)2+ ∴当x=-时,△PAB的面积有最大值,最大值为. 8分 此时yP=×(-)2+×(-)=-. ∴此时P点的坐标为(-,-). 9分
∴直线ON的解析式为y=-x.
由x=-x 2+x,得x1=0,x2=6. ∴N(6,-3). 过点N作NC⊥x轴于C. 在Rt△BCN中,BC=6-4=2,NC=3 ∴NB==. ∵OB=4,∴NB≠OB,∴∠BON≠∠BNO,∴△OBN与 △OAB不相似. 同理,在对称轴左边的抛物线上也不存在符合条件的 点. ∴在x轴下方的抛物线上不存在点N,使△OBN与△OAB相 似. 10分 31.如图,在直角坐标系中,点A的坐标为(-2,0),连结OA,将线段 OA绕原点O顺时针旋转120°,得到线段OB. (1)求点B的坐标; (2)求经过A、O、B三点的抛物线的解析式; (3)在(2)中抛物线的对称轴上是否存在点C,使△BOC的周长 最小?若存在,求出点C的坐标;若不存在,请说明理由. (4)如果点P是(2)中的抛物线上的动点,且在x轴的下方,那么
2012中考数学压轴题精选精析(31-40例)

设N点的横坐标为t,此时点N(t, t2﹣ t+4)(0<t<5),
过点N作NG∥y轴交AC于G;由点A(0,4)和点C(5,0)可求出直线AC的解析式为:y=﹣ x+4;
把x=t代入得:y=﹣ x+4,则G(t,﹣ t+4),
此时:NG=﹣ x+4﹣( t2﹣ t+4)=﹣ t2+ t,
∴四条边的长只能是3、4、5、6的一种情况,
在Rt△AOM中,AM= = =5,
∵抛物线对称轴过点M,
∴在抛物线x>5的图象上有关于点A的对称点与M的距离为5,
即PM=5,此时点P横坐标为6,即AP=6;
故以A、O、M、P为顶点的四边形的四条边长度分别是四个连续的正整数3、4、5、6成立,
即P(6,4);
∴抛物线的解析式为:y=x2+3x;(4分)
(2)∵AC∥x轴,∴点C的纵坐标y=4,
代入y=x2+3x,得方程x2+3x﹣4=0,解得x1=﹣4,x2=1(舍去).
∴C点的坐标为(﹣4,4),且AC=5,(6分)
又△ABC的高为6,∴△ABC的面积= ×5×6=15;(7分)
(3)存在D点使△ABD的面积等于△ABC的面积.
过点C作CD∥AB交抛物线于另一点D.
因为直线AB相应的一次函数是:y=2x+2,且C点的坐标为(﹣4,4),CD∥AB,
所以直线CD相应的一次函数是:y=2x+12.(9分)
解方程组 得 所以点D的坐标是(3,18)(10分)
点评:本题是二次函数的综合题型,其中涉及的到大知识点根据点的坐标求抛物线解析式和双曲线解析式以及三角形的面积求法.关键在于根据点的坐标和相关的知识点求抛物线解析式,曲线解析式和直线解析式
2012中考数学压轴题精选精析(21-30例)

2012中考数学压轴题精选精析(21-30例)21.(2011•湖南邵阳)如图(十一)所示,在平面直角坐标系Oxy 中,已知点A (-94,0),点C (0,3),点B 是x 轴上一点(位于点A 的右侧),以AB 为直径的圆恰好经过....点C . (1)求∠ACB 的度数;(2)已知抛物线y =ax 2+bx +3经过A 、B 两点,求抛物线的解析式;(3)线段BC 上是否存在点D ,使△BOD 为等腰三角形.若存在,则求出所有符条件的点D 的坐标;若不存在,请说明理由.【解题思路】:(1) ∵以AB 为直径的圆恰好经过....点C ∴∠ACB =090 (2) ∵△AOC ∽△ABC ∴OB AO OC∙=2 ∵A (-94,0),点C (0,3),∴49=AO 3=OC ∴OB 4932=∴ 4=OB ∴B(4,0) 把 A 、B 、C 三点坐标代入得 3127312++-=x x y(3)1)OD=OB , D 在OB 的中垂线上,过D 作DH ⊥OB,垂足是H 则H 是OB 中点。
DH=OC 21 OB OH 21 ∴D )23,2(2) BD=BO 过D 作DG ⊥OB,垂足是G ∴OG:OB=CD:CB DG:OC=1:5 ∴ OG:4=1:5 DG:3=1:5 ∴OG=54 DG=53 ∴D(54,53)【点评】:本题考察了相似、勾股定理、抛物线的解析式求解等知识,运用平行于三角形一边的直线截其他两边所得的三角形与原三角形相似构建比例式,求解点到坐标轴的距离,进而得出相应的坐标。
难度中等 24、(2011•湖北荆州)如图甲,分别以两个彼此相邻的正方形OABC 与CDEF 的边OC 、OA 所在直线为x 轴、y 轴建立平面直角坐标系(O 、C 、F 三点在x 轴正半轴上).若⊙P 过A 、B 、E 三点(圆心在x 轴上),抛物线y= 14x2+bx+c 经过A 、C 两点,与x 轴的另一交点为G ,M 是FG 的中点,正方形CDEF 的面积为1.(1)求B 点坐标;(2)求证:ME 是⊙P 的切线;(3)设直线AC 与抛物线对称轴交于N ,Q 点是此轴称轴上不与N 点重合的一动点, ①求△ACQ 周长的最小值;②若FQ=t,S△ACQ=S,直接写出S与t之间的函数关系式.考点:二次函数综合题.分析:(1)如图甲,连接PE、PB,设PC=n,由正方形CDEF的面积为1,可得CD=CF=1,根据圆和正方形的对称性知:OP=PC=n,由PB=PE,根据勾股定理即可求得n的值,继而求得B的坐标;(2)由(1)知A(0,2),C(2,0),即可求得抛物线的解析式,然后求得FM的长,则可得△PEF∽△EMF,则可证得∠PEM=90°,即ME是⊙P的切线;(3)①如图乙,延长AB交抛物线于A′,连CA′交对称轴x=3于Q,连AQ,则有AQ=A′Q,△ACQ周长的最小值为AC+A′C的长,利用勾股定理即可求得△ACQ周长的最小值;②分别当Q点在F点上方时,当Q点在线段FN上时,当Q点在N点下方时去分析即可求得答案.解答:解:(1)如图甲,连接PE、PB,设PC=n,∵正方形CDEF的面积为1,∴CD=CF=1,根据圆和正方形的对称性知:OP=PC=n,∴BC=2PC=2n,∵而PB=PE,∴PB2=BC2+PC2=4n2+n2=5n2,PE2=PF2+EF2=(n+1)2+1,∴5n2=(n+1)2+1,解得:n=1或n=-12(舍去),∴BC=OC=2,∴B点坐标为(2,2);(2)如图甲,由(1)知A(0,2),C(2,0),∵A,C在抛物线上,\∴ {c=214×4+2b+c=0,解得:{c=2b=-32,∴抛物线的解析式为:y= 14x2-32x+2= 14(x-3)2-14,∴抛物线的对称轴为x=3,即EF所在直线,∵C与G关于直线x=3对称,∴CF=FG=1,∴MF= 12FG= 12,在Rt△PEF与Rt△EMF中,∠EFM=∠EFP,∵ FMEF=121=12,EFPF=12,∴ FMEF=EFPF,∴△PEF∽△EMF,∴∴∠EPF=∠FEM,∴∠PEM=∠PEF+∠FEM=∠PEF+∠EPF=90°,∴ME是⊙P的切线;(3)①如图乙,延长AB交抛物线于A′,连CA′交对称轴x=3于Q,连AQ,则有AQ=A′Q,∴△ACQ周长的最小值为AC+A′C的长,∵A与A′关于直线x=3对称,∴A(0,2),A′(6,2),∴A′C=(6-2)2+22=2 5,而AC=22+22=2 2,∴△ACQ周长的最小值为2 2+2 5;②当Q点在F点上方时,S=t+1,当Q点在线段FN上时,S=1-t,当Q点在N点下方时,S=t-1.点评:此题考查了待定系数法求二次函数的解析式,圆的性质,相似三角形的判定与性质以及勾股定理等知识.此题综合性很强,题目难度较大,解题的关键是方程思想、分类讨论与数形结合思想的应用.22、(2011•襄阳)如图,在平面直角坐标系xoy中,AB在x轴上,AB=10,以AB为直径的⊙O'与y轴正半轴交于点C,连接BC,AC.CD是⊙O'的切线,AD丄CD于点D,tan∠CAD=,抛物线y=ax2+bx+c过A,B,C三点.(1)求证:∠CAD=∠CAB;(2)①求抛物线的解析式;②判断抛物线的顶点E是否在直线CD上,并说明理由;(3)在抛物线上是否存在一点P,使四边形PBCA是直角梯形.若存在,直接写出点P 的坐标(不写求解过程);若不存在,请说明理由.考点:二次函数综合题。
2012年中考数学压轴题精选精析

2012年各地中考数学压轴题精选精析(1.2012黄石) 25.(本小题满分10分)已知抛物线1C 的函数解析式为23(0)y ax bx a b =+-<,若抛物线1C 经过点(0,3)-,方程230ax bx a +-=的两根为1x ,2x ,且124x x -=。
(1)求抛物线1C 的顶点坐标. (2)已知实数0x >,请证明:1x x +≥2,并说明x 为何值时才会有12x x+=. (3)若抛物线先向上平移4个单位,再向左平移1个单位后得到抛物线2C ,设1(,)A m y ,2(,)B n y 是2C 上的两个不同点,且满足:090AOB ∠=,0m >,0n <.请你用含有m 的表达式表示出△AOB 的面积S ,并求出S 的最小值及S 取最小值时一次函数OA 的函数解析式。
(参考公式:在平面直角坐标系中,若11(,)P x y ,22(,)Q x y ,则P ,Q 两点间的距离【考点】二次函数综合题. 【专题】压轴题;配方法.【分析】(1)求抛物线的顶点坐标,需要先求出抛物线的解析式,即确定待定系数a 、b 的值.已知抛物线图象与y 轴交点,可确定解析式中的常数项(由此得到a 的值);然后从方程入手求b 的值,题干给出了两根差的绝对值,将其进行适当变形(转化为两根和、两根积的形式),结合根与系数的关系即可求出b 的值. (2)11x x +=,因此将1x x+配成完全平方式,然后根据平方的非负性即可得证.(3)结合(1)的抛物线的解析式以及函数的平移规律,可得出抛物线C 2的解析式;在Rt △OAB 中,由勾股定理可确定m 、n 的关系式,然后用m 列出△AOB 的面积表达式,结合不等式的相关知识可确定△OAB 的最小面积值以及此时m 的值,进而由待定系数法确定一次函数OA 的解析式.【解答】解:(1)∵抛物线过(0,-3)点,∴-3a =-3∴a =1 ……………………………………1分 ∴y=x 2+bx -3∵x 2+bx -3=0的两根为x 1,x 2且21x -x =4∴21221214)(x x x x x x -+=-=4且b <0∴b =-2 ……………………1分 ∴y=x 2-2x -3=(x -1)2-4∴抛物线C1的顶点坐标为(1,-4) ………………………1分 (2)∵x >0,∴0)1(21≥-=-+xx x x ∴,21≥+x x 显然当x =1时,才有,21=+xx ………………………2分 (3)方法一:由平移知识易得C2的解析式为:y =x 2 ………………………1分∴A(m ,m 2),B (n ,n 2) ∵ΔAOB 为Rt Δ ∴OA 2+OB 2=AB 2∴m 2+m 4+n 2+n 4=(m -n )2+(m 2-n 2)2化简得:m n =-1 ……………………1分 ∵SΔAOB =OB OA ∙21=424221n n m m +∙+ ∵m n =-1∴SΔAOB =22221221221mm n m ++=++ =1221121)1(212=∙≥⎪⎭⎫ ⎝⎛+=+m m m m ∴SΔAOB 的最小值为1,此时m =1,A(1,1) ……………………2分 ∴直线OA 的一次函数解析式为y=x ……………………1分方法二:由题意可求抛物线2C 的解析式为:2y x = ··········································· (1分)∴2(,)A m m ,2(,)B n n过点A 、B 作x 轴的垂线,垂足分别为CAOC BOD ACDB S S S S =-- 梯形2222111()()222m n m n m m n n =+--⋅-⋅ 1()2mn m n =--由BOD △ ∽OAC △得 BD ODOC AC=即22n n m m-= ∴1mn =- ········································································································· (1分)∴1n m =-∴1()2S mn m n =--11()2m m=+由(2)知:12m m+≥∴111()2122S m m =+≥⨯=当且仅当1m =,S 取得最小值1此时A 的坐标为(1,1) ·········································································· (2分) ∴一次函数OA 的解析式为y x = ································································· (1分)【点评】该题考查了二次函数解析式的确定、函数图象的平移、不等式的应用等知识,解题过程中完全平方式的变形被多次提及,应熟练掌握并能灵活应用.(2.2012滨州)24.如图,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(﹣2,﹣4),O(0,0),B(2,0)三点.(1)求抛物线y=ax2+bx+c的解析式;(2)若点M是该抛物线对称轴上的一点,求AM+OM的最小值.考点:二次函数综合题。
2012年中考数学压轴题精选(含答案)

(2012年北京市)24、在△ABC 中,BA =BC ,∠BAC =α,M 是AC 的中点,P 是线段BM 上的动点,将线段PA 绕点P 顺时针旋转2α得到线段PQ 。
(1)若α=60°且点P 与点M 重合(如图1),线段CQ 的延长线交射线BM 于点D ,请补全图形,并写出∠CDB 的度数;(2)在图2中,点P 不与点B 、M 重合,线段CQ 的延长线于射线BM 交于点D ,猜想∠CDB 的大小(用含α的代数式表示),并加以证明;(3)对于适当大小的α,当点P 在线段BM 上运动到某一位置(不与点B 、M 重合)时,能使得线段CQ 的延长线与射线BM 交于点D ,且PQ =DQ ,请直接写出α的范围。
图1QM(P)C B APM图2QCBA(答案)(1)o CDB 30=∠ (2)α-=∠o CDB 90 (3)o o 6045<<α (2012年北京市)25、在平面直角坐标系xOy 中,对于任意两点P 1(x 1,y 1)与P 2(x 2,y 2)的“非常距离”,给出如下定义:若|x 1-x 2|≥|y 1-y 2|,则点P 1与点P 2的“非常距离”为|x 1-x 2|; 若|x 1-x 2|<|y 1-y 2|,则点P 1与点P 2的“非常距离”为|y 1-y 2|。
例如:点P 1(1,2),点P 2(3,5),因为|1-3|<|2-5|,所以点P 1与点P 2的“非常距离”为|2-5|=3,也就是图1中线段P 1Q 与线段P 2Q 长度的较大值(点Q 为垂直于y 轴的直线P 1Q 与垂直于x 轴的直线P 2Q 的交点)。
(1)已知点A(-12,0),B 为y 轴上的一个动点,①若点A 与点B 的“非常距离”为2,写出一个满足条件的点B 的坐标; ②直接写出点A 与点B 的“非常距离”的最小值;(2)已知C 是直/线y =34x +3上的一个动点,①如图2,点D 的坐标是(0,1),求点C 与点D 的“非常距离”的最小值及相应的点C 的坐标;②如图3,E 是以原点O 为圆心,1为半径的圆上的一个动点,求点C 与点E 的“非常距离”的最小值及相应的点E 和点C 的坐标。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
易知点F的坐标为(2,2),故BF=2,作PM⊥BF. ∵△PBF是等腰直角三角形,∴PM=BF=1. ∴点P的坐标为(3,3). ∵抛物线经过原点 ∴可设抛物线的解析式为y=ax 2+bx. 又∵抛物线经过点P(3,3)和点D(2,0) ∴ 解得 ∴过O、P、D三点的抛物线的解析式为y=x 2-2x; 7分 (3)由等腰直角三角形的对称性知D点关于∠AOC的平分线的 对称点即为C点.
②连接EQ.在点P、Q运动的过程中,判断有几个时刻使得△CEQ是 等腰三角形? 请直接写出相应的t值。
【004】如图,已知直线 与直线 相交于点 分别交
轴于
两点.矩形
的顶点
分别在直线
上,顶点
都在
轴上,且点
与点
重合. (1)求 的面积; (2)求矩形 的边 与 的长; (3)若矩形 从原点出发,沿 轴的反方向以每秒1个单位长度的速度平移,
F M P E ∴直线BC的解析式为y=-x+3. 当x=1时,y=-1+3=2,∴E(1,2). 当x=m时,y=-m+3,∴P(m,-m+3). 4分 将x=1代入y=-x 2+2x+3,得y=4,∴D(1,4). 将x=m代入y=-x 2+2x+3,得y=-m 2+2m+3. ∴F(m,-m 2+2m+3). 5分 ∴线段DE=4-2=2,线段PF=-m 2+2m+3-(-m+3)= -m 2+3m 6分 ∵PF∥DE,∴当PF=DE时,四边形PEDF为平行四边形. 由-m 2+3m=2,解得:m1=2,m2=1(不合题意,舍 去). ∴当m=2时,四边形PEDF为平行四边形. 7分 ②设直线PF与x轴交于点M. 由B(3,0),O(0,0),可得:OB=OM+MB=3. 则S=S△BPF +S△CPF 8分 =PF·BM+PF·OM =PF·OB =(-m 2+3m)×3 =-m 2+m(0≤m≤3) 即S与m的函数关系式为:S=-m 2+m(0≤m≤3). 9 分
① 过点E作EF⊥AD于点F,交抛物线于点G.当t为何值时,线段EG 最长?
② 连接EQ,在点P、Q运动的过程中,判断有几个时刻使得△CEQ 是等腰三角形?请直接写出相应的t值. 解:(1)点A的坐标为(4,8). 1分
将A(4,8)、C(8,0)两点坐标分别代入y=ax 2+bx, 得 解得a=-,b=4. ∴抛物线的解析式为y=-x 2+4x. 3分
人教版2012年中考数学压轴题精选
【001】如图,已知抛物线(a≠0)经过点,抛物线的顶点为,过作射 线.过顶点平行于轴的直线交射线于点,在轴正半轴上,连结. (1)求该抛物线的解析式; (2)若动点从点出发,以每秒1个长度单位的速度沿射线运动,设点运 动的时间为.问当为何值时,四边形分别为平行四边形?直角梯形?等 腰梯形? (3)若,动点和动点分别从点和点同时出发,分别以每秒1个长度单位 和2个长度单位的速度沿和运动,当其中一个点停止运动时另一个点也 随之停止运动.设它们的运动的时间为,连接,当为何值时,四边形的 面积最小?并求出最小值及此时的长. x y M C D P Q O A B
设移动时间为 秒,矩形
与
重叠部分的面积为
Байду номын сангаас,求
关
的函数关系式,并写出相应的
的取值范围.
A D B E O C F x y y (G) (第26题)
【005】如图1,在等腰梯形中,,是的中点,过点作交于点.,. (1)求点到的距离; (2)点为线段上的一个动点,过作交于点,过作交折线于点,连结, 设.
A D E B F C P N M (第25题)
【006】如图13,二次函数的图象与x轴交于A、B两点,与y轴交于点 C(0,-1),ΔABC的面积为。 (1)求该二次函数的关系式; (2)过y轴上的一点M(0,m)作y轴的垂线,若该垂线与ΔABC的外接
圆有公共点,求m的取值范围; (3)在该二次函数的图象上是否存在点D,使四边形ABCD为直角梯形?
O C F M D E N K y x (第25题图1) O C D K F E N y x M (第25题图2)
【010】如图,抛物线 与 轴交于 两点,与 轴交于C点,且经过点 ,对称轴是直线 ,顶点是 . (1)求抛物线对应的函数表达式; (2)经过 两点作直线与 轴交于点 ,在抛物线上是否存在这样的点 ,使以点 为顶点的四边形为平行四边形?若存在,请求出点
23.如图,在矩形OABC中,已知A、C两点的坐标分别为A(4,0)、
C(0,2),D为OA的中点.设点P是∠AOC平分线上的一个动点(不与 点O重合). (1)试证明:无论点P运动到何处,PC总与PD相等; (2)当点P运动到与点B的距离最小时,试确定过O、P、D三点的抛物 线的解析式; (3)设点E是(2)中所确定抛物线的顶点,当点P运动到何处时,△PDE
22.如图,抛物线y=-x 2+2x+3与x轴相交于A、B两点(点A在点B的左 侧),与y轴相交于点C,顶点为D. (1)直接写出A、B、C三点的坐标和抛物线的对称轴; (2)连结BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点,
过点P作PF∥DE交抛物线于点F,设点P的横坐标为m. ①用含m的代数式表示线段PF的长,并求出当m为何值时,四边
连接EC,它与∠AOC的平分线的交点即为所求的P点(因 为PE+PD=EC,而两点之间线段最短),此时△PED的周 长最小.
∵抛物线y=x 2-2x的顶点E的坐标(1,-1),C点的坐 标(0,2)
设CE所在直线的解析式为y=kx+b 则 解得
∴CE所在直线的解析式为y=-3x+2. 联立,解得,故点P的坐标为(,). △PED的周长即是CE+DE=; 11分 (4)存在点P,使∠CPN=90°,其坐标为(,)或(2, 2). 14分 24.如图1,已知抛物线经过坐标原点O和x轴上另一点E,顶点M的坐标 为(2,4);矩形ABCD的顶点A与点O重合,AD、AB分别在x轴、y轴 上,且AD=2,AB=3. (1)求该抛物线所对应的函数关系式; (2)将矩形ABCD以每秒1个单位长度的速度从图1所示的位置沿x轴的正 方向匀速平行移动,同时一动点P也以相同的速度从点A出发向B匀 速移动,设它们运动的时间为t秒(0≤t≤3),直线AB与该抛物线 的交点为N(如图2所示). ①当t=时,判断点P是否在直线ME上,并说明理由; ②设以P、N、C、D为顶点的多边形面积为S,试问S是否存在最大 值?若存在,求出这个最大值;若不存在,请说明理由.
解:(1)∵因所求抛物线的顶点M的坐标为(2,4)
∴可设其对应的函数关系式为y=a(x -2)2+4. 1分
又抛物线经过坐标原点O(0,0),∴a(0-2)2+4
=0. 2分
解得a=-1. 3分
∴所求函数关系式为y=-(x -2)2+4,即y=-x 2
的坐标;若不存在,请说明理由; (3)设直线
与y轴的交点是
,在线段
上任取一点
(不与
重合),经过
三点的圆交直线
于点
,试判断
的形状,并说明理由; (4)当
是直线
上任意一点时,(3)中的结论是否成立?(请直接写出结论).
O B x y A M
C 1 (第26题图)
2012中考数学压轴题及答案40例(6)
若存在,求出点D的坐标;若不存在,请说明理由。
【007】如图1,在平面直角坐标系中,点O是坐标原点,四边形ABCO是 菱形,点A的坐标为(-3,4), 点C在x轴的正半轴上,直线AC交y轴于点M,AB边交y轴于点H.
(1)求直线AC的解析式; (2)连接BM,如图2,动点P从点A出发,沿折线ABC方向以2个单位 /秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运 动时间为t秒,求S与t之间的函数关系式(要求写出自变量t的取值范 围);
①当点在线段上时(如图2),的形状是否发生改变?若不变,求出的 周长;若改变,请说明理由; ②当点在线段上时(如图3),是否存在点,使为等腰三角形?若存 在,请求出所有满足要求的的值;若不存在,请说明理由.
A D E B F C 图4(备用) A D E B F C 图5(备用) A D E B F C 图1 图2 A D E B F C P N M 图3
(3)在(2)的条件下,当 t为何值时,∠MPB与∠BCO互为余角,并 求此时直线OP与直线AC所夹锐角的正切值.
【008】
如图所示,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AB=BC,E是AB 的中点,CE⊥BD。
(1) 求证:BE=AD; (2) 求证:AC是线段ED的垂直平分线; (3) △DBC是等腰三角形吗?并说明理由。
【003】如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4, 0)、C(8,0)、D(8,8).抛物线y=ax2+bx过A、C两点.
(1)直接写出点A的坐标,并求出抛物线的解析式; (2)动点P从点A出发.沿线段AB向终点B运动,同时点Q从点C出发,沿 线段CD 向终点D运动.速度均为每秒1个单位长度,运动时间为t秒.过点P 作PE⊥AB交AC于点E,①过点E作EF⊥AD于点F,交抛物线于点G.当t为何 值时,线段EG最长?
21.如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4, 0)、C(8,0)、D(8,8).抛物线y=ax 2+bx过A、C两点.
(1)直接写出点A的坐标,并求出抛物线的解析式; (2)动点P从点A出发,沿线段AB向终点B运动,同时点Q从点C出发,沿
线段CD向终点D运动,速度均为每秒1个单位长度,运动时间为t秒. 过点P作PE⊥AB交AC于点E.
A C B P Q E D
图16 (1)当t = 2时,AP = ,点Q到AC的距离是 ; (2)在点P从C向A运动的过程中,求△APQ的面积S与
t的函数关系式;(不必写出t的取值范围) (3)在点E从B向C运动的过程中,四边形QBED能否成
