(完整版)直流电机的基本方程
直流电机的基本方程式

直流电机的基本方程式一.直流发电机的基本方程式以并励机为例:(一).电压平衡方程直流发电机发出的电势E a产生电流I a,I a在电枢回路总电阻R a(包括电枢绕组电阻及两个电刷的接触电阻)上产生压降I a R a,则输出电压U=E a-I a R a,可见发电机E a>U。
电路如图:(二).转矩平衡方程式直流发电机是把机械能转变为电能,因此由原动机输入的机械转矩T1是驱动转矩;电磁转矩T是制动转矩;即使电机空转也存在的、对应电机机械摩擦、铁损耗等的空载转矩T0一定是阻转矩,当驱动=制动时,电机恒速旋转。
因此发电机稳定运行时的转矩平衡方程为:T1=T+ T0(三)功率平衡方程式其功率流程图如图:从原动机输入机械功率P1,扣除了机械方面的损耗p机,就是机转变为电的部分称为电磁功率P M,再扣除了电方面的损耗p电,就是输出的电功率P2=UI,对并励发电机I=I a-I f。
额定时的P2就是P N=U N I N。
其中:p机是机械方面的损耗,它也是电机空载运行时就存在的损耗,故称空载损耗p,它包括了机械摩擦损耗mp、铁耗Fe p、附加损耗ad p(≈0.01~0.05P N),即:p 机=0p =m p +Fe p +ad p ;p 电是电方面的损耗称为铜耗,它包括了电枢回路铜耗cua p =2a I R a 和励磁回路铜耗cuf p =UI 2fU R =2f I =f R ,即p 电=cua p +cuf p 由功率流程图可列功率平衡方程:机械方面:10M P P p =+;电方面:2M cua P P p =--cuf p ;把机械方面的功率平衡方程两边除以Ω,就得到了转矩平衡方程。
其中:T 1=1P Ω;T 0=0P Ω;T =M PΩ。
可见电磁功率M P =T Ω——这是用机械量表示的电磁功率。
把电压平衡方程U =E a -I a R a 的两边乘以I a :UI a = E a I a -2a I R a ∵I a =I +I f ,则:UI a = U(I+I f )= E a I a -2a I R a , ∴UI= E a I a -2a I R a -UI f =E a I a -cua p -cuf p其中:UI 就是P 2;对比电方面的功率平衡方程可知:E a I a 就是电磁功率P M 。
第四章直流电机电枢绕组

一、节距计算
y1
Z 2p
y= =1yk
y2 y1 y
二、绕组展开图
Z为电枢槽数 P为电机的极对数
三、元件连接顺序及并联支路图
空载时气隙磁磁通密度的分布图形
返回
如果不计铁磁材料中的磁压降,则在气隙中各处所消耗的磁通势均
为励磁磁通势。
在极靴下,气隙小,气隙中沿电枢表面上各点磁密较大;在极靴范
围外,气隙增加很多,磁密显著减小,至两极间的几何中性线处磁密为
零。
为一平顶波
直流电机空载磁场的磁密分布
直流电机的空载磁化特性
0
考虑到电机的运行性能 和经济性,直流电机额定运 行的磁通额定值的大小取在 磁化曲线开始弯曲的地方图 中的a点(称为膝部)。
磁电流作用下建立的,这一点与他励发电机不同。并励发电机建立 电压的过程称为自励过程,满足建压的条件称为自励条件。
1、自励条件
曲线1为空载特性曲线,曲线2为励磁回路总电阻R f 特性曲线, 也称场阻线 U f I f R f 。
增大R f ,场阻线变为曲线3时,R f 称为临界 电阻Rcr 。如图所示。
N pN Ea 2a e 60a n Cen
Ce为电动势常数。上式表明直流电机的感应电动势与电机结构、 气隙磁通和电机转速有关。当电机制造好以后,与电机结构有关的常数
Ce不在变化,因此电枢电动势仅与气隙磁通和转速有关,改变转速 和磁通均可改变电枢电动势的大小。
三,直流电机的电磁转矩 定义:根据电磁力定律,当电枢绕组中有电枢电流
直流电机

Tav = f 2 = Bav l ia N 2
Tav
l Ia N 2 p l 2a 2
pN
2a
Ia
CT Ia
大小:T
pN
2 a
Ia
CT Ia
其中:CT
= pN 2πa
为电机的转矩常数
电磁转矩性质:发电机—制动(与转速方向相反); 电动机—驱动(与转速方向相同)。
pm pFe p统称为空载损耗(不变损耗)。
负载损耗:电枢回路电阻损耗 pa ;I电a2 R刷a 接触压降损耗
pb ( 2负Δ载Us损Ia 耗又称可变损耗) 杂散损耗 p:Δ齿槽引起磁场脉动引起的铁耗,一些机械部件切
割磁通产生的铁耗等 pΔ (0.5 ~ 1)%P2
二、直流发电机的基本方程
Bx
B0 x
Bax
物理中性线偏离几何中性线
2.当电刷不在几何中性线上时
电刷从几何中性线偏
移 角,电枢磁动势
轴线也随之移动角, 如图(a)、(b)所示。
这时电枢磁动势可 以分解为两个垂直 分量:交轴电枢磁 动势 Faq 和直轴电 枢磁动势 Fad 。如 图(a)、(b)所示。
交轴磁势和直轴磁势
P1 PM p0 原动机输入给发电机的机械功率 P1
输入直流发电机后扣除空载损耗,其余为电磁功率 空载损耗p0包括:机械摩擦损耗、铁损耗、附加损耗。
p0 pm pFe p ❖电磁功率是转换成电功率的那部分机械功率
将式 U Ea Ia Ra 两边同乘电枢电流:
UIa Ea Ia Ia2 Ra
A Nia
D 在原点O左右x处取磁力线闭
直流电动机稳态运行时的基本方程式和功率关系
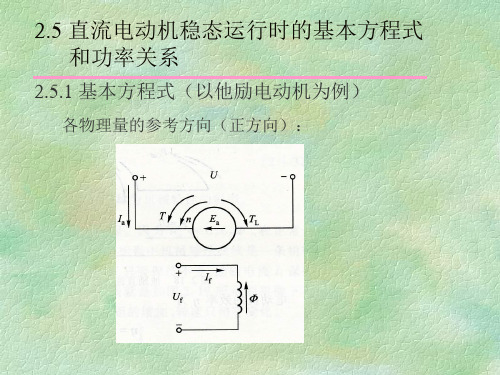
n 0, Ea CeN n 0
UN Ia Ik Ra T CT N I k Tst
⑥ n>n0时为发电机状态,此时 Ea>U, T与n反向,Ia反向, Ea与Ia同向, 向电网送出电 功率。
n
n0 nN
n’0
nN
0
T0
TN
T
2. 人为机械特性分析
根据转速、转矩公式
n U R T 2 Ce CeCT
Ea CE n
T CT I a
可推知:
E a U I a Ra Ra U n T n0 T 2 C e C e C e C e C T
2.6 直流电动机的机械特性
转速与转矩之间的关系n=f(T),直流电动机最重要的特性。
2.6.1 他励直流电动机的机械特性
E a U I a Ra Ra U n T n0 T 2 C e C e C e C e C T
理想空载转速
Ra 2 C e CT
机械特性的斜率
1. 他励直流电动机的固有机械特性
当U=UN,= N,电枢回路无外接电阻时,转速与转 矩之间的关系,称为固有机械特性。
特性的斜率相等,因此各条特性彼此平行。
n
n0
UN U1
固有
U2 UN>U1>U2
0
人为
T
减弱电机主磁通的人为机械特性
保持端电压为额定值不变,电枢回路不串电阻 (Rc=0),只改变励磁电流的机械特性。
表达式:
n n0 N’ N 固有 N> N’ 0 人为
UN Ra n T 2 Ce CeCT n T
UN Ra n T 2 Ce N CeC M N
直流电机的的基本方程式和运行特性
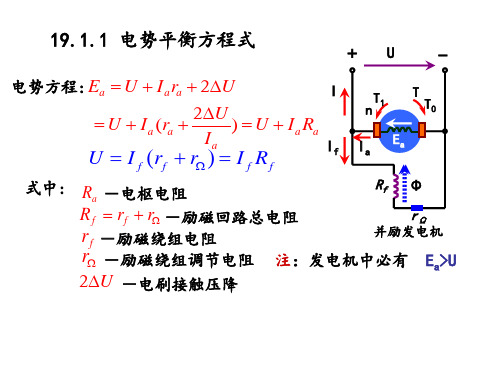
+U -
电势方程: Ea U IaБайду номын сангаасa 2U
I
U
Ia
(ra
2U Ia
)
U
Ia Ra
U I f (rf r ) I f Rf
If
nT1
T T0
Ia Ea
式中: Ra -电枢电阻
Rf Φ
Rf rf r -励磁回路总电阻
rf -励磁绕组电阻
rΩ
并励发电机
r -励磁绕组调节电阻 注:发电机中必有 Ea>U
① 负载特性 n=常数、I=常数时,U=f(If)的关系。其中,当I=0 时的特性U0=f(If)称为发电机的空载特性
② 外特性
n=常数、If=常数(并励时Rf=常数)时,U=f(I) 的关系
③调节特性 n=常数、U=常数时,If=f(I)的关系
19.2.1 它励直流发电机的空载特性 + U
-
定义:n=常数,I=0时,U0=f(If)的关系
P2
其中 p pm pFe pad pCuf pCua
注:额定负载时,直流发电机的效率与容量有关。10kW以下的 小电机,效率为75%~88.5%;10~100kW的电机,效率为85 %~90%;100~1000kW的电机效率为88%~93%
例 一台四极并励直流发电机的额定数据为:PN=6kW, UN=230V,
nN=1450r/min,电枢回路电阻ra=0.92Ω,励磁回路的电阻 Rf=177Ω,2ΔU=2V,损耗pFe+pm=295W。试求额定负载下的 电磁功率、电磁转矩及效率(杂散损耗取输出功率的1%)。
解:额定电流
IN
PN UN
(完整版)无刷直流电机数学模型完整版

电机数学模型以二相导通星形三相六状态为例,分析 BLDC 的数学模型及电磁转矩等特性。
为了便于分析,假定:a) 三相绕组完全对称,气隙磁场为方波,定子电流、转子磁场分布皆对称; b) 忽略齿槽、换相过程和电枢反应等的影响; c) 电枢绕组在定子内表面均匀连续分布;d) 磁路不饱和,不计涡流和磁滞损耗。
则三相绕组的电压平衡方程可表示为:式中:-,「:■「:为定子相绕组电压(V); L L I 为定子相绕组电流(A); -三:为定子相绕组电动势(V); L 为每相绕组的自感(H) ; M 为每相绕组间的 互感(H); p 为微分算子p=d/dt 。
三相绕组为星形连接,且没有中线,则有得到最终电压方程:图•无刷直流电机的等效电路无刷直流电机的电磁转矩方程与普通直流电动机相似, 其电磁转矩大小与磁 通和电流幅值成正比(1)L-M 0 0'r 0d r 0 .5 0 r.L - MT 电=十细⑸所以控制逆变器输出方波电流的幅值即可以控制 BLDC 电机的转矩。
为产 生恒定的电磁转矩,要求定子电流为方波,反电动势为梯形波,且在每半个周期 内,方波电流的持续时间为120°电角度,梯形波反电动势的平顶部分也为120° 电角度,两者应严格同步。
由于在任何时刻,定子只有两相导通,贝U :电磁功率可表示为:二.二 (6)电磁转矩又可表示为:-:二……(7)无刷直流电机的运动方程为:T e -T L -Bto = J^= JPo>其中〔为电磁转矩;幷为负载转矩;B 为阻尼系数;•••为电机机械转速;J 为电机的转动惯量。
传递函数:无刷直流电机的运行特性和传统直流电机基本相同, 其动态结构图可以采用直流 电机通用的动态结构图,如图所示:由无刷直流电机动态结构图可求得其传递函数为= K1 UW ——T L1 + T 狙丫 V '1+T^ L(8)图2.无刷直流电机动态结构图式中:K i为电动势传递系数,•• - — , Ce为电动势系数;K2为转矩传递函数,:- ,R为电动机内阻,Ct为转矩系数;T m为电机时间常数,」7—, G为转子重量,D为转子直径。
直流电机的基本方程式

.直流电机的基本方程式一.直流发电机的基本方程式以并励机为例:(一).电压平衡方程直流发电机发出的电势E产生电流I,I在电枢回路aaa总电阻R(包括电枢绕组电阻及两个电刷的接触电阻)上a产生压降IR,则输出电压U=E-IR,可见发电机E>U。
aaaaaa电路如图:(二).转矩平衡方程式直流发电机是把机械能转变为电能,因此由原动机输入的机械转矩T 是驱动转矩;1电磁转矩T是制动转矩;即使电机空转也存在的、对应电机机械摩擦、铁损耗等的空载转矩T一定是阻转矩,当驱动=制动时,电机恒速旋转。
因此发电机稳定运行时的转矩0平衡方程为:T=T+ T 01(三)功率平衡方程式其功率流程图如图:从原动机输入机械功率P,扣除了机械方面的损耗,就是机转变为电的部分称为电磁p1机功率P,再扣除了电方面的损耗,就是输出的电功率P=UI,对并励发电机p2M电I=I-I。
额定时的P就是P=UI。
Na2fNN其中:是机械方面的损耗,它也是电机空载运行时就存在的损耗,故称空载损耗,pp0机它包括了机械摩擦损耗、铁耗、附加损耗(≈0.01~0.05P),即:ppp N adFem..==++;ppppp adFe0m机是电方面的损耗称为铜耗,它包括了电枢回路铜耗=R和励磁回路铜耗2ppI a acua电2U=UI,即=+pppp2R I==cufcuacuf由功率流程图可列功率平衡方程:电ff R f机械方面:;电方面:-;pP?P?pP?P?p cuaM201Mcuf P;T=把机械方面的功率平衡方程两边除以Ω,就得到了转矩平衡方程。
其中:11?PP TΩ——这是用机械量表示的电磁功率。
;T=。
可见电磁功率==T0M P0 M把电压平衡方程U=E-IR的两边乘以I:UI= EI-R 2I aaaaaaaa a∵I =I+I,则:UI = U(I+I)= EI-R,2I aaaaaff a∴UI= EI-R -UI=EI--其中:UI就是P;对比电方面的功率平衡方程可知:EI 2ppI afaaaa cuacufa就是电磁功率P。
§2.5 直流电动机的基本特性

§2.5 直流电动机的基本特性 2.5.1 基本方程
一、直流电机的可逆性:(图2-30)
1)直流发电机 (原动机以T1拖动电枢以n旋转) Ea和Ia同方向; Ea > U TM与n反方向,TM是制动作用的转矩。 (2)直流电动机
Ea和Ia反方向;(故电动机的电势又叫反电势) Ea < U TM与n同方向,TM是拖动作用的转矩。
+
- +
-
图2-30
直流电机的可逆性
Ia
7.串励电动机机械特性 从电压方程
U Ea I a ( Ra Rs ) Ce n I a ( Ra Rs ) (Ce Kf n Ra Rs )I a
以及
Tem C M I a
CM K f U ( Ra Rs ) Tem
5.串励电动机转速特性( n f ( I a ))
I Ia I f
K f I f K f Ia
n
根据转速公式,可得
Ra Ra UN UN n Ia ' ' Ce Ce Ce I a Ce
Ia
特点:重载时, n很小;轻载时,飞车。
结论:串励电动机不允许在小于15~20%的额定负 载下起动。
火花;电源会发生瞬时跌落。适用于容量 很小的电动机。
ia
n
n
ia
电机学-直流电机

左行
y
yK
K -1 p
右行
y
yK
K 1 p
单波绕组元件
直流电机-电枢绕组
➢ 单叠绕组
并联支路数恒等于2,并联支路数a==1
单波绕组电路图
单波绕组展开图
➢ 总结
直流电机-电枢绕组
直流电机的电枢绕组总是自成回路; 电枢绕组的支路数(2a)永远是成对出现,因为磁极数(2p)是一个偶数;且至少 有2条并联支路;
直流电机-励磁方式
➢ 励磁方式
主磁极的励磁方式有永磁式和电励磁两种。电励磁式是给励磁绕组供电,产生励磁 磁动势而建立主磁场的方式。根据供电方式的不同,它又可以分为他励和自励两类,而自励 又被分为并励、串励和复励三种。
他励
I Ia
并励
I Ia +I f
串励
I Ia =I f
复励
I I f ' =Ia +I f
主磁极的中心线称为直轴,相邻N极和S极的分界线称为
交轴。
直流电机-磁动势和磁场
➢ 电枢磁动势和磁场(电刷位于几何中性线)
N
Hdl D 2x ia
Nia 2x A 2x
D
Fax
1 2
A2x
Ax
Faq
Fa
A
2
τ= D/2p
Bax
0Hax
0
Fax
k
直流电机-磁动势和磁场
➢ 负载气隙磁场(电刷位于几何中性线)
单叠绕组:a= p, 即并联支路对数恒等于电机极对数 单波绕组:a = 1, 即并联支路对数恒等于1 电刷放置的一般原则是空载时通过正、负电刷间的电动势最大,或者说,被电刷 短路的元件中的电动势为零; 对于端接对称的元件,电刷也就放置在主极轴线下的换向片上,电刷总是与位于 几何中线上的导体相接触。
4第二章直流电机_电动势及转矩方程(2.5)

Fx Bxlia
设电枢绕组总导体数为 N , 一个极面下的导体数为 N/(2p),并联支路数为2a(波绕组a=1),电枢总电流为 Ia,有:
ia I a /(2a)
N / 2a k 1
则一个极面下所有导体所受的电磁力为:
FP
N / 2a k 1
f
xk
B
xk a
li lia Bxk
6
直流电机的感应电动势
》 • • • 直流电机电动势的性质: 直流电机的感应电动势与电机结构、气隙磁通及转速有关 发电机——是电源电势(与电枢电流同方向) 电动机——是反电势(与电枢电流反方向)
7
直流电机
二、电磁转矩
设嵌在电枢槽内导体的有效长度为 l,Bx表示任一导体 所在处的磁通密度,ia为导体中流过的电流,则该导体所受 的电磁力为:
直流电机
§2-4 直流电机的基本方程
一、感应电动势
设嵌在电枢槽内导体的有效长度为 l,切割磁通的相对 速度为 ν ,用 Bx 表示任一导体所在处的磁通密度,则该导 体的感应电动势为:
ex Bxl
设电枢绕组总导体数为 N ,并联支路数为 2a (波绕组 a=1),则电枢正负电刷引出的电动势为:
Ea
Ea Ce n
什么关系???
Tem CT I a
- n : r/min - Ω :rad/s – 国际单位 - 关系:
Ω n 2 2 n
60 60
11
直流电机的电动势和电磁转矩公式的关系
1、Ce 和 CT 的关系
Ea
pN Ω CT Ω 2a
Tem CT I a
感应电动势的计算公式为:
Kf—比例常数。
直流电机的基本方程式

直流电机的基本方程式一.直流发电机的基本方程式以并励机为例:(一).电压平衡方程直流发电机发出的电势E a产生电流I a,I a在电枢回路总电阻R a(包括电枢绕组电阻及两个电刷的接触电阻)上产生压降I a R a,则输出电压U=E a-I a R a,可见发电机E a>U。
电路如图:(二).转矩平衡方程式直流发电机是把机械能转变为电能,因此由原动机输入的机械转矩T1是驱动转矩;电磁转矩T是制动转矩;即使电机空转也存在的、对应电机机械摩擦、铁损耗等的空载转矩T0一定是阻转矩,当驱动=制动时,电机恒速旋转。
因此发电机稳定运行时的转矩平衡方程为:T1=T+ T0(三)功率平衡方程式其功率流程图如图:从原动机输入机械功率P1,扣除了机械方面的损耗p机,就是机转变为电的部分称为电磁功率P M,再扣除了电方面的损耗p电,就是输出的电功率P2=UI,对并励发电机I=I a-I f。
额定时的P2就是P N=U N I N。
其中:p机是机械方面的损耗,它也是电机空载运行时就存在的损耗,故称空载损耗p,它包括了机械摩擦损耗mp、铁耗Fe p、附加损耗ad p(≈0.01~0.05P N),即:p 机=0p =m p +Fe p +ad p ;p 电是电方面的损耗称为铜耗,它包括了电枢回路铜耗cua p =2aI R a 和励磁回路铜耗 cuf p =UI 2fU R =2f I =f R ,即p 电=cua p +cuf p 由功率流程图可列功率平衡方程:机械方面:10M P P p =+;电方面:2M cua PP p =--cuf p ; 把机械方面的功率平衡方程两边除以Ω,就得到了转矩平衡方程。
其中:T 1=1P Ω;T 0=0P Ω;T =M PΩ。
可见电磁功率M P =T Ω——这是用机械量表示的电磁功率。
把电压平衡方程U =E a -I a R a 的两边乘以I a :UI a = E a I a -2a I R a ∵I a =I +I f ,则:UI a = U(I+I f )= E a I a -2a I R a , ∴UI= E a I a -2a I R a -UI f =E a I a -cua p -cuf p其中:UI 就是P 2;对比电方面的功率平衡方程可知:E a I a 就是电磁功率P M 。
电机第八章 直流发电机

P
If 继续增加,最后发电 机可自励地建立稳定电压U0。 在P点, U0 = if Rcr ,
Lf di f dt 0
ifRcr
0
If
P点是稳定点,U=U0
U0 Rcr4
4
1
3 2 nN n<n N
左图各场阻线对应的励磁 电阻 Rcr2<Rcr3<Rcr4
Rcr4 是转速为 nN 的空载特 性对应的临界电阻。 临界电阻场阻线与对应空 载特性的稳定点建立的电压略
一、他励发电机运行特性 二、并励发电机运行特性
三、复励发电机运行特性
一 他励发电机运行特性
1、空载特性 2、 外特性
3、调节特性
1、空载特性
怎样测取空载特性? 空载特性测取目的
1、空载特性
n nN
怎样测取空载特性?
实验线路怎样连接?
I 0
U f (I f )
需要什么仪表?
U E a I a Ra
4 E3 E
E0
r
↓E
r
E1
0
If0
If1
If2 If3
If
剩磁 r→ Er → If0 1 E1 →If1 助磁 2 E2 →If2 3
3、励磁回路的总电阻 Rf 应小于与发电机运行 转速相对应的临界电阻。
U0 = if Rcr + L
Lf di f dt 0
di f
f
dt
U0
lf di f dt
T pz 2 a pz 60 a
I a
2 n 60
T1 T T 0
nI a
EaIa
P1 T p 0
电机学 华科电气

Y.Q.Xiong 2006-6 《电机学》第2章 直流电机——直流电动机特性与传动 8
3. 复励电动机的工作特性
复励电动机 试验接线图
速率特性比较
1-并励电动机 2-并励为主的复励电动机 3-串励为主的复励电动机 4-串励电动机 5-差复励电动机
2 = EIa + Ia Ra +UI f = P + pCua + pCuf em
电磁功率 Pem 电枢铜耗 pCua 励磁铜耗 pCuf 电机铁耗 pFe 机械损耗 pmec 附加损耗 pad 输出机械功率 P2
P = Ea Ia em
2 pCua = Ia R a
pCuf =U f = I 2 Rf I f
1. 并励电动机 n = n0 + kjTem
n0 = U 称为理想 CEΦ 空载转速
并励电动机的自然机 械特性接近于一水平 称为硬特性。 线,称为硬特性。
Y.Q.Xiong 2006-6 10
《电机学》第2章 直流电机——直流电动机特性与传动
2.串励电动机 串励电动机
设磁路不饱和
Φ ∝ If = Ia ⇒Tem = CTΦ a ∝Φ2 ⇒Φ ∝ Tem I
Y.Q.Xiong 2006-6 《电机学》第2章 直流电机——直流电动机特性与传动 7
2. 串励电动机的工作特性 n1/4 − nN ∆n = ×100% nN
串励电动机 试验接线图
(U − Ia Ra ) ↓ P ↑⇒P ↑⇒Ia ↑⇒ ⇒n ↓↓ 2 1 If = Ia ⇒ If ↑⇒Φ ↑
U −E U Ist = Ia = = Ra Ra U Ist = Ra + Rst
直流电动机四大方程调速方法和动态模型

30 π
C e。
Tl
L R
2
Tm
GD R 375 C e C m
U d0 RI d E
Te C m I d E Cen
Te T L
n0 n
2
n— 转速(r/min) U— 电枢电压(V) I— 电枢电流(A) ; ; ; R— 电枢回路总电阻() — 励磁磁通(Wb) ; ; Ke— 由电机结构决定的电动势常数。 2 直流调速方法
直流调速电源
G-M 系统工作 原理
G-M 系统特性
1.1 三种常用的可控直流电源 旋转变流机组 静止式可控整流器 直流斩波器或脉宽调制变换器 据前,调压调速是直流调速系统的主要方法,而调节电枢电压需要有专门向电动 机供电的可控直流电源。本节介绍三种常用的可控直流电源。 1.1.1 旋转变流机组(for G-M 系统) --用交流电动机和直流发电机组成机组,获得可调的直流电压 图 1-1 旋转变流机组和由它供电的直流调速系统(G-M 系统)原理图 由原动机(柴油机、交流异步或同步电动机)拖动直流发电机 G 实现变流,由 G 给需要调速的直流电动机 M 供电。 调节 G 的励磁电流 if 即可改变其输出电压 U,从而调节电动机的转速 n 。 这样的调速系统简称 G-M 系统,国际上通称 Ward-Leonard 系统。 图 1-2 G-M 系统中电动机可逆运行的机械特性 1.1.2 静止式可控整流器(for V-M 系统) ——用静止式的可控整流器获得可调的直流电压。 图 1-3 晶闸管-电动机调速系统(V-M 系统)原理图 晶闸管-电动机调速系统(简称 V-M 系统,又称静止的 Ward-Leonard 系统) ,图中 VT 是晶闸管可控整流器,通过调节触发装置 GT 的控制电压 Uc 来移动触发脉冲的相 位,即可改变整流电压 Ud ,从而实现平滑调速。 晶闸管整流装置 经济可靠性有很大提高,技术性能有较大优越性。 晶闸管可控整流器的功率放大倍数在 104 以上, 其门极电流可以直接用晶体管来控 制,不再像直流发电机那样需要较大功率的放大器。 控制作用的快速性,大大提高系统的动态性能。 变流机组是秒级,而晶闸管整流器是毫秒级 可逆 由于晶闸管的单向导电性,它不允许电流反向,给系统的可逆运行造成困难。
电机学直流电机的基本方程

第五节 直流电机的基本方程直流电机的基本方程式包括电系统的电动势平衡方程式、能量系统的功率平衡方程式和机械系统的转矩平衡方程式。
一、直流发电机的基本方程式直流电机的基本方程式与励磁方式有关。
下面以并励直流发电机为例来分析直流发电机的基本方程式。
1.电动势平衡方程式当原动机拖动直流发电机旋转时,电枢绕组切割气隙磁场感应出电动势a E 。
当电机带上负载时,电枢绕组中将有电流a I 流过,取a I 与a E 的参考正方向相同。
根据基尔霍夫第二定律,则有电动势平衡方程式ff s a a a R I U U R I U E =∆++=2式中,U 为并励发电机的端电压,也为加在励磁回路的电压;a R 为电枢绕组的电阻;s U ∆2为一对电刷下的接触压降;f I 为励磁回路的电流;f R 励磁回路的电阻。
对并励直流发电机,根据基尔霍夫第一定律,有电流方程式 f a I I I +=式中,I 为发电机的输出电流,即负载电流。
2.功率平衡方程式并励直流发电机的功率流程图。
图中,1P 为原动机输入的机械功率,除去机械损耗Ωp 、铁耗Fe p 和附加损耗∆p 后,余下的部分转化为电磁功率e P 。
因此有如下功率平衡方程式e e Fe P p P p p p P +=+++=∆Ω01式中,0p 为空载损耗,它等于机械损耗Ωp 、铁耗Fe p 和附加损耗∆p 之和。
其中铁耗Fe p 是由于电枢旋转时交变磁通在电枢铁心内引起的损耗;机械损耗Ωp 是指轴承摩擦损耗、电刷摩擦损耗和转子与空气的摩擦损耗(也称为通风损耗)等;附加损耗∆p 也称为杂散损耗,主要包括结构部件在磁场内旋转而产生的损耗、电枢齿槽的影响使气隙磁通产生脉动而在主极铁心中和电枢铁心中产生的脉动损耗、电枢反应使气隙磁场畸变而在电枢铁心中产生的损耗、由于电流分布不均匀而增加的电刷接触损耗以及换向电流所产生的损耗等,这些损耗难于精确计算,一般进行估算,通常约占额定功率的0.5%~1%。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、直流电机的基本方程式:
(电系统的电势平衡方程式,机械系统的转矩平衡方程式,能量系统的功率平衡方程式。
)
1、电动势平衡方程式:
A、不计磁路饱和效应,并励电动机电枢回路和励磁回路的电势方程式:
B、并励发电机电势方程式:
发电机的大于。
2、转矩平衡方程式:
3、功率方程式:
A、直流电机中的损耗、效率:
损耗有三类:
消耗于导体电阻中。
消耗于摩擦损耗、通风和机械损耗。
消耗于铁心中的损耗。
铁耗:由于电枢旋转时主磁通在电枢铁心内交变而引起的。
铜耗:
电枢回路铜耗
励磁回路铜耗
电刷接触铜耗,为一对电刷总接触电压降。
机械损耗:包
括轴承摩擦损耗、电刷摩擦损耗、定转子和空气的摩擦损耗。
附加损耗:电枢齿、槽存在,使气隙磁通产生脉动,电枢反应使磁场畸变引起的铁耗。
换向电流引起的损耗。
按额定容量的1%计算,无补偿绕组按额定容量的0.5%计算,有补偿绕组在以上损耗中,,随负载变化而变化,称为可变损耗;,,为不变损耗。
电机的效率:
当不变损耗=可变损耗时,取得最大,是的二次曲线。
B、并励电动机的功率方程式:
C、并励发电机的功率方程式:。
