《线性代数》第一章行列式精选习题及解答
(完整word)行列式习题1附答案

命题人或命题小组负责人签名: 教研室(系)主任签名: 分院(部)领导签名:第 1 页 共 4 页《线性代数》第一章练习题一、填空题1、_____________)631254(=τ8 2、要使排列(3729m14n5)为偶排列,则m =___8____, n =____6_____ 3、关于x 的多项式xx x xx 22111---中含23,x x 项的系数分别是 -2,44、 A 为3阶方阵,2=A ,则____________3*=A 1085、四阶行列式)det(ij a 的次对角线元素之积(即41322314a a a a )一项的符号为 +6、求行列式的值 (1)46924692341234=__1000___; (2)131410242121=_0___ ;(3) 2005000200410020030102002200120001--=___2005____;(4) 行列式243012321---中元素0的代数余子式的值为___2____7、648149712551 = 6 ;1252786425941653241111--=1680-8、设矩阵A 为4阶方阵,且|A|=5,则|A *|=__125____,|2A |=__80___,|1-A |= 15。
命题人或命题小组负责人签名: 教研室(系)主任签名: 分院(部)领导签名:第 2 页 共 4 页9、011101110= 2 ;=000100312222210 12 。
10、若方程组⎪⎩⎪⎨⎧=+=+=+a bz cy b az cx ay bx 0 有唯一解,则abc ≠ 011、把行列式的某一列的元素乘以同一数后加到另一列的对应元素上,行列式 值不变 。
12、行列式中在项的项共有214312344214231144434241343332312423222114131211,,24!4a a a a a a a a a a a a a a a a a a a a a a a a =,21431234a a a a 是该行列式的项,符号是 + 。
第一章 行列式答案详解

第一章行列式习题1.1二阶和三阶行列式1.计算下列二阶行列式.()12112-=4(1)5--=()222111x x x x -++22(1)(1)x x x x =-++-321x x =--【分析】考查二阶行列式的计算公式2.计算下列三阶行列式.()1251312204--1301113113123024204===()2a bcb c a c a b 11()1()011b c b ca b c c a a b c c b a ca b a b b c=++=++----333()3c b a c a b c abc a b c a b b c --=++=-----【分析】考查三阶行列式的计算公式或者行列式性质计算三阶行列式3.当x 取何值时,3140010x x x¹.【解析】31210214040(24)0241010x x x x x x xxxx x且===-【分析】考查三阶行列式的计算公式或者行列式性质计算三阶行列式习题1.2排列1.求下列排列的逆序数,并确定它们的奇偶性.()14132;()41324t =,为偶排列()2542316;()5423169t =,为奇排列()3()()246213521n n -L L .()()()(1)2462135212n n n n t +-=L L ,4142443n k k n k k =++⎧⎨=+⎩或时,为奇排列或时,为偶排列【分析】考查逆序数的计算及奇偶排列的概念*2.设排列12n i i i L 的逆序数为k ,求排列121n n i i i i -L 的逆序数.【解析】考虑第m 个数(m=1,2,...,n-1),它与后面n-m 个数的每一个数都有一个“序”,这个序要么是“顺序”,要么是“逆序”。
这样全部的“序”共有:(n-1)+(n-2)+...+2+1=n(n-1)/2个。
12n i i i L 逆序数是k ,那么排列121n n i i i i -L 的逆序是n(n-1)/2-k 【分析】考查逆序概念习题1.3n 阶行列式1.写出四阶行列式中含有因子1123a a 的项.【解析】1123344211233244;a a a a a a a a +-【分析】行列式的定义2.在5阶行列式中,下列各项应取什么符号?()11523314254a a a a a ;()152********,+a a a a a 取“”t =()22132441355a a a a a ;()21324413552,+a a a a a 取“”t =()34153122435a a a a a .()41531224355,a a a a a 取“-”t =【分析】行列式的定义3.设一个n 阶行列式中等于零的元素的个数大于2n n -,试证明该行列式为零.【解析】N 阶行列式共有2n 个元素,等于零的元素的个数大于2n n -,则非零元素个数小于n 个,即一定出现一个0行,则行列式值为0.【分析】行列式的定义4.用行列式的定义计算下列行列式.()1010000200001000n n -L LM M M LML L (23(1)1)112231,11(1)(1)!n n n n n a a a a n τ----=-=- ()2()()1111121211000n n n n a a a a a a --L L MLM M L(1)((1)21)212(1)112(1)1(1)(1)n n n n n n n n n n a a a a a a τ----=-=- 【分析】行列式的定义和主次对角线行列式的结论5.设()11121314212223243132333441424344x a a a a a x a a a f x a a x a a a a a x a --=--,求()f x 中3x 的系数.【解析】根据行列式的定义,3x 系数只能来自于一项11223344()()()()x a x a x a x a ----,即11223344()a a a a -+++【分析】行列式的定义习题1.4n 阶行列式的性质1.用行列式的性质计算下列行列式.()1a x x x x b x xx x c x+++000000a x x x x x x b x xb x x x b x x a x b xc xx c x x x c x x c +=+++=++++2()()()a b x c x x bcx abc ab ac bc x=++-+=+++【分析】各行或各列元素之和相等的行列式+展开定理+三角化方法()22464273271014543443342721621-1321122331299001003279001003270100327190010044310000116100001169001006210029400294c c r r c c c c r r +----===121000011601003272940000000294r r «=-=-【分析】行列式性质+行列式性质+三角化方法()3ab ac aebd cd debf cf ef---1111111111110020204111020002abcdef abcdef abcdef abcdef---=-==-=-【分析】各行或各列元素之和相等的行列式+行列式性质+三角化方法2.将下列行列式化为上三角形行列式,并计算其值.()1111111111111022281111002211110002-==-----【分析】三角化方法的计算()222401120112011204135413505550111221031233123048304832051205102110211----------=-=-=---------112011201120111011101111010102500047001800180031003100025---------=-=-=-=----------【分析】三角化方法的计算3.计算下列行列式.()111100[(1)][(1)]100x a a aa a a a x a x a x a x n a x n a a a x ax x a-=+-=+--L LL L L L M M L M M M L M M M L M L LL 1[(1)]()n x n a x a -=+--10111011120201600022002200220004----=-=-=-----()33312()02()2()0x y x y y x yx yy x y x x y x y x y x y x y xx yxy x yx++-+=+-=+=-+--+--【分析】各行或各列元素之和相等的行列式的计算4.计算下列行列式()112311110010010na a a a L L LM M M LM L ,其中0,2,3,,.i a i n ¹=L 122123211111000110000nn n n a a a a a a a a a a a ---ç==---ççL L L L L LM M M LML 【分析】箭型行列式计算()212111111111111na a a +++L LM M M LML ,其中0,1,2,,.i a i n ¹=L 111121211212211111111100000100000n n n nna aa a a a a a a a a a a a a a a a a +++++-ç===++++çç-L LL L L L L M M M LMM M M L M L L 【分析】利用性质变换为箭型行列式计算5.证明()33by az bz ax bx ayx y z bx ayby az bz ax a b zx y bz ax bx ay by azyzx++++++=++++.【证明】左边by az bz ax bx ayby bz ax bx ay azbz ax bx aybx ayby az bz ax bx by az bz ax ay by az bz axbz ax bx ay by az bz bx ay by az ax bx ay by az+++++++=+++=++++++++++++y bz ax bx ay zbz ax bx ayb x by az bz ax a y by az bz axzbx ay by azx bx ay by az ++++=+++++++++22y bz ax bx zax bx ay y bz ax x z x bx ay b x by az bz a yazbz ax b x by azz a yz bz ax zbx ay by x ay by az z bx ay y xy by az++++=+++=+++++++()223333y bz x z x ay y z x z x y x y z b x byz a y z ax b xy z a yz x a b zx y z bx y x y az z xyxyzy zx=+=+=+【分析】拆项性质+行列式性质6.证明121211221100001000000001n n n n nn n x x x a x a x a x a xa a a a a -------=++++-L L L L M M M L M M LL .【证明】11c n n nD xD a 展开-=+()22121n n n n n n x xD a a x D a x a ----=++=++()3232123232312312121n n n n n n n n n n n n n nx D a x a x a x D a x a x a x a a x a a x a x a x a ----------=+++==+++=++++=++++L L L L 【分析】展开定理+递推发习题1.5行列式的展开1.求行列式30453221--中元素2和2-的代数余子式.【解析】2的代数余子式:313104(1)003A +=-=;2-的代数余子式:323234(1)2953A +-=-=【分析】余子式、代数余子式的概念2.用降阶法计算下列行列式【分析】拉普拉斯展开定理()211122200000000000000=0000000111111231n n na a a a a a a a a nn ------+L L LL MM M L M M MM M L M M L L LL12(1)(1)n nn a a a =+- 【分析】行列式性质+展开定理3.计算下面行列式222244441111a b c d a b c d a b c d .【解析】4D 中各列元素均缺少3次方幂的元素,在4D 中添加3次方幂的一行元素,则产生5阶范德蒙行列式,再适当添加一列得:22222333334444411111()ab c d x f x a b c d x a b c d x a b c d x =按最后一列展开,得2341525354555()f x A xA x A x A x A =++++,因为()()()()0f a f b f c f d ====,所以,,,a b c d 为()f x 的四个根,则()()()()()f x k x a x b x c x d =----由根与系数关系有4555Aa b c d A +++=-,而4545(1)A D D +=-=-,55()()()()()()A b a c a d a c b d b d c =------,则()()()()()()()D a b c d b a c a d a c b d b d c =+++------.【分析】克莱姆法则+展开定理4.已知四阶行列式D 中第1行的元素分别为1,2,0,4-,第3行的元素的余子式依次为6,,19,2x ,试求x 的值.【解析】313233346,,19,2A A x A A ==-==-,由展开定理得:162()019(4)(2)0x ⨯+⨯-+⨯+-⨯-=,解得7x =【分析】代数余子式、余子式+展开定理求11121314及11213141.【解析】1112131411111111016110500164241313042463524130635A A A A -----+++===----------1201048428(1)(1)46136313+--=-=--=---11213141112131411521110513131413M M M M A A A A ---+++=-+-=----152142412000424812812081291210912-----==-=-=------【分析】代数余子式、余子式+展开定理的逆运用习题1.6克莱姆法则1.用克莱姆法则求解下列方程组的解12341234123412342326223832242328x x x x x x x x x x x x x x x x ì++-=ïïïï---=ïíï+-+=ïïï-++=-ïî.【解析】1234324,324,648,324,648D D D D D ====-=-,则12341,2,1,2x x x x ===-=-【分析】克莱姆法则2.设1a ,2a ,3a 互不相同,证明方程组123112233222112233000x x x a x a x a x a x a x a x ì++=ïïï++=íïï++=ïïî只有零解.【解析】系数行列式时范德蒙行列式,因为1a ,2a ,3a 互不相同,则系数行列式非零;再由克莱姆法则可知,该齐次方程组只有零解.【分析】克莱姆法则3.当l 为何值时,齐次线性方程组123122334000x x x x x x x l l ì++=ïïï-+=íïï+=ïïî()1只有零解;()2有非零解.当11λλ≠≠-且时,只有零解;当=1=1λλ-或时,有非零解【分析】克莱姆法则自测题1.填空题(每小题10分,共20分)()1行列式103100204199200395301300600=___2000____.()2已知11111111111111D x---=---,则D 中x 的系数是___4-____.2.计算下列行列式:(每小题15分,共30分)()11(1)(1)(2)220000(1)(1)000000n n n n c nn n D αβαββααββα---==-+-展开()212312323411341(1)3452145221211121n n n n n D n n n +==--(1)(1)1231111101111111101111(1)(1)2211110111111111111n n n n n n nnn n n n n n n n-⨯------++==----(1)(2)1122(1)(1)100100(1)(1)(1)(1)(1)221001000n n n n n n n nn n n n n n n ------⨯-++=⋅-=⋅-⋅-⋅(1)12(1)(1)2n n n n n n --+=-⋅⋅(本题15分)已知2231122D yx=,且1112133M M M +-=,1112131A A A ++=,其中ij M 是D 中元素ij a 的余子式,(1)i j ij ij A M +=-,试求D 的值.【解析】1112133235M M M x y +-=⇒-=111213114A A A y x ++=⇒=⇒=则行列式的值为14.(本题15分)解线性方程组231234231234231234231234x ax a x a x e x bx b x b x ex cx c x c x e x dx d x d x e⎧+++=⎪+++=⎪⎨+++=⎪⎪+++=⎩,其中,,,a b c d 互异.【解析】系数行列式非零,由克莱姆法则可知1234,0,0,0x e x x x ====5.(本题20分)证明:11000100,010001n n a b ab a b ab a b a b a b a ba b++++-=¹+-+L L L M M M L M M L .【解析】上课做为例题已讲过。
第一章 行列式 习题及答案

第一章 行列式习题1. n 阶行列式D 的值为c ,若将D 的第一列移到最后一列,其余各列依次保持原来的次序向左移动,则得到的行列式值为 。
(1(1)n c --)2. n 阶行列式D 的值为c ,若将D 的所有元素改变符号,得到的行列式值为 。
((1)n c -)3. 2(1)(2,1,21,2,,1,)(21)0(23)0122k k N k k k k k k k k --+=-++-+++=+?。
4. 由行列式的定义计算行列式413331233626xx x x xx展开式中4x 和3x 的系数。
(3412, 12x x -)(分析:4x 的系数:四个元素中必须全都包含x 。
第一行只能取11a ,第三行只能取33a ,这样第二、四行只能取22a 和44a ,则此项为(1234)411223344(1)4312N a a a a x x x x x -=⋅⋅⋅=。
3x 的系数:(2134)(4231)3331221334441223314(1)(1)3912N N a a a a a a a a x x x -+-=--=-。
)5. 已知1703,3159,975,10959能被13整除,不直接计算行列式17033159097510959的值,证明他是13的倍数。
证明:12341701703170170341000131531593153159410021309709750979754103109510959109510959l c c l c c l c c l +⋅+⋅=⋅+⋅,能被13整除。
注意,以下两个行列式:170317037033159315915909759759751095910959959≠,所以一定要加到最后一列上。
6. 设行列式311252342011133--=--D ,求11213141243A A A A +--及2123242-++M M M 。
(0和-5)解:112131412112423424301011333A A A A -+--==----。
行列式习题解答

111 (b) c a b(a)(c) (b)1 b 1 (a) a 1 (c) c a2abc abc 0
b c 0
⑥0 1 1 1 0 1 11 2 110 a a2 a3
⑦ b b2 b3 c c2 c3
f ( x) 中旳常数项是(1) 2 31 (1) 3 31 3
x 030 15.已知 0 0 0 2 1, 求 x
0 x00 4 000
x 030
解
0 0
0 x
0 0
2 0
24 x
1, 所以
x
1 24
4 000
16.用行列式性质证明下列等式
证明 ①
a1 kb1 a2 kb2 a3 kb3
00
解 ②此行列式刚好只有处于不同旳行与不同旳列旳
n个非零元素 a12 , a23 , a(n 1)n , an1 ,故非零项只有一项 a12a23 a(n 1)n an1 ,该项所带旳符号为 (1) 23 n1 (1)n1 , 所以 D (1)n11 2 (n 1) n (1)n1 n!
解 ① (38162754) 2 3 0 4 3 1 1 14
所以 38162754 为偶排列
② (3712456) 2 2 0 1 1 1 7
所以 3712456 为奇排列
③ 246 (2n)135 (2n 1)
n (n 1) 2 1 n(n 1) 2
所以当 n 4k 或 n 4k 3 时为偶排列;当n 4k 1
或 n 4k 2 时为奇排列.
6.选择 i, j, k,使排列 21i36 jk97为偶排列.
解 当 i 4, j 8, k 5 时, (214368597 6), 为 为偶排列,当 i 5, j 4, k 8时, (215364897 6), 为偶排列,当 i 8, j 5, k 4时, (218365497 10),
线性代数第1章行列式试卷及答案

第一章 行列式一、单项选择题1.行列式D 非零的充分条件是( D )(A) D 的所有元素非零 (B) D 至少有n 个元素非零 (C) D 的任何两行元素不成比例(D)以D 为系数矩阵的非齐次线性方程组有唯一解 2.二阶行列式1221--k k ≠0的充分必要条件是( C )A .k ≠-1B .k ≠3C .k ≠-1且k ≠3D .k ≠-1或≠3 3.已知2阶行列式2211b a b a =m ,2211c b c b =n ,则222111c a b c a b ++=( B )+n (m+n )4.设行列式==1111034222,1111304z y x zy x 则行列式( A ) A.32D.38 5.下列行列式等于零的是(D )A .100123123- B. 031010300- C . 100003010- D . 261422613-6.行列式111101111011110------第二行第一列元素的代数余子式21A =( B )A .-2B .-1C .1D .28.如果方程组⎪⎩⎪⎨⎧=+=-=-+0404033232321kx x x x x kx x 有非零解,则 k =( B )9.(考研题)行列式0000000a b abc d c d=( B ) A.()2ad bc -B.()2ad bc --C.2222a d b c -D.2222b c a d -二、填空题1.四阶行列式中带负号且含有因子12a 和21a 的项为 44332112a a a a 。
2. 行列式1112344916中(3,2)元素的代数余子式A 32=___-2___.3. 设7343690211118751----=D ,则5A 14+A24+A 44=_______。
解答:5A 14+A 24+A 44=1501343090211115751-=---4.已知行列式011103212=-a ,则数a =____3______.5.若a ,b 是实数,则当a =___且b =___时,有=---10100a b b a 0。
厦门理工学院线性代数第一章行列式参考答案

第一章 行 列 式系 专业 班 姓名 学号 第一节 二阶与三阶行列式 第三节 n 阶行列式的定义一.选择题一.选择题1.若行列式x52231521 = 0,则=x [ C ](A )2 (B )2- (C )3 (D )3-2.线性方程组ôóôòñ=+=+473322121x x x x ,则方程组的解),(21x x = [ C ] (A )(13,5) (B )(13-,5) (C )(13,5-) (D )(5,13--)3.方程093142112=x x根的个数是根的个数是 [ C ](A )0 (B )1 (C )2 (D )3 4.下列构成六阶行列式展开式的各项中,取“+”的有”的有 [ AD ] (A )665144322315a a a a a a (B )655344322611a a a a a a (C )346542165321a a a a a a (D )266544133251a a a a a a5.若55443211)541()1(a a a a a l k l k N -是五阶行列式ij a 的一项,则l k ,的值及该项的符号为[ B ] (A )3,2==l k ,符号为正;,符号为正; (B )3,2==l k ,符号为负;,符号为负; (C )2,3==l k ,符号为正;,符号为正; (D )2,3==l k ,符号为负,符号为负6.下列n (n >2)阶行列式的值必为零的是)阶行列式的值必为零的是 [ B ] (A) 行列式主对角线上的元素全为零行列式主对角线上的元素全为零 (B) 三角形行列式主对角线上有一个元素为零三角形行列式主对角线上有一个元素为零 (C) 行列式零的元素的个数多于n 个 (D) 行列式非零元素的个数小于n 个 二、填空题二、填空题 1.行列式1221--k k 0¹的充分必要条件是的充分必要条件是3,1k k ¹¹- 2.排列36715284的逆序数是的逆序数是 133.已知排列397461t s r 为奇排列,则r = 2,8,5 s = 5,2,8 ,t = 8,5,2 4.在六阶行列式ij a 中,623551461423a a a a a a 应取的符号为应取的符号为 负 。
(完整版)行列式习题1附答案.doc

⋯⋯_ ⋯_ ⋯_ _ ⋯_ _ ⋯_ _ ⋯_ _ ⋯_ _ ⋯_ _ ⋯_ _ ⋯_ _ ⋯_ _ ⋯:⋯号⋯学⋯_ _ ⋯_ _ ⋯_ _ ⋯_ _ ⋯_ _ 线_ 订_ _ 装_ _ ⋯_ _ ⋯_ _ ⋯_ ⋯:⋯名⋯姓⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯:⋯⋯⋯班⋯⋯⋯《线性代数》第一章练习题⋯⋯一、填空⋯⋯⋯1、(631254) _____________ 8⋯⋯⋯2、要使排列(3729m14n5)偶排列, m =___8____, n =____6_____⋯⋯x 1 13 , x 2 的系数分是⋯3、关于x的多式x x x中含 x -2,4⋯1 2 2x⋯⋯4、 A 3方, A 2, 3A* ____________ 108⋯⋯⋯5、四行列式det( a ij)的次角元素之(即a14a23a32a41)一的符号+⋯⋯1 2 1线1234 2346、求行列式的 (1) =__1000 ;(2)2 4 2 =_0___;封2469 469密10 14 13⋯⋯1 2000 2001 2002⋯0 1 0 2003⋯⋯(3)0 1=___2005____;⋯0 20040 0 0 2005⋯⋯1 2 3⋯中元素 0 的代数余子式的___2____⋯(4) 行列式2 1 0⋯3 4 2⋯⋯1 1 1 1⋯1 5 25⋯ 4 2 3 57、 1 7 49 = 6 ;= 1680⋯16 4 9 25⋯1 8 64⋯64 8 27 125⋯⋯矩方,且,,, A 1 1 。
⋯A 4⋯8、|A|=5 | A*| =__125 | 2A| =__80___ | |=50 1 10 1 2 22 2 2 09、 1 0 1 = 2 。
;3 0121 1 01 01 0 0 0bx ay010、若方程cx az b 有唯一解,abc≠0 cy bz a11、把行列式的某一列的元素乘以同一数后加到另一列的元素上,行列式12、行列式a11a12a13a14a21a22a23a24 的共有4! 24, 在a11a23 a14a42, a34a12a31a32a33a34a41a42a43a44a34a12a43 a21 是行列式的,符号是 + 。
第一章 行列式--习题解答

第一章 行列式3.求2111242233634448=D . 【分析】本行列式的特点是第2、3、4行元素均有公因子,可先提出公因子再计算行列式.解 21111211234=120.11211112=⨯⨯D 【注意 “行和相等的行列式的计算方法”】4.求121212--=-n n n n x mx x x x m x D x x x m.【分析】本行列式的特点是各行(列)元素之和相同,故可把第2列至第n 列加到第一列后,提取公因子12()++- n x x x m ,然后化为三角形行列式.【参见同辅P5—例4】解 1221221212211()1---==++---n n n n n n n n x mx x x x x x m x x m x D x x x m x x x m x x m211212100()()()00--=++-=++--- nn n n x x mx x x m x x x m m m.5.求112011111001+=n na D a a,其中120≠n a a a .【分析】本行列式称为箭型行列式,通常可化为三角形行列式来计算.【参见同辅P5—例5.】解 11111212()(2,3,,1)1111100010000=-=-=+-=-∑∑j nj j nj nn j jnc c j n a a a D a a a a a a .6.求2111131111411117=D . 【分析】本行列式可将第一列拆分成两项之和. 解2111111111111131111111311311311020014136+414111411411410030117171711171171170006114136302361854=108.111210101010101001706==+=+=+=++=++D7.求1122334400000000=a b a b D b a b a . 【分析】本行列式各行(列)零元素足够多,可按第一列(行)将行列式展开.【沿边展开】 解1122122114113342233433440000000(1)0(1)00000++==⋅-+⋅-a b a b b a b D a b a b a b b a a b a b a 14142323()().=--a a b b a a b b8.证明121211221100001000000001-------=++++-n n n n nn n x x x a x a x a x a x a a a a a.【分析】考察本题的行列式,n D 与1n D -的结构相同,故可以用递推的方法证明. 证明 按第一列展开212121()-----=+=++=++n n n n n n n n n D xD a x xD a a x D a x a1212121121------==++++=++++ n n n n n n n n x D a x a x a a x a x a x a9.已知4阶行列式2323231211232234334144=D , 求12223242+++A A A A ,其中2(1,2,3,4)=i A i 为D 中第i 行,第2列元素的代数余子式. 【分析】直接计算12223242,,,A A A A 的值,工作量大且容易出错,这类题目可根据行列式的展开性质求解较简单.解 构造新的行列式2323123232323111111112122122212()3133133341441444==-=-范德蒙行列式D10.解方程组212321232123,,.⎧++=⎪++=⎨⎪++=⎩x ax a x d x bx b x d x cx c x d 其中,,a b c 互异.【分析】本题考核克莱姆法则及范德蒙行列式.解 因为系数行列式 22211()()()01==---≠a a D bb b ac a c b cc ,所以方程组有唯一解. 又因为 2212==da a D db b dD dc c , 22221101==d a D db dc , 31101==a dD b d c d ,故由克莱姆法则得 11==D x d D ,220==D x D , 330==Dx D.11.当λ取何值时,齐次线性方程组1231231230,0,0.++=⎧⎪++=⎨⎪++=⎩x x x x x x x x x λλλ有非零解?【分析】本题考查克莱姆法则的推论及含参数的行列式的计算.解 系数行列式 21111(2)(1)11λλλλλ==+-D ,故当210λλ=-=⇔=⇔或时D 齐次线性方程组有非零解.。
(完整版)行列式习题答案

线性代数练习题 第一章 行 列 式系 专业 班 姓名 学号第一节 n 阶 行 列 式一.选择题1.若行列式 = 0,则[ C ]x52231521-=x (A )2 (B )(C )3(D )2-3-2.线性方程组,则方程组的解=[ C ]⎩⎨⎧=+=+473322121x x x x ),(21x x (A )(13,5)(B )(,5)(C )(13,)(D )()13-5-5,13--3.方程根的个数是[ C ]093142112=x x (A )0 (B )1 (C )2 (D )34.下列构成六阶行列式展开式的各项中,取“+”的有 [ A ](A ) (B ) 665144322315a a a a a a 655344322611a a a a a a (C ) (D )346542165321a a a a a a 266544133251a a a a a a 5.若是五阶行列式的一项,则的值及该项的符号为[ B ]55443211)541()1(a a a a a l k l k N -ij a l k ,(A ),符号为正; (B ),符号为负;3,2==l k 3,2==l k (C ),符号为正;(D ),符号为负2,3==l k 2,3==l k 6.下列n (n >2)阶行列式的值必为零的是 [ BD ](A) 行列式主对角线上的元素全为零 (B) 三角形行列式主对角线上有一个元素为零 (C) 行列式零的元素的个数多于n 个 (D) 行列式非零元素的个数小于n 个二、填空题1.行列式的充分必要条件是1221--k k 0≠3,1k k ≠≠-2.排列36715284的逆序数是133.已知排列为奇排列,则r =2,8,5s = 5,2,8,t = 8,5,2397461t s r4.在六阶行列式中,应取的符号为 负 。
ij a 623551461423a a a a a a 三、计算下列行列式:1.=181322133212.=55984131113.yxyx x y x yyx y x +++332()x y =-+4.=100011000001001005.000100002000010n n -1(1)!n n -=-6.0011,22111,111 n n nn a a a a a a --(1)212,11(1)n n n n n a a a --=-线性代数练习题 第一章 行 列 式系专业 班 姓名 学号第二节 行列式的性质一、选择题:1.如果, ,则 [ C ]1333231232221131211==a a a a a a a a a D 3332313123222121131211111232423242324a a a a a a a a a a a a D ---==1D (A )8(B )(C )(D )2412-24-2.如果,,则 [ B ]3333231232221131211==a a a a a a a a a D 2323331322223212212131111352352352a a a a a a a a a a a a D ---==1D (A )18(B ) (C )(D )18-9-27-3. = [ C ]2222222222222222)3()2()1()3()2()1()3()2()1()3()2()1(++++++++++++d d d d c c c c b b b b a a a a (A )8 (B )2(C )0(D )6-二、选择题:1.行列式 12246000 2. 行列式-3=30092280923621534215=11101101101101112.多项式的所有根是0211111)(321321321321=+++++=x a a a a x a a a a x a a a a x f 0,1,2--3.若方程= 0 ,则225143214343314321x x --1,x x =±=4.行列式 5==2100121001210012D 三、计算下列行列式:1.2605232112131412-21214150620.12325062r r +=2.xa a a x a a a x 1[(1)]().n x n a x a -=+--线性代数练习题 第一章 行 列 式系专业 班 姓名 学号第三节 行列式按行(列)展开一、选择题:1.若,则中x 的一次项系数是[D]111111111111101-------=x A A (A )1(B )(C )(D )1-44-2.4阶行列式的值等于 [D ]443322110000000a b a b b a b a (A ) (B )43214321b b b b a a a a -))((43432121b b a a b b a a --(C )(D )43214321b b b b a a a a +))((41413232b b a a b b a a --3.如果,则方程组 的解是 [B]122211211=a a a a ⎩⎨⎧=+-=+-0022221211212111b x a x a b x a x a (A ), (B ),2221211a b a b x =2211112b a b a x =2221211a b a b x -=2211112b a b a x =(C ), (D ),2221211a b a b x ----=2211112b a b a x ----=2221211a b a b x ----=2211112b a b a x -----=二、填空题:1.行列式 中元素3的代数余子式是 -6122305403--2.设行列式,设分布是元素的余子式和代数余子式,4321630211118751=D j j A M 44,j a 4则 =,=-6644434241A A A A +++44434241M M M M +++3.已知四阶行列D 中第三列元素依次为,2,0,1,它们的余子式依次分布为1-5,3,4,则D = -15,7-三、计算行列式:1.321421431432432112341234134101131010141201311123031111310131160.311-==---=-=-2.12111111111na a a +++ ==121111011101110111n a a a+++121111100100100na a a---211112111110010010n c c a a a a a+--+111223211111100001000na a cc a a a a++-+11121101111000000ni ni iia a a c a c a=+++∑1211()(1)nn i i a a a a =+∑或121123113111111000000nn a r r a r r a r r a a a a+------211211212311111000000na a aa a a c c a a a a+++--11122313311111100000ni in nnaa a c c a a a c c a a a a=++++∑1122()(1)nn i ia a a a a =++∑或11221121121110111110111111111(1).n n n n nn i ia a a a a a D a a a a a a a --=++++=+=+=+∑线性代数练习题 第一章 行 列 式系专业 班 姓名学号综 合 练 习一、选择题:1.如果,则 = [ C ]0333231232221131211≠==M a a a a a a a a a D 3332312322211312111222222222a a a a a a a a a D =(A )2 M(B )-2 M(C )8 M(D )-8 M2.若,则项的系数是[ A ]xxx x x x f 171341073221)(----=2x (A )34 (B )25 (C )74 (D )6二、选择题:1.若为五阶行列式带正号的一项,则 i = 2 j = 154435231a a a a a j i 2. 设行列式,则第三行各元素余子式之和的值为 8。
(完整版)行列式练习题及答案

一、填空题1.设自然数从小到大为标准次序,则排列1 3 … )12(-n 2 4 … )2(n 的逆序数为 ,排列1 3 … )12(-n )2(n )22(-n …2的逆序数为 . 2.在6阶行列式中,651456314223a a a a a a 这项的符号为 . 3.所有n 元排列中,奇排列的个数共 个. 二、选择题1.由定义计算行列式nn 00000010020001000ΛΛΛΛΛΛΛΛΛΛ-= ( ). (A )!n(B )!)1(2)1(n n n --(C )!)1(2)2)(1(n n n --- (D )!)1()1(n n n --2.在函数xx x x xx f 21123232101)(=中,3x 的系数是( ).(A )1 (B )-1 (C )2 (D )33.四阶行列式的展开式中含有因子32a 的项,共有( )个. (A )4; (B )2; (C )6; (D )8.三、请按下列不同要求准确写出n 阶行列式)det(ij a D =定义式: 1. 各项以行标为标准顺序排列;2. 各项以列标为标准顺序排列;3. 各项行列标均以任意顺序排列.四、若n 阶行列式中,等于零的元素个数大于n n -2,则此行列式的值等于多少?说明理由.一、填空题1.若D=._____324324324,13332313123222121131211111333231232221131211=---==a a a a a a a a a a a a D a a a a a a a a a 则2.方程229132513232213211x x --=0的根为___________ .二、计算题 1. 8171160451530169144312----- 2.dc b a100110011001---3.abbb a b b b a D n ΛΛΛΛΛΛΛ=4.111113213211211211211nn n n n a a a a x a a a a x a a a a x a a a a x D ΛΛΛΛΛΛΛΛΛΛΛ---+=5.计算n 阶行列式)2(212121222111≥+++++++++=n nx x x n x x x n x x x D n n n n ΛΛΛΛΛΛΛ。
第一章行列式(学生题目简单答案版)
第二部分 线性代数第一章 行列式题型1.1 行列式的计算(88年,数学一)设4阶矩阵234234(,,,)(,,,)A B αγγγβγγγ==,,其中,234,,,,αβγγγ均为4维列向量,且已知行列式41A B ==,,则行列式A B += .【答案】40.(88年,数学三/数学四)1110110110110111= . 【答案】3-.(89年,数学五)行列式1111111111111111x x x x ---+-=--+-- . 【答案】4x .(90年,数学五)设A 为1010⨯矩阵 10010000010000001100000A ⎛⎫⎪⎪⎪= ⎪⎪ ⎪⎝⎭,计算行列式A E λ-,其中E 为10阶单位矩阵,λ为常数.【解析】101010A E λλ-=-.(91年,数学五)n 阶行列式0000000000000000a b a b a a b b a=.【答案】1(1)n n n a b ++-.(96年,数学一)四阶行列式112233440000000a b a b b a b a 的值等于(). (A )12341234a a a a b b b b -. (B )12341234a a a a b b b b +.(C )12123434()()a a b b a a b b --. (D )23231414()()a a b b a a b b --. 【答案】(D ).(96年,数学五)5阶行列式1000110001100011011a aaa D a a a a a---==------ . 【答案】23451a a a a a -+-+-.(97年,数学四)设n 阶矩阵0111110111110111110111110A ⎛⎫⎪⎪ ⎪=⎪ ⎪ ⎪⎪⎪⎝⎭,则A = .【答案】1(1)(1)n n ---.(99年,数学二)记行列式212322212223333245354435743x x x x x x x x x x x x x x x x ---------------为()f x ,则方程()0f x =的根的个数为().(A )1. (B )2. (C )3. (D )4. 【答案】(B ).(00年,数学四)设(1,0,1)T α=-,矩阵T A n αα=,为正整数,则n aE A -= . 【答案】2(2)n a a -.(01年,数学四)设行列式3040222207005322D =--,则第四行各元素余子式之和的值为 .【答案】28-.(14年,数学一/数学二/数学三)行列式00000000a b abc d c d=(). (A )2()ad bc -.(B )2()ad bc --.(C )2222a d b c -.(D )2222b c a d -.【答案】(B ).(15年,数学一)n 阶行列式200212020022012-=-. 【答案】122n +-.(16年,数学一/数学三)行列式10001=0014321λλλλ---+ . 【答案】43223 4.λλλλ++++题型1.2 行列式的计算(二)矩阵的性质(87年,数学一)设A 为n 阶方阵,且A 的行列式0A a =≠,而*A 是A 的伴随矩阵,则*A =().(A )a . (B )1a. (C )1n a -. (D )na . 【答案】(C ).(87年,数学四)设A 为n 阶方阵,k 为常数,则kA k A =.()【答案】(×).(88年,数学四)设A 是三阶方阵,*A 是A 的伴随矩阵,A 的行列式12A =.求行列式1*(3)2A A --的值.【解析】31*12(3)23A A A --⎛⎫-=- ⎪⎝⎭1627=-.(90年,数学五)设A 为n 阶可逆矩阵,*A 是A 的伴随矩阵,则*A =().(A )1n A-. (B )A . (C )n A . (D )1A-.【答案】(A ).(92年,数学四)设A 为m 阶方阵,B 为n 阶方阵,且00A A a B b C B ⎛⎫=== ⎪⎝⎭,,,则C = .【答案】(1)mn ab -.(92年,数学五)已知实矩阵33()ij A a ⨯=满足条件:(Ⅰ)(,1,2,3)ij ij a A i j ==,其中ij A 是ij a 的代数余子式; (Ⅱ)110a ≠. 计算行列式A .【解析】1A =.(93年,数学五)若12312,,,,αααββ都是四维列向量,且四阶行列式1231,,,,m αααβ=1223,,,,n ααβα=则四阶行列式32112,,,()αααββ+等于().(A )m n +. (B )()m n -+. (C )n m -. (D )m n -. 【答案】(C ).(94年,数学一)设A 为n 阶非零方阵,*A 是A 的伴随矩阵,T A 是A 的转置矩阵,当*T A A =时,证明0A ≠.【证明】略. .(95年,数学一)设A 是n 阶矩阵,满足T AA E =(E 是n 阶单位矩阵,T A 是A 的转置矩阵),0A <,求A E +.【解析】0A E +=.(98年,数学四)设,A B 均为n 阶矩阵,23A B ==-,,则*12A B -= .【答案】2123n --.(03年,数学二)设三阶方阵,A B 满足2A B A B E --=,其中E 为三阶单位矩阵,若101020201A ⎛⎫ ⎪= ⎪ ⎪-⎝⎭,则B = .【答案】12.(04年,数学一/数学二)设矩阵210120001A ⎛⎫ ⎪= ⎪ ⎪⎝⎭,矩阵B 满足**2ABA BA E =+,其中*A 为A 的伴随矩阵,E 是单位矩阵,则B = .【答案】19.(05年,数学一/数学二/数学四)设123,,ααα均为三维列向量,记矩阵123(,,)A ααα=,123123123(2439)B ααααααααα=++++++,,.如果1A =,那么B = .【答案】2.(06年,数学一/数学二)设矩阵2112A E ⎛⎫=⎪-⎝⎭,为二阶单位矩阵,矩阵B 满足2BA B E =+,则B = .【答案】2.(06年,数学四)已知12,αα为二维列向量,矩阵1212(2,)A αααα=+-,12(,)B αα=.若行列式,6A =,则B = .【答案】2-.(10年,数学二/数学三)设,A B 为3阶矩阵,且1322A B A B -==+=,,,则1A B -+= .【答案】3.(12年,数学二/数学三)设A 为3阶矩阵,且*3A A =,为A 的伴随矩阵,若交换A 的第一行与第二行得矩阵B ,则*BA = .【答案】27-.(13年,数学一/数学二/数学三)设()ij A a =是3阶非零矩阵,A 为A 的行列式,ijA 为ij a 的代数余子式.若0(123)ij ij a A i j +==,,,,则A = . 【答案】1-.题型1.3 行列式的计算(三)秩数,特征值的性质(91年,数学一)设A 是n 阶正定矩阵,E 是n 阶单位矩阵,证明A E +的行列式大于1. 【证明】略.(98年,数学三)齐次线性方程组2123123123000x x x x x x x x x λλλλ⎧++=⎪++=⎨⎪++=⎩,,,的系数矩阵记为A ,若存在3阶矩阵B O ≠,使得AB O =,则().(A )2λ=-且0B =. (B )2λ=-且0B ≠. (C )1λ=且0B =. (D )1λ=且0B ≠. 【答案】(C ).(99年,数学一/数学二)设A 是m n ⨯矩阵,B 是n m ⨯矩阵,则().(A )当m n >时,必有行列式0AB ≠. (B )当m n >时,必有行列式0AB =.(C )当n m >时,必有行列式0AB ≠. (D )当n m >时,必有行列式0AB =. 【答案】(B ).(00年,数学三)若四阶矩阵A 与B 相似,矩阵A 的特征值为1111,,,2345,则行列式1B E --= .【答案】24.(00年,数学四)已知四阶矩阵A 相似于,B A 的特征值为2,3,4,5.E 为四阶单位矩阵,则B E -= .【答案】24.(08年,数学三)设3阶矩阵A 的特征值是1,2,2,E 为3阶单位矩阵,则14A E --= .【答案】3.(15年,数学二/数学三)设3阶矩阵A 的特征值为2221B A A E -=-+,,,,其中E 为3阶单位矩阵,则行列式B = .【答案】21.。
(完整版)第一章行列式试题及答案

第一章 行列式试题及答案一 选择题 (每小题3分,共30分)⑴ n 元排列 i 1 i 2… i n 经过相邻对换,变为i n … i 2 i 1,则相邻对换的次数为( )(A) n (B) n /2 (C) 2n(D) n (n -1)/2⑵ 在函数()xx x x x x f 2142112---=中,x 3的系数是( )(A) -2 (B) 2 (C) -4 (D) 4⑶ 若D n =det(a ij )=1,则det(-a ij ) = ( )(A) 1 (B) -1 (C) (-1)n (D) (-1)n(n -1)/2⑷ 设nn λλλλλλNO2121=,则n 不可取下面的值是( )(A)7 (B) 2k +1(k ≥2) (C) 2k (k ≥2) (D) 17⑸ 下列行列式等于零的是( )(A)100123123- (B) 031010300- (C) 100003010- (D) 261422613-⑹ 行列式D 非零的充分条件是( ) (A) D 的所有元素非零 (B) D 至少有n 个元素非零 (C) D 的任何两行元素不成比例(D)以D 为系数矩阵的非齐次线性方程组有唯一解 ⑺ =+++111222c bcacbc b ab ac ab a ( )(A) 100010001222+c bc ac bc b ab ac ab a (B) 1111122222+++++c bc ac bc b ab ac ab c bc ac bc b ab ac ab a(C) 101011122222+++++c bc bc b ac abc bc ac bc b ab ac aba(D) 111222bc ac bc ab acab c bc ac bc b ab acab a+⑻ 设a ,b ,c 两两不同,则0222=+++c b a c b a ba a c cb 的充要条件是( )(A) abc =0 (B) a+b+c =0 (C) a =1, b =-1, c =0 (D) a 2=b 2, c =0⑼ 四阶行列式=44332211a b a b b a b a ( )(A) (a 1a 2- b 1b 2) (a 3a 4- b 3b 4) (B) (a 1a 4- b 1b 4) (a 2a 3- b 2b 3) (C) (a 1b 2- a 2b 1) (a 3b 4- a 4b 3) (D) (a 1b 4- a 4b 1) (a 2b 3- a 3b 2)⑽ 齐次线性方程组⎪⎩⎪⎨⎧=-+=+-=-+0302022321321321x x x x x x x x x λ只有零解,则λ应满足的条件是( )(A) λ=0 (B) λ=2 (C) λ=1 (D) λ≠1二 填空 (每小题3分,共15分)⑴ 在五阶行列式中,3524415312a a a a a 的符号是_________。
(完整版)线性代数课后习题答案第1——5章习题详解

第一章 行列式4.计算下列各行列式:(1)⎥⎥⎥⎥⎦⎥⎢⎢⎢⎢⎣⎢7110025*********4; (2)⎥⎥⎥⎥⎦⎥⎢⎢⎢⎢⎣⎢-265232112131412; (3)⎥⎥⎦⎥⎢⎢⎣⎢---ef cf bf de cd bd ae ac ab ; (4)⎥⎥⎥⎥⎦⎥⎢⎢⎢⎢⎣⎢---d c b a100110011001解(1)7110025102021421434327c c c c --0100142310202110214---=34)1(143102211014+-⨯---=143102211014-- 321132c c c c ++1417172001099-=0(2)2605232112131412-24c c -2605032122130412-24r r -0412032122130412- 14r r -0000032122130412-=0(3)ef cf bf de cd bd ae ac ab ---=ec b e c b ec b adf ---=111111111---adfbce =abcdef 4(4)d c b a 100110011001---21ar r +dc b a ab 100110011010---+=12)1)(1(+--dc a ab 10111--+23dc c +010111-+-+cd c ada ab =23)1)(1(+--cdadab +-+111=1++++ad cd ab abcd5.证明: (1)1112222b b a a b ab a +=3)(b a -; (2)bz ay by ax bx az by ax bx az bz ay bx az bz ay by ax +++++++++=y x z x z y z y x b a )(33+;(3)0)3()2()1()3()2()1()3()2()1()3()2()1(2222222222222222=++++++++++++d d d d c c c c b b b b a a a a ;(4)444422221111d c b a d c b a d c b a ))()()()((d b c b d a c a b a -----=))((d c b a d c +++-⋅;(5)1221100000100001a x a a a a x x x n n n +-----n n n n a x a x a x ++++=--111 . 证明(1)00122222221312a b a b a a b a ab a c c c c ------=左边a b a b a b a ab 22)1(22213-----=+21))((a b a a b a b +--=右边=-=3)(b a(2)bz ay by ax z by ax bx az y bx az bz ay x a ++++++分开按第一列左边bzay by ax x by ax bx az z bxaz bz ay y b +++++++ ++++++002y by ax z x bx az y z bz ay x a 分别再分bzay y x by ax x z bxaz z y b +++z y x y x z x z y b y x z x z y z y x a 33+分别再分右边=-+=233)1(yx z x z y zy x b y x z x z y z y x a(3) 2222222222222222)3()2()12()3()2()12()3()2()12()3()2()12(++++++++++++++++=d d d d d c c c c c b b b b b a a a a a 左边9644129644129644129644122222141312++++++++++++---d d d d c c c c b b b b a a a a c c c c c c 964496449644964422222++++++++d d d d c c c c b b b b a a a a 分成二项按第二列964419644196441964412222+++++++++d d d c c c b b b a a a 949494949464222224232423d d c c b b a a c c c c c c c c ----第二项第一项06416416416412222=+ddd c c c bb b a a a (4) 444444422222220001ad a c a b a ad a c a b a ad a c a b a ---------=左边=)()()(222222222222222a d d a c c a b b a d a c a b ad a c a b --------- =)()()(111))()((222a d d a c c a b b a d a c ab a d ac a b ++++++--- =⨯---))()((ad a c a b )()()()()(00122222a b b a d d a b b a c c a b b bd b c a b +-++-++--+ =⨯-----))()()()((b d b c a d a c a b )()()()(112222b d a b bd d b c a b bc c ++++++++=))()()()((d b c b d a c a b a -----))((d c b a d c +++-(5) 用数学归纳法证明.,1,2212122命题成立时当a x a x a x a x D n ++=+-==假设对于)1(-n 阶行列式命题成立,即 ,122111-----++++=n n n n n a x a x a x D:1列展开按第则n D1110010001)1(11----+=+-x xa xD D n n n n 右边=+=-n n a xD 1 所以,对于n 阶行列式命题成立.6.设n 阶行列式)det(ij a D =,把D 上下翻转、或逆时针旋转 90、或依副对角线翻转,依次得n nn n a a a a D 11111 =, 11112n nn n a a a a D = ,11113a a a a D n nnn =,证明D D D D D n n =-==-32)1(21,)1(.证明 )det(ij a D =nnn n nn n nn n a a a a a a a a a a D 2211111111111)1(--==∴ =--=--nnn n nnn n a a a a a a a a 331122111121)1()1( nnn n n n a a a a 111121)1()1()1(---=--D D n n n n 2)1()1()2(21)1()1(--+-+++-=-=同理可证nnn n n n a a a a D 11112)1(2)1(--=D D n n T n n 2)1(2)1()1()1(---=-= D D D D D n n n n n n n n =-=--=-=----)1(2)1(2)1(22)1(3)1()1()1()1(7.计算下列各行列式(阶行列式为k D k ):(1)a aD n 11=,其中对角线上元素都是a ,未写出的元素都是0;(2)xaaax aa a x D n=; (3) 1111)()1()()1(1111n a a a n a a a n a a a D n n n n n n n ------=---+; 提示:利用范德蒙德行列式的结果. (4) nnnnn d c d c b a b a D000011112=; (5)j i a a D ij ij n -==其中),det(;(6)nn a a a D +++=11111111121 ,021≠n a a a 其中.解(1) aa a a a D n 00010000000000001000 =按最后一行展开)1()1(100000000000010000)1(-⨯-+-n n n aa a)1)(1(2)1(--⋅-+n n na aa(再按第一行展开)n n n nn a a a+-⋅-=--+)2)(2(1)1()1(2--=n n a a )1(22-=-a a n(2)将第一行乘)1(-分别加到其余各行,得ax x a ax x a a x x a aa a x D n ------=0000000 再将各列都加到第一列上,得ax ax a x aaa a n x D n ----+=000000000)1( )(])1([1a x a n x n --+=- (3) 从第1+n 行开始,第1+n 行经过n 次相邻对换,换到第1行,第n 行经)1(-n 次对换换到第2行…,经2)1(1)1(+=++-+n n n n 次行交换,得 nn n n n n n n n n a a a n a a a n a a aD )()1()()1(1111)1(1112)1(1-------=---++此行列式为范德蒙德行列式∏≥>≥++++--+--=112)1(1)]1()1[()1(j i n n n n j a i a D∏∏≥>≥+++-++≥>≥++-•-•-=---=111)1(2)1(112)1()][()1()1()]([)1(j i n n n n n j i n n n j i j i∏≥>≥+-=11)(j i n j i(4) nn nnn d c d c b a b a D 011112=nn n n n nd d c d c b a b a a 0000000011111111----展开按第一行0000)1(1111111112c d c d c b a b a b nn n n n nn ----+-+2222 ---n n n n n n D c b D d a 都按最后一行展开由此得递推公式:222)(--=n n n n n n D c b d a D即 ∏=-=ni i i iin D c b da D 222)(而 111111112c b d a d c b a D -==得 ∏=-=ni i i i i n c b d a D 12)((5)j i a ij -=432140123310122210113210)det( --------==n n n n n n n n a D ij n ,3221r r r r --0432111111111111111111111 --------------n n n n,,141312c c c c c c +++152423210222102210002100001---------------n n n n n =212)1()1(----n n n(6)nn a a D a +++=11111111121,,433221c c c c c c ---n n n n a a a a a a a a a a +-------10000100010000100010001000011433221 展开(由下往上)按最后一列))(1(121-+n n a a a a nn n a a a a a a a a a --------00000000000000000000000000022433221 nn n a a a a a a a a ----+--000000000000000001133221 ++ nn n a a a a a a a a -------000000000000000001143322n n n n n n a a a a a a a a a a a a 322321121))(1(++++=---)11)((121∑=+=ni in a a a a8.用克莱姆法则解下列方程组:⎪⎪⎩⎪⎪⎨⎧=+++-=----=+-+=+++;01123,2532,242,5)1(4321432143214321x x x x x x x x x x x x x x x x ⎪⎪⎪⎩⎪⎪⎪⎨⎧=+=++=++=++=+.15,065,065,065,165)2(5454343232121x x x x x x x x x x x x x解 (1)11213513241211111----=D 8120735032101111------=145008130032101111---=1421420005410032101111-=---= 112105132412211151------=D 11210513290501115----=1121023313090509151------=2331309050112109151------=1202300461000112109151-----=14200038100112109151----=142-=112035122412111512-----=D 811507312032701151-------=3139011230023101151-=2842840001910023101151-=----=426110135232422115113-=----=D ; 14202132132212151114=-----=D1,3,2,144332211-========∴DDx D D x D D x D D x (2) 510006510006510006510065=D 展开按最后一行61000510065100655-'D D D ''-'=65 D D D ''-'''-''=6)65(5D D '''-''=3019D D ''''-'''=1146566551141965=⨯-⨯=(,11的余子式中为行列式a D D ',11的余子式中为a D D ''''类推D D ''''''',) 51001651000651000650000611=D 展开按第一列6510065100650006+'D 46+'=D 460319+''''-'''=D 1507=51010651000650000601000152=D 展开按第二列5100651006500061-6510065000610005-365510651065⨯-= 1145108065-=--=51100650000601000051001653=D 展开按第三列51006500061000516500061000510065+6100510656510650061+= 703114619=⨯+=51000601000051000651010654=D 展开按第四列61000510065100655000610005100651--51065106565--=395-= 110051000651000651100655=D 展开按最后一列D '+10005100651006512122111=+= 665212;665395;665703;6651145;665150744321=-==-==∴x x x x x . 9.齐次线性方程组取何值时问,,μλ⎪⎩⎪⎨⎧=++=++=++0200321321321x x x x x x x x x μμλ有非零解?解 μλμμμλ-==12111113D , 齐次线性方程组有非零解,则03=D即 0=-μλμ 得 10==λμ或不难验证,当,10时或==λμ该齐次线性方程组确有非零解.10.齐次线性方程组取何值时问,λ⎪⎩⎪⎨⎧=-++=+-+=+--0)1(0)3(2042)1(321321321x x x x x x x x x λλλ 有非零解?解λλλ----=111132421D λλλλ--+--=101112431)3)(1(2)1(4)3()1(3λλλλλ-------+-=3)1(2)1(23-+-+-=λλλ 齐次线性方程组有非零解,则0=D得 32,0===λλλ或不难验证,当32,0===λλλ或时,该齐次线性方程组确有非零解.第二章 矩阵及其运算1. 已知线性变换:⎪⎩⎪⎨⎧++=++=++=3213321232113235322y y y x y y y x y y y x ,求从变量x 1, x 2, x 3到变量y 1, y 2, y 3的线性变换.解 由已知:⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛221321323513122y y y x x x , 故 ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-3211221323513122x x x y y y ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛----=321423736947y y y , ⎪⎩⎪⎨⎧-+=-+=+--=321332123211423736947x x x y x x x y x x x y .2. 已知两个线性变换⎪⎩⎪⎨⎧++=++-=+=32133212311542322y y y x y y y x y y x , ⎪⎩⎪⎨⎧+-=+=+-=323312211323z z y z z y z z y , 求从z 1, z 2, z 3到x 1, x 2, x 3的线性变换.解 由已知⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛221321514232102y y y x x x ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-=321310102013514232102z z z⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛----=321161109412316z z z , 所以有⎪⎩⎪⎨⎧+--=+-=++-=3213321232111610941236z z z x z z z x z z z x .3. 设⎪⎪⎭⎫ ⎝⎛--=111111111A , ⎪⎪⎭⎫⎝⎛--=150421321B , 求3AB -2A 及A T B . 解 ⎪⎪⎭⎫⎝⎛---⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=-1111111112150421321111111111323A AB ⎪⎪⎭⎫⎝⎛----=⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛-=2294201722213211111111120926508503, ⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=092650850150421321111111111B A T . 4. 计算下列乘积:(1)⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-127075321134; 解 ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-127075321134⎪⎪⎭⎫ ⎝⎛⨯+⨯+⨯⨯+⨯-+⨯⨯+⨯+⨯=102775132)2(71112374⎪⎪⎭⎫ ⎝⎛=49635. (2)⎪⎪⎭⎫⎝⎛123)321(; 解 ⎪⎪⎭⎫⎝⎛123)321(=(1⨯3+2⨯2+3⨯1)=(10).(3))21(312-⎪⎪⎭⎫⎝⎛; 解 )21(312-⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛⨯-⨯⨯-⨯⨯-⨯=23)1(321)1(122)1(2⎪⎪⎭⎫ ⎝⎛---=632142. (4)⎪⎪⎪⎭⎫ ⎝⎛---⎪⎭⎫ ⎝⎛-20413121013143110412 ; 解 ⎪⎪⎪⎭⎫ ⎝⎛---⎪⎭⎫ ⎝⎛-20413121013143110412⎪⎭⎫ ⎝⎛---=6520876. (5)⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛321332313232212131211321)(x x x a a a a a a a a a x x x ; 解⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛321332313232212131211321)(x x x a a a a a a a a a x x x =(a 11x 1+a 12x 2+a 13x 3 a 12x 1+a 22x 2+a 23x 3 a 13x 1+a 23x 2+a 33x 3)⎪⎪⎭⎫ ⎝⎛321x x x322331132112233322222111222x x a x x a x x a x a x a x a +++++=.5. 设⎪⎭⎫ ⎝⎛=3121A , ⎪⎭⎫ ⎝⎛=2101B , 问: (1)AB =BA 吗?解 AB ≠BA .因为⎪⎭⎫ ⎝⎛=6443AB , ⎪⎭⎫ ⎝⎛=8321BA , 所以AB ≠BA .(2)(A +B)2=A 2+2AB +B 2吗?解 (A +B)2≠A 2+2AB +B 2.因为⎪⎭⎫ ⎝⎛=+5222B A , ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=+52225222)(2B A ⎪⎭⎫ ⎝⎛=2914148, 但 ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=++43011288611483222B AB A ⎪⎭⎫ ⎝⎛=27151610, 所以(A +B)2≠A 2+2AB +B 2.(3)(A +B)(A -B)=A 2-B 2吗?解 (A +B)(A -B)≠A 2-B 2.因为⎪⎭⎫ ⎝⎛=+5222B A , ⎪⎭⎫ ⎝⎛=-1020B A , ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=-+906010205222))((B A B A , 而 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=-718243011148322B A , 故(A +B)(A -B)≠A 2-B 2.6. 举反列说明下列命题是错误的:(1)若A 2=0, 则A =0;解 取⎪⎭⎫ ⎝⎛=0010A , 则A 2=0, 但A ≠0. (2)若A 2=A , 则A =0或A =E ;解 取⎪⎭⎫ ⎝⎛=0011A , 则A 2=A , 但A ≠0且A ≠E . (3)若AX =AY , 且A ≠0, 则X =Y .解 取⎪⎭⎫ ⎝⎛=0001A , ⎪⎭⎫ ⎝⎛-=1111X , ⎪⎭⎫ ⎝⎛=1011Y , 则AX =AY , 且A ≠0, 但X ≠Y .7. 设⎪⎭⎫ ⎝⎛=101λA , 求A 2, A 3, ⋅ ⋅ ⋅, A k . 解 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=12011011012λλλA , ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛==1301101120123λλλA A A , ⋅ ⋅ ⋅ ⋅ ⋅ ⋅,⎪⎭⎫ ⎝⎛=101λk A k . 8. 设⎪⎪⎭⎫⎝⎛=λλλ001001A , 求A k . 解 首先观察⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=λλλλλλ0010010010012A ⎪⎪⎭⎫ ⎝⎛=222002012λλλλλ, ⎪⎪⎭⎫ ⎝⎛=⋅=3232323003033λλλλλλA A A , ⎪⎪⎭⎫ ⎝⎛=⋅=43423434004064λλλλλλA A A ,⎪⎪⎭⎫ ⎝⎛=⋅=545345450050105λλλλλλA A A , ⋅ ⋅ ⋅ ⋅ ⋅ ⋅,⎝⎛=k A k k k k k k k k k k λλλλλλ0002)1(121----⎪⎪⎪⎭⎫ . 用数学归纳法证明:当k =2时, 显然成立.假设k 时成立,则k +1时,⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎭⎫ ⎝⎛-=⋅=---+λλλλλλλλλ0010010002)1(1211k k k k k k k k k k k k A A A ⎪⎪⎪⎪⎭⎫ ⎝⎛+++=+-+--+11111100)1(02)1()1(k k k k k k k k k k λλλλλλ, 由数学归纳法原理知:⎪⎪⎪⎪⎭⎫ ⎝⎛-=---k k k k k k k k k k k A λλλλλλ0002)1(121. 9. 设A , B 为n 阶矩阵,且A 为对称矩阵,证明B T AB 也是对称矩阵. 证明 因为A T =A , 所以(B T AB)T =B T (B T A)T =B T A T B =B T AB ,从而B T AB 是对称矩阵.10. 设A , B 都是n 阶对称矩阵,证明AB 是对称矩阵的充分必要条件是AB =BA . 证明 充分性: 因为A T =A , B T =B , 且AB =BA , 所以(AB)T =(BA)T =A T B T =AB ,即AB 是对称矩阵.必要性: 因为A T =A , B T =B , 且(AB)T =AB , 所以AB =(AB)T =B T A T =BA .11. 求下列矩阵的逆矩阵:(1)⎪⎭⎫ ⎝⎛5221; 解 ⎪⎭⎫ ⎝⎛=5221A . |A|=1, 故A -1存在. 因为 ⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛=1225*22122111A A A A A , 故*||11A A A =-⎪⎭⎫ ⎝⎛--=1225. (2)⎪⎭⎫ ⎝⎛-θθθθcos sin sin cos ; 解⎪⎭⎫ ⎝⎛-=θθθθcos sin sin cos A . |A|=1≠0, 故A -1存在. 因为 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛=θθθθcos sin sin cos *22122111A A A A A , 所以*||11A A A =-⎪⎭⎫ ⎝⎛-=θθθθcos sin sin cos . (3)⎪⎪⎭⎫⎝⎛---145243121; 解 ⎪⎪⎭⎫ ⎝⎛---=145243121A . |A|=2≠0, 故A -1存在. 因为 ⎪⎪⎭⎫ ⎝⎛-----=⎪⎪⎭⎫ ⎝⎛=214321613024*332313322212312111A A A A A A A A A A , 所以 *||11A A A =-⎪⎪⎪⎭⎫ ⎝⎛-----=1716213213012.(4)⎪⎪⎪⎭⎫ ⎝⎛n a a a 0021(a 1a 2⋅ ⋅ ⋅a n≠0) .解 ⎪⎪⎪⎭⎫ ⎝⎛=n a a a A 0021, 由对角矩阵的性质知⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=-n a a a A 10011211 . 12. 解下列矩阵方程:(1)⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛12643152X ; 解 ⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=-126431521X ⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛--=12642153⎪⎭⎫ ⎝⎛-=80232. (2)⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛--234311*********X ; 解 1111012112234311-⎪⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛-=X⎪⎪⎭⎫ ⎝⎛---⎪⎭⎫ ⎝⎛-=03323210123431131 ⎪⎪⎭⎫ ⎝⎛---=32538122. (3)⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-101311022141X ;解 11110210132141--⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=X⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=210110131142121 ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=21010366121⎪⎪⎭⎫ ⎝⎛=04111. (4)⎪⎪⎭⎫⎝⎛---=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛021102341010100001100001010X . 解 11010100001021102341100001010--⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛=X⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛=010100001021102341100001010⎪⎪⎭⎫ ⎝⎛---=201431012. 13. 利用逆矩阵解下列线性方程组:(1)⎪⎩⎪⎨⎧=++=++=++3532522132321321321x x x x x x x x x ;解 方程组可表示为⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛321153522321321x x x , 故 ⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-0013211535223211321x x x , 从而有 ⎪⎩⎪⎨⎧===001321x x x .(2)⎪⎩⎪⎨⎧=-+=--=--05231322321321321x x x x x x x x x .解 方程组可表示为⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-----012523312111321x x x ,故 ⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-----=⎪⎪⎭⎫ ⎝⎛-3050125233121111321x x x , 故有 ⎪⎩⎪⎨⎧===305321x x x .14. 设A k =O (k 为正整数), 证明(E -A)-1=E +A +A 2+⋅ ⋅ ⋅+A k -1. 证明 因为A k =O , 所以E -A k =E . 又因为 E -A k =(E -A)(E +A +A 2+⋅ ⋅ ⋅+A k -1),所以 (E -A)(E +A +A 2+⋅ ⋅ ⋅+A k -1)=E , 由定理2推论知(E -A)可逆, 且(E -A)-1=E +A +A 2+⋅ ⋅ ⋅+A k -1.证明 一方面, 有E =(E -A)-1(E -A). 另一方面, 由A k =O , 有E =(E -A)+(A -A 2)+A 2-⋅ ⋅ ⋅-A k -1+(A k -1-A k ) =(E +A +A 2+⋅ ⋅ ⋅+A k -1)(E -A),故 (E -A)-1(E -A)=(E +A +A 2+⋅ ⋅ ⋅+A k -1)(E -A), 两端同时右乘(E -A)-1, 就有(E -A)-1(E -A)=E +A +A 2+⋅ ⋅ ⋅+A k -1.15. 设方阵A 满足A 2-A -2E =O , 证明A 及A +2E 都可逆, 并求A -1及(A +2E)-1.证明 由A 2-A -2E =O 得 A 2-A =2E , 即A(A -E)=2E ,或E E A A =-⋅)(21,由定理2推论知A 可逆, 且)(211E A A -=-.由A 2-A -2E =O 得A 2-A -6E =-4E , 即(A +2E)(A -3E)=-4E ,或E A E E A =-⋅+)3(41)2(由定理2推论知(A +2E)可逆, 且)3(41)2(1A E E A -=+-.证明 由A 2-A -2E =O 得A 2-A =2E , 两端同时取行列式得 |A 2-A|=2,即 |A||A -E|=2, 故 |A|≠0,所以A 可逆, 而A +2E =A 2, |A +2E|=|A 2|=|A|2≠0, 故A +2E 也可逆. 由 A 2-A -2E =O ⇒A(A -E)=2E⇒A -1A(A -E)=2A -1E ⇒)(211E A A -=-,又由 A 2-A -2E =O ⇒(A +2E)A -3(A +2E)=-4E⇒ (A +2E)(A -3E)=-4 E ,所以 (A +2E)-1(A +2E)(A -3E)=-4(A +2 E)-1,)3(41)2(1A E E A -=+-.16. 设A 为3阶矩阵,21||=A , 求|(2A)-1-5A*|.解 因为*||11A A A =-, 所以|||521||*5)2(|111----=-A A A A A |2521|11---=A A=|-2A -1|=(-2)3|A -1|=-8|A|-1=-8⨯2=-16. 17. 设矩阵A 可逆, 证明其伴随阵A*也可逆, 且(A*)-1=(A -1)*.证明 由*||11A A A =-, 得A*=|A|A -1, 所以当A 可逆时, 有|A*|=|A|n |A -1|=|A|n -1≠0,从而A*也可逆.因为A*=|A|A -1, 所以 (A*)-1=|A|-1A .又*)(||)*(||1111---==A A A A A , 所以(A*)-1=|A|-1A =|A|-1|A|(A -1)*=(A -1)*. 18. 设n 阶矩阵A 的伴随矩阵为A*, 证明: (1)若|A|=0, 则|A*|=0; (2)|A*|=|A|n -1. 证明(1)用反证法证明. 假设|A*|≠0, 则有A*(A*)-1=E , 由此得 A =A A*(A*)-1=|A|E(A*)-1=O ,所以A*=O , 这与|A*|≠0矛盾,故当|A|=0时, 有|A*|=0.(2)由于*||11A A A =-, 则AA*=|A|E , 取行列式得到|A||A*|=|A|n . 若|A|≠0, 则|A*|=|A|n -1;若|A|=0, 由(1)知|A*|=0, 此时命题也成立. 因此|A*|=|A|n -1.19. 设⎪⎪⎭⎫⎝⎛-=321011330A , AB =A +2B , 求B .解 由AB =A +2E 可得(A -2E)B =A , 故⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛---=-=--321011330121011332)2(11A E A B ⎪⎪⎭⎫ ⎝⎛-=011321330.20. 设⎪⎪⎭⎫⎝⎛=101020101A , 且AB +E =A 2+B , 求B .解 由AB +E =A 2+B 得 (A -E)B =A 2-E ,即 (A -E)B =(A -E)(A +E).因为01001010100||≠-==-E A , 所以(A -E)可逆, 从而⎪⎪⎭⎫⎝⎛=+=201030102E A B .21. 设A =diag(1, -2, 1), A*BA =2BA -8E , 求B . 解 由A*BA =2BA -8E 得 (A*-2E)BA =-8E , B =-8(A*-2E)-1A -1 =-8[A(A*-2E)]-1 =-8(AA*-2A)-1 =-8(|A|E -2A)-1 =-8(-2E -2A)-1 =4(E +A)-1=4[diag(2, -1, 2)]-1)21 ,1 ,21(diag 4-==2diag(1, -2, 1).22. 已知矩阵A 的伴随阵⎪⎪⎪⎭⎫⎝⎛-=8030010100100001*A , 且ABA -1=BA -1+3E , 求B .解 由|A*|=|A|3=8, 得|A|=2. 由ABA -1=BA -1+3E 得 AB =B +3A ,B =3(A -E)-1A =3[A(E -A -1)]-1A11*)2(6*)21(3---=-=A E A E⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫⎝⎛--=-1030060600600006603001010010000161. 23. 设P -1AP =Λ, 其中⎪⎭⎫ ⎝⎛--=1141P , ⎪⎭⎫ ⎝⎛-=Λ2001, 求A 11.解 由P -1AP =Λ, 得A =P ΛP -1, 所以A 11= A=P Λ11P -1.|P|=3,⎪⎭⎫ ⎝⎛-=1141*P , ⎪⎭⎫ ⎝⎛--=-1141311P ,而 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫⎝⎛-=Λ11111120 012001,故⎪⎪⎪⎭⎫⎝⎛--⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛--=31313431200111411111A ⎪⎭⎫ ⎝⎛--=68468327322731.24. 设AP =P Λ, 其中⎪⎪⎭⎫⎝⎛--=111201111P , ⎪⎪⎭⎫ ⎝⎛-=Λ511, 求ϕ(A)=A 8(5E -6A +A 2).解 ϕ(Λ)=Λ8(5E -6Λ+Λ2)=diag(1,1,58)[diag(5,5,5)-diag(-6,6,30)+diag(1,1,25)] =diag(1,1,58)diag(12,0,0)=12diag(1,0,0). ϕ(A)=P ϕ(Λ)P -1*)(||1P P P Λ=ϕ ⎪⎪⎭⎫⎝⎛------⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---=1213032220000000011112011112⎪⎪⎭⎫⎝⎛=1111111114.25. 设矩阵A 、B 及A +B 都可逆, 证明A -1+B -1也可逆, 并求其逆阵. 证明 因为A -1(A +B)B -1=B -1+A -1=A -1+B -1,而A -1(A +B)B -1是三个可逆矩阵的乘积, 所以A -1(A +B)B -1可逆, 即A -1+B -1可逆.(A -1+B -1)-1=[A -1(A +B)B -1]-1=B(A +B)-1A .26. 计算⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫⎝⎛30003200121013013000120010100121. 解 设⎪⎭⎫ ⎝⎛=10211A , ⎪⎭⎫ ⎝⎛=30122A , ⎪⎭⎫ ⎝⎛-=12131B , ⎪⎭⎫ ⎝⎛--=30322B ,则⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛2121B O B E A O E A ⎪⎭⎫ ⎝⎛+=222111B A O B B A A ,而⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛--+⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=+4225303212131021211B B A ,⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛=90343032301222B A ,所以 ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛2121B O B E A O E A ⎪⎭⎫ ⎝⎛+=222111B A O B B A A ⎪⎪⎪⎭⎫ ⎝⎛---=9000340042102521, 即 ⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫⎝⎛30003200121013013000120010100121⎪⎪⎪⎭⎫ ⎝⎛---=9000340042102521. 27. 取⎪⎭⎫ ⎝⎛==-==1001D C B A , 验证|||||||| D C B A D C B A ≠.解4100120021100101002000021010010110100101==--=--=D C B A , 而01111|||||||| ==D C B A , 故|||||||| D C B A D C B A ≠. 28. 设⎪⎪⎪⎭⎫ ⎝⎛-=22023443O O A , 求|A 8|及A 4. 解 令⎪⎭⎫ ⎝⎛-=34431A , ⎪⎭⎫ ⎝⎛=22022A ,则⎪⎭⎫⎝⎛=21A O O A A ,故8218⎪⎭⎫ ⎝⎛=A O O A A ⎪⎭⎫ ⎝⎛=8281A O O A ,1682818281810||||||||||===A A A A A .⎪⎪⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=464444241422025005O O A O O A A . 29. 设n 阶矩阵A 及s 阶矩阵B 都可逆, 求(1)1-⎪⎭⎫ ⎝⎛O B A O ;解 设⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-43211C C C C O B A O , 则⎪⎭⎫ ⎝⎛O B A O ⎪⎭⎫ ⎝⎛4321C C C C ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=s n E O O E BC BC AC AC 2143. 由此得 ⎪⎩⎪⎨⎧====s n E BC O BC O AC E AC 2143⇒⎪⎩⎪⎨⎧====--121413B C O C O C A C ,所以 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛---O A B O O B A O 111. (2)1-⎪⎭⎫ ⎝⎛B C O A .解 设⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-43211D D D D B C O A , 则⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛++=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛s n E O O E BD CD BD CD AD AD D D D D B C O A 4231214321. 由此得 ⎪⎩⎪⎨⎧=+=+==s n E BD CD O BD CD O AD E AD 423121⇒⎪⎩⎪⎨⎧=-===----14113211B D CA B D O D A D ,所以 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-----11111B CA B O A BC O A . 30. 求下列矩阵的逆阵:(1)⎪⎪⎪⎭⎫⎝⎛2500380000120025; 解 设⎪⎭⎫ ⎝⎛=1225A , ⎪⎭⎫ ⎝⎛=2538B , 则⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛=--5221122511A , ⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛=--8532253811B .于是 ⎪⎪⎪⎭⎫ ⎝⎛----=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫⎝⎛----850032000052002125003800001200251111B A B A .(2)⎪⎪⎪⎭⎫⎝⎛4121031200210001. 解 设⎪⎭⎫ ⎝⎛=2101A , ⎪⎭⎫ ⎝⎛=4103B , ⎪⎭⎫ ⎝⎛=2112C , 则⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫⎝⎛------1111114121031200210001B CA B O A BC O A⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-----=411212458103161210021210001.第三章 矩阵的初等变换与线性方程组1.把下列矩阵化为行最简形矩阵:(1) ⎪⎪⎪⎭⎫ ⎝⎛--340313021201; (2)⎪⎪⎪⎭⎫⎝⎛----174034301320; (3) ⎪⎪⎪⎪⎭⎫⎝⎛---------12433023221453334311; (4)⎪⎪⎪⎪⎭⎫⎝⎛------34732038234202173132.解 (1) ⎪⎪⎪⎭⎫ ⎝⎛--340313*********2)3()2(~r r r r -+-+⎪⎪⎪⎭⎫ ⎝⎛---020*********)2()1(32~-÷-÷r r ⎪⎪⎪⎭⎫ ⎝⎛--01003100120123~r r -⎪⎪⎪⎭⎫⎝⎛--300031001201 33~÷r ⎪⎪⎪⎭⎫ ⎝⎛--100031001201323~r r +⎪⎪⎪⎭⎫ ⎝⎛-1000010012013121)2(~r r r r +-+⎪⎪⎪⎭⎫ ⎝⎛100001000001(2) ⎪⎪⎪⎭⎫ ⎝⎛----1740343013201312)2()3(2~r r r r -+-+⨯⎪⎪⎪⎭⎫ ⎝⎛---31003100132021233~r r r r ++⎪⎪⎪⎭⎫ ⎝⎛000031001002021~÷r ⎪⎪⎪⎭⎫ ⎝⎛000031005010 (3) ⎪⎪⎪⎪⎭⎫⎝⎛---------12433023221453334311 141312323~rr r r rr ---⎪⎪⎪⎪⎭⎫ ⎝⎛--------1010500663008840034311)5()3()4(432~-÷-÷-÷r r r ⎪⎪⎪⎪⎭⎫⎝⎛-----22100221002210034311 2423213~r r r r r r ---⎪⎪⎪⎪⎭⎫⎝⎛---00000000002210032011(4) ⎪⎪⎪⎪⎭⎫⎝⎛------34732038234202173132 242321232~rr r r rr ---⎪⎪⎪⎪⎭⎫ ⎝⎛-----1187701298804202111110141312782~rr r r r r --+⎪⎪⎪⎪⎭⎫⎝⎛--410004100020201111134221)1(~r r r r r --⨯↔⎪⎪⎪⎪⎭⎫ ⎝⎛----0000041000111102020132~rr +⎪⎪⎪⎪⎭⎫⎝⎛--000004100030110202012.设⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛987654321100010101100001010A ,求A 。
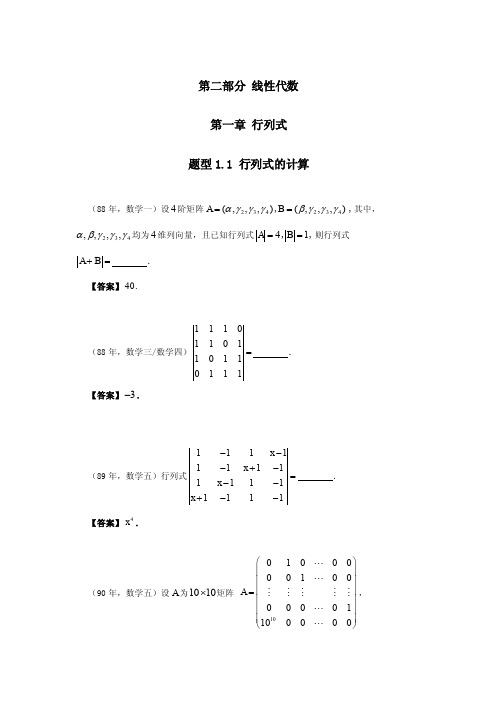
《线性代数》第一章行列式精选习题及解答

4.利用行列式按某一行(列)展开定理计算行列式;
5.利用数学归纳法计算行列式;
6.利用递推公式计算行列式;
7.利用范德蒙行列式的结论计算特殊的行列式;
8.利用加边法计算行列式;
9.综合运用上述方法计算行列式.
1.3 例题分析
例 1.1 排列 14536287 的逆序数为 ( )
(A) 8 (B) 7
因此
(−1Байду номын сангаасt a1n−1a2n−2 Lan−11ann ,其中
t = (n −1)(n − 2) , 2
( 2007 −1)( 2007 − 2 )
D = (−1) 2 2007!= −2007!.
此题也可以按行(列)展开来计算.
例 1.11 计算 n 阶行列式
2 1 1L1
1 2 1L1
Dn = 1 1 2 L 1
⎪⎪a ⎨
21
x1
⎪
+
a22 x2 MM
+L+ MM
a2n xn M
=
0
⎪⎩an1 x1 + an2 x2 + L + ann xn = 0
的系数行列式 D ≠ 0 ,则方程组只有唯一零解.若齐次线性方程组有非零解,则其系数行
列式 D = 0 .
1.2.5 一些常用的行列式
1.上、下三角形行列式等于主对角线上的元素的积.
⎧D i = j
jk
=
ai1 Aj1
+ ai2 Aj2
+ ... + ain Ajn
=
⎨ ⎩
0
i≠ j
其中 Ast 是 ast 的代数余子式.
1.2.4 克拉默法则 1.如果线性非齐次方程组
线性代数 第一章 行列式

第一章 行列式习题答案二、三阶行列式及n 阶行列式的定义部分习题答案1.计算下列二阶行列式(1)23112=; (2)cos sin 1sin cos θθθθ-=;(3)1111121221212222a b a b a b a b ++++1122112211221122a a a b b a b b =+++ 1221122112211221a a a b b a b b ----(4)1112111221222122a ab b a a b b +1122112212211221a a b b a a b b =+--2.计算下列三阶行列式(1)10312126231-=--; (2)11121322233233a a a a a a a 112233112332a a a a a a =-()1122332332a a a a a =- (3)a c bba c cb a3333a b c abc =++- 3.按自然数从小到大为标准次序,求下列各排列的逆序数: (1)3214; (2)614235.123t =+= 112217t =++++=(3)()()()12322524212n n n n ---4.确定,i j ,使6元排列2316i j 为奇排列.解:4,5i j ==,()()23162431655t i j t ==为奇排列. 5.写出4阶行列式中含有1321a a 的项. 解:13213244a a a a ;13213442a a a a -6.按定义计算下列行列式:(1)0001002003004000(4321)(1)2424t =-= (2)000000000000a c db (1342)(1)abcd abcd t =-= 7. 求1230312()123122x xf x x x x-=的展开式中4x 和3x 的系数.4x 的系数为6-;含3x 的项只有(4231)(1)(3)3t x x x -?创,所以3x 的系数为(4231)(1)3(3)119t -?创= 行列式的性质与展开部分习题答案 1.计算下列行列式:(1)200819861964200919871965201019881966;解:32212008198619641110111r r r r D --==(2)123123123111a a a a a a a a a +++; 解:2312323231(1)1111a a D a a a a a a a =+++++各列加到第一列后提取公因式21312312331(1)0101r r r r a a a a a a --=+++123(1)a a a =+++ (3)41232013201116011601110111031023500r r D +--==-- 213314116116(1)111027350818r r r +++--=-=-20=- (4)211201110111611261112112211100100c c D ---==----314110110(1)26126116221223c c -+=-=--=--.(5)00100101D αβαβαβαβαβαβαβ++=++.()401100101D αβαβαβαβαβαβαβαβαβαβαβ+=++-+++ ()()()32212D D D D D a b a b a b a b a b a b 轾=+-=++--臌432234a a b a b ab b =++++2.证明:(1)011=++++=cb adb a dcd a c b d c b a D 11;证明:将D 的各列都加到最后一列再提出公因式有1111(1)01111a b c d a b b c a d b c D a b c d c d a b c d d a b c d a ++==++++=++1111(2)33()ax byay bzaz bx x y z ay bzaz bx ax by a b yz x az bx ax byay bz z xy ++++++=++++.证明:左式12axayaz bybzbx ay bzaz bx ax by ay bzaz bx ax by D D az bx ax by ay bzaz bx ax by ay bz =+++++++=+++++++311r br xyzx y z D a ay bzaz bx ax by a ay bz az bx ax byaz bx ax byay bzazaxay-=+++=++++++23223r br x y z x y z x y z a ay bz az bx ax by a ay az ax a yz x zxyzxyzxy-=+++== 类似有1323322(1)r r r r yz x x y z D b zx y yz x xyzzx y ←−→←−→==-,所以33()ax byay bz az bx x y z ay bzaz bx ax by a b yz x az bx ax byay bzzxy++++++=++++ 3.计算n 阶行列式(1)n D =ab bbb a b bbb a bb b b a ...........................;各行加到第一行后提取公因式有:[]111...1...(1).....................n ba b b D a n b bba bb b b a=+-[]211111 (10)0...0(1)00 0 0...n r br r br a b a n b a b a b---=+---L[]()1(1)n a n b a b -=+--(2)12121212n na n a n D n a ++=+12(0)n a a a ≠ .211212111212121211210012000n n nr r n r r r n r r a a nna naa a n a a a a a a a a a a -----+++++--==--1112221211n n n n i i a na i a a a a a a a a =⎛⎫⎛⎫=++++=+⎪ ⎪⎝⎭⎝⎭∑ 4.利用范德猛行列式计算:1111123414916182764D =.2222333311111234(21)(31)(41)(32)(42)(43)1212341234==------= 克拉默法则部分习题答案1.用克拉默法则解线性方程组(1)122313223(0)0bx ax ab cx bx bc abc cx ax ì-=-ïïï-+= íïï+=ïïî;解:002350b a D cb abc ca-=-=-,212023500ab a D bc c b a bc a --=-= 2220350b ab D bc b ab c ca -==-,220250baab D c bc abc c --=-=-123,,x a x b x c =-==(2)123412341234123432125323348246642x x x x x x x x x x x x x x x x +-+=⎧⎪+-+=⎪⎨-++-=⎪⎪--+=⎩.解:132125321734826164D --==----,1132135323444822164D --==----211212332034826264D --==---,3131125321734426124D ==---,13212533853*******D --==---12342,0,1,5x x x x =-===2.当λ为何值时,齐次线性方程组⎪⎩⎪⎨⎧=+=+-=++0 00433221321x x x x x x x λλλ(1) 仅有零解;(2) 有非零解. 解:3410(1)(3)01D l ll l l=-=--,(1)1l ¹且3l ¹时0D ¹,该齐次线性方程组只有零解。
线性代数习题参考答案

第一章行列式§1 行列式的概念1.填空(1) 排列6427531的逆序数为,该排列为排列。
(2) i= ,j= 时,排列1274i56j9为偶排列。
(3) n阶行列式由项的代数和组成,其中每一项为行列式中位于不同行不同列的n个元素的乘积,若将每一项的各元素所在行标按自然顺序排列,那么列标构成一个n元排列。
若该排列为奇排列,则该项的符号为号;若为偶排列,该项的符号为号。
(4) 在6阶行列式中,含152332445166a a a a a a的项的符号为,含324314516625a a a a a a的项的符号为。
2.用行列式的定义计算下列行列式的值(1)112223323300 0aa aa a解:该行列式的3!项展开式中,有项不为零,它们分别为,所以行列式的值为。
(2)12,121,21,11, 12,100000nn nn n n n n n n n n nnaa aa a aa a a a------解:该行列式展开式中唯一不可能为0的项是,而它的逆序数是,故行列式值为。
3. 证明:在全部n 元排列中,奇排列数与偶排列数相等。
证明:n 元排列共有!n 个,设其中奇排列数有1n 个,偶排列数为2n 个。
对于任意奇排列,交换其任意两个元的位置,就变成偶排列,故一个奇排列与许多偶排列对应,所以有1n 2n ,同理得2n 1n ,所以1n 2n 。
4. 若一个n 阶行列式中等于0的元素个数比n n -2多,则此行列式为0,为什么?5. n 阶行列式中,若负项的个数为偶数,则n 至少为多少?(提示:利用3题的结果)6. 利用对角线法则计算下列三阶行列式(1)201141183---(2)222111ab c a b c§2 行列式的性质1.利用行列式的性质计算系列行列式。
(1) 2141 3121 1232 5062-(2)100 110 011 001abcd ---(3)ab ac ae bd cd de bf cf ef ---2. 证明下列恒等式(1) ()33ax by ay bzaz bx x y z D ay bzaz bx ax by a b yz x az bx ax by ay bzzxy+++=+++=++++ (提示:将行列式按第一列分解为两个行列式之和,再利用性质证明)(2)()()()()()()()()()()()()22222222222222221231230123123a a a a b b b b cc c cd d d d ++++++=++++++(3)1111221100001000001n n n n n n n x x x a x a x a x a a a a x a ------=++++-+ (提示:从最后一列起,后列的x 倍加到前一列)3. 已知四阶行列式D 的第三行元素分别为:1,0,2,4-;第四行元素的对应的余子式依次是2,10,a ,4,求a 的值。
线代第1章练习附答案

1 1 x 1 1
7.求行列式
的值。
1 x 1 1 1
x 1 1 1 1
【分析】 利用行列式的性质,将第 2,3,4 列加到第 1 列上得
1 1 1 x 1 x 1 1 x 1 1 1 1 x 1
1 1 x 1 1 x 1 x 1 1 1 1 x 1 1
x
1 x 1 1 1 x x 1 1 1 1 x 1 1 1
C.k≠-1 且 k≠3 D.k≠-1 或≠3
3.已知 2 阶行列式 a1 a2 =m , b1 b2 =n ,则 b1
b2
=( B )
b1 b2
c1 c2
a1 c1 a2 c2
A.m-n
B.n-m
C.m+n
D.-(m+n)
xyz
2x 2y 2z
4.设行列式 4 0 3 1, 则行列式 4 0 1 ( A )
0 a6
0 a8
0
a2 0 0 的值。 0
a4
【分析】 仿照上题的思路。
a 1
a2
D (a 9)
a5 a6 a7 a8
a3
a4
a 1 a 2
a3 a4 (a 9)
a5 a6
a7 a8
a 1 a 2 a 5 a 6
(a 9)
4(a 9)
a3 a4 a7 a8
11 1 1 5、计算行列式 1 1 1 1 的值。
3
1 0 1
a b0
解答: b a
a 0
b (a2 b2) 0 a=0, b=0
b a
1 0 1
x2 2 3 6. 设 f (x) 1 2x 3 4 ,则 x 2 的系数为 23 。
线性代数习题解答(一)行列式

线性代数习题解答习题一1.计算以下行列式 2223333223(1)(2)53(1)7.15cos sin (2)cos sin 1.sin cos log 1(3)log log 1110.1log 11(4)(1)(1)(1) 1.1113(5)2111123212.120273(6)5415670451201037a a b b b b a a a a a a a a a a a a αααααα-=-⨯-⨯-=---=+==-=-=+=+-+-=+-=-+--=-++-=---=-++-2222456178.0(7)00.01(8)112.1a ba c abc abcbc c b ca abc abc b a +-=--=-+=----=-+++2.解方程(1) 111121.16x x =解 221212281,230,(1)(3)0,1, 3.x x x x x x x x +--=--=+-==-= (2)221220110.12220,20,(2)(1)0.1, 2.x x xx x x x x x x x x -=-++-=+-=+-===- 3.解下面的线性方程组21221222222112123123123131133132(2)()()()(),.().,.235(3)35549521036, 2.424,0,22452x ax a x bx b a b a b x a b a b a b x a b x a a a b ab x ab x a b x x x x x x x x x x x x x x x x x x ⎧+=⎪⎨+=≠⎪⎩-=-=-+=+=-+=-=-⎧⎨=+⎩-+=⎧⎪+-=⎨⎪-+=⎩-=⎧==-==⎨-=⎩=-+解解13123354 1.210x x x x x -=-+=-=⎧⎪=-⎨⎪=⎩12312312320(4)3251324x x x x x x x x x -+=⎧⎪+-=⎨⎪+-=⎩ 解1231231231231233121220 (1) 325 1 (2)32 4 (3)(1)(3)32 4 (4)(4)(2)3219/4 (5)43,3/4.322/4 (6)19/4222/4313/413.327281322/413/28473x x x x x x x x x x x x x x x x x x x x -+=⎧⎪+-=⎨⎪+-=⎩++-=-+=⎧==⎨+=⎩===-==123.281328472834x x x ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩4.求下列个排列的逆序数,并且说明它们的奇偶性: (1)4213 (2)542163(3)134782695 (4)(-1)(-2)21(1)(4213)1+2+1=4,(2)(542163)123039,(3)(134782695)42410,(4)((-1)(-2)21)12(1)(1)/2.4,4142,4n n n n n n n n n n k k n k k ττττ==++++==++==+++-=-=+=+ 解偶排列,3+5.确定i 和j 的值,使得9级排列(1) 1274i 56j 9成偶排列; (2)3972i 15j 4成奇排列.解(1) τ (127435689)=1+2+1+1=5,奇排列, 127485639为偶排列. (2) τ (397261584)=1+3+2+5+3+1+5=20, 397281564为奇排列.6.下列各项,哪些是五阶行列式||ij a 中的一项.若是,试决定该项的符号.132532415431124352244321351254(1)(2);(3)a a a a a a a a a a a a a a a解(1) 1325324154.a a a a a 行号按自然顺序排列,列号排列35214. τ (35214)=2+3+1=6,取正号.(2) 3112435224.a a a a a 列号2重复,不是行列式的项.(3) 43213512541221354354.a a a a a a a a a a =行号按自然序列,列号排列是21534. τ (21534)=1+1+1=3,取符号.7.根据行列式的定义计算下面的行列式:(2(1)1)112(1)2(1)2(1)(1)(1)121(1)/212(1)1010000002000(1)00000100000(1)!(1)!.00000(2)0(1).n n n n n n n n n n n n nn nnn n n n n n n n n a a a a a a a a a a a a a τ-----------=-=-=-((1)(2)1)(1)(2)/2000010000200(3)1000000000(1)!(1)!.n n n n n n nn n τ-----=-=-1111122222331542544455(4)000000.000000a b c d e a b c d e a b a b b a a b a b εε=+= 8.用行列式性质计算下列行列式32153320533205310032053(1)72284721847218410072184320533205310032053132053100721847218410072184172184100(7218432053)4013100.1(2)2()1112()02()0x y x y y x y y x y x x y x yx x yx y x y y x yx x y xy x y x yx+=+=+==-=+++=++++=+-=+--22332()()2().y x yxx y x xy y x y ---=+-+-=-+32222(3)2212()121212()00002().111100111100(4)11110011111111000011011101111()10a b c a b c b c ab ca c a ba b a b c b c ab ac a b a b a b c b c ac a b a b c x x y x x y y yyyyx y y xy y x yy x yxy xy xy xy y xy x y ++++++=++++++=++++++=+++--=+---=----=+=-+=-2.y9。
《线性代数》第一章行列式精选习题及解答

a1 ...
∏ a2
...
... ...
an ...
=
(a j − ai ) .
1≤i< j≤n
a1n−1
a
n−1 2
... ann−1
1.2.6 计算行列式的常用方法
1.利用对角线法则计算行列式,它只适用于 2、3 阶行列式;
2.利用 n 阶行列式定义计算行列式;
3.利用行列式的性质化三角形法计算行列式;
(C) 10 (D) 9
解 在排列 14536287 中,1 排在首位,逆序数为 0;4、5、6、8 各数的前面没有比它们
自身大的数,故这四个数的逆序数为 0;3 的前面比它大的数有 2 个(4、5),故逆序数为 2;
2 的前面比它大的数有 4 个(4、5、3、6),故逆序数为 4;7 的前面比它大的数有 1 个(8),
MM MM
M
11 1 1L2
1 −1 −1 −1 L −1
n +1 0 0 0 L 0
11 0 0L0
求和,故共有 n!项. 1.2.2 行列式的性质
1.行列式和它的转置行列式相等; 2.行列式的两行(列)互换,行列式改变符号; 3.行列式中某行(列)的公因子可提到行列式的的外面,或若以一个数乘行列式等于 用该数乘此行列式的任意一行(列);
4.行列式中若有两行(列)成比例,则该行列式为零; 5.若行列式的某一行(列)的元素都是两数之和,则此行列式等于两个行列式之和, 即
即 ( A31 + A32 + A33 ) + 2( A34 + A35 ) =0. 同理 2( A31 + A32 + A33 ) + ( A34 + A35 ) =0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章 行列式1.1 目的要求1.会求n 元排列的逆序数;2.会用对角线法则计算2阶和3阶行列式; 3.深入领会行列式的定义;4.掌握行列式的性质,并且会正确使用行列式的有关性质化简、计算行列式; 5.灵活掌握行列式按(列)展开; 6.理解代数余字式的定义及性质;7.会用克拉默法则判定线性方程组解的存在性、唯一性及求出方程组的解.1.2 重要公式和结论1.2.1 n 阶行列式的定义n 阶行列式 nnn n n n a a a a a a a a a D (2122221)11211=n n np p p tp p p a a a ...)1(212121)...(∑−=.其中是n 个数12…n 的一个排列,t 是此排列的逆序数,∑表示对所有n 元排列求和,故共有n !项. n p p p ...211.2.2 行列式的性质1.行列式和它的转置行列式相等;2.行列式的两行(列)互换,行列式改变符号;3.行列式中某行(列)的公因子可提到行列式的的外面,或若以一个数乘行列式等于用该数乘此行列式的任意一行(列);4.行列式中若有两行(列)成比例,则该行列式为零;5.若行列式的某一行(列)的元素都是两数之和,则此行列式等于两个行列式之和,即nn n n in i i nnn n n in in i i i i n a a a a a a a a a a a a b a b a b a a a a L MMM L M M M L LMM M L MM M L21211121121221111211=++++nnn n ini i na a ab b b a a a L MMM L M M M L 2121112116. 把行列式的某一行(列)的各元素乘以同一数然后加到另一行(列)对应的元素上去,行列式的值不变. 1.2.3 行列式按行(列)展开设D 为n 阶行列式,则有=∑=nK jkika A 1⎩⎨⎧≠==+++j i ji D A a A a A a jn in j i j i 0...2211=∑=nK jkika A1⎩⎨⎧≠==+++j i ji D A a A a A a jn in j i j i 0 (2211)其中是的代数余子式. st A st a 1.2.4 克拉默法则1.如果线性非齐次方程组⎪⎪⎩⎪⎪⎨⎧=+++=+++=+++nn nn n n n n n n b x a x a x a b x a x a x a b x a x a x a L M M M M M L L 22112222212111212111的系数行列式,则方程组有唯一解0≠D DD x 11=( i=1,2,…,n ),其中是D 中第i 列元素(即的系数)换成方程中右端常数项所构成的行列式.i D i x 2.如果线性齐次方程组⎪⎪⎩⎪⎪⎨⎧=+++=+++=+++000221122221211212111n nn n n n n n n x a x a x a x a x a x a x a x a x a L M M M M M L L的系数行列式,则方程组只有唯一零解.若齐次线性方程组有非零解,则其系数行列式.0≠D 0=D 1.2.5 一些常用的行列式1.上、下三角形行列式等于主对角线上的元素的积.2.设 kk k k a a a a D L M M ML 11111=,nnn nb b b b D L M M M L 11112=,则 211111*********D D b bc c b b c c a a a a nn n nkn n k kkk k =L L M M M MM ML L L MMM L .3.范德蒙行列式)(..................1 (11)11121121i j nj i n nn n n a a aaaa a a −=∏≤<≤−−−.1.2.6 计算行列式的常用方法1.利用对角线法则计算行列式,它只适用于2、3阶行列式; 2.利用n 阶行列式定义计算行列式; 3.利用行列式的性质化三角形法计算行列式; 4.利用行列式按某一行(列)展开定理计算行列式; 5.利用数学归纳法计算行列式; 6.利用递推公式计算行列式;7.利用范德蒙行列式的结论计算特殊的行列式; 8.利用加边法计算行列式; 9.综合运用上述方法计算行列式.1.3 例题分析例1.1 排列14536287的逆序数为 ( )(A) 8 (B) 7 (C) 10 (D) 9解 在排列14536287中,1排在首位,逆序数为0;4、5、6、8各数的前面没有比它们自身大的数,故这四个数的逆序数为0;3的前面比它大的数有2个(4、5),故逆序数为2; 2的前面比它大的数有4个(4、5、3、6),故逆序数为4;7的前面比它大的数有1个(8),故逆序数为1;于是这个排列的逆序数为 t=0+0+2+4+1=7,故正确答案为(B ).例1.2 下列排列中( )是偶排列.(A)54312 (B)51432 (C) 45312 (D) 654321解 按照例1的方法计算知:排列54312的逆序数为9;排列51432的逆序数为7;排列45312的逆序数为8;排列654321的逆序数为15;故正确答案为(C ).例1.3 下列各项中,为某五阶行列式中带正号的项是( ). (A) (B) (C)(D) 5541324413a a a a a 5415413221a a a a a 5214432531a a a a a 5344223115a a a a a 解 由行列式的定义知,每一项应取自不同行不同列的五个元素之积,因此(A)、(B)不是五阶行列式的项,但(C)应取负号,故正确答案为(D ).例1.4 行列式351232113,010101021=−=D D λλλ, 若21D D =,则λ的取值为( ) (A) 2, —1 (B) 1, —1 (C)0, 2 (D)0,1解 按三阶行列式的对角线法则得.若,则,于是0,)1)(1(221=−+=D D λλ21D D =0)1)(1(2=−+λλ1,1−=λ,故正确答案为(B ).例1.5 方程组有唯一解,则( ).⎪⎩⎪⎨⎧=++=++=++111321321321x x x x x x x x x λλλ(A)1−≠λ且2−≠λ (B) 1≠λ且2−≠λ (C) 1≠λ且2≠λ (D) 1−≠λ且2≠λ解 由克拉默法则知,当所给非齐次线性方程组的系数行列式不等于0时,该方程组有唯一解,于是令行列式0)1)(2(1111112≠−+=λλλλλ 即1≠λ且2−≠λ,故正确答案为(B ).例1.6 ==2006200420082006D ( ).分析 对于2、3阶行列式的计算,元素的数值较小时,可以直接采用对角线法则进行计算;但元素的数值较大时,一般不宜直接采用对角线法则进行计算,而是用行列式的性质进行计算.解 此题是一个2阶行列式,虽然可以直接用对角线法则计算,但因数值较大,计算较繁,因此要仔细观察分析,用行列式的性质求解.402221003200622008220062004200820061221=−−+−−−=c c c c D ,故答案为4.例1.7 ==3214214314324321D ( ). 分析 如果行列式的各行(列)数的和相同时,一般首先采用的是将各列(行)加到第一列(行),提取第一列(行)的公因子(简称列(行)加法) .解 这个行列式的特点是各列4个数的和为10 ,于是,各行加到第一行,得===321421431432101010103214214314324321D 101230121012101111103214214314321111−−−−−−= 160400004001210111110=−−−=.例1.8设xx x x x x f 111123111212)(−=,则的系数为( ),的系数为( ). 4x 3x 分析 此类确定系数的题目,首先是利用行列式的定义进行计算.如果用定义比较麻烦时,再考虑用行列式的计算方法进行计算.解 从的表达式和行列式的定义可知,当且仅当的主对角线的4个元素的)(x f )(x f积才能得出,其系数显然是2. 当第一行取4x )1(13=a 或)2(14=a ,则含或的行列式的项中是不出现,含的行列式的项中是不出现,于是含的项只能是含,,,的积,故的系数为13a 14a 3x )2(11x a =3x 3x 12a 21a 33a 44a 3x 1−.故答案为2 ,1−.例1.9 设0123411222641232211154321=D ,则(1)=++333231A A A ( ), (2)=+3534A A ( ), (3)=++++5554535251A A A A A ( ). 分析 此类题目一般不宜算出表达式里每一项的值,而是注意观察要求的表达式的结构,充分利用按行(列)展开的计算方法来进行技巧计算.解 00123411222221112211154321)(23534333231==++++A A A A A (第2,3行相同) 即 =0. 同理 )(2)(3534333231A A A A A ++++)()(23534333231A A A A A ++++=0 于是 0, =++333231A A A =+3534A A 0.011111333336412322111543211111111222641232211154321245554535251=+=++++r r A A A A A 故答案为0,0,0.例1.10 2007000000002006000200500020001000L L L MM MM M M L =D .分析 当行列式中有较多零元素时,一般可以采用行列式的定义或按行(列)展开来计算.解 此行列式刚好只有n 个非零元素,故非零项只有一项:nn n n n a a a a ,,,,112211−−−L nn n n n t a a a a 112211)1(−−−−L ,其中 2)2)(1(−−=n n t ,因此 !2007!2007)1(2)22007)(12007(−=−=−−D .此题也可以按行(列)展开来计算. 例1.11 计算n 阶行列式2111121111211112L M M M M L L L =n D解法1 (行(列)加法)因为这个行列式的每一行的n 个元素的和都为n+1, 所以将第2,3,…,n 列都加到第一列上,得),3,2(,2111121111211111)1(21111211112111111n i r r n n n n n D i n L L M M M ML L L L M M M M L L L =−+=++++=1101000101111)1(+=+n n L M M M M L L L解法2 (加边法))1,,3,2(211111211111211111210000111+=−==+n i c c D D i n n L L M M M M M LL L L11000101001010100011000011000101001001010001111111121+=++++−−−−+n n r r r n L M M M M M LL L L L L M M M M M L L L L . 解法3 (利用行列式的性质)101010100111112),,3,2(21111211112111121L M M M M L L L L L M M M M L L L −−−=−=n i r r D i n11000100010111121+=++++n n c c c n L M M M M L L L L .例 1.12 计算nn n n nn n y x y x y x y x y x y x y x y x y x D +++++++++=111111111212221212111L MM M L L . 解 当n=2时,))((11111212221221112y y x x y x y x y x y x D −−=++++=当n≥3时,111212112122111121111()()()0()()()n nn n n n x y x y x y x x y x x y x x y D x x y x x y x x y +++−−−==−−−L L M M M L n.例1.13 计算nn n n nn n n x x x x x x a a a a a x a D 1122112321100000000000−−−−−−−−+=L L M M M M M M LL其中.),,2,1(0n i x i L ≠≠解 因 )1(11111111x a x x a x a D +=+=+=, 1(221121212112x ax a x x x x a x a D ++=−+=, 归纳推得 )1(1121nn n n x a x a x x x D +++=L L . 用数学归纳法证明上式, 假设当k=n-1时结论成立,即)1(11111211−−−−+++=n n n n x a x a x x x D L L . 则当k=n 时,将按第n 列展开,得n D ))(())(()1(122111−−+−−−−−−+=n n n n n n n x x x x a D x D L 1221111)1()1(−−−+−−−+=n n n n n n n x x x x a D x Ln n nn n n n x a x x x x x D x 12211−−−+=L 1(1121nn n x a x ax x x +++=L L 即当k=n 时结论也成立,故对一切自然数结论都成立.例1.14 计算222111222333n nn nD n n n =L L L M M M L 解 (利用范德蒙行列式计算)1113213211111!−−−==n n n Tnn n n n D D L MMM M LL )]1([)2()24)(23)(1()13)(12(!−−−−−−−−=n n n n n L L L !2)!2()!1(!L −−=n n n .例 1.15 计算 βαβαβαβαβαβαβαβα+++++=L L MM M M ML LL 000000000000n D .解 按第一列把D n 分成两个行列式的和+++++=βαβαβαβαβαβαααL L M M M M M L L L000000000000000n D βαβαβαβαβαβαβαβ++++L L MM MM M LL L0000000000000n n n D D βαβαββαβαβα+=+=−−110000000000000000L L MM M M M L L L (1) +++++=βαβαβαβαβαβααβL L M M M M M L L L000000000000000n D βαβαβαβαβαβαβαα++++L L MM MM M LL L 00000000000000n n n D D αβαβααβαβαβ+=+=−−1100000000000000L L M MM M M L L L (2) (a) 当βα≠时 ,由(1)(2)得 =, 则n n D βα+−1nn D αβ+−1βαβα−−=−nn n D 1.于是 βαβα−−=++11n n n D .(b) 当βα=时,由(1)得 .n n n n n D D ααα)1(1+==+=−L例1.16 设, 证明:0>>>c b a 01222<++abca bc c b a cb a cabc ab . 证明 将行列式的第1行)(c b a ++×,第2行)1(−×,然后加到第3行,得ca bc ab ca bc ab ca bc ab c b a c b a ab ca bc c b a c b a ++++++=222222 222222111)(111)(c b a c b a ca bc ab c b a c b aca bc ab ++=++= ))()()((a b b c a c ca bc ab −−−++=于是,不等式的左边=))()((a b b c a c −−−.由于,从而,0>>>c b a 0)(<−a c 0)(,0)(<−<−a b b c ,因此,当时,0>>>c b a 01222<++abca bc c b a cb a cabc ab .例 1.17 设在上连续,在内可导,试证:至少存在一个)(),(),(x h x g x f ],[b a ),(b a ),(b a ∈ξ,使得0)(=′ξH .其中 )()()()()()()()()()(x h x g x f b h b g b f a h a g a f x H =.证明 由题设知在上连续,在内可导,又由行列式的性质可知,于是由洛尔中值定理可知,至少存在一个)(x H ],[b a ),(b a 0)()(==b H a H ),(b a ∈ξ,使得0)(=′ξH .1.4 独立作业1.4.1 基础训练1.设ij a D =为阶行列式,则在行列式中的符号为( ) . n 11342312n n n a a a a a −L (A) 正 (B) 负 (C) (D) 1)1(−−n 2)1()1(−−n n2.行列式为0的充分条件是( ).n D(A) 零元素的个数大于n; (B) 中各行元素的和为零; n D (C) 次对角线上元素全为零; (D) 主对角线上元素全为零. 3.行列式不为零,利用行列式的性质对进行变换后,行列式的值( ). n D n D (A) 保持不变; (B) 可以变成任何值; (C) 保持不为零; (D)保持相同的正负号.4.方程0881441221111132=−−x x x的根为 ( ).(A) 1,2,2− (B)1,2,3 (C)1,1−,2 (D)0,1,25.如果4333231232221131211==a a a a a a a a a D ,则=−−−−−−=33323331232223211312131********a a a a a a a a a a a a D ( ). (A)-12 (B)12 (C)48 (D)-486.行列式=9092709262514251( ).7.ab b a log 11log = ( ).8.行列式c b d c a b cb a , 则=++312111A A A ( ).9.函数x x x x x f 121312)(−=中,的系数为( ).3x 10.4444333322225432154321543215432111111= ( ).11.49362516362516925169416941, 12.00000000x y y x y x x y D = 13.20000120000001301200101−−=D , 14.xyz zx yyz x 111 15.520003520003520035200035, 16.44342414433323134232221241312111y x y x y x y x y x y x y x y x y x y x y x y x y x y x y x y x ++++++++++++++++17.nn n n a a a a a a b b b b b 13221132100000000−−−−−L M M M M M LL L ,(其中),,2,1(,0n i a i L =≠) 18.n x x x D L M M M M LL L 01001001111021= (),,2,1,0n i x i L =≠ 19.43211111111111111111x x x x ++++, 20.nL M M M ML L L 22223222222222121.211121112L L L L L L =n D .22.当μ取何值时,齐次线性方程组有非零解?⎪⎩⎪⎨⎧=−−+−=−+−=−++0)1(02)3(0)1(42321321321x x x x x x x x x μμμ23.证明αααααααsin )1sin(cos 210001cos 200000cos 210001cos 210001cos 2+=n L L M MM M M LL L (其中0sin ≠α).1.4.2 提高练习1.设A 为n 阶方阵,为*A A 的伴随矩阵,则*A A 为( ) (A) 2A (B) 12−n A(C) nA2 (D) nA2.设A 为n 阶方阵,B 为m 阶方阵,=00A B( ). (A)B A − (B) B A (C) B A mn )1(− (D) B A n m +−)1(3.若xxx x x x g 171341073221)(−−−−=,则的系数为( ). 2x (A) 29 (B) 38 (C) —22 (D) 344.347534453542333322212223212−−−−−−−−−−−−−−−=x x x x x x x x x x x x x x x x g(x),则方程=)(x g 0的根的个数为( ). (A)1 (B)2 (C)3 (D)45.当( )时,方程组只有零解.≠a ⎪⎩⎪⎨⎧=+−=++=+02020z y ax z ax x z ax (A)-1 (B) 0 (C) -2 (D) 26.排列可经过( )次对换后变为排列. n r r r r L 321121r r r r n n n L −−7.四阶行列式中带负号且含有因子和的项为( ).12a 21a 8.设y x ,为实数,则当=x ( ),=y ( )时,010100=−−−x yy x . 9.设A 为4阶方阵,B 为5阶方阵,且,2,2−==B A 则 =−A B ( ),=−B A ( ).10.设A ,B 为n 阶方阵,且,2,3−==B A 则 =−1*3B A ( ). 11.设A 为3阶正交矩阵,0>A ,若73=+B A ,则=+T AB E 21( ). 12.设,则⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=653042001A =+−12A E ( ).13.解方程组011112222212112=nnnnnnn b b b b b b b b b x x x L M M M M L L L ,其中为各不相同的常数. n b b b b ,,,,321L 14.证明:)()()()()()()()()(212222111211x a x a x a x a x a x a x a x a x a dx d nn n n n n L M M M L L =∑=ni nn n n in i i n x a x a x a x a dx d x a dx d x a dx d x a x a x a 1212111211)()()()()()()()()(LM M M L M M M L 15.设xx x x x x x g 620321)(332=,求)(x g ′.16.设17131231533111)(85222−−−−−−=x x x x x x x g ,试证:存在)1,0(∈ξ,使得0)(=′ξg .17.证明:奇数阶反对称矩阵的行列式为零. 18.设z y x ,,是互异的实数,证明:0111333=z y x z y x 的充要条件是0=++z y x . 19.设4322321143113151−=A ,计算44434241A A A A +++的值,其中是)4,3,2,1(4=i A i A 的代数余子式.20.利用克莱默法则求解方程组.⎪⎩⎪⎨⎧=+−=+−=−+3232222321321321x x x x x x x x x 21.求极限111cos sin 3212sin 1231lim23x x x x x x x →.第一章 参考答案1.4 独立作业 1.4.1 基础训练1. (C) 2. (B) 3. (C) 4.(A) 5. (B)6.解=×==17092142512000200070922000425190927092625142515682000.7.0 , 8. 解 0111312111==++cb c a cb A A A ,故答案为09.解 因为在此行列式的展开式中,含有的只有主对角线上的元素的积,故答案为 10.解 由范德蒙行列式得行列式的值为2883x 2−11.解0222222229753169411311971197597531694149362516362516925169416941===.12.解 x y x y x x xyy yxy xyyx y xxy D 0000000000000000−−==22222)(y x xyyx x x yy x y −−=−= 13.解 0131201014200013120101220000120000001301200101−×−=−×−=−−=D 20311243131200014=−−×−=−−×−=14.解 yzx z x y x z y x z x y z x y yzx xy zzx yyz x−−−−=−−−−−−=11))(()(0)(01111=))()((x z z y y x −−−15.解 520003520003520003500003352000352000352000352000325200035200035200035200035+= =5203520035200353252000352000352000350000332000320000320000320000325+=+==L 665 16.解1413121414131213141312121413121144342414433323134232221241312111y y y y y y y x y y y y y y y x y y y y y y y x y y y y y y y x y x y x y x y x y x y x y x y x y x y x y x y x y x y x y x y x −−−+−−−+−−−+−−−+=++++++++++++++++=017.解132111322113210000000)1(00000000−+−−−−−−×−=−−−=n n n n n n n n a a a a b a a a a a a b b b b b D L MMM M MLL L L M M M M M M L L L=−−×+−−−−12221122100n n n n n a a a a a b b b b a L MMM M M LL L ==+−L L 121n n n n nD a a b a a a )(121∑=ni ii n a b a a a L18.解 由第()列的i n i ,,2,1L =ix 1−倍加到第一列上去. nni inx x x x x x x D L MM M ML L LL MM M M LL L 0000000011111001001111021121∑=−===)1(121∑=−n i i n x x x x L19.解43211114321100100111111111111111111x x x x x x x x x x x −−−+=++++432111413121100000001x x x x x x x x x x x x x −−−++++==3214214314324321x x x x x x x x x x x x x x x x ++++20.解 2020012000200021222232222222221−−=n nL MM M M LL L L M M M M L L L 20212002−−=n L M M M ML L =)!2(2−−n 21.解 211121111)1(211121111211121112L LL L L L L L L L L L L L L L L L +=+++==n n n n D n 1101011001)1(+=+=n n L L L L L L22.解 由齐次线性方程组有非零解的条件可知0111213142=−−−−−−μμμ 解之得μ=0,2,3. 于是当μ=0,2,3时,齐次方程组有非零解.⎪⎩⎪⎨⎧=−−+−=−+−=−++0)1(02)3(0)1(42321321321x x x x x x x x x μμμ23.证明 (1)当时,结论显然成立, (2)假设当1=n k n ≤时,结论成立, (3)当时1+=k n11cos 2101cos 200000cos 210001cos 210001cos 2++=k k D αααααL L M M M M ML L Lkk D ααααcos 21010000cos 210001cos 2100001)1(cos 23L M M M M M LL L L −+=ααααααααααsin )2sin(sin sin sin sin cos 2sin )1sin(cos 21+=−=−+=−k k k D k k ααsin ]1)1sin[(++=k 故结论成立. 1.4.2 提高练习1.B , 2.C , 3.D , 4.B , 5.D, 6.2)1(−n n , 7. 44332112a a a a 8.0, 0, 9.32, 64 , 10.2312−−n , 11.277, 12.6 13.提示:用范德蒙行列式将行列式展开求解,答案为i b x =,(n i ,,2,1L =), 14.(用行列式的定义和导数的运算法则)证明))()()()1(()()()()()()()()()(11)(12122221112112211x a x a x a dx dx a x a x a x a x a x a x a x a x a dx d n n p p p p p p t nn n n n n L L M M ML L L ∑−== ))())(()()()1((111)(12211x a x a dx d x a x a n i n p p p p p p p tL L L ∑−=∑=ni nn n n in i i n x a x a x a x a dx d x a dx d x a dx d x a x a x a 1212111211)()()()()()()()()(LMM M L M M M L15.利用(14)的结论进行计算便可得结果,答案为6.2x 16.(用罗尔中值定理证)证明 (1)显然是多项式,故在上连续,在()(x g )(x g ]1,0[)1,0内可导,且 ,从而由罗尔中值定理知,存在0)1()0(==g g )1,0(∈ξ,使得0)(=′ξg . 17.用行列式的性质3的推论(同济四版)18.证明 33333333333301111x z xy xz xy x z x y x x z x y x z y x z y x−−−−=−−−−=0))()()((11))((2222=++−−−=++++−−=z y x y z x z x y xxz z x xy y x z x y 由于z y x ,,是互异的实数,故要使上式成立,当且仅当0=++z y x .19.解 6111132114311315144434241=−=+++A A A A , 20. 11=x ,, 22=x 33=x 21.解 (用罗必塔法则求解)11100013212001230000111231001100sin cos 3212sin 123230cos 11231lim1101cos sin 3212sin 1231lim223230=+=−+=→→x x x x x x x x x x x x x x x x x。
