钢结构基本原理同济第二版沈祖炎重点习题课后答案
钢结构基本原理-同济第二版沈祖炎重点习题课后答案
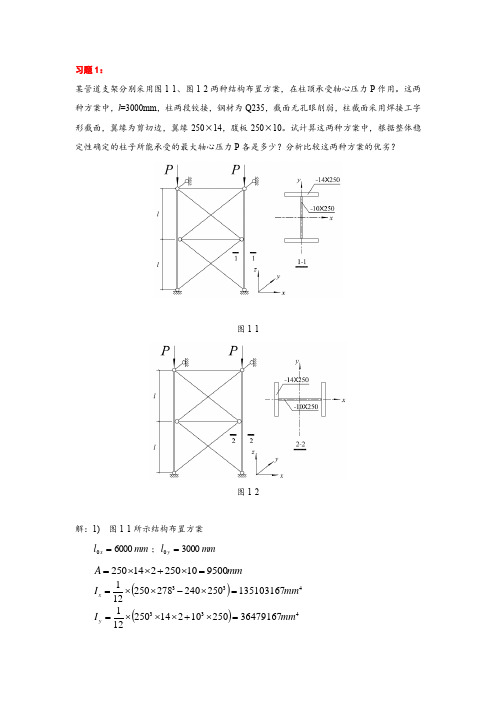
习题1:某管道支架分别采用图1-1、图1-2两种结构布置方案,在柱顶承受轴心压力P 作用。
这两种方案中,l =3000mm ,柱两段铰接,钢材为Q235,截面无孔眼削弱,柱截面采用焊接工字形截面,翼缘为剪切边,翼缘-250×14,腹板-250×10。
试计算这两种方案中,根据整体稳定性确定的柱子所能承受的最大轴心压力P 各是多少?分析比较这两种方案的优劣?图1-1图1-2解:1) 图1-1所示结构布置方案mm l x 60000=;mm l y 30000=mm A 950010250214250=⨯+⨯⨯=()433135103167250240278250121mm I x =⨯-⨯⨯=()4333647916725010214250121mm I y =⨯+⨯⨯⨯=mm A I i x x 3.1199500135103167===;mm AI i y y 0.62950036479167===3.503.11960000===x x x i l λ;4.480.6230000===y y y i l λ此截面对x 轴为b 类,对y 轴为c 类,查表得855.0=x ϕ(附表4-4);785.0=y ϕ(附表4-5)应根据y ϕ确定柱子整体稳定的承载力kN Af P d y 16032159500785.0max =⨯⨯==ϕ2) 图1-2所示结构布置方案mm l x 60000=;mm l y 30000=mm A 9500=;mm i x 0.62=;mm i y 3.119= 8.960.6260000===x x x i l λ;1.253.11930000===y y y i l λ此截面对x 轴为c 类,对y 轴为b 类,查表得478.0=x ϕ(附表4-5);953.0=y ϕ(附表4-4)应根据x ϕ确定柱子整体稳定的承载力kN Af P d x 9762159500478.0max =⨯⨯==ϕ3) 分析比较两种结构布置方案所使用的材料完全相同,但是图1-1所示方案(为下文表述的方便,以后简称方案A )的承载力为1603kN ,而图1-2所示方案(为下文表述的方便,以后简称方案B )的承载力仅为976kN 。
钢结构基本原理课后习题答案
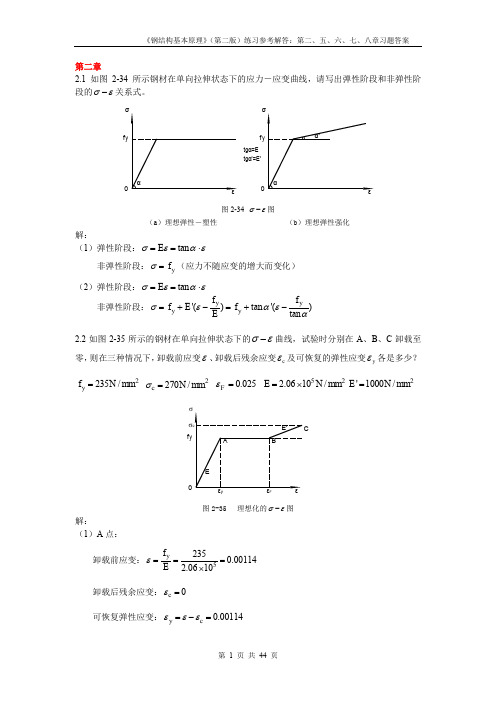
第二章2.1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
tgα'=E'f y 0f y 0tgα=E 图2-34 σε-图(a )理想弹性-塑性(b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化) (2)弹性阶段:tan E σεαε==⋅ 非弹性阶段:'()tan '()tan y y y y f f f E f Eσεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少?2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =f yσF图2-35 理想化的σε-图解:(1)A 点:卸载前应变:52350.001142.0610y f Eε===⨯卸载后残余应变:0c ε=可恢复弹性应变:0.00114y c εεε=-=卸载前应变:0.025F εε== 卸载后残余应变:0.02386y c f Eεε=-=可恢复弹性应变:0.00114y c εεε=-=(3)C 点: 卸载前应变:0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变:0.05869cc Eσεε=-=可恢复弹性应变:0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
2023大学_钢结构基本原理第二版(沈祖炎著)课后答案下载

2023钢结构基本原理第二版(沈祖炎著)课后答
案下载
2023钢结构基本原理第二版(沈祖炎著)课后答案下载
前言
第一章绪论.
第一节钢结构的特点和应用
第二节钢结构设计要求与设计方法
第三节钢结构的发展方向
第四节本课程的主要内容、特点和学习方法
思考题
第二章钢结构的材料
第一节钢结构对材料的要求
第二节钢材的塑性破坏和脆性破坏
第三节钢材的主要性能
第四节影响钢材性能的因素
第五节钢材的疲劳
第六节钢材的种类和规格
思考题
钢结构基本原理第二版(沈祖炎著):内容简介
点击此处下载钢结构基本原理第二版(沈祖炎著)课后答案
钢结构基本原理第二版(沈祖炎著):图书目录
本书主要依据国家标准《钢结构设计规范》(GB 50017--)编写。
全书共分七章,基本内容包括绪论、钢结构的材料、钢结构的'连接、轴心受力构件、受弯构件设计、拉弯压弯构件和钢结构最新技术。
(完整版)钢结构基本原理同济第二版沈祖炎重点习题课后答案

习题1:某管道支架分别采用图1-1、图1-2两种结构布置方案,在柱顶承受轴心压力P 作用。
这两种方案中,l =3000mm ,柱两段铰接,钢材为Q235,截面无孔眼削弱,柱截面采用焊接工字形截面,翼缘为剪切边,翼缘-250×14,腹板-250×10。
试计算这两种方案中,根据整体稳定性确定的柱子所能承受的最大轴心压力P 各是多少?分析比较这两种方案的优劣?图1-1图1-2解:1) 图1-1所示结构布置方案;mm l x 60000=mml y 30000=mmA 950010250214250=⨯+⨯⨯=()433135103167250240278250121mm I x =⨯-⨯⨯=()4333647916725010214250121mm I y =⨯+⨯⨯⨯=;mm A I i x x 3.1199500135103167===mmAI i y y 0.62950036479167===;3.503.11960000===x x x i l λ4.480.6230000===y y y i l λ此截面对x 轴为b 类,对y 轴为c 类,查表得(附表4-4);(附表4-5)855.0=x ϕ785.0=y ϕ应根据确定柱子整体稳定的承载力y ϕkNAf P d y 16032159500785.0max =⨯⨯==ϕ2) 图1-2所示结构布置方案;mm l x 60000=mml y 30000=;;mm A 9500=mm i x 0.62=mmi y 3.119=;8.960.6260000===x x x i l λ1.253.11930000===y y y i l λ此截面对x 轴为c 类,对y 轴为b 类,查表得(附表4-5);(附表4-4)478.0=x ϕ953.0=y ϕ应根据确定柱子整体稳定的承载力x ϕkNAf P d x 9762159500478.0max =⨯⨯==ϕ3) 分析比较两种结构布置方案所使用的材料完全相同,但是图1-1所示方案(为下文表述的方便,以后简称方案A )的承载力为1603kN ,而图1-2所示方案(为下文表述的方便,以后简称方案B )的承载力仅为976kN 。
同济大学钢结构基本原理(沈祖炎)课后习题答案完全版 (1)

第二章2.1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
tgα'=E'f y 0f y 0tgα=E 图2-34 σε-图(a )理想弹性-塑性(b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化) (2)弹性阶段:tan E σεαε==⋅ 非弹性阶段:'()tan '()tan y y y y f f f E f Eσεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少?2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =f yσF图2-35 理想化的σε-图解:(1)A 点:卸载前应变:52350.001142.0610y f Eε===⨯卸载后残余应变:0c ε=可恢复弹性应变:0.00114y c εεε=-=卸载前应变:0.025F εε== 卸载后残余应变:0.02386y c f Eεε=-=可恢复弹性应变:0.00114y c εεε=-=(3)C 点: 卸载前应变:0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变:0.05869cc Eσεε=-=可恢复弹性应变:0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
钢结构基本原理(第二版)习题参考解答第二章

钢结构基本原理(第二版)习题参考解答第二章第二章钢结构的基本材料和构件习题参考解答1. 钢材的基本性能指标有哪些?请简要描述各项性能指标的含义。
答:钢材的基本性能指标包括强度、韧性、可塑性和耐腐蚀性。
- 强度:钢材的强度是指钢材抵抗外力的能力,通常以屈服强度、抗拉强度和抗压强度来表示。
屈服强度是指钢材在受到外力作用时,开始产生塑性变形的应力值;抗拉强度是指钢材在拉伸状态下最大的抵抗外力的应力值;抗压强度是指钢材在受到压缩状态下最大的抵抗外力的应力值。
强度的高低决定了钢材的承载能力。
- 韧性:钢材的韧性是指钢材在受到外力作用时,能够发生塑性变形而不断延展的能力。
韧性的好坏决定了钢结构在受到冲击或震动时的抵抗能力。
- 可塑性:钢材的可塑性是指钢材在受到外力作用时,能够发生塑性变形而不断延展的能力。
可塑性的好坏决定了钢材的加工性能和成型性能。
- 耐腐蚀性:钢材的耐腐蚀性是指钢材在受到各种腐蚀介质(如大气、水、酸等)的侵蚀时,能够保持其力学性能和表面的完整性。
耐腐蚀性的好坏决定了钢结构的使用寿命。
2. 钢材的分类方法有哪些?请简要描述各种分类方法。
答:钢材的分类方法有按化学成分分类、按用途分类和按加工方法分类。
- 按化学成分分类:钢材按化学成分可分为碳素钢、合金钢和不锈钢。
碳素钢的主要成分是碳和铁,其含碳量通常在0.08%~2.11%之间;合金钢是在碳素钢中添加其他合金元素(如铬、钼、锰等)来改善钢材的性能;不锈钢是指含有至少12%的铬元素,在大气或酸性介质中形成一层致密的氧化铬膜,起到防腐蚀的作用。
- 按用途分类:钢材按用途可分为结构钢、机械钢、特种钢和工具钢等。
结构钢是用于制造各种钢结构的钢材,如建筑、桥梁、船舶等;机械钢是用于制造机械零部件的钢材,如轴承、齿轮、轴等;特种钢是用于特殊工作条件下的钢材,如高温、低温、高压等环境下的钢材;工具钢是用于制造各种切削工具和模具的钢材,如刀具、冲压模具等。
- 按加工方法分类:钢材按加工方法可分为热轧钢材、冷轧钢材和锻制钢材。
钢结构基本原理(第二版)习题参考解答第二章
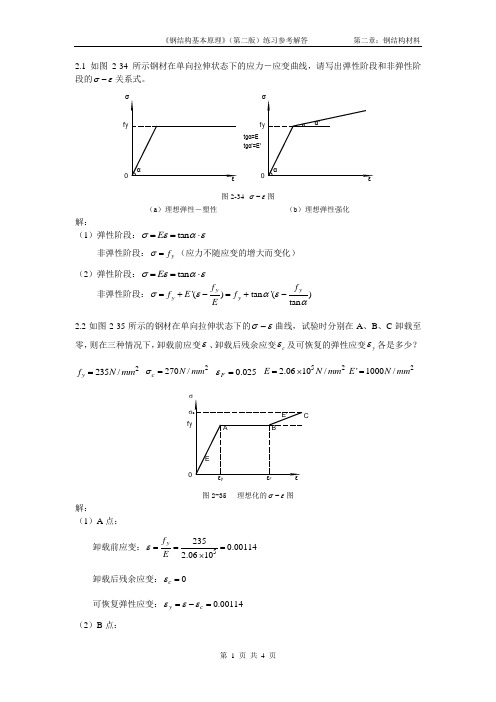
2.1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
tgα'=E'f y0f y 0tgα=E图2-34 σε-图(a )理想弹性-塑性 (b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化)(2)弹性阶段:tan E σεαε==⋅非弹性阶段:'()tan '()tan yyy y f f f E f E σεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少? 2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =f y 0σF图2-35 理想化的σε-图解:(1)A 点:卸载前应变:52350.001142.0610yf E ε===⨯卸载后残余应变:0c ε= 可恢复弹性应变:0.00114y c εεε=-=(2)B 点:卸载前应变:0.025F εε== 卸载后残余应变:0.02386y c f E εε=-= 可恢复弹性应变:0.00114y c εεε=-=(3)C 点:卸载前应变:0.0250.0350.06'c y F f E σεε-=-=+= 卸载后残余应变:0.05869c c E σεε=-= 可恢复弹性应变:0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
同济大学钢结构基本原理(沈祖炎)课后习题答案完全版

同济大学钢结构基本原理(沈祖炎)课后习题答案完全版1. 引言同济大学钢结构基本原理是一门介绍钢结构基本知识和原理的课程。
在学习过程中,课后习题是检验学生掌握程度的重要方式。
本文是同济大学钢结构基本原理(沈祖炎)课后习题的完全版答案。
2. 第一章2.1 选择题1.D2.A3.B4.C5.A2.2 填空题1.拱2.跨度3.支点4.平行5.水平2.3 解答题1.我们可以通过使用方法一和方法二来计算桁架的支反作用力。
方法一使用刚度法,方法二使用Joints法。
具体步骤如下:方法一:–计算桁架的节点刚度矩阵。
–将所有节点刚度矩阵相加得到整个桁架的刚度矩阵。
–构造一个受力平衡的方程组,解得桁架的支反作用力。
方法二:–构造一个支座方程组,解得支座反力。
–通过节点内力平衡,计算出节点的内力。
2.钢结构的主要优点有:–高强度:钢材具有较高的强度和抗拉性能,使得钢结构能够承受较大的荷载。
–轻质:相对于混凝土结构来说,钢结构的自重较轻,可以减少建筑物的结构材料的使用量,降低建筑成本。
–施工速度快:由于钢结构可以在工厂中预制,因此施工速度较快,可以缩短工期,减少施工成本。
–可拆装性好:钢结构可以拆装,便于改建和迁移。
3.塔式起重机是利用强大的垂直支撑能力用高耸的塔架将货物一拉再拉的起重设备。
它是用来适应高空起重和物料搬移的一种机械。
结构上,塔式起重机主要由塔式结构、起升机构、回转机构和顶部配重组成。
其中,塔式结构是起重机的主要承重部分,承担起重机自重和起升机构的荷载。
塔式结构通常使用钢材制作,因为钢材具有较高的强度和抗拉性能,能够承受大的荷载。
此外,塔式起重机的钢结构也具有较好的可拆装性,便于施工和维护。
3. 第二章3.1 选择题1.B2.D3.A4.C5.B3.2 填空题1.核算按简化梁简化支承条件方式2.弹性模量3.建筑结构4.弹性变形5.线弹性3.3 解答题1.三个节点的坐标分别为A(0, 0),B(0, 4),C(4, 0)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题1:某管道支架分别采用图1-1、图1-2两种结构布置方案,在柱顶承受轴心压力P 作用。
这两种方案中,3000,柱两段铰接,钢材为Q235,截面无孔眼削弱,柱截面采用焊接工字形截面,翼缘为剪切边,翼缘-250×14,腹板-250×10。
试计算这两种方案中,根据整体稳定性确定的柱子所能承受的最大轴心压力P 各是多少?分析比较这两种方案的优劣?图1-1图1-2解:1) 图1-1所示结构布置方案mm l x 60000=;mm l y 30000=mm A 950010250214250=⨯+⨯⨯=()433135103167250240278250121mm I x =⨯-⨯⨯=()4333647916725010214250121mm I y =⨯+⨯⨯⨯=mm A I i x x 3.1199500135103167===;mm AI i y y 0.62950036479167===3.503.11960000===x x x i l λ;4.480.6230000===y y y i l λ 此截面对x 轴为b 类,对y 轴为c 类,查表得855.0=x ϕ(附表4-4);785.0=y ϕ(附表4-5)应根据y ϕ确定柱子整体稳定的承载力kN Af P d y 16032159500785.0max =⨯⨯==ϕ2) 图1-2所示结构布置方案mm l x 60000=;mm l y 30000=mm A 9500=;mm i x 0.62=;mm i y 3.119=8.960.6260000===x x x i l λ;1.253.11930000===y y y i l λ 此截面对x 轴为c 类,对y 轴为b 类,查表得478.0=x ϕ(附表4-5);953.0=y ϕ(附表4-4)应根据x ϕ确定柱子整体稳定的承载力kN Af P d x 9762159500478.0max =⨯⨯==ϕ3) 分析比较两种结构布置方案所使用的材料完全相同,但是图1-1所示方案(为下文表述的方便,以后简称方案A )的承载力为1603,而图1-2所示方案(为下文表述的方便,以后简称方案B )的承载力仅为976。
由此,可以判断方案A 更好。
在方案A 中,将柱子截面的强轴与构件较大计算长度所对应的轴取为一致,从而保证了构件相对于截面的两个形心主轴能够实现“等稳定”(稳定系数分别为0.855、0.785)。
在方案B中,构件相对于截面的两个形心主轴的整体稳定系数相差巨大(稳定系数分别为0.478、0.953)。
而构件最终首先相对弱轴发生破坏,尽管构件相对强轴的承载能力很高,但是这个承载力没有发挥的机会。
习题2:如下图所示某焊接工字形等截面简支楼盖梁,截面无削弱,在跨度中点和两端支座处都设有侧向支承,同时在跨度中点截面和两端支座截面处设置有支承加劲肋,材料为Q345钢。
跨中上翼缘作用有集中荷载400(设计值),310(标准值),试对此梁进行强度、刚度及整体稳定验算。
(应考虑构件自重)图2-1解:1、截面几何性质计算214600200121000830014mm A =⨯+⨯+⨯=计算截面形心位置,设截面形心到受压翼缘边缘的距离为y1mm y 45114600102020012514100087300141=⨯⨯+⨯⨯+⨯⨯=mm y 57545110262=-=()()()4922231030342.26575200127451300144515141000810008121mm I x ⨯=-⨯⨯+-⨯⨯+-⨯⨯+⨯⨯=47333109543.3200121218100012130014121mm I y ⨯=⨯⨯+⨯⨯+⨯⨯=mm A I i yy 0.5214600109543.37=⨯==按受压纤维确定的截面模量3691101074.54511030342.2mm W x ⨯=⨯=按受拉纤维确定的截面模量3692100059.45751030342.2mm W x ⨯=⨯=受压翼缘板对x 轴的面积矩()311864800745130014mm S x =-⨯⨯=受拉翼缘板对x 轴的面积矩()321365600657520012mm S x =-⨯⨯=X 轴以上截面对x 轴的面积矩()()3126286767838761864800214451144518mm S S x x =+=-⨯-⨯+=2、梁的内力计算 梁自重标准值m N A g k 8.1347101460078508.92.18.92.16=⨯⨯⨯⨯=⨯⨯=-ρ式中1.2为考虑腹板加劲肋等附加构造用钢材使梁自重增大的系数,9.8为重力加速度。
梁自重设计值m kN m N g g k G 62.14.16178.13472.1≈=⨯==γ梁弯矩设计值m kN M ⋅=+=⨯⨯+⨯⨯=16.1229120016.2912400411262.1812max剪力设计值kN V 72.209400211262.121max =⨯+⨯⨯=(支座截面) 跨中截面的剪力设计值kN V 20040021=⨯=3、强度验算支座截面受到的剪力最大,但此截面所受弯矩为0,故对此截面只需验算抗剪强度2293max max 1809.2981030342.226286761072.209mm N f mm N t I S V v w x x =<=⨯⨯⨯⨯==τ 跨中截面既有较大的剪力,同时还作用有弯矩,另外在此截面上作用有集中荷载。
对此截面的验算应包括截面边缘的正应力验算,截面中和轴位置的剪应力验算,以及腹板与上、下翼缘相交位置的折算应力验算。
截面边缘的正应力验算2266max 3102.292100059.405.11016.1229mm N f mm N W M nx x =<=⨯⨯⨯=γ 跨中截面中和轴位置的剪应力必然小于支座截面中和轴位置的剪应力,支座截面的抗剪强度满足,则跨中截面的抗剪强度必然满足。
由于在跨中截面及支座截面设置有支承加劲肋,因而可以不必验算腹板局部承压强度。
腹板与上翼缘相交位置的折算应力验算()29612.2331030342.2144511016.1229mm N =⨯-⨯⨯=σ 29312.2081030342.2186480010200mm N =⨯⨯⨯⨯=τ0=c σ22222112213108.2352.2032.2333mm N f mm N c c =<=⨯+=+-+τσσσσ腹板与下翼缘相交位置的折算应力验算()29624.3001030342.2125751016.1229mm N =⨯-⨯⨯=σ 29328.1481030342.2136560010200mm N =⨯⨯⨯⨯=τ 222222223105.3018.1434.3003mm N f mm N =<=⨯+=+τσ强度满足要求! 4、刚度验算 跨中最大挠度[]mmlv mm EI l g EI l P v T xk x k T 304003.241030342.21006.2384120003478.151030342.21006.2481200010310384548954953343==<=⨯⨯⨯⨯⨯⨯+⨯⨯⨯⨯⨯⨯=+= 刚度满足要求! 5、整体稳定验算集中荷载产生的弯矩占总弯矩的百分比%6.97%10016.12291200=⨯故按跨度中点作用一个集中荷载查取等效弯矩系数75.1=b β4.1150.5260001===y y i l λ 对单轴对称截面47311015.330014121mm I ⨯=⨯⨯=4632100.820012121mm I ⨯=⨯⨯=7975.0100.81015.31015.3677211=⨯+⨯⨯=+=I I I b α 梁截面属于受压翼缘加强的单轴对称工字形截面,则不对称影响系数()()475.017975.028.0128.0=-⨯⨯=-=b b αηQ345钢屈服强度2345mm N f y =梁的整体稳定系数6.0743.1345235475.010264.4144.1151101074.51026146004.115432075.12354.414320262212>=⨯⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎭⎫ ⎝⎛⨯⨯+⨯⨯⨯⨯=⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎪⎭⎫ ⎝⎛+⋅=y b y x y b b f h t W Ah ηλλβϕ对梁的整体稳定系数进行非弹性修正908.0743.1282.007.1282.007.1=-=-='bbϕϕ 2266max /310/0.265101074.5908.01016.1229mm N f mm N W M x b=<=⨯⨯⨯='ϕ 整体稳定性满足要求! 习题3:图中所示为Q235钢焰切边工字形截面柱,两端铰接,截面无削弱,承受轴心压力的设计值900,跨中集中力设计值为100。
(1) 验算弯矩作用平面内稳定性;(2) 根据弯矩作用平面外稳定性的要求确定此柱至少需要几道侧向支撑杆。
(构件自重可忽略不计)解:(1) 平面内稳定性验算21408064010232012mm A =⨯+⨯⨯=()49331003475.112640310664320mm I x ⨯=⨯-⨯=43365589333123201221210640mm I y =⨯⨯+⨯=3931167023321003475.1mm W x =⨯=mm A I i y y 3.681408065589333=== mm A I i x x 1.271140801003475.19=⨯==3.551.271150000===x x x i l λ,该截面对x ,y 轴均属于b 类,查表得8315.0=x ϕ 0.1=mx β,05.1=x γkN EA N x Ex 3.85013.551.1140801006.214.31.125222=⨯⨯⨯⨯=='λπ m kN M x ⋅=⨯⨯=3751510041()()226312152023.85019008.01311670205.1103750.1140808315.0109008.01mm N f mm N N N W M A N Ex x x xmx x =<=⨯-⨯⨯⨯⨯+⨯⨯='-+γβϕ 平面内稳定性满足要求! (2) 平面外稳定性验算若仅有一道侧向支撑,则mm l oy 7500=8.1093.6875000===y y y l λ,b 类截面,4942.0=y ϕ7960.0235235440008.10907.12354400007.122=⨯-=⋅-=yyb f λϕ226312155.28031167027960.0103750.1140804942.010900mm N f mm N W M A N x b x tx y =<=⨯⨯⨯+⨯⨯=+ϕβϕ面外稳定性不满足要求!若仅有二道侧向支撑,则mm l oy 5000=2.733.6850000===y y y l λ,b 类截面,7308.0=y ϕ9482.0235235440002.7307.12354400007.122=⨯-=⋅-=yyb f λϕ226312154.21431167029482.0103750.1140807308.010900mm N f mm N W M A N x b x tx y =<=⨯⨯⨯+⨯⨯=+ϕβϕ面外稳定性满足要求! 此柱至少需要2道侧向支撑杆。
