数字信号处理实验答案湖南大学经典
数字信号处理实验答案完整版

数字信号处理实验答案 HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】实验一熟悉Matlab环境一、实验目的1.熟悉MATLAB的主要操作命令。
2.学会简单的矩阵输入和数据读写。
3.掌握简单的绘图命令。
4.用MATLAB编程并学会创建函数。
5.观察离散系统的频率响应。
二、实验内容认真阅读本章附录,在MATLAB环境下重新做一遍附录中的例子,体会各条命令的含义。
在熟悉了MATLAB基本命令的基础上,完成以下实验。
上机实验内容:(1)数组的加、减、乘、除和乘方运算。
输入A=[1 2 3 4],B=[3 4 5 6],求C=A+B,D=A-B,E=A.*B,F=A./B,G=A.^B并用stem语句画出A、B、C、D、E、F、G。
clear all;a=[1 2 3 4];b=[3 4 5 6];c=a+b;d=a-b;e=a.*b;f=a./b;g=a.^b;n=1:4;subplot(4,2,1);stem(n,a);xlabel('n');xlim([0 5]);ylabel('A');subplot(4,2,2);stem(n,b);xlabel('n');xlim([0 5]);ylabel('B');subplot(4,2,3);stem(n,c);xlabel('n');xlim([0 5]);ylabel('C');subplot(4,2,4);stem(n,d);xlabel('n');xlim([0 5]);ylabel('D');subplot(4,2,5);stem(n,e);xlabel('n');xlim([0 5]);ylabel('E');subplot(4,2,6);stem(n,f);xlabel('n');xlim([0 5]);ylabel('F');subplot(4,2,7);stem(n,g);xlabel('n');xlim([0 5]);ylabel('G');(2)用MATLAB实现下列序列:a) x(n)= 0≤n≤15b) x(n)=e+3j)n 0≤n≤15c) x(n)=3cosπn+π)+2sinπn+π) 0≤n≤15(n)=x(n+16),绘出四个周期。
(完整word版)数字信号处理上机实验答案(第三版,第十章)

第十章 上机实验数字信号处理是一门理论和实际密切结合的课程,为深入掌握课程内容,最好在学习理论的同时,做习题和上机实验。
上机实验不仅可以帮助读者深入的理解和消化基本理论,而且能锻炼初学者的独立解决问题的能力。
本章在第二版的基础上编写了六个实验,前五个实验属基础理论实验,第六个属应用综合实验。
实验一 系统响应及系统稳定性。
实验二 时域采样与频域采样。
实验三 用FFT 对信号作频谱分析。
实验四 IIR 数字滤波器设计及软件实现。
实验五 FIR 数字滤波器设计与软件实现实验六 应用实验——数字信号处理在双音多频拨号系统中的应用任课教师根据教学进度,安排学生上机进行实验。
建议自学的读者在学习完第一章后作实验一;在学习完第三、四章后作实验二和实验三;实验四IIR 数字滤波器设计及软件实现在。
学习完第六章进行;实验五在学习完第七章后进行。
实验六综合实验在学习完第七章或者再后些进行;实验六为综合实验,在学习完本课程后再进行。
10.1 实验一: 系统响应及系统稳定性1.实验目的(1)掌握 求系统响应的方法。
(2)掌握时域离散系统的时域特性。
(3)分析、观察及检验系统的稳定性。
2.实验原理与方法在时域中,描写系统特性的方法是差分方程和单位脉冲响应,在频域可以用系统函数描述系统特性。
已知输入信号可以由差分方程、单位脉冲响应或系统函数求出系统对于该输入信号的响应,本实验仅在时域求解。
在计算机上适合用递推法求差分方程的解,最简单的方法是采用MA TLAB 语言的工具箱函数filter 函数。
也可以用MATLAB 语言的工具箱函数conv 函数计算输入信号和系统的单位脉冲响应的线性卷积,求出系统的响应。
系统的时域特性指的是系统的线性时不变性质、因果性和稳定性。
重点分析实验系统的稳定性,包括观察系统的暂态响应和稳定响应。
系统的稳定性是指对任意有界的输入信号,系统都能得到有界的系统响应。
或者系统的单位脉冲响应满足绝对可和的条件。
《数字信号处理》第三版课后习题答案

数字信号处理课后答案1.2 教材第一章习题解答1. 用单位脉冲序列()n δ及其加权和表示题1图所示的序列。
解:()(4)2(2)(1)2()(1)2(2)4(3) 0.5(4)2(6)x n n n n n n n n n n δδδδδδδδδ=+++-+++-+-+-+-+-2. 给定信号:25,41()6,040,n n x n n +-≤≤-⎧⎪=≤≤⎨⎪⎩其它(1)画出()x n 序列的波形,标上各序列的值;(2)试用延迟单位脉冲序列及其加权和表示()x n 序列; (3)令1()2(2)x n x n =-,试画出1()x n 波形; (4)令2()2(2)x n x n =+,试画出2()x n 波形; (5)令3()2(2)x n x n =-,试画出3()x n 波形。
解:(1)x(n)的波形如题2解图(一)所示。
(2)()3(4)(3)(2)3(1)6() 6(1)6(2)6(3)6(4)x n n n n n n n n n n δδδδδδδδδ=-+-+++++++-+-+-+-(3)1()x n 的波形是x(n)的波形右移2位,在乘以2,画出图形如题2解图(二)所示。
(4)2()x n 的波形是x(n)的波形左移2位,在乘以2,画出图形如题2解图(三)所示。
(5)画3()x n 时,先画x(-n)的波形,然后再右移2位,3()x n 波形如题2解图(四)所示。
3. 判断下面的序列是否是周期的,若是周期的,确定其周期。
(1)3()cos()78x n A n ππ=-,A 是常数;(2)1()8()j n x n e π-=。
解:(1)3214,73w w ππ==,这是有理数,因此是周期序列,周期是T=14; (2)12,168w wππ==,这是无理数,因此是非周期序列。
5. 设系统分别用下面的差分方程描述,()x n 与()y n 分别表示系统输入和输出,判断系统是否是线性非时变的。
数字信号处理习题及解答

只有在如上周期延拓序列中无混叠的点上, 才满足f(n)=fl(n),所以 f(n)=fl(n)=x(n)*y(n) 7≤n≤19
令
数字信号处理习题及解答
第二章Z变换及离散时间系统分析
3 解答
n≥0时, 因为c内无极点,x(n)=0; n≤-1时, c内有极点0 , 但z=0是一个n阶极点, 改为求
圆外极点留数, 圆外极点有z1=0.5, z2=2, 那么
数字信号处理习题及解答
第二章Z变换及离散时间系统分析 3 解答 (2) 收敛域0.5<|z|<2:
数字信号处理习题及解答
第三章信号的傅里叶变换 1 解答
(1) (2) (3)
数字信号处理习题及解答
第三章信号的傅里叶变换 2 试求如下序列的傅里叶变换:
(1) x1(n)=δ(n-3)
(2)
数字信号处理习题及解答
第三章信号的傅里叶变换 2 解答
(1) (2)
数字信号处理习题及解答
第三章信号的傅里叶变换
第一章离散时间信号与离散时间系统
4 解答
数字信号处理习题及解答
第二章Z变换及离散时间系统分析 1
数字信号处理习题及解答
第二章Z变换及离散时间系统分析 1 解答
数字信号处理习题及解答
第二章Z变换及离散时间系统分析 1 解答
数字信号处理习题及解答
第二章Z变换及离散时间系统分析 2
数字信号处理习题及解答
第二章Z变换及离散时间系统分析 2 解答
数字信号处理习题及解答
第二章Z变换及离散时间系统分析 2 解答
数字信号处理习题及解答
第二章Z变换及离散时间系统分析 3 已知
求出对应X(z)的各种可能的序列表达式。
数字信号处理课后习题答案(全)1-7章

1
4
(2m 5) (n m) 6 (n m)
m4
m0
第 1 章 时域离散信号和时域离散系统
(3) x1(n)的波形是x(n)的波形右移2位, 再乘以2, 画出图形如题2解图 (二)所示。
(4) x2(n)的波形是x(n)的波形左移2位, 再乘以2, 画出图形如题2解图(三) 所示。
因此系统是非线性系统。
第 1 章 时域离散信号和时域离散系统
(6) y(n)=x(n2)
令输入为
输出为
x(n-n0)
y′(n)=x((n-n0)2) y(n-n0)=x((n-n0)2)=y′(n) 故系统是非时变系统。 由于
T[ax1(n)+bx2(n)]=ax1(n2)+bx2(n2) =aT[x1(n)]+bT[x2(n)]
0≤m≤3
-4≤m≤n
非零区间如下:
第 1 章求解: ① n<0时, y(n)=0
② 0≤n≤3时, y(n)= ③ 4≤n≤7时, y(n)= ④ n>7时, y(n)=0
1=n+1
n
1=8-m n0
3
mn4
第 1 章 时域离散信号和时域离散系统
x(m)h(n-m)
m
第 1 章 时域离散信号和时域离散系统
题7图
第 1 章 时域离散信号和时域离散系统
y(n)={-2,-1,-0.5, 2, 1, 4.5, 2, 1; n=-2, -1, 0, 1, 2, 3, 4, 5}
第 1 章 时域离散信号和时域离散系统
解法(二) 采用解析法。 按照题7图写出x(n)和h(n)的表达式分别为
数字信号处理实验答案湖南大学经典

实验二 DFT 和FFT一、实验目的1)认真复习周期序列 DFS、有限长序列DFT 的概念、旋转因子的定义、以及DFS 和DFT的性质等有关内容;复习基2-FFT 的基本算法,混合基-FFT 的基本算法、Chirp-Z 变换的算法等快速傅立叶变换的方法。
2)掌握有限长序列的循环移位、循环卷积的方法,对序列共轭对称性的含义和相关内容加深理解和掌握,掌握利用DFT 分析序列的频谱特性的基本方法。
3)掌握 FFT 算法的基本原理和方法、Chirp-Z 变换的基本原理和方法,掌握利用FFT 分析序列的频谱特性的方法。
4)熟悉利用 MATLAB 进行序列的DFT、FFT 的分析方法。
二、实验内容1)设周期序列( ) { xn =……,0,1,2,3,0,1,2,3,0,1,2,3,……},求该序列的离散傅立叶级数X (k) = DFS[x(n)],并画出DFS 的幅度特性。
主程序:clc;N=4;n=0:N-1;k=0:N-1;xn=[0 1 2 3];Xk=xn*exp(-j*2*pi/N).^(n'*k);stem(k, abs(Xk));xlabel('k');gtext('|X(k)|');分析:由定义可知,对于周期序列,根据离散傅里叶级数公式即可求出,此实验中显示了一个周期的傅里叶级数。
2)设周期方波序列为其中 N 为基波周期,L/N 是占空比。
(1) 用L 和N求| X(k) |的表达式;(2) 当L 和N 分别为:L=5,N=20;L=5,N=40;L=5,N=60 以及L=7,N=60 时画出DFS 的幅度谱;(3) 对以上结果进行讨论,总结其特点和规律。
主程序:L=5,N=20时clc;N=20;xn=[ones(1,5),zeros(1,15)];xn=[xn,xn,xn];n=0:3*N-1;k=0:3*N-1;Xk=xn*exp(-j*2*pi/N).^(n'*k)stem(k,abs(Xk));xlabel('k');title('L=5,N=20时DFS幅度谱');结果:(修改代码中的L和N(x(n)),可以得到其他占空比时DFS的幅度谱)分析:由四组图对比可知,N越大,其频域抽样间隔越小,N为频域的重复周期。
湖南大学数字信号处理实验三

HUNAN UNIVERSITY数字信号处理实验题目:实验三学生姓名: XX学生学号: ********XXX专业班级:通信工程X班实验三IIR 滤波器设计一、实验目的1.认真复习滤波器幅度平方函数的特性,模拟低通滤波器的巴特沃思逼近、切比雪夫型逼近方法;复习从模拟低通到模拟高通、带通、带阻的频率变换法;从模拟滤波器到数字滤波器的脉冲响应不变法、双线性变换法的基本概念、基本理论和基本方法。
2.掌握巴特沃思、切比雪夫模拟低通滤波器的设计方法;利用模拟域频率变换设计模拟高通、带通、带阻滤波器的方法。
3.掌握利用脉冲响应不变法、双线性变换法设计数字滤波器的基本方法;能熟练设计巴特沃思、切比雪夫低通、带通、高通、带阻数字滤波器。
4.熟悉利用MATLAB直接进行各类数字滤波器的设计方法。
二、实验内容a. 设计模拟低通滤波器,通带截止频率为10KHz,阻带截止频率为16KHz,通带最大衰减1dB,阻带最小衰减20dB。
(1) 分别用巴特沃思、切比雪夫I、切比雪夫II型、椭圆型滤波器分别进行设计,并绘制所设计滤波器的幅频和相频特性图。
(2) 在通带截止频率不变的情况下,分别用n=3,4,5,6阶贝塞尔滤波器设计所需的低通滤波器,并绘制其相应的幅频响应和相频响应图。
%'Butter low-pass filter'wp=2*pi*10000;ws=2*pi*16000;Ap=1;As=20;[N,Wc]=buttord(wp,ws,Ap,As,'s'); [B,A]=butter(N,Wc,'s');freqs(B,A);title('Butter low-pass filter');figure%Chebyshev1[N,Wc]=cheb1ord(wp,ws,Ap,As,'s'); [B,A]=cheby1(N,Ap,Wc,'s');freqs(B,A);title('Chebyshev1');figure%Chebyshev2[N,Wc]=cheb2ord(wp,ws,Ap,As,'s'); [B,A]=cheby2(N,Ap,Wc,'s');freqs(B,A);title('Chebyshev2');figure%Elliptic[N,Wc]=ellipord(wp,ws,Ap,As,'s'); [B,A]=ellip(N,Ap,As,Wc,'s');freqs(B,A);title('Elliptic');(2)for n=3:6wn=2*pi*10000; [b,a]=besself(n,wn); figurefreqs(b,a);endb. 设计模拟高通滤波器,通带截止频率为2000Hz,阻带截止频率1500Hz,通带最大衰减为3dB,阻带最小衰减为15dB。
《数字信号处理》第三版课后习题答案

《数字信号处理》第三版课后习题答案数字信号处理课后答案1.2 教材第一章习题解答1. 用单位脉冲序列()n δ及其加权和表示题1图所示的序列。
解:()(4)2(2)(1)2()(1)2(2)4(3)0.5(4)2(6)x n n n n n n n n n n δδδδδδδδδ=+++-+++-+-+-+-+-2. 给定信号:25,41()6,040,n n x n n +-≤≤-??=≤≤其它(1)画出()x n 序列的波形,标上各序列的值;(2)试用延迟单位脉冲序列及其加权和表示()x n 序列;(3)令1()2(2)x n x n =-,试画出1()x n 波形;(4)令2()2(2)x n x n =+,试画出2()x n 波形;(5)令3()2(2)x n x n =-,试画出3()x n 波形。
解:(1)x(n)的波形如题2解图(一)所示。
(2)()3(4)(3)(2)3(1)6()6(1)6(2)6(3)6(4)x n n n n n n n n n n δδδδδδδδδ=-+-+++++++-+-+-+-(3)1()x n 的波形是x(n)的波形右移2位,在乘以2,画出图形如题2解图(二)所示。
(4)2()x n 的波形是x(n)的波形左移2位,在乘以2,画出图形如题2解图(三)所示。
(5)画3()x n 时,先画x(-n)的波形,然后再右移2位,3()x n 波形如题2解图(四)所示。
3. 判断下面的序列是否是周期的,若是周期的,确定其周期。
(1)3()cos()78x n A n ππ=-,A 是常数;(2)1()8()j n x n e π-=。
解:(1)3214,73w w ππ==,这是有理数,因此是周期序列,周期是T=14;(2)12,168w wππ==,这是无理数,因此是非周期序列。
5. 设系统分别用下面的差分方程描述,()x n 与()y n 分别表示系统输入和输出,判断系统是否是线性非时变的。
数字信号处理习题答案及matlab实验详解.pdf

阶跃响应为: y[n] x[n] h[n] x[m]h[n m] h(n m), n m, m 0
m
m0
即 y(0) 0, y(1) 0.25, y(2) 0.5, y(3) 0.75,其余y(n) 1, (n 3)
利用函数 h=impz(b,a,N)和 y=filter(b,a,x)分别绘出冲激和阶跃响应 b=[0,0.25,0.25,0.25,0.25]; a=1; x=ones(1,100); h=impz(b,a,100);y=filter(b,a,x) figure(1) subplot(2,1,1); stem(h,’.’); subplot(2,1,2); plot(y,’.’);
4
解:(1)系统的转移函数是是其单位抽样响应的 Z 变换,因此
H (z)
1 1 z1
1 1 0.3z1
1 1 0.6z1
(1
3 3.8z1 1.08z2 z1)(1 0.3z1)(1 0.6z1)
1
3 1.9
3.8z1 1.08z2 z1 1.08z2 0.18z
3
Z 1
系统的零极点图如下图所示: B=[3,-3.8,1.08]; A=[1,-1.9,1.08,-0.18]; [Z,P,K]=tf2zp(B,A); Zplane(B,A)
5
单位抽样响应:
h(n)
1 2
n1
u
(n
1)
(n)
1
y(n) x(n) * h(n)
2 m1
1 2
m1
e
j (n m)
e
jn
e
jn
e j
1 2 1
2
n
u(n1)
数字信号处理习题及答案解析

==============================绪论==============================1. A/D 8bit 5V 00000000 0V 00000001 20mV 00000010 40mV 00011101 29mV==================第一章 时域离散时间信号与系统==================1.①写出图示序列的表达式答:3)1.5δ(n 2)2δ(n 1)δ(n 2δ(n)1)δ(n x(n)-+---+++= ②用δ(n) 表示y (n )={2,7,19,28,29,15}2. ①求下列周期)54sin()8sin()4()51cos()3()54sin()2()8sin()1(n n n n n ππππ-②判断下面的序列是否是周期的; 若是周期的, 确定其周期。
(1)A是常数 8ππn 73Acos x(n)⎪⎪⎭⎫ ⎝⎛-= (2))81(j e )(π-=n n x 解: (1) 因为ω=73π, 所以314π2=ω, 这是有理数, 因此是周期序列, 周期T =14。
(2) 因为ω=81, 所以ωπ2=16π, 这是无理数, 因此是非周期序列。
③序列)Acos(nw x(n)0ϕ+=是周期序列的条件是是有理数2π/w 0。
3.加法乘法序列{2,3,2,1}与序列{2,3,5,2,1}相加为__{4,6,7,3,1}__,相乘为___{4,9,10,2} 。
移位翻转:①已知x(n)波形,画出x(-n)的波形图。
②尺度变换:已知x(n)波形,画出x(2n)及x(n/2)波形图。
卷积和:①h(n)*求x(n),其他02n 0n 3,h(n)其他03n 0n/2设x(n) 例、⎩⎨⎧≤≤-=⎩⎨⎧≤≤= }23,4,7,4,23{0,h(n)*答案:x(n)=②已知x (n )={1,2,4,3},h (n )={2,3,5}, 求y (n )=x (n )*h (n )x (m )={1,2,4,3},h (m )={2,3,5},则h (-m )={5,3,2}(Step1:翻转)解得y (n )={2,7,19,28,29,15}③(n)x *(n)x 3),求x(n)u(n u(n)x 2),2δ(n 1)3δ(n δ(n)2、已知x 2121=--=-+-+=}{1,4,6,5,2答案:x(n)=4.如果输入信号为,求下述系统的输出信号。
数字信号处理习题解答

y(5)=2*1+1*2=4;y(6)=2*3+1*1+3*2=13 y(7)=1*3+3*1=6;y(8)=3*3=9
y(9)=0;
• N=10圆卷积的结果
10 13 9
6
4
4
1
2
n
0
补充作业
x(n)
22
1
1
n
0
求: (1)x(n)*x(n)的线卷积。
,N=4(不加长)
,N=6(补零加长)
,N=7(补零加长)
作业解答
lfhuang
第一次作业: P104页,3题
...
...
0
n
0
n
第一次作业: P104页,3题
第一次作业: P104页,3题
4
...
1
.k .
0
第二次作业: P104页,4题
第二次作业: P104页,4题
... ... ...
... 图a
n
...
图b n
...
图c n
第二次作业: P104页,4题
3
2
1
1
n
0
周期化
3
2
1
1
n
0
3
3
3
1
2 1
12 1
1
2 1
0
0
n
反折、取主值区间。
3 2
11
0
右平移、相乘、相加 y(0)=1*1+2*1+1*2=5 y(1)=2*3+1*1+3*2=13 y(2)=1*2+2*1+1*3+3*3=16
数字信号处理课后习题答案

数字信号处理课后习题答案数字信号处理课后习题答案数字信号处理是一门重要的学科,它研究如何对数字信号进行处理和分析。
在学习过程中,我们经常会遇到一些习题,通过解答这些习题可以帮助我们更好地理解和掌握数字信号处理的知识。
本文将为大家提供一些数字信号处理课后习题的答案,希望对大家的学习有所帮助。
一、离散时间信号和系统1. 什么是离散时间信号?答:离散时间信号是在离散时间点上取值的信号,它可以用数学上的序列表示。
2. 什么是离散时间系统?答:离散时间系统是对离散时间信号进行处理的系统,它可以用差分方程或差分方程组来描述。
3. 离散时间信号和连续时间信号有何区别?答:离散时间信号是在离散时间点上取值的信号,而连续时间信号是在连续时间上取值的信号。
二、离散时间信号的表示和运算1. 如何表示离散时间信号?答:离散时间信号可以用数学上的序列表示,例如x(n)表示离散时间信号x在时间点n上的取值。
2. 离散时间信号的运算有哪些?答:离散时间信号的运算包括加法、减法、乘法和卷积等。
3. 什么是离散时间信号的卷积?答:离散时间信号的卷积是指两个离散时间信号之间的一种数学运算,它可以表示两个信号之间的线性叠加关系。
三、离散时间系统的性质和稳定性1. 离散时间系统有哪些常见的性质?答:离散时间系统常见的性质包括线性性、时不变性、因果性和稳定性等。
2. 什么是离散时间系统的稳定性?答:离散时间系统的稳定性是指当输入信号有界时,输出信号也有界。
3. 如何判断离散时间系统的稳定性?答:可以通过判断系统的冲激响应的绝对可和性来判断离散时间系统的稳定性。
四、离散傅里叶变换1. 什么是离散傅里叶变换(DFT)?答:离散傅里叶变换是将离散时间信号转换为离散频率信号的一种数学变换。
2. 离散傅里叶变换有何作用?答:离散傅里叶变换可以将时域的信号转换为频域的信号,从而方便对信号的频谱进行分析。
3. 如何计算离散傅里叶变换?答:可以通过对离散时间信号进行离散傅里叶变换公式的计算来得到离散傅里叶变换的结果。
数字信号处理》课后作业参考答案
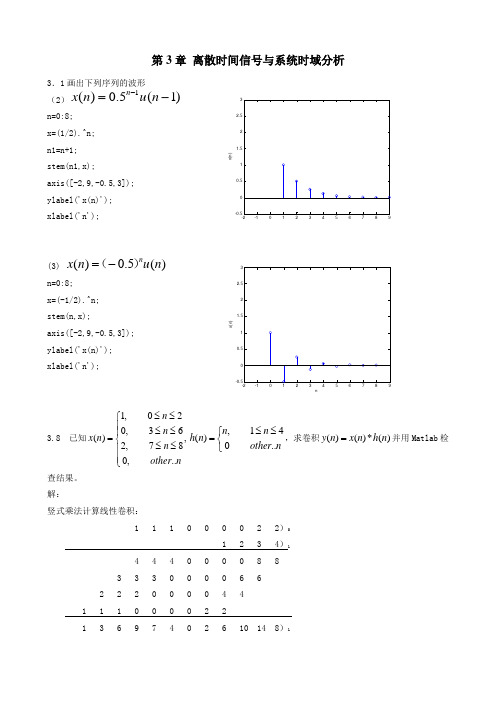
第3章 离散时间信号与系统时域分析3.1画出下列序列的波形(2)1()0.5(1)n x n u n -=- n=0:8; x=(1/2).^n;n1=n+1; stem(n1,x);axis([-2,9,-0.5,3]); ylabel('x(n)'); xlabel('n');(3) ()0.5()nx n u n =-()n=0:8; x=(-1/2).^n;stem(n,x);axis([-2,9,-0.5,3]); ylabel('x(n)'); xlabel('n');3.8 已知1,020,36(),2,780,..n n x n n other n≤≤⎧⎪≤≤⎪=⎨≤≤⎪⎪⎩,14()0..n n h n other n≤≤⎧=⎨⎩,求卷积()()*()y n x n h n =并用Matlab 检查结果。
解:竖式乘法计算线性卷积: 1 1 1 0 0 0 0 2 2)01 2 3 4)14 4 4 0 0 0 0 8 83 3 3 0 0 0 0 6 62 2 2 0 0 0 0 4 41 1 1 0 0 0 02 21 3 6 9 7 4 02 6 10 14 8)1x (n )nx (n )nMatlab 程序:x1=[1 1 1 0 0 0 0 2 2]; n1=0:8; x2=[1 2 3 4]; n2=1:4; n0=n1(1)+n2(1);N=length(n1)+length(n2)-1; n=n0:n0+N-1; x=conv(x1,x2); stem(n,x);ylabel('x(n)=x1(n)*x2(n)');xlabel('n'); 结果:x = 1 3 6 9 7 4 0 2 6 10 14 83.12 (1) 37πx (n )=5sin(n) 解:2214337w πππ==,所以N=14 (2) 326n ππ-x (n )=sin()-sin(n)解:22211213322212,2122612T N w T N w N ππππππ=========,所以(6) 3228n π-x (n )=5sin()-cos(n) 解:22161116313822222()T N w T w x n ππππππ=======,为无理数,所以不是周期序列所以不是周期序列3.20 已知差分方程2()3(1)(2)2()y n y n y n x n --+-=,()4()nx n u n -=,(1)4y -=,(2)10,y -=用Mtalab 编程求系统的完全响应和零状态响应,并画出图形。
数字信号处理习题答案共59页文档

28、目标的坚定是性格中最必要的力 量泉源 之一, 也是成 功的利 器之一 。没有 它,天 才也会 在矛盾 无定的 迷径中 ,徒劳 无功。- -查士 德斐尔 爵士。 29、困难就是机遇。--温斯顿.丘吉 尔。 30、我奋斗,所以我快乐。--格林斯 潘。
16、业余生活要有意义,不要越轨。——华盛顿 17、一个人即使已登上顶峰,也仍要自强不息。——罗素·贝克 18、最大的挑战和突破在于用人,而用人最大的突破在于信任人。——马云 19、自己活着,就是为了使别人过得更美好。——雷锋 20、要掌握书,莫被书掌握;要为生而读,莫为读而生。——布尔沃
《数字信号处理》第三版答案(非常详细完整)

答案很详细,考试前或者平时作业的时候可以好好研究,祝各位考试成功!!电子科技大学微电子与固体电子学陈钢教授著数字信号处理课后答案1.2 教材第一章习题解答1. 用单位脉冲序列()n δ及其加权和表示题1图所示的序列。
解:()(4)2(2)(1)2()(1)2(2)4(3) 0.5(4)2(6)x n n n n n n n n n n δδδδδδδδδ=+++-+++-+-+-+-+-2. 给定信号:25,41()6,040,n n x n n +-≤≤-⎧⎪=≤≤⎨⎪⎩其它(1)画出()x n 序列的波形,标上各序列的值;(2)试用延迟单位脉冲序列及其加权和表示()x n 序列; (3)令1()2(2)x n x n =-,试画出1()x n 波形; (4)令2()2(2)x n x n =+,试画出2()x n 波形; (5)令3()2(2)x n x n =-,试画出3()x n 波形。
解:(1)x(n)的波形如题2解图(一)所示。
(2)()3(4)(3)(2)3(1)6() 6(1)6(2)6(3)6(4)x n n n n n n n n n n δδδδδδδδδ=-+-+++++++-+-+-+-(3)1()x n 的波形是x(n)的波形右移2位,在乘以2,画出图形如题2解图(二)所示。
(4)2()x n 的波形是x(n)的波形左移2位,在乘以2,画出图形如题2解图(三)所示。
(5)画3()x n 时,先画x(-n)的波形,然后再右移2位,3()x n 波形如 5. 设系统分别用下面的差分方程描述,()x n 与()y n 分别表示系统输入和输出,判断系统是否是线性非时变的。
(1)()()2(1)3(2)y n x n x n x n =+-+-; (3)0()()y n x n n =-,0n 为整常数; (5)2()()y n x n =; (7)0()()nm y n x m ==∑。
《数字信号处理》第三版课后习题答案

数字信号处理课后答案1.2 教材第一章习题解答1. 用单位脉冲序列()n δ及其加权和表示题1图所示的序列。
解:()(4)2(2)(1)2()(1)2(2)4(3)0.5(4)2(6)x n n n n n n n n n n δδδδδδδδδ=+++-+++-+-+-+-+-2. 给定信号:25,41()6,040,n n x n n +-≤≤-⎧⎪=≤≤⎨⎪⎩其它(1)画出()x n 序列的波形,标上各序列的值;(2)试用延迟单位脉冲序列及其加权和表示()x n 序列; (3)令1()2(2)x n x n =-,试画出1()x n 波形; (4)令2()2(2)x n x n =+,试画出2()x n 波形; (5)令3()2(2)x n x n =-,试画出3()x n 波形。
解:(1)x(n)的波形如题2解图(一)所示。
(2)()3(4)(3)(2)3(1)6()6(1)6(2)6(3)6(4)x n n n n n n n n n n δδδδδδδδδ=-+-+++++++-+-+-+-(3)1()x n 的波形是x(n)的波形右移2位,在乘以2,画出图形如题2解图(二)所示。
(4)2()x n 的波形是x(n)的波形左移2位,在乘以2,画出图形如题2解图(三)所示。
(5)画3()x n 时,先画x(-n)的波形,然后再右移2位,3()x n 波形如题2解图(四)所示。
3. 判断下面的序列是否是周期的,若是周期的,确定其周期。
(1)3()cos()78x n A n ππ=-,A 是常数;(2)1()8()j n x n e π-=。
解:(1)3214,73w w ππ==,这是有理数,因此是周期序列,周期是T=14; (2)12,168w wππ==,这是无理数,因此是非周期序列。
5. 设系统分别用下面的差分方程描述,()x n 与()y n 分别表示系统输入和输出,判断系统是否是线性非时变的。
数字信号处理实验答案湖南大学经典

实验二DFT 和FFT一、实验目的1)认真复习周期序列DFS、有限长序列DFT 的概念、旋转因子的定义、以及DFS 和DFT的性质等有关内容;复习基2-FFT 的基本算法,混合基-FFT 的基本算法、Chirp-Z 变换的算法等快速傅立叶变换的方法。
2)掌握有限长序列的循环移位、循环卷积的方法,对序列共轭对称性的含义和相关内容加深理解和掌握,掌握利用DFT 分析序列的频谱特性的基本方法。
3)掌握FFT 算法的基本原理和方法、Chirp-Z 变换的基本原理和方法,掌握利用FFT 分析序列的频谱特性的方法。
4)熟悉利用MATLAB 进行序列的DFT、FFT 的分析方法。
二、实验内容1)设周期序列( ) { xn =……,0,1,2,3,0,1,2,3,0,1,2,3,……},求该序列的离散傅立叶级数X (k) = DFS[x(n)],并画出DFS 的幅度特性。
主程序:clc;N=4;n=0:N-1;k=0:N-1;xn=[0 1 2 3];Xk=xn*exp(-j*2*pi/N).^(n'*k);stem(k, abs(Xk));xlabel('k');gtext('|X(k)|');分析:由定义可知,对于周期序列,根据离散傅里叶级数公式即可求出,此实验中显示了一个周期的傅里叶级数。
2)设周期方波序列为其中N 为基波周期,L/N 是占空比。
(1) 用L 和N求| X(k) |的表达式;(2) 当L 和N 分别为:L=5,N=20;L=5,N=40;L=5,N=60 以及L=7,N=60时画出DFS 的幅度谱;(3) 对以上结果进行讨论,总结其特点和规律。
主程序:L=5,N=20时clc;N=20;xn=[ones(1,5),zeros(1,15)];xn=[xn,xn,xn];n=0:3*N-1;k=0:3*N-1;Xk=xn*exp(-j*2*pi/N).^(n'*k)stem(k,abs(Xk));xlabel('k');title('L=5,N=20时DFS幅度谱');结果:(修改代码中的L和N(x(n)),可以得到其他占空比时DFS的幅度谱)分析:由四组图对比可知,N越大,其频域抽样间隔越小,N为频域的重复周期。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验二DFT 和FFT一、实验目的1)认真复习周期序列DFS、有限长序列DFT 的概念、旋转因子的定义、以及DFS 和DFT的性质等有关内容;复习基2-FFT 的基本算法,混合基-FFT 的基本算法、Chirp-Z 变换的算法等快速傅立叶变换的方法。
2)掌握有限长序列的循环移位、循环卷积的方法,对序列共轭对称性的含义和相关内容加深理解和掌握,掌握利用DFT 分析序列的频谱特性的基本方法。
3)掌握FFT 算法的基本原理和方法、Chirp-Z 变换的基本原理和方法,掌握利用FFT 分析序列的频谱特性的方法。
4)熟悉利用MATLAB 进行序列的DFT、FFT 的分析方法。
二、实验内容1)设周期序列( ) { xn =……,0,1,2,3,0,1,2,3,0,1,2,3,……},求该序列的离散傅立叶级数X (k) = DFS[x(n)],并画出DFS 的幅度特性。
主程序:clc;N=4;n=0:N-1;k=0:N-1;xn=[0 1 2 3];Xk=xn*exp(-j*2*pi/N).^(n'*k);stem(k, abs(Xk));xlabel('k');gtext('|X(k)|');分析:由定义可知,对于周期序列,根据离散傅里叶级数公式即可求出,此实验中显示了一个周期的傅里叶级数。
2)设周期方波序列为其中N 为基波周期,L/N 是占空比。
(1) 用L 和N求| X(k) |的表达式;(2) 当L 和N 分别为:L=5,N=20;L=5,N=40;L=5,N=60 以及L=7,N=60时画出DFS 的幅度谱;(3) 对以上结果进行讨论,总结其特点和规律。
主程序:L=5,N=20时clc;N=20;xn=[ones(1,5),zeros(1,15)];xn=[xn,xn,xn];n=0:3*N-1;k=0:3*N-1;Xk=xn*exp(-j*2*pi/N).^(n'*k)stem(k,abs(Xk));xlabel('k');title('L=5,N=20时DFS幅度谱');结果:(修改代码中的L和N(x(n)),可以得到其他占空比时DFS的幅度谱)分析:由四组图对比可知,N越大,其频域抽样间隔越小,N为频域的重复周期。
占空比L/N主要决定第一零点带宽(在一个周期内)。
3)设有限长序列x(n) = {0,1,2,3},计算DTFT[x(n)]=X(ejω),并画出它的幅度谱;然后利用kω=2*pi*k/4,k=0,1,2,3对X(ejω)进行采样,并证明它等于实验a 中的X(k)。
主程序:clc;N=4;xn=[0 1 2 3];n=0:N-1;k=0:N-1;w=2*pi*(0:2047)/2048;Xw=exp(-j*w)+2*exp(-j*2*w)+3*exp(-j*3*w);subplot(211);plot(w/pi,abs(Xw));title('X(ejw)幅度谱');Xk=fft(xn,N);subplot(212);stem(k,abs(Xk),'fill');hold on;plot(N/2*w/pi,abs(Xw));结果:分析:对比第一题的结果可以看出,对离散傅里叶变换的频谱进行抽样,在满足采样定理的条件下,可以无失真的恢复原来的波形。
4)序列x(n)=R4(n),计算DTFT[x(n)]=X(ejω),并绘制其幅度和相位谱。
(1) 计算x(n)的4 点DFT,并绘制DFT 的幅度与相位谱;(2) 将x(n)补零形成8 点序列,计算8 点DFT,并绘制幅度与相位谱,求频率分辨率;(3) 将x(n)补零形成16 点序列,计算16 点DFT,并绘制幅度与相位谱,求频率分辨率;主程序:N1=8; N2=16;k1=0:N1-1;k2=0:N2-1;w=2*pi*(0:2047)/2048;Xw=(1-exp(-j*4*w))./(1-exp(-j*w));%对x(n)的频谱函数采样2048个点可以看做连续的频谱xn=[(n>=0)&(n<4)];X1k=fft(xn,N1);X2k=fft(xn,N2);subplot(321);plot(w/pi,abs(Xw));title('连续函数幅度谱');xlabel('w/pi');subplot(322);plot(w/pi,angle(Xw));title('连续函数相位谱');axis([0,2,-pi,pi]);line([0,2],[0,0]);xlabel('w/pi');subplot(323);stem(k1,abs(X1k),'.');title('X1(k)幅度谱');plot(N1/2*w/pi,abs(Xw));%图形上叠加连续谱的幅度曲线subplot(324)stem(k1,angle(X1k),'.');axis([0,N1,-pi,pi]);line([0,N1],[0,0]);title('X1(k)相位谱');hold on;plot(N1/2*w/pi,angle(Xw));%图形上叠加连续谱的相位曲线subplot(325);stem(k2,abs(X2k),'.');title('X2(k)幅度谱');hold on;plot(N2/2*w/pi,abs(Xw));subplot(326)stem(k2,angle(X2k),'.');axis([0,N2,-pi,pi]);line([0,N2],[0,0]);title('X2(k)相位谱');hold on;plot(N2/2*w/pi,angle(Xw));实验结果:分析:对序列x(n)的N点DFT的物理意义是对其傅里叶变换的频谱在[0,2*pi]上进行N点等间隔的采样。
由实验结果可以看出。
5)序列x(n)=cos(0.48πn)+cos(0.52πn)(1) 求x(n)的10 点DFT,并画出它幅度与相位谱;(2) 求x(n)的100 点DFT,并画出它幅度与相位谱;根据实验结果,讨论DFT 进行谱分析的条件。
主程序:clc;N1=10;k1=0:N1-1;x1=cos(0.48*pi*n1)+cos(0.52*pi*n1); Xk1=fft(x1,10);w=2*pi/10*k1;subplot(311)stem(n1,x1,'.');axis([0,10,-2.5,2.5]);title('信号x(n),0<=n<=9'); subplot(312);stem(k1,abs(Xk1),'.');title('0<=n<=9时幅度谱') subplot(313)stem(k1,angle(Xk1),'.');title('0<=n<=9时相位谱') figure;N2=100;n2=0:N2-1;x2=[x1(1:1:10),zeros(1,90)];Xk2=fft(x2,100);k2=0:N2-1;w2=2*pi/100*k2;stem(n2,x2,'.');axis([0,100,-2.5,2.5]);title('信号x(n)补零N=100'); subplot(312)plot(w2/pi,abs(Xk2));title('0<=n<=99时幅度谱'); subplot(313)stem(k2,angle(Xk2),'.');title('0<=n<=99时相位谱') 实验结果:6)序列x(n)=5(0.9)nR11(n)(1) 求循环反转序列x((-n))11,并绘制x(n)和x((-n))11 的波形;求两序列的DFT,验证DFT 的循环反转性质。
(2) 把序列x(n)分解成圆周共轭奇分量xoc(n)和圆周共轭偶分量xec(n),并求出对应的DFT,验证DFT 的圆周共轭对称性质。
(3) 绘制x((n+4))11R11(n)、x((n-3))15R15(n)和x((n-6))15 的波形,验证序列圆周移位性质。
主程序:clc;N=11;n=0:N-1;x=5*((0.9).^n).*stepseq(0,0,10);subplot(321);stem(n,x,'.');title('原始序列5*(0.9)^n*U(11)');X=fft(x,N);subplot(322)stem(n,abs(X),'.');title('原始序列DFT幅度谱'); subplot(323)stem(n,angle(X),'.');title('原始序列DFT相位谱');x1=[x,zeros(1,N-length(x))];y=x1(mod(-n,N)+1);subplot(324);stem(n,y,'.');title('循环反褶序列x((-n))11');Y=fft(y,N);subplot(325);stem(n,abs(Y),'.');title('循环反褶序列的DFT幅度谱') subplot(326);stem(n,angle(Y),'.');title('循环反褶序列的DFT相位谱')figure(2);xe=0.5*(x+y);xo=0.5*(x-y);Xe=fft(xe,N);Xo=fft(xo,N);subplot(321);stem(n,abs(X),'.');title('原始序列DFT幅度谱'); subplot(322);stem(n,abs(Xo),'.');title('奇对称序列DFT幅度谱'); subplot(323);stem(n,abs(Xe),'.');title('偶对称序列DFT幅度谱'); subplot(324);stem(n,angle(X),'.');title('原始序列DFT相位谱'); subplot(325);stem(n,angle(Xo),'.');title('奇对称序列DFT相位谱'); subplot(326);stem(n,angle(Xe),'.');title('偶对称序列DFT相位谱'); figure(3);n4=0:10;n5=0:14;n6=0:14;x4=cirshftt(x,4,11);x5=cirshftt(x,-3,15);x6=cirshftt(x,-6,15);subplot(311);stem(n4,x4,'.');title('X((n+4))U(11)'); subplot(312);stem(n5,x5,'.');title('X((n-3))U(15)');subplot(313);stem(n4,x4,'.');title('X((n-6))U(15)');实验结果:分析:由实验结果可以知道,实域循环反褶,频域对应共轭。
