机械原理自由度
《机械原理自由度》课件

机械故障诊断
通过运动分析诊断机械故障的原因 和位置。
控制系统设计
利用运动分析结果设计控制系统的 参数和策略。
机构运动分析的实例
平面四杆机构的运动分析
01
通过解析法计算平面四杆机构的自由度,并分析其运动特性。
凸轮机构的运动分析
02
利用实验法测量凸轮机构的位移、速度和加速度,分析其运动
规律。
机器人臂关节的运动分析
03
通过数值法模拟机器人臂关节的运动行为,优化关节的设计参
数。
04
机构动力学分析
机构动力学的基本概念
机构动力学是研究机 械系统中机构运动及 其与力的关系的学科 。
机构动力学的基本概 念包括力、力矩、加 速度、速度和位移等 。
它涉及到系统的平衡 、运动规律、动态响 应等方面的内容。
机构动力学分析的Байду номын сангаас法
空间机构自由度计算
总结词
空间机构自由度计算是机械原理中一个复杂的概念,它涉及到机构在空间中的 运动自由度数。
详细描述
空间机构的自由度计算公式为F=6n-(3PL + Ph),其中n为活动构件数,PL为低 副数,Ph为高副数。与平面机构不同,空间机构需要考虑三个方向的自由度, 因此计算更为复杂。
特殊机构自由度计算
通过建立平面连杆机构的运动学和动力学模型,分析其运动规律 和动态响应。
凸轮机构的动力学分析
研究凸轮机构的动态行为,包括从动件的运动规律和受力情况等。
齿轮机构的动力学分析
分析齿轮机构的动态特性,如振动、冲击和噪声等,以提高齿轮传 动的平稳性和可靠性。
05
机构优化设计
机构优化设计的目标和方法
目标
0918机械原理自由度注意事项
m 个构件在同一处构成复合铰链,实际上构成了
( m-1 ) 个转动副。
F = 3× 5 - 2× 7 =1
例2-7 试计算图2-13所示直线机构的自由度。 B、C、D、F处都是 由三个构件组成的复 合铰链,各有2个转 动副
n7 pl 10 ph 0 F 3 7 2 10 0 1
D 4 C 5 F 6 G B 1 2 3 E I A 7 H
D
虚约束
5 F 6 G H
局部自由度
C
4
B 1
2
3 E
7
I A
n 6 ; PL 8 ; PH 1 F 3n 2 PL PH 3 6 2 8 1 1
例 3 计算图所示机构的自由度 (若存在局部自由度、 复合铰链、虚约束请标出)。
D 4 C 5 F 6 G B 1 2 3 E I A 7 H
D
局部自由度
C
4
5
F 6 G
H
B 1
2
3 E
7
I A
n 6 ; PL 8 ; PH 1 F 3n 2 PL PH 3 6 2 8 1 1
例 4 如图所示, 已知HG=IJ,且相互平行;GL=JK,且相 互平行。计算此机构的自由度 (若存在局部自由度、复 合铰链、虚约束请标出)。
本章结束
例 4 如图所示, 已知HG=IJ,且相互平行;GL=JK,且相 互平行。计算此机构的自由度 (若存在局部自由度、复 合铰链、虚约束请标出)。
I 8 J 9 11
H 7 G 10 C 2 K L E 4 F 5 3 D 1 A 6 B
虚约束
I 8 J 9 11 10 H 7 G
【课程思政优秀案例】《机械原理》:机构自由度的计算

课程思政优秀案例——《机械原理》:机构自由度的计算一、课程和案例的基本情况课程名称:机械原理授课对象:机械类专业大二本科生课程性质:专业核心必修课课程简介:机械原理是机械类专业必修课,以机构设计和分析为主线,培养学生具有一定的机械系统运动方案创新设计能力,教学内容涵盖机构组成理论、运动学、动力学及各种常用机构的设计方法等机构和机器的共性问题,具有较强的综合性和工程实践性,在学生整个学习过程中起着承上启下和培养学生创新思维、综合设计能力及工程实践能力的重要作用。
结合我校人才培养定位及机械类专业特色,机械原理课程不断强化以学生为中心的顶层设计和教学实施,针对课程重点难点,精心设计课堂学习、研究性学习、实验学习和综合性课程实践等教学环节,通过科教融合、资源建设、教学模式改革、课赛结合等,从不同维度提升课程的高阶性、创新性和挑战度,培养学生的创新意识、辩证思维、现代工具应用能力、综合设计能力和解决复杂工程问题能力,并通过学生形成性考核评价和课程质量评价促进课程持续改进。
与此同时,深入挖掘课程育人功能,提出“四融合一示范”课程思政建设思路,将教书育人贯穿于课程教学及实践活动全过程,强化学生在智能制造强国战略中的责任意识和使命担当,实现价值塑造、知识传授和能力培养同向同行。
案例简介:机构结构分析是机构运动分析、力分析和机构设计的基础,是机械系统方案设计和机构创新设计的重要环节。
本案例的教学内容为“机构自由度的计算”,是机构结构分析一章的重点,具体包括“机构具有确定运动的条件、机构自由度的计算和计算平面机构自由度时应注意的事项”,机构自由度计算结果正确与否,直接影响机构运动的可能性和确定性判断,进而影响机构设计方案可行性的评价。
本讲的学习目标:知识传授:①理解平面机构自由度计算公式及其内涵;②准确识别并正确处理机构中的复合铰链、局部自由度和虚约束;③正确运用自由度计算公式计算机构的自由度,并判断其是否具有确定的运动。
机械原理自由度的计算

机械原理自由度的计算机械原理是研究物体在空间中的运动和静止状态的学科,而自由度则是描述一个物体在空间中能够自由运动的能力。
在机械系统中,了解物体的自由度对于设计和分析至关重要。
本文将介绍机械原理自由度的计算方法,帮助读者更好地理解机械系统的运动特性。
首先,我们需要了解自由度的概念。
在机械系统中,一个物体的自由度可以通过其能够在空间中独立运动的轴线数量来描述。
例如,一个刚性物体在三维空间中有6个自由度,分别是三个平移自由度和三个转动自由度。
而在二维平面中,一个刚性物体有3个自由度,分别是两个平移自由度和一个转动自由度。
通过计算物体的自由度,我们可以更好地了解其在空间中的运动特性。
接下来,我们将介绍如何计算机械系统的自由度。
对于一个多连杆机构,我们可以通过以下步骤来计算其自由度:1. 确定机构的运动副数量,首先需要确定机构中所有的运动副数量,包括旋转副和滑动副。
运动副的数量将直接影响机构的自由度。
2. 计算约束数量,接下来需要计算机构中的约束数量,包括固定约束和移动约束。
固定约束会限制物体的运动,而移动约束则会增加机构的自由度。
3. 计算自由度:最后,通过运动副数量和约束数量的对比,我们可以计算出机构的自由度。
自由度的计算公式为:自由度 = 3 (运动副数量) 约束数量。
通过以上步骤,我们可以准确地计算出机械系统的自由度,从而更好地理解其运动特性和设计特点。
在实际工程中,了解机械系统的自由度对于设计和分析都具有重要意义。
通过准确计算自由度,我们可以避免设计中的错误,确保机构的运动性能符合要求。
同时,对于复杂的机械系统,计算自由度也可以帮助工程师更好地理解其结构和运动规律,为系统的优化提供重要参考。
总之,机械原理自由度的计算是机械工程中的重要内容,通过准确计算自由度,我们可以更好地理解机械系统的运动特性,为设计和分析提供重要依据。
希望本文的介绍能够帮助读者更好地理解这一概念,为工程实践提供帮助。
自由度的计算机械原理教案

几个转动副?
计算自由度时,算几个移动副?
机构运动确定吗?
第十二页,共13页。
谢谢大家!
第十三页,共13页。
教学资料整理
• 仅供参考,
• 低副个数Pl=4 • 高副个数Ph=0
• 机构的自由度为
• F=3n-2Pl-Ph=3×3-2×4-0=1
第六页,共13页。
§2-5 平面机构自由度的计算
2. 举例
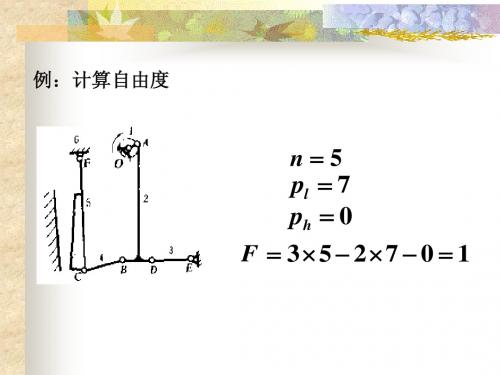
例题二:计算图中所示牛头刨床机构的自由度
活动构件数n=5
低副个数Pl=7
高副个数Ph=0 该机构自由度为
F=3n—2Pl—Ph
=3×5—2×7-0=1
第三页,共13页。
§2-5 平面机构自由度的计算
• 平面机构的自由度
• 机构中各构件相对于机架的所能有的独立运动的数目
1. 计算公式
自由度、约束
一个不受任何约束的构件在平面中的运 动只有三个自由度
一个平面低副引入两个约束
一个平面高副引入一个约束
第四页,共13页。
§2-5 平面机构自由度的计算
1. 计算公式
• 在计算机构自由度时,应注意以下一些情况,否则计算结 果往往会发生错误。
• 1.要除去局部自由度 • 2.要正确计算运动副的数目 • 3. 要除去虚约束
第九页,共13页。
§2-6 计算机构自由度时应注意的事项
• 1. 局部自由度 • 对整个机构运动无关的自由度称为局部自由度。
• 在计算机构自由度时,局部自由度应当舍弃不计。
自由度的计算机械原理教案
课程回顾
• 1.机构运动简图
• 根据机构的运动尺寸,按 一定的比例尺定出各运动副
的位置,采用运动副及常用 机构运动简图符号和构件 的表示方法,将机构运动 传递情况表示出来的简化 图形。
机械原理自由度怎么算

机械原理自由度怎么算
机械系统的自由度是指系统中独立运动的最小数目,通常用f
表示。
机械系统的自由度与其构成的零件数目以及约束条件有关。
对于一个机械系统来说,其自由度f可以通过以下公式计算:
f = 3n - c
其中n表示系统中的运动副数目,c表示系统中的约束条件数目。
运动副是指机械系统中能够实现相对运动的连接件,例如铰链、滑动副、滚动副等。
约束条件是指机械系统中对运动副相对位置或相对运动有限制的表达式,例如固定约束、转动约束、滑动约束等。
在计算自由度时,需要注意的是:
1. 运动副可以是可动的或固定的,但是必须与其他连接件相对运动。
2. 约束条件可以是人为设定的,也可以是由物理条件决定的。
3. 运动副和约束条件的数目可以包括整个系统中的所有连接件,包括外部连接件。
通过计算机械系统的自由度,可以帮助我们理解系统的运动特性和设计过程中的限制条件,从而更好地进行机械设计和分析。
机械原理(第二章 自由度)

§2-5 机构自由度的计算
1.平面机构自由度的计算
(1)计算公式
F=3n-(2pl+ph)
式中:n为机构的活动构件数目;
pl 为机构的低副数目;
ph为机构的高副数目。
3
(2)举例
1)铰链四杆机构
F=3n-(2pl+ph)
=3×3-2×4 =1
3
2)铰链五杆机构
F=3n-(2pl+ph)
4
=3×4-2×5 =2
虚约束的作用: ①改善构件的受力情况,如多个行星轮。 ②增加机构的刚度,如轴与轴承、机床导轨。 ③使机构运动顺利,避免运动不确定,如车轮。
计算图示包装机送纸机构的自由度。
分析: 活 动 构 件 数 n : 复合铰链: 2个低副 局部自由度 2个 虚约束: 1处
E
4 D7
F5G
96 IJ 8
H
B2 C3
轴孔连接(接
触平面)
滑块与导轨联
接(接触平面)
两齿轮轮齿啮 合(齿廓曲面)
运动副元素—两个构件参加接触而构成运动副的表面
面接触的运动副称为低副,
2
转动副 (回转副或铰链)
1
移动副
点接触或线接触的运动副称为高副。
3.平面构件的自由度
当没有约束时,构件作平面运动具有三个自由 度:即可以沿x轴和y轴方向移动,以及绕垂直于 运动平面xOy转动。
2 1
4
2
1 5
3)内燃机机构
F=3n-(2pl+ph) =3×6-2×7 =1
10 C 11
8 ,9 3
7D B
18
4 A1
§2-6 计算平面机构自由度时应注意的事项
1.要正确计算运动副的数目 (1)复合铰链 由m个构件组成的复合铰链,共有(m-1)个转动副。
算自由度的公式

算自由度的公式
1. 平面机构自由度计算公式。
- 对于平面机构,自由度计算公式为F = 3n - 2P_L-P_H。
- 其中n为活动构件数。
- P_L为低副(转动副和移动副)的数目。
- P_H为高副(例如齿轮副、凸轮副等)的数目。
2. 空间机构自由度计算公式(拓展)
- 空间机构自由度的计算相对复杂,常用的公式为F = 6n - 5P_5-4P_4-3P_3-2P_2-P_1。
- 这里n为活动构件数。
- P_5为五级副(相当于有5个相对运动自由度受到约束的运动副)的数目。
- P_4为四级副的数目,以此类推。
在人教版的机械原理相关教材中,平面机构自由度的计算是一个重要的基础内容,在分析机构的运动可能性和确定性方面有着关键的作用。
例如在分析平面连杆机构、凸轮机构等的运动时,通过计算自由度可以判断机构是否具有确定的运动等情况。
机械原理自由度

用F表示,即
F3n2P LP H
1.3.2 机构具有确定相对运动的条件
机构具有确定相对运动的条件: 机构的自由度等于原动件个数。
原动件活 塞,自由 度为1。 将直线运 动变位往 复摆动。
1.3.3 计算平面机构自由度的注意事项
1.复合铰链Biblioteka 1、运动副:两个构件直接接触形成的可动联接。
2、运动副元素:两构件构成运动副时直接接触的点、 线、面部分。
自由度和约束
自由度:构件具有的独立运动的数目 (确定构件位置的独立参变量的数目
约束:对独立运动所加的限制
3、运动副分类: (1)按运动副的接触形式分为低幅和高副 低幅:面与面接触的运动副;接触面压强较低。
以用来表示机构的运动情况,而且还可以根据机构简图
对机构进行运动分析和受力分析,它是一种用简单线条
和符号表示机构的工程图形语言。应表明:机构的种
类,构件的数目及相互传动的路线,运动副的种类、数
目。没有严格按比例绘制的简图称为机构示意图。
• 用途:分析现有机械,构思设计新机械。
运动副与构件的表示方法
1. 构件的种类
处都是3个构件汇交成的 复合铰链,各有二个回转
副,故PL=10。
F 3 n 2 P L P H 3 7 2 1 1 0
F与机构原动件个数相等。因此,当原动件8转动时,圆盘中心 E将确定地沿直线EE’移动。
2.局部自由度
机构中某些构件所具有的自由度仅与其自身的局部运 动有关,并不影响其它构件的运动,则称该自由度为局部 自由度。
得机构
1.4 机构的组成原理和结构分析 1.4.1 平面机构的高副低代
根据一定条件对机构中的高副以低副代替, 称为高副低代。
自由度计算机械原理

利用深度学习技术对复杂机械系统进行自由度预测,实现智 能化分析。
自由度计算在复杂系统中的应用
航空航天领域
对飞行器、卫星等复杂机械系统 的自由度进行精确计算,优化设 计。
机器人领域
对机器人关节、连杆等自由度进 行计算,提高机器人的运动性能 和稳定性。
自由度计算的理论研究与实际应用的结合
机构综合
基于自由度的机构综合方法
01
通过设定机构的自由度要求,可以综合出满足特定运动要求的
机构结构。
机构创新设计
02
利用自由度计算,可以探索新的机构形式,实现更高效、更复
杂的运动功能。
机构优化设计
03
基于自由度计算,可以对现有机构进行优化设计,提高其性能
或降低制造成本。
机构优化
机构尺寸优化
机构运动性能优化
学正解。
运动学逆解
通过自由度计算,确定机器人在 给定的末端执行器位置和姿态下 的关节角度,即求解机器人的运
动学逆解。
雅可比矩阵
基于自由度计算,构建描述机器 人末端执行器速度与关节速度之 间关系的雅可比矩阵,用于机器
人的速度和加速度分析。
机器人动力学分析
动力学正解
基于自由度计算,确定机器人在给定关节力和力矩作用下的末端执 行器加速度、速度和位置变化,即求解机器人的动力学正解。
03 自由度计算在机械设计中 的应用
机构分析
机构自由度计算
通过计算机构的自由度,可以确 定机构在空间中的运动能力,从 而评估其是否能实现特定的运动
要求。
机构运动分析
通过自由度计算,可以分析机构的 运动特性,包括运动范围、速度、 加速度等,为后续的机构设计提供 依据。
机械原理楔块机构自由度

机械原理楔块机构自由度机械原理是研究机械结构和机械运动规律的一门学科,而楔块机构是其中的一种重要的机械原理。
楔块机构是利用楔形零件的变形特性来完成力的传递、定位和固定的机构。
本文将从楔块机构的自由度角度出发,探讨楔块机构的原理和应用。
我们来了解一下楔块机构的自由度。
自由度是指机构中独立运动的最小数目。
对于楔块机构来说,由于楔块的特殊形状和运动特性,其自由度是固定的,即为零。
这是因为楔块只能做直线运动,无法产生旋转运动。
因此,楔块机构在设计和应用时需要考虑其特殊的运动规律和力的传递方式。
楔块机构的主要特点之一是力的传递。
楔块机构通过楔形零件的变形来实现力的传递。
当外界施加力或载荷时,楔形零件会受到压力,从而发生变形。
利用楔形零件的变形特性,可以将外界施加的力传递给其他部件,实现力的定位和固定。
楔块机构广泛应用于各种工程领域,如夹具、刀具、锁紧装置等。
楔块机构的运动规律也是其重要的特点之一。
楔块机构的运动规律可以简单地描述为平移运动。
楔形零件在运动过程中只能沿着一条直线进行平移,不能产生旋转运动。
这种特殊的运动规律使得楔块机构在一些特殊的应用场景中具有独特的优势。
例如,在夹具中,楔块机构可以实现对工件的紧固和定位,确保工件在加工过程中的稳定性和精度。
楔块机构还具有结构简单、工作可靠等特点。
由于楔块机构的运动自由度为零,其结构相对简单,易于制造和维护。
同时,楔块机构的工作可靠性也较高,能够承受较大的载荷和变形,保证力的传递的稳定性和可靠性。
在实际应用中,楔块机构有着广泛的应用。
例如,在汽车制造中,楔块机构常用于发动机的曲轴和连杆的连接,实现动力传递;在建筑工程中,楔块机构常用于起重机的塔臂和基座的连接,确保起重机的稳定性;在工业生产中,楔块机构常用于夹具的设计,实现工件的夹紧和定位。
可以说,楔块机构在各个领域中都发挥着重要的作用。
楔块机构是一种重要的机械原理,其自由度为零。
楔块机构通过楔形零件的变形特性来实现力的传递、定位和固定。
机械原理 课件 §2-5 机构自由度计算
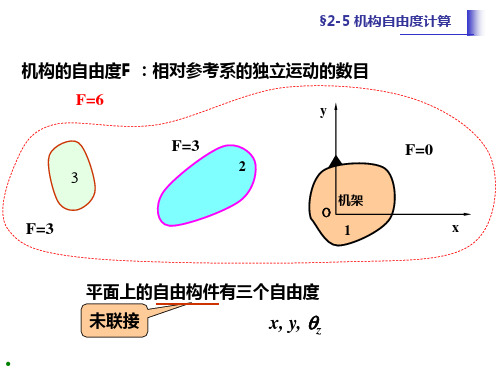
机构的自由度F :相对参考系的独立运动的数目
F=6
F=3 3 F=3
2
y
F=0
机架
O
1
x
平面上的自由构件有三个自由度
未联接
x, y, z
.
机构自由度计算
用转动副与机架连接后剩一个自由度
n=2 pl=3 ph =0
平面低副引入2个约束 平面高副引入1个约束
y
F=2 F=4 F=1 F=3 机构自由度计算公式 F=3n - (2pl + ph ) 活动构件数:n 低副数: pl 高副数: ph
自由度计算注意事项
n=9 pl =11 ph =3 F’=2 p’=1
点划线
作业:2-16 (a)(b)(c)
.
平面机构的组成原理
研究低副机构
F=3n - 2pl
F=1
平面机构的组成原理
n=5 pl =7 F=1
n=2 pl =3 F=0
基本杆组:不可再分的自由度为0的用运动副连接的构件系统 机构由基本杆组联接于原动件和机架上而构成 n=2 , pl =3 F=3n - 2pl =0 n=3 , 无解 n=4 , pl =6 ……
3 1
n=3 pl =3 ph =1 F=2? n=7 pl =6? ph =0 F=9?
2
3 2 1
pl =10
F=1
.
3、虚约束 运动副引入了重复的约束
两构件之间存在多个 *导路互相平行的移动副 *轴线重合的转动副 *法线重合的高副 *不影响机构运动传递的重复部分
自由度计算注意事项
算 一 个 移 动 副
.
例
例:手动冲床 F=3*2-(2*3+0)=0
机械原理基本知识点

机械原理基本知识点2机器里每一个独立的运动单元体称为一个构件。
两个构件直接接触而构成的可动的连接称为运动副。
自由度:机构具有确定运动时所必须给定的独立运动参数的数目。
高副:点线接触,2自由度。
低副:面接触,1自由度。
机械运动简图和机构示意图。
机构自由度:F=3n-(2Pl+Ph-p撇)-F撇(虚约束:重复约束)(局部自由度:产生局部运动而不影响其他构件的运动)复合铰链有n-1个转动副。
低副:移动副,转动副.自由度为1机构具有确定运动条件:原动件数等于其所具有的自由度。
基本杆组:最后不能再拆的最简单的自由度为零的构件组(2构三低,四狗六地)速度瞬心:互作平面相对运动的两构件上瞬时速度相等的重合点,即为两构件的速度瞬心。
(Pij)三心定理:三个作彼此平面平行运动的构件的三个瞬心必位于同一直线上。
科氏加速度----是动点的转动与动点相对运动相互耦合引起的加速度。
科氏加速度的方向垂直于角速度矢量和相对速度矢量。
4运动副中摩擦力的确定:ψ=arctanf.摩擦圆半径ρ=fv·r.运动副中法向反力和摩擦力的合力称为运动副中的总反力。
总反力方向:1总反力与法向反力偏斜一摩擦角ψ。
2总反力Fr21与法向反力偏斜的方向与构件1相对于构件2的相对速度V12的方向相反。
构件组的静定条件:3n=2Pl+Ph总反力方位的确定:1不计摩擦时确定总反力的方向2计摩擦力时总反力与摩擦圆相切3轴承2对轴颈1的总反力对轴颈中心之距离的方向必与轴颈1相对于轴承2的相对较速度w12的方向相反。
(可根据铰接处两者转向判断,摩擦力与之相反,或总反力看作推力,推动摩擦圆与铰接处转向相反。
)5效率=理想比实际。
串联等于相乘,并联分别计算功率,理论功率比实际功率。
运动副自锁条件:作用在轴颈上的驱动力为单力F,且作用于摩擦圆之内,即a<ρ.(力矩小于最大摩擦力矩)移动副自锁条件:作用于滑块的驱动力作用在其摩擦角之内。
6动平衡:惯性力与惯性力矩平衡。
机械原理自由度的定义

机械原理自由度的定义The definition of degrees of freedom in mechanical principles deals with the number of independent movements a system has. 机械原理中对自由度的定义涉及系统具有的独立运动数量。
It is a critical conceptin understanding the behavior and constraints of mechanical systems. 这是理解机械系统行为和约束的重要概念。
Degrees of freedom can be understood as the number of parameters required to uniquely define the configuration of a mechanical system. 自由度可以理解为唯一定义机械系统配置所需的参数数量。
It is essential in design, analysis, and control of mechanical systems in various engineering fields. 在各种工程领域的机械系统的设计、分析和控制中至关重要。
Understanding degrees of freedom is crucial for engineers and researchers to optimize the performance and efficiency of mechanical systems. 理解自由度对于工程师和研究人员来说至关重要,以优化机械系统的性能和效率。
In mechanical systems, degrees of freedom are categorized as translational and rotational. 在机械系统中,自由度被归类为平移和旋转。
机械原理__第1章__平面机构的自由度

1
= 3? 3 2? 3 1 = 2
对于图b) 的机构,有: F=3×2 -2×2 -1=1 事实上,两个机构的运动相同,且F=1
2
1
处理的方法:
计算前先将小滚轮焊接在推杆上 a) b)
§1—3 平面机构自由度的计算
三、虚约束 :对机构的运动不起实际约束作用的约束。 例:平行四边形机构,AB = CD 连杆2作平动,BC线上各点轨迹均为圆 B 2
n K 1
运动副联接前自由度: 3 n 通过运动副联接后,低副产生的约束数 : 2 Pl 高副产生的约束数: 1 Ph
计算公式: F = 3n - 2Pl - Ph
§1—3 平面机构自由度的计算
例1、计算曲柄滑块机构的自由度。 解:活动构件数n= 低副数Pl = 4 高副数Ph = 0 1
原动件数=F 机构运动确定
§1—3 平面机构自由度的计算
例4、计算自由度 ,Ph = 0 解: n = 2, P l =3
F = 3n - 2Pl - Ph = 3? 2 2? 3 0
1 3 例5、计算自由度 2
,Ph = 0 解: n = 3, P l =5
F = 3n - 2Pl - Ph = 3? 3 2? 5 0 = - 1
2
3
4
F = 3n - 2Pl - Ph = 3? 3 2? 4 0
=1
§1—3 平面机构自由度的计算
二、机构具有确定运动的条件 对不同的机构,自由度不同,给定原动件的个数也应不同, 那么,原动件数与自由度有什么关系,才能使机构具有确定的运 动呢? 2 3 例2、计算铰链四杆机构的自由度 1 解:活动构件数n= 3 低副数Pl= 4 高副数Ph= 0 F = 3n - 2Pl - Ph = 3? 3 2? 4 1 4
机械原理机构自由度计算

n
3×n
2 × PL
1 × Ph
计算公式: F=3n-(2PL +Ph )
要求:记住上述公式,并能熟练应用。
例题①计算曲柄滑块机构旳自由度。
解:活动构件数n= 3 低副数PL= 4 高副数PH= 0
1
2
F=3n - 2PL - PH
S3
=3×3 - 2×4
2
3
B
8A
计算成果肯定不对!构件数不会错,肯定是低副数目搞错了!
重庆大学专用
作者: 潘存云教授
1.复合铰链 --两个以上旳构件在同一处以转动 副相联。
两个低副
计算:m个构件, 有m-1转动副。
重庆大学专用
作者: 潘存云教授
例题④重新计算图示圆盘锯机构旳自由度。
上例:在B、C、D、E到处应各有 2 个运动副。
重新计算:n=3, PL=4, PH=0
应用
F=3n - 2PL - PH =3×3 -2×4
=1 尤其注意:此例存在虚约束旳几何条件是:
重庆大学专用
AB=CD=EF
作者: 潘存云教授
出现虚约束旳场合: 1.两构件联接前后,联接点旳轨迹重叠,
作者:潘存云教授
2.两构件构成多种移动副,且 导路平行。
高副数PH= 1
1
F=3n - 2PL - PH =3×2 -2×2-1
=1
重庆大学专用
作者: 潘存云教授
§2-6 自由度计算中旳特殊问题 例题④计算图示圆盘锯机构旳自由度。
解:活动构件数n= 7
D5
F
低副数PL= 6
高副数PH=0
F=3n - 2PL - PH =3×7 -2×6 -0 =9
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
机构分类:闭式链机构和开式链机构。
精品课件
1.2 平面机构的运动简图 1.2.1 机构运动简图及其用途
机构运动简图——用国标规定
的简单符号和线条表示运动副和构 件,并按一定的比例表示运动副的 位置,这种用来说明机构各构件间 相对运动关系的图形,称为机构运 动简图。
必须与原机构具有完全相同的运动特性,它不仅可
精品课件
两构件组成多个平面高副,但接触点之 间的距离为常数
精品课件
(2)两构件上某两点间的距离在运动 过程中始终保持不变。
精品课件
(3)联接构件与被联接构件上联接点 的轨迹重合
精品课件
(4)机
复合铰链:C点;局部自由度:滚在9与活塞4视为一体; 虚约束:E与E1两处移动副,去掉一个虚约束;弹簧 10不影响机构自由度,去掉。
原动件活 塞,自由 度为1。 将直线运 动变位往 复摆动。
精品课件
1.3.3 计算平面机构自由度的注意事项
1.复合铰链
• 两个以上的构件在同一轴线上用转动
副连接起来形成复合铰链。由K个构件 汇交成的复合铰链应当包含(K-1)个回
转副。计算时不可漏算。
计算自由度 F 3n 2 pL pH
3*5 2*7 1
1)固定件或机架;2)原动件;3)从动件 *必须有一个机架,至少有一个原动件,其余为活动构件。
2. 运动副的表示方法
转动副符号
3. 构件的表示方法
移动副符号
高副符号
精品课件
精品课件
精品课件
精品课件
精品课件
精品课件
精品课件
精品课件
精品课件
精品课件
精品课件
精品课件
其他零部件的表示方法可参看GB4460—84“机构运动 简图符号”。
精品课件
得机构
精品课件
1.4 机构的组成原理和结构分析 1.4.1 平面机构的高副低代
根据一定条件对机构中的高副以低副代替, 称为高副低代。
代替条件:代替前后机构自由度不变;瞬时 度和瞬时加速度不变。
方法:一个构件加两个低幅。构件:过接触 点法线,两个低幅:即为接触点圆弧曲率中心。
高副接触有三种:圆弧和圆弧接触;点和圆 弧接触;线和圆弧接触精品。课件
A为复合铰链
精品课件
例:计算图所示圆盘锯主体 机构的自由度。
解 机构中有7个活动构件,
n =7, E,B,C,D 4
处都是3个构件汇交成的 复合铰链,各有二个回转
副,故PL=10。
F 3 n 2 P L P H 3 7 2 1 1 0
F与机构原动件个数相等。因此,当原动件8转动时,圆盘中心 E将确定地沿直线EE’移动。精品课件
精品课件
• 绘制小型压力机机构运动简图
精品课件
精品课件
精品课件
精品课件
精品课件
1.3 平面机构的自由度
• 自由度——可能出现的独立运动称为构件的自由度。 1.3.1 平面机构自由度及其计算公式
设平面机构共有N个构件,低副和高副数目分别为PL和PH,
如将机构中某一构件固定为机架,则机构中的活动构件数为
2.局部自由度 机构中某些构件所具有的自由度仅与其自身的局部运
动有关,并不影响其它构件的运动,则称该自由度为局部 自由度。
发生场合:有滚子的地方,就一定有局部自由度 解决方法:将滚子与安装滚子的构件固结在一起,将 二者视为一个构件。
精品课件
3.虚约束 在特定几何条件或结构条件下,某些运动副所引入的
n=N-1。由于活动构件给机构带进3n个自由度,而机构中全 部运动副所引入的约束总数为2 PL + PH。因此活动构件的自
由度总数减去由运动副引入的约束总数就是该机构的自由度,
用F表示,即
F3n2P LP H
精品课件
1.3.2 机构具有确定相对运动的条件
精品课件
精品课件
机构具有确定相对运动的条件: 机构的自由度等于原动件个数。
约束可能与其它运动副所起的限制作用一致,这种不起独 立限制作用的重复约束为序约束 ,计算自由度时去掉。 虚约束经常出现场合: (1)两构件构成多个运动副时 两构件构成多个转动副,但其轴线相重合:为了改善构件 受力情况。
精品课件
两构件构成多个运动副时,但其导路相互平行或重 合:为了改善构件受力情况。
第1章 平面机构的结构分析
基本要求及重点、难点 运动副及其分类 平面机构运动简图 平面机构的自由度计算
精品课件
基本要求和重点
了解研究机构结构的目的、机构的组成, 熟练掌握运动简图的绘制和机构自由度的 计算,会进行平面机构组成原理和结构分 析
精品课件
1.1 研究机构的目的
1、探讨机构运动的可能性和确定性 2、对机构按结构进行分类,并建立 运动分析和动力分析的一般方法 3、了解机构的组成原理 4、绘制机构运动简图
1、圆弧和圆弧接触 (1)圆形曲线:图示,两构件在c点构成高副,机构 在运动过程中,AO1、BO、O1O长度不变,用一杆 O1O加两副O1和O代替了原高副C。
精品课件
(2)非圆形曲线
由于曲线各处曲率中心的位置不同,故在机构运动中随着 接触点的改变,曲率中心OO1相对于构件1、2的位置及 OO1间的距离也会随之改变。因此对于一般的高副机构, 在不同的位置有不同的瞬时替代机构。实例
高副:点或线接触的运动副。接触面压强较高,易磨损。
常见低幅
常见高副
精品课件
(2)按相对运动形式分平面副和空间副
平面副
空间副
精品课件
运动链
• 由两个或两个以上构件通过运动副联接而 构成的系统。分两类:闭式和开式。
精品课件
开式运动链
精品课件
机构
原动件:按给定运动规律独 力运动的构件。
从动件:其余的活动构件。 机架:固定不动的构件。精品课件
以用来表示机构的运动情况,而且还可以根据机构简图
对机构进行运动分析和受力分析,它是一种用简单线条
和符号表示机构的工程图形语言。应表明:机构的种
类,构件的数目及相互传动的路线,运动副的种类、数 目。没有严格按比例绘制的精品简课件图称为机构示意图。
• 用途:分析现有机械,构思设计新机械。
运动副与构件的表示方法 1. 构件的种类
精品课件
1.2 运动副、运动链和机构
1、运动副:两个构件直接接触形成的可动联接。 2、运动副元素:两构件构成运动副时直接接触的点、
线、面部分。
精品课件
自由度和约束
自由度:构件具有的独立运动的数目 (确定构件位置的独立参变量的数目
约束:对独立运动所加的限制
精品课件
3、运动副分类: (1)按运动副的接触形式分为低幅和高副 低幅:面与面接触的运动副;接触面压强较低。
