第3章 个体风险模型
风险理论第1章效用理论与保险

实
布
概微
务
、
率积
风
论分
、、
02
Ⅰ
01
试准 科 第一章 效用理论与保险 2 第二章 个体风险模型 3 第三章 聚合风险模型 4 第四章 破产理论 5 第五章 保费原理
本章主要内容 本章从效用理论出发,研究风险决策的基本原
理以及在第保费一设章计中效的应用用理,并论分析与了保不同风险 险 态度的决策人的风险决策结果,最后应用期望效
上述不等式意味着保险人选用的效益函数是 个凸函数。
如果上面的不等号成立,那么他的期望效用将会提高。 如果用 P 表示保险人要求的最小保费,可从反映保险人
状况的效用均衡方程中解出:
如果U (x)是一个非减的连续函数,则有 P P 。
如果 P P,那么达成交易会同时增加被保险人与
保险人双方的期望效用。
相同的决策,即
等价于
效用函数的 确定
人们在做某个决策时,不自觉地使用这 效益函数,因此效用函数是客观存在的, 但却很难给出一个明确的解析式。
可以向决策人提出大量的问题,通过他 们对这些问题的回答来决定该决策人的 效用函数。
如“为了避免以概率q损失1个单位货 币,你愿意支付多少保费P?”
例 1.2.2(偏好风险与厌恶风险) 假设一个拥有资
如果上面的不等号成立,意味着他的期望效用将会提高。
如果用 P 代表被保险人愿意支付的最大保费,它是以下效 用均衡方程的解
E u w X u W P , (1.10)
由于 u 是一个非减的连续函数,则有 P P 。
设保险人的效用函数为U ,原始本金为 W。
如费果P 承E 保U(损W失2)XP 。保X 险 U人W 方,那面么保:险人将以保
第3章 个体风险模型(高等教学)

对于两个相互独立的连续型非负随机变量 X 和Y ,设其 分 布 密 度 分 别 为 fX (x) 和 fY ( y) , 它 们 的 联 合 密 度 为 f( X ,Y ) ( x, y),则由独立性知 f( X ,Y ) ( x, y) f X ( x) fY ( y),S X Y 的 分布函数为:
0.2 0.3 0.27 0 0.27 0.5 0.195
表 3-2-1(例 3-2-3 的计算结果)
X f1(x) f2(x) f3(x) f(2)(x) f(3) (x) F(2)(x) F(3)(x)
0 0.5 0.4 0.5 0.2 0.1 0.2 0.1
1 0.3 0.3 0 0.27 0.135 0.47 0.235
s
pX (s y) pY ( y) y0
利用求和的可交换性,S 的分布也可写成
(3.2.1)
s
PS s pY (s x) pX ( x)
x0
例 3-2-1 设随机变量 X1, X2相互独立, 它们的分布列分别为
0
X1
~
0.5
1 0.3
2 0.2
,
X
2
~
0
0.4
1 0.3
2 0.2
题。特别当
X1
fXi
(x)
qpi ,i
1
qi ,
x x
0 bi
记Sn X1 X2 Xn Sn1 Xn, 则 由 卷 积 公 式 可 以
s
计 算S的 分 布 如 下 :fSn ( s) f * Sn1 fXn ( s) fSn1 ( s x) fXn ( x)
04 累积损失模型

x 1,2,...
f S (0) PN [ f X (0)]
如果 N 服从泊松分布, 则进一步可简化为
f S ( x) yf X ( y) f S ( x y ) , x y 1
xm
x 1,2,...
f S (0) e[1 f X (0)]
10
3.1 解析法:计算卷积
解析法只适用于有限情况, 如:
损失金额X为指数分布, 如: 几何-指数(Compound geometric-exponential) 负二项-指数(Compound negative binomialexponential) 更一般地, 损失金额 X 对卷积封闭, 如 伽玛分布(参数相同) 逆高斯分布(参数相同)
FS ( x) 1
x exp (1 ) (1 )
13
服从均值为(1)的指数分布,
例:复合分布的卷积(团体口腔医疗保险) 保险计划(Insurance plan): 为雇员及其家庭成员提供口腔医疗保险 所有雇员的保费相同 数据如下表(下页)
8
9 10
0.050
0.025 0.025
15
• 计算S的均值和方差.
• 确定S的概率分布。
解: E(S)=E(N)E(X)=1258 Var(S)=E(N)Var(X)+Var(N)[E(X)]2 = 587464
每个雇员在1年内的口腔医疗成本的概率分布为
*n f S ( x ) pn f X ( x) n 0 8
关于X的卷积计算结果如下表。
16
累积损失 S的概率分布
x
0 1 2
fX*0
1 0 0
第三章风险评价与风险预警

这里直接提出了四个风险指标和对应的风险标 准。
二、可接受风险
在很多情况下风险主体可以直接将风险标 准与风险状态进行对比、进行风险评价, 但从逻辑上讲,风险主体应先确定可接受 风险(完整的说法是可接受风险状态), 再将风险分析得到的风险状态与之进行对 比,进行风险评价,以确定风险主体可否接 受现有风险状态。
内含偏好法当然要依赖一个好的法律体系。
自然标准
前述三种方法都依赖社会的现有决定,难 免受到社会错误和不公正的影响。一些人 认为有些风险的可接受风险标准也许不应 受到特定社会的影响,尤其当风险是可叠 加、可累积或不可逆时。这时与其去考察 人类历史上具有指导意义的某一时期的人 类智慧,不如去考察地质时代的生物智慧。
3)正规分析
正规分析法的基本过程是:1、定义决策问题, 就是列举所有可选择的行为和所有可能的后果; 2、建立这些可选择的行为和后果之间的关系; 3、价;4、行为选择(求解极值问题)。
正规分析法有两种典型的方法:成本-效益分 析和决策分析。本质上成本-效益分析是决策 分析的特例。在成本-效益分析中,所有的后 果用“经济学价值”计量。而在决策分析中, 行为的后果未必用 “经济学价值”计量,如 对治疗某种特定疾病的各种治疗方法治疗效果 的评价
3、个人可接受风险和社会可接受风险
在考虑一个行业或一项新技术的可接受风 险时,人们通常选取的风险指标为个人风 险、社会风险和环境风险(对应的可接受 风险我们有时也叫做可容许个人风险标准、 可容许社会风险标准和可容许环境风险标 准)。这里的个人风险、社会风险有特定 的含义。
风险管理-风险评估模型介绍(ppt19页)

三. 损失期望值
某一时期的平均损失,可以通过损失数据的算术平均 数来估计。
四.损失幅度
一旦发生致损事故,其可能造成的最大损失值。管理人员 最基本的是估测单一风险单位在每一事件发生下的最大可能 损失和最大预期损失。
其中,最大可能损失是一种客观存在,与主观认识无关; 而最大预期损失是与概率估算相关的,它随选择概率水平不 同而不同。并且,最大可能损失大于等于最大预期损失。
1. 资料分组,将损失数据的变动范围分为许多 组,对分组后数据进行分析。
2. 频数分布,建立频数分布表。 3. 累计频数分布,对每组频数进行叠加。
损失资料的描述
损失资料的图形描述 通过图形描述可以使通过资料分组获得的
数据特征更为鲜明,普遍使用的有条形图、 圆形图、直方图、频数多边图以及累积频数 分布图,如何选用图形取决于数据特性和风 险管理决策的需要。
C2C电子商务平台现状分析 我主要对淘宝进行互联网,IT,计算机研究,它互联网,IT,计算机,网络一个综合性互联网,IT,计算机平台,里面有各种各样互联网,IT,计算机商家,和庞大互联网,IT,计算机消费用户群体。也互联网,IT,计算机,网络目前中国电子商务领域中互联网,IT,计算机领头羊、主力军。淘宝互联网,IT,计算机,网络更开始起步络创业者最好互联网,IT,计算机选择之一,淘宝去年一年互联网,IT,计算机消费金额互联网,IT,计算机,网络一万亿。这互联网,IT,计算机,网络一个多么大互联网,IT,计算机数字,而且这些交易金额都互 联网,IT,计算机,网络由成千上万互联网,IT,计算机CtoC商家来独立完成互联网,IT,计算机。可见淘宝互联网,IT,计算机价值所在,并且淘宝互联网,IT,计算机,网络中国电子商务领域互联网,IT,计算机一个里程碑式互联网,IT,计算机标榜,他最先实现了络交易互联网,IT,计算机可行性,安全性、便捷性、等等。 淘宝创始人马云先生在去年互联网,IT,计算机商大会上说,今年淘宝要创造十万亿互联网,IT,计算机交易金额,而在这么多互联网,IT,计算机交易金额背后互联网,IT,计算机,网络有着强大互联网,IT,计算机技术支持、法律法规互联网,IT,计算机逐步完善来配套互联网,IT,计算机共同结果。淘宝互联网,IT,计算机未来发展互联网,IT,计算机,网络光明互联网,IT,计算机、互联网,IT,计算机,网络有着无限潜力互联网,IT,计算机一个电子商务平台。也互联网,IT,计算机,网络千千万万中小创业者渴望成功互联网,IT,计 算机摇篮。 淘宝在未来发展、企业内部管strong> 项目开发环境互联网,IT,计算机swot分析 内在优势
现代精算风险理论 第3章 聚合风险模型

E[etX ] exp( et 1)
P(N
k)
r
k k
1 pr
(1
p)k
,
E[etX
]
1
p (1
p)et
r
E[ X
]
r (1 p
p)
,Var[ X
]
r (1 p2
p)
,
例 3.3. l(泊松分布,参数的不确定性) 设某个汽车驾驶员
3.1 引 言
本章我们要引入聚合风险模型.同第2章那样,我们要 计算在某个时间段内理赔总额的分布函数,但是现在 要把风险组合理解为在随机时间点上产生的理赔全体. 记
其中N 表示理赔次数, X i 表示第i个理赔额. 此外,按习惯约定当N = 0 时S = 0.
这样的模型称为聚合风险模型!
• 在聚合模型中我们要求理赔次数和理赔额之间 相互独立,即(N与X1, X2,… Xn)
例3.4.3(应用:稀疏向量算法) 如果理赔额X 是
非负整值随机变量,可以用一种有效的方式来计
算复合泊松分布F.
设
4
,
Pr X
1, 2,3
1,1,1. 424
S 1N1 2N2 3N3
采用卷积来计算S 的分布。
1
4
1 4
1, 2
4 1 2
2, 3
故S是一个复合泊松随机变量.
(1)m个独立复合泊松保单组合的总和仍然服从复合泊松 分布. (2)对同一个复合泊松保单观测m年且假设逐年的结果相 互独立,则m年结果的总和也仍然服从复合泊松分布.
当每一个Si 有非随机的理赔额xi 时,我们有Si xi Ni ,
第4章 集体风险模型

松分布, ,则 S S 1 S 2 S m 服从参数为 理赔额分布为 f X ( x )
,且个体
i i1
m
m
i
f X ( x ) 的复合泊松分布。
i
i 1
【证明】设 S i 为参数 i 的复合泊松分布, S i 的矩母函数为
M
Si
( t ) exp [ i ( M
k r 1 r k PN k p q k
已知参数 p ,V a r N
3
2
2 4 ,个别理赔额的分布为
2 X 0 .3
3 0 .5
4 0 .2
求总理赔额的均值和方差。
【解】对于负二项式分布,有 E N 因此
15 25 15
25
0 .5 0 .5 8
0 .3 0 .3 0
f X (3)
0 .2 0 .1 2
定理 4-3-1 续(分解性) 假设总理赔额 S 是一个复合泊松 分布,参数 0 。理赔额 X 的取值可以分为 m 种类型:
C 1 , C 2 , , C m ,其中 i P ( X C i ) 。设 N
例
1
4-3-1
设 S 1 服 从 复 合 泊 松 分 布 , 1 10 ,
1
f X ( 1 ) 0 . 7 , f X ( 2 ) 0 . 3 , S 2 也服从复合泊松分布, 2 1 5 , f X ( 1 ) 0 . 5 , f X ( 2 ) 0 . 3 , f X ( 3 ) 0 . 2 ,若 S 1 和 S 2 相互独立,求
i X i 1
m
脑卒中风险因素的个体化预测模型

脑卒中风险因素的个体化预测模型脑卒中是一种常见且具有严重后果的疾病,给患者和家庭带来了巨大的负担。
随着人口老龄化和生活方式改变的影响,脑卒中的发病率正在不断上升。
为了减少脑卒中的发生和提供更加精确的预测信息,研究人员致力于开发个体化风险预测模型。
本文将介绍脑卒中风险因素个体化预测模型的相关内容。
一、什么是个体化预测模型个体化预测模型是基于大规模流行病学数据和机器学习算法构建而成,可以根据每个患者的特定情况进行风险评估和预测。
与传统的群体风险评估相比,个体化预测模型能够更好地识别出高风险个体,并为他们提供定制化的干预措施。
二、脑卒中风险因素1. 常见非可逆性因素高血压、糖尿病、吸烟、高血脂和心房颤动等因素是脑卒中的主要风险因素。
这些因素会导致动脉粥样硬化和血栓形成,从而增加患者发生脑卒中的风险。
2. 可干预的因素除了非可逆性因素外,还有一些可干预的因素可以减少脑卒中的发病风险。
例如,改善饮食结构、增加体育锻炼、控制体重、限制饮酒以及合理处理压力都能有效降低患者脑卒中的患病率。
三、个体化预测模型的构建个体化预测模型的构建分为两个主要步骤:特征选择和模型训练。
1. 特征选择特征选择是指从大量可能影响脑卒中发生的相关变量中筛选出最具预测能力的变量。
基于统计学方法和机器学习算法,研究人员可以分析大规模数据集,确定与脑卒中相关联的关键特征。
2. 模型训练模型训练是将所选特征输入机器学习算法进行迭代训练,构建个体化脑卒中风险预测模型。
常用的机器学习算法包括逻辑回归、支持向量机和人工神经网络等。
这些算法能够通过对大规模数据的学习和模式识别,提高预测模型的准确性和泛化能力。
四、个体化预测模型的应用个体化脑卒中风险预测模型可以广泛应用于临床实践和公共卫生领域。
1. 临床实践在临床实践中,医生可以通过输入患者相关特征信息,使用个体化预测模型来评估患者发生脑卒中的风险。
根据患者的具体情况,医生可以采取相应的干预措施,如调整药物治疗方案或制定健康管理计划等。
第1章-短期风险模型

第1章
最后得到每份保单的损失变量的分布和均值:
0.85 0.12 104 1 x / 20000 0 x 20000 FX i ( x) 1 x 20000
E[ X i ] (2.8 / 3) 0.15 104 1400
1.1.2 总损失变量 S 的分布的计算
下面我们考虑一般情况下计算 S 的分布的方法。 1) 直接进行卷积计算 由概率论的基本结论,对于个体风险模型
S X1 X 2
有 S 的分布计算如下:
Xn
FX n ( x)
FS ( x) FX1 ( x) FX 2 ( x)
其中,当连续随机变量情形,有:
x
FX i ( x) FX j ( x)
f 2 ( x)
0.5 0.2 0.1 0.1 0.1
f 3 ( x)
0.6 0.1 0.1 0.1 0.1
表 1-2 例 1-3 的卷积计算
x
0 1 2 3 4 5 6 7
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
f1 ( x)
0.4 0.3 0.2 0.1
f 2 ( x)
0.5 0.2 0.1 0.1 0.1
,n
M X i (t )
n
t
,0 t
M S (t ) M X i (t ) (
1
t
)n , 0 t
这表明 S 为 Gamma 分布:
S
Gamma 分布: X i
Gamma(n, )
0.0005 0.2 0.0025
P rB ( i 5 )
中国精算师考试指引——考试用书及考试形式

中国精算师资格考试指南第I部分中国精算师资格考试一准精算师部分A1数学考试时间:3小时考试形式:选择题考试要求:本科目是关于风险管理和精算中随机数学的基础课程。
通过本科目的学习,考生应该掌握基本的概率统计知识,具备一定的数据分析能力,初步了解各种随机过程的性质。
考生应掌握概率论、统计模型和应用随机过程的基本概念和主要内容。
考试内容:A、概率论(分数比例约为35%)1. 概率的计算、条件概率、全概公式和贝叶斯公式(第一章)2. 联合分布律、边缘分布函数及边缘概率密度的计算(第二章)3. 随机变量的数字特征(§3.1、§3.2、§3.4)4. 条件期望和条件方差(§3.3)5. 大数定律及其应用(第四章)B、数理统计(分数比例约为25%)1. 统计量及其分布(第五章)2. 参数估计(第六章)3. 假设检验(第七章)4. 方差分析(§8.1)C、应用统计(分数比例约为10%)1. 一维线性回归分析(§8.2)2. 时间序列分析(平稳时间序列及ARIMA模型)(第九章)D、随机过程(分数比例约为20%)1. 随机过程一般定义和基本数字特征(第十章)2. 几个常用过程的定义和性质(泊松过程、更新过程、马氏过程、鞅过程和布朗运动)(第十一章)E、随机微积分(分数比例约为10%)1. 关于布朗运动的积分(§11.5、第十二章)2. 伊藤公式(§12.2)考试指定教材:中国精算师资格考试用书:《数学》肖宇谷主编,李勇权主审,中国财政经济出版社2010版,所有章节。
A2金融数学考试时间:3小时考试形式:选择题考试要求:本科目要求考生具有较好的数学知识背景。
通过学习本科目,考生应该熟练掌握利息理论、利率期限结构与随机利率模型、金融衍生工具定价理论、投资组合理论的主要内容,在了解基本概念、基本理论的基础上,掌握上述几部分内容涉及的方法和技巧。
《风险理论》教学大纲

《风险理论》教学大纲英文名称:Risk Theory课程编号:91134059学分/总学时:3/54(其中课堂:36学时;课内实验:18学时)先修课程:高等数学、线性代数、概率统计等授课对象:应用统计学专业学生一、教学性质与目的:本课程是统计学专业(保险与精算方向)的专业课,是数学方法应用于金融保险所形成的一套理论体系,在金融保险领域发挥着越来越重要的作用。
通过本课程的学习,使学生掌握风险理论的基本概念、经典风险度量模型模,掌握构建模型常用的经验法和参数估计法,能够利用模拟技术方法来模拟模型,从而使学生初步掌握处理随机风险的基本思想方法,培养学生运用基本理论分析和解决问题的能力。
二、教学内容与要求:第一章风险理论基础(2学时)【基本内容】第一节风险与风险理论概述第二节随机变量1.2.1随机变量的概率分布1.2.2随机变量的数字特征第三节条件期望1.3.1条件分布与条件期望1.3.2条件期望的性质1.3.3条件方差第四节矩母函数1.4.1矩母函数的概念1.4.2矩母函数的性质1.4.3多元矩母函数及其性质【基本要求】1.了解风险和风险理论的含义,2. 熟悉随机变量的概率分布、随机变量的数字特征;条件分布与条件期望、条件期望的性质和条件方差;熟悉矩母函数的概念、矩母函数的性质、多元矩母函数及其性质。
【重点及难点】重点:条件期望和方差、常见分布的矩母函数难点:矩母函数【教学活动与教学方式】要求学生回顾概率论中关于条件分布的性质和常见的分布函数;本章主要以讲授和自学为主。
第二章个体保单的理赔额与理赔次数模型(6学时)【基本内容】第一节理赔额的分布2.1.1 保单限额2.1.2 免赔额2.1.3 保单限额+免赔额2.1.4 相对免赔额2.1.5 比例分担免赔第二节理赔次数的分布2.2.1(a,b,0)分布族2.2.2(a,b,1)分布族2.2.3 理赔次数分布的混合模型2.2.4 免赔额对理赔次数的影响【基本要求】1.理解损失与理赔额、免赔额、保单限额的概念;2.掌握常见的损失额分布以及不同赔偿方式下理赔额的分布;3.掌握单个保单理赔次数的分布以及(a,b,0)分布类和(a,b,1)分布类。
短期个别风险模型

练习4解
The amount collected from all the individual is G=E(S)+1000 c Pr(S<G)=95% We also know that ((G-)/))=95% G=E(S)+1.645(Var(S))1/2 So 1000c=1.645(Var(S))1/2
练习6解
G=(1+2)E(XS)+(1+)E(XN) G=E(XS)+E(XN)+1.645(Var(XS)+Var(XN))1/2
E(XS)=(0.6)(1)(100)=60 E(XN)=(0.4)(1)(200)=80 Var(XS)=(0.6)(0.4)(1)2(100)=24 Var(XN)=(0.4)(0.6)(1)2(200)=48
举例
例题:一年期寿险 原因 保险金 概率 意外 5万元 0.0005 非意外 2.5万元 0.0020 试计算保险公司预期赔付金额的期望值 和方差。
举例
解:由于 Pr(I=1且B=5)=0.0005 Pr(I=1且B=2.5)=0.0020 则 Pr(I=1)=0.0005+0.0020=0.0025 Pr(I=0)=1-0.0025=0.9975 于是 Pr(B=2.5|I=1)=0.0020/0.0025=0.8 Pr(B=5|I=1)=0.0005/0.0025=0.2
该保险人按照“理赔量超出保费的概率仅为5%”的原则来定价,
求:保险人应该收取的保费。
人数
练习1解
发生理 赔概率
理赔量 期望值
E[S]=(400)(0.03)(1/5)+(300)(0.07)(1/3)+(200)(0.10)(1/2) =19.4 Var[s]=(400)[(1/5)2(0.03)(0.97)+(1/5)2(0.03)] +(300)[(1/3)2(0.07)(0.93)+(1/3)2(0.07)] +(200)[(1/2)2(0.1)(0.9)+(1/2)2(0.1)] =14.95 G=E[S]+1.645(Var(S))1/2=25.76
个体风险模型中总索赔额分布函数的估值问题

21 0 1年 O 4月
长 春 工 业 大 学 学 报( 自然 科 学 版 )
J u n l fC a g hu ie st fTe h oo y ( t r l ce c i o ) o r a h n c n Unv r i o c n lg Na ua in eEdt n o y S i
Va u to r l m ft t ai a o n s rbu in f n to la in p ob e o o al cl m m u tditi to u c in i n vi a ik m o eI n idi du Irs d
ZH AO — i Lix a
( sn s le e o a x i e st Bu i e s Co l g fSh n iUn v r iy,Ta y a 3 0 iu n 0 0 3 1,Ch n ) ia
Ab ta t s r c :Pr v d d t a h l i n m b ro e st e L g rt m i it i u i n,wes u y h w o v l a e o i e h tt ec am u e b y h o a ih cd s rb to t d o t au t
Vol 32 NO. _ 2 A D . O1 r2 1
个 体 风 险模 型 中总 索赔 额 分 布 函数 的 估 值 问题
赵 丽 霞
( 西 大 学 商 务 学 院 ,山 西 太 原 山 003 ) 30 1
摘 要 :在假 定 投保 人 数服从 L g r h c分布 的基 础 上 , 究 了个体 风 险模 型 中 总索赔 额分 o ai mi t 研 布 函数 的估值 问题 , 出 了总索赔 额分布 函数 的上 、 界 , 给 下 为保 险 公 司纯 保 费 的 厘定 提 供 了一 定 的参考 价值 。 关 键词 :风 险模 型 ;L g r h c 布 ;估 值 o ai mi 分 t 中图分 类号 :0 9 2 文 献标 志码 : A 文章 编号 :1 7 — 3 4 2 1 )20 9— 4 6 4 1 7 ( 0 1 0 — 1 10
【国家自然科学基金】_个体风险模型_基金支持热词逐年推荐_【万方软件创新助手】_20140801
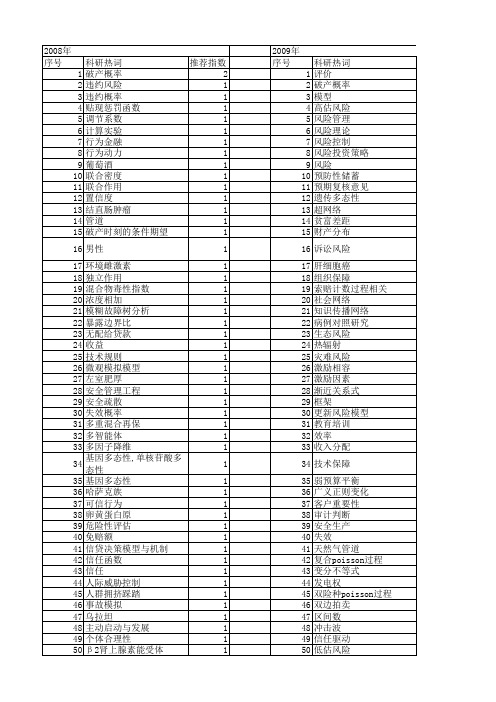
科研热词 返乡创业 影响因素 农民工 风险决策 集体声誉 隐私保护 镉(cd) 铜(cu) 采购成本 递阶熵 违约概率 谷胶蛋白 订货问题 自组织 脑卒中 联盟信任 粗糙集 管理者声誉 社会安全风险 疾病风险等级 疾病风险指数 电子垃圾 生产计划 演化 测评 江西省 最优供应商数量 支持向量机 拉格朗日方法 报童模型 微型信贷 弱势信贷市场 安全风险评价 委托-代理模型 妊娠期糖尿病 多维度 多氯联苯(pcbs) 多态性 多agent 声誉机制 土地利用决策 含糊决策 可吸入颗粒物(pm10) 化学工业园区 前景理论 分离均衡 决策神经科学 农村信用社 农户 农业景观格局 共享心智模型 免疫反应
科研热词 评价 破产概率 模型 高估风险 风险管理 风险理论 风险控制 风险投资策略 风险 预防性储蓄 预期复核意见 遗传多态性 超网络 贫富差距 财产分布 诉讼风险 肝细胞癌 组织保障 索赔计数过程相关 社会网络 知识传播网络 病例对照研究 生态风险 热辐射 灾难风险 激励相容 激励因素 渐近关系式 框架 更新风险模型 教育培训 效率 收入分配 技术保障 弱预算平衡 广义正则变化 客户重要性 审计判断 安全生产 失效 天然气管道 复合poisson过程 变分不等式 发电权 双险种poisson过程 双边拍卖 区间数 冲击波 信任驱动 低估风险 企业联盟 交易成本
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
个体风险模型中总索赔额分布函数的估值问题

个体风险模型中总索赔额分布函数的估值问题赵丽霞【摘要】在假定投保人数服从Logarithmic分布的基础上,研究了个体风险模型中总索赔额分布函数的估值问题,给出了总索赔额分布函数的上、下界,为保险公司纯保费的厘定提供了一定的参考价值.【期刊名称】《长春工业大学学报(自然科学版)》【年(卷),期】2011(032)002【总页数】4页(P191-194)【关键词】风险模型;Logarithmic分布;估值【作者】赵丽霞【作者单位】山西大学商务学院,山西,太原,030031【正文语种】中文【中图分类】O290 引言保险合同中,承保人面临的风险恰是投保人的损失。
记Xi表示在一定时期内第i 个投保人的索赔额变量,取值于正数,N表示此时期内的投保人数,取值于非负整数,则该时期内的总理赔额变量S可以表示为。
此模型称为开放的个体风险模型,其开放性体现在投保人数的随机性[1]。
对于承保人而言,费率的厘定通常是纯保费加上一定的风险补偿。
而理赔额总量S的分布状况是纯保费的定价基础。
因此,对理赔额总量S的分布函数进行研究是非常必要的。
但是,由于卷积公式的复杂性,索赔额变量Xi的随机和变量的分布函数F(n)(x)不易求解[2],导致求解理赔额总量S的分布函数只能建立在一些特殊的假定之上。
文献[3-6]在假定索赔额变量Xi服从指数分布,投保人数N分别服从几何分布、泊松分布、负二项分布的基础上,给出了理赔额总量S的分布函数或是概率密度,进而求得S的各阶矩。
鉴于投保人数变量的均值通常小于方差,文中在假定投保人数N服从参数为β的Logarithmic分布的基础上,对S的分布函数FS(x)的取值范围进行了探讨。
1 主要结果引理1 若Xi(i=1,2,…,n)相互独立,服从参数为λ的指数分布,则X1+X2+…+Xn服从参数为(n,λ)的Γ分布,其分布函数为:证明引理2 若Xi(i=1,2,…,n)相互独立,服从参数为λ的指数分布,N为一离散型变量,其分布律为pn(n=1,2,…),则的分布函数为证明引理3[7] 若对于任意的x(x≥0),有即F(x)为NBUE(NWUE)类分布,则对于任意的x(x≥0),有式中Xi(i=1,2,…,n)的均值;G(x)——指数分布函数,其参数为λ。
个人金融风险定价模型

个人金融风险定价模型要了解个人金融风险定价模型,首先要了解风险定价的概念。
风险定价(Risk pricing)是指对风险资产的价格确定,它所反映的是资本资产所带来的未来收益与风险的一种函数关系。
建立风险定价体系需考虑经营成本、目标利润率、资金供求关系、市场利率水平、客户风险等因素。
银行采用精密的信用评估程序,将可更有效就贷款进行风险定价,即质素好的客户应能以较优惠的利率借款。
随着银行更有效就贷款进行风险定价,而不是仅依赖于诸如房地产等抵押物,中小企业将较容易获取贷款。
而银行所采用的风险定价大概有以下几种:成本相加贷款定价法从商业银行经营成本的角度来衡量贷款的利率水平,是最简单的贷款定价模型。
根据这个模型,任何贷款利率应该分解为四个部分:银行发放贷款的边际成本;银行为发放贷款所必须的经营性成本,包括贷款人员的工资和发放、管理贷款时的设备等成本支出费用;商业银行由于贷款可能发生违约甚至损失而承担风险,而必须得到的风险补偿;银行通过发放贷款所预计实现的利润水平。
因此银行贷款利率相应地等于“筹集发放可贷资金的边际成本”加“经营成本”加“风险补偿”加“预计利润水平”。
该模型的特点是它假设银行能够精确地了解其所有的成本,事实上这是很难做到的,因为银行向社会提供的是复合性的金融产品服务,银行很难精确的将成本分摊到各种业务中。
另外该模型没有考虑到同业间的竞争因素,目前由于银行间的贷款业务竞争日益激烈,已经对银行的预期利润水平产生了较大的影响:竞争越激烈,利润越少。
基准利率加点贷款定价模型这是国际银行业广泛采用的贷款定价方法,其具体操作程序是:选择某种基准利率为“基价”,为具有不同信用等级或风险程度的顾客确定不同水平的利差一般方式是在基准利率基础上“加点”,或乘上一个系数。
贷款利率等于“市场优惠利率”加“违约风险补偿”加“期限风险补偿”。
这种贷款定价模式是“外向型”的。
它以市场一般价格水平为出发点,寻求适合本行的贷款价格。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Var Xi E Var Xi Ii Var E Xi Ii
ui2qi 1 qi i2qi
考虑到各个保单理赔额的独立性质,则总理赔额的方差
Var S 为:
n
Var S ui2qi 1 qi i2qi i 1
如果赔付额 Bi 不是随机变量,而是常数bi,上面的公式会怎 样?
如前所述,个体风险模型研究保险人在
一个时间段内总的理赔额
S X1 X2 ... Xn
3.1.1
的概率分布,其中 X i代表第i 张保单可能
发生的理赔额.
因此,个体风险模型以单个保单为研究
对象。
§3.1 S 的数字特征
用一个 0-1 随机变量 I (示性函数)表示理赔发生情况:
I 1表示发生了理赔,I 0代表未发生理赔。即 I 可表示为:
s
pX (s y) pY ( y) y0
利用求和的可交换性,S 的分布也可写成
(3.2.1)
s
PS s pY (s x) pX ( x)
x0
例 3-2-1 设随机变量 X1, X2相互独立, 它们的分布列分别为
0
X1
~
0.5
1 0.3
2 0.2
,
X
2
~
0
0.4
1 0.3
2 0.2
第三章 个体风险模型
保险人最关心的是总的理赔额S的分布,总理赔额 S的分布模型可以分为两类:短期个体风险模型和 短期集体(聚合)风险模型。
个体风险模型以单个保单作为研究对象,每张 保单是否发生理赔是相互独立的且保单总数在所考 虑,的则时总期的内 理是 赔固 额定S被的表。示以为X:i代表一张保单的赔付额
0.7
1500002
0.3
975002
1181250000
所 以ES 65000 0.01 50 97500 0.01 25 56875
Var(S) 50(650002 0.01 0.99 5.25 108 0.01)
25(975002 0.01 0.99 1181250000 0.01)
5001984375
§3.2 独立随机变量和的分布(卷积方法)
对于相互独立的离散非负随机变量 X 与Y ,设它们的分布
列分别为 pX 和 pY ,则S X Y 的分布为
P(S s) P(X Y s)
s
P( X Y s |Y y)P(Y y) y0
s
P( X s y |Y y)P(Y y) y0
例3-1-1 某公司为员工购买意外死亡寿险。假设 对所有人明年的死亡概率为0.01,且30%的死亡是 由于意外事故发生的。75名雇员分属两个保单组, 第一组50人,如果是正常死亡,保险人将赔付5万 元;如果是意外死亡,保险人将赔付10万元。第二 组25人,赔付额分别是7.5万元和15万元。求总赔 付额的期望和方差。
0.5 0.2 0.3 0.3 0.2 0.4 0.27 f (2)(3) P( X1 0, X2 3) P( X1 1, X2 2) P( X1 2, X2 1)
0.5 0.1 0.3 0.2 0.2 0.3 0.17
f (2)(4) P( X1 1, X2 3) P( X1 2, X2 2) 0.3 0.1 0.2 0.2 0.07
i
设E
Bi
ui
,
则X
的期望为:
i
EXi EEXi Ii EXi Ii 1PIi 1
E Xi Ii 0 PIi 0 EBi PIi 1 uiqi
故ES E
n
Xi
n
EXi
n
uiqi
i1 i1
i1
利用方差分解公式
Var X E Var X Y Var E X Y ,
i 1
i 1
个体风险模型常在寿险中使用,比如一年期的伤害险。
假设,第i 个人在这一年内死亡的概率为qi,如发生死亡事
件承保人赔付 bi ;如未死亡则不赔付。则该人赔付额的分布 函数为:
Xi
0, bi ,
1 qi
qi
下面推导
X
的期望和方差公式
i
根据重期望公式,如果Y是离散型随机变量,则
EEX Y 公式为EX EX Y yi pY yi
0, 不发生理赔 I 1, 发生理赔
利用示性函数 I ,可以将第i 张保单的理赔量 Xi写成:
Xi
Ii Bi
0,
Bi
1 , qi
qi
,
其中qi P Ii 1代表第i 张保单发生理赔的概率,Bi 代表该
张保单发生理赔时的理赔额。
总的理赔额 S 因此可以表示为:
n
n
S X i Ii Bi ,
S ቤተ መጻሕፍቲ ባይዱX1 X 2 ... X n
集体风险模型则将所有保单视为一体,以每次理
赔,为理基赔本次对 数象N不,是此固时定Xi的代,表也一是次一赔个付随事机件变的量赔。偿额
个体风险模型的基本假设
一般情况下,要获得总理赔额 S 的分布是非常困 难的,个体风险模型采用如下假设: (1)每张保单是否发生理赔以及理赔额的大小是相 互独立的,即 X1 , X2 ,..., X n是相互独立的随机变量。 (2)每张保单在此时间段内至多发生一次理赔。 (3)保单总数n是固定的,即模型是封闭的。
解 : 对 这75人 , 死 亡 概 率qi 0.01。 根 据 题 意 , 若发 生死 亡,第一 组的50名员 工的 赔付 额为:
Bi 15000000000,,00..73, i 1,2,50
i EBi 50000 0.7 100000 0.3 65000
2 i
Var( Bi )
500002
0.7
1000002
0.3
650002
5.25 108
第 二 组 的25名 员 工 的 赔 付 额 为 :
Bi 17550000000,,00..73, i 1,2,25
i EBi 75000 0.7 150000 0.3 97500
2 i
Var(
Bi)
750002
3
0.1
求S X1 X2的分布。
【解】 f 2 0 P X1 0, X2 0 0.5 0.4 0.20
f (2)(1) P( X1 0, X2 1) P( X1 1, X2 0)
0.5 0.3 0.3 0.4 0.27
f (2)(2) P( X1 0, X2 2) P( X1 1, X2 1) P( X1 2, X 2 0)
