电磁场与微波技术第一二三章课后习题及部分答案概诉
电磁场与电磁波习题(第三版)习题解答第1-2章

ˆ y ˆ 2 yz z ˆ 的旋度。 1.33 计算矢量场 F xxy
解:
ˆ x F x Fx
ˆ y y Fy
ˆ ˆ z x z x Fz xy
ˆ y y 2 yz
ˆ z z 1
ˆ 2 y xz ˆ x
ˆ yx ˆ ,计算 A A 。 1.35 已知 A xy
2
电磁场与电磁波习题答案 chapter 1~2
Copyright @ ShengQian
dE x, y
S dx '
1/ 2
ˆ x x ' yy ˆ x
1/ 2
2 2 2 0 x x ' y 2 x x ' y 2 ˆ x x ' yy ˆ S x dx ' 2 2 2 0 x x ' y ˆ a 2 S x ˆ x x ' yy dx ' E x, y 2 a 2 2 2 0 x x ' y a 2 ˆ ˆ a2 S y x x x' y S dx ' dx ' 2 2 2 a 2 a 2 2 0 2 0 x x ' y x x ' y 2
D 0 E 0
当r a时
Sa D1n D2 n r a 0
当r b时
C 0C a a
Sb D1n D2 n r b 0
0C C b b
分析,本 题求解面电荷分布时, 法线方向和 D1 , D2 关系不要弄 混,这里公式
电磁场与微波技术第一二三章课后习题及部分答案

第 1 章 习 题1、 求函数()D Cz By Ax u +++=1的等值面方程。
解:根据等值面的定义:标量场中场值相同的空间点组成的曲面称为标量场的等值面,其方程为)( ),,(为常数c c z y x u =。
设常数E ,则,()E D Cz By Ax =+++1, 即:()1=+++D Cz By Ax E针对不同的常数E (不为0),对应不同的等值面。
2、 已知标量场xy u =,求场中与直线042=-+y x 相切的等值线方程。
解:根据等值线的定义可知:要求解标量场与直线相切的等值线方程,即是求解两个方程存在单解的条件,由直线方程可得:42+-=y x ,代入标量场C xy =,得到: 0422=+-C y y ,满足唯一解的条件:02416=⨯⨯-=∆C ,得到:2=C ,因此,满足条件的等值线方程为:2=xy3、 求矢量场z zy y y x xxy A ˆˆˆ222++=的矢量线方程。
解:由矢量线的微分方程:zy x A dz A dy A dx ==本题中,2xy A x =,y x A y 2=,2zy A z =, 则矢量线为:222zy dzy x dy xy dx ==,由此得到三个联立方程:x dy y dx =,z dz x dx =,zy dz x dy =2,解之,得到: 22y x =,z c x 1=,222x c y =,整理, y x ±=,z c x 1=,x c y 3±=它们代表一簇经过坐标原点的直线。
4、 求标量场z y z x u 2322+=在点M (2,0,-1)处沿z z y xy xx t ˆ3ˆˆ242+-=方向的方向导数。
解:由标量场方向导数的定义式:直角坐标系下,标量场u 在可微点M 处沿l 方向的方向导数为γβαcos cos cos zu y u x u l u ∂∂+∂∂+∂∂=∂∂α、β、γ分别是l 方向的方向角,即l 方向与z y xˆˆˆ、、的夹角。
电磁场与微波_毕刚课后习题答案

4 2π 2 ⃗ ⃗ =∯ ⃗ ⃗⃗⃗z − ∯ ⃗ ⃗⃗⃗z + ∯ ⃗ ⃗⃗⃗⃗ ∯ A ∙ dS A ∙ dS A ∙ dS A ∙ dS ∫ (ρ ρ ⃗ + 2zz ) ∙ ρ ⃗ ρdφdz| φ =∫ S S S S 0 0
−Φ ⃗ y
∂ ∂y
∂Aₓ ∂Φ + ∂x Ay ∂y
−
∂Φ Aₓ) z ∂y
∂ΦA = ( ∂y z −
∂ΦAy ∂z
)x ⃗ +
⃗ x (
∂ΦAₓ ∂z
z
∂ ∂z
−
∂ΦAz ∂x
)y ⃗ +(
∂ΦAy ∂x
−
∂ΦAₓ ∂y
)z = |
∂ ∂x
⃗ )=Φ∙ | = 左边,所以∇ × (ΦA
ΦAₓ ΦAy
ΦAz
(∇ × ⃗ A) + ∇ ∙ Φ × ⃗ A。 1-27 已知矢量⃗ A 、⃗ B分别为⃗ A = z²sinφρ ⃗ + z²cosφφ ⃗⃗ + 2zρsinφz 和⃗ B = (3y 2 − 2x)x ⃗ + x²y ⃗ + 2zz,求 (1)哪个矢量可以由一个标量的梯度表示; (2)哪个矢量可以由一个矢量的旋度表示; (3)它们的源分布。 ⃗ = 0,∇ × B ⃗ = 2(x − 3y)z,∇ ∙ A = 2ρsinφ,∇ ∙ B = 0。 解:∇ × A ⃗ 可以由一个标量的梯度表示; (1)A ⃗ 可以由一个矢量的旋度表示; (2)B ⃗ 有散场无旋场,B ⃗ 无散场由旋场。 (3)A 第二章 2-1 半径为a的无限薄带电圆盘上面电荷密度为ρ = r 2,r为圆盘上任意点到圆心的距离,求 圆盘上的总电量。 解:Q = ∬ ρ ∙ dφdr = ∫ r 3 ∙ dr ∙ ∫ dφ = S 0 0
电磁场与波习题答案1-9

第一章绪论1. 光电子器件按功能分为哪几类?每类大致包括哪些器件?光电子器件按功能分为光源器件、光传输器件、光控制器件、光探测器件、光存储器件。
光源器件分为相干光源和非相干光源。
相干光源主要包括激光和非线性光学器件等。
非相干光源包括照明光源、显示光源和信息处理用光源等。
光传输器件分为光学元件(如棱镜、透镜、光栅、分束器等等)、光波导和光纤等。
光控制器件包括调制器、偏转器、光开关、光双稳器件、光路由器等。
光探测器件分为光电导型探测器、光伏型探测器、热伏型探测器、各种传感器等。
光存储器件分为光盘(包括CD、VCD、DVD、LD等)、光驱、光盘塔等。
2.谈谈你对光电子技术的理解。
光电子技术主要研究物质中的电子相互作用及能量相互转换的相关技术,以光源激光化,传输波导(光纤)化,手段电子化,现代电子学中的理论模式和电子学处理方法光学化为特征,是一门新兴的综合性交叉学科。
3.谈谈光电子技术各个发展时期的情况。
20世纪60年代,光电子技术领域最典型的成就是各种激光器的相继问世。
20世纪70年代,光电子技术领域的标志性成果是低损耗光纤的实现,半导体激光器的成熟特别是量子阱激光器的问世以及CCD的问世。
20世纪80年代,出现了大功率量子阱阵列激光器;半导体光学双稳态功能器件的得到了迅速发展;也出现了保偏光纤、光纤传感器,光纤放大器和光纤激光器。
20世纪90年代,掺铒光纤放大器(EDFA)问世,光电子技术在通信领域取得了极大成功,形成了光纤通信产业;。
另外,光电子技术在光存储方面也取得了很大进展,光盘已成为计算机存储数据的重要手段。
21世纪,我们正步入信息化社会,信息与信息交换量的爆炸性增长对信息的采集、传输、处理、存储与显示都提出了严峻的挑战,国家经济与社会的发展,国防实力的增强等都更加依赖于信息的广度、深度和速度。
⒋举出几个你所知道的光电子技术应用实例。
如:光纤通信,光盘存储,光电显示器、光纤传感器、光计算机等等。
微波技术课后习题答案-第二章习题参考答案11
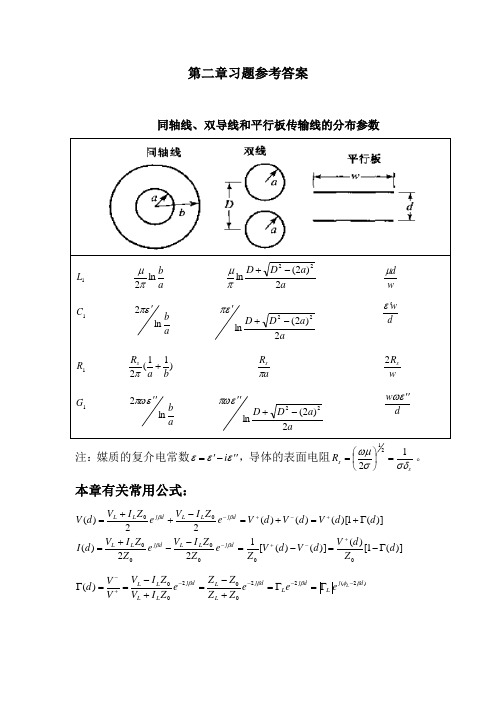
第二章习题参考答案同轴线、双导线和平行板传输线的分布参数注:媒质的复介电常数εεε''-'=i ,导体的表面电阻ss R σδσωμ1221=⎪⎭⎫⎝⎛=。
本章有关常用公式:)](1[)()]()([122)()](1)[()()(22)(00000000d Z d V d V d V Z e Z Z I V e Z Z I V d I d d V d V d V e Z I V e Z I V d V d j L L d j L L dj L L d j L L Γ-=-=--+=Γ+=+=-++=+-+-+-+-ββββ )2(2200200)(d j L d j L dj L L d j L L L L L e e e Z Z Z Z e Z I V Z I V VV d βφβββ----+-Γ=Γ=+-=+-==ΓL Lj L j L L L L L e e Z Z Z Z Z Z Z Z φφΓ=+-=+-=Γ0000dtg jZ Z dtg jZ Z Z d Z L L in ββ++=000)()(1)(1)()()(0d d Z d I d V d Z in Γ-Γ+==LL VV VSWR Γ-Γ+==11minmax2.1无耗或者低耗线的特性阻抗为110C L Z = 平行双导线的特性阻抗:aDa a D D a a D D Z r r rln 11202)2(ln 11202)2(ln 112222000εεεμεπ≈-+=-+=已知平行双导线的直径mm a 22=,间距cm D 10=,周围介质为空气(1=r ε),所以特性阻抗)(6.5521100ln 120ln11200Ω==≈a D Z rε 同轴线的特性阻抗:ab a b Z r rln 60ln 121000εεμεπ==已知同轴线外导体的内直径2mm b 23=,内导体的外直径2mm a 10=,中间填充空气(1=r ε):特性阻抗)(50210223ln 60ln 600Ω===abZ r ε中间填充介质(25.2=r ε):特性阻抗)(3.33210223ln 25.260ln 600Ω===a b Z r ε2.2对于无耗传输线线有相位常数μεωωβ===k C L 11,所以可求出相速度v k C L v p =====μεωβω1111,等于电磁波的传播速度。
微波技术习题解答

微波技术习题解答第1章练习题1.1 无耗传输线的特性阻抗Z0= 100()。
根据给出的已知数据,分别写出传输线上电压、电流的复数和瞬时形式的表达式:(1) R L= 100 (),I L = e j0(mA);(2) R L = 50(),V L = 100e j0(mV);(3) V L = 200e j0 (mV),I L = 0(mA)。
解:本题应用到下列公式:(1)(2)(3)(1) 根据已知条件,可得:V L = I L R L = 100(mV),复数表达式为:瞬时表达式为:(2) 根据已知条件,可得:复数表达式为:瞬时表达式为:(3) 根据已知条件,可得:复数表达式为:瞬时表达式为:1.2 无耗传输线的特性阻抗Z0 = 100(),负载电流I L = j(A),负载阻抗Z L = j100()。
试求:(1) 把传输线上的电压V(z)、电流I(z)写成入射波与反射波之和的形式;(2) 利用欧拉公式改写成纯驻波的形式。
解:根据已知条件,可得:V L = I L Z L = j(j100) = 100(V),1.3 无耗传输线的特性阻抗Z0 = 75(),传输线上电压、电流分布表达式分别为试求:(1) 利用欧拉公式把电压、电流分布表达式改写成入射波与反射波之和的形式;(2) 计算负载电压V L、电流I L和阻抗Z L;(3) 把(1)的结果改写成瞬时值形式。
解:根据已知条件求负载电压和电流:电压入射波和反射波的复振幅为(1) 入射波与反射波之和形式的电压、电流分布表达式(2) 负载电压、电流和阻抗V L = V(0) = 150j75,I L = I(0) = 2 + j(3) 瞬时值形式的电压、电流分布表达式1.4 无耗传输线特性阻抗Z0 = 50(),已知在距离负载z1= p/8处的反射系数为 (z1)= j0.5。
试求(1) 传输线上任意观察点z处的反射系数(z)和等效阻抗Z(z);(2) 利用负载反射系数 L计算负载阻抗Z L;(3) 通过等效阻抗Z(z)计算负载阻抗Z L。
电磁场习题答案

1-8 参照例图 1.1,设有标量 f ( R) ,求证:以 p ′( x ′, y ′, z ′) 为动点时的梯度 ∇ ′f ( R) 间与
以 p ( x, y, z ) 为 动 点 的 梯 度 ∇f ( R ) 间 满 足 关 系 : ∇ ′f ( R ) = −∇f ( R ) 。 其 中
R = r − r′ 。
∇• (AR) 。
答案: ∇ ? R = ; ∇ × R = 0; ∇ × ( R R ) = 0; ∇ ? AR ) = 3 A 。
( )
1-12 证明: ∇ • ( A × B) = B • (∇ × A) − A • (∇ × B) 。 1-13 证明旋度定理(1.47) 。
2 2 1-14 在圆球坐标系中, 已知 A = (sin θ R )a R + R sin θa θ + R sin θ cos ϕa ϕ , 求∇ • A 。
2
坐标原点一侧空间中的电场强度。 答案: E = 8.34( ax − 3a y + 6az ) 2—5
V m。
一点电荷 Q = 50 nC ,位于直角坐标系的原点,求点 (2,, 4 − 5) 处的电通量密度。
答案: D = 2—6
5 (2ax + 4a y − 5az ) 。 54π
两种理想电介质的相对介电常数分别为 ε r1 = 2.5和ε r 2 = 5 ,其分界面为 z = 0 的平 面。若已知介质 1 中的电场强度 E = 3a x + 4 a y + 6 a z ,求:① 介质 2 一侧的电场强 度 E2 和电位移矢量 D2 ;② E2 和 D2 是介质 2 中任意点处的场量表达式吗?为什 么? 答案:① E2 = 3ax + 4a y + 3az ; D2 = ε 0 (15ax + 20a y + 15az ) 。
电磁场微波技术与天线(盛振华版)第二章答案

天线的极化方式分为线极化、圆极化和椭圆极化三种。线极化是指电场矢量或磁场矢量与 地面平行,圆极化是指电场矢量或磁场矢量在垂直于传播方向上的投影为圆,椭圆极化则 是介于两者之间。
天线的主要参数
工作频率
天线的工作频率决定了其应用范围和性能。不同频率的电磁波具有不 同的传播特性和应用场景。
增益
天线的增益表示其在特定方向上对信号的放大能力。增益越高,天线 的定向性和抗干扰能力越强。
电磁场微波技术与天线(盛振华版) 第二章答案
目录
• 电磁场与微波技术的基本概念 • 天线的种类与工作原理 • 电磁场与天线的关系 • 天线的设计与优化 • 实际天线案例分析
01 电磁场与微波技术的基本 概念
电磁场与电磁波
电磁场与电磁波的形成
电磁波的分类
电磁场是由变化的电场和磁场相互激 发而形成的,而电磁波则是在空间传 播的电磁场。
根据频率的不同,电磁波可分为无线 电波、微波、红外线、可见光、紫外 线、X射线和伽马射线等。
电磁波的波动特性
电磁波具有波动性,表现为振荡的电 场和磁场在空间中传播,具有波长、 频率等参数。
微波技术的基本特点
01
02
03
微波的频率范围
微波的频率范围通常在 300MHz到300GHz之间, 是无线电波中较高频段的 组成部分。
探测和定位。
利用微波传输信号,实 现全球定位系统(GPS)
等导航定位服务。
微波可用于加热物体和 治疗某些疾病,如肿瘤
等。
02 天线的种类与工作原理
天线的分类
按工作频段分类
分为超长波天线、长波天线、 中波天线、短波天线、超短波
天线、微波天线等。
按方向性分类
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第 1 章 习 题1、 求函数()D Cz By Ax u +++=1的等值面方程。
解:根据等值面的定义:标量场中场值相同的空间点组成的曲面称为标量场的等值面,其方程为)( ),,(为常数c c z y x u =。
设常数E ,则,()E D Cz By Ax =+++1, 即:()1=+++D Cz By Ax E针对不同的常数E (不为0),对应不同的等值面。
2、 已知标量场xy u =,求场中与直线042=-+y x 相切的等值线方程。
解:根据等值线的定义可知:要求解标量场与直线相切的等值线方程,即是求解两个方程存在单解的条件,由直线方程可得:42+-=y x ,代入标量场C xy =,得到: 0422=+-C y y ,满足唯一解的条件:02416=⨯⨯-=∆C ,得到:2=C ,因此,满足条件的等值线方程为:2=xy3、 求矢量场z zy y y x xxy A ˆˆˆ222++=的矢量线方程。
解:由矢量线的微分方程:zy x A dz A dy A dx ==本题中,2xy A x =,y x A y 2=,2zy A z =, 则矢量线为:222zy dzy x dy xy dx ==,由此得到三个联立方程:x dy y dx =,z dz xdx =,zy dzx dy =2,解之,得到: 22y x =,z c x 1=,222x c y =,整理,y x ±=,z c x 1=,x c y 3±=它们代表一簇经过坐标原点的直线。
4、 求标量场z y z x u 2322+=在点M (2,0,-1)处沿z z y xy xx t ˆ3ˆˆ242+-=方向的方向导数。
解:由标量场方向导数的定义式:直角坐标系下,标量场u 在可微点M 处沿l 方向的方向导数为γβαcos cos cos zuy u x u l u ∂∂+∂∂+∂∂=∂∂α、β、γ分别是l 方向的方向角,即l 方向与z y xˆˆˆ、、的夹角。
αcos 、βcos 、γcos 分别是l 方向的方向余弦。
422==∂∂M M x z x u ,04==∂∂M Mzy y u,1223222=+=∂∂M M y z x z u 令:84222422294)3()()2(zy x x z xy x ++=++=∆则:542cos =∆=M Mx α,0cos 2=∆-=MM xy β,53cos -=Mγ,45360516cos cos cos -=-+=∂∂+∂∂+∂∂=∂∂M MM M z u y u x u t u γβα 5、 求标量场z y x xy z y x u 62332222--++++=在点M (0,0,0) 、点M (1,1,1)处的梯度,并找出场中梯度为0的点。
解:由梯度定义:z zu y y u x x u u ˆˆˆ∂∂+∂∂+∂∂=∇ 则:z z y x y xy x z z u y y u x x u u ˆ)66(ˆ)24(ˆ)32(ˆˆˆ-+-++++=∂∂+∂∂+∂∂=∇z y xu ˆ6ˆ2ˆ3)0,0,0(--=∇ y xu ˆ3ˆ6)1,1,1(+=∇ 若要梯度为零,则需使得梯度中各项分量为零,即:032=++y x 024=-+x y 066=-z解之,得到:1,1,2==-=z y x即,在点(-2,1,1)处,标量场的梯度为零。
6、 设z z y y xx r ˆˆˆ++=,r r =,n 为正整数。
求r ∇、n r ∇、()r f ∇。
解:根据题意及梯度定义:rr z z y y x x r z z y y x x r z y x z y x z y x r =++=++=++∇++=++∇=∇-)ˆˆˆ(1)ˆ2ˆ2ˆ2(121)()(21)(22221222222rnr r r nr rnr r n n n n 211---==∇=∇ rrr f rr f r f )(')(')(=∇=∇ 7、 求矢量场z z y y xx A ˆˆˆ333++=在点M (1,0,-1)处的散度。
解:由题意及散度定义: 222333z y x A ++=⋅∇,将M(1,0,-1)代入:得到:6303=++=⋅∇MA8、 设a为常矢量,z z y y xx r ˆˆˆ++= ,r r =,求()a r ⋅∇、()a r 2⋅∇、()a r n ⋅∇,证明a r a =⋅∇)( 解:由散度运算公式:1)()ra r r a r r ar a r a r⋅=⋅+⋅=⋅∇+⋅∇=⋅∇0 2)()ar r a r r r ar a r a r⋅=⋅+⋅=⋅∇+⋅∇=⋅∇20222223)()ar nr a r r nr r a r nr ar a r a r n n n n n n n⋅=⋅=⋅+⋅∇=⋅∇+⋅∇=⋅∇---21104)证明: 因为:zy x z y x za ya xa z y y y x x z a y a x a r a ++=++⋅++=⋅)ˆˆˆ()ˆˆˆ(且:x a ,y a ,z a 均为常数,所以有:a z a y a xa r a z y x =++=⋅∇ˆˆˆ)( 得证。
9、 设无限长细直导线与z 轴重合,其上有沿正z 轴方向流动的电流I ,导线周围的磁场()()y x xy yx IH ˆˆ222+-+=π计算H⋅∇。
解:由题意及散度的定义:()()y x xy yx IH ˆˆ222+-+⋅∇=⋅∇π22222)(/2-+=∂⎪⎪⎭⎫ ⎝⎛+∂-=∂∂y x xy Ix y x yIx H x ππ22222)(/2-+-=∂⎪⎪⎭⎫ ⎝⎛+∂=∂∂y x xy Iy y x x I y H y ππ∴=∂∂+∂∂=⋅∇y H x H H y x 10、已知xy y x u 222+-=,求u 2∇。
解:由题意及散度运算性质:)(2u u ∇⋅∇=∇y y x xy x z z uy y u x x u u ˆ)22(ˆ)22(ˆˆˆ-++=∂∂+∂∂+∂∂=∇22)ˆ)22(ˆ)22(()(=-=-++⋅∇=∇⋅∇y y x xy x u 所以:02=∇u11、计算下列矢量场的旋度:(1)()()z xyz y xz y x z y x A ˆ2ˆˆ3232+-++= ; (2)z xy y zx xyz A ˆˆˆ222++= ; 解:由矢量场旋度定义式,可得:1)()()()()()z x z y yz xxz z x z y yz x xz xz z y A x A y x A z A x z A y A A A A z y x z y x A x y z x y z zyxˆ3ˆ21ˆ4 ˆ3ˆ21ˆ22 ˆˆˆˆˆˆrot 2222+--+=--+-++=⎪⎪⎭⎫ ⎝⎛∂∂-∂∂+⎪⎭⎫ ⎝⎛∂∂-∂∂+⎪⎪⎭⎫ ⎝⎛∂∂-∂∂=∂∂∂∂=2)()()()z z xz y y yz xx xy z y A x A y x A z A x z A y A A A A z y x zy x A x y z x y z zy x ˆ2ˆ2ˆ2 ˆˆˆˆˆˆrot 222-+-+-=⎪⎪⎭⎫⎝⎛∂∂-∂∂+⎪⎭⎫ ⎝⎛∂∂-∂∂+⎪⎪⎭⎫ ⎝⎛∂∂-∂∂=∂∂∂∂∂=12、已知x e u =,z y y x xz A ˆˆˆ222++=,计算()A u ⨯∇。
解:由题意及矢量的旋度运算公式:())ˆ)2(ˆ)2(ˆ2()ˆ2ˆ2ˆ2ˆˆ()ˆ2ˆ2ˆ2(ˆ2222z x x y y z xy e z x y z x y z x yy e z x y z x y e A xe Au A u A u x xx x ++-+=++++-=+++⨯=⨯∇+⨯∇=⨯∇13、已知z z y y xx r ˆˆˆ++= ,r r =,a 为常矢量,求r ⨯∇、()[]r f r ⨯∇、()[]r f a ⨯∇。
解:1)z ˆ)-(yˆ)-(x ˆ)-(r =∂∂∂∂+∂∂∂∂+∂∂∂∂=⨯∇y x x y xz z z x z yy z2)()[]0)(')(')()()(r f r =⨯=⨯∇=⨯∇=⨯∇+⨯∇=⨯∇rrr r f rr r f rr f rr f r r f3)()[]a r r f rar r r f a r r f ar f ar f a r f r f a⨯=⨯=⨯∇=⨯∇=⨯∇+⨯∇=⨯∇)('1)(')(')()()(14、已知z xy y z xy A ˆˆ2ˆ32++= ,z x x B ˆ4ˆ2-=,求()B A⨯⨯∇。
解:由题意及运算规则,先求出B A⨯,再求旋度:ˆˆˆxy z x y z xy z A B A A A B B B ⨯=22ˆˆˆ 3204xyz y z xy x =- ˆˆˆ ()()()y z z y z x x z x y y x A B A B xA B A B y A B A B z =-+-+- 2322ˆˆˆ =8(12)2z x x y y y x z z -++- ()A B ∇⨯⨯2322ˆˆˆ(8(12)2)z xx y y y x z z =∇⨯-++- 22322232(2)(12)(8)(2)(12)(8)ˆˆˆx z x y y z x z x y y z x y z y z z x x y ⎡⎤⎡⎤⎡⎤∂-∂+∂-∂-∂+∂-=-+-+-⎢⎥⎢⎥⎢⎥∂∂∂∂∂∂⎣⎦⎣⎦⎣⎦22ˆˆ(416)3xz z yx yz =-+ 15、已知位于坐标原点处电量为q 的点电荷产生的电位移矢量D为34r r q D π=,其中z z y y x x r ˆˆˆ++=,r r=,计算D ⨯∇和D ⋅∇。
解:由题意:1)34qrD ()πr ∇⨯=∇⨯ 33r 44q q()r πr πr =∇⨯+∇⨯ 31()4q r πr =∇⨯4 (3)4qr r r π-=-∇⨯43 4q rr πr r-=⨯0=2)34qrD ()πr ∇⋅=∇⋅3 ()4qr r π-=∇⋅ 33()()4q r r r r π--⎡⎤=∇⋅+∇⋅⎣⎦ 43334q r r r r π--⎡⎤=-∇⋅+⎣⎦ 43 334q r r r r πr --⋅⎡⎤=-+⎢⎥⎣⎦ 33334q r r π--⎡⎤=-+⎣⎦ 0(0)r =≠在r=0处,D 无意义,D⋅∇不存在。
16、证明()0=∇⨯∇u ,()0=⨯∇⋅∇A。
证明: 1)由标量场梯度的定义式:z zu y y u x x u u z z y y x x u ˆˆˆˆˆˆ∂∂+∂∂+∂∂=⎪⎪⎭⎫⎝⎛∂∂+∂∂+∂∂=∇ ())ˆˆˆ(z zuy y u x x u u ∂∂+∂∂+∂∂⨯∇=∇⨯∇ 由z y A x A y x A zA x z A y A A x y z x y z ˆˆˆ⎪⎪⎭⎫⎝⎛∂∂-∂∂+⎪⎭⎫ ⎝⎛∂∂-∂∂+⎪⎪⎭⎫ ⎝⎛∂∂-∂∂=⨯∇ 令:z zuy y u x x u A ˆˆˆ∂∂+∂∂+∂∂= 则:()0ˆˆˆ)ˆˆˆ(222222=⎪⎪⎭⎫⎝⎛∂∂∂-∂∂∂+⎪⎪⎭⎫ ⎝⎛∂∂∂-∂∂∂+⎪⎪⎭⎫ ⎝⎛∂∂∂-∂∂∂=∂∂+∂∂+∂∂⨯∇=∇⨯∇zy x u x y u y z x u x z u x y z u z y u z zuy y u x x u u 由此得证。
